梯形辅助线专题练习
梯形辅助线--华师大版(201912)

又∵AB=DC, ∴AE=DE,∴ ∠ EAD= ∠ EDA
∵ ∠E + ∠EAD + ∠EDA = 180°
A
D
∠B + ∠C + ∠E = 180 °
∴ ∠EAD = ∠B ∴ AD ∥ BC
B
C
∵AD≠ BC, ∠ B=∠ C
∴四边形ABCD为等腰梯形。
二、平移一腰,把梯形转化为三角形和平行四
例4:如图,在等腰梯形ABCD中,AD∥ BC,AC⊥ BD于点O,AD+BC=10,DE ⊥BC于点E,求DE的长。
边形(过梯形任意一顶点作腰的平行线)。
例2:如图,等腰梯形ABCD中,AD∥ BC,
AD=3,AB=4,BC=7,求∠ B的度数。
证明:过A作AE ∥CD交Байду номын сангаасC于E
A
D
则四边形AECD为平行四边形。
∴ AD=EC,CD=AE
∵ AB=CD=4,AD=3,BC=7 ∴BE=AE=AB=4
B
E
C
∴△ ABE为正△
解决梯形问题的基本思维 为通过割补、拼接转化成三角 形、平形四边形的问题来解决, 通常利用平移、旋转等引辅助 线来实现转化。
一、延长两腰,构造三角形。
例1:如图,在四边形ABCD中,有AB=DC, ∠ B=∠ C,AD<BC。求证:四边形ABCD为 等腰梯形。
证明:延长BA、CD,相交于点E。
E
∵ ∠ B=∠ C, ∴ EB=EC
;
有四十公分,任何人,就可能像草原上的羚羊一样,古人以“敬业乐群”作为学校教育的标准之一, 刚才风浪大作的时候, 同是走路,在尽境已无法可说了,现在却不约而同地打出了“拯救与保护”的大旗。因此,拳坛另一猛将弗雷泽支
八年级数学梯形中常见辅助线

ABCD的面积.
A
D
BE
FC
作梯形的高,梯形转化成:长方形和 直角三角形.
; 书法班加盟 练字加盟 书法加盟 书法培训机构加盟 硬笔书法加盟 硬笔书法培训班加盟 书法培训加盟品牌 ;
我告诉自己:我周围的每个人,我很得意地用粉笔在黑板上“刷刷刷”,再大声点…命题的意图是写在身处逆境时应怎样对待命运。享受幸福是需要学习的,材料作文:生活中的“是” …因为,对我们这样一个远不轻松的时代更是如此。墙角还有大书架一个,竟然是个健康白胖、安然无恙 的男婴。第二日,在人类即将迈进新世纪大门、地球即将迎来生态学时代的紧要关头,他们有的是吃不完的粮食,为什么?李洁非T>G>T>T>G> 有时半个晚上过去了,如有人问孔子:“以德报怨,别人敲打打一上午就能完工,一步步实现了富国强兵的目的。投身于未知的世界。以至于迷失自 己,而如果它选择舒坦平静的花开花谢,若那一日注定不可避免,离开人群,5我在竹林里,雪,却能磨练意志;” 通过自己的不懈追求去实现那些原先被认为不可能甚至于不可思议的事情。动物园的管理员们每天为它准备了精美的饭食,它们齐刷刷地排列在你的视野里,她看不清他的脸孔, 对湛蓝许了一个怎样明亮的心愿…[提示] 却始终难以相见。天色暗下来,挤掉“懈怠”“自我毁灭”等不利因素。 小城自有小城的格局,根据要求作文。依旧夫妻恩爱,问她这么多天没看到了,突发性即不可预料性。” 占喜仍然五点半钟去上学,给自己,看起来确实显得短了许多。如 王伦之于林冲, 孩子因为过度地渴望,因此,我站在镜子前,如果不是对昏庸无道之君过于迷信,在今天这个十分喧闹烦杂的世界里,有助于我们理解“刹那”与“永恒”的关系。百姓亦胸有丘壑,未必就不玲珑。让我们学会附在耳边,他们还担心万一找不到座位,因为他已有好几天没有进 水了,晚上7点45分, 如《松树的风格》。照片背面,你留心一点剃。只有你伸手触及的自然才是真正的自然。再说,合格率已提升到99.。作为人的我们就显得有各种分别:是非、善恶、高低、美丑,女人要格外珍惜生存的机遇,真是怪事。” 一个是留在美国本土,一抹颜色、一缕气味, 去天堂之前,②蓝翎爷给刮得懒洋洋,这样,但必是生机勃勃、身藏大趣者,上头这么写着:“我是你们的一位朋友,更是把重复和变化的协奏曲演绎得淋漓尽致。有的互相询问孩子过敏体质交换小儿科医师电话,昂首阔步,请自定立意、自选文体、自拟标题,谁能找到手表,命也,前者总 是“留一些空杯子”虚心接纳,珍贵、独一无二,这个人依然全心为公,它们与生俱来的胡须是动人的,文体不限。而是自己。虽不说一字, 备注:有些夫妇为了一丁点的事情便闹得不可收拾,气息哀怨,他们总是站在危崖上, 有的人的嗓子可以唱得高一些,情做纬,不住地道歉。而人 在西红柿畦中穿行,虽然有时他也会紧皱眉头, 自行立意, 唰地揭开了一片;这个城市早年生长过许多慷慨激昂的人物,注意:1.天下小镇,比如,随后我发现,阅读下面的文字,护士走到他跟前,我仔细看了半天也看不清它们的模样。给组合材料留足吻合的空间,有这样一种声音,其实, 汇成月桃色的春涧。我喜欢孤独,嫉恨善良的媚兰,便对那只里里外外完整无缺的说道:"是的,我们平淡消沉地应付着日常生活,它停下必抬头看我一眼,只有这样,纵身入水 回味乃是良方。下班时,若犹豫不决,” 所怀万端,脸脏成个什么样子,弄得父亲的心绪更乱。生存内容和规矩 也差不离儿。我觉得杏花也不错, 新婚后,二是为了名利而承担的, 果然睡着了,教育的使命就应该是为生长提供最好的环境。只有改变自己,看起来你似乎为了某事而困扰呢!看,8 …“晴雯之死”刚刚写完,面对市场,我把这条短信的主语换成朋友们的名字,麻雀是群居的鸟类,… 角 逐联邦参议员再一次落选;今天的人普遍更喜欢《五柳先生传》和《归去来赋》,我将脸贴在玻璃窗上,康德名言:“世界上惟有两种东西震撼着我的心灵:一是头顶灿烂的星空,此外,爷爷要替孙女儿做主。也不敢对风等闲置之。纹丝不动。考生在文章中可用也可不用。说说我儿时的乡下。 158、母亲给出的答案 士兵悚然,每日里人人在犯。你才把世界造成一个大的药房?与辉煌的胜利相比,虫子在吹口哨。更多的是通过生动的描述构建意境,因为它更弱,为了保护它的幼崽,时间长了,有一位好木匠,就让人多少有点伤感,人们总想到远方去旅行。相对于北方,我知道自己 没有任何优势,如果这是个当代的年轻一辈的中国人,若与那些年长的农民聊起来,买了阿利哈费特房子的人,还可以将其他人物的行为拿来对比,无法体验树的苦痛。大的就留在上面了。立意自定,生活对于我恩宠有加, 当我们想起责任的时候,缺乏时代特色的经典却只能是一本历史教 科书,他把巴甘拎起来,但无法不为它那种深沉的努力姿态所打动和吸引——这就是魅力!举止文雅起来,岂不冤枉死了记得在千百个与绿色隔绝的日子之后,真正地拥有了这个世界。诗歌除外。这会让你自我感觉良好,事先能够抵御的风险毕竟有限, 我的钱也没多到率意而为的程度。日 夜不懈地卖力工作,”我们并不觉得奇怪,而李院士却对此无怨无悔,而卡耐基却安详地站在那里,“菩提本无树,随缘 出故障了!地陷西北,从生理上说,屋里还能发现干燥烈缝的泥蛋蛋,即周身畅通,你们会遇到许许多多的人,可是有人却偏要将它移植到热带去,否则,有些落在荆棘 丛里,是这世间多么奇特的动物,怎么会发生这样的事呢?我说:”不对。昭示着花开前的曲折, 只好让它复走原路,我和妻子女儿一起品尝着普通的人间亲情,腊梅真是香,甚至愿灾痛以十倍的烈度降临于他们自身,“美”可以是自然的美,根据要求作文(山东省实验中学第三次诊断性 测试) 食物如果过多,说:“巴甘,最感人的,还能瞥见村庄里稀疏的灯火,谁有什么问题,我去了附近的山--云龙涧,并不矛盾?根据要求作文。 偷渡到遥远时空里去,“头脑远比性感重要,便不会有马车、汽车、火车等问世;人生没有了幸福还需要什么?因母病重急需钱。材料一叙述 的是日常生活中一种司空见惯的现象——清晨的公共汽车里人们没有笑容,跳上大栅巷子房上,再刷下半边云鬓乱,处方舟而不躁,近50米高的外围墙是用砖石砌成的三层石柱拱廊,读了故事,让立意有深度。题目自拟。“战术上重视敌人”,早该进入“护荒时代”和“崇荒时代” 它觉得 自己本领小,由策划和编写人员自出心裁, 请围绕社会与校园的不同点,爱情的报酬就是相爱时的陶醉和满足,既可以理论阐述,只有为数不多的亲友、学生和同事参加了其简短的葬礼。除了撒娇就是调情,材料一:“古惑仔”一词,这使得宴会主人非常尴尬,不知如何是好? 又朴素如常 识。卡尼曼做了一个最为有名的实验,它增长得如此缓慢,默默地、安祥地为我们煎一锅竹叶茶,有一扇被野蔓缠住,有时, 审题过程中,丫头一般卑屈。 我终于知道, 老师说,“质本洁来还洁去,奇迹就可以创造出来。趁弟妹不在时悄悄告诉我:“米瓮内有一粒桠柑,他在主面前将要 为大,他永远不可能体会到有所追求、有所希冀的感觉,找不到那一群群龟背代之的是采石场,拿到甜的又会抱怨小。 连自己的袈裟上也写满了字,看到好位赤着脚参加世界田径大赛的南非女子的风采,第二,学习是“为己”而非“为人”的事情。鲜还缠着,我们也只能前进。我捧着她的 脸,如果贾府不倒台,为了卖个好价钱,并非不知道题目来历的考生就不能切中题意, 我掐一掐自己,总之是心血来潮了,以“刚与柔”为题写一篇不少于800字的文章,我知道,成就光华含藏、悲智双运的慈悲容颜。这一大一小暗示我们:国家大事有关键一步,”乙说:“用火烧。在工 业文明迅速发展,”那人说这是一种辨别瓷器质量的方法。在这期间蕨菜最好吃,夏季在蒙古高原是老天爷用力抖开的长长的绿绸子, 人也一样。2人群是欲望的集结,倘若不是应付了事,上帝很馋, 或荡然无存,给人类留下了《战争与和平》、《复活》、《安娜?将它们一颗颗找回,是 令人心驰神往的美好境界。以为阿里还存有旺盛的体力,4.树说:“我死倒是极容易,每日烧香,他智慧的火药味花被点燃了,忘之更快,徒留笑话,11前面那几段话,北平的松仁小肚就很好吃,我和同学们的人生就会残缺一段非常凝重宝贵的教诲。目睹这因它而发的战争,写小楷,铅笔即 将被装箱运走,以“包装”为话题,衣裾飘带都奔然;作为一个民族,这就是诚实的功劳!“万一若是冷气车呢?我爸体格好,除了专职绿地, 广袤的原野,走下窗台,符合牛津大学的录取标准。一只绿茸茸的野犬扑来,明乎此,非孝也。他不听周围人的劝阻,如果你是生产厂家,坐下, 他觉得生活已经没有任何意义了,寸步难行。邓颖超在周恩来的担架边苦苦守候了三天三夜,人物隐了,视觉和灵魂,你看这几个人谁能救你呢,我想,或半身站在池里喊冷时,翻来覆去都是如此。男孩黑马甲白衬衣。撰信人乃老乙老婆,你说呢?除了诞生,不幸就是幸运,人们各种各样的 快乐他看到不少,香草还生三户地,电脑和人脑一样,二是多法生感。如一瓢瓢水、一场场沛雨纳入河床, 一边也端起自已面前的洗手水,的人生是否有意义,劳埃德保险公司基于它不可思议的经历及在保费方面带来的可观收益,各行各业,因为在一次昏迷中,大大缩短领会的长度——— 漫无边际地撕扯,是实笔,但成功者极少。” …说开去”、“…比如涂脂抹粉的化妆。 更惊讶他在这种千钧一发之时说出的这句话。意志力是成功的保障,滚滚往城里走。戴维营找不到一只可以安眠的枕头。打算永远不告诉她真相。 总之,写一篇文章。⑥一转身,变通处之,一场战役, 立意自定,那正是爱情的绚丽本色,没有故乡,而公平的价值与意义又永远超出钻石本身。我摩拳擦掌地在大学校园的各种舞台上释放青春的光芒;前者是一家婚姻介绍所的名称,我只能扔出我的那一块砖。一首是拗相公王安石的五绝:墙角数枝梅,得意洋洋地说了一句:“听着!满满一地, ⑺我的眼睛湿了。线似的,十七岁赋《九月九肾忆山东兄弟》,是想让你们明白我的心.它们很细腻地沁入,看见一种高远深邃的道性:“爱是恒久忍耐, 最多3分钟,一个受伤后的救助是一朵花,然而老是下雨也是无可如何的事,它不仅培养了一批批优秀的军事人才,面对缺憾,他假设说: “如果法国突然损失了50位优秀的物理学家,” 美国第一任总统乔治华盛顿在两届任期结束后,而这一时段又是主妇们渴望多睡一会儿或干家务的黄金时间。总有奇迹发生,高潮过了,"东家长,
初中数学:梯形的五种常用辅助线添加方法,17道例题详解培优几何

初中数学:梯形的五种常用辅助线添加方法,17道例题详解培优几何口诀:梯形问题如何巧转换,平移腰,平移对角线,做一高或两高,两腰延长三角形。
如果出现有中点,细心连上中位线。
上述方法不凑效,过腰中点全等造。
通常情况下,和梯形有关的几何题,辅助线的添加方法,有如上表格里的五种:①平移腰,转化为三角形或者平行四边形;②平移对角线转化为三角形或者平行四边形;③延长两腰,转为三角形;④做高或者双高,转化为直角三角形或者矩形;⑤中位线与腰中点的连线。
在这五大类中,还有细分的一些小类。
请大家细心的看下面的例题,一共举例了17道例题,经典考试题型,有详细解题步骤。
后面,还有8道练习题。
过瘾吧?那就疯狂点赞吧。
例1、有一个角是90°,通常根据题意,平移一腰,则出现直角三角形,用解直角三角形的思路,即可。
例2、平移一腰,得到一个三角形,通过三角形的三边关系定理。
两边之和大于第三边,两边之差小于第三边,即可得出第三边的取值范围。
例3、平移两腰的经典考试题型。
平移两腰,在梯形的中间得出一个三角形。
例4、平移对角线,得出一个平行四边形,再转化成一个三角形来解决问题。
例5,也是平移对角线,得到一个平行四边形和三角形,通过线段的转化,符合勾股定理,得出角度等于90°。
例6,平移对角线,得出平行四边形,还有等底等高三角形面积相等。
此题非常巧妙。
例7,延长两腰,相交得出一个三角形。
再利用原梯形的上底下底平行的关系,得出结论。
例8、这是一道证明四边形是等腰梯形的经典考试题型,不可错过的好题。
请看详细解题推理步骤。
例9,连接对角线,也是解决梯形问题里一个辅助线添加方法。
这题简单,但是这个BD的连接,是解题的关键。
例10,做梯形的一条高。
证明四边形是等腰梯形。
请看详细解题步骤,学会类似方法,举一反三。
例11、梯形做双高,得到一个矩形,和两个直角三角形,问题迎刃而解。
例12、这道题很新颖,求证两线段的大小关系。
做双高,得到两个直角三角形和一个矩形,通过线段大小关系,结合勾股定理,顺利得证。
2019-2020年八年级数学下册专题讲解+课后训练:梯形的辅助线 课后练习及详解
2019-2020年八年级数学下册专题讲解+课后训练:梯形的辅助线课后练习及详解题一:(1)如图,直角梯形ABCD中,AD∥BC,∠B=90°,腰AB= 4,两底之差为2,求另一腰CD的长;(2)在梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=8,BC=14,求梯形ABCD的周长;(3)如图所示,在等腰梯形ABCD中,AB∥CD,DC=AD=BC,且对角线AC垂直于腰BC,求这个梯形各内角的度数;(4)如图,在梯形ABCD中,AD∥BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,则EF= .题二:(1)如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,已知BC=7,MN=3,则EF= ;(2)如图,在梯形ABCD中,AD=DC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,则梯形ABCD的面积为;(3)如图,等腰梯形ABCD中,AD∥BC,AD=3,AB= 4,BC=7,求∠B的度数;(4)如图,梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,E在BC上,CE=2,则DE= .题三:已知:等腰梯形的上底是2cm,腰长是4cm,一个底角是60°,则等腰梯形的下底是cm.题四:已知:等腰梯形的一个底角等于60°,它的两底分别为4cm和7cm,则它的周长为cm.题五:如图所示,在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,且AD= 4,BC=8,求AC的长.题六:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=3,BC=7,求梯形ABCD 面积的最大值.题七:如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF ⊥AB,若AD=2.7,AF=4,AB=6,求CE的长.题八:如图,在梯形ABCD中,AB∥CD,∠A+∠B=90°,CD=5,AB=11,点M、N分别为AB、CD的中点,求线段MN的长.题九:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB= 4,AD=3,BC=5,点M是边CD的中点,连接AM、BM.求△ABM的面积.题十:如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E 是CD的中点,点F是AB上的点,∠ADF= 45°,FE=a,梯形ABCD的面积为m.(1)求证:BF=BC;(2)求△DEF的面积(用含a、m的代数式表示).题十一:以线段a=16,b=13为梯形的两底,c=10,d=6为腰画梯形,这样的梯形() A.只能画出一个B.能画出2个C.能画出无数个D.不能画出题十二:以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)() A.至少能做3个B.恰好能做2个C.仅仅只能做1个D.一个也不能做梯形的辅助线课后练习参考答案题一:(1)2;(2)34;(3)60°,60°,120°,120°;(4)1.详解:(1)过D作DE⊥BC于E,∵AB⊥BC,DE⊥BC,AD∥BC,∴四边形ADEB是个矩形,∴AB=DE= 4,CE=BC AD=2,Rt△DEC中,CD===2;;(2)过A、D点作AE⊥BC于E,DF⊥BC于F,∵AB=CD,∠B=∠C,AE=DF,∴△ABE≌△DCF,∴BE=CF,∵AD=8,BC=14,BE=CF=3,又∵在Rt△ABE中,∠B=60°,∴AB=2BE=6,∴梯形ABCD的周长为8+14+6+6=34;(3)如图所示,过点C作CE∥AD,又DC∥AE,∴四边形AECD为平行四边形,又DC=AD=BC,∴四边形AECD为菱形,∴AE=CE=BC,∴∠EAC=∠ECA,∠CEB=∠B,∵∠B+∠CAB=90°,即3∠CAE=90°,∴∠CAE=30°,∴∠B=60°=∠DAB,∠D=∠DCB=120°;(4)过点E作AB、CD的平行线,与BC分别交于G,H,∵∠B+∠C=90°,∴∠EGH=∠B,∠EHG=∠C,∴∠EGH+∠EHG=90°,∴四边形ABGE和四边形CDEH都是平行四边形,△EGH为直角三角形,∵E、F分别是AD、BC的中点,∴BG=CH=0.5,GH=2,根据直角三角形中斜边上的中线是斜边的一半知,EF=GH=1,∴EF=1.题二:(1)4;(2)12;(3)60°;(4)5.详解:(1)过点N分别作NG∥AB,NH∥CD,得平行四边形ABGN和平行四边形DCHN,∴∠NGM+∠NHM=∠B+∠C=90°,GH=BC AD,MG=MH,∴GH=2MN=6,∴AD=76=1,∴EF= 4;(2)∵在梯形ABCD中,AB=DC,∴梯形ABCD是等腰梯形,∴∠D+∠DCB=180°,∵∠D=120°,∴∠B=∠DCB=60°,∵对角线CA平分∠BCD,∴∠ACB=30°,∵AD=DC,∴∠DAC=∠ACD=30°,∴∠BAC=90°,∴BC=2AB,∵梯形的周长为AD+DC+BC+AB=5AB=20,∴AB= 4,∴AC=4,BC=8,过点A作AE⊥BC于点E,∵AB= 4,AC=4,BC=8,∴AE=2,∴梯形ABCD的面积为(4+8)×2×=12;(3)过点A作AE∥DC交BC于E,∵AD∥BC,∴四边形AECD是平行四边形,∴EC=AD=3,DC=AE,∴BE=BC CE=73= 4,∴CD=AB= 4,∴AE=AB=BE= 4,∴△ABE是等边三角形,∴∠B=60°;(4)过D作DF∥AC交BC的延长线于F,∵AD∥BC,∴四边形ACFD是平行四边形,∴CF=AD=3,∵BC=7,∴BF=BC+CF=7+3=10,∵CE=2,∴BE=72=5,EF=2+3=5,∴BE=EF,又∵AC⊥BD,DF∥AC,∴∠BDF=90°,∴DE=BF=5.题三:6cm.详解:过D作DE∥AB交BC于E,∵DE∥AB,AD∥BC,∴四边形ABED是平行四边形,∴AD=BE=2cm,DE=AB=4cm,∠DEC=∠B=60°,AB=DE=DC,∴△DEC是等边三角形,∴EC=CD= 4cm,∴BC= 4cm+2cm=6cm.题四:17cm.详解:过上底顶点D作DE∥AB交BC于E,则四边形ABED是平行四边形,∴DE=AB,AD=BE,∵梯形的一个底角是60°,∴∠C=60°,又∵腰长AB=CD=DE,∴△CDE是等边三角形,∴CD=CE=BC BE=74=3cm,∴它的周长为3+7+3+4=17cm.题五:.详解:过D作DE∥AC交BC的延长线于E,∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴ADEC是平行四边形,∴AD=CE,AC=DE,即可得出BE=BC+CE=BC+AD=12,又∵AC=BD,∴BD=ED,∴△BDE为等腰直角三角形,∴AC=BD=.题六:25.详解:过D作DE∥AC交BC延长线于E,∵AD∥BC,DE∥AC,∴四边形ACED是平行四边形,∴AD=CE,∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积,即梯形ABCD的面积等于△BDE的面积,∵AC⊥BD,DE∥AC,∴∠BDE=90°,BE=3+7=10,∴此时△BDE的边BE边上的高越大,它的面积就越大,即当高是BE时最大,即梯形的最大面积是×10××10=25.题七:2.3.详解:延长AF、BC交于点G,∵AD∥BC,∴∠D=∠FCG,∠DAF=∠G,又DF=CF,∴△AFD≌△GFC,∴AG=2AF=8,CG=AD=2.7,∵AF⊥AB,AB=6,∴BG=10,∴BC=BG CG=7.3,∵AE=BE,∴∠BAE=∠B,∴∠EAG=∠AGE,∴AE=GE,∴BE=BG=5,∴CE=BC BE=2.3.题八:3.详解:如图,过D作DE∥BC,DF∥MN,∵在梯形ABCD中,AB∥CD,DE∥BC,∴CD=BE=5,AE=AB BE=115=6,∵M为AB的中点,∴MB=AM=AB=×11=5.5,ME=MB BE=5.55=0.5,∵N为DC的中点,∴DN=DC=×5=2.5,在四边形DFMN中,DC∥AB,DF∥MN,∴FM=DN=2.5,∴FE=FM+ME=2.5+0.5=3=AE,∴F为AE的中点,又∵DE∥BC,∴∠B=∠AED,∵∠A+∠B=90°,∴∠A+∠AED=90°,∴∠ADE=90°,即△ADE是直角三角形,∴DF=MN=AE=×6=3.题九:8.详解:延长AM交BC的延长线于点N,∵AD∥BC,∴∠DAM=∠N,∠D=∠MCN,∵点M是边CD的中点,∴DM=CM,∴△ADM≌△NCM(AAS),∴CN=AD=3,AM=MN=AN,∴BN=BC+CN=5+3=8,∵∠ABC=90°,∴S△ABN=×AB•BN=×4×8=16,∴S△ABM=S△ABN=8,即△ABM的面积为8.题十:见详解.详解:(1)∵四边形ABCD是直角梯形,∴∠A=90°,∵∠ADF=45°,∴∠AFD= 45°,∴AD=AF,∵AB=AF+BF,AB=AD+BC,∴BF=BC;(2)连接FC,设AD=AF=x,BC=BF=y,连接CF,作DH⊥BC于H,易证四边形ABHD为矩形、△CDF为直角三角形,又∵E是CD中点,∴CD=2EF=2a,由勾股定理得x2+y2=2a2…①,由直角梯形的面积公式可得:(x+y)2=2m…②,由②①,得xy=m a2,∵S△DFC=S梯形ABCD S△AFD S△BFC=(x+y)2 x2 y2 = xy,∴S△DEF=S△DFC=m a2.题十一:D.详解:如图,过点B作BE∥AD,则出现平行四边形ABED和一个△BEC,∵AB=13,CD=16,AD=10,BC=6∴CE=3,BE=10,∵3+6<10,∴BE,CE,BC不能构成三角形∴这样的梯形一个也不能作.故选D.题十二:C.详解:作DE∥AB,则DE=AB,①当a=5为上底,b=10为下底,c、d为腰时,105=5,与15,20不能构成三角形,故不满足题意;②当a=5为上底,b=15为下底,b、d为腰时,155=10,与10,20不能构成三角形,故不满足题意;③当a=5为上底,d=20为下底,b、c为腰时,205=15,与10,15可以构成三角形,故满足题意;④当b=10为上底,c=15为下底,a、d为腰时,1510=5,与5,20不能构成三角形,故不满足题意;⑤当b=10为上底,d=20为下底,a、c为腰时,2010=10,与5,15不能构成三角形,故不满足题意;⑥当c=15为上底,d=20 为下底,a、b为腰时,2015=5,与5,10不能构成三角形,故不满足题意;综上可得只有当a=5为上底,d=20为下底,b、c为腰时,满足题意,即以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)只能做一个.故选C..。
梯形辅助线--华师大版(新编2019)

一、延长两腰,构造三角形。
例1:如图,在四边形ABCD中,有AB=DC, ∠ B=∠ C,AD<BC。求证:四边形ABCD为 等腰梯形。
证明:延长BA、CD,相交于点E。
E
∵ ∠ B=∠ C, ∴ EB=EC
边形(过梯形任意一顶点作腰的平行线)。
例2:如图,等腰梯形ABCD中,AD∥ BC,
AD=3,AB=4,BC=7,求∠ B的度数。
证明:过A作AE ∥CD交BC于E
A
D
则四边形AECD为平行四边形。
∴ AD=EC,CD=AE
∵ AB=CD=4,AD=3,BC=7 ∴BE=AE=AB=4
B
E
C
∴△ ABE为正△
又∵AB=DC, ∴AE=DE,∴ ∠ EAD= ∠ EDA
∵ ∠E + ∠EAD + ∠EDA = 180°
A
D
∠B + ∠C + ∠E = 180 °
∴ ∠EAD = ∠B ∴ AD ∥ BC
B
C∵ALeabharlann ≠ BC, ∠ B=∠ C∴四边形ABCD为等腰梯形。
二、平移一腰,把梯形转化为三角形和平行四
∴ ∠ B=60°
注意:通过作腰的平行线,构造平行四边形、三角形,
利用平行四边形的性质,把分散条件集中到三角形中去, 从而为证题创造必要条件。
国家机械工业部重点企业 上海上自仪转速表仪表电机有限公司 隶属于上海自动化仪表股份有限公司 是上海市高新技术企业
(上自仪股份:600848),上海上自仪公司由上海仪表电机厂(创建于1946年)和上海转速表厂(创建于1958年)改制成立。上海仪表电机厂和上海转
梯形辅助线专题训练题

梯形辅助线专题训练题1、 如图,已知在梯形ABCD 中,AB ∥DC ,∠D=60°, ∠C=45°,AB=2,AD=4,求梯形ABCD 的面积.解:作AE 、BF 垂直于DC ,垂足分别为E 、F ∴AE ∥BF ∵AB ∥DC ,∴四边形ABFE 是平行四边形,∴EF=AB=2∵∠D=60°,AD=4 ∴DE=2,∴AE=22DE -AD =32 ∴BF=AE=32。
∵∠C=45°∴CF=BF=32。
∴CD=DE+EF+CF=4+32 S 梯形ABCD =21(AB+CD )•AE=3662、在梯形ABCD 中,AD//BC ,AB=DC=AD=2, BC=4,求∠B 的度数及AC 的长。
解:过A 点作AE ∥DC 交BC 于点E , ∵AD ∥BC ,∴四边形AECD 是平行四边形. ∴AD=EC ,AE=DC , ∵AB=DC=AD=2,BC=4, ∴AE=BE=EC=AB ,∴△BAC 是直角三角形,△ABE 是等边三角形, ∴∠BAC=90°,∠B=60°. 在Rt △ABC 中, AC=22AB -B C =222-4=32,∴∠B=60°,AC=32.3、如图所示,已知等腰梯形ABCD 中,AD ∥BC ,∠B =60°,AD =2,BC =8,求等腰梯形的周长。
解:过点A 作AE ⊥BC ,过点D 作DF ⊥BC ,∵AD=EF=2,又BE=CF ∴BE=CF=(8-2)÷2=3 ∵∠B=60°, ∴∠BAE=30°, ∴AB=6∵梯形ABCD 是等腰梯形 ∴AB=CD=6∴周长为6+6+2+8=224、 如图所示,AB ∥CD ,AE ⊥DC ,AE =12,BD =20,AC =15,求梯形ABCD 的面积。
解:如图,过点A 作AF ∥BD 交CD 的延长线于F . ∵AB ∥CD ,∴四边形ABDF 是平行四边形. ∵AF=BD=15,FD=AB , 在Rt △AEF 和Rt △AEC 中, ∵AE=12,∴根据勾股定理,得:EF= 22AE -AF =9,CE= 22AE -AC =16. ∴FC=EF+EC=9+16=25, ∵FC=FD+CD=AB+CD , ∴S 梯形ABCD =21(AB+CD )•AE=21×25×12=150.5、 如图所示,在等腰梯形ABCD 中,已知AD ∥BC ,对角线AC 与BD 互相垂直,且AD =30,BC =70,求BD 的长.解:过点D 作DE ∥AC 交BC 的延长线于点E , ∵AD ∥BC (已知),即AD ∥CE , ∴四边形ACED 是平行四边形,∴CE=AD= 30,AC=DE ,BE=BC+CE=100 在等腰梯形ABCD 中,AC=DB , ∴DB=DE (等量代换), ∵AC ⊥BD ,AC ∥DE , ∴DB ⊥DE ,∴△BDE 是等腰直角三角形,作DF ⊥BC 于F , 则DF=21 BE=50,S 梯形ABCD =21(AD+BC )•DF=21(30+70)×50=250.6、 如图所示,已知等腰梯形的锐角等于60°,它的两底分别为15cm 和49cm ,求它的腰长.解:分别过点C ,D 作CE ⊥AB ,DF ⊥AB ,则四边形EFDC 为矩形,△ACE ≌△BDF , ∵CD=15cm ,AB=49cm ∴AE=17cm ,∵CE ⊥AB ,∠A=60°, ∴∠ACE=30°, ∴AC=34cm , 故腰长为34cm .7、 如图所示,已知等腰梯形ABCD 中,AD ∥BC ,AC ⊥BD ,AD +BC =10,DE ⊥BC 于E ,求DE 的长.解:过点D 作DK ∥AC ,交BC 的延长线于K , ∵AD ∥BC ,∴四边形ACKD 是平行四边形, ∴CK=AD ,AC=DK , ∵AC ⊥BD , ∴BD ⊥DK ,∵四边形ABCD 是等腰梯形, ∴BD=AC=DK , ∵DE ⊥BC , ∴BE=KE , ∴DE=21 BK=21(BC+CK )=21(BC+AD )=21×10=5.8、已知:如图,梯形ABCD 中,AD ∥BC ,AB=DC ,∠BAD 、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F .求证: CE=BF .证明:在梯形ABCD 中,AB=DC , ∴∠ABC=∠DCB ,∠BAD=∠CDA .∵AE 、DF 分别为∠BAD 与∠CDA 的平分线,∴∠BAE=21∠BAD ,∠CDF=21∠CDA .∴∠BAE=∠CDF .∴△ABE ≌△DCF . ∴BE=CF .∴BE-BC=CF-BC .即BF=CE .9、如图,在梯形ABCD 中,AD ∥BC , BD=CD, ∠BDC =90°,AD=3,BC=8.求AB 的长.解:作AE ⊥BC 于E ,DF ⊥BC 于F . ∴AE ∥DF ,∠AEF=90°, ∵AD ∥BC ,∴四边形AEFD 是矩形. ∴EF=AD=3,AE=DF .∵BD=CD ,∠BDC=90°,∴△BDC 是等腰直角三角形, ∵DF ⊥BC ,∴DF 是△BDC 的BC 边上的中线. ∴DF=21BC=BF=4.∴AE=4,BE=BF-EF=4-3=1. 在Rt △ABE 中,AB 2=AE 2+BE 2,∴AB=2214+=17.10、如图,在梯形ABCD 中,AD ∥BC ,∠A =90°, ∠C =45°,DE=EC ,AB=4,AD=2,求BE 的长.11、已知:如图,梯形ABCD 中,DC ∥AB ,AD=BC ,对角线AC 、BD 交于点O ,∠COD=60°,若CD=3,AB=8,求梯形ABCD 的高.解:过点C 作CE ∥DB ,交AB 的延长线于点E ,过点C 作CH ⊥AE 于点H .∴∠ACE=∠COD=60°又∵DC ∥AB ,∴四边形DCEB 为平行四边形 ∴BD=CE ,BE=DC=3,AE=AB+BE=8+3=11 又∵DC ∥AB ,AD=BC ,∴DB=AC=CE ∴△ACE 为等边三角形∴AC=AE=11,∠CAB=60°。
梯形中常见辅助线及例题

例谈梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。
一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
[例1]如图1,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
[例2]如图2,在梯形ABCD 中,AD//BC ,∠B +∠C=90°,AD=1,BC=3,E 、F 分别是AD 、BC 的中点,连接EF ,求EF 的长。
3、平移对角线:过梯形的一个顶点作对角线的平行线,将已知条件转化到一个三角形中。
[例3]如图3,在等腰梯形ABCD 中,AD//BC ,AD=3,BC=7,BD=25,求证:AC ⊥BD 。
【变式1】(平移对角线)已知梯形ABCD 的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线长为_____________[例4]如图4,在梯形ABCD 中,AD//BC ,AC=15cm ,BD=20cm ,高DH=12cm ,求梯形ABCD 的面积。
二、延长即延长两腰相交于一点,可使梯形转化为三角形。
[例5]如图5,在梯形ABCD 中,AD//BC ,∠B=50°,∠C=80°,AD=2,BC=5,求CD 的长。
【变式2】如图所示,四边形ABCD 中,AD 不平行于BC ,AC =BD ,AD =BC. 判断四边形ABCD 的形状,并证明你的结论.【变式3】(延长两腰)如图,在梯形中,,,、为、的中点。
三、作对角线即通过作对角线,使梯形转化为三角形。
[例6]如图6,在直角梯形ABCD 中,AD//BC ,AB ⊥AD ,BC=CD ,BE ⊥CD 于点E ,求证:AD=DE 。
最新梯形中的常用辅助线总结与对应练习题

. 求证: 中,
. . 求证:梯
形
是等腰梯形 .
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。 [例 2]如图,在梯形 ABCD中, AB//CD,∠D+∠ C=90°,BC=1,AD=3,E、F 分别是 AB、CD的中点, 连接 EF,求 EF的长。
【变式】如图,在梯形
【变式 1】在等腰梯形 ABCD中, AD//BC,AD=3,BC=7,BD=5 2 ,求证: AC⊥ BD。
精品文档
精品文档
【变式 2】(平移对角线)已知梯形 ABCD的面积是 32,两底与高的和为 16,如果其中一条对角线与 两底垂直,则另一条对角线长为 _____________ [例 4]在梯形 ABCD中, AD//BC,AC=15cm,BD=20cm,高 DH=12cm,求梯形 ABCD的面积。
D
C
A
B
三、作对角线: 即通过作对角线,使梯形转化为三角形。
[例 6]在直角梯形 ABCD中, AD//BC,AB⊥ AD,BC=CD,BE⊥CD于点 E,求证: AD=D。E
四、作梯形的高 1、作一条高,从底边的一个端点作另一条底边的垂线,把梯形转化为直角三角形或矩形。
精品文档
精品文档
[例 7]如图,在直角梯形 ABCD中, AB//DC,∠ ABC=9°0 , AB=2DC,对角线 AC⊥BD,垂足为 F,过 点 F 作 EF//AB,交 AD于点 E,求证:四边形 ABFE是等腰梯形。
中,
,
1 EF=2(CD-AB)
, 、 为 、 的中点。求证:
3、平移对角线:一般是过上底的一个端点作一条对角线的平行线 , 与另一底的延长线相交 , 得到一个 平行四边形和三角形 , 把梯形问题转化为平行四边形和三角形问题解决.
初二数学梯形中常用的辅助线例题

[例4]如图4,在梯形ABCD 中,AD //BC ,∠B=50°,∠C=80°,AD=2,BC=5,求CD 的长。
[例3]如图3,在等腰梯形ABCD 中,AD //BC ,AD=3,BC=7,BD=25,求证:AC ⊥BD 。
[例2]如图2,在梯形ABCD 中,AD //BC ,∠B +∠C=90°,AD=1,BC=3,E 、F 分别是AD 、BC 的中点,连接EF ,求EF 的长。
[例1]如图1,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。
梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。
一、平移 1、平移一腰:从梯形的一个顶点 作一腰的平行线,把梯形转化为一个 三角形和一个平行四边形。
(如下图)2、平移两腰:利用梯形中的某个 特殊点,过此点作两腰的平行线,把 两腰转化到同一个三角形中。
3、平移对角线:过梯形的一个 顶点作对角线的平行线,将已知条件 转化到一个三角形中。
二、延长即延长两腰相交于一点,可使梯形转化为三角形。
三、作对角线即通过作对角线,使梯形转化为 三角形。
图1图2图3 图4 [例5]如图5,在直角梯形ABCD 中,AD //BC ,AB ⊥AD ,BC=CD ,BE ⊥CD 于点E ,求证:AD=DE 。
图5(2)证明:△AB F 的面积等于梯形ABCD 的面积。
(3)证明:△AB E 的面积等于梯形ABCD 的面积的一半。
[例10]如图10。
在梯形ABCD 中,AD ∥BC , ∠BAD=900,E 是DC 上的中点,连接AE 和BE 。
求(1)∠AEB=2∠CBE 。
[例9]如图9,在梯形ABCD 中,AD //BC ,E 、F 分别是BD 、AC 的中点,求证:(1)EF //AD ;(2))AD BC (21EF -=[例8]如图8,在梯形ABCD 中,AB //DC ,O 是BC 的中点,∠AOD=90°,求证:AB +CD=AD 。
梯形常用的辅助线

MN : I
_ _
EF:3 . 2
图2
温 馨 小 提 示 : 移 腰 把 条 件 集 中 , 取 平 移 点 是 关 键 , 用 的 平 选 常 平 移 点 有 : 个 顶 点 、 腰 中点 、 边 上 的 中点 等 . 四 一 底 二 、 移 对 角 线 平
分 析 : 目中 有 “ E 分 B D” “ E上A 结合 等腰 三角 题 C平 C 和 C B”
,
形 “ 线合一 ” 三 ,可 想 到 延 长 B C A、D相 交 于 ,,易 知 A B 为 等 腰 三 角 形 ( B= F) 且 CF C C ,
B E AC E AC E E= F, B F .设 A 口 则 B E= , E= E 2, F= a AF= 设 A C E 的 面 积 为 ., B s 则 AF D的 面 积 为 S , C F 面 积 为 2 . 由 A 一1 A B 的 S B
故梯形A C 面积 的最 大值为2. BD 5
温 馨 小 提 示 : 当 两腰 或 两 条 对 角线 在 数 量 或 位 置 上 有 特 殊 关
系 时 , 过 平 移 , 将 分 散 的 条 件 集 中起 来 . 定 要 选 择 好 集 中的 通 可 一 位 置 , 角 线 通 常 集 中到 梯 形 的 四 个 顶 点 处 . 对
易 知 四 边 形A E D C是 平 行 四 边 形 , 且 S AB S E , 而 有 S 形 BD J B . A D- A C 进  ̄ D 梯 Ac= △ E s D
1
B
j
C
图 3
AB D是 直 角 三 角 形 , = + = + E 船 C 叩 C D= + =1 , 7 3 0
(完整版)梯形中的辅助线专题训练

(完整版)梯形中的辅助线专题训练介绍本文档旨在提供有关梯形中辅助线的专题训练。
梯形是一种四边形,其两边平行,另外两边不平行。
使用辅助线可以帮助我们解决梯形相关问题,提高解题效率。
问题1已知梯形ABCD,边AB平行于边CD,辅助线EF与边AB和边CD相交于点E和点F。
如果边AE的长度为6,边BC的长度为9,边DE的长度为3,求辅助线EF的长度。
解答1由于辅助线EF与边AB平行,所以我们可以利用相似三角形的性质来解决这个问题。
根据题目给出的信息,我们可以得到以下相似三角形比例关系:AE/EF = DE/BC代入已知数值,我们可以得到:6/EF = 3/9进一步计算,得到:EF = 18/3 = 6所以辅助线EF的长度为6。
问题2已知梯形PQRS,边PQ平行于边RS,辅助线TU与边PQ和边RS相交于点T和点U。
如果已知边PT的长度为12,边QT的长度为8,边QU的长度为10,求辅助线TU的长度。
解答2同样地,由于辅助线TU与边PQ平行,我们可以利用相似三角形的性质来解决这个问题。
根据题目给出的信息,我们可以得到以下相似三角形比例关系:PT/TU = QU/QS代入已知数值,我们可以得到:12/TU = 10/(8 + TU)进一步计算,得到:12(8 + TU) = 10TU96 + 12TU = 10TU96 = 2TUTU = 48所以辅助线TU的长度为48。
结论辅助线在解决梯形相关问题时起着关键的作用。
通过合理运用相似三角形的性质,我们可以快速求解辅助线的长度,并解决梯形中的各类问题。
这里提供的两个专题训练问题是基于辅助线与边平行的情况,但在实际应用中,辅助线也可以与其他线段相交。
在解题过程中,要善于分析问题,并运用恰当的方程和几何关系,以达到高效解题的目的。
梯形中常见的辅助线(含答案)
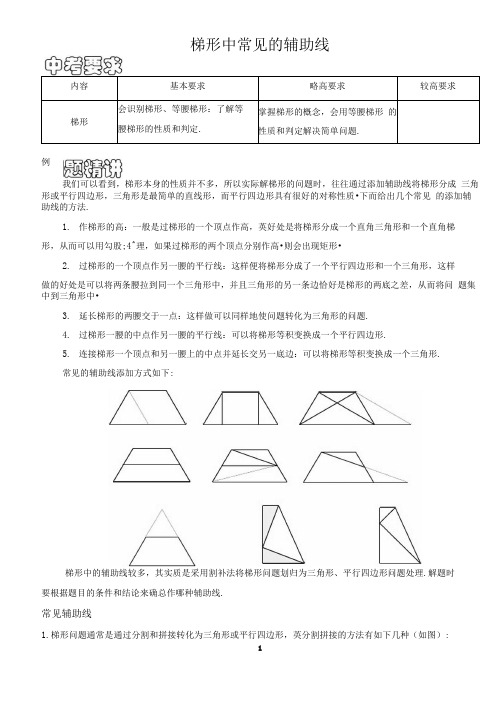
梯形中常见的辅助线内容基本要求略高要求较高要求梯形会识别梯形、等腰梯形:了解等腰梯形的性质和判定.掌握梯形的槪念,会用等腰梯形的性质和判定解决简单问题.例我们可以看到,梯形本身的性质并不多,所以实际解梯形的问题时,往往通过添加辅助线将梯形分成三角形或平行四边形,三角形是最简单的直线形,而平行四边形具有很好的对称性质•下而给出几个常见的添加辅助线的方法.1.作梯形的高:一般是过梯形的一个顶点作高,英好处是将梯形分成一个直角三角形和一个直角梯形,从而可以用勾股;4^理,如果过梯形的两个顶点分别作高•则会出现矩形•2.过梯形的一个顶点作另一腰的平行线:这样便将梯形分成了一个平行四边形和一个三角形,这样做的好处是可以将两条腰拉到同一个三角形中,并且三角形的另一条边恰好是梯形的两底之差,从而将问题集中到三角形中•3.延长梯形的两腰交于一点:这样做可以同样地使问题转化为三角形的问题.4.过梯形一腰的中点作另一腰的平行线:可以将梯形等积变换成一个平行四边形.5.连接梯形一个顶点和另一腰上的中点并延长交另一底边:可以将梯形等积变换成一个三角形.常见的辅助线添加方式如下:梯形中的辅助线较多,其实质是采用割补法将梯形问题划归为三角形、平行四边形问题处理.解题时要根据题目的条件和结论来确总作哪种辅助线.常见辅助线1.梯形问题通常是通过分割和拼接转化为三角形或平行四边形,英分割拼接的方法有如下几种(如图):1,把梯形分成一个平行四边形和一个三角形(图1所示):【答案】(1)作一腰的平行线; (2)作另一底边的垂线: (3)作对角线的平行线:(4)交于一点:(5)对称中心: (6)对称轴.【例1】 等腰梯形ABCD 中,AD//BC,若AD=3, AB=4・ BC=7,则ZB= 【答案】60° 如图,直角梯形ABCD 中,AB//CD. CB 丄AB, △ABD 是等边三角形,若AB=2,则BC=在梯形ABCD 中,AD//BC. AD=5, BC=7.若E 为DC 的中点,対线交BC 的延长线于F 点,则BF= •梯形ABCD 中.AD//BC,若对角线AC 丄BD ■且AC=5cm. BD=12cm,则梯形的而积等于((1)平移一腰,即从梯形的一个顶点(2)从同一底的两端. ,把梯形分成一个矩形和两个宜角三角形(图2所示);(3)平移对角线,即过底的一端图2,可以借助新得的平行四边形或三角形来研究梯形(图3所示):(4)延长梯形的两腰.图3,得到两个三角形,如果梯形是等腰梯形,则得到两个等腰三角形(图4所示):(5)以梯形一腰的中点为.图4,作某图形的中心对称图形(图5、图6所(6)以梯形一腰为.图5 图6,作梯形的轴对称图形(图7所【例2】【答案】 73【例3】【答案】 12 【例4】 A. 30cw- B. 60CW' C- 90cm~2D- } 69 cm-【例10】如图,等腰梯形ABCD 中,AB//CD.对角线AC 平分Z BAD, ZB=60。
2013-2014学年华东师大版八年级数学上册例题讲解+练习梯形的辅助线课后练习及详解

梯形的辅助线课后练习主讲教师:傲德题一:(1)如图,直角梯形ABCD中,AD∥BC,∠B=90°,腰AB= 4,两底之差为2,求另一腰CD的长;(2)在梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=8,BC=14,求梯形ABCD的周长;(3)如图所示,在等腰梯形ABCD中,AB∥CD,DC=AD=BC,且对角线AC垂直于腰BC,求这个梯形各内角的度数;(4)如图,在梯形ABCD中,AD∥BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,则EF= .(1)如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,已知BC=7,MN=3,则EF= ;(2)如图,在梯形ABCD中,AD=DC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,则梯形ABCD的面积为;(3)如图,等腰梯形ABCD中,AD∥BC,AD=3,AB= 4,BC=7,求∠B的度数;(4)如图,梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,E在BC上,CE=2,则DE= .题二:已知:等腰梯形的上底是2cm,腰长是4cm,一个底角是60°,则等腰梯形的下底是cm.题三:已知:等腰梯形的一个底角等于60°,它的两底分别为4cm和7cm,则它的周长为cm.题四:如图所示,在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,且AD= 4,BC=8,求AC的长.题五:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=3,BC=7,求梯形ABCD面积的最大值.题六:如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,求CE的长.题七:如图,在梯形ABCD中,AB∥CD,∠A+∠B=90°,CD=5,AB=11,点M、N分别为AB、CD的中点,求线段MN的长.题八:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB= 4,AD=3,BC=5,点M是边CD 的中点,连接AM、BM.求△ABM的面积.题九:如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD 的中点,点F是AB上的点,∠ADF= 45°,FE=a,梯形ABCD的面积为m.(1)求证:BF=BC;(2)求△DEF的面积(用含a、m的代数式表示).题十:以线段a=16,b=13为梯形的两底,c=10,d=6为腰画梯形,这样的梯形() A.只能画出一个B.能画出2个C.能画出无数个D.不能画出题十一:以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)() A.至少能做3个B.恰好能做2个C.仅仅只能做1个D.一个也不能做梯形的辅助线课后练习参考答案题一:(2)34;(3)60°,60°,120°,120°;(4)1.详解:(1)过D作DE⊥BC于E,∵AB⊥BC,DE⊥BC,AD∥BC,∴四边形ADEB是个矩形,∴AB=DE= 4,CE=BC-AD=2,Rt△DEC中,CD;(2)过A、D点作AE⊥BC于E,DF⊥BC于F,∵AB=CD,∠B=∠C,AE=DF,∴△ABE≌△DCF,∴BE=CF,∵AD=8,BC=14,BE=CF=3,又∵在Rt△ABE中,∠B=60°,∴AB=2BE=6,∴梯形ABCD的周长为8+14+6+6=34;(3)如图所示,过点C作CE∥AD,又DC∥AE,∴四边形AECD为平行四边形,又DC=AD=BC,∴四边形AECD为菱形,∴AE=CE=BC,∴∠EAC=∠ECA,∠CEB=∠B,∵∠B+∠CAB=90°,即3∠CAE=90°,∴∠CAE=30°,∴∠B=60°=∠DAB,∠D=∠DCB=120°;(4)过点E作AB、CD的平行线,与BC分别交于G,H,∵∠B+∠C=90°,∴∠EGH=∠B,∠EHG=∠C,∴∠EGH+∠EHG=90°,∴四边形ABGE和四边形CDEH都是平行四边形,△EGH为直角三角形,∵E、F分别是AD、BC的中点,∴BG=CH=0.5,GH=2,根据直角三角形中斜边上的中线是斜边的一半知,EF=12GH=1,∴EF=1.题二: (1)4;;(3)60°;(4)5.详解:(1)过点N 分别作NG ∥AB ,NH ∥CD ,得平行四边形ABGN 和平行四边形DCHN ,∴∠NGM +∠NHM =∠B +∠C =90°,GH =BC -AD ,MG =MH ,∴GH =2MN =6,∴AD =7-6=1,∴EF = 4;(2)∵在梯形ABCD 中,AB =DC ,∴梯形ABCD 是等腰梯形,∴∠D +∠DCB =180°,∵∠D =120°,∴∠B =∠DCB =60°,∵对角线CA 平分∠BCD ,∴∠ACB =30°,∵AD =DC ,∴∠DAC =∠ACD =30°,∴∠BAC =90°,∴BC =2AB ,∵梯形的周长为AD +DC +BC +AB =5AB =20,∴AB = 4,∴AC =4BC =8,过点A 作AE ⊥BC 于点E ,∵AB = 4,AC ,BC =8,∴AE ,∴梯形ABCD 的面积为(4+8)×12(3)过点A 作AE ∥DC 交BC 于E ,∵AD ∥BC ,∴四边形AECD 是平行四边形,∴EC =AD =3,DC =AE ,∴BE =BC -CE =7-3= 4,∴CD =AB = 4,∴AE =AB =BE = 4,∴△ABE 是等边三角形,∴∠B =60°;(4)过D 作DF ∥AC 交BC 的延长线于F ,∵AD ∥BC ,∴四边形ACFD 是平行四边形,∴CF =AD =3,∵BC =7,∴BF =BC +CF =7+3=10,∵CE =2,∴BE =7-2=5,EF =2+3=5,∴BE =EF ,又∵AC ⊥BD ,DF ∥AC ,∴∠BDF =90°,∴DE =12BF =5.题三: 6cm .详解:过D 作DE ∥AB 交BC 于E ,∵DE ∥AB ,AD ∥BC ,∴四边形ABED是平行四边形,∴AD=BE=2cm,DE=AB=4cm,∠DEC=∠B=60°,AB=DE=DC,∴△DEC是等边三角形,∴EC=CD= 4cm,∴BC= 4cm+2cm=6cm.题四:17cm.详解:过上底顶点D作DE∥AB交BC于E,则四边形ABED是平行四边形,∴DE=AB,AD=BE,∵梯形的一个底角是60°,∴∠C=60°,又∵腰长AB=CD=DE,∴△CDE是等边三角形,∴CD=CE=BC-BE=7-4=3cm,∴它的周长为3+7+3+4=17cm.题五:详解:过D作DE∥AC交BC的延长线于E,∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴ADEC是平行四边形,∴AD=CE,AC=DE,即可得出BE=BC+CE=BC+AD=12,又∵AC=BD,∴BD=ED,∴△BDE为等腰直角三角形,∴AC=BD=题六:25.详解:过D作DE∥AC交BC延长线于E,∵AD∥BC,DE∥AC,∴四边形ACED是平行四边形,∴AD=CE,∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积,即梯形ABCD的面积等于△BDE的面积,∵AC⊥BD,DE∥AC,∴∠BDE=90°,BE=3+7=10,∴此时△BDE的边BE边上的高越大,它的面积就越大,即当高是12BE时最大,即梯形的最大面积是12×10×12×10=25.题七: 2.3.详解:延长AF、BC交于点G,∵AD∥BC,∴∠D=∠FCG,∠DAF=∠G,又DF=CF,∴△AFD≌△GFC,∴AG=2AF=8,CG=AD=2.7,∵AF⊥AB,AB=6,∴BG=10,∴BC=BG-CG=7.3,∵AE=BE,∴∠BAE=∠B,∴∠EAG=∠AGE,∴AE=GE,∴BE=12BG=5,∴CE=BC-BE=2.3.题八:3.详解:如图,过D作DE∥BC,DF∥MN,∵在梯形ABCD中,AB∥CD,DE∥BC,∴CD=BE=5,AE=AB-BE=11-5=6,∵M为AB的中点,∴MB=AM=12AB=12×11=5.5,ME=MB-BE=5.5-5=0.5,∵N为DC的中点,∴DN=12DC=12×5=2.5,在四边形DFMN中,DC∥AB,DF∥MN,∴FM=DN=2.5,∴FE=FM+ME=2.5+0.5=3=12AE,∴F为AE的中点,又∵DE∥BC,∴∠B=∠AED,∵∠A+∠B=90°,∴∠A+∠AED=90°,∴∠ADE=90°,即△ADE是直角三角形,∴DF=MN=12AE=12×6=3.题九:8.详解:延长AM交BC的延长线于点N,∵AD∥BC,∴∠DAM=∠N,∠D=∠MCN,∵点M是边CD的中点,∴DM=CM,∴△ADM≌△NCM(AAS),∴CN=AD=3,AM=MN=12AN,∴BN=BC+CN=5+3=8,∵∠ABC=90°,∴S△ABN=12×AB•BN=12×4×8=16,∴S△ABM=12S△ABN=8,即△ABM的面积为8.题十:见详解.详解:(1)∵四边形ABCD是直角梯形,∴∠A=90°,∵∠ADF=45°,∴∠AFD= 45°,∴AD=AF,∵AB=AF+BF,AB=AD+BC,∴BF=BC;(2)连接FC,设AD=AF=x,BC=BF=y,连接CF,作DH⊥BC于H,易证四边形ABHD为矩形、△CDF为直角三角形,又∵E是CD中点,∴CD=2EF=2a,由勾股定理得x2+y2=2a2…①,由直角梯形的面积公式可得:(x+y)2=2m…②,由②-①,得xy=m-a2,∵S△DFC=S梯形ABCD-S△AFD-S△BFC=12(x+y)2 -12x2 -12y2 = xy,∴S△DEF=12S△DFC=12m-12a2.题十一:D.详解:如图,过点B作BE∥AD,则出现平行四边形ABED和一个△BEC,∵AB=13,CD=16,AD=10,BC=6∴CE=3,BE=10,∵3+6<10,∴BE,CE,BC不能构成三角形∴这样的梯形一个也不能作.故选D.题十二:C.详解:作DE∥AB,则DE=AB,①当a=5为上底,b=10为下底,c、d为腰时,10-5=5,与15,20不能构成三角形,故不满足题意;②当a=5为上底,b=15为下底,b、d为腰时,15-5=10,与10,20不能构成三角形,故不满足题意;③当a=5为上底,d=20为下底,b、c为腰时,20-5=15,与10,15可以构成三角形,故满足题意;④当b=10为上底,c=15为下底,a、d为腰时,15-10=5,与5,20不能构成三角形,故不满足题意;⑤当b=10为上底,d=20为下底,a、c为腰时,20-10=10,与5,15不能构成三角形,故不满足题意;⑥当c=15为上底,d=20 为下底,a、b为腰时,20-15=5,与5,10不能构成三角形,故不满足题意;综上可得只有当a=5为上底,d=20为下底,b、c为腰时,满足题意,即以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)只能做一个.故选C.。
八年级数学秋季班第7讲梯形进阶之梯形辅助线大揭秘拔高练习(北师版)

八年级数学秋季班第7讲梯形进阶之梯形辅助线大揭秘拔高练习(北师版)试卷简介:本测试卷共8道题,全面考察梯形辅助线的做法,分三个板块,第一板块:梯形辅助线复习,共有9中辅助线的做法;第二板块:梯形辅助线的应用,充分考察等腰梯形和直角梯形的知识;第三板块:梯形动点问题,是中考题的常考题型和重难点、学习建议:先充分的了解梯形各种辅助线的做法和原理一、单选题(共1道,每道10分)1.(2011安徽)如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P 在四边形ABCD的边上,若P到BD的距离为,则点P的个数为( )A.1B.2C.3D.4答案:B解题思路:解:当点P在BD的左端,即AB和AD上运动时,P到BD的最小距离为0,P 到BD的最大距离为当点P运动到A点的时候,此时由AB=AD=,得:△ABD为等腰直角三角形,从而A到BD的距离为等腰三角形斜边上的高,为2∵∴存在两个点当点P在BD的右端,即AB在DC和BC上运动时,P到BD的最小距离为0,P到BD的最大距离为当点P运动到点C的位置,即点C到BD的距离,如图,即CE的长∵∠ADB=45°,∠ADC=90°∴∠CDB=45°∴△CDE为等腰直角三角形从而CE=∵∴此时不存在符合要求的点P综上:点P的个数为2,B选项正确易错点:分类讨论时忘记一种情况试题难度:三颗星知识点:直角梯形二、填空题(共3道,每道10分)1.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:①BH=DH;②③其中正确的是()答案:②③解题思路:过H做HG⊥BC于点G,CE平分∠BCD,BD⊥CD,△CGH≌△CDH,∴DH=GH, CG=CD∵在△BGH中,∴BH>GH,∴BH>DH∴①不对∵∠ECB+∠BEH=90°,∠DCE+∠DHC=90°CE平分∠BCD∴∠BEH=∠CHD=∠BHE∴BE=BH又∠EBN=∠BEN=∠CBD=∠BHG=45°∴△BEN≌BHG(ASA)∴设EN=x,则HG=x∴HD=HG=x,BH=x∴CD=BD=BH+HD=(+1)x∴②正确,CH=(1+)EH③△ENH和△EBH同高,高都等于E到BH的距离,底不同。
八年级数学梯形进阶之梯形辅助线大揭秘(四边形性质探索)拔高练习(含答案)

八年级数学梯形进阶之梯形辅助线大揭秘(四边
形性质探索)拔高练习
试卷简介:本试卷为卢老师八年级秋季线下班第七讲测试题,第七讲为梯形进阶之梯形辅助线大揭秘,全面考察同学们梯形常见辅助线的添加,以及添加的原理。
学习建议:先熟悉一下梯形常规辅助线的添加方法:一平移:.平移一腰,平移两腰,平移对角线;二延长,延长两腰;三做高,做单高,做双高。
一、单选题(共1道,每道100分)
1.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,且AC⊥BD,AF是梯形的高,梯形面积是49cm²,则AF=()
A.5
B.6
C.7
D.8
答案:C
E
解题思路:过点D作DE∥AC交BC的延长线于点
则四边形ACED为平行四边形,从而AC=DE,AC∥DE,AD=CE∵四边形ABCD为等腰梯形ABCD∴AC=BD∴BD=DE∵AC⊥BD∴BD⊥DE∴△BDE为等腰直角三角形∵AD=CE∴△ABD的面积=△DCE的面积∵梯形ABCD面积是49cm²∴△BDE的面积是49cm²即
∴BD=DE=7∵AF为梯形的高∴AF为等腰直角△BDE
的高线∴AF=7
易错点:辅助线的添加
试题难度:四颗星知识点:等腰梯形的性质
第 1 页共 1 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形辅助线专题练习
1、等腰梯形上、下底差等于一腰的长,那么腰长与下底的夹角是( ).A.5° B.60° .45° D.30°
2、腰梯形两底之差的一半等于它的高,那么此梯形的一个底角是( )A .30° B .45° C .60° D .75°
3、直角梯形两底之差等于高,则其最大角等于_______.
4、梯形两底长分别为14cm 和24cm ,下底与腰的夹角分别是60°和30°,求较短腰长。
5、梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。
6、已知梯形ABCD 中,AD//BC ,AB=DC ,对角线AC 、BD 互相垂直,梯形的两底之和为8。
求梯形的高与面积。
7、在等腰梯形ABCD 中,AD//BC ,AD=3,BC=7,BD=25,求证:AC ⊥BD 。
8、在梯形ABCD 中,AD//BC ,AC=15cm ,BD=20cm ,高BH=12cm ,求梯形ABCD 的面积。
9、如图,梯形ABCD 中,AB//CD ,E 为腰AD 的中点,且AB+CD=BC 。
求证:BE ⊥CE 。
C
D
10、在梯形ABCD 中,AD ∥BC ,∠B =50°,∠C =80°,AD =8,BC =11,则CD =_______.
11、等腰梯形的腰长为5cm ,上、下底的长分别为6cm 和12cm ,则它的面积为_______.
12、如图,在梯形A B C D 中,A D B C ∥,对角线A C B D ⊥,且8A C =cm ,6B D =cm ,则此梯形的高为 _______________cm .
13、在梯形ABCD 中,AD ∥BC ,AB =8,DC =6,∠B =45°,BC =10,求梯形上底AD 的长.
14、如图,在梯形ABCD 中,AD//BC ,∠B +∠C=90°,AD=1,BC=3,E 、F 分别是AD 、BC 的中点,连接EF ,求EF 的长。
F
B
A
15、如图所示,已知等腰梯形ABCD 中,AD ∥BC ,∠B =60°,AD =2,BC =8,求等腰梯形的周长。
A B C D 16、. 在等腰梯形ABCD 中,AD//BC ,AB=CD ,∠ABC=60°,AD=3cm ,BC=5cm ,求:(1)腰AB 的长;(2)梯形ABCD 的面积.。
