22.1.2学案设计

合集下载

八年级上册语文部编版《22.1 得道多助,失道寡助》名师教学-精品导学案

《得道多助，失道寡助》学案教学目标：1、积累文言知识，掌握古今异义词及词类活用现象。

2、了解《孟子》散文的特点，理解孟子的政治主张。

3、增强对国家团结的政治局面的认识，在现实生活中予以贯彻落实。

教学重点：1、积累文言知识，掌握古今异义词及词类活用现象。

2、理解“天时”地利”“人和”与“得道多助失道寡助”的道理教学难点：理解“天时”地利”“人和”与“得道多助失道寡助”的道理教学时间4课时教学进程第一课时〖教学目标〗1、了解作家作品。

2、掌握生字词3、熟读背诵课文，把握节奏。

一、导入新课记得有首歌曲是这样唱的:“数英雄论成败,古今谁能说明白,千秋功罪任评说,海雨天风独往来,一心要江山图治垂青史,也难说身后骂名滚滚来……有道是得民心者得天下,看江山由谁来主宰……” “得民心者得天下”，这是自古常言.回顾中国几千年王朝更替史，旧王朝腐朽不堪而使民心背离，这时新王朝就顺应民意而夺取天下。

今天我们就来学习课文《得道多助，失道寡助》二、有关资料1、有关作者：孟子（约前372一前289），名轲，字子舆，邹（今山东邹县）人，战国时期思想家、教育家，是儒家思想的代表人物，地位仅次于孔子，被尊为“亚圣”，后世常以“孔孟”并称。

《孟子》是儒家学派的经典著作之一，是孟子及其门人所著散文集，其间杂有弟子的话语。

《孟子》现存“内书”七篇。

2、写作背景战国时期，诸侯各国之间的吞并战争日益激烈，为了求得生存，乃至建立霸业，各国君主不约而同地崇尚武力而不体恤百姓。

面对这种现实，孟子提出了他的治国理想。

三、预习设计1、填空孟子，名，字，时期家学派的代表人物。

被尊为，他主张以统一天下。

2、给加点字注音夫．（）环而攻之米粟．（）域．（）民寡．（）助亲戚畔．（）之3、划分句子的节奏⑴三里之城,七里之郭,环而攻之而不胜。

⑵夫环而攻之,必有得天时者矣,然而不胜者,是天时不如地利也。

⑶城非不高也,池非不深也,兵革非不坚利也,米粟非不多也,委而去之,是地利不如人和也。

第22章二次根式(全章学案)

22.1二次根式(1)教学案学习目标：1．了解二次根式的意义；2. 会运用二次根式的定义判断二次根式是否有意义，即找出二次根式有意义的条件。

并掌握用简单的一元一次不等式解决二次根式中字母的取值问题；学习重点、难点：重点：(1)二次根式的意义；(2)二次根式中字母的取值范围．难点：确定二次根式中字母的取值范围．教材分析及学法指导：二次根式是在算术平方根的基础上引申出来的，因而二次根式的学习实质是平方根知识的巩固与延伸，在学习中要注意二者的结合．学习准备：1．复习提问：请思考什么叫平方根、算术平方根？2．说出下列各式的意义，并计算：，，，，3．观察上面几个式子的特点，请总结它们的被开方数的特点。

学习过程：（一）引入新课：我们已遇到的，，这样的式子是我们这节课研究的内容，引出新课：二次根式。

（二）自主学习交流发现1．自学课本第二页前三段内容，并理解记忆二次根式定义。

2．对于请同学们讨论应该注意的问题，小组交流，引起重视。

选二个小组回答自己小组的观点。

3．例1 当a为实数时，下列各式中哪些是二次根式？（同桌交流答案）4．练习. 判断下列各式，那些是二次根式？（学生回答）676-2-x2m5.例2 x是怎样的实数时，式子在实数范围有意义？（生回答）6. 练习1.完成课本第三页练习2。

练习2.当字母取何值时，下列各式为二次根式：（学生独立完成，小组成员展示）（1）（2）(3) （4）练习3．x是怎样的实数时，下列二次根式有意义？（小组选成员黑板展示）（1）(2)(3)（4）7. 反馈总结交流收获:本节课你的收获是————————————还有的疑惑是——————————————当堂检测：1．判断下列各式是否是二次根式2．a是怎样的实数时，下列各式在实数范围内有意义？课后反思：22.1.1二次根式检测（第一课时）◆随堂检测1、下列式子中，是二次根式的是（）A ．．x2、已知一个正方形的面积是5，那么它的边长是（）A ．5BC ．15D ．以上皆不对3、2=_______； 2=______；2=_______．4＝_______． 5、若y =有意义，则x 的取值范围是． ◆典例分析(1)下列式子，哪些是二次根式，哪些不是二次根式：、1x x>0）1x y+x ≥0，y•≥0）．分析；第二，被开方数是正数或0．解：x>0）、x ≥0，y ≥0）；不是二次1x1x y +．点评：确定一个式子是不是二次根式关键要记住两点：a ≥0的条件(2)当x分析：由二次根式的定义可知，被开方数一定要大于或等于0，所以3x-1≥0，才能有意义．解：由3x-1≥0，得：x ≥13当x ≥13在实数范围内有意义．◆课下作业●拓展提高1、若二次根式26x -+有意义，化简│x-4│-│7-x │．2、若20092009a b ++-=0，求a 2009+b2009的值．3、已知a 、b 为实数，且5a -+2102a -=b+4，求a 、b 的值．4、下列各式中15、3a 、21b -、22a b +、220m +、144-，二次根式的个数是（）．A ．4B ．3C ．2D ．15、使式子2(5)x --有意义的未知数x 有（）个． A ．0 B ．1 C ．2 D ．无数6、若11x x ---2()x y =+，则x －y 的值为（） A ．－1 B ．1 C ．2 D ．3●体验中考1、（2009年贵州省黔东南州）=-2)3(___________2、（2009年湖南怀化）若()22340a b c ---=，则=+-c b a ． 3、（2009年济宁市）已知a 2a -( ) A. a B. a - C. － 1 D. 0 4、(2009年鄂州市)使代数式43--x x 有意义的x 的取值范围是（） A 、x >3 B 、x ≥3C 、 x >4D 、x ≥3且x ≠4随堂检测：1．A . 二次根式应满足两个条件：第一，有二次根号；第二，被开方数是正数或0．所以选A ，而B 中根指数不是2；C 中被开方数x 也可表示负数，无意义；D 是单项式.2. B. 设正方形的边长是x，则25,0,x x x x =∴=>∴=所以选B ；3．4；13；0.主要应用公式2(0)a a =≥进行计算得出：2=4；2=13；2=0．4． 0. 因为与都是二次根式，所以22222210101110,10x x x x x x -≥-≥--∴-=-=且，因为和互为相反数，，所以=0.5. 3x >-.若y =有意义，不仅要考虑被开方数是非负数，必须考虑分式的分母不为零，则30,x +>3x >- 拓展提高：2603,40,70.474(7)3x x x x x x x x -+≥≤-∴-<->∴---=---=-1.解：由得20092009200920092009020090,20090,20090,20090,2009,2009.(2009)20090.a ab a b a b a b ++=+≥-≥∴+=-=∴=-=∴+=-+=2.解：，50505 5. 4.a a a a a b -≥≥≥≤∴=∴=-3.解：由得，由10-2得，4、B2250,505.B x x x B -≥∴-≥∴=5..解：（）），所以只有一个值，选.6..10 1.0 1. 1.0, 1.1(1) 2.C x x x x x x y y x y C -≥≥-≥≤∴=∴+=∴=-∴-=--=解：由得，由1得，所以选.1．-322(4)0,20,30,40;2,3, 4.234 3.a c abc a b c a b c -++-=∴-=-=-=∴===∴-+=-+=2.解：22223..0,0,00,0..D a a a a a D -≥∴≤≥∴=∴=解：由题意知，所以选4..30,40,3 4..D x x x x D -≥-≠∴≥≠解：由题意知且且所以选22.1二次根式(2)教学案学习目标：1≥(0)-(0)a a a a a ≥⎧==⎨<⎩的发现过程，体验归纳、猜想的思想方法。

八(下)22章学案

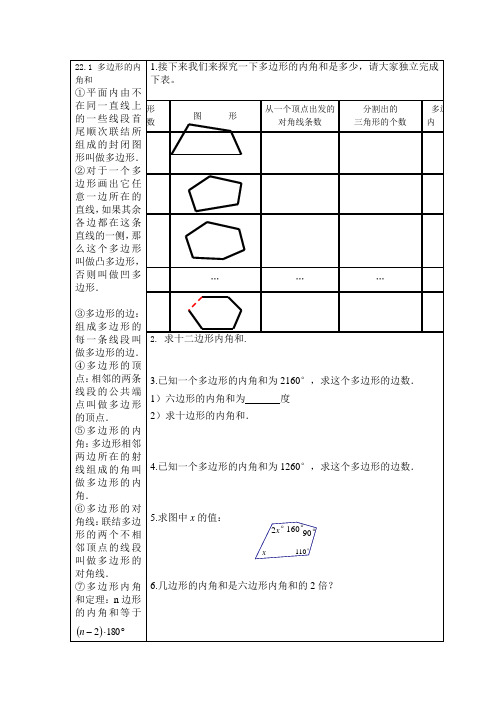
22．3（3）矩形、 1．矩形、菱形的判定菱形的判定矩形的判定 ①有一个角是直四边形矩形角的平行四边形是矩形．有一组邻边相等的平行四边形是菱形．平行四边形矩形
4. 已知：如图，在矩形 ABCD 中，对角线 AC 、 BD 相交于点 O ， ∠ AOD=120 °， AB=4 ，求 BC 的长 .
7. 如图，在菱形 ABCD 中， ∠ BAD=60 °， BD=4 ，则菱形 ABCD 的周长是 .
8. 如图，菱形 ABCD 的对角线相交于 O ， AC=8 ， BD=6 ，则边 AB 的长为 .
22.3（1）特殊的平行四边形 ①有一个角是直角的平行四边形叫做矩形． ②有一组邻边相等的平行四边形叫做菱形． ③ 矩形的四个角都是直角． ④矩形的两条对角线相等． ⑤矩形既是中心对称图形，也是轴对称图形．菱形的性质定理 ⑥菱形的四条边都相等． ⑦ 菱形的对角线互相垂直，并且每一条对角线平分 2. 若矩形的一个内角的平分线把矩形的一条边分成 3cm 和 5cm 的两段，则该矩形的周长为． 1. 在矩形 ABCD 中， AB=3cm ，对角线 AC=5cm ，则矩形 ABCD 的面积 2 是 cm 1 观察并口答平行四边形矩形菱形定义
BE、DF，点 M、N 分别是 BE，DF 的中点，联结 FM、EN，求证：四边形 EMFN 是平行四边形
A
E D N
M B F C
3．已知：如图，ABCD 中，AE，CF 分别平分∠BAD,∠BCD,分别交边 BC、AD 于点 E,F；求证：四边形 AECF 是平行四边形．

(好)第22章_一元二次方程_全章学案

第二十二章一元二次方程一、教材内容一元二次方程概念；解一元二次方程的方法；一元二次方程应用题．二、课标要求1、以分析实际问题中的等量关系并求解其中的未知数为背景,认识一元二次方程及其有关概念.2、根据化归思想,抓住降次这一策略,掌握配方法,公式法和因式分解法等一元二次方程的基本解法.3、经历分析和解决实际问题的过程,体会一元二次方程的数学模型作用,进一步提高在实际问题中运用这种重要数学工具的基本能力.三、教学目标1．知识与技能了解一元二次方程及有关概念；掌握通过配方法、公式法、因式分解法降次──解一元二次方程；掌握依据实际问题建立一元二次方程的数学模型的方法；应用熟练掌握以上知识解决问题．2．过程与方法（1）通过丰富的实例，让学生合作探讨，老师点评分析，建立数学模型．•根据数学模型恰如其分地给出一元二次方程的概念．（2）结合八册上整式中的有关概念介绍一元二次方程的派生概念，如二次项等．（3）通过掌握缺一次项的一元二次方程的解法──直接开方法，•导入用配方法解一元二次方程，又通过大量的练习巩固配方法解一元二次方程．（4）通过用已学的配方法解ax2+bx+c=0（a≠0）导出解一元二次方程的求根公式，接着讨论求根公式的条件：b2－4ac>0，b2－4ac=0，b2－4ac<0．（5）通过复习八年级上册《整式》的第5节因式分解进行知识迁移，解决用因式分解法解一元二次方程，并用练习巩固它．（6）提出、分析问题，建立一元二次方程数学模型，并用解决实际问题．3．情感、态度与价值观经历由事实问题中抽象出一元二次方程等有关概念的过程，体会到通过一元二次方程也是刻画现实世界中的数量关系的一个有效数学模型；经历用配方法、公式法、分解因式法解一元一次方程的过程，使同学们体会到转化等数学思想；经历设置丰富的问题情景，使学生体会到建立数学模型解决实际问题的过程，从而更好地理解方程的意义和作用，激发学生的学习兴趣．四、教学重点与难点教学重点:1. 一元二次方程及其它有关的概念.2．用配方法、公式法、因式分解法降次──解一元二次方程．3. 利用实际问题建立一元二次方程的数学模型,并解决这个问题.教学难点:1．一元二次方程配方法解题．2．用公式法解一元二次方程时的讨论．3．建立一元二次方程实际问题的数学模型；方程解与实际问题解的区别．五、课时划分本单元教学时间约需13课时，具体分配如下：22．1 一元二次方程2课时22．2 降次──解一元二次方程5课时22．3 实际问题与一元二次方程3课时教学活动、习题课、小结3课时22.1.1 《一元二次方程（1）》学案学习目标：1、进一步体会方程是刻画现实世界中数量关系的一个有效数学模型；2、正确理解一元二次方程的概念，掌握一元二次方程的一般形式，并能将一元二次方程转化为一般形式，正确识别二次项系数、一次项系数及常数项。

22.1.1二次函数教案

《22.1.1二次函数》教学设计表任务一：掌握二次函数的定义并解决相关数学问题活动1：下列等式哪些是y关于x的函数?如果是,是什么函数?13)6(123)5()4(2)3(2)2(12)1(222+-=++====+=xyxxyxyxyxyxy（1）学生能快速判断出哪些等式是函数，是什么函数。

若不是函数能说出理由。

（2）能通过活动1中的（5）和（6）来猜想出二次函数的定义。

在质疑和思考中师生共同得出二次函数的一般表达式。

（2）明确二次函数中的二次项系数，一次项系数和常数项。

（4）通过例1学生能独立正确判断出那些函数是二次函数。

对于是二次函数的①⑥能快速正确的说出二次项系数，一次项系数和常数项。

（6）通过例1独立总结或同桌商讨后总结出一个函数是否为二次函数的识别要点。

活动2：利用二次函数的定义求字母的值活动3：二次函数的求值问题（1）能熟练地运用一次函数、正比例函数和二次函数的定义解决数学常考问题。

（3）最少有百分之80的学生能在规定时间（4分钟）书写格式规范并正确的解决第2题和第3题。

95%的学生能得出正确答案。

能快速正确地解决二次函数求值问题任务二：用二次函数解决简单实际应用问题活动1：实际问题中根据几何知识列二次函数解析式（1）95%的学生能准确找出题目中的等量关系。

（2）90%的学生能根据等量关系列出函数解析式并确定自变量的取值范围。

（3）明确解决这类型题目自变量取值范围的方法。

如图,用一段长为40 m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18 m,设AD的长为x m,菜园ABCD的面积为y m2,则y关于自变量x的函数关系式是 ,x的取值1.当m为何值时，函数y=(m-4)x m²-5m+6+mx是关于x的二次函数.2.()273.my m x-=+（1）m取什么值时，此函数是正比例函数？（2）m取什么值时，此函数是二次函数？3.已知函数(1)当k为何值时,该函数为一次函数?(2)当k为何值时,该函数为二次函数?运用：集成：设计：从各地市的月考、模拟考、期中、期末考试试题中精选和改编出能高效考查本节课知识的试题。

22学案设计

22唐雎不辱使命学习目标1.能够结合语境准确辨析课文中重要词语含义。

2.能够把文中重要句子准确翻译成现代汉语。

3.通过讨论、总结,会用自己的话准确分析概括唐雎、秦王两个人物的形象特点,并归纳出学习课文“记言”的史家笔法和简洁传神的人物刻画方法。

学习过程一、课前导学1.作者、背景简介《战国策》是西汉末年刘向编写的一本以记言为主的史书,是一部国别体史书。

它叙事年代上接春秋,下至秦灭六国为止,约240年时间,是我们研究战国时期历史的一部重要著作。

这篇文章记叙了战国末期的一段故事:公元前230年和公元前225年,秦先后灭亡了韩、魏两国;安陵是魏的附庸小国,秦想用诈骗手段并吞安陵。

安陵君拒绝秦王的要求,在秦王不悦的情况下派遣唐雎出使秦国,目的就在于保全国土,解除与秦国之间的矛盾。

2.重点词语归类(1)读一读,写一写唐雎．(jū) 怫．然(fú) 免冠徒跣．(xiǎn) 以头抢．地(qiāng)韩傀．(guī) 休祲．(jìn) 缟．素(ɡǎo) 色挠．(náo)(2)通假字①故不错意也(“错”通“措”,安放)②轻寡人与(“与”通“欤”,语气词“吗”)③仓鹰击于殿上(“仓”通“苍”,青色)(3)词类活用①请广于君(广:形容词活用作动词,扩大,补充)②轻寡人与(轻:形容词活用作动词,轻视,看不起)③天下缟素(缟素:名词作动词,穿戴丧服)④伏尸百万,流血千里(伏、流均为动词的使动用法,“使……伏,使……流”)⑤且秦灭韩亡魏(灭、亡:动词的使动用法,“使……亡”)(4)一词多义①使{秦王使人谓安陵君曰(派遣)安陵君因使唐雎使于秦(前一个是“派遣”,后一个是“出使”)②虽{虽然,受地于先王(虽然,转折连词)虽千里不敢易也(即使,假设连词)③徒{免冠徒跣(光着)徒以有先生也(只,仅仅)④夫{此庸夫之怒也(fū,成年男子,名词)夫专诸之刺王僚也(fú,发语词,无义)⑤以{以头抢地耳(介词,用)而安陵以五十里之地存者(介词,凭借)徒以有先生也(介词,因为)(5)古今异义①岂直五百里哉(古:只,只是;今:不弯曲)②休祲降于天(古:吉祥;今:休息)③长跪而谢之曰(古:道歉;今:感谢)二、学习过程1.给下列加点的字注音。

2022年新课标八年级上册道德与法治《1.2 在社会中成长》教学设计

2022年新课标八年级上册道德与法治《1.2 在社会中成长》教学设计一. 教材分析《道德与法治》是我国初中阶段的一门重要课程，旨在培养学生的道德素养和法律意识。

2022年新课标八年级上册《道德与法治》第一单元的主题是“在社会中成长”，本节课《1.2 在社会中成长》是该单元的第二课。

本节课的主要内容是让学生了解个人与社会的关系，认识到在社会中成长的重要性，以及如何积极地参与社会生活。

二. 学情分析八年级的学生已经具有一定的社会经验和生活常识，对社会现象有一定的观察和思考能力。

但他们对个人与社会的关系的认识还比较模糊，对社会生活的参与度有待提高。

因此，在教学过程中，教师需要以学生的生活经验为切入点，引导学生认识个人与社会的关系，激发他们参与社会生活的热情。

三. 教学目标1.知识与技能：让学生理解个人与社会的关系，知道在社会中成长的重要性，学会在社会生活中与人相处、融入社会。

2.过程与方法：通过调查、讨论、访问等方法，培养学生的实践能力和社会责任感。

3.情感态度与价值观：培养学生热爱社会、积极参与社会生活的情感态度，增强法律意识。

四. 教学重难点1.重点：个人与社会的关系，在社会中成长的重要性。

2.难点：如何引导学生认识个人与社会的关系，激发他们参与社会生活的热情。

五. 教学方法1.情境教学法：通过设置情境，让学生在实践中感受个人与社会的关系，提高他们的社会参与度。

2.案例分析法：通过分析典型案例，让学生深入理解个人与社会的关系，培养他们的法律意识。

3.小组讨论法：引导学生分组讨论，培养他们的合作精神和团队意识。

六. 教学准备1.准备相关案例材料和图片，用于教学演示和讨论。

2.设计好教学过程中的情境设置和实践活动。

3.准备课堂小测验，检验学生对知识的掌握程度。

七. 教学过程1.导入（5分钟）利用图片或视频材料，展示个人与社会的关系，引导学生思考个人与社会的关系，激发他们的学习兴趣。

2.呈现（10分钟）通过案例分析，呈现个人与社会的关系，让学生了解在社会中成长的重要性。

人教版九年级上册 22.1 一元二次函数的图像和性质学案设计

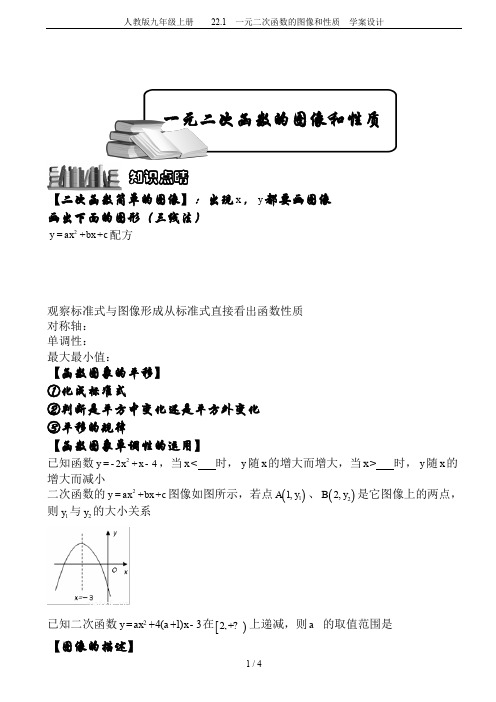
【二次函数简单的图像】：出现x ，y 都要画图像画出下面的图形（三线法）2y ax bx c =++配方观察标准式与图像形成从标准式直接看出函数性质对称轴：单调性：最大最小值：【函数图象的平移】 ①化成标准式②判断是平方中变化还是平方外变化 ③平移的规律【函数图象单调性的运用】已知函数224y x x =-+-，当x < 时，y 随x 的增大而增大，当x > 时，y 随x 的增大而减小二次函数的2y ax bx c =++图像如图所示，若点()11,A y 、()22,B y 是它图像上的两点，则1y 与2y 的大小关系已知二次函数24(1)3y ax a x =++-在[)2,+?上递减，则a 的取值范围是【图像的描述】知识点睛一元二次函数的图像和性质已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->其中所有正确结论的序号是（） A ．①② B ． ①③④ C ．①②③⑤ D ．①②③④⑤3个等量关系根据二次函数图像上三个点的坐标，求出函数的解析式()1,3-，()1,3，()2,6 ()1,1--，()0,2-，()1,1()1,0-，()3,0，()1,5- ()1,2，()3,0，()2,20-已知抛物线经过点(-1，1)和点(2，1)且与x 轴相切． (1)求二次函数的解析式；(2)当x 在什么范围时，y 随x 的增大而增大； (3)当x 在什么范围时，y 随x 的增大而减小．二次函数最值或值域问题（最值只在区间端点和对称轴上）已知函数2142a y x ax =-+-+在区间[0,1]上的最大值是2，求实数a 的值.已知函数2(21)3(0)()a x a f x ax +--?=在区间[23,2]上的最大值为1，求实数a 的值。

22.1.2学案

承德县第二中学八年级数学学科学案
使用日期：年月日
情景引入：一位饱经苍桑的老人，经
过一辈子的辛勤劳动，到晚年的时
候，终于拥有了一块平行四边形的土
地，由于年迈体弱，他决定把这块土
地平均分给他的四个孩子，他是这样
分的：
当四个孩子看到时，争论不休，都认为自己的地少，同学们，你
认为老人这样分合理吗？为什么？
学习新知：
一、探究平行四边形性质
结论：平行四边形的对角
线．
（平行四边形的性质定理2）
定理证明：
已知：如图， ABCD的对角线AC和BD
相交于点O.
求证：OA=OC，OB=OD.
跟踪训练一：
如图，ABCD的对角线AC和BD相
交于点O.图中有哪些三角形全等？
哪些三角形的面积相等？
小结：
1.平行四边形被对角线分成全等的三角形
2.平行四边形被对角线分成4个的相等的小三角形
例2：（先独立试做，再小组交流）
已知:如图所示,O为▱ABCD两条对角线的交点,AC=24 mm,BD=38
mm,BC=28 mm,求△OAD的周长.
AC,BD相交于点O,图中全等三角。

2020九年级数学上册第二十二章二次函数 22.1.2 二次函数y=ax2的图象和性质教案

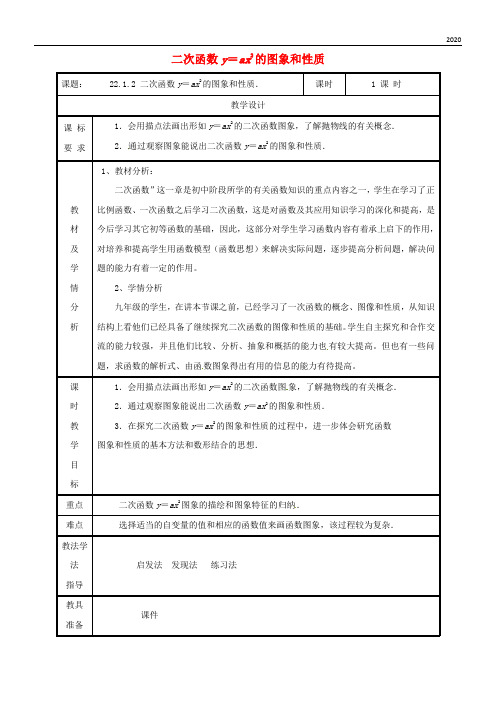
二次函数y＝ax2的图象和性质课题： 22.1.2 二次函数y＝ax2的图象和性质．课时 1 课时教学设计课标要求1．会用描点法画出形如y＝ax2的二次函数图象，了解抛物线的有关概念．2．通过观察图象能说出二次函数y＝ax2的图象和性质．教材及学情分析1、教材分析：二次函数”这一章是初中阶段所学的有关函数知识的重点内容之一，学生在学习了正比例函数、一次函数之后学习二次函数，这是对函数及其应用知识学习的深化和提高，是今后学习其它初等函数的基础，因此，这部分对学生学习函数内容有着承上启下的作用，对培养和提高学生用函数模型（函数思想）来解决实际问题，逐步提高分析问题，解决问题的能力有着一定的作用。

2、学情分析九年级的学生，在讲本节课之前，已经学习了一次函数的概念、图像和性质，从知识结构上看他们已经具备了继续探究二次函数的图像和性质的基础。

学生自主探究和合作交流的能力较强，并且他们比较、分析、抽象和概括的能力也有较大提高。

但也有一些问题，求函数的解析式、由函数图象得出有用的信息的能力有待提高。

课时教学目标1．会用描点法画出形如y＝ax2的二次函数图象，了解抛物线的有关概念．2．通过观察图象能说出二次函数y＝ax2的图象和性质．3．在探究二次函数y＝ax2的图象和性质的过程中，进一步体会研究函数图象和性质的基本方法和数形结合的思想．重点二次函数y＝ax2图象的描绘和图象特征的归纳．难点选择适当的自变量的值和相应的函数值来画函数图象，该过程较为复杂．教法学法指导启发法发现法练习法教具准备课件教学过程提要环节学生要解决的问题或完成的任务师生活动设计意图引入新课一、导入复习1．同学们可以回想一下，一次函数的性质是如何研究的?先画出一次函数的图象，然后观察、分析、归纳得到一次函数的性质．2．我们能否类比研究一次函数性质方法来研究二次函数的性质呢?如果可以，应先研究什么?为研究二次函数的图像和性质做铺垫2020 ax的图象和性质．21x函数的性质，应先研究二次函数的图象．1．二次函数y＝x的图象．…－3 －2 －1 0 1 2 3…9 4 1 0 1 4 9教2＝2x＝－2x方向、对称性、顶点等几个方面分别描述这两个巩固二次函数的概念小结抛物线y＝ax2的对称轴是y轴，顶点是原点．当a＞0时，抛物线的开口向上，顶点是抛物线的最低点；当a＜0时，抛物线的开口向下，顶点是抛物线的最高点．对于抛物线y＝ax2，∣a∣越大，抛物线的开口越小．如果a＞0，当x＜0时，y随x的增大而减小，当x＞0时，y随x的增大而增大；如果a＜0，当x＜0时，y随x的增大而增大，当x＞0时，y随x的增大而减小．板书设计二次函数y＝ax2的图象和性质．一、 ax2+bx+c=0 (a≠0)二、二次函数y＝ax2的图象和性质．1、形状：抛物线2、开口方向：向上3、对称轴：y轴4、顶点：（0，0）作业设计绩优学案1、必做题：1———92、选做题：10题教学反思。

1.2学案设计

第一单元走进化学世界课题2化学是一门以实验为基础的科学学习目标1、认识学习化学的一个重要途径是实验，初步学会对实验现象进行观察和描述的方法。

2、能有意识地从日常生活中发现一些有探究价值的问题，并能在教师指导下根据实验方案进行实验，通过对实验现象的观察和分析得出有价值的结论。

3、能体会到探究活动的乐趣和学习成功的喜悦，并进而体会到化学学习的特点是关注物质的性质、变化、变化过程及其现象等。

自主研学1、化学是一门以为基础的科学，学习化学的一个重要途径是，通过实验以及对实验现象的、和等，可以，学习的方法并获得。

2、蜡烛是由和组成的，是色，味，体(填“液”或“固”)，溶于水(填“能”或“不能”)，质地(填“硬”或“软”)，切下一小块石蜡放入水中会(填“漂浮”或“沉入”)，说明石蜡的密度水(填“大于”或“小于”)。

3、二氧化碳可以使澄清石灰水，而且白色浑浊越多，说明气体中越多。

氧气可以使带火星的木条复燃，木条燃烧越旺，说明氧气的含量。

4、人体的呼吸作用通常是将空气中的吸入体内，通过呼吸作用产生和。

二氧化碳在日常生活中常用作灭火器，说明二氧化碳支持燃烧(填“能”或“不能”)。

合作探究【实验探究1】对蜡烛及其燃烧的探究【实验结论】石蜡为色体，硬度较，加热可熔化、汽化。

石蜡能在空气中燃烧、发光、发热。

其火焰分为层，焰温度最高。

石蜡燃烧生成和。

【交流讨论】（1）火焰分几层？哪层最亮？哪层最暗？哪层温度高？（2）蜡烛燃烧的产物是什么？（3）蜡烛熄灭时，产生的白烟是什么？【实验探究2】对人体吸入的空气和呼出的气体的探究对人体吸入的空气和呼出的气体的探究报告，请你完成。

学以致用1、能使澄清石灰水变浑浊的气体是( )A．空气B．水蒸气 C．氧气D．二氧化碳2、点燃蜡烛，可以观察到蜡烛的火焰分层，最亮，最暗。

取一根火柴梗，拿住一端迅速平放入火焰中，观察并比较火柴梗在火焰的不同部位被烧的情况:部分被烧得最焦，说明火焰温度最高，温度最低。

1.1.2 点、线、面、体导学案 2022-2023学年北师大版数学七年级上册

1.1.2 点、线、面、体导学案2022-2023学年北师大版数学七年级上册一、导入导学案是一种有效的学习工具，它可以帮助我们系统地学习和理解数学知识。

本节课的导学案将帮助你学习和巩固点、线、面、体的概念。

二、知识点回顾在前几节课中，我们已经学习了一些基本的几何概念，例如点、线和面。

现在，我们来回顾一下这些概念的定义：•点：点是空间中没有长度、宽度、厚度的几何对象，它只有一个位置。

•线：线是由无数个点连成的几何对象，它没有厚度，只有长度和方向。

•面：面是由无数个线组成的几何对象，它有长度和宽度，但没有厚度。

三、新知探究3.1 点和线的关系在几何中，点和线之间存在着一种特殊的关系。

一个点可以同时属于多条线，也可以不属于任何一条线。

请思考以下问题：1.一个点能否同时属于两条平行线？2.一个点能否同时属于两条垂直线？3.一个点能否同时属于一条平行线和一条垂直线？3.2 线和面的关系线和面也有一种特殊的关系。

一条线可以同时属于多个面，也可以不属于任何一个面。

请思考以下问题：1.一条线能否同时属于两个平行于彼此的平面？2.一条线能否同时属于两个垂直于彼此的平面？3.一条线能否同时属于一个平面和一个与该平面平行的平面？3.3 点、线和面构成的几何对象除了点、线和面，还有一种更高维度的几何对象，它被称为体。

体由无数个面组成，它有长度、宽度和高度。

请思考以下问题：1.一个点、一条线和一个面能否构成一个体？2.两个点、一条线和一个面能否构成一个体？3.一个点、两条线和一个面能否构成一个体？四、知识总结通过本节课的学习，我们总结了以下几点：1.点是空间中没有长度、宽度、厚度的几何对象，它只有一个位置。

2.线是由无数个点连成的几何对象，它没有厚度，只有长度和方向。

3.面是由无数个线组成的几何对象，它有长度和宽度，但没有厚度。

4.点、线和面在几何中有着特殊的关系和组合方式。

5.体是由无数个面组成的几何对象，它有长度、宽度和高度。

2020高中生物专题22.1.2 植物细胞工程的实际应用学案新人教版选修3

2.1.2 植物细胞工程的实际应用[学习目标] 1.说明植物细胞工程在植物繁殖方面的应用。

2.列举植物细胞工程在作物新品种培育方面的应用。

3.概述细胞产物的工厂化生产的原理。

方式一拯救国家极危植物——虎颜花虎颜花为野牡丹科单种属植物，原产广东，为罕见的野生观赏植物，有重要的科研价值。

虎颜花叶片基生，叶形巨大、美丽，呈心形，上有老虎斑纹，故称虎颜花。

国际自然保护联盟已将虎颜花列为极危物种。

为拯救虎颜花，我国华南植物园的科学家对虎颜花进行了组织培养，获得1万株试管苗，又利用生态恢复技术，使虎颜花成功回归野外。

这体现了植物细胞工程的实际应用。

那么植物细胞工程技术在生产生活中还有哪些方面的应用呢？让我们进入本节的学习，一起来了解吧！方式二具有小灵芝草之称的金钗石斛是一种名贵的中草药，它具有生津益胃、润肺止咳之功效。

金钗石斛的有效化学成分为大黄酚和β－谷甾醇。

那么我们能否在工厂内大量生产这两种物质呢？能！取金钗石斛的茎尖或根尖组织，并培养为愈伤组织再放入液体培养基中进行悬浮培养，获得大量的金钗石斛细胞，从混合液中分离纯化大黄酚和β－谷甾醇即可。

这是植物细胞工程实际应用的一个实例，要了解更多这方面的信息，请跟随教材一起来学习吧。

一、植物繁殖的新途径 1．微型繁殖(1)概念：用于快速繁殖优良品种的植物组织培养技术。

(2)特点⎩⎪⎨⎪⎧①无性繁殖，保持优良品种的遗传特性②高效快速地实现种苗的大量繁殖③可实现产业化生产2．作物脱毒(1)选材部位：无病毒的植物分生区附近的部位。

(2)优点：提高作物的产量和品质。

(3)实例：脱毒马铃薯的培育。

3．人工种子(1)概念：以植物组织培养得到的胚状体、不定芽、顶芽和腋芽等为材料，经过人工薄膜包装得到的种子。

(2)优点①繁殖周期短。

②后代不发生性状分离，能够保持亲本的优良性状。

③不受季节、气候和地域的限制，并可节约土地。

归纳总结关于人工种子(1)各部分的功能针对植物种类和土壤等条件，在人工种子的包裹剂(人工种皮)中应具有适量的养分、无机盐、有机碳源以及农药、抗生素、有益菌等。

广东省陆丰市内湖中学九年级数学上册 22.1 一元二次方程教学案新人教版

22.1 一元二次方程一、教学目标1、了解一元二次方程的概念；一般式ax2+bx+c=0（a≠0）及其派生的概念；2、通过设置问题，建立数学模型，模仿一元一次方程概念给一元二次方程下定义．3、通过生活学习数学，并用数学解决生活中的问题来激发学生的学习热情．二、教学重难点1、重点：一元二次方程的概念及其一般形式和一元二次方程的有关概念并用这些概念解决问题．2、难点：探索一元二次方程的解，培养估算意识能力．三、教学过程（一）自主学习学生活动：列方程．问题1 有一块长方形铁皮，长100cm，宽50cm，在它的四角各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600cm2，那么铁皮各角应切去多大的正方形？分析：设切去的正方形的边长为xcm，则盒底的长为______________，宽为_____________.得方程_______________________________整理得____ ___________________________解：问题2 要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀请多少个队参赛？分析：全部比赛的场数为______________.设应邀请x个队参赛，每个队要与其他____________个队各赛1场，所以全部比赛共_______________场.列方程____________________________化简整理得________________________解：（二）课堂点拨1.学生活动：请口答下面问题．（1）上面三个方程式整理后含有几个未知数？（2）按照整式中的多项式的规定，它们最高次数是几次？小结一元二次方程三要素：①；②；③2.一元二次方程是3.一元二次方程的一般形式： .其中ax2是，是二次项系数；bx是，是一次项系数；是常数项.4.一元一次方程的解（根）：5.范例学习例1：将方程3x(x-1)=5(x+2)化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数及常数项．解：（三）当堂训练1.将方程2（x+1）+（x-2）（x+2）=1化成一元二次方程的一般形式，并写出其中的二次项、二次项系数；一次项、一次项系数；常数项．解：去括号，得：移项，合并得：其中：二次项，二次项系数；一次项，一次项系数；常数项．2.判断下列方程是否为一元二次方程：（1）1-x 2 =0 （2）2( x 2 -1) =3y （3）2x 2 -3x-1=0（4）(x-3) 2 = (x+3) 2 （5）9x 2 =5-4x3.将下列方程化成一元二次方程的一般形式，并指出各项系数．（1）（2x-1）(x-2）=7 （2）3x 2 +5(2x+1)=04.三个连续整数两两相乘，再求和，结果为242，这三个数分别是多少？5.以-2为根的一元二次方程是（）A ．x 2+2x-x=0B ．x 2-x-2=0C ．x 2+x+2=0D ．x 2+x-2=06．求方程322+x =422-x 的二次项系数，一次项系数及常数项.（四）归纳小结本节课你要掌握知识：（五）布置作业1.教材P27习题1、2．2.完成课本28页习题22.1四、教学反思：。

数学：2.2.1(2)教案(新人教A版必修1)

对数（第二课时）一．三维目标：1．知识与技能①通过实例推导对数的运算性质，准确地运用对数运算性质进行运算，求值、化简，并掌握化简求值的技能.②运用对数运算性质解决有关问题.③培养学生分析、综合解决问题的能力.培养学生数学应用的意识和科学分析问题的精神和态度.2. 过程与方法①让学生经历并推理出对数的运算性质.②让学生归纳整理本节所学的知识.3. 情感、态度、和价值观让学生感觉对数运算性质的重要性，增加学生的成功感，增强学习的积极性.二．教学重点、难点重点：对数运算的性质与对数知识的应用难点：正确使用对数的运算性质三．学法和教学用具学法：学生自主推理、讨论和概括，从而更好地完成本节课的三维目标.教学用具：投影仪四．教学过程1．设置情境复习：对数的定义及对数恒等式log b a N b a N =⇔= （a ＞0，且a ≠1，N ＞0），指数的运算性质.;m n m n m n m n a a a a a a +-⋅=÷=();n m n mn ma a a == 2．讲授新课探究：在上课中，我们知道，对数式可看作指数运算的逆运算，你能从指数与对数的关系以及指数运算性质，得出相应的对数运算性质吗？如我们知道m n m n a a a+⋅=，那m n +如何表示，能用对数式运算吗？如：,,m n m n m n a a a M a N a +⋅===设。

于是,m n MN a += 由对数的定义得到 log ,log m n a a M a m M N a n N =⇔==⇔=log m n a MN a m n MN +=⇔+=log log log ()a a a M N MN ∴+=放出投影即：同底对数相加，底数不变，真数相乘提问：你能根据指数的性质按照以上的方法推出对数的其它性质吗？（让学生探究，讨论）如果a ＞0且a ≠1，M ＞0，N ＞0，那么：（1）log log log a a a MN M N =+（2）log log log a a a M M N N=- （3）log log ()n a a M n Mn R =∈ 证明：（1）令,m nM a N a == 则：m n m n M a a a N-=÷= log a M m n N ∴-= 又由,m n M a N a ==log ,log a a m M n N ∴== 即：log log log a a aM M N m n N -=-= （3）0,log ,N n n a n N M M a ≠==时令则log ,bna b n M M a ==则 Nb n na a ∴= Nb ∴= 即log log log a a a M M N N=- 当n =0时，显然成立.log log n a a M n M ∴=提问：1. 在上面的式子中，为什么要规定a ＞0，且a ≠1，M ＞0，N ＞0？1．你能用自己的语言分别表述出以上三个等式吗？例题：1. 判断下列式子是否正确，a ＞0且a ≠1，x ＞0且a ≠1，x ＞0，x ＞y ，则有（1）log log log ()a a a x y x y ⋅=+ （2）log log log ()a a a x y x y -=-（3）log log log a a a x x y y=÷ （4）log log log a a a xy x y =-（5）(log )log n a a x n x = （6）1log log a a x x=- （71log a x n= 例2：用log a x ，log a y ，log a z 表示出（1）（2）小题，并求出（3）、（4）小题的值.（1）log a xy z （2）log a （3）75log (42)z ⨯ （4）分析：利用对数运算性质直接计算：（1）log log log log log log aa a a a a xy xy z x y z z =-=+- （2）2log log log log log log a a a a a a x x ==+ =112log log log 23a a a x y z +- （3）7575222log (42)log 4log 214519⨯=+=+=（4）252lg lg105== 点评：此题关键是要记住对数运算性质的形式，要求学生不要记住公式.让学生完成P 79练习的第1，2，3题提出问题：你能根据对数的定义推导出下面的换底公式吗？a ＞0，且a ≠1，c ＞0，且e ≠1，b ＞0 log log logc a c b b a=先让学生自己探究讨论，教师巡视，最后投影出证明过程.设log ,log ,,M N c c M a N b a c b c ====则且11,()N N M M M a c a a b ====N 所以c 即：log log ,log c a c b N N b M M a==又因为所以：log log log c a c b b a = 小结：以上这个式子换底公式，换的底C 只要满足C ＞0且C ≠1就行了，除此之外，对C 再也没有什么特定的要求.提问：你能用自己的话概括出换底公式吗？说明：我们使用的计算器中，“log ”通常是常用对数. 因此，要使用计算器对数，一定要先用换底公式转化为常用对数. 如：2lg 3log 3lg 2=即计算32log 的值的按键顺序为：“log ”→“3”→“÷”→“log ”→“２” →“=” 再如：在前面要求我国人口达到18亿的年份，就是要计算 1.0118log 13x = 所以 1.0118lg 18lg18lg13 1.2553 1.13913log 13lg1.01lg1.010.043x --===≈ =32.883733()≈年练习：P 79 练习4让学生自己阅读思考P 77~P 78的例5，例的题目，教师点拨.3、归纳小结（1）学习归纳本节（2）你认为学习对数有什么意义？大家议论.2、思考：（1）证明和应用对数运算性质时，应注意哪些问题？（2）222log (3)(5)log (3)log (5)---+-等于吗?。

22.1的教案新部编本

教师学科教案[ 20 – 20 学年度第__学期]任教学科：_____________任教年级：_____________任教老师：_____________xx市实验学校22.1一元二次方程（1课时）教案江苏中学数学组：杨凌冰教学内容：本节课主要学习一元二次方程概念及一元二次方程一般式及有关概念。

教学目标：（一）、知识目标：探索一元二次方程及其相关概念，能够辨别各项系数；能够从实际问题中抽象出方程知识。

(二)、能力目标：1、在探索问题的过程中使学生感受方程是刻画现实世界的一个模型，体会方程与实际生活的联系。

2、培养学生良好的研究问题的习惯，使学生逐步提高自己的数学素养。

（三）、情感态度：通过用一元二次方程解决身边的问题，体会数学知识应用的价值，提高学生学习数学的兴趣，了解数学对促进社会进步和发展人类理性精神的作用。

重、难点：重点：一元二次方程的概念和它的一般形式。

难点：对一元二次方程的一般形式的正确理解及其各项系数的确定。

教学准备教师准备：制作课件，精选习题。

学生准备：复习有关知识，预习本节课内容。

教学过程一、情境引入【问题情境】初二（6）班教室的面积为54平方米，长比宽多3米，求该教室的宽。

【活动方略】教师演示课件，给出题目。

学生根据所学知识，通过分析设出合适的未知数，列出方程回答问题。

【设计意图】由实际问题入手，设置情境问题，激发学生的兴趣，让学生初步感受一元二次方程，同时让学生体会方程这一刻画现实世界的数学模型。

复习回忆：学习过的方程有哪些？你能说出这些方程的定义吗？【设计意图】让学生结合一元一次方程、二元一次方程等总结出二元一次方程的特征。

二、探索新知【活动方略】学生活动：请口答下面问题．（1）上面方程整理后含有几个未知数？（2）按照整式中的多项式的规定，它们最高次数是几次？（3）是等式吗？或与以前多项式一样只有式子？老师点评：（1）都只含一个未知数x；（2）它们的最高次数都是2次的；（3）•都有等号，是方程。