第1章 矢量分析

矢量A的大小为A：A=(A2x+A2y+A2z)1/2
§1 .1 矢量及其代数运算
2 矢量代数运算
矢量相加的平行四边形法则，矢量的加法的坐标分 量是两矢量对应坐标分量之和，矢量加法的结果仍 是矢量 ��
�� � �� � �� � A = ex A x + ey A y + ez A z
� � �� � �� � �� � B = e x Bx + e y B y + e z Bz
� � A = Ae
� � � 其中， A是矢量 A的大小; e 代表矢量 A 的方向。 � � e = A / A 大小等于1。
§1 .1 矢量及其代数运算
1 标量和矢量
一个大小为零的矢量称为空矢（Null Vector）或零矢 （Zero Vector），一个大小为1的矢量称为单位矢量 （Unit Vector）。 在直角坐标系中，用单位矢量 ex、 ey 、 ez 表征矢量分 别沿x、y、z轴分量的方向。
r
r=exX+eyY+ezZ
§1 .1 矢量及其代数运算
1 标量和矢量
X、Y、Z是位置矢量r在x、y、z轴上的投影。
任一矢量A在三维正交坐标系中都可以给出其三个分 量。例如，在直角坐标系中，矢量A的三个分量分别 是Ax、Ay、Az，利用三个单位矢量ex、ey、ez可以将矢 量A表示成：
A=exAx+eyAy+ezAz
§1 .2 标量场的梯度
5 梯度的性质
4）标量场的梯度垂直
于通过该点的等值 面（或切平面）
§1 .2 标量场的梯度
6 梯度运算的基本公式
⎧ ⎪ ⎪∇ ⎪∇ ⎪ ⎪∇ ⎪ ⎨∇ ⎪∇ ⎪ ⎪∇ ⎪ ⎪∇ ⎪ ⎩
c = 0 cu = c ∇ u (u ± v ) = ∇ u ± ∇ v (uv ) = u ∇ v + v ∇ u f (u ) = f ' (u )∇ u × ∇ u = 0
第一章 矢量分析
§1 .1 矢量及其代数运算
1 标量和矢量
电磁场中遇到的绝 大 多 数 物 理 量 ， 能 够 容 易 地 区 分 为 标 量 （Scalar）和矢量(Vector)。一个仅用大小就能够完整描述的物 理量称为标量，例如电压、温度、时间、质量、电荷等。实际 上，所有实数都是标量。一个有大小和方向的物理量称为矢 量，电场、磁场、力、速度、力矩等都是矢量。例如，矢量 A 可以表示成
§1 .4 矢量场的旋度
2 旋度
引入矢量场旋度，定义为：矢量场在M点处的旋度 为一矢量，其数值为包含M点在内的小面元边界的环量 与小面元比值极限的最大值，其方向为极限取得最大 值时小面积元的法线方向，即： � � ⎡ A ⋅ dl ⎤ ∫ � �⎢ ⎥ l rotA = n ⎢lim ⎥ ∆ s ⎢ ∆s →0 ⎥ ⎣ ⎦ Max
§1 .1 矢量及其代数运算
1 标量和矢量
Z
空 间 的 一 点 P(X,Y,Z) 能 够 由 它在三个相互垂直的轴线上 的投影唯一地确定。从原点 指向点 P 的矢量 r 称为位置矢 量 (Position Vector) ， 它 在直角坐标系中表示为
z P(X, Y, Z) Y ay O y
az ax X x
A×B= -B×A A×(B+C)=A×B+A×C
§1 .1 矢量及其代数运算
直角坐标系中的单位矢量有下列关系式：
ex×ey=ez, ey×ez=ex, ez×ex=ey ex×ex=ey×ey=ez×ez= 0
在直角坐标系中，矢量的叉积还可以表示为 ex ey ez A× B = Ax Ay Az Bx By Bz
� � divF ( x, y, z ) = ∇ ⋅ F ( x, y, z )
gradu ( x, y, z ) = ∇u ( x, y, z )
§1 .3 矢量场的散度
3 散度运算的基本公式
⎧∇ ⋅ C = 0(C ) ⎪ ⎪∇ ⋅ (Cf�) = C ⋅ ∇f� ⎪ ⎨∇ ⋅ (αF ) = α∇ ⋅ F (α � � � ⎪∇ ⋅ (φF ) = φ ∇ ⋅ F + F ⋅ ∇ φ ⎪ � � � � ⎪ ⎩∇ ⋅ (F ± G ) = ∇ ⋅ F ± ∇ ⋅ G
�� � � �� � �� � �� � A + B = e x (A x + Bx ) + e y (A y + By ) + ez (A z +Bz ) �� � � �� � �� � �� � A − B = ex (A x − Bx ) + e y (A y − By ) + ez (A z − Bz )
§1 .3 矢量场的散度
Φ>0
表示通过闭合曲 面有净的矢量线 流出 表示通过闭合曲 面有净的矢量线 流入
有正源
Φ<0
有负源
Φ=0
表示流入、流出 的矢量线相等， 或没有矢量线流 入、流出
无源
§1 .3 矢量场的散度
2 散度
为了定量研究场与源之间的关系，需建立场空间任 意点（小体积元）的通量与矢量场（小体积元曲面的 通量）的关系。利用极限方法得到这一关系：
闭曲面
§1 .3 矢量场的散度
1 通量的定义
矢量场对于曲面 ds 的通量为曲 面ds上所有小面积元通的叠加： � � Φ = ∫ dΦ = ∫∫ F (x, y , z ) ⋅ ds
s
� � dΦ＝F ( x, y, z ) ⋅ ds
如果曲面S 为闭合曲面，则 ⎧> 0 ⎪ Φ = ∫∫ F ( x , y , z ) ⋅ d s ＝⎨ = 0 s ⎪< 0 ⎩
§1 .4 矢量场的旋度
1 环量
• 存在另一类不同于通量源的矢量源，它所激发的矢量 场的力线是闭合的，它对于任何闭合曲面的通量为零。 但在场所定义的空间中闭合路径的积分不为零。如磁 场沿任意闭合曲线的积分与通过闭合曲线所围曲面的 电流成正比，即：
∫ B (x , y , z ) ⋅ d L = µ
L
0
I = µ 0 ∫∫ J ( x , y , z ) ⋅ d s
s
上式建立了磁场与电流的关系。
§1 .4 矢量场的旋度
∫ B (x , y , z ) ⋅ d L = µ
L
0பைடு நூலகம்
I = µ 0 ∫∫ J ( x , y , z ) ⋅ d s
s
§1 .4 矢量场的旋度
例：流速场
水流沿平行于水管轴线方向流动
=ex(AyBz-AzBy)+ey(AzBx-AxBz)+ez(AxBy-AyBx)
§1 .2 标量场的梯度
1 场的概念
在自然界中，许多问题是定义在确定空间区域上的， 在该区域上每一点都有确定的量与之对应，我们称在该区 域上定义了一个场。如电荷在其周围空间激发的电场，电 流在周围空间激发的磁场等。如果这个量是标量我们称该 场为标量场；如果这个量是矢量，则称该场为矢量场。如 果场与时间无关，称为静态场，反之为时变场。从数学上 看，场是定义在空间区域上的函数。
§1 .1 矢量及其代数运算
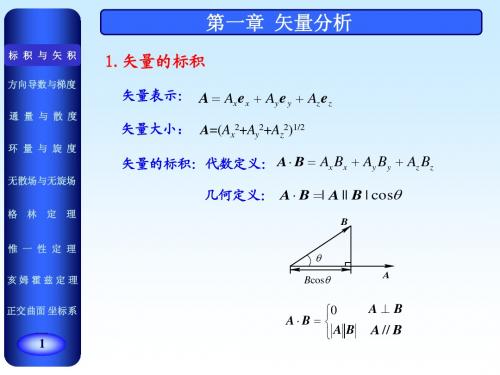
2 矢量的乘积
矢量的乘积包括标量积和矢量积。 1） 标量积 任意两个矢量 A 与 B 的标量积 (Scalar Product) 是一个标 量，它等于两个矢量的大小 与它们夹角的余弦之乘积， 记为
θ B cos θ A B
A·B=ABcosθ
§1 .1 矢量及其代数运算
§1 .2 标量场的梯度
3 方向导数
设一个标量函数场u(x, y, z)在P点可微,则u在P点沿 任意方向的方向导数为 ∂u / ∂l 。它的值与所选取的方
� 向 l 有关, 若
� � � � l = x cos α + y cos β + z cos γ
则
∂u ∂u ∂u ∂u = cos α + cos β + cos γ ∂l ∂x ∂y ∂z
§1 .4 矢量场的旋度
可见, 矢量A的旋度是一个矢量, 其大小是矢量A在 给定点处的最大环量面密度, 其方向就是当面元的取向 � 使环量面密度最大时, 该面元矢量的方向 n 。 它描述 A在该点处的旋涡源强度。 若某区域中各点curlA=0, 称A为无旋场或保守场。
� divF ( x, y, z ) = lim
∆V →0
� � ( ) F x , y , z ⋅ d s ∫∫
s
∆V
∂Fx ∂Fy ∂Fz = + + ∂x ∂y ∂z
称为矢量场的散度。因此散度是矢量通过包含该点的任 意闭合小曲面的通量与曲面元体积之比的极限。
§1 .3 矢量场的散度
2 散度
哈密顿(W.R.Hamilton)引入倒三角算符(读作del(德尔) 或nabla(纳不拉))表示下述矢量形式的微分算子: � ∂ � ∂ � ∂ ∇ = ex + ey + ez ∂x ∂y ∂z 散度 梯度
2 矢量的乘积
2） 矢量积 任意两个矢量A与B的矢量积是一 个矢量，矢量积的大小等于两个 矢量的大小与它们夹角的正弦之 乘积，其方向垂直于矢量A与B组 成的平面，记为
C=A×B=enAB sinθ en=eA×eB （右手螺旋）
§1 .1 矢量及其代数运算
矢量积又称为叉积(Cross Product)，如果两个不为零 的矢量的叉积等于零，则这两个矢量必然相互平 行，或者说，两个相互平行矢量的叉积一定等于零。 矢量的叉积不服从交换律，但服从分配律，即
§1 .2 标量场的梯度
1 场的概念
如果场与时间无关，称为静态场，反之为时变场。 静态标量场和矢量场可分别表示为：
u (x, y , z )