python随机数原理

合集下载

Python随机数种子（randomseed）的使用

Python随机数种⼦（randomseed）的使⽤⽬录1.随机数种⼦2.numpy中的随机数种⼦3.随机数“顺序”的奥秘在科学技术和机器学习等其他算法相关任务中，我们经常需要⽤到随机数，为了把握随机数的⽣成特性，从随机数的随机⽆序中获得确定和秩序。

我们可以利⽤随机数种⼦(random seed)来实现这⼀⽬标，随机数种⼦，可以使得引⼊了随机数的整个程序，在多次运⾏中得到确定的，⼀致的结果。

很多博⽂谈到随机数种⼦，只是简单论及，利⽤随机数种⼦，可以每次⽣成相同的随机数。

想真正⽤好掌握它，对此很容易产⽣疑惑，⽣成相同的随机数数怎么个相同法？随机数种⼦⼜作何⽤处？1. 随机数种⼦下⾯我们从实例中揭开随机数种⼦的神秘⾯纱：import random# print(help(random))def test_random_seed_in_std_lib(seed=0, cnt=3):random.seed(seed)print("test seed: ", seed)for _ in range(cnt):print(random.random())print(random.randint(0,100))print(random.uniform(1, 10))print('\n')test_random_seed_in_std_lib()test seed: 00.8444218515250481979.012195287534180.04048437818077755655.3733492690653140.9182343317851318389.710199954281542test_random_seed_in_std_lib()test seed: 00.8444218515250481979.012195287534180.04048437818077755655.3733492690653140.9182343317851318389.710199954281542test_random_seed_in_std_lib(99)test seed: 990.40397807494366633256.394951906868970.23026272839629136177.83889692857270150.2511510083752201495.777313434770537通过两次运⾏以上程序，我们得到相同的结果，这说明了以下⼏点：1. 在确定了⼀次随机数种⼦后，随机数函数，⽆论任何分布任何类型，在多次重复调⽤中(for循环)⽣成的随机数不同；2. 当再次声明相同的随机数种⼦时(第⼆次调⽤test_random_seed_in_std_lib函数，random.seed(seed)这⼀⾏)，随机数将从“头”开始, 按相同的顺序⽣成随机数。

random底层原理

random底层原理小伙伴们！今天咱们来唠唠这个超有趣的random的底层原理。

你看啊，当我们在程序里用到random的时候，就好像是在跟一个调皮的小精灵打交道。

这个小精灵呢，它的任务就是给我们吐出一些随机的数。

那它到底是怎么做到的呢？其实啊，计算机是个很严谨的家伙，它可不会像我们人类一样，真正意义上的“随心所欲”。

random底层呢，是有一套算法在默默运作的。

就好比是有一个超级神秘的魔法配方。

这个配方里有很多的数学元素哦。

比如说，可能会用到一些很复杂的数学函数，像线性同余法之类的。

这就像是魔法咒语的一部分。

想象一下，计算机的内存就像是一个装满各种魔法材料的大仓库。

random在生成随机数的时候呢，就会从这个仓库里挑选一些“材料”，然后按照那个神秘的数学配方来加工。

比如说，它可能会根据当前的系统时间作为一个起始的“原料”。

因为系统时间可是一直在变的呀，每一个瞬间都不一样，就像天上的云彩，形状时刻在变。

这就给了random一个很好的变化基础。

不过呢，你可别以为这个就是完全随机的啦。

其实严格意义上来说，这是一种伪随机。

为啥叫伪随机呢？因为如果知道了这个魔法配方，而且知道了起始的那些“原料”，理论上是可以预测出接下来的随机数的。

就像是你知道了魔术师的把戏，那他的魔术对你来说就不神秘了。

但是在我们日常使用中，这个伪随机已经足够啦。

比如说你在玩一个猜数字的小游戏，程序用random来生成一个要猜的数字。

这个数字对于我们玩家来说，那就是完全随机的，根本猜不到。

就像每次打开一个抽奖的小盒子，里面的结果是我们无法预知的。

再深入一点看，不同的编程语言可能会对random的底层原理有一些小的调整。

就像不同的厨师做同一道菜，虽然大体的菜谱一样，但是可能会在调料的用量或者烹饪的顺序上有一点点小区别。

不过呢，目的都是一样的，就是给我们提供看起来很随机的数字。

而且哦，random这个小机灵鬼还可以有不同的范围设置。

比如说你想要一个1到10之间的随机数，它就能根据底层的算法，在那个大的随机数空间里，给你挑选出符合这个范围的数字。

随机数的产生原理

随机数的产生原理随机数的产生原理是计算机科学领域中非常重要的一个概念。

在计算机程序开发、密码学、模拟实验等领域都广泛应用着随机数。

首先，我们需要明确随机数的概念。

所谓随机数是指其具有不可预测性和不相关性的数值序列。

也就是说，随机数的产生是不受特定规律、模式或者输入的影响。

在计算机中，由于计算机的运算是通过确定性算法进行的，所以计算机无法自主产生完全随机的数值序列，而只能通过一定的算法来模拟随机数的产生。

常见的随机数生成方法有伪随机数产生器和真随机数产生器。

其中，伪随机数产生器是利用已知的确定性算法生成的数字序列，这些数字序列在某种程度上具有类似随机的性质。

而真随机数产生器则利用物理现象来产生真正的随机数。

首先，我们来介绍一下伪随机数的产生方法。

伪随机数的产生是通过确定性的算法进行的，这个算法需要一个种子作为输入来产生一系列看似随机的数字。

在同一个种子的情况下，这个算法每次产生的数字都是相同的。

因此，为了产生不同的伪随机数序列，通常会使用系统时间等随机的种子。

常见的伪随机数产生算法有线性同余法、梅森旋转算法等。

线性同余法是最常见的伪随机数生成算法之一。

它的原理是通过不断迭代一个初始值（种子）来产生随机数序列。

具体的计算公式为：X(n+1) = (a * X(n) + c) mod m其中，X(n)表示第n个随机数，X(n+1)表示第n+1个随机数，a、c、m为一组给定的常数，mod表示取余操作。

在梅森旋转算法中，使用了一个非常大的2的幂次数作为种子，通过一系列的位操作或异或操作来产生伪随机数。

这种算法的优点是速度快且产生的随机数质量高。

然而，伪随机数产生器是基于已知的算法进行的，其产生的随机数序列是可预测和重现的。

因此，在某些应用场景（如密码学）中，需要使用更加安全和随机的随机数。

那么如何产生真随机数呢？真随机数的产生是利用物理现象的随机性来产生的。

常用的真随机数产生方法包括噪声源、热噪声和量子现象。

pythonrandom随机数的用法

pythonrandom随机数的用法Python中的random模块是一个用于生成随机数的工具。

它提供了多种方法用于生成随机数，包括均匀分布、正态分布等等。

以下是关于Python中random模块的详细介绍：1. random()函数random()函数用于生成一个0到1之间的随机小数。

其语法如下：```pythonimport randomprint(random.random())```实际输出结果为：0.66850377780976952. randint()函数randint()函数用于生成指定范围内的随机整数。

其语法如下：```pythonimport randomprint(random.randint(1,100))```实际输出为1至100之间的随机整数。

3. uniform()函数uniform()函数用于生成指定范围内的随机小数，其语法如下：```pythonimport randomprint(random.uniform(1,10))```实际输出为1至10之间的随机小数。

4. choice()函数choice()函数用于从指定序列中随机选择一个元素。

其语法如下：```pythonimport randomlist=['apple','banana','orange']print(random.choice(list))```实际输出为从list中随机选择一个元素。

5. shuffle()函数shuffle()函数用于将指定序列随机排序。

其语法如下：```pythonimport randomlist=[1,2,3,4,5]random.shuffle(list)print(list)```实际输出为打乱后的list序列。

6. sample()函数sample()函数用于从指定序列中随机选择指定数量的元素。

其语法如下：```pythonimport randomlist=[1,2,3,4,5]print(random.sample(list,3))```实际输出为从list中随机选择3个元素。

python随机数生成原理

python随机数生成原理Python随机数生成原理随机数在计算机科学中是一个非常重要的概念，它被广泛应用于密码学、模拟实验、游戏开发等领域。

在Python中，生成随机数可以通过random模块来实现。

本文将介绍Python随机数生成的原理及其背后的算法。

一、随机数的概念和应用随机数是指在一定范围内没有规律可循的数值。

它的特点是无法预测，具有不确定性。

在计算机科学中，随机数可以用于生成随机密码、模拟随机事件、生成随机样本等。

二、伪随机数生成器计算机无法生成真正的随机数，因为计算机是基于确定性的逻辑运算的。

因此，计算机生成的随机数实际上是伪随机数，也就是一系列看似随机的数字序列。

这些数字序列是通过伪随机数生成器生成的。

Python中的random模块提供了伪随机数生成器，可以生成服从特定分布的随机数。

三、随机数生成的算法Python的random模块基于Mersenne Twister算法实现了伪随机数生成器。

Mersenne Twister算法是一种非常高效且具有良好统计特性的随机数生成算法。

Mersenne Twister算法的原理是使用一个非常长的周期为2^19937-1的Mersenne素数作为随机数生成的种子。

通过对这个种子进行一系列复杂的数学运算，可以生成一组看似随机的数值序列。

这个序列的周期非常长，因此生成的随机数具有很好的随机性。

四、随机数生成的应用1. 生成随机密码随机数可以用于生成随机密码。

通过随机选择字母、数字和特殊字符，可以生成强度较高的密码，提高账户的安全性。

2. 模拟随机事件随机数可以用于模拟随机事件。

例如，在游戏开发中，可以使用随机数生成器来模拟敌人的行动、掉落物品的概率等。

3. 生成随机样本随机数可以用于生成随机样本。

在数据分析和统计学中，随机样本是进行统计推断的重要基础。

通过随机数生成器，可以生成符合特定分布的随机样本，用于进行统计分析。

五、小结本文介绍了Python随机数生成的原理及其背后的算法。

随机数算法原理

随机数算法原理
随机数算法是计算机科学领域的一个重要概念，其原理简单来说
是通过一系列复杂的计算，生成一组看似无序的、无规律的数字序列。

这个数字序列是由计算机的随机数发生器生成的，它是在一段时间内
按无法预测的方式产生的数字序列。

这种序列可以用于密码学、模拟、图形学等领域的应用中。

随机数算法的实现基于伪随机数发生器的原理。

伪随机数发生器
是一种基于数学算法的随机数发生器，它可以通过算法计算出一个看
似无序的数字序列。

这个数字序列会在较长时间内表现出像随机数一
样的性能，但是在短时间内可能会出现规律。

随机数算法的安全性主要取决于伪随机数发生器的质量。

如果伪
随机数发生器的算法不够随机，那么生成的随机数序列可能会出现规律，导致破解算法。

为了保证随机数算法的安全性，开发者们通常会使用硬件随机数
发生器、真随机数发生器或者密钥自动生成器来生成随机数。

这些方
法可以在很大程度上消除随机数算法的弱点和缺陷，从而避免信息泄
露或者黑客攻击等问题的发生。

python生成5个随机数的方法

Python生成5个随机数的方法1.使用ran dom库生成随机数P y th on中的ra nd om库提供了生成随机数的功能。

通过调用r an do m 库中的相关函数，可以生成5个不同范围内的随机数。

首先，我们需要导入r an do m库：i m po rt ra nd om接下来，我们可以使用r an do m库中的函数来生成随机数。

以下是几种常用的方法：1.1生成指定范围内的整数随机数如果我们想要在一个特定的范围内生成整数随机数，可以使用r an do m 库中的`ra nd in t()`函数。

该函数接受两个参数，分别是范围的起始值和结束值。

例如，我们想要生成5个1到10之间的整数随机数，可以使用以下代码：f o ri in ra ng e(5):r a nd om_n um=r an dom.ra nd in t(1,10)p r in t(ra nd om_n um)这段代码会生成5个1到10之间的整数随机数并打印出来。

1.2生成指定范围内的浮点数随机数如果我们想要生成指定范围内的浮点数随机数，可以使用r and o m库中的`u ni fo rm()`函数。

该函数接受两个参数，分别是范围的起始值和结束值。

例如，我们想要生成5个0到1之间的浮点数随机数，可以使用以下代码：f o ri in ra ng e(5):r a nd om_n um=r an dom.un if or m(0,1)p r in t(ra nd om_n um)这段代码会生成5个0到1之间的浮点数随机数并打印出来。

2.使用num py库生成随机数除了ra nd om库，Py t ho n中的n um py库也提供了生成随机数的功能。

n u mp y库中的ra nd om模块可以用于生成各种类型的随机数。

首先，我们需要导入n um py库：i m po rt nu mp ya sn p接下来，我们可以使用n um py库中的函数来生成随机数。

随机数的原理

在实际应用中，随机数被广泛用于模拟、加密、彩票系统等领域。然而，需要注意的是伪随机数并不是真正的随机数，随机数生成算法的质量和种子输入的选择都会对随机数的质量产生影响。
因此，为了获得更为随机的序列，通常会使用真正的随机事件作为种子输入，如量子力学Hale Waihona Puke 随机性或者大型随机数生成器生成的值。
然而，由于计算机程序的本质是可计算的，所以生成的随机数实际上是伪随机数。也就是说，通过固定的算法和种子，随机数序列是可重复的。这是因为计算机程序总是按照一定的规则执行，因此可以预测出随机数序列的下一个数值。
为了增加生成的随机数的随机性，常常使用熵作为种子输入。熵可以是来自外部环境的任意输入，例如硬盘读写的速度、网络传输的延迟等。通过使用熵作为种子输入，RNG算法可以生成更为随机的序列。
随机数的原理
随机数是一种在计算机程序中生成的伪随机序列，其背后的原理是使用一个称为随机数生成器（Random Number Generator，简称RNG）的算法。
RNG算法通常使用一个称为种子（seed）的输入值来初始化。种子可以是任何数据，例如当前的系统时间或用户的输入。然后，RNG算法使用种子来生成一系列看似随机的数值。

python random库生成随机数的方法

python random库生成随机数的方法Python是一种功能强大的编程语言，其中的random库提供了各种生成随机数的方法。

这些方法可以用于模拟数据、密码生成、游戏开发等多个领域。

下面是几种常用的python random库生成随机数的方法：1. random.random()：该方法生成一个大于等于0小于1的随机浮点数。

它采用均匀分布，意味着每个数在[0, 1)范围内出现的概率相等。

2. random.randint(a, b)：该方法生成一个大于等于a小于等于b的随机整数。

参数a和b是整数，a必须小于等于b。

例如，random.randint(1, 10)返回一个1到10之间（包含1和10）的随机整数。

3. random.uniform(a, b)：该方法生成一个大于等于a小于等于b的随机浮点数。

不同于random.random()，random.uniform()可以生成指定范围内的任意浮点数。

4. random.choice(seq)：该方法从非空序列seq中随机选择一个元素并返回。

seq可以是列表、元组、字符串等。

例如，random.choice([1, 2, 3, 4, 5])返回序列中的一个随机元素。

5. random.shuffle(seq)：该方法随机打乱序列seq中元素的顺序。

seq可以是列表、元组等。

它会直接修改原序列，并不返回任何值。

例如，random.shuffle([1, 2, 3, 4, 5])将原序列的元素顺序随机打乱。

以上是常用的几种python random库生成随机数的方法。

通过使用这些方法，我们可以方便地生成各种类型的随机数，满足不同任务需求。

在使用随机数时，我们应该根据具体需求选择合适的方法，并注意边界条件的设置，以确保生成的随机数符合预期。

随机产生[10,50]之间整数的正确表达式

随机产生[10,50]之间整数的正确表达式
（最新版）
目录
1.随机数生成的原理
2.Python 中的 random 模块
3.生成 [10,50] 之间整数的表达式
4.代码示例
正文
1.随机数生成的原理
在计算机程序中，生成随机数主要依赖于随机数生成算法。

这些算法基于统计学原理，例如：线性同余生成器、梅森旋转算法等。

它们可以产生一定范围内的随机整数。

2.Python 中的 random 模块
Python 提供了一个内置的 random 模块，用于生成各种类型的随机数。

我们可以使用 random.randint() 函数生成指定范围内的整数。

3.生成 [10,50] 之间整数的表达式
根据 random 模块中的 random.randint() 函数，我们可以得到生成[10,50] 之间整数的表达式如下：
random.randint(10, 50)
4.代码示例
在 Python 中，我们可以通过以下代码来生成 [10,50] 之间的随机整数：
```python
import random
result = random.randint(10, 50)
print(result)
```
运行上述代码，你将得到一个 [10,50] 之间的随机整数。

详解Python基础random模块随机数的生成

详解Python基础random模块随机数的⽣成随机数参与的应⽤场景⼤家⼀定不会陌⽣，⽐如密码加盐时会在原密码上关联⼀串随机数，蒙特卡洛算法会通过随机数采样等等。

Python内置的random模块提供了⽣成随机数的⽅法，使⽤这些⽅法时需要导⼊random模块。

import random下⾯介绍下Python内置的random模块的⼏种⽣成随机数的⽅法。

1、random.random() 随机⽣成 0 到 1 之间的浮点数[0.0, 1.0) 。

print("random: ", random.random())#random: 0.57140259468991352、random.randint(a , b) 随机⽣成 a 与 b 之间的整数[a, b]。

print("randint: ", random.randint(6,8))#randint: 83、random.randrange(start,stop,step)按步长step随机在上下限范围内取⼀个随机数。

print("randrange: ",random.randrange(20,100,5))#randrange: 854、random.uniform(a, b) 随机⽣成 a 与 b 之间的浮点数[a, b]。

print("uniform: ",random.uniform(5,10))#uniform: 5.1197901633757765、random.choice() 从列表中随机取出⼀个元素，⽐如列表、元祖、字符串等。

注意的是，该⽅法需要参数⾮空，否则会抛出IndexError 的错误。

print("choice: ",random.choice(""))#choice: y6、random.shuffle(items) 把列表 items 中的元素随机打乱。

python random seed原理(一)

python random seed原理(一)Python random seed1. 介绍随机数在计算机编程中具有重要地位。

Python中的random模块提供了生成随机数的函数和方法。

然而，每次运行程序时，生成的随机数序列都是不同的。

为了使随机数的序列可重复，我们可以使用random seed功能。

2. 什么是random seed？在计算机生成随机数时，实际上是通过一系列算法生成的伪随机数。

这些算法是在给定种子(seed)的基础上生成的。

种子(seed)是一个整数值，它确定了随机数的起始点。

如果使用相同的种子(seed)，那么每次运行程序时生成的随机数序列都是相同的。

3. 使用random seed在Python中，我们可以通过random模块来设置随机数的种子(seed)值。

下面是使用random seed的示例代码：import random(123) # 设置随机数种子为123# 生成随机整数print((1, 10))# 生成随机小数print(())# 生成随机元素my_list = [1, 2, 3, 4, 5]print((my_list))当我们将seed设置为123时，无论运行多少次，输出的结果都是一致的。

如果我们将seed的值更改为其他整数，将会生成不同的随机数序列。

4. 为什么要使用random seed？在实际应用中，有时需要使用伪随机数来模拟真实情况。

比如，在测试和调试过程中，将随机数序列固定可以帮助我们重复出现错误以便调试和修复。

此外，如果我们需要对数据进行随机洗牌(shuffling)或随机抽样(sampling)，使用固定的随机数序列可以确保结果的可重复性。

5. 注意事项在使用random seed时，需要注意以下几点：•种子(seed)可以是任意整数。

但为了方便起见，通常使用正整数。

•在同一程序中，如果多次设置相同的seed值，将得到相同的随机数序列。

•默认情况下，如果没有设置seed值，Python会使用系统时间作为种子(seed)值，以确保每次运行程序时都生成不同的随机数序列。

python中随机数的用法

python中随机数的用法在Python中，使用random模块可以生成随机数。

下面是一些常用的随机数生成函数：1. randint(a, b)：生成[a, b]范围内的整数随机数。

2. uniform(a, b)：生成[a, b]范围内的浮点数随机数。

3. random()：生成[0, 1)范围内的浮点数随机数。

4. choice(seq)：从序列seq中随机选择一个元素。

5. shuffle(seq)：将序列seq中的元素打乱顺序。

下面是一些示例代码：```pythonimport random# 生成[1, 10]范围内的整数随机数num = random.randint(1, 10)print(num)# 生成[0, 1)范围内的浮点数随机数num = random.random()print(num)# 从列表中随机选择一个元素lst = [1, 2, 3, 4]item = random.choice(lst)print(item)# 将列表中的元素打乱顺序random.shuffle(lst)print(lst)```需要注意的是，每次运行程序时都会得到不同的结果，因为这些函数都是根据当前时间戳来生成随机种子，所以每次运行结果都不同。

如果需要得到相同的结果，可以通过设置相同的种子来实现。

例如：```pythonimport random# 设置相同种子后，每次运行都会得到相同的结果random.seed(1)num = random.randint(1, 10)print(num)random.seed(1)num = random.randint(1, 10)print(num)```以上就是Python中随机数的用法。

通过这些函数，我们可以方便地生成随机数，从而实现各种随机化操作。

np.random.randint 原理

np.random.randint 原理np.random.randint是NumPy库中的一个函数，用于生成指定范围内的整数随机数。

这个函数基于哈希随机数发生器，实现了均匀分布的整数随机数生成。

本文将介绍np.random.randint的原理、使用方法和注意事项。

一、原理np.random.randint函数基于哈希随机数发生器，生成指定范围内的整数随机数。

哈希随机数发生器是一种基于密码学原理的随机数生成方法，具有高随机性和可预测性。

在np.random.randint函数中，哈希随机数发生器将区间[a,b]映射为一个整数区间[0,n]，其中n是数组参数size的长度。

这样，区间[a,b]中的每个元素都有相同的概率落在生成的整数中。

二、使用方法要使用np.random.randint函数生成指定范围内的整数随机数，需要提供三个参数：最小值a、最大值b和数组参数size。

其中，size表示生成的随机数数组的长度。

以下是一个示例代码：importnumpyasnpprint(np.random.randint(0,10,size=(3,)))输出结果为：[417]这个示例代码生成了一个长度为3的数组，其中每个元素都是从区间[0,9]中随机选取的一个整数。

三、注意事项在使用np.random.randint函数时，需要注意以下几点：1.区间[a,b]中的元素在生成的随机数中具有相同的概率。

这意味着，如果区间[a,b]中存在多个整数，那么它们在生成的随机数中出现的概率相同。

2.生成的随机数数组中的元素个数取决于数组参数size的长度。

如果size 为空或长度为1，则生成的随机数只有一个；如果size为二维数组，则生成的随机数也是一个二维数组。

3.如果最小值a大于最大值b，则np.random.randint函数将返回一个空数组。

因此，在使用np.random.randint函数时，需要确保最小值a小于或等于最大值b。

函数随机百分数

函数随机百分数函数随机百分数是一种常见的编程函数，用于在一定的范围内随机生成百分数。

百分数是指以百为基数的表达方法，常用于描述数字在整个群体中所占的比重。

在实际开发中，函数随机百分数可以被广泛应用于游戏、数据分析和金融等领域。

本文将介绍函数随机百分数的原理、应用场景以及实现方法。

一、函数随机百分数的原理函数随机百分数的原理是通过计算随机数的值，将其转换为对应的百分数。

通常情况下，随机数的取值范围为0到1之间。

因此，我们需要将随机数的值乘以100，得到0到100之间的数字。

如果我们需要生成小数点后一位精度的百分数，可以将结果再除以10。

例如，如果随机数的值为0.789，则将其乘以100得到78.9，再除以10得到7.89%。

在实际开发中，我们还需要考虑百分数的精确度和数量。

例如，在某些游戏中，我们需要随机生成10个0到100之间的整数百分数，且这10个百分数的和为100。

为了满足这个条件，我们可以通过循环控制随机数的取值范围，并在相加的过程中进行调整，以保证结果符合要求。

二、函数随机百分数的应用场景函数随机百分数可以被广泛用于游戏、数据分析和金融等领域。

1.游戏领域在游戏中，函数随机百分数可以被用于生成敌人的血量、攻击力、护甲值等属性。

这些数字通常在一定范围内随机分布，以增加游戏的随机性和可玩性。

例如，在某个RPG游戏中，我们可以对敌人的血量进行随机分配，以增加游戏的挑战难度。

2.数据分析领域在数据分析中，函数随机百分数可以被用于生成模拟数据。

例如，在某个销售预测模型中，我们需要随机生成一批销售数据，并将其插入到模型中进行分析。

通过使用函数随机百分数，我们可以模拟真实的销售情况，并在数据分析中得到更为准确的结果。

3.金融领域在金融领域，函数随机百分数可以被用于生成股票价格、汇率等金融数据。

这些数字通常在一定范围内波动，并且具有一定的趋势性。

例如，在某个股票交易模型中，我们需要随机生成一批股票价格，以进行交易模拟。

python中random.randint的计算方式

random.randint(a, b)是 Python 标准库random中的一个函数，用于生成一个指定范围内的随机整数。

这个函数的计算方式是：
1.参数定义：
o a：表示生成随机数的下限（包含）。

o b：表示生成随机数的上限（包含）。

2.计算过程：random.randint(a, b)内部实现机制会确保生成的随机
数在[a, b]范围内，即生成的随机数至少是a，并且至多是b。

它通过内部算法（通常是线性同余法、Mersenne Twister 等伪随机数生成器算法）产生一个浮点数，然后将其转换为适当的整数值并进行调
整，以确保该值落在给定的整数区间内。

3.返回结果：函数返回的是在这个闭区间[a, b]内的一个等概率随机
整数。

例如：
python
import random
# 生成一个 0 到 9 之间的随机整数
random_number = random.randint(0, 9)
print(random_number) # 可能的输出有：0, 1, 2, ..., 8, 9
注意，尽管我们无法直接查看 Python 标准库中具体的内部实现细节，但可以确信的是其生成的随机数满足均匀分布特性，并且每次调用都能得到一个新的随机值（如果不设置随机种子的话）。

Python——随机数生成模块numpy.random

Python——随机数⽣成模块numpy.random（说明：本⼈只限于收藏，未作他⽤。

由于原作者声明“本⽂为博主原创⽂章，未经博主允许不得转载”，如侵犯版权，请联系删除。

）在数据分析中，数据的获取是第⼀步，numpy.random 模块提供了⾮常全的⾃动产⽣数据API，是学习数据分析的第⼀步。

总体来说，numpy.random模块分为四个部分，对应四种功能：1. 简单随机数：产⽣简单的随机数据，可以是任何维度2. 排列：将所给对象随机排列3. 分布：产⽣指定分布的数据，如⾼斯分布等4. ⽣成器：种随机数种⼦，根据同⼀种⼦产⽣的随机数是相同的以下是详细内容以及代码实例：（以下代码默认已导⼊numpy：import numpy as np ）1. ⽣成器电脑产⽣随机数需要明⽩以下⼏点：1. 随机数是由随机种⼦根据⼀定的计算⽅法计算出来的数值。

所以，只要计算⽅法⼀定，随机种⼦⼀定，那么产⽣的随机数就不会变。

2. 只要⽤户不设置随机种⼦，那么在默认情况下随机种⼦来⾃系统时钟（即定时/计数器的值）3. 随机数产⽣的算法与系统有关，Windows和Linux是不同的，也就是说，即便是随机种⼦⼀样，不同系统产⽣的随机数也不⼀样。

numpy.random 设置种⼦的⽅法有：函数名称函数功能参数说明RandomState定义种⼦类RandomState是⼀个种⼦类，提供了各种种⼦⽅法，最常⽤seedseed([seed])定义全局种⼦参数为整数或者矩阵代码⽰例：np.random.seed(1234) #设置随机种⼦为12342. 简单随机数函数名称函数功能参数说明rand(d0, d1, …, dn)产⽣均匀分布的随机数dn为第n维数据的维度randn(d0, d1, …, dn)产⽣标准正态分布随机数dn为第n维数据的维度randint(low[, high, size,dtype])产⽣随机整数low：最⼩值；high：最⼤值；size：数据个数random_sample([size])在[0,1）内产⽣随机数size：随机数的shape，可以为元祖或者列表，[2,3]表⽰2维随机数，维度为（2,3）random([size])同random_sample([size])同random_sample([size])ranf([size])同random_sample([size])同random_sample([size])sample([size]))同random_sample([size])同random_sample([size]) choice(a[, size, replace, p])从a中随机选择指定数据a：1维数组 size：返回数据形状bytes(length)返回随机位length：位的长度代码⽰例:(1) np.random.rand(2,3) #产⽣2⾏三列均匀分布随机数组Out[7]:array([[ 0.35369993, 0.0086019 , 0.52609906],[ 0.31978928, 0.27069309, 0.21930115]])(2）In [8]: np.random.randn(3,3) #三⾏三列正态分布随机数据Out[8]:array([[ 2.29864491, 0.52591291, -0.80812825],[ 0.37035029, -0.07191693, -0.76625886],[-1.264493 , 1.12006474, -0.45698648]])(3）In [9]: np.random.randint(1,100,[5,5]) #(1,100）以内的5⾏5列随机整数Out[9]:array([[87, 69, 3, 86, 85],[13, 49, 59, 7, 31],[19, 96, 70, 10, 71],[91, 10, 52, 38, 49],[ 8, 21, 55, 96, 34]])(4）In [10]: np.random.random(10) #(0,1）以内10个随机浮点数Out[10]:array([ 0.33846136, 0.06517708, 0.41138166, 0.34638839, 0.41977818,0.37188863, 0.2508949 , 0.89923638, 0.51341298, 0.71233872])(5）In [11]: np.random.choice(10) #[0,10)内随机选择⼀个数Out[11]: 73. 分布numpy.random模块提供了产⽣各种分布随机数的API：函数名称函数功能参数说明beta(a, b[, size])贝塔分布样本，在 [0, 1]内。

pythonnumpy之np.random的随机数函数使用介绍

pythonnumpy之np.random的随机数函数使⽤介绍np.random的随机数函数（1）函数说明rand(d0,d1,..,dn)根据d0‐dn创建随机数数组，浮点数， [0,1)，均匀分布randn(d0,d1,..,dn)根据d0‐dn创建随机数数组，标准正态分布randint(low[,high,shape])根据shape创建随机整数或整数数组，范围是[low, high)seed(s)随机数种⼦， s是给定的种⼦值np.random.randimport numpy as npa = np.random.rand(3, 4, 5)aOut[3]:array([[[0.28576737, 0.96566496, 0.59411491, 0.47805199, 0.97454449],[0.15970049, 0.35184063, 0.66815684, 0.13571458, 0.41168113],[0.66737322, 0.91583297, 0.68033204, 0.49083857, 0.33549182],[0.52797439, 0.23526146, 0.39731129, 0.26576975, 0.26846021]],[[0.46860445, 0.84988491, 0.92614786, 0.76410349, 0.00283208],[0.88036955, 0.01402271, 0.59294569, 0.14080713, 0.72076521],[0.0537956 , 0.08118672, 0.59281986, 0.60544876, 0.77931621],[0.41678215, 0.24321042, 0.25167563, 0.94738625, 0.86642919]],[[0.36137271, 0.21672667, 0.85449629, 0.51065516, 0.16990425],[0.97507815, 0.78870518, 0.36101021, 0.56538782, 0.56392004],[0.93777677, 0.73199966, 0.97342172, 0.42147127, 0.73654324],[0.83139234, 0.00221262, 0.51822612, 0.60964223, 0.83029954]]])np.random.randnb = np.random.randn(3, 4, 5)bOut[5]:array([[[ 0.09170952, -0.36083675, -0.18189783, -0.52370155,-0.61183783],[ 1.05285606, -0.82944771, -0.93438396, 0.32229904,-0.85316565],[ 1.41103666, -0.32534111, -0.02202953, 1.02101228,1.59756695],[-0.33896372, 0.42234042, 0.14297587, -0.70335248,0.29436318]],[[ 0.73454216, 0.35412624, -1.76199508, 1.79502353,1.05694614],[-0.42403323, -0.36551581, 0.54033378, -0.04914723,1.15092556],[ 0.48814148, 1.09265266, 0.65504441, -1.04280834,0.70437122],[ 2.92946803, -1.73066859, -0.30184912, 1.04918753,-1.58460681]],[[ 1.24923498, -0.65467868, -1.30427044, 1.49415265,0.87520623],[-0.26425316, -0.89014489, 0.98409579, 1.13291179,-0.91343016],[-0.71570644, 0.81026219, -0.00906133, 0.90806035,-0.914998 ],[ 0.22115875, -0.81820313, 0.66359573, -0.1490853 ,0.75663096]]])np.random.randintc = np.random.randint(100, 200, (3, 4))cOut[9]:array([[104, 140, 161, 193],[134, 147, 126, 120],[117, 141, 162, 137]])numpy.random.randint的详细⽤法 - python函数的作⽤是，返回⼀个随机整型数，范围从低（包括）到⾼（不包括），即[low, high)。

python中random.randint和random.randrange的区别详解

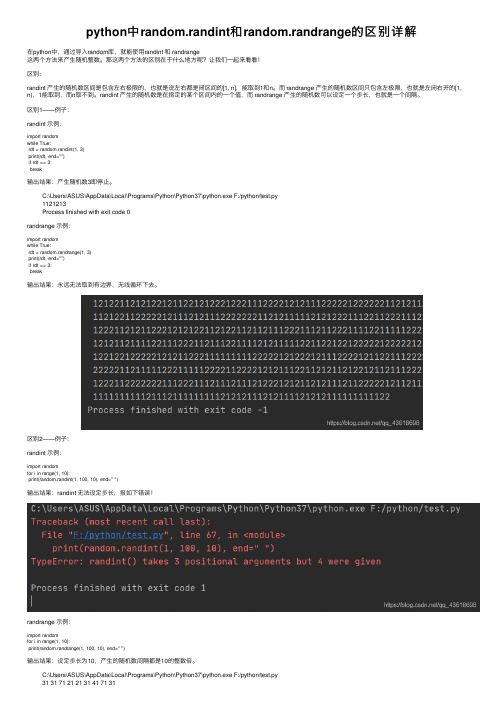
python中random.randint和random.randrange的区别详解在python中，通过导⼊random库，就能使⽤randint 和 randrange这两个⽅法来产⽣随机整数。

那这两个⽅法的区别在于什么地⽅呢？让我们⼀起来看看！区别:randint 产⽣的随机数区间是包含左右极限的，也就是说左右都是闭区间的[1, n]，能取到1和n。

⽽ randrange 产⽣的随机数区间只包含左极限，也就是左闭右开的[1, n)，1能取到，⽽n取不到。

randint 产⽣的随机数是在指定的某个区间内的⼀个值，⽽ randrange 产⽣的随机数可以设定⼀个步长，也就是⼀个间隔。

区别1——例⼦：randint ⽰例：import randomwhile True:rdt = random.randint(1, 3)print(rdt, end="")if rdt == 3:break输出结果：产⽣随机数3即停⽌。

C:\Users\ASUS\AppData\Local\Programs\Python\Python37\python.exe F:/python/test.py1121213Process finished with exit code 0randrange ⽰例：import randomwhile True:rdt = random.randrange(1, 3)print(rdt, end="")if rdt == 3:break输出结果：永远⽆法取到有边界，⽆线循环下去。

区别2——例⼦：randint ⽰例：import randomfor i in range(1, 10):print(random.randint(1, 100, 10), end=" ")输出结果：randint ⽆法设定步长，报如下错误！randrange ⽰例：import randomfor i in range(1, 10):print(random.randrange(1, 100, 10), end=" ")输出结果：设定步长为10，产⽣的随机数间隔都是10的整数倍。

python 随机数函数源代码

python 随机数函数源代码
摘要：
1.Python简介
2.随机数函数的重要性
3.Python随机数函数的源代码
4.随机数函数的应用场景
5.结论
正文：
Python是一种广泛应用于多个领域的编程语言，其简洁的语法和强大的功能使得开发者可以轻松地编写代码。

在各种应用场景中，随机数函数是非常重要的一个组成部分，它们可以帮助开发者生成随机数，从而实现许多有趣的功能。

在Python中，随机数函数的源代码是由内置的random模块提供的。

random模块提供了许多生成随机数的函数，如randint、random、choice 等。

这些函数可以帮助开发者轻松地生成随机数，从而实现诸如抽奖、掷骰子等游戏功能。

以下是random模块中一些随机数函数的源代码：
```python
import random
# 生成一个指定范围内的随机整数
def randint(a, b):
return random.randint(a, b)
# 生成一个0到1之间的随机浮点数
def random():
return random.random()
# 从序列中随机选择一个元素
def choice(seq):
return random.choice(seq)
```
可以看到，Python随机数函数的源代码非常简洁。

这些函数可以广泛应用于各种场景，如游戏开发、数据生成、模拟实验等。

开发者可以根据自己的需求选择合适的随机数函数，从而实现所需的功能。

总之，Python的随机数函数在编程中具有广泛的应用，其源代码简洁易懂。