201403学期信号与系统作业二答案
《信号与系统》课后习题参考答案

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、(1)解:∵系统的微分方程为:)(2)(3)(t e t r t r '=+',∴r(t)的阶数与e(t) 的阶数相等,则h(t)应包含一个)(t δ项。
又∵系统的特征方程为:03=+α,∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程(此时e(t)= )(t δ),得:)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解:①求)(t r zi : ∵系统的特征方程为:0)3)(2(652=++=++αααα,∴特征根:21-=α,32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs :t t e A eA t h 3221)(--+= (t ≥0),可求得:11=A ,12-=A (求解过程略) ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r :)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=,21=C 21=C ∴ 011=-C , ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi , ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解:(1)依题意,得:)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---,两边求导得:)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ (2)∵系统的起始状态保持不变,∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+,∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证:∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时:u(t-3k)为非零值 又∵0≤t ≤3,∴k 取负整数,则:3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(,且311--=e A 。
《信号与系统》2014年秋学期在线作业(二)

10. A. B. C. D. 正确答案:B 满分:4 分 得分:4
11. A. B. C. D. 正确答案:C 满分:4 分 得分:4
4. A. B. C. D. 正确答案:D 满分:4 分 得分:4
5. A. B. C. D. 正确答案:B 满分:4 分 得分:4
14. 拉普拉斯变换中因果信号的收敛域是( )。 A. 收敛轴以左的区域 B. 收敛轴以右的区域 C. 收敛轴间的带状区域 D. 全S平面 正确答案:B 满分:4 分 得分:4
15. A. B. C. D. 正确答案:A 满分:4 分 得分:4
正确答案:B
满分:4 分 得分:4
10. A. 错误 B. 正确 正确答案:B 满分:4 分 得分:4
关闭
2. A. 错误 B. 正确 正确答案:B 满分:4 分 得分:4 3. 信号的傅立叶变换是垃氏变换的特例,存在拉氏变换的信号也一定存在傅立叶变换。 A. 错误 B. 正确 Байду номын сангаас 正确答案:A 满分:4 分 得分:4 4. 理想低通滤波器是因果物理可实现系统。 A. 错误 B. 正确 正确答案:A 满分:4 分 得分:4
2. A. B. C. D. 正确答案:C 满分:4 分 得分:4
3. A. B. C. D. 正确答案:B 满分:4 分 得分:4
201403学期信号与系统作业一答案

201403学期信号与系统作业一答案第1题根据信号定义域的特点可分为连续时间信号和( )。
A、有限时间信号B、离散时间信号C、周期时间信号D、非周期时间信号答案:B第2题根据信号的能量性质可分为能量信号和( )。
A、功率信号B、能量信号C、功率有限信号D、能量有限信号答案:A第3题系统初始状态为零,仅由输入信号引起的响应称为( )。
A、零状态响应B、零输入响应C、全响应D、半状态响应答案:A第4题一个LIT系统,当其初始状态为零时,输入为单位冲击函数所引起的响应称为( )。
A、单位阶跃响应B、阶跃响应C、冲击响应D、单位冲击响应答案:D第5题如果信号功率有限,则称信号为( )。
A、功率有限信号B、能量有限信号C、功率无限信号D、能量无限信号答案:A第6题阻止信号通过的频率范围称为( )。
A、非通带B、通带C、阻带D、非阻带答案:C第7题将信号f(t)变换为( )称为对信号f(t)的平移。
A、f(t–t0)B、f(k–k0)C、f(at)D、f(-t)答案:A第8题理想低通滤波器是( )。
A、物理可实现的B、非因果的C、因果的D、不稳定的答案:B第9题连续周期信号的傅氏变换是( )。
A、连续的B、周期性的C、离散的D、与单周期的相同答案:C第10题下列叙述正确的是( )。
A、各种数字信号都是离散信号B、各种离散信号都是数字信号C、数字信号的幅度只能取1或0D、将模拟信号抽样直接可得数字信号答案:A判断题第11题 s平面的左平面映射到z平面单位圆的外部。
()正确错误答案:错误第12题激励为零,仅由系统的初始状态引起的响应叫做系统的零输入响应。
()正确错误答案:正确第13题当用傅氏级数的有限项和来近似表示信号时,在信号的断点处存在吉布斯现象。
()正确错误答案:正确第14题连续时间LTI系统对周期信号的响应为非周期信号。
()正确错误答案:错误第15题从信号频谱的连续性和离散性来考虑,周期信号的频谱是离散的。
信号与系统考题参考解答(完整版)

《信号与系统》作业参考解答第一章(P16-17)1-3 设)(1t f 和)(2t f 是基本周期分别为1T 和2T 的周期信号。
证明)()()(21t f t f t f +=是周期为T 的周期信号的条件为T nT mT ==21 (m ,n 为正整数) 解:由题知)()(111t f mT t f =+ )()(222t f mT t f =+要使)()()()()(2121t f t f T t f T t f T t f +=+++=+则必须有21nT mT T == (m ,n 为正整数) 1-5 试判断下列信号是否是周期信号。
若是,确定其周期。
(1)t t t f πsin 62sin 3)(+= (2)2)sin ()(t a t f =(8)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2cos 28sin 4cos )(k k k k f πππ解:(1)因为t 2sin 的周期为π,而t πsin 的周期为2。
显然,使方程n m 2=π (m ,n 为正整数)成立的正整数m ,n 是不存在的,所以信号t t t f πsin 62sin 3)(+=是非周期信号。
(2)因为)2cos 1()sin ()(22t a t a t f -==所以信号2)sin ()(t a t f =是周期π=T 的周期信号。
(8)由于)4/cos(k π的周期为8)4//(21==ππN ,)8/sin(k π的周期为16)8//(22==ππN ,)2/cos(k π的周期为4)2//(23==ππN ,且有16412321=⨯=⨯=⨯N N N所以,该信号是周期16=N 的周期信号。
1-10 判断下列系统是否为线性时不变系统,为什么?其中)(t f 、][k f 为输入信号,)(t y 、][k y 为零状态响应。
(1))()()(t f t g t y = (2))()()(2t f t Kf t y += 解:(1)显然,该系统为线性系统。
信号与系统第二章作业解答

A 1, B C 1 rzi (t) 1 (t 1)et (t 0)
2
2 15 已知f1(t) u(t 1) u(t 1), f2 (t) (t 5) (t 5)
f3
(t
)
(t
1 2
)
(t
1 2
),
画出下列各卷积波形.
(1) s1(t) f1(t) f2 (t);
(2) s2 (t) f1(t) f2 (t) f2 (t);
(3) s3 (t) {[ f1(t) f2 (t)][u(t 5) u(t 5)]} f2 (t);
(4) s4 (t) f1(t) f3 (t)
f1(t) f2 (t)
3
2 15 已知f1(t) u(t 1) u(t 1), f2 (t) (t 5) (t 5)
f3
(t)
(t
1 2
)
(t
1), 2
画出下列各卷积波形.
(3) s3(t) {[ f1(t) f2 (t)][u(t 5) u(t 5)]} f2 (t);
f1(t) f2 (t) f2 (t)
f1(t) f2 (t)
4
2 15 已知f1(t) u(t 1) u(t 1),
f
3
(t
)
(t
1 2
)
(t
1) 2
画出下列各卷积波形 .
(4) s4 (t) f1(t) f3 (t)
5
《信号与系统》第二版课后答案_(郑君里)_高等教育出版社
f (t )
1
f (t )
1
(1)
1
(2)
1
f (t ) f (t )
1 1 (3) 1 (4) -1
f (t )
1 3 2
f (t )
(5)
1
(6)
2
3
3
f (t )
1 2 3
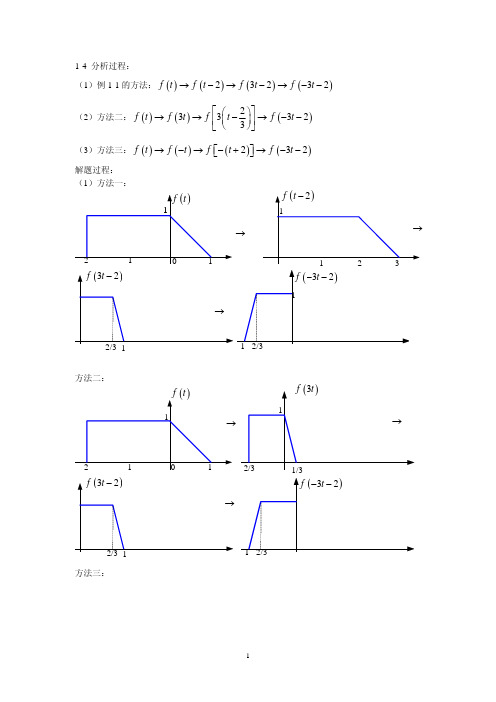
(7) -2 注:1-9、1-12 题中的时域信号均为实因果信号,即 f ( t ) = f ( t ) u ( t ) 1-18 分析过程:任何信号均可分解为奇分量与偶分量之和的形式,即
2
(t )
2
非线性:设 r1 ( t ) = e1
( t ) 、 r2 ( t ) = e2 2 ( t ) ,
2 2 2 2
则⎡ ⎣ c1e1 ( t ) + c2 e2 ( t ) ⎤ ⎦ = c1 e1 ( t ) + c2 e2
2
( t ) + 2c1c2e1 ( t ) e2 ( t ) ≠ c1r1 ( t ) + c2 r2 ( t )
(4) f ( at ) 右移
故(4)运算可以得到正确结果。 注:1-4、1-5 题考察信号时域运算:1-4 题说明采用不同的运算次序可以得到一致的结果; 1-5 题提醒所有的运算是针对自变量 t 进行的。如果先进行尺度变换或者反转变换,再进行 移位变换,一定要注意移位量和移位的方向。 1-9 解题过程: (1) f ( t ) = 2 − e
t0 ⎡ ⎛ t ⎞⎤ : f ⎢ a ⎜ t + 0 ⎟ ⎥ = f ( at + t0 ) ≠ f ( t0 − at ) a ⎣ ⎝ a ⎠⎦ t0 ⎡ ⎛ t ⎞⎤ : f ⎢ − a ⎜ t − 0 ⎟ ⎥ = f ( − at + t0 ) = f ( t0 − at ) a ⎣ ⎝ a ⎠⎦
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
信号与系统课后习题参考答案.pdf

-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
(e)[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 (-1/2)
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则:整个信号的周期为:T = LCM{T1,T2} = π
1.11
j 4πn
解: e 7
→
ω1
=
4πn 7
,则:
2π ω1
=
2π 4π
=7= 2
N1 k
,⇒
N1
=
7
7
j 2πn
e5
→ ω2
信号与系统课后习题与解答第二章
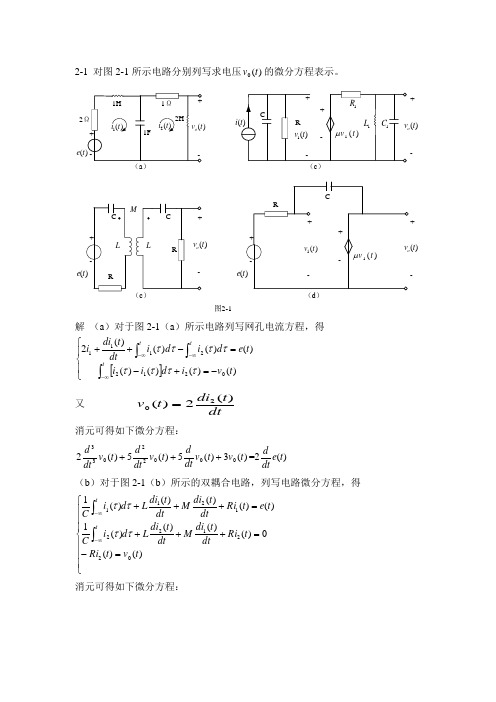
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
信号与系统第二章答案

f (n ) x (n ) y ( n) ,欲使 f (n ) 是周期的,必须有 N 0 kN1 mN 2
(h)
(i)
(j)
x (n ) 2 cos( n / 4) sin( n / 8) 2 sin( n / 2 / 6) x (t ) 2 cos(3t / 4) ,周期信号, T
2 3
。
解:(a)
(b)
x (n ) cos(8 n / 7 2) ,周期信号, Q 0 x (t ) e j ( t 1) ,周期信号, T 2 。
(c)
(a)
h (t 3)
(b)
h (1 2t )
(3) 根据图 P2.1(a) 和(b) 所示的
x (t ) 和 h (t ) ,画出下列各信号的波形图,并加以标注。
(b)
(a)
x(t )h(t )
x(1 t )h(t 1)
(c)
t x (2 )h (t 4) 2
图 P2.1 解:(1) 各信号波形如下图所示:
(d)
x (n ) e j (n / 8 )
(e)
x (n ) (n 3m ) (n 1 3m)
m 0
(f)
x (t ) cos 2 t u (t ) x (t ) Ev cos 2 t u (t )
(g)
x (n ) cos( n / 4) cos( n / 4) x (t ) Ev cos(2 t / 4) u (t )
(b) 不正确。设
x (n ) g (n ) h (n ) ,其中 g ( n) sin
n ,对所有 n , 4
信号与系统第二版课后答案

信号与系统第二版课后答案《信号与系统》(第二版)课后习题解析燕庆明主编高等教育出版社目录第1章习题解析 2 第2章习题解析 5 第3章习题解析15 第4章习题解析22 第5章习题解析30 第6章习题解析40 第7章习题解析48 第8章习题解析54第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?c d题1-1图解 a 、 c 、 d 为连续信号; b 为离散信号; d 为周期信号;其余为非周期信号; a 、 b 、 c 为有始(因果)信号。
1-2 给定题1-2图示信号f t ,试画出下列信号的波形。
[提示:f 2t 表示将f t 波形压缩,f 表示将f t 波形展宽。
]a 2 f t 2b f 2tc fd f t +1题1-2图解以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R、L、C元件可以看成以电流为输入,电压为响应的简单线性系统SR、SL、SC,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解各系统响应与输入的关系可分别表示为;;1-4 如题1-4图示系统由加法器、积分器和放大量为a的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
题1-4图解系统为反馈联接形式。
设加法器的输出为x t ,由于且故有即1-5 已知某系统的输入 f t 与输出y t 的关系为y t | f t |,试判定该系统是否为线性时不变系统?解设T为系统的运算子,则可以表示为:不失一般性,设f t f1 t + f2 t ,则;故有显然即不满足可加性,故为非线性时不变系统。
1-6 判断下列方程所表示的系统的性质。
1 23 4解 1 线性; 2 线性时不变; 3 线性时变; 4 非线性时不变。
1-7 试证明方程所描述的系统为线性系统。
式中a为常量。
证明不失一般性,设输入有两个分量,且则有相加得即可见即满足可加性,齐次性是显然的。
信号与系统课后习题答案汇总

可编辑第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t e t x -= (2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t t x επ= (5) )]4()([4cos )(--=-t t t e t x t εεπ (7) t t t t x 2cos )]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dt d t x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=t d t x ττδ)1()((14) )()(n n n x --=ε 1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t e t x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin )(π=解 功率有限信号。
n 4sinπ是周期序列,周期为8。
(5) )(2sin )(t t t x επ= 解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin )(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sinπ的功率为1/2,因此)(4sin n n επ在),(∞-∞区间上的功率为1/4。
信号与系统习题解答 (2)
| 1 k u[1 k] |
k
k 2
1 | 1 k | ,无界
k 2
是非稳定系统
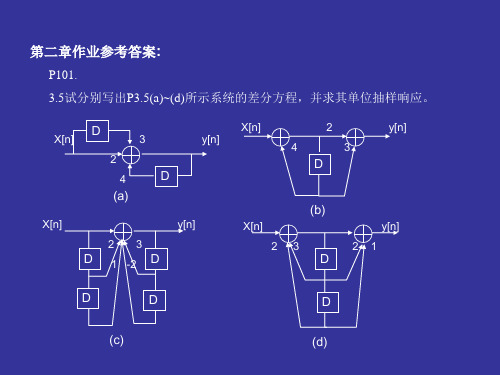
3.26已知二阶LTI离散时间系统的单位抽样响应
n
(a)试写出该系统的h[差n] 分2方 2程2 ;sin
n 4
u[n]
x(t) (t) (t 1) (t 2)
(b)画出该系统的直接I和直接II型模拟图框图.
y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求 hˆ[n] 3hˆ[n 1] 2hˆ[n 2] x[n] [n] 特征方程为 λ2-3λ+2=0,得 λ1=1, λ2=2。
hˆ[n] c1 c2 (2)n
和初始条件 hˆ[0] 1, hˆ[1] 0,得
11221112211?????????????nxnynynynnhnhnh?4sin222nunnhn??????????21?????ttttx???12211242sin224sin22214cos22214sin22214cos4sin222141sin22214sin22221?????????????????????????????????????????????????????????????????????????????????????????nnhnhnnunnunnunnunnunnnunnhnunnhnnxnnnnnnn???????????时解
k
k
是稳定系统
(g) 显然n<0时,h[n]=1,所以是非因果系统;
| h[k] | | u[k 4] u[k 4] |
k
k
| u[k 4] | | u[k 4] | 8,有界
(完整版)信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
信号与系统第二章习题答案

(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
h (t ) = C1e −2t + C2 e t ε (t )
对上式求一阶、二阶导数,得
(
)
h ' (t ) = − 2C1e −2t + C 2e t ε (t ) + C1e −2t + C2 e t δ (t )
(
)
(
t
)
h '' (t ) = 4C1e −2 t + C2 e t ε (t ) + − 2C1e −2t + C 2e t δ (t ) + − 2C1e − 2t
d 2e (t ) d 2i1 (t ) di1 (t ) di 2 (t ) = 4 + 6 + 2 dt 2 dt 2 dt dt
将⑴式、⑸式代入⑽式中,得到:
⑾
对⑾式求导,得到:
⑿
再将⑴式代入⑿式中,得到 i1 (t ) 的微分方程为:
64
d 2e (t ) d 2i1 (t ) di1 (t ) = 4 + 6 + 4i1 (t ) dt 2 dt 2 dt
⑼
再将⑴式代入⑼式中,得到 i 2 (t ) 的微分方程为:
2
d 2i 2 (t ) di 2 (t ) de(t ) + 3 + 2i 2 (t ) = 2 dt dt dt
⑽
对⑹式求一阶导,得到:
di (t ) di (t ) du (t ) de(t ) = 4 1 +2 2 + c dt dt dt dt di (t ) de(t ) = 4 1 + 6i1 (t ) + 2i2 (t ) dt dt
信号与系统课后答案(PDF)
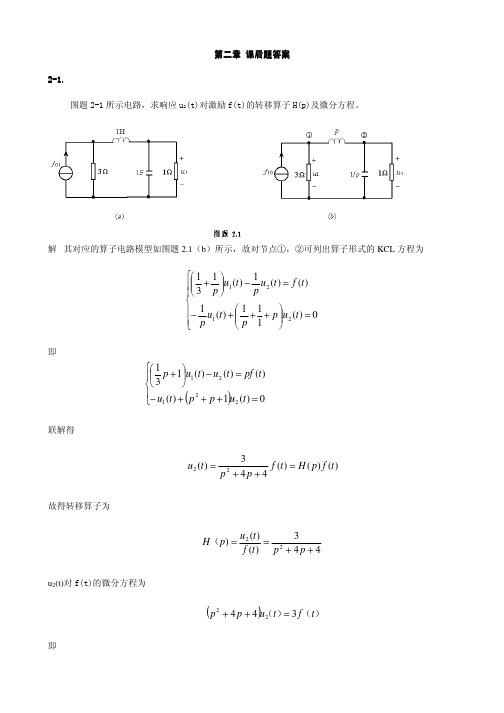
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
信号与系统第2章答案

0 t 1时,
( 2).1 t 2时,
h(t ) h(t 1) h(t 2) h(t ) h(t 1) 1
h(t ) 1 h(t 1) 1 (t 1) 2 t (3).2 t 3时, h(t ) h(t 1) h(t 2) 1
解: (a) 特征方程为 λ2+3λ+2=0 得 λ1=-2, λ2=-1。
(f). (D2+2D+2)y(t)=Dx(t)
则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 2 t+ c2e-t)u(t) h`(t)= (c1+ c2)δ(t)+(-2c1e- 2 t-c2e-t)u(t) h``(t)= (c1+ c2)δ`(t)+(-2c1-c2) δ(t)+ (4c1e- 2 t+c2e-t)u(t)
E 4
e
3 ( t T ) 8
]u (t T )
e
u (t T )
2.22 某LTI系统的输入信号x(t)和其零状态响应yx(t)的 波形如图P2.22所示。(a)求该系囊统的冲激响应 h(t),(b)用积分器,加法器和延时器(T=1s)构成该系统。 解: (a)
0
x(t ) (t ) (t 1) (t 2) t, 0 t 1 y x (t ) 1, 1 t 3 4 t , 3 t 4 x(t ) h(t ) (t ) (t 1) (t 2) h(t ) y x (t ) t, 0 t 1 h(t ) h(t 1) h(t 2) 1, 1 t 3 4 t , 3 t 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
201403学期信号与系统作业二答案
第1题已知某系统的系统函数H(s), 唯一决定该系统冲激响应h(t)函数形式的是( )。
A、H(s)的零点
B、H(s)的极点
C、系统的激励
D、激励与H(s)的极点
答案:B
第2题下列 ( )不是LTI系统的性
质。
A、线性
B、时不变性
C、非因果性
D、稳定性
答案:C
第3题信号的时宽与信号的频宽之间呈
( )。
A、正比关系
B、反比关系
C、平方关系
D、没有关系
答案:B
第4题时域是实偶函数,其傅氏变换一定是
( )。
A、实偶函数
B、纯虚函数
C、任意复函数
D、任意实函数
答案:A
第5题信号〔ε(t)-ε(t-2)〕的拉氏变换的收敛域为 ( )。
A、Re[s]>0
B、Re[s]>2
C、全S平面
D、不存在
答案:C
第6题已知某连续时间系统的系统函数H(s)=1/(s+1),该系统属于什么类型( )。
A、高通滤波器
B、低通滤波器
C、带通滤波器
D、带阻滤波器
答案:B
第7题线性系统具有
()。
A、分解特性
B、零状态线性
C、零输入线性
D、ABC
答案:D
第8题零输入响应是( )。
A、全部自由响应
B、部分自由响应
C、部分零状态响应
D、全响应与强迫响应之差
答案:B
第9题在工程上,从抽样信号恢复原始信号时需要通过的滤波器
( )。
A、高通滤波器
B、低通滤波器
C、带通滤波器
D、带阻滤波器
答案:B
第10题理想低通滤波器一定是
( )。
A、稳定的物理可实现系统
B、稳定的物理不可实现系统
C、不稳定的物理可实现系统
D、不稳定的物理不可实现系统
答案:B
判断题
第11题 H (s)的零点和极点中仅极点决定了h (t) 的函数形式。
()
正确
错误
答案:正确
第12题系统的系统函数为 H(s),若同时存在频响函数H(jω),则该系统必须满足条件稳定系统。
()
正确
错误
答案:正确
第13题对于信号f(t)=sin2Πt的最小采样频率是2Hz。
()
正确
错误
答案:正确
()第14题如果一个系统的幅频响应是常数,那么这个系统就称为全通系统。
正确
错误
答案:正确
第15题偶周期信号的傅氏级数中只有直流项和正弦项。
()
正确
错误
答案:错误
第16题信号时移只会对幅度谱有影响。
()
正确
错误
答案:正确
第17题一个信号存在拉氏变换就一定存在傅氏变换。
()
正确
错误
答案:错误
第18题拉普拉斯变换满足线性性质。
()
正确
错误
答案:错误
第19题所有非周期信号都是能量信号。
()
正确
错误
答案:错误
第20题零状态响应是指系统没有激励时的响应。
()
正确
错误
答案:正确。
