第6章点的复合运动
理论力学习题册答案

理论力学习题册答案班级姓名学号第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
(a)球A(b)杆AB- 1 -(c)杆AB、CD、整体(d)杆AB、CD、整体(e)杆AC、CB、整体(f)杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
(a)球A、球B、整体(b)杆BC、杆AC、整体- 2 -班级姓名学号第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
(a)杆AB、BC、整体(c)杆AB、CD、整体CAFAxDBFAyFBWEW(b)杆ABOriginal Figure、BC、轮E、整体FBD of the entire frame(d)杆BC带铰、杆AC、整体- 3 -(e)杆CE、AH、整体(g)杆AB带轮及较A、整体(f)杆AD、杆DB、整体(h)杆AB、AC、AD、整体- 4 -班级姓名学号第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
点的复合运动

点的合成运动
y’
o’
x’
例2、直升飞机在匀速前进的军舰上降落
y
y’
o’
x’
x
o
点的合成运动
y’ x’
o’
物体的运动的描述结果与所选定的参考系有关。同一物体的运动,在不同的 参考系中看来,可以具有极为不同的运动学特征(具有不同的轨迹、速度、 加速度等)。
相对运动:未知
3、
va ve vr
大小 v1 v2
?
方向 √ √
?
vr va2 ve2 2vave cos60 3.6 m s
arcsin(ve sin 60o ) 46o12
点的合成运动
vr
求解合成运动的速度问题的一般步骤为(P180):
① 选取动点,动系和静系。
B
曲柄-滑块机构
点的合成运动
思考题 动 点:杆上A点。 动系:固连于滑块B。 定系:固连于墙面。 绝对运动? 相对运动? 牵连运动?
点的合成运动
A Bv
点的合成运动
动 点? 动参考系? 绝对运动? 相对运动? 牵连运动?
练习题1
点的合成运动
点的合成运动
点的合成运动
动 点? 动参考系? 绝对运动? 相对运动? 牵连运动?
定系的速度。
点的合成运动
基本概 念
牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
这点称为瞬时重合点或动点的牵连点。 (2)、进一步说明
牵连运动一方面是动系的绝对运动,另一方面对动点来说起 着“牵连”作用。但是带动动点运动的只是动系上在所考察的瞬 时与动点相重合的那一点,该点称为瞬时重合点或牵连点。 (3)、注 意
《理论力学》思考题及习题

《理论力学》思考题及习题宁夏大学机械工程学院技术基础部使用教材:理论力学(Ⅰ).哈尔滨工业大学理论力学教研室,第六版.北京:高等教育出版社.说明:以下各章的思考题及习题的页码和题号均以“哈工大”第六版《理论力学》教材为准。
静力学第一章静力学公理和物体的受力分析思考题:1.合矢与合力概念相同吗?2.几何法求合矢时,分矢与合矢怎样区别?3.力沿任意两个轴分解时的两个分力与力向该二轴的投影大小是否相同?4.二力平衡与作用力、反作用力的概念有什么不同?5.二力杆或二力构件的受力特点是什么?6.不计重力但作用有力偶的杆是二力杆吗?7.三力平衡汇交时怎样确定第三个力的作用线方向?8.画受力图的一般步骤是什么?在画物系中各个分离体的受力图时需要注意什么?9.P18思考题。
习题:P20-21:1-1 (a) (c) (d) (e) (g) (i) (j) (k); 1-2 (a) (d) (f)(i)(m) (o) 第二章平面汇交力系与平面力偶系思考题:1.汇交力系的几何法与解析法在应用上各有什么特点?2.解平衡问题时的一般步骤与注意事项?3.解物系问题时的注意事项?4.P33思考题。
5.力偶的特点与等效条件是什么?6.解力偶系平衡问题时的一般步骤与注意事项?习题:P36-40:2-1;2-3; 2-9; 2--12 (a) (c);2—14;2—17第三章平面任意力系思考题:1.力线平移定理的含义?2.用二矩式、三矩式求解问题时,附加什么条件才能保证物系平衡?3.求解平衡问题时,有哪些技巧可以使计算方便?4.P61思考题。
5.物系问题的解题思路?怎样选取研究对象?怎样列方程?6.销钉既受力又连接两个以上物体时的受力分析需掌握什么原则?7.怎样能做到一个方程求解一个未知数?8.节点法的本质是什么?9.截面法的本质是什么?10.怎样判断零杆?习题:P63-71:3-1;3-4;3-6;3-12(a);3-13;3-22;3-34第四章空间力系思考题:1.空间力系化简结果与平面力系化简结果的关系?2.什么力系有六个平衡方程?什么力系有三个平衡方程?什么力系有两个平衡方程?什么力系只有一个平衡方程?3.计算重心的常用方法。
第六章1 载流子的产生与复合

原子也在不停地进行热振动,这样,对晶体中运动着的电 子产生了散射作用,这种散射的频率非常频繁,大约每秒 发生1012 ~1013 次。
频繁的散射,使得电子在晶体能带的各个电子态之间 不停地跃迁。但是大量的电子在宏观上却表现出了一定的 规律性,费米一狄拉克分布描述了这种规律性。
半导体物理学
第6章
非平衡过剩载流子
非平衡状态,载流子的产生与复合 连续性方程 双极输运 准费米能级 *过剩载流子的寿命 *表面效应
半导体物理学
本章讨论非平衡状态下,半导体中载流子的产生、 复合以及它们的运动规律。
许多重要的半导体效应都是和非平衡态密切相关 的,许多器件就是利用非平衡载流子工作的,
t=0 τ
半导体物理学
过剩少数载流子的复合率
R
' n
d
n
dt
t
r
p0
nt
n t
n0
由于电子和空穴为成对复合,因而
R
' n
Rp'
n t
n0
对于n型半导体的小注入条件
注意过剩少数载 流子寿命和多数 载流子浓度有关
过剩少数载流子空穴的寿命为 p0 rn0 1
Eg
hv
Ev
δp
一块载流子均匀分布的半导体:
在t < 0时,处于热平衡态; 在t = 0时,开始进行光照,假设光子被均匀地吸收,并在半
导体建立起非平衡载流子(过剩电子和过剩空穴),经历一段 时间后达到稳态;
在t = t1时,光照撤除, 在t > t1时,经历一段时间后,样品重新回到热平衡态。
理论力学点的合成运动

例 8-4 曲柄OA以匀角速度 w绕O轴转动,其上
套有小环 M,而小环 M又在固定的大圆环上运动,大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时,小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解:(1)选择动点及 动系: 小环M为动点,动系固连在 OA上。
(2)分析三种运动:绝 对运动为圆周运动,相对运 动为沿OA的直线运动,牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中,设 Oxyz为定系,Oxyz为动系且作平
动,M为动点。动点M在动系中的坐标为 x、y 、z, 动系单位矢量为 i、 j、k。动系平动,i、j、k 的
Oxyz 作某种运动,在瞬时t,动系连同相对轨迹AB在
定系中的I位置,动点则在曲线 AB
上的 M 点。经过时间间 隔 t ,动系运动到定系 中的II位置,动点运动到
点 M。 如果在动系上观
察点M 的运动,则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶,雨滴 以速度 v2 铅直下落,试求雨滴相对于汽车的速度。
v1
解: 因为雨滴相对运动的汽车有运动,所以本题 为点的合成运动问题,可应用点的速度合成定理求解。
点的合成运动

r '
M1(m1)
§8−2 点的速度合成定理
va vr ve
绝对速度 相对速度
M '(m')
牵连速度
z' x'
M2(m2)
速度合成定理 动点的绝对速度等于其相 对速度与牵连速度的矢量 和。
y'
va
r
vr
M(m)
ve r 1
r '
M1(m1)
§8−2 点的速度合成定理
va vr ve
§8−1 合成运动基本概念 合成 本概
动点-摇杆上 A'点。 动系-固连于
'
曲柄OA。
§8−1 合成 合成运动基本概念 本概 练习题 4
动点-滑块 动点 滑块 A 。 动系-固连于 T形槽杆BAC。
§8−1 合成运动基本概念 合成 本概
动点- T形槽 杆上 A'点。 动系-固连于 曲柄OA。
§8−1 合成运动基本概念 合成 本概
试比较其共同点
§8−1 合成运动基本概念 合成 本概
试比较其共同点
§8−1 合成 合成运动基本概念 本概 4. 相对运动 相对运动方程 r r (t )
x x(t )
y y (t )
z z (t )
s s(t )
M
§8−2 点的速度合成定理
y'
解: (1) 运动分析 动点-滑块 M 。
M
动系- Ax'y'固连于摇杆 AB。 定系-固连于机座。 绝对运动-以O为圆心的圆周运动。
x'
相对运动-沿AB的直线运动。 牵连运动-摇杆绕A轴的摆动。
§8−2 点的速度合成定理
点的合成运动

点的合成运动
在此之前,我们研究点的运动时,都是相对于某 一个参考系(定系)而言。但在有些问题中,往往需 要同时在两个不同的参考系中来描述同一点的运动, 而其中一个参考系相对于另一参考系也在运动。
为此,引入动点,动系,定系。并研究同一动点 相对 于两个不同参考系的运动之间的关系。
2013年8月6日
计算有何影响?
2013年8月6日
理论力学CAI
20
选择方法一
动系
动点
2013年8月6日
理论力学CAI
21
选择方法二
动系
动点
2013年8月6日
理论力学CAI
22
动点、动系和定系的选择原则
1. 动点是个确定的点。
2. 动点与动系必须分别选在两个不同的物体上,动点
与动系间有相对运动。
3. 动点相对动系的相对运动轨迹易于直观判断。
例题
已知:AB匀角速度转动。 求:M在导槽EF及BC中运动的速度与加速度。
E
B
C M
A
l F D
2013年8月6日
理论力学CAI
35
y
vB
B
ve
M
E
vM
C
速度分析:
x 动点—M点 动系—BC杆
A
vr
D
l
F
ve = vB = l
v M = ve v r
y : vM = ve sin = l sin x : 0 = vr ve cos
相对轨迹,相对速度vr,相对加速度ar。
2013年8月6日 理论力学CAI
7
牵连运动(entangled motion) :
点的速度合成定理

va v r y
ve *
x
x
va
ve
tan30 2 3e
3
vr
2va
4 3e
3
vABva
2 3e
3
■ 点的速度合成定理 ★ 应用举例
1、选择动点、动系、定系
要选择合适的动点、动系。
解 2、运动分析
题
绝对运动与相对运动都是指点的运动,它可能作
步
直线运动或曲线运动。 牵连运动则是指参考体的运动即刚体的运动,它
O x
牵连点:M′(脚牵印连)点(:甲?板上)
va vr ve 三者关系?
★ 速度合成定理
z y
z o
x
刚性金属丝
y
O
小环
x
动点:小环(沿金属丝滑动)
定系( oxy)z :固定于地面
动系( oxyz ):固连于刚性金属丝
★ 速度合成定理
☆
z
zz
动 系 的
o z y x o x y o
oy
x
运
骤 可能作平动、转动或其它较复杂的运动。
3 、速度分析及其求解
牵连速度:某瞬时动系上与动点相重合的那一点
(称为牵连点)相对于定系的速度;
由 va vrve 作平行四边形,其对角线为v a ;
va vr ve 满足“6-4=2”方可求两个未知量。
■ 点的速度合成定理 ★ 讨论与思考
例 1中
动点:滑块A 动系:固连于O1B杆 绝对运动:绕O点的圆周运动 相对运动:沿滑杆的直线运动
牵连运动:绕O1轴的定轴转动
y
B
x
●A
O1
动点: O1B杆上的A点 动系:固连于OA杆
《理论力学》(范钦珊)习题解答第2篇第46章.doc

(b)第2篇 工程运动学基础第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环 A的运动规律。
解:Rv a a 2ns in ==θ,θs in 2R v a =θθt an co s d d 2tR v a tv a ===,⎰⎰=t v v t R v v 02d t an 1d 0θ t v R R v t s v 00t an t an d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0t an t an ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324t t y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2ar cco s 213ar cs i n y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π== t,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮A习题4-1图习题4-2图习题4-3图e e -t (c)e e -t υ (b)R t R +υ (a)习题4-6图以匀角速度ω转动,如图所示。
刚体的平面运动动力学课后答案

其中: 是从速度瞬心 引向M点的矢径, 为平面图形的角速度矢量。
4、平面图形上各点的加速度
基点法公式:
(7-9)
其中: 。基点法公式建立了平面图形上任意两点的加速度与平面图形的角速度和角加速度间的关系。只要平面图形的角速度和角加速度不同时为零,则其上必存在唯一的一点,其加速度在该瞬时为零,该点称为平面图形的加速度瞬心,用 表示。
(b)
再根据对固定点的冲量矩定理:
系统对固定点A(与铰链A重合且相对地面不动的点)的动量矩为滑块对A点的动量矩和AB杆对A点的动量矩,由于滑块的
动量过A点,因此滑块对A点无动量矩,AB杆对A点的动量矩(也是系统对A点的动量矩)为:
将其代入冲量矩定理有:
(c)
由(a,b,c)三式求解可得:
(滑块的真实方向与图示相反)
其中:aK表示科氏加速度;牵连加速度就是AB杆上C点的加速度,即:
将上述公式在垂直于AB杆的轴上投影有:
科氏加速度 ,由上式可求得:
3-14:取圆盘中心 为动点,半圆盘为动系,动点的绝对运动为直线运动;相对运动为圆周运动;牵连运动为直线平移。
由速度合成定理有:
速度图如图A所示。由于动系平移,所以 ,
根据点的复合运动速度合成定理有:
其中: ,根据几何关系可求得:
AB杆作平面运动,其A点加速度为零,
B点加速度铅垂,由加速度基点法公式可知
由该式可求得
由于A点的加速度为零,AB杆上各点加速度的分布如同定轴转动的加速度分布,AB杆中点的加速度为:
再取AB杆为动系,套筒C为动点,
根据复合运动加速度合成定理有:
3-25设板和圆盘中心O的加速度分别为
,圆盘的角加速度为 ,圆盘上与板
点的复合运动1

42
点的速度合成定理
动点在某瞬时的绝对速度等于它在该瞬时的牵连速 度与相对速度的矢量和。
v a ve v r
*矢量方程式,在平面问题中相当两个标量方程式; *建立了任一瞬时三个运动之间的速度关系,不能求
导,只能求得特殊位置(某瞬时)的速度.一定是以绝对
速度为对角线组成平行四边形. *牵连运动形式不限.
动等。
在复合运动的研究中,参考系(动系)的选择是问题的关
键。恰当的选择参考系,能把复杂的运动分解为若干种简
单运动,或由若干种简单运动组成各种不同的复杂运动。
15
5 动点和动系的选择
基本原则:
1.动点对动系要有相对运动。
2.动点的相对运动轨迹要明确、容易确定。 具体选择方法: 1.选择持续接触点为动点。
7
3 三种速度、加速度
*绝对速度、加速度:va , aa
动点相对定系的速度、加速度;
*相对速度、加速度:vr , ar
动点相对动系的速度、加速度; 动点的牵连点:某瞬时动系上与动点重合的点。
*牵连速度、加速度:ve , ae
牵连点 相对定系的速度、加速度。
8
4.牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
39
三种运动轨迹
设动点M在动系中沿某一曲线 AB如下
三种运动轨迹
40
刚体在定系中运动,动系固结在刚体上。
M1点——t 瞬时动系上与动点重合的点。 z' x' z M,M1 y x O
41
绝对运动轨迹
M' 相对运动轨迹
y'
r a r r M'1
r e
理论力学:第6章 点的合成运动

·1·第6章 点的合成运动6.1 主要内容6.1.1 点的绝对运动、相对运动和牵连运动1.定系和动系若存在两个有相对运动的坐标系,则可指定其中一个为定系,另一个即为动系。
但工程上一般以固定在地面上的坐标系为定系,相对于定系运动着的坐标系称为动系。
2.动点和牵连点动点为研究的对象,牵连点是动点在动系上的重合点,随动点的相对运动而变,是动系上的点,不同瞬时,有不同的牵连点。
3.三种运动的关系动点相对于定系的运动定义为绝对运动;动点相对于动系的运动定义为相对运动;动系相对于定系的运动定义为牵连运动。
本章的主要任务就是建立这三者之间的定量关系,从而用来解决工程实际某些运动分析问题。
6.1.2 点的速度合成定理动点的绝对速度等于它的牵连速度与相对速度的矢量和。
这就是点的速度合成定理。
a e r =+v v v6.1.3 牵连运动为平移时,点的加速度合成定理当牵连运动为平移时,动点的绝对加速度等于牵连加速度与相对加速度的矢量和。
a e r =+a a a6.1.4 牵连运动为转动时,点的加速度合成定理当牵连运动为转动时,动点的绝对加速度等于牵连加速度、相对加速度与科氏加速度的矢量和,这就是牵连运动为转动时点的加速度合成定理。
a e r C =++a a a a其中r C v a ⨯=ω2。
当取平动动系时0=e ω;0=C a 。
6.2 基本要求1.掌握运动合成与分解的基本概念和方法,准确理解本章阐述的若干概念。
2.明确动点与动系的选择原则,能在具体问题中恰当地选择动点与动系,并正确地分析三种运动。
3.熟练掌握点的速度合成定理和牵连运动为平动时的加速度合成定理及其应用。
4.掌握科氏加速度的概念和计算,准确应用牵连运动为转动时的加速度合成定理及其应用。
6.3 重点讨论应用点的合成运动理论解决实际问题时,其关键是正确地选择动点和动系。
选择原则因具体情况不同而略有区别。
常见的问题有三种题型。
1.两个独立运动的物体,研究两者的相对运动。
理论力学习题集
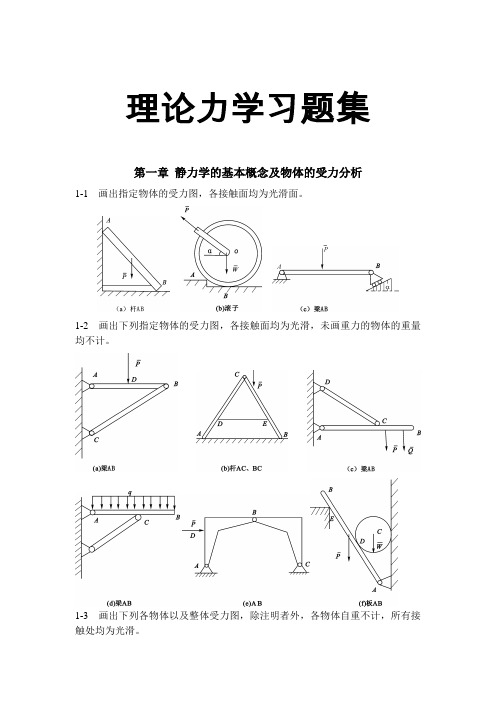
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
第6章 平面机构的运动简图及自由度

解:活塞泵由曲柄1、连杆2、齿扇3、齿条活塞4 和机架5共五个构件组成。曲柄1是原动件,2、3、 4为从动件。当原动件1回转时,活塞在汽缸中作 往复运动。 各构件之间的连接如下:构件1和5、2和1、 3和2、3和5之间为相对转动、分别构成回转副A、 B、C、D。构件3的轮齿与构件4的齿构成平面高 副E。构件4与构件5之间为相对移动,构成移动 副F。 选取适当比例尺,按图a尺寸,用构件和运动 副的规定符号画出机构运动简图,如图6-6b所示。 最后,将图中的机架画上斜线,在原动件上标出 指示运动方向的箭头。
(a)2个自由度机构
(b)1个自由度机构
(c)0个自由度机构
图6-11 不同自由度机构的运动
综上所述,机构具有确定运动的条件是: 机构自由度必须大于零、且其原动件数与机 构自由度必须相等。
6.3.3 计算平面机构自由度时应注意的问题
1.复合铰链 两个以上构件在同一处以转动副相连接, 所构成的运动副称为复合铰链,如图6-12(a), 为三个构件在A处构成复合铰链。由其侧视图612(b)可知,此三构件共组成两个共轴线的 转动副。因此,由K个构件组成复合铰链时, 则组成 (K-1)个共轴线的转动副,即此处的转动 副数为(K-1)个。
表6-1 部分常用机构运动简图符号(GB4460-84)
名称 轴、杆、 连杆等 构件 符号 名称 符号
轴、杆 的固定 支座 (机架)
同一构 件 一个构 件上有 两个转 动副
棘轮 机构
链传 动
一个运 动构件 一个固 定构件 用移动 副相联
外啮 合圆 柱齿 轮传 动
一个运 动构件 与一个 固定构 件用转 动副相 联
P 这样在机构中,n 2 ,Pl 2 ,h 1 ,其自由度为
第六章+运动镜头

第三节 摇镜头
摇镜头,机位不动而通过转动摄像机镜 头光轴(拍摄方向角度)的拍摄方法。 摇镜头:水平摇“横摇”、垂直摇“竖 摇”等 摇镜头以不同的速度来看,有慢摇、快 摇、急摇(甩)等, “摇”镜头由起幅、运动“摇”,落幅 组成。
运动镜头只有中间部分在运动,拍摄时 应注意镜头运动的速度,快慢要适当,尤 其要注意保持速度均匀一致。
镜头在运动,实际上是反映摄像师的思 想在活动:你在想什么,你想让观众看什 么,你想对他们说些什么等等。
第一节
拉镜头
“拉”镜头,通常是指机位不动,镜头光轴 (拍摄方向角度)也不变,通过改变摄像机镜头 的焦距而得到画面景别由小到大,开成景物由近 变远的效果。 /xuyan/show.asp?id=241 /v_show/id_XOTY1MDYw.html /v_show/id_XOTY1MDY0.html “拉”镜头由起幅、运动(拉)、落幅三部分组 成。
作业
• 欣赏影片
第四节 “移”镜头
• “移”镜头是指摄像机作无轴心运动进行拍 摄的方法,一边移动机位一边拍摄,以此 法拍摄的画面能产生特别的空间立体效果。 “移”镜头可分为平移,升降是由上而 下的移动拍摄;进退可以从左而右;升降 是由下而上的移动,拍摄;进退也可视为 “推”,“拉”的摄法。还可以斜向“移” 摄。 “移”镜头由起幅、运动(移)、落幅 组成。
一、表现特征
1.表现局部细节 “推”镜头表现为画框向前运动,画面 视点逐渐前移并靠近主体,反映出多种景 别过渡变化过程。观众在一个镜头内可以 了解到空间整体与局部的变化关系。 2.制约观众视点 “推”镜头所形成的场景空间的连续变 化,具有强烈的视点制约性。同时“推” 镜头保持了时空的统一和连贯性,使主体 与环境的联系具有真实可信性。
理论力学运动学习题及详解
y f 2 (t ) z f 3 (t )
2 2
a x x a y y a z z
2 2 2
v vx v y vz
2
a ax a y az
方向均由相应的方向余弦确定。
第2章 运动学练习
二.基本公式 自然法(轨迹已知时)
运动方程 速度
ae 5 2 0 r 4
5 2a r0 4
B
aC 0
O2
3销钉C固定在AB杆,在滑槽O2D中运动,该瞬时O1A与AB水平,O2D
铅直,且O1A=AC=CB=O2C=r,ω0=常数,求
AB、O2 D、 AB、O2 D .
D
n aCA
(2)加速度分析
AB 0
a 常量, an 0
,点做何种运动( B)。
B.匀变速曲线运动 D.匀变速直线运动
(3)已知点的运动方程为 x 2t 2 4, y 3t 2 3 ,其轨迹方程为(
B)
A.3x 4 y 36 0, C.2 x 2 y 24 0,
第2章 运动学练习
B.3x 2 y 18 0 D.2 x 4 y 36 0
1.选择题:
【练习题】
(4). 如图所示平面机构中,O1A=O2B= r, O1O2 =AB, O1A以匀角速度绕垂直于图 面的O1轴转动,图示瞬时,C点的速度为:( D )
A.
B. C.
Vc 0
Vc r a
2 2
水平向右
O1 A
O2
Vc r0 D. Vc r0
铅直向上 水平向右
2.刚体运动学
基本运动 平面运动
1 关于点的合成运动中动点的选取

高等理科教育关于点的合成运动中动点的选取关于点的合成运动中动点的选取+张东峰陈晓峰(宁夏大学机械工程学院宁夏饭川750021)摘要理论力学中“点的合成运动”一幸占有非常重要的地位,其中关于动点的合理选取更是直接关系到点的速度和加速度的正确求解.文章提出在解决两个物体的接触点不断变化的这一类题目时,动点应选择其相对运动明晰可辨的点作为研究对象。
从而得出正确的速度和加速度。
关键词动点相对运动速度加速度中固分类号G642.4文献标识码A理论力学中“点的合成运动”是运动学部分非常重要的一个内容,它既是进行点的运动分析的一种基本方法,又为学习“刚体的平面运动”作必要的理论准备。
用点的合成运动理论分析点的运动时,当选定了动点、动参考系和定参考系之后,绝对运动、相对运动以及牵连运动即可随之确定.在这三项当中,动点的选取似乎比较简单,在文献中也没有就这个问题作专门的论述,该文献所列例题中的动点的选取或比较直观,或已明确给出,没有更深入的讲解.分析文献中这方面的例题,如图1和图2:c匿田1田2在图1中,OA为曲柄,B为水平板,c为滑杆.选取曲柄OA上的^点作为动点,将动系固定在滑杆C上,则元论曲柄转到任一位置,动点A始终是曲柄的一个端点,而且保持与水平板接触,相对轨迹为水平线.图z中的动点仍可选为曲柄端点A,动系为摇杆O,B,则相对运动为沿o,B方向的直线运动.类似这样的例子比较多,但是对于下面图3所示的情况,又如何选取动点呢?请看下面一例:图3示偏心轮摇杆机构中,摇杆0一^借助弹簧压在半径为尺的偏心轮c上.偏心轮c绕轴0往’嚣薯嚣羿2张00求5--峰06(--196188一)男.陕西洛南人.讲师,主要从事机械设计研究.一87—高等理科教育2004年第2期(总第54期)复摆动,从而带动摇杆绕轴o。
摆动.设OC上00。
时,轮c的角速度为u,角加速度为零,0—60。
.求此时摇杆0。
A的角速度wl和角加速度“1。
这是文献中的一道习题,没有类似的例题可供参考.如果动点选取不当.则无法得出正确答案.现设摇杆01A与偏心轮c的接触点为M,可以看出,随着偏心轮c的运动,接触点M是不断变化的,依次为偏心轮圆周上的各点.如果不加认真分析,将此瞬时(口=60。
机械原理各章问答答案

机械原理问答题1。
什么是机构、机器和机械?答:机构:在运动链中,其中一个件为固定件(机架),一个或几个构件为原动件,其余构件具有确定的相对运动的运动链称为机构。
机器:能代替或减轻人类的体力劳动或转化机械能的机构。
机械:机器和机构的总称。
2.机器有什么特征?答:⑴经过人们精心设计的实物组合体。
⑵各部分之间具有确定的相对运动。
⑶能代替或减轻人的体力劳动,转换机械能.3.机构有什么特征?答:⑴经过人们精心设计的实物组合体。
⑵各部分之间具有确定的相对运动。
4.什么是构件和零件?答:构件:是运动的单元,它可以是一个零件也可以是几个零件的刚性组合。
零件:是制造的单元,加工制造不可再分的个体。
1.什么是平面机构?答:组成机构的所有构件都在同一平面或相互平行的平面上运动。
2。
什么是运动副?平面运动副分几类,各类都有哪些运动副?其约束等于几个?答:运动副:两个构件直接接触而又能产生一定相对运动的联接叫运动副.平面运动副分两类:(1)平面低副(面接触)包括:转动副、移动副,其约束为 2.(2)平面高副(点、线接触)包括:滚子、凸轮、齿轮副等,约束为 1.3。
什么是运动链,分几种?答:若干个构件用运动副联接组成的系统。
分开式链和闭式链。
4。
什么是机架、原动件和从动件?答:机架:支承活动构件运动的固定构件。
原动件:运动规律给定的构件.从动件:随原动件运动,并且具有确定运动的构件。
5.机构确定运动的条件是什么?什么是机构自由度?答:条件:原动件的数目等于机构的自由度数。
机构自由度:机构具有确定运动所需要的独立运动参数。
6 。
平面机构自由度的计算式是怎样表达的?其中符号代表什么?答:F =3n— 2P L—P H其中:n--—-活动构件的数目,P L-—-—低副的数目,p H—-——高副的数目.7.在应用平面机构自由度计算公式时应注意些什么?答:应注意复合铰链、局部自由度、虚约束。
8.什么是复合铰链、局部自由度和虚约束,在计算机构自由度时应如何处理?答:复合铰链:多个构件在同一轴线上组成转动副,计算时,转动副数目为m —1个局部自由度:与整个机构运动无关的自由度,计算时将滚子与其组成转动副的构件假想的焊在一起,预先排除局都自由度。
理论力学第2版范钦珊陈建平主编第6章点的复合运动

例6-7
已知:如图所示平面机构中,曲柄OA=r,以匀角 速度ωO 转动。套筒A沿BC杆滑动。BC=DE,且 BD=CE=l。
求:图示位置时,杆BD的角速度和角加速度。
解: 1.动点:滑块A 动系:BC杆
绝对运动:圆周运动(O点) 相对运动:直线运动(BC) 牵连运动:平移
2.速度
vra vre vrr
点P离圆心O为R时:
r Va
rr V, R)
点评:在不同时刻,点与管重合的点不同,故牵连点的速度 两个时刻是不同的。其中大小的改变是因为相对运动的存 在;方向改变是由于牵连转动引起的。
例6-2
在凸轮机构中已知凸轮以速度 v 直线平动,半径为 R 。
(aa ) (ar ) (ae ) (ac )
坐标系的建立是灵活的,最终建立的方位,依所求问题而定。
例6-6 已知:如图所示平面机构中,铰接在曲柄端A的滑块,可 在丁字形杆的铅直槽DE内滑动。设曲柄以角速度ω作匀速 转动, OA 。r
求:丁字形杆的加速度 aDE 。
D
A Oω φ
va vr ve
大小 ? ? ? 方向 ? ? ?
2)若已知6个量中的4个量,则另外2个量可求出。
3)某些已知量需要分析得出。由于只有3个矢量,可通过矢量 三角形求未知量。
例6-1
已知:直管绕轴O等角速 转动,小球P以常速率u沿 管运动。 求:点P离圆心O为R/3和R时,相对于地面的速度。
2、应尽可能使相对运动轨迹简单或直观。
3、常见情况:
①、一个单独的点在另一个物体上运动,则选该点为动点, 另一物体为载体。
②、两个运动的物体A、B始终有一个接触点P, P与一物体的相对位置始终不变,该物体上的P点为动点; P与另一物体的相对位置随时在变,该物体为载体。
点的复合运动

学习方法 第2章
刚 体 运 动 与 复 合 运 动
要不要预习?
要训练 敏捷的思维能力
这也是学术交流的基本功
2-4 点的复合运动 第2章
刚 体 运 动 与 复 合 运 动
工程实例 复合运动基本定义 三种运动中运动方程之间的关系 矢量的绝对导数和相对导数 速度合成公式 加速度合成公式
r
a ae ar ac
牵连加速度的物理意义 第2章
ae a0 r ( r )
牵连加速度的物理意义? 牵连加速度ve是动参考系(刚体)上与点P 重合的点(牵连点)的瞬时加速度。 牵连加速度ve也可以看成是在该瞬时将P点 固结在动参考刚体上,跟随动参考刚体一 起运动时所具有的加速度,即受动参考刚 体的拖带或牵连而产生的加速度。
y
o
M
t
x
1 x cos t b sin 2t 2 1 y sin t b(1 cos 2t ) 2
b 2 b 2 x (y ) ( ) 2 2
2
所刻轨迹为一圆。
返回
矢量的绝对导数和相对导数 第2章
动系Oxy相对定系OXY作定轴转动
Y y O 时刻t R x R* R R O R — 绝对增量 X Y 时刻t+t R* O y
牵连运动 — 动参考系对于定参考系的运动
绝对运动和相对运动是点的运动,而牵连运 动是刚体的运动(可以是五种运动之一)
动系和定系的选取是人为的,“动” 和“ 定” 是相对的
复合运动基本定义 第2章
定参考系?
刚 体 运 动 与 复 合 运 动
动参考系?
绝对运动? 相对运动? 牵连运动?
