最新三校生高考数学模拟试卷
三校生数学试题及答案

三校生数学试题及答案一、选择题(每题3分,共15分)1. 下列哪个选项不是实数?A. √2B. πC. 0.33333…D. i答案:D2. 一个数的相反数是-5,那么这个数是:A. 5B. -5C. 0D. 10答案:A3. 函数y=2x+3的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:C4. 以下哪个不等式是正确的?A. 3 > 2B. 4 < 3C. 5 ≥ 5D. 6 ≤ 7答案:C5. 一个等差数列的首项是2,公差是3,那么它的第五项是:A. 14B. 17C. 20D. 23答案:A二、填空题(每题2分,共10分)6. 一个圆的半径是5厘米,那么它的周长是________厘米。
答案:31.47. 如果一个三角形的两边长分别是3和4,那么第三边的取值范围是________。
答案:1 < 第三边 < 78. 一个数的平方是25,那么这个数是________。
答案:±59. 函数y=x^2-4x+3的最小值是________。
答案:010. 一个等比数列的首项是2,公比是2,那么它的第四项是________。
答案:16三、解答题(每题10分,共20分)11. 已知函数f(x)=x^2-6x+8,求函数的顶点坐标。
答案:顶点坐标为(3, -1)。
12. 已知等差数列{an}的前三项分别为2,5,8,求该数列的通项公式。
答案:通项公式为an = 3n - 1。
结束语:本试题涵盖了实数、相反数、函数图象、不等式、等差数列等基础数学知识点,旨在考察学生的基础知识掌握情况和计算能力。
希望同学们通过本次练习能够查漏补缺,提高数学解题技巧。
中职三校生高考数学试卷

一、选择题(每题5分,共50分)1. 下列各数中,无理数是()A. √4B. √9C. √16D. √252. 已知等差数列{an}的首项a1=3,公差d=2,则第10项an=()A. 21B. 22C. 23D. 243. 函数f(x) = x^2 - 4x + 4的图像是()A. 抛物线开口向上B. 抛物线开口向下C. 直线D. 没有图像4. 在三角形ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,则角C的大小为()A. 45°B. 60°C. 90°D. 120°5. 下列方程中,无解的是()A. x + 2 = 0B. x^2 - 4 = 0C. x^2 + 4 = 0D. x^2 - 3x + 2 = 06. 已知函数f(x) = 2x + 1,则f(-1)的值为()A. -1B. 0C. 1D. 27. 在直角坐标系中,点P(2,3)关于y轴的对称点为()A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,3)8. 已知数列{an}的前n项和为Sn,若a1=2,a2=4,且an+1 = 2an,则S5的值为()A. 62B. 64C. 66D. 689. 下列不等式中,正确的是()A. 2x + 3 > 5B. 2x - 3 < 5C. 2x + 3 < 5D. 2x - 3 > 510. 已知等比数列{an}的首项a1=1,公比q=2,则第n项an=()A. 2nB. 2n-1C. 2n+1D. 2n-2二、填空题(每题5分,共50分)11. 若等差数列{an}的首项a1=1,公差d=2,则第n项an=________。
12. 函数f(x) = x^2 - 4x + 4的顶点坐标为________。
13. 在三角形ABC中,若a=6,b=8,c=10,则三角形ABC的面积S=________。
人教版三校生高考数学试卷

一、选择题(本大题共20小题,每小题3分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 若集合A={x|-1≤x≤2},集合B={x|x≤-1或x≥2},则A∩B=()A. {x|-1≤x≤2}B. {x|x≤-1或x≥2}C. {x|x=-1或x=2}D. 空集2. 函数f(x)=2x+1在定义域内的单调性为()A. 单调递增B. 单调递减C. 既有单调递增又有单调递减D. 无单调性3. 若log2x+log2(x+1)=2,则x的值为()A. 1B. 2C. 3D. 44. 已知等差数列{an}中,a1=3,d=2,则a10=()A. 21B. 22C. 23D. 245. 下列命题中,正确的是()A. 如果a>b,则a^2>b^2B. 如果a>b,则a-c>b-cC. 如果a>b,则ac>bcD. 如果a>b,则a+c>b+c6. 已知圆的方程为x^2+y^2-2x-4y+5=0,则圆心坐标为()A. (1,2)B. (2,1)C. (1,-2)D. (-2,1)7. 已知向量a=(2,3),向量b=(4,-1),则a·b=()A. 11B. 10C. 9D. 88. 若sinA=1/2,cosB=-1/2,则sin(A+B)=()A. √3/2B. -√3/2C. 1/2D. -1/29. 已知等比数列{an}中,a1=2,q=3,则a5=()A. 54B. 162C. 486D. 145810. 下列函数中,有最大值的是()A. f(x)=x^2B. f(x)=x^3C. f(x)=x^4D. f(x)=x^511. 已知函数f(x)=ax^2+bx+c的图象开口向上,且对称轴为x=1,则a、b、c的关系为()A. a>0,b=0,c=0B. a>0,b=0,c≠0C. a>0,b≠0,c=0D. a>0,b≠0,c≠012. 已知等差数列{an}中,a1=5,d=-3,则an≤0的项数为()A. 3B. 4C. 5D. 613. 下列命题中,正确的是()A. 如果a>b,则a-c>b-cB. 如果a>b,则ac>bcC. 如果a>b,则a+c>b+cD. 如果a>b,则a^2>b^214. 已知圆的方程为x^2+y^2-4x-6y+9=0,则圆心到原点的距离为()A. 2B. 3C. 4D. 515. 已知向量a=(2,3),向量b=(4,-1),则|a-b|=()A. 5B. 6C. 7D. 816. 若sinA=√3/2,cosB=√3/2,则sin(A+B)=()A. 1B. 0C. -1D. 217. 已知等比数列{an}中,a1=3,q=1/3,则a5=()A. 1/243B. 1/81C. 1/27D. 1/918. 下列函数中,有最小值的是()A. f(x)=x^2B. f(x)=x^3C. f(x)=x^4D. f(x)=x^519. 已知函数f(x)=ax^2+bx+c的图象开口向下,且对称轴为x=2,则a、b、c的关系为()A. a<0,b=0,c=0B. a<0,b=0,c≠0C. a<0,b≠0,c=0D. a<0,b≠0,c≠020. 已知等差数列{an}中,a1=5,d=-3,则an≤0的项数为()A. 3B. 4C. 5D. 6二、填空题(本大题共10小题,每小题3分,共30分。
上海数学三校生高考模拟卷-3
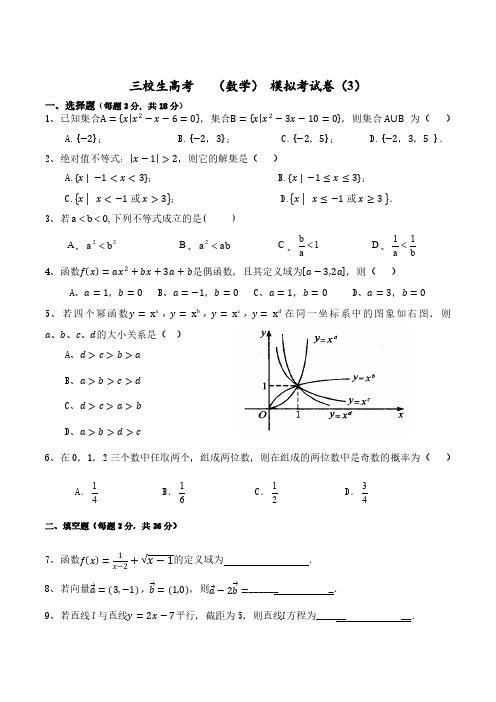
三校生高考 (数学) 模拟考试卷(3)一、选择题(每题3分, 共18分)1、已知集合A =*x |x 2−x −6=0+,集合B =*x |x 2−3x −10=0+,则集合 A⋃B 为( )A.{−2};B.{−2,3};C.{−2,5};D.{−2,3,5 }.2、绝对值不等式:|x −1|>2,则它的解集是( )A.*x | −1<x <3+;B.*x | −1≤x ≤3+;C.{x | x <−1或 x >3};D.{x | x ≤−1或 x ≥3 }.3、若,0<<b a 下列不等式成立的是( )A 、22b a <B 、ab a <2C 、1<a bD 、b a 11<4、函数f (x )=ax 2+bx +3a +b 是偶函数,且其定义域为,a −3,2a -,则( )A 、a =1,b =0B 、a =−1,b =0C 、a =1,b =0D 、a =3,b =05、若四个幂函数y =a x ,y =b x ,y =c x ,y =d x 在同一坐标系中的图象如右图,则a 、b 、c 、d 的大小关系是( )A 、d >c >b >aB 、a >b >c >dC 、d >c >a >bD 、a >b >d >c6、在0,1,2三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为() A .14 B .16 C .12 D .34二、填空题(每题3分,共36分)7、函数f (x )=1x−2+√x −1的定义域为 .8、若向量a ⃗=(3,−1),b ⃗⃗=(1,0),则a ⃗−2b ⃗⃗=______ _.9、若直线 与直线y =2x −7平行,截距为5,则直线 方程为______ __.10、不等式(x+2)(x−7)<0的解集为.11、等差数列*a+中,若a=2,a2+a=13,则数列公差d= ___ __.12、有6名男生,4名女生,现选3名参加比赛,要求至少一男一女,则有种不同选法.13、在∆ABC中,已知sinA:sinB:sinC=3:5:7,且最大边长为14,则∆ABC的面积是 .14、已知角 α 终边上一点 P(−3,4),则 sinα+cosα=。
2024届高三数学仿真模拟卷(全国卷)(理科)(全解全析)

2024年高考第三次模拟考试数学(理科)·全解全析(考试时间:120分钟试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.4.测试范围:高考全部内容5.考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{}24A x x =-≤≤,{}260B x x x =-≥,则A B = ()A .[]2,0-B .[]0,4C .[]2,6-D .[]4,6【答案】A【分析】首先解一元二次不等式求出集合B ,再根据交集的定义计算可得.【详解】由260x x -≥,即()60x x -≥,解得6x ≥或0x ≤,所以{}(][)260,06,B x x x ∞∞=-≥=-⋃+,又{}24A x x =-≤≤,所以[]2,0A B ⋂=-.故选:A 2.已知3i 2z a =(R a ∈,i 是虚数单位),若21322z =,则=a ()A .2B .1C .12D .14【答案】C【分析】运用复数代数运算及两复数相等的性质求解即可.【详解】由题意知,22231(i)i=i2422z a a=+=-+,所以23142a⎧-=⎪⎪=,解得12a=.故选:C.3.如图,已知AM是ABC的边BC上的中线,若AB a=,AC b=,则AM等于()A.()12a b-B.()12a b--C.()12a b+D.()12a b-+【答案】C【分析】根据平面向量线性运算法则计算可得.【详解】因为AM是ABC的边BC上的中线,所以12CM CB=,所以12AM AC CM AC CB=+=+()()()111222AC A CB A AC aBA b=+-=+=+.故选:C4.已知函数()()πtan0,02f x xωϕωϕ⎛⎫=+><<⎝⎭的最小正周期为2π,直线π3x=是()f x图象的一条对称轴,则()f x的单调递减区间为()A.()π5π2π,2πZ66k k k⎛⎤-+∈⎥⎝⎦B.()5π2π2π,2πZ33k k k⎛⎤--∈⎥⎝⎦C.()4ππ2π,2πZ33k k k⎛⎤--∈⎥⎝⎦D.()π2π2π,2πZ33k k k⎛⎤-+∈⎥⎝⎦【答案】B【分析】根据()()πtan0,02f x xωϕωϕ⎛⎫=+><<⎝⎭的最小正周期确定ω的值,根据函数的对称轴求出ϕ,结合正切函数的单调性,列出不等式,即可求得答案.【详解】由于()()πtan 0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的图象是将()tan y x ωϕ=+的图象在x 轴下方部分翻折到x 轴上方,且()tan y x ωϕ=+π0,02ωϕ⎛⎫><<⎪⎝⎭仅有单调递增区间,故()()tan f x x ωϕ=+和()tan y x ωϕ=+的最小正周期相同,均为2π,则π12π,2ωω=∴=,即()1tan 2f x x ϕ⎛⎫=+ ⎪⎝⎭,又直线π3x =是()f x 图象的一条对称轴,则1π1π,Z 232k k ϕ⋅+=∈,即1ππ,Z 26k k ϕ=-∈,结合π02ϕ<<,得π3ϕ=,故()1πtan 23f x x ⎛⎫=+ ⎪⎝⎭,令π1πππ,Z 223k x k k -<+≤∈,则5π2π2π2π,Z 33k x k k -<≤-∈,即()f x 的单调递减区间为()5π2π2π,2πZ 33k k k ⎛⎤--∈ ⎥⎝⎦,故选:B5.已知直线l 过点()1,1A 交圆22:4O x y +=于,C D 两点,则“CD =l 的斜率为0”的()A .必要而不充分条件B .充分必要条件C .充分而不必要条件D .即不充分也不必要条件【答案】A【分析】根据充分性、必要性的定义,结合直线的斜率是否存在进行判断即可.【详解】当直线的斜率等于0时,直线的方程为1y =,代入方程224x y +=中,得x =,显然CD =;当直线的不存在斜率时,直线的方程为1x =,代入方程224x y +=中,得y =CD =因此是必要而不充分条件,故选:A6.甲、乙、丙、丁、戊共5名同学进行唱歌比赛,决出第一名到第五名.丙和丁去询问成绩,回答者对丙说:很遗憾,你和丁都没有得到冠军,对丁说:你当然不会是最差的从这两个回答分析,5人的名次排列方式共有()A .24种B .54种C .96种D .120种【答案】B【分析】根据题意,分2种情况讨论:①丙是最后一名,则丁可以为第二、三、四名,剩下的三人安排在其他三个名次,②丙不是最后一名,丙丁需要排在第二、三、四名,剩下的三人安排在其他三个名次,由加法原理计算可得答案.【详解】根据题意,丙丁都没有得到冠军,而丁不是最后一名,分2种情况讨论:①丙是最后一名,则丁可以为第二、三、四名,即丁有3种情况,剩下的三人安排在其他三个名次,有33A 6=种情况,此时有1863=⨯种名次排列情况;②丙不是最后一名,丙丁需要排在第二、三、四名,有23A 6=种情况,剩下的三人安排在其他三个名次,有33A 6=种情况,此时有6636⨯=种名次排列情况;则一共有361854+=种不同的名次情况,故选:B .7.函数()πln sin 2x x f x x⎛⎫⋅- ⎪⎝⎭=的部分图象大致为()A .B .C.D.【答案】C【分析】先求出函数的定义域和奇偶性,排除BD ,再求出特殊点的函数值,得到答案.【详解】()πln sin ln cos 2x x x x f x x x⎛⎫⋅- ⎪⋅⎝⎭==定义域为()(),00,∞-+∞U ,且()()()ln cos ln cos x x x x f x f x x x-⋅-⋅-==-=--,所以函数()f x 是奇函数,图象关于原点中心对称,排除B 、D .又()ln 2cos 2202f ⋅=<,故A 错误.故选:C .8.祖暅是我国南北朝时期伟大的数学家.祖暅原理用现代语言可以描述为“夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的面积总相等,那么这两个几何体的体积相等”.例如,可以用祖暅原理推导半球的体积公式,如图,底面半径和高都为R 的圆柱与半径为R 的半球放置在同一底平面上,然后在圆柱内挖去一个半径为R ,高为R 的圆锥后得到一个新的几何体,用任何一个平行于底面的平面α去截这两个几何体时,所截得的截面面积总相等,由此可证明半球的体积和新几何体的体积相等.若用平行于半球底面的平面α去截半径为R 的半球,且球心到平面α,则平面α与半球底面之间的几何体的体积是()A .3π24R B .3π24R C .3π12R D .3π12R 【答案】C 【分析】分别求得面α截圆锥时所得小圆锥的体积和平面α与圆柱下底面之间的部分的体积,结合祖暅原理可求得结果.【详解】 平面α截圆柱所得截面圆半径2r =,∴平面α截圆锥时所得小圆锥的体积2311ππ3212V r R R =⋅=,又平面α与圆柱下底面之间的部分的体积为232πV R R R =根据祖暅原理可知:平面α与半球底面之间的几何体体积33321πππ21212V V V R R R =-=-=.故选:C.9.已知函数()21e 3ln ,ln ,ln ,ln 222f x x a f b f c f ⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则()A .a b c <<B .b a c <<C .c<a<bD .a c b<<【答案】B【分析】用定义证明函数()f x 的奇偶性及在()0,1上的单调性,利用函数()f x 的奇偶性及单调性,对数函数ln y x =的性质及对数运算可得结果.【详解】因为函数()f x 的定义域为{}0x x ≠,又()()ln ln f x x x f x -=-==,所以()f x 为偶函数,当01x <<时,任取12x x >,()()12121221ln ln ln ln ln ln 0f x f x x x x x x x -=-=-=-<,即()()12f x f x <,所以()f x 在()0,1上为减函数,因为31ln2ln02>>>,所以()()()113ln ln2ln2ln2ln 22a f f f f f c-⎛⎫⎛⎫===-=<= ⎪ ⎪⎝⎭⎝⎭,即a c <,设3401,1x x <<<,则()4444ln ln ln f x x x x ===,()3333ln ln ln f x x x x ===-,若()()34f x f x =,则34ln ln x x -=,所以341x x =,因为2e ln 2ln212=->,所以22e 11ln e 22ln2ln 2b f f f ⎛⎫ ⎪⎛⎫⎛⎫=== ⎪ ⎪⎪-⎝⎭⎝⎭ ⎪ ⎪⎝⎭,又()21ln21ln202ln22ln2--=>--,即11ln202ln2>>>-,所以()1ln22ln2f f ⎛⎫< ⎪-⎝⎭,即b a <,故选:B.10.已知数列{}n a 满足1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时当为奇数时,若81a=,1a 的所有可能取值构成集合M ,则M 中的元素的个数是()A .7个B .6个C .5个D .4个【答案】B 【分析】由81a=,利用递推关系,分类讨论逆推出1a 的不同取值,进而可得答案.【详解】若81a =,又1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时当为奇数时,根据上述运算法进行逆推,可得72a =,64a =,所以58a =或51a =;若58a =,则4316,32a a ==或35a =;当332a =时,2164,128a a ==或121a =;若35a =时,2110,20a a ==或13a =;当51a =,则4322,4,8a a a ===或21a =;当28a =时,116a =;当21a =时,12a =,故81a=时,1a 的所有可能的取值集合{}2,3,16,20,21,128M =即集合M 中含有6个元素.故选:B11.如图,已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为1(,0)F c -,2(,0)F c ,点A 在C 上,点B 在y 轴上,A ,2F ,B 三点共线,若直线1BF1AF的斜率为C 的离心率是()AB .32CD .3【答案】B【分析】根据斜率及双曲线的对称性得12BF F △为等边三角形,再根据同角间关系求解三角函数值,进而用正弦定理求出121410,33AF c AF c ==,由双曲线定义可得423c a =,从而得到离心率.【详解】由题意,直线1BF12π3BF F ∴∠=,又12BF BF =,所以12BF F △为等边三角形,故12122BF BF F F c ===,2112π2π,33BF F F F A ∠=∠=,在12AF F △中,21tan 0F F A ∠>,则21F F A ∠为锐角,则212111sin 14F F A F F A ∠=∠=,212πsin sin 3A F F A ⎛⎫=+∠= ⎪⎝⎭由正弦定理,12121221sin sin sin F F AF AF AF F AF F A==∠∠,=∴121410,33AF c AF c ==,由122AF AF a -=,得423c a =,32c e a ∴==.故答案选:B .12.已知()f x ,()g x 都是定义在R 上的函数,对任意x ,y 满足()()()()()f x y f x g y g x f y -=-,且()()210f f -=≠,则下列说法正确的是()A .()01f =B .函数()21g x +的图象关于点()1,0对称C .()()110g g +-=D .若()11f =,则()202311n f n ==∑【答案】D【分析】利用赋值法结合题目给定的条件可判断AC ,取()()2π2πsin,cos 33f x xg x x ==可判断B ,对于D ,通过观察选项可以推断()f x 很可能是周期函数,结合()()()(),f x g y g x f y 的特殊性及一些已经证明的结论,想到令1y =-和1y =时可构建出两个式子,两式相加即可得出()()()11f x f x f x ++-=-,进一步得出()f x 是周期函数,从而可求()20231n f n =∑的值.【详解】解:对于A ,令0x y ==,代入已知等式得()()()()()000000f f g g f =-=,得()00f =,故A错误;对于B ,取()()2π2πsin,cos 33f x xg x x ==,满足()()()()()f x y f x g y g x f y -=-及()()210f f -=≠,因为()3cos 2π10g ==≠,所以()g x 的图象不关于点()3,0对称,所以函数()21g x +的图象不关于点()1,0对称,故B 错误;对于C ,令0y =,1x =,代入已知等式得()()()()()11010f f g g f =-,可得()()()()110100f g g f ⎡⎤-=-=⎣⎦,结合()10f ≠得()100g -=,()01g =,再令0x =,代入已知等式得()()()()()00f y f g y g f y -=-,将()00f =,()01g =代入上式,得()()f y f y -=-,所以函数()f x 为奇函数.令1x =,1y =-,代入已知等式,得()()()()()21111f f g g f =---,因为()()11f f -=-,所以()()()()2111f f g g =-+⎡⎤⎣⎦,又因为()()()221f f f =--=-,所以()()()()1111f f g g -=-+⎡⎤⎣⎦,因为()10f ≠,所以()()111g g +-=-,故C 错误;对于D ,分别令1y =-和1y =,代入已知等式,得以下两个等式:()()()()()111f x f x g g x f +=---,()()()()()111f x f x g g x f -=-,两式相加易得()()()11f x f x f x ++-=-,所以有()()()21f x f x f x ++=-+,即:()()()12f x f x f x =-+-+,有:()()()()()()11120f x f x f x f x f x f x -+=++--+-+=,即:()()12f x f x -=+,所以()f x 为周期函数,且周期为3,因为()11f =,所以()21f -=,所以()()221f f =--=-,()()300f f ==,所以()()()1230f f f ++=,所以()()()()()()()2023111232023202311n f n f f f f f f ===++++===∑ ,故D 正确.故选:D.第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分13.已知数列{}n a 的前n 项和2n S n n =+,当9n nS a +取最小值时,n =.【答案】3【分析】根据n S 求得n a ,再结合对勾函数的单调性,即可求得结果.【详解】因为2n S n n =+,则当2n ≥时,()()221112n n n a S S n n n n n -=-=+----=,又当1n =时,112a S ==,满足2n a n =,故2n a n =;则9n n S a +29191222n n n n n ++⎛⎫==++ ⎪⎝⎭,又9y x x=+在()1,3单调递减,在()3,+∞单调递增;故当3n =时,9n n+取得最小值,也即3n =时,9n n S a +取得最小值.故答案为:3.14.若函数()sin 1f x x x ωω=-在[]0,2π上恰有5个零点,且在ππ[,415-上单调递增,则正实数ω的取值范围为.【答案】9542ω≤≤【分析】根据给定条件,利用辅助角公式化简函数()f x ,再利用正弦函数的性质求解即得.【详解】依题意,函数π()2sin(13f x x ω=+-,由()0f x =,得π1sin()32x ω+=,则ππ2π36x k ω+=+或π5π2π,Z 36x k k ω+=+∈,由[0,2π]x ∈,得πππ[,2π333x ωω+∈+,由()f x 在[0,2π]上恰有5个零点,得29ππ37π2π636ω≤+<,解得935412ω≤<,由3ππ22πx ω+≤-≤,得5ππ66x ωω-≤≤,即函数()f x 在5ππ[,66ωω-上单调递增,因此5ππ[,]ππ[,]41566ωω-⊆-,即45π6πω≤--,且π6π15ω≥,解得502ω<≤,所以正实数ω的取值范围为9542ω≤≤.故答案为:9542ω≤≤15.已知52345012345(23)x a a x a x a x a x a x +=+++++,则123452345a a a a a -+-+=.(用数字作答)【答案】15【分析】根据条件,两边求导得到12342345415(23)2345x a a x a x a x a x +=++++,再取=1x -,即可求出结果.【详解】因为52345012345(23)x a a x a x a x a x a x +=+++++,两边求导可得12342345415(23)2345x a a x a x a x a x +=++++,令=1x -,得到23454115(23)2345a a a a a -=-+-+,即12345234515a a a a a -+-+=,故答案为:15.16.已知定义在R 上的函数()f x 满足()4()0f x f x '+>,且(01f =),则下列说法正确的是.①()f x 是奇函数②(0,),()0x f x ∃∈+∞>③41(1)e f >④0x ∀>时,41()e xf x <【答案】②③【分析】根据构造函数的规律由令()()4e xg x f x =,再结合奇函数的性质可得①,求导分析单调性和极值可得②③④.【详解】令()()4e x g x f x =,则()()()()()4444e e e 4x x x g x f x f x f x f x '''=+=+⎡⎤⎣⎦,若()f x 是奇函数,则()()f x f x -=-,取0x =时,即()00f =,但(01f =),故①错误;因为4e 0,(0,)x x >∈+∞恒成立,且()4()0f x f x '+>,所以()0g x '>恒成立,()g x 在(0,)+∞上为单调递增函数,所以()()()()()44110e 101e g g f f f >⇒>⇒>,故②正确;由②可知,③正确;因为()g x 在(0,)+∞上为单调递增函数,所以当0x >时有()()()()0,001g x g g f >==,所以()()441e 1e x xf x f x >⇒>,故④错误;故答案为:②③三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知()sin ,5sin 5sin m B A C =+ ,()5sin 6sin ,sin sin n B C C A =--垂直,其中A ,B ,C 为ABC 的内角.(1)求cos A 的大小;(2)若BC =ABC 的面积的最大值.【答案】(1)35;(2)4.【详解】(1)由()sin ,5sin 5sin m B A C =+ ,()5sin 6sin ,sin sin n B C C A =-- 垂直,得0m n ⋅=,...............1分即sin (5sin 6sin )(5sin 5sin )(sin sin )0B B C A C C A -++-=,整理得2226sin sin sin sin sin 5B C A B C +-=,...............2分在ABC 中,由正弦定理得22265b c a bc +-=,...............3分由余弦定理得2223cos 25b c a A bc +-==,所以cos A 的大小为35................5分(2)由(1)知,在ABC 中,3cos 5A =,则4sin 5A ==,...............6分由22265b c a bc +-=,得22266482555a b c bc bc bc bc ==+-≥-=,即10bc ≤,...................................................................................................8分当且仅当b c =时取等号,...................................................................................................9分因此ABC 的面积12sin 425ABC S bc A bc ==≤ ,..........................................................11分所以ABC 的面积的最大值是4.....................................................12分18.(12分)2016年10月“蓝瘦香菇”等网络新词突然在网络流行,某社区每月都通过问卷形式进行一次网上调查,现从社区随机抽取了60名居民进行调查.已知上网参与问卷调查次数与参与人数的频数分布如下表:参与调查问卷次数[)0,2[)2,4[)4,6[)6,8[)8,10[]10,12参与调查问卷人数814814106(1)若将参与调查问卷不少于4次的居民称为“关注流行语居民”,请你根据频数分布表,完成22⨯列联表,据此调查你是否有99%的把握认为在此社区内“关注流行语与性别有关”?男女合计关注流行语8不关注流行语合计40(2)从被调查的人中按男女比例随机抽取6人,再从选取的6人中选出3人参加政府听证会,求选出的3人为2男1女的概率.附:参考公式()()()()()22n ad bc K a b c d a c b d -=++++及附表()2P K k ≥0.1000.0500.0100.001k 2.706 3.841 6.63510.828【答案】(1)列联表见解析,有99%的把握认为在此社区内“关注流行语与性别有关”;(2)35【详解】(1)依题意,关注流行语居民人数为81410638+++=,不关注流行语居民人数为81422+=,...................................................................................................2分所以22⨯列联表如下:男女合计关注流行语30838不关注流行语101222合计4020602K 的观测值2260(3012108)7.03 6.63540203822K ⨯-⨯=≈>⨯⨯⨯,................................................................4分所以有99%的把握认为在此社区内“关注流行语与性别有关”...................5分(2)依题意,男居民选出406660⨯=(人),.......................................6分记为a b c d ,,,,女居民选出2人,记为,E F ,从6人中任选3人的样本空间{,,,,,,,,,,abc abd abE abF acd acE acF adE adF aEF Ω=,,,,,,,,,}bcd bcE bcF bdE bdF bEF cdE cdF cEF dEF ,共20个,.................................9分选出的3人为2男1女的事件{,,,,,,,,,,,}A abE abF acE acF adE adF bcE bcF bdE bdF cdE cdF =,共12个,...........11分所以选出的3人为2男1女的概率123()205P A ==......................................12分19.(12分)在几何体中,底面ABC 是边长为2的正三角形.⊥AE 平面ABC ,若,5,4,3AE CD BF AE CD BF ===∥∥.(1)求证:平面DEF ⊥平面AEFB ;(2)是否在线段AE 上存在一点P ,使得二面角P DF E --的大小为π3.若存在,求出AP 的长度,若不存在,请说明理由.【答案】(1)证明见解析(2)存在;4AP =-【详解】(1)证明:如图,设,M N 分别为,EF AB 边的中点,连接,,MN DM CN ,..1分因为⊥AE 平面,,5,4,3ABC AE CD BF AE CD BF ===∥∥,所以42AE BFMN CD +===,//MN BF ,进而MN CD ∥,即四边形CNMD 为平行四边形,可得MD CN ∥,......................................3分在底面正三角形ABC 中,N 为AB 边的中点,则CN AB ⊥,......................................4分又⊥AE 平面ABC ,且CN ⊂平面ABC ,所以AE CN ⊥.由于⋂=AE AB A ,且AE AB ⊂、平面ABFE ,所以CN ⊥平面ABFE ......................5分因为,MD CN CN ⊥∥平面ABFE ,则MD ⊥平面ABFE ,又MD ⊂平面DEF ,则平面DEF ⊥平面AEFB .......................................6分(2)如图,以点A为坐标原点,建立空间直角坐标系,则()())0,0,5,0,2,4,E D F .设点()0,0,P t,则)()()1,1,0,2,1,0,2,4DF DE DP t =--=-=--..................8分设平面PDF 的法向量为()1111,,n x y z = ,平面EDF 的法向量为()2222,,n x y z =.由题意知110,0,n DF n DP ⎧⋅=⎪⎨⋅=⎪⎩即()111110,240,y z y t z --=-+-=⎪⎩令12z =,则114,y t x =-=14,2n t ⎫=-⎪⎭ ,......................................9分220,0,n DF n DE ⎧⋅=⎪⎨⋅=⎪⎩即222220,20,y z y z --=-+=⎪⎩取22z =,则)22n = ,...............................10分由121212π1cos ,cos 32n n n n n n ⋅===,28290t t +-=,解得:4t =±-,由于点P 为线段AE 上一点,故05t ≤≤,所以4t =-,......................................11分当4t =-时,二面角P DF E --所成角为锐角,即存在点P 满足,此时4AP =.......................................12分20.(12分)已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2P ⎛⎫ ⎪⎝⎭在椭圆C 上,且PF 垂直于x 轴.(1)求椭圆C 的方程;(2)直线l 斜率存在,交椭圆C 于,A B 两点,,,A B F 三点不共线,且直线AF 和直线BF 关于PF 对称.(ⅰ)证明:直线l 过定点;(ⅱ)求ABF △面积的最大值.【答案】(1)22143x y +=(2)(ⅰ)证明见解析;(ⅱ)4【详解】(1)点31,2P ⎛⎫⎪⎝⎭在椭圆C 上,且PF 垂直于x 轴,则有()1,0F 设椭圆C 的焦距为()20c c >,则1c =,.......................................................................1分点31,2P ⎛⎫ ⎪⎝⎭代入椭圆方程,有()222219191441a b a a +=+=-,解得2a =,则222413b a c =-=-=,所以椭圆C 的方程为22143x y +=...................................................................................3分(2)(ⅰ)设直线l 的方程为y kx m =+,由22143y y k x x m =+⎧⎪⎨⎪+⎩=,消去y ,整理得()2223484120kxkmx m +++-=,因为l 交椭圆C 于,A B 两点,所以()22Δ48430k m =-+>,设()()1122,,,A x y B x y ,所以21212228412,3434km m x x x x k k -+=-=++, (5)分因为直线AF 和直线BF 关于PF 对称,所以()()()()12121212121212220111111AF BF kx x m k x x my y kx m kx m k k x x x x x x +-+-+++=+=+==------所以()()()21212224128222203434m kmkx x m k x x m k m k m k k --+-+-=⨯+-⨯-=++所以222282488860km k km k m mk m --+--=解得4m k =-................................................................................................................7分所以直线l 的方程为()44y kx k k x =-=-,所以直线l 过定点()4,0................................,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,.......8分(ⅱ)设直线l 的方程为4x ny =+,由224143x ny x y =+⎧⎪⎨+=⎪⎩,消去x ,整理得()223424360n y ny +++=,因为l 交椭圆C 于,A B 两点,所以()()()222Δ241443414440n n n =-+=->,解得24n >,........................................................................................................9分1212222436,3434n y y y y n n +=-=++,所以12y y -=所以121331822ABFS y y =⨯-=⨯⨯ .............................10分令()24,0n t t -=>则18184ABC S ==≤,当且仅当163t =时取等号,所以ABF △面积的最大值为4......................................................................12分21.(12分)已知函数()2,0eax x f x a =>.(1)当2a =时,求函数()f x 的单调区间和极值;(2)当0x >时,不等式()()2cos ln ln 4f x f x a x x ⎡⎤-≥-⎣⎦恒成立,求a 的取值范围.【答案】(1)单调递增区间为:(0,1),单调递减区间为:(,0)-∞和(1,)+∞;极大值21(1)f e =,极小值(0)0f =;(2)(]0,2e 【详解】(1)当2a =时,()22=exx f x ()()2222222e e 22(1)=e e x x xxx x x x f x ⋅-⋅⋅--'=......................................2分令()=0f x ',解得0x =或1x =,......................................3分所以()()x f x f x '、、的关系如下表:x(,0)-∞0(0,1)1(1,)+∞()f x '-+-()f x 单调递减0单调递增21e 单调递减所以函数()f x 的单调递增区间为:(0,1),单调递减区间为:(,0)-∞和(1,)+∞;......................................4分极大值21(1)f e=,极小值(0)0f =;......................................5分(2)[]222()cos ln ()ln 4cos ln 2ln 4e eaa x xx x f x f x a x x a x x ⎛⎫-≥-⇔-≥- ⎪⎝⎭ln 2e 2(ln 2)cos(ln 2)0a x x a x x a x x -⇔----≥......................................6分令()e 2cos t g t t t =--,其中ln 2a x x t -=,设l (2)n a x x F x =-,0a >2()2a a x x xF x --='=令()0F x '>,解得:02ax <<,......................................8分所以函数()F x 在0,2a ⎛⎫ ⎪⎝⎭上单调递增,在,2a ⎛⎫+∞ ⎪⎝⎭上单调递减,max ()ln 22a a F x F a a ⎛⎫==- ⎪⎝⎭,且当0x +→时,()F x →-∞,所以函数()F x 的值域为,ln 2a a a ⎛⎤-∞- ⎥⎝⎦;......................................9分又()e 2sin t g t t '=-+,设()e 2sin t h t t =-+,,ln 2a t a a ⎛⎤∈-∞- ⎥⎝⎦,则()e cos t h t t '=+,当0t ≤时,e 1,sin 1t t ≤≤,且等号不同时成立,即()0g t '<恒成立;当0t >时,e 1,cos 1t t >≥-,即()0h t '>恒成立,所以()h t 在(0,)+∞上单调递增,又(0)1g '=-,(1)e 2sin10g '=-+>,所以存在0(0,1)t ∈,使得0()0g t '=,当00t t <<时,()0g t '<,当0t t >时,()0g t '>,所以函数()g t 在0(,)t -∞上单调递减,在0(,)t +∞上单调递增,且(0)0g =......................................11分当ln 02aa a -≤即02e a <≤时,()0g t ≥恒成立,符合题意;当ln02a a a ->即2e a >时,取10min ln ,2a t a a t ⎧⎫=-⎨⎬⎩⎭,必有1()0g t <,不符合题意.综上所述:a 的取值范围为(]0,2e ......................................12分(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22.(10分)在平面直角坐标系xOy 中,曲线C 的参数方程为12cos 2sin x y αα=+⎧⎨=⎩(α为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为sin 42πρθ⎛⎫-= ⎪⎝⎭.(1)求C 的普通方程和l 的直角坐标方程;(2)设直线l 与x 轴相交于点A ,动点B 在C 上,点M 满足AM MB =,点M 的轨迹为E ,试判断曲线C 与曲线E 是否有公共点.若有公共点,求出其直角坐标;若没有公共点,请说明理由.【答案】(1)C 的普通方程为()2214x y -+=,l 直角坐标方程为30x y -+=.(2)存在,坐标为33,,4444⎛⎛--- ⎪ ⎪⎝⎭⎝⎭【详解】(1)由题设曲线C 的参数方程,消参得()2214x y -+=,............................2分由cos ,sin x y ρθρθ==,且)πsin sin cos 4ρθρθρθ⎛⎫-=-=⎪⎝⎭y =30x y -+=,......................................4分∴C 的普通方程为()2214x y -+=,l 直角坐标方程为30x y -+=...............................5分(2)当0y =时,()33,0x A =-⇒-,易知()12cos ,2sin B a a +,设(),M x y ,可得()()3,,2cos 1,2sin AM x y MB a x a y =+=-+-,......................................6分32cos 1cos 1,2sin sin x a x x a AM MB y a y y a +=-+=-⎧⎧=⇒⎨⎨=-=⎩⎩(a 是参数),消参得方程为()2211,x y ++=......................................8分且1,2,1,3E C C E C E r r r r r r ==-=+=,则圆心距离2,d ==得C E C E r r d r r -<<+,则两圆相交,故两圆存在公共点,联立方程组()()22221114x y x y ⎧++=⎪⎨-+=⎪⎩,解得34x y ⎧=-⎪⎪⎨⎪=⎪⎩或34x y ⎧=-⎪⎪⎨⎪=⎪⎩,故坐标为33,,44⎛⎛--- ⎝⎭⎝⎭......................10分选修4-5:不等式选讲23.(10分)已知()2122f x x x x =-+-+.(1)求()2f x ≥的解集;(2)记()f x 的最小值为t ,且2(0,0)3a b t a b +=>>,求证:11254a b a b ⎛⎫⎛⎫++≥ ⎪⎪⎝⎭⎝⎭.【答案】(1)113x x x ⎧⎫≤≥⎨⎬⎩⎭或(2)证明见解析【详解】(1)()2122f x x x x =-+-+,当0x <时,532x -+≥,解得0x <,......................................1分当102x ≤<时,332x -+≥,解得103x ≤≤,......................................2分当112x ≤<时,12x +≥,解得x ∈∅,......................................3分当1x ≥时,532x -≥,解得1x ≥,......................................4分综上所述,()2f x ≥的解集为13x x ⎧≤⎨⎩或}1≥x .......................................5分(3)由已知可得()5301330211<12531x x x x f x x x x x -+<⎧⎪⎪-+≤≤⎪=⎨⎪+≤⎪⎪->⎩,所以当12x =时,()f x 的最小值为32...............................................................................................6分1a b ∴+=,211,24a b a b ab +⎛⎫+=∴≤= ⎪⎝⎭,当且仅当12a b ==取等,......................................8分令t ab =,则104t <≤,211()212225224a b ab a b ab ab t a b ab ab ab t +-⎛⎫⎛⎫++=++=+-=+-≥ ⎪⎪⎝⎭⎝⎭,当且仅当14t =取等,此时12a b ==.......................................10分。
三校生高考模拟数学试卷

一、选择题(本大题共20小题,每小题5分,共100分)1. 下列函数中,在实数域内单调递增的是()A. y = -x^2 + 2xB. y = 2^xC. y = log2xD. y = √x2. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则第15项a15的值为()A. 10B. 15C. 20D. 253. 若复数z满足|z - 1| = |z + 1|,则复数z的实部是()A. 0B. 1C. -1D. 无法确定4. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减5. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极小值为()A. -1B. 0C. 1D. 26. 下列方程组中,无解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 107. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 4868. 下列函数中,在区间(0,+∞)上为减函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x9. 若复数z满足|z - 1| = |z + 1|,则复数z的虚部是()A. 0B. 1C. -1D. 无法确定10. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减11. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极大值为()A. -1B. 0C. 1D. 212. 下列方程组中,有唯一解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1013. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 48614. 下列函数中,在区间(0,+∞)上为增函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x15. 若复数z满足|z - 1| = |z + 1|,则复数z的虚部是()A. 0B. 1C. -1D. 无法确定16. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减17. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极大值为()A. -1B. 0C. 1D. 218. 下列方程组中,无解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1019. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 48620. 下列函数中,在区间(0,+∞)上为减函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x二、填空题(本大题共10小题,每小题5分,共50分)21. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则第15项a15的值为______。
今年三校生高考数学试卷

一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知函数f(x) = 2x - 3,若f(x+1) = 5,则x的值为:A. 2B. 3C. 4D. 52. 若等差数列{an}的前三项分别为2,5,8,则第10项an的值为:A. 19B. 22C. 25D. 283. 在直角坐标系中,点P(2,3)关于直线y=x的对称点为:A. (2,3)B. (3,2)C. (3,-2)D. (-2,3)4. 已知三角形ABC的边长分别为a=3,b=4,c=5,则角A的余弦值为:A. 1/2B. 1/3C. 2/3D. 3/45. 若等比数列{bn}的首项为b1=1,公比为q=2,则第n项bn的值为:A. 2^n - 1B. 2^nC. 2^n + 1D. 2^(n-1)6. 已知函数f(x) = x^2 - 4x + 4,则f(x)的对称轴为:A. x=1B. x=2C. x=3D. x=47. 若等差数列{an}的前n项和为Sn,且a1=1,d=2,则S10的值为:A. 55B. 60C. 65D. 708. 在直角坐标系中,点A(1,2),点B(-3,4)的中点坐标为:A. (-1,3)B. (1,3)C. (-2,3)D. (2,3)9. 已知函数f(x) = log2(x+1),则f(x)的定义域为:A. (-1, +∞)B. [0, +∞)C. (-∞, -1)D. (-1, 0)10. 若函数g(x) = ax^2 + bx + c的图象开口向上,且顶点坐标为(-1,3),则a、b、c的取值范围分别为:A. a>0,b>0,c>0B. a>0,b<0,c>0C. a<0,b<0,c<0D. a<0,b>0,c<0二、填空题(本大题共5小题,每小题10分,共50分。
三校生高考数学模拟试卷

数学试卷 一、 单项选择题(每小题3分,共2×12=24分)1.集合{}{}13,15A x x B x x =-<≤=<<则A B ⋃=( )A .{}15x x -<< B.{}35x x << C. {}11x x -<< D. {}13x x <≤2.不等式24210x x --+≥的解集是( )A .(,7][3,)-∞-⋃+∞B .[7,3]-C .(,3][7,)-∞-⋃+∞D .[3,7]-3.下列函数既是奇函数又是增函数的是( )A .3y x =B .1y x =C .22y x =D .13y x =- 4.已知3log 2=则x=( )A .3B .9C .27D .815.已知{}n a 是等比数列,252,6a a ==则8a =( )A . 12B .18C . 24D .366.已知两点坐标A (-1,2),B (1,-2),则下列各式正确的是( )A .5OA OB →→∙= B .OA BO →→=C .(2,4)AB →=-D .10AB →=7.一个袋子中有7个球,其中3个绿球,4个红球,问从中摸出一个球是红球的概率是( )A .14B .13C .112D .478.如右图,O 为正六边形对角线的交点,则与OA →共线的向量有( )个A .2B .3C .7D .99.已知直线2310x y +-=,则斜率和在y 轴上的截距是() A .21,33- B .21,33- C .21,33 D .21,33-- 10.已知球的大圆周长为6π,求该球的表面积和体积( ) A .9,18ππ B .9,36ππ C .18,36ππD .36,36ππ11.甘肃省3家省属单位被安排某县4个材开展“联村联户,为民富民”活动,要求每家单位至少对口帮助其中1个村且每村只受1家单位帮扶,则不同的安排方法总数是 ( )A .7B .12C .36D .7212.如图为1500辆汽车通过某路段 AO40 50 60 70 80时的速度频率分布直方图,在速度为[60,70]的车辆约有( )辆A .450B .600C .800D .1000二、填空题(每小题3分,共12分)12、已知3cos 5θ=,且θ在第四象限,则sin θ= 13、过点()3,1-且垂直于直线032=+-y x 的直线方程为14、在等差数列}{n a 中,已知42=a ,84=a 则该数列的前10项之和等于15、函数lg(4)3x y x -=-的定义域是 ____________________________.三、解答题(共14分,17、18每题4分,19题6分)16.(6分)解不等式358x -<.17.(6分)已知等差数列{}n a 中,3915,9a a ==-求1a 和20S 的值.18.(7分)求经过点M (3,2),圆心在直线2y x = .。
三校生高考数学模拟试卷

三校生高考数学模拟试卷一、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设集合A = {xx^2 - 3x + 2 = 0},B={1, 2},则A与B的关系是()A. A⊂neqq BB. A = BC. A⊃neqq BD. A∩ B=varnothing2. 函数y=√(x - 1)的定义域是()A. (-∞,1]B. [1,+∞)C. (-∞, 0]D. [0,+∞)3. 若sinα=(3)/(5),且α是第二象限角,则cosα的值为()A. (4)/(5)B. -(4)/(5)C. (3)/(4)D. -(3)/(4)4. 过点(1,2)且斜率为3的直线方程为()A. y - 2 = 3(x - 1)B. y+2=3(x + 1)C. y - 2=-3(x - 1)D. y+2=-3(x + 1)5. 二次函数y = x^2+2x - 3的对称轴为()A. x = - 1B. x = 1C. x = 2D. x=-26. 已知向量→a=(1,2),→b=(3,-1),则→a·→b等于()A. 1B. -1C. 5D. -57. 在等差数列{a_n}中,若a_1=1,d = 2,则a_5的值为()A. 9B. 10C. 11D. 128. 若x>0,则函数y = x+(1)/(x)的最小值是()A. 1B. 2C. 3D. 49. 从5名男生和3名女生中选3人参加某项活动,要求既有男生又有女生,则不同的选法有()种。
A. 45B. 30C. 15D. 1010. 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x^2+1,则f(-1)的值为()A. -2B. 2C. -1D. 1二、填空题(本大题共5小题,每小题4分,共20分)11. 计算log_28=_。
12. 椭圆frac{x^2}{16}+frac{y^2}{9}=1的长半轴长a = _。
最新三校生数学高考模拟试卷

三校生数学高考模拟试卷一、是非选择题。
(对的选A ,错的选B。
每小题3分,共30分)1.如果A={0.1.2.3},B={1},则B ∈A …………………………………………( ) 2.已知直线上两点A (-3,3),B (3,-1),则直线AB 的倾斜角为65π( ) 3.lg 2+lg5=lg7………………………………………………………………………( ) 4.函数f(x)=245x x -+的定义域是【-1,5】…………………………( )5.sin750·sin3750=41-……………………………………………………………( )6.在等比数列{a n }中,a 1=31,a 4=89,则数列的公比为23…………………( )7.若向量32=+,则∥……………………………………( )8.双曲线13422=-y x 的渐近线方程为x y 23±=,焦距为2………………( ) 9.直线l ⊥平面α,直线m ∥平面β,若l ∥m ,则α⊥β………………( )10.二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………( )二、选择题(每小题5分,共40分) 11.函数f(x)=lg(x-3)的定义域是 ( )A.RB.(-3,3)C.(-∞,-3)∪(3,+∞)D.【0,+∞) D.112.以点M (-2,3)为圆心且与x 轴相切的圆的方程( )A.(x +2)2+(y -3)2=4 B . (x -2)2+(y +3)2=4C.(x +2)2+(y -3)2=9 D . (x -2)2+(y +3)2=913.10件产品中,3件次品,甲、乙两人依次各取一件产品,按取后放回,求恰有一件次品的概率为( ) A.10021 B. 241 C. 4521 D. 502114.若函数f(x)在定义域R 上是奇函数,且当x ﹥0时,f(x)=2410x x -,则f(-2)=( ).A. -104B.104C. 1D.10-1215.a=2是直线(a 2-2)x +y=0和直线2x +y +1=0互相平行的( ).A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16.设数列{a n }的前n 项和为2n s n=,则a 8=()A.64B.49C.16D.1517.在直角坐标系中,设A (-2,3),B (-3,-3),现沿x 轴把直角坐标系折成直二面角,则AB 的长为( )A.6B.5C.19D.118.a =(1,2),b =(x ,5),且b a⊥2,则x= ( )A .10B .-10 C.25 D.25-三、填空题(每题5分,共30分)19.已知x ∈(ππ,-),已知sinx=21, 则x= _ 已知tanx=-1,则x= _20.已知正方形ABCD 的边长为2,AP ⊥平面ABCD ,且AP=4,则点P 到BD 的距离 21.过圆3622=+y x 上一点(4,52)的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排,其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级: 姓名: 座号:四、解答题(第25、26、题,每小题10分,第27.28题,每小题15分,共50分)255=8=,<b a ,> =32π,求()()b a b a -∙+2。
三校生高三复习数学试卷

一、选择题(每题5分,共50分)1. 若函数f(x) = 2x - 3在区间[1, 4]上单调递增,则f(3)的值介于下列哪个区间内?A. [1, 2]B. [2, 3]C. [3, 4]D. [4, 5]2. 下列哪个数是方程x^2 - 4x + 3 = 0的根?A. 1B. 2C. 3D. 43. 已知等差数列{an}的前三项分别为a1, a2, a3,若a1 + a2 + a3 = 12,且a2 = 4,则该等差数列的公差为:A. 1B. 2C. 3D. 44. 若函数f(x) = x^3 - 3x^2 + 2x在区间[0, 2]上单调递增,则f(1)的值介于下列哪个区间内?A. [0, 1]B. [1, 2]C. [2, 3]D. [3, 4]5. 已知等比数列{bn}的前三项分别为b1, b2, b3,若b1 = 2,b2 = 4,则该等比数列的公比为:A. 1B. 2C. 4D. 86. 若函数f(x) = ax^2 + bx + c在区间[-1, 2]上单调递增,则下列哪个条件是错误的?A. a > 0B. b > 0C. c > 0D. a + b + c > 07. 已知等差数列{an}的前n项和为Sn,若S10 = 55,S20 = 200,则该等差数列的首项a1为:A. 1B. 2C. 3D. 48. 若函数f(x) = 2x + 1在区间[0, 3]上单调递减,则f(2)的值介于下列哪个区间内?A. [0, 1]B. [1, 2]C. [2, 3]D. [3, 4]的首项b1为:A. 1B. 2C. 3D. 410. 若函数f(x) = ax^2 + bx + c在区间[-1, 2]上单调递增,则下列哪个条件是正确的?A. a > 0B. b > 0C. c > 0D. a + b + c > 0二、填空题(每题5分,共25分)11. 若函数f(x) = 3x^2 - 2x + 1在区间[-1, 2]上单调递增,则f(1)的值为______。
最新三校生数学高考模拟试卷教学内容

三校生数学高考模拟试卷一、是非选择题。
(对的选A ,错的选B。
每小题3分,共30分)1.如果A={0.1.2.3},B={1},则B ∈A …………………………………………( ) 2.已知直线上两点A (-3,3),B (3,-1),则直线AB 的倾斜角为65π( ) 3.lg 2+lg5=lg7………………………………………………………………………( ) 4.函数f(x)=245x x -+的定义域是【-1,5】…………………………( )5.sin750·sin3750=41-……………………………………………………………( )6.在等比数列{a n }中,a 1=31,a 4=89,则数列的公比为23…………………( )7.若向量32=+,则∥……………………………………( )8.双曲线13422=-y x 的渐近线方程为x y 23±=,焦距为2………………( ) 9.直线l ⊥平面α,直线m ∥平面β,若l ∥m ,则α⊥β………………( )10.二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………( )二、选择题(每小题5分,共40分) 11.函数f(x)=lg(x-3)的定义域是 ( )A.RB.(-3,3)C.(-∞,-3)∪(3,+∞)D.【0,+∞) D.112.以点M (-2,3)为圆心且与x 轴相切的圆的方程( )A.(x +2)2+(y -3)2=4 B . (x -2)2+(y +3)2=4C.(x +2)2+(y -3)2=9 D . (x -2)2+(y +3)2=913.10件产品中,3件次品,甲、乙两人依次各取一件产品,按取后放回,求恰有一件次品的概率为( ) A.10021 B. 241 C. 4521 D. 502114.若函数f(x)在定义域R 上是奇函数,且当x ﹥0时,f(x)=2410x x -,则f(-2)=( ).A. -104B.104C. 1D.10-1215.a=2是直线(a 2-2)x +y=0和直线2x +y +1=0互相平行的( ).A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16.设数列{a n }的前n 项和为2n s n=,则a 8=()A.64B.49C.16D.1517.在直角坐标系中,设A (-2,3),B (-3,-3),现沿x 轴把直角坐标系折成直二面角,则AB 的长为( )A.6B.5C.19D.118.a =(1,2),b =(x ,5),且b a⊥2,则x= ( )A .10B .-10 C.25 D.25-三、填空题(每题5分,共30分)19.已知x ∈(ππ,-),已知sinx=21, 则x= _ 已知tanx=-1,则x= _20.已知正方形ABCD 的边长为2,AP ⊥平面ABCD ,且AP=4,则点P 到BD 的距离 21.过圆3622=+y x 上一点(4,52)的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排,其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级: 姓名: 座号:四、解答题(第25、26、题,每小题10分,第27.28题,每小题15分,共50分) 255=8=,<b a ,> =32π,求()()b a b a -•+2。
数学试卷三校生高考

一、选择题(每题4分,共40分)1. 已知函数f(x) = x^2 - 2x + 1,那么f(2)的值为()A. 1B. 3C. 0D. -12. 下列函数中,是奇函数的是()A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = x^43. 已知等差数列{an}的公差为d,若a1 + a2 + a3 = 9,a1 + a2 + a3 + a4 = 18,则d的值为()A. 2B. 3C. 4D. 54. 在△ABC中,角A、B、C的对边分别为a、b、c,若a^2 + b^2 = c^2,则△ABC是()A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形5. 下列方程中,有唯一解的是()A. x^2 + x + 1 = 0B. x^2 - 2x + 1 = 0C. x^2 + 2x + 1 = 0D. x^2 - 4x + 3 = 06. 已知等比数列{an}的公比为q,若a1 + a2 + a3 = 12,a1 a2 a3 = 27,则q的值为()A. 3B. 2C. 1D. -17. 下列函数中,在定义域内单调递增的是()A. f(x) = x^2B. f(x) = 2^xC. f(x) = log2xD. f(x) = x^38. 已知函数f(x) = x^2 - 3x + 2,那么f(-1)的值为()A. 0B. 1C. 2D. -19. 在△ABC中,角A、B、C的对边分别为a、b、c,若a = 3,b = 4,c = 5,则△ABC的面积为()A. 6B. 8C. 10D. 1210. 下列方程中,有无数解的是()A. x^2 + y^2 = 1B. x^2 + y^2 = 4C. x^2 + y^2 = 9D. x^2 + y^2 = 16二、填空题(每题4分,共40分)1. 已知等差数列{an}的首项为a1,公差为d,那么第n项an = _______。
三校生数学模拟试卷一

26.已知 A 0, 4, B x | x2 px q 0 ,若 A B A ,求 p 、 q 的值。
27.设 a (x 1)2 ,b 2x2 2x 1 ,比较 a 与 b 的大小。
A.2, 5
B.2
C.5
14.设全集U x | 4 x 10, x N, A 4, 6,8,10,则 U A =
A.5
B.5, 7
C.7, 9
D.
D.5, 7, 9
15.下列各题中正确的是
A. 若 a b c b ,则 a c C. 若 ab bc ,则 a c
B. 若
a b
30.设U R, A
x | x2 16 0
,
B
x
|
x3 x 1
CU A , CU B 。
学号
21.不等式 2x 3 4 的整数解的解集是
班级
…………………………………………………………………………………………………………
姓名
………………………………………………密…………封…………线………………………………………………
22.已知 A x | x 3, B x | 2 x 7,则 A B
9. p (x 2)(x 3), q x(x 1) ,则 p q …………………………………………( A B )
10.空集是任意集合的真子集 ……………………………………………………………( A B )
二、单项选择题:本大题共 8 题,每小题 5 分,共计 40 分。
11.已知集合 A 1,3,5,7, B 2,3, 4,5,6 ,则 A B
三校生数学考试题及答案

三校生数学考试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程2x+3=7的解?A. x=1B. x=2C. x=3D. x=4答案:B2. 函数y=x^2-4x+4的最小值是多少?A. 0B. 1C. 4D. 7答案:A3. 已知一个等差数列的首项为3,公差为2,那么它的第五项是多少?A. 11B. 13C. 15D. 17答案:C4. 一个圆的半径为5厘米,那么它的面积是多少平方厘米?A. 25πB. 50πC. 75πD. 100π答案:C5. 以下哪个函数是奇函数?A. y=x^2B. y=x^3C. y=x^4D. y=x^5答案:B6. 计算下列极限:\[\lim_{x \to 0} \frac{\sin(x)}{x}\]A. 0B. 1C. πD. 2答案:B7. 一个三角形的两边长分别为3和4,且这两边的夹角为60度,那么这个三角形的面积是多少?A. 3√3B. 4√3C. 6√3D. 8√3答案:A8. 以下哪个不等式是正确的?A. |x| > xB. |x| ≥ xC. |x| < xD. |x| ≤ x答案:B9. 计算下列定积分:\[\int_0^1 x^2 dx\]A. 1/3B. 1/2C. 2/3D. 1答案:A10. 以下哪个选项是不等式x^2 - 4x + 4 ≤ 0的解集?A. (-∞, 2]B. [2, ∞)C. (-∞, 2) ∪ (2, ∞)D. {2}答案:D二、填空题(每题4分,共20分)11. 计算等比数列的前三项和,首项为2,公比为3,和为______。
答案:1412. 已知函数f(x) = 2x - 1,求f(3)的值,结果为______。
答案:513. 一个直角三角形的两直角边长分别为6和8,那么斜边的长度为______。
答案:1014. 计算下列极限:\[\lim_{x \to \infty} \frac{1}{x}\]结果为______。
三校高考数学试卷答案

一、选择题1. 答案:A解析:根据题意,等差数列的公差为d,首项为a1,第n项为an,则有an = a1 + (n-1)d。
将n=5代入,得a5 = a1 + 4d,a6 = a1 + 5d。
由题意得a5 - a6 = -2d,代入选项,只有A选项符合。
2. 答案:C解析:设直线l的方程为y = kx + b,将其代入圆的方程x^2 + y^2 = 4中,得x^2 + (kx + b)^2 = 4。
展开后整理,得(k^2 + 1)x^2 + 2kbx + b^2 - 4 = 0。
由于直线与圆相切,故判别式Δ = 0,即4k^2b^2 - 4(k^2 + 1)(b^2 - 4) = 0。
化简得k^2 = 1,所以k = ±1。
当k = 1时,b = 2;当k = -1时,b = -2。
因此,直线l的方程为y = ±x + 2。
选项C符合题意。
3. 答案:D解析:由题意知,函数f(x) = |x - 1|在x = 1处取得极小值。
因此,f'(1) = 0。
对于分段函数,在分界点处导数不存在,所以f'(1)不存在。
选项D正确。
4. 答案:B解析:设向量a = (x, y),则向量b = (2x - y, 3x + 2y)。
根据向量的数量积公式,有a·b = x(2x - y) + y(3x + 2y) = 2x^2 + 5xy + 2y^2。
要使a·b = 0,即2x^2 + 5xy + 2y^2 = 0。
因为x和y不为零,所以x^2 + y^2 = 0,即x = 0,y = 0。
所以向量a = (0, 0)。
选项B正确。
5. 答案:C解析:根据复数的乘法公式,(a + bi)(c + di) = ac - bd + (ad + bc)i。
将a= 1,b = 2,c = 3,d = 4代入,得(1 + 2i)(3 + 4i) = 13 - 24 + (14 + 23)i = -5 + 10i。
江西省三新协作体2024届高三下学期5月联考数学模拟考试试题

江西省三新协作体2024届高三下学期5月联考数学模拟考试试题一、单选题1.抛物线22y x =的焦点坐标为 A .(1,0)B .1(,0)2C .1(0,)4D .1(0,)82.“生活里没有书籍,就好像没有阳光;智慧里没有书籍,就好像鸟儿没有翅膀.”某学校开展书香校园活动,甲、乙两学生统计某一周内的读书时长数据.若学生甲一周内每天的读书时长(单位:小时)分别为1x ,2x ,…,7x ,其均值和方差分别为x 和2s ,学生乙该周内每天的读书时长均比学生甲多半个小时,则学生乙该周内每天读书时长的均值和方差分别为( ) A .x ,2sB .0.5x +,20.25s +C .0.5x +,20.25s +D .0.5x +,2s3.设随机变量()~2,1,N ξ若(3),P m ξ>=则(13)P ξ<<等于( )A .122m -B .1m -C .12m -D .12m -4.设20183a =,20186b =,201812c =,则数列a ,b ,c ( ) A .是等差数列,但不是等比数列 B .是等比数列,但不是等差数列 C .既是等差数列又是等比数列D .既非等差数列又非等比数列5.已知函数3()2(1)ln 2f x f x x x '=-+-,()f x '是()f x 的导函数,则(1)f =( ) A .1B .2C .12D .12-6.已知实数x ,y 满足:22134x y +=,则12x y -的最大值为( )AB .2CD .57.已知函数()f x 和()g x 的导函数()f x '、()g x '图象分别如图所示,则关于函数()()=-y g x f x 的判断正确的是( )A .有3个极大值点B .有3个极小值点C .有1个极大值点和2个极小值点D .有2个极大值点和1个极小值点8.已知函数()()2cos f x x ωϕ=+0ω>,π02ϕ<<)在0x =处的切线斜率为ω-,若()f x 在()0,π上只有一个零点0x ,则ω的最大值为( )A .52B .136C .2D .53二、多选题9.公差为d 的等差数列{}n a ,其前n 项和为n S ,110S >,120S <,下列说法正确的有( ) A .0d <B .70a >C .{}n S 中5S 最大D .49a a <10.已知函数()1ln f x x x x-+=,给出下列四个结论,其中正确的是( ) A .曲线()y f x =在1x =处的切线方程为10x y ++= B .()f x 恰有2个零点C .()f x 既有最大值,又有最小值D .若120x x >且()()120f x f x +=,则121x x =11.设圆22:(1)(1)3C x y -+-=,直线:3430,l x y P ++=为l 上的动点,过点P 作圆C 的两条切线PA PB 、,切点为,A B M N 、、为圆上任意两点,则下列说法中正确的有( )A .PA 的取值范围为[)1,+∞B .四边形PACBC .满足60APB ∠=o 的点P 有两个D .CAB △三、填空题12.已知成对样本数据()()()()1122,,,,,,3n n x y x y x y n ⋅⋅⋅≥中12,,,n x x x ⋅⋅⋅互不相等,且所有样本点()(),1,2,,i i x y i n =⋅⋅⋅都在直线112y x =-+上,则这组成对样本数据的样本相关系数r =.13.已知函数()()()()ln ,e ,f x x g x x k f x g x ==+≤,则k 的取值范围为14.甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为56和15,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响.随机变量X 表示在3次活动中甲获胜的次数,则(2)P X ≥=;()D X =.四、解答题15.已知函数()()22ln f x x ax x a =+-∈R(1)当0a =时,求函数()f x 的极值;(2)若函数()f x 在区间[]1,2上是减函数,求实数a 的取值范围;16.已知正项数列{}n a 的前n 项和为n S ,且满足:11a =,211n n n a S S ++=+.(1)求数列{}n a 的通项公式; (2)设1(21)(21)n n n b a a =-+,求数列{}n b 的前n 项和n T .17.为了考察学生对高中数学知识的掌握程度,准备了甲、乙两个不透明纸箱.其中,甲箱有2道概念叙述题,2道计算题;乙纸箱中有2道概念叙述题,3道计算题(所有题目均不相同).现有A ,B 两个同学来抽题回答;每个同学在甲或乙两个纸箱中逐个随机抽取两道题作答.每个同学先抽取1道题作答,答完题目后不放回,再抽取一道题作答(不在题目上作答).两道题答题结束后,再将这两道题目放回原纸箱.(1)如果A 同学从甲箱中抽取两道题,则第二题抽到的是概念叙述题的概率;(2)如果A 同学从甲箱中抽取两道题,解答完后,误把题目放到了乙箱中.B 同学接着抽取题目回答,若他从乙箱中抽取两道题目,求第一个题目抽取概念叙述题的概率.18.某公园有一个矩形地块ABCD (如图所示),边ABAD 长4千米.地块的一角是水塘(阴影部分),已知边缘曲线AC 是以A 为顶点,以AD 所在直线为对称轴的抛物线的一部分,现要经过曲线AC 上某一点P (异于A ,C 两点)铺设一条直线隔离带MN ,点,M N 分别在边AB ,BC 上,隔离带占地面积忽略不计且不能穿过水塘.设点P 到边AD 的距离为t (单位:千米),BMN V 的面积为S (单位:平方千米).(1)请以A 为原点,AB 所在的直线为x 轴建立平面直角坐标系,求出S 关于t 的函数解析式; (2)是否存在点P ,使隔离出来的BMN V 的面积S 超过2平方千米?并说明理由.19.公元263年,刘徽首创了用圆的内接正多边形的面积来逼近圆面积的方法,算得n 值为3.14,我国称这种方法为割圆术,直到1200年后,西方人才找到了类似的方法,后人为纪念刘徽的贡献,将3.14称为徽率.我们作单位圆的外切和内接正32n ⨯边形()1,2,3n =L ,记外切正32n ⨯边形周长的一半为n a ,内接正32n ⨯边形周长的一半为n b .通过计算容易得到:32tan n n n a θ=⨯(其中n θ是正32n ⨯边形的一条边所对圆心角的一半)(1)求{}n b 的通项公式; (2)求证:对于任意正整数1111,n n nn a a b +、、依次成等差数列; (3)试问对任意正整数11,n n n n b b a ++、、是否能构成等比数列?说明你的理由.。
2023-2024学年云南省高考数学三校联考模拟试题(一模)含解析

2023-2024学年云南省高考数学三校联考模拟试题(一模)一、单选题1.已知1z ,2z 是方程2220x x +=-的两个复根,则2212z z -=()A .2B .4C .2iD .4i【正确答案】B【分析】利用求根公式求出两个复根,然后利用复数的运算法则及模的公式直接计算即可.【详解】已知1z ,2z 是方程2220x x +=-的两个复根,所以222i1i 22z ±===±,则设11i z =+,21i z =-,所以()()2212121222i 4i 4z z z z z z -=+-=⨯==,故选:B.2.已知集合{}1,0,1A =-,{}2,32B a a a =-+,若{}0A B ⋂=,则=a ()A .0或1B .1或2C .0或2D .0或1或2【正确答案】C【分析】根据集合的并集的结果分类讨论求参数.【详解】由于{}0A B ⋂=,则0B ∈.若0a =,则2322a a -+=,此时{}0,2B =符合题意.若2320a a -+=,则1a =或2,1a =时,{}0,1B =,此时{}0,1A B = 不合题意;2a =时,{}0,2B =符合题意,因此0a =或2,故选:C.3.有7个人排成前后两排照相,前排站3人后排站4人,其中甲同学站在前排,乙同学站在后排的概率为()A .142B .114C .221D .27【正确答案】D【分析】总事件数看成7人站一排,考虑符合题意的情况,从余下5人中选2人与甲站在前排,根据古典概型的计算公式求解即可.【详解】先计算总事件数,可以看成7人站一排有77A 种.现在考虑符合题意的情况,从余下5人中选2人与甲站在前排,乙站在后排有234534C A A 种,概率为23453477C A A 2A 7P ==.故选:D.4.平面向量a 与b 的夹角为2π3,已知()6,8a =- ,10b = ,则向量b 在向量a 上的投影向量的坐标为()A .()3,4-B .()4,3-C .()4,3-D .()3,4-【正确答案】D【分析】利用投影向量的定义结合向量的坐标运算可求得结果.【详解】向量b 在向量a上的投影向量的坐标为()()250cos ,6,83,4100a b b b a a a a ⋅-⋅==⋅-=-,故选:D.5.已知椭圆E :()222210x y a b a b +=>>的左、右焦点分别为1F ,2F (如图),过2F 的直线交E 于P ,Q 两点,且1PF x ⊥轴,229PF F Q =,则E 的离心率为()A.3B .12C.3D.2【正确答案】A【分析】根据题意利用向量可求得点Q 的坐标,结合椭圆方程运算求解.【详解】设椭圆E 的半焦距为()000,,c Q x y >,由题意可得:()22,,,0b P c F c a ⎛⎫- ⎪⎝⎭,则()222002,,,b PF c F Q x c y a ⎛⎫=-=- ⎪⎝⎭uuu r uuu r,因为229PF F Q =uuu r uuu r ,则()02299c x c b y a ⎧=-⎪⎨-=⎪⎩,解得0201199x c b y a ⎧=⎪⎪⎨⎪=-⎪⎩,即211,99b Q c a ⎛⎫- ⎝⎭,且点Q 在椭圆E 上,则4222212181811b c a a b +=,整理得()221211118181e e +-=,解得223e =,即e =.故选:A.6.已知正四棱锥的高为h ,其顶点都在同一球面上,若该球的体积为36π,且3922h ≤≤,则当该正四棱锥体积最大时,高h 的值为()A .2B .32C .4D .92【正确答案】C【分析】根据题意列出体积与高之间的函数关系式,利用导数讨论单调性和最值求解.【详解】如图,设高为h ,底边长为a ,则()222R h R =-+,又34π36π3V R ==球,∴3R =,又39,22h ⎡⎤∈⎢⎣⎦,()()2232111()1823212333V h a h h h h h =⋅=--=-+⎡⎤⎣⎦,()21()6242(4)3V h h h h h '=-+=--,所以当3,42h ⎡⎫∈⎪⎢⎣⎭时,()0V h '>,当94,2h ⎛⎤∈ ⎥⎝⎦时,()0V h '<,所以函数()321()2123V h h h =-+在3,42⎡⎫⎪⎢⎣⎭单调递增,94,2⎛⎤ ⎥⎝⎦单调递减,故max 464|3h V V ===,故选:C.7.定义方程()()f x f x '=的实数根x 叫做函数()f x 的“奋斗点”.若函数()ln g x x =,()32h x x =-的“奋斗点”分别为m ,n ,则m ,n 的大小关系为()A .m n ≥B .m n>C .m n≤D .m n<【正确答案】D【分析】求导,根据“奋斗点”的定义可得1ln m m=,3223n n -=,构造函数,利用导数及零点存在定理求出m 的范围,由223n n =+求出n 的范围,从而可比较大小.【详解】函数()ln g x x =,得()1g x x'=,由题意可得,()()g m g m '=,即1ln m m=.设()1ln H x x x=-,()211H x x x '=--,因为0x >,所以()0H x '<,易得()H x 在()0,∞+上单调递减且()110H =>,()12ln2ln 022H =-=<,故12m <<.由()32h x x =-,()23h x x '=,由题意得:3223n n -=,易知0n ≠,所以2233n n =+>,因为12m <<,所以m n <.故选:D.8.若,x y ∈R )A .2B C .12D 【正确答案】A【分析】设点(),e xP x x 是函数()e x f x x =图象上的点,点(),1Q y y -是直线:1l y x =-上的PQ =,设函数()e xf x x =在点()00,M x y 处的切线1l 与直线l平行,求出函数的导函数,即可得到()()0001e 1x f x x '=+=,再令()()e 11xg x x =+-,利用导数说明函数的单调性,求出函数的零点,即可求出M 点坐标,从而求出min PQ ,从而得解.【详解】设点(),e xP x x 是函数()e x f x x =图象上的点,点(),1Q y y -是直线:1l y x =-上的点,可以转化为P ,Q 两点之间的距离,PQ =,因为()()1e xf x x '=+,设函数()e x f x x =在点()00,M x y 处的切线1l 与直线l 平行,则直线1l 的斜率为1,可得()()0001e 1xf x x '=+=,整理得()00e 110x x +-=,令()()e 11x g x x =+-,则()()e 2xg x x '=+,当<2x -时()0g x '<,当2x >-时()0g x '>,所以()g x 在(),2-∞-上单调递减,在()2,-+∞上单调递增,且当x →-∞时()1g x →-,()00g =,()22e 10g --=--<,当x →+∞时()g x ∞→+,所以()g x 有且仅有一个零点0,∴方程()00e 110xx +-=有且仅有一个解00x =,则()0,0M ,故PQ 的最小值为点()0,0M 到直线:1l y x =-的距离d ==的最小值为2.故选:A.二、多选题9.已知()f x ,()g x 都是定义在R 上且不恒为0的函数,则()A .()()y f x f x =⋅-为偶函数B .()()y g x g x =+-为奇函数C .若()g x 为奇函数,()f x 为偶函数,则()()y f g x =为奇函数D .若()f x 为奇函数,()g x 为偶函数,则()()y f x g x =-为非奇非偶函数【正确答案】AD【分析】根据奇函数和偶函数的定义判断即可.【详解】选项A :设()()()h x f x f x =⋅-,因为()f x 是定义在R 上的函数,所以()h x 的定义域为R ,()()()()h x f x f x h x -=-⋅=,所以()h x 为偶函数,故A 正确;选项B :()()()t x g x g x =+-,因为()g x 是定义在R 上的函数,所以()t x 的定义域为R ,()()()()t x g x g x t x -=-+=,所以()t x 为偶函数,故B 错误;选项C :设()()()m x f g x =,因为()f x ,()g x 都是定义在R 上的函数,所以()m x 的定义域为R ,因为()g x 为奇函数,()f x 为偶函数,所以()()()()()()()()m x f g x f g x f g x m x -=-=-==,所以()m x 为偶函数,故C 错误;选项D :设()()()n x f x g x =-,因为()f x ,()g x 都是定义在R 上的函数,所以()n x 的定义域为R ,()()()()()()()()()()()2n x n x f x g x f x g x f x g x f x g x g x +-=-+---=---=-,因为()g x 是不恒为0的函数,所以()()0n x n x +-=不恒成立,所以()n x 不是奇函数,()()()()()()()()()()()2n x n x f x g x f x g x f x g x f x g x f x --=-----=-++=⎡⎤⎣⎦,因为()f x 是不恒为0的函数,所以()()n x n x =-不恒成立,所以()n x 不是偶函数,所以()n x 是非奇非偶函数,故D 正确,故选:AD.10.已知α,β是两个不同的平面,m ,n ,l 是三条不同的直线,则下列命题正确的是()A .若m α⊥,n α⊥,则//m nB .若//m α,//n α,则//m nC .若αβ⊥,l αβ= ,m α⊂,m l ⊥,则m β⊥D .若l αβ= ,//m α,//m β,则//m l 【正确答案】ACD【分析】根据空间中线、面位置关系逐项分析判断.【详解】对于选项A :因为m α⊥,n α⊥,所以由线面垂直的性质可得m n ∥,故A 正确;对于选项B :若m α∥,n α∥,则m 与n 可能异面或相交或平行,故B 错误;对于选项C :因为αβ⊥,l αβ= ,m α⊂,m l ⊥,由面面垂直的性质定理知,m β⊥,故C 正确;对于选项D :设a αδ= ,且m δ⊂,因为m α∥,则ma ,设b βγ= ,且m γ⊂,因为m β∥,则m b ∥,可得a b ∥,又因为b β⊂,a β⊄,则a β∥,且a α⊂,l αβ= ,则a l ∥,可得m l ∥,故D 正确;故选:ACD.11.在如图所示的平面直角坐标系中,锐角α,β的终边分别与单位圆交于A ,B 两点.则()A .若A 点的横坐标为1213,B 点的纵坐标为45,则()16cos 65αβ+=B .()sin sin sin αβαβ+<+C .()sin sin sin ααββ>++D .以sin α,sin β,()sin αβ+为三边构成的三角形的外接圆的面积为π3【正确答案】AB【分析】根据三角函数定义结合两角和的余弦公式可判断A ;利用两角和的正弦公式结合正余弦函数的性质可判断B ,C ;判断sin α,sin β,()sin αβ+可构成三角形,并结合正余弦定理求得三角形外接圆面积可判断D.【详解】对于A ,由已知得,12cos 13α=,4sin 5β=,α,β为锐角,则5sin 13α=,3cos 5β=,则()1235416cos cos cos sin sin 13513565αβαβαβ+=-=⨯-⨯=,故A 正确;对于B ,∵π,0,2αβ⎛⎫∈ ⎪⎝⎭,()0,παβ+∈,∴()cos 0,1∈α,()cos 0,1β∈,∴()sin cos cos sin si i s n n s n i αβαβαβαβ=+<++,故B 正确;对于C ,∵()()cos 1,1αβ+∈-,∴()()()()sin sin sin cos cos sin sin sin ααββαββαββαββ=+-=+-+<++⎡⎤⎣⎦,故C 错误;对于D ,同理()()()()sin sin sin cos cos sin sin sin βαβααβααβααβα=+-=+-+<++⎡⎤⎣⎦,结合B 、C 可知sin α,sin β,()sin αβ+,可以作为三角形的三边;设该三角形为A B C ''',角A ',B ',C '所对的边长分别为sin α,sin β,()sin αβ+,由余弦定理可得,()()222222sin sin sin sin sin sin cos cos sin cos 2sin sin 2sin sin C αβαβαβαβαβαβαβ+-++-+'=222222sin sin sin cos cos sin 2sin cos cos sin 2sin sin αβαβαβαβαβαβ+---=()()2222sin 1cos sin 1cos cos cos 2sin sin αββααβαβ-+-=-222222sin sin sin sin 2sin sin cos cos cos cos 2sin sin 2sin sin αββααβαβαβαβαβ+=-=-()sin sin cos cos cos αβαβαβ=-=-+,∴()sin sin C αβ'==+,设外接圆半径为R ,则由正弦定理可得()()sin 21sin sin A B R C αβαβ+''==='+,∴12R =,∴π4S =,故D 错误,故选:AB.12.已知长方体1111ABCD A B C D -中,2AB BC ==,1AA =点P 是四边形1111D C B A 内(包含边界)的一动点,设二面角P AD B --的大小为α,直线PB 与平面ABCD 所成的角为β,若αβ=,则()A .点P 的轨迹为一条抛物线B .线段PB 长的最小值为3C .直线1PA 与直线CD 所成角的最大值为π4D .三棱锥11P A BC -体积的最大值为3【正确答案】BCD【分析】作PO ⊥平面ABCD ,OH AD ⊥,根据二面角平面角定义和线面角定义可得PHO PBO ∠=∠,由此可得OH OB =,根据抛物线定义可知O 点轨迹为抛物线的一部分,对应的P 点轨迹也为抛物线的一部分,知A 错误;若PB 取得最小值,则OB 最小,根据抛物线性质可知当O 为AB 中点时,OB 最小,由此可求得PB 最小值,知B 正确;将问题转化为求解OA 与AB 所成角OAB ∠的最大值,建立平面直角坐标系,可知当OA 与抛物线相切时,OAB ∠最大,利用抛物线切线的求法可求得该最大值,知C 正确;由体积桥1111P A BC B PA CV V --=可确定当点O 到AC 的距离最大时,所求体积最大,结合抛物线图形可知当O 为AB 中点时距离最大,由此可求得D 正确.【详解】过点P 作PO ⊥平面ABCD ,垂足为O ,作OH AD ⊥,垂足为H ,对于A ,PO ⊥ 平面ABCD ,AD ⊂平面ABCD ,AD PO ∴⊥,又OH AD ⊥,PO OH O ⋂=,,PO OH ⊂平面POH ,AD ∴⊥平面POH ,PH ⊂ 平面POH ,AD PH ∴⊥,PHO ∴∠即为二面角P AD B --的平面角,即PHO α∠=,又PBO β∠=,PHO PBO ∴∠=∠,OH OB ∴=,O ∴点轨迹为以B 为焦点,AD 为准线的抛物线在四边形ABCD 内(含边界)的部分,则P 点轨迹为以1B 为焦点,11A D 为准线的抛物线在四边形1111D C B A 内(含边界)的部分,A 错误;对于B ,由抛物线性质知:当O 为AB 中点时,min 1OB =,min 3PB ∴=,B 正确;对于C ,1PA 与CD 所成角即为OA 与AB 所成角OAB ∠,在平面ABCD 中,以AB 中点M 为坐标原点,可建立如图所示平面直角坐标系,则当OA 与抛物线相切时,OAB ∠取得最大值;由题意知:抛物线方程为:24y x =,()1,0A -,设切线方程为:1x ty =-,则由214x ty y x =-⎧⎨=⎩得:2440y ty -+=,216160t ∴∆=-=,解得:1t =±,O 在四边形ABCD 内(含边界),结合图形可知:1t =,此时π4OAB Ð=,∴直线1PA 与CD 所成角的最大值为π4,C 正确;对于D ,111111111133P A BC B PA C PA C PA C V V SBB S --==⋅=,11AC =∴若三棱锥11P A BC -的体积最大,则点P 到11AC 的距离最大,即点O 到AC 的距离最大;由C 中图象可知:当O 为AB 中点时,点O 到AC 的距离最大,最大值为142BD =,即点P 到11AC ,()11max13223P A BC V -∴=⨯=,D 正确.故选:BCD.关键点点睛:本题考查立体几何中的轨迹相关问题的求解,解题关键是能够作出二面角的平面角,结合线面角定义确定动点满足到定点的距离等于到定直线的距离,从而确定动点轨迹为抛物线的一部分,进而结合直线与抛物线的知识来进行求解.三、填空题13.在621x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是____________.(用数字作答)【正确答案】15【分析】由题意利用二项展开式的通项公式,求得展开式中常数项【详解】二项式621x x ⎛⎫+ ⎪⎝⎭的展开式的通项公式为()62361661C C rrr r r r T x x x --+⎛⎫== ⎪⎝⎭,令360r -=,即2r =,∴常数项为2615C =.故15.14.假设云南省40万学生数学模拟考试的成绩X 近似服从正态分布()98,100N ,已知某学生成绩排名进入全省前9100名,那么该生的数学成绩不会低于____________分.(参考数据:()0.6827P X μσμσ-<<+=,()220.9545P X μσμσ-<<+=)【正确答案】118【分析】求出从40万名学生任取1名,成绩排名在前9100名的概率,再利用正态分布的对称性求出对应分数作答.【详解】从40万名学生任取1名,成绩排名在前9100名的概率为91000.022********=,因为成绩X 近似服从正态分布()98,100N ,则98μ=,10σ=,()()22781180.9545P X P X μσμσ-<<+=<<=,显然()()1180.510.95450.02275P X ≥=⨯-=,从而数学成绩大于等于118分的人数恰好为9100,所以要进入前9100名,成绩不会低于118分.故11815.已知抛物线C :28x y =,在直线4y =-上任取一点P ,过点P 作抛物线C 的两条切线,切点分别为A ,B ,则原点到直线AB 距离的最大值为____________.【正确答案】4【分析】先根据切线方程得到直线AB 的方程,根据其过定点()0,4可得直线AB 距离的最大值为4.【详解】设()11,A x y ,()22,B x y ,则2118x y =,2228x y =,由28x y =得28x y =,284x x y '==,在A 处的切线方程为()1114x y y x x -=-,即114xy x y =-在B 处的切线方程为()2224x y y x x -=-,即224xy x y =-设(),4P t -,则1144x t y -=-,2244xt y -=-,则直线AB 方程为:44x t y -=-,即44ty x =+,直线AB 恒过定点()0,4,所以原点到直线AB 的距离的最大值为4.故4四、双空题16.定义x 表示与实数x 的距离最近的整数(当x 为两相邻整数的算术平均值时,x 取较大整数),如413=,523=,22=,2.53=,令函数()K x x =,数列{}n a 的通项公式为n a=n 项和为nS ,则6S=______;2025S =______.【正确答案】489【分析】空1:根据数列新定义求出前6项,求和即可;空2:根据数列新定义,数列{}n a 重新分组可得()11111111111111,1,(,),(,,,,,),,(,,,)2222333333n n n,且满足第n 组有2n 个数,且每组中所有数之和为122n n⨯=,根据规律求和即可.【详解】空1:因为()1111a K ==,21a ==,312a ==,()41122a K ==,512a ==,612a ==,所以6111442S =++⨯=;空2:根据()K x x =,当12n ≤≤时,1 1.5≤,则1K=,1n a==,当36n ≤≤时,1.5 2.5<,则2K=,12n a =,当712n ≤≤时,2.5 3.5<<,则3K=,13n a ==,当1320n ≤≤时,3.5 4.5<,则4K=,14n a =,以此类推,将n a=()11111111111111,1,,,,,,,,,,,,,,2222333333n n n ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,第n 组有2n 个数,且每组中所有数之和为122n n⨯=,设2025a =1n +组中,则(22)20252n n+≤,可得(1)2025n n +≤,解得4445n <<,故2025a 在第45组,前面共有44组,共1980项,所以20251244458945S =⨯+⨯=.故4;89.关键点睛:涉及数列新定义问题,关键是理解新定义,利用新定义合理推导,结合数列通项和求和知识解答.五、解答题17.如图,正ABC 是圆柱底面圆O 的内接三角形,其边长为a .AD 是圆O 的直径,PA 是圆柱的母线,E 是AD 与BC 的交点,圆柱的轴截面是正方形.(1)记圆柱的体积为1V ,三棱锥-P ABC 的体积为2V ,求12V V ;(2)设F 是线段PE 上一点,且12FE PF =,求二面角A FC O --的余弦值.【正确答案】(1)π3【分析】(1)利用正弦定理求解圆柱底面圆的半径r 与正ABC 的边长为a 的关系,从而得圆柱的高h 与a 的关系,分别计算体积即可得比值;(2)建立空间直角坐标系,分别求解平面AFC 与平面FCO 的法向量,根据空间向量的坐标运算求解二面角A FC O --的余弦值即可.【详解】(1)已知正ABC 的边长为a ,由正弦定理,2sin 60ar =︒(r 为圆柱底面圆的半径),从而3r OA a ==,由题意,圆柱高23h r a ==,所以231ππ9V r h a ==,232111sin 60326V a h a =⨯︒⨯=,因此12π3V V =.(2)如图,过A 作Ax ⊥平面PAD ,易知Ax ,AD ,AP 两两垂直,以A 为原点建立如图所示的空间直角坐标系A xyz -,设2AD =,则2AP =,1AO =.由于O 为正ABC 的中心,则23AO AE =,于是32AE =,由(1)知正ABC的边长a =,从而BC =则()0,0,0A ,()0,1,0O ,30,,02E ⎛⎫⎪⎝⎭,3,,022C ⎫⎪⎪⎝⎭,()002P ,,,由题意,F 为线段PE 上靠近E 的三等分点,则113120,,20,,33223EF EP ⎛⎫⎛⎫==-=- ⎪ ⎪⎝⎭⎝⎭,于是20,1,3F ⎛⎫ ⎪⎝⎭,20,1,3AF ⎛⎫= ⎪⎝⎭,12,,223FC ⎛⎫=- ⎪ ⎪⎝⎭,1,022CO ⎛⎫=-- ⎪ ⎪⎝⎭ ,设平面AFC 的法向量为()1111,,n x y z =,所以11111111111203312202233n AF y z y x n FC x y z y z ⎧⎧⋅=+==-⎪⎪⎪⎪⇒⎨⎨⎪⎪⋅=+-==-⎪⎪⎩⎩,取11x =-,则132n ⎛=-- ⎝⎭ ,设平面FCO 的法向量为()2222,,n x y z =所以22222222221022012023n CO x y y z n FC x y z ⎧⋅=-=⎪⎧=⎪⎪⇒⎨⎨=⎪⎩⎪⋅+-=⎪⎩,取21x =-,则()2n =- ,所以121212cos,n nn nn n⋅=由图可知二面角A FC O--的夹角为锐角,所以二面角A FC O--的夹角的余弦值为5.18.已知函数()4sin sin6f x x xπωω⎛⎫=+⎪⎝⎭2π.(1)求函数()f x在区间3,34ππ⎡⎤⎢⎥⎣⎦上的值域;(2)在锐角ABC中,角A,B,C的对边分别为a,b,c,且()f A==,c=ABC的面积.【正确答案】(1)[]1,2-(2)3【分析】(1)对函数进行化简,用辅助角公式合为一个三角函数,相邻两条对称轴之间的距离为2π即为半周期,可求出1ω=;(2)由()f A=3Aπ=,由正弦定理求解即可.【详解】(1)()14sin sin4sin cos62f x x x x x xπωωωωω⎫⎛⎫=+-+-⎪⎪⎪⎝⎭⎝⎭)22sin cos1cos2sin2x x x x xωωωωω=+=-+sin222sin23x x xπωωω⎛⎫==-⎪⎝⎭,∵22T Tππ=⇒=,1ω=,()2sin23f x xπ⎛⎫=-⎪⎝⎭,∵334xππ≤≤,72336xπππ≤-≤,∴当7236xππ-=时,()min 1f x=-,当232xππ-=时,()max 2f x=,即()f x的值域为[]1,2-.(2)由()f A=0,2Aπ⎛⎫∈ ⎪⎝⎭,可得3Aπ=,A B=⇒=,0,2Bπ⎛⎫∈ ⎪⎝⎭,∴4Bπ=,∴()62sin sin 4C A B =+=,由sin sin a c a A C =⇒=∴1sin 32ABC S ac B ==+△19.已知数列{}n a 的前n 项和为n S ,11a =,1122n n n S S ++=+,*n ∈N .(1)求数列{}n a 的通项公式;(2)设3n n n b S =,{}n b 的前n 项和为n T ,若对任意的正整数n ,不等式2727n m m T -+>恒成立,求实数m 的取值范围.【正确答案】(1)()21,1,212,2n n n a n n -=⎧=⎨+⋅≥⎩(2)()1,2-【分析】(1)根据等差数列的定义以及,n n a S 的关系求解;(2)利用错位相减法可求得n T ,在根据题意得()2min 727n m m T -+<即可求解.【详解】(1)由1122n n n S S ++=+,得11122n n n n S S ++=+,又111222S a ==,所以数列2n n S ⎧⎫⎨⎬⎩⎭是以12为首项,公差为1的等差数列,∴()1211222n n S n n -=+-=,即()1212n n S n -=-⋅,∴当2n ≥时,()()()1221212232212n n n n n n a S S n n n ----=-=-⋅--⋅=+⋅,又11a =不满足上式,所以()21,1,212,2n n n a n n -=⎧=⎨+⋅≥⎩.(2)由(1)知()1212n n S n -=-⋅,∴()121212323nn nnn b n --⋅⎛⎫⎛⎫==-⋅⎪ ⎪⎝⎭⎝⎭,∴12123212232323nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,①23121232123232323n n T n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,②①−②得:23111222123333323n n n T n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+--⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,整理得()25253nn T n ⎛⎫=-+ ⎪⎝⎭,又因为对任意的正整数n ,2727n m m T -+>恒成立,所以()2min 727n m m T -+<,∵()()11222212527033333n n nn n T T n n n ++⎛⎫⎛⎫⎛⎫⎛⎫-=+-+=+> ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,∴n T 在()0,∞+上单调递增,()1min 13n T T ==,由271273m m -+<,可得12m -<<,所以实数m 的取值范围是()1,2-.20.“学习强国”学台是由中宣部主管,以深入学习宣传为主要内容,立足全体党员,面向全社会的优质平台,现日益成为老百姓了解国家动态,紧跟时代脉搏的热门app .为了了解全民对于“学习强国”使用的情况,现从某单位全体员工中随机抽取3人做问卷调查.已知某单位有N 名员工,其中25是男性,35是女性.(1)当20N =时,求抽出3人中男性员工人数X 的分布列和数学期望;(2)我们知道,当总量N 足够大而抽出的个体足够小时,超几何分布近似为二项分布.现在全市范围内考虑.从N 名员工(男女比例不变)中随机抽取3人,在超几何分布中男性员工恰有2人的概率记作1P ;在二项分布中(即男性员工的人数2~3,5X B ⎛⎫⎪⎝⎭)男性员工恰有2人的概率记作2P .那么当N 至少为多少时,我们可以在误差不超过0.001(即120.001P P -≤)的前提下认为超几何分布近似为二项分布.24.04≈)【正确答案】(1)分布列见解析,数学期望为65(2)N 至少为145时,我们可以在误差不超过0.001(即120.001P P -≤)的前提下认为超几何分布近似为二项分布【分析】(1)利用超几何分布概率模型求出概率,即可列出分布列和求数学期望;(2)利用二项分布概率模型和超几何分布概率模型即可求解.【详解】(1)当20N =时,男性员工有8人,女性员工有12人.X 服从超几何分布,0,1,2,3X =,()312320C 220110C 114057P X ====,()12812320C C 528441C 114095P X ====,()21812320C C 336282C 114095P X ====,()38320C 56143C 1140285P X ====,∴X 的分布列为X0123P11574495289514285数学期望为()11442814601235795952855E X =⨯+⨯+⨯+⨯=.(2)()()()()212355131232C C 111855551C 2512126NNNN N N N N P N N N N N ⎛⎫⎛⎫-⨯- ⎪ ⎪⎝⎭⎝⎭===⋅----,22232336C 0.28855125P ⎛⎫=⋅== ⎪⎝⎭,由于120.001P P -≤,则()()211850.2880.0012512N N N N ⎛⎫- ⎪⎝⎭⋅-≤--,即()()211828950.28925121000N N N N ⎛⎫- ⎪⎝⎭⋅≤=--,即()()2128925289512100018720N N N N ⎛⎫- ⎪⎝⎭≤⨯=--,由题意易知()()120N N -->,从而()()27201289125N N N N ⎛⎫-≤-- ⎪⎝⎭,化简得21475780N N -+≥,又0N >,于是578147N N +≥.由于函数578y x x=+在24.04x =≈处有极小值,从而578y N N=+当25N ≥时单调递增,又578142146.07147142+≈<,578143147.04147143+≈>.因此当143N ≥时符合题意,而又考虑到25N 和35N 都是整数,则N 一定是5的整数倍,于是145N =.即N 至少为145时,我们可以在误差不超过0.001(即120.001P P -≤)的前提下认为超几何分布近似为二项分布.21.已知圆C:(224x y +=,定点)D,如图所示,圆C 上某一点1D 恰好与点D关于直线PQ 对称,设直线PQ 与直线1D C 的交点为T.(1)求证:TC TD -为定值,并求出点T 的轨迹E 方程;(2)设()1,0A -,M 为曲线E 上一点,N 为圆221x y +=上一点(M ,N 均不在x 轴上).直线AM ,AN 的斜率分别记为1k ,2k ,且124k k =-.求证:直线MN 过定点,并求出此定点的坐标.【正确答案】(1)证明见解析,2214y x -=(2)证明见解析,定点坐标为()1,0【分析】(1)根据对称性求得TC TD -为定值,结合双曲线定义求得轨迹E 方程;(2)解一:根据M A ,在双曲线上,用点差法得1111141y x x y -=⋅+,222211y x x y -=-+,代入124k k =-可得122121x y x y y y =--,将MN 方程()y k x m =+代入求得直线MN 恒过定点.解二:分别联立直线与双曲线、圆,求出M N ,的坐标,设定点(),0T t ,由三点共线得1t =,得直线MN 恒过定点.【详解】(1)证明:由图,由点1D 与D 关于PQ 对称,则1TD TD =,所以112TC TD TC TD CD -=-==,故为定值.由2TC TD CD -=<=由双曲线定义知,点T的轨迹为以()C,)D为焦点,实轴长为2的双曲线,设双曲线E 方程为()222210,0x y a b a b -=>>,所以1a =,c =2224b c a =-=,所以双曲线E 的方程为2214y x -=.(2)解一:因为()1,0A -,如图,令()11,M x y ,()22,N x y ,()2211221,4101,y x ⎧-=⎪⎨⎪--=⎩两式相减得:1111141y x x y -=⋅+,同理,()2222221,101,x y ⎧+=⎪⎨-+=⎪⎩两式相减得:222211y x x y -=-+,124k k =-,即2121122121211111444x x k k x y x y y y y y ⎛⎫--=-⇒-=-⋅⋅⇒-=- ⎪⎝⎭,由题知直线MN 斜率一定存在,设直线MN 方程()y k x m =+,则()()()()211122k x m k x m k x m k x m x x +++-=+-,整理得()1212m x x x x =--,所以1m =,故直线MN 恒过定点()1,0.解二:由已知得AM l :()11y k x =+,AN l :()21y k x =+,联立直线方程与双曲线方程()1221,1,4y k x y x ⎧=+⎪⎨-=⎪⎩消去y 整理得()22221114240k x k x k ----=,由韦达定理得212144A M k x x k --=-,所以212144M k x k +=-,即()1121814M M k y k x k =+=-.所以211221148,44k k M k k ⎛⎫+ ⎪--⎝⎭.联立直线方程与圆的方程()2221,1,y k x x y ⎧=+⎨+=⎩消去y 整理得()22222221210k x k x k +++-=,由韦达定理得222211A N k x x k -=+,所以222211N k x k -+=+,即()22222211N N k y k x k =+=+,因为14AN AM k k =-,即2114k k =-,所以2112211168,1616k k N k k ⎛⎫-+- ⎪++⎝⎭,若直线MN 过定点,则由对称性得定点在x 轴上,设定点(),0T t .由三点共线得MT NT k k =,即()()1122222211111122112211884164416161416416k k k k k k t k k t t k k t t k k --+=⇒++-=-++⇒=+-+---+,所以直线MN 过定点()1,0T .方法点睛:圆锥曲线中直线过定点问题通法,是先设出直线方程y kx m =+,通过韦达定理和已知条件若能求出m 为定值可得直线恒过定点,若得到k 和m 的一次函数关系式,代入直线方程即可得到直线恒过定点.此题中由于两点分别是直线与双曲线、圆的交点,故只能求出两交点的坐标,用两点坐标结合直线方程得到直线恒过定点.22.已知函数()()ln 22f x x x =+-+,()e ln x g x a x a =-+.(1)求函数()f x 的极值;(2)请在下列①②中选择一个作答(注意:若选两个分别作答则按选①给分).①若()()f x g x ≤恒成立,求实数a 的取值范围;②若关于x 的方程()()f x g x =有两个实根,求实数a 的取值范围.【正确答案】(1)极大值为3,无极小值(2)选①,[)e,a ∈+∞;选②,a 的取值范围为()0,e 【分析】(1)先求导函数,再根据单调性求解极值即可;(2)把恒成立式子整理化简后,构造函数求导函数结合单调性求解.【详解】(1)函数()f x 的定义域为{}2x x >-,()111022x f x x x --'=-==++,解得=1x -,当2<<1x --时,()0f x ¢>,()f x 单调递增;当1x >-时,()()0,f x f x '<单调递减;所以()()13f x f =-=极大值,无极小值.(2)若选①:由()()f x g x ≤恒成立,即()e ln 2ln 20x a x a -++-≥恒成立,整理得:()ln e ln ln 22x a a x x x ++≥++++,即()()ln 2ln e ln ln 2e x x a a x x ++≥++++,设函数()e x h x x =+,则上式为()()()ln ln 2h x a h x +≥+,因为()e 10x h x '=+>恒成立,所以()h x 单调递增,所以()ln ln 2x a x +≥+,即()ln ln 2a x x ≥+-,令()()ln 2m x x x =+-,()2,x ∈-+∞,则()11122x m x x x +'=-=-++,当()2,1x ∈--时,()0m x '>;当()1,x ∈-+∞时,()0m x '<;所以()m x 在=1x -处取得极大值,()m x 的最大值为()11m -=,故ln 1a ≥,即e a ≥.故当[)e,a ∈+∞时,()()f x g x ≤恒成立.若选择②:由关于x 的方程()()f x g x =有两个实根,得()e ln 2ln 20x a x a -++-=有两个实根,整理得()ln eln ln 22x a a x x x ++=++++,即()()ln 2ln e ln ln 2e x x a a x x ++=++++,设函数()e x h x x =+,则上式为()()()ln ln 2h x a h x +=+,因为()e 10x h x '=+>恒成立,所以()h x 单调递增,所以()ln ln 2x a x +=+,即()ln ln 2a x x =+-,令()()ln 2m x x x =+-,()2,x ∈-+∞,则()11122x m x x x +'=-=-++,当()2,1x ∈--时,()0m x '>;当()1,x ∈-+∞时,()0m x '<;所以()m x 在=1x -处取得极大值,()m x 的最大值为()11m -=,又因为()(),,2,,x m x x m x →+∞→-∞→-→-∞所以要想()ln ln 2a x =+有两个根,只需要ln 1a <,即0e a <<,所以a 的取值范围为()0,e .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三校生高考数学模拟试卷
班级 姓名 学号 得分
第I 卷(选择题 70分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 答案
(请将是非选择题、单项选择题答案写到表格中)
一、是非选择题:本大题共10小题,每小题3分,共30分.对每小题的命题作出选择,
的选A,错的选B.
1. 实数0与集合A={0,1}的关系是.0A ∈ (A B)
2. 点M(1,1)在圆.1)1(2
2
上=+-y x
(A B) 3. 若非零向量.0,//,=•b a b a b a 则满足
(A B) 4. }.10{02<<<+x x x x 的解集是不等式
(A B)
5. 3
4
2tan ,2tan ==θθ则若
(A B)
6. 24lg 25lg =+
(A B) 7. 函数x y πsin = 的最小周期是2
(A B) 8. 若点A,B 到平面a 的距离都等于1,则直线.//a AB
(A B)
9. 当6)32(3
的系数是的展开式中x x +
(A B) 10,等差数列).(125,3,1*
N n n a n ∈-=的通项公式为
(A B)
二、单项选择题:本大题共8小题,每小题5分,共40分.
11. 的离心率为椭圆125
92
2=+y x ( )
A.
5
3 B.
5
4 C.
4
3 D.
4
5 12. 已知的值域是函数x
y 2=( )
A.{}
0≤y y
B. {}
0≥y y
C. {}
0>y y
D. {}
R y y ∈
13. 已知[]()=⋂==B A B A 则集合,5,2,3,0( )
A. (]3,2
B. [)5,0
C. ()3,2
D. []3,2
14. 不等式[]
的最小值为函数2,1,32
-∈+-=x x y ( ) A. -1 B. 0 C. 2 D. 3
15. 的大小关系是,,三个数5
3cos 5cos )8-(cos π
ππ
( ) A.)5
3cos()5cos()8cos(πππ
<<-
B.⎪⎭
⎫
⎝⎛-<<8cos )5cos()53cos(
πππ B.C.⎪⎭
⎫
⎝⎛<-<5cos )8cos()53cos(
πππ
D.⎪⎭
⎫
⎝⎛<<-
5cos )53cos(
)8
cos(πππ
16. 不等式的取值范围是,则是直线与平面所成的角
若θθ( ) A.[)π,0
B. )2
,
0(π
C. )2
,
0[π
D.]2
,
0[π
17. 那么下列说法正确的是如果,b a >( )
A.
1>b
a
B. 2
2b a >
C.
b
a 1
1< D. 33b a > 18. 从1,2,3,4,5,6中任取两个数,则这两个数之和为9的概率是( )
A.
154
B.
51 C. 15
2
D. 15
1
第I 卷(非选择题 80分)
三、填空题:本大题共6小题,每小题5分,共30分.
19.在直角坐标系中,过点(0,1)和(1,0)的直线l 的方程是
20. 在===∠=∠∆AC BC B A ABC ,则,,中,44530
21. 到右焦点的距离为,则点到右焦点的距离为右支上一点若双曲线
p p x x 3116
92
2=- 22. 已知一个圆柱的底面半径为1,高为2,则该圆柱的全面积为 23. 已知向量),1,2(),1,1(-=-=b a =+b a 则
24.甲乙两人投掷飞镖,他们的成绩(环数)如下面的频数条形统计图所示,用甲、乙训练
的成绩的方差大小关系是,乙甲2
2s s
四、
五、解答题:本大题共6小题,25-28小题每小题8分,29-30小题每小题9分,共50分. 25.
26. (本小题满分8分)
的值,求实数若,已知向量m b a m b a ⊥=-=),,1()2,1(
.)()2()()1(cos 11
)()8.26的奇偶性判断函数的定义域;求函数已知函数分(本小题满分x f x f x
x f +=
27. (本小题满分8分) .}{68}{221的通项公式求数列,的前项和,若是递增等比数列已知n n n a S a a a S ==
28. 已(本小题满分8分) 已知).0(0542:2
2>=-+--+m m y x y x C 的方程是
.
0943:)2(;
)1(的值相切,求实数与直线若圆的坐标求圆心m y x l C C =++
29. (本小题满分9分)
.
),1(]1,(),()(2单调递增上上单调递增,在区间在区间已知函数+∞-∞∈++=R b a b ax x x f .
2]0,1[)()2(.
)1(的值,求实数上的最小值为在若的值求实数b x x f a -∈
30. (本小题满分9分)
.1111-AA BC AB C B A ABC ==形,的底面是等腰直角三角如图,已知直三棱柱
(1)求异面直线所成的角与11CC AB .
(2)若M 为线段AC 的中点,N 为线段1
111//:BMC N AB C A 平面平面的中点,求证。
