勾股定理与面积问题
勾股定理与三角形面积的计算

勾股定理与三角形面积的计算勾股定理是数学中一条著名的几何定理,它描述了直角三角形中三个边之间的关系。
根据勾股定理,我们可以通过已知直角三角形的两个边长来计算第三边的长度。
此外,勾股定理还可以应用于计算三角形的面积,为我们解决各种实际问题提供了有力的工具。
一、勾股定理的表述及应用勾股定理可以用以下公式来表述:在一个直角三角形中,设直角边的长度为a和b,斜边的长度为c,则有a^2 + b^2 = c^2。
根据勾股定理,我们可以解决多种实际问题。
例如,已知一个直角三角形的两条直角边的长度为3和4,我们可以通过勾股定理计算出斜边的长度:c^2 = 3^2 + 4^2 = 9 + 16 = 25因此,斜边的长度c为5。
二、三角形面积的计算三角形是几何中常见的形状之一,计算三角形的面积是我们经常遇到的问题之一。
根据勾股定理,我们可以利用三角形的底边和高来计算其面积。
计算三角形面积的公式为:面积 = 底边长度 ×高 / 2。
在这个公式中,底边长度表示为b,高表示为h。
三、应用示例下面以一个具体的应用问题来演示勾股定理和三角形面积的计算。
例题:某个直角三角形的两条直角边分别为5cm和12cm,请计算该直角三角形的斜边长度和面积。
解答:根据勾股定理,斜边的长度c可以通过以下计算得到:c^2 = 5^2 + 12^2 = 25 + 144 = 169因此,斜边的长度c为13cm。
接下来,我们根据三角形面积的计算公式来计算面积。
首先需要确定底边和高的长度。
由于直角边5cm和12cm分别垂直于底边,我们可以选择其中任意一条作为底边。
假设我们选择5cm作为底边,12cm作为高。
根据面积计算公式:面积 = 底边长度 ×高 / 2面积 = 5 × 12 / 2面积 = 60 / 2面积 = 30(平方厘米)因此,该直角三角形的面积为30平方厘米。
四、总结勾股定理与三角形面积的计算是几何学中重要的内容之一。
专题11 解题技巧专题:勾股定理与面积问题、方程思想压轴题七种模型全攻略(解析版)

专题11解题技巧专题:勾股定理与面积问题、方程思想压轴题七种模型全攻略【考点导航】目录【典型例题】 (1)【类型一三角形中,利用面积求斜边上的高】 (1)【考点二结合乘法公式巧求面积或长度】 (6)【考点三巧妙割补求面积】 (9)【考点四“勾股树”及其拓展类型求面积】 (13)【考点五几何图形中的方程思想—折叠问题(利用等边建立方程)】 (19)【考点六几何图形中的方程思想—公边问题(利用公边建立方程)】 (25)【考点七实际问题中的方程思想】 (28)【典型例题】【类型一三角形中,利用面积求斜边上的高】A.8013B.【答案】D【变式训练】A.5【答案】C【分析】根据图形,可以求出根据题意得,13AB AC BC ==,∴1122BD BC ==,在Rt ADB 中,根据勾股定理得,∴22221312AD AB BD =-=-3.(2022·全国·八年级课时练习)如图,在网格中,每个小正方形的边长均为1.点A 、B ,C 都在格点上,若BD 是△ABC 的高,则BD 的长为__________.【答案】ABC 中AB 【分析】如图所述,过点在Rt △ABD 中,可求出【详解】解:如图所述,过点∵ABC 是格点图形,每个小正方形的边长为单位∴3AD =,3BC =,BD ∴在Rt △ABD 中,AB =∵11·22ABC S BC AD == ∴·335BC AD CE AB ⨯===(1)求BC的长.(2)求斜边AB边上的高.BC【答案】(1)=6(2)斜边AB边上的高是【点睛】本题考查勾股定理,三角形的面积,解答本题的关键是明确题意,利用数形结合的思想解答.6.(2023秋·全国·八年级专题练习)在【类型二结合乘法公式巧求面积或长度】例题:已知在Rt ABC 中,90,,C A B C ∠=︒∠∠∠,所对的边分别为a ,b ,c ,若10cm,8cm a b c +==,则Rt ABC 的面积为()A .29cm B .218cm C .224cm D .236cm 【答案】A【解析】【变式训练】1.在ABC 中,AD 是BC 边上的高,4,5AD AB AC ===,则ABC 的面积为()A .18B .24C .18或24D .18或303.直角ABC 三边长分别是x ,1x +和5,则ABC 的面积为__________.【类型三巧妙割补求面积】是直角三角形;(1)求证:ACD(2)求四边形ABCD的面积.【答案】(1)见解析【变式训练】【答案】24平方米【分析】连接AC,根据勾股定理求出据直角三角形的面积公式求出结果即可.∠=︒,4=ADC90AD米,CD=225∴=+=米,AC AD CD(1)求这个四边形草地的面积;(2)如果清理草地杂草,每平方米需要人工费36m【答案】(1)2(2)清理完这块草地杂草需要(2)解:2036720⨯=(元)答:清理完这块草地杂草需要【点睛】本题主要考查了勾股定理,勾股定理的逆定理,解题的关键是掌握直角三角形两直角边的平方和等于斜边平方,两边平方和等于第三边平方的三角形是直角三角形.(1)求线段CD 与BC 的长;(2)求四边形ABCD 的面积;(3)求证:90BCD ∠=︒.【答案】(1)25BC =,(2)292(3)见解析∴22345BD =+=,∵()22225BC CD +=+∴222BC CD BD +=,∴BCD △是直角三角形,且∴90BCD ∠=︒.【点睛】此题考查勾股定理和勾股定理的逆定理,关键是根据勾股定理得出各边的长解答.【类型四“勾股树”及其拓展类型求面积】例题:(2023秋·重庆渝中·八年级重庆巴蜀中学校考期末)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A 、B 、C 、D 的面积分别是6、10、4、6,则最大正方形E 的面积是()A .20B .26C .30D .52【答案】B 【分析】根据正方形的面积公式并结合勾股定理,能够导出正方形A ,B ,C ,D 的面积和即为最大正方形的面积即可.【详解】解:如图:根据勾股定理的几何意义,可得:E F GS S S =+=A B C DS S S S +++=61046+++=26故选B .【点睛】本题考查勾股定理,熟悉勾股定理的几何意义是解题的关键.【变式训练】1.(2023·广西柳州·校考一模)如图,90BDE ∠=︒,正方形BEGC 和正方形AFED 的面积分别是289和225,则以BD 为直径的半圆的面积是()A .16πB .8πC .4πD .2π【答案】B【答案】12;s1+s2=s3(1)如图2,分别以ABC 的三条边为直径向外作半圆,其半圆的面积由小到大分1S 、2S 、3S 3S 有怎样的数量关系,并证明你的结论;(2)分别以直角三角形的三条边为直径作半圆,如图3所示,其面积由小到大分别记作S 1、S 中的探索,直接回答12S S +与3S 有怎样的数量关系;(1)①如图2,3,4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,面积分别为1S ,2S ,3S ,利用勾股定理,判断这3个图形中面积关系满足123S S S +=的有________②如图5,分别以直角三角形三边为直径作半圆,设图中两个月牙形图案(图中阴影部分)的面积分别为2S ,直角三角形面积为3S ,也满足123S S S +=吗?若满足,请证明;若不满足,请求出1S ,关系.(2)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这【点睛】本题考查了勾股定理,勾股树.解题的关键在于正确的表示各部分的面积.【类型五几何图形中的方程思想—折叠问题(利用等边建立方程)】A .54B .74C .15【答案】B【分析】根据图形翻折变换的性质可知,AE BE =【变式训练】1.(2023春·湖北咸宁·八年级校考阶段练习)如图,有一块直角三角形纸片,9043C AC BC ∠=︒==,,,将斜边AB 翻折,使点B 落在直角边AC 的延长线上的点E 处,折痕为AD ,则BD 的长为()A .34【答案】C【分析】利用勾股定理求得则3CD x =-,根据勾股定理可得【答案】103/133【分析】由折叠的性质可得【详解】解:D 是AB 中点,【答案】1或65【分析】分90BFA '∠=︒和90,30,C A BC ∠=︒∠=︒=30,DA E '∠=︒ 60,EA H '∴∠=︒在Rt EHA ' 中,12A H '=在Rt BEH 中,(1)如图①,当A '与点B 重合且3,5BC AB ==.①直接写出AC 的长;②求BCD △的面积.(2)当37A ∠=︒.①A '与点E 在直线AC 的异侧时.如图②,直接写出A EB ∠-∠'②当∥A D BC '时,如图:∵∥A D BC ',90C ∠=︒,∴90ADA '∠=︒,∵ADE V 由A DE ' 折叠所得,∴1452ADE ADA '∠=∠=︒;当A E BC '∥时,如图:∵37A ∠=︒,90C ∠=∴903753B ∠=︒-︒=︒∵ADE V 由A DE ' 折叠所得,∴37A A '∠=∠=︒,综上:ADE ∠的度数分别为【点睛】本题主要考查了勾股定理,三角形那个的内角和定理,折叠的性质,平行线的性质,解题的关键是掌握勾股定理内容,根据勾股定理建立方程求边的长度;掌握三角形是内角和为于与它不相邻的两个内角之和,平行线的性质.【类型六几何图形中的方程思想—公边问题(利用公边建立方程)】例题:如图,在△ABC 中,AB =10,BC =9,AC =17,则BC 边上的高为_______.【答案】8【解析】【分析】作AD BC ⊥交BC 的延长于点D ,在Rt ADB 中,222AD DB AB +=,在Rt ADC 中,222AD DC AC +=,根据2222AB DB AC DC -=-列出方程即可求解.【详解】如图,作AD BC ⊥交BC 的延长于点D ,【变式训练】1.已知:如图,在ABC 中,90C AD ∠=︒,是ABC 的角平分线,35CD BD ==,,则AC =____.【答案】6【分析】作DE AB ⊥,如图,根据角平分线的性质可得3DE CD ==,勾股定理求出BE ,证明()Rt Rt HL ACD AED ≅ ,推出AC AE =,设AC AE x ==,根据勾股定理列出方程即可求出AC .【详解】解:作DE AB ⊥于点E ,如图,∵在ABC 中,90C AD ∠=︒,是ABC 的角平分线,3CD =,∴3DE CD ==,【点睛】本题考查了角平分线的性质、全等三角形的判定和性质以及勾股定理等知识,属于常见题型,熟练掌握上述知识,利用勾股定理得出方程是解题的关键.△和Rt2.如图,在Rt ABC(1)求证:点A在M∠∥,AB(2)若AC DM【答案】(1)见解析(2)5【分析】(1)连接AM在Rt ABC △和Rt ADE △中,∵90B D ∠=∠=︒,AC AE =,BC DE =,Rt Rt (HL)ABC ADE ∴≅ ,AB AD ∴=,AB BM ⊥ ,AD DM ⊥,MA ∴平分BMD ∠,∴点A 在BMD ∠的平分线上;(2)解:AC DM ∥ ,CAM AMD ∴∠=∠,AMB CAM ∴∠=∠,CM AC ∴=,设BC x =,18CM AC x ∴==-,在Rt ABC △中,222AB BC AC +=,22212(18)x x ∴+=-,5x ∴=.5BC ∴=.【点睛】本题考查了全等三角形的判定与性质,角平分线的判定,勾股定理,解决本题的关键是得到Rt Rt (HL)ABC ADE ≅ .【类型七实际问题中的方程思想】例题:(2022·全国·八年级)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地……”翻译成现代文为:如图,秋千绳索OA 悬挂于O 点,静止时竖直下垂,A 点为踏板位置,踏板离地高度为一尺(AC =1尺).将它往前推进两步(EB⊥OC于点E,且EB=10尺),踏板升高到点B位置,此时踏板离地五尺(BD=CE=5尺),则秋千绳索(OA或OB)长______尺.【变式训练】1.(2022·全国·八年级课时练习)如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是()A.50.5寸B.52寸C.101寸D.104寸【答案】C【解析】【分析】取AB的中点O,过D作DE⊥AB于E,根据勾股定理解答即可得到结论.【详解】解:取AB的中点O,过D作DE⊥AB于E,如图2所示:由题意得:OA=OB=AD=BC,设OA=OB=AD=BC=r寸,则AB=2r(寸),DE=10寸,OE=12CD=1寸,∴AE=(r﹣1)寸,在Rt△ADE中,AE2+DE2=AD2,即(r﹣1)2+102=r2,解得:r=50.5,∴2r=101(寸),∴AB=101寸,故选:C.【点睛】本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.2.(2022·河南·金明中小学八年级期中)《九章算术》是我国古代数学名著,有题译文如下:今有门,不知其高宽;有竿,不知其长短.横放,竿比门宽长出4尺;竖放,竿比门高短2尺;斜放,门对角线长恰好倍.问门高、门宽各为多少?3.(2022·重庆市求精中学校八年级期中)在一条东西走向的河的一侧有一村庄C ,河边原有两个取水点A ,B ,其中AB AC =,由于某种原由C 到A 的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H (A 、H 、B 在一条直线上),并新修一条路CH ,测得 1.5CB =千米, 1.2CH =千米,0.9HB =千米.(1)问CH 是否为从村庄C 到河边的最近路?请通过计算加以说明.(2)求原来的路线AC 的长.【答案】(1)CH 是从村庄C 到河边的最近路;理由见解析;(2)原来的路线AC的长为1.25千米.【解析】【分析】(1)根据勾股定理的逆定理证明△CHB是直角三角形即可;(2)设AC=x千米,在Rt△ACH中,由已知得AC=x,AH=x-0.9,CH=1.2,再根据勾股定理解答即可.(1)解:是,理由是:在△CHB中,∵CH2+BH2=1.22+0.92=2.25,BC2=2.25,∴CH2+BH2=BC2,∴△CHB是直角三角形,∴CH是从村庄C到河边的最近路;(2)设AC=x千米,在Rt△ACH中,由已知得AC=x,AH=x-0.9,CH=1.2,由勾股定理得:AC2=AH2+CH2∴x2=(x-0.9)2+1.22,解这个方程,得x=1.25,答:原来的路线AC的长为1.25千米.【点睛】本题考查勾股定理的应用,关键是根据勾股定理的逆定理和定理解答.4.(2022·浙江·浦江县实验中学八年级期中)图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD''.某家装厂设计的折叠床是AB=4cm,BC=8cm,(1)此时CD为_________cm;(2)折叠时,当AB⊥BC′时,四边形ABC′D′的面积为_______cm2.【点睛】。
勾股定理简介及应用

勾股定理简介及应用勾股定理是古希腊数学家毕达哥拉斯在公元前6世纪提出的一条三角形重要的几何定理,它可以用来计算三角形的边长或角度。
勾股定理的表述是:在一个直角三角形中,直角边的平方等于斜边的两个边的平方和。
即a²+ b²= c²,其中a和b是直角三角形的两个直角边,c是斜边。
勾股定理的应用非常广泛,可以用来解决各种实际问题,以下是一些典型的应用:1. 面积计算:勾股定理可以用来计算三角形的面积。
根据定理,面积等于直角边的乘积的一半。
例如,一个直角边长为a,另一个直角边长为b的直角三角形的面积为1/2 * a * b。
2. 边长计算:勾股定理可以用来计算三角形的边长。
如果已知两个边长a和b,可以用勾股定理求解斜边的长度c。
例如,已知一个直角三角形的两条直角边长分别为3和4,可以用勾股定理计算出斜边的长度为5。
3. 角度计算:勾股定理可以用来计算三角形的角度。
根据定理,如果已知三角形的两个边长a和b,并且要求斜边与其中一个直角边之间的角度,可以使用反正弦函数求解。
例如,已知一个直角三角形的两条直角边长分别为3和4,可以用反正弦函数求解出斜边与边长为3的直角边之间的角度。
4. 判断三角形类型:勾股定理可以用来判断三角形的类型。
如果三个边长满足勾股定理,即a²+ b²= c²,那么这个三角形是直角三角形;如果两个边长的平方和小于第三个边长的平方,即a²+ b²< c²,那么这个三角形是钝角三角形;如果两个边长的平方和大于第三个边长的平方,即a²+ b²> c²,那么这个三角形是锐角三角形。
5. 应用于解决实际问题:勾股定理可以用来解决很多实际问题,例如在建筑工程中计算屋顶的坡度和高度、在导航中确定航程和航向、在物理中计算物体的运动轨迹等等。
总结来说,勾股定理是一条非常重要和实用的几何定理,它不仅可以用来计算三角形的边长和角度,还可以用来解决各种实际问题。
勾股定理面积问题
1 S1 S2
2 S2
若变为作其它任意正 多边形,情形会怎样? S3
B
C
S2
a c
B
b
A
S3 A S2
S1
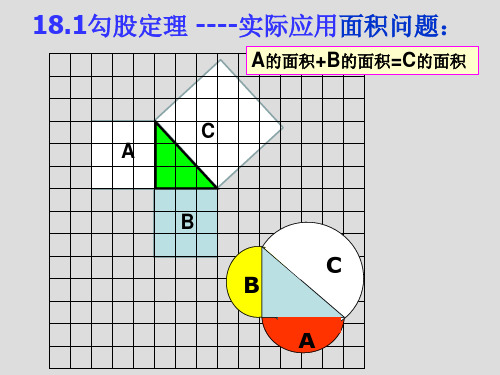
C
S1
四变: 如图,分别以直角△ABC三边 为直径向外作三个半圆,其面积分别用S1、 S2、S3表示,则S1、S2、S3有什么关系? 不难证明S3=S1+S2 .
C S1 a B
S2
b c
A
S3
观察下列图形,正方形1的边长为7,则 正方形2、3、4、5的面积之和为多少? 规律:
18.1勾股定理 ----实际应用面积问题:
A的面积+B的面积=C的面积
C
A
B
B A
C
D
二变:如图,分别以Rt △ABC三边为 斜边向外作三个等腰直角三角形,其面 积分别用S1、S2、S3表示,则S1、S2、S3 之间的关系是 S1 S2 S3,请说理。
C
S3
A
b
a c
S2
B
S1
三变:如图,分别以Rt △ABC三边为 边向外作三个正三角形,其面积分别用 S1、S2、S3表示,则S1、S2、S3之间的关 系是 S1 S2 S3 ,请说理。
2 3 4 5
S2+S3+S4+S5= S1
1
二.y=0 复习面积法证明勾股定理
已知S1=1,S2=3,S3=2,S4=4,求 S5、S6、S7的值
S3
S4
S2
结论:
S1+S2+S3+S4 =S5+S6 =S7
S1
S5
S6
勾股定理的三角形面积计算方法

勾股定理的三角形面积计算方法勾股定理是数学中的一个基本定理,它描述了直角三角形中两条直角边的平方和等于斜边的平方。
根据这个定理,我们可以推导出计算三角形面积的方法。
本文将探讨如何利用勾股定理来计算三角形的面积,并提供一些例题来帮助读者更好地理解。
一、勾股定理简介勾股定理可追溯到古希腊的毕达哥拉斯学派,以其名字命名。
它的数学表达式为:c² = a² + b²,其中c表示斜边的长度,a和b分别表示直角边的长度。
该定理可以用于求解任意直角三角形中的边长,也可以应用于计算三角形的面积。
二、计算三角形面积的方法根据勾股定理,我们可以利用直角三角形的两个直角边的长度来计算其面积。
一般而言,我们可以使用以下公式来计算三角形的面积:面积 = 1/2 * 直角边a * 直角边b其中,直角边a和直角边b分别表示直角三角形的两个直角边的长度。
这个公式的推导过程如下:1. 已知直角边a和直角边b的长度,根据勾股定理可得斜边c的长度:c = √(a² + b²)。
2. 将斜边c代入三角形面积公式:面积= 1/2 * a * b = 1/2 * a * √(c² - a²)。
值得注意的是,我们一般会选择较为简便的方法来计算三角形的面积。
在已知直角边a和直角边b的情况下,可以直接使用公式面积 = 1/2 * a * b来计算三角形的面积。
三、例题解析为了更好地理解利用勾股定理计算三角形面积的方法,我们提供以下例题解析。
例题1:已知直角三角形的直角边a = 3,直角边b = 4,求三角形的面积。
解答:根据上述公式,面积 = 1/2 * a * b。
将已知数据代入公式,可得面积= 1/2 * 3 * 4 = 6。
因此,该直角三角形的面积为6。
例题2:已知直角三角形的直角边a = 5,直角边b = 12,求三角形的面积。
解答:同样地,根据面积 = 1/2 * a * b的公式,代入已知数据可得面积 = 1/2 * 5 * 12 = 30。
怎么用面积证明勾股定理
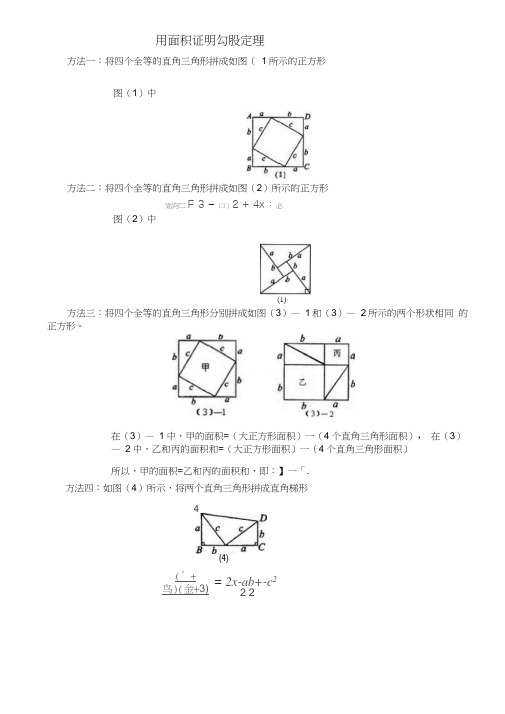
(° + 鸟)(金+3) = 2x-ab+-c 22 2用面积证明勾股定理方法一:将四个全等的直角三角形拼成如图(1所示的正方形方法二:将四个全等的直角三角形拼成如图(2)所示的正方形方法三:将四个全等的直角三角形分别拼成如图(3)— 1和(3)— 2所示的两个形状相同 的正方形。
在(3)— 1中,甲的面积=(大正方形面积)一(4个直角三角形面积), 在(3)— 2中,乙和丙的面积和=(大正方形面积)一(4个直角三角形面积) 所以,甲的面积=乙和丙的面积和,即:】一「.方法四:如图(4)所示,将两个直角三角形拼成直角梯形图(1)中图(2)中‘如阿二F 3 - 口)2 + 4x :必(1)4(4)练习题(一)转化的思想方法我们在求三角形的边或角,或进行推理论证时,常常作垂线,构造直角三角形,将问题转化为直 角三角形问题来解决.49、如图所示,△ ABC 是等腰直角三角形,AB=AC ,D 是斜边BC 的中点,E 、F 分别是AB 、 AC 边上的点,且 DE 丄DF ,若BE=12,CF=5.求线段EF 的长。
50如图,在等腰厶ABC 中,/ ACB=90 °,D 、E 为斜边AB 上的点,且/ DCE=45° 求证:DE 2=AD 2+BE 2。
51如图,在△ A BC 中,52如图,长方形ABCD 中,AB=8,BC=4,将长方形沿AC 折叠,点D 落在点E 处,则重叠部 分厶AFC 的面积是 。
53在厶ABC 中,AB=15 ,AC=20,BC 边上的高A D=12,试求BC 边的长.BCCACAB=13,BC=14,A C=15,则 BC 边上的高 A D=54在厶A BC中,D是BC所在直线上一点,若AB=IO,BD=6,AD=8,AC=17 ,求△ ABC的面积。
55. 若厶ABC三边a b、c满足a2+ b2+ c2+ 338=10a+24b+26c △ ABC是直角三角形吗?为什么?56. 在厶ABC中,BC=1997, AC=1998, AB2=1997+1998,则△ ABC是否为直角三角形?为什么? 注意BC、AC、AB的大小关系。
勾股定理的几何意义从面积关系

勾股定理的几何意义从面积关系勾股定理是几何学中一条重要的定理,它的几何意义不仅仅体现在直角三角形的边长关系上,还可以用来描述三角形的面积关系。
本文将以勾股定理的几何意义为切入点,从面积关系的角度来探讨这一定理。
一、勾股定理的基本形式勾股定理最常见的形式是:直角三角形的斜边的平方等于两个直角边的平方之和。
用公式表示即为:c² = a² + b²,其中c为直角三角形的斜边,a和b为直角三角形的两个直角边。
二、勾股定理的面积关系在直角三角形中,勾股定理不仅仅可以描述边长之间的关系,还能够揭示出三角形的面积关系。
根据勾股定理,我们可以得到以下推论:1. 推论一:直角三角形的面积公式设直角三角形的两个直角边分别为a和b,斜边为c,那么根据勾股定理我们可以得到:c² = a² + b²。
进一步推导,可以得到直角三角形的面积公式:S = 1/2 * a * b,其中S表示三角形的面积。
2. 推论二:直角三角形面积关于斜边的变化规律在直角三角形中,当两个直角边的长度确定时,斜边的长度也随之确定。
我们可以通过勾股定理来分析斜边对于三角形面积的影响。
我们可以看到斜边的长度越大,直角三角形的面积也越大。
这是因为斜边的长度增加,意味着直角三角形的底边和高也会相应增加,从而使面积增大。
当斜边的长度为定值时,直角三角形的面积也达到最大值。
这是因为根据勾股定理可知,斜边与两个直角边之间存在一种最优关系,使得直角三角形的面积取得最大值。
3. 推论三:直角三角形面积关于直角边的变化规律在直角三角形中,当斜边的长度确定时,两个直角边的长度也随之确定。
我们可以通过勾股定理来分析直角边对于三角形面积的影响。
根据勾股定理可知,直角边的长度与斜边的长度呈现一种关联关系。
当一个直角边的长度增加时,另一个直角边的长度会相应减小,从而使直角三角形的面积减小。
反之亦然。
三、勾股定理的应用举例1. 用勾股定理计算直角三角形的面积假设一个直角三角形的直角边分别为3和4,我们可以使用勾股定理来计算斜边的长度:c² = 3² + 4² = 9 + 16 = 25,即c = 5。
求勾股定理中的三角形面积综合练习题

求勾股定理中的三角形面积综合练习题勾股定理是数学中一项重要的几何定理,它是指在直角三角形中,斜边的平方等于两直角边平方和。
根据勾股定理,我们可以计算出三角形的边长、角度以及面积等相关参数。
本文将以练习题的形式,通过求解不同的三角形面积问题,加深对勾股定理的理解与掌握。
练习题一:已知直角三角形ABC,∠C=90°,AB=5cm,BC=12cm,求三角形ABC的面积。
解答:根据勾股定理,可计算出斜边AC的长度:AC = √(AB² + BC²)= √(5² + 12²)= √(25 + 144)= √169= 13由于直角三角形ABC的两条直角边已知,我们可以利用面积公式计算三角形ABC的面积:面积 = 1/2 * 直角边1 * 直角边2= 1/2 * AB * BC= 1/2 * 5 * 12= 30 平方厘米练习题二:已知直角三角形DEF,∠E=90°,DF=8cm,EF=15cm,求三角形DEF的面积和以直角边EF为斜边的矩形面积。
解答:同样根据勾股定理,可以计算出斜边DE的长度:DE = √(DF² + EF²)= √(8² + 15²)= √(64 + 225)= √289= 17三角形DEF的面积可由面积公式计算得出:面积 = 1/2 * 直角边1 * 直角边2= 1/2 * DF * EF= 1/2 * 8 * 15= 60 平方厘米矩形以直角边EF为斜边,所以其长度等于EF,宽度等于直角边DF的长度。
矩形的面积可由公式计算得出:面积 = 长度 * 宽度= EF * DF= 15 * 8= 120 平方厘米练习题三:已知直角三角形GHI,∠H=90°,GH=9cm,HI=40cm,求以斜边HI为直径的圆的面积。
解答:根据勾股定理,可计算出斜边GI的长度:GI = √(GH² + HI²)= √(9² + 40²)= √(81 + 1600)= √1681= 41以斜边HI为直径的圆的半径等于斜边HI的一半,即20cm。
中考数学解题技巧专题勾股定理与面积问题

解题技巧专题:勾股定理与面积问题——全方位求面积,一网搜罗◆类型一 直角三角形中,利用面积求斜边上的高1.(郴州桂阳县期末)在Rt △ABC 中,∠C =90°,AC =9,BC =12,则C 点到AB 的距离为【方法1】( ) A.536 B.365 C.334 D.12252.如图,在2×2的方格中,小正方形的边长是1,点A ,B ,C 都在网格点上,则AB 边上的高为( ) A.355 B.255 C.3510 D.322第2题图 第6题图◆类型二 结合乘法公式巧求面积或周长3.直角三角形的周长为24,斜边长为10,则其面积为( )A.96 B.49 C.24 D.484.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是( ) A.7cm B.10cmC.(5+37)cm D.12cm◆类型三巧妙分割求面积5.如图,已知AB=5,BC=12,CD=13,DA=10,AB⊥BC,求四边形ABCD的面积.◆类型四“勾股树”及其拓展类型中有关面积的计算6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的边长为( )A.14cm B.4cm C.15cm D.3cm7.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )A.4 B.36 C.16 D.55第7题图第8题图8.(青海中考)如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2……按照此规律继续下去,则S 9的值为( )A.⎝ ⎛⎭⎪⎫126B.⎝ ⎛⎭⎪⎫127C.⎝ ⎛⎭⎪⎪⎫226D.⎝ ⎛⎭⎪⎪⎫227 ◆类型五 “赵爽弦图”中有关面积的计算9.“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则大正方形与小正方形的面积差是( )A .9B .36C .27D .34第9题图 第10题图10.(永州零陵区校级模拟)如图是4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边(x >y ),下列四个说法:①x 2+y 2=49;②x -y =2;③2xy +4=49;④x +y =9.其中说法正确的是( )A .①②B .①②③C .①②④D .①②③④参考答案与解析1.B2.A 解析:过点C 作CD ⊥AB 于点D .∵S △ABC =22-12×1×2-12×1×1-12×1×2=32,又∵S △ABC =12AB ·CD ,∴12AB ·CD =32.∵AB =12+22=5,∴CD =355.故选A. 3.C 解析:设该直角三角形的两直角边长分别为a ,b ,则有a +b =14①,a 2+b 2=102②.①两边同时平方,得a 2+b 2+2ab =142,所以2ab =96,所以ab =48,12ab =24.故选C.4.D5.解:连接AC ,过点C 作CE ⊥AD 交AD 于点E .∵AB ⊥BC ,∴∠CBA =90°.在Rt △ABC 中,由勾股定理得AC =AB 2+BC 2=52+122=13.∵CD =13,∴AC =CD ,即△ACD 是等腰三角形.∵CE ⊥AD ,∴AE =12AD =12×10=5.在Rt △ACE 中,由勾股定理得CE =AC 2-AE 2=132-52=12.∴S 四边形ABCD =S △ABC +S △CAD =12AB ·BC +12AD ·CE=12(12×5+10×12)=90. 6.A 7.C8.A 解析:在图中标上字母E ,如图所示.∵正方形ABCD 的边长为2,△CDE 为等腰直角三角形,∴DE 2+CE 2=CD 2,DE =CE ,∴S 2+S 2=S 1.观察,发现规律:S 1=22=4,S 2=12S 1=2,S 3=12S 2=1,S 4=12S 3=12,…,∴S n =⎝ ⎛⎭⎪⎫12n -3.当n =9时,S 9=⎝ ⎛⎭⎪⎫129-3=⎝ ⎛⎭⎪⎫126.故选A.9.B 解析:大正方形的面积为32+62=45,小正方形的面积为(6-3)2=9,则面积差为45-9=36.故选B.10.B 解析:由题意得⎩⎪⎨⎪⎧x 2+y 2=49①,(x -y )2=4②,①-②得2xy =45③,∴2xy +4=49,①+③得x 2+2xy +y 2=94,∴x +y =94,∴①②③正确,④错误.故选B.解题技巧专题:圆中辅助线的作法——形成精准思维模式,快速解题◆类型一 遇弦过圆心作弦的垂线或连半径1.如图,以点O 为圆心的两个圆中,大圆的弦AB 切小圆于点C ,OA 交小圆于点D ,若OD =2,tan ∠OAB =12,则AB 的长是( ) A .4 B .23 C .8 D .43第1题图第2题图2.如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,⊙O的半径为________.◆类型二遇直径添加直径所对的圆周角3.如图,AB是⊙O的直径,C,D,E都是⊙O上的点,则∠ACE+∠BDE等于( )A.60°B.75°C.90°D.120°第3题图第4题图4.如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是________.5.如图,△ABC的顶点均在⊙O上,AD为⊙O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.类型三遇切线连接圆心和切点6.已知⊙O的半径为1,圆心O到直线l的距离为2,过l上任一点A作⊙O的切线,切点为B,则线段AB长度的最小值为( )A.1 B. 2 C. 3 D.27.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为________.8.★如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.(1)求证:∠ADC=∠ABD;(2)求证:AD2=AM·AB;(3)若AM =185,sin ∠ABD =35,求线段BN 的长.。
用面积法证明勾股定理

用面积法证明勾股定理勾股定理是数学中的一个重要定理,它是关于直角三角形的边与斜边之间的关系。
用面积法证明勾股定理是一种经典的证明方法,下面我将简要介绍这个证明过程。
设直角三角形的两条直角边分别为a和b,斜边为c。
我们将这个三角形放在一个长为a、宽为b的矩形内,如下图所示:```---------------| || ||-------------|```首先,我们计算矩形的面积,它等于长乘以宽,即为ab。
接下来,我们将直角三角形内部的直角边分别作为底边和高,可以得到两个矩形,这两个矩形的面积分别为a²和b²,如下图所示:```---------------| a || △ ||-------------|| b |```因此,整个直角三角形的面积等于两个矩形的面积之和,即ab = a² + b²。
进一步,我们观察到斜边c正好可以作为两个矩形的对角线,如下图所示:```---------------| a || △ ||-------------|| b || || ||-------------|```我们知道对角线的长度等于矩形两边长度的平方和开根号,即c = √(a² + b²)。
因此,我们通过面积法证明了勾股定理,即在直角三角形中,直角边的平方和等于斜边的平方,即a² + b² = c²。
这是一个简单而直观的证明方法,通过将直角三角形转化为矩形和计算面积的过程,我们得到了勾股定理的几何解释。
不仅能加深对勾股定理的理解,同时也能让我们以不同的方式思考数学问题。
勾股定理与三角形的面积关系

勾股定理与三角形的面积关系勾股定理是初中数学中最经典的定理之一,它关系到三角形的边长和角度之间的关系。
除此之外,勾股定理还能被应用于计算三角形的面积。
本文将探讨勾股定理与三角形面积的关系,并通过实例说明其应用。
一、勾股定理的定义及应用勾股定理,又称毕达哥拉斯定理,它的数学表述如下:在直角三角形中,直角的边长分别为a、b,斜边的边长为c,那么有a² + b² = c²。
利用勾股定理,我们能够求解未知边长的三角形。
以一个简单的例子来说明:假设我们有一个直角三角形,已知两条直角边的边长分别为3cm和4cm,求斜边的边长。
根据勾股定理,我们可以得出:a² + b² = c²3² + 4² = c²9 + 16 = c²25 = c²因此,斜边的边长c = √25 = 5cm。
通过勾股定理,我们成功求得了三角形的斜边的长度。
二、勾股定理与三角形面积的关系除了求解三角形边长外,勾股定理还能被应用于计算三角形的面积。
在讨论该关系之前,我们先来了解一下三角形的面积公式。
三角形的面积公式为:S = 1/2 ×底 ×高。
其中底表示三角形的底边长度,高表示底边上的高度。
在直角三角形中,底边与高分别为直角边和斜边上的高度。
因此,我们可以借助勾股定理来推导直角三角形的面积公式。
现假设直角三角形的两条直角边分别为a、b,斜边为c。
以a为底边,b为高,代入三角形的面积公式,我们有:S = 1/2 × a × b根据勾股定理,可以得到:c² = a² + b²解方程得到:a² = c² - b²将其代入面积公式,得到:S = 1/2 × (c² - b²) × b整理后可得:S = 1/2 × (c²b - b³)通过以上推导,我们得到了直角三角形面积与两个直角边的关系。
用面积证明勾股定理的原理

用面积证明勾股定理的原理面积证明勾股定理是一种通过对三角形各边的长度进行计算,来验证三条边符合勾股定理的方法。
该方法基于平行四边形面积的性质,可以通过计算三角形各边构成的平行四边形的面积关系,进而推导出勾股定理的原理。
为了证明勾股定理,我们先要了解平行四边形面积的性质。
平行四边形有两条对等的边与一条夹角,我们将这两条对等的边分别称为底边和高。
平行四边形的面积可以通过底边与高的乘积来计算,即S = 底边×高。
我们选取任意一个直角三角形ABC,假设直角边分别为a,b,斜边为c,且直角为C。
首先,我们以c为底边,构造一个平行于直角边a的线段DE,使它与直角边b和斜边c分别交于点D和点E,形成平行四边形ABED。
在这个平行四边形中,线段DE是底边,直角边a是高。
根据平行四边形的面积性质,我们可以计算平行四边形面积S' = DE ×a。
接下来,我们以直角边b为底边,构造一个线段FG,使它与直角边a和斜边c 分别交于点F和点G,形成平行四边形ACGF。
在这个平行四边形中,线段FG 是底边,直角边b是高。
同样地,根据平行四边形的面积性质,我们可以计算平行四边形面积S" = FG ×b。
由于ABED和ACGF是共用一对对等边的平行四边形,它们的面积应该相等,即S' = S"。
因此,我们可以得到以下等式:DE ×a = FG ×b我们将等式两边除以2,得到:(a ×DE) / 2 = (b ×FG) / 2由于直角三角形ABC的面积可以通过斜边c的一半和直角边a与b的乘积来计算,即S = (c ×a ×b) / 2,我们可以将等式转化为:S = S'将S'代入等式,我们可以得到:S = (a ×DE) / 2进一步地,我们可以将DE的长度用斜边c减去GF的长度得到,即DE = c - GF:S = (a ×(c - GF)) / 2通过化简,我们得到:2S = a ×(c - GF)进一步化简为:2S = ac - aGF由于GF的长度等于b,我们可以将等式转化为:2S = ac - ab经过重新排列,我们得到:2S + ab = ac进一步化简为:a²+ b²= c²这正是勾股定理的表达式。
勾股定理知识点与题型总结大全
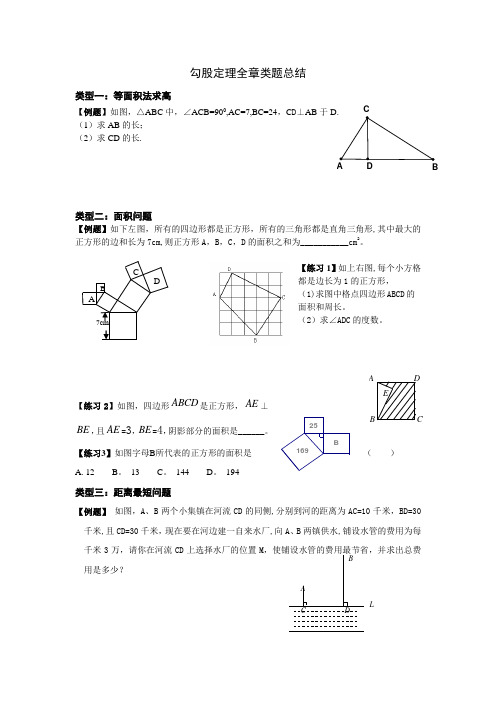
CA BD 勾股定理全章类题总结类型一:等面积法求高【例题】如图,△ABC 中,∠ACB=900,AC=7,BC=24,C D ⊥AB 于D. (1)求AB 的长; (2)求CD 的长.类型二:面积问题【例题】如下左图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A ,B ,C ,D 的面积之和为___________cm 2。
【练习1】如上右图,每个小方格都是边长为1的正方形, (1)求图中格点四边形ABCD 的面积和周长。
(2)求∠ADC 的度数。
【练习2】如图,四边形ABCD 是正方形,AE ⊥BE ,且AE =3,BE =4,阴影部分的面积是______。
【练习3】如图字母B 所代表的正方形的面积是( )A. 12 B 。
13 C 。
144 D 。
194类型三:距离最短问题【例题】 如图,A 、B 两个小集镇在河流CD 的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A 、B 两镇供水,铺设水管的费用为每千米3万,请你在河流CD 上选择水厂的位置M ,使铺设水管的费用最节省,并求出总费用是多少?ABCD7cmBD EB16925A BCDL【练习1】如图,一圆柱体的底面周长为20cm ,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,试求出爬行的最短路程.【练习2】如图,一个牧童在小河的南4km 的A 处牧马,而他正位于他的小屋B的西8km 北7km 处,他想把他的马牵到小河边去饮水,然后回家。
他要完成这件事情所走的最短路程是多少?类型四:判断三角形的形状【例题】如果ΔABC 的三边分别为a 、b 、c ,且满足a 2+b 2+c 2+50=6a+8b+10c ,判断ΔABC 的形状.【练习1】已知△ABC 的三边分别为m 2-n 2,2mn ,m 2+n 2(m,n 为正整数,且m >n),判断△ABC 是否为直角三角形。
《勾股定理》典型练习题

《勾股定理》典型例题分析二、考点剖析考点一:利用勾股定理求面积1、求阴影部分面积:(1)阴影部分是正方形;(2)阴影部分是长方形;(3)阴影部分是半圆.2。
如图,以Rt△ABC的三边为直径分别向外作三个半圆,试探索三个半圆的面积之间的关系.3、如图所示,分别以直角三角形的三边向外作三个正三角形,其面积分别是S1、S 2、S3,则它们之间的关系是( )A.S1—S2= S3 B.S1+ S2= S3C.S2+S3〈S1 D。
S2—S3=S14、四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积。
5、在直线l上依次摆放着七个正方形(如图4所示)。
已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S S12、、S S S S S S341234、,则+++=_____________。
考点二:在直角三角形中,已知两边求第三边1.在直角三角形中,若两直角边的长分别为1cm,2cm ,则斜边长为. 2.(易错题、注意分类的思想)已知直角三角形的两边长为3、2,则另一条边长的平方是3、已知直角三角形两直角边长分别为5和12, 求斜边上的高.4、把直角三角形的两条直角边同时扩大到原来的2倍,则斜边扩大到原来的()A.2倍ﻩﻩB.4倍ﻩC. 6倍ﻩﻩﻩD.8倍5、在Rt△ABC中,∠C=90°①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则Rt△ABC的面积是=________。
6、如果直角三角形的两直角边长分别为1n2-,2n(n〉1),那么它的斜边长是( )A、2nﻩﻩB、n+1ﻩ C、n2-1ﻩD、1n2+7、在Rt△ABC中,a,b,c为三边长,则下列关系中正确的是( )A。
勾股定理与三角形的面积比较利用比例关系解题

勾股定理与三角形的面积比较利用比例关系解题在数学中,勾股定理是一条重要的定理,它描述了直角三角形中直角边的平方和等于斜边的平方。
本文将探讨如何利用勾股定理及比例关系来解决三角形面积的问题。
1. 勾股定理的介绍勾股定理是古希腊数学家毕达哥拉斯在公元前6世纪发现的定理,它被广泛应用于几何学和物理学中。
勾股定理的表达方式为:在直角三角形中,直角边的平方和等于斜边的平方,即a^2 + b^2 = c^2。
2. 利用勾股定理解决三角形面积问题在解决三角形面积的问题时,我们可以利用勾股定理来计算三角形的边长,进而求得三角形的面积。
以一个直角三角形为例,假设直角边的长度分别为a和b,斜边的长度为c。
根据勾股定理可知,a^2 + b^2 = c^2。
假设三角形的底边长度为x,高边长度为y,则三角形的面积可表示为S = 0.5xy。
我们可以通过比例关系来求解x和y的值。
由于三角形的面积与底边和高边成正比,可以利用比例关系建立方程:x:y = a:b。
通过求解比例关系方程,我们可以得到x和y的具体值。
进而代入面积公式S = 0.5xy中,即可得到三角形的面积。
3. 例题解析假设有一个直角三角形,直角边的长度分别为3和4,求该三角形的面积。
根据勾股定理,斜边的长度可计算为c = √(3^2 + 4^2) = 5。
根据比例关系,我们可以得到x:y = a:b = 3:4。
由此可知,x = (3/4) * 5 = 3.75,y = (4/3) * 5 = 6.67。
代入面积公式S = 0.5xy,即可得到该直角三角形的面积为S = 0.5 *3.75 * 6.67 = 12.5。
4. 总结通过利用勾股定理及比例关系解决三角形面积问题,我们可以简化计算过程并获得准确的结果。
在实际应用中,勾股定理及比例关系经常被用于解决各种几何问题,它们的应用范围十分广泛。
以上便是利用比例关系解题时,结合勾股定理计算三角形面积的方法和步骤。
勾股定理与面积问题(初中数学)

第 1 页 共 1 页
典例论坛
勾股定理与面积问题
例题呈现
如图1,直角三角形三边的半圆面积之间有什么关系?
图1
命题意图:本题考查应用勾股定理判断三个半圆面积之间的数量关系.
思路点拨:设出三角形的三边长,根据圆的面积公式求出三个半圆的面积,由勾股定理求出三边之间的关系,即可得出答案.
解:
变式训练:
1.
图2是由两个直角三角形和三个正方形组成的图形.其中两正方形面积分别是S 1=22,S 2=14,AC=
10,则AB=
.
图2 图3
思路点拨:由勾股定理可求出S 3,进一步应用勾股定理求得结果.
解: .
2. 如图3,在Rt △ABC 中,∠C =90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,当AC =4,BC =2时,则阴影部分的面积为( )
A .4
B .4π
C .8π
D .8
思路点拨:根据勾股定理,得AB 2=AC 2+BC 2,由“阴影部分面积=两个小半圆面积之和+△ABC 的面积-大半圆的面积”可求得结果.
解: .
参考答案:【例题呈现】设直角三角形的直角边长分别为a ,b ,斜边长为c ,根据勾股定理,得a 2+b 2=c 2.
表示出斜边上及直角边上的半圆面积,可得出斜边上半圆的面积等于两直角边上的半圆面积之和. 变式训练:1.8 2.A。
利用三角形面积公式证明勾股定理

利用三角形面积公式证明勾股定理在几何学中,勾股定理是一个基本而重要的定理,它揭示了直角三角形的边之间的关系。
本文将利用三角形的面积公式,来证明勾股定理。
为了表达清晰,我们设直角三角形的斜边长为c,直角边长分别为a和b。
根据三角形的面积公式,三角形的面积等于底边乘以高再除以2。
我们可以将直角三角形分为两个直角三角形,分别以a和b作为底边,c作为高。
首先,我们以a作为底边,c作为高来计算三角形的面积。
根据面积公式,这个三角形的面积为:S1 = (a * c) / 2接下来,我们以b作为底边,c作为高来计算三角形的面积。
根据面积公式,这个三角形的面积为:S2 = (b * c) / 2由于直角三角形可以完全由这两个直角三角形组成,所以整个直角三角形的面积即为这两个部分面积的和:S = S1 + S2= (a * c) / 2 + (b * c) / 2= (a * c + b * c) / 2= (a + b) * c / 2然而,我们知道直角三角形的面积也可以由其两条直角边长计算得出。
根据三角形的面积公式,三角形的面积等于底边乘以高再除以2。
以a和b作为直角边,c作为斜边,直角三角形的面积为:S = (a * b) / 2由此可得:(a + b) * c / 2 = (a * b) / 2为了方便推导,我们将上述等式两边同时乘以2,得到:(a + b) * c = a * b进一步展开推导:a * c +b *c = a * ba * c = a *b - b * ca * c =b * (a - c)a / (a - c) =b / c根据相似三角形的性质,如果两个三角形中对应角相等,那么对应边的比例也相等。
因此,在直角三角形ABC中,我们可以得到两个相似三角形ABC和ACD:∠ABC = ∠ACD根据相似三角形的性质:a / (a - c) =b / c通过移项和分数化简,我们可以得到:a /b =c / (a - c)根据比例的性质,如果两个比例相等,其倒数也相等。
利用勾股定理求图形的面积

利用勾股定理求图形的面积江苏刘顿众所周知,勾股定理是我国古代科学文化的一颗明珠,是极其重要的几何定理,它揭示了直角三角形的三边之间的平方关系,对于解决一些与直角三角形相关的问题起到不可低估的作用.下面就运用勾股定理处理图形的面积问题举几例说明.例1已知直角三角形的斜边的长为13,两直角边之比为5∶12.求它的面积.分析与解由于已知直角三角形的斜边的长为13,两直角边之比为5∶12,所以可设两直角边分别为5x、12x,则由勾股定理,得(5x)2+(12x)2=132,解得x=1.即5x=5,12x=12,所以这个直角三角形的面积为12×5×12=30.说明利用勾股定理求得的x有一个负值,应及时将其舍去.例2等腰△ABC的腰长AB=10cm,底BC为16cm,试求这个等腰三角形的面积.分析与解若能求出这个等腰三角形底边上的高,即可顺利地求出其面积了.而由等腰三角形的“三线合一”性质,可以作出底边上的高AD,此时点D也是BC边上的中点,于是在Rt△ABD中,由勾股定理,得AD2=AB2-BD2=102-82=36,所以AD=6.所以这个等腰三角形的面积为12×8×6=24.说明灵活运用等腰三角形和勾股定理的知识是求解本题的关键.例3直角三角形的斜边长为1.5cm,周长为3.6cm,求这个直角三角形的面积.分析与解两直角边长之和为3.6-1.5=2.1,设一条直角边长x,则另一条直角边长为2.1-x,由勾股定理得:x2+(2.1-x)2=1.52,将会用到一元二次方程,没学过.但考虑到关系式(a+b)2=a2+b2+2ab=c2+4S△,即S△=14[ (a+b)2-c2]=14(2.12-1.52)=0.054.所以这个直角三角形的面积是0.054cm2.说明利用关系式(a+b)2=a2+b2+2ab=c2+4S△,这说明两直角边的和、斜边的长和三角形的面积之间存在联系.同样地,在上述三个量中已知两个量可以求出第三个量.例4已知四边形ABCD中,AD∥BC,∠A=90°,AB=8,AD=4,BC=6,试求以DC为边的正方形面积.分析与解依据题意可画出如图所示的图形.要求以DC为边的正方形面积,只要求出DC2,此时可以过点D作DE⊥BC于点E,于是DE=AB=8,BE=AD=4,即CE=2,在Rt△DEC中,由勾股定理,得DC2=DE2+CE2=82+22=68.即以DC为边的正方形面积68.说明正确地画出图形可以降低求解的难度.B C D E 图1 A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解题技巧专题:勾股定理与面积问题
——全方位求面积,一网搜罗
◆类型一 三角形中利用面积法求高
1.直角三角形的两条直角边的长分别为5cm ,12cm ,则斜边上的高线的长为( ) A.8013cm B .13cm C.132cm D.6013cm
2.(2017·乐山中考)点A 、B 、C 在格点图中的位置如图所示,格点小正方形的边长为1,则点C 到线段AB 所在直线的距离是________.
◆类型二 结合乘法公式巧求面积或长度
3.已知Rt △ABC 中,∠C =90°,若a +b =12cm ,c =10cm ,则Rt △ABC 的面积是( )
A .48cm 2
B .24cm 2
C .16cm 2
D .11cm 2
4.若一个直角三角形的面积为6cm 2,斜边长为5cm ,则该直角三角形的周长是( )
A .7cm
B .10cm
C .(5+37)cm
D .12cm
5.(2017·襄阳中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b ,若(a +b)2=21,大正方形的面积为13,则小正方形的面积为( )
A .3
B .4
C .5
D .6
◆类型三 巧妙利用割补法求面积
6.如图,已知AB =5,BC =12,CD =13,DA =10,AB ⊥BC ,求四边形ABCD 的面积.
7.如图,∠B =∠D =90°,∠A =60°,AB =4,CD =2,求四边形ABCD 的面积.【方法6】
◆类型四 利用“勾股树”或“勾股弦图”求面积
8.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm ,则正方形A ,B ,C ,D 的面积之和为________cm 2.
参考答案与解析
1.D
2. 35
5 解析:如图,连接AC ,BC ,设点C 到线段AB 所在直线的距离是h .∵S △ABC =3×3-12×2×1-12×2×1-12×3×3-1=9-1-1-92-1=32,AB =12+22=5,∴12×5h =32,∴h =355.故答案为355
.
3.D 4.D 5.C
6.解:连接AC ,过点C 作CE ⊥AD 交AD 于点E .∵AB ⊥BC ,∴∠CBA =90°.在Rt △ABC 中,由勾股定理得AC =AB 2+BC 2=52+122=13.∵CD =13,∴AC =CD .∵CE ⊥AD ,∴AE =12AD =12
×10=5.在Rt △ACE 中,由勾股定理得CE =AC 2-AE 2=132-52=12.∴S 四边形ABCD =S △ABC +S △CAD =12AB ·BC +12AD ·CE =12×5×12+12
×10×12=90. 7.解:延长AD ,BC 交于点E .∵∠B =90°,∠A =60°,∴∠E =30°.∴AE =2AB =8.在Rt △ABE 中,由勾股定理得BE =AE 2-AB 2=82-42=4 3.∵∠ADC =90°,∴∠CDE =90°,∴CE =2CD =4.在Rt △CDE 中,由勾股定理得DE =CE 2-DC 2=42-22=2 3.∴S
四边形ABCD =S △ABE -S △CDE =12AB ·BE -12CD ·DE =12×4×43-12
×2×23=6 3. 8.81。
