中考数学解题技巧专题:勾股定理与面积问题
中考数学几何模型专题专题六—勾股定理
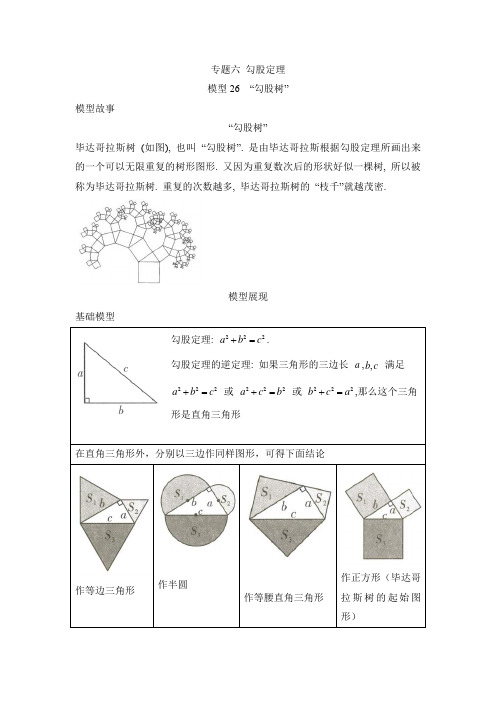
专题六勾股定理模型26 “勾股树”模型故事“勾股树”毕达哥拉斯树(如图), 也叫“勾股树”. 是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形. 又因为重复数次后的形状好似一棵树, 所以被称为毕达哥拉斯树. 重复的次数越多, 毕达哥拉斯树的“枝千”就越茂密.模型展现基础模型勾股定理: 222a b c+=.勾股定理的逆定理: 如果三角形的三边长a,,b c满足222a b c+=或222a c b+=或222b c a+=,那么这个三角形是直角三角形在直角三角形外,分别以三边作同样图形,可得下面结论作等边三角形作半圆作等腰直角三角形作正方形(毕达哥拉斯树的起始图形)怎么用?1. 找模型分别以直角三角形三边为边作相同图形2. 用模型根据勾股定理的关系及等式性质求解, 常用来解决面积问题结论分析:结论: 123S S S +=以作等边三角形为例.证明: 如解图, 过点 D 作 DM AC ⊥ 于点 M ,ACD 是等边三角形, 12AM MC b ∴==, 在 Rt ADM 中, 3tan tan602DM AM DAC AM b ∠=⋅=⋅=, 2111332224S DM AC b b b ∴=⋅⋅=⋅⋅=, 同理可得, 222333,44S a S c ==, ()222212333444S S a b a b ∴+=+=+, Rt ABC 满足 222a b c +=,()222123344S S a b c ∴+=+=.123.S S S ∴+=拓展延伸其余图形的证明, 均是用面积的计算, 然后求和即可, 同学们可以参考给出的证明过程, 自行完成.满分技法以三边分别为边作相同的图形, 解题的基本思想是勾股定理, 但所作图形的性质也是解题的关键.勾股数中常见图形面积公式:1 ;2S =⨯⨯三角形底高2 S =等边三角形边长; 21;2360n r S π=⨯半圆 2 S =正方形边长典例小试例 1 如图,和 AC 为直径的半圆的面积(与模型的作图方法一致), 则123,S S S 和满足的关系式(求面积,可使用结论)为( )A . 123S S S +=B . 123S S S =+C . 123S S S >+D . 123S S S =⋅考什么?圆的面积计算,勾股定理思路点拨满足模型,选填项目中,可直接使用结论,高效解题。
中考数学勾股定理(讲义及答案)附解析

一、选择题1.如图,在ABC ∆中,,90︒=∠=AB AC BAC ,ABC ∠的平分线BD 与边AC 相交于点D ,DE BC ⊥,垂足为E ,若CDE ∆的周长为6,则ABC ∆的面积为( ).A .36B .18C .12D .9 2.如图所示,在中,,,.分别以,,为直径作半圆(以为直径的半圆恰好经过点,则图中阴影部分的面积是( )A .4B .5C .7D .63.如图,在等腰Rt ABC △中,908C AC ∠==°,,F 是AB 边上的中点,点D 、E 分别在AC 、BC 边上运动,且保持AD CE =.连接DE 、DF 、EF .在此运动变化的过程中,下列结论:①DFE △是等腰直角三角形;②四边形CDFE 不可能为正方形;③DE 长度的最小值为4;④四边形CDFE 的面积保持不变;⑤△CDE 面积的最大值为8.其中正确的结论是( )A .①④⑤B .③④⑤C .①③④D .①②③4.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为S 1、S 2、S 3.若S 1+S 2+S 3=15,则S 2的值是( )A .3B .154C .5D .1525.若直角三角形的三边长分别为-a b 、a 、+a b ,且a 、b 都是正整数,则三角形其中一边的长可能为()A .22B .32C .62D .826.如图,A 、B 两点在直线l 的两侧,点A 到直线l 的距离AC=4,点B 到直线l 的距离BD=2,且CD=6,P 为直线CD 上的动点, 则PA PB -的最大值是( )A .62B .22C .210D .67.如图,在△ABC 中,∠ACB =90°,AB 的中垂线交AC 于D ,P 是BD 的中点,若BC =4,AC =8,则S △PBC 为( )A .3B .3.3C .4D .4.58.将一根 24cm 的筷子,置于底面直径为 15cm ,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm ,则 h 的取值范围是( )A .h≤15cmB .h≥8cmC .8cm≤h≤17cmD .7cm≤h≤16cm9.如图,在矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,点B 落在点B ′处,则重叠部分△AFC 的面积为( )A .12B .10C .8D .610.有下列的判断: ①△ABC 中,如果a 2+b 2≠c 2,那么△ABC 不是直角三角形②△ABC 中,如果a 2-b 2=c 2,那么△ABC 是直角三角形③如果△ABC 是直角三角形,那么a 2+b 2=c 2以下说法正确的是( )A .①②B .②③C .①③D .②二、填空题11.如图是一个三级台阶,它的每一级的长、宽和高分别为5 dm 、3 dm 和1 dm ,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物.请你想一想,这只蚂蚁从A 点出发,沿着台阶面爬到B 点的最短路程是 dm .12.如图所示的网格是正方形网格,则ABC ACB ∠+∠=__________°(点A ,B ,C 是网格线交点).13.如图,在△ABC 中,OA =4,OB =3,C 点与A 点关于直线OB 对称,动点P 、Q 分别在线段AC 、AB 上(点P 不与点A 、C 重合),满足∠BPQ =∠BAO.当△PQB 为等腰三角形时,OP 的长度是_____.14.如图,在ABC 中,D 是BC 边中点,106AB AC ==,,4=AD ,则BC 的长是_____________.15.在ABC ∆中,90BAC ∠=︒,以BC 为斜边作等腰直角BCD ∆,连接DA ,若22AB =,42AC =,则DA 的长为______.16.如图在三角形纸片ABC 中,已知∠ABC =90º,AC =5,BC=4,过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的点P 处,折痕为MN ,当点P 在直线l 上移动时,折痕的端点M 、N 也随之移动,若限定端点M 、N 分别在AB 、BC 边上(包括端点)移动,则线段AP 长度的最大值与最小值的差为________________.17.如图,30AOB ∠=︒,点,M N 分别在,OA OB 上,且6,8OM ON ==,点,P Q 分别在,OB OA 上运动,则PM PQ QN ++的最小值为______.18.如图,△ABC 中,AB=AC=13,BC=10,AD 是BAC ∠的角平分线,E 是AD 上的动点,F 是AB 边上的动点,则BE+EF 的最小值为_____.19.在ABC 中,12AB AC ==,30A ∠=︒,点E 是AB 中点,点D 在AC 上,32DE =,将ADE 沿着DE 翻折,点A 的对应点是点F ,直线EF 与AC 交于点G ,那么DGF △的面积=__________.20.如图,在等腰△ABC 中,AB =AC ,底边BC 上的高AD =6cm ,腰AC 上的高BE =4m ,则△ABC 的面积为_____cm 2.三、解答题21.在等边ABC 中,点D 是线段BC 的中点,120,EDF DE ∠=︒与线段AB 相交于点,E DF 与射线AC 相交于点F .()1如图1,若DF AC ⊥,垂足为,4,F AB =求BE 的长;()2如图2,将()1中的EDF ∠绕点D 顺时针旋转一定的角度,DF 仍与线段AC 相交于点F .求证:12BE CF AB +=.()3如图3,将()2中的EDF ∠继续绕点D 顺时针旋转一定的角度,使DF 与线段AC 的延长线交于点,F 作DN AC ⊥于点N ,若,DN FN =设,BE x CF y ==,写出y 关于x 的函数关系式.22.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .(1)若∠AED =20°,则∠DEC = 度;(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.23.如图,在边长为2的等边三角形ABC 中,D 点在边BC 上运动(不与B ,C 重合),点E 在边AB 的延长线上,点F 在边AC 的延长线上,AD DE DF ==. (1)若30AED ∠=︒,则ADB =∠______.(2)求证:BED CDF △≌△.(3)试说明点D 在BC 边上从点B 至点C 的运动过程中,BED 的周长l 是否发生变化?若不变,请求出l 的值,若变,请求出l 的取值范围.24.在等腰Rt △ABC 中,AB =AC ,∠BAC =90°(1)如图1,D ,E 是等腰Rt △ABC 斜边BC 上两动点,且∠DAE =45°,将△ABE 绕点A 逆时针旋转90后,得到△AFC ,连接DF①求证:△AED ≌△AFD ;②当BE =3,CE =7时,求DE 的长;(2)如图2,点D 是等腰Rt △ABC 斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt △ADE ,当BD =3,BC =9时,求DE 的长.25.如图,△ACB 和△ECD 都是等腰直角三角形,∠ACB =∠ECD =90°,点D 在边AB 上,点E 在边AC 的左侧,连接AE .(1)求证:AE =BD ;(2)试探究线段AD 、BD 与CD 之间的数量关系;(3)过点C 作CF ⊥DE 交AB 于点F ,若BD :AF =1:2,CD 36,求线段AB 的长.26.如图, ABD 为边长不变的等腰直角三角形,AB AD =,90BAD ∠=︒,在 ABD外取一点 E ,以A 为直角顶点作等腰直角AEP △,其中 P 在 ABD 内部,90EAP ∠=︒,2AE AP ==,当E 、P 、D 三点共线时,7BP =.下列结论:①E 、P 、D 共线时,点B 到直线AE 的距离为5;②E 、P 、D 共线时, 13ADP ABP S S ∆∆+=+;=532ABD S ∆+③; ④作点 A 关于 BD 的对称点 C ,在 AEP 绕点 A 旋转的过程中,PC 的最小值为5+232-;⑤AEP △绕点A 旋转,当点E 落在AB 上,当点P 落在AD 上时,取BP 上一点N ,使得AN BN =,连接 ED ,则AN ED ⊥.其中正确结论的序号是___.27.如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为k . (1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题?(2)已知ABC 为优三角形,AB c =,AC b =,BC a =,①如图1,若90ACB ∠=︒,b a ≥,6b =,求a 的值.②如图2,若c b a ≥≥,求优比k 的取值范围.(3)已知ABC 是优三角形,且120ABC ∠=︒,4BC =,求ABC 的面积.28.(1)如图1,在Rt ABC ∆中,90ACB ∠=︒,60A ∠=︒,CD 平分ACB ∠.求证:CA AD BC +=.小明为解决上面的问题作了如下思考:作ADC ∆关于直线CD 的对称图形A DC '∆,∵CD 平分ACB ∠,∴A '点落在CB 上,且CA CA '=,A D AD '=.因此,要证的问题转化为只要证出A D A B ''=即可.请根据小明的思考,写出该问题完整的证明过程.(2)参照(1)中小明的思考方法,解答下列问题:如图3,在四边形ABCD 中,AC 平分BAD ∠,10BC CD ==,17AC =,9AD =,求AB 的长.29.已知ABC ∆中,90ACB ∠=︒,AC BC =,过顶点A 作射线AP .(1)当射线AP 在BAC ∠外部时,如图①,点D 在射线AP 上,连结CD 、BD ,已知21AD n =-,21AB n =+,2BD n =(1n >).①试证明ABD ∆是直角三角形;②求线段CD 的长.(用含n 的代数式表示)(2)当射线AP 在BAC ∠内部时,如图②,过点B 作BD AP ⊥于点D ,连结CD ,请写出线段AD 、BD 、CD 的数量关系,并说明理由.30.定义:在△ABC 中,若BC =a ,AC =b ,AB =c ,若a ,b ,c 满足ac +a 2=b 2,则称这个三角形为“类勾股三角形”,请根据以上定义解决下列问题:(1)命题“直角三角形都是类勾股三角形”是 命题(填“真”或“假”);(2)如图1,若等腰三角形ABC 是“类勾股三角形”,其中AB =BC ,AC >AB ,请求∠A 的度数;(3)如图2,在△ABC 中,∠B =2∠A ,且∠C >∠A .①当∠A =32°时,你能把这个三角形分成两个等腰三角形吗?若能,请在图2中画出分割线,并标注被分割后的两个等腰三角形的顶角的度数;若不能,请说明理由; ②请证明△ABC 为“类勾股三角形”.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】利用角平分定理得到DE=AD ,根据三角形内角和得到∠BDE=∠BDA ,再利用角平分线定理得到BE=AB=AC ,根据CDE ∆的周长为6求出AB=6,再根据勾股定理求出218AB =,即可求得ABC ∆的面积.【详解】∵90BAC ︒∠=,∴AB ⊥AD,∵DE BC ⊥,BD 平分ABC ∠,∴DE=AD ,∠BED=90BAC ︒∠=,∴∠BDE=∠BDA ,∴BE=AB=AC ,∵CDE ∆的周长为6,∴DE+CD+CE=AC+CE=BC=6,∵,90︒=∠=AB AC BAC∴22236AB AC BC +==,∴2236AB =, 218AB =,∴ABC ∆的面积=211922AB AC AB ⋅⋅==, 故选:D.【点睛】此题考查角平分线定理的运用,勾股定理求边长,在利用角平分线定理时必须是两个垂直一个平分同时运用,得到到角两边的距离相等的结论. 2.D解析:D【解析】【分析】先利用勾股定理计算BC 的长度,然后阴影部分的面积=以AB 为直径的半圆面积+以BC 为直径的半圆面积+-以AC 为直径的半圆面积. 【详解】解:在中 ∵,, ∴, ∴BC=3,∴阴影部分的面积=以AB 为直径的半圆面积+以BC 为直径的半圆面积+-以AC 为直径的半圆面积=6.故选D. 【点睛】本题考查扇形面积的计算和勾股定理.在本题中解题关键是用重叠法去表示阴影部分的面积. 3.A解析:A【分析】作常规辅助线连接CF ,由SAS 定理可证△CFE 和△ADF 全等,从而可证∠DFE=90°,DF=EF .所以△DEF 是等腰直角三角形;由割补法可知四边形CDFE 的面积保持不变;△DEF 是等腰直角三角形2DF ,当DF 与BC 垂直,即DF 最小时,DE 取最小值42,△CDE 最大的面积等于四边形CDEF 的面积减去△DEF 的最小面积.【详解】连接CF;∵△ABC是等腰直角三角形,∴∠FCB=∠A=45°,CF=AF=FB;∵AD=CE,∴△ADF≌△CEF;∴EF=DF,∠CFE=∠AFD;∵∠AFD+∠CFD=90°,∴∠CFE+∠CFD=∠EFD=90°,∴△EDF是等腰直角三角形.当D. E分别为AC、BC中点时,四边形CDFE是正方形.∵△ADF≌△CEF,∴S△CEF=S△ADF,∴S四边形CEFD=S△AFC.由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;即当DF⊥AC时,DE最小,此时DF=12BC=4.∴22当△CEF面积最大时,此时△DEF的面积最小.此时S△CEF=S四边形CEFD−S△DEF=S△AFC−S△DEF=16−8=8,则结论正确的是①④⑤.故选A.【点睛】本题考查全等三角形的判定与性质, 等腰直角三角形性质.要证明线段或者角相等,一般证明它们所在三角形全等,如果不存在三角形可作辅助线解决问题.4.C解析:C【解析】将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=15,∴得出S1=8y+x,S2=4y+x,S3=x,∴S1+S2+S3=3x+12y=15,即3x+12y=15,x+4y=5,所以S2=x+4y=5,故答案为5.点睛:将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,用x,y表示出S 1,S 2,S 3,再利用S 1+S 2+S 3=15求解是解决问题的关键.5.B解析:B【解析】由题可知(a-b )2+a 2=(a+b )2,解得a=4b ,所以直角三角形三边分别为3b ,4b ,5b ,当b=8时,4b=32,故选B .6.C解析:C【解析】试题解析:作点B 关于直线l 的对称点B ',连接AB '并延长,与直线l 的交点即为使得PA PB -取最大值时对应的点.P此时.PA PB PA PB AB -=-'='过点B '作B E AC '⊥于点,E 如图,四边形B DCE '为矩形,6, 2.B E CD EC B D BD ∴=====''2.AE ∴=22210.AB AE B E ''+=PA PB -的最大值为:210.故答案为:210.7.A解析:A【分析】根据线段垂直平分线的性质得到DA=DB ,根据勾股定理求出BD ,得到CD 的长,根据三角形的面积公式计算,得到答案.【详解】解:∵点D在线段AB的垂直平分线上,∴DA=DB,在Rt△BCD中,BC2+CD2=BD2,即42+(8﹣BD)2=BD2,解得,BD=5,∴CD=8﹣5=3,∴△BCD的面积=12×CD×BC=12×3×4=6,∵P是BD的中点,∴S△PBC=12S△BCD=3,故选:A.【点睛】本题考查的是线段垂直平分线的性质、直角三角形的性质、勾股定理,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.8.C解析:C【分析】筷子浸没在水中的最短距离为水杯高度,最长距离如下图,是筷子斜卧于杯中时,利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时,筷子浸没水中距离最短,为杯高=8cmAD是筷子,AB长是杯子直径,BC是杯子高,当筷子如下图斜卧于杯中时,浸没在水中的距离最长由题意得:AB=15cm,BC=8cm,△ABC是直角三角形∴在Rt△ABC中,根据勾股定理,AC=17cm∴8cm≤h≤17cm故选:C【点睛】本题考查勾股定理在实际生活中的应用,解题关键是将题干中生活实例抽象成数学模型,然后再利用相关知识求解.9.B解析:B【分析】已知AD 为CF 边上的高,要求AFC △的面积,求得FC 即可,求证AFD CFB '△≌△,得B F DF '=,设DF x =,则在Rt AFD △中,根据勾股定理求x ,于是得到CF CD DF =-,即可得到答案.【详解】解:由翻折变换的性质可知,AFD CFB '△≌△,'DF B F ∴=,设DF x =,则8AF CF x ==-,在Rt AFD △中,222AF DF AD =+,即222(8)4x x -=+,解得:3x =,835CF CD FD ∴=-=-=, 1102AFC S AF BC ∴=⋅⋅=△. 故选:B .【点睛】本题考查矩形的性质、折叠的性质、勾股定理等内容,根据折叠的性质得到AFD CFB '△≌△是解题的关键.10.D解析:D【分析】欲判断三角形是否为直角三角形,这里给出三边的长,需要验证两小边的平方和等于最长边的平方即可.【详解】①c 不一定是斜边,故错误;②正确;③若△ABC 是直角三角形,c 不是斜边,则a 2+b 2≠c 2,故错误,所以正确的只有②,故选D.【点睛】本题考查了勾股定理以及勾股定理的逆定理,熟练掌握勾股定理以及勾股定理的逆定理的内容是解题的关键.二、填空题11.【解析】试题分析:将台阶展开,如图,331312,5,AC BC =⨯+⨯==222169,AB AC BC ∴=+=13,AB ∴=即蚂蚁爬行的最短线路为13.dm考点:平面展开:最短路径问题.12.45【分析】如下图,延长BA 至网络中的点D 处,连接CD. ABC ACB DAC ∠+∠=∠,只需证△ADC 是等腰直角三角形即可【详解】如下图,延长BA 至网络中的点D 处,连接CD设正方形网络每一小格的长度为1则根据网络,555BC=5,∴5其中BD 、DC 、BC 边长满足勾股定理逆定理∴∠CDA=90°∵AD=DC∴△ADC 是等腰直角三角形∴∠DAC=45°故答案为:45°【点睛】本题是在网格中考察勾股定理的逆定理,解题关键是延长BA ,构造处△ABC 的外角∠CAD13.1或78【分析】 分为三种情况:①PQ BP =,②BQ QP =,③BQ BP =,由等腰三角形的性质和勾股定理可求解.【详解】解:分为3种情况:①当PB PQ =时,4=OA ,3OB =,∴5BC AB ===, C 点与A 点关于直线OB 对称,BAO BCO ∴∠=∠,BPQ BAO ∠=∠,BPQ BCO ∴∠=∠,APB APQ BPQ BCO CBP ∠=∠+∠=∠+∠,APQ CBP ∴∠=∠,在APQ 和CBP 中,BAO BCP APQ B PQ B P C P ∠=∠⎧⎪∠=∠⎨=⎪⎩, ()APQ CBP AAS ∴△≌△,∴5AP BC ==,1OP AP OA ∴=-=;②当BQ BP =时,BPQ BQP ∠=∠,BPQ BAO ∠=∠,BAO BQP ∴∠=∠,根据三角形外角性质得:BQP BAO ∠>∠,∴这种情况不存在;③当QB QP =时,QBP BPQ BAO ∠=∠=∠,PB PA ∴=,设OP x =,则4PB PA x ==-在Rt OBP △中,222PB OP OB =+,222(4)3x x ∴-=+, 解得:78x =; ∴当PQB △为等腰三角形时,1OP =或78; 【点睛】本题考查了勾股定理,等腰三角形的性质,全等三角形的性质和判定的应用,解题的关键是熟练掌握所学的性质进行解题,注意分类讨论.14.【分析】延长AD至点E,使得DE=AD=4,结合D是中点证得△ADC≌△EDB,进而利用勾股定理逆定理可证得∠E=90°,再利用勾股定理求得BD长进而转化为BC长即可.【详解】解:如图,延长AD至点E,使得DE=AD=4,连接BE,∵D是BC边中点,∴BD=CD,又∵DE=AD,∠ADC=∠EDB,∴△ADC≌△EDB(SAS),∴BE=AC=6,又∵AB=10,∴AE2+BE2=AB2,∴∠E=90°,∴在Rt△BED中,2222=++=,BD BE DE64213∴BC=2BD=13故答案为:13【点睛】本题考查了全等三角形的判定及性质、勾股定理及其逆定理,正确作出辅助线是解决本题的关键.15.6或2.【分析】由于已知没有图形,当Rt△ABC固定后,根据“以BC为斜边作等腰直角△BCD”可知分两种情况讨论:①当D点在BC上方时,如图1,把△ABD绕点D逆时针旋转90°得到△DCE,证明A、C、E三点共线,在等腰Rt△ADE中,利用勾股定理可求AD长;②当D点在BC下方时,如图2,把△BAD绕点D顺时针旋转90°得到△CED,证明过程类似于①求解.【详解】解:分两种情况讨论:①当D点在BC上方时,如图1所示,把△ABD绕点D逆时针旋转90°,得到△DCE,则∠ABD=∠ECD,2,AD=DE,且∠ADE=90°在四边形ACDB中,∠BAC+∠BDC=90°+90°=180°,∴∠ABD+∠ACD=360°-180°=180°,∴∠ACD+∠ECD=180°,∴A、C、E三点共线.∴AE=AC+CE=42+22=62在等腰Rt△ADE中,AD2+DE2=AE2,即2AD2=(62)2,解得AD=6②当D点在BC下方时,如图2所示,把△BAD绕点D顺时针旋转90°得到△CED,则CE=AB=22,∠BAD=∠CED,AD=AE且∠ADE=90°,所以∠EAD=∠AED=45°,∴∠BAD=90°+45°=135°,即∠CED=135°,∴∠CED+∠AED=180°,即A、E、C三点共线.∴AE=AC-CE=42-22=22在等腰Rt△ADE中,2AD2=AE2=8,解得AD=2.故答案为:6或2.【点睛】本题主要考查了旋转的性质、勾股定理,解决这类等边(或共边)的两个三角形问题,一般是通过旋转的方式作辅助线,转化线段使得已知线段于一个特殊三角形中进行求解.1671【分析】分别找到两个极端,当M与A重合时,AP取最大值,当点N与C重合时,AP取最小,即可求出线段AP长度的最大值与最小值之差【详解】如图所示,当M 与A 重合时,AP 取最大值,此时标记为P 1,由折叠的性质易得四边形AP 1NB 是正方形,在Rt △ABC 中,2222AB=AC BC =54=3--,∴AP 的最大值为A P 1=AB=3如图所示,当点N 与C 重合时,AP 取最小,过C 点作CD ⊥直线l 于点D ,可得矩形ABCD ,∴CD=AB=3,AD=BC=4,由折叠的性质有PC=BC=4,在Rt △PCD 中,2222PD=PC CD =43=7--,∴AP 的最小值为AD PD=47-线段AP 长度的最大值与最小值之差为(1AP AP=347=71-- 71【点睛】本题考查勾股定理的折叠问题,可以动手实际操作进行探索.17.10【分析】首先作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M ′N ′,即为MP +PQ +QN 的最小值,易得△ONN ′为等边三角形,△OMM ′为等边三角形,∠N ′OM ′=90°,继而可以求得答案.【详解】作M 关于OB 的对称点M ′,作N 关于OA 的对称点N ′,连接M ′N ′,即为MP +PQ +QN 的最小值.根据轴对称的定义可知:∠N ′OQ =∠M ′OB =30°,∠ONN ′=60°,OM ′=OM =6,ON ′=ON =8,∴△ONN ′为等边三角形,△OMM ′为等边三角形,∴∠N ′OM ′=90°.在Rt △M ′ON ′中,M ′N 22''OM ON +. 故答案为10.【点睛】本题考查了最短路径问题,根据轴对称的定义,找到相等的线段,得到直角三角形是解题的关键.18.12013【解析】 ∵AB=AC ,AD 是角平分线,∴AD ⊥BC ,BD=CD , ∴B 点,C 点关于AD 对称,如图,过C 作CF ⊥AB 于F ,交AD 于E ,则CF=BE+FF 的最小值,根据勾股定理得,AD=12,利用等面积法得:AB ⋅CF=BC ⋅AD ,∴CF=BC AD AB ⋅=101213⨯=12013故答案为12013. 点睛:本题主要考查的是翻折的性质、垂线段最短、勾股定理的应用及三角形面积的等积法.明确当CF ⊥AB 时,CF 有最小值是解题的关键.19.39或639【分析】通过计算E 到AC 的距离即EH 的长度为3,所以根据DE 的长度有两种情况:①当点D 在H 点上方时,②当点D 在H 点下方时,两种情况都是过点E 作EH AC ⊥交AC 于点E ,过点G 作GQ AB ⊥交AB 于点Q ,利用含30°的直角三角形的性质和勾股定理求出AH,DH 的长度,进而可求AD 的长度,然后利用角度之间的关系证明AG GE =,再利用等腰三角形的性质求出GQ 的长度,最后利用2DGF AED AEG SS S =-即可求解. 【详解】①当点D 在H 点上方时,过点E 作EH AC ⊥交AC 于点E ,过点G 作GQ AB ⊥交AB 于点Q ,12AB = ,点E 是AB 中点,162AE AB ∴== . ∵EH AC ⊥,90AHE ∴∠=︒ .30,6A AE ∠=︒=,132EH AE ∴== , 22226333AH AE EH ∴=-=-=. 32DE =,2222(32)33DH DE EH ∴=-=-= ,DH EH ∴=,333AD AH DH =-=,45EDH ∴∠=︒,15AED EDH A ∴∠=∠-∠=︒ .由折叠的性质可知,15DEF AED ∠=∠=︒,230AEG AED ∴∠=∠=︒ ,AEG A ∴∠=∠,AG GE ∴= . 又GQ AE ⊥ ,132AQ AE ∴== . 30A ∠=︒ , 12GQ AG ∴=. 222GQ AQ AG += , 即2223(2)GQ GQ +=, 3GQ ∴= .2DGF AED AEG S S S =- ,112(333)36363922DGF S ∴=⨯⨯-⨯-⨯⨯=-; ②当点D 在H 点下方时,过点E 作EH AC ⊥交AC 于点E ,过点G 作GQ AB ⊥交AB 于点Q ,12AB = ,点E 是AB 中点,162AE AB ∴== . ∵EH AC ⊥,90AHE ∴∠=︒.30,6A AE ∠=︒= ,132EH AE ∴== , 22226333AH AE EH ∴=-=-=.3DE =,3DH ∴=== ,DH EH ∴=,3AD AH DH =+=,45DEH ∴∠=︒ ,90105AED A DEH ∴∠=︒-∠+∠=︒ .由折叠的性质可知,105DEF AED ∠=∠=︒,218030AEG AED ∴∠=∠-︒=︒ ,AEG A ∴∠=∠,AG GE ∴= . 又GQ AE ⊥ ,132AQ AE ∴== . 30A ∠=︒,12GQ AG ∴= . 222GQ AQ AG += , 即2223(2)GQ GQ +=,GQ ∴= .2DGF AED AEG S S S =- ,1123)36922DGF S ∴=⨯⨯⨯-⨯=,综上所述,DGF △的面积为9或9.故答案为:9或9.【点睛】本题主要考查折叠的性质,等腰三角形的判定及性质,等腰直角三角形的性质,勾股定理,含30°的直角三角形的性质,能够作出图形并分情况讨论是解题的关键.20.【分析】根据三角形等面积法求出32AC BC = ,在Rt△ACD 中根据勾股定理得出AC 2=14BC 2+36,依据这两个式子求出AC 、BC 的值.【详解】 ∵AD 是BC 边上的高,BE 是AC 边上的高, ∴12AC•BE=12BC•AD, ∵AD=6,BE =4,∴AC BC =32, ∴22AC BC =94, ∵AB=AC ,AD⊥BC,∴BD=DC =12BC , ∵AC 2﹣CD 2=AD 2,∴AC 2=14BC 2+36, ∴221364BC BC +=94, 整理得,BC 2=3648⨯, 解得:BC=∴△ABC 的面积为12×cm 2故答案为:【点睛】本题考查了三角形的等面积法以及勾股定理的应用,找出AC 与BC 的数量关系是解答此题的关键.三、解答题21.(1)BE =1;(2)见解析;(3)(2y x =【分析】(1)如图1,根据等边三角形的性质和四边形的内角和定理可得∠BED =90°,进而可得∠BDE =30°,然后根据30°角的直角三角形的性质即可求出结果;(2)过点D 作DM ⊥AB 于M ,作DN ⊥AC 于N ,如图2,根据AAS 易证△MBD ≌△NCD ,则有BM =CN ,DM =DN ,进而可根据ASA 证明△EMD ≌△FND ,可得EM =FN ,再根据线段的和差即可推出结论;(3)过点D 作DM ⊥AB 于M ,如图3,同(2)的方法和已知条件可得DM =DN =FN =EM ,然后根据线段的和差关系可得BE +CF =2DM ,BE ﹣CF =2BM ,在Rt △BMD 中,根据30°角的直角三角形的性质可得DMBM ,进而可得BE +CF(BE ﹣CF ),代入x 、y 后整理即得结果.【详解】解:(1)如图1,∵△ABC 是等边三角形,∴∠B =∠C =60°,BC =AC =AB =4.∵点D是线段BC的中点,∴BD=DC=12BC=2.∵DF⊥AC,即∠AFD=90°,∴∠AED=360°﹣60°﹣90°﹣120°=90°,∴∠BED=90°,∴∠BDE=30°,∴BE=12BD=1;(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,则有∠AMD=∠BMD=∠AND=∠CND=90°.∵∠A=60°,∴∠MDN=360°﹣60°﹣90°﹣90°=120°.∵∠EDF=120°,∴∠MDE=∠NDF.在△MBD和△NCD中,∵∠BMD=∠CND,∠B=∠C,BD=CD,∴△MBD≌△NCD(AAS),∴BM=CN,DM=DN.在△EMD和△FND中,∵∠EMD=∠FND,DM=DN,∠MDE=∠NDF,∴△EMD≌△FND(ASA),∴EM=FN,∴BE+CF=BM+EM+CN-FN=BM+CN=2BM=BD=12BC=12AB;(3)过点D作DM⊥AB于M,如图3,同(2)的方法可得:BM=CN,DM=DN,EM=FN.∵DN =FN ,∴DM =DN =FN =EM ,∴BE +CF =BM +EM +FN -CN =NF +EM =2DM =x +y ,BE ﹣CF =BM +EM ﹣(FN -CN )=BM +NC =2BM =x -y ,在Rt △BMD 中,∵∠BDM =30°,∴BD =2BM ,∴DM =22=3BD BM BM -,∴()3x y x y +=-,整理,得()23y x =-.【点睛】本题考查了等边三角形的性质、四边形的内角和定理、全等三角形的判定与性质、30°角的直角三角形的性质以及勾股定理等知识,具有一定的综合性,正确添加辅助线、熟练掌握上述知识是解题的关键.22.(1)45度;(2)∠AEC ﹣∠AED =45°,理由见解析;(3)见解析【分析】(1)由等腰三角形的性质可求∠BAE =140°,可得∠CAE =50°,由等腰三角形的性质可得∠AEC =∠ACE =65°,即可求解;(2)由等腰三角形的性质可求∠BAE =180°﹣2α,可得∠CAE =90°﹣2α,由等腰三角形的性质可得∠AEC =∠ACE =45°+α,可得结论;(3)如图,过点C 作CG ⊥AH 于G ,由等腰直角三角形的性质可得EH 2EF ,CH =2CG ,由“AAS ”可证△AFB ≌△CGA ,可得AF =CG ,由勾股定理可得结论.【详解】解:(1)∵AB =AC ,AE =AB ,∴AB =AC =AE ,∴∠ABE =∠AEB ,∠ACE =∠AEC ,∵∠AED =20°,∴∠ABE =∠AED =20°,∴∠BAE =140°,且∠BAC =90°∴∠CAE =50°,∵∠CAE +∠ACE +∠AEC =180°,且∠ACE =∠AEC ,∴∠AEC =∠ACE =65°,∴∠DEC =∠AEC ﹣∠AED =45°,故答案为:45;(2)猜想:∠AEC ﹣∠AED =45°,理由如下:∵∠AED =∠ABE =α,∴∠BAE =180°﹣2α,∴∠CAE =∠BAE ﹣∠BAC =90°﹣2α,∵∠CAE +∠ACE +∠AEC =180°,且∠ACE =∠AEC ,∴∠AEC =45°+α,∴∠AEC ﹣∠AED =45°;(3)如图,过点C 作CG ⊥AH 于G ,∵∠AEC ﹣∠AED =45°,∴∠FEH =45°,∵AH ⊥BE ,∴∠FHE =∠FEH =45°,∴EF =FH ,且∠EFH =90°,∴EH 2EF ,∵∠FHE =45°,CG ⊥FH ,∴∠GCH =∠FHE =45°,∴GC =GH ,∴CH 2CG ,∵∠BAC =∠CGA =90°,∴∠BAF +∠CAG =90°,∠CAG +∠ACG =90°,∴∠BAF =∠ACG ,且AB =AC ,∠AFB =∠AGC ,∴△AFB ≌△CGA (AAS )∴AF =CG ,∴CH 2AF ,∵在Rt △AEF 中,AE 2=AF 2+EF 2, 2AF )2+2EF )2=2AE 2,∴EH 2+CH 2=2AE 2.【点睛】本题是综合了等腰直角三角形的性质,全等三角形的性质与判定的动点问题,三个问题由易到难,在熟练掌握各个相关知识的基础上找到问题之间的内部联系,层层推进去解答是关键.23.(1)90°;(2)证明见解析;(3)变化,234l +≤<.(1)由等边三角形的性质可得∠ABC=∠ACB=60°,由等腰三角形的性质可求DAE=∠DEA=30°,由三角形内角和定理可求解;(2)根据等腰三角形的性质,可证得∠CDF=∠DEA 和∠EDB=∠DFA ,由此可利用“ASA”证明全等;(3)根据全等三角形的性质可得l =2+AD ,根据AD 的取值范围即可得出l 的取值范围.【详解】解:(1)∵△ABC 是等边三角形,∴AB=AC=BC=2,∠ABC=∠ACB=60°,∵AD=DE∴∠DAE=∠DEA=30°,∴∠ADB=180°-∠BAD-∠ABD=90°,故答案为:90°;(2)∵AD=DE=DF ,∴∠DAE=∠DEA ,∠DAF=∠DFA ,∵∠DAE+∠DAF=∠BAC=60°,∴∠DEA+∠DFA=60°,∵∠ABC=∠DEA+∠EDB=60°,∴∠EDB=∠DFA ,∵∠ACB=∠DFA+∠CDF=60°,∴∠CDF=∠DEA ,在△BDE 和△CFD 中∵CDF DEA DE DF EDB DFA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BDE ≌△CFD (ASA )(3)∵△BDE ≌△CFD ,∴BE=CD ,∴l =BD+BE+DE=BD+CD+AD=BC+AD=2+AD ,当D 点在C 或B 点时,AD=AC=AB=2,此时B 、D 、E 三点在同一条直线上不构成三角形,2+AD=4;当D 点在BC 的中点时,∵AB=AC ,∴BD=112BC =,AD ==此时22l AD =+=综上可知24l +≤<.本题考查全等三角形的性质和判定,勾股定理,等边三角形的性质,等腰三角形的性质,三角形内角和定理.(1)掌握等腰三角形等边对等角是解决此问的关键;(2)中注意角之间的转换;(3)中注意临界点是否可取.24.(1)①见解析;②DE =297;(2)DE 的值为 【分析】(1)①先证明∠DAE =∠DAF ,结合DA =DA ,AE =AF ,即可证明;②如图1中,设DE =x ,则CD =7﹣x .在Rt △DCF 中,由DF 2=CD 2+CF 2,CF =BE =3,可得x 2=(7﹣x )2+32,解方程即可;(2)分两种情形:①当点E 在线段BC 上时,如图2中,连接BE .由△EAD ≌△ADC ,推出∠ABE =∠C =∠ABC =45°,EB =CD =5,推出∠EBD =90°,推出DE 2=BE 2+BD 2=62+32=45,即可解决问题;②当点D 在CB 的延长线上时,如图3中,同法可得DE 2=153.【详解】(1)①如图1中,∵将△ABE 绕点A 逆时针旋转90°后,得到△AFC ,∴△BAE ≌△CAF ,∴AE =AF ,∠BAE =∠CAF ,∵∠BAC =90°,∠EAD =45°,∴∠CAD +∠BAE =∠CAD +∠CAF =45°,∴∠DAE =∠DAF ,∵DA =DA ,AE =AF ,∴△AED ≌△AFD (SAS );②如图1中,设DE =x ,则CD =7﹣x .∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°,∵∠ABE =∠ACF =45°,∴∠DCF =90°,∵△AED ≌△AFD (SAS ),∴DE =DF =x ,∵在Rt △DCF 中, DF 2=CD 2+CF 2,CF =BE =3,∴x 2=(7﹣x )2+32,∴x =297, ∴DE =297; (2)∵BD =3,BC =9,∴分两种情况如下:①当点E 在线段BC 上时,如图2中,连接BE .∵∠BAC=∠EAD=90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE=35;②当点D在CB的延长线上时,如图3中,连接BE.同理可证△DBE是直角三角形,EB=CD=3+9=12,DB=3,∴DE2=EB2+BD2=144+9=153,∴DE=317,综上所述,DE的值为35或317.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.25.(1)见解析;(2)BD2+AD2=2CD2;(3)AB=2+4.【分析】(1)根据等腰直角三角形的性质证明△ACE≌△BCD即可得到结论;(2)利用全等三角形的性质及勾股定理即可证得结论;(3)连接EF,设BD=x,利用(1)、(2)求出EF=3x,再利用勾股定理求出x,即可得到答案.【详解】(1)证明:∵△ACB和△ECD都是等腰直角三角形∴AC=BC,EC=DC,∠ACB=∠ECD=90°∴∠ACB﹣∠ACD=∠ECD﹣∠ACD∴∠ACE=∠BCD,∴△ACE≌△BCD(SAS),∴AE=BD.(2)解:由(1)得△ACE ≌△BCD ,∴∠CAE =∠CBD ,又∵△ABC 是等腰直角三角形,∴∠CAB =∠CBA =∠CAE =45°,∴∠EAD =90°,在Rt △ADE 中,AE 2+AD 2=ED 2,且AE =BD ,∴BD 2+AD 2=ED 2,∵ED =2CD ,∴BD 2+AD 2=2CD 2,(3)解:连接EF ,设BD =x ,∵BD :AF =1:2AF =2x ,∵△ECD 都是等腰直角三角形,CF ⊥DE ,∴DF =EF ,由 (1)、(2)可得,在Rt △FAE 中,EF 22AF AE +22(22)x x +3x , ∵AE 2+AD 2=2CD 2,∴222(223)2(36)x x x ++=,解得x =1,∴AB =2+4.【点睛】此题考查三角形全等的判定及性质,等腰直角三角形的性质,勾股定理.26.②③⑤【分析】①先证得ABE ADP ≅,利用邻补角和等腰直角三角形的性质求得90PEB ∠=︒,利用勾股定理求出BE ,即可求得点B 到直线AE 的距离;②根据①的结论,利用APD ABP ABE APB S S S S ∆∆∆+=+AEP BEP S S ∆∆=+即可求得结论; ③在Rt AHB 中,利用勾股定理求得2AB ,再利用三角形面积公式即可求得ABD S ∆; ④当A P C 、、共线时,PC 最小,利用对称的性质,AB BC =的长,再求得AC 的长,即可求得结论;⑤先证得ABP ADE ≅,得到ABP ADE ∠=∠,根据条件得到ABP NAB ∠=∠,利用互余的关系即可证得结论.【详解】①∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =,45APE AEP ∠=∠=︒, ∴EAB PAD ∠=∠, ∴()ABE ADP SAS ≅,∴180********AEB APD APE ∠=∠=︒-∠=︒-︒=︒,∴1354590PEB AEB AEP ∠=∠-∠=︒-︒=︒,∴222PE BE PB +=,∵2AE AP ==,90EAP ∠=︒, ∴22PE AE ==,∴()22227BE +=, 解得:3BE =,作BH ⊥AE 交AE 的延长线于点H ,∵45AEP ∠=︒,90PEB ∠=︒, ∴180180904545HEB PEB AEP ∠=︒-∠-∠=︒-︒-︒=︒,∴26sin 453HB BE =︒==, ∴点B 到直线AE 6,故①错误; ②由①知:ABE ADP ≅,2EP =,3BE =∴APD ABP ABE APB S S S S ∆∆∆∆+=+AEP BEP S S ∆∆=+1122AE AP PE EB =⨯⨯+⨯⨯ 11222322=⨯ 13=,故②正确;③在Rt AHB 中,由①知:6EH HB ==∴622 AH AE EH=+=+,22222256623AB AH BH⎛⎫⎛⎫=+=++=+⎪ ⎪⎪ ⎪⎭⎝⎭,21153222ABDS AB AD AB∆=⋅==+,故③正确;④因为AC是定值,所以当A P C、、共线时,PC最小,如图,连接BC,∵A C、关于BD的对称,∴523AB BC==+∴225231043AC BC==+=+∴minPC AC AP=-,10432=+⑤∵ABD与AEP都是等腰直角三角形,∴90BAD∠=︒,90EAP∠=︒,AB AD=,AE AP=,在ABP和ADE中,AB ADBAP DAEAP AE=⎧⎪∠=∠⎨⎪=⎩,∴()ABP ADE SAS≅,∴ABP ADE∠=∠,∵AN BN=,∴ABP NAB∠=∠,∴EAN ADE∠=∠,∵90EAN DAN∠+∠=︒,∴90ADE DAN∠+∠=︒,∴AN DE⊥,故⑤正确;综上,②③⑤正确,故答案为:②③⑤.【点睛】本题是三角形的综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理的应用,三角形的面积公式,综合性强,全等三角形的判定和性质的灵活运用是解题的关键.27.(1)该命题是真命题,理由见解析;(2)①a 的值为92;②k 的取值范围为13k ≤<;(3)ABC ∆的面积为2033或1235. 【分析】 (1)根据等边三角形的性质、优三角形和优比的定义即可判断;(2)①先利用勾股定理求出c 的值,再根据优三角形的定义列出,,a b c 的等式,然后求解即可;②类似①分三种情况分析,再根据三角形的三边关系定理得出每种情况下,,a b c 之间的关系,然后根据优比的定义求解即可;(3)如图(见解析),设BD x =,先利用直角三角形的性质、勾股定理求出AC 、AB 的长及ABC ∆面积的表达式,再类似(2),根据优三角形的定义分三种情况分别列出等式,然后解出x 的值,即可得出ABC ∆的面积.【详解】(1)该命题是真命题,理由如下:设等边三角形的三边边长为a则其中两条边的和为2a ,恰好是第三边a 的2倍,满足优三角形的定义,即等边三角形为优三角形又因该两条边相等,则这两条边的比为1,即其优比为1故该命题是真命题;(2)①90,6CB b A ∠=︒=22236c a b a ∴=++根据优三角形的定义,分以下三种情况:当2a b c +=时,26236a a +=+,整理得24360a a -+=,此方程没有实数根。
中考数学专题复习常见模型方法勾股定理相关模型应用
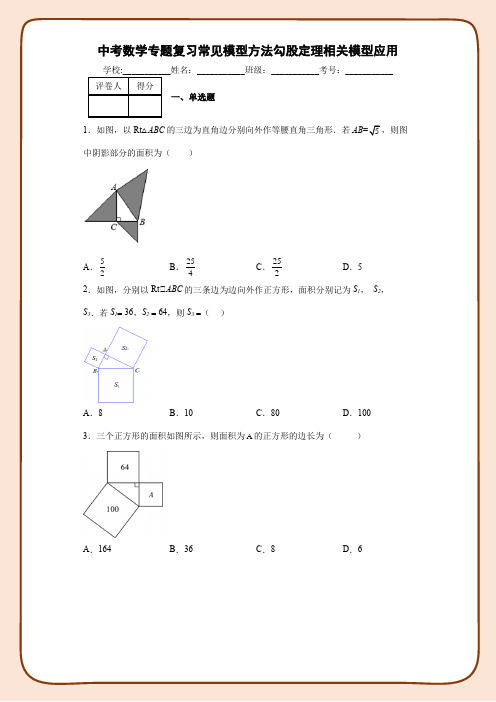
中考数学专题复习常见模型方法勾股定理相关模型应用学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=5,则图中阴影部分的面积为()A.52B.254C.252D.52.如图,分别以Rt△ABC的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1= 36,S2= 64,则S3=()A.8B.10C.80D.100 3.三个正方形的面积如图所示,则面积为A的正方形的边长为()A.164B.36C.8D.64.下图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形G的边长是6cm,则正方形A,B,C,D,E,F,G的面积之和是()A.18cm2B.36cm2C.72cm2D.108cm2 5.如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是()A.13B.47C.47D.136.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了上图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是()A .1B .2021C .2020D .2019 7.设直角三角形的较长直角边长为x ,较短直角边长为y .若 xy =8,大正方形的面积为25,则小正方形的边长为( )A.9B .6 C .4 D .38.如图是“赵爽弦图”,△ABH 、△BCG 、△CDF 和△DAE 是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形,如果AB =10,EF =2,那么AH 等于( )A .8B .6C .4D .59.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a ,较短直角边为b ,则 ab 的值是( )A .4B .6C .8D .10 10.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a ,较短直角边长为b ,若2)21a b +=(,大正方形的面积为13,则小正方形的面积为( )A .3B .4C .5D .611.如图,一竖直的木杆在离地面4米处折断,木杆顶端落在地面离木杆底端3米处,木杆折断之前的高度为().A.7米B.8米C.9米D.12米12.一棵大树在一次强台风中于离地面6米处折断倒下,倒下部分与地面成30夹角,这棵大树在折断前的高度为()A.12米B.18米C.24米D.30米13.如图,一棵大树在离地面3米处折断,树的顶端落在离树干底部4米处,那么这棵树折断之前的高度是()A.8米B.12米C.5米D.5或7米14.如图,一棵高为16m的大树被台风刮数断,若树在地面6m处折断,则树顶端落在离树底部()处A.5m B.7m C.8m D.10m15.如图是一个饮料罐,下底面半径是5,上底面半径是8,高是12,上底面盖子的中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)的取值范围是()A.12≤a≤13B.12≤a≤15C.5≤a≤12D.5≤a≤1316.我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是()A.x2+52 =(x+1)2B.x2+52 =(x﹣1)2C.x2+(x+1)2 =102D.x2+(x﹣1)2=5217.如图,一根长5米的竹竿AB斜靠在竖直的墙上,这时AO为4米,若竹竿的顶端A沿墙下滑2米至C处,则竹竿底端B外移的距离BD()A.小于2米B.等于2米C.大于2米D.以上都不对18.如图,一个梯子AB斜靠在一竖直的墙AO上,测得8AO 米.若梯子的顶端沿墙面向下滑动2米,这时梯子的底端在水平的地面也恰好向外移动2米,则梯子AB的长度为()A.10米B.6米C.7米D.8米19.一架25米长的云梯,斜立在一竖直的墙上,这时梯脚距离墙底端7米.如果梯子的顶端沿墙下滑4米,那么梯脚将水平滑动()A.9米B.15米C.5米D.8米20.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是()A.29B.41C.45D.5321.如图,长方体的长为3cm,宽为2cm,高为4cm,点B到点C的距离为1cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A.4B.5C.29D.3722.如图,正方体的棱长为2,B为一条棱的中点.已知蚂蚁沿正方体的表面从A点出发,到达B点,则它运动的最短路程为()A.10B.4C.17D.523.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为()A.20cm B.2106cm C.(12+234)cm D.18cm24.如图,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)()A.9B.13C.14D.2525.如图,一个底面直径为30cm,高为20cm的糖罐子,一只蚂蚁从A处沿着糖罐的表面爬行到B处,则蚂蚁爬行的最短距离是()A.24cm B.1013cm C.25cm D.30cm26.如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m 处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为()A.1m B.1.1m C.1.2m D.1.3m27.如图所示,有一块直角三角形纸片,△C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.1cm B.1.5cm C.2cm D.3cm28.如图所示的三角形纸片中,90,13,5B AC BC∠=︒==.现将纸片进行折叠,使得顶点B落在AC边上的点D处,折痕为AE,则BE的长为()A.2.4B.2.5C.2.8D.329.如图,在矩形纸片ABCD中,AB=6,AD=8,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则线段EF的长为()A.3B.4C.5D.630.如图所示,沿着AE折叠长方形,使点D落在边BC上的点F处,已知AB=8cm,BC=10cm,则EC的长为()A.3 cm B.4 cm C.5 cm D.6 cm31.如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF长为()A.258cm B.254cm C.252cm D.8cm32.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于点E,8AD=,4AB=,则DE的长为()A.3B.4C.5D.633.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为()A.4B.32C.4.5D.534.在△ABC中,AB=16,AC=14,BC=6,则△ABC的面积为()A.243B.563C.48D.11235.已知在△ABC中,AB=8,AC=7,BC=3,则△B=().A.45°B.37°C.60°D.90°36.已知在△ABC中,AB=7,AC=8,BC=5,则△C=().A.45°B.37°C.60°D.90°37.边长为5,7,8的三角形的最大角和最小角的和是().A.90°B.150°C.135°D.120°评卷人得分二、填空题38.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面________尺高.39.如图,一架长2.5m的梯子斜靠在垂直的墙AO上,这时AO为2m.如果梯子的顶端A沿墙下滑0.5m,那么梯子的底端B向外移动_________m.40.如图,一架13m长的梯子AB斜靠在一竖直的墙AC上,这时AC为12m.如果子的顶端A沿墙下滑7m,那么梯子底端B向外移___m.41.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点1C处(三条棱长如图所示),问最短路线长为_________.42.如图,圆柱体的高为8cm ,底面周长为4cm ,小蚂蚁在圆柱表面爬行,从A 点到B 点,路线如图所示,则最短路程为_____.43.如图,在Rt ABC ∆中,90B =∠,6AB =,8BC =,将ABC ∆折叠,使点B 恰好落在斜边AC 上,与点'B 重合,AE 为折痕,则'EB 的长度是__________.44.如图,在矩形ABCD 中,AB=3,BC=5,在CD 上任取一点E ,连接BE ,将△BCE 沿BE 折叠,使点C 恰好落在AD 边上的点F 处,则CE 的长为_____.45.如图,△ABC 的三边AB ,BC ,CA 的长度分别为3,7,8,则△ABC 的内切圆△的半径为_________.46.在四边形ABCD 中,,7,11,13AC BD AB CD BC ⊥===,则AD =__________.评卷人得分三、解答题47.由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示.根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论△若a>0,b>0且a2+b2为定值,则当a ____ b时,ab取得最大值.拓展:如图所示,在正方形ABCD的四边,,,AB BC CD DA上分别取点,,,E H G F,使得BE CH GD AF===,(1)求证:四边形EHGF是正方形.(2)若//,//,//,//EQ BC HP CD GO DA FR AB,求证四边形ORQP是正方形.48.“风吹树折”问题又称为“折竹抵地”,源自《九章算术》,原文为:“今有竹高一丈,末折抵地,去本三尺.问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远,则折断后的竹子高度为多少尺?(1丈=10尺)49.一阵大风把一根高为9m的树在离地4m处折断,折断处仍相连,此时在离树3.9m处,一头高1m的小马正在吃草,小马有危险吗?为什么?50.读诗求解“ 出水3尺一红莲,风吹花朵齐水面,水面移动有6尺,求水深几何请你算”.51.在平静的湖面上,有一枝荷花,高出水面1米.一阵风吹过来,荷花被吹到一边,花朵齐及水面.已知荷花移动的水平距离为2米,问这里的水深多少米?52.《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”(注:1步=5尺)译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,问绳索有多长.”53.如图所示,在Rt ABC中,90ACB∠=︒,已知6,8,AC BC AD==是ABC的角平分线,求DC的长.54.已知,如图所示,折叠矩形的一边AD ,使点D 落在BC 边的点F 处,如果AB =3cm ,BC =5cm ,求FC 的长.55.如图所示,矩形ABCD 沿直线EF 折叠,使点C 落在边AD 的中点C '处,点B 落在B '处,其中1812AB BC ==,,求FC '的长.56.已知:四边形ABCD 中,BD 、AC 相交于O ,且BD 垂直AC ,求证:2222AB CD AD BC +=+.57.定义,我们把对角线互相垂直的四边形叫做垂美四边形.概念理解:如图△,在四边形ABCD 中,如果AB=AD ,CB=CD ,那么四边形ABCD 是垂美四边形吗?请说明理由.性质探究:如图△,垂美四边形ABCD 两组对边AB 、CD 与BC 、AD 之间有怎样的数量关系?写出你的猜想,并给出证明.问题解决:如图△,分别以Rt△ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连结CE 、BG 、GE .若AC=2,AB=5,则△求证:△AGB△△ACE ;△GE= .58.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD 中,AB AD =,CB CD =,问四边形ABCD 是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD 的对角线AC 、BD 交于点O ,AC BD ⊥.试证明:2222AB CD AD BC +=+;(3)解决问题:如图3,分别以Rt ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连结CE 、BG 、GE .已知4AC =,5AB =,求GE 的长.59.问题情境:如图1,ABC 为等腰直角三角形,90,ACB E ∠=︒是AC 边上的一个动点(点E 与,A C 不重合),以CE 为边在ABC 外作等腰直角,90ECD ECD ∠=︒,连接,BE AD .猜想线段,BE AD 之间的关系.(1)独立思考:请直接写出线段,BE AD 之间的关系.(2)合作交流:“希望”小组受上述问题的启发,将图1中的等腰直角ECD 绕着点C 顺时针方向旋转至如图2的位置,BE 交AC 于点H ,交AD 于点O .(1)中的结论是否仍然成立?请说明理由.(3)拓展延伸:“科技”小组将(2)中的等腰直角ABC 改为,90,8Rt ABC ACB AC ∠=︒=△,6BC =,将等腰直角ECD 改为,90,4,3Rt ECD ECD CD CE ∠=︒==.试猜想22BD AE +是否为定值,结合图3说明理由.参考答案:1.D【解析】【分析】先用直角三角形的边长表示出阴影部分的面积,再根据勾股定理可得:AB 2=AC 2+BC 2,进而可将阴影部分的面积求出.【详解】解:()22222211112222S AC BC AB AB AC BC =++=++阴影, △在Rt△ABC 中,AB 2=AC 2+BC 2=2(5)5=,△AB 2+AC 2+BC 2=10,△S 阴影=12×10=5.故选:D .【点睛】本题考查了勾股定理的知识,能够运用勾股定理证明三个等腰直角三角形的面积之间的关系是解决本题的关键.2.D【解析】【分析】由正方形的面积公式可知S 1=AC 2,S 2=BC 2,S 3=AB 2,在Rt△ABC 中,由勾股定理得AC 2+BC 2=AB 2,即S 1+S 2=S 3,由此可求S 3.【详解】解:△在Rt△ABC 中,AC 2+BC 2=AB 2,又由正方形面积公式得S 1=AC 2,S 2=BC 2,S 3=AB 2,△S 3=S 1+S 2=100.故选:D .【点睛】本题考查了勾股定理及正方形面积公式的运用.关键是明确直角三角形的边长的平方即为相应的正方形的面积.3.D【解析】【分析】已知四边形OGMN和四边形OBCD是正方形,面积分别为64和100,即可求得OG和OD的长,再利用勾股定理即可求得GD的长.【详解】△四边形OGMN和四边形OBCD是正方形,面积分别为64和100△OG2=64,OD2=100△OG=8,OD=10△22221086GD OD OG=-=-=故面积为A的正方形的边长为:6故选:D【点睛】本题考查了正方形的基本性质,四边形各边相等,面积等于边长的平方,本题还考查了利用勾股定理解直角三角形.4.D【解析】【分析】根据正方形的面积公式,运用勾股定理可以证明:6个小正方形的面积和等于最大正方形面积的3倍.【详解】根据勾股定理得到:A与B的面积的和是E的面积;C与D的面积的和是F的面积;而E,F的面积的和是G的面积.即A、B、C、D、E、F的面积之和为3个G的面积.△M的面积是62=36 cm2,△A、B、C、D、E、F的面积之和为36×3=108 cm2.故选D.【点睛】考查了勾股定理,注意运用勾股定理和正方形的面积公式证明结论:6个小正方形的面积和等于最大正方形的面积的2倍.5.B【解析】【分析】设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,根据勾股定理进行求解.【详解】设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:x2=32+52=34,y2=22+32=13,z2=x2+y2=47,即最大正方形E的面积为:z2=47,边长为z=47,故选B.【点睛】本题考查勾股定理,掌握以直角三角形斜边为边长的正方形的面积等于两个以直角边为边长的正方形面积之和是解题的关键.6.B【解析】【分析】根据勾股定理求出“生长”了1次后形成的图形中所有的正方形的面积和,结合图形总结规律,根据规律解答即可.【详解】解:由题意得,正方形A的面积为1,由勾股定理得,正方形B的面积+正方形C的面积=1,△“生长”了1次后形成的图形中所有的正方形的面积和为2,同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为3,△“生长”了3次后形成的图形中所有的正方形的面积和为4,……△“生长”了2020次后形成的图形中所有的正方形的面积和为2021,故选:B.【点睛】本题考查了勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.7.D【解析】【分析】设小正方形的边长为a,根据图形面积关系可得S大正方形=S小正方形+4S直角三角形,再根据xy =8,可列方程求解.【详解】设小正方形的边长为 a (a >0),△ S 大正方形=S 小正方形+4S 直角三角形,S 直角三角形=12x ·y , △ 25=a ²+12×4×8, 所以a =3.故选 D .【点睛】本题考查勾股定理,解题的关键是熟练运用勾股定理以及完全平方公式,本题属于基础题型.8.B【解析】【详解】根据面积的差得出a+b 的值,再利用a ﹣b=2,解得a ,b 的值代入即可.解:△AB=10,EF=2,△大正方形的面积是100,小正方形的面积是4, △四个直角三角形面积和为100﹣4=96,设AE 为a ,DE 为b ,即4×ab=96,△2ab=96,a 2+b 2=100,△(a+b )2=a 2+b 2+2ab=100+96=196,△a+b=14, △a ﹣b=2,解得:a=8,b=6,△AE=8,DE=6,△AH=8﹣2=6.故选B .9.B【解析】【分析】小正方形、大正方形的面积可以分别用a、b 表示,进而两式相减即可求出ab 的值.【详解】由勾股定理,得大正方形的面积为:2217a b +=,又小正方形的面积为2()5a b -= 即2225a b ab +-=△1725ab -=△ab =6故选:B .【点睛】本题是以弦图为背景的计算题,考查了勾股定理,图形的面积,关键是用a、b表示大小正方形的面积.10.C【解析】【详解】解:如图所示,△(a+b)2=21△a2+2ab+b2=21,△大正方形的面积为13,即:a2+b2=13,△2ab=21﹣13=8,△小正方形的面积为13﹣8=5.故选C.11.C【解析】【分析】根据勾股定理求AC的长,从而求木杆折断前的高度.【详解】解:由题意可知,AB=4,BC=3△在Rt△ABC中,225AC=AB+BC=△木杆在折断前的高度为4+5=9米故选:C.【点睛】本题考查勾股定理解直角三角形,正确理解题意进行计算是解题关键.12.B【解析】【分析】如图,由于倒下部分与地面成30°夹角,所以△BAC=30°,由此得到AB=2CB,而离地面5米处折断倒下,即BC=6米,所以得到AB=12米,然后即可求出这棵大树在折断前的高度.【详解】解:如图,△△BAC=30°,△BCA=90°,△AB=2CB,而BC=6米,△AB=12米,△这棵大树在折断前的高度为AB+BC=18米,故选B.【点睛】本题利用了直角三角形中30°的角所对的边是斜边的一半解决问题,解题关键是善于观察题目的信息,利用信息解决问题.13.A【解析】【分析】先根据勾股定理求出折断部分的长,再加上没折断的部分即可.【详解】2234=5米,3+5=8米.故选A.【点睛】本题考查了勾股定理的应用,在直角三角形中,如果两条直角边分别为a和b,斜边为c,那么a2+b2=c2.也就是说,直角三角形两条直角边的平方和等于斜边的平方.14.C【解析】【分析】首先设树顶端落在离树底部x米,根据勾股定理可得62+x2=(16-6)2,再解即可.【详解】设树顶端落在离树底部x米,由题意得:()2226166x+=-,解得:x=8.故选C.【点睛】考查勾股定理的应用,根据勾股定理列出方程是解题的关键. 15.A【解析】【分析】最短距离就是饮料罐的高度,最大距离可根据勾股定理解答.【详解】解:由题意可得:a的最小长度为饮料罐的高,即为12,当吸管斜放时,如图,此时a的长度最大,即为AB,△下底面半径是5,△AB=22512+=13,△a的取值范围是12≤a≤13,故选:A.【点睛】本题考查正确运用勾股定理.主要是运用勾股定理求得a 的最大值,此题比较常见,难度不大.16.A【解析】【分析】首先根据图形将题目中的数字对应起来,再根据题意设出未知数,用勾股定理求解即可.【详解】解:设水池的深度为x 尺,由题意得:x 2+52=(x +1)2,解得:x =12,则x +1=13,答:水深12尺,芦苇长13尺,故选A .【点睛】本题主要考查勾股定理的应用,根据勾股定理列出方程,将其化简成一元一次方程. 17.A【解析】【分析】利用勾股定理可求出OB 、OD 的长,即可得出BD 的长,再根据无理数的估算,估算出BD 的长即可得答案.【详解】△AB=5,OA=4,AC=2,AB=CD=5,△OB=22AB OA -=3,OD=22AB (OA AC)--=21,△BD=21-3,△16<21<25,△4<21<5,△1<21-3<2,即BD 的长小于2米,故选:A .【点睛】本题考查勾股定理的应用及无理数的估算,灵活运用勾股定理、熟练运用“夹逼法”估算无理数是解题关键.18.A【解析】【分析】设BO=xm,利用勾股定理用x表示出AB和CD的长,进而求出x的值,即可求出AB的长度.【详解】解:设BO=xm,依题意,得AC=2,BD=2,AO=8.在Rt△AOB中,根据勾股定理得222228AB AO OB x=+=+,在Rt△COD中,根据勾股定理22222(82)(2),DC CO OD x=+=-++△22228(82)(2),x x+=-++解得x=6,△AB=226810,+=答:梯子AB的长为10m.故选:A.【点睛】本题考查了勾股定理在实际生活中的应用,本题中找到AB=CD是解题的关键.19.D【解析】【分析】利用勾股定理进行解答.求出下滑后梯子低端距离低端的距离,再计算梯子低端滑动的距离.【详解】梯子顶端距离墙角的距离为22257-=24m,24-4=20m,梯子下滑后梯子底端距离墙角的距离为222520=15m,15m-7m=8m,即梯角水平滑动8m,故选D.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键,注意梯子的长度是不变的. 20.B【解析】【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.【详解】如图:根据题意,如上图所示,最短路径有以下三种情况:(1)AB2=(2+3)2+42=41;(2)AB2=32+(4+2)2=45;(3)AB2=22+(4+3)2=53;综上所述,最短路径应为(1)所示,所以AB2=41,即AB=41故选:B【点睛】此题考查的是勾股定理的应用,将长方体从不同角度展开,是解决此类问题的关键,注意不要漏解.21.B【解析】【分析】求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.【详解】解: 将长方体展开,连接A、B,根据两点之间线段最短,BD=1+2=3,AD=4,由勾股定理得:AB=22AD BD+=2234+=5.故选B.【点睛】考查了轴对称−最短路线问题,将长方体展开,根据两点之间线段最短,运用勾股定理解答是关键.22.C【解析】【分析】正方体侧面展开为长方形,确定蚂蚁的起点和终点,根据两点之间线段最短、勾股定理即可求出最短路径长.【详解】解:如图,它运动的最短路程AB=()222+21+=17故选:C【点睛】本题考查了正方体的侧面展开图、两点之间线段最短、勾股定理,掌握正方体的侧面展开图是解题关键.23.A【解析】【分析】平面展开图有两种情况,画出图形利用勾股定理求出MN的长即可.【详解】解:如图1,△AB=18cm,BC=GF=12cm,BF=10cm,点N是FG的中点,△BM=18﹣6=12 cm,BN=10+6=16 cm,△MN=221216+=20 cm;如图2,△AB=18cm,BC=GF=12cm,BF=10cm,点N是FG的中点,△PM=18﹣6+6=18 cm,NP=10 cm,△MN=221810+=424=2106cm.△20<2106,△蚂蚁需要爬行的最短路程为20 cm.故选:A.【点睛】本题考查平面展开图的最短路径问题和勾股定理的应用,解题的关键是将立体图形展为平面图形,利用勾股定理的知识求解.24.B【解析】【分析】要想求得最短路程,首先要把A和B展开到一个平面内.根据两点之间,线段最短求出蚂蚁爬行的最短路程.【详解】解:展开圆柱的半个侧面是矩形,矩形的长是圆柱的底面周长的一半,即4π≈12,矩形的宽是圆柱的高5.根据两点之间线段最短,知最短路程是矩形的对角线的长,即2251213.+=故选:B.【点睛】本题主要考查了平面展开图中最短路径求法,两个不在同一平面内的两个点之间的最短距离时,一定要展开到一个平面内.根据两点之间,线段最短.确定要求的长,再运用勾股定理进行计算.25.C【解析】【分析】根据题意首先将此圆柱展成平面图,根据两点间线段最短,可得AB最短,由勾股定理即可求得需要爬行的最短路程.【详解】解:将此圆柱展成平面图得:△有一圆柱,它的高等于20cm,底面直径等于30πcm,△底面周长=3030ππ⋅=cm,△BC=20cm,AC=12×30=15(cm),△AB=2222201525AC BC+=+=(cm).答:它需要爬行的最短路程为25cm.故选:C.【点睛】本题主要考查平面展开图求最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答是解题关键.26.A【解析】【分析】将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【详解】解:如图,将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,由题意知,A′D=0.6m,A′E=AE=0.2m,△BD=0.9-0.3+0.2=0.8m,△A′B=22'A D BD+=220.60.8+=1(m).故选:A.【点睛】本题考查了平面展开-最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.27.A【解析】【分析】根据勾股定理可将斜边AB的长求出,根据折叠的性质知,AE=AB,已知AC的长,可将CE的长求出.【详解】解:在Rt△ABC中,AB=2222AC BC+=+=435根据折叠的性质可知:AE=AB=5△AC=4△CE=AE﹣AC=1即CE的长为1故选A.考点:勾股定理;翻折变换(折叠问题).28.A【解析】【分析】由△B=90°,AC=13,BC=5,可求得AB的长,设BE=x,由折叠的性质可得:△DEC是直角三角形,ED=BE=x,EC=5−x,CD=1,然后由勾股定理求得BE的长.【详解】解:△△B=90°,AC=13,BC=5,△AB=2212-=,AC BC设BE=x,-=13−12=1,由折叠的性质可得:CD=AC−AD=AC ABDE=BE=x,△ADE=△B=90°,△EC=BC−BE=5−x,在Rt△DEC中,EC2=CD2+DE2,△(5−x)2=1+x2,解得:x=2.4,△BE=2.4.故选:A.【点睛】此题考查了折叠的性质以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想与方程思想的应用.29.A【解析】【分析】根据矩形的性质可得BC=AD,△B=90°,利用勾股定理可求出AC的长,根据折叠的性质可得AF=AB,△B=△AFE=90°,BE=EF,在Rt△CEF中利用勾股定理列方程求出EF的长即可得答案.【详解】△四边形ABCD是矩形,AD=8,△△B=90°,BC=AD=8,△AC=22AB BC+=10,△折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,△BE=EF,AF=AB=6,△AFE=△B=90°,△CF=AC-AF=10﹣6=4,在Rt△CEF中,由勾股定理得,EF2+CF2=CE2,△EF2+CF2=(BC-EF)2,即EF2+42=(8-EF)2,解得:EF=3,故选:A .【点睛】本题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.30.A【解析】【分析】利用矩形的性质和翻折的性质求得AB =CD =8cm ,AD =BC =10cm ,△B =△C =△90°,AF =AD =10cm ,EF =DE ,在Rt、ABF 中,利用勾股定理可得BF ,在Rt、CEF 中,由勾股定理可得CE 的长.【详解】△四边形ABCD 是矩形,△AB =CD =8cm ,AD =BC =10cm ,△B =△90°由折叠的性质可得:AF =AD =10cm ,EF =DE ,在Rt、ABF 中,由勾股定理可得:22221086BF AF AB cm =-=+=在Rt、CEF 中,设EC =xcm ,则EF =DE =(8-x )cm ,FC =BC -BF =4cm , 由勾股定理得:222CE FC EF +=,即()22248x x +=-,解得:3x =△EC 的长为3cm .故选:A .【点睛】本题考查矩形的性质、翻折的性质、勾股定理的应用,解题的关键是熟练掌握上述性质,熟练掌握勾股定理解直角三角形.31.B【解析】【详解】试题解析:设AF=xcm ,则DF=(8-x )cm ,△矩形纸片ABCD 中,AB=6cm ,BC=8cm ,现将其沿EF 对折,使得点C 与点A 重合, △DF=D′F ,在Rt△AD′F中,△AF2=AD′2+D′F2,△x2=62+(8-x)2,解得:x=254(cm).故选B.考点:翻折变换(折叠问题).32.C【解析】【分析】首先根据矩形的性质知道AD△BC,所以△1=△3,由于折叠得到△1=△2,C′D=CD、BC′=BC,所以△2=△3,进而得出BE=DE,设DE=x,在Rt△DEC′中利用勾股定理即可求出DE的长.【详解】解:△四边形ABCD是矩形,△AD△BC,即△1=△3,由折叠可知,△1=△2,C′D=CD=4、BC′=BC=8,△△2=△3,即DE=BE,设DE=x,则EC′=8-x,在Rt△DEC′中,DC'2+EC'2=DE2△42+(8-x)2=x2解得:x=5,△DE的长为5.【点睛】本题主要考查了图形的折叠问题,解题的关键是掌握矩形的性质和折叠的特点,利用勾股定理解题.33.A【解析】【分析】先求出BC′,再由图形折叠特性知,C′F=CF=BC﹣BF=9﹣BF,在Rt△C′BF中,运用勾股定理BF2+BC′2=C′F2求解.。
专题10 勾股定理有关的计算(含答案)

第三章 勾股定理专题10 勾股定理有关的计算知识解读勾股定理:如果直角三角形的两直角边长分别为a ,b ,斜边为c ,那么222c b a =+. 即直角三角形两直角边的平方和等于斜边的平方。
勾股定理几种表达式:在ABC Rt ∆中,90=∠C ,A ∠,B ∠,C ∠的对边分别为a ,b .c ,则222b a c +=,222b c a -=,222a c b -=;22b a c +=,22b c a -=,22a c b -=.勾股定理只有在直角三角形中才适用,如果不是直角三角形,那么三条边之间就没有这种关系。
应用勾股定理的时候,一定要弄清哪条边是直角边,哪条边是斜边.培优学案典例示范一、已知直角三角形的两边关系,常考虑运用方程思想 例1直角三角形的两直角边长的比是4:3,斜边长是25,则它的两直角边长分别是 . 【提示】可设直角三角形的两直角边长分别为x 3和x 4,然后根据勾股定理列出关于x 的方程。
【技巧点评】根据两边关系设未知数,根据勾股定理,列方程求未知数的值,是解决此类问题常用的方法。
跟踪训练1.在ABC Rt ∆中,90=∠C ,30=∠A ,6=b ,则c = ,a = . 二、没有提供图形的几何题,要留意可能出现多解例2在ABC ∆中,13=AB ,15=AC ,BC 边上的高12=AD ,求BC 的长.【提示】本题已知条件的三条线段AB ,AC 和AD ,都是从点A 出发的,需要分两种情况讨论。
【解答】【技巧点评】几何题目如果没有明确图形形状的时候,一般这个图形形状会出现几种情况,解题时需要仔细分析题意,找出所有可能的情况。
跟踪训练2. 已知一个直角三角形的两条边长分别是3和4,则第三边长为 .三、等腰三角形底边上的高例3 如图3-10-1,在ABC ∆中,10==AC AB ,8=BC ,AD 是BC 边上的中线,求AD 的长. 【提示】由于AD 是BC 边上的中线,可知BC AD ⊥,于是由10==AC AB ,8=BC ,利用勾股定理即求.【解答】图3-10-1等腰三角形底边上的高和底边上的中线是同一条线段,根据这一性质,可运用勾股定理求得等腰三角形底边上的高。
2023年中考数学几何专题:勾股定理的应用(解析版)

2023中考数学几何专题:勾股定理的应用(解析版)1. 放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )A .600米 B. 800米 C. 1000米 D. 不能确定【解析】速度一定且相同,路程比=时间比.再用勾股定理,直线距离应该是25分钟的路程.选C.【答案】C2. 一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )A. 9分米B. 15分米C. 5分米D. 8分米 【解析】在初始和结束两个状态下,选定直角三角形,应用勾股定理. 初始时,经计算,可知,梯顶距墙底端24分米.结束时,经计算,可知,梯足距离墙底端15分米.选D. 【答案】D3. 如图,点P 是AOB ∠的角平分线上一点,过点P 作//PC OA 交OB 于点C .若60,4AOB OC ∠==,则点P 到OA 的距离PD 等于__________.【解析】过P 点作PE OB ⊥,并交OB 于点E .∵60,AOB OP ∠=是AOB ∠的角平分线, ∴630BOP ∠==. 又∵//PC OA ,∴60PCB AOB ∠=∠=.∴30OPC BOP BPC ∠==∠=∠.∴14,22PC OC EC PC ====.∴PB =.【答案】4. 将一根长为24cm 的筷子,置于底面直径为5cm ,高为12cm 的圆柱形水杯中,设筷子露在杯子外边的长度为cm h ,则h 的取值范围为PODC B A EP ODC BA【答案】2.3cm5. 如图,是一块直角三角形的土地,现在要在这块地上挖一个正方形蓄水池AEDF ,已知剩余的两直角三角形(阴影部分)的斜边长分别为20cm 和30cm ,则剩余的两个直角三角形(阴影部分)的面积和...为 2cm .【解析】cm AE x =,cm BE a =,cm CF b =,在Rt BDE ∆中,22230900a x +== ① 在Rt CDF ∆中,22220400b x +== ②在Rt ABC ∆中,()()222502500a x b x +++==,即2222222500a ax x b bx x +++++= ③③-①-②得,221200ax bx +=,3002ax bx+=最简单的方法为两个小的直角三角形旋转合并成一个大的直角三角形(正方形的边重合)故130203002⨯⨯=.【答案】3006. 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.【解析】直接应用勾股定理可知,少走了5m.又知2步为1米,所以少走了10步. 【答案】107. 蚂蚁沿图中的折线从A 点爬到D 点,一共爬了多少厘米?(小方格的边长为1厘米)【解析】把折线从A 到D,分三段计算.第1段长为5,第2段长为13,第3段长为10,进行加法计算,所以蚂蚁一共爬了28cm .【答案】28cm8. 在Rt ABC ∆中,90C ∠=︒,若54a b c +==,,则ABC S ∆= . 【解析】 在Rt ABC ∆中,由勾股定理得,222a b c +=. 又有()2222a b a b ab +=++, 所以 ()222a b c ab +-=所以1924ABC S ab ∆==.【答案】94ABC S ∆=9. 如图,Rt ABC ∆中,90CAB ∠=︒,AB AC =,E 、F 为BC 上的点,且45EAF ∠=︒,求证:222EF BE FC =+.【解析】过点A 作线段AD ,使CAF BAD ∠=∠,且AD AF =.在ACF ∆和ABD ∆中, AC AB CAF BAD AF AD =⎧⎪∠=∠⎨⎪=⎩∴ACF ABD ∆∆≌ ∴CF BD =,DBA FCA ∠=∠90DBE DBA ABE FCA ABE ∠=∠+∠=∠+∠=︒ 在ADE ∆和AFE ∆中, 45AE AE EAF EAD AD AF =⎧⎪∠=∠=︒⎨⎪=⎩∴ADE AFE ∆∆≌ ∴ED EF =在Rt BDE ∆中,222DE BD BE =+,∴222EF BE FC =+.【答案】见解析F E C B ADF E CB ACBAD10. 如图,已知Rt △ABC 的周长为26+,其中斜边2AB =,求这个三角形的面积.【解析】在Rt △ABC 中,根据勾股定理,得2222a b +=,即2()24a b ab +-=。
2021中考数学考点归类复习——专题七十三:勾股定理
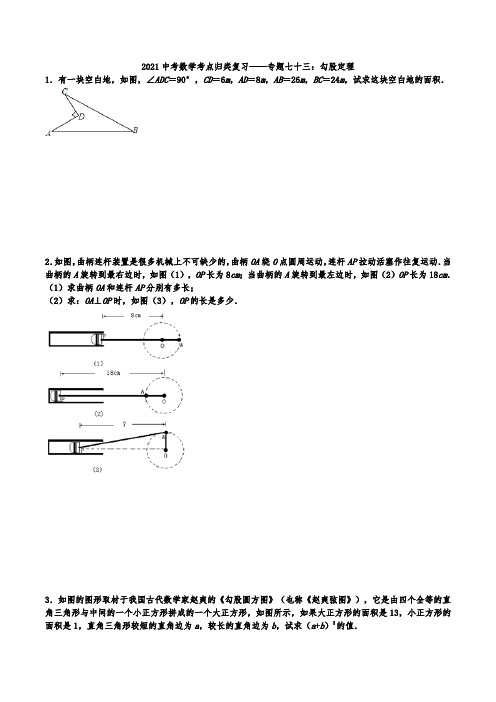
2021中考数学考点归类复习——专题七十三:勾股定理1.有一块空白地,如图,∠ADC=90°,CD=6m,AD=8m,AB=26m,BC=24m,试求这块空白地的面积.2.如图,曲柄连杆装置是很多机械上不可缺少的,曲柄OA绕O点圆周运动,连杆AP拉动活塞作往复运动.当曲柄的A旋转到最右边时,如图(1),OP长为8cm;当曲柄的A旋转到最左边时,如图(2)OP长为18cm.(1)求曲柄OA和连杆AP分别有多长;(2)求:OA⊥OP时,如图(3),OP的长是多少.3.如图的图形取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,试求(a+b)2的值.4.如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM 和BM.(即AM+BM)(如图3)从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?5.如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?6.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.7.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?8.问题背景.在△ABC中,AB=,BC=,AC=,求这个三角形的面积,小辉同学在解答这道题时先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(△ABC的三个顶点都在正方形的顶点处),如图所示,这样不需要求△ABC的高,而借用网格就能计算它的面积.(1)请直接写出△ABC的面积;(2)我们把上述方法叫做构图法,若△ABC中,AB,BC,AC三边的长分别为,,,请你在图2的正方形网格(每个小正方形的边长为a)中画出相应的△ABC.并求其面积.9.如图是一副秋千架,图1是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计),图2是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.10.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.11.在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17,求△ABC的面积.12.利用如图的4×4方格,作出面积为8平方单位的正方形,然后在数轴上表示出实数和﹣.13.如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?14.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米?15.已知,如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2,求证:AB=BC.16.如图,一架2.5米长的梯子AB斜靠在一座建筑物上,梯子底部与建筑物距离BC为0.7米.(1)求梯子上端A到建筑物的底端C的距离(即AC的长);(2)如果梯子的顶端A沿建筑物的墙下滑0.4米(即AA'=0.4米),则梯脚B将外移(即BB'的长)多少米?17.如图1,Rt△ABC中,AC⊥CB,AC=15,AB=25,点D为斜边上动点.(1)如图2,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE;(2)如图3,在点D的运动过程中,连接CD,若△ACD为等腰三角形,求AD.2021中考数学考点归类复习——专题七十三:勾股定理参考答案1.有一块空白地,如图,∠ADC=90°,CD=6m,AD=8m,AB=26m,BC=24m,试求这块空白地的面积.【答案】解:连接AC,在Rt△ACD中,∵CD=6米,AD=8米,BC=24米,AB=26米,∴AC2=AD2+CD2=82+62=100,∴AC=10米,(取正值).在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676.∴AC2+BC2=AB2,∴△ACB为直角三角形,∠ACB=90°.∴S空白=AC×BC﹣AD×CD=×10×24﹣×8×6=96(米2).答:这块空白地的面积是96米2.2.如图,曲柄连杆装置是很多机械上不可缺少的,曲柄OA绕O点圆周运动,连杆AP拉动活塞作往复运动.当曲柄的A旋转到最右边时,如图(1),OP长为8cm;当曲柄的A旋转到最左边时,如图(2)OP长为18cm.(1)求曲柄OA和连杆AP分别有多长;(2)求:OA⊥OP时,如图(3),OP的长是多少.【答案】解:(1)设AP=a,OA=b,由题意,解得,∴AP=13cm,OA=5cm.(2)当OA⊥OP时,在Rt△PAO中,OP===12,∴OP=12cm.3.如图的图形取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,试求(a+b)2的值.【答案】解:∵大正方形的面积是13,小正方形的面积是1,∴直角三角形的斜边的平方为13,∵直角三角形较短的直角边为a,较长的直角边为b,∴a2+b2=13,∵大正方形的面积减去小正方形的面积等于四个直角三角形的面积,∴4×ab=13﹣1,即2ab=12,∴(a+b)2=a2+2ab+b2=13+12=25.4.如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM 和BM.(即AM+BM)(如图3)从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?【答案】解:(1)方案1:AC+AB=1+5=6,方案2:AM+BM=A′B==,∵6<,∴方案1更合适;(2)如图,①AQ1=AB=5或AQ4=AB=5时,CQ1=CQ4==2,∴QG=2+2(舍去)或2﹣2(舍去);②AB=BQ2=5或AB=BQ5=5时,DQ==3,∴QG=3+2=5或3﹣2=1(舍去),③G为CD中点时,当AQ3=BQ3时,(GQ3+2)2+12=(2﹣GQ3)2+42,解得:GQ3=,DQ=.故当DQ=3或时,△ABQ为等腰三角形.5.如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?【答案】解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,∴BC=CA.设AC为x,则OC=9﹣x,由勾股定理得:OB2+OC2=BC2,又∵OA=9,OB=3,∴32+(9﹣x)2=x2,解方程得出x=5.∴机器人行走的路程BC是5cm.6.一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区域,当轮船到A处时测得台风中心移到位于点A正南方的B处,且AB=100海里.若这艘轮船自A处按原速度继续航行,在途中是否会遇到台风?若会,则求出轮船最初遇到台风的时间;若不会,请说明理由.【答案】解:不会受影响,假设途中会遇到台风,且最初遇到的时间为th,此时轮船位于C处,台风中心移到E处,连接CE,则AC=20t,AE=AB﹣BE=100﹣40t,AC2+AE2=EC2.(20t)2+(100﹣40t)2=202,整理得:5t2﹣20t+24=0∵△=(﹣20)2﹣4×5×24<0∴方程无实数根,∴不会受影响.7.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?【答案】解:在直角△ABC中,已知AB=2.5m,BC=0.7m,则AC==2.4m,∵AC=AA1+CA1∴CA1=2m,∵在直角△A1B1C中,AB=A1B1,且A1B1为斜边,∴CB1==1.5m,∴BB1=CB1﹣CB=1.5﹣0.7=0.8m答:梯足向外移动了0.8m.8.问题背景.在△ABC中,AB=,BC=,AC=,求这个三角形的面积,小辉同学在解答这道题时先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(△ABC的三个顶点都在正方形的顶点处),如图所示,这样不需要求△ABC的高,而借用网格就能计算它的面积.(1)请直接写出△ABC的面积;(2)我们把上述方法叫做构图法,若△ABC中,AB,BC,AC三边的长分别为,,,请你在图2的正方形网格(每个小正方形的边长为a)中画出相应的△ABC.并求其面积.【答案】解:(1)S△ABC=3×3﹣×3×1﹣×2×3﹣×1×2=;(2)如图,∵AB==a,BC==2a,AC==a,∴△ABC即为所求作三角形,则S△ABC=2a•4a﹣×a×2a﹣×2a×2a﹣×a×4a=3a2.故答案为:(1).9.如图是一副秋千架,图1是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计),图2是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.【答案】解:设AD=xm,则由题意可得AB=(x﹣0.5)m,AE=(x﹣1)m,在Rt△ABE中,AE2+BE2=AB2,即(x﹣1)2+1.52=(x﹣0.5)2,解得x=3.即秋千支柱AD的高为3m.10.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.【答案】解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,∴BD2+22=6.25,∴BD2=2.25.∵BD>0,∴BD=1.5米.∴CD=BC+BD=0.7+1.5=2.2米.答:小巷的宽度CD为2.2米.11.在△ABC中,D是BC上一点,AB=10,BD=6,AD=8,AC=17,求△ABC的面积.【答案】解:∵BD2+AD2=62+82=102=AB2,∴△ABD是直角三角形,∴AD⊥BC,在Rt△ACD中,CD==15,∴BC=BD+CD=6+15=21,∴S△ABC=BC•AD=×21×8=84.因此△ABC的面积为84.故答案为84.12.利用如图的4×4方格,作出面积为8平方单位的正方形,然后在数轴上表示出实数和﹣.【答案】解:如图,13.如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?【答案】解:根据题意得:AC=CD,∠ABD=90°.在直角三角形ABD中,∵AB=3000,AD=5000,∴BD==4000(m),设CD=AC=x米,BC=4000﹣x(米),在Rt△ABC中,AC2=AB2+BC2,即x2=30002+(4000﹣x)2解得:x=3125,答:该超市与车站D的距离是3125米.14.如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米?【答案】解:在直角三角形AOB中,根据勾股定理,得:OB==6m,根据题意,得:OB′=6+2=8m.又∵梯子的长度不变,∴在Rt△A′OB′中,根据勾股定理,得:OA′==6(m).则AA′=8﹣6=2(m).答:梯顶离路灯2米.15.已知,如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2,求证:AB=BC.【答案】证明:∵∠ABC=90°,∴AB2+BC2=AC2,∵CD⊥AD,∴∠ADC=90°,∴AD2+CD2=AC2,∵AD2+CD2=2AB2,∴AC2=2AB2,∴AB2+BC2=2AB2,∴AB2=BC2,∴AB=BC.16.如图,一架2.5米长的梯子AB斜靠在一座建筑物上,梯子底部与建筑物距离BC为0.7米.(1)求梯子上端A到建筑物的底端C的距离(即AC的长);(2)如果梯子的顶端A沿建筑物的墙下滑0.4米(即AA'=0.4米),则梯脚B将外移(即BB'的长)多少米?【答案】解:(1)在△ABC中,∠ACB=90°,AB=2.5,BC=0.7.根据勾股定理可知答:梯子上端A到建筑物的底端C的距离为2.4米.(2)在△A'B'C'中,∠ACB=90°,A'B'=AB=2.5,A'C=AC﹣AA'=2.4﹣0.4=2 根据勾股定理可知B'C=,B'B=B'C﹣BC=1.5﹣0.7=0.8.答:梯脚B将外移0.8米.17.如图1,Rt△ABC中,AC⊥CB,AC=15,AB=25,点D为斜边上动点.(1)如图2,过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时,求CE;(2)如图3,在点D的运动过程中,连接CD,若△ACD为等腰三角形,求AD.【答案】解:(1)∵AC⊥CB,AC=15,AB=25∴BC=20,∵AE平分∠CAB,∴∠EAC=∠EAD,∵AC⊥CB,DE⊥AB,∴∠EDA=∠ECA=90°,∵AE=AE,∴△ACE≌△ADE(AAS),∴CE=DE,AC=AD=15,设CE=x,则BE=20﹣x,BD=25﹣15=10在Rt△BED中∴x2+102=(20﹣x)2,∴x=7.5,∴CE=7.5.(2)①当AD=AC时,△ACD为等腰三角形∵AC=15,∴AD=AC=15.②当CD=AD时,△ACD为等腰三角形∵CD=AD,∴∠DCA=∠CAD,∵∠CAB+∠B=90°,∠DCA+∠BCD=90°,∴∠B=∠BCD,∴BD=CD,∴CD=BD=DA=12.5,③当CD=AC时,△ACD为等腰三角形,如图1中,作CH⊥BA于点H,则•AB•CH=•AC•BC,∵AC=15,BC=20,AB=25,∴CH=12,在Rt△ACH中,AH==9,∵CD=AC,CH⊥BA,∴DH=HA=9,∴AD=18.。
中考数学解题技巧专题勾股定理与面积问题

解题技巧专题:勾股定理与面积问题——全方位求面积,一网搜罗◆类型一 直角三角形中,利用面积求斜边上的高1.(郴州桂阳县期末)在Rt △ABC 中,∠C =90°,AC =9,BC =12,则C 点到AB 的距离为【方法1】( ) A.536 B.365 C.334 D.12252.如图,在2×2的方格中,小正方形的边长是1,点A ,B ,C 都在网格点上,则AB 边上的高为( ) A.355 B.255 C.3510 D.322第2题图 第6题图◆类型二 结合乘法公式巧求面积或周长3.直角三角形的周长为24,斜边长为10,则其面积为( )A.96 B.49 C.24 D.484.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是( ) A.7cm B.10cmC.(5+37)cm D.12cm◆类型三巧妙分割求面积5.如图,已知AB=5,BC=12,CD=13,DA=10,AB⊥BC,求四边形ABCD的面积.◆类型四“勾股树”及其拓展类型中有关面积的计算6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的边长为( )A.14cm B.4cm C.15cm D.3cm7.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )A.4 B.36 C.16 D.55第7题图第8题图8.(青海中考)如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2……按照此规律继续下去,则S 9的值为( )A.⎝ ⎛⎭⎪⎫126B.⎝ ⎛⎭⎪⎫127C.⎝ ⎛⎭⎪⎪⎫226D.⎝ ⎛⎭⎪⎪⎫227 ◆类型五 “赵爽弦图”中有关面积的计算9.“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则大正方形与小正方形的面积差是( )A .9B .36C .27D .34第9题图 第10题图10.(永州零陵区校级模拟)如图是4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边(x >y ),下列四个说法:①x 2+y 2=49;②x -y =2;③2xy +4=49;④x +y =9.其中说法正确的是( )A .①②B .①②③C .①②④D .①②③④参考答案与解析1.B2.A 解析:过点C 作CD ⊥AB 于点D .∵S △ABC =22-12×1×2-12×1×1-12×1×2=32,又∵S △ABC =12AB ·CD ,∴12AB ·CD =32.∵AB =12+22=5,∴CD =355.故选A. 3.C 解析:设该直角三角形的两直角边长分别为a ,b ,则有a +b =14①,a 2+b 2=102②.①两边同时平方,得a 2+b 2+2ab =142,所以2ab =96,所以ab =48,12ab =24.故选C.4.D5.解:连接AC ,过点C 作CE ⊥AD 交AD 于点E .∵AB ⊥BC ,∴∠CBA =90°.在Rt △ABC 中,由勾股定理得AC =AB 2+BC 2=52+122=13.∵CD =13,∴AC =CD ,即△ACD 是等腰三角形.∵CE ⊥AD ,∴AE =12AD =12×10=5.在Rt △ACE 中,由勾股定理得CE =AC 2-AE 2=132-52=12.∴S 四边形ABCD =S △ABC +S △CAD =12AB ·BC +12AD ·CE=12(12×5+10×12)=90. 6.A 7.C8.A 解析:在图中标上字母E ,如图所示.∵正方形ABCD 的边长为2,△CDE 为等腰直角三角形,∴DE 2+CE 2=CD 2,DE =CE ,∴S 2+S 2=S 1.观察,发现规律:S 1=22=4,S 2=12S 1=2,S 3=12S 2=1,S 4=12S 3=12,…,∴S n =⎝ ⎛⎭⎪⎫12n -3.当n =9时,S 9=⎝ ⎛⎭⎪⎫129-3=⎝ ⎛⎭⎪⎫126.故选A.9.B 解析:大正方形的面积为32+62=45,小正方形的面积为(6-3)2=9,则面积差为45-9=36.故选B.10.B 解析:由题意得⎩⎪⎨⎪⎧x 2+y 2=49①,(x -y )2=4②,①-②得2xy =45③,∴2xy +4=49,①+③得x 2+2xy +y 2=94,∴x +y =94,∴①②③正确,④错误.故选B.解题技巧专题:圆中辅助线的作法——形成精准思维模式,快速解题◆类型一 遇弦过圆心作弦的垂线或连半径1.如图,以点O 为圆心的两个圆中,大圆的弦AB 切小圆于点C ,OA 交小圆于点D ,若OD =2,tan ∠OAB =12,则AB 的长是( ) A .4 B .23 C .8 D .43第1题图第2题图2.如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,⊙O的半径为________.◆类型二遇直径添加直径所对的圆周角3.如图,AB是⊙O的直径,C,D,E都是⊙O上的点,则∠ACE+∠BDE等于( )A.60°B.75°C.90°D.120°第3题图第4题图4.如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是________.5.如图,△ABC的顶点均在⊙O上,AD为⊙O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.类型三遇切线连接圆心和切点6.已知⊙O的半径为1,圆心O到直线l的距离为2,过l上任一点A作⊙O的切线,切点为B,则线段AB长度的最小值为( )A.1 B. 2 C. 3 D.27.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=26°,则∠ACB的度数为________.8.★如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.(1)求证:∠ADC=∠ABD;(2)求证:AD2=AM·AB;(3)若AM =185,sin ∠ABD =35,求线段BN 的长.。
中考数学中的三角形与四边形面积计算技巧总结

中考数学中的三角形与四边形面积计算技巧总结在中考数学考试中,求解三角形与四边形的面积是一个常见的题型。
正确运用计算技巧可以快速准确地得出结果。
本文将总结中考数学中常用的三角形与四边形面积计算技巧,帮助同学们提高解题效率。
一、三角形面积计算技巧1. 直角三角形面积计算直角三角形是最简单的三角形,其面积计算公式为:面积 = 底边长度 ×高其中,底边是直角边,高是与底边垂直的边。
在解题时,可以利用勾股定理求得直角三角形的底边与高,从而计算出面积。
2. 一般三角形面积计算对于一般的三角形,我们可以利用海伦公式计算面积。
海伦公式的表达式为:面积= √[s × (s - a) × (s - b) × (s - c)]其中,s是三角形的半周长,等于三边长之和的一半;a、b、c分别是三角形的边长。
二、四边形面积计算技巧1. 矩形面积计算矩形是一种特殊的四边形,其面积计算公式为:面积 = 长 ×宽矩形的特点是四个角都是直角,且相对的两边长度相等。
在考试中遇到矩形的面积计算问题时,只需知道其长和宽即可直接计算出结果。
2. 平行四边形面积计算平行四边形也是一种常见的四边形,其面积计算公式为:面积 = 底边长度 ×高平行四边形的特点是两对边平行且相等,且相对的两个角也相等。
在计算平行四边形面积时,只需知道底边的长度以及与底边平行的高的长度即可。
3. 梯形面积计算梯形是一种具有两对平行边的四边形,其面积计算公式为:面积 = (上底 + 下底) ×高的一半梯形的关键是知道上底、下底和高的长度,通过将梯形划分为两个三角形和一个矩形,可以利用三角形和矩形的面积计算公式得出最终结果。
4. 菱形面积计算菱形是一种具有四个边相等的四边形,其面积计算公式为:面积 = 对角线1长度 ×对角线2长度的一半在计算菱形面积时,只需知道两条对角线的长度即可。
总结:在中考数学中,掌握三角形与四边形的面积计算技巧对解题非常重要。
中考最大面积求解题技巧

中考最大面积求解题技巧中考最大面积求解题技巧中考数学中,有许多与面积有关的题目,而求解面积最大值是这些题目中常见的一种。
以下是一些求解最大面积题目的技巧和方法。
1. 确定变量及约束条件:首先,我们需要确定一个或多个变量来表示题目中的未知量,然后确定这些变量的取值范围或满足的条件。
这一步是解题的关键,需要根据题目的条件和要求来确定变量和约束条件。
2. 建立面积函数:根据问题的描述,将面积表示为一个函数。
这个函数可能是一个简单的二次函数,也可能是一个复杂的多项式函数,甚至可能是一个三角函数。
根据题目的要求和问题的性质,建立一个准确的面积函数是解决问题的关键。
3. 求解最大值:利用数学的方法求解面积函数的最大值。
常用的方法包括求导法、整式定理法、配方法、柯西不等式等。
这些方法可以根据面积函数的特点和问题的条件来选择使用。
4. 验证最大值:对于求解的最大值,需要进行验证,确保该值满足题目中的所有条件和要求。
如果最大值不满足条件,那么需要重新调整变量或约束条件,重新求解。
5. 给出最大值:先给出面积的表达式,再将问题中的条件代入到表达式中,最后求得最大值,给出答案。
在回答问题时,根据题目的要求给出准确的答案,并合理解释计算过程和结果的意义。
下面通过两个具体的例子来说明上述求解最大面积题目的技巧。
例一:一面墙的长和宽之和为16米,求这面墙与地面围成的矩形的最大面积。
解:设这面墙的长为x米,则宽为16-x米。
根据题目要求,面积函数为A=x(16-x)。
由此可得到面积函数A=f(x)=16x-x^2。
因为这是一个简单的二次函数,我们可以直接进行求解。
首先求解函数的最大值可以通过求导法。
对函数f(x)=16x-x^2求导,得到f'(x)=16-2x。
令f′(x)=0,解得x=8。
说明当长为8米时,面积取得最大值。
然后通过二阶导数判别法来验证最大值。
对f'(x)=16-2x再次求导,得到f′'(x)= -2。
中考数学专题探究-----面积问题(含详细解答)

中考数学专题探究-----面积问题面积问题在中考中占有很重要的地位,一般情况下,计算一些基本图形的面积,可以直接运用图形的面积公式,对于一些不规则的图形面积的计算,可以对图形进行转化,这类问题虽然解题方法比较灵活多样,但难度一般不太大。
但是,在中考压轴题中,有关面积的问题常常以动态的方式出现,经常与函数知识联系起来,有时还需要分类讨论。
因此,对考生要求较高,在解题时,要注意分清其中的变量和不变量,并把运动的过程转化成静止的状态,做到动静结合,以静求动。
考点一:面积的函数关系式问题典型例题:1、(2009年湖南衡阳)如图12,直线4+-=x y 与两坐标轴分别相交于A 、B 点,点M 是线段AB 上任意一点(A 、B 两点除外),过M 分别作MC ⊥OA 于点C ,MD ⊥OB 于D . (1)当点M 在AB 上运动时,你认为四边形OCMD 的周长是否发生变化?并说明理由;(2)当点M 运动到什么位置时,四边形OCMD 的面积有最大值?最大值是多少?(3)当四边形OCMD 为正方形时,将四边形OCMD 沿着x 轴的正方向移动,设平移的距离为)40<<a a (,正方形OCMD 与△AOB 重叠部分的面积为S .试求S 与a 的函数关系式并画出该函数的图象.解:(1)设点M 的横坐标为x ,则点M 的纵坐标为-x+4(0<x<4,x>0,-x+4>0); 则:MC =∣-x+4∣=-x+4,MD =∣x ∣=x ;∴C 四边形OCMD =2(MC+MD )=2(-x+4+x )=8∴当点M 在AB 上运动时,四边形OCMD 的周长不发生变化,总是等于8; (2)根据题意得:S 四边形OCMD =MC ·MD =(-x+4)· x =-x 2+4x =-(x-2)2+4∴四边形OCMD 的面积是关于点M 的横坐标x (0<x<4)的二次函数,并且当x =2,即当点M 运动到线段AB 的中点时,四边形OCMD 的面积最大且最大面积为4; (3)如图10(2),当20≤<a 时,42121422+-=-=a aS ; 如图10(3),当42<≤a 时,22)4(21)4(21-=-=a a S ;∴S 与a 的函数的图象如下图所示:图12(1)图12(2)图12(3)2、(2009宁夏)已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边A B 上沿A B 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作A B 边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒.(1)线段MN 在运动的过程中,t 为何值时,四边形M N Q P 恰为矩形?并求出该矩形的面积; (2)线段MN 在运动的过程中,四边形M N Q P 的面积为S ,运动的时间为t .求四边形M N Q P的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围. 解:(1)过点C 作CD AB ⊥,垂足为D . 则2A D =,当MN 运动到被CD 垂直平分时,四边形M N Q P 是矩形, 即32A M =时,四边形M N Q P 是矩形,32t ∴=秒时,四边形M N Q P 是矩形.tan 60PM AM = °=,M N Q P S ∴=四边形(2)1°当01t <<时,1()2M N Q P S P M Q N M N =+四边形·11)2t ⎤=++⎦2=+))4<≤aC PQBA M NC PQBA MN2°当12t ≤≤时1()2M N Q P S P M Q N M N =+四边形·1)12t ⎤=+-⎦·= 3°当23t <<时,1()2M N Q P S P M Q N M N =+四边形·1))2t t ⎤=-+-⎦=+3、(2010年辽宁丹东)如图,平面直角坐标系中有一直角梯形OMNH ,点H 的坐标为(-8,0),点N 的坐标为(-6,-4).(1)画出直角梯形OMNH 绕点O 旋转180°的图形OABC ,并写出顶点A ,B ,C 的坐标(点M 的对应点为A , 点N 的对应点为B , 点H 的对应点为C ); (2)求出过A ,B ,C 三点的抛物线的表达式;(3)截取CE =OF =AG =m ,且E ,F ,G 分别在线段CO ,OA ,AB 上,求四边形...BEFG 的面积S 与m 之间的函数关系式,并写出自变量m 的取值范围;面积S 是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;(4)在(3)的情况下,四边形BEFG 是否存在邻边相等的情况,若存在,请直接..写出此时m 的值,并指出相等的邻边;若不存在,说明理由.解:(1) 利用中心对称性质,画出梯形OABC . ∵A ,B ,C 三点与M ,N ,H 分别关于点O 中心对称, ∴A (0,4),B (6,4),C (8,0)CPQA M N CPQA MN(2)设过A ,B ,C 三点的抛物线关系式为2y ax bx c =++, ∵抛物线过点A (0,4),∴4c =.则抛物线关系式为24y ax bx =++. 将B (6,4), C (8,0)两点坐标代入关系式,得3664464840a b a b ++=⎧⎨++=⎩,. 解得1432a b ⎧=-⎪⎪⎨⎪=⎪⎩,.所求抛物线关系式为:213442y x x =-++.(3)∵OA =4,OC =8,∴AF =4-m ,OE =8-m .∴AG F EO F BEC EFG B ABC O S S S S S =---△△△四边形梯形 21=OA (AB +OC )12-AF ·AG 12-OE ·OF 12-CE ·OAm m m m m 421)8(21)4(2186421⨯-----+⨯⨯=)(2882+-=m m ( 0<m <4)∵2(4)12S m =-+. ∴当4m =时,S 的取最小值. 又∵0<m <4,∴不存在m 值,使S 的取得最小值. (4)当2m =-+GB =GF ,当2m =时,BE =BG .4、如图所示,菱形ABCD 的边长为6厘米,60B ∠=°.从初始时刻开始,点P 、Q 同时从A 点出发,点P 以1厘米/秒的速度沿A C B →→的方向运动,点Q 以2厘米/秒的速度沿A B C D →→→的方向运动,当点Q 运动到D 点时,P 、Q 两点同时停止运动,设P 、QO MN HA CE FDB↑→ -8(-6,-4)x y运动的时间为x 秒时,APQ △与ABC △重叠部分....的面积为y 平方厘米(这里规定:点和线段是面积为O 的三角形),解答下列问题:(1)点P 、Q 从出发到相遇所用时间是 秒;(2)点P 、Q 从开始运动到停止的过程中,当APQ △是等边三角形时x 的值是 秒; (3)求y 与x 之间的函数关系式. 解:(1)6. (2)8.(3)①当03x <≤时,2111sin 6022222AP Q y S AP AQ x x x ==︒==13△1·····. ②当3x <≤6时,1222222121sin 6021(12-2)22A P Q y S A P P Q A P C Q x x ==︒=△= ····=2.2x -+③当69x ≤≤时,设33P Q 与AC 交于点O . (解法一)过3Q 作3,Q E CB ∥则3CQ E △为等边三角形.33333212..Q E C E C Q x Q E C B C O P EO Q ∴===-∴ ∥△∽△(第28题)Q 1B C D Q 2 P 3 Q 3 EP 2 P 1 O3361,212211(212),33C P O C x O EEQ x O C C E x -∴===-∴==-3333311sin 60sin 6022AQ P AC P C O P y S S C P AC O C C P ===-△△△-S ··°··°111(6)(212)(6)22232x x x =-⨯-⨯--⨯·6.262x x =-+-.(解法二)如右图,过点O 作3OF CP ⊥于点F ,3O G C Q ⊥,于点,G 过点3P 作3P H DC ⊥交DC 延长线于点H .,.A CB ACD O F O G ∠=∠∴=又33,6,2122(6),C P x C Q x x =-=-=-3312C Q P C O Q S S ∴=△△3333321,3113211(212)(6)322(6).6C O P C P Q S S C Q P H x x x ∴==⨯=⨯--=-△△···又331sin 602AC P S C P AC =△··°1(6)6226).2x x =-⨯⨯=-P 3OABC DQ 3G H F3A O P y S ∴=△3326)6)26AC P O C P S S x x =-=---△△262x x =-+-考点2、面积最值问题典型例题:1、(2008年广东广州)如图11,在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2cm ,BC=4cm ,在等腰△PQR 中,∠QPR=120°,底边QR=6cm ,点B 、C 、Q 、R 在同一直线l 上,且C 、Q 两点重合,如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米 (1)当t=4时,求S 的值(2)当4t ≤≤10,求S 与t 的函数关系式,并求出S 的最大值解.(1)t =4时,Q 与B 重合,P 与D 重合, 重合部分是BDC ∆=3232221=⋅⋅(2)当时,如图104≤≤tQB=DP=t-4,CR=6-t,AP=6-t 由PQR ∆∽BQM ∆∽CRN ∆图11得2)324(-=∆∆t S S PQRBQM2)326(t S S PQRCRN -=∆∆22)4(43)324(-=-=∆∆t S t S PQR BQM ,22)6(43)326(t S t S PQR CRN -=-=∆∆S =3255)-(t 23t)-(6434t 4333222+-=---)(当t 取5时,最大值为325当t 取6时,有最大值32 综上所述,最大值为325二、名题精练:1、(2009湖南永州)如图,在平面直角坐标系中,点A C 、的坐标分别为(10)(0--,、,,点B在x 轴上.已知某二次函数的图象经过A 、B 、C 三点,且它的对称轴为直线1x =,点P 为直线BC 下方的二次函数图象上的一个动点(点P 与B 、C 不重合),过点P 作y 轴的平行线交BC 于点F .(1)求该二次函数的解析式;(2)若设点P 的横坐标为m ,用含m 的代数式表示线段P F(3)求PBC △面积的最大值,并求此时点P 的坐标. 解:(1)设二次函数的解析式为2(0)y ax bx c a a b c =++≠,、、为常数,由抛物线的对称性知B 点坐标为(30),,依题意得:093a b c a b c c ⎧-+=⎪++=⎨⎪=⎩(第25题)解得:33a b c ⎧=⎪⎪⎪⎪=-⎨⎪⎪⎪=⎪⎩∴所求二次函数的解析式为233y x x =--(2)P 点的横坐标为m ,P ∴点的纵坐标为233m m --设直线BC 的解析式为(0)y kx b k k b =+≠,、是常数,依题意,得30k b b +=⎧⎪⎨=⎪⎩3k b ⎧=⎪∴⎨⎪=⎩ 故直线BC的解析式为3y x =-∴点F的坐标为3m ⎛-⎝⎭2(03)3PF m ∴=-+<<(3)PBC △的面积12C P F B P F S S S P F B O =+=△△·=2213323228m ⎛⎫⎫⨯-+⨯=--+ ⎪⎪ ⎪⎝⎭⎝⎭∴当32m =时,PBC △的最大面积为8把32m =代入233y m m =--4y =-∴点P的坐标为324⎛⎫-⎪ ⎪⎝⎭,(第25题)2、(2007年淮安)在平面直角坐标系中,放置一个如图所示的直角三角形纸片AOB ,已知OA=2 ∠AOB=30°,D 、E 两点同时从原点O 出发,D 点以每秒3个单位长度的速度沿x 轴的正方向运动,E 点以每秒1个单位长度的速度沿y 轴的正方向运动,设D 、E 两点运动的时间为t 秒。
中考数学章节考点分类突破:第21章-勾股定理(含解析)

(最新最全)2019年全国各地中考数学解析汇编(按章节考点整理)第二十一章 勾股定理21.1 勾股定理(2018广州市,7, 3分)在Rt △ABC 中,∠C=90°,AC=9,BC=12,则点C 到AB 的距离是( ) A.365 B. 1225 C. 94D. 4【解析】首先根据勾股定理求出直角三角形的斜边,利用直角三角形面积的两种求法,求出点C 到AB 的距离。
【答案】由勾股定理得AB==根据面积有等积式11BC=AB CD 22AC ∙∙,于是有CD=365。
【点评】本题用了考查常用的勾股定理,直角三角形根据面积得到的一个等积式,列方程求线段CD 的长。
(2018安徽,10,4分)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )A.10B.54C. 10或54D.10或172 解析:考虑两种情况.要分清从斜边中点向哪个边沿着垂线段过去裁剪的. 解答:解:如下图,54)44()22(22=++⨯,1054)44()32(22=++⨯故选C . 点评:在几何题没有给出图形时,有的同学会忽略掉其中一种情况,错选A 或B ;故解决本题最好先画出图形,运用数形结合和分类讨论的数学思想进行解答,避免出现漏解.(2018四川省南充市,14,4分) 如图,四边形ABCD 中,∠BAD=∠BCD=90°,A B=AD ,若四边形ABCD 的面积是24cm 2,则AC 长是_____________cm.【解析】过点A 作AE ⊥BC 于点E ,AF ⊥CD 交CD 的延长线于点F.则⊿ABE ≌⊿ADF ,得AE=AF ,进一步证明四边形AECF 是正方形,且正方形AECF 与四边形ABCD 的面积相等.则AE =,所以2643AC ===【答案】【点评】本题考查了三角形的全等变换、正方形的性质以及勾股定理.解题的关键是正确的做出旋转的全等变换,将四边形的问题转化成正方形的问题来解决.(2018山东省荷泽市,16(2),6)(2)如图,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA=10,OC=8,在OC 边上取一点D,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D 、E 两点的坐标.【解析】根据折叠问题及矩形的性质,可以利用勾股定理求出线段的长来确定点的坐标.【答案】(1)依题意可知,折痕AD 是四边形OAED 的对称轴,∴在Rt ABE ∆中,10,8AE AO AB ===,6BE =,4CE ∴=,(4,8)E ∴. 在Rt DCE ∆中,222DC CE DE +=,又DE OD =,222(8)4OD OD ∴-+=,5OD ∴=,(0,5)D ∴.【点评】在平面直角坐标系中,求点的坐标实质就是求这个点到两轴的距离,也就是求线段的长,求线段的就是利用勾股定理、三角函数或相似三角形的对应边成比例.(2018贵州贵阳,8,3分)如图,在Rt △ABC 中,∠ACB=90°,AB 的垂直平分线DE 交BC 的延长线于F ,若∠F=30°,DE=1,则EF 的长( )A.3B.2C.3D.1解析:由已知得,BF=2BD=AB ,所以FC=AD,不难得到Rt △FEC ≌Rt △AED,故得EC=ED=1,结合∠F=30°,∠FCE=90°,可得EF=2EC=2.解答:选B .点评:本题主要考查 “直角三角形中30°度角所对的直角边等于斜边的一半”的知识,也涉及到全等三角形的判定与性质,相对综合.(2018浙江省嘉兴市,6,4分)如图,A 、B 两点在河的两岸,要测量这两点之间的距离,测量者在与A 同侧的河岸边选定一点C,测出AC=a 米,∠A=90° , ∠C=40° ,则AB 等于( )米 A. asin4o° B. acos40° C.atan4o° D.tan 40a【解析】如图,在Rt △ABC 中,∵∠A=90° , ∠C=40° , AC=a 米,∴tan40°=AB AC,∴AB =atan4o°, 故选C. 【答案】C.【点评】本题要求适当选用三角函数关系,解直角三角形.22.2 勾股定理的逆定理22.3 直角三角形的性质(2018浙江省湖州市,5,3分)如图,在Rt △ABC 中,∠ACB=900,AB=10,CD 是AB 边上的中线,则CD 的长是( )A.20B.10C.5D.25【解析】直角三角形斜边上的中线等于斜边的一半,故CD=21AB=21×10=5. 【答案】选:C .【点评】此题考查的是直角三角形的性质,属于基础题。
中考数学-勾股定理知识点与常见题型总结

勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证. c ba HG FEDCB A方法二:b ac b a cca b c a b四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证a b ccb a E DCB A3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:A B C 30°D CB A AD B CCB D A题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理222a b c +=解:⑴10AB⑵8BC ==题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴4AC , 2.4AC BC CD AB⋅== DB A C⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm 例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21E DCBA分析:此题将勾股定理与全等三角形的知识结合起来解:作DE AB ⊥于E ,12∠=∠,90C ∠=︒∴ 1.5DE CD ==在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mAB CD E分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD ==答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c = 解:①22221.52 6.25a b +=+=,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒ ②22139b c +=,22516a =,222bc a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状? 解:此三角形是直角三角形 理由:222()264a b a b ab +=+-=,且264c =222a b c ∴+= 所以此三角形是直角三角形。
专题21 勾股定理-2023年中考数学一轮复习热点题型与方法精准突破(解析版)

专题21 勾股定理【考查题型】【知识要点】知识点一勾股定理勾股定理的概念:如果直角三角形的两直角边分别为,,斜边为,那么。
变式:,,,,.适用范围:勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,因而在应用勾股定理时,必须明了所考察的对象是直角三角形。
用拼图的方法验证勾股定理的思路是:1)图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变2)根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理勾股定理的证明方法:方法一(图一):,,化简可证.方法二(图二):四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为大正方形面积为,所以方法三(图三):,,化简得证图一图二图三知识点二勾股数勾股数概念:能够构成直角三角形的三边长的三个正整数称为勾股数,即中,,,为正整数时,称,,为一组勾股数常见的勾股数:如;;;等扩展:用含字母的代数式表示组勾股数:1)(为正整数);2)(为正整数)3)(,为正整数)注意:每组勾股数的相同整数倍,也是勾股数。
知识点三勾股定理的逆定理勾股定理的逆定理内容:如果三角形三边长,,满足,那么这个三角形是直角三角形,其中为斜边【注意】1)勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和与较长边的平方作比较,若它们相等时,以,,为三边的三角形是直角三角形;若,时,以,,为三边的三角形是钝角三角形;若,时,以,,为三边的三角形是锐角三角形;2)定理中,,及只是一种表现形式,不可认为是唯一的,如若三角形三边长,,满足,那么以,,为三边的三角形是直角三角形,但是为斜边3)勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形知识点四直角三角形的性质与判定性质:1)直角三角形的两个锐角互余。
第十七章勾股定理知识与题型总结及测试题含答案

勾股定理知识技能和题型归纳(一)——知识技能一、本章知识内容归纳1、勾股定理——揭示的是平面几何图形本身所蕴含的代数关系。
(1)重视勾股定理的叙述形式:①直角三角形直角边上的两个正方形的面积之和等于斜边上的正方形的面积.②直角三角形斜边长度的平方,等于两个直角边长度平方之和.从这两种形式来看,有“形的勾股定理”和“数的勾股定理”之分。
(2)定理的作用:①已知直角三角形的两边,求第三边。
②证明三角形中的某些线段的平方关系。
,2……的无理数线段的几③作长为n的线段。
(利用勾股定理探究长度为,3何作图方法,并在数轴上将这些点表示出来,进一步反映了数与形的互相表示,加深对无理数概念的认识。
)2、勾股定理的逆定理(1)勾股定理的逆定理的证明方法,通过构造一个三角形与直角三角形全等,达到证明某个角为直角的目的。
(2)逆定理的作用:判定一个三角形是否为直角三角形。
(3)勾股定理的逆定理是把数转化为形,是利用代数计算来证明几何问题。
要注意叙述及书写格式。
运用勾股定理的逆定理的步骤如下:①首先确定最大的边(如c)②验证22b a +与2c 是否具有相等关系:若222c b a =+,则△ABC 是以∠C 为90°的直角三角形。
若222c b a ≠+,则△ABC 不是直角三角形。
补充知识:当222c b a >+时,则是锐角三角形;当222c b a <+时,则是钝角三角形。
(4)通过总结归纳,记住一些常用的勾股数。
如:3,4,5;5,12,13;6,8,10;8,15,17;9,40,41;……以及这些数组的倍数组成的数组。
勾股数组的一般规律: ① 丢番图发现的:式子n m n m mn n m >+-(,2,2222的正整数) ② 毕达哥拉斯发现的:122,22,1222++++n n n n n (1>n 的整数) ③柏拉图发现的:1,1,222+-n n n (1>n 的整数)3、勾股定理与勾股定理逆定理的关系 (1)注意分清应用条件:勾股定理是由直角得到三条边的关系,勾股定理逆定理则是由边的关系来判断一个角是否为直角。
中考数学总复习知识点专题讲解1---勾股定理证明及勾股数应用

大正方形面积=四个直角三角形面积和+小正方形面积
即: (a + b)2 = 4 × 1 ab + c2 .
2 化简得: a2 + b2 = c2 .
图 3 是由图 2 变化位置而来,证法与图 2 一致.
- 2 - / 15
2. 赵爽弦图证明法(如图 4)
b c
a
图 4 赵爽弦图
证法如下:
大正方形面积=四个直角三角形面积和+小正方形面积
图7
【答案】2
【解析】∵
S 1
=
1π 2
AC 2
2
,
S 2
=
1π 2
AB 2
2
,
S 3
=
1π 243;
S 3
=
1π 2
AB 2 2
+
1π 2
BC 2
2
=
1 2
π
AB2
+ BC2 4
又∵△ABC 为直角三角形
∴ AB2 + BC2 =AC2
∴
S 2
+
S 3
=
1π 2
AC 2 4
- 8 - / 15
图 15
图 16
A.9 B.10
C.11
D.12
【答案】B.
【解析】根据正方形的面积公式,结合勾股定理,能够导出正方形 A,B,C,D 的面积
和即为最大正方形的面积. 如图 16,根据勾股定理的几何意义,可得 A、B 的面积和为 S1,C、D 的面积和为 S2, S1+S2=S3,于是 S3=2+5+1+2=10. 故选 B. 【点睛】发现正方形 A,B,C,D 的边长正好是两个直角三角形的四条直角边,根据勾 股定理最终能够证明正方形 A,B,C,D 的面 积和是正方形 E 的面积. 题 9. 如图 17 所示,在△ABC 中,AB=AC=5,BC=6,点 E,F 是中线 AD 上的两点,则 图中阴影部分的面积是 ( )
中考几何题解题技巧

中考几何题解题技巧中考几何题作为数学学科的重要部分,对于学生的成绩有着至关重要的影响。
由于几何题的题型多样,要求学生具备丰富的空间想象力和严谨的逻辑思维能力,因此对于许多学生来说是一个不小的挑战。
掌握正确的解题技巧,能够帮助学生轻松应对各种几何题目,提高解题效率,从而取得好成绩。
一、常见几何题型概述在中考数学试卷中,常见的几何题型主要包括:角的证明、线段的证明、三角形的证明、立体图形的证明等。
这些题型着重考察学生的空间观念和演绎能力。
二、解题技巧与策略角、线段、三角形问题在解决这类问题时,首先要明确题目要求,然后运用相关的定理和公式进行证明。
如角平分线定理、勾股定理、全等三角形判定定理等。
在解题过程中要注意逻辑严谨,每一步都要有明确的依据。
立体图形问题立体图形问题要求学生具备一定的空间想象力和推理能力。
在解决这类问题时,可以尝试将立体图形转化为平面图形,从而简化问题。
此外,要充分考虑图形的对称性、平行性、垂直性等特点,寻找解题突破口。
运用代数方法求解在一些几何题目中,可以通过建立方程或者函数关系来解决。
如角度的度数、线段的长度、三角形的面积等都可以转化为代数问题,运用方程或者函数求解。
三、注意事项与误区纠正学生在面对几何问题时,常常会出现以下误区:忽视定理的适用条件许多学生在使用定理时,不注意检查定理的适用条件,导致定理使用不当或者根本无法使用。
因此,在使用定理之前,一定要仔细阅读定理的适用条件。
跳跃步骤一些学生在解题时,为了图省事或者节省时间,会跳跃一些必要的步骤。
然而,这样的做法往往会导致逻辑断裂,使整个证明过程失去说服力。
因此,在解题时,一定要按照步骤逐一进行。
答案不完整由于部分学生在解题时存在头重脚轻的情况,导致最后的结论没有完整的表述或者干脆没有结论。
这种情况失分是非常可惜的。
因此,在解题时,一定要注意结论的完整性和正确性。
四、实战演练与案例分享例1:如图,点E、F在线段AD上,且△ABC≌△EDF,若∠D=50°,则∠B的度数为()A.80°B.60°C.100°D.90°或80°(分析)由全等三角形的性质得出对应角相等,再由平行线的性质得出答案即可.(解答)解:∵$\bigtriangleup ABC$≌$\bigtriangleup EDF$,∴$\angle D = \angle B = 50^{\circ}$,故可得$\angle B = 180^{\circ} -50^{\circ} \times 2 = 80^{\circ}$故选A.。
中考数学复习:专题4-12 网格中的勾股定理

专题12 网格中的勾股定理【专题综述】网格题型是近几年的常考题型,也是近期各地中考考试的一个热点。
正方形网格中的每一个角都是直角,所以在正方形网格中的计算都可以归结为求任意两个格点之间的长度问题,一般情况下都是设每一个小正方形的边长为1,然后应用勾股定理来进行计算。
【方法解读】一、面积问题例1 如图1所示,在一个有4×4个小正方形组成的正方形网格中,阴影部分的面积与正方形ABCD的面积比是()A、3:4B、5:8C、9:16D、1:2【举一反三】如图,在正方形网格(图中每个小正方形的边长均为1)中,△ABC的三个顶点均在格点上,则△ABC的周长为,面积为.【来源】山东省青岛市第四中学八年级数学上册:1.1探索勾股定理同步练习二、长度问题例2 如图2所示,在△ABC 中,三边a 、b 、c 的大小关系是( )A 、a <b <cB 、c <a <bC 、c <b <aD 、b <a <c【举一反三】勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦。
我国西汉《周髀算经》中周公与商高对话中涉及勾股定理,所以这个定理也有人称商高定理,勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。
我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应。
现在把这个数轴叫做x 轴,同时,增加一个垂直于x 轴的数轴,叫做y 轴,如下图。
这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A 点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A 。
若平面上的点M ()11,x y ,N ()22,x y ,我们定义点M 、N 在x 轴方向上的距离为: 12x x -,点M 、N 在y 轴方向上的距离为: 12y y -。
初中数学平面几何题型的解题技巧研究———以“勾股定理”为例

㊀㊀解题技巧与方法㊀㊀150㊀初中数学平面几何题型的解题技巧研究初中数学平面几何题型的解题技巧研究㊀㊀㊀ 以 勾股定理 为例Һ吴霖杰㊀(泉州市第六中学,福建㊀泉州㊀362000)㊀㊀ʌ摘要ɔ勾股定理作为一个最基本的几何定理,为解答初中数学平面几何题型提供了思路,教师应在初中数学解题教学中,向学生传授勾股定理解题技巧,使学生学会巧妙解题,发散数学思维.文章简要介绍了勾股定理,紧接着分析了勾股定理在初中数学平面几何题型中的实际解题应用技巧,提出利用勾股定理解答周长问题㊁面积问题㊁最短路径问题㊁证明问题等.同时指出,教师应在夯基㊁精讲㊁常练基础上,指导学生利用勾股定理解答初中数学平面几何题型,培养学生的解题能力.ʌ关键词ɔ初中数学;平面几何;解题技巧勾股定理证明了平面直角三角形三边关系问题,即在任何一个平面直角三角形中,两条直角边的平方之和都一定等于斜边的平方.平面几何是初中数学的重点,也是难点.‘义务教育数学课程标准(2022年版)“在数与代数㊁图形与几何㊁统计与概率㊁综合与实践四个领域组织课程内容,平面几何属于图形与几何领域.在该领域,学生应进一步建立几何直观,提升推理能力,解决抽象问题.分析平面几何问题,其解题思路为:将一般图形转化为特殊图形,然后根据特殊图形的特殊规律进行求解.而直角三角形,是转化平面几何图形的最有效图形之一,通过在原图中添加辅助线,构造直角三角形,将平面几何问题转化为直角三角形相关问题,然后利用勾股定理展开计算,不仅有助于学生高效解决问题,而且能够提高学生的数形结合能力,培养其发散思维.教师可以具体的初中数学平面几何题型为例,传授学生勾股定理解题技巧.一㊁勾股定理在初中数学平面几何题型中的解题技巧(一)利用勾股定理解答三角形周长问题例1㊀已知在әABC中,AB=13,AC=15,BC边上的高AD为12,求әABC的周长.解㊀(1)若高AD在әABC的内部,则әABC如图1所示,BC=BD+CD.BD=132-122=5,CD=152-122=9,则BC=9+5=14,әABC的周长=13+15+14=42.(2)若高AD在әABC的外部,则әABC如图2所示,BC=CD-BD,BD=132-122=5,CD=152-122=9,BC=9-5=4,әABC的周长=13+15+4=32.综上,әABC的周长为42或32.图1㊀㊀㊀图2题型与解题技巧分析㊀此题型为初中数学平面几何基础题型.想要确定一个三角形的周长,需要先确定其三边长.但在一些三角形周长问题中,无法通过题目已知条件直接判断其三边长,对此,解题者可构造直角三角形,利用勾股定理降低解题难度.本题给出三角形其中两条边的长度以及另一条边对应的高,解题者可以根据已知条件构造直角三角形,借助勾股定理计算原三角形第三条边的长度,即BC的长.但是根据题目已知条件,无法确定高AD在әABC中的具体位置,应画图并进行分类讨论.当高AD在әABC内部时,先通过勾股定理分别计算出CD与BD的长,再通过求和得到BC的长.当高AD在әABC外部时,需要延长CB,故而在求出CD与BD的长后,需要通过求差得到BC的长.利用勾股定理解答三角形周长问题,关键便在于画图与分类讨论,充分考虑未知边长的每一种可能.㊀图3(二)利用勾股定理解答面积问题例2㊀已知在四边形ABCD中,øB=øD=90ʎ,øA=135ʎ,若AD=23,BC=6,求四边形ABCD的面积.解㊀结合题意可画出如图3所示的四边形ABCD.观察图形,其为不规则图形,无法直接应用已知面积计算公式.但延长DA与CB,可构造出两个等腰直角三角形.在RtәABE中,øABE=90ʎ,øEAB=45ʎ,øBEA=㊀㊀㊀解题技巧与方法151㊀㊀45ʎ,AB=BE.在RtәCDE中,øCDE=90ʎ,øC=øE=45ʎ,CD=DE.令AB=BE=x,则AE=2x,DE=2x+23=CD,CE=6+x.CE2=CD2+DE2,即(6+x)2=2(2x+23)2,解方程可得AB=BE=6-26,DE=CD=62-23,SRtәABE=12㊃AB㊃BE=30-126,SRtәCDE=12㊃DE㊃CD=42-126,S四边形ABCD=SRtәCDE-SRtәABE=(42-126)-(30-126)=12.题型与解题技巧分析㊀初中数学中,一些不规则图形面积问题无法结合已知公式展开计算,而是需要构造直角三角形,将不规则图形转换为两个或两个以上直角三角形,代入勾股定理,具体步骤为:(1)观察图形,分析其特点.(2)引入辅助线,构造直角三角形,确定相关线段长度.(3)借助直角三角形面积间接计算不规则图形面积.本题中,待求图形为不规则四边形,解题者可以延长线段CB,DA,使其延长线交于点E,构造两个直角三角形,确定相关线段长度.之后,通过计算әCDE与әABE的面积差,即可成功求出四边形ABCD的面积.利用勾股定理解答面积问题,关键在于引入辅助线,割补不规则图形,构造直角三角形.(三)利用勾股定理解答最短路径问题例3㊀如图4所示,在一个无盖圆柱形玻璃杯内壁B点有一滴蜂蜜,蜂蜜距玻璃杯底部5cm.玻璃杯整体高度为14cm,底面周长为32cm.若不计玻璃杯厚度,一只蚂蚁在玻璃杯外壁A处出发去吃蜂蜜,最短应爬行多远的距离?(蚂蚁与玻璃杯口的竖直距离为3cm).图4㊀㊀图5解㊀圆柱形玻璃杯的侧面展开图如图5所示,作A点关于线段GF的对称点E,连接BE,即可得到蚂蚁爬行的最短路径长为BE的长.过B作BCʅAE于C,求解BE的长需要将BE置于直角三角形BCE中,BE=CE2+BC2,BC=12ˑ32=16(cm),CE=14+3-5=12(cm),则BE=162+122=20(cm),即蚂蚁最短应爬行20cm的距离.题型与解题技巧分析㊀最短路径问题,是初中数学平面几何题型的特殊形式.解答此类问题,首先需要运用 化曲为直 思想,将题目给出的立体图形转化为平面图形,其次可以利用勾股定理,根据 起点 与 终点 构造直角三角形,分析最短路径.本题为圆柱体的最短路径问题,解题者首先应运用 化曲为直 思想,将圆柱形玻璃杯侧面展开.此时,题目被转化为将军饮马 问题,可以借助对称轴转化蚂蚁爬行路径,构造直角三角形.在此基础上代入已知条件,便可得出蚂蚁的最短爬行距离.利用勾股定理解答立体几何最短路径问题,要注意运用 化曲为直 思想,实现立体几何到平面几何的转化.(四)利用勾股定理解答证明问题㊀图6例4㊀如图6,四边形ABFC为不规则图形.连接BC,ABʅCB.取CF边上一点D,令CDʅAD,AD2=2AB2-CD2.求证:AB=BC.证明㊀观察AD2=2AB2-CD2,其与勾股定理联系紧密.ȵABʅCB,ʑAB2+BC2=AC2.ȵCDʅAD,ʑAD2+CD2=AC2,则AB2+BC2=AD2+CD2,AD2=AB2+BC2-CD2.又AD2=2AB2-CD2,ʑAB2+BC2-CD2=2AB2-CD2,ʑBC2=AB2,又在四边形ABFC中,AB与BC均为具有 正值长度 的线段,故AB=BC得证.题型与解题技巧分析㊀证明问题是初中数学平面几何题型的重要组成部分,包括证明图形线段长度关系㊁角度大小关系㊁直线位置关系等题型.即便题目所给条件较为复杂,解题者也可以从复杂信息中挖掘简单提示,如勾股定理.分析可通过勾股定理进行解答的初中数学平面几何证明问题,其分类如下:(1)题目所给条件未直接体现勾股定理,但证明对象与勾股定理相关.(2)题目所给条件与勾股定理联系紧密.对于前者,解题者应在证明过程中构造直角三角形,将已知条件逐渐转化至同一直角三角形中;对于后者,解题者应寻找或构造直角三角形,直接由勾股定理展开推理,得到边长关系.利用勾股定理解答证明问题时,解题者需要先结合所给条件判断题目特征,再根据题目特征灵活解题.(五)利用勾股定理解答折叠问题㊀图8例5㊀如图7所示,长方形ABCD的长和宽分别为8和6.已知P是宽AD上的一点,现沿着BP折叠әABP,使PE与CD相交于点O,BE与CD相交于点G.如果OD=OE,线段AP的长是多少?解㊀由题意易得,әABPɸәEBP,әODPɸәOEG,由此可得OP=OG,PD=GE,DG=OD+OG=OE+OP=EP.设AP=x,则EP=DG=x,㊀㊀解题技巧与方法㊀㊀152㊀PD=GE=6-x,CG=8-x,BG=2+x.又әBCG为直角三角形,代入勾股定理,得62+(8-x)2=(x+2)2,解得x=4.8,则线段AP的长是4.8.题型与解题技巧分析㊀折叠问题也是常见的初中数学平面几何题型之一,可分为根据折痕求角的度数㊁线段的长㊁重合部分的图形面积等题型.解答折叠问题,不仅需要运用轴对称㊁四边形等知识,而且需要引入勾股定理,具体思路为:(1)根据折痕运用轴对称的性质,确定对应点,分析对应线段位置与大小关系.(2)根据折叠前后的特殊点和线段,构造直角三角形.(3)立足直角三角形,利用勾股定理㊁三角函数计算待求问题.本题为 求线段的长 折叠问题,满足勾股定理解题特点.在长方形ABCD中,折叠前后的对应角与对应边相等.故而想求出线段AP的长度,不妨设未知数x,即AP=x.在此基础上,图中所有线段均可用未知数表示.用相关未知数结合勾股定理列出方程,求出x,便可得到线段AP的长.当然,在题目给出相对简单的条件时,也可以直接运用勾股定理, 跳过 列方程步骤.二㊁初中数学平面几何题型解题技巧的指导要点 以 勾股定理 为例一线教师以勾股定理为切入点研究初中数学平面几何题型的解题技巧,是为了认识初中数学平面几何题型的更多解答方法,更是为了提升教学水平,指导学生从多角度分析和解决初中数学平面几何问题,培养学生的问题解决能力.故而在以上研究基础上,教师应进一步分析初中数学平面几何题型解题技巧的指导要点,下面笔者以勾股定理为例进行阐述.(一)夯基利用勾股定理解答初中数学平面几何题型,要求学生具备扎实的勾股定理知识基础.教师应在此层面上,重视初中数学勾股定理教学,实现 夯基 目标.教师可以在实际教学期间,整合游戏化教学㊁情境教学㊁问题教学㊁任务型教学㊁层次化教学㊁翻转课堂等教学方法,循序渐进地指导学生探究勾股定理,从而使学生充分经历勾股定理的猜想㊁推理㊁认识㊁理解㊁实践㊁掌握过程,形成发散的勾股定理解题思维.比如,在讲解勾股定理时,教师可以借助 赵爽弦图 与 毕达哥拉斯树 创设情境,为学生搭建 数形并茂 的学习平台,指导学生先观察情境中的数学图形,再挖掘和讨论其所蕴含的数学思想.其间,教师应巧妙点拨学生 找规律 ,促使学生发现直角三角形三边的 平方 规律,奠定扎实的勾股定理认知基础.再如,在根据教材例题指导学生运用勾股定理时,教师可鼓励学生扮演 小老师 ,讲解不同题目的分析思路和解题步骤,深化学生思维,强化 夯基 效果.(二)精讲掌握勾股定理在不同初中数学平面几何题型中的解题技巧,要求学生准确区分初中数学平面几何题型与勾股定理的内在联系,建立结构化的思维系统.教师应在此层面上,对涉及勾股定理的初中数学平面几何题型进行精讲,全面启发学生思维.教师应完善初中数学平面几何习题训练,每呈现一个特殊题型,都必须为学生精讲解答过程.对此,教师可以结合课堂互动预案,精心设计动态课件.课上,教师先通过课件呈现题目,鼓励学生自由讨论㊁分享思路.紧接着,教师借助鼠标控制动态课件,依次出示解答步骤.出示题目解答步骤前后,教师都应给予学生充足的讨论时间,然后对学生讨论结果进行补充讲解,使学生准确把握解题技巧.全面讲解例题后,教师还可以设计对比归纳课件,将初中数学平面几何不同题型及其勾股定理解题技巧进行汇总,帮助学生加以区分.(三)常练纸上谈兵不如实际演练,面对初中数学平面几何题型,学生想要快速判断其特点㊁选择正确的勾股定理解题技巧,必须达到熟能生巧的状态.因此,教师应组织学生常练.教师应将 常练 与 题海战术 进行区分,为学生精选典型题目,避免为学生施加过大综合实践压力.对此,教师可以将中考数学真题视为习题资源库,关注历年中考真题,提炼其中的平面几何典型题目,创新设计勾股定理与平面几何测试题,进而对学生定期进行习题训练.在此基础上,教师还可以督促学生整理错题,建立错题集,以便随时查缺补漏,实现巩固练习.结㊀语总之,为提高学生解答初中数学平面几何题型的效率,教师有必要向学生传授勾股定理解题技巧.具体来讲,教师应明确勾股定理的本质及解题价值,总结初中数学中常见的平面几何题型及其勾股定理解题技巧,抓住 夯基 精讲 常练 三大要点对学生进行指导,促使学生创新解决问题,提高解题能力.ʌ参考文献ɔ[1]林劲松.浅析勾股定理的应用探究[J].读写算,2022(36):132-134.[2]赵霞.例析勾股定理常见的应用类型[J].中学数学,2022(20):82-83.[3]万广磊.探究神奇的勾股定理[J].初中生世界,2022(42):44-45.。
中考数学专题复习常见模型方法勾股定理的证明

中考数学专题复习常见模型方法勾股定理的证明学校:___________姓名:___________班级:___________考号:___________评卷人得分一、单选题1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为()A.9B.6C.4D.32.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于()A.8B.6C.4D.53.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a,较短直角边为b,则ab的值是()A.4B.6C.8D.104.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是()A.B.C.D.5.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若12321S S S++=,则S2的值是()A.9B.8C.7D.6评卷人得分二、填空题6.如图,在ABC中,90A∠=︒,则三个半圆面积S1,S2,S3的关系为___________.评卷人得分三、解答题7.如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,H,G,F,使得BE CH GD AF===,求证:四边形EHGF是正方形.8.如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,H,G,F,使得BE CH GD AF===,此外//EQ BC,HP//CD,GO//DA,FR//AB,求证:四边形ORQP是正方形.9.如图所示,在正方形ABCD的四边AB,BC,CD,DA上分别取点E,H,G,F,使得BE CH GD AF===,此外//EQ BC,HP//CD,GO//DA,FR//AB.求证:(1)4AEFABCD EHGFS S S=+正方形正方形;(2)4FREEHGF ORQPS S S=+正方形正方形;(3)ABCD EHGF EHGF ORQPS S S S-=-正方形正方形正方形正方形.10.勾股定理是人类最伟大的十个科学发现之一,在《周髀算经》中就有“若勾三,股四,则弦五”的记载,汉代数学家赵爽为证明勾股定理创制的“赵爽弦图”也流传至今.迄今为止己有400多种证明勾股定理的方法.下面是数学课上创新小组验证过程的一部分.请认真阅读并根据他们的思路将后续的过程补充完整:将两张全等的直角三角形纸片按图所示摆放,其中b a>,点E在线段AC上,点B D、在边AC两侧,试证明:222+= ab c.11.(1)如图1是一个重要公式的几何解释,请你写出这个公式;(2)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(1876年4月1日发表在《新英格兰教育日志》上),现请你尝试证明过程.说明:222C a b=+.12.阅读理解:【问题情境】教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?【探索新知】从面积的角度思考,不难发现:大正方形的面积=小正方形的面积+4个直角三角形的面积.从而得数学等式:(a +b )2=c 2+4×12ab ,化简证得勾股定理:a 2+b 2=c 2.【初步运用】(1)如图1,若b =2a ,则小正方形面积:大正方形面积= ;(2)现将图1中上方的两直角三角形向内折叠,如图2,若a =4,b =6,此时空白部分的面积为 ;(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC =3,求该风车状图案的面积.(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为S 1,S 2,S 3,若S 1+S 2+S 3=40,则S 2= .【迁移运用】如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?带着这个疑问,小丽拼出图5的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a 、b 、c 之间的关系,写出此等量关系式及其推导过程.参考答案:1.D【解析】【分析】已知ab =8可求出四个三角形的面积,用大正方形面积减去四个三角形的面积得到小正方形的面积,根据面积利用算术平方根求小正方形的边长.【详解】a b -由题意可知:中间小正方形的边长为:,11ab 8422=⨯=每一个直角三角形的面积为:, 214ab a b 252(),∴⨯+-= 2a b 25169∴-=-=(),a b 3∴-=,故选D.【点睛】本题考查勾股定理的推导,有较多变形题,解题的关键是找出图形间面积关系,同时熟练运用勾股定理以及完全平方公式,本题属于基础题型.2.B【解析】【详解】根据面积的差得出a+b 的值,再利用a ﹣b=2,解得a ,b 的值代入即可.解:△AB=10,EF=2,△大正方形的面积是100,小正方形的面积是4, △四个直角三角形面积和为100﹣4=96,设AE 为a ,DE 为b ,即4×ab=96, △2ab=96,a 2+b 2=100,△(a+b )2=a 2+b 2+2ab=100+96=196,△a+b=14,△a ﹣b=2,解得:a=8,b=6,△AE=8,DE=6,△AH=8﹣2=6.故选B .3.B【解析】【分析】小正方形、大正方形的面积可以分别用a、b 表示,进而两式相减即可求出ab 的值.【详解】由勾股定理,得大正方形的面积为:2217a b +=,又小正方形的面积为2()5a b -= 即2225a b ab +-=△1725ab -=△ab =6故选:B .【点睛】本题是以弦图为背景的计算题,考查了勾股定理,图形的面积,关键是用a 、b 表示大小正方形的面积.4.D【解析】【分析】利用两个以a 和b 为直角边三角形面积与一个直角边为c 的等腰直角三角形面积和等于上底为a,下第为b,高为(a+b)的梯形面积推导勾股定理可判断A ,利用以a 与b 为两直角边四个全等三角形面积与边长为c 的小正方形面积和等于以a+b 的和为边正方形面积推导勾股定理可判断B , 利用以a 与(a+b )为两直角边四个全等三角形面积与边长为b 的小正方形面积和等于以c 为边正方形面积推导勾股定理可判断C ,利用四个小图形面积和等于大正方形面积推导完全平方公式可判断D .【详解】解: A 、两个以a 和b 为直角边三角形面积与一个直角边为c 的等腰直角三角形面积和等于上底为a,下第为b,高为(a+b)的梯形面积,故()2211112222ab ab c a b ++=+,整理得: 222a b c +=,即能证明勾股定理,故本选项不符合题意;B 、以a 与b 为两直角边四个全等三角形面积与边长为c 的小正方形面积和等于以a+b 的和为边正方形面积,故()22142ab c a b ⨯+=+,整理得: 222a b c +=,即能证明勾股定理,故本选项不符合题意;C 、以a 与(a+b )为两直角边四个全等三角形面积与边长为b 的小正方形面积和等于以c为边正方形面积,()22142a ab bc ⨯++=,整理得: 222a b c +=,即能证明勾股定理,故本选项不符合题意;D 、四个小图形面积和等于大正方形面积,()2222ab a b a b ++=+ ,根据图形证明完全平方公式,不能证明勾股定理,故本选项符合题意;故选:D .【点睛】本题考查利用面积推导勾股定理与完全平方公式,掌握利用面积推导勾股定理与完全平方公公式是关键.5.C【解析】【分析】根据图形的特征得出线段之间的关系,进而利用勾股定理求出各边之间的关系,从而得出答案.【详解】解:△图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为S 1,S 2,S 3, △CG =NG ,CF =DG =NF ,△S 1=(CG +DG )2=CG 2+DG 2+2CG •DG=GF 2+2CG •DG ,S 2=GF 2,S 3=(NG ﹣NF )2=NG 2+NF 2﹣2NG •NF ,△S 1+S 2+S 3=21=GF 2+2CG •DG +GF 2+NG 2+NF 2﹣2NG •NF =3GF 2,△S 2的值是:7.故选:C .【点睛】此题主要考查了勾股定理的应用,根据已知得出S 1+S 2+S 3=21=GF 2+2CG •DG +GF 2+NG 2+NF 2﹣2NG •NF =3GF 2是解决问题的关键.6.123S S S =+【解析】【分析】分别用AB 、BC 和AC 表示出1S 、2S 、3S ,然后根据222BC AB AC =+即可得出1S 、2S 、3S 的关系.【详解】解:在ABC ∆中,90A ∠=︒,222BC AB AC ∴=+,22311()228S AC AC ππ==,22211()228S AB AB ππ==,22111()228S BC BC ππ==, 222321()88S S AC AB BC S ππ∴+=+==,即123S S S =+.故答案为:123S S S =+.【点睛】 本题主要考查了勾股定理的应用.解题的关键是勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.见解析【解析】【分析】 根据正方形的性质证明Rt AEF Rt BHE Rt CGH Rt DFG △≌△≌△≌△,然后证明90FEH ∠=即可得到答案.【详解】解:△四边形ABCD 是正方形△AB CD BC AD ===,90A B C D ∠=∠=∠=∠=︒△BE CH GD FA ===,△AE BH CG FD ===,△Rt AEF Rt BHE Rt CGH Rt DFG △≌△≌△≌△,△EF HE GH FG ===,AFE BEH ∠=∠.△90AEF AFE ∠+∠=,△90AEF BEH ∠+∠=,△90FEH ∠=,△四边形EHGF 是正方形.【点睛】本题主要考查了正方形的性质与判定,全等三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.8.见解析【解析】【分析】根据已知条件得到四边形AFRE 、四边形EBHQ 、四边形HCGP 、四边形FOGD 均为长方形,在根据三角形全等证明即可;【详解】△//EQ BC ,HP//CD ,GO//AD ,FR//AB ,且90A B C D ∠=∠=∠=∠=︒,△四边形AFRE 、四边形EBHQ 、四边形HCGP 、四边形FOGD 均为长方形, △AEF RFE BHE QEH CGH PHG DFG OGF ≌≌≌≌≌≌≌,△FR EQ HP GO ===,ER HQ GP FO ===,△OR RQ QP PO ===,且18090POR FOG ∠=︒-∠=︒,△四边形ORQP 为正方形.【点睛】 本题主要考查了正方形的判定,结合三角形全等的判定与性质、矩形的判定与性质证明是解题的关键.9.(1)证明见解析;(2)证明见解析;(3)证明见解析【解析】【分析】(1)根据正方形的性质证明Rt AEF Rt BHE Rt CGH Rt DFG △≌△≌△≌△,然后证明90FEH ∠=即可得到答案;(2)先证明AEF RFE △≌△,然后同理可以得到RFE QEH PHG OGF △≌△≌△≌△,然后证明四边形ORQP 是正方形,即可得到结论;(3)根据(1)(2)的结论求解即可.【详解】解:(1)△四边形ABCD 是正方形△AB CD BC AD ===,90A B C D ∠=∠=∠=∠=△BE CH GD FA ===,△AE BH CG FD ===,△Rt AEF Rt BHE Rt CGH Rt DFG △≌△≌△≌△,△EF HE GH FG ===,AFE BEH ∠=∠,AEF BHE CGH DFG S S S S ==△△△△=△90AEF AFE ∠+∠=,△90AEF BEH ∠+∠=,△90FEH ∠=,△四边形EHGF 是正方形. △4AEF ABCD EHGF S S S =+正方形正方形(2)△四边形EHGF 是正方形△EH HG GF FE ===,90FEH EHG HGF GFE ∠=∠=∠=∠=△//EQ BC , FR//AB△四边形AERF 是平行四边形△△A =90°△四边形AERF 是矩形△AEF RFE △≌△△90A=ERF=∠∠ 同理可以得到BHE QEH △≌△,CGH PHG △≌△,DFG OGF △≌△△RFE QEH PHG OGF △≌△≌△≌△△RFE QEH PHG OGF S S S S △△△△===,RE QH PG OE ===,RF QE PH OG === △OR RQ QP PO === △90A=ERF=∠∠△90ORQ=∠△四边形ORQP 是正方形△4FRE EHGF ORQP S S S =+正方形正方形(3)△4AEF ABCD EHGF S S S -=△正方形正方形,4FRE EHGF ORQP =S S S -正方形正方形△,又△AEF RFE △≌△△AEF RFE S S △△=△ABCD EHGF EHGF ORQPS S S S-=-正方形正方形正方形正方形【点睛】本题主要考查了正方形的性质与判定,全等三角形的性质与判定,矩形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.10.见解析.【解析】【分析】首先连结BD,作DF BC⊥延长线于F,则AE b a,根据Rt ABC Rt DAE,易证90DAB︒∠=,再根据ADE ABCADFB DFCES S S S四边形四边形,ADB DFBADFBS S S∆∆=+四边形,两者相等,整理即可得证.【详解】证明:连结BD,作DF BC⊥延长线于F,则AE b aADE ABCADFB DFCES S S S四边形四边形1122ab ab b a b2ab b ab=+-2b=Rt ABC Rt DAE∆≅∆AB AD cADE BAC∴∠=∠90ADE DAE90BAC DAE即90DAB︒∠=,△AD AB⊥△ADB DFBADFBS S S∆∆=+四边形21122c a b b a222111222c b a=+-即有:2222111222b c b a△222+=a b c【点睛】本题考查了勾股定理的证明,用两种方法表示出四边形ADFB的面积是解本题的关键.11.(1)222()2a b a ab b+=++;(2)证明见解析.【解析】【分析】(1)根据正方形面积计算公式解答;(2)利用面积法证明即可得到结论.【详解】(1)222()2a b a ab b+=++;(2)如图,△Rt△DEC△Rt△EAB,△△DEC=△EAB,DE=AE,△90EAB AEB∠+∠=︒,△90DEC AEB∠+∠=︒,△△AED为等腰直角三角形,△Rt ABE Rt DCE Rt DEAABCDS S S S=++梯形,△21111()()2222b a a b ab ab c++=++,即22()2a b ab c+=+,△222()2a b a ab b +=++,△22222a ab b ab c ++=+,△222c a b =+.【点睛】此题考查勾股定理的证明,完全平方公式在几何图形中的应用,正确理解各部分图形之间的关系,正确分析它们之间的面积等量关系是解题的关键.12.【初步运用】(1)5:9;(2)28;(3)24;(4)403;【迁移运用】a 2+b 2﹣ab =c 2,证明见解析【解析】【分析】初步运用:(1)如图1,求出小正方形的面积,大正方形的面积即可;(2)根据空白部分的面积=小正方形的面积﹣2个直角三角形的面积计算即可;(3)可设AC =x ,根据勾股定理列出方程可求x ,再根据直角三角形面积公式计算即可求解;(4)根据图形的特征得出四边形MNKT 的面积设为x ,将其余八个全等的三角形面积一个设为y ,从而用x ,y 表示出S 1,S 2,S 3,得出答案即可.迁移运用:根据大正三角形面积=三个全等三角形面积+小正三角形面积,构建关系式即可.【详解】解:【初步运用】(1)由题意:b =2a ,c =5a ,△小正方形面积:大正方形面积=5a 2:9a 2=5:9,故答案为:5:9;(2)空白部分的面积为=52﹣2×12×4×6=28, 故答案为:28;(3)24÷4=6,设AC =x ,依题意有:(x +3)2+32=(6﹣x )2,解得x =1,△面积为:12×(3+1)×3×4=12×4×3×4=24,故该飞镖状图案的面积是24;(4)将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,△正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=40,△S1=8y+x,S2=4y+x,S3=x,△S1+S2+S3=3x+12y=40,△x+4y=403,△S2=x+4y=403,故答案为:403;[迁移运用]结论:a2+b2﹣ab=c2.理由:由题意:大正三角形面积=三个全等三角形面积+小正三角形面积,可得:12(a+b)×k(a+b)=3×12×b×ka+12×c×ck,△(a+b)2=3ab+c2,△a2+b2﹣ab=c2.【点睛】本题考查勾股定理的证明和应用,根据图形得出面积关系是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解题技巧专题:勾股定理与面积问题
——全方位求面积,一网搜罗
◆类型一直角三角形中,利用面积求斜边上的高
1.(郴州桂阳县期末)在Rt△ABC中,∠C=90°,AC=9,BC=12,则C点到AB的距离为【方法1】()
A.
5
36 B.
36
5 C.
33
4 D.
12
25
2.如图,在2×2的方格中,小正方形的边长是1,点A,B,C都在网格点上,则AB 边上的高为()
A.
35
5 B.
25
5 C.
35
10 D.
32
2
第2题图第6题图
◆类型二结合乘法公式巧求面积或周长
3.直角三角形的周长为24,斜边长为10,则其面积为()
A.96 B.49 C.24 D.48
4.若一个直角三角形的面积为6cm2,斜边长为5cm,则该直角三角形的周长是() A.7cm B.10cm
C.(5+37)cm D.12cm
◆类型三巧妙分割求面积
5.如图,已知AB=5,BC=12,CD=13,DA=10,AB⊥BC,求四边形ABCD的面积.
◆类型四“勾股树”及其拓展类型中有关面积的计算
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的边长为()
A.14cm B.4cm C.15cm D.3cm
7.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为()
A.4 B.36 C.16 D.55
第7题图第8题图
8.(青海中考)如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2……按照此规律继续下去,则S9的值为()
A.⎝⎛⎭⎫
1
2
6
B.⎝⎛⎭⎫
1
2
7
C.⎝⎛⎭⎫
2
2
6
D.⎝⎛⎭⎫
2
2
7
◆类型五“赵爽弦图”中有关面积的计算
9.“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则大正方形与小正方形的面积差是() A.9 B.36 C.27 D.34
第9题图第10题图
10.(永州零陵区校级模拟)如图是4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9.其中说法正确的是()
A.①②B.①②③
C.①②④D.①②③④
参考答案与解析
1.B
2.A解析:过点C作CD⊥AB于点D.∵S△ABC=22-
1
2×1×2-
1
2×1×1-
1
2×1×2=
3
2,又∵S△ABC=
1
2AB·CD,∴
1
2AB·CD=
3
2.∵AB=1
2+22=5,∴CD=
35
5.故选A.
3.C解析:设该直角三角形的两直角边长分别为a,b,则有a+b=14①,a2+b2=102②.①两边同时平方,得a2+b2+2ab=142,所以2ab=96,所以ab=48,
1
2ab=24.故选C.
4.D
5.解:连接AC,过点C作CE⊥AD交AD于点E.∵AB⊥BC,∴∠CBA=90°.在Rt△ABC 中,由勾股定理得AC=AB2+BC2=52+122=13.∵CD=13,∴AC=CD,即△ACD是等腰三角形.∵CE⊥AD,∴AE=
1
2AD=
1
2×10=5.在Rt△ACE中,由勾股定理得CE=AC2-AE2=132-52=12.∴S四边形ABCD=S△ABC+S△CAD=
1
2AB·BC+
1
2AD·CE=
1
2(12×5+10×12)=90.
6.A7.C
8.A解析:在图中标上字母E,如图所示.∵正方形ABCD的边长为2,△CDE为等腰直角三角形,∴DE2+CE2=CD2,DE=CE,∴S2+S2=S1.观察,发现规律:S1=22=4,S2=
1
2S1=2,S3=
1
2S2=1,S4=
1
2S3=
1
2,…,∴S n=⎝
⎛
⎭
⎫1
2
n-3
.当n=9时,S9=⎝⎛⎭⎫
1
2
9-3
=⎝⎛⎭⎫
1
2
6
.故选A.
9.B解析:大正方形的面积为32+62=45,小正方形的面积为(6-3)2=9,则面积差为45-9=36.故选B.
10.B解析:由题意得
⎩⎪
⎨
⎪⎧x2+y2=49①,
(x-y)2=4②,
①-②得2xy=45③,∴2xy+4=49,①+③得x2+2xy+y2=94,∴x+y=94,∴①②③正确,④错误.故选B.。
