A星算法求八数码问题实验报告
A星算法求解八数码技术报告

A*算法求解八数码问题●open 表、closed 表数据结构的选择:1)把s放入open表,记f=h,令closed为空表。
2)重复下列过程,直到找到目标节点为止。
若open表为空表,则宣告失败。
3)选取open表中未设置过的具有最小f值的节点为最佳节点bestnode,并把它放入closed表。
4)若bestnode为一目标节点,则成功求得一解。
5)若bestnode不是目标节点,则扩展之,产生后继节点succssor。
6)对每个succssor进行下列过称:a)对每个succssor返回bestnode的指针。
b)计算g(suc)=g(bes)+k(bes,suc)。
c)如果succssore open,称此节点为old,并填到bestnode的后继节点表中。
d)比较新旧路劲代价。
如果g(suc)<g(old),则重新确定old的父辈节点为bestnode,记下较小代价g(old),并修真f(old)值。
e)若至old节点的代价较低或一样,则停止扩展节点。
f)若succssore不再closed表中,则看其是否在closed表中。
g)若succssore在closed表中,则转向(c)。
h)若succssore既不在open表中,又不在closed表中,则把它放入open表中,并添入bestnode后裔表中,然后转向(7)。
i)计算f值j)Go loop●节点的数据结构:static int target[9]={1,2,3,8,0,4,7,6,5}; 全局静态变量,表示目标状态class eight_num{private:int num[9]; 定义八数码的初始状态int not_in_position_num; 定义不在正确位置八数码的个数int deapth; 定义了搜索的深度int eva_function; 评价函数的值,每次选取最小的进行扩展public:eight_num* parent; 指向节点的父节点eight_num* leaf_next; 指向open表的下一个节点eight_num* leaf_pre; 指向open 表的前一个节点初始状态的构造函数eight_num(int init_num[9]);eight_num(int num1,int num2,int num3,int num4,int num5,int num6,int num7,int num8,int num9){}eight_num(void){ }计算启发函数g(n)的值void eight_num::cul_para(void){}显示当前节点的状态void eight_num::show(){}复制当前节点状态到一个另数组中void eight_num::get_numbers_to(int other_num[9]){}设置当前节点状态(欲设置的状态记录的other数组中)void eight_num::set_num(int other_num[9]){}eight_num& eight_num::operator=(eight_num& another_8num){} eight_num& eight_num::operator=(int other_num[9]){}int eight_num::operator==(eight_num& another_8num){}int eight_num::operator==(int other_num[9]){}空格向上移int move_up(int num[9]){}空格向下移int move_down(int num[9]){}空格向左移int move_left(int num[9]){}空格向右移int move_right(int num[9]){}判断可否解出int icansolve(int num[9],int target[9]){}判断有无重复int existed(int num[9],eight_num *where){}寻找估价函数最小的叶子节点eight_num* find_OK_leaf(eight_num* start){}}A*算法求解框图:●分析估价函数对搜索算法的影响:估价函数就是评价函数,它用来评价子结点的好坏,因为准确评价是不可能的,所以称为估值。
A星算法求八数码问题实验报告

A星算法求八数码问题实验报告人工智能实验报告实验名称:八数码问题姓名:xx学号:2012210xxxx计算机学院2014年1月14日一.实验目的掌握A*的思想,启发式搜索,来求解在代价最小的情况下将九宫格从一个状态转为另状态的路径。
二.实验内容给定九宫格的初始状态,要求在有限步的操作内,使其转化为目标状态,且所得到的解是代价最小解(2 8 31 6 47 0 52 8 31 6 47 0 5三、A*算法思想:1、思想:A*算法是一种静态路网中求解最短路最有效的直接搜索方法。
估价值与实际值越接近,估价函数取得就越好2、原理:估价函数公式表示为: f(n)=g(n)+h(n),其中 f(n) 是从初始点经由节点n到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n) 是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
并且如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行此时的搜索效率是最高的。
如果估价值>实际值,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
四、算法流程:Heuristic_Search(启发式搜索)While是从未拓展表中删N为目是,输出路径否,生成n的所有子状态Case:此子状Case:此子状Case:此子状计算该子状记录比已有记录比已有返回五、关键技术:1、使用了CreateChild()函数,求得了任意未拓展九宫格的扩展结点,便于拓展子空间,搜索所有情况。
关键代码:bool CreateChild(NOExtend ns[],NOExtend ne){int i,j,k=0;for(i=0;i<3;i++){for(j=0;j<3;j++){if(ne.cur_sudoku.num[i][j]==0){ //寻找九宫格空缺所在的坐标if(i-1>=0){ //将空格向上移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);//先把未改变的九宫格复制给九宫格数组的某一元素ns[k].cur_sudoku.num[i][j]=ne.cur_sudoku.num[i-1][j];//然后仅改变此二维九宫格的两项值即可ns[k].cur_sudoku.num[i-1][j]=0;ns[k].dx=1;k++;}if(j+1<=2){ //将空格向右移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);ns[k].cur_sudoku.num[i][j]=ns[k].cur_su doku.num[i][j+1];ns[k].cur_sudoku.num[i][j+1]=0;ns[k].dx=1;k++;}if(i+1<=2){ //将空格向下移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);ns[k].cur_sudoku.num[i][j]=ns[k].cur_su doku.num[i+1][j];ns[k].cur_sudoku.num[i+1][j]=0;ns[k].dx=1;k++;}if(j-1>=0){ //将空格向左移动CopySudoku(ns[k].cur_sudoku,ne.cur_sudo ku);ns[k].cur_sudoku.num[i][j]=ns[k].cur_su doku.num[i][j-1];ns[k].cur_sudoku.num[i][j-1]=0;ns[k].dx=1;k++;}return 1;}}}return 0;2、用启发式搜索函数寻找求解路径,运用了A*算法的思想,能够更快的求解出最优解。
数码问题C语言A星算法详细实验报告含代码

一、实验内容和要求八数码问题:在3×3的方格棋盘上,摆放着1到8这八个数码,有1个方格是空的,其初始状态如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。
例如:图1 八数码问题示意图请任选一种盲目搜索算法(广度优先搜索或深度优先搜索)或任选一种启发式搜索方法(全局择优搜索,加权状态图搜索,A 算法或 A* 算法)编程求解八数码问题(初始状态任选)。
选择一个初始状态,画出搜索树,填写相应的OPEN 表和CLOSED表,给出解路径,对实验结果进行分析总结,得出结论。
二、实验目的1. 熟悉人工智能系统中的问题求解过程;2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用;3. 熟悉对八数码问题的建模、求解及编程语言的应用。
三、实验算法A*算法是一种常用的启发式搜索算法。
在A*算法中,一个结点位置的好坏用估价函数来对它进行评估。
A*算法的估价函数可表示为:f'(n) = g'(n) + h'(n)这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h'(n)是n到目标的最短路经的启发值。
由于这个f'(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。
用f(n)作为f'(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。
这样必须满足两个条件:(1)g(n)>=g'(n)(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。
(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。
启发式搜索A星算法的八数码实现报告

1. 请简述人工智能概念于何时何地由何人第一次正式提出?答:1956年夏,在美国的达特茅斯(Dartmouth )学院,由McCarthy (斯坦福大学,MIT )、Minsky (哈佛大学数学和神经学家)、Lochester (IBM 公司)、Shannon (贝尔实验室)四人共同发起,邀请IBM 公司的Moore 、Samuel ,MIT 的Selfridge 、Solomonff ,还有Simon 、Newell 等人参加学术讨论班,在一起共同学习和探讨用机器模拟智能的各种问题,在会上,经McCarthy 提议,决定使用“人工智能”一词来概括这个研究方向。
这次具有历史意义的会议标志着人工智能这个学科的正式诞生。
2.当前人工智能有哪些学派?简述它们在人工智能理论上有何不同之处?a.符号主义: 起源于数理逻辑 基于逻辑推理 认知是符号的处理过程,推理是问题求解过程(核心是知识表示) 无法表示不确知事物和常识问题 Nilssonb.连接主义: 起源于仿生学 基于神经网络 思维是神经元的连接活动而不是符号运算过程(学习算法和网络结构) 用大量非线性并行处理器模拟大脑 Newellc.行为主义: 起源于控制论 基于”感知-行动” 直接利用机器对环境发出作用后环境对作用者的响应为原型(有限状态机,不表示不推理) 能应付复杂环境 MIT Brooks 3.八数码问题初始状态定义估价函数: f(x) = d(x) + h(x),其中:d(x)表示节点x 的深度,h(x)表示节点x 的棋局与目标节点棋局距离的度数。
(1) 使用以上估价函数进行全局择优搜索,列出头三步搜索中的OPEN 表和CLOSED 表全局择优搜索过程如下:(1) 把初始节点S0放入OPEN 表,f(S0)。
(2) 如果OPEN 表为空,则问题无解,退出。
(3) 把OPEN 表的第一个节点(记为节点n)取出放入CLOSED 表。
(4) 考察节点n 是否为目标节点。
AStar算法解决八数码问题

江南大学物联网工程学院实验报告课程名称人工智能实验名称A*算法解决8数码问题实验日期2018.3.20班级计科1501 姓名周启航学号1030415127一、实验目的:修改A*算法,使之能解决N*N矩阵八数码问题问题描述:八数码难题:在3×3方格棋盘上,分别放置了标有数字1,2,3,4,5,6,7,8的八张牌,初始状态S0可自己随机设定,使用的操作有:空格上移,空格左移,空格右移,空格下移。
二、算法描述:1.状态描述八数码的任何一种摆法就是一个状态,所有摆法即为状态集S,他们构成了一个状态空间,其大小为9包括8个数码和一个空格,每个数码就是一个分离的独立的子空间,其所在位置为x:i/3,y:i%3.相应的操作算子就是数码的移动即:将空格向上移UP、将空格向下移DOWN、将空格向左移LEFT、将空格向右移RIGHT,经过一些操作算子后达到目标状态。
2.启发函数设计启发函数为现在的状态中各位置与目标状态各位置数码值不同的个数,例如:现在状态:w=123456780,目标状态为:t=123456708,则h(n)=2.3.规则的判断条件把未扩展的状态存入open表,排序后取出优先状态扩展搜索,将扩展后的存入closed表,循环执行直到扩展出目标状态。
4.算法流程图5.核心代码操作算子:int solve() //搜索过程{P cur;P p;while(!open.empty()){cur=open.top(); //open表open.pop();if(cur.s==t) return cur.id; //达到目标状态,返回当前节点的idint x,y;int ops=0;while(cur.s[ops]!='0') ops++;x=ops/N,y=ops%N; //空格所在位置int r=cur.id;if(x>0){ //空格向上移p.s=cur.s;swap(p.s[ops],p.s[ops-3]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(x<N-1){ //空格向下移p.s=cur.s;swap(p.s[ops],p.s[ops+3]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(y>0){ //空格向左移p.s=cur.s;swap(p.s[ops],p.s[ops-1]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}if(y<N-1){ //空格向右移p.s=cur.s;swap(p.s[ops],p.s[ops+1]);if(!mp[p.s]){p.d=cur.d+1,p.w=calw(p.s),p.id=top+1;open.push(p);stack[++top]=p.s;father[top]=r;mp[p.s]=1;}}}return -1; //搜索失败}int main(){cout<<"请输入棋盘大小N*N\nN:";cin>>N;cout<<"请输入测试的组数:\n";int tt; //测试的组数cin>>tt;for(int k=1;k<=tt;k++){cout<<"Case "<<k<<":\n";int i,j;char a;cout<<"请输入目的状态:\n";cin>>t;p.s="";cout<<"请输入初始状态:\n";for(i=0;i<N;i++){for(j=0;j<N;j++){cin>>a; //输入0~8数码p.s+=a;}}p.d=0,p.w=calw(p.s),p.id=0;father[0]=-1;mp[p.s]=1;stack[0]=p.s;open.push(p); //往open表中加入初始状态节点int id=solve();//调用搜索过程if(id==-1){cout<<"无解!\n";}else{int c=-1;while(id>=0){ //把stack中存的节点按次序放入到record中record[++c]=stack[id];id=father[id];}cout<<"原图:"<<endl;print(c); //输出初始节点cout<<"移动过程: \n\n";for(i=c-1;i>=0;i--){cout<<"Step "<<c-i<<":\n";//输出当前搜索步骤print(i);//输出当前搜索的节点}cout<<"移动结束!\n";mp.clear();while(!open.empty()) open.pop();top=0;cout<<endl;}system("pause\n");return 0;}三、实验结果:四、实验心得:只是做了简单修改,只能解决些简单的问题,过于复杂的还不能实现,不过还是体会到了A*算法的厉害,也见识到了人工智能的神奇,会继续努力学习。
基于启发式搜索算法A星解决八数码问题

int statue[size][size]; //记录当前节点的状态 struct Node * Tparent; //用来构成搜索树,该树由搜索图的反向指针构成 struct Node * opennext; //用来构成 open 表,该指针指向该节点在 open 表中的下一个 节点 struct Node * closenext; //用来构成 open 表,该指针指向该节点在 close 表中的下一个 节点 struct Node * brothernext; //构成兄弟链表,该指针指向该节点在兄弟链表中的下一个节 点 int f; //记录当前节点的 f 函数值 int g; //记录当前节点的 g 函数的值 int h; //记录当前节点的 h 函数的值 };
5
get_bestroute (bestNode); return; }
2.2.7 生成 bestNode 所指节点的后继节点
定义一个后继节点链表,表头为 head_b,将 bestNode 所指节点的不是前驱节点的后继 节点,链接到后继及诶单链表中。getchild 函数可以实现这个功能。
//产生 bestNode 的一切后继节点。。 head head_b; //定义 bestNode 的后继节点表 head_b.next=NULL; getchild (&head_b,bestNode); //产生 bestNode 的子节点,将不是 bestNode 的父节点的
while (head_b.next!=NULL) { Node *tmp=getbrother (&head_b); //从后继节点表中取出一个节点记为 tmp,并从
基于A星算法的8数码问题求解方案设计(1)

基于A星算法的8数码问题求解⽅案设计(1)⼀、问题描述8数码问题⼜称9宫问题,与游戏“华容道”类似。
意在给定的33棋格的8个格⼦内分别放⼀个符号,符号之间互不相同,余下的⼀格为空格。
并且通常把8个符号在棋格上的排列顺序称作8数码的状态。
开始时,规则给定⼀个初始状态和⼀个⽬标状态,并要求被试者对棋格内的符号经过若⼲次移动由初始状态达到⽬标状态,这个过程中只有空格附近的符号可以朝空格的⽅向移动,且每次只能移动⼀个符号。
为⽅便编程和表⽰,本⽂中8个格⼦内的符号分别取1—8的8个数字表⽰,空格⽤0表⽰。
并给定8数码的初始状态和⽬标状态分别如图1、2所⽰。
图1 初始状态图2 ⽬标状态则要求以图1为初始状态,通过交换0和0的上、下、左、右四个⽅位的数字(每次只能和其中⼀个交换),达到图2所⽰⽬标状态。
⼆、实验⽬的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利⽤A*算法求解N数码难题,理解求解流程和搜索顺序。
三、实验任务1)实现类似于如图所⽰N数码难题演⽰程序。
2)⽤你所熟悉的程序语⾔实现,可以B/S实现,也可以C/S实现四、算法设计根据任务要求,本⽂采⽤A*搜索算法。
但要在计算机上通过编程解决该问题,还应当解决该问题在计算机上表⽰的⽅式,并设计合适的启发函数,以提⾼搜索效率。
①状态的表⽰在A*算法中,需要⽤到open表和closed表,特别是在open表中,待扩展节点间有很严格的扩展顺序。
因此在表⽰当前状态的变量中,必须要有能指向下⼀个扩展节点的指针,以完成对open表中元素的索引。
从这⼀点上看,open表中的元素相互间即构成了⼀个线性表,因此初步选定使⽤结构体表⽰问题的状态。
如图3所⽰,表⽰问题的结构体包括表⽰当前节点状态的DATA和指向open 表中下⼀个待扩展节点的指针NEXT。
图3 结构体现在进⼀步考虑DATA中包括的内容:如图1、2所⽰,8数码问题的提出是以⼀个33数表表⽰的,因此本⽂中采⽤⼀个33的⼆维数组s[3][3]表⽰当前状态的具体信息。
人工智能实验一 八数码问题

启发中的估价是用估价函数表示的,如:f(n) = g(n) + h(n) 其中 f(n) 是节点 n 的估价函数,g(n)是在状态空间中从初始节点到 n 节点的实际代价, h(n)是从 n 到目标节点最佳路径的估计代价。 在此八数码问题中,显然 g(n)就是从初始状 态变换到当前状态所移动的步数,估计函数 f(n)我们就可采用当前状态各个数字牌不在目标
附录—源代码及其注释 #include "stdafx.h" #include "iostream.h" #include <time.h> #include <stdio.h> #include <dos.h> #include <conio.h> static int target[9]={1,2,3,8,0,4,7,6,5}; //class definition
eight_num(int init_num[9]); eight_num(int num1,int num2,int num3,int num4,int num5,int num6,int num7,int num8,int num9) {
num[0]=num1; num[1]=num2; num[2]=num3; num[3]=num4; num[4]=num5; num[5]=num6; num[6]=num7; num[7]=num8; num[8]=num9; } eight_num(void) { for (int i=0;i<9;i++)
A-star-算法-八数码问题-C++-报告+代码+详细注释1
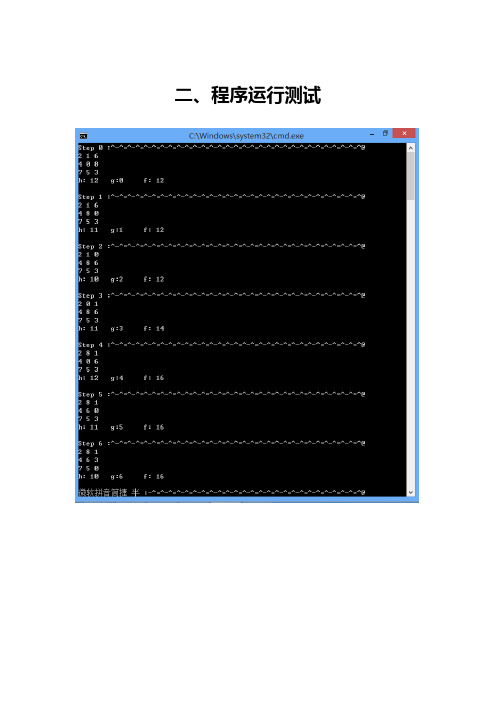
二、程序运行测试A*算法求解八数码问题一、详细设计说明1.评价函数以当前状态下各将牌到目标位置的距离之和作为节点的评价标准。
距离的定义为: “某将牌行下标与目标位置行下标之差的绝对值 + 列下标与目标位置列下标之差的绝对值”。
距离越小, 该节点的效果越好。
某个状态所有将牌到目标位置的距离之和用“h值”表示。
2.主要函数2.1countH(state & st);countH函数功能是计算st状态的h值。
2.2计算过程中将会用到rightPos数组, 数组里记录的是目标状态下, 0~9每个将牌在九宫格里的位置(位置 = 行下标 * 3 + 列下标)。
2.3f(state * p);f()=h()+level2.4look_up_dup(vector<state*> & vec, state * p);2.5在open表或close表中, 是否存在指定状态p, 当找到与p完全相等的节点时, 退出函数。
2.6search(state & start);在open表不为空时, 按f值由小到大对open表中元素进行排序。
调用findZero()函数找到0值元素的位置。
空格可以向上下左右四个方向移动, 前提是移动后不能越过九宫格的边界线。
确定某方向可走后, 空格移动一步, 生成状态p’。
2.7此时, 检查open表中是否已有p’, 若有, 更新p’数据;检查close表中是否已有p’, 若有, 将p’从close表中删除, 添加到open表中。
2.8重复的执行这个过程, 直到某状态的h值为零。
2.9dump_solution(state * q);在终端输出解路径。
// A*算法八数码问题#include"stdafx.h"#include<iostream>#include<vector>#include<time.h>#include<algorithm>using namespace std;const int GRID = 3; //Grid表示表格的行数(列数), 这是3*3的九宫格int rightPos[9] = { 4, 0, 1, 2, 5, 8, 7, 6, 3 };//目标状态时, 若p[i][j]=OMG,那么3*i+j = rightPos[OMG]struct state{int panel[GRID][GRID];int level; //记录深度int h;state * parent;state(int level) :level(level){}bool operator == (state & q){//判断两个状态是否完全相等(对应位置元素相等), 完全相等返回true,否则返回falsefor (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){if (panel[i][j] != q.panel[i][j])return false;}}return true;}state & operator = (state & p){ //以状态p为当前状态赋值, 对应位置元素相同for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++){panel[i][j] = p.panel[i][j];}}return *this;}};void dump_panel(state * p){ //将八数码按3*3矩阵形式输出for (int i = 0; i<GRID; i++){for (int j = 0; j<GRID; j++)cout << p->panel[i][j] << " ";cout << endl;}}int countH(state & st){ //给定状态st, 计算它的h值。
人工智能实验一_八数码问题

用A*算法解决八数码问题1 问题描述1.1 待解决问题的解释八数码游戏(八数码问题)描述为:在3×3组成的九宫格棋盘上,摆有八个将牌,每一个将牌都刻有1-8八个数码中的某一个数码。
棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。
这种游戏求解的问题是:给定一种初始的将牌布局或结构(称初始状态)和一个目标的布局(称目标状态),问如何移动将牌,实现从初始状态到目标状态的转变。
1.2 问题的搜索形式描述(4要素)初始状态:8个数字将牌和空格在九宫格棋盘上的所有格局组成了问题的状态空间。
其中,状态空间中的任一种状态都可以作为初始状态。
后继函数:通过移动空格(上、下、左、右)和周围的任一棋子一次,到达新的合法状态。
目标测试:比较当前状态和目标状态的格局是否一致。
路径消耗:每一步的耗散值为1,因此整个路径的耗散值是从起始状态到目标状态的棋子移动的总步数。
1.3 解决方案介绍(原理)对于八数码问题的解决,首先要考虑是否有答案。
每一个状态可认为是一个1×9的矩阵,问题即通过矩阵的变换,是否可以变换为目标状态对应的矩阵?由数学知识可知,可计算这两个有序数列的逆序值,如果两者都是偶数或奇数,则可通过变换到达,否则,这两个状态不可达。
这样,就可以在具体解决问题之前判断出问题是否可解,从而可以避免不必要的搜索。
如果初始状态可以到达目标状态,那么采取什么样的方法呢?常用的状态空间搜索有深度优先和广度优先。
广度优先是从初始状态一层一层向下找,直到找到目标为止。
深度优先是按照一定的顺序前查找完一个分支,再查找另一个分支,以至找到目标为止。
广度和深度优先搜索有一个很大的缺陷就是他们都是在一个给定的状态空间中穷举。
这在状态空间不大的情况下是很合适的算法,可是当状态空间十分大,且不预测的情况下就不可取了。
他的效率实在太低,甚至不可完成。
由于八数码问题状态空间共有9!个状态,对于八数码问题如果选定了初始状态和目标状态,有9!/2个状态要搜索,考虑到时间和空间的限制,在这里采用A*算法作为搜索策略。
八数码 人工智能实验报告

八数码人工智能实验报告八数码人工智能实验报告引言:八数码是一种经典的数学问题,也是人工智能领域中常用的实验题目之一。
本次实验旨在通过使用搜索算法解决八数码问题,探讨人工智能在解决复杂问题上的应用。
一、问题描述:八数码问题是一种数字排列游戏,使用一个3x3的方格,其中8个方格上各有一个数字,剩下一个方格为空白。
通过移动数字方格,最终将数字按照从小到大的顺序排列,空白方格位于最后一个位置。
例如,初始状态为:1 2 38 47 6 5目标状态为:1 2 34 5 67 8二、算法选择:本次实验采用了A*搜索算法来解决八数码问题。
A*算法是一种启发式搜索算法,通过估计每个搜索节点到达目标状态的代价来进行搜索。
它综合了广度优先搜索和最佳优先搜索的优点,能够高效地找到最优解。
三、实验过程:1. 状态表示:在实验中,我们使用一个3x3的二维数组来表示八数码的状态。
数组中的每个元素代表一个方格的数字,空白方格用0表示。
2. 启发函数:为了评估每个搜索节点到达目标状态的代价,我们需要定义一个启发函数。
本实验中,我们选择了曼哈顿距离作为启发函数。
曼哈顿距离是指每个数字方格与其目标位置之间的水平和垂直距离之和。
3. A*算法:A*算法的核心思想是维护一个优先队列,根据每个搜索节点的估价函数值进行排序。
具体步骤如下:- 将初始状态加入优先队列,并设置初始估价函数值为0。
- 从优先队列中取出估价函数值最小的节点,进行扩展。
- 对于每个扩展节点,计算其估价函数值,并将其加入优先队列。
- 重复上述步骤,直到找到目标状态或者队列为空。
四、实验结果:经过实验,我们发现A*算法能够高效地解决八数码问题。
对于初始状态为随机排列的八数码,A*算法能够在较短的时间内找到最优解。
实验结果表明,A*算法在解决八数码问题上具有较好的性能。
五、实验总结:本次实验通过使用A*搜索算法解决八数码问题,展示了人工智能在解决复杂问题上的应用。
A*算法通过合理的启发函数和优先队列的维护,能够高效地找到最优解。
a算法求解八数码问题 实验报告

题目: a算法求解八数码问题实验报告目录1. 实验目的2. 实验设计3. 实验过程4. 实验结果5. 实验分析6. 实验总结1. 实验目的本实验旨在通过实验验证a算法在求解八数码问题时的效果,并对其进行分析和总结。
2. 实验设计a算法是一种启发式搜索算法,主要用于在图形搜索和有向图中找到最短路径。
在本实验中,我们将使用a算法来解决八数码问题,即在3x3的九宫格中,给定一个初始状态和一个目标状态,通过移动数字的方式将初始状态转变为目标状态。
具体的实验设计如下:1) 实验工具:我们将使用编程语言来实现a算法,并结合九宫格的数据结构来解决八数码问题。
2) 实验流程:我们将设计一个初始状态和一个目标状态,然后通过a 算法来求解初始状态到目标状态的最短路径。
在求解的过程中,我们将记录下每一步的状态变化和移动路径。
3. 实验过程我们在编程语言中实现了a算法,并用于求解八数码问题。
具体的实验过程如下:1) 初始状态和目标状态的设计:我们设计了一个初始状态和一个目标状态,分别为:初始状态:1 2 34 5 67 8 0目标状态:1 2 38 0 42) a算法求解:我们通过a算法来求解初始状态到目标状态的最短路径,并记录下每一步的状态变化和移动路径。
3) 实验结果在实验中,我们成功求解出了初始状态到目标状态的最短路径,并记录下了每一步的状态变化和移动路径。
具体的实验结果如下:初始状态:1 2 34 5 67 8 0目标状态:1 2 38 0 47 6 5求解路径:1. 上移1 2 37 8 62. 左移1 2 3 4 0 5 7 8 63. 下移1 2 3 4 8 5 7 0 64. 右移1 2 3 4 8 5 0 7 65. 上移1 2 3 0 8 5 4 7 61 2 38 0 54 7 67. 下移1 2 38 7 54 0 68. 右移1 2 38 7 54 6 0共计8步,成功从初始状态到目标状态的最短路径。
采用A算法解决八数码问题

人工智能实验一报告题目:采用A*算法解决八数码问题姓名:张博涵学号: 081110317专业:信息与计算科学提交日期: 2014-05-22目录1问题描述........................................................................................................................... - 2 -1.1待解决问题的解释............................................................................................... - 2 -1.2问题的搜索形式描述............................................................................................ - 2 -1.3解决方案介绍(原理)........................................................................................ - 3 -2算法介绍........................................................................................................................... - 4 -2.1A*搜索算法一般介绍............................................................................................ - 4 -2.2 算法伪代码........................................................................................................... - 4 -3算法实现........................................................................................................................... - 5 -3.1 实验环境与问题规模........................................................................................... - 5 -3.2 数据结构............................................................................................................... - 5 -3.3 实验结果............................................................................................................... - 5 -3.4系统中间及最终输出结果.................................................................................... - 7 -4参考文献........................................................................................................................... - 8 - 5附录—源代码及其注释................................................................................................... - 8 -1问题描述所谓八数码问题是指这样一种游戏:将分别标有数字1,2,3,…,8 的八块正方形数码牌任意地放在一块3×3 的数码盘上。
八数码问题实验报告

八数码问题实验报告八数码问题实验报告引言:八数码问题,也被称为九宫格问题,是一种经典的数学谜题。
在一个3x3的方格中,摆放有1至8的数字,其中一个位置为空。
目标是通过交换数字的位置,将数字按照从小到大的顺序排列,最终使得空格位于最后一个位置。
本实验旨在通过编程实现八数码问题的求解,并探讨不同算法在解决该问题上的效果和优劣。
实验步骤:1. 算法选择在本次实验中,我们选择了广度优先搜索算法和A*算法作为求解八数码问题的两种不同方法。
广度优先搜索算法是一种盲目搜索算法,它通过逐层扩展搜索树,直到找到目标状态。
而A*算法则是一种启发式搜索算法,它结合了广度优先搜索和启发式函数,通过评估每个状态的代价来指导搜索过程,以找到最优解。
2. 算法实现我们使用Python语言实现了以上两种算法。
首先,我们定义了一个表示状态的类,并实现了状态的初始化、移动、判断是否达到目标状态等基本操作。
然后,我们分别编写了广度优先搜索算法和A*算法的求解函数。
在广度优先搜索算法中,我们使用队列数据结构来保存待扩展的状态,以实现逐层扩展的效果;在A*算法中,我们使用优先队列来保存待扩展的状态,并根据启发式函数的值进行优先级排序。
3. 实验结果我们使用了多个测试样例来验证两种算法的求解效果。
实验结果表明,广度优先搜索算法能够找到解,但是在面对状态空间较大的情况下,搜索时间会呈指数级增长。
而A*算法则能够更快地找到最优解,其效率相对较高。
然而,A*算法需要选择合适的启发式函数,并且对于某些特殊情况,可能会陷入局部最优解而无法找到最优解。
4. 结果分析通过对比两种算法的求解结果,我们可以发现广度优先搜索算法和A*算法在时间效率和解的质量上存在一定的差异。
广度优先搜索算法适用于状态空间较小的情况,但是在状态空间较大时效率较低;而A*算法则能够在较短的时间内找到最优解,但需要对问题进行合理的建模和启发式函数的选择。
因此,在实际应用中,我们需要根据问题的规模和特点来选择合适的算法。
人工智能-A算法求解8数码问题

实验四 A*算法求解8数码问题一、实验目的熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利用A*算法求解8数码难题,理解求解流程和搜索顺序。
二、实验原理A*算法是一种启发式图搜索算法,其特点在于对估价函数的定义上。
对于一般的启发式图搜索,总是选择估价函数f值最小的节点作为扩展节点。
因此,f 是根据需要找到一条最小代价路径的观点来估算节点的,所以,可考虑每个节点n的估价函数值为两个分量:从起始节点到节点n的实际代价g(n)以及从节点n 到达目标节点的估价代价h(n),且h(n)<=h*(n),h*(n)为n节点到目标节点的最优路径的代价。
八数码问题是在3×3的九宫格棋盘上,排放有8个刻有1~8数码的将牌。
棋盘中有一个空格,允许紧邻空格的某一将牌可以移到空格中,这样通过平移将牌可以将某一将牌布局变换为另一布局。
针对给定的一种初始布局或结构(目标状态),问如何移动将牌,实现从初始状态到目标状态的转变。
如图1所示表示了一个具体的八数码问题求解。
图1 八数码问题的求解三、实验内容1、参考A*算法核心代码,以8数码问题为例实现A*算法的求解程序(编程语言不限),要求设计两种不同的估价函数。
2、在求解8数码问题的A*算法程序中,设置相同的初始状态和目标状态,针对不同的估价函数,求得问题的解,并比较它们对搜索算法性能的影响,包括扩展节点数、生成节点数等。
3、对于8数码问题,设置与图1所示相同的初始状态和目标状态,用宽度优先搜索算法(即令估计代价h(n)=0的A*算法)求得问题的解,记录搜索过程中的扩展节点数、生成节点数。
4、提交实验报告和源程序。
四.实验截图五.源代码#include<iostream>#include"stdio.h"#include"stdlib.h"#include"time.h"#include"string.h"#include<queue>#include<stack>using namespace std;const int N=3;//3*3棋?盘ìconst int Max_Step=32;//最?大洙?搜?索÷深?度èenum Direction{None,Up,Down,Left,Right};//方?向ò,?分?别纄对?应畖上?下?左哩?右?struct Chess//棋?盘ì{int chessNum[N][N];//棋?盘ì数簓码?int Value;//评à估à值μDirection BelockDirec;//所ù屏á蔽?方?向òstruct Chess * Parent;//父?节ú点?};void PrintChess(struct Chess *TheChess);//打洙?印?棋?盘ìstruct Chess * MoveChess(struct Chess * TheChess,Direction Direct,bool CreateNewChess);//移?动ˉ棋?盘ì数簓字?int Appraisal(struct Chess * TheChess,struct Chess * Target);//估à价?函ˉ数簓struct Chess * Search(struct Chess* Begin,struct Chess * Target);//A*搜?索÷函ˉ数簓int main(){//本?程ì序ò的?一?组哩?测a试?数簓据Y为a/*初?始?棋?盘ì*1 4 0**3 5 2**6 7 8**//*目?标括?棋?盘ì*0 1 2**3 4 5**6 7 8**/Chess Target;Chess *Begin,*ChessList;Begin=new Chess;int i;cout<<"请?输?入?初?始?棋?盘ì,?各÷数簓字?用?空?格?隔?开a:阰"<<endl;for(i=0;i<N;i++){for(int j=0;j<N;j++){cin>>Begin->chessNum[i][j];}}cout<<"请?输?入?目?标括?棋?盘ì,?各÷数簓字?用?空?格?隔?开a:阰"<<endl;for(i=0;i<N;i++){for(int j=0;j<N;j++){cin>>Target.chessNum[i][j];}}//获?取?初?始?棋?盘ìAppraisal(Begin,&Target);Begin->Parent=NULL;Begin->BelockDirec=None;Target.Value=0;cout<<"初?始?棋?盘ì:";PrintChess(Begin);cout<<"目?标括?棋?盘ì:";PrintChess(&Target);ChessList=Search(Begin,&Target);//搜?索÷//打洙?印?if(ChessList){/*将?返う?回?的?棋?盘ì列表括?利?用?栈?将?其?倒?叙e*/Chess *p=ChessList;stack<Chess *>Stack;while(p->Parent!=NULL){Stack.push(p);p=p->Parent;}cout<<"搜?索÷结á果?:"<<endl;int num=1;while(!Stack.empty()){cout<<"第台?<<num<<"步?: ";num++;PrintChess(Stack.top());Stack.pop();}cout<<"\n完?成é!"<<endl;}elsecout<<"搜?索÷不?到?结á果?,?搜?索÷深?度è大洙?于?2\n"<<endl;return 0;}//打洙?印?棋?盘ìvoid PrintChess(struct Chess *TheChess){cout<<"(评à估à值μ为a";cout<<TheChess->Value;cout<<")"<<endl;for(int i=0;i<N;i++){cout<<" ";for(int j=0;j<N;j++){cout<<TheChess->chessNum[i][j]<<" ";}cout<<endl;}}//移?动ˉ棋?盘ìstruct Chess * MoveChess(struct Chess * TheChess,Direction Direct,bool CreateNewChess) {struct Chess * NewChess;//获?取?空?闲D格?位?置?int i,j;for(i=0;i<N;i++){bool HasGetBlankCell=false;for(j=0;j<N;j++){if(TheChess->chessNum[i][j]==0){HasGetBlankCell=true;break;}}if(HasGetBlankCell)break;}int ii=i,jj=j;bool AbleMove=true;//判D断?是?否?可é以?移?动ˉswitch(Direct){case Up:i++;if(i>=N)AbleMove=false;break;case Down:i--;if(i<0)AbleMove=false;break;case Left:j++;if(j>=N)AbleMove=false;break;case Right:j--;if(j<0)AbleMove=false;break;};if(!AbleMove)//不?可é以?移?动ˉ则ò返う?回?原-节ú点?{return TheChess;}if(CreateNewChess){NewChess=new Chess();for(int x=0;x<N;x++){for(int y=0;y<N;y++)NewChess->chessNum[x][y]=TheChess->chessNum[x][y];//创洹?建¨新?棋?盘ì,?此?时骸?值μ与?原-棋?盘ì一?致?}}elseNewChess=TheChess;NewChess->chessNum[ii][jj] = NewChess->chessNum[i][j];//移?动ˉ数簓字?NewChess->chessNum[i][j]=0;//将?原-数簓字?位?置?设Θ?置?为a空?格?return NewChess;}//估à价?函ˉ数簓int Appraisal(struct Chess * TheChess,struct Chess * Target){int Value=0;for(int i=0;i<N;i++){for(int j=0;j<N;j++){if(TheChess->chessNum[i][j]!=Target->chessNum[i][j])Value++;}}TheChess->Value=Value;return Value;}//A*搜?索÷函ˉ数簓struct Chess * Search(struct Chess* Begin,struct Chess * Target){Chess *p1,*p2,*p;int Step=0;//深?度èp=NULL;queue<struct Chess *> Queue;Queue.push(Begin);//初?始?棋?盘ì入?队ó//搜?索÷do{p1=(struct Chess *)Queue.front();Queue.pop();//出?队ófor(int i=1;i<=4;i++)//分?别纄从洙?四?个?方?向ò推?导?出?新?子哩?节ú点? {Direction Direct=(Direction)i;if(Direct==p1->BelockDirec)//跳?过y屏á蔽?方?向òcontinue;p2=MoveChess(p1,Direct,true);//移?动ˉ数簓码?if(p2!=p1)//数簓码?是?否?可é以?移?动ˉ{Appraisal(p2,Target);//对?新?节ú点?估à价?if(p2->Value<=p1->Value)//是?否?为a优?越?节ú点?{p2->Parent=p1;switch(Direct)//设Θ?置?屏á蔽?方?向ò,防え?止1往?回?推?{case Up:p2->BelockDirec=Down;break;case Down:p2->BelockDirec=Up;break;case Left:p2->BelockDirec=Right;break;case Right:p2->BelockDirec=Left;break;}Queue.push(p2);//存?储洹?节ú点?到?待鋣处鋦理え?队ó列if(p2->Value==0)//为a0则ò,搜?索÷完?成é{p=p2;i=5;}}else{delete p2;//为a劣ⅷ?质ê节ú点?则ò抛×弃úp2=NULL;}}}Step++;if(Step>Max_Step)return NULL;}while(p==NULL || Queue.size()<=0);return p;}六、实验报告要求1、分析不同的估价函数对A*搜索算法性能的影响等。
采用A算法解决八数码问题

人工智能实验一报告题目:采用A*算法解决八数码问题姓名:XXX学号:10S003028专业:计算机科学与技术提交日期:2011-05-04目录1问题描述 .............................................................................................................................. - 2 -1.1待解决问题的解释.................................................................................................. - 2 -1.2问题的搜索形式描述.............................................................................................. - 3 -1.3解决方案介绍(原理).......................................................................................... - 4 -2算法介绍 .............................................................................................................................. - 5 -2.1A*搜索算法一般介绍 .............................................................................................. - 5 -2.2 算法伪代码 ............................................................................................................. - 6 -3算法实现 .............................................................................................................................. - 7 -3.1 实验环境与问题规模............................................................................................. - 7 -3.2 数据结构.................................................................................................................. - 8 -3.3 实验结果.................................................................................................................. - 8 -3.4系统中间及最终输出结果 ..................................................................................... - 8 -4参考文献 .............................................................................................................................. - 9 -5附录—源代码及其注释................................................................................................... - 10 -1问题描述所谓八数码问题是指这样一种游戏:将分别标有数字1,2,3,…,8 的八块正方形数码牌任意地放在一块3×3 的数码盘上。
人工智能A算法八数码报告

人工智能课程设计报告题目:A*算法解决八数码问题专业:计算机软件与理论1.8数码问题1.1问题描述八数码问题是指这样一种游戏:将分别标有数字1,2,3,…,8 的八块正方形数码牌任意地放在一块3×3 的数码盘上。
放牌时要求不能重叠。
于是,在3×3 的数码盘上出现了一个空格。
现在要求按照每次只能将与空格相邻的数码牌与空格交换的原则,不断移动该空格方块以使其和相邻的方块互换,直至达到所定义的目标状态。
空格方块在中间位置时有上、下、左、右4个方向可移动,在四个角落上有2个方向可移动,在其他位置上有3个方向可移动,问题描述如图1-1所示初始状态过渡状态最终状态图1-1 八数码问题执行过程1.2.八数码问题形式化描述初始状态:初始状态向量:规定向量中各分量对应的位置,各位置上的数字。
把3×3的棋盘按从左到右,从上到下的顺序写成一个一维向量。
我们可以设定初始状态:<1,5,2,4,0,3,6,7,8>后继函数:按照某种规则移动数字得到的新向量。
例如:<1,5,2,4,0,3,6,7,8> <1,0,2,4,5,3,6,7,8>目标测试:新向量是都是目标状态。
即<1,2,3,4,5,6,7,8,0>是目标状态?路径耗散函数:每次移动代价为1,每执行一条规则后总代价加1。
1.3解决方案该问题是一个搜索问题。
它是一种状态到另一种状态的变换。
要解决这个问题,必须先把问题转化为数字描述。
由于八数码是一个3*3的矩阵,但在算法中不实用矩阵,而是将这个矩阵转化为一个一维数组,使用这个一维数组来表示八数码,但是移动时要遵守相关规则。
(1)可用如下形式的规则来表示数字通过空格进行移动:<a1,a2,a3,a4,a5,a6,a7,a8,a9>→<b1,b2,b3,b4,b5,b6,b7,b8,b9>(2)共24条移动规则,对应与每个位置的移动规则。
人工智能A算法八数码报告

人工智能A算法八数码报告
一、什么是人工智能A算法八数码?
二、人工智能A算法八数码原理
八数码问题可以用一个3x3矩阵表示,一个有效路径是由空格移动到另一个位置的路径,它可以在矩阵中上下左右移动,直到所有数字都按从小到大的顺序排列好。
但是,由于有很多种移动的可能性,有效的路径非常难以找到,并且需要大量的计算来完成。
这就是人工智能A算法八数码可以帮助用户解决的问题。
该算法采用了蚁群算法的变种,每个蚂蚁都可以把有效路径拆分成四个状态:移动空格,改变表格上的数字,计算移动的路径,并求出路径的代价(代价是一个函数,用于衡量当前路径和有效路径之间的差异)。
A星算法求解8数码问题实验

成立,则称好h(x)为h*(x)的下界,它表示某种偏于保守的估计。采用h*(x)的下界h(x)为启发函数的A算法,称为A*算法。
针对八数码问题启发函数设计如下:
f(n)=d(n)+p(n) (4)
其中A*算法中的g(n)根据具体情况设计为d(n),意为n节点的深度,而h(n)设计为
其中a算法中得gn根据具体情况设计为dn意为n节点得深gsucgoldsucoldbestndoe得后继结点表中重新确定old得父辈节点为bestnode并修正父辈节点得成功succlosedsuccessor放入openbestnode得后裔失败扩展bestnode产生其后继结点successor选取open表上未设置过得具有最小f值得节点bestnode放入closed是目标节点建立从successor返回bestnode得指针计算gsucgbeskbessucsucopena算法流程图pn意为放错得数码与正确得位置距离之与
int get_successor(structNode * BESTNODE, int direction, struct Node *Successor)//扩展BESTNODE,产生其后继结点SUCCESSOR
{
int i,j,i_0,j_0,temp;
for(i=0; i<3; i++)
for(j=0; j<3; j++)
{ q = head->next;
if(p->f< head->next->f){//考虑插入的节点值比链表的第一个节点值小
p->next = head->next;
head->next = p;
八数码问题C语言A星算法详细实验报告含代码

一、实验容和要求八数码问题:在3×3的方格棋盘上,摆放着1到8这八个数码,有1个方格是空的,其初始状态如图1所示,要求对空格执行空格左移、空格右移、空格上移和空格下移这四个操作使得棋盘从初始状态到目标状态。
例如:(a) 初始状态(b) 目标状态图1 八数码问题示意图请任选一种盲目搜索算法(广度优先搜索或深度优先搜索)或任选一种启发式搜索方法(全局择优搜索,加权状态图搜索,A算法或A* 算法)编程求解八数码问题(初始状态任选)。
选择一个初始状态,画出搜索树,填写相应的OPEN 表和CLOSED表,给出解路径,对实验结果进行分析总结,得出结论。
二、实验目的1. 熟悉人工智能系统中的问题求解过程;2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用;3. 熟悉对八数码问题的建模、求解及编程语言的应用。
三、实验算法A*算法是一种常用的启发式搜索算法。
在A*算法中,一个结点位置的好坏用估价函数来对它进行评估。
A*算法的估价函数可表示为:f'(n) = g'(n) + h'(n)这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h'(n)是n到目标的最短路经的启发值。
由于这个f'(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:f(n) = g(n) + h(n)其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。
在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。
用f(n)作为f'(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。
这样必须满足两个条件:(1)g(n)>=g'(n)(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。
(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人工智能实验报告
实验名称:八数码问题
姓名:xx
学号:*******xx
xx计算机学院
2014年1月14日
一.实验目的
掌握A*的思想,启发式搜索,来求解在代价最小的情况下将九宫格从一个状态转为另状态的路径。
二.实验内容
给定九宫格的初始状态,要求在有限步的操作内,使其转化为目标状态,且所得到的解是代价最小解(
三、A*算法思想:
1、思想:
A*算法是一种静态路网中求解最短路最有效的直接搜索方法。
估价值与实际值越接近,估价函数取得就越好
2、原理:
估价函数公式表示为: f(n)=g(n)+h(n),
其中 f(n) 是从初始点经由节点n到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n) 是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数h(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。
但能得到最优解。
并且如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行此时的搜索效率是最高的。
如果估价值>实际值,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
四、算法流程:
五、关键技术:
1、使用了CreateChild()函数,求得了任意未拓展九宫格的扩展结点,便于拓展子空间,搜索所有情况。
关键代码:
bool CreateChild(NOExtend ns[],NOExtend ne){
int i,j,k=0;
for(i=0;i<3;i++){
for(j=0;j<3;j++){
if(ne.cur_sudoku.num[i][j]==0){ //寻找九宫格空缺所在的坐标
if(i-1>=0){ //将空格向上移动
CopySudoku(ns[k].cur_sudoku,ne.cur_sudoku);//先把未改变的九宫格复制给九宫格数组的某一元素
ns[k].cur_sudoku.num[i][j]=ne.cur_sudoku.num[i-1][j];//然后仅改变此二维九宫格的两项值即可
ns[k].cur_sudoku.num[i-1][j]=0;
ns[k].dx=1;
k++;
}
if(j+1<=2){ //将空格向右移动
CopySudoku(ns[k].cur_sudoku,ne.cur_sudoku);
ns[k].cur_sudoku.num[i][j]=ns[k].cur_sudoku.num[i][j+1];
ns[k].cur_sudoku.num[i][j+1]=0;
ns[k].dx=1;
k++;
}
if(i+1<=2){ //将空格向下移动
CopySudoku(ns[k].cur_sudoku,ne.cur_sudoku);
ns[k].cur_sudoku.num[i][j]=ns[k].cur_sudoku.num[i+1][j];
ns[k].cur_sudoku.num[i+1][j]=0;
ns[k].dx=1;
k++;
}
if(j-1>=0){ //将空格向左移动
CopySudoku(ns[k].cur_sudoku,ne.cur_sudoku);
ns[k].cur_sudoku.num[i][j]=ns[k].cur_sudoku.num[i][j-1];
ns[k].cur_sudoku.num[i][j-1]=0;
ns[k].dx=1;
k++;
}
return 1;
}
}
}
return 0;
2、用启发式搜索函数寻找求解路径,运用了A*算法的思想,能够更快的求解出最优解。
关键代码:
bool Heuristic_Search(Sudoku start,Sudoku end){
int a=0,b=0,c=0;
int count=0;
NOExtend_Sudoku ns; //未扩展结点表
Extended_Sudoku es; //已扩展结点表
Path path; //求解路径
NOExtend father; //定义父节点
ns.no_node[a].cur_sudoku=start; //初始化未拓展结点表
ns.no_node[a].dx=0;
ns.no_node[a].hx=GetHx(ns.no_node[a].cur_sudoku,end);
ns.no_node[a].fx=ns.no_node[a].dx+ns.no_node[a].hx;
a++;
while(a!=0) //当未拓展结点表不为空时
{
father=ns.no_node[0]; //父节点为为拓展表的第一个结点 path.pa[c++]=father; //记录求解路径
DeleteFirst(ns,a); //从未拓展表中删除第一个结点
a--;
if(EqualSudoku(father.cur_sudoku,end)){ //如果找到了目标九宫格则输出求解路径
ShowPath(path,c);
return 1;
}
NOExtend child[4]; //因为九宫格只能拓展上下左右四个方向所以拓展出的结点最多有四个
CreateChild(child,father); //生成父节点的扩展结点if(!CreateChild(child,father))
continue; //如果没有扩展结点就跳出进行下一次循环
for(int i=0;i<4;i++){
if(child[i].dx==1){ //对于父节点可以生成的每个子结点
if(!ExistNOExtend(ns,child[i].cur_sudoku)&&!ExistExtended(es,child[i].cur_s udoku))
{//如果未拓展表和已拓展表中都没有此状态,则添加此状态到未拓展表中
Value(child[i],father,end);//获取此结点的估价值
ns.no_node[a]=child[i];
ns.no_node_father[a]=father;
a++;
continue;
}
if(ExistNOExtend(ns,child[i].cur_sudoku)){
//如果未拓展表中有此状态,此求得当前状态的估价值并且与表中存在的此状态的估价值比较
//若估价值大就放弃此结点,更小,就加入此结点
Value(child[i],father,end);
if(child[i].fx<father.fx){
ns.no_node[a]=child[i];
ns.no_node_father[a]=father;
a++;
continue;
}
}
if(ExistExtended(es,child[i].cur_sudoku)){
//如果已拓展表中有此状态,此求得当前状态的估价值并且与表中存在的此状态的估价值比较
//若估价值大就放弃此结点,更小,就加入此结点
Value(child[i],father,end);
if(child[i].fx<es.node[0].value){//当子状态的价值小与已经扫描过的状态时
ns.no_node[a]=child[i];
ns.no_node_father[a]=father;
a++;//a为未拓展表中的元素个数
continue;
}
}
}
}
es.node[b].cur_sudoku=father.cur_sudoku; //将已经生成完拓展结点的父节点放入已拓展表中
es.node[b].value=father.fx;
b++; //b为已拓展表中的元素个数
SortNoExtend(ns,a); //根据估价函数值,从小到大重新排列未拓展表,每次只搜索估价值最小的结点的路径
if(count++>MAXPATH){
break;
}
}
return 0;
}
六、实验心得
1、学习了新的算法——A*算法,结合了伪代码和网上的一些教程,实现了八数码问题的求解,这是对我编程能力的一种提升,也让我懂了更多做题的方法。
2、在这次实验中,存在着许许多多细节上的小问题,是因为自己的编程基础不牢靠而产生的,通过这次实验又让我懂了许多细节上的问题,以后就不会发生类似的问题了。
