运筹学-第十一章 决策分析1
运筹学决策论

开始结点:应是决策结点 终止:后果 一个简单的决策树
概率枝 状态点
带雨伞 =0.62 不下雨 0.6 下雨 0.4 0.5 下雨 0.4 0.8
后果
0.6
决策点
不带雨伞 0.42 不下雨 0.6 0.3
方案枝
状态点后可 以接方案点
试验
出油 0.85 好 0.6 钻井 不出油 0.15 不钻 井 出油 0.6 不好 0.4 钻井 不出油 0.4 不钻 井
θ1 U11 U21 U31 ┆
θ2 U12 U22 U32 ┆
θ3 U13 U23 U33 ┆
θ4 U14 U24 U34 ┆
┈ ┈ ┈ ┈
该后果相对于决策者的效用,无 量钢,0~1之间的数,U=U (X)——称为效用函数,具体 如何获得决策者的效用函数,后 面章节将具体介绍
状态
行动
A1 A2 A3 ┆
决策是社会科学中用来描述人类进行选择的过程的 术语; 决策是指考虑策略(或方法)来解决目前或未来问 题的智力活动
通过以上定义可以看出:决策是一种有目的的选择行 动,它以人的主观价值判断为依据
决策理论最早与对策一同发展,当前区分依赖于: 对策-多个人之间或人和人之间的决策 决策-人与环境之间对策
不试验 钻井
出油 0.4
不出油 0.6
方案点后可 以接方案点
不钻 井
悲观主义决策准则 乐观主义决策准则 等可能性(Laplace)准则 最小机会损失(最小后悔值、Savage)准则 折中主义准则
§ 6 随机型(风险型)决策准则
6.1随机型决策问题的基本条件和准则
随机性决策问题的基本条件
策 略
运筹学2013年复习

0.1
0.14
0.12
0.26
0.14
0.4
0.16
0.56
0.2
0.76
0.14
0.9
0.1
1
0.04
运筹学:库存决策
E ( y ) (60 * 0.15 110 * 0.25) * 0.04 + (100 * 0.15 70 * 0.25) * 0.1 + (140 * 0.15 30 * 0.25) * 0.12 + 170 * 0.15 * 0.74 19.5 售报员每天的收益期望 为19.5元,一个月的收益期望 为585 元
可以开发
0.9 0.5 0.1
不可开发
0.1 0.5 0.9
运筹学:决策分析
解:
(1)先验分析,由设,利润与概率表为
P( )
i
d
i
j
d1d
1
d2
2
0.2 0.6 0.2
1
80
30 -20
20
20 20
2
3
E (d1 )=80×0.2+30×0.6+(-20) ×0.2=30万元;
E (d2 )=20万元。
运筹学:库存决策
Q
*
2C 3 R P ( ) C1 P R
2 * 1350* 260000* 600000 33868 45 * 0.24 * 340000
运筹学:库存决策
<习题4>
某报社为了扩大销售量,招聘了一大批固定零售售报员,为 了鼓励他们多卖报纸,报社采取的销售策略是:售报员每天 早上从报社设置的售报点以现金买进,每份0.35元,零售价 每份0.5元,利润归售报人所有,如果当天没有售完第二天早 上退还报社,报社按每份报纸0.1元退款,如果某人一个月 (按30天计算)累计订购了7000份,将获得150元的奖金。 某人应聘为售报员,开始他不知道每天应买进多少份报纸, 更不知道能否拿到奖金,报社发行部告诉他一个售报员以前 500天的售报统计数据如表: 问:(1)售报员每天应准备多少份报纸最佳,一个月的收益 的期望值多少? (2)他能否得到奖金,如果一定要得到奖金,一个月的收益 期望值是多少?
第11章决策分析-运筹学PPT课件

运筹学
三.折衷准则 折衷准则又称乐观系数准则或赫威斯准则,是介于悲观准则与乐观准则之间的一个准则。若 决策者对客观情况的评价既不乐观也不悲观,主张将乐观与悲观之间作个折衷,具体做法是 取一个乐观系数α(0<α<1)来反映决策者对状态估计的乐观程度,计算公式如下
u(
A* i0
)
max[
1im
m1 jaxn{aij }
1m jin4{aij }
4 2 3 3 3
2021/2/10
16
第11章 决策分析
试按悲观准则确定其决策方案。
因
u( A1* )
max
1i5
1m jin4{aij
}
4
所以 A为1 最优方案。
一般的,悲观准则可用下式表示
u(
A* i0
)
max
1im
1m jinn{aij }
2021/2/10
运筹学 17
E( A5 )
1 4
(3
5
5
5)
4.50
E( Ai )
1i5
5.50 5.25 5.00 5.50 4.50
运筹学 23
第11章 决策分析
E(
A1 )
E(
A4
)
max{E( i
Ai
)}
5.50
有两个最大期望益损值方案,哪一个更优?
考虑它们的界差:
D( A1) E( A1) 1m jin4{aij} 5.50 4 1.50 D( A4 ) E( A4 ) 1m jin4{aij} 5.50 3 2.50
2021/2/10
运筹学 6
第11章 决策分析
按问题性质和条件划分,决策可分为: • 确定型决策 • 不确定型决策 • 风险型决策 • 竞争型决策
运筹学中的优化理论和决策分析

运筹学中的优化理论和决策分析运筹学是一种科学理论和方法论,主要研究如何制定最优决策,以实现效益最大化。
它主要通过数学模型和计算机仿真等手段,对复杂系统进行优化分析和决策支持,以达到最优化的结果。
优化理论作为运筹学的核心竞争力,是运用数学、工程等学科的方法来解决最优化问题的理论体系,旨在实现最佳决策的目的。
本文将围绕运筹学中的优化理论和决策分析展开讨论。
一、优化理论优化理论是指通过数学分析和计算机仿真等手段,对具有一定复杂性的系统进行分析,从而实现最优化的结果。
优化问题是指在一定的限制条件下,寻求某种指标或目标函数的最优值。
如何处理约束条件和目标函数之间的相互制约关系,是优化问题研究中的核心难题。
因此,优化理论主要通过建立数学模型和算法设计等手段,实现最优决策的目标。
1. 建立数学模型建立数学模型是优化理论的核心。
数学模型通常包括决策变量、目标函数、约束条件等要素。
决策变量是指决策者的选择变量,而目标函数则是指要优化的指标或目标。
约束条件则是指决策制定过程中需要考虑的各类限制因素。
通过将系统建模,可以得到系统的优化方案,并为制定最优决策提供途径。
2. 算法设计算法设计是实现最优化的核心。
常见的算法包括线性规划、非线性规划、动态规划、整数规划等。
不同种类的算法在面对不同的优化问题时,具有各自的优缺点。
因此,在实际应用中,需要根据优化问题特征选择相应的算法进行求解。
3. 求解方法求解方法是指实现算法的具体操作过程,包括求解器、迭代算法、搜索算法等。
求解方法的选择与算法种类密切相关。
通过对数学模型建立算法,并运用求解方法进行求解,可以在有限的时间内得到最优化结果。
二、决策分析决策分析是指对决策问题进行全面、系统地分析,从而为制定最优决策提供支持。
决策分析主要涵盖了决策建模、风险分析、方案评估和数据挖掘四个方面。
1. 决策建模决策建模是指对问题进行抽象、形式化的过程,将现实问题映射到数学模型中进行分析和求解。
运筹学决策分析

运筹学决策分析
决策分析的过程有以下3个阶段。 1. 画决策树 2. 网络计算 3. 检查最优路径与风险特征
PPT文档演模板
运筹学决策分析
1. 画决策树
E1
推出
D1
有利
推出
A 试验 C 0.5
放弃
20
0.5 D2
放弃
不利
推出
E2
PPT文档演模板
0.4 需求大 200 B 0.4 需求小 50
0.2 无需求 -150 0.72 需求大 200 0.24 需求小 50 0.04 无需求 -150
PPT文档演模板
运筹学决策分析
(决策) (事件) 需求数量
订购量
6 7 8 9 10 max
6 * 300 350 3100 1305 2300 20 7 * 2100 305 355 1350 1355 20
8
-4100 2150 400 450 1400 40
9
-6300 4-05 2200 405 455 60
PPT文档演模板
运筹学决策分析
与该产品相关的财务和概率数据显示在下表 中:
需求
损益
概率
(数量) 需求大 需求小 无市场
(万元) 200 50
-150
不试验 有利 不利 0.40 0.72 0.08 0.40 0.24 0.56 0.20 0.04 0.36
市场试验成本 = 20万元
PPT文档演模板
放弃 推出
E2
0
0 0.08 需求大 200 0.56 需求小 50 0.36 无需求
-150
0
运筹学决策分析
3. 检查最优路径与风险特征
风险特征可以汇总为表, 列出可能发生的全 部结果, 指出盈利与亏损的各种可能性, 检 查在EMV值后面是否隐藏着较大的亏损值:
系统工程-决策分析课件

THANKS
感谢观看
系统工程的应用领域
制造业
生产线的规划、设计和优化, 提高生产效率和产品质量。
能源
如核能、太阳能等新能源系统 的规划、建设和运营。
航空航天
如飞机、卫星等复杂系统的设 计、制造和测试。
交通运输
城市交通规划、物流系统优化 等。
信息技术
如软件工程、信息系统设计等 。
系统工程的基本原则
整体性原则
将系统视为一个整体,注重各组成部分之间 的相互关系和作用。
详细描述
决策的定义通常包括目标、条件、方案和选择等要素。决策可以分为不同的类型,如战 略决策、战术决策和操作决策等,也可以根据涉及的领域和范围分为个人决策和组织决
策。
决策过程
总结词
决策过程包括确定目标、收集信息、制 定方案、评估方案和选择最优方案等步 骤。
VS
详细描述
在决策过程中,首先ຫໍສະໝຸດ 要明确目标,然后 通过收集相关信息来了解问题的背景和条 件。接着,制定多个可能的方案,并对这 些方案进行评估和比较。最后,选择最优 方案并实施。
通过优化群决策的流程和方法,提高决策的效率和准确性。
决策支持系统
系统架构
01
构建决策支持系统的基本架构,包括数据层、模型层、应用层
等。
系统功能
02
根据实际需求,设计系统的各项功能,如数据查询、模型计算
、报表生成等。
系统实施
03
根据系统架构和功能要求,进行系统开发和实施工作,确保系
统的正常运行和效果。
决策分析方法
要点一
总结词
决策分析方法包括定性和定量两种方法。定性方法主要依 赖于经验和专业知识,而定量方法则通过数学模型和数据 分析来评估方案。
运筹学 第11章-决策分析

p(N1) = 0.3
S1(大批量生产) S2(中批量生产) S3(小批量生产) 30 20 10
N2(需求量小)
p(N2) = 0.7
-6 -2 5
2
§1 决策的基本概念与决策程序
策略 事件
N1(需求量大)
p(N1) = 0.3
30 20 10
N2(需求量小)
p(N2) = 0.7
三、等可能性准则
• 决策者把各事件的发生看成是等可能的: 则每个事件发生的概率为 1/n, n为事件数 ,然后 计算各行动方案的收益期望值。 用 E(Si)表示第i方 案收益期望值
事件 事件 策略 策略
S1(大批量生产) 1(大批量生产) S2(中批量生产) 2(中批量生产) S3(小批量生产) 3(小批量生产)
EOL(Si)
7.7 7.9 6 (min)
9
§2 风险形决策问题
四、全情报的价值(EVPI)
• 全情报:关于事件的确切消息。 • Expected Value in perfect Information是指决策人为获取全情 报,所能支付的信息费的上限。 前例,当我们不掌握全情报时S3 是最优策略,期望收益为 0.3*10 + 0.7*5 = 6.5万 记 EMV* = 6.5万 若得到全情报时:
1
2
1j2
S1(大批量生产) 30 S1(大批量生产) 10 (30-20) S2(中批量生产) 20 S2(中批量生产) 20 (30-10) S3(小批量生产) 10 S3(小批量生产)
0 (30,理想值)
11 [5-(-6)] -6 7 [5-(-2)] -2 0 (5,理想值)
5
11 10 (min) 20
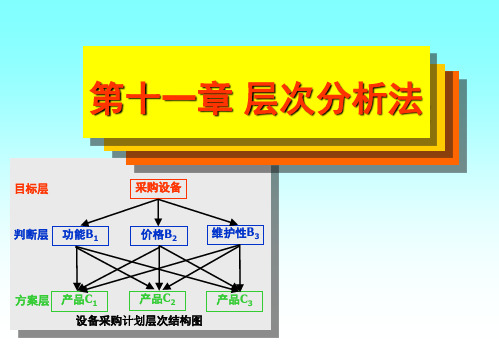
第11章 层次分析法
层次分析法
1 3 2 5 1 1 1 1/ 3 1/ 8 1 1 3 B1 1/ 2 1 2 B 3 1 1/ 3 B3 2 1/ 3 1/ 3 1 8 3 1 1/ 5 1/ 2 1
1 3 4 B4 1 / 3 1 1 1 / 4 1 1
第十一章 层次分析法
目标层 采购设备
判断层
功能B1
价格B2
维护性B3
方案层
产品C1
产品C2
产品C3
设备采购计划层次结构图
层次分析法
层次分析法(AHP, p248)
层次分析法基本简介 层次分析法的基本步骤
1. 建立层次结构模型
2. 构造成对比较阵(判断矩阵)
3. 计算权向量并做一致性检验
4. 计算组合权向量并做组合一致性检验
层次分析法
同理可得方案P2,P3在目标中的组合权重分别为 0.264 和0.456;于是得到方案层对于目标层的权向量为:
w(3)=(0.300,0.264,0.456)T
说明应以P3作为第一选择地点
由上面的计算可得一般的计算步骤如下: 对于 3 个层次的决策问题 ,若第一层只有一个因素 , 第2,3层分别有n,m个因素,记第2层对第1层与第3层 对第2层的权向量分别为:
w(2) ( w1(2) , w2(2) ,..., wn(2) )T
24
层次分析法
wk (3) ( wk1(3) , wk 2(3) ,..., wkm(3) )T , k 1, 2,..., n
以 wk
( 3)
层次分析法的整个过程体现了人的决策思 维的基本特征,即分解、判断与综合,易学易 用,而且定性与定量相结合,便于决策者之间 彼此沟通,是一种十分有效的系统分析方法, 广泛地应用在经济管理规划、能源开发利用与 资源分析、城市产业规划、人才预测、交通运 输、水资源分析利用等方面。 近年来应用领域拓广到经济计划和管理 ,能 源政策和分配,行为科学,军事指挥,运输,农业,教 育,人才,医疗,环境等领域.
运筹学 第十一章

某非确定型决策问题的决策矩阵如表所示:
E1 S1 S2 S3 S4 4 4 15
E2 16 5 19
E3 8 12 14
E4 1 14 13
2 17 8 17 (1)若乐观系数α=0.4,矩阵中的数字是利润,请用非确定 型决策的各种决策准则分别确定出相应的最优方案. (2)若表中的数字为成本,问对应于上述决策准则所选择的 方案有何变化? 某一决策问题的损益矩阵如表,其中矩阵元素为年利润。 事 E E E 件 概 率方案 S S S 40 360 1000 200 360 240 2400 360 200 P P P
某钟表公司计划通过它的销售网抵消一种低价钟表,计划零售 价为每块10元.对这种钟表有三个设计方案:方案Ⅰ需一次投资 10万元,投产后每块成本5元; 方案Ⅱ需一次投资16万元,投产 后每块成本4元; 方案Ⅲ需一次投资25万元,投产后每块成本3 元;该种钟表需求量不确切,但估计有三种可能: E—30 000; E—120 000; E—200 000; (a)建立损益矩阵 (b)分别用乐观法,悲观法及等可能法决定该公司应采用哪一个 设计方案 事件 E E E 方案 Ⅰ Ⅱ Ⅲ 5 2 -4 50 56 59 90 104 115
专业代码
11
专业名 称信息管理与信息系统课程代 码18
知识点 代码
题
干
11181102 某地方书店希望订购最新出版的图书.根据以往经验,新书的 销售量可能为50,100,150或200本.假定每本新书的订购价 为4元,销售价为6元,剩书的处理价为每本2元.要求:(1) 建立损益矩阵;(2)分别用悲观法、乐观法及等可能法决策 该书店应订购的新书数字 ;
有一种游戏分两阶段进行.第一阶段,参加者需先付10元,然 后从含45%白球和55%红球的罐中任摸一球,并决定是否继续第 二阶段.如继续需再付10元,根据第一阶段摸到的球的颜色的 相同颜色罐子中再摸一球.已知白色罐子中含70%蓝球和30%绿 球,红色罐子中含10%的蓝球和90%的绿球.当第二阶段摸到为 蓝色球时,参加者可得50元,如摸到的绿球,或不参加第二阶 段游戏的均无所得.试用决策树法确定参加者的最优策略.
运筹学复习11

线性规划一、判断题1.在线性规划的模型中全部变量要求是整数(✗)2.如果一个线性规划问题有两个不同的最优解,则它有无穷多个最优解。
(✓)3.如果一个线性规划问题有可行解,就一定有最优解。
(✗)4.线性规划的基本类型是“max”型问题。
(✗)5.图解法提供了求解线性规划问题的通用方法。
(✗)6.线性规划问题的可行解集不一定是凸集。
(✗)7.若线性规划问题的可行域无界,则该线性规划问题一定没有最优解。
(✗)8.若线性规划模型的可行域非空有界,则其顶点中必存在最优解。
(✓)9.线性规划数学模型中的决策变量必须是非负的。
(✗)10.凡具备优化、限制、选择条件且能将有关条件用关于决策变量的线性表达式表示出来的问题可以考虑用线性规划模型来处理。
(✓)二、选择题1.建立模型的一个基本理由是去揭晓那些重要的或有关的( B )。
A.数量B.变量C.约束条件D.目标函数2.线性规划模型不包括下列( D )要素。
A.目标函数B.约束条件C.决策变量D.状态变量3.下面( D )不属于构成线性规划问题的必要条件。
A.有一个待实现的目标B.有若干个可供选择的方案C.所有资源具有一定的约束限制D.明确求目标函数的极大值4.关于线性规划模型,下面( D )的叙述正确。
A.约束方程的个数多于一个B.求极大值问题时,约束条件都是小于或等于号C.求极小值问题时,目标函数中变量的系数均为正D.变量的个数一般多于约束方程的个数对偶问题一、判断题1 、任何线性规划问题存在并具有唯一的对偶问题。
(✓)2 、对偶问题的对偶问题一定是原问题。
(✓)3 、如线性规划的原问题存在可行解,则其对偶问题也一定存在可行解。
(✗)4 、如线性规划的对偶问题无可行解,则原问题也一定无可行解。
(✗)5 、若原问题为无界解,则其对偶问题无可行解。
(✓)二、选择题1 、线性规划原问题的目标函数为求极小值型,若其某个变量小于等于0 ,则其对偶问题约束条件为( A )形式。
运筹学课程常见疑难问题及解答

的练习熟练掌握原问题与对偶问题的对应关系。
返回
利用松弛性质求解对偶问题最优解时应注 意什么?
注意给出的线性规划问题是否具备原问题或者对偶问题的标
准形式。对于具备标准形式的线性规划问题,可以直接利用
松弛性质中的描述进行计算。
对于不具备标准形式的线性规划问题,不可以直接利用松弛
以单位矩阵对应的变量作为基变量时,求出的基本解一 定是基本可行解。
迭代时以单位矩阵对应的变量作为基变量,还可以从单
纯形表中直接读出各变量的值。
返回
应用大M法时应注意什么问题?
应用大M法时应注意:
在约束方程中加入人工变量以后,一定要在目标函数中
增加罚函数项;
在求极大的目标函数中,人工变量系数应为-M,相反在
第八章—目标规划
第九章—排队论 第十章—存贮论 第十一章—决策论 第十二章—多目标决策方法 第十三章—在民航应用案例
一般性问题的解答
运筹学在民航运输中的应用情况
参见第十三章内容及平台上的学术文献
如何学好运筹学课程
同一问题求解方法的选择
返回
如何学好运筹学课程?
i=1 m
n m a kj x j b k时, y k 0; a ij yi c j , j 1, , n j=1 的最优解,当且仅当 i=1 m y 0,i 1, , m a y c 时, x 0. i l l il i i=1
返回
什么是满秩矩阵?
如果方阵的行列式非零,则该方阵是满秩矩阵。 某方阵是满秩矩阵时,以该方阵各列作为系数的各变量作为
基变量,其他变量取为常数(计算基本解时取为0)时,则
运筹学-第十一章 决策分析1

解: 设工厂每天生产计划的五个方案 是ai:0个,1000个, 2000个, 3000 个, 4000个。每个方案都会遇到五个 结局Sj是: 0个,1000个, 2000个, 3000个, 4000个。构造益损矩阵如下。 注意:每销售一个产品,可以盈利 0.02元,每销售1000个产品,可以盈 利20元, 当天未卖出1000个产品,损失10元。
2000
3000 4000
0 0.1 0 0 -10 -1 ຫໍສະໝຸດ 20 -2 -30 -3 -40 -4
销售量(事件) 1000 2000 3000 0.2 0.4 0.2 0 0 0 0 0 0 20 20 20 4 8 4
∑Pjaij
max
10 2 0 0 -10 -2
40 16 30 12 20 8
3 等可能准则(Laplace原则)(平 均主义决策) 求出每个行动方案aj在相同概率 状态下各事件的收益的期望值。然后, 比较各行动方案实施后的结果,取具 有最大期望值的决策为最优行动的决 策原则。
产 量 ( 策 略)
0 1000 2000 3000 4000
0 0 -10 -20 -30 -40
二、不确定型决策准则
由于不确定型决策问题所面临 的几个自然状态是不确定,是完全 随机的,这使得不确定型决策,始 终伴随着一定的盲目性。决策者的 经验和性格常常在决策中起主导作 用。
例11 -1 某工厂成批生产某种产品,批发价 格为0 . 05元/个,成本为0 . 03元/个,这 种产品每天生产,当天销售,如果当天卖 不出去,每个损失0 . 01元。已知工厂每天 产量可以是:0个,1000个, 2000个, 3000个, 4000个。根据市场调查和历史 记录表明,这种产品的需要量也可能是: 0个,1000个, 2000个, 3000个, 4000 个。试问领导如何决策?
运筹学 第十一章 决策分析11-5-8

7×10 × 16 销路一般0.3 销路一般 3×10 × -4×10 × 17.5 5×10 × 销路一般0.3 销路一般 2.5×10 × -2.5×10 × 16.5 销路一般0.3 销路一般 3×10 × 1.5×10 × -0.5×10 ×
17.5
扩建现车间 -10
单阶段决策和多阶段决策
追求利润最大,还是损失最小; 追求利润最大,还是损失最小; 有人敢于冒险,有人则力求稳妥。 有人敢于冒险,有人则力求稳妥。
决策的分类 按决策的层次分类: • 按决策的层次分类: 战略型决策:关于全局、影响深远的决策。 战略型决策:关于全局、影响深远的决策。 战术型决策:短期的具体的决策。 战术型决策:短期的具体的决策。 • 按决策出现的频率划分: 按决策出现的频率划分: 程序决策: 经常重复出现的例行决策活动。 程序决策: 经常重复出现的例行决策活动。 非程序决策:指不经常或不重复出现的决策。 非程序决策:指不经常或不重复出现的决策。 • 按决策过程的连续性划分: 按决策过程的连续性划分: 单阶段决策:只有一个阶段。 单阶段决策:只有一个阶段。 多阶段决策:有多个阶段。 多阶段决策:有多个阶段。
实现方法: 实现方法:
表格法 决策树法
(一)、表格法 在例1中 假设已经知道市场销售情况为高、 在例 中,假设已经知道市场销售情况为高、中、低的 概率分别为0.3,0.5,0.2,问如何决策? 概率分别为 ,问如何决策?
自然状态 状态概率 方案 A1 A2 A3 S1 0.3 20 9 6 最优方案 S2 0.5 1 8 5 S3 0.2 -6 0 4 期望收益E(Ai) 期望收益
表格法
自然状态
s1
s2
…
sn
状态概率 损益值 方案
决策分析

“运筹学”课题组
第八章
本章内容重点
决策分析
8.1决策分析概论 8.2不确定型决策
8.3风险型决策分析方法
8.4多属性决策方法
8.5案例分析
8.1决策分析概论
决策存在于社会生活的各个领域,依赖 于决策者个人或群体知识和才能的积累, 诺贝尔经济学奖获得者西蒙有一句名言 “管理就是决策”,强调了决策是管理的 核心。
8.2.2 悲观准则
悲观准则又称最大最小准则,是一 种避险型决策准则。决策者对未来持 悲观态度,认为未来将出现最差的自 然状态。
在一些情况下,由于个人、企业或组 织的财务能力有限,经验不足,承受 不起巨额损失的风险,因此决策时非 常谨慎。 首先,决策者确定每个方案在最差自 然状态下的收益值,然后选择在最差 自然状态下带来最多收益的方案。
指自然状态完全确定,做出的选择结果也 是确定的,比如,通过线性规划得到最优 的生产计划等
-----不确定型决策
指不仅无法确定未来出现哪种自然状态, 而且也无法估计各种自然状态的概率
-----风险型决策
指不能完全确定未来出现何种自然状态, 但可以预测各种自然状态发生的概率
根据决策目标的多寡可分为:
8.2.4 等可能性准则
因无法确知各种自然状态发生的概 率,可以认为它们有同等的可能性, 每一个自然状态发生概率数都是1/状 态数。在此基础上,计算各个方案的 期望收益值,然后进行比较。
例8.4 利用等可能性准则对例8.1的问题进行 决策。 解:题中有三种可能的自然状态,依据等可 能性准则,每种状态出现的概率为1/3。 计算每个方案的收益期望: 大批量 10×1/3+4×1/3+(-2)×1/3=4; 中批量 7×1/3+6×1/3+2×1/3=5; 小批量 4×1/3+2×1/3+1×1/3=7/3。 期望收益中最大值:5(万元)根据等可能 性准则,选择中批量进货为最优方案。
管理运筹学-决策分析

自然状 态
N1
(需求量大)
行动方案
p(N1) = 0.3
S1(大批量生产)
30
S2(中批量生产)
20
S3(小批量生产)
10
N2
(需求量小)
p(N2) = 0.7
-6 -2 5
E(Si)
4.8 4.6 6.5 (max)
9
§2 风险型情况下的决策(续)
三、决策树法
• 过程
(1) 绘制决策树;
(2) 自右到左计算各方案的期望值,将结 果标在方案节点处;
修正先验概率,得到后验概率。如此用决策树方法,可得到 更高期望值的决策方案。
14
§3 效用理论在决策中的应用
• 效用:衡量决策方案的总体指标,反映决策者对决策问
题各种因素的总体看法
• 使用效用值进行决策:首先把要考虑的因素折合成
效用值,然后用决策准则下选出效用值最大的方案,作为 最优方案。
• 例:求下表显示问题的最优方案(万元)
• 一种考虑:
– 由于财务情况不佳,公司无法承受S1中亏损100万的风险,也无法承受S2中 亏损50万以上的风险,结果公司选择S3,即不作任何项目。
• 用效用函数解释:
– 把上表中的最大收益值100万元的效用定为10,U(100) = 10;最小 收益值-100万元的效用定为0,U(-100) = 0; • 对收益60万元确定其效用值:设经理认为使下两项等价的p=0.95 (1)得到确定的收益60万; (2)以 p 的概率得到100万,以 1- p 的概率损失100万。 计算得:U(60)= p*U(100)+(1-p)*U(-100) = 0.95*10+0.05*0 = 9.5
决策分析网上

决策分析复习资料决策分析复习资料第1题:管理科学(Management science)是对与定量因素(quantitative factors)有关的管理问题通过应用科学的方法(scientific approach)进行辅助管理决策制定(aid managerial decision making)的一门学科(discipline)。
对第2题:在随机型决策问题,也就是存在不确定性的决策问题中,决策人可以在各种可能的行动中进行选择;但是有些因素是决策人所无法控制的。
我们把决策问题中决策人无法控制的所有因素,即凡是能够引起决策问题的不确定性的因素,统称作自然状态。
(对)第3题:决策理论是(ABCD )A. 运筹学的一支B. 是经济学和管理科学的重要组成部分C. 是控制论的延伸D. 是社会科学与自然科学的交叉,是典型的软科学第4题:由于经济学家、数学家以及系统科学家的努力,决策分析日益广泛地应用于商业、经济、实用统计、法律、医学、政治等各方面。
(对)第5题:满足以下哪几个条件的决策属于不确定型决策( ABCD)A.存在着一个明确的决策目标 B. 存在着两个或两个以上随机的自然状态C. 存在着可供决策者选择的两个或两个以上的行动方案D. 可求得各方案在各状态下的益损矩阵 E. 能获得各个自然状态发生的概率第6题:标准损失函数有以下哪几种?(ABC)A. 平方损失B. 线性损失C. 0-1损失D. 对数损失第7题:以下(ABCDE)项属于决策的要素A.决策者 B. 分析者 C. 目标 D. 行动空间 E. 结果空间第8题:在下雨带伞问题中的下不下雨是自然状态,在购买火灾保险中的是否发生火灾是自然状态。
(对)第9题:匹兹堡开发公司(PDC)已购得一块地用于建造一个高档的沿河综合商业楼,其位置对繁华的匹兹堡和金三角有很好的景观,所谓金三角是指两条小河汇流成俄亥俄(Ohio)河的地段。
每一个建筑物单元的价格是30万~120万,取决于单元所处楼层、面积以及备选的设施。
6.运筹学-决策分析

决策论(决策分析)Decision Analysis
效用理论在决策中的应用
效用曲线的确定 2、对比提问法:设决策者面临两种可选方案 A1 ,A2 。 A1 表示他 可以无任何风险地得到一笔金额 x ; A2 表示他可以概率 p 得到一 笔金额 y ,或以概率 (1 - p )损失金额 z ;且y > x > z ,设 U ( y )表示金额 y 的效用值。则当决策者认为方案 A1 和 A2 等价 时,应有: p U( y )+(1 - p ) U( z )= U( x ) 上式意味着决策者认为 x 的效用值等价于 y 和 z 的效用期望值。由 于上式含四个变量: y , x , z , p ,通过确定其中三个变量,再 向决策者提问即可获得第四个变量的值。 提问方式大致有以下三种——
22
决策论(决策分析)Decision Analysis
效用理论在决策中的应用
效用曲线的确定 对比提问法在实际应用中经常采用改进的 V – M(Von Neumann – Morgenstern )法(简称 5 点法)。即取 p = 0.5 , 固定 y ,z 利用公式 p U( y )+(1 - p ) U( z )= U( x ) 将 y ,z 改变三次,分别提问三次得到相应的 x 值,即可得到效用 曲线上的三个点,再加上当收益最差时效用为 0 和收益最好时效用 为 1 两个点,则可以得到效用曲线上的 5 个点,根据此 5 点即可绘 出效用曲线的大致图形。
因而基本可以分为以下几种决策准decisionanalysisdecisionanalysis不确定型决策方法悲观准则maxmin准则决策者将从最不利的结果中选择最有利的结果maxmindecisionanalysisdecisionanalysis不确定型决策方法乐观准则maxmax准则决策者总是选择最有利的结果最优方案amaxmax10decisionanalysisdecisionanalysis不确定型决策方法折中准则决策者采用一个乐观系数来选择结果乐观系数maxmax11decisionanalysisdecisionanalysis不确定型决策方法等可能性准则laplace准则该准则由19世纪数学家laplace提出
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.2 不确定型决策
一、不确定型决策 (1)存在着一个明确的决策目标; (2)存在着两个或两个以上随机的自 然状态; (3)存在着可供决策者选择的两个或 两个以上的行动方案; (4)可求得各方案在各状态下的益损 矩阵(函数)。
min max 0 -10 -20 -30 -40 0
2 乐观准则(Hurwicz原则、MaxMax ) (冒险型决策) 对于任何行动方案aj,都认为将是最好的 状态发生,即收益值最大的状态发生。然 后,比较各行动方案实施后的结果,取具 有最大收益值的行动为最优行动的决策原 则,也称为最大最大准则。
事件1的结果 事件1 事件2
策略1
事件2的结果
策略2
事件3的结果 事件3
事件4 事件4的结果
图中符号说明:
表示决策点。决策者应当在决策点 从若干策略中进行决策。 表示事件点。表示在策略确定后, 可能遇到发生不同的事件和状态 ——表示树枝,每一树枝表示一个策 略或事件 树梢,树梢端表示各事件的结果。
风险型决策又称为随机 决策,其信息量介于确定型 决策与不确定型决策之间。 人们对未来的状态既不是一 目了然又不是一无所知,而 是知其发生的概率分布。
• 例:在上例中0~4000的概率分别为0.1、 0.2、0.4、0.2、0.1。 11.3.1 最大收益期望值EMV
产 量 ( 策 略)
0 1000
Max{min(a1j),min{a2j},…,min{amj}}
i j j j
产 量 ( 策 略)
0 1000 2000 3000 4000
0 0 -10 -20 -30 -40
销售量(事件) 1000 2000 3000 4000 0 0 0 0 20 20 20 20 10 40 40 40 0 30 60 60 -10 20 50 80
40 8 60 12 50 10
4000 0.1 0 0 20 2 40 4 60 6 80 8
0 17
28
27 20
28
• 最小机会损失期望值
产 量 ( 策 略)
0 1000
2000
3000 4000
0 0.1 0 0 10 1 20 2 30 3 40 4
销售量(事件) 1000 2000 3000 0.2 0.4 0.2 20 40 60 4 16 12 0 20 40 0 8 8
当前比较流行的两种说法:
由现代管理科学创始人,诺贝 尔奖金获得者,世界著名经济学 家 西 蒙 ( H.A.Simon ): 管 理 就 是决策。 中国社会科学院副院长于光远: 决策就是作决定。
二、完整的决策过程
问题的确定 方案的设计 方案选优 试验实证 普遍实施
反 馈
三、决策要素 决策者:一个或几个人。 方案:必须至少有两个以上可供选
Max{max(a1j), max{a2j} ,…, max{amj}}
i j j j
产 量 ( 策 略)
0 1000 2000 3000 4000
0 0 -10 -20 -30 -40
max max 销售量(事件) 1000 2000 3000 4000 0 0 0 0 0 20 20 20 20 20 10 40 40 40 40 0 30 60 60 60 -10 20 50 80 80 80
3 在机会损失表中,从每一行选一个 最大的值,即每一方案的最大机会损失 值 4 在最大机会损失列中选择最小的,它 所对应的策略即为最小机会损失准则所 得的最优策略。
产 量 ( 策 略)
0 1000 2000 3000 4000
0 0 -10 -20 -30 -40
销售量(事件) 1000 2000 3000 4000 0 0 0 0 20 20 20 20 10 40 40 40 0 30 60 60 -10 20 50 80
对于任何行动方案aj ,都认为将 是最大的后悔值所对应的状态发生。 然后,比较各行动方案实施后的结 果,取具有最小后悔值的行动为最 优行动的决策原则,称为后悔值准 则。
步骤:
1 在收益表中,从事件Sj这一列中找出 一个最大的收益值。
2 构造机会损失表。 用这个最大收益值减去每个策略对应事 件j发生的条件收益值,便得机会损失值。
如果几个决策者的利益 和目标互相对抗,就称为 “对策”; 如果几个决策者的利益 和目标不完全一致,又必须 相互合作,共同决策,则称 为“群体决策”。
根据决策目标的多少分类: 单目标决策 只有一个明确的目标,方案的优劣, 完全由其目标值的大小决定,在追求 经济效益的目标中,目标值越大,方 案就越好。 多目标决策 至少有2个目标;这些目标往往有不同 的度量单位,且相互冲突,不可兼而 得之,这时,仅比较一个目标值的大 小已无法判断方案的优劣。
决策分析
11.1 决策分析概述
• 一、什么叫决策? • 所谓决策,简单地说就是做决定的 意思,详细地说,就是为确定未来某 个行动的目标,根据自己的经验,在 占有一定信息的基础上,借助于科学 的方法和工具,对需要决定的问题的 诸因素进行分析,计算和评价,并从 两个以上的可行方案中,选择一个最 优方案的分析判断过程。
2 决策过程——从枝部到根部。先计算每
个行动下的收益期望值,再比较各行动方 案的值,将最大的期望值保留,同时截去 其他方案的分枝。
例4:某厂试制一种新产品,如果大批
生产,估计销路好的概率为0.7,此时可 获利润1200万元,若销路不好,则将赔 150万元,另一种方案是先建一个小型试 验工厂,先行试销,试验工厂投资约2.8 万元,估计试销销路好的概率为0.8,而 以后转入大批生产时估计销路好的概率 为0.85;但若试销时销路不好,则以后 转入大批生产时估计销路好的概率只有 0.1,试画出该厂决策的决策树?
期望值 max 销售量(事件) 1000 2000 3000 4000 0 0 0 0 0 20 20 20 20 14 10 40 40 40 22 0 30 60 60 24 24 -10 20 50 80 20
4 最小机会损失决策(Savage原 则 )(后悔值准则)
定义:称每个方案aj在事件Si下的 最大可能收益与现收益的差叫机会损 失,又称后悔值或遗憾值。
根据决策结局的多少分类:
确定型决策每个方案只有1个结局。 风险型决策又称“随机型决 策”“统计型决策”,每个方案至 少有2个可能结局,但是各种结局 发生的概率是已知的。 不确定型决策每个方案至少有2个 可能结局,但是各种结局发生的概 率是未知的。
根据决策结构分类: 结构化决策又称“程序化决策”决 策方法有章可循。 非结构化决策又称“非程序化决 策”,决策方法无章可循。 半结构化决策又称“半程序化决 策”,决策方法介于两者之间。 计算机决策支持系统(DSS)主要 解决这一类问题。
解: 设工厂每天生产计划的五个方案 是ai:0个,1000个, 2000个, 3000 个, 4000个。每个方案都会遇到五个 结局Sj是: 0个,1000个, 2000个, 3000个, 4000个。构造益损矩阵如下。 注意:每销售一个产品,可以盈利 0.02元,每销售1000个产品,可以盈 利20元, 当天未卖出1000个产品,损失10元。
择的方案。
客观环境:存在不依决策者主 观意志为转移的客观环境条件 结局:各个方案与可能出现的 状态的相应结果。 评价标准
四、决策分类 根据决策者多少分类 单人决策——这是决策者只有一 人,或是利害关系完全一致的几 个人组成的一个群体。 多人决策——决策者至少2个人, 且他们的目标,利益不完全一致, 甚至相互冲突和矛盾。
2000
3000 4000
0 0.1 0 0 -10 -1 -20 -2 -30 -3 -40 -4
销售量(事件) 1000 2000 3000 0.2 0.4 0.2 0 0 0 0 0 0 20 20 20 4 8 4
∑Pjaij
max
10 2 0 0 -10 -2
40 16 30 12 20 8
乐观主义:
等可能决策准则:
最小机会决策准则:
11.4 风险型决策
一、风险型决策
满足如下五个条件决策称为风险型决策: (1)存在着一个明确的决策目标; (2)存在着两个或两个以上随机状态; (3)存在着可供决策者选择的两个或两个 以上的行动方案; (4)可求得各方案在各状态下的益损矩阵 (函数); (5)找到了随机状态的概率分布。
1
钻井 150万
1
出油0.55 无油0.45
800万
0 出让开采权
160万
在事件1的期望收入: 800*0.55+0*0.45=440万
采用钻井策略,期望收入为440-150=290万
在决策点1处,按MAX(290,160)=290万,决 定该公司的优选策略为钻井。
利用决策树进行决策时要掌握两个步骤: 1 画决策树——从根部到枝部。
例3、某石油公司拟在一片估计含油的 荒地上钻探。如果钻井,费用为150 万,若出油(概率为0.55)收入为 800万,若无油(概率为0.45)则收 入为0。该公司也可以转让开采权, 转让费为160万元,但公司可不担任 何风险。问该公司应如何决策,使其 期望收益值为最大,画出决策树,并 利用决策树来进行决策。
销售量(事件) 0 产 量 ( 策 略) 0 1000 2000 3000 4000 0 -10 -20 -30 -40 1000 2000 3000 0 20 10 0 -10 0 20 40 30 20 0 20 40 60 50 4000 0 20 40 60 80
1 悲观准则(Wald原则、Max Min) (保守型决策) 对于任何行动方案aj,都认为将是最坏 的状态发生,即收益值最小的状态发生。 然后,比较各行动方案实施后的结果, 取具有最大收益值的行动为最优行动的 决策原则,也称为最大最小准则。
