第章教材习题解答
计算机网络第一章习题解答

第一章概述1-01 计算机网络向用户可以提供那些服务?答:连通性和共享1-02 试简述分组交换的要点。
答:采用存储转发的分组交换技术,实质上是在计算机网络的通信过程中动态分配传输线路或信道带宽的一种策略。
它的工作机理是:首先将待发的数据报文划分成若干个大小有限的短数据块,在每个数据块前面加上一些控制信息(即首部),包括诸如数据收发的目的地址、源地址,数据块的序号等,形成一个个分组,然后各分组在交换网内采用“存储转发” 机制将数据从源端发送到目的端,到达目的端后再按照一定的方式方法进行组装成一个数据块。
分组交换网是由若干节点交换机和连接这些交换机的链路组成,每一结点就是一个小型计算机。
基于分组交换的数据通信是实现计算机与计算机之间或计算机与人之间的通信,其通信过程需要定义严格的协议。
分组交换网的主要优点:1、高效。
在分组传输的过程中动态分配传输带宽。
2、灵活。
每个结点均有智能,可根据情况决定路由和对数据做必要的处理。
3、迅速。
以分组作为传送单位,在每个结点存储转发,网络使用高速链路。
4、可靠。
完善的网络协议;分布式多路由的通信子网。
电路交换相比,分组交换的不足之处是:①每一分组在经过每一交换节点时都会产生一定的传输延时,考虑到节点处理分组的能力和分组排队等候处理的时间,以及每一分组经过的路由可能不等同,使得每一分组的传输延时长短不一。
因此,它不适用于一些实时、连续的应用场合,如电话话音、视频图像等数据的传输;②由于每一分组都额外附加一个头信息,从而降低了携带用户数据的通信容量;③分组交换网中的每一节点需要更多地参与对信息转换的处理,如在发送端需要将长报文划分为若干段分组,在接收端必须按序将每个分组组装起来,恢复出原报文数据等,从而降低了数据传输的效率。
1-03 试从多个方面比较电路交换、报文交换和分组交换的主要优缺点。
(教材11—15)1-04 为什么说因特网是自印刷术以来人类通信方面最大的变革?答:融合其他通信网络,在信息化过程中起核心作用,提供最好的连通性和信息共享,第一次提供了各种媒体形式的实时交互能力。
人教版生物七年级上册教材习题答案

教材答案及解析第一单元生物和生物圈第一章认识生物第一节生物的特征第3页【想一想,议一议】因为机器人不像其他生物一样是由细胞构成的(除病毒以外,生物体都是由细胞构成的),也不存在构成细胞的有机物,同时,机器人不具有营养、呼吸、排泄、对外界刺激作出反应、生长和繁殖、遗传和变异的特性,因此机器人不是生物。
第3页【观察与思考】1.尽管生石花的肉质叶看起来像石头,但生石花具有生物的基本特征。
例如,通过观察可以看出,生石花的肉质叶与仙人球的肉质茎类似;生石花能从小长大;生石花能开出各种颜色的花,还能结出种子,表明它能进行繁殖;生石花长有根,可以从土壤中获取水和无机盐等。
查阅生石花的资料可知,生石花是一种植物,因此它是生物。
2.岩洞里的钟乳石尽管能慢慢长大,但这种长大与生物的生长是不同的,它是一些无机物慢慢堆积的结果。
同时钟乳石没有生物所共有的特征,如具有营养、呼吸、排泄、对外界刺激作出反应、繁殖、遗传和变异的特性,因此钟乳石不是生物。
3.要判断一个物体是否有生命,可以看它是不是“活”的,看它是不是具有生命现象。
即看它是否具有生物的基本特征。
生物具有的基本特征是:由细胞构成(除病毒以外)、生活需要营养、能进行呼吸、能排出身体内产生的废物、能对外界刺激作出反应、能生长和繁殖、有遗传和变异的特性等。
第4页【旁栏思考题】植物需要从外界吸收氧气,以维持自身的生存。
生物能进行呼吸,绝大多数生物需要吸入氧气,排出二氧化碳,植物也需要通过呼吸作用分解有机物,消耗氧气,为植物体的各项生命活动提供能量。
第7页【技能训练】在观察时要从宏观到微观,从整体到局部,并及时做好观察记录,有必要时还需要测量。
对于马、牛、驴的外形,可直接用肉眼进行观察。
观察发现马和驴的不同之处主要有:马的体型比驴的体型大,马的鬃毛比驴的长一些,马耳朵短,驴耳朵长,马尾成束,驴尾末端分叉等。
马和牛的相同点主要有:眼睛都较大,都有四肢,都有蹄,体表都被毛,都有尾巴等。
信号与系统课后习题与解答第一章

1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21(a )连续信号(模拟信号);(b )连续(量化)信号;(c )离散信号,数字信号;(d )离散信号;(e )离散信号,数字信号;(f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问)(1);)sin(t e at ω-(2);nT e -(3);)cos(πn (4);为任意值)(00)sin(ωωn (5)。
221⎪⎭⎫ ⎝⎛解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。
1-3 分别求下列各周期信号的周期T :(1);)30t (cos )10t (cos -(2);j10t e (3);2)]8t (5sin [(4)。
[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期;对于分量cos (30t ),其周期。
由于5T 1π=15T 2π=为的最小公倍数,所以此信号的周期。
5π21T T 、5T π=(2)由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。
5102T ππ==(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。
电工技术与电子技术(唐庆玉)第1-4章习题解答
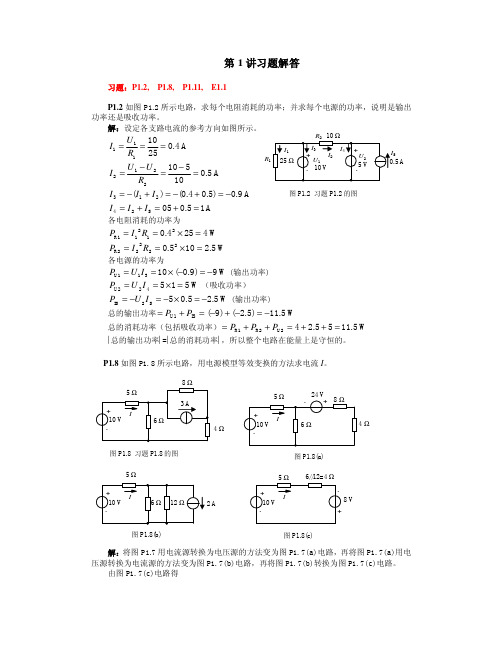
12 − 12 + 6 = 4V VA = 2 1 1 1 + + 3 2 6 6 −8 + 2 4 = 1V VB = 1 1 1 + + 2 4 4 所以 U C = VA − VB = 4 − 1 = 3 V
P1.18 用叠加原理求图 P1.18 电路中的电压 U。
15 mA
+12V 2 kΩ C UC 6 kΩ + −
R1 + − R3 R5 D IS + US − 图 P1.20 习题 P1.20 的图 U1 I 1 U1 R4 B A + C R2 R1 + − R3 R5 D UABO 图 P1.20(a) − B I R4 C R2 I2
A
解:将图 P1.20 电路中的虚线部分单独画出,如图 P1.20(a)所示,求其戴维宁等效电 路。 图 P1.20(a)电路中,
PU1 = U 1 I 3 = 10 × (−0.9) = −9 W (输出功率) PU2 = U 2 I 4 = 5 × 1 = 5 W (吸收功率) PIS = −U 2 I S = −5 × 0.5 = −2.5 W (输出功率) 总的输出功率 = PU1 + PIS = ( −9) + ( −2.5) = −11.5 W
图p114习题p11412v8图p118习题p118英文教材电路原理习题选编清华大学电机系唐庆玉15ma30ma15图p118a英文教材电路原理习题选编清华大学电机系唐庆玉图p118b英文教材电路原理习题选编清华大学电机系唐庆玉15ma30ma图p118c英文教材电路原理习题选编清华大学电机系唐庆玉2002ab图p119b图p119习题p119电路中的虚线部分单独画出如图p1ababop126如图p126所示电路求能获得最大功率的r值是多少k?
《新编大学物理》(上、下册)教材习题答案

答案:[A]
提示: ,
题:
答案:[C]
提示:由时间的相对性, ,长度为
题 :
答案:[D]
提示: 得
题:
答案:[D]
提示: , ,故
题:
答案:[A]
提示: ; ; ;故
二、填空题
题:
答案:
提示:设痕迹之间距离为 ,由公式 ( 为静长度)。则车上观察者测得长度为
题:
答案:(1) ,(2)
提示:(1)相对论质量和相对论动量: ,
简谐振动的表达式为:x= (πt –π/3).
(2)当t=T/4时物体的位置为;x= (π/2–π/3) = π/6 = (m).
速度为;v= -πAsin(π/2–π/3) = πsinπ/6 = (m·s-1).
加速度为:a= dv/dt= -ω2Acos(ωt + φ)= -π2Acos(πt -π/3)= π2cosπ/6 = (m·s-2).
[解答]物体的总能量为:E = Ek+ Ep= (J).
(1)根据能量公式E = kA2/2,得振幅为: = (m).
(2)当动能等于势能时,即Ek= Ep,由于E = Ek+ Ep,可得:E =2Ep,
即 ,解得: = ±(m).
(3)再根据能量公式E = mvm2/2,得物体经过平衡位置的速度为:
(2)速度的最大值为:vm= ωA= π = (m·s-1); 题解答图
加速度的最大值为:am= ω2A= π2= (m·s-2).
(3)弹簧的倔强系数为:k = mω2,最大回复力为:f = kA = mω2A= (N);
振动能量为:E = kA2/2 =mω2A2/2 = ×10-2(J),
必修第1册 人教版新教材高中生物教材课本课后习题参考答案

类的健康服务ꎻ从否定的角度看ꎬ人工合成病毒的研究也可能会合成
都属于无机盐ꎬ它们在饮料中以离子的形式存在ꎮ 运动员在运动中
某些对人类有害的病毒ꎬ如果这些病毒传播开来ꎬ或者被某些人用作
会大量出汗ꎬ出汗时人体会排出大量无机盐ꎬ所以要给他们补充无机
生物武器ꎬ将给人类带来灾难ꎮ
盐ꎮ 无机盐可以调节细胞的生命活动ꎬ也是许多有机物的重要组成
“ 真” 字指“ 真正” 的含义ꎻ从进化的视角看ꎬ真核细胞是由原核细胞进
化而来的ꎮ
练习与应用
概念检测
1.(1) ✕ꎻ (2) √ꎻ (3) √ꎮ
2. Dꎮ
3.提示 根瘤菌是细菌ꎬ属原核生物ꎬ原核细胞没有成形的细胞核ꎬ植
物细胞有成形的细胞核ꎮ
拓展应用
2
高中生物 必修 1 ( 人教版)
1.提示 细胞之所以会有统一性ꎬ 是因为细胞来源于细胞ꎬ即新细胞是
老细胞通过分裂形成的ꎬ所有细胞都来自一类共同的祖先ꎬ所以具有
统一性ꎮ 细胞的多样性是在进化过程中ꎬ由于自然选择等ꎬ细胞出现
结构分化、分别承担不同功能而产生的ꎮ
(1) 支原体与动物细胞结构的区别是:支原体没有成形的细
2.提示
胞核ꎬ只有游离的 DNA 和核糖体一种细胞器ꎮ
别是:植物细胞有细胞壁、液泡ꎬ有些植物细胞还有叶绿体ꎮ
(3) 因为人体皮肤和迎春叶都是由多种组织组成的ꎮ 例如ꎬ人体皮肤
由上皮组织、结缔组织、神经组织和肌肉组织组成ꎬ这些不同的组织
按照一定的次序结合在一起构成行使保护等功能的器官ꎮ
拓展应用
1.提示 可用学生已学过的植物或动物的分类、细胞所具有的结构进
含有大量的 Nꎮ
2.提示 细胞中有些元素含量很少ꎬ但是却有重要作用ꎬ如在玉米细胞
《基础化学》教材习题答案(第3版)

第一章 习题答案1.答:能量单位J 、质量单位μg 、长度单位nm 、温度单位℃、属于SI 单位;其他不是。
2.答:SI 基本单位:m 、kg 、s 、A 、K 、mol 、cd 。
3.答:一切属于国际单位制的单位都是我国的法定计量单位。
根据我国的实际情况,在法定计量单位中还明确规定采用了若干可与国际单位制并用的非国际单位制单位。
第二章习题答案1. 解: 根据)()O H ()O H ()O H (222蔗糖n n n x +=0292m o l .0m o l 342g g0.10)( mol 56.5mol 18.0g g 100)O H (1-1-2=⋅==⋅=蔗糖n n 995.00.0292m o lm o l 56.5mol56.5)O H (2=+=xkPa 33.20.995kPa 34.2)O H ()O H (2*2=⨯==x p p2.解:)B ()O H ()()O H (999.00.1molmol 08mol08)O H ()O H ()O H ()O H (899.00.1molmol 04mol 04)O H ()O H ()O H ()(999.00.1molmol 80mol80)()()()O H (999.00.1mol mol 80mol80)O H ()O H ()O H (*2**2*22*22*2*22*23***2*2*22*21答案为苯苯苯苯苯∴>=+⋅===+⋅===+⋅===+⋅==p p p p x p p p p x p p p p x p p p p x p p 3.解:与人体血浆等渗。
11os f 11os f B f B f f 11-1-1-os L mmol 310L mol 31.0C58.0K58.0L mol 31.0mol kg K 86.1L mol 31.0L00.1mol 147g g33.03mol 74.6g g 30.02mol 58.5g g 50.82-----⋅=⋅=︒-==⋅⨯⋅⋅=≈≈=∆⋅=⋅⨯+⋅⨯+⋅⨯=c T c K c iK b iK T c4.解:K 85.1mol kg K 512.00.510Kmol kg K 86.1mol g 1.28mol kg 0281.00.510K 250g g 00.7mol kg K 512.011b b f B f f 111b A B b B =⋅⋅⋅⋅⋅=∆⋅=⋅=∆⋅=⋅=⨯⨯⋅⋅=∆⋅⋅=-----K T K b K T T m m K MT f = -1.85℃ 5. 解:压略高于人体眼液的渗透kPa 869K 310K mol L kPa 314.8L mol 337.0L mmol 337L mol 337.0mL10001.000LmL 1000mol 61.8g g 00.17mol 161.5g g 00.52111-os 1-1-1-1-os =⨯⋅⋅⋅⨯⋅==⋅=⋅=⨯⋅+⋅⨯=--RT c Πc6. 解:11A fB f B 11A b B b B mol kg 61.1100g0.220K g0.19mol kg K 86.1mol kg 62.1100g 0.0600K g 0.19mol kg .512K 0----⋅=⨯⨯⋅⋅=∆=⋅=⨯⨯⋅⋅=∆=m T m K M m T m K M用两种方法计算该物质的相对分子质量基本相同。
教材第一章习题解答

1. 常见的物质聚集状态有哪几种?各有何特征?如何从它们的微观结构来理解?2. 使用理想气体状态方程的条件是什么?3. 试说明实际气体的范德华方程中各修正项的物理意义。
4. 什么叫临界温度?是否所有气体在室温下加压都可以液化?举例说明。
5. 为什么用高压锅可以缩短食物煮熟的时间?6. 如何区别晶体与非晶体?7. 什么是液晶?液晶态具有哪些特征?举例说明液晶的应用。
8. 什么是等离子体和超高密度态物质?举例说明等离子体的应用。
9. 小水滴和水蒸气混合在一起,它们的化学性质都相同,是否为一个相?10. 在0℃时,一只烧杯中盛有水,水上面浮着一块冰,问水和冰组成的系统有几相?11. 什么是分散系统?分几类?举例说明。
12. 为什么I2能溶于CCl4而不溶于水,而KMnO4可溶于水但不溶于CCl4?13. 难挥发非电解质的稀溶液有哪些依数性?定量关系如何?14. 溶液蒸气压下降的原因是什么?试用蒸气压下降来解释溶液的沸点上升和凝固点下降的现象。
15. 解释下列现象:(1)海鱼放在淡水中会死亡;(2)盐碱地上栽种植物难以生长;(3)雪地里撒些盐,雪就融化了;(4)氯化钙和冰的混合物可作为冷冻剂。
16. 为了行车安全,可在汽车上装备气袋,以便遭到碰撞时使司机不受到伤害。
这种气袋是用氮气充填的,所用氮气是由叠氮化钠与三氧化二铁在火花的引发下反应生成的。
总反应为:6NaN3(s)+Fe2O3(s)→3Na2O(s)+2Fe(s)+9N2(g)在25℃、748mmHg下,要产生75.0L的N2需要叠氮化钠的质量是多少?17. 潜水员的肺中可容纳6.0L空气,在某深海中的压力为980kPa。
在温度37℃条件下,如果潜水员很快升至水面,压力为100kPa,则他的肺将膨胀至多大体积?这样安全吗?18. 在298.2K、10.0L的容器中含有1.00mol N2和3.00mol H2,设气体为理想气体,试求容器中的总压和两种气体的分压?19. 在火星赤道附近中午时温度为20℃,火星大气的主要成分是CO2,其压力约为5mmHg,则其为多少千帕?相同温度下火星上的CO2与地球上的CO2(干空气中,x(CO2)=0.00033)相比,何者更接近理想气体?。
人教版化学教材九年级(上下册)课后习题答案超详细

人教版化学教材九年级(上下册)详细第一章-走进化学世界课题1---化学使世界变得更加绚丽多彩课题2---化学是一门以实验为基础的科学课题3---走进化学实验室第一章小结第二章-我们周围的空气课题1---空气题号解析1 氮气氧气,氮气,氧气点拨:空气的成分注意使用的是体积分数,而不是质量分数。
2(1)B点拨:空气中含量最多的是氮气,且化学性质不活泼。
(2)C液态氧是氧气的液态存在形式,由一种物质组成,属于纯净(3)(3)A臭氧可以用化学式O3表示,有固定的组成,属于纯净物(4) C 点拨:稀有气体性质很不活泼,过去人们认为这些气体不跟其他物质发生化学反应,曾把它们叫做惰性气体。
但随着科学技术的发展,已经发现有些稀有气体在一定条件下也能与某些物质发生化学反应,生成其他物质。
故C项错误。
3 氮气、氧气、二氧化碳、水点拨:此题属于开放性习题,引导学生从具体例子中来初步认识纯净物和混合物。
4 把空水杯或空饮料瓶口向下按入水中,水不能进入杯中或瓶中。
5 去过;感受不一样;在城镇繁华街道附近,空气质量较差,农村广阔的田野空气质量好,清新,安静。
点拨:此题属于开放式的习题,学生答案可有多种,不强求一致。
造成城镇繁华街道附近空气质量差的原因是多方面的,如污染物较多、机动车尾气、尘土、细菌等,噪声也较大。
农村污染物较少,且绿色植物较多,光合作用强一些,所以空气质量好。
6 (1)氧气动植物的呼吸离不开氧气,燃料燃烧离不开氧气,炼钢、气焊以及化工生产和宇宙航行等都要用到氧气。
(2)氮气制硝酸和化肥的主要原料,焊接金属时用氮气作保护气,灯泡中充氮气以延长使用寿命,食品包装时充氮气以防腐等。
(3)稀有气体焊接金属时用稀有气体来隔绝空气,灯泡中充稀有气体以使灯泡耐用;充人灯泡制成多种用途的电光源;用于激光技术;氦可用于制造低温环境;氙可用于医疗麻醉等。
点拨:此题属于开放式的习题,学生可从多方面来认识空气是一种宝贵的自然资源。
万洪文《物理化学》教材习题解答

第一篇化学热力学第一章热力学基本定律.1-1 0.1kg C6H6(l)在,沸点353.35K下蒸发,已知(C6H6) =30.80 kJ mol-1。
试计算此过程Q,W,ΔU和ΔH值。
解:等温等压相变。
n/mol =100/78 , ΔH = Q = n = 39.5 kJ , W= - nRT = -3.77 kJ , ΔU =Q+W=35.7 kJ1-2 设一礼堂的体积是1000m3,室温是290K,气压为pϑ,今欲将温度升至300K,需吸收热量多少?(若将空气视为理想气体,并已知其C p,m为29.29 J K-1·mol-1。
)解:理想气体等压升温(n变)。
Q=nC p,m△T=(1000pϑ)/(8.314×290)×C p,m△T=1.2×107J 1-3 2 mol单原子理想气体,由600K,1.0MPa对抗恒外压绝热膨胀到。
计算该过程的Q、W、ΔU和ΔH。
(Cp ,m=2.5 R)解:理想气体绝热不可逆膨胀Q=0 。
ΔU=W ,即nC V,m(T2-T1)= - p2 (V2-V1), 因V2= nRT2/ p2, V1= nRT1/ p1,求出T2=384K。
ΔU=W=nCV,m(T2-T1)=-5.39kJ ,ΔH=nC p,m(T2-T1)=-8.98 kJ1-4 在298.15K,6×101.3kPa压力下,1 mol单原子理想气体进行绝热膨胀,最后压力为pϑ,若为;(1)可逆膨胀(2)对抗恒外压膨胀,求上述二绝热膨胀过程的气体的最终温度;气体对外界所作的功;气体的热力学能变化及焓变。
(已知C p,m=2.5 R)。
解:(1)绝热可逆膨胀:γ=5/3 , 过程方程p11-γT1γ= p21-γT2γ, T2=145.6 K ,ΔU=W=nC V,m(T2-T1)=-1.9 kJ , ΔH=nC p,m(T2-T1)=-3.17kJ(2)对抗恒外压膨胀,利用ΔU=W ,即nC V,m(T2-T1)= - p2 (V2-V1) ,求出T2=198.8K。
生物化学(第三版)课后习题解答

生物化学(第三版)课后习题解答第一章糖类提要糖类是四大类生物分子之一,广泛存在于生物界,特别是植物界。
糖类在生物体内不仅作为结构成分和主要能源,复合糖中的糖链作为细胞识别的信息分子参与许多生命过程,并因此出现一门新的学科,糖生物学。
多数糖类具有(CHO)n的实验式,其化学本质是多2羟醛、多羟酮及其衍生物。
糖类按其聚合度分为单糖,1个单体;寡糖,含2-20个单体;多糖,含20个以上单体。
同多糖是指仅含一种单糖或单糖衍生物的多糖,杂多糖指含一种以上单糖或加单糖衍生物的多糖。
糖类与蛋白质或脂质共价结合形成的结合物称复合糖或糖复合物。
单糖,除二羟丙酮外,都含有不对称碳原子(C*)或称手性碳原子,含C*的单糖都是不对称分子,当然也是手性分子,因而都具有旋光性,一个C*有两种构型D-和L-型或R-和S-型。
因此含n个C*的单糖有2n个旋光异构体,组成2n-1对不同的对映体。
任一旋光异构体只有一个对映体,其他旋光异构体是它的非对映体,仅有一个C*的构型不同的两个旋光异构体称为差向异构体。
单糖的构型是指离羧基碳最远的那个C*的构型,如果与D-甘油醛构型相同,则属D系糖,反之属L系糖,大多数天然糖是D系糖Fischer E论证了己醛糖旋光异构体的立体化学,并提出了在纸面上表示单糖链状立体结构的Fischer投影式。
许多单糖在水溶液中有变旋现象,这是因为开涟的单糖分子内醇基与醛基或酮基发生可逆亲核加成形成环状半缩醛或半缩酮的缘故。
这种反应经常发生在C5羟基和C1醛基之间,而形成六元环砒喃糖(如砒喃葡糖)或C5经基和C2酮基之间形成五元环呋喃糖(如呋喃果糖)。
成环时由于羰基碳成为新的不对称中心,出现两个异头差向异构体,称α和β异头物,它们通过开链形式发生互变并处于平衡中。
在标准定位的Hsworth式中D-单糖异头碳的羟基在氧环面下方的为α异头物,上方的为β异头物,实际上不像Haworth式所示的那样氧环面上的所有原子都处在同一个平面,吡喃糖环一般采取椅式构象,呋喃糖环采取信封式构象。
电工学第五版第1234 章 习题解答

第1章 习题解答(部分)1.5.3 有一直流电源,其额定功率P N =200 W ,额定电压U N =50 V ,内阻只RN =0.5Ω,负载电阻R0可以调节,其电路如图所示。
试求: (1)额定工作状态下的电流及负载电阻, (2)开路状态下的电源端电压,分析 电源的额定值有额定功率P N 。
额定电压U N 和额定电流I N 。
三者间的关系为 P N =U N I N 。
额定电压U N 是指输出额定电流I N 时的端电压,所以额定功率P N 也就是电源额定工作状态下负载所吸收的功率。
解 (1)额定电流 A U P I N N N 450200===负载电阻 5.12450===N N I U R Ω (2)开路状态下端电压U 0 等于 电源电动势E 。
U 0=E =U N +I N R0=50+4×0.5=52 V1.5.6 一只100V ,8W 的指示灯,现在要接在380V 的电源上,问要串多大阻值的电阻?该电阻应选用多大瓦数的?分析 此题是灯泡和电阻器额定值的应用。
白炽灯电阻值随工作时电压和电流大小而变,但可计算出额定电压下的电阻值。
电阻器的额定值包括电阻值和允许消耗功率。
解 据题给的指示灯额定值可求得额定状态下指示灯电流I N 及电阻只R NΩ≈==≈==1510073.0110A 073.01108N N N N N N U U R U P I串入电阻R 降低指示灯电压,使其在380V 电源上仍保持额定电压U N =110V 工作,故有Ω≈-=-=3710073.01103800N N I U U R 该电阻工作电流为I N =0.073 A,故额定功率为W R I P N R 6.193710073.022≈⨯=⋅=可选额定值为3.7k Ω,20 W 的电阻。
1.5.7在图1.03的两个电路中,要在12V 的直流电源上使6V ,50 mA 的电珠正常发光,应该采用哪 一个联接电路? 解 要使电珠正常发光,必须保证电珠 获得6V ,50mA 电压与电流。
第1章物质聚集状态习题

第一章 物质聚集状态 习 题解答(教材)1.计算在15℃和97 kPa 压力下,15 g 氮气所占有的体积。
解:330132.01097)15273(314.82515PV m nRT =⨯+⨯⨯==2.在20℃和97 kPa 压力下,0.842 g 某气体的体积是0.400 L ,这气体的摩尔质量是多少?解: RT m V M p =13386.52104.010********.8842.0M --⋅=⨯⨯⨯⨯⨯==molg pRT Vm3. 407℃时,2.96 g 氯化汞在 l .00 L 的真空器中蒸发,压力为60 kPa ,求氯化汞的摩尔质量和化学式。
解:由公式PRT Mρ=得,9.278100.110602933148842.0M 33=⨯⨯⨯⨯⨯=-.g ⋅mol -1,M(Hg)=200.59 g ⋅mol -1,25.35==Cl n又25.35131169≈-=x ,所以分子式为HgCl 24.在30℃和 102 kPa 压力下,用 47.0 g 铝和过量的稀硫酸反应可以得到多少升干燥的 氢气?如果上述氢气是在相同条件下的水面上收集的,它的体积是多少? (已知,30℃,液态水的饱和蒸气压为4. 24k kPa )[解:设p 为总压,即常压。
2Al+3H 2SO 4 ==== Al 2(SO 4 )3 + 3H 2 37 347 x 37 :3=47: x x=2.61mol333105.641010215.303314.861.222mPRT n VH H -⨯=⨯⨯⨯== 或)5.64(Lp 总 =O H p 2+P`P` = 102-4. 24k=97.76kPa T 一定,P`V`= P V LP PV V 3.6776.975.64102``=⨯==5,在100 kPa 和 100℃下,混合0.300 L 氢与 0.100 L 氧,然后使之爆炸。
如果爆炸后压力和温度不变,则混合气体的体积是多少? 解: H 2(g) + 1/2O 2(g) = H 2O(l) 0.3 0.10.2 0.1 V(H 2)=0.2L 混合气体的体积0.3L6.在25℃时,初始压力相同的5.0 L 氮和 15 L 氧压缩到体积为 10.0L 的真空容器中, 混合气体的总压力是 150 kPa 试求:(1)两种气体的初始压力;()混合气体中氮和氧的分 压;(3)如果把温度升到210℃,容器的总压力。
管理会计学教材课后习题参考答案
第1章管理会计概述一、选择题1、ABD2、AB3、D4、D5、A第2章成本性态与变动成本法一、选择题1、ACD2、D3、B4、B5、BC6、B7、C8、B9、D 10、D四、计算题1、解:(1)单位变动维修费(b)=(2600-2000)÷(5000-3000)=0.30(元/小时)a=y-bx =2600-0.3×5000=1100(元)或:a=2000-0.3×3000=1100(元)(2)7月份的维修费为:1100+0.30×4600=2480(元)2、(1)收益表摘要第1年第2年第3年合计销售收入240000250000400000890000变动成本变动生产成本120000125000200000445000变动销售成本12000125002000044500变动成本合计132000137500220000489500贡献边际108000112500180000400500期间费用固定生产费用360003600036000108000固定销售费用30000300003000090000期间费用合计660006600066000198000税前净利4200046500114000202500(2)完全成本法下,各期期末存货中的单位固定生产成本如下:第1年=36000÷3000=12(元/件)第2年=36000÷2000=18(元/件)第3年=36000÷4000=9(元/件)完全成本法下各期期末存货吸收的固定生产成本如下:第1年=12×600=7200(元)第2年=18×100=1800(元)第3年=9×100=900(元)完全成本法下各期期初存货释放的固定生产成本如下:第1年=0(元)第2年=7200(元)第3年=1800(元)按利润差额简算法计算完全成本法与变动成本法的各期营业利润差额如下:第1年=7200-0=7200(元)第2年=1800-7200=-5400(元)第3年=900-1800=-900(元)(3)利用简化公式计算完全成本法下的各期营业净利润如下:第1年=42000+7200=49200(元)第2年=46500-5400=41100(元)第3年=114000-900=113100(元)第3章本量利分析一、名词解释1、贡献边际是指产品的销售收入与相应的变动成本之间的差额,也称边际贡献、贡献毛益、边际利润。
图论第一章课后习题解答

bi 个 (i = 1,2,…,s),则有 列。 定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分,称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的 定义 1 如果 V H V G ,E H E G , 重数,则称 H 是 G 的子图,记为 H G 。有时又称 G 是 H 的母图。 当 H G ,但 H G 时,则记为 H G ,且称 H 为 G 的真子图。G 的生成子图是 指满足 V(H) = V(G)的子图 H。 假设 V 是 V 的一个非空子集。以 V 为顶点集,以两端点均在 V 中的边的全体为边集 所组成的子图,称为 G 的由 V 导出的子图,记为 G[ V ];简称为 G 的导出子图,导出子图 G[V\ V ]记为 G V ; 它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。 若 V = {v}, 则把 G-{v}简记为 G–v。 假设 E 是 E 的非空子集。以 E 为边集,以 E 中边的端点全体为顶点集所组成的子图 称为 G 的由 E 导出的子图,记为 G E ;简称为 G 的边导出子图,边集为 E \ E 的 G 的 导出子图简记为 G E 。若 E e ,则用 G–e 来代替 G-{e}。 定理 8 简单图 G 中所有不同的生成子图(包括 G 和空图)的个数是 2m 个。 定义 2 设 G1,G2 是 G 的子图。若 G1 和 G2 无公共顶点,则称它们是不相交的;若 G1 和 G2 无公共边,则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图,其顶点 集为 V(G1)∪V(G2),其边集为 E(G1)∪E(G2);如果 G1 和 G2 是不相交的,有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2,但此时 G1 和 G2 至少要有一个公共顶点。
有机化学(第三版马祥志主编)课后习题问题详解

第一章 绪论习题参考答案1. 某化合物的分子量为60,含碳40.1%、含氮6.7%、含氧53.2%,确定该化合物的分子式。
解:① 由各元素的百分含量,根据下列计算求得实验式1:2:133.3:7.6:34.3162.53:17.6:121.40== 该化合物实验式为:CH 2O② 由分子量计算出该化合物的分子式216121260=+⨯+该化合物的分子式应为实验式的2倍,即:C 2H 4O 22. 在C —H 、C —O 、O —H 、C —Br 、C —N 等共价键中,极性最强的是哪一个? 解:由表1-4可以查得上述共价键极性最强的是O —H 键。
3. 将共价键⑴ C —H ⑵ N —H ⑶ F —H ⑷ O —H 按极性由大到小的顺序进行排列。
解:根据电负性顺序F > O > N > C ,可推知共价键的极性顺序为: F —H > O —H > N —H > C —H4. 化合物CH 3Cl 、CH 4、CHBr 3、HCl 、CH 3OCH 3中,哪个是非极性分子?解:CH 4分子为高度对称的正四面体空间结构,4个C —H 的向量之和为零,因此是非极性分子。
5. 指出下列化合物所含官能团的名称和该化合物所属类型。
CH 3OH(2)碳碳三键,炔烃 羟基 ,酚(4)COOH酮基 ,酮 羧基 ,羧酸(6) CH 3CH 2CHCH 3OH (1) CH 3CH 2C CH(3) CH 3COCH 3(5) CH 3CH 2CHO醛基,醛羟基,醇(7) CH3CH2NH2氨基,胺6. 甲醚(CH3OCH3)分子中,两个O—C键的夹角为111.7°。
甲醚是否为极性分子?若是,用表示偶极矩的方向。
37. 什么叫诱导效应?什么叫共轭效应?各举一例说明之。
(研读教材第11~12页有关容)8. 有机化学中的离子型反应与无机化学中的离子反应有何区别?解:无机化学中的离子反应是指有离子参加的反应,反应物中必须有离子。
河南专升本高数教材(云飞)版第一章函数极限连续课后习题答案

河南专升本(云飞)版高数教材课后习题答案第一章 函数 极限 连续同步练习一一、 选择题 1、 答案:C解:偶次根号下不能取负值,又在分母上,不能为0,可有012>-x ;反三角函数的定义域是[]1,1-,可得1121≤-≤-x.解这个题目只需解不等式组 210011112x x x⎧->⎪⇒≤<⎨-≤-≤⎪⎩,因此选C. 2、 答案:D解:函数相同要求定义域和对应法则都相同. A 中的对应法则不同,x 表示任意实数,而2x 则只是正实数;B 、C 定义域不同. D 只是一个函数的两种不同表达形式. 3、 答案:D解:三角函数都是周期函数,所以A 、C 一定是周期函数,对于B 有22cos 1sin 2xx y -==,显然是周期函数. 4、 答案:D解:求一函数的反函数就是反解出x 即可.对于本题就是由dcx bax y --=解得a cy b dy x --=,再将x ,y 互换即可. 5、 答案:B解:首先反三角函数的定义域是[]1,1-,因此121≤+≤-u ,可得13-≤≤-u ,即123-≤-≤-x ,从而可知x 的取值范围是[]1,1-.二、 填空题 6、 答案:[]πe,1解:)(x f 的定义域是[]π,0,即π≤≤x 0,那么对)(ln x f 来说,有π≤≤x ln 0,由此可解得x 的范围是[]πe,1.7、 答案:x x 22-解:由题目中)1(2)1(34)1(222242+++=++=+x x x x x f ,可知函数t t t f 2)(2+=.再用2-x 来替换t ,即x x x x x f 2)2(2)2()2(22-=-+-=-就可得到结果了. 8、 答案:21x x+ 解:要求)(x f 的表达式,可令x t 1=,即t x 1=.由21)1(xx x f +=可知21)(t t t f +=,所以)(x f =21x x+. 9、 答案:x解:本题已知)(x f 的表达式,求)1(xf 得表达式.所以只需把函数式中的自变量x 换成x1即可.10、答案:π解:正弦函数的周期是π2,x x f sin )(=则是将正弦函数图像中在x 轴以下的部分翻到上面去,具体图形如下由图可知,其周期是π.11、解:()f x 在真数的位置,故有()0f x >,又ln ()f x 在分母上,故ln ()0f x ≠.由此可解得()0f x >且()1f x ≠. 12、答案:11(3)2x y e -=- 解:求反函数就是将原函数中的x 反解出来.由111ln(23)ln(23)1(3)2y y x x y x e -=++⇒+=-⇒=-,再将x 和y 互换位置即可.三、解答题13、求下列函数的定义域.(1)解:由题意可知:cos 0x >;从而解得(2,2)(0,1,2,)22x k k k ππππ∈-+=±±, 所以该函数的定义域就是(2,2)(0,1,2,)22k k k ππππ-+=±±.(2)解:由题意可知:10ln(1)010x x x -≠⎧⎪+≥⎨⎪+>⎩;从而解得)()0,11,x ∈⋃+∞⎡⎣,所以该函数的定义域是)()0,11,⋃+∞⎡⎣.(3)解:由题意可知:2302113x x ⎧-≥⎪⎨--≤≤⎪⎩;从而解得x ⎡∈-⎣,所以该函数的定义域就是⎡-⎣.(4)解:由题意可知:sin 010110x x x x ≥⎧⎪+⎪>⎨-⎪-≠⎪⎩;从而解得)0,1x ∈⎡⎣, 所以该函数的定义域就是)0,1⎡⎣.14、解:因为()f x 的定义域是[]0,1,所以对2()f x 来说就有201x ≤≤,解得有11x -≤≤;对(cos )f x 来说就有0cos 1x ≤≤,解得有[2,2(0,1,2,)22x k k k ππππ⎤∈-+=±±⎥⎦. 所以2()f x 的定义域就是[]1,1-,(cos )f x 的定义域是[2,2(0,1,2,)22k k k ππππ⎤-+=±±⎥⎦.15、解:(1)xf e +的定义域是[]1,1-,也就是说11x -≤≤,从而有1111x e e e -+≤+≤+,所以()f x 的定义域就是11,1e e -⎡⎤++⎣⎦.16、解:因为2()1f x x x =-+,所以2()12f x x x +=-+,所以[]222)1(2)(2)1f f x x x x x +=-+--++(,整理后也就是 []22)1(2)(1)1f f x x x x x +=-+-++(.17、解:令1t x =,即1x t =,则222221111()()(1)11t f f t x t t t t ⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎢⎥===⎢⎥+⎛⎫+⎢⎥ ⎪⎝⎭⎣⎦,所以221()(1)f x x x =+. 18、解:当0x ≤时,()xf x e =,所以11(1)f e e--==,0(0)1f e ==; 当0x π<≤时,()f x x π=,所以(2)2f π=,()f e e π=; 当x π>时,()ln f x x =,所以(2)ln(2)f ππ=. 19、证明:()f x 是奇函数,()g x 是偶函数,其定义域都是D ,则对任意的x D ∈,都有()()f x f x -=-,()()g x g x -=.∴()()()()f x g x f x g x --=-,也就是说()()f x g x 在定义域内是奇函数. 20、解:因为()f x 是(),-∞+∞内的奇函数,所以对任意的(),x ∈-∞+∞,都有()()f x f x -=-.从而有()(22)()(22)()()xx x x F x f x f x F x ---=+-=-+=-,所以可知()F x 在(),-∞+∞内是奇函数.21、解:当1x -∞<<时,()f x x =对应的反函数是x y =,此时1y -∞<<; 当14x ≤≤时,2()f x x =对应的反函数是x =,此时有116y ≤≤;当4x <<+∞,()2x f x =对应的反函数是ln ln 2yx =,此时有16y <<+∞. 所以()f x的反函数就是1,1()16ln ,16ln 2x x f x x x x -⎧-∞<<⎪⎪=≤≤⎨⎪⎪<<+∞⎩.22、将下列复合函数分解成几个简单函数或者基本初等函数. (1)解:32arcsin ,,1y u u v v x ===-. (2)解:2lg ,2y u v v w x x ====+. 23、解:设圆锥的底半径是R ,高是h. 由题意可知:313V R h π=,所以有R =,根据实际情况,可知该函数的定义域是()0,+∞.同步练习二一、选择题 1、 答案:D解:当0x →时,21x →,1sin x 不存在(即∞→x 1),sin 1x x→,()31sin 0x x x +→,无穷小量乘以有界变量极限是0. 2、 答案:C解:当1x →时,101x x -→+,21121x x x -=+→-,11x x +→∞-, e eeexxxx x x x x x x x ====→→--→-→1limln 11limln 11111111lim lim .3、答案:B解:当0x →时,x cos 1-与2x 等价,又因为 ∞==→→21022301lim lim x x x x x ,由定义可知23x 是比2x 低阶的无穷小量,即0x →时,23x 是比x cos 1-低阶的无穷小量. 4、答案:C解:无论x 取何值,函数x sin 、x 1sin 都是有界函数,当0x →时,x x sin 、x x 1sin 都是无穷小量乘以有界变量还是无穷小量,x1显然是无穷大量,A 、B 、D 都正确.5、答案:D解:本题考查两个重要极限中的一个,有e xx x =+∞→)11(lim 和e x x x =+→10)1(lim 这两种形式,通过对照可知答案是D.二、填空题 6、答案:0解:223225252sin lim (2sin )lim lim()2001x x x x x xx x x x x x→∞→∞→∞+++=⋅+=⋅=++. 7、答案:5,2==a m解:由题上已知的极限可知,当∞→x 时,1432++x x 与2++x ax m 是同阶无穷小,故可知2=m ,又53321143lim 2143lim 2222==++++=++++∞→∞→a x xa x x x ax x x x x ,可知5=a . 8、答案:6解:由题意知:13)(lim 3)(lim==∞→∞→x xf xx f x x ,即3)(lim =∞→x xf x ,所以可知6)(2lim =∞→x xf x . 9、答案:βα 解:βαβαααβα=⋅=→→x x x x x x sin lim sin lim00.10、答案:ab e解:ab xad ab axx xadab a x x d bx x e x a xax a x =⎥⎦⎤⎢⎣⎡+=+=++∞→+⋅∞→+∞→∞→)(lim )()1(lim )1(lim )1(lim .11、答案:x解:利用重要极限中的第一个,x x x xx xnn n n n n n nn =⋅==∞→∞→∞→22sinlim 212sinlim 2sin2lim .12、答案:同阶非等价解:当0→x 时,1-xe 与x 等价,故1lim 1lim 220202-=-=-→-→x x x e x x x ,所以12--x e 与2x 是同阶非等价的无穷小量.三、计算题13、求下列极限.(1)解:2121222lim 12222lim 33233=++++=++++∞→∞→n n n n n n n n n n n . (2)解:21)32(32lim 3)2(332lim =-⋅+=-⋅+⋅∞→∞→nn n n n n .(3)解:212lim 2)1(lim ...21lim 2222=+=+=+++∞→∞→∞→nn n n n n n n n n n . (4)解:22lim 2lim 211)211(2121...4121==--∞→+++∞→n n n n .(5)解:)121121...5131311(lim )12)(12(1...531311(lim +--++-+-=++++⋅+⋅∞→∞→n n n n n n 1)1211(lim =--=∞→n n . (6)解:111sin lim1sinlim==∞→∞→nn nn n n .(7)解:34)3234(lim )3234(324)311(lim )311(lim e e nn nn n n n n n ==+=+--⋅∞→-∞→∞→. (8)解:523)1(lim )2)(3()1)(2(lim 623lim 222232-=-+=+-++=--++-→-→-→x x x x x x x x x x x x x x x x .(9)解:)1)(1()1)(2(lim 131lim )1311(lim 2132131++--+=--++=---→→→x x x x x x x x x x x x x 112lim21-=++--=→x x x x .(10)解:1)sin(lim sin lim =--=-→→xx x x x x πππππ.(11)解:)13)(1()13)(13(lim 113lim2121x x x x x x x x x x x x ++--++-+--=----→→ 42)13)(1(2lim)13)(1()1(2lim121-=++-+-=++---=→→x x x x x x x x x . (12)解:e x e x x x x x x x x =++⋅=++=++∞→++∞→+∞→2525)21(3)1221(lim )1221(lim )1232(lim . (13)解:[]33sec 2sec 32)cos 1(lim )cos 1(lim e x x xx xx =+=+→→ππ.(14)解:1ln )1(lim ln )1ln(lim )1ln(lim 10100==⎥⎦⎤⎢⎣⎡+=+=+→→→e x x x x x x x x x ααα.(15)解:111)111(111lim )1(lim ----∞→∞→=⎥⎥⎦⎤⎢⎢⎣⎡+-⋅⎪⎭⎫ ⎝⎛+-=+e x x x x x x x x .(16)解:[]1)11ln(lim )11ln(lim 1lnlim ln )1ln(lim =+=+=+=-+∞→∞→∞→∞→n n n n n nn n n n n n n n . (17)解:)93()93)(93(limsin 93lim 22220220x x x x x x x x -+-+--=--→→61931lim 20=-+=→x x . (18)解:2132421lim 32421)(lim 3242lim222-=+++-=+++-=+++-∞→-∞→-∞→xxx x x x x x x x x x x . (19)解:255sin lim 533sin lim 35sin lim 3sin lim 5sin 3sin lim00000-=-=-=-→→→→→xxx x x x x x x x x x x x x x .(20)解:111lim1ln limln 11111111lim lim -----→-→====→→e eeexxx xx x xx xx x x .14、解:因为x xx tt t t e t x t x x f =⎥⎦⎤⎢⎣⎡+=+=∞→∞→)1(lim )1(lim )()0(≠x ,所以2)2(ln 2ln ==e f .15、解:当0→x 时,2221~11ax ax -+,x x ~sin ,所以12121lim sin 11lim 220220===-+→→a xax x ax x x ,即得2=a . 16、解:由题中极限32lim22=-+-→x ax x x 可知,a x x +-2和2-x 是同阶无穷小量,即当2→x 时,都是无穷小量,故有0)(lim 22=+-→a x x x ,所以可以解得2-=a .17、解:极限值是b ,可知当1-→x 时,423+--x ax x 与1+x 是同阶无穷小量,即有0)4(lim 231=+---→x ax x x ,故得4=a .又b x x x x x x x x x x x x x ==--=+-+-=++---→-→-→10)4)(1(lim 1)4)(1)(1(lim 144lim 11231,即得10=b .18、解:当-→1x 时,+∞→-x 11,从而有211arctan π→-x ;当+→1x 时,-∞→-x11,从而有211arctanπ-→-x .也就是说,2)(lim 1π=-→x f x ,2)(lim 1π-=+→x f x .19、解:当-→1x 时,11)(2--=x x x f ,所以2)1(lim 11lim )(lim 1211=+=--=---→→→x x x x f x x x ; 当+→1x 时,1)1sin()(--=x x x f ,所以有11)1sin(lim )(lim 11=--=++→→x x x f x x .同步训练三一、选择题1、 答案:A解:)(x f 在0x x =处连续需满足三个条件:在0x x =处有定义;)(x f 在0x x =处极限存在;)(x f 在0x x =处的极限值等于该点处得函数值.显然可知)(lim 0x f x x →存在是)(x f 在0x x =处连续的必要而非充分条件.2、 答案:A解:显然0=x 不在函数的定义域内,故一定是间断点.又01sinlim )(lim 0==→→xx x f x x ,也即满足左右极限存在且相等,对照定义可知0=x 是)(x f 的可去间断点. 二、填空题3、 答案:充分必要解:)(x f 在0x x =处连续需满足三个条件:在0x x =处有定义;)(x f 在0x x =处极限存在;)(x f 在0x x =处的极限值等于该点处得函数值.)(0x f 存在就表明)(x f 在0x x =处有定义,等式)()(lim 00x f x f x x =→成立又满足后两条,所以是充分必要条件.4、 答案:a ,一,跳跃解:对已知的函数没有定义的点是a x =,1lim )(lim =--=++→→ax ax x f ax ax ,而 1lim )(lim -=--=--→→ax ax x f ax ax ,显然)(lim )(lim x f x f a x a x -+→→≠,所以由定义可知a x =是)(x f 的第一类间断点,并且是跳跃间断点.5、 答案:一,可去解:1cos 1lim sin lim tan lim)(lim 0000=⋅==→→→→xx x x x x f x x x x .6、 答案:一解:0)(lim 1sin lim )(lim 00=≠==-++→→→x f xxx f x x x ,由定义可知0=x 是)(x f 的第一类间断点.7、答案:](1,-∞-,)[∞+,3 解:32)(2--=x x x f 的定义域是]()[∞+⋃-∞-,31,,又该函数是初等函数复合成的,所以在定义域内是连续的,因此连续区间就是](1,-∞-,)[∞+,3. 8、答案:31 解:)(x f 在0=x 处连续,所以有31)(sin lim sin lim)(lim 000=====→→→x f a ax ax a x ax x f x x x ,所以31=a .9、答案:2解:函数)(x f 在0=x 处连续,所以有22sin lim )(lim )23(lim )(lim 020====+-=--++→→→→xxx f k k x x x f x x x x ,所以2=k . 10、答案:-2解:函数)(x f 在1=x 处连续,因此有a x a x f x x f x x x x -=====--++→→→→πcos lim )(lim 22lim )(lim 1111,所以2-=a .11、答案:2ba =解:函数)(x f 在0=x 处连续,所以有22sin lim )(lim )(lim )(lim 020b x bx x f a bx a x f x x x x ====+=++--→→→→,因此可得到关系式2ba =. 三、解答题12、解:函数)(x f 在0=x 处连续,所以0lim )(lim )0(210===-→→x x x ex f f .13、解:由题意可知,需构造一个分段函数)(x F ,使其在0≠x 时的表达式就是222)31ln()(x x x f +=.6ln )31(lim ln )31ln(lim )(lim )(lim )0(66312022022==⎥⎥⎦⎤⎢⎢⎣⎡+=+===→→→→e x x x f x F F x x xx x x .因此构造的连续函数⎪⎩⎪⎨⎧=≠+=0,60,)31ln()(222x x x x F x .14、解:显然已知函数在每个分段区间内是连续的,关键是区间端点.先考虑点0=x 处,11lim )(lim 1)(lim 00=-===++-→→→x x f x f x x x ,)(x f 在该点处有定义且1)0(=f ,所以0=x 是)(x f 的连续点.再看点3=x ,13lim )(lim 21lim )(lim 3333==≠=-=++--→→→→xx f x x f x x x x ,所以3=x 是)(x f 的第一类间断点,并且是跳跃间断点.因此,)(x f 在()()+∞⋃∞-,33,内连续,3=x 是)(x f 的第一类间断点,并且是跳跃间断点.15、解:显然已知函数在每个分段区间内函数都是连续的,关键是区间端点.先考虑在点1-=x 处,3)3(lim )(lim 2)arcsin (lim )(lim 1111πππ=-=≠=-=--++-→-→-→-→x x f x x f x x x x ,所以1-=x 是函数)(x f 的第一类间断点,并且是跳跃间断点.再看点0=x ,函数在该点处无定义,显然是间断点,并且x x f x x f x x x x ++--→→→→===-=0lim )(lim 0)arcsin (lim )(lim ,所以0=x 是函数)(x f 的第一类间断点,并且是可去间断点.因此可知)(x f 在()()()+∞⋃-⋃-∞-,00,11,上连续;1-=x 是函数)(x f 的第一类间断点,并且是跳跃间断点;0=x 是函数)(x f 的第一类间断点,并且是可去间断点. 16、解:因为)(x f 在()+∞∞-,内是连续的,所以在1=x 处也是连续的.1)(lim )(lim 2)1(1)(lim )(lim 21111+=+====-=-=++--→→→→a x a x f f b x b x f x x x x ,也就是解等式21=-b 和21=+a ,从而有1=a ,3=b . 17、求下列函数的间断点,并指出间断点的类型. (1)解:1-=x 是xxx f +=1)(的无定义点,又因为∞=+=-→-→x x x f x x 1lim )(lim 11,所以1-=x 是)(x f 的第二类间断点,并且是无穷间断点.(2)解: x x x f --=11)(2在1=x 处无定义,又因为2)1(lim 11lim)(lim 1211=+=--=→→→x xx x f x x x ,所以1=x 是)(x f 的第一类间断点,并且是可去间断点. (3)解:1=x 是11arctan)(-=x x f 的无定义点,又因为 211arctan lim )(lim 211arctanlim )(lim 1111ππ-=-=≠=-=--++→→→→x x f x x f x x x x ,所以1=x 是)(x f 的第一类间断点,并且是跳跃间断点.(4)解:21±=x 是142)(22-+=x x x x f 的无定义点,又因为 4112lim 142lim )(lim 21222121=-=-+=-→-→-→x x x x x x f x x x ,∞=-+=→→142lim )(lim 222121x x x x f x x ,所以21-=x 是第一类间断点,并且是可去间断点;21=x 是第二类间断点,并且是无穷间断点. 18、下列函数在0=x 处是否连续? (1)解:)0(0lim )(lim 210f ex f x x x ===-→→,所以0=x 是)(x f 的连续点.(2)解:1sin lim sin lim 1sin lim sin lim )(lim 0000-=-=≠===--+++→→→→→xxx x x x xx x f x x x x x ,所以0=x 是)(x f 的第一类间断点,并且是跳跃间断点.(3)解:xx x f x x x x f x x x x x sin lim )(1)1ln(lim )1ln(lim )(lim 01000+---→→→→===+=+=,所以0=x 是)(x f 的连续点. 19、求下列极限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 质点运动学1.1 一质点沿直线运动,运动方程为x (t ) = 6t 2 - 2t 3.试求: (1)第2s 内的位移和平均速度;(2)1s 末及2s 末的瞬时速度,第2s 内的路程; (3)1s 末的瞬时加速度和第2s 内的平均加速度.解:(1)质点在第1s 末的位移大小为x (1) = 6×12 - 2×13 = 4(m). 在第2s 末的位移大小为x (2) = 6×22 - 2×23 = 8(m). 在第2s 内的位移大小为Δx = x (2) – x (1) = 4(m),经过的时间为Δt = 1s ,所以平均速度大小为v =Δx /Δt = 4(m·s -1).(2)质点的瞬时速度大小为v (t ) = d x /d t = 12t - 6t 2, 因此v (1) = 12×1 - 6×12 = 6(m·s -1),v (2) = 12×2 - 6×22 = 0, 质点在第2s 内的路程等于其位移的大小,即Δs = Δx = 4m .(3)质点的瞬时加速度大小为a (t ) = d v /d t = 12 - 12t , 因此1s 末的瞬时加速度为a (1) = 12 - 12×1 = 0,第2s 内的平均加速度为a = [v (2) - v (1)]/Δt = [0 – 6]/1 = -6(m·s -2). [注意]第几秒内的平均速度和平均加速度的时间间隔都是1秒.1.2 一质点作匀加速直线运动,在t = 10s 内走过路程s = 30m ,而其速度增为n = 5倍.试证加速度为22(1)(1)n sa n t -=+.并由上述数据求出量值.证:依题意得v t = nv o ,根据速度公式v t = v o + at ,得a = (n – 1)v o /t ------- (1) 根据速度与位移的关系式 v t 2 = v o 2 + 2as , 得a = (n 2 – 1)v o 2/2s ------- (2) (1}平方之后除以 (2)式证得22(1)(1)n sa n t -=+.计算得加速度为22(51)30(51)10a -=+= 0.4(m·s -2).1.3 一人乘摩托车跳越一个大矿坑,他以与水平成22.5°的夹角的初速度65m·s -1从西边起跳,准确地落在坑的东边.已知东边比西边低70m ,忽略空气阻力,且取g = 10m·s -2.问: (1)矿坑有多宽?他飞越的时间多长?(2)他在东边落地时的速度?速度与水平面的夹角?解:方法一:分步法.(1)夹角用θ表示,人和车(他)在竖直方向首先做竖直上抛运动,初速度的大小为v y 0 = v 0sin θ = 24.87(m·s -1).取向上的方向为正,根据匀变速直线运动的速度公式v t - v 0 = at ,这里的v 0就是v y 0,a = -g ;当他达到最高点时,v t = 0,所以上升到最高点的时间为t 1 = v y 0/g = 2.49(s).再根据匀变速直线运动的速度和位移的关系式v t 2 - v 02 = 2a s , 可得上升的最大高度为h 1 = v y 02/2g = 30.94(m).他从最高点开始再做自由落体运动,下落的高度为h 2 = h 1 + h = 100.94(m). 根据自由落体运动公式s = gt 2/2,得下落的时间为图1.32t =. 因此他飞越的时间为t = t 1 + t 2 = 6.98(s).他飞越的水平速度为v x 0 = v 0cos θ = 60.05(m·s -1), 所以矿坑的宽度为x = v x 0t = 419.19(m).(2)根据自由落体速度公式可得他落地的竖直速度大小为v y = gt = 69.8(m·s -1), 落地速度为v = (v x 2 + v y 2)1/2 = 92.08(m·s -1), 与水平方向的夹角为φ = arctan(v y /v x ) = 49.30º,方向斜向下.方法二:一步法.取向上的方向为正,他在竖直方向的位移为y = v y 0t - gt 2/2,移项得时间的一元二次方程201sin 02gt v t y θ-+=,解得0(sin t v g θ=. 这里y = -70m ,根号项就是他落地时在竖直方向的速度大小,由于时间应该取正值,所以公式取正根,计算时间为t = 6.98(s). 由此可以求解其他问题.1.4 一个正在沿直线行驶的汽船,关闭发动机后,由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度,即d v /d t = -kv 2,k 为常数. (1)试证在关闭发动机后,船在t 时刻的速度大小为011kt v v =+; (2)试证在时间t 内,船行驶的距离为01ln(1)x v kt k=+. 证:(1)分离变量得2d d vk t v=-, 积分020d d vtv vk t v =-⎰⎰, 可得 011kt v v =+. (2)公式可化为001v v v kt=+,由于v = d x/d t ,所以00001d d d(1)1(1)v x t v kt v kt k v kt ==+++ 积分 00001d d(1)(1)xtx v kt k v kt =++⎰⎰.因此 01ln(1)x v kt k=+. 证毕. [讨论] 当力是速度的函数时,即f = f (v ),根据牛顿第二定律得f = ma .由于a = d 2x /d t 2,而 d x /d t = v ,所以 a = d v /d t ,分离变量得方程 d d ()m vt f v =, 解方程即可求解.在本题中,k 已经包括了质点的质量.如果阻力与速度反向、大小与船速的n 次方成正比,则d v /d t = -kv n . (1)如果n = 1,则得d d vk t v=-,积分得ln v = -kt + C . 当t = 0时,v = v 0,所以C = ln v 0,因此ln v/v 0 = -kt ,得速度为 v = v 0e -kt .而d v = v 0e -kt d t ,积分得0e `ktv x C k-=+-. 当t = 0时,x = 0,所以C` = v 0/k ,因此 0(1-e )ktv x k -=.(2)如果n ≠1,则得d d n vk t v=-,积分得11n v kt C n -=-+-.当t = 0时,v = v 0,所以101n v C n-=-,因此11011(1)n n n kt v v --=+-. 如果n = 2,就是本题的结果.如果n ≠2,可得1(2)/(1)020{[1(1)]1}(2)n n n n n v kt x n v k----+--=-, 读者不妨自证.1.5 一质点沿半径为0.10m 的圆周运动,其角位置(以弧度表示)可用公式表示:θ = 2 + 4t 3.求:(1)t = 2s 时,它的法向加速度和切向加速度;(2)当切向加速度恰为总加速度大小的一半时,θ为何值? (3)在哪一时刻,切向加速度和法向加速度恰有相等的值?解:(1)角速度为ω = d θ/d t = 12t 2 = 48(rad·s -1), 法向加速度为 a n = rω2 = 230.4(m·s -2);角加速度为 β = d ω/d t = 24t = 48(rad·s -2), 切向加速度为 a t = rβ = 4.8(m·s -2). (2)总加速度为a = (a t 2 + a n 2)1/2,当a t = a /2时,有4a t 2 = a t 2 + a n 2,即n a a =2r r ω=, 即22(12)24t = 解得36t =.所以3242(13)t θ=+=+=3.154(rad).(3)当a t = a n 时,可得rβ = rω2,即 24t = (12t 2)2, 解得 t = (1/6)1/3 = 0.55(s).1.6 一飞机在铅直面内飞行,某时刻飞机的速度为v = 300m·s -1,方向与水平线夹角为30°而斜向下,此后飞机的加速度为a =m·s -2,方向与水平前进方向夹角为30°而斜向上,问多长时间后,飞机又回到原来的高度?在此期间飞机在水平方向飞行的距离为多少? 解:建立水平和垂直坐标系,飞机的初速度的大小为v 0x = v 0cos θ,v 0y = v 0sin θ.加速度的大小为a x = a cos α,a y = a sin α.运动方程为2012x x x v t a t =+,2012y y y v t a t =-+.即 201cos cos 2x v t a t θα=⋅+⋅,201sin sin 2y v t a t θα=-⋅+⋅.令y = 0,解得飞机回到原来高度时的时间为t = 0(舍去);02sin sin v t a θα==.将t 代入x 的方程求得x = 9000m .[注意]选择不同的坐标系,例如x 方向沿着a 的方向或者沿着v 0的方向,也能求出相同的结果.1.7 一个半径为R = 1.0m 的轻圆盘,可以绕一水平轴自由转动.一根轻绳绕在盘子的边缘,其自由端拴一物体A .在重力作用下,物体A 从静止开始匀加速地下降,在Δt = 2.0s 内下降的距离h = 0.4m .求物体开始下降后3s 末,圆盘边缘上任一点的切向加速度与法向加速度.解:圆盘边缘的切向加速度大小等于物体A 下落加速度. 由于212t h a t =∆,所以a t = 2h /Δt 2 = 0.2(m·s -2). 物体下降3s 末的速度为v = a t t = 0.6(m·s -1),这也是边缘的线速度,因此法向加速度为2n v a R== 0.36(m·s -2).1.8 一升降机以加速度1.22m·s -2上升,当上升速度为2.44m·s -1时,有一螺帽自升降机的天花板上松落,天花板与升降机的底面相距2.74m .计算: (1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离.解:在螺帽从天花板落到底面时,升降机上升的高度为21012h v t at =+; 螺帽做竖直上抛运动,位移为22012h v t gt =-. 由题意得h = h 1 - h 2,所以21()2h a g t =+,解得时间为t =.算得h 2 = -0.716m ,即螺帽相对于升降机外固定柱子的下降距离为0.716m .[注意]以升降机为参考系,钉子下落时相对加速度为a + g ,而初速度为零,可列方程 h = (a + g )t 2/2,由此可计算钉子落下的时间,进而计算下降距离.1.9 有一架飞机从A 处向东飞到B 处,然后又向西飞回到A 处.已知气流相对于地面的速度为u ,AB 之间的距离为l ,飞机相对于空气的速率v 保持不变.(1)如果u = 0(空气静止),试证来回飞行的时间为02l t v =; (2)如果气流的速度向东,证明来回飞行的总时间为01221/t t u v =-;(3)如果气流的速度向北,证明来回飞行的总时间为2t =.证:(1)飞机飞行来回的速率为v ,路程为2l ,所以飞行时间为t 0 = 2l /v . (2)飞机向东飞行顺风的速率为v + u ,向西飞行逆风的速率为v - u ,所以飞行时间为1222l l vlt v u v u v u=+=+-- 022222/1/1/t l v u v u v ==--. (3)飞机相对地的速度等于相对风的速度加风相对地的速度.为了使飞机沿着AB 之间的直线飞行,就要使其相对地的速度偏向北方,可作矢量三角形,其中沿AB方向的速度大小为V =,所以飞行时间为22l t V ==== 证毕.AAB vv + uv - uABvu uvv1.10 如图所示,一汽车在雨中沿直线行驶,其速度为v 1,下落雨的速度方向与铅直方向的夹角为θ,偏向于汽车前进方向,速度为v 2.今在车后放一长方形物体,问车速v 1为多大时此物体刚好不会被雨水淋湿?解:雨对地的速度2v r 等于雨对车的速度3v r 加车对地的速度1v r,由此可作矢量三角形.根据题意得tan α = l/h . 方法一:利用直角三角形.根据直角三角形得v 1 = v 2sin θ + v 3sin α,其中v 3 = v ⊥/cos α,而v ⊥ = v 2cos θ,因此v 1 = v 2sin θ + v 2cos θsin α/cos α, 即 12(sin cos )lv v hθθ=+. 证毕. 方法二:利用正弦定理.根据正弦定理可得12sin()sin(90)v v θαα=+︒-,所以12sin()cos v v θαα+=2sin cos cos sin cos v θαθαα+=2(sin cos tan )v θθα=+, 即 12(sin cos )lv v hθθ=+.方法三:利用位移关系.将雨滴的速度分解为竖直和水平两个分量,在t 时间内,雨滴的位移为l = (v 1 – v 2sin θ)t ,h = v 2cos θ∙t .两式消去时间t 即得所求. 证毕.图1.101h l α。
