单价数量总价的公式
数量关系计算公式方面

数量关系计算公式方面1、单价×数量=总价2、单产量×数量=总产量3、速度×时间=路程4、工效×时间=工作总量6、 1公里=1千米 1千米=1000米1米=10分米 1分米=10厘米 1厘米=10毫米1平方米=100平方分米 1平方分米=100平方厘米1平方厘米=100平方毫米1立方米=1000立方分米 1立方分米=1000立方厘米1立方厘米=1000立方毫米1吨=1000千克 1千克= 1000克= 1公斤= 1市斤1公顷=10000平方米。
1亩=666.666平方米。
1升=1立方分米=1000毫升 1毫升=1立方厘米8、什么叫比例:表示两个比相等的式子叫做比例。
如3:6=9:189、比例的基本性质:在比例里,两外项之积等于两内项之积。
10、解比例:求比例中的未知项,叫做解比例。
如3:χ=9:1811、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
如:y/x=k( k一定)或kx=y12、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
如:x×y = k( k一定)或k / x = y16、最大公约数:几个数都能被同一个数一次性整除,这个数就叫做这几个数的最大公约数。
(或几个数公有的约数,叫做这几个数的公约数。
其中最大的一个,叫做最大公约数。
)17、互质数:公约数只有1的两个数,叫做互质数。
18、最小公倍数:几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
19、通分:把异分母分数的分别化成和原来分数相等的同分母的分数,叫做通分。
(通分用最小公倍数)20、约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫做约分。
小学数学常用的数量关系式

常用数量关系式1、速度×时间=路程路程÷速度=时间路程÷时间=速度2、单价×数量=总价总价÷单价=数量总价÷数量=单价3、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率4、加数+加数=与与-一个加数=另一个加数5、被减数-减数=差被减数-差=减数差+减数=被减数6、因数×因数=积积÷一个因数=另一个因数7、被除数÷除数=商被除数÷商=除数商×除数=被除数在有余数除法中: (被除数-余数)÷除数=商8、总数÷总份数=平均数9、相遇问题相遇路程=速度与×相遇时间相遇路程=快车速度×相遇时间+慢车速度×相遇时间相遇时间=相遇路程÷速度与速度与=相遇路程÷相遇时间10、利息=本金×利率×时间11、收入-支出=结余单产量×数量=总产量量计量在日常生活、生产劳动与科学研究中,经常要进展各种量计量,我国法定计量单位与国际计量单位一致。
名数;数与单位名称合起来叫做名数。
单名数:只含有一种单位名称名数叫单名数。
复名数:含有两种或两种以上单位名称名数叫复名数。
长度单位换算1千米=1000米 1米=10分米 1分米=10厘米1米=100厘米 1厘米=10毫米面积单位换算1平方千米=1000000平方米 1公顷=10000平方米1平方千米=100公顷1平方米=100平方分米 1平方分米=100平方厘米1平方厘米=100平方毫米体积(容积)单位换算1立方米=1000立方分米 1立方分米=1000立方厘米1立方厘米=1000立方毫米1立方分米=1升 1立方厘米=1毫升 1升=1000毫升质量单位换算1吨=1000 千克 1千克=1000克 1千克=1公斤人民币单位换算1元=10角 1角=10分 1元=100分时间单位换算1世纪=100年 1年=12月=4个季度大月(31天)有:1\3\5\7\8\10\12月小月(30天)有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时 1时=60分 1分=60秒 1时=3600秒练习:填空〔1〕. 1时30分=〔〕时 40分=〔〕时时=〔〕分 0.7时=〔〕分平方米=〔〕平方分米 125克=〔〕千克2 立方分米=〔〕升=〔〕毫升10 .5吨=〔〕吨〔〕千克〔〕元=50元8角1分〔2〕.1米∶10厘米=〔〕∶〔〕=〔〕∶〔〕100毫升∶1升=〔〕∶〔〕=〔〕∶〔〕〔3〕.填上适当计量单位名称。
数量关系计算公式 -完整获奖版

数量关系计算公式总价=单价×数量 总量=单量×数量 路程=速度×时间1.单价=总价÷数量2. 单量=总量÷数量3.速度=路程÷时间 数量=总价÷单价 数量=总量÷单量 时间=路程÷速度工作总量=工作效率×时间 电费=每千瓦时费用×千瓦时数量4.工作效率=工作总量÷时间5.每千瓦时费用=电费÷千瓦时数量 时间=工作总量÷工作效率 千瓦时数量=电费÷每千瓦时费用6. 和=加数+加数7. 积=因数×因数一个加数=和-另一个加数 一个因数=积÷另一个因数 被减数=减数+差 被除数=商×除数8.减数=被减数-差 9.除数=被除数÷商 差=被减数-减数 商=被除数÷除数9.有余数的除法:被除数=商×除数+余数(余数小于除数)10.进率1吨=1000千克1千克= 1000克= 1公斤= 1市斤 1公里=1千米 1平方千米=100公顷 1千米=1000米 1公顷=10000平方米1米=10分米 1平方米=100平方分米1分米=10厘米 1平方分米=100平方厘米1厘米=10毫米 1平方厘米=100平方毫米 1亩=平方米长 度 面积 面积1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米 1升=1立方分米=1000毫升1毫升=1立方厘米7.比:两个数相除就叫做两个数的比。
如:2÷5或3:6或13比的基本性质:比的前项和后项同时乘以或除以一个相同的数 (0除外),比值不变。
8.比例:表示两个比相等的式子叫做比例。
如3:6=9:18比例的基本性质:在比例里,两外项之积等于两内项之积。
9.解比例:求比例中的未知项,叫做解比例。
如3:χ=9:1810.正比例:两种相关联的量,一种量变化,另一种量也随着化,如 果这两种量中相对应的的比值(也就是商k )一定,这两种量就叫 做成正比例的量,它们的关系就叫做正比例关系。
单价、数量、总价之间的关系
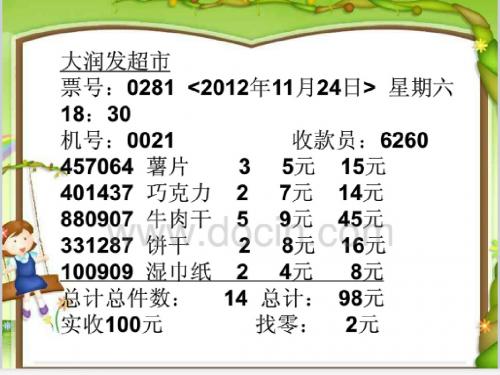
练习
说一说下面已知什么,要求什么? 学校买了四个排球,每个60元,一共用了多少钱?
列式:
思考:
(1)、已知总价和数量,该怎样求单价呢? (2)、已知单价和总价,又该怎样求数量呢?
总价÷数量=单价
总价×单价=数量
BCLeabharlann 归纳总结:今天你有什么收获?
单价×数量=总价 总价÷数量=单价 总价×单价=数量
单价、数量、总价之 间的关系
自学课本52页,回答下列问题:
(1)、通过自学,我知道了:单价是指每件商品的价钱;数量是 指买了多少;总价是指一共用的钱数。 (2)、例题4,它们都是已知单价和数量,要求总价。思考,求 总价,课本上的方法是单价×数量。所以单价、数量、总价之 间的关系是:单价×数量=总价。
小学至初初中数量关系公式

数量关系计算公式1、单价×数量=总价2、单产量×数量=总产量3、速度×时间=路程4、工效×时间=工作总量5、加数+加数=和6、一个加数=和-另一个加数7、被减数-减数=差 8、减数=被减数-差 9、被减数=减数+差10、因数×因数=积 11、一个因数=积÷另一个因数12、被除数÷除数=商 13、除数=被除数÷商 14、被除数=商×除数15、有余数的除法:被除数=商×除数+余数一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。
例:90÷5÷6=90÷(5×6)1公里=1千米 1千米=1000米1米=10分米 1分米=10厘米 1厘米=10毫米1平方米=100平方分米 1平方分米=100平方厘米几何公式1.正方形正方形的周长=边长×4 公式:C=4a正方形的面积=边长×边长公式:S=a×a正方体的体积=边长×边长×边长公式:V=a×a×a2.长方形长方形的周长=(长+宽)×2 公式:C=(a+b)×2长方形的面积=长×宽公式:S=a×b长方体的体积=长×宽×高公式:V=a×b×h3.三角形三角形的面积=底×高÷2 公式:S= a×h÷24.平行四边形平行四边形的面积=底×高公式:S= a×h5.梯形梯形的面积=(上底+下底)×高÷2 公式:S=(a+b)h÷26.圆直径=半径×2 公式:d=2r半径=直径÷2 公式:r= d÷2圆的周长=圆周率×直径公式:c=πd =2πr圆的面积=半径×半径×π公式:S=πrr7.圆柱圆柱的侧面积=底面的周长×高公式:S=ch=πdh=2πrh圆柱的表面积=底面的周长×高+两头的圆的面积公式:S=ch+2s=ch+2πr2圆柱的总体积=底面积×高公式:V=Sh8.圆锥圆锥的总体积=底面积×高×1/3 公式:V=1/3Sh9.三角形内角和=180度算术概念1.加法交换律:两数相加交换加数的位置,和不变。
单价数量合计金额计算公式

单价数量合计金额计算公式在商业和金融领域,计算商品或服务的总价是一个非常重要的计算。
无论是在购买商品时,还是在提供服务时,都需要根据单价和数量来计算出总金额。
在本文中,我们将讨论单价数量合计金额的计算公式,以及如何在实际生活中应用这个公式。
首先,让我们来看一下单价数量合计金额的计算公式。
这个公式非常简单,它只涉及到两个变量:单价和数量。
公式如下:总金额 = 单价×数量。
这个公式非常直观,它表示了单价乘以数量得到总金额。
在这个公式中,单价是指每个单位商品或服务的价格,而数量则是指购买或提供的数量。
将这两个数相乘,就可以得到总金额。
例如,如果某个商品的单价是10元,数量是5个,那么根据上面的公式,总金额就是10元× 5个 = 50元。
这个计算过程非常简单,只需要将单价和数量相乘即可得到结果。
在实际生活中,单价数量合计金额的计算公式可以应用在各种场景中。
首先,它可以应用在购买商品的场景中。
无论是在超市购物,还是在网上购物,我们都需要根据商品的单价和数量来计算总金额。
这个公式可以帮助我们快速准确地计算出总金额,避免因为计算错误而导致购买过多或过少的商品。
此外,这个公式也可以应用在提供服务的场景中。
比如,一个服务提供商需要根据单价和数量来计算客户的总费用。
通过这个公式,服务提供商可以快速准确地计算出客户的总费用,确保不会因为计算错误而导致费用的偏差。
除了在购买商品和提供服务的场景中,单价数量合计金额的计算公式还可以应用在投资和财务管理中。
在投资中,我们经常需要根据投资的单价和数量来计算投资的总金额。
通过这个公式,我们可以快速准确地计算出投资的总金额,帮助我们做出更明智的投资决策。
在财务管理中,这个公式也可以帮助我们计算出各种费用的总金额。
比如,我们可以根据单价和数量来计算出某项费用的总金额,帮助我们更好地控制和管理费用。
总之,单价数量合计金额的计算公式是一个非常重要的公式,在商业和金融领域有着广泛的应用。
总价数量单价的数量关系式

总价、数量、单价的数量关系式【教学目标】1.了解单价、数量、总价的含义,初步理解单价、数量、总价的数量关系,知道“单价×数量=总价”、“总价÷单价=数量”、“总价÷数量=单价”的关系。
2.初步培养运用数学语言、术语表达数量关系的能力。
3.能运用数量关系解决实际问题【教学重点】知道“单价×数量=总价”、“总价÷单价=数量”、“总价÷数量=单价”的关系。
【教学难点】运用“单价×数量=总价”、“总价÷单价=数量”、“总价÷数量=单价”的关系,解决简单的实际生活中的问题。
【教学过程】一、复习导入师:老师知道咱们四(8)班的孩子最聪明了,今天老师出两道题给您们小试身手,您们敢尝试不?师:您们会算这道题不?该怎么列式呢?生:80×3=240师:为什么用乘法呢?生:求3个80就是多少?所以用乘法。
师:这道问题怎么求?生:10×4=40师:也就就是求4个10就是多少。
二、探究新知(一) 理解单价、数量、总价的含义师:在前面的学习中,我们经常会见到一些数量关系,下面我们就来总结一种常见的数量关系。
师:这两个问题有什么共同点?我们先不急着说,老师一步步引导您们。
师:先已知篮球每个80元与鱼每千克10元,那每个表示多少个篮球的价格?鱼呢?生:表示的就是一个篮球的价格与一千克鱼的价格。
师:表示一个的量我们可以称为一件或每件。
师:像篮球、鱼等物品我们都称为商品。
所以我们找到了一个共同点就是已知每件商品的价格。
师:还知道的第二个条件就是什么?生:还知道买了多少件商品。
师:最后要求出什么?生:最后求一共用的钱数。
(二)探索“单价”、“数量”、“总价”三个数量之间的关系。
师:在数学上,每件商品的价格叫做单价,买了多少叫做数量,一共用的钱数叫做总价。
师:您们可以告诉我篮球的单价就是多少元?篮球的数量就是多少个?篮球的总价就是多少元不?生:篮球的单价就是30元,篮球的数量就是8个,篮球的总价就是24元。
小学数学基础知识整理(数量关系篇)

小学数学基础知识整理(数量关系篇)数量关系计算公式方面1、单价×数量=总价2、单产量×数量=总产量3、速度×时间=路程4、工效×时间=工作总量5、加数+加数=和一个加数=和+另一个加数被减数-减数=差减数=被减数-差被减数=减数+差因数×因数=积一个因数=积÷另一个因数被除数÷除数=商除数=被除数÷商被除数=商×除数有余数的除法:被除数=商×除数+余数一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。
例:90÷5÷6=90÷(5×6)6、1公里=1千米1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米1吨=1000千克1千克= 1000克= 1公斤= 1市斤1公顷=10000平方米。
1亩=666.666平方米。
1升=1立方分米=1000毫升1毫升=1立方厘米7、什么叫比:两个数相除就叫做两个数的比。
如:2÷5或3:6或1/3比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
8、什么叫比例:表示两个比相等的式子叫做比例。
如3:6=9:189、比例的基本性质:在比例里,两外项之积等于两内项之积。
10、解比例:求比例中的未知项,叫做解比例。
如3:χ=9:1811、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
如:y/x=k( k一定)或kx=y12、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
总价等于什么公式小学

总价等于什么公式小学一、常用的数量关系1.每份数×份数=总数;总数÷每份数=份数;总数÷份数=每份数2.1倍数×倍数=几倍数;几倍数÷1倍数=倍数;几倍数÷倍数=1倍数3.速度×时间=路程;路程÷速度=时间;路程÷时间=速度4.单价×数量=总价;总价÷单价=数量;总价÷数量=单价5.工作效率×工作时间=工作总量;工作总量÷工作效率=工作时间;工作总量÷工作时间=工作效率6.加数+加数=和;和-一个加数=另一个加数7.被减数-减数=差;被减数-差=减数;差+减数=被减数8.因数×因数=积;积÷一个因数=另一个因数9.被除数÷除数=商;被除数÷商=除数;商×除数=被除数二、小学数学图形计算公式1.正方形C周长S面积a边长周长=边长×4 C=4a 面积=边长×边长S=a×a2.正方体(V:体积S:表面积a:棱长) 表面积=棱长×棱长×6;S=a×a×6;体积=棱长×棱长×棱长;V=a×a×a3.长方形(C周长S面积a边长) 周长=(长+宽)×2;C=2(a+b);面积=长×宽;S=ab4.长方体(V:体积s:面积a:长b: 宽h:高)(1)表面积(长×宽+长×高+宽×高)×2;S=2(ab+ah+bh);(2)体积=长×宽×高;V=abh5.三角形(s面积a底h高) 面积=底×高÷2;s=ah÷2;三角形高=面积×2÷底;三角形底=面积×2÷高6.平行四边形(s面积a底h高) 面积=底×高;s=ah7.梯形(s面积a上底b下底h高) 面积=(上底+下底)×高÷2;s=(a+b)×h÷28.圆形(S面积C周长∏d=直径r=半径) (1)周长=直径×∏=2×∏×半径;C=∏d=2∏r (2)面积=半径×半径×∏9.圆柱体(v:体积h:高s;底面积r:底面半径c:底面周长)(1)侧面积=底面周长×高;(2)表面积=侧面积+底面积×2;(3)体积=底面积×高;(4)体积=侧面积÷2×半径;10.圆锥体(v:体积h:高s;底面积r:底面半径) 体积=底面积×高÷3。
常用的数量关系式

常用的数量关系式1、速度×时间=路程路程÷速度=时间路程÷时间=速度2、单价×数量=总价总价÷单价=数量总价÷数量=单价3、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率4、加数+加数=和和-一个加数=另一个加数5、被减数-减数=差被减数-差=减数差+减数=被减数6、因数×因数=积积÷一个因数=另一个因数6、被除数÷除数=商被除数÷商=除数商×除数=被除数在有余数的除法中: (被除数-余数)÷除数=商7、总数÷总份数=平均数8、相遇问题相遇路程=速度和×相遇时间或相遇路程=快车速度×相遇时间+慢车速度×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间9、利息=本金×利率×时间10、收入-支出=结余单产量×数量=总产量量的计量在日常生活、生产劳动和科学研究中,经常要进行各种量的计量,我国法定计量单位与国际计量单位一致。
名数;数和单位名称合起来叫做名数。
单名数:只含有一种单位名称的名数叫单名数。
复名数:含有两种或两种以上单位名称的名数叫复名数。
×进率高级单位的名数低级单位的名数÷进率长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=1000000平方米1公顷=10000平方米1平方千米=100公顷1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体积(容积)单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米1立方分米=1升1立方厘米=1毫升1升=1000毫升质量单位换算1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月=4个季度大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒练习:填空(1). 1时30分=()时40分=()时时=()分0.7时=()分平方米=()平方分米125克=()千克2 立方分米=()升=()毫升10 吨=()吨()千克()元=50元8角1分(2).1米∶ 10厘米=()∶()=()∶()100毫升∶1升=()∶()=()∶ ()(3).填上适当的计量单位名称。
(完整版)常用的数量关系式

常用的数量关系式1、速度×时间=路程路程÷速度=时间路程÷时间=速度2、单价×数量=总价总价÷单价=数量总价÷数量=单价3、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率4、加数+加数=和和-一个加数=另一个加数5、被减数-减数=差被减数-差=减数差+减数=被减数6、因数×因数=积积÷一个因数=另一个因数6、被除数÷除数=商被除数÷商=除数商×除数=被除数在有余数的除法中: (被除数-余数)÷除数=商7、总数÷总份数=平均数8、相遇问题相遇路程=速度和×相遇时间或相遇路程=快车速度×相遇时间+慢车速度×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间9、利息=本金×利率×时间10、收入-支出=结余单产量×数量=总产量量的计量在日常生活、生产劳动和科学研究中,经常要进行各种量的计量,我国法定计量单位与国际计量单位一致。
名数;数和单位名称合起来叫做名数。
单名数:只含有一种单位名称的名数叫单名数。
复名数:含有两种或两种以上单位名称的名数叫复名数。
×进率高级单位的名数低级单位的名数÷进率长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=1000000平方米1公顷=10000平方米1平方千米=100公顷1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体积(容积)单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米1立方分米=1升1立方厘米=1毫升1升=1000毫升质量单位换算1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月=4个季度大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒练习:填空(1). 1时30分=()时40分=()时时=()分0.7时=()分平方米=()平方分米125克=()千克2 立方分米=()升=()毫升10 吨=()吨()千克()元=50元8角1分(2).1米∶ 10厘米=()∶()=()∶()100毫升∶1升=()∶()=()∶ ()(3).填上适当的计量单位名称。
数量关系计算公式方面

数量关系计算公式方面1、单价×数量=总价2、单产量×数量=总产量3、速度×时间=路程4、工效×时间=工作总量5、加数+加数=和一个加数=和+另一个加数被减数-减数=差减数=被减数-差被减数=减数+差被除数=商×除数被除数÷除数=商除数=被除数÷商因数×因数=积一个因数=积÷另一个因数有余数的除法:被除数=商×除数+余数一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。
6、1公里=1千米1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米1吨=1000千克1千克= 1000克= 1公斤= 1市斤1公顷=10000平方米。
1亩=666.666平方米。
1升=1立方分米=1000毫升1毫升=1立方厘米7、比:两个数相除就叫做两个数的比。
如:比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
8、比例:表示两个比相等的式子叫做比例。
9、比例的基本性质:在比例里,两外项之积等于两内项之积。
10、解比例:求比例中的未知项,叫做解比例。
11、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
如:y/x=k( k一定)或kx=y12、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
如:x×y = k( k一定)或k / x = y百分数:表示一个数是另一个数的百分之几的数,叫做百分数。
百分数也叫做百分率或百分比。
总价数量单价的数量关系式

总价、数量、单价的数量关系式【教学目标】1.了解单价、数量、总价的含义,初步理解单价、数量、总价的数量关系,知道“单价×数量=总价”、“总价÷单价=数量”、“总价÷数量=单价”的关系。
2.初步培养运用数学语言、术语表达数量关系的能力。
3.能运用数量关系解决实际问题【教学重点】知道“单价×数量=总价”、“总价÷单价=数量”、“总价÷数量=单价”的关系。
【教学难点】运用“单价×数量=总价”、“总价÷单价=数量”、“总价÷数量=单价”的关系,解决简单的实际生活中的问题。
【教学过程】一、复习导入师:老师知道咱们四(8)班的孩子最聪明了,今天老师出两道题给你们小试身手,你们敢尝试吗?师:你们会算这道题吗?该怎么列式呢?生:80×3=240师:为什么用乘法呢?生:求3个80是多少?所以用乘法。
师:这道问题怎么求?生:10×4=40师:也就是求4个10是多少。
二、探究新知(一) 理解单价、数量、总价的含义师:在前面的学习中,我们经常会见到一些数量关系,下面我们就来总结一种常见的数量关系。
师:这两个问题有什么共同点?我们先不急着说,老师一步步引导你们。
师:先已知篮球每个80元和鱼每千克10元,那每个表示多少个篮球的价格?鱼呢?生:表示的是一个篮球的价格和一千克鱼的价格。
师:表示一个的量我们可以称为一件或每件。
师:像篮球、鱼等物品我们都称为商品。
所以我们找到了一个共同点是已知每件商品的价格。
师:还知道的第二个条件是什么?生:还知道买了多少件商品。
师:最后要求出什么?生:最后求一共用的钱数。
(二)探索“单价”、“数量”、“总价”三个数量之间的关系。
师:在数学上,每件商品的价格叫做单价,买了多少叫做数量,一共用的钱数叫做总价。
师:你们可以告诉我篮球的单价是多少元?篮球的数量是多少个?篮球的总价是多少元吗?生:篮球的单价是30元,篮球的数量是8个,篮球的总价是24元。
