必修1第一章复习[上学期]新人教版

合集下载

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

（新教材）部编人教版高中数学必修一第一章课后练习和习题汇总（附答案）目录第一章集合与常用逻辑用语.1.1 集合的概念1.2 集合间的基本关系1.3集合的基本运算1.4 充分条件与必要条件1.5全称量词与存在量小结复习参考题1第一章集合与常用逻辑用语1.1集合的概念练习1.判断下列元素的全体是否组成集合，并说明理由:(1)与定点A，B等距离的点;【答案解析】：是集合，因为这些点有确定性.(2)高中学生中的游泳能手.【答案解析】：不是，因为是否能手没有客观性，不好确定.2.用符号“∈”或“∉”填空:0___ N; -3___ N; 0.5__Z; √2__z; ⅓__Q; π__R.【答案解析】：根据自然数,整数,有理数,实数的定义即可判断.0是自然数,则0∈N ;-3不是自然数,则-3∉N ; 0.5,√2 不是整数，则0.5∉Z，√2∉Z;⅓是有理数,则⅓∈Q ;π 是无理数，则π∈R故答案为:(1)∈;(2)∉ ;(3)∉ ;(4)∉ ;(5)∈ ;(6)∈3.用适当的方法表示下列集合:(1)由方程x²-9=0的所有实数根组成的集合;【答案解析】：{-3, 3}.(2)一次函数y=x+3与y=-2x+6图象的交点组成的集合;【答案解析】： {(1, 4)}.(3)不等式4x- 5<3的解集.【答案解析】：{x | x<2}.习题1.1一、复习巩固1.用符号“∈”或“∉”填空:(1)设A为所有亚洲国家组成的集合，则中国____ A,美国____A，印度____A,英国____ A;【答案解析】：设A为所有亚洲国家组成的集合，则:中国∈A，美国∉A,印度∈A，英国∉A.(2)若A={x|x²=x},则-1____A;【答案解析】：A={x|x²=x}={0, 1},则-1∉A.(3)若B={x|x²+x-6=0}，则3____B;【答案解析】：若B={x|x²+x-6=0}={x|(x+3)(x-2)=0}={-3，2}，则3∉B; (4)若C={x∈N|1≤x≤10},则8____C, 9.1____C.【答案解析】：若C={x∈N|1≤x≤10}={1, 2, 3,4，5, 6，7, 8，9，10}，则8∈C, 9.1∉C.2.用列举法表示下列集合:(1)大于1且小于6的整数;【答案解析】：大于1且小于6的整数有4个:2,3,4,5,所以集合为{2,3,4,5}.(2) A={x|(x-1)(x +2)=0};【答案解析】：(x- 1)(x+2)=0的解为x=1或x=-2,所以集合为{1, -2}.(3) B={x∈Z|-3<2x-1<3}.【答案解析】：由-3<2x-1<3,得-1<x<2.又因为x∈Z,所以x=0.或x=1,所以集合为{0,1}.二、综合运用3.把下列集合用另一种方法表示出来:(1) {2，4，6，8, 10};【答案解析】：{x |x=2k, k=1, 2, 3, 4, 5}.(2)由1，2，3这三个数字抽出一部分或全部数字(没有重复)所组成的一切自然数;【答案解析】：{1, 2, 3, 12, 21, 13, 31, 23, 32, 123, 132, 213, 231, 312, 321}.(3) {x∈N|3<x<7};【答案解析】：{4, 5, 6}.(4)中国古代四大发明.【答案解析】：{指南针，活字印刷，造纸术，火药}.4.用适当的方法表示下列集合:(1)二次函数y=x²-4的函数值组成的集合;【答案解析】： {y | y≥-4}.(2)反比例函数y=2/x的自变量组成的集合;【答案解析】：{x | x≠0}.(3)不等式3x≥4- 2x的解集.【答案解析】：{x |x≥4/5}.三、拓广探索5.集合论是德国数学家康托尔于19 世纪末创立的.当时，康托尔在解决涉及无限量研究的数学问题时，越过“数集”限制，提出了一般性的“集合”概念.关于集合论，希尔伯特赞誉其为“数学思想的惊人的产物，在纯粹理性的范畴中人类活动的最美的表现之一”，罗素描述其为“可能是这个时代所能夸耀的最伟大的工作”.请你查阅相关资料，用简短的报告阐述你对这些评价的认识.【答案解析】：略.1.2 集合间的基本关系练习1.写出集合{a, b，c}的所有子集.【答案解析】由0个元素构成的子集: ∅;由1个元素构成的子集: {a}, {b}, {c};由2个元素构成的子集: {a, b}, {a,c}, {b, c};由3个元素构成的子集: {a, b, c};综上，可得集合{a，b, c}的所有子集有: 0, {a}, {b}, {c}, {a, b}, {a,c}, {b, c}, {a, b, c}.2.用适当的符号填空:(1) a__ {a，b，c}; (2) 0__ {x|x²=0};(3) B___ {x∈R|x²+1=0}; (4) {0，1}___N(5) {0}___ {x|x²=x}; (6) {2, 1}___{x|x²-3x+2=0}.【答案解析】：（1）∈；（2）=；（3）=；（4）⊆；（5）⊆；（6）=.3.判断下列两个集合之间的关系:(1) A={x|x<0}， B={x|x<l};(2) A={x|x=3k，k∈N}，B={x|x=6z，z∈N};(3) A={x∈N₋|x是4与10的公倍数}，B={x|x=20m, m∈N₊}.【答案解析】：⫋A B B A A=B习题1.2一、复习巩固1.选用适当的符号填空:(1)若集合A={x|2x-3<3x}, B={x|x≥2},则-4___B，-3___ A， {2}___B，B___ A；【答案解析】：∵集合A= {x|2x-3< 3x}= {x|x>-3},B = {x|x≥2}，则∴-4∉B,-3∉A,{2}B，B A.故答案为:∉，∉,，。

人教版高中数学必修1-第一章知识点知识点归纳[最新版]

知识点总结归纳【最新版】适用于老师、学生、家长一、集合有关概念1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合中元素的三个特性：1.元素的确定性；2.元素的互异性；3.元素的无序性3、集合的表示：{ …} 如{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}1. 用拉丁字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}2．集合的表示方法：列举法与描述法。

非负整数集（即自然数集）记作：N正整数集N*或N+ 整数集Z 有理数集Q 实数集R3.关于“属于”的概念集合的元素通常用小写的拉丁字母表示，如：a是集合A的元素，就说a属于集合A 记作a∈A ，相反，a不属于集合A 记作a∉A•列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

•描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。

用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形}②数学式子描述法：例：不等式x-3>2的解集是{x∈R| x-3>2}或{x| x-3>2}•4、集合的分类：（1）有限集含有有限个元素的集合（2）无限集含有无限个元素的集合（3）空集不含任何元素的集合例：二、集合间的基本关系• 1.“包含”关系—子集注意：有两种可能（1）A是B的一部分；（2）A与B是同一集合。

反之: 集合A不包含于集合B,或集合B不包含集合A,记作A ⊆B或B ⊇A•2．“相等”关系(5≥5，且5≤5，则5=5)实例：设A= B={-1,1} “元素相同”结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时,集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B①子集：任何一个集合是它本身的子集。

A⊆A②真子集:如果A⊆B,且B⊄A那就说集合A是集合B的真子集，记作A⊈B(或B⊉A)③如果A⊆B, B⊆C ,那么A⊆C④如果A⊆B 同时B⊆A 那么A=B3. 不含任何元素的集合叫做空集，记为Φ规定: 空集是任何集合的子集，空集是任何非空集合的真子集。

新人教版高一生物必修一知识点复习总结

高一生物必修一知识点整理第一章走近细胞第一节从生物圈到细胞一、相关概念、细胞：是生物体结构和功能的基本单位。

除了病毒以外，所有生物都是由细胞构成的。

细胞是地球上最基本的生命系统生命系统的结构层次：细胞→组织→器官→系统（植物没有系统）→个体→种群→群落→生态系统→生物圈二、病毒的相关知识：1、病毒（Virus）是一类没有细胞结构的生物体。

主要特征：①、个体微小，一般在10~30nm之间，大多数必须用电子显微镜才能看见；②、仅具有一种类型的核酸，DNA或RNA，没有含两种核酸的病毒；③、专营细胞内寄生生活；④、结构简单，一般由核酸（DNA或RNA）和蛋白质外壳所构成。

2、根据寄生的宿主不同，病毒可分为动物病毒、植物病毒和细菌病毒（即噬菌体）三大类。

根据病毒所含核酸种类的不同分为DNA病毒和RNA病毒。

3、常见的病毒有：人类流感病毒（引起流行性感冒）、SARS病毒、人类免疫缺陷病毒（HIV）[引起艾滋病（AIDS）]、禽流感病毒、乙肝病毒、人类天花病毒、狂犬病毒、烟草花叶病毒等。

第二节细胞的多样性和统一性一、细胞种类：根据细胞内有无以核膜为界限的细胞核，把细胞分为原核细胞和真核细胞二、原核细胞和真核细胞的比较：1、原核细胞：细胞较小，无核膜、无核仁，没有成形的细胞核；遗传物质（一个环状DNA分子）集中的区域称为拟核；没有染色体，DNA 不与蛋白质结合，；细胞器只有核糖体；有细胞壁，成分与真核细胞不同。

2、真核细胞：细胞较大，有核膜、有核仁、有真正的细胞核；有一定数目的染色体（DNA与蛋白质结合而成）；一般有多种细胞器。

3、原核生物：由原核细胞构成的生物。

如：蓝藻、细菌（如硝化细菌、乳酸菌、大肠杆菌、肺炎双球菌）、放线菌、支原体等都属于原核生物。

4、真核生物：由真核细胞构成的生物。

如动物(草履虫、变形虫)、植物、真菌（酵母菌、霉菌、粘菌）等。

三、细胞学说的建立：1、1665 英国人虎克(Robert Hooke)用自己设计与制造的显微镜（放大倍数为40-140倍)观察了软木的薄片，第一次描述了植物细胞的构造，并首次用拉丁文cella（小室)这个词来对细胞命名。

高一上化学人教版必修第一册期末知识点复习总结

第一章物质及其变化一、物质的分类1．根据物质的组成对物质进行分类(1)由同一种元素形成的几种性质不同的单质，叫作这种元素的同素异形体如金刚石、石墨和C60；O2和O3(2)根据物质的组成对物质进行分类——树状分类法(3)从不同的角度对物质进行分类——交叉分类法碳酸钠为钠盐，也为碳酸盐2.根据物质的性质对物质进行分类酸性氧化物碱性氧化物定义能与碱反应生成盐和水的氧化物能与酸反应生成盐和水的氧化物实例CO2、SO3等CaO、Fe2O3等属类大多数非金属氧化物大多数金属氧化物例1 .以下为中学化学中常见的几种物质：①Fe ②熔融NaCl ③NaHSO4 ④CO2 ⑤H2SO4 ⑥酒精⑦KHCO3溶液⑧BaSO4⑨NaOH请回答下面问题。

属于电解质的是（填序号）；属于酸的是；属于盐的是。

二、分散系及其分类1．分散系(1)基本概念(2)分类根据分散质粒子的直径大小分类：2．胶体(1)分类胶体分散剂实例液溶胶液体Fe(OH)3胶体气溶胶气体云、雾固溶胶固体有色玻璃(2)Fe(OH)3胶体的制备在小烧杯中，加入40 mL蒸馏水，加热至沸腾，向沸水中逐滴加入5～6滴FeCl3饱和溶液，继续煮沸至液体呈红褐色，停止加热，即可得到Fe(OH)3胶体。

化学方程式：FeCl 3＋3H 2O=====△Fe(OH)3(胶体)＋3HCl 。

(3)丁达尔效应①实验探究实验操作实验现象原因分析观察到一条光亮的“通路”胶粒的直径为1～100 nm ，能使光波发生散射无明显现象溶液中粒子的直径小于1__nm ，光的散射极其微弱②应用：该效应常用来区分胶体和溶液。

三、物质的转化1．实现物质转化的基本依据：在化学变化过程中，元素不会发生改变。

2．常见单质及其化合物的转化关系 (1)实例探究Ca ――→①CaO ――→②Ca （OH ）2――→③CaCO 3 C ――→④CO 2――→⑤H 2CO 3――→⑥CaCO 3写出上述转化的化学方程式并注明反应类型：序号化学方程式反应类型 ① 2Ca ＋O 2===2CaO 化合反应 ② CaO ＋H 2O===Ca(OH)2化合反应 ③ Ca(OH)2＋CO 2===CaCO 3↓＋H 2O复分解反应 ④ C ＋O 2=====点燃CO 2 化合反应 ⑤ CO 2＋H 2O===H 2CO 3化合反应 ⑥H 2CO 3＋Ca(OH)2===CaCO 3↓＋2H 2O复分解反应(2)探究归纳：单质到盐的转化关系3．确定制取物质的方法 (1)确定依据(2)实例——碱的制备(3)工业生产方法的选择①最适当方法的选择②实例——工业上制取NaOHa．不采用Na2O与H2O反应的原因：Na2O作为原料，来源少、成本高；b．主要采用方法：电解饱和食盐水；c．过去曾采用方法：盐(如Na2CO3)与碱[如Ca(OH)2]反应。

人教版教学课件-新人教[原创]必修1第一章总复习

真核细胞较大(10 μm～100 μm) 没有由核膜包围的典型的细胞核，有成形的、真正的细只是把遗传物质储存、复制的场胞核，有核膜、核仁所称拟核以DNA分子存在以染色体形式存在
只有核糖体
举例
有线粒体等多种细胞器细胞壁不含纤维素，主要成分是细胞壁的主要成分是糖类与蛋白质形成的化合物(肽纤维素和果胶聚糖) 动物植物细菌蓝藻(颤藻念珠藻发菜) 衣藻绿藻红藻硅藻放线菌衣原体支原体真菌(酵母菌霉菌蘑
１．科学发现是很多科学家的共同参与，共同努力的结果２．科学发现的过程离不开技术的支持３．科学发现需要理性思维和实验的结合４．科学学说的建立是一个不断开拓．继承．修正和发展的过程
• 1.下列关于人体生命活动与细胞关系的叙述，错误的是 A.细胞的分裂和分化是人体发育的基础 • B.只有通过精子和卵细胞，子代方能获得亲本的遗传物质 • C.人体是由细胞构成的，所以细胞的生长必然导致人体的生长 • D.人体是由细胞构成的，所以细胞的分裂必然导致人体的生长 • 2.如果把细胞搅碎，细胞将死亡；病毒不具有细胞结构，如果把病毒搅碎，病毒将失去活性，这说明( ) • A.细胞和病毒失活是因为破坏了它们的化学成分 • B.细胞和病毒被搅碎都失活，可见两者的特点是一致的 • C.像病毒这样不具细胞结构的生物的存在，说明生命现象不依赖于细胞结构 • D.生物体的生命活动必须建立在一定的结构基础之上
• • • • •
• 2.细胞的统一性
• 4.成人身体约有1014个细胞。这些细胞大约有20(种不同的类型，根据分化程度的不同，又可分为600多种，但是都有基本相同的结构，这说明( ) • A.体细胞既有多样性，又有统一性 • B.细胞的结构和功能基本相同 • C.200多种不同的类型就是200多种不同的组织 • D.人体细胞的基本结构与草履虫相同 • 5.(05年北京)在以下描述中可以将病毒与其他微生物相区别的是 • A.能够使人或动物患病 B.没有细胞核,仅有核酸 • C.具有寄生性 D.由核酸和蛋白质装配进行增殖

人教版(新教材)高中数学第一册(必修1)精品课件：第一章集合与常用逻辑用语章末复习课

【例1】 (1)设集合A＝{1，2，4}，集合B＝{x|x＝a＋b，a∈A，b∈A}，则集合B中元
素的个数是( )
A.4
B.5
C.6
D.7
(2)已知集合A＝{0，1，2}，则集合B＝{x－y|x∈A，y∈A}中元素的个数是( )
A.1
B.3
ቤተ መጻሕፍቲ ባይዱ
C.5
D.9
解析 (1)∵a∈A，b∈A，x＝a＋b，所以x＝2，3，4，5，6，8，∴B中有6个元素，故选C. (2)当x＝0，y＝0时，x－y＝0；当x＝0，y＝1时，x－y＝－1；当x＝0，y＝2时，x－y ＝－2；当x＝1，y＝0时，x－y＝1；当x＝1，y＝1时，x－y＝0；当x＝1，y＝2时，x －y＝－1；当x＝2，y＝0时，x－y＝2；当x＝2，y＝1时，x－y＝1；当x＝2，y＝2时， x－y＝0.根据集合中元素的互异性知，B中元素有0，－1，－2，1，2，共5个. 答案 (1)C (2)C
【训练4】 (1)若p：x2＋x－6＝0是q：ax＋1＝0的必要不充分条件，则实数a的值为 ________. (2) 若－ a<x< － 1 成立的一个充分不必要条件是－ 2<x< － 1 ，则 a 的取值范围是 ________.
解析 (1)p：x2＋x－6＝0，即x＝2或x＝－3. q：ax＋1＝0，当 a＝0 时，方程无解；当 a≠0 时，x＝－1a. 由题意知p q，q p，故a＝0舍去；
当 a≠0 时，应有－1a＝2 或－1a＝－3，解得 a＝－12或 a＝13. 综上可知，a＝－12或 a＝13. (2)根据充分条件、必要条件与集合间的包含关系，应有{x|－2<x<－1} {x|－a<x< －1}，故有a>2. 答案 (1)－12或13 (2)a>2

人教版高中数学必修一第一章知识点

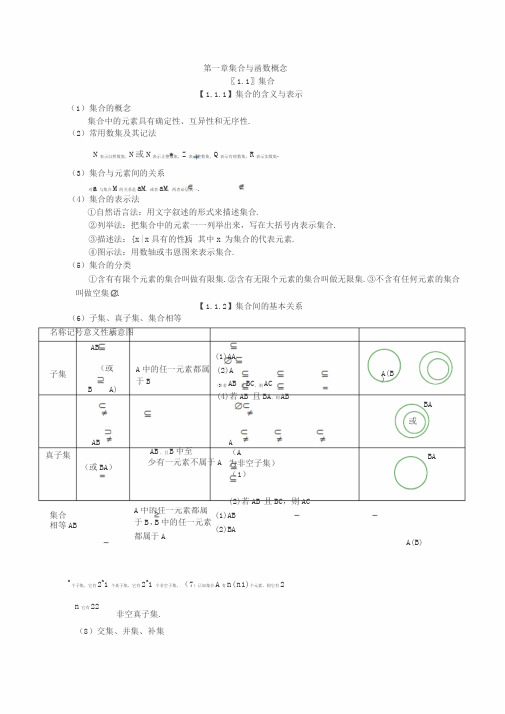
第一章集合与函数概念〖1.1 〗集合【1.1.1 】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性.（ 2）常用数集及其记法N表示自然数集，N或N表示正整数集，Z表示整数集，Q表示有理数集，R表示实数集.（ 3）集合与元素间的关系对象 a 与集合 M 的关系是a M ，或者 a M ，两者必居其一.（4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合 . ③描述法： { x | x具有的性质 } ，其中x为集合的代表元素 .④图示法：用数轴或韦恩图来表示集合.（ 5）集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集 ().【 1.1.2 】集合间的基本关系（ 6）子集、真子集、集合相等名称记号意义性质示意图A B（或子集B A)A B真子集（或B A）A中的任一元素都属于 BA B，且B中至少有一元素不属于 A(1)A A(2)A A(B)BA(3)若A B 且 B C，则A C(4)若A B 且 B A，则 A B或（1） A （A为非空子集）BA(2)若A B 且 B C，则 A CA 中的任一元素都属集合A B于B，B中的任一元素相等都属于 A (1)A BA(B) (2)B A（ 7）已知集合A有n(n1) 个元素，则它有2n个子集，它有 2n1个真子集，它有 2n 1个非空子集，它有 2n2非空真子集.（ 8）交集、并集、补集名称交集并集补集【 1.1.3】集合的基本运算记号意义性质示意图{ x | x A, 且（1）A A AA B（2）AA B（3）A B Ax B}A B B{ x | x A, 或（1）A A AA（2）A ABA B（3）A B Ax B}A B B1A(e A)2A (e U A)UUe A{ x | x U , 且x A}痧( A B)( U A)(?U B)UU痧(A B)(U A)(? B)U U【补充知识】含绝对值的不等式与一元二次不等式的解法（ 1）含绝对值的不等式的解法不等式解集| x | a( a 0){ x | a x a}| x | a(a 0)x | xa 或 x a}把 ax b 看成一个整体，化成| x | a，| ax b |c,| ax b |c(c0)| x | a(a 0) 型不等式来求解（2）一元二次不等式的解法判别式b24ac000二次函数y ax2bx c(a0)的图象O一元二次方程2b b4ac2x1,22a x1 x2bax bx c0( a0)无实根2a（其中x1x2 )的根ax2bx c0(a0){ x | x x1或x x2}{ x | x b }R的解集2aax2bx c 0( a 0){ x | x1x x2}的解集〖1.2 〗函数及其表示【1.2.1 】函数的概念（ 1）函数的概念①设 A、 B 是两个非空的数集，如果按照某种对应法则 f ，对于集合 A 中任何一个数x ，在集合 B中都有唯一确定的数 f ( x) 和它对应，那么这样的对应（包括集合 A ，B 以及 A 到 B 的对应法则 f ）叫做集合 A到 B 的一个函数，记作 f : A B ．②函数的三要素: 定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（ 2）区间的概念及表示法①设 a, b 是两个实数，且a b ，满足 a x b 的实数x的集合叫做闭区间，记做[a,b] ；满足a xb 的实数x的集合叫做开区间，记做(a,b) ；满足a x b ，或 a x b 的实数x的集合叫做半开半闭区间，分别记做[ a,b) ， (a,b] ；满足 x a, x a, x b, x b 的实数 x 的集合分别记做．[a, ),( a,),(, b],(, b)注意：对于集合 { x | a x b} 与区间 (a, b) ，前者 a 可以大于或等于b，而后者必须a b ．（3）求函数的定义域时，一般遵循以下原则：① f ( x) 是整式时，定义域是全体实数．② f ( x) 是分式函数时，定义域是使分母不为零的一切实数．③ f ( x) 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤y tan x 中，x k(k Z ) ．2⑥零（负）指数幂的底数不能为零．⑦若 f ( x) 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知 f (x) 的定义域为 [ a, b] ，其复合函数 f [ g( x)]的定义域应由不等式 a g ( x) b 解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论．⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值．③判别式法：若函数y f ( x) 可以化成一个系数含有y 的关于 x 的二次方程a( y) x2b( y) x c( y)0 ，则在 a( y)0 时，由于 x, y 为实数，故必须有b2 ( y) 4a( y)c( y)0 ，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值．⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值．⑧函数的单调性法．【 1.2.2 】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（ 6）映射的概念①设 A、 B 是两个集合，如果按照某种对应法则 f ，对于集合 A 中任何一个元素，在集合 B 中都有唯一的元素和它对应，那么这样的对应（包括集合 A ， B 以及 A 到 B 的对应法则 f ）叫做集合 A 到B 的映射，记作 f : A B ．②给定一个集合 A 到集合 B 的映射，且 a A, b B ．如果元素 a 和元素b对应，那么我们把元素b 叫做元素a的象，元素a叫做元素 b 的原象．----〖 1.3 〗函数的基本性质【 1.3.1 】单调性与最大（小）值（ 1）函数的单调性①定义及判定方法函数的图象定义性质如果对于属于定义域I 内某个区间上的任意两个自变量y y=f(X)的值 x 1 、x 2 , 当 x 1 < x 2 时，都f(x 2 )．．．有 f(x 1)<f(x 2 ) ，那么就说．．．．．．．．．f(x 1 )f(x) 在这个区间上是增函数．．．．o1x 2xx函数的单调性如果对于属于定义域I 内某yy=f(X)个区间上的任意两个自变量f(x 1)的值 x 1、 x 2 ，当 x 1 < x 2 时，都．．．判定方法（ 1）利用定义（ 2）利用已知函数的单调性（ 3）利用函数图象（在某个区间图象上升为增）（ 4）利用复合函数（ 1）利用定义（ 2）利用已知函数的单调性（ 3）利用函数图象（在有 f(x 1)>f(x 2 ) ，那么就说f(x )．．．．．．．．．2f(x) 在这个区间上是减函数．ox 1x 2．．．x某个区间图象下降为减）（ 4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③ 对于复合函数 yf [ g( x)]，令u g( x)，若y f (u)为增，u g( x)为增，则y f [ g (x)] 为增；若 yf (u) 为减， ug( x) 为减，则 yf [g (x)] 为增；若 y f (u) 为增， ug( x)为减，则yf [ g( x)]为减；若 yf (u)为减，ug( x) 为增，则 yy f [ g (x)] 为减．（ 2）打“√”函数f ( x) x a (a 0) 的图象与性质xf (x) 分别在 ( ,a ] 、 [ a ,) 上为增函数，分别在ox[a, 0) 、 (0, a ] 上为减函数．（ 3）最大（小）值定义①一般地，设函数y f (x) 的定义域为 I ，如果存在实数M 满足：（1）对于任意的 xI ，都有 f ( x)M ；（2）存在 x 0 I ，使得 f (x 0 ) M ．那么，我们称M 是函数 f ( x)的最大值，记作f ( x) M②一般地，设函数y f ( x) 的定义域为 I ，如果存在实数m 满足：（1）对于任意的x I ，都有f (x)m ；（2）存在 x0I ，使得 f ( x0 )m ．那么，我们称 m 是函数 f (x) 的最小值，记作f max (x)m．【1.3.2 】奇偶性（4）函数的奇偶性①定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内（ 1）利用定义（要先任意一个 x，都有f(－x)=－判断定义域是否关于．．．．．．．f(x),那么函数 f(x)叫做奇函原点对称）．．．．．．数．（ 2）利用图象（图象．关于原点对称）函数的奇偶性如果对于函数f(x)定义域内（ 1）利用定义（要先任意一个 x，都有f(－x)=f(x) ,判断定义域是否关于．．．．．．．．．．那么函数 f(x)叫做偶函数．原点对称）．．．（ 2）利用图象（图象关于 y 轴对称）②若函数 f ( x) 为奇函数，且在x 0处有定义，则 f (0)0．③奇函数在 y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（ 1）作图利用描点法作图：①确定函数的定义域；②化解函数解析式；③讨论函数的性质（奇偶性、单调性）；④画出函数的图象．利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象．①平移变换y f ( x)h 0,左移h个单位h0,右移 | h|个单位y f ( x)k 0,上移k个单位k0,下移 | k|个单位②伸缩变换y f (x h) y f (x) ky f ( x)01,伸y f ( x) 1,缩0A1,缩y f ( x) A 1,伸y Af ( x)③对称变换y f ( x)y f ( x)y f ( x)y f ( x) （2）识图x轴f (x)y f (x)y轴f (x)y y原点f ( x)y f ( x)直线y xy f1( x) y去掉y轴左边图象y f (| x |)保留y轴右边图象，并作其关于y轴对称图象保留x轴上方图象y| f ( x) |将x轴下方图象翻折上去对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系．（3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．7。

高一化学必修一第一章重难点：离子反应[新人教版]

高一化学必修一第一章重难点：离子反应[新人教版]高一化学必修一第一章重难点：离子反应[新人教版]亲爱的同学，新学期就要开始了。

怀着梦想，背上行囊，走进英才，又一阶段的学习之旅启程了。

生命的辉煌，在这时奠基；青春作伴，正当立志奋发时！一起来看看高一化学必修一第一章重难点相关内容。

高一化学必修一第一章重难点：离子反应[新人教版]一、离子反应的概念离子反应是指有离子参加的反应。

也就是说，反应物中有离子或生成物中有离子的反应，均为离子反应。

由于中学阶段涉及的问题多数是指水溶液中的变化，所以水溶液中电解质间的相互反应便成了离子反应的常见问题。

但须注意的是，凡是离子化合物，就含有离子，有时固体状态的物质之间(如实验室判氨)或固体与气体之间(如碱石灰与氯化氢)发生的反应，也可以是离子反应，只是通常不书写类似这样过程的离子反应方程式。

在水溶液中发生离子反应的条件即复分解反应的三个条件(有难电离、难溶及易挥发物质生成)和氧化还原反应(比如置换反应等)。

二、离子共存问题凡是能发生反应的离子之间或在水溶液中水解相互促进的离子之间不能大量共存(注意不是完全不能共存，而是不能大量共存)。

一般规律是：A、①B、③ ④C、② ⑤D、① ④[解题分析] 本题全面考查离子共存知识，在题给的六组离子中，第①组ClO-与H+、I-不能大量共存，第②组中NH4+与OH-、HCO3-与OH-不能大量共存，第③④组中各离子可以共存，第⑤组H+与AlO2-、HSO3-不能大量共存，第⑥组中Ca2+与CO32-甚至SO42-不能大量共存。

因此，正确选项应为B。

例2：在pH=1的溶液中，可大量共存的离子组是A、Fe3+、I-、S2-、Cl-B、Al3+、Mg2+、SO42-、Cl-C、K+、Na+、AlO2-、NO3-D、K+、Na+、SO42-、S2O32- [解题分析] 本题先明确了溶液的环境为PH=1的酸性条件下，因此不仅要判断各离子组中离子能否共存，还要判断它们能否与H+大量共存。

人教版高一数学上册第一章复习要点

总结每一章的知识点对学习知识是非常有利的，查字典数学网为您提供的是高一数学上册第一章复习要点，希望可以帮助到你。

第一章集合与函数概念一、集合有关概念1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合的中元素的三个特性：1.元素的确定性;2.元素的互异性;3.元素的无序性说明：(1)对于一个给定的集合，集合中的元素是确定的，任何一个对象或者是或者不是这个给定的集合的元素。

(2)任何一个给定的集合中，任何两个元素都是不同的对象，相同的对象归入一个集合时，仅算一个元素。

(3)集合中的元素是平等的，没有先后顺序，因此判定两个集合是否一样，仅需比较它们的元素是否一样，不需考查排列顺序是否一样。

(4)集合元素的三个特性使集合本身具有了确定性和整体性。

3、集合的表示：{…}如{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}1.用拉丁字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}2.集合的表示方法：列举法与描述法。

注意啊：常用数集及其记法：非负整数集(即自然数集)记作：N正整数集N*或N+整数集Z有理数集Q实数集R关于“属于”的概念集合的元素通常用小写的拉丁字母表示，如：a 是集合A的元素，就说a属于集合A记作a∈A，相反，a不属于集合A记作a?A列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。

用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形}②数学式子描述法：例：不等式x-32的解集是{x?R|x-32}或{x|x-32}4、集合的分类：1.有限集含有有限个元素的集合 2.无限集含有无限个元素的集合3.空集不含任何元素的集合例：{x|x2=-5｝二、集合间的基本关系1.“包含”关系—子集注意：有两种可能(1)A是B的一部分，;(2)A与B是同一集合。

人教版高一地理必修一第一章复习(共158张PPT)

(1)纬度：纬度位置低，太阳高度角大，太阳辐射强。 (2)天气：天气晴朗，阴天少，光照时间长，大气对太阳辐射削弱少，
太阳辐射强。 (3)地势：地势高，空气稀薄，大气对太阳辐射削弱少，太阳辐射强。 (4)大气透明度：大气透明度好，尘埃少、杂质少，太阳辐射强。
青的藏原高因原：成为太阳太辐阳射辐高射值的中分心布及成总从因体东特部征沿：海向西部内
南半球昼夜平分
越往南昼越短越往南昼越长
南极圈内极夜南极圈内极昼
昼夜长短的变化
夏至 •
（北半球）
23．5°
春分 •
秋分 •
春分 • 0º
冬至
•
23．5°
昼渐长昼（渐短昼渐短（昼渐长
昼夜等长
昼最长夜最短
北极圈内极昼）
昼夜等长
昼北最极短圈夜内最极长夜
一架飞机由我国上海（东八区）5月1日18时飞往美国
纽约（西5区），途中需飞行10小时，到达目的地时，
当地时间是
（C）
A、5月2日15时
B、 5月1日19时
C、5月1日15时
D、 5月2日16时
剖析: 8-（-5）=13；
18-13=5；5+10=15
【国际日期变更线】
加一天减一天
【新旧日期范围】
昨天(旧的一天)
自然日界线
今天 (新的一天)
★重要结论：从0时经线开始往东到180°经线为新的一天，往西到180°经线是旧的一天。
0点旧日子
新日子
180° 旧日子
W
E
求新旧日期的范围：新日子范围=180°地方时/24
旧日子范围=1-180°地方时/24

人教版高中数学必修一第一章知识点

第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性.（2）常用数集及其记法N表示自然数集，N或N表示正整数集，Z表示整数集，Q表示有理数集，R表示实数集.（3）集合与元素间的关系对象a与集合M的关系是aM，或者aM，两者必居其一.（4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合.③描述法：{x|x具有的性质}，其中x为集合的代表元素.④图示法：用数轴或韦恩图来表示集合.（5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集().【1.1.2】集合间的基本关系（6）子集、真子集、集合相等名称记号意义性质示意图AB(1)AA子集B （或A)A中的任一元素都属于B(2)A(3)若AB且BC，则AC(4)若AB且BA，则ABA(B)BA或真子集AB（或BA）AB，且B中至少有一元素不属于AA（A为非空子集）（1）(2)若AB且BC，则ACBA集合相等AB A中的任一元素都属于B，B中的任一元素都属于A(1)AB(2)BAA(B)n个子集，它有2n1个真子集，它有2n1个非空子集，（7）已知集合A有n(n1)个元素，则它有2n它有22非空真子集. （8）交集、并集、补集1【1.1.3】集合的基本运算名称记号意义性质示意图AB 交集{x|x A,且（1）AAA（2）AAB（3）ABAxB}ABBAB 并集{x|x A,或（1）AAA（2）AAAB（3）ABAxB}ABB1A(e U A)2()AeAUU补集e U A{x|xU,且xA} 痧U(A B)(U A)(?U B)痧U(AB)(U A)(?U B)【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法不等式解集|x|a(a0){x|axa}|x|a(a0)x|xa或xa}把axb看成一个整体，化成|x|a，|axb|c,|axb|c(c0)|x|a(a0)型不等式来求解（2）一元二次不等式的解法判别式24bac000二次函数2(0)yaxbxcaO的图象一元二次方程20(0)axbxcax1,22bb4ac2abxx122a无实根（其中x1x2)的根20(0) axbxca的解集b{x|xx或xx2}{x|x}12aR 220(0)axbxca的解集{x|xxx}12〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A、B是两个非空的数集，如果按照某种对应法则f，对于集合A中任何一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么这样的对应（包括集合A，B以及A到B的对应法则f）叫做集合A到B的一个函数，记作f:AB．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设a,b是两个实数，且ab，满足a xb的实数x的集合叫做闭区间，记做[a,b]；满足axb的实数x的集合叫做开区间，记做(a,b)；满足a xb，或axb的实数x的集合叫做半开半闭区间，分别记做[a,b)，(a,b]；满足x a,xa,xb,xb的实数x的集合分别记做[a,),(a,),(,b],(,b)．注意：对于集合{x|axb}与区间(a,b)，前者a可以大于或等于b，而后者必须ab．（3）求函数的定义域时，一般遵循以下原则：①f(x)是整式时，定义域是全体实数．②f(x)是分式函数时，定义域是使分母不为零的一切实数．③f(x)是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤ytanx中，()xkkZ．2⑥零（负）指数幂的底数不能为零．⑦若f(x)是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知f(x)的定义域为[a,b]，其复合函数f[g(x)]的定义域应由不等式ag(x)b解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论．⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值．③判别式法：若函数yf(x)可以化成一个系数含有y的关于x的二次方程2a(y)xb(y)xc(y)0，则在a(y)0时，由于x,y为实数，故必须有byaycy，从而确定函数的值域或最值．2()4()()0④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值．⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值．⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A、B是两个集合，如果按照某种对应法则f，对于集合A中任何一个元素，在集合B中都有唯一的元素和它对应，那么这样的对应（包括集合A，B以及A到B的对应法则f）叫做集合A到B的映射，记作f:AB．②给定一个集合A到集合B的映射，且aA,bB．如果元素a和元素b对应，那么我们把元素b叫做元素a的象，元素a叫做元素b的原象．〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法函数的定义图象判定方法性质如果对于属于定义域I 内某（1）利用定义个区间上的任意两个自变量的值x2,当x ． 1、x 1．<．x ．2．时，都y y=f(X) f(x)2（2）利用已知函数的单调性有f ．(x ．．．)．<．f(．x ．．．)．，那么就说 12 f(x)在这个区间上是增函数．．．．f(x)1（3）利用函数图象（在某个区间图o x 1x 2x 象上升为增）函数的（4）利用复合函数单调性（1）利用定义如果对于属于定义域I 内某yy=f(X)（2）利用已知函数的个区间上的任意两个自变量 11、x ．<．x ．的值x2，当x ．2．时，都有f ．(x ．．12．)．，那么就说f(x) 1f(x) 2单调性（3）利用函数图象（在某个区间图f(x)在这个区间上是减函数．．．．o xx 12x象下降为减）（4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数yf[g(x)]，令ug(x)，若yf(u)为增，ug(x)为增，则yf[g(x)]为增；若yf(u)为减，ug(x)为减，则y f[g(x)]为增；若yf(u)为增，ug(x)为减，则y f[g(x)]为减；若yf(u)为减，ug(x)为增，则yyf[g(x)]为减．a（2）打“√”函数()(0)fxxax的图象与性质 f(x)分别在(,a ]、[a ,)上为增函数，分别在ox[a,0)、(0,a]上为减函数．（3）最大（小）值定义①一般地，设函数yf(x)的定义域为I，如果存在实数M满足：（1）对于任意的xI，都有f(x)M；（2）存在x I，使得f(x0)M．那么，我们称M是函数f(x)的最大值，记作0f max(x)M．5②一般地，设函数yf(x)的定义域为I，如果存在实数m满足：（1）对于任意的xI，都有f(x)m；（2）存在x0I，使得f(x0)m．那么，我们称m是函数f(x)的最小值，记作f max(x)m．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内（1）利用定义（要先任意一个x，都有．f(．－．x．．)=．－．判断定义域是否关于f(x)．．．．,那么函数f(x)叫做奇．函．原点对称）数．．（2）利用图象（图象关于原点对称）函数的奇偶性如果对于函数f(x)定义域内（1）利用定义（要先任意一个x，都有f(－．x．．)=．f．(x．)．．,．．判断定义域是否关于那么函数f(x)叫做偶．函．数．．原点对称）（2）利用图象（图象关于y轴对称）②若函数f(x)为奇函数，且在x0处有定义，则f(0)0．③奇函数在y轴两侧相对称的区间增减性相同，偶函数在y轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域；②化解函数解析式；③讨论函数的性质（奇偶性、单调性）；④画出函数的图象．利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象．①平移变换yfxyfxh()h0,h()左移个单位右移|个单位h0,h|yfxyfxk()kk()0,上移个单位下移|个单位k0,k|变换②伸缩01,伸yf(x)yf(x)1,缩6yfxyAfx()0A1,缩()A1,伸③对称变换x轴yf(x)y轴yf(x)yf(x)yf(x)原点直线1yxyf(x)yf(x)yf(x)yf(x)去掉轴左边图象yyf(x)yf(|x|)保留y轴右边图象，并作其关于y轴对称图象保留轴上方图象yfxyfx()x|()|将轴下方图象翻折上去x（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系．（3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．7。

人教版高一数学必修一第一章-知识点与习题讲解

必修1第一章集合与函数基础知识点整理第1讲 §1.1.1 集合的含义与表示¤知识要点：1. 把一些元素组成的总体叫作集合（set ），其元素具有三个特征，即确定性、互异性、无序性.2. 集合的表示方法有两种：列举法，即把集合的元素一一列举出来，并用花括号“{ }”括起来，基本形式为123{,,,,}n a a a a ⋅⋅⋅，适用于有限集或元素间存在规律的无限集.描述法，即用集合所含元素的共同特征来表示，基本形式为{|()x A P x ∈}，既要关注代表元素x ，也要把握其属性()P x ，适用于无限集.3. 通常用大写拉丁字母,,,A B C ⋅⋅⋅表示集合. 要记住一些常见数集的表示，如自然数集N ，正整数集*N 或N +，整数集Z ，有理数集Q ，实数集R .4. 元素与集合之间的关系是属于（belong to ）与不属于（not belong to ），分别用符号∈、∉表示，例如3N ∈，2N -∉.¤例题精讲：【例1】试分别用列举法和描述法表示下列集合：（1）由方程2(23)0x x x --=的所有实数根组成的集合；（2）大于2且小于7的整数.解：（1）用描述法表示为：2{|(23)0}x R x x x ∈--=；用列举法表示为{0,1,3}-.（2）用描述法表示为：{|27}x Z x ∈<<；用列举法表示为{3,4,5,6}.【例2】用适当的符号填空：已知{|32,}A x x k k Z ==+∈，{|61,}B x x m m Z ==-∈，则有：17 A ；－5 A ； 17 B .解：由3217k +=，解得5k Z =∈，所以17A ∈；由325k +=-，解得73k Z =∉，所以5A -∉；由6117m -=，解得3m Z =∈，所以17B ∈. 【例3】试选择适当的方法表示下列集合：（教材P 6 练习题2， P 13 A 组题4）（1）一次函数3y x =+与26y x =-+的图象的交点组成的集合；（2）二次函数24y x =-的函数值组成的集合；（3）反比例函数2y x=的自变量的值组成的集合. 解：（1）3{(,)|}{(1,4)}26y x x y y x =+⎧=⎨=-+⎩. （2）2{|4}{|4}y y x y y =-=≥-. （3）2{|}{|0}x y x x x ==≠.点评：以上代表元素，分别是点、函数值、自变量. 在解题中不能把点的坐标混淆为{1,4}，也注意对比（2）与（3）中的两个集合，自变量的范围和函数值的范围，有着本质上不同，分析时一定要细心.*【例4】已知集合2{|1}2x a A a x +==-有唯一实数解，试用列举法表示集合A ．A B B A A B A B A ． B ． C ． D ．解：化方程212x a x +=-为：2(2)0x x a --+=．应分以下三种情况： ⑴方程有等根且不是2±：由 △=0，得94a =-，此时的解为12x =，合． ⑵方程有一解为2，而另一解不是2-：将2x =代入得2a =-，此时另一解12x =-，合． ⑶方程有一解为2-，而另一解不是2：将2x =-代入得2a =，此时另一解为21x =+，合．综上可知，9{,2,2}4A =--．点评：运用分类讨论思想方法，研究出根的情况，从而列举法表示. 注意分式方程易造成增根的现象.第2讲 §1.1.2 集合间的基本关系¤知识要点：1. 一般地，对于两个集合A 、B ，如果集合A 中的任意一个元素都是集合B 中的元素，则说两个集合有包含关系，其中集合A 是集合B 的子集（subset ），记作A B ⊆（或B A ⊇），读作“A 含于B ”（或“B 包含A ”）.2. 如果集合A 是集合B 的子集（A B ⊆），且集合B 是集合A 的子集（B A ⊇），即集合A 与集合B 的元素是一样的，因此集合A 与集合B 相等，记作A B =.3. 如果集合A B ⊆，但存在元素x B ∈，且x A ∉，则称集合A 是集合B 的真子集（proper subset ），记作A ≠⊂B （或B ≠⊃A ）.4. 不含任何元素的集合叫作空集（empty set ），记作∅，并规定空集是任何集合的子集.5. 性质：A A ⊆；若A B ⊆，B C ⊆，则A C ⊆；若A B A =，则A B ⊆；若A B A =，则B A ⊆.¤例题精讲：【例1】用适当的符号填空：（1）{菱形} {平行四边形}； {等腰三角形} {等边三角形}.（2）∅ 2{|20}x R x ∈+=； 0 {0}； ∅ {0}； N {0}. 解：（1），；（2）=， ∈，，.【例2】设集合1,,}22{|,{|n n x n n A x x B x =∈=+∈==Z}Z ，则下列图形能表示A 与B 关系的是（）. 解：简单列举两个集合的一些元素，3113{,1,,0,,1,,}2222A =⋅⋅⋅---⋅⋅⋅，3113{,,,,,}2222B =⋅⋅⋅--⋅⋅⋅，易知B ≠⊂A ，故答案选A ．另解：由21,}2{|n x n B x +=∈=Z ，易知B ≠⊂A ，故答案选A ．【例3】若集合{}{}2|60,|10M x x x N x ax =+-==-=，且N M ⊆，求实数a 的值. 解：由26023x x x +-=⇒=-或，因此，{}2,3M =-.（i ）若0a =时，得N =∅，此时，N M ⊆；（ii ）若0a ≠时，得1{}N a =. 若N M ⊆,满足1123a a==-或，解得1123a a ==-或. 故所求实数a 的值为0或12或13-. 点评：在考察“A B ⊆”这一关系时，不要忘记“∅” ，因为A =∅时存在A B ⊆. 从而需要分情况讨论. 题中讨论的主线是依据待定的元素进行.【例4】已知集合A ={a ,a +b ,a +2b }，B ={a ,ax ,ax 2}. 若A =B ，求实数x 的值.解：若22a b ax a b ax+=⎧⎨+=⎩⇒a +ax 2-2ax =0, 所以a (x -1)2=0，即a =0或x =1. 当a =0时，集合B 中的元素均为0，故舍去；当x =1时，集合B 中的元素均相同，故舍去.若22a b ax a b ax⎧+=⎨+=⎩⇒2ax 2-ax -a =0. 因为a ≠0，所以2x 2-x -1=0, 即(x -1)(2x +1)=0. 又x ≠1，所以只有12x =-.经检验，此时A =B 成立. 综上所述12x =-.点评：抓住集合相等的定义，分情况进行讨论. 融入方程组思想，结合元素的互异性确定集合.第3讲 §1.1.3 集合的基本运算（一）¤知识要点：集合的基本运算有三种，即交、并、补，学习时先理解概念，并掌握符号等，再B （读作“B （读作“U A （读作“ ¤例题精讲：】设集合,{|15},{|39},,()U U R A x x B x x A B A B ==-≤≤=<<求解：在数轴上表示出集合A 、B ，如右图所示： {|35}A B x x =<≤，(){|1,9}U C A B x x x =<-≥或，【例2】设{|||6}A x Z x =∈≤，{}{}1,2,3,3,4,5,6B C ==，求：（1）()A B C ；（2）()A A B C .解：{}6,5,4,3,2,1,0,1,2,3,4,5,6A =------.（1）又{}3B C =，∴()A B C ={}3；（2）又{}1,2,3,4,5,6B C =，得{}()6,5,4,3,2,1,0A C B C =------. U∴ ()A A C B C {}6,5,4,3,2,1,0=------.【例3】已知集合{|24}A x x =-<<，{|}B x x m =≤，且A B A =，求实数m 的取值范围.解：由A B A =，可得A B ⊆.在数轴上表示集合A 与集合B ，如右图所示：由图形可知，4m ≥. 点评：研究不等式所表示的集合问题，常常由集合之间的关系，得到各端点之间的关系，特别要注意是否含端点的问题.【例4】已知全集*{|10,}U x x x N =<∈且，{2,4,5,8}A =，{1,3,5,8}B =，求()U C A B ，()U C A B ，()()U U C A C B ， ()()U U C A C B ，并比较它们的关系.解：由{1,2,3,4,5,8}A B =，则(){6,7,9}U C A B =.由{5,8}A B =，则(){1,2,3,4,6,7,9}U C A B =由{1,3,6,7,9}U C A =，{2,4,6,7,9}U C B =，则()(){6,7,9}U U C A C B =，()(){1,2,3,4,6,7,9}U U C A C B =.由计算结果可以知道，()()()U U U C A C B C A B =，()()()U U U C A C B C A B =.另解：作出Venn 图，如右图所示，由图形可以直接观察出来结果.点评：可用Venn 图研究()()()U U U C A C B C A B =与()()()U U U C A C B C A B = ，在理解的基础记住此结论，有助于今后迅速解决一些集合问题.第4讲 §1.1.3 集合的基本运算（二） ¤知识要点：1. 含两个集合的Venn 图有四个区域，分别对应着这两个集合运算的结果. 我们需通过Venn 图理解和掌握各区域的集合运算表示，解决一类可用列举法表示的集合运算. 通过图形，我们还可以发现一些集合性质：()()()U U U C A B C A C B =,()()()U U U C A B C A C B =.2. 集合元素个数公式：()()()()n A B n A n B n A B =+-.3. 在研究集合问题时，常常用到分类讨论思想、数形结合思想等. 也常由新的定义考查创新思维.¤例题精讲：【例1】设集合{}{}24,21,,9,5,1A a a B a a =--=--，若{}9A B =，求实数a 的值. 解：由于{}{}24,21,,9,5,1A a a B a a =--=--，且{}9A B =，则有：当219 a -＝时，解得5a ＝，此时={4, 9, 25}={9, 0, 4}A B －，－，不合题意，故舍去；当29a ＝时，解得33a ＝或－.3 ={4,5,9} ={9,2,2}a A B ＝时，－，－－，不合题意，故舍去；3={4, 7 9}={9, 8, 4}a A B ＝－，－－，，－，合题意.所以，3a ＝－.【例2】设集合{|(3)()0,}A x x x a a R =--=∈，{|(4)(1)0}B x x x =--=，求A B , A B .（教材P 14 B 组题2）解：{1,4}B =.当3a =时，{3}A =，则{1,3,4}A B =，A B =∅；当1a =时，{1,3}A =，则{1,3,4}A B =，{1}A B =；当4a =时，{3,4}A =，则{1,3,4}A B =，{4}A B =；-2 4 m x B A当3a ≠且1a ≠且4a ≠时，{3,}A a =，则{1,3,4,}A B a =，A B =∅.点评：集合A 含有参数a ，需要对参数a 进行分情况讨论. 罗列参数a 的各种情况时，需依据集合的性质和影响运算结果的可能而进行分析，不多不少是分类的原则.【例3】设集合A ={x |240x x +=}， B ={x |222(1)10x a x a +++-=，a R ∈}，若A B =B ，求实数a 的值．解：先化简集合A ={4,0}-. 由A B =B ，则B ⊆A ，可知集合B 可为∅，或为{0}，或{－4}，或{4,0}-.(i )若B =∅，则224(1)4(1)0a a ∆=+--<，解得a ＜1-；(ii )若0∈B ，代入得2a 1-=0⇒a =1或a =1-，当a =1时，B =A ，符合题意；当a =1-时，B ={0}⊆A ，也符合题意．(iii )若－4∈B ，代入得2870a a -+=⇒a =7或a =1，当a =1时，已经讨论，符合题意；当a =7时，B ={－12，－4}，不符合题意．综上可得，a =1或a ≤1-．点评：此题考查分类讨论的思想，以及集合间的关系的应用. 通过深刻理解集合表示法的转换，及集合之间的关系，可以把相关问题化归为解方程的问题，这是数学中的化归思想，是重要数学思想方法．解该题时，特别容易出现的错误是遗漏了A =B 和B =∅的情形，从而造成错误．这需要在解题过程中要全方位、多角度审视问题.【例4】对集合A 与B ，若定义{|,}A B x x A x B -=∈∉且，当集合*{|8,}A x x x N =≤∈，集合{|(2)(5)(6)0}B x x x x x =---=时，有A B -= . （由教材P 12 补集定义“集合A 相对于全集U 的补集为{|,}U C A x x x A =∈∉且”而拓展）解：根据题意可知，{1,2,3,4,5,6,7,8}A =，{0,2,5,6}B =由定义{|,}A B x x A x B -=∈∉且，则{1,3,4,7,8}A B -=.点评：运用新定义解题是学习能力的发展，也是一种创新思维的训练，关键是理解定义的实质性内涵，这里新定义的含义是从A 中排除B 的元素. 如果再给定全集U ，则A B -也相当于()U A C B .第5讲 §1.2.1 函数的概念¤知识要点：1. 设A 、B 是非空的数集，如果按某个确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有唯一确定的数y 和它对应，那么就称f ：A →B 为从集合A 到集合B 的一个函数（function ），记作y =()f x ，x A ∈．其中，x 叫自变量，x 的取值范围A 叫作定义域（domain ），与x 的值对应的y 值叫函数值，函数值的集合{()|}f x x A ∈叫值域（range ）.2. 设a 、b 是两个实数，且a <b ，则：{x |a ≤x ≤b }＝[a ,b ] 叫闭区间； {x |a <x <b }＝(a ,b ) 叫开区间；{x |a ≤x <b }＝[,)a b ， {x |a <x ≤b }＝(,]a b ，都叫半开半闭区间.符号：“∞”读“无穷大”；“－∞”读“负无穷大”；“+∞”读“正无穷大”. 则{|}(,)x x a a >=+∞，{|}[,)x x a a ≥=+∞，{|}(,)x x b b <=-∞，{|}(,]x x b b ≤=-∞，(,)R =-∞+∞.3. 决定函数的三个要素是定义域、值域和对应法则. 当且仅当函数定义域、对应法则分别相同时，函数才是同一函数.¤例题精讲：【例1】求下列函数的定义域：（1）121y x =+-；（2）y =.解：（1）由210x +-≠，解得1x ≠-且3x ≠-，所以原函数定义域为(,3)(3,1)(1,)-∞----+∞.（2）由3020x -≥⎧⎪≠，解得3x ≥且9x ≠，所以原函数定义域为[3,9)(9,)+∞.【例2】求下列函数的定义域与值域：（1）3254x y x+=-；（2）22y x x =-++. 解：（1）要使函数有意义，则540x -≠，解得54x ≠. 所以原函数的定义域是5{|}4x x ≠.32112813(45)233233305445445445444x x x y x x x x ++-+==⨯=⨯=-+≠-+=-----，所以值域为3{|}4y y ≠-. （2）22192()24y x x x =-++=--+. 所以原函数的定义域是R ，值域是9(,]4-∞. 【例3】已知函数1()1x f x x-=+. 求：（1）(2)f 的值；（2）()f x 的表达式解：（1）由121x x -=+，解得13x =-，所以1(2)3f =-. （2）设11x t x -=+，解得11t x t -=+，所以1()1t f t t -=+，即1()1x f x x -=+. 点评：此题解法中突出了换元法的思想. 这类问题的函数式没有直接给出，称为抽象函数的研究，常常需要结合换元法、特值代入、方程思想等. 【例4】已知函数22(),1x f x x R x =∈+. （1）求1()()f x f x+的值；（2）计算：111(1)(2)(3)(4)()()()234f f f f f f f ++++++. 解：（1）由2222222221111()()1111111x x x x f x f x x x x x x ++=+=+==+++++. （2）原式11117(1)((2)())((3)())((4)())323422f f f f f f f =++++++=+= 点评：对规律的发现，能使我们实施巧算. 正确探索出前一问的结论，是解答后一问的关键.第6讲 §1.2.2 函数的表示法¤知识要点：1. 函数有三种表示方法：解析法（用数学表达式表示两个变量之间的对应关系，优点：简明，给自变量可求函数值）；图象法（用图象表示两个变量的对应关系，优点：直观形象，反应变化趋势）；列表法（列出表格表示两个变量之间的对应关系，优点：不需计算就可看出函数值）.2. 分段函数的表示法与意义（一个函数，不同范围的x ，对应法则不同）.3. 一般地，设A 、B 是两个非空的集合，如果按某一个确定的对应法则f ，使对于集合A 中的任意一个元素x ，在集合B 中都有唯一确定的元素y 与之对应，那么就称对应:f A B →为从集合A 到集合B 的一个映射（mapping ）．记作“:f A B →”. 判别一个对应是否映射的关键：A 中任意，B 中唯一；对应法则f . ¤例题精讲：【例1】如图，有一块边长为a 的正方形铁皮，将其四个角各截去一个边长为x 的小正方形，然后折成一个无盖的盒子，写出体积V 以x 为自变量的函数式是_____，这个函数的定义域为_______．解：盒子的高为x ，长、宽为2a x －，所以体积为V ＝2(2)x a x －.又由20a x >－，解得2a x <.所以，体积V 以x 为自变量的函数式是2(2)V x a x =－，定义域为{|0}2a x x <<.【例2】已知f (x )=333322x x x x-⎧++⎪⎨+⎪⎩ (,1)(1,)x x ∈-∞∈+∞，求f [f (0)]的值. 解：∵ 0(,1)∈-∞， ∴ f (0)=32. 又 ∵ 32>1，∴ f (32)=(32)3+(32)-3=2+12=52，即f [f (0)]=52.【例3】画出下列函数的图象：（1）|2|y x =-；（教材P 26 练习题3）（2）|1||24|y x x =-++.解：（1）由绝对值的概念，有2,2|2|2,2x x y x x x -≥⎧=-=⎨-<⎩. 所以，函数|2|y x =-的图象如右图所示. （2）33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩，所以，函数|1||24|y x x =-++的图象如右图所示.点评：含有绝对值的函数式，可以采用分零点讨论去绝对值的方法，将函数式化为分段函数，然后根据定义域的分段情况，选择相应的解析式作出函数图象.【例4】函数()[]f x x =的函数值表示不超过x 的最大整数，例如[3.5]4-=-，[2.1]2=，当( 2.5,3]x ∈-时，写出()f x 的解析式，并作出函数的图象.解：3, 2.522,211,10()0,011,122,233,3x x x f x x x x x --<<-⎧⎪--≤<-⎪--≤<⎪=≤<⎨⎪≤<⎪≤<⎪=⎩. 函数图象如右：点评：解题关键是理解符号[]m 的概念，抓住分段函数的对应函数式.第7讲 §1.3.1 函数的单调性 ¤知识要点： 1. 增函数：设函数y =f (x )的定义域为I ，如果对于定义域I 内的某个区间D 内的任意两个自变量x 1，x 2，当x 1<x 2时，都有f (x 1)<f (x 2)，那么就说f (x )在区间D 上是增函数（increasingfunction ）. 仿照增函数的定义可定义减函数.2. 如果函数f (x )在某个区间D 上是增函数或减函数，就说f (x )在这一区间上具有（严格的）单调性，区间D 叫f(x )的单调区间. 在单调区间上，增函数的图象是从左向右是上升的（如右图1），减函数的图象从左向右是下降的（如右图2）. 由此，可以直观观察函数图象上升与下降的变化趋势，得到函数的单调区间及单调性.3. 判断单调性的步骤：设x 1、x 2∈给定区间，且x 1<x 2；→计算f (x 1)－f (x 2) →判断符号→下结论.¤例题精讲：【例1】试用函数单调性的定义判断函数2()1x f x x =-在区间（0，1）上的单调性. 解：任取12,x x ∈(0,1)，且12x x <. 则1221121212222()()()11(1)(1)x x x x f x f x x x x x --=-=----. 由于1201x x <<<，110x -<，210x -<，210x x ->，故12()()0f x f x ->，即12()()f x f x >.所以，函数2()1x f x x =-在（0，1）上是减函数. 【例2】求二次函数2()(0)f x ax bx c a =++<的单调区间及单调性. 解：设任意12,x x R ∈，且12x x <. 则22121122()()()()f x f x ax bx c ax bx c -=++-++221212()()a x x b x x =-+-1212()[()]x x a x x b =-++.若0a <，当122b x x a <≤-时，有120x x -<，12b x x a+<-，即12()0a x x b ++>，从而12()()0f x f x -<，即12()()f x f x <，所以()f x 在(,]2b a-∞-上单调递增. 同理可得()f x 在[,)2b a-+∞上单调递减. 【例3】求下列函数的单调区间：（1）|1||24|y x x =-++；（2）22||3y x x =-++.解：（1）33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩，其图象如右.由图可知，函数在[2,)-+∞上是增函数，在(,2]-∞-上是减函数.（2）22223,02||323,0x x x y x x x x x ⎧-++≥⎪=-++=⎨--+<⎪⎩，其图象如右. 由图可知，函数在(,1]-∞-、[0,1]上是增函数，在[1,0]-、[1,)+∞上是减函数.点评：函数式中含有绝对值，可以采用分零点讨论去绝对值的方法，将函数式化为分段函数. 第2小题也可以由偶函数的对称性，先作y 轴右侧的图象，并把y 轴右侧的图象对折到左侧，得到(||)f x 的图象. 由图象研究单调性，关键在于正确作出函数图象.第8讲 §1.3.1 函数最大（小）值 ¤知识要点： 1. 定义最大值：设函数()y f x =的定义域为I ，如果存在实数M 满足：对于任意的x ∈I ，都有()f x ≤M ；存在x 0∈I ，使得0()f x = M . 那么，称M 是函数()y f x =的最大值（Maximum Value ）. 仿照最大值定义，可以给出最小值（Minimum Value ）的定义.2. 配方法：研究二次函数2(0)y ax bx c a =++≠的最大（小）值，先配方成224()24b ac b y a x a a -=++后，当0a >时，函数取最小值为244ac b a-；当0a <时，函数取最大值244ac b a-. 3. 单调法：一些函数的单调性，比较容易观察出来，或者可以先证明出函数的单调性，再利用函数的单调性求函数的最大值或最小值.4. 图象法：先作出其函数图象后，然后观察图象得到函数的最大值或最小值. ¤例题精讲：【例1】求函数261y x x =++的最大值. 解：配方为2613()24y x =++，由2133()244x ++≥，得260813()24x <≤++. 所以函数的最大值为8.【例2】某商人如果将进货单价为8元的商品按每件10元售出时，每天可售出100件. 现在他采用提高售出价，减少进货量的办法增加利润，已知这种商品每件提价1元，其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚得的利润最大？并求出最大利润.解：设他将售出价定为x 元，则提高了(10)x -元，减少了10(10)x -件，所赚得的利润为(8)[10010(10)]y x x =---.即2210280160010(14)360y x x x =-+-=--+. 当14x =时，max 360y =.所以，他将售出价定为14元时，才能使每天所赚得的利润最大, 最大利润为360元.【例3】求函数21y x x =+-的最小值.解：此函数的定义域为[)1,+∞，且函数在定义域上是增函数，所以当1x =时，min 2112y =+-=，函数的最小值为2.点评：形如y ax b cx d =+±+的函数最大值或最小值，可以用单调性法研究，也可以用换元法研究.【另解】令1x t -=，则0t ≥，21x t =+，所以22115222()48y t t t =++=++，在0t ≥时是增函数，当0t =时，min 2y =，故函数的最小值为2.【例4】求下列函数的最大值和最小值：（1）25332,[,]22y x x x =--∈-；（2）|1||2|y x x =+--.解：（1）二次函数232y x x =--的对称轴为2b x a =-，即1x =-.画出函数的图象，由图可知，当1x =-时，max 4y =；当32x =时，min 94y =-. 所以函数25332,[,]22y x x x =--∈-的最大值为4,最小值为94-. （2） 3 (2)|1||2|2 1 (12)3 (1)x y x x x x x ≥⎧⎪=+--=--<<⎨⎪-≤-⎩.作出函数的图象，由图可知，[3,3]y ∈-. 所以函数的最大值为3, 最小值为-3. 点评：二次函数在闭区间上的最大值或最小值，常根据闭区间与对称轴的关系，结合图象进行分析. 含绝对值的函数，常分零点讨论去绝对值，转化为分段函数进行研究. 分段函数的图象注意分段作出.第9讲 §1.3.2 函数的奇偶性¤知识要点：1. 定义：一般地，对于函数()f x 定义域内的任意一个x ，都有()()f x f x -=，那么函数()f x 叫偶函数（even function ）. 如果对于函数定义域内的任意一个x ，都有()()f x f x -=-），那么函数()f x 叫奇函数（odd function ）.2. 具有奇偶性的函数其定义域关于原点对称，奇函数的图象关于原点中心对称，偶函数图象关于y 轴轴对称.3. 判别方法：先考察定义域是否关于原点对称，再用比较法、计算和差、比商法等判别()f x -与()f x 的关系.¤例题精讲：【例1】判别下列函数的奇偶性：（1）31()f x x x=-；（2）()|1||1|f x x x =-++；（3）23()f x x x =-.解：（1）原函数定义域为{|0}x x ≠，对于定义域的每一个x ，都有3311()()()()f x x x f x x x -=--=--=--，所以为奇函数. （2）原函数定义域为R ，对于定义域的每一个x ，都有()|1||1||1||1|()f x x x x x f x -=--+-+=-++=，所以为偶函数.（3）由于23()()f x x x f x -=+≠±，所以原函数为非奇非偶函数.【例2】已知()f x 是奇函数，()g x 是偶函数，且1()()1f x g x x -=+，求()f x 、()g x . 解：∵ ()f x 是奇函数，()g x 是偶函数，∴ ()()f x f x -=-，()()g x g x -=.则1()()11()()1f x g x x f x g x x ⎧-=⎪⎪+⎨⎪---=⎪-+⎩，即1()()11()()1f x g x x f x g x x ⎧-=⎪⎪+⎨⎪--=⎪-+⎩. 两式相减，解得2()1x f x x =-；两式相加，解得21()1g x x =-.。

期末考试第一单元复习卷【新教材】2020-2021学年人教版(2019)高一上学期生物必修一

高一生物期末复习（第一章）班级姓名一、选择题1．细胞是生命活动的基本单位。

下列选项中不能够支持这一说法的是（）A．草履虫是单细胞生物，能进行运动和分裂B．人体发育离不开细胞的分裂和分化C．离体的叶绿体在一定的条件下能释放氧气D．用手抓握物体需要一系列神经细胞和肌肉细胞的协调配合2．下列有关原核细胞的叙述，错误的是（）A．没有核膜包被的细胞核，有染色质B．蓝细菌细胞内含有叶绿素和藻蓝素C．蓝细菌有细胞壁，但其化学成分与植物细胞细胞壁不同D．原核细胞与真核细胞具有统一性3．新冠病毒是一种RNA病毒，由它引起的新冠肺炎严重威胁全世界人民的生命安全。

下列关于该病毒的叙述，正确的是（）A．新冠病毒没有细胞结构，在分类上属于原核生物B．新冠病毒属于最基本的生命系统C．新冠病毒唯一的细胞器是核糖体D．新冠病毒只能在活细胞中增殖4．细胞学说的创立是生物学发展史上的一个里程碑，被恩格斯列为19世纪自然科学三大发现之一。

下列关于细胞学说内容及意义的描述，错误的是（）A．细胞学说认为细胞是一个有机体B．细胞学说认为新细胞是由老细胞分裂产生的C．细胞学说揭示了动物和植物的统一性D．细胞学说阐明了生物界与非生物界的统一性5．正在肆虐全球的新冠病毒肺炎（COVID-19）是由新型冠状病毒（2019-nCoV）引起的。

该病原体是一种RNA病毒。

下列有关该病毒的叙述，错误的是（）A．该病毒的遗传物质的元素组成有5种B．该病毒属于原核生物C．该病毒的蛋白质组成单位是氨基酸D．该病毒进入人体后，可在肺部细胞中增殖6．下列关于细胞与生命活动关系的叙述，错误的是（）A．引起新型冠状病毒肺炎的病原体无细胞结构，所以其生命活动与细胞无关B．绿藻、酵母菌、草履虫等单细胞生物，只靠一个细胞就可以完成摄食、运动、分裂等多种生命活动C．缩手反射和膝跳反射的完成均需要多种细胞的密切合作D．一切生物的生命活动都在细胞内或细胞参与下完成7．T2噬菌体是一种DNA病毒，有关该病毒的叙述，正确的是（）A．T2噬菌体含DNA和RNA B．T2噬菌体不具有细胞核C．T2噬菌体属于自养型生物D．T2噬菌体能独立合成自身蛋白8．一位动物学家正在研究一种驯鹿的千里踏雪大迁徙行为；一位果树专家正在研究某种果树的丰产措施。

第一章知识点总结高一上学期生物人教版(2019)必修1

生物学必修一第1章知识点总结1.1 细胞是生命活动的基本单位一、细胞学说1. 建立者：和2. 内容：（1）细胞是一个有机体，一切都由细胞发育而来，并由和所构成。

（2）细胞是一个的单位，既有它自己的生命，又能与其他细胞共同组成整体的生命。

（3）新细胞是由老细胞产生。

3．建立过程（连线）a维萨里①用显微镜观察植物的木栓组织，发现并命名细胞b比夏②建立了细胞学说c罗伯特•胡克③通过尸体解剖研究，揭示了人体在器官水平的结构d列文虎克④提出细胞通过分裂产生新细胞，指出所有的细胞都来源于先前存在的细胞e施莱登和施旺⑤通过对器官的解剖观察，指出器官由组织构成f魏尔肖⑥用自制显微镜观察到了细菌、红细胞、精子等活细胞4、科学方法—（包括完全归纳法和不完全归纳法，施莱登和施旺运用的是）5. 意义（细胞学说被恩格斯列为19世纪自然科学三大发现之一）（1）细胞学说揭示了动物和植物的，从而阐明了生物界的；（2）细胞学说使人们认识到植物和动物有着共同的结构基础，打破了之间的壁垒，使解剖学、生理学、胚胎学等学科获得了共同的基础；（2）使生物学的研究进入水平；（3）为后来的确立埋下了伏笔二、细胞是基本的生命系统1、生命活动与细胞的关系（1）单细胞生物依靠独立完成各项生命活动；（2）多细胞生物依赖密切合作，共同完成生命活动（3）病毒细胞结构，必须在细胞中【结论】是生命活动的基本单位；生命活动离不开。

2、生命系统的结构层次细胞→_________→__________→系统→_________→_________→群落→_____________→生物圈【注意】（1）植物没有这一层次；（2）对单细胞生物而言，一个细胞就是一个，因此没有等层次。

（3）生态系统包括生物群落和；（4）最基本/最小的生命系统是；（5）最大的生命系统是。

（5）分子、原子或病毒等都生命系统1.2 细胞的多样性和统一性一、细胞的多样性和统一性（1）细胞的多样性体现在不同细胞的和不同（2）细胞的统一性体现在细胞都有相似的，如细胞膜、细胞质和细胞核二、真核细胞和原核细胞真核细胞与原核细胞的本质区别是：【注】1、如何判断某种菌是细菌：①带“杆”、“球”、“弧”、“螺旋”的都是细菌；②蓝细菌（旧称蓝藻）也属于细菌，如色球蓝细菌、颤蓝细菌、念珠蓝细菌、发菜等；1、细菌中的多数种类是营腐生或生活的生物；2、蓝细菌细胞内含有和，是能进行光合作用的生物（蓝细菌细胞内叶绿体）。

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

威客日付网
[名词解释]复果 [单选]用于连接不同网络的网络设置是（）A.主机B.网卡C.网关D.集中器 [单选,A1型题]寒痰凝滞胸阳不宣之胸痹痛，首选（）A.川楝子B.桂枝C.陈皮D.薤白E.木香 [问答题,简答题]国务院药品监督管理部门负责那些剂型的认证？ [问答题,论述题]什么情况下采用阀门定位器？ [单选]三（四）等水准测量时，尺子的两面都要读数，读数次序为后前前后或（）。A.前后前后B.前前后后C.后前后前D.后后前前 [单选]关于液压调速器的下述叙述中，错误的是（）。A．具有广阔的调速范围B．稳定性好，调节精度与灵敏度高C．它利用飞重离心力直接拉动油量调节机构D．广泛用于大中型柴油机 [问答题,简答题]我国某沿海城市某建设工程项目承包合同形式为采用工程量清单计价的主体总承包总价合同，其工程量清单某章节中包括如下内容：（1）对安装玻璃幕墙工程之指定分包暂定造价RMB1500000.00元，总承包单位对上述工程提供协调及施工设施的配合费用45000.00元。（2）对外围 [多选]下列关于携带伴侣动物出入境说法正确的有（）。A.最多可以携带两只伴侣动物出入境B.出境时持县级以上检疫部门出具的有关证书向检验检疫机构申报C.口岸检验检疫机构对伴侣动物在指定场所进行为期45天的隔离检疫D.进境时向海关申报，并持有输出国或地区官方出具的检疫证书及相 [单选]按照滑行理论，安静时阻碍肌纤蛋白同横桥结合的物质是A．肌凝蛋白B．原肌凝蛋白C．肌钙蛋白ⅡD．肌钙蛋白IE．肌纤蛋白 [单选]涂尔干提出社会学研究七个准则的著作是（）A.《论法的精神》B.《社会学研究方法论》C.《社会体系》D.《社会过程》 [单选]港口与航道工程的技术交底应当做到（）。A.技术交底要填写技术交底记录单B.正式施工前要一次全面交底完毕C.将施工组织设计的主要方案交待清楚D.项目部技术人员清楚设计意图 [单选]以下不属于各级人民法院职权范围内的信访事项的是（）。A.对人民法院工作的建议、批评和意见B.对人民法院工作人员的违法失职行为的报案、申诉、控告或者检举C.对人民法院生效判决、裁定、调解和决定不服的申诉D.对人民法院审判活动中的违法行为的控告或者检举 [单选]关于行政责任的种类的划分方法不包括划分为（）。A.国家侵权责任和国家合同责任B.惩罚性行政责任和补救性行政责任C.制裁性行政责任、强制性行政责任和补救性行政责任D.行政许可责任和行政强制执行责任 [单选,A1型题]不属于促进慢性肾炎恶化因素的是（）A.肾脏基础病变活动B.高脂血症C.高蛋白质饮食D.高血压E.遗传因素 [单选,A2型题,A1/A2型题]当中心体温降到多少度时，肌肉由颤抖变为僵直，失去产热的作用，将会发生死亡（）。A.30～33℃B.32～34℃C.30℃以下D.28～31℃E.0℃ [单选]一个团体旅客，其中有40个成人，10个儿童（均应购买儿童票），按照对团体旅客优惠办法的规定，应购买（）。A、36个成人票，10个儿童票B、38个成人票，8个儿童票C、37个成人票，10个儿童票D、40个成人票，6个儿童票 [多选]下列有关行政法规的说法哪些是正确的？（）A.省、自治区、直辖市人民政府认为需要制定行政法规的，应当在每年年初编制国务院立法工作计划前，向国务院报请立项B.起草行政法规，在赋予行政机关必要的职权的同时，应当规定行政机关行使职权的程序C.起草行政法规，涉及有关管理 [单选]直连螺旋桨并装有极限调速器的船舶主机运转中，当油门一定时，若海面阻力增加，主机的运转工况变化是（）。A．转速降低后稳定工作B．增大供油后稳定工作C．转速增加后稳定工作D．视海面阻力变化大小而定 [单选]WAIS-RC适用于（）岁以上的受测者。A.15B.16C.17D.18 [单选,A2型题,A1/A2型题]结核性脑膜炎的炎性渗出物多聚集于（）.A.大脑表面B.小脑周围C.脑底部D.脊髓膜E.脑室内 [单选]抵押权的实现方式不包括（）。A、拍卖B、变卖C、折价D、在债务履行期届满前，抵押权人与抵押人约定债务人不履行到期债务时抵押财产归债权人所有 [单选]产褥期保健重点不包括以下哪几项（）。A.注意产妇情绪变化B.采用孕产妇营养膳食C.注射乙肝疫苗D.指导母乳喂养E.注意卫生 [单选]何处病变可见肌纤维震颤（）A.肌病B.神经肌肉结合部位C.前角细胞D.上运动神经元病变E.锥体外系统 [单选]某患者进食后发生恶心、呕吐、腹泻。如果在患者粪便标本中分离到一种菌，革兰染色阴性；其生化反应结果是：氧化酶(+)，蔗糖(-)，动力(+)，吲哚(+)，脲酶(-)。则该菌可能是()A．福氏志贺菌B．霍乱弧菌C．大肠埃希菌0157:H7D．副溶血弧菌E．蜡样芽胞杆菌 [单选,A2型题,A1/A2型题]血浆中分子量最大的蛋白质是（）.AACB.HpC.AMGD.CERE.CRP [单选]Battle征是指（）A.颅后窝骨折引起的脑脊液耳漏B.颅中窝底骨折引起的脑脊液鼻漏和耳漏C.颅前窝底骨折引起的眼眶周围的青紫和肿胀D.颅后窝骨折引起的迟发性乳突部皮下淤血斑E.颅中窝底骨折引起的搏动性突眼和颅内血管杂音 [填空题]电梯轿厢运行至上端站，碰下上强迫减速开关，则电梯（）. [单选]锅炉运行时，炉膛可能产生瞬时的压力波动。为了抑制由此而产生的误动作，可在炉膛压力检测时增加（）环节。A、阻尼；B、迟延；C、前馈；D、以上答案都对 [单选]对银行贷款集中度的监管属于（）。A.预防性监管B.援救性监管C.事后补救措施D.机构监管 [单选]与肝细胞癌关系最密切的是（）A.甲型病毒性肝炎B.乙型病毒性肝炎C.戊型病毒性肝炎D.自身免疫性肝炎E.黄疸性肝炎 [问答题,简答题]现场抓斗的检查要点及故障维修。 [单选]目前承担消防产品合格评定的评价机构是（）。A、公安部消防局B、各省、直辖市、自治区公安消防总队C、国家消防产品质量监督检验中心D、公安部消防产品合格评定中心 [单选]农村集体经济审计是基于我国农村（）而产生的一种特殊的审计形式。A.集体所有制B.全民所有制C.股份合作制D.双层经营体制 [单选,A2型题,A1/A2型题]呈小管结构，内含造牙本质细胞芽突的为（）A.牙釉质B.牙本质C.牙骨质D.牙髓E.牙周膜 [单选,A2型题,A1/A2型题]后鼻孔填塞纱球的底部留置丝线主要作用是（）。A.固定纱球B.取出纱球时牵引用C.填塞纱球时牵拉纱球用D.固定于前鼻孔牵拉纱球用E.以上均不正确 [单选]（）是指订货前的库存原料存量。A.期末需存量B.下期需用量C.现有库存量D.日平均消耗量 [问答题,简答题]新建抄表段应注意哪些事项？ [单选]根据所有观测点在堤防上的平面位置和累计沉降量可绘制成（）。A.堤防沉降量平面分布图B.堤防横断面图C.堤防平面图D.堤防纵断面图 [单选]用于承受主要负荷和较强连续振动的设备的垫铁为()。A．成对斜垫铁

必修1第一章复习[上学期]新人教版

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

最新人教版高一数学必修1第一章《复习》教案

人教版高中数学必修1-第一章知识点知识点归纳[最新版]

新人教版高一生物必修一知识点复习总结

最新人教版高一数学上册必修1第一章知识点总结

高一上化学人教版必修第一册期末知识点复习总结

人教版教学课件-新人教[原创]必修1第一章总复习

人教版(新教材)高中数学第一册(必修1)精品课件：第一章集合与常用逻辑用语章末复习课

人教版高中数学必修一第一章知识点

高一化学必修一第一章重难点：离子反应[新人教版]

人教版高一数学上册第一章复习要点

最新人教版高一数学必修1第一章《复习》教案

人教版高一地理必修一第一章复习(共158张PPT)

人教版高中数学必修一第一章知识点

人教版高一数学必修一第一章-知识点与习题讲解

期末考试第一单元复习卷【新教材】2020-2021学年人教版(2019)高一上学期生物必修一

第一章知识点总结高一上学期生物人教版(2019)必修1

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

必修1第一章复习[上学期]新人教版

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

最新人教版高一数学必修1第一章《复习》教案

人教版高中数学必修1-第一章知识点知识点归纳[最新版]

新人教版高一生物必修一知识点复习总结

最新人教版高一数学上册必修1第一章知识点总结

高一上化学人教版必修第一册期末知识点复习总结

人教版教学课件-新人教[原创]必修1第一章总复习

人教版(新教材)高中数学第一册(必修1)精品课件：第一章集合与常用逻辑用语章末复习课

人教版高中数学必修一第一章知识点

高一化学必修一第一章重难点：离子反应[新人教版]

人教版高一数学上册第一章复习要点

最新人教版高一数学必修1第一章《复习》教案

人教版高一地理必修一第一章复习(共158张PPT)

人教版高中数学必修一第一章知识点

人教版高一数学必修一第一章-知识点与习题讲解

期末考试第一单元复习卷【新教材】2020-2021学年人教版(2019)高一上学期生物必修一

第一章知识点总结 高一上学期生物人教版(2019)必修1

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

第一章知识点总结高一上学期生物人教版(2019)必修1