安徽较难点专题:圆中的动点问题及最值问题(选做).ppt
合集下载
2020年安徽中考备考复习课件:选择压轴之几何最值问题(共33张PPT)

若是纯几何的问题,我们则可以将面积利用公式表示出来,然后转化成高或者底的最值,也就是 转化成单线段的最值问题,从而求解。
类型5 “胡不归”问题
典例分析
例6、如图,菱形ABCD中,∠ABC=60°,边长为3,P是对角线BD上的一个动点,则 1 BP+PC的
2
最小值是( )
A. 3
C. 3
B. 3 3
大,即四边形 MANB 的面积最大
类型4 “几何图形面积最值”问题
举一反三
练4-1、如图,点E为边长为8的等边△ABC的BC边上一动点(点E不与B、C重合),以AE为边作等边
△AEF,则△AEF面积的最小值是( )
A.4
B. 8
C.2 3
D. 6 3
类型4 “几何图形面积最值”问题
举一反三
练4-2、如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l, 过点A,B分别作直线l的垂线,垂足分别为点D、C,则四边形ABCD的面积的最大值为( )
▶见定角→找对边(定长)→想“周”角→转“心”角→现“圆”形
【解析】根据已知条件分析得到点 P 在以 AB 为直径的圆上,根据圆的相关性质即可求得 CP 的长的 最小值.故选 B
类型2 “定角对定边”问题
举一反三
练2-1、△ABC中,∠ACB=90°,AC=2,BC=1.点A、C分别在x轴和y轴的正半轴上,当点A在x轴上 运动时,点C也随之在y轴上运动.在整个运动过程中,则点B到原点的最大距离是( )
A.0
B.4
C.6
D.8
【解析】利用轴对称可求出PE+PF的最小值,再分别求出点P与点C、点P与点D重合时PE+PF的值,将其 与9进行比较,根据正方形的对称性即可找出满足条件的点P的个数.所以选D.
类型5 “胡不归”问题
典例分析
例6、如图,菱形ABCD中,∠ABC=60°,边长为3,P是对角线BD上的一个动点,则 1 BP+PC的
2
最小值是( )
A. 3
C. 3
B. 3 3
大,即四边形 MANB 的面积最大
类型4 “几何图形面积最值”问题
举一反三
练4-1、如图,点E为边长为8的等边△ABC的BC边上一动点(点E不与B、C重合),以AE为边作等边
△AEF,则△AEF面积的最小值是( )
A.4
B. 8
C.2 3
D. 6 3
类型4 “几何图形面积最值”问题
举一反三
练4-2、如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l, 过点A,B分别作直线l的垂线,垂足分别为点D、C,则四边形ABCD的面积的最大值为( )
▶见定角→找对边(定长)→想“周”角→转“心”角→现“圆”形
【解析】根据已知条件分析得到点 P 在以 AB 为直径的圆上,根据圆的相关性质即可求得 CP 的长的 最小值.故选 B
类型2 “定角对定边”问题
举一反三
练2-1、△ABC中,∠ACB=90°,AC=2,BC=1.点A、C分别在x轴和y轴的正半轴上,当点A在x轴上 运动时,点C也随之在y轴上运动.在整个运动过程中,则点B到原点的最大距离是( )
A.0
B.4
C.6
D.8
【解析】利用轴对称可求出PE+PF的最小值,再分别求出点P与点C、点P与点D重合时PE+PF的值,将其 与9进行比较,根据正方形的对称性即可找出满足条件的点P的个数.所以选D.
2022安徽中考数学压轴题分析1:动点轨迹与最值问题
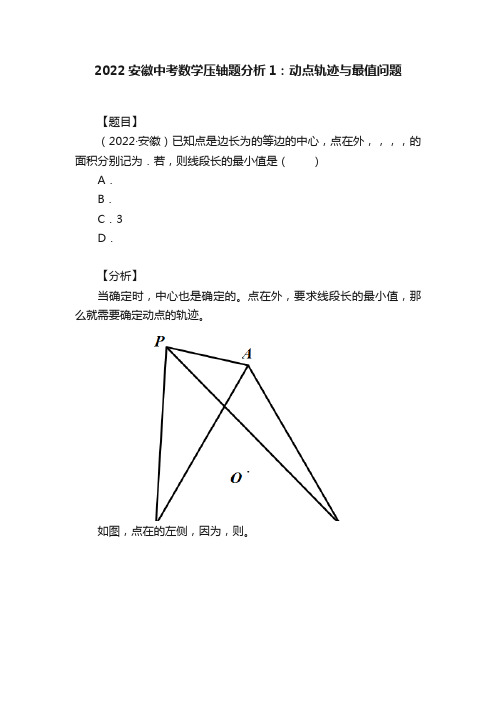
2022安徽中考数学压轴题分析1:动点轨迹与最值问题
【题目】
(2022·安徽)已知点是边长为的等边的中心,点在外,,,,的面积分别记为.若,则线段长的最小值是()
A.
B.
C.3
D.
【分析】
当确定时,中心也是确定的。
点在外,要求线段长的最小值,那么就需要确定动点的轨迹。
如图,点在的左侧,因为,则。
根据三角形的面积公式,可以得到点到的距离为的高的一半。
如图,过点作,垂足为。
因为等边的边长为,所以高为,那么可以得到。
此时可以得到点的轨迹为与平行且相等的线段,过点作该线段的垂线,得到点到该线段的距离,即为此时长的最小值为。
那么只能在该线段上面运动吗?当然不是,往两边分别延长的各边,可以把外的平面分为个区域,所以还需要进行分类讨论,最终确定的最小值。
如图,点的运动路径为六边形,当点在区域①、②和③时,最小
值为。
综上所述,可以得到的最小值为,故答案选择B。
【答案】B
【总结】
本题的关键在于确定点P的轨迹,由于点P到定直线的距离为定值,可以判断其运动路径为线段,轨迹为直线型。
更多动点轨迹问题请看《中考数学压轴题全解析·解答题》12.3第318页。
安徽省2023中考数学第6章圆课件

定理 一条弧所对的圆周角等于它所对的圆心角的⑪
.
常见 图形
结论
∠ACB=⑫
1.在同圆或等圆中,同弧或等弧所对的圆周角⑬
,相等的
圆
周角所对的弧也相等.
推论
2.半圆或直径所对的圆周角是⑭
;90°的圆周角所对的弦
考点4 圆周角定理及其推论
方法指导
根据圆周角定理的推论,涉及直径时,可构造直径所对的圆周角是直角来 进行证明或计算.
考点5 圆内接四边形的概念和定理
一个四边形的四个顶点都在同
一个圆上,这个四边形叫做圆 概念
的内接四边形,这个圆叫做这
个四边形的外接圆.
圆内接四边形的对角⑯
∠A+∠BCD=⑱
,
定理 ,且任何一个外角都等于它的 ∠B+∠D=⑲
,
⑰
.
∠DCE=⑳
方法帮
命题角度1 圆周角定理及其推论
例1 [2021 湖北宜昌]如图,C,D是☉O上直径AB两侧的两点.若∠ABC=25°,则
2.圆的有关概念
同心圆 圆心相同、半径不同的圆叫做同心圆.
等圆 能够重合的两个圆叫做等圆.
圆的任意一条① 半圆 圆.
的两个端点把圆分成两条弧,每一条弧都叫做半
圆上任意两点间的部分叫做圆弧,简称弧,用符号“⌒”表示.大于半圆
弧 的弧叫做②
,如 ;小于半圆的弧叫做③
,如 .
考点1 与圆有关的概念
等弧 在同圆或等圆中,能够互相重合的弧叫做等弧.
例1 如图,在▱ABCD中,∠BCD=30°,BC=4,CD=3,M是AD边的中点,N是AB边上一动点,
将△AMN沿MN所在直线翻折得到△PMN,连接PC,则PC长度的最小值是
2020安徽中考数学专题复习(二):几何图形动点问题PPT下载

2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
例3 如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是
AD上一点,且MD=1,P是BC上一动点,则PM-PO的最大值为( A )
13
例5题解图
2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
模型三 “两点两线”型(两动点+两定点) 【问题】点P、Q是∠AOB的内部两定点,在OA上找点M,在OB上找点N,使 得四边形PQNM周长最小. 【解决思路】要使四边形PQNM周长最小,PQ为定值,即求得PM+MN+NQ 的最小值即可,需将线段PM,MN,NQ三条线段尽可能转化在一条直线上, 因此想到作点P关于OA的对称点,点Q关于OB的对称点.
例4 (2019陕西)如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的
中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为
___2_____.
【解析】如解图,∵四边形ABCD为正方形,∴AB和CB关于对角
线BD对称,作点M关于BD对称的点M′,则点M′在AB上,连接
类型一 最值问题
[2017、2016.10,2015.20,2011.22(3)]
一、利用垂线段最短求线段最值
【问题】A为直线m外一点,求点A到直线m的最短距离. 【解决思路】过点A作AP⊥m,此时点A到直线m的距离最短,即AP的长.
例 如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,点P是边BC上一动点, PE⊥AB,PF⊥AC,垂足分别为点E、F,连接EF,若点M为EF的中点,连接MP, 则PM的最小值是( A )
2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
例3 如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是
AD上一点,且MD=1,P是BC上一动点,则PM-PO的最大值为( A )
13
例5题解图
2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
2020安徽中考数学专题复习(二): 几何图 形动点 问题PPT 下载
模型三 “两点两线”型(两动点+两定点) 【问题】点P、Q是∠AOB的内部两定点,在OA上找点M,在OB上找点N,使 得四边形PQNM周长最小. 【解决思路】要使四边形PQNM周长最小,PQ为定值,即求得PM+MN+NQ 的最小值即可,需将线段PM,MN,NQ三条线段尽可能转化在一条直线上, 因此想到作点P关于OA的对称点,点Q关于OB的对称点.
例4 (2019陕西)如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的
中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为
___2_____.
【解析】如解图,∵四边形ABCD为正方形,∴AB和CB关于对角
线BD对称,作点M关于BD对称的点M′,则点M′在AB上,连接
类型一 最值问题
[2017、2016.10,2015.20,2011.22(3)]
一、利用垂线段最短求线段最值
【问题】A为直线m外一点,求点A到直线m的最短距离. 【解决思路】过点A作AP⊥m,此时点A到直线m的距离最短,即AP的长.
例 如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,点P是边BC上一动点, PE⊥AB,PF⊥AC,垂足分别为点E、F,连接EF,若点M为EF的中点,连接MP, 则PM的最小值是( A )
(新版)安徽省中考数学复习安徽中考重难题型精讲练PPT优质公开课

题型二 几何图形动点问题
类型一 线段最值问题
(10年4考:2017、2016年10题,2015、2011年分别在20题、22题中涉及考查)
典例精讲
一、利用垂线段最短求线段的最值 例1 (2019 安顺改编)如图,在Rt△ABC中,∠BAC=90°,且AB=3,AC= 4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点 N,连接MN,则线段MN的最小值为( )
∵S四边形MANB=S△AMB+S△ANB,∴要使四边形MANB面积最大,则需两个三角形
的高的和最大,当MN为直径时,高最大,四边形MANB面积有最大值,易得
MN⊥AB,∴S四边形MANB的最大值=
1 2
·AB·MN= 1
2
×2
2
×4=4
2
.
【答案】D
例4题解图
题型二 几何图形动点问题
类型三 特定条件问题
A. 5 B.1 5 C. 2 0 D. 1 2
2
2
3
5
例1题图
题型二 几何图形动点问题
【思维教练】分析题干利用已知条件可得四边形AMDN是矩形,根据矩形性质
MN=AD,将求MN的最小值转化为求AD的最小值,再利用垂线段最短即可求
AD的最小值.
【解析】如解图所示,连接AD,∵∠BAC=90°,DM⊥AB,DN⊥AC,∴四边
几何图形动点问题
题型二 几何图形动点问题
满分技法 1. 确定动点轨迹 (1)动点的轨迹为直线:①动点到两定点的距离相等(垂直平分线);②动点到两相 交直线的距离相等(角平分线);③动点和两定点组成的三角形的面积与共底边的 另一三角形面积之间存在倍分关系; (2)动点的轨迹为圆:①以动点为顶点的角为90°(直径所对的圆周角等于90°); ②以动点为顶点的角等于定角的一半(同弧所对的圆周角等于它所对的圆心角的一 半);③一组角相等(同弧所对的圆周角相等;过切点的弦与切线的夹角等于这条 弦所对的圆周角);④到定点的长度相等(如绕某一点旋转,折叠等);⑤与三个定 点组成的四边形的对角和为180°.
