第八章 北航 材料力学 全部课件 习题答案
《材料力学》第八章课后习题参考答案

解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析, 明确各力的大小和方向,以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题,可以画出 相应的示意图或变形图,帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式,能够 准确应用公式进行计算和分析。
检查结果
在解题完成后,要对结果进行检查和 验证,确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题,明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件,选用相应的公式 进行计算。
注意单位换算
在计算过程中,要注意各物理量的单位换算, 确保计算结果的准确性。
检查答案合理性
得出答案后,要检查其是否符合实际情况和 物理规律,避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合,如弯曲与扭转 的组合、拉伸与压缩的组合等,需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构,需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ,需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ,需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。
《材料力学》第8章-组合变形及连接部分的计算-习题解
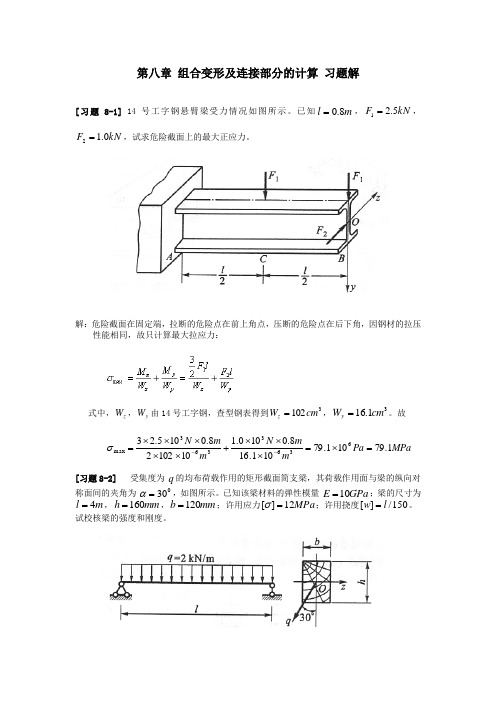
第八章 组合变形及连接部分的计算 习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。
已知m l 8.0=,kN F 5.21=,kN F 0.12=,试求危险截面上的最大正应力。
解:危险截面在固定端,拉断的危险点在前上角点,压断的危险点在后下角,因钢材的拉压性能相同,故只计算最大拉应力:式中,z W ,y W 由14号工字钢,查型钢表得到3102cm W z =,31.16cm W y =。
故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁,其荷载作用面与梁的纵向对称面间的夹角为 030=α,如图所示。
已知该梁材料的弹性模量 GPa E 10=;梁的尺寸为m l 4=,mm h 160=,mm b 120=;许用应力MPa 12][=σ;许用挠度150/][l w =。
试校核梁的强度和刚度。
解:(1)强度校核)/(732.1866.0230cos 0m kN q q y =⨯== (正y 方向↓))/(15.0230sin 0m kN q q z =⨯== (负z 方向←))(464.34732.1818122m kN l q M y zmaz ⋅=⨯⨯== 出现在跨中截面)(241818122m kN l q M z ymaz ⋅=⨯⨯== 出现在跨中截面)(5120001601206161322mm bh W z =⨯⨯==)(3840001201606161322mm hb W y =⨯⨯==最大拉应力出现在左下角点上:yy z z W M W M maxmax max +=σ MPa mmmm N mm mm N 974.1138400010251200010464.33636max=⋅⨯+⋅⨯=σ因为 MPa 974.11max =σ,MPa 12][=σ,即:][max σσ<所以 满足正应力强度条件,即不会拉断或压断,亦即强度上是安全的。
北航材料力学课后习题答案

σ max = 117MPa (在圆孔边缘处)
2-15 图示桁架,承受载荷 F 作用,已知杆的许用应力为[σ ]。若在节点 B 和 C 的
位置保持不变的条件下,试确定使结构重量最轻的α 值(即确定节点 A 的最佳位置)。
解:1.求各杆轴力
题 2-15 图
设杆 AB 和 BC 的轴力分别为 FN1 和 FN2 ,由节点 B 的平衡条件求得
分别为
FN
=
1 2
σmax A
=
1 2
× (100 ×106 Pa) × (0.100m × 0.040m)
=
2.00 ×105 N
=
200kN
Mz
=
FN
(
h 2
−
h )
3
=பைடு நூலகம்
1 6
FN h
=
1 × (200 ×103 N) × (0.100m) 6
= 3.33×103 N ⋅ m
=
3.33kN ⋅ m
2-5 .........................................................................................................................................................2
= 0.2 ×10−3 m 0.100m
= 2.00 ×10−3
rad
α AB
= 0.1×10−3 m = 1.00 ×10−3 0.100m
rad
得 A 点处直角 BAD 的切应变为
γ A = γ BAD = α AD − α AB = 1.00 ×10−3 rad
材料力学(I)第八章

组合变形及连接部分的计算
21
例题 8-7
F Fbs n
而挤压应力为
s bs
Fbs F / n (140 103 N ) / 3 Abs d (10 10 3 m )(16 10 3 m )
292 106 Pa 292 MPa 其值小于许用挤压应力[sbs] 300 MPa,满足 挤压强度条件。
§8-4 扭转和弯曲的组合变形
§8-5 连接件的实用计算法
§8-6 铆钉和螺栓连接的计算
*§8-7 榫齿连接
材料力学(Ⅰ)电子教案组合变形及连 Nhomakorabea部分的计算
3
§8-5 连接件的实用计算法
图a所示为工程中常见的两块铁板用螺栓连接 的形式,现在我们研究问题是---有那些破坏形式。
材料力学(Ⅰ)电子教案
I. 需要保证连接处承压 面的压缩强度,并注意 到木材为正交异性材料, 其斜纹许用压应力小于 顺纹许用压应力。
材料力学(Ⅰ)电子教案
组合变形及连接部分的计算
29
压缩强度条件为
FN sc [s c ] Ac
式中,FN为承压面上的压力;Ac为承压面面积; [sc] 为木材的斜纹许用压应力,下角标 为承压面 上压力[sc]与木纹之间的夹角;木结构设计规范中 对FN随 的变化有规定。
材料力学(Ⅰ)电子教案
组合变形及连接部分的计算
1
第 8 章 组合变形及连接部分的计算
§8-1 概述 §8-2 双对称截面梁在两个相互 垂直平面内的弯曲
§8-2+ 平面弯曲的条件
§I-4 惯性矩和惯性积转轴公式· 截面的主惯性轴和主惯性矩
材料力学(Ⅰ)电子教案
组合变形及连接部分的计算
材料力学作业及练习题参考答案(8、9章)

八章2题: 解:查槽钢表,每根槽钢,A=25.669 cm2,W=141 cm3, 则两根槽钢制成的梁:A=2A=51.538 cm2, W=2W=282 cm3 在B截面左侧的上边缘处: =-FN/A+M/W=-50×103/(51.538×10-4)+37.5×103/(282×10-6) =123.24×106 Pa, 即在该处为拉应力123.24 MPa ; 在B截面左侧的下边缘处: =-FN/A-M/W=-50×103/(51.538×10-4)-37.5×103/(282×10-6) =-142.72×106 Pa, 即在该处为压应力142.72 MPa ; 在B截面右侧的上边缘处: =M/W=37.5×103/(282×10-6)=132.98×106 Pa, 即在该处为拉应力132.98 MPa ; 在B截面右侧的下边缘处: =-M/W=-37.5×103/(282×10-6)=-132.98×106 Pa, 即在该处为压应力132.98 MPa。
(完整版)材料力学课后习题答案
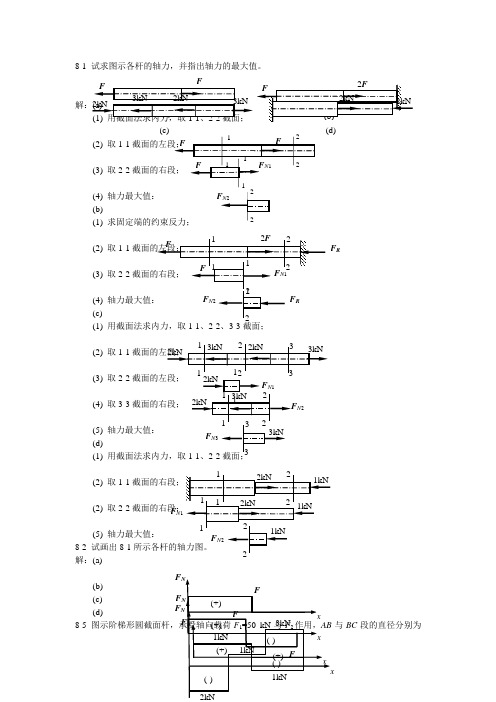
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材料力学课后习题答案详细

N1 N 2 0.5F 0.5 20 10(kN )
10
(2)求 C 点的水平位移与铅垂位移。 变形协调图
A
点的铅垂位移:l1
N1l EA1
10000N 1000mm 210000N / mm2 100mm2
0.476mm
B 点的铅垂位移: l2
材料可认为符合胡克定律,其弹性模量 E 10GPa 。如不计柱的自重,试求:
(1)作轴力图;
(2)各段柱横截面上的应力;
(3)各段柱的纵向线应变;
(4)柱的总变形。
解:(1)作轴力图
N AC 100kN NCB 100 160 260(kN )
轴力图如图所示。
(2)计算各段上的应力
第二章 轴向拉(压)变形
[习题 2-1] 试求图示各杆 1-1 和 2-2 横截面上的轴力,并作轴力图。 (a) 解:(1)求指定截面上的轴力
N11 F N 22 2F F F
(2)作轴力图 轴力图如图所示。
(b) 解:(1)求指定截面上的轴力
N11 2F N 22 2F 2F 0
如以 表示斜截面与横截面的夹角,试求当 0o ,30o ,45o ,60o ,90o 时各斜截面
上的正应力和切应力,并用图表示其方
向。
解:斜截面上的正应力与切应力的公式
为:
5
0 cos 2
0 2
sin 2
式中, 0
N A
10000 N 100mm 2
100MPa ,把
示。
由平平衡条件可得:
X 0
N EG N EA cos 0
(完整版)材料力学课后习题答案
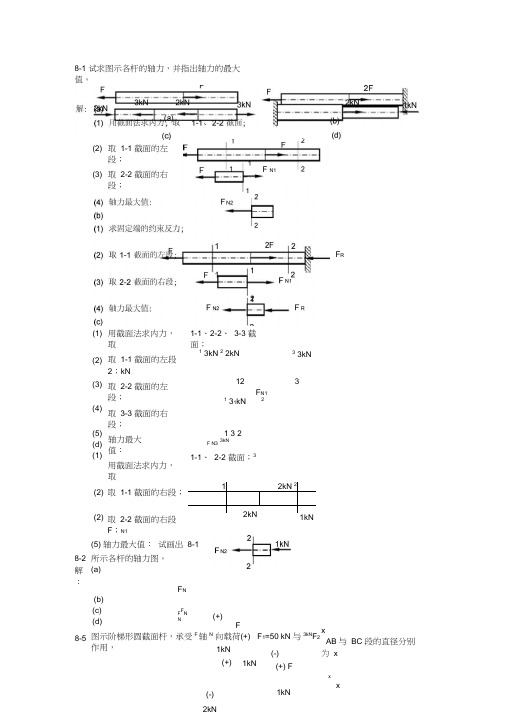
xx8-1 试求图示各杆的轴力,并指出轴力的最大值。
取 1-1 截面的左段;(2) (3) F N1取 2-2 截面的右段;F R用截面法求内力,取1-1、2-2、 3-3 截面;(1) (2) (3) (4)(5)(d)(1)取 1-1 截面的左段2;kN 取 2-2 截面的左段;取 3-3 截面的右段;轴力最大值: 用截面法求内力,取13kN 2 2kN33kN12 3F N11 31kN 21 32 F N33kN1-1、 2-2 截面;38-2 解:8-5 (2) (2) 取 1-1 截面的右段; 取 2-2 截面的右段F ;N112kN 22kN(5) 轴力最大值: 试画出 8-1所示各杆的轴力图。
(a) (b) (c) (d)F NF FN N(+)F图示阶梯形圆截面杆,承受F 轴N 向载荷(+) F 1=50 kN 与3kNF 2作用, 1kN (+) 1kN(-)(+) Fx AB 与 BC 段的直径分别为 x (-)1kN2kNd 1=20 mm 和 d 2=30 mm ,如欲使 AB 与 BC 段横截面上的正应力相同,试求载荷 F 2 之值。
(2) 求 1-1、 2-2 截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷 F=10 kN 作用,杆的横截面面积 A=1000 mm 2,粘接面的方位 角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
l 1l 2解: (1) 用截面法求 AB 、 BC 段的轴力;(2) 分段计F 算个杆向变形;FAC 杆缩短。
2F8-22 图示桁架,杆 1与A 杆 2的横截面面积与材料均相B 同,在节点 A 处承受C 载荷 F 作用。
从解: 8-6 解: (1) 用截面法求出 F 11-1、2-2 截面的轴力;(2) 求 1-1、 2-2 截面的正应A 力 ,利用正应力相B 同 ;题 8-5 图所示圆截面杆,已知载荷 1F 1=200 kN ,F 2=1020 kN ,CAB 段的直径 d 1=40 mm ,如 欲使 AB 与 BC 段横截面上的正应力相同,试求 BC 段的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-18 构件表层一点处的应力如图 a 所示,为了测量应力,在该点沿 0°,45°与 90°
粘贴三个应变片,幷测得相应正应变依次为 0 , 45 与 90 (图 b) 。已知材料的弹性模量为 E, 泊松比为,试根据上述测试应变值,确定该点处的正应力x,y 与切应力x。
题 8-18 图 解:当45°与45°时,相应截面的正应力为 5 x y x y cos90 sin 90 x y 2 2 2 x y x y x y 5 cos(90 ) sin(90 ) 2 2 2 根据广义胡克定律,45°方位的正应变则为
1 ( y x ) E 联立求解式(a) , (b)与(c) ,于是得
σ (
30 10 20sin 90 )MPa 40.0MPa 2 30 10 τ ( sin 90 )MPa 10.0MPa 2
(b)解:由题图所示应力状态可知,
σ x 30MPa,σ y 10MPa,τ x 20MPa,α 22.5
由此可得指定斜截面上的正应力和切应力分别为
Fs F 20kN, | M | Fa 201kN m 20kN m
微体 A,B 和 C 的应力状态依次如图 8-9 a,b 和 c 所示。
图 8-9 对于图 a 所示应力状态,其正应力为
3
σA
|M | 6 20 103 N 6.00 107 Pa 60.0MPa 2 2 Wz 0.050 0.200 m
7
100 80 100 80 cos(120 ) 50sin(120 )( MPa) 128.3 MPa 2 2 根据广义胡克定律,得 30° 的正应变为
60
30
1 ( 60 ) E 30 1 (51.7 106 Pa 0.3 128.3 106 Pa) 0.66 104 9 20010 Pa
板厚的改变量为
μ (σ x σ y ) E
Δδ z
体应变为
0.33 0.010 (80 40) 106 m E 70 109 1.886106 m 0.001886 mm (σ x σ y
θ
由此可得该板件的体积改变量为
(1 2 μ) (σ x σ y σ z ) E
弹性模量 E=200GPa,泊松比 =0.3,试求正应变x,y 与切应变xy,以及 =30°方位的正应 变30°。
题 8-17 图 解:根据广义胡克定律,得
x
y
1 1 ( x y ) (100106 Pa 0.3 80106 Pa) 3.8 104 9 E 20010 Pa
5
由此得
1 ( 45 ) E 45
(a)
1 ( x y )(1 ) 2 (1 ) 2E 根据广义胡克定律还可知,沿 0°与 90°方位的正应变分别为
5
0
90
1 ( x y ) E
(b) (c)
1 1 ( y x ) (80106 Pa 0.3 100106 Pa) 2.5 104 E 200109 Pa 2(1 ) x 2(1 0.3)(50106 Pa) xy x 6.5 104 G E 200109 Pa 斜截面的应力如图 b 所示, x y x y 30 cos2 30 x sin 2 30 2 2 100 80 100 80 cos60 50sin 60 ( MPa) 51.7 MPa 2 2
由此可知,主应力各为
σ1 60.0MPa,
σ 1 的方位角为
σ2 σ3 0
α0 0
对于图 b 所示应力状态,其正应力和切应力分别为
σB τB
极值应力为
| M || y B | 12 20 103 0.050N 3.00 107 Pa 30.0MPa Iz 0.050 0.2003 m 2
σ (
30 10 30 10 cos45 20sin45 )MPa 38.3MPa 2 2 30 10 τ ( sin45 20cos45 )MPa 0 2
(c)解:由题图所示应力状态可知,
σ x 10MPa,σ y 20MPa,τ x 15MPa,α 60
max 1 84.7 MPa
max
1 3 84.7 MPa 4.7 MPa
2 2
44.7 MPa
8-15
在构件表面某点 O 处,沿 0° ,45° ,90° 与 135° 方位粘贴四个应变片,并测得相
应正应变依次为ε = 450×10-6, ε45 = 350×10-6,ε = 100×10-6 与ε = 100×10-6 ,试判 90 0 135 断上述测试结果是否可靠。
800mm,高度 h = 600mm,正应力 x =80MPa, y = 40 MPa,材料为铝,弹性模量 E=70GPa, 泊松比 = 0.33。试求板厚的改变量 与板件的体积改变量 V 。
题 8-16 图
6
解:此为平面应力状态问题。设板厚度方向的正应变为 ε z ,则有
εz
C 84.7 MPa E 4.7 MPa
取 D(20,0)对应于主平面 z,于是,分别以 ED 与 DC 为直径画圆,即得三向应力圆。 可以看出,主应力为
1 C 84.7MPa
2 D 20.0 MPa
3 E 4.7 MPa
而最大正应力与最大切应力则分别为
由于式中 α 为任意值,故原命题得证。
8-7
已知某点 A 处截面 AB 与 AC 的应力如图所示(应力单位为 MPa) ,试用图解法
求主应力的大小及所在截面的方位。
2
题 8-7 图 解:根据题图所给应力,画应力圆如图 8-7 所示。
图 8-7 从所画的应力圆上可以量得两个主应力,它们是:
σ1 69.7MPa, σ 2 9.9MPa
第八章
应力、应变状态分析
8-2
已知应力状态如图所示(应力单位为 MPa) ,试用解析法计算图中指定截面的正
应力与切应力。
题 8-2 图 (a)解:由题图所示应力状态可知,
σ x 30MPa,σ y 10MPa,τ x 20MPa,α 45
将上列数据代入平面应力状态斜截面应力公式,得
σ1 3.00MPa,σ 2 0,σ 3 3.00MPa
σ 1 的方位角为
α0 45
8-12(c)
试画图 a 所示应力状态的三向应力圆,并求主应力、最大正应力与最大
4
切应力。
题 8-12 图 解:显然, σ z 20MPa 为主应力,而其它两个主应力则可由 σ x , τ x 与 σ y 确定(图 b) 。 在 平面内(图 c) ,由坐标(60,40)与(20,-40)分别确定 A 与 B 点,然后,以 AB 为直径画圆,与轴相交于 C 与 E,其横坐标分别为
γ xy (550 700) 106 150106
(d)
将以上所得结果(a),(b)和(d)代入平面应变状态任意方位的正应变公式,计算 ε135 应有 的测量值为
1 1 ε135 ( 450 100) 106 ( 450 100) 106 cos270 2 2 1 6 ( 15010 )sin270 200106 2
8-6
图示双向拉伸应力状态,应力 x y 。试证明任意斜截面上的正应力均等
于 ,而切应力则为零。
题 8-6 图 证明:由题设条件可知,
σ x σ y σ,τ x 0
将上述数据代入平面应力状态斜截面应力公式,则有
σα
σ σ σ σ cos2α 0 σ 2 2 σ σ τα sin 2α 0 0 2
ΔV
(1 2 μ) (σ x σ y σ z )(bhδ ) E (1 2 0.33) (80 40) 106 (0.800 0.600 0.010)m3 70 109 9.33107 m 3 933mm3
x y x
8-17 图 a 所示微体处于平面应力状态, 已知应力 =100MPa, =80MPa, =50 MPa,
由于是平面应力状态,故知
σ3 0
从该应力圆上还可以量得 σ1 的方位角为
α0 23.7
式中负号表示从 AB 面的外法线沿顺时针方向旋转。
8-9
图示悬臂梁,承受载荷 F = 20kN 作用,试绘微体 A,B 与 C 的应力图,并确定
主应力的大小及方位。
题 8-9 图 解:由题图可知,指定截面的剪力与弯矩分别为
FS S z (ω) 12 20 103 0.050 0.050 0.075N 2.25106 Pa 2.25MPa 3 2 I zb 0.050 0.200 0.050m
σ max σ B σB 2 2 30.2 2 2 MPa ( ) τ B [15.0 15.0 2.25 ] MPa σ min 2 2 0.1678
由此可知,主应力为
σ1 30.2 MPa,σ 2 0,σ3 0.1678 MPa
由
tanα0
得 σ 1 的方位角为
τx 2.25 0.07458 σ x σ min 30.00.1678
α0 4.27
对于图 c 应力状态,其切应力为
3FS 3 20103 N 3.00106 Pa 3.00MPa 2 2 A 2 0.050 0.200m 由此得各主应力依次为 τC
ε135 的实际测量值比上述结果小了一半,这说明题中所给测试结果不可靠。
