高等数学下第一章习题课
高等数学课后习题答案--第一章
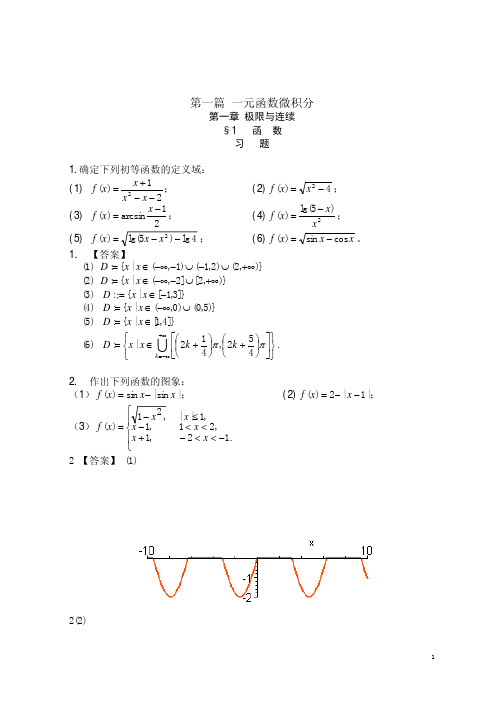
《高等数学》习题参考资料第一篇 一元函数微积分第一章 极限与连续§1 函 数习 题1.确定下列初等函数的定义域:(1) 21)(2−−+=x x x x f ;(2)4)(2−=x x f ;(3) 21arcsin )(−=x x f ;(4)2)5lg()(x x x f −=;(5) 4lg )5lg()(2−−=x x x f ;(6)x x x f cos sin )(−=。
1. 【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象:(1)|sin |sin )(x x x f −=;(2)|1|2)(−−=x x f ;(3)+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性:(1)x x x f ++−=11)(;(2)xxx f x x +−+−=11lg110110)(;(3)x x a a x f x x sin )(++=−;(4))1lg()(2x x x f ++=。
3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。
4. 【答案】 设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5.设函数f 满足:D (f )关于原点对称,且()xc x bf x af =+1)(,其中a ,b ,c 都是常数,||||b a ≠,试证明f 是奇函数。
高等数学第一章课后习题答案

高等数学(本)第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤[]ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x班级 姓名 学号3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()x e x g =,求()[]x g f 和()[]x f g ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x{}结论成立。
高等数学 习题课1-2 极限与连续

xn 1 x
n
( x 0)的连续性。
解 当x [0,1)时, f ( x ) 0;
0, 0 x 1 1 1 即 f ( x) , x 1 当x 1时, f ( x ) ; 2 2 1, x 1 1 当x 1时, f ( x ) lim 1 n 1 n ( ) 1 x
x )
lim
x 0
e x sin 2 x e
2 x
x
2
1
例6 问x 1时, f ( x ) 3 x 2 x 1 ln x
2
是x 1的几阶无穷小 ?
解 f ( x ) 3 x 1 x 1 ln[1 ( x 1)]
lim
x 1
2
n
(2)设x0 1, xn 1
1 xn 1
(n 1, 2,), 试证{ xn }收敛 ,
并求 lim xn。
n
5.求极限
(1) lim
x 0
x 1 cos x
(2) lim
x a
tan x tan a xa xe
(a k
2
)
(3) lim
其中 x=0为跳跃间断点,
例 10 证明: 方程 tanx = x 有无穷多个实根。
分析 从图形看 y=tanx与 y = x 有无穷多个交点。 证 设 f(x) = tan x- x (要在无穷个闭区间上用零点定理)
k Z ,
(1) k
lim
x ( k
2
f ( x ) , lim
8. 设f ( x )在[0,1]上非负连续, 且f (0) f (1) 0, 则对任意实
北科大高数课件第一章

第一章
习题课
8/24
1 2 n ⎛ ⎞ lim ⎜ 2 + 2 + + 2 例5 求极限 ⎟. n→∞ n + n + 1 n +n+2 n +n+n⎠ ⎝ n( n + 1) 1 2 n < 2 + 2 + + 2 解 2 n + n+1 n + n+ 2 n +n+n 2 n +n+n
(
)
n( n + 1) 1 = , 而 lim n→∞ 2 n 2 + n + n 2 n( n + 1) 1 lim = , n→∞ 2 n 2 + n + 1 2
3 ⎛ ⎛ 1 + tan x tan x − sin x ⎞ x 3 ⎞⎞x ⎛ 1 − 1 ⎟ ⎟ = lim ⎜ 1 + 原式 = lim ⎜ 1 + ⎜ x →0 x →0 1 + sin x 1 + sin x ⎟ ⎠⎠ ⎝ ⎠ ⎝ ⎝
1
解
1
∞
1
⎛⎛ tan x − sin x ⎞ = lim ⎜ ⎜ 1 + x →0 ⎜ 1 + sin x ⎟ ⎠ ⎝⎝
第一章
习题课
7/24
x− y x+ y sin x − sin y = 2sin cos 2 2 x+ y x− y sin x + sin y = 2sin cos 2 2 x+ y x− y cos x − cos y = −2sin sin 2 2 x+ y x− y cos x + cos y = 2cos cos 2 2
高等数学(同济第七版下)课后习题及解答

1.设u =a -b +2c ,v =-a +3b -c .试用a ,b ,c 表示2u -3v .解2u -3v =2(a -b +2c )-3(-a +3b -c )=5a -11b +7c .2.如果平面上一个四边形的对角线互相平分,试用向量证明它是平行四边形.证如图8-1,设四边形ABCD 中AC 与BD 交于M ,已知AM =MC ,MB DM =.故DC DM MC MB AM AB =+=+=.即DC AB //且|AB |=|DC |,因此四边形ABCD是平行四边形.3.把△ABC 的BC 边五等分,设分点依次为D 1,D 2,D 3,D 4,再把各分点与点A 连接.试以AB =c ,BC =a 表向量A D 1,A D 2,A D 3,A D4.证如图8-2,根据题意知511=BD a,5121=D D a,5132=D D a,5143=D D a,故A D 1=-(1BD AB +)=-51a -cA D 2=-(2BD AB +)=-52a -c A D 3=-(3BD AB +)=-53a -c A D 4=-(4BD AB +)=-54a -c.4.已知两点M 1(0,1,2)和M 2(1,-1,0).试用坐标表示式表示向量21M M 及-221M M .解21M M =(1-0,-1-1,0-2)=(1,-2,-2).-221M M =-2(1,-2,-2)=(-2,4,4).5.求平行于向量a =(6,7,-6)的单位向量.解向量a 的单位向量为a a ,故平行向量a 的单位向量为±a a =111±(6,7,-6)=⎪⎭⎫ ⎝⎛-±116,117,116,其中11)6(76222=-++=a .6.在空间直角坐标系中,指出下列各点在哪个卦限?A (1,-2,3),B (2,3,-4),C (2,-3,-4),D (-2,-3,1).解A 点在第四卦限,B 点在第五卦限,C 点在第八卦限,D 点在第三卦限.7.在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置:A (3,4,0),B (0,4,3),C (3,0,0),D (0,-1,0).解在坐标面上的点的坐标,其特征是表示坐标的三个有序数中至少有一个为零,比如xOy 面上的点的坐标为(x 0,y 0,0),xOz 面上的点的坐标为(x 0,0,z 0),yOz 面上的点的坐标为(0,y 0,z 0).在坐标轴上的点的坐标,其特征是表示坐标的三个有序数中至少有两个为零,比如x 轴上的点的坐标为(x 0,0,0),y 轴上的点的坐标为(0,y 0,0),z 轴上的点的坐标为(0,0,z 0).A 点在xOy 面上,B 点在yOz 面上,C 点在x 轴上,D 点在y 轴上.8.求点(a ,b ,c )关于(1)各坐标面;(2)各坐标轴;(3)坐标原点的对称点的坐标.解(1)点(a ,b ,c )关于xOy 面的对称点(a ,b ,-c ),为关于yOz 面的对称点为(-a ,b ,c ),关于zOx 面的对称点为(a ,-b ,c ).(2)点(a ,b ,c )关于x 轴的对称点为(a ,-b ,-c ),关于y 轴的对称点为(-a ,b ,-c ),关于z 轴的对称点为(-a ,-b ,c ).(3)点(a ,b ,c )关于坐标原点的对称点是(-a ,-b ,-c ).9.自点P 0),,(000z y x 分别作各坐标面和各坐标轴的垂线,写出各垂足的坐标.解设空间直角坐标系如图8-3,根据题意,P 0F 为点P 0关于xOz面的垂线,垂足F 坐标为),,000(z x ;P 0D 为点P 0关于xOy 面的垂线,垂足D 坐标为),,0(00y x ;P 0E 为点P 0关于yOz 面的垂线,垂足E 坐标为)0(0o z y ,,.P 0A 为点P 0关于x 轴的垂线,垂足A 坐标为),0,0(o x ;P 0B 为点P 0关于y 轴的垂线,垂足B 坐标为)0,,0(0y ;P 0C 为点P 0关于z 轴的垂线,垂足C 坐标为),0,0(0z .10.过点P 0),,(000z y x 分别作平行于z 轴的直线和平行于xOy 面的平面,问在它们上面的点的坐标各有什么特点?解如图8-4,过P 0且平行于z 轴的直线l 上的点的坐标,其特点是,它们的横坐标均相同,纵坐标也均相同.而过点P 0且平行于xOy 面的平面 上的点的坐标,其特点是,它们的竖坐标均相同.11.一边长为a 的正方体放置在xOy 面上,其底面的中心在坐标原点,底面的顶点在x 轴和y 轴上,求它各顶点的坐标.解如图8-5,已知AB=a ,故OA=OB=a 22,于是各顶点的坐标分别为A )0022(,,a ,B (),022,0(a ),C (-a 22,0,0),D (0,-a 22,0),E (a 22,0,a ),F (0,a 22,a ),G (-a 22,0,a ),H (0,-a 22,a ).12.求点M (4,-3,5)到各坐标轴的距离.解点M 到x 轴的距离为d 1=345)3(22=+-,点M 到y 轴的距离为d 2=415422=+,点M 到z 轴的距离为d 3=525)3(422==-+.13.在yOz 面上,求与三点A (3,1,2),B (4,-2,-2),C (0,5,1)等距离的点.解所求点在yOz 面上,不妨设为P (0,y ,z ),点P 与三点A ,B ,C,)2()1(3222-+-+=z y,)2()2(4222++++=z y.)1()5(22-+-=z y==222222)2()2(4)2()1(3++++=-+-+z y z y 22)1()5(-+-=z y ,即.)1()5()2()1(9,)2()2(16)2()1(922222222-+-=-+-+++++=-+-+z y z y z y z y 解上述方程组,得y=1,z=-2.故所求点坐标为(0,1,-2).14.试证明以三点A (4,1,9),B (10,-1,6),C (2,4,3)为顶点的三角形是等腰直角三角形.证由2798)63()14()102(,7)93()14()42(,7)96()11()410(222222222==-+++-==-+-+-==-+--+-=.+==故△ABC 为等腰直角三角形.15.设已知两点为M 1(4,2,1),M 2(3,0,2),计算向量21M M 的模、方向余弦和方向角.解向量21M M =(3-4,0-2,2-1)=(-1,-2,-1),2412-1-222==++=)()(.其方向余弦分别为cos α=-21,cos β=-22,cos γ=21.方向角分别为3,43,32πγπβπα===.16.设向量的方向余弦分别满足(1)cos α=0;(2)cos β=1;(3)cos α=cos β=0,问这些向量与坐标轴或坐标面的关系如何?解(1)由cos α=0得知2πα=,故向量与x 轴垂直,平行于yOz 面.(2)由cos β=1得知β=0,故向量与y 轴同向,垂直于xOz 面.(3)由cos α=cos β=0知2πβα==,故向量垂直于x 轴和y 轴,即与z 轴平行,垂直于xOy 面.17.设向量r 的模是4,它与u 轴的夹角为3π,求r 在u 轴上的投影.解已知|r |=4,则Prj u r=|r |cos θ=4∙cos 3π=4×21=2.18.一向量的终点在点B (2,-1,7),它在x 轴、y 轴和z 轴上的投影依次为4,-4和7,求这向量的起点A 的坐标.解设A 点坐标为(x ,y ,z ),则AB =(2-x ,-1-y ,7-z ),由题意知2-x=4,-1-y=-4,7-z=7,故x=-2,y=3,z=0,因此A 点坐标为(-2,-3,0).19.设m =3i +4j +8k ,n =2i -4j -7k 和p =5i +j -4k .求向量a =4m +3n -p 在x 轴上的投影及在y轴上的分向量.解a=4m+3n-p=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k,a在x轴上的投影为13,在y轴上的分向量为7j.1.设k j i b k j i a -+=--=2,23,求(1)b a b a ⨯⋅及;(2)b a 2b 3a 2-⨯⋅及)(;(3)b a ,的夹角的余弦.解(1)),(),,(1-2,12-1-3⋅=⋅b a ,)()()(31-2-21-13=⨯+⨯+⨯==⨯b a 121213---kj i =(5,1,7).(2)1836)(63)2(-=⨯-=⋅-=⋅-b a b a )14,2,10()7,1,5(2)(22==⨯=⨯b a b a (3222222)1(21)2()1(33),cos(-++-+-+=⋅=b a b a b a 21236143==2.设c b a ,,为单位向量,满足.,0a c c b b a cb a ⋅+⋅+⋅=++求解已知,0,1=++===c b a c b a 故0=++⋅++)()(c b a c b a .即0222222=⋅+⋅+⋅+++a c c b b a c b a .因此23-21222=++-=⋅+⋅+⋅)(c b a a c c b b a 3.已知M 1(1,-1,2),M 2(3,3,1)M 3(3,1,3).求与3221,M M M M 同时垂直的单位向量.解21M M =(3-1,3-(-1),1-2)=(2,4,-1)32M M =(3-3,1-3,3-1)=(0,-2,2)由于3221M M M M ⨯与3221,M M M M 同时垂直,故所求向量可取为M M M M a =)(由3221M M M M ⨯=220142--k j i=(6,-4,-4),17268)4()4(6222==-+-+=⨯知).172,172,173()4,4,6(1721--±=--±=a 4.设质量为100kg 的物体从点M1(3,1,8)沿直线移动到点M2(1,4,2),计算重力所作的功(坐标系长度单位为m ,重力方向为z 轴负方向).解21M M =(1-3,4-1,2-8)=(-2,3,-6)F=(0,0,-100×9.8)=(0,0,-980)W=F ∙21M M =(0,0,-980)∙(-2,3,-6)=5880(J).5.在杠杆上支点O 的一侧与点O 的距离为x 1的点P 1处,有一与1OP 成角1θ的力F 1作用着;在O 的另一侧与点O 的距离为x 2的点P 2处,有一与2OP 成角2θ的力F 2作用着(图8-6),问1θ,2θ,x 1,x 2,21,F F 符合怎样的条件才能使杠杆保持平衡?解如图8-6,已知有固定转轴的物体的平衡条件是力矩的代数和为零,又由对力矩正负符号的规定可得杠杆保持平衡的条件为0sin sin 222111=-θθx F x F ,即222111sin sin θθx F x F =.6.求向量),(4,3-4=a在向量)(1,2,2=b 上的投影.解236122)1,2,2()4,3,4(Pr 222==++⋅-=⋅=b b a a j b .7.设)4,1,2(),2,5,3(=-=b a,问μλ与有怎样的关系,能使b a μλ+与z 轴垂直?解b a μλ+=λ(3,5,-2)+μ(2,1,4)=(μλμλμλ42,5,23+-++).要b a μλ+与z 轴垂直,即要(b a μλ+)⊥(0,0,1),即(b a μλ+)∙(0,0,1)=0,亦即(μλμλμλ42,5,23+-++)∙(0,0,1)=0,故(μλ42+-)=0,因此μλ2=时能使b a μλ+与z 轴垂直.8.试用向量证明直径所对的圆周角是直角.证如图8-7,设AB 是圆O 的直径,C 点在圆周上,要证∠ACB=2π,只要证明0=⋅BCAC 即可.由BC AC ⋅=)()(OC BO OC AO +⋅+=BO OC OC AO BO AO ⋅+⋅+⋅=0=+⋅-⋅+OC AO OC AO .故BC AC⊥,∠ACB为直角.9.已知向量j i c k j i b k j i a 23,32-=+-=+-=和,计算:(1)b c a c b a )()(⋅-⋅(2))()(c b b a +⨯+(3)cb a ⋅⨯)(解(1)8)3,1,1()1,3,2(=-⋅-=⋅ba ,8)0,2,1()1,3,2(=-⋅-=⋅c a ,b c a c b a )()(⋅-⋅)24,8,0()3,1,1(8)0,2,1(8--=---=k i 248--=.(2)b a +=(2,-3,1)+(1,-1,3)=(3,-4,4),c b +=(1,-1,3)+(1,-2,0)=(2,-3,3),)()(c b b a +⨯+332443--=kj i k j --=--=)1,1,0(.(3)c b a ⋅⨯)(.2021311132=---=10.已知k j OBk i OA 3,3+=+=,求△OAB 的面积.解由向量积的几何意义知S △OAB⨯)1,3,3(310301--==⨯kj i OB OA,⨯191)3()3(22=+-+-=S △OAB219=11.已知),,(),,,(),,,(z y x z y x z y x c c c c b b b b a a a a ===,试利用行列式的性质证明:ba c a cbc b a ⋅⨯=⋅⨯=⋅⨯)()()(证因为,)(z yxz y xz y xc c c b b b a a a cb a =⋅⨯zyxz y x z y x a a a c c c b b b a c b =⋅⨯)(=⋅⨯b a c )(zyxz yxz y xb b b a a ac c c ,而由行列式的性质知z yxz y x z y x c c c b b b a a a z yx z y x z y x a a a c c c b b b ==zyxz y x z y x b b b a a a c c c ,故b ac a c b c b a ⋅⨯=⋅⨯=⋅⨯)()()(.12.试用向量证明不等式:332211232221232221b a b a b a b b b a a a ++≥++++,其中321321,,,,,b b b a a a 为任意实数.并指出等号成立的条件.证设向量=a (321,,a a a ),=b (321,,b b b ).由),cos(b a b a ba =⋅b a ≤,从而232221232221332211b b b a a a b a b a b a ++++≤++,当321,,a a a 与321,,b b b 成比例,即332211b a b a b a ==时,上述等式成立.1.求过点(3,0,-1)且与平面012573=-+-z y x 平行的平面方程.解所求平面与已知平面012573=-+-z y x 平行.因此所求平面的法向量可取为n=(3,-7,5),设所求平面为0573=++-D z y x .将点(3,0,-1)代入上式得D=-4.故所求平面方程为04573=-+-z y x .2.求过点M 0(2,9,-6)且与连接坐标原点及点M 0的线段OM 0垂直的平面方程.解.6,9,2(0)-=OM 所求平面与0OM 垂直,可取n=0OM ,设所求平面方程为0692=+-+D z y x .将点M 0(2,9,-6)代入上式得D=-121.故所求平面方程为0121692=--+z y x .3.求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程.解由0121111121212111=+---+----+--z y x ,得023=--z y x ,即为所求平面方程.注设M (x,y,z )为平面上任意一点,)3,2,1)(,,(==i z y x M i i i i 为平面上已知点.由,0)(31211=⨯⋅M M M M MM 即,0131313121212111=---------z z y y x x z z y y x x z z y y x x 它就表示过已知三点M i (i=1,2,3)的平面方程.4.指出下列各平面的特殊位置,并画出各平面:(1)x=0;(2)3y-1=0;(3)2x-3y-6=0;(4)x-3y=0;(5)y+z=1;(6)x-2z=0;(7)6x+5y-z=0.解(1)—(7)的平面分别如图8—8(a )—(g ).(1)x=0表示yOz 坐标面.(2)3y-1=0表示过点(0,31,0)且与y 轴垂直的平面.(3)2x-3y-6=0表示与z 轴平行的平面.(4)x-3y=0表示过z 轴的平面.(5)y+z=1表示平行于x 轴的平面.(6)x-2z=0表示过y 轴的平面.(7)6x+5y-z=0表示过原点的平面.5.求平面0522=++-z y x 与各坐标面的夹角的余弦.解平面的法向量为n=(2,-2,1),设平面与三个坐标面xOy ,yOz ,zOx 的夹角分别为321,,θθθ.则根据平面的方向余弦知,3111)2(2)1,0,0()1,2,2(cos cos 2221=⋅+-+⋅-=⋅==k n k n γθ,3213)0,0,1()1,2,2(cos cos 2=⋅⋅-=⋅==i n i n αθ3213)0,1,0()1,2,2(cos cos 3-=⋅⋅-=⋅==j n j n βθ.6.一平面过点(1,0,-1)且平行于向量)1,1,2(=a 和)0,1,1(-=b ,试求这个平面方程.解所求平面平行于向量a 和b ,可取平面的法向量)3,1,1(011112-=-=⨯=kj i b a n .故所求平面为0)1(3)0(1)1(1=+--⋅+-⋅z y x ,即043=--+z y x .7.求三平面322,02,13=++-=--=++z y x z y x z y x 的交点.解联立三平面方程.322,02,13=++-=--=++z y x z y x z y x 解此方程组得.3,1,1=-==z y x故所求交点为(1,-1,3).8.分别按下列条件求平面方程:(1)平行于xOz 面且经过点(2,-5,3);(2)通过z 轴和点(-3,1,-2);(3)平行于x 轴且经过两点(4,0,-2)和(5,1,7).解(1)所求平面平行于xOz 面,故设所求平面方程为0=+D By .将点(2,-5,3)代入,得05=+-D B ,即B D 5=.因此所求平面方程为05=+B By ,即05=+y .(2)所求平面过z 轴,故设所求平面为0=+By Ax .将点(-3,1,-2)代入,得03=+-B A ,即A B 3=.因此所求平面方程为03=+Ay Ax ,即03=+y x .(3)所求平面平行于x 轴,故设所求平面方程为0=++D Cz By .将点(4,0,-2)及(5,1,7)分别代入方程得2=+-D C 及07=++D C B .D B D C 29,2-==.因此,所求平面方程为0229=++-D z DDy ,即029=--z y .9.求点(1,2,1)到平面01022=-++zy x 的距离.解利用点),,(00o o z y x M 到平面0=+++D Cz By Ax 的距离公式222000C B A DCz By Ax d +++++=.1332211012221222=-=++-⋅+⋅+=1.求过点(4,-1,3)且平行于直线51123-==-z y x 的直线方程.解所求直线与已知直线平行,故所求直线的方向向量)5,1,2(=s ,直线方程即为531124-=+=-z y x .2.求过两点)1,2,3(1-M 和)2,0,1(2-M 的直线方程.解取所求直线的方向向量)1,2,4()12),2(0,31(21-=-----==M M s ,因此所求直线方程为112243-=+=--z y x .3.用对称式方程及参数方程表示直线.42,1=++=+-z y x z y x 解根据题意可知已知直线的方向向量112111-=kj i s ).3,1,2(-=取x=0,代入直线方程得.4,1=+=+-z y z y 解得.25,23==z y 这样就得到直线经过的一点(25,23,0).因此直线的对称式方程为.32512320-=-=--z y x 参数方程为.325,23,2t z t y t x +=+=-=注由于所取的直线上的点可以不同,因此所得到的直线对称式方程或参数方程得表达式也可以是不同的.4.求过点(2,0,-3)且与直线1253,0742=+-+=-+-z y x z y x 垂直的平面方程.解根据题意,所求平面的法向量可取已知直线的方向向量,即),11,14,16(253421-=--==kj i s n 故所求平面方程为.0)3(11)0(14)2(16=++-+--z y x 即.065111416=---z y x 5.求直线0123,09335=-+-=-+-z y x z y x 与直线01883,02322=-++=+-+z y x z y x 的夹角的余弦.解两已知直线的方向向量分别为),1,4,3(1233351-=--=k j i s ),10,5,10(1831222-=-=kj i s 因此,两直线的夹角的余弦212121),(cos cos s s s s s s ⋅== .010)5(10)1(4310154103222222=+-+-++⨯-⨯-⨯=6.证明直线72,72=++-=-+z y x z y x 与直线02,8363=--=-+z y x z y x 平行.证已知直线的方向向量分别是),15,3,9(112363),5,1,3(11212121---=---==--=kj i s k j i s 由123s s -=知两直线互相平行.7.求过点(0,2,4)且与两平面12=+zx 和23=-z y 平行的直线方程.解所求直线与已知的两个平面平行,因此所求直线的方向向量可取),1,3,2(31020121-=-=⨯=kj i n n s 故所求直线方程为.143220-=-=-z y x 注本题也可以这样解:由于所求直线与已知的两个平面平行,则可视所求直线是分别与已知平面平行的两平面的交线,不妨设所求直线为.3,2b z y a z x=-=+将点(0,2,4)代入上式,得.10,8-==b a 故所求直线为.103,82-=-=+z y z x 8.求过点(3,1,-2)且通过直线12354z y x =+=-的平面方程.解利用平面束方程,过直线12354z y x =+=-的平面束方程为,0)23(2354=-+=+=-z y y x λ将点(3,1,-2)代入上式得.2011=λ因此所求平面方程为,0)23(20112354=-+=+=-z y y x即.0592298=---z y x 9.求直线0,03=--=++z y x z y x 与平面01=+--z y x 的夹角.解已知直线的方向向量),2,4,2(111311-=--=k j is 平面的法向量).1,1,1(--=n 设直线与平面的夹角为,ϕ则,0)1()1(1)2(42)1()2()1(412),cos(sin 222222=-+-+-++-⋅-+-⋅+⋅=⋅==n s n s s n ϕ即.0=ϕ10.试确定下列各组中的直线和平面间的关系;(1)37423z y x =-+=-+和3224=--z y x ;(2)723z y x =-=和8723=+-z y x ;(3)431232--=+=-z y x 和.3=++z y x 解设直线的方向向量为s ,平面的法向量为n ,直线与平面的夹角为,ϕ且ns n s s n ⋅==),cos(sin ϕ.(1)),2,2,4(),3,7,2(--=--=ns,0)2()2(43)7()2()2(3)2()7(4)2(sin 222222=-+-+⋅+-+--⋅+-⋅-+⋅-=ϕ则.0=ϕ故直线平行于平面或在平面上,现将直线上的点A (-3,-4,0)代入平面方程,方程不成立.故点A 不在平面上,因此直线不在平面上,直线与平面平行.(2)),7,2,3(),7,2,3(-=-=n s 由于n s =或,17)2(37)2(377)2()2(33sin 222222=+-+⋅+-+⋅+-⋅-+⋅=ϕ知2πϕ=,故直线与平面垂直.(3)),1,1,1(),4,1,3(=-=n s 由于0=⋅n s 或,0111)4(131)4(1113sin 222222=++⋅-++⋅-+⋅+⋅=ϕ知,0=ϕ将直线上的点A (2,-2,3)代入平面方程,方程成立,即点A 在平面上.故直线在平面上.11.求过点(1,2,1)而与两直线1,012=-+-=+-+z y x z y x 和0,02=+-=+-z y x z y x 平行的平面的方程.解两直线的方向向量为),1,1,0(111112),3,2,1(11112121--=--=--=--=kj i s k j is取),1,1,1(11032121--=----=⨯=k j i s s n 则过点(1,2,1),以n 为法向量的平面方程为,0)1(1)2(1)1(1=-⋅--⋅+-⋅-z y x 即.0=+-z y x 12.求点(-1,2,0)在平面012=+-+z y x 上的投影.解作过已知点且与已知平面垂直的直线.该直线与平面的交点即为所求.根据题意,过点(-1,2,0)与平面012=+-+z y x 垂直的直线为,102211--=-=+z y x 将它化为参数方程,,22,1t z t y t x -=+=+-=代入平面方程得,01)()22(21=+--+++-t t t 整理得32-=t .从而所求点(-1,2,0)在平面012=+-+z y x 上的投影为(32,32,35-).13.求点P (3,-1,2)到直线042,01=-+-=+-+z y x z y x 的距离.解直线的方向向量).3,3,0(112111--=--=kj i s 在直线上取点(1,-2,0),这样,直线的方程可表示成参数方程形式.3,32,1t z t y x -=--==(1)又,过点P (3,-1,2),以)3,3,0(--=s 为法向量的平面方程为,0)2(3)1(3=--+-z y 即.01=-+z y (2)将式(1)代入式(2)得21-=t ,于是直线与平面的交点为(23,21,1-),故所求距离为.223)232()211()13(222=-++-+-=d 14.设M 0是直线L 外一点,M 是直线L 上任意一点,且直线的方向向量为s ,试证:点M 0到直线L的距离d =.证如图8-9,点M 0到直线L 的距离为d.由向量积的几何意义知s ⨯表示以M M 0,s 为邻边的平行四边形的面积.而表示以s 为边长的该平面四边形的高,即为点M 0到直线L 的距离.于是d =15.求直线0923,042=---=+-z y x z y x 在平面14=+-z y x 上的投影直线的方程.解作过已知直线的平面束,在该平面束中找出与已知平面垂直的平面,该平面与已知平面的交线即为所求.设过直线0923,042=---=+-z y x z y x 的平面束方程为,0)923(42=---++-z y x z y x λ经整理得.09)21()4()32(=--+--++λλλλz y x 由,01)21()1()4(4)32(=⋅-+-⋅--+⋅+λλλ得1113-=λ.代入平面束方程,得.0117373117=--+z y x 因此所求投影直线的方程为.14,0117373117=+-=--+z y x z y x 16.画出下列各平面所围成的立体的图形.(1);012243,1,2,0,0,0=-++=====z y x y x z y x(2).4,2,1,0,0yz y x z x =====解(1)如图8-10(a );(2)如图8-10(b ).1.一球面过原点及A (4,0,0),B (1,3,0)和C (0,0,-4)三点,求球面的方程及球心的坐标和半径.解设所求球面的方程为2222)()()(R c z b y a x =-+-+-,将已知点的坐标代入上式,得,2222R c b a =++(1),)4(2222R c b a =++-(2),)3()1(2222R c b a =+-+-(3)2222)4(R c b a =+++,(4)联立(1)(2)得,2=a 联立(1)(4)得,2-=c 将2=a 代入(2)(3)并联立得b=1,故R=3.因此所求球面方程为,9)2()1()2(222=++-+-z y x 其中球心坐标为),2,1,2(-半径为3.2.建立以点(1,3,-2)为球心,且通过坐标原点的球面方程.解设以点(1,3,-2)为球心,R 为半径的球面方程为,)2()3()1(2222R z y x =++-+-球面经过原点,故,14)20()30()10(2222=++-+-=R 从而所求球面方程为.14)2()3()1(222=++-+-z y x 3.方程0242222=++-++z y x z y x 表示什么曲面?解将已知方程整理成,)6()1()2()1(2222=++++-z y x所以此方程表示以(1,-2,-1)为球心,以6为半径的球面.4.求与坐标原点O 及点(2,3,4)的距离之比为1:2的点的全体所组成的曲面的方程,它表示怎样的曲面?解设动点坐标为(z y x ,,),根据题意有,21)4()3()2()0()0()0(222222=-+-+--+-+-z y x z y x 化简整理得.)2932()34()1()32(2222=+++++z y x 它表示以(34,1,32---)为球心,以2932为半径的球面.5.将xOz 坐标面上的抛物线x z 52=绕x 轴旋转一周,求所生成的旋转曲面的方程.解以22z y +±代替抛物线方程x z 52=中的z ,得222)(z y +±x 5=,即x z y 522=+.注xOz 面上的曲线0),(=z x F 绕x 轴旋转一周所生成的旋转曲面方程为0),(22=+±z y x F .6.将xOz 坐标面上的圆922=+z x 绕z 轴旋转一周,求所生成的旋转曲面的方程.解以22y x +±代替圆方程922=+z x 中的x ,得,9)(2222=++±z y x 即.9222=++z y x7.将xOy 坐标面上的双曲线369422=-y x分别绕x 轴及y 轴旋转一周,求所生成的旋转曲面的方程.解以22zy +±代替双曲线方程369422=-y x中的y ,得该双曲线绕x 轴旋转一周而生成的旋转曲面方程为,36)(942222=+±-z y x 即.36)(94222=+-z y x 以22zx +±代替双曲线方程369422=-y x中的x ,得该双曲线绕y 轴旋转一周而生成的旋转曲面方程为,369)(42222=-+±y z x 即.369)(4222=-+y z x 8.画出下列各方程所表示的曲面:(1);)2()2(222a y a x =+-(2);19422=+-y x (3);14922=+z x (4);02=-z y (5)22x z-=.解(1)如图8-11(a );(2)如图8-11(b );(3)如图8-11(c );(4)如图8-11(d );(5)如图8-11(e ).9.指出下列方程在平面解析几何中和在空间解析几何中分别表示什么图形:(1);2=x (2);1+=x y (3);422=+y x(4).122=-y x解(1)2=x 在平面解析几何中表示平行于y 轴的一条直线,在空间解析几何中表示与yOz 面平行的平面.(2)1+=x y在平面解析几何中表示斜率为1,y 轴截距也为1的一条直线,在空间解析几何中表示平行于z 轴的平面.(3)422=+y x在平面解析几何中表示圆心在原点,半径为2的圆,在空间解析几何中表示母线平行于z 轴,准线为0,422==+z y x 的圆柱面.(4)122=-y x在平面解析几何中表示以x 轴为实轴,y 轴为虚轴的双曲线,在空间解析几何中表示母线平行于z轴,准线为,122==-z y x 的双曲柱面.10.说明下列旋转曲面是怎样形成的:(1);1994222=++z y x (2);14222=+-z y x (3);1222=--z y x (4).)(222y x a z+=-解(1)1994222=++z y x 表示xOy 面上的椭圆19422=+y x 绕x轴旋转一周而生成的旋转曲面,或表示xOz 面的椭圆19422=+z x 绕x 轴旋转一周而生成的旋转曲面.(2)14222=+-z y x 表示xOy 面上的双曲线1422=-y x 绕y 轴旋转一周而生成的旋转曲面,或表示yOz 面的双曲线1422=+-z y 绕y 轴旋转一周而生成的旋转曲面.(3)1222=--z y x表示xOy 面上的双曲线122=-y x 绕x 轴旋转一周而生成的旋转曲面,或表示xOz 面的双曲线122=-z x 绕x 轴旋转一周而生成的旋转曲面.(4)222)(y x a z+=-表示xOz 面上的直线a x z +=或a x z +-=绕z 轴旋转一周而生成的旋转曲面,或表示yOz 面的直线a y z+=或a y z +-=绕z 轴旋转一周而生成的旋转曲面.11.画出下列方程所表示的曲面:(1);44222=++z y x(2);44222=--z y x(3).94322y x z +=解(1)如图8-12(a );(2)如图8-12(b );(3)如图8-12(c );12.画出下列各曲面所围立体的图形:(1)1,03,0,3,022=+=-=-==y x y x y x z z(在第一卦限内);(2)222222,,0,0,0R z y R y x z y x =+=+===(在第一卦限内).解(1)如图8-13所示;(2)如图8-14所示.1.画出下列曲线在第一卦限内的图形;(1);2,1==y x (2);0,422=---=yxyx z(3).,222222a z x a y x =+=+解(1)如图8-15(a );(2)如图8-15(b );(3)如图8-15(c ).2.指出下列方程组在平面解析几何中与在空间解析几何中分别表示什么图形:(1);32,15-=+=x y x y (2).3,19422==+y y x 解(1)32,15-=+=x y x y 在平面解析几何中表示两直线的交点.在空间解析几何中表示两平面的交线,即空间直线.(2)3,19422==+y y x 在平面解析几何中表示椭圆19422=+y x 与其切线3=y 的交点,即切点.在空间解析几何中表示椭圆柱面19422=+y x 与其切平面3=y 的交线,即空间直线.3.分别求母线平行于x 轴及y 轴而且通过曲线0,162222222=-+=++y z x z y x 的柱面方程.解在,162222222=-+=++y z x z y x 中消去x ,得,16322=-z y 即为母线平行于x 轴且通过已知曲线的柱面方程.在,162222222=-+=++y z x z y x 中消去y ,得,162322=+z x 即为母线平行于y 轴且通过已知曲线多的柱面方程.4.求球面9222=++z y x 与平面1=+z x 的交线在xOy 面上的投影的方程.解在1,9222=+=++z x z y x 中消去z ,得,9)1(222=-++x y x 即,82222=+-y x x它表示母线平行于z轴的柱面,故0,82222==+-z y x x 表示已知交线在xOy 面上的投影的方程.5.将下列曲线的一般方程化为参数方程:(1);,9222x y z y x ==++(2).0,4)1()1(222==+++-z z y x解(1)将x y=代入,9222=++z y x 得,9222=+z x 取,cos 23t x =则,sin 3t z =从而可得该曲线的参数方程tz t y t x sin 3,cos 23,cos 23===(t ≤0˂π2)(2)将z=0代入,4)1()1(222=+++-z y x 得,3)1(22=+-y x 取,cos 31t x =-则,sin 3t y =从而可得该曲线的参数方程0,sin 3,cos 31==+=z t y t x (t ≤0˂π2)6.求螺旋线θθθb z a y a x ===,sin ,cos 在三个坐标面上的投影曲线的直角坐标方程.解由θθsin ,cos a y a x==得,222a y x =+故该螺旋线在xOy 面上的投影曲线的直角坐标方程为,222==+z a y x 由θθb z a y ==,sin 得bza y sin =,故该螺旋线在yOz 面上的投影曲线的直角坐标方程为0,sin ==x bza y 由θθb z a x ==,cos 得,cos b za x =故故该螺旋线在yOz 面上的投影曲线的直角坐标方程为.0,cos ==y bza x 7.求上半球2220y x a z --≤≤与圆柱体a ax y x (22≤+>0)的公共部分在xOy 面和xOz 面上的投影.解如图8-16.所求立体在xOy 面上的投影即为ax y x ≤+22,而由axy x y x a z =+--=22222,得.2ax a z -=故所求立体在xOz 面上的投影为由x 轴,z 轴及曲线ax a z-=2所围成的区域.8.求旋转抛物面)40(22≤≤+=z y x z在三坐标面上的投影解联立422=+=z y x z ,得422=+y x.故旋转抛物面在xOy面上的投影为.0,422=≤+z y x 如图8-17.联立0,22=+=x y x z 得,2y z=故旋转抛物面在yOz 面上的投影为2y z=及4=z 所围成的区域.同理,联立0,22=+=y y x z 得,2x z =故旋转抛物面在xOz 面上的投影为2x z=及4=z 所围成的区域.。
高等数学(同济第七版)课后答案解析

(3)相同、因为定义域、对应法则均相同.
(4)不同、因为定义域不同.
际3.设
求。(寻)“仔)・9(-骨)顽-2).并作出函数L)的囲形.
TT
S,,,T i
1(、)的,形如图丨・1所示.
S4.试让F列陥数在指定区间内的单Wi性:
第一章函故与扱限
(2)j = x+In n(0, *8).证(I) y=/(^)=rL-=-丨+宀(-8』).
F(-T)=/|(-X)+/2(F=/|(对+人(x) =F(x),
枚,(大)为偶函数.
设幻(T),&2(愛)均为奇函数.则幻(-工)=-们(*),幻(-X)=-g2(■*)•令。(])=g]())+&《]),于是
G(-X)=X|(-X)+评2(-X)=■•幻(x) -&2(1)=f),
故c(x)为奇函数.
解因为AC= 20= 15,所以,Ali= /^后IF=25.
Ih20 <2-15 <20・25可知,点P、Q在斜边AH上相讷.
令a + 2% = 15+20 + 25J!;x = 20.即当x= 2()时•点七。相遇.因此•所求函數的定义域为(0.20).
(I )当Ov — vIO时,点P在CR上•点Q在CA上(图1-5).
洎6.&卜血所考虑的函救都是定义在区间U)上的.i止明:
(1)两个偶函数的和是偶函数.两个奇函数的和是奇函数;
(2)两个偶函数的乘枳是偶函数,两个奇函数的乘枳是偶函数,偶函数与奇丽数的乗积是奇函数.
证(1)设J|(X)./2(X)均为偶函数,则乂(-X)”('),(-X)=6(x).今/⑴=/|(^)+/i(x),于是
高等数学(下)课后习题答案

高等数学(下)习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2) s==(3) s=(4) s==.5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).s==故s==xs==ys==.5z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则222222-++-=++--(4)1(7)35(2)z z解得149z=即所求点为M(0,0,149).7. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证:()()++=++a b c a b c.证明:利用三角形法则得证.见图7-1图7-19. 设2,3.u v=-+=-+-a b c a b c 试用a, b, c表示23.u v-解:232(2)3(3)2243935117u v-=-+--+-=-++-+=-+a b c a b ca b c a b ca b c10. 把△ABC的BC边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB=c,BC=a表示向量1D A,2D A,3D A和4D A.解:1115D A BA BD=-=--c a2225D A BA BD=-=--c a3335D A BA BD=-=--c a444.5D A BA BD=-=--c a11. 设向量OM的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M的投影为M',则1Pr j cos604 2.2uOM OM=︒=⨯=12. 一向量的终点为点B(2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A的坐标.解:设此向量的起点A的坐标A(x, y, z),则{4,4,7}{2,1,7}AB x y z =-=----解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0).13. 一向量的起点是P 1(4,0,5),终点是P 2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量.解:(1)12Pr j 3,x x a PP ==12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP == (3) 12cos 14xa PP α== 12cos 14ya PP β==12cos 14za PP γ==(4) 12012{14PPPP ===-e j . 14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R =(1-2+3,2+3-4,3-4+5)=(2,1,4)||==Rcos coscos αβγ=== 15. 求出向量a = i +j +k , b =2i -3j +5k 和c =-2i -j +2k 的模,并分别用单位向量,,a b c e e e 来表达向量a , b , c .解:||==a||==b||3==c, , 3. a b c ==a b c e16. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解:a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k在x 轴上的投影a x =13,在y 轴上分向量为7j .17. 向量r 与三坐标轴交成相等的锐角,求这向量的单位向量e r .解:因αβγ==,故23cos 1 α=,cos αα==则{cos ,cos ,cos })r αβγ===++e i j k . 18. 已知两点M 1(2,5,-3),M 2(3,-2,5),点M 在线段M 1M 2上,且123M M MM =,求向径OM 的坐标.解:设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为,123M M MM = 所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标. 解:设P 的坐标为(x , y , z ),2222||(12)49PA x y z =++-=得2229524x y z z ++=-+126570cos 6, 749z z γ==⇒==又122190cos 2, 749x x α==⇒==123285cos 3, 749y y β==⇒== 故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a , b 的夹角2π3ϕ=,且3,4a b ==,计算: (1) a ·b ; (2) (3a -2b )·(a + 2b ). 解:(1)a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b21. 已知a =(4,-2, 4), b =(6,-3, 2),计算:(1)a ·b ; (2) (2a -3b )·(a + b ); (3)2||-a b解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b(2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b 222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b 36238499=-⨯+=22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影.解:AB ={3,-2,-6},CD ={6,2,3}Pr j CD AB CD AB CD ⋅=4.7==- 23. 设重量为100kg 的物体从点M 1(3, 1, 8)沿直线移动到点M 2(1,4,2),计算重力所作的功(长度单位为m ).解:取重力方向为z 轴负方向,依题意有f ={0,0, -100×9.8}s = 12M M ={-2, 3,-6}故W = f ·s ={0,0,-980}·{-2,3,-6}=5880 (J)24. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角. 解: (a +3b )·(7a -5b )=227||1615||0+⋅-=a a b b ①(a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ② 由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==. 25. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直,求动点的轨迹方程. 解:设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y-1)-4(z-1)=0整理得:2x +3y-4z-1=0即为动点M 的轨迹方程.26. 设a =(-2,7,6),b =(4, -3, -8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a -b ,且a +b ={2,4, -2}a-b ={-6,10,14}又(a +b )·(a-b )= 2×(-6)+4×10+(-2)×14=0故(a +b )⊥(a-b ).27. 已知a =3i +2j -k , b =i -j +2k ,求:(1) a ×b ;(2) 2a ×7b ;(3) 7b ×2a ; (4) a ×a .解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .28. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算:(1) |(a +b )×(a -b )|;(2) |(3a +b )×(a -2b )|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a bπ2||||sin 242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin 842=⨯⨯⨯= 29. 求垂直于向量3i-4j-k 和2i-j +k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||θ⨯===⨯a b a b . 30. 一平行四边形以向量a =(2,1,-1)和b =(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++l l i j k12||||==l l 所以1212||sin 1||||θ⨯===l l l l . 即为所求对角线间夹角的正弦.31. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P -- {2,2,2}MN =--3{1,0,}2MP =- {4,4,4}AC =--{2,0,3}BC =- 22222235233100122MN MP ----⨯=++=++--i j k i j k 44444412208033220AC BC ---⨯=++=++--i j k i j k 故 1()4MN MP AC BC ⨯=⨯. 32. 求同时垂直于向量a =(2,3,4)和横轴的单位向量.解:设横轴向量为b =(x ,0,0)则同时垂直于a ,b 的向量为3442230000x x ⨯=++a b i j k =4x j -3x k故同时垂直于a ,b 的单位向量为1(43)||5⨯=±=±-⨯a b e j k a b . 33. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积. 解:设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ,B ,D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积122S =+. 34. 已知三点A (2,4,1), B (3,7,5), C (4,10,9),证:此三点共线.证明:{1,3,4}AB =,{2,6,8}AC =显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ,B ,C 三点共线.35. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程.解:所求平面与平面3x -2y +6z =11平行故n ={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x -4)-2(y -1)+6(z +2)=0即3x -2y +6z +2=0.36. 求过点M 0(1,7,-3),且与连接坐标原点到点M 0的线段OM 0垂直的平面方程. 解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x -1+7(y -7)-3(z +3)=0即x +7y -3z -59=037. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有121122b b b-++= 得b =2. 故所求平面方程为1424x y z ++= 38. 求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程.解:由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点,有1112121*********x y z --+----+=---+ 化简得x -3y -2z =0即为所求平面方程.39. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x -1=0;(3) 2x -3y -6=0; (4) x –y =0;(5) 2x -3y +4z =0.解:(1) y =0表示xOz 坐标面(如图7-2)(2) 3x -1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z轴且在x轴及y轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x–y=0表示过z轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-6 40. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面. 解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A BA B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.41. 决定参数k的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6);(2)与平面2x-3y+z=0成π4的角. 解:(1)因平面过点(5,-4,6)故有 5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且122123π2cos cos||||42514kkθ⋅-====+⋅n nn n解得2k =±42. 确定下列方程中的l 和m :(1) 平面2x +ly +3z -5=0和平面mx -6y -z +2=0平行; (2) 平面3x -5y +lz -3=0和平面x +3y +2z +5=0垂直. 解:(1)n 1={2,l ,3}, n 2={m ,-6,-1}12232,18613l m l m ⇒==⇒=-=--n n (2) n 1={3, -5, l }, n 2={1,3,2}12315320 6.l l ⊥⇒⨯-⨯+⨯=⇒=n n43. 通过点(1,-1,1)作垂直于两平面x -y +z -1=0和2x +y +z +1=0的平面.解:设所求平面方程为Ax +By +Cz +D =0 其法向量n ={A ,B ,C }n 1={1,-1,1}, n 2={2,1,1}12203203A C A B C A B C CB ⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n n n n 又(1,-1,1)在所求平面上,故A -B +C +D =0,得D =0故所求平面方程为2033CCx y Cz -++= 即2x -y -3z =044. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量. 解:n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 45. 求通过下列两已知点的直线方程: (1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3). 解:(1)两点所确立的一个向量为s ={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s ={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 46. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点(0,7,17),因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为:771719x t y t z t =⎧⎪=-⎨⎪=-⎩47. 求下列直线与平面的交点:(1)11126x y z-+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0. 解:(1)直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为(2,-3,6).(2) 直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为(-2,1,3). 48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩;(2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩解:(1)两直线的方向向量分别为:s 1={5, -3,3}×{3, -2,1}=533321ij k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直,夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x -y +2z -4=0垂直; (2)过点(0,2,4),且与两平面x +2z =1和y -3z =2平行; (3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s ={3,-1,2}故过点(2,-3,4)的直线方程为234312x y z -+-==- (2)所求直线平行两已知平面,且两平面的法向量n 1与n 2不平行,故所求直线平行于两平面的交线,于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n故过点(0,2,4)的直线方程为24231x y z --==- (3)所求直线与已知直线平行,故其方向向量可取为 s ={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z++==--和4x -2y -2z =3; (2)327x y z ==-和3x -2y +7z =8;(3)223314x y z -+-==-和x +y +z =3. 解:平行而不包含. 因为直线的方向向量为s ={-2,-7,3}平面的法向量n ={4,-2,-2},所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上. 51. 求过点(1,-2,1),且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程.解:直线的方向向量为12123111-=++-i j ki j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点(1,-2,3)和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数,又因为所求平面过点(1,-2,3) 故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+= 解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点(-1,2,0)在平面x +2y -z +1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s =n ={1,2,-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0 得23t =-于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(1,2,1)到平面x +2y +2z -10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s =n ={1,2,2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333,且与点(1,2,1)的距离为1d == 即为点到平面的距离. 55. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量即11133211==-=---ij kn s j k 故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d ==56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程. 解:球的半径为22213(2)14.R =++-=设(x ,y ,z )为球面上任一点,则(x -1)2+(y -3)2+(z +2)2=14即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.解:设该动点为M (x ,y ,z ),由题意知222222(2)(0)(3) 3.(4)(6)(6)x y z x y z -+-++=-+++-化简得:8x 2+8y 2+8z 2-68x +108y -114z +779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=. 解:(1)母线平行于z 轴的抛物柱面,如图7-7. (2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8 (3)母线平行于y 轴的椭圆柱面,如图7-9. (4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11. (6)z 轴,如图7-12.图7-11 图7-12 59. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=; (3)222149y z x --=; (4)2221149y z x +-=; (5)22220x y z -+=; (6)22209z x y +-=. 解:(1)半轴分别为1,2,3的椭球面,如图7-13. (2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15. (4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的椭圆锥面,其中心轴是y 轴,如图7-17. (6) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-18.图7-17 图7-1860. 作出下列曲面所围成的立体的图形: (1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0; (3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1. 解:(1)(2)(3)(4)分别如图7-19,7-20,7-21,7-22所示.图7-19 图7-20图7-21 图7-22 61. 求下列曲面和直线的交点:(1) 222181369x y z ++=与342364x y z --+==-; (2) 22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为334624x t y t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1. 得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为4324x t y tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程.解:设(x ,y ,z )为圆上任一点,依题意有2295x y z ⎧+=⎨=±⎩ 即为所求圆的方程.63. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=. 故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线.解:以曲线为准线,母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程. (1) 平面x =2; (2) 平面y =0; (3) 平面y =5; (4) 平面z =2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ⎧==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.66. 求单叶双曲面22211645x y z +-=与平面x -2z +3=0的交线在xOy 平面,yOz 平面及xOz 平面上的投影曲线. 解:以32x z +=代入曲面方程得 x 2+20y 2-24x -116=0.故交线在xOy 平面上的投影为2220241160x y x z ⎧+--=⎨=⎩ 以x =2z -3代入曲面方程,得 20y 2+4z 2-60z -35=0.故交线在yOz 平面上的投影为2220460350y z z x ⎧+--=⎨=⎩ 交线在xOz 平面上的投影为230,0.x z y -+=⎧⎨=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界:(1) {(x ,y )|x ≠0};(2) {(x ,y )|1≤x 2+y 2<4};(3) {(x ,y )|y <x 2};(4) {(x ,y )|(x -1)2+y 2≤1}∪{(x ,y )|(x +1)2+y 2≤1}.解:(1)开集、无界集,聚点集:R 2,边界:{(x ,y )|x =0}. (2)既非开集又非闭集,有界集,聚点集:{(x ,y )|1≤x 2+y 2≤4},边界:{(x ,y )|x 2+y 2=1}∪{(x ,y )| x 2+y 2=4}. (3)开集、区域、无界集,聚点集:{(x ,y )|y ≤x 2},边界:{(x ,y )| y =x 2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x ,y )|(x -1)2+y 2=1}∪{(x ,y )|(x +1)2+y 2=1}. 2. 已知f (x ,y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u vf u v w u w+=+,试求(,,).f x y x y xy +-解:f (x +y , x -y , xy ) =(x +y )xy+(xy )x +y +x -y=(x +y )xy +(xy )2x.4. 求下列各函数的定义域:2(1)ln(21);z y x =-+(2)z=+(3)z =(4)u =+(5)z =(6)ln()z y x =-+(7)u =解:2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>> 2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限:10y x y →→22001(2)lim;x y x y →→+00x y →→0x y →→00sin (5)lim ;x y xyx →→222222001cos()(6)lim .()e x y x y x y x y +→→-++ 解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=001.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O (0,0)处是否连续:33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0,0)点,则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x ,y )=233x y x y -+;(2) f (x ,y )=2222y xy x +-;(3) f (x ,y )=ln(1-x 2-y 2);(4)f (x ,y )=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解:(1)因为当y =-x 时,函数无定义,所以函数在直线y =-x 上的所有点处间断,而在其余点处均连续.(2)因为当y 2=2x 时,函数无定义,所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时,函数无定义,所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数:(1)z =x 2y +2xy;(2)s =22u v uv+;(3)z =x(4)z =lntan x y; (5)z =(1+xy )y; (6)u =z xy;(7)u =arctan(x -y )z; (8)y zu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+ (4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂ 222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y y y x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z z u z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz z u z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .y yzzyy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y=+,求证:3u u x y u x y ∂∂+=∂∂. 证明: 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z z xy z x y∂∂+=∂∂. 证明: 11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1121ex y z y y⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y )=x +(yf x (x ,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z =x 4+ y 4-4x 2y 2; (2)z=arctan y x; (3)z =y x ;(4)z =2ex y+.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,2222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x y z x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x ,y ,z )=xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f -解:2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15.设z =x ln(xy ),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =(3)zy u x =; (4)yzu x =.解:(1)∵2222e 2,e 2x y x y z zx y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解:(1)设f (x ,y )=x 3·y 2,则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =0.02,d y =-0.03,则(1.02)3·(0.97)2=f (1.02,0.97)≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设f (x ,y,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d0.05d0.07(4.05,2.93)(4,3)d(4,3)0.053(0.07)]15(0.01)54.998xyf f f==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=x y,则d f(x,y)=yx y-1d x+x y ln x d y,取x=2,y=1,d x=-0.03,d y=0.05,则1.05d0.03d0.05(1.97)(1.97,1.05)(2,1)d(2,1)20.0393 2.0393.xyf f f=-==≈+=+=19.矩型一边长a=10cm,另一边长b=24cm,当a边增加4mm,而b边缩小1mm时,求对角线长的变化.解:设矩形对角线长为l,则d d).l l x x y y==+当x=10,y=24,d x=0.4,d y=-0.1时,d0.4240.1)0.062l=⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20. 1mol理想气体在温度0℃和1个大气压的标准状态下,体积是22.4L,从这标准状态下将温度升高3℃,压强升高0.015个大气压,问体积大约改变多少?解:由PV=RT得V=RTP,且在标准状态下,R=8.20568×10-2,ΔV≈d v=-2d dRT Rp TP P+=d dV RP TP P-+222.48.20568100.01530.0911-⨯=-⨯+⨯≈-故体积改变量大约为0.09.21. 测得一物体的体积V=4.45cm3,其绝对误差限是0.01cm3,质量m=30.80g,其绝对误差限是0.01g,求由公式mvρ=算出密度ρ的绝对误差与相对误差.解:当V=4.45,m=30.80,d v=0.01,d m=0.01时,22130.801d d d0.010.014.45 4.450.01330.0133mv mv vρ==-+-⨯+⨯≈=-当v=4.45, m=30.80时30.806.92134.45ρ=≈d 0.00192160.19216%ρρ≈=.22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2) z =arc tanx y ,x =u +v ,y =u -v ,求z u ∂∂,z v∂∂; (3) ln(e e )xyu =+,y =x 3,求d d ux; (4) u =x 2+y 2+z 2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx yu v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x yx x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xyu f x y =-(2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xyz xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+ 25. 设22()yz f x y =-,其中f (u )为可导函数,验证:211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f ''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f ''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y ∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,z f x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂由对称性知,22224.z f y f y∂'''=+∂27. 设f 是c 2类函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂ 2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,。
高等数学下教材答案详解

题目:证明函数$f(x)=\begin{cases}x^2-1,\quad x<1\\3x+2,\quad x\geq1\end{cases}$在$x=1$处连续。
解析:要证明函数在$x=1$处连续,需要分别讨论左极限、右极限和函数值是否相等。首先计算左极限,即$$\lim_{x\to1^-}(x^2-1)=(1)^2-1=0$$。然后计算右极限,即$$\lim_{x\to1^+}(3x+2)=3(1)+2=5$$。最后计算$x=1$时的函数值,即$f(1)=3(1)+2=5$。由于左极限、右极限和函数值都相等,因此可以得出结论:函数$f(x)$在$x=1$处连续。
解析:要求函数的极值点,需要先求得函数的导数$f'(x)$。根据乘法法则和指数函数和三角函数求导法则,可以得到$f'(x)=2e^{2x}\sin x+e^{2x}\cos x$。然后,令$f'(x)=0$,解得$x=\frac{3\pi}{2}+k\pi$,其中$k$为整数。将这些解代入原函数$f(x)$,可以得到对应的极值点。
……
通过对高等数学下教材中习题的解析,我们可以更加深入地理解每个章节的内容和知识点。同时,这些答案的详细解析也有助于同学们发现自己在学习过程中的盲点和薄弱环节,从而进行有针对性的补充和提高。希望本文对同学们在学习高等数学下教材时有所帮助,让大家能够更好地掌握这门重要的学科。
总结
通过对高等数学下教材的答案进行详解,本文旨在提供同学们学习和理解教材内容的参考和指导。在学习过程中,同学们可以根据本文的解析,进一步掌握和巩固相关知识点,提升数学能力。当然,本文只是对部分习题进行了解析,同学们在学习过程中还需要充分理解教材中的其他内容,并进行适当的练习和实践。希望本文能够对同学们的学习有所帮助,让大家在高等数学下取得优秀的成绩!
第六版同济大学高等数学上下课后答案详解

|sin x | | x | 3 求 ( ) ( ) ( ) (2) 并作出函数 y(x) 8 设 ( x) 4 6 4 | x | 0 3
的图形 解 ( ) |sin | 1 ( ) |sin | 2 ( ) |sin( )| 2 (2) 0 6 6 2 4 4 2 4 4 2 9 试证下列函数在指定区间内的单调性 (1) y x ( 1) 1 x (2)yxln x (0 ) 证明 (1)对于任意的 x1 x2( 1) 有 1x10 1x20 因为当 x1x2 时
对于映射 g YX 因为对每个 yY 有 g(y)xX 且满足 f(x)f[g(y)]Iy yy 按逆映射的定义 g 是 f 的逆映射 5 设映射 f XY AX 证明 (1)f 1(f(A))A (2)当 f 是单射时 有 f 1(f(A))A 证明 (1)因为 xA f(x)yf(A) f 1(y)xf 1(f(A)) f 1(f(A))A 所以 (2)由(1)知 f 1(f(A))A 另一方面 对于任意的 xf 1(f(A))存在 yf(A) 使 f 1(y)xf(x)y 因为 yf(A)且 f 是单射 所以 xA 这就证明了 f 1(f(A))A 因此 f 1(f(A))A 6 求下列函数的自然定义域 (1) y 3x 2 解 由 3x20 得 x 2 函数的定义域为 [ 2 , ) 3 3 (2) y 1 2 1 x 解 由 1x20 得 x1 函数的定义域为( 1)(1 1)(1 ) (3) y 1 1 x 2 x 解 由 x0 且 1x20 得函数的定义域 D[1 0)(0 1] (4) y
y1 y2
x1 x x1 x2 2 0 1 x1 1 x2 (1 x1)(1 x2 )
高等数学第1章课后习题答案(科学出版社)

第一章 函数、极限、连续习题1-11.求下列函数的自然定义域:(1)321x y x=+-(2) 1arctany x=+(3) 1arccosx y -=;(4) 313 , 1x y x ⎧≠⎪=⎨⎪=⎩. 解:(1)解不等式组23010x x +≥⎧⎨-≠⎩得函数定义域为[3,1)(1,1)(1,)---+∞U U ; (2)解不等式组230x x ⎧-≥⎨≠⎩得函数定义域为[U ;(3)解不等式组2111560x x x -⎧-≤≤⎪⎨⎪-->⎩得函数定义域为[4,2)(3,6]--U ; (4)函数定义域为(,1]-∞.2.已知函数()f x 定义域为[0,1],求(cos ),()() (0)f f x f x c f x c c ++->的定义域.解:函数f要有意义,必须01≤≤,因此f 的定义域为[0,1];同理得函数(cos )f x 定义域为[2π-,2π]22k k ππ+;函数()()f x c f x c ++-要有意义,必须0101x c x c ≤+≤⎧⎨≤-≤⎩,因此,(1)若12c <,定义域为:[],1c c -;(2)若12c =,定义域为:1{}2;(3)若12c >,定义域为:∅. 3.设21()1,||x a f x x x a ⎛⎫-=- ⎪-⎝⎭0,a >求函数值(2),(1)f a f .解:因为21()1||x a f x x x a ⎛⎫-=- ⎪-⎝⎭,所以 21(2)104a f a a a ⎛⎫=-= ⎪⎝⎭,22 ,>1,11(1)10 ,0<<111a a f a a ⎛⎫⎧-=-= ⎪⎨ ⎪-⎩⎝⎭. 4. 证明下列不等式:(1) 对任何x R ∈有 |1||2|1x x -+-≥; (2) 对任何n Z +∈有 111(1)(1)1n n n n++>++;(3) 对任何n Z +∈及实数1a >有 111na a n--≤.证明:(1)由三角不等式得|1||2||1(2)|1x x x x -+-≥---= (2)要证111(1)(1)1n n n n++>++,即要证111n +>+= 111(1)(1)(1)11111n n n n n +++++++<=+++L 得证。
同济高等数学第一章习题课

f (x) b k = lim [ − ] x→+∞ x x ∴ f (x) k = lim x→+∞ x
(或x →−∞)
f (x) b lim x[ −k − ] = 0 x→+∞ x x f (x) b lim [ −k − ] = 0 x→+∞ x x
b = lim [ f (x) − kx]
1
lim(cos x )
x →0
x2
ln cos x ln(1 + cos x − 1) lim = lim 2 x→ 0 x →0 → x x2 cos x − 1 = lim x→ x →0 x2 x2 − 1 = lim 2 = − x →0 x 2 1 2 − 所以, 所以,原式 = e 2
二、无穷小的比较
例11 当 下列函数分别是x的几阶无穷小 时,下列函数分别是 的几阶无穷小
~ ~
x2 2
x
1 2
2x = 1+ x + 1− x
~
x
练习: 练习: P74,3(1) , ( )
求分段函数的极限, 三、求分段函数的极限,判断分段函数的 连续性, 连续性,间断点的类型
例12
解:
1 x>0 x sin x , f ( x) = , 求 lim f ( x ). x x→ 0 → 1 − cos x − x sin 2 , x<0 x2 x 1 − cos x − x sin 2 lim− f ( x ) = lim− x x →0 x →0 x2 x sin 1 − cos x 1 1 2 = lim− − lim− = − =0 x →0 x →0 x2 x2 2 2 1 lim+ f ( x ) = lim+ x sin = 0 x →0 x →0 x lim− f ( x ) = lim+ f ( x ) = 0
高等数学(经管类)下及课后习题答案

1. 指出下列各点所在的坐标轴、坐标面或卦限:A (2,1,-6),B (0,2,0),C (-3,0,5),D (1,-1,-7).解:A 在V 卦限,B 在y 轴上,C 在xOz 平面上,D 在VIII 卦限。
2. 已知点M (-1,2,3),求点M 关于坐标原点、各坐标轴及各坐标面的对称点的坐标. 解:设所求对称点的坐标为(x ,y ,z ),则(1) 由x -1=0,y +2=0,z +3=0,得到点M 关于坐标原点的对称点的坐标为:(1,-2,-3). (2) 由x =-1,y +2=0,z +3=0,得到点M 关于x 轴的对称点的坐标为:(-1,-2,-3). 同理可得:点M 关于y 轴的对称点的坐标为:(1, 2,-3);关于z 轴的对称点的坐标为:(1,-2,3).(3)由x =-1,y =2,z +3=0,得到点M 关于xOy 面的对称点的坐标为:(-1, 2,-3).同理,M 关于yOz 面的对称点的坐标为:(1, 2,3);M 关于zOx 面的对称点的坐标为:(-1,-2,3).3. 在z 轴上求与两点A (-4,1,7)和B (3,5,-2)等距离的点. 解: 设所求的点为M (0,0,z ),依题意有|MA |2=|MB |2,即(-4-0)2+(1-0)2+(7-z)2=(3-0)2+(5-0)2+(-2-z)2.解之得z =11,故所求的点为M (0,0,149). 4. 证明以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 解:由两点距离公式可得21214M M =,2213236,6M M M M ==所以以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 5. 设平面在坐标轴上的截距分别为a =2,b =-3,c =5,求这个平面的方程.解:所求平面方程为1235y x z++=-。
高等数学下册课后习题答案

高等数学下册课后习题答案高等数学下册课后习题答案在学习高等数学下册的过程中,课后习题是非常重要的一部分。
通过解答习题,我们不仅可以巩固课堂知识,还可以提高自己的解题能力和思维能力。
然而,有时候我们会遇到一些难题,对于这些问题,我们需要有一个可以参考的答案。
下面,我将为大家提供一些高等数学下册课后习题的答案,希望对大家的学习有所帮助。
1. 题目:求函数 f(x) = x^3 - 3x^2 + 2x - 1 的极值点和极值。
解答:首先,我们需要求出函数的导数 f'(x)。
对 f(x) 进行求导,得到 f'(x) =3x^2 - 6x + 2。
然后,我们令 f'(x) = 0,解得 x = 1 或 x = 1/3。
接下来,我们需要判断这两个解是否为极值点。
为了判断,我们可以求出f''(x),即 f'(x) 的导数。
对 f'(x) 进行求导,得到 f''(x) = 6x - 6。
当 x = 1 时,f''(x) = 0,此时无法判断是否为极值点。
当 x = 1/3 时,f''(x) = -2,为负数,即 x = 1/3 为极大值点。
所以,函数 f(x) 的极大值点为 x = 1/3,极大值为 f(1/3) = -8/27。
2. 题目:证明数列 {an} 为等差数列,其中 a1 = 2,a2 = 5,a3 = 8。
解答:要证明数列 {an} 为等差数列,我们需要证明其通项公式为 an = a1 + (n - 1)d,其中 d 为公差。
首先,我们可以计算出公差 d。
根据已知条件,a2 - a1 = 5 - 2 = 3,a3 - a2 =8 - 5 = 3。
可以发现,a2 - a1 = a3 - a2,即这两个差值相等。
所以,公差 d = 3。
接下来,我们验证通项公式是否成立。
代入已知条件,an = a1 + (n - 1)d,即an = 2 + (n - 1)3 = 2 + 3n - 3 = 3n - 1。
高等数学课后习题答案--第一章 函数与极限

第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤ []ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由 ][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a ax a ax a a x a x3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()xe x g =,求()[]x gf 和()[]x fg ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}nx 有界, 又,0lim =∞→nn y证明:.0lim =∞→n n n y x{}结论成立。
从而时,有,当自然数即又有对有界,∴=<=-<>∃>∀=≤∀>∃∴∞→ ..0)(,0,0lim ,,0εεεεMM y x y x My N n N y Mx n M x n n n n n n n n n 5. 根据函数的定义证明: ⑴()813lim 3=-→x x8)13(lim 813303,033,33813,03=-<--<-<>∀<-<-=-->∀→x x x x x x x 所以成立时,恒有,当=取故即可。
高等数学(同济大学版) 课程讲解 第一章习题课1教学内容

课时授课计划课次序号:08 一、课题:第一章函数与极限习题课二、课型:习题课三、目的要求:1.加深对函数、极限、连续等基本概念的理解;2.熟练掌握极限的运算方法.四、教学重点:极限运算、两个重要极限、无穷小比较、函数的连续性.教学难点:极限存在准则.五、教学方法及手段:讲练结合,传统教学与多媒体教学相结合.六、参考资料:1.《高等数学释疑解难》,工科数学课程教学指导委员会编,高等教育出版社;2.《高等数学习题课讲义》,同济大学数学教研组主编,高等教育出版社;3.《高等数学教与学参考》,张宏志主编,西北工业大学出版社.七、作业:总复习题一3(2)(3),8(2)(4)(6),10,11,12八、授课记录:九、授课效果分析:第一章 函数与极限习题课一、 主要内容1. 函数函数的概念与特性,反函数,复合函数,基本初等函数,初等函数.2. 极限极限定义、运算、性质,两个重要极限,无穷小比较,极限存在准则.3. 连续函数连续的概念,间断点的类型,初等函数的连续性,闭区间上连续函数的性质,分段函数的连续性.二、典型例题1. 求复合函数例1设()f x =[()]f f x .解[()]f f x ===.2. 利用函数概念求函数表达式例2 设(e )1sin xf x x =++,求()f x .解 令e xt =,则ln x t =,()1ln sin(ln )f t t t =++,()1ln sin(ln )f x x x ∴=++. 例3 设2()sin ,[()]1f x x f x x ϕ==-,求()x ϕ.解 2[()]sin ()1f x x x ϕϕ==-,2()arcsin(1),[x x x ϕ∴=-∈.3. 求00或∞∞型未定式的极限例4 330()lim h x h x h→+-解 []223300()()()()lim limh h x h x x h x h x x x h x h h→→⎡⎤+-+++++-⎣⎦= 222lim ()()3h x h x h x x x →⎡⎤=++++=⎣⎦. 例5 3x →解33(23)92)x x x →→+-=343x x →→===.例6 limx解limlim1x x ==.4.求0⋅∞或∞-∞型未定式的极限例7 1lim x-→解1111lim lim lim(1)2x x x x x ----→→→→===+=. 例8 1lim x →313()11x x --- 解 233211113132lim()lim lim 11111x x x x x x x x x x x →→→++----===----++. 5. 求幂指函数(001,0,∞∞型未定式)的极限例9 32lim 22xx x x →∞-⎛⎫ ⎪-⎝⎭解 22223211lim lim 1lim 1222222x x x xxx x x x x x x --→∞→∞→∞⎡⎤-⎛⎫⎛⎫⎛⎫=+=+⎢⎥ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦2211lim 1e, lim 22222xx x x x x -→∞→∞⎛⎫+==- ⎪--⎝⎭Q ,1232lim e 22xx x x -→∞-⎛⎫∴= ⎪-⎝⎭; 例10 21ln(1)0lim(cos )x x x +→解 1222cos 1cos 111ln(1)ln(1)ln(1)lim(cos )lim(1cos 1)lim (1cos 1)x x x x x x x x x x x --+++→→→⎡⎤=+-=+-⎢⎥⎣⎦, 1cos 1222000cos 112lim(1cos 1)e,lim lim ln(1)2x x x x x x x x x -→→→--+-===-+Q ,211ln(1)20lim(cos )e x x x -+→∴=. 6. 极限的反问题例11 55)(2-++=x bx ax x f (b a ,为常数),问b a ,分别取何值时,有(1)1)(lim =∞→x f x (2)0)(lim =∞→x f x (3)1)(lim 5=→x f x解 (1)1,0==b a (2)0,0==b a(3)由已知得 0)5(lim 25=++→bx ax x ,所以 015=++b a ,代入原式115)1(lim 555lim 525=-=-=-+--→→a ax x x ax ax x x ,所以3,52-==b a . 7. 利用夹逼准则求极限例12 nnnnn 321lim ++∞→解 nn n n 333213⋅≤++≤Θ, 333213⋅≤++≤∴n n n n ,而333lim =⋅∞→n n ,33lim =∞→n , ∴3321lim =++∞→n n n n n8. 利用单调有界准则求极限例13 若x 1,x 2,x n +1n =1,2,…),求lim n n x →∞.解因为12x x ==有21x x >,今设1k k x x ->,则1k k x x +,由数学归纳法知,对于任意正整数n 有1n n x x +>,即数列{}n x 单调递增.又因为12x =<,今设2k x <,则12k x +==,由数学归纳法知,对于任意的正整数 n 有2n x <,即数列{}n x 有上界,由极限收敛准则知lim n n x →∞存在.设lim n n x b →∞=,对等式1n x +=两边取极限得b =22b b =+,解得2b =,1b =-(由极限的保号性,舍去),所以lim 2n n x →∞=. 9. 求n 项和(或积)数列的极限例14 21111lim 3153541n n →∞⎛⎫++++⎪-⎝⎭L解 211111111lim lim 3153541133557(21)(21)n n n n n →∞→∞⎛⎫⎛⎫++++=++++ ⎪ ⎪-⋅⋅⋅-+⎝⎭⎝⎭L L 11111111lim 12335572121n n n →∞⎛⎫=-+-+-++- ⎪-+⎝⎭L 111lim 12212n n →∞⎛⎫=-= ⎪+⎝⎭. 例15 设2coscos cos 222n n x x xx =L ,求lim n n x →∞.解 2sin sincos cos cos sin 222222nn n n n xx x x x xx ==L ,sin (0)2sin 2n n n x x x x ∴=≠, sin sin sin lim limlim(0)2sin 222nnn n n n n n x x xx x x x x →∞→∞→∞∴===≠g .当0x =时,1n x =,lim 1n n x →∞=10. 无穷小的比较与无穷小阶的确定例16 若0→x 时,21cos(e 1)x --和nm x 2等价无穷小,则,m n 各为多少?解 因为当0→x 时,2~cos 12x x -,e 1~xx -,所以222(e 1)1cos(e 1)~2x x ---,从而22224(e 1)()~222x x x -= ,所以 1,4-==m n .例17 0limx→解)()22000112lim x x x x x →→→==4x →==例18 0limx →ln cos 2ln cos3xx解 [][]000ln 1(cos 21)ln cos 2cos 21limlim limln cos3ln cos311(cos31)x x x x x x x x x →→→+--==-+- 22200021(2)1cos 2442lim lim lim .11cos399(3)2x x x x x x x x x →→→-====- 例19 0x → 解2000122lim lim 2sin 24x x x x x xx x →→→+===. 11. 讨论函数的连续性与间断点例20 求下列函数的间断点,并说明类型(1)⎪⎩⎪⎨⎧>≤<-+=-001)1ln()(11x ex x x f x (2)⎪⎪⎩⎪⎪⎨⎧≥-+<π-=01)1(0sin )4()(22x x x x x x x x x f解(1))(x f 的间断点可能为0、1.0=x Θ时,(0)0,f =lim ()lim ln(1)0(0)x x f x x f --→→=+==, 11100lim ()lim (0)x x x f x e e f +--→+→==≠0=∴x 为第一类跳跃间断点.又1=x Θ时,)(x f 在1=x 处无定义,且111lim x x e +-→=+∞,1=∴x 为)(x f 的无穷间断点.(2) ⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅--±=k x ,3,2,1,0都可能为间断点.当0=x 时,20(1)()0,lim ()lim 0(0)1x x x x f x f x f x ++→→+====-,而22000(4)4lim ()lim lim (4)(0)sin x x x x x x f x x f x x πππ---→→→--==-=≠, 0=∴x 为第一类跳跃间断点.当2-=x 时,)(x f 无定义,但π=+π-=-→-→8)2()4(lim)(lim 222x x x x f x x , 2-=∴x 时为可去间断点.当...............5,4,3,1k x ----±=时)(x f 都无定义,且极限为无穷大,因此全为无穷间断点.例21 设⎪⎪⎩⎪⎪⎨⎧<-=>=0)31ln(020sin )(x bx x x x x axx f 问常数b a ,为何值时,)(x f 在0=x 处连续.解 000ln(13)33lim ()lim lim x x x x x f x bx bx b---→→→--===-,000sin lim ()lim lim x x x ax ax f x a x x +++→→→===, 当0lim ()lim ()(0)2x x f x f x f -+→→===,即2,5.1=-=a b 时,)(x f 在0=x 处连续. 12. 闭区间上连续函数性质的应用例22 证明方程ln(1)20xe x +-=至少有一个小于1的正根.证 令()ln(1)2e xf x x =+-,则()f x 在(,)-∞+∞上连续,因而在[0,1]上连续, 且0(0)ln(1)20ln 20e f =+-⨯=>, (1)ln(1)20e f =+-<,由零点定理知,至少存在一点(0,1)ξ∈使得()0f ξ=.即方程ln(1)20xe x +-=至少有一个小于1的正根.三、课后练习1.求下列极限:(1) xx x x tan 2sinlim20→ (2) )sin 1cos (sin lim 0x x x x x -→ (3) n n n n 2)31(lim +-∞→ (4) )1ln()cos 1(1cossin 3lim 20x x x x x x +++→(5) x x x x )1232(lim ++∞→ (6) x x xx x 5sin 3sin lim0+-→ (7) 11sinlim-+∞→x x x x x (8)x x x x sin 1sin 1lim 0--+→2.(1) 已知⎪⎩⎪⎨⎧<->-+=1)1(13)(22x x x A x x f 且)(lim 1x f x → 存在,求常数A .(2) 已知02])2([5lim22=-+--+→x B x A x x ,试求常数A 、B.3. 求下列函数的间断点,并指明其类型.(1))32()1()(11xxe e xf ++= (2))4)(1(2)(---=x x xx f(3)231)(22+--=x x x x f (4))4(2)(22--=x x xx x f4.设⎪⎩⎪⎨⎧≥<-=00cos 22)(x ae x xx x f x ,问a 为何值时,)(x f 在0=x 处连续?5. 设函数)(x f 在],[b a 上连续,b d c a <<<,q p ,为正数.证明:在],[b a 内至少有一点ξ,使()()()()pf c qf d p q f ξ+=+.。
高等数学第一章函数极限练习题

- 17 -
习题课(一)
例7
第 一 章 函 数 极 限 连 续
解
x2 1 ax b] 0. 求常数 a, b, 使得 lim[ x x 1 x2 1 0 lim[ ax b] x x 1 (1 a ) x 2 (b a ) x 1 b lim x x 1 1 a 0, a b 0
第 一 章 函 数 极 限 连 续
x
3 2 1 ) e 3 原式 lim [(1 x 1 x x 1 lim [sin x 1 sin x 1]
x 1 3 x 3 ) ] (
sin x 1 sin x 1 x 1 x 1 x 1 x 1 2 cos sin 2 2 x 1 x 1 | cos | 1 2 1 x 1 x 1 lim sin 0 lim sin x x x 1 x 1 2 所以 原式 0
f A f f f
-6-
2
函数的趋向过程
习题课(一)
定义的四个主要部分
(1) 对任意给定的 , (2) 总存在 ,
第 一 章 函 数 极 限 连 续
(3) 使当 时,
(4) 恒有不等式 成立,
(1),(4)用来刻划函数的趋向过程 (2),(3)用来刻划自变量的趋向过程 (3)起着控制(4)的作用 例5 叙述下列极限的定义 (1) lim xn
1 lim f ( x ) x 0 2
- 20 -
(3)
设 f ( x)
x 1
x 1 e x
习题课(一)
, 考察 lim f ( x ), lim f ( x )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k az bz
(二)空间解析几何 空间直角坐标系
一般方程 旋转曲面
曲线
参数方程 一般方程 参数方程
曲面
平 面
柱
面
直 线
二次曲面
一般方程
对称式方程 点法式方程
1. 空间直线与平面的方程
空间平面
一般式
点法式 截距式
x y z 1 a b c
点 : ( x0 , y0 , z0 ) 法向量 : n ( A , B , C )
L1 M1
L2
M0
M2
L
的方程化为参数方程
设 L 与它们的交点分别为
M1 (t1 , 2 t1 , t1 1),
M 2 (t 2 , 3t 2 4 , 2t 2 1) .
机动 目录 上页 下页 返回 结束
M 0 , M1 , M 2 三点共线
M 0 M1 // M 0 M 2
t1 0 , t 2 2
两向量夹角余弦的坐标表示式
cos
a b
bx b y bz
2
2
2
a x bx a y b y a z bz 0
5、向量积 (叉积、外积) | c || a || b | sin
向量积的坐标表达式
a b ax bx
i
j ay by
4、数量积 (点积、内积) 其中 为a 与b 的夹角 a b | a || b | cos
数量积的坐标表达式
a b a x bx a y b y a z bz
a x bx a y b y a z bz a x a y az
2 2 2
习题课 空间解析几何
一、 内容小结 二、实例分析
机动
目录
上页
下页
返回
结束
一、主要内容
(一)向量代数
(二)空间解析几何
(一)向量代数
向量的 线性运算
向量概念
向量的 表示法
向量的积
数量积 混合积 向量积
向量表示法
向量的分解式: a a x i a y j a z k 在三个坐标轴上的分向量:a x i , a y j , a z k
机动
目录
上页
下页
返回
结束
空间直线
A x B y C z D 0 1 1 1 1 一般式 A2 x B2 y C2 z D2 0
对称式
x x0 m t 参数式 y y0 n t z z0 p t ( x0 , y0 , z0 ) 为直线上一点;
向量的坐标表示式: a {a x , a y , a z }
向量的坐标: a x , a y , a z
其中 a x ,a y , az 分别为向量在 x , y , z 轴上的投影.
向量的加减法、向量与数的乘积等的坐标表达式
a {a x , a y , a z } b {bx , b y , bz } a b {a x bx , a y b y , a z bz } (a x bx )i (a y b y ) j (a z bz )k a b {a x bx , a y b y , a z bz } (a x bx )i (a y b y ) j (a z bz )k a {a x , a y , a z } ( a x )i ( a y ) j ( a z )k
xx y y zz 直线: , s (m , n , p) m n p m n p 垂直:s n 0 A B C 平行: s n 0
sn 夹角公式: sin s n
机动 目录 上页 下页 返回 结束
3. 相关的几个问题
(1) 过直线
A1 x B1 y C1 z D1 0 L: A2 x B2 y C2 z D2 0 的平面束 方程 ( A1 x B1 y C1 z D1 ) ( A2 x B2 y C2 z D2 ) 0
L1
L2
M0
M1 (0 , 0 , 1) , M 2 (2 , 2 , 3) M 1 L x 1 y 1 z 1 L: 1 1 2
M2
机动
目录
上页
下页
返回
结束
取所求平面的法向量
所求为
i j k n s n1 1 1 2 2(3 , 5 , 4) 7 1 4 3 5 4 cos , cos , cos 51 50 50
机动 目录 上页 下页 返回 结束
例. 求过点
且与两直线
都相交的直线 L.
提示: 思路: 先求交点 M1 , M 2 ; 再写直线方程.
s ( m , n , p ) 为直线的方向向量.
机动 目录 上页 下页 返回 结束
2.线面之间的相互关系
面与面的关系 平面
平面 2 : A2 x B2 y C2 z D2 0, n2 ( A2 , B2 , C2 )
垂直: 平行: n1 n2 0
n1 n2 夹角公式: cosθ n1 n2
机动
目录
上页
下页
返回
结束
(2)点 M 0 ( x0 , y0 , z0 ) 到平面 :A x+B y+C z+D = 0
的距离为
M0
d
n
M1
机动
目录
上页
下页
返回
结束
二、典型例题
b j 2k , c 2i 2 j k , 例 已知 a i , 0 0 0 求一单位向量 n , 使 n c , 且 n , a , b 共面. 0 解 设 n xi yj zk , 由题设条件得 0 x2 y2 z2 1 n 1 0 2 x 2 y z 0 n c 2 y z 0 0 n a b 1 2 2 0 解得 n ( i j k ). 3 3 3
例. 求直线
的交点 .
提示: 化直线方程为参数方程
与平面
t
代入平面方程得 t 1
从而确定交点为(1,2,2).
机动 目录 上页 下页 返回 结束
例. 求直线
上的投影直线方程.
在平面
提示:过已知直线的平面束方程
x y z 1 ( x y z 1) 0
即 从中选择 使其与已知平面垂直: 得 1, 从而得投影直线方程 这是投影平面 y z 1 0 x y z 0
A1 A2 B1B2 C1C2 0 A1 B1 C1 A2 B2 C2
机动
目录
上页
下页
返回
结束
线与线的关系
直线 L1:x x1 y y1 z z1 , s (m , n , p ) 1 1 1 1 m1 n1 p1 x x2 y y 2 z z 2 , s2 (m2 , n2 , p2 ) 直线 L2: m2 n2 p2
垂直: 平行: s1 s2 0
s1 s2 夹角公式: cos s1 s2
m1m2 n1n2 p1 p2 0 m1 n1 p1 m 2 n 2 p2
机动
目录
上页
下页
返回
结束
面与线间的关系 平面: Ax By Cz D 0, n ( A , B , C )
机动 目录 上页 下页 返回 结束
2x z 0 例. 设一平面平行于已知直线 x y z 5 0 且垂直于已知平面 7 x y 4 z 3 0 , 求该平面法线的 的方向余弦. 提示: 已知平面的法向量 n1 (7 , 1, 4) 求出已知直线的方向向量
