2019年河北单招文科数学模拟试题(一)【含答案】

合集下载

2019届河北省高三下学期第一次模拟考试文数试卷【含答案及解析】

r13丿
A.二心二MB.h -VFC.■-：?D.:弋壬：「
、填空题
p<0
13.若变量兀宀满足约束条件{x-2y>l，贝V二m.x +f的最小值是
丁-4*03
14.设数列血”}的前川项和为百」，且s，若矶，则k】T•
n弓
15.将函数h：”l2心的图象向右平移个单位后得到函数I、；llLlfI的图象,
第2题【答案】
A
•解析】由题设可知
J=(x|0<x<2}tB= (.v|-卡<x<V?}j贝'JjnB={r|O<r<占} >应选答黑A:
第3题【答案】
D
【解折】m/(3)=5-2-=l」所以
/(/(1))=/(0=^=1,应选答案6
第4题【答案】
6.设等差数列I的前’项和为，若:；== ■:，贝V;一；二（）
A.0B.
C.4D.1
7.一种在实数域和复数域上近似求解方程的方法可以设计如下图所示的程序框图，若输
入的，-，，则输出的结果，—（）
A.小B.
9.下列命题正确的是（）
A.若一直线与两个平面所成角相等，则这两个平面平行
B.若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行
■- :'■■：| ，
经计算二次函数回归模型和线性回归模型的詁|分别约为和，请用说明
选择哪个回归模型更合适，并用此模型预测，超市广告费支出为3万元时的销售额.
7?
参数数据及公式:
L1
工瓦
20.如图，三棱柱」■- 中，“•'丄平面阳2
凉丁二1，•是「的中点.
(1)求证：平面-平面皿也几

河北省高职单招考试数学模拟卷(答案解析)

河北省高职单招考试数学模拟卷一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知复数z 满足()22i z i i -=+，则z 在复平面内对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限2.已知集合{}|21A x y x ==-，集合{}2|B y y x ==，则集合A B = （）A.()1,1 B.[)0,+∞ C.(){}1,1 D.()0,+¥3.已知(),0,x y ∈+∞，4124yx -⎛⎫= ⎪⎝⎭，则xy 的最大值为（）A.2B.98C.32D.944.若不等式20ax bx c ++>的解集为{}|12x x -<<，则不等式()()2112a x b x c ax ++-+<的解集为（）A.{}|21x x -<<B.{}|21x x x <->或C.{}0|3x x x <>或 D.{}|03x x <<5.设()1sin f x x =，()()'21f x f x =，()()'32f x f x =，…，()()'1n n f x f x +=，n N ∈，则()2020f x =（）A.sin xB.sin x- C.cos xD.cos x-6.某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队，平均分到甲、乙两个村进行义务巡诊，其中每个分队都必须有内科医生、外科医生和护士，则不同的分配方案有A.72种B.36种C.24种D.18种7.若幂函数()f x 的图象过点1,22⎛⎫ ⎪ ⎪⎝⎭，则函数()()xf xg x e =的递增区间为（）A.()0,2B.()(),02,-∞+∞C.()2,0-D.()(),20,-∞-+∞ 8.设函数()21f x mx mx =--，若对于[]1,3x ∈，()2f x m >-+恒成立，则实数m 的取值范围（）A.()3,+∞ B.3,7⎛⎫-∞ ⎪⎝⎭ C.(),3-∞ D.3,7⎛⎫+∞ ⎪⎝⎭二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分；部分选对的得3分；有选错的得0分.9.若复数21iz =+，其中i 为虚数单位，则下列结论正确的是（）A.z 的虚部为1-B.||z =C.2z 为纯虚数D.z 的共轭复数为1i--10.下列命题正确的是（）A.“1a >”是“11a<”的必要不充分条件B.命题“()00,x ∃∈+∞，00ln 1x x =-”的否定是“()0,x ∀∈+∞，ln 1x x ≠-”C.若,a b ∈R ，则2b a a b +≥=D.设a R ∈，“1a =”，是“函数()1xxa e f x ae -=+在定义域上是奇函数”的充分不必要条件11.关于11()a b -的说法，正确的是()A.展开式中的二项式系数之和为2048B.展开式中只有第6项的二项式系数最大C.展开式中第6项和第7项的二项式系数最大D.展开式中第6项的系数最小12.如图直角梯形ABCD ，//AB CD ，AB BC ⊥，122BC CD AB ===，E 为AB 中点，以DE 为折痕把ADE 折起，使点A 到达点P 的位置，且PC =．则（）A.平面PED ⊥平面EBCDB.PC ED⊥C.二面角P DC B --的大小为4π D.PC 与平面PED 三、填空题：本题共4小题，每小题5分，共20分.13.从某班6名学生（其中男生4人，女生2人）中任选3人参加学校组织的社会实践活动，设所选三人中男生人数为ξ，则数学期望()E ξ=______.14.如图，在正方体''''ABCD A B C D -中，'BB 的中点为M ，CD 的中点为N ，异面直线AM 与'D N 所成的角是______.15.在()()5122x x -+展开式中，4x 的系数为______.16.关于x 的方程ln 10xkx x--=在(]0,e 上有两个不相等的实根，则实数k 的取值范围______.河北省高职单招考试数学模拟卷答案解析一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知复数z 满足()22i z i i -=+，则z 在复平面内对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】C 【解析】利用复数除法运算求得z ，从而求得z ，由此得到z 对应的坐标，进而求得z 在复平面内对应的点所在象限.【详解】因为()()()2(1)2221322255i i i i i i iz i i i -+++--+--+====--⨯+，所以3155z i =--，z 对应点为31,55⎛⎫-- ⎪⎝⎭，所以z 在复平面内对应的点位于第三象限.故选：C.【点睛】本小题主要考查复数的除法运算，共轭复数，考查复数对应点所在象限的判断，属于基础题目.2.已知集合{}|21A x y x ==-，集合{}2|B y y x ==，则集合A B = （）A.()1,1B.[)0,+∞C.(){}1,1 D.()0,+¥【答案】B 【解析】【分析】先求出集合,A B ，即可求出交集.【详解】{}|21A x y x R ==-= ，{}[)2|0,B y y x ===+∞，[)0,A B ∴=+∞ .故选：B.【点睛】本题考查函数定义域和值域的求法，考查集合交集运算，属于基础题.3.已知(),0,x y ∈+∞，4124yx -⎛⎫= ⎪⎝⎭，则xy 的最大值为（）A.2B.98C.32D.94【答案】A【分析】根据4124yx -⎛⎫= ⎪⎝⎭可得24x y +=，之后利用基本不等式得到2112(2)(2222x y xy x y +=⋅≤=，从而求得结果.【详解】因为(),0,x y ∈+∞，且421224yx y --⎛⎫== ⎪⎝⎭，所以42x y -=-，即24x y+=，所以有2112(2)(2222x y xy x y +=⋅≤=，当且仅当22x y ==时取得最大值2，故选：A.【点睛】该题考查的是有关应用基本不等式求最值的问题，涉及到的知识点有利用基本不等式求积的最大值，属于简单题目.4.若不等式20ax bx c ++>的解集为{}|12x x -<<，则不等式()()2112a x b x c ax ++-+<的解集为（）A.{}|21x x -<<B.{}|21x x x <->或C.{}0|3x x x <>或D.{}|03x x <<【答案】C 【解析】【分析】由题意得0a <，利用韦达定理找到,,a b c 之间的关系，代入所求不等式即可求得.【详解】不等式20ax bx c ++>的解集为{}|12x x -<<，则1x =与2x =是方程20ax bx c ++=的两根，且0a <，由韦达定理知121b a -=-+=，122ca=-⨯=-，即=-b a ，2c a =-，则不等式()()2112a x b x c ax ++-+<可化简为()()21122a x a x a ax +---<，整理得：230ax ax -<，即(3)0ax x -<，由0a <得0x <或3x >，故选：C.【点睛】本题主要考一元二次不等式，属于较易题.5.设()1sin f x x =，()()'21f x f x =，()()'32f x f x =，…，()()'1n n f x f x +=，n N ∈，则()2020f x =（）A.sin xB.sin x- C.cos xD.cos x-【答案】D 【解析】【分析】根据三角函数的导函数和已知定义，依次对其求导，观察得出4()(),n n f x f x n N +=∈，可得解.【详解】1()sin f x x = ，()''1()sin cos f x x x ∴==，'12()()cos f x f x x ==，()23'()(cos )sin f x f x x x '===-，()34'()(sin )cos f x f x x x '==-=-，()45'()(cos )sin f x f x x x '==-=，由此可知：4()(),n n f x f x n N +=∈，24201()()cos f x f x x ∴==-.故选：D.【点晴】本题考查三角函数的导数，依次求三角函数的导数找到所具有的周期性是解决此问题的关键，属于中档题.6.某医院拟派2名内科医生、3名外科医生和3名护士共8人组成两个医疗分队，平均分到甲、乙两个村进行义务巡诊，其中每个分队都必须有内科医生、外科医生和护士，则不同的分配方案有A.72种 B.36种 C.24种 D.18种【答案】B 【解析】【分析】根据条件2名内科医生，每个村一名，3名外科医生和3名护士，平均分成两组，则分1名外科，2名护士和2名外科医生和1名护士，根据排列组合进行计算即可．【详解】2名内科医生，每个村一名，有2种方法，3名外科医生和3名护士，平均分成两组，要求外科医生和护士都有，则分1名外科，2名护士和2名外科医生和1名护士，若甲村有1外科,2名护士,则有1233339C C =⨯=，其余的分到乙村，若甲村有2外科,1名护士,则有2133339C C =⨯=，其余的分到乙村，则总共的分配方案为2×(9+9)=2×18=36种，故选B.【点睛】本题主要考查了分组分配问题，解决这类问题的关键是先分组再分配，属于常考题型.7.若幂函数()f x 的图象过点1,22⎛⎫ ⎪ ⎪⎝⎭，则函数()()x f x g x e =的递增区间为（）A.()0,2B.()(),02,-∞+∞C.()2,0-D.()(),20,-∞-+∞ 【答案】A 【解析】【分析】设()f x x α=，代入点求出α，再求出()g x 的导数()g x '，令()0g x '>，即可求出()g x 的递增区间.【详解】设()f x x α=，代入点122⎛⎫ ⎪ ⎪⎝⎭，则122α⎛⎫= ⎪ ⎪⎝⎭，解得2α=，()2x x g x e∴=，则()2222()x x xxx x xe x e g x e e --'==，令()0g x '>，解得02x <<，∴函数()g x 的递增区间为()0,2.故选：A.【点睛】本题考查待定系数法求幂函数解析式，考查利用导数求函数的单调区间，属于基础题.8.设函数()21f x mx mx =--，若对于[]1,3x ∈，()2f x m >-+恒成立，则实数m 的取值范围（）A.()3,+∞B.3,7⎛⎫-∞ ⎪⎝⎭ C.(),3-∞ D.3,7⎛⎫+∞ ⎪⎝⎭【答案】A 【解析】【分析】由题意变量分离转为231m x x >-+在[]1,3x ∈上恒成立，只需2max31m x x ⎛⎫ ⎪+⎝⎭->，求出最大值即可得到实数m 的取值范围.【详解】由题意，()2f x m >-+可得212mx mx m ->-+-，即()213m x x +>-，当[]1,3x ∈时，[]211,7x x -+∈，所以231m x x >-+在[]1,3x ∈上恒成立，只需2max31m x x ⎛⎫ ⎪+⎝⎭->，当1x =时21x x -+有最小值为1，则231x x -+有最大值为3，则3m >，实数m 的取值范围是()3,+∞，故选：A【点睛】本题考查不等式恒成立问题的解决方法，常用变量分离转为求函数的最值问题，属于基础题.二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分；部分选对的得3分；有选错的得0分.9.若复数21iz =+，其中i 为虚数单位，则下列结论正确的是（）A.z 的虚部为1-B.||z =C.2z 为纯虚数D.z 的共轭复数为1i--【答案】ABC 【解析】【分析】首先利用复数代数形式的乘除运算化简z 后得：1z i =-，然后分别按照四个选项的要求逐一求解判断即可.【详解】因为()()()2122211i 1i 12i i z i i --====-++-，对于A：z 的虚部为1-，正确；对于B：模长z =，正确；对于C：因为22(1)2z i i =-=-，故2z 为纯虚数，正确；对于D：z 的共轭复数为1i +，错误.故选：ABC.【点睛】本题考查复数代数形式的乘除运算，考查复数的有关概念，考查逻辑思维能力和运算能力，侧重考查对基础知识的理解和掌握，属于常考题.10.下列命题正确的是（）A.“1a >”是“11a<”的必要不充分条件B.命题“()00,x ∃∈+∞，00ln 1x x =-”的否定是“()0,x ∀∈+∞，ln 1x x ≠-”C.若,a b ∈R ，则2b a a b +≥=D.设a R ∈，“1a =”，是“函数()1xxa e f x ae-=+在定义域上是奇函数”的充分不必要条件【答案】BD 【解析】【分析】根据不等式的性质可判断A；根据含有量词的否定可判断B；根据基本不等式的适用条件可判断C；根据奇函数的性质可判断D.【详解】对于A，当1a >时，可得11a<，故“1a >”是“11a<”的充分条件，故A 错误；对于B，由特称命题的否定是存在改任意，否定结论可知B 选项正确；对于C，若0ab <时，2b a a b +≤-=-，故C 错误；对于D，当1a =时，1()1xx e f x e -=+，此时()()f x f x -=-，充分性成立，当()1xxa e f x ae -=+为奇函数时，由1()1x x xx a e ae f x ae e a-----==++，()()f x f x -=-可得1a =±，必要性不成立，故D 正确.故选：BD.【点睛】本题考查充分条件与必要条件，考查命题及其关系以及不等关系和不等式，属于基础题.11.关于11()a b -的说法，正确的是()A.展开式中的二项式系数之和为2048B.展开式中只有第6项的二项式系数最大C.展开式中第6项和第7项的二项式系数最大D.展开式中第6项的系数最小【答案】ACD【分析】根据二项式系数的性质即可判断选项A；由n 为奇数可知，展开式中二项式系数最大项为中间两项，据此即可判断选项BC；由展开式中第6项的系数为负数，且其绝对值最大即可判断选项D.【详解】对于选项A：由二项式系数的性质知，11()a b -的二项式系数之和为1122048=，故选项A 正确；因为11()a b -的展开式共有12项，中间两项的二项式系数最大，即第6项和第7项的二项式系数最大，故选项C 正确，选项B 错误；因为展开式中第6项的系数是负数，且绝对值最大，所以展开式中第6项的系数最小，故选项D 正确；故选：ACD【点睛】本题考查利用二项式定理求二项展开式的系数之和、系数最大项、系数最小项及二项式系数最大项；考查运算求解能力；区别二项式系数与系数是求解本题的关键；属于中档题、常考题型.12.如图直角梯形ABCD ，//AB CD ，AB BC ⊥，122BC CD AB ===，E 为AB 中点，以DE 为折痕把ADE 折起，使点A 到达点P 的位置，且PC =．则（）A.平面PED ⊥平面EBCDB.PC ED ⊥C.二面角P DC B --的大小为4π D.PC 与平面PED 【答案】AC【解析】A 中利用折前折后不变可知PD AD =,根据222PD CD PC +=可证CD PD ⊥,可得线面垂直，进而证明面面垂直；B 选项中AED ∠不是直角可知,PD ED 不垂直，故PC ED ⊥错误；C 中二面角P DC B --的平面角为PDE ADE ∠=∠,故正确；D 中PC 与平面PED 所成角为CPD ∠,计算其正切值即可.【详解】A 中,PD AD ===,在三角形PDC 中，222PD CD PC +=，所以PD CD ⊥,又CD DE ⊥，可得CD ⊥平面PED ，CD ⊂平面EBCD ，所以平面PED ⊥平面EBCD ，A 选项正确；B 中，若PC ED ⊥，又ED CD ⊥，可得ED ⊥平面PDC ,则ED PD ⊥,而EDP EDA ∠=∠,显然矛盾，故B 选项错误；C 中，二面角P DC B --的平面角为PDE ∠，根据折前着后不变知=45PDE ADE ∠=∠︒，故C 选项正确；D 中，由上面分析可知，CPD ∠为直线PC 与平面PED 所成角，在t R PCD V 中，2tan 2CD CPD PD ∠==,故D 选项错误.故选：AC【点睛】本题主要考查了线面垂直的判定，二面角，线面角的求法，属于中档题.三、填空题：本题共4小题，每小题5分，共20分.13.从某班6名学生（其中男生4人，女生2人）中任选3人参加学校组织的社会实践活动，设所选三人中男生人数为ξ，则数学期望()E ξ=______.【答案】2【解析】【分析】ξ的可能值为1,2,3，计算概率得到分布列，再计算数学期望得到答案.【详解】ξ的可能值为1,2,3，则()124236115C C p C ξ===；()214236325C C p C ξ⋅===；()3436135C p C ξ===.故分布列为：ξ123p 153515故()1311232555E ξ=⨯+⨯+⨯=.故答案为：2.【点睛】本题考查了概率的计算，分布列，数学期望，意在考查学生的计算能力和应用能力.14.如图，在正方体''''ABCDA B C D -中，'BB 的中点为M ，CD 的中点为N ，异面直线AM 与'D N 所成的角是______.【答案】90︒【解析】【分析】取CC '中点E ，连接ME ，连接ED 交D N '于F ，可知即DFN ∠为异面直线AM 与'D N 所成的角，求出即可.【详解】取CC '中点E ，连接ME ，连接ED 交D N '于F ，在正方体中，可知ME BC AD ∥∥,∴四边形AMED 是平行四边形，AM ED ∴ ，即DFN ∠为异面直线AM 与'D N 所成的角，可知在Rt ECD △和Rt NDD ' 中，,,90EC ND CD DD ECD NDD ''==∠=∠= ,ECD NDD '∴≅ ，CED FND ∴∠=∠,90CED EDC ∠+∠= ,90FND FDN ∴∠+∠= ,90DFN ∴∠= ，即异面直线AM 与'D N 所成的角为90 .故答案为：90 .【点睛】本题考查异面直线所成角的求法，属于基础题.15.在()()5122x x -+展开式中，4x 的系数为______.【答案】80【解析】【分析】将原式化为()()5521212x x x -+-，根据二项式定理，求出()512x -展开式中3x ，4x 的系数，即可得出结果.【详解】()()()()55512221212x x x x x -+=-+-，二项式()512x -的展开式的第1r +项为()152rr r r T C x +=-，令3r =，则()333345280T C x x =-=-，令4r =，则()444455280T C x x =-=，则()()5122x x -+展开式中，4x 的系数为2808080⨯-=.故答案为：80.【点睛】本题主要考查求指定项的系数，熟记二项式定理即可，属于基础题型.16.关于x 的方程ln 10x kx x --=在(]0,e 上有两个不相等的实根，则实数k 的取值范围______.【答案】21,1e e +⎡⎫⎪⎢⎣⎭【解析】【分析】分离参数，构造函数2ln 1(),(0,]x f x x e x x =+∈，利用导数讨论()f x 的单调性，再结合关于x 的方程ln 10x kx x--=在(]0,e 上有两个不相等的实根等价于()y f x =与y k =有两个交点，即可求出k 的取值范围.【详解】ln 10x kx x --= ，2ln 1x k x x ∴=+，设2ln 1(),(0,]x f x x e x x =+∈，312ln ()x x f x x --∴='，设()12ln ,(0,]g x x x x e =--∈，2()10g x x∴=--<'，即()g x 在(]0,e 是减函数，又(1)0g =，∴当01x <<时，()0>g x ，即()0f x '>，当1x e <<时，()0<g x ，即()0f x '<，()f x ∴在()0,1为增函数，在()1,e 为减函数，当0x →时，()f x →-∞，21()(1)1,e e f f e =+=，关于x 的方程ln 10x kx x--=在(]0,e 上有两个不相等的实根等价于()y f x =与y k =有两个交点，由上可知211e k e +< ，∴实数k 的取值范围为21,1e e +⎡⎫⎪⎢⎣⎭.故答案为：21,1e e +⎡⎫⎪⎢⎣⎭.【点睛】本题考查利用导数解决方程根的问题，属于较难题.。

河北省保定市2019年高三(4月)第一次模拟考试文科数学试题(扫描版)

文科数学答案一、选择题：ABDAC BADBCCC 二、填空题：13.1y x =+14.2315.1.216.4516.解：法1：由已知得345OA OB OC = －－，两边平方得45OB OC ∙= －，同理35OA OC ∙= －，OA OB ∙ ＝０所以4()()^5AB AC OB OA OC OA ∙-∙- ＝＝＝法2：以O 为原点建立坐标系。

设A(-1,0),B（cosα,sinα），C（cosβ,sinβ）.代入已知得4sin 5sin 034,cos =0sin =1cos sin -4cs 5cos 355αββααββαβ+=⎧==⎨+=⎩消去得，，，844=1,1-555AB AC AB AC =∴= 则（），（，法3：以AB 所在直线为x 轴，中垂线为y 轴，建立坐标系。

并设A(-a,0),B(a,0),C(b,c),O(0,t),代入3450,OA OB OC ++= 可得12,55a b c t =-=又因为||||||1,OA OB OC === 所以222212()1a t a b c t ⎧+=⎪⇒=⎨+-=⎪⎩4=5AB AC AB AC =∴= 则），三、解答题：17.解析:（1）由2()cos 2cos 1f x x x x =+-，得2()sin cos )(2cos 1)2cos 22sin(26f x x x x x x x π=+-=+=+…3分所以函数()f x 的最小正周期为π……………………………………………………………5分（2）由（1）可知2)62sin(2)(-=+=πA A f ，…………………………………………6分即)∈(,+2-=6+),0(22ππππA k A 解得32=πA .…………………………………………7分由余弦定理得A bc c b a cos 2222-+=,即bc bc c b 31622≥++=，解得316≤bc ,当且仅当433b c ==时等号成立………………………………………10分所以3342331621sin 21=⨯⨯≤=∆A bc S ABC ……………………………………………12分18.解析：(1)如图所示取线段PD 中点H ，连接,NH AH .在PDC ∆中，1,2NH DC NH DC =,因为ABCD 为菱形，M 为中点，所以1,.2AM DC AM DC = 所以,.HN AM HN AM = ……………………………………3分所以四边形AMNH 为平行四边形，所以.MN AH 因为PAD MN PAD AH 面面⊄⊂,,所以MN PAD 平面.………………………6分（2）因为22==PD PA ，AD=4，所以PD AP ⊥,取AD 中点O ,连接PO ，则AD PO ⊥,因为面PAD ⊥面ABCD ,所以ABCD PO 面⊥,则2,4,PO BD ==…………………9分在POB Rt ∆中4PB =，所以72=∆PBD S ，设三棱锥A-PBD 的高为h ，由PBD A ABD P V V --=,得h ⋅⋅=⋅⋅⋅72312164331，解得7214=h ，所以三棱锥A-PBD 的高是7214……………………………………………………12分19.解析：（1）易知抛物线24y x =的焦点为(1,0)，所以椭圆C 的半焦距1c =……2分又因为其离心率为21，所以2a =，故b =…………………………………………4分所以C 的方程为13422=+y x …………………………………………………………………5分(2)法1：由题可知，直线l 斜率存在且不为0，设l 方程为+y kx n =,则有⎩⎨⎧=-++=0124322y x nkx y ，整理得：01248)43(222=-+++n knx x k 。

2019年高职单招语文数学样卷及答案.doc

2019年高职单招语文数学样卷及答案（80分钟完卷）亲爱的同学：祝贺你完成了本学期的数学学习，现在是展示你学习成果之时，请认真答卷，尽情的发挥，相信你是最棒的！单独招生考试语文测试卷样卷一.选择题( 共60分每题5分)1.下列加点字的注音全都正确的一项是( )A.酣(gān)睡袅娜(nà) 开天辟(bì)地B.怯(qiè)懦阡(qiān)陌杳(yǎo)无人烟C.兑(tuō)现耸峙(sì) 坚韧(rěn)不拔D.敷(fù)衍两栖(xī) 蓊蓊(wēng)郁郁2.下列词语中加点的字书写全都正确的一项是( )A.生机勃勃再接再励摇拽多姿B.循序渐近情不自尽没精打彩C.惊心动魄随心所欲无独有偶D.心悦诚伏五体投地刻骨明心3.依次选字填空，答案正确的一项是( )喜上眉( ) ①稍②烧③梢④捎名列前( ) ①茅②矛③卯④袤如火如( ) ①菟②茶③搽④荼惨遭杀( ) ①戳②戮③路④虏A.①②③④B.③①②④C.③②①④D.③①④②4.下列成语中加点的字解释错误的一项是( )A.怨天尤(怨恨)人B.含辛茹(吃)苦C.望穿秋水(比喻眼睛)D.永垂(垂下)不朽5.下列各句标点使用正确的一项是( )A.那个姑娘十八、九岁光景。

B.“行啊，”小王说：“叫我干什么?我就干什么。

”C.节日的北京，到处是人，到处是花，到处是欢声，到处是笑语……D.这本书是他的，还是你的?6.下列句子没有语病的一项是( )A.参加校庆活动的有教师、学生和家长，共计500余人。

B.为避免学生不再发生考试作弊，近期学校对学生加强了组织纪律教育。

C.同学们的欢快笑容与悠扬歌声，至今还在我的耳边回响。

D.那是一张两人的合影，左边是一位英姿飒爽的解放军战士，右边是一位文弱的莘莘学子。

7.下列各句与“皎洁的月亮从云缝后面向下窥探着”所使用的修辞手法相同的一项是( )A.朵朵浪花托起一个个美丽的传说。

B.休闲是人生一枚甘甜的果实。

2019年河北省保定市高考数学一模试卷(文科)

2019年河北省保定市高考数学一模试卷（文科）一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有一项是符合题目要求的1．（5分）若复数z＝，则＝（）A．﹣1+3i B．﹣1﹣3i C．1+3i D．1﹣3i2．（5分）已知cosα＝﹣，且α为第二象限角，则sin2α的值为（）A．B．﹣C．D．﹣3．（5分）设P和Q是两个集合，定义集合P﹣Q＝{x|x∈P，且x∉Q}，如果P＝{x|1＜2x＜4}，Q＝{y|y＝2+sin x，x∈R}，那么P﹣Q＝（）A．{x|0＜x≤1}B．{x|0≤x＜2}C．{x|1≤x＜2}D．{x|0＜x＜1}4．（5分）若方程＝1表示双曲线，则m的取值范围是（）A．m＜2或m＞6B．2＜m＜6C．m＜﹣6或m＞﹣2D．﹣6＜m＜﹣25．（5分）在如图所示的程序框图中，如果输出p＝120，则输入的N＝（）A．3B．4C．5D．66．（5分）已知向量，满足||＝3，||＝2，且，则与的夹角为（）A．30°B．150°C．60°D．120°7．（5分）已知变量x，y满足约束条件则目标函数z＝的取值范围是（）A．[0，2]B．[0，]C．[]D．[0，+∞）8．（5分）一个多面体的三视图如图所示，设在其直观图中，M是AB的中点，则几何体C﹣MEF的体积为（）A．B．C．D．9．（5分）设△ABC的内角A、B、C，满足2sin2A sin2B+sin A sin B＝sin2A sin2B，则cos C＝（）A．﹣B．﹣C．D．10．（5分）已知S、A、B、C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA＝1，AB＝BC＝2，则球O的表面积为（）A．5πB．πC．9πD．π11．（5分）已知数列{a n}的前n项和为S n，若a1＝1，S n＝a n+1，则a11＝（）A．410B．3×48C．3×49D．3×21712．（5分）设函数f（x）＝，则函数g（x）＝f（x）﹣ln（x+e2）的零点个数为（）A．1个B．2个C．3个D．4个二、填空题：本题共4小题，每小题5分，共20分13．（5分）函数y＝x2+e x的图象在点x＝0处的切线方程为14．（5分）从由数字1，2，3所组成的所有两位数中随机抽取一个数，则该数为没有重复数字的两位数的概率为15．（5分）我国古代数学著作《九章算术》中有如下问题：“今有人持金出五关，前关二而税一，次关三而税一，次关四而税一，次关五而税一，次关六而税一．并五关所税，适重一斤．问本持金几何？“其意思为“今有人持金出五关，第1关收税金为总量的，第2关收税金为剩余的，第3关收税金为剩余的，第4关收税金为剩余的，第5关收税金为剩余的，5关所收税金之和恰好重1斤，问原本持金多少？假设原本持金x斤，则x ＝斤．16．（5分）已知点O为△ABC所在平面内的一点，且满足||＝||＝||＝1，3，则＝．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答（一）必考题：共60分17．（12分）已知函数f（x）＝2sin x cos x+2cos2x﹣1（x∈R）．（1）求函数f（x）的最小正周期；（2）在△ABC中，a，b，c分别为内角A，B，C的对边，且f（A）＝﹣2，a＝4，求△ABC面积的最大值．18．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为菱形，∠BAD＝，AB＝4，P A＝PD＝2．（1）若M为线段AB中点，N为线段PC中点，求证：MN∥平面P AD；（2）若平面P AD⊥平面ABCD，求三校锥A﹣PBD的高．19．（12分）已知椭圆C：＝1（a＞b＞0）的右焦点F2与抛物线y2＝4x的焦点重合，且其离心率为．（1）求椭圆C的方程；（2）已知与坐标轴不垂直的直线l与C交于M，N两点，线段MN中点为P，问k MN•k OP（O为坐标原点）是否为定值？请说明理由．20．（12分）为了尽快攻克一项科研课题，某生物研究所分别设立了甲、乙两个研究小组同时进行对比试验，现随机在这两个小组各抽取40个数据作为样本，并规定试验数据落在[495，510）之内的数据为理想数据，否则为不理想数据．试验情况如表所示：（1）根据表中数据作出两个小组样本数据的频率分布直方图；（2）若以频率作为概率，试着估计从两个小组的试验数据中分别任取一个数据，则其恰好是理想数据的概率各是多少？（3）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为抽取的数据为理想数据与对两个研究小组的选择有关？附：K2＝，其中n＝a+b+c+d21．（12分）已知函数f（x）＝alnx﹣+1，a∈R．（1）讨论f（x）的单调性；（2）若（x﹣1）f（x）≥0恒成立，求a的取值范围．选考题：共10分．请考生从第22、23两题中任选一题作答，并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分．[选修4-4：坐标系与参数方程]22．（10分）已知曲线C的极坐标方程是ρ＝，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为（t为参数），曲线M的参数方程是（θ为参数）．（1）写出曲线C和直线l的直角坐标方程；（2）若直线l与曲线C交于A、B两点，P为曲线M上的动点，求△ABP面积的最大值．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣1|﹣|x+a|，a∈R．（1）若a＝2，解不等式f（x）≥1；（2）若x∈（2，4）时，|f（x）|＜|2x+a﹣1|，求a的取值范围．2019年河北省保定市高考数学一模试卷（文科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有一项是符合题目要求的1．【解答】解：∵z＝＝，∴＝﹣1+3i．故选：A．2．【解答】解：∵cosα＝﹣，且α为第二象限角，∴sinα＝＝，则sin2α＝2sinα•cosα＝2••（﹣）＝﹣，故选：B．3．【解答】解：P＝{x|0＜x＜2}，Q＝{y|1≤y≤3}；∴P﹣Q＝{x|0＜x＜1}．故选：D．4．【解答】解：若方程＝1表示双曲线，则（m﹣2）（6﹣m）＜0∴m＜2或m＞6，故选：A．5．【解答】解：第一次p＝1，k＜N成立，k＝2，第二次p＝2，k＜N成立，k＝3，第三次p＝6，k＜N成立，k＝4，第五次p＝24，k＜N成立，k＝5，第六次p＝120，k＜N不成立，输出p＝120，故k≤4不成立，k＝5成立，则N＝5，故选：C．6．【解答】解：∵，；∴；∴；∴；又；∴与的夹角为150°．故选：B．7．【解答】解：变量x，y满足约束条件的可行域如图阴影部分：目标函数z＝的几何意义是可行域内的点与原点连线的斜率：k OA＝2，则目标函数z＝的取值范围是：[0，2]．故选：A．8．【解答】解：由题意可知几何体C﹣MEF的体积：V ADF﹣BCE﹣V F﹣AMCD﹣V E﹣MBC＝＝．故选：D．9．【解答】解：∵2sin2A sin2B+sin A sin B＝sin2A sin2B＝2sin A cos A sin B cos B，又∵sin A sin B≠0，∴可得：2sin A sin B+1＝2cos A cos B，可得：1＝2cos（A+B）＝﹣2cos C，∴解得：cos C＝﹣．故选：B．10．【解答】解：∵SA⊥平面ABC，AB⊥BC，∴四面体S﹣ABC的外接球半径等于以长宽高分别SA，AB，BC三边长的长方体的外接球的半径．∵SA＝1，AB＝2，BC＝2，∴2R＝＝3，即R＝．∴球O的表面积S＝4•πR2＝9π．故选：C．11．【解答】解：由题意，可知：①当n＝1时，a1＝S1＝1；②当n＝2时，a2＝3S1＝3；③当n≥2时，a n＝S n﹣S n﹣1＝，∴，即：a n+1＝4a n．∴数列{a n}从第2项起是以3为首项，4为公比的等比数列．∴∴a11＝3×49．故选：C．12．【解答】解：函数g（x）＝f（x）﹣ln（x+e2）的零点个数即为g（x）＝0，即y＝f（x）和y＝ln（x+e2）的图象交点个数，作出y＝f（x）的图象和y＝ln（x+e2）的图象，可得它们共有3个交点，即零点个数为3．故选：C．二、填空题：本题共4小题，每小题5分，共20分13．【解答】解：函数y＝x2+e x，可得y′＝2x+e x，切线的斜率为：1，切点坐标（0，1），函数y＝x2+e x的图象在点x＝0处的切线方程为：y＝x+1．故答案为：y＝x+1．14．【解答】解：从由数字1，2，3所组成的所有两位数中随机抽取一个数，基本事件个数n＝3×3＝9，该数为没有重复数字的两位数包含的基本事件个数m＝3×2＝6，∴该数为没有重复数字的两位数的概率为p＝＝．故答案为：．15．【解答】解：由题意可知过第一关后剩余，过第二关后剩余•＝，过第三关后剩余＝，过第四关后剩余•＝，过第五关后剩余＝，∴x﹣＝1，解得x＝1.2故答案为：1.216．【解答】解：∵||＝||＝||＝1，3，∴，两边同时平方可得，9+16+24＝25，∴＝0，∵＝，则＝＝（）＝＝0＝，故答案为：．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答（一）必考题：共60分17．【解答】解：（1）函数f（x）＝2sin x cos x+2cos2x﹣1．＝，＝，所以：函数的最小正周期为．（2）由于f（A）＝﹣2，故：，解得：A＝．由余弦定理得：a2＝b2+c2﹣2bc cos A，整理得：16＝b2+c2+bc≥3bc，所以：则：＝．18．【解答】证明：（1）如图所示，取线段PD的中点H，连结NH，AH，在△PDC中，NH∥DC，NH＝，∵ABCD是菱形，M为中点，∴AM∥DC，AM＝，∴HN∥AM，HN＝AM，∴四边形AMNH为平行四边形，∴MN∥AH，∵AH⊂面P AD，MN⊄面P AD，∴MN∥平面P AD．解：（2）∵P A＝PD＝2，AD＝4，∴AP⊥PD，取AD中点O，连结PO，则PO⊥AD，∵面P AD⊥面ABCD，∴PO⊥面ABCD，则PO＝2，BD＝4，在Rt△POB中，PB＝4，∴S△PBD＝＝2，设三棱锥A﹣PBD的高为h，由V P﹣ABD＝V A﹣PBD，得，解得h＝，∴三棱锥A﹣PBD的高为．19．【解答】解：（1）抛物线y2＝4x的焦点为（1，0），∴椭圆C的半焦距为c＝1，又椭圆的离心率e＝，∴a＝2，则b＝．∴椭圆C的方程为；（2）由题意可知，直线l的斜率存在且不为0，设l的方程为y＝kx+m，联立，得（3+4k2）x2+8kmx+4m2﹣12＝0．△＞0即只需n2＜4k2+3．设M（x1，y1），N（x2，y2），则，，∴P（），∴．∴．20．【解答】解：（1）根据题意，画出甲、乙两个小组的频率分布直方图如下；（2）由题意知，甲小组的理想数据为8+14+8＝30，故甲小组的理想数据频率为＝0.75；乙小组的理想数据为12+18+6＝36，故乙小组中理想数据的频率为＝0.9；据此可以估计从甲组数据中任取1个数据，该数据恰好为理想数据的概率为0.75，从乙组数据中任取1个数据，该数据恰好为理想数据的概率为0.9；（3）甲小组的理想数据为30，乙小组的理想数据为36，由此填写列联表如下；由表中数据，计算K2＝≈3.117＞2.706，所以有90%的把握认为抽取的数据为理想数据与对两个小组的选择有关．21．【解答】解：（1）f（x）＝alnx﹣+1的定义域是（0，+∞），f′（x）＝，a≥0时，f′（x）＞0，f（x）在（0，+∞）递增，a＜0时，令f′（x）＞0，解得：0＜x＜﹣，令f′（x）＜0，解得：x，∴f（x）在（0，﹣）递增，在（﹣，+∞）递减；（2）∵f（1）＝0．由（1）可得当a≥0时，f（x）在（0，+∞）递增，x＞1时，f（x）＞0，x＜1时，f（x）＜0．所以，此时（x﹣1）f（x）≥0恒成立，即a≥0符合题意．当a＜0时，f（x）在（0，﹣）递增，在（﹣，+∞）递减，且f（1）＝0；①当﹣时，f（x）在（0，1）递增，在（1，+∞）递减，易知（x﹣1）f（x）≥0不恒成立；②当﹣＜1时，即a＜﹣1时，f（x）在（0，1）上由f（﹣）＞f（1）＝0，易知（x﹣1）f（x）≥0不恒成立；③当﹣时，即﹣1＜a＜0时，，＝﹣，易知（x﹣1）f（x）≥0不恒成立；综上，（x﹣1）f（x）≥0恒成立时，a的取值范围为[0，+∞）．选考题：共10分．请考生从第22、23两题中任选一题作答，并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分．[选修4-4：坐标系与参数方程]22．【解答】解：（1）由题意可知C：x2+y2＝3，直线l的直角坐标方程为y＝x﹣1．（2）将直线l方程代入C的方程并整理得t2+﹣2＝0，设A，B对应的参数分别为t1，t2，则t1+t2＝﹣，t1t2＝﹣2，∴|AB|＝|t1﹣t2|＝，所以点P到直线l的距离d＝＝，所以当sin（﹣θ）＝﹣1时，d的最大值为，即三角形ABP面积最大值为××＝．[选修4-5：不等式选讲]23．【解答】解：（1）当a＝2时，f（x）＝，当x＜﹣2时，由f（x）≥1，得x＜﹣2；当﹣2≤x≤1时，由f（x）≥1得﹣2≤x≤﹣1；当x＞1时，由f（x）≥1，无解；所以不等式f（x）≥1的解集为{x|x≤﹣1}（2）因为|f（x）|＝||x﹣1|﹣|x+a||≤|（x﹣1）+（x+a）|＝|2x+a﹣1|，当且仅当（x﹣1）（x+a）≤0时，等号成立．当（x﹣1）（x+a）＞0时，|f（x）|＜|2x+a﹣1|，记其解集为A，则（2，4）⊆A，①若a≥﹣1，显然成立；②若a＜﹣1，∴A＝（﹣∞，1）∪（﹣a，+∞），∴﹣2≤a≤﹣1，所以a的取值范围是[﹣2，+∞）．。

2019年河北自主招生数学模拟题

∴P（ ≤ξ≤ ）=p（ξ=1）= 故选D 点评：这是一个求概率的问题，根据实际情况写出随机变量对应的变量，求出概率，写出分布列，是一个近几年高考题中经常出现的问题，可以以选择和填空形式出现。
某年段文科班共有4个班级，每班各有40位学生（其中男生8人，女生32人）。若从该年段文科生中以简单随机抽样抽出20人，则下列选项中正确的是（）A、每班至少会有一人被抽中B、抽出来的女生人数一定比男生人数多C、已知小文是男生，小美是女生，则小文被抽中的概率小于小美被抽中的概率D、若学生甲和学生乙在同一班，学生丙在另外一班，则甲、乙两人同时被抽中的概率跟甲、丙两人同时被抽中的概率一样
某单位有职工200名，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组（1－5号，6－10号，…，196－200号）.若第5组抽出的号码为23，则第10组抽出的号码应是 .
答案
48
解析
试题分析：据题意，组距为5，由系统抽样的定义知第10组抽到的号码为：
答案
C
解析
试题分析：根据分层抽样的定义直接计算即可。
解：∵男生36人，女生18人，
∴男生和女生人数比为36：18=2：1，
∴抽取一个容量为9的样本，则抽取的女生人数为
，
故选：C、点评：本题主要考查分层抽样的定义和应用，比较基础。
下面的抽样方法是简单随机抽样的是（）A、在某年明信片销售活动中，规定每100万张为一个开奖组，通过随机抽取的方式确定号码的后四位为2709的为三等奖B、某车间包装一种产品，在自动包装的传送带上，每隔30分钟抽一包产品，称其重量是否合格C、某学校分别从行政人员、教师、后勤人员中抽取2人、14人、4人了解学校机构改革的意见D、用抽签法从10件产品中选取3件进行质量检验

河北省唐山市2019年高考数学一模试卷(文科)含答案解析

河北省唐山市2019年高考数学一模试卷（文科）（解析版）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，有且只有一项符合题目要求．1．设A，B是全集I={1，2，3，4}的子集，A={l，2}，则满足A⊆B的B的个数是（）A．5 B．4 C．3 D．22．复数的虚部为（）A．B．C．﹣D．﹣3．在等差数列{a n}中，a4=2，且a1+a2+…+a10=65，则公差d的值是（）A．4 B．3 C．1 D．24．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（）A．y=﹣B．y=﹣x2C．y=e﹣x+e x D．y=|x+1|5．执行如图的程序框图，输出S的值为（）A．ln4﹣ln3 B．ln5 C．ln5﹣ln4 D．ln46．cosasin（a+）+sinasin（a﹣）=（）A．B．﹣C．D．﹣7．A（，1）为抛物线x2=2py（p＞0）上一点，则A到其焦点F的距离为（）A．B． +C．2 D． +18．在区间[﹣1，1]上随机取一个数x，使cosπx≥的概率为（）A．B．C．D．9．若x，y满足不等式组，则的最大值是（）A．B．1 C．2 D．310．某几何体的三视图如图所示．则其体积积为（）A．8πB．C．9πD．11．F为双曲线Г：﹣=1（a＞0，b＞0）的右焦点，若Г上存在一点P使得△OPF为等边三角形（O为坐标原点），则Г的离心率e为（）A．B．C．D．212．已知函数f（x）=x3﹣3x2+x的极大值为m，极小值为n，则m+n=（）A．0 B．2 C．﹣4 D．﹣2二、填空题：本大题共4小题，每小题5分，共20分，把答案填写在题中横线上．13．S n为等比数列{a n}的前n项和，满足S n=2a n﹣1，则{a n}的公比q=．14．已知向量，满足（﹣）=2，且||=1，||=2，则与的夹角等于．15．直线l：与x轴、y轴分别相交于点A、B，O为坐标原点，则△OAB的内切圆的方程为．16．一个几何体由八个面围成，每个面都是正三角形，有四个顶点在同一平面内且为正方形，若该八面体的棱长为2，所有顶点都在球O上，则球O的表面积为．三、解答题：本大题共70分，其中（17）-（21）题为必考题，（22），（23），（24）题为选考题．解答应写出文字说明、证明过程或演算步骤．17．在如图所示的四边形ABCD中，∠BAD=90°，∠BCD=150°，∠BAC=60°，AC=2，AB=+1．（I）求BC；（Ⅱ）求△ACD的面积．18．为迎接即将举行的集体跳绳比赛，高一年级对甲、乙两个代表队各进行了6轮测试，测试成绩（单位：次/分钟）如表：（Ⅰ）补全茎叶图并指出乙队测试成绩的中位数和众数；（Ⅱ）试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析．19．如图，直四棱柱ABCD﹣A1B1C1D1的棱长均为2，∠BAD=，M为BB1的中点，O l 为上底面对角线的交点．（Ⅰ）求证：O1M⊥平面ACM1；（Ⅱ）求C l到平面ACM的距离．20．已知椭圆C：=1（a＞b＞0）的右焦点为F（2，0），点P（2，）在椭圆上．（Ⅰ）求椭圆C的方程；（Ⅱ）过点F的直线，交椭圆C于A、B两点，点M在椭圆C上，坐标原点O恰为△ABM 的重心，求直线l的方程．21．已知函数f（x）=a（tan x+l）﹣e x．（Ⅰ）若f（x）在x=0处的切线经过点（2，3），求a的值；（Ⅱ）x∈（0，）时，f（x）≥0，求a的取值范围．四.请考生在第（22）、（23）、（24）三题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分．作答时用2B铅笔在答题卡上将所选题号后的方框涂黑．[选修4-1：几何证明选讲]22．如图，AB与圆O相切于点B，CD为圆O上两点，延长AD交圆O于点E，BF∥CD 且交ED于点F（I）证明：△BCE∽△FDB；（Ⅱ）若BE为圆O的直径，∠EBF=∠CBD，BF=2，求ADED．[选修4-4：坐标系与参数方程]23．在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．半圆C （圆心为点C）的极坐标方程为ρ=2sinθ，θ∈（，）．（Ⅰ）求半圆C的参数方程；（Ⅱ）直线l与两坐标轴的交点分别为A，B，其中A（0，﹣2），点D在半圆C上，且直线CD的倾斜角是直线l倾斜角的2倍，若△ABD的面积为4，求点D的直角坐标．[选修4-5：不等式选讲]24．已知函数f（x）=|x+1|﹣a|x﹣l|．（Ⅰ）当a=﹣2时，解不等式f（x）＞5；（Ⅱ）若（x）≤a|x+3|，求a的最小值．2019年河北省唐山市高考数学一模试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，有且只有一项符合题目要求．1．设A，B是全集I={1，2，3，4}的子集，A={l，2}，则满足A⊆B的B的个数是（）A．5 B．4 C．3 D．2【分析】由题意可知：集合B中至少含有元素1，2，即可得出．【解答】解：A，B是全集I={1，2，3，4}的子集，A={l，2}，则满足A⊆B的B为：{1，2}，{1，2，3}，{1，2，4}，{1，2，3，4}．故选：B．【点评】本题考查了集合之间的运算性质、元素与集合之间的关系，考查了推理能力与计算能力，属于基础题．2．复数的虚部为（）A．B．C．﹣D．﹣【分析】直接由复数代数形式的乘除运算化简复数，则答案可求．【解答】解：由=，则复数的虚部为：．故选：A．【点评】本题考查了复数代数形式的乘除运算，是基础题．3．在等差数列{a n}中，a4=2，且a1+a2+…+a10=65，则公差d的值是（）A．4 B．3 C．1 D．2【分析】由已知利用等差数列的通项公式和前n项和公式列出方程组，由此能求出公差．【解答】解：∵在等差数列{a n}中，a4=2，且a1+a2+…+a10=65，∴，解得a1=﹣7，d=3．∴公差d的值是3．故选：B．【点评】本题考查等差数列的公差的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．4．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（）A．y=﹣B．y=﹣x2C．y=e﹣x+e x D．y=|x+1|【分析】根据函数奇偶性和单调性的性质进行判断即可．【解答】解：y=﹣是奇函数，不满足条件．y=﹣x2是偶函数，在区间（0，+∞）上单调递减，不满足条件．y=e﹣x+e x是偶函数，函数的导数y′=﹣e﹣x+e x=，当x＞0时，y′=＞0，函数在区间（0，+∞）上单调递增，满足条件．y=|x+1|为非奇非偶函数，不满足条件．故选：C．【点评】本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．5．执行如图的程序框图，输出S的值为（）A．ln4﹣ln3 B．ln5 C．ln5﹣ln4 D．ln4【分析】由题意，模拟程序框图的运行过程，即可得出该程序输出的结果．【解答】解：根据题意，模拟程序框图的运行过程，可得i=1，S=0满足条件i＜4，S=ln2，i=2满足条件i＜4，S=ln2+ln3﹣ln2=ln3，i=3满足条件i＜4，S=ln3+ln4﹣ln3=ln4，i=4不满足条件i＜4，退出循环，输出S的值为ln4．故选：D．【点评】本题考查了程序框图的应用问题，解题时应模拟程序语言的运行过程，从而得出正确的结论，是基础题．6．cosasin（a+）+sinasin（a﹣）=（）A．B．﹣C．D．﹣【分析】由条件利用两角和的正弦公式，计算求得结果．【解答】解：∵cosasin（a+）+sinasin（a﹣）=cosasin（a+）﹣sinacos[（a﹣）+]=sin（a+）cosa﹣cos（a+）sina=sin[（a+）﹣a]=sin=，故选：A．【点评】本题主要考查两角和的正弦公式的应用，属于基础题．7．A（，1）为抛物线x2=2py（p＞0）上一点，则A到其焦点F的距离为（）A．B． +C．2 D． +1【分析】把A代入抛物线方程解出p，得到抛物线的准线方程，则A到焦点的距离等于A 到准线的距离．【解答】解：把A（，1）代入抛物线方程得：2=2p，∴p=1．∴抛物线的焦点为F（0，）．∴抛物线的准线方程为y=﹣．∴A到准线的距离为1+=．∴AF=．故选：A．【点评】本题考查了抛物线的定义，抛物线的性质，属于基础题．8．在区间[﹣1，1]上随机取一个数x，使cosπx≥的概率为（）A．B．C．D．【分析】求出不等式的等价条件，利用几何概型的概率公式进行求解即可．【解答】解：∵﹣1≤x≤1，∴﹣π≤πx≤π，由cosπx≥得，∴﹣≤πx≤，即﹣≤x≤，则对应的概率P==，故选：A．【点评】本题主要考查几何概型的概率公式的应用，根据不等式的关系求出等价条件是解决本题的关键．9．若x，y满足不等式组，则的最大值是（）A．B．1 C．2 D．3【分析】由题意作平面区域，而的几何意义是阴影内的点（x，y）与原点的连线的斜率，从而求得．【解答】解：由题意作平面区域如下，，的几何意义是阴影内的点（x，y）与原点的连线的斜率，结合图象可知，过点A（1，2）时有最大值，此时==2，故选：C．【点评】本题考查了学生的作图能力及数形结合的思想方法应用，注意的几何意义是阴影内的点（x，y）与原点的连线的斜率．10．某几何体的三视图如图所示．则其体积积为（）A．8πB．C．9πD．【分析】几何体为两个尖头圆柱的组合体．它们可以组合成高为8的圆柱．【解答】解：由三视图可知几何体为两个尖头圆柱的组合体，它们可以组成高为8的圆柱，圆柱的底面半径为1，所以几何体的体积为π×12×8=8π．故选A．【点评】本题考查了空间几何体的三视图和体积计算，属于基础题．11．F为双曲线Г：﹣=1（a＞0，b＞0）的右焦点，若Г上存在一点P使得△OPF为等边三角形（O为坐标原点），则Г的离心率e为（）A．B．C．D．2【分析】先确定等边三角形的边长和点P横坐标，求出点P到右准线的距离d，利用双曲线定义解出离心率e．【解答】解：不妨设F为右焦点，△OPF（O为坐标原点）为等边三角形，故点P横坐标为，∴点P到右准线的距离d=﹣=，△OPF边长为c，∴e==∵e＞1，∴e=+1，故选：C【点评】本题主要考查双曲线的定义、简单性质和标准方程的应用，等边三角形的性质，属于基础题．12．已知函数f（x）=x3﹣3x2+x的极大值为m，极小值为n，则m+n=（）A．0 B．2 C．﹣4 D．﹣2【分析】利用导数工具去解决该函数极值的求解问题，关键要利用导数将原函数的单调区间找出来，即可确定出在哪个点处取得极值，进而得到答案．【解答】解：由题意可得：f′（x）=3x2﹣6x+1，令f′（x）=0，即3x2﹣6x+1=0，解得：x1=，x2=，∴f（x）在（﹣∞，）递增，在（，）递减，在（，+∞）递增，∴x1=是极大值点，x2=是极小值点，∴m+n=f（x1）+f（x2）=（﹣2+）（﹣2﹣）=﹣2，故选：D．【点评】利用导数工具求该函数的极值是解决该题的关键，要先确定出导函数大于0时的实数x的范围，再讨论出函数的单调区间，根据极值的判断方法求出该函数的极值，体现了导数的工具作用．二、填空题：本大题共4小题，每小题5分，共20分，把答案填写在题中横线上．13．S n为等比数列{a n}的前n项和，满足S n=2a n﹣1，则{a n}的公比q=2．【分析】由S n=2a n﹣1，a1=2a1﹣1，a1+a2=2a2﹣1，解得a1，a2，即可得出．【解答】解：由S n=2a n﹣1，a1=2a1﹣1，a1+a2=2a2﹣1，解得a1=1，a2=2．∴等比数列{a n}的公比q=2．故答案为：2．【点评】本题考查了等比数列的通项公式、递推关系，考查了推理能力与计算能力，属于基础题．14．已知向量，满足（﹣）=2，且||=1，||=2，则与的夹角等于．【分析】求出，代入向量夹角公式计算．【解答】解：∵（﹣）==2，∴=﹣1．∴cos＜＞==﹣．∴＜＞=．故答案为：．【点评】本题考查了平面向量的数量积运算，属于基础题．15．直线l：与x轴、y轴分别相交于点A、B，O为坐标原点，则△OAB的内切圆的方程为（x﹣1）2+（y﹣1）2=1．【分析】由题意画出图形，设△OAB的内切圆的圆心为M（m，m），利用圆心到直线l的距离等于圆的半径列式求得m值得答案．【解答】解：由直线方程与x轴、y轴分别相交于点A、B，如图，设△OAB的内切圆的圆心为M（m，m），化直线方程为3x+4y﹣12=0，由题意可得：，解得：m=1．∴△OAB的内切圆的方程为（x﹣1）2+（y﹣1）2=1．故答案为：（x﹣1）2+（y﹣1）2=1．【点评】本题考查圆的标准方程，考查了点到直线距离公式的应用，体现了数形结合的解题思想方法，是基础题．16．一个几何体由八个面围成，每个面都是正三角形，有四个顶点在同一平面内且为正方形，若该八面体的棱长为2，所有顶点都在球O上，则球O的表面积为8π．【分析】根据该八面体的棱长为2，所有顶点都在球O上，确定球O的半径，即可求出球O的表面积．【解答】解：由题意，该八面体的棱长为2，所有顶点都在球O上，所以球O的半径为，所以球O的表面积为=8π．故答案为：8π．【点评】本题考查球的内接几何体，考查球O的表面积，考查学生的计算能力，比较基础．三、解答题：本大题共70分，其中（17）-（21）题为必考题，（22），（23），（24）题为选考题．解答应写出文字说明、证明过程或演算步骤．17．在如图所示的四边形ABCD中，∠BAD=90°，∠BCD=150°，∠BAC=60°，AC=2，AB=+1．（I）求BC；（Ⅱ）求△ACD的面积．【分析】（I）在△ABC中，使用余弦定理即可解出BC；（II）在△ABC中，使用正弦定理解出sin∠ABC，结合角的范围可求∠ACD=75°，AD=AC=2，利用三角形面积公式即可得解．【解答】解：（Ⅰ）在△ABC中，由余弦定理得BC2=AB2+AC2﹣2ABACcos∠BAC=6，所以BC=．…（4分）（Ⅱ）在△ABC中，由正弦定理得=，则sin∠ABC=，又0°＜∠ABC＜120°，所以∠ABC=45°，从而有∠ACB=75°，由∠BCD=150°，得∠ACD=75°，又∠DAC=30°，所以△ACD为等腰三角形，即AD=AC=2，故S△ACD=×2×2×=1．…（12分）【点评】本题主要考查了正弦定理，余弦定理，三角形内角和定理，三角形面积公式在解三角形中的应用，属于中档题．18．为迎接即将举行的集体跳绳比赛，高一年级对甲、乙两个代表队各进行了6轮测试，测试成绩（单位：次/分钟）如表：（Ⅰ）补全茎叶图并指出乙队测试成绩的中位数和众数；（Ⅱ）试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析．【分析】（Ⅰ）根据题意补全茎叶图，求出乙队测试成绩的中位数与众数；（Ⅱ）求出甲、乙二人的平均数与方差，进行比较即可．【解答】解：（Ⅰ）画出茎叶图如下：…（4分）乙队测试成绩的中位数为72，众数为75．…（6分）（Ⅱ）==72，==39；==72，==44，…（10分）因为=，＜，所以甲乙两队水平相当，但甲队发挥较稳定．…（12分）【点评】本题考查了茎叶图的应用问题，也考查了平均数与方差的应用问题，是基础题目．19．如图，直四棱柱ABCD﹣A1B1C1D1的棱长均为2，∠BAD=，M为BB1的中点，O l 为上底面对角线的交点．（Ⅰ）求证：O1M⊥平面ACM1；（Ⅱ）求C l到平面ACM的距离．【分析】（Ⅰ）证明AC⊥O1M，根据勾股定理，证明O1M⊥AM，即可证明：O1M⊥平面ACM1；（Ⅱ）证明C1到平面ACM的距离等于O1到平面ACM的距离，即可求C l到平面ACM的距离．【解答】（Ⅰ）证明：连接AO1，BD∵在直四棱柱ABCD﹣A1B1C1D1中，BB1⊥平面ABCD，AC⊂平面ABCD，∴BB1⊥AC，∵四边形ABCD是边长为2的菱形，∴AC⊥BD，又∵BD∩BB1=B，∴AC⊥平面DBB1D1，又∵O1M⊂平面DBB1D1，∴AC⊥O1M．∵直四棱柱所有棱长均为2，∠BAD=，M为BB1的中点，∴BD=2，AC=2，B1M=BM=1，∴O1M2=O1B12+B1M2=2，AM2=AB2+BM2=5，O1A2=O1A12+A1A2=7，∴O1M2+AM2=O1A2，∴O1M⊥AM．又∵AC∩AM=A，∴O1M⊥平面ACM．…（6分）（Ⅱ）解：∵A1C1∥AC，∴A1C1∥平面ACM，即C1到平面ACM的距离等于O1到平面ACM的距离，由（Ⅰ）得O1M⊥平面ACM，且O1M=，即点C1到平面ACM的距离为．…（12分）【点评】本题考查了线面垂直的判定，点C1到平面ACM的距离的计算，考查学生分析解决问题的能力，属于中档题．20．已知椭圆C：=1（a＞b＞0）的右焦点为F（2，0），点P（2，）在椭圆上．（Ⅰ）求椭圆C的方程；（Ⅱ）过点F的直线，交椭圆C于A、B两点，点M在椭圆C上，坐标原点O恰为△ABM 的重心，求直线l的方程．【分析】（Ⅰ）由题意可得c=2，|PF|=，运用勾股定理可得|PF1|，再由椭圆的定义可得2a，由a，b，c的关系可得b，进而得到椭圆方程；（Ⅱ）显然直线l与x轴不垂直，设l：y=k（x﹣2），A（x1，y1），B（x2，y2），代入椭圆方程，运用韦达定理和三角形的重心坐标公式可得M的坐标，代入椭圆方程，解方程即可得到所求直线的方程．【解答】解：（Ⅰ）由题意可得c=2，左焦点F1（﹣2，0），|PF|=，所以|PF1|==，即2a=|PF|+|PF1|=2，即a2=6，b2=a2﹣c2=2，故椭圆C的方程为+=1；（Ⅱ）显然直线l与x轴不垂直，设l：y=k（x﹣2），A（x1，y1），B（x2，y2）．将l的方程代入C得（1+3k2）x2﹣12k2x+12k2﹣6=0，可得x1+x2=，所以AB的中点N （，），由坐标原点O恰为△ABM的重心，可得M （，）．由点M在C上，可得15k4+2k2﹣1=0，解得k2=或﹣（舍），即k=±．故直线l的方程为y=±（x﹣2）．【点评】本题考查椭圆的方程的求法，注意运用椭圆的定义和a，b，c的关系及点满足椭圆方程，同时考查直线和椭圆方程联立，运用韦达定理和三角形的重心坐标公式，考查运算能力，属于中档题．21．已知函数f（x）=a（tan x+l）﹣e x．（Ⅰ）若f（x）在x=0处的切线经过点（2，3），求a的值；（Ⅱ）x∈（0，）时，f（x）≥0，求a的取值范围．【分析】（Ⅰ）求出函数的导数，求得切线的斜率，由两点的斜率公式解方程可得a；（Ⅱ）由x∈（0，）时，f（x）≥0，得a≥，令g（x）=，求出导数，求得单调区间和最大值，即可得到所求范围．【解答】解：（Ⅰ）f（x）=a（tanx+l）﹣e x的导数为f′（x）=﹣e x，可得f′（0）=a﹣1，又f（0）=a﹣1，所以a﹣1=，解得a=2．（Ⅱ）由x∈（0，）时，f（x）≥0，得a≥，令g（x）=，则g′（x）==，当x∈（0，），g′（x）＞0；x∈（，），g′（x）＜0，所以g （x）的最大值为g（）=，故所求a的取值范围是a≥．【点评】本题考查导数的运用：求切线的斜率和单调区间、极值和最值，考查不等式恒成立问题的解法，注意运用参数分离和构造函数法，转化为求函数的最值问题，属于中档题．四.请考生在第（22）、（23）、（24）三题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分．作答时用2B铅笔在答题卡上将所选题号后的方框涂黑．[选修4-1：几何证明选讲]22．如图，AB与圆O相切于点B，CD为圆O上两点，延长AD交圆O于点E，BF∥CD 且交ED于点F（I）证明：△BCE∽△FDB；（Ⅱ）若BE为圆O的直径，∠EBF=∠CBD，BF=2，求ADED．【分析】（Ⅰ）根据BF∥CD便有∠EDC=∠BFD，再根据同一条弦所对的圆周角相等即可得出∠EBC=∠BFD，∠BCE=∠BDF，这样即可得出：△BCE与△FDB相似；（Ⅱ）根据条件便可得出∠EBC=∠FBD，再由上面即可得出∠FBD=∠BFD，这样即可得出△FDB为等腰直角三角形，从而可求出BD=，根据射影定理即可求出ADED的值．【解答】解：（Ⅰ）证明：∵BF∥CD；∴∠EDC=∠BFD，又∠EBC=∠EDC，∴∠EBC=∠BFD，又∠BCE=∠BDF，∴△BCE∽△FDB．（Ⅱ）因为∠EBF=∠CBD，所以∠EBC=∠FBD，由（Ⅰ）得∠EBC=∠BFD，所以∠FBD=∠BFD，又因为BE为圆O的直径，所以△FDB为等腰直角三角形，BD=BF=，因为AB与圆O相切于B，所以EB⊥AB，即ADED=BD2=2．【点评】考查内错角相等，同条弦所对的圆周角相等，以及三角形相似的判定定理，直径所对的圆周角为直角，以及射影定理．[选修4-4：坐标系与参数方程]23．在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．半圆C （圆心为点C）的极坐标方程为ρ=2sinθ，θ∈（，）．（Ⅰ）求半圆C的参数方程；（Ⅱ）直线l与两坐标轴的交点分别为A，B，其中A（0，﹣2），点D在半圆C上，且直线CD的倾斜角是直线l倾斜角的2倍，若△ABD的面积为4，求点D的直角坐标．【分析】（Ⅰ）由x=ρcosθ，y=ρsinθ，x2+y2=ρ2，代入半圆的极坐标方程，再由同角的平方关系，可得参数方程；（Ⅱ）设直线l的倾斜角为α，可得直线l的方程为y=xtanα﹣2，D（cos2α，1+sin2α），2α∈（0，π）．求得|AB|，运用点到直线的距离公式可得D到AB的距离，再由三角形的面积公式，由三角函数的恒等变换，即可得到所求点的坐标．【解答】解：（Ⅰ）由x=ρcosθ，y=ρsinθ，x2+y2=ρ2，可得半圆C的直角坐标方程为x2+y2=2y，即x2+（y﹣1）2=1（y＞1），它的参数方程是，φ为参数且φ∈（0，π）；（Ⅱ）设直线l的倾斜角为α，则直线l的方程为y=xtanα﹣2，D（cos2α，1+sin2α），2α∈（0，π）．|AB|==，点D到直线l的距离为d===|﹣3cosα﹣sinα|=3cosα+sinα，由△ABD的面积为4，得4=d|AB|==1+3cotα，可得tanα=1，得α=，故点D为（0，2）．【点评】本题考查极坐标方程和参数方程的互化，考查圆的参数方程的运用，直线方程的运用，点到直线的距离公式，同时考查三角函数的恒等变换的运用，属于中档题．[选修4-5：不等式选讲]24．已知函数f（x）=|x+1|﹣a|x﹣l|．（Ⅰ）当a=﹣2时，解不等式f（x）＞5；（Ⅱ）若（x）≤a|x+3|，求a的最小值．【分析】（Ⅰ）将a=2代入f（x），表示出f（x）的分段形式，结合函数的单调性求出不等式的解集即可；（Ⅱ）问题转化为≤，求出a的最小值即可．【解答】解：（Ⅰ）当a=﹣2时，f（x）=，由f（x）的单调性及f（﹣）=f（2）=5，得f（x）＞5的解集为{x|x＜﹣，或x＞2}．…（5分）（Ⅱ）由f（x）≤a|x+3|得a≥，由|x﹣1|+|x+3|≥2|x+1|得≤，得a≥．（当且仅当x≥1或x≤﹣3时等号成立）故a的最小值为．…（10分）【点评】本题考查了解绝对值不等式问题，考查分段函数，是一道中档题．。

2019年河北单招理科数学模拟试题(一)【含答案】

2019年河北单招理科数学模拟试题（一）【含答案】一、选择题：共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A={k∈N|∈N}，B={x|x=2n或x=3n，n∈N}，则A∩B=（）A．{6，9} B．{3，6，9} C．{1，6，9，10} D．{6，9，10}2．若复数z满足z（﹣1+2i）=|1+3i|2，（i为虚数单位），则复数z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．已知命题＞lnx；命题q：∀a＞1，b＞1，logab+2logba≥2，则下列命题中为真命题的是（）A．（¬p）∧q B．p∧q C．p∧（¬q）D．p∨（¬q）4．《九章算术》中有如下问题：“今有勾八步，股一十五步，问勾中容圆，径几何？”其大意：“已知直角三角形两直角边长分别为8步和15步，问其内切圆的直径为多少步？”现若向此三角形内随机投一粒豆子，则豆子落在其内切圆外的概率是（）A．B．C．D．5．已知双曲线过点（2，3），渐进线方程为y=±x，则双曲线的标准方程是（）A．B．C．D．6．将y=cosx的图象上的所有点的纵坐标不变，横坐标缩小到原来的一半，然后再将所得图象向左平移个单位长度，则最后所得图象的解析式为（）A．y=cos（2x+）B．y=cos（+）C．y=sin2x D．y=﹣sin2x7．若实数x、y满足|x|≤y≤1，则x2+y2+2x的最小值为（）A．B．﹣C．D．﹣18．已知一长方体的体对角线的长为l0，这条对角线在长方体一个面上的正投影长为8，则这个长方体体积的最大值为（）A．64 B．128 C．192 D．3849．为了竖一块广告牌，要制造三角形支架，如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了稳固广告牌，要求AC越短越好，则AC最短为（）A．（1+）米B．2米C．（1+）米D．（2+）米10．秦九韶是我国南宋时期著名的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为3，每次输入a的值均为4，输出s的值为484，则输入n的值为（）A．6 B．5 C．4 D．311．在等腰直角三角形ABC中，AB=AC=4，点P是边上异于A，B的一点．光线从点P出发，经BC，CA反射后又回到点P（如图）．若光线QR经过△ABC的重心，则AP等于（）A．2 B．1 C．D．12．椭圆x2+=1（0＜b＜1）的左焦点为F，上顶点为A，右顶点为B，若△FAB的外接圆圆心P（m，n）在直线y=﹣x的左下方，则该椭圆离心率的取值范围为（）A．（，1）B．（，1）C．（0，）D．（0，）二．填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡相应的横线上．13．已知||=4，||=5，=λ+μ（λ，μ∈R），若⊥，⊥（﹣），则=____．14．记“点M（x，y）满足x2+y2≤a（a＞0）”为事件A，记“M（x，y）满足”为事件B ，若P （B|A ）=1，则实数a 的最大值为____．15．已知函数f （x ）=（x+2）（x2+ax ﹣5）的图象关于点（﹣2，0）中心对称，设关于x 的不等式f （x+m ）＜f （x ）的解集为A ，若（﹣5，﹣2）⊆A ，则实数m 的取值范围是____．16．已知数列{an}的首项a1=t ，其前n 项和为Sn ，且满足Sn+Sn+1=n2+2n ，若对∀n ∈N*，an ＜an+1恒成立，则实数t 的取值范围是____．三、解答题：（共5小题，共70分；要求写出必要的文字说明，解题过程和演算步骤）17．（12分）已知向量=（sinωx ﹣cosωx ，1），=（cosωx ，），设函数f （x ）=，若函数f （x ）的图象关于直线x=对称且ω∈[0，2]（Ⅰ）求函数f （x ）的单调递减区间；（Ⅱ）在△ABC 中，角A ，B ，C 的对边分别a ，b ，c ，若a=，f （A ）=1，求b+c 的最大值．18．（12分）某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，在将两组工人的日平均生产件数分成5组：[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率．（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列0.100 0.050 0.01019．（12分）如图1，已知在菱形ABCD 中，∠B=120°，E 为AB 的中点，现将四边形EBCD 沿DE 折起至EBHD ，如图2．（1）求证：DE⊥面ABE；（2）若二面角A﹣DE﹣H的大小为，求平面ABH与平面ADE所成锐二面角的余弦值．20．（12分）已知抛物线C：y2=2px（p＞0）的焦点为F，A为C上位于第一象限的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D．（1）若|FA|=|AD|，当点A的横坐标为时，△ADF为等腰直角三角形，求C的方程；（2）对于（1）中求出的抛物线C，若点，记点B关于x轴的对称点为E，AE交x轴于点P，且AP⊥BP，求证：点P的坐标为（﹣x0，0），并求点P到直线AB 的距离d的取值范围．21．（12分）已知函数，其中a是实数，设A（x1，f（x1）），B（x2，f（x2））为该函数图象上的点，且x1＜x2．（Ⅰ）指出函数f（x）的单调区间；（Ⅱ）若函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值；（Ⅲ）若函数f（x）的图象在点A，B处的切线重合，求a的取值范围．[选修4-4：坐标系与参数方程]22．（10分）已知直线l的参数方程为（t为参数），曲线C的参数方程为（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点P的极坐标为（2，）．（Ⅰ）求直线l以及曲线C的极坐标方程；（Ⅱ）设直线l与曲线C交于A，B两点，求△PAB的面积．[选修4-5：不等式选讲]23．已知函数f（x）=|2x﹣1|+|x+1|，g（x）=|x﹣a|+|x+a|．（Ⅰ）解不等式f（x）＞9；（Ⅱ）∀x1∈R，∃x2∈R，使得f（x1）=g（x2），求实数a的取值范围．2019年河北单招理科数学模拟试题（一）参考答案一、选择题：共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A={k∈N|∈N}，B={x|x=2n或x=3n，n∈N}，则A∩B=（）A．{6，9} B．{3，6，9} C．{1，6，9，10} D．{6，9，10}【考点】1E：交集及其运算．【分析】先分别求出集合A，B，由此利用交集定义能求出A∩B．【解答】解：∵集合A={k∈N|∈N}={1，6，9，10}，B={x|x=2n或x=3n，n∈N}，∴A∩B={6，9，10}．故选：D．【点评】本题考查集合的交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．2．若复数z满足z（﹣1+2i）=|1+3i|2，（i为虚数单位），则复数z在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【考点】A5：复数代数形式的乘除运算．【分析】把已知等式变形，再由复数代数形式的乘法运算化简复数z，求出z在复平面内对应的点的坐标得答案．【解答】解：由z（﹣1+2i）=|1+3i|2，得=，则复数z在复平面内对应的点的坐标为：（﹣2，﹣4），位于第三象限．故选：C．【点评】本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．3．已知命题＞lnx；命题q：∀a＞1，b＞1，logab+2logba≥2，则下列命题中为真命题的是（）A．（¬p）∧q B．p∧q C．p∧（¬q）D．p∨（¬q）【考点】2E：复合命题的真假．【分析】命题＜1＜lnx，可得p是假命题；命题q：∀a＞1，b＞1，logab，logba＞0，转化为logab+2logba=logab+，利用基本不等式的性质即可判断出真假，再利用简易逻辑的判定方法即可得出．【解答】解：命题＜1＜lnx ，因此是假命题；命题q ：∀a ＞1，b ＞1，logab ，logba ＞0，∴logab+2logba=logab+≥2=2，当且仅当logab=时取等号．因此q 是真命题．则下列命题中为真命题的是（￢p ）∧q ．故选：A ．【点评】本题考查了简易逻辑的应用、函数的单调性、基本不等式的性质、转化方法，考查了推理能力与计算能力，属于中档题．4．《九章算术》中有如下问题：“今有勾八步，股一十五步，问勾中容圆，径几何？”其大意：“已知直角三角形两直角边长分别为8步和15步，问其内切圆的直径为多少步？”现若向此三角形内随机投一粒豆子，则豆子落在其内切圆外的概率是（）A ．B ．C ．D ．【考点】CE ：模拟方法估计概率．【分析】求出内切圆半径，计算内切圆和三角形的面积，从而得出答案．【解答】解：直角三角形的斜边长为=17，设内切圆的半径为r ，则8﹣r+15﹣r=17，解得r=3．∴内切圆的面积为πr 2=9π，∴豆子落在内切圆外部的概率P=1﹣=1﹣．故选：D ．【点评】本题考查了几何概型的概率计算，属于基础题．5．已知双曲线过点（2，3），渐进线方程为y=±x ，则双曲线的标准方程是（）A ．B ．C ．D ．【考点】KC：双曲线的简单性质．【分析】根据题意，由双曲线的渐近线方程可以设其方程为﹣x2=λ，将点（2，3）代入其中可得﹣22=λ，解可得λ的值，变形即可得答案．【解答】解：根据题意，双曲线的渐进线方程为y=±x，则可以设其方程为﹣x2=λ，（λ≠0）又由其过点（2，3），则有﹣22=λ，解可得：λ=﹣1，则双曲线的标准方程为：x2﹣=1；故选：C．【点评】本题考查双曲线的几何性质，关键是由渐近线方程设出双曲线的方程．6．将y=cosx的图象上的所有点的纵坐标不变，横坐标缩小到原来的一半，然后再将所得图象向左平移个单位长度，则最后所得图象的解析式为（）A．y=cos（2x+）B．y=cos（+）C．y=sin2x D．y=﹣sin2x【考点】HJ：函数y=Asin（ωx+φ）的图象变换．【分析】利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：将y=cosx的图象上的所有点的纵坐标不变，横坐标缩小到原来的一半，可得y=cos2x的图象；然后再将所得图象向左平移个单位长度，则最后所得图象的解析式为y=cos2（x+）=﹣sin2x，故选：D．【点评】本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．7．若实数x、y满足|x|≤y≤1，则x2+y2+2x的最小值为（）A．B．﹣C．D．﹣1【考点】7C：简单线性规划．【分析】画出约束条件表示的可行域，通过表达式的几何意义，求出表达式的最小值．【解答】解：x，y满足|x|≤y≤1，表示的可行域如图：x2+y2+2x=（x+1）2+y2﹣1它的几何意义是可行域内的点到（﹣1，0）的距离的平方减去1．显然D（﹣1，0）到直线x+y=0的距离最小，最小值为：=，所求表达式的最小值为：=，故选：B．【点评】本题考查线性规划的简单应用，注意约束条件表示的可行域，以及所求表达式的几何意义是解题的关键．8．已知一长方体的体对角线的长为l0，这条对角线在长方体一个面上的正投影长为8，则这个长方体体积的最大值为（）A．64 B．128 C．192 D．384【考点】LF：棱柱、棱锥、棱台的体积．【分析】以投影面为底面，得正方体的高为6，设长方体底面边长分别为a，b，则a2+b2=64，由此能求出这个长方体体积的最大值．【解答】解：以投影面为底面，得到正方体的高为=6，设长方体底面边长分别为a，b，则a2+b2=64，∴这个长方体体积V=6ab≤3（a2+b2）=192．∴这个长方体体积的最大值为192．故选：C．【点评】本题考查长方体的体积的最大值的求法，考查基本不等式、长方体性质等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想，是中档题．9．为了竖一块广告牌，要制造三角形支架，如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了稳固广告牌，要求AC越短越好，则AC最短为（）A．（1+）米B．2米C．（1+）米D．（2+）米【考点】HR：余弦定理；7F：基本不等式．【分析】设BC的长度为x米，AC的长度为y米，依据题意可表示出AB的长度，然后代入到余弦定理中求得x和y的关系式，利用基本不等式求得y的最小值，并求得取等号时x的值．【解答】解：设BC的长度为x米，AC的长度为y米，则AB的长度为（y﹣0.5）米，在△ABC中，依余弦定理得：AB2=AC2+BC2﹣2AC•BCcos∠ACB，即（y﹣0.5）2=y2+x2﹣2yx×，化简，得y（x﹣1）=x2﹣，∵x＞1，∴x﹣1＞0，因此y=，y=（x﹣1）++2≥+2，当且仅当x﹣1=时，取“=”号，即x=1+时，y有最小值2+．故选：D．【点评】本题主要考查了解三角形的实际应用以及基本不等式求最值问题．考查了考生利用数学模型解决实际问题的能力，属于中档题．10．秦九韶是我国南宋时期著名的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为3，每次输入a的值均为4，输出s的值为484，则输入n的值为（）A．6 B．5 C．4 D．3【考点】EF：程序框图．【分析】模拟程序的运行过程，依次写出每次循环得到的s，k的值，由题意可得5＞n≥4，即可得解输入n的值．【解答】解：模拟程序的运行，可得x=3，k=0，s=0，a=4s=4，k=1不满足条件k＞n，执行循环体，a=4，s=16，k=2不满足条件k＞n，执行循环体，a=4，s=52，k=3不满足条件k＞n，执行循环体，a=4，s=160，k=4不满足条件k＞n，执行循环体，a=4，s=484，k=5由题意，此时应该满足条件k＞n，退出循环，输出s的值为484，可得：5＞n≥4，所以输入n的值为4．故选：C．【点评】本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答．11．在等腰直角三角形ABC中，AB=AC=4，点P是边上异于A，B的一点．光线从点P出发，经BC，CA反射后又回到点P（如图）．若光线QR经过△ABC的重心，则AP等于（）A．2 B．1 C．D．【考点】IQ：与直线关于点、直线对称的直线方程．【分析】建立坐标系，设点P的坐标，可得P关于直线BC的对称点P1的坐标，和P关于y 轴的对称点P2的坐标，由P1，Q，R，P2四点共线可得直线的方程，由于过△ABC的重心，代入可得关于a的方程，解之可得P的坐标，进而可得AP的值．【解答】解：以A为原点，AB为x轴，AC为y轴建立直角坐标系如图所示．则A（0，0），B（4，0），C（0，4）．设△ABC的重心为D，则D点坐标为，设P点坐标为（m，0），则P点关于y轴对称点P1为（﹣m，0），因为直线BC方程为x+y﹣4=0，所以P点关于BC的对称点P2为（4，4﹣m），根据光线反射原理，P1，P2均在QR所在直线上，∴，即，解得，或m=0．当m=0时，P点与A点重合，故舍去．∴．故选：D．【点评】本题考查直线与点的对称问题，涉及直线方程的求解以及光的反射原理的应用，属中档题．12．椭圆x2+=1（0＜b＜1）的左焦点为F，上顶点为A，右顶点为B，若△FAB的外接圆圆心P（m，n）在直线y=﹣x的左下方，则该椭圆离心率的取值范围为（）A．（，1）B．（，1）C．（0，）D．（0，）【考点】K4：椭圆的简单性质．【分析】方法一：分别求出线段FA与AB的垂直平分线方程，联立解出圆心坐标P，利用m+n＜0，与离心率计算公式即可得出；方法二：设△FAB的外接圆方程，将三点代入，即可求得P点坐标，由m+n＜0，求得b和c的关系，即可求得椭圆离心率的取值范围．【解答】解：方法一：如图所示，B是右顶点（1，0），上顶点A（0，b），左焦点F（，0），线段FB的垂直平分线为：x=．线段AB的中点（，）．∵kAB=﹣b．∴线段AB的垂直平分线的斜率k=．∴线段AB的垂直平分线方程为：y﹣=（x﹣），把x==m，代入上述方程可得：y==n．由P（m，n）在直线y=﹣x的左下方，则m+n＜0，∴+＞0．化为：b＜，又0＜b＜1，解得：0＜b＜．∴e==c=∈（，1）．∴椭圆离心率的取值范围（，1）．故选A．方法二：设A（0，b），B（a，0），C（﹣c，0），设△FAB的外接圆的方程x2+y2+Dx+Ey+F=0，将A，B，C代入外接圆方程，解得：m=，n=，由P（m，n）在直线y=﹣x的左下方，则m+n＜0，∴+＜0，整理得：1﹣c+b﹣＜0，∴b﹣c+＜0，∴b﹣c＜0，由椭圆的离心率e==c，∴2e2＞1，由0＜e＜1，解得：＜e＜1，∴椭圆离心率的取值范围（，1）．故选A．【点评】本题考查椭圆的简单性质，三角形形外接圆求得求法，考查计算能力，数形结合思想，属于中档题．二．填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡相应的横线上．13．已知||=4，||=5，=λ+μ（λ，μ∈R），若⊥，⊥（﹣），则=．【考点】9T：数量积判断两个平面向量的垂直关系．【分析】由⊥，⊥（﹣），可得•=0，•（﹣）=（λ+μ）•（﹣）=﹣=0，即可得出．【解答】解：∵⊥，⊥（﹣），∴•=0，•（﹣）=（λ+μ）•（﹣）=﹣=0，∴=．故答案为：．【点评】本题考查了向量垂直与数量积的关系，考查了推理能力与计算能力，属于中档题．14．记“点M（x，y）满足x2+y2≤a（a＞0）”为事件A，记“M（x，y）满足”为事件B，若P（B|A）=1，则实数a的最大值为．【考点】7C：简单线性规划．【分析】画出约束条件表示的可行域，利用条件概率，判断圆与可行域的关系，再求出a 的最大值．【解答】解：M（x，y）满足，画出可行域如图所示三角形；记“点M（x，y）满足x2+y2≤a（a＞0）“为事件A，记“M（x，y）满足”为事件B，若P（B|A）=1，说明圆的图形在可行域内部，实数a的最大值是圆与直线x﹣y+1=0相切时对应的值，此时d=r，即=，解得a=，所以实数a的最大值为．故答案为：．【点评】本题考查了线性规划的基本应用问题，利用目标函数的几何意义是解题的关键，是中档题．15．已知函数f（x）=（x+2）（x2+ax﹣5）的图象关于点（﹣2，0）中心对称，设关于x的不等式f（x+m）＜f（x）的解集为A，若（﹣5，﹣2）⊆A，则实数m的取值范围是{3，﹣3}．【考点】18：集合的包含关系判断及应用；3O：函数的图象．【分析】根据题意可知f（﹣4）+f（0）=0，由此可知求出a，f（x+m）﹣f（x）＜0等价于3x2+3（m+4）x+m2+6m+3＜0，利用（﹣5，﹣2）⊆A，即可求出实数m的取值范围．【解答】解：∵函数f（x）=（x+2）（x2+ax﹣5）的图象关于点（﹣2，0）中心对称，∴f（﹣4）+f（0）=0，∴a=4，∴f（x）=（x+2）（x2+4x﹣5）=x3+6x2+3x﹣10，f（x+m）＜f（x）等价于f（x+m）﹣f（x）＜0，f（x+m）﹣f（x）=m[3x2+3（m+4）x+m2+6m+3]若m＞0，f（x+m）﹣f（x）＜0等价于3x2+3（m+4）x+m2+6m+3＜0，由题意3×（﹣5）2﹣15（m+4）+m2+6m+3≤0且3×（﹣2）2﹣6（m+4）+m2+6m+3≤0，∴3≤m≤6且﹣3≤m≤3，∴m=3，同理，m＜0时，m=﹣3，故答案为：{3，﹣3}．【点评】本题考查集合的包含关系，考查函数图象的对称性，考查学生分析解决问题的能力，属于中档题．16．已知数列{an}的首项a1=t，其前n项和为Sn，且满足Sn+Sn+1=n2+2n，若对∀n∈N*，an＜an+1恒成立，则实数t的取值范围是（，）．【考点】8K：数列与不等式的综合．【分析】n=1时，S1+S2=12+2×1，得到a2=3﹣2t，当n≥2时，推导出an+an+1=2n+1，n≥2，由a2+a3=5，得到a3=2t+2，由a3+a4=7，得到a4=5﹣2t，再由对∀n∈N*，an＜an+1恒成立，列出不等式组，能求出实数t的取值范围．【解答】解：∵数列{an}的首项a1=t，其前n项和为Sn，且满足Sn+Sn+1=n2+2n，∴n=1时，S1+S2=12+2×1，即a1+a1+a2=3，∴a2=3﹣2t，∵Sn+Sn+1=n2+2n，①当n≥2时，Sn﹣1+Sn=（n﹣1）2+2（n﹣1），②①﹣②，得：an+an+1=2n+1，n≥2．∴a2+a3=5，∴a3=5﹣a2=5﹣（3﹣2t）=2t+2，a3+a4=7，∴a4=7﹣a3=7﹣（2t+2）=5﹣2t，∵对∀n∈N*，an＜an+1恒成立，∴，即，解得，∴实数t的取值范围是（，）．故答案为：（，）．【点评】本题考查实数的取值范围的求法，考查数列的通项与前n项和的关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．三、解答题：（共5小题，共70分；要求写出必要的文字说明，解题过程和演算步骤）17．（12分）（2017•冀州市校级模拟）已知向量=（sinωx﹣cosωx，1），=（cosωx，），设函数f（x）=，若函数f（x）的图象关于直线x=对称且ω∈[0，2]（Ⅰ）求函数f（x）的单调递减区间；（Ⅱ）在△ABC中，角A，B，C的对边分别a，b，c，若a=，f（A）=1，求b+c的最大值．【考点】HT：三角形中的几何计算；9R：平面向量数量积的运算；GL：三角函数中的恒等变换应用．【分析】（Ⅰ）化简f（x），利用周期公式求出ω得出f（x）的解析式，利用正弦函数的单调性列出不等式解出单调增区间；（Ⅱ）通过f（A）=1，求出A的值，利用余弦定理得到关于b+c的表达式，然后求其最大值．【解答】解：（Ⅰ）f（x）=（sinωx﹣cosωx）cosωx+=sinωx•cosωx﹣cos2ωx+=﹣=sin（2ωx﹣）函数f（x）的图象关于直线x=对称，则则，k∈Z且ω∈[0，2]，则ω=1…（4分）∴f（x）=sin（2x﹣），令2kπ+≤2x﹣+2kπ，解得kπ+，k∈Z∴函数f（x）的单调递减区间为[kπ+，kπ+]，k∈Z．（Ⅱ）f（A）=sin（2A﹣）=1，且A是△ABC内角，∴0＜A＜π，则﹣＜2A﹣，所以2A﹣=，则A=，∵a=，由余弦定理=b2+c2﹣bc=（b+c）2﹣3bc则（b+c）2﹣3bc=3，而bc≤（）2，所以3=（b+c）2﹣3bc≥（b+c）2﹣3×（）2=⇒b+c，当且仅当b=c=时，所以b+c 的最大值为2．【点评】本题考查三角函数的化简求值，解三角形的知识，二倍角公式、两角和的正弦函数、余弦定理的应用，考查计算能力，注意A 的大小求解，是易错点．18．（12分）（2017•冀州市校级模拟）某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，在将两组工人的日平均生产件数分成5组：[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率．（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列0.100 0.050 0.010【分析】（1）根据分层抽样，求得样本中有25周岁以上组工人60名，25周岁以下组工人40人，由频率分布直方图日平均生产件数不足60件的工人中25周岁以上组有3人，25周岁以下组有2人，随机抽取2人，求得所有可能的结果，根据古典概型公式求得至少抽到一名“25周岁以下组”工人的概率；（2）据2×2列联表，代入求临界值的公式，求出观测值，利用观测值同临界值表进行比较，K2≈1.786＜2.706，没有90%的把握认为“生产能手与工人所在的年龄组有关”．【解答】解：（1）由已知得：样本中有25周岁以上组工人60名，25周岁以下组工人40人，所以样本中日平均生产件数不足60件的工人中25周岁以上组有60×0.05=3人，分别记为：A1，A2，A3，25周岁以下组有工人40×0.05=2人，分别记为B1，B2，从中随机抽取2人，所有可能的结果共10种，他们分别是（A1，A2），（A1，A3），（A2，A3），（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B2），（A3，B2），（B1，B2），其中“至少有1名”，25周岁以下组的结果有7种，故所求概率为P=；（2）由频率分别直方图可知：在抽取的100名工人中，“25周岁以上组”中的生产能手60×0.25=15人，“25周岁以下组”中的生产能手40×0.375=15人，所以K2=≈1.786＜2.706．所以没有90%的把握认为“生产能手与工人所在的年龄组有关”．【点评】本题考查根据频率分布直方图的应用，考查独立性检验的概率情况，以及随机分布的概率的计算，考查运算能力，属于中档题．19．（12分）（2017•宜春二模）如图1，已知在菱形ABCD中，∠B=120°，E为AB的中点，现将四边形EBCD沿DE折起至EBHD，如图2．（1）求证：DE⊥面ABE；（2）若二面角A﹣DE﹣H的大小为，求平面ABH与平面ADE所成锐二面角的余弦值．【考点】MT：二面角的平面角及求法；LW：直线与平面垂直的判定．【分析】（1）由已知可得△ABD为正三角形，再由E为AB的中点，得DE⊥AE，DE⊥BE，利用线面垂直的判定可得DE⊥面ABE；（2）以点E为坐标原点，分别以线段ED，EA所在直线为x，y轴，再以过点E且垂直于平面ADE且向上的直线为z轴，建立空间直角坐标系．由二面角A﹣DE﹣H的平面角为，再设AE=1，可得E，A，B，D的坐标，然后分别求出平面ABH与平面ADE的一个法向量，利用两法向量所成角的余弦值求得平面ABH与平面ADE所成锐二面角的余弦值．【解答】（1）证明：∵四边形ABCD为菱形，且∠B=120°，∴△ABD为正三角形，∵E为AB的中点，∴DE⊥AE，DE⊥BE，∴DE⊥面ABE；（2）解：以点E为坐标原点，分别以线段ED，EA所在直线为x，y轴，再以过点E且垂直于平面ADE且向上的直线为z轴，建立空间直角坐标系如图所示．∵DE⊥面ABE，∴∠AEB为二面角A﹣DE﹣H的一个平面角，则，设AE=1，则E（0，0，0），A（0，1，0），B（0，，），D（，0，0），由，得H（），∴，，设平面ABH的法向量为，则，令y=，得．而平面ADE的一个法向量为，设平面ABH与平面ADE所成锐二面角的大小为θ，则cosθ=||=||=．∴平面ABH与平面ADE所成锐二面角的余弦值为．【点评】本题考查直线与平面垂直的判定，考查了空间想象能力和思维能力，训练了利用空间向量求二面角的平面角，是中档题．20．（12分）（2017•冀州市校级模拟）已知抛物线C：y2=2px（p＞0）的焦点为F，A为C 上位于第一象限的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D．（1）若|FA|=|AD|，当点A的横坐标为时，△ADF为等腰直角三角形，求C的方程；（2）对于（1）中求出的抛物线C，若点，记点B关于x轴的对称点为E，AE交x轴于点P，且AP⊥BP，求证：点P的坐标为（﹣x0，0），并求点P到直线AB 的距离d的取值范围．【考点】K8：抛物线的简单性质．【分析】（1）根据抛物线的焦半径公式，求得FD的中点坐标，则+2+=3+2，即可求得p的值，求得抛物线方程；（2）设直线AB的方程，代入抛物线方程，由向量平行即韦达定理，即可求得P点坐标，则△EPB为等腰直角三角形，则kAP=1，由直线的斜率公式可得：y1﹣y2=4，两边平方（y1+y2）2﹣4y1y2=16，m2=1﹣x0，x0＜1，则d=，根据函数的单调性即可求得点P到直线AB的距离d的取值范围．（1）由题意可知F（，0），丨FA丨=3+2+，丨FD丨=丨FA丨=3+4+，【解答】解：则D（3+4++，0），FD的中点坐标（+2+，0），则+2+=3+2，解得：p=2，∴抛物线C：y2=4x；（2）由题意设AB的方程x=my+x0，（m≠0），A（x1，y1），B（x2，y2），E（x2，﹣y2），由，消去x，整理得：y2﹣4my﹣4=0，由x0≥，△=16m2+16x0＞0，y1+y2=4m，y1y2=﹣4x0，设P（xP，0），则=（x2﹣xP，﹣y2），=（x1﹣xP，y1），由∥，则（x2﹣xP）y1+y2（x1﹣xP）=0，即x2y1+y2x1=（y1+y2）xP==，显然y1+y2=4m≠0，∴xP==﹣x0，即P（﹣x0，0），由题意可知△EPB为等腰直角三角形，则kAP=1，即=1，则=1，则y1﹣y2=4，∴（y1+y2）2﹣4y1y2=16，即16m2+16x0=16，则m2=1﹣x0，x0＜1，由x0≥，则≤x0＜1，d===，令=t∈（1，]，则x0=2﹣t2，d==﹣2t，则f（t）=﹣2t，在（1，]上是减函数，∴d∈[，2）．【点评】本题考查抛物线的性质，直线与抛物线的位置关系，考查向量平行，函数单调性与抛物线的应用，考查计算能力，属于中档题．21．（12分）（2013•四川）已知函数，其中a是实数，设A（x1，f（x1）），B（x2，f（x2））为该函数图象上的点，且x1＜x2．（Ⅰ）指出函数f（x）的单调区间；（Ⅱ）若函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值；（Ⅲ）若函数f（x）的图象在点A，B处的切线重合，求a的取值范围．【考点】6B：利用导数研究函数的单调性；6H：利用导数研究曲线上某点切线方程．【分析】（I）利用二次函数的单调性和对数函数的单调性即可得出；（II）利用导数的几何意义即可得到切线的斜率，因为切线互相垂直，可得，即（2x1+2）（2x2+2）=﹣1．可得，再利用基本不等式的性质即可得出；（III）当x1＜x2＜0或0＜x1＜x2时，∵，故不成立，∴x1＜0＜x2．分别写出切线的方程，根据两条直线重合的充要条件即可得出，再利用导数即可得出．．【解答】解：（I）当x＜0时，f（x）=（x+1）2+a，∴f（x）在（﹣∞，﹣1）上单调递减，在[﹣1，0）上单调递增；当x＞0时，f（x）=lnx，在（0，+∞）单调递增．（II）∵x1＜x2＜0，∴f（x）=x2+2x+a，∴f′（x）=2x+2，∴函数f（x）在点A，B处的切线的斜率分别为f′（x1），f′（x2），∵函数f（x）的图象在点A，B处的切线互相垂直，∴，∴（2x1+2）（2x2+2）=﹣1．∴2x1+2＜0，2x2+2＞0，∴=1，当且仅当﹣（2x1+2）=2x2+2=1，即，时等号成立．∴函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值为1．（III）当x1＜x2＜0或0＜x1＜x2时，∵，故不成立，∴x1＜0＜x2．当x1＜0时，函数f（x）在点A（x1，f（x1）），处的切线方程为，即．当x2＞0时，函数f（x）在点B（x2，f（x2））处的切线方程为，即．函数f（x）的图象在点A，B处的切线重合的充要条件是，由①及x1＜0＜x2可得﹣1＜x1＜0，由①②得=．∵函数，y=﹣ln（2x1+2）在区间（﹣1，0）上单调递减，∴a（x1）=在（﹣1，0）上单调递减，且x1→﹣1时，ln（2x1+2）→﹣∞，即﹣ln（2x1+2）→+∞，也即a（x1）→+∞．x1→0，a（x1）→﹣1﹣ln2．∴a的取值范围是（﹣1﹣ln2，+∞）．【点评】本题主要考查了基本函数的性质、利用导数研究函数的单调性、导数的几何意义、基本不等式的性质、直线的位置关系等基础知识，考查了推理论证能力、运算能力、创新意识，考查了函数与方程、分类与整合、转化与化归等思想方法．[选修4-4：坐标系与参数方程]22．（10分）（2017•冀州市校级模拟）已知直线l的参数方程为（t为参数），曲线C的参数方程为（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点P的极坐标为（2，）．（Ⅰ）求直线l以及曲线C的极坐标方程；（Ⅱ）设直线l与曲线C交于A，B两点，求△PAB的面积．【考点】QH：参数方程化成普通方程．【分析】（Ⅰ）直线l的参数方程消去参数t，得到直线l的普通方程为y=，由此能求出直线l的极坐标方程；曲线C的参数方程消去参数θ，得曲线C的普通方程，由此能求出曲线C的极坐标方程．（Ⅱ）由，得到ρ2﹣7ρ+9=0，由韦达定理、弦长公式求出|AB|，△PAB的面积S△PAB=|S△POB﹣S△POA|，由此能求出结果．【解答】解：（Ⅰ）∵直线l的参数方程为（t为参数），消去参数t，得到直线l的普通方程为y=，∴，∴，∴直线l的极坐标方程为（ρ∈R），∵曲线C的参数方程为（θ为参数），∴曲线C的普通方程为：（x﹣1）2+（y﹣2）2=4，则（ρcosθ﹣1）2+（）2=4，则曲线C的极坐标方程为．（Ⅱ）由，得到ρ2﹣7ρ+9=0，设其两根为ρ1，ρ2，则ρ1+ρ2=7，ρ1ρ2=9，∴|AB|=|ρ2﹣ρ1|==，∵点P的极坐标为（），∴|OP|=2，，。

河北省石家庄市2019届高三一模考试数学(文)试题(含答案)

石家庄2019届高中毕业班模拟考试（一）文科数学答案一、选择题A 卷答案：1-5CAACB 6-10CCDBD 11-12DBB 卷答案：1-5CBBCA 6-10CCDAD 11-12DA二、填空题 13. 15 14. ()122y x =- 或()122y x =-- 15. 3121a 16. ⎪⎭⎫ ⎝⎛+∞,103 三、解答题17. 解: （1） ∵△ABC 三内角A 、B 、C 依次成等差数列，∴B=60°设A 、B 、C 所对的边分别为a 、b 、c ,由S =1sin 2ac B 可得12ac =.……2分 ∵sin 3sin C A =，由正弦定理知3c a =，∴2,6a c ==. ……4分△ABC 中，由余弦定理可得2222cos 28b a c ac B =+-=，∴b=即AC的长为……6分（2）∵BD 是AC 边上的中线，∴1()2BD BC BA =+u u u r u u u r u u u r ……8分 ∴2221(2)4BD BC BA BC BA =++⋅u u u r u u u r u u u r u u u r u u u r =221(2cos )4a c ac B ++=221()4a c ac ++ 1(2)94ac ac ≥+=，当且仅当a c =时取“=” ……10分 ∴3BD ≥u u u r ,即BD 长的最小值为3. ……12分18. 解：（1）证明：在PBC ∆中，60o PBC ∠=，2BC =，4PB =，由余弦定理可得PC =222PC BC PB +=Q ，PC BC ∴⊥，…………2分,PC AB AB BC B ⊥⋂=Q 又，PC ABC ∴⊥平面， (4)PC PAC ⊂Q 平面，PAC ABC ∴⊥平面平面。

…………6分（2）设三棱锥-F ACE 的高为1h ，三棱锥-P ABC 的高为h ，F ACE V -=113ACE S h ∆⨯⨯…………7分 =121332ABC S h ∆⨯⨯⨯⨯…………9分 =1133ABC S h ∆⨯⨯⨯=-⨯13P ABC V …………11分所以三棱锥-F ACE 与四棱锥PBEF C -的体积之比为1:2。

2019年河北省高考数学一模试卷(文科)(解析版)

2019年河北省高考数学一模试卷（文科）一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x|x2﹣4x+3＜0}，B={y|y=x2，x∈R}，则A∩B=（）A．∅B．[0，1）∪（3，+∞） C．A D．B2．若复数为纯虚数，则实数a的值为（）A．i B．0 C．1 D．﹣13．设等差数列{a n}的前n项和为S n，a2、a4是方程x2﹣x﹣2=0的两个根，则S5=（）A．B．5 C．D．﹣54．某人午觉醒来，发现表停了，他打开收音机，想听电台报时，他等待的时间不多于10分钟的概率为（）A．B．C．D．5．函数y=cos（4x+）的图象的相邻两个对称中心间的距离为（）A．B．C．D．π6．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此四面体的外接球的体积为（）A．B．3πC．D．π7．函数f（x）=x2﹣elnx的零点个数为（）A．0 B．1 C．2 D．38．设椭圆+=1，双曲线﹣=1，（其中m＞n＞0）的离心率分别为e1，e2，则（）A．e1，e2＞1 B．e1，e2＜1C．e1，e2=1 D．e1，e2与1大小不确定9．程序框图如图：如果上述程序运行的结果S的值比2016小，若使输出的S最大，那么判断框中应填入（）A．k≤10？B．k≥10？C．k≤9？D．k≥9？10．已知函数f（x）的定义域为[﹣2，+∞），且f（4）=f（﹣2）=1，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示．则平面区域所围成的面积是（）A．2 B．3 C．4 D．511．如图，正方体ABCD﹣AB1C1D1的棱长为，以顶点A为球心，2为半径作一个球，则图中球面与正方体的表面相交所得到的两段弧长之和等于（）A．B．C．πD．12．已知平面向量的集合A到B的映射f为f（）=﹣2（•），其中为常向量，若映射f满足f（）•f（）=•对任意，∈A恒成立，则用坐标可能是（）A．B．C．D．二、填空题：本题共4小题，每小题5分，共20分．13．设△ABC的内角A，B，C所对的边长分别为a，b，c且acosB﹣bcosA=c，则的值为．14．已知x＞0，y＞0， ++1=2，则2x+y的最小值为．15．如图，在直角梯形ABCD中，AB∥CD，AB=2，AD=DC=1，P是线段BC上一动点，Q是线段DC上一动点，=λ，=（1﹣λ），则•的取值范围是．16．已知函数f（x）（x∈R）满足f（﹣x）=﹣f（x）=f（4﹣x），当x∈（0，2）时，f（x）=ln（x2﹣x+b）．若函数f（x）在区间[﹣2，2]上有5个零点，则实数b的取值范围是．三、解答题：本题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．已知向量=（sinA，cosA），=（cosB，sinB），=sin2C且A、B、C分别为△ABC的三边a，b，c所对的角．（1）求角C的大小；（2）若sinA，sinC，sinB成等比数列，且=18，求c 的值．．18．某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关，随机抽取了55名市民，得到数据如下表：（Ⅰ）判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关？（Ⅱ）用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率．下面的临界值表供参考：（参考公式：K 2=，其中n=a +b +c +d ） 19．如图，直三棱柱ABC ﹣A 1B 1C 1中，AC ⊥AB ，AB=2AA 1，M 是AB 的中点，△A 1MC 1是等腰三角形，D 为CC 1的中点，E 为BC 上一点．（1）若DE ∥平面A 1MC 1，求；（2）平面A 1MC 1将三棱柱ABC ﹣A 1B 1C 1分成两个部分，求较小部分与较大部分的体积之比．20．如图，已知抛物线C：y2=4x，过焦点F斜率大于零的直线l 交抛物线于A、B两点，且与其准线交于点D．（Ⅰ）若线段AB的长为5，求直线l的方程；（Ⅱ）在C上是否存在点M，使得对任意直线l，直线MA，MD，MB的斜率始终成等差数列，若存在求点M的坐标；若不存在，请说明理由．21．已知函数f（x）=e x﹣1﹣．（Ⅰ）若曲线y=f（x）在（2，f（2））处的切线过（0，﹣1），求a的值；（Ⅱ）求证：当a≤﹣1时，不等式f（x）•lnx≥0在（0，1）∪（1，+∞）上恒成立．请考生在22，23，24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．[选修4-1：几何证明选讲]22．如图，已知AP是⊙O的切线，P为切点，AC是⊙O的割线，与⊙O交于B，C两点，圆心O在∠PAC的内部，点M是BC 的中点．（Ⅰ）证明A，P，O，M四点共圆；（Ⅱ）求∠OAM+∠APM的大小．[选修4-4：坐标系与参数方程]23．在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρsin（θ+）=a，曲线C2的参数方程为，（θ为参数，0≤θ≤π）．（Ⅰ）求C1的直角坐标方程；（Ⅱ）当C1与C2有两个公共点时，求实数a的取值范围．[选修4-5：不等式选讲]24．已知函数f（x）=log2（|x﹣1|+|x﹣5|﹣a）（Ⅰ）当a=5时，求函数f（x）的定义域；（Ⅱ）当函数f（x）的定义域为R时，求实数a的取值范围．参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x|x2﹣4x+3＜0}，B={y|y=x2，x∈R}，则A∩B=（）A．∅B．[0，1）∪（3，+∞） C．A D．B【考点】交集及其运算．【分析】求出A中不等式的解集确定出A，求出B中y的范围确定出B，找出两集合的交集即可．【解答】解：由A中不等式变形得：（x﹣1）（x﹣3）＜0，解得：1＜x＜3，即A=（1，3），由B中y=x2≥0，得到B=[0，+∞），则A∩B=（1，3）=A，故选：C．2．若复数为纯虚数，则实数a的值为（）A．i B．0 C．1 D．﹣1【考点】复数代数形式的乘除运算．【分析】利用复数的运算法则、纯虚数的定义即可得出．【解答】解：复数==﹣i为纯虚数，∴=0，≠0，解得a=1．故选：C．3．设等差数列{a n}的前n项和为S n，a2、a4是方程x2﹣x﹣2=0的两个根，则S5=（）A．B．5 C．D．﹣5【考点】等差数列的前n项和．【分析】根据韦达定理a2+a4=1，通过等差数列的等差性质可知a1+a5=a2+a4，最后把a1+a5代入S5即可得到答案．【解答】解：依题意可知a2+a4=1，∴a1+a5=a2+a4=1∴S5==故答案选A4．某人午觉醒来，发现表停了，他打开收音机，想听电台报时，他等待的时间不多于10分钟的概率为（）A．B．C．D．【考点】几何概型．【分析】由电台整点报时的时刻是任意的知这是一个几何概型，电台整点报时知事件总数包含的时间长度是60，而他等待的时间不多于10分钟的事件包含的时间长度是10，两值一比即可求出所求．【解答】解：设A={等待的时间不多于10分钟}，事件A恰好是打开收音机的时刻位于[50，60]时间段内，因此由几何概型的求概率的公式可得p（A）==，即“等待报时的时间不超过10分钟”的概率为；故选C5．函数y=cos（4x+）的图象的相邻两个对称中心间的距离为（）A．B．C．D．π【考点】余弦函数的图象；余弦函数的对称性．【分析】先根据函数的表达式求出函数的最小正周期，然后根据两向量对称轴间的距离等于半个周期可得答案．【解答】解：对于，T=∴两条相邻对称轴间的距离为=故选B．6．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此四面体的外接球的体积为（）A．B．3πC．D．π【考点】由三视图求面积、体积．【分析】由于正视图、侧视图、俯视图都是边长为1的正方形，所以此四面体一定可以放在棱长为1的正方体中，所以此四面体的外接球即为此正方体的外接球，由此能求出此四面体的外接球的体积．【解答】解：由于正视图、侧视图、俯视图都是边长为1的正方形，所以此四面体一定可以放在正方体中，所以我们可以在正方体中寻找此四面体．如图所示，四面体ABCD满足题意，所以此四面体的外接球即为此正方体的外接球，由题意可知，正方体的棱长为1，所以外接球的半径为R=，所以此四面体的外接球的体积V==．故选C．7．函数f（x）=x2﹣elnx的零点个数为（）A．0 B．1 C．2 D．3【考点】根的存在性及根的个数判断．【分析】求出函数的导数，根据导数求的函数的极小值为f（）＞0，可得函数无零点．【解答】解：∵函数f（x）=x2﹣elnx，∴f′（x）=2x﹣=．令f′（x）=0，解得x=．由于f′（x）在（0，）上小于零，在（，+∞）上大于零，故x=时，函数f（x）取得极小值．由于f（）=﹣eln=﹣ln=（1﹣ln）＞0，所以函数无零点．故选A．8．设椭圆+=1，双曲线﹣=1，（其中m＞n＞0）的离心率分别为e1，e2，则（）A．e1，e2＞1 B．e1，e2＜1C．e1，e2=1 D．e1，e2与1大小不确定【考点】椭圆的简单性质．【分析】由椭圆方程与双曲线方程分别求出椭圆与双曲线的离心率，作积后结合m＞n得答案．【解答】解：在椭圆+=1中，，∴，在双曲线﹣=1中，，∴，∴=．故选：B．9．程序框图如图：如果上述程序运行的结果S的值比2016小，若使输出的S最大，那么判断框中应填入（）A．k≤10？B．k≥10？C．k≤9？D．k≥9？【考点】程序框图．【分析】按照程序框图的流程写出前几次循环的结果判断出当k 为何值时输出，得到判断框中的条件．【解答】解：由题意，模拟执行程序，可得K=12，S=1不满足条件，执行循环体，S=12，K=11不满足条件，执行循环体，S=132，K=10不满足条件，执行循环体，S=1320，K=9不满足条件，执行循环体，S=11880，K=8…观察可得：如果上述程序运行的结果S的值比2016小，若使输出的S最大，那么判断框中应填入K≤9？．故选：C．10．已知函数f（x）的定义域为[﹣2，+∞），且f（4）=f（﹣2）=1，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示．则平面区域所围成的面积是（）A．2 B．3 C．4 D．5【考点】函数的单调性与导数的关系；二元一次不等式（组）与平面区域．【分析】由函数y=f′（x）的图象可得：当x∈（0，+∞）时，f′（x）＞0，此时函数f（x）单调递增．由f（2a+b）＜1，f（4）=1，及f（2a+b）＜1=f（4）．可得2a+b＜4．再利用线性规划的有关知识即可得出．【解答】解：由函数y=f′（x）的图象可得：当x∈[﹣2，0）]时，f′（x）＜0，此时函数f（x）单调递减；当x∈（0，+∞）时，f′（x）＞0，此时函数f（x）单调递增．∵a≥0，b≥0，∴2a+b≥0．又∵f（4）=1，f（2a+b）＜1，∴f（2a+b）＜f（4）．∴0≤2a+b＜4．由，画出图象如图∴阴影部分的面积S==4．故选C．B1C1D1的棱长为，以顶点A为11．如图，正方体ABCD﹣A球心，2为半径作一个球，则图中球面与正方体的表面相交所得到的两段弧长之和等于（）A．B．C．πD．【考点】球内接多面体．【分析】球面与正方体的六个面都相交，所得的交线分为两类：一类在顶点A所在的三个面上，即面AA1B1B、面ABCD和面AA1D1D上；另一类在不过顶点A的三个面上，即面BB1C1C、面CC1D1D和面A1B1C1D1上．由空间几何知识能求出这两段弧的长度之和．【解答】解：如图，球面与正方体的六个面都相交，所得的交线分为两类：一类在顶点A所在的三个面上，即面AA1B1B、面ABCD和面AA1D1D上；另一类在不过顶点A的三个面上，即面BB1C1C、面CC1D1D和面A1B1C1D1上．在面AA1B1B上，交线为弧EF且在过球心A的大圆上，因为=，AE=2，AA则∠A1AE=．同理∠BAF=，所以∠EAF=，故弧EF的长为：2×=，而这样的弧共有三条．在面BB1C1C上，交线为弧FG且在距球心为1的平面与球面相交所得的小圆上，此时，小圆的圆心为B，半径为1，∠FBG=，所以弧FG的长为：1×=．于是，所得的曲线长为： +=．故选：A．12．已知平面向量的集合A到B的映射f为f（）=﹣2（•），其中为常向量，若映射f满足f（）•f（）=•对任意，∈A恒成立，则用坐标可能是（）A．B．C．D．【考点】平面向量数量积的运算；映射．【分析】通过赋值列出关于向量的方程，通过向量的运算法则化简方程，得到满足的条件．【解答】解：令=，则f（）•f（）=•又f（）•f（）=[﹣2（•）]2=2﹣4（•）2+4[（•）]2即﹣4（•）2+4[（•）]2=0，∴（•）2（2﹣1）=0∴=0或||=1，对于选项D，||=1，故选D．二、填空题：本题共4小题，每小题5分，共20分．13．设△ABC的内角A，B，C所对的边长分别为a，b，c且acosB﹣bcosA=c，则的值为4．【考点】正弦定理的应用．【分析】先根据正弦定理得到sinAcosB﹣sinBcosA=sinC，再由两角和与差的正弦公式进行化简可得到sinAcosB=4sinBcosA，然后转化为正切的形式可得到答案．【解答】解：由acosB﹣bcosA=c及正弦定理可得sinAcosB﹣sinBcosA=sinC，即sinAcosB﹣sinBcosA=sin（A+B），即5（sinAcosB﹣sinBcosA）=3（sinAcosB+sinBcosA），即sinAcosB=4sinBcosA，因此tanA=4tanB，所以=4．故答案为：414．已知x＞0，y＞0， ++1=2，则2x+y的最小值为8．【考点】基本不等式．【分析】利用“乘1法”和基本不等式的性质即可得出．【解答】解：∵x＞0，y＞0， ++1=2，∴2x+y=（2x+y）=4+=8，当且仅当y=2x=4时取等号．∴2x+y的最小值为8．故答案为：8．15．如图，在直角梯形ABCD中，AB∥CD，AB=2，AD=DC=1，P是线段BC上一动点，Q是线段DC上一动点，=λ，=（1﹣λ），则•的取值范围是[0，2] ．【考点】平面向量数量积的坐标表示、模、夹角．【分析】通过向量的坐标运算转化为二次函数的单调性即可得出．【解答】解：如图所示，A（0，0），B（2，0），C（1，1），D（0，1）．=（1，1）+（1﹣λ），λ∈[0，1]．=（1，1）+（1﹣λ）（1，﹣1）=（2﹣λ，λ）．==（0，1）+=（0，1）+λ（1，0）=（λ，1）．∴f（λ）==（2﹣λ，λ）•（λ，1）=λ（2﹣λ）+λ=﹣λ2+3λ=，∵λ∈[0，1]，∴f（0）≤f（λ）≤f（1），∴0≤f（λ）≤2．∴•的取值范围是[0，2]．故答案为：[0，2]．16．已知函数f（x）（x∈R）满足f（﹣x）=﹣f（x）=f（4﹣x），当x∈（0，2）时，f（x）=ln（x2﹣x+b）．若函数f（x）在区间[﹣2，2]上有5个零点，则实数b的取值范围是或．【考点】根的存在性及根的个数判断；函数零点的判定定理．【分析】判断函数是奇函数和函数的周期性，可得0、±2是函数f（x）的零点，将函数f（x）在区间[﹣2，2]上的零点个数为5，转化为当x∈（0，2）时，x2﹣x+b＞0恒成立，且x2﹣x+b=1在（0，2）有一解，由此构造关于b的不等式组，解不等式组可得实数b的取值范围．【解答】解：由题意知，f（x）是定义在R上的奇函数，所以f（0）=0，即0是函数f（x）的零点，因为f（x）是定义在R上且以4为周期的周期函数，所以f（﹣2）=f（2），且f（﹣2）=﹣f（2），则f（﹣2）=f（2）=0，即±2也是函数f（x）的零点，因为函数f（x）在区间[﹣2，2]上的零点个数为5，且当x∈（0，2）时，f（x）=ln（x2﹣x+b），所以当x∈（0，2）时，x2﹣x+b＞0恒成立，且x2﹣x+b=1在（0，2）有一解，即或，解得＜b≤1或b=，故答案为：或．三、解答题：本题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．已知向量=（sinA，cosA），=（cosB，sinB），=sin2C且A、B、C分别为△ABC的三边a，b，c所对的角．（1）求角C的大小；（2）若sinA，sinC，sinB成等比数列，且=18，求c 的值．．【考点】平面向量数量积的运算；等比数列的通项公式；正弦定理．【分析】（1）由=sin2C，结合向量的数量积的坐标表示及两角和的正弦公式可求cosC，进而可求C（2）由已知可得，sin2C=sinAsinB，结合正弦定理可得c2=ab，再由向量的数量积的定义可求ab，进而可求c【解答】解：（1）∵=sin2C∴sinAcosB+sinBcosA=sin2C∴sin（A+B）=sinC=sin2C=2sinCcosC∵sinC≠0∴cosC=∵C∈（0，π）∴（2）∵sinA，sinB，sinB成等比数列，∴sin2C=sinAsinB由正弦定理可得c2=ab∵=18，∴==18，∴ab=36∴c2=36，c=618．某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关，随机抽取了55名市民，得到数据如下表：（Ⅰ）判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关？（Ⅱ）用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率．下面的临界值表供参考：（参考公式：K 2=，其中n=a +b +c +d ）【考点】独立性检验的应用．【分析】（Ⅰ）计算K 2的值，与临界值比较，即可得到结论；（II ）确定样本中有4个“大于40岁”的市民，2个“20岁至40岁”的市民，利用列举法确定基本事件，即可求得结论．【解答】解：（1）由公式K2=≈11.978＞7.879，所以有99.5%的把握认为喜欢“人文景观”景点与年龄有关 …（II ）设所抽样本中有m 个“大于40岁”市民，则，得m=4人所以样本中有4个“大于40岁”的市民，2个“20岁至40岁”的市民，分别记作B 1，B 2，B 3，B 4，G 1，G 2．从中任选2人的基本事件有（B1，B2）、（B1，B3）、（B1，B4）、（B1，G1）、（B1，G2）、（B2，B3）、（B2，B4）、（B2，G1）、（B2，G2）、（B3，B4）、（B3，G1）、（B3，G2）、（B4，G1）、（B4，G2）、（G1，G2），共15个，…其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的事件有（B1，G1）、（B1，G2）、（B2，G1）、（B2，G2）、（B3，G1）、（B3，G2）、（B4，G1）、（B4，G2），共8个，所以恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的概率为P=．…19．如图，直三棱柱ABC﹣A1B1C1中，AC⊥AB，AB=2AA1，M是AB的中点，△A1MC1是等腰三角形，D为CC1的中点，E 为BC上一点．（1）若DE∥平面A1MC1，求；（2）平面A1MC1将三棱柱ABC﹣A1B1C1分成两个部分，求较小部分与较大部分的体积之比．【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定．【分析】（1）先证明A1，M，N，C1四点共面，利用DE∥平面A1MC1，可得DE∥C1N，利用D为CC1的中点，即可求；（2）将几何体AA1M﹣CC1N补成三棱柱AA1M﹣CC1F，求出几何体AA1M﹣CC1N的体积、直三棱柱ABC﹣A1B1C1体积，即可求较小部分与较大部分的体积之比．【解答】解：（1）取BC中点为N，连结MN，C1N，…∵M，N分别为AB，CB中点∴MN∥AC∥A1C1，∴A1，M，N，C1四点共面，…且平面BCC1B1∩平面A1MNC1=C1N又DE⊂平面BCC1B1，且DE∥平面A1MC1∴DE∥C1N∵D为CC1的中点，∴E是CN的中点，…∴．…（2）∵三棱柱ABC﹣A1B1C1为直三棱柱，∴AA1⊥平面ABC，又AC⊥AB，则AC⊥平面ABB1A1设AB=2AA1=2，又三角形A1MC1是等腰三角形，所以．如图，将几何体AA1M﹣CC1N补成三棱柱AA1M﹣CC1F∴几何体AA1M﹣CC1N的体积为：…又直三棱柱ABC﹣A1B1C1体积为：…故剩余的几何体棱台BMN﹣B1A1C1的体积为：∴较小部分的体积与较大部分体积之比为：．…20．如图，已知抛物线C：y2=4x，过焦点F斜率大于零的直线l 交抛物线于A、B两点，且与其准线交于点D．（Ⅰ）若线段AB的长为5，求直线l的方程；（Ⅱ）在C上是否存在点M，使得对任意直线l，直线MA，MD，MB的斜率始终成等差数列，若存在求点M的坐标；若不存在，请说明理由．【考点】直线与圆锥曲线的关系；直线的一般式方程．【分析】（Ⅰ）设l：x=my+1，A（x1，y1），B（x2，y2），则联立方程化简可得y2﹣4my﹣4=0，从而可得，从而求直线l的方程；（Ⅱ）设M（a2，2a），则k MA==，k MB=，k MD=，则=，从而可得（a2﹣1）（m+）=0，从而求出点M的坐标．【解答】解：（Ⅰ）焦点F（1，0）∵直线l的斜率不为0，所以设l：x=my+1，A（x1，y1），B（x2，y2）由得y2﹣4my﹣4=0，y1+y2=4m，y1y2=﹣4，，，∴，∴．∴直线l的斜率k2=4，∵k＞0，∴k=2，∴直线l的方程为2x﹣y﹣2=0．（Ⅱ）设M（a2，2a），k MA==，同理，k MB=，k MD=，∵直线MA，MD，MB的斜率始终成等差数列，∴2=+恒成立；∴=，又∵y1+y2=4m，y1y2=﹣4，∴（a2﹣1）（m+）=0，∴a=±1，∴存在点M（1，2）或M（1，﹣2），使得对任意直线l，直线MA，MD，MB的斜率始终成等差数列．21．已知函数f（x）=e x﹣1﹣．（Ⅰ）若曲线y=f（x）在（2，f（2））处的切线过（0，﹣1），求a的值；（Ⅱ）求证：当a≤﹣1时，不等式f（x）•lnx≥0在（0，1）∪（1，+∞）上恒成立．【考点】利用导数求闭区间上函数的最值；利用导数研究曲线上某点切线方程．【分析】（Ⅰ）将x=2代入原函数和导函数，求出切点坐标和切线斜率，得到切线的点斜式方程，将（0，﹣1）代入，可求a的值；（Ⅱ）若证：当a≤﹣1时，不等式f（x）•lnx≥0在（0，1）∪（1，+∞）上恒成立．只需证：（x﹣1）（e x﹣1）﹣ax≥0在（0，+∞）恒成立，设g（x）=（x﹣1）（e x﹣1）﹣ax，x∈[0，+∞），利用导数法求其最值后，可得结论．【解答】解：（Ⅰ）解由x﹣1≠0得：函数f（x）=e x﹣1﹣的定义域为x∈（﹣∞，1）∪（1，+∞），f（2）=e2﹣1﹣2a，，∴f'（2）=e2+a，∴曲线y=f（x）在（2，f（2））处的切线y﹣（e2﹣1﹣2a）=（e2+a）（x﹣2）将（0，﹣1）代入，得﹣1﹣（e2﹣1﹣2a）=﹣2e2﹣2a，解得：证明：（Ⅱ）若证：当a≤﹣1时，不等式f（x）•lnx≥0在（0，1）∪（1，+∞）上恒成立．只需证：在（0，1）∪（1，+∞）上恒成立，∵x∈（0，1）∪（1，+∞）时，恒成立，∴只需证：（x﹣1）（e x﹣1）﹣ax≥0在（0，+∞）恒成立设g（x）=（x﹣1）（e x﹣1）﹣ax，x∈[0，+∞）∵g（0）=0恒成立∴只需证：g（x）≥0在[0，+∞）恒成立∵g'（x）=x•e x﹣1﹣a，g''（x）=（x+1）•e x＞0恒成立，∴g'（x）单调递增，∴g'（x）≥g'（0）=﹣1﹣a≥0∴g（x）单调递增，∴g（x）≥g（0）=0∴g（x）≥0在[0，+∞）恒成立即在（0，1）∪（1，+∞）上恒成立．请考生在22，23，24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．[选修4-1：几何证明选讲]22．如图，已知AP是⊙O的切线，P为切点，AC是⊙O的割线，与⊙O交于B，C两点，圆心O在∠PAC的内部，点M是BC 的中点．（Ⅰ）证明A，P，O，M四点共圆；（Ⅱ）求∠OAM+∠APM的大小．【考点】圆內接多边形的性质与判定．【分析】（1）要证明四点共圆，可根据圆内接四边形判定定理：四边形对角互补，而由AP是⊙O的切线，P为切点，易得∠APO=90°，故解答这题的关键是证明，∠AMO=90°，根据垂径定理不难得到结论．（2）由（1）的结论可知，∠OPM+∠APM=90°，只要能说明∠OPM=∠OAM即可得到结论．【解答】证明：（Ⅰ）连接OP，OM．因为AP与⊙O相切于点P，所以OP⊥AP．因为M是⊙O的弦BC的中点，所以OM⊥BC．于是∠OPA+∠OMA=180°．由圆心O在∠PAC的内部，可知四边形M的对角互补，所以A，P，O，M四点共圆．解：（Ⅱ）由（Ⅰ）得A，P，O，M四点共圆，所以∠OAM=∠OPM．由（Ⅰ）得OP⊥AP．由圆心O在∠PAC的内部，可知∠OPM+∠APM=90°．又∵A，P，O，M四点共圆∴∠OPM=∠OAM所以∠OAM+∠APM=90°．[选修4-4：坐标系与参数方程]23．在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρsin（θ+）=a，曲线C2的参数方程为，（θ为参数，0≤θ≤π）．（Ⅰ）求C1的直角坐标方程；（Ⅱ）当C1与C2有两个公共点时，求实数a的取值范围．【考点】参数方程化成普通方程；直线与圆的位置关系．【分析】（Ⅰ）利用极坐标方程的定义即可求得；（Ⅱ）数形结合：作出图象，根据图象即可求出有两交点时a的范围．【解答】解：（Ⅰ）曲线C1的极坐标方程为ρ（sinθ+cosθ）=a，∴曲线C1的直角坐标方程为x+y﹣a=0．（Ⅱ）曲线C2的直角坐标方程为（x+1）2+（y+1）2=1（﹣1≤y ≤0），为半圆弧，如图所示，曲线C1为一族平行于直线x+y=0的直线，当直线C过点P时，利用得a=﹣2±，舍去a=﹣2﹣，则a=﹣2+，当直线C1过点A、B两点时，a=﹣1，∴由图可知，当﹣1≤a＜﹣2+时，曲线C与曲线C2有两个公共点．[选修4-5：不等式选讲]24．已知函数f（x）=log2（|x﹣1|+|x﹣5|﹣a）（Ⅰ）当a=5时，求函数f（x）的定义域；（Ⅱ）当函数f（x）的定义域为R时，求实数a的取值范围．【考点】绝对值不等式的解法；函数的定义域及其求法；函数的值域．【分析】（1）a=5时，表达式中对数的真数大于0，即|x﹣1|+|x ﹣5|﹣5＞0，分情况讨论不等式的解集，最后取并集即可得到函数f（x）的定义域．（2）函数f（x）的定义域为R，即不等式|x﹣1|+|x﹣5|＞a恒成立，根据绝对值不等式的性质求出左边的最小值，即可得到实数a的取值范围．【解答】解：（Ⅰ）当a=5时，要使函数f（x）有意义，即不等式|x﹣1|+|x﹣5|﹣5＞0成立，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①①当x≤1时，不等式①等价于﹣2x+1＞0，解之得x；②当1＜x≤5时，不等式①等价于﹣1＞0，无实数解；③当x＞5时，不等式①等价于2x﹣11＞0，解之得x综上所述，函数f（x）的定义域为（﹣∞，）∪（，+∞）．（Ⅱ）∵函数f（x）的定义域为R，∴不等式|x﹣1|+|x﹣5|﹣a＞0恒成立，∴只要a＜（|x﹣1|+|x﹣5|）min即可，又∵|x﹣1|+|x﹣5|≥|（x﹣1）﹣（x﹣5）|=4，（当且仅当1≤x≤5时取等号）∴a＜（|x﹣1|+|x﹣5|）min即a＜4，可得实数a的取值范围是（﹣∞，4）．。

河北省沧州市2019届高三普通高等学校招生全国统一模拟考试文科数学试题(解析版)

2019年普通高等学校招生全国统一模拟考试文科数学一、选择题.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，集合，则（）A. B. C. D.【答案】B【解析】【分析】先由且求出，再和集合求交集即可得出结果.【详解】因为，又所以.故选B【点睛】本题主要考查集合的交集，熟记概念即可求解，属于基础题型.2.复数，则（）A. B. C. D.【答案】A【解析】【分析】由复数模的运算法则可知，据此确定复数的模即可.【详解】由复数模的运算法则可得：.本题选择A选项.【点睛】本题主要考查复数的模的运算法则及其应用，属于基础题.3.随着时代的发展，移动通讯技术的进步，各种智能手机不断更新换代，给人们的生活带来了巨大的便利，但与此同时，长时间低头看手机，对人的身体如颈椎、眼睛等会造成一定的损害，“低头族”由此而来.为了了解某群体中“低头族”的比例，现从该群体包括老、中、青三个年龄段的人中采取分层抽样的方法抽取人进行调查，已知这人里老、中、青三个年龄段的分配比例如图所示，则这个群体里老年人人数为（）A. B. C. D.【答案】B【解析】【分析】由题意可知老年人所占的比例为，据此求解老年人的人数即可.【详解】由题意结合分层抽样的定义可知，这个群体里老年人人数为.本题选择B选项.【点睛】本题主要考查统计图表的识别与应用，属于基础题.4.已知直线和平面，则是与异面的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】【分析】由题意，若直线b不在平面内，则b与相交或，充分性不成立，反之，若与异面，一定有直线b不在平面内，据此即可得到正确的结论.【详解】由题意，若直线b不在平面内，则b与相交或，不一定有与异面，反之，若与异面，一定有直线b不在平面内，即是与异面的必要不充分条件.本题选择B选项.【点睛】本题主要考查线面关系有关命题及其应用，充分必要条件的判定等知识，意在考查学生的转化能力和计算求解能力.5.已知，则向量与的夹角为（）A. B. C. D.【答案】D【解析】【分析】由题中条件先求出向量与的数量积，再由即可求出结果.【详解】因为，所以，又，所以，因此，所以，因此向量与的夹角为.故选D【点睛】本题主要考查向量的夹角公式，根据向量的数量积运算，即可求解，属于基础题型.6.若变量满足则使取得最小值的最优解为（）A. B. C. D.【答案】C【解析】【分析】首先绘制不等式组表示的平面区域如图所示，然后结合目标函数的几何意义确定使取得最小值的最优解即可【详解】绘制不等式组表示的平面区域如图所示，目标函数即：，其中z取得最小值时，其几何意义表示直线系在y轴上的截距最小，据此结合目标函数的几何意义可知目标函数在点B处取得最小值，联立直线方程：，可得点的坐标为：.本题选择C选项.【点睛】求线性目标函数z＝ax＋by(ab≠0)的最值，当b＞0时，直线过可行域且在y轴上截距最大时，z值最大，在y轴截距最小时，z值最小；当b＜0时，直线过可行域且在y轴上截距最大时，z值最小，在y轴上截距最小时，z值最大.7.已知等比数列的公比为且成等差数列，若，则为（）A. B. C. D.【答案】A【解析】【分析】先由等比数列的公比为且成等差数列，求出首项，得出通项公式，进而可得出结果. 【详解】因为等比数列的公比为且成等差数列，所以，即，解得，所以，所以,又，因此，所以，解得.故选A【点睛】本题主要考查等比数列，熟记等比数列的通项公式即可，属于基础题型.8.已知函数且满足，则的取值范围为（）A. B. C. D.或【答案】C【解析】【分析】先判断函数的奇偶性和单调性，进而可求出结果.【详解】因为，所以，所以函数为定义在R上的偶函数；又时，单调递减，所以由偶函数的对称可得：时，单调递增，所以由可得，解得.故选C【点睛】本题住考查函数的基本性质，灵活运用函数的单调性和奇偶性即可，属于基础题型.9.为双曲线的左焦点，圆与双曲线的两条渐进线在第一、二象限分别交于两点，若，则双曲线的离心率为（）A. B. C. D.【答案】C【解析】【分析】不妨设，其中，由斜率公式可得，由直线垂直的充分必要条件可知：，据此可得，然后结合双曲线的离心率公式求解离心率即可.【详解】不妨设，其中，由于，故，由于双曲线的渐近线方程为，结合直线垂直的充分必要条件可知：，据此可得：，整理可得，据此可知：，，双曲线的离心率.本题选择C选项.【点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出a，c，代入公式；②只需要根据一个条件得到关于a，b，c的齐次式，结合b2＝c2－a2转化为a，c的齐次式，然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式)，解方程(不等式)即可得e(e的取值范围)．10.中国最早的天文学和数学著作《周髀算经》里提到了七衡，即七个等距的同心圆.七衡的直径和周长都是等差数列，最里面的一圆叫内一衡，外面的圆依次叫次二衡，次三衡，….设内一衡直径为，衡间距为，则次二衡直径为，次三衡直径为，…，执行如下程序框图，则输出的中最大的一个数为（）A. B. C. D.【答案】D【解析】【分析】由题意可知题中所给的程序框图功能为计算并输出的值，结合等差数列的通项公式可得，由均值不等式的结论即可确定输出的中最大的一个数.【详解】由题意可知题中所给的程序框图功能为计算并输出的值，由等差数列通项公式有：，且易知恒成立，则：，当且仅当，即时等号成立.综上可得，输出的中最大的一个数为.本题选择D选项.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．11.已知函数，若函数在上只有三个零点，则的取值范围为（）A. B. C. D.【解析】【分析】先对函数化简整理，再由得到其非负根中较小的几个根，再根据函数在上只有三个零点，即可得出结果.【详解】因为，所以，令得，所以或，即或，则或，则非负根中较小的有：；因为函数在上只有三个零点，所以，解得.故选A【点睛】本题主要考查三角函数的图像和性质，熟记三角函数性质即可，属于常考题型.12.某棱锥的三视图如图所示，则该棱锥的所有棱长之和为（）A. B.C. D.【答案】C【解析】先由三视图还原几何体，再求出各边长度即可.【详解】由三视图还原几何体如下，三棱锥即为该几何体.又由三视图可知，底面是等腰直角三角形，三棱锥的高为2，所以，，，因此该三棱锥的所有棱长之和为.故选C【点睛】本题主要考查几何体的三视图，由三视图还原几何体即可，属于基础题型.二、填空题：本题共4小题.13.已知，则______．【答案】【解析】【分析】先由求出，进而可求出结果.【详解】因为，所以，所以.故答案为【点睛】本题主要考查对数和指数的运算，熟记运算性质即可，属于基础题型.14.高三某宿舍共人，在一次体检中测得其中个人的体重分别为（单位：千克），其中一人因故未测，已知该同学的体重在千克之间，则此次体检中该宿舍成员体重的中位数为的概率为_______．【答案】【解析】【分析】先将测过体重的七人体重数据排序，得到此次体检中该宿舍成员体重的中位数为时，未测体重同学体重的范围，再由该同学的体重区间，即可求出结果.【详解】将七个人的体重按顺序排列如下：，若此次体检中该宿舍成员体重的中位数为，只需未测体重的同学体重要小于等于55，又该同学的体重在千克之间，所以此次体检中该宿舍成员体重的中位数为的概率为.故答案为【点睛】本题主要考查与长度有关的几何概型，熟记概率计算公式即可，属于基础题型.15.直线与曲线有两个公共点，则实数的取值范围是_____．【答案】【解析】【分析】由直线与曲线有两个公共点可得方程有两不等实根，即有两不等实根，令，求出函数的值域即可.【详解】因为直线与曲线有两个公共点，所以方程有两不等实根，即有两不等实根，令，则与函数有两不同交点，因为，所以由得；由得或；因此函数在和上单调递减，在上单调递增，作出函数的简图大致如下：因为；又与函数有两不同交点，所以由图像可得，只需.故答案为【点睛】本题主要考查导数在函数中的应用，只需将函数有交点的问题，转化为方程有零点来处理即可，属于常考题型.16.抛物线的焦点为，准线为，过点的直线与以为圆心且过原点的圆相切于点，直线交直线于点，交抛物线于两点（在之间），则____．【答案】【解析】【分析】先由过点的直线与以为圆心且过原点的圆相切于点，直线交直线于点，求出的长，再由直线的方程与抛物线方程联立，求出点坐标，求出的长，进而可求出的长，即可求出结果.【详解】由题意可得，因为过点的直线与以为圆心且过原点的圆相切于点，所以，，所以在直角三角形中，可得，；因此直线的方程为；又直线交直线于点，所以，因此；又联立得，整理得，解得或，因为在之间且，所以，因此，即,又,所以，所以，所以.故答案为【点睛】本题主要考查抛物线的简单应用，熟记抛物线的性质即可，属于常考题型.三、解答题：解答应写出文字说明、证明过程或演算步骤.17.如图，的内角的对边分别为为线段上一点，的面积为.求：（1）的长；（2）的值.【答案】(1) (2)【解析】【分析】（1）根据，结合余弦定理先求出，进而可得，再由三角形面积公式即可求出结果；（2）根据正弦定理求解即可.【详解】解：（1）由，可知从而由（2）【点睛】本题主要考查解三角形，熟记正弦定理和余弦定理即可，属于基础题型.18.高考改革是教育体制改革中的重点领域和关键环节，全社会极其关注.近年来，在新高考改革中，打破文理分科的“”模式初露端倪.其中“”指必考科目语文、数学、外语，“”指考生根据本人兴趣特长和拟报考学校及专业的要求，从物理、化学、生物、历史、政治、地理六科中选择门作为选考科目，其中语、数、外三门课各占分，选考科目成绩采用“赋分制”，即原始分数不直接用，而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.假定省规定：选考科目按考生成绩从高到低排列，按照占总体的，以此赋分分、分、分、分.为了让学生们体验“赋分制”计算成绩的方法，省某高中高一（）班（共人）举行了以此摸底考试（选考科目全考，单科全班排名，每名学生选三科计算成绩），已知这次摸底考试中的物理成绩（满分分）频率分布直方图，化学成绩（满分分）茎叶图如下图所示，小明同学在这次考试中物理分，化学多分.（1）求小明物理成绩的最后得分；（2）若小明的化学成绩最后得分为分，求小明的原始成绩的可能值；（3）若小明必选物理，其他两科在剩下的五科中任选，求小明此次考试选考科目包括化学的概率.【答案】(1)70分 (2) (3)【解析】【分析】（1）先求出此次考试物理成绩落在内的频率，再由小明的物理成绩即可得出结果；（2）根据选考科目按考生成绩从高到低排列，按照占总体的，以此赋分分、60分、50分、40分，结合茎叶图中数据，即可得出结果；（3）先记物理、化学、生物、历史、地理、政治依次为，用列举法列举出小明的所有可能选法，再列举出小明此次考试选考科目包括化学的选法，基本事件的个数之比就是所求概率.【详解】解：（1），此次考试物理成绩落在内的频率依次为，概率之和为小明的物理成绩为分，大于分.小明物理成绩的最后得分为分.（2）因为40名学生中，赋分分的有人，这六人成绩分别为89,91,92,93,93,96；赋分分的有人,其中包含80多分的共10人，70多分的有4人，分数分别为；因为小明的化学成绩最后得分为分，且小明化学多分，所以小明的原始成绩的可能值为；（3）记物理、化学、生物、历史、地理、政治依次为，小明的所有可能选法有：共种，其中包括化学的有共种，若小明必选物理，其他两科在剩下的五科中任选，所选科目包括化学的概率为.【点睛】本题主要考查频率分布直方图与茎叶图，以及古典概型，熟记古典概型的概率计算公式即可求解，属于常考题型.19.如图，在三棱台中，底面是边长为的等边三角形，上、下底面的面积之比为，侧面底面，并且.（1）平面平面，证明：；（2）求四棱锥的体积.【答案】（1）见证明；（2）【解析】【分析】（1）根据线面平行的性质即可证明出结论成立；（2）先由以及面积之比为相似比的平方，得到与的长度，再过点作交于，证明底面，最后由即可求出结果.【详解】（1）证明：几何体为棱台，平面平面平面，平面平面（2）解：，则面积之比为相似比的平方，而，又过点作交于，由于侧面底面为交线.底面，在中，易求得..【点睛】本题主要考查线面平行的性质以及四棱锥的体积，熟记线面平行的性质定理和棱锥的体积公式即可，属于常考题型.20.如图，菱形的面积为，斜率为的直线交轴于点，且，以线段为长轴，为短轴的椭圆与直线相交于两点（与在轴同侧）.（1）求椭圆的方程；（2）求证：与的交点在定直线上.【答案】（1）（2）见证明【解析】【分析】（1）由题意得到关于a,b的方程组，求解方程组可得，据此确定椭圆方程即可；（2）易得，设直线与椭圆联立可得，求得直线的方程和的方程，联立方程确定交点坐标即可证得题中的结论.【详解】（1）设解得椭圆方程为（2）易得，设直线与椭圆联立，得由得，设，直线的方程为①直线的方程为x ②联立①②消去，得从而命题得证【点睛】解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．21.已知函数.（1）讨论在上的单调性；（2）函数在上单调递增，求实数的取值范围.【答案】（1）见解析（2）【解析】【分析】（1）先对函数求导，分别讨论和即可得出结果；（2）由在上单调递增推出在上恒成立，即，构造函数，由导数的方法研究其单调性即可得出结果.【详解】解：（1）①即时，在上单调递增；②即时，令，得，在上，在上,在上单调递减，在上单调递增.综上：当时，在上单调递增；当时，在上单调递减，在上单调递增.（2）在上单调递增在上恒成立令，由（1）知，在上为增函数，当，即时，在上为增函数，，得，的取值范围为.当，即时，使在上为减函数，在上为增函数，而，使得成立，舍去，综上，实数的取值范围是.【点睛】本题主要考查导数的应用，通常需要用导数的方法研究函数的单调性和最值等，属于常考题型. 22.在直角坐标系中，以为极点，轴为正半轴为极轴建立极坐标系.已知曲线的极坐标方程为，直线与曲线相交于两点，直线过定点且倾斜角为交曲线于两点. （1）把曲线化成直角坐标方程，并求的值；（2）若成等比数列，求直线的倾斜角.【答案】(1) 答案见解析 (2) 或【解析】【分析】（1）将极坐标方程化为直角坐标方程可得C的直角坐标方程为联立直线方程确定MN的长度即可；（2）联立直线的参数方程和C的直角坐标方程可得,结合韦达定理可知.据此得到关于的三角方程，解方程即可确定直线的倾斜角.【详解】（1）得，即曲线的直角坐方程为,直线为，代入，得.（2）直线的参数方程为（为参数），代入得:,即恒成立.设两点对应的参数分别为..由于成等比数列，,从而或.【点睛】本题主要考查极坐标方程与直角坐标方程的转化，直线参数方程的几何意义等知识，意在考查学生的转化能力和计算求解能力.23.已知.（1）解不等式；（2）若，求实数的最大值.【答案】(1) 或 (2) 最大值为【解析】【分析】（1）由题意可得，分类讨论求解不等式的解集即可；（2）原问题等价于恒成立，考查函数的性质确定实数m的最大值即可.【详解】（1）或或得或无解或.所以不等式的解集为或.（2）恒成立恒成立令结合二次函数的性质分析可知，在上单调递减，在上单调递增..实数的最大值为.【点睛】绝对值不等式的解法：法一：利用绝对值不等式的几何意义求解，体现了数形结合的思想；法二：利用“零点分段法”求解，体现了分类讨论的思想；法三：通过构造函数，利用函数的图象求解，体现了函数与方程的思想．。

河北数学(文)解析版-2019年普通高等学校招生全国统一考试

河北数学（文）解析版-2019年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第一卷(选择题)和第二卷(非选择题)两部分。

第一卷1至2页。

第二卷3至4页。

考试结束后，将本试卷和答题卡一并交回。

第一卷本卷须知 1、答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清晰，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目。

2、每题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作．．．．．．答无效。

．．．． 3、第一卷共l2小题，每题5分，共60分。

在每题给出的四个选项中，只有一项为哪一项符合题目要求的。

【一】选择题〔1〕设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =那么075,2,A b a c ==求与=⋂（M N ）ð〔A 〕{}12，〔B 〕{}23，〔C 〕{}2，4 〔D 〕{}1，4【思路点拨】解决此题的关键是掌握集合交并补的计算方法，易求{2,3}M N =,进而求出其补集为{}1，4. 【精讲精析】选D.{2,3},(){1,4}U MN MN =∴=ð.〔2〕函数0)y x =≥的反函数为〔A 〕2()4x y x R =∈ 〔B 〕2(0)4x y x =≥〔C 〕24y x =()x R ∈ 〔D 〕24(0)y x x =≥【思路点拨】先反解用y 表示x,注意要求出y 的取值范围，它是反函数的定义域。

【精讲精析】选 B.在函数0)y x =≥中，0y ≥且反解x 得24y x =，因此0)y x =≥的反函数为2(0)4x y x =≥ 〔3〕权向量a,b 满足a=b=12-,那么2a b +=〔A〔B〔C〔D【思路点拨】此题要把充要条件的概念搞清，注意查找的是通过选项能推出a>b ，而由a>b 推不出选项的选项.〔4〕假设变量x 、y 满足约束条件6321x y x y x +⎧⎪-≤⎨⎪≥⎩，那么23z x y -+的最小值为〔A 〕17〔B 〕14〔C 〕5〔D 〕3【思路点拨】解决此题的关键是作出如右图所示的可行域。

2019单招数学试卷 (1)

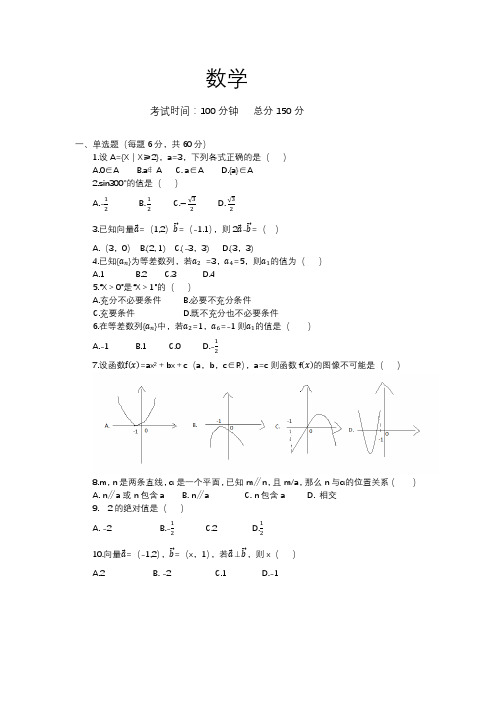
数学考试时间：100分钟总分150分一、单选题（每题6分，共60分）1.设A={X｜X≥2}，a=3，下列各式正确的是（）A.0∈AB.a∉AC. a∈AD.{a}∈A2.sin300°的值是（）A.-12B.12C.−√32D.√323.已知向量a⃗=（1,2）b⃗⃗=（-1.1），则2a⃗-b⃗⃗=（）A.（3，0）B.(2, 1)C.(-3，3)D.(3，3)4.已知{a n}为等差数列，若a2=3，a4=5，则a1的值为（）A.1B.2C.3D.45.“X＞0”是“X＞1”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.在等差数列{a n}中，若a2=1，a6=-1则a1的值是（）A.-1B.1C.0D.-127.设函数f(x)=ax²＋bx＋c（a，b，c∈R），a=c则函数f(x)的图像不可能是（）8.m，n是两条直线，α是一个平面，已知m∥n，且m/a，那么n与α的位置关系（）A. n∥a或n包含aB. n∥aC. n包含aD. 相交9. 2的绝对值是（）A. -2B.-12C.2 D.1210.向量a⃗=（-1,2），b⃗⃗=（x，1），若a⃗⊥b⃗⃗，则x（）A.2B. -2C.1D.-1二、填空题（每题10分，共30分）11．根据程序图输出的的S值为（）12.已知复数Z=3＋4i（i为虚数单位），则｜Z｜=（）13.sin60°=（）三、解答题（每题20分，共60分）14.已知函数f(x)=x²-4x，x∈【1,5】，则f(x)的最大值和最小值是多少。

15.已知全集U={1,2,3,4,5}，其子集A={1，3},B={2，5}求：（1）∁uA；（2）A∪B；( 3 ) A∩B；( 4 ) (∁uA)∪(∁uB)；16.画三视图。

整理2019年河北单招文科数学模拟试题(一)[含答案]

2019年四川单招理科数学模拟试题一含答案
整理表
姓名:
职业工种:
申请级别:
受理机构:
填报日期:
A4打印/ 修订/ 内容可编辑
2019年四川单招理科数学模拟试题（一）【含答案】
一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
二、填空题（每题5分，满分20分，将答案填在答题纸上）
三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）
请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]
[选修4-5：不等式选讲]
2019年四川单招理科数学模拟试题（一）参考答案
一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）
z 轴，建立空间直角坐标系，
请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]
[选修4-5：不等式选讲]
整理丨尼克
本文档信息来自于网络，如您发现内容不准确或不完善，欢迎您联系我修正；如您发现内容涉嫌侵权，请与我们联系，我们将按照相关法律规定及时处理。

职业中学单招考试数学模拟试卷

姓名班级考号…………………………………装……………………………………订……………………………………线……………………………河北省2019年高职单招联考考试六类文化水平考试（数学）模拟试题（B ）1.设全集{}e d c b a U ,,,,=，集合{}d c a A ,,=，{}e d b B ,,=，那么=⋂B C A C U U ( ) A.{}c a , B.{}d C.{}c b , D.Ф2.=-2121616log ( )A.0B.4C.-4D.以上答案都不对3.下列函数中为奇函数的是（）A.xy 3= B.x y 3log = C.23x y = D.x y sin 3= 4.不等式123>-x 的解集是（）A.⎪⎭⎫ ⎝⎛1,31B.()+∞⋃⎪⎭⎫ ⎝⎛∞-,131,C.⎪⎭⎫ ⎝⎛∞-31, D.()+∞,15.若1>a ，则下列结论正确的是（） A.23a a < B.()11->-a a aC.2log 3log a a <D.aa 23<6.在⊿ABC 中，若∠C = 60゜,则=-B A B A sin sin cos cos ( ) A.21 B. 21- C. 23 D. 23-7.在等比数列{}n a 中，若1,973-=-=a a ，则5a 的值是（） A.3或-3 B.3 C.-3 D.不存在8.点()4,3--关于点()1,2-的对称点的坐标是（） A.()2,7 B.⎪⎭⎫⎝⎛--25,21 C.()7,8-- D.()1,6 10.在等差数列{}n a 中，若1264=+a a ，n S 是数列{}n a 前n 项的和，则9S 等于（） A.48 B.54 C.60 D.66二、判断题（每小题3分，共15分） 1. 60︒与︒330角终边相同（）2. 集合错误!未找到引用源。

,用区间表示为()3,2-（） 3. 错误!未找到引用源。

河北省单招数学和语文试卷(含答案)

河北省单招数学和语文试卷（含答案）下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个数学家被称为“几何之父”？A. 欧几里得B. 阿基米德C. 牛顿D. 高斯2. 在《红楼梦》中，下列哪个角色是贾宝玉的表妹？A. 林黛玉B. 薛宝钗C. 王熙凤D. 史湘云3. 下列哪个成语表示“无法挽回的过去”？A. 鞠躬尽瘁B. 亡羊补牢C. 东山再起D. 时光倒流4. 在数学中，下列哪个数被称为“黄金分割数”？A. 3.14B. 1.618C. 2.718D. 1.4145. 下列哪个文学作品是鲁迅的代表作？A. 《红楼梦》B. 《西游记》C. 《呐喊》D. 《三国演义》二、判断题（每题1分，共5分）1. 平方根是一个数的二次方。

2019年河北单招文科数学模拟试题(一)【含答案】

2019年河北单招文科数学模拟试题（一）【含答案】一、选择题（本大题共12个小题，每小题5分，共60分）1．函数与y=ln（2﹣x）的定义域分别为M、N，则M∩N=（）A．（1，2] B．[1，2）C．（﹣∞，1]∪（2，+∞）D．（2，+∞）2．若，则复数z对应的点在（）A．第一象限B．第二象限C．第三象限D．第四象限3．已知向量，，则“m=1”是“”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件4．从编号为1，2，…，79，80的80件产品中，采用系统抽样的方法抽取容量为5的样本，若编号为10的产品在样本中，则该样本中产品的最大编号为（）A．72 B．73 C．74 D．755．已知角α（0°≤α＜360°）终边上一点的坐标为（sin150°，cos150°），则α=（）A．150° B．135° C．300° D．60°6．函数的大致图象是（）A．B．C．D．7．如图是计算的值的程序框图，则图中①②处应填写的语句分别是（）A．n=n+2，i＞16？B．n=n+2，i≥16？C．n=n+1，i＞16？D．n=n+1，i≥16？8．某几何体的三视图如图所示，则其体积为（）A．B．C．D．9．实数x，y满足时，目标函数z=mx+y的最大值等于5，则实数m的值为（）A．﹣1 B．C．2 D．510．三棱锥S﹣ABC中，侧棱SA⊥底面ABC，AB=5，BC=8，∠B=60°，，则该三棱锥的外接球的表面积为（）A．B．C．D．11．已知动点P在椭圆上，若点A的坐标为（3，0），点M满足，，则的最小值是（）A．B．C．D．312．已知函数存在互不相等实数a，b，c，d，有f（a）=f（b）=f（c）=f（d）=m．现给出三个结论：（1）m∈[1，2）；（2）a+b+c+d∈[e﹣3+e﹣1﹣2，e﹣4﹣1），其中e为自然对数的底数；（3）关于x的方程f（x）=x+m恰有三个不等实根．正确结论的个数为（）A．0个B．1个C．2个D．3个二、填空题（每题5分，满分20分，将答案填在答题纸上）13．观察下列式子：，…，根据上述规律，第n个不等式应该为____．14．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，则f（0）的值为____．15．双曲线（a＞0，b＞0）上一点M关于渐进线的对称点恰为右焦点F2，则该双曲线的离心率为____．16．在希腊数学家海伦的著作《测地术》中记载了著名的海伦公式，利用三角形的三条边长求三角形面积，若三角形的三边长为a，b，c，其面积，这里．已知在△ABC中，BC=6，AB=2AC，则△ABC面积的最大值为____．三、解答题17．已知数列{an}满足，n∈N*．（Ⅰ）求数列{an}的通项公式；（Ⅱ）若，Tn=b1+b2+…+bn，求证：对任意的n∈N*，Tn＜1．18．在如图所示的多面体ABCDEF中，ABCD为直角梯形，AB∥CD，∠DAB=90°，四边形ADEF 为等腰梯形，EF∥AD，已知AE⊥EC，AB=AF=EF=2，AD=CD=4．（Ⅰ）求证：CD⊥平面ADEF；（Ⅱ）求多面体ABCDEF的体积．19．天气预报是气象专家根据预测的气象资料和专家们的实际经验，经过分析推断得到的，在现实的生产生活中有着重要的意义．某快餐企业的营销部门经过对数据分析发现，企业经营情况与降雨天数和降雨量的大小有关．（Ⅰ）天气预报说，在今后的三天中，每一天降雨的概率均为40%，该营销部门通过设计模拟实验的方法研究三天中恰有两天降雨的概率，利用计算机产生0到9之间取整数值的随机数，并用1，2，3，4，表示下雨，其余6个数字表示不下雨，产生了20组随机数：907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989求由随机模拟的方法得到的概率值；（Ⅱ）经过数据分析，一天内降雨量的大小x（单位：毫米）与其出售的快餐份数y成线性相关关系，该营销部门统计了降雨量与出售的快餐份数的数据如下：降雨量（毫米） 1 2 3 4 5快餐数（份）50 85 115 140 160试建立y关于x的回归方程，为尽量满足顾客要求又不造成过多浪费，预测降雨量为6毫米时需要准备的快餐份数．（结果四舍五入保留整数）附注：回归方程中斜率和截距的最小二乘估计公式分别为：，．20．在平面直角坐标系xOy中，设圆x2+y2﹣4x=0的圆心为Q．（1）求过点P（0，﹣4）且与圆Q相切的直线的方程；（2）若过点P（0，﹣4）且斜率为k的直线与圆Q相交于不同的两点A，B，以OA、OB为邻边做平行四边形OACB，问是否存在常数k，使得▱OACB为矩形？请说明理由．21．已知函数f（x）=lnx﹣a（x﹣1），g（x）=ex．（1）求证：g（x）≥x+1（x∈R）；（2）设h（x）=f（x+1）+g（x），若x≥0时，h（x）≥1，求实数a的取值范围．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，曲线C1：（α是参数）．在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2：ρcosθ﹣3=0．点P是曲线C1上的动点．（1）求点P到曲线C2的距离的最大值；（2）若曲线C3：θ=交曲线C1于A，B两点，求△ABC1的面积．[选修4-5：不等式选讲]23．已知函数f（x）=|x﹣1|+|x+1|﹣2．（1）求不等式f（x）≥1的解集；（2）若关于x的不等式f（x）≥a2﹣a﹣2在R上恒成立，求实数a的取值范围．2019年河北单招文科数学模拟试题（一）参考答案一、选择题（本大题共12个小题，每小题5分，共60分）1．函数与y=ln（2﹣x）的定义域分别为M、N，则M∩N=（）A．（1，2] B．[1，2）C．（﹣∞，1]∪（2，+∞）D．（2，+∞）【考点】33：函数的定义域及其求法．【分析】分别求函数与y=ln（2﹣x）的定义域，再利用交集的定义写出M∩N．【解答】解：函数的定义域为M={x|x﹣1≥0}={x|x≥1}，函数y=ln（2﹣x）的定义域为N={x|2﹣x＞0}={x|x＜2}，则M∩N={x|1≤x＜2}=[1，2）．故选：B．2．若，则复数z对应的点在（）A．第一象限B．第二象限C．第三象限D．第四象限【考点】A5：复数代数形式的乘除运算．【分析】利用复数的运算法则、几何意义即可得出．【解答】解：==+i，则复数z对应的点在第一象限．故选：A．3．已知向量，，则“m=1”是“”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【考点】2L：必要条件、充分条件与充要条件的判断．【分析】由，可得：m2﹣1=0，解得m，即可判断出结论、【解答】解：由，可得：m2﹣1=0，解得m=±1，∴“m=1”是“”成立的充分不必要条件．故选：A．4．从编号为1，2，…，79，80的80件产品中，采用系统抽样的方法抽取容量为5的样本，若编号为10的产品在样本中，则该样本中产品的最大编号为（）A．72 B．73 C．74 D．75【考点】B4：系统抽样方法．【分析】根据系统抽样的定义求出样本间隔即可得到结论．【解答】解：样本间隔为80÷5=16，因为第一个号码为10，则最大的编号10+4×16=74，故选：C．5．已知角α（0°≤α＜360°）终边上一点的坐标为（sin150°，cos150°），则α=（）A．150° B．135° C．300° D．60°【考点】G9：任意角的三角函数的定义．【分析】利用任意角的三角函数的定义，特殊角的三角函数值，求得α的正切值以及α的范围，可得α的值．【解答】解：∵角α（0°≤α＜360°）终边上一点的坐标为（sin150°，cos150°），即（，﹣），则α为第四象限角，再根据tanα==﹣，∴α=360°﹣60°=300°，故选：C．6．函数的大致图象是（）A．B．C．D．【考点】3O：函数的图象．【分析】判断f（x）的奇偶性，再判断当x＞1时的函数值的符号即可．【解答】解：f（﹣x）===﹣f（x），∴f（x）是奇函数，图象关于原点对称，故A，C错误；又当x＞1时，ln|x|=lnx＞0，∴f（x）＞0，故D错误，故选B．7．如图是计算的值的程序框图，则图中①②处应填写的语句分别是（）A．n=n+2，i＞16？B．n=n+2，i≥16？C．n=n+1，i＞16？D．n=n+1，i≥16？【考点】EF：程序框图．【分析】首先分析，要计算的值需要用到直到型循环结构，按照程序执行运算．【解答】解：①的意图为表示各项的分母，而分母来看相差2，∴n=n+2②的意图是为直到型循环结构构造满足跳出循环的条件，而分母从1到31共16项，∴i＞16故选：A．8．某几何体的三视图如图所示，则其体积为（）A．B．C．D．【考点】L!：由三视图求面积、体积．【分析】由已知三视图得到几何体是一个圆锥沿两条母线切去部分后得到的几何体，因此计算体积．【解答】解：由已知三视图得到几何体是一个圆锥沿两条母线切去部分后得到的几何体，体积为=；故选D．9．实数x，y满足时，目标函数z=mx+y的最大值等于5，则实数m的值为（）A．﹣1 B．C．2 D．5【考点】7C：简单线性规划．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义进行求解即可．【解答】解：由z=mx+y，得y=﹣mx+z，∵标函数z=mx+y的最大值等于5，∴直线y=﹣mx+z最大截距是5，即y=﹣mx+5，则直线y=﹣mx+5过定点（0，5），要使y=﹣mx+z最大截距是5，则必有直线y=﹣mx+z的斜率﹣m＞0，即m＜0，且直线y=﹣mx+5过点B，由得，即B（﹣4，3），代入y=﹣mx+5得4m+5=3，得m=，故选：B．10．三棱锥S﹣ABC中，侧棱SA⊥底面ABC，AB=5，BC=8，∠B=60°，，则该三棱锥的外接球的表面积为（）A．B．C．D．【考点】LG：球的体积和表面积．【分析】由已知结合三棱锥和直三棱柱的几何特征，可得此三棱锥外接球，即为以△ABC为底面以SA为高的直三棱柱的外接球，分别求出棱锥底面半径r，和球心距d，得球的半径R，然后求解表面积．【解答】解：在△ABC中，由AB=5，BC=8，∠B=60°，可得AC==7可得此三棱锥外接球，即为以△ABC为底面以SA为高的直三棱柱的外接球，∵在△ABC中，设△ABC的外接圆半径r，则，r=球心到△ABC的外接圆圆心的距离d=，故球的半径R=，∴三棱锥S﹣ABC外接球的表面积为：4πR2=4=π．故选：B．11．已知动点P在椭圆上，若点A的坐标为（3，0），点M满足，，则的最小值是（）A．B．C．D．3【考点】K4：椭圆的简单性质．【分析】求得椭圆的a，b，c，由题设条件，结合向量的性质，推导出||2=||2﹣1，再由||越小，||越小，能求出||的最小值．【解答】解：椭圆中，a=6，c===3，∵，∴⊥，∴||2=||2﹣||2∵||=1，∴||2=1，∴||2=||2﹣1，∵||=1，∴点M的轨迹为以为以点A为圆心，1为半径的圆，∵||2=||2﹣1，||越小，||越小，结合图形知，当P点为椭圆的右顶点时，||取最小值a﹣c=6﹣3=3，∴||最小值是=2．故选：C．12．已知函数存在互不相等实数a，b，c，d，有f（a）=f（b）=f（c）=f（d）=m．现给出三个结论：（1）m∈[1，2）；（2）a+b+c+d∈[e﹣3+e﹣1﹣2，e﹣4﹣1），其中e为自然对数的底数；（3）关于x的方程f（x）=x+m恰有三个不等实根．正确结论的个数为（）A．0个B．1个C．2个D．3个【考点】54：根的存在性及根的个数判断．【分析】由题意画出函数y=f（x）的图象，数形结合逐一分析三个结论得答案．【解答】解：作出函数的图象如图，若直线y=m与函数y=f（x）的图象相交于四个不同的点，由图可知m∈[1，2），故（1）正确；设y=m与函数y=f（x）的交点自左至右依次为a，b，c，d，由﹣2﹣lnx=1，得x=e﹣3，由﹣2﹣lnx=2，得x=e﹣4，∴c∈（e﹣4，e﹣3]，又﹣2﹣lnc=2+lnd，∴cd=e﹣4，∴a+b+c+d=﹣2+c+在（e﹣4，e﹣3]上是递减函数，∴a+b+c+d∈[e﹣3+e﹣1﹣2，e﹣4﹣1），故（2）正确；设斜率为1的直线与y=lnx+2相切于（x0，lnx0+2），则由，可得x0=1，则切点为（1，2），此时直线方程为y﹣2=1×（x﹣1），即y=x+1，∴当m=1时，直线y=x+m与函数y=f（x）有4个不同交点，即关于x的方程f（x）=x+m有四个不等实根，故（3）错误．∴正确结论的个数是2个．故选：C．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．观察下列式子：，…，根据上述规律，第n个不等式应该为1+++…+＜．【考点】F1：归纳推理．【分析】根据规律，不等式的左边是n+1个自然数倒数的平方的和，右边分母是以2为首项，1为公差的等差数列，分子是以3为首项，2为公差的等差数列，由此可得结论．【解答】解：根据规律，不等式的左边是n+1个自然数倒数的平方的和，右边分母是以2为首项，1为公差的等差数列，分子是以3为首项，2为公差的等差数列，所以第n个不等式应该为1+++…+＜故答案为：1+++…+＜14．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，则f（0）的值为．【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】根据函数f（x）的图象，求出最小正周期T和ω的值，根据五点法画图的定义求出φ的值，写出f（x）的解析式，再计算f（0）的值．【解答】解：根据函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象知，=﹣（﹣）=π，∴T=2π，∴ω==1；根据五点法画图知，x=时，ω•+φ=π，解得φ=，∴f（x）=sin（x+）；∴f（0）=sin=，即f（0）的值为．故答案为：．15．双曲线（a＞0，b＞0）上一点M关于渐进线的对称点恰为右焦点F2，则该双曲线的离心率为．【考点】KC：双曲线的简单性质．【分析】设M（m，n），右焦点F2（c，0），双曲线的一条渐近线方程为y=﹣x，运用两直线垂直的条件：斜率之积为﹣1，以及中点坐标公式，解方程可得m，n，代入双曲线的方程，化简整理，结合双曲线的基本量和离心率公式，计算即可得到所求值．【解答】解：设M（m，n），右焦点F2（c，0），双曲线的一条渐近线方程为y=﹣x，由题意可得﹣•=﹣1①n=﹣•②由①②解得m=，n=﹣，将M（，﹣）代入双曲线的方程，可得：﹣=1，由b2=c2﹣a2，化为（2a2﹣c2）2﹣4a4=a2c2，即为c2=5a2，可得e==．故答案为：．16．在希腊数学家海伦的著作《测地术》中记载了著名的海伦公式，利用三角形的三条边长求三角形面积，若三角形的三边长为a，b，c，其面积，这里．已知在△ABC中，BC=6，AB=2AC，则△ABC面积的最大值为12．【考点】HR：余弦定理．【分析】设b=x，则c=2x，根据海伦面积公式得S△ABC=，由三角形三边关系求得2＜x＜6，由二次函数的性质求得S△ABC取得最大值．【解答】解：∵a=6，设b=x，则c=2x，可得：=3+，∴===由三角形三边关系有：x+2x＞6且x+6＞2x，解得：2＜x＜6，故当x=2时，S△ABC取得最大值12．故答案为：12．三、解答题17．已知数列{an}满足，n∈N*．（Ⅰ）求数列{an}的通项公式；（Ⅱ）若，Tn=b1+b2+…+bn，求证：对任意的n∈N*，Tn＜1．【考点】8E：数列的求和；8H：数列递推式．【分析】（Ⅰ）当n＞1时，，n∈N*…①，…②，①﹣②得，；（Ⅱ）因为，，累加求和即可证明．【解答】解：（Ⅰ）当n＞1时，，n∈N*…①．…②①﹣②得，，当n=1时，a1=2，所以．（Ⅱ）因为，．因此=，所以Tn＜1．18．在如图所示的多面体ABCDEF中，ABCD为直角梯形，AB∥CD，∠DAB=90°，四边形ADEF 为等腰梯形，EF∥AD，已知AE⊥EC，AB=AF=EF=2，AD=CD=4．（Ⅰ）求证：CD⊥平面ADEF；（Ⅱ）求多面体ABCDEF的体积．【考点】LF：棱柱、棱锥、棱台的体积；LW：直线与平面垂直的判定．【分析】（Ⅰ）取AD中点M，连接EM，只需证明AE⊥CD，CD⊥AD，即可得CD⊥平面ADEF．（Ⅱ）作EO⊥AD，可得EO=，连接AC，则VABCDEF=VC﹣ADEF+VF﹣ABC，【解答】解：（Ⅰ）证明：取AD中点M，连接EM，∵AF=EF=DE=2，AD=4，可知EM=AD，∴AE⊥DE，又AE⊥EC，DE∩EC=E∴AE⊥平面CDE，∵CD⊂平面CDE，∴AE⊥CD，又CD⊥AD，AD∩AE=A，∴CD⊥平面ADEF．（Ⅱ）由（1）知CD⊥平面ADEF，CD⊂平面ABCD，∴平面ABCD⊥平面ADEF；作EO⊥AD，∴EO⊥平面ABCD，EO=，连接AC，则VABCDEF=VC﹣ADEF+VF﹣ABC，，，∴．19．天气预报是气象专家根据预测的气象资料和专家们的实际经验，经过分析推断得到的，在现实的生产生活中有着重要的意义．某快餐企业的营销部门经过对数据分析发现，企业经营情况与降雨天数和降雨量的大小有关．（Ⅰ）天气预报说，在今后的三天中，每一天降雨的概率均为40%，该营销部门通过设计模拟实验的方法研究三天中恰有两天降雨的概率，利用计算机产生0到9之间取整数值的随机数，并用1，2，3，4，表示下雨，其余6个数字表示不下雨，产生了20组随机数：907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989求由随机模拟的方法得到的概率值；（Ⅱ）经过数据分析，一天内降雨量的大小x（单位：毫米）与其出售的快餐份数y成线性相关关系，该营销部门统计了降雨量与出售的快餐份数的数据如下：降雨量（毫米） 1 2 3 4 5快餐数（份）50 85 115 140 160试建立y关于x的回归方程，为尽量满足顾客要求又不造成过多浪费，预测降雨量为6毫米时需要准备的快餐份数．（结果四舍五入保留整数）附注：回归方程中斜率和截距的最小二乘估计公式分别为：，．【考点】BK：线性回归方程．【分析】（Ⅰ）找出上述随机数中满足条件的数据，计算对应概率值；（Ⅱ）计算平均数和回归系数，写出y关于x的回归方程，利用回归方程计算x=6时的值即可．【解答】解：（Ⅰ）上述20组随机数中恰好含有1，2，3，4中的两个数的有191 271 932 812 393，共5个，所以三天中恰有两天下雨的概率的近似值为；（Ⅱ）由题意可知，，，；所以，y关于x的回归方程为：．将降雨量x=6代入回归方程得：．所以预测当降雨量为6毫米时需要准备的快餐份数为193份．20．在平面直角坐标系xOy中，设圆x2+y2﹣4x=0的圆心为Q．（1）求过点P（0，﹣4）且与圆Q相切的直线的方程；（2）若过点P（0，﹣4）且斜率为k的直线与圆Q相交于不同的两点A，B，以OA、OB为邻边做平行四边形OACB，问是否存在常数k，使得▱OACB为矩形？请说明理由．【考点】J9：直线与圆的位置关系．【分析】（1）设切线方程为：y=kx﹣4，利用圆心到直线的距离等于半径求出k，即可求过点P（0，﹣4）且与圆Q相切的直线的方程；（2）联立得（1+k2）x2﹣（8k+4）x+16=0，利用韦达定理，结合向量知识，即可得出结论．【解答】解：（1）由题意知，圆心Q坐标为（2，0），半径为2，设切线方程为：y=kx﹣4，所以，由解得所以，所求的切线方程为，或x=0；（2）假设存在满足条件的实数k，则设A（x1，y1），B（x2，y2），联立得（1+k2）x2﹣（8k+4）x+16=0∵△=16（2k+1）2﹣64（1+k2）＞0，∴，∴，且y1+y2=k（x1+x2），∵=（x1+x2，y1+y2），∴，又=，要使平行四边形OACB矩形，则=，所以k=2，∴存在常数k=2，使得平行四边形OACB为矩形．21．已知函数f（x）=lnx﹣a（x﹣1），g（x）=ex．（1）求证：g（x）≥x+1（x∈R）；（2）设h（x）=f（x+1）+g（x），若x≥0时，h（x）≥1，求实数a的取值范围．【考点】6E：利用导数求闭区间上函数的最值；6B：利用导数研究函数的单调性．【分析】（1）构造函数u（x）=ex﹣（x+1），求出导函数u'（x）=ex﹣1，根据导函数求出函数的最小值即可；（2）h（x）=f（x+1）+g（x）=ln（x+1）﹣ax+ex，求出导函数．求出=，得出h'（x）在[0，+∞）上递增，对参数a分类讨论，得出原函数的最小值为1即可．【解答】（1）证明：令u（x）=ex﹣（x+1），则u'（x）=ex﹣1，所以x＜0时u'（x）＜0，x＞0时u'（x）＞0，所以u（x）≥u（0）=0，即ex≥x+1（2）解：h（x）=f（x+1）+g（x）=ln（x+1）﹣ax+ex，．因为=，所以h'（x）在[0，+∞）上递增①当a＞2时，h'（0）=2﹣a＜0，又=则存在x0∈（0，lna），使得h'（x0）=0．所以h（x）在（0，x0）上递减，在（x0，+∞）上递增，又h（x0）＜h（0）=1，所以h（x）≥1不恒成立，不合题意．②当a≤2时，因为h'（0）=2﹣a＞0，所以h'（x）＞0在[0，+∞）上恒成立即h（x）在[0，+∞）上为增函数，所以h（x）≥h（0）=1恒成立，符合题意．综合①②可知，所求实数a的取值范围是（﹣∞，2]．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，曲线C1：（α是参数）．在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2：ρcosθ﹣3=0．点P是曲线C1上的动点．（1）求点P到曲线C2的距离的最大值；（2）若曲线C3：θ=交曲线C1于A，B两点，求△ABC1的面积．【考点】Q4：简单曲线的极坐标方程．【分析】（1）求得C1的标准方程，及曲线C2的标准方程，则圆心C1到x=3距离d，点P 到曲线C2的距离的最大值dmax=R+d=6；（2）将直线l的方程代入C1的方程，求得A和B点坐标，求得丨AB丨，利用点到直线的距离公式，求得C1到AB的距离d，即可求得△ABC1的面积．【解答】解（1）曲线C1：（α是参数）．整理得：（x+2）2+（y+1）2=1曲线C2：ρcosθ﹣3=0，则x=3．则圆心C1到x=3距离d，d=2+3=5，点P到曲线C2的距离的最大值dmax=R+d=6；∴点P到曲线C2的距离的最大值6；（2）若曲线C3：θ=，即y=x，，解得：，，丨AB丨==∴C1到AB的距离d==，则△ABC1的面积S，S=××=．∴△ABC1的面积．[选修4-5：不等式选讲]23．已知函数f（x）=|x﹣1|+|x+1|﹣2．（1）求不等式f（x）≥1的解集；（2）若关于x的不等式f（x）≥a2﹣a﹣2在R上恒成立，求实数a的取值范围．【考点】R4：绝对值三角不等式；R5：绝对值不等式的解法．【分析】（1）分类讨论，去掉绝对值，即可求不等式f（x）≥3的解集；（2）f（x）=|x﹣1|+|x+1|﹣2≥|（x﹣1）﹣（x+1）|﹣2=0，利用关于x的不等式f（x）≥a2﹣a﹣2在R上恒成立，即可求实数a的取值范围．【解答】解：（1）原不等式等价于或或解得：或，∴不等式的解集为或．（2）∵f（x）=|x﹣1|+|x+1|﹣2≥|（x﹣1）﹣（x+1）|﹣2=0，且f（x）≥a2﹣a﹣2在R上恒成立，∴a2﹣a﹣2≤0，解得﹣1≤a≤2，∴实数a的取值范围是﹣1≤a≤2．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。