分式难题汇编附答案
最新最新初中数学—分式的难题汇编含答案

一、选择题1.下列各式:351,,,,12a b x y a b x a b xπ-+++--中,是分式的共有( ) A .1个 B .2个C .3个D .4个2.0.000002019用科学记数法可表示为( )A .0.2019×10﹣5B .2.019×10﹣6C .20.19×10﹣7 D .2019×10﹣9 3.小张在课外阅读中看到这样一条信息:“肥皂泡的厚度约为0.0000007m ”,请你用科学记数法表示肥皂泡的厚度,下列选项正确的是( ) A .0.7 ⨯10-6 mB .0.7 ⨯10-7mC .7 ⨯10-7mD .7 ⨯10-6m4.若x 2-6xy +9y 2=0,那么x yx y-+的值为( ) A .12yB .12y-C .12D .12-5.已知02125,,0.253a b c --⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭,a ,b ,c 的大小关系是( ) A .a >b >cB .b >a >cC .c >a >bD .c >b >a6.下列计算正确的有(). ①0(1)1-= ②21333-⨯= ③()()33m m x x -=- ④2211224x x x ⎛⎫-=-+ ⎪⎝⎭ ⑤22(3)(3)9a b b a a b ---=-A .4个B .3个C .2个D .1个7.把分式a2a b+中的a 、b 都扩大2倍,则分式的值( ) A .缩小14 B .缩小12C .扩大2倍D .不变8.蜜蜂建造的蜂巢坚固省料,其厚度约为0.000073米,0.000073用科学计数法表示为 A .40.7310-⨯ B .47.310-⨯ C .57.310-⨯ D .67.310-⨯9.下列运算中,正确的是( )A .;B .;C .;D .;10.已知x 2-4xy +4y 2=0,则分式x yx y -+的值为( )A .13-B .13C .13yD .y 31-11.将分式2x x y+中的x 、y 都扩大2倍,则分式值( )A .扩大为原来的2倍B .缩小为原来的2倍C .保持不变D .无法确定12.如果把5xy x y+中的x 和y 都扩大为原来的10倍,那么这个分式的值( )A .不变B .扩大为原来的50倍C .扩大为原来的10倍D .缩小为原来的11013.如果把分式2x y zxyz-+中的正数x ,y ,z 都扩大2倍,则分式的值( ) A .不变B .扩大为原来的两倍C .缩小为原来的14D .缩小为原来的1814.(2017河北)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )A .4+446-=B .004+4+4=6C .34+4+4=6D .14446-÷+=15.老师设计了一个接力游戏,用小组合作的方式完成分式的运算,规则是:每人只能看见前一个人给的式子,并进行一步计算,再将结果传递给下一个人,最后完成计算.其中一个组的过程是:老师给甲,甲一步计算后写出结果给乙,乙一步计算后写出结果给丙,丙一步计算后写出结果给丁,丁最后算出结果.接力中,自己负责的一步出现错误的是( )A .甲B .乙C .丙D .丁16.1372x x-+-x 的取值范围是( )A .3<x <72B .3≤x <72C .3≤x ≤72D .x ≥317.用小数表示45.610-⨯为( ) A .5.6000B .0.00056C .0.0056D .0.05618.下列变形正确的是( ) A .()23524a a -=- B .22220x y xy -=C .23322b ab a a-÷=- D .()()222222x y x y x y +-=-19.若23a b =≠0,则代数式(2244b aba -+1)2b a a -÷的值为( ) A .2 B .1C .﹣1D .﹣220.若把分式x xy2中的x 和y 同时扩大为原来的3倍,则分式的值( ) A .扩大3倍B .缩小6倍C .缩小3倍D .保持不变21.下列运算正确的是( ) A .1133a a﹣=B .2322a a a +=C .326()•a a a ﹣=﹣D .32()()a a a ÷﹣﹣=22.使分式211x x -+的值为0,这时x 应为( )A .x =±1 B .x =1C .x =1 且 x≠﹣1D .x 的值不确定23.下列计算:①3362a a a ⋅=;②2352m m m +=;③()224-24a a =-;④()21048a a a a ⋅÷=;⑤()-21-510=;⑥22m a mn a n+=+,其中正确的个数为( ) A .4个 B .3个C .2个D .1个24.若代数式21a 4-在实数范围内有意义,则实数a 的取值范围为( ) A .a 4≠ B .a 2>- C .2a 2-<< D .a 2≠± 25.把0.0813写成科学计教法8.13×10n (n 为整数)的形式,则n 为( ) A .2B .-2C .3D .-3【参考答案】***试卷处理标记,请不要删除一、选择题 1.C【解析】 【分析】根据分式的定义逐一进行判断即可. 【详解】31,,1x a b x a b x ++--是分式 故选:C. 【点睛】本题考查分式的定义,熟练掌握定义是关键.2.B解析:B 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 【详解】0.000002019=2.019×10﹣6, 故选B . 【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.3.C解析:C 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 【详解】解:0.000 000 7=7×10-7. 故选C . 【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.4.C解析:C 【解析】根据完全平方公式求出x 与y 的关系,代入计算即可. 【详解】 x 2-6xy+9y 2=0, (x-3y )2=0, ∴x=3y , 则x y x y -+=3132y y y y -=+, 故选:C . 【点睛】本题考查的是求分式的值,掌握完全平方公式、分式的计算是解题的关键.5.C解析:C 【解析】 【分析】根据负整数指数幂和零指数幂法则计算,比较即可. 【详解】2129==10.25=434a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,,, ∵4>94>1, ∴c >a >b . 故选C . 【点睛】此题考查了负整数指数幂和零指数幂的运算,掌握其运算法则是解答此题的关键.6.C解析:C 【解析】 【分析】直接利用整数指数幂的法则和乘法公式分别计算得出答案. 【详解】解:①0(1)1-=,故①正确;②211333=93-⨯=⨯,故②正确; ③当m 是偶数时,()()333=mm m x x x -=,故③错误;④221124x x x ⎛⎫-=-+ ⎪⎝⎭,故④错误;⑤22(3)(3)9a b b a b a ----=,故⑤错误. 正确的有①②,共2个. 故选C本题考查了整数指数幂的运算法则和乘法公式,熟练掌握幂的各种性质和法则,乘法公式是解题的基础.7.D解析:D【解析】【分析】根据题意进行变形,发现实质上是分子、分母同时扩大2倍,根据分式的基本性质即可判断.【详解】根据题意,得把分式a2a b+中的a、b都扩大2倍,得2a2a a22a2b2(2a b)2a b==⨯+++,根据分式的基本性质,则分式的值不变.故选D.【点睛】此题考查了分式的基本性质.8.C解析:C【解析】【分析】数学术语,a×10的n次幂的形式.将一个数字表示成(a×10的n次幂的形式),其中1≤|a|<10,n表示整数,这种记数方法叫科学记数法。
(专题精选)最新初中数学—分式的难题汇编及答案

一、选择题1.当x =1时,下列分式中值为0的是( ) A .11x - B .222x x -- C .31x x -+ D .11x x -- 2.分式x 5x 6-+ 的值不存在,则x 的取值是 A .x ?6=- B .x 6=C .x 5≠D .x 5=3.下列分式:24a 5b c ,23c 4a b ,25b2ac 中,最简公分母是 A .5abcB .2225a b cC .22220a b cD .22240a b c4.计算: ()332xy ?-一 的结果是A .398x y --B .398x y ---C .391x y 2---D .361x y 2---5.下列运算正确的是( ) A .2-3=-6 B .(-2)3=-6C .(23)-2=49D .2-3=186.在式子:2x、5x y + 、12a - 、1x π-、21x x +中,分式的个数是( ) A .2B .3C .4D .57.如果分式242x x --的值等于0,那么( )A .2x =±B .2x =C .2x =-D .2x ≠8.下列各式从左到右的变形正确的是( )A .221188a a a a ---=-++B .()()221a b a b -+=-C .22x y x y x y+=++ D .052520.11y yx x++=-++9.如果112111S t t =+,212111S t t =-,则12S S =( ) A .1221t t t t +-B .2121t t t t -+C .1221t t t t -+D .1212t t t t +-10.下列各式中的计算正确的是( )A .22b b a a=B .a ba b ++=0 C .a c ab c b+=+ D .a ba b-+-=-1 11.人体中红细胞的直径约为0.000 007 7 m ,用科学记数法表示该数据为 ( )A .7.7×106 B .7.7×107 C .7.7×10-6 D .7.7×10-712.分式 x 22x 6-- 的值等于0,则x 的取值是 A .x 2=B .x ?2=-C .x 3=D .x ?3=-13.在实数范围内有意义,则a 的取值范围是( ) A .4a ≠-B .4a ≥-C .4a >-D .4a >-且0a ≠14.下列分式是最简分式的是( ) A .2426a a -+B .1b ab a++C .22a ba b +-D .22a ba b ++15.化简:32322012220122010201220122013-⨯-+-,结果是( ) A .20102013B .20102012C .20122013D .2011201316.若分式55x x -+的值为0,则x 的值为( ) A .0 B .5C .-5D .±5 17.下列等式或不等式成立的是 ( )A .2332<B .23(3)(2)---<-C .3491031030⨯÷⨯=D .2(0.1)1-->18.()()2323x y z x y z +++-的结果为( ) A .1B .33-+m m C .33m m +- D .33mm + 19.下列分式中:xy x ,2y x -,+-x yx y,22x y x y +-不能再约分化简的分式有( )A .1个B .2个C .3个D .4个20.每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m ,该数值用科学记数法表示为( ) A .51.0510⨯ B .51.0510-⨯C .50.10510-⨯D .410.510-⨯21.下列运算正确的是( )A .a ﹣3÷a ﹣5=a 2 B .(3a 2)3=9a 5 C .(x ﹣1)(1﹣x)=x 2﹣1D .(a+b)2=a 2+b 222.下列说法:①在一个装有2白球和3个红球的袋中摸3个球,摸到红球是必然事12a =--,则12a ≥-; 22a ba b -+是最简分式;其中正确的有()个.A .1个B .2个C .3个D .4个23.若a =-0.32,b =-3-2,c =(-13)-2,d =(-13)0,则它们的大小关系是( ) A .a<c<b<dB .b<a<d<cC .a<b<d<cD .b<a<c<d24.如果把分式232x x y+中的x 和y 都扩大为原来的5倍,那么分式的值( )A .扩大为原来的5倍B .扩大为原来的10倍C .不变D .缩小为原来的1525.如果把分式2xx y-中的x 与y 都扩大2倍,那么分式的值( )A .不变B .扩大2倍C .缩小2倍D .扩大4倍【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】考虑将x=1代入,使分式分子为0,分母不为0,即可得到结果. 【详解】解:当x=1时,下列分式中值为0的是222x x --. 故选B . 【点睛】此题考查了分式的值,熟练掌握运算法则是解本题的关键.2.A解析:A 【解析】 ∵分式56x x -+的值不存在, ∴分式56x x -+无意义, ∴60x +=,解得:6x =-. 故选A.3.C解析:C【解析】根据最简公分母的定义:“通常取各分母的系数的最小公倍数与各分母中所有字母因数的最高次幂的积作为各分母的公分母,这个公分母叫做这几个分式的最简公分母”可知,分式:24a 5b c ,23c 4a b ,25b2ac 的最简公分母是:22220a b c . 故选C.4.B解析:B 【解析】3333939(2)=(-2)8xy x y x y -------=-.故选B.5.D解析:D 【解析】选项A. 2-3=18,A 错. 选项B. (-2)3=-8,B 错.选项C. (23)-2=94 ,C 错误. 选项D. 2-3=18,正确 .所以选D. 6.B解析:B 【解析】 解:分式有2x 、12a -、21x x +共3个.故选B . 点睛:此题主要考查了分式的定义,正确把握分式的定义是解题关键.7.C解析:C 【解析】根据题意得:24020x x ⎧-=⎨-≠⎩,解得:x=−2. 故选C. 8.B解析:B 【解析】解:A .原式=22(1)1(8)8a a a a -++=--- ,错误;B .原式=1,正确;C .原式为最简结果,错误;D .原式=520110yx+-+,错误.故选B .点睛:此题考查了分式的基本性质,熟练掌握分式的基本性质是解本题的关键.9.B解析:B 【解析】∵112111S t t =+,212111S t t =-, ∴S 1=1212t t t t +,S 2=1221t t t t -,∴12112211221221t t s t t t t t t s t t t t +-==+-, 故选B .【点睛】本题考查了分式的混合运算,熟练掌握运算法则是解题的关键.10.D解析:D 【解析】解:A . 22b b a a≠,故A 错误;B . a ba b++=1,故B 错误; C . a c ab c b+≠+,故C 错误; D .a ba b -+-=-1,正确. 故选D .11.C解析:C【解析】绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定,0.000 007 7=7.7×10-6,故选C.12.A解析:A【解析】由题意得:20260xx-=⎧⎨-≠⎩,解得:2x=.故选A.点睛:分式值为0需同时满足两个条件:(1)分子的值为0;(2)分母的值不为0. 13.C解析:C【解析】分析:根据二次根式与分式有意义的条件和分式有意义的条件即可求出a的范围.详解:由题意可知:a+4>0∴a>-4故选C.点睛:解题的关键是正确理解二次根式有意义的条件和分式有意义的条件,本题属于基础题型.14.D解析:D【解析】【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.【详解】A、该分式的分子、分母中含有公因数2,则它不是最简分式.故本选项错误;B、分母为a(b+1),所以该分式的分子、分母中含有公因式(b+1),则它不是最简分式.故本选项错误;C、分母为(a+b)(a-b),所以该分式的分子、分母中含有公因式(a+b),则它不是最简分式.故本选项错误;D、该分式符合最简分式的定义.故本选项正确.故选D.【点睛】本题考查了对最简分式,约分的应用,关键是理解最简分式的定义.15.A解析:A【分析】将所求式子的分子分母前两项提取20122,整理后分子提取2010,分母提取2013,约分后即可得到结果,选出答案. 【详解】原式=32322012220122010201220122013-⨯-+-=2220122012220102012201212013--⨯+-()()=22201220102010201220132013⨯-⨯-=22201020121201320121--()()=20102013,故答案选A. 【点睛】本题主要考查了因式分解的应用,是一道技巧性较强的题,熟练掌握因式分解的方法是解本题的关键.16.B解析:B 【分析】要使分式的值为0,必须分式分子的值为0并且分母的值不为0. 【详解】由式子x -5=0,解得x 5=±. 而x =5时分母5x +≠0,x =-5时分母5x +=0,分式没有意, 即x =5, 故选B. 【点睛】要注意分母的值一定不能为0,分母的值是0时分式没有意义.17.D解析:D 【分析】先进行指数计算,再通过比较即可求出答案. 【详解】解:A 2339;28==,9>8 ,故A 错.B ()()2311;9832----==-,1198>-,故B 错. C 347910310=310⨯÷⨯⨯,故C 错. D ()20.1100--=,100>1, 故D 对.故选D. 【点睛】本题主要考查指数计算和大小比较,题目难度不大,细心做题是关键.18.A解析:A【分析】先计算除法运算,然后进行减法运算即可得出答案. 【详解】 原式=3m m +-6(3)(33)m -+× 32m -= 3m m ++ 33m += 33m m ++=1故答案选A. 【点睛】本题考查的知识点是分式的混合运算,解题的关键是熟练的掌握分式的混合运算.19.B解析:B 【分析】找出各项中分式分子分母中有没有公因式,即可做出判断. 【详解】xyx=y, 22x y x y +-= ()()x y x y x y ++-= 1x y -所以,不能约分化简的有:- 22y x+-x yx y 共两个, 故答案选B. 【点睛】本题考查的知识点是分式的约分,解题的关键是熟练的掌握分式的基本性质.20.B解析:B 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 【详解】0.0000105=1.05×10-5, 故选B . 【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.21.A解析:A 【解析】 【分析】直接利用同底数幂的除法运算法则、积的乘方运算法则、完全平方公式分别化简得出答案. 【详解】A .a ﹣3÷a ﹣5=a 2,故此选项正确;B .(3a 2)3=27a 6,故此选项错误;C .(x ﹣1)(1﹣x )=﹣x 2+2x ﹣1,故此选项错误;D .(a +b )2=a 2+2ab +b 2,故此选项错误. 故选A . 【点睛】本题考查了同底数幂的除法运算法则、积的乘方运算法则、完全平方公式等知识,正确掌握相关运算法则是解题的关键.22.C解析:C 【解析】 【分析】根据必然事件的定义,二次根式的性质,最简分式的定义以及同类二次根式的定义进行判断. 【详解】①在一个装有2白球和3个红球的袋中摸3个球,摸到红球是必然事件,正确.②12a =--,则12a ≤-,错误;4== ④分式22a ba b -+是最简分式,正确;故选:C . 【点睛】本题主要考查了随机事件、二次根式以及命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式.23.B解析:B 【解析】 【分析】首先根据一个数的平方的计算方法,负整数指数幂的运算方法,以及零指数幂的运算方法,分别求出a 、b 、c 、d 的大小;然后根据实数大小比较的方法,判断出它们的大小关系即可. 【详解】∵20 221110.30.09,3,9,1933a b c d--⎛⎫⎛⎫=-=-=-=-=-==-=⎪ ⎪⎝⎭⎝⎭,∴10.0919 9-<-<<,∴b<a<d<c.故选:B.【点睛】考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=1pa(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.24.A解析:A【解析】【分析】x,y都扩大为原来的5倍就是分别变成原来的5倍,变成5x和5y.用5x和5y代替式子中的x和y,看得到的式子与原来的式子的关系.【详解】用5x和5y代替式子中的x和y得:()2255, 151032x xx y x y=++则扩大为原来的5倍.故选:A.【点睛】考查分式的基本性质,掌握分式的基本性质是解题的关键.25.A解析:A【解析】分析:解答此题时,可将分式中的x,y用2x,2y代替,然后计算即可得出结论.详解:依题意得:2222xx y⨯-=222xx y⋅⋅-()=原式.故选A.点睛:本题考查的是对分式的性质的理解和运用,扩大或缩小n倍,就将原来的数乘以n 或除以n.。
最新初中数学—分式的难题汇编含答案解析

一、选择题1.下列分式中:xy x ,2y x -,+-x yx y ,22x y x y+-不能再约分化简的分式有( )A .1个B .2个C .3个D .4个2.下列各式中,正确的是( )A .a m ab m b+=+ B .a b0a b +=+ C .ab 1b 1ac 1c 1--=-- D .22x y 1x y x y-=-+3.下列分式:24a 5b c ,23c 4a b ,25b2ac中,最简公分母是 A .5abcB .2225a b cC .22220a b cD .22240a b c4.计算: ()332xy ?-一 的结果是A .398x y --B .398x y ---C .391x y 2---D .361x y 2---5.下列运算,正确的是 A .0a 0=B .11a a-=C .22a a b b=D .()222a b a b -=-6.下列运算正确的是( ) A .2-3=-6B .(-2)3=-6C .(23)-2=49D .2-3=187.若 a =20170,b =2015×2017﹣20162,c =(﹣23)2016×(32)2017,则下列 a ,b ,c 的大小关系正确的是( ) A .a <b <cB .a <c <bC .b <a <cD .c <b <a8.下面是一位同学所做的5道练习题: ①()325a a = ,②236a a a ⋅=,③22144m m -=, ④()()253aa a -÷-=-,⑤()3339a a -=-,他做对题的个数是 ( )A .1道B .2道C .3道D .4道9.把分式2x-y2xy中的x 、y 都扩大到原来的4倍,则分式的值( ) A .扩大到原来的16倍 B .扩大到原来的4倍 C .缩小到原来的14D .不变10.2018年3月3日,新浪综合网报道:“中科院发明首个抗癌DNA 纳米机器人,可精准阻断肿瘤血管饿死肿瘤!”.中国科学家团队研发出的这种可编程、基于 DNA 折纸技术的纳米机器人大小只有90×60×2nm ,nm 是长度计量单位,1nm=0.000000001米,则2nm 用科学记数法表示为( )A .2×109米B .20×10-8米C .2×10-9米D .2×10-8米 11.在实数范围内有意义,则a 的取值范围是( ) A .4a ≠-B .4a ≥-C .4a >-D .4a >-且0a ≠12.下列分式是最简分式的是( )A .22a a ab+B .63xy aC .211x x -+D .211x x ++13.若0x y y z z xabc a b c---===<,则点P(ab ,bc)不可能在第( )象限 A .一B .二C .三D .四14.下列各式变形正确的是() A .x y x y x y x y -++=---B .22a b a bc d c d--=++ C .0.20.03230.40.0545a b a bc d c d--=++D .a b b ab c c b--=-- 15.已知12x y-=3,分式4322x xy y x xy y +-+-的值为( )A .32 B .0C .23D .9416.下列运算正确的是( ) A .a ﹣3÷a ﹣5=a 2 B .(3a 2)3=9a 5 C .(x ﹣1)(1﹣x)=x 2﹣1D .(a+b)2=a 2+b 217.纳米是一种长度单位,1米=109纳米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示这种花粉的直径为( ) A .3.5×10﹣6米 B .3.5×10﹣5米 C .35×1013米 D .3.5×1013米 18.下列分式中,最简分式是( )A .211x x +-B .2211x x -+C .236212x x -+D .()2--y x x y19.若a =-0.32,b =-3-2,c =(-13)-2,d =(-13)0,则它们的大小关系是( ) A .a<c<b<dB .b<a<d<cC .a<b<d<cD .b<a<c<d20.如果把分式232x x y+中的x 和y 都扩大为原来的5倍,那么分式的值( )A .扩大为原来的5倍B .扩大为原来的10倍C .不变D .缩小为原来的1521.如果2310a a ++=,那么代数式229263a aa a ⎛⎫++⋅ ⎪+⎝⎭的值为( ) A .1B .1-C .2D .2-22.3--2的倒数是( )A .-9B .9C .19D .-1923.下列运算错误的是( )A 4=B .12100-=C 3=- D 2=24.如果a =(﹣99)0,b =(-3)﹣1,c =(﹣2)﹣2,那么a ,b ,c 三数的大小为( ) A .a >b >c B .c >a >bC .c <b <aD .a >c >b25.若分式55x x -+的值为0,则x 的值为( ) A .0B .5C .-5D .±5【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】找出各项中分式分子分母中有没有公因式,即可做出判断. 【详解】xyx=y, 22x y x y +-= ()()x y x y x y ++-= 1x y -所以,不能约分化简的有:- 22y x +-x yx y共两个,故答案选B. 【点睛】本题考查的知识点是分式的约分,解题的关键是熟练的掌握分式的基本性质.2.D解析:D 【解析】A.在分式的分子、分母上同时加上或减去同一个非0的数或式子分式的值要改变,故A 错误;B.a ba b++=1,故B 错误;C.a 不是分子、分母的因式,故C 错误;D.22x y x y --=()()x y x y x y -+-=1x y+;故D 正确.故选D.3.C解析:C 【解析】根据最简公分母的定义:“通常取各分母的系数的最小公倍数与各分母中所有字母因数的最高次幂的积作为各分母的公分母,这个公分母叫做这几个分式的最简公分母”可知,分式:24a 5b c ,23c 4a b ,25b2ac 的最简公分母是:22220a b c . 故选C.4.B解析:B 【解析】3333939(2)=(-2)8xy x y x y -------=-.故选B.5.B解析:B 【解析】A 选项中,因为只有当0a ≠时,01a =,所以A 错误;B 选项中,11=a a-,所以B 正确; C 选项中,22a b的分子与分母没有公因式,不能约分,所以C 错误;D 选项中,222()2a b a ab b -=-+,所以D 错误; 故选B.6.D解析:D 【解析】选项A. 2-3=18,A 错. 选项B. (-2)3=-8,B 错.选项C. (23)-2=94 ,C 错误. 选项D. 2-3=18,正确 .所以选D. 7.C解析:C 【解析】 【详解】解:a =20170=1,b =2015×2017﹣20162=(2016﹣1)(2016+1)﹣20162=20162﹣1-20162=﹣1,c =(﹣23)2016×(32)2017=(﹣23×32)2016×32=32,则b <a <c .故选C . 点睛:本题考查了平方差公式,幂的乘方与积的乘方,以及零指数幂,熟练掌握运算法则及公式是解答本题的关键.8.A解析:A 【解析】分析:原式各项利用幂的乘方,同底数幂的乘法,负整数指数幂法则,单项式除以单项式以及积的乘方计算得到结果,判断即可.详解:①236a a =() ,故①错误;②235a a a ⋅=,故②错误; ③2244mm -=,故③错误; ④523a a a -÷-=-()(),故④正确; ⑤33327a a -=-().故⑤错误.故选A .点睛:本题考查了整式的除法,幂的乘方与积的乘方,零指数幂、负整数指数幂,熟练掌握运算法则是解答本题的关键.9.C解析:C 【解析】分析:把原分式中的x .y 都扩大到原来的4倍后,再约分化简.详解:因为()422441224416242x y x y x y x y xy xy ---⨯⨯==,所以分式的值缩小到原来的14.故选C .点睛:分数可以约分,分式与分数类似,也可以约分,根据分式的基本性质把一个分式的分子与分母的公因式或公因数约去,这种变形称为分式的约分.10.C解析:C【解析】分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 详解:0.000000001×2=2×10﹣9. 故选C .点睛:本题考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.11.C解析:C 【解析】分析:根据二次根式与分式有意义的条件和分式有意义的条件即可求出a 的范围. 详解:由题意可知:a+4>0 ∴a >-4 故选C .点睛:解题的关键是正确理解二次根式有意义的条件和分式有意义的条件,本题属于基础题型.12.D解析:D 【解析】A 选项中,分式的分子、分母中含有公因式a ,因此它不是最简分式.故本选项错误;B 选项中,分式的分子、分母中含有公因数3,因此它不是最简分式.故本选项错误;C 选项中,分子可化为(x +1)(x -1),所以该分式的分子、分母中含有公因式(x +1),因此它不是最简分式.故本选项错误;D 选项中,分式符合最简分式的定义.故本选项正确. 故选:D .点睛:最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,看分子和分母中有无公因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.13.A解析:A 【解析】 【分析】根据有理数的乘法判断出a ,b ,c 中至少有一个是负数,另两个同号,然后求出三个数都是负数时x 、y 、z 的大小关系,得出矛盾,从而判断出a 、b 、c 不能同时是负数,确定出点P 不可能在第一象限. 【详解】 解:∵abc <0,∴a ,b ,c 中至少有一个是负数,另两个同号, 可知三个都是负数或两正数,一个是负数, 当三个都是负数时:若x yabc a-=, 则20x y a bc -=>,即x >y ,同理可得:y >z ,z >x 这三个式子不能同时成立, 即a ,b ,c 不能同时是负数,所以,P(ab,bc)不可能在第一象限.故选:A.【点睛】本题主要考查分式的基本性质和点的坐标的知识,熟悉点的坐标的基本知识是本题的解题关键,确定一个点所在象限,就是确定点的坐标的符号.14.D解析:D【解析】【分析】根据分式的分子分母都乘以或除以同一个不为零的数或者同一个不为零的整式,分式的值不变,可得答案.【详解】A、原式x yx y-=+,所以A选项错误;B、原式=2a bc d-+(),所以B选项错误;C、原式=203405a bc d-+,所以C选项错误;D、a b b ab c c b--=--,所以D选项正确.故选D.【点睛】本题考查了分式基本性质,分式的分子分母都乘以或除以同一个不为零的数或者同一个不为零的整式,分式的值不变.15.A解析:A【解析】【分析】先根据题意得出2x-y=-3xy,再代入原式进行计算即可.【详解】解:∵12x y-=3,∴2x-y=-3xy,∴原式=()()2232x y xyx y xy-+-+,=633xy xyxy xy-+-+,=32xyxy --,=32,故选A.【点睛】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.16.A解析:A【解析】【分析】直接利用同底数幂的除法运算法则、积的乘方运算法则、完全平方公式分别化简得出答案.【详解】A.a﹣3÷a﹣5=a2,故此选项正确;B.(3a2)3=27a6,故此选项错误;C.(x﹣1)(1﹣x)=﹣x2+2x﹣1,故此选项错误;D.(a+b)2=a2+2ab+b2,故此选项错误.故选A.【点睛】本题考查了同底数幂的除法运算法则、积的乘方运算法则、完全平方公式等知识,正确掌握相关运算法则是解题的关键.17.B解析:B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】∵1米=109纳米,某种植物花粉的直径约为35000纳米,∴35000纳米=35000×10﹣9m=3.5×10﹣5m.故选B.【点睛】本题考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.18.B解析:B【分析】利用最简分式的定义判断即可. 【详解】A 、原式=()()11 111x x x x +=+--,不合题意;B 、原式为最简分式,符合题意;C 、原式=()()()666262x x x x +--=+,不合题意,D 、原式=()()2x y x y x x y x--=-,不合题意;故选B . 【点睛】此题考查了最简分式,最简分式为分式的分子分母没有公因式,即不能约分的分式.19.B解析:B 【解析】 【分析】首先根据一个数的平方的计算方法,负整数指数幂的运算方法,以及零指数幂的运算方法,分别求出a 、b 、c 、d 的大小;然后根据实数大小比较的方法,判断出它们的大小关系即可. 【详解】∵2221110.30.09,3,9,1933a b c d --⎛⎫⎛⎫=-=-=-=-=-==-= ⎪ ⎪⎝⎭⎝⎭,∴10.09199-<-<<, ∴b <a <d <c . 故选:B . 【点睛】考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a -p =1p a(a≠0,p 为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a 0=1(a≠0);②00≠1.20.A解析:A 【解析】 【分析】x ,y 都扩大为原来的5倍就是分别变成原来的5倍,变成5x 和5y .用5x 和5y 代替式子中的x 和y ,看得到的式子与原来的式子的关系.【详解】用5x 和5y 代替式子中的x 和y 得:()2255,151032x xx y x y=++则扩大为原来的5倍. 故选:A. 【点睛】考查分式的基本性质,掌握分式的基本性质是解题的关键.21.D解析:D 【分析】根据分式的加法和乘法可以化简题目中的式子,然后根据a 2+3a+1=0,即可求得所求式子的值. 【详解】229263a a a a ⎛⎫++⋅ ⎪+⎝⎭, =22962•3a a a a a +++ =()2232•3a a a a ++ =2a (a+3) =2(a 2+3a ), ∵a 2+3a+1=0, ∴a 2+3a=-1,∴原式=2×(-1)=-2, 故选D . 【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.22.A解析:A 【解析】 【分析】 首先计算3--2=-19,再根据倒数的定义求解即可. 【详解】 ∵3--2=213-=-19,-19的倒数是-9, ∴3--2的倒数是-9, 故选A.【点睛】此题考查了倒数和负整数指数幂,掌握倒数的定义是本题的关键.23.B解析:B【解析】【分析】分别根据立方根及算术平方根的定义对各选项进行逐一解答即可.【详解】A 、∵42=16=4,故本选项正确;B 、12100-110,故本选项错误;C 、∵(-3)3=-273=-,故本选项正确;D =2,故本选项正确.故选B .【点睛】本题考查的是立方根及算术平方根,熟知立方根及算术平方根的定义是解答此题的关键.24.D解析:D【解析】【分析】根据0指数幂、负整数指数幂的运算法则分别求出a 、b 、c 的值即可求得答案.【详解】a =(﹣99)0=1,b =(-3)﹣1=13-,c =(﹣2)﹣2=()21142=-, 11143>>-, 所以a >c >b ,故选D.【点睛】本题考查了实数大小的比较,涉及了0指数幂、负整数指数幂,求出a 、b 、c 的值是解题的关键.25.B解析:B【分析】要使分式的值为0,必须分式分子的值为0并且分母的值不为0.【详解】由式子x -5=0,解得x 5=±.x+≠0,而x=5时分母5x+=0,分式没有意,x=-5时分母5即x=5,故选B.【点睛】要注意分母的值一定不能为0,分母的值是0时分式没有意义.。
分式难题汇编含答案

A.a<c<b<dB.b<a<d<cC.a<b<d<cD.b<a<c<d
【答案】B
【解析】
【分析】
根据正整数指数幂、负整数指数幂以及零次幂的意义分别计算出a,b,c,d的值,再比较大小即可.
【详解】
∵a=-0.22=-0.04,b=-2-2= ,c=(- )-2=4,d=(- )0=1,
【详解】
解:∵式子 有意义
∴
∴x<2
故选:D
【点睛】
本题考查了代数式有意义时字母的取值范围,代数式有意义时字母的取值范围一般从几个方面考虑:①当代数式是整式时,字母可取全体实数;②当代数式是分式时,考虑分式的分母不能为0;③当代数式是二次根式时,被开方数为非负数.
4.如果 ,那么代数式 的值是
A. B. C.2D.3
【答案】A
【解析】
【分析】
根据分式的运算法则即可求出答案.
【详解】
原式= ,
故选A.
【点睛】
本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
20.计算 的结果是( )
A. B. C. D.1
【答案】D
【解析】
原式= = =1,
故选D.
【点睛】本题考查了同分母分式的加减法,熟记法则是解题的关键.
故选D.
【点睛】
本题考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
17.计算 的结果为( )
最新最新初中数学—分式的难题汇编及答案解析

一、选择题1.将分式2a bab+中的a 、b 都扩大为原来的2倍,则分式的值( )A .缩小到原来的12倍 B .扩大为原来的2倍 C .扩大为原来的4倍D .不变2.已知0212,,0.253a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,a ,b ,c 的大小关系是( ) A .a >b >c B .b >a >cC .c >a >bD .c >b >a3.把分式2aa b+中a 、b 都扩大2倍,则分式的值( ) A .扩大4倍B .扩大2倍C .缩小2倍D .不变4.若(x 2﹣ax ﹣b )(x +2)的积不含x 的一次项和二次项,则a b =( ) A .116B .-116C .16D .﹣165.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物。
2.5微米等于0.0000025米,把0.0000025用科学记数法表示为( ) A .0.25×10–5米B .2.5×10–7米C .2.5×10–6米D .25×10–7米6.下列变形正确的是( )A .y x =22y xB .a ac b bc= C .ac a bc b= D .x m xy m y+=+ 7.已知x 2-4xy +4y 2=0,则分式x yx y-+的值为( ) A .13- B .13C .13yD .y 31-8.与分式11a a -+--相等的式子是( ) A .11a a +- B .11a a -+ C .11a a +-- D .11a a --+ 9.下列运算正确的是( )A 3=B .0(2)1-=C .2234a a a +=D .2325a a a ⋅=10.当x =_____ 时,分式11xx-+无意义.( ) A .0B .1C .-1D .211.下列等式从左到右的变形正确的是( )A .22b by x xy= B .2ab b a a =C .22b b a a=D .11b b a a +=+ 12.若x 2-6xy +9y 2=0,那么x yx y-+的值为( )A .12yB .12y-C .12D .12-13.在某次数学小测中,老师给出了5个判断题.如图为张晓亮的答卷,每个小题判断正确得20分,他的得分应是( )A .100分B .80分C .60分D .40分14.下列运算正确的是( ) A .()32622x x -=-B .22133xx -=C .()2x x y x xy --=-+ D .()2222x y x xy y --=-+15.1372x x-+-x 的取值范围是( ) A .3<x <72B .3≤x <72C .3≤x ≤72D .x ≥316.下列结论正确的是( ) A .当23x ≠时,分式132x x +-有意义 B .当x y ≠时,分式222xyx y -有意义C .当0x =时,分式22+xx x的值为0 D .当1x =-时,分式211x x --没有意义17.新冠肺炎疫情爆发以来,口罩成为需求最为迫切的防护物资.在这个关键时刻,我国某企业利用自身优势转产口罩,这背后不仅体现出企业强烈的社会责任感,更是我国人民团结一心抗击疫情的决心.据悉该企业3月份的口罩日产能已达到500万只,预计今后数月内都将保持同样的产能,则3月份(按31天计算)该企业生产的口罩总数量用科学记数法表示为( ) A .71.5510⨯只B .81.5510⨯只C .90.15510⨯只D .6510⨯只18.某种病毒变异后的直径为0.000000102米,将这个数写成科学记数法是( ) A .61.0210-⨯B .60.10210-⨯C .71.0210-⨯D .810210-⨯19.小明家到学校m 千米,若步行从家到学校,需要t 小时;若骑自行车,所用时间比步行少用20分钟,则骑自行车的比步行的速度快了( )A .3(1)m t t -千米/时B .(31)m t t - 千米/时 C .(31)mt t-+ 千米/时 D .13mt - 千米/时 20.使分式211x x -+的值为0,这时x 应为( )A .x =±1 B .x =1C .x =1 且 x≠﹣1D .x 的值不确定21.世界上最小的开花结果植物的果实像一个微小的无花果,质量只有0.000000076克,将0.000000076用科学记数法表示为( ) A .87.610⨯ B .77.610-⨯C .87.610-⨯D .97.610-⨯22.222142x x x÷--的计算结果为( ) A .2x x +B .22x x +C .22x x -D .2(2)x x +23.若代数式21a 4-在实数范围内有意义,则实数a 的取值范围为( ) A .a 4≠B .a 2>-C .2a 2-<<D .a 2≠±24.化简21211a aa a----的结果为( ) A .11a a +- B .a ﹣1 C .a D .125.函数 y=21x x --的自变量 x 的取值范围是( ) A .x > -1且x ≠ 1B .x ≠ 1且x ≠ 2C .x ≥ -1且x ≠ 1D .x ≥ -1【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】用2a ,2b 分别替换掉原分式中的a 、b ,进行计算后与原分式对比即可得出答案. 【详解】用2a ,2b 分别替换掉原分式中的a 、b ,可得:()2221=222822+++=⨯⨯⨯a b a ba b a b ab ab,所以分式缩小到原来的12倍, 故选A. 【点睛】本题考查了分式的基本性质,关键是根据条件正确的替换原式中的字母,然后化简计算.2.C解析:C 【解析】 【分析】根据负整数指数幂和零指数幂法则计算,比较即可. 【详解】2129==10.25=4342a b c --⎛⎛⎫=-== ⎪ ⎝⎭⎝⎭,,, ∵4>94>1, ∴c >a >b . 故选C . 【点睛】此题考查了负整数指数幂和零指数幂的运算,掌握其运算法则是解答此题的关键.3.D解析:D 【解析】 【分析】根据题意进行变形,发现实质上是分子、分母同时扩大2倍,根据分式的基本性质即可判断. 【详解】 根据题意,得把分式2aa b+中的a 、b 都扩大2倍,得2222222()a a a b a b ⋅⋅=++,根据分式的基本性质,则分式的值不变. 故选D . 【点睛】此题考查了分式的基本性质.4.A解析:A 【解析】 【分析】先把原式展开,再根据题意2()(2)x ax b x --+的积不含x 的一次项和二次项,得知20a -=,20a b +=,然后求解即可. 【详解】2322()(2)222x ax b x x x ax ax bx b --+=+---- 32(2)(2)2x a x a b x b =+--+-,2()(2)x ax b x --+的积不含x 的一次项和二次项, ∴2020a a b -=⎧⎨+=⎩,2a ∴=,4b =-,41216b a -∴==. 故选A . 【点睛】本题考查了多项式乘多项式,解题的关键是明确积不含x 的一次项和二次项,即它们的系数为零.5.C解析:C 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.由此即可解答. 【详解】0.0000025=2.5×10﹣6, 故选C . 【点睛】本题考查用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.6.C解析:C 【解析】试题解析:A 、分式的乘方不等于原分式,故A 错误; B 、当c=0时,结果不成立,故B 错误;C 、分式的分子分母都乘或除以同一个不为零的整式,故C 正确;D 、分式的分子分母都加同一个不为零的数,结果发生变化,故D 错误. 故选C .7.B解析:B 【解析】试题解析:∵x 2-4xy+4y 2=0, ∴(x-2y )2=0, ∴x=2y , ∴133x y y x y y -==+. 故选B .8.B解析:B 【分析】根据分式的基本性质即可得出:分式的分子、分母、分式本身的符号,改变其中的任意两个,分式的值不变,据此即可解答. 【详解】 解:原式= 1)(1)a a --+-( =11a a -+故选:B . 【点睛】本题考查分式的基本性质,解题关键是熟练掌握分式的基本性质.9.B解析:B 【分析】直接利用立方根,零指数幂,合并同类项法则同底数幂的乘法法则化简得出答案. 【详解】3≠,无法计算,故此选项错误; B. 0(2)1-=,故此选项正确; C. 22234a a a +=,故此选项错误; D. 2326a a a ⋅=,故此选项错误; 故选:B. 【点睛】此题考查合并同类项,零指数幂,立方根,解题关键在于掌握运算法则.10.C解析:C 【分析】根据分式无意义的条件,分母等于0,列不等式求解即可. 【详解】因为分式11xx-+无意义, 所以1+x =0, 解得x =-1.故选C. 【点睛】本题主要考查分式无意义的条件,解决本题的关键是要熟练掌握分式无意义的条件.11.B解析:B 【分析】根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项. 【详解】 A 、22b by x xy=,其中y≠0,故选项错误; B 、2ab ba a=,其中左边隐含a≠0,故选项正确; C 、2b ab a a =,故选项错误. D 、根据分式基本性质知道11b b aa ++≠,故选项错误; 故选B . 【点睛】此题考查分式的基本性质,解题的关键是熟练掌握分式的基本性质.12.C解析:C 【解析】 【分析】根据完全平方公式求出x 与y 的关系,代入计算即可. 【详解】 x 2-6xy+9y 2=0, (x-3y )2=0, ∴x=3y , 则x y x y -+=3132y y y y -=+, 故选:C . 【点睛】本题考查的是求分式的值,掌握完全平方公式、分式的计算是解题的关键.13.B解析:B 【分析】依据分式的化简,无理数定义,平方根定义,实数的大小比较方法依次判断各小题正确与否即可确定他的得分. 【详解】 因为c ac b++是最简分式不能在进行化简,故第1小题错误,他判断正确得20分; 因为227是分数属于有理数,不是无理数,所以第2小题错误,他判断正确得20分;因为0.6=-,所以第3小题错误,他判断错误不得分;因为23<<,所以112<<,所以第4小题正确,他判断正确得20分;数轴上的点可以表示无理数,故第5小题错误,他判断正确得20分. 故他应得80分,选择B 【点睛】此题考察分式的化简,无理数定义,平方根定义,实数的大小比较方法,熟练掌握才能正确判断.14.C解析:C 【分析】根据积的乘方、负整数指数幂、整式的乘法、完全平方公式逐项判断即可得. 【详解】 A 、()32628x x -=-,此项错误;B 、2233xx-=,此项错误; C 、()2x x y x xy --=-+,此项正确;D 、()()22222x y x y x xy y --=+=++,此项错误; 故选:C . 【点睛】本题考查了积的乘方、负整数指数幂、整式的乘法、完全平方公式,熟练掌握各运算法则和公式是解题关键.15.B解析:B 【分析】根据二次根式的性质,被开方数大于等于0;分母中有字母,分母不为0. 【详解】由题意,得:x ﹣3≥0且7﹣2x >0,解得:3≤x 72<. 故选B . 【点睛】本题考查了二次根式有意义的条件,正确解不等式是解题的关键.解析:A 【分析】根据分式有意义,分母不等于0;分式的值等于0,分子等于0,分母不等于0对各选项分析判断后利用排除法求解. 【详解】A 、分式有意义,3x-2≠0,解得23x ≠,故本选项正确; B 、分式有意义,x 2-y 2≠0,解得x≠±y ,故本选项错误;C 、分式的值等于0,x=0且x 2+2x≠0,解得x=0且x≠0或-2,所以,x=0时分式无意义,故本选项错误;D 、分式没有意义,x-1=0,x=1,故本选项错误. 故选:A . 【点睛】此题考查分式有意义以及分式的值为零的条件,解题关键在于掌握(1)分式无意义⇔分母为零;(2)分式有意义⇔分母不为零;(3)分式值为零⇔分子为零且分母不为零.17.B解析:B 【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数. 【详解】500万×31=5000000×31=155000000=1.55×108(只), 故选:B . 【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.18.C解析:C 【分析】用科学记数法表示比较小的数时,n 的值是第一个不是0的数字前0的个数,包括整数位上的0. 【详解】解:0.000000102=71.0210-⨯. 故选:C . 【点睛】此题考查科学记数法表示较小的数,解题关键在于掌握一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.解析:B【分析】利用速度=路程÷时间分别求得步行的速度和骑自行车的速度,从而利用分式的运算法则求得两者的速度差.【详解】解:步行的速度是:mt(km/h),骑自行车的速度是:31313m mtt=--(km/h),则骑自行车的速度与步行的速度差为:331(31)m m mt t t t-=--.故选:B.【点睛】本题考查了列代数式及分式的加减运用,正确表示出步行和骑自行车的速度是解题的关键.20.B解析:B【分析】使分式211xx-+的值为0,则x2-1=0,且x+1≠0.【详解】使分式211xx-+的值为0,则x2-1=0,且x+1≠0解得x=1故选:B【点睛】考核知识点:考查分式的意义. 要使分式值为0,分子等于0,分母不等于0.21.C解析:C【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.000000076用科学记数法表示为7.6×10-8.故选:C.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.22.B解析:B【分析】先把分母因式分解,再把除法转换为乘法,约分化简得到结果.【详解】222142x x x÷-- =21(2)(2)(2)x x x x ÷+-- =()()()2·222x x x x -+- =22x x +. 故选:B .【点睛】本题主要考查了分式的除法,约分是解答的关键.23.D解析:D【分析】分式有意义时,分母a 2-4≠0.【详解】依题意得:a 2-4≠0,解得a≠±2.故选D .【点睛】本题考查了分式有意义的条件.分式有意义的条件是分母不等于零24.B解析:B【解析】分析:根据同分母分式加减法的运算法则进行计算即可求出答案.详解:原式=21211a a a a -+--, =2(1)1a a --, =a ﹣1故选B .点睛:本题考查同分母分式加减法的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.25.C解析:C【分析】根据分母不能为零且被开方数是非负数,可得答案.【详解】解:由题意得:x-1≠0且x+1≥0,解得:x≥-1且x≠1.故选C.【点睛】本题考查了函数自变量的取值范围,利用分母不能为零且被开方数是非负数得出不等式是解题关键.。
方程与不等式之分式方程难题汇编附解析

方程与不等式之分式方程难题汇编附解析 、选择题1.已知A 、C 两地相距40千米,B 、C 两地相距50千米,甲乙两车分别从 A 、B 两地同时出发到C 地•若乙车每小时比甲车多行驶 为x 千米/小时,依题意列方程正确的是(故选B .故选A【点睛】 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.本题应用 的等量关系为:工作时间 =工作总量 M 效.3.体育测试中,小进和小俊进行 800米跑测试,小进的速度是小俊的1.25倍,小进比小俊少用了 40秒,设小俊的速度是 x 米/秒,则所列方程正确的是()40 A .X 【答案】 【解析】 试题解析: 50x 12 B B . 设乙车的速度为 由题意得,40 50x 12 x40 50x 12 xx 千米/小时, 40 50C.x x 1240 50D .x 12 x则甲车的速度为(x-12) 千米/小时,12千米,则两车同时到达 )C 地.设乙车的速度2.某市在旧城改造过程中,需要整修一段全长 交通所造成的影响,实际工作效率比原计划提高了 计划每小时修路的长度•若设原计划每小时修路24002400°A .8x (1 20%) x 2400 2400 °C.8(1 20%) x x【答案】A 【解析】 【分析】求的是原计划的工效,工作总量为 是:提前8小时完成任务 【详解】原计划用的时间为:B .D.2400m 的道路.为了尽量减少施工对城市20%,结果提前8小时完成任务.求原 xm ,则根据题意可得方程()2400 2400 °8(1 20%) x x2400 2400° 8x (1 20%) x2400,根据工作时间来列等量关系.本题的关键描述语 等量关系为:原计划用的时间 -实际用的时间=8.实际用的时间为:2400 x 1 20%.所列方程为:2400x2400 20%=8.13【详解】 小进跑800米用的时间为-8也 秒,小俊跑800米用的时间为 型 秒,1.25x x•••小进比小俊少用了 40秒,800 800万程是 40,x 1.25x故选C.【点睛】 本题考查了列分式方程解应用题,能找出题目中的相等关系式是解此题的关键.4.从4 , 2 , 1, 0,1, 2, 4, 6这八个数中,随机抽一个数,记为 a .若数a 使关y a 1 3有整数解,确定a 的值即可判断.y 11 y【详解】2 2方程x 2 a 4 x a 0有实数解,•••△ =4(a- 4)2- 4a 2? 0,解得a? 2•满足条件的a 的值为-4, -2, -1, 0, 1, 2 方程y a y 131有整数解,则符合条件的 a 的值的和是( 1 y)A .6B .4C. 2D . 2【答案】 C【解析】【分析】由一兀— .次方程x 2 a4 x a 2 0有实数解,确定a的取值范围, 由分式方程0有实数解.且关于 y 的分式方程A . 4 1.25x 40x 800800 800 40 B.——x 2.25x 800 800 800 800 C.40D .40x1.25x1.25x x【答案】C 【解析】 【分析】先分别表示出小进和小俊跑 800米的时间,再根据小进比小俊少用了 40秒列出方程即可. 于x 的一元二次方程 x22 a 4 x a 2解得y=a+22••• y有整数解--a=-4, 0, 2, 4, 6综上所述,满足条件的a的值为-4, 0, 2,符合条件的a的值的和是-2故选:C【点睛】本题考查了一元二次方程根据方程根的情况确定方程中字母系数的取值范围;以及分式方程解的定义:求出使分式方程中令等号左右两边相等且分母不等于0的未知数的值,这个值叫分式方程的解.5. 若关于x的方程2 —有增根,则a的值为()x 4 x 4A. -4B. 2C. 0D. 4【答案】D【解析】【分析】增根是化为整式方程后产生的不适合分式方程的根•让最简公分母x-4=0,得到x=4.再将x=4代入去分母后的方程即可求出a=4.【详解】解:由分式方程的最简公分母是x-4,•••关于x的方程亠2 —有增根,x 4 x 4••• x-4=0,•••分式方程的增根是x=4.关于x的方程」 2 —去分母得x=2(x-4)+a,x 4 x 4代入x=4得a=4故选D.【点睛】本题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.6. 某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本,求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是()240120240 120A. 4B. 4x 20x x 20 x120 240120 240C.4D. 4x x20x x 20【答案】D【解析】【分析】设第一次买了x本资料,则第二次买了(x+ 20)本资料,由等量关系第二次比第一次优惠了4列出方程即可解答.【详解】解:设第一次买了x本资料,则第二次买了(x + 20)本资料,根据题意可得:120 240 ,4x x 20故选:D【点睛】本题考查由实际问题抽象出分式方程,找到关键描述语,设出未知数,找到等量关系是解题的关键.2x a7. 关于x的分式方程1的解为负数,贝V a 的取值范围是()x 1A. a 1B. a 1 c. a 1 且a 2 D. a 1 且a 2【答案】D【解析】【分析】分式方程去分母转化为整式方程,表示出整式方程的解,根据分式方程解为负数列出关于a的不等式,求出不等式的解集即可确定出a的范围.【详解】分式方程去分母得:x 1 2x a,即x 1 a,因为分式方程解为负数,所以1 a 0,且1 a 1 ,解得:a 1且a 2,故选D.【点睛】本题考查了分式方程的解,熟练掌握解分式方程的一般步骤及注意事项是解题的关键•注意在任何时候都要考虑分母不为0.&新能源汽车环保节能,越来越受到消费者的喜爱•各种品牌相继投放市场•一汽贸公司经销某品牌新能源汽车•去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元•销售数量与去年一整年的相同•销售总额比去年一整年的少20%,今年1~5月【解析】 【分析】首先根据所设今年每辆车的价格,可表示出去年的价格,同样根据销售总额的关系可表示 出今年的销售总额,然后再根据去年和今年 1~5月份销售汽车的数量相同建立方程即可得解• 【详解】•••今年1~5月份每辆车的销售价格为 x 万元, •••去年每辆车的销售价格为(x+1)万元,50005000(1 -20%)则有一|x+ 1x故选A. 【点睛】此题主要考查分式方程的应用,解题的关键是找出题中去年和今年的关系9.某一景点改造工程要限期完成,甲工程队独做可提前一天完成,乙工程队独做要误期6天,现由两工程队合做 4天后,余下的由乙工程队独做,正好如期完成,若设工程期限为x 天,则下面所列方程正确的是 ( )4 x A .1x 1 x 6C.【答案】D 【解析】 【分析】1首先根据工程期限为 x 天,结合题意得出甲每天完成总工程的,而乙每天完成总工程x 11的,据此根据题意最终如期完成了工程进一步列出方程即可x 6【详解】•••工程期限为x 天,1 1•甲每天完成总工程的,乙每天完成总工程的 1份每辆车的销售价格是多少万元 列方程正确的是()50005000(1 - 20%)A .X + 1 X 5000 5000(1 - 20%)C. --------- = ------------------------x * I x【答案】A ?设今年1~5月份每辆车的销售价格为 x 万元•根据题意,B . D .3000 5000(1 + 20%) 50005000(1 + 20%)xx 1 x 6 •••由两工程队合做4天后,余下的由乙工程队独做,正好如期完成,•••可列方程为:x 1 x 6故选:D.1,【点睛】本题主要考查了分式方程的实际应用,根据题意正确找出等量关系是解题关键10.解分式方程2x xx 1 12x1丄时,去分母后所得的方程正确的是(2)A. 2x x 20B. 4x 2x 4 x 1C. 4x2x 4x 1D. 2x x 2 x 1【答案】C【解析】【分析】根据等式的性质,方程两边冋时乘以最简公分母 2 (x-1),整理即可得答案【详解】.2x x21x 11x22x x21x 1x12方程两边同时乘以最简公分母 2 (x-1)得:4x+2(x-2)=x-1,去括号得:4x+2x-4=x-1,故选:C.【点睛】本题考查解分式方程,正确得出最简公分母是解题关键.11.施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是()1000100010001000A. =2B. =2x x 30x 30x1000100010001000C.=2D. =2x x 30x 30x【答案】A【解析】分析:设原计划每天施工x米,则实际每天施工(x+30) 米,根据:原计划所用时间-实际所用时间=2,列出方程即可.详解:设原计划每天施工x米,则实际每天施工(x+30) 米,根据题意,可列方程: =2,1000 1000故选A.x 30点睛:本题考查了由实际问题抽象出分式方程,关键是读懂题意,找出合适的等量关系,列出方程.1 kx 112. 若分式方程2+ = 有增根,则k的值为()x 2 2 xA.- 2B.- 1C. 1D. 2【答案】C【解析】【分析】根据分式方程有增根得到x=2,将其代入化简后的整式方程中求出k即可.【详解】解:分式方程去分母得: 2 (x-2)+1- kx=- 1,由题意将x= 2代入得:1 - 2k=- 1,解得:k= 1.故选:C.【点睛】此题考查分式方程的增根,由增根求方程中其他未知数的值,根据增根的定义得到方程的解是解题的关键•13. 已知甲车行驶35千米与乙车行驶45千米所用时间相同,且乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是| ) 354535 4535 453545A. B. C.D.x x 15x+15 x x-15 x x x+15【答案】D【解析】【分析】首先根据甲车的速度为x千米/小时,表示出乙车的速度为(x+15)千米/小时, 再根据关键是语句甲车行驶35千米与乙车行驶45千米所用时间相同”列出方程即可.【详解】解:设甲车的速度为x千米/小时,则乙车的速度为(x+15)千米/小时,由题意得:35 45x x+15'故选D.【点睛】此题主要考查了分式方程的应用,关键是正确理解题意,表示出甲乙两车的速度,再根据关键是语句列出方程即可•此题用到的公式是:路程谨度=时间.a x a14. 若整数a使关于x的分式方程1 的解为负数,且使关于x 的不等式组x 1 x 1a ) 0无解,则所有满足条件的整数2x 13解分式方程和不等式得出关于x 的值及x 的范围,根据分式方程的解不是增根且为负数和不等式组无解得出 a 的范围,继而可得整数 a 的所有取值,然后相加. 【详解】a) 0无解,2x 13…a £4,•••则所有满足条件的整数 a 的值是:2、3、4,和为9, 故选:C. 【点睛】本题主要考查分式方程的解和一元一次不等式组的解,熟练掌握解分式方程和不等式组的 方法,并根据题意得到a 的范围是解题的关键.2(x a 的值之和是(A . 5【答案】C 【解析】【分析】B . 7 C. 9 D . 10解:解关于x 的分式方程-x汁,得“-2a+1,•/X M ±,•••关于x 的分式方程a 的解为负数,1- 2a+1 v 0,解不等式a) 0,得: x v a ,解不等式2x 1丁,得:•••关于x 的不等式组2(x 15.若关于x 的分式方程 3m 2 x2有增根,则m 的值为(A .1B . 0C. 1D . 23【答案】C 【解析】 【分析】增根是化为整式方程后产生的不适合分式方程的根•所以应先确定增根的可能值,让最简 公分母x - 2= 0,得到x = 2,然后代入化为整式方程的方程,满足即可.【详解】解:方程两边都乘 x - 2, 得 x+m - 3m = 2 (x - 2), •••原方程有增根, •••最简公分母x - 2 = 0, 解得x = 2,当 x = 2 时,2+m - 3m = 0,m = 1,故选:C. 【点睛】本题考查了分式方程的增根,难度适中.确定增根可按如下步骤进行: ① 让最简公分母为0确定可能的增根; ② 化分式方程为整式方程;③ 把可能的增根代入整式方程,使整式方程成立的值即为分式方程的增根.3a a 使得关于x 的方程2的解为非负数,且使得关于y 的不等式x 2 2 x至少有四个整数解,则所有符合条件的整数 a 的和为().解:不等式组整理得:16.若整数3y 2组丁y a 3A . 17【答案】C 【解析】 【分析】表示出不等式组的解集,B . 18 C. 22 D . 25由不等式至少有四个整数解确定出非负数以及分式有意义的条件求出满足题意整数 【详解】a 的值,再由分式方程的解为 a 的值,进而求出之和.600 480 A.x 40600 480 B.x 40由不等式组至少有四个整数解,得到- 1< y^a,解得:a>3即整数a = 3, 4, 5, 6,…,3 a2 一x 2 2 x去分母得:2 (x—2)—3 =—a,7 a解得:x=27 a 7 a- >0且工22 2••• a<7 且a^3,由分式方程的解为非负数以及分式有意义的条件,得到a为4, 5, 6, 7,之和为22.故选:C.【点睛】此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.17. 2017年,全国部分省市实施了免费校车工程”.小明原来骑自行车上学,现在乘校车上学可以从家晚10分钟出发,结果与原来到校时间相同.已知小明家距学校5千米,若校车速度是他骑车速度的2倍,设小明骑车的速度为x千米/时,则下面所列方程正确的为()515551 5 “55“5A. + —=B. = + -C. — + 10 =D.——10 =x62x x2x6x2x x2x 【答案】B【解析】【分析】设小明骑车的速度为x千米/小时,校车速度为2x千米/小时,等量关系为:小明骑车所走的时间减去校车所走的时间=10分钟,据此列方程.【详解】设小明骑车的速度为x千米/小时,校车速度为2x千米/小时,5 5 1由题意得,=—+丄x 2x 6所以答案为B.【点睛】本题考查了分式方程,解题的关键是根据实际问题列出分式方程18.某工厂现在平均每天比原计划多生产40台机器,现在生产600台机器所需的时间与原计划生产480台机器所用的时间相同,设原计划每天生产x台机器,根据题意,下面列出的方程正确的是()x xC. D.——x x 40x x 40【答案】B 【解析】 【分析】由题意分别表达出原来生产 480台机器所需时间和现在生产 600台机器所需时间,然后根据两者相等即可列出方程,再进行判断即可. 【详解】解:设原计划每天生产 x 台机器,根据题意得:480600x x 40故选B . 【点睛】读懂题意,用含x 的代数式表达出原来生产 480台机器所需时间为台机器所需时间为-605天是解答本题的关键.x 40四则运算•若(―3 x =2 x ,则x 的值为(A . -2B . -1I【答案】B 【解析】 【分析】利用题中的新定义变形已知等式,然后解方程即可. 【详解】根据题中的新定义化简得: —9 3x经检验x=- 1是分式方程的解. 故选B . 【点睛】本题考查了新定义和解分式方程,利用了转化的思想,解分式方程注意要检验.20.某车间加工12个零件后,采用新工艺,工效比原来提高了50%,这样加工同样多的零件就少用1小时,那么采用新工艺前每小时加工的零件数为()600 480 600 480 480天和现在生产600x19.对于实数a 、b ,定义一种新运算 ?"为:a3 ab,这里等式右边是通常的D . 2C. 1汽;,去分母得:12 - 6x=27+9x ,解得:x= - 1,A. 3个B. 4个C. 5个D. 6个【答案】B【解析】【分析】根据题意,找出题目的等量关系,列出方程,解方程即可得到答案.【详解】解:根据题意,得:12 12 ,1,x x(1 50%)解得:x 4 ;经检验,x 4是原分式方程的解.•••那么采用新工艺前每小时加工的零件数为4个;故选:B.【点睛】此题主要考查了分式方程的应用,其中找出方程的关键语,找出数量关系是解题的关键.注意解分式方程需要检验.。
(专题精选)初中数学方程与不等式之分式方程难题汇编附解析

(专题精选)初中数学方程与不等式之分式方程难题汇编附解析一、选择题1.解分式方程221112x x x x --=--时,去分母后所得的方程正确的是( ) A .220x x -+= B .4241x x x -+=-C .4241x x x +-=-D .221x x x +-=- 【答案】C【解析】【分析】根据等式的性质,方程两边同时乘以最简公分母2(x-1),整理即可得答案.【详解】 ∵221112x x x x --=--, ∴221112x x x x -+=--, 方程两边同时乘以最简公分母2(x-1)得:4x+2(x-2)=x-1,去括号得:4x+2x-4=x-1,故选:C .【点睛】本题考查解分式方程,正确得出最简公分母是解题关键.2.解分式方程11222x x x -+=--的结果是( ) A .x="2"B .x="3"C .x="4"D .无解【答案】D【解析】【分析】【详解】解:去分母得:1﹣x+2x ﹣4=﹣1,解得:x=2,经检验x=2是增根,分式方程无解.故选D .考点:解分式方程.3.某市从今年1月1日起调整居民用水价格,每立方米水费上涨13,小丽家去年12月份的水费是15元,而今年5月的水费则是30元,已知小丽家今年5月的用水量比去年12月的用水量多35m .求该市今年居民用水的价格.设去年居民用水价格为x 元/3m ,根据题意列方程,正确的是()A.30155113xx-=⎛⎫+⎪⎝⎭B.30155113xx-=⎛⎫-⎪⎝⎭C.15305113xx-=⎛⎫+⎪⎝⎭D.15305113xx-=⎛⎫-⎪⎝⎭【答案】A【解析】【分析】利用总水费÷单价=用水量,结合小丽家今年5月的用水量比去年12月的用水量多5m3得出方程即可.【详解】解:设去年居民用水价格为x元/3m,根据题意得:30155113xx-=⎛⎫+⎪⎝⎭,故选:A.【点睛】此题主要考查了由实际问题抽象出分式方程,正确表示出用水量是解题关键.4.甲、乙两个搬运工搬运某种货物,已知乙比甲每小时多搬运600kg,甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等,求甲、乙两人每小时分别搬运多少千克货物.设甲每小时搬运xkg货物,则可列方程为A.B.C.D.【答案】B【解析】甲种机器人每小时搬运x千克,则乙种机器人每小时搬运(x+600)千克,由题意得:,故选B.【点睛】本题考查了列分时方程解实际问题的运用,解答时根据甲搬运5000kg所用时间与乙搬运8000kg所用时间相等建立方程是关键.5.某工厂现在平均每天比原计划多生产25个零件,现在生产600个零件所需时间与原计划生产450个零件所需时间相同.设原计划平均每天生产x个零件,根据题意可列方程为()A .60045025x x=- B .60045025x x =- C .60045025x x =+ D .60045025x x =+ 【答案】C【解析】【分析】 原计划平均每天生产x 个零件,现在每天生产(x+25)个,根据现在生产600个零件所需时间与原计划生产450个零件所需时间相同即可列出方程.【详解】由题意得:现在每天生产(x+25)个, ∴60045025x x=+, 故选:C.【点睛】 此题考查分式方程的实际应用,正确理解题意是列方程的关键.6.方程24222x x x x =-+-- 的解为( ) A .2B .2或4C .4D .无解 【答案】C【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】去分母得:2x=(x ﹣2)2+4,分解因式得:(x ﹣2)[2﹣(x ﹣2)]=0,解得:x=2或x=4,经检验x=2是增根,分式方程的解为x=4,故选C .【点睛】此题考查了解分式方程,以及分式方程的解,熟练掌握运算法则是解本题的关键.7.已知关于x 的分式方程211x k x x -=--的解为正数,则k 的取值范围为( ) A .20k -<<B .2k >-且1k ≠-C .2k >-D .2k <且1k ≠ 【答案】B【解析】【分析】先用k 表示x ,然后根据x 为正数列出不等式,即可求出答案.【详解】 解:211x k x x-=--Q , 21x k x +∴=-, 2x k ∴=+,Q 该分式方程有解,21k ∴+≠,1k ∴≠-,0x Q >,20k ∴+>,2k ∴>-,2k ∴>-且1k ≠-,故选:B .【点睛】本题考查的是分式方程,熟练掌握分式方程是解题的关键.8.甲、乙两人同时分别从A ,B 两地沿同一条公路骑自行车到C 地.已知A ,C 两地间的距离为110千米,B ,C 两地间的距离为100千米.甲骑自行车的平均速度比乙快2千米/时.结果两人同时到达C 地.求两人的平均速度,为解决此问题,设乙骑自行车的平均速度为x 千米/时.由题意列出方程.其中正确的是( )A .1101002x x=+ B .1101002x x =+ C .1101002x x =- D .1101002x x =- 【答案】A【解析】 设乙骑自行车的平均速度为x 千米/时,则甲骑自行车的平均速度为(x+2)千米/时,根据题意可得等量关系:甲骑110千米所用时间=乙骑100千米所用时间,根据等量关系可列出方程即可.解:设乙骑自行车的平均速度为x 千米/时,由题意得:1102x +=100x, 故选A .9.方程10020x +=6020x-的解为( ) A .x =10B .x =﹣10C .x =5D .x =﹣5 【答案】C【解析】【分析】方程两边同时乘以(20+x)(20﹣x),解得,x=5,经检验,x=5是方程的根.【详解】解:方程两边同时乘以(20+x)(20﹣x),得100(20﹣x)=60(20+x),整理,得8x=40,解得,x=5,经检验,x=5是方程的根,∴原方程的根是x=5;故选:C.【点睛】本题考查分式方程的解法;熟练掌握分式方程的解法,切勿遗漏验根是解题的关键.10.八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是()A.10x-102x=20 B.102x-10x=20 C.10x-102x=13D.102x-10x=13【答案】C【解析】【分析】根据八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,可以列出相应的方程,从而可以得到哪个选项是正确的.【详解】由题意可得,10 x -102x=13,故选:C.【点睛】此题考查由实际问题抽象出分式方程,解题的关键是明确题意,找出题目中的等量关系,列出相应的方程.11.施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是()A.1000100030x x-+=2 B.1000100030x x-+=2C.1000100030x x--=2 D.1000100030x x--=2【答案】A【解析】分析:设原计划每天施工x米,则实际每天施工(x+30)米,根据:原计划所用时间﹣实际所用时间=2,列出方程即可.详解:设原计划每天施工x米,则实际每天施工(x+30)米,根据题意,可列方程:1000100030x x-+=2,故选A.点睛:本题考查了由实际问题抽象出分式方程,关键是读懂题意,找出合适的等量关系,列出方程.12.方程31144xx x--=--的解是()A.-3 B.3 C.4 D.-4【答案】B【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【详解】去分母得:3-x-x+4=1,解得:x=3,经检验x=3是分式方程的解.故选:B.【点睛】此题考查解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.13.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为()A.B.C.D.【答案】C【解析】设每个A型包装箱可以装书x本,则每个B型包装箱可以装书(x+15)本,根据单独使用B型包装箱比单独使用A型包装箱可少用6个,列方程得:,故选C.14.若关于x 的分式方程2233x m x x -=--有增根,则m 的值为( ). A .3B.CD.【答案】D【解析】 解关于x 的方程2233x m x x -=--得:26x m =-, ∵原方程有增根,∴30x -=,即2630m --=,解得:m =故选D.点睛:解这类题时,分两步完成:(1)按解一般分式方程的步骤解方程,用含待定字母的式子表示出方程的根;(2)方程有增根,则把(1)中所得的结果代入最简公分母中,最简公分母的值为0,由此即可求得待定字母的值.15.关于x 的分式方程26344ax x x -+=---的解为正数,且关于x 的不等式组1722x a x x >⎧⎪⎨+≥-⎪⎩有解,则满足上述要求的所有整数a 的绝对值之和为( ) A .12B .14C .16D .18【答案】C【解析】【分析】根据分式方程的解为正数即可得出a <2且a≠1,根据不等式组有解,即可得出a >-5,找出-5<a <2且a≠1中所有的整数,将其相加即可得出结论.【详解】 解分式方程26344ax x x -+=---得:x=43a -, 因为分式方程的解为正数, 所以43a ->0且43a-≠4, 解得:a <3且a≠2, 解不等式1722x a x x >⎧⎪⎨+≥-⎪⎩,得:x≤a+7, ∵不等式组有解,∴a+7>1,解得:a >-6,综上,-6<a <3,且a≠2,则满足上述要求的所有整数a 的绝对值的和为:|-5|+|-4|+|-3|+|-2|+|-1|+|0|+|1|=16,故选:C .【点睛】本题考查了分式方程的解以及解一元一次不等式,根据分式方程的解为正数结合不等式组有解,找出-6<a <3且a≠2是解题的关键.16.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x 千米/小时,根据题意,得 A .25301018060(%)x x -=+ B .253010180(%)x x -=+ C .30251018060(%)x x -=+ D .302510180(%)x x -=+ 【答案】A【解析】若设走路线一时的平均速度为x 千米/小时,根据路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达可列出方程.解:设走路线一时的平均速度为x 千米/小时,()253010180%60x x -=+ 故选A .17.“绿水青山就是金山银山”.某工程队承接了60万平方米的荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了25%,结果提前30天完成了这一任务.设实际工作时每天绿化的面积为x 万平方米,则下面所列方程中正确的是( )A .606030(125%)x x -=+B .606030(125%)x x-=+ C .60(125%)6030x x⨯+-= D .6060(125%)30x x⨯+-= 【答案】C【解析】 分析:设实际工作时每天绿化的面积为x 万平方米,根据工作时间=工作总量÷工作效率结合提前 30 天完成任务,即可得出关于x 的分式方程.详解:设实际工作时每天绿化的面积为x 万平方米,则原来每天绿化的面积为125%x +万依题意得:606030125%x x -=+,即()60125%6030x x ⨯+-=. 故选C .点睛:考查了由实际问题抽象出分式方程.找到关键描述语,找到合适的等量关系是解决问题的关键.18.八年级(1)班全体师生义务植树300棵.原计划每小时植树x 棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是( )A .300300201.2x x -= B .300300201.260x x =- C .300300201.260x x x -=+ D .3002030060 1.2x x -= 【答案】D【解析】【分析】原计划每小时植树x 棵,实际工作效率提高为原计划的1.2倍,故每小时植1.2x 棵,原计划植300棵树可用时300x 小时,实际用了3001.2x 小时,根据关键语句“结果提前20分钟完成任务”可得方程.【详解】设原计划每小时植树x 棵,实际工作效率提高为原计划的1.2倍,故每小时植1.2x 棵,由题意得:3002030060 1.2x x-=, 故选:D .【点睛】 此题主要考查了由实际问题抽象出分式方程,关键是弄清题意,表示出原计划植300棵树所用时间与实际所用时间.19.对于实数a 、b ,定义一种新运算“⊗”为:23a b a ab⊗=-,这里等式右边是通常的四则运算.若32x x ⊗⊗(﹣)=,则x 的值为( )A .-2B .-1C .1D .2 【答案】B【解析】【分析】利用题中的新定义变形已知等式,然后解方程即可.根据题中的新定义化简得:339342x x=+-,去分母得:12﹣6x =27+9x ,解得:x =﹣1,经检验x =﹣1是分式方程的解.故选B .【点睛】本题考查了新定义和解分式方程,利用了转化的思想,解分式方程注意要检验.20.已知关于x 的分式方程13222mx x x -+=--有解,则m 应满足的条件是( ) A . 1 2m m ≠≠且B .2m ≠C .1m =或2m =D .1m ≠或2m ≠ 【答案】A【解析】【分析】分式方程去分母转化为整式方程(m-2)x=-2,由分式方程有解可知m-2≠0,最简公分母x-2≠0,求出x 的值,进一步求出m 的取值即可.【详解】 13222mx x x-+=--, 去分母得,1-(3-mx )=2(x-2)整理得,(m-2)x=-2 ∵分式方程13222mx x x-+=--有解, ∴m-2≠0,即m≠2, ∴22x m -=- ∵分式方程13222mx x x-+=--有解, ∴x-2≠0,即x≠2, ∴222m -≠-,解得,m≠1, 所以,m 的取值为: 1 m ≠且2m ≠故选:A.【点睛】 此题主要考查了分式方程的求解,关键是会解出方程的解,注意隐含条件.。
最新最新初中数学—分式的难题汇编及答案

一、选择题1.下列变形正确的是( )A .()23524a a -=- B .22220x y xy -= C .23322b ab a a-÷=- D .()()222222x y x y x y +-=- 2.如果把5xyx y +中的x 和y 都扩大为原来的10倍,那么这个分式的值( ) A .不变 B .扩大为原来的50倍C .扩大为原来的10倍D .缩小为原来的1103.0.000002019用科学记数法可表示为( )A .0.2019×10﹣5 B .2.019×10﹣6 C .20.19×10﹣7 D .2019×10﹣9 4.小张在课外阅读中看到这样一条信息:“肥皂泡的厚度约为0.0000007m ”,请你用科学记数法表示肥皂泡的厚度,下列选项正确的是( )A .0.7 ⨯10-6 mB .0.7 ⨯10-7mC .7 ⨯10-7mD .7 ⨯10-6m5.已知0212,,0.253a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,a ,b ,c 的大小关系是( ) A .a >b >c B .b >a >c C .c >a >b D .c >b >a6.下列计算正确的有().①0(1)1-= ②21333-⨯= ③()()33m m x x -=- ④2211224x x x ⎛⎫-=-+ ⎪⎝⎭ ⑤22(3)(3)9a b b a a b ---=- A .4个B .3个C .2个D .1个 7.把分式ab a b+中的a 、b 都扩大为原来的3倍,则分式的值( ) A .扩大为原来的6倍 B .不变C .缩小为原来的13 D .扩大为原来的3倍 8.若代数式1x x +有意义,则实数x 的取值范围是( ) A .0x =B .1x =-C .1x ≠D .1x ≠- 9.与分式()()a b a b ---+相等的是( )A .a b a b +-B .a b a b -+C .a b a b +--D .a b a b--+ 10.如果把分式2x y z xyz -+中的正数x ,y ,z 都扩大2倍,则分式的值( ) A .不变B .扩大为原来的两倍C .缩小为原来的14D .缩小为原来的18 11.如果把分式2++a b a b 中的a 和b 都扩大为原来的10倍,那么分式的值( ) A .不变 B .缩小10倍 C .是原来的20倍 D .扩大10倍12.目前,世界上能制造出的小晶体管的长度只有0.00000004m 将0.00000004用科学记数法表示为( )A .3410-⨯B .80.4 10⨯C .8410⨯D .8410-⨯13.如图是数学老师给玲玲留的习题,玲玲经过计算得出的正确结果为( )A .1B .2C .3D .4 14.下列各式中,正确的是( ) A .22x y x y -++=- B .()222x y x y x y x y --=++ C .1a b b ab b ++= D .23193x x x -=-- 15.若23a b =≠0,则代数式(2244b ab a-+1)2b a a -÷的值为( ) A .2 B .1C .﹣1D .﹣2 16.下列运算错误的是( ) A .235a a a ⋅=B .()()422ab ab ab ÷-=C .()222424ab a b -=D .3322a a-= 17.新冠肺炎疫情爆发以来,口罩成为需求最为迫切的防护物资.在这个关键时刻,我国某企业利用自身优势转产口罩,这背后不仅体现出企业强烈的社会责任感,更是我国人民团结一心抗击疫情的决心.据悉该企业3月份的口罩日产能已达到500万只,预计今后数月内都将保持同样的产能,则3月份(按31天计算)该企业生产的口罩总数量用科学记数法表示为( )A .71.5510⨯只B .81.5510⨯只C .90.15510⨯只D .6510⨯只 18.2019年底,我国爆发了新一轮的冠状病毒疫情,冠状病毒直径约80-120纳米,1纳米=1.0×10-9米,用科学记数法表示120纳米,其结果是( )A .1.2×10-9米B .1.2×10-8米C .1.2×10-7米D .1.2×10-6米 19.下列计算:①3362a a a ⋅=;②2352m m m +=;③()224-24a a =-;④()21048a a aa ⋅÷=;⑤()-21-510=;⑥22m a m n a n +=+,其中正确的个数为( ) A .4个B .3个C .2个D .1个 20.222142x x x ÷--的计算结果为( ) A .2x x + B .22x x + C .22x x - D .2(2)x x + 21.若代数式21a 4-在实数范围内有意义,则实数a 的取值范围为( ) A .a 4≠B .a 2>-C .2a 2-<<D .a 2≠± 22.若115a b =,则a b a b -+的值是( ) A .25 B .38 C .35 D .11523.(2017河北)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )A .4+446=B .004+4+4=6C .34+4=6D .14446-=24.化简21211a a a a----的结果为( ) A .11a a +- B .a ﹣1 C .a D .125.已知11(1,2)a x x x =-≠≠,23121111,,,111n n a a a a a a -==⋯⋯=---,则2017a =( )A .21x x --B .12x -C .1x -D .无法确定【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】原式各项计算得到结果,即可作出判断.【详解】A 、原式=4a 6,错误;B 、原式不能合并,错误;C 、原式=−232a,正确; D 、原式=2x 2−4xy +xy−2y 2=2x 2−3xy−2y 2,错误.故选:C .【点睛】此题考查了分式的乘除法,合并同类项,幂的乘方与积的乘方,以及整式的乘法,熟练掌握公式及运算法则是解本题的关键.2.C解析:C【解析】【分析】首先分别判断出x 与y 都扩大为原来的10倍后,分式的分子、分母的变化情况,然后判断出这个代数式的值和原来代数式的值的关系即可.【详解】解:∵x 与y 都扩大为原来的10倍,∴5xy 扩大为原来的100倍,x+y 扩大为原来的10倍, ∴5xy x y+的值扩大为原来的10倍, 即这个代数式的值扩大为原来的10倍.故选:C .【点睛】本题考查分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,要熟练掌握,解答此题的关键是分别判断出分式的分子、分母的变化情况.3.B解析:B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.000002019=2.019×10﹣6,故选B .【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.4.C解析:C【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.000 000 7=7×10-7. 故选C .【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.5.C解析:C【解析】【分析】根据负整数指数幂和零指数幂法则计算,比较即可.【详解】02129==10.25=434a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,,, ∵4>94>1, ∴c >a >b .故选C .【点睛】此题考查了负整数指数幂和零指数幂的运算,掌握其运算法则是解答此题的关键.6.C解析:C【解析】【分析】直接利用整数指数幂的法则和乘法公式分别计算得出答案.【详解】解:①0(1)1-=,故①正确;②211333=93-⨯=⨯,故②正确; ③当m 是偶数时,()()333=m m mx x x -=,故③错误;④221124x x x ⎛⎫-=-+ ⎪⎝⎭,故④错误;⑤22(3)(3)9a b b a b a ----=,故⑤错误.正确的有①②,共2个.故选C【点睛】本题考查了整数指数幂的运算法则和乘法公式,熟练掌握幂的各种性质和法则,乘法公式是解题的基础.7.D解析:D【解析】 试题解析:把分式ab a b +中的a 、b 都扩大为原来的3倍,则33333a b ab a b a b⨯=++,故分式的值扩大3倍.故选D . 8.D解析:D【解析】【分析】根据分式有意义的条件即分母不等于零可得x+1≠0,从而得解.【详解】解:由题意得:x+1≠0,解得:x≠-1,故选:D .【点睛】本题考查分式有意义的条件,解题关键是掌握分式有意义的条件:分母不等于零.9.B解析:B【分析】根据分式的基本性质,分式的分子和分母同时乘以和除以一个不为0的整式,分式的值不变.【详解】解:原分式()()()()()()1=1a b a b a ba b a b a b----⨯--=-+-+⨯-+,故选B.【点睛】本题主要考查分式的基本性质,解决本题的关键是要熟练掌握分式的基本的性质.10.C解析:C【分析】用2x、2y,2z去替换原分式中的x、y和z,利用分式的基本性质化简,再与原分式进行比较即可得到答案.【详解】∵把分式2x y zxyz-+中的正数x,y,z都扩大2倍,∴2222212 22244x y z x y z x y zx y z xyz xyz-⨯+-+-+==⨯⋅⋅.∴分式的值缩小为原来的1 4 .故选:C.【点睛】考查了分式的基本性质,解题关键把字母变化后的值代入式子中,然后化简,再与原式比较,得出结论.11.A解析:A【分析】根据分式的基本性质代入化简即可.【详解】扩大后为:102022=1010)a b a b a b a b a b a b+++=+++10()10(分式的值还是不变故选:A.【点睛】本题考查分式的基本性质,熟练掌握性质是关键.12.D解析:D【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】解:0.000 000 04=4×10-8, 故选:D .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.13.C解析:C【分析】 先将原式通分,可以得到222b a ab ab++,再将分子用完全平方公式进行变形,即可得到()222a b ab ab+-+,最后代入数值计算即可. 【详解】 因为2b a a b++ ()2222222222323233b a ab abb a aba b ab ab=+++=++-=+-⨯=+= 所以选C.【点睛】本题考查的是分式的通分和完全平方公式的变形,能够熟练掌握完全平方公式的变形是解题的关键. 14.B解析:B【分析】根据分式的性质,对每个选项的式子一一判断正误即可.【详解】22x y x y -+-=-,故A 选项错误;()222()()()()x y x y x y x y x y x y x y x y --+-==++++,故B 选项正确; 1b a b a ab b++=,故C 选项错误;23319(3)(3)3x x x x x x --==-+-+,故D 选项错误. 故选:B .【点睛】本题主要考查分式的化简,熟记分式的性质是解题关键. 15.A解析:A【分析】 由23a b =≠0,得2b =3a ,把根据分式运算法则进行化简,再代入已知值计算即可. 【详解】 解:(2244b ab a-+1)2b a a -÷ 222442b ab a a a b a-+=•- 22(2)2a b a a b a-=•- 2b a a -=, ∵23a b =≠0, ∴2b =3a , ∴原式32a a a a a-===2, 故选:A .【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.16.B解析:B【分析】直接运用同底数幂的乘法运算法则、单项式除以单项式运算法则、积的乘方与幂的乘方运算法则以及负整数指数幂的意义分别计算得出答案再进行判断即可.【详解】A . 235a a a ⋅=,计算正确,不符合题意;B . ()()4222ab ab a b ÷-=,原选项计算错误,符合题意;C . ()222424aba b -=,计算正确,不符合题意; D . 3322a a-=,计算正确,不符合题意. 故选:B .【点睛】此题主要考查了幂的运算,熟练掌握运算法则是解题的关键.17.B解析:B【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】500万×31=5000000×31=155000000=1.55×108(只),故选:B .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.18.C解析:C【分析】绝对值小于1的正数利用科学记数法表示,一般形式为a ×10-n ,n 由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:120纳米=120×10-9米=1.2×10-7米,故选:C .【点睛】本题考查用科学记数法表示较小的数(绝对值小于1的正数利用科学记数法表示,一般形式为a ×10-n ,n 由原数左边起第一个不为零的数字前面的0的个数所决定),明确科学记数法的表示方法是解题的关键.19.D解析:D【分析】利用同底数幂相乘、合并同类项、积的乘方、幂的乘方、负整数指数幂以及整式的除法逐个判断即可.【详解】解:①336a a a ⋅=,故①错误;②2m 和3m 不是同类项,不能合并,故②错误;③()()()222224-2-24a a a ==,故③错误;④()2104268a a a a a a ⋅÷==⋅,故④正确;⑤()-21-525=,故⑤错误;⑥22m a m n a n+≠+,故⑥错误;只有1正确. 故答案为D .【点睛】本题考查了同底数幂相乘、合并同类项、积的乘方、幂的乘方、负整数指数幂、整式的除法等知识点,掌握相关运算法则是解答本题的关键.20.B解析:B【分析】先把分母因式分解,再把除法转换为乘法,约分化简得到结果.【详解】222142x x x÷-- =21(2)(2)(2)x x x x ÷+-- =()()()2·222x x x x -+- =22x x +. 故选:B .【点睛】本题主要考查了分式的除法,约分是解答的关键.21.D解析:D【分析】分式有意义时,分母a 2-4≠0.【详解】依题意得:a 2-4≠0,解得a≠±2.故选D .【点睛】本题考查了分式有意义的条件.分式有意义的条件是分母不等于零22.B解析:B【分析】直接根据已知用含x 的式子表示出两数,进而代入化简得出答案.【详解】 解:∵115a b = ∴设11a x =,5b x = ∴11531158a b x x a b x x --==++ 故选:B【点睛】 此类化简求值题目,涉及到的字母a 、b 利用第三个未知数x 设出,代入后得到关于x 的式子进行约分化简即可.将两个字母转化为一个字母是解题的关键.23.D解析:D【详解】∵4+46=,∴选项A 不符合题意;∵4+40+40=6,∴选项B 不符合题意;∵,∴选项C 不符合题意;∵144-=1486≠,∴选项D 符合题意, 故选D . 24.B解析:B【解析】分析:根据同分母分式加减法的运算法则进行计算即可求出答案.详解:原式=21211a a a a -+--, =2(1)1a a --, =a ﹣1故选B .点睛:本题考查同分母分式加减法的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.25.C解析:C【分析】按照规定的运算方法,计算出前几个数的值,进一步找出数字循环的规律,利用规律得出答案即可.【详解】解:∵11(1,2)a x x x =-≠≠,∴2111111(1)2a a x x ===----,321121111()2x a a xx-===----,34111211()1a x x a x===-----… ∴以x−1,12x -,21x x --为一组,依次循环, ∵2017÷3=672…1,∴2017a 的值与a 1的值相同,∴20171a x =-,故选:C .【点睛】此题考查数字的变化规律以及分式的运算,找出数字之间的运算规律,利用规律解决问题是解答此题的关键.。
(专题精选)最新初中数学—分式的难题汇编含答案

一、选择题1.若把分式3xyx y-(,x y均不为0)中的x和y都扩大3倍,则原分式的值是()A.扩大3倍B.缩小至原来的13C.不变D.缩小至原来的162.若把分式x yxy+中的x和y都扩大2倍,那么分式的值()A.扩大2倍B.不变C.缩小2倍D.缩小4倍3.小张在课外阅读中看到这样一条信息:“肥皂泡的厚度约为0.0000007m ”,请你用科学记数法表示肥皂泡的厚度,下列选项正确的是()A.0.7 ⨯10-6m B.0.7 ⨯10-7m C.7 ⨯10-7m D.7 ⨯10-6m4.已知2125,,0.253a b c--⎛⎫⎛⎫=-==⎪⎪ ⎪⎝⎭⎝⎭,a,b,c的大小关系是()A.a>b>c B.b>a>c C.c>a>b D.c>b>a5.把分式a2a b+中的a、b都扩大2倍,则分式的值()A.缩小14B.缩小12C.扩大2倍D.不变6.下列四种说法(1)分式的分子、分母都乘以(或除以),分式的值不变;(2)分式的值能等于零;(3)的最小值为零;其中正确的说法有()A.1个B.2 个C.3 个D.0个7.把分式aba b+中的a、b都扩大为原来的3倍,则分式的值()A.扩大为原来的6倍B.不变C.缩小为原来的13D.扩大为原来的3倍8.与分式11aa-+--相等的式子是()A.11aa+-B.11aa-+C.11aa+--D.11aa--+9.如果把分式2x y zxyz-+中的正数x,y,z都扩大2倍,则分式的值( )A.不变B.扩大为原来的两倍 C.缩小为原来的14D.缩小为原来的1810.如果把分式2++a ba b中的a和b都扩大为原来的10倍,那么分式的值()A .不变B .缩小10倍C .是原来的20倍D .扩大10倍 11.下列运算结果最大的是( ) A .112-⎛⎫ ⎪⎝⎭ B .02 C .12- D .()12- 12.0.000002019用科学记数法可表示为( ) A .0.2019×10﹣5 B .2.019×10﹣6 C .20.19×10﹣7 D .2019×10﹣9 13.下列各分式中,最简分式是( )A .21x x +B .22m n m n-+ C .22a b a b +- D .22x y x y xy ++ 14.下列分式中,属于最简分式的是( ) A .42x B .11x x -- C .211x x +- D .224x x - 15.在某次数学小测中,老师给出了5个判断题.如图为张晓亮的答卷,每个小题判断正确得20分,他的得分应是( )A .100分B .80分C .60分D .40分 16.将分式2a b ab+中的a 、b 都扩大为原来的2倍,则分式的值( ) A .缩小到原来的12倍 B .扩大为原来的2倍C .扩大为原来的4倍D .不变 17.若m+2n =0,则分式22221m n m m mn m m n +⎛⎫+÷⎪--⎝⎭的值为( ) A .32B .﹣3nC .﹣32nD .92 18.若把分式xx y 2中的x 和y 同时扩大为原来的3倍,则分式的值( ) A .扩大3倍 B .缩小6倍 C .缩小3倍 D .保持不变19.下列运算正确的是( )A .1133a a ﹣=B .2322a a a +=C .326()•a a a ﹣=﹣D .32()()a a a ÷﹣﹣= 20.小明家到学校m 千米,若步行从家到学校,需要t 小时;若骑自行车,所用时间比步行少用20分钟,则骑自行车的比步行的速度快了( )A .3(1)m t t -千米/时B .(31)m t t - 千米/时C .(31)m t t -+ 千米/时D .13m t - 千米/时 21.若20.3a =-,23b -=-,021(3)3c d -⎛⎫=-=- ⎪⎝⎭,,则( ) A .a b c d <<< B .b a d c <<< C .a d c b <<< D .c a d b <<< 22.2019年底,我国爆发了新一轮的冠状病毒疫情,冠状病毒直径约80-120纳米,1纳米=1.0×10-9米,用科学记数法表示120纳米,其结果是( ) A .1.2×10-9米 B .1.2×10-8米 C .1.2×10-7米 D .1.2×10-6米 23.若x 取整数,则使分式6321x x +-的值为整数的x 值有( ) A .3个 B .4个C .6个D .8个 24.当x 为任意实数时,下列分式中,一定有意义的是( )A .1xB .11x +C .11x -D .211x + 25.下列运算正确的是( )A .623x x x= B .221x a a x b b ++=++ C .1122x x x x ---=-- D .0.71070.20.323a b a b a b a b --=++【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】将原式中x 变成3x ,将y 变成3y ,再进行化简,与原式相比较即可.【详解】 由题意得3332733333()x y xy xy x y x y x y⋅⋅==⋅---,所以原分式的值扩大了3倍 故选择A.【点睛】此题考察分式的化简,注意结果应化为最简分式后与原分式相比较.2.C解析:C【解析】【分析】根据题意,分式中的x 和y 都扩大2倍,则222()2242x y x y x y x y xy xy +++==⋅; 【详解】 解:由题意,分式x yy x +中的x 和y 都扩大2倍, ∴222()2242x y x y x y x y xy xy+++==⋅; 分式的值是原式的12,即缩小2倍; 故选C .【点睛】本题考查了分式的基本性质,分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,分子、分母、分式本身同时改变两处的符号,分式的值不变. 3.C解析:C【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.000 000 7=7×10-7. 故选C .【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.4.C解析:C【解析】【分析】根据负整数指数幂和零指数幂法则计算,比较即可.【详解】2129==10.25=434a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,,, ∵4>94>1,∴c>a>b.故选C.【点睛】此题考查了负整数指数幂和零指数幂的运算,掌握其运算法则是解答此题的关键.5.D解析:D【解析】【分析】根据题意进行变形,发现实质上是分子、分母同时扩大2倍,根据分式的基本性质即可判断.【详解】根据题意,得把分式a2a b+中的a、b都扩大2倍,得2a2a a22a2b2(2a b)2a b==⨯+++,根据分式的基本性质,则分式的值不变.故选D.【点睛】此题考查了分式的基本性质.6.A解析:A【解析】(1)分式的分子、分母都乘以(或除以)不为零的整式,分式的值不变,故(1)错误;(2)分式的值不能等于零,故②错误;(3)的最小值为零,故(3)正确;故选A.7.D解析:D【解析】试题解析:把分式aba b+中的a、b都扩大为原来的3倍,则33333a b aba b a b⨯=++,故分式的值扩大3倍.故选D.8.B解析:B【分析】根据分式的基本性质即可得出:分式的分子、分母、分式本身的符号,改变其中的任意两个,分式的值不变,据此即可解答.解:原式=1)(1)aa--+-(=11aa-+故选:B.【点睛】本题考查分式的基本性质,解题关键是熟练掌握分式的基本性质.9.C解析:C【分析】用2x、2y,2z去替换原分式中的x、y和z,利用分式的基本性质化简,再与原分式进行比较即可得到答案.【详解】∵把分式2x y zxyz-+中的正数x,y,z都扩大2倍,∴2222212 22244x y z x y z x y zx y z xyz xyz-⨯+-+-+==⨯⋅⋅.∴分式的值缩小为原来的1 4 .故选:C.【点睛】考查了分式的基本性质,解题关键把字母变化后的值代入式子中,然后化简,再与原式比较,得出结论.10.A解析:A【分析】根据分式的基本性质代入化简即可.【详解】扩大后为:102022=1010)a b a b a b a b a b a b+++=+++10()10(分式的值还是不变故选:A.【点睛】本题考查分式的基本性质,熟练掌握性质是关键.11.A解析:A【解析】【分析】直接利用负整数指数幂的性质和零指数幂的性质分别化简得出答案.∵11=22-⎛⎫ ⎪⎝⎭;02=1;12-=12;()12=2--, 2>1>12>-2, ∴运算结果最大的是112-⎛⎫ ⎪⎝⎭, 故选A.【点睛】本题主要考查了负整数指数幂的性质和零指数幂的性质,正确化简各数是解题关键.12.B解析:B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.000002019=2.019×10﹣6,故选B .【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.13.A解析:A【分析】最简分式就是分式的分子和分母没有公因式,也可理解为分式的分子和分母的最大公因式为1.所以判断一个分式是否为最简分式,关键是要看分式的分子和分母的最大公因式是否为1.【详解】解:A. 21x x +,分子分母的最大公因式为1; B. 22m n m n-+,分子分母中含有公因式m+n; C.22a b a b +-,分子分母中含有公因式a+b ; D. 22x y x y xy ++,分子分母中含有公因式x+y【点睛】最简分式首先系数要最简;一个分式是否为最简分式,关键看分子与分母是不是有公因式,但表面不易判断,应将分子、分母分解因式.14.D解析:D【分析】根据最简分式的定义即可判断.【详解】 解:42=2x x,故A 选项错误; ()11=111x x x x ---=---,故B 选项错误; ()()2111==1111x x x x x x ++-+--,故C 选项错误; 224x x -,故D 选项正确. 故选:D【点睛】本题主要考查的是最简分式的定义,正确的掌握最简分式的定义是解题的关键.15.B解析:B【分析】依据分式的化简,无理数定义,平方根定义,实数的大小比较方法依次判断各小题正确与否即可确定他的得分.【详解】 因为c a c b ++是最简分式不能在进行化简,故第1小题错误,他判断正确得20分; 因为227是分数属于有理数,不是无理数,所以第2小题错误,他判断正确得20分;因为0.6=-,所以第3小题错误,他判断错误不得分;因为23<<,所以112<<,所以第4小题正确,他判断正确得20分; 数轴上的点可以表示无理数,故第5小题错误,他判断正确得20分.故他应得80分,选择B【点睛】此题考察分式的化简,无理数定义,平方根定义,实数的大小比较方法,熟练掌握才能正确判断.16.A【分析】用2a ,2b 分别替换掉原分式中的a 、b ,进行计算后与原分式对比即可得出答案.【详解】用2a ,2b 分别替换掉原分式中的a 、b ,可得:()2221=222822+++=⨯⨯⨯a b a b a b a b ab ab ,所以分式缩小到原来的12倍, 故选A.【点睛】本题考查了分式的基本性质,关键是根据条件正确的替换原式中的字母,然后化简计算.17.A解析:A【分析】直接利用分式的混合运算法则进行化简,进而把已知代入求出答案.【详解】 解:原式=2()m n m n m m n ++--•(+)()m n m n m- =3()m m m n -•(+)()m n m n m- =3()m n m+, ∵m+2n =0,∴m =﹣2n , ∴原式=32n n --=32. 故选:A .【点睛】 此题主要考查分式的运算,解题的关键是熟知分式的运算法则.18.D解析:D【分析】 根据题意把分式xx y 2中的x 和y 同时扩大为原来的3倍,将其化简后与原分式进行比价即可做出判断.【详解】 解:∵分式xx y 2中的x 和y 同时扩大为原来的3倍∴()23322333x x x x y x y x y⋅⋅==+++ 则分式的值保持不变.故选:D【点睛】本题考查了分式的基本性质,属于基础题型,能够熟练掌握分式的基本性质是解决问题的关键.19.D解析:D【分析】直接利用负指数幂的性质以及同底数幂的乘除运算法则计算得出答案.【详解】解:A 、133a a-=,故此选项错误; B 、22a a +,不是同类项无法合并; C 、()325a a a -⋅=-,故此选项错误;D 、()()32a a a -÷-=,正确; 故选:D .【点睛】此题考查负指数幂的性质以及同底数幂的乘除运算,正确掌握相关运算法则是解题关键.20.B解析:B【分析】利用速度=路程÷时间分别求得步行的速度和骑自行车的速度,从而利用分式的运算法则求得两者的速度差.【详解】 解:步行的速度是:m t (km /h ),骑自行车的速度是:31313m m t t =--(km /h ), 则骑自行车的速度与步行的速度差为:331(31)m m m t t t t-=--. 故选:B .【点睛】本题考查了列代数式及分式的加减运用,正确表示出步行和骑自行车的速度是解题的关键. 21.B解析:B【分析】分别求出a 、b 、c 、d 的值,比较大小即可.【详解】20.30.09a =-=-2213139b -=-=-=- 01()3c =-=1 2211=(-3))9(3d -==- 故b a d c <<<故选:B【点睛】本题考查正指数与负指数的计算,注意负指数的运算规则.22.C解析:C【分析】绝对值小于1的正数利用科学记数法表示,一般形式为a ×10-n ,n 由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:120纳米=120×10-9米=1.2×10-7米,故选:C .【点睛】本题考查用科学记数法表示较小的数(绝对值小于1的正数利用科学记数法表示,一般形式为a ×10-n ,n 由原数左边起第一个不为零的数字前面的0的个数所决定),明确科学记数法的表示方法是解题的关键.23.B解析:B【分析】 首先把分式转化为6321x +-,则原式的值是整数,即可转化为讨论621x -的整数值有几个的问题.【详解】 6363663212121x x x x x +-+==+---, 当216x -=±或3±或2±或1±时,621x -是整数,即原式是整数. 当216x -=±或2±时,x 的值不是整数,当等于3±或1±是满足条件. 故使分式6321x x +-的值为整数的x 值有4个,是2,0和1±.故选B.【点睛】本题主要考查了分式的值是整数的条件,把原式化简为6321x+-的形式是解决本题的关键.24.D解析:D【分析】根据分式有意义分母不为零分别进行分析即可.【详解】A、当0x=时,分式无意义,故此选项错误;B、当1x=-时,分式无意义,故此选项错误;C、当1x=时,分式无意义,故此选项错误;D、当x为任意实数时,分式都有意义,故此选项正确;故选:D.【点睛】本题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.25.D解析:D【分析】根据分式的基本性质,将每一个分式的分子与分母的公因式约去,再比较即可.【详解】A.633xxx=,故该选项不符合题意;B. 221x a ax b b++≠++,故该选项不符合题意;C.1x122xx x---=--,故该选项不符合题意;D.0.71070.20.323a b a ba b a b--=++,故该选项符合题意;故选:D【点睛】此题考查约分,解题关键在于掌握运算法则.。
最新初中数学分式难题汇编附答案解析

最新初中数学分式难题汇编附答案解析一、选择题1.化简(a ﹣1)÷(1a﹣1)•a 的结果是( ) A .﹣a 2 B .1 C .a 2 D .﹣1【答案】A 【解析】分析:根据分式的混合运算顺序和运算法则计算可得. 详解:原式=(a ﹣1)÷1aa-•a =(a ﹣1)•()1aa --•a=﹣a 2, 故选:A .点睛:本题主要考查分式的混合运算,解题的关键是掌握分式的混合运算顺序和运算法则.2.下列运算中,正确的是( )A .2+=B .632x x x ÷=C .122-=-D .325a a a ⋅=【答案】D 【解析】 【分析】根据实数的加法对A 进行判断;根据同底数幂的乘法对B 进行判断;根据负整数指数幂的意义对C 进行判断;根据同底数幂的除法对D 进行判断. 【详解】解:A 、2不能合并,所以A 选项错误; B 、x 6÷x 3=x 3,所以B 选项错误; C 、2-1=12,所以C 选项错误; D 、a 3•a 2=a 5,所以D 选项正确. 故选:D . 【点睛】此题考查实数的运算,负整数指数幂,同底数幂的乘法与除法,解题关键在于掌握先算乘方,再算乘除,然后进行加减运算;有括号先算括号.3.乐乐所在的四人小组做了下列运算,其中正确的是( )A .2193-⎛⎫-=- ⎪⎝⎭B .()23624a a -=C .623a a a ÷=D .236236a a a ?【答案】B 【解析】 【分析】根据负整数指数幂计算法则,积的乘方计算法则,同底数幂除法法则,单项式乘以单项式计算法则依次判断. 【详解】A 、2913-⎛⎫- ⎪⎭=⎝,故错误; B 、()23624a a -=正确;C 、624a a a ÷=,故错误;D 、235236a a a =⋅, 故选:B. 【点睛】此题考查整式的计算,正确掌握负整数指数幂计算法则,积的乘方计算法则,同底数幂除法法则,单项式乘以单项式计算法则是解题的关键.4.已知24111P Qx x x =+-+-是恒等式,则( ) A .2, 2P Q ==- B .2, 2P Q =-= C .2P Q == D .2P Q ==-【答案】B 【解析】 【分析】首先利用分式的加减运算法则,求得()()2111Qx x x P Q x Q P P ++-=-++-,可得方程组04P Q Q P +=⎧⎨-=⎩,解此方程组即可求得答案. 【详解】 解:∵()()()()()()22111411111P x Q x P Q x Q P P Qx x x x x x -++++-=+==+-+---, ∴()()4P Q x Q P ++-=,∴04P Q Q P +=⎧⎨-=⎩,解之得:22P Q =-⎧⎨=⎩,故选:B . 【点睛】此题考查了分式的加减运算、二元一次方程的解法以及整式相等的性质,解题的关键是掌握分式的加减运算法则.5.若(x ﹣1)0=1成立,则x 的取值范围是( ) A .x =﹣1 B .x =1C .x≠0D .x≠1【答案】D 【解析】试题解析:由题意可知:x-1≠0, x≠1 故选D.6.化简2442x xx x ---得结果是( ) A .26x x -+ B .2x x + C .2x x -+ D .2x x - 【答案】C 【解析】 【分析】先通分,再按照分式的减法法则化简出最简结果即可得答案. 【详解】2442x xx x --- =4(2)(2)(2)(2)(2)x x x x x x x +-+-+-=242(2)(2)x x x x x --+- =(2)(2)(2)x x x x --+-=2xx -+. 故选:C . 【点睛】本题考查分式的减法,同分母分式相加减,只把分子相加减,分母不变;异分母分式相加减,先通分变为同分母分式,再按同分母分式相加减的法则运算.7.关于分式25x x-,下列说法不正确的是( ) A .当x=0时,分式没有意义 B .当x >5时,分式的值为正数 C .当x <5时,分式的值为负数 D .当x=5时,分式的值为0【解析】【分析】此题可化转化为分别求当分式等于0、大于0、小于0、无意义时的x的取值范围,分别计算即可求得解.【详解】A.当x=0时,分母为0,分式没有意义;正确,但不符合题意.B.当x>5时,分式的值为正数;正确,但不符合题意C.当0<x<5时,分式的值为负数;当x=0是分式没有意义,当x<0时,分式的值为负数,原说法错误,符合题意.D.当x=5时,分式的值为0;正确,但不符合题意.故选:C.【点睛】本题主要考查分式的性质的运用,注意分式中分母不为0的隐性条件.8.人的头发直径约为0.00007m,这个数据用科学记数法表示()A.0.7×10﹣4 B.7×10﹣5 C.0.7×104 D.7×105【答案】B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.00007m,这个数据用科学记数法表示7×10﹣5.故选:B.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.9.如果a2+3a﹣2=0,那么代数式()的值为()A.1 B.C.D.【答案】B【解析】【分析】原式括号中两项通分并利用同分母分式的加法法则计算,约分得到最简结果,把已知等式代入计算即可求出值.原式=,由a 2+3a ﹣2=0,得到a 2+3a =2, 则原式=, 故选B . 【点睛】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.10.下列运算中正确的是( )A .62652()a a a a a == B .624282()()a a a a == C .62121022()a a a a a == D .6212622()a a a a a== 【答案】C 【解析】 【分析】根据幂的乘方法则、分式的基本性质及同底数幂除法法则计算即可得答案.【详解】6212122102222()a a a a a a a a a ÷===÷, 故选:C . 【点睛】本题考查幂的乘方及分式的基本性质,幂的乘方,底数不变,指数相乘;分式的分子、分母同时乘以(或除以)一个不为0的整式,分式的值不变;同底数幂相除,底数不变,指数相减;熟练掌握分式的基本性质是解题关键.11.若115a b =,则a b a b-+的值是( ) A .25B .38C .35D .115【答案】B 【解析】 【分析】直接根据已知用含x 的式子表示出两数,进而代入化简得出答案. 【详解】 解:∵115a b =∴设11a x =,5b x =∴11531158a b x x a b x x --==++ 故选:B 【点睛】此类化简求值题目,涉及到的字母a 、b 利用第三个未知数x 设出,代入后得到关于x 的式子进行约分化简即可.将两个字母转化为一个字母是解题的关键.12.世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( ) A .5.6×10﹣1 B .5.6×10﹣2C .5.6×10﹣3D .0.56×10﹣1【答案】B 【解析】 【详解】13.计算211a a a -+-的正确结果是( )A .211a a -- B .211a a --- C .11a - D .11a -- 【答案】A 【解析】 【分析】先将后两项结合起来,然后再化成同分母分式,按同分母分式加减的法则计算就可以了.【详解】211a a a -+-, =2(1)1a a a --- =222111a a a a a -+--- =211a a --. 故选:A. 【点睛】本题考查了数学整体思想的运用,分式的通分和约分的运用,解答的过程中注意符号的运用以及完全平方公式的运用.14.计算-12的结果为( )A .2B .12C .-2D .1-2【答案】B 【解析】 【分析】利用幂次方计算公式即可解答. 【详解】 解:原式=12. 答案选B. 【点睛】本题考查幂次方计算,较为简单.15.一次抽奖活动特等奖的中奖率为150000,把150000用科学记数法表示为( ) A .4510⨯﹣ B .5510⨯﹣C .4210⨯﹣D .5210⨯﹣【答案】D 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 【详解】150000=0.00002=2×10﹣5. 故选D . 【点睛】本题考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.16.式子2a +有意义,则实数a 的取值范围是( ) A .a≥-1 B .a≤1且a≠-2C .a≥1且a≠2D .a>2【答案】B 【解析】 【分析】直接利用二次根式有意义的条件分析得出答案. 【详解】1-a≥0且a+2≠0, 解得:a≤1且a≠-2. 故选:B . 【点睛】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.17.把分式aa b+中的,a b 的值同时扩大为原来的10倍,则分式的值( ) A .不变 B .缩小为原来的110C .扩大为原来的10倍D .扩大为原来的100倍 【答案】A 【解析】 【分析】根据分式的基本性质,把分式aa b+中的x 、y 的值同时扩大为原来的10倍得:1010=101010()a a aa b a b a b=+++,即可得到答案.【详解】 把分式aa b +中的x 、y 的值同时扩大为原来的10倍得: 1010=101010()a a aa b a b a b=+++,即分式aa b +的值不变, 故选:A . 【点睛】本题考查了分式的基本性质,正确掌握分式的基本性质是解题的关键.18.下列分式中,最简分式是( )A .22115xy yB .22x y x y -+C .222x xy y x y -+-D .22x y x y+-【答案】D 【解析】 【分析】根据最简分式的定义即可求出答案. 【详解】解:(A )原式=75xy,故A 不是最简分式; (B )原式=()()x y x y x y+-+=x-y ,故B 不是最简分式;(C )原式=2)x y x y--(=x-y ,故C 不是最简分式; (D) 22x y x y+-的分子分母都不能再进行因式分解、也没有公因式.故选:D . 【点睛】本题考查最简分式,解题关键是正确理解最简分式的定义,本题属于基础题型.19.下列运算中,正确的是( ) A .236x x x ⋅= B .333()ab a b =C .33(2)6a a =D .239-=-【答案】B 【解析】 【分析】分别根据同底数幂的乘法法则,积的乘方法则以及负整数指数幂的运算法则逐一判断即可. 【详解】x 2•x 3=x 5,故选项A 不合题意; (ab )3=a 3b 3,故选项B 符合题意; (2a )3=8a 6,故选项C 不合题意;3−2=19,故选项D 不合题意. 故选:B . 【点睛】此题考查同底数幂的乘法,幂的乘方与积的乘方以及负整数指数幂的计算,熟练掌握幂的运算法则是解题的关键.20.如果30x y -= ,那么代数式()2223x y x x y y ⎛⎫+-÷-⎪⎝⎭的值为( ) A .23B .2C .-2D .3 2【答案】A 【解析】 【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x =3y 代入化简可得.【详解】解:()2223x y x x y y ⎛⎫+-÷- ⎪⎝⎭=()22213xy x y y x y -+-g =()2()13x y y x y --g =3x y y- ∵30x y -=, ∴x=3y , ∴32333x y y y y y --==, 故选:A . 【点睛】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.。
分式重难点专练(解析版)

专题01分式重难点专练(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列分式中不是最简分式的是( )A .293a a ++B .222x y xy y x-+-C .2242x x x -+-D .3333ab a ab b ++【答案】C 【分析】根据最简分式的定义逐一判断即可.【详解】解:A. 293a a ++分子分母没有公因式,不能约分,所以它是最简分式,故A 选项不符合题意;B. 222x y xy y x-+-是最简分式,故B 选项不符合题意;C. 2242x x x -+-=()()()2x)x 221x x -++-(=21x x --,故C 选项符合题意;D. 3333ab a ab b++是最简分式, 故D 选项不符合题意.故应选C.【点睛】本题考查了最简分式的概念及分式的化简,掌握相关知识是解题的关键.2.若分式21aa -的值总是正数,则a 的取值范围是( )A .0a >B .12a >C .102a <<D .0a <或12a >【答案】D 【分析】分两种情况分析:当0a >时210a ->;或当0a p 时,210a -p ,再分别解不等式可得.【详解】若分式21aa -的值总是正数:当0a >时,210a ->,解得12a >;当0a p 时,210a -p ,解得12a <,此时a 的取值范围是0a p ;所以a 的取值范围是0a <或12a >.故选:D .【点睛】考核知识点:分式值的正负.理解分式取值的条件是解的关键点:分式分子和分母的值同号,分式的值为正数.3.下列代数式222222615,,,,321xy y x x y x xx x y x y x x p--+--+++中,最简分式的个数有( )A .1个B .2个C .3个D .4个【答案】A 【分析】根据最简分式的定义对每项进行判断即可.【详解】623xyy x-=-,不是最简分式;22y x x y x y-=---,不是最简分式;22x y x y++,是最简分式;2211211x x x x x --=+++,不是最简分式;5xp,不是分式;∴最简分式的个数有1个故答案为:A .【点睛】本题考查了最简分式的问题,掌握最简分式的定义是解题的关键.4.下列各式中是最简分式的是( )A .55x x--B .2211x x -+C .22222a ab b a b -+-D .128x y【答案】B 【分析】根据最简分式的定义,只要判断出分子分母是否有公因式即可.【详解】A 、该分式的分子分母中含有公因式(x ﹣5),不是最简分式,故本选项不符合题意;B 、该分式符合最简分式的定义,故本选项符合题意;C 、该分式的分子分母中含有公因式(a ﹣b ),不是最简分式,故本选项不符合题意;D 、该分式的分子分母中含有公因数4,不是最简分式,故本选项不符合题意.故选:B .【点睛】此题考查了最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式.5.下列变形从左到右一定正确的是().A .22a ab b -=-B .a ac b bc =C .ax a bx b=D .22a ab b =【答案】C 【分析】根据分式的基本性质依次计算各项后即可解答.【详解】选项A ,根据分式的基本性质,分式的分子和分母都乘以或除以同一个不是0的整式,分式的值不变,分式的分子和分母都减去2不一定成立,选项A 错误;选项B ,当c≠0时,等式才成立,即()0a ac c b bc=¹,选项B 错误;选项C ,axbx 隐含着x≠0,由等式的右边分式的分子和分母都除以x ,根据分式的基本性质得出ax abx b=,选项C 正确;选项D ,当a=2,b=-3时,左边≠右边,选项D 错误.故选C .【点睛】本题考查了分式的基本性质的应用,主要检查学生能否正确运用性质进行变形,熟练运用分式的基本性质是解决问题的关键.6.下列分式是最简分式的是()A.22x xyx-;B.222a ab ba b-+-;C.2211xx+-;D.211xx+-【答案】C【分析】直接利用最简分式的定义进而判断得出答案.【详解】A、22x xyx-=()22x x y x yx--=,不是最简分式,不合题意;B、222a ab ba b-+-=2()a ba ba b-=--,不是最简分式,不合题意;C、2211xx+-无法化简,是最简分式,符合题意;D、21 1x x +-=11(1)(1)1xx x x+=+--,不是最简分式,不合题意.故选:C【点睛】此题主要考查了最简分式,正确把握最简分式的定义是解题关键.7.下列式子正确的是()A.22b ba a=B.0a ba b+=+C.1a ba b-+=--D.0.10.330.22a b a ba b a b--=++【答案】C【分析】根据分式的基本性质,即可解答.【详解】A.分子乘以b,分母乘以a,所以22b ba a¹,故A错误;B.a ba b+=+1,故B错误;C.()a ba ba b a b---+==---1,故C正确;D.0.10.330.2210a b a ba b a b--=++,故D错误.故选C.【点睛】本题考查了分式的基本性质,解决本题的关键是熟记分式的基本性质.8.若分式293xx--的值为0,则x的值是( )A.﹣3B.3C.±3D.0【答案】A【分析】根据分式的值为零的条件可以求出x的值.【详解】解:根据题意,得x2﹣9=0且x﹣3≠0,解得,x=﹣3;故选:A.【点睛】若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.9.分式26 9x-有意义的条件是( )A.x≠3B.x≠9C.x≠±3D.x≠﹣3【答案】C【分析】根据分式有意义的条件是分母不等于零列出关于x的不等式,解之可得.【详解】解:当x2﹣9≠0时,分式有意义,由x2﹣9≠0得:x2≠9,则x≠±3,故选:C.【点睛】本题主要考查了分式有意义的条件,解题的关键是掌握分式有意义的条件是分母不等于零.10.在代数式2p,15x+,221xx--,33x-中,分式有()A.1个B.2个C.3个D.4个【答案】B【分析】根据分式的定义逐个判断即可得.【详解】常数2p是单项式,15x+是多项式,221x x --和33x -都是分式,综上,分式有2个,故选:B .【点睛】本题考查了分式的定义,掌握理解分式的定义是解题关键.11.下列变形不正确的是( )A .1122x x x x +-=---B .b a a bc c--+=-C .a b a bm m-+-=-D .22112323x x x x--=---【答案】A 【分析】答题首先清楚分式的基本性质,然后对各选项进行判断.【详解】解:A 、1122x xx x +--=---,故A 不正确;B 、b a a bc c --+=-,故B 正确;C 、a b a bm m-+-=-,故C 正确;D 、22112323x x x x--=---,故D 正确.故答案为:A .【点睛】本题主要考查了分式的基本性质,掌握分式的基本性质是解题的关键.12.下列各式中,正确的是()A .22a ab b =B .11a ab b+=+C .2233a b a ab b=D .232131a ab b ++=--【答案】C 【分析】利用分式的基本性质变形化简得出答案.【详解】A .22a ab b=,从左边到右边是分子和分母同时平方,不一定相等,故错误;B .11a ab b+=+,从左边到右边分子和分母同时减1,不一定相等,故错误;C .2233a b a ab b=,从左边到右边分子和分母同时除以ab ,分式的值不变,故正确;D .232131a ab b ++=--,从左边到右边分子和分母的部分同时乘以3,不一定相等,故错误.故选:C .【点睛】本题考查分式的性质.熟记分式的性质是解题关键,分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.13.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子1(0)x x x+>的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x ,则另一边长是1x ,矩形的周长是12x x æö+ç÷èø;当矩形成为正方形时,就有1(0)x x x =>,解得1x =,这时矩形的周长124x x æö+=ç÷èø最小,因此1(0)x x x +>的最小值是2.模仿张华的推导,你求得式子24(0)x x x+>的最小值是( ).A .2B .4C .6D .8【答案】B 【解析】在面积是4的矩形中,设矩形的一边长为x ,则另一边是4x,矩形的周长是2(x +4x ),当矩形成为正方形时,就有x =4x ,解得x =2,这时矩形的周长2(x +4x)=8最小,因此x +4x 的最小值是4,而24x x += x +4x ,所以24(0)x x x+>的最小值是4.故选B.点睛:本题关键在于理解已知结论的推导过程.14.如果m 为整数,那么使分式31m m ++的值为整数的m 的值有( )A .2个B .3个C .4个D .5个【答案】C 【分析】分式32111m m m +=+++,讨论21m +就可以了,即1m +是2的约数即可完成.【详解】∵32111m m m +=+++若原分式的值为整数,那么12,1,12m +=--,由12m +=-得,3m =-;由11+=-m 得,2m =-;由11m +=得,0m =;由12m +=得,1m =;∴3,2,0,1m =--,共4个故选C 【点睛】本题主要考查分式的值,熟练掌握相关知识点并全面讨论是解题关键.15.已知:2222233+=´,2333388+=´,244441515+=´,255552424+=´,……,若21010b b a a+=´(a 、b 为正整数)符合前面式子的规律,则a+b 的值是( ).A .109B .218C .326D .436【答案】A 【分析】通过观察已知式子可得分子与第一个加数相同,分母等于分子的平方减1,即可求解.【详解】解:由2222233+=´,2333388+=´,244441515+=´,255552424+=´,……,可知分子与第一个加数相同,分母等于分子的平方减1,∴在21010b ba a+=´中,b =10,a =102-1=99,∴a +b =109,故选:A .【点睛】本题考查数字的变化规律;能够通过所给例子,找到式子的规律是解题的关键.16.若x 是整数,则使分式8221x x +-的值为整数的x 值有( )个.A .2B .3C .4D .5【答案】C 【分析】先将假分式8221x x +-分离可得出6421x +-,根据题意只需21x -是6的整数约数即可.【详解】解:824(21)664212121x x x x x +-+==+---由题意可知,21x -是6的整数约数,∴211,2,3,6,1,2,3,6x -=----解得: 37151,,2,,0,,1,2222x =---,其中x 的值为整数有:0,1,1,2x =-共4个.故选:C .【点睛】本题考查的知识点是分式的值是整数的条件,分离假分式是解此题的关键,通过分离假分式得到6421x +-,从而使问题简单.二、填空题17.如果24422x a bx x x =--+-,那么+a b 的值是______.【答案】0【分析】先将分式方程每一部分的分母通分,然后观察方程的左边和右边,使方程两边的分子部分相同即可解决.【详解】解:224422444x ax a bx bx x x -+=----224()2()44x a b x a b x x --+=--所以4a b -=,0a b +=故答案是:0【点睛】本题考查了分式通分,将方程两边变为同分母,然后比较分子得出结论是解决本题的关键.18.若分式2228x x x ---的值为零,则x 的值为______________.【答案】2【分析】根据分式的值为零的条件可以求出x 的值.【详解】解:由分式的值为零的条件得2-x =0,x 2-2x-8≠0,∴x=±2且x≠4且x≠-2,∴x=2时,分式的值为0,故答案为2.【点睛】本题考查了分式值为0的条件,若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.19.若113x y +=,则分式323x xy yx xy y-+++的值为_________.【答案】74【分析】根据分式基本性质,分子和分母同时除以xy 可得.【详解】()()333322323323111111x xy y xy x xy y y x y x x xy y x xy y xy y x y x-++--+¸-+===++++¸++++若113x y +=则32392744x xy y x xy y -+-==++故答案为:74【点睛】考核知识点:分式基本性质运用.熟练运用分式基本性质是关键.20.当x =_________时,分式242x x--的值为0.【答案】2-【分析】分式有意义的条件是分母不为0;分式的值是0的条件是分母≠0且分子=0.【详解】若分式的值为0,则2-x≠0且24x -=0,即x=-2.故答案为:-2.【点睛】本题考查的是分式有意义的条件:当分母不为0时,分式有意义,并考查了分式值是0的条件.21.如果分式32x x x x--值为零,那么x =_________.【答案】1-【分析】根据分式的值为零,可得30-=x x 且20x x -¹,求解即可.【详解】∵320x x x x-=-∴30-=x x 且20x x -¹∴()()()321110x x x x x x x -=-=+-=且()210x x x x -=-¹∴123011x x x ==-=,,且01x x ¹¹,∴1x =-故答案为:1-.【点睛】本题考查了分式方程的问题,掌握解分式方程的方法是解题的关键.22.分式1753xy x y+中的,x y 同时扩大为原来的3倍,则分式的值扩大为原来的_____________倍.【答案】3【分析】将,x y 同时扩大为原来的3倍得到17353xy x y æö´ç÷+èø,与1753xy x y +进行比较即可.【详解】分式1753xy x y+中的,x y 同时扩大为原来的3倍,可得17335333x yx y´´´+´17353xyx y´=+17353xy x y æö=´ç÷+èø故答案为:3.【点睛】本题考查了分式的运算,掌握分式的运算法则是解题的关键.23.已知213x x =+,则1x x-=__________.【答案】3【分析】将213x x =+两边同时除以x ,即可得出答案.【详解】解:∵213x x=+∴两边同时除以x .,得:13=+x x ∴1-=3x x故答案为:3【点睛】本题考查了代数式求值,利用分式的性质,两边同时除以x ,将式子进行变形是解题的关键.24.下列各式中,最简分式有_____个.①11x -;②422y x +;③3x p ;④10+452a a +;⑤9+73+5p p ;⑥241025y y y ++.【答案】1.【分析】根据最简分式的定义,只要判断出分子分母是否有公因式即可.【详解】①11x-符合最简分式的定义,符合题意.②422y x+ 的分子、分母中含有公因数2,不是最简分式,不符合题意;③3x p ⑤9+73+5p p不是分式,不符合题意;④10+452a a + 的分子、分母中含有公因式(5+2a ),不是最简分式,不符合题意;⑥241025y y y ++的分子、分母中含有公因式(2y+5),不是最简分式,不符合题意;故答案为:1.【点睛】此题考查了最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式.25.当x_____________时,分式21x x x+-的值为0;【答案】=-1【解析】由题意得:x+1=0,且x 2-x≠0,解得:x=-1,故答案为=-1.26.当x=__________时,分式22121x x x --+的值为零.【答案】-1【分析】根据分式的解为0的条件,即可得到答案.【详解】解:∵分式22121x x x --+的值为零,∴2210210x x x ì-=í-+¹î,解得:11x x =±ìí¹î,∴1x =-;故答案为:1-.【点睛】本题主要考查分式的值为0的条件,由于该类型的题易忽略分母不为0这个条件,所以常以这个知识点来命题.27.当x =______时,分式293x x--的值为0.【答案】-3【分析】根据分式的值为零的条件可以求出x 的值.【详解】由分式的值为零的条件得290x -=,30x -¹,由290x -=,得29x =,∴3x =或3x =-,由30x -¹,得3x ¹.综上,得3x =-.故答案是:3-.【点睛】本题考查了分式的值为零的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.28.如果分式126xx--的值为零,那么x=________ .【答案】1【分析】根据分式的值为零可得10x-=,解方程即可得.【详解】由题意得:10x-=,解得1x=,Q分式的分母不能为零,260x\-¹,解得3x¹,1x\=符合题意,故答案为:1.【点睛】本题考查了分式的值为零,正确求出分式的值和掌握分式有意义的条件是解题关键.29.要使分式2xx1+有意义,那么x应满足的条件是________ .【答案】1x¹-【分析】根据分式有意义的条件是分母不等于零可得答案.【详解】由题意得:10x+¹,解得:1x¹-,故答案为:1x¹-.【点睛】本题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.30.已知215aa+=,那么2421aa a=++________.【答案】1 24【分析】将215aa+=变形为21a+=5a,根据完全平方公式将原式的分母变形后代入21a+=5a,即可得到答案.【详解】∵215a a+=,∴21a +=5a ,∴2421a a a =++()()2222222221242451a a a a a a a a ===-+-故答案为:124.【点睛】此题考查分式的化简求值,完全平方公式,根据已知等式变形为21a +=5a ,将所求代数式的分母变形为22(1)aa +-形式,再代入计算是解题的关键.31.化简:22x x x-=_____.【答案】12x -【分析】直接利用分式的性质化简得出答案.【详解】解:22xx x -=(2)x x x -=12x -.故答案为:12x -.【点睛】此题主要考查了分式的化简,熟练掌握运算法则是解答此题的关键.32.已知:x 满足方程11200620061x x =--,则代数式2004200620052007x x -+的值是_____.【答案】20052007-【解析】因为11200620061xx =--,则200420062005200520062006001120072007x x x x x x x --=Þ=Þ=Þ=---+ .故答案:20052007-.33.下列结论:①不论a 为何值时21a a +都有意义;②1a =-时,分式211a a +-的值为0;③若211x x +-的值为负,则x 的取值范围是1x <;④若112x x x x ++¸+有意义,则x 的取值范围是x≠﹣2且x≠0.其中正确的是________【答案】①③【解析】【分析】根据分式有意义的条件对各式进行逐一分析即可.【详解】①正确.∵a 不论为何值不论a 2+2>0,∴不论a 为何值21a a +都有意义;②错误.∵当a =﹣1时,a 2﹣1=1﹣1=0,此时分式无意义,∴此结论错误;③正确.∵若211x x +-的值为负,即x ﹣1<0,即x <1,∴此结论正确;④错误,根据分式成立的意义及除数不能为0的条件可知,若112x x x x++¸+有意义,则x 的取值范围是即20010x x x x ìï+¹ï¹íï+ï¹î,x ≠﹣2,x ≠0且x ≠﹣1,故此结论错误.故答案为:①③.【点睛】本题考查的是分式有意义的条件,解答此题要注意④中除数不能为0,否则会造成误解.34.已知210ab a -+-=,则111(1)(1)(2016)(2016)ab a b a b +++=++++L _______.【答案】20172018【解析】【分析】先根据绝对值的非负性求出a 和b 的值,代入代数式中根据分数的性质对原式进行变形即可求出答案.【详解】∵210ab a -+-=,所以20-=ab ,10a -=∴a =1,b =2,∴原式=111.....122320172018+++´´´ =111111.....22320172018-+-++- =112018- =20172018【点睛】本题考查非负数的性质,绝对值.本题解题关键有两个,①任意数的绝对值都大于或等于0,而两个非负数(或式)的和要等于0,那么这两个数(或式)都要为0;②注意分数的等量变形111(1)1=-++a a a a .35.端午节前后,人们除了吃粽子、插艾叶以外,还会佩减香囊以避邪驱瘟.“行知”精品店也推出了“求真”香囊、“乐群”香囊、“创造”香囊三种产品,所有香囊的外包装都由回收材料制成, 不计成本.其中“求真”香囊的里料是20克艾叶,“乐群”香囊的里料是10克艾叶和20克薄荷,“创造”香囊的里料是20克艾叶和 20 克薄荷.端午节当天,店长发现“乐群”香囊的销量是“求真”香囊的2倍,且“求真”香囊与“乐群”香囊的利润和是“创造”香囊利润的32倍,当天的总利润率是50% .第二天店内促销,“求真”香囊、“乐群”香囊的售价均不变,“创造”香囊的售价打八折,当三种产品的销量分别与前一天相同时,总利润率为___________.【答案】38%【分析】设1g 艾叶成本价为a 元,利润率为x ,1g 薄荷成本价为b 元,利润率为y ,端午节当天“求真”香囊的销量为m 件,则“乐群”香囊的销量为2m 件,“创造”香囊的销量为n 件,先根据利润倍数关系可求出43n m =,再根据端午节当天的总利润率可得2a b ax by ++=,然后根据新的售价和销量列出总利润率的计算式子,化简求值即可得.【详解】设1g 艾叶成本价为a 元,利润率为x ,1g 薄荷成本价为b 元,利润率为y ,端午节当天“求真”香囊的销量为m 件,则“乐群”香囊的销量为2m 件,“创造”香囊的销量为n 件,Q “求真”香囊与“乐群”香囊的利润和是“创造”香囊利润的32倍,3202(1020)(2020)2axm m ax by n ax by \++=+,整理得:43n m =,Q 端午节当天的总利润率是50%,3)(2020)250%202(1020)(2(1020)n ax by am m a b n a b +++\+=++,即54(2020)2350%4202(1020)(2020)3m ax by am m a b m a b ´+=++++,整理得:2a b ax by ++=,Q 第二天店内促销,“求真”香囊、“乐群”香囊的售价均不变,“创造”香囊的售价打八折,且三种产品的销量分别与前一天相同,\第二天总利润率为[][]420(1)210(1)20(1)20(1)20(1)80%314202(1020)(2020)3ma x m a x b y m a x b y ma m a b m a b +++++++++×-++++,[]4620(1)20(1)15110(2020)3m a x b y m a b +++=-+,23()125()a b ax by a b +++=-+,23()2125()a b a b a b +++=-+,69()150()a b a b +=-+,1950=,38%=,故答案为:38%.【点睛】本题考查了分式求值,依据题意,正确设立未知数得出已知等式和所求分式是解题关键.36.若240x y z -+=,4320x y z +-=.则222xy yz zx x y z++++的值为______【答案】16-【分析】先由题意2x−y+4z=0 ,4x+3y−2z=0,得出用含x 的式子分别表示y ,z ,然后带入要求的式中,化简便可求出.【详解】2x-y+4z= 0①,4x+3y- 2z= 0②,将②×2得: 8x+ 6y-4z=0③.①+③得: 10x+ 5y= 0,∴y= -2x ,将y= - 2x 代入①中得:2x- (-2x)+4z=0∴z=-x将y= -2x ,z=-x ,代入上式222xy yz zxx y z ++++=()()()()()()222·22··2x x x x x xx x x -+--+-+-+-=222222224x x x x x x -+-++=226x x -=16-故答案为:16-【点睛】本题考查了分式的化简求值,解题的关键是根据题目,得出用含x 的式子表示y ,z.本题较难,要学会灵活化简.三、解答题37.计算:32222((y y x x-×-.(结果用正整数指数幂的形式表示)【答案】24y 【分析】根据幂的乘方法则是底数不变,指数相乘,负指数次可以把底数变为原来的倒数.负指数变为正的,最后将式子化成最简.【详解】解:原式6222(2y x x y -=×62244y x x y =×24y =.【点睛】本题考查了幂的乘方和负指数幂的预算,解决本题的关键是熟练掌握幂的乘方运算和负指数幂的运算法则.38.(1)3455318x yx y(2)()()2328x y x y --(3)2918933x x x -+- (4)22b a a b --(5)22222222a b c bca b c ab--++-+(6)()()2235221215x y x y x y x y --【答案】(1)216x y ;(2)144x y -;(3)33x -;(4)1a b -+;(5)a b ca b c-+++;(6)2454455x yx y xy -+【分析】(1)根据分式的除法运算法则计算即可;(2)将分式的分子、分母约去相同的因式即可;(3)将分式的分子、分母分别因式分解后约去相同的因式即可;(4)将分式的分母因式分解后约去相同的因式即可;(5)将分式的分子、分母分别应用分组分解法因式分解后约去相同的因式即可;(6)将分式的分母因式分解后约去相同的因式即可.【详解】(1)3455318x y x y 21=6x y;(2)()()2328x y x y --1=4)x y -(144x y=-;(3)2918933x x x -+-29(21)=3(1)x x x -+-23(1)(1)x x -=-3(1)x =-33x =-;(4)22b a a b --()=()()a b a b a b ---+1a b=-+(5)22222222a b c bc a b c ab--++-+222222(2)=2a b bc c a ab b c --+++-2222()()a b c a b c --=+-()()()()a b c a b c a b c a b c -++-=+-++a b ca b c-+=++;(6)()()2235221215x y x y x y x y --()()244=5()x y xy x y x y --+44()5()x y xy x y -=+2454455x yx y xy -=+.【点睛】本题主要考查了分式加减乘除混合运算,解题的关键是对分式的分子与分母分别因式分解,然后约去公因式,分式的约分是分式运算的基础,应重点掌握.39.对于正数x ,规定:()1xf x x =+.例如:11(1)112f ==+,22(2)213f ==+,111212312f æö==ç÷èø+.(1)填空:()3f =________;13f æö=ç÷èø_______;1(4)4æö+=ç÷èøf f _________;(2)猜想:1()æö+=ç÷èøf x f x _________,并证明你的结论;(3)求值:111(1)(2)(2019)(2020)202020192æöæöæö+++×××++++×××++ç÷ç÷ç÷èøèøèøf f f f f f f .【答案】(1)34,14,1;(2)1()1f x f x æö+=ç÷èø,证明见解析;(3)120192.【分析】(1)根据给出的规定计算即可;(2)根据给出的规定证明;(3)运用加法的交换律结合律,再根据规定的运算可求得结果.【详解】解:(1)()3f =33+1 =34,13f æö=ç÷èø131+13=14,,1(4)4æö+=ç÷èøf f 34+14=1,(2)1()1f x f x æö+=ç÷èø,理由为:11111111æö==×=ç÷++èø+x xf x x x x x()1xf x x =+,则111()1111+æö+=+==ç÷+++èøx x f x f x x x x .(3)原式111(2020)(2019)(2)(1)202020192éùéùéùæöæöæö=++++×××+++ç÷ç÷ç÷êúêúêúèøèøèøëûëûëûf f f f f f f 1201912=´+120192=.【点睛】本题考查的是分式的加减,根据题意找出规律是解答此题的关键.40.先化简:221111x x x æö+¸ç÷--èø,再选一个你喜欢的数代入并求值.【答案】11x +,13.【解析】【分析】根据分式的混合运算,先算括号里面的,再算除法,然后取一个分式有意义的数值代入求解即可.【详解】解:原式()()22222111111111x x x x x x x x x x -+--=´=´=-+++,0x Q ¹,1,1-,2x \=时,原式11213==+.【点睛】此题主要考查了分式的化简求值,把分式通分、约分进行化简是关键,代入求值时,代入的数值必须让分式有意义,容易出错.41. 已知22ab a b ab ++=32,求2a -3b 的值.【答案】0【详解】试题分析:根据分式的基本性质,约去分子分母的公因式,得到a 、b 的关系,然后代入求值即可.试题解析:原式=a b =32,∴2a =3b ,∴2a -3b =0.42. 若2a =3b =4c ≠0,求a b c+的值.【答案】54【详解】试题分析:根据比例的基本性质,设出参数,直接代入可求解.试题解析:设a =2k ,b =3k ,c =4k ,k ≠0,∴a b c+=234k k k +=54.43.为进一步落实《中华人民共和国民办教育促进法》,某市教育局拿出了b 元资金建立民办教育发展基金会,其中一部分作为奖金发给了n 所民办学校.奖金分配方案如下:首先将n 所民办学校按去年完成教育、教学工作业绩(假设工作业绩均不相同)从高到低,由1到n 排序,第1所民办学校得奖金bn元,然后再将余额除以n 发给第2所民办学校,按此方法将奖金逐一发给了n 所民办学校.(1)请用n 、b 分别表示第2所、第3所民办学校得到的奖金;(2)设第k 所民办学校所得到的奖金为k a 元(1k n ££),试用k 、n 和b 表示k a (不必证明);(3)比较k a 和1k a +的大小(k=1,2 ,……,1n -),并解释此结果关于奖金分配原则的实际意义.【答案】(1)211()(1)bb a b n n n n =-´=- ,23111()(1(1)b b a b n n n n n=-´-=-;(2)11(1k k b a nn-=- ;(3)1k k a a +> .奖金分配的实际意义:名次越靠后,奖金越少.【解析】【试题分析】(1)根据第1所民办学校得奖金bn元,然后再将余额除以n 发给第2所民办学校,得:22311111((1),()(1)(1).b b b ba b a b n n n n n n n n n=-´=-=-´-=-(2)根据(1)中的两个式子,11(1k k ba n n-=- ;(3)11(1k k b a n n -=-,+11(1)k k ba n n=-,则1111+121111111(1(1)(11(1)(1)(1)0k k k k k k k b b b b ba a n n n n n n n n n n n n----éù-=---=---=-××=-×>êúëû,则+1k k a a >.奖金分配的实际意义:名次越靠后,奖金越少.【试题解析】(1)根据题意得:22311111((1),()(1)(1.bb b ba b a b nn n n n n n n n=-´=-=-´-=- (2)根据(1)中的两个式子,11(1k k ba n n-=- (3)11(1k k b a n n -=-,+11(1)k k ba n n=-,则1111+121111111(1(1)(11(1)(1)(1)0k k k k k k k b b b b ba a n n n n n n n n n n n n----éù-=---=---=-××=-×>êúëû,则+1k k a a >.奖金分配的实际意义:名次越靠后,奖金越少.【方法点睛】本题目是一道分式的实际应用问题,第一个问题有难度,依据奖金的分配规则,写出23a a 、 的表达式;第二问在第一问的基础上,找出规律,直接写出k a 的表达式即可;第三问用作差法比较两个分式的大小,若差为正数,则被减数大于减数;若差为0,则被减数等于减数;若差为负数,则被减数小于减数.44.已知分式2 218 x3 x-+(1)当x取什么值时,分式有意义?(2)当x取什么值时,分式为零?(3)当x取什么值时,分式的值为负数?【答案】(1)x≠-3;(2)x=3;(3)x<3且x≠-3【解析】【分析】(1)根据分式有意义的条件即可求出答案.(2)根据分式值为零的条件是:分子等于零且分母不等于零。
(专题精选)最新初中数学—分式的难题汇编附答案解析

一、选择题1.若分式21x -有意义,则( )A .1x ≠B .1x =C .0x ≠D .0x =2.若(x 2﹣ax ﹣b )(x +2)的积不含x 的一次项和二次项,则a b =( ) A .116B .-116C .16D .﹣163.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物。
2.5微米等于0.0000025米,把0.0000025用科学记数法表示为( ) A .0.25×10–5米B .2.5×10–7米C .2.5×10–6米D .25×10–7米4.下列变形正确的是( )A .y x =22y xB .a acb bc= C .ac a bc b= D .x m xy m y+=+ 5.把分式aba b+中的a 、b 都扩大为原来的3倍,则分式的值( ) A .扩大为原来的6倍 B .不变C .缩小为原来的13D .扩大为原来的3倍6.将分式2x x y+中的x 、y 都扩大2倍,则分式值( )A .扩大为原来的2倍B .缩小为原来的2倍C .保持不变D .无法确定7.若代数式1xx +有意义,则实数x 的取值范围是( ) A .0x = B .1x =-C .1x ≠D .1x ≠-8.与分式11a a -+--相等的式子是( ) A .11a a +- B .11a a -+ C .11a a +-- D .11a a --+ 9.若02018a =,2201720192018b =⨯- , 2017201845()()54c =-⨯ ,则a ,b ,c 的大小关系式( ) A .a b c << B .b c a <<C .c b a <<D .a c b <<10.如果把分式2++a ba b中的a 和b 都扩大为原来的10倍,那么分式的值( ) A .不变B .缩小10倍C .是原来的20倍D .扩大10倍11.使式子x有意义的实数x 的取值范围是( ) A .x ≤3B .x ≤3且x ≠0C .x <3D .x <3且x ≠012.目前,世界上能制造出的小晶体管的长度只有0.00000004m 将0.00000004用科学记数法表示为( ) A .3410-⨯ B .80.4 10⨯C .8410⨯D .8410-⨯13.函数 y =21x x --的自变量 x 的取值范围是( ) A .x > -1且x ≠ 1 B .x ≠ 1且x ≠ 2C .x ≥ -1且x ≠ 1D .x ≥ -114.下列各式:2a b -,3x x +,13,a b a b +-,1()x y m-中,是分式的共有( )A .1个B .2个C .3个D .4个15.若a=20180,b=2016×2018-20172,c=(23-)2016×(32)2017,则a ,b ,c 的大小关系正确的是( ) A .a<b<c B .a<c<b C .b<a<c D .c<b<a16.某种病毒变异后的直径为0.000000102米,将这个数写成科学记数法是( )A .61.0210-⨯B .60.10210-⨯C .71.0210-⨯D .810210-⨯17.下列运算正确的是( ) A .1133a a﹣=B .2322a a a +=C .326()•a a a ﹣=﹣D .32()()a a a ÷﹣﹣=18.下列计算中错误的是( )A .020181=B .224-=C 2=D .1133-=19.若分式242x x --的值为0,则x 等于( )A .±2B .±4 C .-2D .220.222142x x x÷--的计算结果为( ) A .2x x + B .22xx + C .22xx - D .2(2)x x +21.下列等式成立的是( ) A .123a b a b +=+ B .212a b a b =++ C .2ab aab b a b=--D .a aa b a b=--++ 22.(2017河北)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )A .4+446=B .004+4+4=6C .34+4=6D .14446-=23.当x 为任意实数时,下列分式中,一定有意义的是( ) A .1xB .11x + C .11x - D .211x + 24.下列各式中,正确的是( )A .22x y x y -++=-B .()222x y x y x y x y --=++ C .1a b b ab b++= D .23193x x x -=-- 25.函数3y x =+的自变量x 的取值范围是( ) A .3x >-B .3x ≥-C .3x ≠-D .3x ≤-【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】 【分析】根据分式有意义的条件是分母不等于零求解即可. 【详解】 解:∵要使分式21x -有意义 ∴10x -≠1x ∴≠【点睛】本题考查了分式有意义的条件,熟练掌握分式有意义的条件是分母不等于零是解题的关键.2.A解析:A 【解析】 【分析】先把原式展开,再根据题意2()(2)x ax b x --+的积不含x 的一次项和二次项,得知20a -=,20a b +=,然后求解即可. 【详解】2322()(2)222x ax b x x x ax ax bx b --+=+---- 32(2)(2)2x a x a b x b =+--+-,2()(2)x ax b x --+的积不含x 的一次项和二次项, ∴2020a a b -=⎧⎨+=⎩,2a ∴=,4b =-,41216b a -∴==. 故选A . 【点睛】本题考查了多项式乘多项式,解题的关键是明确积不含x 的一次项和二次项,即它们的系数为零.3.C解析:C 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.由此即可解答. 【详解】0.0000025=2.5×10﹣6, 故选C . 【点睛】本题考查用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.4.C【解析】试题解析:A、分式的乘方不等于原分式,故A错误;B、当c=0时,结果不成立,故B错误;C、分式的分子分母都乘或除以同一个不为零的整式,故C正确;D、分式的分子分母都加同一个不为零的数,结果发生变化,故D错误.故选C.5.D解析:D【解析】试题解析:把分式aba b+中的a、b都扩大为原来的3倍,则33333a b aba b a b⨯=++,故分式的值扩大3倍.故选D.6.A解析:A【分析】分别用2x和2y去代换原分式中的x和y,利用分式的基本性质化简与原分式比较即可得答案.【详解】∵将分式2xx y+中的x、y都扩大2倍,∴原式变为2(2)22xx y+=242()xx y+=2×2xx y+,∴扩大为原来的2倍,故选A.【点睛】此题考查的是对分式的性质的理解和运用,分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变,熟练掌握分式的基本性质是解题关键.7.D解析:D【解析】【分析】根据分式有意义的条件即分母不等于零可得x+1≠0,从而得解.【详解】解:由题意得:x+1≠0,解得:x≠-1,故选:D.【点睛】本题考查分式有意义的条件,解题关键是掌握分式有意义的条件:分母不等于零.8.B解析:B 【分析】根据分式的基本性质即可得出:分式的分子、分母、分式本身的符号,改变其中的任意两个,分式的值不变,据此即可解答. 【详解】 解:原式= 1)(1)a a --+-( =11a a -+故选:B . 【点睛】本题考查分式的基本性质,解题关键是熟练掌握分式的基本性质.9.C解析:C 【分析】根据零次幂的性质,平方差公式以及积的乘方法则求出a ,b ,c ,再根据有理数的比较法则判断即可. 【详解】解:020118a ==,2222201720192018(20181)(20181)20182018120181b =⨯-=-+-=--=-,201720182017454555()()()545444c =-⨯=-⨯⨯=-,∵54-<-1<1, ∴c <b <a . 故选:C . 【点睛】本题主要考查了零次幂的性质,平方差公式以及积的乘方,熟练掌握相关运算法则是解题关键.10.A解析:A 【分析】根据分式的基本性质代入化简即可. 【详解】 扩大后为:102022=1010)a b a b a ba b a b a b+++=+++10()10(分式的值还是不变 故选:A.本题考查分式的基本性质,熟练掌握性质是关键.11.B解析:B【分析】直接利用二次根式有意义的条件得出答案.【详解】有意义的实数x的取值范围是:3﹣x≥0,且x≠0,使式子x解得:x≤3且x≠0.故选B.【点睛】此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.12.D解析:D【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:0.000 000 04=4×10-8,故选:D.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.13.C解析:C【分析】根据分母不能为零且被开方数是非负数,可得答案.【详解】解:由题意得:x-1≠0且x+1≥0,解得:x≥-1且x≠1.故选C.【点睛】本题考查了函数自变量的取值范围,利用分母不能为零且被开方数是非负数得出不等式是解题关键.14.C【分析】利用分式的概念:一般地,如果A ,B 表示两个整式,并且B 中含有字母,那么式子A B叫做分式,进行解答即可. 【详解】解:在2a b -,3x x +,13,a b a b +-,1()x y m-中, 3x x +,a b a b +-,1()x y m -是分式,共3个, 故选:C . 【点睛】本题考查了分式,关键是掌握分式的分母必须含有字母,而分子可以含字母,也可以不含字母.15.C解析:C 【分析】首先计算a 、b 、c 的值,再进行比较即可. 【详解】 a=20180=1,b=2016×2018-20172=222(20171)(20171)20172017120171-+-=--=-,20162017201620162016232332333()()()()()323223222c =-⨯=⨯⨯=⨯⨯=,∵-1<1<32, ∴b<a<c , 故选:C. 【点睛】此题考查零次幂定义,平方差公式,同底数幂乘法的逆运算,积的乘方的逆运算,掌握掌握各计算法则是解题的关键.16.C解析:C 【分析】用科学记数法表示比较小的数时,n 的值是第一个不是0的数字前0的个数,包括整数位上的0. 【详解】解:0.000000102=71.0210-⨯. 故选:C . 【点睛】此题考查科学记数法表示较小的数,解题关键在于掌握一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.17.D解析:D 【分析】直接利用负指数幂的性质以及同底数幂的乘除运算法则计算得出答案. 【详解】 解:A 、133aa-=,故此选项错误; B 、22a a +,不是同类项无法合并;C 、()325aa a -⋅=-,故此选项错误; D 、()()32a a a -÷-=,正确;故选:D . 【点睛】此题考查负指数幂的性质以及同底数幂的乘除运算,正确掌握相关运算法则是解题关键.18.B解析:B 【分析】根据零指数幂、指数幂、平方根、负整数指数幂的定义分别验证四个选项即可得到答案. 【详解】解:A 、020181=,任何非零数的零次方都等于1,故A 不是答案; B 、224-=-,故B 是答案;C 2=,故C 不是答案;D 、1133-=,故D 不是答案; 故选:B . 【点睛】本题主要考查了零指数幂、指数幂、平方根、负整数指数幂的定义,熟练掌握各知识点是解题的关键.19.C解析:C 【分析】根据分式为零的条件得到x 2-4=0且x-2≠0,然后分别解方程和不等式即可得到x 的值. 【详解】∵分式242x x --的值为0,∴x 2-4=0且x-2≠0, ∴x=-2.故选:C . 【点睛】本题考查了分式为零的条件:当分式的分子为零且分母不为零时,分式的值为零.20.B解析:B 【分析】先把分母因式分解,再把除法转换为乘法,约分化简得到结果. 【详解】222142x x x÷-- =21(2)(2)(2)x x x x ÷+--=()()()2·222x x x x -+-=22xx +. 故选:B . 【点睛】本题主要考查了分式的除法,约分是解答的关键.21.C解析:C 【分析】根据分式的运算,分别对各选项进行运算得到结果,即可做出判断. 【详解】 A 、221b b a aba +=+,故A 错误; B 、22a b+,分子分母具有相同的因式才可以约分,故B 错误; C 、2()ab ab aab b b a b a b==---,故C 正确; D 、a aa b a b =--+-,故D 错误; 故选C . 【点睛】本题主要考查了分式的运算,熟悉分式的通分以及约分的重要法则是解决本题的关键.22.D解析:D 【详解】∵4+46=,∴选项A 不符合题意;∵4+40+40=6,∴选项B 不符合题意;∵,∴选项C 不符合题意;∵144-=1486≠,∴选项D 符合题意, 故选D . 23.D解析:D【分析】根据分式有意义分母不为零分别进行分析即可.【详解】A 、当0x =时,分式无意义,故此选项错误;B 、当1x =-时,分式无意义,故此选项错误;C 、当1x =时,分式无意义,故此选项错误;D 、当x 为任意实数时,分式都有意义,故此选项正确;故选:D .【点睛】本题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.24.B解析:B【分析】根据分式的性质,对每个选项的式子一一判断正误即可.【详解】22x y x y -+-=-,故A 选项错误; ()222()()()()x y x y x y x y x y x y x y x y --+-==++++,故B 选项正确; 1b a b a ab b++=,故C 选项错误;23319(3)(3)3x x x x x x --==-+-+,故D 选项错误. 故选:B .【点睛】本题主要考查分式的化简,熟记分式的性质是解题关键. 25.A解析:A【分析】根据根式和分母有意义进行判断即可.【详解】要使得该函数有意义分母不能为0且根号内不能为负x+>∴30x>-解得:3故选:A.【点睛】本题主要考查根式和分式的意义,熟练掌握判断有意义的条件是关键.。
新最新初中数学—分式的难题汇编附解析

一、选择题1.生物学家发现一种病毒的长度约为0.00 004mm ,0.00 004用科学记数法表示是( ) A .40.410-⨯ B .5410-⨯C .54010-⨯D .5410⨯2.下列分式:24a 5b c ,23c 4a b ,25b2ac中,最简公分母是 A .5abc B .2225a b cC .22220a b cD .22240a b c3.分式:22x 4- ,x 42x- 中,最简公分母是 A .()()2x 4?42x --B .()()x 2x ?2+C .()()22x 2x 2-+- D .()()2x 2?x 2+-4.计算: ()332xy ?-一 的结果是A .398x y --B .398x y ---C .391x y 2---D .361x y 2---5.在式子:2x、5x y + 、12a - 、1x π-、21x x +中,分式的个数是( ) A .2 B .3 C .4 D .5 6.下列各式从左到右的变形正确的是( )A .221188a a a a ---=-++ B .()()221a b a b -+=-C .22x y x y x y+=++ D .052520.11y yx x ++=-++7.下列各式中,正确的是( ). A .1122b a b a +=++B .22142a a a -=-- C .22111(1)a a a a +-=-- D .11b ba a---=- 8.下列等式成立的是( ) A .|﹣2|=2 B﹣1)0=0C .(﹣12)﹣1=2 D .﹣(﹣2)=﹣29.已知有理式:4x 、4a 、1x y -、34x 、12x 2、1a +4,其中分式有 ( )A .2个B .3个C .4个D .5个10.下列各式中的计算正确的是( )A .22b b a a=B .a ba b++=0 C .a c ab c b+=+ D .a ba b-+-=-111.下列变形正确的是( ).A .1x yx y-+=-- B .x m mx n n+=+ C .22x y x y x y +=++ D .632x x x= 12.下列判断错误..的是( ) A .当23x ≠时,分式132x x +-有意义 B .当a b 时,分式22aba b -有意义 C .当12x =-时,分式214x x+值为0D .当x y ≠时,分式22x yy x--有意义13.人体中红细胞的直径约为0.000 007 7 m ,用科学记数法表示该数据为 ( ) A .7.7×106 B .7.7×107 C .7.7×10-6 D .7.7×10-7 14.如果把分式232x x y+中的x 和y 都扩大为原来的5倍,那么分式的值( )A .扩大为原来的5倍B .扩大为原来的10倍C .不变D .缩小为原来的1515.2018年3月3日,新浪综合网报道:“中科院发明首个抗癌DNA 纳米机器人,可精准阻断肿瘤血管饿死肿瘤!”.中国科学家团队研发出的这种可编程、基于 DNA 折纸技术的纳米机器人大小只有90×60×2nm ,nm 是长度计量单位,1nm=0.000000001米,则2nm 用科学记数法表示为( )A .2×109米B .20×10-8米C .2×10-9米D .2×10-8米 16.已知分式32x x +-有意义,则x 的取值范围是( ) A .x ≠-3B .x≠0C .x≠2D .x=217.化简:32322012220122010201220122013-⨯-+-,结果是( )A .20102013B .20102012C .20122013D .2011201318.若0x y y z z xabc a b c---===<,则点P(ab ,bc)不可能在第( )象限 A .一B .二C .三D .四19.每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m ,该数值用科学记数法表示为( ) A .51.0510⨯ B .51.0510-⨯C .50.10510-⨯D .410.510-⨯20.已知12x y-=3,分式4322x xy y x xy y +-+-的值为( )A .32 B .0C .23D .9421.甲、乙两人分两次在同一粮店内买粮食,两次的单价不同,甲每次购粮100千克,乙每次购粮100元.若规定:谁两次购粮的平均单价低,谁的购粮方式就合算.那么这两次购粮( ) A .甲合算 B .乙合算C .甲、乙一样D .要看两次的价格情况22.纳米是一种长度单位,1米=109纳米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示这种花粉的直径为( ) A .3.5×10﹣6米 B .3.5×10﹣5米 C .35×1013米 D .3.5×1013米 23.若a =-0.32,b =-3-2,c =(-13)-2,d =(-13)0,则它们的大小关系是( ) A .a<c<b<d B .b<a<d<cC .a<b<d<cD .b<a<c<d24.如果把分式2+mm n中的m 和n 都扩大2倍,那么分式的值 ( ) A .扩大4倍B .缩小2倍C .不变D .扩大2倍25.已知a <b ( )A B C .D .【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】解:0.00 004=5410-⨯.故选B .2.C解析:C 【解析】根据最简公分母的定义:“通常取各分母的系数的最小公倍数与各分母中所有字母因数的最高次幂的积作为各分母的公分母,这个公分母叫做这几个分式的最简公分母”可知,分式:24a 5b c ,23c 4a b ,25b2ac 的最简公分母是:22220a b c . 故选C.3.D解析:D 【解析】∵2224(2)(2)x x x =-+-,422(2)x xx x =---, ∴分式22 442xx x --、的最简公分母是:2(2)(2)x x +-. 故选D.4.B解析:B 【解析】3333939(2)=(-2)8xy x y x y -------=-.故选B.5.B解析:B 【解析】 解:分式有2x 、12a -、21x x +共3个.故选B . 点睛:此题主要考查了分式的定义,正确把握分式的定义是解题关键.6.B解析:B 【解析】 解:A .原式=22(1)1(8)8a a a a -++=--- ,错误;B .原式=1,正确;C .原式为最简结果,错误;D .原式=520110yx+-+,错误.故选B .点睛:此题考查了分式的基本性质,熟练掌握分式的基本性质是解本题的关键.7.C解析:C 【解析】解;A .分式的分子分母都乘或除以同一个不为零的整式,故A 错误; B .分子除以(a ﹣2),分母除以(a +2),故B 错误;C .分式的分子分母都乘或除以同一个不为零的整式,分式的值不变,故C 正确;D .分式的分子分母都乘或除以同一个不为零的整式,分式的值不变,故D 错误; 故选C .8.A解析:A 【解析】根据绝对值、零指数幂及负整数指数幂的运算法则,可得: A 、|﹣2|=2,计算正确,故本选项正确;B ﹣1)0=1,原式计算错误,故本选项错误;C 、(﹣12)﹣1=﹣2,原式计算错误,故本选项错误; D 、﹣(﹣2)=2,原式计算错误,故本选项错误; 故选:A .点睛:此题主要考查了绝对值、零指数幂及负整数指数幂的运算法则,灵活运用绝对值、零指数幂及负整数指数幂的运算法则进行计算是解决此类题目的关键.9.B解析:B 【解析】4a 、、34x 、12x 2的分母中均不含有字母,因此它们是整式,而不是分式. 4x、、1x y -、1a +4的分母中含有字母,因此是分式.所以B 选项是正确的.点睛:本题主要考查分式的概念,分式与整式的区别主要在于:分母中是否含有未知数.10.D解析:D 【解析】解:A . 22b b a a≠,故A 错误;B . a ba b++=1,故B 错误; C . a c ab c b+≠+,故C 错误; D .a ba b -+-=-1,正确. 故选D .11.A解析:A 【解析】 试题解析:()1x y x y x y x y-+--==---. 故选A.12.B解析:B【解析】A 、当分母3x-2≠0,即当x≠23时,分式x 13x 2+-有意义.故本选项正确; B 、当分母a 2-b 2≠0,即a≠±b 时,分式22aba b-有意义.故本选项错误; C 、当分子2x+1=0,即x =−12时,分式2x 14x+值为0.故本选项正确; D 、当分母y-x≠0,即x≠y 时,分式22x y y x--有意义.故本选项正确;故选:B .13.C解析:C【解析】绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定, 0.000 007 7=7.7×10-6, 故选C.14.A解析:A 【解析】 【分析】x ,y 都扩大为原来的5倍就是分别变成原来的5倍,变成5x 和5y .用5x 和5y 代替式子中的x 和y ,看得到的式子与原来的式子的关系. 【详解】用5x 和5y 代替式子中的x 和y 得:()2255,151032x x x y x y=++则扩大为原来的5倍. 故选:A. 【点睛】考查分式的基本性质,掌握分式的基本性质是解题的关键.15.C解析:C【解析】分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 详解:0.000000001×2=2×10﹣9. 故选C .点睛:本题考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.16.C解析:C 【解析】分析:根据分式有意义的条件:分母不等于0即可求解. 详解:根据题意得:x-2≠0, 解得:x≠2. 故选C..点睛:本题考查了分式有意义的条件,从以下三个方面透彻理解分式的概念:(1)分式无意义⇔分母为零;(2)分式有意义⇔分母不为零;(3)分式值为零⇔分子为零且分母不为零.17.A解析:A 【分析】将所求式子的分子分母前两项提取20122,整理后分子提取2010,分母提取2013,约分后即可得到结果,选出答案. 【详解】原式=32322012220122010201220122013-⨯-+-=2220122012220102012201212013--⨯+-()()=22201220102010201220132013⨯-⨯-=22201020121201320121--()()=20102013,故答案选A. 【点睛】本题主要考查了因式分解的应用,是一道技巧性较强的题,熟练掌握因式分解的方法是解本题的关键.18.A解析:A 【解析】 【分析】根据有理数的乘法判断出a ,b ,c 中至少有一个是负数,另两个同号,然后求出三个数都是负数时x 、y 、z 的大小关系,得出矛盾,从而判断出a 、b 、c 不能同时是负数,确定出点P 不可能在第一象限. 【详解】 解:∵abc <0,∴a ,b ,c 中至少有一个是负数,另两个同号, 可知三个都是负数或两正数,一个是负数, 当三个都是负数时:若x yabc a-=, 则20x y a bc -=>,即x >y ,同理可得:y >z ,z >x 这三个式子不能同时成立,即a,b,c不能同时是负数,所以,P(ab,bc)不可能在第一象限.故选:A.【点睛】本题主要考查分式的基本性质和点的坐标的知识,熟悉点的坐标的基本知识是本题的解题关键,确定一个点所在象限,就是确定点的坐标的符号.19.B解析:B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.0000105=1.05×10-5,故选B.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.20.A解析:A【解析】【分析】先根据题意得出2x-y=-3xy,再代入原式进行计算即可.【详解】解:∵12x y-=3,∴2x-y=-3xy,∴原式=()()2232x y xyx y xy-+-+,=633xy xyxy xy-+-+,=32xyxy --,=32,故选A.【点睛】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.21.B解析:B【解析】【分析】分别算出两次购粮的平均单价,用做差法比较即可.【详解】解:设第一次购粮时的单价是x元/千克,第二次购粮时的单价是y元/千克,甲两次购粮共花费:100x+100y,一共购买了粮食:100+100=200千克,甲购粮的平均单价是:1001002002x y x y++=;乙两次购粮共花费:100+100=200元,一共购买粮食:()100100100x yx y xy++=(千克),乙购粮的平均单价是:2xyx y+;甲乙购粮的平均单价的差是:()()()()22420 222x y xy x yx y xyx y x y x y>+--+-==+++,即22x y xyx y ++>,所以甲购粮的平均单价高于乙购粮的平均单价,乙的购粮方式更合算,故选B.【点睛】本题考查的知识点是做差法,解题关键是注意一个数的平方为非负数.22.B解析:B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】∵1米=109纳米,某种植物花粉的直径约为35000纳米,∴35000纳米=35000×10﹣9m=3.5×10﹣5m.故选B.【点睛】本题考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.23.B解析:B【解析】 【分析】首先根据一个数的平方的计算方法,负整数指数幂的运算方法,以及零指数幂的运算方法,分别求出a 、b 、c 、d 的大小;然后根据实数大小比较的方法,判断出它们的大小关系即可. 【详解】∵2221110.30.09,3,9,1933a b c d --⎛⎫⎛⎫=-=-=-=-=-==-= ⎪ ⎪⎝⎭⎝⎭, ∴10.09199-<-<<, ∴b <a <d <c . 故选:B . 【点睛】考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a -p =1pa (a≠0,p 为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a 0=1(a≠0);②00≠1.24.C解析:C 【解析】 【分析】根据分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变,可得答案. 【详解】 分式2+m m n 中的m 和n 都扩大2倍,得4222m mm n m n=++,∴分式的值不变, 故选A . 【点睛】本题考查了分式的基本性质,分式的分子分母都乘以(或除以)同一个不为零的数(或整式),分式的值不变.25.D解析:D 【解析】因为a-ba a b-=-故选D.,0,0a aaa a≥⎧==⎨-<⎩,推广此时a可以看做是一个式子,式子整体大于等于0,把绝对值变为括号;式子整体小于0,把绝对值变为括号,前面再加负号.最后去括号,化简.。
(专题精选)最新初中数学—分式的难题汇编附答案

一、选择题1.一种花粉颗粒直径约为0.0000065米,数字0.0000065用科学记数法表示为( ) A .0.65×10﹣5 B .65×10﹣7 C .6.5×10﹣6 D .6.5×10﹣5 2.分式x 22x 6-- 的值等于0,则x 的取值是 A .x 2=B .x ?2=-C .x 3=D .x ?3=-3.下列式子中,错误的是 A .1a a 1a a --=- B .1a a 1a a ---=- C .1a 1aa a---=- D .1a 1aa a+---= 4.计算: ()332xy ?-一 的结果是A .398x y --B .398x y ---C .391x y 2---D .361x y 2---5.下列关于分式的判断,正确的是( ) A .当x =2时,12x x +-的值为零 B .无论x 为何值,231x +的值总为正数 C .无论x 为何值,31x +不可能得整数值 D .当x ≠3时,3x x-有意义 6.下列各式从左到右的变形正确的是( ) A .221188a a a a ---=-++B .()()221a b a b -+=-C .22x y x y x y+=++ D .052520.11y yx x ++=-++7.计算32-的结果是( ) A .-6B .-8C .18-D .188.下列变形正确的是( ).A .11a ab b +=+ B .11a ab b--=-- C .221a b a b a b-=-- D .22()1()a b a b --=-+ 9.已知a <b的结果是( )A B C . D .10.人体中红细胞的直径约为0.000 007 7 m ,用科学记数法表示该数据为 ( ) A .7.7×106 B .7.7×107 C .7.7×10-6 D .7.7×10-7 11.下列约分结果正确的是( ) A .2mgR BLB .a m ab m b+=+ C .22x y x y x y-=-- D .22111m m m m -+-=-+-12.在实数范围内有意义,则x 的取值范围为( ) A .x<-3 B .x ≥-3C .x>2D .x ≥-3,且x ≠213.下列各式:2116,,4,,235x y xx y x π++-中,分式有( ) A .1个B .2个C .3个D .4个14.下列关于分式的判断正确的是 ( ) A .无论x 为何值,231x +的值总为正数 B .无论x 为何值,31x +不可能是整数值 C .当x =2时,12x x +-的值为零 D .当x ≠3时3x x-,有意义 15.(下列化简错误的是( )A )﹣1=2B =2C 52=± D )0=116.下列分式中:xy x ,2y x -,+-x yx y,22x y x y +-不能再约分化简的分式有( )A .1个B .2个C .3个D .4个17.每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m ,该数值用科学记数法表示为( ) A .51.0510⨯ B .51.0510-⨯C .50.10510-⨯D .410.510-⨯18.已知12x y-=3,分式4322x xy yx xy y +-+-的值为( )A .32 B .0C .23D .9419.已知m ﹣1m ,则1m+m 的值为( )A .B C .D .1120.纳米是一种长度单位,1米=109纳米,已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示这种花粉的直径为( )A.3.5×10﹣6米B.3.5×10﹣5米C.35×1013米D.3.5×1013米21.若(1-x)1-3x=1,则x的取值有()个.A.1个B.2个C.3个D.4个22.在12,2x yx-,212x+,m+13,-2x y-中分式的个数有()A.2个B.3个C.4个D.5个23.下列分式从左到右的变形正确的是( )A.2=2x xy yB.22=x xy yC.22=x xx xD.515(2)2x x24.3--2的倒数是()A.-9B.9C.19D.-1925.如果把分式2xx y-中的x与y都扩大2倍,那么分式的值()A.不变B.扩大2倍C.缩小2倍D.扩大4倍【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:0.0000065的小数点向右移动6位得到6.5,所以数字0.0000065用科学记数法表示为6.5×10﹣6,故选C.【点睛】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.解析:A 【解析】由题意得:20260x x -=⎧⎨-≠⎩ ,解得:2x =. 故选A.点睛:分式值为0需同时满足两个条件:(1)分子的值为0;(2)分母的值不为0.3.B解析:B 【解析】 A 选项中,1(1)1a a a a a a ----==--,所以A 正确; B 选项中,1(1)1a a a a a a -----=-=---,所以B 错误; C 选项中,11a aa a ---=-,所以C 正确; D 选项中,11a aa a+---=,所以D 正确. 故选B.4.B解析:B 【解析】3333939(2)=(-2)8xy x y x y -------=-.故选B.5.B解析:B 【解析】A 选项中,因为当2x =时,分式12x x +-无意义,所以本选项错误; B 选项中,因为无论x 取何值,21x +的值始终为正数,则分式231x +的值总为正数,所以本选项正确;C 选项中,因为当2x =时,分式311x =+,所以本选项说法错误; D 选项中,因为0x ≠时,分式3x x-才有意义,所以本选项说法错误; 故选B.6.B【解析】 解:A .原式=22(1)1(8)8a a a a -++=--- ,错误;B .原式=1,正确;C .原式为最简结果,错误;D .原式=520110yx+-+,错误.故选B .点睛:此题考查了分式的基本性质,熟练掌握分式的基本性质是解本题的关键.7.D解析:D 【解析】3311228-==. 故选D. 8.B解析:B 【解析】 A 选项中,11a b ++不能再化简,所以A 中变形错误; B 选项中,11a ab b--=--,所以B 中变形正确; C 选项中,221()()a b a b a b a b a b a b--==-+-+,所以C 中变形错误;D 选项中,2222()()1()()a b a b a b a b --+==++,所以D 中变形错误; 故选B.9.D解析:D 【解析】因为a-ba a b-=-故选D.,0,0a a a a a ≥⎧==⎨-<⎩,推广此时a 可以看做是一个式子,式子整体大于等于0,把绝对值变为括号;式子整体小于0,把绝对值变为括号,前面再加负号.最后去括号,化简.10.C【解析】绝对值小于1的数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定, 0.000 007 7=7.7×10-6, 故选C.11.D解析:D 【解析】A. 282123x x y xy = ,故A 选项错误;B. a mb m++已是最简分式,故B 选项错误;C.22x y x y x y -=+-,故C 选项错误;D. 22111m m m m -+-=-+-,正确, 故选D.12.D解析:D 【分析】根据二次根式有意义的条件和分式有意义的条件得到x+3≥0且x-2≠0,然后求出两个不等式的公共部分即可. 【详解】根据题意得x+3≥0且x−2≠0, 所以x 的取值范围为x ≥−3且x≠2. 故答案选D. 【点睛】本题考查的知识点是二次根式有意义的条件,分式有意义的条件,解题的关键是熟练的掌握二次根式有意义的条件,分式有意义的条件.13.A解析:A 【解析】分析:判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式. 详解:216,,4,,23x y xx y π++的分母中均不含有字母,因此它们是整式,而不是分式.15x -的分母中含有字母,因此是分式. 故选A .点睛:本题主要考查分式的定义,注意π不是字母,6xπ是常数,所以不是分式,是整式.14.A【解析】 【分析】根据分式有意义的条件、分式值为0的条件、分式值是正负等逐一进行分析即可得. 【详解】A 、分母中x 2+1≥1,因而23x 1+的值总为正数,故A 选项正确; B 、当x+1=1或-1时,3x 1+的值是整数,故B 选项错误; C 、当x=2时,分母x-2=0,分式无意义,故C 选项错误; D 、当x=0时,分母x=0,分式无意义,故D 选项错误, 故选A . 【点睛】本题考查了分式的值为零的条件,分式的定义,分式有意义的条件,注意分式的值是正数的条件是分子、分母同号,值是负数的条件是分子、分母异号.15.C解析:C 【解析】 【分析】分别利用负指数幂的性质以及二次根式的性质、零指数幂的性质分别化简得出答案. 【详解】A ﹣1,正确,不合题意;B ,正确,不合题意;C 52=,故此选项错误,符合题意;D 0=1,正确,不合题意; 故选:C . 【点睛】此题主要考查了负指数幂的性质以及二次根式的性质、零指数幂的性质,正确掌握相关运算法则是解题关键.16.B解析:B 【分析】找出各项中分式分子分母中有没有公因式,即可做出判断. 【详解】xyx=y, 22x y x y +-= ()()x y x y x y ++-= 1x y - 所以,不能约分化简的有:- 22y x +-x yx y共两个, 故答案选B. 【点睛】本题考查的知识点是分式的约分,解题的关键是熟练的掌握分式的基本性质.17.B解析:B 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 【详解】0.0000105=1.05×10-5, 故选B . 【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.18.A解析:A 【解析】 【分析】先根据题意得出2x-y=-3xy ,再代入原式进行计算即可. 【详解】 解:∵12x y-=3, ∴2x-y=-3xy , ∴原式=()()2232x y xyx y xy-+-+,=633xy xyxy xy -+-+,=32xyxy --, =32, 故选A .本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.19.A解析:A 【分析】根据完全平方公式即可得到结果. 【详解】1m-=m21m-=7m ⎛⎫∴ ⎪⎝⎭, 221m -2+=7m ∴, 221m +=9m∴,22211m+=m +2+=11m m ⎛⎫∴ ⎪⎝⎭,1m+m ∴=. 故选A. 【点睛】本题主要考查完全平方公式,熟悉掌握公式是关键.20.B解析:B 【解析】 【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10﹣n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 【详解】∵1米=109纳米,某种植物花粉的直径约为35000纳米,∴35000纳米=35000×10﹣9m =3.5×10﹣5m .故选B . 【点睛】本题考查了用科学记数法表示较小的数,一般形式为a ×10﹣n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.21.B解析:B利用零指数幂,乘方的意义判断即可.【详解】解:∵(1-x)1-3x=1,∴1-x≠0,1-3x=0或1-x=1,解得:x=13或x=0,则x的取值有2个,故选B【点睛】本题考查了零指数幂,以及有理数的乘方,熟练掌握运算法则是解题的关键.22.A解析:A【解析】【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式,找到分母中含有字母的式子的个数即可.【详解】解:式子2x yx-,-2x y-中都含有字母是分式.故选:A.【点睛】本题考查分式的概念,分式与整式的区别主要在于:分母中是否含有未知数.23.D解析:D【分析】根据分式的基本性质逐项判断.【详解】解:A、当y=-2时,该等式不成立,故本选项错误;B、当x=-1,y=1时,该等式不成立,故本选项错误;C.22=x xx x--+-,故本选项错误;D、正确.故选D.【点睛】本题考查分式的基本性质,属于基础题型,分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变.24.A解析:A【解析】【分析】首先计算3--2=-19,再根据倒数的定义求解即可. 【详解】∵3--2=213-=-19,-19的倒数是-9, ∴3--2的倒数是-9,故选A.【点睛】此题考查了倒数和负整数指数幂,掌握倒数的定义是本题的关键.25.A解析:A【解析】分析:解答此题时,可将分式中的x ,y 用2x ,2y 代替,然后计算即可得出结论. 详解:依题意得:2222x x y ⨯-=222x x y ⋅⋅-()=原式.故选A . 点睛:本题考查的是对分式的性质的理解和运用,扩大或缩小n 倍,就将原来的数乘以n 或除以n .。
最新最新初中数学—分式的难题汇编附答案解析

一、选择题1.下列各分式中,最简分式是( )A .21x x +B .22m n m n-+C .22a ba b+- D .22x yx y xy ++2.把分式中的、的值同时缩小到原来的,则分式的值( )A .扩大为原来的2倍B .不变C .扩大为原来的4倍D .缩小为原来的一半3.已知02125,,0.253a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,a ,b ,c 的大小关系是( ) A .a >b >c B .b >a >c C .c >a >b D .c >b >a4.若代数式1xx +有意义,则实数x 的取值范围是( ) A .0x = B .1x =-C .1x ≠D .1x ≠-5.与分式()()a b a b ---+相等的是( )A .a ba b+- B .a ba b-+ C .a ba b+-- D .a ba b--+ 6.下列各式:351,,,,12a b x y a b x a b xπ-+++--中,是分式的共有( ) A .1个B .2个C .3个D .4个7.下列各分式的值可能为零的是( ).A .2211m m +-B .11m +C .211m m +-D .211m m -+8.下列运算正确的是( )A .623x x x=B .221x a ax b b++=++ C .1122x xx x ---=-- D .0.71070.20.323a b a ba b a b--=++9.下列分式运算中,正确的是( )A .111x y x y+=+ B .x a ax b b+=+ C .22x y x y x y -=+- D ..a c adb d bc= 10.下列等式从左到右的变形正确的是( )A .22b byx xy= B .2ab b a a =C .22b b a a=D .11b b a a +=+11.若a +b =0, 则ba的值为( ) A .-1 B .0C .1D .-1或无意义12.设2222x 18n x 33x x 9+=+++--,若n 的值为整数,则x 可以取的值得个数是( ) A .5 B .4 C .3 D .2 13.如图是数学老师给玲玲留的习题,玲玲经过计算得出的正确结果为( )A .1B .2C .3D .414.已知1112a b -=,则ab a b-的值是( ) A .12B .12-C .2D .-215.将分式2a bab+中的a 、b 都扩大为原来的2倍,则分式的值( ) A .缩小到原来的12倍 B .扩大为原来的2倍 C .扩大为原来的4倍 D .不变16.1372x x-+-x 的取值范围是( ) A .3<x <72B .3≤x <72C .3≤x ≤72D .x ≥317.下列命题中:①已知两实数a 、b ,如果a >b ,那么a 2>b 2;②同位角相等,两直线平行;③如果两个角是直角,那么这两个角相等;④如果分式332x x -+无意义,那么x =﹣23;这些命题及其逆命题都是真命题的是( ) A .①② B .③④ C .①③ D .②④ 18.用小数表示45.610-⨯为( )A .5.6000B .0.00056C .0.0056D .0.05619.计算33x yx y x y---的结果是( ) A .1B .0C .3D .620.下列变形正确的是( )A .()23524a a -=- B .22220x y xy -=C .23322b ab a a-÷=- D .()()222222x y x y x y +-=-21.将0.00086用科学记数法表示为( ) A .8.6×104 B .8.60×104 C .8.6×10-4 D .8.6×10-6 22.若20.3a =-,23b -=-,021(3)3c d -⎛⎫=-=- ⎪⎝⎭,,则( )A .a b c d <<<B .b a d c <<<C .a d c b <<<D .c a d b <<<23.若222110.2,2,(),()22a b c d --=-=-=-=-,则它们的大小关系是( ) A .a b d c <<< B .b a d c <<< C .a d c b <<<D .c a d b <<<24.使分式211x x -+的值为0,这时x 应为( )A .x =±1 B .x =1C .x =1 且 x≠﹣1D .x 的值不确定25.下列变形中,正确的是( )A .2211x x y y-=-B .22m m n n=C .2()a b a ba b-=-- D .2233x x +=+【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】最简分式就是分式的分子和分母没有公因式,也可理解为分式的分子和分母的最大公因式为1.所以判断一个分式是否为最简分式,关键是要看分式的分子和分母的最大公因式是否为1. 【详解】 解:A.21xx +,分子分母的最大公因式为1; B. 22m n m n-+,分子分母中含有公因式m+n;C.22a ba b +-,分子分母中含有公因式a+b ;D.22x yx y xy ++,分子分母中含有公因式x+y故选:A. 【点睛】最简分式首先系数要最简;一个分式是否为最简分式,关键看分子与分母是不是有公因式,但表面不易判断,应将分子、分母分解因式.2.A解析:A 【解析】 【分析】根据题意可知原来的x 变成,原来的y 变成,在根据分式基本性质可以求得答案.【详解】由题意可知:分式的值扩大为原来的2倍. 故选:A 【点睛】本题考查了分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.3.C解析:C 【解析】 【分析】根据负整数指数幂和零指数幂法则计算,比较即可. 【详解】21295==10.25=434a b c --⎛⎫=-== ⎪⎝⎭⎝⎭,,, ∵4>94>1, ∴c >a >b . 故选C . 【点睛】此题考查了负整数指数幂和零指数幂的运算,掌握其运算法则是解答此题的关键.4.D解析:D 【解析】【分析】根据分式有意义的条件即分母不等于零可得x+1≠0,从而得解. 【详解】解:由题意得:x+1≠0, 解得:x≠-1, 故选:D . 【点睛】本题考查分式有意义的条件,解题关键是掌握分式有意义的条件:分母不等于零.5.B解析:B 【分析】根据分式的基本性质,分式的分子和分母同时乘以和除以一个不为0的整式,分式的值不变. 【详解】解:原分式()()()()()()1=1a b a b a ba b a b a b----⨯--=-+-+⨯-+,故选B. 【点睛】本题主要考查分式的基本性质,解决本题的关键是要熟练掌握分式的基本的性质.6.C解析:C 【解析】 【分析】根据分式的定义逐一进行判断即可. 【详解】31,,1x a b x a b x ++--是分式 故选:C. 【点睛】本题考查分式的定义,熟练掌握定义是关键.7.D解析:D 【分析】根据分式为零的条件进行计算即可. 【详解】解:∵分式有意义且它的值为零, ∴分子为0,分母不为0A. 2m +10≠,分式的值不可能为零,不符合题意;B. 10≠,分式的值不可能为零,不符合题意;C. 2m+1=0m -10⎧⎨≠⎩无解,分式的值不可能为零,不符合题意;D.当 2m -1=0m+10⎧⎨≠⎩,即m=1时,分式的值为零,符合题意;故选:D 【点睛】本题主要考查分式为零的条件,(1)分子的值为零;(2)分母的值不为零;两个条件必须同时具备,缺一不可.8.D解析:D 【分析】根据分式的基本性质,将每一个分式的分子与分母的公因式约去,再比较即可. 【详解】A. 633x x x=,故该选项不符合题意; B.221x a ax b b++≠++,故该选项不符合题意; C. 1x 122x x x ---=--,故该选项不符合题意; D.0.71070.20.323a b a ba b a b --=++,故该选项符合题意;故选:D 【点睛】此题考查约分,解题关键在于掌握运算法则.9.C解析:C 【分析】根据分式的运算法则计算各个选项中的式子,从而可以解答本题. 【详解】解:∵11,x yx y xy ++=故A 错误; (0)x a ax x b b+≠≠+,故B 错误;. 22()()x y x y x y x y x y x y -+-==+--,故C 正确; ∵.a c ac b d bd =,故D 错误. 故选:C【点睛】本题考查分式的混合运算,解答本题的关键是明确分式的混合运算的计算方法.10.B解析:B 【分析】根据分式的基本性质,无论是把分式的分子和分母扩大还是缩小相同的倍数,都不要漏乘(除)分子、分母中的任何一项,且扩大(缩小)的倍数不能为0,并且分式的值不变,由此即可判定选择项. 【详解】A 、22b by x xy=,其中y≠0,故选项错误; B 、2ab ba a=,其中左边隐含a≠0,故选项正确; C 、2b aba a=,故选项错误. D 、根据分式基本性质知道11b b a a ++≠,故选项错误;故选B . 【点睛】此题考查分式的基本性质,解题的关键是熟练掌握分式的基本性质.11.D解析:D 【分析】互为相反数两个数的和为0,同时要考虑到0+0=0,从而进行判断. 【详解】 解:∵a +b =0 ∴a=-b 或a=0,b=0∴ba的值为-1或无意义, 故选:D. 【点睛】掌握互为相反数的两个数的和为0和0+0=0,是本题的解题关键.12.B解析:B 【解析】 【分析】先通分,再加减,最后化简.根据化简结果为整数,确定x 的取值个数. 【详解】n=222218339x x x x ++++-- =()()()()()()()()2323218333333x x x x x x x x x -++-++-+-+-=()()262621833x x x x x ---+++-=()()()2333x x x ++-=23x - 当x-3=±1、±2,即x=4、2、1、5时 分式23x -的值为整数. 故选B . 【点睛】本题考查了异分母分式的加减法及分式为整数的相关知识.解决本题的关键是根据化简结果得到分式值为整数的x 的值.13.C解析:C 【分析】先将原式通分,可以得到222b a ab ab++,再将分子用完全平方公式进行变形,即可得到()222a b abab +-+,最后代入数值计算即可.【详解】因为2b aa b++ ()2222222222323233b a ab ab b a ab a b abab =+++=++-=+-⨯=+=所以选C. 【点睛】本题考查的是分式的通分和完全平方公式的变形,能够熟练掌握完全平方公式的变形是解题的关键.14.D解析:D 【分析】先把已知的式子变形为()2ab b a =-,然后整体代入所求式子约分即得答案. 【详解】 解:∵1112a b -=, ∴()2ab b a =-, ∴()22b a ab a b a b-==---. 故选:D . 【点睛】本题考查了分式的通分与约分,属于常考题目,掌握解答的方法是关键.15.A解析:A 【分析】用2a ,2b 分别替换掉原分式中的a 、b ,进行计算后与原分式对比即可得出答案. 【详解】用2a ,2b 分别替换掉原分式中的a 、b ,可得:()2221=222822+++=⨯⨯⨯a b a ba b a b ab ab,所以分式缩小到原来的12倍, 故选A. 【点睛】本题考查了分式的基本性质,关键是根据条件正确的替换原式中的字母,然后化简计算.16.B解析:B 【分析】根据二次根式的性质,被开方数大于等于0;分母中有字母,分母不为0. 【详解】由题意,得:x ﹣3≥0且7﹣2x >0,解得:3≤x 72<. 故选B . 【点睛】本题考查了二次根式有意义的条件,正确解不等式是解题的关键.17.D解析:D【分析】分别写出四个命题的逆命题,利用反例对①和它的逆命题进行判断;利用平行线的性质和判定对②和它的逆命题进行判断;利用直角的定义对③和它的逆命题进行判断;利用分式有意义的条件对④和它的逆命题进行判断. 【详解】解:①已知两实数a 、b ,如果a >b ,那么a 2>b 2;若a =1,b =﹣2,结论不成立,则命题为假命题,其逆命题为:已知两实数a 、b ,如果a 2>b 2,那么a >b ;若a =﹣2,b =1时,结论不成立,所以逆命题为假命题;②同位角相等,两直线平行;则命题为真命题,其逆命题为:两直线平行,同位角相等,所以逆命题为真命题;③如果两个角是直角,那么这两个角相等;此命题为真命题,其逆命题为:如果两个角相等,那么这两个角是直角,所以逆命题为假命题; ④如果分式332x x -+无意义,那么x =﹣23;此命题为真命题,其逆命题为:如果x =﹣23,那么分式332x x -+无意义,所以逆命题为真命题; 故选:D . 【点睛】此题主要考查命题的判断,解题的关键是熟知实数的性质、平行线的性质、直角的性质及分式的性质.18.B解析:B 【分析】把数据45.610-⨯中5.6的小数点向左移动4位就可以得到. 【详解】解:441=5.6=5.60.0001=0.0005615.6100-⨯⨯⨯. 故选B. 【点睛】本题考查写出用科学记数法表示的原数.(1)科学记数法a ×10n 表示的数,“还原”成通常表示的数,就是把a 的小数点向右移动n 位所得到的数.若科学记数法表示较小的数a ×10-n ,还原为原来的数,需要把a 的小数点向左移动n 位得到原数.(2)把一个数表示成科学记数法的形式及把科学记数法还原是两个互逆的过程,这也可以作为检查用科学记数法表示一个数是否正确的方法.19.C解析:C 【分析】根据同分母的分式加减的法则进行计算即可.【详解】 解:()333=3x y x y x y x y x y--=--- 故选C.【点睛】本题考查了分式的加减法,掌握分式运算的法则是解题的关键.20.C解析:C【分析】原式各项计算得到结果,即可作出判断.【详解】A 、原式=4a 6,错误;B 、原式不能合并,错误;C 、原式=−232a ,正确; D 、原式=2x 2−4xy +xy−2y 2=2x 2−3xy−2y 2,错误.故选:C .【点睛】此题考查了分式的乘除法,合并同类项,幂的乘方与积的乘方,以及整式的乘法,熟练掌握公式及运算法则是解本题的关键.21.C解析:C【解析】【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】将8600用科学记数法表示为:8.6×10-4. 故选:C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.22.B解析:B【分析】分别求出a 、b 、c 、d 的值,比较大小即可.【详解】20.30.09a =-=-2213139b -=-=-=- 01()3c =-=1 2211=(-3))9(3d -==- 故b a d c <<<故选:B【点睛】本题考查正指数与负指数的计算,注意负指数的运算规则.23.B解析:B【分析】根据负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1,可得答案.【详解】∵a=-0.22=-0.04;b=-2-2=-14=-0.25,c=(-12)-2=4,d=(-12)0=1, ∴-0.25<-0.04<1<4,∴b <a <d <c ,故选:B .【点睛】题考查了负整数指数幂,利用负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1是解题关键. 24.B解析:B【分析】 使分式211x x -+的值为0,则x 2-1=0,且x+1≠0. 【详解】 使分式211x x -+的值为0, 则x 2-1=0,且x+1≠0解得x =1故选:B【点睛】考核知识点:考查分式的意义. 要使分式值为0,分子等于0,分母不等于0. 25.C解析:C【分析】根据分式的性质分子分母同时乘(或除以)同一个不为零的整式,分式的值不变,进行判断选择即可.【详解】A,B,D均不符合分式分子分母同时乘(或除以)同一个不为零的整式,分式的值不变的性质,选项C可以将分子分母同时除以(a-b)到()2a ba ba b-=--,故答案选择C.【点睛】本题考查的是分式的基本性质,熟知分式中分子分母同时乘(或除以)同一个不为零的整式,分式的值不变,是解题的关键.。
新最新初中数学—分式的难题汇编及答案

一、选择题1.把分式2n m n +中的m 与n 都扩大3倍,那么这个代数式的值 A .不变 B .扩大3倍 C .扩大6倍 D .缩小到原来的132.计算23x 11x +--的结果是 A .1x 1- B .11x - C .5x 1- D .51x- 3.下列分式约分正确的是( )A .236a a a =B .1-=-+y x y xC .316222=b a abD .m mn m n m 12=++4.当012=-+a a 时,分式2222-21a a a a a ++++的结果是( ) A .25-1- B .251-+ C .1 D .0 5.下列各式、、、+1、中分式有( ) A .2个 B .3个 C .4个 D .5个6.在分式ab a b +(a ,b 为正数)中,字母a ,b 值分别扩大为原来的2倍,则分式的值( )A .扩大为原来的2倍B .缩小为原来的12 C .不变 D .不确定 7.已知,则的值是( )A .B .﹣C .2D .﹣28.化简:(a-2)·22444a a a --+的结果是( ) A .a-2 B .a +2 C .22-+a a D .22+-a a 9.已知+=3,则分式的值为( )A .B .9C .1D .不能确定10.若分式23x x --有意义,则x 满足的条件是( ) A .x ≠0 B .x ≠2 C .x ≠3 D .x ≥3 11.若分式的值为0,则x 的值为( ) A .0B .2C .﹣2D .2或﹣2 12.如果把223y x y-中的x 和y 都扩大5倍,那么分式的值( ) A.扩大5倍 B.不变 C.缩小5倍 D.扩大10倍13.12⎛⎫- ⎪⎝⎭-2的正确结果是( ) A .14 B .14- C .4 D .-414.用科学记数方法表示0.00000601,得( )A .0.601×10-6B .6.01×10-6C .60.1×10-7D .60.1×10-615.若分式的值为0,则x 的值为 A . B . C . D .不存在16.计算222x y x y y x +--的结果是( ) A .1 B .﹣1 C .2x y + D .x y +17.下列各式的约分,正确的是A .1a b a b --=-B .1a b a b--=-- C .22a b a b a b -=-+ D .22a b a b a b-=++ 18.若分式的值为0,则x 的值是( )A .3B -3C .4D .-419.已知115ab a b =+,117bc b c =+,116ca c a =+,则abc ab bc ca ++的值是( ) A .121 B .122 C .123 D .12420.(2015秋•郴州校级期中)下列计算正确的是( ) A .B .•C .x÷y•D .21.在,,中,是分式的有( ) A .0个 B .1个 C .2个 D .3个22.若已知分式22169x x x ---+的值为0,则x ﹣2的值为( ). A .19或﹣1 B .19或1 C .﹣1 D .1 23.计算的结果是( ) A .a+b B .2a+b C .1 D .-124.在函数中,自变量的取值范围是( ) A .>3 B .≥3且≠4 C .>4 D .≥325.若分式211x x -+的值为零,则x 的值为( ) A .0 B .1 C .1- D .±1【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】试题解析:分式2n m n+中的m 与n 都扩大3倍,得 6233n n m n m n=++, 故选A .2.B解析:B【解析】试题分析:先通分,再根据同分母的分式相加减的法则进行计算伯出判断:2323231x 11x 1x 1x 1x 1x-++=-+==------.故选B . 3.D 解析:D【解析】试题分析:A.约分的结果为a3;B.不能进行约分;C.约分的结果为ab 3。
最新初中数学—分式的难题汇编附答案解析
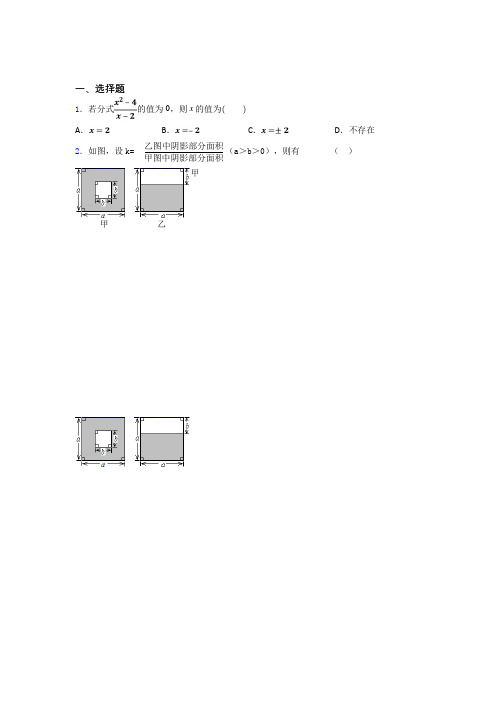
一、选择题1.若分式的值为0,则x 的值为A .B .C .D.不存在2.如图,设k=甲图中阴影部分面积乙图中阴影部分面积(a>b>0),则有()甲乙甲(A )k >2 (B )1<k <2 (C )121<<k (D )210<<k 3.一艘轮船在静水中的最大航速为30千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?设江水的流速为x 千米/时,则可列方程( )A .B .C .D .4.当012=-+a a 时,分式2222-21a a a a a ++++的结果是( ) A .25-1- B .251-+ C .1 D .0 5.下列分式变形中,正确的是( ).A . b a b a b a +=++22B .1-=++-y x y xC . ()()m n n m m n -=--23D .bm am b a = 6.已知:分式的值为零,分式无意义,则的值是( )乙甲A .-5或-2B .-1或-4C .1或4D .5或27.把分式22x y x y -+中的x 、y 都扩大到原来的4倍,则分式的值( )A .扩大到原来的8倍B .扩大到原来的4倍C .缩小到原来的14 D .不变8.若分式的值为零,则x 的值为( )A .0B .﹣2C .2D .﹣2或29.用科学记数方法表示0.0000907,得( )A .49.0710-⨯B .59.0710-⨯C .690.710-⨯D .790.710-⨯ 10.计算4-(-4)0的结果是( )A .3B .0C .8D .4 11.下列各式从左到右的变形正确的是 ( )A .220.220.33a a a a a a --=-- B .11x x x y x y +--=-- C .116321623a a a a --=++ D .22b a a b a b-=-+ 12.计算23x 11x+--的结果是 A .1x 1- B .11x - C .5x 1- D .51x- 13.若分式的值为0,则x 的值为( ) A .0 B .2 C .﹣2 D .2或﹣214.下列变形正确的是( )A .x y y x x y y x--=++ B .222()x y x y y x x y +-=-- C .2a a a ab b+= D .0.250.25a b a b a b a b ++=++ 15.已知空气的单位体积质量是0.001239g /cm 3,则用科学记数法表示该数为( )g /cm 3.A .1.239×10﹣3B .1.2×10﹣3C .1.239×10﹣2D .1.239×10﹣4 16.若式子212x x m -+不论x 取任何数总有意义,则m 的取值范围是( ) A .m≥1 B .m>1 C .m≤1 D .m<117.已知115ab a b =+,117bc b c =+,116ca c a =+,则abc ab bc ca ++的值是( ) A .121 B .122 C .123 D .12418.在,,中,是分式的有( ) A .0个 B .1个 C .2个 D .3个19.在式子x y 3,πa ,13+x ,31+x ,a a 2中,分式有 A .1个 B .2个 C .3个 D .4个20.已知一粒大米的质量约为0.0000021千克,这个数用科学记数法表示为( ) A .0.21×10-5 B .2.1×10-5C .2.1×10-6D .21×10-621.若02(1)2(2)x x ----无意义,则x 的取值范围是( ) A .1x ≠且2x ≠B .1x ≠或2x ≠C .1x =且2x =D .1x =或2x = 22.化简-的结果是( ) A . B . C . D .23.若a >-1,则下列各式中错误..的是( ) A .6a >-6B .2a >-12C .a +1>0D .-5a <-5 24.下列语句:①任何数的零次方都等于1;②如果两条直线被第三条直线所截,那么同位角相等;③一个图形和它经过平移所得的图形中,两组对应点的连线平行且相等;④平行线间的距离处处相等.说法错误的有( )A .1个B .2个C .3个D .4个25.下列算式,计算正确的有( )①10-3=0.0001; ②(0.0001)0=1; ③3a -2=213a; ④(-2)3÷(-2)5=-2-2. A .1个 B .2个 C .3个 D .4个【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】 ∵分式的值为0, ∴,解得:,故选B.点睛:求使分式值为0的字母的取值时,要注意需同时满足两点:(1)分子的值为0;(2)分母的值不为0. 2.C解析:C【解析】试题分析:甲图中阴影部分的面积=22a b -,乙图中阴影部分的面积= ()a a b -,22()1a a b a b k a b a b a b -===--++,∵a >b >0∴0<b a b +<12,∴ 121<<k . 考点:分式的约分. 3.A解析:A【解析】试题分析:因为轮船在静水中的最大航速为30千米/时,江水的流速为x 千米/时,所以轮船在顺流航行中的航速为(30+x )千米/时,轮船在逆流航行的航速为(30-x )千米/时,根据以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,可得:,故选A .考点:列分式方程. 4.C解析:C .【解析】试题分析:先把2222-21a a a a a ++++进行化简得222(1)a a a -+,再把012=-+a a 化简为:2-a 2=a+1,21a a +=,代入即可求值. 试题解析:2222222(2)21(1)a a a a a a a a a a ++-+-=++++ =222(1)a a a -+ ∵012=-+a a∴2-a 2=a+1,21a a +=原式=2211111(1)(1)1a a a a a a a +====+++ 故选C .考点:分式的值. 5.C解析:C【解析】试题分析:分式的约分首先将分子和分母进行因式分解,然后约去公共的因式.A 、B 无法进行约分,C 正确;D 需要保证m 不能为零.考点:分式的约分6.A解析:A【分析】当分式的分子为零,且分母不为零时,则分式的值为零;当分式的分母为零时,则分式无意义.【详解】根据题意可得:,=0,解得:x=-3,y=1或-2,则x+y=-2或-5.【点睛】考核知识点:分式的性质. 7.D解析:D .【解析】试题解析:根据题意得:844(2)2844(2y)2x y x y x y x y x x y ---==+++,即和原式的值相等,故选D .考点:分式的基本性质.8.B解析:B【解析】试题分析:要使分式的值为0,必须分式分子的值为0并且分母的值不为0.解:由分子x 2﹣4=0解得:x=±2. 当x=2时分母x 2﹣2x=4﹣4=0,分式没有意义; 当x=﹣2时分母x 2﹣2x=4+4=8≠0. 所以x=﹣2.故选B .9.B解析:B【详解】解:根据科学记数法的表示—较小的数为10n a ⨯,可知a=9.07,n=-5,即可求解. 故选B【点睛】本题考查科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.10.A解析:A【解析】试题分析:根据零指数幂的性质和有理数的加减法,可求解为:4-(-4)0=4-1=3. 故选A.11.C解析:C【详解】解:A. 220.21020.3103a a a a a a --=--,故原选项错误; B. 11x x x y x y+--=--,故原选项错误; C. 116321623a a a a --=++ ,故此选项正确; D.22b a b a a b-=-+,故原选项错误, 故选C .12.B解析:B【解析】试题分析:先通分,再根据同分母的分式相加减的法则进行计算伯出判断:2323231x 11x 1x 1x 1x 1x-++=-+==------.故选B . 13.B解析:B【解析】根据分式的值为0,分子为0,分母不为0可得 且x+2≠0,解得x=2,故选B.14.D解析:D【解析】A选项错误,x yx y-+=-y xy x-+;B选项错误,x yy x+-=x y y xy x y x+---()()()()=()222y xx y--;C选项错误,2a aab+=1a aab+()=1ab+;D选项正确.故选D.点睛:分式的性质:分式的分子分母乘以或者除以同一个不为零的整式,分式的值不变. 15.A解析:A【解析】根据绝对值小于1的正数也可以利用科学记数法表示方法(一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定)可得:0.001239 =1.239×0.001=1.239×10﹣3,故选A.16.B解析:B【解析】试题解析:分式21 2x x m-+不论x取何值总有意义,则其分母必不等于0,即把分母整理成(a+b)2+k(k>0)的形式为(x2-2x+1)+m-1=(x-1)2+(m-1),因为论x取何值(x2-2x+1)+m-1=(x-1)2+(m-1)都不等于0,所以m-1>0,即m>1.故选B.17.D解析:D【解析】试题解析:由已知得:1115a b+=,1117b c+=,1116c a+=,∴11124 a b c++=,∴原式=11 11124a b c=++,故选D.考点:分式的运算.18.C【解析】解:的分母中不含有字母,因此它们是整式,而不是分式.,的中分母中含有字母,因此是分式.故选:C . 19.C解析:C【解析】试题分析:分式是指分母含有字母的代数式.考点:分式的定义20.C解析:C【解析】0.0000021=2.1×10-6,故选C .21.C解析:C【解析】∵()()02x 12x 2----无意义,∴x −1=0或x −2=0,∴x=1或x=2.故选C. 22.D解析:D【解析】 试题分析:根据分式的加减运算,先确定最简公分母,再通分,然后计算即可,即22(1)(1)(1)111a a a a a a a a +--+=----221111a a a a -+==--. 故选:D23.D解析:D【解析】根据不等式的基本性质可知,A. 6a >−6,正确;B. 2a >12- , 正确; C. a +1>0,正确;D. 根据性质3可知,a >−1两边同乘以−5时,不等式为−5a <5,故D 错误;故选D.24.C【解析】改正:①任何非0数的零次方都等于1;②如果两条平行的直线被第三条直线所截,那么同位角相等;③一个图形和它经过平移所得的图形中,两组对应点的连线平行(或共线)且相等;④正确.故选C.25.A解析:A【解析】分析:本题考查的是负指数幂的运算.解析:①10-3=0.00001,故①错误;②(0.0001)0=1正确;③3a -2=23a,故③错误;④(-2)3÷(-2)5=2-2,故④错误. 故选A.。
(专题精选)最新初中数学—分式的难题汇编及答案解析

一、选择题1.下列运算正确的是( )A .2x -2 = 212xB .a 6÷a 3 =a 2C .(a 2)3 =a 5D .a 3·a =a 4 2.若把分式x y xy +中的x 和y 都扩大2倍,那么分式的值( ) A .扩大2倍 B .不变 C .缩小2倍 D .缩小4倍3.若(x 2﹣ax ﹣b )(x +2)的积不含x 的一次项和二次项,则a b =( )A .116B .-116C .16D .﹣164.纳米是一种长度单位,1纳米810-=米,己知某种植物花粉的直径约为35000纳米,那么用科学记数法表示该种花粉的直径为( )A .43.510⨯米B .43.510-⨯米C .33.510-⨯米D .93.510-⨯5.当x =_____ 时,分式11x x -+无意义.( ) A .0 B .1C .-1D .2 6.化简22222a ab b a b ++-的结果是( ) A .a b a b +- B .b a b - C .a a b + D .b a b+ 7.老师设计了一个接力游戏,用小组合作的方式完成分式的运算,规则是:每人只能看见前一个人给的式子,并进行一步计算,再将结果传递给下一个人,最后完成计算.其中一个组的过程是:老师给甲,甲一步计算后写出结果给乙,乙一步计算后写出结果给丙,丙一步计算后写出结果给丁,丁最后算出结果.接力中,自己负责的一步出现错误的是( )A .甲B .乙C .丙D .丁 8.若把分式3xy x y -(,x y 均不为0)中的x 和y 都扩大3倍,则原分式的值是( ) A .扩大3倍 B .缩小至原来的13 C .不变 D .缩小至原来的169.在某次数学小测中,老师给出了5个判断题.如图为张晓亮的答卷,每个小题判断正确得20分,他的得分应是( )A .100分B .80分C .60分D .40分10.下列命题中: ①已知两实数a 、b ,如果a >b ,那么a 2>b 2;②同位角相等,两直线平行;③如果两个角是直角,那么这两个角相等;④如果分式332x x -+无意义,那么x =﹣23;这些命题及其逆命题都是真命题的是( )A .①②B .③④C .①③D .②④ 11.用小数表示45.610-⨯为( ) A .5.6000 B .0.00056 C .0.0056 D .0.056 12.若a =﹣0.22,b =﹣2-2,c =(﹣12)-2,d =(﹣12)0,则它们的大小关系是( ) A .a <b <c <dB .b <a <d <cC .a <d <c <bD .c <a <d <b 13.下列结论正确的是( )A .当23x ≠时,分式132x x +-有意义 B .当x y ≠时,分式222xy x y -有意义 C .当0x =时,分式22+x x x的值为0 D .当1x =-时,分式211x x --没有意义 14.若式子01(1)k k -+-有意义,则一次函数()11y k x k =-+-的图象可能是( ) A . B . C . D .15.小明家到学校m 千米,若步行从家到学校,需要t 小时;若骑自行车,所用时间比步行少用20分钟,则骑自行车的比步行的速度快了( )A .3(1)m t t -千米/时B .(31)m t t - 千米/时C .(31)m t t -+ 千米/时D .13m t - 千米/时16.若20.3a =-,23b -=-,021(3)3c d -⎛⎫=-=- ⎪⎝⎭,,则( ) A .a b c d <<< B .b a d c <<< C .a d c b <<< D .c a d b <<<17.下列计算中错误的是( )A .020181=B .224-=C .42=D .1133-= 18.下列计算:①3362a a a ⋅=;②2352m m m +=;③()224-24a a =-;④()21048a a aa ⋅÷=;⑤()-21-510=;⑥22m a m n a n +=+,其中正确的个数为( ) A .4个 B .3个C .2个D .1个 19.世界上最小的开花结果植物的果实像一个微小的无花果,质量只有0.000000076克,将0.000000076用科学记数法表示为( )A .87.610⨯B .77.610-⨯C .87.610-⨯D .97.610-⨯ 20.(2017河北)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )A .4+446=B .004+4+4=6C .34+4=6D .14446-= 21.化简:x x y --y x y+,结果正确的是( ) A .1 B .2222x y x y +- C .x y x y -+ D .22x y + 22.下列各式中,正确的是( ) A .22x y x y -++=- B .()222x y x y x y x y --=++ C .1a b b ab b++= D .23193x x x -=-- 23.下列分式中,属于最简分式的是( )A .42xB .11x x --C .211x x +-D .224x x -24.下列各式:2a b -,3x x +,13,a b a b +-,1()x y m -中,是分式的共有( ) A .1个 B .2个 C .3个 D .4个25.若23a b =≠0,则代数式(2244b ab a-+1)2b a a -÷的值为( ) A .2 B .1 C .﹣1 D .﹣2【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据负指数幂、同底数幂的乘法和除法以及幂的乘方的运算法则逐项排除即可.【详解】解:A. 2x -2 = 22x,故选项A 错误; B. a 6÷a 3 =a 3,故选项B 错误;C. (a 2)3 =a 6,故选项C 错误;D. a 3·a =a 4 ,D 正确;故答案为D .【点睛】本题考查了负指数幂、同底数幂的乘法和除法以及幂的乘方的运算法则,掌握相关运算法则是解答本题的关键.2.C解析:C【解析】【分析】根据题意,分式中的x 和y 都扩大2倍,则222()2242x y x y x y x y xy xy+++==⋅; 【详解】 解:由题意,分式x yy x +中的x 和y 都扩大2倍, ∴222()2242x y x y x y x y xy xy+++==⋅; 分式的值是原式的12,即缩小2倍;【点睛】本题考查了分式的基本性质,分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,分子、分母、分式本身同时改变两处的符号,分式的值不变.3.A解析:A【解析】【分析】先把原式展开,再根据题意2()(2)x ax b x --+的积不含x 的一次项和二次项,得知20a -=,20a b +=,然后求解即可.【详解】2322()(2)222x ax b x x x ax ax bx b --+=+----32(2)(2)2x a x a b x b =+--+-,2()(2)x ax b x --+的积不含x 的一次项和二次项,∴2020a a b -=⎧⎨+=⎩, 2a ∴=,4b =-, 41216b a -∴==. 故选A .【点睛】本题考查了多项式乘多项式,解题的关键是明确积不含x 的一次项和二次项,即它们的系数为零.4.B解析:B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】35000纳米=35000×10-8米=3.5×10-4米.故选:B .【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.5.C【分析】根据分式无意义的条件,分母等于0,列不等式求解即可.【详解】 因为分式11x x-+无意义, 所以1+x =0,解得x =-1.故选C.【点睛】 本题主要考查分式无意义的条件,解决本题的关键是要熟练掌握分式无意义的条件.6.A解析:A【分析】利用完全平方公式和平方差公式化简约分即可.【详解】222222()=()()a ab b a b a b a b a b a b a b++++=-+--. 故选A.【点睛】此题主要考查了分式的约分,解题的关键是正确地把分子、分母分解因式.7.B解析:B【分析】找出题中出错的地方即可.【详解】乙同学的过程有误,应为()()22a ab ab b a b a b +-++-, 故选B .【点睛】此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.8.A解析:A【分析】将原式中x 变成3x ,将y 变成3y ,再进行化简,与原式相比较即可.【详解】 由题意得3332733333()x y xy xy x y x y x y⋅⋅==⋅---,所以原分式的值扩大了3倍【点睛】此题考察分式的化简,注意结果应化为最简分式后与原分式相比较.9.B解析:B【分析】依据分式的化简,无理数定义,平方根定义,实数的大小比较方法依次判断各小题正确与否即可确定他的得分.【详解】 因为c a c b ++是最简分式不能在进行化简,故第1小题错误,他判断正确得20分; 因为227是分数属于有理数,不是无理数,所以第2小题错误,他判断正确得20分;因为0.6=-,所以第3小题错误,他判断错误不得分;因为23<<,所以112<<,所以第4小题正确,他判断正确得20分; 数轴上的点可以表示无理数,故第5小题错误,他判断正确得20分.故他应得80分,选择B【点睛】此题考察分式的化简,无理数定义,平方根定义,实数的大小比较方法,熟练掌握才能正确判断.10.D解析:D【分析】分别写出四个命题的逆命题,利用反例对①和它的逆命题进行判断;利用平行线的性质和判定对②和它的逆命题进行判断;利用直角的定义对③和它的逆命题进行判断;利用分式有意义的条件对④和它的逆命题进行判断.【详解】解:①已知两实数a 、b ,如果a >b ,那么a 2>b 2;若a =1,b =﹣2,结论不成立,则命题为假命题,其逆命题为:已知两实数a 、b ,如果a 2>b 2,那么a >b ;若a =﹣2,b =1时,结论不成立,所以逆命题为假命题;②同位角相等,两直线平行;则命题为真命题,其逆命题为:两直线平行,同位角相等,所以逆命题为真命题;③如果两个角是直角,那么这两个角相等;此命题为真命题,其逆命题为:如果两个角相等,那么这两个角是直角,所以逆命题为假命题; ④如果分式332x x -+无意义,那么x =﹣23;此命题为真命题,其逆命题为:如果x =﹣23,那么分式332x x -+无意义,所以逆命题为真命题;【点睛】此题主要考查命题的判断,解题的关键是熟知实数的性质、平行线的性质、直角的性质及分式的性质.11.B解析:B【分析】把数据45.610-⨯中5.6的小数点向左移动4位就可以得到.【详解】 解:441=5.6=5.60.0001=0.0005615.6100-⨯⨯⨯. 故选B.【点睛】本题考查写出用科学记数法表示的原数.(1)科学记数法a ×10n 表示的数,“还原”成通常表示的数,就是把a 的小数点向右移动n 位所得到的数.若科学记数法表示较小的数a ×10-n ,还原为原来的数,需要把a 的小数点向左移动n 位得到原数.(2)把一个数表示成科学记数法的形式及把科学记数法还原是两个互逆的过程,这也可以作为检查用科学记数法表示一个数是否正确的方法.12.B解析:B【解析】【分析】根据负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1,可得答案.【详解】∵a =﹣0.22=﹣0.04;b =﹣2﹣2=﹣14=﹣0.25,c =(﹣12)﹣2=4,d =(﹣12)0=1, ∴﹣0.25<﹣0.04<1<4,∴b <a <d <c ,故选B .【点睛】本题考查了负整数指数幂,熟练掌握负整数指数幂与正整数指数幂互为倒数,非零的零次幂等于1是解题关键. 13.A解析:A【分析】根据分式有意义,分母不等于0;分式的值等于0,分子等于0,分母不等于0对各选项分析判断后利用排除法求解.【详解】A 、分式有意义,3x-2≠0,解得23x ≠,故本选项正确; B 、分式有意义,x 2-y 2≠0,解得x≠±y ,故本选项错误; C 、分式的值等于0,x=0且x 2+2x≠0,解得x=0且x≠0或-2,所以,x=0时分式无意义,故本选项错误;D 、分式没有意义,x-1=0,x=1,故本选项错误.故选:A .【点睛】此题考查分式有意义以及分式的值为零的条件,解题关键在于掌握(1)分式无意义⇔分母为零;(2)分式有意义⇔分母不为零;(3)分式值为零⇔分子为零且分母不为零.14.C解析:C【分析】先求出k 的取值范围,再判断出1k -及1k -的符号,进而可得出结论.【详解】0(1)k -有意义,则1k >.∴10k -<,10k ->,∴一次函数()11y k x k =-+-的图象经过第一、二、四象限.故选:C .【点睛】本题考查的是一次函数的图象,熟知一次函数的图象与系数的关系是解答此题的关键. 15.B解析:B【分析】利用速度=路程÷时间分别求得步行的速度和骑自行车的速度,从而利用分式的运算法则求得两者的速度差.【详解】 解:步行的速度是:m t (km /h ),骑自行车的速度是:31313m m t t =--(km /h ), 则骑自行车的速度与步行的速度差为:331(31)m m m t t t t-=--. 故选:B .【点睛】本题考查了列代数式及分式的加减运用,正确表示出步行和骑自行车的速度是解题的关键.16.B解析:B【分析】分别求出a 、b 、c 、d 的值,比较大小即可.【详解】20.30.09a =-=-2213139b -=-=-=- 01()3c =-=1 2211=(-3))9(3d -==- 故b a d c <<<故选:B【点睛】本题考查正指数与负指数的计算,注意负指数的运算规则.17.B解析:B【分析】根据零指数幂、指数幂、平方根、负整数指数幂的定义分别验证四个选项即可得到答案.【详解】解:A 、020181=,任何非零数的零次方都等于1,故A 不是答案;B 、224-=-,故B 是答案;C 2=,故C 不是答案;D 、1133-=,故D 不是答案; 故选:B .【点睛】本题主要考查了零指数幂、指数幂、平方根、负整数指数幂的定义,熟练掌握各知识点是解题的关键.18.D解析:D【分析】利用同底数幂相乘、合并同类项、积的乘方、幂的乘方、负整数指数幂以及整式的除法逐个判断即可.【详解】解:①336a a a ⋅=,故①错误;②2m 和3m 不是同类项,不能合并,故②错误;③()()()222224-2-24a a a ==,故③错误;④()2104268a a a a a a ⋅÷==⋅,故④正确;⑤()-21-525=,故⑤错误;⑥22m a m n a n+≠+,故⑥错误;只有1正确. 故答案为D .【点睛】本题考查了同底数幂相乘、合并同类项、积的乘方、幂的乘方、负整数指数幂、整式的除法等知识点,掌握相关运算法则是解答本题的关键.19.C解析:C【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.000000076用科学记数法表示为7.6×10-8.故选:C .【点睛】本题考查用科学记数法表示较小的数,一般形式为a ×10-n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.20.D解析:D【详解】∵4+46=,∴选项A 不符合题意;∵4+40+40=6,∴选项B 不符合题意;∵,∴选项C 不符合题意;∵144-=1486≠,∴选项D 符合题意, 故选D . 21.B解析:B【分析】先将分母进行通分,化为(x+y )(x-y )的形式,分子乘上相应的分式,进行化简.【详解】()()()()222222x y x +xy xy-y x +y -=-=x-y x+y x+y x-y x+y x-y x -y 【点睛】本题考查的是分式的混合运算,解题的关键就是熟练掌握运算规则.22.B解析:B【分析】根据分式的性质,对每个选项的式子一一判断正误即可.【详解】22x y x y -+-=-,故A 选项错误; ()222()()()()x y x y x y x y x y x y x y x y --+-==++++,故B 选项正确; 1b a b a ab b++=,故C 选项错误;23319(3)(3)3x x x x x x --==-+-+,故D 选项错误. 故选:B .【点睛】本题主要考查分式的化简,熟记分式的性质是解题关键. 23.D解析:D【分析】根据最简分式的定义即可判断.【详解】 解:42=2x x,故A 选项错误; ()11=111x x x x ---=---,故B 选项错误; ()()2111==1111x x x x x x ++-+--,故C 选项错误; 224x x -,故D 选项正确. 故选:D【点睛】本题主要考查的是最简分式的定义,正确的掌握最简分式的定义是解题的关键.24.C解析:C【分析】利用分式的概念:一般地,如果A ,B 表示两个整式,并且B 中含有字母,那么式子A B叫做分式,进行解答即可.【详解】解:在2a b -,3x x +,13,a b a b +-,1()x y m-中, 3x x +,a b a b +-,1()x y m -是分式,共3个,故选:C .【点睛】 本题考查了分式,关键是掌握分式的分母必须含有字母,而分子可以含字母,也可以不含字母.25.A解析:A【分析】 由23a b =≠0,得2b =3a ,把根据分式运算法则进行化简,再代入已知值计算即可. 【详解】 解:(2244b ab a-+1)2b a a -÷ 222442b ab a a a b a-+=•- 22(2)2a b a a b a-=•- 2b a a -=, ∵23a b =≠0, ∴2b =3a , ∴原式32a a a a a-===2, 故选:A .【点睛】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
把分式 中的x、y的值同时扩大为原来的10倍得:
,
即分式 的值不变,
故选:A.
【点睛】
本题考查了分式的基本性质,正确掌握分式的基本性质是解题的关键.
19.计算 的结果是
A.a-bB.b-aC.1D.-1
【答案】D
【解析】
【分析】
将第二个式子提出一个负号,即可使分母一样,然后化简即可得出答案.
【详解】
则四个实数的大小关系为
因此,最大的数是
故选:C.
【点睛】
本题考查了实数的大小比较法则,掌握大小比较法则是解题关键.
6.要使式子 有意义,则 的取值范围为()
A. B. C. 且 D.
【答案】D
【解析】
【分析】
根据分式有意义的条件可得x+5≠0,再根据二次根式有意义的条件可得x≥0,由此即可求得答案.
【解析】
【分析】
根据负整数指数幂计算法则,积的乘方计算法则,同底数幂除法法则,单项式乘以单项式计算法则依次判断.
【详解】
A、 ,故错误;
B、 正确;
C、 ,故错误;
D、 ,
故选:B.
【点睛】
此题考查整式的计算,正确掌握负整数指数幂计算法则,积的乘方计算法则,同底数幂除法法则,单项式乘以单项式计算法则是解题的关键.
B、 ,故B不符合题意;
C、 ,故C符合题意;
D、 ,故D不符合题意;
故选:C.
【点睛】
此题考查同底数幂的乘除法,平方差公式,熟记法则并根据法则计算是解题关键.
11.若 ,则 的值是()
A. B. C. D.
【答案】B
【解析】
【分析】
直接根据已知用含 的式子表示出两数,进而代入化简得出答案.
【详解】
【详解】
由题意得:x+5≠0,且x≥0,
解得:x≥0,
故选D.
【点睛】
本题考查了分式有意义的条件二次根式有意义的条件,关键是掌握分式有意义的条件是分母不等于零,二次根式中的被开方数是非负数.
7.如果 ,那么代数式 的值是
A. B. C.2D.3
【答案】C
【解析】
分析:先把括号内通分,再把分子分解后约分得到原式 ,然后利用 进行整体代入计算.
3.已知 是恒等式,则()
A. B. C. D.
【答案】B
【解析】
【分析】
首先利用分式的加减运算法则,求得 ,可得方程组 ,解此方程组即可求得答案.
【详解】
解:∵ ,
∴ ,
∴ ,解之得: ,
故选:B.
【点睛】
此题考查了分式的加减运算、二元一次方程的解法以及整式相等的性质,解题的关键是掌握分式的加减运算法则.
A.(﹣x﹣2y)(x+2y)= B. =
C. D.
【答案】D
【解析】
【分析】
根据整式的相关运算法则计算可得.
【详解】
A.(﹣x﹣2y)(x+2y)=﹣(x+2y)2=﹣x2﹣4xy﹣4y2,此选项计算错误;
B.3x﹣1= ,此选项计算错误;
C.(﹣2y2)3=﹣8y6,此选项计算错误;
D.(﹣x)3m÷xm=(﹣1)mx2m,此选项计算正确;
详解:原式
∵
∴
∴原式=2.
故选C.
点睛:考查分式的混合运算,掌握运算法则是解题的关键.注意整体代入法的应用.
8.如果把 中的x与y都扩大为原来的5倍,那么这个代数式的值()
A.不变B.扩大为原来的5倍C.扩大为原来的10倍D.缩小为原来的
【答案】A
【解析】
由题意,得 = =
故选:A.
9.下列各式计算正确的是()
4.若 ,则 的值为()
A. B.1C.-1D.-5
【答案】B
【解析】
【分析】
先将 变形为 ,即 ,再代入求解即可.
【详解】
∵ ,∴ ,即 ,
∴ .故选B.
【点睛】
本题考查分式的化简求值,解题的关键是将 变形为 .
5.在下列四个实数中,最大的数是()
A. B.0C. D.
【答案】C
【解析】
【分析】
根据实数的大小比较法则即可得.
【解析】
【分析】
先将后两项结合起来,然后再化成同分母分式,按照同分母分式加减的法则计算就可以了.
【详解】
原式
.
故选B.
【点睛】
本题考查分式的通分和分式的约分的运用,解题关键在于在解答的过程中注意符号的运用及平方差公式的运用.
17.计算 的结果为()
A. B. C. D.
【答案】B
【解析】
【分析】
利用幂次方计算公式即可解答.
解:∵
∴设 ,
∴
故选:B
【点睛】
此类化简求值题目,涉及到的字母 、 利用第三个未知数 设出,代入后得到关于 的式子进行约分化简即可.将两个字母转化为一个字母是解题的关键.
12.化简(a﹣1)÷( ﹣1)•a的结果是( )
A.﹣a2B.1C.a2D.﹣1
【答案】A
【解析】
分析:根据分式的混合运算顺序和运算法则计算可得.
【详解】
解:原式= .
答案选B.
【点睛】
本题考查幂次方计算,较为简单.
18.把分式 中的 的值同时扩大为原来的10倍,则分式的值()
A.不变B.缩小为原来的
C.扩大为原来的10倍D.扩大为原来的100倍
【答案】A
【解析】
【分析】
根据分式的基本性质,把分式 中的x、y的值同时扩大为原来的10倍得: ,即可得到答案.
详解:原式=(a﹣1)÷ •a
=(a﹣1)• •a
=﹣a2,
故选:A.
点睛:本题主要考查分式的混合运算,解题的关键是掌握分式的混合运算顺序和运算法则.
13.下列计算错误的是()
A. B.
C. D.
【答案】C
【解析】
【分析】
根据同底数幂的乘法法则,积的乘方法则、零次幂、负指数幂进行计算
【详解】
A. ,不符合题意;
【详解】
- = =-1,所以答案选择D.
【点睛】
本题考查了分式的化简,熟悉掌握计算方法是解决本题的关键.
20.生物学家发现某种花粉的直径约为0.0000036毫米,数据0.0000036用科学记数法可表示为()
A. B. C. D.
【答案】A
【解析】
【分析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
B. ,不符合题意;
C. ,原选项错误,符合题意;
D. ,不符合题意;
故选:C
【点睛】
本题考查了同底数幂的乘法法则,积的乘方法则、零次幂、负指数幂,掌握同底数幂的乘法法则,积的乘方法则、零次幂、负指数幂是解题的关键.
14.056用科学记数法表示为:0.056= ,故选B.
15.下列各式中,正确的是()
A.
B.
C.
D.
【答案】B
【解析】
【分析】
根据分式的基本性质分别进行化简即可.
【详解】
解:A、 ,错误;
B、 ,正确;
C、 ,错误;
D、 ,错误.
故选:B.
【点睛】
本题主要考察了分式的基本性质,分式运算时要同时乘除和熟练应用约分是解题的关键.
16.计算 的正确结果是( )
A. B. C. D.
【答案】B
分式难题汇编附答案
一、选择题
1.12×10−3=0.00612,
故选:C.
【点睛】
本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
2.乐乐所在的四人小组做了下列运算,其中正确:D.
【点睛】
本题主要考查整式的运算,解题的关键是掌握整式的运算法则和负整数指数幂的规定.
10.下列运算正确的是()
A. B. C. D.
【答案】C
【解析】
【分析】
根据同底数幂的乘除法,积的乘方,负整数指数幂,平方差公式,可得答案.
【详解】
解:A、不是同底数幂的乘法指数不能相加,故A不符合题意;
