数值计算课后答案
《数值计算方法》习题答案

《数值计算方法》课后题答案详解吉 林 大 学第一章 习 题 答 案1. 已知(1)2,(1)1,(2)1f f f −===,求()f x 的Lagrange 插值多项式。
解:由题意知:()01201212001020211012012202121,1,2;2,1,1()()(1)(2)()()6()()(1)(2)()()2()()(1)(1)()()3(1)(2)(1)(2)()2162nj j j x x x y y y x x x x x x l x x x x x x x x x x l x x x x x x x x x x l x x x x x x x x L x y l x ==−=====−−−−==−−−−+−==−−−−−+−==−−−−+−==×+×−∴∑()2(1)(1)131386x x x x +−+×=−+2. 取节点01210,1,,2x x x ===对x y e −=建立Lagrange 型二次插值函数,并估计差。
解11201201210,1,;1,,2x x x y y e y e −−======1)由题意知:则根据二次Lagrange插值公式得:02011201201021012202110.510.520.51()()()()()()()()()()()()()2(1)(0.5)2(0.5)4(1)(224)(43)1x x x x x x x x x x x x L x y y y x x x x x x x x x x x x x x x x e x x e e e x e e x −−−−−−−−−−−−=++−−−−−−=−−+−−−=+−+−−+22)Lagrange 根据余项定理,其误差为(3)2210122()1|()||()||(1)(0.5)|3!61max |(1)(0.5)|,(0,1)6()(1)(0.5),()330.5030.2113()61()0.2113(0.21131)(0.21130.5)0.008026x f R x x e x x x x x x t x x x x t x x x x t x R x ξξωξ−+≤≤==−−≤−−∈′=−−=−+=−==≤××−×−=∴取 并令 可知当时,有极大值3. 已知函数y =在4, 6.25,9x x x ===处的函数值,试通过一个二次插值函数求的近似值,并估计其误差。
数值计算方法习题答案

《数值计算方法》课后题答案详解吉 林 大 学第一章 习 题 答 案1. 已知(1)2,(1)1,(2)1f f f −===,求()f x 的Lagrange 插值多项式。
解:由题意知:()01201212001020211012012202121,1,2;2,1,1()()(1)(2)()()6()()(1)(2)()()2()()(1)(1)()()3(1)(2)(1)(2)()2162nj j j x x x y y y x x x x x x l x x x x x x x x x x l x x x x x x x x x x l x x x x x x x x L x y l x ==−=====−−−−==−−−−+−==−−−−−+−==−−−−+−==×+×−∴∑()2(1)(1)131386x x x x +−+×=−+2. 取节点01210,1,,2x x x ===对x y e −=建立Lagrange 型二次插值函数,并估计差。
解11201201210,1,;1,,2x x x y y e y e −−======1)由题意知:则根据二次Lagrange插值公式得:02011201201021012202110.510.520.51()()()()()()()()()()()()()2(1)(0.5)2(0.5)4(1)(224)(43)1x x x x x x x x x x x x L x y y y x x x x x x x x x x x x x x x x e x x e e e x e e x −−−−−−−−−−−−=++−−−−−−=−−+−−−=+−+−−+22)Lagrange 根据余项定理,其误差为(3)2210122()1|()||()||(1)(0.5)|3!61max |(1)(0.5)|,(0,1)6()(1)(0.5),()330.5030.2113()61()0.2113(0.21131)(0.21130.5)0.008026x f R x x e x x x x x x t x x x x t x x x x t x R x ξξωξ−+≤≤==−−≤−−∈′=−−=−+=−==≤××−×−=∴取 并令 可知当时,有极大值3. 已知函数y =在4, 6.25,9x x x ===处的函数值,试通过一个二次插值函数求的近似值,并估计其误差。
数值计算方法课后习题答案

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
丁丽娟《数值计算方法》五章课后实验题答案(源程序很详细,且运行无误)

丁丽娟《数值计算方法》五章课后实验题答案(源程序都是自己写的,很详细,且保证运行无误)我做的五章数值实验作业题目如下:第二章:1、2、3、4题第三章:1、2题第四章:1、2题第六章:2、3题第八章:1、2题第二章1:(1) 对A进行列主元素三角分解:function [l u]=myfun(A) n=size(A); for k=1:n for i=k:n sum=0; m=k; for j=1:(k-1) sum=sum+A(i,j)*A(j,k); end s(i)=A(i,k)-sum; if abs(s(m))<abs(s(i)) m=i; end end for j=1:n c=A(m,j); A(m,j)=A(k,j); A(k,j)=c; end for j=k:n sum=0; for r=1:(k-1) sum=sum+A(k,r)*A(r,j); end u(k,j)=A(k,j)-sum; A(k,j)=u(k,j); end for i=1:n l(i,i)=1; end for i=(k+1):n sum=0; for r=1:(k-1) sum=sum+A(i,r)*u(r,k); end l(i,k)=(A(i,k)-sum)/u(k,k); A(i,k)=l(i,k); end end 的列主元素三角分解:求A的列主元素三角分解:>>A=[1 1 1 1 1;1 2 3 4 5;1 3 6 10 15;1 4 10 20 35;1 5 15 35 70]; >>[L,U]=myfun(A) 结果:L = 1.0000 0 0 0 0 1.0000 1.0000 0 0 0 1.0000 0.5000 1.0000 0 0 1.0000 0.7500 0.7500 1.0000 0 1.0000 0.2500 0.7500 -1.0000 1.0000 U = 1.0000 1.0000 1.0000 1.0000 1.0000 0 4.0000 14.0000 34.0000 69.0000 0 0 -2.0000 -8.0000 -20.5000 0 0 0 -0.5000 -2.3750 0 0 0 0 -0.2500 (2) 求矩阵的逆矩阵A -1: inv(A) 结果为:ans = 5 -10 10 -5 1 -10 30 -35 19 -4 10 -35 46 -27 6 -5 19 -27 17 -4 1 -4 6 -4 1 (3)检验结果:E=diag([1 1 1 1 1]) A\E ans = 5 -10 10 -5 1 -10 30 -35 19 -4 10 -35 46 -27 6 -5 19 -27 17 -4 1 -4 6 -4 1 2: 程序:程序:function d=myfun(a,b,c,d,n) for i=2:n l(i)=a(i)/b(i-1); a(i)=l(i); u(i)=b(i)-c(i-1)*a(i); b(i)=u(i); y(i)=d(i)-a(i)*d(i-1); d(i)=y(i); end x(n)=d(n)/b(n); d(n)=x(n); for i=(n-1):-1:1 x(i)=(d(i)-c(i)*d(i+1))/b(i); d(i)=x(i); end 求各段电流量程序:求各段电流量程序:for i=2:8 a(i)=-2; end b=[2 5 5 5 5 5 5 5]; c=[-2 -2 -2 -2 -2 -2 -2]; V=220; R=27; d=[V/R 0 0 0 0 0 0 0]; n=8; I=myfun(a,b,c,d,n) 运行程序得:运行程序得:I = 8.1478 4.0737 2.0365 1.0175 0.5073 0.2506 0.1194 0.0477 3:程序:(1)求矩阵A和向量b的matlab程序:function [A b]=myfun(n) for i=1:n X(i)=1+0.1*i; end for i=1:n for j=1:n A(i,j)=X(i)^(j-1); end end for i=1:n b(i)=sum(A(i,:)); end 求n=5时A1,b1及A1的2-条件数程序运行结果如下:条件数程序运行结果如下: n=5;[A1,b1]=myfun(n) A1 = 1.0000 1.1000 1.2100 1.3310 1.4641 1.0000 1.2000 1.4400 1.7280 2.0736 1.0000 1.3000 1.6900 2.1970 2.8561 1.0000 1.4000 1.9600 2.7440 3.8416 1.0000 1.5000 2.2500 3.3750 5.0625 b1 = 6.1051 7.4416 9.0431 10.9456 13.1875 cond2=cond(A1,2)cond2 = 5.3615e+005 条件数程序运行结果如下:求n=10时A2,b2及A2的2-条件数程序运行结果如下:n=10; [A2,b2]=myfun(n) A2 = 1.0000 1.1000 1.2100 1.3310 1.4641 1.6105 1.7716 1.9487 2.1436 2.3579 1.0000 1.2000 1.4400 1.7280 2.0736 2.4883 2.9860 3.5832 4.2998 5.1598 1.0000 1.3000 1.6900 2.1970 2.8561 3.7129 4.8268 6.2749 8.1573 10.6045 1.0000 1.4000 1.9600 2.7440 3.8416 5.3782 7.5295 10.5414 14.7579 20.6610 1.0000 1.5000 2.2500 3.3750 5.0625 7.5938 11.3906 17.0859 25.6289 38.4434 1.0000 1.6000 2.5600 4.0960 6.5536 10.4858 16.7772 26.8435 42.9497 68.7195 1.0000 1.7000 2.8900 4.9130 8.3521 14.1986 24.1376 41.0339 69.7576 118.5879 1.0000 1.8000 3.2400 5.8320 10.4976 18.8957 34.0122 61.2220 110.1996 198.3593 1.0000 1.9000 3.6100 6.8590 13.0321 24.7610 47.0459 89.3872 169.8356 322.6877 1.0000 2.0000 4.0000 8.0000 16.0000 32.0000 64.0000 128.0000 256.0000 512.0000 b2 = 1.0e+003 * 0.0159 0.0260 0.0426 0.0698 0.1133 0.1816 0.2866 0.4451 0.6801 1.0230 cond2=cond(A2,2) cond2 = 8.6823e+011 条件数程序运行结果如下:求n=20时A3,b3及A3的2-条件数程序运行结果如下:n=20; [A3,b3]=myfun(n) A3 = 1.0e+009 * Columns 1 through 10 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 Columns 11 through 20 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0002 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0003 0.0005 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0003 0.0006 0.0013 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0003 0.0007 0.0015 0.0032 0.0000 0.0000 0.0000 0.0001 0.0001 0.0003 0.0006 0.0014 0.0032 0.0075 0.0000 0.0000 0.0000 0.0001 0.0002 0.0005 0.0012 0.0029 0.0070 0.0167 0.0000 0.0000 0.0001 0.0001 0.0004 0.0009 0.0023 0.0058 0.0146 0.0364 0.0000 0.0000 0.0001 0.0002 0.0006 0.0017 0.0044 0.0113 0.0295 0.0766 0.0000 0.0001 0.0002 0.0004 0.0011 0.0030 0.0080 0.0215 0.0581 0.1570 0.0000 0.0001 0.0002 0.0007 0.0018 0.0051 0.0143 0.0400 0.1119 0.3133 0.0000 0.0001 0.0004 0.0010 0.0030 0.0086 0.0250 0.0726 0.2105 0.6103 0.0001 0.0002 0.0005 0.0016 0.0048 0.0143 0.0430 0.1291 0.3874 1.1623 b3 = 1.0e+009 * Columns 1 through 10 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0002 0.0004 0.0010Columns 11 through 20 0.0025 0.0059 0.0132 0.0287 0.0606 0.1246 0.2494 0.4874 0.9316 1.7434 cond2=cond(A3,2) cond2 =3.2395e+022 由上述运行结果可知:它们是病态的,而且随着n的增大,矩阵的病态变得严重。
数值计算方法与算法第三版课后习题答案

数值计算方法与算法第三版课后习题答案1. 矩阵乘法问题描述给定两个矩阵A和B,尺寸分别为n×m和m×p,求矩阵A 和矩阵B的乘积矩阵C,尺寸为n×p。
算法实现import numpy as npdef matrix_multiplication(A, B):n, m = A.shapem, p = B.shapeC = np.zeros((n, p))for i in range(n):for j in range(p):for k in range(m):C[i][j] += A[i][k] * B[k][j] return C示例A = np.array([[1, 2], [3, 4]])B = np.array([[5, 6], [7, 8]])C = matrix_multiplication(A, B)print(C)输出结果:[[19. 22.][43. 50.]]2. 数值积分问题描述给定一个函数f(x),以及积分区间[a, b],求函数f(x)在区间[a, b]上的定积分值∫abf(x)dx。
算法实现简单的数值积分算法是采用小梯形法,将区间[a, b]均分成n个子区间,然后计算每个子区间的面积,最后将这些子区间面积相加得到定积分值。
def numerical_integration(f, a, b, n):h = (b - a) / nintegral =0for i in range(n):x1 = a + i * hx2 = a + (i +1) * hintegral += (f(x1) + f(x2)) * h /2 return integral示例import mathf =lambda x: math.sin(x)a =0b = math.pin =100result = numerical_integration(f, a, b, n) print(result)输出结果:1.99983550388744363. 非线性方程求解问题描述给定一个非线性方程f(x) = 0,求方程的根x。
数值课后题答案

习 题 一1、解:根据绝对误差限不超过末位数的半个单位,相对误差限为绝对误差限除以有效数字本身,有效数字的位数根据有效数字的定义来求.因此 49×10-2 :E = 0.005; r E = 0.0102; 2位有效数字. 0.0490 :E = 0.00005;r E = 0.00102; 3位有效数字. 490.00 :E = 0.005; r E = 0.0000102;5位有效数字.2、解:722= 3.1428 …… , π = 3.1415 …… , 取它们的相同部分3.14,故有3位有效数字.E = 3.1428 - 3.1415 = 0.0013 ;r E = 14.3E = 14.30013.0 = 0.00041.3、解:101的近似值的首位非0数字1α = 1,因此有 |)(*x E r |)1(10121--⨯⨯=n < = 21× 10-4 , 解之得n > = 5,所以 n = 5 . 4、证:)()(1)()(1)(*11**11**x x x nx E x n x E n n n-=≈--)(11)()(1)()(*****11****x E nx x x n x x x x nx x E x E r nnnn n r =-=-≈=- 5、解:(1)因为=20 4.4721…… ,又=)(*x E |*x x -| = |47.420-| = 0.0021 < 0.01, 所以 =*x 4.47.(2)20的近似值的首位非0数字1α = 4,因此有 |)(*x E r |)1(10421--⨯⨯=n < = 0.01 , 解之得n > = 3 .所以,=*x 4.47. 6、解:设正方形的边长为x ,则其面积为2x y =,由题设知x 的近似值为*x = 10 cm .记*y 为y 的近似值,则)(20)(20)(2)(*****x E x x x x x y E =-=-= < = 0.1,所以)(*x E < = 0.005 cm .7、解:因为)()(*1x x nx x E n n -≈-,所以n x nE x x x n xx E x E r nn nr 01.0)()()(*==-≈=. 9、证:)()()(**t gtE t t gt S S S E =-≈-=t t E gt t t gt S S S S E r )(22/)()(2**=-≈-= 由上述两式易知,结论. 10、解:代入求解,经过计算可知第(3)个计算结果最好.11、解:基本原则为:因式分解,分母分子有理化、三角函数恒等变形…… (1)通分;(2)分子有理化;(3)三角函数恒等变形.12、解: 因为20=x ,41.1*0=x ,所以|*0x x -| < = δ=⨯-21021 于是有|*11x x -| = |110110*00+--x x | = 10|*00x x -| < =δ10 |*22x x -| = |110110*11+--x x | = 10|*11x x -| < =δ210 类推有 |*1010x x -| < =810102110⨯=δ 即计算到10x ,其误差限为δ1010,亦即若在0x 处有误差限为δ,则10x 的误差将扩大1010倍,可见这个计算过程是不稳定的.习 题 二1、 解:只用一种方法.(1)方程组的增广矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----11114423243112 → ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1010411101110112 → ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---11041001110112 → 31=x , 12=x , 13=x . (2)方程组的增广矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------017232221413 → ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--247210250413 → ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--147200250413 → 21=x , 12=x , 2/13=x . (3)适用于计算机编程计算.2、 解:第一步:计算U 的第一行,L 的第一列,得611=u 212=u 113=u 114-=u3/1/112121==u a l 6/1/113131==u a l6/1/114141-==u a l第二步:计算U 的第二行,L 的第二列,得3/1012212222=-=u l a u 3/213212323=-=u l a u 3/114212424=-=u l a u 5/1/)(2212313232=-=u u l a l10/1/)(2212414242=-=u u l a l第三步:计算U 的第三行,L 的第三列,得10/37233213313333=--=u l u l a u 10/9243214313434-=--=u l u l a u 37/9/)(33234213414343-=--=u u l u l a l第四步:计算U 的第四行,得370/9553443244214414444-=---=u l u l u l a u从而, ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----3101141101421126 = ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--137/910/16/1015/16/10013/10001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---370/95500010/910/37003/13/23/1001126 由b LY = , 解得Y =(6,-3,23/5,-955/370)T . 由Y UX = , 解得X =(1,-1,1,-1)T . 3、(1)解:首先检验系数矩阵的对称正定性,这可以通过计算其各阶顺序主子式是否大于零来判断.11a = 3 > 0, 2223= 2 > 0, 301022123 = 4 > 0,所以系数矩阵是对称正定的.记系数矩阵为A ,则平方根法可按如下三步进行:第一步 分解:A = L L T . 由公式计算出矩阵的各元素:311=l 33221=l 3622=l 3331=l 3632-=l 233=l因此, L =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-23633036332003. 第二步 求解方程组LY = b . 解得Y = (335,36,2)T . 第三步 求解方程组L T X = Y . 解得X =(0,2,1)T .(2)解:首先检验系数矩阵的对称正定性,这可以通过计算其各阶顺序主子式是否大于零来判断.11a = 3 > 0,2223= 2 > 0, 1203022323 = 6 > 0,所以系数矩阵是对称正定的.记系数矩阵为A ,则平方根法可按如下三步进行:第一步 分解:A = L L T . 由公式计算出矩阵的各元素:311=l 33221=l 3622=l 331=l 632-=l 333=l因此, L =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-363036332003 . 第二步 求解方程组LY = b . 解得Y = (335,66-,33)T. 第三步 求解方程组L T X = Y . 解得X = (1,21,31)T . 4、解: 对1=i , 2111==a d ;对2=i , 121-=t , 2121-=l , 252-=d ;对3=i , 131=t , 2732=t ,2131=l , 5732-=l ,5273=d .所以数组A 的形式为: ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=527572102521002A 求解方程组LY = b . 解得Y = (4,7,569)T . 求解方程组DL T X = Y . 解得X = (910,97,923)T .5、解:(1)设A = LU = ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1010000000000010010015432l l l l ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡5432106000000000600006006u u u u u计算各元素得: 51=u , 512=l , 1952=u , 1953=l , 19653=u ,65194=l , 652114=u , 211655=l , 2116655=u .求解方程组LY = d . 解得Y = (1,51-,191,651-,211212)T.求解方程组UX = Y . 解得X = (6651509,6651145,665703,665395-,665212)T.(2)设A = LU = ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100100132l l ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡3211001u u u 计算各元素得:51=u ,512=l ,5242=u ,2453=l ,241153=u . 求解方程组LY = d . 解得Y = (17,553,24115)T.求解方程组UX = Y . 解得X = (3,2,1)T. 6、证:(1)(2)相同.因为此方程组的系数矩阵为严格对角占优矩阵,所以雅可比迭代法和相应的高斯-赛德尔迭代法都收敛. (1)雅可比迭代公式:7107271)(3)(2)1(1+--=+k k k x x x14141)(3)(1)1(2+--=+k k k x x x329292)(2)(1)1(3+--=+k k k x x x高斯-赛德尔迭代公式:7107271)(3)(2)1(1+--=+k k k x x x14141)(3)1(1)1(2+--=++k k k x x x329292)1(2)1(1)1(3+--=+++k k k x x x(2)雅可比迭代公式:545152)(3)(2)1(1+-=+k k k x x x525351)(3)(1)1(2++-=+k k k x x x5115152)(2)(1)1(3++=+k k k x x x高斯-赛德尔迭代公式:545152)(3)(2)1(1+-=+k k k x x x525351)(3)1(1)1(2++-=++k k k x x x5115152)1(2)1(1)1(3++=+++k k k x x x7、(1)证:因为此方程组的系数矩阵为严格对角占优矩阵,所以雅可比迭代法和相应的高斯-赛德尔迭代法都收敛。
数值计算课后答案5

习 题 五 解 答1、用矩形公式、梯形公式、抛物线公式计算下列积分,并比较结果。
(1)120(8)4xdx n x =+⎰,(2)20sin (8)x xdx n π=⎰(3)1(4)n =⎰,(4)1(4)x e dxn -=⎰1*、用矩形公式、梯形公式、抛物线公式计算下列积分,并比较结果。
(1)120(4)4x dx n x =+⎰解:解:将区间[0,1]4等分,5个分点上的被积函数值列表如下(取2位小数)(1)矩形法。
用矩形法公式计算(取2位小数)或者 (2)梯形法用梯形法公式计算(取2位小数): (3)抛物线法用抛物线法公式计算(取2位小数):2、用复化梯形公式计算积分841dx x ⎰,由此计算ln2(注:841ln 2dx x=⎰),精度要求为410-。
解:8418ln8ln 4ln ln 24dx x =-==⎰,要求精度为410-,即误差不超过41102ε-=⨯。
将积分区间[4,8]n 等份,则步长844h n n -==在本题中,复化梯形公式的余项为2228484416()()()()12123r h f f f n nηηη--''''''=-=-=-注意到231(),(),()2f x f x x f x x x--'''==-=,所以在[4,8]区间上3()24f x -''≤⨯,则32232161621283346r n n n-⨯≤⨯⨯==⨯, 要使42111062n -≤⨯,需有42421110310577.36757862n n n n n -≤⨯⇒≥⇒≥⇒≥⇒=。
3、用复合梯形公式计算积分()baf x dx ⎰,问将积分区间[a,b]分成多少等份,才能保证误差不超过ε(不计舍入误差)?解:对于复合梯形公式来说,如果()f x ''在积分区间上连续,则其余项为2(),[,]12b a r h f a b ηη-''=-∈,设max ()a x bM f x ≤≤''=,则322()()()1212b a b a Mr h f nη--''=≤ 令32()12b a Mn ε-≤,得n ≥即当1n =+时,能保证计算的精度要求。
最新数值计算课后答案1

习 题 一 解 答1.取3.14,3.15,227,355113作为π的近似值,求各自的绝对误差,相对误差和有效数字的位数。
分析:求绝对误差的方法是按定义直接计算。
求相对误差的一般方法是先求出绝对误差再按定义式计算。
注意,不应先求相对误差再求绝对误差。
有效数字位数可以根据定义来求,即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位,再确定有效数的末位是哪一位,进一步确定有效数字和有效数位。
有了定理2后,可以根据定理2更规范地解答。
根据定理2,首先要将数值转化为科学记数形式,然后解答。
解:(1)绝对误差:e(x)=π-3.14=3.14159265…-3.14=0.00159…≈0.0016。
相对误差:3()0.0016()0.51103.14r e x e x x -==≈⨯ 有效数字:因为π=3.14159265…=0.314159265…×10,3.14=0.314×10,m=1。
而π-3.14=3.14159265…-3.14=0.00159…所以│π-3.14│=0.00159…≤0.005=0.5×10-2=21311101022--⨯=⨯ 所以,3.14作为π的近似值有3个有效数字。
(2)绝对误差:e(x)=π-3.15=3.14159265…-3.14=-0.008407…≈-0.0085。
相对误差:2()0.0085()0.27103.15r e x e x x --==≈-⨯ 有效数字:因为π=3.14159265…=0.314159265…×10,3.15=0.315×10,m=1。
而π-3.15=3.14159265…-3.15=-0.008407…所以│π-3.15│=0.008407……≤0.05=0.5×10-1=11211101022--⨯=⨯ 所以,3.15作为π的近似值有2个有效数字。
(3)绝对误差:22() 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈-L L 相对误差:3()0.0013()0.4110227r e x e x x--==≈-⨯ 有效数字:因为π=3.14159265...=0.314159265 (10)22 3.1428571430.3142857143107==⨯,m=1。
《数值计算方法》课后题答案(湖南大学-曾金平)

习题一1.设x >0相对误差为2%,4x 的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x x f x f x δδ∆=≈得(1)()f x =11()()*2%1%22x x δδδ≈===;(2)4()f x x =时444()()'()4()4*2%8%x x x x x xδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P 关于1212.m nx a a a bb b =±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算 (1)31.97+2.456+0.1352; (2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352 ≈21((0.3197100.245610)0.1352)fl fl ⨯+⨯+ =2(0.3443100.1352)fl ⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl ≈⨯+⨯ = 21(0.3197100.259110)fl ⨯+⨯ =0.3456210⨯易见31.97+2.456+0.1352=0.210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?解:设该正方形的边长为x ,面积为2()f x x =,由(())(())'()()()()f x xf x f x x f x f x δδ∆=≈解得(())()()'()f x f x x xf x δδ≈=2(())(())22f x x f x x xδδ==0.5%5.下面计算y 的公式哪个算得准确些?为什么?(1)已知1x <<,(A )11121xy x x-=-++,(B )22(12)(1)x y x x =++; (2)已知1x >>,(A )y=,(B )y =; (3)已知1x <<,(A )22sin x y x =,(B )1cos 2xy x-=;(4)(A)9y =(B )y =解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算课后习题答案

习 题 一 解 答1.取3.14,3.15,227,355113作为π的近似值,求各自的绝对误差,相对误差和有效数字的位数。
分析:求绝对误差的方法是按定义直接计算。
求相对误差的一般方法是先求出绝对误差再按定义式计算。
注意,不应先求相对误差再求绝对误差。
有效数字位数可以根据定义来求,即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位,再确定有效数的末位是哪一位,进一步确定有效数字和有效数位。
有了定理2后,可以根据定理2更规范地解答。
根据定理2,首先要将数值转化为科学记数形式,然后解答。
解:(1)绝对误差:e(x)=π-3.14=3.14159265…-3.14=0.00159…≈0.0016。
相对误差:3()0.0016()0.51103.14r e x e x x-==≈⨯有效数字:因为π=3.14159265…=0.314159265…×10,3.14=0.314×10,m=1。
而π-3.14=3.14159265…-3.14=0.00159…所以│π-3.14│=0.00159…≤0.005=0.5×10-2=21311101022--⨯=⨯所以,3.14作为π的近似值有3个有效数字。
(2)绝对误差:e(x)=π-3.15=3.14159265…-3.14=-0.008407…≈-0.0085。
相对误差:2()0.0085()0.27103.15r e x e x x--==≈-⨯有效数字:因为π=3.14159265…=0.314159265…×10,3.15=0.315×10,m=1。
而π-3.15=3.14159265…-3.15=-0.008407…所以│π-3.15│=0.008407……≤0.05=0.5×10-1=11211101022--⨯=⨯所以,3.15作为π的近似值有2个有效数字。
(3)绝对误差:22() 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈-相对误差:3()0.0013()0.4110227r e x e x x--==≈-⨯有效数字:因为π=3.14159265...=0.314159265 (10)22 3.1428571430.3142857143107==⨯,m=1。
数值计算课后规范标准答案2
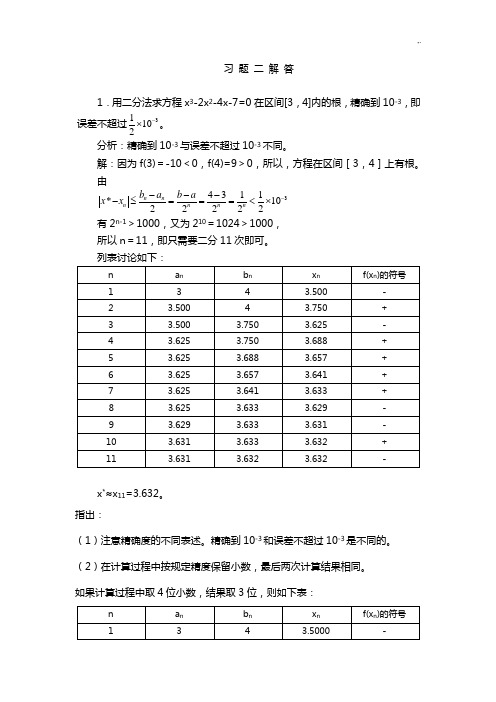
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
数值计算方法教材答案

1习题一1.设x>0相对误差为2%,4x的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x xf x f xδδ∆=≈得(1)()f x=11()()*2%1%22x xδδδ≈===;(2)4()f x x=时444()()'()4()4*2%8%xx x x xxδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P关于1212.m nx a a a bb b=±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算(1)31.97+2.456+0.1352;(2)31.97+(2.456+0.1352)哪个较精确?解:(1)31.97+2.456+0.1352≈21((0.3197100.245610)0.1352)fl fl⨯+⨯+=2(0.3443100.1352)fl⨯+=0.3457210⨯(2)31.97+(2.456+0.1352)21(0.319710(0.245610))fl fl≈⨯+⨯= 21(0.3197100.259110)fl⨯+⨯=0.3456210⨯易见31.97+2.456+0.1352=0.345612210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少?2解:设该正方形的边长为x,面积为2()f x x=,由(())(())'()()()()f x xf x f x xf x f xδδ∆=≈解得(())()()'()f x f xxxf xδδ≈=2(())(())22f x x f xx xδδ==0.5%5.下面计算y的公式哪个算得准确些?为什么?(1)已知1x<<,(A)11121xyx x-=-++,(B)22(12)(1)xyx x=++;(2)已知1x>>,(A)y=,(B)y=;(3)已知1x<<,(A)22sin xyx=,(B)1cos2xyx-=;(4)(A)9y=(B)y=解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算课后全部答案(整合)
目录第一章-----------------------------------------1 第二章-----------------------------------------4 第三章-----------------------------------------9 第四章-----------------------------------------15 第五章-----------------------------------------20 第六章-----------------------------------------27 第七章-----------------------------------------30第一章数值计算中的误差习题一1.1 下列各近似数的绝对误差限是最末位的半个单位,试指出它们各有几位有效数字。
1x =-3.105 , 2x =0.001, 3x =0.100, 4x =253.40, 5x =5000, 6x =5⨯310.答案:4,1,3,6,4,1.1.2 设100>*x >10,x 是*x 的有五位有效数字的的近似数,求x 的绝对误差限。
答案:当10<x<100时,因为有5位有效数字,所以绝对误差限为0.005. 1.3 求下列各近似数的相对误差限和有效数字位数: 1) 123x x x ++,2) 124x x x 3) 24x x 答案:()10.0005e x ≤()20.0005e x ≤()30.0005e x ≤ ()40.005e x ≤ ()50.5e x ≤ ()60.5e x ≤1)()()()()123123e x x x e x e x e x ++=++≤()()()123e x e x e x ++3221.5100.15100.510---≤⨯=⨯≤⨯2123()0.1510x x x ε-++=⨯123123123()()0.0004993...0.0004994r x x x e x x x x x x ε++++==≤++123x x x ++=-3.004 精确到小数点后两位,所以有三位有效数字。
数值计算方法课后习题答案(李庆扬等)

第一章 绪论(12)1、设0>x ,x 的相对误差为δ,求x ln 的误差。
[解]设0*>x 为x 的近似值,则有相对误差为δε=)(*x r ,绝对误差为**)(x x δε=,从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x , 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%,求n x 的相对误差。
[解]设*x 为x 的近似值,则有相对误差为%2)(*=x r ε,绝对误差为**%2)(x x =ε,从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε,相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出它们是几位有效数字:1021.1*1=x ,031.0*2=x ,6.385*3=x ,430.56*4=x ,0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字;0031.0*2=x 有2位有效数字;6.385*3=x 有4位有效数字;430.56*4=x 有5位有效数字;0.17*5⨯=x 有2位有效数字。
4、利用公式(3.3)求下列各近似值的误差限,其中*4*3*2*1,,,x x x x 均为第3题所给的数。
(1)*4*2*1x x x ++; [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε;(2)*3*2*1x x x ;[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε;(3)*4*2/x x 。
数值计算方法答案

数值计算方法习题一(2)习题二(6)习题三(15)习题四(29)习题五(37)习题六(62)习题七(70)2009.9,9习题一1.设x >0相对误差为2%4x 的相对误差。
解:由自变量的误差对函数值引起误差的公式:(())(())'()()()()f x xf x f x x f x f x δδ∆=≈得(1)()f x =11()()*2%1%22x x δδδ≈===;(2)4()f x x =时444()()'()4()4*2%8%x x x x x xδδδ≈===2.设下面各数都是经过四舍五入得到的近似数,即误差不超过最后一位的半个单位,试指出他们各有几位有效数字。
(1)12.1x =;(2)12.10x =;(3)12.100x =。
解:由教材9P 关于1212.m nx a a a bb b =±型数的有效数字的结论,易得上面三个数的有效数字位数分别为:3,4,53.用十进制四位浮点数计算 (1)++; (2)+(+)哪个较精确 解:(1)++ ≈21((0.3197100.245610)0.1352)fl fl ⨯+⨯+=2(0.3443100.1352)fl ⨯+=210⨯(2)+(+)21(0.319710(0.245610))fl fl ≈⨯+⨯ = 21(0.3197100.259110)fl ⨯+⨯ =210⨯易见++=210⨯,故(2)的计算结果较精确。
4.计算正方形面积时,若要求面积的允许相对误差为1%,测量边长所允许的相对误差限为多少解:设该正方形的边长为x ,面积为2()f x x =,由(())(())'()()()()f x xf x f x x f x f x δδ∆=≈解得(())()()'()f x f x x xf x δδ≈=2(())(())22f x x f x x xδδ==%5.下面计算y 的公式哪个算得准确些为什么(1)已知1x <<,(A )11121xy x x-=-++,(B )22(12)(1)x y x x =++; (2)已知1x>>,(A )y=,(B )y = (3)已知1x <<,(A )22sin x y x =,(B )1cos2xy x-=;(4)(A)9y =-(B )y =解:当两个同(异)号相近数相减(加)时,相对误差可能很大,会严重丧失有效数字;当两个数相乘(除)时,大因子(小除数)可能使积(商)的绝对值误差增大许多。
数值计算方法》习题答案

《数值计算方法》课后题答案详解吉 林 大 学第一章 习 题 答 案1. 已知(1)2,(1)1,(2)1f f f −===,求()f x 的Lagrange 插值多项式。
解:由题意知:()01201212001020211012012202121,1,2;2,1,1()()(1)(2)()()6()()(1)(2)()()2()()(1)(1)()()3(1)(2)(1)(2)()2162nj j j x x x y y y x x x x x x l x x x x x x x x x x l x x x x x x x x x x l x x x x x x x x L x y l x ==−=====−−−−==−−−−+−==−−−−−+−==−−−−+−==×+×−∴∑()2(1)(1)131386x x x x +−+×=−+2. 取节点01210,1,,2x x x ===对x y e −=建立Lagrange 型二次插值函数,并估计差。
解11201201210,1,;1,,2x x x y y e y e −−======1)由题意知:则根据二次Lagrange插值公式得:02011201201021012202110.510.520.51()()()()()()()()()()()()()2(1)(0.5)2(0.5)4(1)(224)(43)1x x x x x x x x x x x x L x y y y x x x x x x x x x x x x x x x x e x x e e e x e e x −−−−−−−−−−−−=++−−−−−−=−−+−−−=+−+−−+22)Lagrange 根据余项定理,其误差为(3)2210122()1|()||()||(1)(0.5)|3!61max |(1)(0.5)|,(0,1)6()(1)(0.5),()330.5030.2113()61()0.2113(0.21131)(0.21130.5)0.008026x f R x x e x x x x x x t x x x x t x x x x t x R x ξξωξ−+≤≤==−−≤−−∈′=−−=−+=−==≤××−×−=∴取 并令 可知当时,有极大值3. 已知函数y =在4, 6.25,9x x x ===处的函数值,试通过一个二次插值函数求的近似值,并估计其误差。
数值计算课后答案4

习 题 四 解 答1、设010,1x x ==,写出()x f x e -=的一次插值多项式1()L x ,并估计插值误差。
解:根据已知条件,有设插值函数为1()L x ax b =+,由插值条件,建立线性方程组为1011a b a b e -⨯+=⎧⎨⨯+=⎩ 解之得111a eb -⎧=-⎨=⎩则11()(1)1L x e x -=-+ 因为(),()x x y x e y x e --'''=-= 所以,插值余项为(1)(2)(2)011()()()()()(1)!1()()2!1()()()2!1(0)(1)((0,1))2n r x f x p x f x n f x f x x x x e x x ξξπξπξξ+-=-=+==--=--∈所以010101()max max (1)2111248x r x e x x e ξξ-≤≤≤≤-≤-=⨯⨯=。
2选用合适的三次插值多项式来近似计算f(0.2)和f(0.8)。
解:设三次插值多项式为230123()f x a a x a x a x =+++,由插值条件,建立方程组为230123230123230123230123(0.1)(0.1)(0.1)0.9950.30.30.30.9950.70.70.70.7651.1 1.1 1.10.454a a a a a a a a a a a a a a a a ⎧+⨯-+⨯-+⨯-=⎪+⨯+⨯+⨯=⎪⎨+⨯+⨯+⨯=⎪⎪+⨯+⨯+⨯=⎩即012301230123123012312301230.10.010.0010.9950.10.010.0010.9950.30.090.0270.9950.40.080.02800.70.490.3430.7650.80.480.344 1.761.1 1.21 1.3310.454a a a a a a a a a a a a a a a a a a a a a a a a a a -+-=-+-=⎧⎪+++=++=⎪⇒⎨+++=++=⎪⎪+++=⎩12301231232330.40.720.9880.3110.10.010.0010.9950.40.080.02800.320.288 1.760.384 3.831a a a a a a a a a a a a a ⎧⎪⎪⎨⎪⎪++=-⎩-+-=⎧⎪++=⎪⇒⎨+=⎪⎪-=-⎩解之得 01230.416.293.489.98a a a a =⎧⎪=-⎪⎨=-⎪⎪=⎩ 则所求的三次多项式为23()0.41 6.29 3.489.98f x x x x =--+. 所以2323(0.2)0.41 6.290.2 3.480.29.980.20.91(0.8)0.41 6.290.8 3.480.89.980.8 1.74f f =-⨯-⨯+⨯=-=-⨯-⨯+⨯=-3、设(0,1,2,,)i x i n =是 n+1个互异节点,证明: (1)0()(0,1,2,,)nk k i i i x l x x k n ===∑;(2)0()()0(0,1,2,,)n k i i i x x l x k n =-==∑。
最新数值计算课后答案2
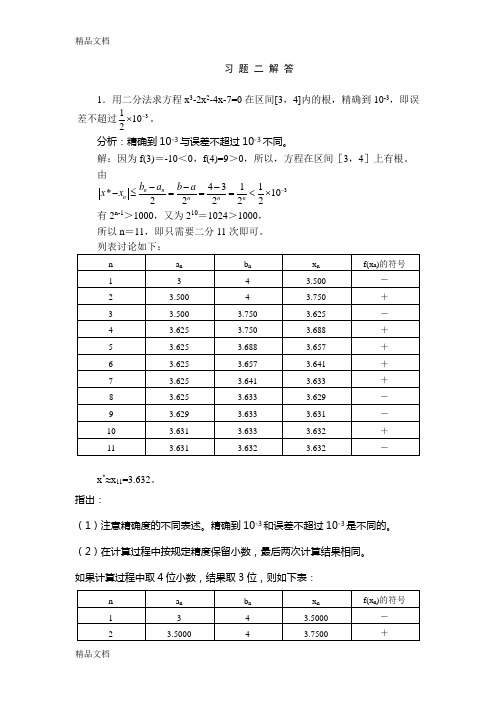
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根;因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 三 解 答1、用高斯消元法解下列方程组。
(1)12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③解:⨯4②+(-)①2,12⨯③+(-)①消去第二、三个方程的1x ,得:1232323231425313222x x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩④⑤⑥ 再由52)4⨯⑥+(-⑤消去此方程组的第三个方程的2x ,得到三角方程组:1232332314272184x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩回代,得:36x =-,21x =-,19x = 所以方程组的解为(9,1,6)T x =--注意:①算法要求,不能化简。
化简则不是严格意义上的消元法,在算法设计上就多出了步骤。
实际上,由于数值计算时用小数进行的,化简既是不必要的也是不能实现的。
无论是顺序消元法还是选主元素消元法都是这样。
②消元法要求采用一般形式,或者说是分量形式,不能用矩阵,以展示消元过程。
要通过练习熟悉消元的过程而不是矩阵变换的技术。
矩阵形式错一点就是全错,也不利于检查。
一般形式或分量形式: 12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③ 矩阵形式123213142541207x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭向量形式 123213142541207x x x -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭③必须是方程组到方程组的变形。
三元方程组的消元过程要有三个方程组,不能变形出单一的方程。
④消元顺序12x x →→L ,不能颠倒。
按为支援在方程组中的排列顺序消元也是存储算法的要求。
实际上,不按顺序消元是不规范的选主元素。
⑤不能化简方程,否则系数矩阵会变化,也不利于算法设计。
(2)1231231231132323110221x x x x x x x x x --=⎧⎪-++=⎨⎪++=-⎩①②③解:⨯23②+()①11,111⨯③+(-)①消去第二、三个方程的1x ,得: 123232311323523569111111252414111111x x x x x x x ⎧--=⎪⎪⎪-=⎨⎪⎪+=-⎪⎩④⑤⑥ 再由2511)5211⨯⑥+(-⑤消去此方程组的第三个方程的2x ,得到三角方程组:123233113235235691111111932235252x x x x x x ⎧⎪--=⎪⎪-=⎨⎪⎪=-⎪⎩回代,得:32122310641,,193193193x x x =-==, 所以方程组的解为 41106223(,,)193193193Tx =-2、将矩阵1020011120110011A ⎛⎫ ⎪⎪= ⎪- ⎪⎝⎭作LU 分解。
解:设1112131421222324313231324142434410001020100001111000201110000011u u u u l u u u A LU l l u u l l l u ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪⎪=== ⎪⎪ ⎪-⎪⎪ ⎪⎝⎭⎝⎭⎝⎭根据矩阵乘法,先求U 的第一行,由11j j a u =,得111213141,0,2,0u u u u ====。
再求L 的第一列,由矩阵乘法,因为1111i i a l u =,所以1111i i a l u =,而111u =,所以11i i l a =,所以2131410,2,0l l l ===。
再求U 的第二行,得 21122211l u u ⨯+⨯=,则22211211001u l u =-⨯=-⨯=,21132333101l u u u ⨯+⨯+⨯=,则 23211311021u l u =-⨯=-⨯=, 21142434441001l u u u u ⨯+⨯+⨯+⨯=,则 24211411001u l u =-⨯=-⨯=,再求L 的第二列,得3112322210000l u l u ⨯+⨯+⨯+⨯=,则 32311200200l l u =-⨯=-⨯=41124222430000l u l u l ⨯+⨯+⨯+⨯=,则 42411200000l l u =-⨯=-⨯=再求U 的第三行,得311332233311l u l u u ⨯+⨯+⨯=-,则33311332231122015u l u l u =--⨯-⨯=--⨯+⨯=-311432243444101l u l u u u ⨯+⨯+⨯+⨯=,则 34311432241120011u l u l u =-⨯-⨯=-⨯-⨯=再求L 的第三列,得411342234333101l u l u l u ⨯+⨯+⨯+⨯=,则4311(10201)55l =-⨯-⨯+⨯=-再求U 的第四行,得4114422443344411l u l u l u u ⨯+⨯+⨯+⨯=,则4441144224433416110001(1)55u l u l u l u =-⨯+⨯+⨯=-⨯-⨯--⨯=所以,矩阵A 的LU 分解为:1000102001000111,201000511600100055L U ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪- ⎪ ⎪⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭指出:用分数而表示元素,不能化成近似小数也不化成小数表示。
3、用LU 分解紧凑格式分解法解方程组。
123457910168109171087157651x x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 解一,用一般格式求解: 将系数矩阵作LU 分解得:10005791062410003555,71171000552213000101105L U ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪⎪ ⎪==- ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭Ly=b 方程组为 1234100061100517111052131015y y y y ⎛⎫ ⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭解之得123411512310y y y y ⎛⎫ ⎪⎛⎫ ⎪- ⎪ ⎪ ⎪ ⎪= ⎪- ⎪ ⎪ ⎪⎝⎭ ⎪⎪⎝⎭同样地,解方程组Ux=y 得1234201253x x x x ⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪= ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭。
解二,用LU 紧凑格式分解法求解: 对增广矩阵三角分解:579101579101579101662418109136810915555571087177110871871552576511765110651579101579101624163555557117155222310515⎛⎫⎛⎫ ⎪⎪⎛⎫⎪ ⎪----⎪ ⎪ ⎪ ⎪→→ ⎪ ⎪⎪-⎪ ⎪⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪ ⎪----- ⎪ ⎪→→---- ⎪ ⎪ ⎪ ⎪⎝⎭241355571171552223131051010⎛⎫ ⎪ ⎪--- ⎪ ⎪---- ⎪ ⎪ ⎪⎪⎝⎭ 原方程组化成同解的上三角方程组为: 12342343445791012413555171522131010x x x x x x x x x x +++=⎧⎪⎪---=-⎪⎪⎨--=-⎪⎪⎪=⎪⎩回代得(20,12,5,3)T x =--。
指出:紧凑格式是直接应用公式进行计算,计算结果保存在A 的相应元素位置。
从算法的角度,紧凑格式实际体现在数据的存储方法上。
由于紧凑格式计算时不再需要A 的前面的元素,因此可以进行。
4、 用列主元的三角分解法解线性方程组。
1231231232213472320x x x x x x x x x -+-=-⎧⎪-+=⎨⎪--=⎩ 解一,列选主元素消元法:先选第一列主元为213a =,将第一个方程与第二个方程交换,消去1x 得:123232334752433371414333x x x x x x x ⎧⎪-+=⎪⎪-=⎨⎪⎪--=-⎪⎩再选第二列主元为3273a =-,交换第二、三两个方程,消去2x 得三角形方程组:1232333477141433312633x x x x x x ⎧⎪-+=⎪⎪--=-⎨⎪⎪-=-⎪⎩回代求得方程组的解312x =,21x =,12x =所以方程组的解为1(2,1,)2T x =。
解二,列主元素三角分解法:21233247122132471(,)32471221221323202320232033247324722714143203333311522121337A b r r r r ⎛⎫ ⎪-----⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪=-↔---→--- ⎪ ⎪ ⎪ ⎪ ⎪---- ⎪⎝⎭⎝⎭ ⎪--⎝⎭⎛⎫⎛⎫ ⎪ -- ⎪ ⎪ ↔--→--- ⎪ ⎪ ⎪ -------⎝⎭⎝⎭u u u u u u u r u u u u u u u r 32472714143333154237⎛⎫⎪ ⎪-⎪ ⎪⎪ ⎪→---⎪ ⎪⎪ ⎪⎪ ⎪----⎝⎭同解的三角形方程组为1232333477141433342x x x x x x -+=⎧⎪⎪--=-⎨⎪⎪-=-⎩回代求得方程组的解312x =,21x =,12x =所以方程组的解为1(2,1,)2T x =。
精品文档说明:用矩阵讨论中,矩阵元素进行了化简。
5.用追赶法解方程组2111210,12101210120A b -⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪⎪ ⎪==-- ⎪ ⎪-- ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭。
分析: 三对角矩阵11221n n n A αβγαβγα-⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭O O O 可以分解如下形式的两个矩阵:11222331111,1n n n u l u L l U u l u βββ-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪== ⎪ ⎪⎪⎪ ⎪ ⎪⎝⎭⎝⎭OO O O 。
即11112222233111111n n n n n n u l u l u l u βαββγαββγα--⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎪⎝⎭⎝⎭O OO O O O O 由矩阵乘法规则,有 1111(2,3,)(2,3,,)i ii i i i i u l i n u u l i n αγαβ--⎧=⎪⎪==⎨⎪⎪=-=⎩L L , 这样可以求出矩阵L 和U 的所有元素。
设有系数矩阵为A 的方程组: 12,(,,)T n Ax b b b b b ==L , 这样的方程组称为三对角方程组。
三对角方程组经LU 分解分解为 ,Ly b Ux y ==, 求解之111,2,3,,ii i i y b y b l y i n -=⎧⎨=-=⎩L , 1(),1,2,,1n n nii i i i x y u x y x u i n n β+=⎧⎨=-=--⎩L 这就是所谓追赶法。
