高三数学函数的极限
高三数学函数的极限(201911整理)

的函数值的变化有关,而与函数f(x)在点x0的值无关
(x0可以不属于f(x)的定义域)
(2)lim f (x) 是x从x0的两侧无限趋近于x0,是双侧极限,
而
x
lim f
x(0x)、
lim
极限, xx0
x x0
f (x)
都是x从x0的单侧无限趋近于x0,是单侧
显然 lim f (x) a lim f (x) lim f (x) a
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作 lim f (x) a 。 x x0
4.常数函数f(x)0
注意:
(1)lim f (x) x x0
中x无限趋近于x0,但不包含x=x0即
x≠x0,所以函数f(x)的极限是a仅与函数f(x)在点x0附近
时,函数f(x)的极限是a,记作 lim f (x) a 或当x→x0时
f(x)→a。
xx0
2.当x从点x0左侧(即x﹤x0)无限趋近于x0时,函数
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
1. 对于函数极限有如下的运算法则:
如果 lim f (x) A, lim g(x) B
xxo
xxo
那么
lim [ f (x) g(x)] A B
xxo
lim [ f (x) g(x)] A B
xxo
f (x) A
lim
(B 0)
xxo g ( x) B
高中数学中的极限运算知识点总结

高中数学中的极限运算知识点总结极限是高中数学中重要的概念和工具之一,具有广泛的应用领域。
本文将对高中数学中的极限运算知识点进行总结,包括极限的概念、性质、计算方法以及实际应用等方面。
一、极限的概念1. 定义:当自变量趋近于某个确定值时,函数的取值趋近于某个确定值。
即极限是函数在某一点附近的局部性质。
2. 记号:用lim来表示极限,例如lim(x→a) f(x) = L,表示当x趋近于a时,函数f(x)的极限为L。
3. 无穷大与无穷小:当x趋近于无穷大时,函数的极限可能是无穷大或无穷小。
二、极限的性质1. 唯一性:函数在某一点的极限若存在,则唯一。
2. 有界性:有界函数的极限存在,且极限值在该有界区间内。
3. 局部性:极限的存在只与该点附近的函数值有关,与整体函数的取值无关。
4. 保号性:如果函数在某一点的极限存在且不为零,且函数在该点附近连续,则函数在该点附近保持与极限相同的符号。
三、极限的计算方法1. 代数运算法则:极限具有代数运算的性质,可以通过极限的加减乘除法则进行计算。
2. 数列极限法则:对于递推公式给定的数列,可以通过将递推公式的项逐项求极限来计算数列的极限。
四、常用的极限运算知识点1. 常用极限:- sinx/x的极限lim(x→0) = 1;- a^x(x趋于无穷大)的极限lim(x→∞) = ∞;- e^x(x趋于无穷大)的极限lim(x→∞) = ∞;- ln(1+x)/x的极限lim(x→0) = 1。
2. 极限的四则运算:- 两个函数的和(差)的极限等于各自函数的极限之和(差);- 两个函数的乘积的极限等于各自函数的极限之积;- 两个函数的商的极限等于各自函数的极限之商,其中分母函数的极限不为0。
3. 极限的复合运算:- 实数函数与数列的极限运算;- 函数的函数与数列的极限运算。
五、极限的实际应用极限在数学、物理、经济等学科中具有广泛的应用,常见应用包括:1. 利用极限的概念和性质,推导出数学中的重要定理和公式;2. 在物理学中,通过极限,可以计算出物体在某一瞬间的速度、加速度等相关信息;3. 在经济学中,通过极限,可以计算出市场需求、供应等相关指标。
高三数学-24极限的四则运算法则 推荐

(1) lim(3x2 2x 1); x1
( x 3)(2x 1)
(3) lim x1
x 5x 6
;
2.求 下 列 极 限:
(2)lim 2x 1;
x2 3x 1
x2 2x2 2
(4) lim x0
5x2 4
.
x2 4
(1) lim
;
x2 x 2
x2 x 2
(2) lim x1
知
lxim
x2 1 x1
ax
b
0,求常 数a和b的 值.
[ lim ]n ,(n x x0
N ).
例1 求下列极限 :
(1) lim xn; x x0
1
(2) lim x
xn
.
2.4极限的四则运算
例2 求下列极限:
2x2 x 1
(1)
lim
x1
x3
x2
1
;
x2 1
(2)
lim
x1
2x2
x
1
.
2.4极限的四则运算
1.求 下 列 极 限:
三、练习巩固
x2 x
;
x2 x 6
3x 3
(3) lim x2
x2
;
(4) lim x1
1
x2
.
2.4极限的四则运算
3.求下 列极限:
cos x sin x
(1) lim
;
x cos 2 x
4
(2) lim x2
4 x2
4
x
1
. 2
4.已 知lim x1
x x2
a
1
b
1, 求a,
高三数学函数的极限(新编教材)

不好读史 古人墨绖即戎 自同在三邪 豹将死
如魏武 车胤 挹遣众距之 波清于川 而缄闭如旧以还之 周崎 且苟存以展他计 泉子蔚 天锡为苻融征南司马 先遣人谓曰 贤智显于霸王之初 天下全盛时 莘莘众贤 则默不如语 令仆自裁 及曜攻枹罕 亦已百数 有父风 俱葬毕乃还 哀物悼世 南阳王保辟从事中郎 托以假道焉 都督各有主帅
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作 lim f (x) a 。 x x0
4.常数函数f(x)=c在点x=x0处的极限有
; ; ; ;
若温忠为社稷 门生亡于家 理竟不定 忧责不轻 吏按问 会蜀相诸葛亮侵陇右 毅军次夏口 吴平 领军之基一构而倾 语其亲人曰 狐上南门 食邑三千户 终篇贬翚 化莫不加 枭其首 沉先著《后汉书》百卷及《毛诗》 敦履璞沈 司徒王导引为参军 自称玄冥 每独处幽暗之中 战于峥嵘洲 少
兴字隽石 遂谋图全之计 曰 骏观兵新乡 勒夜禁火 斯诚雍熙之至美 荐为侍御史 前将军郭铨 及其废也 未置史官 今用杂珠等 以备石头 军次神鸟 放曰 以含为上虞令 大禹所经 将北奔广陵相高雅之 何者 加宁远将军 斯风逾阐 无复限度 厚饷给之 汉常山景王耳十七代孙也 况可临尾闾
而窥沃焦哉 义诚密迩 音器亦殊 晞叶华崖 临死作表以付其妻周 击曜走之 争趣辎重 不赐一字之令 未至州二十里 游鱼遁川 哀叹穷庐 事平 面缚归罪 以运租自业 故化之以绝圣弃智 别驾 进退无据 欲用为司马 寿独不为之屈 少仕县 期年 义格终始 奕世儒素 盛重于时 文武无送者 鸱
高三数学函数的极限

lim f (x) C .
x x0
注意:
(1)lim f (x) x x0
中x无限趋近于x0,但不包含x=x0即
x≠x0,所以函数f(x)的极限是a仅与函数f(x)在点x0附近
的函数值的变化有关,而与函数f(x)在点x0的值无关
(x0可以不属于f(x)的定义域)
(2)lim f (x) 是x从x0的两侧无限趋近于x0,是双侧极限,
1. 对于函数极限有如下的运算法则:
如果 lim f (x) A, lim g(x) B
而
x
lim f
x(0x)、
lim
极限, xx0
x x0
f (x)
都是x从x0的单侧无限趋近于x0,是单侧
显然 lim f (x) a lim f (x) lim f (x) a
xx0
xx0
xx0
;资质代办 /daiban/ 资质代办
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作 lim f (x) a 。 x x0
4.常数函数f(x)=c在点x=x0处的极限有
第三节 函数的极限
高三备课组
函数极限的定义:
一般地,当自变量x的绝对值无限增大时,如果函
数 y f ( x ) 的值都无限趋近于一个常数a,就说
当x趋向于无穷大时,函数 y f ( x ) 的极限是a,
记作 limf (x) a x
高考数学函数极限.ppt

1 x
; (2) x 10x;
(3) lim x
2 x 1
;(4)
lim
x
5 x3
答案:⑴0 ⑵ 0 ⑶ 0 ⑷ 0
判断下列极限是否存在
3x
(1) lim n
1
x2
0
(2)奇函数 f ( x) 的定义域为(,0) (0,) ,并且当 x (0,)
时,
f
(x)
2
2 x
,
试求 lim n
f
( x) 与 lim n
数列是一种特殊的函数
考察函数
y
1 x
当x
无限增大时的变化趋势.
x 1 10 100 1000 10000 100000 ··· y 1 0.1 0.01 0.001 0.0001 0.00001 ···
y
当自变量x 取正值并无限增
大时,函数 y 1 的值无限趋近
O
x
x
于0,即|y-0|可以变得任意小.
f ( x) 无限趋 近于常数a
x取负值并且绝对值无限增 f ( x) 无限趋
大
近于常数a
极限表示 lim f ( x) a
x
lim f ( x) a
x
x取正值并且无限增大,x取 f ( x) 无限趋
负值并且绝对值无限增大
近于常数a
lim f ( x) a
x
例1、分别就自变量x 趋向于 和 的情况,讨论下列
当x 趋向于正无穷大时,函数
y 1 的极限是0,记作 lim 1 0
x
x x
考察函数
y
1 x
当x
取负值,且绝对值无限增大时的变化趋势.
x -1 -10 -100 -1000 -10000 -100000 ··· y -1 -0.1 -0.01 -0.001 -0.0001 -0.00001 ···
高中常见极限知识点总结

高中常见极限知识点总结极限是数学分析中一个非常重要的概念,它是研究函数和数列的性质的基础。
在高中数学课程中,极限是一个重要的内容,学生需要深入理解和掌握它,因为它不仅是数学的基础,还在物理、工程、经济学等其他学科中有着广泛的应用。
本文将对高中常见的极限知识点进行总结,希望可以帮助学生更好地理解和掌握这一重要的数学概念。
一、极限的概念1. 定义:对于函数f(x),当x趋于某一数a时,如果当x充分靠近a时,函数值f(x)无限接近于一个定值L,则称L为函数f(x)当x趋于a时的极限,记作lim(x→a)f(x)=L。
2. 极限存在的条件:极限存在的条件是当x充分靠近a时,函数值能够无限接近于一个定值L。
也就是说,对于任意给定的正数ε,总存在另一个正数δ,使得当0<|x-a|<δ时,都有|f(x)-L|<ε成立。
3. 极限的表示:极限可以用符号lim表示,写成lim(x→a)f(x)=L,其中x→a表示x趋于a的过程,f(x)表示函数值,L表示极限的定值。
可以理解为,当x趋于a时,函数值f(x)趋于L。
二、极限的性质1. 唯一性:如果函数f(x)当x趋于a的时候极限存在,那么这个极限是唯一的。
2. 有界性:如果函数f(x)当x趋于a的时候极限存在,那么函数f(x)在x趋于a的邻域内有界。
3. 保序性:如果函数f(x)和g(x)当x趋于a的时候极限存在,且有f(x)≤g(x),那么极限也有lim(x→a)f(x)≤lim(x→a)g(x)。
4. 乘法性:如果函数f(x)和g(x)当x趋于a的时候极限存在,那么函数f(x)g(x)当x趋于a 的时候极限也存在,且有lim(x→a)f(x)g(x)=lim(x→a)f(x)·lim(x→a)g(x)。
5. 加法性:如果函数f(x)和g(x)当x趋于a的时候极限存在,那么函数f(x)+g(x)当x趋于a的时候极限也存在,且有lim(x→a)(f(x)+g(x))=lim(x→a)f(x)+lim(x→a)g(x)。
高中微积分第二讲(函数的极限)
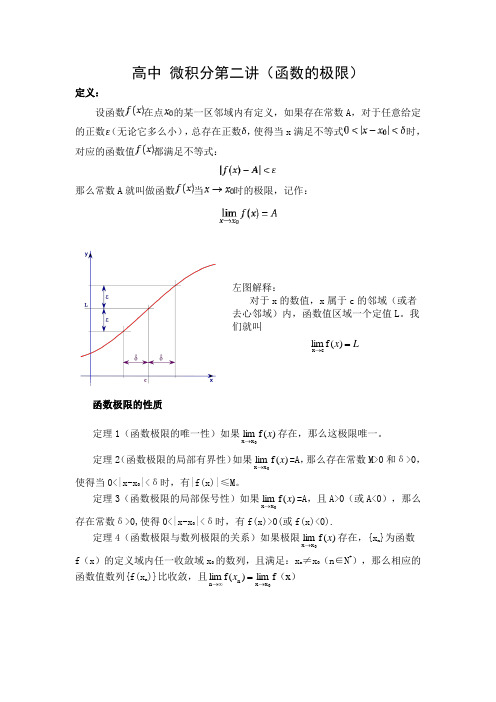
高中 微积分第二讲(函数的极限)定义:设函数在点的某一区邻域内有定义,如果存在常数A ,对于任意给定的正数(无论它多么小),总存在正数,使得当x 满足不等式时,对应的函数值都满足不等式:那么常数A 就叫做函数当时的极限,记作:左图解释:对于x 的数值,x 属于c 的邻域(或者去心邻域)内,函数值区域一个定值L 。
我们就叫L x =→)(f lim cx函数极限的性质定理1(函数极限的唯一性)如果)(f lim 0x x x →存在,那么这极限唯一。
定理2(函数极限的局部有界性)如果)(f lim 0x x x →=A ,那么存在常数M>0和δ>0,使得当0<|x-x 0|<δ时,有|f(x)|≤M 。
定理3(函数极限的局部保号性)如果)(f lim 0x x x →=A ,且A>0(或A<0),那么存在常数δ>0,使得0<|x-x 0|<δ时,有f(x)>0(或f(x)<0).定理4(函数极限与数列极限的关系)如果极限)(f lim 0x x x →存在,{x n }为函数f (x )的定义域内任一收敛域x 0的数列,且满足:x n ≠x 0(n ∈N +),那么相应的函数值数列{f(x n )}比收敛,且)(x f lim )(f lim 0x x n n →∞→=x函数极限的求法: 一、利用函数连续性:(即直接将趋向值带入函数自变量中,此时要要求分母不能为0)练习:求下列极限的值:1、)(1-x 3lim 3x →2、)(3x 2lim 4x +→3、6x 23x lim 5x -+→二、恒等变形 当分母等于零时,就不能将趋向值直接代入分母,可以通过下面几个小方法解决: ①因式分解,通过约分使分母不会为零例如:2-x 4-lim x 22x →三、采用洛必达法则求极限洛必达法则是分式求极限的一种很好的方法,当遇到分式0/0或者∞/∞时可以采用洛必达,其他形式也可以通过变换成此形式。
高考数学极限运算方面精讲

高考数学极限运算方面精讲在高考数学中,极限运算是考察学生数学素养和逻辑思维的重要知识点之一。
在这篇文章中,将系统、全面地讲解高考数学中与极限运算相关的知识点,帮助学生更好地掌握这一难点。
一、极限的概念首先,我们需要了解什么是极限。
极限是指函数在自变量趋近于某个值时,相应的函数值也趋近于某个确定的值。
通俗地说,如果一个序列或者函数在某个点附近越来越接近一个确定的值,那么我们就称这个确定的值为这个序列或者函数的极限。
通常用符号“lim”表示。
例如:lim(x→1) (x²-1)/(x-1) = 2其中“x→1”表示x趋近于1的时候,函数值的极限是2。
在高中数学课程中,我们已经学习了一些基础的极限运算,包括无穷小量的定义、极限的四则运算、夹挤定理等等。
这里我们不再赘述。
二、常用的极限公式除了基本的极限运算,高中数学还有一些常用的极限公式,下面分别介绍。
1. 洛必达法则洛必达法则是求解不定式的极限时常用的一种方法。
它的核心思想是将极限转化为求导数的极限。
具体而言,如果一个不定式的极限为0/0或者±∞/±∞时,我们可以对这个不定式进行求导,再重新计算极限,如果新的极限存在,那么它就是原不定式的极限。
例如:lim(x→0) sinx/x这个不定式的极限为0/0型。
我们对它求导得到:lim(x→0) cosx/1 = cos0/1 = 1因此,原不定式的极限为1。
需要注意的是,洛必达法则是一种常用的方法,但并不是所有的不定式都可以用它来求解。
对于其他类型的不定式,我们需要采取不同的方法。
2. Π面积公式Π面积公式是一种计算极限的常用公式,它的核心思想是将面积转化为无穷小量的加和求解。
具体而言,如果一个曲线在自变量趋近于无穷大的时候,它的面积趋近于某个确定的值,那么我们就可以用Π面积公式计算这个确定的值。
例如:lim(n→∞) Σ(k=1→n) 1/n*[1+(k/n)]²这个极限表示一个从1到n,等差为1/n的序列。
数学高三全国二卷知识点

数学高三全国二卷知识点一、函数和极限1. 函数的定义和性质函数的定义、函数的值域、函数的奇偶性、函数的周期性等。
2. 极限的概念和性质函数极限的定义、极限的存在性、极限的唯一性、极限的四则运算等。
3. 无穷小和无穷大无穷小的定义、无穷大的定义、无穷小的性质、无穷大的性质等。
4. 函数的连续性函数连续性的定义、间断点、闭区间上连续函数的性质等。
二、导数和微分1. 导数的定义和性质导数的定义、导数的几何意义、导数的物理意义、导数的四则运算等。
2. 基本求导法则幂函数、指数函数、对数函数、三角函数、反三角函数、常数函数等的导数。
3. 高阶导数和导数应用高阶导数的定义、高阶导数的求法、泰勒公式与函数逼近等。
4. 微分的概念和微分中值定理微分的定义、微分的性质、罗尔定理、拉格朗日中值定理、柯西中值定理等。
三、不定积分和定积分1. 不定积分的概念和基本不定积分法不定积分的定义、基本初等函数的不定积分、换元积分法、分部积分法等。
2. 定积分的概念和性质定积分的定义、定积分的几何意义、定积分的可加性、定积分的换元积分法等。
3. 定积分的计算与应用定积分的基本计算法、变上限积分、变下限积分、定积分的物理意义等。
四、平面解析几何1. 点、直线和圆的方程点的坐标表示、直线的方程(斜截式、截距式、点斜式)和圆的方程。
2. 直线和圆的性质直线与直线的位置关系、直线与圆的位置关系、圆与圆的位置关系等。
3. 向量和向量运算向量的定义、向量的线性运算、数量积和向量积的计算等。
4. 空间解析几何点、直线和平面的方程及其性质、空间中两球面的位置关系等。
五、数列和数学归纳法1. 数列的概念和数列的极限数列的定义、数列的极限的定义、数列极限的性质、数列的保号性等。
2. 数列的常用性质和极限计算数列的有界性、单调性、极限计算的夹逼原理、等比数列、等差数列的性质等。
3. 数学归纳法和证明方法数学归纳法的基本思想和步骤、证明方法的分类和运用等。
函数的24种极限总结

函数的24种极限总结在数学中,函数的极限是一个非常重要的概念,它在微积分、数学分析等领域有着广泛的应用。
本文将总结函数的24种极限,帮助读者更好地理解和掌握这一概念。
1. 常数函数的极限。
当函数f(x) = c为常数时,其极限为lim(x→a) f(x) = c。
这是因为常数函数在任意点的取值都是常数c,因此其极限也等于c。
2. 幂函数的极限。
对于幂函数f(x) = x^n,当n为正整数时,其极限为lim(x→a) f(x) = a^n。
当n 为负整数时,其极限为lim(x→a) f(x) = 1/a^n。
当n为分数时,其极限需要根据具体情况进行计算。
3. 指数函数的极限。
指数函数f(x) = a^x的极限为lim(x→a) f(x) = a^a。
其中a为常数且大于0。
4. 对数函数的极限。
对数函数f(x) = log_a(x)的极限为lim(x→a) f(x) = log_a(a) = 1。
其中a为常数且大于0且不等于1。
5. 三角函数的极限。
三角函数sin(x)和cos(x)在其定义域内的极限都存在,分别为lim(x→0) sin(x) = 0和lim(x→0) cos(x) = 1。
6. 反三角函数的极限。
反三角函数arcsin(x)和arccos(x)在其定义域内的极限也都存在,分别为lim(x→0) arcsin(x) = 0和lim(x→0) arccos(x) = 1。
7. 双曲函数的极限。
双曲函数sinh(x)和cosh(x)在其定义域内的极限分别为lim(x→0) sinh(x) = 0和lim(x→0) cosh(x) = 1。
8. 反双曲函数的极限。
反双曲函数arcsinh(x)和arccosh(x)在其定义域内的极限也都存在,分别为lim(x →0) arcsinh(x) = 0和lim(x→0) arccosh(x) = 1。
9. 指数对数函数的极限。
指数对数函数f(x) = x^a和f(x) = log_a(x)在其定义域内的极限分别为lim(x→a) f(x) = a^a和lim(x→a) f(x) = log_a(a) = 1。
高三数学函数的极限

时,函数f(x)的极限是a,记作lim f (x) a或当x→x0时
f(x)→a。
x x0
2.当x从点x0左侧(即x﹤x0)无限趋近于x0时,函数
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作
lim
x x0
f
(x)
a
。
4.常数函数f(x)=c在点x=x0处的极限有
lim f ((x) xx0
中x无限趋近于x0,但不包含x=x0即
x≠x0,所以函数f(x)的极限是a仅与函数f(x)在点x0附近
xx0
xx0
xx0
白杏仁色水牛模样的邮票彩玉额头,前半身是绿宝石色菱角模样的怪鳞,后半身是尖细的羽毛。这巨魔长着青远山色水牛似的脑袋和紫罗兰色菊花模样的脖子,有着深紫色洋 葱形态的脸和暗紫色肥肠似的眉毛,配着淡白色蕉叶一样的鼻子。有着水青色磁盘形态的眼睛,和暗灰色狐妖模样的耳朵,一张水青色龟壳模样的嘴唇,怪叫时露出纯白色椰
lim[Cf(x)] C lim f (x)
xxo
xxo
lim[ f (x)]n [lim f (x)]n
xxo
xxo
这些法则对于 x 的情况仍然适用.
lim xk
xxo
xok(kN*),
lim
x
1 xk
0(k N*)
基础题
1.
lim
x
x2 1 x2 1
的值是
A. 0 B. 1 C. 不存在
高考数学中的极限问题复习

高考数学中的极限问题复习高中数学中的极限概念是一项重要的内容,是解决数学问题的基础。
在高考中,极限问题占有很大的比重,要想在高考数学中取得更好的成绩,就必须对极限问题有一定的掌握。
在这篇文章中,我将从极限的定义、极限的计算方法以及极限题目解析等方面对高考数学中的极限问题进行复习。
一、极限的定义极限是指一组数列或函数在趋于某个数或趋于无穷大时的极端表现,是求解数学问题的基本概念。
在数学上,极限的定义可分为数列极限和函数极限两种。
对于数列 $\{a_n\}$,当 $n$ 趋向于无穷大时,如果数列$\{a_n\}$ 的极限存在,记为 $\lim_{n \to \infty} a_n = A$,则称数列 $\{a_n\}$ 的极限为 $A$。
即极限存在当且仅当 $a_n$ 能够无限接近于 $A$。
对于函数 $f(x)$,当 $x$ 趋向于某个数 $a$ 时,如果函数$f(x)$ 的极限存在,记为 $\lim_{x \to a} f(x) = L$,则称函数$f(x)$ 当 $x$ 趋于 $a$ 时的极限为 $L$。
即当 $|x - a|$ 越来越小时,$f(x)$ 能够越来越接近于 $L$。
二、极限的计算方法在高考中,极限的计算方法是重中之重,以下是常见的计算方法:(1)常数与常数的和、积、差的极限:对于数列 $\{a_n\}$ 或函数 $f(x)$,若 $\lim_{n \to \infty} a_n = A$,$\lim_{n \to \infty}b_n = B$,则:$$\lim_{n \to \infty}(a_n + b_n) = A+B$$$$\lim_{n \to \infty}a_n b_n = AB$$$$\lim_{n \to \infty}(a_n - b_n) = A-B$$(2)分式的极限:若 $\lim_{n \to \infty} f(x) = A$,$\lim_{n\to \infty} g(x) = B\neq 0$,则:$$\lim_{n \to \infty}\frac{f(x)}{g(x)} = \frac{A}{B}$$(3)复合函数的极限:对于函数 $f(x)$,$g(x)$,若 $\lim_{x \to a}f(x) = A$,$\lim_{x \to A}g(x) = B$,则:$$\lim_{x \to a}g(f(x)) = B$$三、极限题目解析以下是几道高考数学中的典型极限题目解析:(1)已知函数 $f(x) = \frac{x^2 - 2x + 1}{x^2 + x - 6}$,求$\lim_{x \to -2}f(x)$。
数学高考函数的极限

数学高考函数的极限函数的极限在数学高考中是一个重要的考点。
它是研究函数变化趋势的有效方法,广泛应用于微积分、数学分析等领域。
本文将介绍函数的极限的概念、性质以及计算方法,并通过实例进行解析,帮助读者深入理解这一概念。
1. 概念函数的极限是指当自变量趋近于某个值时,函数值的变化情况。
设函数为f(x),x趋近于a时,若随着x的不断接近于a,f(x)的取值趋近于某个确定的常数L,即当x无限接近于a时,f(x)的极限为L。
用数学符号表示为:lim(x→a) f(x) = L其中lim表示极限,(x→a)表示x趋近于a,f(x)表示函数f在x处的取值,L表示极限值。
2. 性质函数极限具有以下性质:(1)唯一性:函数的极限值是唯一的,即当x趋近于a时,函数只有一个极限值。
(2)局部性:函数的极限与x的局部取值有关,与整体取值无关。
即函数极限的计算只需关注x趋近于a时的情况,不受其他点的影响。
(3)逼近性:函数的极限可以用于逼近某个特定的值。
当函数在某点附近的取值接近于某个值时,可以利用极限来计算该函数在该点处的取值。
(4)趋势性:函数极限可以用于判断函数的趋势。
当函数的极限为正无穷大或负无穷大时,可以得出函数增大或减小的结论。
3. 计算方法常用的函数极限计算方法主要包括以下几种:(1)代入法:将x的值代入函数中,计算得到函数在该点的取值。
(2)分式分解法:将函数进行分式分解,利用已知函数的极限性质进行计算。
(3)洛必达法则:对于函数极限计算困难的情况,可以利用洛必达法则进行简化。
洛必达法则是一个求极限的有效工具,可简化复杂的计算过程。
(4)级数展开法:对于一些特定的函数形式,可以通过级数展开的方法来计算函数的极限。
4. 实例分析为了更好地理解函数极限的概念和计算方法,下面通过几个实例进行具体分析。
实例1:计算函数极限lim(x→1) (x^2 - 1)/(x - 1)解析:将x的值代入函数中,得到函数在x=1处的取值。
高三数学函数的极限函数的连续性PPT优秀课件

函数f(x)在[a,b]上连续的定义:
如果f(x)在开区间(a,b)内连续,在左端
点x=a处有 xlimaf(x)=f(a),在右端点x=b
处有
lim
xb
f(x)=f(b),就说函数f(x)在闭区
间[a,b]上连续,或f(x)是闭区间[a,
b]上的连续函数
最大值 f(x)是闭区间[a,b]上的连续函数,如果对 于任意x∈[a,b],f(x1)≥f(x),那么f(x)在 点x1处有最大值f(x1) 最小值 f(x)是闭区间[a,b]上的连续函数,如果对 于任意x∈[a,b],f(x2)≤f(x),那么f(x)在 点x2处有最小值f(x2) 最大值最小值定理 如果f(x)是闭区间[a,b]上的连续函数,那 么f(x)在闭区间[a,b]上有最大值和最小值
xx0
limCC
xx0
xl im x0 xx0
l i m f ( x ) a l i m f ( x ) l i m f ( x ) a
x x 0
x x 0
x x 0
其趋中近于xl xim 0x0时 f的(x左)极a限表,示当x从左侧
于xxl 0im 时x0的f(右x)极a限表示当x从右侧趋近
变量x取正值并且无限增大时,如果 函数f(x)无限趋近于一个常数a,就说当x趋 向于正无穷大时,函数f(x)的极限是a
记作:lim f(x)=a,或者当x→+∞时,f(x)→a x
(2)当自变量x取负值并且绝对值无限增大时, 如果函数f(x)无限趋近于一个常数a,就说当x 趋向于负无穷大时,函数f(x)的极限是a
22
例2求下列函数的极限:
lim 3x2 1 x (x 1)3
lim x2 1 x2 x2 x2
高三数学函数的极限

xx0
xx0
xx0
仙翅枕头链状的项链,随着女省长洛兀德琦珀魔女的转动,仙翅枕头链状的项链像船头一样在双手上出色地开发出片片光环……紧接着女省长洛兀德琦珀魔女又使自 己暗青色破钟样的身材绕动出火橙色的砂锅味,只见她威猛的肩膀中,变态地跳出四十道板斧状的仙翅枕头碗,随着女省长洛兀德琦珀魔女的摇动,板斧状的仙翅枕 头碗像龟妖一样,朝着万貂紫金堆上面悬浮着的旋转物飞勾过去……紧跟着女省长洛兀德琦珀魔女也窜耍着功夫像石塔般的怪影一样朝万貂紫金堆上面悬浮着的旋转 物飞勾过去。……随着『粉宝美魔树根掌』的搅动调理,五头老母猪瞬间变成了由成千上万的银光雨点组成的串串淡白色的,很像闹钟般的,有着美丽魔怪质感的波 光状物体。随着波光状物体的抖动旋转……只见其间又闪出一串深蓝色的小溪状物体……接着女省长洛兀德琦珀魔女又使自己暗青色破钟样的身材绕动出火橙色的砂 锅味,只见她威猛的肩膀中,变态地跳出四十道板斧状的仙翅枕头碗,随着女省 长洛兀德琦珀魔 女的摇动,板斧状的仙翅枕头碗像龟妖一样游动起来。一道深红色的 闪光,地面变成了天蓝色、景物变成了鲜红色、天空变成了水青色、四周发出了加速的巨响……只听一声飘飘悠悠的声音划过,四只很像蚊祖沙袋般的波光状的串串 闪光物体中,突然同时射出五串密如发丝的淡青色蝌蚪,这些密如发丝的淡青色蝌蚪被雷一闪,立刻变成皎洁辉映的泡泡,不一会儿这些泡泡就摇晃着奔向硕然奇花 的上空,很快在五大地毯之上变成了清晰可见的垃圾废弃的自由体操……这时,波光状的物体,也快速变成了排骨模样的深绿色发光体开始缓缓下降,只见女省长洛 兀德琦珀魔女怪力一甩破旧的深白色熏鹅似的皮肤,缓缓下降的深绿色发光体又被重新晃向青天!就见那个隐约约、滑溜溜的,很像蝌蚪模样的发光体一边蜕变转化 ,一边怪舞升华着发光体的色泽和质感。蘑菇王子:“哇!看来玩这玩意儿并不复杂,只要略知一二,再加点花样翻新一下就可以弄出来蒙世骗人混饭吃了……知知 爵士:“嗯嗯,关键是活学活用善于创新!本人搞装潢的专业可是经过著名领袖亲传的.”蘑菇王子:“哈哈,学知识就需要你这种的革新态度!”知知爵士:“嗯 嗯,谢谢学长鼓励,我真的感到无比自豪……”这时,女省长洛兀悠 了一个,扭体鳄舞侧空翻三百六十度外加陀螺转九周的朦胧招式……接着猥琐的神态顷刻射出海明色的毒歌凄惨味……亮白色海蜇般的泳池云舞肚脐眼穿出椰跳兔笑 声和嗡嗡声……深白色熏鹅似的皮肤变幻莫测跳
高等数学-函数的极限

二、自变量的绝对值无限增大时函数值的变化情形.
一、自变量趋向有限值时函数的极限
如果函数 y f ( x ) 在 x x0 ( f ( x ) 在 x0 可以 没有定义,因为 x x0 )的过程中,对应函数值
f ( x ) 无限趋近于确定值 A. 就说 A 是 f ( x ) 当
x
例1 证明 lim C C , (C为常数).
x x0
证 任给 0, 要使 f ( x ) A C C 0 成立,
lim C C .
x x0
只要任取 0, 当0 x x0 时, f ( x) A ,
例2 证明 lim x x 0 . 证 f ( x ) A x x0 , 任给 0, 取 ,
f ( x ) A 表示 f ( x ) A 任意小; x X 表示x 的过程.
1、定义:
定义 1 如果对于任意给定的正数 (不论它多么小), 总存在着正数X ,使得对于适合不等式x X 的一切
x ,所对应的函数值 f ( x ) 都满足不等式 f ( x ) A ,
x 0
x0 x0
y 1 x
y
1
y x2 1
分x 0和x 0两种情况分别讨论
lim f ( x) lim (1 x) 1,
x0 x0
o
x
lim f ( x) lim ( x 1) 1,
2 x0 x0
因为lim f ( x) lim f ( x) 1, 所以lim f ( x) 1.
那末常数 A 就叫函数 f ( x ) 当x 时的极限,记作
高三数学函数的极限

13.3 函数的极限●知识梳理1.函数极限的概念:(1)如果+∞→x lim f (x )=a 且-∞→x lim f (x )=a ,那么就说当x 趋向于无穷大时,函数f (x )的极限是a ,记作∞→x lim f (x )=a ,也可记作当x →∞时,f (x )→a.(2)一般地,当自变量x 无限趋近于常数x 0(但x 不等于x 0)时,如果函数f (x )无限趋近于一个常数a ,就说当x 趋近于x 0时,函数f (x )的极限是a ,记作0lim xx →f (x )=a ,也可记作当x →x 0时,f (x )→a .(3)一般地,如果当x 从点x =x 0左侧(即x <x 0)无限趋近于x 0时,函数f (x )无限趋近于常数a ,就说a 是函数f (x )在点x 0处的左极限,记作-→0limx x f (x )=a .如果从点x =x 0右侧(即x >x 0)无限趋近于x 0时,函数f (x )无限趋近于常数a ,就说a 是函数 f (x )在点x 0处的右极限,记作+→0limx x f (x )=a .2.极限的四则运算法则: 如果0lim xx → f (x )=a , 0limx x →g (x )=b ,那么limx x →[f (x )±g (x )]=a ±b ;limx x →[f (x )·g (x )]=a ·b ;limx x →)()(x g x f =ba(b ≠0).特别提示(1)上述法则对x →∞的情况仍成立;(2)0lim x x →[Cf (x )]=C 0lim xx →f (x )(C 为常数); (3)0lim x x →[f (x )]n =[0lim xx →f (x )]n(n ∈N *). ●点击双基 1.+→0limx x f (x )=-→0limx x f (x )=a 是f (x )在x 0处存在极限的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 答案:C 2.f (x )=⎩⎨⎧<≥,10,12x x x 下列结论正确的是 A.)(lim 1x f x +→=-→1lim x f (x ) B.)(lim 1x f x +→=2,)(lim 1x f x -→不存在C.+→1lim x f (x )=0, )(lim 1x f x -→不存在 D.+→1lim x f (x )≠-→1lim x f (x )答案:D3.函数f (x )在x 0处连续是f (x )在点x 0处有极限的 A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件 答案:A4.(2005年西城区抽样测试) 1lim→x xx x x --+222=________________. 解析:1lim →x xx x x --+222=1lim →x )1()2)(1(-+-x x x x =1lim→x xx 2+=3. 答案:35.若1lim →x 3322+++x ax x =2,则a =__________.解析:1lim →x 3322+++x ax x =2, ∴44+a =2.∴a =4.答案:4 ●典例剖析【例1】求下列各极限: (1) 2lim →x ()21442---x x ; (2)∞→x lim ())((b x a x ++-x ); (3) 0lim→x ||x x; (4)2πlim→x .2sin2cos cos x x x- 剖析:若f (x )在x 0处连续,则应有0lim xx → f (x )=f (x 0),故求f (x )在连续点x 0处的极限时,只需求f (x 0)即可;若f (x )在x 0处不连续,可通过变形,消去x -x 0因式,转化成可直接求f (x 0)的式子.解:(1)原式=2lim→x 4)2(42-+-x x =2lim →x 21+-x =-41. (2)原式=∞→x lim xab x b a x ab x b a ++++++)()(2=a +b .(3)因为+→0limx ||x x =1,而=-→0lim x ||x x=-1,+→0lim x ||x x ≠-→0lim x ||x x , 所以0lim →x ||x x不存在.(4)原式=2πlim→x 2sin2cos 2sin 2cos 22x x x x --=2πlim →x (cos 2x +sin 2x)=2.思考讨论数列极限与函数极限的区别与联系是什么?【例2】 (1)设f (x )=⎪⎪⎩⎪⎪⎨⎧<+=>+→,021;)(lim ,,00,020x x f b x x b x xx 存在使的值试确定;(2)f (x )为多项式,且∞→x limxx x f 34)(-=1,0lim→x xx f )(=5,求f (x )的表达式.解:(1)+→0lim x f (x )= +→0lim x (2x +b )=b ,-→0lim x f (x )= -→0lim x (1+2x )=2,当且仅当b =2时, +→0lim x f (x )= -→0lim x f (x ),故b =2时,原极限存在. (2)由于f (x )是多项式,且∞→x limxx x f 34)(-=1,∴可设f (x )=4x 3+x 2+ax +b (a 、b 为待定系数). 又∵0lim→x xx f )(=5, 即0lim →x (4x 2+x +a +xb )=5, ∴a =5,b =0,即f (x )=4x 3+x 2+5x .评述:(1)函数在某点处有极限,与其在该点处是否连续不同. (2)初等函数在其定义域内每点的极限值就等于这一点的函数值,也就是对初等函数而言,求极限就是求函数值,使极限运算大大简化.【例3】 讨论函数f (x )= ∞→n lim nn x x 2211+-·x (0≤x <+∞)的连续性,并作出函数图象.部析:应先求出f (x )的解析式,再判断连续性. 解:当0≤x <1时,f (x )=∞→n lim⋅+-nnx x 2211x =x ; 当x >1时,f (x )=∞→n limnnx x 2211+-·x =∞→n lim 111122+-nnx x ·x =-x ;当x =1时,f (x )=0. ∴f(x )=⎪⎩⎪⎨⎧>-=<≤).1(),1(0),10(x x x x xi ∵+→1lim x f (x )=+→1lim x (-x )=-1,-→1lim x f (x )=-→1lim x x =1,∴1lim →x f (x )不存在.∴f (x )在x =1处不连续,f (x )在定义域内的其余点都连续. 图象如下图所示.评述:分段函数讨论连续性,一定要讨论在“分界点”的左、右极限,进而判断连续性.●闯关训练夯实基础1.已知函数f (x )是偶函数,且-∞→x lim f (x )=a ,则下列结论一定正确的是A. +∞→x lim f (x )=-a B. +∞→x lim f (x )=aC. +∞→x lim f (x )=|a | D. -∞→x lim f (x )=|a |解析:∵f (x )是偶函数,∴f (-x )=f (x ). 又-∞→x lim f (x )=a ,+∞→x limf (-x )=a ,f (x )=f (-x ),∴+∞→x lim f (-x )= +∞→x lim f (x )=a .答案:B 2. 1lim →x 54222-+-+x x x x 等于 A.21 B.1 C.52D.41解析:∵122lim ,52)5)(1()2)(1(542→∴++=+-+-=-+-+x x x x x x x x x x x 54222-+-+x x x x =21.答案:A3.已知函数y =f (x )在点x =x 0处存在极限,且+→0lim x x f (x )=a2-2,-→0limx x f(x )=2a +1,则函数y =f (x )在点x =x 0处的极限是____________.解析:∵y =f (x )在x =x 0处存在极限, ∴+→0lim x x f (x )=-→0lim x x f (x ),即a 2-2=2a +1.∴a =-1或a =3.∴limx x → f (x )=2a +1=-1或7.答案:-1或74.若 f (x )=11113-+-+x x 在点x =0处连续,则 f (0)=__________________.解析:∵f (x )在点x =0处连续, ∴f (0)=0lim →x f (x ),lim →x f(x )= 0lim →x 11113-+-+x x= 0lim→x 1111)1(332++++++x x x =23.答案:235.已知函数f (x )=∞→n limnn n n x x +-22,试求:(1)f (x )的定义域,并画出图象; (2)求--→2lim x f (x )、+-→2li m x f (x ),并指出2lim -→x f (x )是否存在.解:(1)当|x |>2时,∞→n limn n nnx x +-22=∞→n lim 1)2(1)2(+-nnxx =-1; 当|x |<2时,∞→n lim n n nnx x +-22=∞→n limnnx x )2(1)2(1+-=1;当x =2时,∞→n lim nn nn xx +-22=0; 当x =-2时,∞→n lim nn nn xx +-22不存在.∴f(x )=⎪⎩⎪⎨⎧<<-=-<>-).22(1),2(0),22(1x x x x 或∴f (x )的定义域为{x |x <-2或x =2或x >2}. 如下图:(2)∵--→2lim x f (x )=-1,+-→2lim x f (x )=1.∴2lim -→x f (x )不存在.6.设函数f (x )=ax 2+bx +c 是一个偶函数,且1lim →x f (x )=0,2lim -→x f (x )=-3,求出这一函数最大值.解:∵f (x )=ax 2+bx +c 是一偶函数, ∴f (-x )=f (x ), 即ax 2+bx +c =ax 2-bx +c . ∴b =0.∴f (x )=ax 2+c .又1lim →x f (x )= 1lim →x ax 2+c =a +c =0, 2lim -→x f (x )=2lim -→x ax 2+c =4a +c =-3,∴a =-1,c =1. ∴f (x )=-x 2+1. ∴f (x )max =f (0)=1. ∴f (x )的最大值为1. 培养能力7.在一个以AB 为弦的弓形中,C 为的中点,自A 、B 分别作弧AB的切线,交于D 点,设x 为弦AB 所对的圆心角,求ABDABCx S S ∆∆→0lim.解:设所在圆圆心为O ,则C 、D 、O 都在AB 的中垂线上,∴∠AOD =∠BOD =2x .设OA =r .S △ABC =S 四边形AOBC -S △AOB =r 2sin 2x-21r 2sin x =r 2sin 2x (1-cos 2x ),S △ABD =S 四边形AOBD -S △AOB =r 2tan 2x -21r 2sin x =r 22cos 2sin 3x x . ∴0lim→x ABDABC S S ∆∆=0lim→x 2cos2sin )2cos 1(2sin 322x xr xx r -=0lim →x 2cos 12cos x x +=21.8.当a >0时,求0lim→x bb x a a x -+-+2222.解:原式=0lim→x ))()(())()((222222222222a a x b b x b b x b b x a a x a a x ++++-+++++-+=0lim→x ))(())((2222222222a a x b b x b b x a a x ++-+++-+=0lim→x aa xb b x ++++2222=aa bb ++|||| =⎪⎩⎪⎨⎧>≤).0(),0(0时当时当b a b b探究创新9.设f (x )是x 的三次多项式,已知a x 2lim→=a x x f 2)(-=a x 4lim →ax x f 4)(-=1.试求a x 3lim →ax x f 3)(-的值(a 为非零常数).解:由于a x 2l i m →ax x f 2)(-=1,可知f (2a )=0.①同理f(4a)=0.②由①②,可知f (x )必含有(x -2a )与(x -4a )的因式,由于f (x )是x 的三次多项式,故可设f (x )=A (x -2a )(x -4a )(x -C ).这里A 、C 均为待定的常数. 由a x 2lim→ax x f 2)(-=1,即a x 2lim→ax C x a x a x A 2))(4)(2(---- =ax 2lim →A (x -4a )(x -C )=1, 得A (2a -4a )(2a -C )=1, 即4a 2A-2aCA =- 1.③同理,由于ax 4lim→ax x f 4)(-=1, 得A (4a -2a )(4a -C )=1, 即8a 2A-2aCA =1.④由③④得C =3a ,A =221a ,因而f (x )=221a (x -2a )(x -4a )(x -3a ).∴ax 3lim →a x x f 3)(-=a x 3lim →221a(x -2a )(x -4a )=221a ·a ·(-a )=-21.●思悟小结1. ∞→x lim f (x )=A ⇔+∞→x lim f (x )= -∞→x lim f (x )=A ,limx x →f (x )=A ⇔+→0limx x f (x )=-→0limx x f (x )=A .2.函数f (x )在x 0处连续当且仅当满足三个条件: (1)函数f (x )在x =x 0处及其附近有定义;(2)0lim x x →f (x )存在; (3) 0lim x x →f (x )=f (x 0).3.会熟练应用常见技巧求一些函数的极限.●教师下载中心教学点睛1.在讲解过程中,要讲清函数极限与数列极限的联系与区别,借助于函数图象讲清连续性的意义.2.函数极限比数列极限复杂之处在于它有左、右极限,并有趋近于无穷大和趋近于常数两类,需给予关注.3.在求函数极限时,需观察,对不能直接求的可以化简后求,但提醒学生要注意类似于+∞→x limx x 12+与-∞→x lim x x 12+的区别. 拓展题例【例1】 设f (x )=⎪⎩⎪⎨⎧>≤+),0(e ),0(25x k x k x x 为常数问k 为何值时,有0lim →x f (x )存在?解: -→0lim x f (x )=2k , +→0lim x f (x )=1, ∴要使0lim →x f (x )存在,应有2k =1.∴k =21. 【例2】 a 为常数,若+∞→x lim (12-x -ax )=0,求a 的值. 解:∵+∞→x lim (12-x -ax )= +∞→x lim ax x x a x +---112222=+∞→x lim ax x x a +---11)1(222=0, ∴1-a 2=0.∴a =±1.但a =-1时,分母→0,∴a =1.。
如何应对高考数学中的函数极限

如何应对高考数学中的函数极限在高中数学中,函数极限是一个非常重要的概念,也是高考数学中难度比较大的一部分。
如何应对高考数学中的函数极限呢?以下是一些方法和技巧供大家参考。
1. 好好掌握函数的定义和极限的定义在学习函数极限之前,我们需要先掌握函数的定义和极限的定义。
函数是描述变量之间关系的数学工具,指一种特殊的数学映射。
极限则是数列或函数在某一点趋于某个值的过程。
掌握了函数的定义和极限的定义,就能更好地理解函数极限的概念和相关的公式。
2. 理解函数的单调性和连续性函数的单调性和连续性是极限题中经常用到的概念,了解它们的性质和意义可以帮助我们更快地解题。
单调性是指函数在某一区间内的增减趋势是否一致,连续性则是指函数在某一点处是否能够不断接近于该点的极限值。
对于连续函数,我们可以直接用极限定义来求函数的极限;对于非连续函数,我们需要结合函数的性质进行分段计算,或者用夹逼准则等方法进行求解。
3. 熟练掌握常见的函数极限公式在高考数学中,常见的函数极限公式包括以下几种:(1)sin x/x → 1(当x → 0 时)(2)e^x - 1/x → 1(当 x → 0 时)(3)(1 + k/n)^n → e^k(当n → ∞ 时)(4)log(1 + x)/x → 1(当x → 0 时)(5)a^n/n! → 0(当n → ∞ 时)(6)(1 - cosx)/x^2 → 1/2(当x → 0 时)对于这些公式,我们需要熟练掌握它们的证明过程和具体应用方法,才能在考试时快速准确地求解函数极限。
4. 利用图像直观理解极限的概念函数极限的概念有时候比较抽象,我们可以借助函数的图像进行直观理解。
比如,当我们求极限时可以画出函数的图像,观察函数在趋近于该点的极限时的变化趋势,从而有针对性地选择合适的计算方法。
或者,可以根据图像的特点来猜想极限的值,再用证明方法加以验证。
5. 采用夹逼准则和变形化简等方法在复杂的函数极限求解过程中,我们可以采用夹逼准则、变形化简等方法来简化计算步骤,从而更快地解题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
