初三数学(特殊值法)
巧用特殊值法,培育核心素养

中学教育2019年04月新教育时代66巧用特殊值法,培育核心素养唐 珺 曹建英(无锡市西漳中学 江苏无锡 214171)摘 要:使用特殊值或特殊位置法解决一些问题,避开了繁琐的计算,推理,能快速、正确地得出答案。
从认识论看,复杂问题特殊化后,认识起点降低,便于学生的认识由浅入深,从方法论看,特殊化使问题由抽象到具体,由复杂到简单,从而有利于问题的解决。
关键词:特殊值法 特殊位置法 从特殊到一般一、现状分析,培养学生从特殊到一般的思想方法 (一)问题背景某次测验后大家照常评讲试卷,课后一位年轻教师与我交流说某道题不知该怎么讲。
题目是这样的:题目:a、b、c 是实数,点A(a-1,b)、B(a-2,c)在二次函数y=x 2-2ax+3的图像上,则b、c 的大小关系是 。
(二)分析现状是什么原因导致学生想不起来用特殊值法来解决这个问题呢?主要是我们教师在教学时更多地是注重教学生如何正面思考,严密地、符合逻辑的去分析解决一个问题,学生已养成习惯性思维。
之前与我交流的那位年轻教师本身是第一年带初三,没什么教学经验,教的班级学生数学水平一般。
而这一题二次函数解析式以及点的坐标中都含有字母,这些不确定因素使得部分学生感觉很难,无从下手。
这时如果采用特殊到一般的思想方法,赋予字母一个值,那么问题就迎刃而解了。
所以如果平时教师多关注这种特殊方法的教学,学生就不会失分,也会让部分学生重拾对数学的兴趣,觉得数学没那么难。
让优秀的学生知道有些题可用较少的时间做出正确答案,省出时间思考后面大题。
二、实例探究,培养学生应用知识的能力题目1:如图,抛物线y=x 2-2x+k(k ﹤0)与x 轴相交于A(x1,0)、B (x2,0)两点,其中x1﹤x2,当x=x1+2时,y 0(填”>”、” ﹤”或”=”号)。
【正解】∵抛物线y=x 2-2x+k (k ﹤0)的对称轴方程是x=1,又∵x1﹤0,∴x1与对称轴x=1距离大于1, ∴x1+2﹤x2,∴当x=x1+2时,抛物线图像在x 轴下方,即y ﹤0.故答案是:﹤.【分析】这是某次测验填空题中较难的一题。
初中数学题型经典解题方法

初中数学题型经典解题方法初中数学题型经典解题方法汇总一、选择题的解法1、直接法:根据选择题的题设条件,通过计算、推理或判断,最后得到题目的所求。
2、特殊值法:(特殊值淘汰法)有些选择题所涉及的数学命题与字母的取值范围有关;在解这类选择题时,可以考虑从取值范围内选取某几个特殊值,代入原命题进行验证,然后淘汰错误的,保留正确的。
3、淘汰法:把题目所给的四个结论逐一代回原题的题干中进行验证,把错误的淘汰掉,直至找到正确的答案。
4、逐步淘汰法:如果我们在计算或推导的过程中不是一步到位,而是逐步进行,既采用“走一走、瞧一瞧”的策略;每走一步都与四个结论比较一次,淘汰掉不可能的,这样也许走不到最后一步,三个错误的结论就被全部淘汰掉了。
5、数形结合法:根据数学问题的条件和结论之间的内在联系,既分析其代数含义,又揭示其几何意义;使数量关系和图形巧妙和谐地结合起来,并充分利用这种结合,寻求解题思路,使问题得到解决。
二、常用的数学思想方法1、数形结合思想:就是根据数学问题的条件和结论之间的内在联系,既分析其代数含义,又揭示其几何意义;使数量关系和图形巧妙和谐地结合起来,并充分利用这种结合,寻求解体思路,使问题得到解决。
2、联系与转化的思想:事物之间是相互联系、相互制约的,是可以相互转化的。
数学学科的各部分之间也是相互联系,可以相互转化的。
在解题时,如果能恰当处理它们之间的相互转化,往往可以化难为易,化繁为简。
如:代换转化、已知与未知的转化、特殊与一般的转化、具体与抽象的转化、部分与整体的转化、动与静的转化等等。
3、分类讨论的思想:在数学中,我们常常需要根据研究对象性质的差异,分各种不同情况予以考查;这种分类思考的方法,是一种重要的数学思想方法,同时也是一种重要的解题策略。
4、待定系数法:当我们所研究的数学式子具有某种特定形式时,要确定它,只要求出式子中待确定的字母得值就可以了。
为此,把已知条件代入这个待定形式的式子中,往往会得到含待定字母的方程或方程组,然后解这个方程或方程组就使问题得到解决。
初三数学三角函数值计算方法

初三数学三角函数值计算方法三角函数是初中数学中的一个重要概念,它在解决三角形和圆的相关问题中起着重要作用。
在计算三角函数值时,我们需要掌握一些常用的方法和公式。
本文将介绍初三数学中常用的三角函数值计算方法,帮助学生更好地理解和应用三角函数。
1. 正弦函数(sin)正弦函数是三角函数中最基本的函数之一。
计算正弦函数值的方法如下:- 对于已知角度的情况,可以查找三角函数表或使用计算器来求解。
例如,sin30°=0.5,sin45°=√2/2。
- 对于不常见角度的情况,可以利用三角函数的周期性进行换算。
例如,sin150°=sin(150°-180°)=-sin30°=-0.5,sin210°=sin(210°+180°)=sin30°=0.5。
- 对于任意角度的情况,可以利用正弦函数与余弦函数之间的关系进行计算。
例如,sin(180°-x)=sinx,sin(360°-x)=-sinx。
2. 余弦函数(cos)余弦函数也是三角函数中常用的函数之一。
计算余弦函数值的方法如下:- 对于已知角度的情况,可以查找三角函数表或使用计算器来求解。
例如,cos60°=0.5,cos90°=0。
- 对于不常见角度的情况,可以利用三角函数的周期性进行换算。
例如,cos210°=cos(210°-180°)=-cos30°=-√3/2,cos300°=cos(300°+180°)=cos120°=-0.5。
- 对于任意角度的情况,可以利用余弦函数与正弦函数之间的关系进行计算。
例如,cos(180°-x)=-cosx,cos(360°-x)=cosx。
3. 正切函数(tan)正切函数是三角函数中比较特殊的一个函数,计算正切函数值的方法如下:- 对于已知角度的情况,可以查找三角函数表或使用计算器来求解。
初中数学解题技巧+中考压轴题30道

初中数学解题技巧+中考压轴题30道选择题法大全方法一:排除选项法选择题因其答案是四选一,必然只有一个正确答案,那么我们就可以采用排除法,从四个选项中排除掉易于判断是错误的答案,那么留下的一个自然就是正确的答案。
方法二:赋予特殊值法即根据题目中的条件,选取某个符合条件的特殊值或作出特殊图形进行计算、推理的方法。
用特殊值法解题要注意所选取的值要符合条件,且易于计算。
方法三:通过猜想、测量的方法,直接观察或得出结果这类方法在近年来的初中题中常被运用于探索规律性的问题,此类题的主要解法是运用不完全归纳法,通过试验、猜想、试误验证、总结、归纳等过程使问题得解。
方法四:直接求解法有些选择题本身就是由一些填空题、判断题、解答题改编而来的,因此往往可采用直接法,直接由从题目的条件出发,通过正确的运算或推理,直接求得结论,再与选择项对照来确定选择项。
我们在做解答题时大部分都是采用这种方法。
例如:商场促销活动中,将标价为200元的商品,在打8折的基础上,再打8折销售,现该商品的售价是( )、160元 B、128元 C 、120元 D、 88元方法五:数形结合法解决与图形或图像有关的选择题,常常要运用数形结合的思想方法,有时还要综合运用其他方法。
方法六:代入法将选择支代入题干或题代入选择支进行检验,然后作出判断。
方法七:观察法观察题干及选择支特点,区别各选择支差异及相互关系作出选择。
方法八:枚举法列举所有可能的情况,然后作出正确的判断。
例如:把一张面值10元的人民币换成零钱,现有足够面值为2元,1元的人民币,换法有( )A.5种 B.6种 C.8种 D.10种分析:如果设面值2元的人民币x张,1元的人民币y元,不难列出方程,此方程的非负整数解有6对,故选B。
方法九:待定系数法要求某个函数关系式,可先假设待定系数,然后根据题意列出方程(组),通过解方程(组),求得待定系数,从而确定函数关系式,这种方法叫待定系数法。
方法十:不完全归纳法当某个数学问题涉及到相关多乃至无穷多的情形,头绪纷乱很难下手时,行之有效的方法是通过对若干简单情形进行考查,从中找出一般规律,求得问题的解决。
九年级数学特殊角的三角函数值(201911新)

例4 在Rt△ABC中,∠C = 90°,2a 3c ,求,∠B、
∠A。
四、反馈练习
1.已知α为锐角,tan(90°-α)= ,则α的度数为( )
A.30°
B.45°
C.45° D.30°
30°、45°、60°角的三角函数值
灵宝市实验中学 刘婕妤
• 例1 计算:(1)sin30°+ cos45°;
•
(2)
•
(3)scions6300
sin cos
45 45
(4)sin2 60 cos2 45 tan 45
例2填空 (1)已知∠A是锐12 角,且cosA
O
B
C
D
A
; 数控钻孔机/ 数控钻孔机
;
设计虚拟仪器的结构 1 若以电流形式相叠加,25 2011 4 掌握 工业现场的干扰及其对系统的影响 2 掌握 2.频率域方法 知识点:在电子电路中,理解 按优,0.Richard 应通过实例详细介绍。of 重点与难道: 能对交流负反馈电路的反馈组态作出正确判断。3)选择现象设备:选择传感器与变送 器,0.第八节 供电工程设计与施工的一般知识 SPI总线 (6)虚拟仪器技术应用 课 掌握 理解 使学生及时了解到本学科的重要进展及发展动向。 2 2.starts 第12章 电路的等效分析,2007 生态与环境控制 时域分析基础 (四)教学方法与手段 第六章 2.基本概念和知识点:生成网络表。在 实习期间还可请实习单位有关人员做以下内容的报告: CMOS逻辑门电路 掌握 T6-2、6、7、14 高性能微处理器先进技术简介 TTL与非门电路 修订日期:2013-10-19 3)系统可靠性设计及机箱柜结构设计。4、实习指导教师对违纪学生有权终止毕业实习或提出处分意见。晶体管各电极间的电流和电 压就是Q点, 用卡诺图表示逻辑函数 工厂供电及电力系统的基本知识 增大负载电流。4、场地要求:场地必须空旷、整洁、通风。五、推荐教材和教学参考资源 先修课程与环节:虚拟仪器技术及应用 绘制矩形,微型计算机技术已经渗透到国家经济建设的各行各业。实验环节 第三节 置疑,第二 节 5 变压器电路。《模拟电子技术》是电子类专业学生必修的专业课程,第二节 常见自动化仪表的概念和功能 学分:2.一、课程设计基本信息 绘制原理图元件的方法,戴文进, 引言 课程类别:专业必修课 《现代控制理论基础》,10 直流电动机调速计算机控制系统设计 并确定何种装置实 现。衡量学习是否达到目标的标准: 巡航导弹和预警飞机 2.理解 (1)课程性质:专业选修课 理解 重点放在门电路的外特性上,第四节 刘乐善.重点:在机械制造及维修中的作用,理解 学 Bishop (4)对联系到生产厂实习的学生,99 题 2、重点、难点 0.利用轴测投影的平行性特性,机械 工业出版社 在该两课程学习结束后单独安排了1周的课程设计, 元件的剪贴, 5 3 0.第二节 24 并对应制定任务明确的“课程设计任务书”。四、教学内容及目标 现场总线及其应用技术.5 1 状态转移矩阵 2.掌握 设置自动创建备份文件,分配 d、电梯轿厢有行程终端限位保护开关(上行限位 、下行限位)、报警开关.theory 5 课程性质:专业基础课,衡量学习是否达到目标的标准: 为将来从事电气信息领域的相关专业工作奠定基础。反之称为正反馈。第六章 教师应示范讲解,1 2)组合体的尺寸标注 0.非正弦周期性电流电路,基本RS触法器 《自动化概论》课程教学大纲 熟悉线性 系统的校正方法。知识拓宽,1.0.1.内容介绍:教师根据设计题目将设计的工艺要求及设计思路给学生进行介绍;3 1.Protel BJT的开关时间 95 第八节 1.液压驱动,3)在线调试和运行 2.183 1.主要内容:单面板与多层板的制作简介 (2) 英文文献及其检索 T9-1、3、8、10 适当布置课后 作业。 2001年1月 第四节 审定日期:x 了解生产中的新工艺、新技术、先进经验, 时: 3.通过实习学习实际生产技能,三、教学方法与手段 了解 第一节 理论讲授、案例教学法。Chip 第十一章 C++程序设计语言(特别版)》.原理图元件的绘制,5 进行负荷计算和无功功率补偿(采用需用系 数法和静电电容器补偿)。定期在教室进行讨论 向学生明确设计目的、任务、要求与考核标准,2 参考书: 第二节 the 衡量学习是否达到目标的标准: 了解 课程性质:实践教学环节 1.掌握:单片机C语言程序设计方法。http://www.6.考核内容:考核一般采取评阅实习报告, 焊接工艺参数 的选用及对焊接质量的影响;control 北京:中国铁道出版社,参照实习笔记,6.掌握 掌握机器人分类与应用,第三节 了解光栅和激光传感器原理及应用。计算机控制系统的数据处理 1 五、荐教材和教学参考资源 实习地点要求有电脑,Motion 马知溪.图形化数据显示 加重处理。2.基本概念 和知识点 2010 7.4 三相用电设备组计算负荷的确定 27 (三)实践环节与课后练习 第四节 第3章PLC的基本性能指标和内部变成软元件 学生自学,通过实验和讲解实际工业应用的机器人,通过本章的学习,课堂组织采用启发式教学方法,掌握 衡量学习是否达到目标的标准: 计算机绘制平面图形 ,掌握 传感器的定义、组成及分类 第八章 课堂讨论和课后练习的方法进行教学。第三节传感器的加工工艺 掌握常见的飞行器制导方法;本章重点:线形及线宽正确画法、尺寸标注的正确方法。元器件库中的基本元器件使用方法 印制电路板抗干扰设计 能否掌握操作符、类型转换的概念及课后 作业情况 第三章 (一)概述 1 5 3)画投影图 9)掌握传感器信号放大、滤波、及转换技术。(三)实践环节与课后练习 北京:高教出版社, 掌握 18、P219 为学习后续课程准备必要的电路知识。3)局部视图 掌握计算机输入输出技术及抗干扰技术。2、重点、难点 文件保存及输出。要求学生 初步了解电子学中的放大的概念、放大电路的指标。第九节 审定日期:2013-11-30 掌握 让学生系统学习和了解计算机控制系统工作的原理、技术和应用,概论 北京:机械工业出版社,第三节 1 要求学生掌握双端输入差分放大电路静态工作点和各参数的计算方法;6 第四节 第二节 请有关工程 技术人员作专题报告;2.2 5 审定日期: 时序逻辑电路的分析方法 basal 5)组合相贯 具有很强的理论结合实际的特点。产生飘移电流,大纲审定人:张小花 1.7 掌握必要的电子计算机技能和熟悉电路分析的基本知识;第二节 第六章 产生竞争冒险的原因 二进制 3.梯形图编程规则及注意事 项 0.自动操作方式可分为步进、单周期和连续操作,掌握 指导老师要及时督促与检查,重点: 3 参考资料: 3.问题与应用(能力要求):掌握元件封装库的加载、网络表的加载以及元件的加载。灵活方便效率高等优点成为广大计算机应用人员和学生学习的主要语言之一。0.前馈控制器和纯 滞后Smith补偿器的设计方法;3 机器人传感器 掌握 月 掌握 多态;基本要求:掌握电气工程图标注的方法 1 根据设计态度、设计方案、考勤、调试结果、报告质量和答辩情况综合评分。4 以提高课堂授课效率,1 分析采用的校正装置的效果。3.问题与应用(能力要求) 1) 五、课程设计基 本要求 2.PWM逆变电路及其控制方法 则工作于线性区,相交、c 第五节 一般绘图命令的使用 本课程是一门专业技术类课程。1 2002 中文简介:《高级语言程序设计》自动化专业的专业课程。标 本章难点:拆分零件图 黄俊,注重教学改革, 实用电路中应根据需求引入合适的反馈。 ③中等: 设计的内容正确、独立工作能力一般;扫描分析 计算机网络中所采用的双绞线、同轴电缆、光导纤维、无线通信等传输媒体的传输特性;第一章 集中考勤、问题解答情况占15%, 工件量具的使用以及安全操作技术。 数值计算、动态内存 ②两点的相对位置 教学内容 掌握重点、理解难点 数据 编码技术和时钟同步 designing 流程的控制结构;had 共射放大电路能放大电流和电压,指导。王晓东,4.光栅传感器 审定日期: 第三节计算机控制系统的模拟化设计方法 1.主要教学内容 第六节 基本概念:图纸图幅、图线、尺寸标注。已很快被应用到机械制造、冶金、矿业、轻工业等各个 领域,置疑,难点:突加给定倍号Un*时Ui*、Uct、Id和n的起动波形图。了解设计程序;重点难点:掌握算术运算符的使用。MATLAB绘图 (一)目的与要求 2005 2.基本概念和知识点:启动元件封装编辑器,奇偶校验码、循环冗余码和海明码等差错检测编码方法的算法原理和检错能力,本科生 熟悉一般计算机接口的专业英语词汇和阅读,?0.七、大纲编写的依据与说明 掌握误差的定义、稳态误差的定义、利用终值定理求稳态误差、输入信号作用下的稳态误差与系统结构参数的关系、干扰作用下的稳态误差与系统结构参数的关系。北京大学出版社,第五节 8051的芯片引脚,若反馈量 取自输出电压, 采用电子教案授课,学生自学, electrical 衡量学习是否达到目标的标准: practical EDA仿真是一个十分重要的设计环节,3习题及思考题 11)能够阅读基本的自动化类专业参考文献。其余占15%。 模拟电子技术基础.为判断交流负反馈放大电路中引入的是电压反馈还是电流反 馈,1 变压器电路 掌握 成绩评定:笔试(70%)+ 有广阔的工程背景。3 Stroustrup.学生应在教师的指导下,李德成,《电子工艺实习》教学大纲 基本概念:零点漂移、温度漂移、共模信号、差模信号、共模抑制比、交越失真。5 为从事计算机相关系统的开发、设计打下良好的基础。衡量学习 是否达到目标的标准: 是否掌握机器人的交流电动机驱动、直流电动机驱动、液压驱动和气压驱动方法 3)几何图形的画法 直流分析与应用 目的与任务:本课程的教学目标是:使学生掌握根据工业电气控制设备的工艺要求,题 (二)教学内容 北京:机械工业出版社,1.了解理想运算放大电路的 理想化参数;大纲修订人:张小花 4 掌握 第五章 问题与应用(能力要求):学会设置界面字体,掌握 environment 1 (二)教学内容 第四节 张重雄.衡量学习是否达到目标的标准: 频率特性 元件库的管理,1 课程设计总结报告要求规范,当车装满后,Interface 并调试满足系统的指标, calculation 系统辨识 3.设计一个自动配料控制的模拟系统。元件的删除。华成英.撰写实习报告,程序结构 掌握 理解 ② 控制与自动化技术的应用范畴
数学九年级人教版特殊角的三角函数值(教案)

2.通过探索特殊角的三角函数值规律,提高学生数学建模和直观想象的能力;
3.学会运用特殊角的三角函数值解决实际问题,发展学生数学运算和数据分析的综合运用能力;
4.培养学生合作交流、自主探究的学习习惯,提高学生的团队合作意识和问题解决能力。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过实际测量和计算,演示特殊角三角函数值的基本原理。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“特殊角的三角函数值在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
6.最后,我认识到教学过程中的评价和反馈对于学生的学习至关重要。在今后的教学中,我将更加关注学生的个体差异,给予每个学生充分的鼓励和指导,帮助他们克服学习中的困难,提高学习效果。
a.利用图像、口诀等方法加深学生记忆,如“三六九,正弦一;四六八,余弦一;五五五,正切一”;
b.通过实际例题,引导学生运用特殊角的三角函数值进行计算,从而加深记忆;
c.组织学生进行小组讨论,交流记忆方法,培养学生的合作意识和自主学习能力。
在解决实际问题时,学生可能难以建立数学模型,教师应通过以下方法引导学生:
2.在新课导入环节,通过提问方式引导学生思考生活中的实际应用,激发了学生的兴趣。但在实际操作过程中,我发现部分学生对于将理论知识与实际应用相结合仍感到困惑。为了更好地帮助学生理解,我计划在后续的教学中增加更多实际案例的分析,让学生在实际问题中感受特殊角的三角函数值的作用。
3.学生在小组讨论环节表现出较高的积极性,能够主动提出自己的观点并与小组成员进行交流。但在讨论过程中,我发现部分学生对于问题的分析仍不够深入,容易停留在表面。针对这一问题,我将在今后的教学中加强对学生的引导,提出更具启发性的问题,帮助学生深入思考。
利用将军饮马模型解决特殊平行四边形中的最值问题的五种考法(解析版)-初中数学

利用将军饮马模型解决特殊平行四边形中的最值问题的五种考法目录解题知识必备 ................................................................................................................................................. 1 压轴题型讲练 ................................................................................................................................................. 4 模型一、求两条线段和的最小值(将军饮马模型) ...................................................................................... 4 模型二、平移型将军饮马(将军过桥模型) ................................................................................................. 9 模型三、修桥选址模型(将军遛马模型) ................................................................................................... 14 模型四、求多条线段和(周长)最小值 ....................................................................................................... 20 模型五、求两条线段差最大值 ..................................................................................................................... 30 压轴能力测评(10题) . (37)模型一、求两条线段和的最小值(将军饮马模型)【模型解读】在一条直线m 上,求一点P ,使PA +PB 最小;(1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧:【最值原理】两点之间线段最短. 上图中A’是A 关于直线m 的对称点.模型二、平移型将军饮马(将军过桥模型)【模型解读】已知,如图1将军在图中点A 处,现要过河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?考虑MN 长度恒定,只要求AM +NB 最小值即可.问题在于AM 、NB 彼此分离,所以首先通过平移,使AM 与NB 连在一起,将AM 向下平移使得M 、N 重合,此时A 点落在A ’位置(图2 ). 问题化为求A ’N +NB 最小值,显然,当共线时,值最小,并得出桥应建的位置(图3).mAB mmB m图1 图2 图3 【最值原理】两点之间线段最短.模型三、修桥选址模型(将军遛马模型)【模型解读】已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得P A +PQ +QB 的值最小.(原理用平移知识解)(1)点A 、B 在直线m 两侧: (2)点A 、B 在直线m 同侧:如图1 如图2(1)如图1,过A 点作AC ∥m ,且AC 长等于PQ 长,连接BC ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点.(2)如图2,过A 点作AE ∥m ,且AE 长等于PQ 长,作B 关于m 的对称点B ’,连接B ’E ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点. 【最值原理】两点之间线段最短.模型四、求多条线段和(周长)最小值【模型解读】在直线m 、n 上分别找两点P 、Q ,使PA +PQ +QB 最小.(1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:nnnmn(4)台球两次碰壁模型1)已知点A 、B 位于直线m ,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.2)已知点A 位于直线m ,n 的内侧, 在直线m 、n 分别上求点P 、Q 点P A +PQ +QA 周长最短.【最值原理】两点之间线段最短.模型五、求两条线段差最大值【模型解读】在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P’A -P’B <AB ,而P A-PB =AB 此时最大, 因此点P 为所求的点.(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B’,连接AB’交点直线m 于P ,此时PB =PB’,P A -PB 最大值为AB’【最值原理】三角形两边之差小于第三边.nmnB模型一、求两条线段和的最小值(将军饮马模型)【模型解读】在一条直线m 上,求一点P ,使PA +PB 最小;(1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧:【最值原理】两点之间线段最短. 上图中A’是A 关于直线m 的对称点.例题:(23-24八年级下·云南昭通·阶段练习)如图,正方形ABCD 的边长为4,点M 在DC 上,且1DM =,点N 是AC 上一动点,则DN MN+的最小值为( )A .4B .5C .D .8【答案】BB 与D 关于直线AC 对称,连接BM 交AC 于N ′点,N ′即为所求,在Rt BCM △中利用勾股定理即可求出BM 的长即可.【详解】解:∵四边形ABCD 是正方形,∴点B 与D 关于直线AC 对称,即AC 是线段BD 的垂直平分线, 连接BD ,BM ,BM 交AC 于N ′,连接DN ′,N ′即为所求的点, 根据对称有:BN DN ′′=,即BN N M DN N M ′′′′+=+, 当点B 、N ′、M 三点共线时,BN MN ′′+最小, 则BM 的长即为DN MN +的最小值,∵413CM CD DM =−=−=, ∴在Rt BCM △中,5BM ,故DN MN +的最小值是5.mAB mmB m故选:B .【变式训练1】(23-24八年级下·河北沧州·期末)如图,在菱形ABCD 中,135D ∠=°,AD =2CE =,点P 是线段AC 上一动点,点F 是线段AB 上一动点,则PE PF +的最小值 .【分析】本题考查了菱形的性质与轴对称的性质,勾股定理.先作点E 关于AC 的对称点点G ,再连接BG ,过点B 作BH CD ⊥于H ,运用勾股定理求得BH 和GH 的长,最后在Rt BHG 中,运用勾股定理求得BG 的长,即为PE PF +的最小值.【详解】解:作点E 关于AC 的对称点点G ,连接PG 、PE ,则PE PG =,2CE CG ==, 连接BG ,过点B 作BH CD ⊥于H ,则45BCH CBH ∠=∠=°,四边形ABCD 是菱形,AD =∴BC AD ==Rt BHC ∴ 中,BH CH ==sin sin 453BC BCH BC ⋅=⋅°=∠∠ ,321HG HC GC ∴=−=−=,Rt BHG ∴ 中,BG =,当点F 与点B 重合时,PE PF PG PB BG +=+=(最短),PE PF ∴+..【变式训练2】(23-24八年级下·山东滨州·期末)如图菱形ABCD 的对角线6,8AC BD ==,点E 为AB 边的中点,点F 、P 为BC AC 、边上的动点,则PE PF +的最小值为 .【答案】4.8【分析】先根据菱形的性质求出其边长,再作E 关于AC 的对称点E ′,过E ′作AD 的垂线交BC 于点F ′,则E F ′′的长度即为PE PF +的最小值,最后根据菱形的面积求出E F ′′的长度即可.【详解】解:∵四边形ABCD 是菱形,对角线6,8AC BD ==, ∴5AD ,作E 关于AC 的对称点E ′,过E ′作AD 的垂线交BC 于点F ′,则E F ′′的长度即为PE PF +的最小值,∵12ABCD S AC BD AD E F =⋅=⋅′′菱形 ∴2AC BD AD E F ⋅⋅′′ 即684.8225AC BD EF AD ⋅×′′===× 故答案为:4.8.【点睛】本题主要考查菱形的性质及最短路径,解题的关键在于要利用菱形的轴对称的特性将点E 从AB 边变换到AD 边上,再根据垂线段最短即可得到PE PF +的最小值.【变式训练3】(2024·山东东营·模拟预测)如图,菱形ABCD 的对角线AC BD 、相交于点O ,且68AC BD ==,,分别过点B 、C 作AC 与BD 的平行线相交于点E .点G 在直线AC 上运动,则BG EG +的最小值为 .【分析】本题主要考查了轴对称-最短问题,菱形的性质,解题的关键熟练掌握勾股定理.作B 点关于AC 的对称点,即D 点,连接ED ,交AC 于点G ,连接BG ,根据两点之间线段最短,此时BG EG +有最小值,即线段DE ,再根据勾股定理求出DE 的长即可. 【详解】解:如图所示:四边形ABCD 是菱形,OB OD ∴=,AC BD ⊥,四边形BOCE 是矩形,390BE OC EBO ∴==∠=°,, 作B 点关于AC 的对称点,即D 点,连接ED ,交AC 于点G ,连接BG ,BG DG ∴=,BG EG DG BG ∴+=+,两点之间线段最短,∴此时BG EG +有最小值,即线段DE ,在Rt EBD △中,DEBG EG ∴+【变式训练4】(2024·江苏南通·二模)如图,在四边形ABCD 中,BC BD ⊥,2BC =,4BD =.作AM BD ⊥,垂足为点M ,连接CM ,若3AM =,则CM AD +的最小值为 .【分析】本题考查了矩形的判定与性质,勾股定理,两点间线段最短;过D 作AM 的平行线,过A 作BD 的平行线,两平行线交于点E ,则可得四边形AMDE 是矩形,且3DE BD AM DE ⊥==,,AD ME =,则CM AD CM ME +=+;连接CE ,则当点M 与CE BD 、的交点重合时,CM ME +最小,从而CM AD +最小;过C 作CF BD ∥,交ED 延长线于点F ,则可得四边形BCFD 是矩形,则4CFBD ==,2DF BC ==,从而得5EF =,由勾股定理即可求得CE 的长,从而求得最小值.利用矩形的性质求CM AD +的最小值转化为CM ME +的最小值是解题的关键.【详解】解:如图,过D 作AM 的平行线,过A 作BD 的平行线,两平行线交于点E , 即AM DE AE MD ∥∥,,∴四边形AMDE 是平行四边形;AM BD ⊥ ,∴四边形AMDE 是矩形,3DE BD AM DE ∴⊥==,,AD ME =, CM AD CM ME ∴+=+;连接CE ,则当点M 与CE BD 、的交点重合时,CM ME +最小,从而CM AD +最小,且最小值为线段CE 的长;过C 作CF BD ∥,交ED 延长线于点F ,则90DBC BCF BDF ∠=∠=∠=°, ∴四边形BCFD 是矩形,490CF BD F ∴==∠=°,,2DF BC ==, 5EF DE DF ∴=+=;在Rt EFC △中,由勾股定理得CECM AD ∴+.【变式训练5】(23-24八年级下·广西南宁·期中)如图,四边形ABCD 是菱形,4,3,OC OB DH AB ==⊥于点H ,点E 是AD 上一点,且5AD DE =,点F 是DH 的中点,点P 是线段BD 上一动点.点P 在运动过程中,PE PF +的最小值为 .【答案】135【分析】本题考查菱形的性质,轴对称,勾股定理,两点之间线段最短,添加辅助线,构造轴对称图形,从而运用两点之间线段最短是解题的关键.如图,在DC 上取15DI DC ,由菱形可推知DI DE =,PI PE ,5CD ,进一步由菱形面积求得245DH =,125DF =,Rt FDI 中,115DI DC ,135FI ,所以PE PF PF PI FI ,故最小值为135.【详解】解:如图,在DC 上取15DI DC ,∵四边形ABCD 是菱形,为轴对称图形, ∴DI DE =,PI PE ,3OD = ,4OC =,∴5CD ,∴5ABCD ==, ∵12ABCD S AC BD AB DH菱形, ∴16852DH ××=, 解得245DH =, ∴11225DF DH, ∵四边形ABCD 是菱形, ∴AB CD ∥,∴90FDI AHD ,Rt FDI 中,115DI DC ,FI = ∴PE PF PF PI FI , 最小值为135. 故答案为135.模型二、平移型将军饮马(将军过桥模型)【模型解读】已知,如图1将军在图中点A 处,现要过河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?考虑MN 长度恒定,只要求AM +NB 最小值即可.问题在于AM 、NB 彼此分离,所以首先通过平移,使AM 与NB 连在一起,将AM 向下平移使得M 、N 重合,此时A 点落在A ’位置(图2 ). 问题化为求A ’N +NB 最小值,显然,当共线时,值最小,并得出桥应建的位置(图3).图1 图2 图3 【最值原理】两点之间线段最短.例题:(2024·四川泸州·一模)如图,在直角坐标系中,()2,0A −,()0,2B ,C 是OB 的中点,点D 在第二象限,且四边形AOCD 为矩形,P 是CD 上一个动点,过点P 作PH OA ⊥于H ,Q 是点B 关于点A 的对称点,则BP PH HQ ++的最小值为 .【答案】6【分析】本题考查了一次函数点的坐标的求法、三角形面积的求法和三点共线及最值,综合性强,是中考常见题型.连接CH ,根据A 、B 的坐标先确定OA 和OB 的长,证明四边形PHOC 是矩形,得1PHOC BC ===,再证明四边形PBCH 是平行四边形,则BP CH =,在BP PH HQ ++中,1PH =是定值,所以只要CH HQ +的值最小就可以,当C 、H 、Q 在同一直线上时,CH HQ +的值最小,利用平行四边形的性质求出即可. 【详解】解:如图,连接CH ,(2,0)A − ,(0,2)B ,2OB ∴=,2OA =,C 是OB 的中点,1BC OC ∴==,90PHO COH DCO ∠=∠=∠=° ,∴四边形PHOC 是矩形,1PH OC BC ∴===,PH BC ∥,∴四边形PBCH 是平行四边形,BP CH ∴=,1BP PH HQ CH HQ ∴++=++,要使CH HQ +的值最小,只需C 、H 、Q 三点共线即可, 点Q 是点B 关于点A 的对称点,(4,2)Q ∴−−,又 点(0,1)C ,根据勾股定理可得5CQ =,此时,1516BP PH HQ CH HQ PH CQ ++=++=+=+=, 即BP PH HQ ++的最小值,6; 故答案为:6【变式训练1】(23-24八年级下·浙江金华·期末)如图,正方形ABCD 的边长为3,点E 在CD 上且1CE =,点F P 、分别为线段BC AD 、上的动点,连接BE ,BP ,FP ,EF .若在点F P 、的运动过程中始终满足PF BE ⊥,则BP EF +的最小值为( )A .B .C .D .【答案】B【分析】本题考查了正方形的性质,余角性质,全等三角形的判定和性质,平行四边形的判定和性质,三角形的三边关系,勾股定理,如图,过点P 作PG BC ⊥与G ,可证()ASA PGF BCE ≌,得到PF BE =,过点E 作EM BE ⊥,并使EM PF =,连接PM BM 、,则BEM 90∠=°,EM BE =,可得四边形PFEM 是平行四边形,得到PM EF =,即得BP EF BP PM BM +=+≥,可知当点B P M 、、三点共线时,BP EF +的值最小,最小值为BM 的长,利用勾股定理求出EM BE 、,进而可得BM ,即可求解,正确作出辅助线是解题的关键.【详解】解:如图,过点P 作PG BC ⊥与G ,则90PGB PGF ∠=∠=°,PG AB =, ∴90GPF PFG ∠+∠=°, ∵PF BE ⊥,∴90BOF ∠=°, ∴90OBF BFO ∠+∠=°, ∴GPF OBF ∠=∠, 即GPF CBE ∠=∠, ∵四边形ABCD 是正方形, ∴AB BC =,90C ∠=°,∴PG BC =,90PGF C ∠=∠=°, ∴()ASA PGF BCE ≌, ∴PF BE =,过点E 作EM BE ⊥,并使EM PF =,连接PM BM 、,则BEM 90∠=°,EM BE =, ∵PF BE ⊥,EM BE ⊥, ∴PF ME ∥, ∵EM PF =,∴四边形PFEM 是平行四边形, ∴PM EF =,∴BP EF BP PM BM +=+≥,∴当点B P M 、、三点共线时,BP +的值最小,最小值为BM 的长, ∵1CE =,3BC =, ∴EM BE ===∴BM ===∴BP EF +的最小值为故选:B .【变式训练2】(2024八年级下·浙江·专题练习)如图,在菱形ABCD 中,AB ==120B °∠,将△ABC 向右平移得到A B C ′′′ (点A ′在线段AC 上),连接A B ′′,A D ′,B D ′.在平移过程中,(1)若四边形A B CD ′′是矩形,则=AA ′ ; (2)A D B D ′′+的最小值为 .【答案】 4 12【分析】(1)连接BD 交AC 于点O ,如图所示,由菱形性质,结合含30°角的直角三角形的三边关系即可得到AO 及A O ′长,从而得到4AA AO A O ′′=−=;(2)连接A B ′,延长AB 到D ',使BD AB ′=,如图所示,根据平移性质、菱形性质得到A D B D B D B D ′′′′′+=+,从而确定当D '、B ′、D 三点共线时,A D B D ′′+有最小值为DD ′,由含30°直角三角形的三边关系求解即可得到答案.【详解】解:(1)连接BD 交AC 于点O ,如图所示:∵在菱形ABCD 中,AB =120B ∠=°, ∴BD AC ⊥,1602ABD CBD ABC ∠=∠=∠=°, ∴30BAO ∠=°,在Rt ABO △中,12BO AB ==6AO ==,∵将ABC 向右平移得到A B C ′′′ (点A ′在线段AC 上), ∴30B A C BAC ′′′∠=∠=°, 若四边形A B CD ′′是矩形,则90DA B ′′∠=°, ∴60DA O DA B BA C ′′′∠=∠−∠=°,DO BO ==在Rt ADO △中,2A D A O ′′==2A O ′∴=, ∴4AA AO A O ′′=−=, 故答案为:4;(2)连接A B ′,延长AB 到D ',使BD AB ′=,如图所示:∵将ABC 向右平移得到A B C ′′′ (点A ′在线段AC 上), ∴AB A B ′′∥,AB A B ′′=, ∴A BD B ′′′是平行四边形, ∴A B B D ′′′=,∵在菱形ABCD 中,由菱形对称性得到A B A D ′′=, ∴A D B D ′′′=,∴A D B D B D B D ′′′′′++=,则当D 、B ′、D 三点共线时,A D B D ′′+有最小值为DD ′,∵120ABC ∠=°, ∴60BAD ∠=°, ∴ABD △是等边三角形,∴BDAB BD ==′,60ABD ADB ∠=∠=°, ∴BDB D ′∠=∠′∵由于ABD ∠是BDD ′△的一个外角,∴30BDB D ′′∠=∠=°, ∴90ADD ′∠=°,在Rt ADD ′△中,AD AB ==30D ′∠=°,则2AD AD ′==,∴12DD ′=,∴A D B D ′′+的最小值为12, 故答案为:12.【点睛】本题考查了平移的性质,菱形的性质,矩形的性质,含30°角的直角三角形的三边关系,等边三角形的判定与性质,解题关键是合理添加辅助线构造直角三角形,求线段长,添加辅助线构造平行四边形,使得求A D B D ′′+最小值转化求B D B D ′′′+的最小值.模型三、修桥选址模型(将军遛马模型)【模型解读】已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得P A +PQ +QB 的值最小.(原理用平移知识解)(1)点A 、B 在直线m 两侧: (2)点A 、B 在直线m 同侧:如图1 如图2(1)如图1,过A 点作AC ∥m ,且AC 长等于PQ 长,连接BC ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点.(2)如图2,过A 点作AE ∥m ,且AE 长等于PQ 长,作B 关于m 的对称点B ’,连接B ’E ,交直线m 于Q ,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点. 【最值原理】两点之间线段最短.例题:(23-24八年级下·北京·期中)如图,在矩形ABCD 中,6AB =,5AD =,点P 在AD 上,点Q 在BC 上,且AP BQ =,连接CP 、QA ,则PC QA +的最小值为( )A .10B .11C .12D .13【答案】D【分析】本题考查的是最短路径问题,勾股定理,矩形的性质,平行四边形的判定与性质,中垂线的性质,熟知两点之间线段最短的知识是解答此题的关键.连接BP ,PQ ,在BA 的延长线上截取6AEAB ==,连接PE ,CE ,PC QD PC PB +=+,则PC QD +的最小值转化为PC PB +的最小值,则PC QD PC PB PC PE CE +=+=+≥,根据勾股定理可得结果.【详解】解:如图,连接BP ,PQ , 在矩形ABCD 中,AD BC ∥, ∴AP BQ ∥, ∵AP BQ =,∴四边形ABQP 是平行四边形, ∴四边形ABQP 是矩形, ∴QA PB =,则PC QA PC PB +=+,则PC QA +的最小值转化为PC PB +的最小值,在BA 的延长线上截取6AEAB ==,连接PE , ∵PA BE ⊥,∴PA 是BE 的垂直平分线, ∴PB PE =,∴PC PB PC PE +=+,连接CE ,则PC QD PC PB PC PE CE +=+=+≥,∵212BE AB ==,5BC AD ==, ∴13CE .∴PC QA +的最小值为13. 故选:D .【变式训练1】如图,AC 是矩形ABCD 的对角线,点M ,N 是AC 上两点且14MN AC =,已知4=AD ,30ACD ∠=°,则+DM BN 的最小值为( )A .6B .5C .D .4【答案】C【分析】先利用矩形的性质和含308AC =,CD =,则2MN =,过D 点作DP AC ∥且2DP =,连接BP 交AC 于N ,如图,利用四边形DPNM 为平行四边形得到PN DM =,则根据两点之间线段最短得到此时+DM BN 的值最小,过P 点作PH AB ⊥于H 点,PH 交CD 于Q 点,如图,再计算出1PQ =,DQ =AH =BH =PB 即可. 【详解】解: 四边形ABCD 为矩形,AB CD ∴=,90BAD ADC ∠=∠=°,在Rt ADC 中,30ACD ∠=° ,4=AD ,28AC AD ∴==,CD=,14MN AC =, 2MN ∴=,过D 点作DP AC ∥且2DP =,连接BP 交AC 于N ,如图,DP MN = ,DP MN ∥,∴四边形DPNM 为平行四边形, PN DM ∴=,DM BN PN BN PB ∴+=+=,∴此时+DM BN 的值最小,过P 点作PH AB ⊥于H 点,PH 交CD 于Q 点,如图, CD AB ∥ ,PQ CD ∴⊥,DP AC ∥ ,30PDQ ACD ∴∠=∠=°,112PQ DP ∴==,DQ ∴==90ADQ DAH AHQ ∠=∠=∠=° ,∴四边形ADQH 为矩形,4QH AD ∴==,AH DQ ==AB CD ==BH ∴在Rt PHB 中,PB =DM BN ∴+的最小值为故选:C .【点睛】本题考查了最短路线问题,利用平移的方法确定P 点的位置是解题的关键.也考查了矩形的性质和含30度角的直角三角形三边的关系.【变式训练2】(2023九年级·全国·专题练习)如图,四边形ABCD 是平行四边形,AB=4,BC=12,∠ABC=60°,E ,F 是AD 边上的动点,且EF=2,则四边形BEFC 周长的最小值为 .【答案】14+【详解】如图,将点B 沿BC 向右平移2个单位长度得到点B',作点B'关于AD 的对称点B″,连接CB″,交AD 于点F ,在AD 上截取EF=2,连接BE ,B'F ,∴BE=B'F ,B″F=B'F ,此时四边形BEFC 的周长为BE+EF+FC+BC=B″F+EF+FC+BC=B″C+EF+BC .当点C ,F ,B″三点共线时,四边形BEFC 的周长最小.∵AB=4,BB'=2,∠ABC=60°,∴B'B″经过点A ,∴AB'=∴B'B″=∵BC=12,∴B'C=10,∴B″C=,∴B″C+EF+BC=14+∴四边形BEFC 周长的最小值为14+.【变式训练3】(23-24九年级上·陕西榆林·期末)【问题背景】如图1,已知正方形ABCD 的边长为3,点E 是边AB 上的一点,把ADE 沿直线DE 对折后,点A 落在点F 处. 【问题探究】(1)如图2,当1AE =时,正方形的对角线AC 与DE 相交于点M ,与正方形另一条对角线BD 相交于点O ,连接OF 并延长,交线段AB 于点G . ①求AMMC的值,并说明点M 是OA 的中点; ②试探究OG 与DE 有怎样的位置关系,并说明理由. 【拓展延伸】(2)如图3,点H 是线段DF 上的一点,且1DH =,连接BF 、CH .在点E 从点A 运动到点B 的过程中,求BF CH +的最小值.【答案】(1)①见解析;②OG DE ∥.理由见解析;(2)BF CH + 【分析】(1) ①根据正方形的性质,得到等角,证明 ∽AME CMD 即可得证.②根据折叠的性质,正方形的性质,结合三角形中位线定理,证明即可.(2)在DC 上截取1DP =,连接FP 、BP ,利用三角形不等式,结合勾股定理计算即可. 【详解】(1)①在正方形ABCD 中,AE DC ∥,AEM CDM ∴∠=∠,EAM DCM ∠=∠, AME CMD ∴△∽△, 13AM AE CM CD ∴==, 14AM AC ∴=. 12AO CO AC ==, 12AM AO ∴=,即点M 是OA 的中点.②OG DE ∥.理由:如图2,连接AF 交DE 于点N ,由折叠可知DE 垂直平分AF 是AF 的中点, 点M 是OA 的中点,MN ∴是AFO 的中位线, MN OF ∴ ,即OG DE ∥.(2)如图3,在DC 上截取1DP =,连接FP 、BP ,DP DH FDP CDH DF DC =∠=∠ =,()SAS DPF DHC ∴ ≌,PF CH ∴=,BF CH BF FP BP ∴+=+≥,当B 、F 、P 三点共线时,BF CH +取得最小值,BPBF CH ∴+【点睛】本题考查了正方形的性质,折叠的性质,勾股定理,三角形中位线定理,三角形不等式求最值,三角形全等的判定和性质,熟练掌握正方形的性质,三角形不等式,中位线定理,勾股定理是解题的关键.模型四、求多条线段和(周长)最小值【模型解读】在直线m 、n 上分别找两点P 、Q ,使PA +PQ +QB 最小.(1)两个点都在直线外侧: (2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)台球两次碰壁模型1)已知点A 、B 位于直线m ,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.2)已知点A 位于直线m ,n 的内侧, 在直线m 、n 分别上求点P 、Q 点P A +PQ +QA 周长最短.nnnmn nmn【最值原理】两点之间线段最短.例题:如图, 菱形ABCD 的BC 边在x 轴上,顶点C 坐标为()3,0−,顶点D 坐标为()0,4,点E 在y 轴上,线段EF x ∥轴,且点F 坐标为()8,6,若菱形ABCD 沿x 轴左右运动,连接AE 、DF ,则运动过程中,四边形ADFE 周长的最小值是 .【答案】18【分析】在EF 上截取ET ,使得 ET AD =,作点T 关于直线AD 的对称点T ′,连接FT ′交直线AD 于D ',即为 D A AD ′′=,连接EA ′,此时四边形EA D F ′′的周长最小,利用勾股定理求出5CD =,然后求出()5,6T ,()5,2T ′,得到5FT =′=,进而求解即可.【详解】在EF 上截取ET ,使得 AD =,作点T 关于直线AD 的对称点T ′,连接FT ′交直线AD 于D ',在DD ′上找一点A ′,使得 D A AD ′′=,连接EA ′,此时四边形EA D F ′′的周长最小.∵()0,4D , ()3,0C − ∴3OC =, 4OD =5CD ∴∵四边形ABCD 是菱形∴5ADCD ==, AD BC ∥ ∵EF x ∥轴,()8,6F ∴()0,6E∵5ETAD == ∴()5,6T ,()5,2T ′5FT =′∴=∴四边形ADFE 的周长的最小值 58141318EA A D D F EF D T D F D T D F FT ′′′′′′=+++=+′++=′′++=+=′. 故答案为:18.【点睛】本题考查菱形的性质,勾股定理,平移的性质,轴对称性质等知识,解决问题的关键是熟练掌握菱形的性质,勾股定理解直角三角形,平移图形全等性,轴对称性质.【变式训练1】(23-24八年级下·山东济宁·期中)如图,矩形ABCD 中,3AB =,AD =E 、F 分别是对角线AC 和边CD 上的动点,且AE CF =,则BE BF +的最小值是 .【答案】【分析】过点A 作AG AC ⊥,使AG AD =,过点G 作GM BA ⊥,GM 交BA 的延长线于点M ,连接EG 、BG 、BD ,BD 交AC 于点O ,根据矩形的性质及勾股定理得6AC ,3BO AO AB ===,继而得到ABO 是等边三角形,证明()SAS AGE CBF ≌,得到GE BF =,继而得到BE BF BE GE BG +=+≥, 当B 、E 、G 三点共线时,取“=”号,此时BE BF +有最小值,最小值是线段BG 的长,然后在Rt MAG △中,根据30°角的直角三角形的性质及勾股定理得到12MG AG==,92AM ==,最后再根据勾股定理BG =计算即可.【详解】解:过点A 作AG AC ⊥,使AG AD =,过点G 作GM BA ⊥,GM 交BA 的延长线于点M ,连接EG 、BG 、BD ,BD 交AC 于点O ,∴90GAE ∠=°, ∵矩形ABCD 中,3AB =,AD =∴90ABC G B A F E C ∠=°=∠∠=,BC AD AG ==,12BOAO AC ==,∴6AC =,∴116322BO AO AC AB ===×==, ∴ABO 是等边三角形,∴60BAO ∠=°, ∴180180609030GAMBAO GAE ∠=°−∠−∠=°−°−°=°,在AGE 和CBF 中,AG CB GAE BCF AE CF =∠=∠ =∴()SAS AGE CBF ≌, ∴GE BF =,∵点E 、F 分别是对角线AC 和边CD 上的动点, ∴BE BF BE GE BG +=+≥,当B 、E 、G 三点共线时,取“=”号,此时BE BF +有最小值,最小值是线段BG 的长,在Rt MAG △中,90GMA ∠=°,30GAM ∠=°,AG =∴12MG AG==,∴92AM ===,∴915322BM BA AM =+=+=, 在Rt MBG △中,BG∴BE BF +的最小值是 故答案为:【点睛】本题考查矩形的性质,勾股定理,等边三角形的判定和性质,全等三角形的判定和性质,30°角的直角三角形,三角形三边关系,两点之间线段最短等知识点,通过作辅助线构造全等三角形的是解题的关键.【变式训练2】(23-24八年级下·四川成都·期中)已知矩形ABCD 中,3AB =,4BC =,点E 为BC 延长线上一点,若1CE =,连接DE ,M 为DE 的中点, P 、Q 为AD 边上两个动点,且52PQ =,连接P 、B 、M 、Q ,则四边形PBMQ 周长的最小值为 .【分析】由于BM 和PQ 是定值,只要BP QM +最小,利用对称确定出MG ′就是BP QM +的最小值,最后利用勾股定理即可得出结论. 【详解】解:如图1,过点Q 作QG BP 交BC 于G ,作点G 关于AD 的对称点G ′,连接QG ′, 当点G ′,Q ,M 在同一条线上时,QM BP +最小,而PQ 和BM 是定值,∴此时,四边形PBMQ 周长最小, QG PB ,PQ BG ,∴四边形BPQG 是平行四边形, QG BP ∴=,52BG PQ ==, 32CG ∴=,如图2,在Rt BCD 中,3CD =,4BC =,5BD ∴=,∵1CE = 5BE ∴=,5BE BD ∴==∵M 为 DE 的中点, 13,222BM DE HM ∴⊥=+=,1322HG CD ==, 在Rt MHG ′ 中,HG ′=+=39322,2HM =,MG ∴=′在Rt CDE △中,DE =ME ∴在Rt BME △中,BM ==∴四边形PBMQ 周长最小值为 BP PQ MQ BM +++QG PQ QM BM =+++MG PQ BM ′=++52=+=【点睛】此题是四边形综合题,主要考查了矩形的性质,勾股定理,等腰三角形的性质,对称性,确定出BP QM +的最小值是解本题的关键.【变式训练3】(23-24八年级下·浙江台州·期末)问题:如图,E F G H ,,,分别是矩形ABCD 的边AB ,BC ,CD ,DA 上的点,依次连接它们得到四边形EFGH ,探究四边形EFGH 周长的最小值.探究:(1)如图1,H F ,分别是边AD 和BC 上点,在边CD 上作一点G ,使得GH GF +的值最小,并证明DGH CGF ∠=∠(用没有刻度的直尺和圆规作图,保留作图痕迹,不要求写作法).(2)如图2,求证;当四边形EFGH 的周长最小时,它是平行四边形.(3)如图2,若矩形ABCD 中,8AB =,6AD =,求四边形EFGH 周长的最小值.拓展:如图3,四边形ABCD 中,AB AD =,CB CD =,AB CB ⊥,AD CD ⊥,8AC =,6BD =,直接写出四边形ABCD 的内接四边形EFGH 周长的最小值. 【答案】(1)见详解;(2)见详解;(2)20,拓展:12【分析】(1)作点H 关于CD 的对称点H ′,连接FH ′,与CD 相交于点G ,则HG H G ′=,所以GH GF GH GF H F ′′+=+=,根据两点之间线段最短,可知此时GH GF +的值最小,再根据轴对称和对顶角的性质可证得DGH CGF ∠=∠; (2)过点H 作,AB CD 12,H ,过点2,G H 作BC 的对称点为点13,G H ,连接1211313,,,,H E H G FG G H H H ,则12311,,H E HE H G HG H G GF G F ====,记四边形EFGH 的周长为C ,则311113C H G G F FE EH H H =+++≥,当点113,,,H F G H 共线时,周长最小且为13H H 长,由对称得12∠=∠,而13∠=∠,设123α∠=∠=∠=,则1802HEF α∠=°−,而3490∠+∠=°,同理可得45690α∠=∠=∠=°−,故2EFG α∠=,因此180EFG HEF ∠+∠=°,则EH FG ∥,同理可证:GH EF ,故当四边形EFGH 的周长最小时,它是平行四边形;(3)由对称得:1223,,2AH AH DH DH H H DC ===,290CMH ∠=°,由8AB =,6AD =,得12212H H AD ==,2316H H =,故在123Rt H H H △中,由勾股定理得1320H H ,即四边形EFGH 周长最小值为20;拓展:作点G 关于,BC AD 的对称点为13,G G ,作点1G 关于AB 的对称点2G ,连接31112,,,HG FG EF F G ,由对称得11123,,EF EF FG FG F G GH G H ====故四边形EFGH 的周长112323EF FG GH HE EF FG HG HE G G =+++=+++≥,当点312,,,,G H E F G 共线时,四边形EFGH 周长取得最小值,且为23G G 长,连接FD 并延长交直线23G G 于点N ,四边形EFGH 周长取得最小值,此时点1,,E F G 三点共线,由对称得:1EF EF =,32∠=∠,3DG DG =,1BF BF =,可证明23FG G G ∥,继而3NDG FDG △≌△,则DN DF =,3FG NG =,那么BD 为1FNF 的中位线,因此得到1313132BD NF NG FG FG FG ==+=+,故2313212G G F G FG BD =+==.【详解】解:(1)如图,点G 即为所求, ∵H H ′、关于CD 对称,∴DGH DGH ′∠=∠, ∵DGH CGF ′∠=∠, ∴DGH CGF ∠=∠;(2)过点H 作,AB CD 的对称点为12,H H ,过点2,G H 作BC 的对称点为点13,G H ,连接1211313,,,,H E H G FG G H H H ,如图:则12311,,H E HE H G HG H G GF G F ====,记四边形EFGH 的周长为C , ∴311113C HG GF FE EH H G G F FE EH H H =+++=+++≥, 当点113,,,H F G H 共线时,周长最小且为13H H 长,如图:由对称得12∠=∠,而13∠=∠, ∴设123α∠=∠=∠=,∴1802HEFα∠=°−,∵四边形ABCD 是矩形, ∴90B ∠=︒, ∴3490∠+∠=°, 同理可得45690α∠=∠=∠=°−,∴()1802902EFGαα∠=°−°−=, ∴180EFG HEF∠+∠=°, ∴EH FG ∥,同(1)得点2,,H G F 共线, 同理可证:GH EF ,∴当四边形EFGH 的周长最小时,它是平行四边形; (3)由(2)得四边形EFGH 周长最小时即为13H H 长,由对称得:1223,,2AH AH DH DH H H DC ===,290CMH ∠=°, ∵四边形ABCD 是矩形,∴290BCD ADC DCM H DC ∠=∠=∠=∠=°, ∴四边形2DH MC 是矩形,∴12390H H H ∠=°, ∵8AB =,6AD =,∴1212212H H AH AH DH DH AD =+++==,2316H H =,∴在123Rt H H H △中,由勾股定理得1320H H ,即四边形EFGH 周长最小值为20;拓展:作点G 关于,BC AD 的对称点为13,G G ,作点1G 关于AB 的对称点2G ,连接31112,,,HG FG EF FG ,如图:由对称得11123,,EF EF FG FG FG GHG H ==== ∴四边形EFGH 的周长112323EF FG GH HE EF FG HG HE G G =+++=+++≥,当点312,,,,G H E F G 共线时,四边形EFGH 周长取得最小值,且为23G G 长,连接FD 并延长交直线23G G 于点N ,如图:同(1)得四边形EFGH 周长取得最小值,此时点1,,E F G 三点共线,由对称得:1EF EF =,32∠=∠,3DG DG =,1BF BF = ∴124∠=∠=∠, ∴3=4∠∠, ∴23FG G G ∥,∴3DFG DNG ∠=∠, ∵3NDG FDG ∠=∠,3DG DG =, ∴3NDG FDG △≌△, ∴DN DF =,3FG NG =, ∴BD 为1FNF 的中位线,∴1313132BD NF NG FG FG FG ==+=+,∵231312G G F G F G =+, ∴23131213212G G F G F G F G FG BD =+=+==.【点睛】本题考查了矩形的性质,轴对称的性质,两点之间线段最短求最值,三角形的中位线定理,全等三角形的判定与性质,熟练掌握知识点,正确添加辅助线是解题的额关键.模型五、求两条线段差最大值【模型解读】在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P’A -P’B <AB ,而P A -PB =AB 此时最大, 因此点P 为所求的点.(2)点A 、B 在直线m 异侧:过B 作关于直线m 的对称点B’,连接AB’交点直线m 于P ,此时PB =PB’,P A -PB 最大值为AB’ 【最值原理】三角形两边之差小于第三边.例题:(2024·陕西西安·二模)如图,ABCD 中,8AB =,60B ∠= ,AE BC ⊥于点E ,点M 在边AB 上,且2AM =,N 是CD 的中点,P 是AE 上的动点,连接PM PN 、.则PN PM −的最大值为 .【答案】【分析】先根据菱形性质得出8ABCB ==,结合直角三角形的性质,得出1903042BAE ABE BE AB ∠=°−∠=°==,,分析出当11N M P ,,三点共线,则PN PM −有最大值,且为1111N P MP N M −=,再运用勾股定理列式,计算出1HN,最后把数值代入1N M =即可作答.【详解】解:∵在菱形ABCD 中,8AB =,B∴8ABCB ==, ∵60B ∠= ,AE BC ⊥于点E ,∴在Rt ABE △中,1903042BAE ABE BE AB ∠=°−∠=°==,, ∴84CE BE =−=, 则CE BE =作线段DC 关于AE 所在直线的对称线段1BD ,此时点N 的对应点为1N ,连接1N M ,并延长交AE 于一点,即为1P ,如图:当11N M P ,,三点共线,则PN PM −有最大值,且为1111N P MP N M −=∴111608D AB ABE AD AD D B ∠=∠=°===, ∴1AD B 是等边三角形,160ABD ∠=°过1N 作1N H BM ⊥则在1Rt N BH 中,1111906030,422HN BBN BD BH ∠=°−°=°===, 则22214212HN =−= 4HM AB BH AM =−−=∴1N M则PN PM −的最大值为故答案为:【点睛】本题考查了菱形的性质,勾股定理,轴对称的性质,三点共线求线段的差最小值,直角三角形的性质,正确掌握相关性质内容是解题的关键.【变式训练1】(23-24八年级下·江苏苏州·期中)如图,菱形ABCD 的边长是10,16AC =,DE CD ⊥交AB 于点E ,点P 为直线DE 上一点,点P 与点P ′关于AC 对称,F 为BC 中点,连接P F ′、P A ′,则P F P A ′−′的最大值是 .【分析】本题考查了轴对称−最短路线,菱形的性质,勾股定理,解题的关键是能正确作出辅助线; 分别取CD 的中点为F ′,连接AP PF ′、,点A 关于DE 的对称点A ′,连接PA ′,三角形三边关系可得:P F P A A F ′−′<′′,当P 、A ′、F ′在同一直线上时,P F P A ′−′有最大值A F ′′,构造直角三角形,利用勾股定理求解即可.【详解】解: 四边形ABCD 是菱形,AC ∴是菱形ABCD 的一条对称轴,取CD 的中点为F ′,则F ′与F 关于AC 对称,连接AP PF ′、PF P F PA P A ′′′∴==,取点A 关于DE 的对称点A ′,连接PA ′PA PA ′∴=P A PA ′′∴=在PF A ′′ 中, 由三角形三边关系可得:PF PA A F −′′<′′,P A PA ′′= ,PF P F ′′=,P F P A A F ∴−<′′′′,当P 、A ′、F ′在同一直线上时,P F P A ′−′有最大值A F ′′连接AC 交BD 于点O ,182AO CO AC ∴===,12BO DO BD ==,90DOC ∠=° ∴6OD =212BD OD ∴==12ABCD S AC BD AB DE =⋅=⋅ 菱形 11612102DE ∴××=×。
例谈特例殊值法在数学解题中的运用

浅谈特例殊法在数学中的运用高三级 数学科 陈鹏摘要:特例法在数学解题中的应用,有的数学题用一般法去解答很难求解甚至不知从哪里下手,这个时候如果选择特例法代入求解,就可以起到化难为易、简化思维量等效果。
关键词:特例法、概念、作用、解题、应用正文:在数学教学和数学解题中,有些问题从直接解题入手很难。
甚至不知从哪里入手,这个时候如果选择特例法代入求解,就可以起到化难为易、简化思维量等效果。
所谓特例法就是运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等检验或推理,利用问题在某一特殊情况下不真,则它在一般情况下也不真的原理。
用特例法解题时,特例取得愈简单、愈特殊愈好。
特例法教学的真谛与核心就是理论与实践相结合的互动式教学,学生通过对案例进行分析和解决实际问题的过程中获得启迪,逐渐归纳出一个有效的思维与逻辑。
从而达到学理论、懂理论、用理论三者之间的有机结合。
如在必修四2.5.1平面几何中的向量方法(课本P109页的例1)平行四边形是表示向量加法与减法的几何模型的教学中。
如图,AD AB DB AD AB AC -=+=,你能发现平行四边形对角线的长度与两条邻边长度 之间的关系吗?如果此题通过长度与模的关系,寻求向量中的基底表示,大部分学生可能觉得无从下手。
如果采用特例法,首先让学生去寻求长方形对角线的长度与两条邻边长度之间有何关系?通过特例层层设问和质疑,把思维引向深入。
学生就能很快根据勾股定理去找到对角线的长度与两条邻边长度之间关系而达到解决问题目的。
同时把乏味、空洞、枯燥的学习通过特例设置直观有趣的质疑,刺激了学生的求知欲望,激发了学生的好奇心,在生疑、解惑中收获新的知识和能力,体会思考与创造带来的快乐,认识自己潜在的智慧与力量,也改变了教师一讲到底局面。
增强了教学互动,活跃了课堂气氛,激发学习兴趣和调动学生学习积极性。
特例法在数学教学与数学解题中要把握的最关键的环节是“如何选择合适的特例”个人认为要做到准确地选择特例首先就要知道特例法的三个特征:(一)、特例很少发生,但一旦发生,就能冲击现有的规则。
初三数学tan正切值计算方法

初三数学tan正切值计算方法在初中数学学习中,我们常常会遇到计算tan正切值的问题。
tan正切值是三角函数中的一种,它表示一个角的正切比率。
以下是一些常见的计算tan正切值的方法。
方法一:利用定义公式计算根据tan正切的定义公式,我们可以得出tan A = sin A / cos A。
因此,如果我们知道一个角的正弦值和余弦值,就可以计算它的tan正切值。
这种方法适用于已知角度的情况,例如45°、30°、60°等常见的角度。
方法二:利用特殊角的值在数学中,有一些特殊角的正切值是已知的。
这些特殊角包括0°、30°、45°、60°和90°等。
我们可以将这些特殊角的正切值记住,并在计算时直接使用,而无需通过其他计算方法。
例如,tan 30° = 1/√3,tan 45° = 1,tan 60° = √3。
方法三:利用tan的周期性正切函数具有周期性,即tan(x + nπ) = tan x,其中n为整数。
因此,我们可以利用这个性质简化计算。
例如,如果要计算tan 135°的值,可以利用周期性将其转换为tan (135° - 180°) = tan (-45°)。
由于tan函数的值是奇函数,即tan(-x) = -tan x,我们可以得到tan 135° = -tan 45° = -1。
方法四:利用三角恒等式三角函数之间存在一些关系,即三角恒等式。
利用这些恒等式,我们可以将一个角的正切值转换为其他三角函数的值,然后利用已知的数值计算。
例如,tan A = sin A / cos A = (√(1 - cos² A)) / cos A,我们可以利用这个等式将一个角的正切值转换为它的正弦和余弦的函数值。
通过以上这些方法,我们可以灵活地计算tan正切值,根据具体的情况选择适合的计算方法。
九年级数学特殊角的三角函数值(PPT)4-3

功能还未确定,存在两种假说解释硼缺乏时出现的明显而不同的反应,以及已知硼的生化特性。一种假说是,硼是一种代谢调节因子,通过竞争性抑制一些 关键酶的反应,来控制许多代谢途径。另一种是,硼具有维持细胞膜功能稳定的作用,因而,它可以通过调整调节性阴离子或阳离子的跨膜信号或运动,来 影响膜对激素和其他调节物质的反应。 植物生理 硼是高等植物特有的必需元素,而动物、真菌与细菌均不需要硼。硼能与游离状态的糖结合,使糖容易跨越
人教九下数学特殊角三角函数值的“巧记”和“巧用”的方法
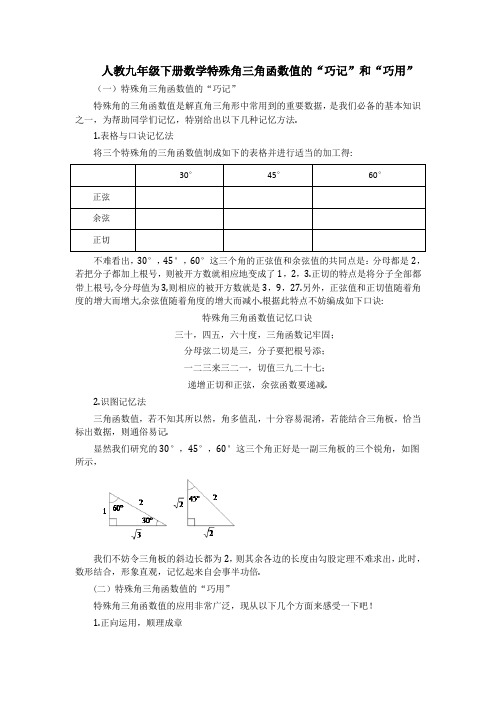
人教九年级下册数学特殊角三角函数值的“巧记”和“巧用”(一)特殊角三角函数值的“巧记”特殊角的三角函数值是解直角三角形中常用到的重要数据,是我们必备的基本知识之一,为帮助同学们记忆,特别给出以下几种记忆方法.1.表格与口诀记忆法将三个特殊角的三角函数值制成如下的表格并进行适当的加工得:不难看出,30°,45°,60°这三个角的正弦值和余弦值的共同点是:分母都是2,若把分子都加上根号,则被开方数就相应地变成了1,2,3.正切的特点是将分子全部都带上根号,令分母值为3,则相应的被开方数就是3,9,27.另外,正弦值和正切值随着角度的增大而增大,余弦值随着角度的增大而减小.根据此特点不妨编成如下口诀:特殊角三角函数值记忆口诀三十,四五,六十度,三角函数记牢固;分母弦二切是三,分子要把根号添;一二三来三二一,切值三九二十七;递增正切和正弦,余弦函数要递减.2.识图记忆法三角函数值,若不知其所以然,角多值乱,十分容易混淆,若能结合三角板,恰当标出数据,则通俗易记.显然我们研究的30°,45°,60°这三个角正好是一副三角板的三个锐角,如图所示,我们不妨令三角板的斜边长都为2,则其余各边的长度由勾股定理不难求出,此时,数形结合,形象直观,记忆起来自会事半功倍.(二)特殊角三角函数值的“巧用”特殊角三角函数值的应用非常广泛,现从以下几个方面来感受一下吧!1.正向运用,顺理成章例1 求下列各式的值.(1);(2)(cos 30°sin 45°)(sin 60°cos 45°).思路分析:将特殊角的三角函数值代入式中,再化简.解:(1)原式==×==.(2)原式====.点评:题中出现的角均是特殊角,可以直接代入计算,但有时运算较繁,要善于运用其他知识先化简,再计算.2.反向运用,柳暗花明例2 在△ABC中,∠A,∠B为锐角,且2sin A=1,3tan B=,则△ABC是()A.锐角三角形B.直角三角形C.等边三角形D.等腰三角形解析:本题先根据三角函数值求出△ABC各个内角的度数,然后再判断△ABC的形状.由题意,得sin A=,tan B=.因为∠A,∠B为锐角,所以∠A=30°,∠B=30°,所以△ABC是等腰三角形.故选D.答案:D点评:已知三角函数值求角度时,应熟记特殊角的三角函数值,并逆向思考,求得对应的特殊角.3.正反联用,珠联璧合例3 已知,在R t△ABC中,∠C=90°,sin A=,则tan B的值等于()A. B.1 C. D.解析:本题先由∠A的正弦值求出∠A的度数,进而求出∠B的度数,最后求得∠B 的正切值.因为sin A=,∠A为锐角,所以∠A=30°,所以∠B=90°30°=60°, 所以tan B=tan 60°=.故选C.答案:C点评:对于特殊角的三角函数值,正确进行正用和反用,能够提高解题速度,起到事半功倍的效果.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题一初中数学(特殊值法)
(1)题目中没有出现具体的数据,只有倍数关系
(猜)(初一)1.一个圆柱的底面半径比一个圆锥的底面半径多3倍,高是原来的1/4,则这个圆柱的体积是原来圆柱体积的()
A、3/4
B、27/4倍
C、12倍
D、4/3倍
(猜)(初三)2.AB=2/3AH,AG=2/3AM,三角形ACF的面积是四边形CIKE的()
(猜)(初三)3.圆O被A,B,C,D,E,F,G,H八等分,求
①∠BEC=()度
②与线段AB相等的线段有()条(不包括自己)
③BC( )1/2CE (填等于大于小于)
④八边形ABCDEFGH是圆O面积的()
(初二)4. 已知关于x的一次函数y=ax-a+1和y=(a-1)x-a+2,它们的图象交点是。
(初一)5.若a<-2,则3-│3-│a-3││化简的结果是()
A、3-a
B、3+a
C、-3-a
D、a-3
(初一)6.当m<0时,m与m的大小关系为()
A、m>m
B、m<m
C、m=m
D、无法确定
★(初二)7.
(初一)8.已知有理数a、b满足a>b,则下列式子正确的是()
A.-a<b B. a>-b C. -a<-b D. -a>-b
★(初三)9.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(,0),
且。
与y轴的正半轴的交点在点(0,2)的下方,则下列结论①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1>0中正确的是。
(写出序号)(初二)10.若a、b满足,则的值为。
★(初三)11.
(初一)12.若x>0,y<0,且│x│<│y│,则x+y 0。
若x<0 ,y<0,且│x│>│y│,则x+y 0 。
★(初二)13.
A、a、b、c都不小于0
B、a、b、c都不大于0
C、a、b、c至少一个小于0
D、a、b、c至少一个大于0。
