高中数学必修一 《4 3 对数》集体备课导学案
人教A版(2019)高中数学必修第一册4.3.1对数的概念教学设计
4.3.1 对数的概念16、17世纪之交，苏格兰数学家纳皮尔在研究天文学的过程中发明了对数，为数学家们在运算中赢得了时间与精力．对数发明20多年后法国数学家笛卡尔开始使用指数符号，数学家们开始关注指、对数之间的关系．直到18世纪，瑞士数学家欧拉才发现了指数与对数的互逆关系，他首先使用y= 来定义．至此，人们彻底揭示了对数本质，完善了指、对数的知识体系和数学运算体系．对数的发明先于指数，也成为数学史上的珍闻．事实上，对数的本质是一种运算．随着人们对指数的认识的不断深入，总会遇到诸如“在方程=2中求解x”的问题，即“已知底数和幂的值，求指数”．在数学运算体系的建立过程中，人们也经历了多次类似的情况，例如在加法运算中已知一个加数与和，求另一个加数时引入了“差”的概念；在乘法运算中已知一个因数与积，求另一个因数时引入了“商”的概念；在乘方运算中已知指数与幂，求底数时引入了“数的n次方根”的概念．欧拉指出：“对数源出于指数”，也就是说对数与指数之间存在必然的联系：当a>0，且a≠1时，．利用这一关系，我们可以实现对数式与指数式之间的互化．代数学的根源在于运算，“运算中的不变性、规律性”是发现“代数性质”的引路人，通过这种互化运算，我们可以得出对数的下列性质：当对数中的真数N为负数或者0时，对数没有意义．这是由于在实数范围内，正数的任何次幂都是正数．因而=N中的N总是正数．（2）（a>0，a≠1）．指数式中存在着诸如及的性质，将这两个指数式化为对数式即可得到对数的上述性质．从对数的发明过程可以看到，社会生产、科学技术的需要是数学发展的主要动力．建立对数与指数之间联系的过程表明，使用较好的符号体系和运算规则不仅对数学的发展至关重要，而且可以大大减轻人们的思维负担．因此，本节课的教学重点是：以“指数与对数的关系”为指引，发现和应用对数的概念．学情分析：本节课第一个学习难点是对数概念，虽然学生可以根据以往经验提出新概念建立的必要性，但是就像差、商、数的n次方根等概念的提出一样，每一次新概念的提出都与学生以前的认知产生矛盾，因此需要适应和熟悉，而这样的过程在对数这一概念上显得尤为漫长．在以往的学习过程中，涉及“差”的概念的减法是加法的逆运算，涉及“商”的概念的除法是乘法的逆运算，涉及“数的n次方根”的概念的开方运算是乘方的逆运算，对于对数这一概念，可以类比以往的互逆运算的关系进行认识．即使这样，减法、除法、开方等运算还是比较直观、容易理解的，但是由于对数所处运算级别较高，因此在教学中需要反复训练，使得学生尽快熟悉．第二个学习难点是在对指、对数的关系的认识上，学生往往只在表面上认识了对数概念，没有紧扣定义，充分发掘定义中指、对数之间的关系．为此可以借助图表、式中连线等简单直观的方式对指、对数式进行对照，在此过程中学生可以进一步理解对数概念，揭示指、对数之间的关系，特别是在对字母x的认识中可以明确“对数即指数”这一本质；也可以借助已有知识进行突破，例如借助指数函数中的变量对应关系揭示指、对数之间的关系．教学目标：1.了解对数产生的历史及背景，体会对数概念提出的必要性，发展数学人文素养；2.经历概念的形成过程，理解对数的概念，发展数学抽象核心素养；3.理解指、对数的关系，掌握指、对数式的互化，发展数学运算核心素养．教学重点：对数的概念；对数式与指数式的互化。
高中数学《对数》导学案 北师大版必修1(1)
第5课时对数1.理解对数的概念,能够进行指数式与对数式的互化.2.了解常用对数与自然对数的意义.3.熟记对数的运算性质及使用条件,理解对数恒等式.4.能熟练地运用对数的运算性质进行计算,掌握对数的换底公式,并利用它进行恒等变换.实例1:一尺之锤,日取其半,万世不竭.(1)取4次,还有多长?(2)取多少次,还有0.125尺?实例2:假设2008年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产总值达到翻两番的目标?问题1:根据上述情境,我们由指数函数来了解对数函数的意义:(1)取4次之后,还剩下()4= ,我们设取x次后还剩下0.125尺,那么列出方程()x=0.125⇒x= .(2)设经过x年国民生产总值达到翻两番的目标,那么 (1+8%)x=4,两边取常用对数可得:x lg 1.08=lg 4, 解得x=≈(年).问题2:两种特殊的对数(1)常用对数,以10为底,log10N写成;(2)自然对数,以e为底(e为无理数,e=2.71828…),log e N写成.问题3:对数具有的运算性质:当a>0且a≠1,M>0,N>0时,有:(1)log a(MN)= + ;(2)log a= - ;(3)log a M n= ;(4)= .问题4:对数换底公式:(1)log a b= (a>0且a≠1,c>0且c≠1,b>0).(2)推论: log a b=;lo b m=log a b.1.对数式log a-2(5-a)=b,实数a的取值范围是().A.(-∞,5)B.(2,5)C.(2,3)∪(3,5)D.(2,+∞)2.式子的值为().A. B. C.2 D.33.(log32+log92)(log43+log83)= .4.已知log73=a,log74=b,试用a,b表示log4948.对数的概念及其运算性质求使log64x=-成立的x的值.换底公式的应用(1)若log34·log48·log8m=log416,则m的值为().A. B.9 C.18 D.27(2)已知log189=a,18b=5,求log3645.用指数幂的运算性质求值已知二次函数f(x)=lg a·x2+2x+4lg a的最大值为3,求a的值.已知log2(log3x)=1,求x的值.当m a=n b= 时,+=1.(其中m,n为大于0且不为1的正数,a,b为不等于0的实数)设方程lg2x+(lg 2+lg 3)·lg x+lg 2·lg 3=0的两个根是x1、x2,求x1x2的值.1.25=32化为对数式为().A.log52=32B.log532=2C.log232=5D.log322=52.计算等于().A.B.4 C.3 D.3.lg 50+lg 2·lg 5+lg22= .4.已知方程x2+x·log26+log23=0的两根分别为α和β,求()α·()β的值.(2012年·安徽卷)(log29)·(log34)等于().A.B.C.2 D.4考题变式(我来改编):答案第5课时对数知识体系梳理问题1:(1)3(2)18问题2:(1)lg N (2)ln N问题3:(1)log a M log a N (2)log a M log a N (3)n log a M (4)N 问题4:(1)基础学习交流1.C根据对数式的意义得不等式组∴2<a<5且a≠3.2.A∵log89==log23,∴原式=.3.原式=(log32+log32)(log23+log23)=log32·log23=.4.解:log4948====.重点难点探究探究一:【解析】由对数的定义,可得x=6=(43=4-2=.【小结】指数式a b=N与对数式log a N=b(a>0,且a≠1)是相同三个量的同一种数量关系的两种不同表达形式,这两种形式在同一问题中可以相互等价转化.探究二:【解析】(1)由换底公式可得··==log3m,∴有log3m=log442=2,即m=32=9.(2)(法一)因为18b=5,所以log185=b,于是log3645=====.(法二)因为18b=5,所以log185=b,又log189=a,于是log3645===.(法三)因为log189=a,18b=5,所以lg 9=a lg 18,lg 5=b lg 18.所以log3645=====.【答案】(1)B【小结】(1)利用换底公式时,注意各个字母的取值范围,注意换底公式的正用、逆用、变换用,要灵活掌握.(2)在解题过程中,根据问题的需要将指数式转化为对数式,或者将对数式转化为指数式的运算,这正是数学转化思想的具体体现,转化思想是中学重要的数学思想,要注意学习体会,逐步达到灵活运用的目的.探究三:【解析】f(x)=lg a·(x+)2-+4lg a.由题知:⇒lg a=-,∴a=1.【小结】先通过配方求出最大值,再列出关于lg a的方程,最后转化为指数式求出a.思维拓展应用应用一:∵log2(log3x)=1,∴log3x=21=2,x=32=9.应用二:mn 令m a=n b=k,∴a=log m k,b=log n k,∴+=log k m+log k n=log k(mn).∵+=1,∴log k(mn)=1,∴k=mn.应用三:由题意知lg x1、lg x2是关于lg x的一元二次方程lg2x+(lg 2+lg 3)·lg x+lg 2·lg 3=0的两根,由韦达定理得:lg x1+lg x2=-(lg 2+lg 3)=-lg 6=lg.即lg x1x2=lg,x1x2=.基础智能检测1.C由a b=N⇒log a N=b,知选C.2.A==.3.2∵lg 5=1-lg 2,∴原式=2-lg 2+lg 2(1-lg 2)+lg22=2.4.解:由题意知:α·β=log23,α+β=-log26,∴()α·()β=()α+β=(=(2-2=()-2=()-2=36.全新视角拓展D(log29)·(log34)=×=×=4.思维导图构建log a M+log a N log a M-log a N n·log a M。
人教A版高中数学第一册(必修1)教学设计1：4.3.1 对数的概念教案
4.3.1 对数的概念课程标准：通过具体实例，理解对数的概念，了解常用对数与自然对数．理解对数的简单性质．教学重点：1.对数的概念，指数式与对数式的互化.2.对数的简单性质．教学难点：对数概念的理解，指数式与对数式之间的熟练转化.知识导学知识点一对数的概念(1)对数的概念：如果a x＝N(a>0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝log a N，其中a叫做对数的底数，N叫做真数．(2)两种特殊的对数①常用对数：通常以10为底的对数叫做常用对数，N的常用对数log10N简记为lg N；②自然对数：以e为底的对数称为自然对数，N的自然对数log e N简记为ln N(其中e＝2.71828…)．知识点二对数与指数的关系(1)对数的基本性质①零和负数没有对数，即真数N>0；②1的对数为0，即log a1＝0(a>0，且a≠1)；③底数的对数等于1，即log a a＝1(a>0，且a≠1)．(2)两个重要的对数恒等式①a log a N＝N(a>0，且a≠1，N>0)；②log a a N＝N(a>0，且a≠1)．新知拓展在对数的概念中为什么规定a>0且a≠1(1)若a<0，则当N为某些值时，x的值不存在，如：x＝log(－2)8不存在．(2)若a＝0，①当N≠0时，x的值不存在．如：log03(可理解为0的多少次幂是3)不存在；②当N＝0时，x可以是任意正实数，是不唯一的，即log00有无数个值．(3)若a＝1，①当N≠1时，x的值不存在．如：log13不存在；②当N＝1时，x可以为任意实数，是不唯一的，即log11有无数个值．因此规定a>0，且a≠1.评价自测1．判一判(正确的打“√”，错误的打“×”) (1)因为(－2)4＝16，所以log (－2)16＝4.( ) (2)对数式log 32与log 23的意义一样．( )(3)对于同一个正数，当底不同时，它的对数也不相同．( ) (4)等式log a 1＝0对于任意实数a 恒成立．( ) 【答案】 (1)× (2)× (3)× (4)× 2．做一做(请把正确的答案写在横线上) (1)若5x ＝2019，则x ＝________. (2)lg 10＝________；ln e ＝________. (3)将log 3a ＝2化为指数式为________． 【答案】 (1)log 52019 (2)1 1 (3)32＝a核心素养提成题型一对数的概念例1 (1)使对数log 2(－2x ＋1)有意义的x 的取值范围为( ) A.⎝⎛⎭⎫0，12 B.⎝⎛⎭⎫12，＋∞ C.⎝⎛⎭⎫－∞，12 D.⎝⎛⎭⎫－∞，－12 (2)在对数式b ＝log a －2(5－a )中，实数a 的取值范围是( ) A ．a >5或a <2 B ．2<a <5 C ．2<a <3或3<a <5D ．3<a <4【解析】 (1)要使对数log 2(－2x ＋1)有意义，只要使真数－2x ＋1>0即可，即x <12，所以x的取值范围为⎝⎛⎭⎫－∞，12，故选C. (2)由题意，得⎩⎪⎨⎪⎧a －2>0，a －2≠1，5－a >0，解得2<a <3或3<a <5.【答案】 (1)C (2)C 金版点睛对数有意义的条件对数有意义的两个条件：①底数大于零且不等于1；②对数的真数必须大于零． 跟踪训练1 (1)函数f (x )＝lg (x ＋1)x －1中x 的取值范围是( )A ．(－1，＋∞)B ．[－1，＋∞)C ．(－1,1)∪(1，＋∞)D ．[－1,1)∪(1，＋∞)(2)若log (2x －1)(x ＋2)有意义，求x 的取值范围． (1)【答案】C【解析】(1)要使函数有意义，必有⎩⎪⎨⎪⎧x ＋1>0，x －1≠0，解得x >－1且x ≠1，故选C.(2)解：若对数有意义，则真数大于0，底数大于0且不等于1， 所以⎩⎪⎨⎪⎧x ＋2>0，2x －1>0，2x －1≠1，解得x >12，且x ≠1.即x 的取值范围是⎩⎨⎧⎭⎬⎫x ⎪⎪x >12，且x ≠1. 题型二指数式与对数式的互化例2 (1)将下列指数式改写成对数式：24＝16；2－5＝132；34＝81；⎝⎛⎭⎫12m ＝n ； (2)将下列对数式改写成指数式：log 5125＝3；log 1216＝－4；ln a ＝b ；lg 1000＝3.解：(1)log 216＝4；log 2132＝－5；log 381＝4；log 12n ＝m .(2)53＝125；⎝⎛⎭⎫12－4＝16；e b ＝a ；103＝1000. 金版点睛由指数式a b ＝N 可以写成log a N ＝b (a >0，且a ≠1)，这是指数式与对数式互化的依据．对数式与指数式是同一种数量关系的两种不同表达形式．具体对应如下：跟踪训练2 (1)若a ＝log 23，则2a ＋2－a ＝________； (2)将下列指数式化为对数式，对数式化为指数式： ①log 216＝4；②log 3x ＝6；③43＝64. (1)【答案】103【解析】因为a ＝log 23，所以2a ＝3，则2a ＋2－a ＝3＋3－1＝103.(2)解：①24＝16；②(3)6＝x ；③log 464＝3. 题型三对数性质的应用 例3 (1)给出下列各式： ①lg (lg 10)＝0； ②lg (ln e)＝0；③若10＝lg x ，则x ＝10； ④由log 25x ＝12，得x ＝±5.其中，正确的是________(把正确的序号都填上)； (2)求下列各式中x 的值： ①log 2(log 5x )＝0；②log 3(lg x )＝1； ③log (2－1) (2－1)＝x ；④3x ＋3＝2.(1)【答案】①②【解析】∵lg 10＝1，∴lg (lg 10)＝lg 1＝0，①正确；∵ln e ＝1，∴lg (ln e)＝lg 1＝0，②正确；若10＝lg x ，则x ＝1010，③错误；由log 25x ＝12，得x ＝25 12 ＝5，④错误．故填①②.(2)解：①∵log 2(log 5x )＝0. ∴log 5x ＝20＝1，∴x ＝51＝5.②∵log 3(lg x )＝1，∴lg x ＝31＝3，∴x ＝103＝1000. ③∵log (2－1) (2－1)＝x ，∴(2－1)x ＝2－1， ∴x ＝1.④∵x ＋3＝log 32，∴x ＝log 32－3. 金版点睛对数性质在计算中的应用(1)对数的常用性质：log a a ＝1，log a 1＝0(a >0，且a ≠1)．(2)使用对数的性质时，有时需要将底数或真数进行变形后才能运用；对于多重对数符号的，可以先把内层视为整体，逐层使用对数的性质． 跟踪训练3 (1)若log 2(x 2－7x ＋13)＝0，求x 的值； (2)已知log 2[log 3(log 4x )]＝log 3[log 4(log 2y )]＝0，求x ＋y 的值． 解：(1)因为log 2(x 2－7x ＋13)＝0， 所以x 2－7x ＋13＝1，即x 2－7x ＋12＝0， 解得x ＝4或x ＝3.(2)因为log 2[log 3(log 4x )]＝0， 所以log 3(log 4x )＝1，所以log 4x ＝3.所以x ＝43＝64.同理求得y ＝16.所以x ＋y ＝80. 题型四对数恒等式的应用 例4 求下列各式的值：(1)5log 54；(2)3log 34－2；(3)24＋log 25. 解：(1)设5log 54＝x ，则log 54＝log 5x ，∴x ＝4. (2)∵3log 34＝4，∴3log 34－2＝3log 34×3－2＝4×19＝49.(3)∵2log 25＝5，∴24＋log 25＝24×2log 25＝16×5＝80. 金版点睛运用对数恒等式时的注意事项(1)对于对数恒等式a log a N ＝N (a >0，且a ≠1，N >0)要注意格式：①它们是同底的；②指数中含有对数形式；③其值为对数的真数．(2)对于指数中含有对数值的式子进行化简，应充分考虑对数恒等式的应用． 跟踪训练4 求31＋log 36－24＋log 23＋103lg 3＋⎝⎛⎭⎫19log 34的值． 解：原式＝31×3log 36－24×2log 23＋(10lg 3)3＋3－2×log 34 ＝3×6－16×3＋33＋(3log 34)－2 ＝18－48＋27＋116＝－4716.随堂水平达标1．若a >0，且a ≠1，c >0，则将a b ＝c 化为对数式为( ) A ．log a b ＝c B ．log a c ＝b C ．log b c ＝a D ．log c a ＝b【答案】 B【解析】 由对数的定义直接可得log a c ＝b . 2．已知log x 16＝2，则x 等于( ) A ．±4 B ．4 C ．256 D ．2 【答案】 B【解析】 ∵x 2＝16且x >0，x ≠1，∴x ＝4.故选B. 3．若log 3181＝x ，则x ＝________.【答案】 －4【解析】 ∵log 3181＝log 33－4，∴3x ＝3－4，∴x ＝－4.4．式子2log 25＋log 32 1的值为________．【答案】 5【解析】 由对数性质知，2log 25＝5，log 32 1＝0，故原式＝5.5．求下列各式中x 的值： (1)若log 31＋2x3＝1，求x 的值；(2)若log 2019(x 2－1)＝0，求x 的值． 解 (1)∵log 31＋2x 3＝1，∴1＋2x3＝3，∴1＋2x ＝9，∴x ＝4. (2)∵log 2019(x 2－1)＝0， ∴x 2－1＝1，即x 2＝2.∴x ＝±2.。
数学高一(北师大)必修1教案 3.4对数
3.4对数教案第1课时对数●三维目标1．知识与技能(1)理解对数的概念，了解对数与指数的关系．(2)理解和掌握对数的性质．(3)掌握对数式与指数式的关系．2．过程与方法通过与指数式的比较，引出对数定义与性质．3．情感、态度与价值观(1)学会对数式与指数式的互化，从而培养学生的类比、分析、归纳能力．(2)通过对数的运算法则的学习，培养学生的严谨的思维品质．(3)在学习过程中培养学生探究的意识．●重点难点重点：对数的概念和对数式与指数式的互化．难点：对数基本性质的理解．本节用一课时完成，重点研究对数的概念、性质，难点是对数性质及其推导过程．教材以2000年国民经济生产总值增幅为背景，引入对数概念，在使学生认识引进对数必要性的同时，强化学生的数学应用意识．“思考交流”旨在引导学生进一步理清指数式与对数式之间的关系，明确1和底数对数的特点，深化真数取值范围的理解，为对数函数学习打下伏笔．常用对数及自然对数是对数的特例，由此进一步体现数学与现实生活的紧密联系，进一步加强学生学习数学的决心．●教学建议根据教材及学情特点，本课以探究式教学法为主，辅之以讨论法和自学辅导法．以问题为主线，力求创设有效的教学情境，引导学生在观察中思考，在思考中探索，在探索中发现，在发现中收获，在收获中创新，在创新中升华．通过具有一定层次梯度的问题序列，多角度、全方位训练学生思维的聚敛性和发散性．同时注重信息技术与数学课程的整合，借助多媒体设备进行辅助教学．●教学流程创设情境，导入新课，引导学生按照解决数学问题的常规步骤建构方程⇒引导观察，探索本质，建构对数概念，完成例1及变式训练⇒加深概念理解，让学生学会指数与对数的互化，完成例2及其变式训练⇒适时分化，揭示概念本质，探索对数性质a log a N＝N⇒结合例3及其变式训练，巩固对数的性质⇒归纳整理，进行课堂小结，整体认识本节课所学知识⇒完成当堂双基达标，巩固所学知识并进行反馈矫正(见学生用书第45页)课标解读1.理解对数的概念．(重点)2．掌握指数式与对数式的互化．(重点)3．理解并掌握对数的基本性质．(难点、易混点)对数的定义1．若2x＝16，(13)x ＝9，x 的值分别为多少？【提示】 4，－2.2．若2x＝3，(13)x ＝2，你现在还能求得x 吗？【提示】 不能．3．若2x＝0，(13)x ＝－1，则这样的x 存在吗？【提示】 不存在．1．一般地，如果a b＝N (a >0且a ≠1)，那么数b 叫作以a 为底N 的对数，记作b ＝log a N ，其中a 叫作对数的底数，N 叫作真数．2．几种常见对数对数形式 特点记法 一般对数 以a (a >0且a ≠1)为底的对数 log a N 自然对数 以__e __为底的对数 ln N 常用对数以__10__为底的对数lg N对数的性质及恒等式1．当a >0且a ≠1时，log a (－2)，log a 0存在吗？为什么？由此能得到什么结论？ 【提示】 不存在，因为log a (－2)，log a 0对应的指数式分别为a x＝－2，a x＝0，而a x>0，所以a x＝－2，a x＝0中的x 值不存在，由此能得到的结论是：0和负数没有对数．2．若a b＝N ，则b ＝log a N ，二者组合可得什么等式？ 【提示】 对数恒等式：a log a N ＝N .对数恒等式 a log a N ＝__N __对数的性质底的对数等于__1__，即log a a ＝__1__ 1的对数等于__0__，即log a 1＝__0__ 零和负数没有对数(见学生用书第46页)对数的概念(1－a )【思路探究】 根据对数的概念列出实数a 满足的不等式组，再解不等式组即可 .【自主解答】 由于对数log (1－a )(a ＋2)有意义，则有⎩⎪⎨⎪⎧a ＋2>0，1－a >0，1－a ≠1，解得－2<a <0或0<a <1.所以实数a 的取值范围是(－2,0)∪(0,1)．1．正确理解对数的概念：(1)底数大于0且不等于1，真数大于0.(2)明确指数式和对数式的区别和联系，以及二者之间的相互转化．2．求对数式中有关参数的范围时，根据对数中对底数和真数的要求列出不等式组解出即可．若对数log 3a (－2a ＋1)有意义，则a 的取值范围是________． 【解析】 根据题意可得⎩⎪⎨⎪⎧－2a ＋1>0，3a >0，3a ≠1，解得0<a <12，a ≠13.所以a 的取值范围是(0，13)∪(13，12)． 【答案】 (0，13)∪(13，12)指数式与对数式的互化求下列各式中x 的值： (1)log 16x ＝－2； (2)log x 27＝34；(3)log 4(log 3x )＝0.【思路探究】 利用对数的定义，把各个对数式化为指数式，即可解得x 的值． 【自主解答】 (1)由log 16x ＝－2，得x ＝16－2＝(116)2＝1256，故x ＝1256.(2)由log x 27＝34，得 x 34＝27，即x 34＝33，∴x 14＝3，∴x ＝34＝81.(3)由log 4(log 3x )＝0，得log 3x ＝1，故x ＝3.1．首先掌握指数式与对数式的关系，即a b＝N ⇔b ＝log a N .2．对数的定义是对数式和指数式互化的依据，在互化过程中应注意各自的位置及表示方式．另外，解形如log a [log b (log c x )]＝m 的方程时，一般是按由外往里去掉对数符号的顺序解决．将下列指数式化为对数式，对数式化为指数式： (1)2－7＝1128；(2)33＝27；(3)10－1＝0.1；(4)log 1232＝－5；(5)lg 0.001＝－3.【解】 (1)log 21128＝－7；(2)log 327＝3；(3)lg0.1＝－1；(4)(12)－5＝32；(5)10－3＝0.001.求值(1)log 327；(2)81－log 85；(3)22＋log 25＋log a 1.【思路探究】 对于(1)可设log 327＝x ，利用对数式与指数式的互化，求x ；(2)(3)可利用对数的基本性质及对数恒等式求其值．【自主解答】 (1)设log 327＝x ，则3x＝27＝33， 所以x ＝3，即log 327＝3.(2)法一 81－log 85＝8log 88－log 85＝8log 88÷8log 85＝8÷5＝85.法二 81－log 85＝88log 85＝85.(3)∵22＋log25＝22×2log25＝4×5＝20.∴原式＝20＋0＝20.1．求单个对数的值，可先把对数式化为指数式，再利用指数的有关运算转化为同底数的幂的形式求值．2．利用对数恒等式化简求值时，必须使幂底数和对数的底数保持一致．求下列各对数式的值：(1)log416；(2)log5(lg 10)；(3)log22log21.【解】(1)设log416＝x，则4x＝16＝42，∴x＝2，即log416＝2.(2)log5(lg 10)＝log51＝0.(3)log22log21＝log21＝0.第2课时对数的运算性质●三维目标1．知识与技能(1)通过实例推导对数的运算性质，准确地运用对数运算性质进行运算、求值、化简，并掌握化简求值的技能．(2)运用对数运算性质解决有关问题．2．过程与方法(1)让学生经历并推理出对数的运算性质．(2)让学生归纳整理本节所学的知识．3．情感、态度与价值观让学生感受对数运算性质的重要性，增加学生的成功感，增强学习的积极性．●重点难点重点：对数运算的性质与对数知识的应用．难点：能灵活的使用对数的运算性质进行化简和求值．对数运算是指数运算的逆运算，由平方根的乘方法则过渡到对数的运算法则，通过类比推导深入理解对数运算性质的公式结构．●教学建议遵循教师的主导作用和学生的主体地位相统一的教学规律，采用引导发现式的教学方法，通过在教学过程中铺垫、提问，启发学生通过类比主动思考、合作探究来达到对对数运算性质及应用技巧的发现和接受．●教学流程复习对数的概念，对数式和指数式的互化及对数恒等式，引入新课⇒联系已知，形成台阶，借助指数的运算性质得出对数的运算性质⇒根据对数的运算性质，完成例1及其变式训练⇒在运算过程中，列举反例，强化对运算性质的记忆⇒灵活运用性质和法则，解决带有附加条件的对数式求值问题，完成例2及其变式训练⇒归纳整理，进行课堂小结，整体认识本节课所学知识⇒完成当堂双基达标，巩固所学知识并进行反馈矫正(见学生用书第47页)课标解读1.掌握对数的运算性质．(重点)2．能灵活使用对数的运算性质进行化简求值．(难点)对数的运算性质1．我们知道am ＋n＝a m ·a n，那么log a M ·N ＝log a M ·log a N 正确吗？举例说明．【提示】 不正确，例如log 24＝log 22×2＝log 22·log 22＝1×1＝1，而log 24＝2. 2．你能推出log a (MN )(M >0，N >0)表达式吗？ 【提示】 能． 令a m＝M ，a n＝N ， ∴MN ＝am ＋n由对数的定义知log a M ＝m ，log a N ＝n ，log a (MN )＝m ＋n ， ∴log a (MN )＝log a M ＋log a N .如果a ＞0且a ≠1，M ＞0，N ＞0，则 1．log a (MN )＝log a M ＋log a N . 2．log a M n＝n log a M (n ∈R)． 3．log a M N＝log a M －log a N .(见学生用书第48页)对数运算性质的应用计算下列各式的值：(1)log 2748＋log 212－12log 242＋(12)log 23； (2)lg 52＋23lg 8＋lg 5·lg 20＋(lg 2)2.【思路探究】 解答本题的关键是活用对数的运算性质．【自主解答】 (1)原式＝log 27×1248×42＋2－log 23＝log 212＋13＝－12＋13＝－16.(2)原式＝2lg 5＋2lg 2＋lg 5(1＋lg 2)＋(lg 2)2＝2(lg 5＋lg 2)＋lg 5＋lg 2(lg 5＋lg 2) ＝2＋lg 5＋lg 2＝2＋1＝3.对数式的化简求值常用的方法与技巧： 1．对于同底对数的化简方法错误!)2．对于常用对数的化简要充分利用“lg 2＋lg 5＝1”、“lg 2＝1－lg 5”、“lg 5＝1－lg 2”来解题．计算：(1)log 327＋lg 25＋lg 4＋7log 72＋(－9.8)0； (2)(lg 5)2＋(lg 2)(lg 50)．【解】 (1)原式＝log 3332＋lg 52＋lg 22＋2＋1＝32＋2(lg 5＋lg 2)＋3 ＝32＋2lg 10＋3＝32＋2＋3＝132. (2)原式＝(lg 5)2＋(lg 2)(lg 52＋lg 2) ＝(lg 5)2＋2lg 2lg 5＋(lg 2)2＝(lg 5＋lg 2)2＝(lg 10)2＝1.带有附加条件的对数式求值565656(2)已知lg 2＝0.301 0，lg 3＝0.477 1，求lg 45的值． 【思路探究】 利用条件――→观察式子的结构特征分解待求对 数的真数――→利用运算性质结果【自主解答】 (1)∵log 567＝a ，∴log 568＝log 56567＝log 5656－log 567＝1－a .log 5698＝log 56(49×2)＝log 56(72×2)＝log 5672＋log 562 ＝2log 567＋log 56813＝2log 567＋13log 568＝2a ＋13(1－a )＝1＋5a3.(2)法一 lg 45＝12lg 45＝12lg 902＝12(lg 9＋lg 10－lg 2)＝12(2lg 3＋1－lg 2)＝lg 3＋12－12lg 2 ＝0.477 1＋0.5－0.150 5＝0.826 6. 法二 lg 45＝12lg 45＝12lg(5×9)＝12(lg 5＋2lg 3)＝12(1－lg 2＋2lg 3) ＝12－12lg 2＋lg 3＝0.826 6.将待求式子用已知式子中的对数表示，关键是建立对数式底数与真数的联系，在运算过程中应注意运算性质和法则的灵活运用．(1)设a ＝lg(1＋17)，b ＝lg(1＋149)，用a ，b 表示lg 2，lg 7.(2)已知lg 2＝0.301 0，lg 3＝0.477 1，lg x ＝－2＋0.778 1，求x . 【解】 (1)∵a ＝lg(1＋17)＝lg 237＝3lg 2－lg 7，b ＝lg(1＋149)＝lg 5049＝lg 1022×72＝2－lg 2－2lg 7，∴lg 2＝17(2a －b ＋2)，lg 7＝17(－a －3b ＋6)．(2)∵lg 2＝0.301 0，lg 3＝0.477 1， ∴lg x ＝－2＋0.778 1＝－2＋0.301 0＋0.477 1 ＝－2＋lg 2＋lg 3＝－2＋lg 6＝lg(6×10－2)， ∴x ＝6×10－2.4.2 换底公式●三维目标1．知识与技能(1)通过实例推导换底公式．(2)会用换底公式进行化简与求值．2．过程与方法通过设置问题串的方式，让学生通过在问题的引导下自主学习、合作学习经历推导对数的换底公式的过程，培养学生分析、综合解决问题的能力．在换底公式的应用的过程中，引导学生自己思考发现规律，提高学生的探索发现并总结问题的能力．3．情感、态度与价值观让学生探索研究对数的换底公式，培养学生的探究意识，培养学生的严谨的思维品质，感受对数的广泛应用，增强学习的积极性．培养学生数学应用意识和科学分析问题的精神和态度．●重点难点重点：对数的运算性质及换底公式及其应用．难点：正确使用对数的运算性质和换底公式．教材注重从实际问题中开始探讨，有利于培养学生的思维素质，激发学生学习数学的兴趣与欲望．教材中从特殊到一般，推导、证明、应用对数的换底公式，培养学生分析、综合解决问题的能力．教学中要充分发挥课本这些材料的作用．●教学建议本课主要学习对数换底公式，它在以后的学习中有着非常重要的应用，由于对数的运算法则是在同底的基础上，因此利用对数换底公式把不同底数的对数转化为同底显得非常重要，有时也可以逆用对数的换底公式达到我们的目的，特别是实际问题的应用更为广泛，因此要反复训练，授课时要激发学生的学习兴趣，多应用多媒体的教学手段．●教学流程复习对数的定义及运算性质并引入新课题⇒根据教材中的问题，探究出解决的方法，得到换底公式⇒完成换底公式的证明，加深对换底公式的理解⇒利用换底公式化简求值，完成例1及其变式训练⇒运用换底公式，用已知对数表示其他对数，完成例2及其互动探究⇒利用换底公式解决实际问题，完成例3及其变式训练⇒归纳整理，进行课堂小结，整体认识本节课所学知识⇒完成当堂双基达标，巩固所学知识并进行反馈矫正(见学生用书第49页)课标解读1.能推导出对数的换底公式．(重点)2．会用对数换底公式进行化简与求值．(难点易混点)对数换底公式已知对数log 864，log 264，log 28，log 464，log 48. 1．你能计算出它们各自的值吗？【提示】 log 864＝2，log 264＝6，log 28＝3，log 464＝3，log 48＝32.2．对数log 864的值与对数log 264和log 28的值有什么关系？ 【提示】 log 864＝log 264log 28.3．对数log 864的值与对数log 464和log 48的值有什么关系？ 【提示】 log 864＝log 464log 48.换底公式：log b N ＝log a Nlog a b(a ，b ＞0，a ，b ≠1，N ＞0)．(见学生用书第49页)利用换底公式化简求值(1)化简：log 225·log 3116·log 519.(2)计算：(log 43＋log 83)lg 2lg 3.【思路探究】 由于所给式子的底数不同，可考虑用换底公式统一底数，然后化简求值． 【自主解答】 (1)原式＝log 252·log 32－4·log 53－2＝2lg 5lg 2·－4lg 2lg 3·－2lg 3lg 5＝16.(2)原式＝(lg 3lg 4＋lg 3lg 8)·lg 2lg 3＝(12lg 2＋13lg 2)·lg 2＝56.利用换底公式计算、化简、求值问题的思路：一是先利用对数的运算法则及性质进行部分运算，最后再换成统一底．二是一次性地统一换为常用对数(或自然对数)，再化简、通分、求值．计算：(1)log 1627·log 8132； (2)(log 32＋log 92)(log 43＋log 83)．【解】 (1)原式＝lg 27lg 16·lg 32lg 81＝3lg 34lg 2·5lg 24lg 3＝1516.(2)原式＝(lg 2lg 3＋lg 22lg 3)(lg 32lg 2＋lg 33lg 2)＝3lg 22lg 3·5lg 36lg 2＝54.用已知对数表示其他对数1836【思路探究】 运用换底公式，统一化为以18为底的对数． 【自主解答】 法一 因为log 189＝a ，所以9＝18a， 又5＝18b，所以log 3645＝log 2×18(5×9) ＝log 2×1818a ＋b ＝(a ＋b )·log 2×1818.又因为log 2×1818＝1log 1818×2＝11＋log 182＝11＋log 18189＝11＋1－log 189＝12－a，所以原式＝a ＋b2－a.法二 ∵18b＝5，∴log 185＝b .∴log3645＝log1845log1836＝log185×9log184×9＝log185＋log1892log182＋log189＝a＋b2log18189＋log189＝a＋b2－2log189＋log189＝a＋b2－a.用已知对数的值表示所求对数的值，要注意以下几点：1．增强目标意识，合理地把所求向已知条件靠拢，巧妙代换；2．巧用换底公式，灵活“换底”是解决这种类型问题的关键；3．注意一些派生公式的使用．若本例条件不变，求log92545(用a，b表示)．【解】由18b＝5，得log185＝b，∴log92545＝log1845log18925＝log185＋log189log189－log1825＝b＋aa－2b.对数的实际应用设光线原来的强度为a，通过x块玻璃板以后的强度值为y.(1)试写出y关于x的函数关系式；(2)至少通过多少块玻璃板以后，光线强度减弱到原来光线强度的12以下？(lg 2＝0.3010，lg 3＝0.4771)【思路点拨】 (1)根据x ＝1,2,3时的光线强度值归纳出y 与x 的关系式． (2)可通过解不等式求解．【自主解答】 (1)当x ＝1时，y ＝0.9a ， 当x ＝2时，y ＝0.92a ， 当x ＝3时，y ＝0.93a ，则经过x 块玻璃板后，光线强度值为y ＝0.9xa (x ∈N)． (2)由题意得0.9x a ＜12a ，则0.9x＜12，∴x ＞log 0.912＝lg 12lg 0.9＝－lg 22lg 3－1＝－0.30102×0.477 1－1≈6.57.即至少通过7块玻璃板后，光线强度减弱到原来强度的12以下．1．本题通过归纳得到y 与x 的关系式，这是一种常用的方法． 2．解对数应用题的一般步骤：某种汽车安全行驶的稳定性系数μ随使用年数t 的变化规律是μ＝μ0e－λt，其中μ0，λ是正常数．经检测，当t＝2时，μ＝0.90 μ0，则当稳定性系数降为0.50μ0时，该种汽车已使用的年数为__________(结果精确到1，参考数据：lg 2＝0.301 0，lg 3＝0.477 1)．【解】由0.90μ0＝μ0(e－λ)2，得e－λ＝0.90，又0.50μ0＝μ0(e－λ)t，则12＝(0.90)t，两边取常用对数，得lg12＝t2lg 0.90，故t＝2lg 21－2lg 3＝2×0.301 01－2×0.477 1≈13. 【答案】13。
《对数的概念》教学设计、导学案、同步练习
第四章指数函数与对数函数《4.3.1对数的概念》教学设计【教材分析】本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.3.1节《对数的概念》。
从内容上看它是学生了指数幂运算的基础上，通过实际问题的提出，从而建立对数的概念。
其研究和学习过程，与先前学习加法与减法、乘法与除法类似。
由指数运算进而提出对数运算，本节为后续的对数函数奠定基础。
培养学生数学运算、数学抽象、逻辑推理和数学建模的核心素养。
【教学目标与核心素养】【教学重难点】教学重点：对数的概念、指数式与对数的互化教学难点：由于对数符号是直接引入的，带有“规定”的性质，且这种符号比较抽象，不易为学生接受，因此，对对数符号的认识会形成教学中的难点。
【教学过程】上述问题实际上就是从2=1.11x，3=1.11x，4=1.11x，…中分别求出x，即已知底数和幂的值，求指数．这是本节要学习的对数．对数的发明：对数的创始人是苏格兰数学家纳皮尔（Napier，1550年~1617年）。
他发明了供天文计算作参考的对数，并于1614年在爱丁堡出版了《奇妙的对数定律说明书》，公布了他的发明。
恩格斯把对数的发明与解析几何的创始，微积分的建立并称为17世纪数学的三大成就。
（二）、探索新知1．对数(1)指数式与对数式的互化及有关概念：(2)底数a的范围是________________.2．常用对数与自然对数3．对数的基本性质(1)负数和零没有对数．(2)log a1＝0(a>0，且a＝1(a>0，且a≠1)．a≠1)．(3)loga思考：为什么零和负数没有对数？[提示] 由对数的定义：a x＝N(a>0且a≠1)，则总有N>0，所以转化为对数式x＝log a N时，不存在N≤0的情况．1．思考辨析(1)log a N是log a与N的乘积．( )(2)(－2)3＝－8可化为log(－2)(－8)＝3.( ) (3)对数运算的实质是求幂指数．( )[答案] (1)×(2)×(3)√2．若a2＝M(a>0且a≠1)，则有( )A．log2M＝a B．logaM＝2C．log22＝M D．log2a＝MB[∵a2＝M，∴log a M＝2，故选B.]（三）典例解析例1 将下列指数形式化为对数形式,对数形式化为指数形式：(1)54＝625;(2)2－7＝1128；(3)(12)m＝5.73(4)log1232＝－5；(5)lg1000＝3；(6)ln10＝2.303[解] (1)由54＝625，可得log5625＝4.(2)由2－7＝1128，可得log21128＝－7.(3)由(12)m＝5.73，可得log125.73＝m，(4)由log1232＝－5，可得⎝⎛⎭⎪⎫12－5＝32.(5)由lg1000＝3，可得103＝1000.(6)由ln10＝2.303，可得e2.303＝10.[规律方法] 指数式与对数式互化的方法将指数式化为对数式，只需要将幂作为真数，指数当成对数值，底数不变，写出对数式；将对数式化为指数式，只需将真数作为幂，对数作为指数，底数不变，写出指数式；1．将下列指数式化为对数式，对数式化为指数式：(1)3－2＝19；(2)⎝⎛⎭⎪⎫14－2＝16；(3)log1327＝－3;(4)log x64(1)B(2)10 [(1)由5log(2x－1)＝25得2x－1＝25，所5以x＝13，故选B.(2)由log(lg x)＝0得lg x＝1，∴x＝10.]3归纳总结:1.利用对数性质求解的2类问题的解法（1）求多重对数式的值解题方法是由内到外，如求log a log b c的值，先求log b c的值，再求log a log b c的值.（2）已知多重对数式的值，求变量值，应从外到内求，逐步脱去“log”后再求解.2.性质a log a N＝N与log a a b＝b的作用（1）a log a N＝N的作用在于能把任意一个正实数转化为以a,为底的指数形式.（2）log a a b＝b的作用在于能把以a为底的指数转化为一个实数《4.3.1 对数的概念》导学案【学习目标】1.理解对数的概念，掌握对数的性质，能进行简单的对数计算．2.理解指数式与对数式的等价关系，会进行对数式与指数式的互化．3.理解常用对数、自然对数的概念及记法．【重点难点】教学重点：理解对数的概念,掌握指数式与对数式的等价关系，会进行对数式与指数式的互化教学难点：掌握对数的性质，能进行简单的对数计算．【知识梳理】1．对数(1)指数式与对数式的互化及有关概念：(2)底数a的范围是________________.【学习过程】问题提出：在4.2.1的问题1中，通过指数幂运算，我们能从y＝1.11x中求出经过4年后Ｂ地景区的游客人次为2001年的倍数y．反之，如果要求经过多少年游客人次是2001年的2倍，3倍，4倍，…，那么该如何解决？上述问题实际上就是从2=1.11x，3=1.11x，4=1.11x，…中分别求出x，即已知底数和幂的值，求指数．这是本节要学习的对数．对数的发明：对数的创始人是苏格兰数学家纳皮尔（Napier，1550年~1617年）。
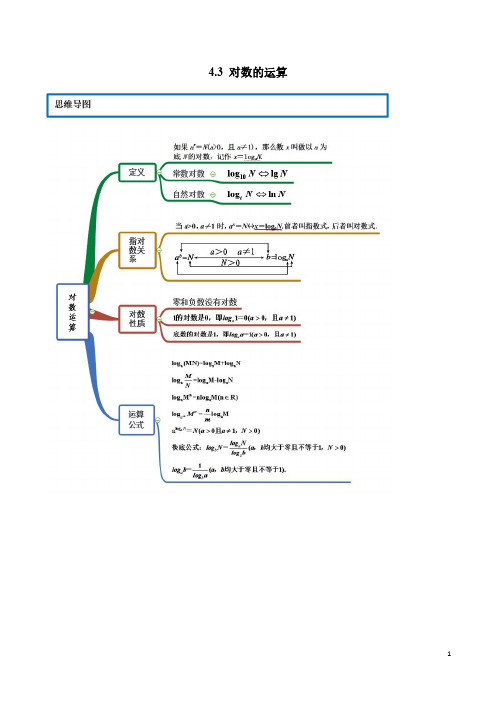
2020高一数学新教材必修1教案学案 4.3 对数解析版
2
3
lg3＋2lg9＋3lg 27－lg 3
③55
. ④lg5·lg8000＋(lg2 3)2＋lg0.06－lg6；
lg81－lg27
⑤lg 2＋lg3－lg 10. lg1.8
⑥ log 2 3 ( 3 2 ) 2log16 9 ；
⑦ (lg 5)2 lg 2 lg 5 lg 2 .
⑧log2 8＋4 3＋log2 8－4 3；
48
.
（2）若 26a＝33b＝62c，求证：1＋2＝3. abc
【答案】（1）
log 49
48
2b 2
a
.（2）见解析
【解析】（1）
1 7
a
1 , a 3
lg 3 lg 7
.
∵
log7
4
b,
∴b
lg lg
4 7
.则
log 49
48
ቤተ መጻሕፍቲ ባይዱ
lg lg
48 49
lg lg
4 7
lg 3 2 lg 7
b
a 2
4.3 对数的运算
1
运用一 指数对数的转化
【例 1】(1)根据对数定义，将下列指数式写成对数式：
①3x＝ 1 ； 27
1 ② 4 x＝64
1 ③ 2 x＝ 1 ；
16
④5
1 2
＝
1
.
5
(2)根据对数定义，把下列对数式写成指数式：
①loga1＝0(a>0，a≠1)；②log161＝－1；③ln 10＝x. 24
＝6lo5g32×52log32＝2152.
【触类旁通】
1.化简(log43＋log83)llgg23；
高一数学必修一对数与对数运算导学案
高一数学对数与对数运算导学案 课题：《 对数与对数的运算(1)》编写：审核：时间：一、教学目标1、理解对数的概念；2、能够说明对数与指数的关系；3、掌握对数式与指数式的相互转化.教学重点：对数的概念，对数式与指数式的相互转化 教学难点：对数概念的理解． 二、问题导学（一）指数函数检测1. 625的4次方根是，(122--⎡⎤⎢⎥⎣⎦= ． 2. .已知1122a a-+=3，则1a a -+= ；（2）22a a -+= ；（3）33221122a a a a----= ．3. 化简3225()4-=；= ；2115113366221()(3)()3a b a b a b -÷= ．4.函数xy 523-=的定义域为 ；值域为 ．5.已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性；（2）求f (x )的值域；（3）判断f (x )单调性并证明. （二）新知识1、对数的概念三、问题探究问题1：假设2002年我国国民生产总值为a 亿元，如果每年平均增长8%，那么经过多少年国民生产总值是2002年的2倍？()?2%81=⇒=+⋅x a a x也就是已知底数和幂的值，求指数．你能看得出来吗？怎样求呢？ 新知：1. 对数的概念.一般地，如果N a x =)1,0(≠>a a ，那么数 x 叫做以a 为底 N 的对数. 记作 ，其中a 叫做对数的底数，N 叫做真数. 2. 对数与指数的关系.一般地，如果(a ＞0, a ≠1)的b 次幂等于N ，就是N a b =，那么数b 叫做以a为底N 的对数，记作b N a =log ，3. 常用对数.我们通常将以10为底的对数叫做常用对数，并把常用对数10log N 简记为lg N例如：5log 10简记作lg5； 5.3log 10简记作 .4. 自然对数.在科学技术中常使用以无理数……为底的对数，以e 为底的对数叫自然对数，并把自然对数N e log 简记作N ln⇔=N a b例如：3log e 简记作3ln ； 10log e 简记作 ．反思：1.是不是所有的实数都有对数？b N a =log 中的N 可以取哪些值？负数与零是否有对数？为什么？ 2.=1log a ， =a a log .3.底数的取值范围是 ,真数的取值范围 ．4.=na a log ，=na alog ．【典型例题】例1．将下列指数式写成对数式，对数式写成指数式．（1）62554=； （2）73.531=m）（ ； （3）416log 21-= ； （4）303.210ln =．例2．求下列各式中的x 的值．（1）32log 64-=x ； （2）68log =x ； （3）x =100lg ； （4）x e =-2ln ．例3．计算．（1）27log 9； （2）81log 3； （3）125log 5； （4）()()32log 32-+．例4（全程设计例1） 四、课堂训练（全程设计42页1-6题） 五、自主小结六、课后反思课题：《 对数与对数的运算(2)》编写：审核：时间：一、教学目标1、掌握对数的运算性质；2、理解推导这些法则的依据和过程；3、能运用对数运算法则解决问题. 教学重点：运用对数运算法则解决问题。
2024春新教材高中数学4.3.1对数的概念教学设计新人教A版必修第一册
课后作业
1.请用自然语言描述对数的定义，并尝试用生活中的例子来说明对数的概念。
答案：对数的定义是：如果一个非零实数a的指数是b，那么数b叫做a的以10为底的对数，记作b=log10a。例如，如果5的指数是2，那么2叫做5的以10为底的对数，记作2=log105。
-提问与讨论：针对不懂的问题或新的想法，勇敢提问并参与讨论。
教学方法/手段/资源：
-讲授法：通过详细讲解，帮助学生理解对数的知识点。
-实践活动法：设计实践活动，让学生在实践中掌握对数技能。
-合作学习法：通过小组讨论等活动，培养学生的团队合作意识和沟通能力。
作用与目的：
-帮助学生深入理解对数的知识点，掌握对数技能。
最后，我意识到在教学过程中，我可能过于注重知识的传授，而忽视了学生的思维和创造力的发展。因此，在未来的教学中，我应该更加注重培养学生的思维能力和创造力，通过设计更多的启发性和探究性的问题，引导学生自主思考和创新。
答案：log10(2×10^4)=log10(2) + log10(10^4)=2 + 4=6。
4.请计算下面的问题：如果一个数增长20%，那么原来的数是多少？
答案：原来的数是1/1.2=0.8333...。
5.请将下面的单位转换为千克：如果一个物体重200磅，那么它的重量是多少千克？
答案：1磅=0.453592千克，所以200磅=200×0.453592=90.7184千克。
2.能力培养：学生在学习过程中，通过解决问题和实际应用，培养了数学抽象、逻辑推理、数学建模和数学运算等能力。例如，学生能够将实际问题转化为对数模型，运用对数运算公式进行计算，并能够对结果进行合理的解释和分析。
高中数学北师大版必修1-4对数教案
对数教学目标：1、理解对数的定义及常用对数。
2、掌握对数的运算性质。
3、掌握换底公式及对数式变形，理解自然对数。
重点：对数的定义及对数的运算性质。
难点：换底公式及对数式变形 教学过程：一、对数及性质1、对数与指数的关系N x N a a x log =⇒=2、对数的性质① 和 没有对数，②1的对数是 ，即)1,1(1log ≠>=a a a 且③底数的对数是 ，即应用：1、指数式与对数式的转换()()()()()3001.0lg 5532log 41.010*********212117-=-====--a()()()1641864476log 6233=⎪⎭⎫⎝⎛==-x2、指数的性质()()()()()[]0lg log ln 31lg log 20)(log log 12335===x x x3、若的值求y x m y m x 24121,2log ,log +==4、的值求设n m a a a n m +==2,3log ,2log二、对数的运算 1、对数的运算性质()()()()===∙n a a a M NMN M log 3log 2log 12、换底公式及推论若c>0且c ≠1，则abb c c a log log log =（a>0，且a ≠1，b>0） 推论：()()()()=∙∙=∙==d c b a b a a c b a b a n a n a mnlog log log 4log log 3log 2log 1应用：1、对数运算性质()()()348log 348log 358log 932log 2log 2251lg 5lg 32lg 41223log 3335-++-+--+2、换底公式的应用：()()()()45log ,518,9log 28log 4log 2log 5log 25log 125log :13618125255842求已知计算==++∙++ba3、对数方程的求解()()()()()()()010lg lg 32log 12log 2)3(log 12log 13225522=-+-=+=+x x x x x x 、、4、已知()的值。
高中数学 《对数的概念》导学案 苏教版必修1
高一Ⅱ部数学班级 学号 姓名【学习任务】1. 了解对数的概念，理解指数式与对数式的相互关系，能熟练进行指数式与对数式的互化。
2. 了解常用对数与自然对数以及这两种对数符号的记法。
3. 了解对数恒等式，并能运用恒等式进行计算。
【课前预习】对数概念：1.一般地，如果a (0,1a a >≠)的b 次幂等于N ，即b a N =，那么数b 叫做 ，记作log a N b =．其中，a 叫做对数的 ，N 叫做 ．例如：2339 log 92=⇒=，读作：以3为底9的对数为2 ．〔1〕概念分析：对数式log a b N =中各字母的取值范围：a ： 0,1a a >≠ ；b ： b R ∈ ； N ：0N > ．〔2〕零和负数没有对数；1的对数为0，即log 10a =〔0a >且1≠a 〕；底数的对数为1，即log 1a a =〔0a >且1≠a 〕．2.以10为底的对数称为 ，以e 为底的对数称为3.log b a a = log a N a =【合作探究】学点1.指数式和对数式互化1.将以下指数式写成对数式： 4211 5625 10 81 () 5.731003a m e -===①②③④＝2.将以下对数式写成指数式： 2121 log 16 4 log 7 lg 0.01 2 ln10 2.303128=-=-=-①②③④＝学点2.求对数值3.求以下对数的值〔1〕72log 4 〔2〕〔3〕)381(log 3学点3.求未知数的值4. 求以下各式中x 的值〔1〕log 42x =． 〔2〕3133log [log (log )]0x =【自我检测】1.完成以下指数式与对数式的互化：〔1〕26416=-⇔ ， 〔2〕73.5)31(=m ⇔ ， 〔3〕0.5log 164=-⇔ ， 〔4〕7128log 2=⇔ ， 〔5〕201.0lg -=⇔ ， 〔6〕303.210ln =⇔ ．2．求以下对数的值〔1〕1162log = ，〔2〕01.0lg = ，〔3〕ln e = ， 〔4〕 2.5log 6.25= ，〔5〕21)log (322)-+=3.假设1log a a -有意义，那么a 的取值范围为4.求以下各式中x 的值：〔1〕2log 4x =， 〔2〕2log 4x =， 〔3〕532log [log (log )]0x =5.计算〔1〕3(2log 2)3+= 〔2〕52log 35=〔3〕235log [log (log 125)]=6.0a >且1a ≠，log 2a m =，log 3a n =，求2m n a+的值。
高中数学 34对数(一)导学案 北师大版必修1 学案
陕西省咸阳市泾阳县云阳中学高中数学 3.4对数（一）导学案 北师大版必修 1【学习目标】1. 知道对数的概念。
2. 能够说明对数式与指数式的关系，会对数式与指数式的相互转化。
3 热情投入学习，体会成功的快乐。
【学习重点】知道对数概念,明确对数运算是指数运算的逆运算. 能够进行对数式与指数式的互化。
【学法指导】1．请同学们认真阅读课本78-79页，规范完成导学案内容，用红笔做好疑难标记。
2．本学案分为Ａ、Ｂ、Ｃ、三个层次，其中ＡＢ必须都完成；Ｃ层供有余力的同学选作。
3. 抓住对数式与指数的关系这一关键。
4. 在课堂上联系课本知识和学过的知识，小组合作、讨论完成导学案上的内容，组长负责，拿出讨论结果，准备展示、点评。
【学习过程】 （一） 基础学习（A ）1阅读课本第78页试写出对数的定义，及对数式中各字母的名称。
2.写出指数式与对数式的关系及各字母的取值范围。
3.把下列指数式化为对数式，对数式化为指数式：;3127)4(;212)3(;322)2(;82)1(31153====--.4811log )8(;241log )7(;3125log )6(;29log )5(3253-=-===4.你知道什么是常用对数吗？N 的常用对数可以简记为什么？个 性 笔 记5.你知道什么是自然对数吗？N 的自然对数可以简记为什么？（二）学习探究（B ） 探究一：对数的性质1、1log 3= 、1lg = 、1log 5.0= 、1ln = 、 你发现了什么？能证明你的结论吗？2. 3log 3= 、10lg = 、3.0log 3.0= 、e ln = 、 你又发现了什么？能证明你的结论吗？3.零和负数有没有对数？为什么？探究二：N a N a =log ，为什么？求值：3log 22= 、6.0log 77= 、8log4.04.0= 、探究三: 求下列各式的值：（三）巩固提高（C ）求下列各式中x 的值：（温馨提示：试利用指数式与对数式的互化完成.）（1）642log 3x =； （2）log 86x =-；（3）lg 4x =； （4）3ln e x =（四）达标检测（A ）1． 将下列指数式化成对数式，对数式化成指数式. （1）53243=； （2）51232-=； （3）01.0102=-（4）10=e ； （5）12log 164=-； （6）2log 1287=；（7）1ln =e （8）4982732=⎪⎭⎫⎝⎛(B)4. 对数式2log (5)a a b --=中，实数a 的取值范围是（ ）. A ．(,5)-∞B ．(2,5)C ．(2,)+∞D ． (2,3)(3,5)(B)5. 计算：21log (322)++= .(B)6. 若log (21)1x +=-，则x =________，若2log 8y =，则y =__【教与学的反思】本节课有哪些收获？请写下来，与组内的同学分享。
2013北师大版必修一3.4《对数》word教案
§4.1 对数及其运算（第一课时）一．教学目标：1．知识技能：①理解对数的概念，了解对数与指数的关系；②理解和掌握对数的性质；③掌握对数式与指数式的关系 .2. 过程与方法：通过与指数式的比较，引出对数定义与性质 .3．情感、态度、价值观（1）学会对数式与指数式的互化，从而培养学生的类比、分析、归纳能力.（2）通过对数的运算法则的学习，培养学生的严谨的思维品质 .（3）在学习过程中培养学生探究的意识.（4）让学生理解平均之间的内在联系，培养分析、解决问题的能力.二．重点与难点：（1）重点：对数式与指数式的互化及对数的性质（2）难点：推导对数性质的三．学法与教具：（1）学法：讲授法、讨论法、类比分析与发现（2）教具：投影仪四．教学过程：1．对数的概念一般地，若(0,1)x a N a a =>≠且，那么数x 叫做以a 为底N 的对数，记作log a x N =a 叫做对数的底数，N 叫做真数.举例：如：24416,2log 16==则，读作2是以4为底，16的对数.1242=，则41log 22=，读作12是以4为底2的对数. 提问：你们还能找到那些对数的例子2．对数式与指数式的互化在对数的概念中，要注意：（1）底数的限制a ＞0，且a ≠1（2）log xa a N N x =⇔=指数式⇔对数式幂底数←a →对数底数指 数←x →对数幂 ←N →真数说明：对数式log a N 可看作一记号，表示底为a （a ＞0，且a ≠1），幂为N 的指数工表示方程xa N =（a ＞0，且a ≠1）的解. 也可以看作一种运算，即已知底为a （a ＞0，且a ≠1）幂为N ，求幂指数的运算. 因此，对数式log a N 又可看幂运算的逆运算。
3．思考交流p79归纳小结：对数的定义 log (b N a a N b a =⇔=＞0且a ≠1）1的对数是零，负数和零没有对数对数的性质 l o g 1a a = a ＞0且a ≠1 log a N a N =通常将以10为底的对数称为常用对数，10log N 常记为lg N .以无理数e=2.71828…为底的对数称为自然对数，log e N 常记为ln N .例题分析例1将下列指数式写成对数式:(1) 54 =625; (2) 3-3=1/27;(3)84/3=16; (4) 5a =15.例2将下列对数式写成指数式:(1) ㏒1/216=-4;(2) ㏒3243=5;(3) ㏒1/31/27=3;(4) lg0.1=-1.例3 求下列各式的值:(1)㏒525(2) ㏒1/232(3)3㏒310;(4)㏑1,(5) ㏒ 2.52.5.练习p80 1,2,3作业习题3-4 1,2课后反思：§4.1 对数及其运算（第二课时）一．教学目标：1．知识与技能①通过实例推导对数的运算性质，准确地运用对数运算性质进行运算， 求值、化简，并掌握化简求值的技能.②运用对数运算性质解决有关问题.③培养学生分析、综合解决问题的能力.培养学生数学应用的意识和科学分析问题的精神和态度.2. 过程与方法①让学生经历并推理出对数的运算性质.②让学生归纳整理本节所学的知识.3. 情感、态度、和价值观让学生感觉对数运算性质的重要性，增加学生的成功感，增强学习的积极性.二．教学重点、难点重点：对数运算的性质与对数知识的应用难点：正确使用对数的运算性质三．学法和教学用具学法：学生自主推理、讨论和概括，从而更好地完成本节课的教学目标.教学用具：投影仪四．教学过程：1．设置情境复习：对数的定义及对数恒等式log b a N b a N =⇔= （a ＞0，且a ≠1，N ＞0）， 指数的运算性质.;m n m n m n m n a a a a a a +-⋅=÷=();n m n mn ma a a == 2．讲授新课探究：在上课中，我们知道，对数式可看作指数运算的逆运算，你能从指数与对数的关系以及指数运算性质，得出相应的对数运算性质吗？如我们知道m n m n a a a+⋅=，那m n+如何表示，能用对数式运算吗？如：,,m n m n m n a a a M a N a +⋅===设。
人教版(新教材)高中数学第一册(必修1)：4.3.1 对数的概念学案
4.3 对数4.3.1 对数的概念课标要求素养要求1.理解对数的概念.2.知道自然对数和常用对数.3.通过阅读材料，了解对数的发现历史以及对简化运算的作用.. 1.会用对数的定义进行对数式与指数式的互化.2.理解和掌握对数的性质，会求简单的对数值，发展数学抽象及数学运算素养教材知识探究某种细胞分裂时，由1个分裂成2个，2个分裂成4个，….问题依次类推，那么1个这样的细胞分裂x次得到细胞个数N是多少？分裂多少次得到细胞个数为8个，256个呢？如果已知细胞分裂后的个数N，如何求分裂次数呢？提示2x个，3次，8次；由2x＝N可知当N已知时，x的值即为分裂次数.1.对数的概念（1）对数的概念一般地，如果a x=N(a>0,且a≠1)，那么数x叫做以a为底N的对数，记作x=log a N，其中a叫做对数的底数，N叫做真数.(2)常用对数与自然对数熟记无理数e的大小，在后面估算中经常用到通常，我们将以10为底的对数叫做常用对数，并把log10N记为lg__N，另外，在科技、经济以及社会生活中经常使用以无理数e＝2.718 28…为底数的对数，以e为底的对数称为自然对数，并把log e N记为ln__N.2.对数与指数的关系易得a log a N＝N，log a a b＝b.根据对数的定义，可以得到对数与指数之间的关系：当a>0，且a≠1时，a x＝N x＝log a N.3.对数的有关结论对数的有关结论是解题的重要依据(1)零和负数没有对数；(2)1的对数为零，即log a1＝0(a>0且a≠1)；(3)底数的对数为1，即log a a＝1(a>0且a≠1)教材拓展补遗『微判断』1.根据对数的定义，因为(－2)4＝16，所以log(－2)16＝4.(×)提示因为对数的底数a应满足a>0且a≠1，所以错误.2.对数式log32与log23的意义一样.(×)提示log32表示以3为底2的对数，log23表示以2为底3的对数，所以错误.3.对数的运算实质是求幂指数.(√)『微训练』1.若log3(2x－1)＝0，则x＝________.『解析』若log3(2x－1)＝0，则2x－1＝1，即x＝1.『答案』 12.若log x8＝3，则x＝________.『解析』由指对互化知x3＝8，所以x＝2.『答 案』 2 『微思考』1.任何一个指数式都可以化为对数式吗？ 提示 不是，如(－3)2＝9，不能写成log (－3)9＝2. 2.在对数的定义中为什么不能取a ≤0及a ＝1呢？提示 ①a <0，N 取某些值时，log a N 不存在，如根据指数的运算性质可知，不存在实数x 使⎝ ⎛⎭⎪⎫－12x＝2成立，所以log －122不存在，所以a 不能小于0.②a ＝0，N ≠0时，不存在实数x 使a x ＝N ，无法定义log a N ；N ＝0时，任意非零实数x ，有a x ＝N 成立，log a N 不确定.③a ＝1，N ≠1时，log a N 不存在；N ＝1，log a 1有无数个值，不能确定.题型一 对数的定义及其应用『例1』 (1)在对数式y ＝log (x －2)(4－x )中，实数x 的取值范围是________. (2)将下列指数式、对数式互化. 指对互化的重要依据a b ＝N log a N ＝b①54＝625；②log 216＝4；③10－2＝0.01；④log5125＝6.(1)『解 析』由题意可知⎩⎪⎨⎪⎧4－x >0，x －2>0，x －2≠1，解得2<x <4且x ≠3.『答 案』 (2，3)∪(3，4)(2)解 ①由54＝625，得log 5625＝4. ②由log 216＝4，得24＝16. ③由10－2＝0.01，得lg 0.01＝－2. ④由log5125＝6，得(5)6＝125.规律方法 指数式与对数式互化的思路(1)指数式化为对数式：将指数式的幂作为真数，指数作为对数，底数不变，写出对数式.(2)对数式化为指数式：将对数式的真数作为幂，对数作为指数，底数不变，写出指数式.『训练1』 将下列指数式、对数式互化： (1)43＝64；(2)ln a ＝b ；(3)⎝ ⎛⎭⎪⎫12m＝n ；(4)lg 1 000＝3.解 (1)因为43＝64，所以log 464＝3； (2)因为ln a ＝b ，所以e b ＝a ；(3)因为⎝ ⎛⎭⎪⎫12m＝n ，所以log 12n ＝m ；(4)因为lg 1 000＝3，所以103＝1 000. 题型二 对数相关结论的应用『例2』 求下列各式中的x 的值. 利用对数的结论由外层到内层求解 (1)log 2(log 3x )＝0； (2)log 5(log 2x )＝1； (3)log (3＋1)23－1＝x . 解 (1)因为log 2(log 3x )＝0，所以log 3x ＝1，所以x ＝3. (2)因为log 5(log 2x )＝1，所以log 2x ＝5，所以x ＝25＝32. (3)23－1＝2（3＋1）2＝3＋1，所以log (3＋1)23－1＝log (3＋1)(3＋1)＝1.∴x ＝1.规律方法 求解此类问题时，应根据对数的两个结论log a 1＝0和log a a ＝1(a >0且a ≠1)，进行变形求解，若已知对数值求真数，则可将其化为指数式运算. 『训练2』 求下列各式中的x 的值. (1)log 8『log 7(log 2x )』＝0； (2)log 2『log 3(log 2x )』＝1.解 (1)由log 8『log 7(log 2x )』＝0，得log 7(log 2x )＝1， 即log 2x ＝7，∴x ＝27.(2)由log 2『log 3(log 2x )』＝1，∴log 3(log 2x )＝2，∴log 2x ＝9，∴x ＝29. 题型三 利用指数式与对数式的互化求值 『例3』 (1)求下列各式的值.①log 981＝________.②log 0.41＝________.③ln e 2＝________. (2)求下列各式中x 的值. 注意指对互化关系式在解题中的应用①log64x＝－2 3；②log x8＝6；③lg 100＝x；④－ln e2＝x.(1)『解析』①设log981＝x，所以9x＝81＝92，故x＝2，即log981＝2；②设log0.41＝x，所以0.4x＝1＝0.40，故x＝0，即log0.41＝0；③设ln e2＝x，所以e x ＝e2，故x＝2，即ln e2＝2.『答案』①2②0③2(2)解①由log64x＝－23得x＝64－23＝43×(－23)＝4－2＝116；②由log x8＝6，得x6＝8，又x>0，即x＝816＝23×16＝2；③由lg 100＝x，得10x＝100＝102，即x＝2；④由－ln e2＝x，得ln e2＝－x，所以e－x＝e2，－x＝2，x＝－2.规律方法对数式中求值的基本思想和方法(1)基本思想在一定条件下求对数的值，或求对数式中参数字母的值，要注意利用方程思想求解.(2)基本方法①将对数式化为指数式，构建方程转化为指数问题.②利用幂的运算性质和指数的性质计算.『训练3』利用指数式、对数式的互化求下列各式中的x值.(1)log2x＝－12；(2)log x25＝2；(3)log5x2＝2；(4)2log3x＝4.解(1)由log2x＝－12，得2－12＝x，∴x＝22.(2)由log x25＝2，得x2＝25.∵x>0，且x≠1，∴x＝5.(3)由log5x2＝2，得x2＝52，∴x＝±5.∵52＝25>0，(－5)2＝25>0，∴x＝5或x＝－5.(4)由2log3x＝4＝22，得log3x＝2，所以x＝32，即x＝9.一、素养落地1.通过学习对数、常用对数、自然对数的概念，提升数学抽象素养.通过运用对数的结论求简单的对数值，提升数学运算素养.2.对数概念与指数概念有关，指数式和对数式是互逆的，即a b＝N log a N＝b(a>0，且a≠1，N>0)，据此可得记住这两个式子有利于简化运算两个常用恒等式：(1)log a a b＝b；(2)a log a N＝N.3.在关系式a x＝N中，已知a和x求N的运算称为求幂运算，而如果已知a和N 求x的运算就是对数运算，两个式子实质相同而形式不同，互为逆运算.二、素养训练1.有下列说法：(1)只有正数有对数；(2)任何一个指数式都可以化成对数式；(3)以5为底25的对数等于±2；(4)3log3(－5)＝－5成立.其中正确的个数为() A.0 B.1C.2D.3『解析』(1)正确；(2)，(3)，(4)不正确.『答案』 B2.使对数log a(－2a＋1)有意义的a的取值范围为()A.a>12且a≠1 B.0<a<12C.a>0且a≠1D.a<1 2『解 析』由题意知⎩⎪⎨⎪⎧－2a ＋1>0，a >0，a ≠1，解得0<a <12.『答 案』 B3.方程lg(2x －3)＝1的解为________.『解 析』 由lg(2x －3)＝1知2x －3＝10，解得x ＝132. 『答 案』 1324.计算：2log 23＋2log 31－3log 77＋3ln 1＝________. 『解 析』 原式＝3＋2×0－3×1＋3×0＝0. 『答 案』 05.把下列指数式化为对数式，对数式化为指数式. (1)2－3＝18；(2)⎝ ⎛⎭⎪⎫17a＝b ；(3)lg 11 000＝－3；(4)ln 10＝x .解 (1)由2－3＝18可得log 218＝－3； (2)由⎝ ⎛⎭⎪⎫17a＝b 得log 17b ＝a ；(3)由lg 11 000＝－3可得10－3＝11 000； (4)由ln 10＝x 可得e x ＝10.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 指数函数与对数函数
4.3.2 对数的运算
1.理解对数的运算性质．(重点)
2.能用换底公式将一般对数转化成自然对数或常用对数．(难点)
3.会运用运算性质进行一些简单的化简与证明．(易混点)
重点：对数的运算性质
难点：对数的运算性质的探究是教学的难点，突破这个难点的关键是抓住指数式与对数式之间的联系，启发学生进行转化。
1．对数
(1)指数式与对数式的互化及有关概念：
(2)底数a 的范围是________________.
2.
3.a
b b
c c a log log log =(a ＞0，且a ≠1；c ＞0，且c ≠1；b ＞0)．
问题提出：在引入对数之后，自然应研究对数的运算性质．你认为可以怎样研究？
我们知道了对数与指数间的关系，能否利用指数幂运算性质得出相应的对数运算性质呢？
探究一：对数的运算性质
回顾指数幂的运算性质：
n m n m a a a +=⋅，n m n m a a a -=÷，mn n m a a =)(．
把指对数互化的式子具体化：
设m a M =，n a N =，
于是有,m n MN a ,m n n mn M
a M a N n N m M a a ==log ,log ．
根据对数的定义有：n m a
n m a +=+log ，n m a n m a -=-log ，mn a mn a =log ． 于是有对数的运算性质：
如果0>a ，且1≠a 时，M>0，N>0，那么：
（1）log ()
a M N
；（积的对数等于两对数的和） （2）log a M N ；（商的对数等于两对数的差）
（3）log n a M
；（R n ∈）．（幂的对数等于幂指数乘以底数的对数） 1．思考辨析
(1)积、商的对数可以化为对数的和、差．( )
(2)log a (xy )＝log a x ·log a y .( )
(3)log 2(－3)2＝2log 2(－3)．( )
例1．求下列各式的值
（1）log 84＋log 82；（2）log 510－log 52 （3）log 2（47×25）
跟踪训练1 计算下列各式的值：
(1)12lg 3249－43
lg 8＋lg 245； (2)lg 52＋23
lg 8＋lg 5·lg 20＋(lg 2)2； (3)lg 2＋lg 3－lg 10lg 1.8
. ().ln ,ln ,ln 1ln x y z xy z 例2用表示下列各式
探究二：换底公式
问题1：前面我们学习了常用对数和自然对数，我们知道任意不等于1的正数都可以作为对数的底，能否
将其它底的对数转换为以10或e 为底的对数？
把问题一般化，能否把以a 为底转化为以c 为底？
探究：设p b a =log ，则b a p =，对此等式两边取以c 为底的对数，得到：
b a
c p c log log =，根据对数的性质，有：b a p c c log log =，所以
a b p c c log log =． 即
a b
b c c a log log log =
．其中0>a ，且1≠a ，0>c ，且1≠c ． 公式log a b ；称为换底公式．
用换底公式可以很方便地利用计算器进行对数的数值计算．
问题2：在4.2.1的问题1中，求经过多少年B 地景区的游客人次是2001年的2倍，就是计算 x =log 1.112 的值。
例3.尽管目前人类还无法准确预报地震，但科学家通过研究，已经对地震有所了解，例如，地震时释放出的能量E （单位：焦耳）与地震里氏震M 之间的关系为
2011年3月11日，日本东北部海域发生里氏9.0级地震，它所释放出来的能量是2008年5月12日我国汶川发生里氏8.0级地震的多少倍（精确到1）？
跟踪训练2求值：
(1)log 23·log 35·log 516； (2)(log 32＋log 92)(log 43＋log 83)．
1．计算：log 153－log 62＋log 155－log 63＝( )
A ．－2
B ．0
C ．1
D ．2
2．计算log 92·log 43＝( )
A ．4
B ．2 C.12 D.14
3．设10a ＝2，lg 3＝b ，则log 26＝( )
A.b a
B.a ＋b a
C ．ab
D ．a ＋b 4． log 816＝________.
5．计算：(1)log 535－2log 573
＋log 57－log 51.8； (2)log 2748＋log 212－12
log 242－1.
lg 4.8 1.5E M =+
1.对数的运算法则。
2.利用定义及指数运算证明对数的运算法则。
3.对数运算法则的应用。
4.换底公式的证明及应用。
参考答案：
二、学习过程
思考辨析 1. [答案] (1)√ (2)× (3)×
例1.解：（1）log 84＋log 82＝log 88＝1.
（2）log 510－log 52＝log 55＝1
(3) log 2（47×25）= log 2219 =19
跟踪训练1[解] (1)原式＝12(5lg 2－2lg 7)－43·3
2lg 2＋12(2lg 7＋lg 5)
＝52lg 2－lg 7－2lg 2＋lg 7＋1
2lg 5
＝12lg 2＋12lg 5＝1
2(lg 2＋lg 5)＝12lg 10＝1
2.
(2)原式＝2lg 5＋2lg 2＋lg 5(2lg 2＋lg 5)＋(lg 2)2
＝2lg 10＋(lg 5＋lg 2)2＝2＋(lg 10)2＝2＋1＝3.
(3)原式＝12lg 2＋lg 9－lg 10lg 1.8＝lg 18
102lg 1.8＝lg 1.8
2lg 1.8＝1
2.
例2.[解] ()()1ln ln ln ln ln ln xy
xy z x z z =-=+-
()(2332ln x y
x y z z =-23ln 1
1
2ln ln ln 23x y z x y z
=+=+-
问题2：换底公式可得;x =log 1.112=lg2
lg1.11，
利用计算工具，可得x =lg2
lg1.11≈6.64≈7，
由此可得，大约经过7年，B 地景区的
游客人次就达到2001年的2倍，类似地，可以求出游客人次是2001年的3倍，4倍，:…所需要的年数。
例3解:设里氏9.0级和里氏8.0级地震的能量分别为E
1和E 2
设里利用计算工具可得，
虽然里氏9.0级和里氏8.0级地震仅相差1级，但前者释放出的能量却是后者的约32倍。
跟踪训练2.[解] (1)原式＝lg 3lg 2·lg 5lg 3·lg 16lg 5＝lg 16lg 2＝4lg 2lg 2
＝4. (2)原式＝⎝⎛⎭⎫lg 2lg 3＋lg 2lg 9⎝⎛⎭⎫lg 3lg 4＋lg 3lg 8
＝⎝⎛⎭⎫lg 2lg 3＋lg 22lg 3⎝⎛⎭⎫lg 32lg 2＋lg 33lg 2＝3lg 22lg 3·5lg 36lg 2＝54
.. 三、达标检测
1.【答案】B [原式＝log 15(3×5)－log 6(2×3)＝1－1＝0.]
2.【答案】D [log 92·log 43＝lg 2lg 9·lg 3lg 4＝14
.] 3.【答案】B [∵10a ＝2，∴lg 2＝a ，
∴log 26＝lg 6lg 2＝lg 2＋lg 3lg 2＝a ＋b a
.] 4.【答案】43 [log 816＝log 2324＝43
.] 5【答案】(1)原式＝log 5(5×7)－2(log 57－log 53)＋log 57－log 595
＝log 55＋log 57－2log 57＋2log 53＋log 57－2log 53＋log 55＝2.
(2)原式＝log 2748
＋log 212－log 242－log 22 ＝log 2
7×1248×42×2＝log 2122
＝log 22－32＝－32. lg 4.8 1.5,E M 由=+12lg 4.8 1.59.0,
lg 4.8 1.58.0E E 可得；=+⨯=+⨯1122
lg lg -lg = 4.8 1.59.0- 4.8 1.58.0=E E E E 于是（）（）1.5
=+⨯+⨯1.5121032E E =≈。