人口模型预测数学建模作业
数学建模作业

题目在5.6节人口预测和控制模型中,总和出育率)(t β和生育模式),(t r h 是两种控制人口增长的手段。
试说明我国目前的人口政策,如提倡一对夫妇只生一个孩子、晚婚晚育,以及生育第二胎的一些规定,可以怎样通过这两种手段加以实施。
摘 要针对中国人口的实际特点,建立人口分布函数。
收集数据得到中国人口随年份变化的增长率,解决中国人口中短期和长期的人口预测与控制问题。
首先,将人口的预测问题转化为对出生率的预测,通过对数据的分析研究,发现影响人口增长的主要因素可归结为出生率及生育模式的变化,并依次建立不同参数随时间变化的递推数学模型从而讨论各个参数对人口增长的影响。
利用Gamma 函数拟合死亡率对年龄的分布,建立人口分布函数模型,由于概率分布是相对稳定的。
所以对人口预测而言其结果具有可控性,由此可以为我国的计划生育政策作出贡献。
关键词:人口控制;人口分布函数;生育模式一、问题重述在5.6节人口预测和控制模型中,总和出育率)(t β和生育模式),(t r h 是两种控制人口增长的手段。
试说明我国目前的人口政策,如提倡一对夫妇只生一个孩子、晚婚晚育,以及生育第二胎的一些规定,可以怎样通过这两种手段加以实施。
二、问题分析据了解,我国人口总数占世界人口总数的22%,居世界第一,虽然在二十世纪八十年代就已经开始控制人口,但人口增长的脚步依然没有停下,人口老年化问题也越来越严重,所以现在开始提倡一对夫妻只能生一个孩子、晚婚晚育以及定下了一些关于第二胎的政策。
所以,考虑用微分方程中生育率和生育模式来求解问题。
三、模型假设1.时刻t 年龄小于r 的人口2.在社会安定的局面下和不太长的时间里,死亡率大致与时间无关3.无重大天灾人祸,死亡率出生率大致与时间无关。
4.人口统计数据不存在大的误差。
四、符号说明1.人口分布函数记作),(t r F ;2.婴儿的出生率记为)(),0(t f t p =;3.时刻t 、年龄r 的人的死亡率记为),(t r μ;4.dr t r p t r ),(),(μ表示时刻t 年龄在[]dr r r +,内单位时间的死亡人数;5.)(0r p 是人口调查得到的已知函数;6.婴儿的出生率记为)(t f ;五、模型建立由问题假设我们可以得到各个年龄段的人口数,即人口分布函数为: ds t s p t r F r⎰=0),(),(由于在社会安定的局面下和不太长的时间里,死亡率大致与时间无关,于是可近似的假设)(),(r t r μμ=因为)(0r p 与)(r μ可由人口统计数据得到,所以),(t r μ可由)0,(r μ粗略估计,为了预测和控制人口的发展状况,我们需要关注和可以用作控制的就是婴儿的出生率)(t f ,因此我们主要通过讨论)(t f 来研究人口的研究与控制。
数学建模人口模型人口预测

关于计划生育政策调整对人口数量、结构及其影响的研究【摘要】本文着重于讨论两个问题:1、从目前中国人口现状出发,对于中国未来人口数量进行预测。
2、针对深圳市讨论单独二胎政策对未来人口数量、结构及其对教育、劳动力供给与就业、养老等方面的影响。
对于问题1从中国的实际情况和人口增长的特点出发,针对中国未来人口的老龄化、出生人口性别比以及乡村人口城镇化等,提出了 Logistic 、灰色预测、等方法进行建模预测。
首先,本文建立了 Logistic 阻滞增长模型,在最简单的假设下,依照中国人口的历史数据,运用线形最小二乘法对其进行拟合, 对 2014 至 2040 年的人口数目进行了预测, 得出在 2040 年时,中国人口有 14.32 亿。
在此模型中,由于并没有考虑人口的年龄、 出生人数男女比例等因素,只是粗略的进行了预测,所以只对中短期人口做了预测,理 论上很好,实用性不强,有一定的局限性。
然后, 为了减少人口的出生和死亡这些随机事件对预测的影响, 本文建立了 GM(1,1) 灰色预测模型,对 2014 至 2040 年的人口数目进行了预测,同时还用 2002 至 2013 年的 人口数据对模型进行了误差检验,结果表明,此模型的精度较高,适合中长期的预测, 得出 2040 年时,中国人口有 14.22 亿。
与阻滞增长模型相同,本模型也没有考虑年龄 一类的因素,只是做出了人口总数的预测,没有进一步深入。
对于问题2针对深圳市人口结构中非户籍人口比重大,流动人口多这一特点,我们采用了灰色GM(1,1)模型,通过matlab 对深圳市自2001至2010年的数据进行拟合,发现其人口变化近似呈线性增长,线性相关系数高达0.99,我们就此认定其为线性相关并给出线性方程。
同理,针对其非户籍人口,我们进行matlab 拟合发现,其为非线性相关,并得出相关函数。
并做出了拟合函数0.0419775(1)17255.816531.2t X t e ⨯+=⨯-。
基于人口增长模型的数学建模(DOC)

数学建模论文题目:人口增长模型的确定专业、姓名:专业、姓名:专业、姓名:人口增长模型摘要随着人口的增加,人们越来越认识到资源的有限性,人口与资源之间的矛盾日渐突出,人口问题已成为世界上最被关注的问题之一。
问题给出了1790—1980年间美国的人口数据,通过分析近两百年的美国人口统计数据表,得知每10年的人口数的变化。
预测美国未来的人口。
对于问题我们选择建立Logistic模型(模型2)现实中,影响人口的因素很多,人口也不能无限的增长下去,Logistic 模型引进常数N 表示自然资源和环境所能承受的最大人口数,因而得到了一个贝努利方程的初值问题公式,从实际效果来看,这个公式较好的符合实际情况的发展,随着时间的递增,人口不是无限增长的,而是趋近于一个数,这个即为最大承受数。
我们还同时对数据作了深入的探讨,作数据分析预测,通过观测比较选择一个比较好的拟合模型(模型3)进行预测。
预测接下来的每隔十年五次人口数量,分别为251.4949, 273.5988 , 293.4904 , 310.9222 325.8466。
关键词:人口预测Logistic模型指数模型一、问题重述1790-1980年间美国每隔10年的人口记录如下表所示。
试用以上数据建立马尔萨斯(Malthus)人口指数增长模型,并对接下来的每隔十年预测五次人口数量,并查阅实际数据进行比对分析。
如果数据不相符,再对以上模型进行改进,寻找更为合适的模型进行预测。
二、问题分析人口预测是一个相当复杂的问题,影响人口增长除了人口数与可利用资源外,还与医药卫生条件的改善,人们生育观念的变化等因素有关…….可以采取几套不同的假设,做出不同的预测方案,进行比较。
人口预测可按预测期长短分为短期预测 (5年以下)、中期预测(5~20年)和长期预测(20~50年)。
在参数的确定和结果讨论方面,必须对中短期和长期预测这两种情况分开讨论。
中短期预测中所用的各项参数以实际调查所得数据为基础,根据以往变动趋势可较准确加以估计,推算结果容易接近实际,现实意义较大。
数学建模习题中国人口增长预测

中国人口增长预测本题是一个人口发展预测的问题。
人口发展与一般种群增长一样,是由自然增长率决定的。
然而,人类个体是一种社会的个体,所以人口发展有自己的特点。
想到人口的迁移,性别比例,城镇化等。
同时,人口发展受政策的影响,例如计划生育;也要受到人们意识的影响,像生育意识等。
但是从社会层面上看,生育意识在整个社会上体现为妇女的生育模式,进而可以特别地去考虑。
思考方法:首先,数据的处理。
在经过EXCEL分析和验证后,适当修正题中的个别有误数据后,利用有效数据进行建模求解,在此过程中,我们提取出死亡率、生育率等感念,且把人的一生按年龄分为青年期、衰老期等阶段。
这是求解人口增长模型的必要过程和方法。
其次,模型建立。
和一般的预测模型一样,本模型也是个预测模型,所以考虑到用题目所给的五年的信息,来推测今后几十年的人口的总数和结构情况。
对此,我们选用差分方程模型和数据参数拟合等方法。
同时,将死亡率与出生率分开分别计算和拟合,通过五年的实际数据拟合出相应函数的参数,再利用此函数进行评估和预测。
最后,利用已有信息以及上述所求出的对应函数和方程,对中短期与长期进行估计和预测,进而得出人口结构、人口比例、人口数量等一系列的相关数据。
以下是解答过程:1.数据说明:x:表示最大的年龄;mi=1,2,3,4,5,6 其中1表示市男性,2表示市女性,3表示镇男性,4表示镇女性,5表示乡男性,6表示乡女性;A :表示婴儿性别比例矩阵;* :表示点乘;P(x,t):表示t时刻年龄为x的人口数量;ibir(x,t):表示t时刻年龄为x的出生率;i)(,i dea x t:表示t时刻年龄为x的死亡率;)(i t k:表示t时刻婴儿的死亡率;tra(x,t):表示t时刻年龄为x的人口迁出率;i2.假设条件1. 假设国内社会环境稳定,无异常大量死亡或出生情况发生,人口比例,人口总数不会出现突变状况; 2. 假设只存在乡向城镇迁出,不存在其他迁移方式,且不同年龄段迁移率相同; 3. 假设不考虑国家之间的迁入与迁出,把中国内部看为一个封闭的模型; 4. 对于90岁以上的人都按照90岁处理; 5. 假设只存在乡向城镇迁出,不存在其他迁移方式,且不同年龄段迁出率相同,按照0.6%均匀增长。
数学建模作业6

[beta,r,J]=nlinfit(t',x','renkou1',beta0);
beta
y=renkou1(beta,t)
[YY,delta]=nlpredci('renkou1',t',beta,r,J);
plot(t,x,'b*',t,YY,'r')
error=abs(y-x)
42.3671
33.6329
1910
92.0
52.6268
39.3732
1920
106.5
65.3711
41.1289
1930
123.2
81.2016
41.9984
1940
131.7
100.8656
30.8344
1950
150.7
125.2915
25.4085
1960
179.3
155.6324
23.6676
佛山科学技术学院
上机报告
课程名称数学建模
上机项目人口模型
专业班级
一、问题提出
人口问题是当前世界上人们最关心的问题之一。认识人口数量的变化规律,作出较准确的预报,是有效控制人口增长的前提。
要求:分别建立并求解两个最基本的人口模型,即:指数增长模型和Logistic模型,并利用表1给出的近两百年的人口统计数据,画出图形拟合数据,对模型做出检验,最后用它预报2000年的人口。
f=renkou2(beta,t)
plot(t,x,'r*',t,f)
error=abs(f-x)
画图:
(根据拟合出的数据和原来数据填写表格)
6.2 人口增长模型 数学建模

一、粮食生产 19501950-1984 世界粮食产量的增幅超过人口增 长速度。但84年以后粮食产量增幅一直落后 长速度。但84年以后粮食产量增幅一直落后 于人口增长速度。 原因:缺少新垦土、灌溉量减少、土地生 产率的提高越来越难。
二、水资源的匮乏 国际水资源管理研究预测,到2050年, 国际水资源管理研究预测,到2050年, 约有10亿人口将面临缺水的状况。 约有10亿人口将面临缺水的状况。 三、海洋捕捞
2005年11月 世界人口状况报告》 2005年11月《世界人口状况报告》显示目 前世界总人口为64.647亿,我国占了约20% 前世界总人口为64.647亿,我国占了约20% 2050年世界人口将达77-112亿,若采取94 2050年世界人口将达77-112亿,若采取94 亿的预测值。会带来什么影响?
例题2齐次微分方程3一阶线性非线性微分方程其他模型malthusmalthus11模型假设模型假设33美国的实际人口数据美国的实际人口数据22模型建立模型建立33模型检验分析模型检验分析1人口预测人口预测22景区游客人数增长景区游客人数增长3城市人口增长城市人口增长
第六章鱼类减少
饲料
渔业养殖
四、森林覆盖率、生物多样性、能源危机等等
2、复习
1、微分方程:含有导数 或微分的方程 2、微分方程的类型:
(1)可分离变量的微分方程,形如 dy = f ( x) ⋅ g ( y ) dx
(2)齐次微分方程 (3)一阶线性、非线性微分方程 其他
例题 模型
2、模型建立
3、模型分析检验
美国的实际人口数据
二、阻滞增长模型
1、 模型假设 设人口增长率r是人口数N的线性递减函数, 记为r ( N ), K 是自然资源和环境条件的最大人 口容量,r 表示人口很少时的增长率(固有增 长率)
数学建模-人口增长模型
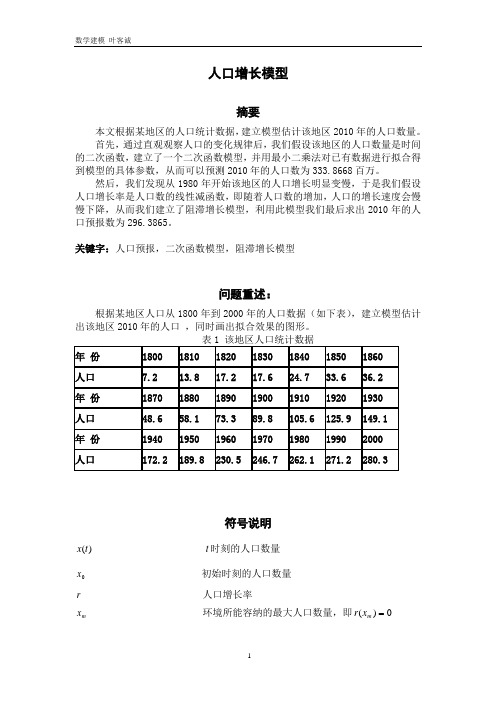
人口增长模型摘要本文根据某地区的人口统计数据,建立模型估计该地区2010年的人口数量。
首先,通过直观观察人口的变化规律后,我们假设该地区的人口数量是时间的二次函数,建立了一个二次函数模型,并用最小二乘法对已有数据进行拟合得到模型的具体参数,从而可以预测2010年的人口数为333.8668百万。
然后,我们发现从1980年开始该地区的人口增长明显变慢,于是我们假设人口增长率是人口数的线性减函数,即随着人口数的增加,人口的增长速度会慢慢下降,从而我们建立了阻滞增长模型,利用此模型我们最后求出2010年的人口预报数为296.3865。
关键字:人口预报,二次函数模型,阻滞增长模型问题重述:根据某地区人口从1800年到2000年的人口数据(如下表),建立模型估计出该地区2010年的人口 ,同时画出拟合效果的图形。
符号说明)(t x t 时刻的人口数量 0x 初始时刻的人口数量 r 人口增长率m x 环境所能容纳的最大人口数量,即0)( m x r问题分析首先,我们运用Matlab软件[1]编程(见附件1),绘制出1800年到2000年的人口数据图,如图1。
18001820184018601880190019201940196019802000图1 1800年到2000年的人口数据图从图1我们可以看出1800年到2000年的人口数是呈现增长的趋势的,而且类似二次函数增长。
所以我们可以建立了一个二次函数模型,并用最小二乘法对已有数据进行拟合得到模型的具体参数。
于是我们假设人口增长率是人口数的线性减函数,即随着人口数的增加,人口的增长速度会慢慢下降,从而我们可以建立一个阻滞增长模型。
模型建立模型一:二次函数模型我们假设该地区t时刻的人口数量的人口数量)(tx是时间t的二次函数,即:2()=++x t at bt c我们可以根据最小二乘法,利用已有数据拟合得到具体参数。
即,要求a、b和c,使得以下函数达到最小值:221(,,)()ni i i i E a b c at bt c x ==++-∑其中i x 是i t 时刻该地区的人口数,即有:2222)3.28020002000...)2.718001800(),,(-+⋅+⋅++-+⋅+⋅=c b a c b a c b a E令0,0,0E E E a b c∂∂∂===∂∂∂,可以得到三个关于a 、b 和c 的一次方程,从而可解得a 、b 和c 。
数学建模人口模型

实验一 人口模型与混沌实验目的1.了解Logistic 模型的基本概念。
2.了解的1(1)n n n x rx x +=-分叉和混沌现象。
3.学习、掌握MATLAB 软件有关命令。
实验步骤及结果1. 根据离散Logistic 模型)t (x )x )t (x (r )t (x x )t (x )t (x m -+=+=+11∆t=0,1,2,…,预测出2005-2011年我国的人口总数,其中r =0.029,=m x1950838861。
实验结果如下图所示:r =0.029,=m x 19508388612. 讨论简化的logistic 迭代方程))t (x )(t (rx )t (x -=+11,对于不同的r 和x0观察数列的收敛情况,分别给出t-x 坐标系下图形。
当x(1)=0.4,r 分别为0.7,1.5,3.2时实验结果如下图所示:3、绘制Feigenbaum 图过程:为了观察r 对迭代格式))t (x )(t (rx )t (x -=+11的影响,将区间(0,4]以步长r ∆离散化。
对每个离散的r 值进行迭代,忽略前50个迭代值,把点5152100(,),(,),,(,)r x r x r x 显示在坐标平面上。
实验结果如下:实验代码:1.x=[2005:1:2011];y(1)=126743;r=0.029;k=1950838861;for i=1:11y(i+1)=y(i)+r*(1-y(i)/k)*y(i); endplot(x,y(6:12),'+');hold on2.x=[1:19];y(1)=0.4;r=3.2;for i=1:18y(i+1)=r*(1-y(i))*y(i);plot(x(i),y(i),'+');hold onendxlabel('t');ylabel('x');title('r=3.2,x(1)=0.4')3.for r=[0.005:0.005:4]x(1)=0.6;t=linspace(r,r,100);for j=1:99x(j+1)=r*x(j)*(1-x(j));endhold onplot(t,x,'r+','markersize',0.5); endxlabel('t');ylabel('x');title('r(0,4),x(0.6)')。
数学建模习题-人口问题

数学建模报告——浙江省人口增长预测模型的建立与分析问题综述:为了加快中国的经济建设进程,全面落实科学的发展观,按照构建社会主义和谐社会的要求,实现人口与经济社会资源环境的协调和可持续发展。
我们确定人口发展战略,必须既着眼于人口本身的问题,又处理好人口与经济社会资源环境之间的相互关系,构建社会主义和谐社会,统筹解决人口数量、素质、结构、分布等问题。
人口增长预测的研究是国家(地区)制定未来人口发展目标和生育政策等有关人口政策的基础,对于经济计划的制定和社会战略目标的决策具有重要参考价值。
一般的人口预测统计学模型,其预测精度难以保证。
所以选择一个好的人口预测模型,首先应符合人口基本理论和数学建模的要求,这是选择模型的关键,其次要保证模型数据可得一致性与可比性,在数据预测检验阶段应充分拟合原始数据。
浙江省是人口大省、地域小省(资源小省),虽然从“资源小省、经济小省(国家投入小省)、工业小省”迅速发展成为“经济大省”,但人口问题始终是制约浙江省发展的关键因素之一。
根据已有数据,运用数学建模的方法,对浙江省做出分析和预测是一个重要问题。
近年来浙江省的人口发展出现了一些新的特点,例如,老龄化进程加速、出生人口性别比持续升高,以及乡村人口城镇化等因素,这些都影响着浙江省人口的增长。
从浙江省的实际情况和人口增长的特点出发, 建立浙江省人口增长的数学模型,并由此对浙江省人口增长的中短期和长期趋势做出预测。
解:假设:不考虑特别年份的特殊性,例如特大自然灾害等对人口增长的影响;在研究 Logistic生物模型,假设其研究对象p(t) {p(t)表示在t时刻种群的大小}是连续的;不考虑男女出生比例对人口增长的影响。
模型建立:1.短期人口预测影响人口增长的因素有很多,有经济、政策、科学技术、自然环境等,这些众多的因素之间的关系难以准确描述出来, 它们对人口增长的作用不是用几个指标就能精确计算出来的。
人口系统具有明显的灰色性, 是一个部分信息已知而部分信息未知的系统。
人口增长的预测(数学建模论文)-论文

人口增长的预测(数学建模论文) - 论文人口增长的预测(数学建模论文) - 论文关键字:人口增长稳定曲线预测运动模型方程平衡点人口数一题目: 请在人口增长的简单模型的基础上。
; (1)找到现有的描述人口增长,与控制人口增长的模型;; (2)深入分析现有的数学模型,并通过计算机进行仿真验证;; (3)选择一个你们认为较好的数学模型,并应用该模型对未来20年的某一地区或国家的人口作出有关预测;; (4)就人口增长模型给报刊写一篇,对控制人口的策略进行论述。
二摘要:本次建模是依照已知普查数据,利用Lgisti模型,对中国人口的增长进行预测。
首先假设人口增长符合Lgisti模型,即引入常数,用来表示自然环境条件所能容许的最大人口数。
并假设净增长率为,即净增长率随着人口数N(t)增长而减小,当N(t) 时,净增长率趋于零。
按照这个假设,。
用参数 ,3.0,r=0.0386, =1908, =14.5。
画出N=N(t)的图像,作为人口增长模型的一种近似。
做微分方程解的定性分析,求出N=N(t)的驻点和拐点,按照函数作图方法列出定性分析表,作出相轨迹的运动图。
当初始人口时,方程的解单调递增到地趋向,这意味着如果使用Lgisti模型描述人口增长,则人口发展地总趋势是渐增到最大人口数,因此可作为人口的预测值,也称谓平衡点。
用导数做稳定分析,为判断平衡点是否为稳定,可在平面上绘制f(x)的图象,然后像函数绘图那样,用导数进行定性分析,通过图看出人口数N(t)按时间是递增的,当人口数未达到饱和状态的时候,将逐渐地趋向,这意味着是稳定的平衡点。
按该模型,未来人口的数量将随着时间的演化,从初始状态出发达到极限状态,这样就给出了人口的未来预测。
三问题的提出1( althus模型英国统计学家althus(1766,1834)发现人口增长率是一个常数。
设t时刻人口为N(t),因为人口总数很大,可近似把N(t)当作连续变量处理。
以人口预测为例初试数学建模

答疑解惑239以人口预测为例初试数学建模★纪秀浩本文研究“二孩”政策对我国人口发展的影响问题,对于预测未来30年人口数的问题,分别对“单独二孩”和“全部二孩”政策首先建立灰色预测模型,将近5年的人口数据做累加合成,得到近似指数规律的数据,然后建立leslie 模型,将用灰色预测模型算出来的数据代入leslie 模型中,得到leslie 矩阵,进而预测出未来30年我国的人口数;通过搜集中国统计局各个年龄段的结构比例以及老年人口占全部人口的比重,预测未来30年老龄化程度。
本课题是研究单独二胎和全面二胎对未来人口的影响,所以我们要用到最新的数据并对未来30年做一个预测,由于需要的数据很少,所以我们必须用已有的数据做一些预测,本次预测方法采用灰色模型矩阵来进行预测,灰色模型它的优点就在于根据已有的少量数据,对事物的发展规律做一个模糊性的描述,来预测后边未知的数据,当然在此之前我们还要把之前的数据进行一些累加,以弱化原始数据的影响,而且大大的减少了原始数据的随机性,从而呈现出比较明显的变化规律。
得到了一个初步的数据后,我们可以用Leslie 模型在MATLAB 的基础上编程求解,在图中呈现不开放二胎和单独二胎政策和全面二胎政策的一些发展趋势,并定量的分析两种政策下对未来国家总人口及老龄化的影响。
一、灰色GM(1,1)模型为了研究“二孩”政策对我国人口发展的影响问题,对于预测未来30年人口数的问题,通过搜集统计局近5年的数据人口[1],分别对“单独二孩”和“全部二孩”政策首先建立灰色预测模型,将近5年的人口数据做累加合成,得到近似指数规律的数据,将已知的2006年至2010年出生人口性别比数据作为已知数据向量0x ,(0)125{(0),(0),,(0)}x x x x = ,先对五年的数据进行一次累加。
以减少对后边数据的影响,并得到新的向量表达式:1(1)(0) (1,2,,30),kk jj x xk ===∑ 令x为生成的新向量,(1)1230{(1),(1),,(1)}x x x x = ,在新向量x 的基础上建立灰色方程为(t)(1)dx cx v d t+= (1)式(1)为灰色一阶微分方程,一般记做(1,1)G M,其中,c v为未知参数。
数学建模_人口模型与预测

人口模型与预测摘要人口的增长是当前世界上引起普遍关注的问题,作为世界上人口最多的国家,我国的人口问题是十分突出的,由于人口基数大,尽管我国已经实行了20多年的计划生育政策,人口的增长依然很快,巨大的人口压力给我国的社会、政治、经济、医疗、就业等带来了一系列的问题。
因此,研究和解决人口问题在我国显得尤为重要。
我们经常在报刊上看见关于人口增长的预报,说到本世纪末,或到下世纪中叶,全世界(或某地区)的人口将达到多少亿。
你可能注意到不同报刊对同一时间人口的预报在数字上长有较大的区别,这显然是由于用了不同的人口模型计算的结果。
人类社会进入20世纪以来,在科学技术和生产力飞速发展的同时,世界人口也以空前的规模增长。
人口每增加十亿的时间,由一百年缩短为十二三年.我们赖以生存的地球,已经携带着它的60亿子民踏入21世纪.长期以来,人类的繁殖一直在自发地进行着,只是由于人口数量的迅速膨胀和环境质量的急剧恶化,人们才猛然醒悟,开始研究人类和自然的关系、人口数量的变化规律,以及如何进行人口控制等问题本文建立两个模型(1)中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)中国人口的Logistic模型,并用该模型进行预测,与实际人口数据进行比较。
而且利用MATLAB图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线和两种预测模型的误差比较图,并分别标出其误差。
关键词指数增长模型Logistic模型MATLAB软件人口增长预测1 问题的提出下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(0=t ),1016540=N 万人,200000=m N 万人。
要求:(1)建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
(2)建立中国人口的Logistic 模型,并用该模型进行预测,与实际人口数据进行比较。
(3)利用MATLAB 图形,标出中国人口的实际统计数据,并画出两种模型的预测曲线。
数学建模人口预测模型

• 生育率, [i1 , i2 ] 为育龄区间, ki (t ) 为第t 年 i 岁人口 的女性比, 则第t 年的出生人数为
f (t ) bi (t )ki (t ) xi (t )
i i1
i2
(2)
• 记 d00 (t ) 为第t 年婴儿死亡率,即第t 年出生但未活到 人口统计时刻的婴儿比例 (婴儿死亡率通常较高, 在人 口统计和建模中一般都不能忽略),
• 于是
f (t ) x0 (t ) d 00 (t ) f (t )
x0 (t ) (1 d00 (t )) f (t )
(3)
对于i=0将(2),(3)代入(1)得:
x1 (t 1) (1 d00 (t ))( 1 d0 (t )) bi (t )ki (t ) xi (t )
• 人口发展方程 时间以年为单位,年龄按周岁计算,设最 大年龄为 m岁,记 xi (t ) 为第t 年i岁(满 i 周岁而不到i+1 周岁)的人数, t 0,1,2,, i 0,1,2,, m .只考虑由 于生育, 老化和死亡引起的人口演变,而不计迁移等社会 因素的影响. 记 d i (t ) 为第 t年 i 岁人口的死亡率,即
• 的增长率, 不涉及年龄结构. 但在实际上, 在人口预测 这人口按年龄分布状况是十分重要的,因为不同年龄人 的生育率和死亡率有着很大的差别. 两个国家或地区目 前人口总数一样,如果一个国家或地区年青人的比例高 于另一个国家或地区,那么两者人口的发展状况将大不 一样. 因此考虑人口按年龄的分布, 除了时间是一个变 量, 年龄也是一个变量. • 如果用连续性模型来描述它, 就要用偏微分方程来 描述. 但在实际应用中连续模型很不方便, 需要建立 相应的离散模型. 因为作为已知的输入数据是离散的, 要得到的输出数据也是离散的, 再者对连续模型求解也 是非常困难的.因此我们选择建立一个离散性模型来描 述, 用差分方程来实现它. •
人口模型预测数学建模作业修订

人口模型预测数学建模作业修订YUKI was compiled on the morning of December 16, 2020上传是为了分析数学的乐趣,请粘贴复制的时候也多思考哈。
为了更多的学子们。
2014年数学建模论文第二套题目:人口增长模型的确定专业、姓名:土木135提交日期: 2015/7/2晚上题目:人口增长模型的确定摘要对美国人口数据的变化进行拟合,并进行未来人口预测,在第一个模型中,考虑到人口连续变化的规律,用微分方程的方法解出其数量随时间变化的方程,用matlab里的cftool工具箱求出参数,即人口净增长率r=,对该模型与实际数据进行对比,并计算了从1980年后每隔10年的人口数据,与实际对比,有很大出入。
因此又改进出更为符合实际的阻滞增长模型,应用微分方程里的分离变量法和积分法解出其数量随时间变化的方程,求出参数人口增长率r=和人口所能容纳最大值m x=,与实际数据对比,拟合得很好,并预测出1980年后每隔10年的人口数据,与实际对比,比较符合。
为了便于比较两个模型与实际数据的描述情况作对比,又做出了两个模型与实际数据的对比图,以及两个模型的误差图。
关键词:人口预测微分方程马尔萨斯人口增长模型阻滞增长模型一、问题重述1790-1980年间美国每隔10年的人口记录如下表所示。
表1 人口记录表试用以上数据建立马尔萨斯(Malthus)人口指数增长模型,并对接下来的每隔十年预测五次人口数量,并查阅实际数据进行比对分析。
如果数据不相符,再对以上模型进行改进,寻找更为合适的模型进行预测。
二、问题分析由于题目已经说明首先用马尔萨斯人口增长模型来刻划,列出人口增长指数增长方程并求解,并进行未来50年内人口数据预测,但发现与实际数据有较大出入。
考虑到实际的人口增长率是受实际情况制约的,因此,使人口增长率为一变化的线性递减函数,列出人口增长微分方程,求出其方程解,并预测未来五十年内人口实际数据。
数学模型作业:人口模型

数学模型报告2邓曌 100244105作业1 用1900年至2000年的数据拟合指数增长模型,计算并作图,观察结果。
年份19001910192019301940195019601970198019902000实际人口7692106.5123.2131.7150.7179.3204226.5251.4281.4 表1模型建立:记时刻t 的人口为x(t),当考察一个国家或一个较大地区的人口时, x(t)是一个很大的整数。
为了讨论方便,我们将x(t)视为连续、可微函数。
记初始时刻的人口为x0.基本假设 :人口(相对)增长率 r 是常数x(t):时刻t 的人口t r t x t x t t x ∆=-∆+)()()( (1) 0)0(,x x rx dtdx == (2) rt e x t x 0)(= ,t t r r x e x t x )1()()(00+≈= (3)rt e x t x 0)(=的参数r 和x 0可以用表1的数据估计。
为了利用简单的线性最小二乘法,将(3)式取对数,可得:0ln ,ln ,x a x y a rt y ==+= (4)模型求解:以1900年至2000年的数据拟合(4)MATLAB 编程代码:>> t=1900:10:2000;x=[76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4 281.4];y=log(x);p=polyfit(t,y,1);x0=exp(p(2));r=p(1);plot(t,x,'r:o');hold on;x1=x0*exp(r*t);plot(t,x1);disp(['x0=',num2str(x0),',r=',num2str(r)]);结果得:x0=1.9618e-09,r=0.0128611900191019201930194019501960197019801990200050100150200250300图1由图1可以看出,蓝色拟合曲线表示曲线拟合的很好,用这个模型基本上能够描述十九世纪以前美国人口的增长。
数学建模作业-人口增长模型

论文结构合理,模型建立详细,思想明确,论述清楚程序和拟合是文章的亮点,模型建立完了没有做误差分析,如果补完整是一篇很不错的文章。
摘要•随着科学技术的发展,国内资金积累量在不断增加,但是中国人口近几年还是呈增加的趋势,这样就会影响人均收入。
由于国民收入是资金积累的一部分,国民收入变化可以反映资金积累的变化。
因此研究资金积累、国民收入与人口增长的关系可以转化成研究资金积累与人口增长的关系。
若国民平均收入与按人口平均资金积累成正比,说明仅当资金积累的相对增长率大于人口的相对增长率时,国民平均收入才是增长的。
所以认识资金积累与人口增长的关系,对国民平均收入的增长有重大意义。
本文通过微分方程建立三个模型,即人口Malthus模型、资金积累指数模型、资金积累增长率与人口增长率的二次曲线模型。
通过资金积累与人口增长的关系来分析国民平均收入。
关键词:资金积累人口增长国民平均收入资金积累增长率人口增长率一、问题的重述资金积累、国民收入、与人口增长的关系:(1)若国民平均收入x与按人口平均资金积累y成正比,说明仅当总资金积累的相对增长率k大于人口的相对增长率r时,国民平均收入才是增长的. (2)作出k(x)和r(x)的示意图,分析人口激增会引起什么后果.二、问题分析人均国民收入主要与国家资金总积累量和总人口数有关,若总人口数的增长率大于资金积累增长率,则增长的资金不能使每一位国民增加收入,只能使少量国民收入增加,因此,总体来说,国家人均收入实际上是减少的。
三、模型假设假设总资金增长和人口增长均为指数增长,资金积累增长率和人口增长率为二次曲线模型。
四、符号说明a为国民收入在总资金积累中所占比例;y(t)为总资金积累量;N(t)为总人口数;Nm为人口的峰值;x(t) 为人均国民收入;r 为人口增长率;k 为资金积累增长率。
五、模型的建立与求解(1)人口增长模型曲线如图1所示:图1通过图形,用MATLAB 编程可建立指数增长模型6110)()(⨯+=⨯tet N αα 其中0127.01=α 0058.02=α(2)总资金积累模型曲线如图2所示:图2由曲线可知资金增长是呈指数整长的并通过MATLAB编程得到指数模型:y(t)=(0.001+e x003.0) 106。
数学建模实例人口预报问题

数学建模实例:人口预报问题1.问题人口问题是当前世界上人们最关心的问题之一.认识人口数量的变化规律,作出较准确的预报,是有效控制人口增长的前提.下面介绍两个最基本的人口模型,并利用表1给出的近两百年的美国人口统计数据,对模型做出检验,最后用它预报2000年、2010年美国人口.表1 美国人口统计数据2.指数增长模型(马尔萨斯人口模型)此模型由英国人口学家马尔萨斯(Malthus1766~1834)于1798年提出. [1] 假设:人口增长率r 是常数(或单位时间内人口的增长量与当时的人口成正比).[2] 建立模型: 记时刻t=0时人口数为x 0, 时刻t 的人口为()t x ,由于量大,()t x 可视为连续、可微函数.t 到t t ∆+时间内人口的增量为:()()()t rx tt x t t x =∆-∆+于是()t x 满足微分方程:()⎪⎩⎪⎨⎧==00x x rx dt dx(1)[3] 模型求解: 解微分方程(1)得()rt e x t x 0= (2)表明:∞→t 时,()∞→t x (r>0).[4] 模型的参数估计:要用模型的结果(2)来预报人口,必须对其中的参数r 进行估计,这可以用表1的数据通过拟合得到.拟合的具体方法见本书第16章或第18章.通过表中1790-1980的数据拟合得:r=0.307. [5] 模型检验:将x 0=3.9,r=0.307 代入公式(2),求出用指数增长模型预测的1810-1920的人口数,见表2.表2 美国实际人口与按指数增长模型计算的人口比较年以后的误差越来越大.分析原因,该模型的结果说明人口将以指数规律无限增长.而事实上,随着人口的增加,自然资源、环境条件等因素对人口增长的限制作用越来越显著.如果当人口较少时人口的自然增长率可以看作常数的话,那么当人口增加到一定数量以后,这个增长率就要随着人口增加而减少.于是应该对指数增长模型关于人口净增长率是常数的假设进行修改.下面的模型是在修改的模型中著名的一个.3. 阻滞增长模型(Logistic 模型)[1]假设:(a )人口增长率r 为人口()t x 的函数()x r (减函数),最简单假定()0, ,>-=s r sx r x r (线性函数),r 叫做固有增长率.(b )自然资源和环境条件年容纳的最大人口容量m x . [2]建立模型: 当mx x =时,增长率应为0,即()m x r =0,于是m x rs =,代入()sxr x r -=得:()⎪⎪⎭⎫⎝⎛-=m x x r x r 1 (3)将(3)式代入(1)得:模型为: ()⎪⎩⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛-=001xx x x x r dt dx m (4)[3] 模型的求解: 解方程组(4)得()rt m me x x x t x -⎪⎪⎭⎫ ⎝⎛-+=110 (5)根据方程(4)作出x dtdx~ 曲线图,见图1-1,由该图可看出人口增长率随人口数的变化规律.根据结果(5)作出x~t 曲线,见图1-2,由该图可看出人口数随时间的变化规律.[4] 模型的参数估计:利用表1中1790-1980的数据对r 和x m 拟合得:r=0.2072, x m =464. [5] 模型检验:将r=0.2072, x m =464代入公式(5),求出用指数增长模型预测的1800-1990的人口数,见表3第3、4列.也可将方程(4)离散化,得)())(1()()()1(t x x t x r t x x t x t x m-+=∆+=+ t=0,1,2,… (6) 用公式(6)预测1800-1990的人口数,结果见表3第5、6列.表3 美国实际人口与按阻滞增长模型计算的人口比较图1-2 x~t 曲线现应用该模型预测人口.用表1中1790-1990年的全部数据重新估计参数,可得r=0.2083, x m=457.6. 用公式(6)作预测得:x(2000)=275; x(2010)=297.9.也可用公式(5)进行预测.。
数学建模人口预测

摘 要中国是一个人口大国,人口问题与我国的经济发展等方面息息相关。
随着我国人口数量的不断变化,人口的老龄化问题也日益突显,政策的调整不可或缺。
从当初实行计划生育政策到逐步放开生育政策再到全面实行二孩政策,我国人口发展呈现了一些新特点。
本文旨在通过多种预测方法对“全面二孩政策”下的人口数量及其结构进行预测,筛选出了经济发展的指标,并分人口结构对经济发展的影响,结论如下:针对问题一,本文参考中国国家统计局等官方资料的数据统计出各年人口总数、自然增长率等数据,建立了logistic 模型,得出人口总数的变化公式,然后建立GM(1,1)预测模型,预测2016年的人口总数,再利用SPSS 进行回归、曲线估计,得出最为符合的方程式,再利用MATLAB 函数拟合工具箱对所得数据进行拟合。
预测出2017-2030年间人口先增后减,在2021年达到峰值。
针对问题二,通过建立BP 神经网络模型,利用GM(1,1)灰色预测处理人口结构数据得到训练及测试数据集,将数据BP 神经网络算法进行多次训练,最终得到具有相当精度的稳定预测结果。
提取相当数量的经济指标并对其进行主成分分析降维处理,之后对主要经济指标及人口结构指标进行多元回归分析得到2020-2030年人口结构对经济发展的影响。
针对问题三,关键词:灰色预测 BP 神经网络 Leslie 人口结构预测模型问题假设1.将我国看做一个封闭系统,没有人口的迁入和迁出2.人口增长只与人口基数、生育率、死亡率等有关3.没有大规模战争及瘟疫等传染性疾病4.假设短期内没有外来物种对人类生存造成影响5.假设所有数据均为准确数据6.假设2050年前医疗水平和科学技术不会对人类的死亡率、出生率造成影响模型符号说明: r : 人口自然增长率 x :总人口数0x :初始年份的人口数量t :时间)()0(k x :灰色预测的原始序列 )(ˆ)0(k x:灰色预测的原始数列预测值 ij x :第i 个指标的第j 个数据i d :第i 岁的死亡率i b :第i 岁的生育率问题一 模型建立首先,我们建立了logistics 模型,具体如下)0(x x rxdtdx == 其次,建立GM(1,1)预测模型GM(1,1)是一阶微分方程模型,其形式为:u ax dtdx=+ 离散形式:u k x a k x =+++∆))1(())1(()1()1(预测公式:a u e a u x k xka ˆˆˆˆ)1()1(ˆˆ)1()1(+⎥⎦⎤⎢⎣⎡-=+- 由导数可知:tt x t t x dt dx t ∆-∆+=→∆)()(lim0 当t ∆很小并且取很小的1单位时,则近似的有:txt x t x ∆∆=-+)()1( 写成离散形式:))1(()()1()1(+∆=-+=∆∆k x k x k x tx由于tx ∆∆)1(涉及到累加列)1(x 的两个时刻的数值,因此,)()1(i x 取前后两个时刻的平均代替更为合理,即将)()(i x i 替换为)]()1([21)1().,...,3,2()],1()([21).,...,3,2()],1()([21)1()1()1()()()()()(k x k x k x n i i x i x x n i i x i x i i i i i ++=+=-+==-+))1(()()1()1(+∆=-+=∆∆k x k x k x txu k x a k x =+++∆))1(())1(()1()1()]()1([21)1()1()1()1(k x k x k x ++=+整理可得 u k x k x a k x+++-=+))]1()((21[)1()1()1()0(表示为矩阵形式:⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⋯-+-⋯+-+-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⋯u a n x n x x x x x n x x x 111)]1()([21)]2()3([21)]1()2([21)()3()2()1()1()1()1()1()1()0()0()0( 不妨令T n x x xy ))(),3(),2(()0()0()0(,⋯=令⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⋯-+-⋯+-+-=u a U n x n x x x x x B ,111)]1()([21)]2()3([21)]1()2([21)1()1()1()1()1()1( 则y B B B ua U BU Y T T 1)(ˆˆˆ-=⎥⎦⎤⎢⎣⎡==,模型求解1.对logistics 模型进行求解 得到总人口变化公式:rte x x 0= (0x 为初始年份人口数,21≥t )2.利用GM (1,1)模型,根据1996-2015年中国总人口数据,对2016年总人口数进行预测。
数学建模作业 求解常微分方程和人口模型问题

实验报告课程名称:数学建模课题名称:求解常微分方程与人口模型专业:信息与计算科学姓名:胡家炜班级:123132完成日期: 2016年 6 月10 日一.求解微分方程的通解(1). dsolve('2*x^2*y*Dy=y^2+1','x')ans =(exp(C3 - 1/x) - 1)^(1/2)-(exp(C3 - 1/x) - 1)^(1/2)i-i(2). dsolve('Dy=(y+x)/(y-x)','x')ans =x + 2^(1/2)*(x^2 + C12)^(1/2)x - 2^(1/2)*(x^2 + C12)^(1/2)(3). dsolve('Dy=cos(y/x)+y/x','x')ans =(pi*x)/2-x*log(-(exp(C25 + log(x)) - i)/(exp(C25 + log(x))*i - 1))*i (4). dsolve('(x*cos(y)+sin(2*y))*Dy=1','x')ans =-asin(x/2 + lambertw(0, -(C30*exp(- x/2 - 1))/2) + 1)(5). dsolve('D2y+3*Dy-y=exp(x)*cos(2*x)','x')ans =C32*exp(x*(13^(1/2)/2 - 3/2)) + C33*exp(-x*(13^(1/2)/2 + 3/2)) + (13^(1/2)*exp(x*(13^(1/2)/2-3/2))*exp((5*x)/2(13^(1/2)*x)/2)*(2*sin(2*x) - cos(2*x)*(13^(1/2)/2 - 5/2)))/(13*((13^(1/2)/2 - 5/2)^2 +4))-(13^(1/2)*exp(x*(13^(1/2)/2+3/2))*exp((5*x)/2+(13^(1/2)*x)/2)*(2 *sin(2*x)+cos(2*x)*(13^(1/2)/2+5/2)))/(13*((13^(1/2)/2 + 5/2)^2 + 4))(6)dsolve('D2y+4*y=x+1+sin(x)','x')ans =cos(2*x)*(cos(2*x)/4 - sin(2*x)/8 + sin(3*x)/12 - sin(x)/4 + (x*cos(2*x))/4 - 1/4) + sin(2*x)*(cos(2*x)/8 - cos(3*x)/12 + sin(2*x)/4 + cos(x)/4 + (x*sin(2*x))/4 + 1/8) + C35*cos(2*x) +C36*sin(2*x)二.求初值问题的解(1). dsolve('x^2+2*x*y-y^2+(y^2+2*x*y-x^2)*Dy=0','y(1)=1','x') ans =(x*((- 4*x^2 + 4*x + 1)/x^2)^(1/2))/2 + 1/2(2). dsolve('D2x+2*n*Dx+a^2*x=0','x(0)=x0','Dx(0)=V0')ans =(exp(-t*(n - (-(a + n)*(a - n))^(1/2)))*(V0 + n*x0 + x0*(-(a + n)*(a - n))^(1/2)))/(2*(-(a + n)*(a - n))^(1/2)) - (exp(-t*(n + (-(a + n)*(a - n))^(1/2)))*(V0 + n*x0 - x0*(-(a + n)*(a - n))^(1/2)))/(2*(-(a + n)*(a - n))^(1/2))三.给出函数f(x)=sinx+cosx在x=0点的7阶taylor展开式以及在x=1处的5阶taylor展开式。
人口普查问题的数学建模

人口普查问题的数学建模在实际的城市管理与城市发展过程中,往往要对城市人口和农村人口发展趋势做出预判,以对城市土地管理、公共设施等资源进行合理分配与规划。
因此,需要用数学的方法来对城市人口发展趋势作出预测。
一、问题的提出现有一地区,农村人口300万,城市人口100万,每年有20%的农村人口移居城市,每年有10%的城市居民移居农村,假设该地区总人口不变,且人口迁移规律也不变,求:⑴一年后该地区农村人口和城市人口的数量⑵5年后该地区的人口状况⑶给出若干年后该地区人口状况的预测。
二、符号约定设城市人口为A0=1000000,农村人口为B0=3000000n年后的城市人口为A n,n年后农村人口为B n每年有比率为a的农村人口移居城市(a=20%)每年有比率为b的城市居民移居农村(b=10%)假设A n+B n=4000000不变三、问题的分析⑴要求得一年后该地区农村人口和城市人口的数量,这些条件都已知,分别是A0、B0、a和b,故可以求解。
⑵要求得5年后该地区的人口状况,须知道4年后城市人口A4与农村人口B4各是多少,以及每年有多少农村人口移居城市,又有多少城市居民移居农村。
每年农村人口移居城市的比率以及城市居民移居农村的比率已知,分别为a和b。
⑶要求得若干年后该地区人口状况的预测,可设为n年后。
须知道最初城市人口A0与农村人口为B0各是多少,以及每年有多少农村人口移居城市,又有多少城市居民移居农村。
而n年后城市人口A n与农村人口B n可由An=A n-1*(1-b)+B n-1*a,Bn=A n-1*b+B n-1*(1-a)递推得出,故可以求解。
四、基本假设⑴所普查城市和农村人口的总数目不变,总和是300万。
⑵最初城市人口A0是100万,农村人口A0是200万,然后根据每年向城市和农村迁移的比率来计算以后每年城市和农村的人口。
⑶下一年的人口是用上一年的人口减去上一年的人口乘以迁移率。
五、模型建立于求解/*tc2.0下运行的模型*//*程序下An,Bn分别为所求n年后城市人口与农村人口*/#include<stdio.h>#include<math.h>AB(int n){float An=1000000,Bn=3000000,A,B;int i;for(i=1;i<=n;i++){A=An;B=Bn;An=A*0.9+B*0.2;Bn=A*0.1+B*0.8;}printf("city:A%d=%.2f\ncontruy:B%d=%.2f\nA%d+B%d=%.0f",n,An,n,Bn,n,n,An+Bn);}/*求城市人口与农村人口状况的函数*/Ch(){clrscr();printf("If you want to play input....1;\n");printf("Exit.........................0.\n\n");printf("Please choose 1or0:");}Play(){int n;clrscr();printf("Please input years n(n>0):");scanf("%d",&n);AB(n);getch();clrscr();}main(){int t;Ch();while((t=getchar())!='0'){if(t=='1'){Play();Ch();}}}六、模型的进一步分析要建立若干年后该地区的人口数量问题的模型,首先要知道每年的前一年的人口数量,然后根据城市和农村人口的迁移率来计算下一年的城市和农村人口,总之每年城市和农村的总人口总是相等的,否责就计算错了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上传是为了分析数学的乐趣,请粘贴复制的时候也多思考哈。
为了更多的学子们2014 年数学建模论文第二套题目:人口增长模型的确定专业、姓名:土木135提交日期:2015/7/2 晚上题目:人口增长模型的确定摘要对美国人口数据的变化进行拟合,并进行未来人口预测,在第一个模型中,考虑到人口连续变化的规律,用微分方程的方法解出其数量随时间变化的方程,用 matlab 里的 cftool 工具箱求出参数,即人口净增长率 r=, 对该模型与实际数据进行对比,并计算了从 1980年后每隔10 年的人口数据,与实际对比,有很大出入。
因此又改进出更为符合实际的阻滞增长模型,应用微分方程里的分离变量法和积分法解出其数量随时间变化的方程,求出参数人口增长率r=和人口所能容纳最大值 x m =, 与实际数据对比,拟合得很好,并预测出 1980年后每隔 10 年的人口数据,与实际对比,比较符合。
为了便于比较两个模型与实际数据的描述情况作对比,又做出了两个模型与实际数据的对比图,以及两个模型的误差图。
关键词:人口预测微分方程马尔萨斯人口增长模型阻滞增长模型一、问题重述1790-1980 年间美国每隔 10 年的人口记录如下表所示表 1 人口记录表试用以上数据建立马尔萨斯 (Malthus) 人口指数增长模型,并对接下来的每隔十年预测五次人口数量,并查阅实际数据进行比对分析。
如果数据不相符,再对以上模型进行改进,寻找更为合适的模型进行预测。
二、问题分析由于题目已经说明首先用马尔萨斯人口增长模型来刻划,列出人口增长指数增长方程并求解,并进行未来 50 年内人口数据预测,但发现与实际数据有较大出入。
考虑到实际的人口增长率是受实际情况制约的,因此,使人口增长率为一变化的线性递减函数,列出人口增长微分方程,求出其方程解,并预测未来五十年内人口实际数据。
三、问题假设1. 假设所给的数据真实可靠 ;2. 各个年龄段的性别比例大致保持不变3. 人口变化不受外界大的因素的影响;4. 马尔萨斯人口模型( 1)单位时间的人口增长率 r 为常数; (2)将 x(t) 视为 t 的连续可微函数。
5. 改进后的模型(阻滞增长模型)(1) 人口净增长率 r 为变化量。
四、变量说明x(t) t 时刻的人口数量x 1790初始时刻的人口数量 r 人口净增长率 x m 环境所能容纳的最大人口数量,即 r(x m ) 0五、模型建立1.马尔萨斯人口增长模型t=1790 时的人口数为 x 1790 , 在 t 到 t+Δt 这一时间间隔内,人口的增长为则得到可建立含初始条件的微分 方程 x'(t) =rx(t) , x(1790) x 1790 =(省略 10^6)其解为 x(t) x1790er (t 1790)2.阻滞增长模型 假设人口增长生长率为人口 x(t) 的线性递减函数,即 x m 。
假设自然资源和环境条件所能承受的最大人口容量为x m ,显然,当 x x m 时, r(x m ) r xr m 0。
所以 s r /r m 。
因此有r(x) r rx / r m 。
于是建立下列微分方程 x'(t) r(1 x(t))x(t) ,x m11 x(1790) 3.9。
把上式化为 ( )dx rd(t 1790)。
分离常 x x x mx mm i 于 由 ) t ( x数并积分得到:x m。
x m r(t 1790)1 ( 1)ex1790六、模型求解1. 马尔萨斯模型求解参数估计 :r 可以用实际数据的线性最小二乘法求解,对于x(t) x1790e r (t 1790),直接求解是比较麻烦的,因此在两边取对数,即lnx(t) ln x1790 r(t 1790) ,记lnx(t) y ,ln x1790 ln3.9 1.36 =a。
则原方程化为 (x) = *exp(r*(t-1790)) 。
利用 1790 —1900 年的数据进行拟合,得到 r=. 所以也能求出方程程序见附录 1。
但本题还可以应用matlab 里的 cftool 工具箱求参数,在命令行中输入得到更精确的解:General model:f(x) = *exp(r*(t-1790))Coefficients (with 95% confidence bounds):r=,得到如图所示结果,其中蓝线表示马尔萨斯人口模型预测人口数据,正方形黑点表示实际人口数据。
图 1. 马尔萨斯人口模型与实际人口数据则每隔 10 年预测人口为 : x1990 332.1 , x2000 412.8 , x2010 517.7, x2020 646.5, x2030 799.3 ,然而查阅相关年份美国实际人口数据, 1990年为百万, 2000年为百万,2010年为百万。
对于 2020年和 2030年实际还没有统计,因为没有发生,但通过前三个数据就可以看出马尔萨斯模型预测人口与实际有很大出入,所以必须对该模型做出改进,得到更符合实际的预测模型。
2. 阻滞增长模型求解通过对x '(t )求导得拐点在x x m / 2时,人口增长速度最大。
在问题分析已经得到该模型的表达式,运用 matlab 里的 cftool 工具箱拟合求出参数 General model:f(x) = a*+*exp(-r*(t-1790)))Coefficients (with 95% confidence bounds):模型预测数据,黑点表示实际人口数据 图 2. 组织增长模型预测数据与实际人口数据根据该方程预测得到 x 1990 , x 2000 , x 2010 , x 2020 , x 2030 .其中 1990, 2000,2010 年这三年的预测人口数斗鱼实际人口数据很接近。
但还是有一定的误差,模 型也存在一定的改进程度才能更符合实际情况。
但从图形看,与实际拟合的很好。
3. 为了便于比较两种模型与实际数据的直观对比, 编出程序附录 2把他们放在一个坐标 系里。
图 3. 两个模型与实际人口数据的对比图形虽然直观,但不具体,因此应算出两种模型与实际的误差值比较,程序见附录 3. 得到下图。
图 4. 马尔萨斯模型与阻滞增长模型误差的比较 从图中可以看出阻滞增长模型的误差更小。
七、结果分析1. 马尔萨斯模型结果分析则 每 隔 10 年 预 测 人 口 为 : x 1990 332.1 , x 2000 412.8 , x 2010 517.7, x 2020 646.5, x 2030 799.3 ,然而查阅相关年份美国实际人 口数据, 1990年为百万, 2000年为百万, 2010年为百万。
对于 2020年和 2030年实际 还没有统计,因为没有发生,但通过前三个数据就可以看出马尔萨斯模型预测人口与实 际有很大出入,所以必须对该模型做出改进,得到更符合实际的预测模型。
2. 阻滞增长模型结果分析根据该方程预测得到 x 1990 , x 2000 , x 2010 , x 2020 , x 2030 . 其中 1990年实际人口为百万, 2000 年为百万, 2010 年为百万,这三年的预测人口数与实际人口 因此 x 285.9 285.9 3.9 1)e 0.02858( t 1790) 并得到如下图, 蓝线表示组织增长数据很接近。
但还是有一定的误差,模型也存在一定的改进程度才能更符合实际情况。
但从图形看,与实际拟合的比较好。
八,模型的评价与推广Malthus 数学模型在短期内具有较好的准确度,简易易行,但是不能准确的预测处人口长期的发展趋势,不具有预测人口长期增长数量的能力。
为此,结合资料,考虑到一些实际因素,建立了能很好滴预测人口数量增长的 logstic 模型。
在人口增长的整个过程中 logistic 模型预测的数据与题中所给数据能很好地在误差范围内,几乎一致。
但由于也存在误差,因此也可以通过相关多项式拟合出其方程,也是可以的,比如二次多项式,但次数不一定越高越好,应使模型所预的数据与实际数据更接近,才是比较好的模型。
logistic 模型在人口预测中,在医疗卫生中可以预测寻找某一疾病的危险因素(以及疾病的发展趋势),预测自然界中种群数量的增长等都发挥着巨大的作用。
九、参考文献[1] 王玉英王建国史加荣鲁萍 . 数学建模及其软件实现北京:清华大学出版社 ,2015.[2] 赵凤群戴芳王小侠肖艳婷数学实验基础西安理工大学理学院2013十、附录程序 1 马尔萨斯模型的线性解法t0=[1790:10:1980];X0=[ ];plot(t,x, 'o' );n=1;a=polyfit(t0,x0,n);y=log(x);p=poly2sym(a)程序 2 人口数量实际值与两种模型预测数据对比图clear;t=[1790:10:1980];nx1=*exp.*(t-1790)); nx2=./ (1+*exp.*(t-1790)));plot(t,x, 'r' ,t,nx1, 'b' ,t,nx2, 'g' );legend( ' 实际值 ' , ' 马尔萨斯模型 ' , '? 阻滞增长模型 ' ) 程序 3 两种模型误差散点图x=[ ];clear; t=[1790:10:1980]; x=[ ];nx1=*exp.*(t-1790)); nx2=./(1+*exp.*(t-1790)));W1=(x-nx1)./x;W2=(x-nx2)./x; plot(t,W1, '*' ,t,W2, 'x' ); legend( ' 马尔萨斯模型误差 ' ,' 阻滞增长模型误差 ' )。
