第7章定量分析中的误差及有效数字答案
分析化学:第七章 定量分析概论

➢ 固体——质量分数
wB
mB mS
例:Fe = 0.5643 或 Fe = 56.43 %
低含量:g / g , ng / g
➢ 气体——体积百分数
空气中的成分 氮气占78%,氧气占21%,稀有气体占
0.94%,二氧化碳占0.03%,其他占0.03%
13
➢ 液体
物质的量浓度 (cB) mol / dm3
➢ Quatitative or quantitative? ➢ How much object (sample) ? ➢ Matrix of composition? ➢ Single or multi-component? ➢ Time available? ➢ Sample supply repeatedly? ➢ Destruction or non-destruction? ➢ Look for a continuous system? ➢
0.01~ 1ml
超微量分析 <0.1mg <0.01ml
7.1.4 定量分析的基本步骤 1.问题提出
2.样品的采集
5.计算分 析结果
3.试样的分解
4.样品的测定
一、分析问题的确定
➢ Nature of sample ? Analyte? Ion? Molecules? Function group?
(1)定性分析 鉴定物质有哪些粒子组成;即“有什么?”
(2)定量分析 测定物质中有关组份的相对含量;“有多少”
(3)结构分析 研究物质组成中各成份元素的价态、官能团和结构。 主要测定物质的分子结构和晶体结构。
7.1.3 分析方法的分类
2. 根据对象不同:
有机分析;无机分析。
3. 根据分析原理的不同:
无机及分析化学第七章 定量分析方法概述课后练习与答案

第七章分析化学概论一、选择题1.消除测量过程中的偶然误差的方法是( )A.空白实验 B.对照实验 C.增加平行测定次数 D.校正仪器2. 下列物质可采用直接法配制标准溶液的是 ( )A.NaOH B.HCl C.无水Na2CO3 D.KMnO43.下列说法错误的是 ( )A.系统误差又称为可测误差 B.系统误差具有单向性C.方法误差属于系统误差 D.偶然误差可完全消除4.下列属于偶然误差的是 ( )A.使用生锈的砝码称量B.标定HCl时所用Na2CO3不纯C.所用试剂含待测组分D.滴定管读数时最后一位估计不准5.05.2010 .01250.0的有效数字位数为( )A.4 B.2C.3 D.16.pH=10.02的有效数字位数为 ( )A.4 B.2C.3 D.无法确定7.用失去结晶水的Na2B4O7.10H2O标定HCl溶液,则测得的浓度会 ( ) A.偏高B.偏低C.与实际浓度一致D.无法确定8.滴定分析中,指示剂颜色发生突变的这一点称为 ( )A.化学计量点B.滴定终点C.既是化学计量点,也是滴定终点D.以上都不对9.测定CaCO3含量时,先加入一定量并且过量的HCl溶液,然后用NaOH标准溶液滴定剩余的HCl溶液,此滴定方式属于( )A.直接滴定B.返滴定C.置换滴定D.简接滴定10.常量分析的试样用量为 ( )A .大于1.0gB .1.0~10gC .大于0.1gD .小于0.1g11.滴定分析中,滴定管的读数误差为±0.01mL ,滴定管的一次滴定需读初、终两次读数,可能引起的最大误差为±0.02mL ,为使滴定的相对误差小于0.1%,终点时消耗的滴定剂的体积至少为 ( )A .10mLB .15mLC .20mLD .无法确定12.用25mL 常量酸碱滴定管进行滴定,结果记录正确的是( )A .18.2B .18.20C .18D .18.00013.已知T HCI/NaON =0.004000 g/ml 、则C HCI 为( )A .0.1000mol/LB .0.004000g/mlC .0.003600g/mlD .0.1097mol/L14.滴定管的读数误差为±0.02ml,若滴定时用去滴定液20.00ml ,则相对误差是( )A .±0.1%B .±0.01%C .±1.0%D .±0.001%15.在标定NaOH 溶液浓度时,某同学的四次测定结果分别为0.1023 mol ·L -1、0.1024 mol ·L -1、0.1022 mol ·L -1、0.1023 mol ·L -1,而实际结果应为0.1088 mol ·L -1,该学生的测定结果 ( )A .准确度较好,但精密度较差B .准确度较差,但精密度较好C .准确度较差,精密度也较差D .系统误差小,偶然误差大16.在定量分析结果的一般表示方法中,通常要求( )A .d R ≤2%B .d R ≤0.02%C .d R ≥0.2% D.d R ≤0.2% 17.T A/B 表示的意义是 ( )A .100ml 标准溶液A 中所含溶质的质量B .1ml 标准溶液A 中所含溶质的质量C .1L 标准溶液A 相当于被测物质B 的质量D .1ml 标准溶液A 相当于被测物质的质量18.T HCl/NaOH =0.003000g/ml ,终点时HCl 消耗40.00 ml ,试样中NaOH 的质量为( )A .0.1200gB .0.01200gC .0.001200gD .0.1200mg19.欲配制1000ml 0.1mol/L HCl 溶液,应取浓盐酸(12mol/L HCl)( )ml 。
误差计算带答案技术总结

误差计算带答案技术总结各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢是XX最新发布的《误差计算带答案技术总结》的详细范文参考文章,好的范文应该跟大家分享,重新整理了一下发到这里[http://]。
篇一:误差计算(带答案)1、(C)2、(B)3、(A)4、(A)5、(A)6、(D)7、(C)8、(A)9、(C)10、(A)11、(C)12、(D)14、(A)15、(B)16、(A)17、(B)18、(C)19、(C)20、(B)21、(A)22、(A)23、(D)24、(B)25、(B)第五章测量误差(练习题)一、选择题1、对某一量进行观测后得到一组观测值,则该量的最或是值为这组观测值的(C)。
A.最大值B.最小值C.算术平均值D.中间值2、观测三角形三个内角后,将它们求和并减去180°所得的三角形闭合差为(B)。
A.中误差B.真误差C.相对误差D.系统误差3、系统误差具有的特点为(A)。
A.偶然性B.统计性C.累积性D.抵偿性4、在相同的观测条件下测得同一水平角角值为:173°58′58”、173°59′02”、173°59′04”、173°59′06”、173°59′10”,最全面的范文参考写作网站则观测值的中误差为(A)。
A.±”B.±”C.±”D.±”5、一组测量值的中误差越小,表明测量精度越(A)A.高B.低C.精度与中误差没有关系D.无法确定6、边长测量往返测差值的绝对值与边长平均值的比值称为(D)。
A.系统误差B.平均中误差C.偶然误差D.相对误差7、对三角形三个内角等精度观测,已知测角中误差为10″,则三角形闭合差的中误差为(C)。
A.10″ B.30″C.″D.″8、两段距离及其中误差为:D1=±,D2=±,比较它们的测距精度为(A)。
A.D1精度高B.两者精度相同(转载于: XX:误差计算带答案技术总结)C.D2精度高D.无法比较9、设某三角形三个内角中两个角的测角中误差为±4″和±3″,则求算的第三个角的中误差为(C)。
定量分析中的误差及数据处理

(3)试剂误差 所用试剂纯度差,有杂质。
例:去离子水不合格 试剂级别不合适
(4)主观误差 操作人员主观因素造成。
例:指示剂颜色辨别偏深或偏浅 滴定管读数位置不正确
2. 偶然误差产生的原因 (1)偶然因素 (2)滴定管读数
平均偏差:
d
1 n
n
| xi
i 1
x
|
相对平均偏差: d 100 % x
特点:简单
缺点:大偏差得不到应有反映
2. 标准偏差 标准偏差的计算分两种情况:
(1) 当测定次数趋于无穷大时:
总体标准偏差 : X 2 / n
μ 为无限多次测定 的平均值(总体平均值), 即
lim
n
1 n
n i 1
3. 过失误差产生的原因
(三) 误差减免方法 1. 系统误差的减免 方法误差—— 采用标准方法,对比实验 仪器误差—— 校正仪器 试剂误差—— 作空白实验 2. 偶然误差的减免 增加平行测定的次数
思考题:
1.下列叙述错误的是:
A.方法误差属于系统误差 B.系统误差包括操作误差 C.系统误差又称可测误差 D.系统误差呈正态分布 E. 系统误差具有单向性
定量分析中的误差和数据处理
分析测试的误差与偏差 误差产生的原因及其减免方法 分析结果的数据处理 分析测试结果准确度的的评价 有效数字及其运算规则
一、分析测试的误差与偏差
误差和准确度 偏差和精密度 准确度和精密度的关系
1.误差和准确度
准确度: 测定值与真实值的接近程度。 准确度的高低用误差来衡量。
C 20.6,20.9,21.1,21.0 D 20.8,20.6
第7章-多组定量资料的比较思考与练习参考答案

第7章 多组定量资料的比较思考与练习参考答案一、最佳选择题1. 完全随机设计资料的方差分析中,必然有( C )。
A. 组间SS >组内SSB. 组内组间总MS MS MS +=C. 总ss=组间SS +组内SSD. 组内组间MS MS >E. 组间组内νν> 2. 定量资料两样本均数的比较,可采用( D )。
A. t 检验B.F 检验C. Bonferroni 检验D. t 检验与F 检验均可E. LSD 检验3. 当组数等于2时,对于同一资料,方差分析结果与t 检验结果相比,( C )。
A. t 检验结果更为准确B. 方差分析结果更为准确C. 完全等价且F t =D. 完全等价且t F =E. 两者结果可能出现矛盾4. 若单因素方差分析结果为),(01.021ννF F >,则统计推断是( D )。
A. 各样本均数都不相等B. 各样本均数不全相等C. 各总体均数都不相等D. 各总体均数不全相等E. 各总体均数全相等 5. 完全随机设计资料的方差分析中,组间均方表示( C )。
A. 抽样误差的大小B. 处理效应的大小C. 处理效应和抽样误差综合结果D. N 个数据的离散程度E. 随机因素的效应大小 6. 多样本定量资料比较,当分布类型不清时应选择( D )。
A. 方差分析B. t 检验C. Z 检验D. Kruskal-Wallis 检验E. Wilcoxon 检验7. 多组样本比较的Kruskal-Wallis 检验中,当相同秩次较多时,如果用H 值而不用校正后的c H 值,则会( C )。
A . 提高检验的灵敏度B .把一些无差别的总体推断成有差别 C. 把一些有差别的总体推断成无差别 D .Ⅰ、Ⅱ类错误概率不变E. 以上说法均不对二、思考题1. 方差分析的基本思想和应用条件是什么?答:方差分析的基本思想是,对于不同设计的方差分析,其思想都一样,即均将处理间平均变异与误差平均变异比较。
定量分析中的误差及

2021/7/30
精选ppt课件
22
一、产生误差的原因
准确度:实验值与真实值之间相符合的 程度。
误差越小,准确度越高; 误差越大,准确度越低。
2021/7/30
精选ppt课件
6
一、准确度与误差
例2:测定值57.30,真实值57.34 测定值为80.35,真实值80.39
求:绝对误差(E),相对误差(RE)
讨论:绝对误差与相对误差的不同?
2021/7/30
精选ppt课件
8
二、精密度与偏差
精密度:相同条件下几次重复测定结 果彼此相符合的程度。
精密度大小由偏差表示。 偏差愈小,精密度愈高。
2021/7/30
精选ppt课件
9
二、精密度与偏差
偏差 算术平均偏差 偏差的表示 标准偏差 极差 公差
2021/7/30
精选ppt课件
10
二、精密度与偏差
1.偏差 _
…,n)
n
_ __
相对平均偏差(d%)= (d / x ) × 100%
算术平均偏差:是指单项测定值与平均值的偏差 (取绝对值)之和,除以测定次数。
2021/7/30
精选ppt课件
12
二、精密度与偏差
例4:55.51,55.50,55.46,55.49,55.51
__ _ 求:x,d,d%
J解:
_ X=55.49
仪器分析(第三版)课后题答案第七章
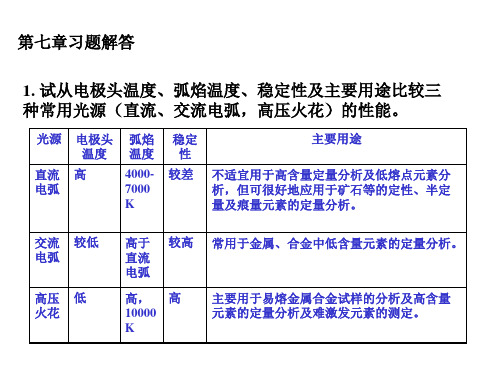
5. 光谱定性分析的基本原理是什么?进行光谱定性分析时可 光谱定性分析的基本原理是什么? 以有哪几种方法?说明各个方法的基本原理和使用场合。 以有哪几种方法?说明各个方法的基本原理和使用场合。 解:由于各种元素的原子结构不同,在光源的激发下,可以 由于各种元素的原子结构不同,在光源的激发下, 产生各自的特征谱线, 产生各自的特征谱线,其波长是由每种元素的原子性质决定 具有特征性和唯一性, 的,具有特征性和唯一性,因此可以通过检查谱片上有无特 征谱线的出现来确定该元素是否存在, 征谱线的出现来确定该元素是否存在,这就是光谱定性分析 的基础。 的基础。 进行光谱定性分析有以下三种方法: 进行光谱定性分析有以下三种方法: (1)比较法。将要检出元素的纯物质或纯化合物与试样并列 )比较法。 摄谱于同一感光板上, 摄谱于同一感光板上,在映谱仪上检查试样光谱与纯物质光 若两者谱线出现在同一波长位置上, 谱。若两者谱线出现在同一波长位置上,即可说明某一元素 的某条谱线存在。本方法简单易行, 的某条谱线存在。本方法简单易行,但只适用于试样中指定 组分的定性。 组分的定性。
10. 试述光谱半定量分析的基本原理,如何进行? 试述光谱半定量分析的基本原理,如何进行? 解:光谱半定量分析主要有三种方法. 光谱半定量分析主要有三种方法. (1)谱线呈现法,当分析元素含量降低时,该元素的谱线 谱线呈现法,当分析元素含量降低时, 数目也会逐渐减少, 数目也会逐渐减少,可以根据一定实验条件下出现特征谱线 的数目来进行半定量分析. 的数目来进行半定量分析. (2)谱线强度比较法.可以将被测元素配制成不同浓度 谱线强度比较法. 的标准系列,然后分别与试样同时摄谱, 的标准系列,然后分别与试样同时摄谱,并控制相同的摄 谱条件, 谱条件,通过比较被测元素的灵敏线与标准试样中该元素 的相应谱线的黑度,用目视进行比较,进行半定量分析. 的相应谱线的黑度,用目视进行比较,进行半定量分析.
分析化学课后习题答案第七章

第七章重量分析法和沉淀滴定法思考题1.沉淀形式和称量形式有何区别?试举例说明之。
答:在重量分析法中,沉淀是经过烘干或灼烧后再称量的。
沉淀形式是被测物与沉淀剂反应生成的沉淀物质,称量形式是沉淀经过烘干或灼烧后能够进行称量的物质。
有些情况下,由于在烘干或灼烧过程中可能发生化学变化,使沉淀转化为另一物质。
故沉淀形式和称量形式可以相同,也可以不相同。
例如:BaSO4,2+其沉淀形式和称量形式相同,而在测定Mg时,沉淀形式是MgNH4PO4·6H2O,灼烧后所得的称量形式却是Mg2P2O7。
2.为了使沉淀定量完全,必须加人过量沉淀剂,为什么又不能过量太多?答:在重量分析法中,为使沉淀完全,常加入过量的沉淀剂,这样可以利用共同离子效应来降低沉淀的溶解度。
沉淀剂过量的程度,应根据沉淀剂的性质来确定。
若沉淀剂不易挥发,应过量20%~50%;若沉淀剂易挥发,则可过量多些,甚至过量100%。
但沉淀剂不能过量太多,否则可能发生盐效应、配位效应等,反而使沉淀的溶解度增大。
3.影响沉淀溶解度的因素有哪些?它们是怎样发生影响的?在分析工作中,对于复杂的情况,应如何考虑主要影响因素?答:影响沉淀溶解度的因素有:共同离子效应,盐效应,酸效应,配位效应,温度,溶剂,沉淀颗粒大小和结构等。
共同离子效应能够降低沉淀的溶解度;盐效应通过改变溶液的离子强度使沉淀的溶解度增+加;酸效应是由于溶液中H浓度的大小对弱酸、多元酸或难溶酸离解平衡的影响来影响沉淀的溶解度。
若沉淀是强酸盐,如BaSO4,AgCl等,其溶解度受酸度影响不大,若沉淀是弱酸或多元酸盐[如CaC2O4、Ca3(PO4)2]或难溶酸(如硅酸、钨酸)以及与有机沉淀剂形成的沉淀,则酸效应就很显著。
除沉淀是难溶酸外,其他沉淀的溶解度往往随着溶液酸度的增加而增加;配位效应是配位剂与生成沉淀的离子形成配合物,是沉淀的溶解度增大的现象。
因为溶解是一吸热过程,所以绝大多数沉淀的溶解度岁温度的升高而增大。
中南大学《分析化学》网上(课程)作业一及参考答案

(一) 单选题1.用分度值为0.1g的台秤称取20g的物品,最多可以记录()位有效数字。
(A) 1 (B) 2 (C) 3 (D) 4参考答案:(C)2.在滴定管上读取溶液的体积为24mL,应该记录为()。
(A) 24mL (B) 24.0mL (C) 24.00mL (D) 24.000mL参考答案:(C)3.可用下列何种方法减免分析测试中的系统误差()。
(A) 进行仪器校正(B) 增加测定次数(C) 认真细心操作析(D) 测定时保证环境的湿度一致参考答案:(A)4.滴定管可估读到±0.01mL,若要求滴定的相对误差小于0.1%,至少应耗用体积()毫升。
(A) 10(B) 20(C) 30(D) 40参考答案:(B)5.称得某物质质量为0.5180g,它表示该物实际质量是(0.5180±0.0002)g,其相对误差为()。
(A) ±0.04%(B) ±0.03%(C) ±0.004%(D) 0.04%参考答案:(A)6.下列表述中,最能说明随机误差小的是()。
(A) 高精密度(B) 与已知的质量分数的试样多次分析结果的平均值一致(C) 标准差大(D) 仔细校正所用砝码和容量仪器等参考答案:(A)7.下列有关随机误差的叙述中不正确的是()。
(A) 随机误差具有随机性(B) 随机误差具有单向性(C) 随机误差在分析中是无法避免的(D) 随机误差是由一些不确定的偶然因素造成的参考答案:(B)8.分析Si02的质量分数得到两个数据:35.01%,35.42%,按有效数字规则其平均值应表示为()。
(A) 35.215% (B) 35.22% (C) 35.2% (D) 35%参考答案:(C)9.定量分析中,精密度与准确度之间的关系是()。
(A) 精密度高,准确度必然高(B) 准确度高,精密度也就高(C) 高精密度是保证准确度的前提(D) 准确度是保证精密度的前提参考答案:(C)10.在滴定分析测定中,属偶然误差的是()。
定量分析中的误差及有效数字练习题

11误差表示分析结果的_______;偏差表示分析结果的_______。
答案:准确度好坏;精密度高低
12多次分析结果的重现性愈好,则分析的精密度愈_______。
答案:高
13用相同的方法对同一个试样平行测定多次,得到的n次测定结果相互接近的程度,称为_______。测定值与真值之间接近的程度,称为_______。
答案: A, C, E
2提高分析结果准确度的方法是()。
A:做空白试验B:增加平行测定的次数C:校正仪器D:使用纯度为98%的基准物
E:选择合适的分析方法
答案: A, B, C, E
3系统误差产生的原因有()。
A:仪器误差B:方法误差C:偶然误差D:试剂误差E:操作误差
答案: A, B, D, E
4准确度的高低用()大小来表示。
9不加试样,按照试样分析步骤和条件平行进行的分析试验,称为_______。通过它主要可以消除由试剂、蒸馏水及器皿引入的杂质造成的_______。
答案:空白试验。仪器和试剂误差
10系统误差的减免是采用校正仪器以及做_______试验、试验和空白试验等办法减免的,而偶然误差则是采用增加_______的办法,减小偶然误差。
19下列一组分析结果的平均偏差为( )。55.51 55.50 55.46 55.49 55.51
A: 55.49B: 0.016C: 0.028D: 0.008
答案: B
20托盘天平读数误差在2克以内,分析样品应称至( )克才能保证称样相对误差为1%。
A: 100克B: 200克C: 150克D: 50克
答案: B
6测定精密度好,表示().
A:系统误差小B:偶然误差小C:相对误差小D:标准偏差小
化验员培训系列7误差分析及数据处理

▪ 但进行多次测定,便会发现偶然误差具有很多的规律性
(象核外电子运动一样),概率统计学就是研究其规律的一 门学科,后面会部分的讲授。特点:
▪ 有一矿石试样,在相同条件下用吸光光度法测定其中铜
的质量分数,共有100个测量值。
▪ a:正负误差出现的概率相等。 ▪ b:小误差出现的机会大,大误差出现的概率小。
▪ 如何尽量减少误差,误差所允许的范围有多大,误差有何
规律性,这是这一节所要学习的内容,
▪ 掌握误差的规律性,有利于既快速又准确地完成测定任务。
例如,用不同类型的天平称量同一试样,所得称量结果如 表3-1所示:
使用的仪器 误差范围(g)称量结果(g) 真值的范围 (g)
台天平
± 0.1
5.1
5.1±0.1
二、减小测量误差
▪ 由于容量分析和重量分析要求相对误差< 2 ‰ ,即要有
四位有效数字,最后一位为可疑值。根据误差传递原理 (由于结果的计算一般都有各步骤测量结果的相互乘除) 每一步测定步骤的结果都应有四位有效数字。
▪ 如称量时,分析天平的称量误差为0.0001,滴定管的读
数准确至0.01 ml, 要使误差小于1 ‰, 试样的重量和 滴定的体积就不能太小。
法进行分析以资对照,也可以用不同的分析方法,或者由 不同单位的化验人员分析同一试样来互相对照,标准试样 组成应尽量与试样组成相近。
▪ 如,在进行新的分析方法研究时,常用标准试样来检验方
法的准确度,或用国家规定的标准方法对同一试样进行分 析。
▪ 又如,在工厂的产品检验中,为了检查分析人员的操作规
范化或仪器等是否存在系统误差,常用标准试样给分析人 员做,或同一试样给不同分析人员做,这叫“内检”,将 试样送交外单位进行对照分析,这叫“外检”。
定量分析中的误差和数据处理

定量分析中的误差和数据处理自测题一.填空题1.系统误差的特征是:,,,。
2.随机误差的特征是:,,,。
3.在分析过程中,下列情况各造成何种(系统、随机)误差(或过失)?(1)天平两臂不等长,引起。
(2)称量过程中天平零点略有变动,是。
(3)过滤沉淀时出现穿滤现象,是。
(4)读取滴定管最后一位时,估测不准,是。
(5)蒸馏水中含有微量杂质,引起。
(6)重量分析中,有共沉淀现象,是。
4.测定饲料中淀粉含量,数据为20.01%,20.03%,20.04%,20.05%。
则淀粉含量的平均值为;测定的平均偏差为;相对平均偏差为;极差为。
5.总体平均值μ是当测量次数为时,各测定值的值。
若没误差,总体平均值就是值。
6.测定次数n为时,标准偏差S的表达式为,式中的n –1被称为。
7.对某一溶液中NaOH的浓度测定4次,其结果分别是:0.2043, 0.2039, 0.2049, 0.2041mol/L。
则这一组测量的平均值x为,平均偏差d为,标准偏差S为。
由结果可知,同一组测量值的标准偏差值比平均偏差值,说明标准偏差对于更敏感。
8.检验分析结果的平均值与标准值之间是否存在显著性差异,应当用检验法;判断同一试样的两组测定结果的平均值之间是否存在显著性差异,应先用检验法判断两组数据的是否有显著性差异,再进一步用检验法判断平均值之间是否有显著性差异。
9.25.5508有位有效数字,若保留3位有效数字,应按的原则修约为。
计算下式0.1001(25.450821.52)246.432.03591000⨯-⨯⨯并按有效数字保留原则所得的结果为。
10.根据有效数字修约规则计算下列各式:pH = 3.25,[H+] = ;pH = 6.74,[H+] = ;[H+] = 1.02×10-5,pH = 。
[H+] = 3.45×10-5,pH = 。
二. 正误判断题1.测定方法的准确度高,精密度一定高。
2.测定方法的精密度高,不一定能保证准确度也高。
定量分析误差范文

定量分析误差范文引言:1.仪器误差:精密仪器在设计、生产和使用过程中都难免出现一定的误差,例如测量仪器的刻度不准确或灵敏度不均匀,都会引起定量分析结果的误差。
2.人为误差:在进行定量分析实验时,操作人员的技术水平和经验都可能会产生误差。
比如,分析前不完全洗净实验设备,导致前后两次实验结果不一致;又或者在样本制备过程中,误差地加入了其他物质,导致结果偏差。
二、误差的影响因素:1.实验条件:实验环境的温度、湿度、光照等因素都会对定量分析结果产生一定的影响。
例如,在温度较高的条件下进行溶解实验,会导致反应速率加快,进而影响溶解度的测量结果。
2.样品质量:样品的纯度、含水量、杂质等因素都会对定量分析结果产生影响。
例如,在测定食品中其中一种成分的含量时,如果样品本身含有其他成分的杂质,就会导致实际测量出的该成分含量低于真实值。
3.数据处理方法:对于定量分析结果的数据处理方法也会对结果准确性产生影响。
例如,使用不恰当的统计方法或者对数据处理过程中出现漏算或重复计算等错误,都会导致结果偏差。
三、解决误差的方法和建议:1.选用合适的仪器和设备:在进行定量分析实验前,要仔细选择合适的仪器和设备,并保证其准确性和稳定性。
同时,在使用过程中要进行仪器的校准和维护,以减小仪器误差的影响。
2.确保实验条件的一致性:在进行定量分析实验时,尽可能保持实验条件的一致性,例如温度、湿度等环境因素,以减小其对结果的影响。
3.提高操作人员的技术水平:操作人员要具备扎实的理论基础和丰富的实验经验,在实验操作过程中严格按照标准操作程序进行,减小人为误差的产生。
4.样品制备和处理的标准化:在进行定量分析实验前,要对样品进行合适的制备和处理,保证样品的纯度和质量。
同时要规范操作流程,减小样品制备过程中的误差。
5.合理选择数据处理方法:对于定量分析结果的数据处理,要选择合适的统计学方法,并进行严谨的计算过程,以确保结果的准确性。
6.多次重复实验:在进行定量分析时,可通过多次重复实验来取平均值或者计算标准差,以提高结果的可靠性。
定量分析中的误差

二、在有效数字中“0”的意义
1、“0”在第一个不为零的数字前面时,只起定位作
用,不是有效数字, 2、“0”在数字中间或最末一位不为零的数字后 面时 ,是有效数字 如: 一个物体重0.0060g,有 2位 有效数字。 若用毫克表示为6.0mg,仍为 2位 有效数字
0.02003 四位
0.010500 五位
i 1
n
2
n 1
di
i 1
n
2
n 1
3、相对标准偏差(变异系数):标准偏差 在平均值中所占 的百分率
相对标准偏差 s 100% x
有甲乙两组数据,其各次测定的偏差分别为
甲组: +0.11、-0.73*、+0.24、+0.51 *、-0.14、0.00、+0.30、-0.21 n1=8
奇数还是偶数
均入
例:将下列数字修约为4位有效数字。 14.4350 27.1652 约。 14.44 27.17 157.450 157.4
在确定修约位数后,应 一次 修约获得结果,不得多次连续修
四、有效数字运算规则
1、加减运算
几个数相加或相减时,它们的和或差的有效数字的保留应
以小数点
后位数最少(即绝对误差最大)的数为准。
1 2 n n 1 2 n i 1 i
相对平均偏差是 平均偏差 在平均值中所占的百分率
相对平均偏差 d 100% x
平均偏差不计正负号,而各次测得值的偏差是有 正负 的
(三)标准偏差
1、总体标准偏差:σ =
( )
i 1
n
2
n
2、标准偏差:(s)测定次数n<20
s
( xi x )
使分析结果总是偏高或偏低,在多次平行测定中
定量分析中误差及数据处理
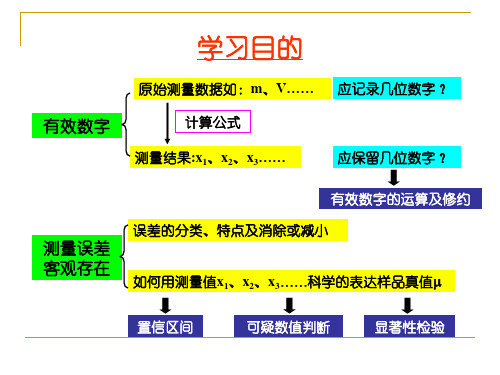
系统误差的来源及消除
方法误差:方法选择不适当,如重量法中沉淀剂选择不当 —选用其他方法或校正
试剂误差:不纯或存在干扰物质 —更换试剂或做空白实验扣除
仪器误差:如刻度不准、砝码磨损等 —校正
主观误差:如颜色观察、读数习惯等 —加强技术训练
系统误差和随机误差的比较
项目
系统误差
随机误差
产生原因 固定因素,有时不存在
不定因素,总是存在
分类 性质
方法误差、仪器误差、试剂误 环境的变化因素、主
差、主观误差
观的变化因素等
重现性、单向性(周期性)、 服从概率统计规律、
可测性
不可测性
影响
准确度
精密度
消除/减小 校正(理论上可消除)
的方法
增加测定的次数 (减小)
容量瓶和移液管体积不准确
系统误差;校正
❖试剂中含有微量的被测组分 天平零点有微小的变动 读取滴定体积时最后一位估读略有不准 读取滴定体积时眼睛习惯性仰视
系统误差;提纯或空白实验 随机误差 随机误差 系统误差;加强训练
滴定时不慎从锥形瓶中溅出一滴溶液 用定性滤纸代替定量滤纸
过失;重做 系统误差;改用定量滤纸
很重要,但由于实际计算很困难,且在通常的分析测定中
较少应用,因此不作要求。
3-2 误差的传递(2)
虽然不要求掌握由测量值的误差来估算分析结果误差, 但应当 知道测量过程中误差是不断积累的,最终误差主要由误差最大 的那一步决定,因此设计实验时应使分析各环节的测量误差基 本接近,以使分析测定准确、快速进行。
3-1 误差的基本概念(5)
公差(允许差):是由多次测定所得的一系列数据中最大 值和最小值的允许界限,生产部门对分析结果误差允许的 一种限量。
资料:分析化学中的误差与数据处理习题-上交

2.1定量分析中误差的基本概念2.1.1 误差、误差的分类及其特点1. 从精密度好就可以判定分析结果可靠的前提是(B)A、偶然误差小B、系统误差小C、平均偏差小D、标准偏差小2. 下列叙述正确的是(A)A、准确度高,一定需要精密度高B、进行分析时,过失误差是不可避免的C、精密度高,准确度一定高D、精密度高,系统误差一定小3. 下列叙述错误的是(D)A、方法误差属于系统误差B、系统误差包括操作误差C、系统误差又称可测误差D、系统误差呈正态分布4. 下列各项造成偶然误差的是(D)A、天平称量时把13.659g记录为13.569gB、称量时不正确地估计天平的平衡点C、称量时有吸湿的固体时湿度有变化D、在称量时天平的平衡点稍有变动5. 下列叙述中正确的是(A)A、误差是以真值为标准的,偏差是以平均值为标准的,实际工作中获得的“误差”,实际上仍然是偏差B、随机误差是可以测量的C、精密度高,则该测定的准确度一定会高D、系统误差没有重复性,不可避免6.下列各项中属于过失误差的是(A)A、实验中错误区别两个样品滴定终点时橙色的深浅B、滴定时温度有波动C、滴定时大气压力有波动D、称量吸湿性固体样品时动作稍慢7. 对某试样进行3次平行测定,其平均含量为0.3060.若其实值为0.3030,则(0.3060-0.3030)=0.0030是误差。
(C)A、相对误差B、相对偏差C、绝对误差D、绝对偏差8. 分析结果出现下列情况,属于系统误差。
(C)A、试样未充分混匀B、滴定时有液滴溅出C、称量时试样吸收了空气中的水分D、天平零点稍有变动9. 精密度和准确度的关系是(D)A、精确度高,准确度一定高B、准确度高,精密度一定高C、二者之间无关系D、准确度高,精密度不一定高10. 下列情况中,使分析结果产生正误差的是(B)A、以HCl标准溶液滴定某碱样,所用滴定管未用原液润洗B、用于标定标准溶液的基准物在称量时吸潮了C、以失去部分结晶水的硼砂为基准物,标定盐酸溶液的浓度D 、以EDTA 标准溶液滴定钙镁含量时,滴定速度过快11. 分析某样品得到四个分析数据,为了衡量其精密度优劣,可用 表示 (C )A 、相对误差B 、绝对误差C 、平均偏差D 、相对误差12. 由测量所得的下列计算式中,每一个数据最后一位都有±1的绝对误差,在计算结果x 中引入的相对误差最大的数据为x (A)A 、0.0670B 、30.20C 、45.820D 、300013. 下列叙述错误的是 (C)A 、误差是以真值为标准的,偏差是以平均值为标准的,实际工作中获得的所谓“误差”,实质上仍是偏差B 、对某项测定来说,它的系统误差大小是不可测量的C 、对偶然误差来说,大小相近的正误差和负误差出现的机会是均等的D 、标准偏差是用数理统计方法处理测定的数据而获得的14. 下列叙述中正确的是 (D)A 、偏差是测定值与真实值的差值B 、算术平均偏差又称相对平均偏差C 、相对平均偏差的表达式为1n n n x x d n =-=∑D 、相对平均偏差的表达式为100%d x⨯ 2.1.2 偶然误差分布的数理统计规律1. 分析测定中的偶然误差,就统计规律来讲,以下不符合的是 (A)A 、数值固定不变 C 、大误差出现的概率小,小误差出现的概率大B 、数值随机可变 D 、数值相等的正、负误差出现的概率均等2. 从误差的正态分布曲线可知,标准偏差在±2之内的测定结果占全部分析结果的(C)A 、68.3%B 、86.3%C 、95.5%D 、99.7%3. 分析数据的可靠性随平行测定次数的增加而提高,但达到一定次数后,再增加测定次数也就没有意义了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考题1. 指出在下列情况下,各会引起哪种误差如果是系统误差,应该用什么方法减免(1) 砝码被腐蚀;答:引起系统误差(仪器误差),采用校准砝码、更换砝码。
(2) 天平的两臂不等长;答:引起系统误差(仪器误差),采用校正仪器(天平两臂等长)或更换仪器。
(3) 容量瓶和移液管不配套;答:引起系统误差(仪器误差),采用校正仪器(相对校正也可)或更换仪器。
(4) 试剂中含有微量的被测组分;答:引起系统误差(试剂误差),采用空白试验,减去空白值。
(5) 天平的零点有微小变动;答:随机(偶然)误差。
(6) 读取滴定管体积时最后一位数字估计不准;答:随机(偶然)误差。
采用读数卡和多练习,提高读数的准确度。
(7) 滴定时不慎从锥形瓶中溅出一滴溶液;答:过失,弃去该数据,重做实验。
(8) 标定HCl 溶液用的NaOH 标准溶液中吸入CO2。
答:系统误差(试剂误差)。
终点时加热,除去CO2,再滴至稳定的终点(半分钟不褪色)。
2. 判断下列说法是否正确(1) 要求分析结果达到%的准确度,即指分析结果的相对误差为%。
(2) 分析结果的精密度高就说明准确度高。
(3) 由试剂不纯造成的误差属于偶然误差。
(4) 偏差越大,说明精密度越高。
(5) 准确度高,要求精密度高。
(6) 系统误差呈正态分布。
(7) 精密度高,准确度一定高。
(8) 分析工作中,要求分析误差为零。
(9) 偏差是指测定值与真实值之差。
(10) 随机误差影响测定结果的精密度。
(11) 在分析数据中,所有的“0”均为有效数字。
(12) 方法误差属于系统误差。
(13) 有效数字中每一位数字都是准确的。
(14) 有效数字中的末位数字是估计值,不是测定结果。
(15) 有效数字的位数多少,反映了测量值相对误差的大小。
(16) 有效数字的位数与采用的单位有关。
(17) 对某试样平行测定多次,可以减少系统误差。
(18) Q检验法可以检验测试数据的系统误差。
答:(1) 对;(2) 错;(3) 错;(4) 错;(5) 对;(6) 错;(7) 错;(8) 错;(9) 错;(10) 对;(11) 错;(12) 对;(13) 错;(14) 对;(15) 对;(16) 错;(17) 错;(18) 错3. 单选题(1) 准确度和精密度的正确关系是……………………..……………………………………………….( )(A) 准确度不高,精密度一定不会高 (B) 准确度高,要求精密度也高(C) 精密度高,准确度一定高 (D) 两者没有关系(2) 从精密度好就可判断分析结果准确度的前提是…………………..……………………………….( )(A) 偶然误差小 (B) 系统误差小 (C) 操作误差不存在(D) 相对偏差小(3) 以下是有关系统误差叙述,错误的是………………………………...…………………………….( )(A) 误差可以估计其大小 (B) 误差是可以测定的(C) 在同一条件下重复测定中,正负误差出现的机会相等 (D) 它对分析结果影响比较恒定(4) 测定精密度好,表示………….…………………………………..………………………………….( )(A) 系统误差小 (B) 偶然误差小 (C) 相对误差小 (D) 标准偏差小(5) 下列叙述中错误的是…………….……………………………………..…………………………….( )(A) 方法误差属于系统误差 (B) 系统误差具有单向性(C) 系统误差呈正态分布 (D) 系统误差又称可测误差(6) 下列因素中,产生系统误差的是………………………………………….………………………….( )(A) 称量时未关天平门 (B) 砝码稍有侵蚀(C) 滴定管末端有气泡 (D) 滴定管最后一位读数估计不准(7) 下列情况所引起的误差中,不属于系统误差的是……..………………..………………………….( )(A) 移液管转移溶液后残留量稍有不同 (B): 称量时使用的砝码锈蚀(C) 天平的两臂不等长 (D) 试剂里含微量的被测组分(8) 下述说法不正确的是……..…..………………..…………………….………………………………. ( )(A) 偶然误差是无法避免的 (B) 偶然误差具有随机性(C) 偶然误差的出现符合正态分布 (D) 偶然误差小,精密度不一定高(9) 下列叙述正确的是……….…………………..………………………………………………………. ( )(A) 溶液pH为,读数有四位有效数字 (B) 0.0150g试样的质量有4位有效数字(C) 测量数据的最后一位数字不是准确值(D) 从50mL滴定管中,可以准确放出标准溶液(10) 分析天平的称样误差约为0.0002克,如使测量时相对误差达到%,试样至少应该称……….( )(A) 0.1000克以上 (B) 0.1000克以下 (C) 0.2克以上(D) 0.2克以下(11) 精密度的高低用()的大小表示………………………..………………………………………….( )(A) 误差 (B) 相对误差 (C) 偏差 (D) 准确度(12) 分析实验中由于试剂不纯而引起的误差属于…………………..…………….……………..…….( )(A): 系统误差 (B) 过失 (C) 偶然误差 (D)方法误差(13) 四次测定结果:、、、,其分析结果的平均值为……………………….( )(A) (B) (C) % (D) %(14) 配制一定摩尔浓度的NaOH溶液时,造成所配溶液浓度偏高的原因是…..…………………….( )(A) 所用NaOH固体已经潮解 (B): 向容量瓶倒水未至刻度线(C) 有少量的NaOH溶液残留在烧杯中 (D) 用带游码的托盘天平称NaOH固体时误用“左码右物”(15) 四次测定结果:、、、、,其分析结果的平均偏差为………..………….( )(A) (B) (C) (D)(16) 托盘天平读数误差在2克以内,分析样品应称至( )克才能保证称样相对误差为1% 。
…..…….( )(A) 100克 (B) 200克 (C) 150克 (D) 50克(17) 滴定时,不慎从锥形瓶中溅失少许试液,是属于…………………….……..…………………….( )(A) 系统误差 (B) 偶然误差 (C) 过失 (D) 方法误差(18) 绝对偏差是指单项测定与( )的差值。
…………………….……………..…..…………………….( )(A) 真实值 (B): 测定次数 (C) 平均值 (D) 绝对误差(19) 要求滴定分析时的相对误差为%,50mL滴定管的读数误差约为毫升,滴定时所用液体体积至少要( )亳升。
…………………………………………………….……………..…..…………………….( )(A) 15毫升 (B) 10毫升 (C) 5毫升 (D) 20毫升(20) 四次测定结果:、、、,其分析结果的变异系数(相对标准偏差)为………….( )(A) % (B) % (C) % (D) %(21) 四次测定结果:、、、,其分析结果的标准偏差为…………….…………….( )(A) (B) (C) (D)(22) pH=有( )位有效数字。
………………………………………….…..…..…………………….( )(A) 4 (B) 3 (C) 2 (D) 1(23) 增加测定次数可以减少…………………………………………………...…..…………………….( )(A) 系统误差 (B) 过失 (C) 操作误差 (D) 偶然误差答案:(1) B;(2) BD;(3) C;(4) B;(5) C;(6) B;(7) A;(8) D;(9) C;(10) C;(11) C;(12) A;(13) B;(14) B;(15) B;(16) B;(17) C;(18) C;(19) B;(20) C;(21) C;(22) B;;(23) D4. 多选题(1) 下列情况引起的误差,属于系统误差的有………………..……………...…..…………………….( )(A) 砝码腐蚀 (B)天平零点稍有变动(C) 读取滴定管读数时,最后一位数字估测不准(D) 以含量约98%的金属锌作为基准物质标定EDTA的浓度(2) 提高分析结果准确度的方法是………………..…………………………...…..…………………….( )(A) 做空白试验 (B) 增加平行测定的次数 (C) 校正仪器 (D 使用纯度为98%的基准物(E) 选择合适的分析方法(3) 系统误差产生的原因有………………………….………………………...…..…….……………….( )(A) 仪器误差 (B) 方法误差 (C) 偶然误差 (D) 试剂误差 (E) 操作误差(4) 准确度的高低用( )大小来表示。
…………………………………….……..………………….( )(A) 相对偏差 (B) 相对误差 (C) 标准偏差 (D) 绝对误差 (E) 平均偏差答案:(1) AD ;(2) ABCE ;(3) ABDE ;(4) B, D5. 甲乙二人同时分析一矿物试样中含硫量,每次称取试样3.5g ,分析结果报告为:甲:%,%乙:%,% 。
习 题1. 如果分析天平的称量误差为±,拟分别称取试样0.1g 和1g 左右,称量的相对误差各为多少这些结果说明了什么问题【解】因分析天平的称量误差为±。
故读数的绝对误差E a =±0.0002g相对误差:%2.0%1001000.00002.01.0±=⨯±=g g g r E%02.0%1000000.10002.01±=⨯±=g g g r E这说明,两物体称量的绝对误差相等,但他们的相对误差并不相同。
也就是说,当被测定的量较大时,相对误差就比较小,测定的准确程度也就比较高。
2. 滴定管的读数误差为±。
如果滴定中用去标准溶液的体积分别为2mL 和20mL 左右,读数的相对误差各是多少从相对误差的大小说明了什么问题 【解】因滴定管的读数误差为±,故读数的绝对误差E a =±相对误差:%1%100202.02±=⨯±=mLmLmL r E%1.0%1002002.020±=⨯±=mLmL mL r E这说明,量取两溶液的绝对误差相等,但他们的相对误差并不相同。
也就是说,当被测定的量较大时,测量的相对误差较小,测定的准确程度也就较高。
3. 已知某标准样品中含KBr 的分数w (KBr)=,甲、乙两人的分析结果为:甲:、、;乙:、、。
分别计算甲、乙两人测定的平均值、绝对误差、相对误差和平均偏差,并比较其准确度和精密度。
