中位线定理证明题
专题22 三角形中位线定理应用问题(解析版)

专题22 三角形中位线定理应用问题1.三角形中位线的定义:连接三角形两边中点的线段叫做三角形的中位线。
2.三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
3.对三角形中位线的深刻理解(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的. (3)三角形的中位线不同于三角形的中线.【例题1】(2020•福建)如图,面积为1的等边三角形ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,则△DEF 的面积是( )A .1B .12C .13D .14 【答案】D【解析】根据三角形的中位线定理和相似三角形的判定和性质定理即可得到结论.∵D ,E ,F 分别是AB ,BC ,CA 的中点,1214∴DE =12AC ,DF =12BC ,EF =12AB ,∴DF BC =EF AB =DE AC =12,∴△DEF ∽△ABC ,∴S △DEFS △ABC =(DE AC )2=(12)2=14, ∵等边三角形ABC 的面积为1,∴△DEF 的面积是14.【对点练习】(2019内蒙古赤峰)如图,菱形ABCD 周长为20,对角线AC 、BD 相交于点O ,E 是CD 的中点,则OE 的长是( )A .2.5B .3C .4D .5【答案】A .【解析】∵四边形ABCD 为菱形,∴CD =BC ==5,且O 为BD 的中点, ∵E 为CD 的中点,∴OE 为△BCD 的中位线,∴OE =CB =2.5。
【点拨】掌握菱形特点,根据三角形中位线定理解决问题。
【例题2】(2020•临沂)如图,在△ABC 中,D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,H 为AF 与DG 的交点.若AC =6,则DH = .【解析】1.【分析】由三等分点的定义与平行线的性质得出BE =DE =AD ,BF =GF =CG ,AH =HF ,DH 是△AEF 的中位线,易证△BEF ∽△BAC ,得EF AC =BE AB ,解得EF =2,则DH =12EF =1. 【解析】∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC ,∴△BEF ∽△BAC ,∴EF AC =BE AB ,即EF 6=BE 3BE ,解得:EF =2,∴DH =12EF =12×2=1,【对点练习】(2019广西梧州)如图,已知在△ABC 中,D 、E 分别是AB 、AC 的中点,F 、G 分别是AD 、AE 的中点,且FG =2cm ,则BC 的长度是 cm .【答案】8.【解析】利用三角形中位线定理求得FG=DE,DE=BC.如图,∵△ADE中,F、G分别是AD、AE的中点,∴DE=2FG=4cm,∵D,E分别是AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=8cm【点拨】连续两次应用三角形中位线定理处理本题,是关键。
三角形中位线定理专练

三角形中位线定理专练1.如图,在△ ABC中,D是AB上一点,且AD=AC,AE⊥ CD,垂足是E,F 是CB的中点.求证:BD=2EF.2.如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△ EFG是等腰三角形.3.在△ ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.4.如图,BE,CF是△ ABC的角平分线,AN⊥ BE于N,AM⊥ CF于M,求证:MN∥ BC.5.如图,BM、CN分别平分△ABC的外角∠ ABD、∠ ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)6.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠ DHF=∠ DEF.7.如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD 的中点,且AC=BD.求证:OM=ON.8.如图,M是△ ABC的边BC的中点,AN平分∠ BAC,BN⊥ AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ ABC的周长.三角形中位线定理专练参考答案与试题解析一.解答题(共8小题)1.(2014?山东模拟)如图,在△ABC中,D是AB上一点,且AD=AC,AE⊥CD,垂足是E,F是CB的中点.求证:BD=2EF.【考点】三角形中位线定理.菁优网版权所有【专题】常规题型.【分析】根据三角形的中位线定理,在三角形中准确应用,并且求证E为CD 的中点,再求证EF为△BCD的中位线.【解答】证明:在△ACD中,因为AD=AC 且AE⊥CD,所以根据等腰三角形中底边的垂线与底边的交点即中点,可以证明:E为CD的中点,又因为F是CB的中点,所以,EF∥BD,且EF为△BCD的中位线,因此EF=BD,即BD=2EF.【点评】此题主要是中位线定理在三角形中的应用,考查在三角形中位线为对应边长的的定理.2.(2015春?天津校级期中)如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△EFG是等腰三角形.【考点】三角形中位线定理;等腰三角形的判定.菁优网版权所有【专题】证明题.【分析】由于E,F,G分别是AB,CD,AC的中点,利用中位线定理,GF=AD,GE=BC,又因为AD=BC,所以GF=GE.【解答】证明:∵E,F,G分别是AB,CD,AC的中点.∴GF=AD,GE=BC.又∵AD=BC,∴GF=GE,即△EFG是等腰三角形.【点评】本题通过给出的中点,利用中位线定理,证得边相等,从而证明等腰三角形,是一道基础题.3.(2015秋?青岛校级月考)在△ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.【考点】三角形中位线定理;平行四边形的判定.菁优网版权所有【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,MN∥BC且MN=BC,从而得到EF∥MN且EF=MN,再根据一组对边平行且相等的四边形是平行四边形判断.【解答】解:四边形MNEF是平行四边形.理由如下:∵BE、CF是中线,∴E、F分别是AC、AB的中点,∴EF是△ABC的中位线,∴EF∥BC且EF=BC,∵M、N分别是BO、CO中点,∴MN是△OBC的中位线,∴MN∥BC且MN=BC,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,熟记定理并准确识图是解题的关键.4.(2015春?泗洪县校级期中)如图,BE,CF是△ABC的角平分线,AN⊥BE 于N,AM⊥CF于M,求证:MN∥BC.【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】延长AN、AM分别交BC于点D、G,根据BE为∠ABC的角平分线,BE⊥AG可知∠BAN=∠BGN故△ABG为等腰三角形,所以BN也为等腰三角形的中线,即AM=GN.同理AM=DM,根据三角形中位线定理即可得出结论.【解答】证明:延长AN、AM分别交BC于点D、G.∵BE为∠ABC的角平分线,BE⊥AG,∴∠BAG=∠BGA,∴△ABG为等腰三角形,∴BN也为等腰三角形的中线,即AN=GN.同理AM=DM,∴MN为△ADG的中位线,∴MN∥BC.【点评】本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.5.(2015春?富顺县校级月考)如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】首先通过△ABM≌△DBM,得到AB=DB,AM=DM,同理:AN=EN,AC=CE,再根据三角形的中位线定理即可得到结果.【解答】证明:∵AM⊥BM,∴∠AMB=∠DMB=90°,∵BM平分∠ABD,∴∠ABM=∠DBM,在△ABM与△DBM中,,∴△ABM≌△DBM(asa),∴AB=DB,AM=DM,同理:AN=EN,AC=CE,∴MN=DE=(DB+BC+CE)=(AB+BC+AC).【点评】本题考查了三角形的中位线定理,全等三角形的判定与性质,证明三角形全等是解题的关键.6.(2014?宿迁)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF.【考点】三角形中位线定理;直角三角形斜边上的中线;平行四边形的判定.菁优网版权所有【专题】证明题;几何综合题.【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AB,DE∥AC,再根据平行四边形的定义证明即可;(2)根据平行四边形的对角相等可得∠DEF=∠BAC,根据直角三角形斜边上的中线等于斜边的一半可得DH=AD,FH=AF,再根据等边对等角可得∠DAH=∠DHA,∠FAH=∠FHA,然后求出∠DHF=∠BAC,等量代换即可得到∠DHF=∠DEF.【解答】证明:(1)∵点D,E,F分别是AB,BC,CA的中点,∴DE、EF都是△ABC的中位线,∴EF∥AB,DE∥AC,∴四边形ADEF是平行四边形;(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BA C,∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,∴∠DAH=∠DHA,∠FAH=∠FHA,∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,∴∠DHF=∠BAC,∴∠DHF=∠DEF.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,平行四边形的判定与性质,熟记各性质并准确识图是解题的关键.7.(2014?丹阳市校级模拟)如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD的中点,且AC=BD.求证:OM=ON.【考点】三角形中位线定理;平行线的性质;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】取AD的中点G,连接EG,FG,构造三角形的中位线,根据三角形的中位线定理进行证明即可.【解答】证明:取AD的中点G,连接EG,FG,∵G、F分别为AD、CD的中点,∴GF是△ACD的中位线,∴GF=AC,同理可得,GE=BD,∵AC=BD,∴GF=GE=AC=BD.∴∠GFN=∠GEM,又∵EG∥OM,FG∥ON,∴∠OMN=∠GEM=∠GFN=∠ONM,∴OM=ON.【点评】本题考查了三角形的中位线性质定理,解题的关键是构造三角形的中位线.运用三角形的中位线的数量关系和位置关系进行分析证明.8.(2013?永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN 于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【分析】(1)证明△ABN≌△ADN,即可得出结论;(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.【解答】(1)证明:在△ABN和△ADN中,∵,∴△ABN≌△ADN(ASA),∴BN=DN.(2)解:∵△ABN≌△ADN,∴AD=AB=10,又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.【点评】本题考查了三角形的中位线定理及等腰三角形的判定,注意培养自己的敏感性,一般出现高、角平分线重合的情况,都需要找到等腰三角形.。
10、三角形的中位线定理

三角形的中位线定理【知识要点】问题1、什么是三角形的中线?什么是三角形的中位线?三角形有几条中位线?问题2、A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但又无法直接去测量,怎么办?例(1):如图已知,在△ABC中,点D,E分别是△ABC的边AB、AC中点,求证:DE∥BC,且DE=1/2BC.三角形的中位线定理:.应用:已知:如图所示,在四边形ABCD中,E、F、H、M分别是AB、BC、CD、DA的中点.求证:(1)AC和HG的关系;(2)AC和EF的关系;(3)四边形EFHM是平行四边形.【例题讲解】考点1、中位线定理的概念例题1、如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长是多少?训练1、如图, E、F分别是ABCD 的两边AB、CD的中点, AF交DE于P, BF交CE于Q,则PQ与AB 的关系是 .考点2、中位线定理解决周长相关的问题例题2、如图,点D、E、F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为()A.5 B.10 C.20 D.40训练1、如果一个三角形的周长为10,那么连接各边中点所成的三角形的周长为()A.4B.5C.6D.12例题2-1、如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:①线段MN的长;②∥PAB的周长;③∥PMN的面积;④直线MN,AB之间的距离;⑤∥APB 的大小.其中会随点P的移动而变化的是()训练1、如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.7 B.9 C.10 D.11训练2、如图,E、F、G、H分别是四边形ABCD各边的中点,对角线AC、BD的长分别为7和9,则四边形EFGH的周长是______.训练3、如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是________.已知第一个三角形的周长为1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,以此类推,则第50个三角形的周长为()A.()50B.()51C.()49D.()48考点3、中点四边形问题例题3、证明:顺次连接四边形各边重点所得到的四边形一定是();思考:什么情况下得到的平行四边形可以成为矩形?原来四边形的两条对角线连接四边中点所得到的四边形矩形菱形正方形平行四边形练习1.△ABC中,AB=3,BC=5,CA=7,顺次连结三边中点得△DEF的周长为_________.2.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形3.若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是()A.矩形B.等腰梯形C.对角线相等的四边形D.对角线互相垂直的四边形4.顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【及时训练】1、如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为()3.在△ABC中,D、E分别是BC、AC中点,BF平分△ABC.交DE于点F.AB=8,BC=6,则EF的长为()A.1B.2C.3D.44.平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A.3cm B.6cm C.9cm D.12cm5.如图所示,在△ABC中,△A=60°,BD、CE分别是AC、AB上的高,H是BD、CE的交点,求△BHC的度数.6.如图,△ABC中,AB>AC,AD平分△BAC,CD△AD,点E是BC的中点,若AB=12,AC=10,求DE的长.7.如图,在△ABCD中,AB=3,AD=4,E是CD的中点,则EO等于()A.3B.4C.1.5D.28.如图,在△ABC中,AD=DE=EF=FB,DG△EH△FI△BC,已知BC=a,则DG+EH+FI的长是()A.B.C.2a D.9.(1)回顾定理:如图1,在△ABC中,DE是△ABC的中位线.那么DE与BC的关系有.(2)运用定理:如图2,在四边形ABCD中,△ABC=50°,△BCD=40°,点F为AC的中点,点E为BD的中点.若AB=4,CD=6,求EF的长.【课堂总结】1.2.3.4.【课上练习】1.如图,在∥ABC中,点D,E分别是AB,AC的中点,∥A=50°,∥ADE=60°,则∥C的度数为()A.50°B.60°C.70°D.80°3.如图,∥ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=4,AO=3,则四边形DEFG的周长为()A.6B.7C.8D.125.如图,∥ABC中,D,E分别是边AB,AC的中点.若DE=2,则BC=()A.2B.3C.4D.56.如图,等边∥ABC中,点D、E分别为边AB、AC的中点,则∥DEC的度数为()A.30°B.60°C.120°D.150°7.如图∥ABC中,D、E分别是边AB、AC的中点,已知DE=5,则BC的长为()A.8B.9C.10D.118.如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()AB=24m B.MN△AB C.△CMN△△CAB D.CM:MA=1:25.如图,D是△ABC内一点,E、F、G、H分别是AB、AC、CD、BD的中点,求证:四边形EFGH是平行四边形.【课后练习】【要点梳理】要点一、三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于第三边,并且等于第三边的一半.要点诠释:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.要点二、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点诠释:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.。
三角形中位线专项训练(30道)(解析版)

专题9.7 三角形中位线专项训练(30道)【苏科版】1.(2021秋•淅川县期末)如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为()A.2B.5C.7D.9【分析】根据三角形的中位线定理得出EF=12DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,N与A重合时,DN最小,从而求得EF的最大值为6.5,最小值是2.5,可解答.【解答】解:连接DN,∵ED=EM,MF=FN,∴EF=12DN,∴DN最大时,EF最大,DN最小时,EF最小,∵N与B重合时DN最大,此时DN=DB=√AD2+BD2=√52+122=13,∴EF的最大值为6.5.∵∠A=90°,AD=5,∴DN≥5,∴EF≥2.5,∴EF长度的可能为5;故选:B.2.(2021秋•渝中区校级期末)如图,在△ABC中,AB=CB=6,BD⊥AC于点D,F在BC上且BF=2,连接AF,E为AF的中点,连接DE,则DE的长为()A.1B.2C.3D.4【分析】根据等腰三角形的性质得到AD=DC,根据三角形中位线定理解答即可.【解答】解:∵CB=6,BF=2,∴FC=6﹣2=4,∵BA=BC,BD⊥AC,∴AD=DC,∵AE=EF,∴DE是△AFC的中位线,∴DE=12FC=12×4=2,故选:B.3.(2021秋•龙岗区校级期末)如图,四边形ABCD中,E,F分别是边AB,CD的中点,则AD,BC和EF的关系是()A.AD+BC>2EF B.AD+BC≥2EF C.AD+BC<2EF D.AD+BC≤2EF【分析】取AC的中点G,连接EF,EG,GF,根据三角形中位线定理求出EG=12BC,GF=12AD,再利用三角形三边关系:两边之和大于第三边,即可得出AD,BC和EF的关系.【解答】解:如图,取AC的中点G,连接EF,EG,GF,∵E,F分别是边AB,CD的中点,∴EG,GF分别是△ABC和△ACD的中位线,∴EG=12BC,GF=12AD,在△EGF中,由三角形三边关系得EG+GF>EF,即12BC+12AD>EF,∴AD +BC >2EF ,当AD ∥BC 时,点E 、F 、G 在同一条直线上,∴AD +BC =2EF ,所以四边形ABCD 中,E ,F 分别是边AB ,CD 的中点,则AD ,BC 和EF 的关系是AD +BC ≥2EF .故选:B .4.(2021秋•荆门期末)如图,△ABC 的周长为20,点D ,E 在边BC 上,∠ABC 的平分线垂直于AE ,垂足为N ,∠ACB 的平分线垂直于AD ,垂足为M ,若BC =8,则MN 的长度为( )A .32B .2C .52 D .3【分析】证明△BNA ≌△BNE ,得到BE =BA ,AN =NE ,同理得到CD =CA ,AM =MD ,求出DE ,根据三角形中位线定理计算即可.【解答】解:在△BNA 和△BNE 中,{∠NBA =∠NBE BN =BN ∠BNA =∠BNE,∴△BNA ≌△BNE (ASA )∴BE =BA ,AN =NE ,同理,CD =CA ,AM =MD ,∴DE =BE +CD ﹣BC =BA +CA ﹣BC =20﹣8﹣8=4,∵AN =NE ,AM =MD ,∴MN =12DE =2,故选:B .5.(2021秋•宛城区期中)如图,在△ABC 中,∠A =90°,AC >AB >4,点D 、E 分别在边AB 、AC 上,BD =4,CE =3,取DE 、BC 的中点M 、N ,线段MN 的长为( )A .2.5B .3C .4D .5【分析】如图,作CH ∥AB ,连接DN ,延长DN 交CH 于H ,连接EH ,首先证明CH =BD ,∠ECH =90°,解直角三角形求出EH ,利用三角形中位线定理即可解决问题.【解答】解:作CH ∥AB ,连接DN 并延长交CH 于H ,连接EH ,∵BD ∥CH ,∴∠B =∠NCH ,∠ECH +∠A =180°,∵∠A =90°,∴∠ECH =∠A =90°,在△DNB 和△HNC 中,{∠B =∠NCH BN =CN ∠DNB =∠HNC,∴△DNB ≌△HNC (ASA ),∴CH =BD =4,DN =NH ,在Rt △CEH 中,CH =4,CE =3,∴EH =√CH 2+CE 2=√42+32=5,∵DM =ME ,DN =NH ,∴MN =12EH =2.5,故选:A .6.(2021•丹东模拟)如图,在△ABC 中,CE 是中线,CD 是角平分线,AF ⊥CD 交CD延长线于点F ,AC =7,BC =4,则EF 的长为( )A .1.5B .2C .2.5D .3【分析】延长AF 、BC 交于点G ,证明△ACF ≌△GCF ,根据全等三角形的性质得到CG =AC =7,AF =FG ,求出BG ,根据三角形中位线定理解答即可.【解答】解:延长AF 、BC 交于点G ,∵CD 是△ABC 的角平分线,∴∠ACF =∠BCF ,在△ACF 和△GCF 中,{∠ACF =∠GCF CF =CF ∠AFC =∠GFC =90°,∴△ACF ≌△GCF (ASA ),∴CG =AC =7,AF =FG ,∴BG =CG ﹣CB =3,∵AE =EB ,AF =FG ,∴EF =12BG =1.5,故选:A .7.(2021•碑林区校级模拟)如图,AD 为△ABC 的角平分线,BE ⊥AD 于E ,F 为BC 中点,连接EF ,若∠BAC =80°,∠EBD =20°,则∠EFD =( )A .26°B .28°C .30°D .32°【分析】延长BE 交AC 于G ,证△ABE ≌△AGE (ASA ),得BE =GE ,再由三角形中位线定理得EF ∥GC ,则∠EFD =∠C ,然后求出∠ABC =∠ABE +∠EBD =70°,即可解决问题.【解答】解:延长BE 交AC 于G ,如图所示:∵AD 平分∠BAC ,∠BAC =80°,∴∠BAE =∠GAE =12∠BAC =40°,∵BE ⊥AD ,∴∠BEA =∠GEA =90°,∵AE =AE ,∴△ABE ≌△AGE (ASA ),∴BE =GE ,∵F 为BC 的中点,∴EF 是△BCG 的中位线,∴EF ∥GC ,∴∠EFD =∠C ,∵∠BEA =90°,∴∠ABE =90°﹣∠BAE =90°﹣40°=50°,∴∠ABC =∠ABE +∠EBD =50°+20°=70°,∴∠EFD =∠C =180°﹣∠BAC ﹣∠ABC =180°﹣80°﹣70°=30°,故选:C .8.(2021秋•广饶县期末)如图,AD 是△ABC 的中线,E 是AD 的中点,F 是BE 延长线与AC 的交点,若AC =4,则AF =( )A .85 B .43 C .1 D .23 【分析】取EF 的中点H ,连接DH ,根据三角形中位线定理得到DH =12FC ,DH ∥AC ,证明△AEF ≌△DEH ,根据全等三角形的性质得到AF =DH ,计算即可.【解答】解:取EF 的中点H ,连接DH , ∵BD =DC ,BH =HF ,∴DH =12FC ,DH ∥AC ,∴∠HDE =∠F AE ,在△AEF 和△DEH 中,{∠AEF =∠DEH AE =DE ∠EAF =∠EDH,∴△AEF ≌△DEH (ASA ), ∴AF =DH ,∴AF =12FC , ∵AC =4,∴AF =43,故选:B .9.(2021春•平邑县期末)如图,在△ABC 中,AB =8,AC =6,AD 、AE 分别是其角平分线和中线,过点C 作CG ⊥AD 于F ,交AB 于G ,连接EF ,则线段EF 的长为( )A .1B .2C .32D .12【分析】证明△AFG ≌△AFC ,得到GF =FC ,根据三角形中位线定理计算即可.【解答】解:∵AD 是∠BAC 的角平分线,∴∠GAF =∠CAF ,∵CG ⊥AD ,∴∠AFG =∠AFC =90°,在△AFG 和△AFC 中,{∠AFG =∠AFC AF =AF ∠FAG =∠FAC,∴△AFG≌△AFC(ASA),∴GF=FC,AG=AC=6,∴GB=AB﹣AG=2,∵GF=FC,BE=EC,∴EF=12GB=1,故选:A.10.(2021春•宽城县期末)如图,E,F是四边形ABCD两边AB,CD的中点,G,H是对角线AC,BD的中点,若EH=6,则以下结论不正确的是()A.BC=12B.GF=6C.AD=12D.EH∥GF【分析】先判定EH为△ABD的中位线,GF为△ADC的中位线,然后根据三角形中位线性质对各选项进行判断.【解答】解:∵点E为AB的中点,点H为BD的中点,∴EH为△ABD的中位线,∴EH=12AD,EH∥AD,∵点F为CD的中点,点G为AC的中点,∴GF为△ADC的中位线,∴GF=12AD,GF∥AD,∴GF=EH=6,AD=2EH=12,EH∥GF,所以A选项符合题意,B选项、C选项和D 选项不符合题意.故选:A.二.填空题(共10小题)11.(2021秋•莱阳市期末)如图,D、E分别为△ABC的边AB、AC的中点.连接DE,过点B作BF平分∠ABC,交DE于点F.若EF=4,AD=7,则BC的长为22.【分析】根据三角形中位线定理得到DE ∥BC ,DE =12BC ,BD =AD =7,根据平行线的性质、角平分线的定义得到∠DBF =∠FBC ,根据等腰三角形的判定定理得到DF =BD =7,计算即可.【解答】解:∵D 、E 分别为△ABC 的边AB 、AC 的中点,∴DE ∥BC ,DE =12BC ,BD =AD =7,∴∠DFB =∠FBC ,∵BF 平分∠ABC ,∴∠DFB =∠DBF ,∴∠DBF =∠FBC ,∴DF =BD =7,∴DE =DF +EF =11,∴BC =2DE =22,故答案为:22.12.(2021秋•让胡路区校级期末)如图,△ABC 的周长为64,E 、F 、G 分别为AB 、AC 、BC 的中点,A ′、B ′、C ′分别为EF 、EG 、GF 的中点,△A ′B ′C ′的周长为 16 .如果△ABC 、△EFG 、△A ′B ′C ′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n 个三角形的周长是 27﹣n .【分析】根据E 、F 、G 分别为AB 、AC 、BC 的中点,可以判断EF 、FG 、EG 为三角形中位线,利用中位线定理求出EF 、FG 、EG 与BC 、AB 、CA 的长度关系即可求得△EFG 的周长是△ABC 周长的一半,△A ′B ′C ′的周长是△EFG 的周长的一半,以此类推,可以求得第n 个三角形的周长.【解答】解:∵如图,△ABC 的周长为64,E 、F 、G 分别为AB 、AC 、BC 的中点, ∴EF 、FG 、EG 为三角形中位线,∴EF =12BC ,EG =12AC ,FG =12AB ,∴EF +FG +EG =12(BC +AC +AB ),即△EFG 的周长是△ABC 周长的一半.同理,△A ′B ′C ′的周长是△EFG 的周长的一半,即△A ′B ′C ′的周长为14×64=16.以此类推,第n 个小三角形的周长是第一个三角形周长的64×(12)n ﹣1=27﹣n故答案是:27﹣n .13.(2021春•安徽月考)如图,在四边形ABCD 中,AD =BC ,∠DAB =50°,∠CBA =70°,P 、M 、N 分别是AB 、AC 、BD 的中点,若BC =6,则△PMN 的周长是 9 .【分析】根据三角形中位线定理得到PM ∥BC ,PM =12BC =3,PN ∥AD ,PN =12AD =3,根据等边三角形的判定和性质定理解答即可.【解答】解:∵P 、M 分别是AB 、AC 的中点,∴PM ∥BC ,PM =12BC =3,∴∠APM =∠CBA =70°,同理可得:PN ∥AD ,PN =12AD =3,∴∠BPN =∠DAB =50°,∴PM =PN =3,∠MPN =180°﹣50°﹣70°=60°,∴△PMN 为等边三角形,∴△PMN 的周长为9,故答案为:9.14.(2021秋•长春期中)如图所示,在△ABC 中,BC >AC ,点D 在BC 上,DC =AC =10,且AD BD =32,作∠ACB 的平分线CF 交AD 于点F ,CF =8,E 是AB 的中点,连接EF ,则EF 的长为 4 .【分析】根据等腰三角形的性质得到F 为AD 的中点,CF ⊥AD ,根据勾股定理得到DF =√CD 2−CF 2=6,根据三角形的中位线定理即可得到结论.【解答】解:∵DC =AC =10,∠ACB 的平分线CF 交AD 于F ,∴F 为AD 的中点,CF ⊥AD ,∴∠CFD =90°,∵DC =10,CF =8,∴DF =√CD 2−CF 2=6,∴AD =2DF =12,∵AD BD =32,∴BD =8,∵点E 是AB 的中点, ∴EF 为△ABD 的中位线,∴EF =12BD =4,故答案为:4.15.(2021•商丘四模)如图,四边形ABCD 中,点E 、F 分别为AD 、BC 的中点,延长FE交CD 延长线于点G ,交BA 延长线于点H ,若∠BHF 与∠CGF 互余,AB =4,CD =6,则EF 的长为 √13 .【分析】根据三角形的中位线定理和勾股定理解答即可.【解答】解:连接BD ,取BD 的中点M ,连接EM ,FM ,∵E 、F 分别为AD 、BC 的中点,M 为BD 的中点,∴EM ,MF 分别为△ADB 、△BCD 的中位线,∴EM ∥AB ,MF ∥DC ,EM =12AB =2,MF =12DC =3,∵MF ∥DC ,∴∠FGC =∠EFM ,∵EM ∥AB ,∴∠FEM =∠FHB ,∵∠BHF 与∠CGF 互余,∴∠CGF +∠BHF =∠EFM +∠FEM =90°,∴∠EMF =180°﹣∠EFM ﹣∠FEM =90°,∴△EMF 是直角三角形,∴EF=√EM2+FM2=√22+32=√13,故答案为:√13.16.(2021•香坊区校级开学)如图,在△ABC中,E是AB的中点,D是AC上一点,连接DE,BH⊥AC于H,若2∠ADE=90°﹣∠HBC,AD:BC=4:3,CD=2,则BC的长为6.【分析】如图,延长AC至N,使CN=BC,连接BN,由等腰三角形的性质可得∠ADE =∠N,可证DE∥BN,由三角形中位线定理可得AD=DN,即可求解.【解答】解:如图,延长AC至N,使CN=BC,连接BN,∵2∠ADE=90°﹣∠HBC,∠BCA=90°﹣∠HBC,∴∠BCA=2∠ADE,∵CN=BC,∴∠N=∠CBN,∴∠BCA=∠N+∠CBN=2∠N,∴∠ADE=∠N,∴DE∥BN,又∵E是AB的中点,∴DE是△ABN的中位线,∴AD=DN,∵AD:BC=4:3,∴设AD=DN=4x,BC=CN=3x,∴CD=DN﹣CN=x=2,∴BC=6,故答案为6.17.(2021春•牡丹区期末)如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=13,AC=8,则DF的长为 2.5.【分析】延长CF交AB于点G,判断出AF垂直平分CG,得到AC=AG,根据三角形中位线定理解答.【解答】解:延长CF交AB于点G,∵AE平分∠BAC,∴∠GAF=∠CAF,∴AF垂直平分CG,∴AC=AG,GF=CF,又∵点D是BC中点,∴DF是△CBG的中位线,∴DF=12BG=12(AB﹣AG)=12(AB﹣AC)=2.5,故答案为:2.5.18.(2021春•洛阳期末)如图,D是△ABC的边BC的中点,AE平分∠BAC,BE⊥AE于点E,且AB=10cm,DE=2cm,则AC的长为6cm.【分析】延长AC 、BE 交于点F ,证明△AEB ≌△AEF ,根据全等三角形的性质得到AF =AB =10cm ,BE =EF ,根据三角形中位线定理计算即可.【解答】解:延长AC 、BE 交于点F ,∵AE 平分∠BAC ,∴∠BAE =∠CAE ,在△AEB 和△AEF 中,{∠BAE =∠FAE AE =AE ∠AEB =∠AEF =90°,∴△AEB ≌△AEF (ASA ),∴AF =AB =10(cm ),BE =EF ,∵BD =DC ,DE =2cm ,∴CF =2DE =4(cm ),∴AC =AF ﹣CF =6(cm ),故答案为:6.19.(2021春•盐湖区校级期末)如图,在四边形ABCD 中,AB =CD ,M 、N 、P 分别是AD 、BC 、BD 的中点,若∠MPN =130°,则∠NMP 的度数为 25° .【分析】根据中位线定理和已知,易证明△PMN 是等腰三角形,根据等腰三角形的性质和三角形内角和定理即可求出∠PMN 的度数.【解答】解:在四边形ABCD 中,M 、N 、P 分别是AD 、BC 、BD 的中点,∴PN ,PM 分别是△CDB 与△DAB 的中位线,∴PM =12AB ,PN =12DC ,PM ∥AB ,PN ∥DC ,∵AB =CD , ∴PM =PN ,∴△PMN 是等腰三角形,∵∠MPN=130°,∴∠PMN=180°−130°2=25°.故答案为:25°.20.(2021春•虹口区校级期末)如图,在△ABC中,BM、CN平分∠ABC和∠ACB的外角,AM⊥BM于M,AN⊥CN于N,AB=10,BC=13,AC=6,则MN= 4.5.【分析】延长AM交BC于点G,根据BM为∠ABC的平分线,AM⊥BM得出∠BAM=∠G,故△ABG为等腰三角形,所以AM=GM.同理AN=DN,根据三角形中位线定理即可求得MN.【解答】解:延长AM交BC于点G,延长AN交BC延长线于点D,∵BM为∠ABC的平分线,∴∠CBM=∠ABM,∵BM⊥AG,∴∠ABM+∠BAM=90°,∠MGB+∠CBM=90°,∴∠BAM=∠MGB,∴△ABG为等腰三角形,∴AM=GM.BG=AB=10,同理AN=DN,CD=AC=6,∴MN为△ADG的中位线,∴MN=12DG=12(BC﹣BG+CD)=12(BC﹣AB+AC)=12(13﹣10+6)=4.5.故答案为:4.5.三.解答题(共10小题)21.(2019春•岐山县期末)△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.【分析】连接DE,FG,由BD与CE为中位线,利用中位线定理得到ED与BC平行,FG与BC平行,且都等于BC的一半,等量代换得到ED与FG平行且相等,进而得到四边形EFGD为平行四边形,利用平行四边形的性质即可得证.【解答】证明:连接DE,FG,∵BD,CE是△ABC的中线,∴D,E是AB,AC的中点,∴DE∥BC,DE=12BC,同理:FG∥BC,FG=12BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.22.(2021秋•桓台县期末)如图,在四边形ABCD中,E,F分别是AD,BC的中点.(1)若AB=6,CD=8,∠ABD=30°,∠BDC=120°,求EF的长;(2)若∠BDC﹣∠ABD=90°,求证:AB2+CD2=4EF2.【分析】(1)取BD的中点P,利用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理来求EF的长度;(2)如图,取BD的中点P,连接EP、FP.用三角形中位线定理可以求得EP、FP的长度,然后利用勾股定理即可得到结论.【解答】(1)解:如图,取BD的中点P,连接EP、FP.∵E,F分别是AD、BC的中点,AB=6,CD=8,∴PE ∥AB ,且PE =12AB =3,PF ∥CD 且PF =12CD =4.又∵∠ABD =30°,∠BDC =120°,∴∠EPD =∠ABD =30°,∠DPF =180°﹣∠BDC =60°,∴∠EPF =∠EPD +∠DPF =90°,在直角△EPF 中,由勾股定理得到:EF =√EP 2+PF 2=√32+42=5,即EF =5;(2)证明:如图,取BD 的中点P ,连接EP 、FP .∵E ,F 分别是AD 、BC 的中点,∴PE ∥AB ,且PE =12AB ,PF ∥CD 且PF =12CD .∴∠EPD =∠ABD ,∠BPF =∠BDC ,∴∠DPF =180°﹣∠BPF =180°﹣∠BDC ,∵∠BDC ﹣∠ABD =90°,∴∠BDC =90°+∠ABD ,∴∠EPF =∠EPD +∠DPF =∠ABD +180°﹣∠BDC =∠ABD +180°﹣(90°+∠ABD )=90°,∴PE 2+PF 2=(12AB )2+(12CD )2=EF 2,∴AB 2+CD 2=4EF 2.23.(2021秋•莱州市期末)已知:如图,在四边形ABCD 中,对角线AC 、BD 相交于点O ,且AC =BD ,E 、F 分别是AB 、CD 的中点,EF 分别交BD 、AC 于点G 、H .求证:OG =OH .【分析】取BC 边的中点M ,连接EM ,FM ,则根据三角形的中位线定理,即可证得△EMF 是等腰三角形,根据等边对等角,即可证得∠MEF =∠MFE ,然后根据平行线的性质证得∠OGH =∠OHG ,根据等角对等边即可证得.【解答】解:取BC边的中点M,连接EM,FM,∵M、F分别是BC、CD的中点,∴MF∥BD,MF=12BD,同理:ME∥AC,ME=12AC,∵AC=BD∴ME=MF∴∠MEF=∠MFE,∵MF∥BD,∴∠MFE=∠OGH,同理,∠MEF=∠OHG,∴∠OGH=∠OHG∴OG=OH.24.(2021春•抚州期末)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.(1)求证:CE=DE;(2)若点F为BC的中点,求EF的长.【分析】(1)根据ASA证明△AEC和△AED全等,进而利用全等三角形的性质解答即可;(2)根据勾股定理得出AB,进而利用三角形中位线定理解答即可.【解答】(1)证明:∵AE平分∠CAB,∴∠CAE=∠BAE,∵CE⊥AE,∴∠AEC =∠AED =90°,在△AEC 和△AED 中,{∠CAE =∠DAE AE =AE ∠AEC =∠AED,∴△AEC ≌△AED (ASA ),∴CE =DE ;(2)在Rt △ABC 中,∵AC =6,BC =8,∴AB =√AC 2+BC 2=√62+82=10,∵△AEC ≌△AED ,∴AD =AC =6,∴BD =AB ﹣AD =4,∵点E 为CD 中点,点F 为BC 中点,∴EF =12BD =2.25.(2021春•秦都区期末)如图,在△ABC 中,AB =AC ,点D 、E 分别是边AB 、AC 上的点,连接BE 、DE ,∠ADE =∠AED ,点F 、G 、H 分别为BE 、DE 、BC 的中点.求证:FG =FH .【分析】根据等腰三角形的判定定理得到AD =AE ,根据线段的和差得到BD =CE ,根据三角形的中位线定理即可得到结论.【解答】证明:∵∠ADE =∠AED ,∴AD =AE ,∵AB =AC ,∴AB ﹣AD =AC ﹣AE ,即BD =CE ,∵点F 、G 、H 分别为BE 、DE 、BC 的中点,∴FG 是△EDB 的中位线,FH 是△BCE 的中位线,∴FG =12BD ,FH =12CE ,∴FG =FH .26.(2021春•泰兴市月考)如图,在四边形ABCD 中,AB =CD ,E 、F 分别是BC 、AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M、N,证明:∠BME=∠CNE.【分析】连接BD,取BD的中点H,连接HE,HF,根据三角形的中位线的性质得到FH∥BM,FH=12AB,EH∥CN,EH=12CD,根据平行线的性质得到∠BME=∠HFE,∠CNE=∠HEF,根据等腰三角形的性质得到∠HFE=∠HEF,等量代换即可得到结论.【解答】证明:连接BD,取BD的中点H,连接HE,HF,∵E、F分别是BC、AD的中点,∴FH∥BM,FH=12AB,EH∥CN,EH=12CD,∴∠BME=∠HFE,∠CNE=∠HEF,∵AB=CD,∴FH=EH,∴∠HFE=∠HEF,∴∠BME=∠CNE.27.(2021春•沈北新区期末)如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=12CF.【分析】过D 作DG ∥AC ,可证明△AEF ≌△DEG ,可得AF =DG ,由三角形中位线定理可得DG =12CF ,可证得结论.【解答】证明:如图,过D 作DG ∥AC ,则∠EAF =∠EDG ,∵AD 是△ABC 的中线,∴D 为BC 中点, ∴G 为BF 中点,∴DG =12CF ,∵E 为AD 中点,∴AE =DE ,在△AEF 和△DEG 中,{∠EAF =∠EDG AE =DE ∠AEF =∠DEG,∴△AEF ≌△DEG (ASA ), ∴DG =AF ,∴AF =12CF .28.(2021春•莆田期末)如图,已知四边形ABCD 的对角线AC 与BD 相交于点O ,且AC=BD ,M 、N 分别是AB 、CD 的中点,MN 分别交BD 、AC 于点E 、F .你能说出OE 与OF 的大小关系并加以证明吗?【分析】此题要构造三角形的中位线,根据三角形的中位线定理进行证明.【解答】解:相等.理由如下:取AD 的中点G ,连接MG ,NG ,∵G 、N 分别为AD 、CD 的中点, ∴GN 是△ACD 的中位线,∴GN =12AC ,同理可得,GM=12BD,∵AC=BD,∴GN=GM=12AC=12BD.∴∠GMN=∠GNM,又∵MG∥OE,NG∥OF,∴∠OEF=∠GMN=∠GNM=∠OFE,∴OE=OF.29.(2021春•城固县期末)如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD 的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.【分析】根据三角形中位线定理得到EG=12AC,EG∥AC,FG=12BD,FG∥BD,根据平行线的性质、等腰三角形的性质和判定定理证明结论.【解答】证明:∵E,G为AB、BC中点,∴EG=12AC,EG∥AC,∴∠FEG=∠OQP,同理,FG=12BD,FG∥BD,∴∠EFG=∠OPQ,∵AC=BD,∴EG=FG,∴∠FEG=∠EFG,∴∠OPQ=∠OQP,∴OP=OQ.30.(2021春•三水区期末)如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.(1)求证:FG=FH;(2)若∠A=90°,求证:FG⊥FH;(3)若∠A=80°,求∠GFH的度数.【分析】(1)由中点性质及AB=AC,得到BD=EC,再由中位线性质证明FG∥BD,GF=12BD,FH∥EC,FH=12EC,从而得到FG=FH;(2)由(1)FG∥BD,FH∥EC,再由∠A=90°,可证FG⊥FH;(3)由(1)FG∥BD,∠A=80°,可求得∠FKC,再由FH∥EC,可求得∠GFH的度数.【解答】(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点∴BD=EC∵点F,G,H分别为BE,DE,BC的中点∴FG∥BD,GF=12 BDFH∥EC,FH=12 EC∴FG=FH;(2)证明:由(1)FG∥BD又∵∠A=90°∴FG⊥AC∵FH∥EC∴FG⊥FH;(3)解:延长FG交AC于点K,∵FG∥BD,∠A=80°∴∠FKC=∠A=80°∵FH∥EC∴∠GFH=180°﹣∠FKC=100°。
2021年九年级数学中考复习分类专题:三角形中位线定理(二)

2021年九年级数学中考复习分类专题:三角形中位线定理(二)一.选择题1.如图,屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则BC和DE的长分别等于()A.2m,2m B.4m,2m C.2m,4m D.4m,4m2.如图,△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()A.3 B.4 C.5 D.63.如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tan C 等于()A.B.C.D.4.如图,在△ABC中,AB=8,∠C=90°,∠A=30°,D、E分别为AB、AC边上的中点,则DE的长为()A.2 B.3 C.2D.45.如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.B.5 C.3 D.46.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形……,如此操作下去,那么,第6个三角形的直角顶点坐标为()A.(﹣,)B.(﹣,)C.(﹣,)D.(﹣,)7.如图所示,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=8,MN=3,则AC的长是()A.12 B.14 C.16 D.188.如图,在Rt△ABC中,∠B=90°,BC=3,AB=4,点D,E分别是AB,AC的中点,CF 平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为()A.4 B.5 C.5.5 D.69.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为()A.8 B.6 C.4 D.510.如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A.B.C.D.二.填空题11.如图所示,在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E、F分别为MB、BC 的中点,若EF=1,则AB=.12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,点D是AC边上的一点,且AD=2,以AD为直角边作等腰直角三角形ADE,连接BE并取BE的中点F,连接CF,则CF的长为.13.如图,在△ABC中,AD平分∠BAC,BD⊥AD,点E是BC的中点,连结DE,且AB=6,AC =10,则DE=.14.如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为.15.在△ABC中,CD⊥AB于点D,E,F分别为BC,AC的中点,连接DF、DE、EF,若△ABC 周长为6,则△DEF周长为.16.如图,四边形ABCD中,∠BMF+∠CNF=90°,E、F分别是AD、BC的中点,AB=5,CD =12,则EF=.三.解答题17.在Rt△ABC中,∠ACB=90°,中线AE与中线CD交于点O,AB=6.(1)求证:AO:OE=2:1;(2)求OC的长.18.如图,在△ABC中,AB=BC=12cm,∠ABC=80°,BD是∠ABC的平分线,DE∥BC.(1)求∠EDB的度数;(2)求DE的长.19.在△ABC中,∠BAC=90°,延长BA到D,使AD=AB,点E、F分别为边BC、AC的中点.(1)求证:DF=BE;(2)若CF=2,CE=.求tan∠ADF.20.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.(1)求证:CD∥AB;(2)求证:△BDE≌△ACE;(3)若O为AB中点,求证:OF=BE.21.如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B 重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于F.(1)求证:BF=FD;(2)∠A在什么范围内变化时,四边形ACFE是梯形,并说明理由;(3)∠A在什么范围内变化时,线段DE上存在点G,满足条件DG=DA,并说明理由.22.如图1,已知E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,连接EF、FG、GH、HE.(1)求证:四边形EFGH是平行四边形(提示:可连接AC或BD);(2)在电脑上用适当的应用程序画出图1,然后用鼠标拖动点D,当点D在原四边形ABCD的内部,在原四边形ABCD的外部时,图1依次变为图2、图3.图2、图3中四边形EFGH 还是平行四边形吗?选择其中之一说明理由.23.已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;(2)如图1,若CB=a,CE=2a,求BM,ME的长;(3)如图2,当∠BCE=45°时,求证:BM=ME.参考答案一.选择题1.解:∵BC⊥AF,∠A=30°,∴BC=AB=4m,∵BC、DE垂直于横梁AC,∴DE∥BC,又D是AB的中点,∴DE=BC=2m,即:BC=4m,DE=2m.故选:B.2.解:∵D,E分别是BC,AC的中点,∴DE∥AB,∴∠BFD=∠ABF,∵BF平分∠ABC,∴∠DBF=∠ABF,∴∠BFD=∠DBF,∴DF=DB=BC=3,故选:A.3.解:连接BD,∵E、F分别是AB、AD中点,∴BD=2EF=4,∵BD2+CD2=25,BC2=25,∴BD2+CD2=BC2,∴∠BDC=90°,∴tan C==,故选:A.4.解:∵AB=8,∠C=90°,∠A=30°,∴BC=4,∵D、E分别为AB、AC边上的中点,∴DE=BC=2,故选:A.5.解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=26﹣BC=30﹣12=18,∴DE=BE+CD﹣BC=6,∴PQ=DE=3.故选:C.6.解:由题意:第1个三角形的直角顶点坐标:(﹣2,2);第2个三角形的直角顶点坐标:(﹣1,1);第3个三角形的第1个三角形的直角顶点坐标:(﹣,);第4个三角形的直角顶点坐标:(﹣,);第5个三角形的直角顶点坐标:(﹣,);第6个三角形的直角顶点坐标:(﹣,);故选:A.7.解:延长BN交AC于D,在△ANB和△AND中,,∴△ANB≌△AND,∴AD=AB=8,BN=ND,∵M是△ABC的边BC的中点,∴DC=2MN=6,∴AC=AD+CD=14,故选:B.8.解:∵∠B=90°,BC=3,AB=4,∴AC==5,∵D,E分别是AB,AC的中点,∴DE=BC=,EC=AC=,DE∥BC,∴∠FCM=∠EFC,∵CF平分Rt△ABC的一个外角∠ACM,∴∠FCM=∠FCE,∴∠EFC=∠FCE,∴EF=EC=,∴DF=DE+EF=4,故选:A.9.解:如图,连结DN,∵DE=EM,FN=FM,∴EF=DN,当点N与点B重合时,DN的值最大即EF最大,在Rt△ABD中,∵∠A=90°,AD=6,AB=8,∴BD==10,∴EF的最大值=BD=5.故选:D.10.解:如图,取BC的中点H,连接BE、FH、GH,∵∠BAD=∠CAE=90°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠BAE=∠DAC,在△ABE和△ADC中,,∴△ABE≌△ADC(SAS),∴BE=CD,∠ABE=∠ADC,∴∠BDC+∠DBE=∠BDA+∠ABD=90°,∴BE⊥CD,又∵F、G分别是线段BD和CE的中点,∴FH、GH分别是△BCD和△BCE的中位线,∴FH∥CD且FH=CD,GH∥BE且GH=BE,∴△HFG是等腰直角三角形,∴=,∴=.故选:B.二.填空题(共6小题)11.解:∵E、F分别为MB、BC的中点,∴CM=2EF=2,∵∠ACB=90°,CM是斜边AB上的中线,∴AB=2CM=4,故答案为:4.12.解:延长AE、BC交于点H,∵△ADE是等腰直角三角形,∴∠HAC=45°,AE=AD=2,∴CH=AC=BC,AH=AC=6,∴EH=AH﹣AE=4,∵BC=CH,BF=FE,∴FC=EH=2,故答案为:2.13.解:延长BD交AC于F,在△ADB和△ADF中,,∴△ADB≌△ADF(ASA)∴AF=AB=6,BD=DF,∴FC=AC﹣AF=4,∵BD=DF,BE=EC,∴DE=FC=2,故答案为:2.14.解:当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,∵△A′BC与△ABC关于BC所在直线对称,∴A'C=AC=2,∠ACB=∠A'CB,∵点D,E分别为AB,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠BDE=∠MAN=90°,∴∠BDE=∠A'EF,∴AB∥A'E,∴∠ABC=∠A'EB,∴∠A'BC=∠A'EB,∴A'B=A'E,Rt△A'CB中,∵E是斜边BC的中点,∴BC=2A'E,由勾股定理得:AB2=BC2﹣AC2,∴AE′=,∴AB=;②当∠A'FE=90°时,如图2,∵∠ADF=∠A=∠DFC=90°,∴∠ACF=90°,∵△A′BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC是等腰直角三角形,∴AB=AC=2;综上所述,AB的长为或2;故答案为:或2.15.解:∵在△ABC中,CD⊥AB于点D,E,F分别为AC,BC的中点,∴DE=BC=4.5,DF=AC,EF=AB,∴△DEF的周长=(AB+BC+AC)=×6=3.故答案为:3.16.解:连接BD,取BD的中点H,连接EH,HF,∵E、F分别是AD、BC的中点,∴EH∥AB,EH=AB=,HF∥CD,HF=CD=6,∴∠HEF=∠BMF,∠HFE=∠CNF,∵∠BMF+∠CNF=90°,∴∠HEF+∠HFE=90°,∴∠EHF=90°,∴EF===,故答案为:.三.解答题(共7小题)17.(1)证明:连接DE则DE是△ABC的中位线,DE∥AC,DE=AC∴∠OAC=∠OED,∠OCA=∠ODE∴△OAC∽△OED∴AO:OE=OC:OD=AC:DE=2:1(2)解:CD是Rt△ABC斜边AB上的中线,AB=6 ∴CD=AB=3由(1)可知,OC:OD=2:1∴OC=CD=2.18.解:(1)∵BD是∠ABC的平分线,∴∠ABD=∠CBD=∠ABC,∵DE∥BC,∴∠EDB=∠DBC=∠ABC=40°.(2)∵AB=BC,BD是∠ABC的平分线,∴D为AC的中点,∵DE∥BC,∴E为AB的中点,∴DE=AB=6cm.19.(1)证明:∵F,E是AC,BC的中点,∴FE=AB(中位线定理);∵AD=AB,∴AD=FE,∵点F是AC中点,∴AF=FC,又∠DAF=∠CFE=90°,∴△DAF≌△FEC,∴DF=EC,∴DF=BE;(2)解:∵CF=2,CE=,∴EF=1,∴tan∠ADF=tan∠CEF=2.20.证明:(1)∵BD=CD,∴∠BCD=∠1;∵∠1=∠2,∴∠BCD=∠2;∴CD∥AB.(2)∵CD∥AB,∴∠CDA=∠3.∵∠BCD=∠2=∠3,∴BE=AE.且∠CDA=∠BCD,∴DE=CE.在△BDE和△ACE中,∵.∴△BDE≌△ACE(SAS);(3)∵△BDE≌△ACE,∴∠4=∠1,∠ACE=∠BDE=90°∴∠ACH=90°﹣∠BCH;又∵CH⊥AB,∴∠2=90°﹣∠BCH;∴∠ACH=∠2=∠1=∠4,∴AF=CF;∵∠AEC=90°﹣∠4,∠ECF=90°﹣∠ACH,又∵∠ACH=∠4,∴∠AEC=∠ECF;∴CF=EF;∴EF=AF;∵O为AB中点,∴OF为△ABE的中位线;∴OF=BE.21.(1)证明:在Rt△AEB中,∵AC=BC,∴CE=AB,∴CB=CE,∴∠CEB=∠CBE.∵∠CEF=∠CBF=90°,∴∠BEF=∠EBF,∴EF=BF.∵∠BEF+∠FED=90°,∠EBD+∠EDB=90°,∴∠FED=∠EDF.∴BF=FD;(2)解:由(1)BF=FD,而BC=CA,∴CF∥AD,即AE∥CF.若AC∥EF,则AC=EF,∴BC=BF.∴BA=BD,∠A=45°.∴0°<∠A<90°且∠A≠45°时,四边形ACFE为梯形;(3)解:作GH⊥BD,垂足为H,则GH∥AB.∵DG=DA,∴DH=DB.又F为BD中点,∴H为DF的中点.∴GH为DF的中垂线.∴∠GDF=∠GFD.∵点G在ED上,∴∠EFD≥∠GFD.∵∠EFD+∠FDE+∠DEF=180°,∴∠GFD+∠FDE+∠DEF≤180度.∴3∠EDF≤180度.∴∠EDF≤60度.又∠A+∠EDF=90°,∴30°≤∠A<90°.∴当30°≤∠A<90°时,DE上存在点G,满足条件DG=DA.22.(1)证明:如图1,连接AC,∵E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,∴EF是△ABC的中位线,GH是△DAC的中位线,∴EF∥AC,;HG∥AC,.∴EF GH,∴四边形EFGH是平行四边形;(2)解:四边形EFGH均为平行四边形.证明(以图2为例):连接AC.在△BAC中,∵E、F分别为AB、BC的中点,∴EF∥AC,;在△DAC中,∵G、H分别为AD、CD的中点,∴HG∥AC,.∴EF平行且等于GH.∴四边形EFGH是平行四边形;23.(1)证法一:如答图1a,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,∴AB=BC=BD,∴点B为线段AD的中点,又∵点M为线段AF的中点,∴BM为△ADF的中位线,∴BM∥CF.证法二:如答图1b,延长BM交EF于D,∵∠ABC=∠CEF=90°,∴AB⊥CE,EF⊥CE,∴AB∥EF,∴∠BAM=∠DFM,∵M是AF的中点,∴AM=MF,在△ABM和△FDM中,,∴△ABM≌△FDM(ASA),∴AB=DF,∵BE=CE﹣BC,DE=EF﹣DF,∴BE=DE,∴△BDE是等腰直角三角形,∴∠EBM=45°,∵在等腰直角△CEF中,∠ECF=45°,∴∠EBM=∠ECF,∴MB∥CF;(2)解法一:如答图2a所示,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,∴AB=BC=BD=a,AC=CD=a,∴点B为AD中点,又点M为AF中点,∴BM=DF.分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,∴CE=EF=GE=2a,CG=CF=a,∴点E为FG中点,又点M为AF中点,∴ME=AG.∵CG=CF=a,CA=CD=a,∴AG=DF=a,∴BM=ME=×a=a.解法二:如答图1b.∵CB=a,CE=2a,∴BE=CE﹣CB=2a﹣a=a,∵△ABM≌△FDM,∴BM=DM,又∵△BED是等腰直角三角形,∴△BEM是等腰直角三角形,∴BM=ME=BE=a;(3)证法一:如答图3a,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,∴AB=BC=BD,AC=CD,∴点B为AD中点,又点M为AF中点,∴BM=DF.延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,∴CE=EF=EG,CF=CG,∴点E为FG中点,又点M为AF中点,∴ME=AG.在△ACG与△DCF中,,∴△ACG≌△DCF(SAS),∴DF=AG,∴BM=ME.证法二:如答图3b,延长BM交CF于D,连接BE、DE,∵∠BCE=45°,∴∠ACD=45°×2+45°=135°∴∠BAC+∠ACF=45°+135°=180°,∴AB∥CF,∴∠BAM=∠DFM,∵M是AF的中点,∴AM=FM,在△ABM和△FDM中,,∴△ABM≌△FDM(ASA),∴AB=DF,BM=DM,∴AB=BC=DF,在△BCE和△DFE中,,∴△BCE≌△DFE(SAS),∴BE=DE,∠BEC=∠DEF,∴∠BED=∠BEC+∠CED=∠DEF+∠CED=∠CEF=90°,∴△BDE是等腰直角三角形,又∵BM=DM,∴BM=ME=BD,故BM=ME.。
(完整版)三角形的中位线经典练习题及其答案

八年级三角形的中位线练习题及其答案1.连结三角形___________的线段叫做三角形的中位线. 2.三角形的中位线______于第三边,并且等于_______. 3.一个三角形的中位线有_________条. 4。
如图△ABC 中,D 、E 分别是AB 、AC 的中点,则线段CD 是△ABC 的___, 线段DE 是△ABC _______5、如图,D 、E 、F 分别是△ABC 各边的中点 (1)如果EF =4cm ,那么BC =__cm 如果AB =10cm ,那么DF =___cm(2)中线AD 与中位线EF 的关系是___6.如图1所示,EF 是△ABC 的中位线,若BC=8cm ,则EF=_______cm .(1) (2) (3) (4)7.三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点所围成的三角形的周长是_________cm . 8.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______. 9.若三角形的三条中位线长分别为2cm ,3cm,4cm,则原三角形的周长为( ) A .4。
5cm B .18cm C .9cm D .36cm10.如图2所示,A ,B 两点分别位于一个池塘的两端,小聪想用绳子测量A ,B 间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A ,B 的点C ,找到AC ,BC 的中点D,E ,并且测出DE 的长为10m ,则A ,B 间的距离为( )A .15mB .25mC .30mD .20m11.已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形,•再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( ) A 、20081 B 、20091 C 、220081 D 、22009112.如图3所示,已知四边形ABCD ,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减少 C .线段EF 的长不变 D .线段EF 的长不能确定13.如图4,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,AB=6,AC=4,则四边形AEDF•的周长是( ) A .10 B .20 C .30 D .4014.如图所示,□ ABCD 的对角线AC ,BD 相交于点O ,AE=EB ,求证:OE ∥BC .15.已知矩形ABCD 中,AB =4cm ,AD =10cm ,点P 在边BC 上移动,点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点。
北师大版八年级下册数学 6.3三角形中位线定理的认识(含解析)

三角形中位线定理的认识一、选择题1、Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为()A.10cm B.3cm C.4cm D.5cm2、如图,点D、E、F分别为△ABC各边中点,下列说法正确的是()A.DE=DFB.EF=ABC.S△ABD=S△ACD D.AD平分∠BAC3、如图,已知矩形ABCD,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当P在BC上从B向C移动而R不动时,那么下列结论成立的是( )A .线段EF的长逐渐增大B .线段EF的长逐渐减少C .线段EF的长不变D .线段EF的长不能确定4、如图,已知四边形ABCD中,R、P 分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D 移动而点R不动时,那么下列结论成立的是( )A .线段EF的长逐渐增大B .线段EF的长逐渐减少C .线段EF的长不变D .线段EF的长与点P的位置有关5、如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是()A.15米B.20米C.25米D.30米6、如图,▱ABCD中,对角线AC、BD相交于点O,E是AD的中点,连接OE,如果AB=8,那么OE为()A.6B.4C.3D.27、如图,D,E,F分别为△ABC三边的中点,则图中平行四边形共有()个.A.2B.3C.4D.58、如图,在△ABC中,点D、E、F分别是三边的中点,那么平移△ADE可以得到()A.△DBF和△DEF B.△DBF和△ABCC.△DEF和△CEF D.△DBF和△EFC9、如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若BD平分∠ABC,则下列结论错误的是()A.BC=2BE B.∠A=∠EDA C.BC=2AD D.BD⊥AC10、如图,在△ABC中,D是AB的中点,E是AC的中点,那么的值是()A.B.C.D.11、等边三角形的一条中线与一条中位线的比值是()A.3:1B.:2D.:1C.:12、如图,D,E,F分别为△ABC三边的中点,且AB=AC≠BC,那么△DEF为()A.等边三角形B.等腰直角三角形C.等腰三角形D.不等边三角形13、如图,ABCD是等腰梯形,对角线AC与BD交于O点,AD=2,M、N分别是OB、OC的中点,AN与DM互相平分,则BC等于()A.1B.2C.3D.414、如图1,在△ABC中,D、E分别是AB、AC的中点,将△ADE沿线段DE向下折叠,得到图2.下列关于图2的四个结论中,不一定成立的是()A.点A落在BC边的中点B.∠B+∠1+∠C=180°C.△DBA是等腰三角形D.DE∥BC15、三角形的三条中位线长分别为6,8,10,则该三角形为()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定16、如图,在Rt△ABC中,∠ACB=90°,D、E分别为AC、AB的中点,连DE、CE.则下列结论中不一定正确的是()A.ED∥BC B.ED⊥AC C.∠ACE=∠BCE D.AE=CE二、填空题17、如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA,OB的中点M,N,测得MN=32m,则A,B两点间的距离是__________m.18、如图,若D,E分别是AB,AC中点,现测得DE的长为10米,则池塘的宽BC是__________米。
2021年中考复习分类专题练习:三角形中位线定理综合运用(二)(含答案)

2021年中考复习分类专题练习:三角形中位线定理综合运用(二)Megan 一.选择题1.如图,在△ABC中,点E、F分别为AB、AC的中点.若△ABC的周长为6,则△AEF的周长为()A.12 B.3 C.4 D.不能确定2.如图在△ABC中,M是BC中点,AP是∠A平分线,BP⊥AP于P,AB=12,AC=22,则MP 长为()A.3 B.4 C.5 D.63.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度()A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大4.如图,在△ABC中,D,E分别是AB,AC边的中点,若DE=2,则BC的长度是()A.6 B.5 C.4 D.35.如图,在△ABC中,D、E分别是AB、AC的中点,BC=16,F是线段DE上一点,连接AF、CF,DE=4DF,若∠AFC=90°,则AC的长度是()A.6 B.8 C.10 D.126.如图,在▱ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A.3cm B.6cm C.9cm D.12cm7.如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD 于F,交AB于G,连接EF,则线段EF的长为()A.1 B.C.D.8.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B 之间的距离为()A.30m B.70m C.105m D.140m9.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC 于点E.若DF=5,BC=16,则线段EF的长为()A.4 B.3 C.2 D.110.如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则的值等于()A.B.C.D.11.如图,△ABC中,M是BC的中点,AD平分∠BAC,BD⊥AD于点D,若AB=12,AC=16,则MD等于()A.4 B.3 C.2 D.112.如图,D是△ABC内一点,BD⊥CD,E、F、G、H分别是边AB、BD、CD、AC的中点.若AD=10,BD=8,CD=6,则四边形EFGH的周长是()A.24 B.20 C.12 D.10二.填空题13.如图,在△ABC中,AB=AC,BC=6,点F是BC的中点,点D是AB的中点,连接AF和DF,若△DBF的周长是11,则AB=.14.如图,EF是△ABC的中位线,将△AEF沿中线AD方向平移到△A1E1F1的位置,使E1F1与BC边重合,已知△AEF的面积为7,则图中阴影部分的面积为.15.如图,D是△ABC内一点,BD⊥CD,E,F,G,H分别是AB,BD,CD,AC的中点.若AD =5,BD=4,CD=3,则四边形EFGH的周长是.16.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE=.17.△ABC中,∠ACB=90°,BD=AC,M、N分别为CD、AB的中点,CD=2,MN=2,则CN=.三.解答题18.如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=BC 求证:D、E分别是AB、AC的中点.19.在△ABC中,∠ACB=90°,AC=.以BC为底作等腰直角△BCD,E是CD的中点,求证:AE⊥EB.20.证明:三角形中位线定理.已知:如图,D,E分别是△ABC的边AB,AC的中点.求证:.证明:21.已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)如图1,当CB 与CE 在同一直线上时,求证:MB ∥CF ;(2)如图1,若CB =a ,CE =2a ,求BM ,ME 的长;(3)如图2,当∠BCE =45°时,求证:BM =ME .22.如图,在△ABC 中,AB <AC ,点D 、F 分别为BC 、AC 的中点,E 点在边AC 上,连接DE ,过点B 作DE 的垂线交AC 于点G ,垂足为点H ,且△CDE 与四边形ABDE 的周长相等,设AC =b ,AB =c .(1)求线段CE 的长度;(2)求证:DF =EF ;(3)若S △BDH =S △EGH ,求的值.23.如图,E 、F 、G 、H 分别为四边形ABCD 四边之中点.(1)求证:四边形EFGH 为平行四边形;(2)当AC 、BD 满足 时,四边形EFGH 为菱形.当AC 、BD 满足 时,四边形EFGH 为矩形.当AC 、BD 满足 时,四边形EFGH 为正方形.参考答案一.选择题1.解:∵点E、F分别为AB、AC的中点.∴EF=BC,EA=BA,AF=AC,∵△ABC的周长为6,即AB+AB+BC=6,∴△AEF的周长=AE+AF+EF=(AB+AC+BC)=3,故选:B.2.解:延长BP交AC于N∵AP是∠BAC的角平分线,BP⊥AP于P,∴∠BAP=∠NAP,∠APB=∠APN=90°,∴△ABP≌△ANP(ASA),∴AN=AB=12,BP=PN,∴CN=AC﹣AN=22﹣12=10,∵BP=PN,BM=CM,∴PM是△BNC的中位线,∴PM=CN=5.故选:C.3.解:连接AQ,∵点Q是边BC上的定点,∴AQ的大小不变,∵E,F分别是AP,PQ的中点,∴EF=AQ,∴线段EF的长度保持不变,故选:A.4.解:∵在△ABC中,D,E分别是AB,AC边的中点,∴DE是△ABC的中位线,∵DE=2,∴BC的长度是:4.故选:C.5.解:∵D、E分别是AB、AC的中点,∴DE=BC=8,∵DE=4DF,∴DF=DE=2,∴EF=DE﹣DF=6,∵∠AFC=90°,点E是AC的中点,∴AC=2EF=12,故选:D.6.解:∵四边形ABCD是平行四边形,∴OA=OC;又∵点E是BC的中点,∴BE=CE,∴AB=2OE=2×3=6(cm)故选:B.7.解:∵AD是∠BAC平分线,∴∠BAD=∠CAD,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA)∴AG=AC=3,GF=FC,∴GB=AB﹣AG=1,∵CF=FG,CE=EB,∴EF是△CGB的中位线,∴EF=GB=,故选:C.8.解:∵D、E分别是AC、BC的中点,∴DE是△ABC的中位线,根据三角形的中位线定理,得:AB=2DE=70m.故选:B.9.解:延长AF交BC于H,在△AFB和△HFB中,,∴△AFB≌△HFB,∴AF=FH,又AD=DB,∴BH=2DF=10,DF∥BC,∴HC=BC﹣BH=6,∵DF∥BC,AF=FH,∴EF=HC=3,故选:B.10.解:如图,取BC的中点H,连接BE、FH、GH,∵∠BAD=∠CAE=90°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠BAE=∠DAC,在△ABE和△ADC中,,∴△ABE≌△ADC(SAS),∴BE=CD,∠ABE=∠ADC,∴∠BDC+∠DBE=∠BDA+∠ABD=90°,∴BE⊥CD,又∵F、G分别是线段BD和CE的中点,∴FH、GH分别是△BCD和△BCE的中位线,∴FH∥CD且FH=CD,GH∥BE且GH=BE,∴△HFG是等腰直角三角形,∴=,∴=.故选:B.11.解:延长BD交AC于H,∵AD平分∠BAC,BD⊥AD,∴BD=DH,AH=AB=12,∴HC=AC﹣AH=4,∵M是BC中点,BD=DH,∴MD=CH=2,故选:C.12.解:∵BD⊥CD,BD=8,CD=6,∴BC===10,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=BC,EF=GH=AD,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=10,∴四边形EFGH的周长=10+10=20,故选:B.二.填空题(共5小题)13.解:∵AB=AC,AF⊥BC,∴BF=CF=BC=×6=3,∵AF⊥BC,点D是AB的中点,∴AB=2BD=2DF,∵△DBF的周长是11,∴DB=DF=×(11﹣3)=4,∴AB=2DF=2×4=8.故答案为:8.14.解:∵EF是△ABC的中位线,∴EF∥BC,EF=BC.∴△AEF∽△ACB.∴=()2=.∴△ABC的面积=28.∴图中阴影部分的面积为28﹣7﹣7=14.故答案为:14.15.解:在Rt△BDC中,BD=4,CD=3,∴BC==5,∵F,G分别是BD,CD的中点,∴FG是△DBC的中位线,∴FG=BC=2.5,同理,EF=AD=2.5,EH=BC=2.5,HG=AD=2.5,∴四边形EFGH的周长=FG+EF+EH+HG=10,故答案为:10.16.解:如图,∵在Rt△ABC中,∠ABC=90°,F为CA的中点,BF=5,∴AC=2BF=10.又∵D、E分别为AB、BC的中点,∴DE是Rt△ABC的中位线,∴DE=AC=5.故答案是:5.17.解:过点N作NE⊥BC于点E,则NE∥AC,又N是AB的中点,∴NE=AC,BE=(2+BD)=(2+AC)=1+AC,∴EM=MD+DE=1+BD﹣BE=AC,∴NE=ME,由勾股定理得,MN2=ME2+NE2,即(2)2=ME2+NE2,解得,NE=ME=2,∴CN===.故答案为:.三.解答题(共6小题)18.证明:作BF∥AC交ED的延长线于点F,∵DE∥BC,∴四边形BCEF是平行四边形,∴BC=EF=2ED,AC∥BF,EC=BF,∴ED=DF,∠A=∠DBF,∴在△ADE与△BDF中,,∴△ADE≌△BDF(AAS)∴AD=BD,AE=BF=EC,即D、E分别是AB、AC的中点.19.证明:过E作EF∥BC交BD于F.∵∠ACE=∠ACB+∠BCE=135°,∠DFE=∠DBC=45°,∴∠EFB=135°.又EF=BC,EF∥BC,AC=BC,∴EF=AC,CE=FB.∴△EFB≌△ACE.∴∠CEA=∠DBE.又∵∠DBE+∠DEB=90°,∴∠DEB+∠CEA=90°.故∠AEB=90°.∴AE⊥EB.20.求证:DE∥BC,DE=BC.证明:延长DE至点F,使EF=DE连接CF.∵E是AC的中点,∴AE=CE.在△ADE与△CFE中,∵,∴△ADE≌△CFE(SAS),∴AD=CF,∠ADE=∠F,∴BD∥CF,∴四边形BCFD是平行四边形,∴DF∥BC,DF=BC,∴DE∥BC,DE=BC.故答案为:DE∥BC,DE=BC.21.(1)证法一:如答图1a,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,∴AB=BC=BD,∴点B为线段AD的中点,又∵点M为线段AF的中点,∴BM为△ADF的中位线,∴BM∥CF.证法二:如答图1b,延长BM交EF于D,∵∠ABC=∠CEF=90°,∴AB⊥CE,EF⊥CE,∴AB∥EF,∴∠BAM=∠DFM,∵M是AF的中点,∴AM=MF,在△ABM和△FDM中,,∴△ABM≌△FDM(ASA),∴AB=DF,∵BE=CE﹣BC,DE=EF﹣DF,∴BE=DE,∴△BDE是等腰直角三角形,∴∠EBM=45°,∵在等腰直角△CEF中,∠ECF=45°,∴∠EBM=∠ECF,∴MB∥CF;(2)解法一:如答图2a所示,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,∴AB=BC=BD=a,AC=CD=a,∴点B为AD中点,又点M为AF中点,∴BM=DF.分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,∴CE=EF=GE=2a,CG=CF=a,∴点E为FG中点,又点M为AF中点,∴ME=AG.∵CG=CF=a,CA=CD=a,∴AG=DF=a,∴BM=ME=×a=a.解法二:如答图1b.∵CB=a,CE=2a,∴BE=CE﹣CB=2a﹣a=a,∵△ABM≌△FDM,∴BM=DM,又∵△BED是等腰直角三角形,∴△BEM是等腰直角三角形,∴BM=ME=BE=a;(3)证法一:如答图3a,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,∴AB=BC=BD,AC=CD,∴点B为AD中点,又点M为AF中点,∴BM=DF.延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,∴CE=EF=EG,CF=CG,∴点E为FG中点,又点M为AF中点,∴ME=AG.在△ACG与△DCF中,,∴△ACG≌△DCF(SAS),∴DF=AG,∴BM=ME.证法二:如答图3b,延长BM交CF于D,连接BE、DE,∵∠BCE=45°,∴∠ACD=45°×2+45°=135°∴∠BAC+∠ACF=45°+135°=180°,∴AB∥CF,∴∠BAM=∠DFM,∵M是AF的中点,∴AM=FM,在△ABM和△FDM中,,∴△ABM≌△FDM(ASA),∴AB=DF,BM=DM,∴AB=BC=DF,在△BCE和△DFE中,,∴△BCE≌△DFE(SAS),∴BE=DE,∠BEC=∠DEF,∴∠BED=∠BEC+∠CED=∠DEF+∠CED=∠CEF=90°,∴△BDE是等腰直角三角形,又∵BM=DM,∴BM=ME=BD,故BM=ME.22.(1)解:∵点D为BC的中点,∴BD=CD,∵△CDE与四边形ABDE的周长相等,∴CD+DE+CE=AB+BD+DE+AE,∴CE=AB+AE=AB+(AC﹣EC),∴2CE=AC+AB=b+c,∴CE=(b+c);(2)证明:∵点D、F分别为BC、AC的中点,∴DF是△CAB的中位线,∴DF=AB=c,AF=AC=b,由(1)知:CE=(b+c),∴AE=b﹣CE=b﹣(b+c)=(b﹣c),∴EF=AF﹣AE=b﹣(b﹣c)=c,∴DF=EF;(3)解:连接BE、DG,如图所示:∵S△BDH =S△EGH,∴S△BDG =S△DEG,∴BE∥DG,∵DF是△CAB的中位线,∴DF∥AB,=,∴△ABE∽△FDG,∴==,∴FG=AE=×(b﹣c)=(b﹣c),过点A作AP⊥BG于P,∵DF∥AB,∴∠DFC=∠BAC,∵∠DFC=∠DEF+∠EDF,EF=DF,∴∠DEF=∠EDF,∴∠BAP+∠PAC=2∠DEF,∵ED⊥BG,AP⊥BG,∴DE∥AP,∴∠PAC=∠DEF,∴∠BAP=∠DEF=∠PAC,∵AP⊥BG,∴AB=AG=c,∴CG=b﹣c,∴CF=b=FG+CG=(b﹣c)+(b﹣c),∴3b=5c,∴=.23.(1)证明:如图,连接BD,∵E、F、G、H分别为四边形ABCD四边之中点,∴EH是△ABD的中位线,FG是△BCD的中位线,∴EH∥BD 且EH=BD,FG∥BD 且FG=BD,∴EH∥FG且EH=FG,∴四边形EFGH为平行四边形;(2)解:连接AC,同理可得EF∥AC且EF=AC,所以,AC=BD时,四边形EFGH为菱形;AC⊥BD时,四边形EFGH为矩形;AC=BD且AC⊥BD时,四边形EFGH为正方形.故答案为:AC=BD;AC⊥BD;AC=BD且AC⊥BD.。
三角形的中线及中位线性质的运用举例

直角三角形斜边上中线性质的运用在直角三角形中有这样一个十分重要而又运用广泛的性质:直角三角形中,斜边上的中线等于斜边的一半.下面就这一性质的应用举例说明.例1 如图1,已知,△ABC 中,CE ⊥AD 于E ,BD ⊥AD 于D ,BM =CM .求证:ME =MD .分析 要证明ME =MD 首先想到的要证明两个角相等,可没有足够的条件,但有中点和垂线,于是想到通过辅助线构造直角三角形,利用直角三角形斜边上的中线性质证明.证明 延长DM 与CE 交于N .因为CE ⊥AD 于E ,BD ⊥AD 于D , 所以CE ∥BD ,即∠NCM =∠DBM ,又∠CMN =∠BMD ,BM =CM ,所以△CMN ≌△BMD , 所以NM =DM ,即M 为ND 中点.因为CE ⊥AD 于E ,所以△NED 为直角三角形,所以ME =12ND ,所以ME =MD .例2 如图2,BD 、CE 是高,G 、F 分别是BC 、DE 的中点,求证:FG ⊥DE .分析 有三角形高就会想到直角三角形,有中点当然会联想到直角三角形斜边上的中点性质和等腰三角形的性质,于是,连结DG 、EG ,可得DG 、EG 分别是Rt △BDC 和Rt △BEC 的中线,可知△GDE 是等腰三角形,进而由F 是DE 的中点,即FG ⊥DE .证明 因为BD 、CE 是高,所以∠BDC =∠BEC =90°, 即△BDC 和△BEC 都是直角三角形. 又因为G 是BC 的中点,所以DG =EG =12BC ,即△GDE 是等腰三角形. 因为F 是DE 的中点,所以GF 是等腰三角形GDE 的底边DE 上的中线, 所以由等腰三角形的“三线合一”,得GF 也是底边DE 上的高线,EDBCA FG图2N ED CBAM图1所以FG ⊥DE .例3 如图3所示,点E 、F 分别为正方形ABCD 边AB 、BC 的中点,DF 、CE 交于点M ,CE 的延长线交DA 的延长线于G ,试探索:(1)DF 与CE 的位置关系;(2)MA 与DG 的大小关系.分析(1)要探索DF 与CE 的位置关系,由图可以猜想到DF ⊥CE ,而由条件可以证明△EBC ≌△FCD ,则有∠ECB =∠FDC ,即可证明DF ⊥CE .(2)仍然通过观察分析图形,可以猜想MA =12DG ,而事实上,由(1)可知△DMG 是直角三角形,再由条件可得△GAE ≌△CBE ,即得GA =CB ,于是利用直角三角形斜边上的中线性质即可证明.解(1)DF ⊥CE .理由:因为点E 、F 分别为正方形ABCD 边AB 、BC 的中点, 所以∠B =∠FCD =90°,BE =12AB ,CF =12BC ,而AB =BC =CD ,即BE =CF , 所以△EBC ≌△FCD ,所以∠ECB =∠FDC ,而∠DFC +∠FDC =90°,所以∠DFC +∠FCM =90°, 即∠CMF =90°,所以DF ⊥CE . (2)MA =12DG .理由:因为F 是AB 的中点,所以AE =BE , 又∠GAE =∠B ,∠AEG =∠BEC ,所以△GAE ≌△CBE ,所以GA =CB . 而由(1)可知△DMG 是直角三角形,所以MA =12DG . 例4 已知:如图4,□ABCD 中,对角线AC 、BD 相交于点O ,EF ⊥AC ,O 是垂足,EF 分别交AB 、CD 于点E 、F ,且BE =OE =12AE .求证:□ABCD 是矩形.EDBCA FGM 图3图4ABCEGFOD分析 要证□ABCD 是矩形,只要证AC =BD 或OA =OB 即可.由BE =OE =12AE ,可作出Rt △AOE 斜边上的中线OG ,这样可证得△AOG ≌△BOE ,于是证得OA =OB .证明 取AE 的中点G ,连结OG ,所以Rt △AOE 中,OG =12AE =AG , 因为BE =OE =12AE ,所以OE =OG ,AG =BE ,即∠OGE =∠OEG , 所以∠AGO =∠OEB ,所以△AGO ≌△BEO ,所以OA =OB ,又四边形ABCD 是平行四边形,所以AC =2OA ,BD =2OB ,即AC =BD , 所以□ABCD 是矩形.综上所述,利用直角三角形斜边上中线的性质解题时,应依据条件,贯例图形,通过分析,把问题转化为证明线段相等,或通过辅助线,构造出直角三角形,利用“直角三角形斜边上的中线等于斜边的一半”,同时兼用全等三角形的知识,从而逐步逼近结论.在几何证明中,另外,熟练地识别图形、善于构造图形,并运用图形的性质进行推理论证是十分重要的.下面一道题目供同学们自己练习:如图6所示,在梯形ABCD 中,AB ∥CD ,∠C +∠D =90°,E 、F 为AB 、CD 的中点.求证:CD -AB =2EF .提示:作EM ∥AD 交CD 于M ,EN ∥BC 交CD 于N .利用直角三角形斜边上中线等斜边的一半.图6FEDCBA聚焦中位线定理的运用中位线定理是三角形一个重要定理.有一个特点,在同一个题设下有两个结论:一个结论是表明两条线段的位置关系(平行),另一个结论是表明两条线段的数量关系(一半).在应用这个定理时,不一定同时需要两个结论,有时需要平行,有时需要倍分关系.可以根据具体情况,按需选用.现举例说明中位线定理的运用.一、用于证明平行例1 在△ABC 中,BD 平分∠ABC ,A D ⊥BD,垂足为D ,AE=EC. 求证:DE ∥BC.图1CFEDBA证明:延长AD 交BC 于点F. 因为BD 平分∠ABC , 所以∠ABD =∠CBD. 因为A D ⊥BD,所以∠BDA =∠BDF=900. 又BD=BD,所以△BDA ≌△BDF(ASA). 所以AD=DF.又因为AE=EC,所以DE ∥FC, 即DE ∥BC (三角形的中位线定理). 二、用于证明角相等例2 如图2,四边形ABCD 中,对角线AC 、BD 相交于O ,已知AC=BD,M,N 分别是AD 、BC 的中点,MN 与AC 、BD 分别交于E 、F 点.求证:∠AEN=∠BFM.图24312FEBAP NMCD分析:可取CD 或AB 的中点构造中位线. 证明:可取AB 的中点P ,连接PM 、PN. 因为AM=MD,AP=BP,BN=NC, 所以MPBD 21,PN AC 21(三角形中位线定理). 所以∠1=∠3,∠2=∠4. 又因为AC=BD, 所以MP=NP, ∠3=∠4, 所以∠1=∠2.所以∠AEN=∠BFM (等角的补角相等). 三、用于证明线段相等例3 如图3,△ABC 的AB 、AC 向形外作正三角形ABD 和ACE,分别取BD 、BC 、CE 的中点P 、M 、Q.求证:PM=QM.图3QPCAD分析:中点P 、M 所在线段DB 、CB 有公共端点B ,若连接它们的另一端D 、C ,则PM 使成为△BCD 的中位线,同理连接BE 之后MQ 也成为△BEC 的中位线,通过中位线定理的传递,问题转化为证明DC 与BE 相等.证明过程由同学们自己完成!四、用于证明线段的特殊关系例4 如图4,已知四边形ABCD 中,E 、F 、G 、H 分别为AB 、CD 、AC 、BD 的中点,且E 、F 、G 、H 不在同一条直线上,求证:EF 和GH 互相平分.分析:要证明EF 和GH 互相平分,可证明四边形EGFH 是平行四边形;有中点,可考虑利用中位线定理.图4GHBE ACFD证明:连接EG 、GF 、FH 、HE. 因为AE=EB, BH=HD, 所以EH AD 21. 同理FG AD 21. 所以EHFG.所以四边形EGFH 是平行四边形. 所以EF 和GH 互相平分.巧用中线的性质解题我们知道三角形的一条中线将三角形分成的两个三角形等底同高,这样的两个三角形的面积相等.下面我们利用上述性质来巧解以下问题.一、巧算式子的值例1 在数学活动中,小明为了求23411112222++++ (1)2n +的值(结果用n 表示),设计了如图1所示的几何图形.请你利用这个几何图形求23411112222++++ (1)2n +的值.图1解析:从图中可以看出大三角形的面积为1,根据三角形的中线把它分成两个面积相等的三角形可知,23411112222++++…12n +12n +表示:组成面积为1的大三角形的所有小三角形的面积之和,于是23411112222++++ (12)n +112n =-.【点评】此题运用“数形结合思想”,借助三角形的面积来求数的运算. 二、求图形的面积例2 如图2,长方形ABCD 的长为a ,宽为b ,E 、F 分别是BC 和CD 的中点,DE 、BF 交于点G ,求四边形ABGD 的面积.图2 解析:连接CG ,不难得出BCFSDCE S=4ab=,从而BEGDFG S S=,由E 、F 分别是BC 和CD 的中点,可得△DGF、△CFG、△CEG、△BEG的面积相等,因此S四边形ABGDab=-4ab43⨯23=ab.【点评】本题的难度较大,通过连接CG,巧妙地把四边形ABGD以外的部分分成四个面积相等的三角形.像CG这样原题中没有,但我们在解题的过程中用它来“辅助”解决问题的线,称之为“辅助线”.三、巧等分土地例3.有一块三角形优良品种试验基地,如图3所示,•由于引进四个优良品种进行对比试验,需将这块土地分成面积相等的四块,请你制定出两种以上的划分方案供选择(画图说明).图3解析:可根据中线的特征,先分为两个面积相等的三角形,然后再依次等分.方案1:如答图(1),在BC上取D、E、F,使BD=ED=EF=FC,连接AE、ED、•AF.(1) (2) (3)方案2:如答图2,分别取AB、BC、CA的中点D、E、F,连接DE、EF、DF.方案3:如答图3,分别取BC的中点D,CD的中点E,AB的中点F,连接AD、AE、DF.【点评】三角形面积计算公式为12×底×高,因此解题的关键是找出底、高分别相等的四个三角形.对于本题,同学们!你还有别的方法吗?试试看.。
三角形中位线定理

。
。B
E
例1:
Байду номын сангаас
已知点O是△ABC内一点,D、E、F、G分 别是AO、BO、CB、CA的中点。
求证:四边形DEFG是平行四边形
C
G
F
O
D A
E B
练习:求证:顺次连结四边形四条边的中点,所得的 四边形是平行四边形
已知:在四边形ABCD中,E.F.G.H 分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形 E
A
D。 。E
B
图1
C
B
D 。 4 。F 53 。
A 图2 E
1.如图1:在△ABC中,DE是中位线 (1)若∠ADE=60°,
则∠B= 60 度,为什么?
(2)若BC=8cm,
则DE= 4 cm,为什么?
2.如图2:在△ABC中,D、E、F分别 是各边中点
AB=6cm,AC=8cm,BC=10cm,
:三角形的中位线平行于第三边,并且等于第三边的 一半
已知:在△ABC 中,DE是△ABC 的中位线 求证:DE ∥ BC,且DE=1/2BC
证明:延 长DE 到 F,使EF=DE ,
A
连 结CF.
D
E
F
B
C
A
D
E
B
C
如果 DE是△ABC的中位线 那么 ⑴ DE∥BC,
⑵ DE=1/2BC
① 证明平行问题 ② 证明一条线段是另一条线段 的2倍或1/2
则△DEF的周长= 12 cm.
C △DEF面积是_________
思考:
如图,在A、B外选一点C,连结AC和BC,
并分别找出AC和BC的中点D、E,如果能测 量出DE的长度,也就能知道AB的距离了。
中位线习题及答案
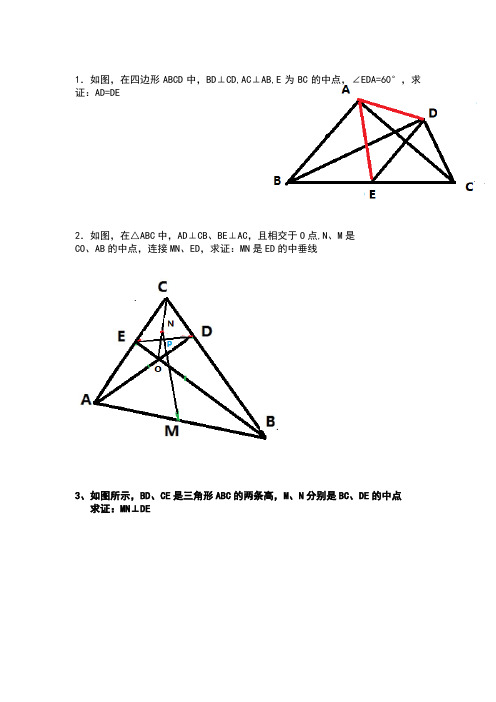
1.如图,在四边形ABCD中,BD⊥CD,AC⊥AB,E为BC的中点,∠EDA=60°,求证:AD=DE2.如图,在△ABC中,AD⊥CB、BE⊥AC,且相交于O点,N、M是CO、AB的中点,连接MN、ED,求证:MN是ED的中垂线3、如图所示,BD、CE是三角形ABC的两条高,M、N分别是BC、DE的中点求证:MN⊥DENMEDCA4、如图,四边形ABCD中,∠DAB=∠DCB=90o,点M、N分别是BD、AC的中点。
MN、AC的位置关系如何证明你的猜想。
NMDCBA5.已知:点B、C分别在射线OA、OD上,AB=CD,△PAB的面积等于△PCD的面积。
求证:OP平分∠AOD。
6、如图,在△ABC 中,∠ABC=60°,AD 、CE 分别平分∠BAC 、∠ACB ,求证:AC=AE+CD .7、如图1,在正方形ABCD 和正方形CGEF (CG >BC )中,点B ,C ,G 在同一直线上,点M 是AE 的中点.(1)探究线段MD ,MF 的位置及数量关系,并证明.(2)若将图1中的正方形CGEF 绕点C 顺时针旋转,使D ,C ,G 三点在一条直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化写出你的猜想并加以证明.(3)将图1中的正方形CGEF 绕点C 顺时针旋转,使正方形CGEF 的对角线CE 恰好与正方形ABCD 的边BC 在同一条直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化写出你的猜想并加以证明.8.已知:在ABC ∆中,AC BC >,动点D 绕ABC ∆的顶点A 逆时针旋转,且BC AD =,连结DC .过AB 、DC 的中点E 、F 作直线,直线EF 与直线AD 、BC 分别相交于点M 、N .(1)如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连结HE 、HF ,根据三角形中位线定理和平行线的性质,可得结论BNE AMF ∠=∠(不需证明). (2)当点D 旋转到图2或图3中的位置时,AMF ∠与BNE ∠有何数量关系请分别写出猜想,并任选一种情况证明.分析:取AC 的中点H ,连接HE 、HF ,当点D 旋转到图2中的位置时,由F 为DC 的中点,E 为AB 的中点,根据三角形中位线的性质得到FH ∥AD ,且FH=1/2AD ;HE ∥BC ,且HE=1/2BC ,得到∠HFE=∠AMF ,∠HEF=∠ENB ,HE=HF ,则∠HEF=∠HFE ,所以∠AMF=∠BNE ;当点D 旋转到图3中的位置时,同理可证得∠AMF=∠BNE . 解:取AC 的中点H ,连接HE 、HF ,如图,当点D 旋转到图2中的位置时,∵F 为DC 的中点,E 为AB 的中点,∴FH ∥AD ,且FH=1/2AD ;HE ∥BC ,且HE=1/2BC ,∴∠HFE=∠AMF ,∠HEF=∠ENB ,HE=HF , ∴∠HEF=∠HFE ,∴∠AMF=∠BNE ;当点D 旋转到图3中的位置时,用同样的方法可证明∠HFE=∠AME ,∠HEF=∠BNE ,而∠HFE=∠HEF ,∴∠AME=∠BNE ,而∠AMF+∠AME=180°,∴∠AMF+∠BNE=180°.故答案为:∠AMF=∠BNE 或∠AMF+∠BNE=18010、如图1,在四边形ABCD 中,AB=CD ,E 、F 分别是BC 、AD 的中点,连接EF 并延长,分别与BA 、CD 的延长线交于点M 、N ,则∠B M E =∠C N E (不需证明).(温馨提示:在图1中,连接BD ,取BD 的中点H ,连接HE 、HF ,根据三角形中位线定理,证明HE =HF ,从而∠1=∠2,再利用平行线性质,可证得∠B M E =∠图2 图3图1 H MF C D MN F A C D M N FA B C D (N)C N E.)问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△O MN的形状,请直接写出结论;问题二:如图3,在△AB C中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EF C=60°,连接GD,判断△AGD的形状并证明.解:(1)取AC中点P,连接PF,PE,可知PE=AB/ 2 ,PE∥AB,∴∠PEF=∠ANF,同理PF=CD / 2 ,PF∥CD,∴∠PFE=∠CME,又PE=PF,∴∠PFE=∠PEF,∴∠OMN=∠ONM,∴△OMN为等腰三角形.(2)判断出△AGD是直角三角形.证明:如图连接BD,取BD的中点H,连接HF、HE,∵F是AD的中点,∴HF∥AB,HF=1/2AB,同理,HE∥CD,HE=1/2CD,∵AB=CD∴HF=HE,∵∠EFC=60°,∴∠HEF=60°,∴∠HEF=∠HFE=60°,∴△EHF是等边三角形,∴∠3=∠EFC=∠AFG=60°,∴△AGF是等边三角形.∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°∴∠AGD=90°即△AGD是直角三角形.。
三角形的中位线练习题(含答案)
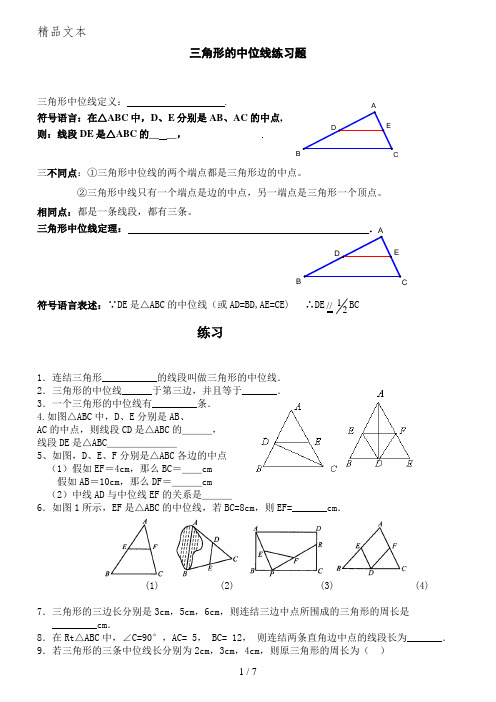
三角形的中位线练习题三角形中位线定义: .符号语言:在△ABC 中,D 、E 分别是AB 、AC 的中点, 则:线段DE 是△ABC 的__ __,三不同点:①三角形中位线的两个端点都是三角形边的中点。
②三角形中线只有一个端点是边的中点,另一端点是三角形一个顶点。
相同点:都是一条线段,都有三条。
三角形中位线定理: .符号语言表述:∵DE 是△ABC 的中位线(或AD=BD,AE=CE) ∴DE //21BC练习1.连结三角形___________的线段叫做三角形的中位线. 2.三角形的中位线______于第三边,并且等于_______. 3.一个三角形的中位线有_________条. 4.如图△ABC 中,D 、E 分别是AB 、AC 的中点,则线段CD 是△ABC 的___, 线段DE 是△ABC _______5、如图,D 、E 、F 分别是△ABC 各边的中点 (1)假如EF =4cm ,那么BC =__cm 假如AB =10cm ,那么DF =___cm (2)中线AD 与中位线EF 的关系是___6.如图1所示,EF 是△ABC 的中位线,若BC=8cm ,则EF=_______cm .(1) (2) (3) (4)7.三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点所围成的三角形的周长是_________cm .8.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______. 9.若三角形的三条中位线长分别为2cm ,3cm ,4cm ,则原三角形的周长为( )E DBEDAA .4.5cmB .18cmC .9cmD .36cm10.如图2所示,A ,B 两点分别位于一个池塘的两端,小聪想用绳子测量A ,B 间的距离,但绳子不够长,一位同学帮他想了一个方法:先在地上取一个可以直接到达A ,B 的点C ,找到AC ,BC 的中点D ,E ,并且测出DE 的长为10m ,则A ,B 间的距离为( ) A .15m B .25m C .30m D .20m11.已知△ABC 的周长为1,连结△ABC 的三边中点构成其次个三角形,•再连结其次个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( ) A 、20081 B 、20091 C 、220081 D 、22009112.如图3所示,已知四边形ABCD ,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC 上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是( ) A .线段EF 的长渐渐增大 B .线段EF 的长渐渐削减 C .线段EF 的长不变 D .线段EF 的长不能确定13.如图4,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,AB=6,AC=4,则四边形AEDF•的周长是( )A .10B .20C .30D .4014.如图所示,□ ABCD 的对角线AC ,BD 相交于点O ,AE=EB ,求证:OE ∥BC .15.已知矩形ABCD 中,AB =4cm ,AD =10cm ,点P 在边BC 上移动,点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点.求证:EF +GH =5cm ;16.如图所示,在△ABC 中,点D 在BC 上且CD=CA ,CF 平分∠ACB ,AE=EB ,求证:EF=12BD .BG A E FH D C 图5 17.如图所示,已知在□ABCD 中,E ,F 分别是AD ,BC 的中点,求证:MN ∥BC .18.已知:如图,四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点. 求证:四边形EFGH 是平行四边形.19.如图,点E ,F ,G ,H 分别是CD ,BC ,AB ,DA 的中点。
专题15 三角形的中位线(含答案)

专题15 三角形的中位线知识解读三角形的中位线定理,反映了三角形的中位线与第三边的双重关系:(1)位置关系,三角形的中位线平行于第三边;(2)数量关系,三角形的中位线等于第三边长的一半。
位置关系可证明两直线平行;数量关系可证明线段的倍分关系。
培优学案典例示范一、中位线反映了线段间的平行和数量关系1.如图4-15-1,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()图4-15-1A.2B.3C.52D.4【提示】由于D,E分别是BC,AC的中点,所以DE是△ABC的中位线,根据中位线定6理可知DE∥AB,所以∠BFD=∠ABF;又由于BF平分∠ABC,所以∠ABF=∠CBF,就可证得△BDF为等腰三角形,要求DF 的长,只需求BD的长即可.【技巧点评】当题中有中点时,特别是一个三角形中出现两边中点时,我们常常考虑运用三角形的中位线来解决问题.本题是采用中位线来证明两直线平行.跟踪训练1.如图4-15-2,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.7B.9C.10D.11图4-15-2 2.如图4-15-3,已知E为平行四边形ABCD中DC边的延长线的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF.求证:AB=2OF.图4-15-3【提示】点O是平行四边形两条对角线的交点,所以点O是线段AC的中点,要证明AB=2OF,我们只需证明点F是BC的中点,即证明OF是△ABC的中位线,证明F是BC的中点有两种方法,方法一是证明四边形ABEC是平行四边形,利用平行四边形的对角线互相平分来证明;方法二是证明△ABFQ△ECF,利用全等三角形对应边相等来证明.【解答】【技巧点评】由于中位线等于三角形第三边长的一半,因此当需要证明某一线段是另一线段的一半或两倍,且题中出现中点的时候,常常考虑使用中位线定理.跟踪训练2.如图4-15-4,平行四边形ABCD中,M、N分别是AB、CD的中点,AN与DM相交于点P,BN与CM 相交于点Q.试说明PQ与MN互相平分.图4-15-4二、补全三角形,使得中点连线段成为中位线例3如图4-15-5,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,四边形MNPQ是平行四边形吗?为什么?【提示】点P、点N分别是CD,BD的中点,很显然PN是△BCD的中位线,所以考虑连接BC,将△BCD补全,然后运用中位线定理解决问题.【解答】图4-15-5 【技巧点评】当一个图形中出现具有公共端点的两条线段的中点时,可考虑连接另外两个端点,构造三角形,使得中点连线段成为中位线.跟踪训练3.如图4-15-6,在△ABC中,E、F分别是AB、BC的中点,G、H是AC的三等分点,EG、FH的延长线相交于点D.求证:四边形ABCD是平行四边形.【解答】图4-15-6三、由一个中点构造中位线解决问题例4如图4-15-7,已知四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是()图4-15-7A.1<MN<5B.1<MN≤5C.12<MN52<D.12<MN52【提示】M,N虽然是AD,BC的中点,但MN却不是三角形的中位线,可考虑连接BD,取BD的中点G,线段GM和GN可以看成△ABD和△BCD的中位线,利用中位线可求得GM、GN的长分别为1和1.5.在△GMN中利用三角形两边之和大于第三边以及两边之差小于第三边可求得MN的范围.【技巧点评】当图形中出现中点的时候,就可能应用中位线知识解决问题,如果没有中位线,应考虑构造中位线解决问题.跟踪训练4.如图4-15-8所示.D,E分别在AB,AC上,BD=CE,BE,CD的中点分别是M,N,直线MN分别交AB,AC于P,Q.求证:AP=AQ.【解答】图4-15-8拓展延伸例5 在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.(1)如图4-15-9①,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;(2)如图4-15-9②,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.图4-15-9【提示】(1)延长DF交AB于点G,根据三角形中位线的判定得出点G为AB的中点,根据中位线的性质及已知条件AC=BC,得出DC=DG,从而EC=FG,易证∠ECF=∠GFH=90°-∠DFC,∠CEF=∠FGH=135°,由AAS证出△CEF≌△FGH.∴CF=FH.(2)通过证明△CEF≌△FGH得出.【解答】跟踪训练5.如图4-15-10,D 是△ABC 中AB 边上的中点,△ACE 和△BCF 分别是以AC ,BC 为斜边的等腰直角三角形,连接DE ,DF.求证:DE=DF.【解答】EABFCD图4-15-10竞赛链接例6(武汉竞赛试题)如图4-15-11,在△ABC 中,∠ABC,∠ACB 的平分线 BE ,CF 相交于O ,AGLBE 于G ,AHLCF 于H. (1)求证:GH/∥BC;(2)若AB=9厘米,AC=14厘米,BC=18厘米,求GH 的长度。
专题12 三角形中位线定理-2020-2021学年八年级数学下册常考题专练(人教版)(解析版)

专题12三角形中位线定理★知识归纳●三角形的中位线1.连接三角形两边中点的线段叫做三角形的中位线.2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.要点梳理:(1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系.(2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的12,每个小三角形的面积为原三角形面积的14.(3)三角形的中位线不同于三角形的中线.★实操夯实一.选择题(共18小题)1.如图,在△ABC中,AB=3,BC=6,AC=4,点D,E分别是边AB,CB的中点,那么DE的长为()A.1.5B.2C.3D.4【解答】解:∵点D,E分别是边AB,CB的中点,∴DE=AC=2,故选:B.2.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE等于()A.AB B.AC C.AB D.AC【解答】解:如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.又∵点D是AB的中点,∴EF=AE.∵∠DEF=∠BFC=180°﹣∠AED=180°﹣(90°+∠C)=90°﹣∠C,∴∠FBC=∠BFC,∴BC=FC,∴BC+2AE=AC.故选:B.3.如图,在△ABC中,E,F分别为AC,BC中点,若AB=6,BC=7,AC=8,则EF=()A.3B.3.5C.4D.4.5【解答】解:∵E,F分别为AC,BC中点,∴EF是△ABC的中位线,∴EF=AB=×6=3,故选:A.4.如图,平地上A、B两点被池塘隔开,测量员在岸边选一点C,并分别找到AC和BC的中点M、N,测量得MN =8米,则A、B两点间的距离为()A.4米B.24米C.16米D.48米【解答】解:∵点M、N分别为AC和BC的中点,∴MN是△ABC的中位线,∴AB=2MN=16(米),故选:C.5.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为()A.2B.4C.6D.8【解答】解:∵BD平分∠ABC,∴∠ABD=∠CBD,∵EF是△ABC的中位线,∴EF∥BC,BC=2EF,∴∠EDB=∠CBD,∴∠ABD=∠EDB,∴ED=EB=3,∴EF=ED+DF=4,∴BC=2EF=8,故选:D.6.一个三角形的三条中位线的长为6、7、8,则此三角形的周长为()A.10.5B.21C.42D.63【解答】解:∵三角形的三条中位线的长为6、7、8,∴三角形的三边长分别为12、14、16,∴此三角形的周长=12+14+16=42,故选:C.7.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度()A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大【解答】解:连接AQ,∵点Q是边BC上的定点,∴AQ的大小不变,∵E,F分别是AP,PQ的中点,∴EF=AQ,∴线段EF的长度保持不变,故选:A.8.如图,△ABC中,D,E分别是BC,AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是()A.3B.4C.5D.6【解答】解:∵D,E分别是BC,AC的中点,∴DE∥AB,∴∠BFD=∠ABF,∵BF平分∠ABC,∴∠DBF=∠ABF,∴∠BFD=∠DBF,∴DF=DB=BC=3,故选:A.9.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是()A.2B.3C.4D.5【解答】解:∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∵BC=14,∴DE=BC=7,∵∠AFB=90°,AB=8,∴DF=AB=4,∴EF=DE﹣DF=7﹣4=3,故选:B.10.△ABC中,点D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED=()A.22°B.68°C.96°D.112°【解答】解:∵点D、E分别是△ABC的边AB、AC的中点,∴DE∥BC,∴∠AED=∠C,∵∠C=68°,∴∠AED=∠C=68°.故选:B.11.如图,△ABC中,D、E分别是AB、AC边的中点,延长DE至F,使EF=DF,若BC=8,则DF的长为()A.6B.8C.4D.【解答】解:∵D、E分别是AB、AC边的中点,∴DE=BC=4,∵EF=DF,∴EF=2,∴DF=6,故选:A.12.如图,在直角三角形ABC中,∠C=90°,点E、F分别为AC和AB的中点,AF=5,AE=4,则BC=()A.3B.6C.8D.10【解答】解:∵点E、F分别为AC和AB的中点,∴EF∥BC,BC=2EF,∴∠AEF=∠C=90°,∴EF===3,∴BC=6,故选:B.13.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3B.4C.5D.6【解答】解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=DE=4.故选:B.14.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()A.B.2C.D.3【解答】解:延长BC到E使BE=AD,则四边形ABED是平行四边形,∵BC=3,AD=6,∴C是BE的中点,∵M是BD的中点,∴CM=DE=AB,∵AC⊥BC,∴AB===5,∴CM=,故选:C.15.如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为()A.50°B.25°C.15°D.20°【解答】解:∵在四边形ABCD中,M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM=AB,PN=DC,PM∥AB,PN∥DC,∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN==25°.故选:B.16.如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE =2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是()A.①②④B.①③④C.①②③D.①②③④【解答】解:①∵CB是三角形ACE的中线,∴AE=2AB,又AB=AC,∴AE=2AC.故此选项正确;②取CE的中点F,连接BF.∵AB=BE,CF=EF,∴BF∥AC,BF=AC.∴∠CBF=∠ACB.∵AC=AB,∴∠ACB=∠ABC.∴∠CBF=∠DBC.又∵CD是三角形ABC的中线,∴AC=AB=2BD.∴BD=BF.又∵BC=BC,∴△BCD≌△BCF,∴CF=CD.∴CE=2CD.故此选项正确.③若要∠ACD=∠BCE,则需∠ACB=∠DCE,又∠ACB=∠ABC=∠BCE+∠E=∠DCE,则需∠E=∠BCD.根据②中的全等,得∠BCD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故此选项错误;④根据②中的全等,知此选项正确.故选:A.17.如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①AD⊥BC;②AE∥BC;③AE=AG;④AD2+AE2=4AG2.其中正确结论的个数是()A.1B.2C.3D.4【解答】解:连接EC,∵AB=AC,AD是∠BAC的平分线,∴AD⊥BC,故①正确;∵AB=AC,∴∠B=∠ACB,∵AE平分∠F AC,∴∠F AC=2∠F AE,∵∠F AC=∠B+∠ACB,∴∠F AE=∠B,∴AE∥BC,故②正确;∵AE∥BC,DE∥AB,∴四边形ABDE是平行四边形,∴AE=BD,∵AB=AC,AD⊥BC,∴CD=BD,∴AE=CD,∵AE∥BC,∠ADC=90°,∴四边形ADCE是矩形,∴AC=DE,AG=CG,DG=EG,∴DG=AG=CG=EG,在Rt△AED中,AD2+AE2=DE2=AC2=(2AG)2=4AG2,故④正确;∵AE=BD=BC,AG=AC,∴AG=AE错误(已知没有条件AC=BC),故③错误;即正确的个数是3个,故选:C.18.如图,△ABC中,AB>AC,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则①EF∥AB;②∠BCG=(∠ACB﹣∠ABC);③EF=(AB﹣AC);④(AB﹣AC)<AE<(AB+AC).其中正确的是()A.①②③④B.①②C.②③④D.①③④【解答】解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC=90°,在△AFG和△AFC中∴△AFG≌△AFC(ASA),∴GF=CF,∵AE为△ABC的中线,∴BE=CE,∴EF∥AB,故①正确;∵△AFG≌△AFC,∴∠AGC=∠ACG,∠AGF=∠ACF,∵∠AGC=∠B+∠BCG,∴∠ACG=∠B+∠BCG,∴∠BCG=∠ACB﹣∠ACG=∠ACB﹣(∠B+∠BCG),∴2∠BCG=∠ACB﹣∠B,∴∠BCG=(∠ACB﹣∠B),故②正确;∵△AFG≌△AFC,∴AC=AG,∴BG=AB﹣AG=AB﹣AC,∵F、E分别是CG、BC的中点,∴EF=BG,∴EF=(AB﹣AC),故③正确;∵∠AFG=90°,∴∠EAF<90°,∵∠AFE=∠AFG+∠EFG>90°,∴∠AFE>∠EAF,∴AE>EF,∵EF=(AB﹣AC),∴(AB﹣AC)<AE,延长AE到M,使AE=EM,连接BM,∵在△ACE和△MBE中∴△ACE≌△MBE(SAS),∴AC=MB,在△ABM中,AM<AB+MB=AB+AC,∵AE=EM,∴2AE<AB+AC,∴AE<(AB+AC),即(AB﹣AC)<AE<(AB+AC),故④正确;故选:A.二.填空题(共6小题)19.如图,在△ABC中,点D,E,F分别是边AB,BC,CA上的中点,且AB=10cm,AC=16cm,则四边形ADEF 的周长等于26cm.【解答】解:∵点D,E,F分别是边AB,BC,CA上的中点,∴DE,EF都是△ABC的中位线,∴DE=AC=8cm,DE∥AC,EF=AB=5cm,EF∥AB,∴四边形ADEF是平行四边形,∴四边形ADEF的周长=2(DE+EF)=2×13=26(cm).故答案为:26.20.如图,△ABC的面积为4,分别取AC,BC两边的中点A1,B1,记△A1B1C的面积为S1;再分别取A1C,B1C 的中点A2,B2,记△A2B2C的面积为S2,再分别取A2C,B2C的中点A3,B3,记△A3B3C的面积为S3;则S3的值等于.【解答】解:∵点A1,B1是AC,BC两边的中点,∴A1B1是△ABC的中位线,∴A1B1=AB,A1B1∥AB,∴△CA1B1∽△CAB,∴=()2=,∵△ABC的面积为4,∴S1=1,同理可得,S3=,故答案为:.21.如图,四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=35°,则∠PFE的度数是35°.【解答】解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,∴FP,PE分别是△CDB与△DAB的中位线,∴PF=BC,PE=AD,∵AD=BC,∴PF=PE,故△EPF是等腰三角形.∵∠PEF=35°,∴∠PEF=∠PFE=35°,故答案为:35°.22.如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN=13.【解答】解:连接BD,取BD的中点F,连接MF、NF,如图所示:∵M、N、F分别是AB、DE、BD的中点,∴NF、MF分别是△BDE、△ABD的中位线,∴NF∥BE,MF∥AD,NF=BE=5,MF=AD=12,∵∠ACB=90°,∴AD⊥BC,∵MF∥AD,∴MF⊥BC,∵NF∥BE,∴NF⊥MF,在Rt△MNF中,由勾股定理得:MN===13;故答案为:13.23.如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是33.【解答】解:∵第一次操作后,三角形共有4个;第二次操作后,三角形共有4+3=7个;第三次操作后,三角形共有4+3+3=10个;…∴第n次操作后,三角形共有4+3(n﹣1)=3n+1个;当3n+1=100时,解得:n=33,故答案为:33.24.如图,在△ABC中,BF平分∠ABC,AG⊥BF,垂足为点D,交BC于点G,E为AC的中点,连接DE,DE =2.5cm,AB=4cm,则BC的长为9cm.【解答】解:∵BF平分∠ABC,AG⊥BF,∴△ABG是等腰三角形,∴AB=GB=4cm,∵BF平分∠ABC,∴AD=DG,∵E为AC的中点,∴DE是△AGB的中位线,∴DE=CG,∴CG=2DE=5cm,∴BC=BG+CG=4+5=9cm,故答案为:9三.解答题(共6小题)25.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC.(1)利用直尺与圆规先作∠ACB的平分线,交AD于F点,再作线段AB的垂直平分线,交AB于点E,最后连接EF.(2)若线段BD的长为6,求线段EF的长.【解答】解:(1)所作图形如下:(2)∵CF平分∠ACB∴∠ACF=∠BCF又∵DC=AC∴CF是△ACD的中线∴点F是AD的中点∵点E是AB的垂直平分线与AB的交点∴点E是AB的中点∴EF是△ABD中位线∴EF=BD=326.在△ABC中,E是AC边上一点,线段BE垂直∠BAC的平分线于D点,点M为BC边的中点,连接DM.(1)求证:DM=CE;(2)若AD=6,BD=8,DM=2,求AC的长.【解答】(1)证明:在△ADB和△ADE中,,∴△ADB≌△ADE(ASA)∴AE=AB,BD=DE,∵BD=DE,BM=MC,∴DM=CE;(2)解:在Rt△ADB中,AB==10,∴AE=10,由(1)得,CE=2DM=4,∴AC=CE+AE=14.27.如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.(1)求证:DE=CF;(2)求EF的长.【解答】解:(1)∵D、E分别为AB、AC的中点,∴DE∥BC,DE=BC,∵EF∥CD∴四边形DEFC是平行四边形,∴DE=CF.(2)∵四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.28.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.【解答】证明:如图,连接BD,作BD的中点M,连接EM、FM.∵点E是AD的中点,∴在△ABD中,EM∥AB,EM=AB,∴∠MEF=∠P同理可证:FM∥CD,FM=CD.∴∠MFQ=∠CQF,又∵AB=CD,∴EM=FM,∴∠MEF=∠MFE,∴∠P=∠CQF..29.△ABC的中线BD、CE相交于O,F,G分别是BO、CO的中点,求证:EF∥DG,且EF=DG.【解答】证明:连接DE,FG,∵BD、CE是△ABC的中线,∴D,E是AB,AC边中点,∴DE∥BC,DE=BC,同理:FG∥BC,FG=BC,∴DE∥FG,DE=FG,∴四边形DEFG是平行四边形,∴EF∥DG,EF=DG.30.如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=CF.【解答】证明:如图,过D作DG∥AC,则∠EAF=∠EDG,∵AD是△ABC的中线,∴D为BC中点,∴G为BF中点,∴DG=CF,∵E为AD中点,∴AE=DE,在△AEF和△DEG中,,∴△AEF≌△DEG(ASA),∴DG=AF,∴AF=CF.。
3角形中位线定理

3角形中位线定理三角形中位线定理,是在三角形中,与三条相邻边的中点相连的线段,它们构成的三个交点都在同一点上。
本文将从定理的证明、推广应用、例题等三个方面进行阐述。
一、定理的证明证明思路:设三角形ABC的三边分别为a、b、c,D为BC的中点,E为AC的中点,F 为AB的中点,则连接AD、BE、CF的交点为G。
则需证明AD、BE、CF三条线段的交点G是一个固定点。
证明:由于D、E、F都是各边中点,可得:∵ D是BC的中点,∴ BD = DC;又∵ G是AD与BE的交点,故可以得出:∵ D、E分别为BC和AC的中点,∴ DE // AC,同时AE = EC,∴ △AED与△CEB 相似。
$\frac{GA}{BD}=\frac{GC}{CE}$又 $\because BD=DC$ , $\therefore GA=GC$同理可得:于是,我们得到了两个相等的值:GA=GC,GB=GC。
由此,可知三角形GAC是一个等腰三角形,且AG与CF之间的线段垂直于CF,同理可得:因为三角形GAC、GBA、CBG均拥有最长边CG,所以它们就构成了一个共同的圆,而这个圆的中心就是点G。
因此可以得知:三角形ABC的三边中位线的交点G是一个固定点。
二、推广应用利用中位线定理,我们可以推导容易证明的三条定理和一个相关问题:中位线长定值定理、七分线长定值定理、以及在四边形中应用中位线定理、解决中位线问题。
1. 中位线长定值定理在三角形中,如果其中一条中位线相等,那么这个三角形就是等边三角形。
设△ABC为等边三角形,则BD、AE、CF三条中位线的长度均为$\frac{1}{2}$边长,又 $\because BD=AE=CF$ ,所以可以得到:BD=AE=CF=$\frac{1}{2}$a=a,同理可得:b=c=a。
在三角形中,三条中位线可将它们所在线段的长分为1:2:3的比例。
首先,由于三角形的三角形内部对角线互不交于同一点,那么三角形内部的线段AB、AC、BC是不会共线的。
中位线——打开解证明题思路的金钥匙

AF F = C.
分析 : 是 R AC F斜 边 上 的 中点 , t B 由
中点可联 想 到中线 , 自然 想 到连接 MF ME, 、
很容易证得 ME MF = .也 就是 AME F为等 腰 三角形. AME Ⅳ为 F底边上 的中点 , 等腰三 角 形底 边 上 的 中线 , 也是 底边 上 的高 , 于是 即
3 E A .
等腰 三角 形底 边 上 的 中线是 底边 上 的高 , 也 是 顶 角 的平分 线 ,得 A I C /B D- 0 , D.B , A - 。 _ _ 6
/B 3 。 _ = 0.又在直 角三角形 中,0角所 对 的直 3。
无解 , k的值. 求 错解 : 去分母得 k 1 一 k x 1= . (一 )3 (+ ) 7
于 求证 : A
F C.
求证 : 上E 删 E
D
C
图 3
分析 : 遇到 这种 情形 , 当再 找一 个 中 应 点, 然后应用 三角形的 中位线 定理. 中给 出 题
图 2
了B C的中点 D, 可再 找边 F C的 中点 , F 设 C
的 中点 为 G, 连接 D 可证得 D / B . 因 G, G / F又 为 E是 A 的中 点 。 G/E 。所以 F是 A D D / F G
因此 , 同学们在解题 时要 注意概念 、 性质 、
±时, 1 解得k 一 ,={. l ÷ J一 = i } 2
U 二
定 理使用 的前提 条件 等 问题 ,从而 顺利地 越
过题设 陷阱 , 避免不必要 的错误 .
分析 : 对于形 如 a= x b的方程 , a O b 当 = ,≠
利用中位线定理证明线段关系

利用中位线定理证明线段关系:
1.如图:在△ABC中,BD平分∠ABC,A D⊥BD于点D,E为AC的中点,求证:
DE∥BC.
2.如图:△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点,判断:EF和DG的数量和位置关系。
3.如图,△ABC中,D,E,F分别为BC,AC,AB边的中点,试证明AD,EF 互相平分.
4.如图所示,在△ABC中,点D在BC上,且CD=CA,CF平分∠ACB,AE=EB.
求证EF=BD.
菱形的判定:
1、AD是△ABC的角平分线,DE//AC,DF//AB.求证:四边形AEDF是菱形。
2、□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,四边形AFCE是否是菱形?为什么?
3.如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.
4.(提升题)如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.
在运动过程中,四边形AQCP可能是菱形吗?如果可能,那么经过多少秒后,四边形AQCP是菱形?
5.在△ABC中,∠BAC=90°,延长BA到点D,使AD=1/2AB,点E,F分别为BC,AC
的中点,求证:DF=BE。
中位线定理证明题
v1.0可编辑可修改中位线定理证明题1、如图,若AB//CD , E、F分别是BC、且AB a , CD b,求EF的长4、如图,在ABC中,B 2 C,AD BC,垂足为D,M是BC的中点,AB 10cm,求MD的长5、如图,D E、F分别是ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P Q两点,求PQ : BE的值2、已知矩形ABCD 中,AB 15cm,BC 8cm, E、F、G、H分别是AB、BC、CD、DA的中点,求四边形EFGH的周长和面积6、如图,在ABC中,AD平分BAC,BD AD,DE//AC,交AB 于E,若AB 5,求DE 的长3、如图,已知四边形ABCD中,AD // BC,若DAB的角平分线AE交CD于E,连结BE,且BE平分ABC,求证:AB AD BC 7、连接凸四边形一组对边中点的线段等于另一组对边和的一半,问这个凸四边形是什么四边形试证明你的结论11、如图,已知梯形 ABCD 中,AB//CD , DAB D 90, ACB 是14、如图,在 ABC 中, BAC 120,以AB 、AC 为向形外作等边三角 形ABD 和ACE ,M 为AD 中点,N 为AE 中点,P 为BC 中点,试求 MPN8、分别以 ABC 的边AC 和BC 为一边,在 ABC 外作正方形ACDE 和 CBFG ,点P 是EF 的中点,如图,求证:点 P 到边AB 的距离是AB 的一半9、如图,在梯形ABCD 中,AD//BC , B 30 ,N 分别是AB 、BC 、CD 、DA 的中点,已知BC 7 ,3EFm ,求梯形的下底 4AB 的长12、如图,梯形 ABCD 的面积是12,求此梯形四边的 中点组成的四边形 EFGH 的面积10、如图,已知梯形 ABCD 中,AD // BC , DCB ADC 90,E 为 AB13、如图,已知A 为DE 的中点,设 DBC 、 ABC 、 EBC 的面积分别为S 1、DEAE BE ,BF CF ,CG DG ,DH AH1 11 1EF - AC , FG - BD , GH AC HE-BD2 22215、如图,以 ABC 的边AB 、AC 为斜边向外作直角三角形 ABD 和ACE , 矩形ABCD 中 ,AC BD , EF FG GH HE ,且使 ABD ACE ,M 是BC 的中点,求证: DM EM 四边形EFGH 是菱形,在Rt ABC 中, AC 一 AB 2BC 2 .152 82 17(cm)2、解:连结AC 、BD60(cm 2)四边形EFGH 的周长为34cm , S 菱形E FGH 3、证明:取 AB 中点F ,连结EF中位线定理证明题答案:1、解:连结 AC ,取AC 中点G ,连结EG 、FGE 、F 分别是BC 、AD 的中点 EG 、FG 分别是 ACB 、ACD 的中位线 AD // BC CBE EBA AF BF ABE EAB ,CE EG //AB ,EG -AB 2 FG//CD ,FG -CD2AB//CD , EG//FG E 、F 、G 三点在一条直线上EF FGEG - (CD2DAB CBA 180DAE BAE 90, DE, 4、解:取AB 中点N ,连结 在Rt ABD 中, DN BNNDB ,BMDNMNDB AEB 90,EFDN 、-AB 2MNCM , AN 2 NMDNMD , ND MD ,EF - AB 2CBN ,NMD NDB DNMAB 10cm , MD5cmv1.0可编辑可修改5、解: BD CD , BF AF , DF//AC , BD CD,DP//CE 垂足分别是M 、N 、Q 、H在BCE 中,可得 BP EP ,DP EM // PQ // CH // FN , EP FP PD EG ,在 QPD 和 QEG QPD QEG ,PD EG , QDP QGE PQ : BE 1:41 CE , AE2 QPD 也 QEG , QP QE , 2 QP - PE BE 4 CE,EG AGMQ NQ , PQ2(EM2FN )6、解: 延长BD 、AC 相交于K ,在 ABD 和 AKD EAC 90 , EAM BAC 90 EAMAEM 90 ,AEM BACEAM AHC 90 , AE也 ACH , EM ACAH ,同理可得FH BHAB AH BH EM BH ,1 2, AD AD , ADB ADK 90 ,ABD 也 AKDPQ - AB29、过点 N 作 NG//AB , NH //CD ,分别交 BC 于G 、H ,BD KD , AB AKAD//BC1 DE//AC , BE AE , DE - AK ,27、证明:连结BD ,取BD 中点M ,连结EME 、F 分别是AB 、CD 的中点AB FM5, DE -EM EM1 1— AD , FM -BC ,且 EM // AD , FM // BC 2 21FM (AD BC), EF EM FM , M 点在 EF 上2BC // AD , 四边形ABCD 是平行四边形或梯形8、证明:作 EM AB , FN AB , PQ AB , CH AB ,ANBG,AB//NG , ND NGM B , NHMCB 30 ,C60NGM NHM 90GNH 90BM CM : ,AN DNGM HMGH 2MN6,AD AN四边形ABGN 、NHCD 是平行四边形HC , NH //CDv1.0可编辑可修改21 EF 是梯形ABCD 的中位线, EF (AD BC) 42 10、证明:取 CD 中点F ,连结EF AE BE , EF // BC , DCB 90 , EFD 90 EFCD , EF 是CD 的垂直平分线, CE DES四边形EFGH613、解:分别过 D 、A 、E 作BC 的垂线,垂足分别为 M 、H 、N ,则 DM // AH // EN ,AH S 1 1-(DM EN)21S 3 - BC DM2 AD AE ,1BC EN 211、解:在等边 CAB 中,AC AB , CAB 60DAB 90 DAC 30 S 2-(S 1 S 3) 2在 Rt ACD 中,CD ^AC 2 EF 是梯形的中位线, EF ^AB 21 (CD 2AB)14、证明:连结DE 、 MN 、 BM 、 CN BAC 120,EAC 60,〔(〔AB 2 2 AB) 3m 4 AB m , 梯形的下底 AB 的长为m 12、解:连结 BD 、 AC , 取BD 中点O BACBAC连结EO 、HO EH // BD四边形 AEOH 、EBOH 、 EODH 都是平行四边形S AEH S EOH S ODH S EBO ,SAEH1 ABD4同理可得 S CFG1SS CBD , S 1SDHG S ACD , S BEF 1SS ABC444EO//ADHO//AB , AE BE ,AHDHEAC 180 DAB 180 E 三点共线,(易证全等)AMDM ,AN EN,AB DB , AC CE , BMCCNB 90BP CP ,MP 1 BC2MN MP NP在BAC 和 DAE 中,MNBMNPDABD 三点共线BC DE1 DE 21 -CB 2AD ,CN AE1 BCv1.0可编辑可修改延长CE至Q,使EQ EC连结AP、AQ、PC 、QBAD DB ,AE CEAP AB,AQ ACABD ACEDAB CAE又PAD DAB ,CAEPAB QAC ,PACPAC也BAQPC BQMD、ME为中位线1MD PC , ME2 】BQ 2MD ME EAQ BAQMNP是等边三角形MPN 6015、证明:延长BD至P,使DP。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中位线定理证明题1、 如图,若CD AB //,E 、F 分别是BC 、AD 的中点, 且a AB =,b CD =,求EF 的长2、已知矩形ABCD 中,cm AB 15=,cm BC 8=,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,求四边形EFGH 的周长和面积3、 如图,已知四边形ABCD 中,BC AD //, 若DAB ∠的角平分线AE 交CD 于E ,连结BE , 且BE 平分ABC ∠,求证:BC AD AB +=4、如图,在ABC ∆中,C B ∠=∠2,BC AD ⊥,垂足为D ,M 是BC 的中点,cm AB 10=,求MD 的长5、 如图,D 、E 、F 分别是ABC ∆三边的中点,G 是AE 的中点,BE 与DF 、DG 分别交于P 、Q 两点,求BE PQ :的值6、 如图,在ABC ∆中,AD 平分BAC ∠,AD BD ⊥,AC DE //,交AB 于E ,若5=AB ,求DE 的长7、连接凸四边形一组对边中点的线段等于另一组对边和的一半,问这个凸四边形是什么四边形试证明你的结论8、分别以ABC ∆的边AC 和BC 为一边,在ABC ∆外作正方形ACDE 和CBFG ,点P 是EF 的中点,如图,求证:点P 到边AB 的距离是AB 的一半9、如图,在梯形ABCD 中,BC AD //,︒=∠30B ,︒=∠60C ,E 、M 、F 、N 分别是AB 、BC 、CD 、DA 的中点,已知7=BC ,3=MN ,求EF 的值10、如图,已知梯形ABCD 中,BC AD //,︒=∠=∠90ADC DCB ,E 为AB 中点,求证:DE CE =11、如图,已知梯形ABCD 中,CD AB //,︒=∠=∠90D DAB ,ACB ∆是等边三角形,梯形中位线m EF 43=,求梯形的下底AB 的长12、如图,梯形ABCD 的面积是12,求此梯形四边的中点组成的四边形EFGH 的面积13、如图,已知A 为DE 的中点,设DBC ∆、ABC ∆、EBC ∆的面积分别为1S 、2S 、3S ,求1S 、2S 、3S 之间的关系14、如图,在ABC ∆中,︒=∠120BAC ,以AB 、AC 为向形外作等边三角形ABD 和ACE ,M 为AD 中点,N 为AE 中点,P 为BC 中点,试求MPN ∠的度数15、如图,以ABC ∆的边AB 、AC 为斜边向外作直角三角形ABD 和ACE ,且使ACE ABD ∠=∠,M 是BC 的中点,求证:EM DM =中位线定理证明题答案:1、解:连结AC ,取AC 中点G ,连结EG 、FGE 、F 分别是BC 、AD 的中点∴EG 、FG 分别是ACB ∆、ACD ∆的中位线 ∴AB EG //,AB EG 21=,CD FG //,CD FG 21= CD AB //,∴FG EG //,∴E 、F 、G 三点在一条直线上)(21AB CD EG FG EF -=-=∴, a AB =,b CD =,∴)(21a b EF -=2、解:连结AC 、BDBE AE =,CF BF =,DG CG =,AH DH =AC EF 21=∴,BD FG 21=,AC GH 21=,BD HE 21= 矩形ABCD 中,BD AC =,HE GH FG EF ===∴, ∴四边形EFGH 是菱形,在ABC Rt ∆中,)(178152222cm BC AB AC =+=+=∴四边形EFGH 的周长为cm 34,)(602cm S EFGH =菱形3、证明:取AB 中点F ,连结EFBC AD //,∴︒=∠+∠180CBA DAB ABE CBE ∠=∠,BAE DAE ∠=∠∴︒=∠=∠90EAB EBA ,∴︒=∠90AEB ,AB EF 21=∴ BF AF =,DE CE =,)(21BC AD EF +=∴,BC AD AB +=∴ 4、解:取AB 中点N ,连结DN 、MN 在ABD Rt ∆中,AB BN DN 21==, NDB B ∠=∠∴,BN AN CM BM ==, ,AC MN //∴,C NMD ∠=∠∴ C B ∠=∠2 ,NMD NDB ∠=∠∴2,NMD DNM NDB ∠+∠=∠ NMD DNM ∠=∠∴,MD ND =∴, cm AB 10=,cm MD 5=∴5、解: CD BD =,AF BF =,∴AC DF //,CE DP CD BD //,= 在BCE ∆中,可得EP BP =,∴CE DP 21=,AG EG CE AE ==, ∴EG PD =,在QPD ∆和QEG ∆中QEG QPD ∠=∠,EG PD =, QGE QDP ∠=∠QPD ∆∴≌QEG ∆,QE QP =∴,BE PE QP 4121==∴,4:1:=∴BE PQ6、解:延长BD 、AC 相交于K ,在ABD ∆和AKD ∆中21∠=∠,AD AD =,︒=∠=∠90ADK ADB ,ABD ∆∴≌AKD ∆ KD BD =∴,AK AB =AC DE // ,AE BE =∴,AK DE 21=∴,5=AB ,25=∴DE7、证明:连结BD ,取BD 中点M ,连结EM 、FME 、F 分别是AB 、CD 的中点∴AD EM 21=,BC FM 21=,且AD EM //,BC FM // ∴)(21BC AD FM EM +=+,FM EM EF +=∴,M ∴点在EF 上AD BC //∴,∴四边形ABCD 是平行四边形或梯形8、证明:作AB EM ⊥,AB FN ⊥,AB PQ ⊥,AB CH ⊥,垂足分别是M 、N 、Q 、H∴FN CH PQ EM //////,FP EP = , ∴NQ MQ =,)(21FN EM PQ +=∴ ︒=∠90EAC ,︒=∠+∠∴90BAC EAM︒=∠+∠90AEM EAM ,BAC AEM ∠=∠∴ ︒=∠=∠90AHC M ,AC AE =EAM ∆∴≌ACH ∆,AH EM =∴,同理可得BH FH = BH EM BH AH AB +=+=∴,AB PQ 21=∴ 9、过点N 作AB NG //,CD NH //,分别交BC 于G 、H ,BC AD //∴四边形ABGN 、NHCD 是平行四边形∴BG AN =,NG AB //,HC ND =,CD NH //B NGM ∠=∠ ,C NHM ∠=∠︒=∠30B ,︒=∠60C︒=∠+∠∴90NHM NGM ︒=∠∴90GNHCM BM = ,DN AN = HM GM =∴62==∴MN GH ,1=-=+=∴GH BC ND AN ADv1.0 可编辑可修改∴EF 是梯形ABCD 的中位线,∴4)(2=+=BC AD EF 10、证明:取CD 中点F ,连结EFBE AE = ,∴BC EF //,︒=∠90DCB ,︒=∠∴90EFD CD EF ⊥∴,∴EF 是CD 的垂直平分线,DE CE =∴11、解:在等边CAB ∆中,AB AC =,︒=∠60CAB︒=∠90DAB ,︒=∠∴30DAC∴在ACD Rt ∆中,AB AC CD 2121==EF 是梯形的中位线,)(21AB CD EF +=∴m AB AB 43)21(21=+∴ m AB =∴,∴梯形的下底AB 的长为m12、解:连结BD 、AC ,取BD 中点O 连结EO 、HOBE AE = ,DH AH =,AD EO //∴,AB HO //,BD EH //∴四边形AEOH 、EBOH 、EODH 都是平行四边形EBO ODH EOH AEH S S S S ∆∆∆∆===∴,ABD AEH S S ∆∆=∴41同理可得CBD CFG S S ∆∆=41,ACD DHG S S ∆∆=41,ABC BEF S S ∆∆=416=∴EFGH S 四边形13、解:分别过D 、A 、E 作BC 的垂线,垂足分别为M 、H 、N , 则EN AH DM ////,AE AD = ,NH MH =∴)(21EN DM AH +=∴,23122212121S AH BC EN BC DM BC S S =⋅=⋅+⋅=+∴)(21312S S S +=∴14、证明:连结DE 、MN 、BM 、CN︒=∠120BAC ,︒=∠60EAC ,︒=∠60DAB ︒=∠+∠∴180EAC BAC ︒=∠+∠180DAB BACB ∴、A 、E 三点共线,C 、A 、D 三点共线在BAC ∆和DAE ∆中,(易证全等),DE BC =∴DM AM = ,EN AN =,CB DE MN 2121==∴ DB AB = ,CE AC =,AD BM ⊥∴,AE CN ⊥ ︒=∠=∠∴90CNB BMCCP BP = ,BC MP 21=∴,BC NP 21=NP MP MN ==∴v1.0 可编辑可修改MNP ∆∴是等边三角形 ︒=∠∴60MPN15、证明:延长BD 至P ,使DB DP = 延长CE 至Q ,使EC EQ = 连结AP 、AQ 、PC 、QBDB AD ⊥ ,CE AE ⊥ AB AP =∴,AC AQ = ACE ABD ∠=∠ CAE DAB ∠=∠∴又DAB PAD ∠=∠ ,EAQ CAE ∠=∠QAC PAB ∠=∠∴,BAQ PAC ∠=∠∴PAC ∆∴≌BAQ ∆BQ PC =∴MD 、ME 为中位线PC MD 21=∴,BQ ME 21= ME MD =∴。
