4第四讲误差传播定律
误差传播定律

测值中误差乘积的平方和的平方根。
例4:已知矩形的宽x=30m,其中误差mx=±0.005m,矩形的长y=50m, 其中误差my=±0.008m,计算矩形面积S及其中误差ms。
解:矩形面积 S=xy 由题意:求各观测值偏导数: f y
x
f x y
mz
(
f X 1
)2
m12
(
二、和或差的函数
设和或差函数为: z x y
即: mz
m
2 x
m
2 y
式中:Z为x、y的和或差的函数;x、y为独立观测值;mx、my为x、y的
中误差,mZ为Z的中误。
结论:两观测值代数和或差的函数中误差等于两观测值的中误差的 平方和的平方根。
z x1 x2 xn
即:
mz
(
f X 1
)2
m12
(
f X 2
)2
m
2 2
(
f X n
)2
m
2 n
式中:xi (i=1,2…n)为独立观测值;已知其中误差为mi(i=1 2…n), mz为z的中误差;xf(i i=l,2…n)是函数对各个变量所取的偏导数。
结论:一般函数中误差等于按每个观测值所求的偏导数与相应观
阐述观测值中误差与观测值函数中误差之间关系的定律,就称为误差传播定律。
一、倍数函数
设倍数函数为:zm2 z kk x2mx2
即:mz kmx
式中:Z为观测值X的函数(也就是未知量的间接观测值);K为常数;X为 直接观测值;mx为X的中误差;mZ为Z的中误差。
结论:倍数函数的中误差(观测值与常数乘积的中误差),等于 观测值中误差乘常数。
测量平差测量误差及其传播定律课件

地理信息获取
通过平差测量原理,获取高精度 地理信息数据,为地理信息系统
提供基础数据。
科学研究
在物理、化学、生物等领域,利 用平差测量原理对各种实验数据
进行处理和分析。
CHAPTER 03
误差传播定律
误差传播定律的定义
误差传播定律是测量平差中用来描述测量误差之间相互关系 的定律。它表明,当对一个或多个观测值进行数学运算时, 误差会按照一定的规律传播。
测量误差的来源
01
02
03
04
测量设备误差
设备精度、磨损、老化等因素 导致误差。
环境误差
温度、湿度、气压、风速等环 境因素影响测量结果。
操作误差
操作人员技能水平、操作习惯 等因素导致误差。
观测误差
观测过程中产生的随机误差和 系统误差。
测量误差的分类
系统误差
可预测且相对稳定的误差,如设 备误差。
随机误差
实例三:距离测量误差分析
总结词
距离测量误差主要来源于仪器误差、 人为误差和外界环境因素。
详细描述
仪器误差包括固定误差和比例误差; 人为误差包括读数误差和记录误差; 外界环境因素包括温度、气压和湿度 等气象因素的影响。
THANKS FOR WATCHING
感谢您的观看
总结词
水准测量误差主要来源于仪器误差、 人为误差和外界环境因素。
详细描述
仪器误差包括望远镜调焦误差、十字 丝分划板误差等;人为误差包括读数 误差和仪器对中误差;外界环境因素 包括大气折射和地球曲率的影响。
实例二:角度测量误差分析
总结词
角度测量误差主要来源于仪器误差、人为误差和目标偏心。
详细描述
测量平差测量误差及其传播定律课件

数据预处理
数据清洗 数据转换 数据集成
数据处理方法
统计分析 数据挖掘 预测分析
数据后处理
结果验证
1பைடு நூலகம்
报告生成
2
数据存储
3
CHAPTER
测量误差实例分析
实例一:水准测量误差分析
总结词
详细描述
仪器误差包括望远镜调焦误差、十字 丝分划板误差等;人为误差包括读数 误差和仪器对中误差;外界环境因素 包括大气折射和地球曲率的影响。
测量平差测量误差及 其传播定律课件
• 测量误差概述 • 平差测量原理 • 误差传播定律 • 测量数据处理 • 测量误差实例分析
CHAPTER
测量误差概述
测量误差的定义
测量误差
不可避免性
测量结果与被测量真值之间的差异。
由于受到多种因素的影响,测量误差 不可避免。
产生原因
测量设备、环境、操作方法、人员等 因素的影响。
实例二:角度测量误差分析
总结词
角度测量误差主要来源于仪器误差、人为误差和目标偏心。
详细描述
仪器误差包括照准误差、度盘刻划误差等;人为误差包括瞄准误差和读数误差; 目标偏心则是指目标偏离了理想位置,导致观测值失真。
实例三:距离测量误差分析
总结词
详细描述
WATCHING
测量误差的来源
01
测量设备误差
02
环境误差
03
操作误差
04
观测误差
测量误差的分类
系统误差
随机误差 过失误差
CHAPTER
平差测量原理
平差测量基本概念
01
02
平差测量
测量误差
03 误差传播定律
4第四讲误差传播定律(精)

误差传播定律在实际工作中有许多未知量不能直接观测而求其值,需要由观测值间接计算岀来。
例如某未知点B的高程H B,是由起始点A 的高程比加上从A点到B点间进行了若干站水准測量而得来的观測高差h】……厲求和得出的。
这时未知点B的高程H。
是各独立观测值的函数。
那么如何根据观测值的中误差去求观测值函数的中课差呢?阐述观測值中谋莖与观测值函数中谋差之间关系的定律,称为误差传播定律。
1、和差函数设有函数:z=x±yZ 为x 、y 的和或差的函数,x 、y 为独立观测值,已知其中课差为 m& m y ,求Z 的中泯差mz 。
设x 、y^z 的真课差分别为亠、△舟亠则 A. =△、+△、, 若对x 、y 均观测了n 次,则(2 1,2……对将上式平方,得= A 2.… + △[讨 ±2A r A v ,(i = 1,2……n)由于亠、亠均为假然误差,其符号为正或负的机会相 同,因为Ay 为独立误差,它们出现的正・负号互不相 关,所以其乘积亠Ay 也具有正负机会相同的性质,在求 [心]时其正值与负值有互相抵消的可能;当n 愈大时, 上式中最后一项[g ] /n 将趋近于零,即 lim lA r A r l 1 - ^ = 0/? —>oo n将满足上式的误差A 禺为互相独立的误差,简称独立 误差,相应的观测值称为独立观測值。
对于独立观测值来说, 即使n 是有限量,由于 罰 式残存的值不大,一般就 观测值的函数求和,并除以n,得k J =忽视它的影响。
根据中谀療是义;得两观测值代数和的中谋差平方,等于两观测值中误差的平方之和。
当z是一组观测值X】、兀…%代数和(差)的函数时,即Z = X}±X2^^^±X n可以得出函数Z的中误差平方为7H:= 〃彳+加;+・・・+加[Z X| x2 xn结论:n个)WU值代数和(差)的中谋差平方,等于n个观灣值中误差平方之和。
误差传播定律

dz
f x1
dx1
f x2
dx2
f xi
dxi
f xn
dxn
,分别求出 f
xi
(3)将
f xi
、m
i
带入关系式(5—6)求出
m
z
根据关系式(5—6)可导出下列简单函数式的中误差传 播公式(见表5—2)。
5/15/2019
表5—2 简单函数式的中误差传播公式
解: 1)首先列出函数式 D Lcos
2)水平距离
D 247.50 cos10o34' 243.303m
这是一个非线性函数,所以对函数式进行全微分
3)先求出各偏导值如下
5/15/2019
D COS10O34' 0.9830 L D L sin10o34' 247.50 sin10o34' 45.3864
f xi
dxi
f xn
dxn
如将上式中的微分量“d”改用真误差“△”,则得
5/15/2019
z
f x1
x1
f x2
x2
f xi
xi
f xn
xn
式中
f xi
为函数z分别对各变量
xi
的偏导数,并将观测值xi
代入偏导数后求出的数值,故均为常数。
函数 名称
函数式
中误差传播公式
备
注
倍数 函数
z kx
mz kmx
和差 函数
z x1 x2 xn
k
mz mx21 mx22 mx2n 为
绪论2误差传播定律

智能化技术应用
随着人工智能等技术的 发展,未来误差传播定 律的研究将更加注重智 能化技术的应用,如利 用机器学习等方法进行
误差预测和控制。
实验与理论相结合
未来研究将更加注重实 验与理论的相结合,通 过实验验证理论的正确 性和可靠性,推动误差 传播定律在实际应用中
误差控制
为了控制误差的累积和传播,提高测 量结果的准确性,需要研究和掌握误 差传播规律。
学科发展
随着测量科学和技术的不断发展,对 误差传播规律的研究逐渐深入,形成 了较为完善的理论体系。
02
误差传播定律数学表达式
单一观测值误差传播公式
误差传播定律描述了测量误差在数据处理过程中的传 递规律。对于单一观测值,其误差传播公式可表示为
缺乏统一的理论框架
目前,误差传播定律的研究缺乏统一的理论框架,不同领域和方法 之间的融合不够,限制了其应用范围和效果。
实验验证不足
误差传播定律的实验验证相对较少,缺乏充分的实验数据支持,使 得理论成果在实际应用中的可靠性受到质疑。
未来发展趋势及前景预测
第一季度
第二季度
第三季度
第四季度
跨学科融合研究
输标02入题
$$sigma_y = |f'(x)| cdot sigma_x$$
01
03
该公式表明,函数 $y$ 的误差与 $x$ 的测量误差及 函数在该点的导数有关。当 $|f'(x)|$ 较大时,即使
$sigma_x$ 很小,$sigma_y$ 也可能较大。
04
其中,$sigma_y$ 为函数 $y = f(x)$ 的误差,$f'(x)$ 为函数在点 $x$ 处的导数,程测量中,误差传播定律用 于评估测量结果的可靠性和精度, 指导测量方案的设计和实施。
4-误差传播律习题课

x2
y1
x2 y2
x2 ym
xn y1 xn y2 xn ym
2 i
02Qii
ji 02Qij
2 j
02Q jj
观测值向量 L 的协因数阵 n1
Q11 Q12 Q1n
QXX
n,n
Q21
• 问:可设多少个测站?
• 4、有一个角度测了20 回,得中误差 为 ±0。42〞。
• 问:需要再增加多少测回,其中误差 可达 ±0。28〞。
• 5、以相同精度测定支导线各转折角 L1、L2。。。LN ,观测中误差为 σ。
• 设起始方位角α无误差。
• 求:导线边A-1,1-2,2-3,…(n-1)B的方位角的中误差。
Qn1
Q22
Qn2
Q2n
Qnn
DXX
Q 2
0 XX
三、二观、观测测值值函线性数函的数误的方差差传播
1、线性函数 :
X
n,1
[X1,
X
2,...X n
]T
,
DXX
Z K X K0
t ,1
t , n n,1
t ,1
Y F X F0
r ,1
r , n n,1
• 6、设附合水准线路长 SAB=80km , 每公里观测高差的权为 1 。设A、B 点高程无误差。
• 求:最弱点平差前后的高程的权。
• 7、对 A 角观测 4 次,每次观测中误观测中误差 为 ±4〞。
•
根据公式:
第四节误差传播定律第五节算术平均值及中误差资料

讨论一般函数,设有函数
其中
z f(
x1、x2
x1、x2 xn)
xn 为独立观测值。
中误差分别为: m1、m2 mn
设 x1、x2 xn 分别有真误差 x1、x2 xn
相应函数 随之产生真误差
根据变量的误差与函数的误差之间的关系近似用全微分表达求函数的全 微分,舍取二次以上各项得:
K22m22
K
m 2 2
nn
[例题]:丈量得倾斜距离s=50.00m,其中误差 ms 0.05,并测得倾斜角
150000,其中误差 m 30 ,求相应水平距离D及其中误差。
解:首先列出函数式 D=Scos 水平距离D=50∙cos15ْ =48.296m 这是个非线性函数,所以要用公式(6-9)求函数的中误差。先求出个偏导数如下:
n
所以
lim n
x
X
在有限次观测时,所求得观测值 是接近真值的值,因此算术平均值是 观测量的最可靠值。(最或然值)
二、算术平均值的中误差
在同精度观测条件下,得观测值L1、L2┉Ln,中误差 均相同为m,算术平均值如下。
x
L
n
1 n
L1
1 n
L2
1 n
Ln
根据误差传播定律中误差式为:
2 n2
按级数展开取第一项得:
x2
n2
m2 n
代入得: m2 vv
由以上可得:
m2 vv
n 1
m
vv
n1
(白塞尔公式)
M
vv
n(n 1)
D cos cos15 0.9659 D s sin 50 sin 15 12.9410
误差传播定律

例二:某房屋长边量得结果为80±0.02mm,短边量得 结果为40±0.01mm,求房屋面积中误差 解:第一步:列出圆的数学方程
S=a×b
第二步:将方程进行微分,(有两个变量则需全微分) 省略 第三步:将微分转化为方程
ms a mb b ma
2 2 2 2
2
m s 1 . 13 m
• 例一:量地圆半径R=31.3mm,其中误差mR =±0.3mm,试求圆面积的中误差。
解:第一步:列出圆的数学方程
S=π R2
第二步:将方程进行微分,(有两个变量则需全微分)
ds=2πRdR
如果不会微分没关系,直接跳到第三步
第三步:将微分转化为方程
M s 2 R ) m R (
2 2 2
习题: 1、在1:500的地形图上量的两点之间距离d=234.5mm及 其中误差md=±0.2mm,求两点之间地面水平距离D的值 及其中误差。 2、设对某一三角形观测了α、β角,测角中误差分别为 mα=±3.5″,mβ=±6.2″,求γ角的中误差。 3、采用两次仪高法进行水准测量,每次读数包含瞄准误 差、估读误差、及气泡居中不准误差。他们数值分别为 m瞄=1.1mm、m估=2.5mm、m气=1.5mm,试求: ①一次仪器测定高差h0的中误差mh1 ②两次仪器高测得高差之差Δh的中误差mΔh ③测站高差平均值h的中误差mh
m s 59 mm
关于第三步的解释 我理解的求全微分其核心内容就是: 一、数学方程中只有一个变量,将 此项求导后平方,再乘以其中误差 的平方即可 二、对于两个及以上变量,将函数 每一个可引起误差的变量分别拿出, 将其余变量看做系数然后求导,求 导后将其平方,再乘以该变量中误 差的平方即可。
例三:三角高程测量h=Dtanα,测得α=20° ,mα=±1′, D=250m,mD=±0.13m,求mh
误差传递定义

误差传递定义
测量中,某些结果,要通过一系列的测量操作步骤并分析运算后获得的。
而其中的每一个步骤可能发生的误差都会对分析结果产生不同程度的影响,称为误差的传递;
误差:测量值与真实值之间的差异称,物理实验离不开对物理量的测量,测量有直接的,也有间接的。
由于仪器、实验条件、环境等因素的限制,测量不可能无限精确,物理量的测量值与客观存在的真实值之间总会存在着一定的差异,这种差异就是测量误差。
误差是不可避免的,只能减小。
1、加法中的误差传递:
即:若有X=u±v,则X的均方差为:σX^2 =sqrt(σu^2+σv ^2)。
2、乘法中的误差传递:
3、除法中的误差传递:
4、有限次幂的误差的传播:
可以使用蒙特卡罗法来验证其误差,如下面的程序用来验证出发的误差:N=1e6。
x=10+randn(N,1)。
y=5+randn(N,1)*2。
std(x./y)。
mean(x./y)。
imu 误差传递公式推导

imu 误差传递公式推导摘要:1.引言2.误差传递公式的基本概念3.误差传递公式的推导过程4.误差传递公式的应用实例5.结论正文:【引言】在科学实验和工程计算中,我们常常需要处理测量数据,而测量过程中总会存在一定的误差。
为了评价测量结果的可靠性,研究误差传递规律显得尤为重要。
本文将介绍误差传递公式的推导及其应用,以帮助我们更好地理解测量误差对结果的影响。
【误差传递公式的基本概念】误差传递公式是描述测量结果误差与各测量量之间关系的一种数学表达式。
在国际单位制(SI)中,误差传递公式可以表示为:Δ量= Δ测量值/ 灵敏度其中,Δ量表示测量结果的误差,Δ测量值表示测量值的误差,灵敏度表示测量装置对被测量物理量的敏感程度。
【误差传递公式的推导过程】误差传递公式的推导过程相对简单。
以单一变量为例,假设测量值为x,真实值为x0,测量误差为Δx,则有:x = x0 + Δx对上式两边求导,得到:Δx/Δx0 = d(x)/dx - d(x0)/dx其中,d(x)/dx和d(x0)/dx分别表示x和x0对测量过程中的变量求导。
根据灵敏度的定义,我们有:d(x)/dx = 灵敏度将其代入上式,可得:Δx/Δx0 = 灵敏度- 灵敏度0其中,灵敏度0表示测量装置对真实值的灵敏度。
整理得到误差传递公式:Δ量= Δx / 灵敏度= (灵敏度- 灵敏度0)Δx0 / 灵敏度【误差传递公式的应用实例】以测量长度为例,假设使用一把尺子测量长度,其灵敏度为1cm/mm。
若测量结果为20cm,实际长度为20.01cm,测量误差为0.01cm。
根据误差传递公式,我们可以计算出:Δ量= Δx / 灵敏度= 0.01cm / 1cm/mm = 0.01mm这意味着,测量结果的误差为0.01mm,小于实际误差的1/10。
在实际应用中,我们可以根据误差传递公式评估测量结果的可靠性,并根据需要采取相应的措施减小误差。
【结论】误差传递公式是描述测量结果误差与各测量量之间关系的重要工具。
误差传递公式

误差传递公式的推导设间接测得量),,(321xxxfN=,式中321,,xxx均为彼此相互独立的直接测得量,每一直接测得量为等精度多次测量,且只含随机误差,那么间接测得量N的最可信赖值(用平均值N表示)为),,(321f=①算术合成法求误差传递公式绝对误差传递公式:332211xxfxxfxxfN∆∂∂+∆∂∂+∆∂∂=∆相对误差传递公式:332211lnlnlnxxfxxfxxfNN∆∂∂+∆∂∂+∆∂∂=∆②方和根合成法求标准偏差传递公式标准偏差传递公式:223222221321xxxNSxfSxfSxfS⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫⎝⎛∂∂=相对偏差传递公式:223222221321lnlnlnxxxN SxfSxfSxfNS⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫⎝⎛∂∂+⎪⎪⎭⎫⎝⎛∂∂=例1:已知cbaz31-+=,其中aaa∆±=,bbb∆±=,ccc∆±=,求z的平均值和误差传递公式。
解:平均值:cbaz31-+=;z分别对各直接量求一阶偏导数:1=∂∂a z ,1=∂∂b z ,31-=∂∂c z , 得误差传递公式:c b a c c z b b z a a z z ∆+∆+∆=∆∂∂+∆∂∂+∆∂∂=∆31。
例2:已知h d m 24πρ=,其中m m m ∆±=,d d d ∆±=,h h h ∆±=,求h 的平均值和误差传递公式。
解:平均值:h d m 24πρ=; 对公式hd m 24πρ=两边取自然对数: h d m ln ln 2ln 4ln ln --+=πρ, ρln 分别对各直接量求一阶偏导数:m m 1ln =∂∂ρ,d d 2ln -=∂∂ρ,hh 1ln -=∂∂ρ, 得误差传递公式:h hd d m m h h d d m m ∆+∆+∆=∆∂∂+∆∂∂+∆∂∂=∆121ln ln ln ρρρρρ。
工程测量误差传播定律三步走的步骤

工程测量误差传播定律三步走的步骤
工程测量误差传播定律三步走的步骤为:
1. 计算单个偏差的影响
首先,需要计算出每个测量量的偏差,即实际值与标准值之间的差异。
偏差可以表示为δX。
然后,需要计算出这个偏差对于最终结果的影响,即偏差δX的传递率。
2. 计算总体偏差的贡献
接下来,需要计算出所有偏差的总体贡献,即误差平方和,表示为δX^2。
这个数值代表了所有偏差对于最终结果的综合影响。
3. 计算最终结果的误差范围
最后,需要将总体偏差的贡献转化为标准偏差,表示为σX。
这个数值代表了最终结果的误差范围,即结果的忠实度。
通常情况下,结果的误差范围是标准偏差值的2-3倍,这取决于测量的精度和测量的数量。
误差传递基本公式

误差传递基本公式
误差传递是指在数学模型中,当输入数据存在误差时,这个误差会如何传递到输出结果中。
对于一个复杂的数学模型,计算误差传递可能会很困难,但是对于一些简单的模型,可以使用误差传递基本公式来计算。
对于一个函数f(x) ,其中x 是输入变量,y 是输出变量,假设x 的误差为Δx ,则根据误差传递基本公式,输出变量y 的误差Δy 可以通过以下公式计算:
Δy = |f'(x)| * Δx
其中f'(x) 表示函数f(x) 在点x 处的导数。
这个公式表明,输出变量y 的误差与输入变量x 的误差成正比,并且与函数f(x) 在点x 处的斜率(即导数)有关。
斜率越大,误差传递的影响就越大。
需要注意的是,误差传递基本公式只适用于一阶导数可导的函数,对于高阶导数不可导的函数,需要使用更加复杂的方法来计算误差传递。
此外,该公式也假设了输入变量的误差是小量,即Δx 很小,所以对于较大的误差,可能需要考虑其他因素。
总之,误差传递基本公式是一种简单而常用的方法,用于计算输入误差如何传递到输出结果中。
第4讲观测向量的精度
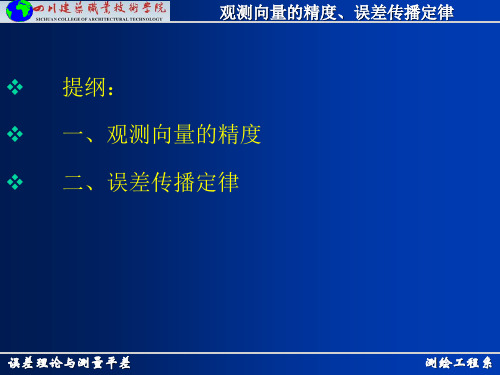
i j
E(i
j
)
lim
n
i j n
ij=0
表示观测量L
i和观测量L
之间线性无关
j
ij
0
表示观测量L i和观测量L
之间线性相关
j
误差理论与测量平差
测绘工程系
一、观测向量的精度
观测向量的精度、误差传播定律
பைடு நூலகம்
观测向量的方差阵 若有n个观测值L1,L2,…,Ln,将它们表示成一个向量
(i=1、2、3…n)
误差理论与测量平差
测绘工程系
二、误差传播定律
观测向量的精度、误差传播定律
对上式由1加到n得: [2Z ] K2[2X ]
两边同时除以n得: [2Z ] K2[2X ]
n
n
当n趋向于无穷时极限得形式为:lim [2Z ] K2 lim [2X ]
n n
L (L1, L2,称, L为n )T观测向量。观测向量的精度一般用方差阵 来表示。
DLL
2 1
21
.
12
2 2
.
. .
1n 2n
. .
n1
n2
.
2 n
DLL
2 1
0
.
0
2 2
.
. . .
0
0
.
和h2,我们通过中误差的定义式通常求的是观测值h1和h2的中
误差,HP2=HA+h1+h2 HP2的中误差怎么计算?观测值函数的
数值分析中的误差传播理论

数值分析中的误差传播理论数值分析是一门应用数学领域的重要学科,旨在通过利用数值方法解决实际问题。
然而,在数值计算中,由于各种因素的影响,我们无法完全避免误差的产生。
误差传播理论是数值分析中一种重要的理论工具,旨在帮助我们理解和控制误差的产生和传播过程。
一、误差及其分类在数值计算中,由于测量和计算过程中的不确定性,我们得到的结果往往与真实值存在一定的偏差,我们称之为误差。
根据误差产生的原因和性质,误差可以分为以下几类:1. 舍入误差:由于计算机存储空间的有限性,无法精确表示某些实数,从而导致舍入误差的产生。
舍入误差是最常见的一类误差,通常通过保留足够的有效数字或采用更高的精度计算来减小。
2. 截断误差:当我们使用近似方法计算某个函数或数值时,由于截断计算过程中的无穷级数或无穷小量,截断误差会被引入。
减小截断误差的常用方法是增加计算的步骤或者使用更高阶的近似方法。
3. 模型误差:数值计算往往需要建立数学模型来描述实际问题,而模型本身的不准确性会引入模型误差。
模型误差可以通过改进数学模型或采用更适合实际情况的模型来减小。
二、误差传播的基本原理误差传播理论是基于线性近似的思想,它假设误差在传播过程中是线性累积的。
根据误差传播的基本原理,我们可以通过对误差的传播规律进行研究,从而评估计算结果的可靠性。
误差传播理论的基本公式为:δf = |∂f/∂x₁|δx₁ + |∂f/∂x₂|δx₂ + ... + |∂f/∂xₙ|δxₙ其中,δf表示函数f的误差,δx₁、δx₂、...、δxₙ表示自变量x₁、x₂、...、xₙ的误差,|∂f/∂x₁|、|∂f/∂x₂|、...、|∂f/∂xₙ|表示函数f对自变量的偏导数。
该公式表明,函数f的误差δf由自变量的误差δx₁、δx₂、...、δxₙ以及函数f对各自变量的偏导数共同决定。
三、利用误差传播理论进行数值计算在实际的数值计算中,我们可以利用误差传播理论来评估计算结果的误差范围,并采取相应的措施来减小误差。
