三角函数公式默写表
三角函数默写

(3)利用五点法画出函数 y 3cos
1 x 图象. 6 2
(4)画出 y | cos x | , y sin | x | 图象.
5.(1)已知 sin
1 ,且 为第二象限角,求 cos , tan . 3
(2)已知 tan 3 ,且 为第二象限角,求 sin ,cos .
1.三角函数值 sin0°=sin30°=sin45°=sin60°=sin90°= cos0°= tan0°= cos30°= tan30°= cos45°= tan45°= cos60°= tan60°= cos90°=
2.三角函数的诱导公式(k∈Z) 公式一:sin(α+k*2π)=cos(α+k*2π)= tan(α+k*2π)= 公式二:sin(π+α) = 公式三:sin(-α) = 公式四:sin(π-α) = 公式五:sin(π/2-α) = cos(π+α) = cos(-α) = cos(π-α) = cos(π/2-α) = tan(π+α)= tan (-α)= tan(π-α) =
y sin x
y cos xy Fra bibliotek tan x图象
定义域 值域 奇偶性 最小正周期 增区间 减区间 对称轴方程 对称中心
4.图象变换 (1) y 3cos
1 x 图象如何由 y cos x 图象变换得到. 6 2
(2)求函数 y 3cos
1 x 的增减区间、对称中心、对称轴方程. 6 2
公式六:sin(π/2+α)=cos(π/2+α)= sin(π/2+α)= cos(π/2+α)= sin(π/2-α)= cot(π/2-α)= tan(3π/2+α)= cos(3π/2-α)= 3.三角函数 名称 tan(π/2+α)= cos(π/2-α)= sin(3π/2+α)= cot(3π/2+α)= tan(3π/2-α)= cot(π/2+α)= tan(π/2-α)= cos(3π/2+α)= sin(3π/2-α)= cot(3π/2-α)=
(完整版)三角函数公式大全

三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦函数:r y=αsin 余弦函数:r x =αcos 正切函数:x y =αtan余切函数:y x =αcot 正割函数:xr=αsec余割函数:yr=αcsc二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα cos(2kπ+α)=cosαtan(2kπ+α)=tanα cot(2kπ+α)=cotα (其中k∈Z) 公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin(απ-2)=cosα cos(απ-2)=sinα tan(απ-2)=cotα cot(απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin(απ+2)=cosα cos(απ+2)=-sinαtan(απ+2)=-cotα cot(απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系:sin(απ-23)=-cosα cos(απ-23)=-sinαtan(απ-23)=cotα cot(απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin(απ+23)=-cosα cos(απ+23)=sinαtan(απ+23)=-cotα cot(απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
三角函数公式表大全

三角函数公式表大全以下是常用的三角函数公式表:1. 正弦函数(Sine Function):- 正弦函数的定义:sinθ = 对边/斜边- 余弦函数与正弦函数的关系:cosθ = 邻边/斜边- 正弦函数的倒数:cosecθ = 1/sinθ- 余弦函数的倒数:secθ = 1/cosθ- 正弦函数的平方:sin^2θ + cos^2θ = 1- 正弦函数的和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ- 正弦函数的倍角公式:sin2θ = 2sinθcosθ2. 余弦函数(Cosine Function):- 余弦函数的定义:cosθ = 邻边/斜边- 正弦函数与余弦函数的关系:sinθ = 对边/斜边- 余弦函数的倒数:secθ = 1/cosθ- 正弦函数的倒数:cosecθ = 1/sinθ- 余弦函数的平方:cos^2θ + sin^2θ = 1- 余弦函数的和差公式:cos(α ± β) = cosαcosβ ∓sinαsinβ- 余弦函数的倍角公式:cos2θ = cos^2θ - sin^2θ3. 正切函数(Tangent Function):- 正切函数的定义:tanθ = 对边/邻边= sinθ/cosθ- 正切函数的倒数:cotθ = 1/tanθ = cosθ/sinθ- 正切函数与正弦、余弦的关系:tanθ = sinθ/cosθ = (对边/斜边) / (邻边/斜边) = 对边/邻边- 正切函数的和差公式:tan(α ± β) = (tanα ± tanβ) / (1 ∓tanαtanβ)4. 反三角函数:- 反正弦函数(Arcsine Function):sin⁻¹(x) = θ,其中-π/2 ≤ θ ≤ π/2- 反余弦函数(Arccosine Function):cos⁻¹(x) = θ,其中0 ≤ θ ≤ π- 反正切函数(Arctangent Function):tan⁻¹(x) = θ,其中-π/2 < θ < π/2这些是常用的三角函数公式,可以根据具体的问题和需要,灵活运用这些公式进行计算和推导。
三角函数公式(必记忆)

tan(A+B) =
tan(A-B) =
cot(A+B) =
cot(A-B) =
倍角公式
tan2A =
Sin2A=2SinA•CosA
Cos2A = Cos2A-Sin2A=2Cos2A-1=1-2sana=
其它公式
a•sina+b•cosa= ×sin(a+c) [其中tanc= ]
a•sin(a)-b•cos(a) = ×cos(a-c) [其中tan(c)= ]
两角和公式
sin(A+B) = sinAcosB+cosAsinB
sin(A-B) = sinAcosB-cosAsinB
cos(A+B) = cosAcosB-sinAsinB
cosasinb = [sin(a+b)-sin(a-b)]
三角函数公式(记忆)
诱导公式
sin(-a) = -sina
cos(-a) = cosa
sin( -a) = cosa
cos( -a) = sina
sin( +a) = cosa
cos( +a) = -sina
sin(π-a) = sina
cos(π-a) = -cosa
sin(π+a) = -sina
公式六:
±α及 ±α与α的三角函数值之间的关系:
sin( +α)= cosα
cos( +α)= -sinα
tan( +α)= -cotα
cot( +α)= -tanα
sin( -α)= cosα
三角函数公式表(全)

三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1 sinα ·cscα=1 sinα/cosα=tanαsin2α+cos2α=11+tan2α=sec2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=co sαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=———----———1-tanα ·tanβtanα-tanβtan(α-β)=—————-------—1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2) cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式Sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2] cos α+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2 ] 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)。
高中生必备实用三角函数公式总表

x | x 2k arcsin a, k Z
a 1
x | x k 1 arcsin a, k Z
k
cosx a
a 1 a 1
x | x 2k arccosa, k Z x | x 2k arccosa, k Z
3
⒕和差化积公式: ① sin sin 2 sin
2 2 cos ③ cos cos 2 cos 2 2 cos
② sin sin 2 cos
2
sin
2
2
④ cos cos 2 sin
4R
=
a 2 sin B sin C b 2 sin A sin C c 2 sin Asin B = = =pr= p( p a)( p b)( p c) 2 sin B 2 sin C 2 sin A
2
(其中 p 1 (a b c) , r 为三角形内切圆半径) ⒌同角关系:
tg tg 1 tg tg
② cos( ) cos cos sin sin ④ tg tg tg( )(1 tg tg )
⑤ tg ( )
tg tg tg tg tg tg 其中当 A+B+C=π 时,有: 1 tg tg tg tg tg tg
⒊ 余 弦 定 理 : a 2 =b 2 +c 2 -2bc cos A c 2 =a 2 +b 2 -2ab cos C
2 2 2 2
⒋S⊿= 1 a ha = 1 ab sin C = 1 bc sin A = 1 ac sin B = abc =2R 2 sin A sin B sin C
完整三角函数公式表

三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secαsin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=c otαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβ2tan(α/2) sinα=——————1+tan2(α/2)1-tan2(α/2) cosα=——————tan(α+β)=——————1-tanα ·tanβtanα-tanβtan(α-β)=——————1+tanα ·tanβ1+tan2(α/2)2tan(α/2) tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式α+βα-βsinα+sinβ=2sin———·cos———2 2α+βα-βsinα-sinβ=2cos———·sin———2 2α+βα-βcosα+cosβ=2cos———·cos———2 2α+βα-βcosα-cosβ=-2sin———·sin———2 2 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=—-[cos(α+β)-cos(α-β)]2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y =2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =三角形中三角函数基本定理Tag:三角函数点击: 1522 【正弦定理】式中R为ABC的外接圆半径(图1.3).【余弦定理】【勾股定理】在直角三角形(C为直角)中,勾方加股方等于弦方(图1.4),即勾股定理也称商高定理,外国书刊中称毕达哥拉斯定理.【正切定理】或【半角与边长的关系公式】式中,r为ABC的内切圆半径,且式中S为ABC的面积.。
三角函数默写(含答案)

sin(p + a ) = - sina c(p +a ) = tana
sin(3p -a ) = - cosa 2
sin(3p + a ) = - cosa 2
cos(3p -a ) = - sina tan(3p -a ) = cota
2
2
cos(3p + a ) = sina tan(3p + a ) = - cota
p sin(
+a)
=
cosa
2
sin(p -a ) = sina
cos(p -a ) = sina 2
cos(p + a ) = - sina 2
cos(p -a ) = - cosa
tan(p -a ) = cot a 2
tan(p + a ) = - cota 2
tan(p -a ) = - tana
2
2
披荆斩棘 勇往直前 加油!
敏哥数学
二、和差化积、和差化积
爱敏哥 爱数学
sin(a + b ) = sina cos b + cosa sin b sin(a - b ) = sina cos b - cosa sin b cos(a + b ) = cosa cos b - sina sin b cos(a - b ) = cosa cos b + sina sin b
敏哥数学
三角函数默写(答案版)
爱敏哥 爱数学
一、诱导公式
sin(-a ) = - sina
cos(-a ) = cosa
tan(-a ) = - tana
sin(2p + a ) = sina
完整三角函数公式表

完整三角函数公式表
以下是完整的三角函数公式表:
1.正弦函数(Sine Function):
o sin(θ) = 对边 / 斜边
o cos(θ) = 邻边 / 斜边
o tan(θ) = 对边 / 邻边
2.余弦函数(Cosine Function):
o cos(θ) = 邻边 / 斜边
o sec(θ) = 斜边 / 邻边
3.正切函数(Tangent Function):
o tan(θ) = 对边 / 邻边
o cot(θ) = 邻边 / 对边
4.反正弦函数(Arcsine Function):
o arcsin(x) = θ,其中 sin(θ) = x
5.反余弦函数(Arccosine Function):
o arccos(x) = θ,其中 cos(θ) = x
6.反正切函数(Arctangent Function):
o arctan(x) = θ,其中 tan(θ) = x
7.余切函数(Cotangent Function):
o cot(θ) = 邻边 / 对边
o csc(θ) = 斜边 / 对边
这些是常见的三角函数及其反函数。
通过使用这些公式,您可以计算给定角度的三角函数值或根据给定的三角函数值计算相应的角度。
请注意,这里列出的公式适用于弧度制下的角度,如果您需要在度数制下使用,需要进行相应的转换。
三角函数公式表(全)

(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法"对角线上两个函数的积为1 ;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin (— a )= —sin a COS (― a )= COs a tan (— a )= —tanaCOt (— a )=—COt asin ( n /2 — a)= COS a COS ( n /2 — a)= sin a tan (n /2 — a)= COt a COt ( n /2 —a)= tan a sin ( n — a )= sin aCOS ( n — a )=—COSatan ( n — a)=—tan aCOt ( n— a )=—COt asin( 3 n /2 — a)=—COS aCOS (3 n /2 —a)=—sin atan (3 n /2 —a)= cot aCOt (3 n /2 —a)= tan asin (2 n — a ) =—sin aCOS (2 n — a )= COS atan (2 n — a ) =—tan aCOt (2 n — a ) = —COt a倒数关系:tan a • cot a =1Sin a • CSC a =1 三角函数公式表同角三角函数的基本关系式商的关系: 平方关系: sin a /cos a = tanaSin 2a + COS 2a=1 1 + tan 2a =sec2asin ( n /2 +a)= COS a sin ( n + a )=—sina sin( 3 n /2 + a)=—COS asin (2k n + a )= sin acos ( n /2 + a ) =— sin a cos ( n + a )=— cos a cos (3 n /2 + a )= sin a cos (2k n + a ) = cosatan (n /2 + a) = — cota tan ( n + a)= tan a tan (3 n /2 + a )=— cot a tan (2k n + a ) = tanacot ( n /2 + a ) =— tana cot ( n+ a )= cot a cot (3 n /2 + a )=— tan acot (2k n + a ) = cota(其中k € Z)两角和与差的三角函数公式 sin ( a+B )= sin a cos 3 + cos a sin 3 sin ( a — 3 )= sin a cos 3 — cos asin 3 cos (a+ 3)= cos a cos 3 — sin a sin 3 cos (a — 3)= cos a cos 3 + sin a sin 3 tan a + tan 3 tan ( a+ 3 )= — 1 — tan a • tan 3 tan a — tan 3 tan ( a — 3 )= -------- ----- 1 + tan a • tan 3半角的正弦、余弦和正切公式 万能公式2tan( a /2)sin a = ----------1 + tan 2(a /2)1 — tan 2( a /2)cos a = ----------1 + tan 2(a /2)2tan( a /2)tan a = ----------1 — tan 2(a/2)三角函数的降幕公式二倍角的正弦、余弦和正切公式sin2 a = 2sin a COS a cos2 a = cos 2 a — sin 2 a= 2cos 2a — 1 = 1 — 2sin 2 a 2ta n a tan2 a = --------- 1 — tan 2a 三角函数的和差化积公式Sin a +sin 3 =2sin[( a + 3 )/2] • cos[( a - 3 )/2] sin a -sin 3 =2cos[( a + 3 )/2] • sin[ ( a - 3 )/2] cos a +cos 3 =2cos[( a + 3 )/2] • COS[ ( a - 3)/2] cos a -cos 3 =-2sin[( a + 3 )/2] • sin[( a -3 )/2] .2 1 - cos2otsin & = -------------231+ cos 2acos ot = --- --2三倍角的正弦、余弦和正切公式sin3 a = 3sin a — 4sin 3acos3 a = 4cos 3a — 3cosa3tan a — tan 3atan3 a = ----------1 — 3ta n 2a三角函数的积化和差公式sinacoscos a cos 3 = -[sin (a + B)+ sin (a — 3)]2 1sin 3 = -[sin (a + 3)— sin (a — 3)]2 1-cos 3 = -[cos (a + 3)+ cos (a — 3 )]sin a • sin 3=—-[cos (a+ B )—cos (a — 3 )]2化asin a ± bcos a为一个角的一个三角函数的形式(辅助角的三角函数的公式)(其中①角所在象限由尔占的符号确定4角的值*tar^=-确定) aTHANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求。
必记最全高中三角函数公式表
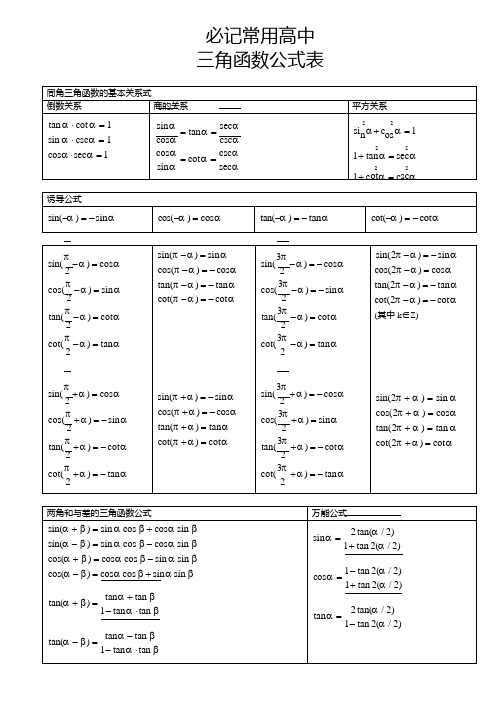
1 sin( ) sin( ) 2 1 cos sin sin( ) sin( ) 2 1 cos cos cos( ) cos( ) 2 1 sin sin cos( ) cos( ) 2 sin cos
1 cos sin( ) 2 2 1 cos cos( ) 2 2 1 cos 1 cos sin tan( ) 2 1 cos sin 1 cos
sin
1 cos 2 2 2 1 cos 2 cos 2
sin( ) sin cos cos sin sin( ) sin cos cos sin cos( ) cos cos sin sin cos( ) cos cos sin sin tan( ) tan tan 1 tan tan tan tan 1 tan tan
三角函数的和差化积公式
三角函数的积化和差公式
cos 2 2 sin sin 2 cos sin 2 2 cos cos 2 cos cos 2 2 cos cos 2 sin sin 2 2
2
二倍角的正弦、余弦和正切公式
三倍角的正弦、余弦和正切公式
sin 2 2 sin cos cos 2 cos 2 sin 2 2 cos 2 1 1 2 sin 2 tan 2 2 tan 1 tan 2
sin 3 3sin 4 sin 3 cos 3 4 cos 3 3 cos . tan 3 3 tan tan 3 1 3 tan 2
《三角函数》公式记忆表

《三角函数》公式记忆表————————————————————————————————作者: ————————————————————————————————日期:ﻩ口诀:“奇变偶不变,符号看象限”;《三角函数》公式记忆表 P RZ 制作 10.06.12一、诱导公式:212(1)sin ,sin()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩212(1)s ,s()2(1)sin ,nn co n co απαα+⎧-⎪+=⎨⎪-⎩ 第一组:ααπsin )2sin(=+k ααπcos )2cos(=+k ααπtan )2tan(=+k第二组:απαsin )sin(-=± απαcos )cos(-=± απαtan )tan(=± 第三组:ααπsin )sin(=- ααπcos )cos(-=- ααπtan )tan(-=- 第四组:ααsin )sin(-=- ααcos )cos(=- ααtan )tan(-=- 第五组:ααπcos )2sin(=- ααπsin )2cos(=- ααπcot )2tan(=-第六组:ααπcos )2sin(=+ ααπsin )2cos(-=+ ααπcot )2tan(-=+ 第七组:ααπcos )23sin(-=- ααπsin )23cos(-=- ααπcot )23tan(=-第八组:ααπcos )23sin(-=+ ααπsin )23cos(=+ ααπcot )23tan(-=+(n 为偶数)(n 为偶数)正切线正弦线余弦线α二、同角三角函数的基本关系式: 1、平方关系:黑色倒三角形里上面两个顶点函数值的平方和等于下面顶点函数值的平方。
1cos sin 22=+αα αα22sec tan 1=+ αα22csc cot 1=+2、商数关系:每个顶点处的函数值等于两相邻顶点函数值的乘积。
三角函数公式大全(表格分类)

三角函数公式大全(表格分类) 诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(pi/2-a)=cos(a)cos(pi/2-a)=sin(a)sin(pi/2+a)=cos(a)cos(pi/2+a)=-sin(a)sin(pi-a)=sin(a)cos(pi-a)=-cos(a)sin(pi+a)=-sin(a)cos(pi+a)=-cos(a)tgA=tanA=sinA/cosA两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b)) tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b)) 三角函数和差化积公式sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式sin(2a)=2sin(a)cos(a)cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a) 半角公式sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式sin(a)=(2tan(a/2))/(1+tan^2(a/2))cos(a)=(1-tan^2(a/2))/(1+tan^2(a/2))tan(a)=(2tan(a/2))/(1-tan^2(a/2))其它公式a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)[其中,tan(c)=b/a]a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)[其中,tan(c)=a/b]1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=(e^a-e^(-a))/2cosh(a)=(e^a+e^(-a))/2tgh(a)=sinh(a)/cosh(a)。
(完整版)专升本三角函数公式表

(完整版)专升本三角函数公式表三角函数公式表同角三角函数的基本关系式倒数关系:商的关系:平方关系:tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secαsin2α+cos2α=11+tan2α=sec2α1+cot2α=csc2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积.”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=——-——-—--1-tanα ·tanβtanα-tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2)cosα=——-——-1+tan2(α/2)2tan(α/2)tanα=---—--1-tan2(α/2)(完整版)专升本三角函数公式表tan(α-β)=——————1+tanα ·tanβ半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=-———-1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=—--———1-3tan2α三角函数的和差化积公式三角函数的积化和差公式(完整版)专升本三角函数公式表α+βα-βsinα+sinβ=2sin-——·cos-——2 2α+βα-βsinα-sinβ=2cos-——·sin———2 2α+βα-βcosα+cosβ=2cos—-—·cos—--2 2α+βα-βcosα-cosβ=-2sin—-—·sin-—-2 21sinα ·cosβ=———[sin(α+β)+sin(α-β)] 21cosα ·sinβ=--—[sin(α+β)-sin(α-β)] 21cosα ·cosβ=-—-[cos(α+β)+cos(α-β)]21sinα ·sinβ=—-—[cos(α+β)-cos(α-β)] 2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)Sec a133222不存在Csc a不存在223321。
