n阶魔方阵c源代码
魔方阵算法及C语言实现

魔方阵算法及C语言实现1 魔方阵概念魔方阵是指由1,2,3……n2填充的,每一行、每一列、对角线之和均相等的方阵,阶数n = 3,4,5…。
魔方阵也称为幻方阵。
例如三阶魔方阵为:魔方阵有什么的规律呢?魔方阵分为奇幻方和偶幻方。
而偶幻方又分为是4的倍数(如4,8,12……)和不是4的倍数(如6,10,14……)两种。
下面分别进行介绍。
2 奇魔方的算法2.1 奇魔方的规律与算法奇魔方(阶数n = 2 * m + 1,m =1,2,3……)规律如下:1.数字1位于方阵中的第一行中间一列;2.数字a(1 < a ≤ n2)所在行数比a-1行数少1,若a-1的行数为1,则a的行数为n;3.数字a(1 < a ≤ n2)所在列数比a-1列数大1,若a-1的列数为n,则a的列数为1;4.如果a-1是n的倍数,则a(1 < a ≤ n2)的行数比a-1行数大1,列数与a-1相同。
2.2 奇魔方算法的C语言实现1 #include <stdio.h> 2// Author: / 3// N为魔方阶数 4#define N 115 6int main()7{8int a[N][N]; 9int i;10 int col,row;1112 col = (N-1)/2;13 row = 0;1415a[row][col] = 1;1617for(i = 2; i <= N*N; i++)18 {19if((i-1)%N == 0 )20 {21 row++;22 }23else24 {25// if row = 0, then row = N-1, or row = row - 126 row--;27 row = (row+N)%N;2829// if col = N, then col = 0, or col = col + 130 col ++;31 col %= N;32 }33 a[row][col] = i;34 }35for(row = 0;row<N;row++)36 {37for(col = 0;col < N; col ++)38{39 printf("%6d",a[row][col]);40 }41printf("\n");42 }43return0;44 }3 偶魔方的算法偶魔方的情况比较特殊,分为阶数n = 4 * m(m =1,2,3……)的情况和阶数n = 4 * m + 2(m = 1,2,3……)情况两种。
C语言程序设计100例之(29):拉丁方阵

C语言程序设计100例之(29):拉丁方阵例29 拉丁方阵问题描述构造NXN 阶的拉丁方阵,使方阵中的每一行和每一列中数字1到N只出现一次。
如N=4时:1 2 3 42 3 4 13 4 1 24 1 2 3输入格式一个正整数n(2<=n<=9)。
输出格式生成的n*n阶方阵。
输入样例4输出样例1 2 3 42 3 4 13 4 1 24 1 2 3(1)编程思路。
观察给出的例子,可以发现:若将每一行中第一列的数字和最后一列的数字连起来构成一个环,则该环正好是由1到N顺序构成;对于第i行,这个环的开始数字为i。
按照此规律可以很容易的写出程序。
(2)源程序。
#include <stdio.h>int main(){int n;scanf("%d",&n);int i,k,t;for(i=0; i<n; i++){t=i%n; // 确定该拉丁方阵第i行的第一个元素的值for(k=0; k<n; k++) // 按照环的形式输出该行中的各个元素printf("%d ",(k+t)%n+1);printf("\n");}return 0;}习题2929-1 奇数阶魔方本题选自杭州电子科技大学OJ题库(/showproblem.php?pid=1998)Problem Description一个n 阶方阵的元素是1,2,...,n^2,它的每行,每列和2条对角线上元素的和相等,这样的方阵叫魔方。
n为奇数时我们有1种构造方法,叫做“右上方” ,例如下面给出n=3,5,7时的魔方。
38 1 63 5 74 9 2517 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9730 39 48 1 10 19 2838 47 7 9 18 27 2946 6 8 17 26 35 375 14 16 25 34 36 4513 15 24 33 42 44 421 23 32 41 43 3 1222 31 40 49 2 11 20第1行中间的数总是1,最后1行中间的数是n^2,他的右边是2,从这三个魔方,你可看出“右上方”是何意。
魔方程序C语言代码

#include <windows.h>#include <gl/gl.h>#include <gl/glu.h>#include <gl/glut.h>//小方块的结构,包括小方块在x,y,z上的旋转角度,颜色数组下标,小方块的三维坐标。
struct rcube{int xr;int yr;int zr;int cl[6];GLfloat x;GLfloat y;GLfloat z;};struct rcube rc[3][3][3];struct rcube *temp[3][3];//颜色数组GLfloat color[6][3]={{1.0,0.0,0.0},{0.0,1.0,0.0},{0.0,0.0,1.0},{1.0,1.0,0.0},{1.0,0.0,1.0},{0.0,1.0,1.0}};int tempc[3][3][6];//有关旋转的一些变量GLfloat xRot = 10.0f;GLfloat yRot = 10.0f;int rotateType=0;int rotateOK=0;int rotateRate=50;int rotate=0;/////////////////////////////////////////////////////////////////////////////// //画小方块void drawcube(int cl[6]){glBegin(GL_QUADS);//右面glColor3fv(color[cl[0]]);glVertex3f(0.14f,-0.14f,-0.14f);glVertex3f(0.14f,0.14f,-0.14f);glVertex3f(0.14f,0.14f,0.14f);glVertex3f(0.14f,-0.14f,0.14f);//左面glColor3fv(color[cl[1]]);glVertex3f(-0.14f,-0.14f,0.14f);glVertex3f(-0.14f,0.14f,0.14f);glVertex3f(-0.14f,0.14f,-0.14f);glVertex3f(-0.14f,-0.14f,-0.14f);//前面glColor3fv(color[cl[2]]);glVertex3f(-0.14f,0.14f,0.14f);glVertex3f(-0.14f,-0.14f,0.14f);glVertex3f(0.14f,-0.14f,0.14f);glVertex3f(0.14f,0.14f,0.14f);//后面glColor3fv(color[cl[3]]);glVertex3f(-0.14f,0.14f,-0.14f);glVertex3f(0.14f,0.14f,-0.14f);glVertex3f(0.14f,-0.14f,-0.14f);glVertex3f(-0.14f,-0.14f,-0.14f);//上面glColor3fv(color[cl[4]]);glVertex3f(-0.14f,0.14f,-0.14f);glVertex3f(-0.14f,0.14f,0.14f);glVertex3f(0.14f,0.14f,0.14f);glVertex3f(0.14f,0.14f,-0.14f);//下面glColor3fv(color[cl[5]]);glVertex3f(-0.14f,-0.14f,-0.14f);glVertex3f(0.14f,-0.14f,-0.14f);glVertex3f(0.14f,-0.14f,0.14f);glVertex3f(-0.14f,-0.14f,0.14f);glEnd();glFlush();}//窗口刷新时被调用。
编程魔方

else if(a[i]==3)cout<<"R";
else if(a[i]==4)cout<<"r";
else if(a[i]==5)cout<<"U";
else if(a[i]==6)cout<<"u";
}cout<<" 共"<<k<<"步 ";j++;if(j%3==0)cout<<"\n";
for(a[8]=1;a[8]<=6;a[8]++)
{
if(b<=7)a[8]=0;
if(a[8]!=0&&a[9]!=0&&(a[8]==a[9]&&a[9]==a[10]||(a[8]+a[9]+1)%4==0&&(a[8]-a[9])*(a[8]-a[9])==1))continue;
for(a[5]=1;a[5]<=6;a[5]++)
{
if(b<=4)a[5]=0;
if(a[5]!=0&&a[6]!=0&&(a[5]==a[6]&&a[6]==a[7]||(a[5]+a[6]+1)%4==0&&(a[5]-a[6])*(a[5]-a[6])==1))continue;
魔方程序C语言代码

魔方程序C语言代码#include <windows.h>#include <gl/gl.h>#include <gl/glu.h>#include <gl/glut.h>//小方块的结构,包括小方块在x,y,z上的旋转角度,颜色数组下标,小方块的三维坐标。
struct rcube{int xr;int yr;int zr;int cl[6];GLfloat x;GLfloat y;GLfloat z;};struct rcube rc[3][3][3];struct rcube *temp[3][3];//颜色数组GLfloatcolor[6][3]={{1.0,0.0,0.0},{0.0,1.0,0.0}, {0.0,0.0,1.0},{1.0,1.0,0.0},{1.0,0.0,1.0},{0.0,1.0,1.0} };int tempc[3][3][6];//有关旋转的一些变量GLfloat xRot = 10.0f;GLfloat yRot = 10.0f;int rotateType=0;int rotateOK=0;int rotateRate=50;int rotate=0;///////////////////////////////////////// ////////////////////////////////////// //画小方块void drawcube(int cl[6]){glBegin(GL_QUADS);//右面glColor3fv(color[cl[0]]);glVertex3f(0.14f,-0.14f,-0.14f); glVertex3f(0.14f,0.14f,-0.14f);glVertex3f(0.14f,0.14f,0.14f);glVertex3f(0.14f,-0.14f,0.14f);//左面glColor3fv(color[cl[1]]);glVertex3f(-0.14f,-0.14f,0.14f);glVertex3f(-0.14f,0.14f,0.14f);glVertex3f(-0.14f,0.14f,-0.14f);glVertex3f(-0.14f,-0.14f,-0.14f); //前面glColor3fv(color[cl[2]]);glVertex3f(-0.14f,0.14f,0.14f);glVertex3f(-0.14f,-0.14f,0.14f);glVertex3f(0.14f,-0.14f,0.14f);glVertex3f(0.14f,0.14f,0.14f);//后面glColor3fv(color[cl[3]]);glVertex3f(-0.14f,0.14f,-0.14f);glVertex3f(0.14f,0.14f,-0.14f);glVertex3f(0.14f,-0.14f,-0.14f);glVertex3f(-0.14f,-0.14f,-0.14f); //上面glColor3fv(color[cl[4]]);glVertex3f(-0.14f,0.14f,-0.14f);glVertex3f(-0.14f,0.14f,0.14f);glVertex3f(0.14f,0.14f,0.14f);glVertex3f(0.14f,0.14f,-0.14f);//下面glColor3fv(color[cl[5]]);glVertex3f(-0.14f,-0.14f,-0.14f); glVertex3f(0.14f,-0.14f,-0.14f);glVertex3f(0.14f,-0.14f,0.14f);glVertex3f(-0.14f,-0.14f,0.14f);glEnd();glFlush();}//窗口刷新时被调用。
魔方阵 C语言

一、幻方按照阶数可分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
二、奇数阶幻方(劳伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:(1)每一个数放在前一个数的右上一格;(2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在底行且最左列;(5)如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:三、单偶数阶幻方(斯特拉兹法)所谓单偶阶幻方就是当n不可以被4整除时的偶阶幻方,即4K+2阶幻方。
如(n=6,10,14……)的幻方。
单偶数阶幻方最经典的填法是斯特拉兹法。
填写的方法是:以10阶幻方为例。
这时,k=2。
(1)把魔方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。
用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
(2)在A象限的中间行、中间格开始,按自左向右的方向,标出k格。
A象限的其它行则标出最左边的k格。
将这些格,和C象限相对位置上的数互换位置。
(3)在B象限所有行的中间格,自右向左,标出k-1格。
(注:6阶幻方由于k-1=0,所以不用再作B、D象限的数据交换),将这些格,和D象限相对位置上的数互换位置。
四、源代码如下,已加详细注释#include<stdio.h>#include<stdlib.h>int array[15][15];intinit(int degree) //初始化{inti;int j;for(i=0; i<=degree+1; i++)for(j=0; j<=degree+1; j++)array[i][j] = 0;return 0;}inttest_print(int x, int y, int w, int h) //测试用的,输出以(x,y)为原点,宽为w,高为h,这个区域的数值{inti;int j;for(i=y; i<=y+h-1; i++){for(j=x; j<=x+w-1; j++){printf("%2d ",array[i][j]);}printf("\n");}return 0;}intlao_bo_er(int degree, int x, int y, intnum) //劳伯法{inti;int j;int k;i = y;j = degree/2 + x;for(k=num; k<=num+degree*degree-1; k++){array[i][j] = k;if((k-num+1)%degree == 0){ //如果这个数所要放的格已经有数填入i = (i-y+1)%degree+y;}else{ //每一个数放在前一个数的右上一格i = (i-y-1+degree)%degree+y;j = (j-x+1)%degree+x;}}return 0;}intseq_range(int degree) //把数字按顺序填{inti;int j;intnum;num = 1;for(i=1; i<=degree; i++){for(j=1; j<=degree; j++){array[i][j] = num++;}}return 0;}intsi_te_la_zi(int degree, int x, int y, intnum) //斯特拉兹法{intdeg;int k;int temp;inti;int j;deg = degree/2;lao_bo_er(deg, x, y, num); //用罗伯法,依次在A象限,D象限,B象限,C象限按奇数阶幻方的填法填数lao_bo_er(deg, x+deg, y, num+2*deg*deg);lao_bo_er(deg, x, y+deg, num+3*deg*deg);lao_bo_er(deg, x+deg, y+deg, num+deg*deg);k = (degree-2)/4;for(i=1; i<=deg; i++){ //A象限和C象限对换数据for(j=1; j<=k; j++){temp = array[i][j];array[i][j] = array[i+deg][j];array[i+deg][j]=temp;}for(j=deg+deg/2+1; j>=deg+deg/2-k+3; j--){temp = array[i][j];array[i][j] = array[i+deg][j];array[i+deg][j]=temp;}}for(i=j=1; j<=deg/2+k; j++){ //B象限和D象限对换数据temp = array[i+deg/2][j];array[i+deg/2][j] = array[i+deg+deg/2][j];array[i+deg+deg/2][j]=temp;}return 0;}inthai_er_fa(int degree) //海尔法{inti;int j;int complement;intdeg;seq_range(degree);complement = degree*degree+1;deg = degree/4;for(i=0; i<deg; i++){for(j=0; j<deg; j++){ //对角线上的数字换成和它互补的数array[i*4+1][j*4+1] = complement -array[i*4+1][j*4+1];array[i*4+1][j*4+4] = complement -array[i*4+1][j*4+4];array[i*4+4][j*4+1] = complement -array[i*4+4][j*4+1];array[i*4+4][j*4+4] = complement -array[i*4+4][j*4+4];array[i*4+2][j*4+2] = complement -array[i*4+2][j*4+2];array[i*4+2][j*4+3] = complement -array[i*4+2][j*4+3];array[i*4+3][j*4+2] = complement -array[i*4+3][j*4+2];array[i*4+3][j*4+3] = complement -array[i*4+3][j*4+3];}}return 0;}int main(){int degree;printf("please input the degree\n");scanf("%d",°ree);init(degree);if(degree%2 == 1){ //奇数阶幻方lao_bo_er(degree,1,1,1);test_print(1,1,degree,degree);}else if(degree%4 == 2){ //双偶阶幻方si_te_la_zi(degree, 1, 1, 1);test_print(1,1,degree,degree);}else{ //单偶阶幻方hai_er_fa(degree);test_print(1,1,degree,degree);}return 0;}。
输出魔方阵

for(j=0;j<n;j++)a[n][i]+=a[j][i];
for(i=0;i<n;i++)a[n][n]+=a[i][i];//主对角线的和
}
void main()
{
int n;
int a[M][M]={0};
printf("魔方阵的阶数n=");//n为大于2的任意整数
}
}
//三、当n为单偶数(n=4k+2)时,可把方阵分为4个2k+1的小方阵,编号如下:
//1.各小方阵按奇数阶算法依次填入A(1…[2k+1]2)、B([2k+1]2+1…2[2k+1]2)、C(…)、D(…4[2k+1]2);
//2.将A与D换:A中间格始向右取k格;A最左边的k列(除中行);
//3.将C与B互换:从C的中间列开始向左数k-1列。
MagicOdd(a,0,m,2*m*m+1,m);//C阵(右上)
MagicOdd(a,m,0,3*m*m+1,m);//D阵(左下)
for(j=k;j<m-1;j++){//从A的中间格开始向右数k格...
t=a[k][j];
a[k][j]=a[k+m][j];//...与D对应位置交换
a[k+m][j]=t;
}
void MagicSev(int a[M][M],int st,int n)//单偶4k+2阶魔方阵,起始数st
{
int m=n/2,k=m/2;//将原矩阵分为2×2的方阵
C语言实现魔方阵

C语言实现魔方阵魔方阵(Magic Square)是一个古老且有趣的数学问题,它是一个正方形矩阵,其中每行、每列以及对角线上的元素之和都相等。
例如,下面是一个3阶魔方阵:```816357492```实现魔方阵的算法有多种,下面我们将介绍一种基于C语言的实现方法。
首先,我们需要设计一个函数来检查生成的矩阵是否是魔方阵。
这个函数的输入是一个二维数组和魔方阵的阶数,输出是一个布尔值,表示输入的矩阵是否是魔方阵。
下面是这个函数的实现:```c#include <stdbool.h>bool checkMagicSquare(int **matrix, int n)int sum = n * (n * n + 1) / 2;//检查每行的和for (int i = 0; i < n; i++)for (int j = 0; j < n; j++) rowSum += matrix[i][j];}if (rowSum != sum)return false;}}//检查每列的和for (int i = 0; i < n; i++) int colSum = 0;for (int j = 0; j < n; j++) colSum += matrix[j][i];}if (colSum != sum)return false;}}//检查主对角线的和for (int i = 0; i < n; i++)diagSum += matrix[i][i];}if (diagSum != sum)return false;}//检查副对角线的和int antiDiagSum = 0;for (int i = 0; i < n; i++) antiDiagSum += matrix[i][n - 1 - i]; }if (antiDiagSum != sum)return false;}return true;```接下来,我们使用一个递归函数来生成魔方阵。
任意阶魔方阵算法(c语言)

任意阶魔方阵算法2009-03-19 11:45:00| 分类:我的文章|字号大中小订阅我一直就对魔方阵很感兴趣,特别是知道了奇数阶魔方阵的罗伯特算法后,就特别想知道偶数阶魔方阵应有什么算法。
当时书上说偶数阶魔方阵比较复杂。
都没有什么说明。
因此这个问题一直搁在我心里很久,已差不多快忘记了。
今天突然又想到了这个问题。
于是我开始在网上搜寻,看能不能找到什么好的算法。
记得在高中的时候,我就做过魔方阵,当时我从三阶一直做到过八阶方阵,不过用的是人工的方法。
到大学的时候我知道了罗伯特算法后,我就用程序将算法写了出来。
于是我今天准备把偶数阶的魔方阵也写出来。
在网上终于找到了一个比较好的算法。
将该算法用C写了出来。
供大家分亨。
1、奇数阶幻方n为奇数(n=3,5,7,9,11……) (n=2*k+1,k=1,2,3,4,5……)奇数阶幻方最经典的填法是罗伯特法(也有人称之为楼梯方)。
填写方法是这样:把1(或最小的数)放在第一行正中;按以下规律排列剩下的n*n-1个数:(1)、每一个数放在前一个数的右上一格;(2)、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;(3)、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;(4)、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;(5)、如果这个数所要放的格已经有数填入,处理方法同(4)。
这种写法总是先向“右上”的方向,象是在爬楼梯。
2、双偶阶幻方n为偶数,且能被4整除(n=4,8,12,16,20……) (n=4k,k=1,2,3,4,5……)先说明一个定义:互补:如果两个数字的和,等于幻方最大数和最小数的和,即n*n+1,称为互补。
先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:1 2 3 45 6 7 89 10 11 1213 14 15 16这个方阵的对角线,已经用蓝色标出。
C语言---魔方阵

C语⾔---魔⽅阵魔⽅阵的定义:在n*n的⽅阵中,每⼀⾏的和=每⼀列的和=对⾓线的和。
(本⽂中涉及的n为⼤于3的奇数)。
例如3*3的魔⽅阵为:5*5的魔⽅阵为:如何写魔⽅阵呢?1.数字1位于第⼀⾏的正中间2.下⼀个数放到上⼀个数的右上⾓(即上⼀⾏下⼀列),若⽆上⼀⾏则放到最后⼀⾏,若⽆下⼀列则放到第⼀列3.若新位置已经放了数,则将其放⼊该数的正下⽅(即下⼀⾏的同⼀列)C语⾔代码:1int magicMatrix() {2 printf("请输⼊你想⽣成的魔⽅阵阶数:(⼤于3的奇数)\n");3int i,c,r;4 scanf("%d",&i);5int arr[i][i];6for(int n=0; n<i; n++) {7for(int m=0; m<i; m++) {8 arr[n][m]=0;9 }10 }11 c=0;12 r=i/2;13 arr[c][r] = 1;// 魔⽅阵的第⼀⾏最中间的数为114int k=i*i;15for(int j=2; j<=k; j++) {16int h=c,l=r; //记录原来的位置17if(c==0) {18 c=i-1;19 } else {20 c=c-1;21 }22if(r==i-1) {23 r=0;24 } else {25 r=r+1;26 }27if(arr[c][r]!=0) {28 c=h+1;29 r=l;30 }31 printf("c=%d,r=%d,j=%d\n",c,r,j);32 arr[c][r]=j;33 }34 printf("\n");35for(int n=0; n<i; n++) {36for(int m=0; m<i; m++) {37 printf("%d\t",arr[n][m]);38 }39 printf("\n");40 }41 }计算下⼀个数字的位置时,如果位置已经被占,就在该数的下⼀⾏同⼀列,所以代码中每次计算要记录该数的位置。
C语言魔方阵的三种实现方法

C语⾔魔⽅阵的三种实现⽅法⽬录魔⽅阵:1.奇数阶魔⽅阵2.偶数阶魔⽅阵(n=4K)3.偶数阶魔⽅阵(n=4K+2)魔⽅阵:把1到n*n排成n⾏n列⽅阵,使⽅阵中的每⼀⾏、每⼀列以及对⾓线上的数之和都相同,即为n阶魔⽅阵。
根据魔⽅阵的规律,我将它分为三种情况。
1.奇数阶魔⽅阵规律:第⼀个数放在第⼀⾏的中间,下⼀个数放在上⼀个数的上⼀⾏下⼀列,若该位置已经有了数字即放在上个数的下⾯⼀⾏的相同列⽤C语⾔编程如下:⽰例:n=5;#include<stdio.h>#include<stdlib.h>#include<assert.h>void Magic1(){#define ROW 5#define COL ROWassert(ROW % 2 != 0); //判断n是否为奇数int arr[ROW][COL] = { 0 }; //定义⼆维数组int currow = 0;int curcol = COL / 2;arr[currow][curcol] = 1;for (int i = 2; i <= ROW * COL; i++){if (arr[(currow - 1 + ROW) % ROW][(curcol + 1) % COL] == 0) //按照规律赋值{currow = (currow - 1 + ROW) % ROW;curcol = (curcol + 1) % COL;}else{currow = (currow + 1) % ROW;}arr[currow][curcol] = i;}for (int i = 0; i < ROW; i++) //打印魔⽅阵{for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}}int main(){Magic1();return 0;}结果:2.偶数阶魔⽅阵(n=4K)规律:按数字从⼩到⼤,即1,2,3……n顺序对魔⽅阵从左到右,从上到下进⾏填充;将魔⽅阵分成若⼲个4×4⼦⽅阵(如:8阶魔⽅阵可分成四个4×4⼦⽅阵),将⼦⽅阵对⾓线上的元素取出;将取出的元素按从⼤到⼩的顺序依次填充到n×n⽅阵的空缺处。
C#输出N阶魔方方阵(带校验)[原创]
![C#输出N阶魔方方阵(带校验)[原创]](https://img.taocdn.com/s3/m/7fa0bb32492fb4daa58da0116c175f0e7dd1195a.png)
C#输出N阶魔⽅⽅阵(带校验)[原创]昨天同事发了个图⽚过来,要求输出N阶魔⽅的,横竖跟对⾓线的和都相等!所以就研究了⼀下,感觉⾥⾯的算法⽐较容易把⼈搞晕,C#代码如下:using System;namespace MagiCube{class Program{static void Main(string[] args){int n = 0;bool parseOK = false;bool exit = false;do{do{try{Console.Clear();Console.WriteLine("请输⼊魔⽅的阶数:");n = Int32.Parse(Console.ReadLine());if (n < 3 || n > 99){Console.WriteLine("输⼊的数字不能⼩于3或⼤于99,请重试!");Console.ReadKey();parseOK = false;continue;}parseOK = true;}catch (FormatException){Console.WriteLine("输⼊的不是整数,请重试!");parseOK = false;Console.ReadKey();}} while (!parseOK);GetData(n, true);Console.WriteLine("是否继续运⾏?(按“Y”继续,否则退出!)");exit = (Console.ReadKey().Key.ToString().ToLower() == "y" ? false : true);} while (!exit);}public static void GetData(int n,bool checkSum) //根据n的值决定调⽤的函数,并输出结果{int[,] N = new int[n, n];if (n % 2 != 0) //n为基数时{N = Odd(n);}else if (n % 4 == 0) //n为4的倍数时{N = Even(n);}else if (n % 4 == 2) //n为⾮4的倍数的其他偶数时(n%4==2){N = Even2(n);}//else//{// Console.WriteLine("⽆法处理数字 {0} !", n);//}Console.WriteLine(new string('=', 50));Print(N);if (checkSum){Console.WriteLine(new string('=', 50));CheckSum(N);}Console.WriteLine(new string('=', 50));}public static void CheckSum(int[,] N) //输出N阶魔⽅每⾏每列及对⾓线的和{int row = N.GetLength(0);int col = N.GetLength(1);int sumrow = 0;int sumcol = 0;int sumdia = 0;for (int x = 0; x < row; x++){for (int y = 0; y < col; y++){sumrow += N[x, y];sumcol += N[y, x];}Console.WriteLine("⾏{0}:{1},列{0}:{1}", x + 1, sumrow, x + 1, sumcol);sumrow = 0;sumcol = 0;}for (int m = 0; m < row; m++){sumdia += N[m, m];}Console.Write("对⾓线1:{0},", sumdia);sumdia = 0;int i = 0;for (int j = (col - 1); j >= 0; j--){sumdia += N[i, j];}Console.WriteLine("对⾓线2:{0}", sumdia);}public static int[,] Odd(int n) //n为基数时{int[,] N = new int[n, n];int x = 0;int y = (n - 1) / 2;for (int i = 1; i <= n * n; i++){x = (x < 0 ? (n + x) : (x > (n - 1) ? (x - n) : x));y = (y > (n - 1) ? (y - n) : (y < 0 ? (n + y) : y));if (N[x, y] == 0){if ((i % n) == 0 && i != 1){N[x++, y] = i;}else{N[x--, y++] = i;}}}return N;}public static int[,] Even(int n) //n为4的倍数时{int[,] N = new int[n, n];/*消去对⾓线法* 适⽤:四之倍数阶魔⽅阵* ⽅法:(1)先将整个⽅阵划分成k*k个4阶⽅阵,然后在每个4阶⽅阵的对⾓线上做记号* (2)由左⽽右、由上⽽下,遇到没有记号的位置才填数字,但不管是否填⼊数字,每移动⼀格数字都要加1 * (3)⾃右下⾓开始,由右⽽左、由下⽽上,遇到没有数字的位置就填⼊数字,但每移动⼀格数字都要加1 * 参考:/article/DailyBlog/479.htm*/for (int x = 0; x < n; x += 4){for (int y = 0; y < n; y += 4){N[x, y] = 1;N[x + 3, y + 3] = 1;N[x + 1, y + 1] = 1;N[x + 2, y + 2] = 1;N[x, y + 3] = 1;N[x + 3, y] = 1;N[x + 1, y + 2] = 1;N[x + 2, y + 1] = 1;}}int m = n * n;for (int i = 1; i <= n * n; i++){if (N[(i - 1) / n, (i - 1) % n] != 1){N[(i - 1) / n, (i - 1) % n] = i;}else{N[(i - 1) / n, (i - 1) % n] = m;}m--;}return N;}public static int[,] Even2(int n) //n为⾮4的倍数的其他偶数时(n%4==2) {/* n为⾮4的倍数的其他偶数时,划分成四个奇数⽅阵⽰意图* |* B区(次⼩) | C区(次⼤)* ---------------------------* D区(最⼤) | A区(最⼩)* |*/int[,] N = new int[n, n];int[,] initN = Odd(n / 2);int v = n * n / 4;for (int x = 0; x < n / 2; x++){for (int y = 0; y < n / 2; y++){N[x + n / 2, y + n / 2] = initN[x, y]; //A区N[x, y] = initN[x, y] + v; //B区N[x, y + n / 2] = initN[x, y] + 2 * v; //C区N[x + n / 2, y] = initN[x, y] + 3 * v; //D区}}int tmp;int m = (n - 2) / 4;if (m > 1){for (int i = 0; i <= m - 2; i++){for (int j = 0; j < n / 2; j++){tmp = N[i, j];N[i, j] = N[i, n / 2 + j];N[i, n / 2 + j] = tmp;}}}for (int i = n - m; i < n; i++){for (int j = 0; j < n / 2; j++){tmp = N[i, j];N[i, j] = N[i, n / 2 + j];N[i, n / 2 + j] = tmp;}}tmp = N[n / 2 + m, m];N[n / 2 + m, m] = N[n / 2 + m, n / 2 + m];N[n / 2 + m, n / 2 + m] = tmp;tmp = N[n - 1, m];N[n - 1, m] = N[n - 1, n / 2 + m];N[n - 1, n / 2 + m] = tmp;return N;}public static void Print(int[,] N){int maxLength = 4;int preLen = 0;for (int i = 0; i < N.GetLength(0); i++){for (int j = 0; j < N.GetLength(1); j++){Console.Write(new String(' ', maxLength - preLen));Console.Write(N[i, j]);preLen = N[i, j].ToString().Length;}for (int k = 0; k < maxLength - 2; k++){Console.WriteLine("");}preLen = 0; }}}}。
用Python简陋模拟n阶魔方
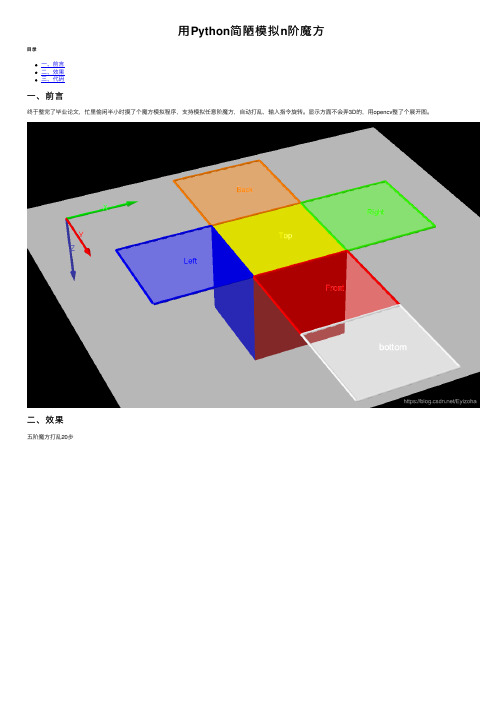
⽤Python简陋模拟n阶魔⽅⽬录⼀、前⾔⼆、效果三、代码⼀、前⾔终于整完了毕业论⽂,忙⾥偷闲半⼩时摸了个魔⽅模拟程序,⽀持模拟任意阶魔⽅,⾃动打乱,输⼊指令旋转。
显⽰⽅⾯不会弄3D的,⽤opencv整了个展开图。
⼆、效果五阶魔⽅打乱20步震撼⼈⼼50阶,打乱100步三、代码import cv2import numpy as npfrom random import randintclass Cube:def __init__(self, order=3, size=50): # 魔⽅阶数、显⽰尺⼨self.img = np.zeros((4 * size * order, 3 * size * order, 3), dtype=np.uint8)self.order = orderself.size = sizeself.len = size * orderself.top = [['y'] * order for _ in range(order)]self.front = [['r'] * order for _ in range(order)]self.left = [['b'] * order for _ in range(order)]self.right = [['g'] * order for _ in range(order)]self.back = [['o'] * order for _ in range(order)]self.bottom = [['w'] * order for _ in range(order)]self.axis_rotate = (self.base_rotate_x, self.base_rotate_y, self.base_rotate_z)self.color = {'y': (0, 255, 255), 'r': (0, 0, 255), 'b': (255, 0, 0),'g': (0, 255, 0), 'o': (0, 128, 255), 'w': (255, 255, 255)}def check(self): # 检测魔⽅是否还原for i in range(self.order):for j in range(self.order):if self.top[i][j] != self.top[0][0]:return Falseif self.back[i][j] != self.back[0][0]:return Falseif self.front[i][j] != self.front[0][0]:return Falseif self.left[i][j] != self.left[0][0]:return Falseif self.right[i][j] != self.right[0][0]:return Falseif self.bottom[i][j] != self.bottom[0][0]:return Falsereturn Truedef show(self, wait=0): # 显⽰魔⽅展开图for i in range(self.order):for j in range(self.order):# backx, y = self.len + i * self.size, j * self.sizecv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), self.color[self.back[j][i]], -1) cv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), (10, 10, 10), 1)# leftx, y = i * self.size, self.len + j * self.sizecv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), self.color[self.left[j][i]], -1)cv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), (10, 10, 10), 1)# topx, y = self.len + i * self.size, self.len + j * self.sizecv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), self.color[self.top[j][i]], -1)cv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), (10, 10, 10), 1)# rightx, y = 2 * self.len + i * self.size, self.len + j * self.sizecv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), self.color[self.right[j][i]], -1)cv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), (10, 10, 10), 1)# frontx, y = self.len + i * self.size, 2 * self.len + j * self.sizecv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), self.color[self.front[j][i]], -1)cv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), (10, 10, 10), 1)# bottomx, y = self.len + i * self.size, 3 * self.len + j * self.sizecv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), self.color[self.bottom[j][i]], -1)cv2.rectangle(self.img, (x, y), (x + self.size, y + self.size), (10, 10, 10), 1)cv2.imshow('cube', self.img)cv2.waitKey(wait)def shuffle(self, times): # 打乱魔⽅for _ in range(times):self.rotate(randint(0, 2), randint(0, self.order - 1), randint(0, 3))def rotate(self, axis, index, times): # 旋转魔⽅:axis轴,第index层,逆时针times次for _ in range(times):self.axis_rotate[axis](index)def count(self, color='y'):count = 0for i in range(self.order):for j in range(self.order):if self.top[i][j] == color:count += 1return count@staticmethoddef _column_trans(surface, index, col):for i, r in enumerate(surface):r[index] = col[i]def base_rotate_x(self, index):if index == 0:self.left = [list(c) for c in zip(*self.left)][::-1]elif index == self.order - 1:self.right = [list(c)[::-1] for c in zip(*self.right)]temp = [r[index] for r in self.top]self._column_trans(self.top, index, [r[index] for r in self.front])self._column_trans(self.front, index, [r[index] for r in self.bottom])self._column_trans(self.bottom, index, [r[index] for r in self.back])self._column_trans(self.back, index, temp)def base_rotate_y(self, index):if index == 0:self.back = [list(c)[::-1] for c in zip(*self.back)]elif index == self.order - 1:self.front = [list(c) for c in zip(*self.front)][::-1]temp = self.left[index][::-1]self.left[index] = self.top[index]self.top[index] = self.right[index]self.right[index] = self.bottom[self.order - index - 1][::-1]self.bottom[self.order - index - 1] = tempdef base_rotate_z(self, index):if index == 0:self.top = [list(c) for c in zip(*self.top)][::-1]elif index == self.order - 1:self.bottom = [list(c)[::-1] for c in zip(*self.bottom)]temp = self.front[index][::-1]self.front[index] = [r[self.order - index - 1] for r in self.left]self._column_trans(self.left, self.order - index - 1, self.back[self.order - index - 1][::-1])self.back[self.order - index - 1] = [r[index] for r in self.right]self._column_trans(self.right, index, temp)cube = Cube(3, 50)cube.shuffle(100)while True:cube.show(1)cube.rotate(*(int(c) for c in input('axis,index,times:').split()))if cube.check():breakprint('Congratulations')cube.show(0)到此这篇关于⽤Python简陋模拟n阶魔⽅的⽂章就介绍到这了,更多相关pytho模拟魔⽅内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持!。
n阶魔阵程序源代码

#include "stdafx.h"#include <vector>using namespace std;void OddMagicSquare(vector<vector<int> > &matrix, int n);void DoublyEvenMagicSquare(vector<vector<int> > &matrix, int n);void SinglyEvenMagicSquare(vector<vector<int> > &matrix, int n);void MagicSquare(vector<vector<int> > &matrix, int n); void PrintMagicSquare(vector<vector<int> > &matrix, int n);int main(int argc, char* argv[]){int n;printf("Enter order of square: ");scanf("%d", &n);vector<vector<int> > matrix(n, vector<int> (n, 0));if (n<3){printf("\nError: n must be greater than 2\n\n");return -1;}MagicSquare(matrix, n);//Print resultsPrintMagicSquare(matrix, n);return 0;}void MagicSquare(vector<vector<int> > &matrix,int n) {if (n%2==1) //n is OddOddMagicSquare(matrix, n);else //n is evenif (n%4==0) //doubly even orderDoublyEvenMagicSquare(matrix, n);else //singly even orderSinglyEvenMagicSquare(matrix, n);}void OddMagicSquare(vector<vector<int> > &matrix, int n){int nsqr = n * n;int i=0, j=n/2; // start positionfor (int k=1; k<=nsqr; ++k){matrix[i][j] = k;i--;j++;if (k%n == 0){i += 2;--j;}else{if (j==n)j -= n;else if (i<0)i += n;}}}void DoublyEvenMagicSquare(vector<vector<int> > &matrix, int n){vector<vector<int> > I(n, vector<int> (n, 0));vector<vector<int> > J(n, vector<int> (n, 0));int i, j;//prepare I, Jint index=1;for (i=0; i<n; i++)for (j=0; j<n; j++){I[i][j]=((i+1)%4)/2;J[j][i]=((i+1)%4)/2;matrix[i][j]=index;index++;}for (i=0; i<n; i++)for (j=0; j<n; j++){if (I[i][j]==J[i][j])matrix[i][j]=n*n+1-matrix[i][j];}}void SinglyEvenMagicSquare(vector<vector<int> > &matrix, int n){int p=n/2;vector<vector<int> > M(p, vector<int> (p, 0)); MagicSquare(M, p);int i, j, k;for (i=0; i<p; i++)for (j=0; j<p; j++){matrix[i][j]=M[i][j];matrix[i+p][j]=M[i][j]+3*p*p;matrix[i][j+p]=M[i][j]+2*p*p;matrix[i+p][j+p]=M[i][j]+p*p; }if (n==2)return;vector<int> I(p, 0);vector<int> J;for (i=0; i<p; i++)I[i]=i+1;k=(n-2)/4;for (i=1; i<=k; i++)J.push_back(i);for (i=n-k+2; i<=n; i++)J.push_back(i);int temp;for (i=1; i<=p; i++)for (j=1; j<=J.size(); j++){temp=matrix[i-1][J[j-1]-1];matrix[i-1][J[j-1]-1]=matrix[i+p-1][J[j-1]-1];matrix[i+p-1][J[j-1]-1]=temp;}//j=1, i//i=k+1, k+1+pi=k;j=0;temp=matrix[i][j]; matrix[i][j]=matrix[i+p][j]; matrix[i+p][j]=temp;j=i;temp=matrix[i+p][j]; matrix[i+p][j]=matrix[i][j]; matrix[i][j]=temp;}void PrintMagicSquare(vector<vector<int> > &matrix, int n){for (int i=0; i<n; i++){for (int j=0; j<n; j++)printf(" %3d", matrix[i][j]);printf("\n");}printf("\n\n");}。
魔方算法源代码

#include ""#include ""int color[6][9]={4,4,4,4,4,4,4,4,4,2,2,2,2,2,2,2,2,2,14,14,14,14,14,14,14,14,14,15,15,15,15,15,15,15,15,15,7,7,7,7,7,7,7,7,7,9,9,9,9,9,9,9,9,9};int column[6][9]={195,255,315,345,375,315,255,225,285, 180,180,180,240,300,300,300,240,240, 345,345,345,375,405,405,405,375,375, 470,470,470,530,590,590,590,530,530, 55,55,55,85,115,115,115,85,85,195,255,315,345,375,315,255,225,285}; int row[6][9]={135,135,135,105,75,75,75,105,105,180,240,300,300,300,240,180,180,240,165,225,285,255,225,165,105,135,185,90,150,210,210,210,150,90,90,150,165,225,285,255,225,165,105,135,185,425,425,425,395,365,365,365,395,395}; void boxinit(){setcolor(CYAN);moveto(150,150);lineto(330,150);line(150,210,330,210);line(150,330,330,330); line(180,120,360,120); line(210,90,390,90); line(240,60,420,60); line(360,120,360,300); line(390,90,390,270); line(420,60,420,240); line(330,210,420,120); line(330,270,420,180); line(330,330,420,240); line(330,150,420,60); line(330,150,330,330); line(270,150,270,330); line(210,150,210,330); line(150,150,150,330); line(150,150,240,60); line(210,150,300,60); line(270,150,360,60);moveto(40,150);lineto(130,60);lineto(130,240);lineto(40,330);lineto(40,150);line(70,120,70,300); line(100,90,100,270);line(40,270,130,180);moveto(440,60);lineto(620,60);lineto(620,240);lineto(440,240);lineto(440,60);line(440,120,620,120); line(440,180,620,180); line(500,60,500,240); line(560,60,560,240);moveto(150,440);lineto(330,440);lineto(420,350);lineto(240,350);lineto(150,440);line(210,440,300,350); line(270,440,360,350); line(180,410,360,410); line(210,380,390,380); }void temp(){ delay(1);}void upcolor(){int i,j;for(i=0;i<6;i++)for(j=0;j<9;j++){setfillstyle(1,color[i][j]);floodfill(column[i][j],row[i][j],CYAN);temp();}}//该函数实现边面转90度的功能//bt为要转的边面void borderturn(int bt){int x1,x2;x1=color[bt][0];x2=color[bt][1];color[bt][0]=color[bt][2];color[bt][1]=color[bt][3];color[bt][2]=color[bt][4];color[bt][3]=color[bt][5];color[bt][4]=color[bt][6];color[bt][5]=color[bt][7];color[bt][6]=x1;color[bt][7]=x2;}//该函数实现中间面转90度的功能//x1,x2,x3,x4为旋转涉及到的面参数,x5-x16为正方形参数说明是哪个正方形参与了旋转//其中x5,x6,x7为x1面的//x8,x9,x10为x2面的//x11,x12,x13为x3面的//x14,x15,x16为x4面的//中间面旋转涉及到四个面的变化void medturn(int x1,int x2,int x3,int x4,int x5,int x6,int x7,int x8,int x9,int x10,int x11,int x12,int x13,int x14,int x15,int x16) {int y1,y2,y3;y1=color[x1][x5];y2=color[x1][x6];y3=color[x1][x7];color[x1][x5]=color[x2][x8];color[x1][x6]=color[x2][x9];color[x1][x7]=color[x2][x10];color[x2][x8]=color[x3][x11];color[x2][x9]=color[x3][x12];color[x2][x10]=color[x3][x13];color[x3][x11]=color[x4][x14];color[x3][x12]=color[x4][x15];color[x3][x13]=color[x4][x16];color[x4][x14]=y1;color[x4][x15]=y2;color[x4][x16]=y3;}//函数实现UP面顺时针转90*i度的功能void turn1(int i){int k;for(k=0;k<i;k++){borderturn(0);medturn(1,2,3,4,0,7,6,0,7,6,6,7,0,6,7,0);}}//函数实现UP面和DOWN面中间层顺时针转90*i度的功能void turn2(int i){int k;for(k=0;k<i;k++){medturn(1,2,3,4,1,8,5,1,8,5,5,8,1,5,8,1);}}//函数实现DOWN面顺时针转90*i度的功能void turn3(int i){int k;for(k=0;k<i;k++){borderturn(5);medturn(1,2,3,4,2,3,4,2,3,4,4,3,2,4,3,2);}}//函数实现FRONT面顺时针转90*i度的功能void turn4(int i){int k;for(k=0;k<i;k++){borderturn(1);medturn(4,5,2,0,0,1,2,0,1,2,2,1,0,2,1,0);}}//函数实现FRONT面和BACK面的中间层顺时针转90*i度的功能void turn5(int i){int k;for(k=0;k<i;k++){medturn(4,5,2,0,7,8,3,7,8,3,3,8,7,3,8,7);}}//函数实现BACK面顺时针转90*i度的功能void turn6(int i){int k;for(k=0;k<i;k++){borderturn(3);medturn(4,5,2,0,6,5,4,6,5,4,4,5,6,4,5,6);}}//函数实现RIGHT面顺时针转90*i度的功能void turn7(int i){int k;for(k=0;k<i;k++){borderturn(2);medturn(1,5,3,0,6,5,4,2,3,4,4,5,6,4,3,2);}}//函数实现LEFT面和RIGHT面的中间层顺时针转90*i度的功能void turn8(int i){int k;for(k=0;k<i;k++){medturn(1,5,3,0,7,8,3,1,8,5,3,8,7,5,8,1);}}//函数实现LEFT面顺时针转90*i度的功能void turn9(int i){int k;for(k=0;k<i;k++){borderturn(4);medturn(1,5,3,0,0,1,2,0,7,6,2,1,0,6,7,0); }}//实现i次L-E'-L'-U-L-E-L'-U'功能void turna(int i){int k;for(k=0;k<i;k++){turn9(1);//Lturn2(3);//E'turn9(3);//L'turn1(1);//Uturn9(1);//Lturn2(1);//Eturn9(3);//L'turn1(3);//U'}}//实现i次R-E-R'-U'-R-E'-U功能void turnb(int i){int k;for(k=0;k<i;k++){turn7(1);//Rturn2(1);//Eturn7(3);//R'turn1(3);//U'turn7(1);//Rturn2(3);//E'turn7(3);//R'turn1(1);//U }}void turnc(int i) {int k;for(k=0;k<i;k++){ turn7(1);turn9(1);turn1(3);turn9(3);turn1(1);turn7(3);turn1(3);turn9(1);turn1(1);turn9(3);}}void turnd(int i){int k;for(k=0;k<i;k++){ turn9(1);turn7(1);turn1(1);turn7(3);turn1(3);turn9(3);turn1(1);turn7(1);turn1(3);turn7(3);}}void turne(int i) {int k;for(k=0;k<i;k++){ turn7(3);turn3(1);turn7(1);turn3(3);turn4(1);turn3(3);turn4(3);}}void turnf(int i) {int k;for(k=0;k<i;k++){ turn4(1);turn2(1);turn9(1);turn2(3);turn4(1);}}void turnc1(int i) {int k;for(k=0;k<i;k++){ turn4(3);turn2(3);turn7(1);turn2(1);turn4(3);}}void turnd1(int i) {int k;for(k=0;k<i;k++){ turn8(1);turn9(1);turnd(1);turn8(3);turn9(3);}}void turnb1(int i){int k;for(k=0;k<i;k++){turn7(1);turnd(1);turn7(3);}}void turnlast(){int k,total,k1,total1,i,j,c0,c1,c2,c3,c4,c5; c0=color[0][8];c5=color[5][8];/*对好第一层的十字架 */total=0;while(total<5){i=0;while(color[5][1]!=c5){turn4(1);if(i>4) break;i++;}if(i==5){i=0;while(color[5][1]!=c5){turn1(1);if(i<4) turn4(2);else {turn5(1);turn6(1);turn8(3);turn6(3);turn5(3);}if(i>7) break;i++;}if(i==8){i=0;while(color[5][1]!=c5){turn2(1);if(i<4) turn4(1);else turn4(3);if(i>7) break;i++;}if(i==8){}else {total++;turn1(1);turn2(1);turn3(1);}}else {total++;turn1(1);turn2(1);turn3(1);}}else {total++;turn1(1);turn2(1);turn3(1);}}c0=color[0][8];c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];c5=color[5][8];while(color[3][3]!=c3) {turn3(1);}upcolor();if(color[4][3]==c1) turnf(1);else if(color[2][3]==c1) turnc1(1);if(color[4][3]!=c4) {turn5(2); turn1(2); turn5(2);}upcolor();/*对好第一层的十字架end*//*对好第一层*/total=0;k=0;while(total<4){c1=color[1][8];c4=color[4][8];i=0;while(color[1][2]==c1 && color[4][2]==c4 && color[5][0]==c5){ turn2(1); turn3(1); turn1(1);c1=color[1][8];c4=color[4][8];if(i>4) break;i++;}while(color[1][2]!=c1 || color[4][2]!=c4 || color[5][0]!=c5){ i=0;while(color[1][2]!=c1 || color[4][2]!=c4 || color[5][0]!=c5){ turn9(2); turnc(1); turn9(2); turn1(1);if(i>3) break;i++;}if(i<4) total++;turn2(1); turn3(1);c1=color[1][8];c4=color[4][8];}if(k>100) break;k++;}upcolor();/*对好第一层end*/c0=color[0][8];c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];/*开始对第二层 */while(color[2][5]!=c2 || color[3][5]!=c3 || color[3][1]!=c3 || color[4][5]!=c4 || color[4][1]!=c4 || color[1][1]!=c1 || color[1][5]!=c1 || color[2][1]!=c2){ /*当看到顶层有第二层的东西就将其放下去*/for(k=0;k<4;k++){i=0;while(color[0][1]==c0 || color[1][7]==c0){turn1(1);if(i>4) break;i++;}if(i<5){i=0;while(color[1][7]!=c3){turn2(1);c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];if(i>4) break;i++;}if(i<5){if(color[1][7]==c3){if(color[0][1]==c2) turna(1);if (color[0][1]==c4) turnb(1);}}}}upcolor();total=0;k=0;c0=color[0][8];c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];/*使第二层远角做成不符*/i=0;while(color[2][5]==c2 && color[3][5]==c3){ turn2(1);turn3(1);c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];if(i>4) break;i++;}k=0;if(color[2][5]!=c2 || color[3][5]!=c3){turna(2);turn2(1);turn3(1);k=1;c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];}i=0;while(color[0][1]!=c2 || color[1][7]!=c3){ turn2(1);k++;c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];if(i>3) break;i++;}if(color[0][1]==c2 && color[1][7]==c3){turna(1);if(k<4){turn2(4-k);c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];}}upcolor();if(total>10) break;total++;}i=0;while(color[1][3]!=color[1][8]){ turn2(1);if(i>4) break;i++;}upcolor();/*对好第二层end*//* 对好第三层的四个角*/c0=color[0][8];c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];j=0;while((color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4) ||(color[0][6]!=c0 || color[3][0]!=c3 || color[4][6]!=c4) ||(color[0][2]!=c0 || color[2][0]!=c2 || color[1][6]!=c1)){/*将近角对好*/k=0;while(color[0][2]!=c0 || color[2][0]!=c2 || color[1][6]!=c1){i=0;while(color[0][2]!=c0 || color[2][0]!=c2 || color[1][6]!=c1){turn1(1);if(i>4) break;i++;}if(i>4) turnc(1);if(k>16) break;k++;}upcolor();k1=0;while(color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4 ||color[0][6]!=c0 || color[3][0]!=c3 || color[4][6]!=c4){/*将左角对好*/k=0;while(color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4){turnd(1);i=0;while((i<3)&&(color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4)) { turnd(1);i++;}if((i==3)&&(color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4)) { turn1(1);turnc((k % 3));turn1(3);}if(k>15) break;k++;}upcolor();/*还是没有对好*/if((k>15)&&(color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4)){turn1(1);turnc(1);turn1(3);turnd(1);}else{/*将远角对好*/i=0;while((i<3)&&(color[0][6]!=c0 || color[3][0]!=c3 || color[4][6]!=c4)) { turn1(1);turnc(1);turn1(3);turnd(1);i++;}/*没有对好*/if((i==3)&&(color[0][6]!=c0 || color[3][0]!=c3 || color[4][6]!=c4)){ turn1(1);turnc(1);turn1(3);}}upcolor();if(k1>4) break;k1++;}/*还是没有对好*/if((k1>4)&&(color[0][6]!=c0 || color[3][0]!=c3 || color[4][6]!=c4 || color[0][0]!=c0 || color[1][0]!=c1 || color[4][0]!=c4)){ turn1(1);turn2(1);turn3(1);c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];}if(j>16) break;j++;}upcolor();/* 对好第三层的四个角end*//*对好第三层的十字*/k1=0;while(color[0][1]!=c0 || color[1][7]!=c1 || color[0][3]!=c0 || color[3][7]!=c3 ||color[0][5]!=c0 || color[2][7]!=c2 || color[0][7]!=c0 || color[4][7]!=c4){/*找一个已经对好的边*/k1=0;while((k1<4)&&(color[3][7]!=c3 || color[0][5]!=c0)){k=0;while((k<4)&&(color[3][7]!=c3 || color[0][5]!=c0)){i=0;while((i<4)&&(color[3][7]!=c3 || color[0][5]!=c0)){turn1(1);turn2(1);turn3(1);c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];i++;}/*没有找到,变换一下角度*/if((i==4)&&(color[3][7]!=c3 || color[0][5]!=c0)){turna(1);turn1(3);turna(1);turn1(1);}k++;}/*还是没有找到,翻转一下*/if((k==4)&&(color[3][7]!=c3 || color[0][5]!=c0)){turna(1);turn2(3);turnb(1);turn2(1);turna(2);}k1++;}turn1(1);turn2(1);turn3(1);c1=color[1][8];c2=color[2][8];c3=color[3][8];c4=color[4][8];upcolor();/*对另外三边*/k=0;while((k<16)&&(color[0][1]!=c0 || color[1][7]!=c1 || color[0][3]!=c0 ||color[2][7]!=c2 || color[0][7]!=c0 || color[4][7]!=c4)){ i=0;while((i<3)&&(color[0][1]!=c0 || color[1][7]!=c1 || color[0][3]!=c0 || color[2][7]!=c2 || color[0][7]!=c0 || color[4][7]!=c4)){ turna(1);turn1(3);turna(1);turn1(1);i++;}/*还是没有对好,翻转一下*/if((i==3)&&(color[0][1]!=c0 || color[1][7]!=c1 || color[0][3]!=c0 || color[2][7]!=c2 || color[0][7]!=c0 || color[4][7]!=c4)){turn1(3);turn2(3);turn3(3);turna(1);turn2(3);turnb(1);turn2(1);turna(2);turn1(1);turn2(1);turn3(1);}k++;}/*还是没有对好,打乱,重新来过*/if((k==16)&&(color[0][1]!=c0 || color[1][7]!=c1 || color[0][3]!=c0 || color[2][7]!=c2 || color[0][7]!=c0 || color[4][7]!=c4)){ turna(1);turn2(3);turn3(3);turnb(1);turn2(1);turna(2);}if(k1>16) break;k1++;}/*将底对齐*/i=0;while(color[1][3]!=c1){turn3(1);if(i>4) break;i++;}upcolor();}main(){int driver,mode;int bkcolor[6][9];int i,j,b;char a;FILE *fp;driver=DETECT;mode=0;initgraph(&driver,&mode,"bgi");setbkcolor(1);for(i=0;i<6;i++)for(j=0;j<9;j++)bkcolor[i][j]=color[i][j];gotoxy(10,15);printf("Are you continue last game\n\tpress 'n' another"); if((a=getch())!='n'){fp=fopen("","r");b=getc(fp);for(i=0;i<6;i++)for(j=0;j<9;j++) {color[i][j]=b;b=getc(fp);}fclose(fp);}cleardevice();boxinit();upcolor();while((a=getch())!='q'){switch (a) {case '0':for(i=0;i<6;i++)for(j=0;j<9;j++)color[i][j]=bkcolor[i][j]; upcolor();break;case '1':turn1(1);upcolor();break;case '2':turn2(1);upcolor();break;case '3':turn3(1);upcolor();break;case '4':turn4(1);upcolor();break;case '5':turn5(1); upcolor(); break;case '6':turn6(1); upcolor(); break;case '7':turn7(1); upcolor(); break;case '8':turn8(1); upcolor(); break;case '9':turn9(1); upcolor(); break;case 'a':turna(1); upcolor(); break;case 'b':turnb(1); upcolor(); break;case 'c':turnc(1); upcolor(); break;case 'd':turnd(1); upcolor(); break;case 'e':turne(1); upcolor(); break;case 'f':turnf(1); upcolor(); break;case 'g':turnd1(1); upcolor(); break;case 'h':turnc1(1); upcolor(); break;case 'i':turnb1(1); upcolor();break;case 'l':turnlast();break;}}gotoxy(10,2);printf("Are you memery this game\n\tpress 'n' exit without memery"); if((a=getch())!='n'){fp=fopen("","w");for(i=0;i<6;i++)for(j=0;j<9;j++)putc(color[i][j],fp);fclose(fp);}closegraph();}。
c语言魔方数

#include "stdio.h"#include "stdlib.h"/*最大范围限制*/#define N 30void f_2K1(int **z,int n);void f_4k(int **z,int n);void f_4k2(int **z,int n);void main(){int **a;int i,j,n,c;printf("请输入魔方数阶数n (2~%d):",N);do{scanf("%d",&n);if(n>N)printf("阶数太大请调整:");}while(n>N);/*定义动态a[n][n]*/a=(int **)malloc(n*sizeof(int *));for(i=0;i<n;i++)a[i]=(int *)malloc(n*sizeof(int));for(i=0;i<=n-1;i++)for(j=0;j<=n-1;j++)a[i][j]=0;/*判断类型*/c=n%4;switch(c){case 0:printf("为4k型阵\n");f_4k(a,n);break;case 2:printf("为4k+2型阵\n");f_4k2(a,n);break;case 1:case 3:printf("为2k+1型阵\n");f_2K1(a,n);break;}/*输出*/for(i=0;i<=n-1;i++){for(j=0;j<=n-1;j++)printf("%5d",a[i][j]);printf("\n");}/*释放a[n][n]*/for(i=0;i<n;i++)free(a[i]);free(a);}/*4k型阵*/void f_4k(int **z,int n){int k,i,j,t;k=1;for(i=0;i<=n-1;i++)for(j=0;j<=n-1;j++){z[i][j]=k;k=k+1;}for(i=0;i<=n/2-1;i++)for(j=0;j<=n-1;j++){if(i==j){t=z[i][j];z[i][j]=z[n-i-1][n-j-1];z[n-i-1][n-j-1]=t;}if(i+j==n-1){t=z[i][j];z[i][j]=z[j][i];z[j][i]=t;}}}/*4k+2型阵*/void f_4k2(int **z,int n) {int m,i=0,j,p,k,t;n=n/2;m=(n+1)/2;j=m-1;for(p=1;p<=n*n;p++){z[i][j]=p;if(i-1<0)i=n-1;else i=i-1;if(j+1>n-1)j=0;else j=j+1;if(z[i][j]!=0){if(i+2==n)i=0;if(i+2==n+1)i=1;else i=i+2;if(j-1<0)j=n-1;else j=j-1;}}for(i=0;i<=n-1;i++)for(j=0;j<=n-1;j++){z[i+n][j]=z[i][j]+3*n*n;z[i][j+n]=z[i][j]+2*n*n;z[i+n][j+n]=z[i][j]+n*n;}n=n*2,k=(n-2)/4;for(i=0;i<=n/2-1;i++)for(j=0;j<=n-1;j++){if(j<=k-1||j>=n/2+k+2){t=z[i][j];z[i][j]=z[n/2+i][j];z[n/2+i][j]=t;}}t=z[k][0];z[k][0]=z[k+n/2][0];z[k+n/2][0]=t;t=z[k][k];z[k][k]=z[k+n/2][k];z[k+n/2][k]=t;}/*2k+1型阵*/void f_2K1(int **z,int n) {int m,i=0,j,p;m=(n+1)/2;j=m-1;for(p=1;p<=n*n;p++){z[i][j]=p;if(i-1<0)i=n-1;else i=i-1;if(j+1>n-1)j=0;else j=j+1;if(z[i][j]!=0){if(i+2==n)i=0;if(i+2==n+1)i=1;else i=i+2;if(j-1<0)j=n-1;else j=j-1;}}}。
C语言程序编程:输入奇数,输出n阶幻方矩阵(5篇)

C语言程序编程:输入奇数,输出n阶幻方矩阵(5篇)第一篇:C语言程序编程:输入奇数,输出n阶幻方矩阵#include #define MAX 100void huanFang(int n){int a[MAX][MAX]={0};//初始化数组都为0 int i,j;int m,k;//当前位置 int p,q;//下一个位置 int data=0;m=0;k=n/2;while(data q=k+1;//右if(p<0&&q=0){//上出框//printf(“qian shang chu: p=%d,q=%dn”,p,q);p=n-1;//下边放//printf(“hou shang chu: p=%d,q=%dn”,p,q);}else if(p>=0&&p//printf(“qian youchu: p=%d,q=%dn”,p,q);q=0;//左边放//printf(“hou youchu: p=%d,q=%dn”,p,q);}else if(p<0&&q==n){//斜出框//printf(“qian xiechu: p=%d,q=%dn”,p,q);p=m+1;//下格填q=k;//printf(“hou xiechu: p=%d,q=%dn”,p,q);} if(a[p][q]!=0){//排重//printf(“qian chongpai: p=%d,q=%dn”,p,q);p=m+1;//下格填q=k;//printf(“hou chongpai: p=%d,q=%dn”,p,q);} m=p;k=q;}for(i=0;iprintf(“%d ”,a[i][j]);}printf(“n”);} }void main(){ int n;//判断是否输入的是奇数while(1){printf(“please input n jie,n is oddn”);scanf(“%d”,&n);if(n%2==1)break;} huanFang(n);}第二篇:浅谈小学英语课堂中的语言输入与输出浅谈小学英语课堂中的语言输入与输出《义务教育英语课程标准》指出:现代外语教育注重语言学习的过程,强调语言学习的实践性,主张学生在语境中接触、体验和理解真实语言,并在此基础上学习和运用语言。
n阶螺旋矩阵c语言

n阶螺旋矩阵c语言n阶螺旋矩阵是一种特殊的矩阵排列方式,它按照螺旋的方式从外到内依次填充数字。
在这篇文章中,我将介绍如何使用C语言编写一个生成n阶螺旋矩阵的程序。
首先,我们需要定义一个二维数组来表示螺旋矩阵。
假设n为奇数,我们可以创建一个n×n的二维数组来存储螺旋矩阵的元素。
接下来,我们需要定义四个变量来表示矩阵的边界,分别是top、bottom、left和right。
初始时,top和left都为0,bottom和right都为n-1。
接下来,我们需要定义一个变量num来表示当前要填充的数字。
初始时,num为1。
然后,我们需要使用一个循环来不断填充矩阵的元素,直到num达到n×n为止。
在循环中,我们首先从左到右填充矩阵的上边界,即从left到right。
填充完成后,我们将top加1,表示上边界向下移动一行。
然后,我们从上到下填充矩阵的右边界,即从top到bottom。
填充完成后,我们将right减1,表示右边界向左移动一列。
接下来,我们从右到左填充矩阵的下边界,即从right到left。
填充完成后,我们将bottom减1,表示下边界向上移动一行。
最后,我们从下到上填充矩阵的左边界,即从bottom到top。
填充完成后,我们将left加1,表示左边界向右移动一列。
在每次填充矩阵元素时,我们将num的值赋给当前位置的元素,并将num加1。
填充完成后,我们继续下一轮循环,直到num达到n×n为止。
最后,我们可以使用一个嵌套的循环来打印生成的螺旋矩阵。
外层循环控制行数,内层循环控制列数。
通过遍历二维数组的每个元素,我们可以将其打印出来。
下面是一个完整的C语言程序示例:```c#include <stdio.h>#define MAX_SIZE 100void generateSpiralMatrix(int n, int matrix[MAX_SIZE][MAX_SIZE]) {int top = 0, bottom = n - 1, left = 0, right = n - 1;int num = 1;while (num <= n * n) {for (int i = left; i <= right; i++) {matrix[top][i] = num++;}top++;for (int i = top; i <= bottom; i++) {matrix[i][right] = num++;}right--;for (int i = right; i >= left; i--) {matrix[bottom][i] = num++;}bottom--;for (int i = bottom; i >= top; i--) {matrix[i][left] = num++;}left++;}}void printMatrix(int n, int matrix[MAX_SIZE][MAX_SIZE]) { for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {printf("%3d ", matrix[i][j]);}printf("\n");}}int main() {int n;printf("请输入n的值:");scanf("%d", &n);int matrix[MAX_SIZE][MAX_SIZE];generateSpiralMatrix(n, matrix);printMatrix(n, matrix);return 0;}```通过运行上述程序,我们可以输入n的值,然后生成并打印出对应的n阶螺旋矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include <stdio.h>
#include <windows.h>
#define N 12 //N大于或等于三
void uneven()//N为奇数
{
int A[N][N]={0},B[N*N+1],x=0,y=N/2,a,b,n;
for (n=1;n<=N*N;n++)
B[n]=n;
A[x][y]=B[1];
for (n=2;n<=N*N;n++)
{
a=x;
b=y;
x-=1;
y+=1;
if (x==-1) x=N-1;
if (y==N) y=0;
if (A[x][y]!=0) {x=a+1;y=b;}
if (x==N ) x=0;
A[x][y]=B[n];
}
for (x=0;x<N;x++)
{
for (y=0;y<N;y++)
{
printf("%3d ",A[x][y]);
}
printf("\n\n");
}
}
void even()//N为偶数,且能被四整除
{
int a[N][N],n=1,i,j,x=1,y=1;
for (i=0;i<N;i++)
for (j=0;j<N;j++)
{
a[i][j]=n;
n++;
}
for (i=0;i<N;i++)
{
for (j=0;j<N;j++)
{
switch (y)
{
case 1:
case 4:if (x==1 || x==4) a[i][j]=N*N-a[i][j]+1;break;
case 2:
case 3:if (x==2 || x==3) a[i][j]=N*N-a[i][j]+1;break;
default:break;
}
x++;
if (x==5) x=1;
}
y++; if (y==5) y=1;
}
for (i=0;i<N;i++)
{
for (j=0;j<N;j++)
printf("%3d ",a[i][j]);
printf("\n\n");
}
}
void evens()//N为偶数,且不能被四整除
{
int a[N][N],i[N/2][N/2]={0},j[N/2][N/2]={0},m[N/2][N/2]={0},n[N/2][N/2]={0};
int b,d,k,x,y,z;
x=0;y=N/4;
i[x][y]=1;
for (z=2;z<=N*N/4;z++)
{
d=x;
b=y;
x-=1;
y+=1;
if (x==-1) x=N/2-1;
if (y==N/2) y=0;
if (i[x][y]!=0) {x=d+1;y=b;}
if (x==N/2 ) x=0;
i[x][y]=z;
}
x=0;y=N/4;
j[x][y]=N*N/2+1;
for (z=2;z<=N*N/4;z++)
{
d=x;
b=y;
x-=1;
y+=1;
if (x==-1) x=N/2-1;
if (y==N/2) y=0;
if (j[x][y]!=0) {x=d+1;y=b;}
if (x==N/2 ) x=0;
j[x][y]=z+N*N/2;
}
x=0;y=N/4;
m[x][y]=N*N*3/4+1;
for (z=2;z<=N*N/4;z++)
{
d=x;
b=y;
x-=1;
y+=1;
if (x==-1) x=N/2-1;
if (y==N/2) y=0;
if (m[x][y]!=0) {x=d+1;y=b;}
if (x==N/2 ) x=0;
m[x][y]=z+N*N*3/4;
}
x=0;y=N/4;
n[x][y]=N*N/4+1;
for (z=2;z<=N*N/4;z++)
{
d=x;
b=y;
x-=1;
y+=1;
if (x==-1) x=N/2-1;
if (y==N/2) y=0;
if (n[x][y]!=0) {x=d+1;y=b;}
if (x==N/2 ) x=0;
n[x][y]=z+N*N/4;
}
k=(N-2)/4;
for (y=N/4,b=0;b<k;b++,y++) {
z=i[N/4][y];
i[N/4][y]=m[N/4][y];
m[N/4][y]=z;
}
for (x=0;x<N/2;x++)
for (y=0;y<k;y++)
{
if (x==N/4)
continue;
z=i[x][y];
i[x][y]=m[x][y];
m[x][y]=z;
}
for (y=N/4,b=0;b<k-1;y--,b++)
for (x=0;x<N/2;x++)
{
z=j[x][y];
j[x][y]=n[x][y];
n[x][y]=z;
}
for (x=0;x<N/2;x++)
for (y=0;y<N/2;y++)
a[x][y]=i[x][y];
for (x=0;x<N/2;x++)
for (y=N/2;y<N;y++)
a[x][y]=j[x][y-N/2];
for (x=N/2;x<N;x++)
for (y=0;y<N/2;y++)
a[x][y]=m[x-N/2][y];
for (x=N/2;x<N;x++)
for (y=N/2;y<N;y++)
a[x][y]=n[x-N/2][y-N/2]; for (x=0;x<N;x++)
{
for (y=0;y<N;y++)
printf("%3d ",a[x][y]);
printf("\n\n");
}
}
int main()
{
int a;
if (N%2!=0)
a=1;
else
if (N%4==0)
a=2;
else
a=3;
switch (a)
{
case 1:uneven();break;
case 2:even();break;
case 3:evens();break;
default:putchar('\a');
}
system("pause");
return 0;
}。
