地基中的附加应力计算 34页PPT文档
合集下载
地基中附加应力计算

§3 土体中的应力计算
小结
应力状态
自重应力
水平地基中的自重应力
的计算
土力学中应力符号的规定 地基中的应力状态 应力应变关系的假定
影响因素 基底压力分布 实用简化计算
基底压力计算
附加应力 的计算
因素:底面形状;荷载分 布;计算点位置
'u
饱和土的有效应力
土的变形与强度都
原理
只取决于有效应力
34
y
x
x
M’
R βz
M
z R2 r2 z2 x2 y2 z2
k
3
2
[1
(r
1 / z)2 ]5/ 2
z
k
P z2
集中力作用下的 应力分布系数
查表3-1
4
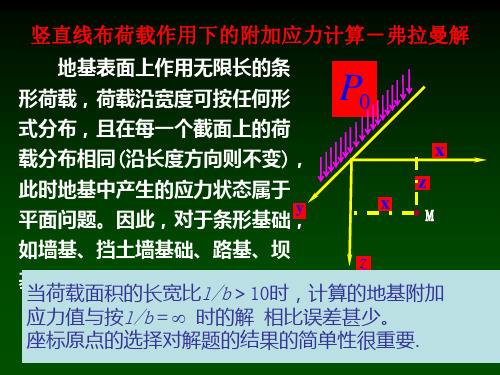
§3 土体中的应力计算 §3.4 地基中附加应力的计算
一. 竖直集中力作用下的附加应力计算-布辛内斯克课题
z
k
P z2
特点
k
3
2
[1
(r
圆内积 分
竖直线布荷载 宽度积分 圆形面积竖直均布荷载
条形面积竖直均布荷载
2
§3 土体中的应力计算 §3.4 地基中附加应力的计算
一. 竖直集中力作用下的附加应力计算-
P
o
αr
x R
布辛内斯克(J.Boussinesq)课题
x
y M’
βz
z
zx
y
xy
x
M
y yz
z R2 r2 z2 x2 y2 z2 r / z tg
l z
0
——圆形面积均布荷载作用时园心点下
§3 土体中的应力计算 §3.3 地基中附加应力的计
地基中的附加应力ppt课件

本章主要内容
2.1 概述 2.2 土的自重应力 2.3 自重应力系 有效应力原理 2.4 基底接触应力分布及简化计算 2.5 地基中的附加应力—空间问题的解及其应用 2.6 地基中的附加应力—平面问题的解及其应用 2.7 非均质和各向异性地基中的附加应力 2.8 其他条件下地基中的应力计算
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
1-1面
土的自重应力
c1z γ 1 h 1 1.2 8 3 2 .5 = 4.5 5 k 8p aO
2-2面
h1=2.5m r1=18.23KN/m3
1
1
σ cz24σ 5cz1 .5γ12 h882 .62 282.82kh2p =2.0 am r2=18.62KN/m3
3-3面
2
2
h3=1.5m r1 '=9.80KN/m3
影响基底接触应力分布图形的因素
基底接触应力及简化计算
•大小 •方向 •分布
荷载条件
地基条件
•土类 •密度 •土层结构等
基础条件
•刚度 •形状 •大小 •埋深
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
支承建筑物荷载的土层称为地基 与建筑物基础底面直接接触的土层称为持力层 将持力层下面的土层称为下卧层
F 基础
概述
地基
G
主
持力层(受力层)
要
下卧层
受 力
层
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
地基中的附加应力计算

冻胀力
寒冷地区,地基土中的水分冻结膨胀,对基础产生冻胀力。
膨胀土胀缩
膨胀土在湿度变化时会发生体积胀缩,对基础产生附加应力。
地面堆载
地面上的堆载会对地基产生额外的压力,增加地基中的附加应力 。
03 附加应力的计算方法
弹性力学方法
弹性力学方法基于弹性力学理 论,将地基视为弹性体,通过 求解弹性力学方程来计算附加 应力。
02
在地基表面,水平向附加应力最大,随着离地表距 离的增加,应力逐渐减小。
03
水平向附加应力的分布还受到地基土的性质、基础 形状和荷载大小等因素的影响。
垂直向附加应力分布
01
垂直向附加应力在地基中的分布通常呈现出 先增大后减小的趋势。
02
03
在地基表面,由于荷载的作用,垂直向附加 应力较大。
随着深度的增加,垂直向附加应力逐渐减小 ,直至某一深度处达到最小值。
03
准确计算地基中的附加应力可以为工程师提供重要的设 计依据,确保建筑物的稳定性和安全性。
附加应力的定义和重要性
附加应力是指建筑物或其他 荷载在地基中引起的超过原 有应力的那部分应力。
附加应力的大小和分布直接 影响地基的变形和稳定性。
对于不同类型和性质的地基 土,附加应力的计算和评估 方法也有所不同。
工程处理措施及效果评价
处理措施
针对地基中的附加应力问题,采取了以下处理措施:对地基 进行加固处理,提高地基的承载力;采用桩基础,将建筑物 荷载传递至更深层的土层中;加强建筑物的结构刚度,减小 荷载对地基的影响。
效果评价
经过处理措施的实施,地基中的附加应力得到了有效控制, 建筑物的沉降和倾斜等变形指标均满足规范要求。同时,通 过对处理前后地基性状进行对比分析,发现处理措施对改善 地基性状具有显著效果。
地基中的附加应力计算
σ K p ,σ
K p ,
K
s XZ
p
s 0
z x s 式中 n , m K 为附加应力系数可查表 B B
任意形状基底受各种分布形式荷载的作 用下地基中附加应力的计算
• 感应图:
感应图
AB Z
Z 0.005NP0
土体中的应力集中与应力扩散
B
H
均匀
B
H 均匀
b 2
K xz F ( x, B, z )
Z K z P0, X
附加应力系数 K x p0 xz K xz p0 ,
式中 K z K x K xz为附加应力系数可根据 m和n查表
查表
(P94表3.6.1)
Kz Kx K xz
Kz Kx
附加应力等值线
条形面积三角形荷载
dP
3
dP p0 d
3
2 p0 z d d z 2 2 2 [(x ) z ]
2 p0 z d d z 2 2 2 [(x ) z ]
3
计算原理
dP p0 d
z
b
0
2 z 3 p 0 d [(x ) 2 z 2 ] 2
2P0 z 3 z (x2 z 2 )2
X
2P0 x 2 z (x 2 z 2 )2
dP1
2
B
p 0 d
xz zx
s z s Z
2P0 xz 2 2 2 (x z )
s 0 s X s X s 0
B dP2 p0 d B
s xz
B
H
硬 成层 均匀
软
4.4地基附加应力的计算

过程:取元素面积 dA rdrd ,
则均布荷载可等效为一个集中荷 载 dQ p0dA P0rdrd 。在圆面 积范围内求积分可得 z 值:
z
A
d z
3 p0 z3
2
2 0
r0 0
(r2
l2
rdrd - 2r/cos
z2 )5/2
c p0
l 0
x dxdy
b
b
0 ( x2 y2 z2 )5
mnp
2
1 m2 n2
(1 m2 )
m2 1 n2
m2
t1 p
t1 ——应力系数,是 l / b 和 z / b 的函数,可制成表备查。
同理,可以求得荷载最大值边的角点下深度z处N点的竖向应
b 0.5
b 0.5
查表得应力系数 c =0.1202
zG GADH GBCH (0.2016-0.1202) 100=8.1kPa
6、 矩形面积上作用三角形分布荷载时竖向应力的计算
目的:在矩形面积上作用三角形分布布荷载
p x b
p ,求荷载为
零的角点下某深度处
M点的竖向应力 z值。
的 z值,并绘出分布图;
解:
z (m) r (m) r/z
z
Q z2
(kPa)
0
0
0 0.4775
∞
1
0
0 0.4775
95.5
3
0
0 0.4775
23.9
4
0
0 0.4775
10.6
5
0
0 0.4775
则均布荷载可等效为一个集中荷 载 dQ p0dA P0rdrd 。在圆面 积范围内求积分可得 z 值:
z
A
d z
3 p0 z3
2
2 0
r0 0
(r2
l2
rdrd - 2r/cos
z2 )5/2
c p0
l 0
x dxdy
b
b
0 ( x2 y2 z2 )5
mnp
2
1 m2 n2
(1 m2 )
m2 1 n2
m2
t1 p
t1 ——应力系数,是 l / b 和 z / b 的函数,可制成表备查。
同理,可以求得荷载最大值边的角点下深度z处N点的竖向应
b 0.5
b 0.5
查表得应力系数 c =0.1202
zG GADH GBCH (0.2016-0.1202) 100=8.1kPa
6、 矩形面积上作用三角形分布荷载时竖向应力的计算
目的:在矩形面积上作用三角形分布布荷载
p x b
p ,求荷载为
零的角点下某深度处
M点的竖向应力 z值。
的 z值,并绘出分布图;
解:
z (m) r (m) r/z
z
Q z2
(kPa)
0
0
0 0.4775
∞
1
0
0 0.4775
95.5
3
0
0 0.4775
23.9
4
0
0 0.4775
10.6
5
0
0 0.4775
《地基中的应力》PPT课件

(z 2) t 2 pt
t1 F(z / a) t2
a--圆形面积的半径
查表3.5.6
44
3.6平面问题条件下的地基附加应力(l/B>=10)
利用费拉曼理论
45
46
3.6.2条形基底均布荷载作用下地基附加应力
σz zsp0
s z
F( x b
,
z) b
查表3.6.1
y
B
p
x
z
x
M
z
47
3.6.3条形基底三角形分布荷载作用下地基附加应力
作用位置离墙基础前缘A点3.2m;因
土压力等作用墙背受到水平力,
H 400KN/其m 作用点距离基底面2.4m 。设地基土重度为19kN/m3,若不计
1.5m
A
墙后填土附加应力的影响,试求因P
,H作用基础中心点下深度z=7.2m处 z
M点的附加应力。
3.2m
P 2400KN/m
H 400KN/m
εx εy 0 σx σy
根据弹性力学中广义虎克定律:εx
1 E
σx
υ
σy
σz
0
σcx σcy K 0σcz
σx
1
ν
ν
σ
z
k0σz
9
2.计算点在地下水位以下
地下水位以下用浮容重γ’
地面
σcz γH1 γ'H2
γ' γsat γ w
H1
地下水位
H2
sz
sx
sy
10
3.成层土中自重应力
σz
s t
p
T
查表3.6.2
pt
ts
F( x b
t1 F(z / a) t2
a--圆形面积的半径
查表3.5.6
44
3.6平面问题条件下的地基附加应力(l/B>=10)
利用费拉曼理论
45
46
3.6.2条形基底均布荷载作用下地基附加应力
σz zsp0
s z
F( x b
,
z) b
查表3.6.1
y
B
p
x
z
x
M
z
47
3.6.3条形基底三角形分布荷载作用下地基附加应力
作用位置离墙基础前缘A点3.2m;因
土压力等作用墙背受到水平力,
H 400KN/其m 作用点距离基底面2.4m 。设地基土重度为19kN/m3,若不计
1.5m
A
墙后填土附加应力的影响,试求因P
,H作用基础中心点下深度z=7.2m处 z
M点的附加应力。
3.2m
P 2400KN/m
H 400KN/m
εx εy 0 σx σy
根据弹性力学中广义虎克定律:εx
1 E
σx
υ
σy
σz
0
σcx σcy K 0σcz
σx
1
ν
ν
σ
z
k0σz
9
2.计算点在地下水位以下
地下水位以下用浮容重γ’
地面
σcz γH1 γ'H2
γ' γsat γ w
H1
地下水位
H2
sz
sx
sy
10
3.成层土中自重应力
σz
s t
p
T
查表3.6.2
pt
ts
F( x b
水利工程土力学教学课件:任务4.3地基中的附加应力

z 10m :
8
z zi 4 0.045 0.047 0.368kPa i 1
地基附加应力计算
水平向集中力作用下附加应力计算
Qo
r
x R
—西罗提(Cerruti)课题
x
y
z
z
y
x
M y
z
地基附加应力计算
水平向集中力作用下附加应力计算 —西罗提(Cerruti)课题
z
3Q
2R5
3. 土中任意点的竖向附加应力——角点法
基本方法:
将荷载作用 面积分块
各分块产生的 竖向附加应力
叠加
土中任意点的 竖向附加应力
角点下竖向附加 应力计算公式
地基附加应力计算
矩形面积竖向均布荷载作用下附加应力计算
3. 土中任意点的竖向附加应力——角点法
a
h
d 情况一:M点投影在矩形荷载
作用面积范围之内
等值线(应力泡)
集中荷载作用下的地面沉降
s Q(1 2 ) E0r
E0 —土的变形模量
—土的泊松比
例题 4.3
在地表面作用集中力Q=200kN,计 算地面深度z=3m处水平面上竖向法向应 力σz分布,以及距Q作用点r=1m处竖直 面上竖向法向应力σz分布。
解答
解答
例题 4.4
O
有一矩形基础,b=2m,l=4m, 作用均布荷载p=10kPa,计算矩形 基础中点O下深度z=2m及10m处 的竖应力σz 值。
地基附加应力计算
均布线荷载作用下附加应力计算—弗拉曼(Flamant)解
M
地基附加应力计算
均布条形荷载作用下附加应力计算
z u p
应力系数
u
8
z zi 4 0.045 0.047 0.368kPa i 1
地基附加应力计算
水平向集中力作用下附加应力计算
Qo
r
x R
—西罗提(Cerruti)课题
x
y
z
z
y
x
M y
z
地基附加应力计算
水平向集中力作用下附加应力计算 —西罗提(Cerruti)课题
z
3Q
2R5
3. 土中任意点的竖向附加应力——角点法
基本方法:
将荷载作用 面积分块
各分块产生的 竖向附加应力
叠加
土中任意点的 竖向附加应力
角点下竖向附加 应力计算公式
地基附加应力计算
矩形面积竖向均布荷载作用下附加应力计算
3. 土中任意点的竖向附加应力——角点法
a
h
d 情况一:M点投影在矩形荷载
作用面积范围之内
等值线(应力泡)
集中荷载作用下的地面沉降
s Q(1 2 ) E0r
E0 —土的变形模量
—土的泊松比
例题 4.3
在地表面作用集中力Q=200kN,计 算地面深度z=3m处水平面上竖向法向应 力σz分布,以及距Q作用点r=1m处竖直 面上竖向法向应力σz分布。
解答
解答
例题 4.4
O
有一矩形基础,b=2m,l=4m, 作用均布荷载p=10kPa,计算矩形 基础中点O下深度z=2m及10m处 的竖应力σz 值。
地基附加应力计算
均布线荷载作用下附加应力计算—弗拉曼(Flamant)解
M
地基附加应力计算
均布条形荷载作用下附加应力计算
z u p
应力系数
u
地基附加应力的计算

2.3 竖向荷载作用下地基附加 应力的计算
2.3 地基附加应力的计算
• 附加应力:建筑物荷载(p0)在地基中产生的应力。
• 计算假定:地基土为均质,各向同性,用弹性理论 计算。
2.3.1 竖向集中荷载作用下 土中附加应力的计算
布辛奈斯克(法)公式:
y
P z
。
z2
α—附加应力计算系数与(r,z有关)
z c p0 基底附加压力
l
0
式中:αC—矩形荷载下附加应力 计算系数(与l/b,z/b有关);
σz
M(z)
p0—基底附加压力。
z
b
p0 x
2.3 地基附加应力的计算
(二)矩形均布荷载下任意角点处 的附加应力计算------角点法
叠加原理
角点下垂直附加 应力的计算公式
地基中任意点的附加应力
计算系数(与x/b,z/b有关)。
本章小结
自重应力:
cz z
基底压力:
pmax pmin
F
G A
(1
6e ) l
基底附加压力: p0 p cz p 0d
附加应力:
z c p0
天然地面
本章小结
基础底面
自重应力 分布曲线
附加应力 分布曲线
地基应力分布示意图
P x
r
σz
M(x,y,z)
z
2.3 地基附加应力的计算
集中荷载作用下地基中附加应力分布规律: 1.在集中力作用线上,附加应力随着深度Z的增加而递减; 2.在某一水平面上,即Z一定时,附加应力随r的增大而减 少; 3.当离集中力作用线某一距离r时,z=0, σz=0,z↑, σz先增加后减小; P
2.3 地基附加应力的计算
• 附加应力:建筑物荷载(p0)在地基中产生的应力。
• 计算假定:地基土为均质,各向同性,用弹性理论 计算。
2.3.1 竖向集中荷载作用下 土中附加应力的计算
布辛奈斯克(法)公式:
y
P z
。
z2
α—附加应力计算系数与(r,z有关)
z c p0 基底附加压力
l
0
式中:αC—矩形荷载下附加应力 计算系数(与l/b,z/b有关);
σz
M(z)
p0—基底附加压力。
z
b
p0 x
2.3 地基附加应力的计算
(二)矩形均布荷载下任意角点处 的附加应力计算------角点法
叠加原理
角点下垂直附加 应力的计算公式
地基中任意点的附加应力
计算系数(与x/b,z/b有关)。
本章小结
自重应力:
cz z
基底压力:
pmax pmin
F
G A
(1
6e ) l
基底附加压力: p0 p cz p 0d
附加应力:
z c p0
天然地面
本章小结
基础底面
自重应力 分布曲线
附加应力 分布曲线
地基应力分布示意图
P x
r
σz
M(x,y,z)
z
2.3 地基附加应力的计算
集中荷载作用下地基中附加应力分布规律: 1.在集中力作用线上,附加应力随着深度Z的增加而递减; 2.在某一水平面上,即Z一定时,附加应力随r的增大而减 少; 3.当离集中力作用线某一距离r时,z=0, σz=0,z↑, σz先增加后减小; P
地基中的附加应力
1.5m 2m
0 =18.5kN/m3
荷载偏心距 e=M/(F+G)
基础及上覆 土重G= GAd 140.3kPa
319.7kPa
pmax pmin
1.基底压力计算
条形基础取单 位长度计算
F G 6e 1 bl l
分析步骤Ⅱ:
F=400kN/m 0.1m M=20kN •m
基础底面长宽 比l / b→∞
理想 情况
条形基础
实际 情况
基础底面长宽 比l / b≥10
pdy布辛涅斯克解
线积分
z
2 pz 3
x 2 z 2
2
几种不同分布荷载计算Ⅰ
均布荷载情况
p
b/2 b/2 x z
z K sz p
Ksz ,Ktz条形基底竖向附 加应力系数, 均为m ,n 的函数,其中m=x/b, n=z/b,可查表得到
x
附加应力系数
P K 2 z
z
z
1885年法国学者布 辛涅斯克解
3Pz3 3P 3 z cos q 5 2 2R 2R
附加应力分布规律
距离地面越深,附加应力的分布范围越广 在集中力作用线上的附加应力最大,向两侧逐渐 减小 同一竖向线上的附加应力随深度而变化 在集中力作用线上,当z=0时,σz→∞,随着深 度增加,σz逐渐减小 竖向集中力作用引起的附加应力向深部向四周无 限传播,在传播过程中,应力强度不断降低(应 力扩散)
地基中的附加应力
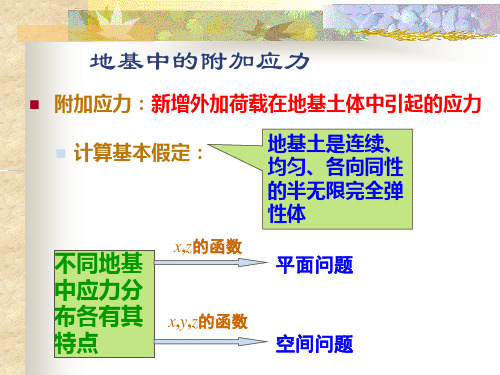
附加应力:新增外加荷载在地基土体中引起的应力
计算基本假定:
地基土是连续、 均匀、各向同性 的半无限完全弹 性体
不同地基 中应力分 布各有其 特点
精编地基中的附加应力计算资料

第二章 土体应力计算
【解】(1)求作用于基底面上的力及偏心距。将Fh移至基底面,根据 静力等效,需加力矩。设合力作用点离基底前缘A点的水平距离为x,利 用合力矩定理,即
Fv·x= Fv×3.2-Fh ×2.4 则 x=(3.2 Fv-2.4 Fh )/Fv=3.2-2.4 ×400 / 2400
=2.8(m) 于是合力偏心距e=b/2-2.8=0.2(m);合力作用点位于基底面中点的 左侧0.2m。 (2)求基底压力。这属于平面问题应用式(2-13),得竖向基底压力
第二章 土体应力计算
应用式(2-17),得 ph=Fh/b=400/6=66.7kPa (3)求基底净压力(基底附加应力)。对于梯形分布的竖向基底压力应用 图2-23所示方法可得竖向基底净压力如下
pn=pmin-γod=320-19×1.5=291.5kPa pt=pmax-pmin=480-320=160kPa
图4-3 集中荷载作用下地基中应力
Valentin Joseph Boussinesq (1842-1929)
法国著名物理家和数学家,对数学物理、流体力 学和固体力学都有贡献。
竖向集中力作用下地基附加应力
弹性力学解答 Boussinesq 解
竖向集中力作用下地基附加应力
z
3Pz 3
2R5
六 条形基底均布荷载作用下地基附加应力
条形基底三角形分布荷载作用下地基附加应力
p pt b
条形基底受水平荷载作用时附加应力
第二章 土体应力计算
基底作用有倾 斜偏心荷载时
平面问题: 注意:(1)原点
(2)X轴正向
第二章 土体应力计算
【例题2-3】如图所示的挡土墙,基础底面 宽度为6m,埋置于地面下1.5m处。每米墙自 重及其上部其他竖向荷载Fv= 2400kN/m,作 用位置离墙基础前缘A点3.2m;因土压力等作 用墙背受到水平力Fh=400kN/m,其作用点距 离基底面2.4m。设地基土重度为19kN/m3, 若不计墙后填土附加应力的影响,试求因Fv ,Fh作用基础中心点及前缘A点下深度 z=7.2m处M点,N点的附加应力。
地基中的附加应力

3. “角点法”的实质是什么?
4.若基础底面的压力不变,增加基础埋置深度后土中附 加应力有何变化?
地基基础
角点法
(a)
(b)
(c)
(d)
1)o点在荷载面边缘:
z (Kc1 Kc2 ) p0
2)o在荷载面内:
z (Kc1 Kc2 Kc3 Kc4 ) p0
角点法
(a)
(b)
3)o点在荷载边缘外侧:
(c)
(d)
z (Kofbg Kc2 Koecg Kc4 ) p0
4)o点在荷载面角点外侧:
实际上,地基是弹性塑性体和各向异性体。
3.问题类型: (1)空间问题(如集中力、矩形荷载、圆形荷载);(2)平 面问题(如线荷载、条形荷载l/b>10)
(二)不同面积上受各种分布荷载作用下,附加应力的计算方法 1.竖向集中力下的地基附加应力
(1)布辛奈斯克(Boussinesq)解答 半空间任意点M(x,y,z)处的六个应力分量和三个位移分量:
矩形 z
条形 xz
(三)非均质和各向异性地基中的附加应力 1.变形模量随深度增大的地基(非均质地基)。 2.薄交互层地基(各向异性地基)。 3.双层地基(非均质地基)。
应力集中 (一)
应上 力硬
扩下
散软
应力扩散
应上 力软 集下 中硬
(三)
均(质 二)
思考题
1.何谓有效自重应力?
2.在集中荷载作用下,地基中附加应力的分布有何规律? 相邻两基础下的附加应力是否会彼此影响?
地基基础
(一)定义与假设
1.定义:由建筑物荷载在地基中产生的应力,叫做附加应力。 2.假设:目前采用的附加应力计算方法是根据弹性理论推导出来的。
4.若基础底面的压力不变,增加基础埋置深度后土中附 加应力有何变化?
地基基础
角点法
(a)
(b)
(c)
(d)
1)o点在荷载面边缘:
z (Kc1 Kc2 ) p0
2)o在荷载面内:
z (Kc1 Kc2 Kc3 Kc4 ) p0
角点法
(a)
(b)
3)o点在荷载边缘外侧:
(c)
(d)
z (Kofbg Kc2 Koecg Kc4 ) p0
4)o点在荷载面角点外侧:
实际上,地基是弹性塑性体和各向异性体。
3.问题类型: (1)空间问题(如集中力、矩形荷载、圆形荷载);(2)平 面问题(如线荷载、条形荷载l/b>10)
(二)不同面积上受各种分布荷载作用下,附加应力的计算方法 1.竖向集中力下的地基附加应力
(1)布辛奈斯克(Boussinesq)解答 半空间任意点M(x,y,z)处的六个应力分量和三个位移分量:
矩形 z
条形 xz
(三)非均质和各向异性地基中的附加应力 1.变形模量随深度增大的地基(非均质地基)。 2.薄交互层地基(各向异性地基)。 3.双层地基(非均质地基)。
应力集中 (一)
应上 力硬
扩下
散软
应力扩散
应上 力软 集下 中硬
(三)
均(质 二)
思考题
1.何谓有效自重应力?
2.在集中荷载作用下,地基中附加应力的分布有何规律? 相邻两基础下的附加应力是否会彼此影响?
地基基础
(一)定义与假设
1.定义:由建筑物荷载在地基中产生的应力,叫做附加应力。 2.假设:目前采用的附加应力计算方法是根据弹性理论推导出来的。
地基附加应力的计算

,则式(2-13)可改写为
1.1竖 向集 中力 作用 下的 地基 附加 应力
2.集中力作用下的σz分布特征
图2-13 集中力作用下土中的应力σz的分布
1.1竖 向集 中力 作用 下的 地基 附加 应力
2.集中力作用下的σz分布特征
在集中力P作用 在r>0的竖直线 线上的σz分布 上的σz分布
1)
1.角点下任意深度的附加应力
图2-17 矩形均布荷载作用时角点下的附加应力σz
1.2矩 形面 积上 均布 荷载 作用 下的 地基 附加 应力
2.非角点下任意深度的附加应力
当矩形面积上均布荷载作用下的附加应力计算点不 位于角点下时,可通过角点下的应力计算公式(2 1 5)和应力叠加原理求得。例如,求非角点Q下任意深 度的附加应力时,可通过Q点将荷载面积划分为几块 小矩形面积,使Q点为每块小矩形面积的共同角点, 利用式(2 15)分别求出Q点下同一深度在每个小矩 形均布荷载作用下的应力值,然后利用叠加原理求出 总的附加应力,这就是角点法。如图2 18所示,角 点法可分为四种情况。
2)
在一定深度z处 的水平面上的
σz分布
3)
1.1竖 向集 中力 作用 下的 地基 附加 应力
2.集中力作用下的σz分布特征 图2-14集中力作用下σz的等值线
1.1竖 向集 中力 作用 下的 地基 附加 应力
3.多个集中力作用下的σz
图2-15 两个集中力作用下σz的叠加
1.1竖 向集 中力 作用 下的 地基 附加 应力
土力学与中应力
1.1竖 向集 中力 作用 下的 地基 附加 应力
1.计算公式
法国J.布辛奈斯克(Boussinesq,1885)运用弹性理论 推出了这些应力分量的解,其中竖向正应力 σz在建筑工程 中对基础沉降计算意义最大,其表达式为
1.1竖 向集 中力 作用 下的 地基 附加 应力
2.集中力作用下的σz分布特征
图2-13 集中力作用下土中的应力σz的分布
1.1竖 向集 中力 作用 下的 地基 附加 应力
2.集中力作用下的σz分布特征
在集中力P作用 在r>0的竖直线 线上的σz分布 上的σz分布
1)
1.角点下任意深度的附加应力
图2-17 矩形均布荷载作用时角点下的附加应力σz
1.2矩 形面 积上 均布 荷载 作用 下的 地基 附加 应力
2.非角点下任意深度的附加应力
当矩形面积上均布荷载作用下的附加应力计算点不 位于角点下时,可通过角点下的应力计算公式(2 1 5)和应力叠加原理求得。例如,求非角点Q下任意深 度的附加应力时,可通过Q点将荷载面积划分为几块 小矩形面积,使Q点为每块小矩形面积的共同角点, 利用式(2 15)分别求出Q点下同一深度在每个小矩 形均布荷载作用下的应力值,然后利用叠加原理求出 总的附加应力,这就是角点法。如图2 18所示,角 点法可分为四种情况。
2)
在一定深度z处 的水平面上的
σz分布
3)
1.1竖 向集 中力 作用 下的 地基 附加 应力
2.集中力作用下的σz分布特征 图2-14集中力作用下σz的等值线
1.1竖 向集 中力 作用 下的 地基 附加 应力
3.多个集中力作用下的σz
图2-15 两个集中力作用下σz的叠加
1.1竖 向集 中力 作用 下的 地基 附加 应力
土力学与中应力
1.1竖 向集 中力 作用 下的 地基 附加 应力
1.计算公式
法国J.布辛奈斯克(Boussinesq,1885)运用弹性理论 推出了这些应力分量的解,其中竖向正应力 σz在建筑工程 中对基础沉降计算意义最大,其表达式为
土体中的应力计算—附加应力的计算(土力学课件)

土中任意点所受的附加应力
z 2 p
x
p x
z z
x z
二、条形面积受均布荷载土中附加应力
2.条形面积受三角形荷载作用下的附加应力
土中任意点所受的附加应力
z 3 p
-x 0
z x
p x
z
注意坐标系的建立,以荷载0为坐标原点,向荷 载增大的方向为正方向。
二、条形面积受均布荷载土中附加应力
3.圆形面积均布荷载作用下的竖向附加应力
(1)距离地面越深, 附加应力的分布范围 越广,r/z=2.5范围内。
(2)在距地面为z的平 面上,集中力作用线 下的附加应力最大, 向两侧逐渐减小。
集中力作用下附加应力分布图
一、竖直集中荷载作用下的地基附加应力计算
1、附加应力分布规律
(3)距P作用线为r竖直 线上的附加应力随深 度先增加再减小。
171
332 kPa
134
条形荷载作用下土中附加应力
(1)p1=134kPa
+x
+x
+(x 2)p2=198kPa
-x
z x1 x/b z/b
x2 x/b z/b
00 0 0 1
134 1 0.5 0 0.500 99 233
1 0 0 0.5 0.820 110 1 0.5 0.5 0.410 81 191
条形荷载作用下 土中附加应力
条形荷载作用下土中附加应力
条形荷载作用下土中附加应力
1.条形面积受均布荷载作用下的土中竖向附加应力
土中任意点所受的附加应力 x
z 2 p
2 ——条形均布荷载作用
下的竖向附加应力系数
2 (x / b, z / b)
z 2 p
x
p x
z z
x z
二、条形面积受均布荷载土中附加应力
2.条形面积受三角形荷载作用下的附加应力
土中任意点所受的附加应力
z 3 p
-x 0
z x
p x
z
注意坐标系的建立,以荷载0为坐标原点,向荷 载增大的方向为正方向。
二、条形面积受均布荷载土中附加应力
3.圆形面积均布荷载作用下的竖向附加应力
(1)距离地面越深, 附加应力的分布范围 越广,r/z=2.5范围内。
(2)在距地面为z的平 面上,集中力作用线 下的附加应力最大, 向两侧逐渐减小。
集中力作用下附加应力分布图
一、竖直集中荷载作用下的地基附加应力计算
1、附加应力分布规律
(3)距P作用线为r竖直 线上的附加应力随深 度先增加再减小。
171
332 kPa
134
条形荷载作用下土中附加应力
(1)p1=134kPa
+x
+x
+(x 2)p2=198kPa
-x
z x1 x/b z/b
x2 x/b z/b
00 0 0 1
134 1 0.5 0 0.500 99 233
1 0 0 0.5 0.820 110 1 0.5 0.5 0.410 81 191
条形荷载作用下 土中附加应力
条形荷载作用下土中附加应力
条形荷载作用下土中附加应力
1.条形面积受均布荷载作用下的土中竖向附加应力
土中任意点所受的附加应力 x
z 2 p
2 ——条形均布荷载作用
下的竖向附加应力系数
2 (x / b, z / b)
地基中的附加应力计算36页PPT

ห้องสมุดไป่ตู้
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
地基中的附加应力计算
61、辍学如磨刀之石,不见其损,日 有所亏 。 62、奇文共欣赞,疑义相与析。
63、暧暧远人村,依依墟里烟,狗吠 深巷中 ,鸡鸣 桑树颠 。 64、一生复能几,倏如流电惊。 65、少无适俗韵,性本爱丘山。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
地基中的附加应力计算
61、辍学如磨刀之石,不见其损,日 有所亏 。 62、奇文共欣赞,疑义相与析。
63、暧暧远人村,依依墟里烟,狗吠 深巷中 ,鸡鸣 桑树颠 。 64、一生复能几,倏如流电惊。 65、少无适俗韵,性本爱丘山。
谢谢你的阅读
地基中的附加应力计算ppt课件

其加中应K力zI系、数K。zII、z K zII( IK 、z K zIVK 为z 相 应K 于z 面积 IK 、z I V I、) p III、IV 的角点附
z 4Kz p
角点法计算恣意位置附加应力
ed
c
(c) O点在荷载面的边缘外侧:
荷载面〔abcd〕= 面积Ⅰ〔ofbg〕- 面积Ⅱ〔ofah〕
x
2pcos2
z
sin2
可见解与 y 无关,xz即在zx与y2轴pzc垂os直3的s恣in意平面上的应力形状均一样。
六 条形基底均布荷载作用下地基附加应力
条形基底三角形分布荷载作用下地基附加应力
p
pt
b
条形基底受程度荷载作用时附加应力
第二章 土体应力计算
基底作用有倾 斜偏心荷载时
平面问题: 留意:〔1〕原点
使O 成为划分出的各个新矩形的公共角点,然后再根据迭加原理计算。
共有以下四种情况: (a) O点在荷载面的边缘:
Ⅱ
O
其中KzI 、KzII 为z相 应于 o 面 积 Ⅰo 和 Ⅱ( K 的z 角 点K 附z 加) 应p 力系数。
Ⅰ
(b) O点在荷载面内:
ⅣⅢ
当 O 位于荷载中心,那么有:
ⅠO Ⅱ
竖向集中力作用下地基附加应力
z
K
F z2
竖向集中力作用竖向附加应力系数
竖向集中力作用下地基附加应力
在竖向集中力作用 下,地基附加应力 越深越小,越远越 小,Z=0为奇特点, 无法计算附加应力
应力叠加原理〔等代荷载法〕
由于集中力作用下地基中的附加应力 σz是荷载的一次函数,因此当假设干 竖向集中力Fi作用于地表时,运用叠 加原理,地基中z深度任一点M的附加 应力σz应为各集中力单独作用时在该 点所引起的附加应力总和。
3.6.1竖向集中荷载作用下地基中附加应力.PPT - test

地基中竖向附加应力分布规律将地基中应力相同的点连成线就称为应力等值线也称应的等值线图应力等值线如果有若干个竖向集中荷载f作用在地基表面时则采用叠加原理地面下深度z处某点m的竖向附加应力土力学soilmechanics廖红建教授主讲
3.6 地基中的附加应力
3.6.1 竖向集中荷载作用下 地基中附加应力
(a)
该应力是使地基土压缩变形
产生沉降的原因。
R2=r2+z2
土力学 Soil Mechanics
根据几何关系 R2=r2+z2 ,改写(a)式为:
z
3F
2 z2
1
1 r
z
2 5/2
F z2
3
2
1
1 r
z
2 5/2
(b)
α为竖向集中荷载作用下应力系数,是r/z的函数, 可查相关应力系数表获得。
(c)
αi —根据(ri/z)查表而得;
ri— 第i个集中荷载作用点到M点的水平距离。
地基中竖向附加应力分布规律
z
3F
2 z2
1
1 r
z
2 5/2
F z2
(b)
在集中力作用线上(r=0), 沿着z轴,σz值随深度增加而减 小。
当z一定时,在同一水平面上 ,随着与集中力作用线水平距 离r的增大,σz值减小。 在离集中力作用线某一距离r 时 , 在 地 表 处 σz 从 零 开 始 随 深 度增加而增大,但到一定深度 后又减小。
应力等值线
将地基中应力相同的 点连成线,就称为应 力等值线,也称“应 力泡”。
地基中的附加应力σz 的等值线图
土力学 Soil Mechanics
如果有若干个竖向集中荷载Fi 作用在地基表面时, 则采用叠加原理,地面下 深度z处,某点M的竖向附加
3.6 地基中的附加应力
3.6.1 竖向集中荷载作用下 地基中附加应力
(a)
该应力是使地基土压缩变形
产生沉降的原因。
R2=r2+z2
土力学 Soil Mechanics
根据几何关系 R2=r2+z2 ,改写(a)式为:
z
3F
2 z2
1
1 r
z
2 5/2
F z2
3
2
1
1 r
z
2 5/2
(b)
α为竖向集中荷载作用下应力系数,是r/z的函数, 可查相关应力系数表获得。
(c)
αi —根据(ri/z)查表而得;
ri— 第i个集中荷载作用点到M点的水平距离。
地基中竖向附加应力分布规律
z
3F
2 z2
1
1 r
z
2 5/2
F z2
(b)
在集中力作用线上(r=0), 沿着z轴,σz值随深度增加而减 小。
当z一定时,在同一水平面上 ,随着与集中力作用线水平距 离r的增大,σz值减小。 在离集中力作用线某一距离r 时 , 在 地 表 处 σz 从 零 开 始 随 深 度增加而增大,但到一定深度 后又减小。
应力等值线
将地基中应力相同的 点连成线,就称为应 力等值线,也称“应 力泡”。
地基中的附加应力σz 的等值线图
土力学 Soil Mechanics
如果有若干个竖向集中荷载Fi 作用在地基表面时, 则采用叠加原理,地面下 深度z处,某点M的竖向附加
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b) O点在荷载面内:
ⅠO Ⅱ
z ( K z K z K z K z V ) p
当 O 位于荷载中心,则有:z 4Kzp
其中KzI 、KzII、KzIII 、KzIV 为相应于面积 I、II、III、IV 的角点 附加应力系数。
角点法计算任意位置附加应力
应力叠加原理应用
将基底面基底净压力 的分布划分为若干小 块面积并将其上的分 布荷载合成为小的集 中力,即可应用公式 (2-24)计算。
这种方法适用于基底 面不规则的情况,每 块面积划分得越小, 计算精度就越高。
二 矩形基础底面铅直荷载下的附加应力
1.竖直均布压力作用举行基底角点下的附加应力
ed
c
(c) O点在荷载面的边缘外侧:
o
荷载面(abcd)= 面积Ⅰ(ofbg)- 面积Ⅱ(ofah)
h
g
+ 面积Ⅲ(oecg)- 面积Ⅳ(oedh) f a b
则:
z ( K c K c K c K c V ) p
(d) O点在荷载面的角点外侧
ed
c
荷载面(abcd)= 面积Ⅰ(ohce)- 面积Ⅱ(ohbf) f a
(3)求A点下1m深处竖向附加应力σzA。
A点是ACbG,AdaG两块矩形的公共角点,这两块面积相
等,长度l宽度b均相同,故其附加应力系数Ks相同。根据l
,b,z的值可得
l/b=2 /2=1
z/b=1/2=0.5
查表2-1应用线性插值方法可得Ks=0.2315,所以
σzA=2 Kspn=2×0.2315 ×131=60.65(kPa)
(4)求H点下1m深度处竖向应力σzH。 H点是HGbQ, HSaG,HAcQ,HAdS的公共角点。σzH是由四块面积各 自引起的附加应力的叠加。对于HGbQ,HSaG两块面积
,长度l宽度b均相同,由例图
l/b=2.5/2=1.25
z/b=1/2=0.5
查表2-2,利用双向线性插值得Ks=0.2350
R r2z2
竖向集中力作用下地基附加应力
z
K
F z2
竖向集中力作用竖向附加应力系数
竖向集中力作用下地基附加应力
在竖向集中力作用 下,地基附加应力 越深越小,越远越 小,Z=0为奇异点, 无法计算附加应力
应力叠加原理(等代荷载法)
由于集中力作用下地基中的附加应力 σz是荷载的一次函数,因此当若干竖 向集中力Fi作用于地表时,应用叠加 原理,地基中z深度任一点M的附加应 力σz应为各集中力单独作用时在该点 所引起的附加应力总和。
对于HAcQ,HAdS两块面积,长度l宽度b均相同,由例 图
l/b=2/0.5=4 z/b=1/0.5=2 查表2-2,得Ks=0.1350,则σzH可按叠加原理求得: σzH=(2×0.2350- 2×0.1350 )×131=26.2(kPa)
矩形面积基底受三角形分布荷载时角点下的附加 应力
竖直均布压力作用举行基底角点下的附加应力
Ks是竖直均布压力矩形基底角点下的附 加应力系数,它是m,n的函数,其中 m=l/b,n=z/b。l是矩形的长边,b是矩 形的短边,z是从基底起算的深度,pn是 基底净压力。
Ks可直接查表
表4-4 矩形均布荷载角点下竖向附
加应力系数Kz1
角点法计算任意位置附加应力
b
则:
- 面积Ⅲ(ogde)+ 面积Ⅳ(ogaf) o z ( K z K z K z K z V ) p
g
h
必须注意: 在角点法中,查附加应力系数时所用的 l 和 b 均指划 分后的新矩形(如ofbg、ohce等)的长和宽。
角点法计算任意位置附加应力
【例题2-2】如图所示,矩形基底长为4m、宽为2m,基 础埋深为0.5m,基础两侧土的重度为18kN/m3,由上部中 心荷载和基础自重计算的基底均布压力为140kPa。试求基 础中心O点下及A点下、H点下z=1m深度处的竖向附加应 力。 【解】 (1)先求基底净压力(基底附加应力)pn,由已知条件
x p pt b
dz
3z3ptxdxdy
2R5b
R x2y2z2
矩形面积基底受三角形分布荷载时角点下的附加 应力
根据等代荷载法原 理,将基底面积划 分成无穷多块,每 块面积趋向于无穷
小,将σz用积分 表示
竖直均布压力作用举行基底角点下的附加应力
将 Байду номын сангаас x2y2z2
lb
z dz Kz1pn
00
代入并沿整个基底面
积积分,即可得到竖
直均布压力作用矩形
基底角点O下z深度处
所引起的附加应力
图4-3 集中荷载作用下地基中应力
Valentin Joseph Boussinesq (1842-1929)
法国著名物理家和数学家,对数学物理、流体力 学和固体力学都有贡献。
竖向集中力作用下地基附加应力
弹性力学解答 Boussinesq 解
竖向集中力作用下地基附加应力
z
3Pz 3
2R 5
第二章 土体应力计算
地基中的附加应力计算
附加应力:由外荷引起的土中应力。
一 地表集中力下地基中附加应力
虽然理论上的集中力实际上是不存在的,但集中力作用下 弹性半空间地基理论解(即布辛涅斯克解)是求解其他 形式荷载作用下地基中附加应力分布的基础。 (一)布辛涅斯克解(法国Boussinesq,1885)
pn=p-γod=140-18×0.5=131kPa
(2)求O点下1m深处地基附加应力 σzo。O点是矩形面积OGbE,OGaF ,OAdF,OAcE的共同角点。这四块 面积相等,长度l宽度b均相同,故其 附加应力系数Ks相同。根据l,b,z的 值可得
l/b=2 /1=2
z/b=1/1=1
查表2-2得Ks=0.2019,所以 σzo=4 Kspn=4×0.2019 ×131= 104.75(kPa)
角点法:即通过计算点o将原矩形荷载分成若干个新矩形荷载,从而使 O 成为划分出的各个新矩形的公共角点,然后再根据迭加原理计算。共 有以下四种情况:
Ⅱ
(a) O点在荷载面的边缘:
z o o ( K z K z )p
O
Ⅰ
其中KzI 、KzII 为相应于面积Ⅰ和Ⅱ的角点附加应力系数。 Ⅳ Ⅲ
