完整word版,八年级四边形几何证明提高题(经典)
完整版八年级数学四边形证明题专项练习

卓越个性化教案GFJW0901学生姓名彭年级初二授课时间教师姓名刘课时2课题四边形证明题专题教学目标熟悉四边形的性质和判定,了解线段和角度证明的方法。
重点掌握各种特殊四边形的性质和判定。
熟悉线段和角度数量关系的证明方法难点运用平行、三角形全等、特殊三角形性质、四边形性质进行证明。
【课堂练习】:1.:在矩形ABCD中,AE BD于E,DAE=3∠BAE,求:∠EAC的度数。
2.:直角梯形ABCD中,BC=CD=a且∠BCD=60,E、F分别为梯形的腰AB、DC的中点,求:EF的长。
3、:在等腰梯形ABCD中,AB∥DC,AD=BC,E、F分别为AD、BC的中点,BD平分∠ABC交EF于G,EG=18,GF=10求:等腰梯形ABCD的周长。
A DE FB CD CE G FA BE4、:梯形ABCD中,AB∥CD,以AD,AC为邻边作平行四边形ACED,DC延长线交BE于F,求证:F是BE的中点。
5、:梯形ABCD中,AB∥CD,ACCB,AC平分∠A,又∠B=60,梯形的周长是20cm,求:AB的长。
A6、从平行四边形四边形ABCD的各顶点作对角线的垂线AE、BF、CG、DH,垂足分别是E、F、G、H,求证:EF∥GH。
AD C FA BD CBD CFOH GB卓越个性化教学讲义7、:梯形ABCD的对角线的交点为E假设在平行边的一边长线上取一点F,使S ABC=S EBF,求证:DF∥AC。
8、在正方形ABCD中,直线EF平行于 G对角线AC,与边AB、BC的交点为E、F,在DA的延长线上取一点G,使AG=AD,假设EG与DF的交点为H,求证:AH与正方形的边长相等。
9、假设以直角三角形ABC的边AB为边,在三角形ABC的外部作正方形ABDE,AF是BC边的高,延长FA使AG=BC,求证:BG=CD。
BC的延A DEB C F A DEHB F CGEDA10、正方形ABCD,E、F分别是AB、AD延长线上的一点,且AE=AF=AC,EF交BC于G,交AC于K,交CD于H,求证:EG=GC=CH=HF。
人教版八年级数学下册 特殊平行四边形 解答题训练(word版含解析)

人教版八年级数学下册《18-2特殊平行四边形》解答题优生辅导训练(附答案)1.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M、N.(1)求证:四边形BNDM是菱形;(2)若BD=24,菱形BNDM的面积为120,求菱形BNDM的周长.2.如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC.(1)求证:四边形AECD是菱形;(2)过点E作EF⊥CD于点F,若AB=3,BC=5,求EF的长.3.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)若AD=10,EC=4,求AC的长度.4.如图,在菱形ABCD中,AB=4,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.(1)求证:△NED≌△MEA.(2)当AM的值为何值时,四边形AMDN是矩形?并说明理由.5.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G为EF 中点,连接BD、DG.(1)试判断△ECF的形状,并说明理由;(2)求∠BDG的度数.6.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC、BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.(1)求证:四边形ABCD是菱形;(2)若AB=6,BD=8,求CE的长.7.如图,在正方形ABCD中,E,F分别在边AB,BC上,△DEF是等边三角形,连接BD交EF于点G.(1)求证:BE=BF;(2)若DE=2,求BD的长.8.如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF,过点D作DG⊥CF于点G.(1)求证:四边形ADCF是平行四边形;(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?(3)在(2)的条件下,若AB=6,BC=10,求DG的长.9.如图,在正方形ABCD中,AB=,E为正方形ABCD内一点,DE=AB,∠EDC=α(0°<α<90°),连结CE,AE,过点D作DF⊥AE,垂足为点F,交CE的延长线于点G,连结AG.(1)当α=20°时,则∠AEC=;(2)判断△AEG的形状,并说明理由;(3)当GF=1时,求CE的长.10.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于点H,连接CH,过点C作CG⊥HC交AE于点G.(1)若点F在边CD上,如图1.①证明:∠DAH=∠DCH;②猜想线段CG与EF的关系并说明理由;(2)取DF中点M,连结MG,若MG=4,正方形边长为6,求BE的长.11.在△ABC中,过A作BC的平行线,交∠ACB的平分线于点D,点E是BC上一点,连接DE,交AB于点F,∠CAD+∠BED=180°.(1)如图1,求证:四边形ACED是菱形;(2)如图2,若∠ACB=90°,BC=2AC,点G、H分别是AD、AC边中点,连接CG、EG、EH,不添加字母和辅助线,直接写出图中与△CEH所有的全等的三角形.12.如图,四边形ABCD为正方形,E为AD上一点,连接BE,∠AEB=60°,M为BE的中点,过点M的直线交AB、CD于P、Q.(1)如图1,当PQ⊥BE时,求证:BP=2AP;(2)如图2,若∠APQ为锐角,且PQ=BE,延长BE、CD交于点N,请你猜想QM与QN的数量关系,并说明理由.13.如图,点G在正方形ABCD的边CD上,且四边形CEFG也是正方形,连接BG,DE,AF,取AF的中点M,连接CM.求证:(1)BG=DE;(2)CM=AF.14.如图,在正方形ABCD中,点E是BC上一点,点F是CD延长线上的一点,且BE=DF,连接AE、AF、EF.(1)求证:AE=AF;(2)已知∠AEB=75°,若点P是EF的中点,连接CP,DP,求∠CPD的度数.15.如图,点O为矩形ABCD对角线的交点,过点D作DE⊥AC于点E,过点B作BF∥AC,交DE的延长线于F,在BF的延长线上取FG=OD,连接AG,OF.(1)求证:四边形AOFG为菱形;(2)若AD=5,DF=8,求BG的长.16.已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.17.如图,▱ABCD,BE⊥AD于E,交AC于M,DF⊥BC于F,交AC于N,连接DM、BN.(1)求证:△ABM≌△CDN;(2)当▱ABCD是菱形时,判断四边形MBND的形状,并说明理由.18.如图,矩形ABCD中,对角线AC、BD相交于点O,BD的垂直平分线分别交边AD、BC于点E、F,连接BE、DF.(1)求证:四边形BEDF是菱形;(2)若∠BOC=120°,AB=6,求FC的长.19.如图,在△ABC中,∠ABC=90°,点O是斜边AC的中点,过点O作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD、DE.(1)求证:四边形ABCD是矩形;(2)若BC=3,∠BAC=30°,求DE的长.20.如图,四边形ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC 于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度.参考答案1.(1)证明:∵AD∥BC,∴∠DMO=∠BNO,∵MN是对角线BD的垂直平分线,∴OB=OD,MN⊥BD,在△MOD和△NOB中,,∴△MOD≌△NOB(AAS),∴OM=ON,∵OB=OD,∴四边形BNDM是平行四边形,∵MN⊥BD,∴四边形BNDM是菱形;(2)解:∵菱形BNDM的面积为120=×BD×MN,∴MN=10,∵四边形BNDM是菱形,BD=24,MN=10,∴BM=BN=DM=DN,OB=BD=12,OM=MN=5,在Rt△BOM中,由勾股定理得:BM===13,∴菱形BNDM的周长=4BM=4×13=52.2.证明:(1)∵∠BAC=90°,E是BC的中点,∴AE=BC=CE,又∵AD∥BC,AE∥DC,∴四边形AECD是平行四边形.∴四边形AECD是菱形.(2)过点A作AG⊥BC于点G,∵AB=3,BC=5,∴AC=,∵,∴,∴AG=,又∵S菱形AECD=CD•EF=CE•AG,∵CD=CE,∴EF=AG=.3.(1)证明:∵四边形ABCD是菱形,∴AD∥BC且AD=BC,∵BE=CF,∴BC=EF,∴AD=EF,∵AD∥EF,∴四边形AEFD是平行四边形,∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;(2)∵四边形ABCD是菱形,AD=10,∴AD=AB=BC=10,∵EC=4,∴BE=10﹣4=6,在Rt△ABE中,AE=,在Rt△AEC中,AC=.4.(1)证明:∵四边形ABCD为菱形,∴CD∥AB,∴∠DNE=∠AME,∵E为AD的中点,∴DE=AE,在△NED和△MEA中,∴△NDE≌△MAE(AAS);(2)当AM=2时,四边形AMDN是矩形.理由如下:由(1)知△NED≌△MEA,∴NE=ME,又∵DE=AE,∴四边形AMDN是平行四边形,∵菱形ABCD,AB=4,E为AD中点,∴AE=2=AM,又∵∠DAB=60°,∴△MEA为等边三角形,∴AE=ME,∴AD=MN,∴平行四边形AMDN为矩形.5.(1)解:△ECF是等腰直角三角形;理由如下:∵四边形ABCD是矩形,∴AD∥BC,∠DAB=∠ABC=∠BCD=90°,∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠DAE=∠BAE=45°,∴∠BEA=∠BAE=45°,∴∠CEF=45°,AB=BE,∴∠F=90°﹣45°=45°,∴EC=FC,又∵∠ECF=90°,∴△ECF是等腰直角三角形;(2)∵四边形ABCD是矩形,∴AB=CD,∵AB=BE,∴BE=CD,∵EC=FC,∠ECF=90°,∴CG=EF=EG,∠ECG=∠ECF=45°,∴∠DCG=90°+45°=135°,∵∠BEG=180°﹣45°=135°,∴∠DCG=∠BEG,在△DCG和△BEG中,,∴△DCG≌△BEG(SAS),∴DG=BG,∠DGC=∠BGE,∴∠BGD=∠EGC=90°,又∵DG=BG,∴∠BDG=45°.6.(1)证明:∵AB∥CD,∴∠OAB=∠DCA,∵AC为∠DAB的平分线,∴∠OAB=∠DAC,∴∠DCA=∠DAC,∴CD=AD,∵AB∥CD,∴四边形ABCD是平行四边形,∵AD=AB,∴▱ABCD是菱形;(2)解:∵四边形ABCD是菱形,BD=8,∴OA=OC,BD⊥AC,OB=OD=BD=4,∴∠AOB=90°,∴OA===2,∴AC=2OA=4,∴菱形ABCD的面积=AC×BD=×4×8=16,∵CE⊥AB,∴菱形ABCD的面积=AB×CE=6CE=16,∴CE=.7.(1)证明:∵四边形ABCD为正方形,∴AD=CD=AB=BC,∠A=∠C=90°,∵△DEF为等边三角形,∴DE=DF,在Rt△ADE和Rt△CDF中,,∴Rt△ADE≌Rt△CDF(HL),∴AE=CF.又∵AB=BC,∴AB﹣AE=BC﹣CF,∴BE=BF;(2)解:由(1)可知BE=BF,∴△BEF为等腰直角三角形,∵四边形ABCD为正方形,∴BD平分∠ABC,∴点G为EF的中点,BD⊥EF,∵△DEF为等边三角形,DE=2,∴EF=DE=2,BG=EG=1,在Rt△EDG中,由勾股定理得,DG===,∴BD=BG+DG=1+.8.证明:(1)∵点D、E分别是边BC、AC的中点,∴DE∥AB,∵AF∥BC,∴四边形ABDF是平行四边形,∴AF=BD,则AF=DC,∵AF∥BC,∴四边形ADCF是平行四边形;(2)当△ABC是直角三角形时,四边形ADCF是菱形,理由:∵点D是边BC的中点,△ABC是直角三角形,∴AD=DC,∴平行四边形ADCF是菱形;(3)∵△ABC是直角三角形,AB=6,BC=10,BD=DC,∴AD=DC=5,AC=,∵四边形ADCF是菱形,∴AC⊥DF,∴DE=,∴,即,解得:DG=.9.解:(1)∵四边形ABCD是正方形,∴∠ADC=90°,AB=AD=DC,∵∠CDE=20°,∴∠ADE=70°,∵DE=AB,∴DC=DE,DA=DE,∴∠DEC=∠DCE=×(180°﹣20°)=80°,∠DAE=∠DEA=×(180°﹣70°)=55°,∴∠AEC=∠AED+∠DEC=80°+55°=135°,故答案为:135°;(2)结论:△AEG是等腰直角三角形.理由:∵AD=DE,DF⊥AE,∴DG是AE的垂直平分线,∴AG=GE,∴∠GAE=∠GEA,∵DE=DC=AD,∴∠DAE=∠DEA,∠DEC=∠DCE,∵∠DAE+∠DEA+∠DEC+∠DCE+∠ADC=360°,∴∠DEA+∠DEC=135°,∴∠GEA=45°,∴∠GAE=∠GEA=45°,∴∠AGE=90°,∴△AEG为等腰直角三角形.(3)如图,连接AC,∵四边形ABCD是正方形,∴AC=AB=,∵△AEG为等腰直角三角形,GF⊥AE,∴GF=AF=EF=1,∴AG=GE=,∵AC2=AG2+GC2,∴10=2+(EC+)2,∴EC=(负根已经舍弃).10.证明:(1)①∵四边形ABCD是正方形,∴∠ADB=∠CDB=45°,AD=DC,在△ADH和△CDH中,,∴△ADH≌△CDH(SAS),∴∠DAH=∠DCH;②结论:EF=2CG,理由如下:∵△DAH≌△DCH,∴∠DAF=∠DCH,∵CG⊥HC,∴∠FCG+∠DCH=90°,∴∠FCG+∠DAF=90°,∵∠DF A+∠DAF=90°,∠DF A=∠CFG,∴∠CFG=∠FCG,∴GF=GC,∵∠GCE+∠GCF=90°,∠CFG+∠E=90°,∴∠GCE=∠GCF,∴CG=GE,∴EF=2CG;(2)①如图,当点F在线段CD上时,连接DE.∵∠GFC=∠GCF,∠GEC+∠GFC=90°,∠GCF+∠GCE=90°,∴∠GCE=∠GEC,∴EG=GC=FG,∵FG=GE,FM=MD,∴DE=2MG=8,在Rt△DCE中,CE===2,∴BE=BC+CE=6+2;②如图,当点F在线段DC的延长线上时,连接DE.同法可知GM是△DEC的中位线,∴DE=2GM=6,在Rt△DCE中,CE=2,∴BE=BC﹣CE=6﹣2综上所述,BE的长为6+2或6﹣2.11.(1)证明:∵AD∥BC,∴∠ADC=∠BCD,∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠ADE=∠DEB,∵∠DEB+∠DEC=180°,∠DEB+∠CAD=180°,∴∠DEC=∠DAC,∴∠ADE+∠DAC=180°,∴DE∥AC,∴四边形ACED是菱形;(2)解:∵∠ACB=90°,∴菱形ACED是正方形,∴∠D=∠CAG=∠DEC=90°,AC=AD=CE,∵G是AD的中点,H是AC边中点,∴AG=DG=CE,∴△EDG≌△CAG≌△ECH(SAS),∵BC=2AC,∴BE=CE=AD,∵AD∥BE,∴∠B=∠DAF,∵∠AFE=∠BFE,∴△BFE≌△AFD(AAS),∵AD=CE=BE,∴△BEF≌△ECH,∴图中与△CEH全等的三角形有△ADF,△EDG,△CAG,△EBF.12.(1)证明:连接PE,如图1,∵点M是BE的中点,PQ⊥BE,∴PQ垂直平分BE,∴PB=PE,∴∠PEB=∠PBE=90°﹣∠AEB=90°﹣60°=30°,∴∠APE=∠PBE+∠PEB=60°,∴∠AEP=90°﹣∠APE=90°﹣60°=30°,∵∠A=90°,∴BP=EP=2AP;(2)解:NQ=2MQ或NQ=MQ.理由如下:分两种情况:如图3所示,过点Q作QF⊥AB于点F,交BN于点G,则FQ=CB,∵正方形ABCD中,AB=BC,∴FQ=AB.在Rt△ABE和Rt△FQP中,,∴Rt△ABE≌Rt△FQP(HL),∴∠FQP=∠ABE=30°,又∵∠MGQ=∠BGF=∠AEB=60°,∴∠GMQ=90°,∵CD∥AB.∴∠N=∠ABE=30°,∴NQ=2MQ;如图2所示,过点Q作QF⊥AB于点F,则QF=CB,同理可证:△ABE≌△FQP,此时∠FPQ=∠AEB=60°,又∵∠FPQ=∠ABE+∠PMB=60°,∠N=∠ABE=30°,∴∠EMQ=∠PMB=30°,∴∠N=∠EMQ,∴NQ=MQ.13.(1)证明∵四边形ABCD,四边形CEFG都是正方形,∴BC=CD,CG=CE,在Rt△BGC和Rt△DEC中,∴Rt△BGC≌Rt△DEC(HL),∴BG=DE,(2)连接AC,FC,∴∠ACD=∠FCD=45°,∠ACF=90°,∴△ACF为直角三角形,又∵M是AF的中点,∴CM=AF.14.(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠ABC=∠ADC=∠ADF=90°,在△ABE和△ADF中,∴△ABE≌△ADF(SAS);∴AE=AF,(2)连接AP,∵△ABE≌△ADF,∴∠BAE=∠DAF,∠F AE=90°,在Rt△EAF和Rt△ECF中,P是EF中点,∴P A=PC=PE=PF=EF,又∵AE=AF,∠AEB=75°,∴∠AEP=45°,∠CEP=∠ECP=60°,∴∠DCP=30°,在△APD和△CPD中,∴△APD≌△CPD(SSS),∴∠CDP=45°,∴∠CPD=180°﹣30°﹣45°=105°.15.证明:(1)∵四边形ABCD是矩形,∴OA=OB=OC=OD,∵DE⊥AC,BF∥AC,∴OF=OD=OA,∵FG=OD,∴FG=OA,∵FG∥OA,∴四边形AOFG为菱形;(2)∵AD=5,DF=8,∴DE=EF=4,AE=3,在Rt△DEO中,设OE=x,由勾股定理得:(x+3)2﹣42=x2,解得:x=,∴OD=,OE=,∴BF=2OE=,FG=OD=,∴BG=GF+BF=.16.(1)证明:∵AF∥BC,∴∠AFE=∠DBE,∵E是AD的中点,∴AE=DE,在△AEF和△DEB中,,∴△AEF≌△DEB(AAS);(2)解:当AB=AC时,四边形ADCF是正方形,理由:由(1)知,△AEF≌△DEB,∴AF=DB,∵D是BC的中点,∴DB=DC,∴AF=DC,∵AF∥BC,∴四边形ADCF是平行四边形,∵∠BAC=90°,D是BC的中点,∴AD=DC=BC,∴四边形ADCF是菱形,∵AB=AC,D是BC的中点,∴AD⊥BC,∴四边形ADCF是正方形.17.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠DAB=∠DCB,∴∠BAC=∠DCA,∵BE⊥AD,DF⊥BC,∴∠DAB+∠ABM=90°,∠DCB+∠CDN=90°,又∵∠DAB=∠DCB,∴∠ABM=∠CDN,在△ABM和△CDN中,,∴△ABM≌△CDN(ASA);(2)解:四边形MBND是菱形,理由如下:∵BE⊥AD,DF⊥BC,AD∥BC,∴BE∥DF,由(1)知△ABM≌△CDN,∴BM=DN,∴四边形MBND是平行四边形,连接BD,如图所示:∵四边形ABCD是菱形,∴AC⊥BD,即MN⊥BD,∴平行四边形MBND是菱形.18.(1)证明:∵EF垂直平分BD,∴EB=ED,FB=FD,BO=DO,∵四边形ABCD是矩形,∴∠OBF=∠ODE,∵∠DOE=∠BOF,∴△EOD≌△FOB(AAS),∴DE=BF,∴EB=ED=FB=FD,∴四边形BEDF是菱形;(2)解:∵四边形ABCD是矩形,∴OB=OC,CD=AB=6,∴∠OBC=∠OCB,∵∠BOC=120°,∴∠OBC=∠OCB=30°,∵四边形EBFD为菱形,∴FB=FD,∴∠FBD=∠FDB=30°,∴∠DFC=60°,∴∠FDC=30°,设CF=x,则FD=2x,根据勾股定理得:(2x)2﹣x2=62,解得:x=2,∴FC的长为2.19.(1)证明:∵点O是AC的中点,∴OA=OC,∵AD∥BC,∴∠DAO=∠BCO,∠ADO=∠CBO,在△OAD与△OCB中,,∴△OAD≌△OCB(AAS),∴AD=BC,∴四边形ABCD是平行四边形,∵∠ABC=90°,∴平行四边形ABCD是矩形;(2)解:∵四边形ABCD是矩形,∴AD=BC=3,∵∠ABC=90°,∠BAC=30°,∴AC=2BC=6,∴OA=3,∵OE⊥AC,∴∠AOE=90°,∵∠BAC=30°,∴OE=OA=,∴AE=2OE=2,∴DE===.20.(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在△EQF和△EPD中,,∴△EQF≌△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)如图2中,在Rt△ABC中,AC=AB=2,∵CE=,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,∴四边形DECG是正方形,∴CG=CE=.。
八年级四边形几何证明提高题经典

八年级四边形几何证明提高题经典Revised by BLUE on the afternoon of December 12,2020.几何证明提高题1、如图,在四边形ABCD 中,AB=AD ,CB=CD ,E 是CD 上一点,BE 交AC 于F ,连接DF .(1)若AB ∥CD ,试证明四边形ABCD 是菱形;(2)在(2)的条件下,试确定E 点的位置,使得∠EFD=∠BCD ,并说明理由. 2、已知:如图平行四边形ABCD ,DE ⊥AC ,AM ⊥BD ,BN ⊥AC ,CF ⊥BD求证:MN ∥EF 3、已知:如图菱形ABCD ,E 是BC 上一点,AE 、BD 交于F ,若AE=AB ,∠DAE=2∠BAE 求证:BE=AF4、已知:如图正方形ABCD ,P 、Q 分别是BC 、DC 上的点,若∠1=∠2 求证:PB+QD=PA5、已知:如图正方形ABCD ,AC 、BD 交于点O ,E 、F 分别是BC 、OD 的中点 求证:AF ⊥EF6已知:如图,//AB CD ,AE ED =,BF FC =,//EM AF 交DC 于M ,求证:FM AE =。
7、已知:如图,⊿ABC 中,E 、F 分别是AB 、BC 中点,M 、N 是AC 上两点,EM 、FN交于D ,若AM=MN=N C ,求证:四边形ABCD 是平行四边形。
8、已知:如图,12∠=∠,3AB AC =,BE AD ⊥,求证:AD DE =。
9、已知:如图,//AB CD ,090D ∠=,BE EC DC ==,求证:3AEC BAE ∠=∠。
10、已知:如图,AD BC ⊥,2B C ∠=∠,BE EC =,求证:12DE AB =。
11、已知:如图,AB DC =,AE DE =,BF FC =,FE 交BA 、CD 的延长线于G 、H ,求证:12∠=∠。
12、已知:如图,//AB CD ,090ADC ∠=,BE EC =,求证:2AED EDC ∠=∠。
完整word初二数学平行四边形压轴几何证明题

初二数学平行四边形:几何证明题 GH、HE.CD、DA的中点,顺次连接EF、FG、E1.在四边形ABCD中,、F、G、H分别是AB、BC、C 1)请判断四边形EFGH的形状,并给予证明;(GD 是菱形,并说明理由。
2)试探究当满足什么条件时,使四边形EFGH(FHB E ABC沿顺时针方向旋转90°得到△A.ABC中,∠ACB=90°,AC=BC=10,将△ABC绕点B2.如图,在直角三角形11.C的长度是,∠CBA的度数是(1)线段A111 CBAC 是平行四边形.(2)连接CC,求证:四边形CAA 11111B CQ. BC于的中点,PO的延长线交为ABCD中,点P是线段AD上一动点,OBD如图,矩形3. OP=OQ;(1)求证:t运动时间为.设点PD厘米/秒的速度向D运动(不与重合)A2()若AD=8厘米,AB=6厘米,P从点出发,以1 是菱形.t为何值时,四边形PBQD秒,请用t表示PD的长;并求PD AOC B QGFC.与点C重合,得△E是BC边上的高,将△ABE沿BC方向平移,使点AE4.已知:如图,在□ABCD 中,?DG;⑴求证:BE. 是菱形?证明你的结论与BC满足什么数量关系时,四边形ABFG,当B ⑵若∠?60?AB G ADBCFEF.AE交BC的延长线于点E∥BC,为CD的中点,连结AE、BE,BE⊥AE,延长5. 如图,在四边形ABCD中,AD AD;)FC=求证:(1DA .BC+ADAB(2)=EFB CBE,CE.BC,D是的中点,连结AD,在AD的延长线上取一点E,连结6.如图,在△ABC中,AB=AC ACE)求证:△ABE≌△(1 满足什么数量关系时,四边形ABEC是菱形?并说明理由.(2)当AE 与AD BAEDCF.的延长线与CD的延长线交于点的中点,ABCD中,点E是边ADBE7.如图,在平行四边形F DFE )求证:△ABE≌△(1.ABDF的形状,并说明理由BD2)连结、AF,判断四边形(EADBCFACEDFABDEDABCBCACAB∥8. 如图,已知点在△于的边上,交∥交.于,DFAE 1)求证:;=A AEDFBACAD 2()若的形状,并说明理由.平分∠,试判断四边形E FC B DFE,BDDEBF?上两点,且9. 如图,在平行四边形中,点是对角线. 1)写出图中每一对你认为全等的三角形;( 1)中的任意一对全等三角形进行证明.(2)选择(A DF E BCAC. 、BF、CF,并延长DE至点F,使EF=DE.连接BCAD10.在梯形ABCD中,∥BC,AB=DC,过点D 作DE⊥,垂足为点E )求证:四边形ABFC是平行四边形;1(2CEBE?DE?. ABFC是矩形,(2)若求证:四边形 DACE BFAE. 的外角平分线,BE⊥BACAEAB=AC11.如图,△ABC中,,AD、分别是∠BAC和∠BAEDA(1)求证:⊥(DE与是否相等?并说明理由。
最新八级数学四边形证明(四边形的质探索拔高练习

八级数学四边形证明(四边形的质探索)拔高练习八年级数学四边形证明(四边形的性质探索)拔高练习试卷简介:本测试卷共5道选择题,综合考察同学们对四边形这一章节的掌握。
一、单选题(共5道,每道10分)1.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF= ,则平行四边形ABCD的周长是()A.4B.8C.16D.102.菱形的周长为16,两邻角度数的比为1∶2,此菱形的面积为()A.B.C.D.3.四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是()A.OA=OB=OC=OD,AC⊥BDB.AB∥CD,AC=BDC.AD∥BC,∠A=∠CD.OA=OC,OB=OD,AB=BC4.(2010盐城)小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D 点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M 处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD长与宽的比值为()A.B.2C.D.5.如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是()A.①②⑤B.①④⑤C.③⑤D.①③④⑤。
经典初二数学几何证明题

A DB C E最新中考数学几何证明(平行四边形,菱形矩形正方形)经典 1.(本题10分)如图,已知: ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC∠的平分线BG 交CE 于F ,交AD 于G .求证:AE DG =.2.在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED . (1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数.3.(本小题满分5分)如图,在△ABC 中,点D 、E 分别在边AC 、AB 上,BD=CE ,∠DBC=∠求证:AB=AC 。
4.(本小题满分7分)如图,在△ABC 中,AB=AC ,D 为BC 中点,四边形ABDE 是平行四边形。
是矩形。
5.(10分)在□ABCD 中,AC 是一条对角线,∠B =∠CAD ,延长BC 至点接DE .(1)求证:四边形ABED 是等腰梯形.(2)若AB =AD =4,求梯形ABED 的面积. 6、(本小题7分)如图,点A 、E 、B 、D 在同一条直线上,AE=DB ,AC=DF ,AC ∥DF. 请探索BC 与EF 有怎样的位置关系?并说明理由。
7.如图,已知BE ⊥AD ,CF ⊥AD ,且BE =CF .(1) 请你判断AD 是△ABC 的中线还是角平分线?请证明你的结论.(2)连接BF 、CE ,若四边形BFCE 是菱形,则△ABC 添加一个条件 ▲8.(广东广州,18,9分)如图5,在等腰梯形ABCD 中,AD ∥BC .求证:∠A +∠C =180°10.如图,C 是线段AB 的中点,CD 平分∠ACE ,CE 平分∠BCD ,CD=CE .(1)求证:△ACD≌△BCE;(2)若∠D=50°,求∠B 的度数. 11.(本题6分)如图,在△ABC 中,D 是BC 边上的点(不与B ,C 重合),F ,E 分别是AD 及其延长线上的点,CF ∥BE. 请你添加一个条件,使△BDE ≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是: ▲ ;(2)证明:.12.(8分)如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形ABCD 是平行四边形,并予以证明.(写出一种即可)B A CBD FE(第11题)B CDE F A 关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B . 已知:在四边形ABCD 中, , ; 求证:四边形ABCD 是平行四边形. 13.(本题满分9分)将三角形纸片ABC (AB >AC )沿过点A 的直线折叠,使得AC 落在AB 边上,折痕为AD ,展平纸片,如图(1);再次折叠该三角形纸片,使得点A 与点D 重合,折痕为EF ,再次展平后连接DE 、DF ,如图2,证明:四边形AEDF 是菱形.14.如图10,已知ABC ADE Rt △≌Rt △,90ABC ADE ∠=∠=°,BC 与DE 相交于点F ,连接CD ,EB .(1)图中还有几对全等三角形,请你一一列举. (2)求证:.CF EF = 15.(本小题满分8分)如图,已知:点B 、F 、C 、E 在一条直线上,FB =CE ,AC=DF .能否由上面的已知条件证明AB ∥ED ?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件.......,添加到已知条件中,使AB ∥ED 成立,并给出证明. 供选择的三个条件(请从其中选择一个): ①AB =ED ; ②BC =EF ; ③∠ACB =∠DFE . 16.(6分)已知:正方形ABCD 中,E 、F 分别是边CD 、DA 上的点,且CE =DF ,AE 与BF 交于点M . (1)求证:△ABF ≌△DAE ;(2)找出图中与△ABM 相似的所有三角形(不添加任何辅助线).17.(6分)如图,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CF 交AD 于点F .点E 是AB 的中点,连接EF .(1)求证:EF ∥BC ;(2)若△ABD 的面积是6,求四边形BDFE 的面积.18.(本小题满分8分)如图,四边形ABCD 的对角线AC 、DB 相交于点O ,现给出如下三个条件:AB CD(1)(2) ABDCCDBF AE图10 DE(第15题)A EB DA G EB CF D AB DC AC DB OBC OCB ==∠=∠①②③.(1)请你再增加一个..条件:________,使得四边形ABCD 为矩形(不添加其它字母和辅助线,只填一个即可,不必证明);(2)请你从①②③中选择两个条件________(用序号表示,只填一种情况),使得AOB DOC △≌△,并加以证明.19.如图,在直角梯形ABCD 中,AD ∥BC ,∠A =90o ,AB =AD =6,DE ⊥CD交AB 于E ,DF 平分∠CDE 交BC 于F ,连接EF . (1)证明:CF =EF ; (2)当tan ∠ADE = 13时,求EF 的长.20.(10分)如图,在□ABCD 中,E 、F 分别是边AB 、CD的中点,AG ∥BD 交CB 的延长线于点G .(1)求证:△ADE ∽≌△CBF ;(2)若四边形BEDF 是菱形,则四边形AGBD 是什么特 殊四边形?请说明你的理由. 21.(本题满分8分)如图,在ABCD 中,点E 、F 是对角线AC 上两点,且CF AE =.求证:FDE EBF =∠.22.(8分)如图,四边形ABCD 是矩形,∠EDC=∠CAB , ∠DEC=90°。
完整word初二数学平行四边形压轴几何证明题

初二数学平行四边形:几何证明题 GH 、HE. CD DA 的中点,顺次连接EF 、 FG E1.在四边形ABCD 中,、F 、G H 分别是AB BC C 1 )请判断四边形 EFGH 的形状,并给 予证明;(G D 是菱形,并说明理由。
2)试探究当满足什么条件时,使四边形EFGH (F HB E ABC 沿顺时针方向旋转 90°得到△ A . ABC 中,/ ACB=90°,AC=BC=1Q 将厶ABC 绕点B2.如图, 在直角三角形 *. C 的长度是 ,/ CBA 的度数是(1)线段A- _____________________ CBAC是平行四边形.(2)连接CC 求证:四边形 CAA milQ. BC 于的中点, PO 的延长线交为 ABCD 中,点P 是线段AD 上一动点,OBD 如图,矩形3.OP=OQ ; (1)求证:t 运动时间为.设点PD 厘米/秒的速度向D 运动(不与重合)A2 ()若AD=8 厘米,AB=6厘米,P 从点岀发,以1是菱形.t 为何值时,四边形 PBQD 秒,请用t 表示PD 的GFC. 与点C 重合,得△ E 是BC 边上的高,将△ ABE 沿BC 方向平移,使点 AE4.已知:如图,在口 ABCD 中,?DG ⑴求证:BE.是菱形?证明你的结论与 BC 满足什么数量关系时,四边形 ABFG 当B ⑵若/ ?50?\BG ADB C F EF . AE交BC的延长线于点E// BC,为CD的中点,连结AE、BE, BE X AE,延长5.如图,在四边形ABCD 中, AD AD;FC=求证:(1DA . BC+ ADAB( 2)=EBE , CE.BC, D是的中点,连结AD,在AD的延长线上取一点E,连结6.如图,在厶ABC中,AB=AC ACE求证:△ ABE^^(1满足什么数量关系时,四边形ABEC是菱形?并说明理由.(2)当AE 与ADBAEDCF.的延长线与CD的延长线交于点的中点,ABCD中,点E是边ADBE7.如图,在平行四边形 F DFE )求证:△ ABE^^( 1.ABDF的形状,并说明理由BD2)连结、AF,判断四边形(EADBFACEDFABDEDABCBCACAB 如图,已知点在△于的边上,交//交•于, AEDFBACAD ()若的形状,并说明理由•平分/,试判断四边形E FFE , BDDEBF?上两点,且9.如图,在平行四边形中,点是对角线.1 )写岀图中每一对你AC.、BF 、CF ,并延长 DE 至点 F ,使 EF=DE.连接 BCAD10.在梯形 ABCD 中,/ BC,AB=DC 过点 D 作DEI ,垂足为点 E )求证:四边形 ABFC 是平行四边形;1 (2CEBEQE? ABFC 是矩形,(2) 若求证:四边形 D ADFAE 1 )求证:;=A(2)选择(A DAE.的外角平分线,BE丄BACAEAB=AC11如图,△ ABC中,,AD 分别是/ BAC和/ B AEDA( 1)求证:丄(DE与是否相等?并说明理由。
初二四边形几何拓展证明题

6(2010 山东莱芜)在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.(1)如图①,试判断四边形EGFH的形状,并说明理由;(2)如图②,当EF⊥GH时,四边形EGFH的形状是;(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是;(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.1.(2005年海淀区)如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD 于F.求证:BE=CF.11.(2005年广东省)如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC 的中点,E、F分别是BM、CM的中点.⑴求证:四边形MENF是菱形;⑵若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,并证明你的结论.16.(2005年河北省)已知线段AC=8,BD=6.HGFEODCBA图①HGFEODCBA图②AB CDOEFGH图③AB CDOEFG H图④⑴已知线段AC 垂直于线段BD.设图甲、图乙和图丙中的四边形ABCD 的面积分别为S 1、S 2和S 3,则S 1=__________,S 2=_________,S 3=___________;⑵如图丁,对于线段AC 与线段BD 垂直相交(垂足O 不与点A ,C ,B ,D 重合)的任意情形,请你就四边形ABCD 面积的大小提出猜想,并证明你的猜想; ⑶当线段BD 与AC (或CA )的延长线垂直相交时,猜想顺次连结A ,B ,C ,D ,A 所围成的封闭图形的面积是多少?18.(2005年河南省)如图,梯形ABCD 中,AD∥BC,AB =DC ,P 为梯形ABCD 外一点,PA 、PD 分别交线段BC 于点E 、F ,且PA =PD.⑴写出图中三对你认为全等的三角形(不再添加辅助线); ⑵选择你在⑴中写出的全等三角形中的任意一对进行证明.21.(2005年黑龙江省)已知矩形ABCD 和点P ,当点P 在图1中的位置时,则有结论:S △PBC =S △PAC +S △PCD .理由:过点P 作EF⊥BC,分别交AD 、BC 于E 、F 两点.∵S △PBC +S △PAD =BC·PF+AD·PE=BC (PF +PE )=BC·EF=S 矩形ABCD ,又∵S △PAC +S △PCD +S PAD =S 矩形ABCD , ∴S △PBC +S △PAD =S △PAC +S △PCD +S PAD . ∴S △PBC =S △PAC +S △PCD .请你参照上述信息,当点P 分别在图2、图3中的位置时,S △PBC 、S △PAC 、S △PCD 又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.22.(2005年大连市)在数学活动中,小明为了求的值(结果用n表示),设计如图1所示的几何图形.⑴请你利用这个几何图形求的值为___________;⑵请你利用图形2,再设计一个能求的值的几何图形.23.(2005年济南市)如图,已知ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F.⑴求证:CD=FA;⑵若使∠F=∠BCF,ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并进行证明(不要再增添辅助线).27.(2004年黑龙江省宁安市)如图,四边形ABCD中,点E在边CD上,连结AE、BE. 给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.⑴用序号写出一个真命题(书写形式如:如果×××,那么×××),并给出证明;⑵用序号再写出三个真命题(不要求证明);29.(2004年河北省)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.⑴当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时(如图1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;⑵当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在⑴中得到的结论还成立吗?简要说明理由.19.(2005年辽宁省11市)如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(点E不与B、C两点重合),EF∥BD 交AC于点F,EG∥AC交BD于点G.⑴求证:四边形EFOG的周长等于2OB;⑵请你将上述题目的条件“梯形ABCD中,AD∥BC,AB=DC”改为另一种四边形,其他条件不变,使得结论“四边形EFOG的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证,不必证明.12.(2005年浙江省)请将四个全等直角梯形(如图)拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法).26.(2004年青海省湟中县)阅读材料:如图1,在四边形ABCD中,对角线AC⊥BD,垂足为P.求证:S四边形ABCD=AC·BD.∴S四边形ABCD =S△ACD+S△ACB=AC·PD+AC·BP=AC(PD+PB)=AC·BD解答问题:⑴上述证明得到的性质可叙述为______________________________________________;⑵已知:如图2,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,AD =3cm,BC=7cm,利用上述的性质求梯形的面积.30.(2004年贵阳市)如图,四边形ABCD 中,AC =6,BD =8且AC⊥BD,顺次连接四边形ABCD 各边中点,得到四边形A 1B 1C 1D 1;再顺次连接四边形A 1B 1C 1D 1各边中点,得到四边形A 2B 2C 2D 2……如此进行下去得到四边形A n B n C n D n . ⑴证明:四边形A 1B 1C 1D 1是矩形;⑵写出四边形A 1B 1C 1D 1和四边形A 2B 2C 2D 2的面积; ⑶写出四边形A n B n C n D n 的面积;14.把“直角三角形、等腰三角形、等腰直角三角形”填入下列相应的空格上.(1)正方形可以由两个能够完全重合的 拼合而成; (2)菱形可以由两个能够完全重合的 拼合而成; (3)矩形可以由两个能够完全重合的 拼合而成.40.如图19-13,在△ABC 中,点O 是AC 边上的一动点, 过点O 作直线MN //BC , 设MN 交∠BCA 的平分线 于点E ,交∠BCA 的外角平分线于点F . (1)说明EO =FO ;(2)当点O 运动到何处时,四边形AECF 是矩形?说明你的结论.49.如图19-22,已知平行四边形ABCD ,AE 平分∠DAB 交DC 于E ,BF 平分∠ABC交DC 于F ,DC =6c m ,AD =2c m ,求DE 、EF 、FC 的长.A EBC F ONMD图19-13图19-22。
完整word版,几何证明题和应用题的复习(八年级上册湘教版)

几何证明题和应用题的复习(八年级上册湘教版)1、已知:如图,点D 在等边三角形ABC 的边AB 上,延长BC 至点E 使CE =AD ,连接DE 交AC 于点F ,求证:FD =FE 。
2、在Rt △ABC 中,AB =AC ,∠BAC =90°,O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论。
3、如图,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE=BD , 连结EC 、ED ,求证:CE=DE4、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 平分∠ABC ,DE ⊥BC 且BC =10,求△DCE 的周长。
AB COM NCBA D E F 5、如图所示,已知点D 是等边三角形ABC 的边BC 延长线上的一点,∠EBC=∠DAC ,CE ∥AB 。
求证:△CDE 是等边三角形。
AEBC6、如图,小红用一张长方形纸片ABCD 进行折纸,已知该纸片宽AB 为8cm 长BC 为10cm .当小红折叠时,顶点D 落在BC 边上的点F 处(折痕为AE ).想一想,此时EC 有多长?•7、如图,在△ABC 中,∠ABC=60°,AD 、CE 分别平分∠BAC 、∠ACB ,求证:AC=AE+CD .8、如图,ABC ∆为等边三角形,点,M N 分别在,BC AC 上,且BM CN =,AM 与BN 交于Q 点。
求AQN ∠ 的度数。
9、如图a ,△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共顶点C ,连接AF 和BE(1)线段AF 和BE 有怎样的大小关系?请证明你的结论; (2)将图a 中的△CEF 绕点C 旋转一定的角度,得到图b ,(1)中的结论还成立吗?作出判断并说明理由.10、为支援灾区,宁波市政府组织了20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运一种救灾物资且必须装满.根据表中提供的信息,解答下列问题:物资种类食品药品生活用品每辆汽车运载量(吨) 6 5 4每吨所需运费(元/吨)120 160 110(1)设装运食品的车辆数为x,装运药品的车辆数为y.求y与x的函数关系式;(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么车辆的安排有几种方案?并写出每种安排方案;(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?并求出最少总运费.11、甲、乙两人准备整理一批新到的实验器材.若甲单独整理需要40分钟完工:若甲、乙共同整理20分钟后,乙需再单独整理20分钟才能完工.(1)问乙单独整理多少分钟完工?(2)若乙因工作需要,他的整理时间不超过30分钟,则甲至少整理多少分钟才能完工?12、如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.13、如图,∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于E点.求证:∠E=∠A.14、如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.15、我市某学习机营销商经营某品牌A、B两种型号的学习机.用10000元可进货A型号的学习机5个,B型号的学习机10个;用11000元可进货A型号的学习机10个,B型号的学习机5个.(1)求A、B两种型号的学习机每个分别为多少元?(2)若该学习机营销商销售1个A型号的学习机可获利120元,销售1个B型号的学习机可获利90元,该学习机营销商准备用不超过30000元购进A、B两种型号的学习机共40个,且这两种型号的学习机全部售出后总获利不低于4440元,问有几种进货方案?这几种进货方案中,该学习机营销商将这些型号的学习机全部售出后,获利最大的是哪种方案?最大利润是多少?16、某厂有甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种现配制这种饮料10千克,要求至少含有4200单位的维生素C,并要求购买甲、乙两种原料的费用不超过72元,(1)设需用x千克甲种原料,写出x应满足的不等式组。
八年级数学-四边形经典练习提高题含答案

梯形菱形正方形综合练习(含答案)1、如图,在矩形ABCD 中,AB = 3,AD = 4,P 是AD 上不与A 、D 重合的一动点,PE ⊥AC ,PF ⊥BD ,E 、F 为垂足,则PE + PF 的值为( )A 、2B 、2.4C 、2.5D 、2.62、下列命题正确的是( )A 、 两邻边相等的四边形是菱形B 、一条对角线平分一个内角的平行四边形是菱形C 、对角线垂直且一组邻边相等的四边形是菱形D 、对角线垂直的四边形是菱形3、已知菱形的周长是高的8倍,则菱形较大的一个角是( )A 、100°B 、120°C 、135°D 、150°4.如图梯形ABCD 的两底长为AD =6,BC =10,中线为EF , 且∠B =90︒,若P 为AB 上的一点,且PE 将梯形ABCD 分成面积相同的两区域,则△EFP 与 梯形ABCD 的面积比为何?(A) 1:6 (B) 1:10 (C) 1:12 (D) 1:16 。
5.如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E 、F ,AD =4,BC =8,则AE +EF 等于()A .9B .10C .11D .126.如图,在等腰梯形ABCD 中,AB ∥CD , 对角线AC ⊥BC ,∠B =60º,BC =2cm ,则梯形ABCD的面积为( )D C B AEF P ACB D (第3题图)60°30°D C B AA .33cm 2B .6 cm 2 C.36cm 2D .12 cm 2 7.(1)梯形ABCD 中,AD ∥BC ,AB=CD=AD=2,∠B=60°,则下底BC 的长是( )A .3B .4C . 2D .5(2)已知等腰梯形的底角为45o ,高为2,上底为2,则其面积为(A )2 (B )6 (C )8 (D )128.如图,在等腰梯形ABCD 中,AC ⊥BD ,AC =6cm ,则等腰梯形ABCD 的面积为_____cm 2.9,在等腰梯形ABCD 中,AD ∥BC ,CD AD AB ==,若︒=∠60ABC ,12=BC ,则梯形ABCD 的周长为____________。
八年级数学四边形证明(四边形性质探索)拔高练习(含答案)

八年级数学四边形证明(四边形性质探索)拔高练
习
试卷简介:本卷共一道证明题,时间20分钟,满分100分。
学习建议:认真领会四边形证明的特征,寻找有利条件进行证明。
一、证明题(共1道,每道100分)
1.如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)证明:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
答案:(1)证明:∵AB∥CE ∴∠BAF=∠CEF,∠ABF=∠FCE 又∵AB=CD=CE ∴△ABF≌△ECF(ASA)(2)由△ABF≌△ECF得:AB=EC 再由题意中AB∥EC可得:四边形ABEC为平行四边形∵BC∥AD ∴∠D=∠BCE ∵∠AFC=2∠D ∴∠AFC=2∠BCE ∵∠AFC为△EFC的一个外角∴∠AFC=∠BCE+∠FEC 从而∠BCE=∠FEC,即EF=FC ∴AE=BC ∴四边形ABEC为矩形
解题思路:观察图形找矩形的判别条件
易错点:∠AFC=2∠D怎样运用
试题难度:四颗星知识点:平行四边形的判定
第 1 页共 1 页。
四边形几何证明综合应用

四边形几何证明综合应用第一篇:四边形几何证明综合应用1.已知:如图,E、F在ABCD的对角线BD上,BF=DE,B求证:四边形AECF是平行四边形.C2.如图,P是边长为1的正方形ABCD对角线AC上一动点(P 与A、C不重合),点E在射线BC上,且PE=PB.(1)求证:① PE =PD ;② PE⊥PD;(2)设AP=x, △PBE的面积为y.① 求出y关于x的函数关系式,并写出x的取值范围;② 当x取何值时,y取得最大值,并求出这个最大值.BED3.如图,在四边形ABCD中,点E是线段AD上的任意一点(E 与A,D不重合),G,F,H分别是BE,BC,CE的中点.(1)证明四边形EGFH是平行四边形;(2)在(1)的条件下,若EF⊥BC,且EF=证明平行四边形EGFH 是正方形.EHDBC,2BFC4.如图,在直角梯形ABCD 中,AD//BC,∠B=900,AB=8cm,AD=24cm,BC=26cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒.求:(1).t为何值时,四边形PQCD为平行四边形?(2).t为何值时,四边形ABQP为矩形?5.如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.(1)求∠2的度数.(2)求证:BO=BE.ABC6.已知:如图,D是△ABC的边BC上的中点,DE⊥AC,DF⊥AB,垂足分别为E、F,且BF=CE.当∠A满足什么条件时,四边形AFDE是正方形?请证明你的结论.7.如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.8.已知:如图,在正方形ABCD中,AC、BD交于点O,延长CB到点F,使BF=BC,连结DF交AB于E.求证:OE=()BF(在括号中填人一个适当的常数,再证明).9.(12分)已知:如图,在△ABC中,AB=AC,若将△ABC绕点C 顺时针旋转180°得到△FEC.(1)试猜想线段AE与BF有何关系?说明理由.(2)若△ABC的面积为3 cm2,请求四边形ABFE的面积.(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.10.已知:等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD相交与点O。
四边形几何证明题精选含解析
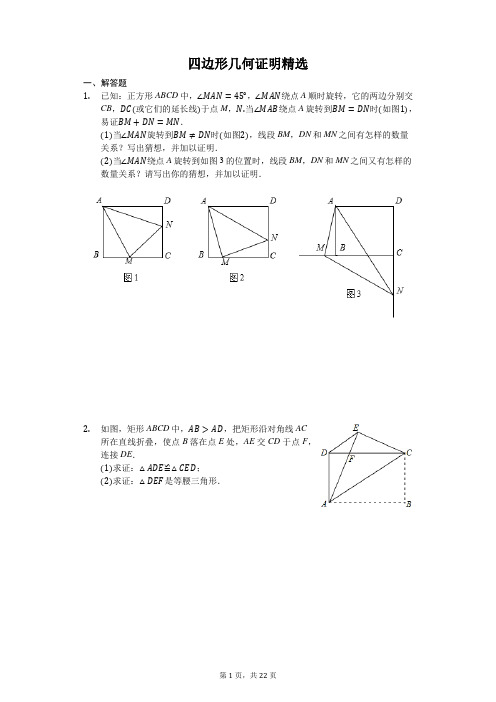
四边形几何证明精选一、解答题1.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAB绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请写出你的猜想,并加以证明.2.如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△ADE≌△CED;(2)求证:△DEF是等腰三角形.3.【问题情境】如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.【探究展示】(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.(2)如图2,若点E是BC边上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.【拓展延伸】(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.4.如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.(1)求证:△PCE是等腰直角三角形;(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.5.如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;(2)判断△CEF的形状,并说明理由.6.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;(2)将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并证明你的判断.7.如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.8.如图所示,E、F分别为平行四边形ABCD边AB、CD的中点,AG//DB交CB的延长线于点G.(1)求证:DE//BF;(2)若∠G=90°,判断四边形DEBF的形状,并说明理由.9.如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.求证:(1)△ADA′≌△CDE;(2)直线CE是线段AA′的垂直平分线.10.如图,在▱ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.11.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.12.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF//BC交CD于点O.(1)求证:OE=OF;(2)若点O为CD的中点,求证:四边形DECF是矩形.13.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.14.如图1,四边形ABCD是正方形,点G是BC边上任意一点.DE⊥AG于点E,BF//DE且交AG于点F.(1)求证:AE=BF;(2)如图2,如果点G是BC延长线上一点,其余条件不变,则线段AF、BF、EF有什么数量关系?请证明出你的结论.15.如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;(2)若AC=10,CF=6,求线段AG的长度.16.已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB延长线于点F,其它条件不变,OE=OF还成立吗?17.如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.(1)求证:四边形BEDF是平行四边形;(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.18.如图,EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.(1)求证:四边形BFDE是菱形;(2)若ED=5,BD=8,求菱形BFDE的面积.19.如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.(1)求证:四边形AECF为平行四边形;(2)当四边形AECF为菱形,M点为BC的中点时,求∠CBD的度数.20.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH//BC分别交AF,CD于G,H两点.(1)求证:DE=DC;(2)求证:AF⊥BF;答案和解析1.【答案】解:(1)BM +DN =MN 成立.证明:如图,把△ADN 绕点A 顺时针旋转90°,得到△ABE ,则可证得E 、B 、M 三点共线(图形画正确).∴∠EAM =90°−∠NAM =90°−45°=45°,又∵∠NAM =45°,∴在△AEM 与△ANM 中,{AE =AN ∠EAM =∠NAM AM =AM,∴△AEM≌△ANM(SAS),∴ME =MN ,∵ME =BE +BM =DN +BM ,∴DN +BM =MN ;(2)DN −BM =MN .在线段DN 上截取DQ =BM ,在△ADQ 与△ABM 中,∵{AD =AB∠ADQ =∠ABM DQ =MB,∴△ADQ≌△ABM(SAS),∴∠DAQ =∠BAM ,∴∠QAN =∠MAN .在△AMN 和△AQN 中,{AQ =AM ∠QAN =∠MAN AN =AN,∴△AMN≌△AQN(SAS),∴MN =QN ,∴DN −BM =MN .【解析】(1)结论:BM +DN =MN 成立,证得B 、E 、M 三点共线即可得到△AEM≌△ANM ,从而证得ME =MN .(2)结论:DN −BM =MN.首先证明△ADQ≌△ABM ,得DQ =BM ,再证明△AMN≌△AQN(SAS),得MN =QN ,本题考查正方形的性质、旋转变换等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.2.【答案】证明:(1)∵四边形ABCD 是矩形,∴AD =BC ,AB =CD .由折叠的性质可得:BC =CE ,AB =AE ,∴AD =CE ,AE =CD .在△ADE 和△CED 中,{AD =CEAE =CD DE =ED,∴△ADE≌△CED(SSS).(2)由(1)得△ADE≌△CED,∴∠DEA=∠EDC,即∠DEF=∠EDF,∴EF=DF,∴△DEF是等腰三角形.【解析】(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD= CE、AE=CD,进而即可证出△ADE≌△CED(SSS);(2)根据全等三角形的性质可得出∠DEF=∠EDF,利用等边对等角可得出EF=DF,由此即可证出△DEF是等腰三角形.本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质,解题的关键是:(1)根据矩形的性质结合折叠的性质找出AD=CE、AE=CD;(2)利用全等三角形的性质找出∠DEF=∠EDF.3.【答案】(1)证明:取AB的中点M,连结EM,如图1:∵M是AB的中点,E是BC的中点,∴在正方形ABCD中,AM=EC,∵CF是∠DCG的平分线,∴∠ECF=90°+45°=135°,∵BM=BE,∴∠BME=45°,∴∠AME=∠ECF=135°,∵∠BEA+∠CEF=90°,∠MAE+∠BEA=90°,∴∠MAE=∠CEF,在△AME与△ECF中,{∠MAE=∠CEF AM=EC∠AME=∠ECF,∴△AME≌△ECF(ASA),∴∠BAE+∠EFC=∠FCG=∠DCF;(2)证明:取AB上的任意一点M,使得AM=EC,连结EM,如图2:∵AE⊥EF,AB⊥BC,∴∠BAE+∠BEA=90°,∠BEA+∠CEF=90°,∴∠MAE=∠CEF,∵AM=EC,∴在正方形ABCD中,BM=BE,∴∠AME=∠ECF=135°,在△AME与△ECF中,{∠MAE=∠CEF AM=EC∠AME=∠ECF,∴△AME≌△ECF(ASA),∴∠BAE+∠EFC=∠FCG=∠DCF;(3)证明:取BA延长线上的一点N使得AN=CE,如图3:∵AN=CE,AB⊥BC,∴∠ANE=45°,∴∠ECF=∠ANE=45°,∵AD//BE,∴∠DAE=∠BEA,∵NA⊥AD,AE⊥EF,∴∠NAE=∠CEF,在△ANE与△ECF中,{∠NAE=∠CEFAN=CE∠ANE=∠ECF,∴△ANE≌△ECF(ASA),∴AE=EF.【解析】(1)取AB的中点M,连结EM,根据正方形的性质和全等三角形的判定证明即可;(2)在AB上取一点M,使AM=EC,连接EM,根据已知条件利用ASA判定△AME≌△ECF,利用全等三角形的性质证明即可.(3)在BA的延长线上取一点N,使AN=CE,连接NE,根据已知利用ASA判定△ANE≌△ECF,利用全等三角形的性质证明即可.此题主要考查全等三角形的判定和性质,关键是熟练掌握正方形的性质,角平分线的性质及全等三角形的判定方法.4.【答案】(1)证明:如图1中,∵四边形ABCD是正方形,∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,在△PDA和△PDC中,{PD=PD∠PDA=∠PDC DA=DC,∴△PDA≌△PDC,∴PA=PC,∠3=∠1,∵PA=PE,∴∠2=∠3,∴∠1=∠2,∵∠EDF=90°,∠DFE=∠PFC,∴∠FPC=∠EDF=90°,∴△PEC是等腰直角三角形.(2)解:如图2中,结论:△PCE是等边三角形.理由:∵四边形ABCD是菱形,∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,在△PDA和△PDC中,{PD=PD∠PDA=∠PDC DA=DC,∴△PDA≌△PDC,∴PA=PC,∠3=∠1,∵PA=PE,∴∠2=∠3,PA=PE=PC,∴∠1=∠2,∵∠DFE=∠PFC,∴∠EPC=∠EDC,∵∠ADC=120°,∴∠EDC=60°,∴∠EPC=60°,∵PE=PC,∴△PEC是等边三角形.【解析】本题考查正方形的性质、菱形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.(1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=∠EDF=90°,推出△PEC是等腰直角三角形;(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA=PE= PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形.5.【答案】(1)证明:∵四边形ABCD是正方形,∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,∴∠ABC−∠CBF=∠EBF−∠CBF,∴∠ABF=∠CBE.在△ABF和△CBE中,有{AB=CB∠ABF=∠CBE BF=BE,∴△ABF≌△CBE(SAS).(2)解:△CEF是直角三角形.理由如下:∵△EBF是等腰直角三角形,∴∠BFE=∠FEB=45°,∴∠AFB=180°−∠BFE=135°,又∵△ABF≌△CBE,∴∠CEB=∠AFB=135°,∴∠CEF=∠CEB−∠FEB=135°−45°=90°,∴△CEF是直角三角形.【解析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB= 135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.本题考查了正方形的性质.全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)根据判定定理SAS证明△ABF≌△CBE;(2)通过角的计算得出∠CEF=90°.本题属于中档题,难度不大,解决该题型题目时,通过正方形和等腰三角形的性质找出相等的边,再通过角的计算找出相等的角,以此来证明两三角形全等是关键.6.【答案】解:(1)延长BG交DE于点H,在△BCG与△DCE中,{BC=DC∠BCG=∠DCECG=CE,∴△BCG≌△DCE(SAS),∴∠GBC=∠EDC,BG=DE,∵∠BGC=∠DGH,∴∠DHB=∠BCG=90°,∴BG⊥DE;(2)BG=DE,BG⊥DE仍然成立如图2,∠BCD+∠DCG=∠ECG+∠DCG,即∠BCG=∠DCE,在△BCG与△DCE中,{BC=DC∠BCG=∠DCE CG=CE,∴△BCG≌△DCE(SAS),∵∠BHC=∠DHG,∴∠BCD=∠DOB=90°,即BG⊥DE【解析】(1)延长BG交DE于点H,易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠DHB=90°;(2)易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠BCD=90°.本题主要考查正方形,涉及正方形的性质,旋转的性质,全等三角形的判定与性质,综合程度较高,需要学生根据所学知识灵活解答.7.【答案】证明:如图所示:(1)∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,在△BAF和△DAF中,{AB=AD ∠BAF=∠DAF AF=AF ,∴△BAF≌△DAF(SAS),∴BF=DF;(2)∵BE的垂直平分线FG交对角AC于点F,∴BF=EF,∵BF=DF,∴EF=DF,∴∠FDE=∠FED,∵△BAF≌△DAF,∴∠ABF=∠FDE,∴∠ABF=∠FED,∵∠FED+∠FEA=180°,∴∠ABF+∠FEA=180°,∴∠BAE+∠BFE=180°,∴∠BFE=90°,∴BF⊥FE.【解析】(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF≌△DAF,得出对应边相等即可;(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE= 90°即可.本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、四边形内角和定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.8.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB//CD,AB=CD.∵点E、F分别是AB、CD的中点,∴BE=12AB,DF=12CD.∴BE=DF,BE//DF,∴四边形DFBE是平行四边形,(2)解:四边形DEBF 是菱形;理由如下:∵∠G =90°,AG//BD ,AD//BG ,∴四边形AGBD 是矩形,∴∠ADB =90°,在Rt △ADB 中∵E 为AB 的中点,∴AE =BE =DE ,∵四边形DFBE 是平行四边形,∴四边形DEBF 是菱形.【解析】(1)根据已知条件证明BE =DF ,BE//DF ,从而得出四边形DFBE 是平行四边形,即可证明DE//BF ,(2)先证明DE =BE ,再根据邻边相等的平行四边形是菱形,从而得出结论.本题主要考查了平行四边形的性质、菱形的判定,直角三角形的性质:在直角三角形中斜边中线等于斜边一半,比较综合,难度适中.9.【答案】证明:(1)∵四边形ABCD 是正方形,∴AD =CD ,∠ADC =90°,∴∠A′DE =90°,根据旋转的方法可得:∠EA′D =45°,∴∠A′ED =45°,∴A′D =ED ,在△AA′D 和△CED 中{AD =CD∠ADA′=∠CDE A′D =ED,∴△ADA′≌△CDE(SAS);(2)由正方形的性质及旋转,得CD =CB′,∠CB′E =∠CDE =90°,又CE =CE ,∴Rt △CEB′≌Rt △CED∴∠B′CE =∠DCE ,∵AC =A′C∴直线CE 是线段AA′的垂直平分线.【解析】(1)根据正方形的性质可得AD =CD ,∠ADC =90°,∠EA′D =45°,则∠A′DE =90°,再计算出∠A′ED =45°,根据等角对等边可得A′D =ED ,即可利用SAS 证明△ADA′≌△CDE ;(2)首先由AC =A′C ,可得点C 在AA′的垂直平分线上;再证明△AEB′≌△A′ED ,可得AE =A′E ,进而得到点E 也在AA′的垂直平分线上,再根据两点确定一条直线可得直线CE 是线段AA′的垂直平分线.此题主要考查了正方形的性质,以及旋转的性质,关键是熟练掌握正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;找准旋转后相等的线段.10.【答案】(1)证明:∵四边形ABCD 是平行四边形,∴AB//DF ,∴∠BAF =∠CFA .∵E 为BC 的中点,在△AEB和△FEC中,{∠BAE=∠CFA ∠AEB=∠FEC BE=EC,∴△AEB≌△FEC(AAS)∴AB=CF;(2)解:当BC=AF时,四边形ABFC是矩形,理由:∵AB=CF,AB‖CF,∴四边形ABFC是平行四边形,∵BC=AF,∴四边形ABFC是矩形.【解析】此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,正确得出△AEB≌△FEC(AAS)是解题关键.(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;(2)首先得出四边形ABFC是平行四边形,进而得出答案.11.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,∴四边形AEBD是平行四边形,∵AB=AC,AD是∠BAC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;(2)当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,∴AD=BD=CD,∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.【解析】(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识,熟练掌握正方形和矩形的判定是解题关键.12.【答案】证明:(1)∵CE平分∠BCD、CF平分∠GCD,∴∠BCE=∠DCE,∠DCF=∠GCF,∵EF//BC,∴∠BCE=∠FEC,∠EFC=∠GCF,∴∠DCE=∠FEC,∠EFC=∠DCF,∴OE=OC,OF=OC,∴OE=OF;(2)∵点O为CD的中点,∴OD=OC,又OE=OF,∵CE平分∠BCD、CF平分∠GCD,∴∠DCE=12∠BCD,∠DCF=12∠DCG,,即∠ECF=90°,∴四边形DECF是矩形.【解析】本题利用了角平分线的定义、平行线的性质、等角对等边、等量代换、平行四边形的判定、矩形的判定.(1)由于CE平分∠BCD,那么∠DCE=∠BCE,而EF//BC,于是∠FEC=∠BCE,等量代换∠FEC=∠DCE,那么OE=OC,同理OC=OF,等量代换有OE=OF;(2)由于O是CD中点,故OD=OC,而OE=OF,那么易证四边形DECF是平行四边形,又CE、CF是∠BCD、∠DCG的角平分线,∠BCD+∠DCG=180°那么易得∠ECF=90°,从而可证四边形DECF是矩形.13.【答案】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE//AC,AC=2DE,∵EF=2DE,∴EF//AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE;(2)解:当∠B=30°时,四边形ACEF是菱形;理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC=12AB=AE,∴△AEC是等边三角形,∴AC=CE,又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.【解析】(1)由三角形中位线定理得出DE//AC,AC=2DE,求出EF//AC,EF=AC,得出四边形ACEF是平行四边形,即可得出AF=CE;(2)由直角三角形的性质得出∠BAC=60°,AC=12AB=AE,证出△AEC是等边三角形,得出AC=CE,即可得出结论.本题考查了平行四边形的判定与性质、菱形的判定、三角形中位线定理、直角三角形斜边上的中线性质、等边三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形是等边三角形是解决问题的关键.14.【答案】(1)证明:∵四边形ABCD是正方形,BF⊥AG,DE⊥AG,∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,{∠BAF=∠ADE∠AFB=∠DEA=90°DA=AB,∴△ABF≌△DAE(AAS),∴BF=AE,(2)AF+EF=BF;∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,{∠BAF=∠ADE∠AFB=∠DEA=90°DA=AB,∴△ABF≌△DAE(AAS),∴BF=AE,AF=DE,∴AF+EF=BF.【解析】(1)根据正方形的四条边都相等可得DA=AB,再根据同角的余角相等求出∠BAF=∠ADE,然后利用“角角边”证明△ABF和△DAE全等,再根据全等三角形对应边相等可得BF=AE,AF=DE,然后根据图形列式整理即可得证;(2)根据题意作出图形,然后根据(1)的结论可得BF=AE,AF=DE,然后结合图形写出结论即可.本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,熟记正方形的四条边都相等,每一个角都是直角,然后求出三角形全等是解题的关键.15.【答案】(1)证明:∵AG//BD,BD=FG,∴四边形BGFD是平行四边形,∵CE⊥BD∴CE⊥AG,又∵BD为AC的中线,∴BD=DF=12AC,∴四边形BDFG是菱形;(2)解:∵四边形BDFG是菱形,∠ABC=90°,点D为AC的中点,∴GF=DF=12AC=5,∵CF⊥AG,∴AF=√AC2−CF2=√102−62=8,∴AG=AF+GF=8+5=13.【解析】(1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形;(2)由菱形的性质求得GF=DF=12AC=5,由勾股定理得AF的长,继而求得AG的长.本题主要考查了菱形的判定与性质、直角三角形斜边的中线的性质以及勾股定理,注意掌握数形结合思想是解答此题的关键.16.【答案】①证明:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,{∠BOE=∠AOF OB=OA ∠OBE=∠OAF ,∴△BOE≌△AOF(ASA),∴OE=OF;②解:OE=OF还成立;理由如下:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,{∠BOE=∠AOF OB=OA ∠OBE=∠OAF ,∴△BOE≌△AOF(ASA),∴OE=OF.【解析】本题考查了正方形的性质、全等三角形的判定与性质有关知识.①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.17.【答案】证明:(1)∵四边形ABCD是矩形,∴AB//DC、AD//BC,∴∠ABD=∠CDB,∵BE平分∠ABD、DF平分∠BDC,∴∠EBD=12∠ABD,∠FDB=12∠BDC,∴∠EBD=∠FDB,∴BE//DF,又∵AD//BC,∴四边形BEDF是平行四边形;(2)当∠ABE=30°时,四边形BEDF是菱形,∵BE平分∠ABD,∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,∵四边形ABCD是矩形,∴∠A=90°,∴∠EDB=90°−∠ABD=30°,∴∠EDB=∠EBD=30°,∴EB=ED,∴四边形BEDF是菱形.【解析】(1)由矩形可得∠ABD=∠CDB,结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB,即可知BE//DF,根据AD//BC即可得证;(2)当∠ABE=30°时,四边形BEDF是菱形,由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°,结合∠A=90°可得∠EDB=∠EBD=30°,即EB=ED,即可得证.本题主要考查矩形的性质、平行四边形、菱形,熟练掌握矩形的性质、平行四边形的判定与菱形的判定是解题的关键.18.【答案】(1)证明:∵EF垂直平分BD,∴OB=OD,∵四边形ABCD为平行四边形,∴AD//BC,∴∠EDO=∠FBO,∠DOE=∠BOF,∴△DOE≌△BOF(ASA),∴OE=OF,∴四边形AFCE为菱形;(2)解:∵BD=8,∴OD=4且ED=5,∴EO=3,∴S菱形BFDE =12BD×EF=EO·BD=3×8=24.【解析】本题主要考查平行四边形的性质、垂直平分线的性质,全等三角形的判定与性质以及菱形的判定与性质.(1)先证明△DOE≌△BOF,得出OE=OF,再根据EF垂直平分BD,可得出四边形BFDE 为菱形;(2)根据勾股定理可得出OE的长,根据菱形的面积求解即可.19.【答案】(1)证明∵四边形ABCD是平行四边形(已知),∴BC//AD(平行四边形的对边相互平行),∴∠ADE=∠CBD,AD=BC又∵AM丄BC(已知),∴AM⊥AD;∵CN丄AD(已知),∴AM//CN,∴AE//CF;在△ADE和△CBF中,{∠DAE=∠BCF AD=CB∠ADF=∠CBE∴△ADE≌△CBF(ASA),∴AE=CF(全等三角形的对应边相等),∴四边形AECF为平行四边形(对边平行且相等的四边形是平行四边形);(2)如图,连接AC交BF于点0,当四边形AECF为菱形时,则AC与EF互相垂直平分,∵BO=OD(平行四边形的对角线相互平分),∴AC与BD互相垂直平分,∴▱ABCD是菱形(对角线相互垂直平分的平行四边形是菱形),∴AB=BC(菱形的邻边相等);∵M是BC的中点,AM丄BC(已知),∴AB=AC(等腰三角形的性质),∴△ABC为等边三角形,∴∠ABC=60°,∠CBD=30°.【解析】(1)根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE//CF;然后由全等三角形的判定定理ASA推知△ADE≌△CBF;最后根据全等三角形的对应边相等知AE=CF,所以一组对边平行且相等的四边形是平行四边形;(2)根据M是BC的中点,AM丄BC(已知),可证明△ABC为等边三角形,然后根据三线合一定理即可求解.本题综合考查了全等三角形的判定与性质、菱形的判定与性质以及等边三角形的判定与性质等知识点.20.【答案】解:(1)∵四边形ABCD是矩形,∴AB//CD,∴∠DCE=∠CEB,∵EC平分∠DEB,∴∠DEC=∠CEB,∴∠DCE=∠DEC,∴DE=DC;(2)如图,连接DF,∵DE=DC,F为CE的中点,∴DF⊥EC,∴∠DFC=90°,在矩形ABCD中,AB=DC,∠ABC=90°,∴BF=CF=EF=12EC,∴∠ABF=∠CEB,∵∠DCE=∠CEB,∴∠ABF=∠DCF,在△ABF和△DCF中,{BF=CF∠ABF=∠DCF AB=DC,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,∴AF⊥BF;(3)CE=4√7.理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,∵EH//BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,∵∠ABF=∠CEB,∴∠BAF=∠FEH,∵∠EFG=∠AFE,∴△EFG∽△AFE,∴GFEF =EFAF,即EF2=AF⋅GF,∵AF⋅GF=28,∴EF=2√7,∴CE=2EF=4√7.【解析】(1)根据平行线的性质以及角平分线的定义,即可得到∠DCE=∠DEC,进而得出DE=DC;(2)连接DF,根据等腰三角形的性质得出∠DFC=90°,再根据直角三角形斜边上中线的性质得出BF=CF=EF=12EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;(3)根据等角的余角相等可得∠BAF=∠FEH,再根据公共角∠EFG=∠AFE,即可判定△EFG∽△AFE,进而得出EF2=AF⋅GF=28,求得EF=2√7,即可得到CE=2EF= 4√7.本题属于四边形综合题,主要考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质的综合应用,解决问题的关键是作辅助线,构造全等三角形.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.。
八年级 四边形 综合拔高训练 能力提升(含完整答案与解析)

1.如图,在四边形ABCD中,AB=CD,点E在DC的延长线上,连接BE交AD于点F,BE平分∠ABC,BC=EC,作FG⊥BA延长线于点G.(1)求证:四边形ABCD为平行四边形;(2)若F为AD中点,EF=6,BC=2,求GF的长.2.在四边形ABCD中,点E、F在对角线AC上,连接DE、BF,DE∥BF,DE=BF,AF =CE.(1)如图1,求证:四边形ABCD是平行四边形;(2)如图2,∠ABC=90°,DE⊥AC,连接BE、DF,请直接写出所有的全等的直角三角形.3.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,点O是AB的中点,连接DO 并延长到点E,使OE=OD,连接AE、BD.(1)求证:四边形AEBD是矩形;(2)当∠BAC=90°时,判断四边形AEBD的形状,并证明你的结论.4.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.(1)求证:四边形GHCD为平行四边形.(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.5.如图1,▱ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.(1)求证:四边形ABCD是菱形;(2)若∠ADC=60°,BE=2,求BD的长.6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接AE交OD于点F,连接CE、OE.(1)求证:四边形OCED为矩形;(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.7.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=,OE=2,求四边形ABCD的面积.8.如图,在△ABC中,AB=AC,AD是BC边的中线,AG平分△ABC的外角∠BAF,BE ⊥AG,垂足为E.(1)求证:四边形ADBE是矩形;(2)连结DE,交AB于点O,若BC=8,AO=,则△ABC的面积是:.9.如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作OE⊥BC交BC于点E.过点O作FG⊥AB交AB、CD于点F、G.(1)如图1,若BC=5,OE=3,求平行四边形ABCD的面积;(2)如图2,若∠ACB=45°,求证:AF+FO=EG.10.如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)求证:四边形AFHD为平行四边形;(3)连接EH,交BC于点O,若OC=OH,求证:EF⊥EG.答案与解析1.如图,在四边形ABCD中,AB=CD,点E在DC的延长线上,连接BE交AD于点F,BE平分∠ABC,BC=EC,作FG⊥BA延长线于点G.(1)求证:四边形ABCD为平行四边形;(2)若F为AD中点,EF=6,BC=2,求GF的长.【解答】(1)证明:∵BE平分∠ABC,BC=EC,∴∠ABF=∠CBE,∠CBE=∠E,∴∠ABF=∠E,∴AB∥CD,又∵AB=CD,∴四边形ABCD为平行四边形;(2)解:由(1)得:四边形ABCD为平行四边形,∴AD=BC=2,∵F为AD中点,∴AF=DF=,在△ABF和△DEF中,,∴△ABF≌△DEF(AAS),∴BF=EF=6,AB=DE,∵AB=CD,∴AB=CD=DE=CE=BC=,∵FG⊥AB,∴∠G=90°,∴GF2=AF2﹣AG2=BF2﹣BG2,即()2﹣AG2=62﹣(+AG)2,解得:AG=,∴GF==.【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解题的关键.2.在四边形ABCD中,点E、F在对角线AC上,连接DE、BF,DE∥BF,DE=BF,AF =CE.(1)如图1,求证:四边形ABCD是平行四边形;(2)如图2,∠ABC=90°,DE⊥AC,连接BE、DF,请直接写出所有的全等的直角三角形.【解答】(1)证明:∵DE∥BF,∴∠AFB=∠CED,在△ABF和△CDE中,,∴△ABF≌△CDE(SAS),∴AB=CD,∠BAF=∠DCE,∴AB∥CD,∴四边形ABCD是平行四边形;(2)解:图中所有的全等的直角三角形为△ABC≌△CDA,△ABF≌△CDE,△BEF≌△DFE,△BCF≌△DAE,理由如下:∵DE⊥AC,∴∠AED=∠CED=90°,由(1)得:△ABF≌△CDE,AB=CD,四边形ABCD是平行四边形,∴∠AFB=∠CED=90°,∴∠BFC=90°,∵∠ABC=90°,∴四边形ABCD是矩形,∴AD=BC,∠CDA=90°,在△ABC和△CDA中,,∴△ABC≌△CDA(SAS);同理:△ABF≌△CDE(SAS),△BEF≌△DFE(SAS),△BCF≌△DAE(SAS).【点评】本题考查了平行四边形的判定与性质、矩形的判定与性质、全等三角形的判定与性质等知识;熟练掌握平行四边形的判定与性质,证明三角形全等是解题的关键.3.如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,点O是AB的中点,连接DO 并延长到点E,使OE=OD,连接AE、BD.(1)求证:四边形AEBD是矩形;(2)当∠BAC=90°时,判断四边形AEBD的形状,并证明你的结论.【解答】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,∴四边形AEBD是平行四边形,∵AB=AC,AD是∠BAC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;(2)∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,∴AD=BD=CD,∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.【点评】此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识,熟练掌握正方形和矩形的判定是解题关键.4.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.(1)求证:四边形GHCD为平行四边形.(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.【解答】解:(1)证明:∵四边形ABCD是正方形,∴AD=DC,∠GAD=∠DCE=90°,在△GAD和△ECD中,,∴△GAD≌△ECD(SAS),∴DE=DG,∠GDA=∠EDC,∴∠GDA+∠ADF=∠EDC+∠ADF,即∠GDF=∠ADC=90°,∵DE⊥CH,∴∠DFH=∠CDF=90°,∴DG∥CH,∵∠HCB+∠HCD=∠EDC+∠DCF=90°,∴∠HCB=∠EDC,在△HBC和△ECD中,,∴△HBC和△ECD(ASA)∴CH=DE,∴DG=CH,∵DG∥CH,∴四边形GHCD为平行四边形;(2)∵△HBC≌△ECD,∴∠BHC=∠CED,∵∠ECF+∠FEC=90°,∴∠FEC,∠BHC与∠ECF互余;∵AD∥BC,∴∠ADE=∠DEC,∴∠ADE与∠ECF互余;∵∠DGA=∠CHB,∴∠DGA与∠ECF互余;∵∠DCF+∠ECF=90°,∴∠DCF与∠ECF互余;∴与∠ECF互余的角有:∠FEC、∠DCF、∠BHC、∠DGA、∠ADE.【点评】本题考查了全等三角形的性质和判定,平行线的性质和判定,正方形性质的应用,主要考查学生的推理能力.5.如图1,▱ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.(1)求证:四边形ABCD是菱形;(2)若∠ADC=60°,BE=2,求BD的长.【解答】(1)证明:∵AE∥BD,BE∥AC,∴四边形AEBO是平行四边形,∵四边形ABCD是平行四边形,∴DC=AB.∵OE=CD,∴OE=AB.∴平行四边形AEBO是矩形,∴∠BOA=90°.∴AC⊥BD.∴平行四边形ABCD是菱形;(2)解:由(1)得:四边形AEBO是矩形,四边形ABCD是菱形,∴OA=BE=2,AC⊥BD,BO=DO,∠ADO=30°,∴OD=OA=2,∴BD=2OD=4.【点评】本题考查了菱形的判定和性质,矩形的判定和性质,直角三角形的性质,平行四边形的判定与性质等知识;灵活运用有关性质是解题的关键.6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接AE交OD于点F,连接CE、OE.(1)求证:四边形OCED为矩形;(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.【解答】(1)证明:四边形ABCD是菱形,∴OA=OC=AC,AD=CD,∵DE∥AC且DE=AC,∴DE=OA=OC,∴四边形OADE、四边形OCED都是平行四边形,∵AC⊥BD,∴四边形OCED是矩形;(2)解:∵在菱形ABCD中,∠ABC=60°,∴AC=AB=6,∴在矩形OCED中,CE=OD==3.∴在Rt△ACE中,AE==3.【点评】本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用.注意证得四边形OCED是平行四边形,四边形OCED是矩形是关键.7.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=,OE=2,求四边形ABCD的面积.【解答】(1)证明:∵AB∥DC,∴∠ABD=∠CDB,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠CDB=∠CBD,∴BC=CD,且AB=BC,∴CD=AB,且AB∥CD,∴四边形ABCD是平行四边形,∵AB=BC,∴四边形ABCD是菱形;(2)解:由(1)得:四边形ABCD是菱形,∴OA=OC,BD⊥AC,BO=DO,∵CE⊥AB,∴AC=2OE=4,∴OA=2,∴OB===1,∴BD=2OB=2,∴菱形ABCD的面积=AC×BD=×4×2=4.【点评】本题考查了菱形的判定和性质,角平分线的定义,勾股定理,直角三角形的性质等知识;证明四边形ABCD为菱形是解本题的关键.8.如图,在△ABC中,AB=AC,AD是BC边的中线,AG平分△ABC的外角∠BAF,BE ⊥AG,垂足为E.(1)求证:四边形ADBE是矩形;(2)连结DE,交AB于点O,若BC=8,AO=,则△ABC的面积是:12.【解答】(1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,∴AD⊥BC,∠BAD=∠CAD,∴∠ADB=90°,∵AG为△ABC的外角∠BAF的平分线,∴∠BAE=∠F AE,∴∠DAE=90°,∵BE⊥AG,∴∠AEB=90°,∴四边形ADBE为矩形;(2)解:∵AD是BC边的中线,BC=8,∴BD=CD=4,由(1)得:四边形ADBE是矩形,∴AB=DE=2AO=5,在Rt△ABD中,AD===3,∴△ABC的面积=BC×AD=×8×3=12;故答案为:12.【点评】此题考查了矩形的判定与性质、等腰三角形的性质、勾股定理等知识;熟练掌握矩形的判定与性质是解题的关键.9.如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作OE⊥BC交BC于点E.过点O作FG⊥AB交AB、CD于点F、G.(1)如图1,若BC=5,OE=3,求平行四边形ABCD的面积;(2)如图2,若∠ACB=45°,求证:AF+FO=EG.【解答】解:(1)连接BD,∵平行四边形ABCD,∴BD过点O,∴S△OBC=BC•OE=×5×3=∴平行四边形ABCD的面积=4S△OBC=30;(2)过点E作EH⊥EG,与GC的延长线交于点H,如图2,∵OE⊥BC,∴∠OEG+∠OEC=∠GEC+∠CEH=90°,∴∠OEG=∠CEH,∵∠ACB=45°,∴∠COE=45°,∴OE=CE,∵平行四边形ABCD中,AB∥CD,又FG⊥AB,∴FG⊥CD,∴∠EOG+∠ECG=360°﹣90°﹣90°=180°,∵∠ECH+∠ECG=180°,∴∠EOG=∠ECH,∴△OEG≌△CEH(ASA),∴OG=CH,EG=EH,∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∴∠OAF=∠OCG,∵∠AOF=∠COG,∴△OAF≌△OCG(ASA),∴AF=CG,OF=OG,∵CG+CH=GH,∴AF+OF=GH,∵∠GEH=90°,EG=EH,∴GH=,∴AF+OF=EG.【点评】本题主要考查了平行四边形的性质,全等三角形的性质与判定,勾股定理,三角形的面积公式,关键是证明全等三角形.10.如图,点E为▱ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)求证:四边形AFHD为平行四边形;(3)连接EH,交BC于点O,若OC=OH,求证:EF⊥EG.【解答】(1)解:∵四边形ABCD是平行四边形,∴∠BAE=∠BCD=70°,AD∥BC,∵∠DCE=20°,∵AB∥CD,∴∠CDE=180°﹣∠BAE=110°,∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∠BAE=∠BCD,∵BF=BE,CG=CE,∴BC是△EFG的中位线,∴BC∥FG,BC=FG,∵H为FG的中点,∴FH=FG,∴BC∥FH,BC=FH,∴AD∥FH,AD∥FH,∴四边形AFHD是平行四边形;(3)证明:连接EH,CH,∵CE=CG,FH=HG,∴CH=EF,CH∥EF,∵EB=BF=EF,∴BE=CH,∴四边形EBHC是平行四边形,∴OB=OC,OE=OH,∵OC=OH,∴OE=OB=OC=BC,∴△BCE是直角三角形,∴∠FEG=90°,∴EF⊥EG.【点评】本题考查了平行四边形的判定与性质、三角形中位线定理、等腰三角形的性质以及三角形内角和定理;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.。
完整word版,八年级四边形几何证明提高题(经典)
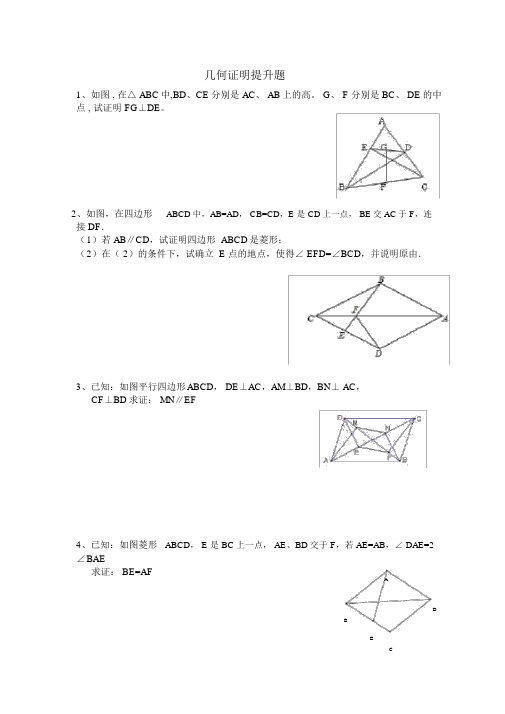
几何证明提升题1、如图 , 在△ ABC中,BD、CE分别是 AC、 AB上的高。
G、 F 分别是 BC、 DE的中点 , 试证明 FG⊥DE。
2、如图,在四边形ABCD中,AB=AD, CB=CD,E 是 CD上一点, BE交 AC于 F,连接 DF.(1)若 AB∥CD,试证明四边形 ABCD是菱形;(2)在( 2)的条件下,试确立 E 点的地点,使得∠ EFD=∠BCD,并说明原由.3、已知:如图平行四边形ABCD, DE⊥AC,AM⊥BD,BN⊥ AC,CF⊥BD求证: MN∥EF4、已知:如图菱形ABCD, E 是 BC上一点, AE、BD交于 F,若 AE=AB,∠ DAE=2 ∠BAE求证: BE=AFADBEC5、已知:如图正方形ABCD,P、Q分别是 BC、DC上的点,若∠1=∠2 求证: PB+QD=PAAD12QB CP6、已知:如图正方形ABCD,AC、 BD交于点 O,E、F 分别是 BC、OD的中点求证: AF⊥EFDAFOB CE7、已知:如图,,AB=BC,D、E 分别是 AB、BC上一点,DM AE 交 AC于 M,BN AE 交 AC于 N,若 BD BE 求证: MN NC 。
8、已知:如图, AB / /CD , AE ED , BF FC , EM / / AF 交 DC于 M,求证: FM AE 。
10、已知:如图,⊿ ABC 中,E、F 分别是 AB、BC中点, M、N是 AC上两点,EM、FN交于 D,若 AM=MN=NC,求证:四边形 ABCD是平行四边形。
11、已知:如图,1 2 , AB 3AC , BE AD ,求证: AD DE 。
12、已知:如图, AB / /CD ,D 900,BE EC DC ,求证:AEC 3 BAE 。
113、已知:如图, AD BC , B 2 C , BE EC ,求证: DE AB 。
214、已知:如图, AB DC , AE DE , BF FC ,FE 交 BA、CD的延伸线于 G、H,求证: 1 2 。
(完整版)初二上几何证明题100题专题训练(可编辑修改word版)
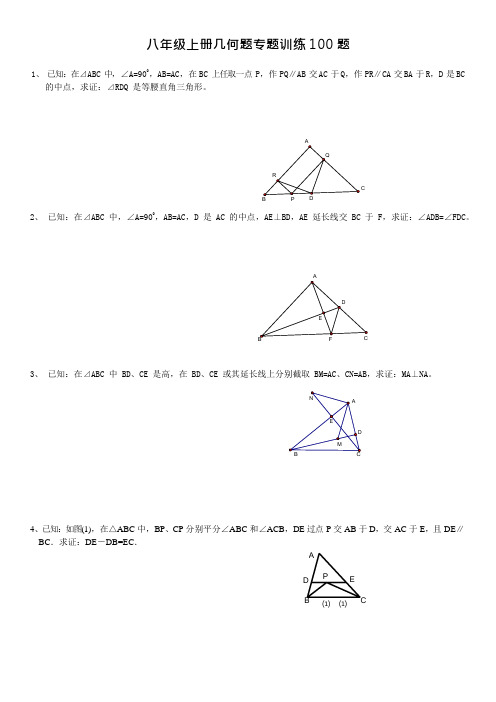
A D P E 八年级上册几何题专题训练 100 题1、 已知:在⊿ABC 中,∠A=900,AB=AC ,在 BC 上任取一点 P ,作 PQ∥AB 交 AC 于 Q ,作 PR∥CA 交 BA 于 R ,D 是 BC的中点,求证:⊿RDQ 是等腰直角三角形。
C2、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是 AC 的中点,AE⊥BD,AE 延长线交 BC 于 F ,求证:∠ADB=∠FDC。
3、 已知:在⊿ABC 中 BD 、CE 是高,在 BD 、CE 或其延长线上分别截取 BM=AC 、CN=AB ,求证:MA⊥NA。
4、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点 P 交 AB 于 D ,交 AC 于 E ,且 DE ∥ BC .求证:DE -DB=EC .BC5、在Rt△ABC 中,AB=AC,∠BAC=90°,O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A、B、C 的距离的大小关系(不要求证明);(2)如果点M、N 分别在线段AB、AC 上移动,在移动中保持AN=BM,请判断△OMN 的形状,并证明你的结论。
CNOA M B6、如图,△ABC 为等边三角形,延长BC 到D,延长BA 到E,AE=BD,连结EC、ED,求证:CE=DE7、如图,等腰三角形ABC 中,AB=AC,∠A=90°,BD 平分∠ABC,DE⊥BC 且BC=10,求△DCE 的周长。
8.如图,已知△EAB≌△DCE,AB,EC 分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.9.如图,点 E、A、B、F 在同一条直线上,AD 与BC 交于点 O, 已知∠CAE=∠DBF,AC=BD.求证:∠C=∠DC DOE B10.如图,OP 平分∠AOB,且OA=OB.(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);(2)从(1)中任选一个结论进行证明.11.已知:如图,AB=AC,DB=DC,AD 的延长线交 BC 于点E,求证:BE=EC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明提高题
1、如图,在△ABC 中,BD 、CE 分别是AC 、AB 上的高。
G 、F 分别是BC 、DE 的中点,试证明FG ⊥DE 。
2、如图,在四边形ABCD 中,AB=AD ,CB=CD ,E 是CD 上一点,BE 交AC 于F ,连接DF .
(1)若AB ∥CD ,试证明四边形ABCD 是菱形;
(2)在(2)的条件下,试确定E 点的位置,使得∠EFD=∠BCD ,并说明理由.
3、已知:如图平行四边形ABCD ,DE ⊥AC ,AM ⊥BD ,BN ⊥AC ,CF ⊥BD 求证:MN ∥EF
4、已知:如图菱形ABCD ,E 是BC 上一点,AE 、BD 交于F ,若AE=AB ,∠DAE=2∠BAE
求证:BE=AF
A
B
E
5、已知:如图正方形ABCD ,P 、Q 分别是BC 、DC 上的点,若∠1=∠2 求证:PB+QD=PA
6、已知:如图正方形ABCD ,AC 、BD 交于点O ,E 、F 分别是BC 、OD 的中点 求证:AF ⊥EF
7、已知:如图,,AB=BC ,D 、E 分别是AB 、BC 上一点,DM AE ⊥交AC 于M , BN AE ⊥交AC 于N ,若BD BE =求证:MN NC =。
8、已知:如图,//AB CD ,AE ED =,BF FC =,//EM AF 交DC 于M , 求证:FM AE =。
21C A P F O A
D
10、已知:如图,⊿ABC 中,E 、F 分别是AB 、BC 中点,M 、N 是AC 上两点,EM 、FN 交于D ,若AM=MN=NC ,求证:四边形ABCD 是平行四边形。
11、已知:如图,12∠=∠,3AB AC =,BE AD ⊥,求证:AD DE =。
12、已知:如图,//AB CD ,090D ∠=,BE EC DC ==,求证:3AEC BAE ∠=∠。
13、已知:如图,AD BC ⊥,2B C ∠=∠,BE EC =,求证:1
2
DE AB =。
14、已知:如图,AB DC =,AE DE =,BF FC =,FE 交BA 、CD 的延长线于G 、H ,求证:12∠=∠。
15、已知:如图,//AB CD ,090ADC ∠=,BE EC =,求证:2AED EDC ∠=∠。
16、已知:如图,正方形ABCD 中,E 是DC 上一点,DF ⊥AE 交BC 于F 求证:OE ⊥OF
17、如图,在四边形ABCD 中,AB=DC ,E 、F 分别是AD 、BC 的中点,G 、H 分别是BD 、AC 的中点,猜一猜EF 与GH 的位置关系,并证明你的结论.
O
F
E
D
C
B
A
18、如图,分别以△ABC 的三边为边长,在BC 的同侧作等边三角形ABD ,等边三角形BCE ,等边三角形ACF ,连接DE ,EF 。
求证:四边形ADEF 是平行四边形。
19、如图,点G 是正方形ABCD 对角线CA 的延长线上任意一点,以线段AG 为边作一个正方形AEFG ,线段EB 和GD 相交于点H . (1)求证:EB=GD ;
(2)判断EB 与GD 的位置关系,并说明理由;
(3)若AB=2,AG=错误!未找到引用源。
2,求EB 的长.
20、如图,以矩形OABC 的顶点O 为原点,OA 所在的直线为x 轴,OC 所在的直线为y 轴,建立平面直角坐标系.已知OA =3,OC =2,点E 是AB 的中点,在OA 上取一点D ,将△BDA 沿BD 翻折,使点A 落在BC 边上的点F 处. (1)直接写出点E 、F 的坐标;
(2)在x 轴、y 轴上是否分别存在点M 、N ,使得四边形MNFE 的周 长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
E
F
D
C
A。
