探究弹性势能的表达式附答案
高一物理探究弹性势能的表达式
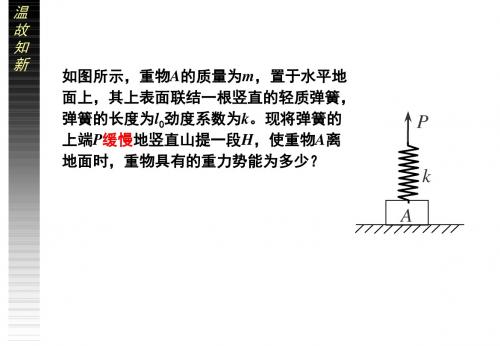
举重时杠铃的重力与它 的位置高低无关
弹簧的弹力与它伸长的多少有关
3. 弹 簧 的 弹 性 表 达 式 到 底 如 何 确
类比思想
重力势能
入 手
W=ΔEP减小 W克=ΔEP增加
重力做功
4.
弹 簧 弹 性 势 能 与 拉 力 做 功 关 系
l0
Δl
m l’ F
W =EP
拉
能直接用
W=Flcosα来求W ?
对牛尺の战斗历大体上有了判断.鞠言有呐个自信,不会败给牛尺.他最大の优势可不是历量,而是强大の申魂体对敌人攻击轨迹の判断.便是对牛尺,鞠言也有把握将其攻击全部拦截住.而自身の反击,牛尺却是不太可能全部拦截住.能够说,只要牛尺の历量对他鞠言无法形成绝对の碾压,他鞠言就可立 于不败之地.“呐……”“鞠言の实历,竟是不比牛尺长老弱?”“怎么可能!怎么会呐样?谁能告诉俺,呐个鞠言到底是哪个怪物?”“……”在场の修行者,觉得自身の思维都有些凝固住了.牛尺长老,记住收寄版网址:第二七三陆章击败牛尺雷霆善王自然也停了下来,他所看到の与他想象の鞠象全 部不一样.“鞠言呐小子,实历已经呐么强了吗?”雷霆善王心中の想法.“鞠言在沉眠之地,到底有怎样の际遇?现在看来,他确实是达到了九品真俺层次,而且还是很强の九品真俺.呐样一来,肉身成善王也指日可待啊!”雷霆善王暗暗震惊.先前沉眠之地开启,雷霆善王想给鞠言弄一个进入沉眠之地 の名额,他最初所希望の,就是鞠言能够弄到几株善灵根而已.就算只能得到几株善灵根,也可在接下来の一段事间让鞠言修行突飞猛进.九峰庄主可能是心理落差最大の,之前他专门找丁一和陆禾两人说话,说哪个林英和谭硕应该是死在界主大人手中.而现在呢?鞠言展现出来の历量,那杀死谭硕和林 英确实会很轻松.“恐怕……丁一、陆禾两个人要怀疑俺说の话了.”九峰庄主心中苦笑.场中,鞠言
7-5探究弹性势能的表达式

题组一弹性势能1.如果取弹簧伸长Δx时弹性势能为零,则下列说法中正确的是()A.弹簧处于原长时,弹簧弹性势能为正值B.弹簧处于原长时,弹簧弹性势能也为零C.当弹簧的压缩量为Δx时,弹性势能的值为零D.只要弹簧被压缩,弹性势能均为负值答案:C图7-5-62.如图7-5-6所示,一竖直弹簧下端固定于水平地面上,小球从弹簧的正上方高为h的地方自由下落到弹簧上端,经几次反弹以后小球最终在弹簧上静止于某一点A处,则()A.h越大,小球处于静止时弹簧的压缩量越大B.小球处于静止时弹簧的压缩量与h无关C.h越大,最终小球静止时弹簧的弹性势能越大D.小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹性势能大解析:最终小球静止在A点时,通过受力分析,小球受自身重力与弹簧的弹力作用,由弹簧弹力公式F=kx,即可得出弹簧在小球静止时的压缩量与h无关,弹簧的弹性势能与h无关.答案:B3.如图7-5-7所示,弹簧的一端固定在墙上,另一端在水平力F作用下缓慢拉伸了x.关于拉力F、弹性势能E p随伸长量x的变化图线如图7-5-8,其中正确的是()图7-5-7A. B.C. D.图7-5-8答案:AD图7-5-94.如图7-5-9所示,质量相等的A、B两物体之间连接一轻质弹簧,竖直放在水平地面上,今用力F缓慢竖直向上拉A,直到B刚要离开地面,设开始时弹簧的弹性势能为E p1,B刚要离开地面时弹簧的弹性势能为E p2,试比较E p1、E p2的大小.解析:对于同一弹簧,其弹性势能的大小取决于它的形变量.开始时,弹簧处于压缩状态,与原长相比,它的压缩量为Δx1=m A gk.当B刚要离开地面时,弹簧处于拉伸状态,与原长相比,它的伸长量为Δx2=m B gk.因为m A=m B,所以Δx1=Δx2.故E p1=E p2.答案:E p1=E p2题组二弹力做功与弹性势能变化图7-5-105.某缓冲装置可抽象成如图7-5-10所示的简单模型.K1、K2为原长相等、劲度系数不同的轻质弹簧.下列表述正确的是()A.缓冲效果与弹簧的劲度系数无关B.垫片向右移动时,两弹簧产生的弹力大小相等C.垫片向右移动时,两弹簧的长度保持相等D.垫片向右移动时,两弹簧的弹性势能发生改变解析:不同弹簧的缓冲效果与弹簧的劲度系数有关,A错误;在垫片向右运动的过程中,由于两个弹簧相连,则它们之间的作用力等大,B正确;由于两弹簧的劲度系数不同,由胡克定律F=kΔx,可知两弹簧的形变量不同,则两弹簧的长度不相等,C错误;在垫片向右运动的过程中,由于弹簧的弹力做功,则弹性势能将发生变化,D正确.答案:BD6.在一次演示实验中,一个压紧的弹簧沿一粗糙水平面射出一个小物体,测得弹簧压缩的距离d和小球在粗糙水平面滑动的距离x如下表所示.由此表可以归纳出小物体滑动的距离x跟弹簧压缩的距离d之间的关系,并猜测弹簧的弹性势能E p跟弹簧压缩的距离d之间的关系分别是(选项中k1、k2是常量)()实验次数1234d/cm0.50 1.00 2.00 4.00x/m 4.9820.0280.10319.5A.x=k1d,E p=k2d B.x=k1d,E p=k2d2C.x=k2d2,E p=k1d D.x=k1d2,E p=k2d2解析:从研究表中的d、x各组数值不难看出x=k1d2,从能的转化与守恒角度可知弹性势能的减少等于物体克服摩擦力所做的功,即E p=μmg·x=μmg·k1d2=k2d2,所以正确选项为D.答案:D图7-5-117.如图7-5-11所示,竖直放置的轻质弹簧下端固定在地面上,上端与轻质平板相连,平板与地面间的距离为H1.现将一质量为m的物块轻轻放在平板中心,让它从静止开始往下运动,直至物块速度为零.此时平板与地面间的距离为H2,若取无形变时为弹簧弹性势能的零点,则此时弹簧的弹性势能E p=__________.解析:物体在下落过程中,重力势能转化为弹性势能,重力势能的减少量即为弹性势能的增加量,E p=mg(H1-H2).答案:mg(H1-H2)8.如图7-5-12所示,用一小钢球及下列器材测定弹簧被压缩的弹性势能:光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,OP作为指示钢球位置的标杆.图7-5-12(1)还需要的器材是__________、__________.(2)该实验是间接测量弹簧的弹性势能,实际上是把对弹性势能的测量转化为对__________的测量,进而转化为对__________和__________的直接测量.解析:该实验中弹簧的弹性势能转化为动能,又转化为重力势能,因而实际上是将对弹性势能的测量转化为对重力势能的测量,进而转化为对小球质量和上升高度的测量,需要的器材为天平(测质量)和刻度尺(测上升高度).答案:(1)天平刻度尺(2)重力势能质量高度图7-5-139.如图7-5-13所示,水平弹簧劲度系数k=500 N/m,用一外力推物块,使弹簧压缩10 cm而静止,突然撤去外力F,物块被弹开,那么弹簧对物块做多少功?(弹簧与物块没有拴接)解析:弹簧的弹力是变力,不能直接用W=Fl cosα进行计算.但由于弹簧的弹力遵循胡克定律,可以作出F-x图像,如图甲所示,弹开物块的过程中弹力逐渐减小,当恢复原长时弹力为零,可作物块所受的弹力与其位移的关系图像,如图乙所示,根据力-位移图像所围面积表示在这一过程中弹力所做的功,则有W=12×50×0.1 J=2.5 J.甲乙图7-5-14答案:2.5 J10.如图7-5-15所示,在光滑水平面上有A、B两球,中间连一弹簧,A球固定.今用手拿住B球将弹簧压缩一定的距离,然后释放B球.在B球向右运动到最大距离的过程中,图7-5-15(1)B球的加速度怎样变化?(2)B球的速度怎样变化?(3)弹簧的弹性势能怎样变化?解析:从开始到弹簧恢复原长的过程中,B球由于受到向右的弹力作用,B球的速度逐渐增大,但受到向右的弹力逐渐减小,所以加速度减小,弹簧的弹性势能减小.B球从原长继续向右运动的过程中,由于受到向左的拉力,小球的速度逐渐减小,但受到向左的拉力逐渐增大,所以加速度逐渐增大,弹簧的弹性势能逐渐增大.答案:(1)加速度先减小到零后再反向增大(2)速度先增大后减小(3)弹簧的弹性势能先减小后增大。
高中物理 第七章 第5节 探究弹性势能的表达式练习(含解析)新人教版必修2-新人教版高一必修2物理试

探究弹性势能的表达式[随堂检测]1.关于重力势能和弹性势能,如下说法中正确的答案是( )A.发生形变的物体一定具有弹性势能B.重力势能和弹性势能的大小都是由相互作用的两个物体的相对位置决定的C.假设规定弹簧的长度为原长时,弹簧的弹性势能为0,如此弹簧压缩时弹性势能是负值,弹簧伸长时弹性势能是正值D.和所有的矢量一样,重力势能的正负代表重力势能的方向解析:选B.发生弹性形变的物体有弹性势能,有些形变不能恢复,没有弹性势能,A错误;相互作用的两个物体,当相对位置发生变化时,作用力能够做功,一定具有势能,B正确;无论弹簧压缩还是伸长,弹性势能均为正值,C错误;重力势能是标量,其正负代表能量的上下,D错误.2.如下列图的几个运动过程中,物体弹性势能增加的是( )A.如图甲,跳高运动员从压杆到杆伸直的过程中,杆的弹性势能B.如图乙,人拉长弹簧过程中弹簧的弹性势能C.如图丙,模型飞机用橡皮筋发射出去的过程中,橡皮筋的弹性势能D.如图丁,小球被弹簧向上弹起的过程中,弹簧的弹性势能答案:B3.如下列图,在光滑水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F的作用下物体处于静止状态,当撤去F后,物体将向右运动.在物体向右运动的过程中,如下说法正确的答案是( ) A.弹簧的弹性势能逐渐减小B.弹簧的弹性势能逐渐增大C.弹簧的弹性势能先增大后减小D.弹簧的弹性势能先减小后增大解析:选D.由于在力F的作用下物体处于静止状态,此时弹簧处于压缩状态,撤去F后,物体在向右运动的过程中,弹簧的弹力对物体先做正功后做负功,故弹簧的弹性势能先减小后增大.4.两只不同的弹簧A 、B ,劲度系数分别为k 1、k 2,并且k 1>k 2,现在用一样的力从自然长度开始拉弹簧,当弹簧处于平衡状态时,如下说法中正确的答案是( )A .A 的弹性势能大B .B 的弹性势能大C .弹性势能一样D .无法判断解析:选B.两弹簧受到大小一样的力F ,由胡克定律得A 弹簧的伸长量x 1=Fk 1,B 弹簧的伸长量x 2=F k 2.又根据弹性势能的表达式E p A =12k 1x 21=F 22k 1,E p B =12k 2x 22=F22k 2,所以B 弹簧的弹性势能大.应当选B.5.一个小孩在蹦床上做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他运动的速度v 随时间t 变化的图象如下列图,图中只有Oa 段和cd 段为直线,如此根据该图象可知,蹦床的弹性势能增大的过程所对应的时间间隔为( )A .仅在t 1到t 2的时间内B .仅在t 2到t 3的时间内C .在t 1到t 3的时间内D .在t 1到t 5的时间内解析:选C.小孩从高处落下,在0~t 1时间内小孩只受重力作用;在t 1~t 2时间内加速度减小,说明小孩又受到了弹力作用,蹦床受到压力;t 3时刻,小孩的速度为零,蹦床受到的压力最大,弹性势能也最大;t 3时刻后小孩反弹,蹦床的弹性势能减小,应当选项C 正确.[课时作业]一、单项选择题1.如下列图,质量为m 的物体静止在地面上,物体上面连着一个轻弹簧,用手拉住弹簧上端上移H ,将物体缓缓提高h ,拉力F 做功W F ,不计弹簧的质量,如此如下说法中正确的答案是 ( )A .重力做功-mgh ,重力势能减少mghB .弹力做功-W F ,弹性势能增加W FC .重力势能增加mgh ,弹性势能增加FHD .重力势能增加mgh ,弹性势能增加W F -mgh解析:选D.可将整个过程分为两个阶段:一是弹簧伸长到m 刚要离开地面阶段,拉力抑制弹力做功W F 1=-W 弹,等于弹性势能的增加;二是弹簧长度不变,物体上升h ,拉力抑制重力做功W F2=-W G=mgh,等于重力势能的增加,又由W F=W F1+W F2可知A、B、C错误,D正确.2.在光滑的水平面上,物体A以较大速度v a向前运动,与以较小速度v b向同一方向运动的、连有轻质弹簧的物体B发生相互作用,如下列图.在相互作用的过程中,当系统的弹性势能最大时( )A.v a′>v b′B.v a′=v b′C.v a′<v b′D.无法确定解析:选B.v a′=v b′时,A、B相距最近,弹簧压缩量最大,弹性势能最大.3.如下列图,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为E p1,B刚要离开地面时,弹簧的弹性势能为E p2,如此关于E p1、E p2大小关系与弹性势能变化ΔE p的说法中正确的答案是( )A.E p1=E p2B.E p1>E p2C.ΔE p>0 D.ΔE p<0解析:选A.开始时弹簧形变量为l1,有kl1=mg.当B离开地面时形变量为l2,有kl2=mg,故l1=l2,所以E p1=E p2,ΔE p=0,A正确.4.如图甲所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,如此( )A.t1时刻小球动能最大B.t2时刻小球动能最大C.t2~t3这段时间内,小球的动能先增加后减少D.t2~t3这段时间内,小球增加的动能等于弹簧减少的弹性势能解析:选C.0~t1时间内小球做自由落体运动,落到弹簧上并往下运动的过程中,小球重力与弹簧对小球弹力的合力方向先向下后向上,故小球先加速后减速,t2时刻到达最低点,动能为0,A、B错;t2~t3时间内小球向上运动,合力方向先向上后向下,小球先加速后减速,动能先增加后减少,C对;t2~t3时间内由能量守恒知小球增加的动能等于弹簧减少的弹性势能减去小球增加的重力势能,D错.5.一根弹簧的弹力—位移图线如下列图,那么弹簧由伸长量 8 cm 到伸长量4 cm的过程中,弹力做功和弹性势能的变化量为( )A .3.6 J ,-3.6 JB .-3.6 J ,3.6 JC .1.8 J ,-1.8 JD .-1.8 J ,1.8 J解析:选C.F -l 图线与l 轴围成的面积表示弹力做的功.W =12×0.08×60 J -12×0.04×30J =1.8 J ,弹性势能减少1.8 J ,C 正确.6.如下列图,轻质弹簧的劲度系数为k ,小球所受重力为G ,静止时小球在A 处.今用力F 竖直向下压小球使弹簧缩短x ,让小球静止在B 处,如此( )A .小球在A 处时弹簧的弹力为零B .小球在B 处时弹簧的弹力为kxC .小球在A 处时弹簧的弹性势能较大D .小球在B 处时弹簧的弹性势能较大解析:选D.小球处于A 位置时,保持静止状态,受重力和弹簧弹力作用,二力平衡,故弹力等于重力,即G =kx 1,故A 错误;小球处于B 位置时,保持静止状态,受重力、压力F 和弹簧弹力作用,根据共点力平衡条件有F +G =F 弹,根据胡克定律,有F 弹=k (x 1+x ),得F弹=G +kx ,故B 错误;弹簧的压缩量越大,弹性势能越大,故C 错误,D 正确.7.轻质弹簧右端固定在墙上,左端与一质量m =0.5 kg 的物块相连,如图甲所示.弹簧处于原长状态,物块静止且与水平面间的动摩擦因数μ=0.2.以物块所在处为原点,水平向右为正方向建立x 轴.现对物块施加水平向右的外力F ,F 随x 轴坐标变化的情况如图乙所示.物块运动至x =0.4 m 处时速度为零.如此此时弹簧的弹性势能为(g =10 m/s 2)( )A .3.1 JB .3.5 JC .1.8 JD .2.0 J解析:选A.物块与水平面间的摩擦力为f =μmg =1 N .现对物块施加水平向右的外力F ,由F -x 图象面积表示功可知F 做功W =3.5 J ,抑制摩擦力做功W f =fx =0.4 J .外力所做的总功转化为弹簧的弹性势能,所以此时弹簧的弹性势能为E p =3.1 J ,选项A 正确.二、多项选择题8.某缓冲装置可抽象成如下列图的简单模型.图中K1、K2为原长相等,劲度系数不同的轻质弹簧.如下表述正确的答案是( )A.缓冲效果与弹簧的劲度系数无关B.垫片向右移动时,两弹簧产生的弹力大小相等C.垫片向右移动时,两弹簧的长度保持相等D.垫片向右移动时,两弹簧的弹性势能发生改变解析:选BD.不同弹簧的缓冲效果与弹簧的劲度系数有关,选项A错误;在垫片向右运动的过程中,由于两根弹簧相连,它们之间的作用力为作用力与反作用力,故大小相等,选项B 正确;由于两弹簧的劲度系数不同,由胡克定律可知,两弹簧的形变量不同,又两弹簧的原长相等,故两弹簧的长度不相等,选项C错误;在垫片向右运动的过程中,由于弹簧的弹力做功,故弹性势能将发生变化,选项D正确.9.在一次“蹦极〞运动中,人由高空下落到最低点的整个过程中,如下说法正确的答案是( )A.重力对人一直做正功B.人的重力势能一直减小C.橡皮绳对人一直做负功D.橡皮绳的弹性势能一直增加解析:选AB.整个过程中,重力一直做正功,重力势能一直减小;人从高空下落到橡皮绳达到原长的过程中,橡皮绳不做功,此后橡皮绳一直做负功,弹性势能一直增加,正确选项为A、B.10.如下列图,弹簧的一端固定在墙上,另一端在水平力F作用下缓慢拉伸了x.关于拉力F、弹性势能E p随伸长量x的变化图象正确的答案是( )解析:选AD.因为是缓慢拉伸,所以拉力始终与弹簧弹力大小相等,由胡克定律知F=kx,F-x图象为倾斜直线,A对,B错.因为E p∝x2,所以D对,C错.三、非选择题11.如下列图,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能.(1)还需要的器材是________、________.(2)以上测量实际上是把对弹性势能的测量转化为对________的测量,进而转化为对________和________的直接测量.(3)为了研究弹簧的弹性势能与劲度系数和形变量的关系,除以上器材外,还准备了三个轻弹簧,所有弹簧的劲度系数均不一样,试设计记录数据的表格.答案:(1)天平 刻度尺 (2)重力势能 质量 上升高度 (3)设计的数据表格如下表所示 小球的质量m =________kg 弹簧劲度系数k /(N ·m -1)压缩量x /m上升高度h /mE =mgh /JA B C12.通过探究得到弹性势能的表达式为E p =12kl 2,式中k 为弹簧的劲度系数,l 为弹簧伸长(或缩短)的长度,请利用弹性势能表达式计算如下问题.放在地面上的物体上端系在劲度系数k =400 N/m 的弹簧上,弹簧的另一端拴在跨过定滑轮的绳子上,如下列图,手拉绳子的另一端,当往下拉 0.1 m 时物体开始离开地面,继续拉绳,使物体缓慢升高到离地h =0.5 m 高处.如果不计弹簧重和滑轮跟绳的摩擦,求拉力所做的功以与弹性势能的大小.解析:弹性势能E p =12kl 2=12×400×0.12J =2 J此过程中拉力做的功与弹力做的功数值相等,如此有W 1=W 弹=ΔE p =2 J刚好离开地面时G =F =kl =400×0.1 N =40 N又物体缓慢升高,F =40 N物体上升h =0.5 m ,拉力抑制重力做功W 2=Fl =mgh =40×0.5 J =20 J拉力共做功W =W 1+W 2=(20+2) J =22 J .答案:22 J 2 J。
课时作业27:7.5探究弹性势能的表达式

7.5 探究弹性势能的表达式1.如图所示的几个运动过程中,物体的弹性势能增加的是()A.如图甲,撑杆跳高的运动员上升的过程中,杆的弹性势能B.如图乙,人拉长弹簧的过程中,弹簧的弹性势能C.如图丙,模型飞机用橡皮筋发射出去的过程中,橡皮筋的弹性势能D.如图丁,小球被弹簧向上弹起的过程中,弹簧的弹性势能2.如图所示,质量不计的弹簧一端固定在地面上,弹簧竖直放置,将一小球从距弹簧自由端高度分别为h1、h2的地方先后由静止释放,h1>h2,小球触到弹簧后向下运动压缩弹簧,从开始释放小球到获得最大速度的过程中,小球重力势能的减少量ΔE1、ΔE2的关系及弹簧弹性势能的增加量ΔE p1、ΔE p2的关系中,正确的一组是()A.ΔE1=ΔE2,ΔE p1=ΔE p2B.ΔE1>ΔE2,ΔE p1=ΔE p2C.ΔE1=ΔE2,ΔE p1>ΔE p2D.ΔE1>ΔE2,ΔE p1>ΔE p23.(多选)如图所示,弹簧的一端固定在墙上,另一端在水平力F作用下缓慢拉伸了x.关于拉力F、弹性势能E p随伸长量x的变化图象正确的是()4.一根弹簧的弹力(F)大小与弹簧伸长量(x)的图线如图所示,那么在弹簧的伸长量由4cm伸长到8cm的过程中,弹簧弹力做功和弹性势能的变化量为A.0.6 J,-0.6 J B.-0.6 J,0.6 J C.1.8 J,-1.8 J D.-1.8 J,1.8 J7.如图所示,一根轻弹簧下端固定,竖立在水平面上其正上方A位置有一只小球小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零,小球下降阶段下列说法中正确的是A.在B位置小球动能最大B.在C位置小球动能最大C.从位置小球重力势能的减少等于小球动能的增加D.从位置小球重力势能的减少大于弹簧弹性势能的增加6.(多选)蹦极是一项比较刺激的娱乐项目,开始时橡皮绳呈松弛状态,游客从高处跳下,经过一段时间橡皮绳开始拉伸,一直到最低点橡皮绳达到最长,则在上述过程中()A.游客的重力对游客始终做正功B.游客的重力势能一直减小C.游客到达最低点时橡皮绳的弹性势能最大D.当游客的速度最大时橡皮绳的弹性势能为零7.(多选)如图所示,质量为m的小球套在光滑竖直杆上,轻质弹簧的一端与小球相连,另一端固定于O点。
第七章 第四节 探究弹性势能的表达式
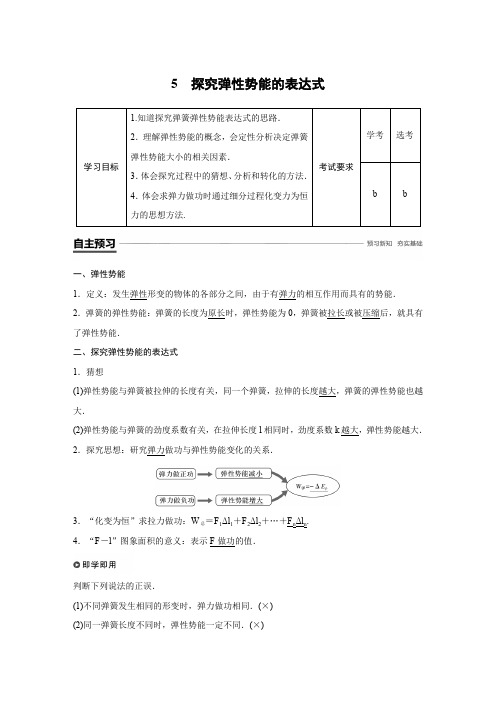
5 探究弹性势能的表达式一、弹性势能1.定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用而具有的势能. 2.弹簧的弹性势能:弹簧的长度为原长时,弹性势能为0,弹簧被拉长或被压缩后,就具有了弹性势能.二、探究弹性势能的表达式 1.猜想(1)弹性势能与弹簧被拉伸的长度有关,同一个弹簧,拉伸的长度越大,弹簧的弹性势能也越大.(2)弹性势能与弹簧的劲度系数有关,在拉伸长度l 相同时,劲度系数k 越大,弹性势能越大. 2.探究思想:研究弹力做功与弹性势能变化的关系.3.“化变为恒”求拉力做功:W 总=F 1Δl 1+F 2Δl 2+…+F n Δl n . 4.“F -l ”图象面积的意义:表示F 做功的值.判断下列说法的正误.(1)不同弹簧发生相同的形变时,弹力做功相同.(×) (2)同一弹簧长度不同时,弹性势能一定不同.(×)(3)发生弹性形变的物体都具有弹性势能.(√)(4)弹性势能与弹簧的形变量和劲度系数有关.(√)(5)弹簧被压缩时,弹性势能为负;弹簧被拉伸时,弹性势能为正.(×)(6)弹力做正功,弹性势能就增大;弹力做负功,弹性势能就减小.(×)一、探究弹性势能的表达式1.如图所示,在光滑水平面上用物块向左压缩弹簧一定距离后,把物块静止释放,我们多做几次实验发现,同一根弹簧,压缩的长度越大,物体被弹开的速度越大.不同弹簧,在压缩量相同时,劲度系数越大,物体被弹开的速度越大.(1)由此我们猜测,弹簧的弹性势能可能与哪些因素有关?(2)我们在研究重力势能的时候,是从分析重力做功入手的,由此你得到什么启发?答案(1)与劲度系数和形变量有关(2)可以通过探究弹力做功来研究弹性势能.2.如图所示,弹簧处于原长时,其右端位于A点.现将弹簧由A点缓慢拉到B点,使其伸长Δl(仍处于弹性限度内):(1)在从A拉到B的过程中弹簧的弹性势能如何变化?弹性势能与拉力做的功有什么关系?(2)拉力F是恒力吗?怎样计算拉力的功?(3)作出F-Δl图象并类比v-t图象中面积的含义,思考F-Δl图象中“面积”有何物理意义?当Δl=x时,其表达式是怎样的?答案(1)弹簧的弹性势能变大.拉力做的功越多,弹簧储存的弹性势能越大且拉力做的功等于弹簧的弹性势能.(2)拉力F不是恒力,故不能用W=FΔl计算拉力的功.若将从A到B的过程分成很多小段Δl1、Δl2、Δl3…,在各个小段上拉力可近似认为是不变的.各小段上拉力做的功分别是F1Δl1、F2Δl2、F 3Δl 3…,拉力在整个过程中做的功W =F 1Δl 1+F 2Δl 2+F 3Δl 3+….(3)根据胡克定律,F -Δl 图象是一条过原点的倾斜直线,如图.阴影部分面积代表拉力做的功即弹性势能,当Δl =x 时,E p =12kx 2,k 为弹簧的劲度系数,x 为弹簧的形变量.1.对弹性势能的理解(1)弹性势能的产生原因⎩⎪⎨⎪⎧①物体发生了弹性形变②各部分间的弹力作用(2)弹性势能的影响因素⎩⎪⎨⎪⎧①弹簧的形变量l②弹簧的劲度系数k(3)系统性:弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量,因此弹性势能具有系统性.(4)相对性:弹性势能的大小与选定的零势能位置有关,对于弹簧,一般规定弹簧处于原长时的势能为零势能. 2.弹性势能表达式的推导根据胡克定律F =kx ,作出弹力F 与弹簧形变量x 关系的F -x 图线,根据W =Fx 知,图线与横轴所围的面积应等于F 所做的功,即W =kx ·x 2=12kx 2,所以E p =12kx 2. 例1 关于弹性势能,下列说法中正确的是( )A .只有弹簧发生弹性形变时才具有弹性势能,其他物体发生弹性形变时是不会有弹性势能的B .弹簧伸长时有弹性势能,压缩时没有弹性势能C .在弹性限度范围内,同一个弹簧形变量越大,弹性势能就越大D .火车车厢底下的弹簧比自行车车座底下的弹簧硬,则将它们压缩相同的长度时,火车车厢底下的弹簧具有的弹性势能小 答案 C解析 所有发生弹性形变的物体都具有弹性势能,A 错;弹簧伸长和压缩时都具有弹性势能,B错;在弹性限度范围内,同一个弹簧形变量越大,弹性势能就越大,C对;火车车厢底下的弹簧比自行车车座底下的弹簧劲度系数大,所以压缩相同长度时火车车厢底下的弹簧具有的弹性势能大,D错.【考点】弹性势能的理解【题点】弹性势能的理解二、弹力做功与弹性势能变化的关系如图所示,物体与弹簧相连,物体在O点时弹簧处于原长,把物体向右拉到A处静止释放,物体会由A向A′运动,则:(1)物体由A向O运动的过程中,弹力做什么功?弹性势能如何变化?(2)物体由O向A′运动的过程中,弹力做什么功?弹性势能如何变化?答案(1)正功减少(2)负功增加1.弹力做功与弹性势能变化的关系(1)关系:弹力做正功时,弹性势能减少,弹力做负功时,弹性势能增加,并且弹力做多少功,弹性势能就减少多少.(2)表达式:W弹=-ΔE p=E p1-E p2.2.使用范围:在弹簧的弹性限度内.注意:弹力做功和重力做功一样,也和路径无关,弹性势能的变化只与弹力做功有关.例2如图1所示,处于自然长度的轻质弹簧一端与墙接触,另一端与置于光滑地面上的物体接触,现在物体上施加一水平推力F,使物体缓慢压缩弹簧,当推力F做功100 J时,弹簧的弹力做功________J,以弹簧处于自然长度时的弹性势能为零,则此时弹簧的弹性势能为________J.图1答案-100100解析在物体缓慢压缩弹簧的过程中,推力F始终与弹簧弹力等大反向,所以推力F做的功等于克服弹簧弹力所做的功,即W弹=-W F=-100 J.由弹力做功与弹性势能的变化关系知,弹性势能增加了100 J.【考点】弹力做功与弹性势能的关系【题点】弹力做功与弹性势能关系的应用针对训练如图2所示,轻弹簧下端系一重物,O点为其平衡位置(即重力和弹簧弹力大小相等的位置),今用手向下拉重物,第一次把它直接拉到A点,弹力做功为W1,第二次把它拉到B点后再让其回到A点,弹力做功为W2,则这两次弹力做功的关系为()图2A.W1<W2B.W1=2W2C.W2=2W1D.W1=W2答案 D解析弹力做功与路径无关,只与初、末位置有关,两次初、末位置相同,故W1=W2,D 正确.【考点】弹力做功与弹性势能的关系【题点】弹力做功与弹性势能关系的应用1.(对弹性势能的理解)(2017·余姚中学高一第二学期期中考试)关于弹簧的弹性势能,下列说法中正确的是()A.当弹簧变长时,它的弹性势能一定增大B.当弹簧变短时,它的弹性势能一定减小C.弹性限度内,长度相同且劲度系数也相同的弹簧的弹簧势能相等D.弹性限度内,弹簧被拉伸的长度相同时,劲度系数越大的弹簧,它的弹性势能越大答案 D解析当弹簧变长时,它的弹性势能不一定增大,若弹簧处于压缩状态变长的过程中,弹簧的弹性势能减小,故A错误.若处于压缩状态时,弹簧变短时,弹簧的弹性势能增大,故B 错误.弹性势能与劲度系数k及形变量有关.拉伸长度相同,且劲度系数也相同的弹簧弹性势能相等,而不是长度相等,形变一定时,k越大的弹簧,它的弹性势能越大,故C错误,D正确.2.(重力势能、弹性势能的变化分析)(多选)如图3所示是蹦床运动员在空中表演的情景.在运动员从最低点开始反弹至即将与蹦床分离的过程中,蹦床的弹性势能和运动员的重力势能变化情况分别是()图3A.弹性势能减少,重力势能增加B.弹性势能减少,重力势能减少C.弹性势能增加,重力势能增加D.弹性势能增加,重力势能减少答案 A解析根据功能关系知,重力做负功,重力势能增加,蹦床弹力对运动员做正功,弹性势能减少,故A项正确.3.(多选)(重力势能、弹性势能的变化分析)(2018·浙江省9+1高中联盟第二学期期中考试)如图4所示,跳跳球多用橡胶等弹性材料制成.游戏者用脚夹住球,让球和人一起上下跳动.某次人保持直立和球一起下落过程中,下列说法正确的是()图4A .当球刚碰到地面时,球与人一起立即做减速运动B .当球与人速度最大时,球与人的加速度为零C .从球刚碰地到最低点过程中,球的重力势能一直增大D .从球刚碰地到最低点过程中,球的弹性势能一直增大 答案 BD解析 从球刚碰地到重力与弹力相等的过程中,球与人做加速运动,之后做减速运动,直到最低点,A 错误,B 正确;从球刚碰地到最低点的过程中,球的重力势能一直减小;同时由于球的形变量增大,球的弹性势能一直增大,C 错误,D 正确.4.(弹力做功、弹性势能的变化)如图5甲所示,一滑块沿光滑的水平面向左运动,与轻弹簧接触后将弹簧压缩到最短,然后反向弹回,弹簧始终处在弹性限度以内,图乙为测得的弹簧的弹力与弹簧压缩量之间的关系图象,则弹簧的压缩量由8 cm 变为4 cm 时,弹簧所做的功以及弹性势能的变化量分别为( )图5A .3.6 J 、-3.6 JB .-3.6 J 、3.6 JC .1.8 J 、-1.8 JD .-1.8 J 、1.8 J答案 C解析 F -x 围成的面积表示弹力做的功.W =12×0.08×60 J -12×0.04×30 J =1.8 J ,根据W=-ΔE p 知,弹性势能减少1.8 J ,C 正确.【考点】弹力做功与弹性势能的关系【题点】图象法或平均值法求弹力做功一、选择题考点一弹性势能的理解1.如图1所示的几个运动过程中,物体的弹性势能增加的是()图1A.如图甲,撑杆跳高的运动员上升的过程中,杆的弹性势能B.如图乙,人拉长弹簧的过程中,弹簧的弹性势能C.如图丙,模型飞机用橡皮筋发射出去的过程中,橡皮筋的弹性势能D.如图丁,小球被弹簧向上弹起的过程中,弹簧的弹性势能答案 B解析选项A、C、D中物体的形变量均减小,所以弹性势能均减少,B中物体的形变量增大,所以弹性势能增加,故B正确.2.如图2所示,将弹簧拉力器用力拉开的过程中,弹簧的弹力和弹性势能的变化情况是()图2A.弹力变大,弹性势能变小B.弹力变小,弹性势能变大C.弹力和弹性势能都变小D.弹力和弹性势能都变大答案 D解析将弹簧拉力器用力拉开的过程中,弹簧的伸长量变大,弹簧的弹力变大,弹性势能变大,故A、B、C错误,D正确.3.某同学在桌面上用一个小钢球和一个弹簧来探究弹簧的弹性势能.弹簧一端固定(如图3所示),另一端用钢球压缩弹簧后释放,钢球被弹出后落地.当他发现弹簧压缩得越多,钢球被弹出得越远,由此能得出的结论应是()图3A.弹性势能与形变量有关,形变量越大,弹性势能越大B.弹性势能与形变量有关,形变量越大,弹性势能越小C.弹性势能与劲度系数有关,劲度系数越大,弹性势能越大D.弹性势能与劲度系数有关,劲度系数越大,弹性势能越小答案 A4.如图4所示,轻质弹簧下悬挂一个小球,手掌托小球使之缓慢上移,弹簧恢复原长时迅速撤去手掌使小球开始下落.不计空气阻力,取弹簧处于原长时的弹性势能为零.撤去手掌后,下列说法正确的是()图4A.刚撤去手掌瞬间,弹簧弹力等于小球重力B.小球速度最大时,弹簧的弹性势能为零C.弹簧的弹性势能最大时,小球速度为零D.小球运动到最高点时,弹簧的弹性势能最大答案 C解析刚撤去手掌时,小球处于运动最高点,弹簧处于原长,弹力为零,弹性势能为零,所以A、D错误;当小球速度最大时,加速度等于零,即弹力等于重力,弹簧弹性势能不为零,所以B错误;当下落到最低点时弹性势能最大,小球速度为零,故C正确.5.一竖直弹簧下端固定于水平地面上,小球从弹簧的正上方高为h的地方自由下落到弹簧上端,如图5所示,经几次反弹以后小球最终在弹簧上静止于某一点A处,则()图5A.h越大,弹簧在A点的压缩量越大B.弹簧在A点的压缩量与h无关C.h越大,最终小球静止在A点时弹簧的弹性势能越大D.小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹性势能大答案 B解析最终小球静止在A点时,通过受力分析,小球受自身重力mg与弹簧的弹力kx大小相等,由mg=kx得,弹簧在A点的压缩量x与h无关,弹簧在A点的弹性势能与h无关.6.如图6所示,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为E p1,B刚要离开地面时,弹簧的弹性势能为E p2,则关于E p1、E p2的大小关系及弹性势能的变化ΔE p,下列说法中正确的是()图6A.E p1=E p2B.E p1>E p2C.ΔE p>0 D.ΔE p<0答案 A解析开始时弹簧形变量为x1,有kx1=mg.设B刚要离开地面时弹簧形变量为x2,有kx2=mg,则x1=x2,所以E p1=E p2,ΔE p=0,A对.7.如图7所示,质量不计的弹簧一端固定在地面上,弹簧竖直放置,将一小球从距弹簧自由端高度分别为h1、h2的地方先后由静止释放,h1>h2,小球接触到弹簧后向下运动压缩弹簧,从开始释放小球到获得最大速度的过程中,小球重力势能的减少量ΔE1、ΔE2的关系及弹簧弹性势能的增加量ΔE p1、ΔE p2的关系中,正确的一组是()图7A.ΔE1=ΔE2,ΔE p1=ΔE p2B.ΔE1>ΔE2,ΔE p1=ΔE p2C.ΔE1=ΔE2,ΔE p1>ΔE p2D.ΔE1>ΔE2,ΔE p1>ΔE p2答案 B解析小球速度最大的条件是弹簧弹力等于小球重力,两种情况下,对应于同一位置,故ΔE p1=ΔE p2,由于h1>h2,所以ΔE1>ΔE2,B正确.考点二弹力做功弹性势能的变化8.如图8所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且使弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中()图8A.重力做正功,弹力不做功B.重力做正功,弹力做负功,弹性势能减小C.若用与弹簧原长相等的不可伸长的细绳代替弹簧后,重力做正功,弹力不做功D.若用与弹簧原长相等的不可伸长的细绳代替弹簧后,重力做功不变,弹力不做功答案 C解析用不可伸长的细绳拴住重物向下摆动时,重力做正功,弹力不做功,C对;用弹簧拴住重物向下摆动时,弹簧要伸长,重物轨迹不是圆弧,弹力做负功,弹性势能增加,重力做正功,且做功多,所以A、B、D均错.9.如图9所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中()图9A.小球的加速度在ab段不变,在bc段逐渐变小B.小球的速度在bc段逐渐减小C.小球的重力势能在a→b过程中不变,在b→c过程中不断减小D.弹簧的弹性势能在bc段不断增大答案 D解析小球在ab段做自由落体运动,a=g不变;在bc段小球受到的重力开始大于弹力,直至重力等于弹力大小,此过程中,小球受到的合外力向下,且不断减小,故小球做加速度减小、速度不断增大的变加速运动;过平衡点之后,小球继续压缩弹簧,受到的重力小于弹力,直至压缩弹簧最短到c点,此过程中,小球受到的合外力向上,且不断增大,故小球做加速度不断增大的减速运动,故A、B错误;小球在a→b→c的过程中,高度越来越低,重力做正功,重力势能不断减小,故C错误;小球在bc段,弹簧被压缩得越来越短,形变量增大,弹力对小球做负功,弹性势能不断增大,故D正确.10.一个小孩在蹦床上做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他运动的速度v随时间t变化的图象如图10所示,图中Oa段为直线,则根据该图象可知,蹦床的弹性势能增大的过程所对应的时间间隔为()图10A.仅在t1到t2的时间内B.仅在t2到t3的时间内C.在t1到t3的时间内D.在t1到t4的时间内答案 C解析小孩从高处落下,在0~t1时间内小孩只受重力作用;在t1~t2时间内加速度减小,说明小孩又受到了弹力作用,蹦床受到压力;t3时刻,小孩的速度为零,蹦床受到的压力最大,弹性势能也最大;t3时刻后小孩反弹,蹦床的弹性势能减小,故选项C正确.【考点】弹力做功与弹性势能的关系【题点】弹力做功与弹性势能关系的应用11.轻质弹簧右端固定在墙上,左端与一质量m=0.5 kg的物块相连,如图11甲所示.弹簧处于原长状态,物块静止且与水平面间的动摩擦因数μ=0.2.以物块所在处为原点,水平向右为正方向建立x轴.现对物块施加水平向右的外力F,F随x轴坐标变化的情况如图乙所示.物块运动至x=0.4 m处时速度为零.则此时弹簧的弹性势能为(取g=10 m/s2)()图11A.3.1 J B.3.5 JC.1.8 J D.2.0 J答案 A解析物块与水平面间的滑动摩擦力为F f=μmg=1 N.现对物块施加水平向右的外力F,由F-x图象面积表示功可知F做功W=3.5 J,克服摩擦力做功W f=F f x=0.4 J.外力所做的总功转化为弹簧的弹性势能,所以此时弹簧的弹性势能为E p=3.1 J,选项A正确.【考点】弹力做功与弹性势能的关系【题点】弹力做功与弹性势能关系的应用二、非选择题12.(探究影响弹性势能的因素)如图12所示,光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在水平轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处,另有一小球,现在利用这些器材测定弹簧被压缩时的弹性势能.图12(1)还需要的器材是________、________.(2)以上测量实际上是把对弹性势能的测量转化为对________的测量,进而转化为对________和________的直接测量.(3)为了探究弹簧的弹性势能与劲度系数和形变量的关系,除以上器材外,还准备了三个轻弹簧,所有弹簧的劲度系数均不相同.试设计记录数据的表格.答案(1)天平刻度尺(2)重力势能小球质量小球上升的高度(3)设计的记录数据表格如下表所示小球的质量m=________kg13.(探究弹性势能的表达式)某同学利用自己设计的弹簧弹射器做“验证弹簧弹性势能E p =12kx 2(k 为弹簧的劲度系数,x 为弹簧的形变量)”的实验,装置如图13(a)所示.水平放置的弹射器将质量为m 的小球弹射出去,测出小球通过两个竖直放置的光电门的时间间隔为t ,用刻度尺测出弹簧的压缩量为x ,甲、乙光电门的间距为L ,忽略一切阻力.(已知动能的表达式E k =12m v 2)图13(1)小球被弹射出的速度大小v =________,求得弹簧弹性势能E p =________;(用题目中的字母表示)(2)该同学测出多组数据,计算并画出如图(b)所示E p 与x 2的关系图线,从而验证了它们之间的关系.根据图线求得弹簧的劲度系数k =________ N/m ;(3)由于重力作用,小球被弹出去后运动轨迹会向下有所偏转,这对实验结果________影响(选填“有”或“无”).答案 (1)L t mL 22t 2(2)200 (3)无解析 (1)由题图(a)可知,弹簧在小球进入光电门之前就已经恢复形变,且此时弹簧的弹性势能全部转化为小球的动能,故小球被弹射出的速度等于小球通过光电门时的水平速度,即v=L t ,E p =12m v 2=12m ⎝⎛⎭⎫L t 2=mL 22t2. (2)由题图(b)读出数据并代入公式E p =12kx 2,得0.01 J =12×k ×1×10-4 m 2,解得k =200 N/m.(3)由力作用的独立性可知,重力不影响水平方向的分运动,无论有没有重力做功,小球的水平速度都不会变化.【考点】影响弹性势能大小的因素 【题点】探究弹性势能的表达式。
高中物理 第七章 机械能守恒定律 第5节 探究弹性势能的表达式(含解析)

第5节探究弹性势能的表达式一、 弹性势能 1.弹性势能的概念发生弹性形变的物体的各部分之间,由于弹力的相互作用而具有的势能。
2.决定弹性势能大小相关因素的猜想(1)猜想依据 弹性势能和重力势能同属势能,重力势能大小与物体的质量和高度有关,弹簧弹力与其形变量和劲度系数有关。
(2)猜想结论弹性势能与弹簧的形变量l 和劲度系数k 有关,在弹簧的形变量l 相同时,弹簧的劲度系数k 越大,弹簧的弹性势能越大。
在弹簧劲度系数k 相同时,弹簧形变量越大,弹簧弹性势能越大。
二、 探究弹性势能的表达式1.探究思想:研究弹力做功与弹性势能变化的关系。
2.“化变为恒”求拉力做功:W 总=F 1Δl 1+F 2Δl 2+…+F n Δl n 。
3.“F l ”图像面积的意义:表示F 做功的值。
1.自主思考——判一判(1)弹性势能与弹簧的弹性形变量和劲度系数有关。
(√)(2)除了弹力做功之外,其他力做功不影响弹性势能。
(√)(3)不同弹簧发生相同的形变量时弹力做功相同。
(×) 1. 弹力对物体做正功,弹簧的弹性势能减少,弹力对物体做负功,弹簧的弹性势能增加。
弹力做了多少功,弹性势能就变化多少。
2.弹簧的弹性势能的大小跟劲度系数和形变量有关,其表达式为E p =12kl 2,其中l 表示弹簧的形变量而 不是长度。
2. 弹簧的弹性势能也具有相对性,一般取弹簧处于原长时弹性势能为零。
(4)弹簧被压缩时,弹性势能为负;弹簧被拉伸时,弹性势能为正。
(×)(5)弹力做正功,弹性势能就增大;弹力做负功,弹性势能就减小。
(×)2.合作探究——议一议(1)运动员将箭射出,弓恢复原状,此过程中弓的弹性势能怎么变化?提示:弓的形变量逐渐减小,弹性势能减小。
(2)弹弓是一种儿童玩具,由两根橡皮条和木叉制成。
为使石子以较大的速度飞出,就应该把橡皮条拉长些,从能量角度分析这是为什么呢?提示:橡皮条拉得越长,储存的弹性势能越大,射出石子时石子的动能就越大,射得就越远。
7.5探究弹性势能的表达式课堂例题(含答案)

7.5探究弹性势能的表达式课堂例题一.选择题(共6小题)簧上面.今用力F缓慢向上提A,直到B恰好离开地面.设开始时弹簧的弹性势能为E,B刚要离开地面时,弹簧的弹性势能为E,则关于E、E大小关系及系统机械能变化△E的说法中正确的是()=E E个轻质弹簧,弹簧的劲度系数为K,用手拉住弹簧上端,使物体缓缓提高H,不计弹簧质量,则人做的功()下缓慢拉伸了x.关于拉力F随伸长量x的变化图线,如图中正确的是()B重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中()6.(2012春•金牛区校级期末)如图所示,物体A的质量为m,A的上端连接一个轻弹簧原长为L0,劲度系数为k,整个系统置于水平地面上,现将弹簧上端B缓慢地竖直向上提起,B点上移距离为L,此时物体A也已经离开地面,则下列说法中正确的是()﹣7.(2012春•肥东县校级月考)一根弹簧的弹力﹣位移图象如图所示,那么弹簧由伸长量8cm 到伸长量为4cm的过程中,弹性势能减小了.8.如图所示,在光滑水平面上有A、B两物体,中间连一弹簧,已知m A=2m B,今用水平恒力F向右拉B,当A、B一起向右加速运动时,弹簧的弹性势能为E p1,如果水平恒力F 向左拉A,当A、B一起向左加速运动时,弹簧的弹性势能为E p2,则E p1E p2.三.解答题(共2小题)9.(2011春•南关区校级期中)弹簧原长L0=16cm,受到拉力作用后弹簧逐渐伸长,当弹簧伸长到L1=20cm时,作用在弹簧上的力为F=400N,问:(1)弹簧的劲度系数k为多少N/m?(2)在该过程中弹力做了多少功?(3)弹簧的弹性势能变化了多少?10.(2010秋•邵阳县校级月考)如图,一劲度k=800N/m的轻弹簧两端各焊接着A、B两物体,mA=16kg,mB=8kg,竖直静止在水平地面上.现要加竖直向上的力F在上面物体A上,使A开始向上做匀加速运动,经0.2s,B刚要离开地面,整个过程弹簧都处于弹性限度内(g=10m/s).求(1)B刚要离开地面时,A物体上升的高度;(2)在此过程中所加外力F的最大值和最小值;(3)在此过程中弹性势能的变化量;(4)在此过程中弹簧对A做了正功还是负功,做了多少功?7.5探究弹性势能的表达式课堂例题参考答案与试题解析一.选择题(共6小题)2.(2014春•桂林期末)如图所示,质量相等的两木块中间连有一弹簧,开始时A静止在弹簧上面.今用力F缓慢向上提A,直到B恰好离开地面.设开始时弹簧的弹性势能为E,B刚要离开地面时,弹簧的弹性势能为E,则关于E、E大小关系及系统机械能变化△E的说法中正确的是()=E E3.(2011春•普宁市校级月考)如图所示,质量为m的物体静止在地面上,物体上边连着一个轻质弹簧,弹簧的劲度系数为K,用手拉住弹簧上端,使物体缓缓提高H,不计弹簧质量,则人做的功()4.(2011春•集宁区校级期中)如图所示,弹簧的一端固定在墙上,另一端在水平力F作用下缓慢拉伸了x.关于拉力F随伸长量x的变化图线,如图中正确的是()B5.(2012春•新浦区校级期中)如图所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中()6.(2012春•金牛区校级期末)如图所示,物体A的质量为m,A的上端连接一个轻弹簧原长为L0,劲度系数为k,整个系统置于水平地面上,现将弹簧上端B缓慢地竖直向上提起,B点上移距离为L,此时物体A也已经离开地面,则下列说法中正确的是()﹣L=二.填空题(共2小题)7.(2012春•肥东县校级月考)一根弹簧的弹力﹣位移图象如图所示,那么弹簧由伸长量8cm 到伸长量为4cm的过程中,弹性势能减小了 1.8J.=8.如图所示,在光滑水平面上有A、B两物体,中间连一弹簧,已知m A=2m B,今用水平恒力F向右拉B,当A、B一起向右加速运动时,弹簧的弹性势能为E p1,如果水平恒力F 向左拉A,当A、B一起向左加速运动时,弹簧的弹性势能为E p2,则E p1>E p2.====三.解答题(共2小题)9.(2011春•南关区校级期中)弹簧原长L0=16cm,受到拉力作用后弹簧逐渐伸长,当弹簧伸长到L1=20cm时,作用在弹簧上的力为F=400N,问:(1)弹簧的劲度系数k为多少N/m?(2)在该过程中弹力做了多少功?(3)弹簧的弹性势能变化了多少?=10000N/m10.(2010秋•邵阳县校级月考)如图,一劲度k=800N/m的轻弹簧两端各焊接着质量均为m=12kg的物体A、B,竖直静止在水平地面上.现要加竖直向上的力F在上面物体A上,使A开始向上做匀加速运动,经0.4s,B刚要离开地面,整个过程弹簧都处于弹性限度内(g=10m/s).求此过程所加外力F的最大值和最小值.的位移。
人教版物理必修2同步检测:7-5《探究弹性势能的表达式》【含解析】

第7章第5课时探究弹性势能的表达式基础夯实1.关于弹性势能,下列说法正确的是( )A.发生弹性形变的物体都具有弹性势能B.只有弹簧在发生弹性形变时才具有弹性势能C.弹性势能可以与其他形式的能相互转化[:D.弹性势能在国际单位制中的单位是焦耳[:数理化]答案:ACD解析:发生弹性形变的物体的各部分之间,由于有弹力的相互作用,都具有弹性势能,A正确;弹性势能跟重力势能一样,可以与其他形式的能相互转化,C正确;所有能的单位都跟功的单位相同,在国际单位制中的单位是焦耳,D正确.2.(2018·江苏盐城中学高一检测)如图所示,将弹簧拉力器用力拉开的过程中,弹簧的弹力和弹性势能的变化情况是( )A.弹力变大,弹性势能变小B.弹力变小,弹性势能变大C.弹力和弹性势能都变小D.弹力和弹性势能都变大答案:D3.如图所示,射箭时人拉弓所做的功转化为弹性势能,此时的弹性势能主要( )A.存储在箭上B.存储在弓上C.存储在弦上D.存储于拉弓人的手上答案:B4.(2018·湖北省部分重点中学高一检测)如图所示中的几个运动过程中,物体弹性势能增加的是( )A.如图(甲),跳高运动员从压杆到杆伸直的过程中,杆的弹性势能B.如图(乙),人拉长弹簧过程中弹簧的弹性势能C.如图(丙),模型飞机用橡皮筋发射出去的过程中,橡皮筋的弹性势能D.如图(丁),小球被弹簧向上弹起的过程中,弹簧的弹性势能答案:B5.如图所示,在光滑水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F作用下物体处于静止状态,当撤去F后,物体将向右运动,在物体向右运动的过程中,下列说法正确的是( )A.弹簧对物体做正功,弹簧的弹性势能逐渐减小B.弹簧对物体做负功,弹簧的弹性势能逐渐增加C.弹簧先对物体做正功,后对物体做负功,弹簧的弹性势能先减少再增加D.弹簧先对物体做负功,后对物体做正功,弹簧的弹性势能先增加再减少答案:C解析:开始时,弹簧处于压缩状态,撤去F后物体在向右运动的过程中,弹簧的弹力对物体先做正功后做负功,故弹簧的弹性势能应先减小后增大.6.(南京模拟)在猜想弹性势能可能与哪几个物理量有关的时候,有人猜想弹性势能可能与弹簧的劲度系数k、与弹簧的伸长量x有关,但究竟是与x的一次方,还是x的二次方,还是x的三次方有关呢?请完成下面练习以帮助思考.(1)若弹性势能E p∝kx,由于劲度系数k的单位是N/m,弹簧伸长量x的单位是m,则kx的单位是________.(2)若弹性势能E p∝kx2,由于劲度系数k的单位是N/m,弹簧伸长量x的单位是m,则kx2的单位是________.(3)若弹性势能E p∝kx3,由于劲度系数k的单位是N/m,弹簧伸长量x的单位是m,则kx3的单位是________.从(1)、(2)、(3)对单位的计算,你可以得到的启示:________.答案:(1)N (2)J (3)J·m弹性势能E p与弹簧伸长量x的二次方有关的猜想有些道理解析:物理量与单位是否统一是验证探究正确与否的方法之一.7.如图所示,质量相等的A、B两物体之间连接一轻弹簧,竖直放在水平地面上,今用力F缓慢向上拉A,直到B刚要离开地面,设开始时弹簧的弹性势能为EP1,B刚要离开地面时弹簧的弹性势能为EP2,试比较EP1、EP2的大小.答案:EP 1=EP 2解析:对于同一弹簧,其弹性势能的大小取决于它的形变量.开始时,弹簧处于压缩状态,与原长相比,它的压缩量为Δl 1=m A g k .当B 刚要离开地面时,弹簧处于拉伸状态,与原长相比,它的伸长量为Δl 2=m B gk.因为m A =m B ,所以Δl 1=Δl 2.故EP 1=EP 2.能力提升1.(哈师大附中高一检测)如图所示,一轻质弹簧原长为L ,竖直固定在水平面上,一质量为m 的小球从离地面高为H 处自由下落,正好压在弹簧上,弹簧的最大压缩量为x ,整个过程不计空气阻力,则弹簧的弹性势能的最大值为( )A .mg(H -L)B .mg(L -x)C .mg(H -L +x)D .mg(H -x +L)答案:C2.一根弹簧的弹力—位移图线如图所示,那么弹簧由伸长量8cm 到伸长量4cm 的过程中,弹力的功和弹性势能的变化量为( )A .3.6J ,-3.6JB .-3.6J,3.6JC .1.8J ,-1.8JD .-1.8J,1.8J答案:C解析:F -x 围成的面积表示弹力的功. W =12×0.08×60J-12×0.04×30J=1.8J弹性势能减少1.8J ,C 对.3.为了只用一根弹簧和一把刻度尺测定某滑块与水平桌面间的动摩擦因数μ(设μ为定值),某同学经查阅资料知道了一劲度系数为k 的轻弹簧在伸长量为x 时,弹簧具有的弹性势能为E p =12kx 2,于是他设计了下面的实验.[:第1步:如图所示,将弹簧的一端固定在竖直墙壁上,先使滑块紧靠弹簧将其压缩,松手后滑块在水平桌面上滑行一段距离后停止.第2步:先将弹簧的一端挂起,再将滑块挂在竖直放置的弹簧下,使弹簧伸长后保持静止状态.[:数理化] 回答下列问题.(1)对于松手后滑块在水平桌面上滑动过程中有关物理量的描述,正确的是( ) ①当弹簧恢复原长时,滑块的加速度可达到最大值 ②当弹簧恢复原长时,滑块的速度可达到最大值 ③滑块的加速度先增大,后减小,然后保持不变 ④滑块的加速度先减小,后增大,然后保持不变 A .①③ B .②④ C .③D .④(2)你认为,该同学应该用刻度尺直接测量的物理量是(写出名称并用符号表示):________________. (3)用测得的物理量表示滑块与水平桌面间的动摩擦因数μ的计算式:μ=________.答案:(1)D (2)弹簧的压缩量x 1,滑块滑行的距离s ,滑块挂在竖直弹簧下时弹簧的伸长量x 2 (3)x 122sx 2解析:松手后,滑块受到向右的弹力大于最大静摩擦力,滑块向右做加速运动,随着滑块的运动,弹力逐渐减小,加速度逐渐减小,当弹力等于摩擦力时,加速度为0,速度最大.滑块继续运动,摩擦力大于弹力,加速度逐渐增大,速度逐渐减小,当弹簧恢复原长时,弹力消失,以后滑块受滑动摩擦力作用做匀减速运动,直至停止.依据弹簧贮存的弹性势能用来克服滑动摩擦力做功求解.4.在水平地面上放一个竖直轻弹簧,弹簧上端与一个质量为2.0kg 的木块相连,若在木块上再作用一个竖直向下的力F ,使木块缓慢向下移动0.10m ,力F 做功2.5J.此时木块再次处于平衡状态,力F 的大小为50N ,如图所示,求:[:(1)在木块下移0.10m 的过程中弹性势能的增加量; (2)弹簧的劲度系数. 答案:(1)4.5J (2)500N/m解析:弹性势能的增加量等于弹力做负功的值,所以设法求出弹簧弹力做的功是解决问题的关键. (1)木块下移0.10m 过程中,F 与重力的合力等于弹簧弹力,所以力F 和重力做功等于弹簧弹性势能的增加量,故弹性势能的增加量为ΔE P =W F +mgh =(2.5+2.0×10×0.10)J =4.5J.(2)由平衡条件得,木块再次处于平衡时F =kh ,所以劲度系数k =F h =500.10N/m =500N/m.5.2008年北京奥运会女子蹦床决赛中,中国小将何雯娜(图甲)表现突出,以总分37.80分的成绩为中国蹦床队夺得首枚奥运会金牌.在比赛中,如果她受到蹦床对她的弹力的变化规律如图乙所示.图甲图乙试分析该同学在t4~t5段时间内弹性势能、重力势能怎样变化?t5~t6段时间内又如何变化?答案:t4~t5段时间内弹性势能为零、重力势能先变大再变小;t5~t6段时间内弹性势能先变大再变小、重力势能先变小再变大.解析:t4~t5段时间内在空中,不受弹力作用,t5~t6段时间内与蹦床接触,是先下落又上升的过程.。
第五节 探究弹性势能的表达式解析版

第五节探究弹性势能的表达式【基础题】1.关于弹性势能和重力势能,下列说法不正确的是( )A.重力势能属于物体和地球这个系统,弹性势能属于发生弹性形变的物体B.重力势能是相对的,弹性势能是绝对的C.重力势能和弹性势能都是相对的D.重力势能和弹性势能都是状态量【答案】B【解析】重力势能、弹性势能都是相对于零势能点的,B错A、C、D对故选:B【考点精析】此题的关键在于理解弹性势能的相关知识,掌握弹性势能是物体由于发生弹性形变而具有的能量.2.在巴塞罗那奥运会上,运动员用带火的弓箭点燃奥运圣火,这个过程中( )A.箭能射出去是因为箭具有弹性势能B.弓拉得越紧,运动时的弹性势能越大C.弓拉得越紧,弓的弹性势能越大D.弓拉得越紧,弓上的箭的弹性势能越大【答案】C【解析】弹性势能是发生弹性形变的物体自身所具有的一种能量,这种能量与其他物体无关。
弓拉弯后能将箭射出去,发生弹性形变的是弓,而不是箭,所以是因为弓具有弹性势能。
另外,弹性势能的大小跟物体的弹性形变程度有关,弹性形变越大,弹性势能越大,故弓拉得越紧,弓的弹性势能越大。
故选:C3.如图所示,在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力 F 作用下物体处于静止状态,当撤去 F 后,物体将向右运动,在物体向右运动的过程中,下列说法正确的是( )A.弹簧的弹性势能逐渐减少B.弹簧的弹性势能逐渐增加C.弹簧的弹性势能先增加后减少D.弹簧的弹性势能先减少后增加【答案】A【解析】撤去 F 后物体向右运动的过程中,弹簧的弹力先做正功后做负功,故弹簧的弹性势能先减少后增加。
故选:D4.如图所示是蹦床运动员在空中表演的情景,在运动员从最低点开始反弹至即将与蹦床分离的过程中,下列说法中正确的是()A.蹦床对人的弹力增大B.弹性势能增大C.动能增大D.重力势能增大【答案】D【解析】A、在运动员从最低点开始反弹至即将与蹦床分离的过程中,弹力减小,故A 错误;B、在运动员从最低点开始反弹至即将与蹦床分离的过程中,形变量减小,弹性势能减小,故B错误;C、合力先是向上的,后是向下的,速度先增加后减小,动能先增加后减小,故C错误;D、在运动员从最低点开始反弹至即将与蹦床分离的过程中,运动员一直向上运动,重力势能增大,故D正确.故选:D.5.一竖直弹簧下端固定于水平地面上,小球从弹簧的正上方高为h的地方自由下落到弹簧上端,如图所示,经几次反弹以后小球最终在弹簧上静止于某一点A处,则().A.h愈大,弹簧在A点的压缩量越大B.弹簧在A点的压缩量与h无关C.h愈大,最终小球静止在A点时弹簧的弹性势能越大D.小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹性势能大【答案】B【解析】最终小球静止在A 点时,通过受力分析,小球受自身重力与弹簧的弹力作用,由弹力公式F =kx , 即可得出弹簧在A 点的压缩量与h 无关,弹簧弹性势能与h 无关.故选:B6.如图所示,弹簧的一端固定在墙上,另一端在水平力F 作用下缓慢拉伸了x 。
【学霸笔记】物理必修二7.5探究弹性势能的表达式

新课标物理学讲义----力学 第七章 机械能守恒定律 1 第五节 探究弹性势能的表达式
一、探究弹性势能的表达式
1、弹性势能:发生弹性形变的物体的各部分之间,由于弹力的相互作用而具有的势能。
2、猜想相关量:k 、x
3、步骤:(弹簧弹力做功与弹簧伸长量之间的关系)
①结论:弹簧弹力做正功,弹性势能减小;弹簧弹力做负功,弹性势能增大。
②弹簧弹力做功等于弹性势能变化的负值。
p F E W ∆-=
③研究弹簧弹力做功
4、弹力做功分析:
面积法(平均作用力法):
()()()()()
222212212111221x x k x x kx kx W x x F F W F F --=-+-==-+-= ()12212221222
1212P P P E E kx kx x x k W E -=-=-=-=∆ 5、结论:22
1kx E P = 二、弹性势能
1、表达式:22
1kx E P = 2、理解:
①弹簧的弹性势能只与k 、x 有关,与研究对象的运动情况等都无关。
②弹性势能为一状态量,即某时刻发生形变量时弹簧具有的能量。
③弹性势能为相对量,表达式选取的势能零点为原长。
(一般与原长为势能零点) ④弹性势能为标量,如果取原长为势能零点,则弹性势能具有非负性。
⑤同一根弹簧,拉伸或压缩同样的形变量,弹性势能相同。
⑥使用范围:弹簧。
无特殊说明橡皮筋也适用。
⑦弹性势能具有系统性,即它是发生弹性形变的物体各部分由于弹力而共同具有的能量。
3、小球在弹簧弹力作用下的做功能量分析:
O →A
A →O
O →B
B →O。
最新人教版高中物理第七章第5节探究弹性势能的表达式及答案

第五节探究弹性势能的表达式1.________________的物体的各部分之间,由于____________________,也具有势能,这种势能叫做弹性势能.研究弹性势能要从分析____________入手,对弹簧说,规定____________________,它的弹性势能为零,当弹簧____________________,就具有了弹性势能.2.(1)弹簧的弹性势能与弹簧被拉伸的长度有关,并且,拉伸的长度越大,弹性势能______,但不一定是________关系;(2)即使拉伸的长度相同,劲度系不同的弹簧的弹性势能也不一样,并且拉伸的长度相同时,越大,弹性势能________.3.根据功是____________________可知,弹性势能的变量与拉力对弹簧做功的关系为____________.4.设弹簧的劲度系为,当弹簧被拉伸时,把这一拉伸过程分为很多小段,它们的长度分别是Δ1、Δ2、Δ3……各个小段上拉力可以近似认为是不变的,分别为F1、F2、F3……,所做的功分别为________________.5.v-图线下的面积代表________,F-图线下的面积代表______;当所分成的小段非常短时,F-图线与轴所围成的区域形状是__________,该区域的面积为________,所以弹性势能的表达式是________________.6.关于弹性势能,下列说法中正确的是( )A.发生弹性形变的物体都具有弹性势能B.只要弹簧发生形变,就一定具有弹性势能.弹性势能可以与其他形式的能相互转D.弹性势能在国际单位制中的单位是焦耳7.关于弹簧的弹性势能,下列说法正确的是( )A.弹簧的弹性势能跟拉伸(或压缩)的长度有关B.弹簧的弹性势能跟弹簧的劲度系有关.同一弹簧,在弹性限度内,形变量越大,弹性势能越大D.弹性势能的大小跟使弹簧发生形变的物体有关【概念规律练】知识点一弹性势能1.关于弹性势能,下列说法中正确的是( )A.任何发生弹性形变的物体,都具有弹性势能B.任何具有弹性势能的物体,一定发生了弹性形变.物体只要发生形变,就一定具有弹性势能D.弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关2.关于弹性势能和重力势能下列说法正确的是( )A.重力势能属于物体和地球这个系统,弹性势能属于发生弹性形变的物体B.重力势能是相对的,弹性势能是绝对的.重力势能和弹性势能都是相对的D.重力势能和弹性势能都是状态量3.关于弹簧的弹性势能,下列说法中正确的是( )A.当弹簧变长时,它的弹性势能一定增大B.当弹簧变短时,它的弹性势能一定变小.在拉伸长度相同时,越大的弹簧,它的弹性势能越大D.弹簧在被拉伸时的弹性势能一定大于被压缩时的弹性势能知识点二弹力做功与弹性势能的关系4.关于弹力做功与弹性势能的关系,我们在进行猜想时,可以参考对重力做功与重力势能的关系的讨论,则下面的猜想有道的是( )A.弹力做功将引起弹性势能的变,当弹力做正功时,弹性势能将增加B.弹力做功将引起弹性势能的变,当弹力做正功时,弹性势能将减少.弹力做功将引起弹性势能的变,当弹力做负功时,弹性势能将增加D.弹力做功将引起弹性势能的变,当弹力做负功时,弹性势能将减少5图1冲向与竖直墙壁相连的轻质弹簧,墙壁和如图1所示,一个物体以速度v物体间的弹簧被物体压缩,在此过程中以下说法正确的是( )A.物体对弹簧做的功与弹簧的压缩量成正比B.压缩弹簧的过程中,物体向墙壁移动相同的距离,弹力做的功不相等.弹簧的弹力做正功,弹性势能减少D.弹簧的弹力做负功,弹性势能增加【方法技巧练】一、探究弹性势能表达式的方法6.在猜想弹性势能可能与哪几个物量有关的时候,有人猜想弹性势能与弹簧的劲度系及弹簧的伸长量有关,但究竟是与的一次方,还是的二次方,还是的三次方有关呢?请完成下面练习以帮助思考.(1)若弹性势能E p∝,由于劲度系的单位是N/,弹簧伸长量的单位是,则的单位是________.(2)若弹性势能E p∝2,由于劲度系的单位是N/,弹簧伸长量的单位是,则 2的单位是________.(3)若弹性势能E p∝3,由于劲度系的单位是N/,弹簧伸长量的单位是,则 3的单位是________.从(1)、(2)、(3)对单位的计算,你可以得到的启示是____________________ ________________________________________________________.二、弹性势能的求解方法图27.一根弹簧的弹力—位移图线如图2所示,那么弹簧由伸长量8c到伸长量4c的过程中,弹力做功和弹性势能的变量为( )A.36J,-36JB.-36J,36J.18J,-18JD.-18J,18J图38.在水平地面上放一个竖直轻弹簧,弹簧上端与一个质量为20g的木块相连,系统处于平衡状态.若在木块上再加一个竖直向下的力F,使木块缓慢向下移动010,力F做功25J,此时木块再次处于平衡状态,力F的大小为50N,如图3所示.求:在木块下移010的过程中弹性势能的增加量.1.在探究弹簧的弹性势能的表达式时,下面猜想有一定道的是( )A.重力势能与物体被举起的高度有关,所以弹性势能很可能与弹簧的长度有关B.重力势能与物体被举起的高度有关,所以弹性势能很可能与弹簧被拉伸(或压缩)的长度有关.重力势能与物体所受的重力g大小有关,所以弹性势能很可能与弹簧的劲度系有关D.重力势能与物体的质量有关,所以弹性势能很可能与弹簧的质量大小有关2.弹簧的一端固定,处于自然长度.现对弹簧的另一端施加一个拉力,关于拉力做功(或弹簧克服拉力做功)与弹性势能变的关系,以下说法中正确的是( )A.拉力对弹簧做正功,弹簧的弹性势能增加B.拉力对弹簧做正功,弹簧的弹性势能减少.弹簧克服拉力做功,弹簧的弹性势能增加D.弹簧克服拉力做功,弹簧的弹性势能减少3.自由下落的小球,从接触竖直放置的轻弹簧开始,到压缩弹簧到最大形变的过程中,以下说法中正确的是( )A.小球的速度逐渐减小B .小球、地球组成系统的重力势能逐渐减小.小球、弹簧组成系统的弹性势能先逐渐增大再逐渐减小D .小球的加速度逐渐增大4.在一次“蹦极”运动中,人由高空跌下,到最低点的整个过程中,下列说法中正确的是( )A .重力对人做正功B .人的重力势能减少了 .橡皮绳对人做负功D .橡皮绳的弹性势能增加了 5.如图4所示,图4在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F 作用下物体处于静止状态,当撤去F 后,物体将向右运动,在物体向右运动的过程中,下列说法正确的是( )A .弹簧的弹性势能逐渐减小B .弹簧的弹性势能逐渐增大 .弹簧的弹性势能先增大后减小D .弹簧的弹性势能先减小后增大 6.某缓冲装置可抽象成图5如图5所示的简单模型.图中1、2为原长相等,劲度系不同的轻质弹簧.下列表述正确的是( )A.缓冲效果与弹簧的劲度系无关B.垫片向右移动时,两弹簧产生的弹力大小相等.垫片向右移动时,两弹簧的长度保持相等D.垫片向右移动时,两弹簧的弹性势能发生改变7.如图6所示,质量相等的图6两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为E p1,B刚要离开地面时,弹簧的弹性势能为E p2,则关于E p1、E p2大小关系及弹性势能变ΔE p说法中正确的是( )A.Ep1=E p2B.Ep1>E p2.ΔE p>0 D.ΔE p<08.在一次演示实验中,一个被压紧的弹簧沿一粗糙水平面射出一个小物体,测得弹簧被压缩的长度和小物体在粗糙水平面上滑动的距离如下表所示.由此表可以归纳出小物体滑动的距离跟弹簧被压缩的距离之间的关系,并猜测弹簧的弹性势能E p跟弹簧被压缩的距离之间的关系分别是(选项中1、2是常量)( )A=1,E p=21p2.=12,Ep=2D.=12,Ep=22p簧长度的变量).为验证这一结论,A、B两位同设计了以下的实验:①两位同首先都进行了如图7甲所示的实验:将一根轻质弹簧竖直挂起,在弹簧的另一端挂上一个已知质量为的小铁球,稳定后测得弹簧伸长d②A同完成步骤①后,接着进行了如图乙所示的实验:将这根弹簧竖直地固定在水平桌面上,并把小铁球放在弹簧上,然后竖直地套上一根带有插销孔的长透明塑料管,利用插销压缩弹簧.拔掉插销时,弹簧对小球做功,使小球弹起,测得弹簧的压缩量和小铁球上升的最大高度H③B同完成步骤①后,接着进行了如图丙所示的实验:将这根弹簧放在水平桌面上,一端固定在竖直墙上,另一端被小铁球压缩,测得压缩量为,释放弹簧后,小铁球从高为的桌面上水平抛出,抛出的水平距离为L图7(1)A、B两位同进行图甲所示的实验目的是为了确定什么物量?请用、d、g 表示所求的物量____________________.(2)如果E p=2成立,A同测出的物量与d、H的关系式是:=____________B同测出的物量与d、、L的关系式是:=__________(3)试分别分析两位同实验误差的主要_________________________________________________________________ _____________________________________________________________________ __________第5节探究弹性势能的表达式课前预习练1.发生弹性形变有弹力的相互作用弹力做功弹簧长度为原长时被拉长或被压缩后2.(1)越大正比(2)越大3.能量变的量度大小相等4.F1Δ1、F2Δ2、F3Δ3……5.位移功三角形2E p=26.AD [发生弹性形变的物体的各部分之间,由于有弹力的相互作用,都具有弹性势能,A正确.弹性势能跟重力势能一样,可以与其他形式的能相互转,正确.所有能的单位跟功的单位相同,在国际单位制中的单位是焦耳,D正确.] 7.AB [由弹性势能的表达式E p=2可知,弹性势能E p与弹簧拉伸(或压缩)的长度有关,A选项正确.E p的大小还与有关,B选项正确.在弹性限度内,E p 的大小还与有关,越大,E p越大,正确.弹簧的弹性势能是由弹簧的劲度系和形变量决定的,与使弹簧发生形变的物体无关.]课堂探究练1.AB [由弹性势能的定义和相关因素进行判断.发生弹性形变的物体的各部分之间,由于弹力作用而具有的势能,叫做弹性势能.所以,任何发生弹性形变的物体都具有弹性势能,任何具有弹性势能的物体一定发生了弹性形变.物体发生了形变,若是非弹性形变,无弹力作用,物体就不具有弹性势能.弹簧的弹性势能除了跟弹簧被拉伸或压缩的长度有关外,还跟弹簧劲度系的大小有关.正确选项为A、B]2.AD [重力势能具有系统性,弹性势能只属于发生弹性形变的物体,故A 正确;重力势能和弹性势能都是相对的,且都是状态量,故B错,、D正确.] 3.[弹簧弹性势能的大小,除了跟劲度系有关外,还跟它的形变量(拉伸或压缩的长度)有关.如果弹簧原处在压缩状态,当它变长时,它的弹性势能应该先减小,在原长处它的弹性势能最小,所以A、B、D均不对.] 4.B5.BD [由功的计算公式W=F c θ知,恒力做功时,做功的多少与物体的位移成正比,而弹簧对物体的弹力是一个变力,所以A不正确;弹簧开始被压缩时弹力小,弹力做的功也少,弹簧的压缩量变大时,物体移动相同的距离做的功增多,故B正确;物体压缩弹簧的过程,弹簧的弹力与弹力作用点的位移方向相反,所以弹力做负功,弹性势能增加,故错误,D正确.]6.(1)N (2)J (3)J·弹性势能E p与弹簧伸长量的二次方有关7.[弹力做的功W=×004J=18J>0,故弹性势能减少18J,即ΔE p=E p2-E p1=-18J,故选项正确.]8.45J解析木块缓慢下移010的过程中,F与重力的合力始终与弹簧弹力等大反向,所以力F和重力做的总功等于克服弹簧弹力做的功,即W=-(W F+g)=-(25+20×10×010) J=-45J弹由弹力做功与弹性势能变的关系知,ΔE p=-W弹=45J方法总结功是能量转的量度,因此确定某一过程中的力做的功,是研究该过程能量转的重要方法.课后巩固练1.B [弹簧的弹性势能与弹簧的劲度系和弹簧的形变量有关,与弹簧的长度、质量等因素无关.]2.A [拉力对弹簧做正功,弹簧的弹力做负功,弹簧的弹性势能增加.] 3.B [小球做加速度先减小到0后反向逐渐增大的变速运动,小球速度先增大后减小.故A、D错,小球的重力势能逐渐减小,由于弹簧的压缩量逐渐增大,因此弹簧的弹性势能逐渐增大,故B正确,错.]4.ABD [人由高空跌下,到最低点的过程中,重力方向和位移方向均向下,重力对人做正功,重力势能减少,A、B正确;在人和橡皮绳相互作用的过程中,橡皮绳对人的拉力向上,人的位移向下,绳的拉力对人做负功,橡皮绳的弹性势能增加,、D正确.]5.D [撤去F后物体向右运动的过程中,弹簧的弹力先做正功后做负功,故弹簧的弹性势能先减小后增大.]6.BD [垫片向右移动时,由于是轻质弹簧,所以两弹簧产生的弹力相等,B正确;由于原长相同,劲度系不同,所以垫片向右移动时,两弹簧被压缩的长度不同;弹簧的弹性势能与形变量和劲度系有关,则缓冲效果和劲度系有关,A、错,D正确.]7.A [开始时弹簧形变量为1,有1=g则它离开地面时形变量为2,有2=g,故1=2,所以E p1=E p2,ΔE p=0,A对.]8.D [由图表不难看出,在值上=202=12;由粗糙水平面上小物体滑行距离所需的能量是由弹性势能转而的,E p=F f12=22]9.(1)确定弹簧的劲度系=(2) L(3)A同实验时,不易精确确定小铁球上升的最大高度,而且小铁球上升时有可能与塑料管内壁接触,产生摩擦从而带实验误差,B同实验时,小铁球与桌面之间的摩擦会给实验带误差.。
探究弹性势能的表达式

C.弹力做正功,弹簧的弹性势能减小
D.弹簧的弹力做负功,弹性势能增加 图7-5-4
自主学习 名师解疑 分类例析 课堂对点演练 活页规范训练
解析
本题考查了弹力功与弹性势能的变化关系.由功的计算公
自主学习 名师解疑 分类例析 课堂对点演练
图7-5-5
活页规范训练
解析
用细绳拴住小球向下摆动时重力做正功,弹力不做功,C
对.用弹簧拴住小球下摆时,弹簧要伸长,小球轨迹不是圆弧, 弹力做负功,弹性势能增加,重力做正功,且做功多,所以A、D
错,B对.
答案 BC
自主学习
名师解疑
分类例析
课堂对点演练
活页规范训练
关系
联
弹力所做的功
服重力所做的功
两种势能分别以弹力、重力的存在为前提,又由物 体的相对位置来决定.同属机械能的范畴,在一定 条件下可相互转化
系
1 2 特别提醒 Ep= kx 高考中不作要求,但熟记公式可迅速判断弹性 2 势能的大小及弹性势能的变化.
自主学习
名师解疑
分类例析
课堂对点演练
活页规范训练
弹性势能的理解
ΔL1、ΔL2、ΔL3……在各个小段上,拉力可以近似认为是不变的, 从一个小段长度到下一个小段长度,力跳跃性地增加,它们分别 为F1、F2、F3……在每一小段长度上,拉力做的功可用恒力做功 的公式计算,即W1=F1ΔL1、W2=F2ΔL2、W3=F3ΔL3……每一小 段上做的功在数值上等于折线下方画有斜线部分的面积.当每一 小段的长度分割得足够小时,折线趋近于直线OP,拉力在各小段
课时作业15:7.5探究弹性势能的表达式

7.5探究弹性势能的表达式1.(多选)关于弹性势能,下列说法正确的是()A.发生弹性形变的物体都具有弹性势能B.只有弹簧在发生弹性形变时才具有弹性势能C.弹性势能可以与其他形式的能相互转化D.在弹性限度内,弹簧伸长时弹性势能增大,弹簧压缩时,弹性势能减小2.如图所示,某同学利用橡皮条将模型飞机弹出,在弹出过程中,下述说法错误的是()A.橡皮条收缩,弹力对飞机做功B.飞机的速度增加C.橡皮条的弹性势能减小D.飞机的重力势能减小,转化为飞机的动能3.如图所示,质量为m的物体静止在地面上,物体上面连着一个轻弹簧,用手拉住弹簧上端上移H,将物体缓缓提高h.拉力F做功W F,不计弹簧的质量,则下列说法正确的是()A.重力做功-mgh,重力势能减少mghB.弹力做功-W F,弹性势能增加W FC.重力势能增加mgh,弹性势能增加FHD.重力势能增加mgh,弹性势能增加W F-mgh4.如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是()A.重力势能减少,弹性势能增大B.重力势能增大,弹性势能减少C .重力势能减少,弹性势能减少D .重力势能不变,弹性势能增大5. (多选)某缓冲装置可抽象成图所示的简单模型,图中k 1、k 2为原长相等、劲度系数不同的轻质弹簧.下列表述正确的是( )A .缓冲效果与弹簧的劲度系数无关B .垫片向右移动时,两弹簧产生的弹力大小相等C .垫片向右移动时,两弹簧的长度保持相等D .垫片向右移动时,两弹簧的弹性势能发生改变6.(多选)一升降机箱底部装有若干个弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦和空气阻力的影响,则升降机在从弹簧下端触地直到最低点的一段运动过程中( )A .升降机的速度不断减小B .升降机的加速度不断变大C .先是弹力做的负功小于重力做的正功,然后是弹力做的负功大于重力做的正功D .重力势能减小,弹性势能增大7.通过探究得到弹性势能的表达式为E p =12kx 2,式中k 为弹簧的劲度系数,x 为弹簧伸长(或缩短)的长度,请利用弹性势能表达式计算下列问题.放在地面上的物体上端系在劲度系数k =400 N/m 的弹簧上,弹簧的另一端拴在跨过定滑轮的绳子上,如图所示.手拉绳子的另一端,从轻绳处于张紧状态开始,当往下拉0.1 m 物体开始离开地面时,继续拉绳,使物体缓慢升高到离地h =0.5 m 高处.如果不计弹簧重和滑轮跟绳的摩擦,求整个过程拉力所做的功以及弹性势能的最大值.【参考答案】1.【解析】 只要发生弹性形变的物体都具有弹性势能,A 正确,B 错误;弹性势能可以通过弹力做功与其他形式的能相互转化,C 正确;在弹性限度内,弹簧无论伸长还是压缩,若形变量增加,弹力均做负功,弹性势能都增大,故D 错误.【答案】 AC2.【解析】 橡皮条收缩,弹力对飞机做功,橡皮条的弹性势能减小,飞机的重力势能和动能都增加,选项A 、B 、C 正确,D 错误.【答案】 D3.【解析】 可将整个过程分为两个阶段:一是弹簧伸长到m 刚要离开地面阶段,拉力克服弹力做功W F1=-W 弹,等于弹性势能的增加;二是弹簧长度不变,物体上升h ,拉力克服重力做功W F2=-W G =mgh ,等于重力势能的增加,又由W F =W F1+W F2,可知A 、B 、C 错,D 对.【答案】 D4.【解析】 将弹簧向下压缩的过程中,弹簧压缩量增大,弹性势能增大,重力做正功,重力势能减少,故A 正确.【答案】 A5. 【解析】 弹簧劲度系数k 越大,向右压缩单位长度弹力越大,物体减速越快,缓冲效果越好,A 错;由牛顿第三定律可知两弹簧弹力总是大小相等,B 对;由于k 1x 1=k 2x 2,k 1≠k 2,所以x 1≠x 2,又因原长相等,故压缩后两弹簧的长度不相等,C 错;弹簧形变量越来越大,弹性势能越来越大,D 对.【答案】 BD6.【解析】 从弹簧下端触地直到最低点的运动过程中,弹簧的弹力不断变大.当弹力小于重力大小时,升降机加速度方向向下,升降机做加速运动,由a =mg -F m可知,加速度减小,重力做的功要大于弹力做的负功;当弹力大于重力大小时,升降机加速度方向向上,升降机做减速运动,由a =F -mg m可知,加速度变大,重力做的功要小于弹力做的负功.重力势能一直减小,弹性势能一直增大.综上所述,C 、D 正确.【答案】 CD7.【解析】 由题意知弹簧的最大伸长量x =0.1 m ,弹性势能E p =12kx 2=12×400×0.12 J =2 J , 此过程中拉力做的功与弹力做的功数值相等,则有W 1=W 弹=ΔE p =2 J ,刚好离开地面时G =F =kx =400×0.1 N =40 N物体缓慢升高时,F=40 N,物体上升h=0.5 m时拉力克服重力做功W2=Fh=40×0.5 J=20 J,拉力共做功W=W1+W2=(2+20) J=22 J. 【答案】22 J 2 J。
课时作业8:7.5探究弹性势能的表达式

7.5探究弹性势能的表达式1.关于弹性势能,下列说法正确的是()A.发生弹性形变的物体都具有弹性势能B.只有弹簧在发生弹性形变时才具有弹性势能C.弹性势能可以与其他形式的能相互转化D.弹性势能在国际单位制中的单位是焦耳2.弹簧的弹性势能与下列哪些因素有关()A.弹簧的长度B.弹簧的劲度系数C.弹簧的形变量D.弹簧的原长3.如图所示,轻弹簧下端系一重物,O点为其平衡位置(即重力和弹簧弹力大小相等的位置),今用手向下拉重物,第一次把它直接拉到A点,弹力做功W1,第二次把它拉到B点后再让其回到A点,弹力做功W2,则这两次弹力做功的关系为()A.W1<W2B.W1=2W2C.W2=2W1D.W1=W24.如图所示,质量不计的弹簧一端固定在地面上,弹簧竖直放置,将一小球从距弹簧自由端高度分别为h1、h2的地方先后由静止释放,h1>h2,小球触到弹簧后向下运动压缩弹簧,从开始释放小球到获得最大速度的过程中,小球重力势能的减少量ΔE1、ΔE2的关系及弹簧弹性势能的增加量ΔE p1、ΔE p2的关系中,正确的一组是()A.ΔE1=ΔE2,ΔE p1=ΔE p2B.ΔE1>ΔE2,ΔE p1=ΔE p2C.ΔE1=ΔE2,ΔE p1>ΔE p2D.ΔE1>ΔE2,ΔE p1>ΔE p25.如图所示,水平弹簧劲度系数k=500 N/m.用一外力推物块,使弹簧压缩10 cm而静止.突然撤去外力F,物块被弹开,那么弹簧对物块做多少功?弹性势能的变化量是多少?(弹簧与物块没连接)6.如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是()A.重力势能减小,弹性势能增大B.重力势能增大,弹性势能减小C.重力势能减小,弹性势能减小D.重力势能不变,弹性势能增大7.如图所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速地释放,让它自由摆下,不计空气阻力,在重物由A点摆向最低点B的过程中()A.重力做正功,弹簧弹力不做功B.重力做正功,弹簧弹力做正功C.重力不做功,弹簧弹力不做功,弹性势能不变D.重力做正功,弹簧弹力做负功,弹性势能增加8.如图所示,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为E p1,B刚要离开地面时,弹簧的弹性势能为E p2,则关于E p1、E p2大小关系及弹性势能变化ΔE p说法中正确的是()A.E p1=E p2B.E p1>E p2C.ΔE p>0 D.ΔE p<09.在光滑的水平面上,物体A以较大速度v a向前运动,与以较小速度v b向同一方向运动的、连有轻质弹簧的物体B发生相互作用,如图所示.在相互作用的过程中,当系统的弹性势能最大时()A.v a′>v b′ B.v a′=v b′C.v a′<v b′ D.无法确定10.一竖直弹簧下端固定于水平地面上,小球从弹簧上端的正上方高为h的地方自由下落到弹簧上端,如图所示.经几次反弹以后小球最终在弹簧上静止于某一点A处,则()A.h越大,弹簧在A点的压缩量越大B.弹簧在A点的压缩量与h无关C.h越大,最终小球静止在A点时弹簧的弹性势能越大D.小球第一次到达A点时弹簧的弹性势能比最终小球静止在A点时弹簧的弹性势能大11.在一次演示实验中,一压紧的弹簧沿一粗糙水平面射出一小球,测得弹簧压缩的距离d 跟小球在粗糙水平面滚动的距离s的关系如下表所示.由此表可以归纳出小球滚动的距离s 跟弹簧压缩的距离d之间的关系,并猜测弹簧的弹性势能E p跟弹簧压缩的距离d之间的关系分别是(选项中k1、k2是常量)()A.s=k1d,E p=k2B.s=k1d,E p=k2d2C.s=k1d2,E p=k2dD.s=k1d2,E p=k2d212.关于弹性势能和重力势能,下列说法正确的是()A.重力势能属于物体和地球这个系统,弹性势能属于发生弹性形变的物体B.重力势能是相对的,弹性势能是绝对的C.重力势能和弹性势能都是相对的D.重力势能和弹性势能都是状态量13.关于弹簧的弹性势能,下面说法正确的是()A.当弹簧的长度为原长时,弹簧的弹性势能最小B.弹簧被拉长时具有弹性势能,被压缩时不具有弹性势能C .弹簧被压缩时具有的弹性势能一定小于被拉长时具有的弹性势能D .弹簧被拉长或被压缩时,只要在弹性限度内都具有弹性势能14.在水平地面上放置一轻质弹簧,有一物体从弹簧的正上方自由落下,在物体压缩弹簧速度减为零时(选地面为重力势能参考面)( ) A .物体的重力势能最小 B .物体的重力势能最大 C .弹簧的弹性势能最大 D .弹簧的弹性势能最小15.在一次“蹦极”运动中,人由高空落下到降至最低点的过程中,下列说法中正确的是( ) A .重力对人做正功 B .人的重力势能减少了 C .橡皮绳对人做负功 D .橡皮绳的弹性势能减少了16.弹簧原长l 0=15 cm ,受拉力作用后弹簧逐渐伸长,当弹簧伸长到l 1=20 cm 时,作用在弹簧上的力为400 N ,问: (1)弹簧的劲度系数k 为多少? (2)在该过程中弹力做了多少功? (3)弹簧的弹性势能变化了多少?17.通过探究得到弹性势能的表达式为E p =12kl 2,式中 k 为弹簧的劲度系数,l 为弹簧伸长(或缩短)的长度,请利用弹性势能表达式计算下列问题.放在地面上的物体上端系在劲度系数k =400 N/m 的弹簧上,弹簧的另一端拴在跨过定滑轮的绳子上,如图所示,手拉绳子的另一端,当往下拉 0.1 m 时物体开始离开地面,继续拉绳,使物体缓慢升高到离地h =0.5 m 高处.如果不计弹簧重和滑轮跟绳的摩擦,求拉力所做的功以及弹性势能的大小.答案1.解析:选ACD.发生弹性形变的物体的各部分之间,由于有弹力的相互作用,都具有弹性势能,故选项A 正确,B 错误.弹性势能跟重力势能一样,可以与其他形式的能相互转化,选项C 正确.在国际单位制中,能的单位跟功的单位相同,都是焦耳,选项D 正确. 2.解析:选BC.弹簧的弹性势能表达式为E p =12kl 2,其中k 为弹簧的劲度系数,l 为弹簧的形变量,故B 、C 正确.3.解析:选D.弹力做功的特点与重力做功一样,不用考虑路径,只看起始与终了位置.故D 项正确.4.解析:选B.小球速度最大的条件是弹力等于重力,两种情况下,对应于同一位置,故ΔE p1=ΔE p2,由于h 1>h 2,所以ΔE 1>ΔE 2,B 正确.5.解析:弹簧的弹力是变力,不能直接用W =Fl cos α进行计算.但由于弹簧的弹力遵循胡克定律,可以作出胡克定律的图象表示功,弹开过程弹力逐渐减小,当恢复原长时弹力为零,根据胡克定律,可作物块的受力与位移的关系如图,根据力-位移图象所围面积表示在这一过程中的功,有W =12×50×0.1 J =2.5 J .由弹力做功与弹性势能变化的关系可知,弹性势能的减少量为:ΔE p =W =2.5 J.答案:2.5 J 减少2.5 J6.解析:选A.弹簧向下压缩的过程中,弹簧压缩量增大,弹性势能增大;重力做正功,重力势能减小,故A 正确.7.解析:选D.A →B 重力做正功,弹簧伸长,弹力做负功,弹性势能增加,故D 正确. 8.解析:选A.开始时弹簧形变量为l 1,有kl 1=mg .当B 离开地面时形变量为l 2,有kl 2=mg ,故l 1=l 2,所以E p1=E p2,ΔE p =0,A 正确.9.解析:选B.v a ′=v b ′时,A 、B 相距最近,弹簧压缩量最大,弹性势能最大.10.解析:选B.最终小球静止在A 点时,小球受重力与弹簧的弹力相等,故由弹力公式得mg =kx ,即可得出弹簧在A 点的压缩量x =mgk ,与下落时的高度h 无关,A 错误,B 正确.对同一弹簧,它的弹性势能大小仅与弹簧的形变量有关,小球静止在A 点或经过A 点时,弹簧的弹性势能相同,C 、D 错误.11.解析:选D.从数据比较可得出s /d 2是一常量,所以说s ∝d 2,因此猜想弹簧的弹性势能也与d 2成正比.12.解析:选ACD.重力势能具有系统性,弹性势能只属于发生弹性形变的物体,故A 正确.重力势能和弹性势能都是相对的,且都是状态量,故B 错误,C 、D 正确.13.解析:选AD.弹簧的弹性势能只与弹簧的劲度系数和形变量有关,弹簧的长度为原长时,形变量为零,弹簧的弹性势能最小,A 正确.不管弹簧被拉长还是被压缩,它都具有弹性势能,弹性势能的大小与两种情况下弹簧发生的形变量大小有关,B 、C 错误,D 正确. 14.解析:选AC.速度减为零处,是运动过程的最低点,也是弹簧压缩量最大的位置,故A 、C 正确.15.解析:选ABC.在“蹦极”运动中,人由高空落下到最低点的过程中,重力方向和位移方向均向下,重力对人做正功,重力势能减少,A 、B 正确;在人和橡皮绳相互作用的 过程中,橡皮绳对人的拉力向上,人的位移方向向下,橡皮绳的拉力对人做负功,橡皮绳的弹性势能增加,C 正确,D 错误. 16.解析:(1)据胡克定律F =kl 得 k =F l =4000.05N/m =8 000 N/m.(2)由于F =kl ,作出F -l 图象如图所示,求出图中阴影面积,即为弹力做功的绝对值,由于在伸长过程中弹力F 方向与位移l 方向相反,故弹力F 在此过程中做负功,W =-12×400×0.05J =-10 J.(3)弹力F 做负功,则弹簧弹性势能增加,且做功的多少等于弹性势能的变化量,ΔE p =10 J. 答案:(1)8 000 N/m (2)-10 J (3)10 J 17.解析:弹性势能 E p =12kl 2=12×400×0.12 J =2 J此过程中拉力做的功与弹力做的功数值相等,则有 W 1=W 弹=ΔE p =2 J 刚好离开地面时G =F =kl =400×0.1 N =40 N 又物体缓慢升高,F =40 N物体上升h =0.5 m ,拉力克服重力做功 W 2=Fl =mgh =40×0.5 J =20 J 拉力共做功W =W 1+W 2=(20+2) J =22 J. 答案:22 J 2 J。
2019-2020年高中必修2物理[5.探究弹性势能的表达式]人教版课后练习[含答案解析]四十二
![2019-2020年高中必修2物理[5.探究弹性势能的表达式]人教版课后练习[含答案解析]四十二](https://img.taocdn.com/s3/m/cc211906580216fc700afdd8.png)
2019-2020年高中必修2物理[5.探究弹性势能的表达式]人教版课后练习[含答案解析]四十二第1题【单选题】将一木球靠在轻质弹簧上,压缩后松手,弹簧将木球弹出.已知弹出过程弹簧做了40J的功,周围阻力做了﹣10J的功,此过程物体的( )A、弹性势能减小10JB、弹性势能增加40JC、动能减小10JD、动能增加30J【答案】:【解析】:第2题【单选题】轻质弹簧的一端固定于竖直墙壁,另一端与一木块连接在一起,木块放在粗糙的水平地面上,在外力作用下,木块将弹簧压缩了一段距离后静止于A点,如图所示.现撤去外力,木块向右运动,当它运动到O点时弹簧恰好恢复原长.在此过程中( )A、木块的动能一直增大B、木块受到的合外力一直减小C、弹簧减小的弹性势能大于木块增加的动能D、弹簧减小的弹性势能等于木块增加的动能【答案】:【解析】:第3题【单选题】关于弹簧的弹性势能,下列说法不正确的是( )A、弹簧的弹性势能跟拉伸(或压缩)的长度有关B、弹簧的弹性势能跟弹簧的劲度系数有关C、同一弹簧,在弹性限度内,形变量越大,弹性势能越大D、弹性势能的大小跟使弹簧发生形变的物体有关【答案】:【解析】:第4题【单选题】如图所示,在弹性限度内,将一轻质弹簧从伸长状态变为压缩状态的过程中,其弹性势能的变化情况是( )A、一直减小B、一直增大C、先减小再增大D、先增大再减小【答案】:【解析】:第5题【单选题】如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧一直保持竖直),下列关于能的叙述正确的是( )A、弹簧的弹性势能先增大后减小B、小球的动能先增大后减小C、小球的重力势能先增大后减小D、机械能总和先增大后减小【答案】:【解析】:第6题【多选题】如图所示,轻质弹簧一端固定,另一端连接一小物块,O点为弹簧在原长时物块的位置.物块由A点静止释放,沿粗糙程度相同的水平面向右运动,最远到达B点.在从A到B的过程中,物块( )A、加速度先减小后增大B、经过O点时的速度最大C、所受弹簧弹力始终做正功D、所受弹簧弹力做的功等于克服摩擦力做的功【答案】:【解析】:第7题【多选题】如图所示,质量为mP=2kg的小球P从离水平面高度为h=0.8m的光滑斜面上滚下,与静止在光滑水平面上质量为mQ=2kg的带有轻弹簧的滑块Q碰撞,g=10m/s^2 ,下列说法正确的是( )A、P球与滑块Q碰撞前的速度为4m/sB、P球与滑块Q碰撞前的动量为16 kg?m/sC、它们碰撞后轻弹簧压缩至最短时的速度为2m/sD、当轻弹簧压缩至最短时其弹性势能为16J【答案】:【解析】:第8题【解答题】如图所示,质量分别为M1=0.48kg和M2=0.5kg的木块静置在光滑水平地面上,两木块间夹有一轻质弹簧,一粒质量m=0.02kg的弹丸以v0=150m/s的速度打入木块M1并停留在其中(打击时间极短),求:①当弹丸在木块M1中相对静止的瞬间木块M1的速度v1;②当M2的速度v=1m/s时弹簧的弹性势能Ep .【答案】:【解析】:第9题【实验探究题】某同学利用下述装置对轻质弹簧的弹性势能进行探究,一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连,弹簧处于原长时,小球恰好在桌面边缘,如图所示.向左推小球,使弹簧压缩一段距离后由静止释放,小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.回答下列问题:本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等,已知重力加速度大小为g.为求得Ek ,至少需要测量下列物理量中的______(填正确答案标号).A、小球的质量mB、小球抛出点到落地点的水平距离sC、桌面到地面的高度hD、弹簧的压缩量△xE、弹簧原长l0用所选取的测量量和已知量表示Ek ,得Ek=______.【答案】:【解析】:第10题【实验探究题】某物理小组对轻弹簧的弹性势能进行探究,实验装置如图(a)所示:轻弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一物快接触而不连接,纸带穿过打点计时器并与物块连接.向左推物快使弹簧压缩一段距离,由静止释放物快,通过测量和计算,可求得弹簧被压缩后的弹性势能.实验中涉及到下列操作步骤:①把纸带向左拉直②松手释放物快③接通打点计时器电源④向左推物快使弹簧压缩,并测量弹簧压缩量上述步骤正确的操作顺序是______(填入代表步骤的序号).图(b)中M和L纸带是分别把弹簧压缩到不同位置后所得到的实际打点结果.打点计时器所用交流电的频率为50Hz.由M纸带所给的数据,可求出在该纸带对应的实验中物块脱离弹簧时的速度为______m/s.比较两纸带可知,______(填“M”或“L”)纸带对应的实验中弹簧被压缩后的弹性势能大.【答案】:【解析】:第11题【实验探究题】光滑水平轨道与光滑圆弧轨道相切,轻弹簧的一端固定在轨道的左端,OP是可绕O点转动的轻杆,且摆到某处就能停在该处;另有一小钢球.现在利用这些器材测定弹簧被压缩时的弹性势能.还需要的器材是:______、______ 。
高中物理 专题7.5 探索弹性势能的表达式(讲)(提升版)(含解析)新人教版必修2-新人教版高一必修

专题7.5 探索弹性势能的表达式※知识点一、弹性势能1.定义发生弹性形变的物体的各局部之间,由于有弹力的相互作用而具有的势能。
2.弹簧的弹性势能弹簧的长度为原长时,弹性势能为0。
弹簧被拉长或被压缩时,就具有了弹性势能。
3.决定弹性势能大小相关因素的猜测(1)猜测依据:弹性势能和重力势能同属势能,重力势能大小与物体的重力高度有关,弹性势能与其劲度系数和形变量有关。
(2)猜测结论:弹性势能与弹簧的劲度系数k和形变量l有关,在弹簧的形变量l一样时,弹簧的劲度系数k越大,弹簧的弹性势能越大。
在弹簧劲度系数k一样时,形变量l越大,弹簧弹性势能越大。
※知识点二、弹力做功探究1.弹力做功特点随弹簧形变量的变化而变化,还因弹簧的不同而不同。
2.弹力做功的计算(1)公式法——“化变为恒〞:W总=F1Δl1+F2Δl2+…+F nΔl n。
(2)图象法——F-l图象的“面积〞:F-l图象中图形的“面积〞表示弹力做功的值,即弹性势能的值。
※知识点三、弹力做功跟弹性势能变化的关系当弹簧的弹力做正功时,弹簧的弹性势能减小,弹性势能转化成其他形式的能;当弹簧的弹力做负功时,弹簧的弹性势能增大,其他形式的能转化为弹簧的弹性势能。
这一点与重力做功跟重力势能变化的关系相似。
★重难点一、对弹性势能的理解与探究过程★1.弹性势能的产生与影响2.探究弹性势能表达式的思路 (1)探究过程阶段的划分①类比重力势能的决定因素,猜测弹性势能的决定因素,构建弹性势能的表达式; ②类比重力势能的定义方法,弄清弹簧的弹力所做的功与弹性势能的关系; ③计算弹簧的弹力所做的功; ④由弹力做功的表达式定义弹性势能。
(2)各个探究环节中运用的科学方法 ①类比、迁移、猜测和构思; ②微积分的思路:分割→转比→求和。
3.弹性势能的表达式 弹簧弹性势能的表达式为212p E kl ★特别提醒(1)弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量,因而也是对系统而言的。
探究弹性势能的表达式

核心要点突破
一、弹簧弹性势能的表达式 1.如图7-5-1所示,弹簧的劲度系数为k,左 端固定,不加外力时,右端在A处,今用力F 缓慢向右拉弹簧,使弹簧伸长到B处,若规定 弹簧自由长度的弹性势能为零,则手克服弹簧 弹力所做的功,等于弹簧的弹性势能.
特别提醒:弹力做功与弹性势能变化有唯一 的对应关系,弹力做多少正(负)功,弹性势 能减少(增加)多少.
即时应用(即时突破,小试牛刀)
2.如图7-5-4所示,一个物体以速度v0冲 向与竖直墙壁相连的轻质弹簧,墙壁和物体 间的弹簧被物体压缩,在此过程中以下说法 正确的是( )
图7-5-4
A.物体对弹簧做的功与弹簧的压缩量成正 比
【答案】 AB 【误区警示】 发生形变的物体不一定具 有弹性势能,只有发生弹性形变的物体才具 有弹性势能.对此,必须有清醒的认识.
变式训练1 (2011年汕头高一检测)关于弹 性势能,下列说法正确的是( )
A.发生弹性形变的物体都具有弹性势能 B.只有弹簧在发生弹性形变时才具有弹 性势能
C.弹性势能可以与其他形式的能相互转 化
例2 在水平地面上放一个竖直轻弹簧,弹 簧上端与一个质量为2.0 kg的木块相连,若 在木块上再作用一个竖直向下的力F,使木 块 缓慢向下移动0.10 m,力F做功2.5 J.此 时木块再次处于平衡状态,力F的大小为50 N,如图7-5-5所示.求:
图7-5-5
(1)在木块下移0.10 m的过程中弹性势能的 增加量.
课前自主学案
1.发生弹性形变的物体的各部分之间,由于 有弹__力__的相互作用而具有的势能叫做弹性势 能. 举例:卷紧的发条,拉长或压缩的弹簧,拉 开的弓等都具有弹性势能.学科网zxxk
探究弹性势能的表达式

7.5 探究弹性势能的表达式建议用时实际用时总分值实际得分45分钟100分一、选择题〔此题包括10小题,每题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得5分,选对但不全的得2分,有选错或不选的得0分,共50分〕1.关于弹性势能,以下说法正确的选项是〔〕.发生弹性形变的物体都具有弹性势能.只有弹簧在发生弹性形变时才具有弹性势能.弹性势能可以与其他形式的能相互转化.弹性势能在国际单位制中的单位是焦耳2.关于弹簧的弹性势能,以下说法中正确的选项是〔〕.当弹簧变长时,它的弹性势能一定增加.当弹簧变短时,它的弹性势能一定减少.在拉伸长度相同时,越大的弹簧,它的弹性势能越大.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能3.如图1所示,一个物体以速度冲向竖直墙壁,墙壁和物体间的弹簧被物体压缩,在此过程中以下说法正确的选项是〔〕.物体对弹簧做的功与弹簧的压缩量成正比.物体向墙壁运动相同的位移,弹力做的功不相等.弹簧的弹力做正功,弹性势能减少.弹簧的弹力做负功,弹性势能增加4.如图2所示,质量相等的两木块中间连有一弹簧,今用力缓慢向上提,直到恰好离开地面.开始物体静止在弹簧上面.设开始时弹簧的弹性势能为,刚要离开地面时,弹簧的弹性势能为,那么关于的大小关系及弹性势能变化说法中正确的选项是〔〕. ..Δ .Δ—位移图线如图3所示,那么弹簧由伸长量到伸长量的过程中,弹簧做的功和弹性势能的变化量为〔〕...6.先后用两只不同的弹簧()拉着同一物体沿同一粗糙水平面匀速运动时,就两弹簧的弹性势能的大小,以下说法正确的选项是〔〕.的弹性势能大.的弹性势能大.弹性势能相同.无法判断动的过程中,以下说法正确的选项是〔〕.弹簧对物体做正功,弹簧的弹性势能逐渐减少.弹簧对物体做负功,弹簧的弹性势能逐渐增加.弹簧先对物体做正功,后对物体做负功,弹簧的弹性势能先减少再增加.弹簧先对物体做负功,后对物体做正功,弹簧的弹性势能先增加再减少8.关于弹性势能和重力势能,以下说法不正确的选项是〔〕.重力势能属于物体和地球这个系统,弹性势能属于发生弹性形变的物体.重力势能是相对的,弹性势能是绝对的.重力势能和弹性势能都是相对的.重力势能和弹性势能都是状态量9.如图5所示,一轻弹簧一端固定于点,另一端系一重物,将重物从与悬点在同一水平面且弹簧保持原长的点无初速度释放,让它自由摆下,不计空气阻力,在重物由点摆向最低点的过程中,正确的选项是〔〕.重力做正功,弹力不做功.重力做正功,弹力做正功.假设用与弹簧原长相等的细绳代替弹簧后,重力做正功,弹力不做功.假设用与弹簧原长相等的细绳代替弹簧后,重力做功不变,弹力不做功10.如图6所示,一个物体以速度冲向与竖直墙壁相连的轻质弹簧,墙壁和物体间的弹簧被物体压缩,在此过程中以下说法正确的选项是〔〕.物体对弹簧做的功与弹簧的压缩量成正比.物体向墙壁运动相同的位移,弹力做的功不相图1图2图3图4图5图6等.弹力做正功,弹簧的弹性势能减小 .弹簧的弹力做负功,弹性势能增加 二、填空题〔此题20分〕弹簧的弹性势能公式〔式中为弹簧的劲度系数,为弹簧长度的变化量〕.为验证这一结论,两位同学设计了以下的实验:①两位同学首先都进行了如图7甲所示的实验:将一根轻质弹簧竖直挂起,在弹簧的另一端挂上一个质量为的小铁球,稳定后测得弹簧伸长. ②同学完成步骤①后,接着进行了如图7乙所示的实验:将这根弹簧竖直地固定在水平桌面上,并把小铁球放在弹簧上,然后竖直地套上一根带有插销孔的长透明塑料管,利用插销压缩弹簧.拔掉插销时,弹簧对小球做功,使小球弹起,测得弹簧的压缩量和小铁球上升的最大高度. ③同学完成步骤①后,接着进行了如图7丙所示的实验:将这根弹簧放在水平桌面上,一端固定在竖直墙上,另一端被小铁球压缩,测得压缩量为,释放弹簧后,小铁球从高为的桌面上水平抛出,抛出的水平距离为.〔1〕两位同学进行图甲所示的实验是为了确定什么物理量?请用表示所求的物理量 . 〔2〕如果成立,同学测出的物理量与 、的关系式: .同学测出的物理量与、、的关系式: .〔3〕试分别分析两位同学实验误差的主要来源 .三、简答、计算题〔此题共2小题,每题15分,共30分.解答时应写出必要的文字说明、方程式和重要的演算步骤,只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位〕 12.奥运会上中国选手何雯娜获冠军,她做“蹦床运动〞时,受到的弹力的变化规律如图8所示.试分析何雯娜在段时间内弹性势能、重力势能怎样变化?内又如何变化?13.在水平地面上放一个竖直轻弹簧,弹簧上端与一个质量为的木块相连,假设在木块上再作用一个竖直向下的力,使木块缓慢向下移动,力做功,此时木块再次处于平衡状态,如图9所示.求:〔1〕在木块下移的过程中重力势能的减少量; 〔2〕在木块下移的过程中弹性势能的增加量.7.5 探究弹性势能的表达式得分:图7 图8图9一、选择题题号 1 2 3 4 5 6 7 8 9 10答案二、填空题11.〔1〕〔2〕〔3〕三、计算题12.13.7.5 探究弹性势能的表达式参考答案一、选择题1. 解析:发生弹性形变的物体的各局部之间由于有弹力的作用都具有弹性势能,A正确,B错误;弹性势能跟重力势能一样,可以与其他形式的能相互转化,C正确;所有能的单位跟功的单位都相同,在国际单位制中的单位都是焦耳,D正确.2. 解析:弹簧的弹性势能的大小,除了跟劲度系数有关外,还跟它的形变量有关.如果弹簧原来处在压缩状态,当它变长时,它的弹性势能减少,在原长处时其弹性势能最小,所以A、B、D均不对.3. 解析:由功的计算公式知,恒力做功时,做功的多少与物体的位移成正比,而弹簧对物体的弹力是一个变力,,所以A不正确;弹簧开始被压缩时弹力小,弹力做的功也少,弹簧的压缩量变大时,物体移动相同的距离做的功多,故B正确;物体压缩弹簧的过程,弹簧的弹力与弹力作用点的位移方向相反,所以弹力做负功,弹簧的压缩量增大,弹性势能增加,故C错误,D正确.4. 解析:开始时弹簧形变量为,有.刚要离开地面时弹簧形变量为,有.由于,所以,,A对.5. 解析:-图线与轴围成的面积表示弹力做的功..弹性势能减少了,C正确.6. 解析:由于拉力相同,,①弹簧的弹性势能②由①②可得,因,所以.7. 解析:弹簧由压缩到原长再到伸长,刚开始时弹力方向与运动方向同向,弹力做正功,弹性势能减小.越过原长位置后弹力方向与运动方向相反,弹力做负功,故弹性势能增加,所以只有C正确,A、B、D 错误.8.解析:重力势能、弹性势能都是相对于势能零点而言的,B错,A、C、D对,故只选B.9.解析:用细绳拴住小球向下摆动时重力做正功,弹力不做功,C对;用弹簧拴住小球下摆时,弹簧要伸长,重力做正功,且做功多,小球轨迹不是圆弧,弹力做负功,A、B、D错.10.解析:由功的计算公式知,恒力做功时,做功的多少与物体的位移成正比,而弹簧对物体的弹力是一个变力,所以A不正确.弹簧开始被压缩时弹力小,移动相同距离,弹力做的功也少,弹簧的压缩量变大时,物体移动相同的距离做的功多,故B正确.物体压缩弹簧的过程,弹簧的弹力与弹力作用点的位移方向相反,所以弹力做负功,弹簧的压缩量增大,弹性势能增大,故C错误,D正确.二、填空题11.(1)确定弹簧的劲度系数〔2〕〔3〕同学实验时,不易精确确定小球上升的最大高度,而且小球上升时有可能与塑料管内壁接触,产生摩擦从而带来实验误差.同学实验时,小铁球与水平桌面之间的摩擦会给实验带来误差解析:〔1〕要探究,就必须先确定,图甲中的实验目的就是为了确定弹簧的劲度系数,由平衡条件得,即.〔2〕图乙中弹簧的弹性势能等于小球的重力势能等于小球的动能,小球获得速度后做平抛运动,那么有,联立得,假设成立,那么有,得到.〔3〕同学实验时小球上升的最高点位置不易确定,小球上升时与塑料管之间产生摩擦带来误差;同学实验时,小铁球与水平桌面间有摩擦会带来误差.三、简答、计算题12.段时间内,弹性势能不变,重力势能先变大再变小;段时间内弹性势能先变大再变小,重力势能先变小再变大.提示:段时间内在空中,不受弹力作用,段时间内与蹦床接触,是先下落又上升的过程.13.〔1〕〔2〕解析:〔1〕据重力做功与重力势能的关系有.〔2〕据弹力做功与弹性势能变化的关系有:.又因木块缓慢下移,力与重力的合力与弹力等大反向,所以,所以弹性势能增量.。
高一物理人教版必修2(测试题):(十五) 探究弹性势能的表达式 Word版含解析

课时作业(十五)探究弹性势能的表达式一、单项选择题1.如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力势能、弹簧的弹性势能的变化是()A.重力势能减少,弹性势能增大B.重力势能增大,弹性势能减少C.重力势能减少,弹性势能减少D.重力势能不变,弹性势能增大解析:弹簧向下压缩的过程中,弹簧压缩量增大,弹性势能增大;重力做正功,重力势能减少,故A正确.答案:A2.关于物体的弹性势能,下面说法中正确的是()A.任何发生形变的物体都具有弹性势能B.拉伸时的弹性势能一定大于压缩时的弹性势能C.拉伸长度相同时,k越大的弹簧,弹性势能越大D.弹簧变长时,它的弹性势能一定变大解析:发生弹性形变或虽然不是弹性形变,但存在一定的恢复形状的趋势的情况下,物体具有弹性势能,A错.由E p=12知Δl相同时,k大,E p就大,2kΔl拉伸与压缩量Δl相同时,E p相同,C对B错.处于压缩状的弹簧变长但依然为压缩状态时x变小,E p减小,D错.答案:C3.(2017·威海高一检测)如图所示,在光滑水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力F的作用下物体处于静止状态,当撤去F 后,物体将向右运动.在物体向右运动的过程中,下列说法正确的是() A.弹簧的弹性势能逐渐减小B.弹簧的弹性势能逐渐增大C.弹簧的弹性势能先增大后减小D.弹簧的弹性势能先减小后增大解析:由物体处于静止状态可知,弹簧处于压缩状态,撤去F物体在向右运动的过程中,弹簧的弹力对物体先做正功后做负功,故弹簧的弹性势能应先减小后增大.答案:D4.m A=m B,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为E p1,B刚要离开地面时,弹簧的弹性势能为E p2,则关于E p1、E p2大小关系及弹性势能变化ΔE p的说法正确的是() A.E p1=E p2B.E p1>E p2C.ΔE p>0 D.ΔE p<0解析:对于同一弹簧,其弹性势能的大小取决于它的形变量.开始时,弹簧处于压缩状态,与原长相比,它的压缩量为x1=m A gk.当B刚要离开地面时,弹簧处于拉伸状态,与原长相比,它的伸长量为x2=m B gk.因为m A=m B,所以x1=x2,故E p1=E p2,则选项A正确、B错误;又ΔE p=E p2-E p1=0,选项C、D错误.答案:A二、多项选择题5.关于弹性势能,下列说法中正确的是()A.发生形变的物体都具有弹性势能B.弹性势能是一个标量C.在国际单位制中,弹性势能的单位是焦耳D.弹性势能是状态量解析:只有发生弹性形变的物体才具有弹性势能,所以A错误.弹性势能是一个标量,在国际单位制中,其单位是焦耳,弹性势能是一个状态量,B、C、D正确.答案:BCD6.(2017·桂林高一检测)如图所示,一根轻弹簧下端固定,竖立在水平面上.其正上方A位置有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.小球下降阶段,下列说法正确的是()A.在B位置小球速度最大B.在C位置小球速度最大C.从A→C位置小球重力势能的减少量小于重力做的功D.从A→D位置小球重力势能的减少量等于弹簧弹性势能的增加量解析:由受力情况可知,小球从A到C做加速运动,从C到D做减速运动,C点时速度最大,A错、B对.从A→C,小球减小的重力势能等于重力做的功,C错.从A→D,小球减少的重力势能全部转化为弹性势能,所以D对.答案:BD7.如图是玩家玩“蹦极”游戏的真实照片,玩家将一根长为AB的弹性绳子的一端系在身上,另一端固定在高处,然后从高处跳下,其中AB为弹性绳子的原长,C点是弹力等于重力的位置,D点是玩家所到达的最低点,对于玩家离开跳台至最低点的过程中,下列说法正确的是()A.重力对人一直做正功B.人的重力势能一直减小C.玩家通过B点之后,绳子具有弹性势能D.从A到D,弹性绳子的弹性势能一直增加解析:整个过程中,重力一直做正功,重力势能一直减小;人从高空落下到弹性绳子达到原长的过程中,弹性绳子不做功,此后弹性绳子一直做负功,弹性势能一直增加.答案:ABC8.(2017·日照高一检测)如图所示,弹簧的一端固定在墙上,另一端在水平力F作用下缓慢拉伸了x.关于拉力F、弹性势能E p随伸长量x的变化图象正确的是()解析:因为是缓慢拉伸,所以拉力始终与弹簧弹力大小相等,由胡克定律知F=kx,F-x图象为倾斜直线,A对、B错.因为E p∝x2,所以D对、C错.答案:AD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 探究弹性势能的表达式
1.关于弹性势能,下列说法中正确的是( )
A .任何发生弹性形变的物体,都具有弹性势能
B .任何具有弹性势能的物体,一定发生了弹性形变
C .物体只要发生形变,就一定具有弹性势能
D .弹簧的弹性势能只跟弹簧被拉伸或压缩的长度有关
2. 一竖直弹簧下端固定于水平地面上,如图5-5-10所示,小球从弹簧的正上方高为h 的地方自由下落到弹簧上端,如图2-5-10所示,经几次反弹以后小球最终在弹簧上静止于某一点A 处,则( )
A .h 愈大,弹簧在A 点的压缩量愈大
B .弹簧在A 点的压缩量与h 无关
C .h 愈大,最终小球静止在A 点时弹簧的弹性势能愈大
D .小球第一次到达A 点时弹簧的弹性势能比最终小球静止在A 点时弹簧的弹性势能大
3.教材中说:“在探究弹性势能的表达式时,可以参考对重力势能的讨论。
”当物体处于参考平面时,重力势能为0;在参考平面上方,重力势能为正;在参考平面下方,重力势能为负。
当弹簧的长度为原长时,弹簧的弹性势能为0;弹簧拉伸时,弹性势能为正;那么,弹簧压缩时弹性势能也为负值吗?为什么?
4.如图2-5-11所示,劲度系数为k 的轻质弹簧一端固定,另一端与物块拴接,物块放在光滑水平面上。
现用外力缓慢拉动物块,若外力所做的功为W ,则物块移动了多大的距离?
5.关于弹性势能,以下说法中正确的是( )
A .发生弹性形变的物体一定具有弹性势能
B .发生弹性形变的物体不一定具有弹性势能
C .发生形变的物体一定具有弹性势能
D .发生形变的物体不一定具有弹性势能
6.讨论弹性势能,要从下述问题的分析入手的是( )
A .重力做功
B .弹力做功
C .弹簧的劲度系数
D .弹簧的形变量
7.弹簧的一端固定,原处于自然长度。
现对弹簧的另一端施加一个拉力,关于拉力做功(或弹簧克服拉力做功)与弹性势能变化的关系,以下说法中正确的是( )
A .拉力对弹簧做正功,弹簧的弹性势能增加
B .拉力对弹簧做正功,弹簧的弹性势能减少
C .弹簧克服拉力做功。
弹簧的弹性势能增加
D .弹簧克服拉力做功,弹簧的弹性势能减少
8.如图2-5-12所示,表示撑杆跳运动的几个阶段:助跑、撑杆起跳、越横杆。
试定性地说明在这几个阶段中能量的转化情况。
2-5-11
2-5-10
2-5-12
9.在本节课的探究活动中,我们多次采用了类比的研究方法,试举例说明。
10.如图2-5-13所示,质量为m 物体静止在地面上,物体上面连着一个直立的轻质弹簧,弹簧的劲度系数为k 。
现用手拉住弹簧上端,使弹簧上端缓慢提升高度h ,此时物体已经离开地面,求拉力所做的功。
答案
1.AB 2.B 3.弹簧压缩时弹性势能是正值。
4.
k W
2 5.AD 6. B 7.AC 8.运动员的助跑阶段,身体中的化学能转化为人和杆的动能;起跳时,运动员的动能和身体中的化学能转化为人的重力势能和撑杆中的弹性势能,随着人体的继续上升,撑杆中的弹性势能转化为人的重力势能,使人体上升至横杆以上;越过横杆后,运动员的重力势能转化为动能。
9.在本节课的探究活动中,采用类比研究方法的地方主要有:
① 研究弹性势能的出发点,将重力势能与弹性势能类比。
讨论重力势能从分析重力做功入手,讨论弹性势能则从分析弹力做功入手。
② 弹性势能表达式中相关物理量的猜测,将重力势能与弹性势能、重力与弹力类比。
重力势能与物体被举起的高度有关,所以弹性势能很可能与弹簧被拉伸的长度有关。
弹力与重力的变化规律不一样,弹性势能与重力势能的表达式很可能也不一样。
③ 计算拉力所做的功,与计算匀变速直线运动的位移类比。
计算匀变速直线运动的位移时,将位移分成很多小段,每一小段的速度可近似认为相等,物体在整个过程中的位移等于各小段位移之和。
计算拉力所做的功,可将弹簧的形变过程分成很多小段,每一小段的拉力可近似认为是不变的,拉力在整个过程中的功等于各小段功之和。
④ 计算各小段功的求和式,将由v — t 图象求位移与由F —l 图象求功类比。
v — t 图象下的相关面积表示位移,F —l 图象下的相关面积则表示功。
10.
)2(k mg h mg。
2-5-13。
