高等数学 极限存在的判断准则
同济大学高等数学§1.3.1 极限存在准则

xn 单调增加(或单调减少)。
单调增加和单调减少的数列统称为单调数列。
定理2(单调有界原理): 单调增加(减少)有上(下)界的数列必定有极限。
x1 x2 x3 xn xn1 a M
x
定理的几何解释:若数列{xn } 单调增加且有上界,即
n
n
※夹逼定理在肯定{yn} 收敛的同时也给出了其极
限当值n,在N实1 时际,应有用x时n ,a若nlim, y从n 而不a易求得xn,,则将yn 适当当n缩小N、2 时放,大有,z得n 两a个具,有从相而同zn极限a的辅,助数列
{x取n}N,{mzna}x,(N即1, 可N求2 )出,nl则im当ynn 。N 时,有
a xn yn zn a yn a ,
故 lim yn a 。
n
例 1.(1) a1,a2,, ak 为 k 个给定的正数, 求 lim n a1n a2n ak n 。
n
解:设a max{a1, a2 ,, ak } ,则
a n an n a1n a2n ak n n kan a n k ,
∵ lim a a , lim a n k a ,
n
n
∴ lim n a1n a2n ak n a 。
n
lim n k 1
n
(2)求 lim 1 352n1. n 2 4 6 2n
解:令 xn
1 3 5 () 2n 1
246
2n
,
yn
2 4 6 () 2n ,
357
2n 1
定理3(Cauchy 收敛准则):
数列an 收敛的充分必要条件是
0 N N使得m, n N有 am - an 。
高等数学第3章第3节函数极限存在条件

§3 函数极限存在条件引 言在讨论数列极限存在条件时,我们曾向大家介绍过“单调有界定理”和“柯西收敛准则”.我们说数列是特殊的函数,那么对于函数是否也有类似的结果呢?或者说能否从函数值的变化趋势来判断其极限的存在性呢?这是本节的主要任务.本节的结论只对0x x →这种类型的函数极限进行论述,但其结论对其它类型的函数极限也是成立的. 首先介绍一个很主要的结果——海涅(Heine)定理(归结原则).一、归结原则定理1(Heine 定理) 设f 在00(;)U x δ'内有定义,0lim ()x x f x →存在⇔对任何含于00(;)U x δ'且以0x 为极限的数列{}n x ,极限lim ()n n f x →∞都存在且相等.注1.{}()n f x 是数列,lim ()n n f x →∞是数列的极限.所以这个定理把函数()f x 的极限归结为数列{}()n f x 的极限问题来讨论,所以称之为“归结原则”.由此,可由数列极限的性质来推断函数极限性质. 注2.从Heine 定理可以得到一个说明0lim ()x x f x →不存在的方法,即“若可找到一个数列{}n x ,0lim n n x x →∞=,使得lim ()n n f x →∞不存在;”或“找到两个都以0x 为极限的数列{}{},n n x x ''',使l i m (),l i m (n n n n f x f x →∞→∞'''都存在但不相等,则0lim ()x x f x →不存在. 例1 证明01lim sinx x→不存在. 注3.对于00,,,x x x x x x +-→→→+∞→-∞这四种类型的单侧极限,相应的归结原则可表示为更强的形式.如当0x x +→时有:定理2 设函数f 在0x 的某空心邻域00()U x +内有定义,0lim ()x x f x A +→= ⇔对任何以0x 为极限的递减数列{}00()n x U x +⊂,有lim ()n n f x A →∞=.二、单调有界定理相应于数列极限的单调有界定理,关于上述四类单侧极限也有相应的定理.现以0x x +→这种类型为例叙述如下:定理3 设f 为定义有00()U x +上的单调有界函数,则右极限0lim ()x x f x +→存在.注:定理3可更具体地叙述如下:f 为定义在00()U x +上的函数,若(1)f 在00()U x +上递增有下界,则0l i m ()x x f x +→存在,且0()lim ()inf ()x x x U x f x f x ++→∈=;(2)f 在00()U x +上递减有上界,则0lim ()x x f x +→存在,且00()lim ()sup ()x x x U x f x f x ++→∈=. 三 函数极限的Cauchy 收敛准则定理4(Cauchy 准则) 设函数f 在00(;)U x δ'内有定义,0lim ()x x f x →存在⇔任给0ε>,存在正数()δδ'<,使得对任何00,(;)x x U x δ'''∈有|()()|f x f x ε'''-<.注:按照Cauchy 准则,可以写出0lim ()x x f x →不存在的充要条件:存在0ε>,对任意(0)δ>,存在00,(;)x x U x δ'''∈使得|()()|f x f x ε'''-≥.例:用Cauchy 准则说明01lim sinx x→不存在. 综上所述:Heine 定理和Cauchy 准则是说明极限不存在的很方便的工具. 作业:p55. 1, 2, 4.。
关于大学高等数学函数极限和连续

第一章 函数、极限和连续§ 函数一、 主要内容 ㈠ 函数的概念1. 函数的定义: y=fx, x ∈D定义域: Df, 值域: Zf.2.分段函数: ⎩⎨⎧∈∈=21)()(D x x g D x x f y 3.隐函数: Fx,y= 04.反函数: y=fx → x=φy=f -1y y=f -1 x定理:如果函数: y=fx, Df=X, Zf=Y 是严格单调增加或减少的; 则它必定存在反函数:y=f -1x, Df -1=Y, Zf -1=X且也是严格单调增加或减少的;㈡ 函数的几何特性1.函数的单调性: y=fx,x ∈D,x 1、x 2∈D 当x 1<x 2时,若fx 1≤fx 2,则称fx 在D 内单调增加 ;若fx 1≥fx 2,则称fx 在D 内单调减少 ;若fx 1<fx 2,则称fx 在D 内严格单调增加 ;若fx 1>fx 2,则称fx 在D 内严格单调减少 ;2.函数的奇偶性:Df 关于原点对称 偶函数:f-x=fx 奇函数:f-x=-fx3.函数的周期性:周期函数:fx+T=fx, x ∈-∞,+∞ 周期:T ——最小的正数4.函数的有界性: |fx|≤M , x ∈a,b ㈢ 基本初等函数1.常数函数: y=c , c 为常数2.幂函数: y=x n , n 为实数3.指数函数: y=a x , a >0、a ≠14.对数函数: y=log a x ,a >0、a ≠15.三角函数: y=sin x , y=con xy=tan x , y=cot x y=sec x , y=csc x6.反三角函数:y=arcsin x, y=arccon x y=arctan x, y=arccot x ㈣ 复合函数和初等函数1.复合函数: y=fu , u=φxy=f φx , x ∈X2.初等函数:由基本初等函数经过有限次的四则运算加、减、乘、除和复合所构成的,并且能用一个数学式子表示的函数§ 极 限一、 主要内容 ㈠极限的概念1. 数列的极限:Aynn =∞→lim称数列{}n y 以常数A 为极限; 或称数列{}n y 收敛于A.定理: 若{}n y 的极限存在⇒{}n y 必定有界.2.函数的极限:⑴当∞→x 时,)(x f 的极限:⑵当0x x →时,)(x f 的极限:左极限:Ax f x x =-→)(lim 0右极限:A x f x x =+→)(lim 0⑶函数极限存的充要条件:定理:AxfxfAxfxxxxxx==⇔=+-→→→)(lim)(lim)(lim㈡无穷大量和无穷小量1.无穷大量:+∞=)(lim xf称在该变化过程中)(xf为无穷大量;X再某个变化过程是指:2.无穷小量:)(lim=xf称在该变化过程中)(xf为无穷小量;3.无穷大量与无穷小量的关系:定理:)0)((,)(1lim)(lim≠+∞=⇔=xfxfxf4.无穷小量的比较:lim,0lim==βα⑴若lim=αβ,则称β是比α较高阶的无穷小量;⑵若c=αβlimc为常数,则称β与α同阶的无穷小量;⑶若1lim=αβ,则称β与α是等价的无穷小量,记作:β~α;⑷若∞=αβlim ,则称β是比α较低阶的无穷小量; 定理:若:;,2211~~βαβα则:2121limlim ββαα=㈢两面夹定理1. 数列极限存在的判定准则:设:n n n z x y ≤≤ n=1、2、3…且: a z y n n n n ==∞→∞→lim lim则: a x n n =∞→lim2. 函数极限存在的判定准则: 设:对于点x 0的某个邻域内的一切点 点x 0除外有:且:Ax h x g x x x x ==→→)(lim )(lim 0则:A x f x x =→)(lim 0㈣极限的运算规则若:B x v A x u ==)(lim ,)(lim则:①B A x v x u x v x u ±=±=±)(lim )(lim )]()(lim[②B A x v x u x v x u ⋅=⋅=⋅)(lim )(lim )]()(lim[③BA x v x u x v x u ==)(lim )(lim )()(lim )0)((lim ≠x v 推论:①)]()()(lim [21x u x u x u n ±±±②)(lim )](lim[x u c x u c ⋅=⋅③nnx u x u )]([lim )](lim [=㈤两个重要极限1.1sin lim 0=→xxx 或 1)()(sin lim 0)(=→x x x ϕϕϕ 2.e xxx =+∞→)11(lim e x xx =+→10)1(lim§ 连续一、主要内容㈠ 函数的连续性 1. 函数在0x 处连续:)(x f 在0x 的邻域内有定义,1o 0)]()([lim lim 000=-∆+=∆→∆→∆x f x x f y x x2o)()(lim 00x f x f x x =→左连续:)()(lim 00x f x f x x =-→右连续:)()(lim 00x f x f x x =+→2. 函数在0x 处连续的必要条件:定理:)(x f 在0x 处连续⇒)(x f 在0x 处极限存在3. 函数在0x 处连续的充要条件:定理:)()(lim )(lim )()(lim 000x f x f x f x f x f x x x x x x ==⇔=+-→→→4. 函数在[]b a ,上连续:)(x f 在[]b a ,上每一点都连续;在端点a 和b 连续是指:)()(lim a f x f ax =+→ 左端点右连续;)()(lim b f x f b x =-→ 右端点左连续;a + 0b - x 5. 函数的间断点:若)(x f 在0x 处不连续,则0x 为)(x f 的间断点;间断点有三种情况:1o)(x f在0x 处无定义;2o)(lim 0x f x x →不存在;3o)(x f在0x 处有定义,且)(lim 0x f x x →存在,但)()(lim 00x f x f x x ≠→;两类间断点的判断: 1o 第一类间断点:特点:)(lim 0x f x x -→和)(lim 0x f x x +→都存在;可去间断点:)(lim 0x f x x →存在,但)()(lim 00x f x f x x ≠→,或)(x f在0x 处无定义;2o 第二类间断点:特点:)(lim 0x f x x -→和)(lim 0x f x x +→至少有一个为∞,或)(lim 0x f x x →振荡不存在;无穷间断点:)(lim 0x f x x -→和)(lim 0x f x x +→至少有一个为∞㈡函数在0x 处连续的性质1.连续函数的四则运算:设)()(lim 00x f x f x x =→,)()(lim 00x g x g x x =→1o)()()]()([lim 000x g x f x g x f x x ±=±→2o)()()]()([lim 000x g x f x g x f x x ⋅=⋅→3o)()()()(lim 000x g x f x g x f x x =→ ⎪⎭⎫ ⎝⎛≠→0)(lim 0x g x x2. 复合函数的连续性:则:)]([)](lim [)]([lim 00x f x f x f x x x x ϕϕϕ==→→3.反函数的连续性:㈢函数在],[b a 上连续的性质1.最大值与最小值定理:)(x f 在],[b a 上连续⇒)(x f 在],[b a 上一定存在最大值与最小值;fx0 a b xm-M0 ab x2.有界定理:) (xf在],[ba上连续⇒)(x f在],[b a上一定有界;3.介值定理:) (xf在],[ba上连续⇒在),(b a内至少存在一点ξ,使得:cf=)(ξ,其中:Mcm≤≤y yCfx0 a ξm0 a ξ1 ξ2 b x 推论:)(x f 在],[b a 上连续,且)(a f 与)(b f 异号⇒在),(b a 内至少存在一点ξ,使得:0)(=ξf ;4.初等函数的连续性:初等函数在其定域区间内都是连续的; 第二章 一元函数微分学 § 导数与微分 一、主要内容 ㈠导数的概念1.导数:)(x f y =在0x 的某个邻域内有定义, 2.左导数:00)()(lim )(0x x x f x f x f x x --='-→- 右导数:00)()(lim )(0x x x f x f x f x x --='+→+ 定理:)(x f 在0x 的左或右邻域上连续在其内可导,且极限存在;则:)(lim )(00x f x f x x '='-→-或:)(lim )(00x f x f x x '='+→+3.函数可导的必要条件:定理:)(x f 在0x 处可导⇒)(x f 在0x 处连续4. 函数可导的充要条件:定理:)(00x f y x x '='=存在)()(00x f x f +-'='⇒,且存在;5.导函数: ),(x f y '=' ),(b a x ∈)(x f 在),(b a 内处处可导; y )(0x f '6.导数的几何性质: y ∆)(0x f '是曲线)(x f y =上点 ∆()00,y x M 处切线的斜率; o x 0㈡求导法则 1.基本求导公式: 2.导数的四则运算: 1o v u v u '±'='±)(2ov u v u v u '⋅+⋅'='⋅)(3o2v v u v u v u '⋅-⋅'='⎪⎭⎫⎝⎛ )0(≠v 3.复合函数的导数:dxdu du dy dx dy ⋅=,或 )()]([})]([{x x f x f ϕϕϕ'⋅'=' ☆注意})]([{'x f ϕ与)]([x f ϕ'的区别:})]([{'x f ϕ表示复合函数对自变量x 求导;)]([x f ϕ'表示复合函数对中间变量)(x ϕ求导;4.高阶导数:)(),(),()3(x f x f x f 或'''''函数的n 阶导数等于其n-1导数的导数; ㈢微分的概念 1.微分:)(x f 在x 的某个邻域内有定义,其中:)(x A 与x ∆无关,)(x o ∆是比x ∆较高阶的无穷小量,即:0)(lim 0=∆∆→∆x x o x 则称)(x f y =在x 处可微,记作:2.导数与微分的等价关系: 定理:)(x f 在x 处可微)(x f ⇒在x 处可导,且:)()(x A x f ='3.微分形式不变性:不论u 是自变量,还是中间变量,函数的微分dy 都具有相同的形式;§ 中值定理及导数的应用 一、主要内容 ㈠中值定理1.罗尔定理: )(x f 满足条件:y)(ξf ' )(x fa o ξb x a o x2.拉格朗日定理:)(x f 满足条件:㈡罗必塔法则:∞∞,型未定式 定理:)(x f 和)(x g 满足条件:1o)或)或∞=∞=→→(0)(lim (0)(lim x g x f ax ax ;2o 在点a 的某个邻域内可导,且0)(≠'x g ;3o)(或∞=''∞→,)()(lim )(A x g x f a x则:)(或∞=''=∞→∞→,)()(lim )()(lim )()(A x g x f x g x f a x a x☆注意:1o 法则的意义:把函数之比的极限化成了它们导数之比的极限; 2o若不满足法则的条件,不能使用法则;即不是型或∞∞型时,不可求导;3o 应用法则时,要分别对分子、分母 求导,而不是对整个分式求导; 4o 若)(x f '和)(x g '还满足法则的条件,可以继续使用法则,即: 5o 若函数是∞-∞∞⋅,0型可采用代数变形,化成或∞∞型;若是0,0,1∞∞型可采用对数或指数变形,化成或∞∞型;㈢导数的应用 1.切线方程和法线方程:设:),(),(00y x M x f y =切线方程:))((000x x x f y y -'=-法线方程:)0)((),()(10000≠'-'-=-x f x x x f y y 2. 曲线的单调性:⑴),(0)(b a x x f ∈≥'内单调增加;在),()(b a x f ⇒⑵),(0)(b a x x f ∈>'内严格单调增加;在),(b a ⇒3.函数的极值: ⑴极值的定义:设)(x f 在),(b a 内有定义,0x 是),(b a 内的一点;若对于x 的某个邻域内的任意点x x ≠,都有:则称)(0x f 是)(x f 的一个极大值或极小值,称x 为)(x f 的极大值点或极小值点;⑵极值存在的必要条件:定理:)()(.2)()(.1=⇒⎭⎬⎫'xfxfxfxf存在。
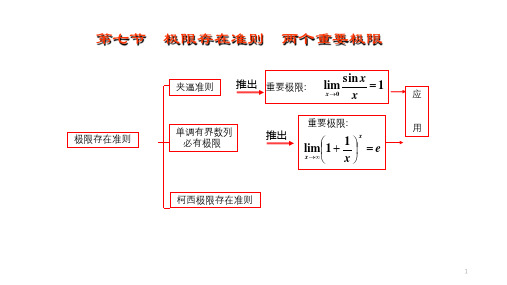
高等数学1-6极限存在准则,两种重要极限

xn a 成立,
该准则可以推广到函数的极限
准则 I'
如果当 x U ( x0 ) (或 | x | M )时,有
(1) g( x ) f ( x ) h( x ),
(2) lim g ( x ) A,
x x0 ( x ) x x0 ( x )
o
lim h( x ) A,
lim 那么 x x f ( x ) 存在, 且等于 A .
( x )
0
准则 I 和准则 I’ 称为夹逼准则. 注意: 利用夹逼准则求极限关键是构造出 yn与 zn
( g( x ), h( x )), 并且 yn ( g ( x ))与zn ( h( x )) 的极限
1 x lim (1 ) e . x x
1 x 再证 xlim (1 ) e , x
令 t x,
1 x lim (1 ) e . x x
1 x 1 t t t lim (1 ) lim(1 ) lim( ) x t t t 1 x t 1 t lim(1 ) lim(1 1 )t 1 (1 1 ) e. t t 1 t t 1 t 1 1 令t , x
复习
1. 无穷小与无穷大的定义
2. 无穷小与函数极限的关系 3. 无穷小与无穷大的关系
几点注意:
1. 无穷小和无穷大是相对于过程而言的;
2. 无穷小(大) 是变量,不能与很小(大)的数混淆; 3. 零是唯一可作为无穷小的数; 4. 无界变量未必是无穷大.
1. 极限运算法则
(1) 无穷小运算法则 (2) 极限四则运算法则 (3) 复合函数极限运算法则
arcsin x . 例5. 求 lim x 0 x
高等数学极限存在准则

x x0 ( x )
x x0 ( x )
那末 lim f ( x)存在, 且等于A. x x0 ( x)
A
A
A
(( 1 x0
y h( x) y f (x) y g(x)
x0
)) 2
x0
准则 Ⅰ和准则 Ⅰ'称为夹逼准则. 问题: 1. 怎样使用数列夹逼准则?
回答:关键是构造数列 yn和 zn,使得对于一切正整
于是有sin x BD, x 弧 AB, tan x AC,
sin x x tan x, 即 cos x sin x 1, x
上式对于 x 0也成立. 2
当 0 x 时,
2
0 cos x 1 1 cos x
2sin2 x 2
2( x)2
x2 ,
22
lim x 2 0, lim(1 cos x) 0,
x x
3. lim xsin 1 _0___ ;
x0
x
作业
2. lim xsin 1 __1__ ;
x
x
4. lim (1 1)n _e___1;
n n
P55 1 (4),(5),(6) ; 2 (2),(3),(4) ; 4 (4) , (5)
第七节 目录 上页 下页 返回 结束
xn
存在.
xn1
3 xn ,
xn21 3 xn ,
lim
n
x2 n1
lim(3
n
xn ),
A2 3 A, 解得 A 1 13 , A 1 13 (舍去)
2
2
lim n
xn
1
2
13 .
二、两个重要极限
(1) lim sin x 1 x0 x
高等数学 第1章 第七节 极限存在准则 两个重要极限
则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,(舍去)
lim n
xn
3.
14
3.两个重要极限的应用
例6: 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解: lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知:
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明:
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x
高等数学函数极限存在的判别法则

1 1 1 1 1 1 1 1 1 x x x 1 x
x
x
x
x
1 1 x
1 x
1 由 lim 1 e 知 n n
0
若 xn x0 n , 则有
判 别 准 则 II 的 充分性证明要 用反证法证明 ,证明从略.
f ( xn ) A( n ).
x 这里 0 可代表 x0 , x0 , , , 和 .
sin x 极限不存在. 例4 证明 xlim
3 x 1
3 x 1
1 1 lim 1 1 x x x
x
3
e 3 1 0 e 3 .
数列极限是特殊的函数极限,由函数极限的定义,若
lim f ( x ) A, 则对任何 xn x0 ( n ), 有 x x
x 0 x 0
sin x 1. 由判别准则I,知 lim x 0 x
图1.6.1
第二个重要极限:
1 lim 1 e x x
n
x
1 第二个重要极限要通过 lim 1 e 和定理1得到, n n
有兴趣研究其证明方法可参阅有关教材,我们只给出
高等数学多媒体课件
§1.6 函数极限存在的判别法则
由于函数极限的变量取值的连续性,导致函 数极限存在的判别法则和数列极限存在的判别法 有相似,但又有许多不同. 判别准则I (两边夹法则) 若 0 0, 使得当
x U ( x0 , 0 ) 时, h( x ) f ( x ) g ( x ), 且
函数极限存在的充要条件

函数极限存在的充要条件函数极限存在的充要条件在高等数学中,函数极限是一个重要的概念,它是描述函数在某些特定点上的行为情况的工具。
函数极限的存在性是判断函数在某点处是否连续的关键因素。
接下来我们将介绍函数极限存在的充要条件,以及如何利用这些条件来计算函数的极限。
在介绍函数极限存在的充要条件之前,先回顾一下什么是函数极限。
对于给定的函数f(x),如果当自变量x无限接近一个给定的实数a时,相应的函数值f(x)也无限接近于一个实数L,那么我们称L为f(x)在x=a处的极限,记作f(x)——>L(x——>a)。
数学符号表示为:当x——>a时,f(x)——>L接下来是函数极限存在的充要条件:充要条件1:局部有界性如果函数f(x)在x=a点的某个小邻域内有界,即存在正实数M,使得对于所有x∈(a-δ,a+δ)(δ>0),都有|f(x)|≤M,那么函数f(x)在x=a处的极限存在。
这个定理的意义在于,如果函数在x=a附近不会变得太大或太小,我们可以认为它在a点处的极限存在,而不必考虑它的确切值。
此外,这个定理也叫做Bellman定理,是一种非常有用的工具,可以用来推导出其他更复杂的定理和性质。
充要条件2:逐点有界性如果函数f(x)在整个定义域X内都是有界的,即存在正实数M,使得对于所有x∈X,都有|f(x)|≤M,那么函数f(x)在x=a处的极限存在。
这个定理的作用在于,它给出了函数极限存在的一个非常强的条件,可以帮助我们快速判断函数是否具有极限。
注意,这里的定义域X可以是有限或无限的,但是函数必须在这个定义域内都有定义才能使用这个定理。
充要条件3:局部单调性如果函数f(x)在x=a点的某个小邻域内是单调的,并且这个邻域内有一个确界,那么函数f(x)在x=a处的极限存在。
此外,如果在这个邻域内,函数的单调性和确界性质可以保持,则极限值等于函数的确界或小于它。
这个定理的思想是比较显然的:如果函数在x=a的某个邻域内单调,那么它在这个邻域中的行为应该是比较稳定的,不会跳跃或震荡。
极限存在准则与两个重要极限

100 000 2.718 27 100 000 2.718 30
1 000 000 2.718 28 1 000 000 2.718 28
e e
1.2 准则Ⅱ与第二个重要极限
因此,
lim
x
1
1 x
x
e
.
e 是无理数,它的值是 2.718 28 .在 1.1 中提到的指数函数 y ex 及自然对数 y ln x 中的
(2) lim g(x) lim h(x) A ,
xx0
xx0
则有 lim f (x) A . xx0
1.1 准则Ⅰ与第一个重要极限
作为准则Ⅰ及准则Ⅰ'的应用,下面证明一个重要极限: lim sin x 1 . x0 x
证明 在图所示的单位圆中,设圆心角 BOA x , AD 切圆 O 于 A , 且与 OB 延长线相交于 D ,于是有
3 1
x 1
1
lim
x 1
3
x
2x 1
2x
lim
x
2x 2x
3 1
lim
x
1 1
3
x
2x
1 x 2x
1
3
e2
1
e2
e.
1.7 无穷小阶的比较
在 1.4 节中我们已经知道,两个无穷小的和、差及乘积仍是无穷小.但是关于两
个无穷小的商却会出现不同的情况.例如,当 x 0 时,2x , x2 ,sin x 都是无穷小
an1
1
n
1
n1
1
1
1
21!1
n
1
1
1 3!
1
1 n
1
高等数学 第六节 极限存在准则 两个重要极限

1 + 2 +⋯+ n < I n 2 2 2 n +n n +n n +n < 1 + 2 +⋯+ n , n2 + 1 n2 + 1 n2 + 1
+ 即 1 + 22 ⋯ + n < In < 1 + 2 + ⋯ + n , n +n n2 + 1
n(n + 1) n(n + 1) < In < , 2 2 2(n + 1) 2(n + n)
n
或 lim(1+ x)
x→0
1 x
=e .
e = 2.7182818284 59045⋯ (无理数 ⋯ )
sin x =1 . 2) . lim x→0 x
弦长 AB = 2 sin x , 弧长 AB = 2 x , 切线长 CD = 2 tan x .
F
A C
x
B
E
D
7
sin x < x < tan x . ( x > 0)
∀ε > 0 , ∃ N1 , 当 n > N1 时, A − ε < yn < A + ε ;
∃ N 2 , 当 n > N 2 时, A − ε < zn < A + ε , 从而 , 当 n > max{ N1 , N 2 } 时 ,
A − ε < yn ≤ xn ≤ z n < A + ε
n→∞
13
uk + uk uk −1 − uk −1 − uk −1uk uk uk−1 = − (1 + uk ) (1 + uk −1 ) 1+ uk 1+ uk−1 uk − uk −1 = > 0 ⇒ uk +1 > uk , { un } 单调增加 . (1 + uk ) (1 + uk −1 )
高等数学1.7 极限存在准则 两个重要极限

一、准则 I
准则 I: 如果数列{xn }、{yn}及{zn}满足下列条件:
( ynxnzn(n=1,2,3,…),
lim (2) lim yn=a,n zn=a,
n
lim 那么数列{xn }的极限存在,且 x n=a . n
.
例8
sin x . x x tan x 求 lim . x0 x 1 - cos x 例 2 求 lim . 2 x 0 x
求 lim
5 求 lim
6
7
7 x + 5x - 3 3x 2 - 2 x - 1 求 lim . x 2 x 3 - x 2 + 5 2x 3 - x 2 + 5 求 lim . 2 x 3 x - 2 x - 1
例2 求lim
1 - cos x . 2 x 0 x
2
解
x sin x 2 x sin 2 sin 1 1 1 - cos x 2 2 = lim 2 = lim lim = lim x0 x0 x2 2 x 0 1 2 2 x 0 x x2 2 2 1 2 1 = 1 = . 2 2
n
根据准则II,数列{x n}必有极限. 这个极限我们用e 来表示.即
lim 1 + n 1 =e . n
n
e 是个无理数,它的值是e=2.718281828459045 ···.
还可证明
1 lim1 + =e . x x
x
第二个重要极限: lim1 + x
准则 I: 如果函数g(x)、f(x)及h(x)满足下列条件:
极限的定义与极限存在的判定方法

极限的定义与极限存在的判定方法极限是高等数学中最基础和最重要的概念之一,是计算微积分、微分方程等高级数学问题的基础。
极限的存在性也是判断函数是否可导、连续等重要性质的基础。
那么,什么是极限?极限存在的判定方法又有哪些呢?一、极限的定义极限的定义是通过无穷小和无穷大的概念来描述的。
对于一个函数f(x),当x趋近于a时,若f(x)可以无限接近于一个确定的数L,则称函数f(x)在x趋近于a时的极限为L,记作:$\lim\limits_{x\rightarrow a}f(x)=L$其中,a为x的极限点。
如果对于任意一个ε>0,都存在一个δ>0,使得当0<|x-a|<δ时,有|f(x)-L|<ε,那么称L为f(x)在x=a时的极限。
二、极限存在的判定方法1. 函数存在左、右极限且相等当a为函数f(x)的间断点,但其左右极限都存在且相等,则f(x)在x=a时的极限存在。
例如:$\lim\limits_{x\rightarrow0}\frac{\sin{x}}{x}=1$在x=0时,函数的左右极限均为1。
2. 夹逼准则对于函数f(x),若存在两个函数g(x)和h(x),满足当x趋近于a 时,g(x)≤f(x)≤h(x),且$\lim\limits_{x\rightarrowa}g(x)=\lim\limits_{x\rightarrow a}h(x)=L$,则函数f(x)在x=a时的极限存在,且等于L。
例如:$\lim\limits_{x\rightarrow0}x\sin(\frac{1}{x})=0$证明:由于|x|≥0,所以-1≤sin(x)≤1,于是有$-|x|\leq x\sin(\frac{1}{x})\leq |x|,\ \ x\neq0$当x趋近于0时,左右两边的夹逼条件都成立,因此可以得到$\lim\limits_{x\rightarrow0}-|x|\leq\lim\limits_{x\rightarrow0}x\sin(\frac{1}{x})\leq\lim\limits_{x\rightarrow0}|x|$即$0\leq \lim\limits_{x\rightarrow0}x\sin(\frac{1}{x})\leq 0$由夹逼准则,可得$\lim\limits_{x\rightarrow0}x\sin(\frac{1}{x})=0$3. 函数具有保号性如果当x趋近于a时,函数f(x)的极限存在,且极限不为0,则函数f(x)在x=a时的符号和极限的符号相同。
高等数学教案(极限部分)4 极限存在准则与两个重要极限

n →∞
8
如右图, 当 n > N 0 = 5 , 数列 x n = 右图
ln n n
2
有界、 有界、
但收敛很慢. 单调递减有极限, 单调递减有极限 且 lim xn = 0, 但收敛很慢 n →∞
2 1.5 1 0.5
2000
4000
6000
8000
10000
9
设
2 1.5 1 0.5 -1 -0.5 -1 1
o 函数图形如上, 函数图形如上 它在 ( − 1, 3) 有界且分段单调, 有界且分段单调,
请观察函数在每一点的单侧极限都存在, 请观察函数在每一点的单侧极限都存在 如
x → 2− 0
x 2 − 1 x ∈ [−1, 0) x ∈ [0,1) 2x f ( x) = , −2 x + 4 x ∈ [1, 2) 0.8 x − 1 x ∈ [2, 3)
101520253002040608如左图数列有界20004000600080001000005如右图数列有界它在有界且分段单调函数图形如上请观察函数在每一点的单侧极限都存在10505数列单调下降有下设其极限值为a存在所以120204060802040608证明重要极限1如图先考虑一个很明显的几何事实
1 − cos x lim , 2 x →0 x
1 1 = ⋅1⋅1 = 2 2
15
解
x tan x 1 x2 1 x sin x lim = lim ⋅ 2 ⋅ x →0 2 − 2cos x 2 x →0 1 − cos x x cos x
1 x 1 1 sin x 1 = lim ⋅ ⋅ = ⋅ 2 ⋅1⋅ = 1 2 x →0 1 − cos x x cos x 2 1
高等数学 第二章 极限和导数2-6极限存在准则 两个重要极限

所以 lim ( 3 n +
n→ ∞
1 9n )n
= 9.
2 例2 求 lim x x , 其 中 [ x ]是 不 超 过 x 的 x→ 0 最 大 整 数. 2 2 2 解Q ( x ≠ 0) −1< ≤ x x x 2 o 1 当x > 0时, 2 − x < x x ≤ 2 ( x > 0)
x2 )2 = → 0, ( x → 0) 2
∴
x→ 0+
lim ( 1 − cos x ) = 0
即
x→ 0
lim cos x = 1
sin x lim =1 x→ 0 x
例5 解
1 − cos 2 x . 求 lim x → 0 x sin x
0 型 0
2 1 − cos 2 x 2 sin x lim = lim x → 0 x sin x x → 0 x sin x
n→ ∞
lim x n = a ( ≤ M )
a
(单调减少有下界 单调减少有下界) 单调减少有下界
n→ ∞
lim x n = b ( ≥ m )
( 证明略 )
b
准 则 I I ′ ( 单 调 有 界 准 则) 若 f ( x ) 是 ( a , b )内 的 单调有界函数,
则 lim f ( x )与 lim f ( x ) 都 存 在 。
2 lim x = 2 x→ 0− x
故 2 lim x = 2 . x→ 0 x
x → x0 − f ( x0 )
lim f ( x ) = A ⇔ = f
+ ( x0 )
2 −1< x
2 2 ≤ x x
极限存在法则 两重要极限

高等数学( 高等数学(上)
1 [ x] 1 x 1 [ x]+1 (1 + ) ≤ (1 + ) ≤ (1 + ) , [ x] + 1 x [ x] 1 [ x]+1 1 [ x] 1 而 lim (1 + ) = lim (1 + ) ⋅ lim (1 + ) x→+∞ x→+∞ x→+∞ [ x] [ x] [ x] =
高等数学( 高等数学(上)
例 2 证明 lim
n→∞
n
n
n =1
n(n − 1) 2 n(n − 1) 2 n xn + ... + xn > xn ⇒ n = (1 + xn ) = 1 + nxn + 2 2 2 2 2 2 lim = 0. ; n→∞ ⇒ xn < ⇒ 0 < xn < n −1 n−1 n−1 由夹逼准则⇒lim xn = 0 ⇒ lim n n = 1.
数列{xn}
单调增加 ,若 x1 ≤ x2 ≤ ⋅ ⋅ ⋅ ≤ xn ≤ ⋅ ⋅ ⋅ 单调减少 ,若 x1 ≥ x2 ≥ ⋅ ⋅ ⋅ ≥ xn ≥ ⋅ ⋅ ⋅
准则Ⅱ(单调有界收敛准则)单调有界数列必有极限. 准则Ⅱ(单调有界收敛准则)单调有界数列必有极限. Ⅱ(单调有界收敛准则 几何解释: 几何解释:
第六节
极限存在准则
两个重要极限
夹逼准则) 准则 I (夹逼准则) 如果{ x n }, y n } 及 { z n } { 满足下列条件: 满足下列条件: (1) yn ≤ xn ≤ zn (2) lim yn = a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n lim 由此可得 n→ ∞ a
( a > 0)
n n n ⇒ lim a =1 由 1 a n ( n a 时 ) ≤ ≤ ≥ (1) 当 a ≥ 1 时, n→ ∞
∴ lim n a = lim (2) 当 0 < a < 1 时,
n→ ∞
1 1a
n→ ∞ n
=
1
n→ ∞
1 >1 a
lim n 1 a
第三节 极限存在的判别准则
1. 夹逼性定理 2. 单调有界性定理 3. 小结、作业
1/17
一. 夹逼定理
定理1 设有数列 { x n }, { yn }, { z n },满足: (1) ∃N , n > N : zn ≤ xn ≤ yn (2) lim yn = lim z n = A, 则ຫໍສະໝຸດ n→ ∞2 2解
n
<
1
++
<
2
,
注:1) 求n项和的数列极限时常用夹逼准则。 2) 使用夹逼准则时需要对极限的值有个猜测。
3/17
n 例2 再求 lim n→∞
n
证: 由AG不等式 :
( n − 2) + 2 n ⋅1 ⋅ 1 n n ≤ 1≤ n = n 1 n n− 2 2 n lim ≤ 1+ , ( n ≥ 2). ⇒ n→ ∞ n = 1. n
n →∞
由保序性, ∃N, ∀n > N :
n
a < aε .
两边取对数,得
log a n < ε. n
n n
当n → ∞时,下列无穷大量阶的 比较有
log a n n a (a > 1) n! n
k
例4 解
设 x n = n 1 + 2 n + 3 n , 求 lim x n
n→ ∞
1) x n ≤ β , ∀n ∈ {1,2}; 2) ∀ε > 0, ∃N : x N > β − ε .
{x n }单调增, 故 ∀n > N , 有 x n > x N > β − ε ,
而 x n ≤ β < β + ε , 于是 ∀n > N , 有 β − ε < x n < β + ε ,
思考题
1 1 1 (1) 证明不等式 < ln(1 + ) < ; n+1 n n
1 1 1 ( 2) 设 x n = 1 + + + + − ln n, 证明{x n }收敛。 2 3 n
1 [ln( k + 1) − ln k ] <∑ , 提示: 由(1)得, ∑ k =1 k =1 k 1 1 1 > 0, 有下界. 即 ln( n + 1) < 1 + + + , ∴ x n+1 > n +1 2 n
1 1 1 1 1 n lim n = lim ⋅ ⋅ ⋅ = lim = 0. n→∞ n→∞ n n →∞ 1 2 n n!
二. 单调有界数列收敛定理
定理2 若数列 {x n }单调增 (减 )且有上(下)界,
则 {x n }必收敛 .
证明 设 {x n }有上界,则必有上确界 :β = sup{x n }, 由上确界定义知:
a ∴ lim = 0. n →∞ n!
n
a[a ] a → 0, ( n → ∞ ). ≤ ⋅ [a ]! n
5/17
nk ( 3) x n = n , ( a > 1, k ∈ N + ). a
解
n
不妨设 a > 1, 记a = 1 + α (α
n
> 0)
k +1 k +1 a = (1 + α ) ≥ C n α
设 lim x n = a , 且a ≥
n→ ∞
A > 0.
对 x n +1
∴ lim x n =
n→ ∞
1 A 2 ( ) a a = a + ⇒ = A, 即 a = 两边求极限,得 2 a
1 A = ( xn + ) 2 xn
A.
A.
例3 证明数列 x1 = 3 , xn + 1 = 3 + xn 的极限存在并求 lim xn .
1 n+1 = (1 + ) = x n+1 , (∀n ≥ 2). ∴{x n }单调增。 n+1 n+ 2
=4
故{x n }有上界。
1 n (1 + ) = e 由此得 {x n }收敛, 并记 lim n →∞ n
1 n+1 解法二 作辅助数列 y n = (1 + ) n
( n > 2k )
n k = n ⋅ ( n − 1) ( n − k ) ≥ n( ) ( k + 1)! k +1 2
n k 2 k ( k + 1)! 1 0< n ≤ a α k +1 n nk ∴ lim n = 0. n→∞ a
α
k +1
α
k +1 `
0,( n → ∞ ).
log a n =0 利用极限性质可证得 lim n→∞ n 事实上,∀ε > 0 ⇒ a ε > 1, 而 lim n a = 1 < a ε ,
5 12 29 而a1 = 2, a 2 = , a 3 = , a4 = , 故 a1 < a 3 , a 2 > a4 , 2 5 12
∴{a 2 n−1 }单调增,有上界;{a 2 n }单调减,有下界;
都收敛 . 设 lim a 2 n −1 = A, lim a 2 n = B ,
n→∞ n→∞
n→ ∞
lim x n = A
{yn }, {zn }在具体应 注意 定理中满足条件的
. 放大或缩小找出的
n→ ∞
, 而是通过对{x n }的适当 用时不是事先给出
例1 求 lim (
n→ ∞
1 n +1
2
+
1 n +2
2
++
1
2
1 n +n n
2
).
n +n n +1 n +n n +1 1 n n 1 又 lim 2 = lim = 1, lim = 1, lim = 2 n→ ∞ n + n n→ ∞ n→ ∞ n + 1 n→ ∞ 1 1 1+ 1+ 2 n n 1 1 1 由夹逼定理得 lim ( 2 + ++ ) = 1. 2 2 n→ ∞ n +1 n +2 n +n
n ( n + 1) + 1 n n+1 1 n+1 ) ⋅1 ≤ =( yn n+1 n+2
n+ 2
1 = , y n+1
即 y n+1 ≤ y n , {y n }单调减 , 又 y n ≥ 0,有下界,
由此得{y n }收敛。
1 n+1 (1 + ) 1 n n ∴ lim(1 + ) = lim = lim y n = e . n →∞ n →∞ n →∞ 1 n 1+ n
解
a1 = 2, 则 a n ≥ 2, ( n = 1,2, ), 又
1 1 a n−1 = 2+ a n +1 = 2 + = 2+ 1 an 2 a + 1 n − 1 2+ a n−1 a n−1 + 1 = 3− < 3, 2a n−1 + 1 ∴ 2 ≤ a n ≤ 3, 即 {a n }为有界 .
4/17
1.
例3 求下列数列的极限
n! ! n (1) x n = n ; (由前面讨论知lim n = 0) n→∞ n n n a ( 2) x n = ; n! 证: ∀n > [a ],
a a a a a a an ≤ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 0< 1 2 [a ] [a ] + 1 [a ] + 2 n n!
n →∞
1 n 例 5 数 e 的存在性 设 xn = (1 + ) , 求 lim x n n→ ∞ n
1 n(1 + ) + 1 n 解 设 xn = (1 + 1 )n ⋅ 1 ≤ ( ) n+1 n n+1
1 1 n(1 + ) + 2 ⋅ 1 n 1 n 1 2 n 2 又 x n = (1 + ) = 4 (1 + ) ( ) ≤ 4 n+2 n n 2
设 lim x n = a , 对 x n = n + 3 x n−1两边求极限得 n→∞ 2n − 1
1 a = a ⇒ a = 0, ∴ lim x n = 0. n→∞ 2
例 2 设 A > 0 , x1 > 0, x n+1
试证 { x n } 收敛 , 并求此极限 .
A 1 = ( x n + ), ( n = 1,2, ) xn 2
3 = n 3 n < xn < n 3 ⋅ 3 n = 3 ⋅ n 3 → 3, ( n → ∞ ),
lim x n = 3.
n→∞
