经典例题二次函数根的分布

合集下载

微专题11 二次函数根的分布问题(解析版)

微专题11二次函数根的分布问题【方法技巧与总结】1、实系数一元二次方程20(0)ax bx c a ++=≠的实根符号与系数之间的关系（1）方程有两个不等正根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=->⎨⎪⎪=>⎪⎩（2）方程有两个不等负根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=-<⎨⎪⎪=>⎪⎩（3）方程有一正根和一负根，设两根为12,x x ⇔120cx x a=<2、一元二次方程20(0)ax bx c a ++=≠的根的分布问题一般情况下需要从以下4个方面考虑：（1）开口方向；（2）判别式；（3）对称轴2bx a=-与区间端点的关系；（4）区间端点函数值的正负．设12,x x 为实系数方程20(0)ax bx c a ++=>的两根，则一元二次20(0)ax bx c a ++=>的根的分布与其限定条件如表所示．根的分布图像限定条件12m x x <<02()0b m a f m ∆>⎧⎪⎪->⎨⎪⎪>⎩12x m x <<()0f m <12x x m<<02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪>⎩在区间(,)m n 内没有实根∆<12120x x m x x m∆==≤=≥或02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪≥⎩02()0b n a f n ∆>⎧⎪⎪->⎨⎪⎪≥⎩()0()0f m f n ≤⎧⎨≤⎩在区间(,)m n 内有且只有一个实根()0()0f m f n >⎧⎨<⎩()0()0f mf n<⎧⎨>⎩在区间(,)m n内有两个不等实根2()0()0bm naf mf n∆>⎧⎪⎪<-<⎪⎨⎪>⎪>⎪⎩【题型归纳目录】题型一：正负根问题题型二：根在区间的分布问题题型三：整数根问题题型四：范围问题【典型例题】题型一：正负根问题例1．（2022·河南·郑州市回民高级中学高一阶段练习）已知m为实数，命题甲：关于x的不等式240mx mx+-<的解集为R；命题乙：关于x的方程22200x mx m-++=有两个不相等的负实数根．若甲、乙至少有一个为真命题，求实数m的取值范围为_______．【答案】(20,0]-【解析】由命题甲：关于x的不等式240mx mx+-<的解集为R，当0m=时，不等式40-<恒成立；当0m≠时，则满足2160mm m<⎧⎨∆=+<⎩，解得160m-<<，综上可得160m-<≤．由命题乙：关于x的方程22200x mx m-++=有两个不相等的负实数根，则满足2121244(20)020200m m x x m x x m ⎧∆=-+>⎪+=<⎨⎪=+>⎩，整理得2200020m m m m ⎧-->⎪<⎨⎪>-⎩，所以45020m m m m <->⎧⎪<⎨⎪>-⎩或，解得204m -<<-．所以甲、乙至少有一个为真命题时，有160m -<≤或204m -<<-，可得200m -<≤，即实数m 的取值范围为(20,0]-．故答案为：(20,0]-．例2．（2022·全国·高一单元测试）关于x 的方程2210ax x ++=的实数根中有且只有一个负实数根的充要条件为____________.【答案】0a ≤或1a =【解析】若方程2210ax x ++=有且仅有一个负实数根，则当0a =时，12x =-，符合题意.当0a ≠时，方程2210ax x ++=有实数根，则440a ∆=-≥，解得1a ≤，当1a =时，方程有且仅有一个负实数根1x =-，当1a <且0a ≠时，若方程有且仅有一个负实数根，则10a<，即0a <.所以当0a ≤或1a =时，关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根.综上，“关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根”的充要条件为“0a ≤或1a =”.故答案为：0a ≤或1a =.例3．（2022·甘肃·兰化一中高一阶段练习）若一元二次方程2330kx kx k ++-=的两根都是负数，求k 的取值范围为___________.【答案】125k ≤-或3k >【解析】首先0k ≠，设方程2330kx kx k ++-=的两根为12,x x ，则12121200,00x x x x x x +<⎧<<⇔⎨>⎩，所以2Δ94(3)03030k k k kkk k⎧⎪=--≥⎪⎪-<⎨⎪-⎪>⎪⎩，又0k ≠，解得125k ≤-或3k >．故答案为：125k ≤-或3k >．例4．（2022·全国·高一专题练习）已知关于x 的二次方程2(21)210m x mx m +-+-=有一正数根和一负数根，则实数m 的取值范围是_____．【答案】112m -<<【解析】由题意知，二次方程有一正根和一负根，得2101021m m m +≠⎧⎪-⎨<⎪+⎩，解得112m -<<.故答案为：112m -<<例5．（2022·河南·高一阶段练习）（1）若不等式210ax bx +-<的解集是113x x ⎧⎫-<<⎨⎬⎩⎭∣，求,a b 的值；（2）若31b a =--，且关于x 的方程210+-=ax bx 有两个不同的负根，求a 的取值范围.【解析】（1）由题意可得1-和13是方程210+-=ax bx 的两个实根，则11,31113b a a ⎧-+=-⎪⎪⎨-⎪-⨯=⎪⎩解得3,2a b ==.（2）因为31b a =--，所以()23110ax a x -+-=，由题可知Δ0>，则1a <-或19a >-，由题意，方程有两个负根，即310,10,a a a +⎧<⎪⎪⎨-⎪>⎪⎩解得103-<<a .综上，实数a 的取值范围是109aa ⎧⎫-<<⎨⎬⎩⎭∣.例6．（2022·辽宁·沈阳市第八十三中学高一阶段练习）已知1x ､2x 是一元二次方程24410kx kx k -++=的两个实数根．(1)若1x ､2x 均为正根，求实数k 的取值范围；(2)是否存在实数k ，使得()()12123222x x x x --=-成立？若存在，求出k 的值；若不能存在，请说明理由．【解析】（1）由题意，一元二次方程有两个正根1x ､2x 故20,(4)16(+1)0k k k k ≠∆=-≥，即0k ≤，且121210104x x k x x k +=>⎧⎪+⎨=>⎪⎩，解得：1k <-．（2）由题意，当0∆≥，即0k ≤时，有121211,4k x x x x k++==()()2221212121212129(1)93222+252()92442k k x x x x x x x x x x x x k k ++--=-=+-=-=-=-解得：95k =，与0k ≤矛盾.故不存在实数k ，使得()()12123222x x x x --=-成立题型二：根在区间的分布问题例7．（2022·全国·高一专题练习）已知一元二次方程x 2＋ax ＋1＝0的一个根在(0，1)内，另一个根在(1，2)内，则实数a 的取值范围为________．【答案】5(,2)2--【解析】设f (x )＝x 2＋ax ＋1，由题意知(0)10(1)20(2)520f f a f a =>⎧⎪=+<⎨⎪=+>⎩，解得－52<a <－2.故答案为：5(,2)2--.例8．（2022·全国·高一课时练习）已知关于x 的方程220x x a -+=．(1)当a 为何值时，方程的一个根大于1，另一个根小于1？(2)当a 为何值时，方程的一个根大于1-且小于1，另一个根大于2且小于3？(3)当a 为何值时，方程的两个根都大于0？【解析】（1）二次函数22y x x a =-+的图象是开口向上的抛物线，故方程220x x a -+=的一个根大于1，另一个根小于1，则2120a -+<，解得1a <，所以a 的取值范围是{}1a a <．（2）方程220x x a -+=的一个根大于1-且小于1，另一个根大于2且小于3，作满足题意的二次函数22y x x a =-+的大致图象，由图知，120120440960a a a a ++>⎧⎪-+<⎪⎨-+<⎪⎪-+>⎩，解得30a -<<．所以a 的取值范围是{}30a a -<<．（3）方程220x x a -+=的两个根都大于0，则Δ4400a a =-≥⎧⎨>⎩，解得01a <≤，所以a 的取值范围是{}01a a <≤．例9．（2022·全国·高一专题练习）已知关于x 的一元二次方程2220x ax a -++=，当a 为何值时，该方程：有不同的两根且两根在(1,3)内．【解析】令2()22f x x ax a =-++，因为方程2220x ax a -++=有不同的两根且两根在(1,3)内，所以213Δ44(2)0(1)30(3)1150a a a f a f a <<⎧⎪=-+>⎪⎨=->⎪⎪=->⎩，解得1125<<a ，故答案为：112,5⎛⎫⎪⎝⎭例10．（2022·江苏·高一专题练习）已知二次函数()2221R y x tx t t =-+-∈.(1)若该二次函数有两个互为相反数的零点，解不等式22210x tx t -+-≥；(2)若关于x 的方程22210x tx t -+-=的两个实根均大于2-且小于4，求实数t 的取值范围．【解析】（1）设二次函数()2221y x tx t t =-+-∈R 的两个零点分别为1x ，2x ，由已知得120x x +=，而122x x t +=，所以20t =，故0=t ，不等式22210x tx t -+-≥即210x -≥，解得1≥x 或1x ≤-，故不等式的解集为{1x x ≥或}1≤-x .（2）因为方程22210x tx t -+-=的两个实根均大于2-且小于4，所以()()()()222222Δ2t 4t 102t 422t 2t 1042t 4t 10⎧=---≥⎪⎪-<<⎨⎪--⨯-+->⎪-⨯+->⎩，即2240244308150t t t t t ≥⎧⎪-<<⎪⎨++>⎪⎪-+>⎩，解得：13t -<<，即实数t 的取值范围为{}13t t -<<.例11．（2022·全国·高一单元测试）求实数m 的范围，使关于x 的方程()221 260.x m x m +-++=(1)有两个实根，且一个比2大，一个比2小；(2)有两个实根 αβ，，且满足014αβ<<<<；(3)至少有一个正根.【答案】(1)1m <-(2)7554m -<<-(3)1m ≤-【分析】设()()22126y f x x m x m ==+-++，一元二次方程根的分布主要从对称轴、判别式、端点值、开口方向这几个方面来确定.（1）设()()22126y f x x m x m ==+-++．依题意有()20f <，即()441260m m +-++<，得1m <-．（2）设()()22126y f x x m x m ==+-++．依题意有()()()02601450410140f m f m f m ⎧=+>⎪=+<⎨⎪=+>⎩，解得7554m -<<-．（3）设()()22126y f x x m x m ==+-++．方程至少有一个正根，则有三种可能：①有两个正根，此时可得()()Δ0002102f m ⎧⎪≥⎪⎪>⎨⎪-⎪>⎪-⎩，即153.311m m m m m ≤-≥⎧⎪>-∴-<≤-⎨⎪<⎩或．②有一个正根，一个负根，此时可得()00f <，得3m <-．③有一个正根，另一根为0，此时可得()6203210m m m +=⎧∴=-⎨-<⎩，．综上所述，得1m ≤-．例12．（2022·上海市七宝中学高一阶段练习）方程()2271320x a x a a -++--=的一个根在区间()0,1上，另一个根在区间()1,2上，则实数a 的取值范围为___________.【答案】()()2,13,4--【解析】令()()227132f x x a x a a =-++--，因为程()2271320x a x a a -++--=的一个根在区间()0,1上，另一个根在区间()1,2上，所以()()()001020f f f ⎧>⎪<⎨⎪>⎩，即()22220713202821320a a a a a a a a ⎧-->⎪--+--<⎨⎪-++-->⎩，解得21a -<<-或34a <<，所以实数a 的取值范围为()()2,13,4--.故答案为：()()2,13,4--.例13．（2022·全国·高一专题练习）关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根，则实数a 的取值范围是_____．【答案】16(5,]3【解析】关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根，令()()214f x x a x =--+，则有()()()2Δ1160113216031630a a f a f a ⎧=-->⎪-⎪<<⎪⎨⎪=-≥⎪=-≥⎪⎩，解得1653a <≤，所以实数a 的取值范围是16(5,]3.故答案为：16(5,]3例14．（2022·全国·高一单元测试）方程()2250x a x a --+-=的两根都大于2，则实数 a 的取值范围是_____．【答案】54a -<≤-【解析】由题意，方程()2250x a x a +=－－－的两根都大于 2，令()()225f x x a x a =+－－－，可得()020222f a⎧⎪≥⎪>⎨⎪-⎪>⎩，即2165024a a a ⎧≥⎪+>⎨⎪->⎩，解得54a <≤－－．故答案为：54a -<≤-.例15．（2022·全国·高一专题练习）已知关于x 的方程220ax x ++=的两个实根一个小于0，另一个大于1，则实数a 的取值范围是_____．【答案】()3,0-【解析】显然0a ≠，关于x 的方程220ax x ++=对应的二次函数()22f x ax x =++当0a >时，二次函数()22f x ax x =++的图象开口向上，因为220ax x ++=的两个实根一个小于0，另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0，另一个大于1，所以()()0010f f ⎧<⎪⎨<⎪⎩，即2030a <⎧⎨+<⎩，解得a ∈∅；②当0a <时，二次函数()22f x ax x =++的图象开口向下，因为220ax x ++=的两个实根一个小于0，另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0，另一个大于1，所以()()0010f f ⎧>⎪⎨>⎪⎩，即2030a >⎧⎨+>⎩，解得30a -<<．；综上所述，实数a 的范围是()3,0-．故答案为：()3,0-．例16．（2022·全国·高一专题练习）已知方程()()22110x a x a a -+++=的两根分别在区间()0,1，()1,3之内，则实数a 的取值范围为______．【答案】()0,1.【解析】方程()()()()2211010x a x a a x a x a ⎡⎤+++=⇒--+=⎣⎦－∴方程两根为12,1x a x a ==+，若要满足题意，则01113a a <<⎧⎨<+<⎩，解得01a <<，故答案为：()0,1.例17．（2022·上海·高一专题练习）方程2240x ax -+=的两根均大于1，则实数a 的取值范围是_______【答案】5[2,)2【解析】2240x ax -+=的两个根都大于121520Δ4160a a a >⎧⎪∴->⎨⎪=-≥⎩，解得522a ≤<可求得实数a 的取值范围为5[2,2故答案为：5[2,)2例18．（2022·湖北·华中师大一附中高一开学考试）关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x <<，那么a 的取值范围是（）A ．2275a -<<B ．25a >C ．27a <-D ．2011a -<<【答案】D【解析】当0a =时，()2290ax a x a +++=即为20x =，不符合题意；故0a ≠，()2290ax a x a +++=即为22190x x a ⎛⎫+++= ⎪⎝⎭，令2219y x x a ⎛⎫=+++ ⎪⎝⎭，由于关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ，且121x x <<，则()229y ax a x a =+++与x 轴有两个交点，且分布在1的两侧，故1x =时，0y <，即211190a ⎛⎫++⨯+< ⎪⎝⎭，解得211a<-，故2011a -<<，故选：D例19．（2022·全国·高一课时练习）关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内，则实数m 的取值范围是（）A ．13,22⎡⎤⎢⎥⎣⎦B ．12,23⎛⎤ ⎥⎝⎦C ．1,22⎡⎫⎪⎢⎣⎭D．{12,623⎛⎤⋃- ⎥⎝⎦【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为：()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1)，则需要满足：①()()010f f ⋅<，()()21320m m --<，解得：1223m <<；②函数()f x 刚好经过点()0,0或者()1,0，另一个零点属于(0,1)，把点()0,0代入()2(2)21f x x m x m =+-+-，解得：12m =，此时方程为2302x x -=，两根为0，32，而()30,12∉，不合题意，舍去把点()1,0代入()2(2)21f x x m x m =+-+-，解得：23m =，此时方程为23410x x -+=，两根为1，13，而()10,13∈，故符合题意；③函数与x 轴只有一个交点，横坐标属于(0,1)，()2(2)4210m m ∆=---=，解得6m =±当6m =+2(2)210x m x m +-+-=的根为2-若6m =-2(2)210x m x m +-+-=2，符合题意综上：实数m的取值范围为{12,623⎛⎤⋃- ⎥⎝⎦故选：D题型三：整数根问题例20．（2022·上海市实验学校高一开学考试）已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ，使得()()12123222x x x x --=-成立？若存在，求出k 的值；若不存在，请说明理由；(2)求使12212x x x x +-的值为整数的实数k 的整数值.【解析】（1）假设存在实数k ，使得()()12123222x x x x --=-成立，一元二次方程24410kx kx k -++=的两个实数根，()2400Δ(4)441160k k k k k k ≠⎧∴⇒<⎨=--⋅+=-⎩，(不要忽略判别式的要求)，由韦达定理得1212114x x k x x k +=⎧⎪+⎨=⎪⎩，()()()()2221212121212129322252942k x x x x x x x x x x x x k +∴--=+-=+-=-=-，95k ⇒=但0k <，∴不存在实数k ，使得()()12123222x x x x --=-成立.（2）()22212121221121244224411x x x x x x k x x x x x x k k +++-==-=-=-++，∴要使其值是整数，只需要1k +能被4整除，故1124k +=±±±，，，即021335k =---，，，，，，0k <，235k ∴=---，，.例21．（2022·上海·高三专题练习）已知,a Z ∈关于x 的一元二次不等式260x x a -+≤的解集中有且仅有3个整数，则所有符合条件的a 的值之和是（）A ．13B ．18C ．21D ．26【答案】C【解析】设2()6f x x x a =-+，其图象为开口向上，对称轴为3x =的抛物线，根据题意可得，3640a ∆=->，解得9a <，因为()0f x ≤解集中有且仅有3个整数，结合二次函数的对称性可得(2)0(1)0f f ≤⎧⎨>⎩，即4120160a a -+≤⎧⎨-+>⎩，解得58a <≤，又,a Z ∈所以a =6，7，8，所以符合题意的a 的值之和6+7+8=21.故选：C例22．（多选题）（2022·全国·高一课时练习）已知a ∈Z ，关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数，则a 的值可以是（）A ．5B ．6C ．7D ．9【答案】BC【解析】设()26f x x x a =-+，函数图象开口向上，且对称轴为3x =，因此关于x 的一元二次不等式x 2－6x ＋a ≤0的解集中有且仅有3个整数时，需满足()()2010f f ⎧≤⎪⎨>⎪⎩，即2226201610a a ⎧-⨯+≤⎨-⨯+>⎩，解得58a <≤，又因为a ∈Z ，所以6a =或7或8，故选：BC.例23．（2022·全国·高一专题练习）若方程()22460x kx x --+=有两个不相等的实根，则k 可取的最大整数值是______.【答案】1【解析】方程化为()221860k x x --+=，由()Δ6424210k =-->，12k ≠解得116k <，所以k 最大整数值是1.故答案为：1.题型四：范围问题例24．（2022·上海·高一专题练习）已知t 是实数，若a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，则()()2211a b --的最小值是___________.【答案】3-【解析】a ，b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根，∴可得2a b +=，10ab t =-≥，1t ∴≥，又()4410t ∆=--≥，可得2t ≤，12t ∴≤≤，又()()()()()()222222211121a b ab a b ab a b ab --=-++=-+++()()()()2221114211a b t t ∴--=--+-+，24t =-，又12t ≤≤，2340t ∴-≤-≤，故答案为：3-．例25．（2022·吉林省实验中学高一阶段练习）设方程240x mx m -+=的两实根分别为12,x x .(1)当1m =时，求1211+x x 的值；(2)若120,0x x >>，求实数m 的取值范围及124x x +的最小值.【解析】（1）当1m =时，方程为2410x x -+=，2(4)4120∆=--=>，所以12124,1x x x x +=⋅=，122112114x x x x x x ∴+⋅+==.（2）因为240x mx m -+=两根120,0x x >>，所以21212Δ1640400m m x x m x x m ⎧=-≥⎪+=>⎨⎪⋅=>⎩，解得14m ≥.因为12124x x x x +=，120,0x x >>，所以12114x x +=，所以211212121241111194(4)()(5)54444x x x x x x x x x x ⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭，当且仅当21124x x x x =，即1233,48x x ==时等号成立，此时91324m =>符合题意，124x x ∴+的最小值为94.例26．（2022·北京海淀·高一期末）已知函数()22f x x bx c =++（b ，c 为实数），()()1012f f -=.若方程()0f x =有两个正实数根1x ，2x ，则1211+x x 的最小值是（）A ．4B ．2C ．1D ．12【答案】B【解析】因为函数()22f x x bx c =++（b ，c 为实数），()()1012f f -=，所以1012200288b c b c +=++-，解得4b =-，所以()224f x x x c -+=，因为方程()0f x =有两个正实数根1x ，2x ，所以()Δ168000c f c =-≥⎧⎨=>⎩，解得02c <≤，所以121212112422x x c x x x x c =++==≥，当c =2时，等号成立，所以其最小值是2，故选：B例27．（2022·江苏·高一）已知关于x 的方程230x kx k -++=有两个正根，那么两个根的倒数和最小值是（）A ．-2B ．23C ．89D ．1【答案】B【解析】由题意可得∆2()4(3)0k k =--+ ，解得6k 或2k ≤-，设两个为1x ，2x ，由两根为正根可得12120·30x x k x x k +=>⎧⎨=+>⎩，解得0k >，综上知，6k .故两个根的倒数和为12121211x x x x x x ++=1331k k k==++，6k ，∴1106k < ，3102k < ，故33112k <+，∴12331k+，故两个根的倒数和的最小值是23.故选：B例28．（2022·上海·华师大二附中高一期中）已知实数a b <，关于x 的不等式()210x a b x ab -+++<的解集为()12,x x ，则实数a 、b 、1x 、2x 从小到大的排列是()A ．12a x x b <<<B ．12x a b x <<<C ．12a x b x <<<D ．12x a x b<<<【答案】A【解析】由题可得：12x x a b +=+，121x x ab =+.由a b <，12x x <，设1x a m =+，则2x b m =-.所以212()()()1a m b m ab m b a m ab x x =+-=+--=+，所以2()1m b a m --=，21m m b a+=-.又a b <，所以0b a ->，所以0m >.故1x a >，2x b <.又12x x <，故12a x x b <<<.故选：A.例29．（2022·福建厦门·高一期末）已知函数()()11f x x x a =-⋅--，a R ∈．(1)若0a =，解不等式()1f x <；(2)若函数()f x 恰有三个零点1x ，2x ，3x ，求123111x x x ++的取值范围．【解析】(1)当0a =时，原不等式可化为()120x x -⋅-<…①．（ⅰ）当0x ≥时，①式化为220x x --<，解得12x -<<，所以02x ≤<；（ⅱ）当0x <时，①式化为220x x -+>，解得x ∈R ，所以0x <．综上，原不等式的解集为(),2-∞．(2)依题意，()()()2211,11,x a x a x af x x a x a x a ⎧-++--<⎪=⎨-++-≥⎪⎩．因为()10f a =-<，且二次函数()211y x a x a =-++-开口向上，所以当x a ≥时，函数()f x 有且仅有一个零点．所以x a <时，函数()f x 恰有两个零点．所以()()()21,21410,10.a a a a f a +⎧<⎪⎪⎪=+-+>⎨⎪=-<⎪⎪⎩解得3a >．不妨设123x x x <<，所以1x ，2x 是方程()2110x a x a -++--=的两相异实根，则12121,1x x a x x a +=+⎧⎨=+⎩，所以121212111x x x x x x ++==．因为3x 是方程()2110x a x a -++-=的根，且312a x +>，由求根公式得3x =因为函数()g a ()3,+∞上单调递增，所以()332x g >=31012x <<-．所以123111x x x ++．所以a 的取值范围是21,22⎛- ⎝⎭．【过关测试】一、单选题1．（2022·江苏·高一专题练习）已知p ：a m <（其中R a ∈，m ∈Z ），q ：关于x 的一元二次方程2210ax x ++=有一正一负两个根.若p 是q 的充分不必要条件，则m 的最大值为（）A ．1B ．0C ．1-D ．2【答案】C【解析】因为2210ax x ++=有一正一负两个根，所以224010a a ⎧∆=->⎪⎨<⎪⎩，解得0a <.因为p 是q 的充分不必要条件，所以0m <，且m ∈Z ，则m 的最大值为1-.故选：C2．（2022·江苏·高一专题练习）已知方程2(2)50x m x m +-+-=有两个不相等的实数根，且两个实数根都大于2，则实数m 的取值范围是（）A ．(5,4)(4,)--+∞B ．(5,)-+∞C ．(5,4)--D ．(4,2)(4,)--+∞【答案】C【解析】令()2(2)5mf x m x x =+-+-由题可知：()()()()2Δ02450442222242250520m m m m m m m m m m f >⎧⎧--⨯->><-⎧⎪⎪-⎪⎪>⇒<-⇒<-⎨⎨⎨⎪⎪⎪+-⨯+->>-⎩>⎩⎪⎩或则54m -<<-，即(5,4)m ∈--故选：C3．（2021·北京·北师大实验中学高一期中）设方程2610x x -+=的两个不等实根分别为12,x x ，则12||x x -=（）A ．3B ．6C．D．【答案】D【解析】2610x x -+=，364320∆=-=>，故121261x x x x +=⎧⎨=⎩，12||x x -===.故选：D.4．（2021·江苏·高一课时练习）设a 为实数，若方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解，则a 的取值范围是（）.A ．(,0)(1,)-∞⋃+∞B ．(1,0)-C ．1,03⎛⎫- ⎪⎝⎭D ．1,0(1,)3⎛⎫-+∞ ⎪⎝⎭【答案】C【解析】令2()2g x x ax a =-+，由方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解可得244011(1)0(1)0a a a g g ⎧∆=->⎪-<<⎪⎨->⎪⎪>⎩，即011131a a a a <⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩或111131a a a a >⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩，解得103-<<a ，故选：C5．（2022·全国·高一课时练习）一元二次方程()22100ax x a ++=≠有一个正实数根和一个负实数根的一个充分不必要条件是()A ．0a <B ．0a >C ．1a <-D ．2a <【答案】C【解析】由题意，不妨设2()21f x ax x =++，因为(0)10=>f ，且()22100ax x a ++=≠有一个正实数根和一个负实数根，所以2()21f x ax x =++的图像开口向下，即0a <，故对于选项ABCD ，只有C 选项：1a <-是0a <的充分不必要条件.故选：C.6．（2021·四川·树德中学高一阶段练习）设集合{}2320A x x x =-+<，集合{}2210B x ax x =--=，若A B ⋂≠∅，则实数a 的取值范围是（）A ．34,43⎡⎫⎪⎢⎣⎭B ．5,34⎛⎫ ⎪⎝⎭C ．3,4⎡⎫+∞⎪⎢⎣⎭D ．(1,)+∞【答案】B【解析】由题意，{}2320{|12}A x x x x x =-+<=<<若AB ⋂≠∅，即方程2210ax x --=存在根在区间(1,2)（1）若102102a x x =∴--=∴=-，不成立；（2）若0a ≠，由于0x =不为方程的根，故0x ≠，则222221211210(1)1x ax x a x x x x+--=⇔==+=+-由于21115(1,2)(,1)(1)1(,3)24x x x ∈∴∈∴+-∈综上，实数a 的取值范围是5,34⎛⎫⎪⎝⎭故选：B7．（2022·全国·高一课时练习）要使关于x 的方程()22120x a x a +-+-=的一根比1大且另一根比1小，则实数a 的取值范围是（）A ．{}12a a -<<B ．{}21a a -<<C ．{}2a a <-D ．{}1a a >【答案】B【解析】由题意可得()2211220a a a a +-+-=+-<，解得21a -<<.故选：B.8．（2021·甘肃·天水市第一中学高一阶段练习）已知一元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，则m 的值为（）A ．4-B ．5-C ．6-D ．7-【答案】A【解析】因为元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ，2x ，且12013x x <<<<，令2()(1)1f x x m x =+++，则由题意可得(0)0(1)0(3)0f f f >⎧⎪<⎨⎪>⎩，即10,30,1330,m m >⎧⎪+<⎨⎪+>⎩解得1333m -<<-，又m Z ∈，可得4m =-.故选：A 二、多选题9．（2022·江苏南通·高一开学考试）已知不等式20(0)x ax b a ++>>的解集是{}|x x d ≠，则下列四个结论中正确的是（）.A ．24a b=B ．若不等式2+x ax b c +<的解集为(3,1)-，则7a b c ++=C ．若不等式20x ax b +-<的解集为12(,)x x ，则120x x >D ．若不等式2x ax b c ++<的解集为12(,)x x ，且12||4x x -=，则4c =【答案】ABD【解析】由题意，不等式20(0)x ax b a ++>>的解集是{}|x x d ≠，所以240a b ∆=-=，24a b ∴=，所以A 正确；对于B ：2+x ax b c +<变形为2+0x ax b c +-<，其解集为(3,1)-，所以231 314 a b c a b -+=-⎧⎪-⨯=-⎨⎪=⎩，得214a b c =⎧⎪=⎨⎪=⎩，故7a b c ++=成立，所以B 正确；对于C ：若不等式20x ax b +-<的解集为12(,)x x ，由韦达定理知：21204a x xb =-=-<，所以C 错误；对于D ：若不等式2x ax bc ++<的解集为12(,)x x ，即20x ax b c ++-<的解集为12(,)x x ，由韦达定理知：21212,4a x x a x x b c c +=-=-=，则12||4x x -==，解得4c =，所以D 正确.故选：D.10．（2021·江苏·海安高级中学高一阶段练习）一元二次方程240x x m -+=有正数根的充分不必要条件是（）A ．4m =B ．5m =C ．1m =D ．12=-m 【答案】ACD【解析】设()24f x x x m =-+，则二次函数()f x 的图象的对称轴为2x =．当4m =时，方程即()224420x x x -+=-=，求得2x =，满足方程有正根，但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故4m =是方程240x x m -+=有正数根的充分不必要条件，故A 满足条件；当5m =时，方程即()224521x x x -+=-=-，求得x ∈∅，不满足方程有正实数根，故5m =不是方程240x x m -+=有正数根的充分条件，故排除B ．当1m =时，方程即()224123x x x -+=-=，求得2=±x 但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故1m =方程240x x m -+=有正数根的充分不必要条件，故C 满足条件；当12=-m 时，方程即24120x x --=，求得2x =-，或6x =，满足方程有正根，但由方程240x x m -+=有正数根，可得()240f m =-≤，即4m ≤，故12=-m 方程240x x m -+=有正数根的充分不必要条件，故D 满足条件，故选：ACD ．11．（2022·湖南湖南·高一期末）若方程220x x λ++=在区间()1,0-上有实数根，则实数λ的取值可以是（）A ．3-B ．18C ．14D ．1【答案】BC【解析】由题意22x x λ=--在(1,0)-上有解．∵(1,0)x ∈-，∴222(1)1(0,1)x x x λ=--=-++∈，故选：BC ．12．（2021·全国·高一专题练习）已知关于x 的方程()230x m x m +-+=，则下列结论中正确的是（）A ．方程()230x m x m +-+=有一个正根一个负根的充要条件是{}0m m m ∈<B ．方程()230x m x m +-+=有两个正实数根的充要条件是{}01m m m ∈<≤C ．方程()230x m x m +-+=无实数根的充要条件是{}1m m m ∈>D ．当m =3时，方程()230x m x m +-+=的两个实数根之和为0【答案】AB【解析】对A ，当0x =时，函数2(3)y x m x m =+-+的值为m ，由二次函数的图象知，方程有一正一负根的充要条件是{}|0m m m ∈<，故A 正确；对B ，若方程()230x m x m +-+=有两个正实数根1x ，2x ，即()2121234030,0,m m x x m x x m ⎧∆=--≥⎪+=->⎨⎪=>⎩解得：01m <≤，故B 正确；对C ，方程()230x m x m +-+=无实数根，即()2340m m ∆=--<，解得：19m <<，方程()230x m x m +-+=无实数根的充要条件是{}19m m m ∈<<，故C 错误；对D ，当3m =时，方程为230x +=，无实数根，故D 错误.故答案为：AB.13．（2021·江苏·高一专题练习）已知一元二次方程()()21102x m x m Z +++=∈有两个实数根12,x x ，且12013x x <<<<，则m 的值为（）A ．-2B ．-3C ．-4D ．-5【答案】BC 【解析】设()()2112f x x m x =+++，由12013x x <<<<，可得()()()()10200110110230193102f f m f m ⎧>⎪⎧>⎪⎪⎪<⇒+++<⎨⎨⎪⎪>⎩⎪+++>⎪⎩，解得：25562m -<<-，又因为m Z ∈，得3m =-或4m =-，故选：BC.三、填空题14．（2022·安徽省蚌埠第三中学高一开学考试）关于x 的方程210x ax ++=的一根大于1，一根小于1，则a 的取值范围是：__________________．【答案】a <-2【解析】∵关于x 的方程210x ax ++=的一根大于1，另一根小于1，令2()1=++f x x ax ，则(1)20f a =+<，求得2a <-，故答案为：2a <-15．（2021·北京师大附中高一期中）若关于x 的一元二次方程2240x ax -+=有两个实根，且一个实根小于1，另一个实根大于2，则实数a 的取值范围是________．【答案】（52，＋∞）【解析】设2()24f x x ax =-+，由题意2Δ4160(1)1240(2)4440a f a f a ⎧=->⎪=-+<⎨⎪=-+<⎩，解得52a >，故答案为：5(,)2+∞．16．（2021·上海·复旦附中高一期中）若关于x 的方程220x kx -+=的一根大于－1，另一根小于－1，则实数k 的取值范围为______．【答案】(),3-∞-【解析】由题意，关于x 的方程220x kx -+=的一根大于-1，另一根小于-1，设()22f x x kx =-+，根据二次函数的性质，可得()130f k -=+<，解得3k <-，所以实数k 的取值范围为(),3-∞-.故答案为：(),3-∞-.17．（2020·上海·高一专题练习）已知集合()(){}2|320,A x x x x x R =-+-≤∈，{}2|120,B x x ax x R =--≤∈，若A B ⊆，则实数a 的取值范围是______________．【答案】[]1,1-【解析】由()()2320x x x -+-≤，得23020x x x ⎧-≥⎪⎨+-≤⎪⎩或23020x x x ⎧-≤⎪⎨+-≥⎪⎩，解得13x ≤≤，所以集合{|31A x x =-≤≤-或}13x ≤≤，因为A B ⊆，令()212f x x ax =--，则()()3030f f ⎧-≤⎪⎨≤⎪⎩，即9312093120a a +-≤⎧⎨--≤⎩，解得11a -≤≤，所以实数a 的取值范围是[]1,1-故答案为：[]1,1-四、解答题18．（2022·全国·高一期中）命题:p 关于x 的方程20x x m ++=有两个相异负根；命题():0,q x ∃∈+∞，2390x mx -+<．(1)若命题q 为假命题，求实数m 的取值范围；(2)若这两个命题有且仅有一个为真命题，求实数m 的取值范围．【解析】（1）若命题q 为假命题，则对()0,x ∀∈+∞，2390x mx -+≥为真命题；239mx x ∴≤+，即93m x x ≤+；96x x +≥（当且仅当9x x =，即3x =时取等号），36m ∴≤，解得：2m ≤，∴实数m 的取值范围为(],2-∞.（2）由（1）知：若命题q为真命题，则2m >；若命题p 为真命题，则Δ1400m m =->⎧⎨>⎩，解得：104m <<；若p 真q 假，则104m <<；若p 假q 真，则2m >；综上所述：实数m 的取值范围为()10,2,4⎛⎫+∞ ⎪⎝⎭.19．（2022·湖南·高一课时练习）若一元二次方程2570x x a --=的一个根在区间()1,0-内，另一个根在区间()1,2内，求实数a 的取值范围．【解析】令2()57f x x x a =--，则根据题意得(1)057012(0)000(1)0202(2)0201406f a a f a a f a a f a a ->⇒+->⇒<⎧⎪<⇒-⇒⎪⎨<⇒--⇒-⎪⎪>⇒-->⇒<⎩，∴06a <<.故实数a 的取值范围(0,6).20．（2021·辽宁·昌图县第一高级中学高一期中）1.已知()()2213f x x a x =+-+．(1)如果方程()0f x =在()0,3有两个根，求实数a 的取值范围；(2)如果[]1,2x ∃∈，()0f x >成立，求实数a 的取值范围．【解析】(1)()()2213f x x a x =+-+的对称轴为1x a=-要想方程()0f x =在()0,3有两个根，需要满足()()()100001330f a f a f ⎧-<⎪>⎪⎨<-<⎪⎪>⎩解得：(1,1a ∈--(2)[]1,2x ∃∈，()22130x a x +-+>成立，即3122x a x ⎛⎫->-+ ⎪⎝⎭在[]1,2x ∈上有解，只需1a -大于()322x g x x ⎛⎫=-+ ⎪⎝⎭的最小值，其中()322x g x x ⎛⎫=-+ ⎪⎝⎭为对勾函数，在x ⎡∈⎣上单调递增，在)x ∈上单调递减，又()131222g ⎛⎫=-+=- ⎪⎝⎭，()2372244g ⎛⎫=-+=- ⎪⎝⎭，所以最小值为()12g =-故12a ->-，解得：1a >-，实数a 的取值范围为()1,-+∞21．（2021·上海市七宝中学高一阶段练习）设二次函数()2f x ax bx c =++，其中R a b c ∈、、.(1)若()21,94b a c a =+=+，且关于x 的不等式()28200-+<x x f x 的解集为R ，求a 的取值范围；(2)若Z a b c ∈、、，且()()01f f 、均为奇数，求证：方程()0f x =无整数根；(3)若21,21,a b k c k ==-=，当方程()0f x =有两个大于1的不等根时求k 的取值范围.【解析】（1）∵()22820440x x x -+=-+>∴()()221940f x ax a x a =++++<在R 上恒成立∵0a ≠，则()()20Δ414940a a a a <⎧⎪⎨=+-+<⎪⎩，解得12a <-综上所述：a 的取值范围为1,2⎛⎫-∞- ⎪⎝⎭.（2）∵()()0,1f c f a b c ==++，则c 为奇数，a b +为偶数当Z x ∈时，则有：1.若a b 、均为偶数时，则2ax bx +为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根2.若a b 、均为奇数时，则有①若x 为偶数时，则2ax bx +为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根②若x 为奇数时，则()2ax bx x ax b +=+为偶数∴()20f x ax bx c =++≠，即方程()0f x =无整数根综上所述：方程()0f x =无整数根（3）()()2221f x x k x k =+-+由题意可得()()222Δ21402112120k k k f k k ⎧=-->⎪-⎪->⎨⎪=+>⎪⎩，解得2k <-则k 的取值范围为(),2∞--.。

二次函数性质及根的分布

二次函数的性质及根的分布
判别式△＝b2－ 4ac
二次函数
△＞0
△＝0
y＝ax2＋bx＋ c(a＞0)的图像
一 ax2＋bx+c=0
元二
(a≠0)的根
次
不
等 ax2＋bx＋c>0
式的
(a＞0)
解
集 ax2＋bx+c<0
(a＞0)
有两相异实根：有两相等实根x1
x1,2＝
＝x2＝-
x＜x1或x＞x2
或 (x1－m)(x2－m)＞０， (x1－m)＋(x2－m)>０．
(3)若x1＜m＜x2，则应有 f(m)＜０，或 (x1－m)(x2－m)＜０．
y
x1 m x2
O
x
(4)若m＜x1＜x2＜n，则应有 y Δ＝b2－４ac＞０，
f(m)＞０，
f(n)＞０，
x1
x2
m＜－
b 2a
＜n.
mO
n
x
(5)若x1＜m＜n＜x2，则应有
19
2
解之得
４a＋２b＋c＝19
2
a=2
b＝２, c＝－
5 2
b2－４ac－１２a＝０
5 ∴ f(x)＝２x2＋２x－2 ．
解二
∵ f（－３）＝f（２）＝
19 2
，
∴ 抛物线y＝f(x)的对称轴为x＝ 3 2 ，即x＝－ 1 ，
2
2
故其顶点坐标为（－ 1 ，－３）．
2
1
设 ∵ ∴
f(x)＝a(x＋ 21)2－３．
Ａ.１
Ｂ. 3
2
Ｃ. 5 4
Ｄ.
4 3
4．若二次函数f(x)＝－２x2＋４x＋t的图像顶点的纵坐标等

二次函数根的分布

特点二：(1)-(5)都是两根在同一区间内；(6)-(10) 都是两根在不同的区间内。
现在的问题变成了“如何解决这两类问题？”
分成两组研究: 第一组：(1)-(5) 第二组：(6)-(10)
问题二：方程满足下列条件x2+（m-3)x+m=0，求m的范围。
（2）有两个负根
解法一：设方程的两实根分别为x1、x2，则
（6）一个正根，一个负根
解法一：设方程的两实根分别为x1、x2，则
( m 3)2 4m 0
x1x2 m 0
m m0
问题二：方程满足下列条件x2+（m-3)x+m=0，求m的范围。
（6）一个正根，一个负根
解法二：设f(x)＝ x2＋(m－3)x＋m，要使二次函数与x轴的交点分别在x轴的正、负半轴，由图像知只需满足：
思路：通过换元，转化为一元二次方程根的分布问题
解：设t＝2x，则t∈(0,+∞)
t2 (m 3)t m 0 (1)
问题转化为方程（1）有两相异正实根，求m的取值范围。
设 f (t) t2 (m 3)t m ，则
＝(3-m)2 -4m 0

- b =- 3-m >0 2a 2 f ( 0 )=m>0
一元二次方程ax2+bx+c=0 （a>0）根的分布
两个根都小于k
小
y
两个根都大于k
y
两个根都在（k1.k2)内
y
kx
k
x
k1 O
kx 2
结
0
0

b 2a

k

第四节二次函数根的分布问题

第四课二次函数零点的分布问题二次函数的图象及其应用研究一元二次方程的根的分布问题，一般情况下需要考虑三个方面：(1)一元二次方程根的________；(2)相应二次函数区间端点______________；(3)相应二次函数图象的对称轴_________与______的位置关系．设x1，x2是实系数一元二次方程ax2＋bx＋c＝0(a>0)的两根，则x1，x2的分布范围与二次方程系数之间的关系如下表所示.根的分布x1<x2<k k<x1<x2x1<k<x2图象等价条件f(k)<0根的分布x1，x2∈(k1，k2)k1<x1<k2<x2<k3在区间(k1，k2)内有且仅有一个根图象等价条件f(k1)f(k2)<0或Δ＝0 且－b2a∈(k1，k2)考点一二次函数的单调性与对称性例一函数f(x)＝2x2－mx＋3，当x∈[－2，＋∞)时是增函数，则m的取值范围是() A．[－8，＋∞)B．[8，＋∞)C．(－∞，－8]D．(－∞，8]若f(x)＝x2－x＋a，f(－m)<0，则f(m＋1)的值()A．是正数B．是负数C．是非负数D．与m有关练习：1若函数f(x)＝(a2－2a－3)x2＋(a－3)x＋1的定义域和值域都为R，则a的取值范围是()A．a＝－1或3 B．a＝－1C．a＞3或a＜－1 D．－1＜a＜32已知函数y＝x2－4ax(1≤x≤3)是单调递增函数，则实数a的取值范围是3函数y＝x2＋bx＋c，x∈[0，＋∞)是单调函数的充要条件是()A．b≥0B．b≤0C．b>0D．b<04如果函数f(x)＝x2＋bx＋c对任意实数t都有f(2＋t)＝f(2－t)，那么()A．f(2)<f(1)<f(4) B．f(1)<f(2)<f(4)C．f(2)<f(4)<f(1) D．f(4)<f(2)<f(1)考点二二次方程根的分布问题例一：已知函数f(x)＝mx2＋(m－3)x＋1在原点右侧至少有一个零点，求实数m的取值范围．练习1：已知函数f(x)＝x2－(2a－1)x＋a2－2的图象与x轴的非负半轴至少有一个交点，求a的取值范围练习2：若关于x 的方程3tx 2＋(3－7t)x ＋4＝0的两个实根α，β满足0<α<1<β<2，实数t 的取值范围是______．练习3若方程x 2＋(k －2)x ＋2k －1＝0的两根中，一根在0和1之间，另一根在1和2之间，则实数k 的取值范围是______________ .练习四若关于x 的方程x 2＋mx ＋1＝0有两个不相等的实数根，则实数m 的取值范围是() A ．(－1,1) B ．(－2,2)C ．(－∞，－2)∪(2，＋∞)D ．(－∞，－1)∪(1，＋∞)考点三二次函数图像的应用例三直线y ＝2与曲线y ＝x 2－|x |＋a 有四个交点，则a 的取值范围是( )A.⎝⎛⎭⎫34，1B.⎝⎛⎭⎫1，54C.⎝⎛⎭⎫2，74D.⎝⎛⎭⎫2，94练习：1已知二次函数f (x )满足f (x ＋1)－f (x )＝2x ，且f (0)＝1.(1)求f (x )的解析式；(2)在区间[－1,1]上，f (x )的图象恒在y ＝2x ＋m 的图象上方，试确定实数m 的范围．练习 2．对实数a 和b ，定义运算“ ”：a b ＝设函数f(x)＝(x 2－2) (x －1)，x ∈R.若函数y ＝f(x)－c 的图象与x 轴恰有两个公共点，则实数c 的取值范围是 ( )A ．(－1,1]∪(2，＋∞)B ．(－2，－1]∪(1,2]C ．(－∞，－2)∪(1,2]D ．[－2，－1]考点4 二次函数最值问题例4 求二次函数f(x)＝x 2－2x ＋3在区间[t ，t ＋1](t ∈R)上的最大值与最小值．不等式f(x)=a x 2-x-c>0的解集为{x |-2<x <1},则函数f(x )在区间[1，2]上的最小值为__________．点评：讨论二次函数的区间最值问题：(1)注意对称轴与区间的相对位置；(2)注意相应抛物线的开口方向．具体地说，二次函数f(x)＝ax 2＋bx ＋c 在区间[α，β]上的最值一般分为三种情况讨论：①对称轴x ＝－在区间左边，函数在此区间上具有单调性；②对称轴在区间之内；③对称轴在区间右边，函数在此区间上具有单调性．要注意系数a 的符号对抛物线开口方向的影响．⊗⊗⊗,,,.-≤⎧⎨->⎩a a b 1b a b 1b2a。

高一数学二次函数根的分布专题归类精练

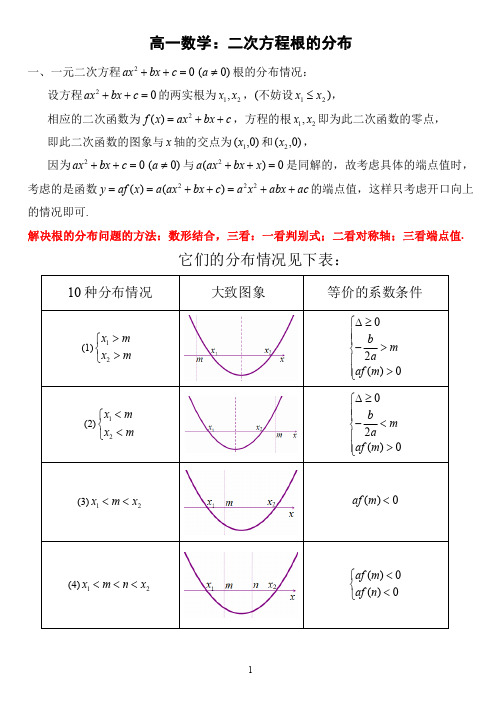
高一数学：二次方程根的分布一、一元二次方程02=++c bx ax )0(≠a 根的分布情况：设方程02=++c bx ax 的两实根为12,x x ，(不妨设21x x ≤)，相应的二次函数为c bx ax x f ++=2)(，方程的根12,x x 即为此二次函数的零点，即此二次函数的图象与x 轴的交点为)0,(1x 和)0,(2x ，因为02=++c bx ax )0(≠a 与0)(2=++x bx ax a 是同解的，故考虑具体的端点值时，考虑的是函数ac abx x a c bx ax a x af y ++=++==222)()(的端点值，这样只考虑开口向上的情况即可.解决根的分布问题的方法：数形结合，三看：一看判别式；二看对称轴；三看端点值.它们的分布情况见下表：如上图，只是可以过两端点，注注2：对于端点值是否可取，最好单独讨论；注3：以上11种情况都有相应的等价形式，对于具体题中的条件，往往是几种情况合在一起的，这时需要分类讨论，此时莫忘注1，注2 .特别注意下列两种情况：一. 函数)(x f 在()n m ,内仅有一个零点，可分：（1）方程0)(=x f 有且只有一根（两根重合时），且这个根在区间()n m ,内，即0∆=，此时由0∆=可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数的值.（2）若()0f m =，可以确定的求出相应的系数（或得到一个关系），从而可以求出另外一根，若这另外的一根在区间()n m ,内，则满足条件；若不在，则这种情况不成立.（3）若()0f n =时，同理.（4）以上三种都讨论完了，只剩下一种情况，即只要0)()(<n f m f 即可.例1：已知624)(2++-=m mx x x f 在区间()3,0-内有且仅有一个零点，求m 的取值范围.解：①当0∆=时，即()2164260m m -+=，得出1m =-或32m =，当1m =-时，根()23,0x =-∈-，即1m =-满足题意；当32m =时，根()33,0x =∉-，故32m =不满足题意； ②当0151462129)3(=+=+++=-m m m f ，解得：1415-=m ，由韦达定理的两根之积为72767156232=+-=+=⨯-m x ，即)0,3(792-∈-=x ，满足条件，故1415-=m 合适； ③当062)0(=+=m f ，解得：3-=m ，由韦达定理的两根之和为12402-==+m x ，即)0,3(122-∉-=x ，不满足条件，故3-=m （舍）；④当0)0()3(<⋅-f f 时，即0)62)(1514(<++m m ，得出14153-<<-m ，必满足条件. 综上所述所求m 的取值范围是：14153-≤<-m ，或1m =-. 注：你能发现这个题的巧解吗？二. 函数)(x f 在],[n m 内仅有一个零点，可同上分析.即先讨论0=∆（即方程两根重合）时的情况，验证相应的根是否合适；再看取到端点值时的情况，此时已知一根，由韦达定理易得另一根，验证是否满足条件；最后0)()(<n f m f 即可！熟练之后，此次序可以灵活变通，只是请注意分类要不重不漏！例2：已知624)(2++-=m mx x x f 在区间]0,3[-内有且仅有一个零点，求m 的取值范围. 解：①当0∆=时，即()2164260m m -+=，得出1m =-或32m =，当1m =-时，根]0,3[2-∈-=x ，即1m =-满足题意；当32m =时，根]0,3[3-∉=x ，故32m =不满足题意； ②当0151462129)3(=+=+++=-m m m f ，解得：1415-=m ，由韦达定理的两根之积为72767156232=+-=+=⨯-m x ，即)0,3(792-∈-=x ，不满足条件，故1415-=m （舍）；③当062)0(=+=m f ，解得：3-=m ，由韦达定理的两根之和为12402-==+m x ，即)0,3(122-∉-=x ，满足条件，故3-=m 合适；④当0)0()3(<⋅-f f 时，即0)62)(1514(<++m m ，得出14153-<<-m ，必满足条件. 综上所述所求m 的取值范围是：14153-<≤-m ，或1m =-. 注：你能发现这个题的巧解吗？注：讨论端点时，如果遇到下列情况，前参看下列题的处理办法！例3：已知方程02)2(2=++-x m mx 在区间()1,3上有一根，求m 的取值范围. 解：当0=m 时，易知方程仅有一个根为1，不满足条件当0≠m 时，令2)2()(2++-=x m mx x f ，因为()10f =，所以()()()22212mx m x x mx -++=--，故另一根为2m，由213m <<，得223m <<即为所求. 例4：已知方程02)2(2=++-x m mx 在区间]3,1[上有一根，求m 的取值范围. 解：当0=m 时，易知方程仅有一个根为1，满足条件；当0≠m 时，令)2)(1(2)2()(2--=++-=mx x x m mx x f ，必有一根为1 故另一根2m ，当12=m，即2=m 时合适；否则必须满足：12<m 或32>m ，解得：0<m ，或320<<m ，或2>m综上所述，所求m 的取值范围是32<m 或2≥m .注：你能发现这两个题的巧解吗？以后再赘述吧，先抱歉了！二．根的分布经典题归类讲解例1、①m 取何实数值时，方程0)1(22=++-m x m x 有两个不等正实根.②m 取何实数值时，方程013422=-++m mx x 有两个负数根.③m 取何实数值时，关于x 的方程05)2(2=-+-+m x m x 的两个实根都大于2. 解：①令=)(x f m x m x ++-)1(22，其图像开口向上，对称轴为41+=m x ，判别式为168)1(22+-=-+=∆m m m m原条件⎪⎪⎩⎪⎪⎨⎧>=>+>+-=∆⇔0)0(0410162m f m m m 解得：2230-<<m 或223+>m ，即为所求.②令=)(x f 13422-++m mx x ，其图像开口向上，对称轴为m x -=，判别式为)1)(21(16)2123(16)13(81622--=+-=--=∆m m m m m m . 原条件⎪⎪⎩⎪⎪⎨⎧>-=<-≥--=∆⇔013)0(00)1)(21(16m f m m m 解得：2131≤<m 或1≥m ，即为所求.③令=)(x f m x m x -+-+5)2(2，其图像开口向上，对称轴为21m x -=，判别式为)4)(4(16)5(4)2(22-+=-=---=∆m m m m m .原条件⎪⎪⎩⎪⎪⎨⎧>+=-+-+=>-≥-+=∆⇔055424)2(2210)4)(4(m m m f m m m 解得：45-≤<-m ，即为所求.例2、①已知二次方程012)12(2=-+-+m mx x m 有一正根和一负根，求实数m 的取值范围.②已知二次函数33)42()2(2+++-+=m x m x m y 与x 轴有两个交点，一个在1=x 的左侧，一个在1=x 的右侧，求实数m 的取值范围.③m 取何实数值时，关于x 的方程05)2(2=-+-+m x m x 的一个实根大于2，另一个实根小于2.解：①令=)(x f 12)12(2-+-+m mx x m ，其图像开口方向不明，原条件0)1)(12()0()12(<-+=+⇔m f m ，解得：21->m . 即为所求. 注：利用两个之积012121<+-=m x x ，也可以快速得出！②令=)(x f 33)42()2(2+++-+m x m x m ，其图像开口方向不明，原条件0)12)(2()33422)(2()1()2(<++=++--++=+⇔m m m m m m f m ，解得：212-<<-m . 即为所求. 注：利用0)1)(1(21<--x x ，即021212422331)(2121<++=+++-++=++-m m m m m m x x x x 也可得.③令=)(x f m x m x -+-+5)2(2，其图像开口向上，原条件055424)2(<+=-+-+=⇔m m m f 解得：5-<m ，即为所求.注：利用0)2)(2(21<--x x ，即054)2(254)(22121<+=+---=++-m m m x x x x 也可得. 例3．①已知关于x 的方程：022=+-a ax x 有两个实根βα,，且满足2,10><<βα，求实数a 的取值范围．②已知关于x 的方程：062)1(22=-++--m m mx x m 有两个实根βα,，且满足βα<<<10，求实数m 的取值范围．③已知关于x 的方程：0532=+-a x x 有两个实根βα,，且满足)3,1(),0,2(∈-∈βα，求实数a 的取值范围．解：①令=)(x f a ax x +-22，其图像开口向上，画图可得：原条件⎪⎩⎪⎨⎧<-=<-=>=⇔034)2(01)1(0)0(a f a f a f 解得：34>a ，即为所求.②令=)(x f 62)1(22-++--m m mx x m ，其图像开口方向不明，画图可得：原条件⎩⎨⎧<->-⇔0)1()1(0)0()1(f m f m ，即⎪⎩⎪⎨⎧<-++--->-+-⇔0)621)(1(0)6)(1(22m m m m m m m m即⎩⎨⎧<+-->+--⇔0)7)(7)(1(0)3)(2)(1(m m m m m m 解得：73-<<-m 或72<<m ，即为所求.③令=)(x f a x x +-532，其图像开口向上，画图可得：原条件⎪⎪⎩⎪⎪⎨⎧>+=+-=<-=+-=<=>+=++=-⇔0121527)3(022)1(0)0(0221012)2(a a f a a f a f a a f 解得：012<<-a ，即为所求.例4、①已知方程03222=+++m mx x 的两个不等实根都在区间)2,0(内，求实数m 的取值范围.②已知方程03222=+++m mx x 的两个不等实根都在区间]2,0[之外，求实数m 的取值范围. 解：令322)(2+++=m mx x x f ，其图像开口向上，对称轴为m x -=，由判别式0)3)(1(4)32(4)32(4422>-+=--=+-=∆m m m m m m ，得：1-<m 或3>m①的条件⎪⎪⎩⎪⎪⎨⎧>+=>+=<-<>∆⇔076)2(032)0(200m f m f m ，即⎪⎪⎪⎩⎪⎪⎪⎨⎧->-><<->-<⇔67230231m m m m m 或解得：167-<<-m 即为所求.②的条件可分为：两根都小于0，或两根都大于2，或一根小于0，一根大于2，三种情况故⎪⎩⎪⎨⎧>+=<->∆⇔032)0(00m f m 或⎪⎩⎪⎨⎧>+=>->∆076)2(20m f m 或⎩⎨⎧<+=<+=076)2(032)0(m f m f解得：3>m ，或无解，或23-<m ，故所求m 的取值范围是：23-<m 或3>m . 例5：已知集合}0107|{2≤+-=x x x A ，}05)2(|{2≤-+--=m x m x x B ，且A B ⊆，求实数m 的取值范围.解：首先}52|{≤≤=x x A ；当∅=B 时，即不等式05)2(2≤-+--m x m x 无解，即0)5(4)2(2<---=∆m m 即：0162<-m ，解得：44<<-m ； -----（1）当∅≠B 时，即不等式05)2(2≤-+--m x m x 有解，其形式必为21x x x ≤≤；其中21,x x 为方程05)2(2=-+--m x m x 的两个根，（不妨设21x x ≤）按条件，只要5221≤≤≤x x 即可满足A B ⊆；按照根的分布的理论，此时只要满足：⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-+--=≥-+--=≤-≤≥-=∆05)2(525)5(05)2(24)2(52220162m m f m m f m m即⎪⎪⎩⎪⎪⎨⎧-≥-≥-≤≤-≥-≤55284,4m m m m m 或，解得：45-≤≤-m ，-----（2）由（1）（2）可得：所求的m 的取值范围是45≤≤-m .三．自己练习巩固提升1．设有一元二次方程02)1(22=++-+m x m x ．试问：(1)m 为何值时，有一正根、一负根．(2)m 为何值时，有一根大于1、另一根小于1． (3)m 为何值时，有两正根． (4)m 为何值时，有两负根．(5)m 为何值时，仅有一根在[1，4]内.2. 关于x 的方程012=-++a ax x 有异号的两个实根，求a 的取值范围.3.如果方程032)3(22=-+++a x a x 的两个实根中一根大于3,另一根小于3，求实数a 的取值范围. 4.若方程07)1(82=-+++m x m x 有两个负根，求实数a 的取值范围. 5. 关于x 的方程0422=-+-a ax x 有两个正根，求a 的取值范围.6.设关于x 的方程0)(44222=+++-n m x n m x 有一个实根大于-1，另一个实根小于-1，则n m ,必须满足什么关系.7. 设关于x 的方程023222=---k x kx 有两个实根都在]0,2[-之间，求k 的取值范围.8.关于x 的方程02)13(72=--+-m x m x 的两个实根21,x x 满足2021<<<x x ，求m 的范围. 9.①已知方程065)9(222=+-+-+a a x a x 的一根小于0，另一根大于2，求实数a 的取值范围.②已知方程065)9(222=+-+-+a a x a x 的存在小于2的根，求实数a 的取值范围.。

二次函数根的分布

即(2a 3)(a 2) 0 由 x a 1 2得
3 a 2, 2
a2
(1)1 a
2时,
x
(a
1)(a
2)
2(a
2)
(2)
3 2
a
x [6,12)
1时, x (1 a)(a
2)x2([a9, 4
22)3) 4
例3.已知函数f(x)=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧，求实数m的取值范围 .
1 2
时,
x
a,
01 1 2X=a
01
x
x
X=a
y有最大值a2, x 1时, y有最小值f (1) 2a 1.
2.若关于x的方程 x2 (a 1)x 1 0 有两个相
等的实数根,且两根在区间[0,2]上,求实数a的范围.
解:设f (x) x2 (a 1)x 1(如图)
(a 1)2 4 0
(1)试写出g(t)的函数表达式； (2)作g(t)的图象并写出g(t)的最小值
解: f (x) (x 2)2 8
8 1 t 2
g(t
)
f (t) t2 4t 4(t 2)
f (t 1) (t 1)2 4(t 1) 4(t 1)
【巩固练习】
1.当a 0,0 x 1时,求函数f (x) x2 2ax的最大最小值.
3.关于x的方程x2+(a2-1)x+(a-2)=0的一根比1大,
另一根比1小，则有( C )
(A)-1＜a＜1 (B)a＜-2或a＞1 (C)-2＜a＜1 (D)a＜-1或a＞2
4.设x,y是关于m的方程m2-2am+a+6=0的两个实

二次函数根的分布

k 0
k9
பைடு நூலகம்
(k 3) 0
例题：已知方程x2 (k 3)x k 0 求满足下列条件的k的范围？
3、一个正根，一个负根
设f x x2 (k 3)x k，则
0

f
(0)

0
f (0) 0
k 0
0
x1
x2
例题：已知方程x2 (k 3)x k 0 求满足下列条件的k的范围？
设 f x x2 (k 3)x k,则
f
(0)

f
(1)

0
或0

-
k2
3

2
0
0 k 1
0
x1
2
x2
练习： 1、若方程x2 (k 3)x k 0 的两根都小于1，求k的取 x1 x2 0
-1
值范围？
2、若方程7x2 k 13x k 2 k 2 0的两根分别在0，1和1，2内，求k的取值范围？
1
0
2
4、有两个根都大于1 解：设x2 (k 3)x k 0的两根为 x1, x2，则
0

x1

x2
1
x1 x2 2
反例：x1

3,
x2

1 2
例题：已知方程x2 (k 3)x k 0 求满足下列条件的k的范围？
4、有两个根都大于1
设 f x x2 (k 3)x k，则
0
(k 3)2 4k 0

f
b
2a (1)

【经典例题】二次函数根的分布

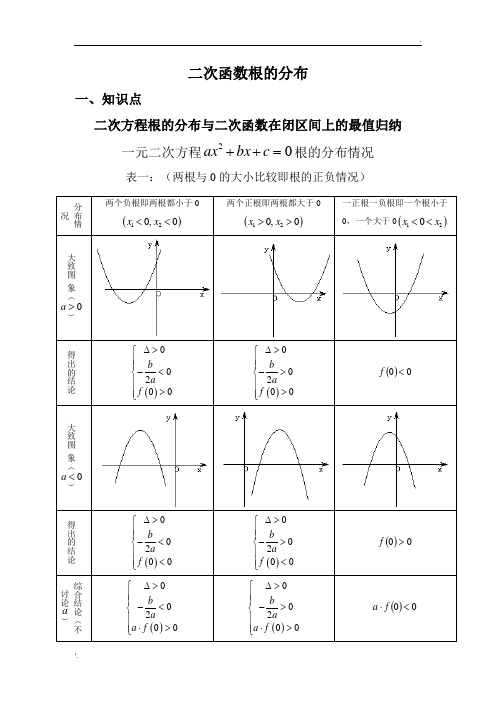
二次函数根的分布一、知识点二次方程根的分布与二次函数在闭区间上的最值归纳一元二次方程02=++c bx ax 根的分布情况表一：（两根与0的大小比较即根的正负情况）分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（0>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a表二：（两根与k 的大小比较）分布情况两根都小于k 即k x k x <<21, 两根都大于k 即k x k x >>21, 一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a ）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk表三：（根在区间上的分布）二、经典例题分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种）一根在()n m ,内，另一根在()q p ,内，q p n m <<<大致图象（>a ）得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象（<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 综合结论（不讨论a ）——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f例1：（实根与分布条件）已知βα, 是方程024)12(2=-+-+m x m x 的两个根，且βα<<2 ，求实数m 的取值范围。

二次函数中根的分布问题

一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）k k k根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

如方程()2220mx m x -++=在区间()1,3上有一根，因为()10f =，所以()()()22212mx m x x mx -++=--，另一根为2m ，由213m<<得223m <<即为所求； 2︒ 方程有且只有一根，且这个根在区间()n m ,内，即0∆=，此时由0∆=可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数。

如方程24260x mx m -++=有且一根在区间()3,0-内，求m 的取值范围。

分析：①由()()300f f -<即()()141530m m ++<得出15314m -<<-；②由0∆=即()2164260m m -+=得出1m =-或32m =，当1m =-时，根()23,0x =-∈-，即1m =-满足题意；当32m =时，根()33,0x =∉-，故32m =不满足题意；综上分析，得出15314m -<<-或1m =-例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根，求实数m 的取值范围。

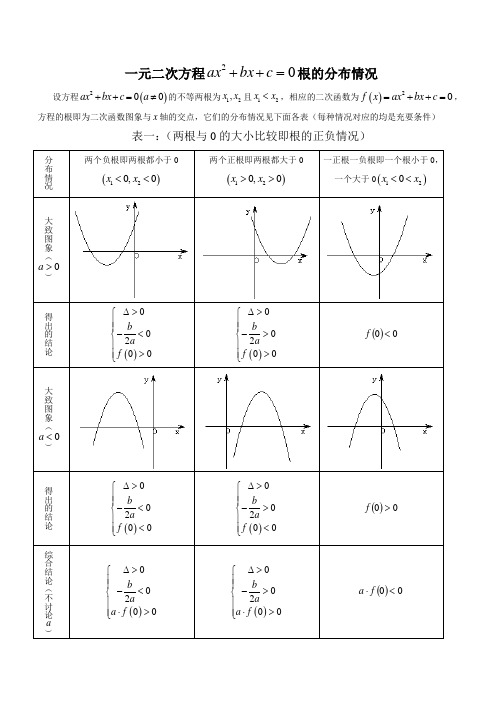
二次函数根的分布

二次函数根的分布本文介绍了一元二次方程根的分布情况以及与二次函数在闭区间上的最值归纳。

设方程 $ax^2+bx+c$ 的不等两根为$x_1,x_2$，且 $x_1<x_2$，相应的二次函数为$f(x)=ax^2+bx+c$，方程的根即为二次函数图象与 $x$ 轴的交点。

根的分布情况可归纳为三种情况，每种情况对应的均是充要条件。

第一种情况是两个负根即两根都小于 $0$，或两个正根即两根都大于 $0$，或一个正根一负根即一个根小于 $0$，一个大于 $0$。

此时，当 $a>0$ 时，$f(x)$ 最小值为$\frac{\Delta}{4a}$，当 $a<0$ 时，$f(x)$ 最大值为$\frac{\Delta}{4a}$。

第二种情况是两根与 $k$ 的大小比较，即两根都小于 $k$，或两根都大于$k$，或一个根小于$k$，一个大于$k$。

此时，当 $a>0$ 时，$f(k)$ 最小值为 $a(k-x_1)(k-x_2)$，当 $a<0$ 时，$f(k)$ 最大值为 $a(k-x_1)(k-x_2)$。

第三种情况是根在区间上的分布，包括两根都在$(m,n)$ 内，一根在 $(m,n)$ 内，另一根在 $(p,q)$，或两根有且仅有一根在 $(m,n)$ 内。

此时，当 $a>0$ 时，$f(x)$ 最小值为 $f\left(\frac{x_1+x_2}{2}\right)$，当 $a<0$ 时，$f(x)$ 最大值为 $f\left(\frac{x_1+x_2}{2}\right)$。

经过观察得出，文章中存在大量格式错误和重复内容，需要进行整理和删减。

同时，需要对每段话进行简单的改写，以提高可读性。

根据图像，可以得出以下结论：1.当mf(n)且f(n)>b，则有f(m)*f(n)<2a；若有f(m)<f(n)且f(n)<b，则有f(m)*f(n)<2a；若有f(m)<f(n)<b，则有f(m)*f(n)<f(p)*f(q)。

二次函数根的分布

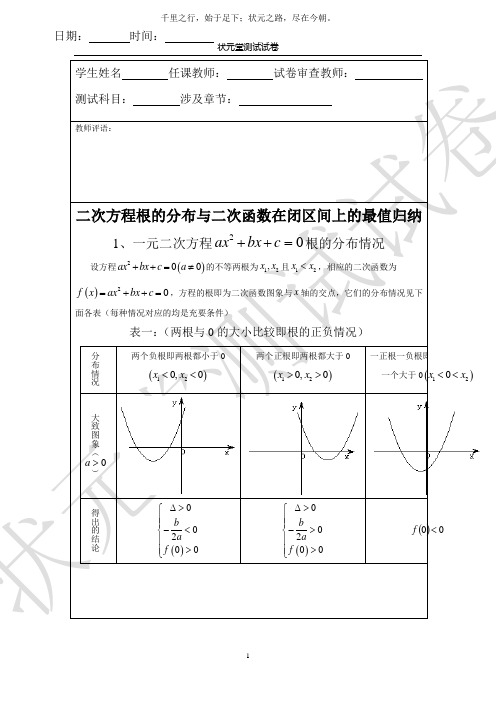
状元堂测试试卷学生姓名任课教师：试卷审查教师：测试科目：涉及章节：教师评语：二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一一个大于0()120x x <<大致图象（0>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200ba f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f 日期：时间：大致图象（<a ）得出的结论 ()00200ba f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200ba f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a ）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a表二：（两根与k 的大小比较）分布情况两根都小于k 即 k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ，一k1xk x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020bk a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f kkk大致图象（<a ）得出的结论()020bk a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020bk a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a ）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f a表三：（根在区间上的分布）分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种）一根在()n m ,内，另一()q p ,内，q p n m <<<大致图象（>a ）得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()000f m f n fp f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n fp f q <⎧⎪⎨<⎪⎩大致图象（<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()000f m f n fp f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n fp f q <⎧⎪⎨<⎪⎩综合结论（不讨论a ）——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n < 不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

二次函数根分布问题

一元3x2 5x a 0的一个根大于 2且小于0，另一个根大于1且小于3，求实数a的取值范围
练习 1、已知关于x的方程 x2 2m x 2m 1 0; 若方程有两个根，其中一个根在区间（ 1,0）内，；另一根在区间（ 1,2）内，求m的取值范围
例题2、已知关于x的方程 x2 2m x 2m 1 0; 若方程有两个实根，且一个大于4，一个小于4，求m的取值范围
练习2、已知关于x的方程 x2 （ 2 m 1 ）x 2m 6 0; 若方程有两个实根，且一个比2大，一个比2小，求m的取值范围
题型二：两根正负
例题3、已知关于x的方程 x2 2mx 2m 1 0; 若方程有一正一负两个根，求实数m的取值范围
练习3、已知关于x的方程 x2 2mx 2m 1 0; 若方程有且仅有一个正实根，求实数m的取值范围
题型三：两根在某个区间中
例题4、已知关于 x的方程 x2 2mx 2m 1 0; 若方程有两个实根，且都在区间 [0,4)内，求m的取值范围
练习4、已知关于 x的方程2 x2 （ 2 2a 1 ）x a 2 0; 若方程有两个实根，且都在区间 3与3之间，求实数 a的取值范围
题型四：在某个区间中考虑根的情况
练习5、已知关于x的方程 x2 2ax 2 0; 在区间 [0,4]上至少有一个零点，求实数a的取值范围

经典例题二次函数根的分布(供参考)

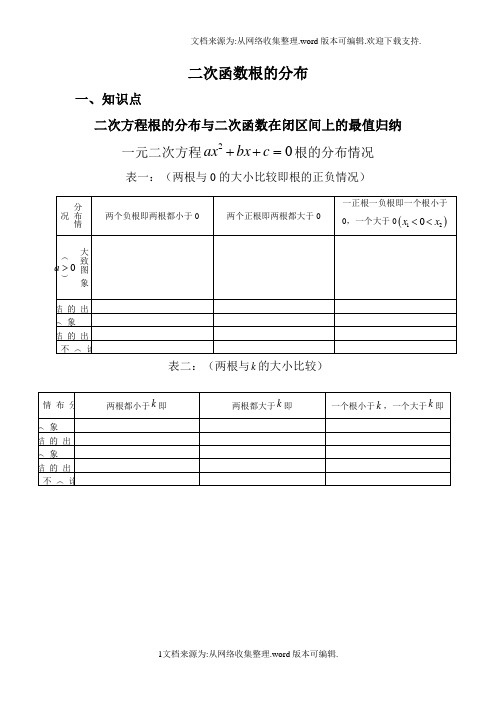
二次函数根的分布一、知识点二次方程根的分布与二次函数在闭区间上的最值归纳一元二次方程02=++c bx ax 根的分布情况表一：（两根与0的大小比较即根的正负情况）表二：（两根与k 的大小比较）论论论论表三：（根在区间上的分布）二、经典例题例1：（实根与分布条件）已知βα,是方程024)12(2=-+-+m x m x 的两个根，且βα<<2 ，求实数m 的取值范围。

变式：关于x 的方程012)1(22=-+-mx x m 的两个根，一个小于0，一个大于1，求m 的取值范围。

例2：（动轴定区间）函数32)(2--=ax x x f 在区间[]2,1上是单调函数，则a 的取值范围是？变式2：函数32)(2+-=kx x x f 在[]+∞-,1上是增函数，求实数k 的取值范围。

列3：（定轴动区间）求函数12)(2--=ax x x f 在[]2,0上的值域。

变式3：已知函数2244)(22+-+-=a a ax x x f 在区间[]2,0上有最小值3，求实数a 的取值范围。

例4：（定轴动区间）已知二次函数32)(2--=x x x f ，若)(x f 在[]1,+t t 上的最小值为)(t g ，求)(t g 的表达式。

变式4：已知二次函数)(x f 满足)1()1(x f x f -=+，且1)1(,0)0(==f f ，若)(x f 在区间[]n m ,上的值域是[]n m ,，求n m ,的值。

例5：（恒成立问题）已知函数1)(2-+=mx x x f ，若对于任意[]1,+∈m m x ，都有0)(<x f 成立，求实数m 的取值范围。

变式5：已知函数1)(2+-=mx x x f 在)2,21(上恒大于0，求实数m 的取值范围。

三、课后练习1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根，求实数m 的取值范围。

2、函数()()2220f x ax ax b a =-++≠在[]2,3上有最大值5和最小值2，求,a b 的值。

二次函数中根地分布问的题目

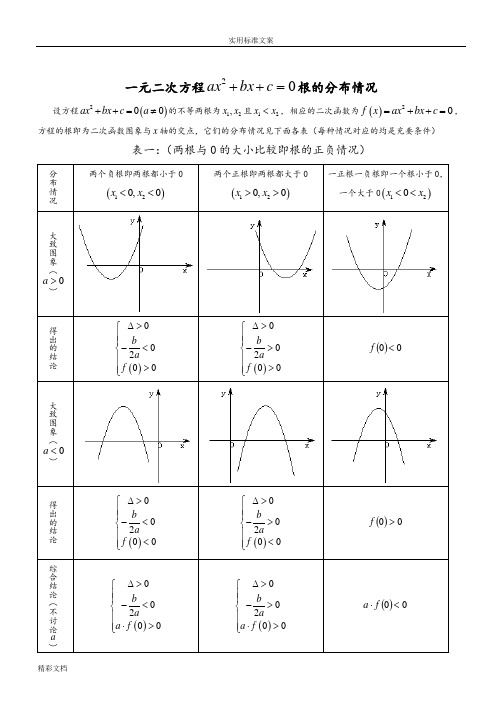
一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种）一根在()n m ,内，另一根在()q p ,内，q p n m <<<大致图象（>a ）得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象（<a ）得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩综合结论（不讨论a）——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩；（2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

高中数学例题：一元二次方程根的分布

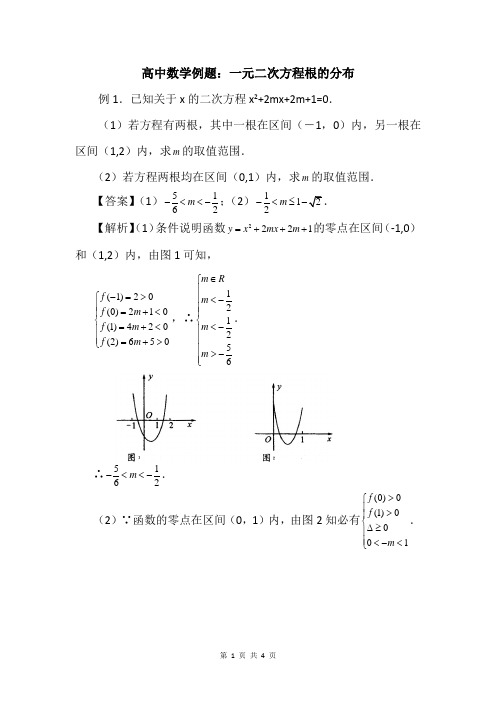
高中数学例题：一元二次方程根的分布例1．已知关于x 的二次方程x 2+2mx+2m+1=0．（1）若方程有两根，其中一根在区间（―1，0）内，另一根在区间（1,2）内，求m 的取值范围．（2）若方程两根均在区间（0,1）内，求m 的取值范围．【答案】（1）5162m -<<-；（2）112m -<≤．【解析】（1）条件说明函数2221y x mx m =+++的零点在区间（-1,0）和（1,2）内，由图1可知，(1)20(0)210(1)420(2)650f f m f m f m -=>⎧⎪=+<⎪⎨=+<⎪⎪=+>⎩，∴121256m R m m m ∈⎧⎪⎪<-⎪⎪⎨<-⎪⎪⎪>-⎪⎩． ∴5162m -<<-．（2）∵函数的零点在区间（0，1）内，由图2知必有(0)0(1)0001f f m >⎧⎪>⎪⎨∆≥⎪⎪<-<⎩．∴12121110m m m m m ⎧>-⎪⎪⎪>-⎨⎪≥+≤⎪⎪-<<⎩．∴112m -<≤【总结升华】本例两个小题均可以用解方程的方法求解，但很繁琐，而利用函数的性质和图象求解就变得非常直观简捷．“方程与函数思想”“数形结合思想”是数学中的两个重要思想，解题中要注意应用．探究本例中若方程的二次项系数含有参数（mx 2+2x+m+2=0，m ≠0），如何求解？可以用分类讨论方法求解，即讨论m ＞0和m ＜0，结合图象求解；注意讨论过程中，函数端点值的符号与m 的正负有关，因此也可用下面方法求解．即设2()22(0)g x mx x m m =+++≠，则在（1）中有(1)0(0)0(1)0(2)0m g m g m g m g ⋅->⎧⎪⋅<⎪⎨⋅<⎪⎪⋅>⎩，在（2）中有(0)0(1)00101m g m g m ⋅>⎧⎪⋅>⎪⎪∆≥⎨⎪⎪<-<⎪⎩．例2．若二次函数y=―x 2+mx ―1的图象与两端点为A （0，3），B （3，0）的线段AB 有两个不同的交点，求m 的取值范围．【答案】 103,3⎛⎤ ⎥⎝⎦【解析】先求出线段AB 的方程，之后将图象交点问题转化为方程组解的问题，再将方程组解的问题转化为二次函数在区间上有零点的问题，最后通过不等式组求得m 范围．线段AB 的方程为x+y=3（0≤x ≤3），由题意得方程组23(03) 1 x y x y x mx +=≤≤⎧⎨=-+-⎩①②有两组实解． ①代入②得x 2－(m+1)x+4=0（0≤x ≤3）有两个实根，令2()(1)4f x x m x =-++．因此问题转化为二次函数2()(1)4f x x m x =-++在x ∈[0，3]上有两个不同的实根，故有 2(1)1601032(0)40(3)93(1)40m m f f m ⎧∆=+->⎪+⎪<<⎪⎨⎪=>⎪=-++≥⎪⎩，解得1033m <≤．故m 的取值范围是103,3⎛⎤ ⎥⎝⎦．【总结升华】本题解法体现了函数与方程的思想：从列方程（组）开始，通过消元得到一元二次方程，对这个方程实根的研究转化为二次函数f(x)在[0，3]的实根，又转化为二次函数f(x)在[0，3]上与x 轴有两个交点的问题，最后建立m 的不等式组求出m 的取值范围，整个解题过程充满了对函数、方程和不等式的研究和转化，充分体现了函数方程思想的应用．举一反三：【变式1】关于x 的方程ax 2―2(a+1)x+a ―1=0，求a 为何值时：（1）方程有一根；（2）方程有一正一负根；（3）方程两根都大于1；（4）方程有一根大于1，一根小于1．【答案】（1）0a =或13a =-（2）01a <<（3）不存在实数a （4）0a >【解析】（1）当a=0时，方程变为―2x ―1=0，即12x =-，符合题意；当0a ≠时，方程为二次方程，因为方程有一根，所以1240a ∆=+=，解得13a =-．综上可知，当0a =或13a =-时，关于x 的方程ax 2―2(a+1)x+a ―1=0有一根．（2）因为方程有一正一负根，所以由根与系数的关系得10a a -<．又1240,a ∆=+>解得01a <<．（3）方程两根都大于1，图象大致如图所以必须满足0,0,2(1)1,2(1)0.a a a f >⎧⎪∆>⎪⎪+⎨>⎪⎪>⎪⎩或0,0,2(1)1,2(1)0.a a a f <⎧⎪∆>⎪⎪+⎨>⎪⎪<⎪⎩两不等式组均无解．所以不存在实数a ，使方程两根都大于1．（4）因为方程有一根大于1，一根小于1，图象大致如图所以必须满足0,(1)0a f >⎧⎨<⎩或0,(1)0a f <⎧⎨>⎩解得0a >．。