点线面的投影答案.
第二节点线面的投影

47
投影面垂直面
V c'
b'
V
a'
A a"
C
c" W
b´
O
B a
b"
c
b
H
Y
c´
a´
CA
B
a
C
b
c a
W b
48
(1) 投影面垂直面的投影特性
β
γ YH
γ α
YW
YH
βα YW
49
H
是什么位置的平面?
b
b
为什么?
铅垂面 a 积聚性
γ
投影特性: a
c c
βc b
a 主、左视图 类似性
在它垂直的投影面上的投影积聚成直线。该直线与投 影轴的夹角反映空间平面与另外两投影面夹角的大小。
面投影。
●a ● b
18
各种位置直线的投影
正平线(平行于V面) 投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
平行于某一投影面而 与其余两投影面倾斜
统称特殊 位置直线
正垂线(垂直于V面)
投影面垂直线 侧垂线(垂直于W面) 垂直于某一投影面
铅垂线(垂直于H面)
一般位置直线 与三个投影面都倾斜的直线
c
交,但 “交点”不符合
2
●
b 空间一个点的投影规律。
●
a
●
1
3(4 )
d
(2) “交点”是两直线
Ⅰ、Ⅱ在V面 是重影点。
上的一 对重影点的投影,
用其可帮助判断两直线
的空间位置。
40
例、判定两直线是否相交
Z
画法几何(点线面)习题解答

4′1′ ) (′ 2
′
34 2 ( ) 1
18页
3-17.作一水平线MN与H面相距15mm, 3-16。作直线MN,使它与直线AB平行, 并与直线CD、EF都相交 。 e 并与 、 相交。 c b a n n m d
m c n d c b a m b b
15
a a
d
f f
c d m
画法几何习题解答画法几何习题解答吉林建筑工程学院制图教研室点线面投影变换部分页号题号251页号题号10312133714381214383415391215393416310111631213173141831516退出退出页号题号18317181931913193194620320222032123203242521326223272822329302233132233333423335362433738243394026411226413426423页号题号34423344243542526365123653375453856739589退出退出点击题号进入题解页号题号274452746728481228483429491229493430495631410113141213324141532416173341834334193542036421373442223
( )
正垂线 (4) (5)
水平线 (6)
铅垂线
一般线
正平线
侧平线
13页
3-8.根据已知条件,求直线
的三面投影。 2)已知 为正平线及点 的两面投影, 点 在点 的右下方。
Z
(1)已知 为水平线及点 的两面投影, ,点 在点 的右后方,且在 面上。
Z
=30
a
a a Y
画法几何(点线面)习题解答
d′
c′
b′
c′
a′ d′
(d)
a
b(c)
a
c(d)
b
20页
3-21. 求点M到直线AB的距离。 3-24. 已知直线A B与CD垂直相交, AB=40mm,求V面投影。
a′ n′
b′ m′
b
n
a
m
b′
c′ a′
c
d′
a
b
d
20页
3-24. 以BC为底边作等腰三角形,3-25. 已知A D为等腰直角△ABC的高,
b′
a′
b a
c′
a′
c
a
24页
b′
c
b
3-39.已知AB为平面对H面的最大斜度 线,平面的α=30,求作该平面的两面投 影.
b′
3-40.已知△ABC平面的AB边为该平面相 对于V面的最大斜度线,并知点C比点A 高10mm,且距W面50mm,完成该平面的V、W 面投影.
c′ a′
c′
c″
c
b
a′
前上方,求AB的V、H面投影。
3-13.已知直线AB及点C的两面投 影,在直线上AB上取一点D, 使AD=AC。
30 ′
β ′
′
′
′
′
16页
3-14 判别两直线的相对位置。
(1)
b
(2)
d ac
bd c
a
AB与CD 交错
c
(3)
a d b
(4)
d
b
c a
b d
c a
AB与CD 相交 d b
c a
b
a″
a
b′ mm
点线面的投影分析

点的投影规律: (1)点的正面投影和水平投影的连线
垂直于OX 轴。即ss’⊥ OX
(2)点的正面投影和侧面投影的连线
垂直于OZ 轴。即s’s” ⊥ OZ (3)点的水平投影到OX轴的距离等于
侧面投影到OZ 的距离。
退出 节目录
§2-3 立体表面上点、线、面的投影分析
一、点的投影分析
影面。
退出 节目录
§2-3 立体表面上点、线、面的投影分析
三、平面的投影分析
1.一般位置平面 投影特性:
(1)三个投影都不 反映平面实形。 (2)三个投影均对 投影轴倾斜。
退出 节目录
§2-3 立体表面上点、线、面的投影分析 三、平面的投影分析
2.投影面平行面 投影特性:
(1)在所平行 的投影面上投 影反映实形。 (2)其他两个 投影面上的投 影积聚为直线, 且分别平行于 相应的投影轴。
2.投影面平行面 投影特性:
(1)在所平行 的投影面上投 影反映实形。 (2)其他两个 投影面上的投 影积聚为直线, 且分别平行于 相应的投影轴。
平行于侧面的平面称为侧平面
退出 节目录
§2-3 立体表面上点、线、面的投影分析 三、平面的投影分析
3.投影面垂直面 投影特性:
(1)在所垂直的投 影面内投影积聚 为一段斜线。 (2)其他两个投影 面上的投影均为 缩小的类似形。
平行于侧面的直线称为侧平线
退出 节目录
§2-3 立体表面上点、线、面的投影分析
二、直线的投影分析
3.投影面垂直线 投影特性:
(1)在所垂直的 投影面上投影积 聚为一点。
(2)其他两个投 影面上的投影反 映实长,且分别 垂直于相应的投 影轴。
垂直于水平面的直线称为铅垂线
北京工业大学工程图学习题集答案_图文

返回
P12-5
5. 过点K作直线KC与AB线段垂直相交。
P12-6
6. 过点K作直线KC与AB线段垂直相交。
P12-7
7. 求点K到直线AB的距离。
P12-8
判断两直线的相对位置
相交
平行
交叉
交叉
返回
P13-1
完成平面和点的投影
并判断平面与投影面的位置
一般位置平面
返回
P13-1
完成平面和点的投影
求作A(20,30,15),B(10,20,0) C(30,0,30)三点的三面投影
返回
P6-4
求作各点的三面投影
返回
P7-5 已知B点在A点左方15,且X=Y=Z,点C比点B低10, 且X坐标比点B大5,X=Y,求作B,C两点的三面投影,并比较A
和B,C和D,E和F的相对位置
P26-4 4. 求两三角形ABC、DEF平面的交线,并判断可见性。
P26-5 求点D到三角形ABC的距离,并求垂足K的投影 返回
P26-6 6. 求直线MN与三角形ABC平面的交点,并判断可见性。
P27-7
试用一段管路 KF将GH和EF 连接起来。 (1)求KL最短距
离实长 (2)求KL的投影
返回
P7-7
已知A,B,C,D四点的投影图,求作
它们的轴侧图。并写出各点的空间位置
点 象限
返回
已知点A的两面投影,点B与点A对称于V面
P7-8
点C与点A对称于X面,求作B点与C点的
两面投影图,并画出A,B,C三点的轴侧图
返回
求作侧平线AB(距W面20,与H面
P8-1
夹角30,实长为25)的三面投影
分析曲面立体的相贯线,补全褚投影
土木工程制图讲义点线面投影篇7

c a
ad
b 根据直线与平面垂直的
投影规律,过点S作水
s
平 线 SC , 使 其 水 平 投 影scab;再过点S作正
平 线 SD , 使 其 正 面 投
s
影s d a b ,则相 交 两 直 线 SCSD 所 确
定的平面即为所求。
c
b
3.平面与平面垂直
几何条件:
若一直线垂直于某平面,则包含 这条直线的一切平面都垂直于该平面。
m
k 2a
直则平K面G,即则为该所直求线。 必定与另一平面垂
实长
直。
△kg
4— 已知三直线AB、CD、EF,求作一
直线MN与CD、EF相交且与AB平行。
e' b'
分析:所求的直线MN
2' m' p'
d'
分ABB析,平于:EM与行所NAA求一BB的平,定直行属M线N的于一M与平N定A面平B属P行 平, 行的M平N面与P交,叉M两MN直与线交C叉D两、
综合作图举例
3、 投影作图——根据解题思路及解题步 骤,找出相应的各种基本作图原理和 作图方法进行投影作图;
4 、题解讨论——必要时,还应对题解进 行讨论,证明答案确能满足题目要求 的几何条件或解答的存在性,是唯一 解还是多解等。
二 举例
1 — 已知矩形ABCD的一边两投影和
其邻边一投影,完成矩形投影图。
的 平M行作线直与线CADB的(平或行EF线) 相 交与于C点D (N ,或即EF为)所相求交的 直线于M点N。N , 即 为 所 求 的
直线MN。
5—已知直角三角形ABC的直角边AB,其斜 边BC属于直线BM,求作此直角三角形。
2' d' m' c'
画法几何点线面投影的习题
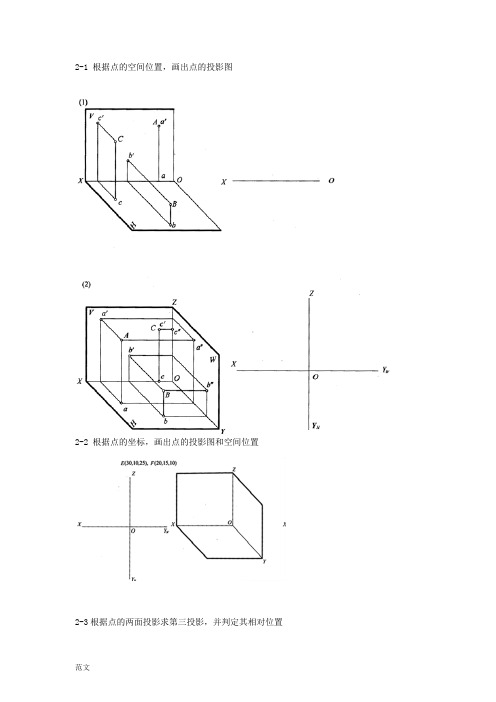
2-1 根据点的空间位置,画出点的投影图2-2 根据点的坐标,画出点的投影图和空间位置2-3根据点的两面投影求第三投影,并判定其相对位置2-4 已知点B 在点A 的正上方10,点C 在点B 的正左方10,求A 、B 、C 的三面投影,并标明其可见性。
b'b b”c'c” c( a” ) ( )ab”A AA BBB c ׳dC CCDD2-5 已知长方体的投影图,试判定棱线AB、AC、CD与投影面的相对位置,并标明其侧面投影。
2-6 注出三棱锥SABC各棱线的水平和正面投影,并判定它们属于哪类直线。
2-7求直线AB的第三投影。
2-8 分别求出直线CD和EF的实长及其倾角α和β。
2-9 已知直线AB与V面的倾角β=300,求其水平投影ab。
2-10 判定点K是否在直线AB上。
不在2-11 判定下列直线的相对位置(平行、相交、交叉)2-12 求点M到直线AB的距离。
2-13求一距H面为20的水平线,与两交叉直线AB、CD相交2-14判定两条交叉直线AB、CD对V、W面重影点的可见性2-15试求两条直线AB、CD之间的距离2-16已知正方形ABCD的对角线位于侧平线EF上,试完成该正方形的正面、侧面投影2-17求下列平面的第三投影,并判定它们与投影面的相对位置2-18试判定A、B两点是否在下列平面内2-19 完成平面五边形的正面投影2-20判定3条相互平行的直线是否在同一平面内通过作图可知:左边两条平行直线可确定一平面,右边的平行线没有过该平面上的某一点,所以三条平行线不在同一平面。
2-21已知直线CD在⊿ABC平面内,试求c′d′2-22试在⊿ABC内取一点K,使K距H面、V面均为20。
形体投影(点线面体)

点、线、面、体投影特征强化训练(学习互动、评价部分)已知一几何形体及三个投影面及其投影一、线:学习阶段:点选任意两点连线,观察三个投影特征。
评价阶段:连接体上两点成线,使之成为:不同空间位置的直线,包括:一般位置直线、特殊位置直面——垂直线(铅垂线、正垂线、侧垂线)、平行线(水平线、正平线、侧平线)。
知识拓展、提升阶段:根据已知直线投影特征,判断直线空间位置。
包括一条直线、两条直线二、面:已知一几何形体及三个投影面学习阶段:点选任意三点连线成面,观察平面的三个投影特征。
评价阶段:1.连接体上三点成面,使之成为:不同空间位置的平面,包括:一般位置平面、特殊位置平面——垂直平面(铅垂平面、正垂平面、侧垂平面)、平行面(水平面、正平面、侧平面)。
2.选择体上任意一条直线和直线外一点形成平面,使之成为不同空间位置的平面,包括:一般位置平面、特殊位置平面——垂直平面(铅垂平面、正垂平面、侧垂平面)、平行面(水平面、正平面、侧平面)。
3.选择体上任意两条平行直线形成平面,使之成为不同空间位置的平面,包括:一般位置平面、特殊位置平面——垂直平面(铅垂平面、正垂平面、侧垂平面)、平行面(水平面、正平面、侧平面)。
4.选择体上任意两个平面,判断两平面空间位置,如果相交,找出交线。
知识拓展、提升阶段:根据已知平面投影特征,判断平面空间位置。
包括一个平面、两个平面、多个平面。
三、体:学习阶段:1.不同的基本几何形体的投影特征学习:平面体、曲面体;2.基本几何形体不同摆放位置的投影变化3.简单组合体的投影特征学习:选择正确三面正投影图;评价阶段:1.已知形体两投影,分析求出第三投影2.补全三面正投影图;3.已知形体两投影,列出与两投影相同的不同形体提升、综合训练阶段:建筑构件,细部照片抽象成组合体,选择摆放位置,进行三视图投影。
鼠标点选菜单设定的旋转角度,形体翻转到位,同步呈现投射线三个投影面呈现投影,形体位置发生变化投影同步改变,同时二维三视图同步呈现。
点、线、面的投影问题

点的投影
点的正投影
点的正投影定义:点在投影面上的投影 点的正投影性质:与原点等距,与投影线垂直 点的正投影的作法:通过原点和投影面的垂线与投影面的交点作为投影 点的正投影的特性:不改变点的形状和大小
点的斜投影
定义:点在非 正投影面上的
投影
性质:与点的 空间位置和投
影方向有关
计算方法:根 据点的坐标和 投影方向计算
添加标题
添加标题
添加标题
添加标题
点在直线上的投影:点在直线上 的投影是该点与直线平行的线段
投影的性质:投影具有真实性、 类似性和积聚性
线的投影
直线的正投影
直线在平面上的投影是一条直线
直线与平面平行或重合时,投影 为一条直线
添加标题
添加标题
添加标题
添加标题
直线与平面垂直时,投影为一点
直线与平面斜交时,投影为一条 斜线
线的投影与空间位置关系
平行线:在投 影面上,投影 线与线段平行, 且长度保持不
变
垂直线:在投 影面上,投影 线与线段垂直,
长度缩短
斜线:在投影 面上,投影线 与线段斜交, 长度缩短,角
度变化
曲线:在投影 面上,曲线的 投影可能为直 线、圆或椭圆 等形状,取决 于曲线的形状
和空间位置
面的投影
平面的正投影
直线的斜投影
定义:直线在投影面上的投影称 为直线的斜投影
分类:根据直线与投影面的关系, 分为正投影和斜投影
添加标题
添加标题
添加标题
添加标题
性质:直线的斜投影反映直线的 方向,但长度可能发生变化
应用:在工程制图中,常利用斜 投影法绘制三维物体的二维图形
直线的透视投影
建筑工程制图---点线面-的投影---点共31页文档

2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
建筑工程制图---点线面-的投影---点 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
点线面的投影试题
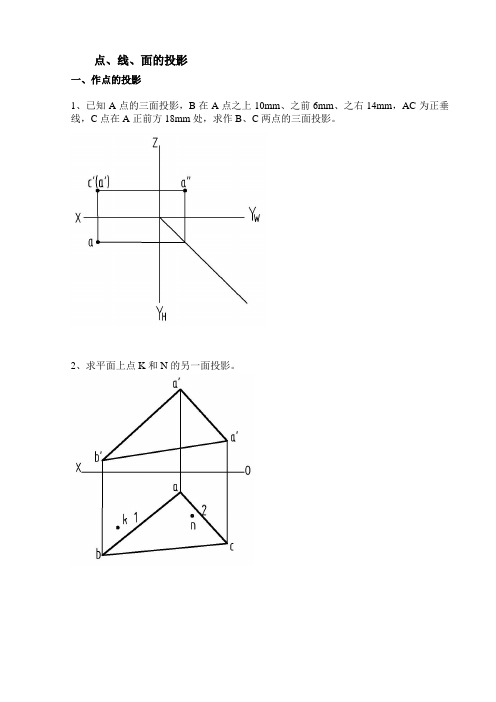
点、线、面的投影一、作点的投影1、已知A点的三面投影,B在A点之上10mm、之前6mm、之右14mm,AC为正垂线,C点在A正前方18mm处,求作B、C两点的三面投影。
2、求平面上点K和N的另一面投影。
3、已知A、B、C三点的两面投影,试求其第三面投影。
4、已知A、B、C三点的两面投影,求各点的第三面投影。
5、已知点A在V面之前15,点B在H面之上20,点C在V面上,点D在H面上,点E在投影轴上,补全诸点的V、H两面投影。
6、已知点A(40,20,30),作A点的直观图。
7、已知空间点A、B、C的坐标分别为(10,5,15)、(5,0,10)、(0,10,0)试绘制A、B、C在三面投影图中投影。
8、已知点A(10,10,30)、点B(0,15,20),点C在点A的左方10,下放15,前方10,求点A、B、C的三面投影。
9、已知A点的两面投影,B点在A点左方20mm,前方15mm,上方15mm,求作线段AB的三面投影。
10、按立体图作诸点的两面投影。
11、按照立体图作诸点的三面投影。
12、已知点A在V面之前36,点B在H面之上10,点C在V面上,点D在H面上,点E在投影轴上,补全诸点的两面投影。
二、直线的投影13、已知直线AB与CD相交,求作CD。
14、求直线CD真长及对V面、W面的倾角β、γ。
15、求下列直线的第三面投影,并判断空间位置。
AB 是线16、求下列直线的第三面投影,并判断空间位置。
EF是线18、求下列直线的第三面投影,并判断空间位置。
AB是线。
20、求下列直线的第三面投影,并判断空间位置。
AB是线。
21、点M在直线AB上,且距H面15。
绘出点M在V、H面上的投影。
22、补全直线的三面投影,并判断其空间位置AB是线CD是线23、补全直线的三面投影,并判断其空间位置。
AB是线CD是线24、作直线的三面的投影;(1)水平线AB,从点A向左,向前, 长18,β=30°。
(2)正垂线CD,从点C向后,长12。
点线面的投影

总之,投影是数学、物理和其他学科中非常重要的概念和方法,它可以帮助我们更好地理解三维物体或场景在二维平面上的表现和描述,以及解决各种实际问题
-
感谢观看
日期:XXXX
汇报人:XXXX
添加标题内容
点线面的投影
-
点的投影
1ቤተ መጻሕፍቲ ባይዱ
点的投影
在二维空间中,点的投影是指该点在空间中投射到某个平面上的点。对于一个点,我们只需要知道其x和y坐标即可确定其在二维平面上的位置
例如,假设有一个点P(1, 2),我们想将它投影到x-y平面上。我们可以将y坐标保持不变,x坐标变为0,得到投影点P'(0, 2)
线的投影
4
除了上述基本的投影方法,还有一些更复杂的投影方法,例如透视投影和斜投影
5
透视投影是一种模拟人眼视线的投影方法,可以产生一种物体距离观察者越远越小的视觉效果。在建筑、城市规划等领域中,透视投影被广泛用于制作三维场景的效果图
平面的投影
1
斜投影是一种将物体按照一定的角度斜着投影到平面上的方法。它可以将物体在某个方向上的尺寸放大或缩小,产生一种变形的效果。斜投影通常用于制作漫画、插画等艺术作品
1
平面的投影是指一个平面在空间中投射到某个平面上的面。平面的投影通常是在二维平面上绘制三维物体的表面
2
例如,假设有一个平面π通过点P(1, 2, 3)和Q(4, 5, 6)。我们想将它投影到x-y平面上。我们可以将所有点的z坐标变为0,得到投影面π'
3
总结一下,点的投影是它在空间中投射到某个平面上的点,线的投影是它在空间中投射到某个平面上的线,平面的投影是它在空间中投射到某个平面上的面。这些投影都是为了在二维平面上表现三维物体或场景
点线面投影规律

点线面投影规律《点线面投影规律指南》咱们来聊聊点线面投影规律这事儿,可别一听就觉得头疼,这就像咱们日常生活里的一些小奥秘,弄明白了还挺有趣的。
先说说点的投影吧。
点就像一个小蚂蚁在空间里,它投影到某个平面上的时候,就好像小蚂蚁在灯光下的影子。
这个影子可只有一个哦。
不管是从哪个方向投影,点的投影始终是一个点。
你想啊,一个孤零零的小蚂蚁,不管光线从哪儿照过来,它在地上的影子就是那么一个小小的点,不可能变成别的形状。
这多简单直接啊,就像我们做人有时候也要直来直去,不要搞那些弯弯绕绕的。
再来看线的投影。
线就像是一条小绳子,要是这条小绳子平行于投影面,那它的投影就和它本身差不多长,就像你把一根直直的筷子平行放在桌子上,它在桌面上的影子和筷子本身长度没差多少。
可要是这根“小绳子”垂直于投影面呢,那它的投影就变成一个点啦,这就好比你把那根筷子垂直地立在桌面上,从正上方看,你看到的就只是一个点,这是不是很神奇呢?还有啊,要是这线是倾斜于投影面的,那它的投影长度就会发生变化,就像你斜着放那根筷子,影子就变长或者变短了。
这就像生活中的事情啊,有时候换个角度,东西就变样了。
面的投影就更有趣了。
面就像一张小纸片。
要是这个面平行于投影面,那它的投影就和这个面一模一样,大小形状都不变,就好像你把一张平整的纸平行放在地上,它在地上的影子就是那张纸的模样。
要是这个面垂直于投影面呢,它的投影就变成一条线了,这就像你把那张纸立起来,从侧面看,你就只能看到一条线了。
要是这个面是倾斜的呢,那它的投影形状和大小都会发生变化,就像你把那张纸斜着放,影子就不是原来纸的形状了,可能变得扁一点或者长一点。
这就好比我们看东西,有时候从不同的角度看一个东西,它看起来就完全不一样了。
我们可以把这些投影规律想象成拍照。
你看啊,点就是画面里一个小小的点,怎么拍都是个点。
线呢,就像是一根树枝,平行拍的时候树枝长长的,垂直拍就成了一个小点,斜着拍树枝就变形了。
点线面投影的习题

科目:建筑制图班级:姓名:总分:一、填空(30)1、投影规律的三等关系是指“、、”。
2、投影面垂直线有、、三种3、工程上常采用的投影法是和,其中投影法按投射线与投影面是否垂直又分为和法。
4、当直线平行于投影面时,其投影,这种性质叫真实性,当直线垂直投影面时,其投影,这种性质叫积聚性,当平面倾斜于投影面时,其投影,这种性质叫缩短性。
5、正立投影面用字母表示,水平投影面用字母表示。
侧立投影面用字母表示。
6、直线按其对三个投影面的相对位置关系不同,可分为、、、。
二、选择题(30)1、下列投影法中不属于平行投影法的是()A、中心投影法B、正投影法C、斜投影法2、当一条直线平行于投影面时,在该投影面上反映()A、实形性B、类似性C、积聚性3、当一条直线垂直于投影面时,在该投影面上反映()A、实形性B、类似性C、积聚性4、在三视图中,主视图反映物体的()A、长和宽B、长和高C、宽和高5、主视图与俯视图()A、长对正B、高平齐C、宽相等6、主视图与左视图()A、长对正B、高平齐C、宽相等7、为了将物体的外部形状表达清楚,一般采用()个视图来表达。
A、三B、四C、五8、三视图是采用()得到的A、中心投影法B、正投影法C、斜投影法9、当一个面平行于一个投影面时,必()于另外两个投影面A、平行B、垂直C、倾斜10、当一条线垂直于一个投影面时,必()于另外两个投影面A、平行B、垂直C、倾斜11、投射方向垂直于投影面,所得到的平行投影称为_______。
A 正投影B 斜投影C 平行投影D 中心投影12、直线AB的V、H面投影均反映实长,该直线为( )。
A.水平线B.正垂线C.侧平线D.侧垂线13、某直线的V面投影反映实长,该直线为()。
A.水平线B.正平线C.侧平线D.铅垂线14、直线AB的W面投影反映实长,该直线为( )。
A.水平线B.正平线C.侧平线D.侧垂线15、直线AB的正面投影反映为一点,该直线为( )。
A.水平线B.正平线C.铅垂线D.正垂线三、判断题(10分)1、两点的V投影能反映出点在空间的上下、左右关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知平面上一点K的一个投影,作出此平面的第三投影及点K的其他两个投影。
2-1-3-7
在已知平面内作一点D,使其距H面30,距W面20。
2-1-3-8
已知平面 ABCDE 的一个投影,求作另一个投影。
2-1-3-9
完成平面图形 ABCDEFGH 的另一个投影。
2-1-3-10
三角形 EFG 位于平面 ABCD 内,求作 ABCD 及 EFG 水平投影。
点的投影
2-1-1-1
已知A、B、C、D四点的投影图,画出它们的直观图,并说明其空间位置。
此处错误, 应为虚线。
2-1-1-2
已知A、B、C各点对投影面的距离,画出它们的三面投影图和直观图。
2-1-1-3 已知点A的坐标(40,15,0),画出其三面投影并作出点B和点C的三面投影。 ⑴ 点B ——在点A右面20,前面15,上面20; ⑵ 点C ——在点A左面10,后面15,上面15
2-1-1-4
已知点A的两投影,点A、B对称于V、W两面角的分角面,求 a″和点B的三面投影。
直线的投影
2-1-2-1 影。
已知三脚架的两个投影,试判断S1S2、S2A、S2B各为何种位置直线,并作出它们的侧面投
2-1-2-2
已知线段AB的实长L及其一个投影,求作其另一投影。
2-1-2-3
平面的投影
2-1-3-1
已知平面的两个投影,求作第三投影。
2-1-3-2
已知平面的两个投影,求作第三投影。
2-1-3-3
已知平面的两个投影,求作第三投影。
2-1-3-4
已知平面的两个投影,求作第三投影。
2-1-3-5
已知平面上一点K的一个投影,作出此平面的第三投影及点K的其他两个投影。
2-1-3-6
在线段AB上取一点C,使A、C两点之间的距离为C两点之间的距离为20。
*2-1-2-5
在线段AB上取一点C,使它与H面和V面的距离相等;再取一点D,使 Zd:Yd = 2:1 。
2-1-2-6
已知直线 CD = DE ,试求直线 DE 的水平投影。
2-1-2-7
过点C作AB的平行线CD,实长为20(先作出AB的水平投影,后作CD的三面投影)。
2-1-2-8
作水平线与两已知直线 AB 和 CD 相交并与H面相距 25。
2-1-2-9
作一直线MN与已知直线CD、EF相交,同时与AB平行(点M在CD上,点N在EF上)。
2-1-2-10
过点C作一直线MN与直线 AB 和 OX 轴都相交。
