浙江大学 春夏学期《电磁场与电磁波》期末考试试卷及答案
《电磁场与电磁波》期末复习题及答案

《电磁场与电磁波》期末复习题及答案一,单项选择题1.电磁波的极化特性由__B ___决定。
A.磁场强度B.电场强度C.电场强度和磁场强度D. 矢量磁位2.下述关于介质中静电场的基本方程不正确的是__D ___A. ρ??=DB. 0??=EC. 0C d ?=? E lD.0S q d ε?=? E S 3. 一半径为a 的圆环(环面法向矢量z = n e )通过电流I ,则圆环中心处的磁感应强度B 为__D ___A. 02r Ia μe B.02I a φμe C. 02z Ia μe D. 02z I a μπe4. 下列关于电力线的描述正确的是__D ___A.是表示电子在电场中运动的轨迹B. 只能表示E 的方向,不能表示E 的大小C. 曲线上各点E 的量值是恒定的D. 既能表示E 的方向,又能表示E 的大小5. 0??=B 说明__A ___A. 磁场是无旋场B. 磁场是无散场C. 空间不存在电流D. 以上都不是6. 下列关于交变电磁场描述正确的是__C ___A. 电场和磁场振幅相同,方向不同B. 电场和磁场振幅不同,方向相同C. 电场和磁场处处正交D. 电场和磁场振幅相同,方向也相同7.关于时变电磁场的叙述中,不正确的是:(D )A. 电场是有旋场B. 电场和磁场相互激发C.电荷可以激发电场D. 磁场是有源场8. 以下关于在导电媒质中传播的电磁波的叙述中,正确的是__B ___A. 不再是平面波B. 电场和磁场不同相C.振幅不变D. 以TE波形式传播9. 两个载流线圈之间存在互感,对互感没有影响的是_C ____A. 线圈的尺寸B. 两个线圈的相对位置C. 线圈上的电流D. 空间介质10. 用镜像法求解静电场边值问题时,判断镜像电荷的选取是否正确的根据__C ___A. 镜像电荷是否对称B.电位?所满足的方程是否改变C. 边界条件是否保持不变D. 同时选择B和C11. 区域V全部全部用非导电媒质填充,当此区域中的电磁场能量减少时,一定是_A ___A. 能量流出了区域B.能量在区域中被损耗C.电磁场做了功D. 同时选择A和C12. 磁感应强度为(32)x y z B axe y z e ze =+-+ , 试确定常数a 的值。
浙江大学电磁场与电磁波——2011期末考试

0
2(no ne )
,
B. 线极化波,极化方向旋转了 45 度 D. 线极化波,极化方向旋转了 90 度 B ) B.使天线的辐射变得更集中 D.使用低驻波比的设备 ~3~
C. 线极化波,极化方向不变 20. 天线增益是如何获得的? (
A.在天线系统中使用功率放大器 C.使用高效率的天线馈线
二、 (15 分)如下图为微波放大器的输入匹配电路。用双电纳匹配器进行匹配,两并联开路 支线 S1、S2 的间距为 7.5mm,第一个并联支线 S1 离开晶体管输入端为 6.04mm。已知微带线 的有效相对介电常数为 4,特征阻抗为 50,工作频率为 5GHz。测得晶体管输入端处的 电压反射系数为 0.75 150 。 S2 In S1 (1) 求微带线的波导波长g (1 分) 解: g
1 1 m z 方向: S z Re E y H* Re E0 sin x 2 2 a
2 k E m x z 0 sin 2 2 a 0
(4)解:根据 J s n H 求内壁上的电流分布: j m J s x 0 y 0 H z x 0 y 0 E0 e jkz z 0 a j m J s x a y0 H z x a y 0 E0 cos(m )e jkz z 0 a
~7~
四、 (15 分)如图所示,矩形空腔谐振器沿 z 方向用=3.250、=0 的介质填充了 1/3 空间, x 和 y 方向宽度分别为 a=2cm 和 b=1cm。已知谐振频率 f0=15GHz,工作模式为 TE101 模。问: (1) x 方向的传播常数和特征阻抗 kx、Zcx; (2 分) (2) 画出 z 方向的等效电路,求各段的传播常数和特征阻 抗; (6 分) (7 分) a l/3 x (1)解: l z b y
《电磁场与电磁波》试题含答案

�
区域 1 图3
区域 2
《电磁场与电磁波》试题 2
一、填空题(每小题 1 分,共 10 分)
1.在均匀各向同性线性媒质中,设媒质的介电常数为 ε ,则电位移矢量 D 和电场 E 满足的 方程为: 。
�
�
2.设线性各向同性的均匀媒质中电位为 φ ,媒质的介电常数为 ε ,电荷体密度为 所满足的方程为 。 。 分量等于零。
U 0 ,其余三面电位为零,
(1) 写出电位满足的方程和电位函数的边界条件 (2) 求槽内的电位分布
b
a
图1
五、综合题 (10 分)
21.设沿 + z 方向传播的均匀平面电磁波垂直入射到理想导体,如图 2 所示,该电磁波为沿
x 方向的线极化,设电场强度幅度为 E0 ,传播常数为 β 。
(5) 试写出均匀平面电磁波入射波电场的表达式; (6) 求出反射系数。
图1 20.设时变电磁场的电场强度和磁场强度分别为:
� � E = E 0 cos(ωt − φ e )
� � H = H 0 cos(ωt − φ m )
(1) 写出电场强度和磁场强度的复数表达式
� � 1 � S av = E 0 × H 0 cos(φ e − φ m ) 2 (2) 证明其坡印廷矢量的平均值为:
5.在无源区域中,变化的电场产生磁场,变化的磁场产生电场,使电磁场以 播出去,即电磁波。 6.随时间变化的电磁场称为 场。 。
的形式传
7.从场角度来讲,电流是电流密度矢量场的
8.一个微小电流环,设其半径为 a 、电流为 I ,则磁偶极矩矢量的大小为 9.电介质中的束缚电荷在外加
电磁场与电磁波波试卷3套含答案

《电磁场与电磁波》试卷1一. 填空题〔每空2分,共40分〕1.矢量场的环流量有两种特性:一是环流量为0,表明这个矢量场 无漩涡流动 。
另一个是环流量不为0,表明矢量场的 流体沿着闭合回做漩涡流动 。
2.带电导体内静电场值为 0 ,从电位的角度来说,导体是一个 等电位体 ,电荷分布在导体的 表面 。
3.分离变量法是一种重要的求解微分方程的方法,这种方法要求待求的偏微分方程的解可以表示为 3个 函数的乘积,而且每个函数仅是 一个 坐标的函数,这样可以把偏微分方程化为 常微分方程 来求解。
4.求解边值问题时的边界条件分为3类,第一类为 整个边界上的电位函数为已知 ,这种条件成为狄利克莱条件。
第二类为已知 整个边界上的电位法向导数 ,成为诺伊曼条件。
第三类条件为 部分边界上的电位为已知,另一部分边界上电位法向导数已知 ,称为混合边界条件。
在每种边界条件下,方程的解是 唯一的 。
5.无界的介质空间中场的基本变量B 和H 是 连续可导的 ,当遇到不同介质的分界面时,B 和H 经过分解面时要发生 突变 ,用公式表示就是12()0n B B ⋅-=,12()s n H H J ⨯-=。
6.亥姆霍兹定理可以对Maxwell 方程做一个简单的解释:矢量场的 旋度 ,和 散度 都表示矢量场的源,Maxwell 方程表明了 电磁场 和它们的 源 之间的关系。
二.简述和计算题〔60分〕1.简述均匀导波系统上传播的电磁波的模式。
〔10分〕答:〔1〕在电磁波传播方向上没有电场和磁场分量,即电场和磁场完全在横平面内,这种模式的电磁波称为横电磁波,简称TEM 波。
〔2〕在电磁波传播方向上有电场和但没有磁场分量,即磁场在横平面内,这种模式的电磁波称为横磁波,简称TM 波。
因为它只有纵向电场分量,又成为电波或E 波。
〔3〕在电磁波传播方向上有磁场但没有电场分量,即电场在横平面内,这种模式的电磁波称为横电波,简称TE 波。
因为它只有纵向磁场分量,又成为磁波或M 波。
电磁场与电磁波期末试卷A卷答案

淮海工学院10 - 11 学年第 2 学期电磁场与电磁波期末试卷(A闭卷)答案及评分标准1.任一矢量A的旋度的散度一定等于零。
(√)2.任一无旋场一定可以表示为一个标量场的梯度。
(√)3.在两种介质形成的边界上,磁通密度的法向分量是不连续的。
(×)4.恒定电流场是一个无散场。
(√)5.电磁波的波长描述相位随空间的变化特性。
(√)6.在两介质边界上,若不存在自由电荷,电通密度的法向分量总是连续的。
(√)7.对任意频率的电磁波,海水均可视为良导体。
(×)8.全天候雷达使用的是线极化电磁波。
(×)9.均匀平面波在导电媒质中传播时,电磁场的振幅将随着传播距离的增加而按指数规律衰减。
(√)10.不仅电流可以产生磁场,变化的电场也可以产生磁场。
(√)二、单项选择题(本大题共10小题,每题3分,共30分)1.设点电荷位于金属直角劈上方,如图所示,则镜像电荷和其所在的位置为[ A ]。
A、-q(-1,2,0);q(-1,-2,0) ;-q(1,-2,0)B、q(-1,2,0);q(-1,-2,0); q(1,-2,0)C、q(-1,2,0);-q(-1,-2,0); q(1,-2,0);D、-q(-1,2,0);q(-1,-2,0); q(1,-2,0)。
2.用镜像法求解静电场边值问题时,判断镜像电荷设置是否正确的依据是[ C ]。
A、镜像电荷的位置是否与原电荷对称;B、镜像电荷是否与原电荷等值异号;C、待求区域内的电位函数所满足的方程与边界条件是否保持不变;D、镜像电荷的数量是否等于原电荷的数量。
3.已知真空中均匀平面波的电场强度复矢量为2π()120 (V/m)j zE z e eπ-=x则其磁场强度的复矢量为[ A ]A、2π=(/)j zyH e e A m-;B、2π=(/)j zyH e e A m;C、2π=(/)j zxH e e A m-;D、2π=-(/)j zyH e e A m-4.空气(介电常数为10εε=)与电介质(介电常数为204εε=)的分界面是0z=的平面。
《电磁场与电磁波》期末考试参考题

1、一半径为a 的均匀带电圆环,电荷总量为q ,求圆环轴线上离环中心o 点为z 处的电场强度E。
解:设圆环电荷线密度为λ,再在圆环上任取微元dl ,则dl dq λ=∴圆环上点电荷元dq 在p 处产生的电场强度为204RdqE d πε=根据对称性原理可,整个圆环在p 点产生的场强为沿轴线方向分量之和,即()232202044cos za dl z RzR dq E d E d z +===πελπεθ∴ ()⎰+=lz dl za z E 232204πελ又a dl lπ2=⎰ λπa q 2=∴ ()232204za zq E z +=πε2、在介电常数为ε的无限大约均匀介质中,有一半径为a 的带电q 的导体球,求储存在介质中的静电能量。
解:导体在空间各点产生的电场为)(4)0(02a r r q E a r E r w >=<<=πε故静电能量为a q dr r r q dV E dV E D W V V πεππεεε844212121202222=⎪⎭⎫ ⎝⎛==•=⎰⎰⎰∞ 3、一电荷面密度为σ的“无限大”平面,在距离平面a 的一点的场强大小的一半是由平面上的一个半径为R 的圆面积范围内的电荷所产生。
圆半径的大小。
解:电荷面密度为σ的“无限大”平面,在其周围任意点的场强为:2εσ=E 以图中O 点为圆心,取半径为r 的环形圆,其电量为:rdr dq πσ2=它在距离平面为a 的一点处产生的场强为:()2/32202ra ardrdE +=εσ则半径为R 的圆面积内的电荷在该点的场强为:()⎪⎪⎭⎫⎝⎛+-=+=⎰22002/322122R a a r ardra E Rεσεσ 0220412εσεσ=⎪⎪⎭⎫ ⎝⎛+-R a a∴ a R 3=4、已知两半径分别为a 和)(a b b >的同轴圆柱构成的电容器,其电位差为V 。
试证:将半径分别为a 和b ,介电常数为ε的介质管拉进电容器时,拉力为abV F ln )(20εεπ-=证明:内外导体间的电场为ab r V E r ln=插入介质管后的能量变化为a b zV dz dr r a b r B dV E W z b a v ln )(ln 2)(21)(21200222020εεππεεεε-=⎪⎭⎫ ⎝⎛-=-=⎰⎰⎰ 式中z 为介质管拉进电容器内的长度。
电磁场与电磁波期末考试试题库

2I 1I 1l l⨯•《电磁场与电磁波》自测试题1.介电常数为ε的均匀线性介质中,电荷的分布为()r ρ,则空间任一点E ∇= ____________, D ∇= _____________。
2. /ρε;ρ1. 线电流1I 与2I 垂直穿过纸面,如图所示。
已知11I A =,试问1.l H dl =⎰__ _______;若.0lH dl =⎰, 则2I=_____ ____。
2. 1-; 1A1. 镜像法是用等效的 代替原来场问题的边界,该方法的理论依据是___。
2. 镜像电荷; 唯一性定理1. 在导电媒质中, 电磁波的相速随频率改变的现象称为_____________, 这样的媒质又称为_________ 。
2. 色散; 色散媒质1. 已知自由空间一均匀平面波, 其磁场强度为0cos()y H e H t x ωβ=+, 则电场强度的方向为__________, 能流密度的方向为__________。
2. z e ; x e -1. 传输线的工作状态有________ ____、_______ _____、____________三种,其中________ ____状态不传递电磁能量。
2. 行波; 驻波; 混合波;驻波1. 真空中有一边长为的正六角 形,六个顶点都放有点电荷。
则在图示两种情形 下,在六角形中心点处的场强大小为图中____________________;图中____________________。
2. ;1. 平行板空气电容器中,电位(其中 a 、b 、c 与 d 为常数), 则电场强度__________________,电荷体密度_____________________。
2.;1. 在静电场中,位于原点处的电荷场中的电场强度线是一族以原点为中心的__________________ 线, 等位线为一族_________________。
2. 射 ; 同心圆1. 损耗媒质中的平面波 , 其传播系数 可表示为__________ 的复数形式,其中表 示衰减的为___________。
电磁波与电磁场期末复习题(试题+答案)汇编

电磁波与电磁场期末试题一、填空题(20分)1.旋度矢量的散度恒等与零,梯度矢量的旋度恒等与零。
2.在理想导体与介质分界面上,法线矢量n 由理想导体2指向介质1,则磁场满足的边界条件:01=⋅B n,s J H n =⨯1 。
3.在静电场中,导体表面的电荷密度σ与导体外的电位函数ϕ满足的关系式n ∂∂=ϕεσ-。
4.极化介质体积内的束缚电荷密度σ与极化强度P 之间的关系式为P ⋅-∇=σ。
5.在解析法求解静态场的边值问题中,分离变量法是求解拉普拉斯方程的最基本方法;在某些特定情况下,还可用镜像法求拉普拉斯方程的特解。
6.若密绕的线圈匝数为N ,则产生的磁通为单匝时的N 倍,其自感为单匝的2N 倍。
7.麦克斯韦关于位移电流的假说反映出变化的电场要产生磁场。
8.表征时变场中电磁能量的守恒关系是坡印廷定理。
9.如果将导波装置的两端短路,使电磁波在两端来回反射以产生振荡的装置称为谐振腔。
10.写出下列两种情况下,介电常数为ε的均匀无界媒质中电场强度的量值随距离r 的变化规律:带电金属球(带电荷量为Q )E =24rQπε;无限长线电荷(电荷线密度为λ)E =rπελ2。
11.电介质的极性分子在无外电场作用下,所有正、负电荷的作用中心不相重合,而形成电偶极子,但由于电偶极矩方向不规则,电偶极矩的矢量和为零。
在外电场作用下,极性分子的电矩发生转向,使电偶极矩的矢量和不再为零,而产生极化。
12.根据场的唯一性定理在静态场的边值问题中,只要满足给定的边界条件,则泊松方程或拉普拉斯方程的解是唯一的。
二、判断题(每空2分,共10分)1.应用分离变量法求解电、磁场问题时,要求整个场域内媒质必须是均匀、线性的。
(×)2.一个点电荷Q 放在球形高斯面中心处。
如果此电荷被移开原来的球心,但仍在球内,则通过这个球面的电通量将会改变。
(×)3.在线性磁介质中,由IL ψ= 的关系可知,电感系数不仅与导线的几何尺寸、材料特性有关,还与通过线圈的电流有关。
电磁场与电磁波复习试卷答案

《电磁场与电磁波》试题(1)参考答案二、简答题 (每小题5分,共20分)11.答:意义:随时间变化的磁场可以产生电场。
(3分)其积分形式为:S d t Bl d E C S⋅∂∂-=⋅⎰⎰ (2分) 12.答:在静电场中,在给定的边界条件下,拉普拉斯方程或泊松方程的解是唯一的,这一定理称为唯一性定理。
(3分)它的意义:给出了定解的充要条件:既满足方程又满足边界条件的解是正确的。
13.答:电磁波包络或能量的传播速度称为群速。
(3分)群速g v 与相速p v 的关系式为: ωωd dvv v v pp pg -=1 (2分)14.答:位移电流:tDJ d ∂∂=位移电流产生磁效应代表了变化的电场能够产生磁场,使麦克斯韦能够预言电磁场以波的形式传播,为现代通信打下理论基础。
三、计算题 (每小题10 分,共30分)15.按要求完成下列题目(1)判断矢量函数y x e xz ey B ˆˆ2+-= 是否是某区域的磁通量密度? (2)如果是,求相应的电流分布。
解:(1)根据散度的表达式zB y B x B B zy x ∂∂+∂∂+∂∂=⋅∇ (3分) 将矢量函数B代入,显然有0=⋅∇B(1分)故:该矢量函数为某区域的磁通量密度。
(1分) (2)电流分布为:()[]分)(分)(分)(1ˆ2ˆ120ˆˆˆ2102z x z y x ez y e x xzy z yx e e e BJ ++-=-∂∂∂∂∂∂=⨯∇=μμ16.矢量z y x e ˆe ˆe ˆA 32-+=,z y x e e e B ˆˆ3ˆ5--= ,求 (1)B A+ (2)B A⋅解:(1)z y x e ˆe ˆeˆB A 427--=+(5分) (2)103310=+-=⋅B A(5分) 17.在无源的自由空间中,电场强度复矢量的表达式为 ()jkz y x e E e E eE --=004ˆ3ˆ(1) 试写出其时间表达式; (2) 说明电磁波的传播方向;解:(1)该电场的时间表达式为:()()tj eE t z E ωRe ,= (3分)()()()kz t E e E et z E y x --=ωcos 4ˆ3ˆ,00(2分) (2)由于相位因子为jkze-,其等相位面在xoy 平面,传播方向为z 轴方向。
大学电磁场与电磁波-电磁波试卷电磁场与电磁波试题及答案

20XX年复习资料大学复习资料专业:班级:科目老师:日期:物理与电信工程学院20XX09 /20XX20XXXX 学年(2)学期期末考试试卷《电磁场与电磁波》 试卷(A 卷)专业 年级 班级 姓名 学号题号 一二三总分得分一、 单项选择题 (每小题2分,共20XX 分)1 两个矢量的矢量积(叉乘)满足以下运算规律( ) A 交换律; B 分配率;C 结合率;D 以上均不满足。
2 以下关于边界条件的描述,正确的是( )A 电场强度切向分量连续;B 电位移矢量切向分量连续;C 电场强度法向分量连续;D 电位移矢量法向分量连续。
3 对于像电荷,下列说法正确的是( )A 像电荷是虚拟电荷,必须置于所求区域之内;B 像电荷是虚拟电荷,必须置于所求区域之外;C 像电荷是真实电荷,必须置于所求区域之内;D 像电荷是真实电荷,必须置于所求区域之外。
4 磁场的散度恒等于零,即0B ∇⋅=,这说明( )A 磁场线有头有尾;B 磁荷是存在的;C 存在磁单极;D 通过任一闭合曲面的磁通量恒等于零。
5时变电磁场的特点是( )A 时变电磁场各自独立;B 时变电磁场是一个不可分离的整体;C 时变电磁场不随时间变化;D 时变电磁场是保守场。
6 下列关于媒质的说法正确的是( )A 均匀、线性、各向异性的无耗媒质一定是色散媒质;B 均匀、线性、各向异性的无耗媒质不一定是色散媒质;C 有损耗导电媒质一定是非色散媒质;D 有损耗导电媒质一定是色散媒质。
7 一平面电磁波从一理想介质斜入射到一理想导体的表面,则在理想介质中传播的是( )A 纯驻波;B 在法线方向上合成波的场量是驻波;C 在法线方向上合成波的场量是行波;D 是均匀平面波。
8 对于处于静电平衡状态的导体,下列说法不正确的是( ) A 导体为等位体; B 导体内部电场为0;C 导体表面切向电场为0;D 导体内部可能存在感应电荷。
9 自由空间中所传输的均匀平面波,是( )A TE 波;B TM 波;C TEM 波;D 以上都不是。
浙江大学 春夏学期《电磁场与电磁波》期末考试试卷及答案
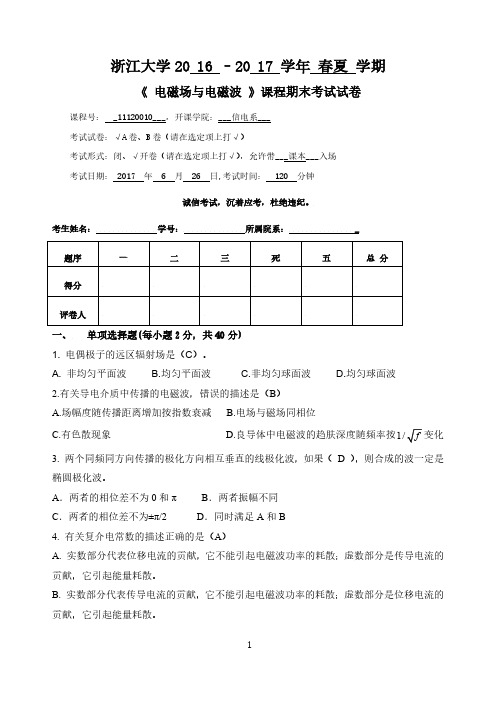
z015.02103 mW / m2
(3)透射波
E2 x0Em2e j2z x01.21510e j1.66z x012.15e j1.66zmV / m
5
H2
1 2
z0
x0 Em2e j2z
1 238.44
y
012.15e
j1.66
z
y0 51103 e j1.66zmA / m
A.都是连续的 B. 不连续的;连续的 C. 连续的;不连续的 D.都不连续
8. z=0 是空气( 0 )与介质( 2 30 )的分界面,若已知空气中的电场强度 E1 3x0 3z0 , 则介质中的电场强度应为(C)。
A. E2 3x0 9z0
B. E2 x0 3z0
D. 实数部分代表传导电流的贡献,它引起电磁波功率的耗散;虚数部分是位移电流的贡献,
它不能引起能量耗散。
5. 有关天线增益和天线方向性的描述,不正确的是(B)
A.天线增益考虑了天线材料中的欧姆损耗,而天线方向性则没有;
B.天线增益是馈入天线电磁信号的放大倍数,方向性是指波束的指向方向;
C.方向图主瓣越窄,副瓣越小,天线方向性就越大,天线增益也越高
浙江大学 20 16 –20 17 学年 春夏 学期
《 电磁场与电磁波 》课程期末考试试卷
浙江大学电磁场与电磁波期末考试题(2011-2012)

浙江大学20 11 –20 12 学年 春夏 学期《 电磁场与电磁波 》课程期末考试试卷课程号: _11120010_______,开课学院:___信电系________ 考试试卷:√A 卷、B 卷(请在选定项上打√)考试形式:闭、√开卷(请在选定项上打√),允许带___课本___入场 考试日期: 2012 年 6 月 19 日,考试时间: 120 分钟诚信考试,沉着应考,杜绝违纪。
考生姓名: 学号: 所属院系: _一、单项选择题(每小题2分,共30分)1. 对于二个在同一线性介质中传播的电磁波,下列描述正确的是( D ) A. 一个波的电场会影响另一波的磁场 B. 一个波的磁场会影响另一波的电场 C. 二个波的电场和磁场相互都有影响 D. 一个波的传播并不影响另一个波的传播2. 有关天线增益的描述,不正确的是 ( B )A .与天线方向图有密切的关系B .馈入天线电磁信号的放大倍数C .方向图主瓣越窄,副瓣越小,增益越高D .天线把输入功率集中辐射的程度 3. 用铁锤敲打矩形空腔谐振器的顶部,使之略有凹陷,问其谐振频率( C )A. 变小B. 不变C. 变大D. 不一定4. 如右图所示。
同样一个负载,接特征阻抗为100Ω和50Ω的传输线时在阻抗圆图上的位置分别是( B )A .M 、N B. N 、M C. N 、Q D. M 、P5.用于微波炉加热食物的容器,其材料的主要特点是( A )A. 导电率很小B. 介电常数很大C. 介电常数是复数D. 损耗正切很大6. 二个金属空腔谐振器,形状尺寸完全相同,一个材料是铝,一个材料是铜,比较二者的品质因素, 正确的是( B )A .铝腔大 B. 铜腔大 C. 二者一样大 D. 频率低时铜腔大,频率高时铝腔大7. 各向同性介质是指:( A )A. ε、μ、σ与电磁波在空间传播的方向性无关;B. ε、μ、σ与电磁波在空间传播的方向性有关C. 不同方向的E 、H 相同D. 不同传播方向的能量相同8. 两个同频同方向传播的极化方向相互垂直的线极化波,如果( D ),则合成的波一定是椭圆极化波。
《电磁场与电磁波》试题含答案

ρ V ,电位
3.时变电磁场中,坡印廷矢量的数学表达式为 4.在理想导体的表面,电场强度的
5.表达式
� � � ( ) A r ⋅ d S ∫
S
� � A 称为矢量场 ( r ) 穿过闭合曲面 S 的
。 。 。 。 。 场,因此,它可用磁矢
6.电磁波从一种媒质入射到理想导体表面时,电磁波将发生 7.静电场是保守场,故电场强度沿任一条闭合路径的积分等于 8.如果两个不等于零的矢量的点积等于零,则此两个矢量必然相互 9.对横电磁波而言,在波的传播方向上电场、磁场分量为 10.由恒定电流产生的磁场称为恒定磁场,恒定磁场是 位函数的旋度来表示。
5.在无源区域中,变化的电场产生磁场,变化的磁场产生电场,使电磁场以 播出去,即电磁波。 6.随时间变化的电磁场称为 场。 。
的形式传
7.从场角度来讲,电流是电流密度矢量场的
8.一个微小电流环,设其半径为 a 、电流为 I ,则磁偶极矩矢量的大小为 9.电介质中的束缚电荷在外加
。
作用下,完全脱离分子的内部束缚力时,我们把这种
18.均匀带电导体球,半径为 a ,带电量为 Q 。试求 (1) 球内任一点的电场强度 (2) 球外任一点的电位移矢量。 19.设无限长直导线与矩形回路共面, (如图 1 所示) , (1)判断通过矩形回路中的磁感应强度的方向(在图中标出) ; (2)设矩形回路的法向为穿出纸面,求通过矩形回路中的磁通量。
《电磁场与电磁波》试题 1
填空题(每小题 1 分,共 10 分)
1.在均匀各向同性线性媒质中,设媒质的导磁率为 µ ,则磁感应强度 B 和磁场 H 满足的 方程为: 。
2
�
�
2.设线性各向同性的均匀媒质中, ∇ φ = 0 称为
电磁场与电磁波期末考试复习试题4套(部分含答案)

电磁场与电磁波期末考试复习资料11.圆柱坐标系中单位矢量,。
2.对于矢量A ,若,则=+∙y x a y x a x )(2,=⨯x z a y a x 2。
3.给定两个矢量z y x a a a A 32-+=,z y a a B +-=4,则矢量A 的单位矢量为,矢量B A ⋅=。
4.已知直角坐标系中点P 1(5,-2,1),P 2(3,1,2),则P1的位置矢量为,P1到P2的距离矢量为。
5.已知球坐标系中单位矢量。
6.在两半无限大导电平面组成的直角劈形中间放置一点电荷,此时点电荷的镜像电荷个数为。
7.点电荷q 在自由空间任一点r 处电场强度为。
8.静电场中导体内的电场为,电场强度与电位函数的关系为。
9.高斯散度定理的积分式为,它广泛的用于将一个封闭面积分变成等价的体积分,或者将一个体积分变成等价的封闭面积分。
10.已知任意一个矢量场A ,则其旋度的散度为。
11.真空中静电场的基本方程的微分形式为、、。
12.分析恒定磁场时,在无界真空中,两个基本场变量为,它们之间的关系为。
13.斯托克斯定理为,它表明矢量场A 的旋度沿曲面S 的方向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。
14.任意一个标量场u ,则其梯度的旋度为。
15.对于某一矢量 ,它的散度定义式为,用哈密顿算子表示为。
16.介质中静电场的基本方程的积分式为,,。
17.介质中恒定磁场的基本方程的微分形式为、、。
18.介质中恒定磁场的基本方程的积分式为,,。
19.静电场中两种介质分界面的边界条件是,。
20.在无限大的导体平面上方d 处放一点电荷q ,则其镜像电荷电量为,位置位于;如果一个点电荷置于两平行导体中间,则此点电荷有镜像电荷。
21.矢量场223z a yz a y x a A z y x ++=在点P(1,1,0)的散度为。
22.一个半径为a 的接地导体球,一点电荷q 位于距球心d 处,则其镜像电荷带电量为,位置位于;当点电荷q 向无限远处运动时,其镜像电荷向运动。
电磁波期末考试题集及答案详解

电磁场与电磁波练习1、一半径为a 的均匀带电圆环,电荷总量为q ,求圆环轴线上离环中心 o 点为z 处的电场强度E 。
解:(1)如图所示,环上任一点电荷元dq 在P 点产生的场强为dE积分得到dq 2 dr 由习题2. 1的结果可知该回环在轴线上 P 点处的场强为称性可知,整个圆环在P 点产生的场强只有z 分量,即zdqdE z dE cosdq zo R 24 o a 2 3z 2 2dq3dl4 o a 2z 2 2 1324 o a 2 z 2 2qz3A22石4 o a z 2 2、半径为a 的圆面上均匀带电,电荷面密度为(2)在保持 不变的情况下,当 a 0和,试求:(1)轴线上离圆心为z 处的场强, a时结果如何?(3)在保持总电荷时结果如何?r 的圆环,它所带的电荷量为z2q a不变的情况下,当a 0和a半径为当 a ,则 E z (10)2 0 2 0⑶若保持q a 2不变,当a 0时,此带电圆面可视为一点电荷。
则E z 普。
当a时,0,则E z 0的静电能量为W证:在内外导体间介质中的电场为E汀(a r b)沿同轴线单位长度的储能为1 WE?DdV e E 2dV2 2 2e b2 dr In 22 r4 adEzdq rdr 则整个均匀带电圆面在轴线上E z(2)若不变,当aor 2z"2or 2P 点出产生的场强为z a rdr0 时,则 E z (1 1)3、有一同轴圆柱导体,其内导体半径为a ,外导体内表面的半径为b ,其间填充介电常数为 的介质,现将同轴导体充电,使每米长带电荷 。
试证明储存在每米长同轴导体间z4、在介电常数为的无限大约均匀介质中,有一半径为a的带电q的导体球,求储存在介质中的静电能量。
解:导体在空间各点产生的电场为E w 0 (0 r a)E r J (r a)r r故静电能量为5、真空中一半径为 R 的圆球空间内,分布有体密度为以图中O 点为圆心,取半径为r 叶dr 的环形面积,其电量为:dq 2 rdr它在距离平面为a 的一点处产生的场强为:ardrdEk 严则半径为R 的圆面积内的电荷在该点的场强为:a R rdr, a由题意: E37212 0 2 23/22: 2 _2D ?EdVq 4 r 21224 2 vE vdVdr量。
电磁波与电磁场期末复习题(试题+答案)

电磁波与电磁场期末试题一、填空题(20分)1.旋度矢量的散度恒等与零,梯度矢量的旋度恒等与零。
2.在理想导体与介质分界面上,法线矢量n r由理想导体2指向介质1,则磁场满足的边界条件:01=⋅B n ρρ,s J H n =⨯1ρρ。
3.在静电场中,导体表面的电荷密度σ与导体外的电位函数ϕ满足的关系式n ∂∂=ϕεσ-。
4.极化介质体积内的束缚电荷密度σ与极化强度P 之间的关系式为P ⋅-∇=σ。
5.在解析法求解静态场的边值问题中,分离变量法是求解拉普拉斯方程的最基本方法;在某些特定情况下,还可用镜像法求拉普拉斯方程的特解。
6.若密绕的线圈匝数为N ,则产生的磁通为单匝时的N 倍,其自感为单匝的2N 倍。
7.麦克斯韦关于位移电流的假说反映出变化的电场要产生磁场。
8.表征时变场中电磁能量的守恒关系是坡印廷定理。
9.如果将导波装置的两端短路,使电磁波在两端来回反射以产生振荡的装置称为谐振腔。
10.写出下列两种情况下,介电常数为ε的均匀无界媒质中电场强度的量值随距离r 的变化规律:带电金属球(带电荷量为Q )E =24r Qπε;无限长线电荷(电荷线密度为λ)E =rπελ2。
11.电介质的极性分子在无外电场作用下,所有正、负电荷的作用中心不相重合,而形成电偶极子,但由于电偶极矩方向不规则,电偶极矩的矢量和为零。
在外电场作用下,极性分子的电矩发生转向,使电偶极矩的矢量和不再为零,而产生极化。
12.根据场的唯一性定理在静态场的边值问题中,只要满足给定的边界条件,则泊松方程或拉普拉斯方程的解是唯一的。
二、判断题(每空2分,共10分)1.应用分离变量法求解电、磁场问题时,要求整个场域内媒质必须是均匀、线性的。
(×)2.一个点电荷Q 放在球形高斯面中心处。
如果此电荷被移开原来的球心,但仍在球内,则通过这个球面的电通量将会改变。
(×)3.在线性磁介质中,由IL ψ=的关系可知,电感系数不仅与导线的几何尺寸、材料特性有关,还与通过线圈的电流有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:平面波的工作频率 f 为:
f c 3108 0.5 (兆赫) air 600
A.都是连续的 B. 不连续的;连续的 C. 连续的;不连续的 D.都不连续
8. z=0 是空气( 0 )与介质( 2 30 )的分界面,若已知空气中的电场强度 E1 3x0 3z0 , 则介质中的电场强度应为(C)。
A. E2 3x0 9z0
B. E2 x0 3z0
C. E2 3x0 z0
A.2a
B. 2b
C.4a
D.4b
20. 若抛物面天线直径为2m,有效面积为1.6 m2 ,工作频率为6GHz,则天线增益为(A)。
A. 39dB
B.66dB
C. 33dB
D.78dB
二、 一余弦平面电磁波垂直向下传播,由空气射到海面,已知在空气中的波长为 600 米, 海水中的电导率 1S/m、r 80 ,r 1 。试求波透入海水中后的波长、相速、相位常数 与波阻抗。(15 分)
C. 数值孔径较大光纤模间色散较大 D. 数值孔径较大纤芯和包层相对折射率差较大
12. 下面对于趋肤效应的说法错误的是(D)
A. 趋肤深度是指波进入到导体内,幅度衰减为导体表面幅度的 1/e 处的深度
2
B.媒质导电性越好,趋肤深度越小。
C. 频率越高,趋肤深度越小。
D.媒质导电性越好,波在媒质中的衰减越慢。
13.一传输线其终端反射系数为0.2,则驻波系数为(B)
A.1
B.1.5
C.2
D.2.5
14.E(r)和H(r)分别是电场和磁场的复矢量形式,则时间平均坡印廷矢量为:( A )
A. 1 Re[E(r) H (r)] 2
B. 1 Re[E(r) H (r)] 2
C. Re[E(r) H (r)]
D. Re[E(r) H (r)]
诚信考试,沉着应考,杜绝违纪。
考生姓名:
学号:
所属院系:
_
题序
一
二
三
死
五
总分
得分
评卷人
一、 单项选择题(每小题 2 分,共 40 分)
1. 电偶极子的远区辐射场是(C)。
A. 非均匀平面波 B.均匀平面波
C.非均匀球面波
2.有关导电介质中传播的电磁波,错误的描述是(B)
A.场幅度随传播距离增加按指数衰减 B.电场与磁场同相位
D. E2 9x0 3z0
9. 截面尺寸为 ab(b<a/2)的矩形波导,TE10 波在其中传播的条件为(C) 。(注:为工作 波长)
A. 0 a
B. 2b 2a
C. a 2a
D. 2a
10. 长度为 l 的传输线将负载连接到振荡频率为 f 的正弦电压源,假定线路上的波速为 2108
A. 实数部分代表位移电流的贡献,它不能引起电磁波功率的耗散;虚数部分是传导电流的
贡献,它引起能量耗散。
B. 实数部分代表传导电流的贡献,它不能引起电磁波功率的耗散;虚数部分是位移电流的
贡献,它引起能量耗散。
1
C. 实数部分代表位移电流的贡献,它,
它不能引起能量耗散。
D.天线方向性和增益都表示了天线把输入功率集中辐射的程度
6. 下面的说法不正确的是(C)
A. 相速是指信号恒定相位点的移动速度 B. 在导电媒质中,相速与频率有关
C. 相速代表信号的能量传播的速度
D. 群速是指信号包络上恒定相位点的移动速度
7. 在不同介质分界面上电场强度的法向分量和切向分量分别是(B)
D. 实数部分代表传导电流的贡献,它引起电磁波功率的耗散;虚数部分是位移电流的贡献,
它不能引起能量耗散。
5. 有关天线增益和天线方向性的描述,不正确的是(B)
A.天线增益考虑了天线材料中的欧姆损耗,而天线方向性则没有;
B.天线增益是馈入天线电磁信号的放大倍数,方向性是指波束的指向方向;
C.方向图主瓣越窄,副瓣越小,天线方向性就越大,天线增益也越高
D.均匀球面波
C.有色散现象
D.良导体中电磁波的趋肤深度随频率按1/ f 变化
3. 两个同频同方向传播的极化方向相互垂直的线极化波,如果( D ),则合成的波一定是
椭圆极化波。
A.两者的相位差不为 0 和 π B.两者振幅不同
C.两者的相位差不为±π/2
D.同时满足 A 和 B
4. 有关复介电常数的描述正确的是(A)
D. , d 4
18.一段传输线,其中电压驻波系数恒定为 ,沿线各参考面上能出现的最大电纳为(B)。
A、 2 1 2
B、 2 1 2
C、 2 1
D、 2 1
19. 矩形波导管边长分别为a、b(已知),内填相对介电常数为4的介质,该波导管能传播
的电磁波最大真空波长为(C)。
15.传输线特征阻抗为50 ,电压为U (z) 10e jkz 5e jkz ,则电流 I(z) 为(D):
A. 0.1e jkz 0.2e jkz B. 0.1e jkz 0.2e jkz C. 0.2e jkz 0.1e jkz D. 0.2e jkz 0.1e jkz
16.均匀平面波由介质垂直入射到理想导体表面时,产生全反射,入射波与反射波叠加将形
浙江大学 20 16 –20 17 学年 春夏 学期
《 电磁场与电磁波 》课程期末考试试卷
课程号: _11120010___,开课学院:___信电系___ 考试试卷:√A 卷、B 卷(请在选定项上打√) 考试形式:闭、√开卷(请在选定项上打√),允许带___课本___入场 考试日期: 2017 年 6 月 26 日,考试时间: 120 分钟
m/s,对于以下情况,可以忽略传输线影响的是(A)
A. l=20cm, f=10kHz
B. l=50km, f=600Hz
C. l=20cm, f=300MHz
D. l=1mm, f=100GHz
11. 有关光纤的数值孔径描述不正确的是(A )
A.数值孔径较大光纤传输带宽较大 B. 数值孔径较大光纤聚光能力较强
成驻波,其电场强度的波节位置和磁场的波节位置(B)
A.相同
B.相差λ/4
C.相差λ/2
D.相差λ
17. 有一个二单元天线阵,两个单元为线天线,沿 z 轴排列,相隔距离为 d,天线的激励幅
度相同,相位差为 ,哪种情况下,沿 z 轴的辐射为零(C)
A. , d 22
B. , d 2
C. , d 24
