09-10年山东大学线性代数期末试题及答案.
完整word版线性代数考试题及答案解析

WORD格式整理……_…_学年第一学期期末考试-20102009_…__…_试卷《线性代数》…__…__…_分钟完卷。
分,1201、本试卷共6页,五个大题,满分100答卷说明:_…_…__…号2、闭卷考试。
…学)线(_总分五三四一二_…__…题号_…__…_分数_…__…_…________________ :_____________ 总分人:评阅人…_名…姓…) 分分,共24一、单项选择题。
(每小题得分……)级封班(11?31_…__…111?3__?…行列式【】1._1?311…__…_3111?_…_业……专3021(B) (D)(A) (C) …__…__…???A?A32?3?A阶方阵,数2. 】设,为,则【_…__)_6?624?24 (D) (A) (C) (B) _密_系(n,BA,阶方阵,则下列式子一定正确的是【】3.已知为…__…__…_222B?2(A?B)AB?A?BAAB? (A) (B)_…_…__…_22B?A?B?B)(A?)(A BA?AB (D) (C)_…__…_…_?0??aA?A3A【】4.设,则为阶方阵, _…__……243aaaa (D) (A) ( B) (C)AB等价,则有 5.设矩阵与【】专业技术参考资料WORD格式整理R(A)?R(B)R(A)?R(B) (A) (B)R(A)?R(B)R(A)R(B)的大小不能确定 (C) 和 (D)n Ax?0Ax?0A r有非零解的系数矩阵【】6.设,则元齐次线性方程组的秩为的充分必要条件是r?nr?nr?n nr? (B) (C) (D) (A)a,a,,a(m?2) 向量组】【 7. 线性相关的充分必要条件是m21a,a,,a (A) 中至少有一个零向量m12a,a,,a (B) 中至少有两个向量成比例m12a,a,,a m?1(C) 个向量线性表示中每个向量都能由其余m21a,a,,a m?1(D) 个向量线性表示中至少有一个向量可由其余m21n A与对角阵相似的充分必要条件是阶方阵】8. 【nn)?R(A A个互不相同的特征值有(A) (B)n AA一定是对称阵个线性无关的特征向量 (D)(C)有) 分,共15二、填空题。
土木工程线性代数山东大学网络教育考试模拟题及答案

09年11月期末本科《线性代数》参考解答线性代数模拟题1一.单选题.1.下列( )是4级偶排列.(A ) 4321; (B) 4123; (C) 1324; (D) 2341. 答:A2. 如果1333231232221131211==a a a a a a a a a D ,3332313123222121131211111324324324a a a a a a a a a a a a D ---=,那么=1D ( ). (A ) 8; (B) 12-; (C) 24; (D) 24-. 答:D3. 设A 与B 均为n n ⨯矩阵,满足O AB =,则必有( ). 答:C(A )O A =或O B =; (B )O B A =+; (C )0=A 或0=B ; (D )0=+B A .4. 设A 为n 阶方阵)3(≥n ,而*A 是A 的伴随矩阵,又k 为常数,且1,0±≠k ,则必有()*kA 等于( ). 答:B (A )*kA ; (B )*1A k n -; (C )*A k n ; (D )*1A k -.5.向量组s ααα,....,,21线性相关的充要条件是( ) 答:C(A )s ααα,....,,21中有一零向量 (B) s ααα,....,,21中任意两个向量的分量成比例(C) s ααα,....,,21中有一个向量是其余向量的线性组合 (D) s ααα,....,,21中任意一个向量都是其余向量的线性组合6. 已知21,ββ是非齐次方程组b Ax =的两个不同解,21,αα是0=Ax 的基础解系,21,k k 为任意常数,则b Ax =的通解为( ) 答:B(A) 2)(2121211ββααα-+++k k ; (B) 2)(2121211ββααα++-+k k(C) 2)(2121211ββββα-+++k k ; (D) 2)(2121211ββββα++++k k7. λ=2是A 的特征值,则(A 2/3)-1的一个特征值是( ) 答:B(A)4/3 (B)3/4 (C)1/2 (D)1/48. 若四阶矩阵A 与B 相似,矩阵A 的特征值为1/2,1/3,1/4,1/5,则行列式|B -1-I|=( )(A)0 (B)24 (C)60 (D)120 答:B9. 若A 是( ),则A 必有A A ='. 答:A(A )对角矩阵; (B) 三角矩阵; (C) 可逆矩阵; (D) 正交矩阵. 10. 若A 为可逆矩阵,下列( )恒正确. 答:A(A )()A A '='22; (B)()1122--=A A ; (C)[][]111)()(---''='A A ;(D)[][]'=''---111)()(A A . 二.计算题或证明题1. 设矩阵 ⎪⎪⎪⎭⎫⎝⎛----=3241223k kA (1)当k 为何值时,存在可逆矩阵P ,使得P -1AP 为对角矩阵?(2)求出P 及相应的对角矩阵。
2009-2010学年线代B期末试卷答案

同济大学课程考核试卷(A 卷) 2009—2010学年第一学期课名:线性代数B 考试考查:考试一、填空题(每空3分,共24分)1、设1α、2α、3α均为3维列向量,已知矩阵123(,,)A ααα=,()123123123927,248B ααααααααα=++++++,3,且1A =,那么B = -12.解:由矩阵之间的关系,我们可以得到1321941278B A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,对等式两边取行列式,有 1321941278B A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦。
所以得到-12B =2、 设分块矩阵A O C O B ⎛⎫=⎪⎝⎭, ,A B 均为方阵,则下列命题中正确的个数为4.(A).若,A B 均可逆, 则C 也可逆. (B).若,A B 均为对称阵, 则C 也为对称阵. (C).若,A B 均为正交阵, 则C 也为正交阵. (D).若,A B 均可对角化, 则C 也可对角化. 解:A. 若,A B 均可逆,说明,A B 的行列式都不为0,则我们可以根据拉普拉斯定理求出C的行列式为A B ,所以可知C 的行列式也不为0,即C 可逆.B .若,A B 均为对称阵,则有,TTA AB B ==,对矩阵C 取转置,根据对角阵性质有T TT A O A O C C O B O B ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,所以C 也是对称阵。
C .若,A B 均为正交阵, 则有,T T A A E B B E ==,固T T TT T A O A O A A O C C E O B O B O B B ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭。
所以C 也为正交阵. D .若,A B 均可对角化,则有-1-112,A P P B Q Q =Λ=Λ,则-1-111-1-122=O P O P P O P O C O O Q OQ Q O Q Λ⎛⎫⎛⎫Λ⎛⎫⎛⎫= ⎪ ⎪ ⎪⎪ΛΛ⎝⎭⎝⎭⎝⎭⎝⎭,令P O M O Q ⎛⎫= ⎪⎝⎭,则原式可看成-1-111-12P P O C M M OQ Q ⎛⎫Λ==Λ ⎪Λ⎝⎭ 固以上4个全对(考试里出现全对的情况还是第一次见)3、设2341345145617891D =,则D 的第一列上所有元素的代数余子式之和为0. 解:直接利用代数余子式性质,求113411451015611891D == 4、设向量组(I):12,,,r ααα 可由向量组(II):12,,,s βββ 线性表示,则D 成立.(注:此题单选)(A).当r s <时,向量组(II )必线性相关 (B).当r s >时,向量组(II )必线性相关(C).当r s <时,向量组(I )必线性相关 (D).当r s >时,向量组(I )必线性相关解:直接分析,举反例,A 反例1201,,,10200r r ααα⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦,(), ()12100,,,0103001s s βββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦ ,;B 反例()12100,,,0103001s s βββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦ ,,121000,,,010040011r r ααα⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦ ,();C 反例1201,,,10200r r ααα⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦ ,(),()12100,,,0103001s s βββ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦,;D.正确,这个很显然。
大一线性代数期末考试试卷+答案

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=TA A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 s n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示 ④ s ααα,,, 21中不含零向量3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
大一线性代数期末考试试卷+答案

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ ααα,,, 中任一个向量都不能用其余向量线性表示④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
线性代数课后习题答案山大

线性代数课后习题答案山大
《线性代数课后习题答案山大》
在学习线性代数课程的过程中,课后习题是巩固知识、提高能力的重要环节。
为了帮助学生更好地掌握线性代数的知识,我们整理了一些课后习题的答案,
以便同学们在学习中进行参考和对比。
1. 矩阵A与B的乘积AB存在的充要条件是什么?如果AB存在,它的秩是多少?答:矩阵A的列数等于矩阵B的行数时,AB存在。
如果AB存在,它的秩等于
矩阵A的秩。
2. 设A为n阶方阵,证明:A与A'的秩相等。
答:A与A'的秩相等是因为A与A'的秩都等于A的秩。
3. 设A为n阶方阵,证明:A与A'的行秩相等。
答:A与A'的行秩相等是因为A与A'的行空间相同。
4. 设A为n阶方阵,证明:A与A'的列秩相等。
答:A与A'的列秩相等是因为A与A'的列空间相同。
5. 设A为n阶方阵,证明:A与A'的零空间维数之和等于n。
答:A与A'的零空间维数之和等于n是因为A与A'的秩加上零空间维数等于n。
通过以上习题答案的整理,我们可以更好地理解线性代数中的一些概念和定理。
希望同学们在学习线性代数的过程中,能够加深对知识点的理解,提高解题能力,为今后的学习和工作打下坚实的基础。
线性代数期末考试题库及答案

2、n2, 当 n 为偶数时为偶排列,当 n 为奇数时为奇排列. 4、29.
1、12.
2、 x2 y2 .
4
∑ 3、 x = 0 或 − ai . i =1
4、 λ = ±1, 2 .
三、证明题
证明提示: 由于 f(x)是关于 x 的二次多项式,在[0,1]中可导,又可计算出 f (0) = f (1) = 0 ,
3、解方程 D4( x) =
a1 a1
a1 + x
a2 a2 a2 + x a2
a3 a3 + x
a3 a3
a4 + x a4 = 0 . a4 a4
4、已知下列齐次线性方程组有非零解,求参数λ的值。
(5
− λ)x1 −6 x1
−4 x2 +(7 − λ )x2
−7 x3 +11x3
=0 =0
6 x1
(B)若 AX=0有非零解,则 AX=b有无穷多解;
(C)若 AX=b有无穷多个解,则 AX=0仅有零解;
(D)若 AX=b有无穷多个解,则 AX=0有非零解。
(7)非齐次线性方程组 AX=b中未知量个数为 n,方程个数为 m,系数矩阵 A的秩为 r,则
()
(A)r=m时,方程组 AX=b有解; (B)r=n时,方程组 AX=b有唯一解;
《线性代数》补充练习二
一、选择题:
(1)设 n阶方阵 A的秩 r<n,则在 A的 n个行向量中( )
(A)必有 r个行向量线性无关; (B)任意 r个行向量均可构成极大无关组;
(C)任意 r个行向量均线性无关;(D)任一个行向量均可由其他 r个行向量线性表示
(2)若向量组α,β,γ线性无关;α,β,δ线性相关,则( )
线性代数期末考试试卷+答案.pdf

一、填空题
1. 5
2.
1
3. s s , n n
4. 相关
5. A 3E
二、判断正误
1. ×
2. √
3. √
4.
√
5. ×
三、单项选择题
1. ③
2. ③
3. ③ 4.
② 5.
①
四、计算题
1.
xa b
c
d
a xb c
d
a b xc d
a
b
c xd
1b
1 xb (x a b c d)
1b
1b
xabcd b
求 B。
解 . (A 2E)B A
( A 2E) 1
2 11
2 2 1,
11 1
B (A 2E) 1 A
5 22 4 32 22 3
1 10 0
3.
设B
01 00
1 0, 11
00 0 1
求 。 X (C B)' E,
2134
C
0 0
2 0
1 2
3 1
且矩阵
0002
满足关系式
4. 问 a 取 何 值 时 , 下 列 向 量 组 线 性 相 关 ?
线性代数期末考试试卷 +答案
大学生校园网— 线性代数 综合测试题
×××大学线性代数期末考试题
一、填空题(将正确答案填在题中横线上。每小题
2
分,共 10 分)
1 31
1. 若 0 5 x 0 ,则
12 2
__________。
x1 x 2 x3 0
2.若齐次线性方程组 x1 x2 x3 0 只有零解,则 应
2 11
线性代数 期末测试题及其答案
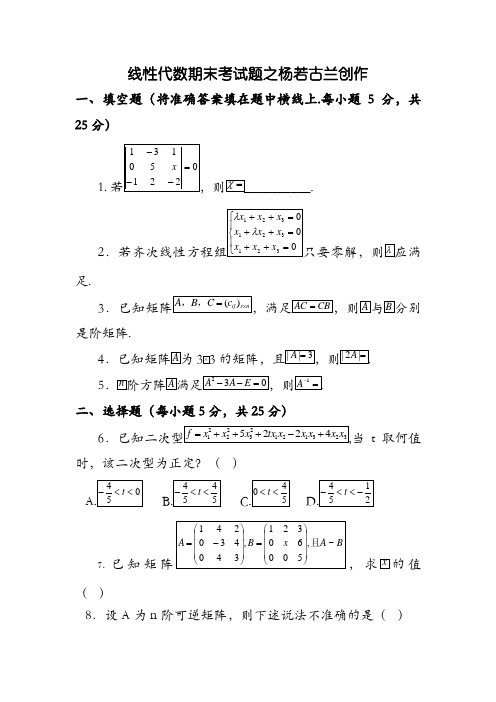
线性代数期末考试题之杨若古兰创作一、填空题(将准确答案填在题中横线上.每小题5分,共25分)1.2足.3是阶矩阵.45二、选择题(每小题5分,共25分)6当t 取何值时,该二次型为正定?( )7.已知矩阵,求的值( )8.设A 为n 阶可逆矩阵,则下述说法不准确的是( )A的行向量组线性相干9.过点(0,2,4行的直线方程为()10其特征值为()三、解答题(每小题10分,共50分)11.矩足关系式12.问取何值时,以下向量组线性相干?解和有没有量多解?当方程组有没有量多解时求其通解.14.求此向量组的秩和一个极大有关组,并将其余向量用该极大有关组线性暗示. 15.证实其中线性代数期末考试题答案一、填空题1. 5.解析:采取对角线法则,考查常识点:行列式的计算.难度系数:解析:要使该现行方程组只要零解,考查常识点:线性方程组的求解难度系数:解析;,,,阶矩阵.考查常识点:n 阶矩阵的性质难度系数: 4. 24解析:由题可知3考查常识点:矩阵的运算 难度系数: 解析:考查常识点:求解矩阵的逆矩阵 难度系数:二、选择题 6. A解析:由题可知,该二次型矩阵为,而此时,该二次型正定.考查常识点:二次型正定的判断难度系数7. C解析:由矩阵特征值性质有1-3+3=1+x+5,可解得x=-5. 考查常识点:n 阶矩阵特征值的性质 难度系数:8. D解析:由题可知,A 为n 阶可逆矩阵,则A 的行向量组线性有关.考查常识点:n 阶可逆矩阵的性质 难度系数:9. A.解析:由题可知,两平面法向量分别为,则所求直线的方向向量为考查常识点:求空间平面交线平行的直线方程 难度系数:10. C.考查常识点:求解矩阵的特征值三、解答题11.解:考查常识点:矩阵方程的运算求解难度系数:12.解:.考查常识点:向量组的线性相干性难度系数:13.解:③当时,有没有量多组解,通解为考查常识点:线性方程组的求解14.解:由题可知,且线性关系为考查常识点:向量组的秩与最大有关组难度系数:15.证实:由题可知,考查常识点:n 阶方阵的性质难度系数:。
山东大学网络教育线性代数-专期末考试试题及参考答案

一、填空题(36分)
1、若矩阵A 满足__A T =A_,则称A 为对称矩阵.
2、设A ,B 是两个3阶矩阵,且det A=-2.det B=-1.则
=. 32 3、
,则齐次线性方程组AX-0必有_
非零__解 4、设mxn 矩阵A 的秩为r ,则非齐次线性方程组Ax=B 有解的充分必要条件是_()B A R r =__
5、二次型)(.,,.........2,1n x x x f ,如果对任意一组不全为零的实数n c c c ,......2,1,
0),......,(21>n c c c f 则称)(.,,.........2,1n x x x f 为___正定__
6、如果向量a.β是正交的,则(a.β)=._0_
7、设AB 是两个3阶矩阵,且det A=-2.det B=-1,则
. 32 8、若数
为矩阵A 的特征值,则齐次线性方程组AX=0必有__非零___解 10、设A.B 是两个3阶矩阵,且det A=-2.det B=-1,则
32 11、设mxn 矩阵A 的秩为r.则非齐次线性方程组Ax=B 有解的充分必要条件是
_()B A R r =__ 12、设A 是mxn 矩阵,B 是pxm 矩阵,则
是_p n ⨯_ 矩阵.
二、计算题(107分)
13、解线性方程组:
解: 该线性方程组的增广矩阵()⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛------=05986741212060311512b A ()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------1155912001230072106031~1510912002120135706031~95109127702120135706031~b A。
线性代数期末试题及答案

8.设A 为三阶方阵, 且3=A , 则 12-=A .一、填空题(每小题2分,共20分)1.行列式=-203297302233241.2.设014111112--=D ,则=++333231A A A .3.设 , 231102 ⎪⎪⎭⎫ ⎝⎛-=A , 102324171⎪⎪⎪⎭⎫ ⎝⎛-=B 则= )( TAB . 4.设052=-+I A A ,则=+-1)2(I A .5.已知矩阵⎪⎪⎪⎭⎫⎝⎛-=100120121A ,*A 是A 的伴随矩阵,则=-1*)(A .6.A 、A 分别为线性方程组b AX =的系数矩阵与增广矩阵,则线性方程组b AX =有解的充分必要条件是 .7.设⎪⎪⎪⎭⎫ ⎝⎛-=30511132a A ,且秩(A )=2,则=a .9.向量组1(1,2,1,1),T α=-,)0,3,0,2(2T=αT )1,4,2,1(3--=α的秩等于 . 10.设21,αα是)3(≥n n 元齐次线性方程组OAX =的基础解系,则=)(A r .二、选择题(每小题2分,共20分)1.已知101yxy x aA =,则A 中元素a 的代数余子式11A 等于( ).A.1- B .1 C .a - D .a2.已知4阶矩阵A 的第三列的元素依次为2,2,3,1-,它们的余子式的值分别为1,1,2,3-,则=A ( ).A .3B .3-C .5D .5-3.B A ,均为n 阶矩阵,且2222)(BAB AB A ++=+,则必有( ).A.B A = B .I A = C .I B = D .BA AB =4.设A 、B 均为n 阶矩阵,满足O AB =,则必有( ).A.0=+B A B .))B r A r ((= C .O A =或O B = D .0=A 或0=B5.设33⨯阶矩阵),,(1γβα=A ,),,(2γβα=B ,其中γβαα,,,21均为3维列向量,若2=A ,1-=B ,则=+B A ( ).A.4 B .4- C .2 D .16.设B AX =为n 个未知数m 个方程的线性方程组,,)(r A r =下列命题中正确的是( ).A .当n m =时,B AX =有唯一解 B .当n r =时,B AX =有唯一解C .当m r =时,B AX =有解D .当n r <时,B AX =有无穷多解7.若齐次线性方程组⎪⎩⎪⎨⎧=λ++=+λ+=++λ000321321321x x x x x x x x x 有非零解,则=λ( ).A .1或2B .1或-2C .-1或2D .-1或-28.n 阶矩阵A 的秩r n =的充分必要条件是A 中( ).A.所有的r 阶子式都不等于零 B .所有的1r +阶子式都不等于零 C.有一个r 阶子式不等于零 D .有一个r 阶子式不等于零, 且所有1r +阶子式都等于零9.设向量组,),,1(21T a a =α,),,1(22T b b =αT c c ),,1(23=α,则321,,ααα线性无关的充分必要条件是 ( ).A.c b a ,,全不为0 B .c b a ,,不全为0 C .c b a ,,互不相等 D .c b a ,,不全相等10.已知21,ββ为b AX =的两个不同的解,21,αα为其齐次方程组0A X =基础解系,21,k k 为任意常数,则方程组b AX =的通解可表成( ).A.2)(2121211ββααα-+++k kB .2)(2121211ββααα++-+k k线性代数期末试题答案一、填空题(每小题2分,共20分)1.52.03. ⎪⎪⎪⎭⎫⎝⎛-1031314170 4. )(31I A - 5.1/211/2011/2001/2-⎛⎫⎪⎪ ⎪⎝⎭6.)()(A r A r =7.6=a8. 38 9.2 10.2-n二、选择题(每小题2分,共20分)1.B2.C3.D4.D5.A6.C7.B8.D9.C 10.B 三、(8分)解:3211324-824823592373(1)373125212412411131D -===-----18361836(1)1313241=-=-=-四、(10分)解:(1)⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-=14191269629303212114321011324TAA (2)⎪⎪⎪⎭⎫⎝⎛-----=--461351341)2(1E A (3) 由XA AX2+=,得A XE A =-)2(A E A X 1)2(--=⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫⎝⎛-----=9122692683321011324461351341五、(12分)解:将方程组的增广矩阵A 用初等行变换化为阶梯矩阵:22112411411242110228018211240134(1)(4)00(4)2k k k k k k k k k k k ⎡⎤⎢⎥----⎡⎤⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=-→-→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎣⎦⎣⎦+-⎢⎥-⎣⎦A所以,⑴ 当1k≠-且4k ≠时,()()3r r ==A A ,此时线性方程组有唯一解.⑵ 当1k =-时,()2=A r ,()3=A r ,此时线性方程组无解.⑶ 当4k=时,()()2==A A r r ,此时线性方程组有无穷多组解.此时,原线性方程组化为132334x x x x =-⎧⎨=-⎩ 因此,原线性方程组的通解为13233334x x x x x x=-⎧⎪=-⎨⎪=⎩或者写为123034101x x C x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x (C R)∈六、(10分)解:记向量组4321,,,αααα对应矩阵为A 并化为行阶梯形矩阵为12341223122324130212(,,,)12030013062300002634000A αααα--⎛⎫⎛⎫⎪ ⎪-----⎪ ⎪ ⎪ ⎪==→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭所以向量组4321,,,αααα的秩为3且它的一个最大无关组为:123,,ααα或124,,ααα1004101020013000000A -⎛⎫⎪ ⎪- ⎪→⎪ ⎪ ⎪ ⎪⎝⎭41231432αααα=--+ 七、(12分)解:(1).⎪⎪⎪⎪⎪⎭⎫⎝⎛--------→⎪⎪⎪⎪⎪⎭⎫⎝⎛--------=61826239131039131024511810957245113322311312A⎪⎪⎪⎪⎪⎭⎫⎝⎛----→0000000039131015801为自由未知量。
大一线性代数期末考试试卷+答案

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分) 1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0100100000010010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=TA A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 s n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示 ④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
线性代数期末考试试题C及解答

一、(36分)填空(2分 18)
1、四阶行列式 的展开式中有一项 ,此项前面应带的的符号
为;三阶行列式 第三行元素的代数余子式之和 =。
2、当 时,向量组
线性相关,此时向量组 , , 的一个极大无关组为。
3、设向量 ,则 , ,矩阵 的秩 。
4、设 为四阶方阵,且 =2,则 =, (其中 为矩阵 的伴随矩阵), 的行向量组线性关。
1、计算四阶行列式:
2、已知矩阵 , 满足矩阵方程 ,
求矩阵 。
共6页第3页
3、设三阶矩阵 ,且 ,
求:(1) ;(2)
4、已知 为三阶矩阵 的特征值, 为 属于特征值 的特征向量,求 的值;并判断 能否与对角形矩阵相似,说明理由。
共6页第4页
三、(12分)设线性方程组 。
问: 取何值时,方程组有无穷多解;此时求出方程组的通解。
共6页第5页
四、(15分)设二次型 ,
1、写出此二次型的系数矩阵 ;
2、 取何值时,此二次型正定;
3、当 时,该二次型在正交变换 下化为标准形 ,求出此正交变换 。
共6页第6页
五、(10分)证明题(5分+5分)
1、 阶矩阵 满足 。求证:矩阵 可逆,并求 。
2、 中,向量组 线性无关, 为 阶矩阵,使向量组 线性相关,问矩阵 应满足什么条件,并给出证明。
5、 为 矩阵,齐次线性方程组 有非零解的充分必要条ቤተ መጻሕፍቲ ባይዱ为,
此时 的一个基础解系中含个解向量。
6、设二阶矩阵 ,且对角形矩阵 ,则 ;又矩阵 与 相似,则 , 。
7、设三阶矩阵 , 且矩阵 均不可逆,则 的三个特征值为,又实对称矩阵 与 相似,则二次型 的秩为,且此二次型的规范形是。
山东交通学院期末考试 线性代数 课程试卷答案和评分标准 ( E )卷

…
线 所以当 1且 10 时 方程组有唯一解;
…
… …
要使方程组有无穷多解 必须 R(A) 3,即必须 1 10 0且1 0,
… …
所以当 1或 10 时 方程组有无穷多解
---------------------(4 分)
…
…
…
试卷适用班级 理工科 09 级、专升本 10 级 、路专 09 级等 班级
所以 f 为负定。
--------------(7 分)
…
34 0
…
…
… …
2.设 A 为 3 阶矩阵 A* 为 A 的伴随矩阵,| A |
1
则
A*
1
.
…
2
4
…
…
…
1 0 1 1 2 3
1 2 2
密 … … …
3.设
A
0
10456 Nhomakorabea则
A
4
5
2
0 0 1 7 8 9
7 8 2
…
…
…
1 0 0
… … 封 … …
4.设
A
0
1
0
A* 为 A 的伴随矩阵,则 R A* 3 .
2
6
0
2 0 4
所以 K 可逆 故有 A BK 1 --------------(3 分) 所以向量组1, 2 , , n 能由向量组 1, 2 , , n 线性表示。
-------------------------- (4 分)
因为
5 2
a11 5 0
2
26 0 | A | 80 0 6
2. 设 A, B 均为 n 阶方阵,下面结论正确的是
山大工程制图期末测试题

答案:本科线性代数测试题(一)一、填空题),,2,1,0________(010001000100011111.11210n i a a a a a a i nn=≠=-).1()1(000001111)1()1()1()1(10211021211021∑∑∑===⋅⋅-⨯+-⨯-⨯ni in ni in nni ina a a a a a a a a a a a a a a D a n a a -故应填-=-=而得其值,即化为上三角行列式,从至第一列,可把行列式加列,第,,第三列把行列式中第二列解.____20012021.2=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==-A B A B AB ,则,其中已知.20001210211)(10000210210)(04100002020)(11⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-=-=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-=--∴≠=-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-=-=---E B B A E B E B E B E B BE B A A B AB ,则且可逆,其中由解.______**)(3______,*23_____,*)(_____,**)(____,*____223.3111=-=-=====---A A A A A A A AA A ,,则阶阵,且为设.2214116442233)(321)1(432323412)(16)(442122221311111123114169213131,,-,,,所以应填====解==-=-=--=⋅-=-=-=⋅-=-========⋅⋅-**------*----*+-**-*--A A A A A A A A A AAA A A A AAAA AAA AA A AAn n._____)(3010202012)(34.4=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==⨯AB r B A r A A ,则,而的秩矩阵,且是设 .2)()(0||==≠A r AB r B ,所以因为解二、选择题))((D)())((C)(B)(A)(0000000.14141323243432121432143214321432144332211b b a a b b a a b b a a b b a a b b b b a a a a b b b b a a a a a b a b b a b a ----+-=).D ())((00000000000000.32324141332244113322441144332211故应选====列式,然后计算把行列式化为块对角行首先根据行列式的性质解b b a a b b a a a b b a a b b a a b b a a b b a a b a b b a b a D --⋅)D ()C (2)B (3)A (,,.2222EEEC B A E CA BC AB n C B A =++===,则阶方阵,且均为设).A (3))(()())(()())(()(222222故应选所以,因为解ECB A E EE BC CA C AB C C EEE AB BC B CA B B E EE CA AB A BC A A =++============ababab ab C O BA OC b B a A n B m A mnnm )()()()(,则阶方阵,且为阶方阵,为设D C )1(B )1(A ,,.3---=⎥⎦⎤⎢⎣⎡===+).B (.)1()1()1()1(21)2()1(故应选由拉普拉斯定理的代数余子为阶子式利用拉普拉斯定理解ab A B OBA O C AA B n mnmnmnnm m -=-⋅==-=-++++++++3D)(2C)(1B)(0A)(0)(,111111111111111)(.4---------=的根为=则设x f xx f.30)()3(4)1(48,21202022001111)(;)1(-=+-=+--=+----=-⨯x x f x x x x f 的根为=故行展开得行加至第四行并按第一加至第二、三行,第一第一行解1)()D (2)()C (2)()B (2)()A (2)(0.5≥≤<=-==B r B r B r B r n A r AB n B A ,则,若阶方阵,满足均为、已知).C (.2)2(0)()()(0)(0.)()()(故应选得,,则根据由不等式解=--+=-+≤==-+≥n n A r n AB r B r AB r AB n B r A r AB r三、计算、证明题.1111111111111111.1--+---+---x x x x 计算:441101110000001111111111111111x x xx x x x x xxx x x x x xD x ===,则再提出第一列的公因子将各列加到第一列后,解---=----------+---482200020000340043.2A A A 及,求设⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡===⋅-==464444224114121141688822000200005000051022023443M OO M M OO M AAA解.21431312.3⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=λB 求下列矩阵的秩:.3)(033;2)(023300110431410110431415504312131243121431312=≠=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=B r B r B ,故阶子式不为有时,-当,所以阶子式不为时有=显然,当-------解λλλλλλλ.,20012031)3(;:)2(;,:)1(.,,.4A B BA AB n E E A B A AB n B A 求矩阵已知证明阶单位矩阵为其中为可逆矩阵证明且阶方阵为设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==-+= .)())(()1(1E B E A E A EE B E A E E B A AB B A AB -=--=--=+--+=-可逆,且这说明矩阵即得由证明.))(())(()1()2(BA AB E B A BA E B A AB E A E B E B E A =+--+----=--从而=即知由.,1)2(;1)1(:,,,,.52是不可逆矩阵时当证明转置的是维非零列向量是阶单位矩阵是其中设A A An n E E A TTTT==⇔=-=ξξξξξξξξξ..)1(.1.)2(.1.00)1()2()2()2(2))(()1(1211222是不可逆矩阵故矛盾这与,从而,得,等式两端同时左乘知此时,由为可逆的时,=假设当用反证法所以只有是非零列向量,故因为,亦即,即证明A E E A E A A AAAA A AA E E A AE E E E E ATTTT TtTT T T TTTTT TTT≠-=====≠=--=--=--=--=+-=--=---ξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξξ.0:,,,.6=>⨯⨯AB n m m n B n m A 试证且矩阵为矩阵为设{}。
