风险、收益和资产定价模型 (ppt 34页)

合集下载

资本资产定价模型PPT课件

资产定价的随机过程
随机过程的基本概念
随机过程是描述一系列随机事件的数学模型，其中每个事件的发生都具有不确定性。在资产定价的上下文中，随机过程通常用于描述资产价格的变动。
资本资产定价模型的随机过程
资本资产定价模型假设资产价格的变动遵循随机过程，并且这种变动与资产的预期回报和风险有关。通过建立适当的随机过程模型，可以进一步研究资产价格的动态行为和风险特征。
发展历程
起源
资本资产定价模型起源于20世纪60年代，由经济学家威廉·夏普、约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中，CAPM经历了多次修订和完善，以适应金融市场的变化。
应用
资本资产定价模型被广泛应用于投资组合管理、风险评估和资本预算等领域。
发展历程
起源
资本资产定价模型起源于20世纪60年代，由经济学家威廉·夏普、约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中，CAPM经历了多次修订和完善，以适应金融市场的变化。
应用
资本资产定价模型被广泛应用于投资组合管本资产定价模型用于确定投资组合的风险和预期回报，帮助投资者在风险和回报之间做出权衡。
风险评估
通过CAPM，投资者可以评估特定资产或投资组合的风险，并与其他资产或基准进行比较。
主要发现
是一种用于评估风险和预期回报之间关系的金融模型，主要用于投资组合管理和风险评估。
CAPM的核心思想
资本的预期收益率由两部分组成，一部分是无风险利率，另一部分是风险溢价，即风险超过无风险资产的部分。
目的和目标
目的
通过理解CAPM，投资者可以更准确地评估投资的风险和预期回报，从而做出更明智的投资决策。

第5讲风险收益与资本资产定价模型

Corporate Finance
第4讲、风险、收益与资本资产定价模型
4.1收益的计量 (收益率与风险) 4.2 投资组合收益和风险计量
4.3风险和期望收益的关系
–资本资产定价模型（CAPM模型）
Though this be madness, yet there is method in it.
William Shakespeare
?
红利 ? 资本利得初始市场价值
? 股利收益率 ? 资本利得收益率
收益：示例
? 假设你一年前购买了沃尔玛公司(WMT)的100股股票，当时的股价是$25 。上一年你得到股利$20 (=每股 20分 ×100股)。如果年末股价达到$30，你做得如何？
? Quite well. 你的投资金额是：$25 × 100 = $2,500. 年末你的股票价值是$3,000，并且现金股利是$20。所以美元总收入是$520 = $20 + ($3,000 – $2,500)。
Source: ? Stocks, Bonds, Bills, and Inflation
2000 Yearbook? , Ibbotson Associates, Inc., Chicago (annually updates work by
Roger G. Ibbotson and Rex A. Sinquefield). All rights reserved.
n
n
n
? ? ? 样本协方差 v ? pi (xi ? x )( yi ? y ), x ? pi xi , y ? pi yi
i?1
i?1
i?1
相关系数 ? ? cov(x, y) ? 1 ? ? ? 1

资本资产定价模型(CAPM模型)ppt课件

ppt课件
12
β值及其经济含义
证券市场线也可以用另一种方式来表明：
i
E(ri ) rf E(rm ) rf
i
Cov(ri , rm ) /Var(rm )
im
/
2 m
系数是表示了某只证券相对于市场组合的风险度量。
➢ 由于无风险资产与有效组合的协方差一定为零，则任何无风险资产的值也一定为零。同时任何值为零的资产的超额回报率也一定为零。
因此，对于有效组合来说，可以用两种指标来度量其风险，而对于非有效组合来说，只能用β系数来度量其风险，标准差是一种错误度量
ppt课件
11
资本市场线与证券市场线的内在关系
资本市场线表示的是无风险资产与有效率风险资产再组合后的有效资产组合期望收益与总风险之间的关系，因此在资本市场线上的点就是有效组合；而证券市场线表明的是任何一种单个资产或者组合的期望收益与其系统风险之间的关系，因此在证券市场线上的点不一定在资本市场线上。
rC (1 wA wB )rf wArA wBrB rC rf wA (rA rf ) wB (rB rf )
E(rC rf ) wA[E(rA) rf ] wB[E(rB ) rf ]
(wAA wBB )[E(rM ) rf ]
ppt课件
17
β值及其经济含义
例：假定市场投资组合的风险溢价为8%，其标准差为22%。如果某一资产25%投资于通用汽车公司股票，
ppt课件
26
我们可以对 rp j 给出另一种解释。由于拥有股票j的风险
为 jm ，即 j乘上市场风险 m是j所带来的风险，而每
单位风险的价格为：
P rm rf m
所以，承担风险资产j的所需求的风险溢价应为：

管理学投资学PPT第章资本资产定价模型

问题：
❖若某一个股票未包含在最优资产组合中，
会怎样？
2024/6/29
21
图 9.1 The Efficient Frontier and the
Capital Market Line
2024/6/29
22
9.1.2 消极策略的有效性
理由：
❖市场的有效性
❖投资于市场投资组合指数这样一个消极策略是有
26
▪ β系数。美国经济学家威廉·夏普提出的风险衡量
指标。
▪
用它反映资产组合波动性与市场波动性关系（
在一般情况下，将某个具有一定权威性的股指（
市场组合）作为测量股票β值的基准）。
▪ 如果β值为1.1，表明该股票波动性要比市场大盘
高10 ％，说明该股票的风险大于整个市场的风险
，当然它的收益也应该大于市场收益，因此是进
则其收益 - 风险比率为：
wGE [ E (rGE ) rf ] E (rGE ) r f

wGE Cov(rGE , rM ) Cov(rGE , rM )
2024/6/29
25
9.1.4 单个证券的期望收益
市场组合M与CML相切，其收益风险比率为：
E (rM ) rf

2
M
(风险的市场价格)
率应该增加的数量。
▪ 在金融世界里，任何资产组合都不可能超越CML
。由于单个资产一般来说，并不是最优的资产组
合，因此，单个资产也位于该直线的下方。
2024/6/29
14
证券市场线
▪ 资本市场线描述了有效组合的预期收益率和标准
差之间的均衡关系―有效资产组合定价模型。
▪ 问题：
▪ （1）单个风险资产的预期收益率和标准差之间

第五章-资本资产定价模型PPT课件

第五章资本资产定价模型
2021/3/12
1
第五章资本资产定价模型
资本资产定价模型(CAPM)是现代金融学的奠基石。 CAPM由威廉·夏普、约翰·林特、简·莫辛分别于 1964、1965、1966年独立提出。研究当投资者按照Markowitz建议的方式行动时，市场达到均衡时资产的预期收益率与风险之间的关系。
2021/3/12
9
二、相关的推导
（二）所有投资者都选择市场资产组合作为他们的最优风险资产组合。
由于投资者按照马可维茨的方法进行投资选择，其持有的组合是最优风险资产组合，因此它一定在有效边界上，而且与最优资本配置线相切。
市场组合与无风险资产构成的资本配置线被称为资本市场线。(CML，Capital Market Line)
•资本资产定价模型的基本形式：
并定义系数：
任意风险资产的风险溢价与市场组合的风险溢价成正比，
该比例系数称为 ᵝ系数，衡量的是单位资产对市场组合
风险的202贡1/3/献12 率。
16
实际上，我们可以从ᵝ取值的大小来区分股票类型：
ᵝ>1的股票被称为“攻击性股票”，市场上升时其
升幅较大；
ᵝ<1的股票被称为“防御性股票”，市场上升时其升
2021/3/12
10
E(r)
rf •
0
2021/3/12
M
•
•B
•A
11
哪一条资本市场线是最优的呢？
2021/3/12
12
为什么所有的投资者都持有市场资产组合
• 投资者在一个什么样的价位上才愿意将该只股票纳入其最优风险资产组合。当某只股票需求为零时，股价会下跌，直至它对于投资者的吸引力超过任意其它一只股票的吸引力，并进入到投资者的最优资产组合的构成之中，从而使该股票价格回升到某一均衡水平

第三章资产风险与收益分析

第二节

均值和方差分析
风险――收益的数学度量证券之间关联性――协方差与相关系数资产组合方差的计算

投资组合风险分散
均值――方差准则（MVC）
一、风险――收益的数学度量
收益的度量资产收益率单个资产
持有期收益率算术平均收益率几何平均收益率
资产组合
（二）效用函数的应用――风险态度
• 消费者的偏好是指消费者根据自身的愿望对不同消费束之间的一个排序。 • 无差异曲线――偏好的图形描述 • 效用函数――偏好的数学表示
消费者偏好
效用及效用函数
（二）效用函数的应用――风险态度
• 对待风险的态度可以分为三类：风险厌恶型、风险中性型和风险偏好型。 • 在不确定性效用分析中，经常以彩票为例来说
将标准差转变为变异系数后，可以将不同预期报酬率的投资进行比较。例1：中国联通（600050）和中兴通讯（000063）
二、资产风险之间关联度――协方差与相关系数
1、协方差
如果已知证券 i 和证券 j 的收益率的联合分
布，则其协方差记作 Cov(ri , rj ) 。
协方差是测算两个随机变量之间相互关系的
票价格上涨至200元，但时隔1年，在第2年年末它又跌回到了100 元。假定这期间公司没有派发过股息，这样，第1年的投资收益率为100％（R1＝（200-100）/100=1=100%），第2年的投资收益率则为－50%(R2= (100-200)/200=-0.5＝－50％)。用算术平均收益率来计算，这两年的平均收益率为25％，而实际上，在整个投资期间，投资者并未赚到任何净收益。
ij ＝1，两个收益率完全正相关； ij ＝－1，两个收益率完全负相关； ij ＝0，两个收益率无任何关系。

风险与收益分析 (PPT 39张)

（1）当β ＝1时，表示该资产的收益率与市场平均收益率呈相同比例的变化，其风险情况与市场组合的风险情况一致；（2）如果β ＞1，说明该资产收益率的变动幅度大于市场组合收益率的变动幅度，该资产的风险大于整个市场组合的风险；（3）如果β ＜1，说明该资产收益率的变动幅度小于市场组合收益率的变动幅度，该资产的风险程度小于整个市场投资组合的风险。
判断题
按照资本资产定价模型，某项资产的风险收益率是等于该资产的系统风险系数与市场风险溢酬的乘积。【答案】√ 【解析】根据R＝Rf＋β ×(Rm－Rf)，可见，某项资产的风险收益率＝该资产的β 系数×市场风险溢酬。
计算分析题
某公司拟进行股票投资，计划购买A、B、C三种股票，并分别设计了甲乙两种投资组合。已知三种股票的β 系数分别为1.5、1.0和0.5，它们在甲种投资组合下的投资比重为50%、30%和20%；乙种投资组合的风险收益率为3.4%。同期市场上所有股票的平均收益率为12%，无风险收益率为8%。要求：（1）根据Ａ、Ｂ、Ｃ股票的β 系数，分别评价这三种股票相对于市场投资组合而言投资风险大小。（2）按照资本资产定价模型计算A股票的必要收益率。（3）计算甲种投资组合的β 系数和风险收益率。（4）计算乙种投资组合的β 系数和必要收益率。（5）比较甲乙两种投资组合的β 系数，评价它们的投资风险大小。（2005年）
3.风险中立者
风险中立者通常既不回避风险也不主动追求风险，他们选择资产的惟一标准是预期收益的大小，而不管风险状况如何。
单项选择题
某投资者选择资产的惟一标准是预期收益的大小，而不管风险状况如何，则该投资者属于（）。（2008年） A.风险爱好者 B.风险回避者 C.风险追求者 D. 风险中立者【答案】D 【解析】风险中立者既不回避风险，也不主动追求风险。他们选择资产的惟一标准是预期收益的大小，而不管风险状况如何，这是因为所有预期收益相同的资产将给他们带来同样的效用。

第6讲资本资产定价模型(CAPM) (《金融经济学》PPT课件)

第6讲资本资产定价模型（CAPM）
6.1 从组合选择到市场均衡
《
金
融经
市场组合M是什么样的？
济学
市场组合就是包含了所有风险资产的整个市场
二
五讲
这么个依赖于大量前提条件（各类资产的收益波动状况）的复杂均值方差优化
》配
问题的结果M，怎么会这么巧就和现实中的整个市场一模一样？
套课
但结果就是这么巧，也必须这么巧
对市场所做的简化假设
五讲
没有交易成本（佣金、买卖价差等）
》
配套
没有税收
课件
所有资产都可以任意交易，并且无限可分
完全竞争：所有人都是价格的接受者，没有影响价格的能力
对投资者的假设（所有人都求解均值-方差问题）
所有人都以均值方差的方式选择投资组合：偏好更高的期望回报率，以及更低的回报率波动率
i
市场组合M处，否则与CML
市场组合
定义矛盾
σ
0
7
6.4 CAPM的第二种论证
基于组合构建的CAPM论证（续）
《
金
融经
济
学
由曲线与CML在M处相切得dE到(rw)
E(rM ) rf
二五
d (rw ) w0
M
由求导法则及E(r )的表达式可知讲
》
配
套
课
件
wdE(rw ) dE(rw ) d (rw ) dw
所有资产（包括无风险资产）都可以任意买空卖空
一致预期：所有人针对相同的时间区间（1期）考虑投资问题，并对资产的预期回报率和预期波动率状况{E(r1̃ ), E(r2̃ ), ..., E(rñ ), σ(r1̃ ), σ(r2̃ ), ..., σ(rñ )}有相同预期

资本资产定价模型(1).ppt

n
(Ri R )2 Pi
i1
而期望收益
n
R Ri Pi
i 1
11
标准离差的局限
只能用来比较期望报酬率相同的各项投资的风险程度。如果期望报酬不同，则不能比较。
12
标准离差率
v
R
超级技术公司v=25.86%/17.5%=1.48 慢行公司v=11.5%/5.5%=2.09
13
协方差和相关系数
i 1
Corr( R A ,
RB
)
Cov(RA, RB
A B
)
15
相关系数的数值例子
16
17
协方差的涵义
在任何经济状况下，如果两个公司股票的可能收益一般都高于或低于各自的期望收益，表明两个公司股票的收益呈正相关关系或趋势，结果协方差为正值。
在任何经济状况下，如果两个公司股票的可能收益，当一个高于其期望收益，而另一个低于其期望收益时，表明两个公司股票的收益呈负相关关系或趋势，结果协方差为负值。
收益和风险：资本资产定价模型
1
风险资产的特征
期望收益。它是指一个持有一种资产（证券）的投资者期望在下一个时期所能获得的收益。
2
风险资产的特征
方差和标准差。评价资产（证券）风险的方法有很多，其中最为常用的是方差。方差是一种资产（证券）的收益与其平均收益的离差的平方和的平均数。标准差是方差的平方根。
24
组合的方差和标准差
由A和B两种证券构成的投资组合的方差
是：
投资组合的方差取决于组合中各种证券的方差和每两种证券之间的协方差。
25
组合的方差和标准差
在证券方差给定的情况下：
➢ 如果两种证券收益之间相互关系或协方差为正，组合的方差就上升；

第章收益和风险资本资产定价模型

• The standard deviation of returns is a measure of total risk
• For well-diversified portfolios, unsystematic risk is very small
• Consequently, the total risk for a diversified portfolio is essentially equivalent to the systematic risk
return for the portfolio? •DCLK: 2/15 = .133
– DCLK: 19.69% – KO: 5.25% – INTC: 16.65%
•KO: 3/15 = .2 •INTC: 4/15 = .267
– KEI: 18.24%
•KEI: 6/15 = .4
• E(RP) = .133(19.69) + .2(5.25) + .267(16.65) + .4(18.24) = 15.41%
– 可风险风险又称非系统性风险或公司特有风险，是通过投
资组合可以分散掉的风险。Includes such things as labor strikes, part shortages, etc.
Total Risk
• Total risk = systematic risk + unsystematic risk
2024/8/2
19
10.3 投资组合的收益和风险
– 当由两种证券构成投资组合时，只要ρAB<1，投资组合的标准差就小于这两种证券各自的标准差的加
权平均数，也就是投资组合多元化的效应就会发生

第11章收益和风险：资本资产定价模型

投资于股票的 %
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50.00% 55% 60% 65% 70% 75% 80% 85% 90% 95% 100%
风险
8.2% 7.0% 5.9% 4.8% 3.7% 2.6% 1.4% 0.4% 0.9% 2.0% 3.08% 4.2% 5.3% 6.4% 7.6% 8.7% 9.8% 10.9% 12.1% 13.2% 14.3%
方差
标准差协方差
6.68
25.84
1.32
11.49 -0.4875
σ 12 =0.19-1.09-2.19+1.14/4=-0.4875
12 =-0.004875/(0.2584×0.1149)=-0.1641
Portfolio Risk
2 2 2 Portfolio Variance x1 σ 1 x2 σ σ 2) 2 2 2( x1x 2ρ 12σ 1
2015-6-13
11.2单项资产的风险与收益
2. 计算预期收益率
两家公司的预期收益率分别为多少？
2015-6-13
11.2单项资产的风险与收益
3. 计算标准差
（1）计算预期收益率（3）计算方差
（2）计算离差
（4）计算标准差
两家公司的标准差分别为多少？
2015-6-13
11.2单项资产的风险与收益
2015-6-13
11.3投资组合的风险与收益
从以上两张图可以看出，当股票收益完全负相关时，所有风险都能被分散掉；而当股票收益完全正相关时，风险无法分散。若投资组合包含的股票多于两只，通常情况下，投资组合的风险将随所包含股票的数量的增加而降低。

财务风险控制ppt34张课件

ZJGSU
F分数模式列式
F=-0.1774+1.1091X1+0.1074X2 +1.9271X3+0.0302X4+0.4961X5
式中： X1——期末营运资本/期末总资产； X2——期末留存收益/期末总资产； X3——（税后收益+折旧）/平均总负债； X4——期末股东权益市场价值/期末总负债； X5——（税后收益+利息+折旧）/平均总资产。
F分数模式以0.0274为临界点：若某一特定公司的F分数低于0.0274，则被预测为破产公司；反之，若F分数高于 0.0274，则公司将被预测为可继续生存的公司
ZJGSU
结束语
在激烈的市场竞争中，风险与机遇同在，风险与收益并存。企业应尽最大可能抓住机遇，规避风险，创造收益，才能在竞争中立于不败之地．
债比率要适度；（2）负债内部（即长短期债务）结构要
合理；（3）横向资本结构要合理，即企业资本
来源与资产的对应关系要合理。
ZJGSU
设计资本结构，控制筹资风险？
——关键点之一：负债比率要适度
负债比率为什么要适度?——负债是把“双刃剑”。
什么叫适度？理论上讲，负债比率以50%左右为宜，大于
100%为资不抵债。原因？例如：浙江海纳
三、投资风险
投资是通过垫付资金以获取经济利益为目的的财务行为。
公司投资方式简介
现金
流动资产投资
应收账款存货
投
资
方
式
长
期
投
资
固定资产
项目投资无形资产
对外项目投资
金融投资
股票、债券
基金
ZJGSU
金融衍生工具

第四章风险、收益和资产定价模型(金融市场学-人民银行,杜金富)

ei为证券i 的非系统性收益
这样，根据APT模型，证券的随机收益率有如下的关系：
Ri=E（Ri）+β
ih+β i2+F2+ei

通过数学计算，可以推算出均衡定价的条件： ifjE（rfl）式中： ri— 证券 i 高于无风险利率的超额回报； β ifj—— 第 i 种证券对第j 个因素的敏感性； rfj—第j个系统性因素的高于无风险利率的超额回报，这一回报可以看作第j个系统性风险的价格（或风险溢价）。

套利定价理论模型
为了描述 APT 模型，在这里我们假定一个资产组合中包括了三种证券，这三种证券受两种因素的影响。其中： Ri为证券i（i=1,2,3,）的随机收益率 E（Ri）为证券i（i=1,2,3,）的预期收益 β ih为第i种证券对第h个因素的敏感性指数 Fn为影响三种证券共同的第n种影响因素

表4—3
包含20种股票的资产组合标准差和预测的极限值的关系
股票组别含20种股票的资产组合的标准差各组股票的平均 β 值极限值
A+ A AB+ B B-及C
3.94 4.17 4.52 4.45 5.27 5.32
0.74 0.80 0.89 0.87 1.24 1.23
R(ri)= β
将公式扩展为H个影响因素，i个证券，则有如下关系式：
E(ri)= β
if1E（rfl）+β if2E（rf2）+β ifj
E（rfj）
这个公式即APT模型。

资产组合系统风险性=β pσ
m

资产组合的β 值则可以通过单个证券的β 值及在资产组合中每项资产所占的比重予以确定：

资本资产定价模型CAPM.pptx

0.0205
14.3%
债券基金
回报率离标差准平差方
17%
1.00%
7%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
14.3% 0.0205
9
第10页/共73页
协方差
衡量资产同步变动的程度
考虑如下的乘积：
[r股票(s)-E(r股票)][r债券(s)-E(r债券)]
协方差的定义
Cov(r股票,r债券) = S P(s)[r股票(s)-E(r股票)][r债券(s)-E(r债
26
第27页/共73页
10.4 两个资产的有效集
股票在组合的比率
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50.00% 55% 60% 65% 70% 75% 80% 85% 90% 95% 100%
风险
8.2% 7.0% 5.9% 4.8% 3.7% 2.6% 1.4% 0.4% 0.9% 2.0% 3.08% 4.2% 5.3% 6.4% 7.6% 8.7% 9.8% 10.9% 12.1% 13.2% 14.3%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
2.05% 1 (3.24% 0.01% 2.89%) 3
8
第9页/共73页
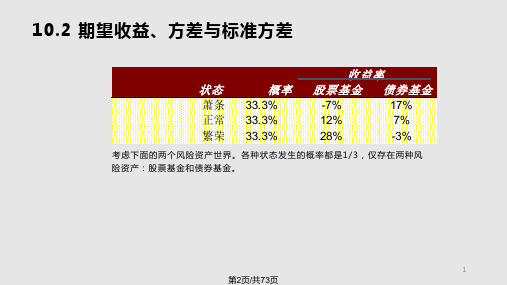
10.2 期望收益、方差与标准方差
状态
萧条正常繁荣
期望收益方差标准差
股票基金
回报率离标差准平差方
-7%
3.24%
12%
0.01%
28%
2.89%
11.00%
24
第25页/共73页

资产定价模型课件.ppt

w iri c ,
i1
n
wi 1
i1
第16页，共36页。
4- 16
投资者最佳组合点的选择
• 投资者如何在有效组合中进行选择呢？
– 这取决于他们的投资收益与风险的偏好。 – 投资者的收益与风险偏好可用无差异曲线来描述。
– 所谓无差异是指一个相对较高的收益必然伴随着较高的风险，而一个相对较低的收益却只承受较低的风险，这对投资者的效用是相等的。
第34页，共36页。
4- 34
证券均衡定价
• SML为我们提供了一种方便地判断证券是否合理定价的
标准。
– “合理定价”的证券一定位于SML上；
– “错误定价”的证券则分布在SML上方或下方。
• 证券实际期望收益率与均衡期望收益率之间的差额称
为证券的α值。
– 根据α值的正负及大小，可以判断证券是否定价合理以及定价偏离的程度。
假定投资组合中各成分证券的标准差及权重一定，投资组合风险的高低就取决于成分证券间的相关系数。成份证券相关系数越大，投资组合的相关度高，风险也越大；相反，相关系数小，投资组合的相关度低，风险也就小。
第10页，共36页。
4- 10
证券组合数量与资产组合的风险
• 投资组合具有降低非系统性风险的功能，但风险降低的极限为分散掉全部非系统性风险，而系统
第22页，共36页。
4- 22
3.分散投资可以消除组合的非系统风险，但不能消除系统风险。一个充分分散的证券组合收益率的变化基本上代表了市场收益率的变化，其预期收益率是对不可分散的系统风险的补偿。
4.投资者决策的关键是正确计算预期收益率、风险（方差或标准差）、相关系数或协方差，通过比较决定有效组合，并从中选择最优组合。

收益和风险资本资产定价模型

•
路漫漫其悠远
组合的期望报酬率（%）
Q 1
M
N 2
路漫漫其悠远
组合的标准差（%）由无风险资产和风险资产组合构成的组合的收益与风险的关系
•
• 这些投资是否有效？在可行集以下的无效
•
路漫漫其悠远
组合的期望报酬率（%）
风险偏好者 5 风险厌恶者 A
Q 4 1M
资本市场线 N
2
路漫漫其悠远
组合的标准差（%）由无风险资产和风险资产组合构成的组合的收益与风险的关系
•
风险厌恶者，减少风险资产的投资比例风险偏好者，加大风险资产的投资比例
•
路漫漫其悠远
• 注：红线代表“资本市场线”，描述了由无风险资产和风险资产构成的投资组合的有效边界测度风险的工具：整个资产组合的标准差
•
路漫漫其悠远
6.4 资本资产定价模型
• 6.4.1 市场均衡组合共同期望假定：所有的投资者可以获得相似的信息源
• 投资组合的贝塔系数
•
路漫漫其悠远
• 例14，甲公司持有A、B、C三种股票，在由上述股票组成的证券投资组合中，各股票所占比重分别为50%、30%和20%，其系数分别为2.1、1.0和0.5。求该证券组合的值解：
•
路漫漫其悠远
• 2、资本资产定价模型（CAPM）是现代金融市场价格理论的支柱
•
路漫漫其悠远
• 但如下情况可能会发生：观望的人偶尔也会下注
如何使得“风险厌恶者”参与赌局？
•
路漫漫其悠远
• 改变规则：人头，赌客输，庄家赢100美金；字
，庄家输，赌客赢200美金。
村户可能会考虑参与赌局
•

第四章风险与收益《财务管理》PPT课件

Cov(X ,Y) XY E[(X EX ) (Y EY)]
其中，E(X )为随机变量X的期望值。
一、单个证券的期望收益、方差和协方差
当X和Y都是满足离散型分布的随机变量时，协方差的数学公式也可以表示为
n
Cov( X ,Y ) XY ( Xt X ) (Yt Y ) Pt
（2）连续型分布的方差计算公式
假设 X 为服从连续型分布的随机变量，其分布函数为 f (x) ，其取值范围在区间a,b（注意，此处 a可为，可为）。以 D X 表示其方差，那么，D X 的计算公式为
D
X
b
a [x
E(x)]2
f
x
dx
二、风险的度量
（五）变异系数
变异系数的定义是随机变量标准差与期望值之间的比值的绝对值，其含义是获得一个单位收益率条件下的离散程度。其计算公式如下：
第四章风险与收益
第一节收益
一、收益值二、收益率三、持有期间收益率四、股票的平均收益和无风险收益率
一、收益值
（一）收益值的含义收益值是衡量收益的一种方法，它从货币价值的角度对
投资收益进行考察。
（二）收益值的表现形式购买股票是最为典型的投资。投资收益表现为股利收入和资本利得这两者之和。
了将资金分配于资产1和资产2之间所有可能得到的组合。
三、两种资产组合的有效集
（一）最小方差组合
曲线上最左端的点所代表的组合具有最小的方差，也即最小标准差。换句话说，该点上的组合是所有投资者可能构造的组合中标准差最小的，因而被定义为“最小方差组合”，用mvp来表示。
当投资者非常偏好风险时，可以选择曲线最右边点，如点B。
wn为其相应的权重。
二、投资组合的收益和风险

收益和风险资本资产定价模型CAPM课件

阿尔法系数（α）
阿尔法系数代表资产收益率与市场组合收益率之间的差异。正值阿尔法表示资产收益率高于市场组合，而负值阿尔法则表示资产收益率低于市场组合。
04
CAPM模型应用实例分析
股票市场CAPM应用案例
估计股票预期收益率
01
利用CAPM模型计算个股或股票组合的预期收益率，并与实际
收益率进行比较。
风险管理
详细解释CAPM模型在风险管理中的应用，包括计算资产的系统性风险、评估投资组合的风险水平等。
学习目标与要求
掌握CAPM模型的基本原理和计算方法
通过学习CAPM模型的基本概念、假设条件和计算过程，掌握运用CAPM模型进行资产定价的基本方法。
理解CAPM模型的应用场景和局限性
了解CAPM模型在不同市场环境和资产类型下的应用效果，认识CAPM模型的局限性和适用范围。
息做出最佳决策，追求效用最大化。
市场是有效的
02 CAPM模型假设市场是有效的，即所有信息都是公开
可用的，并且价格反映了所有可用信息。
投资者可以无限制地借贷
03
CAPM模型假设投资者可以无限制地以无风险利率借
贷，这意味着他们可以通过杠杆操作来增加预期收益
。
CAPM模型中关键参数解释
贝塔系数（β）
贝塔系数衡量了资产收益率与市场组合收益率之间的相关性。贝塔系数大于1 的资产比市场组合更具风险，而贝塔系数小于1的资产则相对较为安全。
假设条件过于理想化
如市场完全有效、投资者理性等，现实中难以满足。
单一风险因子不足
CAPM仅考虑市场风险，忽略其他可能影响资产收益的风险因子。
估计误差与模型检验问题
实际数据可能存在误差，影响模型参数估计和检验结果。