六大基本初等函数图像及其性质
(完整版)六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。
b.2. 4.a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) nm n m a a a +=⋅(2)nm n m aa a -=÷b.y(1)()a a nn= ; (2)当n 为奇数时,a a nn=当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及性质
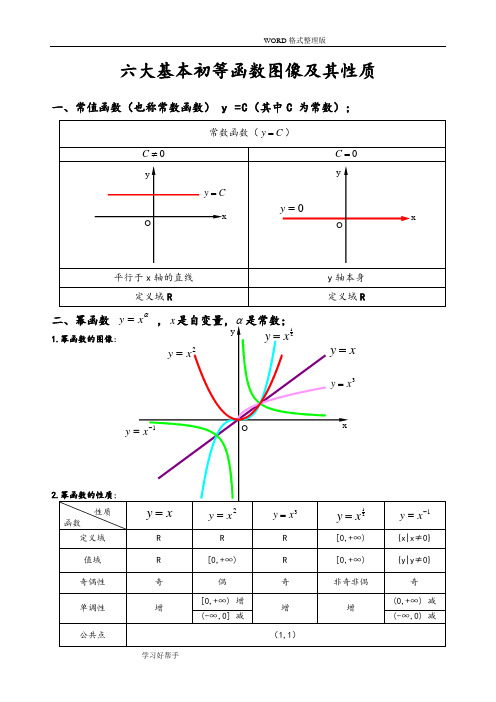
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质

,
的函数图像关于y轴对称。
时,a值越大,
的图像越靠近y轴;
时,a值越大,
的图像越远离y轴。
4.指数的运算法那么〔公式〕;
;
(1)
(2)
(3)
(4)
b.根式的性质;
(1) ; (2)当n为奇数时,
当n为偶数时,
c.分数指数幂;
(1)
(2)
四、对数函数 ( 是常数且 ),定义域 [无界]
六大根本初等函数图像及其性质
一、常值函数〔也称常数函数〕y =C〔其中C为常数〕;
常数函数〔 〕
y
y
O
O
平行于x轴的直线
y轴本身
定义域R
定义域R
二、 幂函数 , 是自变量, 是常数;
:
2.幂函数的性质;
性质
函数
定义域
R
R
R
[0,+∞)
{x|x≠0}
值域
R
[0,+∞)
R
[0,+∞)
{y|y≠0}
奇偶性
3〕当α为正有理数 时,n为偶数时函数的定义域为〔0, +∞〕,n为奇数时函数的定义域为〔-∞,+∞〕,函数的图形均经过原点和〔1 ,1〕;
4〕如果m>n图形于x轴相切,如果m<n,图形于y轴相切,且m为偶数时,还跟y轴对称;m,n均为奇数时,跟原点对称;
5〕当α为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
1.对数的概念:如果a(a>0,a≠1)的b次幂等于N,就是 ,那么数b叫做以a为底N的对数,记作 ,其中a叫做对数的底数,N叫做真数,式子 叫做对数式。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数定义域为区间为),(+∞-∞∈x ,他们图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)2)3)1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;21xy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1)n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnmaaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及其性质(可编辑修改word版)

1. 幂函数的图像:2. 幂函数的性质;性质函数 定义域 y R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R O奇偶性 奇 偶奇 [0,+∞)x非奇非偶 {y|y ≠0}奇 单调性 增[0,+∞) 增 (-∞,0] 减增 增(0,+∞) 减 (-∞,0) 减公共点(1,1)六 大 基 本 初 等 函 数 图 像 及 其 性 质一、常值函数(也称常数函数) y =C (其中 C 为常数);常数函数( y = C )C ≠ 0 C = 0 yOxyxO平行于 x 轴的直线y 轴本身 定义域 R定义域 R二、幂函数 y = x , x 是自变量,是常数;1) 当α为正整数时,函数的定义域为区间为 x ∈ (-∞,+∞) ,他们的图形都经过原点,并当α>1 时在原点处与 x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于 y 轴对称;2) 当α为负整数时。
函数的定义域为除去 x=0 的所有实数; 3) 当α为正有理数m 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的n定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4) 如果 m>n 图形于 x 轴相切,如果 m<n,图形于 y 轴相切,且 m 为偶数时,还跟 y 轴对称;m ,n 均为奇数时,跟原点对称;(0,1) Oxb.1.当 a > 1 时,a 值越大, y = ax在(- ∞,+ ∞)是减函数在(- ∞,+ ∞)是增函数单调性公共点奇偶性 O值域非奇非偶性质定义域(0,1) R (0,1)过点(0,1),即 x = 0 时, y = 15) 当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除 x=0 以外的一切实数。
三、指数函数 y = a x( x 是自变量, a 是常数且a > 0 , a ≠1),定义域是 R ; [无界函数]1. 指数函数的图象:2. 指数函数的性质;yyx(0,+∞) Ox1) 当 a > 1 时函数为单调增,当 0 < a < 1时函数为单调减; 2) 不论 x 为何值, y 总是正的,图形在 x 轴上方;3) 当 x = 0 时, y = 1,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质
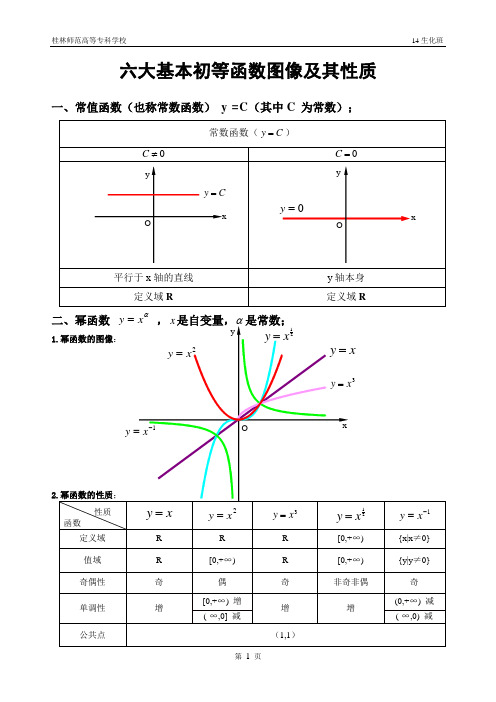
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
(完整版)六大基本初等函数图像与性质
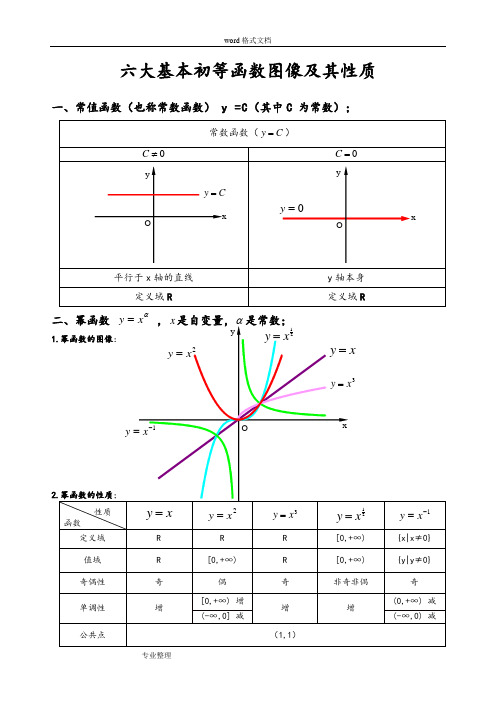
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
六大基本初等函数图像及其性质_9000
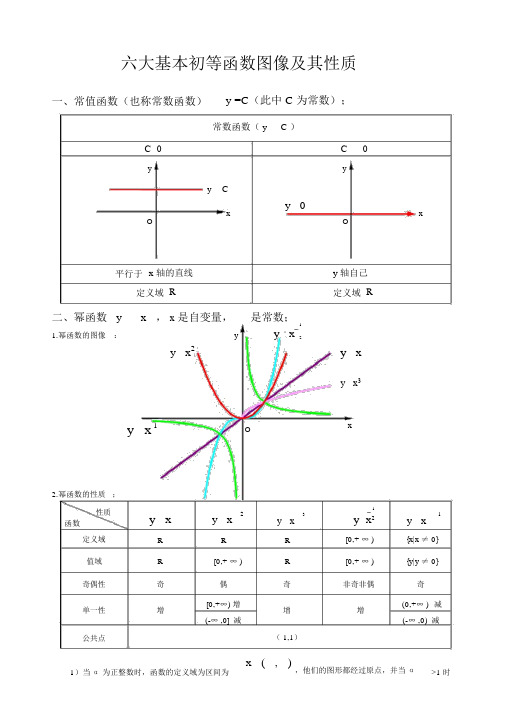
六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C(此中 C 为常数);常数函数( y C )C 0C0y yy Cx y 0xO O平行于x 轴的直线y 轴自己定义域R定义域R 二、幂函数 y x ,x是自变量,是常数;1y y x1.幂函数的图像:2y x2y xy x3y x1O x2.幂函数的性质;性质y x y x231y x1y x y x2函数定义域R R R[0,+ ∞ ){x|x ≠ 0}值域R[0,+ ∞ )R[0,+ ∞ ){y|y ≠ 0}奇偶性奇偶奇非奇非偶奇单一性增[0,+∞) 增增增(0,+∞ )减(-∞ ,0] 减(-∞ ,0)减公共点( 1,1)1)当α为正整数时,函数的定义域为区间为x ( , ),他们的图形都经过原点,并当α>1 时在原点处与x 轴相切。
且α为奇数时,图形对于原点对称;α为偶数时图形对于y 轴对称;2)当α为负整数时。
函数的定义域为除掉x=0 的全部实数;3)当α为正有理数m时,n为偶数时函数的定义域为(0, +∞),n为奇数时函数的定义域为(-n∞ ,+∞),函数的图形均经过原点和( 1 ,1);4)假如 m>n 图形于 x 轴相切,假如m<n,图形于 y 轴相切,且m 为偶数时,还跟y 轴对称; m, n均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一确实数;n 为奇数时,定义域为去除 x=0 之外的一确实数。
三、指数函数 y a x(x是自变量,a是常数且a0, a1),定义域是 R ;[ 无界函数 ]1.指数函数的图象:yy a x y a xy(a 1)(0a1)(0,1)y1(0,1)y1 O x O x2.指数函数的性质;性质y a x(a1)y a x(0 a 1)函数定义域R值域(0,+∞)奇偶性非奇非偶公共点过点 (0,1),即 x0 时,y 1单一性在(,)是增函数在(,)是减函数1 )当a 1时函数为单调增 , 当0a 1时函数为单调减;2 )不论x为何值 ,y 总是正的,图形在 x 轴上方;3 )当x 0时 , y 1, 所以它的图形通过 (0,1) 点。
六大基本初等函数图像及其性质
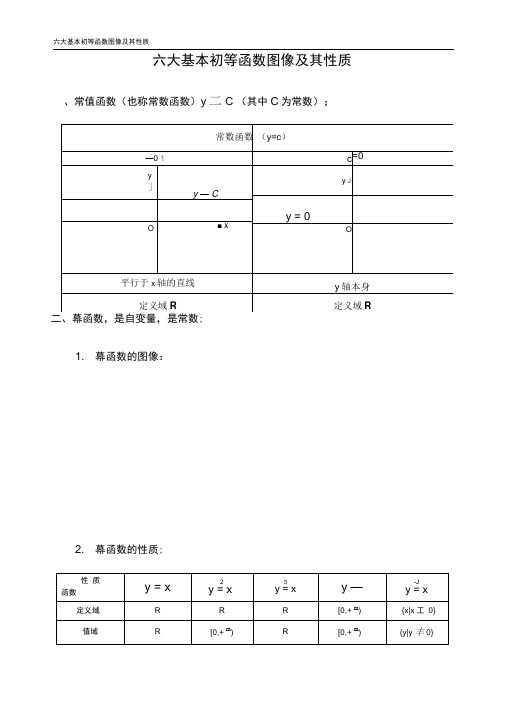
六大基本初等函数图像及其性质、常值函数(也称常数函数)y二C (其中C为常数);二、幕函数,是自变量,是常数;1. 幕函数的图像:2. 幕函数的性质;奇偶性奇偶奇非奇非偶奇[0,+ X)增增增(0,+ X )减单调性增(-X ,0]减(-X ,0)减公共点(1,1)1)当a为正整数时,函数的定义域为区间为,他们的图形都经过原点,并当a >1时在原点处与X轴相切。
且a为奇数时,图形关于原点对称;a为偶数时图形关于y轴对称;2)当a为负整数时。
函数的定义域为除去X=0的所有实数;3)当a为正有理数时,n为偶数时函数的定义域为(0, + X), n为奇数时函数的定义域为(-X,+ X),函数的图形均经过原点和(1 ,1 );4)如果m>n图形于x轴相切,如果m<n,图形于y轴相切,且m为偶数时, 还跟y轴对称;m n均为奇数时,跟原点对称;5)当a为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数(是自变量,是常数且,),定义域是R ;[无界函数]1. 指数函数的图象:2.指数函数的性质;性质函数xy = a (a > 1)xY = a (0 c a c 1)定义域 R 值域(0, + %) 奇偶性 非奇非偶公共点过点(0, 1),即 x = 0时,y = 1单调性在(-, +立)是增函数在(-°0 ,)是减函数1) 当时函数为单调增,当时函数为单调减; 2) 不论为何值,总是正的,图形在轴上方; 3) 当时,,所以它的图形通过(0,1)点。
3. (选,补充)指数函数值的大小比较; a. 底数互为倒数的两个指数函数的函数图像关于y 轴对称b. 1.当时,a 值越大,i yf(x) =2h(x) =3xO(0,1)六大基本初等函数图像及其性质的图像越靠近y 轴;四、对数函数(是常数且),定义域[无界]b.2.当时,a 值越大,的图像越远离y 轴。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:3y2.幂函数的性质;1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数yxx a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,xay =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) nm n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4)()n n n b a ab =b.根式的性质;f xxxx g ⎪⎫ ⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
六大基本初等函数图像及性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减;2)不论x 为何值,y总是正的,图形在x 轴上方;3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,xay =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4)()nn n b a ab =yxf x xxx g ⎪⎫ ⎛=1)(b.根式的性质;(1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a an m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六大基本初等函数图像及其性质
一、常值函数(也称常数函数) y =C (其中C 为常数);
α
1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;
2)当α为负整数时。
函数的定义域为除去x=0的所有实数;
3)当α为正有理数
n
m
时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);
4)如果m>n 图形于x
轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;
5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数x
a y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;
[无界函数]
1.指数函数的图象:
2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*
N ∈a ;
a.底数互为倒数的两个指数函数
x a x f =)(,x
a x f ⎪⎭
⎫
⎝⎛=1)(
的函数图像关于y 轴对称。
y 的图像越靠近y 轴;
b.2.当1
0<
<a时,a值越大,
x
a y=
的图像越远离y轴。
4.指数的运算法则(公式);
a.整数指数幂的运算性质),,0(Q n m a ∈≥;
(1) n m n m a a a +=⋅
(2) n
m n m
a
a a -=÷
(3)
()
()
m
n nm n m a
a
a ==
(4) ()
n
n
n
b
a a
b =
b.根式的性质;
(1)
()a a n
n
= ; (2)当n 为奇数时,
a a n
n =
当n 为偶数时,⎩⎨⎧<-≥==)
0(0)
(a a a a a a n
n
c.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a a
n m n
m
(2))
1,,,0(1
1*>∈>=
=-
n Z n m a a a
a
n
m
n
m n
m 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域
),0(+∞∈x [无界]
1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b =,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
对数函数
x y a log =与指数函数x a y =互为反函数,所以x y a log =的图
象与x a y =的图象关于直线
x y =对称。
2.常用对数:N 10log 的对数叫做常用对数,为了简便,N 的常用对数记作N lg 。
3.自然对数:使用以无理数7182.2=e 为底的对数叫做自然对数,为了简便,N 的自然对数N e log 简记作N ln 。
4.对数函数的图象:
1)对数函数的图形为于y 轴的右方,并过点(1,0);
2)当1>a 时,在区间(0,1),y 的值为负,图形位于x 的下方;在区间(1, +∞),y 值为正,图形位于x 轴上方,在定义域是单调增函数。
1<a 在实际中很少用到。
6.(选,补充)对数函数值的大小比较*
N ∈a ;
a.底数互为倒数的两个对数函数
x y a log =,x y a
1log =
的函数图像关于x 轴对称。
b.1. 当1>a 时,a
的图像越靠近x 轴;
x x f a log )(=
a.如果a >0,a ≠1,M >0,N >0,那么:
b.对数恒等式:
c.换底公式: (1)b
N
N a a b log log log =
(1,0≠>a a ,一般常常换为e 或10为底的对数,即N b log =
b
N b lg log =
)
(2)由公式和运算性质推倒的结论:
d.对数运算性质
(1)1的对数是零,即01log =a ;同理01ln =或01lg = (2)底数的对数等于1,即1log =a a ;同理1ln =e 或110lg =
五、三角函数
1.正弦函数
x y sin =,有界函数,定义域),(+∞-∞∈x ,值域]1,1[+-∈y
图象:五点作图法:0,
2
π,π,23π,π2
2.余弦函数x y cos =,有界函数,定义域),(+∞-∞∈x ,值域]
1,1[+-∈y
图象:五点作图法:0,2
π,π,23π,π2
3.正、余弦函数的性质;
六、反三角函数
1.反正弦函数x y arcsin =,无界函数,定义域[-1,1],值域],0[π
A.反正弦函数的概念:正弦函数x y sin =在区间⎥⎦
⎤
⎢⎣⎡-2,2ππ上的反函数称为
反正弦函数,记为x
y arcsin =
2.反余弦弦函数
x y arccos =,无界函数,定义域[-1,1],值域],0[π
B.反余弦函数的概念:余弦函数x y cos =在区间[]π,0上的反函数称为反余
4.反正切函数x y arctan =,有界函数,定义域),(+∞-∞∈x ,值域⎪⎭
⎫
⎝⎛-2,2ππ
C.反正切函数的概念:正切函数x y tan =在区间⎪⎭
⎫
⎝⎛-2,2ππ上的反函数称为
反正切函数,记为x y arctan =
5.反余切函数x arc y cot =,有界函数,定义域),(+∞-∞∈x ,值域()π,0
D.反余切函数的概念:余切函数x y cot =在区间()π,0上的反函数称为反余切函数,记为x arc y cot =
一、任意角的三角函数
在角α的终边上任取..
一点),(y x P ,记:2
2y x r +=。
正弦:r
y
=αsin 余弦:r x =αcos
正切:x
y
=
αtan 余切:y x =αcot
正割:x
r
=
αsec 余割:y r =αcsc
二、同角三角函数的基本关系式
倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα
商数关系:αααcos sin tan =,α
ααsin cos cot =
平方关系:1cos sin
22
=+αα,αα22sec tan 1=+,
αα22csc cot 1=+ 三、诱导公式
x 轴上的角,口诀:函数名不变,符号看象限;
y 轴上的角,口诀:函数名改变,符号看象限。
四、和角公式和差角公式五、二倍角公式
二倍角的余弦公式常用变形:(规律:降幂扩角,升幂缩角)
22cos 1cos 2αα+=,2
2sin 1sin 2αα+=,
α
α
ααα2cos 12sin 2sin 2cos 1tan +=-=
六、三倍角公式
七、和差化积公式
八、辅助角公式
其中:角 的终边所在的象限与点)
a所在的象限相同,
(b
,
2
2sin b a b +=
ϕ,2
2cos b
a a
+=
ϕ,a b
=ϕtan 九、三角函数的周期公式
函数)sin(ϕω+=x A y ,R x ∈及函数)cos(ϕω+=x A y ,R x ∈(A,ϕω,,为常数,且0,0>≠ωA )
周期: ω
π
2=
T
函数)tan(ϕω+=x A y ,Z k k x ∈+
≠,2
π
π(A,ϕω,,为常数,且0,0>≠ωA )
周期: ω
π
=
T 十、正弦定理
R C c
B b A a 2sin sin sin ===(R 为AB
C ∆外接圆半径) 十一、余弦定理
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
