平面直角坐标系中的面积计算(专题)

平面直角坐标系中的面积计算专题

平面直角坐标系中的面积计算知识点一：已知点的坐标求图形面积类型一：平面直角坐标系中三角形的面积①三角形有一边在坐标轴上例1：平面直角坐标系中，A(4，-4)， B(1，0)，C(6，0). 求△ABC 的面积. x yO A (4,-4)B (1,0)C (6,0)例2：平面直角坐标系中，A(0，3)， B(0，-3)，C(2，1). 求△ABC 的面积. x y123–1–2123–1–2–3OCB A②三角形有一边平行于坐标轴例3：平面直角坐标系中，A(-2，3)， B(-2，-3)，C(2，1). 求△ABC 的面积.xy –1–2–3123–1–2–3123OA （-2,3）B (-2,-3)C (2,1)③三角形没有一边平行于坐标轴变式1.保持A 、C 不动，改变点B 的位置：B (0，-3), 求△ABC 的面积. x y –1–2–3–4123–1–2–31234OA (-2,3）C (2,1）B x y –1–2–3–4123–1–2–31234O A (-2,3）C (2,1）B x y –1–2–3–4123–1–2–31234O A (-2,3）C (2,1）B练习：如图中，A 、B 两点的坐标分别为（2，3）、（4，1），求△ABO 的面积．类型二：平面直角坐标系中不规则多边形的面积例4：平面直角坐标系中，A(-3，-2)，B(3，-2)，C(1，3)，D(-2，1)，求四边形ABCD 的面积. xyO A (-3,-2)B (3,-2)C (1,3)D (-2,1)练习：如图，已知四边形ABCD 四个顶点的坐标分别是A （-5，2），B （1，5），C （5，-2），D （-4，-5）.求四边形ABCD 的面积.知识点二：已知图形面积求点的坐标例5：（1）▲ABC 的两个顶点分别为A （2，3），B （-2，0），且▲ABC 的面积为9，若点C 在x 轴上，求点C 的坐标.（2）已知A （1，0），B （0，3），点P 在x 轴上，且▲PAB 的面积为6，求点P 的坐标.（3）已知O （0，0），B （3，2），点A 在坐标轴上，且6=∆OAB S ，求A 点的坐标.练习1.如图A （﹣4，0），B （6，0），C （2，4），D （﹣3，2）．（1）求四边形ABCD 的面积；（2）在y 轴上找一点P ，使△APB 的面积等于四边形的一半．求P 点坐标．练习2.如图，已知A （﹣2，0），B （4，0），C （2，4），D （0，2）（1）求三角形ABC 的面积；（2）设P 为坐标轴上一点，若S △APC ＝S △ABC ，求P 点的坐标．练习3.如图，已知三点A （0，1），B （2，0），C （4，3）（1）求三角形ABC 的面积；（2）设点P 在坐标轴上，且三角形ABP 与三角形ABC 的面积相等，求点P 的坐标．。

专题在平面直角坐标系中求图形的面积(四大题型)(原卷版)

解题技巧提炼
1.上面题主要考查坐标与图形性质，解题的关键是明确题意，画出相应的图形，利用数形结合的思想解答．
2.由于点的位置不明确，因此在解题时要注意分情况讨论.
【变式41】已知点A（1，0），B（0，2），点P在x轴的负半轴上，且△PAB的面积为5，则点P的坐标为（）
A．（0，﹣4）B．（0，﹣8）C．（﹣4，0）D．（6，0）
（2）直接写出A1，B1，C1三点的坐标；
（3）求△ABC的面积．
【例题3】（2022春•长安区校级月考）如图所示，在平面直角坐标系中，点A（4，0），B（3，4），C（0，2），则四边形ABCO的面积为（）
A．9B．10C．11D．12
解题技巧提炼
1、当四边形的其中有一边在坐标轴上（或与坐标轴平行）时，可以用分割法；
【变式45】（2022秋•渭滨区期末）如图所示，在平面直角坐标系中，已知A（0，1）、B（2，0）、C（4，3）．
（1）在平面直角坐标系中画出△ABC，则△ABC的面积是；
（2）若点D与点C关于y轴对称，则点D的坐标为；
（3）已知P为x轴上一点，若△ABP的面积为1，求点P的坐标．
【变式46】（2022•天津模拟）如图，在平面直角坐标系中，已知A（a，0），B（b，0），其中a，b满足|a+1|+（b﹣3）2＝0．
【变式24】（2022春•雷州市期末）如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标；
（2）求出S△ABC．
【变式25】在如图所示的正方形网格中，每个小正方形的边长均为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（﹣4，5）、（﹣1，3）．
（1）请在如图所示的网格平面内画出平面直角坐标系；

平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

平面直角坐标系中如何求几何图形的面积

图1图2图3平面直角坐标系中如何求几何图形的面积一、求三角形的面积1、有一边在坐标轴上或平行于坐标轴例1：如图1，平面直角坐标系中，△ABC 的顶点坐标分别为（-3,0）、（0,3）、（0，-1），你能求出三角形ABC 的面积吗2、无边在坐标轴上或平行于坐标轴例2：如图2，平面直角坐标系中，已知点A （-3，-1）、B （1,3）、C （2，-3），你能求出三角形ABC 的面积吗归纳：求三角形面积的关键是确定某条边及这条边上的高，如果在坐标系中，某个三角形中有一条边在坐标轴上或平行于坐标轴，则根据这条边的两个顶点的坐标易求出这边的长，根据这条边的相对的顶点可求出他的高。

二、求四边形的面积例3：如图3，你能求出四边形ABCD 的面积吗分析：四边形ABCD 是不规则的四边形，面积不能直接求出，我们可以利用分割或补形来求。

归纳：会将图形转化为有边与坐标轴平行的图形进行计算。

怎样确定点的坐标一、象限点解决有关象限点问题的关键是熟记各象限的符号特征，由第一到底四象限点的符号特征分别为（+，+）、（-，+）、（-，-）、（+，-）。

例1：已知点M （a 3-9,1-a ）在第三象限，且它的坐标都是整数，则a =（）A 、1B 、2C 、3D 、0二、轴上的点解决有关轴上点问题的关键是把握“0”的特征，x 轴上点的纵坐标为0，可记为（x ，0）；y 轴上点的横坐标为0，可记为（0，y ）；原点可记为（0,0）。

例2：点P （m+3,m+1）在直角坐标系的x 轴上，则P 点的坐标为（）A 、（0，-2）B 、（2,0）C 、（4,0）D 、（0，-4）三、象限角平分线上的点所谓象限角平分线上的点，就是各象限坐标轴夹角平分线上的点。

解决这类问题的关键是掌握“y x =”的特征，一、三象限角平分线上点的横、纵坐标相等，可记为（x ，x ）；二、四象限角平分线上的点横、纵坐标互为相反数，可记为（x ，-x ）。

平面直角坐标系中三角形面积的求法(例题及对应练习)

.；.例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

《平面直角坐标系》之知坐标,求面积习题(学生版)

重点强化专题：知坐标，求面积重点强化1有一边在坐标轴上（或平行于坐标轴）的三角形的面积1．已知：在图中，已知点A、B、C的坐标，分别求三角形ABC的面积．（1）A（﹣1，0），B（3，0），C（4，﹣3）；（2）A（2，0），B（0，1），C（0，4）．重点强化2三条边均不在坐标轴上（且不平行于坐标轴）的三角形的面积2．已知三角形三个顶点坐标，求三角形面积通常有以下三种方法：方法1：直接法．计算三角形一边的长，并求出该边上的高．方法2：补形法．将三角形面积转化成若干个特殊的四边形和三角形的面积的和与差．方法3：分割法．选择一条恰当的直线，将三角形分割成两个便于计算面积的三角形．现给出三点坐标A（﹣1，4），B（2，2），C（4，﹣1），请你选择一种方法计算△ABC的面积，你的答案是S＝．3．△ABC中，A（﹣1，4），B（﹣4，﹣1），C（1，1），求△ABC的面积．4．已知点A（1，4）、B（3，﹣1），C（﹣4，﹣2），求以A、B、C三点为顶点的三角形的面积．5．如图，在直角坐标系中，描出四个点A（﹣3，﹣2），B（2，﹣2），C（﹣2，1），D（3，1），连接AB，DC，CA．（1）观察图形，线段AB和线段CD有什么数量关系和位置关系？（2）在线段AB上任意取一点P，则线段CP的最小值是多少？（3）求四边形ABCD的面积．6．如图，请在平面直角坐标系中描出下列各点：A（1，3），B（3，1），C（﹣3，1），D（﹣1，﹣1）．（1）连接AB，CD，两线段有怎样的位置关系？（2）线段CD可由线段AB经过怎样的变化得到？（3）连接AC，BD，求四边形ABDC的面积．7．在图中A（2，﹣4）、B（4，﹣3）、C（5，0），求四边形ABCO的面积．8．已知：四边形ABCD各顶点坐标为A（﹣4，﹣2），B（4，﹣2），C（3，1），D（0，3）．（1）在平面直角坐标系中画出四边形ABCD；（2）求四边形ABCD的面积．（3）如果把原来的四边形ABCD各个顶点横坐标减2，纵坐标加3，所得图形的面积是多少？9．如图，每个小正方形的边长为单位长度1．（1）写出多边形ABCDEF各个顶点A、B、C、D、E、F的坐标；（2）点C与E的坐标什么关系？（3）直线CE与两坐标轴有怎样的位置关系？难点突破知面积，求坐标10．已知点A（1，0）、B（0，2），点P在x轴负半轴上，且三角形PAB的面积为5，求点P的坐标．11．已知点A（1，0），B（0，2），若点P在y轴负半轴上，且△PAB的面积为5，求点P的坐标．12．如图所示，点A的坐标为A（0，a），将点A向右平移b个单位得到点B，其中a，b满足：（3a﹣6）2+|a+b﹣5|＝0．；（1）求点B的坐标并求△AOB的面积S△AOB＝2S△AOD？若存在，求出D点的坐标；（2）在x轴上是否存在一点D，使得S△AOB若不存在，说明理由．13．如图，在平面直角坐标系中，已知S△ABO＝8，OA＝OB，BC＝12，点P的坐标是（a，6）．（1）求△ABC三个顶点的坐标；（2）连接PA、PB，并用含字母a的式子表示△PAB的面积；（3）是否存在点P，使△PAB的面积等于△ABC的面积？如果存在，求出点P的坐标．。

平面直角坐标系中三角形面积的计算

平面直角坐标系中三角形面积的计算设直角坐标系中的三角形的三个顶点分别为A(x1,y1)，B(x2,y2)，C(x3,y3)。

我们可以利用向量的性质和行列式的方法求出三角形的面积。

首先，我们计算向量AB和向量AC的坐标分量分别为(u,v)和(w,z)。

则有：u=x2-x1v=y2-y1w=x3-x1z=y3-y1然后，根据向量的性质，可以计算向量AB与向量AC的叉积的大小，即面积的两倍：2*面积=，u*z-v*w最后，我们可以通过取绝对值并除以2来得到三角形的面积，即：面积=，u*z-v*w，/2这就是通过向量的方法计算三角形面积的基本公式。

下面我们通过一个具体的例子来演示一下计算三角形面积的过程。

设直角坐标系中的三角形的三个顶点分别为A(2,3)，B(5,6)，C(8,1)。

我们将依次计算向量AB和向量AC的坐标分量：u=5-2=3v=6-3=3w=8-2=6z=1-3=-2然后，根据公式面积=，u*z-v*w，/2，我们计算：面积=，3*(-2)-3*6，/2=，-6-18，/2=24/2=12所以，三角形ABC的面积为12平方单位。

除了向量方法，我们还可以使用行列式的方式来计算三角形的面积。

具体步骤如下：1.将三个顶点的坐标按照行列式的顺序排列，构成一个3×3的矩阵：x1y1x2y2x3y32.计算矩阵的行列式的值。

3.取行列式的绝对值并除以2，即为三角形的面积。

以上就是使用行列式方法计算三角形面积的基本步骤。

总结起来，平面直角坐标系中三角形的面积可以通过向量或行列式的方法进行计算。

这些方法都是基于向量叉积的性质和行列式的性质进行推导和计算的。

无论是哪一种方法，核心思想都是通过计算向量叉积的大小来获得三角形的面积。

如何求平面直角坐标系中三角形的面积

如何求平面直角坐标系中三角形的面积在平面直角坐标系中，求解三角形的面积是几何学中的基本问题之一。

下面将介绍两种求解平面直角坐标系中三角形面积的方法。

方法一：行列式法行列式法是一种常用的求解三角形面积的方法。

设三角形的顶点为A(x1, y1)，B(x2, y2)，C(x3, y3)。

首先将三个顶点的坐标依次排列成行：A(x1, y1) B(x2, y2) C(x3, y3)然后将A点的坐标复制到下方形成两行：A(x1, y1) B(x2, y2) C(x3, y3)A(x1, y1) B(x2, y2) C(x3, y3)接下来按照主对角线往右上方的方向连线，并将相乘的结果写在对应的线上：A(x1, y1) B(x2, y2) C(x3, y3)A(x1, y1) B(x2, y2) C(x3, y3)计算两条斜线上的乘积之和，再减去两条副对角线上的乘积之和，最后除以2即可得到三角形的面积。

行列式法的计算较为繁琐，但是适用于所有类型的三角形。

方法二：海伦公式海伦公式是通过三角形的边长来求解三角形面积的一种方法。

假设三角形的三边长度分别为a、b、c，半周长为p。

首先计算半周长p：p = (a + b + c) / 2然后套用海伦公式进行计算：面积S = √(p * (p - a) * (p - b) * (p - c))海伦公式较为简单，适用于已知三边长度的情况。

根据不同的题目要求和数据提供的形式，可以选择适合的方法进行计算。

总之，无论使用哪种方法，都可以准确求解平面直角坐标系中三角形的面积。

三角形的面积计算在实际生活中有着广泛的应用。

例如，在建筑工程中，需要计算地基的面积以确定施工方案；在地理测量学中，需要求解地理图形的面积和边长，以准确描述地理实体特征。

因此，掌握求解三角形面积的方法是十分重要的。

总结起来，通过行列式法和海伦公式，我们可以准确求解平面直角坐标系中的三角形面积。

无论是使用繁琐的行列式法，还是简便的海伦公式，都能满足求解三角形面积的需求。

平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题我们要注意其中的解题方法和解题技巧.现一、有一边在坐标轴上例1如图1，平面直角坐标系中，△ ABC的顶点坐标分别为(— 3 , 0),(0, 3),( 0,—1),你能求岀三角形ABC的面积吗？1~.解题时丄丄丄 1 1(AD+CE X DE- 2 ADX DB-M CE X BE= X( 4+6)X 5 —2 X4X 4—X^6 X 1 = 14.平面直角坐标系中的面积问题(提高篇)4、在平面直角坐标系中，△ ABC的顶点坐标分别为A (1, -1) , B (-1 ,4), C (-3 , 1), (1)求厶ABC 的面积；(2)将厶ABC先向下平移2个单位长度,再向右平移3个单位长度，求线段AB扫过的面积。

“割补法”的应用-、已知点的坐标，求图形的面积。

1、在平面直角坐标系中，△ ABC的顶点坐标分别为A (-2, -2), B (0 , -1) , C ( 1 , 1),求厶ABC 的面积。

分析：根据三个顶点的坐标特征可以看岀，△ ABC的边y轴上,由图形可得BC= 4,点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3,然后根据三角形的面积公式求解解：因为B(0,3),C(0,-1), 所以BC=3- (-1 ) =4.因为A(-3,0), 所以A点到y轴的距离，即BC边上的高为3,S iAiC=-BC^AO =丄汀恋二6二、有一边与坐标轴平行例2 如图2,三角形ABC三个顶点的坐标分别为A(4, 1), B (4, 5), C (-1 , 2), 求三角形ABC的面积.2、在平面直角坐标系中，四边形ABCD (-4, -2) B (4, -2) C (2, 2) D (-2 , 3)分析：由A (4 , 1), B (4, 5)两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的咼CD,则D点的横坐标与A点的横坐标相同，也是4,这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A, B两点的横坐标相同，所以边AB// y轴，所以AB=5-1=4.作AB边上的咼CD,则D点的横坐标为4,所以<y—X4X5 = 10所以.三、三边均不与坐标轴平行例3如图2,平面直角坐标系中，已知点A (-3，-1)，B( 1，3)，C(2,-3)，你能求岀三角形ABC的面积吗？CD=4- (-1 ) =5，TFh-llH丿丄i—『J-l]bJnNJ・rE3分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形(长方形)的上下底(长)与其中一坐标轴平行，高(宽)与另一坐标轴平行.这样，梯形(长方形)的面积容易求岀，再减去围在梯形(长方形)内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D E,则四边形ADEC为梯形.因为A (-3 , -1 ), B (1,1*7 —3) , C (2, -3 )，所以AD= 4, CE=6, DB=4, BE=1, DE= 5.所以亠-=-ABC的面积为12,求点C的坐标的各个顶点的坐标分别为A求这个四边形的面积。

初二数学平面直角坐标系面积问题

初二数学平面直角坐标系面积问题一、概述在初中数学学习中，平面直角坐标系是一个重要的概念。

在这个坐标系中，我们可以通过两个数值来确定平面上的一个点的位置，进而计算出所需图形的面积。

本文将从初二数学的角度出发，探讨平面直角坐标系下的面积问题，并为大家解析面积问题的解题思路和方法。

希望能够对同学们的学习有所帮助。

二、平面直角坐标系下的基本概念1. 坐标系平面直角坐标系由两条相互垂直的直线，它们被称为坐标轴，通常用x 和y来表示。

这两条坐标轴把平面分成了四个部分，它们分别是第一象限、第二象限、第三象限和第四象限。

2. 点的坐标在平面直角坐标系中，我们可以用一个有序数对(x, y)来表示一个点P 的坐标，其中x为点P在x轴上的坐标，y为点P在y轴上的坐标。

3. 面积的计算在平面直角坐标系中，我们可以通过连接坐标轴上的点和直线，来确定一个图形的面积。

面积的计算方法有很多种，例如利用基本几何图形的面积公式进行计算，或者利用积分的方法进行计算。

三、常见的面积计算题型1. 长方形的面积计算我们来看一个简单的例子。

如果给出了一个长方形的两个顶点的坐标，我们要计算这个长方形的面积该怎么做呢？解题思路：（1）首先计算长方形的边长，可以利用坐标点之间的距离公式进行计算。

（2）根据长方形的面积公式S=长×宽，计算出长方形的面积。

2. 三角形的面积计算另外一个常见的题型是给出三角形的三个顶点的坐标，要求计算三角形的面积。

解题思路：（1）利用三角形的面积公式S=（1/2）×底边长度×高，计算出三角形的面积。

（2）可以利用向量运算的方法进行计算，例如计算三角形的两条边的向量，然后利用向量叉乘的方法得到三角形的面积。

3. 多边形的面积计算对于给出多边形的各个顶点的坐标，要求计算多边形的面积这样的题型，我们可以采用分割成若干个三角形，再分别计算每个三角形的面积，最后将各个三角形的面积相加来得到多边形的面积。

直角坐标系中的面积问题

直角坐标系中的面积问题在平面直角坐标系中，常常要求与面积相关的问题，在解与面积相关的问题时，常常用点到x 轴、y 轴的距离或两点之间的距离，实行求解．例1 在如图1所示的方格纸中，每个小方格都是边长为1的正方形，点A 、B 是方格纸中的两个格点（即正方形的顶点），在5×5的方格纸中，找出格点C ，使△ABC 的面积为两个平方单位，则满足条件的格点C 的个数是（） A ．5 B ．4 C ．3 D ．2解析:如图2，由三角形ABC 的面积为22221=⨯⨯得点C 1、C 2、C 3，由三角形ABC 的面积为21421=⨯⨯得点C 4，由三角形ABC 的面积为221212121=⨯⨯+⨯⨯得点C 5．故满足条件的格点C 共有5个．评注:解决三角形面面积积问题的基本方法是面积公式法．例2 已知点A(0，0)，B(4，0)，点C 在y 轴上，且△ABC 的面积为5，则点C 的坐标为_______．解析：有已知点A 为原点，点B 在x 轴正上方，因为点C 在y 轴上，有两种情况，如图3，因为△ABC 的面积为5，而三角形的面积公式为高底⨯⨯21．所以△ABC的面积=AC AB ⨯⨯21，又因为A(0，0)，B(4，0)，所以AB=4，代入求得AC=25．因为点C 在y 轴上，有两种情况，∴设点C 坐标为(0，|y|)．∵AB=|4|=4，AC=|y|．又△ABC 的面积=AC AB ⨯⨯21，得.4215y ⨯⨯=∴25=y ，即25=y 或25-=y ． ∴C 点坐标为(0，25)或(0， -25)．评注：此题利用三角形的面积关系求点的坐标，解这类问题时，要会利用点的坐标求出所需线段的长度，如此题中利用点A(0，0)，B(4，0)，得出AB=4．因为点C 的位置不确定，所以在解决问题时，要考虑几种可能的情况，此题中点C 的位置有两种情况，所以求出的点C 的坐标有两个，在解题时很容易出错，应引起重视．例3 如图4，在平面直角坐标系中， △ABC 的顶点A(4，3)，B(3，1)，C(1，2)，则△ABC 的面积为_________．分析:此题求△ABC 的面积，而已知条件是△ABC 三个顶点的坐标，在解决这类问题时，通常使用转化方法，转化成规则的图形，先求出规则图形的面积，再求出△ABC 的面积，如图5，先求出长方形AEFG 的面积，再求出三个直角三角形的面积，长方形与三个直角三角形的面积差就是△ABC 的面积，从图中能够看出A(4，3)，E(1，3)，F(1，1)，G(4，1)，所以AE=3，EF=2，长方形的面积为:2×3=6， △AEC 的面积=,23312121=⨯⨯=⨯⨯EC AE △BFC 的面积=,1212121=⨯⨯=⨯⨯FC BF图3图4图5AB 图1 AB C 1C 2C 3C 5C 4图2△ABG 的面积=,1212121=⨯⨯=⨯⨯BG AG ∴△ABC 的面积=2511236=---．评注:此题求三角形的面积使用了重要的数学思想-----转化思想．通过转化把复杂的问题简单化，此题通过转化，把△ABC 补成一个长方形，先求出长方形AEFG 的面积，在求出三个直角三角形的面积，长方形与三个直角三角形的面积差就是△ABC 的面积，这样使解决问题的过程变得简单．此题还能够求求出梯形ACFG 的面积，减去二个直角三角形的面积，也能够得到△ABC 的面积．在平面直角坐标系中，解决与面积相关的问题时，要会求出点到坐标轴的距离，在求面积时，要会应用转化方法，将图形补成规则的图形或将图形分割成规则图形实行求解．。

(完整版)平面直角坐标系中的面积问题

平面直角坐标系中的面积问题
陈玲萍
问题1 已知平面直角坐标系中，点A（1，-2）， B（-4，-2），C（1,3）.
则①线段AB与x轴的位置关系平行，线段 AB的长度为 5 ； ②线段AC与y轴的位置关系平行，线段 AC的长度为 5 。
平行x轴的直线上的AB两点间的距离为：AB= xA xB 平行y轴的直线上的AC两点间的距离为：AC= yA yC
AD
44 2
8
（2）A（0,5），B（0,3），C（3,1）；
如图，过点C做CD⊥AB
∵A（0,5），B（0,3），C（3,1）
∴CD=3，AB=2
∴
SABC
1 ABCD 1 23 3
2
2
小结
平面直角坐标系中，求三角形的面积，关键在于找到平行x轴或平行y轴的线段作为规则图形的底和高。
F
∴BE=3,CF=3
∴ SABC SABD SACD
1 AD• BE 1 AD• CF
E
2
2
1 33 1 33
2
2
9
F
E
补
补
割
问题4
在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，0)，A(5，0)，B(3，4)， C(0，3),计算这个四边形的面积。
方法总结
割
割
割
补
补
问题2
• 求下列三角形的面积： • （1）A（1,4），B（0,0），C（4,0）； • （2）A（0,5），B（0,3），C（3,1）；
（1）A（1,4），B（0,0），C（4,0）；由图，过点A作AD⊥BC
∵A（1,4），B（0,0），C（4,0）
∴AD=4，BC=4

平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

小专题(四)：平面直角坐标系中图形面积的求法

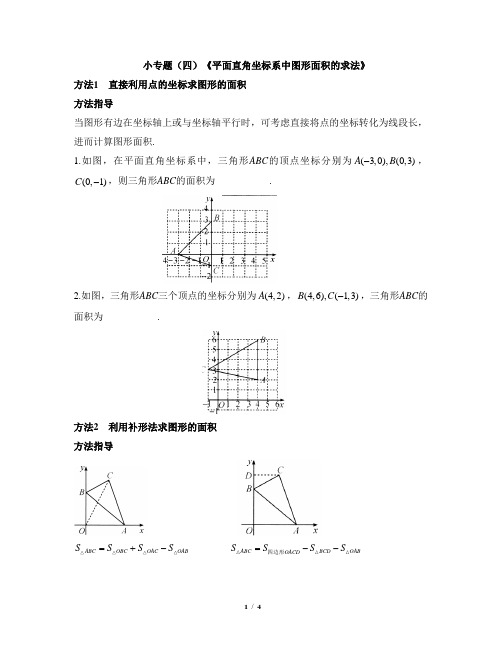
小专题（四）《平面直角坐标系中图形面积的求法》方法1 直接利用点的坐标求图形的面积方法指导当图形有边在坐标轴上或与坐标轴平行时，可考虑直接将点的坐标转化为线段长，进而计算图形面积.1.如图，在平面直角坐标系中，三角形ABC 的顶点坐标分别为(3,0),(0,3)A B -，(0,1)C -，则三角形ABC 的面积为___________.2.如图，三角形ABC 三个顶点的坐标分别为(4,2)A ，(4,6),(1,3)B C -，三角形ABC 的面积为___________.方法2 利用补形法求图形的面积方法指导ABCOBCOACOABSSSS=+- ABCBCDOABOACD SS SS=--四边形ABCACDOABOBCD SS SS=+-四边形 ABCACDBCEOABOADE SS SSS--=-四边形3.如图，在平面直角坐标系中，已知点(3,1)A --，(1,3),(2,3)B C -，你能求出三角形ABC 的面积吗？方法3 利用分割法求图形的面积ACDOACB ODCB S SS =+四边形四边形 ADEBCFABCD EFCD S SSS =++四边形四边形4.在如图所示的平面直角坐标系中，四边形OABC 各顶点的坐标分别是(0,0)O ，(4,10),(12,8),(14,0)A B C ---，求四边形OABC 的面积.方法4 根据已知图形的面积利用逆向思维求点的坐标方法指导已知坐标系中图形的面积，求点的坐标时，可将点的横（纵）坐标转化为到坐标轴的距离，利用面积来解决线段数量关系，从而求出点的坐标.5.如图，(1,0),(1,4)-，点B在x轴上，且3A CAB=.（1）点B的坐标为_____________；（2）三角形ABC的面积为_____________；（3）在y轴上是否存在点P，使以A B P，，三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由.参考答案 1.6 2.10 3.解：14.4.解：过点A 作AD x ⊥轴，垂足为D ，过点B 作BE x ⊥轴，垂足为E ，则(4,0)D -，(12,0)E -.8,10,4,8,2BE AD OD DE CE ∴=====.111()222OABC AOD BCE ABED S S S S OD AD CE BE BE AD DE ∴=++=⋅+⋅++⋅=四边形三角形三角形梯形11141028(810)8100222⨯⨯+⨯⨯+⨯+⨯=. 5.解：（1）(2,0)或(4,0)-（2）6（3）设点P 到x 轴的距离为h ，则13102h ⨯=，解得203h =.①当点P 在y 轴正半轴时，点P 的坐标为200,3⎛⎫⎪⎝⎭；②当点P 在y 轴负半轴时，点P 的坐标为200,3⎛⎫- ⎪⎝⎭.综上所述，点P 的坐标为20200,0,33⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭或.。

平面直角坐标系中的图形面积问题

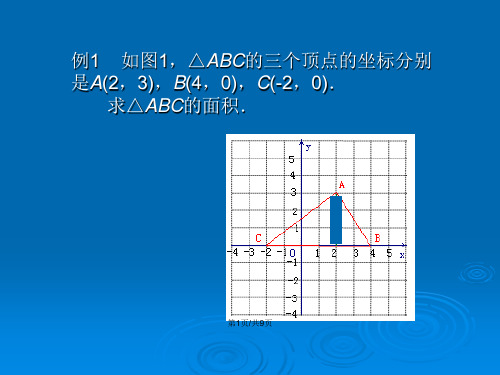
例3 如图3，平面直角坐标系中，已知 △ABC三个顶点的坐标分别是A(-3，-1)， B(1，3)，C(2，-3)．
求△ABC的面积．
第6页/共9页
例4 如图，四边形ABCD的四个顶点的坐标分别是A(4， 2)，B(4，-2)，C(0，-4)， D(0，1)．求四边形ABCD的面积．
第7页/共9页
例1 如图1，△ABC的三个顶点的坐标分别是A(2，3)，B(4，0)，C(-2，0)．
求△ABC的面积．
第1页/共9页
例1 如图1，△ABC的三个顶点的坐标分别是A(2，3)，B(4，0)，C(-2，0)．
求△ABC的面积．Zxxk
第2页/共9页
例2 如图，平面直角坐标系中，已知点A(-3，-2)，B(0，3)，C(-3，2)．
求△ABC的面积．
第3页/共9页
例2 如图，平面直角坐标系中，已知点A(-3，-2)，B(0，3)，C(-3，2)．
求△ABC的面积．
第4页/共9页
例3 如图3，平面直角坐标系中，已知 △ABC三个顶点的坐标分别是A(-3，-1)， B(1，3)，C(2，-3)．
求△ABC的面积．
第5页/共9页
例4 如图，四边形ABCD的四个顶点的坐标分别是A(4，2)，B(4，-2)，C(0，4)，D(0，1)．
Zx。xk
求四边形ABCD的面积．
第8页/共9页

专题05平面直角坐标系中求图形面积(解析版)

专题05平面直角坐标系中求图形面积类型一、直接用公式求面积例1.如图，在平面直角坐标系中，点()0,4A b 为y 轴正半轴上一点，点()3,0B b 是x 轴正半轴上一点，其中b 满足()316b +=．（1）求点A ，B 的坐标．（2）点C 为x 轴上一点，且ABC 的面积为12，求C 点的坐标．【答案】（1）()0,4A ，()3,0B ；（2）点C 的坐标为()3,0-或()9,0【解析】（1）由()316b +=得1b =，∴()04A ，，()30B ，．（2）设点C 的坐标为()0x ，，则3BC x =-，由1（）可知4OA =，∴1432ABC S x =⨯⨯-= 12，解得：9x =或3-．∴点C 的坐标为()30-，或()90，．【变式训练1】在平面直角坐标系中，已知点(),0A a ，(),0B b ，a 、b 满足方程组24a b a b +=-⎧⎨-=-⎩，（1）求A 、B 两点的坐标；（2）C 为y 轴正半轴上一点，且6ABC S = ，请求出C 的坐标．【答案】（1）A （-3，0），B （1，0）；（2）C （0，3）【解析】（1）解方程组24a b a b +=-⎧⎨-=-⎩，解得：31a b =-⎧⎨=⎩，∴A （-3，0），B （1，0）；（2）由（1）可知：AB =4，∵S △ABC =12AB •OC =6，∴12×4×OC =6，解得OC =3，∴C （0，3）．故答案为：（1）A （-3，0），B （1，0）；（2）C （0，3）类型二、割补法求面积例1.如图，三角形ABC 的面积等于（）A ．12B ．1122C ．13D ．1132【答案】D【解析】过点A 作AD x ⊥轴于D ，如图所示：由题意可得，3BO =，3OC =，6AD =，3CD =，∴6OD =，∴ABC BOC ACDBODA S S S S ∆∆∆=--梯形111()222BO AD OD BO OC CD AD=+⋅-⋅⋅-⋅⋅111(36)63336222=+⨯-⨯⨯-⨯⨯54918222=--272=，即272ABC S ∆=，故选：D ．【变式训练1】如图，连接AB 、BC 、AC ，则△ABC 的面积是（）A ．312B ．3C ．212D ．2【答案】C【解析】长方形AGDE 的面积为：3×2=6，AGC 的面积：3×1÷2=1.5，CDB △的面积：2×1÷2=1，ABE △的面积：2×1÷2=1，故ABC 的面积为：6-1.5-1-1=2.5，故答案为：C ；【变式训练2】如图，三角形ABO 中，()2,3A --，()2,1B -，A B O ''' 是ABO 平移之后得到的图形，并且O 的对应点O '的坐标为()5,4．（1）作出ABO 平移之后的图形A B O ''' ，并写出A '、B '两点的坐标分别为A '______，B '_____；（2）()00,P x y 为ABO 中任意一点，则平移后对应点P 的坐标为______．（3）求ABO 的面积；【解析】（1）如图，△A 'B 'O '即为所求，A '、B '两点的坐标分别（3，1），（7，3）．故答案为：（3，1），（7，3）．（2）点P '的坐标为（x 0+5，y 0+4）．故答案为：（x 0+5，y 0+4）．（3）S △ABO =3×4-12×2×3-12×1×2-12×4×2=4．【变式训练3】在平面直角坐标系xoy 中，△ABC 的位置如图所示，点A ，B ，C 都在格点上．（1）分别写出下列顶点的坐标：A ________；B ________；（2）请在图中画出△ABC 关于y 轴对称的图形△A ′B ′C ′；（3）计算出△ABC 的面积．【答案】（1）(-1,6)，(-2,0)；（2）见解析；（3）152【解析】（1）由图知，点A 的坐标为(-1,6)，点B 的坐标为(-2,0)，故答案为：(-1,6)，(-2,0)（2）由图得，点C 的坐标为(-4,3)，则点A 、B 、C 关于y 轴的对称点A ′，B ′，C ′坐标分别为(1,6)，(2,0)，(4,3)，依次连接A ′，B ′，C ′，即得△A ′B ′C ′，所得图形如图所示（3）过A 、C 作x 轴的垂线，垂足分别为D 、E则ABC AOD CED ADEC S S S S =-- 梯形111(36)31623222=⨯+⨯-⨯⨯-⨯⨯152=类型三、点的存在性问题例1.如图，在平面直角坐标系中，点B ，C 的坐标分别为(),2a a -、()3,2a a ，其中0a >，点A 为BC 的中点，若4BC =，解决下列问题：（1）BC 所在直线与x 轴的位置关系是；（2）求出a 的值，并写出点A ，C 的坐标；（3）在y 轴上是否存在一点P ，使得三角形PAC 的面积等于5？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）平行；（2）()1,2A ，()3,2C ；（3）存在，P 点坐标为()0,3-或()0,7【解析】（1）∵点B ，C 的坐标分别为(),2a a -、()3,2a a ，∴BC 所在直线与x 轴的位置关系是平行．故答案为：平行．（2）∵4BC =，∴()34a a --=，∴1a =，∴B （-1，2），C （3，2），∵A 为BC 的中点，∴()1,2A ．（3）存在点P ．设()0,P m ，∵2AC =，∴12252m ⨯⨯-=，∴3m =-或7.∴P 为()0,3-或()0,7．【变式训练1】如图，在直角坐标系中，已知()0,2A ，()3,0B ，()3,4C 三点．（1）求四边形AOBC 的面积；（2）是否存在点()0.5P x x ,，使2ABC AOBC S S = 四边形？若存在，求出点P 的坐标．若不存在，请说明理由．【答案】（1）9；（2）存在，()189P --,或(18,9)【解析】如图，∵34C （，），∴33CD ==．∵()34C ，，30B （，），∴404CB =-=，∴4312DCBO S =⨯=四边形．∵()04D ，，()02A ，，∴422DA =-=，∴11236322DCA S =⨯⨯=⨯= ．∵DCA AOBC DCBO S S S =- 四边形四边形，∴1239AOBC S =-=四边形．（2）由（1）得1239AOBC S =-=四边形设存在点()0.5P x x ，，使△AOP 的面积为四边形AOBC 的面积的两倍．∵△AOP 的面积=122x x ⨯⨯=，∴29x =⨯，∴18x =±∴存在点P （18，9）或（-18，-9），使△AOP 的面积为四边形AOBC 的面积的两倍．【变式训练2】如图，A （0，3）是直角坐标系y 轴上一点，动点P 从原点O 出发，沿x 轴正半轴运动，速度为每秒2个单位长度，以P 为直角顶点在第一象限内作等腰Rt △APB ．设P 点的运动时间为t 秒．（1）若AB ∥x 轴，求t 的值；（2）如图2，当t ＝2时，坐标平面内有一点M （不与A 重合）使得以M 、P 、B 为顶点的三角形和△ABP 全等，请直接写出点M 的坐标．【答案】（1）t 的值为1.5；（2）点M 的坐标为（3，7），（8，﹣3），（11，1）．【解析】（1）过点B 作BC ⊥x 轴于点C ，如图所示．∵AO⊥x轴，BC⊥x轴，且AB∥x轴，∴四边形ABCO为矩形，∴AO=BC=3，∵△APB为等腰直角三角形，∴AP=BP，∠PAB=∠PBA=45°，∴∠OAP=90°-∠PAB=45°，∴△AOP为等腰直角三角形，∴OA=OP=3，∴t=3÷2=1.5（秒），故t的值为1.5；（2）当t=2时，OP=4，①如图3，若△ABP≌△MBP，则AP=PM，过点M作MD⊥OP于点D，∵∠AOP=∠PDM，∠APO=∠DPM，∴△AOP≌△MDP（AAS），∴OA=DM=3，OP=PD=4，∴M（8，-3）；②如图，若△ABP≌△MPB，连接AM，则AP=PB=BM，∠APB=∠MBP=90︒，∴AP∥MB，且AP=MB，∴四边形APBM是平行四边形，y轴于点E，又∠APB=∠MBP=90︒，∴四边形APBM是正方形，∴AP=AM，过点M作ME⊥同理可证△AOP≌△MEA（AAS），∴OA=EM=3，OP=AE=4，∴M（3，7）；③如图，若△ABP≌△MPB，则AP=BP=BM，过点M 、B 分别作x 轴的垂线，垂足分别为点F 、G ，过点M 作MH ⊥BF 于点H ，∴四边形FGMH 是矩形，∴MH =FG ，MG =HF ，同理可证△AOP ≌△PFB ≌△BHM （AAS ），∴OA =PF =BH =3，OP =BF =MH =4，∴MG =HF =BF -BH =1，OG =OP +PF +FG =11，∴M （11，1）；综合以上可得点M 的坐标为（3，7），（8，-3），（11，1）．【变式训练3】在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为()1,0，点D 的坐标为()0,2．延长CB 交x 轴于点1A ，作第1个正方形111A B C C ；延长11C B 交x 轴于点2A ，作第2个正方形2221A B C C ，…，按这样的规律进行下去，第2021个正方形的面积是______．【答案】404235(2⨯【解析】()()1,0,0,2,A D 正方形ABCD ，1,2OA OD ∴==,,AD AB ===190,DAO ADO DAO BAA ∠+∠=︒=∠+∠1,ADO BAA ∴∠=∠190,DOA ABA ∠=∠=︒ 1,AOD A BA ∴ ∽1,AO OD A B AB ∴=15,2AO AB A B OD ∴== 正方形111A B C C，1113222A B A C ∴====⨯同理可得：22232442A B ⎛⎫=+==⨯ ⎪⎝⎭33332A B ⎛⎫= ⎪⎝⎭······20212021202132A B ⎛⎫= ⎪⎝⎭所以第2021个正方形的面积是22021404233=5.22⎡⎛⎫⎛⎫⨯⎢ ⎪ ⎪⎝⎭⎝⎭⎢⎣⎦故答案为：404235.2⎛⎫⨯ ⎪⎝⎭。

求平面直角坐标系中三角形的面积

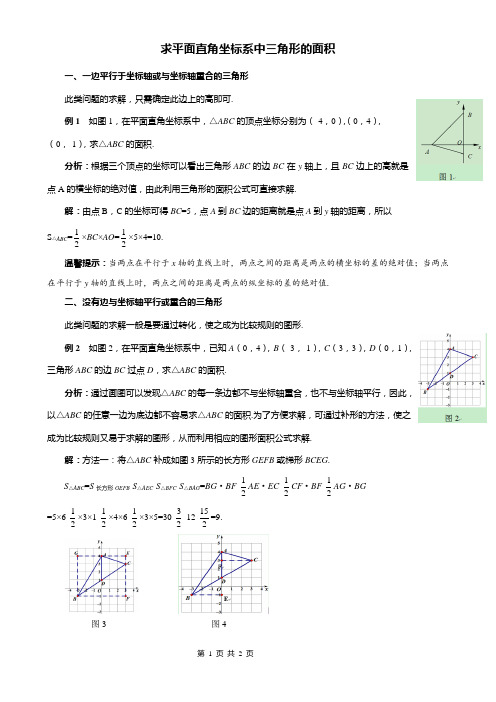
求平面直角坐标系中三角形的面积一、一边平行于坐标轴或与坐标轴重合的三角形此类问题的求解，只需确定此边上的高即可.例1 如图1，在平面直角坐标系中，△ABC的顶点坐标分别为（-4，0），（0，4），（0，-1），求△ABC的面积.分析：根据三个顶点的坐标可以看出三角形ABC的边BC在y轴上，且BC边上的高就是点A的横坐标的绝对值，由此利用三角形的面积公式可直接求解.解：由点B，C的坐标可得BC=5，点A到BC边的距离就是点A到y轴的距离，所以S△ABC=12×BC×AO=12×5×4=10.温馨提示：当两点在平行于x轴的直线上时，两点之间的距离是两点的横坐标的差的绝对值；当两点在平行于y轴的直线上时，两点之间的距离是两点的纵坐标的差的绝对值.二、没有边与坐标轴平行或重合的三角形此类问题的求解一般是要通过转化，使之成为比较规则的图形.例2 如图2，在平面直角坐标系中，已知A（0，4），B（-3，-1），C（3，3），D（0，1），三角形ABC的边BC过点D，求△ABC的面积.分析：通过画图可以发现△ABC的每一条边都不与坐标轴重合，也不与坐标轴平行，因此，以△ABC的任意一边为底边都不容易求△ABC的面积.为了方便求解，可通过补形的方法，使之成为比较规则又易于求解的图形，从而利用相应的图形面积公式求解.解：方法一：将△ABC补成如图3所示的长方形GEFB或梯形BCEG.S△ABC=S长方形GEFB-S△AEC-S△BFC-S△BAG=BG·BF-12AE·EC-12CF·BF-12AG·BG=5×6-12×3×1-12×4×6-12×3×5=30-32-12-152=9.图3 图4方法二：如图4，分割成两个三角形，根据铅垂线与水平线求三角形的面积.S△ABC= S△ABD+ S△ACD=12AD·BE+12AD·CF=12×3×3+12×3×3=92+92=9.牛刀小试：如图5，在平面直角坐标系中，△ABC的顶点坐标分别为A（2，0），B（0，4），C（-3，2），求△ABC的面积.图5答案：如图6，过点C作CD⊥x轴于点D，则S△A BC=S梯形O BC D+S△O A B-S△A C D=12×（2+4）×3+12×2×4-12×5×2=8.图6。