用旋转法………作辅助线证明平面几何题.
2018_2019学年八年级数学第15课图形与证明例题课件
失误防范
中考题中与三角形有关的综合题:
类型一:构造法添加辅助线 当题目中的结论在现有图形中难以解决时,我们自然会考虑添加辅助线, 而构造全等三角形来转化线段或角是我们常用的方法之一. 类型二:在变化的图中探究同一类问题 这类问题往往是方法的延续,而第一问是很容易入手的,因此对比第一 问,利用第一问的方法就可以解决后面的问题.
重点中学与你有约
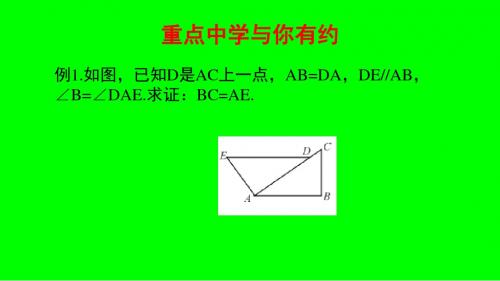
例1.如图,已知D是AC上一点,AB=DA,DE//AB, ∠B=∠DAE.求证:BC=AE.
解题技巧
解: ∵DE//AB, ∴∠CAB=∠ADE
在△ABC和△DAE中,
CAB ADE
AB
DA
B DAE
△ABC △DAE(ASA )
∴BC=AE.
掌重握要三结角论形:
2
重要结论:
全等三角
一三四二 读解悟联
关形键熟的词练性:掌质握, 直垂中求关全形直形中的角线点线系所定断全本键等的角斜线应三,,段.学理三等题.三判三边性用角之性,角是的角定角上质.形间质判形解关,,
重要方法:
综合法
举一反三
已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点 (点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足 分别为E、F,点O为AC的中点. (1)当点P与点O重合时如图1,求证:OE=OF (2)直线BP绕点B逆时针方向旋转,当点P在对角线AC上时,且 ∠OFE=30°时,如图2,猜想线段CF、AE、OE之间有怎样的数量 关系?并给予证明. (3)当点P在对角线CA的 延长线上时,且∠OFE=30° 时,如图3,猜想线段CF、 AE、OE之间有怎样的数量 关系?直接写出结论即可.
∵AB=AC, ∴∠C=∠ABC=36°,∴∠CDE=72°, ∴∠CDE=∠CED=72°,∴CD=CE, 则BC=BE+EC=AB+CD;
初中数学《利用旋转添加辅助线》讲义及练习

板块 考试要求A 级要求B 级要求C 级要求全等三角形的性质及判定会识别全等三角形掌握全等三角形的概念、判定和性质,会用全等三角形的性质和判定解决简单问题会运用全等三角形的性质和判定解决有关问题基本知识把图形G 绕平面上的一个定点O 旋转一个角度θ,得到图形G ',这样的由图形G 到G '变换叫做旋转变换,点O 叫做旋转中心,θ叫做旋转角,G '叫做G 的象;G 叫做G '的原象,无论是什么图形,在旋转变换下,象与原象是全等形.很明显,旋转变换具有以下基本性质:①旋转变换的对应点到旋转中心的距离相等; ②对应直线的交角等于旋转角.旋转变换多用在等腰三角形、正三角形、正方形等较规则的图形上,其功能还是把分散的条件盯对集中,以便于诸条件的综合与推演.重点:本节的重点是全等三角形的概念和性质以及判定,全等三角形的性质是以后证明三角形问题的基础,也是学好全章的关键。
同时全等三角形的判定也是本章的重点,特别是几种判定方法,尤其是当在直角三角形中时,HL 的判定是整个直角三角形的重点难点:本节的难点是全等三角形性质和判定定理的灵活应用。
为了能熟练的应用性质定理及其推论,要把性质定理和推论的条件和结论弄清楚,哪几个是条件,决定哪个结论,如何用数学符号表示,即书写格式,都要在讲练中反复强化重、难点知识点睛中考要求第十二讲利用旋转添加辅助线【例1】 如图,等边三角形ABC ∆与等边DEC ∆共顶点于C 点.求证:AE BD =.DECBA【解析】 ∵ABC ∆是等边三角形,∴60ACB ∠=︒,AC BC =.∴60BCD DCA ∠+∠=︒,同理60ACE DCA ∠+∠=︒,DC EC =.∴BCD ACE ∠=∠ 在BCD ∆与ACE ∆ 中, BC AC BCD ACE DC EC =⎧⎪∠=∠⎨⎪=⎩∴BCD ACE ∆∆≌,∴BD AE =.【巩固】(2008年全国初中数学联赛武汉CASIO 杯选拔赛)如图,ABD ∆和CED ∆均为等边三角形,AC BC =,AC BC ⊥.若2BE =,则CD = .图6DECBA【解析】 31-.易知CDB ∆≌CDA ∆≌EDB ∆,从而2BC AC BE ===,2AB =, 由CDA CDB ∠=∠知CD 是ABD ∆一条高的一部分,不难算出答案为31-.【例2】 (1997年安徽省初中数学竞赛题)在等腰Rt ABC ∆的斜边AB 上取两点M 、N ,使45MCN ∠=︒,记AM m =,MN x =,BN n =,则以x 、m 、n 为边长的三角形的形状是( ).A .锐角三角形B .直角三角形C .钝角三角形D .随x 、m 、n 的变化而变化MNCBAMDNCBA【解析】 如图,将CBN ∆绕点C 顺时针旋转90︒,得CAD ∆,连结MD ,则AD BN n ==,CD CN =,ACD BCN =∠∠,∴MCD ACM ACD =+∠∠∠ACM BCN =∠+∠904545MCN =-==∠. ∴MDC MNC ∆∆≌,∴MD MN x ==又易得454590DAM ∠=+︒=,∴在Rt AMD ∆中,有222m n x +=,故应选(B )例题精讲【例3】 (通州区2009一模第25题)请阅读下列材料:已知:如图1在Rt ABC ∆中,90BAC ∠=︒,AB AC =,点D 、E 分别为线段BC 上两动点,若45DAE ∠=︒.探究线段BD 、DE 、EC 三条线段之间的数量关系.小明的思路是:把AEC ∆绕点A 顺时针旋转90︒,得到ABE '∆,连结E D ', 使问题得到解决.请你参考小明的思路探究并解决下列问题:⑴ 猜想BD 、DE 、EC 三条线段之间存在的数量关系式,并对你的猜想给予证明;⑵ 当动点E 在线段BC 上,动点D 运动在线段CB 延长线上时,如图2,其它条件不变,⑴中探究的结论是否发生改变?请说明你的猜想并给予证明.图1ABCDE图2AB CDE【解析】 ⑴ 222DE BD EC =+证明:根据AEC ∆绕点A 顺时针旋转90︒得到ABE '∆ ∴AEC ABE '∆∆≌∴BE EC '=,AE AE '=,C ABE '∠=∠,EAC E AB '∠=∠ 在Rt ABC ∆中 ∵AB AC =∴45ABC ACB ∠=∠=︒ ∴90ABC ABE '∠+∠=︒ 即90E BD '∠=︒∴222E B BD E D ''+= 又∵45DAE ∠=︒∴45BAD EAC ∠+∠=︒ ∴45E AB BAD '∠+∠=︒ 即45E AD '∠=︒∴AED AED '∆∆≌ ∴DE DE '=∴222DE BD EC =+E'EDCBAFEDCB A⑵ 关系式222DE BD EC =+仍然成立证明:将ADB ∆沿直线AD 对折,得AFD ∆,连FE ∴AFD ABD ∆∆≌∴AF AB =,FD DB =FAD BAD ∠=∠,AFD ABD ∠=∠ 又∵AB AC =,∴AF AC =∵45FAE FAD DAE FAD ∠=∠+∠=∠+︒()9045EAC BAC BAE DAE DAB DAB ∠=∠-∠=︒-∠-∠=︒+∠ ∴FAE EAC ∠=∠ 又∵AE AE = ∴AFE ACE ∆∆≌∴FE EC =,45AFE ACE ∠=∠=︒ 180135AFD ABD ABC ∠=∠=︒-∠=︒∴1354590DFE AFD AFE ∠=∠-∠=︒-︒=︒ ∴在Rt DFE ∆中222DF FE DE +=即222DE BD EC =+【例4】 E 、F 分别是正方形ABCD 的边BC 、CD 上的点,且45EAF =︒∠,AH EF ⊥,H 为垂足,求证:AH AB =.CHF ED BACH FEGD BA【解析】 延长CB 至G ,使BG DF =,连结AG ,易证ABG ADF △≌△,BAG DAF =∠∠,AG AF =.再证AEG AEF △≌△,全等三角形的对应高相等(利用三角形全等可证得),则有AH AB =.【巩固】如图,正方形ABCD 的边长为1,点F 在线段CD 上运动,AE 平分BAF ∠交BC 边于点E .⑴求证:AF DF BE =+.⑵设DF x =(01x ≤≤),ADF ∆与ABE ∆的面积和S 是否存在最大值?若存在,求出此时x 的值及S .若不存在,请说明理由.FEDC BAGABC DEF【解析】 ⑴ 证明: 如图,延长CB 至点G ,使得BG DF =,连结AG .因为ABCD 是正方形,所以在Rt ADF ∆和Rt ABG ∆中,AD AB =, 90ADF ABG ∠=∠=°,DF BG =. ∴Rt Rt (SAS)ADF ABG ∆∆≌, ∴AF AG =,DAF BAG ∠=∠. 又 ∵ AE 是BAF ∠的平分线. ∴EAF BAE ∠=∠,∴DAF EAF BAG BAE ∠+∠=∠+∠. 即EAD GAE ∠=∠.∵AD BC ∥,∴GEA EAD ∠=∠, ∴GEA GAE ∠=∠,∴AG GE =. 即AG BG BE =+.∴AF BG BE =+,得证.⑵ ADF ABE S S S ∆∆=+1122DF AD BE AB =⋅+⋅.∵1AD AB ==,∴()12S DF BE =+由⑴知,AF DF BE =+,所以12S AF =.在Rt ADF ∆中,1AD =,DF x =,∴AF =∴S 由上式可知,当2x 达到最大值时,S 最大.而01x ≤≤, 所以,当1x =时,S.【巩固】如图所示,在四边形ABCD 中,AB =BC ,∠A =∠C =90°,∠B =135°,K 、N 分别是AB 、BC 上的点,若△BKN 的周长为AB 的2倍,求∠KDN 的度数.N K DCB AFNKEDCB A【解析】 延长BC 至F ,使得CF =AB ,在CF 上取点E ,使得CE =AK ,连接BD 、DE 、DF .∵AB ⊥AD ,BC ⊥CD ,AB =BC ∴Rt △ADB ≌Rt △CDB ∴AD =CD∵AD =CD ,AK =CE ,AB ⊥AD ,BC ⊥CD ∴△ADK ≌△CDE ∴DK =DE∵BK +BN +KN =2AB ,BF =BN +EF +EN =2AB ,EF =CF -CE =AB -AK =BK ∴KN =EN∴△NDK ≌△NDE∴∠KDN =∠EDN =∠CDE +∠NDC =∠CDE +∠ADK∵∠ABC =135° ∴∠KDN =12(180°-135°)=22.5° 点评:本题的辅助线可以看作是将△ADB 割下来,放到△CDF 处,从而将不规则的图形转化为规则的图形,进而利用线段之间的等量关系求解.【例5】 在等边ABC ∆的两边AB ,AC 所在直线上分别有两点M ,N ,D 为ABC ∆外一点,且60MDN ∠=︒,120BDC ∠=︒,BD CD =,探究:当点M ,N 分别在直线AB ,AC 上移动时,BM ,NC ,MN 之间的数量关系及AMN ∆的周长与等边ABC ∆的周长L 的关系.图③图②图①ABCD MNABCD MNN M D CBA⑴如图①,当点M ,N 在边AB ,AC 上,且DM =DN 时,BM ,NC ,MN 之间的数量关系式__________;此时LQ=__________⑵如图②,当点M ,N 在边AB ,AC 上,且DN DM ≠时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;⑶如图③,当点M ,N 分别在边AB ,CA 的延长线上时,若AN =x ,则Q =_________(用x ,L 表示)【解析】 B M +NC =MN ;32=LQ EABC DM N(2)猜想:仍然成立证明:如图,延长AC 至E ,使CE =BM ,连接DE ,120BD CD BDC =∠=︒且, 30DBC DCB ∴∠=∠=︒由ABC ∆是等边三角形,90MBD NCD ∴∠=∠=︒,()MBD ECD SAS ∴∆∆≌ ,DM DE BDM CDE ∴=∠=∠,60EDN BDC MDN ∴∠=∠-∠=︒ 在MDN ∆与EDN ∆中 DM DE MDN EDN DN DN =⎧⎪∠=⎨⎪=⎩()MDN EDN SAS ∴∆∆≌ MN NE NC BM ∴==+AMN ∆的周长Q AM AN MN =++=()()AM BM AN NC +++=2AB AC AB += 而等边ABC ∆的周长3L AB = 23Q L ∴= (3)223x L +【巩固】(1)如图25-1,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD .求证:EF =BE +FD ;FED CBA(2) 如图25-2在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD , (1)中的结论是否仍然成立?不用证明. FED CBAF EDCBA(3) 如图25-3在四边形ABCD 中,AB =AD ,∠B +∠ADC =180°,E 、F 分别是边BC 、CD 延长线上的点,且∠EAF =12∠BAD , (1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.GFED CBAGFEDCBA【解析】 证明:延长EB 到G ,使BG =DF ,联结AG .∵∠ABG =∠ABC =∠D =90°, AB =AD , ∴△ABG ≌△ADF .∴AG =AF , ∠1=∠2.∴∠1+∠3=∠2+∠3=∠EAF =12∠BAD .∴∠GAE =∠EAF . 又AE =AE ,∴△AEG ≌△AEF . ∴EG =EF . ∵EG =BE +BG . ∴EF = BE +FD(2) (1)中的结论EF = BE +FD 仍然成立.(3)结论EF =BE +FD 不成立,应当是EF =BE -FD 证明:在BE 上截取BG , 使BG =DF ,连接AG . ∵∠B +∠ADC =180°, ∠ADF +∠ADC =180°, ∴∠B =∠ADF . ∵AB =AD ,∴△ABG ≌△ADF .∴∠BAG =∠DAF ,AG =AF .∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =12∠BAD .∴∠GAE =∠EAF . ∵AE =AE ,∴△AEG ≌△AEF . ∴EG =EF ∵EG =BE -BG【例6】 (2005年四川省中考题)如图,等腰直角三角形ABC 中,90B =︒∠,AB a =,O 为AC 中点,EO OF ⊥.求证:BE BF +为定值.OBEC F A 4321OB ECF A【解析】 连结OB 由上可知,1290+∠=︒∠,2390∠+=∠,13∠=∠,而445C =∠=︒∠,OB OC =.∴OBE OCF ∆∆≌,∴BE FC =,∴BE BF CF BF BC a +=+==.【巩固】等腰直角三角形ABC ,90ABC =︒∠,AB a =,O 为AC 中点,45EOF =︒∠,试猜想,BE 、BF 、EF 三者的关系.OBE C FA OB EG C F A【解析】 如图,过点O 作OG OE ⊥,交BC 于G ,连结OB ,易知OGC OBE ∆∆≌,∵BE CG =,又∵EO OG =,45EOF FOG =∠=∠,OF OF =, ∴OEF OGF ∆∆≌,∴EF FG =∴BE BF EF CG BF FG AB a ++=++==又∵90B =︒∠,∴BE 、BF 、EF 又存在另一关系式222BF BE EF +=【例7】 如图所示.正方形ABCD 中,在边CD 上任取一点Q ,连AQ ,过D 作DP ⊥AQ ,交AQ 于R ,交BC 于P ,正方形对角线交点为O ,连OP ,OQ .求证:OP ⊥OQ .QRPOD CBA【解析】 欲证OP ⊥OQ ,即证明∠COP +∠COQ =90°.然而,∠COQ +∠QOD =90°,因此只需证明∠COP =∠DOQ 即可.这归结为证明△COP ≌△DOQ ,又归结为证明CP =DQ ,最后,再归结为证明△ADQ ≌△DCP 的问题.证 在正方形ABCD 中,因为AQ ⊥DP ,所以,在Rt △ADQ 与Rt △RDQ 中有∠RDQ =∠QAD .所以,在Rt △ADQ 与Rt △DCP 中有AD =DC ,∠ADQ =∠DCP =90°,∠QAD =∠PDC , 所以△ADQ ≌△DCP (ASA ),DQ =CP .又在△DOQ 与△COP 中,DO =CO ,∠ODQ =∠OCP =45°, 所以△DOQ ≌△COP (SAS ),∠DOQ =∠COP .从而∠POQ =∠COP +∠COQ =∠DOQ +∠COQ =∠COD =90°, 即OP ⊥OQ .说明 (1)利用特殊图形的特殊性质,常可发现有用的条件,如正方形对角线互相垂直,对角线与边成45°角,及OA =OB =OC =OD 等均在推证全等三角形中被用到.(2)两个三角形的全等与对应元素相等,这两者互为因果,这是利用全等三角形证明问题的基本技巧.【巩固】如图,正方形OGHK 绕正方形ABCD 中点O 旋转,其交点为E 、F ,求证:AE CF AB +=.54321OHBE DK G CFA【解析】 正方形ABCD 中,1245∠==︒∠,OA OB =而3490∠+=︒∠,4590∠+=︒∠ ∴35=∠∠,∴AOE BOF ∆∆≌∴AE BF =,∴AE FC BF FC BC AB +=+==【例8】 (2004河北)如图,已知点E 是正方形ABCD 的边CD 上一点,点F 是CB 的延长线上一点,且EA AF ⊥. 求证:DE BF =.D CBEFA【解析】 证明:因为四边形ABCD 是正方形,所以AB AD =,90BAD ADE ABF ︒∠=∠=∠=.因为EA AF ⊥,所以90BAF BAE BAE DAE ︒∠+∠=∠+∠=,所以BAF DAE ∠=∠,故Rt ABF ∆≌Rt ADE ∆,故DE BF =.【巩固】如图所示,在四边形ABCD 中,90ADC ABC ∠=∠=︒,AD CD =,DP AB ⊥于P ,若四边形ABCD的面积是16,求DP 的长.PDC BAABCDEP【解析】 如图,过点D 作DE DP ⊥,延长BC 交DE 于点E ,容易证得ADP CDE ∆∆≌(实际上就是把ADP∆逆时针旋转90︒,得到正方形DPBE )∵正方形DPBE 的面积等于四边形ABCD 面积为16,∴4DP =.【例9】 已知:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.求证:AN BM =.M D NEC BFA【解析】 ∵ACM ∆、CBN ∆是等边三角形,∴MC AC =,CN CB =,ACN MCB ∠=∠ ∴ACN MCB ∆∆≌,∴AN BM =【点评】此题放在例题之前回忆,此题是旋转中的基本图形.【巩固】如图,B ,C ,E 三点共线,且ABC ∆与DCE ∆是等边三角形,连结BD ,AE 分别交AC ,DC于M ,N 点.求证:CM CN =.NMEDCBA【解析】 ∵ABC ∆与DCE ∆都是等边三角形∴BC AC =,CD CE =及60ACB DCE ∠=∠=︒ ∵B ,C ,E 三点共线∴180BCD DCE ∠+∠=︒,180BCA ACE ∠+∠=︒ ∴120BCD ACE ∠=∠=︒ 在BCD ∆与ACE ∆中 BC AC BCD ACE DC EC =⎧⎪∠=∠⎨⎪=⎩∴BCD ACE ∆∆≌, ∴CAN CBM ∠=∠∵120BCD ACE ∠=∠=︒,60BCM NCE ∠=∠=︒ ∴60ACD ∠=︒在BCM ∆与ACN ∆中 60BC AC BCM ACN CBM CAN =⎧⎪∠==︒⎨⎪∠=∠⎩∴BCM ACN ∆∆≌,∴CM CN =.【巩固】已知:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.求证:CF 平分AFB ∠.M D NEC BFAGM H D NEC BF A【解析】 过点C 作CG AN ⊥于G ,CH BM ⊥于H ,由ACN MCB ∆∆≌,利用AAS 进而再证BCH NCD ∆∆≌,可得到CG CH =,故CF 平分AFB ∠.【巩固】如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.请你证明: ⑴AN BM =; ⑵DE AB ∥;⑶CF 平分AFB ∠.M D NEC BFA【解析】 此图是旋转中的基本图形.其中蕴含了许多等量关系.60MCN ∠=与三角形各内角相等,及平行线所形成的内错角及同位角相等; 全等三角形推导出来的对应角相等… 推到而得的:AFC BFC ∠=∠;AN BM =,CD CE =,AD ME =,ND BE =; AM CN ∥,CM BN ∥;DE AB ∥ACN MCB ∆∆≌,ADC MCE ∆∆≌,NDC BEC ∆∆≌; DEC ∆为等边三角形.⑴∵ACM ∆、CBN ∆是等边三角形,∴MC AC =,CN CB =,ACN MCB ∠=∠ ∴ACN MCB ∆∆≌,∴AN BM =⑵由ACN MCB ∆∆≌易推得NDC BEC ∆∆≌,所以CD CE =,又60MCN ∠=, 进而可得DEC ∆为等边三角形.易得DE AB ∥.⑶过点C 作CG AN ⊥于G ,CH BM ⊥于H ,由ACN MCB ∆∆≌,利用AAS 进而再证BCH NCD ∆∆≌,可得AFC BFC ∠=∠,故CF 平分AFB ∠.【例10】 如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形,D 是AN 中点,E 是BM 中点,求证:CDE ∆是等边三角形.M DNECBA【解析】 ∵ACN MCB ∆∆≌,∴AN BM =,ABM ANC ∠=∠ 又∵D 、E 分别是AN 、BM 的中点,∴BCE NCD ∆∆≌,∴CE CD =,BCE NCD ∠=∠∴60DCE NCD NCE BCE NCE NCB ∠=∠+∠=∠+∠=∠= ∴CDE ∆是等边三角形【巩固】(2008年全国初中数学竞赛海南区初赛)如下图,在线段AE 同侧作两个等边三角形ABC ∆和CDE ∆(120ACE ∠<°),点P 与点M 分别是线段BE 和AD 的中点,则CPM ∆是( )PMBC DEAA .钝角三角形B .直角三角形C .等边三角形D .非等腰三角形【解析】 易得ACD BCE ∆∆≌.所以BCE ∆可以看成是ACD ∆绕着点C 顺时针旋转60︒而得到的.又M 为线段AD 中点,P 为线段BE 中点,故CP 就是CM 绕着点C 顺时针旋转60°而得.所以CP CM =且,60PCM ∠=°,故CPM ∆是等边三角形,选C .【例11】 平面上三个正三角形ACF ,ABD ,BCE 两两共只有一个顶点,求证:EF 与CD 互相平分.FEDBCA【解析】 连接DE 与DF∵DBA EBC ∠=∠,BAD CAF ∠=∠ ∴DBE ABC ∠=∠,BAC DAF ∠=∠ ∴在DBE ∆与ABC ∆中 DB AB DBE ABC BE BC =⎧⎪∠=∠⎨⎪=⎩∴(SAS)DBE ABC ∆∆≌ ∴DE CA FC == 在D FA ∆与BCA ∆中 DA BA DAF BAC AF AC =⎧⎪∠=∠⎨⎪=⎩∴(SAS)DFA BCA ∆∆≌ ∴DF BC EC ==∴DECF 为平行四边形, ∴EF ,CD 互相平分.【例12】 已知:如图,ABC ∆、CDE ∆、EHK ∆都是等边三角形,且A 、D 、K 共线,AD DK =.求证:HBD ∆也是等边三角形.EKHCDBAMAB DCH KE【解析】 连结EB ,∵CE CD =,CE EA =,BE AD =,所以BE AD =,并且BE 与AD 的夹角为60︒, 延长EB 交AK 于M ,则360300EBH BHD HDE BED HDM MDE MED ∠=︒-∠-∠-∠=︒-∠-∠-∠ ()180********HDM MDE MED HDM HDK =︒-∠+︒-︒-∠-∠=︒-∠=.又因为HK AD BE ==,BH HD =. 所以BEH DKH ∆∆≌. 所以HK HE =,EHD EHD DHK BHE ∠=∠+∠=∠.【例13】 (1997年安徽省竞赛题)如图,在△ABC 外面作正方形ABEF 与ACGH ,AD 为△ABC 的高,其反向延长线交FH 于M ,求证:(1)CF BH =;(2)MH MF =M EFHGD CBA【解析】 证明△ABH ≌△AFC ;(2)作P MD FP 于⊥,Q MD HQ 于⊥,先证△AFP ≌△BAD ,△ACD ≌△HAQ ,再证△FPM ≌△HQM【巩固】(2008年怀化市初中毕业学业考试试卷)如图,四边形ABCD 、DEFG 都是正方形,连接AE 、CG .求证:AE CG =.G FE DCBA【解析】 ∵ADC EDG ∠=∠∴CDG ADE ∠=∠ 在CDG ∆和ADE ∆中 CD AD CDG ADE DG DE =⎧⎪∠=∠⎨⎪=⎩∴CDG ADE ∆∆≌ ∴AE CG =【巩固】以△ABC 的两边AB 、AC 为边向外作正方形ABDE 、ACFG ,求证:CE =BG ,且CE ⊥BG .OGFEDCBA 【解析】 易证△AEC ≌△ABG ,故∠ACE =∠AGB ,又AC ⊥AG ,∠AOG =∠BOC ,故CE ⊥BG .【例14】 (北京市初二数学竞赛试题) 如图所示,在五边形ABCDE 中,90B E ∠=∠=︒,AB CD AE ===1BC DE +=,求此五边形的面积.EDCBAF EDCBA【解析】 我们马上就会想到连接AC 、AD ,因为其中有两个直角三角形,但又发现直接求各三角形的面积并不容易,至此思路中断. 我们回到已知条件中去,注意到1BC DE +=,这一条件应当如何利用?联想到在证明线段相等时我们常用的“截长补短法”,那么可否把BC 拼接到DE 的一端且使EF BC =呢(如图所示)?据此,连接AF ,则发现ABC ∆≌AEF ∆,且1FD =,AF AC =,AE AB =,ADF ∆是底、高各为1的三角形,其面积为12,而ACD ∆与AFD ∆全等,从而可知此五边形的面积为1.【巩固】(江苏省数学竞赛试题)如图,已知五边形ABCDE 中,∠ABC =∠AED =90°,AB =CD =AE =BC +DE =2.求该五边形的面积.EDCBAFEDCBA【解析】 延长CB 至F ,使得BF =DE ,连接AF 、AC 、AD .∵∠ABC =∠AED =90°,AB =AE ,BF =DE ∴△ABF ≌△AED ∴AF =AD∵CD = BC +DE =BC +BF =CF ,AC =AC ∴△ACF ≌△ACD ∵AB =CD =CF =2∴该五边形的面积为16.点评:本题可看作将五边形ABCDE 分割成三块,通过割补重新组合成一个规则的图形.【巩固】(希望杯全国数学邀请赛初二第二试试题) 在五边形ABCDE 中,已知AB AE =,BC DE CD +=,180ABC AED ∠+∠=,连接AD .求证:AD 平分CDE ∠.EDCBAFEDCBA【解析】 连接AC .由于AB AE =,180ABC AED ∠+∠=.我们以A 为中心,将ABC ∆逆时针旋转到AEF ∆的位置.因AB AE =,所以B 点与E 点重合,而180AEF AED ABC AED ∠+∠=∠+∠=,所以D 、E 、F 在一条直线上,C 点旋转后落在点F 的位置,且AF AC =,EF BC =. 所以DF DE EF DE BC CD =+=+=. 在ACD ∆与AFD ∆中,因为AC AF =,CD FD =,AD AD =, 故ACD ∆≌AFD ∆,因此ADC ADF ∠=∠,即AD 平分CDE ∠.【例15】 (2008山东)在梯形ABCD 中,AB CD ∥,90A ∠=︒,2AB =,3BC =,1CD =,E 是AD 中点,试判断EC 与EB 的位置关系,并写出推理过程.ABCDE FE DCBA【解析】 延长BE 交CD 延长线于点F .E ∵是AD 中点,DE AE =∴,AB CD ∵∥,90A ∠=︒,90EDF EAB ∠=∠=︒∴,ABE DFE ∠=∠ 在AEB ∆和FED ∆中, ABE DFE EAB EDF AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∵ AEB FED ∆∆∴≌,FE BE =∴又2,3,1AB BC CD ===∵,CF BC =∴ 在FCE ∆和BCE ∆中, FC BC CE CE FE BE =⎧⎪=⎨⎪=⎩∵ FCE BCE ∆∆∴≌,CE EB ⊥∴【习题1】如图,已知ABC ∆和ADE ∆都是等边三角形,B 、C 、D 在一条直线上,试说明CE 与AC CD+相等的理由.EDCBA【解析】 ∵AC AB =,CAE BAD ∠=∠,AE AD =∴AEC ADB ∆∆≌ ∴CE BD =又∵BD BC CD AC CD =+=+ ∴CE AC CD =+【习题2】(湖北省黄冈市2008年初中毕业生升学考试)已知:如图,点E 是正方形ABCD 的边AB 上任意一点,过点D 作DF DE ⊥交BC 的延长线于点F .求证:DE DF =.FEDCBA【解析】 ∵ADC EDF ∠=∠∴ADE CDF ∠=∠ 在ADE ∆和CDF ∆中 DAE DCF AD CDADE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADE CDF ∆∆≌ ∴DE DF =【习题3】如图,正方形ABCD 的边长为1,AB 、AD 上各存一点P 、Q ,若△APQ 的周长为2,求∠PCQ 的度数.Q P DCBAQP FDCBA【解析】 把△CDQ 绕点C 旋转90°到△CBF 的位置,CQ =CF .∵AQ +AP +QP =2,家庭作业又AQ +QD +AP +PB =2,∴QD +BP =QP .又DQ =BF ,∴PQ =PF .∴QCP FCP ∆∆≌.∴∠QCP =∠FCP . 又∵∠QCF =90°,∴∠PCQ =45°.【习题4】已知:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.CG 、CH 分别是ACN ∆、MCB ∆ 的高.求证:CG CH =.HG NM C BA【解析】 由ACN MCB ∆∆≌,利用AAS 进而再证BCH NCD ∆∆≌,可得到CG CH =.【备选1】(北京市数学竞赛试题,天津市数学竞赛试题) 如图所示,ABC ∆是边长为1的正三角形,BDC∆是顶角为120的等腰三角形,以D 为顶点作一个60的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.NM DCBA NM ED C BA【解析】 如图所示,延长AC 到E 使CE BM =.在BDM ∆与CDE ∆中,因为BD CD =,90MBD ECD ∠=∠=,BM CE =, 所以BDM CDE ∆∆≌,故MD ED =.因为120BDC ∠=,60MDN ∠=,所以60BDM NDC ∠+∠=. 又因为BDM CDE ∠=∠,所以60MDN EDN ∠=∠=.在MND ∆与END ∆中,DN DN =,60MDN EDN ∠=∠=,D M D E =, 所以MND END ∆∆≌,则NE MN =,所以AMN ∆的周长为2.【备选2】在等腰直角ABC ∆中,90ACB ∠=,AC BC =,M 是AB 的中点,点P 从B 出发向C 运动,MQ MP ⊥ 交AC 于点Q ,试说明MPQ ∆的形状和面积将如何变化.月测备选APMCQ BAP MC QB【解析】 连接CM .因为AC BC =且90ACB ∠=,所以45B ∠=.因为M 是AB 的中点,所以90AMC BMC ∠=∠=,45ACM ∠=且CM BM =,则ACM B ∠=∠. 因为MQ MP ⊥,所以90QMC CMP PMB ∠=-∠=∠,所以QCM PBM ∆∆≌, 所以QM PM =.因此MPQ ∆是等腰直角三角形,在P 的运动过程中形状不变. MPQ ∆的面积与边MP 的大小有关.当点P 从B 出发到BC 中点时,面积由大变小; 当P 是BC 中点时,三角形的面积最小;P 继续向点C 运动时,面积又由小变大.【备选3】如图,正方形ABCD 中,FAD FAE ∠=∠.求证:BE DF AE +=.FED CBA FEDMCBA【解析】 延长CB 至M ,使得BM D F =,连接AM .易证得:ABM ADF ∆∆≌,从而可得:AFD BAF EAF BAE BAM BAE EAM ∠=∠=∠+∠=∠+∠=∠, AM B EAM ∠=∠,故AE EM BE BM BE DF ==+=+.【备选4】等边ABD ∆和等边CBD ∆的边长均为1,E 是BE AD ⊥上异于A D 、的任意一点,F 是CD 上一点,满足1AE CF +=,当E F 、移动时,试判断BEF ∆的形状.DFE CBA【解析】 由条件1AE CF +=,且1DF CF +=,得AE DF =.因为AB DB =,60A BDF ∠=∠=,所以ABE DBF ∆∆≌, 因此BE BF =,ABE DBF ∠=∠.因为60EBF EBD DBF EBD ABE ABD ∠=∠+∠=∠+∠=∠=, 所以BEF ∆为等边三角形.。
用旋转法………作辅助线证明平面几何题.

用旋转法………作辅助线证明平面几何题旋转法就是在图形具有等邻边特征时,可以把图形的某部分绕等邻边的公共端点,旋转另一位置的引辅助线的方法。
1、旋转方法主要用途是把分散的元素通过旋转集中起来,从而为证题创造必要的条件。
2、旋转时要注意旋转中心、旋转方向、旋转角度的大小(三要素:中心、方向、大小);3、旋转方法常用于竺腰三角形、等边三角形及正方形等图形中。
例1:例2 已知,在Rt ABC 中;∠BAC=90︒;D为BC边上任意一点,求证:2AD2=BD2+CD2.证明:把ABD绕点A逆时钍方向旋转90︒,得∆ACE,则ABD≅∆ACE,∴BD=CE,∠B=∠ACE;∠BAD=∠CAE, AD=AE。
又∠BAC=90︒;∴∠DAE=90︒所以: D E2=AD2+AE2=2AD2。
因为:∠B+∠ACB=90︒所以:∠DCE=90︒CD2+CE2=DE2=2AD2即: 2AD2=BD2+CD2。
注:也可以把ADC顺时针方向旋转90︒来证明。
注CD已知,P 为等边ABC 内一点,PA=5,PB=4,PC=3,求∠BPC 的度数。
证明:把ABP 绕点B 顺时钍方向旋转90︒,得∆CBD ,则ABP ≅∆CBD ,∴, ∠ABP=∠CBD ,所以 ∠BAP+∠PBC=∠CBD+∠PBC=60︒,所以 BPD 为等边三角形。
∠PBD=60︒所以: C D 2=PD 2+PC 2。
因为: ∠DPC=90︒所以: ∠BPC=∠BPD+∠DPC=60︒+90︒=150︒注:也可以把CAP 绕点C 逆时针方向旋转60︒来证明。
DC例3:如图:在正方形ABCD 中,E 为AD 边上一点,BF 平分∠CBE 交CD 于F 点。
求证:BE=CF+AE证明:把ABE 绕点B 顺时针方向旋转90︒得BCN 。
则:ABE ≅BCN ,所以:∠ABE=∠CBN ,BE=BN ,AE=CN 。
因为:四边形ABCD 是正方形,所以:CD AB ,∠NFB=NBF因为:∠ABF=∠ABE+∠EBF ,∠NBF=∠NBC+∠CBF ,而:∠EBF=∠FBC ;∠NBF=∠NFB 所以:BN=NF=CN+CF 所以:BE=AE+CF 。
几何证明题辅助线的添加-平移、旋转、翻折的应用

几何证明题中的辅助线添加
——平移、旋转、翻折的应用
一、图形的平移
平移的特征是把线段、直线、三角形等等图形 从一个地方移动到另一个地方,通过平移可以 将图形中一些分散的条件汇集到一起,也可以 把不太明朗的关系明朗化。特别是对于有些条 件比较隐蔽的几何题,往往能起到“柳暗花明 又一村”的效果。由于线段或直线在平移过程 中保持着线段的长短和角的大小不变,这一结 论对于将题目中的有用条件集中到一起从而能 比较容易的添加出辅助线以达到解题的目的很 有好处。
例4、如图四,已知△ABC中,点M是
BC边上的中点,过M作∠BAC的平分线
AD的平行线交AB于F,交CA的延长线于
E点。
E
求证:BF=CE
A F
B
MD
C
N
例5、设P为等边三角形ABC内的一 点,且PA=5,PB=4,PC=3,
求此等边三角形的边长.
A
E
P
B
C
D 图五
例6、在等腰直角三角形ABC中E、D 分别是直角边BC、AC上的点,且 CE=CD。过C、D作AE的垂线交斜边 AB于L、K,求证:BL=LK.
F
C
E
D
B
L
K
A
图六
三、图形的翻折
翻折就是将图形中的一部分沿着一条直线 进行翻折。通过翻折可以构造出轴对称图 形并充分利用轴对称图形的性质进行解题。 例如等腰三角形、等腰梯形等等。它的基 本特点是各个对称点到对称轴的距离相等, 因此利用图中的已知相等线段并以其对称 轴为对称轴构造轴对称图形是一种常见的 辅助线添加方法。
A
B
E
FC
图九 D
A
D
巧用旋转法解几何题资料讲解

巧用旋转法解几何题将一个图形绕着某一点旋转一个角度的图形变换叫做旋转,由旋转的性质可知旋转前后的图形全等,对应点到旋转中心的连线所组成的夹角等于旋转角。
旋转法是在图形具有公共端点的相等的线段特征时,可以把图形的某部分绕相等的线段的公共端点,旋转另一位置的引辅助线的方法,主要用途是把分散的元素通过旋转集中起来,从而为证题创造必要的条件。
旋转方法常用于等腰三角形、等边三角形及正方形等图形中。
现就旋转法在几何证题中的应用举例加以说明,供同学们参考。
例1.如图,在Rt△ABC中,∠C=90°,D是AB的中点,E,F分别AC和BC上,且DE⊥DF,求证:EF2=AE2+BF2分析:从所证的结论来看,令人联想到勾股定理,但注意到EF,AE,BF三条线段不在同一个三角形中,由于D是中点,我们可以考虑以D为旋转中心,将BF旋转到和AE相邻的位置,构造一个直角三角形,问题便迎刃而解。
证明:延长FD到G,使DG=DF,连接AG,EG∵AD=DB,∠ADG=∠BDF∴⊿ADG≌⊿BDF(SAS)∴∠DAG=∠DBF,BF=AG∴AG∥BC∵∠C=90°∴∠EAG=90°∴EG2=AE2+AG2=AE2+BF2∵DE⊥DF∴EG=EF∴EF2=AE2+BF2例2,如图2,在⊿ABC中,∠ACB=90°,AC=BC,P是⊿ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数.分析:题目已知条件中给出了三条线段的长度和一个直角,但已知的三条线段不在同一三角形中,故可考虑通过旋转变换移至一个三角形中,由于⊿ACB是等腰直角三角形,宜以直角顶点C为旋转中心。
解:作MC⊥CP,使MC=CP,连接PM,BM∵∠ACB=90°,∠PCM=90°∴∠1=∠2∵AC=BC , ∴⊿CAP ≌⊿CBM (SAS )∴MB=AP=3∵PC=MC ,∠PCM=90°∴∠MPC=45°由勾股定理PM==22MC PC =22PC =22, 在⊿MPB 中,PB 2+PM 2=(22)2+12=9=BM 2∴⊿MPB 是直角三角形∴∠BPC=∠CPM+∠MPB=45°+90°=135°例3,如图3,直角三角形ABC 中,AB=AC ,∠BAC=90°,∠EAF=45°,求证:EF 2=BE 2+CF 2分析:本题求证的结论和例1十分相似,无法直接用勾股定理,可通过旋转变换将BE ,CF 转移到同一个直角三角形中,由于⊿BAC 是等腰直角三角形,不妨以A 为旋转中心,将∠BAE 和∠CAF 合在一起,取零为整。
小学平面几何常考题型总结(含解题套路)

小学平面几何常考题型总结(含解题套路)小学曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
规则图形的面积及周长都有相应的公式直接计算,家长应确保孩子对这些计算公式烂熟于心。
实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算,一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
先看三道例题感受一下:例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米. 解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积. 例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如:下图,求阴影部分的面积。
102条作几何辅助线的规律,以后再也不怕了!

102条作几何辅助线的规律,以后再也不怕了!几何中,同学们最头疼的就是做辅助线了,所以,今天数姐整理了做辅助线的102条规律,从此,再也不怕了!规律1.如果平面上有n(n≥2)个点,其中任何三点都不在同一直线上,那么每两点画一条直线,一共可以画出n(n-1)条.规律2.平面上的n条直线最多可把平面分成〔n(n+1)+1〕个部分.规律3.如果一条直线上有n个点,那么在这个图形中共有线段的条数为n(n-1)条.规律4.线段(或延长线)上任一点分线段为两段,这两条线段的中点的距离等于线段长的一半.规律5.有公共端点的n条射线所构成的交点的个数一共有n(n-1)个.规律6.如果平面内有n条直线都经过同一点,则可构成小于平角的角共有2n(n-1)个.规律7.如果平面内有n条直线都经过同一点,则可构成n(n-1)对对顶角.规律8.平面上若有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形一共可作出n(n-1)(n-2)个.规律9.互为邻补角的两个角平分线所成的角的度数为90°.规律10.平面上有n条直线相交,最多交点的个数为n(n-1)个.规律11.互为补角中较小角的余角等于这两个互为补角的角的差的一半.规律12.当两直线平行时,同位角的角平分线互相平行,内错角的角平分线互相平行,同旁内角的角平分线互相垂直.规律13.已知AB∥DE,如图⑴~⑹,规律如下:规律14.成“8”字形的两个三角形的一对内角平分线相交所成的角等于另两个内角和的一半.规律15.在利用三角形三边关系证明线段不等关系时,如果直接证不出来,可连结两点或延长某边构造三角形,使结论中出现的线段在一个或几个三角形中,再利用三边关系定理及不等式性质证题.注意:利用三角形三边关系定理及推论证题时,常通过引辅助线,把求证的量(或与求证有关的量)移到同一个或几个三角形中去然后再证题.规律16.三角形的一个内角平分线与一个外角平分线相交所成的锐角,等于第三个内角的一半.规律17.三角形的两个内角平分线相交所成的钝角等于90o加上第三个内角的一半.规律18.三角形的两个外角平分线相交所成的锐角等于90o减去第三个内角的一半.规律19.从三角形的一个顶点作高线和角平分线,它们所夹的角等于三角形另外两个角差(的绝对值)的一半.注意:同学们在学习几何时,可以把自己证完的题进行适当变换,从而使自己通过解一道题掌握一类题,提高自己举一反三、灵活应变的能力.规律20.在利用三角形的外角大于任何和它不相邻的内角证明角的不等关系时,如果直接证不出来,可连结两点或延长某边,构造三角形,使求证的大角在某个三角形外角的位置上,小角处在内角的位置上,再利用外角定理证题.规律21.有角平分线时常在角两边截取相等的线段,构造全等三角形.规律22.有以线段中点为端点的线段时,常加倍延长此线段构造全等三角形.规律23.在三角形中有中线时,常加倍延长中线构造全等三角形.规律24.截长补短作辅助线的方法截长法:在较长的线段上截取一条线段等于较短线段;补短法:延长较短线段和较长线段相等.这两种方法统称截长补短法.当已知或求证中涉及到线段a、b、c、d有下列情况之一时用此种方法:①a>b②a±b = c③a±b = c±d规律25.证明两条线段相等的步骤:①观察要证线段在哪两个可能全等的三角形中,然后证这两个三角形全等。
平面几何辅助线之旋转专题

平面几何辅助线之旋转专题类型一:060造等边的边长,求内部一点是等边如图ABC ,5PB ,4PA ,3PC ,ABC P ,.1∆===∆的度数求若外一点是等边如图APB ,5PC ,4PB ,3PA ,ABC P ,,2∠===∆2220AC BC DC :,30BCD ,AD BD AB ,ABCD ,,3=+=∠==求证中四边形如图类型二:旋转090,造垂直的面积求四边形的长度为另一条对角线都是直角和其中和直角三角形分为等腰直角三角形被对角线四边形如图ABCD ,2AC ,C A ,CBD ABD BD ABCD ,,4∠∠的长求为一边作正方形以中如图PD ,ABCD AB ,4PB ,2PA ,45APB ,PAB ,,50===∠∆GHCG :)2(DFDE :)1(,H AB CG ,EF G ,F BC ,DE DF ,AC E ,AB D ,90ACB ,BC AC ,ABC ,,60==⊥=∠=∆证明证明于点交延长的中点为点于交直线任意一点上是直线若的中点为中如图CEAF BE :ABEFB ,AD F ,CD ABCD E ,,7==∠求证平分且上的点是边上任意一点的边是正方形如图的面积求四边形若为等腰直角三角形求证连接得到顺时针旋转绕点将中已知如图ACED ,2AC ,1BC )2(ACD :)1(CE,CD ,AED ,90A ABC ,135ACB ,ABC ,,800==∆∆∆=∠∆类型三:旋0180,造中心对称______,,86,O ,O ,ABCD ,,9则阴影部分的面积为时和长分别为当菱形的两条对角线的分成阴影和空白部分点的三条直线将菱形过是两条对角线的交点是菱形四边形如图的度数求边上的中线为中在如图BAC ,AC AD ,BC AD ,AC 2AB ,ABC ,,10∠⊥=∆的长度求出线段若不变则说明变化规律若变化的长度是否发生变化线段在移动过程中试问当动点于点作于点交连接且的延长线上在线段动点不重合与点点上在线段动点连接线段擦去折痕的条件下在如图的长求边的面积比为与若连接交于点已知折痕与边如图点处边上的落在使得顶点折叠将矩形的一条边已知矩形EF ,,,?EF ,N M,E,BP MF F,PB MN PM,BN ,AB N )A P,M (AP M BP,OP,AO,,(1),(2)CD 4,:1PDA OCP OA,OP,AP,,O BC ,)1(,P CD B ,ABCD ,8AD ABCD ,11⊥=∆∆=类型四:大角夹半角.______,AC AF 3AE :,AB 2AD ,)3(2FHAE :H,AD CH C 2AB,AD ,(2)ACAF AE ACF,BCE :AB,AD ,(1))F(E,AD AB,,C 60,ABCD 60,)120BAD (ABCD 120,,120000=+==⊥==+∆≅∆==∠t t 则的值为常数探究得若如图深入探究求证于点作过点若如图类比发现②①求证若如图初步尝试不包括线段的端点于点在的两直线分别交线段较短的直角边和斜边所重合角的顶点始终与点且所在平面内旋转在平行四边形的直角三角板如图放置将一块含进行探究的平行四边形为某学习小组对有一内角数学活动课上?AMN )2(NCBM MN :)1(,MN ,N AC ,M AB ,60D ,120BDC ,BDC ,3ABC ,,1300的周长为多少求证连接于点交于点使其两边分别交角为顶点作一个以且是等腰三角形的等边三角形是边长为如图∆+==∠∆∆类型五:旋转任意角它说明理由的差使它的面积等于形以已知点为顶点的多边请你在图中确定一个连接中如图,S S ,,CE ,AC AB ,AE AD ,DAE BAC ,ABC ,,14ADE ABC 0∆∆-===∠=∠∆a 的长求连接且面积之比为菱形使菱形为边作一个菱形以线段延长线上的任意一点对角线是菱形点如图DG ,DG ,5106AF 8,EC 5,:2ABCD,~AEFG ,AEFG AE ,CA ABCD E ,,15==的长求线段时②当①求证于点交延长如图时逆时针旋转绕点当正方形请说明理由若不成立请证明若成立成立吗如图时逆时旋转绕点当正方形成立此时边上分别在是正方形四边形是等腰直角三角形如图BG ,2AD ,4AB CFBD :,G CF BD ,,45A ADEF (2),:,?CF BD ,,)90(0A ADEF (1)CF BD CF,BD ,AC AB,F D,,ADEF ,ABC ,,16000==⊥=<<⊥=∆θθ的值求值时为最大当在旋转过程中逆时针方向旋转绕点将正方形若连接作正方形的中点是点是等腰直角三角形已知如图AF ,AE ,,D DEFG ,2DE BC ,AE ,DEFG ,BC D ,90BAC ,ABC ,,170===∠∆,?MN DN BM,,A MAN (2),?MN DN BM,,DN BM A MAN ,(1)MNDN BM ,DN BM A AMN ,N,M,)(DC ,CB ,A MAN ,45MAN ,ABCD ,,180请直接写出你的猜想系之间又有怎样的数量关和线段旋转到如图的位置时绕点当并加以证明写出猜想之间有怎样的数量关系和线段时旋转到绕点当如图易证时旋转到绕点当如图于点或它们的延长线它的两边分别交顺时针旋转绕点中正方形已知∠≠∠=+=∠∠=∠并证明关系请写出它们之间的数量若不成立请证明若成立中的结论是否仍然成立且上的点分别边中在四边形如图不用证明中的结论是否仍然成立上的点且分别是边中在四边形如图求证且上的点分别是边中在正方形拓展,,:,?)1(,BAD 21EAF ,CD BC,F E,,180ADC B ,AD AB ,ABCD ,)3(?)1(,BAD 21EAF CD BC,F E,,180D B ,AD AB ,ABCD ,)2(FD BE EF :,BAD 21EAF ,CD BC,F E,,90D B ,AD AB ,ABCD )1(,000∠=∠=∠+∠=∠=∠=∠+∠=+=∠=∠=∠=∠=类型一:旋造等边,60031225)23()3234(CD AD AC ,ACD R ,323CD PC PD 23PC 21CD ,30CPD DAP ,AP CD C 150PQB AQP AQB APC 90PQB 5PB ,3QB ,4PQ ,PQB 4AP PQ ,60AQP APQ 3PC QB ,4AP AQ ,60PAQ ,APC AQB ,PQ AQB,60A APC ,:,122222200000+=++=+=∆=-====∠⊥=∠+∠=∠=∠=∠===∆===∠∆=====∠∠=∠∆∆中在因此则的延长线于点交作过点故中在从而是等边三角形故则连接得到逆时针旋转绕点等如图【答案】解t 000000306090APB ,90BPM 3MP ,5BM ,4PB PACMAB ,PAC MAB AMP 60MAP ,MA PA ,MP ,MAB 60A PAC ,:,2=-=∠=∠∴===∴∆≅∆∠=∠∴∆∴=∠=∆∆为等边三角形由旋转可知连接得到逆时针旋转绕点将如图【答案】解222222000000AC BC DC ACDE ,BC CE DE CE DC ,DCE R 906030BCE BCD DCE 60BCE CEBE BC ,BCE ACDE ,60CBE ,BE BC CE ,DBF 60B ABC ,:,3=+===+∆∴=+=∠+∠=∠∴=∠∴==∆∴==∠=∴∆∆ 又中在即是等边三角形连接得到顺时针旋转绕点将如图【答案】证明t 类型二:旋造垂直,9002222S S 'ACC ACC'AC'AC C'D,C,180ABC ADC ADC ADC 'CDC :'C C ,D B ,90A ABC ,:,4'ACC ABCD 00=÷⨯==∴∆∴=∴=∠+∠=∠+∠=∠∆四边形的面积是等腰直角三角形又在同一条直线上则有点到重合与使点选择绕将三角形如图【答案】解 5242PB 'PP B 'P PD 2'PP ,2PA 90PB 'P ,45'APP ,90'PAP A'P PA ,B P'PD ,AB 'P PAD AB 'P 90A PAD ,ABCD ,:,522220000=+=+==∴===∠=∠=∠∴==≅∆∆∆ 可得得到旋转顺时针绕点可将为正方形因为四边形如图【答案】解GHCG GDGH HDGGHD 90GDC HDG ,90GCD GHD 90CDH ABCD CDGGCD DGCG FGEG DG EF G ,90EDF FGEG CG EF G ,90ACB DG,)2(DFDE CDFADE CDF ADE CD AD DCF A CDF ADE R CDFADE 90CDF EDC EDF DEDF 90CDF 45DAE DCF ,90EDC EDA ABCD BCAC BDAD CD BCAC ,AB D ,90ACB CD,)1(:,600000000=∴=∠∴∠=∠∴=∠+∠=∠+∠∴=∠∴⊥∠=∠∴=∴==∴=∠==∴=∠=∴∆≅∆∴⎪⎩⎪⎨⎧∠=∠=∠=∠∆∆∠=∠∴=∠+∠=∠∴⊥==∠=∠=∠+∠∴⊥∴===∴==∠ 又的中点为的中点为连接如图中和在又的中点为连接如图【答案】证明t CEAF CE CG EG BE GEBG EBGFBC 5BC//AD EBGFBC 43423221CGAF ,31,G 5BCGABF BCG ,90B BAF ,:,70+=+==∴∠=∠∴∠=∠=∠∴∠=∠∠+∠=∠+∠∴∠=∠∴∠=∠=∠=∠∠=∠∴∆≅∆∴∆∆ 即得到点逆时针旋转绕将如图【答案】证明221122212221DE CD 21AD AC 21S S S 1BC DE 90ADC ADE CDE 135ADE ,)1(22AD AC CD 2AD AC ,45ACD ADC ACD ,:)2(ACD ADAC ,90CAD AEDABC 90ABC AED ,:)1(,8CDE ACD ADEC 022000+=⨯⨯⨯+⨯⨯=⋅+⋅=+=∴===∠-∠=∠∴=∠=+=∴===∠=∠∴∆∆∴==∠∴∆≅∆∴∆≅∆∆∆四边形知由是等腰直角三角形如图解是等腰直角三角形得到的旋转如图证明【答案】 类型三:旋造中心对称,180012122421O 248621,86:12,9故答案为阴影部分的面积点是菱形两条对角线的交菱形的面积和分别为菱形的两条对角线的长解析【答案】=⨯=∴=⨯⨯=∴ 00001209030EAC ABAE BAC 30BAE BE AB 21,2BE AB ,2AC AB 90EAC E BEAC EDBADC DCDB ,EDB ADC ,DE DA EDB ADC DCDB ,BC AD 90EAC ,AC AD BE ,AD DE ,E AD ,:,10=+=∠+∠=∠∴=∠∴==∴==∠=∠∴=∴∆≅∆∴=∠=∠=∆∆=∴=∠∴⊥=即中和在平分连接使到点延长如图【答案】解52, EF ,N M,,)1(52PB 21EF 5448PB 90C 8,BC 4,PC :(1)PB 21QB 21PQ 21QF EQ EF QB 21QF )AAS (NFB MFQ NB MQ BNF QMF BFN QFM NFB MFQ BNFQMF AN //MQ PQ 21EQ PQME ,MQ MP QMBN ,PM BN MQMP MQPABP APB AN//MQ ,AB AP ,Q PB ,AN //MQ ,,EF )2(10CD 102OP AP AB 5:4)8(90C ,PCO R 8CO ,OP 4AD 21CP 2141DA CP PA OP 4:1PDA OCP PDA~OCP CD 32902190B APO 903190D C ABCD ,)1(:,112202220它的长度为的长度不变线段在移动过程中当点的条件下在中的结论可得由中和在于点交作如图的长度不发生变化线段的长为边解得由勾股定理得中在则设的面积比为与又由折叠可得是矩形四边形如图【答案】解∴==∴=+=∴=∠===+=+=∴=∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠∠=∠∆∆∠=∠∴=∴⊥==∴==∴∠=∠=∠∴=∴===∴=+-==∠∆-====∴===∴∆∆∆∆∴∠=∠∠=∠∴=∠+∠∴=∠=∠=∠+∠∴=∠=∠∴ x x x t x x类型四:大角交半角2FHAE CHACFH AE HCF~ACE ACECHF 60ECF 60ACH 30CAD 90ACD BAC 90ACD AD CD AC 32CH AH AC ADCH 3DH AD AH 42AB AD 3CH ,2CD ,DH ,:(2)ACAB BE AE AF AE AFBE ACF,BCE ACFBCE ACFBCE AC BC CAFB ACF BCE ACFBCE 60ACE ACF ACE BCE 60ECF ACBC ,60ACB ,60CAD B ACD ,ABC ABAD 60B D 120BAD ,ABCD ,:)1(,1202222200000=∴=∴∆∆∴∠=∠∴=∠=∠∴=∠∴=∠=∠∴=∠∴=+∴=+=∴⊥=-=∴==∴=====∴∴∆≅∆∆≅∆∴⎪⎩⎪⎨⎧∠=∠=∠=∠∆∆∠=∠∴=∠+∠=∠+∠∴=∠==∠=∠=∠∴∆∆∴==∠=∠∴=∠ xxx x 由题意得,设如图证明+=+=②中和在都是等边三角形是平行四边形四边形①如图证明【答案】7732123314AC AF 3AE 3414AM 3HN 3AH FN 33HN 3AHN AM EM )FN NH AH (3)AM EM (3AF AE 3212AH ,33AM a3,HC CM HM ,22CN HC 30CHN AHM 90M ,60MAH ,3EM ,3CM ,6FN ,NC 31EM FN CM CN 3CNCM AB AD CN AD CM AB EMFN CM CN CEM~CFN 90CNF M AECCFN 180CFN AFC 180AFC EAEC 180EAF ECF H AD CM ,M BA ,BABA CM ,N AD CN ,7)3(000故答案为则设=3,=交于点与延长线于交于作如图==+∴=-+=-++==-++-====∴==-===∴=∠=∠∴=∠=∠======∴=∴⋅⋅=∴∆∆∴=∠=∠∠=∠∴=∠+∠=∠+∠∴=∠+∠⊥⊥a a a a a HN a a b a a6AC AB AN CN MB AM MN AN AM :AMN CNMB BF MB MF MN )SAS (DMF DMN DN DF NDM FDM DM DM DMF DMN 60CDN BDM 60MDN CNBF ,DN DF ,CDN BDF CDNBDF BDF120D CND ,90DCA DBA 60BCA BAC ABC 3ABC 30DBC BCD 120BDC ,BDC :)1(,13000=+=+++=++∆∴+=+==∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆=∠+∠∴=∠==∠=∠∴∆≅∆∴∆∆=∠=∠∴=∠=∠=∠∴∆=∠=∠∴=∠∆的周长是中和在得到逆时针旋转绕点将如图得等边三角形是边长为且是等腰三角形证明【答案】 类型五:旋转任意角ADEABC ADEABD ACE ABD ADEABD ABCE BCED ACEAVBD 0ADE ABC S S S S S S S S S S S S CAE,BAD AC AB CAE BAD AE AD CAE BAD CAEBAD DACDAE DAC BAC DAE BAC :S S BCED BD,:,14∆∆∆∆∆∆∆∆∆∆∆∆-=--+=--=∴=∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∠-∠=∠-∠∴=∠=∠=四边形四边形中和则在即理由的差的面积等于则四边形连接如图【答案】解α26BE DG 2615OB OE BE EOB R 13)10(OA AB OB AOB R ,AC BD ABCD 10AB 2AE ,5:2AB :AE 5OA AE OE 268AC EC AE ,32AC OA 6AC 5106AF 5:2AG :AF 5:2ABCD,~AEFG BEDG BAE DAB A DAG ,ABCD ~AEFG ,O AC BD ,:,1522222222==∴=+=+=∆∴=-=-=∆⊥=∴===+=∴=-=-==÷=∴=∴==∴=∴∆∠∆∴中在中在中菱形又且又且面积之比为菱形菱形的度数可以得到顺时针旋转绕点将菱形于点交连接如图【答案】解t t CFBD )SAS (CAF BAD AFAD CAF BAD ACAB CAF BAD CAFBAD DACDAF CAF DACBAC BAD 90DAF BAC ,AF AD ,AC AB ,ADEF ,ABC ,:BCF )1(,160=∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∴∠-∠=∠∠-∠=∠=∠=∠==∴∆中和在是正方形四边形是等腰直角三角形如图理由成立【答案】5108CG BC BG BGC R CG3843104CG CM BA BM CMG ~BMA 3104AM AB BM 38344AM AC CM 34AB 31AM 31CN FN FCN tan AB AM ABM tan ABM R 24AC AB BC ,3AN AC CN ,4AB AC ,ABC 1AE 21FN AN 2DE AD AE 2DE AD ,ADEF ,N AC FN ,:CFBD 90BAC BGC CMG~BMA CMGBMA GCMABM CAFBAD ,M AC BG ,:)2(222222220=-=∆∴=∴=∴∆∆=+==-=-=∴==∴====∠∆∴=+==-=∴==∆===∴=+=∴==⊥⊥∴=∠=∠∴∆∆∴∠=∠∠=∠∴∆≅∆中,在中在中在等腰直角中在正方形于点作过点如图②解于点交设如图①证明t t F 1323EF AE AF AEF R 90E ,DEFG 321DE AD AE ,1BC 21AD ,2BC ,BC D ,90BAC ,ABC ,AE ,AE D ,E D,A,,:,17222200=+=+=∆∴=∠=+=+===∴==∠∆中在中正方形此时的中点是点是等腰直角三角形的长最大上时在线段且点三点在一条直线上当如图【答案】解tFDBE EF BGBE EG EFEG AEFAEG AEAE EAFGAE BAD 21EAF EAD DAF EAD BAG AFAG ,DAF BAG ADFABG ADAB ADFB 180ADC ADF ,180ADC B AG,DF BG ,BG BE ,:FDBE EF ,FD BE EF )3(,FD BE EF )1)(2(FDBE EF BGBE EG EFEG AEFAEG AEAE EAFGAE BAD21EAF EAFBAD 323121,AF AG ADFABG ADAB ,90D ABC ABG AG,DF BG ,G EB ,)1(,MNBM DN ,AEN AMN ,ADE ABM ,AE ,MB DE DC ,)2(,,AEN AMN ,ADE ABM ,BM DE ,AE ,E ND ,,MN DN BM )1(:,18000-=∴-=∴=∴∆≅∆∴=∠=∠∴∠=∠=∠+∠=∠+∠∴=∠=∠∴∆≅∆∴=∠=∠∴=∠+∠=∠+∠=-=+=+=+=∴+==∴∆≅∆∴=∠=∠∴=∠=∠-∠=∠+∠=∠+∠∴∠=∠=∴∆≅∆∴==∠=∠=∠==-∆≅∆∆≅∆=∆≅∆∆≅∆==+ 连接使上截取在如图证明应当是不成立结论仍然成立中的结论又连接使到延长如图【答案】拓展可得到结论同理再证易证连接上截取在如图即可得出结论再证易证使连接到延长如图【答案】解类型一:旋造等边,60031225)23()3234(CD AD AC ,ACD R ,323CD PC PD 23PC 21CD ,30CPD DAP ,AP CD C 150PQB AQP AQB APC 90PQB 5PB ,3QB ,4PQ ,PQB 4AP PQ ,60AQP APQ 3PC QB ,4AP AQ ,60PAQ ,APC AQB ,PQ AQB,60A APC ,:,122222200000+=++=+=∆=-====∠⊥=∠+∠=∠=∠=∠===∆===∠∆=====∠∠=∠∆∆中在因此则的延长线于点交作过点故中在从而是等边三角形故则连接得到逆时针旋转绕点等如图【答案】解t 000000306090APB ,90BPM 3MP ,5BM ,4PB PACMAB ,PAC MAB AMP 60MAP ,MA PA ,MP ,MAB 60A PAC ,:,2=-=∠=∠∴===∴∆≅∆∠=∠∴∆∴=∠=∆∆为等边三角形由旋转可知连接得到逆时针旋转绕点将如图【答案】解222222000000AC BC DC ACDE ,BC CE DE CE DC ,DCE R 906030BCE BCD DCE 60BCE CEBE BC ,BCE ACDE ,60CBE ,BE BC CE ,DBF 60B ABC ,:,3=+===+∆∴=+=∠+∠=∠∴=∠∴==∆∴==∠=∴∆∆ 又中在即是等边三角形连接得到顺时针旋转绕点将如图【答案】证明t 类型二:旋造垂直,9002222S S 'ACC ACC'AC'AC C'D,C,180ABC ADC ADC ADC 'CDC :'C C ,D B ,90A ABC ,:,4'ACC ABCD 00=÷⨯==∴∆∴=∴=∠+∠=∠+∠=∠∆四边形的面积是等腰直角三角形又在同一条直线上则有点到重合与使点选择绕将三角形如图【答案】解 5242PB 'PP B 'P PD 2'PP ,2PA 90PB 'P ,45'APP ,90'PAP A'P PA ,B P'PD ,AB 'P PAD AB 'P 90A PAD ,ABCD ,:,522220000=+=+==∴===∠=∠=∠∴==≅∆∆∆ 可得得到旋转顺时针绕点可将为正方形因为四边形如图【答案】解GHCG GDGH HDGGHD 90GDC HDG ,90GCD GHD 90CDH ABCD CDGGCD DGCG FGEG DG EF G ,90EDF FGEG CG EF G ,90ACB DG,)2(DFDE CDFADE CDF ADE CD AD DCF A CDF ADE R CDFADE 90CDF EDC EDF DEDF 90CDF 45DAE DCF ,90EDC EDA ABCD BCAC BDAD CD BCAC ,AB D ,90ACB CD,)1(:,600000000=∴=∠∴∠=∠∴=∠+∠=∠+∠∴=∠∴⊥∠=∠∴=∴==∴=∠==∴=∠=∴∆≅∆∴⎪⎩⎪⎨⎧∠=∠=∠=∠∆∆∠=∠∴=∠+∠=∠∴⊥==∠=∠=∠+∠∴⊥∴===∴==∠ 又的中点为的中点为连接如图中和在又的中点为连接如图【答案】证明t CEAF CE CG EG BE GEBG EBGFBC 5BC//AD EBGFBC 43423221CGAF ,31,G 5BCGABF BCG ,90B BAF ,:,70+=+==∴∠=∠∴∠=∠=∠∴∠=∠∠+∠=∠+∠∴∠=∠∴∠=∠=∠=∠∠=∠∴∆≅∆∴∆∆ 即得到点逆时针旋转绕将如图【答案】证明221122212221DE CD 21AD AC 21S S S 1BC DE 90ADC ADE CDE 135ADE ,)1(22AD AC CD 2AD AC ,45ACD ADC ACD ,:)2(ACD ADAC ,90CAD AEDABC 90ABC AED ,:)1(,8CDE ACD ADEC 022000+=⨯⨯⨯+⨯⨯=⋅+⋅=+=∴===∠-∠=∠∴=∠=+=∴===∠=∠∴∆∆∴==∠∴∆≅∆∴∆≅∆∆∆四边形知由是等腰直角三角形如图解是等腰直角三角形得到的旋转如图证明【答案】 类型三:旋造中心对称,180012122421O 248621,86:12,9故答案为阴影部分的面积点是菱形两条对角线的交菱形的面积和分别为菱形的两条对角线的长解析【答案】=⨯=∴=⨯⨯=∴ 00001209030EAC ABAE BAC 30BAE BE AB 21,2BE AB ,2AC AB 90EAC E BEAC EDBADC DCDB ,EDB ADC ,DE DA EDB ADC DCDB ,BC AD 90EAC ,AC AD BE ,AD DE ,E AD ,:,10=+=∠+∠=∠∴=∠∴==∴==∠=∠∴=∴∆≅∆∴=∠=∠=∆∆=∴=∠∴⊥=即中和在平分连接使到点延长如图【答案】解52, EF ,N M,,)1(52PB 21EF 5448PB 90C 8,BC 4,PC :(1)PB 21QB 21PQ 21QF EQ EF QB 21QF )AAS (NFB MFQ NB MQ BNF QMF BFN QFM NFB MFQ BNFQMF AN //MQ PQ 21EQ PQME ,MQ MP QMBN ,PM BN MQMP MQPABP APB AN//MQ ,AB AP ,Q PB ,AN //MQ ,,EF )2(10CD 102OP AP AB 5:4)8(90C ,PCO R 8CO ,OP 4AD 21CP 2141DA CP PA OP 4:1PDA OCP PDA~OCP CD 32902190B APO 903190D C ABCD ,)1(:,112202220它的长度为的长度不变线段在移动过程中当点的条件下在中的结论可得由中和在于点交作如图的长度不发生变化线段的长为边解得由勾股定理得中在则设的面积比为与又由折叠可得是矩形四边形如图【答案】解∴==∴=+=∴=∠===+=+=∴=∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠∠=∠∆∆∠=∠∴=∴⊥==∴==∴∠=∠=∠∴=∴===∴=+-==∠∆-====∴===∴∆∆∆∆∴∠=∠∠=∠∴=∠+∠∴=∠=∠=∠+∠∴=∠=∠∴ x x x t x x类型四:大角交半角2FHAE CHACFH AE HCF~ACE ACECHF 60ECF 60ACH 30CAD 90ACD BAC 90ACD AD CD AC 32CH AH AC ADCH 3DH AD AH 42AB AD 3CH ,2CD ,DH ,:(2)ACAB BE AE AF AE AFBE ACF,BCE ACFBCE ACFBCE AC BC CAFB ACF BCE ACFBCE 60ACE ACF ACE BCE 60ECF ACBC ,60ACB ,60CAD B ACD ,ABC ABAD 60B D 120BAD ,ABCD ,:)1(,1202222200000=∴=∴∆∆∴∠=∠∴=∠=∠∴=∠∴=∠=∠∴=∠∴=+∴=+=∴⊥=-=∴==∴=====∴∴∆≅∆∆≅∆∴⎪⎩⎪⎨⎧∠=∠=∠=∠∆∆∠=∠∴=∠+∠=∠+∠∴=∠==∠=∠=∠∴∆∆∴==∠=∠∴=∠ xxx x 由题意得,设如图证明+=+=②中和在都是等边三角形是平行四边形四边形①如图证明【答案】7732123314AC AF 3AE 3414AM 3HN 3AH FN 33HN 3AHN AM EM )FN NH AH (3)AM EM (3AF AE 3212AH ,33AM a3,HC CM HM ,22CN HC 30CHN AHM 90M ,60MAH ,3EM ,3CM ,6FN ,NC 31EM FN CM CN 3CNCM AB AD CN AD CM AB EMFN CM CN CEM~CFN 90CNF M AECCFN 180CFN AFC 180AFC EAEC 180EAF ECF H AD CM ,M BA ,BABA CM ,N AD CN ,7)3(000故答案为则设=3,=交于点与延长线于交于作如图==+∴=-+=-++==-++-====∴==-===∴=∠=∠∴=∠=∠======∴=∴⋅⋅=∴∆∆∴=∠=∠∠=∠∴=∠+∠=∠+∠∴=∠+∠⊥⊥a a a a a HN a a b a a6AC AB AN CN MB AM MN AN AM :AMN CNMB BF MB MF MN )SAS (DMF DMN DN DF NDM FDM DM DM DMF DMN 60CDN BDM 60MDN CNBF ,DN DF ,CDN BDF CDNBDF BDF120D CND ,90DCA DBA 60BCA BAC ABC 3ABC 30DBC BCD 120BDC ,BDC :)1(,13000=+=+++=++∆∴+=+==∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆=∠+∠∴=∠==∠=∠∴∆≅∆∴∆∆=∠=∠∴=∠=∠=∠∴∆=∠=∠∴=∠∆的周长是中和在得到逆时针旋转绕点将如图得等边三角形是边长为且是等腰三角形证明【答案】 类型五:旋转任意角ADEABC ADEABD ACE ABD ADEABD ABCE BCED ACEAVBD 0ADE ABC S S S S S S S S S S S S CAE,BAD AC AB CAE BAD AE AD CAE BAD CAEBAD DACDAE DAC BAC DAE BAC :S S BCED BD,:,14∆∆∆∆∆∆∆∆∆∆∆∆-=--+=--=∴=∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∠-∠=∠-∠∴=∠=∠=四边形四边形中和则在即理由的差的面积等于则四边形连接如图【答案】解α26BE DG 2615OB OE BE EOB R 13)10(OA AB OB AOB R ,AC BD ABCD 10AB 2AE ,5:2AB :AE 5OA AE OE 268AC EC AE ,32AC OA 6AC 5106AF 5:2AG :AF 5:2ABCD,~AEFG BEDG BAE DAB A DAG ,ABCD ~AEFG ,O AC BD ,:,1522222222==∴=+=+=∆∴=-=-=∆⊥=∴===+=∴=-=-==÷=∴=∴==∴=∴∆∠∆∴中在中在中菱形又且又且面积之比为菱形菱形的度数可以得到顺时针旋转绕点将菱形于点交连接如图【答案】解t t CFBD )SAS (CAF BAD AFAD CAF BAD ACAB CAF BAD CAFBAD DACDAF CAF DACBAC BAD 90DAF BAC ,AF AD ,AC AB ,ADEF ,ABC ,:BCF )1(,160=∴∆≅∆∴⎪⎩⎪⎨⎧=∠=∠=∆∆∠=∠∴∠-∠=∠∠-∠=∠=∠=∠==∴∆中和在是正方形四边形是等腰直角三角形如图理由成立【答案】5108CG BC BG BGC R CG3843104CG CM BA BM CMG ~BMA 3104AM AB BM 38344AM AC CM 34AB 31AM 31CN FN FCN tan AB AM ABM tan ABM R 24AC AB BC ,3AN AC CN ,4AB AC ,ABC 1AE 21FN AN 2DE AD AE 2DE AD ,ADEF ,N AC FN ,:CFBD 90BAC BGC CMG~BMA CMGBMA GCMABM CAFBAD ,M AC BG ,:)2(222222220=-=∆∴=∴=∴∆∆=+==-=-=∴==∴====∠∆∴=+==-=∴==∆===∴=+=∴==⊥⊥∴=∠=∠∴∆∆∴∠=∠∠=∠∴∆≅∆中,在中在中在等腰直角中在正方形于点作过点如图②解于点交设如图①证明t t F 1323EF AE AF AEF R 90E ,DEFG 321DE AD AE ,1BC 21AD ,2BC ,BC D ,90BAC ,ABC ,AE ,AE D ,E D,A,,:,17222200=+=+=∆∴=∠=+=+===∴==∠∆中在中正方形此时的中点是点是等腰直角三角形的长最大上时在线段且点三点在一条直线上当如图【答案】解tFD BE EF BGBE EG EFEG AEFAEG AEAE EAFGAE BAD 21EAF EAD DAF EAD BAG AFAG ,DAF BAG ADFABG ADAB ADFB 180ADC ADF ,180ADC B AG,DF BG ,BG BE ,:FDBE EF ,FD BE EF )3(,FD BE EF )1)(2(FDBE EF BGBE EG EFEG AEFAEG AEAE EAFGAE BAD21EAF EAFBAD 323121,AF AG ADFABG ADAB ,90D ABC ABG AG,DF BG ,G EB ,)1(,MNBM DN ,AEN AMN ,ADE ABM ,AE ,MB DE DC ,)2(,,AEN AMN ,ADE ABM ,BM DE ,AE ,E ND ,,MN DN BM )1(:,18000-=∴-=∴=∴∆≅∆∴=∠=∠∴∠=∠=∠+∠=∠+∠∴=∠=∠∴∆≅∆∴=∠=∠∴=∠+∠=∠+∠=-=+=+=+=∴+==∴∆≅∆∴=∠=∠∴=∠=∠-∠=∠+∠=∠+∠∴∠=∠=∴∆≅∆∴==∠=∠=∠==-∆≅∆∆≅∆=∆≅∆∆≅∆==+ 连接使上截取在如图证明应当是不成立结论仍然成立中的结论又连接使到延长如图【答案】拓展可得到结论同理再证易证连接上截取在如图即可得出结论再证易证使连接到延长如图【答案】解。
用旋转作辅助线证明几何题专题训练课

用旋转作辅助线证明几何题专题训练课(对 2018 年广州市中考第 25 题的解读与变式训练)授课班级初三设计者Gu zi设计时间2018 年 10 月 18 日专题设计背景分析(2018 广州中考第 25 题)如图,在四边形 ABCD 中,∠B=60°,∠D=30°,AB=BC (1)求∠A+∠C 的度数(2)连接 BD,探究 AD,BD,CD 三者之间的数量关系,并说明理由(3)若 AB=1,点E 在四边形 ABCD 内部运动,且满足AE²=BE²+CE²,求点 E 运动路径的长度。
本题位于 2018 年广州中考数学第 25 题,全卷的最后一题,是一道难题。
本题条件较少,措词简单,图形简单仅仅只有一个不规则的四边形,第一问非常容易,学生都很容易接受,考察四边形内角和定理,但这个问题其实意味深远,给学生第二问以脚手架,并且别处心裁,学生很难联想到270°的用法原来是利用360°-270°=90°,得到我们熟知的直角,虚者实之,妙不可言。
第二问探究三边之间的关系,很容易联想到割长补短等解题策略,但题者给出出乎意料的处理方法,题目条件中的连接 BD,让题目中的∠D=30°的特殊角给破坏了,引人深思。
学生若能从已知AB=BC 中顿悟到用旋转辅助线将△BCD 逆时针旋转为△BAG破解了270°转化到90°,所有问题都迎刃而解,精彩绝伦。
本题第 3 问,已知三边的关系,求点 E 与定点 A,B 形成的角度。
题者让学生求解 E 的运动路径,也就是考察学生对弧长公式的理解与掌握程度。
一个题目将四边形,三角形,圆,旋转等多个章节有机得结合在一起,从不同维度考察学生的数学素养。
对于此题目 2,3 问辅助线做法是比较有难度的。
笔者进行反思,为了降低难度,达到训练的目的整理了三道变式题进行专题训练。
10解题技巧专题巧用旋转进行计算

10解题技巧专题巧用旋转进行计算在解题过程中,有时我们可以巧用旋转来进行计算,以简化问题、加快解题速度。
下面将介绍几种巧用旋转进行计算的技巧。
1.点的旋转:对于一个点(x,y),我们可以将其逆时针旋转θ度得到新的点(x',y'),计算方法如下:x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ这种技巧可以用来求解两点之间的距离、判断点的位置关系等问题。
2.向量的旋转:对于一个向量(x,y),我们同样可以将其逆时针旋转θ度得到新的向量(x',y'),计算方法与点的旋转类似。
x' = x * cosθ - y * sinθy' = x * sinθ + y * cosθ这种技巧可以用来求解向量的和、点积、叉积等问题。
3. 复数的旋转:对于一个复数a + bi,我们可以将其旋转θ度得到新的复数c + di,计算方法同样类似。
c = (a + bi) * cosθd = (a + bi) * sinθ这种技巧可以用来求解复数的乘法、除法等问题。
4.矩阵的旋转:对于一个二维矩阵,我们可以将其逆时针旋转θ度得到新的矩阵,计算方法如下:对于一个点(x,y)在原矩阵中的位置(i,j),新矩阵中该点的位置为:i' = j * sinθ + i * cosθj' = j * cosθ - i * sinθ这种技巧可以用来求解矩阵的转置、乘法、快速幂等问题。
在实际应用中,我们可以根据具体问题选择合适的旋转方法。
例如,在计算几何中,通过旋转可以使问题简化为求解两点之间的距离或者判断一些点是否在条直线上,从而简化问题的求解过程。
在矩阵运算中,可以通过旋转将矩阵进行转置或者快速幂运算,提高运算效率。
巧用旋转进行计算可以节省时间、简化问题,但在应用时也需要注意旋转角度的选择和计算的正确性。
在实际解题过程中,可以通过举例或者推导来验证旋转计算的正确性,避免出现错误的结果。
最新旋转法解几何证明题分类解析
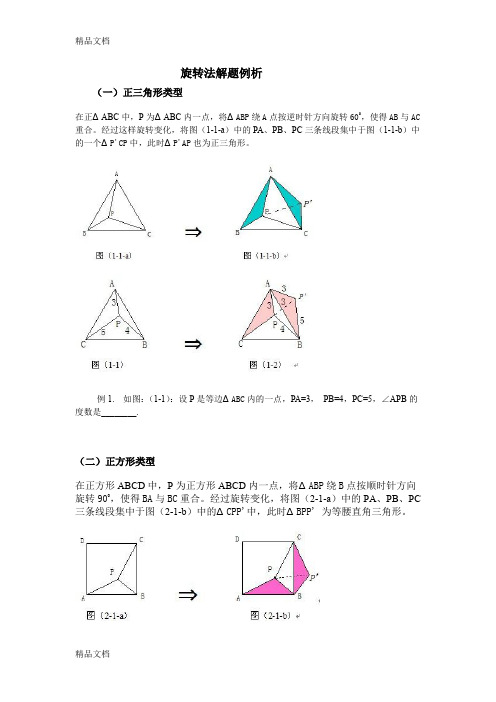
旋转法解题例析(一)正三角形类型在正ΔABC中,P为ΔABC内一点,将ΔABP绕A点按逆时针方向旋转600,使得AB与AC 重合。
经过这样旋转变化,将图(1-1-a)中的PA、PB、PC三条线段集中于图(1-1-b)中的一个ΔP'CP中,此时ΔP'AP也为正三角形。
例1. 如图:(1-1):设P是等边ΔABC内的一点,PA=3,PB=4,PC=5,∠APB的度数是________.(二)正方形类型在正方形ABCD中,P为正方形ABCD内一点,将ΔABP绕B点按顺时针方向旋转900,使得BA与BC重合。
经过旋转变化,将图(2-1-a)中的PA、PB、PC 三条线段集中于图(2-1-b)中的ΔCPP'中,此时ΔBPP'为等腰直角三角形。
例4 如图,P 是正方形ABCD 内一点,且满足PA :PD :PC=1:2:3,则∠APD= . 分析与解:设PA=k ,则PD=2k ,PC=3k(k>0),而PA 、PD 、PC 三条线段较为分散,故可考虑旋转法,目的就是将三条线段以等线段替换方式集中在一个三角形中.3、直角三角形例1 如图,在△ABC 中,∠C=90°,AC=BC ,M 、N 是斜边AB 上的点,且∠MCN= 45°,AM=3,BN=5,则MN= .分析:基于在△ABC 中,∠C=90°,AC=BC 及AM 、BN 、MN 共线特点的考虑,选择旋转法解答,目的就是设法将这三条线段以等线段替换的方式集中在一个三角形中例2 如图,四边形ABCD 中, ∠BAD=∠ACB=90°,AB=AD ,AC =4BC ,设CD 的长为x ,四边 形ABCD 的面积为y ,则y 与x 之间的函数关系式为( )A .2225y x =B .2425y x =C .225y x =D .245y x =练习:如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=()A.2 B.3 C.D.2 如图,P是等边三角形△ABC内一点,∠APC、∠BPC、∠BPA的大小之比是5:6:7,则以PA、PB、PC的长为边的三角形三个内角从小到大依次是.分析与解:易得∠APC=100°,∠BPC=120°,∠BPA=140°.欲求以PA、PB、PC的长为边的三角形三个内角,因为三条线段分散,故可考虑旋转法,目的就是将三条线段通过等线段替换方式集中在一个三角形中.4、与边的中点相关的问题例5在△ABC中,AB=7,AC=5,AD是BC边的中线,求AD的取值范围.例6如图,在正方形ABCD中,E是AB边的点,G、F分别是AD、BC边上的点,且AG=1,BF=2,∠GEF=90°,则GF的长是.练习:1. 如图:(1-1):设P 是等边ΔABC 内的一点,PC=3, PB=4,PA=5,∠APB 的度数是________.APCB2如图,P 为正方形ABCD 内一点,123PA PD PC ===,,,将PDC ∆绕着D 点按逆时针旋转90︒到PQD ∆ 的位置。
利用旋转巧解几何题

利用旋转巧解几何题将一个图形绕着某一点旋转一个角度的图形变换叫做旋转,由旋转的性质可知旋转前后的图形全等,对应点到旋转中心的连线所组成的夹角等于旋转角,利用其性质可以解一些几何题,对同学们在解此类问题时有所帮助,下面举例说明。
一、旋转在解三角形中的应用例1 如图1所示,P是等边三角形ABC内的一个点,PA=2,PB=,PC=4,求△ABC的边长。
图1分析:PA、PB、PC比较分散,可利用旋转将PA、PB、PC放在一个三角形中,为此可将△BPA绕B点逆时针方向旋转60°可得△BHC。
解:把△BPA绕B点逆时针方向旋转60°得到△BHC。
因为BP=BH,∠PBH=60°所以△BPH是等边三角形所以∠BPH=60°,所以BP=PH又因为HC=PA=2,PC=4所以所以△HCP是Rt△,所以∠CHP=90°又因为HC=2,PC=4所以∠HPC=30°又因为∠BPH=60°,所以∠CPB=90°在Rt△BPC中,=12+16=28,那么△ABC的边长为。
例2 如图2,O是等边三角形ABC内一点,已知:∠AOB=115°,∠BOC=125°,则以线段OA、OB、OC为边构成三角形的各角度数是多少?图2解:可将△BOC绕B点按逆时针方向旋转60°可得△BMA。
因为BO=BM,∠MBO=60°所以△BOM是等边三角形,所以∠1=∠2=60°又因为∠AOB=115°,所以∠MOA=55°又因为∠AMB=∠COB=125°所以∠AMO=65°又因为AM=OC,MO=BO所以△AMO正好是以AO、OC、BO为边组成的三角形,所以∠MAO=180°-(55°+65°)=180°-120°=60°即:以线段OA、OB、OC为边构成三角形的各角的度数分别为55°、65°、60°。
几何证明题辅助线的技巧和方法

几何证明题辅助线的技巧和方法
在解决几何证明题时,辅助线是一种常用且有效的工具。
它可以帮助我们发现
隐藏的几何关系,简化证明过程,并提供新的角度来解决问题。
以下是几种常见的辅助线技巧和方法,可用于解决几何证明题。
1. 平行线辅助线法:当题目涉及到平行线时,我们可以通过引入一条平行线作
为辅助线,从而构建出平行线之间的相似三角形或平行四边形。
这样,我们可以得出相应的角度和边的关系,进而证明几何问题。
2. 三角形中线辅助线法:三角形的中线是连接一个顶点与对应中点的线段。
通
过引入三角形中线作为辅助线,我们可以将原问题转化为直角三角形的性质或平行线的性质。
这种方法常常用于证明三角形的等边、等腰等性质。
3. 垂直线辅助线法:当题目涉及到垂直线时,我们可以通过引入一条垂直线作
为辅助线,从而构建出垂直角、直角三角形或平行四边形。
通过利用垂直线的性质,我们可以得到角度、边长等关系,进而解决问题。
4. 内切圆辅助线法:对于一个给定的三角形,可以通过引入其内切圆作为辅助线,来简化证明过程。
内切圆与三角形的的边相切于三个点,这些点可以提供有用的几何关系,如正方形的性质、垂直线的性质等。
5. 类似三角形辅助线法:当计算角度或证明形状相似时,引入类似三角形作为
辅助线可以大大简化证明过程。
通过找到两个或多个类似的三角形,我们可以得到两个三角形的边长比例,并据此解决问题。
总之,辅助线是几何证明中的有效工具,它们可以帮助我们发现关键的几何关系,简化证明过程,并提供新的角度来解决问题。
通过灵活运用各种辅助线技巧和方法,我们可以更加轻松地解决各种几何证明题。
初中几何旋转经典例题

初中几何旋转经典例题 旋转是初中几何学中的重要概念之一,它涉及到物体在平面上以一定角度绕旋转中心旋转的运动。
在几何学中,旋转可以通过不同的方法来表示和计算,而初中几何旋转的例题则是学生们常见的练习题目类型之一。
下面将介绍几个经典的例题,以帮助学生们更好地理解初中几何旋转的概念和运用。
例题1:如图所示,长方形ABCD的顶点A经过顺时针旋转90°后得到顶点A',连接AA'所得线段与BC延长线的交点为E。
求证:线段BD与线段AE互相垂直。
解析:首先,我们可以通过观察图形得知旋转中心为矩形的中心点。
由于顶点A经过顺时针旋转90°后得到顶点A',所以图形经过旋转后变成了一个正方形。
因此,线段BD与直线AE是正方形的对角线,而正方形的对角线互相垂直。
因此,线段BD与线段AE互相垂直,得证。
例题2:如图所示,正方形ABCD的顶点A经过顺时针旋转60°后得到顶点A',连接AA'所得线段与AC相交于点E。
求证:线段BE与BC垂直,并且线段BE的长度等于线段BC的一半。
解析:首先,我们可以观察图形得知旋转中心为正方形的中心点。
由于顶点A经过顺时针旋转60°后得到顶点A',所以图形经过旋转后变为一个新的正方形。
连接AA'所得线段与AC相交于点E,根据旋转的特性,线段AE与直线AC重合。
因此,线段BE与线段AC互相垂直,并且线段BE的长度等于线段BC的一半,得证。
例题3:如图所示,正方形ABCD的顶点A经过顺时针旋转120°后得到顶点A',连接AA'所得线段与AC延长线的交点为E。
求证:直线BE平分线段AC。
解析:同样地,我们可以观察图形得知旋转中心为正方形的中心点。
由于顶点A经过顺时针旋转120°后得到顶点A',所以图形经过旋转后变成了一个新的正方形。
连接AA'所得线段与AC延长线相交于点E,根据旋转的特性,线段AE与直线AC平行。
第10招旋转问题中作辅助线的技巧课件人教版九年级上册极速提分法

∴△ADP是直角三角形,且∠ADP=90°, ∴∠BDA=∠BDP+∠ADP=60°+90°=150°, ∴∠BPC=∠BDA=150°.
【点方法】 利用旋转作辅助线构造出直角三角形和等边三角形是解
本题的关键.
3. (1)如图①,在四边形ABCD中,AB=AD, ∠BAD=120°,∠B=∠ADC=90°,且∠EAF= 60°,探究图中线段BE,EF,FD之间的数量关系, 小明同学的方法是将△ABE绕点A逆时针旋转120° 到△ADG的位置,然后证明△AFE≌△AFG,从而 得出结论:_______E_F__=__B_E_+__F_.D
解:如图②,连接BD,由于AD=CD,∠ADC=60°, 因此可将△BCD绕点D顺时针旋转60°,得到△B′AD, 连接BB′,过点B′作B′E⊥AB,交BA的延长线于点E, 由旋转的性质可得△BCD≌△B′AD, ∴S四边形ABCD=S四边形BDB′A. ∵∠ABC=75°,∠ADC=60°,
∴∠BCD+∠BAD=360°-∠ABC-∠ADC= 360°-75°-60°=225°, ∴∠B′AD+∠BAD=∠BCD+∠BAD=225°, ∴∠BAB′=360°-(∠B′AD+∠BAD)= 360°-225°=135°, ∴∠B′AE=180°-∠BAB′=180°-135°=45°, ∴△B′EA是等腰直角三角形.
∴∠BAD+∠DAB′=180°,即点B,A,B′三点共线, ∴△BDB′是等边三角形.
(2)在(1)的基础上,求四边形ABCD的面积;
解:由(1)知,△BCD≌△B′AD, ∴S四边形ABCD=S△BDB′,AB′=BC=1, ∴BB′=AB+AB′=2+1=3. ∵△BDB′是等边三角形,∴BD=BB′=3.
(2)如图②,在四边形 ABCD 中,AB=AD,∠B+∠D= 180°,E,F 分别是边 BC,CD 上的点,且∠EAF=12 ∠BAD,(1)中得出的结论是否仍然成立?并说明理由.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用旋转法………作辅助线证明平面几何题
旋转法就是在图形具有等邻边特征时,可以把图形的某部分绕等邻边的公共端点,旋转另一位置的引辅助线的方法。
1、旋转方法主要用途是把分散的元素通过旋转集中起来,从而为证题创造必要的条
件。
2、旋转时要注意旋转中心、旋转方向、旋转角度的大小(三要素:中心、方向、大小);
3、旋转方法常用于竺腰三角形、等边三角形及正方形等图形中。
例1:
例2 已知,在Rt ABC 中;∠BAC=90︒;
D为BC边上任意一点,求证:2AD2=BD2+CD2.
证明:把ABD绕点A逆时钍方向旋转90︒,得∆ACE,则ABD≅∆ACE,∴BD=CE,∠B=∠ACE;
∠BAD=∠CAE, AD=AE。
又∠BAC=90︒;∴∠DAE=90︒
所以: D E2=AD2+AE2=2AD2。
因为:∠B+∠ACB=90︒
所以:∠DCE=90︒
CD2+CE2=DE2=2AD2
即: 2AD2=BD2+CD2。
注:也可以把ADC顺时针方向旋转90︒来证明。
注
C
D
已知,P 为等边ABC 内一点,PA=5,PB=4,PC=3,求∠BPC 的度数。
证明:把ABP 绕点B 顺时钍方向旋转90︒,得∆CBD ,则ABP ≅∆CBD ,∴, ∠ABP=∠CBD ,所以 ∠BAP+∠PBC=∠CBD+∠PBC=60︒,所以 BPD 为等边三角形。
∠PBD=60︒所以: C D 2=PD 2+PC 2。
因为: ∠DPC=90︒
所以: ∠BPC=∠BPD+∠DPC=60︒+90︒=150︒
注:也可以把CAP 绕点C 逆时针方向旋转60︒来证明。
D
C
例3:
如图:在正方形ABCD 中,E 为AD 边上一点,BF 平分∠CBE 交CD 于F 点。
求证:BE=CF+AE
证明:把ABE 绕点B 顺时针方向旋转90︒得BCN 。
则:ABE ≅BCN ,所以: ∠ABE=∠CBN ,BE=BN ,AE=CN 。
因为:四边形ABCD 是正方形,所以:CD AB ,∠NFB=NBF
因为:∠ABF=∠ABE+∠EBF ,∠NBF=∠NBC+∠CBF ,而:∠EBF=∠FBC ;∠NBF=∠NFB 所以:BN=NF=CN+CF 所以:BE=AE+CF 。
注:也可以把BCF 绕点B 逆时针方向旋转90︒来证明。
