工程力学第3章
合集下载
工程力学(静力学与材料力学)第三章力偶系详解

FB
r M2 0 ∑ M = 0 , FA sin
M 2 2r FA
M2 = 4M1 = 8kNm
2M 1 FO FB FA 8kN r
• 作业3-1,3-4,3-8
考虑CB部分为二力构件,得:
FC FA FB FC
例3-4
图示机构自重不记。圆轮上的销子 A 放在 摇杆 BC上的光滑导槽内。M 1 = 2kNm,OA = r = 0.5m 。图示位置OA⊥OB,α = 30°,且系统平衡。 求作用于摇杆 BC 上力偶的矩 M 2 及 O、B 支座的反 力。 解:受力分析
M1
R
F1
M
F2
2
M1 + M2 = rBA×F1 + rBA×F2 = rBA×( F1 + F2 ) = rBA×R = M
如有n个力偶,按上法依次合成, 最后得一力偶,合力偶矩矢为 M = M1 +M2 + … +Mn = ∑M I
B
rBA
A
F2
F1
任意个力偶可以合成为一个 合力偶,这个合力偶矩矢等于各 分力偶矩矢的矢量和。 M = M 1+ M 2+ … + M n = ∑M i
性质三
证:
力偶没有合力
仍用反证法,即假定力偶有合力,那么总可 找到一个与此力大小相等,方向相反而作用线 共线的力与此力平衡,即力与力偶相平衡。与 性质二矛盾。
性质一、二和三告诉我们力偶只能与力偶等 效而不能与单个力等效。
•力偶只能与力偶相平衡 力偶只能与力偶相平衡
§3-4 力偶系的合成
设有两个力偶,由性质一,将 力偶中两力分别移到两力偶作用面 交线上的两点 A 和 B,可得到两个 汇交力系,其合力分别为R 、 R ’ 。
工程力学I-第3章 力矩与平面力偶系

D
x
§3-2 关于力偶的概念
力偶:一对等值、反向而不共线的平行力,用 符号(F ,F′)表示。
力偶臂:两个力作用
线之间的垂直距离d。
F’
F
力偶的作用面:两个 力作用线所决定的平 面
§3-2 关于力偶的概念
F F
d
d
F
d
F
F
F
转动游戏方向盘
拧水龙头
扳手拧螺母
§3-2 关于力偶的概念
Q AABD AABC 显然, 并注意到力偶矩的转向也相同, 则有M ( F , F ) M ( P, P) P
M (P 1, P 1 ) M ( P, P ) 显然, 1, P 1) 从而有M ,( F , F ) M ( P
P1
力偶等效
M ( F , F ) M ( P 1, P 1)
(1)力对点之矩,不仅取决于力的大小,还与矩心的位置有关。
(2)力对任一点之矩,不因该力的作用点沿其作用线移动而改变。 *(3)力的大小等于零或其作用线通过矩心时,力矩等于零。 (4)互成平衡的两个力对同一点之矩的代数和为零。
Mo(F)=±Fd
§3-1 关于力矩的概念及其计算
合力矩定理:
y Fy
(3)将力P和P’沿各自的作用 线移至任意点A’,B’,根 据力的可传性原理,有 (P,P’) =(P1,P1’) 。
§3-2 关于力偶的概念
(4) A′
P1′ b F′ A A F B Q′ D P′ B′ C
M (F , F ) AB BD 2 AABD ,
M(P, P') AB BC 2 AABC
工程力学第三章 受力分析(课堂PPT)

1
31
解:
1.杆AB的受力图。
2. 活塞和连杆的受力图。
E D
B
Aq
C q
B
FBA
A
FA
3. 压块 C 的受力图。
q
FCB
FAB
q
C FCx
F
B
q
FBC
1 FCy
32
例题7
D
A
K
q
C
E
BⅠ Ⅱ
P
如图所示平面构架,由杆AB , DE及DB铰接而成。钢绳一端拴 在K处,另一端绕过定滑轮Ⅰ和 动滑轮Ⅱ后拴在销钉B上。重物 的重量为P,各杆和滑轮的自重 不计。(1)试分别画出各杆, 各滑轮,销钉B以及整个系统的 受力图;(2)画出销钉B与滑轮 Ⅰ一起的受力图;(3)画出杆 AB ,滑轮Ⅰ ,Ⅱ ,钢绳和重物 作为一个系统时的受力图
处必有力,力的方向由约束类型而定。
要注意力是物体之间的相互机械作用。因此对 2、不要多画力 于受力体所受的每一个力,都应能明确地指出
它是哪一个施力体施加的。
1
18
3、不要画错力的方向 约束反力的方向必须严格地按照约束的类型来画,不 能单凭直观或根据主动力的方向来简单推想。在分析 两物体之间的作用力与反作用力时,要注意,作用力 的方向一旦确定,反作用力的方向一定要与之相反, 不要把箭头方向画错。
BB
D
F
A
C
1
7
解: 1. 杆 BC 的受力图。
BB
D
F
A
C
1
FB B
C
FC
8
2. 杆AB 的受力图。
BB
D
F
A
正交分解
工程力学 第3章 力偶系
M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论:两个力偶的合成仍然为力偶,且
第三章 力偶系
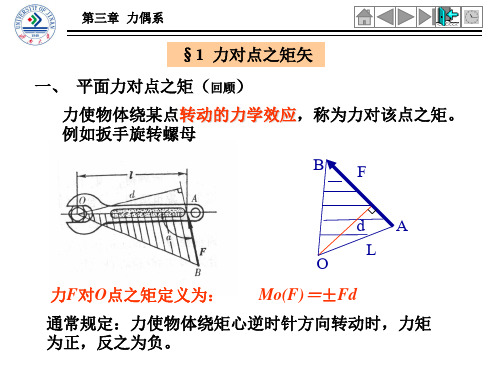
§1 力对点之矩矢 一、 平面力对点之矩(回顾)
力使物体绕某点转动的力学效应,称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为: Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩 为正,反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素:
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反,但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义:在力学中把这样一对等值、反向而不共线的平行力 称为力偶,用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
力对点之矩在各坐标轴上的投影
MO z
O xr
工程力学(第三章)

MR
y
MR Mz cos MR
§3-6
力偶系的平衡条件
M 0
平衡: 力偶系平衡的充要条件是 其合力偶矩矢为零。
即:力偶系平衡
一、平面力偶系的平衡条件
M R M(代数和) i
M 0
平面力偶系的平衡方程
§3-6
力偶系的平衡条件
M 0
平衡: 力偶系平衡的充要条件是 其合力偶矩矢为零。
力对点之矩矢
作用: 用来度量力使物体绕某点转动效应的量。
(代数量) 一、平面中力对点之矩(力矩)
F
O
h
定义:M O
F Fh
正负号规定: 力使物体绕矩心逆转为正,顺转为负。
作用: 用来度量力使物体绕某点转动效应的量。 1、平面问题
(代数量) 力矩作用面
矩心 O h
力臂
定义: M O F Fh
A
O x
y
Fx
z
y
Fy
x
A x, y, z ,
F Fx , Fy , Fz
(一)、力对点的矩
1、平面问题
MO
F Fh
MO F
O
h
z
F
F
2、空间问题
MO F r F
x
(二)、力对轴的矩
空间: 力偶对空间任一点的矩矢恒等于力偶矩矢, 而与矩心位置无关。
性质二 力偶可在其作用面内任意移转,或移到另
一平行平面,而不改变对刚体的作用效应。
= =
F
F
F
F
工程力学基础第3章 力系的静力等效和简化

二、力系简化的最终结果 根据力系主矢和主矩的性质,力系可最终简化为下列四种情形 1 2 3 4 平衡力系 即与零力系等效。其条件为主矢F′R=0,主矩M 该力偶称为力系的合力偶。力系存在合力 该力称为力系的合力。
O=0 单一等效力偶 单一等效力 力螺旋 偶的条件为主矢F′R≠0,主矩MO≠0。 在最一般的情况下,力系的主矢和主矩不垂直
三、平面力系的简化结果
(1)沿直线路面行驶的汽车,若不考虑由于路面不平引起的
左右摇摆和侧滑,则由汽车所受的重力、空气阻力及地面对车 轮的约束力构成的空间力系将对称于汽车的纵向对称面。将该 力系向汽车的纵向对称面简化,就可得到一个平面一般力系, 如图3-11 (2)工厂车间里的桥式起重机,梁的自重、起重机小车的自 重和起吊物的重量均作用在梁的纵向对称面内。梁两端四个车 轮的约束力也对称于该平面,故该力系可简化为梁纵向对称面 内的一个平面力系,如图3-12所示。
图3-3
力的平移定理
可以把作用于刚体上点A的力F平行移动到任一
点O,同时附加一个力偶,其力偶矩矢M等于力F对点O的力矩
矢,即M=MO(F),则平移后得到的新力系与原力系等效, 如图3-4 力的平移定理可以直接用等效力系定理来证明。反之,作用于 同一刚体的同一平面内的一个力和一个力偶(即力偶矩矢和力 矢垂直时),可以用一个力等效代替。
(一般)力系,这是力系的最一般的形式。当力系中各力的作 用线位于同一平面内时,称为平面(一般)力系,这是工程实 际中常见的重要情形。有些空间力系通过等效转换的方法也可 以变为平面力系。如果力系中各力的作用线交于一点,则称为 汇交力系。如果力系全部由力偶组成,则称为力偶系。汇交力 系和力偶系也有空间和平面两种情形,汇交力系和力偶系是两
图3-4
工程力学第三章力矩与平面力偶系

位置无关,因此力偶对刚体的效
应用力偶 矩度量。
F
A B
d
F'
x
O
mO ( F ) mO ( F ') F ( x d ) F 'x F d
4.力偶的表示方法
用力和力偶臂表示,或用带箭头的弧线表示,箭头表示 力偶的转向,M表示力偶的大小。
第三章力矩与平面力偶系
湖南工业大学土木工程学院
y
Fx
x
则
r cos x, r sin y
mo ( F ) xFy yFx
湖南工业大学土木工程学院
( )
a
第三章力矩与平面力偶系
§3-1力矩的概念和计算
mo (F ) xFy yFx
若作用在
( )
a
y
Fy
F
F2 、 A 点上的是一个汇交力系( F1 、 则可将每个力对 o 点之矩相加,有 Fn ), o
r
d
,
x
A
y
Fx
m (F ) x F
o
y
y Fx
(b)
x
由式( a ),该汇交力系的合力 R 它对矩心的矩
F
m0 (R) xRy yRx x Fy y Fx ( c )
比较( b )、( c )两式有
mo (R) M o (F )
第三章力矩与平面力偶系 湖南工业大学土木工程学院
l
A
o
第三章力矩与平面力偶系 湖南工业大学土木工程学院
d
F
力矩计算
简支刚架如图所示,荷载F=15kN,α=45 ,尺寸如图。试分别计 算F对A、B两点之矩。
工程力学教学课件 第3章 平面任意力系

A
MA
FAx
A
简 化
2021/7/22
FAy
11
一、简化结果分析
3.2
平
面 任
F1
A1
F2
O A n A2
M O FR'
O
意
Fn
力
系 的 简 化
1 . F R ' 0 ,M o 0
2 . F R ' 0 ,M O 0
结 果
3 . F R ' 0 ,M O 0 4 . F R ' 0 ,M O 0
的 简 化
此时主矩与简化中心的位置无关。
3、主矢不等于零,主矩等于零 (F R ' 0 ,M O 0 )
结 果
此时平面力系简化为一合力,作用在简化
中心,其大小和方向等于原力系的主矢,即
FRF
2021/7/22
13
一、简化结果分析
3.2 4、主矢和主矩均不等于零 (F R ' 0 ,M O 0 )
平
此时还可进一步简化为一合力。
面
任
FR'
FR'
FR
FR
意 力
O M O O
O
d
O
O
O
d
系 的 简 化
FR'' M O m O ( F R ) F R d F R 'd 于是
d M
F
由主矩的定义知:M O m O (F i)
O ' R
结 所以:
m O (F R ) m O (F i)
果 结论:平面任意力系的合力对作用面内任一点之矩
杆所受的力。
A
45
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 力矩和平面力偶系 图3-4
第3章 力矩和平面力偶系
这样由两个大小相等、方向相反且不共线的平行力组成的 力系称为力偶。力偶用符号(F,F′)表示,两力之间的垂直距离d 称为力偶臂, 如图3-5所示。 力偶两力作用线所决定的平面称 为力偶的作用面,力偶使物体转动的方向称为力偶的转向。 实 践证明,力偶只能对物体产生转动效应,而不能使物体产生移 动效应。力偶对物体的转动效应,可用力偶中的力与力偶臂的 乘积再冠以适当的正负号来确定,称为力偶矩,记做M(F,F′), 或简写为M,
解:(1) 求三个主动力偶的合力偶矩
M Mi M1 M2 M3
13.5 13.5 17 44N m
负号表示合力偶矩为顺时针方向。
第3章 力矩和平面力偶系 图 3-10
第3章 力矩和平面力偶系 (2) 求两个螺栓所受的力。
选工件为研究对象,工件受三个主动力偶作用和两个螺栓的 反力作用而平衡,故两个螺栓的反力FA与FB必然组成为一力偶, 设它们的方向如图所示, 由平面力偶系的平衡条件,有
根据合力矩定理,力F对A点之矩
M A (F ) M A (F1 ) M A (F2 ) F1l1 F2l2 F (l1 cos150 l2 sin150 ) 3970N cm 39.7N m
负号说明力F使手柄绕A点顺时针转动。
第3章 力矩和平面力偶系 图3-3
设在刚体上作用一力F,如图3-11所示,由经验可知,当力 F通过刚体的重心C时,刚体只发生移动。如果将力F平行移动到 刚体上任一点D,则刚体既发生移动,又发生转动,即作用效果
发生改变。那么,在什么条件下,力平行移动后与未移动前对 刚体的作用效果等效呢?力的平移定理解决了这一问题。
第3章 力矩和平面力偶系 图3-11
合力矩定理 平面汇交力系的合力对平面内任一点之矩, 等于力系中各分力对同一点之矩的代数和。 即
M O (FR ) M O (F1 ) M O (F2 ) M O (Fn ) M O (Fi )
(3-3)
第3章 力矩和平面力偶系 例3-1 一齿轮受到啮合力Fn作用,Fn=980N,齿轮的压力 角α=20°,节圆直径D=0.16 m,如图3-2(a)所示。试计算Fn对轴 心O的力矩。
(3-6)
这就是平面力偶系的平衡方程,用这个方程可以求解一个未知量。
第3章 力矩和平面力偶系 例3-3 图3-9(a)所示简支梁AB上,受作用线相距为d=20 cm的两反向力F与F′组成的力偶和力偶矩为M的力偶的作用。 若F=F′=100N, M=40 N·m,梁长l=1m,求支座A和B的约束反 力。
d
20N
所以 FB FA 20N ,方向如图3-9(b)所示。
第3章 力矩和平面力偶系
例 3-4 多刀钻床在水平工件上钻孔(图3-10),每个钻头的 切削刀刃作用于工件的力在水平面内构成一力偶。已知切制三 个孔对工件的力偶矩分别为 M1 M 2 13.5N m, M3 17N m。 求工件受到的合力偶矩。如果工件在A、B两处用螺栓固定,A 和B之间的距离,试求两个螺栓在工件平面内所受的力。
图 3-9
第3章 力矩和平面力偶系
解 取梁AB为研究对象,因为只受主动力偶作用,而力偶
只能用力偶来平衡,故两支座反力必构成一对力偶。现已知FB 的方向,则FA与FB平行且反向,如图3-9(b)所示。由平面力偶系 的平衡条件, 有
Mi 0
FA l F d M 0
解得
FA
M
F l
第3章 力矩和平面力偶系 图3-6
第3章 力矩和平面力偶系 性质二 力偶对其作用面内任意点的矩恒等于此力偶的力
偶矩,而与矩心的位置无关。 证明 如图3-5所示,在力偶(F,F′)的二力作用点A、B连
线上任意取一点O为矩心,并设O点到力F的距离为x, 按力矩 定义,F与F′对O点的力矩和为
MO (F) MO (F) Fx F(x d ) Fd
点加一对平衡力F′和F″,并使它们与力F平行,而且F′=-F″=F,
如图3-12(b)所示,显然,它们对刚体的作用与原来的一个力F对
刚体的作用等效。在这三个力中,力F与F″组成一对力偶(F, F″)。
于是,原来作用在A点的力,现在被一个作用在B点的力F′和一
个附加力偶(F, F″)所取代,如图3-12(c)所示, 此附加力偶的力
第3章 力矩和平面力偶系
力的平移定理 作用于刚体上某点的力,可以平行移动到 刚体内任意一点,但同时必须附加一个力偶,此附加力偶的力 偶矩等于原力对平移点的力矩,力偶的转向决定于原力对平移 点的力矩的转动方向。
证明 如图3-12(a)所示,假设有一力F作用在刚体上A点,
要把它平移到刚体上另一点B处。根据加减平衡力系原理,在B
Mi 0
解得
FAl M1 M 2 M 3 0
FA
M1 M2 l
M3
220N
所以 FB FA 220N ,方向如图3-10所示。
第3章 力矩和平面力偶系
3.3 力的平移定理
力对物体的作用效果取决于力的三要素:力的大小、方向 和作用点。当力沿其作用线移动时,力对刚体的作用效果不变。 但是,如果保持力的大小、方向不变,将力的作用线平行移动 到另一位置,则力对刚体的作用效果将发生改变。
力对点之矩,简称力矩,以符号MO(F)表示,即
MO (F) F d
(3-1)
式中O点称为矩心,O点到在力F的作用线的垂直距离d称为力
臂,正负号的规定如下:力使物体绕矩心作逆时针转动时力矩
为正,反之为负。由此式可见,平面内力对点之矩,只取决于
力矩的大小及其正负号,说明力矩是代数量。
第3章 力矩和平面力偶系 图 3-1
即
MO (F ) MO (F ) M (F, F )
第3章 力矩和平面力偶系
性质三 保持力偶的转向和力偶矩的大小不变, 力偶可 以在其作用面内任意移动和转动, 而不会改变它对刚体的作 用效应。
力偶的这一性质说明力偶对物体的作用与力偶在作用面内 的位置无关。须指出,这一性质只适用于刚体而不适用于变形 体。
Ft Fn cos
根据合力矩定理
Fr Fn sin
M O(Fn ) M O (Ft ) M O (Fr )
因为径向力Fr过矩心O,故MO(Fr)=0,于是
M O (Fn ) M O (Ft ) F
D 2
Fn
D cos
2
73.7N m
第3章 力矩和平面力偶系
例3-2 手动剪断机的结构及尺寸如图3-3所示。设l1=80cm, l2=8cm,α=15°,被剪物体放在刃口K处,在B处施加F=50 N的 作用力。试求在图示位置时力F对A点之矩。
解 本题用合力矩定理求解较为方便,将力F分解为垂直于 手柄方向的分力F1和沿手柄方向的分力F2,得
F1 F cos F2 F sin
思考题3-2图
第3章 力矩和平面力偶系 3-3 能否用力在坐标轴上的投影的代数和为零来判断力偶系 的平衡?如图所示刚体上,作用二力偶(F, F′)和(F1, F1′), 它们 在x轴和y轴上投影的代数和都等于零, 刚体是否平衡? 为什么?
第3章 力矩和平面力偶系
3.2 平 面 力 偶 系
3.2.1 力偶及其基本性质 1. 力偶的概念 在日常生活及生产实践中,常见到物体受一对大小相等、
方向相反但不在同一作用线上的平行力作用,而使物体产生转 动效应的情况, 如人用手拧水龙头开关(图3-4(a))、司机 用双手转动方向盘(图3-4(b))、 钳工用丝锥攻螺纹(图34(c))等。
第3章 力矩和平面力偶系 图3-5
第3章 力矩和平面力偶系
1. 力偶的性质 根据力偶的定义,力偶具有以下一些性质。 性质一 力偶在任意轴上投影的代数和为零,如图3-6,故力 偶无合力,力偶不能与一个力等效,也不能用一个力平衡。
力偶无合力,故力偶对物体的平移运动不会产生任何影响, 力与力偶相互不能代替,不能构成平衡。因此,力与力偶是静 力学中的两种基本元素。
图 3-2
第3章 力矩和平面力偶系
解
(1)
力臂:
h D cos
2
由式(3-1)得力Fn对O点之矩:
MO
(Fn
)
Fn
h
Fn
D 2
cos
73.7N m
负号表示力Fn使齿轮绕O点做顺时针转动。
第3章 力矩和平面力偶系
(2) 应用合力矩定理。
将力Fn分解为圆周力Ft和径向力Fr,如图3-2(b)所示, 则
第3章 力矩和平面力偶系
性质四 只要保持力偶的转向和力偶臂的大小不变, 可 以同时改变力偶中力的大小和力偶臂的长短, 而不会改变力 偶对刚体的作用效应。
力偶的这一性质说明力偶中力或力偶臂都不是力偶的特征 量,只有力偶矩才是力偶作用的度量。因此,力偶可以用一段 带箭头的弧线表示, 其中弧线所在平面表示力偶的作用面, 箭头指向表示力偶的转向,再标注力偶矩的大小。图3-7表示 力偶矩为M的一个力偶,四种表示方法等效。
第3章 力矩和平面力偶系
3.1 力对点之矩及合力矩定理
以扳手拧紧螺母为例(如图3-1所示),人施于扳手上的力
F使扳手和螺母一起绕转动中心O点转动,即产生转动效应。 由
经验可知,转动效应的大小不仅与力F的大小和方向有关,且与
转动中心O点到力F作用线的垂直距离d有关。因此,力F对扳手
的转动效应可用乘积F·d冠以适当的正负号来度量。这个量称为
偶矩大小为
M M B (F ) Fd (3-7)
第3章 力矩和平面力偶系 图3-12
第3章 力矩和平面力偶系 图3-13
