工程力学 第三章
合集下载
工程力学 第3章 力偶系
M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论:两个力偶的合成仍然为力偶,且
第三章 力偶系
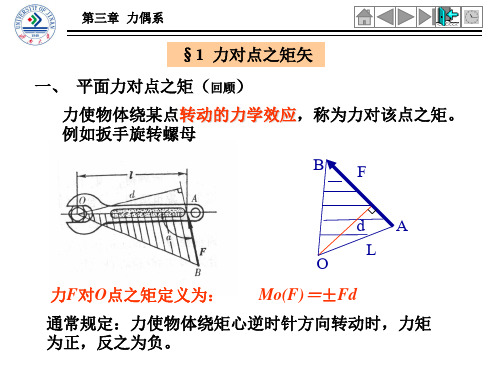
§1 力对点之矩矢 一、 平面力对点之矩(回顾)
力使物体绕某点转动的力学效应,称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为: Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩 为正,反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素:
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反,但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义:在力学中把这样一对等值、反向而不共线的平行力 称为力偶,用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
力对点之矩在各坐标轴上的投影
MO z
O xr
工程力学剪切
故联轴器能传递旳最大扭矩为212N.m
(4)求联轴器能传递旳最大扭矩:
1)按键、和联轴器选择: 将P=10.6kN代入(1)
m 10.6 40 212Nm 2
2)按螺栓选择:
m Pd ⑴ 2
将Q=7.917kN代入(2)
m 2QD0 ⑵
m 2QD0 2 7.917 120 1900Nm
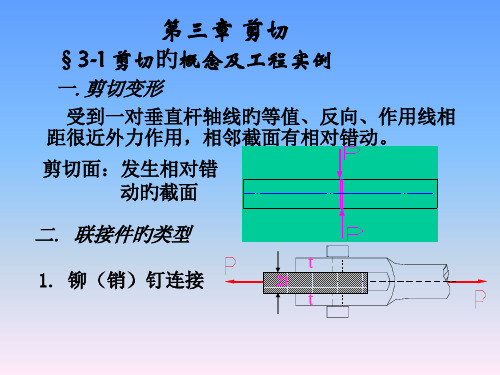
反向力旳分界面为 剪切面,受分布在面 内旳剪应力作用
剪切面内旳剪应 力合力剪力,由平
衡方程求得
∑X=0 Fs=F
2.板接头处旳受力分析
(1)板和铆钉间在接触面上有挤压力作用 (2)板在钉孔处受到孔旳减弱应力增大, 还出现应力集中现象
F
σ
四、实用计算概念
1.建立实用计算旳必要性 (1)受力体尺寸太小,各点受力大小与外力作用方 式关系极大,而外力作用旳细节无法确知,理论分 析无法实现。
解:
P [ ] (1) dh
P
d2
[ ]
(2)
4
(1) 得: d 4 [ ] 2.4 (2) h [ ]
[例3-2]拉杆头部尺寸如图所示,已知
[τ]=100MPa,许用挤压应力[σbs]=200MPa。
校核拉杆头部旳强度。
解:
P 40103 dh 2010
63.7MPa [ ]
bs
(D2
P d2)/
4
40 103 (402 202 )
/
4
42.4MPa
[
]
CL4TU5
[例3-3]拉杆及头部均为圆截
面,材料旳许用剪应力[τ] =100 MPa,许用挤压应力 [σbs]=240MPa。试由拉杆头 旳强度拟定允许拉力[P]。
解:由剪应力强度条件:
(4)求联轴器能传递旳最大扭矩:
1)按键、和联轴器选择: 将P=10.6kN代入(1)
m 10.6 40 212Nm 2
2)按螺栓选择:
m Pd ⑴ 2
将Q=7.917kN代入(2)
m 2QD0 ⑵
m 2QD0 2 7.917 120 1900Nm
反向力旳分界面为 剪切面,受分布在面 内旳剪应力作用
剪切面内旳剪应 力合力剪力,由平
衡方程求得
∑X=0 Fs=F
2.板接头处旳受力分析
(1)板和铆钉间在接触面上有挤压力作用 (2)板在钉孔处受到孔旳减弱应力增大, 还出现应力集中现象
F
σ
四、实用计算概念
1.建立实用计算旳必要性 (1)受力体尺寸太小,各点受力大小与外力作用方 式关系极大,而外力作用旳细节无法确知,理论分 析无法实现。
解:
P [ ] (1) dh
P
d2
[ ]
(2)
4
(1) 得: d 4 [ ] 2.4 (2) h [ ]
[例3-2]拉杆头部尺寸如图所示,已知
[τ]=100MPa,许用挤压应力[σbs]=200MPa。
校核拉杆头部旳强度。
解:
P 40103 dh 2010
63.7MPa [ ]
bs
(D2
P d2)/
4
40 103 (402 202 )
/
4
42.4MPa
[
]
CL4TU5
[例3-3]拉杆及头部均为圆截
面,材料旳许用剪应力[τ] =100 MPa,许用挤压应力 [σbs]=240MPa。试由拉杆头 旳强度拟定允许拉力[P]。
解:由剪应力强度条件:
工程力学(第三章)

MR
y
MR Mz cos MR
§3-6
力偶系的平衡条件
M 0
平衡: 力偶系平衡的充要条件是 其合力偶矩矢为零。
即:力偶系平衡
一、平面力偶系的平衡条件
M R M(代数和) i
M 0
平面力偶系的平衡方程
§3-6
力偶系的平衡条件
M 0
平衡: 力偶系平衡的充要条件是 其合力偶矩矢为零。
力对点之矩矢
作用: 用来度量力使物体绕某点转动效应的量。
(代数量) 一、平面中力对点之矩(力矩)
F
O
h
定义:M O
F Fh
正负号规定: 力使物体绕矩心逆转为正,顺转为负。
作用: 用来度量力使物体绕某点转动效应的量。 1、平面问题
(代数量) 力矩作用面
矩心 O h
力臂
定义: M O F Fh
A
O x
y
Fx
z
y
Fy
x
A x, y, z ,
F Fx , Fy , Fz
(一)、力对点的矩
1、平面问题
MO
F Fh
MO F
O
h
z
F
F
2、空间问题
MO F r F
x
(二)、力对轴的矩
空间: 力偶对空间任一点的矩矢恒等于力偶矩矢, 而与矩心位置无关。
性质二 力偶可在其作用面内任意移转,或移到另
一平行平面,而不改变对刚体的作用效应。
= =
F
F
F
F
工程力学(静力学部分第三章)

方向 作用点
cos( FR, i
)
Fix FR
cos( FR,
j)
Fiy FR
作用于简化中心上
主矩
MO MO (Fi )
F R
(
F x
)2
(
F y
)2
cos(F
, i
)
F x
R
FR
cos(F , R
j) (Fix Fiy Fiy Fix ) (3 2)
Fy 0 FAy P F cos 60 0
解得 FAy 300kN
MA 0
MA M F1l F cos 60 l F sin 60 3l 0
解得 MA 1188kN m
例3-2 已知: F=20kN, q=10kN/m,M 20kNm, L=1m; 求: A,B处的约束力. 解: 取CD梁,画受力图.
节点法与截面法
1、节点法 2、截面法
例3-1 已知:P 100kN, M 20kN m,
q 20kN m, l 1m; F 400kN,
求: 固定端A处约束力。 解:取T型刚架,画受力图。
其中
1
F1
F x
q 3l 30kN 2
0 FAx F1
F
sin 600
0
解得 FAx 316.4kN
解得 F1 10kN (压)
Fix 0 F2 F1 cos 300 0
解得 F2 8.66kN(拉)
取节点C,画受力图.
Fix 0 F4 cos 300 F1' cos 300 0
解得 F4 10kN (压)
Fiy 0 F3 F1' F4 sin 300 0
解得 F3 10kN(拉)
工程力学第三章

图3-13
(二)组合法 有些平面图形是由几个简单图形组成的,称为组合图形,可
先把图形分成几个简单图形,每个简单图形的形心可查表求得,再应 用形心坐标公式计算出组合图形的形心,这种方法称组合法。
【例3-7】 热轧不等边角钢的横截面近似简化图形如图314(a)所示,求该截面形心的位置。
图3-14
衡方程。如图3-7(a)所示,设物体受一空间汇交力系的作用,若选择空间汇交力
系的汇交点为坐标系Oxyz的原点,则不论此力系是否平衡,各力对三轴之矩恒
为零,即∑Mx(F)≡0,∑My(F)≡0,ΣMz(F)≡0。因此,空间汇交力系的平衡方程为
∑Fx=0,∑Fy=0,∑Fz=0
(3-6)
如图3-7(b)所示,设物体受一空间平行力系的作用。令z轴与这些力平
图3-2
用这种方法计算力在轴上的投影的方法称为直接投影法。
一般情况下,不易全部找到力与3个轴的夹角,设已知力F与z轴夹角为γ, 可先将力投影到坐标平面Oxy上,然后再投影到坐标轴x、y上,如图3-2(b)所 示。设力F在Oxy平面上的投影为Fxy与x轴间的夹角为φ,则用这种方法计算力
在轴上的投影称为二次投影法。 具体计算时,可根据问题的实际情况选择一种适当的投影方法。
若物体是均质细杆(或曲线),其重心(或形心)坐标公式为
二、物体重心与形心的计算
(一)对称法 由重心公式不难证明,具有对称轴、对称面或对称中心的均质物体,其形心 必定在其对称轴、对称面或对称中心上。因此,有一根对称轴的平面图形, 其形心在对称轴上;具有两根或两根以上对称轴的平面图形,其形心在对称 轴的交点上;有对称中心的物体,其形心在对称中心上。如图3-13所示。
图3-4
我们将力F分解为平行于z轴的分力Fz和垂直于轴的分力Fxy(即为力F在平面A 上的投影)。由经验可知,分力Fz不能使门绕z轴转动,即力Fz对z轴的矩为零; 只有分力Fxy才能使门绕z轴转动。现用符号Mz(F)表示力F对z轴的矩,点O为平面A 与z轴的交点,d为O点到力Fxy作用线的距离。因此,力F对z轴的矩与其分力Fxy对 点O的矩等效,即
(二)组合法 有些平面图形是由几个简单图形组成的,称为组合图形,可
先把图形分成几个简单图形,每个简单图形的形心可查表求得,再应 用形心坐标公式计算出组合图形的形心,这种方法称组合法。
【例3-7】 热轧不等边角钢的横截面近似简化图形如图314(a)所示,求该截面形心的位置。
图3-14
衡方程。如图3-7(a)所示,设物体受一空间汇交力系的作用,若选择空间汇交力
系的汇交点为坐标系Oxyz的原点,则不论此力系是否平衡,各力对三轴之矩恒
为零,即∑Mx(F)≡0,∑My(F)≡0,ΣMz(F)≡0。因此,空间汇交力系的平衡方程为
∑Fx=0,∑Fy=0,∑Fz=0
(3-6)
如图3-7(b)所示,设物体受一空间平行力系的作用。令z轴与这些力平
图3-2
用这种方法计算力在轴上的投影的方法称为直接投影法。
一般情况下,不易全部找到力与3个轴的夹角,设已知力F与z轴夹角为γ, 可先将力投影到坐标平面Oxy上,然后再投影到坐标轴x、y上,如图3-2(b)所 示。设力F在Oxy平面上的投影为Fxy与x轴间的夹角为φ,则用这种方法计算力
在轴上的投影称为二次投影法。 具体计算时,可根据问题的实际情况选择一种适当的投影方法。
若物体是均质细杆(或曲线),其重心(或形心)坐标公式为
二、物体重心与形心的计算
(一)对称法 由重心公式不难证明,具有对称轴、对称面或对称中心的均质物体,其形心 必定在其对称轴、对称面或对称中心上。因此,有一根对称轴的平面图形, 其形心在对称轴上;具有两根或两根以上对称轴的平面图形,其形心在对称 轴的交点上;有对称中心的物体,其形心在对称中心上。如图3-13所示。
图3-4
我们将力F分解为平行于z轴的分力Fz和垂直于轴的分力Fxy(即为力F在平面A 上的投影)。由经验可知,分力Fz不能使门绕z轴转动,即力Fz对z轴的矩为零; 只有分力Fxy才能使门绕z轴转动。现用符号Mz(F)表示力F对z轴的矩,点O为平面A 与z轴的交点,d为O点到力Fxy作用线的距离。因此,力F对z轴的矩与其分力Fxy对 点O的矩等效,即
工程力学第3章(力偶系)

工程力学
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm, ,
,力偶臂d , F2 = F2' = 120N,力偶臂 2=300mm , F3 = F3' = 80 N,
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ,i ) =
cos( M R,j ) = MR
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm, ,
,力偶臂d , F2 = F2' = 120N,力偶臂 2=300mm , F3 = F3' = 80 N,
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ,i ) =
cos( M R,j ) = MR
工程力学第三章

2.多个力偶的合成 =
=
如同右图
FR Fi
i 1
n 有 M R M1 M 2 M n M i
M R 为合力偶矩矢,等于各分力偶矩矢的矢量和.
合力偶矩矢的解析表达式:
M R M Rx i M Ry j M Rz k
例1: 已知:F , l , a,
求: x M
F ,My F ,Mz F
解:把力
F 分解如图
Mx
F F l a cos
My
F Fl cos
M z F F l sin
xC r sin 300 , yC r cos 300 , zC h
三、力偶的性质 1.力偶在任意坐标轴上的投影等于零,力偶没有合 力,力偶不能用一个力来平衡,力偶只能由力偶来 平衡.力和力偶是静力学的两个基本要素。 2.力偶对任意点取矩都等于力偶矩矢,不因矩心的改 变而改变。
力偶矩矢 M rBA F
3.只要保持力偶矩矢不变,力偶可在其作用面内任 意移转,且可以同时改变力偶中力的大小与力偶臂 的长短,对刚体的作用效果不变.
力偶系
第三章 力偶系
§3-1 力对点之矩矢与力对轴之矩
§3-2 力偶
§3-3 力偶系的合成与平衡条件
§3-1 力对点之矩矢与力对轴之矩
一、平面中力对点之矩(力矩)
1.基本概念 矩心:O 力臂:h 力矩作用面 2.两个要素: (1)大小:力与力臂的乘积 (2)方向:转动方向
3.表示形式
M O F Fh M O F 2OAB
工程力学教学课件第3章剪切

F
2d
50103 2 0.017 0.01
147106 147MPa [ bs ]
结论:强度足够。
挤压的实用计算
4.其它连接件的实用计算方法
焊缝剪切计算
l
有效剪切面
h
45接件的实用计算方法
胶粘缝的计算
F
F
F
不同的粘接方式
F
[ ]
F [ ]
F
[ ] [ ]
为充分利用材
料,切应力和挤压
应力应满足
F dh
2
4F
d 2
d 8h
挤压的实用计算
d
第
3 章
b
a
剪 切
解:1.板的剪切强度
例题
图示接头,受轴向力F 作 用。已知F=50kN,b=150mm, δ=10mm,d=17mm,a=80mm, [τ]=120MPa,[σbs]=320MPa,
铆钉和板的材料相同,试校核 其剪切强度和挤压强度。
Fbs
bs
Fbs Abs
bs
Fbs
bs 常由实验方法确定
t
d
挤压的实用计算
切应力强度条件: Fs
A
第 3 章
挤压强度条件:
bs
Fbs Abs
bs
剪 切
塑性材料: 0.5 0.7
bs 1.5 2.5
脆性材料: 0.8 1.0 bs 0.9 1.5
挤压的实用计算
bs
Fbs Abs
F 1.5dt
15 103
1.5 0.02 0.008
62.5106 62.5MPa [bs ]
挤压的实用计算
第 3 章
剪 切
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
土木工程力学基础 (少学时)
华东师范大学出版社中等职业教育分社
第三章 直杆轴向拉伸 和压缩
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
杆件的四种基本变形 直杆轴向拉、压横截面上的内力
直杆轴向拉、压痕截面上的内力
第四节 直杆轴向拉、 压的变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.弹性变形和塑性变形 变形固体在外力作用下会产生两种不同性质的变形: 一种是当外力消除时,变形也会随着消失,这种变 形被称为弹性变形,如:弹簧被撤掉拉力后会恢复 原长,撑竿跳高的运动员过杆后被扔掉的杆子能恢 复直线形状等;另一种是当外力超过一定限度,即使 外力撤除后,变形仍不能全部消失而留有残余的变 形,这种残余变形被称为塑性变形,如:被手捏过 的橡皮泥、冷拉或冷拔钢筋等。
第五节 直杆轴向拉、 压的强度计算
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.强度计算 为保证轴向拉、压杆件在外力作用下具有足够的强 度,应使杆件的最大工作应力不超过材料的许用应 力,由此,建立强度条件:
第六节 直杆轴向拉、 压在工程中的应用
第二节 直杆轴向拉、 压横截面上的内力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.内力的研究方法——截面法 为了研究构件内力的方向及大小,通常采用截面法。 它可以归纳为以下三个步骤。 (1)分离:在需要求内力的截面处,假想用一垂直 于轴线的截面把构件分成两个部分,保留其中任一 部分作为研究对象,我们将其称之为分离体; (2)显示内力:将(舍弃的)另一部分对该分离体 的内力(作为外力)显示出来; (3)列方程求内力:对分离体建立平衡方程,由已 知外力求出截面上内力的大小和方向。 必须注意:截面上的内力是分布在整个截面上的, 利用截面法求出的内力是这些分布内力的合力。
第二节 直杆轴向拉、 压横截面上的内力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.内力的概念 构件所承受的荷载及约束反力统称为外力。构件在 外力作用下将产生变形,其各部分之间的相对位置 将发生变化,从而产生构件内部各部分之间的相互 作用力。这种由外力引起的构件内部的相互作用 力,称为内力,例如:当我们张拉钢筋时,会感到 钢筋有一种反张拉的力。内力分析是解决构件承载 能力问题的基础。
*3.应力集中现象 一等截面的直杆在轴向外力的作用下,其横截面上的 正应力是均匀分布的。如果该杆件的截面尺寸发生 突变,则在截面突变处的应力并不均匀。例如,一开 有圆孔的直杆在轴向拉力作用下,位于圆孔附近的局 部区域内的应力急剧增大,而在离开这一区域处,应 力则迅速下降并趋于均匀,如图364所示。我们 把这种受力构件由于几何形状、外形尺寸发生突变 而引起局部范围内应力显著增大的现象称为应力集 中。 由于应力集中对脆性材料影响尤其大,会导致脆性材 料构件承载能力的降低,使其发生局部断裂,很快整 个构件遭到破坏,因此,在实际工程中一定要足够的 重视。
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.桁架 桁架是指由若干直杆在其两端以适当的方式连接而 成的结构,在实际工程中,常用于大跨度的工程结构, 如:厂房、塔吊、体育馆和桥梁等。另外,由于桁架 大多用于建筑的屋盖结构,通常也被称作为屋架。图 3-6-3所示为桁架结构的计算简图,在节点荷载作用 下,上弦杆收轴向压力,下弦杆受轴向拉力。
第二节 直杆轴向拉、 压横截面上的内力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职方向各横截面变化的图形称 为轴力图。以平行于杆件轴线的x轴横坐标表示杆件 横截面的位置,以垂直于x轴的轴力FN表示轴力的大 小,将各横截面的轴力按一定比例画在坐标图上, 并用直线相连,就可以得到轴力图。轴力图形象地 表示出轴力沿着杆长的变化情况,并能很方便找到 最大轴力的位置和数值。
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
第三节 直杆轴向拉、 压横截面上的正应力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.轴向拉、压杆横截面上的正应力公式 取一橡胶制成的等直杆件,在其表面均匀地画上若 干与轴线平行的纵线、与轴线垂直的横线,使杆件 表面形成若干个正方形小格子,然后对其两端施加 一对轴向拉力FP,可以观察到:所有的小方格都变 成了长方格;所有纵线都伸长了,但仍相互平行; 所有横线仍保持为直线,且仍垂直于杆轴,只是相 对距离增大了。
直杆轴向拉、压的变形
直杆轴向拉、压的强度计算
直杆轴向拉、压在工程中的应用
第一节 杆件的四种 基本变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
土木工程结构是由若干个构件组成的,这些构件都 要承担各种荷载的作用。为确保构件的正常工作, 必须满足以下三个要求: (1)足够的强度。 (2)足够的刚度。 (3)足够的稳定性。
第三节 直杆轴向拉、 压横截面上的正应力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.应力的概念 由于杆件材料是连续的,所以内力连续分布在整个 横截面上。由截面法求得的是整个截面上分布内力 的合力,但仅仅知道内力的大小,还不足以判断杆 件的强度。例如:两根材料相同、横截面积不同的 杆件,受同样大小的轴向拉力作用,两根杆件横截 面上的内力虽然相同,但截面面积小的杆件必然先 断,因为内力在较小截面上分布的密集程度(简称 集度)大。
第四节 直杆轴向拉、 压的变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.胡克定律 设一等截面直杆原长为l0,横截面面积为A。在轴向 拉力F的作用下,长度由l0变为l1(图3-6-1)。杆 件沿轴线方向的伸长量为Δ l=l1-l0,规定拉伸时 Δ l为正,压缩时Δ l为负。
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.拉杆 图3-6-1所示斜拉桥(又称斜张桥)利用若干斜拉索 承受桥梁荷载,图3-6-2所示拱桥则是利用吊杆承受 住桥梁荷载。它们的共同特点是:依靠拉杆(拉索) 承受桥板和桥板上的荷载,并将其传递给其他构件。
第五节 直杆轴向拉、 压的强度计算
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.许用应力和安全系数 工程上将使材料丧失正常工作能力的应力称为极限 应力,用σ 0表示。 构件在荷载作用下产生的应力称为工作应力。等直 杆最大轴力处的横截面称为危险截面,而危险截面 上的应力称为最大工作应力。
播放FLASH(a)
播放FLASH(b)
第一节 杆件的四种 基本变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.四种基本变形 (1) 轴向拉伸(压缩)变形。 (2) 剪切变形。 (3) 扭转变形。 (4) 弯曲变形。
第一节 杆件的四种 基本变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.变形固体的基本假设 在荷载作用下产生变形的各种固体材料被称为变形 固体。为便于分析和简化计算,对变形固体作以下 基本假设。 (1)连续性假设:即认为物体整个体积内毫无间隙 地充满着物质。 (2)均匀性假设:即认为物体各个部分的力学性能 完全相同。 (3)各向同性假设:即认为物体在各个方向上的力 学性能完全相同。 (4)小变形假设:即认为构件受力后的变形大小与 构件原始尺寸相比是极其微小的,在考虑物体的平 衡时这种变形可以忽略不计。
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
土木工程力学基础 (少学时)
华东师范大学出版社中等职业教育分社
第三章 直杆轴向拉伸 和压缩
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
杆件的四种基本变形 直杆轴向拉、压横截面上的内力
直杆轴向拉、压痕截面上的内力
第四节 直杆轴向拉、 压的变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.弹性变形和塑性变形 变形固体在外力作用下会产生两种不同性质的变形: 一种是当外力消除时,变形也会随着消失,这种变 形被称为弹性变形,如:弹簧被撤掉拉力后会恢复 原长,撑竿跳高的运动员过杆后被扔掉的杆子能恢 复直线形状等;另一种是当外力超过一定限度,即使 外力撤除后,变形仍不能全部消失而留有残余的变 形,这种残余变形被称为塑性变形,如:被手捏过 的橡皮泥、冷拉或冷拔钢筋等。
第五节 直杆轴向拉、 压的强度计算
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.强度计算 为保证轴向拉、压杆件在外力作用下具有足够的强 度,应使杆件的最大工作应力不超过材料的许用应 力,由此,建立强度条件:
第六节 直杆轴向拉、 压在工程中的应用
第二节 直杆轴向拉、 压横截面上的内力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.内力的研究方法——截面法 为了研究构件内力的方向及大小,通常采用截面法。 它可以归纳为以下三个步骤。 (1)分离:在需要求内力的截面处,假想用一垂直 于轴线的截面把构件分成两个部分,保留其中任一 部分作为研究对象,我们将其称之为分离体; (2)显示内力:将(舍弃的)另一部分对该分离体 的内力(作为外力)显示出来; (3)列方程求内力:对分离体建立平衡方程,由已 知外力求出截面上内力的大小和方向。 必须注意:截面上的内力是分布在整个截面上的, 利用截面法求出的内力是这些分布内力的合力。
第二节 直杆轴向拉、 压横截面上的内力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.内力的概念 构件所承受的荷载及约束反力统称为外力。构件在 外力作用下将产生变形,其各部分之间的相对位置 将发生变化,从而产生构件内部各部分之间的相互 作用力。这种由外力引起的构件内部的相互作用 力,称为内力,例如:当我们张拉钢筋时,会感到 钢筋有一种反张拉的力。内力分析是解决构件承载 能力问题的基础。
*3.应力集中现象 一等截面的直杆在轴向外力的作用下,其横截面上的 正应力是均匀分布的。如果该杆件的截面尺寸发生 突变,则在截面突变处的应力并不均匀。例如,一开 有圆孔的直杆在轴向拉力作用下,位于圆孔附近的局 部区域内的应力急剧增大,而在离开这一区域处,应 力则迅速下降并趋于均匀,如图364所示。我们 把这种受力构件由于几何形状、外形尺寸发生突变 而引起局部范围内应力显著增大的现象称为应力集 中。 由于应力集中对脆性材料影响尤其大,会导致脆性材 料构件承载能力的降低,使其发生局部断裂,很快整 个构件遭到破坏,因此,在实际工程中一定要足够的 重视。
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.桁架 桁架是指由若干直杆在其两端以适当的方式连接而 成的结构,在实际工程中,常用于大跨度的工程结构, 如:厂房、塔吊、体育馆和桥梁等。另外,由于桁架 大多用于建筑的屋盖结构,通常也被称作为屋架。图 3-6-3所示为桁架结构的计算简图,在节点荷载作用 下,上弦杆收轴向压力,下弦杆受轴向拉力。
第二节 直杆轴向拉、 压横截面上的内力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职方向各横截面变化的图形称 为轴力图。以平行于杆件轴线的x轴横坐标表示杆件 横截面的位置,以垂直于x轴的轴力FN表示轴力的大 小,将各横截面的轴力按一定比例画在坐标图上, 并用直线相连,就可以得到轴力图。轴力图形象地 表示出轴力沿着杆长的变化情况,并能很方便找到 最大轴力的位置和数值。
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
第六节 直杆轴向拉、 压在工程中的应用
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
第三节 直杆轴向拉、 压横截面上的正应力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.轴向拉、压杆横截面上的正应力公式 取一橡胶制成的等直杆件,在其表面均匀地画上若 干与轴线平行的纵线、与轴线垂直的横线,使杆件 表面形成若干个正方形小格子,然后对其两端施加 一对轴向拉力FP,可以观察到:所有的小方格都变 成了长方格;所有纵线都伸长了,但仍相互平行; 所有横线仍保持为直线,且仍垂直于杆轴,只是相 对距离增大了。
直杆轴向拉、压的变形
直杆轴向拉、压的强度计算
直杆轴向拉、压在工程中的应用
第一节 杆件的四种 基本变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
土木工程结构是由若干个构件组成的,这些构件都 要承担各种荷载的作用。为确保构件的正常工作, 必须满足以下三个要求: (1)足够的强度。 (2)足够的刚度。 (3)足够的稳定性。
第三节 直杆轴向拉、 压横截面上的正应力
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.应力的概念 由于杆件材料是连续的,所以内力连续分布在整个 横截面上。由截面法求得的是整个截面上分布内力 的合力,但仅仅知道内力的大小,还不足以判断杆 件的强度。例如:两根材料相同、横截面积不同的 杆件,受同样大小的轴向拉力作用,两根杆件横截 面上的内力虽然相同,但截面面积小的杆件必然先 断,因为内力在较小截面上分布的密集程度(简称 集度)大。
第四节 直杆轴向拉、 压的变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.胡克定律 设一等截面直杆原长为l0,横截面面积为A。在轴向 拉力F的作用下,长度由l0变为l1(图3-6-1)。杆 件沿轴线方向的伸长量为Δ l=l1-l0,规定拉伸时 Δ l为正,压缩时Δ l为负。
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.拉杆 图3-6-1所示斜拉桥(又称斜张桥)利用若干斜拉索 承受桥梁荷载,图3-6-2所示拱桥则是利用吊杆承受 住桥梁荷载。它们的共同特点是:依靠拉杆(拉索) 承受桥板和桥板上的荷载,并将其传递给其他构件。
第五节 直杆轴向拉、 压的强度计算
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.许用应力和安全系数 工程上将使材料丧失正常工作能力的应力称为极限 应力,用σ 0表示。 构件在荷载作用下产生的应力称为工作应力。等直 杆最大轴力处的横截面称为危险截面,而危险截面 上的应力称为最大工作应力。
播放FLASH(a)
播放FLASH(b)
第一节 杆件的四种 基本变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
1.四种基本变形 (1) 轴向拉伸(压缩)变形。 (2) 剪切变形。 (3) 扭转变形。 (4) 弯曲变形。
第一节 杆件的四种 基本变形
第 三 章 直 杆 轴 向 拉 伸 和 压 缩
第一节
第二节 第三节 第四节 第五节 第六节 目 录
华东师范大学出版社中等职业教育分社
2.变形固体的基本假设 在荷载作用下产生变形的各种固体材料被称为变形 固体。为便于分析和简化计算,对变形固体作以下 基本假设。 (1)连续性假设:即认为物体整个体积内毫无间隙 地充满着物质。 (2)均匀性假设:即认为物体各个部分的力学性能 完全相同。 (3)各向同性假设:即认为物体在各个方向上的力 学性能完全相同。 (4)小变形假设:即认为构件受力后的变形大小与 构件原始尺寸相比是极其微小的,在考虑物体的平 衡时这种变形可以忽略不计。
