六年级奥数比较大小
小学数学奥数解题技巧-三到六年级 比较法

通过对应用题条件之间的比较,或难解题与易解题 的比较,找出它们的联系与区别,研究产生联系与 区别的原因,从而发现解题思路的解题方法叫做比 较法。 在用比较法解应用题时,有些条件可直接比较,有 些条件不能直接比较。在条件不能直接比较时,可 借助画图、列表等方法比较,也可适当变换题目的 陈述方式及数量的大小,创造条件比较。 (一)在同一道题内比较 在同一道题内比较,就是在同一道题的条件与条件、 数量与数量之间的比较,不涉及其他题目。 1.直接比较
3.列表比较 有些应用题适于借助列表的方法比较条件。在用列 表的方法比较条件时,要把题中的条件摘录下来, 尽量按“同事横对,同名竖对”的格式排列成表。 这就是说,要尽量使同一件事情的数量横着对齐, 使单位名称相同的数量竖着对齐。
3.列表比较 有些应用题适于借助列表的方法比较条件。在用列 表的方法比较条件时,要把题中的条件摘录下来, 尽量按“同事横对,同名竖对”的格式排列成表。 这就是说,要尽量使同一件事情的数量横着对齐, 使单位名称相同的数量竖着对齐。
【例题】 甲、乙两人共需做140个零件,甲做了自己任务的80%, 乙做了自己任务的75%,这时甲、乙共剩下32个零件未完成。求甲、 乙两人各需做多少个零件?
【点拔】 已知“甲做了自己任务的80%,乙做了自己任务的75%”后共剩下 32个零件,甲、乙两人所做零件个数不相等,因此,甲所做零件的80% 与乙所做零件的75%不可直接比较。此时就要创造条件比较了。 已知甲做自己任务的80%,假设乙也做自己任务的80%,那么甲乙 就共剩下零件:140×(1-80%)=28(个) 这比原来已知的“甲、乙共剩下32个零件”少:32-28=4(个) 这4个所对应的分率是:80%-75%=5% 所以,乙需做的零件是:4÷5%=80(个) 甲需做的零件是:140-80=60(个)
六年级奥数题:比

比的奥数一、 填空题1、 4:( )=2016=( ) 10=( )%2、 在3:5里,如果前项加上6,要使比值不变,后项应加 .3、某生产队有一块正方形菜地,边长120米,在总面积中种植西红柿、南瓜、茄子面积的比是25:1:21,三种蔬菜各种了 亩.4、买甲、乙两种铅笔共210支,甲种铅笔每支价值3分,乙种铅笔每支价值4分,两种铅笔用去的钱相同,甲种铅笔买了 支.5、车库中停放若干辆双轮摩托车和四轮小卧车,车的辆数与车的轮子数的比是2:5.问:摩托车的辆数与小卧车的辆数的比是 .6、光明小学有三个年级,一年级学生占全校学生人数的25%,二年级与三年级学生人数的比是3:4,已知一年级比三年级学生少40人,一年级有学生 人.7、水泥、石子、黄砂各有6吨,用水泥、石子、黄砂按5:3:2拌制某种混凝土,若用完石子,水泥缺 吨.黄砂多 吨.8、已知甲、乙两数的比为5:3,并且它们最大公约数与最小公倍数的和是1040,那么甲数是多少,乙数是多少.9、有一块铜锌合金,其中铜与锌的比是2:3.现在加入锌6克,共得新合金36克,求在新合金内铜与锌的比.10、一段路程分成上坡、平路、下坡三段,各段路程长之比依次是1:2:3.某人走各段路所用时间之比依次是4:5:6.已知他上坡时速度为每小时3千米.路程全长50千米.问:此人走完全程用了多少时间?二、练习题1、有一个长方体,长与宽的比是2:1,宽与高的比是3:2,已知这个长方体的全部棱长之和是220cm。
求这个长方体的体积。
2、三批货物共值152万元,第一、二、三批货物的重量比为2:4:3,单位重量的价格比为6:5:2,这三批货物各值多少万元?3、一班和二班的人数之比是8:7,如果将一班的8名同学调到二班去,则一班和二班的人数比变为4:5。
求原来两班的人数。
4、某商贩按大个鸡蛋每个3角6分,小个鸡蛋每个2角8分卖出了一批鸡蛋,共收入214元,已知他卖出的大个鸡蛋与小个鸡蛋的个数比是8:5,他卖出大个鸡蛋与小个鸡蛋各多少个?5、某商店购进一批小兔和小狗玩具,共80只,已卖出小兔只数的15与小狗只数的23,共30只,购进小兔和小狗的只数比是几?6、搬运一批货物,甲车单独运要运6次,乙车每次可运7.2吨。
小学六年级奥数 第四章 分数的比较大小

第四章分数大小的比较知识要点分数大小的比较方法有很多,主要有通分、倒数比较、相减比较、相除比较、交叉相乘等。
通分:(1)统一分母,比较分子,分子越大分数越大。
(2)统一分子,比较分母,分母越小分数越大。
倒数比较:倒数大的分数小于倒数小的分数。
相减比较:有两个分数ba与dc,若ba-dc>0,则ba>dc;若ba-dc<0,则ba<dc。
相除比较:分数ba与dc,若ba÷dc的商为真分数,则ba<dc;若商为假分数,则ba>dc。
交叉相乘:分数ba与dc,若bc>ad,则ba>dc。
除了以上几种方法,还有用“1”减法、公式法、化小数比较等等。
典例巧解例1 有五个分数23,58,1523,1017,1219,请按从小到大的顺序排列。
点拨此题若统一分母比较麻烦,而分子的最小公倍数很容易找出为60,故统一分子。
解23=6090,58=6096,1523=6092,1017=60102,1219=6095,因为60102<6096<6095<6092<6090,所以1017<58<1219<1523<23。
例2 比较99999959999997和66666616666663的大小。
点拨一可利用求倒数的方法比较。
解99999959999997的倒数是99999979999995=1+29999995,66666616666663的倒数是66666636666661=1+26666661比较倒数右边的结果知1+26666661>1+29999995,所以66666636666661>99999979999995,即99999959999997>66666616666663。
点拨二由于这两个分数的分子和分母都很接近,且都相差2,可以找到一个标准数。
这两个分数的大小都比1略小,则可用“1”做减法。
解99999959999997=1-29999997,66666616666663=1-26666663。
由于29999997<26666663,在被减数相同的情况下,减数越小,说明差越大,所以99999959999997>66666616666663。
六年级比较与估值(奥数拓展)-运算第5讲

比较与估值(奥数拓展)1.小数之间的大小比较在小数的末尾添上适当的“0”,使它们都变成小数位数相同的小数(如果是循环小数,就把它改写成一般写法的形式),从高位比起。
2.分数之间的大小比较常见方法:1、通分法(通分子、通分母)2、比倒数:与1相减比较法(1)真分数:与1相减,差大的分数小(2)假分数:与1相减,差大的分数大4、两数相除进行比较5、化成小数进行比较3.估值常用方法1)放缩法:为求出某数的整数部分,设法放大或缩小,将结果确定在两个接近数之间,从而估算出结果。
2)变换结构:将算式变形为便于估算的形式。
3)估值步骤(估算和式整数部分):a.找出和式中最小的项和最大的项,并找出项数。
b.令和式结果等于Ac.最小的数×个数 < A < 最大的数×个数d.求出A的整数部分。
例1、典型例题【针对练习1.1】【针对练习1.2】【针对练习1.3】例2、【针对练习2.1】【针对练习2.2】【针对练习2.3】例3、如果A=20012002.2003×20002001.2002,B=20012002.2002×20002001.2003,比较A和B大小。
关系是A_____B(填“>”=“<”).【针对练习3.1】如果M=10011002.1003×10001001.1002,N=10011002.1002×10001001.1003,那么M和N的大小关系是M____N(填“>”,“=”,“<”).A.>B.=C.<D.不确定【针对练习3.2】已知A=1798.57×634.98,B=1798.56×634.99,试比较A和B的大小关系是A____B(填“>”,“=”,“<”).A.>B.=C.<D.不确定例4、【针对练习4.2】【针对练习4.2】例5、【针对练习5.1】【针对练习5.1】比2/7大比1/3小的分数有无数多个,则分子为27的分数有多少个?【针对练习5.2】要使不等式:成立5/9 <9/□<1,方框内的最大自然数可以是多少?例6、【针对练习6.1】【针对练习6.2】【针对练习6.3】A=8.8+8.98+8.998+8.9998+8.99998,A的整数部分是________.例7、有15个正整数,去掉最大的数后平均数等于2.5,去掉最小的数后平均数等于3.0,最大数与最小数之差为______.【针对练习7.1】有30个正整数,去掉最大的数后平均数等于10.8,去掉最小的数后平均数等于12.8,最大数与最小数之差为_________.【针对练习7.2】有51个正整数,去掉最大的数后平均数等于17.8,去掉最小的数后平均数等于20.1,最大数与最小数之差为________.例8、有一道题目要求17个自然数的平均数,结果保留两位小数,冬冬的计算结果是11.28,老师说这个数百分位上的数字错了,其他数位上的数都正确,请问:正确答案是多少?【针对练习8.1】老师在黑板上写了七个自然数,让小明计算它们的平均数(保留小数点后面两位).小明计算出的答数是14.73,老师说:“除最后一位数字外其它都对了.”那么,正确的得数应是__________.【针对练习8.2】小东在计算11个整数的平均数(保留两位小数时),得数为15.33,老师说最后一位数字错了,那么正确的得数是多少?【针对练习8.3】老师在黑板上写了13个自然数,让小明计算平均数(保留两位小数)。
(完整word版)六年级奥数知识点大汇总(良心出品必属精品)

六年级奥数知识点大汇总1、六年级奥数知识点讲解:不定方程2、六年级奥数知识点:约数与倍数3、六年级奥数知识点:数的整除4、六年级奥数知识点:余数及其应用5、六年级奥数知识点:余数问题6、六年级奥数知识点:分数与百分数的应用7、六年奥级数知识点:分数大小的比较8、六年级奥数知识点:完全平方数9、六年级奥数知识点讲解:称球问题10、六年级奥数知识点讲解:质数与合数11、六年级奥数知识点讲解:二进制及其应用12、六年级奥数知识点讲解:定义新运算13、六年级奥数知识点讲解:周期循环数14、六年级奥数知识点讲解:牛吃草问题15、六年级奥数知识点讲解:鸡兔同笼问题16、六年级奥数知识点讲解:归一问题17、六年级奥数知识点讲解:逻辑推理问题18、六年级奥数知识点讲解:几何面积19、六年级奥数知识点讲解:时钟问题20、六年级奥数知识点讲解:浓度与配比21、六年级奥数知识点讲解:经济问题22、六年级奥数知识点讲解:简单方程23、六年级奥数知识点讲解:循环小数24、六年级奥数知识点:综合行程问题25、六年级奥数知识点讲解:工程问题26、六年级奥数知识点讲解:比和比例27、六年级奥数知识点讲解:加法原理28、六年级奥数知识讲解:数列求和29、六年级奥数知识讲解:抽屉原理30、六年级奥数知识点讲解:平均数问题31、六年级奥数知识点讲解:盈亏问题32、六年级奥数知识点讲解:植树问题33、六年级奥数知识点讲解:年龄问题的三大特征34、小学奥数知识点总结之:和差倍问题35、小学奥数知识点总结之:分数拆分1、六年级奥数知识点讲解:不定方程不定方程一次不定方程:含有两个未知数的一个方程,叫做二元一次方程,由于它的解不唯一,所以也叫做二元一次不定方程;常规方法:观察法、试验法、枚举法;多元不定方程:含有三个未知数的方程叫三元一次方程,它的解也不唯一;多元不定方程解法:根据已知条件确定一个未知数的值,或者消去一个未知数,这样就把三元一次方程变成二元一次不定方程,按照二元一次不定方程解即可;涉及知识点:列方程、数的整除、大小比较;解不定方程的步骤:1、列方程;2、消元;3、写出表达式;4、确定范围;5、确定特征;6、确定答案;技巧总结:A、写出表达式的技巧:用特征不明显的未知数表示特征明显的未知数,同时考虑用范围小的未知数表示范围大的未知数;B、消元技巧:消掉范围大的未知数;2、六年级奥数知识点:约数与倍数约数和倍数:若整数a能够被b整除,a叫做b的倍数,b就叫做a 的约数。
小学六年级奥数教程题目

奥数教程(六年级)第一讲 分数的计算例1 计算:4.3695.3)5.3694.3(2009-⨯+⨯⨯ (提示:转化成分母相同) 例2 计算:1341321318428.44.22.113913313118628.106.32.1⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯ (提示:找分子分母共同点,变形)例3 计算:10241195121172561151281136411132191617815413211+++++++++(提示:先合并再相加) 例4 计算:)1099()988()877()766()655()544()433()322()211(-⨯-⨯-⨯-⨯-⨯-⨯-⨯-⨯-(提示:先求差)例5 计算:23191713111917132223171311132613117455⨯⨯+⨯⨯+⨯⨯+⨯⨯(分子分解质因数,约分) 例6 计算:()123...891098...32199...531)100...642(22222222++++++++++++++++-++++第二讲 分数的大小比较例1 分数75、1715、94、12440、309103中,哪一个最大?(提示:化简,统一分子)例2 在□内填上相同的自然数,使不等式3619613111>++++ 成立,此时□内的数的最大值是几?例3 若A=12009200912+-, B=2220082009200820091+⨯-,比较A 与B 的大小。
(提示:比较分母)例4 不求和,比较200520022004200420032005+与200520022003200420032006+的大小。
例5 在下列□内填两个相邻的整数,使不等式成立。
□<10191817161514131211+++++++++<□ 例6 已知A=21771 (21611216011)+++,求A 的整数部分是多少?第三讲 巧算分数的和例1 计算:50491...431321211⨯++⨯+⨯+⨯ 例2 计算:100981...861641421⨯++⨯+⨯+⨯ 例3 计算:10099981...43213211⨯⨯++⨯⨯+⨯⨯ 例4 计算:10099...3211...4321132112111++++++++++++++++例5 计算:2019...4321...54321432132121++++++++++++++++ 例6 计算:⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+++9911...311211991 (41131121141)3112113121121 第四讲 繁分数例1 计算:20072008200820091200920092009122⨯+-+-÷ 例2 计算:41322111+++例3 规定□表示选择两数中较大的数的运算,△表示选择两数中较小的数的运算。
小学六年级奥数第24讲 比较大小(含答案分析)

第24讲 比较大小一、知识要点我们已经掌握了基本的比较整数、小数、分数大小的方法。
本周将进一步研究如何比较一些较复杂的数或式子的值的大小。
解答这种类型的题目,需要将原题进行各种形式的转化,再利用一些不等式的性质进行推理判断。
如:a >b >0,那么a 的平方>b 的平方;如果a >b >0,那么1a<1b;如果a b>1,b >0,那么a >b 等等。
比较大小时,如果要比较的分数都接近1时,可先用1减去原分数,再根据被减数相等(都是1),减数越小,差越大的道理判断原分数的大小。
如果两个数的倒数接近,可以先用1分别除以这两个数。
再根据被除数相等,商越小,除数越大的道理判断原数的大小。
除了将比较大小转化为比差、比商等形式外,还常常要根据算式的特点将它作适当的变形后再进行判断。
二、精讲精练 【例题1】比较777773777778 和888884888889的大小。
这两个分数的分子与分母各不相同,不能直接比较大小,使用通分的方法又太麻烦。
由于这里的两个分数都接近1,所以我们可先用1分别减去以上分数,再比较所得差的大小,然后再判断原来分数的大小。
因为1-777773777778 =5777778 ,1-888884888889 =58888895777778 >5888889 所以777773777778 <888884888889。
练习1: 1、比较77777757777777 和66666616666663的大小。
2、将9876598766 ,98769877 ,987988 ,9899按从小到大的顺序排列出来。
3、比较235861235862 和652971652974的大小。
【例题2】比较1111111 和111111111哪个分数大? 可以先用1分别除以这两个分数,再比较所得商的大小,最后判断原分数的大小。
因为1÷1111111 =1111111 =1011111÷111111111 =111111111 =1011111101111 >1011111 所以1111111 <111111111练习2: 1、比较A =3331666 和B =33166的大小2、比较111111110222222221 和444444443888888887的大小3、比较88888878888889 和99999919999994的大小。
小学六年级奥数《比较分数的大小》课件+习题

比较分数的大小
2021年3月17日
你有多少种比较分数大小的方法呢?
常用的比较分数大小的方法:
一、通分比较法
• 先统一分母,再比较分子, 分子越大分数越大。
• 先统一分子,再比较分母, 分母越小分数越大。
比较 7 与 3 的大小 94
① 先 统 一 分 母 :① 先 统 一 分 子 :
7 4 28 9 4 36
666667
777778
①先化为倒数
666667 1 2 666665 666665 777778 1 2 777776 777776
②倒数大的,小于倒数小的分数 666665< 777776 666667 777778
常用的比较分数大小的方法:
三、相减比较法
• 比较两个分数的大小,可先计算它们的差: • 差大于0,则前者大于后者; • 差小于0,则后者大于前者。
7 3 21 9 3 27
3 9 27 4 9 36
3 7 21 4 7 28
②比较大小: ②比较大小:
7> 27 9 36
7> 27 9 36
练习:
比较 5 、15 、4 、40 、103 的大小 7 17 9 124 309
能约分的先约分: 40 10 、103 1 124 31 309 3
分子5、15、4、10、1,最小公倍数是60。
常用的比较分数大小的方法:
二、倒数比较法
• 倒数大的分数, 小于倒数小的分数。
比较 111 与 1111 的大小 1111 11111
①化为倒数
111 的倒数:1111 1110 1 10 1
1111
111 111
111
1111 的倒数是:11111 11110 1 10 1
13小学六年级奥数题-专题训练之比和比例应用题

小学六年级奥数题:专题训练之比和比例应用题例1、乘坐某路汽车成年人票价3元,儿童票价2元,残疾人票价1元,某天乘车的成年人、儿童和残疾人的人数比是50:20:1,共收得票款26740元,这天乘车中成年人、儿童和残疾人各有多少人?提示:单价比:成年人:儿童:残疾人=3:2:1人数比:50:20:1[练习]甲乙两人走同一段路,甲要20分钟,乙要15分钟,现在甲、乙两人分别同时从相距840米的两地相向而行,相遇时,甲、乙各走了多少米?例2、“希望小学”搞了一次募捐活动,她们用募捐所得的钱购买了甲、乙、丙三种商品,这三种商品的单价分别为30元、15元和10元。
已知购得的甲商品与乙商品的数量之比为5:6,乙商品与丙商品的数量之比为4:11,且购买丙商品比购买甲商品多花了210元。
提示:根据已知条件可先求三种商品的数量比。
[练习]一种什锦糖是由酥糖、奶糖和水果糖按5:4:3的比例混合而成,酥糖、奶糖和水果糖的单价比是11:8:7,要合成这样的什锦糖120千克,什锦糖每千克32.4元,混合前的酥糖每千克是多少元?例3、A、B、C是三个顺次咬合的齿轮。
当A转4圈时,B恰好转3圈;当B转4圈时,C恰好转5圈,问这三个齿轮的齿数的最小数分别是多少?提示:根据已知条件已知A、B、C转速与齿数的积都相等,即它们的转速与齿数成反比例。
习题:1、甲、乙、丙三个平行四边形的底之比是4:5:6,高之比是3:2:1,已知三个平行四边形的面积和是140平方分米,那么甲、乙、丙三个平行四边形的面积各是多少?2、甲、乙、丙三个三角形的面积之比是8:9:10,高之比是2:3:4,对应的底之比是多少?3、某校四、五年级参加数学竞赛的人数相等,四年级获奖人数与未获奖人数的比是1:4,五年级获奖人数与未获奖人数的比是2:7;两个年级中获奖与未获奖人数的比是多少?4、盒子里共有红、白、黑三种颜色的彩球共68个,红球与白球个数的比是1:2,白球与黑球个数的比是3:4,红球有多少个?二年级奥数测试题一、找规律填数(1)、10,7,4,()(2)、2,5,(),11,14,()(3)、8、15、10、13、12、11、()、()(4)、3、6、5、10、9、()、()(5)、1、6、16、()、51、76二、填空1、学校有两个鸽棚,甲棚里有13只,乙棚里有27只,()棚里的鸽子送给()棚里()只,这样,两个棚里的鸽子同样多。
六年级上册奥数试题:第4讲 最大与最小 全国通用(含答案)

第4讲最大与最小知识网络人们经常考虑有关“最”的问题,如最大、最小、最多、最少、最快、最慢等。
这类求最大值、最小值的问题是一类重要典型的问题,我们在实际生产和生活中经常遇到。
在本书的学习中我们经常要用到以下几个重要结论:(1)两个数的和一定,那么当这两个数的差最小时,它们的积最大。
(2)三个数a、b、c,如果a+b+c一定,只有当a=b=c时,a×b×c的积才能最大。
(3)两个数的积一定,那么当两个数的差最小时,它们的和最小。
(4)在所有周长相等的n边形中,以正n边形的面积最大。
(5)在周长相等的封闭平面图形中,以圆的面积为最大。
(6)在棱长的和一定的长方体中,以长、宽、高都相等的长方体,即正方体的体积最大。
(7)在所有表面积一定的几何体中,球体体积最大。
重点·难点本节所涉及的题型较多,但一般都要求根据一个不变量来确定另一变量的最大值或最小值。
如何根据题意,灵活运用不同的方法来求出表达式,再求最值,或直接求最值是本讲的重点。
这就要求我们不能太急于入手,不妨从一些比较简单的现象或数字开始,找出规律,进而解决问题。
学法指导解决本节问题的方法和策略常常因题而异,归纳起来有以下几种常用的方法:(1)从极端情形入手。
(2)枚举比较。
(3)分析推理。
(4)构造。
[例1]不能写成两个不同的奇合数之和的最大偶数为多少?思路剖析两个最小的不同的奇合数为9和15,9+15=24,因此小于24的偶数都不能写成两个不同的奇合数之和。
下面我们只需要考虑大于24的偶数即可。
15后面的一个奇合数为21,9+21=30,所以比24大比30小的偶数也不能写成两个不同的奇合数之和。
32也不能,34=9+25,36=9+27,38不能,40=15+25,42=15=27,44=9+35,…此时初步确定不能写成两个不同的奇合数之和的最大偶数为38。
解答根据以上分析,我们初步确定所求的最大偶数为38,下面我们给予证明。
六年级奥数-比较分数的大小-

聪明屋:苍蝇散步一只苍蝇和它的孩子在一个秃头上散步,过了一会儿,它若有所思的说:“孩子们,时间过得真快啊,我像你们这么大的时候,这儿只是一条小道。
”第三讲 比较分数的大小一、 考点、热点回顾对于两个不同的分数,有分母相同,分子相同以及分子、分母都不相同三种情况,其中前两种情况判别大小的方法是:(1)分母相同的两个分数,分子大的那个分数比较大;(2)分子相同的两个分数,分母大的那个分数比较小。
(3)分子、分母都不同的两个分数,通常是采用通分的方法,使它们的分母相同,化为第一种情况,再比较大小。
由于要比较的分数千差万别,所以通分的方法不一定是最简捷的。
下面我们介绍另外几种方法:1、“通分子”。
当两个已知分数的分母的最小公倍数比较大,而分子的最小公倍数比较小时,可以把它们化成同分子的分数,再比较大小,这种方法比通分的方法简便。
2、化为小数。
3、先约分,后比较。
有时已知分数不是最简分数,可以先约分。
4、根据倒数比较大小,倒数大的分数小5、若两个真分数的分母与分子的差相等、则分母(子)大的分数较大;若两个假分数的分子与分母的差相等,则分母(子)小的分数较大。
6、借助第三个数进行比较。
有以下几种情况:(1)对于分数m 和n ,若m >k ,k >n ,则m >n 。
(2)对于分数m 和n ,若m-k >n-k ,则m >n 。
(3)对于分数m 和n ,若k-m <k-n ,则m >n 。
注意:(2)与(3)的差别在于,(2)中借助的数k 小于原来的两个分数m 和n ;(3)中借助的数k 大于原来的两个分数m 和n 。
(4)把两个已知分数的分母、分子分别相加,得到一个新分数。
新分数一定介于两个已知分数之间,即比其中一个分数大,比另一个分数小。
7、交叉相乘法:如比较b d a c和的大小,交叉相乘后,如果ac bd >,那么说明a b 大. 8、基准数法:最常用的是把1选为基准数,还有常用的像1123,这样的分数. 9、两数相减法:两个分数相减,如0a b ->,则a 大;反之则b 大.两数相除法:两个分数相除,如1a b ÷>,则a 大;反之则b 大.二、典型例题例1、 比较分数3214和5316的大小例2、 将下列分数按由大到小的顺序排列。
奥数六年级-第2讲-分数的大小比较

第2讲 分数的大小比较知识点、重点、难点比较两个分数的大小,有两种基本方法,第一种是:如果两个分数分母相同,分子大的分数较大;第二种是:如果两个分数分子相同,分母小的分数较大;或者统一分母,或者统一分子,再进行比较。
有时候可另辟蹊径,例如(6)相除比较,若商是真分数,则被除数小于除数,若商是假分数,则被除数大于除数;化为小数比较等等。
在解题中必须认真分析;要学会多角度、多侧面思考问题、灵活动用解题方法,不断开阔解题思路,提高解题能力.课前训练1. 若A =12344×98766,B =12345×98765,比较A 和B 的大小。
2.比较下列各组分数的大小4027___2513 20318___13112 638___516 3611___247 33333___3333333 31483145___12371234 480481___346347 21192113___219213 例题精讲例1 比较分数7761572514和的大小。
提示:通分子比较.7761572514,10864108751086421014776141577615,1087521015725151472514,210]15,14[<>=⨯⨯==⨯⨯==所以因为 跟踪练习:比较分数53163214和的大小。
例2 比较分数1111111111111111和的大小. 提示:倒数法比较(倒数比较,倒数大的分数小于倒数小的分数)。
1111111111111111,1111111011111101111111011111111111111101111111<>所以因为。
的倒数是;的倒数是 跟踪练习:比较分数456789152347654321218191和的大小。
例3比较下列各组分数的大小(1)235231673669和 (2)9999100019991001和 提示:作差比较,如果减去的分数小,那么所得的差就大,原来的分数就大,作和比较,如果加上的分数小,则和小,这个分数就小,加上的分数大,则和大,这个分数就大。
(完整版)六年级奥数知识点大汇总

六年级奥数知识点大汇总1、六年级奥数知识点讲解:不定方程2、六年级奥数知识点:约数与倍数3、六年级奥数知识点:数的整除4、六年级奥数知识点:余数及其应用5、六年级奥数知识点:余数问题6、六年级奥数知识点:分数与百分数的应用7、六年奥级数知识点:分数大小的比较8、六年级奥数知识点:完全平方数9、六年级奥数知识点讲解:称球问题10、六年级奥数知识点讲解:质数与合数11、六年级奥数知识点讲解:二进制及其应用12、六年级奥数知识点讲解:定义新运算13、六年级奥数知识点讲解:周期循环数14、六年级奥数知识点讲解:牛吃草问题15、六年级奥数知识点讲解:鸡兔同笼问题16、六年级奥数知识点讲解:归一问题17、六年级奥数知识点讲解:逻辑推理问题18、六年级奥数知识点讲解:几何面积19、六年级奥数知识点讲解:时钟问题20、六年级奥数知识点讲解:浓度与配比21、六年级奥数知识点讲解:经济问题22、六年级奥数知识点讲解:简单方程24、六年级奥数知识点:综合行程问题25、六年级奥数知识点讲解:工程问题26、六年级奥数知识点讲解:比和比例27、六年级奥数知识点讲解:加法原理28、六年级奥数知识讲解:数列求和29、六年级奥数知识讲解:抽屉原理30、六年级奥数知识点讲解:平均数问题31、六年级奥数知识点讲解:盈亏问题32、六年级奥数知识点讲解:植树问题33、六年级奥数知识点讲解:年龄问题的三大特征34、小学奥数知识点总结之:和差倍问题35、小学奥数知识点总结之:分数拆分1、六年级奥数知识点讲解:不定方程不定方程一次不定方程:含有两个未知数的一个方程,叫做二元一次方程,由于它的解不唯一,所以也叫做二元一次不定方程;常规方法:观察法、试验法、枚举法;多元不定方程:含有三个未知数的方程叫三元一次方程,它的解也不唯一;多元不定方程解法:根据已知条件确定一个未知数的值,或者消去一个未知数,这样就把三元一次方程变成二元一次不定方程,按照二元一次不定方程解即可;涉及知识点:列方程、数的整除、大小比较;解不定方程的步骤:1、列方程;2、消元;3、写出表达式;4、确定范围;5、确定特征;6、确定答案;技巧总结:A、写出表达式的技巧:用特征不明显的未知数表示特征明显的未知数,同时考虑用范围小的未知数表示范围大的未知数;B、消元技巧:消掉范围大的未知数;约数和倍数:若整数a能够被b整除,a叫做b的倍数,b就叫做a的约数。
六年级下册奥数试题最大与最小全国通用(含答案)

第八讲最大与最小在实际生活与生产实践中,人们总是想用最少的财力、物力、人力以及时间等在可能的范围内取得最佳效益。
况且,在许多现实问题中有时很难确定或者就不需要具体的每个数值,有时只关心最大、最小等极值。
这一讲就来研究某个量在一定条件下取得最大值或最小值问题。
这类问题题目中经常出现“最小”、“至少”、“至多”等术语。
经常只能根据具体问题,综合运用所学知识进行求解。
例1某校六年级一班准备用100元钱买圣诞树装饰品。
在花店这样的装饰品成束出售,由20朵花组成的花束每束价值4元,由35朵花组成的花束每束价值6元,由50朵花组成的花束每束价值9元,请问每种花束各买多少才能买到最多的花朵?分析:想用100元钱买到最多的花朵,题目中有三种花束:A种:由20朵花组成的花束价值4元B种:由35朵花组成的花束价值6元C种:由50朵花组成的花束每束价值9元平均1元钱可买A种花朵5朵或B种花朵5.8朵或C种花朵5.5朵,为了买到最多的花朵,应该多买B种花束解:经分析可知由35朵花组成的B种花束中的花朵最便宜,宜多买。
由于每束6元,故100元钱可买16束,还剩4元钱,这4元钱恰好买一束由20朵花组成的A种花束,这时共买花朵:16×35+20=580(朵),若B种花束少买几束,增加A种或C种花束的数量,都不能使花朵数达到580朵。
因此,应买由35朵花组成的花束16束和由20朵花组成的花束1束,可使花朵数量最多:580朵。
说明:此题也可设A种、B种、C种花束各买x束、y束、z束时,可使花朵最多,列方程:4x+6y+9z=100,x,y,z是自然数可以先缩小字母的取值范围。
例如12元能买3束A种花束或2束B种花束,分别得到60朵花和70朵花,于是很清楚在最优解中A种花束不应超过2束。
同理,比较B种花束和C种花束,发现要使花朵最多,C种花束不应超过1束,即x≦2,z≦1,下面只有很少的几种情况了,可以一一列举,同样可以求得x=1,z=0,y=16例2有一类自然数,从第三个数字开始,每个数字恰好是它前面两个数字之和,如134,1459等等,求这类数中最大的自然数和最小的自然数。
奥数六年级--第2讲--分数的比较大小
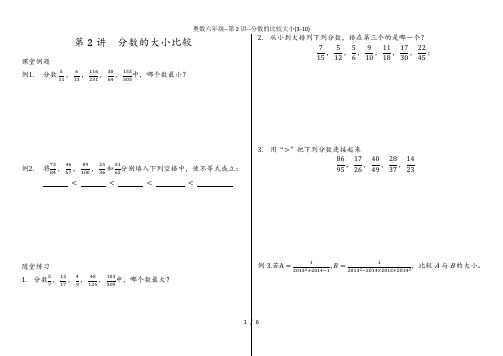
第2讲分数的大小比较课堂例题例1.分数511,613,116231,3064,153305中,哪个数最小?例2.将7384,4657,89100,2536和5162分别填入下列空格中,使不等式成立:< < < <随堂练习1.分数57,1517,49,40124,103309中,哪个数最大?2.从小到大排列下列分数,排在第三个的是哪一个?715,512,56,910,1118,1730,2245;3.用“>”把下列分数连接起来8695,1726,4049,2837,1423例3.若A=120132+2014−1,B=120132−2014×2013+20142,比较A与B的大小。
1/ 6例4.不求和,比较201320112012+201220092013与201420112012+201120092013的大小。
练习4.已知:a×1100÷153.75÷123=b÷100×56×0.375,比较a,b的大小。
练习5.若A=120132−2014−1,B=120132+2014×2013−20142,比较A和B的大小。
练习6.不求差,比较201320112012−201220092013与201420112012−201120092013的大小。
例5.在下列中填两个相邻的整数,使不等式成立。
< 1+12+13+14+15+16+17+18+19+110<例6.已知A=112160+12161+∙∙∙+12177,求A的整数部分是多少?2/ 63 / 6练习7.在横线上填入两个相邻的自然数,使不等式成立。
< (1101+1102+1103+∙∙∙+1150)×3 <练习8.求与(1+1797×1)+(1+1797×2)+(1+1797×3)+∙∙∙+(1+1797×15)最接近的整数。
六年级奥数比的实际运用

比的实际运用例1、两个相同的瓶子装满酒精溶液,甲瓶中酒精与水的体积比是3︰1,而乙瓶中的酒精与水的体积比是4︰1。
若把两瓶溶液混合,混合液中酒精与水的体积比是多少?训练:两个相同的瓶子都装满酒精溶液,A瓶中酒精与水的体积比1:2,而B瓶中酒精与水的体积比是1:3,现把两个瓶子中的酒精溶液充分混合,混合液中酒精与水的体积之比是多少?例2、某村饲养的鸡与猪的只数比为26︰5,羊与马的只数比为25︰9,猪和马的只数比为10︰3,求鸡、猪、马羊的只数比是多少?训练:如果甲︰乙=2︰3,乙︰丙=2︰3,那么甲︰乙︰丙是多少?例3、有大小两瓶油共重2.7千克,把大瓶的1/4倒给小瓶后,大瓶的油与小瓶的油的重量比是3∶2,求大小瓶里原有油多少千克?训练:甲乙两桶油共130千克,从甲桶倒出2/7给乙桶后,甲桶与乙桶油的比为7∶6,原来两桶各有多少千克?例4、甲乙两个长方形,它们的周长相等,甲的长与宽之比是3∶2,乙的长与宽之比是7∶5,求甲与乙的面积比。
训练:如图,ABCD是一个梯形,E是BC的中点,线段DE把梯形分成甲、乙两部分,它们的面积之比是7:4,求上底AB与下底CD的长度之比。
例5、有甲、乙、丙三枚长短不相同的钉子,甲与乙的长度之比是6:5。
如果将甲钉子的2/3钉入墙内,甲与丙钉入墙内的长度之比是5:4,而它们留在墙外的部分一样长。
问:甲、乙、丙的长度比是多少?训练:某团体有100名会员,男会员与女会员的人数比是14∶11,会员分成三个组,甲组人数与乙丙两组人数之和一样多,各组男会员与女会员人数之比是甲:12∶13、乙:5∶3、丙:2∶1,那么丙组有多少名男会员?例6、甲乙两个仓库共存粮240吨,其中甲仓存粮的1/3与乙仓存粮的1/5相等,甲乙两仓各存粮多少吨?训练:箱子里有两种不同颜色的皮球,红球个数的4/9等于白球个数的5/6,已知红球个数比白球个数多21个,两种球各有多少个?例7、一条路全长60千米,分成上坡、平路、下坡3段,各段路程长的比依次是1:2:3。
六年级奥数比较数的大小

例1、求数 的整数部分.
例2、求数 的整数部分是几?
例3、已知 ,求 的整数部分.
P(Practice-Oriented)——实战演练
课堂狙击
1、如果 ,那么A和B中较大的数是.
2、有8个数, , , , , 是其中6个,如果按从小到大的顺序排列时,第4个数是 ,那么按从大到小排列时,第4个数是哪一个数?
7、有一列数,第一个数是133,第二个数是57,从第三个数开始,每个数都是它前面两个数的平均数,那么,第16个数的整数部分是_______.
1、(第五届华杯赛口试)图中有两个黑色的正方形,两个白色的正方形,它们的面积已在图中标出(单位:厘米 ).黑色的两个正方形面积大还是白色的两个正方形面积大?请说明理由.
3、将 、 、 、 、 从小到大排列,第三个数是________.
4、甲、乙两个天平上都放着一定重量的物体,问:哪—个是平衡的?
5、 =10.8+10.98+10.998+10.9998+10.99998, 的整数部分是。
6、有13个自然数,它们的平均值利用四舍五入精确到小数点后一位是26.9.那么,精确到小数点后两位数是多少?
重要结论:
①对于两个真分数,如果分子和分母相差相同的数,则分子和分母都大的分数比较大;
②对于两个假分数,如果分子和分母相差相同的数,则分子和分母都小的分数比较大.
放缩法
在实际解题的过程中,我们还会用到其它一些思路!同学们要根据具体情况展开思维!
三、数的估算时常用方法
(1)放缩法:为求出某数的整数部分,设法放大或缩小.使结果介于某两个接近数之间,从而估算结果.
三、数的估算时常用方法
(1)放缩法:为求出某数的整数部分,设法放大或缩小.使结果介于某两个接近数之间,从而估算结果.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们已经掌握了基本的比较整数、小数、分数大小的方法。
本周将进一步研究如何比较一些较复杂的数或式子的值的大小。
解答这种类型的题目,需要将原题进行各种形式的转化,再利用一些不等式的性质进行推理判断。
如:a >b >0,那么a 的平方>b 的平方;如果a >b >0,那么1a <1b ;如果a b>1,b >0,那么a >b 等等。
比较大小时,如果要比较的分数都接近1时,可先用1减去原分数,再根据被减数相等(都是1),减数越小,差越大的道理判断原分数的大小。
如果两个数的倒数接近,可以先用1分别除以这两个数。
再根据被除数相等,商越小,除数越大的道理判断原数的大小。
除了将比较大小转化为比差、比商等形式外,还常常要根据算式的特点将它作适当的变形后再进行判断。
比较777773777778 和888884888889的大小。
这两个分数的分子与分母各不相同,不能直接比较大小,使用通分的方法又太麻烦。
由于这里的两个分数都接近1,所以我们可先用1分别减去以上分数,再比较所得差的大小,然后再判断原来分数的大小。
因为1-777773777778 =5777778 ,1-888884888889 =58888895777778 >5888889所以777773777778 <888884888889。
1.比较77777757777777 和66666616666663的大小。
2.将9876598766 ,98769877 ,987988 ,9899按从小到大的顺序排列出来。
挑战自我例题1专题简析:比较大小3.比较235861235862 和652971652974 的大小。
比较1111111 和111111111哪个分数大? 可以先用1分别除以这两个分数,再比较所得商的大小,最后判断原分数的大小。
因为1÷1111111 =1111111 =1011111÷111111111 =111111111 =1011111101111 >1011111所以1111111 <1111111111、比较A =3331666 和B =33166的大小2、比较111111110222222221 和444444443888888887的大小3、比较88888878888889 和99999919999994的大小。
比较1234598761 和1234698765的大小。
两个分数中的分子与分子、分母与分母都较为接近,可以根据通分的原理,用交叉相乘法比较分数的大小。
因为12345×98765例题3挑战自我例题212346×98761=12345×98761+98760而 98761>49380所以12346×98761>12345×98765 则1234598761 <1234698765 1.比较176257 和177259的大小。
2.如果A =2222133332 ,B =4444366665,那么A 与B 中较大的数是_______.3.试比较12345679876543 与1234567198765431的大小。
已知A ×15×1199 =B ×23 ÷34 ×15=C ×15.2÷45 =D ×14.8×7374。
A 、B 、C 、D 四个数中最大的是_______. 求A 、B 、C 、D 四个数中最大的数,就要找15×1199 ,23 ÷34 ×15,15.2÷45 ,14.8×7374中最小的。
15×1199>15 15.2÷45>15 23 ÷34 ×15=131314.8×7374=14.6 答:因为23 ÷34×15的积最小,所以B 最大。
1、已知A ×123 =B ×90%=C ÷75%=D ×45 =E ÷115。
把A 、B 、C 、D 、E 这5个数从小到大排列,第二个数是______.挑战自我例题4挑战自我A 2、有八个数,0.5●1●,23 ,59 ,0.51●,2447 ,1325 是其中的六个数,如果从小到大排列时,第四个数是0.5111…,那么从大到小排列时,第四个数是哪个?3、在下面四个算式中,最大的得数是几?(1)(117 +119 )×20 (2)(124 +129)×30 (3)(131 +137 )×40 (4)(141 +147)×50图24-1中有两个红色的正方形,两个蓝色的正方形,它们的面积已在图中标出(单位:平方厘米)。
问:红色的两个正方形面积大还是蓝色的两个正方形面积大?红 蓝红 蓝通过计算结果再比较大小自然是可以,但比较麻烦。
我们可以采取间接比较的方法。
19972-19972 =(1997+1966)×(1997-1996)=399319932-19922 =(1993+1992)×(1993-1992)=3985() 因为19972-19972 >19932-19922所以 19972+19972 >19932+199221.如图24-2所示,有两个红色的圆和两个蓝色的圆。
红色的两圆的直径分别是1992厘米和1949厘米,蓝色的两圆的直径分别是1990厘米和1951厘米。
问:红色的两圆面积之和大,还是蓝色的两圆面积之和大?2.如图24-3所示,正方形被一条曲线分成了A 、B 两部分,如果x >y ,是比较A 、B 两部分周长的大小。
3.问12 ×34 ×56 ×78 ×…×99100 与110相比,哪个更大?为什么?挑战自我例题519962 199221993219972图24-2 图24-3人们碰到的各种优化问题、高效低耗问题,最终都表现为数学上的极值问题,即小学阶段的最大最小问题。
最大最小问题设计到的知识多,灵活性强,解题时要善于综合运用所学的各种知识。
a 和b 是小于100的两个不同的自然数,求a -b a+b的最大值。
根据题意,应使分子尽可能大,使分母尽可能小。
所以b=1;由b=1可知,分母比分子大2,也就是说,所有的分数再添两个分数单位就等于1,可见应使所求分数的分数单位尽可能小,因此a=99a -b a+b 的最大值是99-199+1 =4950答:a -b a+b 的最大值是4950。
1.设x 和y 是选自前100个自然数的两个不同的数,求x -y x+y的最大值。
2.a 和b 是小于50的两个不同的自然数,且a >b ,求a -b a+b的最小值。
3.设x 和y 是选自前200个自然数的两个不同的数,且x >y ,①求x+y x -y 的最大值;②求x+y x -y的最小值。
挑战自我例题专题简析:最大最小问题有甲、乙两个两位数,甲数27 等于乙数的23。
这两个两位数的差最多是多少? 甲数:乙数=23 :27=7:3,甲数的7份,乙数的3份。
由甲是两位数可知,每份的数量最大是14,甲数与乙数相差4份,所以,甲、乙两数的差是14×(7-3)=56答:这两个两位数的差最多是56。
1.有甲、乙两个两位数,甲数的310 等于乙数的45。
这两个两位数的差最多是多少?2.甲、乙两数都是三位数,如果甲数的56 恰好等于乙数的14。
这两个两位数的和最小是多少?3.加工某种机器零件要三道工序,专做第一、二、三道工序的工人每小时分别能做48个、32个、28个,要使每天三道工序完成的个数相同,至少要安排多少工人?如果两个四位数的差等于8921,就是说这两个四位数组成一个数对。
问:这样的数对共有多少个?在这些数对中,被减数最大是9999,此时减数是9999-8921=1078,被减数和减数同时减去1后,又得到一个满足题意条件的四位数对。
为了保证减数是四位数,最多可以减去78,因此,这样的数对共有78+1=79个。
答:这样的数对共有79个。
1.两个四位数的差是8921。
这两个四位数的和的最大值是多少?2.如果两个三位数的和是525,就说这两个三位数组成一个数对。
那么这样的数对共有多少个?组成这样的数对的两个数的差最小是多少?最大是多少?3.如果两个四位数的差是3456,就说这两个数组成一个数对。
那么,这样的数对共有多少个?组成这样的数对的两个数的和最大是多少?最小是少?挑战自我例题3挑战自我例题2三个连续自然数,后面两个数的积与前面两个数的积之差是114。
这三个数中最小的是多少? 因为:最大数×中间数-最小数×中间数=114,即:(最大数-最小数)×中间数=114而三个连续自然数中,最大数-最小数=2,因此,中间数是114÷2=57,最小数是57-1=56答:最小数是56。
1.三个连续的奇数,后两个数的积与前两个数的积之差是252。
三个数中最小的数是______.2.a 、b 、c 是从小到大排列的三个数,且a -b =b -c ,前两个数的积与后两个数的积之差是280。
如果b =35,那么c 是_____。
3.被分数67 ,514 ,1021除得的结果都是整数的最小分数是______。
三个数字能组成6个不同的三位数。
这6个三位数的和是2886。
求所有这样的6个三位数中的最小的三位数。
因为三个数字分别在百位、十位、个位各出现了2次。
所以,2886÷222能得到三个数字的和。
设三个数字为a 、b 、c ,那么6个不同的三位数的和为abc+acb+bac+bca+cab+cba=(a+b+c )×100×2+(a+b+c )×100×2+(a+b+c )×100×2=(a+b+c )×222=2886即a+b+c =2886÷222=13答:所有这样的6个三位数中,最小的三位数是139。
挑战自我例题5挑战自我例题42.有三个数字能组成6个不同的三位数。
这6个不同的三位数的和是2220。
所有这样的6个三位数中最小的一个是多少?3.用a、b、c能组成6个不同的三位数。
这6个三位数相加的和是2886。
已知a、b、c三个数字中,最大的数字是最小数字的2倍,这6个三位数中最小的数是多少?。
