(完整版)全等三角形证明中考题精选(有答案)
全等三角形证明中考题精选[有答案解析]
![全等三角形证明中考题精选[有答案解析]](https://img.taocdn.com/s3/m/abb0f9f733687e21ae45a9aa.png)
全等三角形证明中考题精选[有答案解析]七年级数学下---全等三角形证明题1如图,已知人。
是厶ABC勺中线,分别过点B、C作BEL AD于点E,CF丄AD交AD的延长线于点F,求证:BE=CF2•如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中/(1)操作发现:如图2,固定△ ABC使厶DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是_____________②设△ BDC的面积为$,△ AEC的面积为S,则(2)猜想论证S与S2的数量关系是 _____________当厶DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S与S2的数量关系仍然成立,并尝试分别作出了△BDC ffiA AEC中BC CE边上的高,请你证明小明的猜想.(3)拓展探究已知/ABC=60,点D是角平分线上一点,BD=CD=, DE// AB交BC于点E (如图4).若在射线BA 上存在点F,使S A DC=S BDE,请直接写出相应的BF的长.3.如图,把一个直角三角形ACB(/ACB=90 )绕着顶点B顺时针旋转60°,使得点C旋转到AB 边上的一点D,点A旋转到点E的位置.F, G分别是BD BE上的点,BF=BG延长CF与DG交于点H. (1)求证:CF=DG (2)求出/ FHG勺度数.全等三角形证明中考题精选[有答案解析]4•如图所示,在△ ABC 中,D E 分别是AB AC 上的点,DE// BQ 如图①,然后将厶ADE 绕A 点顺 时针旋转一定角度,得到图②,然后将 BD CE 分别延长至M N,使DM=BD EN=CE 得到图③, 请解答下列问题:(1)若AB=AC 请探究下列数量关系:① 在图②中,BD 与CE的数量关系是_ _ ;② 在图③中,猜想AM 与 AN 的数量关系、/ MAN 与/BAC 的数量关系,并证明你的猜想;(2)若AB=I?AC( k > 1),按上述操作方法,得到图④,请继续探究: AM 与 AN 的数量关系、/ MAN 与/BAC 的数量关系,直接写出你的猜想,不必证明.4. (1)如图,在△ ABC ffiA ADE 中, AB 二AC AD=AE Z BAC K DAE=90 .① 当点D 在AC 上时,如图1,线段BD CE 有怎样的数量关系和位置关系? 直接写出你猜想的结论;② 将图1中的△ ADE 绕点A 顺时针旋转口角(O °VaV 90°),如图2,线段BD CE 有怎样的数量 关系和位置关系?请说明理由.(2)当厶ABC^P ^ADE 满足下面甲、乙、丙中的哪个条件时,使线段 BD CE 在(1)中的位置关系 仍然成立?不必说明理由.甲: AB AC=AD AE=1, / BAC K DA 字90°;乙:AB AC=AD AE M 1,K BAC K DAE=90 ;丙: 6. CD 经过/ BCA 顶点C 的一条直线,CA=CB E, F 分别是直线CD 上两点,且/ BEC K CFA Ka.(1)若直线CD 经过/ BCA 的内部,且E, F 在射线CD 上,请解决下面两个问题:①如图 1,若/ BCA=90 , Ka =90°,则 BE ______________ CF; EF ___________ |BE - AF| (填“〉”, “v”或“=”);②如图2,若0°<Z BCA : 180°,请添加一个关于Ka 与/ BCA 关系的条件—AB: AC=AD AE M 1,/ BAC K DAE^ 90E__________ ,使①中的两个结论仍然成立,并证明两个结论成立.7. 如图,已知 AB=AC (1)若 CE=BD 求证:GE=G ;⑵若CE=mBD (m 为正数),试猜想GE 与 GD 有何关系.(只写结论,不证明)8. (1)已知:如图①,在△ AOBf^A COD 中, OA=OJ 3OC=OD / AOB M COD=60,求证:① AC=BD ②/ APB=6(度;(2)如图②,在△ AOBf^A COD 中,若 OA=OBOC=O , / AOB M COD a ,贝U AC 与 BD 间的等量关系式为 _____________ ; Z APB 的大小为 _____________ ;(3)如图③,在△ AOBf^ACOD 中,若 OA=?OBOC=?OD(k > 1),Z AOB ZCOD a ,贝U AC 与 BD间的等量关系式为 10.已知:EG// AF, AB=AC DE=DF 求证:BE=CF参考答案与试题解析(2)如图3,若直线CD 经过/ BCA 的外部,/ a =Z BCA 请提出EF, BE AF 三条线段数量关系的 合理猜想(不要求证明)•Z APB 的大小为 _____2. 解:(1)①DEC绕点C旋转点D恰好落在AB边上,••• AC=CD:/ BAC=90 -Z B=90°- 30° =60°,二厶ACD是等边三角形,•••/ ACD=60,又TZ CDE Z BAC=60 ,:Z ACD Z CDE 二DE// AC;②T Z B=30°,Z C=90,二CD=AC=AB /• BD=AD=AC2根据等边三角形的性质,△ ACD的边AC AD上的高相等,•••△ BDC的面积和△ AEC的面积相等(等底等高的三角形的面积相等),即S=S2;故答案为:DE// AC S=S;(2)如图,•「△ DEC是由厶ABC绕点C旋转得到,••• BC=CE AC=CD T Z ACN Z BCN=90,Z DCM Z BCN=180 - 90° =90°,•••Z ACN Z DCM T在厶ACNm DCM中,fZACM=ZDCHI ZCND=ZH=90°,[AC=CD•△ACN^A DCM( AAS, • AN=DM•△ BDC的面积和△ AEC的面积相等(等底等高的三角形的面积相等),即S i=S2;3、解(1)证明:•••在厶CBF ft^ DBG K答.fBC=BD答《二,:BF=BG•△CBF^A DBG( SAS , • CF=DQ(2)解:•••△ CBF^A DBG •Z BCF Z BDG又T Z CFB Z DFH •Z DHF Z CBF=60 ,•Z FHG=180 -Z DHF=180 - 60°=120°.4、解答:解:(1)①结论:BD=CE BDL CE②结论:BD=CE BDL CE;理由如下:T Z BAC Z DAE=90• Z BAC-Z DAC Z DAE-Z DAC 即Z BAD Z CAE ft^ ABD与△ ACE中, AB=ACT*4皿ZCAE •△ABD^A ACE(SAS • BD=CEb AD=AE延长BD交AC于F,交CE于H.在厶ABF 与厶HCF 中,T Z ABF=/ HCF Z AFB=/ HFC •Z CHF Z BAF=90••• BDL CE(2)结论:乙.AB AC=AD AE / BAC K DAE=905.6.解答:解:(1)①IK BCA=90,/a =90°,.・.K BCE K CBE=90,/ BCE K ACF=90 , • K CBE K ACF v CA=CB K BEC K CFA •△ BCE^A CAF •- BE=CF EF=|BE- AF|. ②所填的条件是:Ka +K BCA=180 . I AE=AD 卩. 7 •••△ CAE^A BAD( SAS , AC 二 AB • / ACE K ABD v DM=BD EN=CE • BM=CN 在厶 ABM ffiA ACN 中, r 瓏二 CN ••• ZAC14=ZAbr 〔AB 二AC • △ ABMm ACN( SAS , • AM=AN •/ BAM K CAN 即K MAN K BAC (2)AM=?AN 在厶BADfy CAE 中 解答: / CAE=/ BAD K MAN K BAC全等三角形证明中考题精选[有答案解析]证明:在厶 BCE 中,/ CBE# BCE=180 -Z BEC=180 — /a. v/ BCA=180 —/a,•••/ CBE Z BCE Z BCA 又v/ ACF Z BCE Z BCA CBE Z ACF又v BC=CA / BEC Z CFA •△BCE^A CAF( AAS •- BE=CF CE=AF又v EF=C- CE, • EF=|BE- AF|.(2) EF=BE+AF7.解证明:(1)过D作DF// CE交BC于F,答: 贝UZ E=Z GDF v AB=AC •/ ACB Z ABC/ DF/ CE •/ DFB Z ACB•Z DFB Z ACB Z ABC • DF=DB v CE=BD •- DF=CE 在厶GDF^ GEC中, (ZE 二ZGDFI ZDGF=ZEGC ,[DF=EC•△GDF^A GEC(AAS. • GE=GD• / AOB Z BOC Z COD Z BOC 即:/ AOC Z BOD 答:又v OA=OB OC=OD •△ AOC^A BOD • AC=BD②由①得:/ OAC Z OBDv/ AEO Z PEB / APB=180 — (/ BEP+Z OBD, / AOB=180 —(/ OAC Z AEO , • Z APB Z AOB=60 .(2) AC=BD a(3) AC=?BD 180°—a.。
全等三角形证明题及答案(15道)

全等三角形的判定与性质.
7.如图,D、E分别是AB、AC上的点,且 AB=AC,AD=AE.求证:∠B=∠C.
在△ABE和△ACD中, ∵ AB=AC ∠A=∠A AE=AD , ∴△ABE≌△ACD〔SAS〕, ∴∠B=∠C.
证明:∵AB∥DE, ∴∠B=∠DEF. ∵BE=CF, ∴BC=EF. ∵∠ACB=∠F, ∴ ∠B=∠DEF BC=EF∠ACB=∠F , ∴△ABC≌△DEF.
全等三角形的判定;平行线的性质.
10.:如图,E、F在AC上,AD∥CB且AD=CB,∠D=∠B. 求证:AE=CF.
证明:∵AD∥CB, ∴∠A=∠C, 在△ADF和△CBE中, ∠A=∠C AD=CB ∠D=∠B , ∴△ADF≌△CBE〔ASA〕, ∴AF=CE, ∴AF+EF=CE+EF,即AE=CF.
∴△BCF≌△CBD〔ASA〕. 全等三角形的判定.
如图,在△ABC中,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F,BE=CF. 求证:AD是△ABC的角平分线.
证明:∵DE⊥AB,DF⊥AC, ∴Rt△BDE=Rt△DCF=90°. BD=DC BE=CF , ∴Rt△BDE≌Rt△DCF〔HL〕, ∴DE=DF, 又∵DE⊥AB,DF⊥AC, ∴AD是角平分线.
系和位置关系?并加以证明.
• 证明:∵AB∥CD, • ∴∠A=∠D, • ∵在△ABF和△DCE中 • AB=CD ∠A=∠D
AF=DE , • ∴△ABF≌△DCE, • ∴CE=BF,
中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道
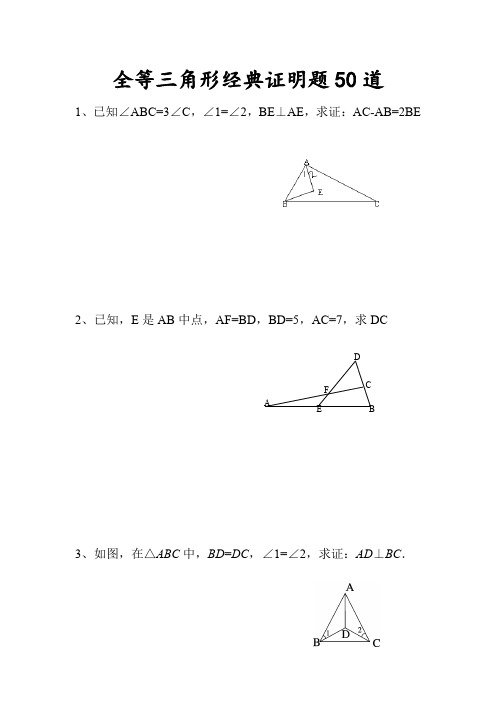
全等三角形经典证明题50道1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .FAEDC B4.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA5.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PCEDBA6.(6分)如图①,E、F分别为线段AC上的两个动点,且DE ⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .OEDCB AFE D CB A25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
证明:∵DF=CE , ∵DF-EF=CE-EF , 即DE=CF ,在∵AED 和∵BFC 中,∵ AD=BC , ∵D=∵C ,DE=CF ∵∵AED ∵∵BFC (SAS )26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道

全等三角形经典证明题50道1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .FAEDC B4.如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA5.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.PCEDBA6.(6分)如图①,E、F分别为线段AC上的两个动点,且DE ⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于点M.(1)求证:MB=MD,ME=MF(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .OEDCB AFE D CB A25、如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
证明:∵DF=CE , ∵DF-EF=CE-EF , 即DE=CF ,在∵AED 和∵BFC 中,∵ AD=BC , ∵D=∵C ,DE=CF ∵∵AED ∵∵BFC (SAS )26、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD 之蔡仲巾千创作解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:AD B C延长CD与P,使D为CP中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴ AB=AE。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点GCG∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD≌△CGDEF =CG∠CGD =∠EFD 又,EF∥AB∴,∠EFD =∠1∠1=∠2∴∠CGD=∠2∴△AGC 为等腰三角形,AC =CG 又 EF =CG∴EF=AC5. 已知:AD 平分∠BAC,AC=AB+BD ,求证:∠B=2∠CB ACDF21 E A证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴B D=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF ,CE =CE ,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC 平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS )∴AD=AF∴AE=AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE 中 AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=2AD B C8. 已知:D 是AB 中点,∠ACB=90°,求证:解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE 中 AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=2 9. 已知:BC=DE ,∠B=∠E,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形证明经典40题含答案(供参考)

1.已知:AB=4, AC=2, D是BC中点,AD是整数,求AD的长.解:延长AD到E使AD=DEYD是BC中点ABD=DC^EAACD和厶BDE中AD=DEZBDE=ZADCBD=DCAAACD^ABDEAAC=BE=2•••在△ ABE 中AB-BE<AE<AB+BEVAB=4即4・2V2ADV4+21<AD<3AAD=22.已知:BC=ED, ZB二ZE, ZC=ZD, F 是CD 中点,求证:Z1 = Z2证明:连接BF和EF••• BC=ED.CF=DE ZBCF=ZEDF・•.三角形BCF全等于三角形EDF(边角边)••• BF=EEZCBF=ZDEF连接BE在三角形BEF中,BF=EF••• ZEBF=ZBEFo••• ZABC=ZAEDc••• ZABE=ZAEBo/. AB=AEo在三角形ABF和三角形AEF中AB=AE.BF=EEZABF=ZABE+ZEBF=ZAEB+ZBEF=ZAEF ・•.三角形ABF和三角形AEF全等。
••• ZBAF=ZEAF(Zl=Z2)o3.已知:Z1=Z2, CD=DE, EF//AB,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG/7EF,可得,ZEFD=CGDDE=DCZFDE=ZGDC (对顶角)•••△ EFD^ACGDEF=CGZCGD=ZEFD又,EF〃AB•••, ZEFD=Z1Z1=Z2AZCGD=Z2・•・△ AGC为等腰三角形,AC=CG又EF=CG・・・EF=AC4.已知:AD 平分ZBAC, AC=AB+BD,求证:ZB=2ZC证明:延长AB取点E,使AE=AC,连接DE TAD 平分ZBAC •••ZEAD=ZCADVAE=AC, AD=ADAAAED^AACD (SAS)AZE=ZCVAC=AB+BDAAE = AB+BDVAE = AB+BE•••BD = BEAZBDE=ZEAZABC=2ZEAZABC=2ZC5.已知:AC 平分ZBAD, CE丄AB, ZB+ZD=180° ,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CFICE丄ABAZCEB = ZCEF=90°VEB=EF, CE=CE,AACEB^ACEF(SAS)AZB = ZCFEVZB4-ZD=180° , ZCFE+ZCFA=180°AZD=ZCFAVAC 平分ZBADAZDAC=ZFACVAC=ACAAADC^AAFC (SAS)•••AD = AF•••AE=AF+FE=AD+BE6.如图,四边形ABCD中,AB〃DC, BE、CE分别平分ZABC、ZBCD,且点E在AD 上。
全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案)1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=22.已知:D是AB中点,∠ACB=90°,求证:12 CD AB延长CD与P,使D为CP中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP为平行四边形又∠ACB=90∴平行四边形ACBP为矩形∴AB=CP=1/2AB3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三角形ABF和三角形AEF全等。
A DBC∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC∠FDE =∠GDC (对顶角) ∴△EFD ≌△CGD EF =CG∠CGD =∠EFD 又,EF ∥AB∴,∠EFD =∠1 ∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS ) ∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E∵∠ABC =∠E+∠BDE ∴∠ABC =2∠EABA CDF2 1 E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学下---全等三角形证明题
1.如图,已知AD 是△ABC 的中线,分别过点B 、C 作BE⊥AD 于点E ,CF⊥AD 交AD 的延长线于点F ,求证:BE=CF
.
2.如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC 绕点C 旋转,当点D 恰好落在AB 边上时,填空:
①线段DE 与AC 的位置关系是 _________ ;
②设△BDC 的面积为S 1,△AEC 的面积为S 2,则S 1与S 2的数量关系是 _________ .
(2)猜想论证
当△DEC 绕点C 旋转到如图3所示的位置时,小明猜想(1)中S 1与S 2的数量关系仍然成立,并尝
试分别作出了△BDC 和△AEC 中BC 、CE 边上的高,请你证明小明的猜想.(3)拓展探究
已知∠ABC=60°,点D 是角平分线上一点,BD=CD=4,DE∥AB 交BC 于点E (如图4).若在射线BA 上存在点F ,使S △DCF =S △BDE ,请直接写出相应的BF 的长.
3.如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB 边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.
4.如图所示,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,如图①,然后将△ADE绕A点顺时针旋转一定角度,得到图②,然后将BD、CE分别延长至M、N,使DM=BD,EN=CE,得到图③,请解答下列问题:(1)若AB=AC,请探究下列数量关系:
①在图②中,BD与CE的数量关系是 _________ ;
②在图③中,猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)若AB=k•AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN 与∠BAC的数量关系,直接写出你的猜想,不必证明.
4.(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数
量关系和位置关系?请说明理由.
(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;
乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.
6.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE _________ CF;EF _________ |BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 _________ ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
r
7.如图,已知AB=AC ,(1)若CE=BD ,求证:GE=GD ;
(2)若CE=m•BD (m 为正数),试猜想GE 与GD 有何关系.(只写结论,不证明)
8.(1)已知:如图①,在△AOB 和△COD 中,OA=OB ,OC=OD ,∠AOB=∠COD=60°,求证:①AC=BD;②∠APB=60度;
(2)如图②,在△AOB 和△COD 中,若OA=OB ,OC=OD ,∠AOB=∠COD=α,则AC 与BD 间的等量关
系式为 _________ ;∠APB 的大小为 _________ ;
(3)如图③,在△AOB 和△COD 中,若OA=k•OB ,OC=k•OD (k >1),∠AOB=∠COD=α,则AC 与BD
间的等量关系式为 _________ ;∠APB 的大小为
10.已知:EG∥AF,AB=AC ,DE=DF ;求证:
BE=CF
i m
e n d
A
l l t h i n g
s i
n t h
e i r
b e
i 参考答案与试题解析
2.解:(1)①∵△DEC 绕点C 旋转点D 恰好落在AB 边上,
∴AC=CD,∵∠BAC=90°﹣∠B=90°﹣30°=60°,∴△ACD 是等边三角形,∴∠ACD=60°,又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;②∵∠B=30°,∠C=90°,∴CD=AC=AB ,∴BD=AD=AC,根据等边三角形的性质,△ACD 的边AC 、AD 上的高相等,
∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),
即S 1=S 2;故答案为:DE∥AC;S 1=S 2;
(2)如图,∵△DEC 是由△ABC 绕点C 旋转得到,
∴BC=CE,AC=CD ,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN 和△DCM 中,
,
∴△ACN≌△DCM(AAS ),∴AN=DM,
∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2;
3、解答:
(1)证明:∵在△CBF 和△DBG 中,,
∴△CBF≌△DBG(SAS ),∴CF=DG;
(2)解:∵△CBF≌△DBG,∴∠BCF=∠BDG,又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°,
∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.
4、
解答:解:(1)①结论:BD=CE ,BD⊥CE;
②结论:BD=CE ,BD⊥CE;理由如下:∵∠BAC=∠DAE=90°
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE 在△ABD 与△ACE 中,∵
∴△ABD≌△ACE(SAS )∴BD=CE
e a n d
A
l l t h i n g
s i
n t h
e i r
b e
i n g
a r e g
o o d f o r
s o
5.
在△ABF 与△HCF 中,∵∠ABF=∠HCF,∠AFB=∠HFC;∴∠CHF=∠BAF=90°∴BD⊥CE(2)结论:乙.AB :AC=AD :AE ,∠BAC=∠DAE=90°
解答:解:(1)①BD=CE;②AM=AN,∠MAN=∠BAC,∵∠DAE=∠BAC,∴∠CAE=∠BAD,
在△BAD 和△CAE 中∵
∴△CAE≌△BAD(SAS ),
∴∠ACE=∠ABD,∵DM=BD ,EN=CE ,∴BM=CN,
在△ABM 和△ACN 中,∵
∴△ABM≌△ACN(SAS ),∴AM=AN,∴∠BAM=∠CAN,即∠MAN=∠BAC;
(2)AM=k•AN ,
∠MAN=∠BAC.
6.
解答:解:(1)①∵∠BCA=90°,∠α=90°,∴∠BCE+∠CBE=90°,∠BCE+∠ACF=90°,∴∠CBE=∠ACF,∵CA=CB,∠BEC=∠CFA;∴△BCE≌△
CAF,∴BE=CF;EF=|BE﹣AF|.
②所填的条件是:∠α+∠BCA=180°.
证明:在△BCE中,∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α.∵∠BCA=180°
﹣∠α,
∴∠CBE+∠BCE=∠BCA.又∵∠ACF+∠BCE=∠BCA,∴∠CBE=∠ACF,
又∵BC=CA,∠BEC=∠CFA,∴△BCE≌△CAF(AAS)∴BE=CF,CE=AF,
又∵EF=CF﹣CE,∴EF=|BE﹣AF|.
t h i n g
s i
n t h
e i r
b e
i n g
a r e g
o o d f
7.解答:证明:(1)过D 作DF∥CE,交BC 于F ,
则∠E=∠GDF.∵AB=AC,∴∠ACB=∠ABC∵DF∥CE,∴∠DFB=∠ACB,
∴∠DFB=∠ACB=∠ABC.∴DF=DB.∵CE=BD,∴DF=CE,在△GDF 和△GEC 中,
,
∴△GDF≌△GEC(AAS ).∴GE=GD.(2)GE=m•GD .
9.解答:解:(1)①∵∠AOB=∠COD=60°,∴∠AOB+∠BOC=∠COD+∠BOC.即:
∠AOC=∠BOD.
又∵OA=OB,OC=OD ,∴△AOC≌△BOD.∴AC=BD.②由①得:∠OAC=∠OBD,
∵∠AEO=∠PEB,∠APB=180°﹣(∠BEP+∠OBD),∠AOB=180°﹣(∠OAC+∠AEO),
∴∠APB=∠AOB=60°.
(2)AC=BD ,α (3)AC=k•BD ,180°﹣α.。
