初二三角形证明的中考题
全等三角形的判定中考题
全等三角形的判定中考题一、已知两个三角形两边及夹角分别相等，根据哪种全等判定定理可以确定这两个三角形全等？A. SSS（三边相等）B. SAS（两边及夹角相等）C. ASA（两角及夹边相等）D. AAS（两角及非夹边相等）（答案：B）二、在△ABC与△DEF中，若∠A=∠D，∠C=∠F，且AC=DF，则依据哪个判定定理可证明两三角形全等？A. SSSB. SASC. ASAD. AAS（答案：C）三、若△PQR与△STU中，PQ=ST，QR=TU，且∠Q=∠T，但∠Q并非PQ与QR的夹角，则根据哪个判定不能直接证明两三角形全等？A. SSSB. SASC. ASAD. 以上均不可（答案：D）四、两个三角形中，如果两个角和一条边分别相等，且这条边是这两个角的夹边，应使用哪个全等判定定理？A. SSSB. SASC. ASAD. AAS（答案：C）五、在△ABC与△MNP中，若AB=MN，BC=NP，且∠B=∠N，但∠B不是AB和BC的夹角，则不能直接通过哪个判定证明两三角形全等？A. SSSB. SASC. AASD. 以上都不是直接证明的依据（答案：B）六、若两个三角形的两个角及非夹边分别相等，应依据哪个全等判定定理来确定它们全等？A. SSSB. SASC. ASAD. AAS（答案：D）七、在△XYZ与△LMN中，若XY=LM，YZ=MN，且∠YZX=∠LMN，但∠YZX并非XY与YZ的夹角，则不能直接应用哪个全等判定？A. SSSB. SAS（答案）C. 这种情况无法判定三角形全等D. AAS八、已知△ABC与△DEF中，∠A=∠D，∠B=∠E，若要证明两三角形全等，还需满足以下条件中的哪一个？A. AB=DEB. AC=EF（非夹角对应的边）C. BC=DF（夹角对应的边，即SAS情况）（答案）D. ∠C=∠F（已有两角相等，再加一角无法判定全等）。
中考数学相似三角形分类专练 证明相似三角形中的对应线段成比例重难点专练(解析版)
同上，AB可以与DE对应，也可以与DF对应，∴相似比可能是 ，也可能是 ，C不一定成立；
∵∠A=∠D，即∠A与∠D是对应角，∴它们的对边一定是对应比，即BC与EF是对应比，
∴相似比为 ，∴D一定成立，
故选D．
【考点知悉】
本题考查相似三角形的性质，注意相似三角形的性质是针对对应角和对应边而言的．
17．如图，点D、E分别在 的边AB、AC上，且 ，若DE=3，BC=6，AC=8，则 _______．
18．如图，点D、E、F分别位于△ABC的三边上，满足DE∥BC，EF∥AB，如果AD：DB=3：2，那么BF：FC=_____．
19．如图，在△ABC中，AB＝9，AC＝6，D为AB边上一点，且△ABC∽△ACD，则AD＝__．
∴这个三角形的边长扩大到原来的4倍,
故选B.
【考点知悉】
本题考查了相似三角形的相似比和周长比之间的关系,属于简单题,熟练掌握相似三角形的性质是解题关键.
10．D
【思路点拨】
根据①直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项.②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项,进行判断即可.
30．如图， ， ， ， ，则 ________．
31．如图，△ABC中，DE∥BC, ,△ADE的面积为8，则△ABC的面积为______
三、解答题
32．已知：如图，AB是半圆O的直径，弦CD∥AB，动点P、Q分别在线段OC、CD上，且DQ＝OP，AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与点C、D不重合)，AB＝20，cos∠AOC＝ .设OP＝x，△CPF的面积为y.
∴ ，
初二证明题考试题及答案
初二证明题考试题及答案一、选择题1. 已知在△ABC中，AB=AC，点D在BC上，且BD=DC，那么下列说法正确的是：A. AD是△ABC的中线B. AD是△ABC的角平分线C. AD是△ABC的高线D. AD是△ABC的中线、角平分线和高线答案：D2. 在等腰三角形中，如果顶角的角平分线也是底边的高线，那么这个三角形是：A. 等边三角形B. 等腰三角形C. 直角三角形D. 不能确定答案：A二、填空题1. 在平行四边形ABCD中，若∠A=60°，则∠B的度数为______。
答案：120°2. 已知等腰三角形的底边长为6cm，腰长为5cm，那么它的高线长度为______。
答案：4cm三、解答题1. 已知在△ABC中，AB=AC，点D在BC上，且BD=DC，求证：AD是△ABC的中线、角平分线和高线。
证明：因为AB=AC，所以△ABC是等腰三角形。
又因为BD=DC，所以D是BC的中点，故AD是△ABC的中线。
在△ABD和△ACD中，有AB=AC，BD=DC，AD=AD，根据SSS（边边边）全等条件，可得△ABD≌△ACD。
因此，∠BAD=∠CAD，所以AD是△ABC的角平分线。
又因为△ABD≌△ACD，所以∠ADB=∠ADC，即AD是△ABC的高线。
综上所述，AD是△ABC的中线、角平分线和高线。
2. 在等腰三角形ABC中，AB=AC，点D是底边BC上的一点，使得AD 是底边BC的高线，求证：BD=DC。
证明：因为AB=AC，所以△ABC是等腰三角形。
又因为AD是底边BC的高线，根据等腰三角形的性质，底边的高线也是底边的中线，所以BD=DC。
因此，BD=DC得证。
中考数学专题复习八几何证明题
专题八：几何证明题问题解析几何证明题重在训练学生应用数学语言合情推理能力;几何证明题和计算题在中考中占有重要地位．根据新的课程标准;对几何证明题证明的方法技巧上要降低;繁琐性、难度方面要降低．但是注重考查学生的基础把握推理能力;所以几何证明题是目前常考的题型．热点探究类型一：关于三角形的综合证明题例题12016·四川南充已知△ABN和△ACM位置如图所示;AB=AC;AD=AE;∠1=∠2．1求证：BD=CE；2求证：∠M=∠N．分析1由SAS证明△ABD≌△ACE;得出对应边相等即可2证出∠BAN=∠CAM;由全等三角形的性质得出∠B=∠C;由AAS证明△ACM≌△ABN;得出对应角相等即可．解答1证明：在△ABD和△ACE中;;∴△ABD≌△ACESAS;∴BD=CE；2证明：∵∠1=∠2;∴∠1+∠DAE=∠2+∠DAE;即∠BAN=∠CAM;由1得：△ABD≌△ACE;∴∠B=∠C;在△ACM和△ABN中;;∴△ACM≌△ABNASA;∴∠M=∠N．点评本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．类型二：关于四边形的综合证明题例题22016·山东省滨州市·10分如图;BD是△ABC的角平分线;它的垂直平分线分别交AB;BD;BC 于点E;F;G;连接ED;DG．1请判断四边形EBGD的形状;并说明理由；2若∠ABC=30°;∠C=45°;ED=2;点H是BD上的一个动点;求HG+HC的最小值．考点平行四边形的判定与性质；角平分线的性质．分析1结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EMC中;求出EM、MC即可解决问题．解答解：1四边形EBGD是菱形．理由：∵EG垂直平分BD;∴EB=ED;GB=GD;∴∠EBD=∠EDB;∵∠EBD=∠DBC;∴∠EDF=∠GBF;在△EFD和△GFB中;;∴△EFD≌△GFB;∴ED=BG;∴BE=ED=DG=GB;∴四边形EBGD是菱形．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EBM中;∵∠EMB=90°;∠EBM=30°;EB=ED=2;∴EM=BE=;∵DE∥BC;EM⊥BC;DN⊥BC;∴EM∥DN;EM=DN=;MN=DE=2;在RT△DNC中;∵∠DNC=90°;∠DCN=45°;∴∠NDC=∠NCD=45°;∴DN=NC=;∴MC=3;在RT△EMC中;∵∠EMC=90°;EM=．MC=3;∴EC===10．∵HG+HC=EH+HC=EC;∴HG+HC的最小值为10．点评本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识;解题的关键是利用对称找到点H的位置;属于中考常考题型．同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．类型三：关于圆的综合证明题例题32016·山东潍坊正方形ABCD内接于⊙O;如图所示;在劣弧上取一点E;连接DE、BE;过点D作DF∥BE交⊙O于点F;连接BF、AF;且AF与DE相交于点G;求证：1四边形EBFD是矩形；2DG=BE．考点正方形的性质；矩形的判定；圆周角定理．分析1直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°;∠BFD=∠BCD=90°;∠EDF=90°;进而得出答案；2直接利用正方形的性质的度数是90°;进而得出BE=DF;则BE=DG．解答证明：1∵正方形ABCD内接于⊙O;∴∠BED=∠BAD=90°;∠BFD=∠BCD=90°;又∵DF∥BE;∴∠EDF+∠BED=180°;∴∠EDF=90°;∴四边形EBFD是矩形；2∵正方形ABCD内接于⊙O;∴的度数是90°;∴∠AFD=45°;又∵∠GDF=90°;∴∠DGF=∠DFC=45°;∴DG=DF;又∵在矩形EBFD中;BE=D同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．类型四：关于相似三角形的证明问题例题42016·黑龙江齐齐哈尔·8分如图;在△ABC中;AD⊥BC;BE⊥AC;垂足分别为D;E;AD与BE 相交于点F．1求证：△ACD∽△BFD；2当tan∠ABD=1;AC=3时;求BF的长．考点相似三角形的判定与性质．分析1由∠C+∠DBF=90°;∠C+∠DAC=90°;推出∠DBF=∠DAC;由此即可证明．2先证明AD=BD;由△ACD∽△BFD;得==1;即可解决问题．解答1证明：∵AD⊥BC;BE⊥AC;∴∠BDF=∠ADC=∠BEC=90°;∴∠C+∠DBF=90°;∠C+∠DAC=90°;∴∠DBF=∠DAC;∴△ACD∽△BFD．2∵tan∠ABD=1;∠ADB=90°∴=1;∴AD=BD;∵△ACD∽△BFD;∴==1;∴BF=AC=3．同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．3. 烟台市 2015 中考 -23如图;以△ABC 的一边AB 为直径的半圆与其它两边AC;BC 的交点分别为D 、E;且=．1试判断△ABC 的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD 的值．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD 中;E 、F 分别为边AB 、CD 的中点;BD 是对角线．1求证：△ADE ≌△CBF ；2若∠ADB 是直角;则四边形BEDF 是什么四边形 证明你的结论．5. 烟台市 2014 中考 -24如图;AB 是⊙O 的直径;延长AB 至P;使BP=OB;BD 垂直于弦BC;垂足为点B;点D 在PC 上．设∠PCB=α;∠POC=β．求证：tanα tan=．DCEF B A 图66. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．7. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE 交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．参考答案类型一：关于三角形的综合证明题同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．考点等腰三角形的性质．分析1①通过角的计算找出∠ACD=∠BCE;再结合△ACB和△DCE均为等腰三角形可得出“AC=BC;DC=EC”;利用全等三角形的判定SAS即可证出△ACD≌△BCE;由此即可得出结论AD=BE；②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC;再通过角的计算即可算出∠AEB的度数；2根据等腰三角形的性质结合顶角的度数;即可得出底角的度数;利用1的结论;通过解直角三角形即可求出线段AD、DE的长度;二者相加即可证出结论．解答1①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°;∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB;∠DCE=∠DCB+∠BCE;∴∠ACD=∠BCE．∵△AC B和△DCE均为等腰三角形;∴AC=BC;DC=EC．在△ACD和△BCE中;有;∴△ACD≌△BCESAS;∴AD=BE．②解：∵△ACD≌△BCE;∴∠ADC=∠BEC．∵点A;D;E在同一直线上;且∠CDE=50°;∴∠ADC=180°﹣∠CDE=130°;∴∠BEC=130°．∵∠BEC=∠CED+∠AEB;且∠CED=50°;∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．2证明：∵△ACB和△DCE均为等腰三角形;且∠ACB=∠DCE=120°;∴∠CDM=∠CEM=×180°﹣120°=30°．∵CM⊥DE;∴∠CMD=90°;DM=EM．在Rt△CMD中;∠CMD=90°;∠CDM=30°;∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°;∠BEC=∠CEM+∠AEB;∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°;∴∠BEN=180°﹣120°=60°．在Rt△BNE中;∠BNE=90°;∠BEN=60°;∴BE==BN．∵AD=BE;AE=AD+DE;∴AE=BE+DE=BN+2CM．点评本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算;解题的关键是：1通过角的计算结合等腰三角形的性质证出△ACD≌△BCE；2找出线段AD、DE的长．本题属于中档题;难度不大;但稍显繁琐;解决该题型题目时;利用角的计算找出相等的角;再利用等腰三角形的性质找出相等的边或角;最后根据全等三角形的判定定理证出三角形全是关键．类型二：关于四边形的综合证明题同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．考点正方形的性质．分析1根据正方形的性质以及勾股定理即可求得；2根据等腰三角形三线合一的性质证得CE⊥AF;进一步得出∠BAF=∠BCN;然后通过证得△ABF≌△CBN得出AF=CN;进而证得△ABF∽△COM;根据相似三角形的性质和正方形的性质即可证得CN= CM．解答解：1∵四边形ABCD是正方形;∴△ABD是等腰直角三角形;∴2AB2=BD2;∵BD=;∴AB=1;∴正方形ABCD的边长为1；2CN=CM．证明：∵CF=CA;AF是∠ACF的平分线;∴CE⊥AF;∴∠AEN=∠CBN=90°;∵∠ANE=∠CNB;∴∠BAF=∠BCN;在△ABF和△CBN中;;∴△ABF≌△CBNAAS;∴AF=CN;∵∠BAF=∠BCN;∠ACN=∠BCN;∴∠BAF=∠OCM;∵四边形ABCD是正方形;∴AC⊥BD;∴∠ABF=∠COM=90°;∴△ABF∽△COM;∴=;∴==;即CN=CM．类型三：关于圆的综合证明题同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．思路分析：本题考查了切线的判定;垂径定理以及相似三角形的判定与性质等知识点．故对于题1可以连接OD;BD;由AB为圆O的直径;得到∠ADB为直角;从而得出三角形BCD为直角三角形;E为斜边BC 的中点;利用斜边上的中线等于斜边的一半;得到CE=DE;利用等边对等角得到一对角相等;再由OA=OD;利用等边对等角得到一对角相等;由直角三角形ABC中两锐角互余;利用等角的余角相等得到∠ADO与∠CDE互余;可得出∠ODE为直角;即DE垂直于半径OD;可得出DE为圆O的切线；对于题2首先可证明OE是△ABC的中位线;则AC=2OE;然后证明△ABC∽△BDC;根据相似三角形的对应边的比相等;即可证得；对于题3在直角△ABC中;利用勾股定理求得AC的长;之后根据三角形中位线定理OE的长即可求得．解题过程：1证明：连接OD;BD;∵AB为圆O的直径;∴∠ADB=90°;在Rt△BDC中;E为斜边BC的中点;∴CE=DE=BE=12 BC;∴∠C=∠CDE;∵OA=OD;∴∠A=∠ADO;∵∠ABC=90°;即∠C+∠A=90°;∴∠ADO+∠CDE=90°;即∠ODE=90°;∴DE⊥OD;又OD为圆的半径;∴DE为⊙O的切线；2证明：∵E是BC的中点;O点是AB的中点; ∴OE是△ABC的中位线;∴AC=2OE;∵∠C=∠C;∠ABC=∠BDC;∴△ABC∽△BDC;∴BC ACCD BC=;即BC2=AC CD．∴BC2=2CD OE；3解：∵cos∠BAD=35;∴sin∠BAC=45 BCAC=;又∵BE=6;E是BC的中点;即BC=12;∴AC=15．又∵AC=2OE;∴OE=12AC=152．规律总结：熟练把握切线的判定;垂径定理以及相似三角形的判定与性质等知识点是解决本题的关键．要证某线是圆的切线;已知此线过圆上某点;连接圆心与这点即为半径;再证垂直即可．类型四：关于相似三角形的证明问题同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．考点相似形综合;考查相似三角形的判定和性质;平行线的性质;三角形中位线性质;勾股定理..答案 1证△ACP∽△ABC即可；2①BP＝5；②71解析1证明：∵∠ACP＝∠B;∠BAC＝∠CAP;∴△ACP∽△ABC;∴AC：AB＝AP：AC;∴AC2＝AP·AB；2①如图;作CQ∥BM交AB延长线于Q;设BP＝x;则P Q＝2x∵∠PBM＝∠ACP;∠PAC＝∠CAQ;∴△APC∽△ACQ;由AC2＝AP·AQ得：22＝3－x35即BP②如图：作CQ⊥AB 于点Q;作CP 0＝CP 交AB 于点P 0;∵AC ＝2;∴AQ＝1;CQ ＝BQ; 设P0Q ＝PQ ＝1－x;BP －1＋x;∵∠BPM＝∠CP 0A ;∠BMP＝∠CAP 0;∴△AP 0C∽△MPB;∴00AP P C MP BP =;∴MP P0C ＝2012P C ==AP 0 BP ＝1＋x;解得x ∴BP ＝－11-．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．考点正方形的性质；全等三角形的判定与性质．分析1根据正方形的性质得出AD=BA;∠BAQ=∠ADP;再根据已知条件得到∠AQB=∠DPA;判定△AQB≌△DPA 并得出结论；2根据AQ ﹣AP=PQ 和全等三角形的对应边相等进行判断分析．解答解：1∵正方形ABCD∴AD=BA;∠BAD=90°;即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE 于点Q;DP⊥AQ 于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPAAAS∴AP=BQ2①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．考点三角形例行;特殊四边形的性质与判定..1证明：∵点E 是AD 的中点;∴AE ＝DE ．∵AF ∥BC;∴∠AFE ＝∠DCE;∠FAE ＝∠CDE ．∴△EAF ≌△EDC ．∴AF ＝DC ．∵AF ＝BD;∴BD ＝DC;即D 是BC 的中点．2四边形AFBD 是矩形．证明如下：∵AF ∥BD;AF ＝BD;∴四边形AFBD 是平行四边形．∵AB ＝AC;又由1可知D 是BC 的中点;∴AD ⊥BC ．DC EF B A图6∴□AFBD是矩形．3. 烟台市 2015 中考 -23如图;以△ABC的一边AB为直径的半圆与其它两边AC;BC的交点分别为D、E;且=．1试判断△ABC的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD的值．思路分析：1连结AE;如图;根据圆周角定理;由=得∠DAE=∠BAE;由AB为直径得∠AEB=90°;根据等腰三角形的判定方法即可得△ABC为等腰三角形；2由等腰三角形的性质得BE=CE=BC=6;再在Rt△ABE中利用勾股定理计算出AE=8;接着由AB为直径得到∠ADB=90°;则可利用面积法计算出BD=;然后在Rt△ABD中利用勾股定理计算出AD=;再根据正弦的定义求解．解题过程：解：1△ABC为等腰三角形．理由如下：连结AE;如图;∵=;∴∠DAE=∠BAE;即AE平分∠BAC;∵AB为直径;∴∠AEB=90°;∴AE⊥BC;∴△ABC为等腰三角形；2∵△ABC为等腰三角形;AE⊥BC;∴BE=CE=BC=×12=6;在Rt△ABE中;∵AB=10;BE=6;∴AE==8;∵AB为直径;∴∠ADB=90°;∴AE BC=BD AC;∴BD==;在Rt△ABD中;∵AB=10;BD=;∴AD==;∴sin∠ABD===．规律总结：本题考查了圆周角定理：在同圆或等圆中;同弧或等弧所对的圆周角相等;都等于这条弧所对的圆心角的一半．推论：半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径．也考查了等腰三角形的判定与性质和勾股定理．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD中;E、F分别为边AB、CD的中点;BD是对角线．1求证：△ADE≌△CBF；2若∠ADB是直角;则四边形BEDF是什么四边形证明你的结论．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．分析：1由四边形ABCD是平行四边形;即可得AD=BC;AB=CD;∠A=∠C;又由E、F分别为边AB、CD的中点;可证得AE=CF;然后由SAS;即可判定△ADE≌△CBF；2先证明BE与DF平行且相等;然后根据一组对边平行且相等的四边形是平行四边形;再连接EF;可以证明四边形AEFD是平行四边形;所以AD∥EF;又AD⊥BD;所以BD⊥EF;根据菱形的判定可以得到四边形是菱形．解答：1证明：∵四边形ABCD是平行四边形;∴AD=BC;AB=CD;∠A=∠C;∵E、F分别为边AB、CD的中点;∴AE=AB;CF=CD;∴AE=CF;在△ADE和△CBF中;∵;∴△ADE≌△CBFSAS；2若∠ADB是直角;则四边形BEDF是菱形;理由如下：解：由1可得BE=DF;又∵AB∥C D;∴BE∥DF;BE=DF;∴四边形BEDF是平行四边形;连接EF;在 ABCD中;E、F分别为边AB、CD的中点;∴DF∥AE;DF=AE;∴四边形AEFD是平行四边形;∴EF∥AD;∵∠ADB是直角;∴AD⊥BD;∴EF⊥BD;又∵四边形BFDE是平行四边形;∴四边形BFDE是菱形．点评：本题主要考查了平行四边形的性质;全等三角形的判定以及菱形的判定;利用好E、F 是中点是解题的关键．5. 烟台市 2014 中考 -24如图;AB是⊙O的直径;延长AB至P;使BP=OB;BD垂直于弦BC;垂足为点B;点D在PC上．设∠PCB=α;∠POC=β．求证：tanα tan=．解析：连接AC先求出△PBD∽△PAC;再求出=;最后得到tanα tan=．解答：证明：连接AC;则∠A=∠POC=;∵AB是⊙O的直径;∴∠ACB=90°;∴tanα=;BD∥AC;∴∠PBD=∠A;∵∠P=∠P;∴△PBD∽△PAC;∴=;∵PB=0B=OA;∴=;∴tana tan===．点评：本题主要考查了相似三角形的判定与性质及圆周角的知识;本题解题的关键是求出△PBD∽△PAC;再求出tanα tan=．6. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．所有分析： 1先根据EQ⊥BO;EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH;故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE;故可得出结论；2由勾股定理求出BP的长;根据EF是BP的垂直平分线可知BQ=BP;再根据锐角三角函数的定义得出QF=BQ的长;由1知;△APB≌△HFE;故EF=BP=4;再根据EQ=EF﹣QF即可得出结论．解答： 1证明：∵EQ⊥BO;EH⊥AB;∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH;∴△EMQ∽△BMH;∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中;;∴△APB≌△HFE;∴HF=AP；2解：由勾股定理得;BP===4．∵EF是BP的垂直平分线;∴BQ=BP=2;∴QF=BQ tan∠FBQ=BQ tan∠ABP=2×=．由1知;△APB≌△HFE;∴EF=BP=4;∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质;熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．7.8. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．考点：切线的判定．分析： 1如图;连接OE．欲证明PE是⊙O的切线;只需推知OE⊥PE即可；2由圆周角定理得到∠AEB=∠CED=90°;根据“同角的余角相等”推知∠3=∠4;结合已知条件证得结论；3设EF=x;则CF=2x;在RT△OEF中;根据勾股定理得出52=x2+2x﹣52;求得EF=4;进而求得BE=8;CF=8;在RT△AEB中;根据勾股定理求得AE=6;然后根据△AEB∽△EFP;得出=;求得PF=;即可求得PD的长．解答： 1证明：如图;连接OE．∵CD是圆O的直径;∴∠CED=90°．∵OC=OE;∴∠1=∠2．又∵∠PED=∠C;即∠PED=∠1;∴∠PED=∠2;∴∠PED+∠OED=∠2+∠OED=90°;即∠OEP=90°; ∴OE⊥EP;又∵点E在圆上;∴PE是⊙O的切线；2证明：∵AB、CD为⊙O的直径;∴∠AEB=∠CED=90°;∴∠3=∠4同角的余角相等．又∵∠PED=∠1;∴∠PED=∠4;即ED平分∠BEP；3解：设EF=x;则CF=2x;∵⊙O的半径为5;∴OF=2x﹣5;在RT△OEF中;OE2=OF2+EF2;即52=x2+2x﹣52;解得x=4;∴EF=4;∴BE=2EF=8;CF=2EF=8;∴DF=CD﹣CF=10﹣8=2;∵AB为⊙O的直径;∴∠AEB=90°;∵AB=10;BE=8;∴AE=6;∵∠BEP=∠A;∠EFP=∠AEB=90°;∴△AEB∽△EFP;∴=;即=;∴PF=;∴PD=PF﹣DF=﹣2=．点评：本题考查了切线的判定和性质;圆周角定理的应用;勾股定理的应用;三角形相似的判定和性质;熟练掌握性质定理是解题的关键．。
山东数学中考分类汇编--有关三角形的综合证明题
有关三角形的综合证明题1．（（2018年滨州）已知，在△ABC中，∠A＝90°，AB＝AC，点D为BC的中点．（1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF，求证：BE＝AF；（2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF，那么BE＝AF吗？请利用图②说明理由．2．（2017年东营）如图，在等腰三角形ABC中，∠BAC＝120°，AB＝AC＝2，点D是BC 边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE＝30°．（1）求证：△ABD∽△DCE；（2）设BD＝x，AE＝y，求y关于x的函数关系式并写出自变量x的取值范围；（3）当△ADE是等腰三角形时，求AE的长．3.（2021年东营）已知点O是线段AB的中点，点P是直线l上的任意一点，分别过点A和点B作直线l的垂线，垂足分别为点C和点D．我们定义垂足与中点之间的距离为“足中距”．（1）[猜想验证]如图1，当点P与点O重合时，请你猜想、验证后直接写出“足中距”OC和OD的数量关系是．（2）[探究证明]如图2，当点P是线段AB上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明；若不成立，请说明理由．（3）[拓展延伸]如图3，①当点P是线段BA延长线上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明；若不成立，请说明理由；②若∠COD＝60°，请直接写出线段AC、BD、OC之间的数量关系．4．（2020•菏泽）如图，在△ABC中，∠ACB＝90°，点E在AC的延长线上，ED⊥AB于点D，若BC＝ED，求证：CE＝DB．5.（2018•菏泽）如图，AB∥CD，AB=CD，CE=BF．请写出DF与AE的数量关系，并证明你的结论．6．（2022•菏泽）如图1，在△ABC中，∠ABC＝45°，AD⊥BC于点D，在DA上取点E，使DE＝DC，连接BE、CE．（1）直接写出CE与AB的位置关系；（2）如图2，将△BED绕点D旋转，得到△B′E′D（点B′、E′分别与点B、E对应），连接CE′、AB′，在△BED旋转的过程中CE′与AB′的位置关系与（1）中的CE与AB的位置关系是否一致？请说明理由；（3）如图3，当△BED绕点D顺时针旋转30°时，射线CE′与AD、AB′分别交于点G、F，若CG＝FG，DC＝，求AB′的长．7.（2017年莱芜）已知△ABC与△DEC是两个大小不同的等腰直角三角形．（1）如图①所示，连接AE，DB，试判断线段AE和DB的数量和位置关系，并说明理由；（2）如图②所示，连接DB，将线段DB绕D点顺时针旋转90°到DF，连接AF，试判断线段DE和AF的数量和位置关系，并说明理由8.（2018年莱芜）已知△ABC中，AB＝AC，∠BAC＝90°，D、E分别是AB、AC的中点，将△ADE绕点A按顺时针方向旋转一个角度α（0°＜α＜90°）得到△AD'E′，连接BD′、CE′，如图1．（1）求证：BD′＝CE'；（2）如图2，当α＝60°时，设AB与D′E′交于点F，求的值．9、（2019年莱芜）如图，已知等边△ABC，CD⊥AB于D，AF⊥AC，E为线段CD上一点，且CE＝AF，连接BE，BF，EG⊥BF于G，连接DG．（1）求证：BE＝BF；（2）试说明DG与AF的位置关系和数量关系．10.（2017年聊城）如图，已知AB∥DE，AB＝DE，BE＝CF，求证：AC∥DF．11.（2017临沂）数学课上，张老师出示了问题：如图1，AC，BD是四边形ABCD 的对角线，若∠ACB=∠ACD=∠ABD=∠ADB=60°，则线段BC，CD，AC三者之间有何等量关系？经过思考，小明展示了一种正确的思路：如图2，延长CB到E，使BE=CD，连接AE，证得△ABE≌△ADC，从而容易证明△ACE是等边三角形，故AC=CE，所以AC=BC+CD．小亮展示了另一种正确的思路：如图3，将△ABC绕着点A逆时针旋转60°，使AB与AD重合，从而容易证明△ACF是等边三角形，故AC=CF，所以AC=BC+CD．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图4，如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小颖提出的问题，请你写出结论，并给出证明．（2）小华提出：如图5，如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小华提出的问题，请你写出结论，不用证明．12．（2020•泰安）若△ABC和△AED均为等腰三角形，且∠BAC＝∠EAD＝90°．（1）如图（1），点B是DE的中点，判定四边形BEAC的形状，并说明理由；（2）如图（2），若点G是EC的中点，连接GB并延长至点F，使CF＝CD．求证：①EB＝DC，②∠EBG＝∠BFC．13．（2020•泰安）小明将两个直角三角形纸片如图（1）那样拼放在同一平面上，抽象出如图（2）的平面图形，∠ACB与∠ECD恰好为对顶角，∠ABC＝∠CDE＝90°，连接BD，AB＝BD，点F是线段CE上一点．探究发现：（1）当点F为线段CE的中点时，连接DF（如图（2）），小明经过探究，得到结论：BD ⊥DF．你认为此结论是否成立？．（填“是”或“否”）拓展延伸：（2）将（1）中的条件与结论互换，即：BD⊥DF，则点F为线段CE的中点．请判断此结论是否成立．若成立，请写出证明过程；若不成立，请说明理由．问题解决：（3）若AB＝6，CE＝9，求AD的长．14．（2021•威海）（1）已知△ABC，△ADE如图①摆放，点B，C，D在同一条直线上，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝45°．连接BE，过点A作AF⊥BD，垂足为点F，直线AF交BE于点G．求证：BG＝EG．（2）已知△ABC，△ADE如图②摆放，∠BAC＝∠DAE＝90°，∠ACB＝∠ADE＝30°．连接BE，CD，过点A作AF⊥BE，垂足为点F，直线AF交CD于点G．求的值．15．（2022•威海）回顾：用数学的思维思考（1）如图1，在△ABC中，AB＝AC．①BD，CE是△ABC的角平分线．求证：BD＝CE．②点D，E分别是边AC，AB的中点，连接BD，CE．求证：BD＝CE．（从①②两题中选择一题加以证明）猜想：用数学的眼光观察经过做题反思，小明同学认为：在△ABC中，AB＝AC，D为边AC上一动点（不与点A，C重合）．对于点D在边AC上的任意位置，在另一边AB上总能找到一个与其对应的点E，使得BD＝CE．进而提出问题：若点D，E分别运动到边AC，AB的延长线上，BD与CE还相等吗？请解决下面的问题：（2）如图2，在△ABC中，AB＝AC，点D，E分别在边AC，AB的延长线上，请添加一个条件（不再添加新的字母），使得BD＝CE，并证明．探究：用数学的语言表达（3）如图3，在△ABC中，AB＝AC＝2，∠A＝36°，E为边AB上任意一点（不与点A，B重合），F为边AC延长线上一点．判断BF与CE能否相等．若能，求CF的取值范围；若不能，说明理由．16.（2022烟台）（1）【问题呈现】如图1，△ABC和△ADE都是等边三角形，连接BD，CE．求证：BD＝CE．（2）【类比探究】如图2，△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°．连接BD，CE．请直接写出BDCE的值．（3）【拓展提升】如图3，△ABC和△ADE都是直角三角形，∠ABC＝∠ADE＝90°，且AB BC＝AD DE ＝34．连接BD，CE．①求BDCE的值；②延长CE交BD于点F，交AB于点G．求sin∠BFC的值．17. （2020烟台）（12分）如图，在等边三角形ABC中，点E是边AC上一定点，点D是直【问题解决】如图1，若点D在边BC上，求证：CE+CF＝CD；【类比探究】如图2，若点D在边BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．18.（2019烟台）【问题探究】（1）如图1，△ABC和△DEC均为等腰直角三角形，∠ACB＝∠DCE＝90°，点B，D，E 在同一直线上，连接AD，BD．①请探究AD与BD之间的位置关系：；②若AC＝BC＝，DC＝CE＝，则线段AD的长为；【拓展延伸】（2）如图2，△ABC和△DEC均为直角三角形，∠ACB＝∠DCE＝90°，AC＝，BC＝，CD＝，CE＝1．将△DCE绕点C在平面内顺时针旋转，设旋转角∠BCD为α（0°≤α＜360°），作直线BD，连接AD，当点B，D，E在同一直线上时，画出图形，并求线段AD 的长．19．（2017烟台）【操作发现】（1）如图1，△ABC为等边三角形，现将三角板中的60°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于30°），旋转后三角板的一直角边与AB交于点D，在三角板斜边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=30°，连接AF，EF．①求∠EAF的度数；②DE与EF相等吗？请说明理由；【类比探究】（2）如图2，△ABC为等腰直角三角形，∠ACB=90°，先将三角板的90°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于45°），旋转后三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=45°，连接AF，EF，请直接写出探究结果：①求∠EAF的度数；②线段AE，ED，DB之间的数量关系．20．（2019枣庄）在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN ＝AM．21．（2020枣庄）在△ABC中，∠ACB＝90°，CD是中线，AC＝BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AC交于点M，DE与BC交于点N．（1）如图1，若CE＝CF，求证：DE＝DF；（2）如图2，在∠EDF绕点D旋转的过程中，试证明CD2＝CE•CF恒成立；（3）若CD＝2，CF＝，求DN的长．22．（2022枣庄）已知△ABC中，∠ACB＝90°，AC＝BC＝4cm，点P从点A出发，沿AB方向以每秒cm的速度向终点B运动，同时动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，设运动的时间为t秒．（1）如图①，若PQ⊥BC，求t的值；（2）如图②，将△PQC沿BC翻折至△P′QC，当t为何值时，四边形QPCP′为菱形？23.（2018淄博）（1）操作发现：如图①，小明画了一个等腰三角形ABC，其中AB=AC，在△ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN．小明发现了：线段GM与GN的数量关系是；位置关系是．（2）类比思考：如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB＞AC，其它条件不变，小明发现的上述结论还成立吗？请说明理由．（3）深入研究：如图③，小明在（2）的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其它条件不变，试判断△GMN的形状，并给与证明．24、（2019淄博）已知，在如图所示的“风筝”图案中，AB＝AD，AC＝AE，∠BAE＝∠DAC．求证：∠E＝∠C．25．（2018淄博）已知：如图，△ABC是任意一个三角形，求证：∠A+∠B+∠C=180°．。
全等三角形证明中考题精选[有答案解析]
![全等三角形证明中考题精选[有答案解析]](https://img.taocdn.com/s3/m/abb0f9f733687e21ae45a9aa.png)
全等三角形证明中考题精选［有答案解析］七年级数学下---全等三角形证明题1如图，已知人。
是厶ABC勺中线，分别过点B、C作BEL AD于点E,CF丄AD交AD的延长线于点F,求证：BE=CF2•如图1,将两个完全相同的三角形纸片ABC和DEC重合放置，其中/(1)操作发现：如图2,固定△ ABC使厶DEC绕点C旋转，当点D恰好落在AB边上时，填空:①线段DE与AC的位置关系是_____________②设△ BDC的面积为$,△ AEC的面积为S，则(2)猜想论证S与S2的数量关系是 _____________当厶DEC绕点C旋转到如图3所示的位置时，小明猜想(1)中S与S2的数量关系仍然成立，并尝试分别作出了△BDC ffiA AEC中BC CE边上的高，请你证明小明的猜想.(3)拓展探究已知/ABC=60，点D是角平分线上一点，BD=CD=, DE// AB交BC于点E (如图4).若在射线BA 上存在点F,使S A DC=S BDE,请直接写出相应的BF的长.3.如图，把一个直角三角形ACB(/ACB=90 )绕着顶点B顺时针旋转60°,使得点C旋转到AB 边上的一点D,点A旋转到点E的位置.F, G分别是BD BE上的点，BF=BG延长CF与DG交于点H. (1)求证：CF=DG (2)求出/ FHG勺度数.全等三角形证明中考题精选［有答案解析］4•如图所示，在△ ABC 中，D E 分别是AB AC 上的点，DE// BQ 如图①，然后将厶ADE 绕A 点顺 时针旋转一定角度，得到图②，然后将 BD CE 分别延长至M N,使DM=BD EN=CE 得到图③， 请解答下列问题：(1)若AB=AC 请探究下列数量关系：① 在图②中，BD 与CE的数量关系是_ _ ;② 在图③中，猜想AM 与 AN 的数量关系、/ MAN 与/BAC 的数量关系，并证明你的猜想；(2)若AB=I?AC( k > 1)，按上述操作方法，得到图④，请继续探究： AM 与 AN 的数量关系、/ MAN 与/BAC 的数量关系，直接写出你的猜想，不必证明.4. (1)如图，在△ ABC ffiA ADE 中, AB 二AC AD=AE Z BAC K DAE=90 .① 当点D 在AC 上时，如图1,线段BD CE 有怎样的数量关系和位置关系？ 直接写出你猜想的结论；② 将图1中的△ ADE 绕点A 顺时针旋转口角(O °VaV 90°)，如图2，线段BD CE 有怎样的数量 关系和位置关系？请说明理由.(2)当厶ABC^P ^ADE 满足下面甲、乙、丙中的哪个条件时，使线段 BD CE 在(1)中的位置关系 仍然成立？不必说明理由.甲： AB AC=AD AE=1, / BAC K DA 字90°;乙：AB AC=AD AE M 1，K BAC K DAE=90 ;丙: 6. CD 经过/ BCA 顶点C 的一条直线，CA=CB E, F 分别是直线CD 上两点，且/ BEC K CFA Ka.(1)若直线CD 经过/ BCA 的内部，且E, F 在射线CD 上，请解决下面两个问题:①如图 1,若/ BCA=90 , Ka =90°,则 BE ______________ CF; EF ___________ |BE - AF| (填“〉”, “v”或“=”)；②如图2,若0°<Z BCA ： 180°,请添加一个关于Ka 与/ BCA 关系的条件—AB: AC=AD AE M 1，/ BAC K DAE^ 90E__________ ，使①中的两个结论仍然成立，并证明两个结论成立.7. 如图，已知 AB=AC （1）若 CE=BD 求证：GE=G ；⑵若CE=mBD （m 为正数），试猜想GE 与 GD 有何关系.（只写结论，不证明）8. (1)已知：如图①，在△ AOBf^A COD 中, OA=OJ 3OC=OD / AOB M COD=60，求证：① AC=BD ②/ APB=6（度；（2）如图②，在△ AOBf^A COD 中，若 OA=OBOC=O , / AOB M COD a ，贝U AC 与 BD 间的等量关系式为 _____________ ; Z APB 的大小为 _____________ ;(3)如图③，在△ AOBf^ACOD 中，若 OA=?OBOC=?OD(k > 1)，Z AOB ZCOD a ，贝U AC 与 BD间的等量关系式为 10.已知：EG// AF, AB=AC DE=DF 求证：BE=CF参考答案与试题解析（2）如图3,若直线CD 经过/ BCA 的外部，/ a =Z BCA 请提出EF, BE AF 三条线段数量关系的 合理猜想（不要求证明）•Z APB 的大小为 _____2. 解：（1）①DEC绕点C旋转点D恰好落在AB边上，••• AC=CD：/ BAC=90 -Z B=90°- 30° =60°,二厶ACD是等边三角形，•••/ ACD=60，又TZ CDE Z BAC=60 ,：Z ACD Z CDE 二DE// AC;②T Z B=30°,Z C=90，二CD=AC=AB /• BD=AD=AC2根据等边三角形的性质，△ ACD的边AC AD上的高相等，•••△ BDC的面积和△ AEC的面积相等（等底等高的三角形的面积相等），即S=S2;故答案为：DE// AC S=S;（2）如图，•「△ DEC是由厶ABC绕点C旋转得到，••• BC=CE AC=CD T Z ACN Z BCN=90，Z DCM Z BCN=180 - 90° =90°,•••Z ACN Z DCM T在厶ACNm DCM中,fZACM=ZDCHI ZCND=ZH=90°,［AC=CD•△ACN^A DCM（ AAS, • AN=DM•△ BDC的面积和△ AEC的面积相等（等底等高的三角形的面积相等），即S i=S2;3、解(1)证明：•••在厶CBF ft^ DBG K答.fBC=BD答《二,:BF=BG•△CBF^A DBG( SAS , • CF=DQ(2)解：•••△ CBF^A DBG •Z BCF Z BDG又T Z CFB Z DFH •Z DHF Z CBF=60 ,•Z FHG=180 -Z DHF=180 - 60°=120°.4、解答：解：(1)①结论：BD=CE BDL CE②结论：BD=CE BDL CE;理由如下：T Z BAC Z DAE=90• Z BAC-Z DAC Z DAE-Z DAC 即Z BAD Z CAE ft^ ABD与△ ACE中, AB=ACT*4皿ZCAE •△ABD^A ACE(SAS • BD=CEb AD=AE延长BD交AC于F,交CE于H.在厶ABF 与厶HCF 中，T Z ABF=/ HCF Z AFB=/ HFC •Z CHF Z BAF=90••• BDL CE(2)结论：乙.AB AC=AD AE / BAC K DAE=905.6.解答：解：(1)①IK BCA=90，/a =90°,.・.K BCE K CBE=90，/ BCE K ACF=90 , • K CBE K ACF v CA=CB K BEC K CFA •△ BCE^A CAF •- BE=CF EF=|BE- AF|. ②所填的条件是：Ka +K BCA=180 . I AE=AD 卩. 7 •••△ CAE^A BAD( SAS , AC 二 AB • / ACE K ABD v DM=BD EN=CE • BM=CN 在厶 ABM ffiA ACN 中, r 瓏二 CN ••• ZAC14=ZAbr 〔AB 二AC • △ ABMm ACN( SAS , • AM=AN •/ BAM K CAN 即K MAN K BAC (2)AM=?AN 在厶BADfy CAE 中 解答: / CAE=/ BAD K MAN K BAC全等三角形证明中考题精选［有答案解析］证明：在厶 BCE 中，/ CBE# BCE=180 -Z BEC=180 — /a. v/ BCA=180 —/a,•••/ CBE Z BCE Z BCA 又v/ ACF Z BCE Z BCA CBE Z ACF又v BC=CA / BEC Z CFA •△BCE^A CAF( AAS •- BE=CF CE=AF又v EF=C- CE, • EF=|BE- AF|.(2) EF=BE+AF7.解证明：(1)过D作DF// CE交BC于F,答: 贝UZ E=Z GDF v AB=AC •/ ACB Z ABC/ DF/ CE •/ DFB Z ACB•Z DFB Z ACB Z ABC • DF=DB v CE=BD •- DF=CE 在厶GDF^ GEC中, (ZE 二ZGDFI ZDGF=ZEGC ,［DF=EC•△GDF^A GEC(AAS. • GE=GD• / AOB Z BOC Z COD Z BOC 即：/ AOC Z BOD 答：又v OA=OB OC=OD •△ AOC^A BOD • AC=BD②由①得：/ OAC Z OBDv/ AEO Z PEB / APB=180 — (/ BEP+Z OBD, / AOB=180 —(/ OAC Z AEO , • Z APB Z AOB=60 .(2) AC=BD a(3) AC=?BD 180°—a.。
八年级上册三角形相关证明题大全(适用于复习巩固)
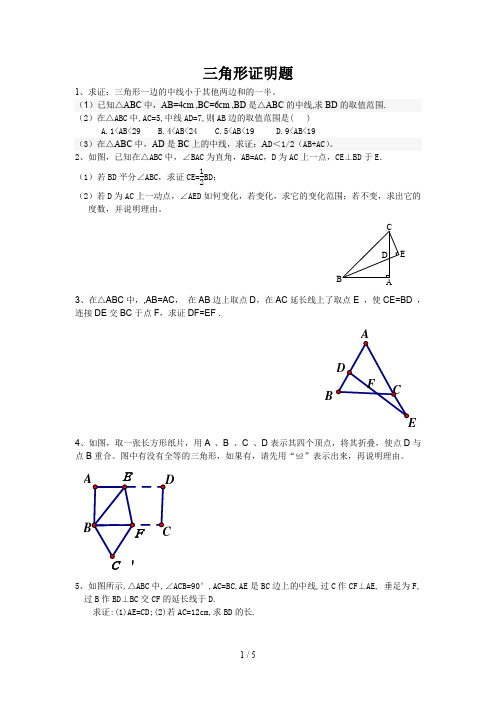
三角形证明题1、求证：三角形一边的中线小于其他两边和的一半。
（1）已知△ABC 中，AB=4cm ,BC=6cm ,BD 是△ABC 的中线,求BD 的取值范围. （2）在△ABC 中,AC=5,中线AD=7,则AB 边的取值范围是( ) A.1<AB<29 B.4<AB<24 C.5<AB<19 D.9<AB<19 （3）在△ABC 中，AD 是BC 上的中线，求证：A D ＜1/2（AB+AC ）。
2、如图，已知在△ABC 中，∠BAC 为直角，AB=AC ，D 为AC 上一点，CE ⊥BD 于E ． （1）若BD 平分∠ABC ，求证CE=12BD ；（2）若D 为AC 上一动点，∠AED 如何变化，若变化，求它的变化范围；若不变，求出它的度数，并说明理由。
EDC BA3、在△ABC 中，,AB=AC ， 在AB 边上取点D ，在AC 延长线上了取点E ，使CE=BD ， 连接DE 交BC 于点F ，求证DF=EF .FC BA ED4、如图，取一张长方形纸片，用A 、B 、C 、D 表示其四个顶点，将其折叠，使点D 与点B 重合。
图中有没有全等的三角形，如果有，请先用“≌”表示出来，再说明理由。
ABDCＣ｀ＥＦ5、如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF ⊥AE, 垂足为F,过B 作BD ⊥BC 交CF 的延长线于D.求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.EDCBAF6、在△ABC 中，AB=AC ，∠BAC=90°，BD 是中线，AF ⊥BD ，F 是垂足，过点C 作AB 的平行线交AF 的延长线于点E 。
求证：（1）∠ABD=∠FAD ；（2）AB=2CEF ACBED7、如图所示，AB=AC ，A D ⊥BC 于D ，且AB+AC+BC=50，而AB+BD+AD=40，则AD 为多少？AD CB8、如图，在△ABC 中，D 是BC 的中点，E 、F 分别是AB 、AC 上的点，且FD ⊥ED ，求证：BE+CF ﹥EFA BCDF E9、ABCD 为正方形，CE 平分∠DCF ，M 为线段BC 上的点，连接AM 、ME ，问：AM 和ME 有何大小关系？当M 点在射线BC 上运动时，AM 和ME 的大小关系改变吗？10、如图，在△ABC 中，AD ⊥BC ，CE ⊥AB ，垂足分别为D 、E ，AD 、CE 交于点H ，已知EH=EB=3，AE=4，则CH 的长是多少？为什么？D HE BA C11、如图, 已知△ABC 中, ∠BAC=900, AB=AC, AE 是过A 的一条直线, 且B 、C 在A 、E 的异侧, BD ⊥AE 于D, CE ⊥AE 于E (1)试说明: BD=DE+CE.(2) 若直线AE 绕A 点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 为什么？(3) 若直线AE 绕A 点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 请直接写出结果, 不需说明.12、在△ABC 中∠BAC 是锐角，AB=AC ，AD 和BE 是高，它们交于点H ，且AE=BE ； （1）求证：AH=2BD ； （2）若将∠BAC 改为钝角，其余条件不变，上述的结论还成立？若成立，请证明；若不成立，请说明理由； 13、如图所示,已知D 是等腰△ABC 底边BC 上的一点,它到两腰AB 、AC 的距离分别为DE 、DF,CM ⊥AB,垂足为M,请你探索一下线段DE 、DF 、CM 三者之间的数量关系, 并给予证明.E D CBAMF14、在Rt △ABC 中，AB=AC ，∠BAC=90°，O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系，并说明理由.(2)若点M 、N 分别是AB 、AC 上的点，且BM=AN ，试判断△OMN 形状，并证明你的结论.15、如图22⑴，AB=CD ，AD=BC ，O 为AC 中点，过O 点的直线分别与AD 、BC 相交于点M 、N ，那么∠1与∠2有什么关系？请说明理由。
中考复习初中数学几何证明经典试题(含答案)
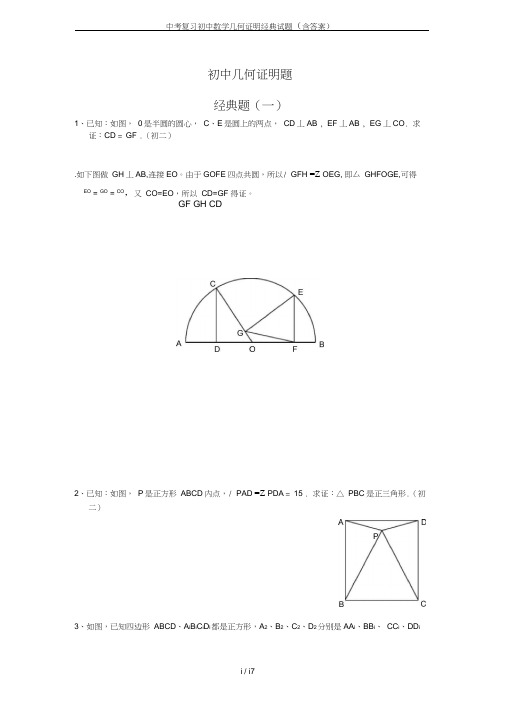
初中几何证明题经典题（一）1、已知：如图，0是半圆的圆心，C、E是圆上的两点，CD丄AB , EF丄AB , EG丄CO. 求证：CD = GF .（初二）.如下图做GH丄AB,连接EO。
由于GOFE四点共圆，所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO，又CO=EO，所以CD=GF 得证。
GF GH CD2、已知：如图，P是正方形ABCD内点，/ PAD =Z PDA = 15°. 求证：△ PBC是正三角形.（初二）3、如图，已知四边形ABCD、A i B i C i D i都是正方形，A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证：AP = AQ .（初二）3、如果上题把直线 MN 由圆外平移至圆内，则由此可得以下命题:设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN P 、Q .4、 1、求证：四边形 A 2B 2C 2D 2是正方形.（初二）已知: 求证: 如图，在四边形 的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中，AD = BC , M 、N 分别是 AB 、CD 的中点，AD 、BC 于E 、F .经典题（二）已知： (1) 求证：AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心 （各边高线的交点），0为外心，且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线，过O 作OA 丄MN 于A ，自A 引圆的两条直线，交圆于DCGN求证：AP = AQ .（初二）ECAM NP4、如图，分别以厶 ABC 的AC 和BC 为一边，在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ，点P 是EF 的中点.求证：点P 到边AB 的距离等于 AB 的一半.（初二）经典题（二）1、如图，四边形 ABCD 为正方形, 求证：CE = CF .（初二）2、如图，四边形 ABCD 为正方形，DE // AC ,且CE = CA ，直线EC 交DA 延长线于F . 求证：AE = AF .（初二）DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图，PC 切圆0于C , AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形，求证： AB • CD + AD • BC = AC • BD .（初三）B 、D .求证: AB = DC , BC = AD .（初三）1、已知：△ ABC 是正三角形，P 是三角形内一点 求：/ APB 的度数.（初二）2、设P 是平行四边形 ABCD 内部的一点，且/求证：/ PAB = Z PCB .（初二）4、平行四边形 ABCD 中，设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证：/ DPA =Z DPC .（初二）AO DB EFC求证:4、如图，△ ABC 中，/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点，/ DCA = 30°, / EBA = 20°，求/ BED 的度数. LiB C经典题（一）1•如下图做GH丄AB,连接E0。
八年级上册数学全等三角形证明题
八年级上册数学全等三角形证明题一、全等三角形证明题1 20题及解析。
（一）题目1。
1. 题目。
已知：如图，在△ABC中，AD是BC边上的中线，E是AD上一点，且BE = AC，延长BE交AC于F。
求证：AF = EF。
2. 解析。
证明：延长AD到G，使DG = AD，连接BG。
因为AD是BC边上的中线，所以BD = CD。
在△BDG和△CDA中，BD = CD，∠BDG = ∠CDA（对顶角相等），DG = DA。
根据SAS（边角边）全等判定定理，可得△BDG≌△CDA。
所以BG = AC，∠G = ∠CAD。
又因为BE = AC，所以BG = BE。
所以∠G = ∠BEG。
因为∠BEG = ∠AEF（对顶角相等），所以∠AEF = ∠CAD。
所以AF = EF。
（二）题目2。
1. 题目。
如图，在△ABC和△DEF中，AB = DE，BE = CF，∠B = ∠DEF。
求证：AC = DF。
2. 解析。
因为BE = CF，所以BE + EC = CF+EC，即BC = EF。
在△ABC和△DEF中，AB = DE，∠B = ∠DEF，BC = EF。
根据SAS全等判定定理，可得△ABC≌△DEF。
所以AC = DF。
（三）题目3。
1. 题目。
已知：如图，AB = CD，AE = DF，CE = FB。
求证：AF = DE。
2. 解析。
因为CE = FB，所以CE + EF = FB + EF，即CF = BE。
在△AEB和△DFC中，AB = CD，AE = DF，BE = CF。
根据SSS（边边边）全等判定定理，可得△AEB≌△DFC。
所以∠B = ∠C。
在△ABF和△DCE中，AB = CD，∠B = ∠C，BF = CE。
根据SAS全等判定定理，可得△ABF≌△DCE。
所以AF = DE。
（四）题目4。
1. 题目。
如图，在Rt△ABC中，∠ACB = 90°，CA = CB，D是AC上一点，E在BC的延长线上，且AE = BD，BD的延长线与AE交于点F。
初二数学 三角形全等中考真题含解析
DEF一、选择题1．如图所示， ∠E = ∠F = 90，∠B = ∠C ， AE = AF ，结论：① EM = FN ；② CD = DN ；③ ∠FAN = ∠EAM ；④△ACN ≌△ABM ．其中正确的有A.1 个 B ．2 个 C ．3 个 D ．4 个【答案】C2．如图 2 所示，AB = AC ，要说明△ADC≌△AEB，需添加的条件不．能．是（ )BCA ．∠B ＝∠CB. AD = AEC ．∠ADC＝∠AEBD. DC = BE【答案】D3.如图 2 所示，在Rt ∆ABC 中， ∠A = 90︒ , BD 平分∠ABC ， 交 AC 于点 D ,且AB = 4, BD = 5 ,则点D 到 BC 的距离是：（A ）3（B ）4（C ）5（D ）6【答案】A4．如图3，Rt△ABC 中，∠C=90°，∠ABC 的平分线BD交AC 于D，若CD=3cm，则点D 到AB 的距离DE 是A．5cm B．4cm C．3cm D．2cm【答案】C5．如图，△A BC≌△D E F，BE=4，A E=1，则DE的长是（）A．5 B．4 C．3 D．2【答案】A二、填空题1．如图，已知AC=FE，BC=DE，点A、D、B、F 在一条直线上，要使△ ABC ≌△ FDE ，还需添加一．个．条件，这个条件可以是．ADCB EF第（13）题【答案】∠C=∠E（答案不惟一，也可以是AB=FD或AD=FB）2．（2010 广西钦州市）如图，在△ABC 和△BAD 中，BC = AD，请你再补充一个条件，使△ABC≌△BAD．你补充的条件是_ ▲ _（只填一个）．C DA B第8 题【答案】AC =BD 或∠CBA＝∠DAB三、解答题CF1．如图，C 是线段 AB 的中点，CD 平分∠ACE ，CE 平分 ∠BCD ，CD=CE ．(1) 求证：△ ACD ≌△ BCE ；(2)若∠D=50°，求∠B 的度数．【答案】2．如图，已知：点 B 、F 、C 、E 在一条直线上，FB =CE ，AC =DF ．能否由上面的已知条件证明 AB ∥ED ？如果能，请给出证明；如果不能，请从下列三个条件中选择一．个．合．适．的．条．件．，添加到已知条件中，使 AB ∥ED 成立，并给出证明． 供选择的三个条件（请从其中选择一个）：①AB =ED ； ②BC =EF ； ③∠ACB =∠DFE ．ABED（第 25 题）FDE ( 第 18 题⎨⎩【答案】解：由上面两条件不能证明AB//ED.有两种添加方法.第一种：FB=CE，AC=DF 添加①AB=ED证明：因为FB=CE，所以BC=EF，又AC=EF，AB=ED，所以ABC≅DEF所以∠ABC=∠DEF 所以AB//ED第二种：FB=CE，AC=DF 添加③∠ACB=∠DFE证明：因为FB=CE，所以BC=EF，又∠ACB=∠DFE AC=EF，所以ABC ≅DEF 所以∠ABC=∠DEF 所以AB//ED3．如图，在△ABC 中，D是BC 边上的点（不与B，C 重合），F，E 分别是AD及其延长线上的点，CF∥BE. 请你添加一个条件，使△B D E≌△C A D F (不再添加其它线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是：▲； B C（2）证明：【答案】解：（1）BD=DC(或点D是线段BC 的中点)，FD=ED，CF=BE中任选一个即可﹒（2）以BD =DC 为例进行证明：∵CF∥BE，∴∠FCD﹦∠EBD．又∵ BD =DC ，∠FDC﹦∠EDB，∴△BDE≌△CDF．4．（1）如图，点B、E、C、F 在一条直线上，BC＝EF，AB∥DE，∠A＝∠D．求证：△ABC≌△DEF．(第 17(1)题)【答案】证明：∵ AB∥DE．∴ ∠B＝∠DEF．在△ABC 和△DEF 中，⎧∠B =∠DEF，⎪∠A =∠D，⎪BC =EF．∴ △ABC ≌△DEF ．5．如图，分别过点 C 、B 作△ABC 的 BC 边上的中线 AD 及其延长线的垂线，垂足分 别为 E 、F ．求证：BF =CE ．【答案】∵CE ⊥AF ，FB ⊥AF ，∴∠DEC ＝∠DFB ＝90°又∵AD 为 BC 边上的中线，∴BD ＝CD ， 且∠EDC ＝∠FDB （对顶角相等） ∴所以△BFD ≌△C D E （AAS ），∴BF =CE ． 6．如图，已知 AD 是△A BC 的角平分线，在不添加任何辅助线的前提下，要使△AE D≌△AFD ，需添加一个条件是：，并给予证明.ABD C【答案】解法一：添加条件：AE ＝AF ，证明：在△AED 与△AFD 中，∵AE＝AF ，∠EAD＝∠FAD，AD ＝AD ，∴△AED≌△AFD（SAS ）.解法二：添加条件：∠EDA＝∠FDA，证明：在△AED 与△AFD 中，∵∠EAD＝∠FAD，AD ＝AD ，∠EDA＝∠FDA ∴△AED≌△AFD（ASA ）.EF⎨⎩7．如图，B，F，C，E 在同一条直线上，点A，D在直线BE 的两侧，AB∥DE，AC∥DF，BF=CE．求证：AC=DF【答案】证明：∵AB∥DE，∴∠ABC=∠DEF∵AC∥DF，∴∠ABC=∠DEF∵BF=CE，∴BC=EF∴△ABC≌△DEF∴AC=DF8．已知：如图，点C 是线段 AB 的中点，CE=CD，∠ACD=∠BCE,求证：AE=BD．【答案】证明：∵点 C 是线段 AB 的中点，∴AC=BC，∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠BCD,题 20 图⎧AC =BC在△ACE 和△BCD 中，⎪∠ACE =∠BCD ，⎪CE∴△A CE≌△BCD（SAS），∴AE=BD.=CD9．已知：如图，点A、B、C、D在同一条直线上，EA⊥AD，FD⊥AD，AE=DF，AB=DC．求证：∠ACE=∠DBF．⎨⎩EBCD⎨ ⎩【答案】证明：∵AB =DC∴AC =DB∵EA ⊥AD ，FD ⊥AD ∴∠A =∠D =90° 在△EAC 与△FDB 中⎧EA = FD ⎪∠A = ∠D ⎪AC = DB ∴△EAC ≌△FDB ∴∠ACE =∠DBF ．10．如图，点 A 、E 、B 、D 在同一条直线上，AE ＝DB ，AC ＝DF ，AC ∥DF .请探索 BC 与 EF 有怎样的位置关系？并说明理由．FAD【答案】解：BC ∥EF ．理由如下：∵AE ＝DB ，∴AE ＋BE ＝DB ＋BE ，∴AD ＝DE .∵AC ∥DF ， ∴∠A ＝∠D ，∵AC ＝DF ， ∴△ACB ≌△DFE ，∴∠FED ＝∠CBA ，∴BC ∥EF ． 11．如图，点 B 、D 、C 、F 在一条直线上，且 BC = FD ，A B = E F .（1） 请你只添加一个条件（不再加辅助线），使△A BC ≌△E FD ，你添加的条件是 ； （2） 添加了条件后，证明△ABC ≌△EFD.ABFE【答案】（1）∠B = ∠F 或 AB ∥EF 或 AC = ED .（2）证明：当∠B = ∠F 时在△ABC 和△EFD 中⎧A B = E⎪∠B = ∠F ⎪BC = FD求证：⑴ △ABC ≌△DEF ；⑵ BE ＝CF ．∴△ABC ≌△EFD (SAS)12．如图 4，已知 AC ∥DF ，且 BE =CF . （1） 请你只添加一．个．条件，使△ ABC ≌△D EF ，你添加的条件是；（2）添加条件后，证明△ ABC ≌△DEF.【答案】（１）添加的条件是 AC ＝DF （或 AB ∥D E 、∠B ＝∠D E F 、∠A ＝∠D ）（有一个即可）（２）证明：∵AC ∥DF ，∴∠ACB ＝∠F ，∵BE=CF ，∴BC ＝EF ，在△ ABC 和△ DEF 中，⎧BC = EF ⎪⎨∠ACB = ∠F ⎪⎩AC = DF ，∴△ABC ≌△DEF. 13．如图， ∠BAC = ∠ABD .（1） 要使OC = OD ，可以添加的条件为：或 ；（写出 2 个符合题意的条件即可）（2） 请选择(1)中你所添加的一个条件，证明OC = OD .CD【答案】解：（1）答案不唯一. 如∠C = ∠D ，或∠ABC = ∠BAD ，或∠OAD = ∠OBC ，或 AC = BD . ……4 分说明：2 空全填对者，给 4 分；只填 1 空且对者，给 2 分. （2）答案不唯一. 如选 AC = BD 证明 OC=OD.证明: ∵ ∠BAC = ∠ABD ，∴ OA=OB. ……………………6 分 DC又 AC = BD ， O∴ AC-OA=BD-OB ，或 AO+OC=BO+OD. AB∴ OC = OD......................................................... 8 分14．已知：点B 、E 、C 、F 在同一直线上，AB ＝DE ，∠A ＝∠D ，AC ∥ DF ．O AB⎨⎩【答案】证明：(1)∵AC ∥DF∴∠ACB ＝∠F ...................................................................................................... 2 分 在△ABC 与△DEF 中⎧∠ACB = ∠F ⎪∠A = ∠D ⎪ AB = DE ∴△ABC≌△DEF ................................................... 6 分(2) ∵△ABC≌△DEF∴BC=EF ∴BC–EC=EF –EC即 BE=CF ......................................................... 10 分 15．如图，已知点E ，C 在线段 BF 上， BE = CF ，请在下列四个等式中，①AB ＝DE ，②∠ACB ＝∠F ，③∠A ＝∠D ，④AC ＝DF ．选出两．个．作为条件，推出 △ABC ≌△DEF ．并予以证明．（写出一种即可）已知： ， ． 求证： △ABC≌△DEF ．证明：A DBECF【答案】解：已知：①④（或②③、或②④） .........3 分AD证明：若选①④ ∵ BE = CFB EC C ∴ BE + EC = CF + EC ,即BC = EF ． .............................. 5 分在△ABC 和△DEF 中AB ＝DE ，BC ＝EF ，AC ＝DF ． ..................... 8 分∴ △ABC ≌△DEF ． .......................... 9 分 16．八（1）班同学上数学活动课，利用角尺平分一个角（如图）.设计了如下方案：⎨⎩（Ⅰ）∠AOB 是一个任意角，将角尺的直角顶点 P 介于射线 OA 、OB 之间，移动角尺使角尺两边相同的刻度与 M 、N 重合，即 PM=PN ，过角尺顶点 P 的射线 OP 就是∠AOB 的平分线. （Ⅱ）∠AOB 是一个任意角，在边 OA 、OB 上分别取 OM=ON ，将角尺的直角顶点 P 介于射线 OA 、OB 之间，移动角尺使角尺两边相同的刻度与 M 、N 重合，即 PM=PN ，过角尺顶点 P 的射线 OP 就是∠AOB 的平分线.（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由. （2） 在方案（Ⅰ）PM=PN 的情况下，继续移动角尺，同时使 PM⊥OA，PN⊥OB.此方案是否可行？请说明理由.【答案】解：（1）方案（Ⅰ）不可行.缺少证明三角形全等的条件. …………………………… 2 分（2）方案（Ⅱ）可行 ...................... 3 分证明：在△OPM 和△OPN 中⎧OM = OP ⎪PM = PN ⎪ OP = OP ∴△OPM≌△OPN(SSS)∴∠AOP=∠BOP(全等三角形对应角相等) ............................................. 5 分（3）当∠AOB 是直角时，此方案可行 ...................... 6 分∵四边形内角和为 360°，又若 PM⊥OA,PN⊥OB, ∠OMP=∠ONP=90°, ∠MPN=90°,∴∠AOB=90° ∵若 PM⊥OA,PN⊥OB, 且 PM=PN∴OP 为∠AOB 的平分线.(到角两边距离相等的点在这个角的角平分线上) 当∠AOB 不为直角时，此方案不可行 .......... 8 分 17．如图，AB 是∠D AC 的平分线，且 AD =AC 。
八年级三角形的证明题
八年级三角形的证明题一、等腰三角形性质相关证明题（8题）1. 已知：在△ABC中，AB = AC，AD是BC边上的中线。
求证：AD⊥BC。
- 证明：- 因为AB = AC，AD是BC边上的中线，所以BD = DC（中线的定义）。
- 在△ABD和△ACD中，AB = AC（已知），BD = CD（已证），AD = AD（公共边）。
- 所以△ABD≌△ACD（SSS）。
- 则∠ADB=∠ADC（全等三角形对应角相等）。
- 又因为∠ADB + ∠ADC = 180°（平角的定义），所以∠ADB = ∠ADC = 90°，即AD⊥BC。
2. 已知：在等腰△ABC中，AB = AC，∠A = 36°，求证：∠B = 72°。
- 证明：- 因为AB = AC，所以∠B = ∠C（等腰三角形两底角相等）。
- 又因为∠A+∠B + ∠C = 180°（三角形内角和定理），∠A = 36°。
- 设∠B = x，则∠C = x，可得方程36°+x + x = 180°。
- 2x=180° - 36°，2x = 144°，解得x = 72°，即∠B = 72°。
3. 已知：在△ABC中，AB = AC，D是AC上一点，且AD = BD = BC。
求∠A的度数。
- 证明：- 设∠A=x，因为AD = BD，所以∠ABD = ∠A=x（等边对等角）。
- 则∠BDC=∠A + ∠ABD = 2x（三角形外角性质）。
- 因为BD = BC，所以∠C = ∠BDC = 2x。
- 又因为AB = AC，所以∠ABC = ∠C = 2x。
- 根据三角形内角和定理，∠A+∠ABC+∠C = 180°，即x + 2x+2x = 180°。
- 5x = 180°，解得x = 36°，所以∠A = 36°。
中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道
全等三角形经典证明题50道1、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE2、已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC3、如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．FAEDC B4．如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA5．（5分）如图，已知AD∥BC，∠P AB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．PCEDBA6．（6分）如图①，E、F分别为线段AC上的两个动点，且DE ⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．7．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：8．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．OEDCB AFE D CB A25、如图：DF=CE ，AD=BC ，∠D=∠C 。
求证：△AED ≌△BFC 。
证明：∵DF=CE ， ∵DF-EF=CE-EF ， 即DE=CF ，在∵AED 和∵BFC 中，∵ AD=BC ， ∵D=∵C ，DE=CF ∵∵AED ∵∵BFC （SAS ）26、（10分）如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。
求证：AM 是△ABC 的中线。
中考数学打基础系列 三角形的基本计算与证明 专题
备战中考数学打基础专题练习系列（三角形的基本计算与证明）专题总分：120分建议用时：100分钟一、选择题（30分）题号 1 2 3 4 5 6 7 8 9 10选项1. 下列长度的3根小木棒不能搭成三角形的是（）A. 2cm，3cm，4cmB.1cm，2cm，3cmC. 3cm， 4cm，5cmD. 4cm，5cm， 6cm2. 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是( )A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形3.如图，四个图形中，线段BE是△ABC的高的图是（）4.如图，已知BD是△ABC的一条中线，△ABD与△BCD的周长分别为21，12，则AB－BC的长是（）.A.6B.7C.8D.95. 如图,在△ABC中,AB=AC,点D,E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是( )A.4B.5C.6D.76. 如图,在平面直角坐标系中,已知A(0,√3),B(-2,-√3),△ABC 是等边三角形,AD 是BC 边上的高,则点C 的坐标是 ( )A.(2,-√3)B.(-2,√3)C.(2,-2)D.(-2,2)7. 如图,D,E,F 分别是等边三角形ABC 各边上的点,且AD=BE=CF,则△DEF 的形状是( )A.等边三角形B.腰和底边不相等的等腰三角形C.直角三角形D.不等边三角形8.如图，将一张三角形纸片ABC 的一角折叠，使点A 落在△ABC 外的A′处，折痕为DE ，如果∠A=α，∠CEA′=β，∠BDA′=γ，那么下列式子中正确的是（ ）A ．γ=2α+βB ．γ=α+2βC ．γ=α+βD ．γ=180°-α-β12AB C9.一个多边形割去一个角后，得到的多边形的内角和为1440°，则这个多边形原来的边数为（）A．9 B．10 C．11 D．以上都有可能10. 如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为S△ABC ，S△ADF，S△BEF，且S△ABC=12，则S△ADF-S△BEF=( )A.1B.2C.3D.4二、填空题（32分）11. 在等腰三角形ABC中，AB=AC，AC边上的中线BD将这个三角形的周长分为15和12两部分，则底边BC的长为_________．12. 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为_________．13. 如图，在△ABC中，CD平分∠ACB，DE∥BC，交AC于点E.若∠AED＝50°，则∠D的度数为 .14.如图，在△ABC中，∠ACB＝90°，AC＜BC．分别以点A，B为圆心，大于12 AB的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH．若BC＝3，则△AFH的周长为_____．15.如图，在△ABC 中，已知点D ，E ，F 分别为边BC ，AD ，CE 的中点，且 S △ABC =4 cm 2，那么阴影部分的面积是_________．16. 如图，在△ABC 中，AB ＝5，BC ＝10，△ABC 的高AD 与CE 的比是 .17.用一条宽度相等的足够长的纸条打一个结（如图1所示），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE ．图中，∠BAC ＝ 度．18. 如图,在等边△ABC 中,D 是边AC 上一点,连接BD.将△BCD 绕点B 逆时针旋转60°,得到△BAE,连接ED.若BC=10,BD=9,则△AED 的周长是________.三、解答题（58分）A BC DEF19. 已知△ABC 中，DE ∥BC ，∠AED=50°，CD 平分∠ACB ，求∠CDE 的度数．20. 如图，已知：AD 平分BAC ∠，EF 垂直平分AD ，交BC 延长线于F ，连结AF 。
八年级全等三角形简单证明题及答案(15道)
∴BC=ED．
全等三角形的判定与性 质．
01
如图，在△ABC中， ∠C=90°，点D是AB边上的 一点，DM⊥AB，且 DM=AC，过点M作 ME∥BC交AB于点E．求证： △ABC≌△MED。
02
证明：∵MD⊥AB，
∴∠MDE=∠C=90°，
∵ME∥BC，
∴∠B=∠MED，
在△ABC与△MED中， ∠B=∠MED ∠C=∠EDM DM=AC ，
∠D=∠B ， ∴△ADF≌△CBE（ASA）， ∴AF=CE， ∴AF+EF=CE+EF，即
AE=CF．
全等三角形的判定与性 质．
11.在△ABC中，AB=CB，∠ABC=90°，F为AB延 长线上一点，点E在BC上，且AE=CF．求证： Rt△ABE≌Rt△CBF；
证明：∵∠ABC=90°，
角平分线的性质；全等三角形的判定与性质．
全等三角形的判定．
如图，在△ABC中， AB=AC，AD平分 ∠BAC．求证： ∠DBC=∠DCB．
解：∵AD平分∠BAC， ∴∠BAD=∠CAD． ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD
AD=AD ， ∴△ACD≌△ABD， ∴BD=CD， ∴∠DBC=∠DCB．
：∵AC平分∠BAD，
∴∠BAC=∠DAC，
在△ABC和△ADC中， AB=AD ∠BAC=∠DAC AC=AC ，
∴△ABC≌△ADC．
全等三角形的判定．
9.如图，已知 点E，C在线段
BF上， BE=CF， AB∥DE， ∠ACB=∠F．
求证： △ABC≌△DEF
．
证明：∵AB∥DE，
∴∠B=∠DEF．
全等三角形的判定与性质．
2022年中考数学真题分类汇编：三角形类几何证明题(含答案)
2022年中考数学真题汇编三角形类几何证明题1.(2022·江苏省南通市)如图，AC和BD相交于点O，OA=OC，OB=OD．(1)求证：∠A=∠C；(2)求证：AB//CD．2.(2022·西藏)如图，已知AD平分∠BAC，AB=AC.求证：△ABD≌△ACD．3.(2022·湖南省益阳市)如图，在Rt△ABC中，∠B=90°，CD//AB，DE⊥AC于点E，且CE=AB.求证：△CED≌△ABC．4.(2022·辽宁省大连市)如图，在△ABC中，∠ACB=90°，BC=4，点D在AC上，CD=3，连接DB，AD=DB，点P是边AC上一动点(点P不与点A，D，C重合)，过点P作AC的垂线，与AB相交于点Q，连接DQ，设AP=x，△PDQ与△ABD重叠部分的面积为S．(1)求AC的长；(2)求S关于x的函数解析式，并直接写出自变量x的取值范围．5.(2022·黑龙江省牡丹江市)如图，△ABC和△DEF，点E，F在直线BC上，AB=DF，∠A=∠D，∠B=∠F.如图①，易证：BC+BE=BF.请解答下列问题：(1)如图②，如图③，请猜想BC，BE，BF之间的数量关系，并直接写出猜想结论；(2)请选择(1)中任意一种结论进行证明；(3)若AB=6，CE=2，∠F=60°，S△ABC=12√3，则BC=______，BF=______．6.(2022·广西壮族自治区柳州市)如图，点A，D，C，F在同一条直线上，AB=DE，BC=EF.有下列三个条件：①AC=DF，②∠ABC=∠DEF，③∠ACB=∠DFE．(1)请在上述三个条件中选取一个条件，使得△ABC≌△DEF．你选取的条件为(填写序号)______(只需选一个条件，多选不得分)，你判定△ABC ≌△DEF的依据是______(填“SSS”或“SAS”或“ASA”或“AAS”)；(2)利用(1)的结论△ABC≌△DEF.求证：AB//DE．7.(2022·上海市)如图所示，在等腰三角形ABC中，AB=AC，点E，F在线段BC上，点Q在线段AB上，且CF=BE，AE2=AQ⋅AB．求证：(1)∠CAE=∠BAF；(2)CF⋅FQ=AF⋅BQ．8.(2022·广西壮族自治区河池市)如图，点A，F，C，D在同一直线上，AB=DE，AF=CD，BC=EF．(1)求证：∠ACB=∠DFE；(2)连接BF，CE，直接判断四边形BFEC的形状．9.(2022·吉林省长春市)图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．(1)网格中△ABC的形状是______；(2)在图①中确定一点D，连结DB、DC，使△DBC与△ABC全等；(3)在图②中△ABC的边BC上确定一点E，连结AE，使△ABE∽△CBA；(4)在图③中△ABC的边AB上确定一点P，在边BC上确定一点Q，连结PQ，使△PBQ∽△ABC，且相似比为1：2．10.(2022·北京市)下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明．三角形内角和定理：三角形三个内角的和等于180°．已知：如图，△ABC，求证：∠A+∠B+∠C=180°．方法一证明：如图，过点A作DE//BC．方法二证明：如图，过点C作CD//AB．11.(2022·山东省青岛市)已知：Rt△ABC，∠B=90°．求作：点P，使点P在△ABC内部．且PB=PC，∠PBC=45°．12.(2022·贵州省铜仁市)如图，点C在BD上，AB⊥BD，ED⊥BD，AC⊥CE，AB=CD.求证：△ABC≌△CDE．13.(2022·北京市)在△ABC中，∠ACB=90°，D为△ABC内一点，连接BD，DC，延长DC到点E，使得CE=DC．(1)如图1，延长BC到点F，使得CF=BC，连接AF，EF.若AF⊥EF，求证：BD⊥AF；(2)连接AE，交BD的延长线于点H，连接CH，依题意补全图2.若AB2=AE2+BD2，用等式表示线段CD与CH的数量关系，并证明．14.(2022·吉林省)如图，AB=AC，∠BAD=∠CAD.求证：BD=CD．15.(2022·广东省云浮市)如图，已知∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E.求证：△OPD≌△OPE．16.(2022·黑龙江省鹤岗市)△ABC和△ADE都是等边三角形．(1)将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+PC=PB)成立(不需证明)；(2)将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；(3)将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？直接写出结论，不需要证明．17.(2022·湖南省长沙市)如图，AC平分∠BAD，CB⊥AB，CD⊥AD，垂足分别为B，D．(1)求证：△ABC≌△ADC；(2)若AB=4，CD=3，求四边形ABCD的面积．18.(2022·内蒙古自治区赤峰市)如图，已知Rt△ABC中，∠ACB=90°，AB=8，BC=5．(1)作BC的垂直平分线，分别交AB、BC于点D、H；(要求：尺规作图，不写作法，保留作图痕迹)(2)在(1)的条件下，连接CD，求△BCD的周长．19.(2022·福建省)如图，点B，F，C，E在同一条直线上，BF=EC，AB=DE，∠B=∠E.求证：∠A=∠D．20.(2022·广西壮族自治区玉林市)问题情境：在数学探究活动中，老师给出了如图的图形及下面三个等式：①AB=AC；②DB=DC；③∠BAD=∠CAD.若以其中两个等式作为已知条件，能否得到余下一个等式成立？解决方案：探究△ABD与△ACD全等．问题解决：(1)当选择①②作为已知条件时，△ABD与△ACD全等吗？______(填“全等”或“不全等”)，理由是______；(2)当任意选择两个等式作为已知条件时，请用画树状图法或列表法求△ABD≌△ACD的概率．21.(2022·四川省宜宾市)已知：如图，点A、D、C、F在同一直线上，AB//DE，∠B=∠E，BC=EF.求证：AD=CF．22.(2022·陕西省)如图，在△ABC中，点D在边BC上，CD=AB，DE//AB，∠DCE=∠A.求证：DE=BC．23.(2022·湖南省衡阳市)如图，在△ABC中，AB=AC，D、E是BC边上的点，且BD=CE.求证：AD=AE．24.(2022·四川省乐山市)如图，B是线段AC的中点，AD//BE，BD//CE.求证：△ABD≌△BCE．25.(2022·浙江省杭州市)如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE.已知∠A=50°，∠ACE=30°．(1)求证：CE=CM．(2)若AB=4，求线段FC的长．参考答案1.证明：(1)在△AOB和△COD中，{OA=OC∠AOB=∠CODOB=OD,∴△AOB≌△COD(SAS)，∴∠A=∠C；(2)由(1)得∠A=∠C，∴AB//CD．2.证明：∵AD平分∠BAC，∴∠BAD=∠CAD，在△ABD和△ACD中，{AB=AC∠BAD=∠CAD AD=AD，∴△ABD≌△ACD(SAS)．3.证明：∵DE⊥AC，∠B=90°，∴∠DEC=∠B=90°，∵CD//AB，∴∠A=∠DCE，在△CED和△ABC中，{∠DCE=∠A CE=AB∠DEC=∠B，∴△CED≌△ABC(ASA)．4.解：(1)在Rt△BCD中，BC=4，CD=3，∴BD=√BC2+CD2=5，又∵AD=BD，∴AC=AD+CD=5+3=8；(2)当点P在点D的左侧时，即0<x<5，如图1，此时阴影部分的面积就是△PQD的面积，∵PQ⊥AC，BC⊥AC，∴PQ//BC，∴△ABC∽△AQP，∴APPQ =ACBC=84=2，设AP=x，则PQ=12x，PD=AD−AP=5−x，∴S阴影部分=S△PQD=12(5−x)×12x=−14x2+54x；当点P在点D的右侧时，即5<x<8，如图2，由(1)得，AP=x，PQ=12x，则PD=x−5，∵PQ//BC，∴△DPE∽△DCB，∴DPEP =DCBC=34，∴PE=43(x−5)，∴S阴影部分=S△PQD−S△DPE=12(x−5)×12x−12(x−5)×43(x−5)=−512x2+2512x−503；答：S关于x的函数解析式为：当0<x<5时，S=−14x2+54x；当5<x<8时，S=−512x2+2512x−503．5.814或186.①SSS7.证明：(1)∵AB=AC，∴∠B=∠C，∵CF=BE，∴CF−EF=BE−EF，即CE=BF，在△ACE和△ABF中，{AC=AB∠C=∠BCE=BF，∴△ACE≌△ABF(SAS)，∴∠CAE=∠BAF；(2)∵△ACE≌△ABF，∴AE=AF，∠CAE=∠BAF，∵AE2=AQ⋅AB，AC=AB，∴AEAQ =ACAF，∴△ACE∽AFQ，∴∠AEC=∠AQF，∴∠AEF=∠BQF，∵AE=AF，∴∠AEF=∠AFE，∴∠BQF=∠AFE，∵∠B=∠C，∴△CAF∽△BFQ，∴CFBQ =AFFQ，即CF⋅FQ=AF⋅BQ．8.(1)证明：∵AF=CD，∴AF+CF=CD+CF，即AC=DF，在△ABC和△DEF中，{AB=DE BC=EF AC=DF，∴△ABC≌△DEF(SSS)，∴∠ACB=∠DFE；(2)解：如图，四边形BFEC是平行四边形，理由如下：由(1)可知，∠ACB=∠DFE，∴BC//EF，又∵BC=EF，∴四边形BFEC是平行四边形．9.直角三角形10.证明：方法一：∵DE//BC，∴∠B=∠BAD，∠C=∠CAE，∵∠BAD+∠BAC+∠CAE=180°，∴∠B+∠BAC+∠C=180°；方法二：延长BC，如图，∵CD//AB，∴∠A=∠ACD，∠B=∠DCE，∵∠ACB+∠ACD+∠DCE=180°，∴∠A+∠ACD+∠B=180°．11.解：①先作出线段BC的垂直平分线EF；②再作出∠ABC的角平分线BM，EF与BM的交点为P；则P即为所求作的点．12.证明：∵AB⊥BD，ED⊥BD，AC⊥CE，∴∠B=∠D=∠ACE=90°，∴∠DCE+∠DEC=90°，∠BCA+∠DCE=90°，∴∠BCA=∠DEC，在△ABC和△CDE中，{∠BCA=∠DEC ∠B=∠DAB=CD，∴△ABC≌△CDE(AAS)．13.(1)证明：在△BCD和△FCE中，{BC=CF∠BCD=∠FCE CD=CE，∴△BCD≌△FCE(SAS)，∴∠DBC=∠EFC，∴BD//EF，∵AF⊥EF，∴BD⊥AF；(2)解：由题意补全图形如下：CD=CH．证明：延长BC到F，使CF=BC，连接AF，EF，∵AC⊥BF，BC=CF，∴AB=AF，由(1)可知BD//EF，BD=EF，∵AB2=AE2+BD2，∴AF2=AE2+EF2，∴∠AEF=90°，∴AE⊥EF，∴BD⊥AE，∴∠DHE=90°，又∵CD=CE，∴CH=CD=CE．14.证明：在△ABD与△ACD中，{AB=AC∠BAD=∠CAD AD=AD，∴△ABD≌△ACD(SAS)，∴BD=CD．15.证明：∵∠AOC=∠BOC，PD⊥OA，PE⊥OB，∴PD=PE，在Rt△OPD和Rt△OPE中，{OP=OPPD=PE，∴Rt△OPD≌Rt△OPE(HL)．16.解：(2)PB=PA+PC，理由如下：如图②，在BP上截取BF=PC，连接AF，∵△ABC、△ADE都是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAC+∠CAD=∠CAD+∠DAE，即∠DAB=∠EAC，∴△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，∵AB=AC，BF=CP，∴△BAF≌△CAP(SAS)，∴AF=AP，∠BAF=∠CAP，∴∠BAC=∠PAF=90°，∴△AFP是等边三角形，∴PF=PA，∴PB=BF+PF=PC+PA；(3)PC=PA+PB，理由如下：如图③，在PC上截取CM=PB，连接AM，同理得：△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，∵AB=AC，PB=CM，∴△AMC≌△APB(SAS)，∴AM=AP，∠BAP=∠CAM，∴∠BAC=∠PAM=60°，∴△AMP是等边三角形，∴PM=PA，∴PC=PM+CM=PA+PB．17.(1)证明：∵AC平分∠BAD，∴∠BAC=∠DAC，∵CB⊥AB，CD⊥AD，∴∠B=90°=∠D，在△ABC和△ADC中，{∠B=∠D∠BAC=∠DAC AC=AC，∴△ABC≌△ADC(AAS)；(2)解：由(1)知：△ABC≌△ADC，∴BC=CD=3，S△ABC=S△ADC，∴S△ABC=12AB⋅BC=12×4×3=6，∴S△ADC=6，∴S四边形ABCD=S△ABC+S△ADC=12，答：四边形ABCD的面积是12．18.解：(1)如图，DH为所作；(2)∵DH垂直平分AB，∴DC=DB，∴∠B=∠DCB，∵∠B+∠A=90°，∠DCB+∠DCA=90°，∴∠A=∠DCA，∴DC=DA，∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13．19.证明：∵BF=EC，∴BF+CF=EC+CF，即BC=EF，在△ABC和△DEF中，{AB=DE∠B=∠EBC=EF，∴△ABC≌△DEF(SAS)，∴∠A=∠D．20.全等三边对应相等的两个三角形全等21.证明：∵AB//DE，∴∠A=∠EDF．在△ABC和△DEF中，{∠A=∠EDF ∠B=∠EBC=EF，∴△ABC≌△DEF(AAS)．∴AC=DF，∴AC−DC=DF−DC，即：AD=CF．22.证明：∵DE//AB，∴∠EDC=∠B，在△CDE和△ABC中，{∠EDC=∠B CD=AB∠DCE=∠A，∴△CDE≌△ABC(ASA)，∴DE=BC．23.证明：∵AB=AC，∴∠B=∠C，在△ABD和△ACE中，{AB=AC ∠B=∠C BD=CE，∴△ABD≌△ACE(SAS)，∴AD=AE．24.证明：∵点B为线段AC的中点，∴AB=BC，∵AD//BE，∴∠A=∠EBC，∵BD//CE，∴∠C=∠DBA，在△ABD与△BCE中，{∠A=∠EBC AB=BC∠DBA=∠C，∴△ABD≌△BCE.(ASA)．25.(1)证明：∵∠ACB=90°，点M为边AB的中点，∴MC=MA=MB，∴∠MCA=∠A，∠MCB=∠B，∵∠A=50°，∴∠MCA=50°，∠MCB=∠B=40°，∴∠EMC=∠MCB+∠B=80°，∵∠ACE=30°，∴∠MEC=∠A+∠ACE=50°，∴∠MEC=∠EMC，∴CE=CM；(2)解：∵AB=4，∴CE=CM=1AB=2，2∵EF⊥AC，∠ACE=30°，∴FC=CE⋅cos30°=√3．。
全等三角形证明中考题精选(有答案)
新人教版八年级上学期全等三角形证明题一．解答题（共10小题）1．（泉州）如图，已知AD是△ABC的中线，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．2．（河南）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是_________；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是_________．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC=60°，点D是角平分线上一点，BD=CD=4，DE∥AB交BC于点E（如图4）．若在射线BA 上存在点F，使S△DCF=S△BDE，请直接写出相应的BF的长．3．（大庆）如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．（1）求证：CF=DG；（2）求出∠FHG的度数．4．（阜新）（1）如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°．①当点D在AC上时，如图1，线段BD、CE有怎样的数量关系和位置关系？直接写出你猜想的结论；②将图1中的△ADE绕点A顺时针旋转α角（0°＜α＜90°），如图2，线段BD、CE有怎样的数量关系和位置关系？请说明理由．（2）当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时，使线段BD、CE在（1）中的位置关系仍然成立？不必说明理由．甲：AB：AC=AD：AE=1，∠BAC=∠DAE≠90°；乙：AB：AC=AD：AE≠1，∠BAC=∠DAE=90°；丙：AB：AC=AD：AE≠1，∠BAC=∠DAE≠90°．5．（仙桃）如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE 绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM=BD，EN=CE，得到图③，请解答下列问题：（1）若AB=AC，请探究下列数量关系：①在图②中，BD与CE的数量关系是_________；②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN 与∠BAC的数量关系，直接写出你的猜想，不必证明．6．（四川）CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：①如图1，若∠BCA=90°，∠α=90°，则BE_________CF；EF_________|BE﹣AF|（填“＞”，“＜”或“=”）；②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件_________，使①中的两个结论仍然成立，并证明两个结论成立．（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．7．（绍兴）课外兴趣小组活动时，许老师出示了如下问题：如图1，己知四边形ABCD中，AC平分∠DAB，∠DAB=60°，∠B与∠D互补，求证：AB+AD=AC．小敏反复探索，不得其解．她想，若将四边形ABCD 特殊化，看如何解决该问题．（1）特殊情况入手添加条件：“∠B=∠D”，如图2，可证AB+AD=AC；（请你完成此证明）（2）解决原来问题受到（1）的启发，在原问题中，添加辅助线：如图3，过C点分别作AB、AD的垂线，垂足分别为E、F．（请你补全证明）8．（常德）如图，已知AB=AC，（1）若CE=BD，求证：GE=GD；（2）若CE=m•BD（m为正数），试猜想GE与GD有何关系．（只写结论，不证明）9．（泰安）（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°，求证：①AC=BD；②∠APB=60度；（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为_________；∠APB的大小为_________；（3）如图③，在△AOB和△COD中，若OA=k•OB，OC=k•OD（k＞1），∠AOB=∠COD=α，则AC与BD间的等量关系式为_________；∠APB的大小为10．（南宁）（A类）如图，DE⊥AB、DF⊥AC．垂足分别为E、F．请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②BD=CD；③BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BD=CD求证：BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BE=CF求证：BD=CD已知：DE⊥AB、DF⊥AC，垂足分别为E、F，BD=CD，BE=CF求证：AB=AC（B类）如图，EG∥AF，请你从下面三个条件中，再选两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②DE=DF；③BE=CF已知：EG∥AF，AB=AC，DE=DF求证：BE=CF新人教版八年级上学期全等三角形证明题参考答案与试题解析一．解答题（共10小题）1．（泉州）如图，已知AD是△ABC的中线，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．考点：全等三角形的判定与性质．专题：证明题．分析：根据中线的定义可得BD=CD，然后利用“角角边”证明△BDE和△CDF全等，根据全等三角形对应边相等即可得证．解答：证明：∵AD是△ABC的中线，∴BD=CD，∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD=90°，在△BDE和△CDF中，，∴△BDE≌△CDF（AAS），∴BE=CF．点评：本题考查了全等三角形的判定与性质，利用三角形全等证明边相等是常用的方法之一，要熟练掌握并灵活运用．2．（河南）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1=S2．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC=60°，点D是角平分线上一点，BD=CD=4，DE∥AB交BC于点E（如图4）．若在射线BA 上存在点F，使S△DCF=S△BDE，请直接写出相应的BF的长．考点：全等三角形的判定与性质．专题：几何综合题；压轴题．分析：（1）①根据旋转的性质可得AC=CD，然后求出△ACD是等边三角形，根据等边三角形的性质可得∠ACD=60°，然后根据内错角相等，两直线平行解答；②根据等边三角形的性质可得AC=AD，再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=AB，然后求出AC=BE，再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离，然后根据等底等高的三角形的面积相等解答；（2）根据旋转的性质可得BC=CE，AC=CD，再求出∠ACN=∠DCM，然后利用“角角边”证明△ACN 和△DCM全等，根据全等三角形对应边相等可得AN=DM，然后利用等底等高的三角形的面积相等证明；（3）过点D作DF1∥BE，求出四边形BEDF1是菱形，根据菱形的对边相等可得BE=DF1，然后根据等底等高的三角形的面积相等可知点F1为所求的点，过点D作DF2⊥BD，求出∠F1DF2=60°，从而得到△DF1F2是等边三角形，然后求出DF1=DF2，再求出∠CDF1=∠CDF2，利用“边角边”证明△CDF1和△CDF2全等，根据全等三角形的面积相等可得点F2也是所求的点，然后在等腰△BDE 中求出BE的长，即可得解．解答：解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC=CD，∵∠BAC=90°﹣∠B=90°﹣30°=60°，∴△ACD是等边三角形，∴∠ACD=60°，又∵∠CDE=∠BAC=60°，∴∠ACD=∠CDE，∴DE∥AC；②∵∠B=30°，∠C=90°，∴BD=AD=AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；故答案为：DE∥AC；S1=S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC=CE，AC=CD，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°﹣90°=90°，∴∠ACN=∠DCM，∵在△ACN和△DCM中，，∴△ACN≌△DCM（AAS），∴AN=DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF=S△BDE，过点D作DF2⊥BD，∵∠ABC=60°，∴∠F1DF2=∠ABC=60°，∴△DF1F2是等边三角形，∴DF1=DF2，∵BD=CD，∠ABC=60°，点D是角平分线上一点，∴∠DBC=∠DCB=×60°=30°，∴∠CDF1=180°﹣30°=150°，∠CDF2=360°﹣150°﹣60°=150°，∴∠CDF1=∠CDF2，∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=×60°=30°，又∵BD=4，∴BE=×4÷cos30°=2÷=，∴BF1=，BF2=BF1+F1F2=+=，故BF的长为或．点评：本题考查了全等三角形的判定与性质，三角形的面积，等边三角形的判定与性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟练掌握等底等高的三角形的面积相等，以及全等三角形的面积相等是解题的关键，（3）要注意符合条件的点F有两个．3．（大庆）如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．（1）求证：CF=DG；（2）求出∠FHG的度数．考点：全等三角形的判定与性质．分析：（1）在△CBF和△DBG中，利用SAS即可证得两个三角形全等，利用全等三角形的对应边相等即可证得；（2）根据全等三角形的对应角相等，即可证得∠DHF=∠CBF=60°，从而求解．解答：（1）证明：∵在△CBF和△DBG中，，∴△CBF≌△DBG（SAS），∴CF=DG；（2）解：∵△CBF≌△DBG，∴∠BCF=∠BDG，又∵∠CFB=∠DFH，∴∠DHF=∠CBF=60°，∴∠FHG=180°﹣∠DHF=180°﹣60°=120°．点评：本题考查了全等三角形的判定与性质，正确证明三角形全等是关键．4．（阜新）（1）如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°．①当点D在AC上时，如图1，线段BD、CE有怎样的数量关系和位置关系？直接写出你猜想的结论；②将图1中的△ADE绕点A顺时针旋转α角（0°＜α＜90°），如图2，线段BD、CE有怎样的数量关系和位置关系？请说明理由．（2）当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时，使线段BD、CE在（1）中的位置关系仍然成立？不必说明理由．甲：AB：AC=AD：AE=1，∠BAC=∠DAE≠90°；乙：AB：AC=AD：AE≠1，∠BAC=∠DAE=90°；丙：AB：AC=AD：AE≠1，∠BAC=∠DAE≠90°．考点：全等三角形的判定与性质．专题：几何综合题；压轴题．分析：（1）①BD=CE，BD⊥CE．根据全等三角形的判定定理SAS推知△ABD≌△ACE，然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA；然后在△ABD和△CDF中，由三角形内角和定理可以求得∠CFD=90°，即BD⊥CF；②BD=CE，BD⊥CE．根据全等三角形的判定定理SAS推知△ABD≌△ACE，然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA；作辅助线（延长BD交AC于F，交CE 于H）BH构建对顶角∠ABF=∠HCF，再根据三角形内角和定理证得∠BHC=90°；（2）根据结论①、②的证明过程知，∠BAC=∠DFC（或∠FHC=90°）时，该结论成立了，所以本条件中的∠BAC=∠DAE≠90°不合适．解答：解：（1）①结论：BD=CE，BD⊥CE；②结论：BD=CE，BD⊥CE…1分理由如下：∵∠BAC=∠DAE=90°∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE…1分在△ABD与△ACE中，∵∴△ABD≌△ACE（SAS）∴BD=CE…1分延长BD交AC于F，交CE于H．在△ABF与△HCF中，∵∠ABF=∠HCF，∠AFB=∠HFC∴∠CHF=∠BAF=90°∴BD⊥CE…3分（2）结论：乙．AB：AC=AD：AE，∠BAC=∠DAE=90°…2分点评：本题考查了全等三角形的判定与性质．SSS，SAS，ASA，AAS，HL均可作为判定三角形全等的定理．注意：在全等的判定中，没有AAA（角角角）和SSA（边边角）（特例：直角三角形为HL，因为勾股定理，只要确定了斜边和一条直角边，另一直角边也确定，属于SSS），因为这两种情况都不能唯一确定三角形的形状；另外三条中线（或高、角平分线）分别对应相等的两个三角形也全等．5．（仙桃）如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，然后将△ADE 绕A点顺时针旋转一定角度，得到图②，然后将BD、CE分别延长至M、N，使DM=BD，EN=CE，得到图③，请解答下列问题：（1）若AB=AC，请探究下列数量关系：①在图②中，BD与CE的数量关系是；②在图③中，猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系，并证明你的猜想；（2）若AB=k•AC（k＞1），按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、∠MAN 与∠BAC的数量关系，直接写出你的猜想，不必证明．考点：全等三角形的判定．专题：压轴题；探究型．分析：（1）①根据题意和旋转的性质可知△AEC≌△ADB，所以BD=CE；②根据题意可知∠CAE=BAD，AB=AC，AD=AE，所以得到△BAD≌△CAE，在△ABM和△ACN中，DM=BD，EN=CE，可证△ABM≌△ACN，所以AM=AN，即∠MAN=∠BAC．（2）直接类比（1）中结果可知AM=k•AN，∠MAN=∠BAC．解答：解：（1）①BD=CE；②AM=AN，∠MAN=∠BAC，∵∠DAE=∠BAC，∴∠CAE=∠BAD，在△BAD和△CAE中∵∴△CAE≌△BAD（SAS），∴∠ACE=∠ABD，∵DM=BD，EN=CE，∴BM=CN，在△ABM和△ACN中，∵∴△ABM≌△ACN（SAS），∴AM=AN，∴∠BAM=∠CAN，即∠MAN=∠BAC；（2）AM=k•AN，∠MAN=∠BAC．点评：本题考查三角形全等的判定方法和性质．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．本题还要会根据所求的结论运用类比的方法求得同类题目．6．（台州）CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：①如图1，若∠BCA=90°，∠α=90°，则BE=CF；EF=|BE﹣AF|（填“＞”，“＜”或“=”）；②如图2，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件∠α+∠BCA=180°，使①中的两个结论仍然成立，并证明两个结论成立．（2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．考点：直角三角形全等的判定；三角形内角和定理．专题：几何综合题；压轴题．分析：由题意推出∠CBE=∠ACF，再由AAS定理证△BCE≌△CAF，继而得答案．解答：解：（1）①∵∠BCA=90°，∠α=90°，∴∠BCE+∠CBE=90°，∠BCE+∠ACF=90°，∴∠CBE=∠ACF，∵CA=CB，∠BEC=∠CFA；∴△BCE≌△CAF，∴BE=CF；EF=|BE﹣AF|．②所填的条件是：∠α+∠BCA=180°．证明：在△BCE中，∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α．∵∠BCA=180°﹣∠α，∴∠CBE+∠BCE=∠BCA．又∵∠ACF+∠BCE=∠BCA，∴∠CBE=∠ACF，又∵BC=CA，∠BEC=∠CFA，∴△BCE≌△CAF（AAS）∴BE=CF，CE=AF，又∵EF=CF﹣CE，∴EF=|BE﹣AF|．（2）EF=BE+AF．点评：本题综合考查全等三角形、等边三角形和四边形的有关知识．注意对三角形全等，相似的综合应用．7．（绍兴）课外兴趣小组活动时，许老师出示了如下问题：如图1，己知四边形ABCD中，AC平分∠DAB，∠DAB=60°，∠B与∠D互补，求证：AB+AD=AC．小敏反复探索，不得其解．她想，若将四边形ABCD 特殊化，看如何解决该问题．（1）特殊情况入手添加条件：“∠B=∠D”，如图2，可证AB+AD=AC；（请你完成此证明）（2）解决原来问题受到（1）的启发，在原问题中，添加辅助线：如图3，过C点分别作AB、AD的垂线，垂足分别为E、F．（请你补全证明）考点：直角三角形全等的判定．专题：证明题；压轴题；开放型．分析：（1）如果：“∠B=∠D”，根据∠B与∠D互补，那么∠B=∠D=90°，又因为∠DAC=∠BAC=30°，因此我们可在直角三角形ADC和ABC中得出AD=AB=AC，那么AD+AB=AC．（2）按（1）的思路，作好辅助线后，我们只要证明三角形CFD和BCD全等即可得到（1）的条件．根据AAS可证两三角形全等，DF=BE．然后按照（1）的解法进行计算即可．解答：证明：（1）∵∠B与∠D互补，∠B=∠D，∴∠B=∠D=90°，∠CAD=∠CAB=∠DAB=30°，∵在△ADC中，cos30°=，在△ABC中，cos30°=，∴AB=AC，AD=．∴AB+AD=．（2）由（1）知，AE+AF=AC，∵AC为角平分线，CF⊥CD，CE⊥AB，∴CE=CF．而∠ABC与∠D互补，∠ABC与∠CBE也互补，∴∠D=∠CBE．∵在Rt△CDF与Rt△CBE中，∴Rt△CDF≌Rt△CBE．∴DF=BE．∴AB+AD=AB+（AF+FD）=（AB+BE）+AF=AE+AF=AC．点评：本题考查了直角三角形全等的判定及性质；通过辅助线来构建全等三角形是解题的常用方法，也是解决本题的关键．8．（常德）如图，已知AB=AC，（1）若CE=BD，求证：GE=GD；（2）若CE=m•BD（m为正数），试猜想GE与GD有何关系．（只写结论，不证明）考点：全等三角形的判定与性质．专题：证明题；压轴题；探究型．分析：（1）要证GE=GD，需证△GDF≌△GEC，由已知条件可根据AAS判定．（2）若CE=m•BD（m为正数），那么GE=m•GD．解答：证明：（1）过D作DF∥CE，交BC于F，则∠E=∠GDF．∵AB=AC，∴∠ACB=∠ABC∵DF∥CE，∴∠DFB=∠ACB，∴∠DFB=∠ACB=∠ABC．∴DF=DB．∵CE=BD，∴DF=CE，在△GDF和△GEC中，，∴△GDF≌△GEC（AAS）．∴GE=GD．（2）GE=m•GD．点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．本题的辅助线是解决题目的关键．9．（泰安）（1）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=60°，求证：①AC=BD；②∠APB=60度；（2）如图②，在△AOB和△COD中，若OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系式为AC=BD；∠APB的大小为α；（3）如图③，在△AOB和△COD中，若OA=k•OB，OC=k•OD（k＞1），∠AOB=∠COD=α，则AC与BD间的等量关系式为AC=k•BD；∠APB的大小为180°﹣α．考点：全等三角形的判定；三角形内角和定理．专题：探究型．分析：（1）分析结论AC=BD可知，需要证明△AOC≌△BOD，围绕这个目标找全等的条件；（2）与图①比较，图形条件发生了变化，仍然可以证明△AOC≌△BOD，方法类似；（3）转化为证明△AOC∽△BOD．解答：解：（1）①∵∠AOB=∠COD=60°，∴∠AOB+∠BOC=∠COD+∠BOC．即：∠AOC=∠BOD．又∵OA=OB，OC=OD，∴△AOC≌△BOD．∴AC=BD．②由①得：∠OAC=∠OBD，∵∠AEO=∠PEB，∠APB=180°﹣（∠BEP+∠OBD），∠AOB=180°﹣（∠OAC+∠AEO），∴∠APB=∠AOB=60°．（2）AC=BD，α（3）AC=k•BD，180°﹣α．点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．10．（南宁）（A类）如图，DE⊥AB、DF⊥AC．垂足分别为E、F．请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②BD=CD；③BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BD=CD求证：BE=CF已知：DE⊥AB、DF⊥AC，垂足分别为E、F，AB=AC，BE=CF求证：BD=CD已知：DE⊥AB、DF⊥AC，垂足分别为E、F，BD=CD，BE=CF求证：AB=AC（B类）如图，EG∥AF，请你从下面三个条件中，再选两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．①AB=AC；②DE=DF；③BE=CF已知：EG∥AF，AB=AC，DE=DF求证：BE=CF友情提醒：若两题都做的同学，请你确认以哪类题记分，你的选择是A类类题．考点：全等三角形的判定与性质．专题：证明题；开放型．分析：本题是开放题，应先确定选择哪对三角形，对应三角形全等条件求解；再根据全等三角形的性质得出结论．解答：解：（A类）已知：…，AB=AC，BD=CD求证：BE=CF．证明：∵AB=AC，∴∠B=∠C．∵DE⊥AB，DF⊥AC，∴∠BED=∠CFD=90°．在△BDE和△CDF中∴△BDE≌△CDF．∴BE=CF．已知：…，AB=AC，DE=DF，求证：BE=CF．证明：∵EG∥AF，∴∠GED=∠F，∠BGE=∠BCA．∵AB=AC，∴∠B=∠BCA，∴∠B=∠BGE，∴BE=EG．在△DEG和△DFC中∴△DEG≌△DFC，∴EG=CF，∴BE=CF．点评：这是一道考查三角形全等的识别方法的开放性题目，答案可有多种．同时还考查了全等三角形的性质．。
中考数学专题复习：三角形的证明
中考数学专题复习：三角形的证明一．选择题1．下列语句中错误的是（）A. 角的大小与角两边的长短无关B. 过两点有且只有一条直线C. 若线段，则一定是的中点D. 与两点之间的距离是指连接．两点间的线段的长度2．如图，在△ABC中，AB＝AC＝5，BC＝6，△ABC和△ACB角平分线交于点O，则AO的长度为（）A．2.5B．3C．D．3．把一副三角尺ABC与BDE按如图所示那样拼在一起，△ABC＝60°，△C＝△DBE ＝90°，其中A，D，B三点在同一直线上，BM为△ABC的平分线，BN为△CBE 的平分线，则△MBN的度数是（）A．55°B．30°C．45°D．60°4．如图，△ABC中△ACB＝90°，且CD△AB．△B＝60°，则△1等于（）A．30°B．40°C．50°D．60°5．若点在线段的垂直平分线上，，则( ).A. B. 无法确定 C. D.6．如图，在△ABC中，△ACB＝90°，△B＝15°，DE垂直平分AB，交BC于点E，AE＝6cm，则AC＝（）A．6cm B．5cm C．4cm D．3cm7．如图，在△ABC中，△C＝90°，AD是△BAC的角平分线，E是边AB上一点，若CD＝6，则DE的长可以是（）A．1B．3C．5D．78．下列命题：△一组对边平行，另一组对边相等的四边形是平行四边形；△对角线互相垂直且平分的四边形是菱形；△一个角为90°且一组邻边相等的四边形是正方形；△对角线相等的平行四边形是矩形．其中真命题的个数是（）A．1B．2C．3D．49．在△ABC中，有下列条件：△△A+△B＝△C；△△A：△B：△C＝1：2：3；△△A＝2△B＝3△C；△△A＝△B＝△C．其中能确定△ABC是直角三角形的条件有（）A．1个B．2个C．3个D．4个10．如图，DE是△ABC中AC边的垂直平分线，若BC＝4cm，AB＝5cm，则△EBC 的周长为（）A．8cm B．9cm C．10cm D．11cm11．某一实验装置的截面图如图所示，上方装置可看做一长方形，其侧面与水平线的夹角为，下方是一个直径为，高为的圆柱形容器，若使容器中的液面与上方装置相接触，则容器中液体的高度至少应为（）A. B. C. D.12．用反证法证明命题“三角形中必有一个内角小于或等于60°时，首先应该假设（）A．三角形中每个内角都大于60°B．三角形中至少有一个内角大于60°C．三角形中每个内角都大于或等于60°D．三角形中每一个内角都小于成等于60°二．填空题13．如图，点A．O．E在同一直线上，△AOB＝40°，△EOD＝28°46′，OD平分△COE，则△COB的度数为__________．14．如图，△ABC中，AB＝8，BC＝10，BD是△ABC的角平分线，DE△AB于点E，若DE＝4，则三角形ABC的面积为__________．15．如图，OP平分△AOB，△AOP＝15°，PC△OB，PD△OB于点D，PD＝4，则PC等于__________．16．如图，在△ABC中，△ABC和△ACB的平分线交于点E，过点E作MN△BC 交AB于M，交AC于N，若BM+CN＝10，则线段MN的长为__________．17．说明命题“如果a．b．c是△ABC的三边，那么长为a﹣1．b﹣1．c﹣1的三条线段能构成三角形”是假命题的反例可以是a＝2，b＝2，c＝__________．18．用反证法证明“已知五个正数的和等于1，求证：这五个正数中至少有一个大于或等于”时，首先要假设__________．三．解答题19．如图：△AOB＝160°，OC是△AOB的平分线，OD是△COB的平分线，求△COD 的度数．20．已知：如图，△AOB及M．N两点．请你在△AOB内部找一点P，使它到角的两边和到点M．N的距离分别相等（保留作图痕迹）．21．如图，已知：AD是△BAC的平分线，AB＝BD，过点B作BE△AC，与AD 交于点F．（1）求证：AC△BD；（2）若AE＝2，AB＝3，BF＝，求△ABF中AB边上的高．22．如图，在△ABC和△DCB中，AC与BD交于点E，现有三个条件：△AB＝DC；△△A＝△D，△△1＝△2，请你从三个条件中选出两个作为条件，另一个作为结论，组成一个真命题，并给予证明．（1）条件是__________；结论是__________（填序号）；（2）证明．23．如图所示，在△ABC中．AB＝AC．△A＝36°，DE垂直平分AB交AC于点D，垂足为点E，求证：AD＝BC．24．如图，在四边形中，已知为的角平分线，，．两点分别在．上，且.请完整说明为什么四边形的面积为四边形的一半．25．已知等边△ABC和点P，设点P到△ABC三边AB．AC．BC的距离分别为h1，h2，h3，△ABC的高为h．（1）若点P在一边BC上[如图△]，此时h3＝0，求证：h1+h2+h3＝h；（2）当点P在△ABC内[如图△]，以及点P在△ABC外[如图△]这两种情况时，上述结论是否成立？若成立，请予以证明；若不成立，h1，h2，h3与h之间又有怎样的关系，请说出你的猜想，并说明理由．参考答案13．82°28′14．3615．816．1017．3（答案不唯一）18．这五个数都小于19．解：△OC是△AOB的平分线，△AOB＝160°，△△COB＝△AOB＝80°，又△OD是△COB的平分线，△△COD＝△COB＝40°．20．解：点P就是所求的点．如果能正确画出角平分线和中垂线的给满分21．（1）证明：△AD是△BAC的平分线，△△CAD＝△BAD，△AB＝BD，△△BDA＝△BAD，△△CAD＝△BDA，△AC△BD；（2）解：作FG△AB于G，在Rt△ABE中，AE＝2，AB＝3，△BE＝＝＝，△FE＝BE﹣BF＝﹣＝，△AD是△BAC的平分线，BE△AC，作FG△AB，△FG＝FE＝，即△ABF中AB边上的高为．22．解：（1）条件是：△AB＝DC；△△A＝△D，结论是△△1＝△2；（2）证明如下：在△ABE与△DEC中，△△ABE△△DEC（AAS），△BE＝EC，△△1＝△2．故答案为：△△；△23．证明：△△ABC中，AB＝AC，△A＝36°，△△ABC＝72°，△DE是线段AB的垂直平分线，△AD＝BD，△△A＝△ABD＝36°，△△CDB＝△A+△ABD＝72°，△△CDB＝△C，△BD＝BC，△AD＝BC．24．解：分别作于，于，△为的角平分线，△，△，△，又△，△，△，△，△，△四边形的面积，四边形的面积，△四边形的面积，又△四边形的面积，△四边形的面积，△四边形的面积为四边形的面积的一半．25．解：（1）如图1，连接AP，则S△ABC＝S△ABP+S△APC △BC•AM＝AB•PD+AC•PF即BC•h＝AB•h1+AC•h2又△△ABC是等边三角形△BC＝AB＝AC，△h＝h1+h2；（2）点P在△ABC内时，h＝h1+h2+h3，理由如下：如图2，连接AP．BP．CP，则S△ABC＝S△ABP+S△BPC+S△ACP △BC•AM＝AB•PD+AC•PE+BC•PF即BC•h＝AB•h1+AC•h2+BC•h3又△△ABC是等边三角形，△BC＝AB＝AC．△h＝h1+h2+h3；点P在△ABC外时，h＝h1+h2﹣h3．理由如下：如图3，连接PB，PC，P A由三角形的面积公式得：S△ABC＝S△P AB+S△P AC﹣S△PBC，即BC•AM＝AB•PD+AC•PE﹣BC•PF，△AB＝BC＝AC，△h1+h2﹣h3＝h，即h1+h2﹣h3＝h．。
八年级全等三角形简单证明题及解答(5道)
汇报人：XX
目 录
• 题目一：基本的全等三角形证明 • 题目二：利用角平分线性质证明 • 题目三：通过边边边条件证明 • 题目四：结合中线性质进行证明 • 题目五：综合应用多种性质证明 • 总结与拓展
01
题目一：基本的全等三角形证明
题目描述
• 已知三角形$ABC$和三角形$DEF$，其中$AB = DE$，$AC = DF$，$\angle BAC = \angle EDF$。求证：$\triangle ABC \cong \triangle DEF$。
由第二步可知，△BDE∽△CFD。
详细解答
4. 第四步，根据相似三角形的性质，对应边成比例，所以BD/CF=DE/DF。
5. 第五步，因为BD=AD（已知），所以AD/CF=DE/DF。又因为AE/EC=DE/EF（已知）， 所以AD/CF=AE/EC。
6. 第六步，交叉相乘得AD*EC=AE*CF，即AE/AD=EC/CF。又因为∠A=∠ACF（对顶角相 等），所以△ADE∽△ACF。
第三步，根据相似三 角形的性质，有 AB/AC = BD/DC。
综上，我们证明了 AB/AC = BD/DC。
03
题目三：通过边边边条件证明
题目描述
已知
△ABC和△DEF中，AB = DE，BC = EF，AC = DF。
求证
△ABC ≌ △DEF。
题目描述
【分析】
本题主要考察全等三角形的判定方法——边边边条件。根据已知条件，我们可以 直接应用边边边定理来证明两个三角形全等。
题目描述
01
【解答】
02
证明
03
04
∵ 在△ABC和△DEF中，AB = DE，BC = EF，AC = DF（已
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章三角形的证明测试卷（源于中考的试题）参考答案与试题解析一．选择题（共9小题）1．（2013?郴州）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．25°B．30°C．35°D．40°解答：解：∵在Rt△ACB中，∠ACB=90°，∠A=25°，∴∠B=90°﹣25°=65°，∵△CDB′由△CDB反折而成，∴∠CB′D=∠B=65°，∵∠CB′D是△AB′D的外角，∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°．故选D．2．（2012?潍坊）轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行半小时到达C处，在C 处观测灯塔A位于北偏东60°方向上，则C处与灯塔A的距离是（）海里．A．25B．25C．50D．25解答：解：根据题意，∠1=∠2=30°，∵∠ACD=60°，∴∠ACB=30°+60°=90°，∴∠CBA=75°﹣30°=45°，∴△ABC为等腰直角三角形，∵BC=50×=25，∴AC=BC=25（海里）．故选D．3．（2011?贵阳）如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（）A．B．C．D．7解答：解：根据垂线段最短，可知AP的长不可小于3；∵△ABC中，∠C=90°，AC=3，∠B=30°，∴AB=6，∴AP的长不能大于6．故选D．4．（2012?铜仁地区）如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（）A．6B．7C．8D．9考点：等腰三角形的判定与性质；平行线的性质．分析：由∠ABC、∠ACB的平分线相交于点E，∠MBE=∠EBC，∠ECN=∠ECB，利用两直线平行，内错角相等，利用等量代换可∠MBE=∠MEB，∠NEC=∠ECN，然后即可求得结论．解答：解：∵∠ABC、∠ACB的平分线相交于点E，∴∠MBE=∠EBC，∠ECN=∠ECB，∵MN∥BC，∴∠EBC=∠MEB，∠NEC=∠ECB，∴∠MBE=∠MEB，∠NEC=∠ECN，∴BM=ME，EN=CN，∴MN=ME+EN，即MN=BM+CN．∵BM+CN=9∴MN=9，故选D．5．（2011?恩施州）如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）A．11B．C．7D．考点：角平分线的性质；全等三角形的判定与性质．专题：计算题；压轴题．分析：作DM=DE交AC于M，作DN⊥AC，利用角平分线的性质得到DN=DF，将三角形EDF的面积转化为三角形DNM的面积来求．解答：解：作DM=DE交AC于M，作DN⊥AC，∵DE=DG，DM=DE，∴DM=DG，∵AD是△ABC的角平分线，DF⊥AB，∴DF=DN，在Rt△DEF和Rt△DMN中，，∴Rt△DEF≌Rt△DMN（HL），∵△ADG和△AED的面积分别为50和39，∴S△MDG=S△ADG﹣S△ADM=50﹣39=11，S△DNM=S△DEF=S△MDG==故选B．点评：本题考查了角平分线的性质及全等三角形的判定及性质，解题的关键是正确地作出辅助线，将所求的三角形的面积转化为另外的三角形的面积来求．6．（2012?广州）在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（）A．B．C．D．解答：解：根据题意画出相应的图形，如图所示：在Rt△ABC中，AC=9，BC=12，根据勾股定理得：AB==15，过C作CD⊥AB，交AB于点D，又S△ABC=AC?BC=AB?CD，∴CD===，则点C到AB的距离是．故选A7．（2007?芜湖）如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE 交于点H，已知EH=EB=3，AE=4，则CH的长是（）A．1B．2C．3D．4解答：解：在△ABC中，AD⊥BC，CE⊥AB，∴∠AEH=∠ADB=90°；∵∠EAH+∠AHE=90°，∠DHC+∠BCH=90°，∵∠EHA=∠DHC（对顶角相等），∴∠EAH=∠DCH（等量代换）；∵在△BCE和△HAE中，∴△AEH≌△CEB（AAS）；∴AE=CE；∵EH=EB=3，AE=4，∴CH=CE﹣EH=AE﹣EH=4﹣3=1．故选A．8．（2011?泰安）如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（）A．B．C．D．6解答：解：∵△CEO是△CEB翻折而成，∴BC=OC，BE=OE，∠B=∠COE=90°，∴EO⊥AC，∵O是矩形ABCD的中心，∴OE是AC的垂直平分线，AC=2BC=2×3=6，∴AE=CE，在Rt△ABC中，AC2=AB2+BC2，即62=AB2+32，解得AB=3，在Rt△AOE中，设OE=x，则AE=3﹣x，AE2=AO2+OE2，即（3﹣x）2=32+x2，解得x=，∴AE=EC=3﹣=2．故选A．9．（2012?深圳）如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A6B6A7的边长为（）A．6B．12C．32D．64解答：解：∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°，∵∠MON=30°，∴∠1=180°﹣120°﹣30°=30°，又∵∠3=60°，∴∠5=180°﹣60°﹣30°=90°，∵∠MON=∠1=30°，∴OA1=A1B1=1，∴A2B1=1，∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°，∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴A2B2=2B1A2，B3A3=2B2A3，∴A3B3=4B1A2=4，A4B4=8B1A2=8，A5B5=16B1A2=16，以此类推：A6B6=32B1A2=32．故选：C．二．填空题（共8小题）10．（2011?怀化）如图，在△ABC中，AB=AC，∠BAC的角平分线交BC边于点D，AB=5，BC=6，则AD= 4 ．考点：勾股定理；等腰三角形的性质．分析：首先根据等腰三角形的性质：等腰三角形的三线合一，求出DB=DC=CB，AD⊥BC，再利用勾股定理求出AD的长．解答：解：∵AB=AC，AD是∠BAC的角平分线，∴DB=DC=CB=3，AD⊥BC，在Rt△ABD中，∵AD2+BD2=AB2，∴AD==4，故答案为：4．点评：此题主要考查了等腰三角形的性质与勾股定理的应用，做题的关键是根据等腰三角形的性质证出△ADB是直角三角形．11．（2011?衡阳）如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为7 ．考点：翻折变换（折叠问题）；勾股定理．专题：压轴题；探究型．分析：先根据勾股定理求出BC的长，再根据图形翻折变换的性质得出AE=CE，进而求出△ABE的周长．解答：解：∵在△ABC中，∠B=90°，AB=3，AC=5，∴BC===4，∵△ADE是△CDE翻折而成，∴AE=CE，∴AE+BE=BC=4，∴△ABE的周长=AB+BC=3+4=7．故答案为：7．点评：本题考查的是图形翻折变换的性质，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．12．（2010?滨州）如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD 上的动点，E是AC边上一点，若AE=2，EM+CM的最小值为．考点：轴对称-最短路线问题；勾股定理．专题：压轴题；动点型．分析：要求EM+CM的最小值，需考虑通过作辅助线转化EM，CM的值，从而找出其最小值求解．解答：解：连接BE，与AD交于点M．则BE就是EM+CM的最小值．取CE中点F，连接DF．∵等边△ABC的边长为6，AE=2，∴CE=AC﹣AE=6﹣2=4，∴CF=EF=AE=2，又∵AD是BC边上的中线，∴DF是△BCE的中位线，∴BE=2DF，BE∥DF，又∵E为AF的中点，∴M为AD的中点，∴ME是△ADF的中位线，∴DF=2ME，∴BE=2DF=4ME，∴BM=BE﹣ME=4ME﹣ME=3ME，∴BE=BM．在直角△BDM中，BD=BC=3，DM=AD=，∴BM==，∴BE=．∵EM+CM=BE∴EM+CM的最小值为．点评：考查等边三角形的性质和轴对称及勾股定理等知识的综合应用．13．（2013?泰安）如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC 于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是 2 ．考点：含30度角的直角三角形；线段垂直平分线的性质．专题：压轴题．分析：根据同角的余角相等、等腰△ABE的性质推知∠DBE=30°，则在直角△DBE中由“30度角所对的直角边是斜边的一半”即可求得线段BE的长度．解答：解：∵∠ACB=90°，FD⊥AB，∴∠ACB=∠FDB=90°，∵∠F=30°，∴∠A=∠F=30°（同角的余角相等）．又AB的垂直平分线DE交AC于E，∴∠EBA=∠A=30°，∴直角△DBE中，BE=2DE=2．故答案是：2．点评：本题考查了线段垂直平分线的性质、含30度角的直角三角形．解题的难点是推知∠EBA=30°．14．（2013?黔西南州）如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG=CD，DF=DE，则∠E=15 度．考点：等边三角形的性质；三角形的外角性质；等腰三角形的性质．专题：压轴题．分析：根据等边三角形三个角相等，可知∠ACB=60°，根据等腰三角形底角相等即可得出∠E的度数．解答：解：∵△ABC是等边三角形，∴∠ACB=60°，∠ACD=120°，∵CG=CD，∴∠CDG=30°，∠FDE=150°，∵DF=DE，∴∠E=15°．故答案为：15．点评：本题考查了等边三角形的性质，互补两角和为180°以及等腰三角形的性质，难度适中．15．（2005?绵阳）如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 5 cm．考点：等腰三角形的判定与性质；平行线的性质．专题：压轴题．分析：分别利用角平分线的性质和平行线的判定，求得△DBP和△ECP为等腰三角形，由等腰三角形的性质得BD=PD，CE=PE，那么△PDE的周长就转化为BC边的长，即为5cm．解答：解：∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABP=∠PBD，∠ACP=∠PCE，∵PD∥AB，PE∥AC，∴∠ABP=∠BPD，∠ACP=∠CPE，∴∠PBD=∠BPD，∠PCE=∠CPE，∴BD=PD，CE=PE，∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm．答：△PDE的周长是5cm．点评：此题主要考查了平行线的判定，角平分线的性质及等腰三角形的性质等知识点．本题的关键是将△PDE的周长就转化为BC边的长．17．（2005?十堰）如图中的螺旋由一系列直角三角形组成，则第n个三角形的面积为．考点：勾股定理．专题：规律型．分析：根据勾股定理，逐一进行计算，从中寻求规律，进行解答．解答：解：根据勾股定理：第一个三角形中：OA12=1+1，S1=1×1÷2；第二个三角形中：OA22=OA12+1=1+1+1，S2=OA1×1÷2=×1÷2；第三个三角形中：OA32=OA22+1=1+1+1+1，S3=OA2×1÷2=×1÷2；…第n个三角形中：S n=×1÷2=．点评：本题主要考查了勾股定理的应用，要注意图中三角形的面积的变化规律．三．解答题（共5小题）18．（2013?温州）如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．（1）求证：△ACD≌△AED；（2）若∠B=30°，CD=1，求BD的长．考点：全等三角形的判定与性质；角平分线的性质；含30度角的直角三角形．分析：（1）根据角平分线性质求出CD=DE，根据HL定理求出另三角形全等即可；（2）求出∠DEB=90°，DE=1，根据含30度角的直角三角形性质求出即可．解答：（1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，∴CD=ED，∠DEA=∠C=90°，∵在Rt△ACD和Rt△AED中∴Rt△ACD≌Rt△AED（HL）；（2）解：∵DC=DE=1，DE⊥AB，∴∠DEB=90°，∵∠B=30°，∴BD=2DE=2．点评：本题考查了全等三角形的判定，角平分线性质，含30度角的直角三角形性质的应用，注意：角平分线上的点到角两边的距离相等．19．（2013?沈阳）如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF．（1）求证：BF=2AE；（2）若CD=，求AD的长．考点：全等三角形的判定与性质；勾股定理．专题：证明题；压轴题．分析：（1）先判定出△ABD是等腰直角三角形，根据等腰直角三角形的性质可得AD=BD，再根据同角的余角相等求出∠CAD=∠CBE，然后利用“角边角”证明△ADC和△BDF全等，根据全等三角形对应边相等可得BF=AC，再根据等腰三角形三线合一的性质可得AC=2AF，从而得证；（2）根据全等三角形对应边相等可得DF=CD，然后利用勾股定理列式求出CF，再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=CF，然后根据AD=AF+DF代入数据即可得解．解答：（1）证明：∵AD⊥BC，∠BAD=45°，∴△ABD是等腰直角三角形，∴AD=BD，∵BE⊥AC，AD⊥BC，∴∠CAD+∠ACD=90°，∠CBE+∠ACD=90°，∴∠CAD=∠CBE，在△ADC和△BDF中，，∴△ADC≌△BDF（ASA），∴BF=AC，∵AB=BC，BE⊥AC，∴AC=2AE，∴BF=2AE；（2）解：∵△ADC≌△BDF，∴DF=CD=，在Rt△CDF中，CF===2，∵BE⊥AC，AE=EC，∴AF=CF=2，∴AD=AF+DF=2+．点评：本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，等腰三角形三线合一的性质，勾股定理的应用，以及线段垂直平分线上的点到线段两端点的距离相的性质，熟记各性质并准确识图是解题的关键．22．（2013?铜仁地区）如图，△ABC和△ADE都是等腰三角形，且∠BAC=90°，∠DAE=90°，B，C，D在同一条直线上．求证：BD=CE．考点：全等三角形的判定与性质；等腰直角三角形．专题：证明题．分析：求出AD=AE，AB=AC，∠DAB=∠EAC，根据SAS证出△ADB≌△AEC即可．解答：证明：∵△ABC和△ADE都是等腰直角三角形∴AD=AE，AB=AC，又∵∠EAC=90°+∠CAD，∠DAB=90°+∠CAD，∴∠DAB=∠EAC，∵在△ADB和△AEC中∴△ADB≌△AEC（SAS），∴BD=CE．点评：本题考查了等腰直角三角形性质，全等三角形的性质和判定的应用，关键是推出△ADB≌△AEC．。