kruskal算法求最小生成树

求无向图的最小生成树算法——Prim与Kruskal

求无向图的最小生成树算法——Prim与Kruskal一.Prim算法1.算法思想对于图G=(V,E)，用Prim算法求最小生成树T=(S,TE)的流程如下① 初始化：设S、TE为空集，任选节点K加入S。

② 选取一条权值最小的边（X,Y），其中X∈S，且not (Y∈S）即，选取一条权值最小的、连接着S中一点与S外一点的边。

将Y加入S中，边（X，Y）加入TE中重复② 直到V=S即所有G中的点都在S中，此时的T为G的最小生成树。

由此流程可见，Prim算法求最小生成树时任何时候的T都是一颗树。

2.实现显然，Prim算法的主要运行时间花在过程②的选边中。

看起来复杂度是O(VE)=O(V^3)不是么，效率也太低了吧……为了比较快速地选边，我们用两个数组lowcost、closest动态地维护每一个点到S的最短距离。

在某一状态下，lowcost[i]表示所有与i相连且另一端点在S中的边中的权值最小值，closest[i]表示在S中且与i相连的点中与i之间距离最小的点。

显然，lowcost[i]=w(i,closest[i])。

需要注意的是两个数组记录的都是边而不是路径。

若i没有边直接连向S，则lowcost[i]=∞。

另外，若i已在S 中，则lowcost[i]=0。

设出发点为x。

初始时对于任意k∈V，closest[k]=x，lowcost[k]=w（k,x）【w（i，j）表示i、j间的距离。

初始化时，若两点间没有边则w（i，j）赋为一个足够大的整数（如maxint），并且所有点到自身的距离赋为0，即w（i，i）=0】每一次找出lowcost中不为0的最小值lowcost[i]，然后把i加入S（即lowcost[i]:=0），然后对于图中所有点k，若w(k,i)<lowcost[k]，则把lowcost[k]赋为w(k,i)，把closest[k]赋为i。

【由于s中所有点的lowcost都为0，所以只影响到s以外的点】以上操作重复|V|-1次结束。

Kruskal克鲁斯卡尔最小生成树算法（贪心算法）

Kruskal克鲁斯卡尔最⼩⽣成树算法（贪⼼算法）1. /*2. * Introduction to Algorithms3. * Chapter 23 --- MST.Kruskal4. * Tanky Woo @ 5. * 2012.1.76. */7.8. #include <iostream>9. #include <algorithm>10. using namespace std;11.12. const int maxint = 999999;13.14. typedef struct Road{15. int c1, c2;// a到b16. int value;//权值17. }Road;18.19. int no;20. int line;//记录实际关系数21. Road road[100];//设⼀个⽐较⼤的值，实际看输⼊最⼩⽣成树中：边数e=n-122. int node[101];//最⼩⽣成树：n顶点数23.24. bool myCmp(const Road &a,const Road &b)25. {26. if(a.value < b.value)27. return 1;28. return 0;29. }30.31. //node[2]=1 node[8]=1 ,node[3]=1,共同的祖先,如果(3,8)加进去，则构成回路，不要32. //有点像并查集33. int Find_Set(int n)34. {35. if(node[n]==-1)36. return n;37. return node[n]= Find_Set(node[n]);38. }39.40. bool Merge(int s1,int s2)41. {42. int r1 = Find_Set(s1);43. int r2 = Find_Set(s2);44. if(r1 == r2)//如果相等证明构成回路，则直接返回⼀个0,不要把顶点加进来(下⼀步是加进去的)45. return 0;46. if(r1 < r2)47. node[r2]= r1;48. else49. node[r1]= r2;50. return 1;51. }52.53. int main()54. {55. freopen("input.txt","r", stdin);56. //初始化全为-157. memset(node,-1, sizeof(node));58. scanf("%d",&no);59. scanf("%d",&line);60. int i;61. for(i=0; i<line; ++i)62. {63. cin >> road[i].c1 >> road[i].c2 >> road[i].value;64. }65. sort(road, road+line, myCmp);66. int sum = 0, count = 0;// sum是MST的值，count是记录已使⽤的点数67. for(i=0; i<line; ++i)68. {69. if(Merge(road[i].c1, road[i].c2))//如果返回的为0,则证明构成回路，不要加进70. {71. count ++;72. sum += road[i].value;73. }74. if(count == no-1)//e=n-1已经连通，可以退出75. break;76. }77. cout << sum << endl;78. return 0;79. }80.81.82. /*83. input.txt:84. 985. 1486. 1 2 487. 1 8 888. 2 3 889. 2 8 1190. 3 4 791. 3 6 492. 3 9 293. 4 5 994. 4 6 1495. 5 6 1096. 6 7 297. 7 8 198. 7 9 699. 8 9 7100. */。

最小生成树(Kruskal算法)

三、方案解决：
在本题中我们将采用 Kruskal 算法来构造最小生成树。从题目所给赋权图中我们可以得到该图的邻接矩阵为：
⎡ 0 20 0 0 0 23 1 ⎤ ⎢20 0 15 0 0 0 4 ⎥ ⎢ ⎥ ⎢ 0 15 0 3 0 0 9 ⎥ ⎢ ⎥ G = ⎢ 0 0 3 0 17 0 16 ⎥ ⎢ 0 0 0 17 0 28 25⎥ ⎢ ⎥ ⎢ 23 0 0 0 28 0 36⎥ ⎢ 1 4 9 16 25 36 0 ⎥ ⎣ ⎦
-3-
6.选择造价第五小的序号为 5 的边，即 S 23 ，由于加入后边 S 23 ， S 27 ， S37 将构成回路，因此舍弃该边如图所示：
7.选择造价第六小的序号为 6 的边，即 S 47 ，由于加入后边 S34 ， S37 ， S 47 将构成回路，因此舍弃该边如图所示：
8.选择造价第七小的序号为 7 的边，即 S 45 ，加入 T 中，此时 T={{6},{ S17 ， S34 ， S 27 ， S37 ，
S 45 ， S16 }}，Cost=34+23=57
如图所示：
11.算法结束此时，所有顶点已包含在树中，整棵最小生成树已经构造完成。即应该在城市{（1,7），（2,7），（3,7），（3,4），（4,5），（1,6）}之间建造通信道路，可使得城市间相互通信又造价费用最小，此时可以得到其最小的费用为 57 万元
-7-
edges[k].end = j; edges[k].weight = G->arc[i][j].weight; k++; } } } sort(edges, G); for (i = 1; i <= G->arcnum; i++) { parent[i] = 0; } printf("最小生成树为:\n"); for (i = 1; i <= G->arcnum; i++)//核心部分 { n = Find(parent, edges[i].begin); m = Find(parent, edges[i].end); if (n != m) { parent[n] = m; printf("< %d, %d > %d\n", edges[i].begin, edges[i].end, edges[i].weight); Mincost+=edges[i].weight; } } printf("使各城市间能够通信的最小费用为：Mincost=%d\n",Mincost); } int Find(int *parent, int f) { while ( parent[f] > 0) { f = parent[f]; } return f; }

② kruskal最小生成树算法的定义和实现

Krskal最小生成树算法是一种用来解决图论中最小生成树问题的算法。

它采用了一种贪心的策略，即每一步都选择权值最小的边，并且保证选择的边不会构成环，直到生成一棵最小生成树为止。

1. 算法的定义kruskal最小生成树算法的定义如下：输入：一个连通无向图G=(V,E)，其中V是顶点集合，E是边的集合，每条边都有一个权值。

输出：G的最小生成树算法步骤：① 将图G的所有边按照权值从小到大进行排序。

② 初始化一个空的边集合T，该集合用来存放最小生成树的边。

③ 依次遍历排序后的边集合，对于每一条边e=(u,v)，如果将该边添加到T中不会构成环，则将其添加到T中。

④ 重复步骤③，直到T中的边数等于V-1为止，此时T就是G的最小生成树。

2. 算法的实现下面是kruskal最小生成树算法的具体实现过程：```pythonclass UnionFind:def __init__(self, n):self.parent = [i for i in range(n)]def find(self, x):if self.parent[x] != x:self.parent[x] = self.find(self.parent[x]) return self.parent[x]def union(self, x, y):root_x = self.find(x)root_y = self.find(y)if root_x != root_y:self.parent[root_x] = root_ydef kruskal(graph):edges = []for u in range(len(graph)):for v in range(u+1, len(graph)):if graph[u][v] != 0:edges.append((u, v, graph[u][v])) edges.sort(key=lambda x: x[2])n = len(graph)result = []uf = UnionFind(n)for edge in edges:u, v, weight = edgeif uf.find(u) != uf.find(v):uf.union(u, v)result.append((u, v, weight))if len(result) == n - 1:breakreturn result```以上代码实现了kruskal最小生成树算法，其中使用了UnionFind类来实现并查集的功能，以判断是否构成环。

c语言数据结构kruskal算法两种构造最小生成树算法

c语言数据结构kruskal算法两种构造最小生成树算法1. 引言1.1 概述本篇文章将讨论C语言数据结构中的Kruskal算法以及它的两种构造最小生成树的方法。

数据结构是计算机科学中至关重要的概念，它用于组织和存储数据以便于使用和操作。

C语言是一种广泛应用于系统开发和嵌入式软件的编程语言，而Kruskal算法则是解决图论中最小生成树问题的一种有效方法。

1.2 文章结构本文共分为五个部分。

首先，我们将介绍C语言中的数据结构，包括其概念、在C语言中的实现以及在算法中应用的重要性。

接下来，我们将对Kruskal算法进行简要介绍，包括最小生成树的概念和应用场景、Kruskal算法原理及思路以及详细步骤解析。

然后，我们将探讨Kruskal算法的两种构造最小生成树的方法：按边权重顺序遍历并加入最小生成树中和使用并查集维护连通性信息并进行判断和合并操作。

最后，我们将总结评估这两种方法，并讨论适用情景与选择依据。

文章最后将给出结论与总结，并对该算法的效率、应用案例以及未来的可扩展和改进方向进行分析。

1.3 目的本文旨在深入介绍C语言数据结构中Kruskal算法的两种构造最小生成树的方法，并对它们进行比较与选择依据分析。

通过阅读本文，读者将能够理解数据结构在算法中的应用、掌握Kruskal算法的原理和步骤，并了解如何选择合适的构造最小生成树方法。

此外，本文还将讨论该算法的效率、实际应用案例以及未来可能的发展方向，以便读者更全面地了解该算法并从中受益。

2. C语言数据结构简介：2.1 数据结构概念数据结构是计算机存储、组织和管理数据的方式。

它涉及到如何将不同类型的数据元素组合在一起，以便有效地进行操作和处理。

常见的数据结构包括数组、链表、栈、队列、树等。

2.2 C语言中的数据结构C语言提供了基本的数据类型，如整型、浮点型和字符型等，同时还支持用户自定义的数据结构。

通过使用struct关键字可以定义自己的复合类型，其中可以包含多个不同类型的成员变量。

Kruskal算法计算最小生成树（java）

J avaMan_chen的专栏K ruskal算法计算最小生成树(java)分类：算法 2012-12-04 17:15 243人阅读评论(2) 收藏举报kruskalKruskal克鲁斯卡尔最小生成树最小生成树定义：每一个无向图可拆分成多个子图，在这些子图中，如果图的各个顶点没有形成回路，则是图的一颗生成树。

最小生成树的意识是树的相邻节点距离之和最小。

应用场景：张三被选为他们镇的镇长！他其中一个竞选承诺就是在镇上建立起互联网，并连接到所有的农场。

张三已经给他的农场安排了一条高速的网络线路，他想把这条线路共享给其他农场。

为了用最小的消费，他想铺设最短的光纤去连接所有的农场，问要如何实现。

算法实现：有关最小生成树的问题常见的算法有两种，分别是Kruskal(克鲁斯卡尔)算法和Prim(普里姆)算法，本文讲解Kruskal算法的实现Kruskal算法的计算流程大致如下：1.将无向图的边按距离长短递增式排序，放到集合中2.遍历该集合，找出最短的边，加入到结果生成树的集合中3.如果结果生成树出现回路，则放弃这条边4.重新执行步骤2，直至所有顶点被遍历可以看出在每次遍历过程中采用了贪心算法算法实例图：代码实现：Edge类用与封装无向图中每条边的信息public class Edge implements Comparable<Edge>{private String start;private String end;private int distance;public Edge(String start,String end,int distance){this.start=start;this.end=end;this.distance=distance;}public String getStart() {return start;}public void setStart(String start) {this.start = start;}public String getEnd() {return end;}public void setEnd(String end) {this.end = end;}public int getDistance() {return distance;}public void setDistance(int distance) {this.distance = distance;}@Overridepublic String toString() {return start + "->" + end;}@Overridepublic int compareTo(Edge obj) {int targetDis=obj.getDistance();return distance>targetDis?1:(distance==targetDis?0:-1);}}MapBuilder类用于构建数据源(数据源结构如上图所示)：public class MapBuilder {public TreeSet<Edge> build(){TreeSet<Edge> edges=new TreeSet<Edge>();edges.add(new Edge("A","B",1));edges.add(new Edge("A","C",4));edges.add(new Edge("A","F",6));edges.add(new Edge("B","D",8));edges.add(new Edge("B","E",3));edges.add(new Edge("C","F",5));edges.add(new Edge("C","E",9));edges.add(new Edge("D","E",7));edges.add(new Edge("D","F",10));edges.add(new Edge("E","F",2));return edges;}public int getPointNum(){return 6;}}Kruskal类用于计算最小生成树public class Kruskal {private Set<String> points=new HashSet<String>();private List<Edge> treeEdges=new ArrayList<Edge>();public void buildTree(){MapBuilder builder=new MapBuilder();TreeSet<Edge> edges=builder.build();int pointNum=builder.getPointNum();for(Edge edge:edges){if(isCircle(edge)){continue;}else{//没有出现回路,将这条边加入treeEdges集合treeEdges.add(edge);//如果边数等于定点数-1,则遍历结束if(treeEdges.size()==pointNum-1){return;}}}}public void printTreeInfo(){int totalDistance=0;for(Edge edge:treeEdges){totalDistance+=edge.getDistance();System.out.println(edge.toString());}System.out.println("总路径长度:"+totalDistance);}private boolean isCircle(Edge edge){int size=points.size();if(!points.contains(edge.getStart())){size++;}if(!points.contains(edge.getEnd())){size++;}if(size==treeEdges.size()+1){return true;}else{points.add(edge.getStart());points.add(edge.getEnd());return false;}}}Main类用于测试Kruskal算法public class Main {public static void main(String[] args) {Kruskal test=new Kruskal();test.buildTree();test.printTreeInfo();}}打印输出：A->BE->FB->EA->CD->E总路径长度:17。

Kruskal算法求最小生成树

荆楚理工学院课程设计成果学院:_______计算机工程学院__________ 班级: 14计算机科学与技术一班学生姓名: 陈志杰学号: 2014407020137设计地点（单位）_____B5101_________ ____________设计题目:克鲁斯卡尔算法求最小生成树__________________________________完成日期：2015年1月6日指导教师评语: ______________ ____________________________________________________________________________________________________________ ___________________________________________________________________________________________ ___________________________ __________ _成绩(五级记分制):_____ _ __________教师签名:__________ _______________注：介于A和C之间为B级，低于C为D级和E级。

按各项指标打分后，总分在90～100为优，80～89为良，70～79为中，60～69为及格，60分以下为不及格。

目录1 需求分析 (1)1.1系统目标 (1)1.2主体功能 (1)1.3开发环境 (1)2 概要设计 (1)2.1功能模块划分 (1)2.2 系统流程图 (2)3 详细设计 (3)3.1 数据结构 (3)3.2 模块设计 (3)4测试 (3)4.1 测试数据 (3)4.2测试分析 (4)5总结与体会 (6)5.1总结： (6)5.2体会： (6)参考文献 (7)附录全部代码 (8)1 需求分析1.1系统目标Kruskal算法是一种按照网中边的权值递增的顺序构造最小生成树的方法。

用Kruskal算法求无向图的最小生成树

用Kruskal算法求无向图的最小生成树该图用邻接矩阵表示，邻接表原理与之相同。

可以指出的是，对于有向图，算法可以做得更加简单，因为对无向图的“回边”情况的处理比有向图回边情况的处理要复杂一些。

图1：输入示例图二：输入时若两点之间没有公共边，则将权值设置为-1。

程序设置处理的最大点数为10。

图三：注意到Kruskal算法的解答结果有时候不是唯一的，这个结果和对图遍历时的顺序有关，但是必需注意的是所有的最小生成树其网络代价和是一样的。

下面是源代码：/* Kruskal.cCopyright (c) 2002, 2006 by ctu_85All Rights Reserved.*//* I am sorry to say that the situation of unconnected graph is not concerned */ #include "stdio.h"#define maxver 10#define maxright 100int G[maxver][maxver],record=0,touched[maxver][maxver];int circle=0;int FindCircle(int,int,int,int);int main(){int path[maxver][2],used[maxver][maxver];int i,j,k,t,min=maxright,exsit=0;int v1,v2,num,temp,status=0;restart:printf("Please enter the number of vertex(s) in the graph:\n"); scanf("%d",&num);if(num>maxver||num<0){printf("Error!Please reinput!\n");goto restart;}for(j=0;j<num;j++)for(k=0;k<num;k++){if(j==k){G[j][k]=maxright;used[j][k]=1;touched[j][k]=0;}elseif(j<k){re:printf("Please input the right between vertex %d and vertex %d,if no edge exists please input -1:\n",j+1,k+1); scanf("%d",&temp);if(temp>=maxright||temp<-1){printf("Invalid input!\n"); goto re;}if(temp==-1)temp=maxright;G[j][k]=G[k][j]=temp;used[j][k]=used[k][j]=0; touched[j][k]=touched[k][j]=0; }}for(j=0;j<num;j++){path[j][0]=0;path[j][1]=0;}for(j=0;j<num;j++) {status=0;for(k=0;k<num;k++) if(G[j][k]<maxright) {status=1; break;}if(status==0) break;}for(i=0;i<num-1&&status;i++) {for(j=0;j<num;j++)for(k=0;k<num;k++)if(G[j][k]<min&&!used[j][k]) {v1=j;v2=k;min=G[j][k];}if(!used[v1][v2]){used[v1][v2]=1;used[v2][v1]=1;touched[v1][v2]=1;touched[v2][v1]=1;path[i][0]=v1;path[i][1]=v2;for(t=0;t<record;t++)FindCircle(path[t][0],path[t][0],num,path[t][0]); if(circle){/*if a circle exsits,roll back*/circle=0;i--;exsit=0;touched[v1][v2]=0;touched[v2][v1]=0;min=maxright;}else{record++;min=maxright;}}}if(!status)printf("We cannot deal with it because the graph is not connected!\n");else{for(i=0;i<num-1;i++)printf("Path %d:vertex %d to vertex %d\n",i+1,path[i][0]+1,path[i][1]+1); }return 1;}int FindCircle(int start,int begin,int times,int pre){ /* to judge whether a circle is produced*/int i;for(i=0;i<times;i++)if(touched[begin][i]==1){if(i==start&&pre!=start){circle=1;return 1;break;}elseif(pre!=i)FindCircle(start,i,times,begin); elsecontinue;}return 1;}。

最小生成树kruskal算法例题

最小生成树kruskal算法例题最小生成树（Minimum Spanning Tree，简称MST）是图论中的一个重要概念，它是指在一个连通图中，找到一棵包含所有顶点且边权值之和最小的树。

Kruskal算法是一种常用的求解最小生成树的算法，下面我们通过一个例题来详细介绍Kruskal算法的具体步骤和实现过程。

假设有一个无向连通图，其中包含6个顶点和9条边，每条边都有对应的权值。

我们的目标是找到一棵最小生成树。

首先，我们需要将所有的边按照权值从小到大进行排序。

然后，从权值最小的边开始，依次判断这条边的两个顶点是否在同一个连通分量中。

如果不在同一个连通分量中，就将这条边加入最小生成树中，并将这两个顶点合并到同一个连通分量中。

重复这个过程，直到最小生成树中包含了所有的顶点。

下面是具体的步骤：1. 将所有的边按照权值从小到大进行排序。

2. 创建一个并查集，用于判断两个顶点是否在同一个连通分量中。

3. 从权值最小的边开始遍历，依次判断这条边的两个顶点是否在同一个连通分量中。

4. 如果两个顶点不在同一个连通分量中，将这条边加入最小生成树中，并将这两个顶点合并到同一个连通分量中。

5. 重复步骤3和步骤4，直到最小生成树中包含了所有的顶点。

下面我们通过一个具体的例题来演示Kruskal算法的实现过程。

假设有一个无向连通图，其中包含6个顶点A、B、C、D、E、F，以及9条边，每条边的权值如下：AB: 2AC: 3AD: 1BC: 4BD: 5BE: 6CD: 7CE: 8DE: 9首先，将所有的边按照权值从小到大进行排序：AD: 1AB: 2AC: 3BC: 4BD: 5BE: 6CD: 7CE: 8DE: 9然后，创建一个并查集，用于判断两个顶点是否在同一个连通分量中。

接下来，从权值最小的边AD开始遍历，判断顶点A和顶点D是否在同一个连通分量中。

由于初始时每个顶点都是一个独立的连通分量，所以A和D不在同一个连通分量中。

kruskal算法求最小生成树

数据结构课程设计Kruskal算法求最小生成树学院：班级：学号；姓名；指导老师；完成日期：目录(一)需求分析———————————(二)概要设计———————————(三)详细设计———————————(四)主函数设计—————————(五)经验体会——————————- （六）源代码及调试分析————————1、需求分析运用kruskal算法求最小生成树最短路径：①输入任意源点，求到其余顶点的最短路径。

②输入任意对顶点，求这两点之间的最短路径和所有路径。

2、概要设计首先要确定图的存储形式。

经过的题目要求的初步分析，发现该题的主要操作是路径的输出，因此采用数组（邻接矩阵）的方法构造无向图，比较方便以后的编程。

从而求得最小生成树。

3、函数详细设计（1）构造无向图本题中为了能够求得最小生成树，先要构造无向图，并且用领结矩阵的形式表现出来。

void Create(MGraph &G) //采用数组（邻接矩阵）表示法，构造无向图G。

{int i,j,k,w;char v1[10],v2[10];scanf("%d%d",&G.vexnum,&G.arcnum); //输入定点数和边数for(i=0; i<G.vexnum; i++)scanf("%s", G.vexs[i]);for(i=0; i<G.vexnum; i++) //初始化邻接矩阵{for(j=0; j<G.vexnum; j++)G.arcs[i][j] = INF;}for(k=0; k<G.arcnum; k++) //构造邻接矩阵{scanf("%s%s%d",v1,v2,&w); //输入一条边依附的顶点及权值i = Locate(G,v1); //确定v1在G中的位置j = Locate(G,v2); //确定v2在G中的位置G.arcs[i][j] = w; //弧<v1,v2>的权值G.arcs[j][i] = w; //弧<v2,v1>是权值}for(i=0; i<G.vexnum; i++){for(j=0; j<G.vexnum; j++){printf("%6d ",G.arcs[i][j]);}printf("\n");}}（2） kruskal算法。

数据结构-kruskal算法求最小生成树实验报告

一、问题简述题目：图的操作。

要求：用kruskal算法求最小生成树。

最短路径：①输入任意源点，求到其余顶点的最短路径。

②输入任意对顶点，求这两点之间的最短路径和所有路径。

二、程序设计思想首先要确定图的存储形式。

经过的题目要求的初步分析，发现该题的主要操作是路径的输出，因此采用边集数组（每个元素是一个结构体，包括起点、终点和权值）和邻接矩阵比较方便以后的编程。

其次是kruskal算法。

该算法的主要步骤是：GENERNIC-MIT(G,W)1. A←2. while A没有形成一棵生成树3 do 找出A的一条安全边(u,v);4.A←A∪{(u,v)};5.return A算法设置了集合A，该集合一直是某最小生成树的子集。

在每步决定是否把边(u,v)添加到集合A中，其添加条件是A∪{(u,v)}仍然是最小生成树的子集。

我们称这样的边为A 的安全边，因为可以安全地把它添加到A中而不会破坏上述条件。

然后就是Dijkstra算法。

Dijkstra算法基本思路是：假设每个点都有一对标号 (dj , pj)，其中dj是从起源点s到点j的最短路径的长度 (从顶点到其本身的最短路径是零路(没有弧的路)，其长度等于零)；pj则是从s到j的最短路径中j点的前一点。

求解从起源点s到点j的最短路径算法的基本过程如下：1) 初始化。

起源点设置为：① ds =0, ps为空;②所有其他点: di=∞, pi=?;③标记起源点s，记k=s,其他所有点设为未标记的。

2) 检验从所有已标记的点k到其直接连接的未标记的点j的距离，并设置：d j =min［dj, dk+lkj］式中，lkj是从点k到j的直接连接距离。

3) 选取下一个点。

从所有未标记的结点中，选取dj中最小的一个i：di =min［dj, 所有未标记的点j］点i就被选为最短路径中的一点，并设为已标记的。

4) 找到点i的前一点。

从已标记的点中找到直接连接到点i的点j*，作为前一点,设置：i=j*5) 标记点i。

最小生成树的方法

最小生成树的方法
最小生成树（Minimum Spanning Tree）是指在一个带权无向连通图中，找到一个包含所有顶点且总权值最小的树。

常用的方法有以下几种：
1. Prim算法（普里姆算法）：从一个起始顶点开始，逐步扩展生成树，每次选择一个与当前生成树距离最小的顶点加入，直到所有顶点都被包含在生成树中。

2. Kruskal算法（克鲁斯卡尔算法）：首先将图的所有边按照权值从小到大排序，然后依次选择权值最小的边加入生成树中，但要保证加入边后不会形成环，直到生成树中包含所有顶点，或者图中的所有边都被考虑过。

3. Boruvka算法（博鲁卡尔算法）：将图的所有顶点分成多个不相交的集合，每个集合中的顶点组成一棵生成树，然后每次选择具有最小权值且连接两个不同集合的边加入生成树中，直到只剩下一个集合。

4. Jarnik算法（加尔尼克算法）：也称为更改版的Prim算法，首先选择一个起始顶点加入生成树中，然后通过比较当前生成树中的顶点到其他顶点的距离，选择一个距离最小的顶点加入生成树，重复该过程直到所有顶点都被包含在生成树中。

这些方法都可以得到最小生成树，但在某些情况下，它们的效率和性能可能会不同。

选择合适的方法取决于具体的应用场景和图的特征。

克鲁斯卡尔(Kruskal)算法求无向网的最小生成树数据结构报告

数据结构上机报告（1) 姓名：张可心学号：14030188030 班级：1403018一、题目描述用克鲁斯卡尔（Kruskal）算法求无向网的最小生成树，分析你的算法的时空复杂度，必须有过程说明。

输入：输入数据第一行为两个正整数n和m，分别表示顶点数和边数。

后面紧跟m行数据，每行数据是一条边的信息，包括三个数字，分别表示该边的两个顶点和边上的权值。

输出：按顺序输出Kruskal算法求得的最小生成树的边集，每行一条边，包括三个数字，分别是该边的两个顶点和边上的权值，其中第一个顶点的编号应小于第二个顶点的编号。

示例输入8 111 2 31 4 51 6 182 4 72 5 63 5 103 8 204 6 154 7 115 7 85 8 12示例输出1 2 31 4 52 5 65 7 83 5 105 8 124 6 15二、解题思路（1）假定每对顶点表示图的一条边，每条边对应一个权值；（2）输入每条边的顶点和权值；（3）输入每条边后，计算出最小生成树；（4）打印最小生成树边的顶点及权值。

三、源代码#include<stdio.h>#include<stdlib.h>typedef struct {int a,b,value;}node;int stcmp(const void *p,const void *q){node *a=(node *)p;node *b=(node *)q;if(a->value>b->value){return 1;}else if(a->value==b->value){return 0;}else{return -1;}}int root(int a,int *b){for(;a!=b[a];a=b[a]);return a;}bool isgroup(int a,int b,int *c){if(root(a,c)==root(b,c))return true;return false;}void add(int a,int tob,int *c){c[root(a,c)]=root(tob,c);}int main (){int n,m;scanf("%d %d",&n,&m);node no[m];for(int u=0;u<m;u++){scanf("%d",&(no[u].a));scanf("%d",&(no[u].b));scanf("%d",&(no[u].value));}qsort(no,m,sizeof(no[0]),stcmp);int bcj[n+1];for(int u=1;u<=n;u++){bcj[u]=u;}int i=0;int cc=n;for(;i<m;i++){if(!isgroup(no[i].a,no[i].b,bcj)){add(no[i].a,no[i].b,bcj);cc--;printf("%d %d %d\n",no[i].a,no[i].b,no[i].value);}if(cc==1)break;}return 0;}四、运行结果。

kruskal算法求最小生成树

kruskal算法求最小生成树课题：用kruskal算法求最小生成树。

编译工具：Visual Studio 2017kruskal算法基本思想：先构造一个只含n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集E中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。

依次类推，直到森林中只有一棵树，也即子图中含有n-1 条边为止。

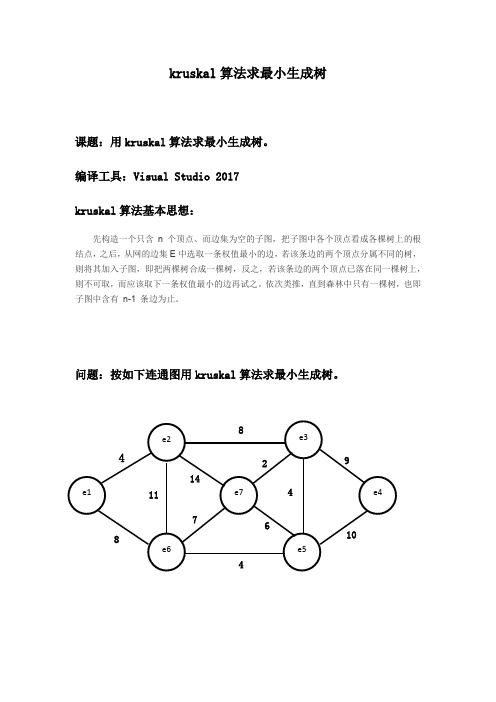
问题：按如下连通图用kruskal算法求最小生成树。

程序源码：#include <iostream>#include <algorithm>using namespace std;const int N = 100;int nodeset[N];int n, m;struct Edge { //定义结构体.int u;int v;int w;}e[N*N];bool comp(Edge x, Edge y) { //配合sort()方法对权值进行升序。

return x.w < y.w;}void Init(int n) //对集合号nodeset数组进行初始化. {for (int i = 1; i <= n; i++)nodeset[i] = i;}int Merge(int a, int b) //将e[i].u结点传递给a; e[i].v结点传递给b. {int p = nodeset[a]; //p为a结点的集结号，int q = nodeset[b]; //q为b 结点的集结号.if (p == q) return 0; //判断结点间是否回环。

若两个结点的集结号相同，则不操作，直接返回。

for (int i = 1; i <= n; i++)//若两个结点的集结号不相同，检查所有结点，把集合号是q的改为p.{if (nodeset[i] == q)nodeset[i] = p;}return 1;}int Kruskal(int n){int ans = 0;for (int i = 1; i<=m; i++)if (Merge(e[i].u, e[i].v)){cout << "A结点：" << e[i].u << "一>B结点：" << e[i].v << endl; //输出满足条件的各结点ans += e[i].w;n--;if (n == 1)return ans;}return 0;}int main() {cout << "输入总结点数(n)和总边数(m)：" << endl;cin >> n >> m;Init(n);cout << "输入结点数(u),(v)和权值(w)：" << endl;for (int i = 1; i <= m; i++)cin >> e[i].u >> e[i].v >> e[i].w;sort(e+1, e + m+1, comp);int ans = Kruskal(n);cout << "最小的花费是：" << ans << endl;return 0;}源码流程解析：(1)在main（）中，输入结点数n与边m，n=7，m=12。

数据结构Kruskal算法求解最小生成树

数据结构Kruskal算法求解最小生成树#include<stdio.h>#include<stdlib.h>#include<malloc.h>#define MAX 100struct Node{int vertex1;int vertex2;int weight;struct Node *next;};typedef struct Node * Edge;Edge head = NULL;int visited[MAX];Edge read(){int v1, v2, w;Edge newNode = NULL, pointer = NULL;while(1){scanf("%d %d %d", &v1, &v2, &w);if(v1 == -1 || v2 == -1 || w == -1)break;newNode = (Edge)malloc(sizeof(struct Node));newNode->vertex1 = v1;newNode->vertex2 = v2;newNode->weight = w;newNode->next = NULL;pointer = head;if(pointer == NULL)head = newNode;else{if(newNode->weight < pointer->weight){newNode->next = pointer;head = newNode;}else{while(pointer != NULL && pointer->next != NULL){if(pointer->weight < newNode->weight && newNode->weight < pointer->next->weight){newNode->next = pointer->next;pointer->next = newNode;break;}pointer = pointer->next;}pointer->next = newNode;}}}return head;}void printLink(Edge edge){Edge pointer = edge;printf("\n\n图中所有边按权值递增的排序如下: \n");while(pointer != NULL){printf("[%d %d]", pointer->vertex1, pointer->vertex2);printf("(%d)",pointer->weight);if(pointer->next != NULL)printf(" ==> ");pointer = pointer->next;}printf("\n");}void kruskal(Edge edge, int vexnum){int visitedEdgeNum = 0, weight = 0;printf("\n最小生成树的路径为: \n");while(visitedEdgeNum < vexnum){if(visited[edge->vertex1] == 0 || visited[edge->vertex2] == 0){ printf("[%d %d]", edge->vertex1, edge->vertex2);printf("(%d) ",edge->weight);weight += edge->weight; visitedEdgeNum++;visited[edge->vertex1] = 1;visited[edge->vertex2] = 1;}edge = edge->next;if(edge == NULL){break;}}printf("\n\n最短路径长度为：%d \n\n", weight);}void main(){int vexnum, i;Edge edge = NULL;printf("请输入定点个数、各顶点和权值：\n输入形式如下：n i j w ... -1 -1 -1\nn 表示图的顶点个数，i j w 表示从顶点i 到顶点j 的权为w 的一条边，均以-1结尾。

Prim算法和Kruskal算法介绍

Prim算法和Kruskal算法介绍⼀、Prim算法普利姆(Prim)算法适⽤于求解⽆向图中的(Minimum Cost Spanning Tree)。

下⾯是Prim算法构造最⼩⽣成树的过程图解。

选择⼀个节点开始，⽐如V1进⼊集合U，剩下的集合的V-U包括剩下的节点，然后寻找从集合U到集合V-U最近的路径。

这⾥有三条路径分别是权重为6到V2，权重为5到V4以及权重为1到V3，显然到通过V3连接⽽集合U和集合V-U是最近的，选择V3进⼊集合U。

同样继续选择到V-U的路径，此时有6条可选路径，分别是权为6到V2【从V1】，权为5到V4【从V1】，权为5到V2【从V3】，权为5到V4【从V3】，权为6到V5【从V3】，权为4到V6【从V3】。

选择出从V3到V6的路径并将V6添加⾄集合U中。

按照这种⽅法依次将V4，V2和V5添加到集合U直到U和全体节点结合V相等，或者说V-U集合为空时结束，这时选出的n-1条边即为最⼩⽣成树。

⼆、Kruskal算法克鲁斯卡尔(Kruskal)算法是另⼀种求解最⼩⽣成树的算法。

下⾯是Kruskal算法构造最⼩⽣成树的过程图解。

Kruskal则是采取另⼀种思路，即从边⼊⼿。

⾸先n个顶点分别视为n个连通分量，然后选择⼀条权重最⼩的边，如果边的两端分属于两个连通分量，就把这个边加⼊集合E，否则舍去这条边⽽选择下⼀条代价最⼩的边，依次类推，直到所有节点都在同⼀个连通分量上。

三、对⽐假设⽹中有n个节点和e条边，普利姆算法的时间复杂度是O(n^2)，克鲁斯卡尔算法的时间复杂度是O(eloge)，可以看出前者与⽹中的边数⽆关，⽽后者相反。

因此，普利姆算法适⽤于边稠密的⽹络⽽克鲁斯卡尔算法适⽤于求解边稀疏的⽹。

kruskal算法求最小生成树

求无向图的最小生成树算法——Prim与Kruskal

Kruskal克鲁斯卡尔最小生成树算法（贪心算法）

最小生成树(Kruskal算法)

② kruskal最小生成树算法的定义和实现

c语言数据结构kruskal算法两种构造最小生成树算法

Kruskal算法计算最小生成树（java）

Kruskal算法求最小生成树

用Kruskal算法求无向图的最小生成树

最小生成树kruskal算法例题

kruskal算法求最小生成树

数据结构-kruskal算法求最小生成树 实验报告

最小生成树的方法

克鲁斯卡尔(Kruskal)算法求无向网的最小生成树数据结构报告

kruskal算法求最小生成树

数据结构Kruskal算法求解最小生成树

Prim算法和Kruskal算法介绍

数据结构-kruskal算法求最小生成树实验报告