2020中考数学几何探究题解析
2020年中考数学冲刺专题:几何探究和证明(含答案)

2020中考数学冲刺专题:几何探究与证明(含答案)1.如图①,已知在正方形ABCD中,E为对角线BD上一点,过点E作EF⊥BD 交BC于点F,连接DF,G为DF中点,连接EG,CG.第1题图(1)求证:EG=CG;(2)将图①中△BEF绕点B逆时针旋转45°,则点F落在对角线BD上,如图②,取DF中点G,连接EG,CG.问EG和CG相等吗?若相等,请给出证明;若不相等,请说明理由;(3)将图①中△BEF绕B点旋转任意角度,如图③,再连接相应的线段,问线段EG和CG有何关系?(请直接写出答案)(1)证明:∵在正方形ABCD中,∴∠BCD=90°.∵EF⊥BD,∴∠FED=90°. ∵G为DF中点,∴EG=12DF,CG=12DF.∴EG=CG;(2)解:EG=CG.证明:如解图①,延长EF交CD于点H,连接GH,第1题解图①∵在正方形ABCD中,∴∠ABC=90°,BD平分∠ABC,∴∠EBF=12∠ABC=45°.∵EF⊥AB,∴∠FEB=90°,∴∠EFB=90°-∠EBF=45°,∴∠EBF=∠EFB,∴BE=FE.∵∠BCD=∠ABC=∠BEF=90°,∴四边形EBCH是矩形,∴HC=EB=EF,∠FHC=90°,∴∠FHD=180°-∠FHC=90°. ∵CD∥EB,∴∠HDF=∠EBF=45°,∴∠DFH=90°-∠HDF=45°,∴∠HDF=∠DFH,∴HD=FH.∵G为DF中点,∠DHF=45°,∴∠DHG=12∴∠GHC=180°-∠DHG=135°.∵∠EFG=180°-∠DFH=135°,∴∠GHC=∠EFG,∵在Rt△DHF中,G为DF中点,∴GH=12DF=GF,∴△EFG≌△CHG(SAS),∴EG=CG;(3)解:EG=CG,EG⊥CG.【解法提示】如解图③,理由如下:第1题解图②过点F作CD的平行线并延长CG交于点M,连接EM、EC,过点F作FN 垂直于AB于点N,∵G为FD中点,易证△CDG≌△MFG,得到CD=FM,又∵BE=EF,∴∠EBF=∠EFB,∴∠EFM=180°-45°-∠BFH=135°-∠BFH,∠EBC=∠EBF+∠FBH=45°+90°-∠BFH=135°-∠BFH,∴∠EFM=∠EBC,∴△EFM≌△EBC(SAS),∴∠FEM=∠BEC,EM=EC,∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形,∵G为CM中点,∴EG=CG,EG⊥CG.2. 如图,在△ABC中,∠ACB=90°,过点A作射线AP⊥AB,点D是线段AC上一动点(不与点A、C重合),连接BD,过点D作DE⊥BD,交射线AP于点E.(1)如图①,当∠BAC=45°时,则线段AE与线段CD之间的数量关系为________;(2)如图②,当∠BAC=30°时,猜想线段AE与线段CD之间的数量关系,并说明理由;(3)当∠BAC=α时,直接写出线段AE与线段CD的数量关系(用含α的三角函数表示).第2题图解:(1)AE=2CD;【解法提示】如解图①,在BC上取一点G,使AD=BG,连接DG,∵∠BAC=45°,∠ACB=90°,∴△ACB是等腰直角三角形,∴AC=BC,∴AC-CD=BC-BG,即CD=CG,∴△CDG是等腰直角三角形,∴DG=2CD,∠DGC=45°,∴∠DGB=135°,∵AP⊥AB,∴∠BAP=90°,∴∠DAE =90°+45°=135°,∴∠DAE =∠DGB ,∵DE ⊥DB ,∴∠EDB =90°,∴∠EDA +∠BDC =90°,∵∠BDC +∠DBC =90°,∴∠EDA =∠DBC ,∴△EAD ≌△DGB (ASA),∴AE =DG ,∴AE =2CD ;(2)猜想:AE =2CD ,理由是:如解图②,过点D 作DF ∥AB ,交BC 于点F ,则∠FDC =∠BAC =30°,AD CD =BF CF ,∴AD BF =CD CF ,∵AP ⊥AB ,DE ⊥BD ,∴∠BAP =∠BDE =90°,∵∠ADE +∠BDE +∠BDC =180°,∴∠ADE +∠BDC =90°,∵∠ACB =90°,∠FDC =30°,∴∠DBC +∠BDC =90°,CF =12DF ,∴∠ADE =∠DBC ,∵∠DAE =∠BAC +∠BAP ,∠BFD =∠FDC +∠ACB ,∴∠DAE =∠BFD ,∴△DAE ∽△BFD ,∴AD BF =AE FD ,∴CD CF =AE FD ,∴DF CF =AE CD ,∴AE CD =2,即AE =2CD ;(3)CD =AE ·sin α,【解法提示】如解图③,过点D 作DF ∥AB ,交BC 于点F ,则∠FDC =∠BAC=α,AD CD =BF CF ,∴AD BF =CD CF ,∵AP ⊥AB ,DE ⊥BD ,∴∠BAP =∠BDE =90°,∵∠ADE +∠BDE +∠BDC =180°,∴∠ADE +∠BDC =90°,∵∠ACB =90°,∠FDC =α,∴∠DBC +∠BDC =90°,sin ∠FDC =sin α=CF DF ,∴∠ADE =∠DBC ,∵∠DAE =∠BAC +∠BAP ,∠BFD =∠FDC +∠ACB ,∴∠DAE =∠BFD ,∴△DAE ∽△BFD ,∴AD BF =AE FD ,∴CD CF =AE FD ,∴CD AE =CF FD =sin α,∴CD =AE ·sin α.第2题解图3.已知在正方形ABCD 中,点E 在直线AB 上,点F 在直线BC 上,连接DE 、DF ,∠EDF =45°.(1)如图①,点E ,点F 分别在线段AB ,BC 上时,直接写出AE ,CF ,EF 的数量关系 ;(2)如图②,点E 在AB 的延长线上,点F 在BC 的延长线上,求AE ,CF ,EF 的数量关系;(3)如图③,在(2)的条件下,若AE=2AB=8,求EF的长.第3题图解:(1)EF=AE+CF.【解法提示】∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠C=∠ADC=∠DAB=90°,如解图①:延长BA,使AM=CF,且AD=CD,∠C=∠MAD,∴△AMD≌△CFD(SAS),∴∠ADM=∠CDF,DM=DF,∵∠EDF=45°,∴∠ADE+∠FDC=45°,∴∠ADM+∠ADE=45°=∠MDE,∴∠MDE=∠FDE,且DM=DF,DE=DE,∴△EDF≌△EDM(SAS),∴EF=EM,∵EM=AM+AE=AE+CF,∴EF=AE+CF;第3题解图①第3题解图②(2)如解图②:在AB上截取AM=CF,∵AD=CD,AM=CF,∠A=∠DCF=90°,∴△ADM≌△CDF(SAS),∴DM=DF,∠ADM=∠CDF,∵∠ADM+∠MDC=90°,∴∠CDF+∠MDC=90°,即∠MDF=90°,∵∠EDF=45°,∴∠EDF=∠MDE=45°,且DM=DF,DE=DE,∴△MDE≌△FDE(SAS),∴EF=EM,∵AE=AM+ME,∴AE=CF+EF;(3)∵AE=2AB=8,∴AB=BC=BE=4,∵AE=CF+EF,∴CF=8-EF,在Rt△BEF中,EF2=BE2+BF2,∴EF2=16+(4+8-EF)2,∴EF=203.4. 在菱形ABCD中,P为直线AD上的点,Q为直线CD上的点,分别连接PC,PQ,且PC=PQ.(1)若∠B=60°,点P在线段DA上,点Q在线段CD的延长线上,如图①,证明:DQ+PD=AB;(2)若∠B=60°,点P在线段DA的延长线上,点Q在线段CD上,如图②,猜想线段DQ,PD和AB之间有怎样的数量关系,并给予证明;(3)若∠B=120°,点P在线段DA上,点Q在线段CD的延长线上,如图③,猜想线段DQ,PD和AB之间有怎样的数量关系?并给予证明.第4题图(1)证明:如解图①,在CD上取CH=DQ,连接PH,∵PC=PQ,∴∠PCQ=∠PQC,∵CH=DQ,∴△PCH≌△PQD(SAS),∴PH=PD,∵四边形ABCD是菱形,∴CD=AB,∠PDC=∠B=60°,∴△PHD是等边三角形,∴PD=HD,∴PD+DQ=DH+CH=CD=AB;(2)解:猜想PD-DQ=AB.证明:如解图②,延长CA到点M,使得AM=AP,连接PM. ∵四边形ABCD是菱形,∠B=60°,∴△ABC,△ACD都是等边三角形,∴∠CAD=∠P AM=60°,∴△P AM是等边三角形,∴AM=PM,∠M=∠ACD=60°,∴PM∥CD,∴∠PCD+∠CPM=180°,∵PC=PQ,∴∠PCQ=∠PQC,∵∠PQC+∠PQD=180°,∴∠CPM=∠PQD,∴△PCM≌△QPD(AAS),∴CM=PD,PM=DQ=AM,∵CM=AC+AM=AB+DQ,∴PD-DQ=AB;(3)解:猜想:DQ-PD=AB.证明:如解图③,在DQ上截取DM=DP,连接PM. ∵∠B=∠ADC=120°,∴∠PDM=60°,∴△PDM是等边三角形,∴PD=PM,∠PMC=∠PDQ=60°,∵PC=PQ,∴∠PCM=∠Q,∴△PCM≌△PQD(AAS),∴CM=DQ,∴CD+DM=DQ,∴AB+PD=DQ,即DQ-PD=AB.第4题解图5.在△ABC 中,已知AB >AC ,AD 平分∠BAC 交BC 于点D ,点E 在DC 的延长线上,且DE BD =k ,过点E 作EF ∥AB 交AC 的延长线于点F .(1)如图①,当k =1时,求证:AF +EF =AB ;(2)如图②,当k =2时,直接写出线段AF 、EF 、AB 之间满足的数量关系:________;(3)如图③,当DE BD =k 时,请猜想线段AF 、EF 、AB 之间满足的数量关系(含k ),并证明你的结论.第5题图(1)证明:如解图①,延长AD 、EF 交于点G ,当k =1时,DE =BD ,∵EF ∥AB ,∴∠BAD =∠EGD ,在△ABD 与△GED 中,⎩⎪⎨⎪⎧∠BAD =∠EGD ∠BDA =∠EDG BD =ED,∴△ABD ≌GED (AAS),∴AB =GE ,又∵AD 平分∠BAC ,∴∠BAD =∠DAC ,∴∠FGD =∠DAC ,∴AF =GF ,∵GF +EF =GE ,∴AF +EF =AB;(2)解:AF+EF=2AB.【解法提示】如解图②,延长AD、EF交于点G,当k=2时,∵EF∥AB,∴∠BAD=∠EGD,又∵∠BDA=∠EDG,∴△ABD∽△GED,∴GEAB =DEDB=2,即GE=2AB,又∵AD平分∠BAC,∴∠BAD=∠DAC,∵∠FGD=∠DAC,∴AF=GF,∵GF+EF=GE,∴AF+EF=2AB;(3)解:猜想:AF+EF=kAB.证明:如解图③,延长AD、EF交于点G,当DEBD=k时,∵EF∥AB,∴∠BAD=∠EGD,又∵∠BDA=∠EDG,∴△ABD∽△GED,∴GE AB =DEBD=k,即GE=kAB,又∵AD平分∠BAC,∴∠BAD=∠DAC,∴∠FGD=∠DAC,∴AF=GF,∵GF+EF=GE,∴AF+EF=kAB.第5题解图类型二两条线段之间的数量关系与位置关系证明6. 如图,已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,连接BE,点F为BE的中点,连接CF,DF.(1)如图①,点D在AC上,延长DF,交BC于点G,请判断线段CF,DF 有怎样的数量关系和位置关系?并说明理由;(2)将图①中的△ADE绕点A旋转到图②位置,延长DF至G使GF=DF,DG与AB交于点O,连接BG,CG,DC,请判断(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.第6题图解:(1)DF=CF,DF⊥CF;理由:∵∠ADE=∠ACB=90°,∴DE∥BC,∴∠DEF=∠GBF,∠EDF=∠BGF.∵F为BE中点,∴EF=BF,∴△DEF≌△GBF(AAS),∴DE=GB,DF=GF.∵AD=DE,∴AD=GB,∵AC =BC ,∴AC -AD =BC -GB ,∴DC =GC .∵∠ACB =90°,∴△DCG 是等腰直角三角形,∵DF =GF ,∴DF =CF ,DF ⊥CF ;(2)(1)中的结论仍然成立,理由是:在△FDE 和△FGB 中,⎩⎪⎨⎪⎧DF =FG ∠DFE =∠GFB EF =FB,∴△FDE ≌△FGB (SAS),∴∠DEF =∠GBF ,DE =GB ,∴BG ∥DE ,如解图,延长DE 交BC 于点M ,∵DE ∥BG ,∴∠CBG =∠DMB ,∵∠ADE =∠ACB =90°,∴∠DAC +∠DMC =180°,∴∠DMB =∠DAC =∠CBG ,在△CAD 和△CBG 中,∵⎩⎪⎨⎪⎧AD =BG ∠DAC =∠GBC AC =BC,∴△CAD ≌△CBG (SAS),∴CD =CG ,∠DCA =∠GCB ,∴∠DCG =∠BCG +∠BCD =∠ACD +∠BCD =∠ACB =90°,∵DF =GF ,∴DF =CF ,DF ⊥CF .第6题解图7. 在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点CD不重合),连接AE,平移△ADE使点D移动到点C得到△BCF,过点F作FG⊥BD 于点G,连接AG,EG.第7题图(1)如图①,若点E在线段CD上,试猜想AG与EG的数量关系和位置关系;(2)如图②,若点E在线段CD的延长线上其余条件不变时,猜想(1)中的结论是否仍然成立,请你给出证明;(3)若点E 在线段DC 的延长线上且∠AGF =120°,正方形ABCD 的边长为2,直接写出DE 的长度.(1)解:AG =EG ,AG ⊥EG ,理由如下:由平移得EF =CD =AD ,∵BD 是正方形ABCD 的对角线,∴∠ADB =∠CDB =45°,∵FG ⊥BD ,∴∠DGF =90°,∴∠GFD +∠CDB =90°,∴∠DFG =45°,∴GD =GF ,在△AGD 和△EGF 中,⎩⎪⎨⎪⎧AD =EF ∠ADG =∠EFG DG =FG,∴△AGD ≌△EGF (SAS),∴AG =EG ,∠AGD =∠EGF ,∴∠AGE =∠AGD +∠DGE =∠EGF +∠DGE =90°,∴AG ⊥EG ;(2)解:(1)中结论仍然成立.证明:由平移得EF =CD =AD ,∵BD 是正方形ABCD 的对角线,∴∠ADB =∠CDB =45°,∵FG ⊥BD ,∴∠DGF =90°,∴∠GFD +∠CDB =90°,∴∠DFG =45°,∴GD =GF ,在△AGD 和△EGF 中,⎩⎪⎨⎪⎧AD =EF ∠ADG =∠EFG DG =FG,∴△AGD ≌△EGF (SAS),∴AG =EG ,∠AGD =∠EGF ,∴∠AGE=∠AGD-∠DGE=∠EGF-∠DGE=90°,∴AG⊥EG;(3)DE=2 3.【解法提示】同(1)可得,AG=EG,AG⊥EG,∴∠GEA=45°,∵∠AGF=120°,∴∠AGB=∠EGF=30°,又∵∠GFD=45°,∴∠CEG=∠EFG+∠EGF=75°,∴∠AED=∠CEG-∠GEA=30°,在Rt△ADE中,AD=2,∴DE=2 3.第7题解图8.在矩形ABCD中,已知AD>AB.在边AD上取点E,使AE=AB,连接CE,过点E作EF⊥CE,与直线AB交于点F.猜想:如图①,当点F在边AB上时,线段AF与DE的大小关系为________;探究:如图②,当点F 在边AB 的延长线上时,EF 与边BC 交于点G .判断线段AF 与DE 的大小关系,并加以证明;应用:如图②,若AB =2,AD =5,利用探究得到的结论,求线段BG 的长.第8题图解:猜想:AF =DE ;【解法提示】∵∠CEF =90°,∴∠AEF +∠CED =90°,∵∠AFE +∠AEF =90°,∴∠AFE =∠CED ,∠AEF =∠DCE ,∵AE =AB ,AB =CD ,∴AE =CD ,∴在△AEF和△DCE 中,⎩⎪⎨⎪⎧∠AEF =∠DCE ∠AFE =∠EDC AE =CD,∴△AEF ≌△DCE ,∴AF =DE ;探究:AF =DE ,证明:∵∠A =∠FEC =∠D =90°,∴∠AEF =∠DCE ,在△AEF 和△DCE 中,⎩⎪⎨⎪⎧∠A =∠D AE =CD∠AEF =∠DCE, ∴△AEF ≌△DCE (ASA),∴AF =DE .应用:∵△AEF ≌△DCE ,∴AE =CD =AB =2,AF =DE =3,FB =F A -AB =1,∵BG ∥AD ,∴BG AE =FB F A ,∴BG 2=13,∴BG =23.9 已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与点B 、C 重合),以AD 为边作等边△ADE (顶点A 、D 、E 按逆时针方向排列),连接CE .(1)如图①,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;第9题图(2)如图②,当点D在边BC的延长线上且其他条件不变时,结论AC=CE +CD是否成立?若不成立请写出AC、CE、CD之间存在的数量关系并说明理由;(3)如图③,当点D在边BC的反向延长线上且其他条件不变时,直接写出AC、CE、CD之间存在的数量关系.(1)证明:①∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,∴∠BAC-∠CAD=∠DAE-∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,⎩⎪⎨⎪⎧AB =AC ∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS),∴BD =CE ;②∵BC =BD +CD ,AC =BC ,BD =CE , ∴AC =CE +CD ;(2)解:AC =CE +CD 不成立,AC 、CE 、CD 之间存在的数量关系是AC =CE -CD . 理由:∵△ABC 和△ADE 都是等边三角形,∴AB =AC =BC ,AD =AE ,∠BAC =∠DAE =60°, ∴∠BAC +∠CAD =∠DAE +∠CAD ,即∠BAD =∠CAE ,在△ABD 和△ACE 中,⎩⎪⎨⎪⎧AB =AC ∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS),∴BD =CE ,∵BC =BD -CD ,∴BC =CE -CD ,∵AC =BC ,∴AC =CE -CD ;(3)解:AC 、CE 、CD 之间存在的数量关系是AC =CD -CE .【解法提示】∵△ABC 和△ADE 是等边三角形,∴AD =AE ,AB =AC ,∵∠DAE =∠BAC =60°,∴∠DAB =∠EAC ,∴在△ADB 和△AEC 中,⎩⎪⎨⎪⎧AD =AE ∠DAB =∠EAC AB =AC,∴△ADB ≌△AEC ,∵BD =CE ,∵CD =BD +BC ,∴BC =CD -CE ,∴AC =CD -CE .10. 已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B 、C 重合),以AD 为边作∠DAF =60°,在射线AF 上截取点F ,使AF =AD ,过点D 作DE ∥AF ,过点F 作EF ∥AD ,DE 、EF 交于点E ,连接CF ,(1)如图①,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)如图②,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图③,当点D在边CB的延长线上且其他条件不变时,并直接写出AC、CF、CD之间存在的数量关系.第10题图(1)证明:∵△ABC是等边三角形,∴AB=AC=BC,∠BAC=∠DAF=60°,∴∠BAC-∠DAC=∠DAF-∠DAC,∴∠BAD=∠CAF,∵在△BAD 和△CAF 中⎩⎪⎨⎪⎧AB =AC ∠BAD =∠CAF AD =AF,∴△BAD ≌△CAF (SAS),∴CF =BD ,∴CF +CD =BD +CD =BC =AC ,即①BD =CF ,②AC =CF +CD ;(2)解:AC =CF +CD 不成立,AC 、CF 、CD 之间存在的数量关系是AC =CF -CD ,理由是:由(1)知:AB =AC =BC ,AD =AF ,∠BAC =∠DAF =60°, ∴∠BAC +∠DAC =∠DAF +∠DAC ,即∠BAD =∠CAF ,∵在△BAD 和△CAF 中,⎩⎪⎨⎪⎧AB =AC ∠BAD =∠CAF AD =AF,∴△BAD ≌△CAF (SAS),∴BD =CF ,∴CF -CD =BD -CD =BC =AC ,即AC =CF -CD ;(3)解:AC =CD -CF .【解法提示】理由是:∵∠BAC =∠DAF =60°, ∴∠DAB =∠CAF ,∵在△BAD 和△CAF 中, ⎩⎪⎨⎪⎧AB =AC∠DAB =∠F AC AD =AF,∴△BAD ≌△CAF (SAS),∴CF =BD ,∴CD -CF =CD -BD =BC =AC ,即AC =CD -CF .。
最新九年级数学中考复习:几何探究题--线段问题含答案

(1)猜想线段AE和BG的关系,请直接写出你的结论;
(2)将正方形DEFG绕点D顺时针方向旋转一定角度后(旋转角大于0°,小于或等于360°),如图2,判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
问题探究:
(1)如图1,若 、 都是直角,把 绕点A逆时针旋转90°至 ,使AB与AD重合,则 ______度,线段BE、DF和EF之间的数量关系为______;
问题再探:
(2)如图2,若 、 都不是直角,但满足 ,线段BE、DF和EF之间的数量关系是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
(1)如图1,求∠BDC的度数(用含α的式子表示).
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接 .将直线l绕点A旋转,当线段BF的长取得最大值时,直接写出tan∠FBC的值..
17.(1)发现问题:如图1,在等腰直角三角形ABC中,∠ACB=90°,点F为BC上一点,以BF为边作正方形BFED,点E在AB上,若AC=BC=2,BF= ,则 =;
②当点D到直线BC的距离等于2时,DG的长为;
③当以点A、C、D、B为顶点的四边形时矩形时,点P在线段DG上,且∠CPG与∠A互余,连接CP,则直线CP与AB所夹锐角的正切值为.
11.有公共顶点A的正方形ABCD与正方形AEGF按如图1所示放置,点E,F分别在边AB和AD上,DE,M是BF的中点
【观察猜想】
(2)如图2,点D在AC左侧且在点A上方,连接BE交CD于点M,F为BE上一点,连接DF,过点F作FG∥AC交BC延长线于点G,连接GM,EG,AD.若∠EDF+∠EBG=∠DEB,GM=BM.求证:AD=EF.
2020中考数学专项训练4.代数与几何综合题(附解析)

代数与几何综合题类型一动点型探究题1.如图①,已知Rt △ABC 中,∠C =90°,AC =8cm ,BC =6cm ,点P 由B 出发沿BA 方向向点A 匀速运动,同时点Q 由A 出发沿AC 方向向点C 匀速运动,它们的速度均为2cm/s.以AQ 、PQ 为边作四边形AQPD ,连接DQ ,交AB 于点E .设运动的时间为t (单位:s)(0<t ≤4),解答下列问题:(1)用含有t 的代数式表示AE =____;(2)如图②,当t 为何值时,四边形AQPD 为菱形;(3)求运动过程中,四边形AQPD 的面积的最大值.第1题图解:(1)5-t ;【解法提示】∵在Rt △ABC 中,∠C =90°,AC =8cm ,BC =6cm ,∴由勾股定理得:AB =10cm ,∵点P 由B 出发沿BA 方向向点A 匀速运动,速度为2cm/s ,∴BP =2t cm ,∴AP =AB -BP =10-2t ,∵四边形AQPD 为平行四边形,∴AE =12AP =5-t .(2)如解图①,当四边形AQPD 是菱形时,DQ ⊥AP ,则cos ∠BAC =AE AQ =AC AB,即5-t 2t =810,解得t =2513,∴当t =2513时,四边形AQPD 是菱形;(3)如解图②,作PM ⊥AC 于M ,设平行四边形AQPD 的面积为S .∵PM ∥BC ,∴△APM ∽△ABC ,∴AP AB =PM BC ,即10-2t 10=PM 6,∴PM =65(5-t ),∴S =AQ ·PM =2t ·65(5-t )=-125t 2+12t=15255122+⎪⎭⎫ ⎝⎛--t (0<t ≤4),∵-125<0,∴当t =52时,S 有最大值,最大值为15cm 2.第1题解图2.已知,在Rt△ABC中,∠ACB=90°,BC=AC,AB=6,D是AB的中点,动点E从点D出发,在AB边上向左或右运动,以CE为边向左侧作正方形CEFG,直线BG,FE相交于点N(点E向左运动时如图①,点E向右运动时如图②).(1)在点E的运动过程中,直线BG与CD的位置关系为________;(2)设DE=x,NB=y,求y与x之间的函数关系式,并求出y的最大值;(3)如图②,当DE的长度为3时,求∠BFE的度数.第2题图解:(1)BG∥CD;【解法提示】∵四边形EFGC是正方形,∴CG=CE,∠GCE=∠GFE=∠FEC =90°,∵∠ACB=∠GCE=90°,∴∠GCB=∠ECA,∵GC=CE,CB=CA,∴△CAE≌△CBG.又∵∠ACB=90°,BC=AC,D是AB的中点,∴∠CBG=∠CAE=45°,∠BCD=45°,∴∠CBG=∠BCD,∴BG∥CD.(2)∵CB=CA,CD⊥AB,∠ACB=90°,∴CD=BD=AD=3,∠CBA=∠A=45°,易得△CAE≌△CBG,∴∠CBG =∠A =45°,∴∠GBA =∠GBC +∠CBA =90°.∵∠BEN +∠BNE =90°,∠BEN +∠CED =90°,∴∠BNE =∠CED ,∵∠EBN =∠CDE =90°,∴△NBE ∽△EDC ,∴BN ED =BE CD ,∴y x =3-x 3,∴y =-31(x -32)2+34,∵-31<0,∴x =32时,y 的最大值为34;(3)如解图,作FH ⊥AB 于点H .∵CB =CA ,BD =CD ,∠BCA =90°,∴CD ⊥AB ,CD =BD =AD =3,∴tan ∠DCE =DE CD =33,∴∠DCE =30°,∵四边形EFGC 是正方形,∴EF=EC,∵∠CDE=∠EHF=90°,易证∠DCE=∠HEF,∴△CDE≌△EHF,∴∠DCE=∠HEF=30°,FH=DE,CD=EH,∵CD=BD,∴BD=EH,∴BH=DE=FH,∴△BHF是等腰直角三角形,∴∠BFH=45°,∵∠EFH=90°-∠HEF=60°,∴∠BFE=∠BFH+∠EFH=105°.第2题解图3.如图,在直角梯形ABCD中,∠A=∠D=90°,AB=8cm,CD=10cm,AD =6cm,点E从点A出发,沿A→D→C方向运动,运动速度为2cm/s,点F 同时从点A出发,沿A→B方向运动,运动速度为1cm/s.设运动时间为t(s),△CEF的面积为S(cm2).(1)当0≤t≤3时,t=________,EF=10.(2)当0≤t≤3时(如图①),求S与t的函数关系式,并化为S=a(t-h)2+k的形式,指出当t为何值时,S有最大值,最大值为多少?(3)当3≤t≤8时(如图②),求S与t的函数关系式,并求出当t为何值时,S有最大值,最大值为多少?第3题图解:(1)2;【解法提示】根据题意知,AF=t,AE=2t,∵∠A=90°,∴AF2+AE2=EF2,即t2+(2t)2=(10)2,解得:t=2(负值舍去).(2)当0≤t≤3时,如解图①,过点C作CP⊥AB,交AB延长线于点P,第3题解图①∵∠A=∠D=90°,∴四边形APCD是矩形,则CP=AD=6cm,∵AB=8cm,AD=6cm,∴BF =(8-t )cm ,DE =(6-2t )cm ,则S =S 梯形ABCD -S △AEF -S △CBF -S △CDE=12×(8+10)×6-12×t ×2t -12×(8-t )×6-12×(6-2t )×10=-t 2+13t=-(t -132)2+1694,即S =-(t -132)2+1694,∵当t <132时,S 随t 的增大而增大,∴当t =3时,S 取得最大值,最大值为30;(3)当3≤t ≤8时,如解图②,过点F 作FQ ⊥CD 于点Q ,第3题解图②由∠A =∠D =90°,知四边形ADQF 是矩形,∴FQ =AD =6cm ,∵AD +DE =2t ,AD =6cm ,CD =10cm ,∴CE =(16-2t )cm ,则此时S =12×(16-2t )×6=48-6t ,∵-6<0,∴S 随t 的增大而减小,∴当t =3时,S 取得最大值,最大值为30cm 2.4.如图,在Rt △ABC 中,∠ACB =90°,AC =8,BC =6,CD ⊥AB 于点D .点P 从点D 出发,沿线段DC 向点C 运动,点Q 从点C 出发,沿线段CA 向点A 运动,两点同时出发,速度都为每秒1个单位长度,当点P 运动到C 时,两点都停止.设运动时间为t 秒.(1)①求线段CD 的长;②求证:△CBD ∽△ABC ;(2)设△CPQ 的面积为S ,求S 与t 之间的函数关系式,并求出S 的最大值;(3)是否存在某一时刻t ,使得△CPQ 为等腰三角形?若存在,请直接写出满足条件的t 的值;若不存在,请说明理由.(1)①解:∵∠ACB =90°,AC =8,BC =6,∴AB =10,∵CD ⊥AB ,∴S △ABC =12BC ·AC =12AB ·CD ,∴CD =BC ·AC AB =6×810=524,∴线段CD 的长为524;②证明:∵∠B =∠B ,∠CDB =∠BCA =90°,∴△CBD ∽△ABC ;(2)解:如解图②,过点P 作PH ⊥AC ,垂足为H ,由题可知DP =t ,CQ =t ,则CP =524-t ,∵∠ACB =∠CDB =90°,∴∠HCP =90°-∠DCB =∠B ,∵PH ⊥AC ,∴∠CHP =90°,∴∠CHP =∠ACB ,∴△CHP ∽△BCA ,∴PH AC =PC BA,∴PH 8=10524t -,∴PH =9625-45t ,∴S =12CQ ·PH =12t (9625-45t )=-25(t -125)2+288125,∵52-<0,∴当t =125时,S 最大=288125;(3)存在,t =125或14.455或2411.【解法提示】①若CQ =CP ,如解图①,则t =524-t .解得:t =125;②若PQ =PC ,如解图②所示.∵PQ =PC ,PH ⊥QC ,∴QH =CH =12QC =t 2.∵△CHP ∽△BCA .∴CH BC =CP AB .∴t 26=10524t -,解得t =14455;③若QC =QP ,如解图③,过点Q 作QE ⊥CP ,垂足为E ,同理可得:t =2411.综上所述:当t 为524秒或14455秒或2411秒时,△CPQ 为等腰三角形.第4题解图5.如图,在矩形ABCD 中,AB =6cm ,BC =8cm.如果点E 由点B 出发沿BC 方向向点C 匀速运动,同时点F 由点D 出发沿DA 方向向点A 匀速运动,它们的速度分别为2cm/s 和1cm/s.FQ ⊥BC ,分别交AC 、BC 于点P 和Q ,设运动时间为t (s)(0<t <4).(1)连接EF 、DQ ,若四边形EQDF 为平行四边形,求t 的值;(2)连接EP ,设△EPC 的面积为y cm 2,求y 与t 的函数关系式,并求y 的最大值;(3)若△EPQ 与△ADC 相似,请直接写出t 的值.解:(1)在矩形ABCD 中,∵AB =6cm ,BC =8cm ,∴CD =AB =6cm ,AD =BC =8cm ,∠BAD =∠ADC =∠DCB =∠B =90°,在Rt △ABC 中,由勾股定理得:AC =10,∵FQ ⊥BC ,∴∠FQC =90°,∴四边形CDFQ 是矩形,∴DF =QC ,FQ =DC =6cm ,由题意知,BE =2t ,QC =DF =t ,∴EQ =BC -BE -QC =8-3t ,∵四边形EQDF 为平行四边形,∴FD =EQ ,即t =8-3t ,解得t =2;(2)∵∠FQC =90°,∠B =90°,∴∠FQC =∠B ,∴PQ ∥AB ,∴△CPQ ∽△CAB ,∴PQ AB =QC BC,即PQ 6=t 8,∴PQ =34t ,∵S △EPC =12EC ·PQ ,∴y =12·(8-2t )·34t =-34t 2+3t =-34(t -2)2+3,即y =-34(t -2)2+3,∵a =-34<0,∴当t =2时,y 有最大值,y 的最大值为3;(3)t 的值为2或12857或12839.【解法提示】分两种情况讨论:若E 在FQ 左边,①当△EPQ ∽△ACD 时,可得:PQ CD =EQ AD ,即34t 6=8-3t 8,解得t =2;②当△EPQ ∽△CAD 时,可得:PQ AD =EQ CD ,即34t 8=8-3t 6,解得t =12857.若E 在FQ 右边,③当△EPQ ∽△ACD 时,可得:PQ CD =EQ AD ,即34t 6=3t -88,解得t =4(舍去);④当△EPQ ∽△CAD 时,可得:PQ AD =EQ CD ,即34t 8=3t -86,解得t =12839.综上所述,若△EPQ 与△ADC 相似,则t的值为:2或12857或12839.类型二动线型探究题6.如图,在△ABC 中,∠C =90°,∠A =60°,AC =2cm.长为1cm 的线段MN 在△ABC 的边AB 上沿AB 方向以1cm/s 的速度向点B 运动(运动前点M 与点A 重合).过M ,N 分别作AB 的垂线交直角边于P ,Q 两点,线段MN 运动的时间为t s.(1)若△AMP 的面积为y ,写出y 与t 的函数关系式(写出自变量t 的取值范围),并求出y 的最大值;(2)在线段MN 运动过程中,四边形MNQP 有可能成为矩形吗?若有可能,求出此时t 的值;若不可能,说明理由;(3)t 为何值时,以C ,P ,Q 为顶点的三角形与△ABC 相似?第6题图解:(1)当点P 在AC 上时,∵AM =t ,∴PM =AM ·tan60°=3t ,∴y =12t ·3t =32t 2(0<t ≤1),当t =1时,y 最大=32;当点P 在BC 上时,PM =BM ·tan 30°=33(4-t ),∴y =12t ·33(4-t )=-36t 2+233t =-36(t -2)2+233(1<t <3),当t =2s 时,y 最大=233,综上所述,y0<t ≤12+233t ,1<t <3,∴当t =2s 时,y 最大=233;(2)∵AC =2,∴AB =4,∴BN =AB -AM -MN =4-t -1=3-t .∴QN =BN ·tan 30°=33(3-t ),由题知,若要四边形MNQP 为矩形,需PM =QN ,且P ,Q 分别在AC ,BC 上,即3t =33(3-t ),∴t =34,∴当t =34s 时,四边形MNQP 为矩形.(3)由(2)知,当t =34s 时,四边形MNQP 为矩形,此时PQ ∥AB ,∴△PQC ∽△ABC ,除此之外,当∠CPQ =∠B =30°时,△QPC ∽△ABC ,此时CQ CP =tan 30°=33,∵AM AP =cos 60°=12,∴AP =2AM =2t ,∴CP =2-2t ,∵BN BQ =cos 30°=32,∴BQ =BN 32=233(3-t ),又BC =23,∴CQ =23-233(3-t )=23t 3,∴23t 32-2t =33,解得t =12,∴当t =12s 或34s 时,以C ,P ,Q 为顶点的三角形与△ABC 相似.7.如图,在△ABC 中,AB =AC =5cm,BC=6cm,AD是BC边上的高.点P由C出发沿CA方向匀速运动.速度为1cm/s.同时,直线EF由BC出发沿DA方向匀速运动,速度为1cm/s,EF//BC,并且EF分别交AB、AD、AC于点E,Q,F,连接PQ.若设运动时间为t(s)(0<t<4),解答下列问题:(1)当t为何值时,四边形BDFE是平行四边形?(2)设四边形QDCP的面积为y(cm2),求出y与t之间的函数关系式;(3)是否存在某一时刻t,使点Q在线段AP的垂直平分线上?若存在,求出此时点F到直线PQ的距离h;若不存在,请说明理由.第7题图解:(1)如解图①,连接DF,第7题解图①∵AB=AC=5,BC=6,AD⊥BC,∴BD=CD=3,在Rt△ABD中AD=52-32=4,∵EF //BC ,∴△AEF ∽△ABC ,∴EF BC =AQ AD,∴EF 6=4-t 4,∴EF =32(4-t ),∵EF //BD ,∴当EF =BD 时,四边形EFDB 是平行四边形,∴32(4-t )=3,∴t =2,∴当t =2s 时,四边形EFDB 是平行四边形;(2)如解图②,作PN ⊥AD 于N ,第7题解图②∵PN //DC ,∴PN DC =AP AC,∴PN 3=5-t 5,∴PN =35(5-t ),∴y =12DC ·AD -12AQ ·PN =6-12(4-t )·35(5-t )=6-(310t 2-2710t +6)=-310t 2+2710t (0<t <4);(3)存在.理由如下:如解图③,作QN ⊥AC 于N ,作FH ⊥PQ 于H .第7题解图③∵当QN 为AP 的垂直平分线时QA =QP ,QN ⊥AP ,∴AN =NP =12AP =12(5-t ),由题意cos ∠CAD =AD AC =AN AQ,∴12(5-t )4-t=45,∴t =73,∴当t =73s 时,点Q 在线段AP 的垂直平分线上.∵sin ∠FPH =FH PF =sin ∠CAD =35,∵PA =5-73=83,AF =AQ ÷45=2512,∴PF =712,∴FH =720.∴点F 到直线PQ 的距离h =720(cm).类型三动图型探究题8.如图①,在平行四边形ABCD 中,连接BD ,AD =6cm ,BD =8cm ,∠DBC =90°,现将△AEF 沿BD 的方向匀速平移,速度为2cm/s ,同时,点G 从点D 出发,沿DC 的方向匀速移动,速度为2cm/s.当△AEF 停止移动时,点G 也停止运动,连接AD ,AG ,EG ,过点E 作EH ⊥CD 于点H ,如图②所示,设△AEF 的移动时间为t (s)(0<t <4).(1)当t =1时,求EH 的长度;(2)若EG ⊥AG ,求证:EG 2=AE ·HG ;(3)设△AGD 的面积为y (cm 2),当t 为何值时,y 可取得最大值,并求y 的最大值.第8题图解:(1)∵四边形ABCD 是平行四边形,∴AD ∥BC ,又∠DBC =90°,∴∠ADB =90°,又AD =6cm ,BD =8cm ,由勾股定理得,AB =AD 2+BD 2=10cm ,当t =1时,EB =2cm ,则DE =8-2=6cm ,∵EH ⊥CD ,∠DBC =90°,∴△DEH ∽△DCB ,∴DE DC =EH BC ,即610=EH 6,解得EH =3.6cm ;(2)∵∠CDB =∠AEF ,∴AE ∥CD ,∴∠AEG =∠EGH ,又EG ⊥AG ,EH ⊥CD ,∴△AGE ∽△EHG ,∴EG HG =AE EG,∴EG 2=AE ·HG ;(3)由(1)得,△DEH ∽△DCB ,∴DE CD =EH BC ,即8-2t 10=EH 6,解得,EH =24-6t 5,∴y =12×DG ×EH =-6t 2+24t 5=-65t 2+245t =-65(t -2)2+245,∴当t =2时,y 的最大值为245.9.把Rt △ABC 和Rt △DEF 按如图①摆放(点C 与点E 重合),点B 、C (E )、F 在同一条直线上.已知:∠ACB =∠EDF =90°,∠DEF =45°,AC =8cm ,BC =6cm ,EF =10cm.如图②,△DEF 从图①的位置出发,以1cm/s 的速度沿CB 向△ABC 匀速移动,在△DEF 移动的同时,点P 从△ABC 的顶点A 出发,以2cm/s 的速度沿AB 向点B 匀速移动;当点P 移动到点B 时,点P 停止移动,△DEF 也随之停止移动.DE 与AC 交于点Q ,连接PQ ,设移动时间为t (s).(1)用含t 的代数式表示线段AP 和AQ 的长,并写出t 的取值范围;(2)连接PE ,设四边形APEQ 的面积为y (cm 2),试求出y 的最大值;(3)当t 为何值时,△APQ 是等腰三角形.第9题图解:(1)AP =2t ,∵∠EDF =90°,∠DEF =45°,∴∠CQE =45°=∠DEF ,∴CQ =CE =t ,∴AQ =8-t ,t 的取值范围是:0≤t ≤5;(2)如解图①,过点P 作PG ⊥x 轴于G ,可求得AB =10,sin B =45,PB =10-2t ,EB =6-t ,∴PG =PB sin B =45(10-2t ),∴y =S △ABC -S △PBE -S △QCE=12×6×8-12(6-t )×45(10-2t )-12t 2=-1310t 2+445t =-1310(t -4413)2+96865,∴当t =4413(s)(在0≤t ≤5内),y 有最大值,y 最大值=96865(cm 2);第9题解图(3)若AP =AQ ,则有2t =8-t 解得:t =83(s),若AP =PQ ,如解图②:过点P 作PH ⊥AC ,则AH =QH =8-t 2,PH ∥BC ,∴△APH ∽△ABC ,∴AP AH =AB AC ,即2t 8-t 2=108,解得:t =4021(s),若AQ =PQ ,如解图③:过点Q 作QI ⊥AB ,则AI =PI =12AP =t ,∵∠AIQ =∠ACB =90°∠A =∠A ,∴△AQI ∽△ABC ∴AI AQ =AC AB 即t 8-t =810,解得:t =329(s),综上所述,当t =83(s)或4021(s)或329(s)时,△APQ 是等腰三角形.10.如图①,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图①所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图②,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:(1)连接CG,求证:△CGH∽△AGK;(2)连接HK,求证:KH∥EF;(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.第10题图(1)证明:在Rt△ABC中,CG⊥AB,∠B=30°,∴∠GCH=∠GAK=60°,又∠CGH=∠AGK=α,∴△CGH∽△AGK;(2)证明:由(1)得△CGH∽△AGK,∴GH GK =CG AG.在Rt △ACG 中,tan ∠CAG =CG AG =3,∴GH GK = 3.在Rt △KHG 中,tan ∠GKH =GH GK =3,∴∠GKH =60°.∵在Rt △EFG 中,∠F =30°,∴∠E =60°,∴∠GKH =∠E ,∴KH ∥EF ;(3)解:由(1)得△CGH ∽△AGK ,∴CH AK =CG AG .由(2)知CG AG =3,∴CH AK = 3.∴CH =3AK =3x ,在Rt △ABC 中,∠B =30°,∴AC =12AB =2,∴CK =AC -AK =2-x ,∴y =12CK ·CH =12(2-x )·3x =-32x 2+3x ,又y =-32x 2+3x =-32(x -1)2+32,(0<x <2)∴当x =1时,y 有最大值为32.。
中考数学题型八 几何图形探究题

例2 (2020·东营)如图①,在等腰三角形ABC中,∠A=120°,AB=AC,
点D,E分别在边AB,AC上,AD=AE,连接BE,点M,N,P分别为DE,
BE,BC的中点.
(1)观察猜想 图①中,线段NM,NP的数量关系是___N__M_=__N__P____,∠MNP的大小为 ____6_0_°___;
2. (2020·泰安)小明将两个直角三角形纸片如图①那样拼放在同一平面上, 抽象出如图②的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC= ∠CDE=90°,连接BD,AB=BD,点F是线段CE上一点.
探究发现: (1)当点F为线段CE的中点时,连接DF(如图②),小明经过探究,得到结 论:BD⊥DF.你认为此结论是否成立?_是___.(填“是”或“否” )
又∵AB=BC,∴∠ACB=∠CAB=∠FAE, ∵EF∥BC,∴∠F=∠FCB, ∴EF=AE,∴AE=FE=FM+ME=CF+BC;
(3)解:CF=18或CF=6, 当DE=2AE=6时,题图①中,由(1)得:AE=3,BC=AB=BD+DE +AE=15, ∴CF=AE+BC=3+15=18; 题图②中,由(2)得:AE=AD=3,BC=AB=BD+AD=9,∴CF= BC-AE=9-3=6; 题图③中,DE小于AE,故不存在.故答案为18或6.
拓展创新:解:AD 的长为 5 .[解法提示]如解图②,过点 A 作 AB 的垂线, 过点 D 作 AD 的垂线,两垂线交于点 M,连接 BM,∵∠BAD=30°,∴∠DAM =60°,∴∠AMD=30°,
∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴MBDD
=DDCA ,又∠BDC=∠ADM,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM
2020年九年级中考数学 压轴专题 几何探究题(含答案)

2020中考数学 压轴专题 几何探究题(含答案)1. 我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.第1题图(1)概念理解:请你根据定义举一个“等邻角四边形的”例子;(2)问题探究:如图①,在等邻角四边形ABCD 中,∠DAB =∠ABC ,AD 、BC 的中垂线恰好交于AB 边上一点P ,连接AC 、BD ,试探究AC 与BD 的数量关系,并说明理由.(3)应用拓展:如图②,在Rt △ABC 与Rt △ABD 中,∠C =∠D =90°,BC =BD =3,AB =5,将Rt △ABD 绕着点A 顺时针旋转角α(0°)得到Rt △AB ′D ′(如图③),当凸四边形AD ′BC 为“等邻角四边形”时,求出它的面积.解:(1)矩形;(答案不唯一)(2)AC =BD ;如解图①所示,连接PD 、PC , ∵PE 是AD 的垂直平分线,PF 是BC 的垂直平分线, ∴P A =PD ,PB =PC ,∴∠P AD =∠PDA ,∠PBC =∠PCB ,∴∠DPB =180°-∠DP A =∠P AD +∠PDA =2∠P AD ,同理可得∠APC =2∠PBC , ∵∠DAB =∠ABC ,即∠P AD =∠PBC ,∴∠APC =∠DPB ,在△APC 和△DPB 中,⎩⎪⎨⎪⎧PA =PD ∠APC =∠DPB PB =PC,△APC ≌△DPB (SAS), ∴ AC =BD .第1题解图①(3)①当∠AD ′B =∠D ′BC 时,如解图②所示,延长AD ′交CB 的延长线于点E ,过点D ′作DF ⊥CE 于点F , ∠ED ′B =∠EBD ′, ∴EB =ED ′,∵∠C =∠EFD ′,∠EAC =∠ED ′F , ∴△ED ′F ∽△EAC , 则D ′F AC =ED ′AE, 设EB =ED ′=x ,由勾股定理可知,在Rt △ACB 中,AC =AB 2-BC 2=52-32=4,则AD ′=4,CE =3+x ,AE =4+x ,在Rt △ACE 中,AC 2+CE 2=AE 2,即42+(3+x )2=(4+x )2, 整理得:2x -9=0,解得x =92,EB =ED ′=92,∴AE =172,∴D ′F 4=92112,∴D ′F =3617,S 四边形AD ′BC =S △ACE -S △D ′BE =12AC ·CE -12D ′F ·BE =12×4×(3+92)-12×92×3617=15-8117=17417;第1题解图②②当∠D ′BC =90°时,如解图③所示,过点D ′作D ′E ⊥AC ,交AC 于点E , ∴四边形ECBD ′是矩形,∴ED ′=BC =3,在Rt △AED ′中,根据勾股定理得AE =AD′2-ED′2=42-32=7,∵S 四边形AD ′BC =S △AED ′+S 矩形ECBD ′=12AE ·ED ′+EC ·BC =372+12-37=12-372.综上所述,当凸四边形AD 为等邻角四边形时,它的面积为17417或12-372.第1题解图③2. (1)发现 如图①,点A 为线段BC 外一动点,且BC =a ,AB =b .填空:当点A 位于________时,线段AC 的长取得最大值,且最大值为________(用含有a ,b 的式子表示); (2)应用 点A 为线段BC 外一动点,且BC =3,AB =1.如图②所示,分别以AB ,AC 为边作等边三角形ABD 和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值;(3)拓展如图③,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且P A=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.第2题图(1)解:CB的延长线上,a+b;【解法提示】∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.(2)解:①DC=BE,理由如下:∵△ABD和△ACE均为等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,∴△CAD≌△EAB(SAS),∴DC=BE;②BE长的最大值是4;【解法提示】∵线段BE长的最大值=线段CD的最大值,由(1)知,当线段CD的长取得最大值时,点D在CB 的延长线上,∴CD长的最大值为BD+BC=AB+BC=4.(3)解:AM长的最大值是3+22,点P的坐标是(2-2,2).【解法提示】如解图①,构造△BNP≌△MAP,则NB=AM,P A=PN,∴∠APN=90°,由(1)得出当点N在BA的延长线上时,NB有最大值(如解图②),可得AN=22,∴AM=NB=3+22,过点P作PE⊥x轴于点E,PE=AE=2,∴点P的坐标是(2-2,2).第2题解图3.如图,△ABC是边长为4 cm的等边三角形,边AB在射线OM上,且OA=6 cm.点D从O点出发,沿OM的方向以1 cm/s的速度运动.当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.(1)求证:△CDE是等边三角形;(2)当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;(3)当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.第3题图(1)证明:∵△BCE是由△ACD逆时针旋转60°得到的,∴CD=CE,∠DCE=60°,∴△CDE是等边三角形;(2)解:存在.理由如下:∵△BCE是由△ACD逆时针旋转60°得到的,∴AD=BE,又∵△CDE是等边三角形,∴DE=CD,∴C△BDE=BD+BE+DE=BD+AD+CD=AB+CD,∵AB=4为定值,∴当CD最小,即CD⊥AB时,△BDE的周长最小,∵△ABC是等边三角形,∴当CD最小,即CD⊥AB时,易得CD=23,∴△BDE的最小周长为23+4;(3)解:存在.理由如下:如解图,过点C作CF⊥OM于点F,则CF=23,∴BD=||t-6,t-10,BE=AD=||DE=CD=CF2+DF2=12+(t-8)2,①当∠DEB=90°时,BD2=BE2+DE2,即(t-10)2=(t-6)2+12+(t-8)2,第3题解图解得t1=2,t2=6(不合题意,舍去);②当∠EBD=90°时,DE2=BD2+BE2,即12+(t-8)2=(t-10)2+(t-6)2,解得t3=6,t4=10(两者均不合题意,舍去);③当∠BDE=90°时,BE2=BD2+DE2,即(t-6)2=(t-10)2+12+(t-8)2,解得t5=14,t6=10(舍去).综上所述,存在以D、E、B为顶点的三角形是直角三角形,此时t=2或14.4.如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图①),△ABD不动.(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图②),证明:MB=MC;(2)若将图①中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图③),判断并直接写出MB、MC的数量关系;(3)在(2)中,若∠CAE的大小改变(图④),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.第4题图(1)证明:如解图①,连接AM,由已知得△ABD≌△ACE,第4题解图①∴ AD =AE , AB =AC , ∠BAD =∠CAE , 又∵MD =ME ,∴∠MAD =∠MAE (三线合一), ∴∠MAD -∠BAD =∠MAE -∠CAE , 即∠BAM =∠CAM , 在△ABM 和△ACM 中, ⎩⎪⎨⎪⎧AB =AC ∠BAM =∠CAM AM =AM, ∴△ABM ≌△ACM (SAS ), ∴MB =MC ;第4题解图②(2)解:MB =MC ;【解法提示】如解图②,延长DB 、AE 相交于点E ′,延长EC 交AD 于点F , ∴BD =BE ′,CE =CF ,又∵M 是ED 的中点,B 是DE ′的中点, ∴MB ∥AE ′,∴∠MBC =∠CAE ,同理:MC ∥AD , ∴∠BCM =∠BAD , 又∵∠BAD =∠CAE , ∴∠MBC =∠BCM , ∴MB =MC .(3)解:MB =MC 还成立.理由如下: 如解图③,延长BM 交CE 于点F ,第4题解图③∵CE ∥BD , ∴∠MDB =∠MEF , ∠MBD =∠MFE , 又∵M 是DE 的中点, ∴MD =ME ,在△MDB 和△MEF 中, ⎩⎪⎨⎪⎧∠MBD =∠MFE ∠MDB =∠MEF MD =ME, ∴△MDB ≌△MEF (AAS), ∴MB =MF =12BF ,又∵∠ACE =90°,∴∠BCF =90°, ∴MC =12BF ,∴MB=MC.5.在正方形ABCD中,点E是对角线AC上的动点(与点A,C不重合),连接BE.(1)将射线BE绕点B顺时针方向旋转45°,交直线AC于点F.①依题意补全图①;②小研通过观察、实验,发现线段AE,FC,EF存在以下数量关系:AE与FC的平方和等于EF的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:想法1:将线段BF绕点B逆时针旋转90°,得到线段BM,要证AE,FC,EF的数量关系,只需证AE,AM,EM的数量关系.想法2:将△ABE沿BE翻折,得到△NBE,要证AE,FC,EF的关系,只需证EN,FN,EF的关系.…请你参考上面的想法,用等式表示线段AE,FC,EF的数量关系并证明;(一种方法即可)(2)如图②,若将直线..AC于点F.小研完成作图后,发现直线AC上存在三..BE绕点B顺时针旋转135°,交直线条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.第5题图解:(1)①补全图形,如解图①;图① 图②第5题解图②AE 2+FC 2=EF 2;证明:如解图②,过B 作MB ⊥BF 于点B ,使BM =BF ,连接AM 、EM ,∵四边形ABCD 是正方形,∴∠ABC =90°,∠1=∠2=45°,AB =BC ,∵∠3=45°,∴∠MBE =∠3=45°,在△MBE 和△FBE 中,⎩⎪⎨⎪⎧BM =BF ∠MBE =∠3BE =BE,∴△MBE ≌△FBE (SAS ),∴EM =EF ,∵∠4=90°-∠ABF ,∠5=90°-∠ABF ,∴∠4=∠5,在△AMB 和△CFB 中,⎩⎪⎨⎪⎧BM =BF ∠4=∠5AB =CB,∴△AMB ≌△CFB (SAS),∴AM =FC ,∠6=∠2=45°,∴∠MAE =∠6+∠1=90°,在Rt △MAE 中,AE 2+AM 2=EM 2,∴AE 2+FC 2=EF 2;(2)AF 2+EC 2=EF 2.【解法提示】如解图③,过B 作MB ⊥BE ,使BM =BE ,连接ME 、MF 、AM ,∵直线BE 绕点B 顺时针旋转135°,交直线AC 于点F ,∴∠FBE =45°,∴∠MBF =90°-45°=45°,∴∠FBE =∠MBF ,在△MBF 和△EBF 中,⎩⎪⎨⎪⎧BM =BE ∠MBF =∠FBE ,BF =BF∴△MBF ≌△EBF (SAS),∴MF =EF ,∵∠MBA =90°-∠ABE ,∠EBC =90°-∠ABE ,∴∠MBA =∠EBC ,在△AMB 和△CBE 中,⎩⎪⎨⎪⎧BM =BE ∠MBA =∠EBC AB =CB,∴△AMB ≌△CEB (SAS ),∴AM =EC ,∠BAM =∠BCE =45°,∴∠MAE =∠BAM +∠BAC =90°,∴∠MAF =90°,在Rt △MAF 中,AF 2+AM 2=MF 2,∴AF 2+EC 2=EF 2.第5题解图③6.在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.(1)依题意补全图形;(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;想法3:由等腰三角形三线合一,可得AD是∠BAC的平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF;…请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.解:(1)补全图形,如解图①;第6题解图(2)想法1:证明:如解图②,过点D作DG∥AB,交AC于点G,∵点D是BC边的中点,∴DG=12AB,∴△CDG是等边三角形,∴∠EDB+∠EDG=120°,∵∠FDG+∠EDG=120°,∴∠EDB=∠FDG,∵BD=DG,∠B=∠FGD=60°,∴△BDE≌△GDF,∴DE=DF;想法2:证明:如解图③,连接AD,作点E关于线段AD的对称点P,点P在边AC上,∵点D是BC边的中点,AB=AC,∴直线AD是△ABC的对称轴,∴△ADE≌△ADP,∴DE=DP,∠AED=∠APD,∵∠BAC+∠EDF=180°,∴∠AED+∠AFD=180°,∵∠APD+∠DPF=180°,∴∠AFD=∠DPF,∴DP=DF,∴DE=DF;第6题解图想法3:证明:如解图④,连接AD,过D作DM⊥AB于点M,DN⊥AC于点N,∵点D是BC边的中点,∴AD平分∠BAC,∵DM⊥AB于点M,DN⊥AC于点N,∴DM=DN,∵∠A=60°,∴∠MDE+∠EDN=120°,∵∠FDN+∠EDN=120°,∴∠MDE =∠FDN ,∴Rt △MDE ≌Rt △NDF ,∴DE =DF ;(3)当点F 在AC 边上时,BE +CF =12AB ;当点F 在AC 的延长线上时,BE -CF =12AB . 【解法提示】①当点F 在AC 边上时,如解图⑤,过点D 作DM ⊥AB 于点M ,作DN ⊥AC 于点N , ∵∠B =∠C =60°,BD =DC ,∠BDM =∠CDN =30°,∴△BDM ≌△CDN ,∴BM =CN ,DM =DN ,又∵∠EDF =120°=∠MDN ,∴∠EDM =∠NDF ,又∵∠EMD =∠FND =90°,∴△EDM ≌△FDN ,∴ME =NF ,∴BE +CF =BM +EM +NC -FN =2BM =BD =12AB ;图⑤ 图⑥第6题解图②当点F 在AC 的延长线上时,如解图⑥,过D 作DM ⊥AB 于点M ,作DN ⊥AC 于点N ,∵∠B =∠DCN =60°,BD =DC ,∠BDM =∠CDN =30°,∴△BDM ≌△CDN ,∴BM =CN ,DM =DN ,又∵∠EDF =120°=∠MDN ,∴∠EDM =∠NDF ,又∵∠EMD =∠FND =90°,∴△EDM ≌△FDN ,∴ME =NF ,∴BE -CF =BM +EM -(FN -CN )=2BM =BD =12AB ,综上所述,当点F 在AC 边上时,BE +CF =12AB ;当点F 在AC 的延长线上时,BE -CF =12AB . 7. 我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图①,在△ABC 中,AO 是BC 边上的中线,AB 与AC 的“极化值”就等于AO 2-BO 2的值,可记为ABAC =AO 2-BO 2.第7题图(1)在图①中,若∠BAC =90°,AB =8,AC =6,AO 是BC 边上的中线,则ABAC=________,OCOA=________;(2)如图②,在△ABC中,AB=AC=4,∠BAC=120°,求AB AC、BA BC的值;(3)如图③,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=13A A O,已知ABAC=14,BN BA=10,求△ABC的面积.解:(1)0 ,7;【解法提示】∵∠BAC=90°,AB=8,AC=6,∴BC=AB2+AC2=10,在Rt△ABC中,AO是BC边上的中线,∴AO=BO=5,∴AB AC=AO2-BO2=0,如解图①,取AC的中点D ,连接OD ,则OD ∥AB ,OD =12AB =4,CD =12AC =3,∴OC OA =OD 2-CD 2=16-9=7.第7题解图(2)如解图②,作底边BC 上的中线AE ,由题意可知AE 是∠BAC 的平分线、BC 边上的高. ∵AB =ΑC =4,∠BAC =120°,∴在Rt △ABE 中,∠AEB =90°,∠ABC =30°,∴AE =12×4=2,BE =32×4=23, ∴AB AC =AE 2-BE 2=22-(23)2=-8.过点B作AC边上中线BM,过点M作MN⊥BC于点N,∴AM=CM=1×4=2.2在Rt△MNC中,∠MNC=90°,∠C=30°,×2=1,CN=22-12= 3.∴MN=12∵BC=2BE=43,∴BN=BC-CN=43-3=33,BM2=12+(33)2=28.∴BA BC=BM2-AM2=28-22=24;(3)如解图③,过点B作△ABN的AN边上中线BM,∵在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=13AO,第7题解图③∴AM=MN=NO,AO⊥BC,即AO=3NO.∵AB A AC =14,BNBA =10,∴ AO 2-BO 2=14,即(3ON )2-BO 2=9ON 2-BO 2=14,①∵BM 2-MN 2=OM 2+BO 2-MN 2=(2ON )2+BO 2-ON 2=3ON 2+BO 2=10,②由①、②得⎩⎪⎨⎪⎧9ON 2-BO 2=143ON 2+BO 2=10, ∴ON 2=2,即ON =2,BO =2,∴BC =4,AO =32,∴S △ABC =12BC ·AO =12×4×32=6 2. 8. 问题发现:如图①,在△ABC 中,∠ACB =90°,分别以AC 、BC 为边向外侧作正方形ACDE 和正方形BCFG .(1)△ABC和△DCF面积的关系是________;(请在横线上填写“相等”或“不相等”)(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图②给出证明;若不成立,请说明理由;(3)解决问题:如图③,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CD JI、正方形DA LK;运用(2)中的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.第8题图解:(1)相等;【解法提示】∵四边形ACDE和四边形BCFG是正方形,∴AC=DC,BC=FC,∠ACD=∠BCF=90°,∵∠ACB=90°,∴∠DCF=90°=∠ACB.∴12AC·BC=12DC·CF,∴S△ABC=S△DFC.(2)成立.理由如下:如解图,延长BC到点P,过点A作AP⊥BP于点P,过点D作DQ⊥FC于点Q,∴∠APC=∠DQC=90°.∵四边形ACDE,四边形BCFG均为正方形,∴AC=CD,BC=CF,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ.第8题解图在△APC 和△DQC 中,⎩⎪⎨⎪⎧∠APC =∠DQC ∠ACP =∠DCQ AC =DC,∴△APC ≌△DQC (AAS),∴AP =DQ .又∵S △ABC =12BC ·AP ,S △DFC =12FC ·DQ , ∴S △ABC =S △DFC ;(3)图中阴影部分的面积和有最大值.理由如下:由(2)中的结论可知:S △K D J =S △ADC ,S △FBG =S △ABC ,S △AE L =S △ABD ,S △CH I =S △BDC ,∴S 阴影=S △K DJ +S △FBG +S △AEL +S △CHI =S △ADC +S △ABC +S △ABD +S △BDC =2S 四边形ABCD .设AC =m ,则BD =10-m ,∵AC ⊥BD ,∴S 四边形ABCD =12AC ·BD =12m ·(10-m )=-12m 2+5m =-12(m -5)2+252. ∵-12<0,∴S四边形ABCD有最大值,最大值为252.=25,∴S阴影=2×252∴阴影部分的面积和有最大值,最大值为25.9.问题背景如图①,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE ≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.类比探究如图②,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F 三点不重合).(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)△DEF是否为正三角形?请说明理由;(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.第9题图解:(1)△ABD≌△BCE≌△CAF.证明:如解图①,第9题解图①∵△ABC为正三角形,∴∠CAB=∠ABC=∠BCA=60°,AB=BC.∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,而∠2=∠3,∴∠ABD=∠BCE.又∵∠1=∠2,∴△ABD≌△BCE(ASA);(2)△DEF是正三角形.理由如下:∵△ABD≌△BCE≌△CAF,∴∠ADB=∠BEC=∠CF A,∴∠FDE=∠DEF=∠EFD,∴△DEF是正三角形;(3)如解图②,作AG⊥BD,交BD延长线于点G,第9题解图②由△DEF 是正三角形得到∠ADG =60°,(或者∠ADG =∠1+∠ABD =∠2+∠ABD =60°.)∴在Rt △ADG 中,DG =12b ,AG =32b . ∴在Rt △ABG 中,c 2=(a +12b )2+(32b )2, ∴c 2=a 2+ab +b 2.10. 在△ABC 中,∠ACB =90°,AC =3,BC =4,将△ABC 绕顶点C 顺时针旋转,旋转角为θ(0°<θ<180°),得到△A ′B ′C .(1)设△ACA ′和△BCB ′的面积分别为S 1和S 2.若θ=40°,请求出S 1S 2的值; (2)如图①,设A ′B ′与CB 相交于点D ,且AB ∥CB ′:①求证:CD =B ′D ;②求BD 的长;(3)如图②,设AC 中点为点M ,A ′B ′中点为点N ,连接MN ,MN 是否存在最大值,若存在,求出MN 的值,判断出此时AA ′与BB ′的位置关系;若不存在,请说明理由.第10题图(1)解: ∵△ABC 绕顶点C 顺时针旋转40°,得到△A ′B ′C , ∴CA =CA ′,CB =CB ′,∠ACA ′=∠BCB ′=θ,∴△ACA ′∽△BCB ′,∴S △ACA ′∶S △BCB ′=AC 2∶BC 2=32∶42=9∶16;∴S 1S 2=916; (2)①证明:∵AB ∥B ′C ,∴∠ABC =∠BCB ′;由旋转的性质得∠ABC =∠DB ′C ,即∠BCB ′ =∠DB ′C ;∴CD =B ′D ;②解:根据勾股定理可得A ′B ′=AB =5,据题意可得∠BCB ′ +∠BCA ′ =∠DB ′C +∠CA ′B ′=90°,∴∠BCA ′ =∠CA ′B ′,∴CD =A ′D =B ′D =12A ′B ′=52, ∴ BD =BC -CD =32; (3)解:存在,∵∠A ′CB ′=90°,点M 为AC 的中点,∴CM =12AC =32, ∵△A ′B ′C 是由△ABC 绕顶点C 顺时针旋转所得,∴A ′B ′=AB =5,第10题解图如解图,连接CN ,可得MN ≤CM +CN ,∴只有当点N 在MC 的延长线上时,MN =CM +CN ,此时MN 最大,∵点N 为A ′B ′的中点,∴CN =12 A ′B ′=52,MN =CM +CN =4, 即MN 的最大值为4.此时AA ′⊥BB ′.。
中考数学 精讲篇 中考压轴题重难点突破六 几何综合探究题 类型二

∴∠AEB=90°, ∵AE2+BE2=AB2,且 DE=2,AD=BE, ∴(AD+2)2+AD2=(2 5)2+(2 5)2. 解得 AD= 19-1 或 AD=- 19-1(舍去); 如解图 3,A,D,E 三点在同一直线上, 且点 D 在 AE 的延长线上, ∵∠BCF=∠ACE=90°-∠ACF,BC=AC,CF=CE, ∴△BCF≌△ACE(SAS),∴∠BFC=∠AEC,
(2)证明:在等边△ABC 中,AC=BC,∠ACB=60°, 由旋转可得 CP=CQ,∠PCQ=60°, ∴∠ACB=∠PCQ, ∴∠ACP+∠PCB=∠BCQ+∠PCB,即∠ACP=∠BCQ,
∴△ACP≌△BCQ(SAS), ∴AP=BQ,∠CBQ=∠CAP=90°, ∴BQ=AP=AC=BC,
②如图 2,过 A 点作 AM⊥GD,垂足为 M,交 FE 于点 N, ∵四边形 DEFG 是正方形, ∴DE=GD=GF=EF=2,由①得△AGD≌△CED, ∴AG=CE,AD=CD.
又∵CE=CD,∴AG=AD=CD=4, 1
∵AM⊥GD,∴GM=2GD=1,
又∵∠FGD=∠F=90°, ∴四边形 GMNF 是矩形, ∴MN=GF=2,在 Rt△AGM 中,AM= AG2-GM2= 42-12= 15,
∵∠CFE=∠CED=45°, ∴∠BFC+∠CFE=∠AEC+∠CED=180°, ∴点 B,F,E 在同一条直线上. ∵AC=BC,∠ACD=∠BCE=90°+∠ACE,CD=CE,∴△ACD≌△BCE(SAS), ∴AD=BE,∵AE2+BE2=AB2, ∴(AD-2)2+AD2=(2 5)2+(2 5)2. 解得 AD= 19+1 或 AD=- 19+1(舍去). 综上所述,AD 的长为 19-1 或 19+1.
2020年中考数学一轮复习题型09几何类比、拓展、探究题(原卷版)

题型09 几何类比、拓展、探究题一、解答题1.如图1,ABC ∆(12AC BC AC <<)绕点C 顺时针旋转得DEC ∆,射线AB 交射线DE 于点F . (1)AFD ∠与BCE ∠的关系是 ;(2)如图2,当旋转角为60°时,点D ,点B 与线段AC 的中点O 恰好在同一直线上,延长DO 至点G ,使OG OD =,连接GC .①AFD ∠与GCD ∠的关系是 ,请说明理由;②如图3,连接,AE BE ,若45ACB ∠=o ,4CE =,求线段AE 的长度.2.(问题)如图1,在Rt ABC V 中,90,ACB AC BC ∠=︒=,过点C 作直线l 平行于AB .90EDF ∠=︒,点D 在直线l 上移动,角的一边DE 始终经过点B ,另一边DF 与AC 交于点P ,研究DP 和DB 的数量关系.(探究发现)(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D 移动到使点P 与点C 重合时,通过推理就可以得到DP DB =,请写出证明过程;(数学思考)(2)如图3,若点P 是AC 上的任意一点(不含端点A C 、),受(1)的启发,这个小组过点D 作DG CD ⊥交BC 于点G ,就可以证明DP DB =,请完成证明过程;(拓展引申)(3)如图4,在(1)的条件下,M 是AB 边上任意一点(不含端点A B 、),N 是射线BD 上一点,且AM BN =,连接MN 与BC 交于点Q ,这个数学兴趣小组经过多次取M 点反复进行实验,发现点M 在某一位置时BQ 的值最大.若4AC BC ==,请你直接写出BQ 的最大值.3.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.(1)温故:如图 1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,若BC=6 ,AD=4,求正方形PQMN的边长.(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图 2,任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结B N′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”.(3)推理:证明图2 中的四边形PQMN是正方形.(4)拓展:在(2)的条件下,于波利业线B N上截取NE=NM,连结EQ,EM(如图 3).当tan∠NBM=34时,猜想∠QEM的度数,并尝试证明.请帮助小波解决“温故”、“推理”、“拓展”中的问题.4.问题提出:如图,图①是一张由三个边长为1 的小正方形组成的“L”形纸片,图②是一张a×b的方格纸(a×b的方格纸指边长分别为a,b的矩形,被分成a×b个边长为 1 的小正方形,其中a≥2 ,b≥2,且a,b为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.探究一:把图①放置在2× 2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图③,对于2×2的方格纸,要用图①盖住其中的三个小正方形,显然有4 种不同的放置方法.探究二:把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图④,在3×2的方格纸中,共可以找到2 个位置不同的2 ×2方格,依据探究一的结论可知,把图①放置在3×2 的方格纸中,使它恰好盖住其中的三个小正方形,共有2 ×4=8种不同的放置方法.探究三:把图①放置在a ×2 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑤,在a ×2 的方格纸中,共可以找到______个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a× 2 的方格纸中,使它恰好盖住其中的三个小正方形,共有______种不同的放置方法.探究四:把图①放置在a ×3 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑥,在a ×3 的方格纸中,共可以找到______个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a ×3 的方格纸中,使它恰好盖住其中的三个小正方形,共有_____种不同的放置方法.……问题解决:把图①放置在a ×b的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)问题拓展:如图,图⑦是一个由4 个棱长为1 的小立方体构成的几何体,图⑧是一个长、宽、高分别为a,b,c(a≥2 ,b≥2 ,c≥2 ,且a,b,c是正整数)的长方体,被分成了a×b×c个棱长为1 的小立方体.在图⑧的不同位置共可以找到______个图⑦这样的几何体.5.在ABC ∆中,90BAC ∠=︒,AB AC =,AD BC ⊥于点D ,(1)如图1,点M ,N 分别在AD ,AB 上,且90BMN ∠=︒,当30AMN ∠=︒,2AB =时,求线段AM 的长;(2)如图2,点E ,F 分别在AB ,AC 上,且90EDF ∠=︒,求证:BE AF =;(3)如图3,点M 在AD 的延长线上,点N 在AC 上,且90BMN ∠=︒,求证:AB AN +=;6.如图,正方形ABDE 和BCFG 的边AB ,BC 在同一条直线上,且2AB BC =,取EF 的中点M ,连接MD ,MG ,MB .(1)试证明DM MG ⊥,并求MBMG的值. (2)如图,将如图中的正方形变为菱形,设()2090EAB αα∠=<<︒,其它条件不变,问(1)中MBMG的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.7.定义:有一组邻边相等且对角互补的四边形叫做等补四边形. 理解:()1如图1,点A B C ,,在O e 上,ABC ∠的平分线交O e 于点D ,连接AD CD ,.求证:四边形ABCD 是等补四边形; 探究:()2如图2,在等补四边形ABCD 中AB AD ,=,连接AC AC ,是否平分?BCD ∠请说明理由. 运用:()3如图3,在等补四边形ABCD 中,AB AD =,其外角EAD ∠的平分线交CD 的延长线于点105F CD AF ,=,=,求DF 的长.8.已知V ABC 内接于O e ,BAC ∠的平分线交O e 于点D ,连接DB ,DC .(1)如图①,当120BAC ∠=o 时,请直接写出线段AB ,AC ,AD 之间满足的等量关系式: ; (2)如图②,当90BAC ∠=o 时,试探究线段AB ,AC ,AD 之间满足的等量关系,并证明你的结论; (3)如图③,若BC =5,BD =4,求ADAB AC+ 的值.9.如图,在ABC ∆中,AB BC =,AD BC ⊥于点D ,BE AC ⊥于点E ,AD 与BE 交于点F ,BH AB ⊥于点B ,点M 是BC 的中点,连接FM 并延长交BH 于点H .(1)如图①所示,若30ABC ∠=o ,求证:DF BH +=; (2)如图②所示,若45ABC ∠=o ,如图③所示,若60ABC ∠=o (点M 与点D 重合),猜想线段DF 、BH 与BD 之间又有怎样的数量关系?请直接写出你的猜想,不需证明.10.将在同一平面内如图放置的两块三角板绕公共顶点A旋转,连接BC,DE.探究S△ABC与S△ADC的比是否为定值.(1)两块三角板是完全相同的等腰直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图①)(2)一块是等腰直角三角板,另一块是含有30°角的直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图②)(3)两块三角板中,∠BAE+∠CAD=180°,AB=a,AE=b,AC=m,AD=n(a,b,m,n为常数),S△ABC:S△ADE是否为定值?如果是,用含a,b,m,n的式子表示此定值(直接写出结论,不写推理过程),如果不是,说明理由.(图③)11.如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD 中,AB AD =,CB CD =,问四边形ABCD 是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD 的对角线AC 、BD 交于点O ,AC BD ⊥.试证明:2222AB CD AD BC +=+;(3)解决问题:如图3,分别以Rt ACB V 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ,连结CE 、BG 、GE .已知4AC =,5AB =,求GE 的长.12.(1)数学理解:如图①,△ABC是等腰直角三角形,过斜边AB的中点D作正方形DECF,分别交BC,AC于点E,F,求AB,BE,AF之间的数量关系;(2)问题解决:如图②,在任意直角△ABC内,找一点D,过点D作正方形DECF,分别交BC,AC于点E,F,若AB=BE+AF,求∠ADB的度数;(3)联系拓广:如图③,在(2)的条件下,分别延长ED,FD,交AB于点M,N,求MN,AM,BN的数量关系.13.如图,正方形ABCD 的边长为2,E 为AB 的中点,P 是BA 延长线上的一点,连接PC 交AD 于点F ,AP FD =.(1)求AFAP的值; (2)如图1,连接EC ,在线段EC 上取一点M ,使EM EB =,连接MF ,求证:MF PF =; (3)如图2,过点E 作EN CD ⊥于点N ,在线段EN 上取一点Q ,使AQ AP =,连接BQ ,BN .将AQB ∆绕点A 旋转,使点Q 旋转后的对应点'Q 落在边AD 上.请判断点B 旋转后的对应点'B 是否落在线段BN 上,并说明理由.14.在ABC ∆中,90ABC ∠=︒,ABn BC=,M 是BC 上一点,连接AM (1)如图1,若1n =,N 是AB 延长线上一点,CN 与AM 垂直,求证:BM BN =(2)过点B 作BP AM ⊥,P 为垂足,连接CP 并延长交AB 于点Q . ①如图2,若1n =,求证:CP BMPQ BQ=②如图3,若M 是BC 的中点,直接写出tan BPQ ∠的值(用含n 的式子表示)15.⑴如图1,E 是正方形ABCD 边AB 上的一点,连接BD DE 、,将BDE ∠绕着点D 逆时针旋转90°,旋转后角的两边分别与射线BC 交于点F 和点G . ①线段DB 和DG 的数量关系是 ; ②写出线段BE BF 、和DB 之间的数量关系.⑵当四边形ABCD 为菱形,ADC 60∠=o ,点E 是菱形ABCD 边AB 所在直线上的一点,连接BD DE 、,将BDE ∠绕着点D 逆时针旋转120°,旋转后角的两边分别与射线BC 交于点F 和点G .①如图2,点E 在线段上时,请探究线段BE BF 、和BD 之间的数量关系,写出结论并给出证明; ②如图3,点E 在线段AB 的延长线上时,DE 交射线BC 于点M ;若 BE 1,AB 2==,直接写出线段GM 的长度.16.教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.例2 如图,在ABC ∆中,,D E 分别是边,BC AB 的中点,,AD CE 相交于点G ,求证:13GE GD CE AD ==,证明:连结ED .请根据教材提示,结合图①,写出完整的证明过程.结论应用:在ABCD Y 中,对角线AC BD 、交于点O ,E 为边BC 的中点,AE 、BD 交于点F . (1)如图②,若ABCD Y 为正方形,且6AB =,则OF 的长为 . (2)如图③,连结DE 交AC 于点G ,若四边形OFEG 的面积为12,则ABCD Y 的面积为 .17.如图1,在矩形ABCD 中,BC =3,动点P 从B 出发,以每秒1个单位的速度,沿射线BC 方向移动,作PAB ∆关于直线PA 的对称'PAB ∆,设点P 的运动时间为()t s(1)若AB =①如图2,当点B ’落在AC 上时,显然△PCB ’是直角三角形,求此时t 的值②是否存在异于图2的时刻,使得△PCB ’是直角三角形?若存在,请直接写出所有符合题意的t 的值?若不存在,请说明理由(2)当P 点不与C 点重合时,若直线PB ’与直线CD 相交于点M ,且当t <3时存在某一时刻有结论∠P AM =45°成立,试探究:对于t >3的任意时刻,结论∠P AM =45°是否总是成立?请说明理由.18.在等腰三角形ABC ∆中,AB AC =,作CM AB ⊥交AB 于点M ,BN AC ⊥交AC 于点N . (1)在图1中,求证:BMC CNB ∆≅∆;(2)在图2中的线段CB 上取一动点P ,过P 作//PE AB 交CM 于点E ,作//PF AC 交BN 于点F ,求证:PE PF BM +=;(3)在图3中动点P 在线段CB 的延长线上,类似(2)过P 作//PE AB 交CM 的延长线于点E ,作//PF AC 交NB 的延长线于点F ,求证:···AM PF OM BN AM PE +=.19.问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.问题探究:在“问题情境”的基础上,(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P落在点P'处.若正方形ABCD的边长为4 ,AD的中点为S,求P'S的最小值.问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD 沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=52,请直接写出FH的长.20.箭头四角形,模型规律:如图1,延长CO 交AB 于点D ,则1BOC B A C B ∠∠+∠∠+∠+∠==..因为凹四边形ABOC 形似箭头,其四角具有“BOC A B C ∠∠+∠+∠=”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:(1)直接应用:①如图2,A B C D E F ∠+∠+∠+∠+∠+∠= .②如图3,ABE ACE ∠∠、的2等分线(即角平分线)BF CF 、交于点F ,已知12050BEC BAC ∠=∠=o o ,,则BFC ∠=③如图4,i i BO CO 、分别为ABO ACO ∠∠、的2019等分线12320172018i =⋯(,,,,,).它们的交点从上到下依次为1232018O O O O ⋯、、、、.已知BOC m BAC n ∠=∠=o o ,,则1000BO C ∠= 度 (2)拓展应用:如图5,在四边形ABCD 中,2BC CD BCD BAD =∠=∠,.O 是四边形ABCD 内一点,且OA OB OD ==.求证:四边形OBCD 是菱形.21.如图1,在Rt △ABC 中,∠B =90°,BC =2AB =8,点D ,E 分别是边BC ,AC 的中点,连接DE ,将△EDC 绕点C 按顺时针方向旋转,记旋转角为α. (1)问题发现 ① 当0α︒=时,AEBD= ;② 当时,AEBD= (2)拓展探究试判断:当0°≤α<360°时,AEDB的大小有无变化?请仅就图2的情况给出证明. (3)问题解决当△EDC 旋转至A 、D 、E 三点共线时,直接写出线段BD 的长.22.操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.(1)如图1,求证:BE=BF;(2)特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;(3)类比探究:若DE=a,CF=b.①如图3,当点P在线段EF的延长线上运动时,试用含a、b的式子表示QM与QN之间的数量关系,并证明;②如图4,当点P在线段FE的延长线上运动时,请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)23.如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,.CD)24.(1)(探究发现)如图1,EOF ∠的顶点O 在正方形ABCD 两条对角线的交点处,90EOF ︒∠=,将EOF ∠绕点O 旋转,旋转过程中,EOF ∠的两边分别与正方形ABCD 的边BC 和CD 交于点E 和点F (点F 与点C ,D 不重合).则,,CE CF BC 之间满足的数量关系是 . (2)(类比应用)如图2,若将(1)中的“正方形ABCD ”改为“120BCD ∠=o 的菱形ABCD ”,其他条件不变,当60EOF ∠=o 时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由. (3)(拓展延伸)如图3,120BOD =o ∠,34OD =,4OB =,OA 平分BOD ∠,AB =且2OB OA >,点C 是OB 上一点,60CAD ∠=o ,求OC 的长.25.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).①条边成比例的两个凸四边形相似;( 命题) ②三个角分别相等的两个凸四边形相似;( 命题) ③两个大小不同的正方形相似.( 命题)(2)如图1,在四边形ABCD 和四边形A 1B 1C 1D 1中,∠ABC =∠A 1B 1C 1,∠BCD =∠B 1C 1D 1,111111AB BC CDA B B C C D ==,求证:四边形ABCD 与四边形A 1B 1C 1D 1相似.(3)如图2,四边形ABCD 中,AB ∥CD ,AC 与BD 相交于点O ,过点O 作EF ∥AB 分别交AD ,BC 于点E ,F .记四边形ABFE 的面积为S 1,四边形EFDE 的面积为S 2,若四边形ABFE 与四边形EFCD 相似,求21S S 的值.26.在△ABC 中,已知D 是BC 边的中点,G 是△ABC 的重心,过G 点的直线分别交AB 、AC 于点E 、F .(1)如图1,当EF ∥BC 时,求证:1BE CFAE AF+=; (2)如图2,当EF 和BC 不平行,且点E 、F 分别在线段AB 、AC 上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.(3)如图3,当点E 在AB 的延长线上或点F 在AC 的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.27.如图,在等腰Rt ABC V 中,90,ACB AB ∠==o 点D ,E 分别在边AB ,BC 上,将线段ED 绕点E 按逆时针方向旋转90º得到EF .(1)如图1,若AD BD =,点E 与点C 重合,AF 与DC 相交于点O .求证:2BD DO =. (2)已知点G 为AF 的中点.①如图2,若,2AD BD CE ==,求DG 的长.②若6AD BD =,是否存在点E ,使得DEG △是直角三角形?若存在,求CE 的长;若不存在,试说明理由.28.(1)方法选择如图①,四边形ABCD 是O e 的内接四边形,连接AC ,BD ,AB BC AC ==.求证:BD AD CD =+. 小颖认为可用截长法证明:在DB 上截取DM AD =,连接AM …小军认为可用补短法证明:延长CD 至点N ,使得DN AD =…请你选择一种方法证明.(2)类比探究(探究1)如图②,四边形ABCD 是O e 的内接四边形,连接AC ,BD ,BC 是O e 的直径,AB AC =.试用等式表示线段AD ,BD ,CD 之间的数量关系,并证明你的结论.(探究2)如图③,四边形ABCD 是O e 的内接四边形,连接AC ,BD .若BC 是O e 的直径,30ABC ∠=︒,则线段AD ,BD ,CD 之间的等量关系式是______.(3)拓展猜想如图④,四边形ABCD 是O e 的内接四边形,连接AC ,BD .若BC 是O e 的直径,::::BC AC AB a b c =,则线段AD ,BD ,CD 之间的等量关系式是______.29.(1)证明推断:如图(1),在正方形ABCD 中,点E ,Q 分别在边BC ,AB 上,DQ AE ⊥于点O ,点G ,F 分别在边CD ,AB 上,GF AE ⊥.①求证:DQ AE =; ②推断:GF AE的值为 ; (2)类比探究:如图(2),在矩形ABCD 中,BC k AB =(k 为常数).将矩形ABCD 沿GF 折叠,使点A 落在BC 边上的点E 处,得到四边形FEPG ,EP 交CD 于点H ,连接AE 交GF 于点O .试探究GF 与AE CP 之间的数量关系,并说明理由;(3)拓展应用:在(2)的条件下,连接CP ,当23k =时,若3tan 4CGP ∠=,GF =CP 的长.30.在ABC ∆,CA CB =,ACB α∠=.点P 是平面内不与点A ,C 重合的任意一点.连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,BD ,CP .(1)观察猜想如图1,当60α︒=时,BD CP 的值是 ,直线BD 与直线CP 相交所成的较小角的度数是 . (2)类比探究如图2,当90α︒=时,请写出BD CP 的值及直线BD 与直线CP 相交所成的小角的度数,并就图2的情形说明理由.(3)解决问题当90α︒=时,若点E ,F 分别是CA ,CB 的中点,点P 在直线EF 上,请直接写出点C ,P ,D 在同一直线上时AD CP的值.。
2020年九年级数学中考几何探究型问题:线段最值问题——“费马点”问题(含答案)

几何探究型问题(针对第25题)线段最值问题“费马点”问题【问题背景】“费马点”——就是到三角形三个顶点的距离之和最小的点.“费马点”问题在中考考查时主要隐藏在求PA+PB+PC的最小值问题,通常将某三角形绕点旋转一定的角度,从而将三条线段转化在同一条直线上,利用两点之间线段最短解决问题.【模型分析】对于一个各角不超过120°的三角形,“费马点”是对各边的张角都是120°的点,对于有一个角超过120°的三角形,费马点就是这个内角的顶点.费马点P使它到△ABC三个顶点的距离之和PA+PB+PC最小,这就是所谓的“费马”问题.如图,将△APC绕点A逆时针旋转60°到△AP′C′,则可以构造出等边三角形APP′,从而得到AP=PP′,CP=C′P′,所以将PA+PB+PC的值转化为PP′+PB+P′C′的值,则线段BC′的长即为所求的最小值.例题1.如图,已知点P为等边三角形ABC外接圆的劣弧BC上任意一点,求证:PB+PC=PA.证明:如答图,在P A上截取PM=PC,连接CM.∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,BC =AC .∵∠ABC =∠APC ,∴∠MPC =60°,∴△MPC 是等边三角形,∴∠MCP =60°,MC =PC ,∴∠ACM =∠BCP .在△BPC 和△AMC 中,⎩⎪⎨⎪⎧ BC =AC ,∠BCP =∠ACM ,PC =MC ,∴△BPC ≌△AMC (SAS),∴BP =AM ,∴PB +PC =AM +PM =P A .2.已知三个村庄A ,B ,C 构成了如图所示的△ABC(其中∠A ,∠B ,∠C 均小于120°),现选取一点P 作为打水井,使水井P 到三个村庄A ,B ,C 所铺设的输水管总长度最小.求输水管总长度的最小值.解:如答图,以BC 为边在△ABC 的外部作等边三角形BCD ,连接AD .∴AD 的长就是△ABC 的费马距离.易得∠ABD =90°,∴AD =AB 2+BD 2=5(km).答:输水管总长度的最小值为5 km.练习(2019·陕师大附中六模)问题提出(1)如图1,在△ABC 中,BC =2,将△ABC 绕点B 顺时针旋转60°得到△A ′BC ′,则CC ′=______.【解答】由旋转的性质可知∠CBC ′=60°,BC ′=BC ,则∠△BCC ′是等边三角形,故CC ′=BC =2.问题探究(2)如图2,在△ABC中,AB=BC=3,∠ABC=30°,点P为△ABC内一点,连接PA,PB,PC,求PA+PB+PC的最小值,并说明理由.解题思路将△ABP绕点B逆时针旋转60°得到△EBF,连接PF,EC.易证PA+PB+PC=EF+PF+PC;由PC+PF+EF≥EC,推出当点P,F在直线EC上时,PA+PB+PC的值最小,即为EC的长,求出EC的长即可解决问题.【解答】如答图1,将△ABP绕点B逆时针旋转60°得到△EBF,连接PF,EC.由旋转的性质可知△PBF是等边三角形,∴PB=PF.∵P A=EF,∴P A+PB+PC=EF+PF+PC.∵PC+PF+EF≥EC,∴当点P,F在直线EC上时,P A+PB+PC的值最小,易得BC=BE=BA=3,∠CBE=90°,∴EC=2BC=32,∴P A+PB+PC的最小值为3 2.问题解决(3)如图3,在四边形ABCD中,AD∥BC,AB=6,AD=4,∠ABC=∠BCD=60°.在四边形ABCD内部有一点P,满足∠APD=120°,连接BP,CP,点Q为△BPC内的任意一点,是否存在一点P和一点Q,使得PQ+BQ+CQ有最小值?若存在,请求出这个最小值;若不存在,请说明理由.解题思路将△PBQ绕点B逆时针旋转60°得到△EBG,则PQ=EG,△BQG是等边三角形,易知PQ+BQ+CQ=EG+GQ+QC≥EC,推出当EC取得最小值时,PQ +BQ +CQ 的值最小.延长BA 交CD 的延长线于点S ,作△ADS 的外接圆⊙O ,将线段BO ,BP 绕点B 逆时针旋转60°得到线段BO ′,BE ,连接EO ′,OB ,OP .易证△BEO ′≌△BPO(SAS),推出EO ′=OP =433,故点E 在以点O ′为圆心,433为半径的圆上,则当点E 在线段CO ′上时,EC 的值最小,最小值为CO ′-EO ′的长.【解答】如答图2,将△PBQ 绕点B 逆时针旋转60°得到△EBG ,连接GQ ,EC ,则PQ =EG ,△BQG 是等边三角形,∴BQ =QG ,∴PQ +BQ +CQ =EG +GQ +QC ≥EC ,∴当EC 取得最小值时,PQ +BQ +CQ 的值最小.如答图3,延长BA 交CD 的延长线于点S ,作△ADS 的外接圆⊙O ,连接OB .将线段BO ,BP 绕点B 逆时针旋转60°得到线段BO ′,BE ,连接EO ′,OP.易证△BEO ′≌△BPO (SAS),∴EO ′=PO .∵∠APD +∠ASD =180°,∴A ,P ,D ,S 四点共圆,∴OP =433,∴EO ′=433, ∴点E 在以点O ′为圆心,433为半径的圆上, ∴当点E 在线段CO ′上时,EC 的值最小,最小值为CO ′-EO ′的长,连接OO ′,延长OO ′到点R ,使得O ′R =OO ′,连接BR ,则∠OBR =90°,作RH ⊥CB 交CB 的延长线于点H ,O ′T ⊥CH 于点T ,OM ⊥BC 于点M .易知在Rt △OBM 中,BM =5,OM =1133, ∴OB =OM 2+BM 2=1433, ∴BR =3OB =14.易知△BHR ∽△OMB ,∴RH BM =BR OB,∴RH =5 3.∵HR ∥O ′T ∥OM ,OO ′=RO ′,∴TM =TH ,∴O ′T =RH +OM 2=1333,∴BT =O ′B 2-O ′T 2=3, ∴CO ′=CT 2+O ′T 2=2633, ∴CE =CO ′-EO ′=2633-433=2233, ∴PQ +BQ +CQ 的最小值为2233.类型三 “阿氏圆”问题【问题背景】“PA +k ·PB ”型的最值问题是近几年中考考查的热点,更是一个难点.当k 的值为1时,即可转化为“PA +PB ”之和最短问题,就可用我们常见的“将军饮马”问题模型来处理,即可以转化为轴对称问题来处理.当k 取任意不为1的正数时,此类问题的处理通常以动点P 的运动轨迹不同来分类,一般分为两类研究,即点P 在直线上运动和点P 在圆上运动.其中点P 在圆周上运动的类型称之为“阿氏圆”问题.【模型分析】如图1,⊙O 的半径为r ,点A ,B 都在⊙O 外,P 为⊙O 上一动点,已知r =k ·OB ,连接PA ,PB ,则当PA +k ·PB 的值最小时,点P 的位置如何确定?如图2,在线段OB 上截取OC ,使OC =k ·r ,则可证明△BPO 与△PCO 相似,即k ·PB =PC .故求PA +k ·PB 的最小值可以转化为PA +PC 的最小值,其中A ,C 为定点,P 为动点,当点P ,A ,C 共线时,PA +PC 的值最小,如图3.“阿氏圆”模型解题策略:第一步:连接动点与圆心O(一般将含有k 的线段两端点分别与圆心O 相连),即连接OB ,OP ;第二步:计算线段OP 与OB 及OP 与OA 的线段比,找到线段比为k 的情况,如例子中的OP OB =k ; 第三步:在OB 上取点C ,使得OC OP =OP OB ;第四步:连接AC ,与⊙O 的交点即为点P .例题如图,在Rt △ABC 中,∠ACB =90°,CB =4,CA =6,⊙C 的半径为2,P 为圆上一动点,连接AP ,BP ,求AP +12BP 的最小值. 解:如答图,连接CP ,在CB 上取点D ,使CD =1,连接AD ,PD .∵CD CP =CP BC =12,∠PCD =∠BCD , ∴△PCD ∽△BCP ,∴PD BP =12, ∴PD =12BP ,∴AP +12BP =AP +PD , ∴要使AP +12BP 最小,则AP +PD 最小, 当点A ,P ,D 在同一条直线时,AP +PD 最小,即AP +12BP 的最小值为AD 的长. 在Rt △ACD 中,∵CD =1,AC =6,∴AD =AC 2+CD 2=37,∴AP +12BP 的最小值为37. 练习问题提出(1)如图1,已知线段AB 和BC ,AB =2,BC =5,则线段AC 的最小值为______.解题思路当点A 在线段BC 上时,线段AC 有最小值.【解答】∵当点A 在线段BC 上时,线段AC 有最小值,∴线段AC 的最小值为5-2=3.问题探究(2)如图2,已知在扇形COD 中,∠COD =90°,DO =CO =6,A 是OC的中点,延长OC 到点F ,使CF =OC ,P 是CD ︵上的动点,点B 是OD 上的一点,BD =1.①求证:△OAP ∽△OPF .解题思路由题意可得OA OP =OP OF =12,由相似三角形的判定可得△OAP ∽△OPF . 【解答】∵A 是OC 的中点,DO =CO =6=OP ,∴OA OP =12. ∵CF =OC ,∴OF =2OC =2OP ,∴OP OF =12, ∴OA OP =OP OF,且∠AOP =∠POF ,∴△OAP ∽△OPF .②求BP +2AP 的最小值.解题思路由相似三角形的性质可得PF =2AP ,可得BP +2AP =BP +PF ,即当F ,P ,B 三点共线时,BP +2AP 有最小值,最小值为BF 的长,由勾股定理即可求解.【解答】∵△OAP ∽△OPF ,∴AP PF =OP OF =12, ∴PF =2AP .∵BP +2AP =BP +PF ,∴当F ,P ,B 三点共线时,BP +2AP 有最小值,最小值为BF 的长.∵DO =CO =6,BD =1,∴BO =5,OF =12,∴BF =OB 2+OF 2=13.问题解决(3)如图3,有一个形状为四边形ABCD 的人工湖,BC =9千米,CD =4千米,∠BCD =150°,现计划在湖中选取一处建造一座假山P ,且BP =3千米,为方便游客观光,从C ,D 分别建小桥PD ,PC .已知建桥PD 每千米的造价是3万元,建桥PC 每千米的造价是1万元,建桥PD 和PC 的总造价是否存在最小值?若存在,请确定点P 的位置,并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)解题思路以点B 为圆心,3为半径作圆交AB 于点E ,交BC 于点F ,点P 为EF ︵上一点,连接BP ,PC ,PD ,在BC 上截取BM =1,连接MD ,PM ,过点D 作DG ⊥CB ,可证△BPM ∽△BCP ,可得PC =3PM ,当点P 在线段MD 上时,建桥PD 和PC 的总造价有最小值,由勾股定理可求MD 的值,即可求出建桥PD 和PC 的总造价的最小值.【解答】存在.如答图,以点B 为圆心,3为半径作圆交AB 于点E ,交BC 于点F ,P 为EF ︵上一点,连接BP ,PC ,PD ,在BC 上截取BM =1,连接MD ,PM ,过点D 作DG ⊥BC 交BC 的延长线于点G .∵BM BP =13=BP BC,且∠PBM =∠CBP , ∴△BPM ∽△BCP ,∴PM CP =BM BP =13,∴PC =3PM . ∵建桥PD 和PC 的总造价为3PD +PC =3PD +3PM =3(PD +PM ),∴当点P 在线段MD 上时,建桥PD 和PC 的总造价有最小值.∵∠BCD =150°,∴∠DCG =30°.∵DG ⊥BC ,∴DG =12DC =23(千米),CG =3DG =6(千米), ∴MG =BC +CG -BM =9+6-1=14(千米),∴MD =DG 2+MG 2=413(千米),∴建桥PD 和PC 的总造价的最小值为3×413=1213万元.作业5.(2019·交大附中三模)问题提出(1)如图1,点M ,N 是直线l 外两点,在直线l 上找一点K ,使得MK +NK 最小. 问题探究(2)如图2,在等边三角形ABC 内有一点P ,且P A =3,PB =4,PC =5,求∠APB 的度数.问题解决(3)如图3,矩形ABCD是某公园的平面图,AB=30 3 米,BC=60米,现需要在对角线BD上修一凉亭E,使得到公园出口A,B,C的距离之和最小.问:是否存在这样的点E?若存在,请画出点E的位置,并求出EA+EB+EC的最小值;若不存在,请说明理由.解:(1)如答图1,连接MN,与直线l交于点K,点K即为所求.(2)如答图2,把△APB绕点A逆时针旋转60°得到△AP′C,连接PP′.由旋转的性质,得P′A=P A=3,P′C=PB=4,∠P AP′=60°,∠AP′C=∠APB,∴△APP′是等边三角形,∴PP′=P A=3,∠AP′P=60°.∵PP′2+P′C2=32+42=25,PC2=52=25,∴PP′2+P′C2=PC2,∴△PP′C为直角三角形,且∠PP′C=90°,∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°,∴∠APB=∠AP′C=150°.(3)存在.如答图3,把△ABE绕点B逆时针旋转60°得到△A′BE′,连接EE′.答图由旋转的性质,得A′B=AB=30 3 米,BE′=BE,A′E′=AE,∠E′BE=60°,∠A′BA=60°,∴△E′BE是等边三角形,∴BE=EE′,∴EA +EB +EC =A ′E ′+EE ′+EC .根据两点之间线段最短,可知当EA +EB +EC =A ′C 时最短,连接A ′C ,与BD 的交点E 2即为所求,此时EA +EB +EC 最短,最短距离为A ′C 的长度.过点A ′作A ′G ⊥CB 交CB 的延长线于点G . ∵∠A ′BG =90°-∠A ′BA =90°-60°=30°, A ′G =12A ′B =12AB =12×303=153(米),∴GB =3A ′G =3×153=45(米), ∴GC =GB +BC =45+60=105(米).在Rt △A ′GC 中,A ′C =A ′G 2+GC 2=(153)2+1052=3013(米), 因此EA +EB +EC 的最小值为3013 米. 6.问题提出(1)如图1,已知△OAB 中,OB =3,将△OAB 绕点O 逆时针旋转90°得△OA ′B ′,连接BB ′,则BB ′=问题探究(2)如图2,已知△ABC 是边长为43的等边三角形,以BC 为边向外作等边三角形BCD ,P 为△ABC 内一点,将线段CP 绕点C 逆时针旋转60°,点P 的对应点为点Q .①求证:△DCQ ≌△BCP . ②求P A +PB +PC 的最小值. 问题解决(3)如图3,某货运场为一个矩形场地ABCD ,其中AB =500米,AD =800米,顶点A ,D 为两个出口,现在想在货运广场内建一个货物堆放平台P ,在BC 边上(含B ,C 两点)开一个货物入口M ,并修建三条专用车道P A ,PD ,PM .若修建每米专用车道的费用为10 000元,当M ,P 建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留根号)解:(1)由旋转的性质,得∠BOB ′=90°,OB =OB ′=3, 根据勾股定理,得BB ′=3 2. (2)①证明:∵△BDC 是等边三角形, ∴CD =CB ,∠DCB =60°.由旋转的性质,得∠PCQ =60°,PC =QC , ∴∠DCQ =∠BCP .在△DCQ 和△BCP 中,⎩⎪⎨⎪⎧CD =CB ,∠DCQ =∠BCP ,CQ =CP ,∴△DCQ ≌△BCP (SAS). ②如答图1,连接AD ,PQ . ∵PC =CQ ,∠PCQ =60°,∴△CPQ 是等边三角形,∴PQ =PC , 由①知DQ =PB ,∴P A +PB +PC =P A +QD +PQ ,由两点之间线段最短,得P A +QD +PQ ≥AD , ∴P A +PB +PC ≥AD ,∴当点A ,P ,Q ,D 在同一条直线上时,P A +PB +PC 取得最小值,即为AD 的长,过点D 作DE ⊥AC ,交AC 的延长线于点E . ∵△ABC 是边长为43的等边三角形, ∴CB =AC =43,∠BCA =60°, ∴CD =CB =43,∠DCE =60°, ∴DE =6,∠DAE =∠ADC =30°, ∴AD =12,即P A +PB +PC 的最小值为12.答图(3)如答图2,将△ADP 绕点A 逆时针旋转60°,得△AD ′P ′.由(2)知,当点M ,P ,P ′,D ′在同一条直线上时,P A +PM +PD 最小,最小值为D ′M 的长.∵M 在BC 上,∴当D ′M ⊥BC 时,D ′M 取得最小值. 设D ′M 交AD 于点E ,连接DD ′,AM ,DM . 易知△ADD ′是等边三角形,∴EM =AB =500米, ∴BM =400米,PM =EM -PE =(500-40033)米,∴D ′E =32AD =4003(米),∴D ′M =(4003+500)米, ∴最少费用为10 000×(4003+500)= 1 000 000(43+5)元.∴当M 建在BC 的中点(BM =400米)处,点P 在过M 且垂直于BC 的直线上,且在M上方(500-40033)米处时,修建专用车道的费用最少,最少费用为1 000 000(43+5)元.类型三 “阿氏圆”问题7.(2018·西工大附中三模) 问题提出(1)如图1,在△ABC 中,AB =AC ,BD 是AC 边的中线,请用尺规作图作出AB 边的中线CE ,并证明BD =CE ;问题探究(2)如图2,已知点P 是边长为6的正方形ABCD 内部一动点,P A =3,求PC +12PD 的最小值;问题解决(3)如图3,在矩形ABCD 中,AB =18,BC =25,点M 是矩形内部一动点,MA =15,当MC +35MD 最小时,画出点M 的位置,并求出MC +35MD 的最小值.解:(1)如答图1,线段EC 即为所求.证明:∵AB =AC ,AE =EB ,AD =CD ,∴AE =AD , 在△BAD 和△CAE 中,⎩⎪⎨⎪⎧AB =AC ,∠A =∠A ,AD =AE ,答图1∴△BAD ≌△CAE (SAS),∴BD =CE . (2)如答图2,在AD 上截取AE ,使得AE =32.∵P A 2=9,AE ·AD =32×6=9,∴P A 2=AE ·AD ,∴P A AD =AEP A.∵∠P AE =∠DAP ,∴△P AE ∽△DAP , ∴PE DP =P A DA =12,∴PE =12PD , ∴PC +12PD =PC +PE .∵PC +PE ≥EC ,∴PC +12PD 的最小值即为EC 的长,在Rt △CDE 中,∵∠CDE =90°,CD =6,DE =92,∴EC =62+(92)2=152,∴PC +12PD 的最小值为152.答图(3)如答图3,在AD 上截取AE ,使得AE =9. ∵MA 2=225,AE ·AD =9×25=225,∴MA 2=AE ·AD ,∴MA AD =AEMA.∵∠MAE =∠DAM ,∴△MAE ∽△DAM , ∴EM MD =MA DA =1525=35,∴ME =35MD , ∴MC +35MD =MC +ME .∵MC +ME ≥EC ,∴MC +35MD 的最小值即为EC 的长.如答图3,以点A 为圆心,AM 长为半径画弧,交EC 于点M ′,点M ′即为所求. 在Rt △CDE 中,∵∠CDE =90°,CD =18,DE =16, ∴EC =162+182=2145, ∴MC +35MD 的最小值为2145.8.(1)如图1,已知正方形ABCD 的边长为4,⊙B 的半径为2,P 是⊙B 上的一个动点,求PD +12PC 的最小值和PD -12PC 的最大值;(2)如图2,已知正方形ABCD 的边长为9,⊙B 的半径为6,P 是⊙B 上的一个动点,那么PD +23PC 的最小值为,PD -23PC 的最大值为(3)如图3,已知菱形ABCD 的边长为4,∠B =60°,⊙B 的半径为2,P 是⊙B 上的一个动点,那么PD +12PC 的最小值为,PD -12PC 的最大值为解:(1)如答图1,在BC 上取一点G ,使得BG =1,连接PB ,PG ,DG .∵PB BG =CBPB=2,∠PBG =∠CBP , ∴△PBG ∽△CBP , ∴PG CP =BG BP =12,∴PG =12PC , ∴PD +12PC =PD +PG .∵PD +PG ≥DG ,∴当D ,P ,G 三点共线时,PD +12PC 的值最小,最小值为DG =42+32=5.∵PD -12PC =PD -PG ≤DG ,∴如答图2,当点P 在DG 的延长线上时,PD -12PC 的值最大,最大值为5.答图(2)106,106.【解法提示】如答图3,在BC 上取一点G ,使BG =4,连接PG ,PB ,DG . ∵PB BG =64=32,CB PB =96=32,∴PB BG =CB BP. ∵∠PBG =∠CBP ,∴△PBG ∽△CBP , ∴PG CP =BG BP =23, ∴PG =23PC ,∴PD +23PC =DP +PG .∵DP +PG ≥DG ,∴当D ,P ,G 三点共线时,PD +23PC 的值最小,最小值为DG =52+92=106.∵PD -23PC =PD -PG ≤DG ,∴当点P 在DG 的延长线上时,PD -12PC 的值最大,最大值为106.答图(3)37,37.【解法提示】如答图4,在BC 上取一点G ,使得BG =1,连接PB ,PG ,DG ,作DF ⊥BC 交BC 的延长线于点F .∵PB BG =21=2,BC PB =42=2,∴PB BG =CB BP. ∵∠PBG =∠CBP ,∴△PBG ∽△CBP , ∴PG CP =BG BP =12, ∴PG =12PC ,∴PD +12PC =DP +PG .∵DP +PG ≥DG ,∴当D ,P ,G 三点共线时,PD +12PC 的值最小,最小值为DG 的长.在Rt △CDF 中,∵∠DCF =60°,CD =4, ∴DF =CD ·sin60°=23,CF =2,∴在Rt △GDF 中,DG =(23)2+52=37. ∴PD +12PC 的最小值为37.∵PD -12PC =PD -PG ≤DG ,∴当点P 在DG 的延长线上时,PD -12PC 的值最大,最大值为37.。
2020中考数学 几何专项突破:等腰三角形和直角三角形(含详解版)

2020中考数学几何专项突破等腰三角形和直角三角形(含答案)典例探究例1 如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是()A.70°B.55°C.50°D.40°例2 已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为()A.16 B.20或16 C.20 D.12例3 已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD=1,连接DE,则DE =.例4 如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.(1)求证:BE=CE;(2)若BE的延长线交AC于点F,且BF⊥AC,垂足为F,如图2,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.巩固练习1、若等腰三角形的一个内角为50°,则这个等腰三角形顶角的度数为 .2.在△ABC中,AB=AC,D为AC边上一点,且BD=BC=AD.则∠A等于()A.30° B.36° C.45° D.72°3. 已知:如图,AC和BD相交于点O,AB∥CD,OA=OB,求证:OC=OD4. 如图,已知P、Q是△ABC边BC上两点,且BP=PQ=AP=AQ=QC,求∠BAC的度数。
5.已知:如图,在△ABC中,∠B=∠C,D、E、F分别为AB,BC,AC上的点,且BD=CE,∠DEF=∠B。
求证:△DEF是等腰三角形。
AB CDE图1AB CDEF图26.若三角形一边上的中线等于这条边的一半,则这个三角形的形状是.7.在直角三角形中,若一锐角为30°,而斜边与30°角所对的边的和为15cm,则斜边的长为()A、3cmB、 7.5cmC、10cmD、12cm8. 如图,已知△ABC为等边三角形,D、E、F分别在边BC、CA、AB上,且△DEF是等边三角形(1)除已知相等的边以外,请你猜想还有哪些相等的线段,并证明你的猜想是正确的。
2020年中考数学热点冲刺8 动态几何问题(含解析)

热点专题8动点几何问题考向1图形的运动与最值1. (2019 江苏省连云港市)如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则的最大值是.【解析】如图,过点P作PE⊙BD交AB的延长线于E,⊙⊙AEP=⊙ABD,⊙APE⊙⊙ATB,⊙,⊙AB=4,⊙AE=AB+BE=4+BE,⊙,⊙BE最大时,最大,⊙四边形ABCD是矩形,⊙BC=AD=3,CD=AB=4,过点C作CH⊙BD于H,交PE于M,并延长交AB于G,⊙BD是⊙C的切线,⊙⊙GME=90°,在Rt⊙BCD中,BD==5,⊙⊙BHC=⊙BCD=90°,⊙CBH=⊙DBC,⊙⊙BHC⊙⊙BCD,⊙,⊙,⊙BH=,CH=,⊙⊙BHG=⊙BAD=90°,⊙GBH=⊙DBA,⊙⊙BHG⊙⊙BAD,⊙=,⊙,⊙HG=,BG=,在Rt⊙GME中,GM=EG•sin⊙AEP=EG×=EG,而BE=GE﹣BG=GE﹣,⊙GE最大时,BE最大,⊙GM最大时,BE最大,⊙GM=HG+HM=+HM,即:HM最大时,BE最大,延长MC交⊙C于P',此时,HM最大=HP'=2CH=,⊙GP'=HP'+HG=,过点P'作P'F⊙BD交AB的延长线于F,⊙BE最大时,点E落在点F处,即:BE 最大=BF ,在Rt⊙GP 'F 中,FG ====,⊙BF =FG ﹣BG =8, ⊙最大值为1+=3,故答案为:3.2. (2019 江苏省无锡市)如图,在ABC ∆中,5AB AC ==,BC =D 为边AB 上一动点(B 点除外),以CD 为一边作正方形CDEF ,连接BE ,则BDE ∆面积的最大值为 .【解析】过D 作DG ⊙BC 于G ,过A 作AN ⊙BC 于N ,过E 作EH ⊙HG 于H ,延长ED 交BC 于M .易证⊙EHD ⊙⊙DGC ,可设DG =HE =x ,⊙AB =AC =5,BC =AN ⊙BC ,⊙BN =12BC =,AN ⊙G ⊙BC ,AN ⊙BC , ⊙DG ⊙AN , ⊙2BG BNDG AN==,⊙BG =2x ,CG =HD =- 2x ;易证⊙HED ⊙⊙GMD ,于是HE HDGM GD =,x GM =MG 2= ,所以S ⊙BDE= 12BM ×HD =12×(2x 2)×(4- 2x )=252x -+=2582x ⎛-+ ⎝⎭,当x 时,S ⊙BDE 的最大值为8. 因此本题答案为8. 3. (2019 江苏省宿迁市)如图,⊙MAN =60°,若⊙ABC 的顶点B 在射线AM 上,且AB =2,点C 在射线AN 上运动,当⊙ABC 是锐角三角形时,BC 的取值范围是 .【解析】如图,过点B作BC1⊙AN,垂足为C1,BC2⊙AM,交AN于点C2在Rt⊙ABC1中,AB=2,⊙A=60°⊙⊙ABC1=30°⊙AC1=AB=1,由勾股定理得:BC1=,在Rt⊙ABC2中,AB=2,⊙A=60°⊙⊙AC2B=30°⊙AC2=4,由勾股定理得:BC2=2,当⊙ABC是锐角三角形时,点C在C1C2上移动,此时<BC<2.故答案为:<BC<2.4. (2019 江苏省宿迁市)如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边⊙EFG,连接CG,则CG的最小值为.【解析】由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动将⊙EFB绕点E旋转60°,使EF与EG重合,得到⊙EFB⊙⊙EHG从而可知⊙EBH为等边三角形,点G在垂直于HE的直线HN上作CM⊙HN,则CM即为CG的最小值作EP⊙CM,可知四边形HEPM为矩形,则CM=MP+CP=HE+EC=1+=故答案为.5.(2019 江苏省扬州市)如图,已知等边⊙ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合).直线1是经过点P的一条直线,把⊙ABC沿直线1折叠,点B的对应点是点B′.(1)如图1,当PB=4时,若点B′恰好在AC边上,则AB′的长度为;(2)如图2,当PB=5时,若直线1⊙AC,则BB′的长度为;(3)如图3,点P在AB边上运动过程中,若直线1始终垂直于AC,⊙ACB′的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)当PB=6时,在直线1变化过程中,求⊙ACB′面积的最大值.【解析】(1)如图1中,⊙⊙ABC是等边三角形,⊙⊙A=60°,AB=BC=AC=8,⊙PB=4,⊙PB′=PB=P A=4,⊙⊙A=60°,⊙⊙APB′是等边三角形,⊙AB′=AP=4.故答案为4.(2)如图2中,设直线l交BC于点E.连接BB′交PE于O.⊙PE⊙AC,⊙⊙BPE=⊙A=60°,⊙BEP=⊙C=60°,⊙⊙PEB是等边三角形,⊙PB=5,⊙⊙B,B′关于PE对称,⊙BB′⊙PE,BB′=2OB⊙OB=PB•sin60°=,⊙BB′=5.故答案为5.(3)如图3中,结论:面积不变.⊙B,B′关于直线l对称,⊙BB′⊙直线l,⊙直线l ⊙AC , ⊙AC ⊙BB ′, ⊙S ⊙ACB ′=S ⊙ACB =•82=16.(4)如图4中,当B ′P ⊙AC 时,⊙ACB ′的面积最大,设直线PB ′交AC 于E ,在Rt⊙APE 中,⊙P A =2,⊙P AE =60°, ⊙PE =P A •sin60°=,⊙B ′E =6+,⊙S ⊙ACB ′的最大值=×8×(6+)=4+24.6. (2019 江苏省苏州市) 已知矩形ABCD 中,AB =5cm ,点P 为对角线AC 上的一点,且AP=.如图⊙,动点M 从点A 出发,在矩形边上沿着A B C →→的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s ),APM ∆的面积为S (cm²),S 与t 的函数关系如图⊙所示:(1)直接写出动点M 的运动速度为 /cm s ,BC 的长度为 cm ;(2)如图⊙,动点M 重新从点A 出发,在矩形边上,按原来的速度和方向匀速运动.同时,另一个动点N 从点D 出发,在矩形边上沿着D C B →→的方向匀速运动,设动点N 的运动速度为()/v cm s .已知两动点M 、N 经过时间()x s 在线段BC 上相遇(不包含点C ),动点M 、N 相遇后立即停止运动,记此时APM DPN ∆∆与的面积为()()2212,S cm S cm . ⊙求动点N 运动速度()/v cm s 的取值范围;⊙试探究12S S ⋅是否存在最大值.若存在,求出12S S ⋅的最大值并确定运动速度时间x 的值;若不存在,请说明理由.【解析】(1)2/cm s ;10cm(2)⊙解:⊙在边BC 上相遇,且不包含C 点 ⊙57.515 2.5C vB v⎧⎪⎪⎨⎪≥⎪⎩<在点在点⊙2/6/3cm s v cm s ≤<⊙如右图12()PAD CDM ABM N ABCD S S S S S S ∆∆∆+=---(N )矩形()()5152525751022x x ⨯-⨯-=---=15过M 点做MH ⊙AC,则12MH CM ==①(图)PBCDAS (cm²)t (s )②图O2.57.515-2x2x-5(N )⊙ ⊙22S x =()122152S S x x ⋅=-+⋅ =2430x x -+ =215225444x ⎛⎫--+ ⎪⎝⎭因为152.57.54<<,所以当154x =时,12S S ⋅取最大值2254.7. (2019 江苏省扬州市)如图,四边形ABCD 是矩形,AB =20,BC =10,以CD 为一边向矩形外部作等腰直角⊙GDC ,⊙G =90°.点M 在线段AB 上,且AM =a ,点P 沿折线AD ﹣DG 运动,点Q 沿折线BC ﹣CG 运动(与点G 不重合),在运动过程中始终保持线段PQ ⊙A B .设PQ 与AB 之间的距离为x . (1)若a =12.⊙如图1,当点P 在线段AD 上时,若四边形AMQP 的面积为48,则x 的值为 ; ⊙在运动过程中,求四边形AMQP 的最大面积;(2)如图2,若点P 在线段DG 上时,要使四边形AMQP 的面积始终不小于50,求a 的取值范围.【解析】 ⊙P 在线段AD 上,PQ =AB =20,AP =x ,AM =12,112152S MH AP x =⋅=-+四边形AMQP的面积=(12+20)x=48,解得:x=3;故答案为:3;⊙当P,在AD上运动时,P到D点时四边形AMQP面积最大,为直角梯形,⊙0<x≤10时,四边形AMQP面积的最大值=(12+20)10=160,当P在DG上运动,10<x≤20,四边形AMQP为不规则梯形,作PH⊙AB于M,交CD于N,作GE⊙CD于E,交AB于F,如图2所示:则PM=x,PN=x﹣10,EF=BC=10,⊙⊙GDC是等腰直角三角形,⊙DE=CE,GE=CD=10,⊙GF=GE+EF=20,⊙GH=20﹣x,由题意得:PQ⊙CD,⊙⊙GPQ⊙⊙GDC,⊙=,即=,解得:PQ=40﹣2x,⊙梯形AMQP的面积=(12+40﹣2x)×x=﹣x2+26x=﹣(x﹣13)2+169,⊙当x=13时,四边形AMQP的面积最大=169;(2)解:P在DG上,则10≤x≤20,AM=a,PQ=40﹣2x,梯形AMQP的面积S=(a+40﹣2x)×x=﹣x2+x,对称轴为:x=10+,⊙0≤x≤20,⊙10≤10+≤15,对称轴在10和15之间,⊙10≤x≤20,二次函数图象开口向下,⊙当x=20时,S最小,⊙﹣202+×20≥50,⊙a≥5;综上所述,a的取值范围为5≤a≤20.考向2动点与函数的结合问题1.(2019 江苏省连云港市)如图,在平面直角坐标系xOy中,抛物线L1:y=x2+bx+c过点C(0,﹣3),与抛物线L2:y=﹣x2﹣x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点.(1)求抛物线L1对应的函数表达式;(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;(3)设点R为抛物线L1上另一个动点,且CA平分⊙PCR.若OQ⊙PR,求出点Q的坐标.【解析】(1)将x=2代入y=﹣x2﹣x+2,得y=﹣3,故点A的坐标为(2,﹣3),将A(2,﹣1),C(0,﹣3)代入y=x2+bx+c,得,解得,⊙抛物线L1:y=x2﹣2x﹣3;(2)设点P的坐标为(x,x2﹣2x﹣3),第一种情况:AC为平行四边形的一条边,⊙当点Q在点P右侧时,则点Q的坐标为(x+2,﹣2x﹣3),将Q(x+2,﹣2x﹣3)代入y=﹣x2﹣x+2,得﹣2x﹣3=﹣(x+2)2﹣(x+2)+2,解得,x=0或x=﹣1,因为x=0时,点P与C重合,不符合题意,所以舍去,此时点P的坐标为(﹣1,0);⊙当点Q在点P左侧时,则点Q的坐标为(x﹣2,x2﹣2x﹣3),将Q(x﹣2,x2﹣2x﹣3)代入y=﹣x2﹣x+2,得y=﹣x2﹣x+2,得x2﹣2x﹣3=﹣(x﹣2)2﹣(x﹣2)+2,解得,x=3,或x=﹣,此时点P的坐标为(3,0)或(﹣,);第二种情况:当AC为平行四边形的一条对角线时,由AC的中点坐标为(1,﹣3),得PQ的中点坐标为(1,﹣3),故点Q的坐标为(2﹣x,﹣x2+2x﹣3),将Q(2﹣x,﹣x2+2x﹣3)代入y=﹣x2﹣x+2,得﹣x2+2x﹣3═﹣(2﹣x)2﹣(2﹣x)+2,解得,x=0或x=﹣3,因为x=0时,点P与点C重合,不符合题意,所以舍去,此时点P的坐标为(﹣3,12),综上所述,点P的坐标为(﹣1,0)或(3,0)或(﹣,)或(﹣3,12);(3)当点P在y轴左侧时,抛物线L1不存在点R使得CA平分⊙PCR,当点P在y轴右侧时,不妨设点P在CA的上方,点R在CA的下方,过点P、R分别作y轴的垂线,垂足分别为S、T,过点P作PH⊙TR于点H,则有⊙PSC=⊙RTC=90°,由CA平分⊙PCR,得⊙PCA=⊙RCA,则⊙PCS=⊙RCT,⊙⊙PSC⊙⊙RTC,⊙,设点P坐标为(x1,),点R坐标为(x2,),所以有,整理得,x1+x2=4,在Rt⊙PRH中,tan⊙PRH==过点Q作QK⊙x轴于点K,设点Q坐标为(m,),若OQ⊙PR,则需⊙QOK=⊙PRH,所以tan⊙QOK=tan⊙PRH=2,所以2m=,解得,m=,所以点Q坐标为(,﹣7+)或(,﹣7﹣).2.(2019 江苏省常州市)已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.(1)写出下列图形的宽距:⊙半径为1的圆:;⊙如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“:;(2)如图2,在平面直角坐标系中,已知点A(﹣1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.⊙若d=2,用直尺和圆规画出点C所在的区域并求它的面积(所在区域用阴影表示);⊙若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.【解析】(1)⊙半径为1的圆的宽距离为1,故答案为1.⊙如图1,正方形ABCD的边长为2,设半圆的圆心为O,点P是⊙O上一点,连接OP,PC,OC.在Rt⊙ODC中,OC===⊙OP+OC≥PC,⊙PC≤1+,⊙这个“窗户形“的宽距为1+.故答案为1+.(2)⊙如图2﹣1中,点C所在的区域是图中正方形AEBF,面积为2.⊙如图2﹣2中,当点M在y轴的右侧时,连接AM,作MT⊙x轴于T.⊙AC≤AM+CM,又⊙5≤d≤8,⊙当d=5时.AM=4,⊙AT==2,此时M(2﹣1,2),当d=8时.AM=7,⊙AT==2,此时M(2﹣1,2),⊙满足条件的点M的横坐标的范围为2﹣1≤x≤2﹣1.当点M在y轴的左侧时,满足条件的点M的横坐标的范围为﹣2+1≤x﹣2+1.考向3运动过程中的定值问题1.(2019 江苏省宿迁市)如图⊙,在钝角⊙ABC中,⊙ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将⊙BDE绕点B逆时针方向旋转α度(0≤α≤180).(1)如图⊙,当0<α<180时,连接AD、CE.求证:⊙BDA⊙⊙BEC;(2)如图⊙,直线CE、AD交于点G.在旋转过程中,⊙AGC的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)将⊙BDE从图⊙位置绕点B逆时针方向旋转180°,求点G的运动路程.【解析】(1)如图⊙中,由图⊙,⊙点D为边AB中点,点E为边BC中点,⊙DE⊙AC,⊙=,⊙=,⊙⊙DBE=⊙ABC,⊙⊙DBA=⊙EBC,⊙⊙DBA⊙⊙EBC.(2)⊙AGC的大小不发生变化,⊙AGC=30°.理由:如图⊙中,设AB交CG于点O.⊙⊙DBA⊙⊙EBC,⊙⊙DAB=⊙ECB,⊙⊙DAB+⊙AOG+⊙G=180°,⊙ECB+⊙COB+⊙ABC=180°,⊙AOG=⊙COB,⊙⊙G=⊙ABC=30°.(3)如图⊙﹣1中.设AB的中点为K,连接DK,以AC为边向右作等边⊙ACO,连接OG,OB.以O为圆心,OA为半径作⊙O,⊙⊙AGC=30°,⊙AOC=60°,⊙⊙AGC=⊙AOC,⊙点G在⊙O上运动,以B 为圆心,BD 为半径作⊙B ,当直线与⊙B 相切时,BD ⊙AD , ⊙⊙ADB =90°, ⊙BK =AK , ⊙DK =BK =AK , ⊙BD =BK , ⊙BD =DK =BK , ⊙⊙BDK 是等边三角形, ⊙⊙DBK =60°, ⊙⊙DAB =30°,⊙⊙DOG =2⊙DAB =60°, ⊙的长==,观察图象可知,点G 的运动路程是的长的两倍=.2.(2019 江苏省无锡市)如图1,在矩形ABCD 中,3BC =,动点P 从B 出发,以每秒1个单位的速度,沿射线BC 方向移动,作PAB ∆关于直线PA 的对称PAB ∆',设点P 的运动时间为()t s .(1)若AB =⊙如图2,当点B '落在AC 上时,显然PAB ∆'是直角三角形,求此时t 的值;⊙是否存在异于图2的时刻,使得PCB ∆'是直角三角形?若存在,请直接写出所有符合题意的t 的值?若不存在,请说明理由.(2)当P 点不与C 点重合时,若直线PB '与直线CD 相交于点M ,且当3t <时存在某一时刻有结论45PAM ∠=︒成立,试探究:对于3t >的任意时刻,结论“45PAM ∠=︒”是否总是成立?请说明理由.【解析】(1)⊙勾股求的易证CB P CBA'V:V,故''43B P=解得⊙1°如图,当⊙PCB’=90 °时,在⊙PCB’中采用勾股得:222(3)t t+-=,解得t=22°如图,当⊙PCB’=90 °时,在⊙PCB’中采用勾股得:222(3)t t+-=,解得t=6B'CB'CBA A BDPD33°当⊙CPB’=90 °时,易证四边形ABP’为正方形,解得(2)如图,⊙⊙PAM=45°⊙⊙2+⊙3=45°,⊙1+⊙4=45°又⊙翻折⊙⊙1=⊙2,⊙3=⊙4又⊙⊙ADM=⊙AB’M(AAS)⊙AD=AB’=AB即四边形ABCD是正方形如图,设⊙APB=xB'CA BDA⊙⊙PAB=90°-x ⊙⊙DAP=x易证⊙MDA⊙⊙B’AM (HL ) ⊙⊙BAM=⊙DAM ⊙翻折⊙⊙PAB=⊙PAB’=90°-x⊙⊙DAB’=⊙PAB’-⊙DAP=90°-2x ⊙⊙DAM=21⊙DAB’=45°-x ⊙⊙MAP=⊙DAM+⊙PAD=45°4321MB'BCB'A D PP。
中考数学重难点题型:12道几何探究题解析

中考数学重难点题型---12道几何探究题解析考点1 三角形几何探究1.如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.(1)若△ABC 是“准互余三角形”,∠C >90°,∠A =60°,则∠B =15°;(2)如图1,在Rt △ABC 中,∠ACB =90°,AC =4,BC =5.若AD 是∠BAC 的平分线,不难证明△ABD 是“准互余三角形”.试问在边BC 上是否存在点E(异于点D),使得△ABE 也是“准互余三角形”?若存在,请求出BE 的长;若不存在,请说明理由.(3)如图2,在四边形ABCD 中,AB =7,CD =12,BD ⊥CD ,∠ABD =2∠BCD ,且△ABC 是“准互余三角形”,求对角线AC 的长.解:(1)∵△ABC 是“准互余三角形”,∠C >90°,∠A =60°,∴2∠B +∠A =90°,解得∠B =15°. (2)如答图1,在Rt △ABC 中,∵∠B +∠BAC =90°,∠BAC =2∠BAD ,∴∠B +2∠BAD =90°, ∴△ABD 是“准互余三角形”. ∵△ABE 也是“准互余三角形”, ∴只有2∠B +∠BAE =90°.∵∠B +∠BAE +∠EAC =90°,∴∠CAE =∠B. ∵∠C =∠C =90°,∴△CAE ∽△CBA ,∴CA 2=CE·CB, ∴CE =165,∴BE =5-165=95.(3)如答图2,将△BCD沿BC翻折得到△BCF,∴CF=CD=12,∠BCF=∠BCD,∠CBF=∠CBD.∵∠ABD=2∠BCD,∠BCD+∠CBD=90°,∴∠ABD+∠DBC+∠CBF=180°,∴点A,B,F共线,∴∠A+∠ACF=90°,∴2∠ACB+∠CAB≠90°,∴只有2∠BAC+∠ACB=90°,∴∠FCB=∠FAC.∵∠F=∠F,∴△FCB∽△FAC,∴CF2=FB·FA,设FB=x,则有x(x+7)=122,∴x=9或x=-16(舍去),∴AF=7+9=16,在Rt△ACF中,AC=AF2+CF2=162+122=20.2.将一副三角尺按图1摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,BC=2 3 cm.(1)求GC的长;(2)如图2,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过H,C作AB的垂线,垂足分别为M,N,通过观察,猜想MD与ND的数量关系,并验证你的猜想.(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.解:(1)在Rt△ABC中,∵BC=23,∠B=60°,∴AC=BC·tan60°=6,AB=2BC=43,在Rt△ADG中,AG=ADcos30°=4,∴CG=AC-AG=6-4=2.(2)结论:DM+DN=2 3.理由:∵HM⊥AB,CN⊥AB,∴∠AMH=∠DMH=∠CNB=∠CND=90°.∵∠A+∠B=90°,∠B+∠BCN=90°,∴∠A=∠BCN,∴△AHM∽△CBN,∴AMCN=HMBN①,同理可证:△DHM∽△CDN,∴DNMH=CNDM②由①②可得AM·BN=DN·DM,∴DMAM=BNDN,∴DM+AMAM=BN+DNDN,∴ADAM=BDDN.∵AD=BD,∴AM=DN,∴DM+DN=AM+DM=AD=2 3.第2题答图(3)如答图,作GK∥DE交AB于K.在△AGK中,AG=GK=4,∠A=∠GKD=30°,作GH⊥AB于H.则AH=AG·cos30°=23,可得AK=2AH=43,此时K与B重合.∴DD′=DB=2 3.考点2四边形几何探究3.我们定义:有一组邻角相等且对角线相等的凸四边形叫做邻对等四边形.概念理解(1)我们所学过的特殊四边形中的邻对等四边形是矩形或正方形; 性质探究(2)如图1,在邻对等四边形ABCD 中,∠ABC =∠DCB ,AC =DB ,AB>CD ,求证:∠BAC 与∠CDB 互补;拓展应用(3)如图2,在四边形ABCD 中,∠BCD =2∠B ,AC =BC =5,AB =6,CD =4.在BC 的延长线上是否存在一点E ,使得四边形ABED 为邻对等四边形?如果存在,求出DE 的长;如果不存在,说明理由.(1)解:矩形或正方形.(2)证明:如答图1,延长CD 至E ,使CE =BA ,连接BE.在△ABC 和△ECB 中,⎩⎨⎧AB =EC ,∠ABC =∠ECB ,BC =CB ,∴△ABC ≌△ECB(SAS), ∴BE =CA ,∠BAC =∠E.∵AC =DB ,∴BD =BE ,∴∠BDE =∠E ,∴∠CDB +∠BDE =∠CDB +∠E =∠BAC +∠CDB =180°,即∠BAC 与∠CDB 互补.(3)解:存在这样一点E ,使得四边形ABED 为邻对等四边形,如答图2,在BC 的延长线上取一点E ,使得CE =CD =4,连接DE ,AE ,BD ,则四边形ABED 为邻对等四边形.理由如下:∵CE =CD ,∴∠CDE =∠CED. ∵∠BCD =2∠ABC ,∴∠ABC =∠DEB ,∴∠ACE =∠BCD.在△ACE 和△BCD 中,⎩⎨⎧AC =BC ,∠ACE =∠BCD ,CE =CD ,∴△ACE ≌△BCD(SAS),∴BD =AE ,四边形ABED 为邻对等四边形. ∵∠CBA =∠CAB =∠CDE =∠CED , ∴△ABC ∽△DEC , ∴AB BC =65=DE CE =DE 4,∴DE =245.4.将矩形ABCD 绕点A 顺时针旋转α(0°<α<360°),得到矩形AEFG.(1)如图,当点E 在BD 上时.求证:FD =CD ;(2)当α为何值时,GC =GB ?画出图形,并说明理由.解:(1)由旋转可得,AE =AB ,∠AEF =∠ABC =∠DAB =90°,EF =BC =AD ,∴∠AEB =∠ABE. ∵∠ABE +∠EDA =90°=∠AEB +∠DEF , ∴∠EDA =∠DEF.∵DE =ED ,∴△AED ≌△FDE(SAS), ∴DF =AE ,∵AE =AB =CD ,∴CD =DF.(2)当GB =GC 时,点G 在BC 的垂直平分线上,分两种情况讨论: ①当点G 在AD 右侧时,如答图1,取BC 的中点H ,连接GH 交AD 于M , ∵GC =GB ,∴GH ⊥BC ,∴四边形ABHM 是矩形, ∴AM =BH =12AD =12AG ,∴GM 垂直平分AD ,∴GD =GA =DA , ∴△ADG 是等边三角形,∴∠DAG =60°, ∴旋转角α=60°;②当点G 在AD 左侧时,如答图2,同理可得△ADG 是等边三角形,∴∠DAG =60°, ∴旋转角α=360°-60°=300°. 综上,α为60°或300°时,GC =GB.5.如图1,边长为4的正方形ABCD 中,点E 在AB 边上(不与点A ,B 重合),点F 在BC 边上(不与点B ,C 重合).第一次操作:将线段EF 绕点F 顺时针旋转,当点E 落在正方形上时,记为点G ; 第二次操作:将线段FG 绕点G 顺时针旋转,当点F 落在正方形上时,记为点H ; 依此操作下去…(1)图2中的△EFD 是经过两次操作后得到的,其形状为等边三角形,求此时线段EF 的长; (2)若经过三次操作可得到四边形EFGH.①请判断四边形EFGH 的形状为正方形,此时AE 与BF 的数量关系是AE =BF ;②以①中的结论为前提,设AE 的长为x ,四边形EFGH 的面积为y ,求y 与x 的函数关系式及面积y 的取值范围.解:(1)如题图2,由旋转性质可知EF =DF =DE ,则△DEF 为等边三角形. 在Rt △ADE 和Rt △CDF 中,⎩⎨⎧AD =CD ,DE =DF ,∴Rt △ADE ≌Rt △CDF(HL).∴AE =CF. 设AE =CF =x ,则BE =BF =4-x ∴△BEF 为等腰直角三角形.∴DE =DF =EF =2(4-x).在Rt △ADE 中,由勾股定理得AE 2+AD 2=DE 2,即x 2+42=[2(4-x)]2, 解得x 1=8-43,x 2=8+43(舍去). ∴EF =2(4-x)=46-4 2.△DEF 的形状为等边三角形,EF 的长为46-4 2.第5题答图(2)①四边形EFGH 的形状为正方形,此时AE =BF.理由如下:依题意画出图形,如答图所示,连接EG ,FH ,作HN ⊥BC 于N ,GM ⊥AB 于M. 由旋转性质可知,EF =FG =GH =HE , ∴四边形EFGH 是菱形, 由△EGM ≌△FHN ,可知EG =FH ,∴四边形EFGH 的形状为正方形,∴∠HEF =90°. ∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3. ∵∠3+∠4=90°,∠2+∠3=90°,∴∠2=∠4.在△AEH 和△BFE 中,⎩⎨⎧∠1=∠3,EH =EF ,∠2=∠4,∴△AEH ≌△BFE(ASA),∴AE =BF.②利用①中结论,易证△AEH ,△BFE ,△CGF ,△DHG 均为全等三角形, ∴BF =CG =DH =AE =x ,AH =BE =CF =DG =4-x.∴y =S 正方形ABCD -4S △AEH =4×4-4×12·x·(4-x)=2x 2-8x +16,∴y =2x 2-8x +16(0<x <4).∵y =2x 2-8x +16=2(x -2)2+8,∴当x =2时,y 取得最小值8;当x =0或4时,y =16.∴y的取值范围为8≤y<16.6.提出问题如图,已知在矩形ABCD中,AB=2,BC=3,点P是线段AD边上的一动点(不与端点A,D重合),连接PC,过点P作PE⊥PC交AB于点E,在点P的运动过程中,图中各角和线段之间是否存在某种关系和规律?特殊求解当点E为AB的中点,且AP>AE时,求证:PE=PC.深入探究当点P在AD上运动时,对应的点E也随之在AB上运动,求整个运动过程中BE的取值范围.解:特殊求解∵PE⊥PC,∴∠APE+∠DPC=90°.∵∠D=90°,∴∠DPC+∠DCP=90°.∴∠APE=∠DCP.∵∠A=∠D=90°,∴△APE∽△DCP,∴APDC=AEDP.设AP=x,则有DP=3-x.而AE=BE=1,∴x(3-x)=2×1,解得x1=2,x2=1.∵AP>AE,∴AP=2,AE=PD=1,∴△APE≌△DCP,∴PE=PC.深入探究设AP=x,AE=y,由AP·DP=AE·DC,可得x(3-x)=2y.∴y=12x(3-x)=-12x2+32x=-12(x-32)2+98.∴在0<x<3范围内,当x =32时,y 最大=98.∵当AE =y 取得最大值时,BE 取得最小值为2-98=78,∴BE 的取值范围为78≤BE<2.7.已知Rt △OAB ,∠OAB =90°,∠ABO =30°,斜边OB =4,将Rt △OAB 绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC =60°;(2)如图1,连接AC ,作OP ⊥AC ,垂足为P ,求OP 的长度;(3)如图2,点M ,N 同时从点O 出发,在△OCB 边上运动,M 沿O→C→B 路径匀速运动,N 沿O→B→C 路径匀速运动,当两点相遇时运动停止,已知点M 的运动速度为1.5单位/秒,点N 的运动速度为1单位/秒,设运动时间为x 秒,△OMN 的面积为y ,求当x 为何值时y 取得最大值.最大值为多少?解:(1)由旋转性质可知OB =OC ,∠BOC =60°, ∴△OBC 是等边三角形,∴∠OBC =60°.第7题答图1(2)如答图1中, ∵OB =4,∠ABO =30°, ∴OA =12OB =2,AB =3OA =23,∴S △AOC =12·OA·AB=12×2×23=2 3.∵△BOC 是等边三角形,∴∠OBC =60°,∠ABC =∠ABO +∠OBC =90°, ∴AC =AB 2+BC 2=2r(32+42)=27,∴OP =2S △AOC AC =4327=2217.第7题答图2(3)①当0<x≤83时,M 在OC 上运动,N 在OB 上运动,此时过点N 作NE ⊥OC 且交OC 于点E.如答图2,则NE =ON·sin60°=32x ,∴S △OMN =12·OM·NE=12×1.5x×32x ,∴y =338x 2,∴当x =83时,y 有最大值,最大值为833.第7题答图3②当83<x≤4时,M 在BC 上运动,N 在OB 上运动.如答图3,作MH ⊥OB 于H.则BM =8-1.5x ,MH =BM·sin60°=32(8-1.5x),∴y =12×ON×MH=-338x 2+23x.当x =83时,y 取得最大值,最大值为833.第7题答图4③当4<x≤4.8时,M,N都在BC上运动,作OG⊥BC于G.如答图4,MN=12-2.5x,OG=AB=23,∴y=12·MN·OG=123-532x,当x=4时,y有最大值,最大值为2 3.综上所述,y有最大值,最大值为83 3.8.在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E 的位置随着点P的位置变化而变化.(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是PB=EC,CE与AD 的位置关系是CE⊥AD;(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);(3)如图4,当点P在线段BD的延长线上时,连接BE.若AB=23,BE=219,求四边形ADPE的面积.解:(1)结论:PB=EC,CE⊥AD.理由:如答图1中,连接AC.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.∵△APE是等边三角形,∴AB=AC,AP=AE,∠BAC=∠PAE=60°,∴△BAP≌△CAE,∴BP=CE,∠ABP=∠ACE=30°,延长CE交AD于H,∵∠CAH=60°,∴∠CAH+∠ACH=90°,∴∠AHC=90°,即CE⊥AD.第8题答图2(2)结论仍然成立.理由:如答图2,连接AC交BD于O,设CE交AD于H.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°.∵△APE是等边三角形,∴AB=AC,AP=AE,∠BAC=∠PAE=60°,∴△BAP≌△CAE,∴BP=CE,∠ABP=∠ACE=30°,∵∠CAH=60°,∴∠CAH+∠ACH=90°,∴∠AHC=90°,即CE⊥AD.(3)如答图3,连接AC 交BD 于点O ,连接CE 交AD 于点H , 由(2)可知EC ⊥AD ,CE =BP , 在菱形ABCD 中,AD ∥BC , ∴EC ⊥BC.∵BC =AB =23,BE =219, ∴在Rt △BCE 中,EC =2r(192-2r(3)2)=8,∴BP =CE =8.∵AC 与BD 是菱形的对角线, ∴∠ABD =12∠ABC =30°,AC ⊥BD ,∴BD =2BO =2AB·cos30°=6,∴OA =12AB =3,DP =BP -BD =8-6=2,∴OP =OD +DP =5,在Rt △AOP 中,AP =AO 2+OP 2=27, ∴S 四边形ADPE =S △ADP +S △AEP =12DP·AO+34·AP 2=12×2×3+34×(27)2=8 3.考点3 三角形、四边形混合几何探究9.我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF ,BE 是△ABC 的中线,AF ⊥BE ,垂足为P ,像△ABC 这样的三角形均称为“中垂三角形”,设BC =a ,AC =b ,AB =c.特例探索(1)如图1,当∠ABE =45°,c =22时,a =____25____,b =____25____. 如图2,当∠ABE =30°,c =4时,a =____213____,b =____27____. 归纳证明(2)请你观察(1)中的计算结果,猜想a 2,b 2,c 2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.拓展应用(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=25,AB=3,求AF的长.解:(1)∵AF⊥BE,∠ABE=45°,∴AP=BP=22AB=2.∵AF,BE是△ABC的中线,∴EF∥AB,EF=12AB=2,∴∠PFE=∠PEF=45°,∴PE=PF=1.在Rt△FPB和Rt△PEA中,AE=BF=12+22=5,∴AC=BC=25,∴a=b=2 5.如答图1,连接EF.同理可得EF=12×4=2.∵EF∥AB,∴△PEF∽△PBA,∴PFAP=PEPB=EFAB=12.在Rt△ABP中,AB=4,∠ABP=30°,∴AP=2,PB=23,∴PF=1,PE= 3.在Rt△APE和Rt△BPF中,AE=7,BF=13,∴a=213,b=27.(2)猜想:a2+b2=5c2,证明如下:如答图2,连接EF.设∠ABP=α,∴AP=csinα,PB=ccosα,由(1)同理可得PF=12PA=csinα2,PE=12PB=ccosα2, ∴AE 2=AP 2+PE 2=c 2sin 2α+c 2cos 2α4,BF 2=PB 2+PF 2=c 2cos 2α+c 2sin 2α4,∴(b 2)2=c 2sin 2α+c 2cos 2α4,(a 2)2=c 2sin 2α4+c 2cos 2α,∴a 24+b 24=c 2sin 2α4+c 2cos 2α+c 2sin 2α+c 2cos 2α4, ∴a 2+b 2=5c 2.(3)如答图3,连接AC ,EF 交于点H ,AC 与BE 交于点Q ,设BE 与AF 的交点为P. ∵点E ,G 分别是AD ,CD 的中点,∴EG ∥AC. ∵BE ⊥EG ,∴BE ⊥AC.∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC =25,∴∠EAH =∠FCH. ∵E ,F 分别是AD ,BC 的中点, ∴AE =12AD ,BF =12BC ,∴AE =BF =CF =12AD = 5.∵AE ∥BF ,∴四边形ABFE 是平行四边形, ∴EF =AB =3,AP =PF.在△AEH 和△CFH 中,⎩⎨⎧∠EAH =∠FCH ,∠AHE =∠FHC ,AE =CF ,∴△AEH ≌△CFH ,∴EH =FH ,∴EP ,AH 分别是△AFE 的中线,由(2)的结论得AF 2+EF 2=5AE 2,或连接F 与AB 的中点M ,证MF 垂直BP ,构造出“中垂三角形”,由AB =3,BC =12AD =5及(2)中的结论,直接可求AF.10.我们定义:如图1,在△ABC 中,把AB 绕点A 顺时针旋转α(0°<α<180°)得到AB′,把AC 绕点A 逆时针旋转β得到AC′,连接B′C′.当α+β=180°时,我们称△AB′C′是△ABC 的“旋补三角形”,△AB′C′边B′C′上的中线AD 叫做△ABC 的“旋补中线”,点A 叫做“旋补中心”.特例感知(1)在图2,图3中,△AB′C′是△ABC 的“旋补三角形”,AD 是△ABC 的“旋补中线”. ①如图2,当△ABC 为等边三角形时,AD 与BC 的数量关系为AD =12BC ;②如图3,当∠BAC =90°,BC =8时,则AD 长为4. 猜想论证(2)在图1中,当△ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明. 拓展应用(3)如图4,在四边形ABCD ,∠C =90°,∠D =150°,BC =12,CD =23,DA =6.在四边形内部是否存在点P ,使△PDC 是△PAB 的“旋补三角形”?若存在,给予证明,并求△PAB 的“旋补中线”长;若不存在,说明理由.图1 图2 图3 图4解:(1)①∵△ABC 是等边三角形,∴AB =BC =AC =AB′=AC′.∵DB′=DC′, ∴AD ⊥B′C′.∵∠BAC =60°,∠BAC +∠B′AC′=180°, ∴∠B′AC′=120°,∴∠B′=∠C′=30°, ∴AD =12AB′=12BC.②∵∠BAC =90°,∠BAC +∠B′AC′=180°,∴∠B′AC′=∠BAC=90°.∵AB=AB′,AC=AC′,∴△BAC≌△B′AC′,∴BC=B′C′.∵B′D=DC′,∴AD=12B′C′=12BC=4.(2)结论:AD=12 BC.证明如下:如答图1,延长AD到M,使得AD=DM,连接B′M,C′M.∵B′D=DC′,AD=DM,∴四边形AC′MB′是平行四边形,∴AC′=B′M=AC.第10题答图1∵∠BAC+∠B′AC′=180°,∠B′AC′+∠AB′M=180°,∴∠BAC=∠MB′A.∵AB=AB′,∴△BAC≌△AB′M,∴BC=AM,∴AD=12 BC.(3)存在.理由:如答图2,延长AD交BC的延长线于M,作BE⊥AD于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA,PD,PC,作△PCD的中线PN,第10题答图2连接DF交PC于O.∵∠ADC=150°,∴∠MDC=30°.在Rt△DCM中,CD=23,∠DCM=90°,∠MDC=30°,∴CM=2,DM=4,∠M=60°.在Rt△BEM中,∠BEM=90°,BM=14,∠MBE=30°,∴EM=12BM=7,∴DE=EM-DM=3.∵AD=6,∴AE=DE.∵BE⊥AD,∴PA=PD,PB=PC.在Rt△CDF中,CD=23,CF=6,∴tan∠CDF=3,∴∠CDF=60°=∠CPF,易证△FCP≌△CFD,∴CD=PF.∵CD∥PF.∴四边形CDPF是矩形,∴∠CDP=90°,∴∠ADP=∠ADC-∠CDP=60°,∴△ADP是等边三角形,∴∠ADP=60°.∵∠BPF=∠CPF=60°,∴∠BPC=120°,∴∠APD+∠BPC=180°,∴△PDC是△PAB的“旋补三角形”.在Rt△PDN中,∠PDN=90°,PD=AD=6,DN=3,∴PN=DN2+PD2=r(32+62)=39.考点4 多边形几何探究11.【图形定义】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”;【探究证明】(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形.(2)如图2,求证:∠OAB=∠OAE′;【归纳猜想】(3)图1、图2中的“叠弦角”的度数分别为15°,24°;(4)图n中,“叠弦三角形”是等边三角形(填“是”或“不是”);(5)图n中,“叠弦角”的度数为60°-180°n.(用含n的式子表示)解:(1)∵四边形ABCD是正方形,由旋转知,AD=AD′,∠D=∠D′=90°,∠DAD′=∠OAP=60°,∴∠DAP=∠D′AO,∴△APD≌△AOD′(ASA),∴AP=AO.∵∠OAP=60°,∴△AOP是等边三角形;第11题答图(2)如答图,作AM⊥DE于M,作AN⊥CB于N.∵五边形ABCDE是正五边形,由旋转知,AE=AE′,∠E=∠E′=108°,∠EAE′=∠OAP=60°,∴∠EAP=∠E′AO.在Rt△AEM和Rt△ABN中,∠AEM=∠ABN=72°,AE=AB,∴Rt△AEM≌Rt△ABN (AAS),∴∠EAM =∠BAN ,AM =AN.在Rt △APM 和Rt △AON 中,AP =AO ,AM =AN , ∴Rt △APM ≌Rt △AON (HL), ∴∠PAM =∠OAN ,∴∠PAE =∠OAB, ∴∠OAE′=∠OAB.(3)由(1)知,△APD ≌△AOD′, ∴∠DAP =∠D′AO.在Rt △AD′O 和Rt △ABO 中,⎩⎨⎧AD′=AB ,AO =AO ,∴Rt △AD′O≌Rt △ABO(HL), ∴∠D′AO=∠BAO.由旋转得,∠DAD′=60°.∵∠DAB =90°, ∴∠D′AB=∠DAB -∠DAD′=30°, ∴∠D′AO=12∠D′AB=15°,∵题图2的多边形是正五边形, ∴∠EAB =5-2×180°5=108°,∴∠E′AB=∠EAB -∠EAE′=108°-60°=48°, ∴同理可得,∠E′AO=12∠E′AB=24°.(4)是(5)同(3)的方法得,∠OAB =[(n -2)×180°÷n-60°]÷2=60°-180°n.考点5 圆形几何探究12.如图,在半径为3 cm 的⊙O 中,A ,B ,C 三点在圆上,∠BAC =75°.点P 从点B 开始以π5cm/s 的速度在劣弧BC 上运动,且运动时间为t s ,∠AOB =90°,∠BOP =n°.(1)求n与t之间的函数关系式,并求t的取值范围;(2)试探究:当点P运动多少秒时,①在BP,PC,CA,AB四条线段中有两条相互平行?②以P,B,A,C四点中的三点为顶点的三角形是等腰三角形?解:(1)∵∠BOP=n°,∴π5t=3πn180,n=12t.当n=150时,150=12t,t=12.5.∴t的取值范围为0≤t≤12.5.(2)①∠BOP=n°,n=12t.如答图1,当BP∥AC时,t=5.理由:∵∠PBA=180°-75°=105°,∠OBA=45°,∴∠OBP=60°.∵OB=OP,∴∠BOP=60°,∴60=12t,t=5.如答图2,当PC∥AB时,t=10.理由:易得∠PBA=∠BAC=75°,∴∠PBO=∠BPO=30°,∴∠BOP=120°,∴120=12t,t=10.综上所述,当点P的运动时间为5 s时,BP∥AC.当点P的运动时间为10 s时,PC∥AB.②在△ABP中,以AB为腰时(如答图3),∠BPA=∠BAP=45°,∠BOP=90°,∴t=7.5. 以AB为底边时(如答图4),∠BPA=45°,∠BAP=67.5°,∠BOP=2×67.5°=135°,∴t=11.25.如答图5,在△APC中,易得∠AOC=120°,∴∠APC=60°,△APC是等边三角形.∴∠AOP=120°,∴∠BOP=30°,t=2.5.如答图6,在△BPC中,∠BPC=105°,只有BP=PC这种情况.此时点P是弧BC的中心,∴∠BOP=75°,t=6.25.综上所述,当点P的运动时间为7.5 s或11.25 s时,△ABP为等腰三角形;当点P的运动时间为2.5 s时,△APC为等边三角形;当点P的运动时间为6.25 s时,△BPC为等腰三角形.。
《几何综合探究问题》(共48题)中考专项配套练习(重庆专用)

5年(2016-2020)中考1年模拟数学试题分项详解(重庆专用)专题13 几何综合探究问题(共48题)一.解析题(共10小题)1.(2020•重庆)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.(1)求证:CF=√22AD;(2)如图2所示,在点D运动的过程中,当BD=2CD时,分别延长CF,BA,相交于点G,猜想AG 与BC存在的数量关系,并证明你猜想的结论;(3)在点D运动的过程中,在线段AD上存在一点P,使P A+PB+PC的值最小.当P A+PB+PC的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.2.(2020•重庆)△ABC为等边三角形,AB=8,AD⊥BC于点D,E为线段AD上一点,AE=2√3.以AE 为边在直线AD右侧构造等边三角形AEF,连接CE,N为CE的中点.(1)如图1,EF与AC交于点G,连接NG,求线段NG的长;(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接DN,MN.当30°<α<120°时,猜想∠DNM的大小是否为定值,并证明你的结论;(3)连接BN,在△AEF绕点A逆时针旋转过程中,当线段BN最大时,请直接写出△ADN的面五年中考真题积.3.(2019•重庆)如图,在平行四边形ABCD中,点E在边BC上,连接AE,EM⊥AE,垂足为E,交CD 于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.(1)若DP=2AP=4,CP=√17,CD=5,求△ACD的面积.(2)若AE=BN,AN=CE,求证:AD=√2CM+2CE.4.(2019•重庆)在▱ABCD中,BE平分∠ABC交AD于点E.(1)如图1,若∠D=30°,AB=√6,求△ABE的面积;(2)如图2,过点A作AF⊥DC,交DC的延长线于点F,分别交BE,BC于点G,H,且AB=AF.求证:ED﹣AG=FC.5.(2018•重庆)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=√2CG.6.(2018•重庆)如图,在▱ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.(1)若BC=12√2,AB=13,求AF的长;(2)求证:EB=EH.7.(2017•重庆)在△ABM中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.(1)如图1,若AB=3√2,BC=5,求AC的长;(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.8.(2017•重庆)如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.(1)如图1,若AB=4√2,BE=5,求AE的长;(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.9.(2016•重庆)在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.(1)若AB =2√2,求BC 的长;(2)如图1,当点G 在AC 上时,求证:BD =12CG ;(3)如图2,当点G 在AC 的垂直平分线上时,直接写出ABCG 的值.10.(2016•重庆)已知△ABC 是等腰直角三角形,∠BAC =90°,CD =12BC ,DE ⊥CE ,DE =CE ,连接AE ,点M 是AE 的中点.(1)如图1,若点D 在BC 边上,连接CM ,当AB =4时,求CM 的长;(2)如图2,若点D 在△ABC 的内部,连接BD ,点N 是BD 中点,连接MN ,NE ,求证:MN ⊥AE ; (3)如图3,将图2中的△CDE 绕点C 逆时针旋转,使∠BCD =30°,连接BD ,点N 是BD 中点,连接MN ,探索MNAC 的值并直接写出结果.一.解答题(共38小题)1.(2020•渝中区校级二模)如图,CA =CB ,∠ACB =90°,点D 为AB 的中点,连接CD ;点E 为CD 的中点,EF =EG =EC ,且∠FEG =90°;点O 为CB 的中点,直线GO 与直线CF 交于点N .(1)如图1,若∠FCD =30°,OC =√2,求CF 的长;(2)连接BG 并延长至点M ,使BG =MG ,连接CM .①如图2,若NG ⊥MB ,求证:AB =√10CM ;②如图3,当点G 、F 、B 共线时,BM 交AC 于点H ,AH =14AC ,请直接写出FCMH 的值.一年模拟新题2.(2020•渝中区二模)如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,E为线段CD上一点(不含端点),连接AE,设F为AE的中点,作CG⊥CF交直线AB于点G.(1)猜想:线段AG、BC、EC之间有何等量关系?并加以证明;(2)如果将题设中的条件“E为线段CD上一点(不含端点)”改变为“E为直线CD上任意一点”,试探究发现线段AG、BC、EC之间有怎样的等量关系,请直接写出你的结论,不用证明.3.(2020•沙坪坝区校级一模)在△ABC中,AE⊥CD且AE=CD,∠CAE+2∠BAE=90°.(1)如图1,若△ACE为等边三角形,CD=2√3,求AB的长;(2)如图2,作EG⊥AB,求证:AD=√2BE;(3)如图3,作EG⊥AB,当点D与点G重合时,连接BF,请直接写出BF与EC之间的数量关系.4.(2020•南岸区模拟)如图,在△ABC中,∠BAC=90°,AB=AC=6,AD⊥BC于点D.点G是射线AD上一点.(1)若GE⊥GF,点E,F分别在AB,AC上,当点G与点D重合时,如图①所示,容易证明AE+AF=√2AD.当点G在线段AD外时,如图②所示,点E与点B重合,猜想并证明AE,AF与AG存在的数量关系.(2)当点G在线段AD上时,AG+BG+CG的值是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.5.(2020•南岸区校级模拟)△ABC与△ADE都是等边三角形,DE与AC交于点P,点P恰为DE的中点,延长AD交BC于点F,连结BD、CD,取CD的中点Q,连结PQ.求证:PQ=12BD.(1)如图1,理清思路,完成解答:本题证明的思路可以用下列框图表示:根据上述思路,请你完整地书写本题的证明过程;(2)如图2,特殊位置,求线段长:若点P为AC的中点,连接PF,已知PQ=√3,求PF的长.(3)知识迁移,探索新知:若点P是线段AC上任意一点,直接写出PF与CD的数量关系.6.(2020•九龙坡区校级模拟)【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF =BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F 在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.7.(2019•渝中区校级一模)已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF,CF.(1)如图1,点D在AC上,请你判断此时线段DF,CF的关系,并证明你的判断;(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45时,若AD=DE=2,AB=6,求此时线段CF的长.8.(2019•重庆模拟)一节数学课后,老师布置了一道课后练习:△ABC是等边三角形,点D是线段BC上的点,点E为△ABC的外角平分线上一点,且∠ADE=60°,如图①,当点D是线段BC上(除B,C 外)任意一点时,求证:AD=DE(1)理清思路,完成解答本题证明思路可以用下列框图表:根据上述思路,请你完整地书写本题的证明过程;(2)特殊位置,计算求解当点D为BC的中点时,等边△ABC的边长为6,求出DE的长;(3)知识迁移,探索新知当点D在线段BC的延长线上,且满足CD=BC时,若AB=2,请直接写出△ADE的面积(不必写解答过程)9.(2020•南岸区校级模拟)如图1,直角三角形△ABC中,∠ACB=90°,AC=4,∠A=60°,O为BC中点,将△ABC 绕O 点旋转180°得到△DCB .一动点P 从A 出发,以每秒1的速度沿A →B →D 的路线匀速运动,过点P 作直线PM ⊥AC 交折线段A ﹣C ﹣D 于M .(1)如图2,当点P 运动2秒时,另一动点Q 也从A 出发沿A →B →D 的路线运动,且在AB 上以每秒1的速度匀速运动,在BD 上以每秒2的速度匀速运动,过Q 作直线QN ∥PM 交折线段A ﹣C ﹣D 于N ,设点Q 的运动时间为t 秒,(0<t <10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.(2)如图3,当点P 开始运动的同时,另一动点R 从B 处出发沿B →C →D 的路线运动,且在BC 上以每秒√32的速度匀速运动,在CD 上以每秒2的速度匀速运动,是否存在这样的P 、R .使△BPR 为等腰三角形?若存在,直接写出点P 运动的时间m 的值,若不存在请说明理由.10.(2019秋•沙坪坝区校级期末)如图,在菱形ABCD 中,∠ABC =60°,连接AC ,动点P 从A 点出发沿射线AB 方向运动,同时动点Q 从B 点出发以与P 点相同的速度沿射线BC 方向运动,连接AQ ,CP ,直线AQ 与直线CP 交于点H .(1)如图1,当P ,Q 两点分别在线段AB 和线段BC 上时,直接写出∠CHQ 的度数;(2)如图2,当P ,Q 两点分别运动到线段AB 和线段BC 的延长线上时,试问(1)问中的结论是否成立:若成立请说明理由,若不成立,请求出∠CHQ 的度数;(3)如图3,在(2)问的前提下,连接DH ,过点D 作DE ⊥PH 交PH 延长线于点E .求证:AH ﹣CE =12DH .11.(2020春•沙坪坝区校级月考)如图,正方形ABCD 中,对角线AC ,BD 交于点O ,点E ,点F 分别在线段OB ,线段AB 上,且AF =OE ,连接AE 交OF 于G ,连接DG 交AO 于H .(1)如图1,若点E为线段BO中点,AE=√5,求BF的长;(2)如图2,若AE平分∠BAC,求证:FG=HG;(3)如图3,点E在线段BO(含端点)上运动,连接HE,当线段HE长度取得最大值时,直接写出cos ∠HDO的值.12.(2020•沙坪坝区自主招生)在▱ABCD中,AF平分∠BAD交BC于点F,∠BAC=90°,点E是对角线AC上的点,连结BE.(1)如图1.若AB=AE,BF=3,求BE的长;(2)如图2,若AB=AE,点G是BE的中点,∠F AG=∠BFG,求证:AB=√10FG;(3)如图3,以点E为直角顶点,在BE的右下方作等腰直角△BEM,若点E从点A出发,沿AC运动到点C停止,设在点E运动过程中,BM的中点N经过的路径长为m,AC的长为n,请直接写出nm的值.13.(2020•巴南区自主招生)已知,在矩形ABCD中,AB=2,点E在边BC上,且AE⊥DE,AE=DE,点F是BC的延长线上一点,AF与DE相交于点G,DH⊥AF,垂足为H,DH的延长线与BC相交于点K.(1)如图1,求AD的长;(2)如图2,连接KG,求证:AG=DK+KG;(3)如图3,设△ADM与△ADH关于AD对称,点N、Q分别是MA、MD的中点,请直接写出BN+NQ 的最大值.14.(2020•南岸区自主招生)如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM ⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.(1)求证:AE=√2NE+ME;(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.猜想CH与FH存在的数量关系,并证明你的结论;(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.15.(2020•北碚区自主招生)如图1,在正方形ABCD中,对角线AC、BD相交于点O,点E为线段BO上一点,连接CE,将CE绕点C顺时针旋转90°得到CF,连接EF交CD于点G.(1)若AB=4,BE=√2,求△CEF的面积.(2)如图2,线段FE的延长线交AB于点H,过点F作FM⊥CD于点M,求证:BH+MG=√22BE;(3)如图3,点E为射线OD上一点,线段FE的延长线交直线CD于点G,交直线AB于点H,过点F 作FM垂直直线CD于点M,请直接写出线段BH、MG、BE的数量关系.16.(2019秋•九龙坡区校级期末)已知,在平行四边形ABCD中,∠D=60°,点F,G在边BC上,且AF=AG.(1)如图1,若AG平分∠F AC,∠AFC=5∠BAF,且AF=4,求线段AC的长;(2)如图2,点E在边AB上,且BE=EF,证明:AE=BG;(3)在(2)的条件下,连接CE(如图3),若∠AEC=∠ACD,你能得到AD,FG,BE怎样的数量关系?试证明你的猜想.17.(2020春•沙坪坝区校级月考)如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,到达A点停止运动;同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,到达D点停止运动,设点E移动的时间为t(秒).(1)当t=1时,求四边形BCFE的面积;(2)设四边形BCFE的面积为S,求S与t之间的关系式,并写出t的取值范围;(3)若F点到达D点后立即返回,并在线段CD上往返运动,当E点到达A点时它们同时停止运动,求当t为何值时,以E,F,D三点为顶点的三角形是等腰三角形,并求出此的等腰三角形的面积S△EDF.18.(2020春•沙坪坝区校级月考)已知,在▱ABCD中,AB⊥BD,AB=BD,E为射线BC上一点,连接AE 交BD于点F.(1)如图1,若点E与点C重合,且AF=2√5,求AD的长;(2)如图2,当点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH.求证:AF=DH+FH;(3)如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G,M为AG的中点,点N在BC边上且BN=1,已知AB=4√2,请直接写出MN的最小值.19.(2020春•沙坪坝区校级月考)已知:在△ABC中,∠C=90°,BC=AC.(1)如图1,若点D、E分别在BC、AC边上,且CD=CE,连接AD、BE,点O、M、N分别是AB、AD、BE的中点.求证:△OMN是等腰直⻆三角形;(2)将图1中△CDE绕着点C顺时针旋转90°如图2,O、M、N分别为AB、AD、BE中点,则(1)中的结论是否成⽴,并说明理由;(3)如图3,将图1中△CDE绕着点C顺时针旋转,记旋转⻆为α(0<α<360°),O、M、N分别为AB、AD、BE中点,当MN=√10,请求出四边形ABED的⽴积.20.(2019秋•九龙坡区期末)(1)如图1,四边形EFGH中,FE=EH,∠EFG+∠EHG=180°,点A,B分别在边FG,GH上,且∠AEB=12∠FEH,求证:AB=AF+BH.(2)如图2,四边形EFGH中,FE=EH,点M在边EH上,连接FM,EN平分∠FEH交FM于点N,∠ENM=α,∠FGH=180°﹣2α,连接GN,HN.①找出图中与NH相等的线段,并加以证明;②求∠NGH的度数(用含α的式子表示).21.(2019秋•吉州区期末)【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)直接写出AM、AD、MC三条线段的数量关系:;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.22.(2019春•江北区校级期中)如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,点A (﹣2,0),线段AB=8,线段AD=6,且∠BAD=60°,AD与y的交点记为E,连接BE.(1)求▱ABCD的面积.(2)如图2,在线段BE上有两个动点G、K(G在K点上方),且KG=√3,点F为BC中点,点P为线段CD上一动点,当FG+GK+KP的值最小时,求出此时P点的坐标;此时在y轴上找一点H,x轴上线一点M,使得PH+HM−√22AM取得最小值,请求出PH+HM−√22AM的最小值.(3)如图3,将△AOE沿射线EB平移到△A′O'E'的位置,线段E′A′的中点N落在x轴上,此时再将△A′O'E'绕平面内某点W旋转90°,旋转后的三角形记为△A''O''E'',若△A''O''E'恰好只有两个顶点同时落在直线BC和直线BE上,且△A''E''B''的边均不在直线BC或直线BE上,请求出满足条件的W的坐标.23.(2019秋•北碚区校级月考)已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.(1)如图①,若tan∠ADM=34,MN=3,求BC的长;(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.24.(2019秋•沙坪坝区校级月考)如图,在平行四边形ABCD中,过A作AE⊥CD于点E,点G,F分别为AD,BC上一点,连接CG交AE于点H,连接AF,AF=AH,∠GCF=∠F AE=45°.(1)若tan∠DAE=23,GH=4,求AF的长;(2)求证:AG+√2GH=GC.25.(2020春•北碚区校级期末)已知在△ABC和△ADE中,∠ACB+∠AED=180°,CA=CB,EA=ED,AB=3.(1)如图1,若∠ACB=90°,B、A、D三点共线,连接CE:①若CE=5√22,求BD长度;②如图2,若点F是BD中点,连接CF,EF,求证:CE=√2EF;(2)如图3,若点D在线段BC上,且∠CAB=2∠EAD,试直接写出△AED面积的最小值.26.(2020春•重庆期末)已知三角形ABC中,∠ACB=90°,点D(0,﹣4),M(4,﹣4).(1)如图1,若点C与点O重合,A(﹣2,2)、B(4,4),求△ABC的面积;(2)如图2,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,若∠AOG=55°,求∠CEF的度数;(3)如图3,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,N为AC上一点,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,∠NEC+∠CEF=180°,求证:∠NEF=2∠AOG.27.(2020春•沙坪坝区校级月考)已知Rt△ABC中,∠ACB=90°,以AC为斜边作Rt△AEC,∠AEC=90°,AB与CE相交于点D.(1)如图1,AB平分∠CAE,BD=4,CD=5,求AC;(2)如图2,若AC=BC,点F在EA的延长线上,连接FB、FC,FB与CE相交于点G,且∠EAD=∠ACF,求证:AF=2GE;(3)如图3,在(2)的条件下,CE的中垂线与AB相交于点Q,连接EQ,若∠DEQ+2∠ACE=90°,请直接写出线段FC、ED、EQ的关系.28.(2020春•沙坪坝区校级月考)已知等腰直角△ABC中,AB=AC,∠BAC=90°,点D是AC边上一点,以BD为边作等腰直角△BDE,其中BD=BE,∠DBE=90°,边AB与DE交于点F,点G是BC上一点.(1)如图1,若DG⊥DE,连接FG.①若∠ABD=30°,DE=√6+√2,求BF的长度;②求证:DG=EF﹣FG;(2)如图2,若DG⊥BD,EP⊥BE交BA的延长线于点P,连接PG,请猜想线段PG,DG,PE之间的数量关系,并证明.29.(2020春•沙坪坝区校级月考)如图,在等边△ABC中,延长AB至点D,延长AC交BD的中垂线于点E,连接BE,DE.(1)如图1,若DE=3√10,BC=2√3,求CE的长;(2)如图2,连接CD交BE于点M,在CE上取一点F,连接DF交BE于点N,且DF=CD,求证:AB=12EF;(3)在(2)的条件下,若∠AED=45°,直接写出线段BD,EF,ED的等量关系.30.(2020春•沙坪坝区校级月考)在△ABC中,AC=BC,点G是直线BC上一点,CF⊥AG,垂足为点E,BF⊥CF于点F,点D为AB的中点,连接DF.(1)如图1,如果∠ACB=90°,且G在CB边上,设CF交AB于点R,且E为CR的中点,若CG=1,求线段BG的长;(2)如图2,如果∠ACB=90°,且G在CB边上,求证:EF=√2DF;(3)如图3,如果∠ACB=60°,且G在CB的延长线上,∠BAG=15°,请探究线段EF、BD之间的数量关系,并直接写出你的结论.31.(2020春•沙坪坝区校级月考)如图所示,△ABC为等边三角形,点D,点E分别在CA,CB的延长线上,连接BD,DE,DB=DE.(1)如图1,若CA:AD=3:7,BE=4,求EC的长;(2)如图2,点F在AC上,连接BE,∠DBF=60°,连接EF,①求证:BF+EF=BD;②如图3,若∠BDE=30°,直接写出EFBF的值.32.(2020春•沙坪坝区校级月考)在△ABC,△CDE中,∠BAC=∠DEC=90°,连接BD,F为BD中点,连接AF,EF.(1)如图1,若A,C,E三点在同一直线上,∠ABC=∠EDC=45°,已知AB=3,DE=5,求线段AF的长;(2)如图2,若∠ABC=∠EDC=45°,求证:△AEF为等腰直角三角形;(3)如图3,若∠ABC=∠EDC=30°,请判断△AEF的形状,并说明理由.33.(2019秋•渝中区校级期末)如图,在△ABC中,∠ABC=30°,以AC为边作等边△ACD,连接BD.(1)如图1,若∠ACB=90°,AB=4,求△BCD的面积;(2)如图2,若∠ACB<90°,点E为BD中点,连接AE、CE,且AE⊥CE,延长BC至点F,连接AF,使得∠F=30°,求证:AF=CE+√3AE.34.(2020春•南岸区期末)把△ABC绕着点A逆时针旋转α,得到△ADE.(1)如图1,当点B恰好在ED的延长线上时,若α=60°,求∠ABC的度数;(2)如图2,当点C恰好在ED的延长线上时,求证:CA平分∠BCE;(3)如图3,连接CD,如果DE=DC,连接EC与AB的延长线交于点F,直接写出∠F的度数(用含α的式子表示).35.(2020春•渝中区期末)如图,在正方形ABCD中,E为CD边上一点,以DE为边向外作正方形DEFG,将正方形DEFG绕点D顺时针旋转,连接AG.(1)如图1,若AD=2√3、DE=2,当∠ADG=150°时,求AG的长;(2)如图2,正方形DEFG绕点D旋转的过程中,取AG的中点M,连接DM、CE,猜想:DM和CE 之间有何等量关系?并利用图2加以证明.36.(2020春•沙坪坝区校级月考)在菱形ABCD中,∠ABC=60°,点M是对角线BD上一动点,将线段CM绕点C顺时针旋转120°到CN,连接DN,连接NM并延长,分别交AB、CD于点P、Q.(1)如图1,若CM⊥BD且PQ=4√3,求菱形ABCD的面积;(2)如图2,求证:PM=QN.37.(2019秋•江津区期末)如图,四边形ABCD是平行四边形,AC=CD,∠BAC=90°,点E为BC边上一点,将AE绕点A顺时针旋转90°后得到线段AF,连接FB,FB⊥BC.且FB的延长线与AE的延长线交于点G,点E是AG的中点.(1)若BG=2,BE=1,求FG的长;(2)求证:√2AB=BG+2BE.38.(2020春•渝北区期中)如图1,光线照射在光滑表面上时会发生反射现象,入射光线与镜面的夹角等于出射光线与镜面的夹角,即∠1=∠2.(1)如图1,AB、BC为两个平面镜,∠B=90°,一束光线l经两次反射后,经点D,由从点E射出,求证:DM∥EN;(2)如图2,AB、BC为两个平面镜,∠B=122°,一束光线l经两次反射后,经点D,且由从点E射出,且EN⊥AB,求∠ADM的度数;(3)如图3,已知FL∥GS,FG⊥GS,∠LPK=∠SQK=30°,∠PKQ绕点K顺时针旋转,旋转速度为5°/秒,记旋转角α(0<α≤360°),同时,射线FG绕点F顺时针旋转,旋转速度为3°/秒,记旋转角β(0<β≤360°),当FG所在直线平行于∠PKQ边所在直线时,直接写出对应时间t的所有值.。
2020中考数学专题1——几何模型之双子型-含答案
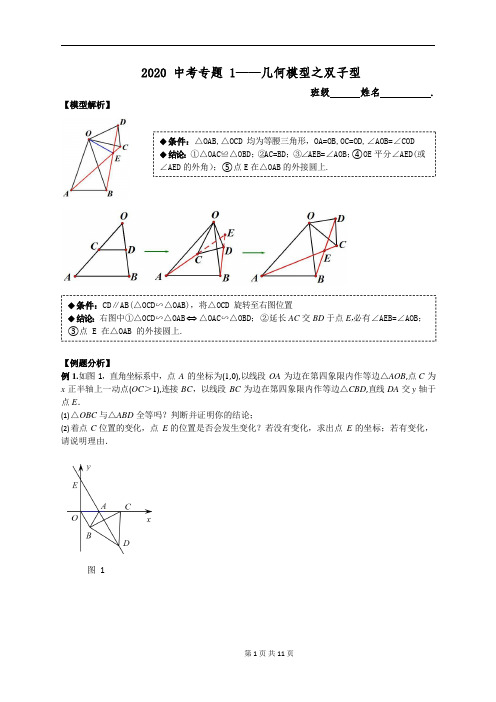
◆条件:CD∥AB(△OCD∽△OAB),将△OCD 旋转至右图位置◆结论:右图中①△OCD∽△OAB △OAC∽△OBD;②延长AC交BD于点E,必有∠AEB=∠AOB;③点 E 在△OAB 的外接圆上.【模型解析】2020 中考专题 1——几何模型之双子型班级姓名.【例题分析】例1.如图1,直角坐标系中,点A 的坐标为(1,0),以线段OA 为边在第四象限内作等边△AOB,点C 为x 正半轴上一动点(OC>1),连接BC,以线段BC 为边在第四象限内作等边△CBD,直线DA 交y 轴于点E.(1)△OBC 与△ABD 全等吗?判断并证明你的结论;(2)着点C 位置的变化,点E 的位置是否会发生变化?若没有变化,求出点E 的坐标;若有变化,请说明理由.图 1◆条件:△OAB,△OCD 均为等腰三角形,OA=OB,OC=OD,∠AOB=∠COD◆结论:①△OAC≌△OBD;②AC=BD;③∠AEB=∠AOB;④OE平分∠AED(或∠AED的外角);⑤点E在△OAB的外接圆上.3例2.如图 2-1,在Rt△ABC 中,∠B=90°,cosC=5,点6D、E 分别是边BC、AC 的中点,连接DE,AE将△EDC 绕点C 按顺时针方向旋转,记旋转角为θ.当0°≤θ<360°时,仅就图2-2 的情况给出证明.图2-1 图2-2的大小有无变化?请BD例3.如图3 所示,在四边形ABCD 中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD 的长为.图3 图4例4.如图4,在△ABC 中,∠ABC=60°,AB=2 ,BC=8,以AC 为腰,点A 为顶点作等腰△ACD,且∠DAC=120°,则BD 的长为.【巩固练习】1.如图1,△ABC 和△ADE 都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O 为AC 中点,若点D 在直线BC 上运动,连接OE,则在点D 运动过程中,线段OE 的最小值是为()A1B.C.1.2 2图1 图22.如图2,△ABC 为等边三角形,AB=2,点D 为BC 边上的动点,连接AD,以AD 为一边向右作等边△ADE,连接CE. (1)在点D 从点B 运动到点C 的过程中,点E 运动的路径长为;(2)在点D 的运动过程中,是否存在∠DEC=60°,若存在,求出BD 的长,若不存在,请说明理由.(3)取AC 中点P,连接PE,在点D 的运动过程中,求PE 的最小值.2D. 23.在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图3-1,当点C1在线段C A的延长线上时,求∠CC1A1的度数;(2)如图3-2,连接AA1,CC1.若△A1BA1的面积为4,求△CBC1的面积;图3-1 图3-24.【提出问题】(1)如图4-1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM 为边作等边△AMN,连结CN.求证:BM=CN.【类比探究】(2)如图4-2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论BM=CN 还成立吗?请说明理由.【拓展延伸】(3)如图4-3,在等腰△ABC 中,BA=BC,AB=6,AC=4,点M 是BC 上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究BM与CN的数量关系,并说明理由.图4-1 图4-2 图4-35.如图5,正方形ABCD、BGFE 边长分别为2、1,正方形BGFE 绕点B 旋转,直线AE、GC 相交于点H.(1)在正方形BGFE绕点B旋转过程中,∠AHC的大小是否始终为90°,请说明理由;(2)连接DH、BH,在正方形BGFE 绕点B 旋转过程中,求DH 的最大值;图5 备用图6.如图6-1,已知点A(0,-3)和x 轴上的动点C(m,0),△AOB 和△BCD 都是等边三角形.(1)在C 点运动的过程中,始终有两点的距离等于OC 的长度,请将它找出来,并说明理由.(2)如图6-2,将△BCD 沿CD 翻折得△ECD,当点C 在x 轴上运动时,设点E(x,y),请你用m 来表示点E 的坐标并求出点E 运动时所在图象的解析式.(3)在C 点运动的过程中,当m 时,直接写出△ABD 是等腰三角形时E 点的坐标.图1 图237.【问题探究】(1)如图7-1,锐角△ABC 中分别以AB、AC 为边向外作等腰△ABE 和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD 与CE 的大小关系,并说明理由.【深入探究】(2)如图7-2,四边形ABCD 中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45°,求BD 的长.(3)如图7-3,在(2)的条件下,当△ACD 在线段AC 的左侧时,求BD 的长.图7-1 图7-2 图7-38.(1)如图8-1,已知△ABC,以AB、AC 为边分别向△ABC 外作等边△ABD 和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法,保留作图痕迹),并证明:BE=CD;(2)如图8-2,利用(1)中的方法解决如下问题:在四边形ABCD 中,AD=3,BD=2,∠ABC=∠ACB=∠ADB=45°,求BD 的长;(3)如图8-3,四边形ABCD中,∠BAC=90°,∠ADB=∠ABC=α,tanα=4,B D=5,AD=12,求BD 3的长.图8-1 图8-2 图8-32020 中考专题1——几何模型之双子型参考答案例1.解:①全等.理由:∵△AOB 和△CBD 是等边三角形,∴OB=AB,∠OBA=∠OAB=60°,BC=BD,∠CBD=60°,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,在△OBC 和△ABD 中,∵,∴△OBC≌△ABD(SAS).②不变.理由:∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,又∵∠OAB=60°,∴∠OAE=180°﹣∠OAB﹣∠BAD=60°,∴Rt△OEA 中,AE=2OA=2,∴OE=,∴点E的位置不会发生变化,E的坐标为E(0,).例2.当0°≤α<360°时,的大小没有变化,∵∠ECD=∠ACB,∴∠ECA=∠DCB,又∵==,∴△ECA∽△DCB,∴==;例3.解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,在△BAD 与△CAD′中,,∴△BAD≌△CAD′(SAS),∴BD=CD′,∠DAD′=90°,由勾股定理得DD′==3 ,∠D′DA+∠ADC=90°,由勾股定理得CD′==,∴BD=CD′=.故答案为:.例4.解:以A 为旋转中心,把△BAC 逆时针旋转120°,得到△EAD,连接BE,作AP⊥BE 于P,则∠BAE=120°,AB=AE,∴∠ABE=∠AEB=30°,∴BP=AB•cos∠ABP=3,∠AEB=90°,∴BE=2BP=6,在Rt△BED 中,BD==10,故答案为:10.【巩固训练】1. 解:设 Q 是 AB 的中点,连接 DQ ,∵∠BAC =∠DAE =90°,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC ,即∠BAD =∠CAE , ∵AB =AC =2,O 为 AC 中点,∴AQ =AO , 在△AQD 和△AOE 中,,∴△AQD ≌△AOE (SAS ),∴QD =OE ,∵点 D 在直线 BC 上运动,∴当 QD ⊥BC 时,QD 最小,∵△ABC 是等腰直角三角形,∴∠B =45°, ∵QD ⊥BC ,∴△QBD 是等腰直角三角形,∴QD =QB ,∵QB = AB =1,∴QD =,∴线段 OE 的最小值是为.故选:B .2. 解:(1)△ABD ≌△ACE 可得 BD =CE ,E 的运动路径的长即 D 的运动路径长,BC =2.(2) ∠DEC =60°相当于∠AEC =∠ADB =120°,即∠EDC =0°,此时点 D 与点 B 重合.因此不存在.(3) ∠ACE =60°,当 PE ⊥CE 时取最小值.PE =PC cos 60°=1.23. 解:(1)由旋转的性质可得:∠A 1C 1B =∠ACB =45°,BC =BC 1, ∴∠CC 1B =∠C 1CB =45°,∴∠CC 1A 1=∠CC 1B +∠A 1C 1B =45°+45°=90°. (2)∵△ABC ≌△A 1BC 1,∴BA =BA 1,BC =BC 1,∠ABC =∠A 1BC 1,∴,∠ABC +∠ABC 1=∠A 1BC 1+∠ABC 1,∴∠ABA 1=∠CBC 1,∴△ABA 1∽△CBC 1.∴,∵S △ABA 1=4,∴S △CBC 1= ;4.(1)证明:∵△ABC 、△AMN 是等边三角形, ∴AB =AC ,AM =AN ,∠BAC =∠MAN =60°, ∴∠BAM =∠CAN ,∵在△BAM 和△CAN 中,∴△BAM ≌△CAN (SAS ), ∴∠ABC =∠ACN .(2) 解:结论∠ABC =∠ACN 仍成立;理由如下:∵△ABC 、△AMN 是等边三角形,∴AB =AC ,AM =AN ,∠BAC =∠MAN =60°,∴∠BAM =∠CAN ,∵在△BAM 和△CAN 中,∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN.(3)解:∠ABC=∠ACN;理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,∴底角∠BAC=∠MAN,∴△ABC∽△AMN,∴=,又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN,∴△BAM∽△CAN,∴∠ABC=∠ACN.5.解:(1)是,理由如下:如图,由旋转知,∠ABE=CBG,在正方形ABCD,BGFE 中,AB=BC,BE=BG,∠ADC=∠BCD=∠BAD=∠ABC=90°,∴△ABE≌△CBG,∴∠BAE=∠BCG,记AH 与BC 的交点为点P,∵∠APB=∠CPH,∠ABC+∠BAE+∠APB=180°∠AHC+∠BCG+∠CPH=180°,∴∠AHC=∠ABC=90°,(2)DH≤DE+EG=BD=2 26.解:(1)连接AD,如图1所示.A、D 两点间的距离始终等于OC 的长度.理由如下:∵△AOB 和△BCD 都是等边三角形,∴AB=OB,BD=BC,∠ABO=∠CBD=60°,∵∠ABD=∠ABO+∠OBD,∠OBC=∠OBD+∠DBC,∴∠ABD=∠OBC.在△ABD 和△OBC 中,有,∴△ABD≌△OBC(SAS),∴AD=OC.(2)过D 作DF⊥y 轴于F,连接BE,如图2 所示.由(1)可知△ABD≌△OBC,∴AD=OC=m,∠DAF=∠BAO﹣∠BAD=60°﹣(90°﹣60°)=30°∴DF=AD•sin∠DAF=m,AF=AD•cos∠DAF=m,∵A(0,﹣3),∴D(m,m﹣3).∵将△BCD 沿CD 翻折得△ECD 且△BCD 是等边三角形,∴四边形BCED 是菱形,∴BE、CD 互相平分.∵△AOB是等边三角形,且点O(0,0),点A(0,﹣3),∴点B(,﹣),∴E(m﹣,m﹣).∵m﹣=(m﹣),∴点E在图形y=x上运动.(3)∵点A(0,﹣3),点B(,﹣),点D(m,m﹣3),∴AB=3,AD=m,BD==,△ABD 为等腰三角形分三种情况:①当AB=AD 时,有3=m,此时点E的坐标为(﹣,﹣);②当AB=BD 时,有3=,解得:m=0(舍去),或m=3,此时点E的坐标为(3,3);③当AD=BD 时,有m=,解得:m=(舍去).综上可知:在C 点运动的过程中,当m>时,△ABD是等腰三角形时E点的坐标为(﹣,﹣)或(3,3).7.解:(1)BD=CE.理由是:∵∠BAE=∠CAD,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC 和△BAD 中,,∴△EAC≌△BAD,∴BD=CE;(2)如图2,在△ABC 的外部,以A 为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.∵∠ACD=∠ADC=45°,∴AC=AD,∠CAD=90°,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC 和△BAD 中,,∴△EAC≌△BAD,∴BD=CE.∵AE=AB=7,∴BE==7 ,∠ABE=∠AEB=45°,又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°=90°,∴EC===,∴BD=CE=.(3)如图3,在线段AC 的右侧过点A 作AE⊥AB 于点A,交BC 的延长线于点E,连接BE.∵AE⊥AB,∴∠BAE=90°,又∵∠ABC=45°,∴∠E=∠ABC=45°,∴AE=AB=7,BE==7 ,又∵∠ACD=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,在△EAC 和△BAD 中,,∴△EAC≌△BAD,∴BD=CE,∵BC=3,∴BD=CE=(7 ﹣3)cm.8.解:(1)如图1,分别以点A、B为圆心,以AB为半径画弧,交于点D,连接AD、BD,再分别以A、C 为圆心,以AC 为半径画弧,交于点E,连接AE、CE则△ABD、△ACE 就是所求作的等边三角形;证明:如图1,∵△ABD 和△ACE 都是等边三角形,∴AD=AB,AC=AE,∠DAB=∠EAC=60°,∴∠DAC=∠BAE,∴△DAC≌△BAE(SAS),∴BE=CD;(2)如图2,过A 作AE⊥AD,使AD=AE=3,连接DE、CE,由勾股定理得:DE==3 ,∴∠EDA=45°,∵∠ADC=45°,∴∠EDC=∠EDA+∠ADC=90°,∵∠ACB=∠ABC=45°,∴∠CAB=90°,∴∠CAB+∠DAC=∠EAD+∠DAC,即∠EAC=∠DAB,∵AE=AD,AC=AB,∴△DAB≌△EAC(SAS),∴EC=BD,在Rt△DCE 中,EC===,∴BD=EC=;(3)如图3,作直角三角形DAE,使得∠DAE=90°,∠DEA=∠ACB,连接EC,容易得到△DAE∽△BAC,∴,即,∵∠DAE=∠BAC=90°,∴∠DAE+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,∴△EAC∽△DAB,∴,在△DCE 中,∠ADC=∠ACB,∠EDA=∠ABC,∴∠EDC=90°,∵,AD=12,∴AE=9,∠DAE=90°,∴DE==15,CE==5 ,由△EAC∽△DAB,∴BD=.第 11 页共 11 页。
中考数学压轴题:几何探究题

几何探究题(10道)1.如图①,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.(1)判断BF与AC的数量关系并说明理由.(2)如图②,将△ACD沿线段AD对折,点C落在BD 上的点M,AM与BE相交于点N,当DE∥AM时,①求证:AE=EC;②求∠MAC的度数以及线段NE与AC的数量关系.第1题图解:(1)BF=AC,理由是:∵AD⊥BC,BE⊥AC,∴∠ADB=∠AEF=90°,∵∠ABC=45°,∴△ABD是等腰直角三角形,∴AD =BD ,∵∠AFE =∠BFD ,∴∠DAC =∠EBC ,在△ADC 和△BDF 中,⎪⎩⎪⎨⎧︒=∠=∠=∠=∠90BDF ADC BDAD DBF DAC , ∴△ADC ≌△BDF (ASA ),∴BF =AC ;(2)①由折叠得:MD =DC ,∵DE ∥AM ,∴AE =EC ,②∵AE =EC ,BE ⊥AC ,∴AB =BC ,由(1)得:△ADC ≌△BDF ,∵△ADC ≌△ADM ,∴△BDF ≌△ADM ,∴∠DBF=∠MAD=22.5°,∴∠MAC=2∠MAD=45°,∵∠NEA=90°,∴△AEN是等腰直角三角形,1AC.∴EN=AE=EC,∴EN=22.在长方形ABCD中,点E是AD的中点,将△ABE沿BE折叠后得到对应的△GBE,将BG延长交直线DC于点F.(1)如果点G在长方形ABCD的内部,如图①所示.①求证:GF=DF;1DC,AD=4,求AB的长度.②若DF=2(2)如果点G在长方形ABCD的外部,如图②所示,AD的值. DF=kDC(k>1).请用含k的代数式表示AB第2题图解:(1)①连接EF ,如解图第2题解图根据翻折的性质得,∠EGF =∠A =90°,EG =AE =ED , 在Rt △EGF 和Rt △EDF 中,⎩⎨⎧==EF EF ED EG , ∴Rt △EGF ≌Rt △EDF (HL ),∴GF =DF ;②由①知,GF =DF ,设DF =x ,BC =y ,则GF =x ,AD =y , ∵DC =2DF ,∴CF =x ,DC =AB =BG =2x ,∴BF =BG +GF =3x ;在Rt △BCF 中,BC 2+CF 2=BF 2,即y 2+x 2=(3x )2 ∴y =22x ,∴ABAD =x y 2=2;∵AD=4,(2)由(1)知,GF=DF,设DF=x,BC=y,则GF=x,AD=y,在Rt△BCF中,BC2+CF2=BF2,3.将一副三角尺按图①摆放,等腰直角三角尺的直角边DF 恰好垂直平分AB,与AC相交于点G,BC=23cm.(1)求GC的长;(2)如图②,将△DEF绕点D顺时针旋转,使直角边DF 经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想;(3)在(2)的条件下,将△DEF沿DB方向平移得到△D'E'F',当D'E'恰好经过(1)中的点G时,请直接写出DD'的长度.第3题图解:(1)在Rt△ABC中,∠BAC=30°,BC=23cm,∴AC=23×3=6cm,AB=43cm,又∵AD=BD,GD⊥AB,∴AD=23cm,在Rt△ADG中,∠BAC=30°,∴DG=2cm,AG=4cm,∴GC=AC-AG=6-4=2cm;(2)MD=ND,证明如下:∵D是AB的中点,∠ACB=90°,∠A=30°,∴BC=BD=AD,∵∠B=60°,∴△CDB为等边三角形.1BD,∵CN⊥BD,∴DN=NB=2在△ADH中,∠HDA=180°-60°-90°=30°,∴∠HDA=∠A=30°,1AD,∴MD=ND;∵HM⊥AB,∴AM=MD=2(3)DD'=23cm.【解法提示】如解图,连接GD,GB;∵GD垂直平分AB,∴AG=BG,∴∠GBA=∠A=30°,∠E'D'A=30°,当点D'与点B 重合时,点G在D'E'上,∴DD'=DB=23cm.第3题解图4.(1)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.①若AB=6,AE=4,BD=2,则CF= ;②求证:△EBD∽△DCF.(2)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示,问:点D是否存在某一位置,使BD的ED平分∠BEF且FD平分∠CFE?若存在,求出BC 值;若不存在,请说明理由.(3)如图③,在等腰△ABC中,AB=AC,点O为BC 边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为(用含α的表达式表示).图①图②图③第4题图解:(1)①4;【解法提示】∵△ABC是等边三角形,∴AB=BC=AC=6,∠B=∠C=60°.∵AE=4,∴BE=2,则BE=BD,∴△BDE是等边三角形,∴∠BED=60°,又∵∠EDF=60°,∴∠CDF=180°-∠EDF-∠B=60°,则∠CDF=∠C=60°,∴△CDF是等边三角形,∴CF=CD=BC-BD=6-2=4.②证明:∵∠EDF=60°,∠B=60°,∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,∴∠BED=∠CDF.又∠B=∠C=60°,∴△EBD∽△DCF;(2)存在,如解图①,过D作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别是M、G、N,第4题解图①∵ED 平分∠BEF 且FD 平分∠CFE .∴DM =DG =DN .又∠B =∠C =60°,∠BMD =∠CND =90°,∴△BDM ≌△CDN ,∴BD =CD ,即点D 是BC 的中点,∴BC BD =21; (3)如解图②,连接AO ,作OG ⊥BE ,OD ⊥EF ,OH ⊥CF ,垂足分别是G 、D 、H .第4题解图②则∠BGO =∠CHO =90°,∵AB =AC ,O 是BC 的中点,∴∠B =∠C ,OB =OC ,∴△OBG ≌△OCH ,∴OG =OH ,GB =CH ,∠BOG =∠COH =90°-α, 则∠GOH =180°-(∠BOG +∠COH )=2α,∴∠EOF =∠B =α,由(2)题可猜想应用EF =ED +DF =GE +FH (可通过半角旋转证明),则C △AEF =AE +EF +AF =AE +EG +FH +AF =AG +AH =2AG , 设AB =m ,则OB =mcosα,GB =mcos 2α.ααcos cos )(222m m m m OB AB AG OB AB AG C C ABC AEF +-=+=+=∆∆=1-cos α. 5.如图,Rt △ACB 中,∠ACB =90°,AC =BC ,E 点为射线CB 上一动点,连接AE ,作AF ⊥AE 且AF =AE .(1)如图①,过F 点作FD ⊥AC 交AC 于D 点,求证:FD =BC ;(2)如图②,连接BF 交AC 于G 点,若AG =3,CG =1,求证:E 点为BC 中点;(3)当E 点在射线CB 上,连接BF 与直线AC 交于G 点,若BC =4,BE =3,直接写出CGAG 的值.第5题图 (1)证明:∵FD ⊥AC ,∴∠FDA =90°, ∴∠DFA +∠DAF =90°, 同理,∵AF ⊥AE ,∴∠CAE +∠DAF =90°,∴∠DFA =∠CAE ,在△AFD 和△EAC 中,⎪⎩⎪⎨⎧=∠=∠︒=∠=∠AE AF EACAFD ECA ADF 90, ∴△AFD ≌△EAC (AAS ),∴DF =AC ,∵AC =BC ,∴FD =BC ;(2)如解图①,过点F 作FD ⊥AC 于点D ,第5题解图①由(1)得,FD =AC =BC ,AD =CE ,在△FDG 和△BCG 中,⎪⎩⎪⎨⎧=︒=∠=∠∠=∠BC FD BCG FDG BGC FGD 90, ∴△FDG ≌△BCG (AAS ),∴DG =CG =1,∴AD =2,∴CE =2,∵BC =AC =AG +CG =4,∴E 点为BC 中点;(3)311或35.【解法提示】当点E 在CB 的延长线上时,过F 作FD ⊥AG 与AG 的延长线交于点D ,如解图②,第5题解图②BC =AC =4,CE =CB +BE =7,由(1)(2)知:△ADF ≌△ECA ,△GDF ≌△GCB , ∴CG =GD ,AD =CE =7,∴CG =DG =1.5, ∴CG AG =5.15.14+=311, 同理,当点E 在线段BC 上时,CG AG =5.15.14-=35. 6.如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D 为AB 延长线上一点,连接CD ,过A 分别作AM ⊥CD ,垂足为M ,交BC 于点N ,作AP ⊥BC ,垂足为P ,交CD 于点Q .(1)求证:AN =CQ ;(2)如图,点E 在BA 的延长线上,且AE =BD ,连接EN 并延长交CD 于点F ,求证:DQ =EN ;(3)在(2)的条件下,当AE =32AB 时,求FNEN 的值.第6题图证明:(1)∵AP ⊥BC ,AM ⊥CD ,∴∠APN =∠CPQ =90°,∴∠PNA +∠NAP =∠NAP +∠CQP =90°,∴∠PNA =∠CQP ,∵AB =AC ,∠BAC =90°,∴AP =PC ,∴△APN ≌△CPQ (ASA ),∴AN =CQ ;(2)如解图①,连接BQ ,第6题解图① 由(1)知:AP 是BC 的垂直平分线, ∴BQ =CQ , ∵AN =CQ ,∴AN =BQ ,∵BQ =CQ ,∴∠QBC =∠QCB =∠NAP ,∵∠PBA =∠PAB =45°,∴∠QBA =∠BAN ,∴∠DBQ =∠NAE ,在△DBQ 和△NAE 中,⎪⎩⎪⎨⎧=∠=∠=AE BD EAN DBQ AN BQ , ∴△DBQ ≌△EAN (SAS ),∴DQ =EN ; (3)∵AE =32AB ,即AB AE =32, ∴设AE =2x ,AB =3x ,则BD =2x ,DC =34x ,如解图②,过E 作EH ⊥AM ,交MA 的延长线于H ,第6题解图②∴∠H =∠AMD =90°,∴EH ∥DC ,∴△AHE ∽△AMD ,∴52322=+==x x x AD AE AM AH , ∵∠MAC =∠CDA ,∠ACN =∠DAQ =45°,∴△DQA ∽△ANC ,∴3535===x x AN DQ AC AD ,由(2)知:CQ=AN,∴设AH=8m,AM=20m,AN=17m,则MN=3m,∵EH∥FM,∴△EHN∽△FMN,7.如图,点P是正方形ABCD外一点,连接PA、PD,作BM⊥PA,垂足为E,使BM=PA,再作CN⊥PD,垂足为F,使CN=PD,连接PM、PN.(1)如图①,当PA=PD时,直接写出线段PM、PN的位置关系和数量关系;(2)在(1)的条件下,若∠APD=40°,则∠ABM= ;(3)如图②,当PA≠PD时,(1)中的结论是否仍然成立,若成立,请给出证明;若不成立,请说明理由.第7题图解:(1)结论:PM=PN,PM⊥PN.理由:如解图①,连接AM,DN.第7题解图①∵四边形ABCD是正方形,∴AB =BC =CD =AD ,∴∠BAD =90°,∵PE ⊥BM ,∴∠AEB =90°,∴∠PAD +∠EAB =90°,∠EAB +∠ABE =90°, ∴∠PAD =∠ABE ,∵PA =PD ,在△PAD 和△ABE 中,⎪⎩⎪⎨⎧=∠=∠=BAAD ABM PAD BMPA , ∴△PAD ≌△MBA (SAS ),∴AM =PD ,∠AMB =∠APD ,∴MA =MB =PA =PD ,同理可证:ND =NC =PA =PD ,∠DNC =∠APD ,∴∠AME =∠DNF ,∵∠AME +∠MAE =90°,∠DNF +∠NDF =90°, ∴∠MAE =∠NDF ,∴∠PAM =∠PDN ,∴△PAM≌△PDN(SAS),∴PM=PN,∠APM=∠DPN=∠AMP=∠DNP,∵∠AME+∠MAE=90°,∠MAE=∠AMP+∠APM=∠APM+∠NPD,∴∠APD+∠APM+∠NPD=90°,∴∠MPN=90°,∴MP⊥PN.(2)70°;【解法提示】∵PA=PD,∠P=40°,∴∠PAD=∠PDA=70°,由(1)可知:∠ABM=∠PAD=70°.(3)结论仍然成立,理由如下:如解图②,连接MA,延长MA交PF于点Q.第7题解图②由(1)可知:∠PAD=∠ABM,在△PAD 和△ABM 中,⎪⎩⎪⎨⎧=∠=∠=BA AD ABM PAD BM PA ∵PA =BM ,AD =BA ,∴△PAD ≌△MBA (SAS ),∴AM =PD ,∠ADP =∠MAB ,∵四边形ABCD 是正方形,∴∠BAD =∠ADC =90°,AB =AD =CD ,∵∠MAB +∠QAD =90°,∴∠QAD +∠ADP =90°,∴∠AQD =90°,∵PF ⊥CN ,∴∠AQD =∠DFC =90°,∴∠ADQ +∠CDF =90°,∠CDF +∠DCF =90°,∴∠ADQ =∠DCF ,在△ADQ 和△DCF 中,⎪⎩⎪⎨⎧=∠=∠∠=∠CD AD DCF ADQ DFC AQD ,∴△AQD ≌△DFC (AAS ),∴AQ =DF ,DQ =CF ,∵PD =CN ,∴PQ =FN ,MQ =PF ,∵∠MQP =∠PFN =90°,∴△MQP ≌△PFN (SAS ),∴PM =PN ,∠MPQ =∠N ,∵∠N +∠FPN =90°,∴∠MPQ +∠FPN =90°,∴∠MPN =90°,∴PM ⊥PN .8、在Rt △ABC 中,∠ACB =90°,∠B =30°,M 为AB 中点,点P 为BC 延长线上一点,CP <BC ,连接PM ,AC =n ,CP =m .(1)如图①,将射线MP 绕点M 逆时针旋转60°交CA 延长线于点D ,且BC =AD +CP.①在图中找出与∠MDC相等的角,并加以证明;m的值;②求n(2)如图②,若将射线MP绕点M顺时针旋转60°交AC延长线于点H,求CH的长(用含有m,n的式子表示)第8题图①第8题图②解:(1)①结论:∠ADM=∠PMA.理由:如解图①,连接CM.∵∠ACB=90°,∠B=30°,∴∠BAC=60°,∵BM=MA,∴CM=MA=BM,∴△AMC是等边三角形,∴∠AMC=∠PMN=60°,∴∠PMC=∠AMD,∵∠BAC=∠AMD+∠ADM=60°,∠AMP+∠PMC=60°∴∠ADM=∠PMA.第8题解图①②如解图①,连接CM、作CK∥AB交PM于点K.∵CK∥AB,由(1)知△AMC是等边三角形,∴∠MAC=∠MCA=∠AMC=60°,MA=MC,∵CK∥AB,∴∠ACK=∠MAC=60°,∠AMK=∠MKC,∴∠DAM=∠MCK=120°,∵∠ADM=∠AMP,∴∠MKC=∠MDA,在△MCK 和△MAD 中,⎪⎩⎪⎨⎧=∠=∠∠=∠MCMA MAD MCK MDAMKC ,∴△MCK ≌△MAD ,∵CK ∥BM ,∴△PKC ∽△PMB ,∴AD =CK ,∵BC =AD +PC ,整理得:m 2+mn -3n 2=0,(3)如解图②,连接CM 、作CK ∥AB 交PM 于点K .第8题解图② ∵∠PMH =∠ACM =60°, ∴∠PMC +∠CMH =∠CMH +∠H ,∴∠CMK =∠H ,∵∠HCM =∠MCK =120°,∴△HCM ∽△MCK ,∴CK CM MC HC =, ∴nm mnn n HC 3+=, ∴HC =mn mn 23+. 9. 已知四边形ABCD 是正方形,△BEF 是等腰直角三角形,∠BEF =90°,BE =EF ,连接DF ,G 为DF 的中点,连接EG,CG,EC.(1)如图①,若点E在CB边的延长线上,直接写出EC的值;EG与GC的位置关系及GC(2)将图①中的△BEF绕点B顺时针旋转至图②所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图①中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=2,当E,F,D三点共线时,求DF的长及tan∠ABF的值.第9题图EC=2,解:(1)EG⊥CG,GC理由如下:如解图①,过G作GH⊥EC于点H,∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,∵G 为DF 中点, ∴H 为EC 中点, ∴EG =GC ,GH =21(EF +DC )=21(EB +BC ), 即GH =EH =HC ,∴∠EGC =90°,即△EGC 是等腰直角三角形, ∴GC EC =2;第9题解图① 第9题解图② (2)解:结论还成立,理由如下:如图②,延长EG 到H ,使EG =GH ,连接CH 、EC ,延长CD 交EH 于点N ,过E 作BC 的垂线交CB 延长线于点R ,交DF 延长线于点Q ,∵在△EFG 和△HDG 中,⎪⎩⎪⎨⎧=∠=∠=HG EG DGH FGE GD GF ,∴△EFG ≌△HDG (SAS ),∴DH =EF =BE ,∠FEG =∠DHG ,∴EF ∥DH ,又易证ER ∥CD ,∴∠1=∠2,∴∠1=∠2=90°-∠3=∠4,∴∠EBC =180°-∠4=180°-∠1=∠HDC ,在△EBC 和△HDC 中,⎪⎩⎪⎨⎧=∠=∠=CD BC HDC EBC DH BE ,∴△EBC ≌△HDC .∴CE =CH ,∠BCE =∠DCH ,∴∠ECH =∠DCH +∠ECD =∠BCE +∠ECD =∠BCD =90°,∴△ECH 是等腰直角三角形, ∵G 为EH 的中点,∴EG ⊥GC ,GCEC =2, 即(1)中的结论仍然成立;(3)解:如解图③,连接BD ,第9题解图③∵在正方形ABCD 中,AB =2,∴BD =2,∴cos ∠DBE =BD BE =21, ∴∠DBE =60°,∴∠ABE =∠DBE -∠ABD =15°,∴∠ABF =45°-15°=30°,∴tan ∠ABF =33,∴DE =3BE =3, ∴DF =DE -EF =3-1.10.在△ABC 和△ADE 中,AB =AC ,∠BAC =120°,∠ADE =90°,∠DAE =60°,F 为BC 中点,连接BE 、DF ,G 、H 分别为BE ,DF 的中点,连接GH .(1)如图①,若D 在△ABC 的边AB 上时,请直接写出线段GH 与HF 的位置关系 ,HFGH = . (2)如图②,将图①中的△ADE 绕A 点逆时针旋转至图②所示位置,其他条件不变,(1)中结论是否改变?请说明理由;(3)如图③,将图①中的△ADE 绕A 点顺时针旋转至图③所示位置,若C 、D 、E 三点共线,且AE =2,AC =5,求线段BE 的长.图① 图② 图③第10题图 解:(1)如解图①,连接DG ,FG .第10题解图①∵AB =AC ,BF =CF ,∴AF ⊥BC ,∴∠BAF =∠CAF =60°,∵ED ⊥AB ,∴∠BFE =∠BDE =90°,∵BG =GE ,∴DG =21BE ,GF =21BE ,∴DG =FG ,∵DH =HF ,∴GH ⊥DF ,∵∠BAE =60°,∴∠ABE +∠AEB =120°,∵DG=BG=GF=GE,∴∠GBD=∠GDB,∠GEF=∠GFE,∴∠BGD+∠EGF=120°,∴∠DGF=60°,∴△DGF是等边三角形,GH=tan60°=3.∴HF(2)结论不变.理由:如解图②,延长ED至S,使DS=DE,连接AS,BS,CE,FG,DG.第10题解图②∵∠ADE=90°,DS=DE,∴AS=AE,∠DAE=∠DAS=60°,∴∠BAC=∠SAE=120°,∴∠SAB=∠EAC,∵AB=AC,∴△ABS≌△ACE.∴BS=CE,∠ABS=∠ACE,∵F,G分别为BC,BE中点,∴DG=FG,∵H为DF中点,∴GH⊥HF,延长SB交CE延长线于T,∵∠ABS+∠ABT=∠ACE+∠ABT=180°,∴∠BAC+∠T=180°,∴∠T=60°,延长FG交BT于P,∴∠T=∠BPF=∠DGF=60°,(3)如解图③,延长ED到H,使得DH=DE,连接AH,BH,作BM⊥EC于M,设BC交AH于点O.第10题解图③∵AD⊥EH,ED=DH,∴AE=AH,∴∠AEH=∠AHE=30°,∴∠EAH=∠BAC=120°,∴∠BAH=∠CAE,∵AB=AC,AH=AE,∴△BAH≌△CAE(SAS),∴∠BHA=∠AEC=30°,BH=CE,∴∠OBA=∠OHC=30°,∵∠AOB =∠COH ,∴△AOB ∽△COH ,∴△AOC ∽△BOH ,∴∠BHO =∠AOC =30°,∴∠BHE =30°+30°=60°,在Rt △ADE 中,∵AE =2,∠AED =30°,在Rt △EBM 中,11)1233()]332(21[22=-++=.。
【中考冲刺】2020中考数学专题总复习:专题五 几何的证明与综合应用

角三角形,∴DF= 2 AD,∴ DF = 2,∴ EB = 2.
AD
AD
栏目索引
栏目索引
方法技巧
与三角形有关的证明与综合应用主要涉及证三角形全等和相似,看到证明
线段相等,要想到全等,看到证明线段之间成比例,要想到三角形相似,这是一种
定性思维,其中三角形相似有以下几种基本结构.
常见 结构
A字型
X字型 母子型
栏目索引
DEB CDF, DBE CFD, ED DC,
∴△DBE≌△CFD(AAS),
∴EB=DF,∴EB=AD.
(3) EB = 2 .理由如下:作DF∥BC交AC于点F,如图3所示,同(1),得△DBE≌
AD
△CFD(AAS),∴EB=DF,∵△ABC是等腰直角三角形,DF∥BC,∴△ADF是等腰直
(2)DH⊥HG.证明:如图,延长GH交CD于点N,
栏目索引
∵FG⊥AD,CD⊥AD,∴FG∥CD.∴∠GFC=∠HCN,∠FGH=∠HNC.∴△FGH
∽△CNH.∴ FG = FH = GH ,
CN CH NH
又∵CH=FH,∴GH=HN,NC=FG.∴AG=FG=NC.又∵AD=CD,∴GD=DN,∴DH⊥
AG AC,
即∠GAB=∠CAE,在△GAB和△CAE中, GAB CAE,∴△GAB≌△CAE
AB AE,
栏目索引
(SAS), ∴∠ABG=∠AEC,又∵∠AEC+∠AME=90°,∴∠ABG+∠BMN=90°,∴∠BNM= 90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2=CB2+GE2, ∵AC=4,AB=5, ∴BC=3,CG=4 2 ,BE=5 2 ,∴GE2=CG2+BE2-CB2=73,∴GE= 73 .
江西省2020届中考数学单元专题练之几何探究题附全解全析

江西省2020届中考数学单元专题练之几何探究题【题型解读】几何探究题为江西近10年的必考题型,题位在解答题最后两道题中的一道.考查类型有:(1)操作探究问题(3次);(2)旋转探究问题(3次);(3)新定义探究问题(2次);(4)动点探究问题(2次);主要设问有:(1)求线段长;(2)判断图形的形状;(3)求角度;(4)判断两条线段的数量和位置关系并证明.类型一操作探究问题1.如图,在正方形ABCD中,点E、F是正方形内两点,BE∥DF,EF⊥BE.为探索研究这个图形的特殊性质,某数学学习小组经历了如下过程:●初步体验如图①,连接BD,若BE=DF,求证:EF与BD互相平分.●规律探究(1)在图①中,(BE+DF)2+EF2=________AB2;(2)如图②,若BE≠DF,其他条件不变,(1)中的数量关系是否会发生变化?如果不会,请证明你的结论;如果会发生变化,请说明理由.●拓展应用如图③,若AB=4,∠DPB=135°,2BP+2PD=46,求PD的长.第1题图2. 如图①,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为,P是半径OB上的一动点,Q是上的一动点,连接PQ.发现:当∠POQ=________时,PQ有最大值,最大值为________;思考:(1)如图②,若P是OB中点,且QP⊥OB于点P,求的长;(2)如图③,将扇形AOB沿折痕AP折叠,使点B的对应点恰好落在OA的延长线上,求阴影部分的面积;探究:如图④,将扇形OAB沿PQ折叠,使折叠后的恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.第2题图3. 综合与实践 问题情境:数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图①所示的长方形纸条ABCD ,其中AD =BC =1,AB =CD =5.然后在纸条上任意画一条截线段MN ,将纸片沿MN 折叠,MB 与DN 交于点K ,得到△MNK ,如图②所示:深入探究: (1)若∠1=70°,求∠MKN 的度数;(2)试判断△MNK 的形状;若改变折痕MN 的位置,△MNK 的形状是否发生变化,请说明理由;拓展应用:(3)爱动脑筋的小明在研究△MNK 的面积时,发现KN 边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN 的面积最小值为12,求此时∠1的度数;(4)小明继续动手操作,发现了△MNK 面积的最大值.请你求出这个最大值.第3题图4. 如图,在矩形ABCD 中,将矩形折叠,使点B 落在边AD (含端点)上,落点记为点E ,这时折痕与边BC 或者边CD (含端点)交于点F ,然后展开铺平,连接BE 、EF .(1)操作发现:①在矩形ABCD 中,任意折叠所得的△BEF 是一个______三角形; ②当折痕经过点A 时,cos ∠BEF 的值为________; (2)深入探究:在矩形ABCD 中,AB =3,BC =23,①当△BEF是等边三角形时,求出BE的长度;②在任意折叠中,△BEF的面积是否存在最大值,若存在,求出EF的长;若不存在,请说明理由.第4题图5. 如图①,已知△ABC中,∠BAC=90°,AB=AC,在∠BAC内部作∠MAN=45°,AM、AN分别交BC于点M、N.【操作】(1)将△ABM绕点A逆时针旋转90°,使AB边与AC边重合,把旋转后点M的对应点记作点Q,得到△ACQ,请在图①中画出△ACQ;(不写画法)【探究】(2)在(1)中所作图的基础上,连接NQ,①求证:MN=NQ;②写出线段BM,MN和NC之间满足的数量关系,并简要说明理由;【拓展】如图②,在等腰△DEF中,∠EDF=45°,DE=DF,点P是EF边上任意一点(不与点E,F重合),连接DP,以DP为腰向两侧分别作顶角均为45°的等腰△DPG和等腰△DPH,分别交DE、DF于点K、L,连接GH,分别交DE、DF于点S、T,(3)线段GS,ST和TH之间满足的数量关系是________;(4)设DK=a,DE=b,求DP的值.(用a、b表示)第5题图6.现有三角形纸板ABC, AC=BC=6,∠ACB=90°,将该三角形纸板放在足够大的圆中移动,⊙O交直线AB于点D,连接DO并延长交⊙O于点E,连接AE.(1)操作发现:如图①,当⊙O经过A、C两点,且圆心O在△ABC内部时,连接CD、CE,①试判断CD与CE的数量关系,并说明理由;②求AE+AD的值;(2)数学思考:如图②,当⊙O 经过A 、C 两点,且圆心O 在△ABC 外部时,连接CD 、CE ,求AE -AD 的值;(3)问题解决:如图③,点F 为CA 延长线上一点,且AC =3AF .当⊙O 经过A ,F 两点,且圆心O 在△ABC 外部时,连接DF ,EF ,①猜想AE 、AD 之间的数量关系,并证明;②连接CE ,是否存在△AEC 为直角三角形?若存在,请直接写出⊙O 的半径;若不存在,请说明理由.第6题图类型二 旋转探究问题1. 在△ABC 中,∠ACB =90°,AC =3,BC =4,将△ABC 绕顶点C 顺时针旋转,旋转角为θ(0°<θ<180°),得到△A ′B ′C .(1)设△ACA ′和△BCB ′的面积分别为S 1和S 2.若θ=40°,请求出S 1S 2的值;(2)如图①,设A ′B ′与CB 相交于点D ,且AB ∥CB ′: ①求证:CD =B ′D ; ②求BD 的长;(3)如图②,设AC 中点为点M ,A ′B ′中点为点N ,连接MN ,MN 是否存在最大值,若存在,求出MN 的值,判断出此时AA ′与BB ′的位置关系;若不存在,请说明理由.第1题图2. 如图①,在△ABC中,AC=BC=22,∠ACB=90°,点D、E分别是AC、BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,旋转角为α,连接AD′、BE′.(1)如图①,若0°<α<90°.①求证:AD′=BE′;②当AD′∥CE′时,求BE′的长;(2)如图②,若90°<α<180°,当点D′落在线段BE′上时,求sin∠CBE′的值;(3)如图③,将△CDE绕点C旋转一周,在旋转过程中,若AD′与直线BE′相交于点P,M为AB的中点,那么在整个旋转过程中,求PM扫过的图形面积.第2题图3. 如图①,边长为6的等边△ABC中,点D在AB边上(不与点A,B重合),点E在BC 边上(不与点B,C重合).第一次操作:将线段DE绕点E顺时针旋转,当点D落在三角形上时,记为点F;第二次操作:将线段EF绕点F顺时针旋转,当点E落在三角形上时,记为点G;依次操作下去….(1)如图②中的四边形DEFG是经过三次操作后得到的,且DE⊥EC.①四边形DEFG的形状为________;②若BE=CF,求线段DE的长;(2)若经过两次操作可得到△DEF如图③.①请判断△DEF的形状为________,此时AD与BE的数量关系是________;②以①中的结论为前提,设AD的长为x,△DEF的面积为y,求y与x的函数关系式;(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.第3题图4. 已知△ABC与△DEF均为透明的完全一样的等腰直角三角板,且AC=BC=2,∠C =∠E=90°.在数学活动课上,小颖同学用这两块三角板进行探究活动.操作:使点D落在线段AB的中点处并使DF过点B(如图①),然后将△DEF绕点D顺时针旋转,直至点E落在CB的延长线上时结束操作,在此过程中,射线ED与射线CA交于点N,射线CB与DF相交于点M,连接MN(如图②,图③).(1)如图②,若AB∥MN,求证:△ADN≌△BDM;(2)如图②,在以上操作过程中,求证:AN·BM的值不会发生变化;(3)①如图③,在以上操作过程中,ND始终平分∠ANM吗?若平分,请加以证明;若不平分,请说明理由;②设AN=m,请直接写出△DMN的面积(用含m的式子表示).第4题图5. 如图①,把边长为2的正方形纸片ABCD沿对角线BD剪开,将△BCD平移得到△DEF,使得BC边与AD边重合,如图②所示,固定△ABC,将△EFD绕点A顺时针旋转,当ED边与AB边重合时,旋转停止.不考虑旋转开始和结束时重合的情况,设ED、EF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图③所示.(1)图②四边形ABCF的形状是________,连接BF,则BF=________;(2)在旋转过程中,∠CEF+∠CHE的度数为________;(3)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图③所示的情况说明理由);(4)当x为何值时,△AGH是等腰三角形?(直接写出答案,不必说明理由)第5题图6.将两张完全相同的平行四边行纸片按如图①所示放置(其中点E在BC上,点A在BG 上,AB=BE=4,BC=BG=23+2,∠B=60°,▱ABCD固定不动,将▱GBEF绕点B顺时针旋转,旋转角为α(0°<α<360°).(1)如图①,连接AF,求AF的长.(2)如图②,当▱GBEF绕点B旋转到点F与点D重合时,AD与BG相交于点M,BC与ED相交于点N,求证:四边形BMDN是菱形.(3)如图③,在旋转过程中,当旋转角α为多少度时,以点C,G,D,F为顶点的四边形是正方形?是矩形?请给予证明.第6题图类型三 新定义探究问题1. 如图①,P 为△ABC 内一点,连接P A 、PB 、PC ,若△PBC 与△CAB 相似,那么就称点P 为△ABC 的黄金点.(1)在下列三角形中,一定没有黄金点的是( ) A . 锐角三角形 B . 钝角三角形 C . 等腰三角形 D . 直角三角形(2)如图②,已知Rt △ABC 中,∠ACB =90°,∠ABC >∠A ,CD 是AB 上的中线,过点B 作BE ⊥CD ,垂足为点E ,试说明点E 是△ABC 的黄金点;(3)如图③,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,BC =4. ①若点P 1是△ABC 的黄金点,求AP 1的长;②若点P 1是△ABC 的黄金点,点P 2是△P 1BC 的黄金点, 点P 3是△P 1P 2C 的黄金点,点P 4是△P 1P 2 P 3的黄金点,…,以此类推,请求出△P 2016P 2017P 2018的周长.第1题图2. 我们知道若线段上的一个点把这条线段分割为两部分,其中一部分与全长之比等于5-12时,则这个点称为黄金分割点.类比三角形中线的定义,我们规定:连接一个顶点和它对边的黄金分割点的线段叫做这个三角形的黄金线.(1)如图①,已知CD 是△ABC 的黄金线(AD >BD ),△ABC 的面积为4,则△BCD 的面积为________;(2)如图②,在△ABC 中,∠A =36°,AB =AC =1,过B 点作BD 平分∠ABC ,与AC 相交于点D ,求证:BD 是△ABC 的黄金线;(3)如图③, BE 、CD 是△ABC 的黄金线(AD >BD ,AE >CE ),BE 、CD 相交于点O . ①设△BOD 与△COE 的面积分别为S 1、S 2,试猜想S 1、S 2的数量关系,并说明理由;②求ODCD的值.第2题图3.如果在两个相似但不全等的三角形中,其中一个三角形的一边等于另一个三角形的一边,那么,我们称这两个三角形为梦幻三角形,例如:(如图①所示)△ABC 的三边长分别为a 、b 、c ,(如图②所示)△A 1B 1C 1的三边长分别为a 1、b 1、c 1,且△ABC ∽△A 1B 1C 1,c =a 1,那么我们将△ABC 与△A 1B 1C 1称为梦幻三角形.(1)若△ABC 与△A 1B 1C 1为梦幻三角形,且相似比为k (k >1),求证:a =kc ; (2)如图③,在△ABC 中,∠ACB =80°,∠B =60°,CD 平分∠ACB 交AB 于点D ,求证:△CBD 与△ABC 为梦幻三角形;(3)如图④,△ABC 内接于⊙O ,且AB 为⊙O 的直径,∠ACB 的平分线交⊙O 于点D ,过点D 作⊙O 的切线PD 交CA 的延长线于点P ,过点C 作CF ⊥PD 于点F ,与AD 相交于点E ,且△ACE 与△ADC 刚好构成梦幻三角形.①若AE ·AD =36,BC =8,求线段AD 的长;②若CDAB=m ,请直接写出PC 与PD 的数量关系(用含m 的式子表示,不必说明理由).第3题图4.阅读理解如图①,在正n边形A1A2A3…A n的边A2A3上任取一不与点A2重合的动点B2,并以线段A1B2为边在线段A1A2上方作一正n边形A1B2B3…B n,把正n边形A1B2B3…B n叫正n边形A1A2A3…A n的准位似图形,点A3称为准位似中心.特例论证(1)如图②,已知正三角形A1A2A3的准位似图形为正三角形A1B2B3,试证明:随着点B2的运动,∠B3A3A1的大小始终不变.数学思考(2)如图③,已知正方形A1A2A3A4的准位似图形为正方形A1B2B3B4,随着点B2的运动,∠B3A3A4的大小是否始终不变?若不变,请求出∠B3A3A4的大小;若改变,请说明理由.归纳猜想(3)在图①的情况下:①试猜想∠B3A3A4的大小是否会发生改变?若不改变,用含n的代数式表示出∠B3A3A4的大小(不要求证明);若会改变,请说明理由;②∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠B n A n A1=________.(用含n的代数式表示)第4题图类型四 动点探究问题1.在四边形OABC 中,AB ∥OC ,∠OAB =90°, ∠OCB =60°,AB =2,OA =2 3.(1)如图①,连接OB ,请直接写出OB 的长度;(2)如图②,过点O 作OH ⊥BC 于点H .动点P 从点H 出发,沿线段HO 向点O 运动,动点Q 从点O 出发,沿线段OA 向点A 运动,两点同时出发,速度都为每秒1个单位长度,设点P 运动的时间为t 秒,△OPQ 的面积为S (平方单位).①求S 与t 之间的函数关系式;②设PQ 与OB 交于点M ,当△OPM 为等腰三角形时,试求出△OPQ 的面积S 的值.第1题图2. 如图,点O 为正方形ABCD 的中心,AB =2,点E 为AB 上的一动点,DF ⊥DE 于点D ,DF 与BC 的延长线相交于点F . OM ⊥DE 于点M , ON ⊥DF 于点N .(1)求证:DE =DF ;(2)在点E 的运动过程中,OM 2+ON 2是否是一个定值,如果是,请求出 OM 2+ON 2的值,若不是,请说明理由;(3)如图②,若DE 与AC 相交于点P ,DF 的延长线与AC 的延长线相交于点Q ,求证: AP CQ =DP DQ.第2题图3. 如图①,在等腰△ABC中,∠BAC=90°,AB=AC,点D是BC边上的动点,P为AB边上的动点,连接DP,以DP为边构造△DEP,∠DPE=90°,PD=PE.(1)如图②,若点P与点A重合,①求证:CD=BE;②猜想BD、CD与PD之间的数量关系,并说明理由;(2)如图③,若BP=2AP时,AC=62,设DP2=y,BD=x.①求y关于x的函数关系式;②连接CP,请问是否存在△CDP为等腰三角形?若存在,请求出△DPE的面积;若不存在,请说明理由.第3题图4. 如图,在锐角△ABC中,AB=8,BC=6,CD⊥AB于点D,点E是AC的中点,连接DE.(1)如图①,①当DE∥BC时,则cos∠B的值为________;②当DE⊥AC时,求sin∠B的值;(2)设△ACD的面积为S,求S-AC2的最大值;(3)如图②,M、F为线段AB上的两动点,在运动的过程中,EF始终与CM平行,延长FE到点P,随着∠B的变化,是否存在∠DEP=k∠A(k为正整数)?若存在,请直接写出tan∠MCA的取值范围;若不存在,请说明理由.第4题图江西省2020届中考数学单元专题练之几何探究题答案全解全析类型一操作探究问题1.解:●初步体验证明:如解图①,连接BD交EF于点O,连接DE、BF,第1题解图∵BE=DF,BE∥DF,∴四边形BFDE是平行四边形,∴EF与BD互相平分.●规律探究(1) 2;(2)(1)中的数量关系不会发生变化.理由如下:如解图①,过点D作BE的垂线,与BE的延长线交于点M,连接BD,第1题解图①∵BE∥DF,EF⊥BE,DM⊥BM,∴EF∥DM,∴四边形EFDM是矩形,∴DF=EM,EF=DM,BM=BE+DF,∵在正方形ABCD中,∴BD=2AB,∵BD2=BM2+DM2,∴(BE+DF)2+EF2=2AB2.●拓展应用如解图②,过点P作EP⊥DP,过点B作BE⊥EP,第1题解图②∵∠DPB=135°,∴∠EPB=45°,即△EBP为等腰直角三角形,∴PB=2BE,∵2BP+2PD=46,∴2·2BE +2PD =46, ∴BE +PD =26,设PE =BE =x ,则有(BE +PD )2+x 2= 2AB 2,即(26)2+x 2=32, 解得x =±22(负值舍去), ∴PD =26-BE =26-2 2. 2. 解:发现:90°,102;【解法提示】∵点Q 在AB ︵上,点P 在OB 上,∴当PQ 取最大值时,点Q 与点A 重合,点P 与点B 重合, 此时∠POQ =90°,PQ =OA 2+OB 2=10 2.思考:(1)如解图①,连接OQ ,则OP =12OB =12OQ ,∵QP ⊥OB , ∴cos ∠QOP =OP OQ =12∴∠QOP =60°,∴l BQ ︵=60180π×10=103π ;第2题解图①(2)由折叠的性质可得,BP =B ′P ,AB ′=AB =102, 在Rt △B ′OP 中,OP 2+(102-10)2=(10-OP )2, 解得OP =102-10, S 阴影=S 扇形AOB -2S △AOP =90360π×102-2×12×10× (102-10)=25π-1002+100;探究:如解图②,找点O 关于PQ 的对称点O ′,连接OO ′、O ′B 、O ′C 、O ′P ,OO ′与PQ 交于点M ,则OM =O ′M ,OO ′⊥PQ ,O ′P =OP =6,第2题解图②∵点O ′是B ′Q ︵所在圆的圆心, ∴O ′C =OB =10,∵折叠后的B ′Q ︵恰好与半径OA 相切于C 点,∴O ′C ⊥AO , ∴O ′C ∥OB ,∴四边形OCO ′B 是矩形,在Rt △O ′BP 中,O ′B =62-42=2 5在Rt △OBO ′中,OO ′=102+(25)2=230, ∴OM =12OO ′=12×230=30,即点O 到折痕PQ 的距离为30.3. 解:深入探究:(1)∵折叠前的四边形ABCD 是矩形, ∴AM ∥DN ,∴∠KNM =∠KMN =∠1=70°, ∴∠MKN =40°;(2)△MNK 为等腰三角形;不发生变化; 理由如下:∵AM ∥DN , ∴∠1=∠MNK ,∵将纸片沿MN 折叠, ∴∠1=∠KMN , ∴∠MNK =∠KMN , ∴KM =KN ,∴△MNK 始终为等腰三角形;拓展应用:(3)如解图①,当△KMN 的面积最小值为12时,KN =KM =BC =1,∴KM ⊥KN ,第3题解图①∵∠NMB =∠KMN ,∠KMB =90°, ∴∠1=∠NMB =45°,同理将纸条向下折叠时,∠1=∠NMB =135°, ∴∠1=45°或∠1=135°; (4)分两种情况:情况一:如解图②,将矩形纸片对折,使点B 与D 重合,此时点K 也与D 重合,第3题解图②设MK =MB =x ,则AM =5-x ,在Rt △AMK 中,由勾股定理得12+(5-x )2=x 2, 解得x =2.6,∴MK =NK =2.6,(由(2)可得)∴S △MNK =12×1×2.6=1.3;情况二:如解图③,将矩形纸片沿对角线AC 对折,此时折痕即为AC ,第3题解图③设MK =AK =CK =x ,则DK =5-x . 同理可得MK =NK =2.6, ∵MD =1,∴S △MNK =12×1×2.6=1.3,∴△MNK 的面积最大值为1.3. 4. 解:(1)①等腰;【解法提示】由折叠的性质可知BF =EF ,∴△BEF 为等腰三角形. ②22; 【解法提示】由折叠的性质可知∠BEF =∠EBF =45°, ∴cos ∠BEF =22; (2)①当△BEF 是等边三角形时,则∠ABE =30°, ∵AB =3,∴cos ∠ABE =AB BE =32,∴BE =2;②根据题意可得矩形ABCD 的面积为6; 第一种情况:当点F 在边BC 上时,此时可得S △BEF ≤12S 矩形ABCD ,即当点F 与点C 重合时,S △BEF 存在最大值,最大值为3;由折叠可知CE =CB =23,即EF = 23; 第二种情况:当点F 在边CD 上时,如解图,过点F 作FH ∥BC 交AB 于点H ,交BE 于点K ,第4题解图∵S △EKF =12KF ·AH ≤12HF ·AH =12S 矩形AHFD ,S △BKF =12KF ·BH ≤12HF ·BH =12S 矩形BCFH ,∴S △BEF ≤12S 矩形ABCD =3,即当点F 为CD 中点时,△BEF 的面积最大,此时,点E 与点A 重合,△BEF 面积最大为3, ∴EF =AD 2+DF 2=(23)2+(32)2=512, 综上所述,当△BEF 的最大面积为3时,EF 的长为23或512. 5. (1) 解:如解图①,△ACQ 即为所求;第5题解图①(2)①证明:由旋转可得,△ABM ≌ △ACQ ,∴AM =AQ ,∠BAM =∠CAQ , ∵∠MAN =45°,∠BAC = 90°, ∴∠BAM +∠NAC =45°, ∴∠CAQ +∠NAC =45°,即∠NAQ =45°, 在△MAN 和△QAN 中, ⎩⎪⎨⎪⎧AM =AQ ∠MAN =∠QAN ,AN =AN∴△MAN ≌△QAN (SAS ), ∴MN =NQ ;② 解:MN 2=BM 2+NC 2; 理由如下:由①中可知,MN =NQ ,MB =CQ ,又∵∠NCQ =∠NCA +ACQ =∠NCA +∠ABM =45°+45°=90°, ∴在Rt △NCQ 中,NQ 2=CQ 2+NC 2,即MN 2=BM 2+NC 2; (3)解:ST 2=GS 2+TH 2;【解法提示】如解图③,连接SP 、PT ,用(2)中的方法可证△DGS ≌△DPT ,△GSP ≌△PTH ,∴GS =PT ,TH =SP ,由题意易知GH ⊥PD ,△SPT 为直角三角形, ∴ST 2=PT 2+SP 2=GS 2+TH 2.(4)解:如解图③,∵DE =DF ,DG =DP ,∠EDF =∠GDP =45°,第5题解图③∴∠DPK =∠DEP , 又∵∠PDK =∠EDP , ∴△DPK ∽△DEP ,∴DPDE=DKDP,即DP2=DK·DE,∵DK=a, DE=b,∴DP=ab.6.解:(1)①CD=CE,理由如下:∵AC=BC=6,∠ACB=90°,∴∠CAB=45°,∴∠CED=∠CAB=45°,又∵DE是⊙O的直径,∴∠ECD=90°,∴∠CDE=∠CED=45°,∴CD=CE;②由题意可得∠ECD=∠ACB=90°,∴∠ECA=∠BCD,又∵AC=BC=6,CD=CE,∴△ECA≌△DCB,∴AE=BD,∴AE+AD=BD+AD=AB,在Rt△ABC中,由勾股定理可得AB=62,即AE+AD的值为62;(2)∵DE是⊙O的直径,∴∠DAE=∠DCE=90°,又∵AC=BC,∠ACB=90°,∴∠CAB=∠B=45°,∠ECA=∠DCB,∠CEA=∠ADC∴∠EAC=∠B=45°,∴△ECA≌△DCB,∴AE=BD,∴AE-AD=BD-AD=AB,在Rt△ABC中,由勾股定理可得AB=62,即AE-AD的值为62;(3)①AD-AE=22,证明如下:第6题解图①∵DE是⊙O的直径,∴∠DFE=90°,如解图①,过点F作FM⊥AF于点F,交AD于点M,∴∠DFM=∠EF A,又∵∠MAF=∠CAB=45°,∴∠AMF=45°,∴AF=MF,又∵∠FDM=∠FEA,∴△FDM ≌△FEA (AAS), ∴AE =DM ,∴AD -AE =AD -DM =AM ,由AC =3AF ,AC =6可得AF =2,在Rt △AMF 中,由勾股定理可得AM =22,即AD -AE 的值为22; ②存在,⊙O 的半径为5.6或17. 【解法提示】由①可得CF =8, 如解图②,当∠ECA =90°时,△AEC 为直角三角形, 可证EC =AC =6,在Rt △ECF 中,由勾股定理可得EF =10,在Rt △EDF 中,由勾股定理可得DE =102,即⊙O 的半径为52, 如解图③,当∠AEC =90°时,△AEC 为直角三角形, 过点E 作EH ⊥AC 于点H ,可得EH =AH =3, ∴FH =5,第6题解图在Rt △EHF 中,由勾股定理可得EF =34,在Rt △EDF 中,由勾股定理可得DE =217,即⊙O 的半径为17.类型二 旋转探究问题1. (1)解: ∵△ABC 绕顶点C 顺时针旋转40°,得到△A ′B ′C , ∴CA =CA ′,CB =CB ′,∠ACA ′=∠BCB ′=θ, ∴△ACA ′∽△BCB ′,∴S △ACA ′∶S △BCB ′=AC 2∶BC 2=32∶42=9∶16; ∴S 1S 2=916; (2)①证明:∵AB ∥B ′C , ∴∠ABC =∠BCB ′;由旋转的性质得∠ABC =∠DB ′C , 即∠BCB ′ =∠DB ′C ; ∴CD =B ′D ;②解:根据勾股定理可得A ′B ′=AB =5,据题意可得∠BCB ′ +∠BCA ′ =∠DB ′C +∠CA ′B ′=90°, ∴∠BCA ′ =∠CA ′B ′,∴CD =A ′D =B ′D =12A ′B ′=52 ,∴ BD =BC -CD =32;(3)解:存在,∵∠A ′CB ′=90°,点M 为AC 的中点,∴CM =12AC =32,∵△A ′B ′C 是由△ABC 绕顶点C 顺时针旋转所得,∴A ′B ′=AB =5,第1题解图如解图,连接CN ,可得MN ≤CM +CN ,∴只有当点N 在MC 的延长线上时,MN =CM +CN ,此时MN 最大, ∵点N 为A ′B ′的中点,∴CN =12 A ′B ′=52,MN =CM +CN =4,即MN 的最大值为4.此时AA ′⊥BB ′.2. (1)证明:①∵AC =BC ,D , E 分别是 AC ,BC 的中点, ∴CD =CE ,由旋转可得∠D ′CE ′=∠DCE =90°,CD =CD ′,CE =CE ′, ∴∠ACD ′=∠BCE ′,CD ′=CE ′, ∴△ACD ′≌ △BCE ′, ∴AD ′=BE ′;②解:∵AD ′∥CE ′,∴∠AD ′C =∠E ′CD ′=90°, ∵AC =2CD ′,∴∠CAD ′=30°, ∴ AD ′=cos 30°×AC =32×22=6, 由①得BE ′=AD ′= 6 ;第2题解图①(2)解:根据题意可得CD ′=CE ′= 2 ,∵△CD ′E ′是等腰直角三角形,CD ′=CE ′= 2 , ∴D ′E ′=2,如解图①,作CK ⊥BE ′于点K .可得KD ′=E ′K , ∴CK =12D ′E ′=1,∴sin ∠CBE ′=CK BC =122=24;(3)解:如解图②,连接PM ,由(1)得△ACD ′≌ △BCE ′,第2题解图②∴∠P AC =∠E ′BC ,AD ′=BE ′, 又∠P AC +∠ACB =∠PBC +∠APB , ∴∠APB =∠ACB =90°, 设AD ′=x ,则BD ′=x -2,在△ABD ′中可得AD ′2+BD ′2=AB 2,即x 2+(x -2)2=42, 解得x 1=7+1,x 2=-7+1 (舍去), ∴BD ′=7-1,∴S △BD ′M =S △ABD′2=(7+1)(7-1)4=32,由轴对称性可得PM 扫过的图形面积为:180π×22360-32×2=2π-3.3. 解: (1)①正方形;【解法提示】由旋转性质可知DE =EF =FG =DG , ∴四边形DEFG 为菱形, ∴DG ∥BC . 又∵DE ⊥EC ,∴四边形DEFG 为正方形. ②∵四边形DEFG 为正方形, ∴DG ∥BC .∴∠ADG =∠B ,∠AGD =∠C . ∵△ABC 为等边三角形, ∴∠B =∠C =60°.∴△ADG 为等边三角形. ∴AD = DG =DE .又∵BD =DE sin ∠B =DE sin 60°=233DE ,∴BD +AD =233DE +DE =6.解得DE =1823+3=123-18.(2)①等边三角形,相等;②据题意可得△ADF ≌△BED ≌△CFE ,AD =x ,BD =6-x , 如解图①,过点D 作DG ⊥BC 于点G , 可得DG =sin ∠B ·BD =32(6-x ), y =S △ABC -3S △BDE =12×33×6-3×x 2×32(6-x ),化简得y =334x 2-932x +9 3.图①图② 第3题解图(3)如解图②,经过多次操作可得到首尾顺次相接的多边形,其最大边数是6,它可能为正多边形,边长为2.4. (1)证明:据题意可得∠CAB =∠CBA ,AD =BD , ∴∠NAB =∠MBA ,又∵AB ∥MN ,AC =BC ,∴AC AN =BC BM,即AN =BM , ∴△ADN ≌△BDM (SAS );(2)证明:据题意可得AD =BD =2, 由(1)得∠NAB =∠MBA =135°,∠EDM = 45°,∴∠AND +∠ADN =∠EDB +∠BDM =45°, ∴∠AND =∠BDM , ∴△ADN ∽△BMD , ∴AD BM =ANBD,即AN ·BM =AD ·BD =2·2=2, ∴AN ·BM 的值不会发生变化;(3)解:①平分.证明:由(2)可得∠ADN +∠BDM =45°, ∴∠MDN =∠DAN =135°, 又∵△ADN ∽△BMD , ∴AN BD =ND DM , 又∵AD =BD , ∴AN AD =ND DM, ∴△ADN ∽△DNM ,∴∠AND =∠DNM ,即ND 始终平分∠ANM ; ②S △DMN =m 2+2m +22m;【解法提示】由(2)可得:AN ·BM =2,AN =m , ∴BM =2m,如解图,分别过点D 作AC 、MN 、CM 的垂线,垂足分别为H 、H ′、H ″ ,第4题解图∵ND 平分∠ANM ,且DH ⊥CA ,DH ′⊥MN 在Rt △ABC 中,DH ∥BC ,AD =BD 可得DH ′=DH =BC2=1,同理DH ″=1,∴S △DMN =S △CMN -S △ADN -S △ABC -S △DMB =12·CN ·CM -12·AN ·DH -12·AC ·BC -12·BM ·DH ″ =12×(2+m )×(2+2m )-12×m ×1-12×2×2-12×2m ×1 =m 2+2m +22m.∴△DMN 的面积为m 2+2m +22m.5. 解:(1)平行四边形;25;【解法提示】依题意可知,正方形ABCD 沿对角线剪开后为第5题解图①两个等腰直角三角形,当ED 边与AB 边重合时,AB =DF ,BC =EF ,∴四边形ABCF 是平行四边形,设AD 与BF 交于点O ,如解图①,可知AO =DO =12AD =1,∴BO =AB 2+AO 2=5,∴BF =2 5. (2)45°或135°;【解法提示】当△EFD 转到如解图②所示的位置时,∠CEF +∠CHE =∠ACB =45°;当△EFD 旋转到如解图③所示的位置时,∠CEF +∠CHE =180°-∠C =135°,综上可知,∠CEF +∠CHE 的度数为45°或135°.第5题解图(3)由题意知∠DEF =∠ACB =∠B =45°,∴∠DAC +∠CAH =45°,∠AHB +∠CAH =∠ACB =45°, ∴∠DAC =∠AHB ,∴△AGC ∽△HAB , ∴AC HB =GCAB ,∴2y =x 2,∴y =4x(0≤x <22); (4)当x 为2或2时,△AGH 是等腰三角形. 【解法提示】由题意可得△AGC ∽△HGA .∴要使△AGH 是等腰三角形,只要△AGC 是等腰三角形即可.第5题解图分三种情况讨论,①如解图④,当CG =AG ,此时CG =2, ②如解图⑤,当CG =AC ,此时CG =2,③如解图⑥,当AG =AC ,此时ED 与AB 重合,不合题意,舍去. 综上所述,当x =2或2时,△AGH 是等腰三角形.6. (1)解:如解图①,连接DF ,过点F 作FH ⊥AD 于点H .第6题解图①∵四边形ABCD 和四边形BEFG 是平行四边形. ∴AK ∥BE ,AB ∥EK .∴四边形ABEK 是平行四边形. ∵AB =BE ,∴四边形ABEK 是菱形.∴DK =FK =23+2-4=23-2,∠FKD =∠AKE =∠B =60°, ∴△FKD 是等边三角形. ∵FH ⊥AD ,∴KH =12DK =3-1,FH =3-3,在Rt △AFH 中,AH =4+3-1=3+3, ∴AF =AH 2+FH 2=(3+3)2+(3-3)2=24=2 6.(2)证明:∵四边形ABCD 和四边形GBEF 是平行四边形,∴四边形BMDN 是平行四边形.∵∠A =∠G ,∠AMB =∠GMD ,AB =GD . ∴△ABM ≌△GDM (AAS ). ∴BM =DM .∴四边形BMDN 是菱形.(3)解:①如解图①,当旋转角α为30°时,四边形CGDF 是正方形(此时也是矩形).第6题解图② 证明:∵BG =BC ,∠ABG =∠α=30°, ∴∠GBC =60°-30°=30°, ∴∠BGC =∠BCG =75°, ∴∠GCO =∠CGO =45°, ∴OG =OC ,∠GOC =90°,如解图②,过点G 作GN ⊥BC 于点N , 在Rt △BNG 中,∠GBC =30°, ∴GN =12BG =3+1,BN =3GN =3+ 3.∴NC =BC -BN =23+2-(3+3)=3-1. ∴GC =GN 2+NC 2=(3+1)2+(3-1)2=8=22,∴OG =OC =CG 2=222=2,∴OD =OF =4-2=2, ∴OD =OC =OG =OF , ∴四边形CGDF 是矩形, ∵GF ⊥CD ,∴四边形CGDF 是正方形;②如解图③,当旋转角α为300°时,四边形CGFD 是矩形.第6题解图③证明:∵∠α=300°,∴点E 与点A 重合,∠CBG =120°. ∵BC =BG ,∴∠GCD =120°-30°=90°.∵四边形ABCD 和四边形GBEF 是平行四边形, ∴CD ∥AB ,AB ∥GF ,AB =CD ,AB =GF , ∴CD ∥GF ,CD =GF ,∴四边形CGFD 是平行四边形, ∵∠GCD =90°,∴四边形CGFD 是矩形.类型三 新定义探究问题1. 解: (1)C ;(2)∵在Rt △ABC 中,∠ACB =90°,CD 是AB 上的中线, ∴CD =12AB ,∴CD =BD ,∴∠BCE =∠ABC , ∵BE ⊥CD , ∴∠BEC =90°, ∴∠BEC =∠ACB , ∴△BCE ∽△ABC ,∴点E 是△ABC 的黄金点;(3)①据题意可得∠P 1CB =60°,∠BP 1C =90°,AC =43, ∴P 1C =cos ∠P 1CB ·BC =cos 60°·BC =2,如解图,过点P 1作P 1D ⊥AC 于点D ,连接AP 1,可得∠P 1CD =30°, ∴P 1D =12P 1C =1,CD = 3 ,∴ AD =AC -CD =33,在Rt △AP 1D 中,根据勾股定理可得AP 1=(33)2+12=27;第1题解图②据题意可得△P 1BC ∽△CAB , ∴C △P 1BC C △CAB=BC AB =12, 同理可得C △P 2CP 1C △P 1BC =P 1C BC =12,即 C △P 2CP 1C △CAB=P 1C AB =14, ∴C △P 2016P 2017P 2018C △CBA=P 2017P 2018AB =122016,可得△CAB 的周长为12+43,∴△P 2016P 2017P 2018的周长为3+3220142. (1)解: 6-25;【解法提示】∵CD 是△ABC 的黄金线(AD >BD ), ∴AD AB =5-12, ∵S △ABC =4, ∴S △ADC =5-12×4=25-2, ∴S △BCD =S △ABC -S △ADC =6-25; (2)证明:∵∠A =36°,AB =AC , ∴∠ABC =∠C =72°,∵过点B 作BD 平分∠ABC ,与AC 相交于点D , ∴∠CBD =∠A =36°,∠BDC =∠C =72°, ∴AD =BD =BC , ∴△BCD ∽△ABC , ∴CD BC =BDAC ,即1-AD BC =1-BC BC =BC 1, 解得BC =5-12, ∴AD =5-12, ∴AD AC =5-12, ∴D 点是AC 的黄金分割点, ∴BD 是△ABC 的黄金线; (3)解:①S 1=S 2.理由如下:如解图,连接ED ,第2题解图据题意得:AD AB =AEAC =5-12,∴S △ABE S △ABC =S △ACD S △ABC=5-12,∴S △ABE =S △ACD ,∴ S △COE =S △BOD ,即S 1=S 2; ②由①得AD AB =AE AC, 又∵∠A 为公共角, ∴△ADE ∽△ABC ,∴∠DEA =∠BCA ,DE BC =AEAC =5-12, ∴DE ∥BC ,∴△ODE ∽△OCB , ∴OD OC =DEBC =5-12, ∴OD CD =5-15+1=(5-1)24. 3. (1)证明:根据题意可得△ABC ∽△A 1B 1C 1,且相似比为k (k >1), ∴aa 1=k ,即a =ka 1, 又∵c =a 1, ∴a =kc ;(2)证明:根据题意得∠A =40°, ∵CD 平分∠ACB ,∴∠BCD =12∠ACB =40°,即∠BCD =∠A ,又∵∠B =∠B , ∴△CBD ∽△ABC , 又∵BC 是公共边,∴△CBD 与△ABC 为梦幻三角形;(3)解:①∵△ACE 与△ADC 刚好构成梦幻三角形, ∴△ACE ∽△ADC , ∴AC AD =AEAC,即AC 2=AE ·AD =36, ∴AC =6,∵AB 为⊙O 的直径, ∴∠ACB =90°, 又∵BC =8,∴由勾股定理可得AB =10, 如解图,连接OD ,又∵∠ACB 的平分线交⊙O 于点D , ∴∠ACD =45°, ∴∠AOD =90°,∴∠OAD =∠ADO =45°,∵OD =5, ∴AD =52; ②PCPD=2m ;第3题解图【解法提示】根据题意可得AD =22AB , ∴CD AD =CD 2AB2=2·CD AB =2m , ∵PD 是⊙O 的切线, ∴∠ODP =90°, ∴∠ADP =45°,即∠ADP =∠PCD , 又∵∠P =∠P ,∴△ADP ∽△DCP ,且DP 为两三角形的公共边, ∴PC PD =CDDA=2m . 4. (1)证明:∵△A 1A 2A 3与△A 1B 2B 3都是正三角形, ∴A 1A 2=A 1A 3,A 1B 2=A 1B 3,∠A 2A 1A 3=∠B 2A 1B 3=60°, ∴∠A 2A 1B 2=∠A 3A 1B 3,∴△A 2A 1B 2≌△A 3A 1B 3(SAS ), ∴∠B 3A 3A 1=∠A 2=60°;∴随着点B 2的运动,∠B 3A 3A 1的大小始终不变,为60°. (2)解:∠B 3A 3A 4的大小不变.如解图,在边A 1A 2上取点D ,使A 1D =A 3B 2,连接B 2D .第4题解图∵四边形A 1A 2A 3A 4与四边形A 1B 2B 3B 4都是正方形, ∴A 1B 2=B 2B 3,∠A 1B 2B 3=∠A 1A 2A 3=90°, ∴∠A 3B 2B 3+∠A 1B 2A 2=90°, ∠A 2A 1B 2+∠A 1B 2A 2=90°, ∴∠A 3B 2B 3=∠A 2A 1B 2, ∴△A 3B 2B 3≌△DA 1B 2, ∴∠B 2A 3B 3=∠A 1DB 2, ∵A 1A 2=A 2A 3,A 1D =A 3B 2, ∴A 2B 2=A 2D .又∵∠A 1A 2A 3=90°,∴△DA 2B 2为等腰直角三角形, ∴∠A 1DB 2=135°, ∴∠B 2A 3B 3=135°, ∵∠A 4A 3A 2=90°, ∴∠B 3A 3A 4=45°,∴∠B 3A 3A 4的大小始终不变,为45°; (3)解:①∠B 3A 3A 4的大小不会发生改变,始终为180°n;②90°(n -1)(n -2)n.【解法提示】∠B 3A 3A 4+∠B 4A 4A 5+B 5A 5A 6+…+∠B n A n A 1=180°n ×1+180°n×2+180°n ×3+…180°n ×(n -2)=180°n ×[1+2+3+…+(n -2)]=90°(n -1)(n -2)n. 类型四 动点探究问题1. 解:(1)OB =4;(2)①∵AB =2,OB =4,∠OAB =90°,∴∠ABO =60°,又∵∠OCB =60°,∴△BOC 为等边三角形,∴OH =OBcos 30°=4×32=23, ∴OP =OH -PH =23-t ,如解图①,过P 点作PE ⊥OA ,垂足为点E ,第1题解图①则EP =OPcos 30°=3-32t , ∴S =12·OQ ·EP =12·t ·(3-32t )=-34t 2+32t (0<t <23);②若△OPM 为等腰三角形:(ⅰ)若OM =PM ,如解图②,则∠MPO =∠MOP =∠POC ,第1题解图②∴PQ ∥OC ,过点P 作PK ⊥OC 于点K , ∴OQ =PK =OP 2,即t =3-t2,解得:t =233,此时S =-34×(233)2+32×233=233; (ⅱ)若OP =OM ,如解图③,则∠OPM =∠OMP =75°,第1题解图③∴∠OQP =∠OMP -∠QOM =75°-30°=45°,此时EQ =EP ,即t -(3-12t )=3-32t , 解得:t =2,此时S =-34×22+32×2=3-3; (ⅲ)若OP =PM ,∠POM =∠PMO =∠AOB ,则PQ ∥OA ,此时点Q 在AB 上,不满足题意,舍去.综上所述,当△OPM 为等腰三角形时,△OPM 的面积为233或2. 2. (1)证明:根据题意得AD =CD ,∠ADC =∠DCF =∠DAB =90°,又∵DF ⊥DE 于点D ,∴∠ADE =∠CDF ,∴△ADE ≌△CDF ,∴DE =DF ;(2)解: OM 2+ON 2 的值为定值;理由:∵OM ⊥DE 于点M , ON ⊥DF 于点N ,∴四边形DMON 为矩形,∴DN =OM ,如解图①,连接OD ,可得OM 2+DM 2=OD 2,即OM 2+ON 2=OD 2,第2题解图①∵点O 为正方形ABCD 的中心,AB =2,∴OD =2,即OM 2+ON 2=OD 2=2;(3)证明:由正方形的性质可得∠DAC =45°,如解图②,过点Q 作C ′Q ⊥AQ 于点Q ,QC ′与DC 的延长线相交于点C ′,第2题解图②可得∠C ′=45°,即∠DAC =∠C ′,CQ =C ′Q ,又∠ADE +∠EDC =∠QDC ′+∠EDC =90°,∴∠ADE =∠QDC ′,∴△ADP ∽△C ′DQ ,∴AP C ′Q =AP CQ =DP DQ. 3. (1)①证明:据题意可得∠EAB +∠BAD =∠CAD +∠BAD =90°,∴∠EAB =∠CAD ,又AB =AC ,AD =AE ,∴△ABE ≌△ACD ,∴CD =BE ;②解:猜想:CD 2+BD 2=2PD 2.理由:据题意可得∠ABC =∠C =45°,由①可得∠ABE =∠C =45°,即∠EBD =90°,∴BE 2+BD 2=PE 2+PD 2,即CD 2+BD 2=2PD 2;(2)解:①据题意可得BP =42,如解图,过点P 作PF ∥AC ,PF 与BC 相交于点F ,第3题解图可得BF =BP sin 45°=42×22=8, 由(1)可得△PBE ≌△PFD ,∴DF =BE ,∠ABE =∠PFD =45°,∴∠EBD =90°,∴BE 2+BD 2=PE 2+PD 2,∴DF 2+BD 2=2PD 2,即2y =x 2+(8-x )2,化简得y =x 2-8x +32;②存在;理由如下:据题意可得BC =12,CD =12-x ,AP =22, 在Rt △ACP 中,可得:CP =(62)2+(22)2=45, 当CD =DP 时,△CDP 为等腰三角形,此时,可得 y =12-x ,即x 2-8x +32=(12-x )2,解得x =7,∴y =x 2-8x +32=72-8×7+32=25,∴S △DPE =252; 当CP =CD 时,△CDP 为等腰三角形;此时,可得12-x =45,解得x =12-45,∴y =x 2-8x +32=(12-45)2-8×(12-45)+32=160-645,∴S △DPE =160-6452=80-325,综上,△DPE 的面积为252或(80-325). 4. 解:(1)① 23; 【解法提示】∵E 是AC 的中点,∴当DE ∥BC 时,D 为AB 的中点,即BD =12AB =4, 又∵CD ⊥AB ,∴cos ∠B =BD BC =46=23. ②∵点E 是AC 的中点,∴当DE ⊥AC 时,DE 为AC 的垂直平分线,∴CD =AD ,设CD =AD =x ,则BD =8-x ,在Rt △BCD 中,根据勾股定理得:(8-x )2+x 2=62,解得x 1=4+2,x 2=4-2,∴sin ∠B =CD BC =4+26或4-26; (2)∵CD ⊥AB ,∴ S -AC 2=AD ·CD 2-(AD 2+CD 2)=-(AD 2+CD 2-2AD ·CD )-3AD ·CD 2, ∴ S -AC 2=-(AD -CD )2-3AD ·CD 2, ∴当AD =CD 时,S -AC 2的值最大,最大值为-3AD ·CD 2, 由(1)可知:-3AD ·CD 2= -3×(4-2)22=122-27; (3)34<tan ∠MCA <377. 【解法提示】当∠ABC 为直角时,根据勾股定理可得AC =10,此时可得 tan ∠A =BC AB =68=34. 当∠ACB 为直角时,根据勾股定理可得AC =27 ,此时可得tan ∠A =BC AC =627=377. ∵△ABC 是锐角三角形,∴34<tan ∠A <377. 由题意可知∠DEP =∠DEC +∠CEP =2∠A +∠CEP ,又∵∠DEP =k ∠A ,且k 为正整数,∴k =3,即∠CEP =∠AEF =∠A ,又∵EF始终与CM平行,∴∠MCA=∠AEF=∠A,∴34<tan∠MCA<377.。
2020年九年级数学中考几何探究型问题:线段最值问题——“费马点”问题(包含答案)

几何探究型问题(针对第25题)线段最值问题“费马点”问题【问题背景】“费马点”——就是到三角形三个顶点的距离之和最小的点.“费马点”问题在中考考查时主要隐藏在求PA+PB+PC的最小值问题,通常将某三角形绕点旋转一定的角度,从而将三条线段转化在同一条直线上,利用两点之间线段最短解决问题.【模型分析】对于一个各角不超过120°的三角形,“费马点”是对各边的张角都是120°的点,对于有一个角超过120°的三角形,费马点就是这个内角的顶点.费马点P使它到△ABC三个顶点的距离之和PA+PB+PC最小,这就是所谓的“费马”问题.如图,将△APC绕点A逆时针旋转60°到△AP′C′,则可以构造出等边三角形APP′,从而得到AP=PP′,CP=C′P′,所以将PA+PB+PC的值转化为PP′+PB+P′C′的值,则线段BC′的长即为所求的最小值.例题1.如图,已知点P为等边三角形ABC外接圆的劣弧BC上任意一点,求证:PB+PC=PA.证明:如答图,在P A上截取PM=PC,连接CM.∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,BC =AC .∵∠ABC =∠APC ,∴∠MPC =60°,∴△MPC 是等边三角形,∴∠MCP =60°,MC =PC ,∴∠ACM =∠BCP .在△BPC 和△AMC 中,⎩⎪⎨⎪⎧BC =AC ,∠BCP =∠ACM ,PC =MC ,∴△BPC ≌△AMC (SAS),∴BP =AM ,∴PB +PC =AM +PM =P A .2.已知三个村庄A ,B ,C 构成了如图所示的△ABC(其中∠A ,∠B ,∠C 均小于120°),现选取一点P 作为打水井,使水井P 到三个村庄A ,B ,C 所铺设的输水管总长度最小.求输水管总长度的最小值.解:如答图,以BC 为边在△ABC 的外部作等边三角形BCD ,连接AD .∴AD 的长就是△ABC 的费马距离. 易得∠ABD =90°,∴AD =AB 2+BD 2=5(km).答:输水管总长度的最小值为5 km.练习(2019·陕师大附中六模)问题提出(1)如图1,在△ABC 中,BC =2,将△ABC 绕点B 顺时针旋转60°得到△A ′BC ′,则CC ′=______.【解答】由旋转的性质可知∠CBC ′=60°,BC ′=BC ,则∠△BCC ′是等边三角形,故CC ′=BC =2.问题探究(2)如图2,在△ABC中,AB=BC=3,∠ABC=30°,点P为△ABC内一点,连接PA,PB,PC,求PA+PB+PC的最小值,并说明理由.解题思路将△ABP绕点B逆时针旋转60°得到△EBF,连接PF,EC.易证PA+PB+PC=EF+PF+PC;由PC+PF+EF≥EC,推出当点P,F在直线EC上时,PA+PB+PC的值最小,即为EC的长,求出EC的长即可解决问题.【解答】如答图1,将△ABP绕点B逆时针旋转60°得到△EBF,连接PF,EC.由旋转的性质可知△PBF是等边三角形,∴PB=PF.∵P A=EF,∴P A+PB+PC=EF+PF+PC.∵PC+PF+EF≥EC,∴当点P,F在直线EC上时,P A+PB+PC的值最小,易得BC=BE=BA=3,∠CBE=90°,∴EC=2BC=32,∴P A+PB+PC的最小值为3 2.问题解决(3)如图3,在四边形ABCD中,AD∥BC,AB=6,AD=4,∠ABC=∠BCD=60°.在四边形ABCD内部有一点P,满足∠APD=120°,连接BP,CP,点Q为△BPC内的任意一点,是否存在一点P和一点Q,使得PQ+BQ+CQ有最小值?若存在,请求出这个最小值;若不存在,请说明理由.解题思路将△PBQ绕点B逆时针旋转60°得到△EBG,则PQ=EG,△BQG是等边三角形,易知PQ+BQ+CQ=EG+GQ+QC≥EC,推出当EC取得最小值时,PQ +BQ +CQ 的值最小.延长BA 交CD 的延长线于点S ,作△ADS 的外接圆⊙O ,将线段BO ,BP 绕点B 逆时针旋转60°得到线段BO ′,BE ,连接EO ′,OB ,OP .易证△BEO ′≌△BPO(SAS),推出EO ′=OP =433,故点E 在以点O ′为圆心,433为半径的圆上,则当点E 在线段CO ′上时,EC 的值最小,最小值为CO ′-EO ′的长.【解答】如答图2,将△PBQ 绕点B 逆时针旋转60°得到△EBG ,连接GQ ,EC ,则PQ =EG ,△BQG 是等边三角形,∴BQ =QG ,∴PQ +BQ +CQ =EG +GQ +QC ≥EC ,∴当EC 取得最小值时,PQ +BQ +CQ 的值最小.如答图3,延长BA 交CD 的延长线于点S ,作△ADS 的外接圆⊙O ,连接OB .将线段BO ,BP 绕点B 逆时针旋转60°得到线段BO ′,BE ,连接EO ′,OP.易证△BEO ′≌△BPO (SAS),∴EO ′=PO .∵∠APD +∠ASD =180°,∴A ,P ,D ,S 四点共圆,∴OP =433,∴EO ′=433, ∴点E 在以点O ′为圆心,433为半径的圆上, ∴当点E 在线段CO ′上时,EC 的值最小,最小值为CO ′-EO ′的长,连接OO ′,延长OO ′到点R ,使得O ′R =OO ′,连接BR ,则∠OBR =90°,作RH ⊥CB 交CB 的延长线于点H ,O ′T ⊥CH 于点T ,OM ⊥BC 于点M .易知在Rt △OBM 中,BM =5,OM =1133, ∴OB =OM 2+BM 2=1433, ∴BR =3OB =14.易知△BHR ∽△OMB ,∴RH BM =BR OB,∴RH =5 3.∵HR ∥O ′T ∥OM ,OO ′=RO ′,∴TM =TH ,∴O ′T =RH +OM 2=1333,∴BT =O ′B 2-O ′T 2=3, ∴CO ′=CT 2+O ′T 2=2633, ∴CE =CO ′-EO ′=2633-433=2233, ∴PQ +BQ +CQ 的最小值为2233.类型三 “阿氏圆”问题【问题背景】“PA +k ·PB ”型的最值问题是近几年中考考查的热点,更是一个难点.当k 的值为1时,即可转化为“PA +PB ”之和最短问题,就可用我们常见的“将军饮马”问题模型来处理,即可以转化为轴对称问题来处理.当k 取任意不为1的正数时,此类问题的处理通常以动点P 的运动轨迹不同来分类,一般分为两类研究,即点P 在直线上运动和点P 在圆上运动.其中点P 在圆周上运动的类型称之为“阿氏圆”问题.【模型分析】如图1,⊙O 的半径为r ,点A ,B 都在⊙O 外,P 为⊙O 上一动点,已知r =k ·OB ,连接PA ,PB ,则当PA +k ·PB 的值最小时,点P 的位置如何确定?如图2,在线段OB 上截取OC ,使OC =k ·r ,则可证明△BPO 与△PCO 相似,即k ·PB =PC .故求PA +k ·PB 的最小值可以转化为PA +PC 的最小值,其中A ,C 为定点,P 为动点,当点P ,A ,C 共线时,PA +PC 的值最小,如图3.“阿氏圆”模型解题策略:第一步:连接动点与圆心O(一般将含有k 的线段两端点分别与圆心O 相连),即连接OB ,OP ;第二步:计算线段OP 与OB 及OP 与OA 的线段比,找到线段比为k 的情况,如例子中的OP OB =k ; 第三步:在OB 上取点C ,使得OC OP =OP OB ;第四步:连接AC ,与⊙O 的交点即为点P .例题如图,在Rt △ABC 中,∠ACB =90°,CB =4,CA =6,⊙C 的半径为2,P 为圆上一动点,连接AP ,BP ,求AP +12BP 的最小值. 解:如答图,连接CP ,在CB 上取点D ,使CD =1,连接AD ,PD .∵CD CP =CP BC =12,∠PCD =∠BCD , ∴△PCD ∽△BCP ,∴PD BP =12, ∴PD =12BP ,∴AP +12BP =AP +PD , ∴要使AP +12BP 最小,则AP +PD 最小, 当点A ,P ,D 在同一条直线时,AP +PD 最小,即AP +12BP 的最小值为AD 的长. 在Rt △ACD 中,∵CD =1,AC =6,∴AD =AC 2+CD 2=37,∴AP +12BP 的最小值为37. 练习问题提出(1)如图1,已知线段AB 和BC ,AB =2,BC =5,则线段AC 的最小值为______.解题思路当点A 在线段BC 上时,线段AC 有最小值.【解答】∵当点A 在线段BC 上时,线段AC 有最小值,∴线段AC 的最小值为5-2=3.问题探究(2)如图2,已知在扇形COD 中,∠COD =90°,DO =CO =6,A 是OC的中点,延长OC 到点F ,使CF =OC ,P 是CD ︵上的动点,点B 是OD 上的一点,BD =1.①求证:△OAP ∽△OPF .解题思路由题意可得OA OP =OP OF =12,由相似三角形的判定可得△OAP ∽△OPF . 【解答】∵A 是OC 的中点,DO =CO =6=OP ,∴OA OP =12. ∵CF =OC ,∴OF =2OC =2OP ,∴OP OF =12, ∴OA OP =OP OF,且∠AOP =∠POF ,∴△OAP ∽△OPF .②求BP +2AP 的最小值.解题思路由相似三角形的性质可得PF =2AP ,可得BP +2AP =BP +PF ,即当F ,P ,B 三点共线时,BP +2AP 有最小值,最小值为BF 的长,由勾股定理即可求解.【解答】∵△OAP ∽△OPF ,∴AP PF =OP OF =12, ∴PF =2AP .∵BP +2AP =BP +PF ,∴当F ,P ,B 三点共线时,BP +2AP 有最小值,最小值为BF 的长.∵DO =CO =6,BD =1,∴BO =5,OF =12,∴BF =OB 2+OF 2=13.问题解决(3)如图3,有一个形状为四边形ABCD 的人工湖,BC =9千米,CD =4千米,∠BCD =150°,现计划在湖中选取一处建造一座假山P ,且BP =3千米,为方便游客观光,从C ,D 分别建小桥PD ,PC .已知建桥PD 每千米的造价是3万元,建桥PC 每千米的造价是1万元,建桥PD 和PC 的总造价是否存在最小值?若存在,请确定点P 的位置,并求出总造价的最小值,若不存在,请说明理由.(桥的宽度忽略不计)解题思路以点B 为圆心,3为半径作圆交AB 于点E ,交BC 于点F ,点P 为EF ︵上一点,连接BP ,PC ,PD ,在BC 上截取BM =1,连接MD ,PM ,过点D 作DG ⊥CB ,可证△BPM ∽△BCP ,可得PC =3PM ,当点P 在线段MD 上时,建桥PD 和PC 的总造价有最小值,由勾股定理可求MD 的值,即可求出建桥PD 和PC 的总造价的最小值.【解答】存在.如答图,以点B 为圆心,3为半径作圆交AB 于点E ,交BC 于点F ,P 为EF ︵上一点,连接BP ,PC ,PD ,在BC 上截取BM =1,连接MD ,PM ,过点D 作DG ⊥BC 交BC 的延长线于点G .∵BM BP =13=BP BC,且∠PBM =∠CBP , ∴△BPM ∽△BCP ,∴PM CP =BM BP =13,∴PC =3PM . ∵建桥PD 和PC 的总造价为3PD +PC =3PD +3PM =3(PD +PM ),∴当点P 在线段MD 上时,建桥PD 和PC 的总造价有最小值.∵∠BCD =150°,∴∠DCG =30°.∵DG ⊥BC ,∴DG =12DC =23(千米),CG =3DG =6(千米), ∴MG =BC +CG -BM =9+6-1=14(千米),∴MD =DG 2+MG 2=413(千米),∴建桥PD 和PC 的总造价的最小值为3×413=1213万元.作业5.(2019·交大附中三模)问题提出(1)如图1,点M ,N 是直线l 外两点,在直线l 上找一点K ,使得MK +NK 最小. 问题探究(2)如图2,在等边三角形ABC 内有一点P ,且P A =3,PB =4,PC =5,求∠APB 的度数.问题解决(3)如图3,矩形ABCD是某公园的平面图,AB=30 3 米,BC=60米,现需要在对角线BD上修一凉亭E,使得到公园出口A,B,C的距离之和最小.问:是否存在这样的点E?若存在,请画出点E的位置,并求出EA+EB+EC的最小值;若不存在,请说明理由.解:(1)如答图1,连接MN,与直线l交于点K,点K即为所求.(2)如答图2,把△APB绕点A逆时针旋转60°得到△AP′C,连接PP′.由旋转的性质,得P′A=P A=3,P′C=PB=4,∠P AP′=60°,∠AP′C=∠APB,∴△APP′是等边三角形,∴PP′=P A=3,∠AP′P=60°.∵PP′2+P′C2=32+42=25,PC2=52=25,∴PP′2+P′C2=PC2,∴△PP′C为直角三角形,且∠PP′C=90°,∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°,∴∠APB=∠AP′C=150°.(3)存在.如答图3,把△ABE绕点B逆时针旋转60°得到△A′BE′,连接EE′.答图由旋转的性质,得A′B=AB=30 3 米,BE′=BE,A′E′=AE,∠E′BE=60°,∠A′BA=60°,∴△E′BE是等边三角形,∴BE=EE′,∴EA +EB +EC =A ′E ′+EE ′+EC .根据两点之间线段最短,可知当EA +EB +EC =A ′C 时最短,连接A ′C ,与BD 的交点E 2即为所求,此时EA +EB +EC 最短,最短距离为A ′C 的长度.过点A ′作A ′G ⊥CB 交CB 的延长线于点G . ∵∠A ′BG =90°-∠A ′BA =90°-60°=30°, A ′G =12A ′B =12AB =12×303=153(米),∴GB =3A ′G =3×153=45(米), ∴GC =GB +BC =45+60=105(米).在Rt △A ′GC 中,A ′C =A ′G 2+GC 2=(153)2+1052=3013(米), 因此EA +EB +EC 的最小值为3013 米. 6.问题提出(1)如图1,已知△OAB 中,OB =3,将△OAB 绕点O 逆时针旋转90°得△OA ′B ′,连接BB ′,则BB ′=问题探究(2)如图2,已知△ABC 是边长为43的等边三角形,以BC 为边向外作等边三角形BCD ,P 为△ABC 内一点,将线段CP 绕点C 逆时针旋转60°,点P 的对应点为点Q .①求证:△DCQ ≌△BCP . ②求P A +PB +PC 的最小值. 问题解决(3)如图3,某货运场为一个矩形场地ABCD ,其中AB =500米,AD =800米,顶点A ,D 为两个出口,现在想在货运广场内建一个货物堆放平台P ,在BC 边上(含B ,C 两点)开一个货物入口M ,并修建三条专用车道P A ,PD ,PM .若修建每米专用车道的费用为10 000元,当M ,P 建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留根号)解:(1)由旋转的性质,得∠BOB ′=90°,OB =OB ′=3, 根据勾股定理,得BB ′=3 2. (2)①证明:∵△BDC 是等边三角形, ∴CD =CB ,∠DCB =60°.由旋转的性质,得∠PCQ =60°,PC =QC , ∴∠DCQ =∠BCP .在△DCQ 和△BCP 中,⎩⎪⎨⎪⎧CD =CB ,∠DCQ =∠BCP ,CQ =CP ,∴△DCQ ≌△BCP (SAS). ②如答图1,连接AD ,PQ . ∵PC =CQ ,∠PCQ =60°,∴△CPQ 是等边三角形,∴PQ =PC , 由①知DQ =PB ,∴P A +PB +PC =P A +QD +PQ ,由两点之间线段最短,得P A +QD +PQ ≥AD , ∴P A +PB +PC ≥AD ,∴当点A ,P ,Q ,D 在同一条直线上时,P A +PB +PC 取得最小值,即为AD 的长,过点D 作DE ⊥AC ,交AC 的延长线于点E . ∵△ABC 是边长为43的等边三角形, ∴CB =AC =43,∠BCA =60°, ∴CD =CB =43,∠DCE =60°, ∴DE =6,∠DAE =∠ADC =30°, ∴AD =12,即P A +PB +PC 的最小值为12.答图(3)如答图2,将△ADP 绕点A 逆时针旋转60°,得△AD ′P ′.由(2)知,当点M ,P ,P ′,D ′在同一条直线上时,P A +PM +PD 最小,最小值为D ′M 的长.∵M 在BC 上,∴当D ′M ⊥BC 时,D ′M 取得最小值. 设D ′M 交AD 于点E ,连接DD ′,AM ,DM . 易知△ADD ′是等边三角形,∴EM =AB =500米, ∴BM =400米,PM =EM -PE =(500-40033)米,∴D ′E =32AD =4003(米),∴D ′M =(4003+500)米, ∴最少费用为10 000×(4003+500)= 1 000 000(43+5)元.∴当M 建在BC 的中点(BM =400米)处,点P 在过M 且垂直于BC 的直线上,且在M上方(500-40033)米处时,修建专用车道的费用最少,最少费用为1 000 000(43+5)元.类型三 “阿氏圆”问题7.(2018·西工大附中三模) 问题提出(1)如图1,在△ABC 中,AB =AC ,BD 是AC 边的中线,请用尺规作图作出AB 边的中线CE ,并证明BD =CE ;问题探究(2)如图2,已知点P 是边长为6的正方形ABCD 内部一动点,P A =3,求PC +12PD 的最小值;问题解决(3)如图3,在矩形ABCD 中,AB =18,BC =25,点M 是矩形内部一动点,MA =15,当MC +35MD 最小时,画出点M 的位置,并求出MC +35MD 的最小值.解:(1)如答图1,线段EC 即为所求.证明:∵AB =AC ,AE =EB ,AD =CD ,∴AE =AD , 在△BAD 和△CAE 中,⎩⎪⎨⎪⎧AB =AC ,∠A =∠A ,AD =AE ,答图1∴△BAD ≌△CAE (SAS),∴BD =CE . (2)如答图2,在AD 上截取AE ,使得AE =32.∵P A 2=9,AE ·AD =32×6=9,∴P A 2=AE ·AD ,∴P A AD =AEP A.∵∠P AE =∠DAP ,∴△P AE ∽△DAP , ∴PE DP =P A DA =12,∴PE =12PD , ∴PC +12PD =PC +PE .∵PC +PE ≥EC ,∴PC +12PD 的最小值即为EC 的长,在Rt △CDE 中,∵∠CDE =90°,CD =6,DE =92,∴EC =62+(92)2=152,∴PC +12PD 的最小值为152.答图(3)如答图3,在AD 上截取AE ,使得AE =9. ∵MA 2=225,AE ·AD =9×25=225,∴MA 2=AE ·AD ,∴MA AD =AEMA.∵∠MAE =∠DAM ,∴△MAE ∽△DAM , ∴EM MD =MA DA =1525=35,∴ME =35MD , ∴MC +35MD =MC +ME .∵MC +ME ≥EC ,∴MC +35MD 的最小值即为EC 的长.如答图3,以点A 为圆心,AM 长为半径画弧,交EC 于点M ′,点M ′即为所求. 在Rt △CDE 中,∵∠CDE =90°,CD =18,DE =16, ∴EC =162+182=2145, ∴MC +35MD 的最小值为2145.8.(1)如图1,已知正方形ABCD 的边长为4,⊙B 的半径为2,P 是⊙B 上的一个动点,求PD +12PC 的最小值和PD -12PC 的最大值;(2)如图2,已知正方形ABCD 的边长为9,⊙B 的半径为6,P 是⊙B 上的一个动点,那么PD +23PC 的最小值为,PD -23PC 的最大值为(3)如图3,已知菱形ABCD 的边长为4,∠B =60°,⊙B 的半径为2,P 是⊙B 上的一个动点,那么PD +12PC 的最小值为,PD -12PC 的最大值为解:(1)如答图1,在BC 上取一点G ,使得BG =1,连接PB ,PG ,DG .∵PB BG =CBPB=2,∠PBG =∠CBP , ∴△PBG ∽△CBP , ∴PG CP =BG BP =12,∴PG =12PC , ∴PD +12PC =PD +PG .∵PD +PG ≥DG ,∴当D ,P ,G 三点共线时,PD +12PC 的值最小,最小值为DG =42+32=5.∵PD -12PC =PD -PG ≤DG ,∴如答图2,当点P 在DG 的延长线上时,PD -12PC 的值最大,最大值为5.答图(2)106,106.【解法提示】如答图3,在BC 上取一点G ,使BG =4,连接PG ,PB ,DG . ∵PB BG =64=32,CB PB =96=32,∴PB BG =CB BP. ∵∠PBG =∠CBP ,∴△PBG ∽△CBP , ∴PG CP =BG BP =23, ∴PG =23PC ,∴PD +23PC =DP +PG .∵DP +PG ≥DG ,∴当D ,P ,G 三点共线时,PD +23PC 的值最小,最小值为DG =52+92=106.∵PD -23PC =PD -PG ≤DG ,∴当点P 在DG 的延长线上时,PD -12PC 的值最大,最大值为106.答图(3)37,37.【解法提示】如答图4,在BC 上取一点G ,使得BG =1,连接PB ,PG ,DG ,作DF ⊥BC 交BC 的延长线于点F .∵PB BG =21=2,BC PB =42=2,∴PB BG =CB BP. ∵∠PBG =∠CBP ,∴△PBG ∽△CBP , ∴PG CP =BG BP =12, ∴PG =12PC ,∴PD +12PC =DP +PG .∵DP +PG ≥DG ,∴当D ,P ,G 三点共线时,PD +12PC 的值最小,最小值为DG 的长.在Rt △CDF 中,∵∠DCF =60°,CD =4, ∴DF =CD ·sin60°=23,CF =2,∴在Rt △GDF 中,DG =(23)2+52=37. ∴PD +12PC 的最小值为37.∵PD -12PC =PD -PG ≤DG ,∴当点P 在DG 的延长线上时,PD -12PC 的值最大,最大值为37.。
中考数学重难点题型--几何探究题解析

中考数学重难点题型--几何探究题解析
考点1三角形几何探究
1.如果三角形的两个内角α与。
满足2α+。
=90°,那么我们称这样的三角形为“准互余三角形”
(1)若βABC是“准互余三角形”,LC>90°,ζA=60°,贝l jζ·B=丘。
;
(2)如图i,在RtLABC中,4乙ACB=90°,AC=4, BC=S.若A D是ζBAC的平分线,不难证明LA BD是“准互余三角形?试问在边BC上是否存在点E(异于点D),使得LABE也是“准互余三角形”?若存在,请求出B E的长;若不存在,请说明理由.
(3)如图2,在四边形ABCD中,AB=7,CD= 12, BD.lCD,ζABD=2L乙BCD,且LABC是“准互余三角形”,求对角线AC的长
A
A可
B
解:or:LABC是“准互余三角形”,ζC>90°,ζA=60°,二2L乙B十ζA=90°,解得ζB=l5°.
(2)如答图l,在RtLABC中,·.·ζB+LBAC=90°,LBAC=2ζBAD,二ζB +2LBAD=90°’。
专题八 几何证明之四边形中的三角形全等问题 2020年中考数学冲刺难点突破 几何证明问题(解析版)

2020年中考数学冲刺难点突破几何证明问题专题八几何证明之四边形中的三角形全等问题1、如图1,已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.(1)连接GD,求证DG=BE;(2)连接FC,求tan∠FCN的值;(3)如图2,将图1中正方形ABCD改为矩形ABCD,AB=3,BC=8,E是线段BC上一动点(不含端点B,C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.当点E由B向C运动时,判断tan∠FCN的值是否为定值?若是,求出该定值;若不是,请说明理由.解:(1)如图1,∵正方形ABCD和正方形AEFG中,∴∠BAD=∠EAG=90°,AB=AD,AE=AG,∴△BAE≌△GAD(SAS),∴DG=BE;(2)如图2,过点F作FM⊥BN于M,则∠B=∠AEF=∠FME=90°,∴∠BAE+∠AEB=∠FEM+∠AEB=90°,即∠BAE=∠FEM,又AE=EF,∴△BAE≌△MEF(ASA),∴FM=BE,EM=AB,又BE+EC=AB,EM=EC+CM,∴CM=FM,在Rt△FCM中,tan∠FCN==1;(3)如图2,过点F作FM⊥BN于M,则∠B=∠AEF=∠FME=90°,∴∠BAE+∠AEB=∠FEM+∠AEB=90°,同理可证∠GAD=∠FEM,又AG=EF,∴△DAG≌△MEF,△BAE∽△MEF,∴EM=AD=BC=8,=,设BE=a,则EM=EC+CM=BC=BE+EC,∴CM=BE=a,∴=,∴FM=,∴tan∠FCN===,即tan∠FCN的值为定值.2、【操作发现】如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.【拓展】(3)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN,已知∠MAN=45°,BN=1,求DM的长.【实践探究】(1)解:∵四边形ABCD是正方形,∴AB=CD=AD,∠BAD=∠C=∠D=90°,由旋转得:△ABE≌△ADM,∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,即∠EAM=90°,∵∠MAN=45°,∴∠EAN=90°﹣45°=45°,∴∠MAN=∠EAN,在△AMN和△EAN中,,∴△AMN≌△EAN(SAS),∴MN=EN.∵EN=BE+BN=DM+BN,∴MN=BN+DM.在Rt△CMN中,MN===5,则BN+DM=5,设正方形ABCD的边长为x,则BN=BC﹣CN=x﹣3,DM=CD﹣CM=x﹣4,∴x﹣3+x﹣4=5,解得:x=6,即正方形ABCD的边长是6;故答案为:6;(2)EF2=BE2+DF2,理由如下:如图②,将△AFD绕点A顺时针旋转90°,点D与点B重合,得到△ABH,连结EH,∴∠ADF=∠ABH,DF=BH,∠DAF=∠BAH,AH=AF,∵∠EAF=45°,∴∠DAF+∠BAE=45°=∠BAH+∠BAE,∴∠HAE=45°=∠EAF,又∵AH=AF,AE=AE,∴△EAH≌△EAF(SAS),∴HE=EF,∵BN=DM,BN∥DM,∴四边形BMDN是平行四边形,∴DN∥BM,∴∠AND=∠ABM,∵∠ADN+∠AND=90°,∴∠ABH+∠ABM=90°=∠HBM,∴BE2+BH2=HE2,∴EF2=BE2+DF2;(3)如图③,延长AB至P,使BP=BN=1,过P作BC的平行线交DC的延长线于Q,延长AN交PQ 于E,连接EM,则四边形APQD是正方形,∴PQ=DQ=AP=AB+BP=4,设DM=x,则MQ=4﹣x,∵PQ∥BC,∴△ABN∽△APE,∴,∴PE=BN=,∴EQ=PQ﹣PE=4﹣=,由(1)得:EM=PE+DM=+x,在Rt△QEM中,由勾股定理得:()2+(4﹣x)2=(+x)2,解得:x=2,即DM的长是2.3、如图,将▱ABCD的边AB延长到点E,使BE=AB,连接DE,交BC边于点F.(1)求证:△BEF≌△CDF;(2)连接BD、CE,请探究:当∠BFD与∠A之间满足怎样的数量关系时,能使四边形BECD成为矩形?为什么?(1)证明:∵四边形ABCD是平行四边形,∵AB=CD,AB∥CD.∵BE=AB,∴BE=CD.∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,在△BEF与△CDF中,,∴△BEF≌△CDF(ASA);(2)解:∠BFD=2∠A时,四边形BECD成为矩形.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠A=∠DCB,∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,∴BF=CF,EF=DF,∵∠BFD=2∠A,∴∠BFD=2∠DCF,∴∠DCF=∠FDC,∴DF=CF,∴DE=BC,∴四边形BECD是矩形.4、已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.(1)求证:△BAD≌△CAE;(2)若∠ABC=30°,求∠MEC的度数;(3)求证:四边形MBDE是平行四边形.(1)证明:∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°﹣2∠ABC,∵以AD、AE为腰做等腰三角形ADE,∴AD=AE,∴∠ADE=∠AED,∴∠DAE=180°﹣2∠ADE,∵∠ADE=∠ABC,∴∠BAC=∠DAE,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS);(2)解:∵AB=AC,∴∠ACB=∠ABC=30°,∵△BAD≌△CAE,∴∠ABD=∠ACE=30°,∴∠ACB=∠ACE=30°,∴∠ECB=∠ACB+∠ACE=60°,∵EM∥BC,∴∠MEC+∠ECD=180°,∴∠MEC=180°﹣60°=120°;(3)证明:∵△BAD≌△CAE,∴DB=CE,∠ABD=∠ACE,∵AB=AC,∴∠ABD=∠ACB,∴∠ACB=∠ACE,∵EM∥BC,∴∠EMC=∠ACB,∴∠ACE=∠EMC,∴ME=EC,∴DB=ME,又∵EM∥BD,∴四边形MBDE是平行四边形.5、如图,在四边形ABCD中,∠A=90°,AD∥BC,BC=BD,CE⊥BD,垂足为E.(1)求证:△ABD≌△ECB;(2)若AD=4,CE=3,求CD的长.证明:(1)∵AD∥BC,∴∠ADB=∠EBC,∵CE⊥BD,∠A=90°,∴∠A=∠BEC=90°,在△ABD和△ECB中,,∴△ABD≌△ECB(AAS);(2)∵△ABD≌△ECB,∴AB=CE=3,∵AD=4,∴在Rt△ABD中,由勾股定理可得:BD=5,∵△BD≌△ECB,∴D=BE=4,∴DE=BD﹣BE=1,∴在Rt△CDE中,由勾股定理得:CD=.6、已知:矩形ABCD中,点E、F为对角线AC上两点,AF=CE.(1)如图1,求证:BE∥DF;(2)如图2,当AB=BE=AD时,连接DE、BF,在不添加任何辅助线的情况下,请直接写出四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.(1)证明:∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∴∠DAF=∠BCE,在△AFD和△CEB中,,∴△AFD≌△CEB(SAS),∴∠AFD=∠CEB,∴BE∥DF;(2)解:△ABF,△CDE,△ADF,△BCE;理由如下:由(1)得:△AFD≌△CEB,同理:△ABF≌△CDE(SAS),∴△AFD的面积=△CEB的面积,△ABF的面积=△CDE的面积,作BG⊥AC于G,如图2所示:∵四边形ABCD是矩形,∴∠ABC=90°,BC=AD,∵AB=BE=AD,∴AB=BE=BC,∴BC=2AB,AC==AB,AG=EG,∵△ABC的面积=AC×BG=AB×BC,∴BG===AB,∴AG===AB,∴AE=2AG=AB,∵AF=CE,∴△ABF的面积=△BCE的面积,CF=AE=AB,∴AF=AC﹣CF=AB﹣AB=AB,∴△ABF的面积=AF×BG=×AB×AB=AB2,∵矩形ABCD的面积=AB×BC=AB×2AB=2AB2,∴△ABF的面积=矩形ABCD面积的,∴△ABF的面积=△CDE的面积=△ADF的面积=△BCE的面积=矩形ABCD面积的.7、如图,在平行四边形ABCD中,点G在CD上,点H在AB上,且DG=BH,点E.F在AC上,且AE=CF.连接GF,FH,HE,EG.(1)求证:△CFG≌△AEH;(2)若AG=GC,则四边形EHFG是什么特殊四边形?请说明理由.证明:(1)∵在平行四边形ABCD中,AB∥CD,AB=CD,∴∠GCF=∠HAE,∵DG=BH,∴GC=AH,在△CFG与△AEH中,,∴△CFG≌△AEH(SAS);(2)∵△CFG≌△AEH,∴GF=EH,∠AEH=∠GFC,∴∠FEH=∠EFG,∴四边形EGFH是平行四边形,∵AG=GC,∴∠GAE=∠GCF,在△GAE与△GCF中,∴△GAE≌△GCF(SAS),∴EG=GF,∴平行四边形EGFH是菱形.8、如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD边上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.(1)求证:△BDF≌△CDE.(2)若DE=BC,求证:四边形BECF是正方形.(1)证明:∵AD是BC边上的中线,AB=AC,∴BD=CD,∴∠DBF=∠DCE,∵∠BDF=∠CDE,∴△BDF≌△CDE(ASA);(2)证明:∵△BDF≌△CDE,∴BF=CE,DE=DF,∵BF∥CE,∴四边形BECF是平行四边形,∵AB=AC,AD是中线,∴四边形BECF是菱形,∵DE=BC,DE=DF=EF,∴EF=BC,∴四边形BECF是正方形.9、阅读材料:教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力,要增强学生的创新精神和综合素质.王老师想尝试改变教学方法,将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中,引导同学们解决菱形中的一个问题时,采用了以下过程(请解决王老师提出的问题):先出示问题(1):如图1,在等边三角形ABC中,D为BC上一点,E为AC上一点,如果BD=CE,连接AD、BE,AD、BE相交于点P,求∠APE的度数.学习,王老师请同学们说说自己的收获.小明说发现一个结论:在这个等边三角形ABC中,只要满足BD=CE,则∠APE的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形ABCD中,∠A=60°,E为BC上一点,F为CD上一点,BE=CF,连接DE、BF,DE、BF相交于点P,如果DP=4,BP=3,求出菱形的边长.问题(3):通过以上的学习请写出你得到的启示(一条即可).解:问题(1)∵△ABC是等边三角形,∴∠ABD=∠C=60°,AB=BC,在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),∴∠BAD=∠EBC,∵∠APE=∠ABP+∠BAP,∴∠APE=∠ABP+∠EBC=∠ABC=60°;问题(2)过点D作DG⊥BF交BF于点G,如图2所示:∵四边形ABCD是菱形,∴∠C=∠A=60°,BC=CD,∴△BCD是等边三角形,∴BC=CD=BD,由(1)可知∠DPG=60°,在Rt△DPG中,sin60°=,即=,解得:DG=2,cos60°=,即=,解得:PG=2,∴BG=BP+PG=3+2=5,在Rt△BDG中,由勾股定理得:BD2=BG2+DG2=52+(2)2=37,∴BD=,∴BC=BD=,∴菱形的边长为;问题(3)平时应该注意基本图形的积累,在学习过程中做个有心人.10、如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.(1)求证:BP=CQ;(2)若BP=PC,求AN的长;(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.解:(1)证明:∵∠ABC=90°∴∠BAP+∠APB=90°∵BQ⊥AP∴∠APB+∠QBC=90°,∴∠QBC=∠BAP,在△ABP于△BCQ中,,∴△ABP≌△BCQ(ASA),∴BP=CQ,(2)由翻折可知,AB=BC',连接BN,在Rt△ABN和Rt△C'BN中,AB=BC',BN=BN,∴Rt△ABN≌△Rt△C'BN(HL),∴AN=NC',∵BP=PC,AB=8,∴BP=2=CQ,CP=DQ=6,设AN=NC'=a,则DN=8﹣a,∴在Rt△NDQ中,(8﹣a)2+62=(a+2)2解得:a=4.8,即AN=4.8.(3)解:过Q点作QG⊥BM于G,由(1)知BP=CQ=BG=x,BM=MQ.设MQ=BM=y,则MG=y﹣x,∴在Rt△MQG中,y2=82+(y﹣x)2,∴.∴S△BMC′=S△BMQ﹣S△BC'Q==,=.11、已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B、C重合),以AD为边做正方形ADEF,连接CF.(1)如图①,当点D在线段BC上时,直接写出线段CF、BC、CD之间的数量关系.(2)如图②,当点D在线段BC的延长线上时,其他件不变,则(1)中的三条线段之间的数量关系还成立吗?如成立,请予以证明,如不成立,请说明理由;(3)如图③,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC两侧,其他条件不变;若正方形ADEF的边长为4,对角线AE、DF相交于点O,连接OC,请直接写出OC的长度.解:(1)∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,∴∠BAD=∠CAF,∵在△BAD和△CAF中,,∴△BAD≌△CAF(SAS),∴BD=CF,∵BD+CD=BC,∴CF+CD=BC;故答案为:CF+CD=BC;(2)CF+CD=BC不成立,存在CF﹣CD=BC;理由:∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,∴∠BAD=∠CAF,∵在△BAD和△CAF中,,∴△BAD≌△CAF(SAS)∴BD=CF∴BC+CD=CF,∴CF﹣CD=BC;(3)∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,∴∠BAD=∠CAF,∵在△BAD和△CAF中,,∴△BAD≌△CAF(SAS),∴∠ACF=∠ABD,∵∠ABC=45°,∴∠ABD=135°,∴∠ACF=∠ABD=135°,∴∠FCD=135°﹣45°=90°,∴△FCD是直角三角形.∵正方形ADEF的边长4且对角线AE、DF相交于点O.∴DF=AD=4,O为DF中点.∴Rt△CDF中,OC=DF=×=.13、已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;(2)如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD.①求∠BDE的度数;②若正方形ABCD的边长是,请求出△BCG的面积.(1)证明:∵四边形ABCD和四边形CEFG为正方形,∴BC=DC,CG=CE,∠BCD=∠GCE=90°.∴∠BCD+∠DCG=∠GCE+∠DCG,∴∠BCG=∠DCE.在△BCG和△DCE中,,∴△BCG≌△DCE(SAS).∴BG=DE;(2)解:①连接BE,如图2所示:由(1)可知:BG=DE,∵CG∥BD,∴∠DCG=∠BDC=45°,∴∠BCG=∠BCD+∠DCG=90°+45°=135°,∵∠GCE=90°,∴∠BCE=360°﹣∠BCG﹣∠GCE=360°﹣135°﹣90°=135°,∴∠BCG=∠BCE,在△BCG和△BCE中,,∴△BCG≌△BCE(SAS),∴BG=BE,∵BG=BD=DE,∴BD=BE=DE,∴△BDE为等边三角形,∴∠BDE=60°;②延长EC交BD于点H,过点G作GN⊥BC于N,如图3所示:在△BCE和△DCE中,,∴△BCE≌△BCG(SSS),∴∠BEC=∠DEC,∴EH⊥BD,BH=BD,∵BC=CD=,∴BD=BC=2,∴BE=2,BH=1,∴CH=1,在Rt△BHE中,由勾股定理得:EH===,∴CE=﹣1,∵∠BCG=135°,∴∠GCN=45°,∴△GCN是等腰直角三角形,∴GN=CG=(﹣1),∴S△BCG=BC•GN=××(﹣1)=.15、利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.(1)如图①,B,C,D三点共线,AB⊥BD于点B,DE⊥BD于点D,AC⊥CE,且AC=CE.若AB+DE=6,求BD的长.(2)如图②,在平面直角坐标系中,△ABC为等腰直角三角形,直角顶点C的坐标为(1,0),点A 的坐标为(﹣2,1).求直线AB与y轴的交点坐标.(3)如图③,∠ACB=90°,OC平分∠AOB,若点B坐标为(b,0),点A坐标为(0,a).则S四边形AOBC=.(只需写出结果,用含a,b的式子表示)解:(1)∵AB⊥BD,DE⊥BD,AC⊥CE,∴∠ABC=∠CDE=∠ACE=90°,∴∠A+∠ACB=90°,∠ECD+∠ACB=180°﹣∠ACE=90°,∴∠A=∠ECD,在△ABC和△CDE中,,∴△ABC≌△CDE(AAS),∴AB=CD,BC=DE,∴BD=CD+BC=AB+DE=6;(2)过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,如图②所示:∵△ABC为等腰直角三角形∴∠ADC=∠CEB=∠ACB=90°,AC=CB,∴∠DAC+∠ACD=90°,∠ECB+∠ACD=180°﹣∠ACB=90°,∴∠DAC=∠ECB,在△ADC和△CEB中,,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,∵点C的坐标为(1,0),点A的坐标为(﹣2,1),∴CO=1,AD=1,DO=2,∴OE=OC+CE=OC+AD=2,BE=CD=CO+DO=3,∴点B的坐标为(2,3),设直线AB的解析式为y=kx+b,将A、B两点的坐标代入,得,解得:,∴直线AB的解析式为:y=x+2,当x=0时,解得y=2,∴直线AB与y轴的交点坐标为(0,2);(3)过点C作CD⊥y轴于D,CE⊥x轴于E,如图③所示:∵OC平分∠AOB,∴CD=CE∴四边形OECD是正方形∴∠DCE=90°,OD=OE,∵∠ACB=90°,∴∠DCA+∠ACE=∠ECB+∠ACE=90°,∴∠DCA=∠ECB,在△DCA和△ECB中,,∴△DCA≌△ECB(ASA),∴DA=EB,S△DCA=S△ECB,∵点B坐标为(b,0),点A坐标为(0,a),∴OB=b,OA=a,∵OD=OE,∴OA+DA=OB﹣BE,即a+DA=b﹣DA,∴DA=,∴OD=OA+DA=a+=,∴S=S四边形AOEC+S△ECB=S四边形AOEC+S△DCA=S正方形DOEC=OD2=()2=,四边形AOBC故答案为:.16、如图1,将边长为2的正方形OABC如图放置在直角坐标系中.(1)如图2,若将正方形OABC绕点O顺时针旋转30°时,求点A的坐标;(2)如图3,若将正方形OABC绕点O顺时针旋转75°时,求点B的坐标.解:(1)过点A作AD⊥x轴于点D,如图2所示:则∠AOD=30°,∵正方形OABC的边长为2,∴AO=2,∴AD=AO=1,∴OD===,∴点A的坐标为:(,﹣1);(2)连接OB,过点B作BE⊥x轴于点E,如图3所示:则∠AOE=75°,∵四边形OABC是正方形,∴∠AOB=45°,OB=AO=2,在Rt△BOE中,∠BOE=∠AOE﹣∠AOB=30°,∴BE=OB=,OE=BE=,∴点B的坐标为(,﹣).。
2020中考数学二轮复习课件:专题八 几何综合探究题

2.
填空:①线段DE与AC的位置关系是
;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系
是
.
21
123456
解题知识解读
题型分类突破
素养训练提高
(2)当△DEC绕点C旋转到图3所示的位置时,小智猜想(1)中S1与S2的 数量关系仍然成立,并尝试作DM⊥BC,AN⊥CE,垂足分别为M,N,请
∵△ABC,△DEF都为等腰直角三角形,D是BC中 点,∴AD=BD,DF=DE,∠ADB+∠ADF=∠FDE+∠ADF,即
∠BDF=∠ADE,
∴△ADE≌△BDF, ∴AE=BF,
19
解题知识解读
题型分类突破
素养训练提高
123456
(3)当BC=2,在(2)的条件下,当α°=90°时,AE值最大,如图所示:
∠ACN=∠DCM,
∵在△ACN和△DCM 中,∠ACN=∠DCM,∠CMD=∠N,AC=DC,∴△ACN≌△DCM(AAS ),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三
角形的面积相等),即S1=S2.
23
123456
解题知识解读
题型分类突破
素养训练提高
∵BD∠=AB∠C12=A6B0C°=,F310D°∥,∠BFE2,D∴B∠=9F02°F,∴1D∠=∠F1ADBFC2==∠60A°,B∵CB=F610=°,DF1,∠F1 ∴△DF1F2是等边三角形,∴DF1=DF2,
BF,AE的数量关系,并说明理由.
(3)若BC=2,在(2)的条件下,当α°=
°时,AE值最大?并求此时
点A到EF三等分点的距离(画出示意图,并写出求算过程).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020中考数学几何探究题解析
分析:
第一小题比较简单,一看就知道是个正方形;
第二小题看图的话,感觉像是两个线段相等,那么要证明F是CE'中点,而这个时候要注意FE'是在正方形中的,所以要懂得线段的转换;
第三小题只有两个线段长度,咋一看感觉应该有难度吧,但是如果善于发现,就很容易找到突破口了。
解答:
(1)正方形
理由:BE=BE',
∠EBE'=∠BE'F=90°
所以BE//FE'
同时可得EF//BE'
所以四边形FEBE'是矩形,
同时又邻边相等
所以正方形成立;
(2)分析的时候已经说了,不能忘记FE'是在刚才的正方形中的,而同时两个线段都在线段CE'上,所以要好好研究这个CE'
根据旋转可知CE'=AE
而题中刚好又给了DA=DE
这不等腰三角形吗
有等腰三角形,那么首先就想到了三线合一,干脆画出来
如图,作DH⊥AE于H,则AH=EH
别忘了刚才的AE=CE'
现在AE倒被分成了两个线段的线段,
那么如果F是CE'中点,那么CF和FE'不是就和AH、EH一样吗所以我们如果能够得到FE'等于AE的一半不是也行嘛
根据条件可以得证
△DAH≌△ABE
所以AH=BE=BE'
现在正方形派上用场了,所以FE'=BE=AH=HE
即AE=2FE'
那么CE'=2FE'
所以CF=FE'
(3)这一小题给出的两个线段其实是有联系的,不知道看到这的你是否发现了
CF=3,AB=15
看看CF在什么位置,不是在刚才的CE'上吗,凑上FE'就刚好变成CE'了,而CE'=AE,同时还有FE'=BE,
所以我们如果假设FEBE'的边长为x,
那么BE=x,AE=CE'=3+x,AB=15
勾股定理走起,
可得x²+(3+x)²=15²
根据经验可以直接判断BE=9,AE=12,符合3、4、5的比例嘛
现在知道了BE和AE,那么题上让求DE,
我们可以让DE处于直角三角形,利用勾股定理解决
这里可以过D向AE作垂线,也可以过E向AD作垂线,
前者刚好能构造出前面用过的全等,所以作DM⊥AE于M
那么可得AM=9,DM=12,
所以ME=3,
那么Rt△DME中,
DE=3√17
学完这道题,同学们就应该记牢出现正方形的时候,要能想到利用正方形的四边相等进行线段转换,同时有直角的时候千万不能忘记勾股定理。
