陕西师范大一数学分析期末考试题
大一上数学分析期末考试题及答案

大一上数学分析期末考试题及答案一、选择题(每题3分,共30分)1. 极限的定义是:如果对于任意的正数ε,都存在正整数N,使得当n>N时,都有|a_n - A| < ε,则称序列{a_n}的极限为A。
A. 正确B. 错误答案:A2. 函数f(x)=x^2在区间(-∞, +∞)上是单调递增的。
A. 正确B. 错误答案:B3. 函数f(x)=x^3在区间(-∞, +∞)上是单调递增的。
A. 正确B. 错误答案:A4. 函数f(x)=sin(x)在区间[0, π]上是单调递增的。
A. 正确B. 错误答案:B5. 函数f(x)=x^2在区间[0, +∞)上是单调递增的。
A. 正确B. 错误答案:A6. 函数f(x)=x^3在区间(-∞, +∞)上是单调递增的。
A. 正确B. 错误答案:A7. 函数f(x)=e^x在区间(-∞, +∞)上是单调递增的。
A. 正确B. 错误答案:A8. 函数f(x)=ln(x)在区间(0, +∞)上是单调递增的。
A. 正确B. 错误答案:A9. 函数f(x)=1/x在区间(0, +∞)上是单调递减的。
A. 正确B. 错误答案:B10. 函数f(x)=x^2在区间(-∞, 0)上是单调递减的。
A. 正确B. 错误答案:A二、填空题(每题4分,共20分)11. 极限lim(x→0) (sin(x)/x) = ________。
答案:112. 极限lim(x→+∞) (1/x) = ________。
答案:013. 极限lim(x→0) (1 - cos(x))/x^2 = ________。
答案:1/214. 函数f(x)=x^3在x=0处的导数为 ________。
答案:015. 函数f(x)=e^x在x=0处的导数为 ________。
答案:1三、计算题(每题10分,共40分)16. 计算极限lim(x→0) (tan(x) - sin(x))/x^3。
解:利用洛必达法则,对分子分母分别求导三次,得到极限为1/2。
陕西师范大学考研数学分析真题2019
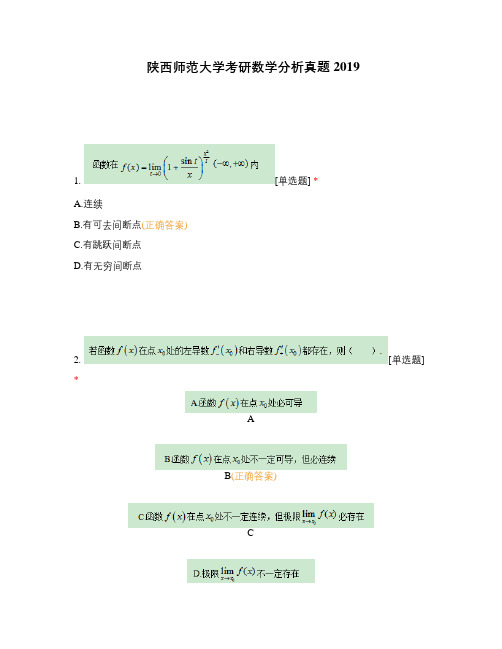
陕西师范大学考研数学分析真题20191. [单选题] *A.连续B.有可去间断点(正确答案)C.有跳跃间断点D.有无穷间断点2. [单选题] *AB(正确答案)CD3. [单选题] *AB(正确答案)CD4. [单选题] *A(正确答案)BCD5. [单选题] *AB(正确答案)CD6. [单选题] *A.①②B.③④C.②④(正确答案)D.①③7.[单选题] *AB(正确答案)CD8.[单选题] *ABCD(正确答案)9. [单选题] *ABCD(正确答案)10.[单选题] *ABCD(正确答案)11.[填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:-1)12. [填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:1/12)13.[填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3;本题的两个答案之间用“,”隔开_________________________________(答案:2,0)14. [填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:2)15.[填空题] *答案若为分数,请用“/”作分数线,示例:三分之一写作1/3_________________________________(答案:10/3)。
大一上学期高等数学期末试题及解答

Q( x) sin x , x
y
e
1 x
dx
s
in x
x
e
1 x
dx
dx
C
eln x sin x eln x dx C
x
1 x
sin x x
x dx
C
1 cos x C .
x
把y( ) 1代入通解,得 C 1.
故特解为
y 1 ( cos x 1).
x
四、计算题(每小题9分,共36分)
则f (ln x)定义域是 [1, e] .
知识点:复合函数的定义域
分析 0 ln x 1, 1 x e
一、 填空题(每小题3分,共15分) 2. 已知y x x ,则y _______ .
知识点:对数求导法
解 ln y x ln x , y =lnx 1, y
y xx (ln x 1).
( A) p 1,q 2; (B) p 2,q 3;
(C) p 2,q 1; (D) p 3,q 2 .
解: 特征方程为:r2 pr q 0 , 把特征根 r1 1 , r2 2 1 p q 0 分别代入特征方程,得 4 2 p q 0
解得
p 3,q 2 .
4. 求曲线y e x ( x 0)与y 0, x 0围成的
右边无限伸展的图形绕轴旋转一周所得立体的体积.
知识点: 反常积分,定积分的应用,旋转体的体积,
解 V + πy2dx + πe2xdx
0
0
π e2x 2
|0+
π. 2
五、解答题(每小题10分,共20分)
1. 在抛物线y x2 (0 x 1)上找一点P,使经过P的
数学分析上学期期末考试试题(及答案)

数学分析上学期期末考试试题(及答案)一、选择题(每小题2分,共20分)1. 下列哪个不是测度论中的重要定理?A. 开集的性质B. 测度的可贸易性C. 有限可加性定理D. 外测度的定义2. 设函数f(x)在[a, b]上可导,下列关于f(x)的结论中正确的是:A. f(x)在[a, b]上一定为增函数B. f(x)在[a, b]上一定为减函数C. f(x)在[a, b]上既可以是增函数也可以是减函数D. f(x)在[a, b]上一定为周期函数3. 以下哪个不是级数收敛的充要条件?A. 极限一致有界B. 积分收敛C. 极限值为零D. 部分和有界4. 若函数序列fn(x)在[a, b]上一致收敛于f(x),则f(x)在[a, b]上一定是A. 递增的B. 递减的C. 周期函数D. 连续函数5. 下列哪个不是积分的线性性质?A. ∫[a, b](f+g)(x)dx = ∫[a, b]f(x)dx + ∫[a, b]g(x)dxB. ∫[a, b]cf(x)dx = c∫[a, b]f(x)dx (c为常数)C. ∫[a, b]f(x)g(x)dx = ∫[a, b]f(x)dx * ∫[a, b]g(x)dxD. ∫[a, b]f(x)dx = -∫[b, a]f(x)dx6. 函数f(x)=|x|/(x^2+9)的不可导点是A. x=-3B. x=3C. x=-3和x=-sqrt(3)D. x=-3和x=sqrt(3)7. 设函数u(x, y)具有二阶连续偏导数,下列哪个条件可以确保u(x, y)为调和函数?A. u_xx + u_yy = 0B. u_xx + u_yy = 1C. u_xx - u_yy = 0D. u_xx - u_yy = 18. 设实数α为2π的有理数倍数,函数f(x)的周期为2π,下列哪个函数一定是f(x)的周期函数?A. f(x + α)B. f(x - α)C. f(-x)D. f(x/2)9. 设f(x)在区间[a, b]上一阶可导,且f(a)=f(b)=0,若存在c∈(a,b)使得f(c)=0,则函数f(x)在[a, b]上的其中一个极值点为A. aB. bC. cD. 以上都可能是10. 函数f(x)对任意的x∈(-∞, +∞)满足f'(x) = f(x),若f(x)在x=0处的值为2,则f(1)的值为A. -1B. 0C. 1D. 2二、填空题(每小题5分,共20分)1. 若函数f(x)可导,则f(x)________是可测的,且__________是可测的。
2022-2023学年陕西省陕西师大附中数学高一上期末预测试题含解析

可得函数为
y
sin
1 2
x
6
.
故答案为:
y
sin
1 2
x
6
.
15、 0 a 5 21 2
【解析】首先根据函数的解析式确定 a 0 ,再利用换元法将函数
f (x) a 2x3 a a 2x 1在区间 (0, ) 上有两个不同的零点的问题,转化为方程
a2t2 6at 1 a 0 区间 (1, ) 上有两个不同 根的问题,由此列出不等式组解得答案.
D. f (x) 3x 4
6. cos150 =() A. 1
2
C. 2 2
B. 3 2
1 D.
2
7.函数 f (x) 2x 的定义域为( )
A.[1, )
C.0,
B. 0,
D.R
8.已知直线 l 过 A(2, 1) , B(1,3) 两点,则直线 l 的斜率为
A. 3
3
B.
4
4
C. 4
不变),所得图象的函数解析式为________.
15.若函数 f (x) a 2x3 a a 2x 1在区间 (0, ) 上有两个不同的零点,则实数 a 的取值范围是_________.
16.已知幂函数
y
f
(
x)
的图象过点
3,
1 9
,则
f (2)
___________.
三、解答题:本大题共 5 小题,共 70 分。解答时应写出文字说明、证明过程或演算步骤。 17.甲乙两人用两颗质地均匀的骰子(各面依次标有数字 1、2、3、4、5、6 的正方体)做游戏,规则如下:若掷出的
用到的变形,也是解决问题时简化解题过程的关键所在
数学分析期末考试试题

数学分析期末考试试题一、选择题(每题2分,共20分)1. 函数f(x)=x^2-3x+2在区间[1,3]上的最大值是:A. 0B. 2C. 4D. 62. 以下哪个选项不是闭区间[a, b]上连续函数的性质?A. 有界性B. 保号性C. 介值性D. 可微性3. 函数f(x)=sin(x)在x=0处的导数是:A. 0B. 1C. -1D. 24. 函数f(x)=x^3+2x^2-3x+1在x=-1处的泰勒展开式(展开到x^2项)是:A. -1+2x-x^2B. 1-2x+x^2C. -1+2x+x^2D. 1+2x-x^25. 以下哪个级数是发散的?A. 1 - 1/2 + 1/3 - 1/4 + ...B. 1^2 + 1/2^2 + 1/3^2 + ...C. 1 - 1/2 + 1/4 - 1/8 + ...D. 1 - 1/2^2 + 1/3^2 - 1/4^2 + ...6. 函数f(x)=x^2在x=1处的高阶导数f^(n)(x)(n≥2)是:A. 0B. 1C. 2D. 47. 函数f(x)=e^x的原函数是:A. e^x + CB. ln(x) + CC. sin(e^x) + CD. cos(e^x) + C8. 函数f(x)=x^2在[0,1]上的定积分是:A. 1/3B. 1/2C. 1D. 2/39. 函数f(x)=|x|在x=0处的导数是:A. 1B. -1C. 0D. 不存在10. 以下哪个函数是周期函数?A. f(x)=x^2B. f(x)=e^xC. f(x)=sin(x)D. f(x)=ln(x)二、填空题(每题2分,共10分)11. 若函数f(x)=x^3-6x^2+11x-6在x=2处取得极小值,则f'(2)=_________。
12. 若函数f(x)=x^3+bx^2+cx+d在x=-1处取得最大值,则b=_________。
13. 函数f(x)=ln(x)的原函数是_________。
数学分析试题(一)答案及评分标准 - 陕西师范大学

数学分析试题(一)答案及评分标准一、填空(每题3分)1. ]10,0(2.2)()(x f x f −+,2)()(x f x f −− 3.52 4.,1=a 1−=b 5.0二、求极限(每题5分)1.=++++++∞→n n 313131212121222L L lim )(lim )(lim n n n n 31313121212122++++++∞→∞→L L ……………………………(1分) =3113113121121121−−−−∞→∞→))((lim ))((lim n n n n ……………………………………………………………(2分) 2=……………………………………………………………………………(2分) 2.))()((lim 22221111n n nn ++++∞→L 22221211110n n n n n +≤++++≤)()(L ……………………………………………(2分) 利用夹逼原则,…………………………………………………………………(1分) 可求得021111222=++++∞→))()((lim n n n n L .……………………………………(2分) 3.=−−++∞→902070155863)()()(lim x x x x 9090207090155863()()(lim xx x x x x −−++∞→………………………(2分)=902070155863)()()(lim xx x x −−++∞→…………………………………………………..(1分) 902070583⋅=…………………………………………………………………..(2分) 4.x x x sin )(tan lim 0→= ………………………………………………..(1分) )ln(tan sin lim x x x e 0→x x x x e tan ln sin lim lim 00→→=x x x x e sin tan ln lim lim 100→→=………………………………………………(1分)x x x e sin sec lim 20→−=…………………………………………………………………(2分) 10==e ………………………………………………………………………(1分)5.))cos cos cos (cos lim (lim n n x x x x x 22220L ∞→→ n n n x x x x x x x x x x 22222222212sin cos cos cos sin cos cos cos sin sin L L +==== …………………………………………………………………………………..(2分)=∞→)cos cos cos (cos lim n n x x x x 2222L 12122+∞→⋅n n n x x sin sin lim …………………………….(1分) 12122+∞→⋅n n n x x sin sin lim =x x x xn n n 2222sin sin lim ⋅∞→x x 22sin =………………………………...(1分) ))cos cos cos (cos lim (lim n n x x x x x 22220L ∞→→=1220=→x x x sin lim …………………………(1分) 6.)sin (lim x x x 22011−→=)sin sin (lim xx x x x 22220−→………………………………………..(1分) =)sin sin (lim xx x x x 22220−→=x x x x x x x 2222220sin sin sin lim +−→……………………………….(1分) xx x x x x x 22222220cos sin sin cos lim++−=→……………………………………………(1分) xx x x x x x 2226232220sin cos sin sin lim −+−=→…………………………………………(1分) 31−=.…………………………………………………………………………(1分) 三、计算(每题5分)1.22xx x x x x y tan sec )tan (−=′=′ 2.)ln )11(ln()1111(ln 2′−−−=′−++−−+=′x x x x xx y ………通过分母有理化先将化简………………………………………………………………………………..(2分) y xx x x x x 1111111222−−⋅−−=′−−−)ln )(ln(………………………………(2分) 2111111x x x x xx y −=′−++−−+=′)(ln ……………………………………………(1分)3.……………………………………………………...(2分))()(ln sin sin ′=′=′x x x e x y )ln (sin )(sin ln sin ′⋅=′x x e e xinx x x …………………………………………………..(1分) )sin ln (cos )ln (sin sin sin xx x x x x x e y x xinx +=′⋅=′………………………………..(2分) 4.,则……………………………………………...(1分) 31x x f =−)(31)()(+=x x f 213()(+=′x x f )…………………………………………………………………(2分) 2)2(3)1(+=+′x x f ………………………………………………………………(1分) 231x x f =−′)(…………………………………………………………………..(1分)5.,则⎪⎩⎪⎨⎧==ta y t a x 33sin cos t t t a t t a dx dy tan sin cos cos sin −=−=2233……………………………(2分) ⎪⎩⎪⎨⎧−==x dxdy t a x tan cos 3,则t t a t t a x dx y d sin cos sin cos sec 42222313=−−=…………………...(3分) 6.设,由于x x x y −=ln x x x x y ln )ln (=′−=′………………………………(3分)xdx dy ln =……………………………………………………………………(2分)四、由于∞=−+−→13221x x x x ))((lim,1=x 是垂直渐近线……………………(1分) 21322=−+−∞→xx x x x )())((lim ……………………………………………………….(2分)=−−+−∞→)))(((lim x x x x x 2132241124=−−∞→x x x lim ……………………………….(2分) 因此也具有斜渐近线42+=x y .……………………………………..(1分) 五、x x x f 2ln )(=,由0222=−=′xx x x f ln ln )(,可解出1=x ,……..(2分) 2e 当时,;当时,10<<x 0<′)(x f 21e x <<0>′)(x f ;当时, x e <20<′)(x f ……………………………………………………………………………………(2分) 所以是的极小值,1=x f 01=)(f ;是的极大值,. 2e x =f 224−=e e f )(…………………………………………………………………………………….(2分) 六、证:令⎪⎩⎪⎨⎧=∈=0120x x x x x f ,],(,sin )(π…………………………………………(1分) f 在],[20π上连续.当),(20π∈x 时,022<−=−=′xx x x x x x x x f )tan (cos sin cos )(, 所以在f ],[20π上严格递减,………………………………………………..(3分) 因此),(20π∈x 时, 1022=<<=)()()(f x f f ππ 即x x x<<sin π2.…………………………….(2分)七、不妨假设在上不恒正也不恒负,…………………………..(1分) f ],[b a 即存在,满足],[,b a x x ∈′′′0>′)(x f ,0<′′)(x f ,…………………………(2分) 由连续函数的介值定理,……………………………………………………(2分) 则存在),(x x x ′′′∈0,使得00=)(x f ………………………………………….(1分) 这与已知矛盾.……………………………………………………………….(1分)。
大一上册期末高等数学试卷

一、选择题(每题5分,共20分)1. 下列函数中,在区间(0,+∞)上单调递减的是:A. f(x) = x^2B. f(x) = e^xC. f(x) = ln(x)D. f(x) = 1/x2. 函数y = x^3 - 6x + 9的极值点为:A. x = -1B. x = 1C. x = -3D. x = 33. 下列积分中,结果为π的是:A. ∫(0 to π) sin(x) dxB. ∫(0 to π) cos(x) dxC. ∫(0 to π) tan(x) dxD. ∫(0 to π) cot(x) dx4. 设f(x) = x^3 - 3x,则f(x)的导数f'(x)为:A. 3x^2 - 3B. 3x^2 - 2xC. 3x^2 + 2xD. 3x^2 + 35. 下列级数中,收敛的是:A. ∑(n=1 to ∞) (1/n^2)B. ∑(n=1 to ∞) (1/n)C. ∑(n=1 to ∞) (1/n^3)D. ∑(n=1 to ∞) (n^2)二、填空题(每题5分,共20分)1. 函数f(x) = 2x^3 - 3x^2 + x在x=1处的导数值为______。
2. 极限lim(x→0) (sin(x)/x) 的值为______。
3. 若f(x) = x^2 + 1,则f'(x) = ______。
4. 函数y = e^x的导数y' = ______。
5. 级数∑(n=1 to ∞) (1/n^2) 的和为______。
三、解答题(每题10分,共40分)1. 求函数f(x) = x^3 - 3x^2 + 4x的导数。
2. 求函数y = ln(x^2 + 1)的导数。
3. 计算极限lim(x→∞) (1/x^2 + 1/x^3)。
4. 求函数y = e^(2x)的积分。
四、应用题(每题10分,共20分)1. 一辆汽车以v = 20m/s的速度匀速行驶,当刹车后,每秒减速5m/s,求汽车停止前行驶的距离。
陕西师范大一数学分析期末考试题

A、N 是唯一的 C、前 N 项有 | x n − a |≥ ε
B、N 是 ε 的函数 D、必有对任何 N, | x n − a |< ε
学院: 适用班级: 学院: 数学与计算机科学学院 适用班级: 一 二 三 四 五 六 七 八 九 总分
11、当 x → 0 时, sec x − 1 是 A、高阶无穷小 12、 lim n + 3
π π , 上满足罗尔定理的点 ξ = 4 4
,凸性区间是 17、证明不等式:当 x > 0 时, 1 + x ln( x + 1 + x 2 ) > 1 + x 2 18、若 f (x ) 在区间 I 上存在有界导数,即 ∀x ∈ I , | f ′( x ) |≤ M ,则 f ′(x ) 在 I 上一致连续。
B、 1 −
A、 1 −
1 cos y 2
1 cos x 2
C、
2 2 − cos y
D、
2 2 − cos x
8、曲线 y = ln(e −
1 ) 具有 x
B、一条斜渐近线 C、两条垂直渐近线 D、两条斜渐近线
A、一条垂直渐近线 9、 lim
2x = x →0 | x |
B、-2 C、0 D、不存在
A、2
iiiiii4lncosxy?在???????44??上满足罗尔定理的点?5曲线xxy12??的拐点是凸性区间是6曲线xxy1??与x轴交点处的切线方程为二单项选择题每小题3分共15分7设xxysin21??则?dydxaycos211?bxcos211?cycos22?dxcos22?8曲线1lnxey??具有a一条垂直渐近线b一条斜渐近线c两条垂直渐近线d两条斜渐近线9??2lim0xxxa2b2c0d不存在10在数列极限axnn???lim的n??定义中an是唯一的bn是?的函数c前n项有???axnd必有对任何n???axn11当0?x时sec1x?是22x的a高阶无穷小b低阶无穷小c同阶无穷小c等价无穷小三计算题每小题6分共30分12nnxn3lim3???13xxxarctan2lim???141??xxy求y?1521arcsinxy??求dy16xxyarctan?求yd2四证明题每小题10分共20分17证明不等式
2022-2023学年陕西省西安市陕西师范大学附属中学高一上数学期末检测模拟试题含解析

【解析】因为函数 在区间 上单调递减,所以 时, 恒成立,即 ,故选A.
2、B
【解析】由题意可得 , , 在 递增,分别讨论 , , , , ,结合 的单调性,可得 的范围
【详解】函数 是定义在 上的奇函数,在区间 上单调递增,且 (1) ,
可得 , , 在 递增,
若 时, 成立;若 ,则 成立;
(2)选择合适的公式进行化简求值
19、(1)见解析; (2)见解析.
【解析】(1)根据线面平行的判定定理可证明 平面 ;
(2)根据面面垂直的判定定理即可证明平面 平面 .
【详解】(1)证明:连结 ,在 中, , 分别是 , 的中点,
为 的中位线,
.
在 , , 分别是 , 的中点,
是 的中位线,
,
.
平面 ,
4、C
【解析】对于A、B、D均可能出现 ,而对于C是正确的
5、A
【解析】设对称点为 ,则 ,则 ,故选A.
6、C
【解析】根据题意,列出所有可能,结合古典概率,即可求解.
【详解】甲、乙、丙3人投中与否的所有情况为:(中,中,中),(中,中,不中),(中,不中,中),
(中,不中,不中),(不中,中,中),(不中,中,不中),(不中,不中,中),
(Ⅱ)推导出 , ,从而 平面 , ,同理 ,由此能证明 平面AB1D1,从而 平面
【详解】(Ⅰ)连接BC1,∵正方体ABCD-A1B1C1D1中,AB∥C1D1,AB=C1D1,∴四边形ABC1D1是平行四边形,∴AD1∥BC1.又∵E,G分别是BC,CC1的中点,∴EG∥BC1,∴EG∥AD1.又∵EG⊄平面AB1D1,AD1⊂平面AB1D1,∴EG∥平面AB1D1.同理EF∥平面AB1D1,且EG∩EF=E,EG⊂平面EFG,EF⊂平面EFG,∴平面AB1D1∥平面EFG.
大一数学分析复习题

方法一:应用数列极限的定义(证明题)用定义求数列极限有几种模式: (1),作差,解方程,解出,则取或(2)将a a n -适当放大,解出()εf n >; (3)作适当变形,找出所需N 的要求。
方法二:常用方法:约去零因子求极限,分子分母同除求极限,分子(母)有理化求极限方法三(迫敛性)设收敛数列都以为极限,数列满足:存在正整数,当时有:则数列{}c n收敛,且。
方法四:(单调有界定理)在实系数中,有界的单调数列必有极限。
方法五:两个重要极限是和方法六:(柯西收敛准则)数列收敛的充要条件是:对任给的,存在正整数N,使得当n,m时,有方法七:Stolz定理:设n>N时,且,若(为有限数或无穷大),则方法八:形如数列极限方法九:用等价无穷小量代换求极限(等价无穷小量代换,只能代换极限式中的因式..),常见等价无穷小有:当时,,;方法十:用罗必塔法则求极限,用对数恒等式求极限,数列极限转化成函数极限求解。
算术-几何-调和平均不等式:对记(算术平均值)(几何平均值)(调和平均值)有均值不等式:等号当且仅当时成立. (3) Bernoulli 不等式: (在中学已用数学归纳法证明过)对由二项展开式(4)Cauchy-Schwarz 不等式:(),有(5),;;;导数微分及应用习题判断:1、若可微,且为上的偶函数,则必为][l l-上的偶函数;,()2 若是上的奇函数,则)f'必为[]l l,-上的偶函数;()(xx点的极限存在3、如果函数在点的左、右极限都存在,则函数在()x点可导;()4、若函数)f在(x(xf在点连续,则)5、若函数)(x f 在点0x x =连续,则)(x f 在0x 点的极限一定存在;( )6、若函数)(x f 在点0x x =可微,则)(x f 在0x 点可导 ; ( )7、如果函数()x f y = 在 0x 点 的左、右 极限都存在,则)(x f 在0x 点可导 ;( )8、若函数)(x f 在点0x x =连续,则函数()x f y = 在 0x 点 的左、右 极限都存在且相等;( )9、若)(x f 在0x 点不可导,则函数)(x f 在点0x x =一定不连续;( ) 10、若函数)(x f 在点0x x =不可微,则)(x f 在0x 点不可导 ; ( ) 11、若函数)(x f 在点0x x =不可微,则)(x f 的左、右 极限一定不存在;( )12、设函数)(x f 在0x 点可导,导数为,则( )13、设函数)(x f 在0x 点可导,导数为)(0x f ',则( )14、设函数)(x f 在0x 点可导,导数为)(0x f ',则( ) 15、函数在处不可导;( )16、函数1-=x y 在1=x 处不连续;( ) 17. 若)(0x f '存在,且,则( )18、若)(x f 在上可导,则)(x f 在],[b a 上有界; ( )19、若)(x f 在0x 点导数不存在,则曲线在点处没有切线;( ) 20、曲线上点处的法线的斜率为;( )21.设)(x f y =在0x x =可微,则当时,是关于高阶的无穷小;( ) 22、若,则)(x f 在处不可导;( )23、若)0()()()(lim2+∞<<=--→l l a x a f x f ax ,则)(x f 在a x =处可导但;( ) 24、若)0()()()(lim2+∞<<=--→l l a x a f x f ax ,则)(x f 在a x =处可导且;( ) 25、若,则; ( )1.设)(x f 在0x x =的某个邻域内具有二阶连续导数,则( ).A 、0;B 、)(0x f ';C 、;D 、;.2、设在0x 的邻域内连续,且有,则( ).A 、0;B 、;C 、;D 、.3.设,则( ). A 、; B 、; C 、; D 、.4.设)(x f 在1=x 点处可微,,则( ).A 、2;B 、1;C 、0;D 、.5.设,其中)(x f 为二阶可导函数,则( ).A 、;B 、;C 、;D 、.6.如果在区间内,,则在),(b a 内)(x f 与)(x ϕ( ).A 、仅相差一个常数;B 、完全相等;C 、均为常数;D 、为常数).7.设)(x f 为可导的偶函数,则)(x f '为( ).A 、偶函数;B 、可能是偶函数;C 、奇函数;D 、非奇非偶函数.8、设()x f 在0x x =处可导,则( ). A 、0; B 、; C 、; D 、)(0x f '.9、设,则( ).A 、-3;B 、3;C 、0;D 、∞. 10、设()x f 在区间),(b a 内连续,,则在点0x 处()x f ( ).A 、极限存在且可导;B 、极限不存在,但可导;C 、极限存在,但不一定可导;D 、极限不一定存在. 11.设,则在处()x f ( ).A 、 无定义;B 、不连续;C 、连续且可导;D 、连续但不可导. 12、设,在0=x 可导,则必有( ).A、;B、;C、;D、.13、,则在0x处的导数().=A、0;B、-1;C、不存在;D、1.14、可微的周期函数其导数().A、一定是周期函数,且周期不变;B、一定是周期函数,但周期可能发生变化;C、不一定是周期函数; D、一定不是周期函数.15、设()xf为可微的偶函数,且对任意的,则().A、;B、;C、2;D、-2.16.曲线上,切线平行于直线的点的坐标为().A、(1,-3);B、(3,-3);C、(-1,5);D、(2,0).''y().17、设,其中为可微函数,则=A、;B、;C、;D、.18、设,则().A、;B、;C、;D、.19.设)f为可微函数,若,则().(uA、;B、;C、;D、.20、下列函数中导数等于的是().A、;B、;C、;D、.21、曲线在点处的切线与直线垂直,则此曲线在点M 处的切线方程为( ). A 、;B 、;C 、; D 、.22.设,则( ).A 、;B 、;C 、2;D 、.23、设,则=''y ( ).A 、;B 、; C 、; D 、.24、下列函数中在点0=x 连续且可导的是( ).A 、;B 、;C 、;D 、.25、设方程确定是的函数,则( ).A 、;B 、1;C 、;D 、0.26.其中为可微函数,则=22dxyd ( ).A 、;B 、;C 、;D 、.27.设,其中l 为有限值,则()x f 在a x =处( ).A 、可导且0)(='a f ;B 、可导但0)(≠'a f ;C 、不一定可导;D 、肯定不可导.28.曲线在点M 处的切线斜率为3,则M 点的坐标为( ).A 、(1,0);B 、(0,1);C 、(1,3);D 、(1,-2). 29、设,则=dy ( ).A 、;B 、; C 、; D 、.30.设具有二阶导数,,则=''y ( ). A 、; B 、; C 、; D 、.31、函数,则()x f 在0=x 处( ).A 、间断;B 、连续但不可导;C 、连续且导数为0;D 、连续且导数为-1. 32.设,在0=x 可导,则的值为( ).A 、; B 、1,2=-=b a ; C 、1,2==b a ; D 、.33、,则( ).A 、;B 、;C 、6;D 、-6.34.若)(x f 在0x 处不可导,则)(x f 在0x 点( ).A 、无意义;B 、左、右极限不相等;C 、不一定可导;D 、不可微. 35、若,则( ).A 、;B 、; C 、; D 、.36.若,且,则=)(x f ( ).A 、; B 、; C 、; D 、.37、设函数 ,则=')0(f ( ).A 、-1;B 、;C 、1;D 、. 38.,在0=x 处( ).A 、不可导;B 、连续且可导;C 、不连续但可导;D 、不连续.39、设,则)(x f 的有关论证正确的是( ).A 、)(x f 在点0=x 处可微;B 、,C 、,D 、)(x f 在点0=x 处可导.40.设(其中 为常数),则( ). A 、; B 、0; C 、1; D 、x . 41、设(其中 n a a a ,,,21 为常数),则( ). A 、!n ; B 、0; C 、1; D 、x .42.设,则( ).A 、;B 、;C 、;D 、0.43.设函数,则函数)(x f 在0=x 处( ).A 、不连续;B 、连续,不可导;C 、可导,但不连续;D 、可导且导数也存在.44、设,则=22dxy d ( ). A 、;B 、;C 、;D 、.45.已知函数,则函数)(x f 在点0=x 处的导数( ). A 、; B 、; C 、; D 、不存在.46.设,则( ). A 、21; B 、; C 、1; D 、0. 47.设,则( ). A 、0; B 、1; C 、-1; D 、2.48、设,则=+)1(n y ( ). A 、; B 、; C 、; D 、0. 49、设,则( ). A 、; B 、; C 、; D 、. 50.下列命题中正确的是( ).A 、若,则有;B 、若)()(x g x f =,则有)()(x g x f '='; C 、若,则; D 、若0)(0=x f ;则0)(0='x f .51.)(x f y 在点0x 处的左、右导数存在且相等是)(x f 在点0x 处可导的 ( ).A 、必要条件;B 、充分条件;C 、充分必要条件;D 、无关条件.52.设函数,则为( ).A 、2;B 、3;C 、-1;D 、不存在.1. × ;2.∨;3、×;4、×;5、∨;6、∨;7、 × ;8、 ∨ ;9、 × ;10、 ∨ ;11、×;12、×;13、 ∨ ;14、×;15、∨ ;16、×;17、 ∨ ;18、∨ ;19、×;20、∨ ;21、 ∨ ;22、×;23、×;24、∨;25、× ;1、D ;2、B ;3、D ;4、A ;5、C ;6、A ;7、C ;8、B ;9、A ;10、C ;11、D ;12、D ;13、;C ;14、A ;15、B ;16、B ;17、D ;18、C ;19、D ;20、B ;21、A ;22、B ;23、D ;24、C ;25、B ;26、C ;27、A ;28、D ;29、B ;30、D ;31、D ;32、C ;33、C ;34、D ;35、A ;36、C ;37、C ;38、B ;39、C ;40、B ;41、A ;42、B ;43、B ;44、B ;45、D ;46、D ;47、D ;48、B ;49、A ;50、B ;51、C ;52、D.中值定理和罗比达法则★1.下列函数在给定区间上是否满足罗尔定理的所有条件?如满足,请求出满足定理的数值。
数学分析大一上学期考试试题 A

(x)
x2 5x
4 2
在点
x0
2 连续。
2.证明 f (x) cos 2x 在[0,) 上一致连续。
3.设函数 f (x) 在a,b上可导,证明:存在 (a,b) ,使得 2 f (b) f (a) (b2 a2 ) f ( )
(10)求
x y
t t
2 2
sin t, cos t;
的一阶导。
三、讨论题(共 20 分)
1.讨论函数 f (x) ex 1 的间断点,并指出其类型。
x(x 2)
2.讨论极限 lim sin 1 是否存在。
x0
x
四、证明题(共 30 分)
1.用“ ”定义验证函数
f
n n2 1 n2 2
n2 n
x x 1
(3)求 lim x0
1 tan x 1 sin x ;
ln(1 x3 )
3
(4)求 lim
x 11;
x0 x 1 1
x2
(5)求
limx0cos源自x x4e2
(提示:可先考虑泰勒公式);
(6)设 lim x1人人网仅提供信息存储空间仅对用户上传内容的表现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
数学分析第一学期期末考试试卷(A 卷)
一、叙述题(共 10 分)
1.下确界;
2.叙述闭区间套定理。
二、计算题(共 40 分)
(1)求 lim[ 1 1 1 ];(2)求 lim( x 1)x ;
x2 ax x2 x
b
4
,求
西安市陕西师范大学附属中学2022-2023学年高一下学期期末考试数学试题含答案

陕西师大附中2022—2023 学年度第二学期高一年级期终考试数学学科试题一、单项选择题:本题共8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求.2.在ABC中,2BD BC=,3BE BA=,且,若CP xCA yCB=+ )R∈,则y+=()B.35C..已知函数()()1fA.B.C.D.++”模式,即语文、数学、外语必选,物理、历史二选7.2022年某省新高考将实行“312)图(1)π++929分.在每小题给出的选项中,有多项符合题目要求.全部选对的得4分,部分选对的得2分,有选错的得0分.9.制造业PMI指数反映制造业的整体增长或衰退,制造业PMI指数的临界点为50%.我国2021年10月至2022年10月制造业PMI指数如图所示,则()A.2022年10月中国制造业PMI指数为49.2%,比上月下降0.9个百分点,低于临界点B.2021年10月至2022年10月中国制造业PMI指数的极差为2.9%C.2021年10月至2022年10月中国制造业PMI指数的众数为50.2%.12EF AB = .34AF AB AD =-+.34BE AB AD =+ .()()22916BE AF AD AB ⋅=-.在ABC 中,内角A ,C 所对的边分别为a ,b ,c ,根据下列条件判断三角形的情况,则正确的是( 19b =,45A =︒,C ︒,有两解 B .3a =,2b =3=,2b =,则AB AC ⋅=______ y x a =+的图象有且只有一个交点,分。
解答应写出文字说明、证明过程或演算步骤.在ABC中a的大小;(2)若,试判断ABC的形状.分)已知z是复数,均为实数,其中的共轭复数z;m对应的点在第三象限,求实数60,PA⊥2(2)求点分)已知函数(f x(2)若()12f x =,()23f x =,()128f x x =,求a 的值; (3)x ∀∈R ,()212x x f x -+≤恒成立,求a 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A、2
B、 1 −
A、 1 −
1 cos y 2
1 cos x 2
C、
2 2 − cos y
D、
2 2 − cos x
8、曲线 y = ln(e −
1 ) 具有 x
B、一条斜渐近线 C、两条垂直渐近线 D、两条斜渐近线
A、一条垂直渐近线 9、 lim
2x = x →0 | x |
B、-2 C、0 D、不存在
宜春学院
命题人: 命题人: 审核人: 审核人:
-
学年第
学期模拟试卷 学期模拟试卷 模拟
(A/B)考试方式: 闭 (开/闭) A/B)考试方式:
10、在数列极限 lim x n = a 的 ε − N 定义中
n →∞
课程名称: 数学分析( 试卷类型: 课程名称: 数学分析(一)试卷类型:
题号 分数
承诺:我将严格遵守考场纪律,并知道考试违纪、作弊的严重性,承担由此引起的一切后果。 专业 班级 学号 学生姓名:
A、N 是唯一的 C、前 N 项有 | x n − a |≥ ε
B、N 是 ε 的函数 D、必有对任何 N, | x n − a |< ε
学院: 适用班级: 学院: 数学与计算机科学学院 适用班级: 一 二 三 四 五 六 七 八 九 总分
11、当 x → 0 时, sec x − 1 是 A、高阶无穷小 12、 lim n + 3
2
B、低阶无穷小
三、计算题(每小题 6 分,共 30 分)
13、 lim (
x→∞
2
π
arctan x) x
第 1 页 ii iii
14、 y = x x +1 ,求 y ′ 16、 y = x arctan x ,求 d 2 y
15、 y = arcsin 1 − x 2 ,求 dy
四、证明题(每小题 10 分,共 20 分)
n 3 x→∞ n
x2 的 2
C、同阶无穷小 C、等价无穷小
评卷人 一、填空题(每空 2 分,共 20 分) x+2 1、 f ( 、 lim x sin x cos = , 65 的近似值= x →0 x
3、函数 f (x ) 在点 x0 处连续有三层含义:i 4、 y = ln(cos x) 在 − 5、曲线 y = x +
π π , 上满足罗尔定理的点 ξ = 4 4
,凸性区间是 17、证明不等式:当 x > 0 时, 1 + x ln( x + 1 + x 2 ) > 1 + x 2 18、若 f (x ) 在区间 I 上存在有界导数,即 ∀x ∈ I , | f ′( x ) |≤ M ,则 f ′(x ) 在 I 上一致连续。
1 的拐点是 x
1 6、曲线 y = x − 与 x 轴交点处的切线方程为 x
五、综合题(15 分)
共 1 页 19、列表利用导数研究函数 y = x (ln x − 2) 的性态,并作出函数图象。
二、单项选择题(每小题 3 分,共 15 分)
7、设 y = x −
1 dx sin x ,则 = 2 dy
