初中数学竞赛——正方形和梯形
初中数学竞赛专项训练(5)及答案

图9-3初中数学竞赛专项训练(9)(面积及等积变换)一、选择题:1、如图9-1,在梯形ABCD 中,AB ∥CD ,AC 与BD 交于O ,点P 在AB 的延长线上,且BP =CD ,则图形中面积相等的三角形有 ( ) A. 3对 B. 4对 C. 5对 D. 6对2、如图9-2,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE ,设AF 、CE 交于点G ,则ABCDAGCD S S 矩形四边形等于( )A.65 B.54 C.43 D.32 3、设△ABC 的面积为1,D 是边AB 上一点,且AB AD =31,若在边AC 上取一点E ,使四边形DECB 的面积为43,则EA CE 的值为 ( )A. 21B. 31C. 41D. 514、如图9-3,在△ABC 中,∠ACB =90°,分别以AC 、AB 为边,在△ABC 外作正方形ACEF 和正方形AGHB ,作CK ⊥AB ,分别交AB 和GH 于D 和K ,则正方形ACEF 的面积S 1与矩形AGKD 的面积S 2的大小关系是 ( ) A. S 1=S 2 B. S 1>S 2C. S 1<S 2D. 不能确定,与ABAC的大小有关5、如图9-4,四边形ABCD 中,∠A =60°,∠B =∠D =90°, AD =8,AB =7,则BC+CD 等于 ( )A. 36B. 53C. 43D. 336、如图9-5,若将左边正方形剪成四块,恰能拼成右边的矩形,设a =1,则正方形的面积为 ( ) 2537+A.B.253+C.215+ D.图9-1 F图9-2 A B C D 图9-4图9-5CD图9-6图9-7图9-10图9-11图9-122)21(+7、如图9-6,矩形ABCD 中,AB =a ,BC =b ,M 是BC 的中点,DE ⊥AM ,E 为垂足,则DE =( ) A.2242b a ab + B.224b a ab +C. 2242ba ab + D. 224ba ab +8、O 为△ABC 内一点,AO 、BO 、CO 及其延长线把△ABC 分成六个小三角形,它们的面积如图9-7所示,则S △ABC =( ) A. 292 B. 315 C. 322 D. 357 二、填空题1、如图9-8,梯形ABCD 的中位线EF 的长为a ,高为h ,则图中阴影部分的面积为___2、如图9-9,若等腰三角形的底边上的高等于18cm ,腰上的中线等于15cm ,则这个等腰三角形的面积等于____3、如图9-10,在△ABC 中,CE ∶EB =1∶2,DE ∥AC ,若△ABC 的面积为S ,则△ADE 的面积为_____4、如图9-11,已知D 、E 分别是△ABC 的边BC 、CA 上的点,且BD =4,DC =1,AE =5,EC =2。
初中数学竞赛:图形与面积(含例题练习及答案)

初中数学竞赛:图形与面积一、直线图形的面积在小学数学中我们学习了几种简单图形的面积计算方法,数学竞赛中的面积问题不但具有直观性,而且变换精巧,妙趣横生,对开发智力、发展能力非常有益。
图形的面积是图形所占平面部分的大小的度量。
它有如下两条性质:1.两个可以完全重合的图形的面积相等;2.图形被分成若干部分时,各部分面积之和等于图形的面积。
对图形面积的计算,一些主要的面积公式应当熟记。
如:正方形面积=边长×边长;矩形面积=长×宽;平行四边形面积=底×高; 三角形面积=底×高÷2;梯形面积=(上底+下底)×高÷2。
此外,以下事实也非常有用,它对提高解题速度非常有益。
1.等腰三角形底边上的高线平分三角形面积;2.三角形一边上的中线平分这个三角形的面积;3.平行四边形的对角线平分它的面积;4.等底等高的两个三角形面积相等。
解决图形面积的主要方法有:1.观察图形,分析图形,找出图形中所包含的基本图形;2.对某些图形,在保持其面积不变的条件下改变其形状或位置(叫做等积变形);3.作出适当的辅助线,铺路搭桥,沟通联系;4.把图形进行割补(叫做割补法)。
例1 你会用几种不同的方法把一个三角形的面积平均分成4等份吗?解:最容易想到的是将△ABC 的底边4等分,如左下图构成4个小三角形,面积都为原来的三 角形面积的41。
另外,先将三角形△ABC 的面积2等分(如右上图),即取BC 的中点D ,连接AD ,则S △ABD=S △ADC ,然后再将这两个小三角形分别2等分,分得的4个小三角形各自的面积为原来大三角形面积的41。
还 有许多方法,如下面的三种。
请你再想出几种不同的方法。
例2 右图中每个小方格面积都是1cm2,那么六边形ABCDEF 的面积是多少平方厘米?分析:解决这类问题常用割补法,把图形分成几个简单的容易求出面积的图形,分别求出面积。
也可以求出六边形外空白处的面积,从总面积中减去空白处的面积,就是六边形的面积。
初1数学竞赛教程含例题练习及答案⑹ (4)

初一数学竞赛讲座第6讲 图形与面积一、直线图形的面积在小学数学中我们学习了几种简单图形的面积计算方法, 数学竞赛中的面积问题不但具有直观性, 而且变换精巧, 妙趣横生, 对开发智力、发展能力非常有益。
图形的面积是图形所占平面部分的大小的度量。
它有如下两条性质:1.两个可以完全重合的图形的面积相等;2.图形被分成若干部分时, 各部分面积之和等于图形的面积。
对图形面积的计算, 一些主要的面积公式应当熟记。
如:正方形面积=边长×边长;矩形面积=长×宽;平行四边形面积=底×高; 三角形面积=底×高÷2;梯形面积=(上底+下底)×高÷2。
此外, 以下事实也非常有用, 它对提高解题速度非常有益。
1.等腰三角形底边上的高线平分三角形面积;2.三角形一边上的中线平分这个三角形的面积;3.平行四边形的对角线平分它的面积;4.等底等高的两个三角形面积相等。
解决图形面积的主要方法有:1.观察图形, 分析图形, 找出图形中所包含的基本图形;2.对某些图形, 在保持其面积不变的条件下改变其形状或位置(叫做等积变形);3.作出适当的辅助线, 铺路搭桥, 沟通联系;4.把图形进行割补(叫做割补法)。
例1 你会用几种不同的方法把一个三角形的面积平均分成4等份吗?解:最容易想到的是将△ABC 的底边4等分,如左下图构成4个小三角形, 面积都为原来的三 角形面积的41。
另外, 先将三角形△ABC 的面积2等分(如右上图), 即取BC 的中点D, 连接AD,则S △ABD =S △ADC , 然后再将这两个小三角形分别2等分, 分得的4个小三角形各 自的面积为原来大三角形面积的41。
还 有许多方法, 如下面的三种。
请你再想出几种不同的方法。
例2 右图中每个小方格面积都是1cm 2, 那么六边形ABCDEF 的面积是多少平方厘米?分析:解决这类问题常用割补法, 把图形分成几个简单的容易求出面积的图形, 分别求出面积。
全国初中数学联赛 专题 正方形
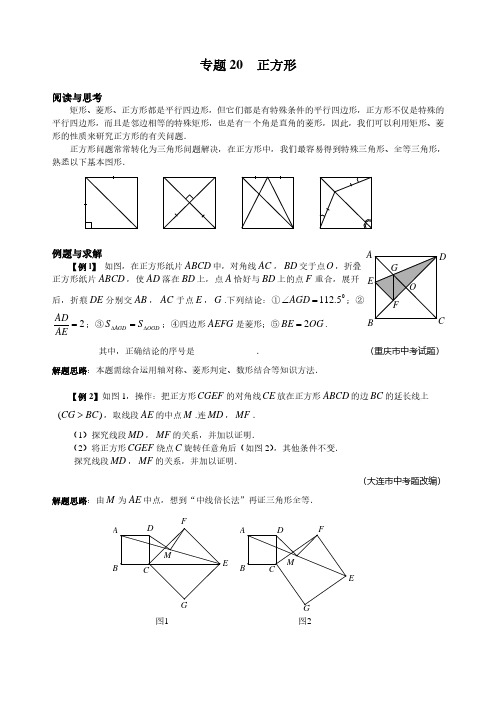
ABCDE FGO 专题20 正方形阅读与思考矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的平行四边形,而且是邻边相等的特殊矩形,也是有一个角是直角的菱形,因此,我们可以利用矩形、菱形的性质来研究正方形的有关问题.正方形问题常常转化为三角形问题解决,在正方形中,我们最容易得到特殊三角形、全等三角形,熟悉以下基本图形.例题与求解【例l 】 如图,在正方形纸片ABCD 中,对角线AC ,BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰好与BD 上的点F 重合,展开后,折痕DE 分别交AB ,AC 于点E ,G .下列结论:①05.112=∠AGD ;②2=AEAD;③OGD AGD S S ∆∆=;④四边形AEFG 是菱形;⑤OG BE 2=. 其中,正确结论的序号是______________. (重庆市中考试题)解题思路:本题需综合运用轴对称、菱形判定、数形结合等知识方法.【例2】如图1,操作:把正方形CGEF 的对角线CE 放在正方形ABCD 的边BC 的延长线上)(BC CG >,取线段AE 的中点M .连MD ,MF .(1)探究线段MD ,MF 的关系,并加以证明. (2)将正方形CGEF 绕点C 旋转任意角后(如图2),其他条件不变. 探究线段MD ,MF 的关系,并加以证明.(大连市中考题改编) 解题思路:由M 为AE 中点,想到“中线倍长法”再证三角形全等.图2图1MFEGMFGABDCECD BA【例3】如图,正方形ABCD 中,E ,F 是AB ,BC 边上两点,且FC AE EF +=,EF DG ⊥于G ,求证:DA DG =.(重庆市竞赛试题)解题思路:构造FC AE +的线段是解本例的关键.GF B CA DE【例4】 如图,正方形ABCD 被两条与边平行的线段EF 、GH 分割成四个小矩形,P 是EF 与GH 的交点,若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定HAF ∠的大小,并证明你的结论.(北京市竞赛试题) 解题思路:先猜测HAF ∠的大小,再作出证明,解题的关键是由条件及图形推出隐含的线段间的关系.【例5】 如图,在正方形ABCD 中,E ,F 分别是边BC ,CD 上的点,满足DF BE EF +=,AF AE ,分别与对角线BD 交于点N M ,.求证:(1)045=∠EAF ;(2)222DN BM MN +=. (四川省竞赛试题)解题思路:对于(1),可作辅助线,创造条件,再通过三角形全等,即可解答;对于(2),很容易联想到直角三角形三边关系.M NEBCDAFA B CDE F GHP【例6】已知 :正方形ABCD 中,045=∠MAN ,MAN ∠绕点A 顺时针旋转,它的两边分别交CB ,DC (或它们的延长线)于点N M ,.当MAN ∠绕点A 旋转到DN BM =时(如图1),易证MN DN BM =+.(1)当MAN ∠绕点A 旋转到DN BM ≠时(如图2),线段DN BM ,和MN 之间有怎样的数量关系?写出猜想,并加以证明;(2)当MAN ∠绕点A 旋转到如图3的位置时,线段DN BM ,和MN 之间又有怎样的数量关系?请直接写出你的猜想.(黑龙江省中考试题)解题思路:对于(2),构造BM DN −是解题的关键.能力训练A 级1. 如图,若四边形ABCD 是正方形,CDE ∆是等边三角形,则EAB ∠的度数为__________.(北京市竞赛试题)2. 四边形ABCD 的对角线BD AC 、相交于点O ,给出以下题设条件: ①DA CD BC AB ===;②BD AC DO CO BO AO ⊥===,; ③BD AC DO BO CO AO ⊥==,,;ABCDMN图3ABCDMN图2ABCDMN图1④DA CD BC AB ==,.其中,能判定它是正方形的题设条件是______________. (把你认为正确的序号都填在横线上)(浙江省中考试题)3.如图,边长为1的两个正方形互相重合,按住一个不动,将另一个绕顶点A 顺时针旋转030,则这两个正方形重叠部分的面积是__________.(青岛市中考试题)B CDA E第1题图 第3题图 第4题图4.如图,P 是正方形ABCD 内一点,将ABP ∆绕点B 顺时针方向旋转至能与'CBP ∆重合,若3=PB ,则'PP =__________. (河南省中考试题)5.将n 个边长都为cm 1的正方形按如图所示摆放,点n A A A Λ,,21分别是正方形的中心,则n 个正方形重叠形成的重叠部分的面积和为( )A .241cm B .24cm n C. 241cm n − D. 2)41(cm n(晋江市中考试题)A 5A 3A 4A 2A 1OB F ECA第5题图 第6题图ABCDPP ''ABCDC 'D 'A '6. 如图,以BCA Rt ∆的斜边BC 为一边在BCA ∆的同侧作正方形BCEF ,设正方形的中心为O ,连接AO ,如果26,4==AO AB ,则AC 的长为( )A . 12B .8 C.34 D. 28(浙江省竞赛试题)7.如图,正方形ABCD 中,035,=∠=MCE MN CE ,那么ANM ∠是( ) A .045 B .055 C. 065 D. 0758.如图,正方形ABCD 的面积为256,点F 在AD 上,点E 在AB 的延长线上,CEF Rt ∆的面积为200,则BE 的值是( )A .15B .12C .11D .10第8题图第7题图ABMBCD ACD E FNE9.如图,在正方形ABCD 中,E 是AD 边的中点,BD 与CE 交于F 点,求证:BE AF ⊥.FEB CDA10. 如图,在正方形ABCD 中,E 是AB 边的中点,F 是AD 上的一点,且AD AF 41= . 求证:CE 平分BCF ∠.BCADE F11. 如图,已知P 是正方形ABCD 对角线BD 上一点,F E BC PF DC PE ,,,⊥⊥分别是垂足. 求证:EF AP =.(扬州市中考试题)FEBCAD P12.(1)如图1,已知正方形ABCD 和正方形)(BC CG CGEF >,G C B ,,在同一条直线上,M 为线段AE 的中点.探究:线段MF MD ,的关系.(2)如图2,若将正方形CGEF 绕点C 顺时针旋转045,使得正方形CGEF 的对角线CE 在正方形ABCD 的边BC 的延长线上,M 为AE 的中点.试问:(1)中探究的结论是否成立?若成立,请证明;若不成立,请说明理由.(大连市中考试题)图1 图2B 级1. 如图,在四边形ABCD 中,090,=∠=∠=ABC ADC DC AD ,AB DE ⊥于E ,若四边形ABCDEFGMABCDEFGMABCD 的面积为8,则DE 的长为__________.2.如图,M 是边长为1的正方形ABCD 内一点,若02290,21=∠=−CMD MB MA ,则=∠MCD __________.(北京市竞赛试题)第3题图第1题图第2题图OCB EBC AE B DADMFAC3.如图,在ABC Rt ∆中,3,900==∠AC C ,以AB 为一边向三角形外作正方形ABEF ,正方形的中心为O ,且24=OC ,则BC 的长为__________.(“希望杯”邀请赛试题)4.如图:边长一定的正方形ABCD ,Q 是CD 上一动点,AQ 交BD 于M ,过M 作AQ MN ⊥交BC 于N 点,作BD NP ⊥于点P ,连接NQ ,下列结论:①MN AM =;②BD MP 21=; ③NQ DQ BN =+;④BMBNAB +为定值,其中一定成立的是( )A . ①②③B .①②④ C. ②③④ D. ①②③④ 5.如图,ABCD 是正方形,AC BF //,AEFC 是菱形,则ACF ∠与F ∠度数的比值是( ) A . 3 B .4 C. 5 D. 不是整数6.一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )A .58 B .527C. 8D. 65E.35(美国高中考试题)第7题图第5题图第4题图第6题图Q BCFABPNMBC DACDDA QE P7.如图,正方形ABCD 中,8=AB ,Q 是CD 的中点,设α=∠DAQ ,在CD 上取一点P ,使α2=∠BAP ,则CP 的长度等于 ( )A . 1B .2 C. 3 D.3(“希望杯”邀请赛试题)8.已知正方形ABCD 中,M 是AB 中点,E 是AB 延长线上一点,DM MN ⊥且交CBE ∠平分线于N (如图1)(1)求证:MN MD =;(2)若将上述条件中的“M 是AB 中点”改为“M 是AB 上任意一点”其余条件不变(如图2),(1)中结论是否成立?如果成立,请证明;如果不成立,请说明理由;(3)如图2,点M 是AB 的延长线上(除B 点外)的任意一点,其他条件不变,则(1)中结论是否成立?如果成立,请证明;如果不成立,请说明理由;(临汾市中考试题)E 图3图2图1N NAB N M ABA B DCCDEDCE MM`9.已知,10,10<<<<b a 求证:22)1()1()1()1(22222222≥−+−+−+++−++b a b a b a b a .10.如果,点N M ,分别在正方形ABCD 的边CD BC ,上,已知MCN ∆的周长等于正方形ABCD 周长的一半,求MAN ∠的度数. (“祖冲之杯”邀请赛试题)A BDC MN11.如图,两张大小适当的正方形纸片,重叠地放在一起,重叠部分是一个凸八边形ABCDEFGH ,对角线CG AE ,分这个八边形为四个小的凸四边形,请你证明:CG AE ⊥,且CG AE =.(北京市竞赛试题)CBAHGFED12.如图,正方形MNBC 内有一点A ,以AC AB ,为边向ABC ∆外作正方形ABRT 和正方形ACPQ ,连接BP RM ,.求证:RM BP //.(武汉市竞赛试题)MNPQT BCAR。
全国初三初中数学竞赛测试带答案解析

全国初三初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)842.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.1003.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.4.若不等式ax2+7x-1>2x+5对-1≤a≤1恒成立,则x的取值范围是( ).A.2≤x≤3B.2<x<3C.-1≤x≤1D.-1<x<15.在Rt△ABC中,∠B=60°,∠C=90°,AB=1,分别以AB、BC、CA为边长向△ABC外作等边△ABR、等边△BCP、等边△CAQ,联结QR交AB于点T.则△PRT的面积等于( ).(A) (B) (C) (D)6.在3×5的棋盘上,一枚棋子每次可以沿水平或者垂直方向移动一小格,但不可以沿任何斜对角线移动.从某些待定的格子开始,要求棋子经过全部的小正方格恰好一次,但不必回到原来出发的小方格上.在这15个小方格中,有( )个可以是这枚棋子出发的小方格.A.6B.8C.9D.10二、填空题1.正方形ABCD的边长为5,E为边BC上一点,使得BE=3,P是对角线BD上的一点,使得PE+PC的值最小.则PB= .2.设a、b、c为整数,且对一切实数x,(x-a)(x-8)+1="(x-b)(x-c)" 恒成立.则a+b+c的值为 .3.如图,在以O为圆心的两个同心圆图2中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP= 1,MA=AB=BC,则△MBQ的面积为 .4.从1, 2,…, 2 006中,至少要取出个奇数,才能保证其中必定存在两个数,它们的和为2 008.三、解答题1.(20分)实数x、y、z、w满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.2.(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.3.(25分)在中,有多少个不同的整数(其中,[x]表示不大于x的最大整数)?全国初三初中数学竞赛测试答案及解析一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)84【答案】D【解析】分析:首先设BC=a,AC=b,由勾股定理与正方形的性质,可得:a2+b2=352,Rt△AFE∽Rt△ACB,再由相似三角形的对应边成比例,可得12(a+b)=ab,解方程组即可求得.解答:解:如图,设BC=a,AC=b,则a2+b2=352=1225.①又Rt△AFE∽Rt△ACB,所以=,即=,故12(a+b)=ab.②由①②得(a+b)2=a2+b2+2ab=1225+24(a+b),解得a+b=49(另一个解-25舍去),所以a+b+c=49+35=84.故答案为D.2.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.100【答案】C【解析】由于9=10-1,99=100-1,…,所以n="9+99+999+…+" =10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.解:n=9+99+999+…+=10+102+103+…1099-99×1,=1111111…10(99个1)-99,=11111…1011(99个1).所以在十进制表示中,数码1有99个.故答案为:99.根据式中数据的特点将式中的数据变为10的n次方相加的形式是完成本题的关键.3.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.【答案】D【解析】本题考查二次函数与一元二次方程关系的综合应用问题。
正方形 梯形经典例题

第 1 页 共 4 页A BCD EFD CBAEGF 正方形 梯形常见经典例题 例题讲解:1.已知:如图所示,在正方形ABCD 中,E 、F 分别是AD 、DC 的 交点,AF 、BE 交于点G ,连结CG ,求证:ΔCGB 是等腰三角形。
2.如图正方形ABCD 中,E 为AD 边上的中点,过A 作AF ⊥BE ,交CD 边于F ,M 是AD 边上一点,且有BM =DM +CD .⑴求证:点F 是CD 边的中点; ⑵求证:∠MBC =2∠ABE .3.如图,已知正方形ABCD ,M 是AB 边上一点,连DM ,作MN ⊥DM 交∠CBE 的平分线于N. (1)求证:MN = MD ;(2)连DN 交BC 于F ,求证:MN 平分∠FME ;4.如图所示,在直角梯形ABCD 中,∠ABC=90°,AD ∥BC ,AB=BC ,E 是AB 的中点,CE ⊥BD 。
(1) 求证:BE=AD ;求证:AC 是线段ED 的垂直平分线; (2) △DBC 是等腰三角形吗?并说明理由。
5.梯形ABCD 中,AD //BC ,M 、N 分别是底AD 和BC 的中点, ∠B +∠C =90°,BC =18,AD =6,求EF 的长进而探究一般规律, 若BC =x ,AD =y ,那么 EF 为多少?6梯形上下底长分别为1和4,两条对角线长分别为3和4,则此梯形面积为 .7如图,梯形 ABCD 中,AD //BC ,E 是CD 的中点,EF ⊥AB 于点F ,AB =6cm ,EF =5cm ,试求梯形 ABCD 的面积.MFECDBABCDMNAEA DCB第 2 页 共 4 页A BCDABCPO mn 练习题:1.正方形具有而矩形不一定具有的特征是()A .四个角都是直角B .对角线互相平分C .对角线互相垂直D .对角线相等 2.在四边形ABCD 中,AC 、BD 相交于O ,能判定这个四边形是平行四边形的是( ) A .AO =BO =CO =DO ,AC ⊥BD B .AB ∥CD ,AC =BD C .AO =BO ,∠A =∠CD .AO =CO ,BO =DO ,AB =BC3.下列图形中,既是轴对称图形,又是中心对称图形的是()A .平行四边形B .等腰三角形C .等边三角形D .菱形4.梯形上底长为6cm ,过上底一个顶点引一腰的平行线交下底所得三角形周长为5cm ,那么这个梯形周长为( )5.四边形四个内角的度数之比为2︰2︰1︰3,则此四边形是( ) A .任意四边形;B .任意梯形;C .等腰梯形;D .直角梯形; 6.下列命题正确的是( )A .对角线相等且互相平分的四边形是菱形B .对角线相等且互相垂直的四边形是菱形C .对角线相等且互相平分的四边形是矩形D .对角线相等的四边形是等腰梯形 7.顺次连接等腰梯形四边中点所得四边形是( )A .菱形B .正方形C .矩形D .等腰梯形 8.若等腰梯形的两底差等于一腰长,那么它的腰与下底的夹角为 9.等腰梯形的上底与高相等,下底是上底的3倍,则底角的度数是( )A .30º和150 ºB .45º和135ºC .60º和120ºD . 都是90º10.用两个全等的直角三角形拼下列图形:①矩形;②菱形;③正方形;④平行四边形;⑤等腰三角形;⑥等腰梯形,其中一定能拼成的图形是…( ) A .①②③B .①④⑤C .①②⑤D .②⑤⑥ 11.对角线互相垂直且相等的四边形一定是……( )A .正方形B .矩形C .菱形D .以上均不对12.连接等腰梯形各边中点所得四边形是 13.一组对边相等,另一组对边平行的四边形是…………( )A .梯形B .等腰梯形C .平行四边形D .等腰梯形或平行四边形14.如图,已知梯形ABCD 中,AB ∥CD ,AD ⊥CD ,若腰BC =15,对角线AC =20,且AC ⊥BC ,则AB = ,AD = ,CD = ,ABCD S 梯形 . 15.如图,已知:直线m ∥n ,A 、B 为直线n 上两点,C 、P 为直线m上两点.⑴请写出图中面积相等的各对三角形:____________.⑵如果A 、B 、C 、为三个定点,点P 在m 上移动,那么,无论P 点移第 3 页 共 4 页DC BA动到任何位置,总有_______与△ABC 的面积相等.16.等腰梯形ABCD 中,AD ∥BC ,AD =5cm ,BC =9cm ,∠C =60°,则梯形的腰长是 cm . 17.已知一个梯形的面积为22 cm 2,高为2 cm ,则该梯形的中位线的长等于________cm . 18.如图,在正方形ABCD 中,∠DAF =25°,AF 交对角线BD 于E 点,则∠BEC =( )19.如图,E 是正方形ABCD 外一点,AE=AD ,∠ADE =75°, 求∠AEB 的度数。
初中数学-梯形和正方形典型例题

(2)若 ADC 的周长为16cm,AE 3cm, AC EC 3cm ,求四边形 ADCE 的周长.
分析:(1)由角平分线和平行线可得到一些相等的角,如 OAD ODA . 从而有 OA OD ,再由 AC DE 推导出 OCE OEC ,则容易得出结论 AD // CE ,∵ AD CE ,∴能证出四边形 ADCE 是梯形,再由已知条件容易证出 ADE DAC ,因 此有 AE DC ,所以可证出四边形 ADCE 是等腰梯形.
形中,过 A 作 AE // CD 交 BC 于 E,得到一个 AECD 和 ABE . 那么由已知条件易知 ABE 是等边三角形,则由 BE BC AD ,就可以解决问题了.
解答:过点 A 作 AE // CD 交 BC 于 E,
∵四边形 ABCD 是等腰梯形,
∴ B C 60 (等腰梯形同一底上的两个角相等) 又∵ AD // BC, AE // CD ,
例 01.如图,已知:四边形 ABCD 是等腰梯形,其中 AD BC ,若 AD 5 ,CD 2 , AB 8 .
求:梯形 ABCD 的面积.
分析:由已知条件知,梯形 ABCD 是等腰梯形,由于等腰梯形是一个轴对称图形,由
图中的辅助线很容易想到 AE BF . 在此基础上应用勾股定理,就可以解决问题. 解答:过点 D、C 作 DE AB 于 E, CF AB 于 F. 则根据等腰梯形的轴对称性可知: AE BF .
(2)因为四边形 ADCE 是等腰梯形,由给出条件容易求出四边形 ADCE 的周长.
证明:(1)∵ AB // ED (已知), ∴ BAD ADE (两直线平行,内错角相等) 又∵ BAD CAD (角平分线定义), ∴ CAD ADE . ∴ OA OD (等角对等边) ∵ AC DE (已知), ∴ AC OA DE OD 即 OE OC ∴ OEC OCE (等边对等角) 又∵ AOD COE (对顶角相等), ∴ CAD OCE ∴ AD // CE (内错角相等,两直线平行) 而 AD CE , ∴ 四边形 ADCE 是梯形. 又∵ CAD ADE, AD AD, AC DE ,
全国各地初中(九年级)数学竞赛《几何》真题大全 (附答案)

全国各地初中(九年级)数学竞赛专题大全竞赛专题7 几何一、单选题 1.(2021·全国·九年级竞赛)某种产品由甲、乙、丙三种元件构成,如图为生产效率最高,在表示工人分配的扇形图中,生产甲、乙、丙元件的工人数量所对应的扇形圆心角的大小依次是( ).A .120,180,60︒︒︒B .108,144,108︒︒︒C .90,180,90︒︒︒D .72,216,720︒︒︒2.(2021·全国·九年级竞赛)如图所示,一次函数y kx b =+的图象过点(1,4)P 且与x 轴和y 轴的正半轴交于AB 、两点,点O 为坐标原点,当AOB 的面积最小时,k ,b 的值为( )A .4k =-,8b =B .4k =-,4b =C .2k =-,4b =D .2k =-,2b =3.(2021·全国·九年级竞赛)如图,已知DEF 的边长分别为3,2,正六边形网格由24个边长为2的正三角形组成,以这些正三角形的顶点画ABC ,使得ABC DEF ∽△△,相似比为ABk DE=,那么k 的不同值共有( )个.A .1B .2C .3D .4二、填空题4.(2021·全国·九年级竞赛)如图所示,正方形ABCD 的边长为10cm ,点E 在边CB 的延长线上且10cm EB =,点P 在边CD 上运动,EP 与AB 的交点为F .设cm DP x =,EFB △与四边形AFPD 的面积和为2cm y ,那么y 与x 之间的函数关系式是________.5.(2021·全国·九年级竞赛)把两个半径为5及一个半径为8的圆形纸片放在桌面上,使它们两两外切.若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于________. 6.(2021·全国·九年级竞赛)由一次函数2,2y x y x =+=-+和x 轴围成的三角形与圆心在(1,1)、半径为1的圆构成的图形覆盖的面积等于______.7.(2021·全国·九年级竞赛)某广场地面铺满了边长为36cm 的正六边形地砖,现向上抛掷半径为3cm 的圆碟,圆碟落地后与地面不相交的概率大约是_________. 三、解答题8.(2021·全国·九年级竞赛)平面上7个点,它们之间可以连一些线段,使7个点中任意三点必存在两点有线段相连.问最少要连几条线段?证明你的结论.9.(2021·全国·九年级竞赛)在直径为5的圆内放入10个点,证明其中必有两点的距离小于2.10.(2021·全国·九年级竞赛)设1M 是凸五边形12345A A A A A ,将1M 沿1i A A 方向平移,使1A 移到i A 得到凸五边形(2,3,4,5)i M i =.证明:12345,,,,M M M M M 中至少有两个图形,它们有公共内点.11.(2021·全国·九年级竞赛)在圆周上任取21个点,证明:以这些点为端点的弧中至少存在100条不超过120︒的弧.12.(2021·全国·九年级竞赛)两人A 和B 相约在12点与下午1点之间在某地会面,先到的人要等候另一人20分钟,过时就可以离开.如果每人可在指定的一小时内任何时刻到达,并且两人到达的时刻是彼此独立的(即一人到达的时刻与另一人到达的时刻没有影响),试计算两人能会面的概率.13.(2021·全国·九年级竞赛)平面上给出n个不全共线的点,求证:存在一条直线l,它恰通过其中两个点.14.(2021·全国·九年级竞赛)已知A,B,C,D为平面上两两距离不超过1的任意4点,今欲作一圆覆盖这4点(即A,B,C,D在圆内或圆周上)问圆的半径最小该是多少?试证明之.15.(2021·全国·九年级竞赛)任意凸四边形ABCD中总存在一条对角线和一条边,以它们为直径的两个圆可以覆盖这个四边形.16.(2021·全国·九年级竞赛)设甲是边长为1的正三角形纸片,乙是边长为1的正方形纸片,丙是边长为1的正五边形纸片,丁是边长为1的正六边形纸片.证明:(1)不能用甲、乙、丙合起来盖住一个半径为1的圆;(2)能用甲、乙、丙、丁合起来盖住一个半径为1的圆.17.(2021·全国·九年级竞赛)在一个半径等于6的圆内任意放入六个半径等于1的小圆.证明:其中总还有一块空位置,可以完整地放入一个半径为1的小圆.18.(2021·全国·九年级竞赛)将4张圆形纸片放在桌面上,使得其题中任何3张圆形纸片都有公共点,那么这4张圆形纸片是否一定有公共点?证明你的结论.19.(2021·全国·九年级竞赛)平面上给定了若干个圆,它们覆盖的面积为1.证明:从中可选出若干个两两不重叠的圆,使它们覆盖的面积不小于19.20.(2021·全国·九年级竞赛)证明:一个边长为5的正方形可以被3个边长为4的正方形所覆盖.21.(2021·全国·九年级竞赛)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).(1)当30α=︒时,通过计算说明此溶液是否会溢出;(2)现需要倒出不少于33000cm的溶液,当α等于60︒时,能实现要求吗?通过计算说明理由.22.(2021·全国·九年级竞赛)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头停泊,它们在一昼夜内到达的时间是等可能的,如果甲的停泊时间是1小时,乙的停泊时间是2小时,求它们中任何一艘都不需要等候码头空出的概率(精确到0.001).23.(2021·全国·九年级竞赛)把长为a 的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.24.(2022·福建·九年级竞赛)如图,四边形ABCD 是平行四边形,∠DAC =45°,以线段AC 为直径的圆与AB 和AD 的延长线分别交于点E 和F ,过点B 作AC 的垂线,垂足为H .求证:E ,H ,F 三点共线.竞赛专题7 几何答案解析一、单选题 1.(2021·全国·九年级竞赛)某种产品由甲、乙、丙三种元件构成,如图为生产效率最高,在表示工人分配的扇形图中,生产甲、乙、丙元件的工人数量所对应的扇形圆心角的大小依次是( ).A .120,180,60︒︒︒B .108,144,108︒︒︒C .90,180,90︒︒︒D .72,216,720︒︒︒【答案】B 【详解】解 设分配生产甲、乙、丙3种元件的人数分别为x 人,y 人,z 人,于是每小时生产甲、乙、丙三种元件的个数分别为50,30,20x y z .为了提高效率应使生产出来的元件全部组成成品而没有剩余.设共可组成k 件成品,则503020504020x y z k ===,即4,,3x k y k z k ===,从而4::1::13:4:33x y z ==.设在扇形图中生产甲、乙、丙三种元件的圆心角分别为,,αβγ,则3336036036010834310x x y z α=⨯︒=⨯︒=⨯︒=︒++++,4436036036014434310y x y z β=⨯︒=⨯︒=⨯︒=︒++++,3336036036010834310z x y z γ=⨯︒=⨯︒=⨯︒=︒++++.故应选B .2.(2021·全国·九年级竞赛)如图所示,一次函数y kx b =+的图象过点(1,4)P 且与x 轴和y 轴的正半轴交于A B 、两点,点O 为坐标原点,当AOB 的面积最小时,k ,b 的值为( )A .4k =-,8b =B .4k =-,4b =C .2k =-,4b =D .2k =-,2b =【答案】A 【详解】解 因函数y kx b =+的图象过点(1,4)P ,所以4,4k b b k =+=-,于是(4)y kx k =+-. 令0y =得4,0k A k -⎛⎫⎪⎝⎭. 令0x =得(0,4)B k -.连OP ,得 114122OABOAP OPBSSSOA OB =+=⨯⨯+⨯⨯ 14141(4)22k k k -=⨯⨯+⨯⨯- 11642k k ⎛⎫=-+ ⎪⎝⎭.显然0k <.令k u =-,则0u >,于是116116442822OABSu u u u⎛⎫=++≥+⨯⨯= ⎪⎝⎭.等号成立当且仅当16(0)u u u=>,即4u =,这时4,48k b k =-=-=. 故选A .注:OAB 的面积也可用114(4)22OABk SOA OB k k-=⨯⨯=⨯⨯-算出. 3.(2021·全国·九年级竞赛)如图,已知DEF 的边长分别为3,2,正六边形网格由24个边长为2的正三角形组成,以这些正三角形的顶点画ABC ,使得ABC DEF ∽△△,相似比为ABk DE=,那么k 的不同值共有( )个.A .1B .2C .3D .4【答案】C 【详解】作图知与DEF 相似的三角形,而相似比不同的三角形只有如图所示的三种,故选C .二、填空题4.(2021·全国·九年级竞赛)如图所示,正方形ABCD 的边长为10cm ,点E 在边CB 的延长线上且10cm EB =,点P 在边CD 上运动,EP 与AB 的交点为F .设cm DP x =,EFB △与四边形AFPD 的面积和为2cm y ,那么y 与x 之间的函数关系式是________.【答案】550(010)y x x =+<< 【详解】解 由DP x =得10PC x =-. 又12BF BE PC EC ==,即11(10),10(10)22BF x AF BF x =-=-=+, 所以EFBAFPD y SS =+四边形11()22BE BF AF DP AD =⨯⨯++⨯ 111110(10)(10)102222x x x ⎡⎤=⨯⨯-+++⨯⎢⎥⎣⎦550(010)x x =+<<. 故应填550(010)y x x =+<<.5.(2021·全国·九年级竞赛)把两个半径为5及一个半径为8的圆形纸片放在桌面上,使它们两两外切.若要用一个大圆形纸片把这三个圆形纸片完全盖住,则这个大圆形纸片的最小半径等于________. 【答案】1133.【详解】如图,设1O 的半径为8,2O ,3O 的半径为5,切点为A .由对称性,能盖住这3个圆的最小圆形纸片的中心O 在对称轴1O A 上,且与已知三个圆内切.若设这个圆形纸片的半径为r ,则在12Rt O O A 中22221122(85)512O A OO O A =-=+-=,在2Rt OO A 中,25OO r =-,1112(8)OA O A OO r =-=--,25O A =,于是,由22222OO O A OA =+得222(5)5(128)r r -=+-+,由此解出4011333r ==,即所求圆形纸片的最小半径等于1133.6.(2021·全国·九年级竞赛)由一次函数2,2y x y x =+=-+和x 轴围成的三角形与圆心在(1,1)、半径为1的圆构成的图形覆盖的面积等于______. 【答案】42π+【详解】如图,所覆盖面积2 114214222ABCS S S ππ=+=⨯⨯+⋅=+半圆.故答案为:42π+.7.(2021·全国·九年级竞赛)某广场地面铺满了边长为36cm 的正六边形地砖,现向上抛掷半径为3cm 的圆碟,圆碟落地后与地面不相交的概率大约是_________. 【答案】49【详解】解 要使圆碟与地砖的边缘不相交的条件是落地后圆碟的中心到正六边形地砖ABCDEF 的任何一边的距离不小于圆的半径63cm ,也就是圆碟的中心必落在与地砖ABCDEF 同中心且边与地砖边彼此平行、距离为63111111A B C D E F 内(图6-1).作OG AB ⊥于G ,交11A B 于1G 且163cm GG =,所以33336183OG AB ====1118363123OG OG GG =-==而113OG =,所以1132433OA ===,故11124A B OA ==. 设正六边形ABCDEF 和111111A B C D E F 的面积分别为S 和1S ,则所求概率为22211122224243639S A B p S AB =====.故应填49. 三、解答题8.(2021·全国·九年级竞赛)平面上7个点,它们之间可以连一些线段,使7个点中任意三点必存在两点有线段相连.问最少要连几条线段?证明你的结论.【答案】9条,见解析 【详解】解法一:设最少要连n 条线段,如图4-3中7个点之间共连有9条线段,其中任意三点间必有两点连有线段,故9n ≤.另一方面,我们证明9n ≥,下面分4种情形讨论: (1)若7点中存在一点1A 不与其他6点237,,,A A A 连线,则依题意1A ,i A ,j A (27)i j ≤<≤中必有2点连线,于是只可能i A 与j A 连有线,即237,,,A A A 这6点中任意两点连有线,图中一共连了65152⨯=条线. (2)若7点中存在一点1A 只连出一条线段,设1A 仅与2A 连有线而与其余5点3A ,4A ,5A ,6A ,7A ,没有连线,则同(1)可知3A ,4A ,5A ,6A ,7A 这5点中任意两点连有线,至少连有54102⨯=条线.(3)若每点出发至少连出2条线,且有一点恰连出2条线.设该点为1A ,它连出的两条线为12A A ,13A A ,则不与1A 相连的4个点每两点连有线,要连4362⨯=条线,而2A 连出的线段至少2条,除21A A 外,至少还有一条,所以此时至少要连6219++=条线. (4)若每点至少连出3条线,则至少要连73102⨯>条线. 综上所述,最少要连9条线段.解法二:设7点中从1A 出发所连的线段最少,只有k 条,设它们是121311,,,k A A A A A A +,其余6k -个点126,,,k B B B -都与1A 没有连线,于是对任意2点i B ,j B (16)i j k ≤<≤-,由已知条件知1A ,i B ,j B 中必有2点连有线,而1A 与i B ,1A 与j B 没有连线,故只可能i B 与j B 连有线,即16,,k B B -中每点与其余5k -点连有线,于是从各点连出的线段数的总和不少于(1)(6)(5)k k k k ++--221030k k =-+.但上述计数中每条线段计算了2次,故图中所连线段至少为()21210302k k -+=22551522k ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭22151522⎛⎫⎛⎫≥+- ⎪ ⎪⎝⎭⎝⎭1569=-=,即至少要连9条线段. 另一方面,如图4-3中,7点中连有9条线段时满足题设条件. 综上所述,最少要连9条线段.9.(2021·全国·九年级竞赛)在直径为5的圆内放入10个点,证明其中必有两点的距离小于2. 【答案】见解析 【详解】分析 把圆等分为9个扇形显然不行(虽然必有一扇形内至少有2点,但不保证它们的距离小于2),因此,我们先作一个与已知圆同心的小圆(其直径必须小于2,但不能太小),然后将余下的圆环部分8等分. 证明 设O 是已知圆心,如图,以O 为圆心作半径为0.9的圆,再将余下的圆环8等分,于是将已知圆面分成了9个部分,由抽屉原理知其中必有一部分内至少有已知10点中的101129-⎡⎤+=⎢⎥⎣⎦点,M N ,若,M N 在小圆内,则220.9 1.82MN OC ≤=⨯=<. 若,M N 同在一个扇面形内,则由余弦定理,有222cos45MN AC OC OA OC OA ≤+-⋅︒0.81 6.2520.9 2.50.7 3.912+-⨯⨯⨯<.从例2可以看出,分割图形制造“抽屉”时,可能不是将图形等分为几部分,而是要求分割的每一部分图形都具有所需要的性质(例2中每一部分图形内任意两点的距离都小于2),读者应用这种方法解题时,应该注意到这一点.10.(2021·全国·九年级竞赛)设1M 是凸五边形12345A A A A A ,将1M 沿1i A A 方向平移,使1A 移到i A 得到凸五边形(2,3,4,5)i M i =.证明:12345,,,,M M M M M 中至少有两个图形,它们有公共内点.【答案】见解析 【详解】证明 如图,以1A 为位似中心,以2:1为相似比作1M 的位似图形M ,则M 仍为凸五边形且1M 在M 内.下面我们证明2345,,,M M M M 都在M 内,例如先证4M 在M 内.设P 是4M 内任意一点,它是1M 内的点Q 经过平移得到的,于是14QP A A ∥,故14A A PQ 为平行四边形,又R 是14A A PQ 的两条对角线的交点,因Q 和4A 属于1M ,且1M 是凸五边形,故R 属于M ,而111,:2:1A R RP A P A R ==,故P 属于M .又P 是M ,内任意一点,所以4M 包含在M 之内,同理235,,M M M 都包含在M 内,设12345,,,,M M M M M 及M 的面积分别为12345,,,,S S S S S 及S ,则2123451152S S S S S S S S ++++=>⋅=.于是,由图形重叠原理知,12345,,,,M M M M M 中至少有两个图形,它们有公共内点.11.(2021·全国·九年级竞赛)在圆周上任取21个点,证明:以这些点为端点的弧中至少存在100条不超过120︒的弧.【答案】见解析 【详解】证明:我们称不超过120︒的弧为好弧.不妨设以1A 为端点的好弧最少,并且设它只有1n -条,它们是12131,,,n A A A A A A ,从而以231,,,n A A A -为端点的好弧都至少有1n -条,故以这n 个点为端点的好弧至少有1(1)2n n ⋅-条,除这n 个点外,其余21n -个点记为1221,,,n n A A A ++,从中任取两点,(121)i j A A n i j +≤<≤.因1i j A A A ,至少有一个内角不超过60︒,故11,,i j i j A A A A A A 中至少有一条弧不超过260120⨯︒=︒,根据1A 的取法,这条弧不能是1i A A 和1j A A ,而只能是j i A A ,即j i A A 是好弧.可见以1221,,,n n A A A ++中任意两点,(121)i j A A n i j +≤<≤为端点的弧都为好弧.这样的好弧有1(21)(20)2n n ⋅--条.综上所述知好弧至少有2211213991399(1)(21)(20)100222424y n n n n n ⎛⎫⎛⎫=⋅-+⋅--=-+≥+= ⎪ ⎪⎝⎭⎝⎭条.当10n =或11时,y 取到最小值100,于是结论成立.12.(2021·全国·九年级竞赛)两人A 和B 相约在12点与下午1点之间在某地会面,先到的人要等候另一人20分钟,过时就可以离开.如果每人可在指定的一小时内任何时刻到达,并且两人到达的时刻是彼此独立的(即一人到达的时刻与另一人到达的时刻没有影响),试计算两人能会面的概率. 【答案】59 【详解】解 我们用,x y 分别表示,A B 到达的时刻,而两人能会面的充分必要条件为20x y -≤,其中060,060x y ≤≤≤≤.我们用平面直角坐标系中的点(),x y 表示,A B 到达的时刻(从中午12点以后算起,以分为单位),于是所有可能结果是一个边长为60的正方形OABC .代表能够会面的点都落在图中画有阴影线的区域H 内(图6-2),于是21260240402H ADE OABC S S S =-⨯=-⨯⨯⨯正方形 226040=-,故两人能会面的概率为22226040251()6039HOABC S p S -===-=正方形. 答:两人能会面的概率等于59. 13.(2021·全国·九年级竞赛)平面上给出n 个不全共线的点,求证:存在一条直线l ,它恰通过其中两个点.【答案】见解析【详解】证明:平面上只有有限点,过每两点作一直线只有有限点直线,每条直线与不在这条直线上的点(由已知条件知这样的点必存在)配成对,则这样的点只有有限个,每个点线对中都有该点到直线的距离,记这些距离最小的点对为(,)P l ,则l 为所求.实际上,设l 上有不少于3个给定的已知点,则过P 作PA l ⊥于A (如图),则在l 上A 的某一侧(包括A )必有2个已知点,设为,M N (M 可能与A 重合,连PN ,并M 作MQ PN ⊥于Q ,过A 作AR PN ⊥于R ,则MQ AR AP d ≤<=,这与AP d =最小矛盾,于是结论得证.注 本题是英国著名数学家希尔维斯特(J.J. Sylvester)在其逝世前不久提出的一个有趣的问题.这个貌似简单的问题,当时困扰过不少的数学家,并且这状况持续350年之久,直到1933年,伽莱(T. Callai)给出了一个非常复杂的证明.不久以后,凯里(L. M. Kelly) 才给出上述很简单的证明,其证法的关键就是利用极端原理.14.(2021·全国·九年级竞赛)已知A ,B ,C ,D 为平面上两两距离不超过1的任意4点,今欲作一圆覆盖这4点(即A ,B ,C ,D 在圆内或圆周上)问圆的半径最小该是多少?试证明之. 3 【详解】注意最不利的情形点A 、B 、C 、D 中有3点构成边长等于1的正三角形,覆盖此三角形的圆的半径不小33 (1)A 、B 、C 、D 共线,这时4点在一条长度不超过1的线段内,结论显然成立;(2)A 、B 、C 、D 中有3点(例如A 、B 、C )构成一个三角形,第4点D 在此三角形内,不妨设60C ∠≥︒,以AB 为弦作圆O ,使AB 所对的弓形弧(含C 的一侧)为60︒,则此圆O 覆盖A 、B 、C 、D 4点.作此圆直径2AE R =,则22222(2)1R R AE BE AB -=-=≤,即3R ≤,故A 、B 、C 、D 4点被一个半径不大3 (3)A 、B 、C 、D 是一个凸四边形的4个顶点,则A C ∠+∠,B D ∠+∠中必有一个不小于180︒,不妨设180B D ∠+∠≥︒,同(2)可证ABC 的外接圆半径3≤180B D ∠+∠≥︒知D 点也在这个圆内或圆周上,故A 、B 、C 、D 3 315.(2021·全国·九年级竞赛)任意凸四边形ABCD 中总存在一条对角线和一条边,以它们为直径的两个圆可以覆盖这个四边形.【答案】见解析【详解】四边形的4个内角中至少有一个90≥︒,不妨设90A ∠≥︒,以对角BD 为直径的圆O 必覆盖ABD △.若90C ∠≥︒,圆O 覆盖四边形ABCD 结论成立,若90C ∠>︒,则C 在圆外,圆O 与CD 、CB 中至少一条线段相交,不妨设圆O 与CD 交于E ,于点分别以BD 、BC 为直径的两个圆覆盖四边形ABCD .16.(2021·全国·九年级竞赛)设甲是边长为1的正三角形纸片,乙是边长为1的正方形纸片,丙是边长为1的正五边形纸片,丁是边长为1的正六边形纸片.证明:(1)不能用甲、乙、丙合起来盖住一个半径为1的圆;(2)能用甲、乙、丙、丁合起来盖住一个半径为1的圆.【答案】(1)见解析;(2)见解析【详解】(1)因为对于半径为1的圆,边长为1的正三角形至多盖住60︒的弧,边长为1的正方形至多盖住90︒的弧,边长为1的正五边形至多盖住120︒的弧(因边长为1的正五边形对角线的长<边长为1的正六边形对角线的长3=,而6090120360︒+︒+︒<︒,所以甲、乙、丙合起来不得盖住半径为1的圆.(2)如图所示,用甲、乙、丙、丁合起来可盖住半径为1的圆.17.(2021·全国·九年级竞赛)在一个半径等于6的圆内任意放入六个半径等于1的小圆.证明:其中总还有一块空位置,可以完整地放入一个半径为1的小圆.【答案】见解析【详解】分析 与证明设半径为6的大圆O 内任意放入6个半径为1的小圆,则小圆圆心都在以O 为中心,615-=为半径的圆内.如果大圆内无论怎样再放入一个半径为1的小圆7O ,都要与6个小圆中某个(16)i O i ≤≤重叠,那么7112i O O ≤+≤,即半径为5的圆将被6个半径为2的圆所覆盖.由图形重叠原理知6个小圆的总面积将不小于半径为5的圆的面积.但实际上226224255ππππ⋅=<=⋅,得到矛盾,于是命题得证.注:本例的证题关键是将外圆缩小,而将里圆扩大,这是解决嵌入问题的一种技巧,即收缩与膨胀技巧或裁边与镶边技巧.18.(2021·全国·九年级竞赛)将4张圆形纸片放在桌面上,使得其题中任何3张圆形纸片都有公共点,那么这4张圆形纸片是否一定有公共点?证明你的结论.【答案】见解析.【解析】【分析】【详解】设4张圆形纸片是(1,2,3,4)k O k ,其中1O ,2O ,3O 有公共点1A ,1O ,2O ,4O 有公共点2A ,1O ,3O ,4O 有公共点3A ,2O ,3O ,4O 公共点4A .(1)若1A ,2A ,3A ,4A 共线(如图顺序),因为1A ,3A 都是圆形纸片1O 与3O 的公共点,故线段13A A 在圆形纸片1O 与2O 的公共部分内,又24A A 都是圆形纸片2O 与4O 的公共点,故线段24A A 在圆形纸片2O 与4O 的公共部分内,所以线段23A A 上任意一点都是这4张圆形纸片的公共点.(2)若1A ,2A ,3A ,4A 中有一点在以其余3点为顶点的三角形的边界上或内部(如图).因为1A ,2A ,3A 都在1O 内,故123A A A △被圆形纸片1O 所覆盖,从而4A 在圆形纸片1O 内,而4A 是圆形纸片2O ,3O ,4O 的公共点,所以4A 是这张圆形纸片的公共点.(3)若1A ,2A ,3A ,4A 是一个凸四边形的4个顶点(如图),同上可知线段13A A 在圆形纸片1O 与3O 的公共部分内,线段24A A 在圆形纸片2O 与4O 的公共部分内,所以13A A 与24A A 的交点是这4张圆形纸片的公共点.总之,这4张圆形纸片一定有公共点.19.(2021·全国·九年级竞赛)平面上给定了若干个圆,它们覆盖的面积为1.证明:从中可选出若干个两两不重叠的圆,使它们覆盖的面积不小于19. 【答案】见解析.【解析】【分析】【详解】从给定圆中选出半径最大的圆1O ,其半径为1r ,面积为1S ,则与圆1O 有重叠的圆连同圆1O 一起覆盖的面积()211139M r S π≤=,即1119S M ≥.然后去掉与圆1O 重叠的圆,再从剩下的圆(圆1O 除外)选出半径最大的圆2O ,其半径为2r ,并将与圆2O 有重叠的圆去掉.这样经过有限步可得有限个两两不重叠的圆1O ,2O ,…k O ,它们覆盖的面积为()12121199k k S S S M M M ++⋅⋅⋅+≥++⋅⋅⋅+=. 20.(2021·全国·九年级竞赛)证明:一个边长为5的正方形可以被3个边长为4的正方形所覆盖.【答案】见解析.【解析】【分析】【详解】设正方形ABCD 的边长为5,先放置一个边长为4的正方形CEFG ,其中C 为原正方形ABCD 的一个顶点,E 在边CD 上,F 在正方形ABCD 内,G 在边CB 上.连AF ,再放置第二个边长为4的正方形111AB C D ,其中A 是原正方形的一个顶点,且使D 在射线11D C 上(如图),由勾股定理有:2211D D AD AD =-2211543D C =-=<.故D 在线段11D C 内,且1111431C D D C D D =-=-=.设11B C 与CD 交于H ,则1541DE CD CE DC DH =-=-==<,故E 在线段DH 内,从而E 被正方形111AB C D 覆盖.又11145B AD B AC FAD ∠>∠=︒=∠,即AF 在1B AD 内,且1224AF DE AB ==,故F 也被正方形111AB C D 覆盖,这就证明了梯形AFED 可以被一个边长为4的正方形111AB C D 所覆盖.同理,梯形AFGB 也可以被一个边长为4的正方形222AB C D 所覆盖,于是正方形ABCD 可被3个边长为4的正方形所覆盖. 21.(2021·全国·九年级竞赛)如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm 的正方形,高为30cm ,内有20cm 深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).(1)当30α=︒时,通过计算说明此溶液是否会溢出;(2)现需要倒出不少于33000cm 的溶液,当α等于60︒时,能实现要求吗?通过计算说明理由.【答案】(1)不会溢出,理由见解析;(2)不能实现要求,见解析.【解析】【分析】【详解】(1)当30α=︒时,如图a ,过C 作//CF BP 交AD 所在直线于F .在Rt CDF △中,20330,20cm,30cm FCD CD DF ∠=︒==<,所以点F 在线段AD 上,20330AF =此时容器内能容纳的溶液量为()3 ()203320203030201040003cm 2ABCF AF BC AB S ⎛⎫⎛+⋅=⋅=⋅⋅= ⎪ ⎪ ⎝⎭⎝⎭梯形.而容器中原有溶液量为()32020208000cm ⨯⨯=.因为3400038000⎛> ⎝⎭,所以当30α=︒时溶液不会溢出. (2)如图b ,当60α=︒时,过C 作//CF BP 交AB 所在直线于F .在Rt CBF △中,30cm 30BC BCF =∠=︒,,10320cm BF =<,所以点F 在线段AB 上,故溶液纵截面为Rt BFC △.因211503cm 2BFC S BC BF =⨯⨯=,容器内溶液量为315032030003cm =,倒出的溶液量为3(80003)3000cm -<,所以不能实现要求. 22.(2021·全国·九年级竞赛)甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头停泊,它们在一昼夜内到达的时间是等可能的,如果甲的停泊时间是1小时,乙的停泊时间是2小时,求它们中任何一艘都不需要等候码头空出的概率(精确到0.001).【答案】0.879.【解析】【分析】【详解】设自当天零时算起,甲、乙两船到达码头的时刻分别是x 和y ,则必须024,024x y ≤≤≤≤.我们视(),x y 为平面直角坐标系内的点,于是点(),x y 落在一个面积为224S =的正方形OABC 的内部或边界上(如下图).如果轮船不需要等候码头空出,那么当船甲先到时,船乙应迟来1个小时以上,即1y x -≥,即1y x ≥+;当船乙先到时,船甲应迟来2个小时以上,即2x y -≥,即2y x ≤-,即点(),x y 应在直线1y x =+的上方且在直线2y x =-的下方,也就是点(),x y 应在如图所示的两个三角形ADE 和CFG △中某一个的内部或边界上,故所求概率ADE CFGABCD S S p S +=四边形.而24123,24222CG CF AD AE ==-===-=,所以211222223231103220.879241152p ⨯⨯+⨯⨯===. 答:两船中任何一艘都不需要等候码头空出的概率为0.879.23.(2021·全国·九年级竞赛)把长为a 的线段任意分成3条线段,求这3条线段能够构成一个三角形的3条边的概率.【答案】14【解析】【分析】【详解】解 设其中两条线段的长为,x y ,则第3条线段的长为()a x y -+,于是,x y 的取值范围是0,0,0,0,0()0.x a x a y a y a a x y a x y a ⎧<<<<⎧⎪⎪<<⇔<<⎨⎨⎪⎪<-+<<+<⎩⎩ ① 要使3条线段构成一个三角形的3条边,其充要条件是其中任意一条线段的长度小于其余两条线段的长度之和.这等价于每条线段的长度都小于2a ,即 0,0,220,0,220().22a a x x a a y y a a a x y x y a ⎧⎧<<<<⎪⎪⎪⎪⎪⎪<<⇔<<⎨⎨⎪⎪⎪⎪<-+<<+<⎪⎪⎩⎩ ②将(),x y 视为平面直角坐标系的坐标,则满足条件①的点(),x y 在以()()()0,0,,0,0,O A a B a 为顶点的OAB 内.而满足条件②的点(),x y 在以(,),(0,),,0()2222a a a a C D E 为顶点的CDE △内,故所求概率为11222142CDE OAB a a CD DE Sp S a a OA OB ⨯⨯⨯====⨯⨯⨯.答:3条线段能构成一个三角形的三边的概率为14. 24.(2022·福建·九年级竞赛)如图,四边形ABCD 是平行四边形,∠DAC =45°,以线段AC 为直径的圆与AB 和AD 的延长线分别交于点E 和F ,过点B 作AC 的垂线,垂足为H .求证:E ,H ,F 三点共线.【答案】见解析【解析】【分析】如图:证明P ,A ,B ,C 四点共圆.可得CBE APC ∠=∠.①,证明C ,E ,B ,H 四点共圆,可得CHE CBE ∠=∠.②,证明C ,H ,F ,P 四点共圆,可得180APC CHF ∠=︒-∠.③,由①②③代换可得180CHE CHF ∠+∠=︒.可得结论;【详解】如图,延长BH 与直线AD 相交于点P ,连接CP .因为45DAC ∠=︒,BP AC ⊥,所以45BPA ∠=︒.又45BCADAC∠=∠=︒,所以BPA BCA ∠=∠,于是P ,A ,B ,C 四点共圆.所以CBE APC ∠=∠.①连接CE ,由AC 为圆直径,得90CEA CHB ∠=︒=∠,所以C ,E ,B ,H 四点共圆,于是CHE CBE ∠=∠.②连接CF ,由AC 为圆直径,得90CFP CHP ∠=︒=∠,所以C ,H ,F ,P 四点共圆,于是180APC CHF ∠=︒-∠.③由②,①,③,得180CHE CBE APC CHF ∠=∠=∠=︒-∠,所以180CHE CHF ∠+∠=︒.所以E ,H ,F 三点共线.【点睛】本题考查了圆内接罩边形的判断及性质,难度较大,解题的关键是构造圆内接四边形.。
初一数学竞赛专讲第⑹讲含例题及答案:图形与面积

3.在右图的4×7的方格纸板上画有如阴 影所示的“6”字,阴影边缘是线段或圆孤。
7
保证原创精品 已受版权保护
问:阴影面积占纸板面积的几分之几? 4.在右下图中,六边形ABCDEF的面积是
54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ的 面积。
解:由图可知,阴影部分是由三个直径不同的半
圆周所围成,所以其周长为
说明:实际上,该图形中两个小半圆的直径之和等于大半圆的直径,因而它们的 周长也正好等于大半圆的半圆周。 推而广之,若n个小圆的直径之和等于大圆的直径,即:d1+d2+d3+…+dn=D, 那么这些小圆的周长之和也等于大圆的周长,即 πd1+πd2+πd3+…+πdn=π(d1+d2+d3+…+dn)=πD。 例8 某开发区的大标语牌上,要画出如下图所示(图形阴影部分)的三种标点符 号:句号、逗号、问号。已知大圆半径为R,小圆半径为r,且R=2r。若均匀用料,则 哪一个标点符号的油漆用得多?哪一个标点符号的油漆用得少?
例12 已知右图中正方形的面积是12cm2,求图中里外两个 圆的面积。
分析:计算圆面积,要知道半径。先考虑内圆面积。内圆 的直径与正方形的边长相等,但正方形的边长是未知的。根据 已知正方形的面积是12cm2,可以推出内圆直径的平方为12cm2, 再求内圆面积就不难了。 外圆的直径是正方形的对角线,设外圆半径为R,则正方形面积等于由一条对角线 分成的两个等腰直角三角形的面积之和。再由正方形面积=2R×R÷2×2=2R2,2R2=12, 便可求出外圆面积。 解:设内圆半径为r,由正方形面积为12cm2,正方形边长为2r,得 (2r)2=12,r2=3。
八年级数学竞赛专题训练21 梯形(附答案)

八年级数学竞赛专题训练21 梯形阅读与思考梯形是一类具有一组对边平行而另一组对边不平行的特殊四边形,梯形的主要内容是等腰梯形、直角梯形等相关概念及性质.解决梯形问题的基本思路是:通过适当添加辅助线,把梯形转化为三角形或平行四边形,常见的辅助线的方法有:(1)过一个顶点作一腰的平行线(平移腰);(2)过一个顶点作一条对角线的平行线(平移对角线);(3)过较短底的一个顶点作另一底的垂线;(4)延长两腰,使它们的延长线交于一点,将梯形还原为三角形.如图所示:例题与求解【例1】如图,在四边形ABCD中,AB//CD,∠D=2∠B,AD和CD的长度分别为a,b,那么AB的长是___________. (荆州市竞赛试题)解题思路:平移一腰,构造平行四边形、特殊三角形.AB【例2】如图1,四边形ABCD是等腰梯形,AB//CD.由四个这样的等腰梯形可以拼出图2所示的平行四边形.(1)求四边形ABCD四个内角的度数;(2)试探究四边形ABCD 四条边之间存在的等量关系,并说明理由;(3)现有图1中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图. (山东省中考试题) 解题思路:对于(1)、(2),在观察的基础上易得出结论,探寻上、下底和腰及上、下底之间的关系,从作出梯形的常见辅助线入手;对于(3),在(2)的基础上,展开想象的翅膀,就可设计出若干种图形.图2图1A【例3】如图,在等腰梯形ABCD 中,AD//BC ,AB =DC ,且AC ⊥BD ,AF 是梯形的高,梯形的面积是49cm 2,求梯形的高.(内蒙古自治区东四盟中考试题) 解题思路:由于题目条件中涉及对角线位置关系,不妨从平移对角线入手.B【例4】 如图,在等腰梯形ABCD 中,AB//DC ,AB =998,DC =1001,AD =1999,点P 在线段AD 上,问:满足条件∠BPC =900的点P 有多少个?(全国初中数学联赛试题) 解题思路:根据AB +DC =AD 这一关系,可以在AD 上取点构造等腰三角形.D【例5】如图,在等腰梯形ABCD中,CD//AB,对角线AC,BD相交于O,∠ACD=600,点S,P,Q分别为OD,OA,BC的中点.(1)求证:△PQS是等边三角形;(2)若AB=5,CD=3,求△PQS的面积;(3)若△PQS的面积与△AOD的面积的比是7:8,求梯形上、下两底的比CD:AB.(“希望杯”邀请赛试题)解题思路:多个中点给人以广泛的联想:等腰三角形性质、直角三角形斜边中线、三角形中位线等.A【例6】如图,分别以△ABC的边AC和BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到边AB的距离是AB的一半.(山东省竞赛试题)解题思路:本题考查了梯形中位线定理、全等三角形的判定与性质.关键是要构造能运用条件EP=PF的图形.EF能力训练A级1. 等腰梯形中,上底:腰:下底=1:2:3,则下底角的度数是__________.(天津市中考试题)2. 如图,直角梯形ABCD中,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转900至DE,连接AE,则△ADE的面积为______________. (宁波市中考试题)3.如图,在等腰梯形ABCD 中,AB//CD ,∠A =060,∠1=∠2,且梯形的周长为30cm ,则这个等腰梯形的腰长为______________.第3题图第4题图第2题图ABAB4.如图,梯形ABCD 中,AD//BC ,EF 是中位线,G 是BC 边上任一点,如果222cm S GEF =∆,那么梯形ABCD 的面积为__________. (成都市中考试题)5.等腰梯形的两条对角线互相垂直,则梯形的高h 和中位线的长m 之间的关系是 ( )A .m >hB .m =hC .m <hD .无法确定6. 梯形ABCD 中,AB//DC ,AB =5,BC =23,∠BCD =045,∠CDA =060,则DC 的长度是( )A .3327+B .8 C.219 D.38+ E. 338+(美国高中考试题)7.如图,在等腰梯形ABCD 中,AC =BC +AD ,则∠DBC 的度数是 ( )A.300B.450C.600D.900(陕西省中考试第7题图第8题图BBAC第9题图B8.如图,在直角梯形ABCD 中,AD//BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当P A +PD 取最小值时,△APD 中边AP 上的高为( )A .17172 B .17174 C .17178 D .3 (鄂州市中考试题)9.如图,在等腰梯形ABCD 中,AD //BC ,AB =CD ,点P 为BC 边上一点,PE ⊥AB ,PF ⊥CD ,BG ⊥CD ,垂足分别为E ,F ,G .求证 :PE +PF =BG .(哈尔滨市中考试题)10. 如图,在梯形ABCD 中,AD//BC ,E ,F 分别为AB ,AC 中点,BD 与EF 相交于G .求证:)(21AD BC GF -=.BC11.如图,等腰三角形ABC 中,AB =AC ,点E 、F 分别是AB 、AC 的中点,CE ⊥BF 于点O . 求证:(1)四边形EBCF 是等腰梯形;(2)2222BE BC EF =+. (深圳市中考试题)B12.如图1,在等腰梯形ABCD 中,AD//BC ,E 是AB 的中点,过点E 作EF//BC 交CD 于点F ,AB =4,BC =6,∠B =060.(1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM ⊥EF 交BC 于点M ,过M 作MN//AB 交折线ADC 于点N ,连接PN ,设EP =x .①当点N 在线段AD 上时(如图2),△PMN 的形状是否发生改变?若不变,求出△PMN 的周长;若改变,请说明理由.②当点N 在线段DC 上时(如图3),是否存在点P ,使△PMN 为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由. (江西省中考试题)图5(备用图)图4(备用图)图2图1图3B B BC B BB 级1. 如图,在梯形ABCD 中,AB//DC ,AD =BC ,AB =10,CD =4,延长BD 到E ,使DE =DB ,作 EF ⊥AB 交BA 的延长线于点F ,则AF =__________.(山东省竞赛试题)第2题图第1题图EBF2.如图,在梯形ABCD 中,AD//BC ,AB =DC =10cm ,AC 与BD 相交于G ,且∠AGD =060,设E 为CG 中点,F 是AB 中点,则EF 长为_________.(“希望杯”邀请赛试题)3.用四条线段:7,9,13,14====d c b a 作为四条边,构成一个梯形,则在所构成的梯形中,中位线的长的最大值为_________. (湖北赛区选拔赛试题)4.如图,梯形ABCD 的两条对角线AC ,BD 相交于O 点,且AO :CO =3:2,则两条对角线将梯形分成的四个小三角形面积之比为=∆∆∆∆AOB COB DOC AOD S S S S :::_________. (安徽省中考试题)MABBC第4题图 第5题图 第6题图5.如图,在四边形ABCD 中,AD//BC ,E 是AB 的中点,若△DEC 的面积为S ,则四边形ABCD 的面积为 ( )A .S 25 B .2S C .S 47 D .S 49(重庆市竞赛试题)6.如图,在梯形ABCD 中,AD//BC ,∠B =020,∠C =070,E ,M ,F ,N 分别为AB ,BC ,CD , DA 的中点,已知BC =7,MN =3,则EF 的值为 ( )A .4B .214C .5D .6 (全国初中数学联赛试题)7.如图,梯形ABCD 中,AB//DC ,E 是AD 的中点,有以下四个命题:①若AB +DC =BC ,则∠BEC =090;②若∠BEC =090,则AB +DC =BC ;③若BE 是∠ABC 的平分线,则∠BEC =090; ④若AB +DC =BC ,则CE 是∠DCB 的平分线.其中真命题的个数是 ( )A .1个B .2个C .3个D .4个(重庆市竞赛试题)第8题图第7题图NDAC B8.如图,四边形ABCD 是一梯形,AB//CD ,∠ABC =090,AB =9cm ,BC =8cm ,CD =7cm ,M 是AD 的中点,从M 作AD 的垂线交BC 于N ,则BN 的长等于 ( )A .1cmB .1.5cmC .2cmD .2.5cm(“希望杯”邀请赛试题)9.如图,在梯形ABCD 中,AB//DC ,M 是腰BC 的中点,MN ⊥AD .求证:AD MN S ABCD ⋅=四边形(山东省竞赛试题)AB10.如图,在梯形ABCD 中,AD//BC ,分别以两腰AB ,CD 为边向两边作正方形ABGE 和正方形DCHF ,设线段AD 的垂直平分线l 交线段EF 于点M.求证:点M 为EF 的中点.(全国初中数学联赛试题)GH11.已知一个直角梯形的上底是3,下底是7,且两条对角线的长都是整数,求此直角梯形的面积.(“东方航空杯”上海市竞赛试题)12.如图1,平面直角坐标系中,反比例函数)0,0(>>=x k xky 的图象经过矩形OABD 的边BD 的三等分点(BD DF 31=)交AB 于E ,AB =12,四边形OEBF 的面积为16. (1)求k 值.(2)已知)0,13(C ,点P 从A 出发以0.5cm/s 速度沿AB 、BD 向D 运动,点Q 从C 同时出发,以1.5cm/s 的速度沿CO ,OA ,AB 向B 运动,其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,经过多少时间,四边形PQCB 为等腰梯形(如图2).(3)在(2)条件下,在梯形PQCB 内是否有一点M ,使过M 且与PB ,CQ 分别交于S ,T 的直线把PQCB 的面积分成相等的两部分,若存在,请写出点M 的坐标及CM 的长度;若不存在,请说明理由.图2图1专题21梯形例1 a +b例2⑴上底角为120°,下底角为60°;⑵梯形的上底等于下底的一半,且等于腰长; ⑶能拼出菱形,以下图形供参考:例3 7cm 提示:过A 作AE ∥BD 交CB 延长线于E ,则S △AEC =S 梯形ABCD . 例4(1)如图a ,若E 为AD 中点,则∠BEC =90°且CE,BE 分别平分∠BCD ,∠ABC ; ⑵如图b ,在BC 上取一点M ,使AB =MB ,连结AM,DM ,则∠AMD =90°; ⑶如图c ,将a ,b 组合,则四边形GEHM 为矩形.图a 图b 图c ∴当P 为AD 中点时,可以证明∠BPC =90°;在AD 上截取AP =AB ,可以证明∠BPC =90°,故满足条件∠BPC =90°的点P 有2个.例5⑴连结SC,PB .∴△OCD,△OAB 均为等边三角形,S ,P ,Q 分别为OD,OA,BC 中点, ∴SQ =12BC =12AD =SP =PQ .故△SPQ 为等边三角形.⑵∵SB =12DO +OB =132,CS =323,BC =7.∴△SPQ 的边长SQ =12BC =72.∴S △SPQ =34×(72)2=49316.(3)设CD =a ,AB =b (a <b ),BC 2=SC 2+BS 2=(32a )2+(b +a2)2=a 2+b 2+ab . ∴S △SPQ =316(a 2+ab +b 2).又S △AOD S △COD =b a ,则S △AOD =34ab . 又S △AOD S △COD =b a ,则S △AOD =34ab .∵S △PQS S △AOD =78,∴8×316 (a 2+ab +b 2)=7×34ab . 即2a 2-5ab +2b 2=0,化简得a b =12. 故CD :AB =1:2.例6如图,分别过E,F ,C,P 作AB 的垂线,垂足依次为R ,S ,T ,Q ,则PQ 就是点P 到AB 的距离,且有ER ∥PQ ∥CT ∥FS ,故四边形ERSF 为直角梯形,PQ =12(ER +FS ).易证Rt △AER ≌Rt △CAT ,Rt △BFS ≌Rt △CBT ,∴ER =AT ,FS =BT ,又AT +BT =AB =ER +FS , 故PQ =12AB .A 级1.60°2.33.6cm4.82cm 25.B6.D7.C8.C 提示:如图,作点D 关于直线BC 的对称点D ',连结DD '交BC 于E ,连结AD '交BC 于P ,过D 作DF ⊥AP 于F ,故P A +PD 此时最小.由BE =AD =2,EC =3,则可得:DE =4,∴DD '=8,则AD '=217. 又∵AD '·DF =AD ·DD ',则DF =81717.9.提示:过P 点作PQ ⊥BG 于Q ,证明PE =BQ .10.提示:连结DF 并延长交于BC 于H ,则GF =12BH ,AD =CH . 11.略12.⑴ 3⑵①当点N 在线段AD 上运动时,△PMN 形状不发生改变,其周长为3+7+4.②当点在线段DC 上运动时,△PMN 的形状发生改变,但MNC 恒为等边三角形,过E 作EG BC 于G 。
初三数学完美正方巧妙构造
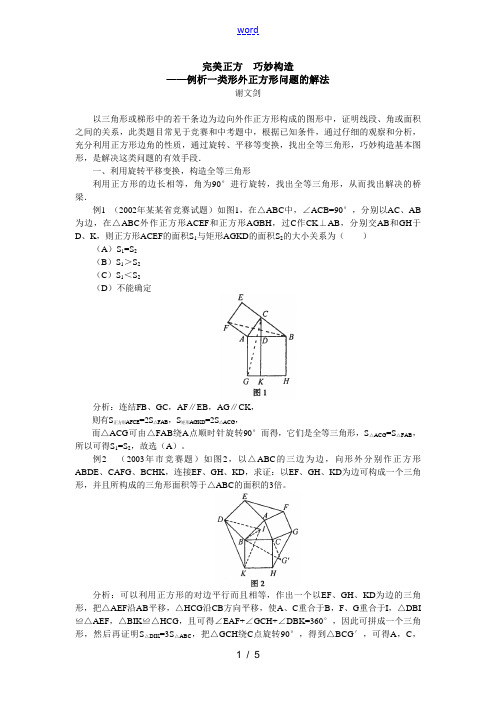
完美正方巧妙构造——例析一类形外正方形问题的解法谢文剑以三角形或梯形中的若干条边为边向外作正方形构成的图形中,证明线段、角或面积之间的关系,此类题目常见于竞赛和中考题中,根据已知条件,通过仔细的观察和分析,充分利用正方形边角的性质,通过旋转、平移等变换,找出全等三角形,巧妙构造基本图形,是解决这类问题的有效手段.一、利用旋转平移变换,构造全等三角形利用正方形的边长相等,角为90°进行旋转,找出全等三角形,从而找出解决的桥梁.例1 (2002年某某省竞赛试题)如图1,在△ABC中,∠ACB=90°,分别以AC、AB 为边,在△ABC外作正方形ACEF和正方形AGBH,过C作CK⊥AB,分别交AB和GH于D、K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系为()(A)S1=S2(B)S1>S2(C)S1<S2(D)不能确定分析:连结FB、GC,AF∥EB,AG∥CK,则有S正方形AFCE=2S△FAB,S矩形AGKD=2S△ACG,而△ACG可由△FAB绕A点顺时针旋转90°而得,它们是全等三角形,S△ACG=S△FAB,所以可得S1=S2,故选(A)。
例2 (2003年市竞赛题)如图2,以△ABC的三边为边,向形外分别作正方形ABDE、CAFG、BCHK,连接EF、GH、KD,求证:以EF、GH、KD为边可构成一个三角形,并且所构成的三角形面积等于△ABC的面积的3倍。
分析:可以利用正方形的对边平行而且相等,作出一个以EF、GH、KD为边的三角形,把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,△DBI ≌△AEF,△BIK≌△HCG,且可得∠EAF+∠GCH+∠DBK=360°,因此可拼成一个三角形,然后再证明S△DIK=3S△ABC,把△GCH绕C点旋转90°,得到△BCG′,可得A,C,G ′在一条直线上,且C 为AG ′的中点。
第25讲 特殊四边形-正方形与梯形(课件)中考数学一轮复习(全国通用)

∴ = Р = 6 − 2 = 4, ⊥ ,
1
∴ = 2 ,
由勾股定理得: = 2 + 2 = 4 2,
∴ = 2 2,
故选:B.
考点一 正方形的性质与判定
题型03 根据正方形的性质求面积
【例3】(2023·河南省直辖县级单位·统考二模)四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发
又∵点又是正方形1 1 1 的一个顶点,∴∠A1OC1=90°,
∴∠AOE+∠EOB=∠EOB+∠BOF=90°,∴∠AOE =∠FOB,
∠ = ∠
在△ AOE 和△ BOF 中,
,
=
∠ = ∠
∴△ AOE≌△ BOF(ASA)
,
1
∴S1=S 四边形 EOFB=S△ EOB+S△ BOF= S△ EOB+S△ AOE=S△ AOB=4 2 .
中考数学一轮复习
第25讲 特殊四边形-正方形与梯形
目录
C
O
N
T
E
N
T
S
01
02
考情分析
知识建构
03
考点精讲
第一部分
考情分析
考点要求
新课标要求
正方形的性 ➢ 探索并证明正方形的性质定理.
质与判定
四边形之间
➢ 探索并证明正方形的判定定理.
命题预测
正方形是特殊平行四边形中比较重要的图形,也
是几何图形中难度比较大的几个图形之一,年年都
∴∠BAC=∠DAC,
故答案为:=.
考点一 正方形的性质与判定
题型11 根据正方形的性质与判定求线段长
新课标八年级数学竞赛讲座7 菱形矩形正方形和梯形

培优专题7 菱形、矩形、正方形和梯形菱形、矩形、正方形都是特殊的平行四边形,它们除了具有平行四边形的性质外,各自都有相应的特性,如菱形四边相等、对角线互相垂直,且平分对角;矩形四个角都是直角且对角线相等;正方形是最特殊的平行四边形,它具有菱形和矩形的所有特性,可以说是菱形、矩形的完美结合体,也是最基本的正多边形之一.梯形是现实生活中比较常见的图形之一,也是考查平行四边形和直角三角形非常好的载体,因此在中考数学测试和初中数学竞赛中这些特殊的四边形都是考查的重要内容.例1 如果将长方形纸片ABCD,沿EF折叠,如图,延长C′E交AD于H,连结GH,那么EF与GH互相垂直平分吗?分析要说明EF与GH互相垂直平分,只须说明四边形FGEH是菱形即可.解:∵FH`∥GE,FG∥EH,∴四边形FGEH为平行四边形,由题意知:△GEF≌△HFE.∴FG=FH,EG=EH.∴四边形GEHF为菱形.∴EF、GH互相垂直平分.练习11.如图1,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,•∠BAE=18°,则∠CEF=________.(1) (2) (3)2.如图2,四边形ABCD是正方形,对角线AC、BD相交于O,四边形BEFD是菱形,若正方形的边长为6,则菱形的面积为________.3.如图3,ABCD是正方形,E为BF上一点,四边形AFEC•恰是一个菱形,•则∠EAB=________.例2 矩形一边长为5,另一边长小于4,将矩形折起来,使两对角顶点重合,•如图,若折痕EF分析关键弄清“折痕”特点,即在对角线的中垂线上.此问题转化为就矩形ABCD中,已知AD=5,过对角线AC的中点O作AC的垂线EF,分别交AD于F,BC于E,若求AB的长的问题.解:设AB=x,BE=y,连结AE.则AE=CE=5-y.在Rt△ABE中,AB2+BE2=AE2,即x2+y2=(5-y)2.得y=22510x-,AE=5-y=22510x+.又在Rt△AOE中,AO=12EO=12代入AE2=AO2+OE2得,(22510x+)2=)2+2.即x4+25x2-150=0.解之得,x2=5,x2=-30(舍去)∴练习21.如图4,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,•设折痕为EF,试确定重叠部分的△AEF的面积是__________.(4) (5)2.如图5所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF•交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是________.3.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使AD=2,求AG .例3 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM ⊥EF ,•垂足为M ,AM=AB ,则有EF=BE+DF ,为什么?分析要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可.理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用,∴△ABE ≌△AME .∴BE=ME .同理可得,△ADF ≌△AMF .∴DF=MF .∴EF=ME+MF=BE+DF .练习31.如图6,点A 在线段BG 上,四边形ABCD 与DEFG 都是正方形,•其边长分别为3cm 和5cm ,则△CDE 的面积为________c m 2.(6) (7)2.你可以依次剪6张正方形纸片,拼成如图7所示图形.•如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,•那么正方形⑤的面积为________.3.如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?例4 如图,等腰梯形ABCD 中,AD ∥BC ,BD 平分∠ABC ,∠C=30°,求AD :BC 的值. 分析 添加辅助线,使等腰梯形ABCD•的问题转化为平行四边形和等腰三角形的问题. 解:过D 作DF ∥AB 交BC 于F ,过D 作DE ⊥BC 于E ,则四边形ABFD 为平行四边形. 设AD=a ,则AD=BF=a .∵BD 平分∠ABC ,∴AD=AB=DF=DC=a .在Rt △DEC 中,∠C=30°,∵DE=2a ,. 又∵, ∴(a . ∴AD :BC=a :(a=):2练习41.用长为1、4、4、5的线段为边作梯形,那么这个梯形的面积等于_______.2.用一块面积为900cm2的等腰梯形彩纸做风筝,为牢固起见,•用竹条做梯形的对角线,对角线恰好互相垂直,那么梯形对角线至少需______cm.3.如图,一块直角梯形的钢板,两底长分别是4cm、•10cm,•且有一个内角为60°,问是否能将铁板任意翻转,使从一个直径为8.7cm的圆洞中穿过?例5 如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE•⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长.分析连结PO,则PE、PF可分别看作是OD、OA边上的高,而OA=OD,故只需求出△AOP、△DOP的面积即可.解:连结OP.由矩形ABCD,AD=12,AB=5.∴AC=BD=2OA=2OB=13.∴OA=OD=6.5.而S矩形=12×5=60.∴S△AOD=14×60=15.∴S△AOP +S△DOP =15.即12×OA×PF+12×OD×PE=15.∴12×6.5×(PE+PF)=15.∴PE+PF=60 13.练习51.如图8,等腰梯形ABCD中,上底AD=2,下底BC=8,M是腰AB的中点,若MD⊥CD,•则梯形的面积为________.(8) (9)2.如图9,已知正方形ABCD的面积为35平方厘米,E、F分别为边AB、BC上的点.AF、CE相交于G,并且△ABF的面积为14平方厘米,△BCE的面积为5平方厘米,•那么四边形BEGF的面积是________.3.如图,在 ABCD中,在AD、CD上各取一点E、F,使AF=CE,AF与CE相交于P,•则PB平分∠APC.答案:练习11.18° 2.363.连结BD交AC于点O,作EM⊥AC于点M.设正方形边长为a,则又∵AC∥BF,BO⊥AC,EM⊥AC,∴BO=EM=12.在Rt△AEM中,,EM=2a.∴∠CAE=30°.则∠EAB=15°.练习21.7516cm2.2.纸条长为6cm,宽为.3.作GM⊥BD,垂足为M.由题意可知∠ADG=GDM,则△ADG≌△MDG.∴DM=DA=2. AC=GM又易知:GM=BM.而),∴AG=BM=2).练习31.6c m2. 2.36.3.过P作EF⊥AB于F交DC于E.设PF=x,则EF=10+x,BF=12(10+x).由PB2=PF2+BF2.可得:102=x2+14(x+10)2.故x=6.S正方形ABCD=162=256.练习41.10.2.3.过D作DE⊥BC于E,则BE=4,EC=6,由∠C=60°,知CD=2EC=12,由于BC>8.7,DE>8.7,故这两个方向不能穿过圆洞.过B作BF⊥CD,有CF=12BC=5.得=8.7.故沿CD方向可穿过圆洞.练习51.2.42027cm2(面积法).3.连结BF、BE.过B作BM⊥AF于M,BN⊥CE于N.则有S△ABF=S△BCE=12S ABCD.即12×AF×BM=12×CE×BN.∵AF=CE∴BM=BN∴点B在∠APC的平分线上.即PB平分∠APC.练习5-1的详解:方法一:过D作DQ⊥BC于Q,作CD中点N,连结MN,交DQ于S MN为梯形ABCD中位线,∴MN=5,MN‖BC∴MS为梯形ABQD中位线∴MS=7/2,S为DQ中点,∵DQ⊥BC,MN‖BC,∴DQ⊥MN设DS=SQ=a,则MS²+DS²=MD²,则MD²=49/4 + a²,SN为△DQC中位线∴SN=3/2∴DN²=9/4 +a²∵MD⊥CD∴MD²+DN²=MN²∴49/4 + a²+ 9/4 +a²=25 解得a=√21 /2,DQ=√21,S=1/2(2+8)*√21=5√21方法二:延长DM,BC交于点N。
八年级数学竞赛例题专题-梯形

八年级数学竞赛例题专题-梯形专题21 梯形阅读与思考梯形是一类具有一组对边平行而另一组对边不平行的特殊四边形,梯形的主要内容是等腰梯形、直角梯形等相关概念及性质.解决梯形问题的基本思路是:通过适当添加辅助线,把梯形转化为三角形或平行四边形,常见的辅助线的方法有:(1)过一个顶点作一腰的平行线(平移腰);(2)过一个顶点作一条对角线的平行线(平移对角线);(3)过较短底的一个顶点作另一底的垂线;(4)延长两腰,使它们的延长线交于一点,将梯形还原为三角形.如图所示:例题与求解【例1】如图,在四边形ABCD中,AB//CD,∠D=2∠B,AD和CD的长度分别为,,那么AB的长是___________. (荆州市竞赛试题)解题思路:平移一腰,构造平行四边形、特殊三角形.【例2】如图1,四边形ABCD是等腰梯形,AB//CD.由四个这样的等腰梯形可以拼出图2所示的平行四边形.(1)求四边形ABCD四个内角的度数;(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;(3)现有图1中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.(山东省中考试题)解题思路:对于(1)、(2),在观察的基础上易得出结论,探寻上、下底和腰及上、下底之间的关系,从作出梯形的常见辅助线入手;对于(3),在(2)的基础上,展开想象的翅膀,就可设计出若干种图形.【例3】如图,在等腰梯形ABCD中,AD//BC,AB=DC,且AC⊥BD,AF是梯形的高,梯形的面积是49cm2,求梯形的高.(内蒙古自治区东四盟中考试题)解题思路:由于题目条件中涉及对角线位置关系,不妨从平移对角线入手.【例4】如图,在等腰梯形ABCD中,AB//DC,AB=998,DC=1001,AD=1999,点P在线段AD上,问:满足条件∠BPC=900的点P有多少个?(全国初中数学联赛试题)解题思路:根据AB+DC=AD这一关系,可以在AD上取点构造等腰三角形.【例5】如图,在等腰梯形ABCD中,CD//AB,对角线AC,BD相交于O,∠ACD=600,点S,P,Q分别为OD,OA,BC的中点.(1)求证:△PQS是等边三角形;(2)若AB=5,CD=3,求△PQS的面积;(3)若△PQS的面积与△AOD的面积的比是7:8,求梯形上、下两底的比CD:AB.(“希望杯”邀请赛试题)解题思路:多个中点给人以广泛的联想:等腰三角形性质、直角三角形斜边中线、三角形中位线等.【例6】如图,分别以△ABC的边AC和BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到边AB的距离是AB的一半.(山东省竞赛试题)解题思路:本题考查了梯形中位线定理、全等三角形的判定与性质.关键是要构造能运用条件EP=PF的图形.能力训练A 级等腰梯形中,上底:腰:下底=1:2:3,则下底角的度数是__________.(天津市中考试题)2. 如图,直角梯形ABCD中,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转900至DE,连接AE,则△ADE的面积为______________. (宁波市中考试题)3.如图,在等腰梯形ABCD中,AB//CD,∠A=,∠1=∠2,且梯形的周长为30cm,则这个等腰梯形的腰长为______________.4.如图,梯形ABCD中,AD//BC,EF是中位线,G是BC边上任一点,如果,那么梯形ABCD的面积为__________. (成都市中考试题)5.等腰梯形的两条对角线互相垂直,则梯形的高和中位线的长之间的关系是 ( )A.> B.= C.< D.无法确定梯形ABCD中,AB//DC,AB=5,BC=,∠BCD=,∠CDA=,则DC的长度是( )A . B.8 C. D(美国高中考试题).如图,在等腰梯形ABCD中,AC=BC+AD,则∠DBC的度数是 ( )A.300B.450C.600D.900(陕西省中考试8.如图,在直角梯形ABCD中,AD//BC,AB⊥BC,AD=2,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,△APD中边AP上的高为( )A. B. C. D.(鄂州市中考试题)9.如图,在等腰梯形ABCD中,AD//BC,AB=CD,点P为BC边上一点,PE⊥AB,PF⊥CD,BG⊥CD,垂足分别为E,F,G.求证:PE+PF=BG.(哈尔滨市中考试题)10. 如图,在梯形ABCD中,AD//BC,E,F分别为AB,AC 中点,BD与EF相交于G.求证:.11.如图,等腰三角形ABC中,AB=AC,点E、F分别是AB、AC的中点,CE⊥BF于点O.求证:(1)四边形EBCF是等腰梯形;(2).(深圳市中考试题)12.如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=.(1)求点E到BC的距离;(2)点P为线段EF上的一个动点,过P作PM⊥EF交BC于点M,过M作MN//AB交折线ADC于点N,连接PN,设EP=.①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN的周长;若改变,请说明理由.②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的的值;若不存在,请说明理由.(江西省中考试题) B 级如图,在梯形ABCD中,AB//DC,AD=BC,AB=10,CD=4,延长BD到E,使DE=DB,作EF⊥AB交BA的延长线于点F,则AF=__________.(山东省竞赛试题)2.如图,在梯形ABCD中,AD//BC,AB=DC=10cm,AC与BD相交于G,且∠AGD=,设E为CG中点,F是AB中点,则EF长为_________.(“希望杯”邀请赛试题)3.用四条线段:作为四条边,构成一个梯形,则在所构成的梯形中,中位线的长的最大值为_________.(湖北赛区选拔赛试题)4.如图,梯形ABCD的两条对角线AC,BD相交于O点,且AO:CO=3:2,则两条对角线将梯形分成的四个小三角形面积之比为 _________. (安徽省中考试题)第4题图第5题图第6题图5.如图,在四边形ABCD中,AD//BC,E是AB的中点,若△DEC的面积为S,则四边形ABCD的面积为 ( )A. B.2S C. D.(重庆市竞赛试题)6.如图,在梯形ABCD中,AD//BC,∠B=,∠C=,E,M,F,N分别为AB,BC,CD,DA的中点,已知BC=7,MN=3,则EF的值为 ( ) A.4 B. C.5 D.(全国初中数学联赛试题)7.如图,梯形ABCD中,AB//DC,E是AD的中点,有以下四个命题:①若AB+DC=BC,则∠BEC=;②若∠BEC=,则AB+DC=BC;③若BE是∠ABC的平分线,则∠BEC=;④若AB+DC=BC,则CE是∠DCB的平分线.其中真命题的个数是 ( )A.1个 B.2个 C.3个 D.4个(重庆市竞赛试题)8.如图,四边形ABCD是一梯形,AB//CD,∠ABC=,AB =9cm,BC=8cm,CD=7cm,M是AD的中点,从M作AD的垂线交BC于N,则BN的长等于 ( )A.1cm B.1.5cm C.2cm D.2(“希望杯”邀请赛试题)9.如图,在梯形ABCD中,AB//DC,M是腰BC的中点,MN⊥AD.求证:(山东省竞赛试题)10.如图,在梯形ABCD中,AD//BC,分别以两腰AB,CD为边向两边作正方形ABGE和正方形DCHF,设线段AD的垂直平分线交线段EF于点M.求证:点M为EF的中点.(全国初中数学联赛试题)11.已知一个直角梯形的上底是3,下底是7,且两条对角线的长都是整数,求此直角梯形的面积.(“东方航空杯”上海市竞赛试题)12.如图1,平面直角坐标系中,反比例函数的图象经过矩形OABD的边BD的三等分点()交AB于E,AB=12,四边形OEBF的面积为(1)求值.(2)已知,点P从A出发以0.5cm/s速度沿AB、BD向D运动,点Q从C同时出发,以1.5cm/s的速度沿CO,OA,AB向B运动,其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,经过多少时间,四边形PQCB为等腰梯形(如图2).(3)在(2)条件下,在梯形PQCB内是否有一点M,使过M且与PB,CQ分别交于S,T的直线把PQCB的面积分成相等的两部分,若存在,请写出点M的坐标及CM的长度;若不存在,请说明理由.。
初中数学竞赛——正方形和梯形

第3讲正方形和梯形知识总结归纳一.正方形的定义:定义:邻边相等的矩形叫正方形,或者有一个角为直角的菱形叫正方形.正方形既是矩形又是菱形.二.正方形的性质:正方形具有四边形、平行四边形、矩形、菱形的一切性质.(1)边:四条边都相等,邻边垂直,对边平行.(2)角:四个角都是直角.(3)对角线:对角线相等且互相垂直平分,每条对角线平分一组对角.(4)对称性:正方形是轴对称图形,有4条对称轴.(5)特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的的夹角是45;正方形的两条对角线把正方形分成四个全等的等腰直角三角形.三.正方形的判定:(1)有一组邻边相等的矩形是正方形.(2)有一个角是直角的菱形是正方形.四.梯形的相关定义:(1)梯形的定义:一组对边平行,另一组对边不平行的四边形叫做梯形.(2)梯形的腰:梯形中不平行的两边叫梯形的腰.(3)梯形的高:梯形两底间的距离角梯形的高.(4)等腰梯形:两腰相等的梯形叫等腰梯形,(5)直角梯形:有一个角是直角的梯形叫等腰梯形.五.等腰梯形的性质:(1)等腰梯形是轴对称图形,上下底中点所在的直线是对称轴.(2)等腰梯形同一底边上的两个角相等.(3)等腰梯形的两条对角线相等.六.等腰梯形的判定:(1)同一底边上两个角相等的梯形是等腰梯形.(2)对角线相等的梯形是等腰梯形.七.梯形的中位线:(1)定义:连结梯形两腰中点的线段叫做三角形的中位线.(2)梯形的中位线定理:梯形的中位线平行于梯形的上下底,且等于上下底之和的一半.典型例题一. 正方形【例1】 如图,正方形ABCD 中,EBC △是正三角形,求∠EAD 的度数.【例2】 如图,在正方形ABCD 中,P 为对角线BD 上的一点,PE BC ⊥于E ,PF CD ⊥于F ,求证:AP EF =.【例3】 如图,正方形ABCD 中,E 是AB 上一点,BF ⊥CE 于G 交AD 于F ,求证:CE =BF .【例4】 如图,正方形ABCD 中,E 是BC 的中点,AE 与BD 相交于F ,求证:CF DE ⊥.【例5】 如图,在正方形ABCD 中,E 为BD 上一点,AE 的延长线交BC 的延长线于F ,交CD 于H ,F DCBAP EGDCBA F EFE DCBAABCDEG 为FH 的中点,求证:EC CG ⊥。
初中数学初赛竞赛试卷

一、选择题(每题5分,共20分)1. 下列数中,有理数是()A. $\sqrt{2}$B. $\pi$C. $\frac{1}{3}$D. $\sqrt{5}$2. 下列图形中,是轴对称图形的是()A. 长方形B. 等边三角形C. 正方形D. 梯形3. 已知 $a=2$,$b=-3$,则 $a^2+b^2$ 的值为()A. 5B. 6C. 7D. 84. 下列方程中,无解的是()A. $2x+3=7$B. $3x-4=2$C. $x+5=10$D. $5x-2=0$5. 已知 $\angle A=30^\circ$,$\angle B=60^\circ$,则 $\angle C$ 的度数为()A. $30^\circ$B. $60^\circ$C. $90^\circ$D. $120^\circ$二、填空题(每题5分,共20分)6. 若 $a=3$,$b=-2$,则 $a^2+b^2$ 的值为______。
7. 已知 $x^2-4x+4=0$,则 $x$ 的值为______。
8. 下列图形中,是等腰三角形的图形是______。
9. 若 $\angle A$ 和 $\angle B$ 是邻补角,且 $\angle A=45^\circ$,则$\angle B$ 的度数为______。
10. 已知 $a=2$,$b=3$,则 $a^2+b^2$ 的值为______。
三、解答题(每题10分,共30分)11. (1)计算:$\frac{5}{6}+\frac{3}{4}-\frac{1}{3}$;(2)化简:$a^2-2a+1$。
12. (1)已知 $x=2$,求 $2x^2-3x+1$ 的值;(2)若 $x^2-2x+1=0$,求 $x^2+2x+1$ 的值。
13. (1)已知 $a=3$,$b=-2$,求 $a^2+b^2$ 的值;(2)若 $a^2-2a+1=0$,求 $a^2+2a+1$ 的值。
人教版初二数学下册正方形梯形知识点总结及例题

正方形一周强化一、一周学问概述、正方形的定义及性质有一组邻边相等并且有一个角是直角的平行四边形叫正方形.从定义可知,正方形既是一种特别的矩形〔有一组邻边相等的矩形〕,又是一种特别的菱形〔有一个角是直角的菱形〕,因此它具有矩形和菱形的全部性质.正方形被对角线分成的三角形,都是等腰直角三角形.、正方形的断定从平行四边形动身:有一组邻边相等且有一个角是直角的平行四边形是正方形.从矩形动身:有一组邻边相等的矩形是正方形.从菱形动身:有一个角是直角的菱形是正方形.、平行四边形、矩形、菱形、正方形的关系正方形、矩形、菱形都是特别的平行四边形,它们的包含关系如图.二、重难点学问归纳正方形的断定和性质的综合运用是重点.几种特别的平行四边形的断定的恰中选择是难点.三、例题解析、利用正方形对角线的性质解题例、如图,在正方形中,点、在上,且.请猜测四边形的形态,并对你的猜测给出合理的说明.解:四边形为菱形.理由如下:连结交于点.∵四边形为正方形,又,∴.∴四边形是平行四边形.又∵⊥∴四边形为菱形点拨:正方形的对角线相互垂直平分且相等的性质,会为解题带来许多便利.例、如图,正方形的对角线交于点,是上任一点,⊥于点,交于点.求证:.证明:∵四边形为正方形,∴对角线、相互垂直平分于点,即,⊥.又⊥,∴∠∠.点拨:这里主要是应用正方形对角线相互垂直平分来破题的.、利用正方形的轴对称性解题例、如图,、分别是正方形的边、上的点,、分别及对角线相交于点、.假设∠°,求∠+∠的度数.解:在四边形中,∵及、及均关于直线对称,又五边形内角和为°,点拨:利用正方形的对称性作角和线段的转化非常快捷,如图中∠∠,∠∠,,等.例、,如图,在正方形中,点在上.解:〔〕∵点在上,点、关于对称,∴.〔〕能用文字概括为“正方形一条对角线上的一点和另一条对角线的两端间隔相等〞.〔〕能.证明:连结,由〔〕可知,又∵⊥,⊥,∴∠∠°.又∵∠°,∴四边形是矩形,点拨:该题〔〕的结论是一个常用到的正方形的性质,也可用对称的学问或证△≌△得到,在例中该图已经出现过;第〔〕小题的证明思路是,抓住正方形是轴对称图形这一特点,把正方形沿对称轴翻折,使翻折到,把要证转化为只要证,从而到达把分散的条件集中到一块的目的.、利用旋转法解决有关正方形问题例、如图,正方形的边长,为上一点,连结,作⊥交的延长线于点,作⊥交于点.假设,求的长.解:△绕点旋转°后可以得到△,点拨:分析条件⊥,⊥,,于是可以将△旋转,旋转本质还是两个三角形全等.例、如图,在一正方形花池内须要装一只喷头,且满意︰︰︰︰.求∠的度数.解:将△绕点顺时针旋转°得△′,连结′.∴可设′,′,.又△′为等腰直角三角形,又(),∴′+′.故∠′°+°°.点拨:这里是通过旋转,将分散的条件集中起来,再由三角形边及边的关系,求出有关角的大小.、构造正方形解题例、如图,⊥,⊥,是上一点,,,,∠°,∠°.求的长.解:过作的垂线交延长线于点,那么又,∴△是等边三角形,又∠°-(°+°)°,点拨:此题是通过补图,构造正方形求解.、利用正方形性质解选择题例、如图,有两个正方形和一个等边三角形,那么图中度数为°的角有〔〕.个.个.个.个解:如图.∵△′为正三角形,四边形、四边形′′′均为正方形,在四边形′中,易知∠′°-°×-°°.故∠′∠′°.应选.点评:此题极易误选.梯形一周强化一、一周学问概述、梯形的概念梯形是指一组对边平行而另一组对边不平行的四边形,这两个条件缺一不行.换一种说法就是,一组对边平行且不相等的四边形是梯形.等腰梯形和直角梯形是两种特别梯形.、等腰梯形的性质及断定()等腰梯形的性质①等腰梯形是轴对称图形,它只有一条对称轴,底边的垂直平分线是它的对称轴;②等腰梯形同一底边上的两个角相等;③等腰梯形的两条对角线相等.()等腰梯形的断定同一底上两个角相等的梯形是等腰梯形.、梯形中常见协助线作法()平移一腰,使两腰、两底角集中于同一个三角形中,并且得出两底之差(如图());()平移一条对角线,使两条对角线及两底之和构成一个三角形,并且能得出两底之和(如图());()延长两腰交于一点,将梯形转化为三角形(如图());()作梯形的高,将梯形转化为矩形及直角三角形(如图());()延长顶点及一腰中点的连线交底边于一点,将梯形转化为三角形,并且集中了两底(如图());()将梯形割补为平行四边形(如图());二、重难点学问归纳、驾驭梯形、等腰梯形、直角梯形等有关概念,并理解它们之间的关系.、探究等腰梯形的有关性质和常用判别方法,并能运用它们进展有关的证明和计算.、通过对梯形协助线的探究,学会将未知问题转化为问题,培育化归意识.三、典型例题剖析、干脆利用等腰梯形的性质或断定解题例、如图,为等腰梯形的下底上一点,⊥,⊥,,为垂足,⊥,为垂足.求证:+.证明:过点作⊥于点.∵⊥,⊥,∴四边形是矩形.∵四边形为等腰梯形,∴∠∠.又⊥,公共,∴△≌△.∴.点拨:要证线段的和差问题,通常可以考虑用“截长法〞或“补短法〞来完成,本例采纳的是“截长法〞.例、如图,矩形中,、分别是、的中点.求证:四边形是等腰梯形.证明:∵四边形是矩形,又、分别是、中点,∴∥.又,∴四边形是梯形.又,∴△≌△().∴∠∠又∠∠,∴∠∠∴梯形是等腰梯形.点拨:这里是先依据梯形定义,断定四边形是梯形,再证同一底上两底角相等.例、如图,四边形中,,,≠.求证:四边形是等腰梯形.证明:过点作∥交边于点.∵,,,又∥,∴∠∠∴四边形是平行四边形.∴∥.又,且≠,∴四边形为等腰梯形.点拨:断定一个随意四边形为等腰梯形,假如不能干脆运用等腰梯形的断定定理,一般的方法是通过作协助线,将此四边形分解为熟识的多边形,此例就是通过作平行线,将四边形分解成为一个平行四边形和一个等腰三角形.、梯形协助线的作法例、如图,在等腰梯形中,∥,,,.求∠的度数.解:过点作∥交于点,∵∥,∴四边形是平行四边形.又,∴∴△是等边三角形.∴∠°点拨:过顶点作一腰的平行线,把梯形化为平行四边形和三角形,转化的目的是把条件都集中到以∠为内角的三角形中.例、如图,在梯形中,∥,且+,为的中点.求证:⊥.证明:延长交的延长线于点.∵为中点,∥,∴△≌△.由等腰三角形“三线合一〞知,⊥.点拨:依据证题的须要,集中梯形的两底也是常用的添加协助线的方法.本例也可以先延长至,使,再证、、共线.例、如图,梯形中,∥,对角线⊥,且,,求该梯形上下底的和.解:过作∥交的延长线于点.∵∥,∴,.在△中,点拨:过顶点作一条对角线的平行线,把两条对角线的数量关系和位置关系集中到一个三角形中,将求梯形上下底的长转化为求直角三角形斜边的长.例、如图,在等腰梯形中,∥,,且⊥,是梯形的高,梯形的面积是.求梯形的高.解法:如图(甲),过作∥交的延长线于点.又∵四边形是等腰梯形,∴.∴.∴△是等腰直角三角形.又是斜边上的高,故也为斜边上的中线.解法:设梯形的两条对角线相交于点,过作⊥于点,延长交于点(如图(乙)).∵,,公共,又∵⊥,∴△是等腰直角三角形.∴.同理.以下解答过程及解法一样.解法:过作⊥于点(如图(丙)).∵梯形是等腰梯形,∴,∠∠.又∵,∴△≌△,∴∠∠.又∵⊥,∴∠∠°.∴△和△都是等腰直角三角形.∴,,以下解答过程及解法一样.点拨:此题的三种解法都是利用等腰直角三角形的性质或全等三角形的性质来证明该梯形的高就等于该梯形的中位线的长.因此,在等腰梯形中,假设两条对角线垂直,那么这个梯形的高就等于中位线的长,梯形的面积就等于高的平方.例、如图,在等腰梯形中,∥.()假设,,梯形的高是,求梯形的周长;()假设,,梯形的高是,梯形的周长为,那么;(请用含的代数式表示;答案干脆写在横线上,不要求证明)()假设,,,求证:⊥.解:()分别过点、作⊥,⊥,垂足分别为、,那么.又,∴∴梯形的周长为++×.()过点作∥,交的延长线于点.∵∥,∴四边形是平行四边形.而+++,点评:()是作等腰梯形的两条高,构造直角三角形,运用勾股定理求腰长;由()知在等腰梯形中,对角线相互垂直或要证对角线相互垂直,一般的方法就是平移一腰.。
初中数学竞赛培训讲义-第十二讲-与矩形、菱形、正方形、梯形相关的竞赛题

HFGPE DC BAFPEDCBA FE DCB AF EDCBA初中数学竞赛培训讲义第十二讲 与矩形、菱形、正方形、梯形相关的竞赛题矩形、菱形、正方形、梯形是特殊的四边形,它除具有平行四边形的性质外,还具有一些特殊的几何性质,本将就开始研究与这些特殊的四边形相关的竞赛题.一 矩形的性质与判定的应用 例 1 如图,设P 是等腰直角ABC 斜边AB 上任意一点,PEAC 于点E ,PFBC 于点F ,PGEF 与点G ,延长GP 并在其延长线上取点D ,使PDPC ,求证:PCBD 且BCBD例2 在矩形ABCD 中,已知12,5,AD AB P 是AD 边上任意一点,PEBD 于E ,PFAC 于F ,求PE PF 的值.练习1、已知矩形ABCD 中,6,8AB BC ,将BCD 沿BD 对折,点C 落至E 处,AD 交BE 于点F ,求DEF 的面积.2、如图,在平行四边形ABCD 中,75,ABC AF BC 于F ,AF 交BD 于E ,若2DEAB ,求AED 的大小.OE DCB AFED CBAFED CBAG FEDB CA3、如图,矩形ABCD 的对角线相交于点O ,AE 平分BAD 交BC 于E ,15CAE,求BOE 的度数.二 菱形的性质与判定的应用 例 3 四边形ABCD 是菱形,AEF 是正三角形,点,E F 分别在边,BC CD 上,且ABAE ,求B 的度数.练习1、如图,菱形ABCD 中,点,E F 分别在边,BC CD 上,60B ,60AEF,(1)求证:AEF 是正三角形(2)若3,4BE EC,求AEF 的面积.2、如图,ABC 中,90,,BACAD BC D 为垂足,在BC 上取BE BA ,作EFBC 交AC 于F ,联接BF 交AD 于G ,求证:四边形AGEF 是菱形FEODCBAHGFED CB AH GFEDCB AFEDCBA三 正方形的性质与判定的应用 1、正方形中的全等构造例4 如图,,E F 分别是正方形ABCD 的边,CD AD 上的点,且CE DF ,,AE BF相交于点O ,下列结论:①AE BF ,②AE BF ,③AOOE ,④AOB DEOF S S ∆=四边形,正确的有练习1、将边长为12cm 的正方形ABCD 折叠,使点A 落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13cm ,求线段CE 的长.2、如图,已知正方形ABCD 的边长为6,菱形EFGH 的三个顶点,,E G H 分别落在正方形的边,,AB CD DA 上,2,1AH CG ==,求FCG ∆的面积.2、正方形中的特殊直角三角形例5 如图,BF 平行于正方形ABCD 的对角线AC ,点E 在BF 上,且AE AC =,CF ∥AE ,求BCF ∠的值.GFDCBAPEDCBAQP EDCBA练习1、正方形ABCD 的面积为64,BCE ∆是等边三角形,F 是CE 的中点,,AE BF 交于点G ,联接CG ,求CG 的长.2、如图,两块边长为a 的正方形中心互相重合,记露出的一个三角形为ABC ∆,A ∠为直角,(1)求证:ABC ∆的周长为定值.(2)若60ABC ∠=︒,求ABC ∆的面积.3、正方形中的对称性的应用例6 如图,正方形ABCD 中,2AB =,E 是CD 的中点,P 是对角线上BD 一点,求CP PE +的最小值.练习如图,正方形ABCD 中,E 是BC 上一点,2,4BE EC ==,,P Q 分别在线段,BD DC 上,求周长的最小值.DCBAACD B_ A _ _ E 四 梯形的性质及常见辅助线的作法 1、平移两腰例 已知一个梯形的4条边长分别为1,2,3,4,求此梯形的面积.练习 如图,梯形ABCD 中,AD ∥BC ,AD <BC ,∠B +∠C =90°,E 为AD 的中点,F 为BC 的中点,求证:EF =12(BC -AD )2、作梯形的高例 如图,在梯形ABCD 中,AD ∥BC ,AB =CD =AD ,∠ADC =120°(1)求证:BD ⊥DC ;(2)若AB =4,求梯形ABCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
!
【例29】如图, 是正方形 边 边上任意一点,过 作 的垂线交正方形的外角 的平分线于 ,求证: .
:
【例30】 是正方形 的边 的中点,作 , 在 上.求证: .
.
【例31】如图,在梯形 中, ,两条对角线相交于 , ,且 , ,求证: .
:
【例32】如图所示, 是正方形, 为 上的一点,四边形 恰好是一个菱形,则求 .
;
【例24】 如图,梯形 中, ,对角线 ,且 ,求梯形的中位线的长度。
…
四.综合提高
【例25】如图,等腰直角 中, , 是 的中点, 于 交 于 ,求证: .
^
【例26】如图所示,等腰梯形 中, ,对角线 、 相交于 , ,点 、 、 分别是 、 、 的中点.
【例27】(1)求证: 是等边三角形;
;
典型例题
一.正方形
【例1】如图,正方形ABCD中, 是正三角形,求∠EAD的度数.
~
【例2】 如图,在正方形 中, 为对角线 上的一点, 于 , 于 ,求证: .
【例3】^
【例4】如图,正方形ABCD中,E是AB上一点,BF⊥CE于G交AD于F,求证:CE=BF.
【例5】…
【例6】如图,正方形 中, 是 的中点, 与 相交于 ,求证: .
&
作业
1.判断下列说法正确的是( )
A.四条边相等的四边形是正方形
B.两条对角线相等且互相垂直的四边形是正方形
·
C.两条对角线分别平分一组对角的四形
2.下列哪个图形不是轴对称图形( )
A.等腰梯形
B.等腰三角形
C.矩形
D.平行四边形
3.等腰梯形四个内角之比可能是( )
(1)梯形的定义:一组对边平行,另一组对边不平行的四边形叫做梯形.
,
(2)梯形的腰:梯形中不平行的两边叫梯形的腰.
(3)梯形的高:梯形两底间的距离角梯形的高.
(4)等腰梯形:两腰相等的梯形叫等腰梯形,
(5)直角梯形:有一个角是直角的梯形叫等腰梯形.
五.等腰梯形的性质:
(1)等腰梯形是轴对称图形,上下底中点所在的直线是对称轴.
【例16】如图,在梯形 中, , , , ,延长 至 ,使 ,作 交 的延长线于点 ,求 的长度.
、
}
【例17】(
【例18】 如图,梯形 中, ,求对角线 之长。
;
【例19】如图,在直角梯形 中, , 的中垂线 交 边于 ,交 延长线于 ,求证: 。
"
三.梯形的中位线
【例20】如图,等腰梯形 中,对角线 ,垂足为 , 于 , 是梯形的中位线,求证: .
(2)等腰梯形同一底边上的两个角相等.
(3)等腰梯形的两条对角线相等.
六.?
七.等腰梯形的判定:
(1)同一底边上两个角相等的梯形是等腰梯形.
(2)对角线相等的梯形是等腰梯形.
八.梯形的中位线:
(1)定义:连结梯形两腰中点的线段叫做三角形的中位线.
(2)梯形的中位线定理:梯形的中位线平行于梯形的上下底,且等于上下底之和的一半.
【例43】
}
【例44】~
【例45】正方形 对角线交于 , 的平分线交 于 ,交 于 ,求证: .
?
【例46】 如图,在直角梯形 中, , . 为 边上一点,且 .求证: .
。
【例47】在正方形 中,已知 、 分别是边 、 上的点,满足 , 、 分别与对角线 交于 、 .求证:
(1) ;
{
(2) .
—
【例48】已知 ,向外作正方形 和 ,直线 垂直 于 ,反向延长交 于 ,求证: 是 的中点.
¥
【例49】如图(1),在 中, ,点 、 是线段 上两动点,且 ,
,垂足为 , 的延长线交 于点 ,直线 与直线 相交于点 .
(1)试判断 的形状,并加以证明.
》
(2)若点 、 是直线 上两动点,其他条件不变,试判断 的形状,并说明理由.
(4)对称性:正方形是轴对称图形,有 条对称轴.
(5)特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的的夹角是 ;正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
三.正方形的判定:
(1)有一组邻边相等的矩形是正方形.
(2)有一个角是直角的菱形是正方形.
四.梯形的相关定义:
(
【例21】如图,梯形 的中位线 与对角线 、 分别交于点 、 ,设梯形 的周长为 ,四边形 的周长为 .若 ,试求 的值.
,
【例22】 如图, 外一条直线 , 、 、 分别是各边中点 、 、 、 都垂直 于 、 、 、 ,求证: .
、
【例23】如图,直角梯形 中, , , , 是 的中点.若 , ,求 的面积.
<
【例33】 如图, 是 的中线,分别以 、 为边向外作正方形 、 .
【例34】求证: .
》
~
【例35】如图,直角梯形 中, , . 为 边上一点,且 .求证: .
…
【例36】 四边形 是正方形,四边形 是菱形, 、 、 在一直线上.求证: 、 三等分 .
?
~
【例37】如图,在梯形 中, , .求证: .
-
\
【例38】 如图,梯形 中, , , 为 上一点,且 , ,求 .
、
|
【例39】 是正方形 的边 的中点,点 分对角线 的比为 ,证明: .
\
【例40】如图,在正方形 中, 、 分别是 、 的中点,求证: .
[
【例41】如图,直角梯形 中, , , , 是 上一点, , ,求 .
·
【例42】 正方形 中, 为 的中点, 为 上的点,且 .求证: .
第3讲正方形和梯形
知识总结归纳
一.正方形的定义:
定义:邻边相等的矩形叫正方形,或者有一个角为直角的菱形叫正方形.正方形既是矩形又是菱形.
二.正方形的性质:
正方形具有四边形、平行四边形、矩形、菱形的一切性质.
(1)边:四条边都相等,邻边垂直,对边平行.
(2)角:四个角都是直角.
|
(3)对角线:对角线相等且互相垂直平分,每条对角线平分一组对角.
(
A.
B.
C.
D.
4.如图,在四边形 中, , , , 于 .
求证: .
…
5.如图所示,正方形 对角线 与 相交于 , ∥ ,且分别与 交于 .试探讨 与 之间的关系,写出你所得到的结论的证明过程.
6.如图,在正方形 中, 是 的中点, 与 交于 点,求证: .
【
7.如图,梯形 中, ,点 是 的中点,且 ,求证:四边形 是等腰梯形.
13.如图,在梯形 中, , , , 是 上一点,且 , .求 的长.
8.如图,设 正方形 的对角线 ,在 延长线上取一点 ,使 , 与 交于 ,求证: 正方形的边长.
9.如图,在梯形 中, , ,求证: .
10. 如图,在梯形 中, , , 是 的中点,且 .求证: 到 的距离等于 .
11. 在梯形 中, ( ), , , 在 上, ,若 ,求 的长.
12.如图, ,在 的内部有一个正方形 ,点 、 分别在射线 、 上,点 是 上任意一点,在 的内部做正方形 .连结 ,猜一猜 的度数是多少并证明你的结论;
!
【例12】如图,已知直角梯形 , ,腰 的长为 , ,则该梯形另一腰 的长是多少
【例13】等腰梯形的一角为 ,上底为 ,下底为 ,则它的腰长是多少
(
【例14】如图,在梯形 中, ,对角线 、 交于 , ,求证: .
#
【例15】如图,在等腰梯形 中,已知 ,对角线 与 互相垂直,且 , ,求等腰梯形的面积.
【例7】\
【例8】如图,在正方形 中, 为 上一点, 的延长线交 的延长线于 ,交 于 , 为 的中点,求证: 。
【例9】:
【例10】如图,在正方形 中,点 在 上, , ,点 在 上,求 与 和的最小值.
%
二.梯形
【例11】已知,等腰梯形 中, , 平分 .
(1)求证: .
~
(2)若 , ,求梯形的周长.
